Активные и реактивные силы: Активные и реактивные силы — БилдоМан

Содержание

Внешние силы и нагрузки

Все внешние силы (нагрузки), действующие на изучаемое тело, следует рассматривать как проявление взаимодействия его с окружающими телами, которое представляется в виде сил или пар сил (моментов).

Все внешние силы (нагрузки) могут рассматриваться как сосредоточенные или распределённые.

В природе сосредоточенных сил не бывает. Все реальные тела практически контактируют через небольшие площадки. Однако принцип Сен-Венана позволяет распределенную нагрузку заменить равнодействующей силой, что упрощает расчёт.

Сосредоточенные нагрузки выражаются в ньютонах [H] и обозначается буквой F.

Распределённые нагрузки обозначаются буквой q и они бывают:

поверхностными (например, давление ветра, воды на стенку). Размерность [FL^-2].
объёмными. Их размерность [FL^-3].
распределенными по длине (например, силу тяжести стержня, учитывая небольшие размеры его поперечного сечения, рассматривают как распределённую нагрузку по длине). Размерность [FL^-1].

Сосредоточенные и распределённые нагрузки могут быть как статическими, так и динамическими.

Статическими называются нагрузки, которые изменяют свою величину или точку приложения с очень небольшой скоростью, так что возникающими при этом ускорениями можно пренебречь.

Динамическими называются нагрузки, изменяющиеся во времени с большой скоростью. Возникшие при этом силы инерции могут многократно превосходить те же нагрузки, приложенные статически.

Законы изменения нагрузок во времени могут иметь весьма сложный характер.

В сопротивлении материалов основным изучаемым элементом конструкции является брус – тело, у которого один из линейных размеров (длина) значительно превышает два других, определяющих поперечное сечение. При работе конструкции ее элементы воспринимают внешние силы и действие их передают друг другу.

Классификация внешних нагрузок

Внешние силы делятся на активные и реактивные (реакции связей).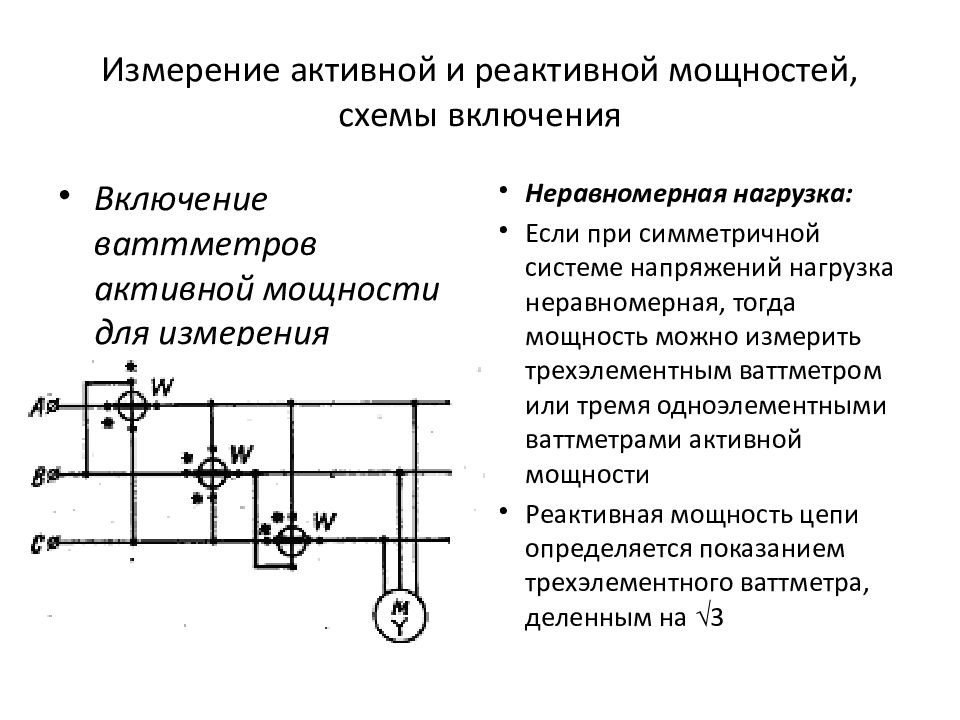 Активные связи принято называть нагрузками.

По способу приложения нагрузки бывают объемные и поверхностные, распределенные и сосредоточенные, по характеру изменения в процессе приложения – статические, динамические и повторно-переменные, по продолжительности действия – постоянные и временные.

Примеры решения задач >
Внутренние силовые факторы >

Активные силы и реакции связей . 46. Силы внешние и внутренние

Введение в динамику механической системы. Механическая система. Классификация сил, действующих на механическую систему силы активные (задаваемые) и реакции связей силы внешние и внутренние. Свойства внутренних сил. Масса системы. Центр масс радиус-вектор и координата центра масс. [c.8]
С и с т е м а с идеальными связями. Рассмотрим систему, на которую наложены связи, не изменяющиеся со временем. Разделим все действующие на точки системы внешние и внутренние силы на активные и реакции связей.

Тогда уравнение (49) можно представить в виде [c.308]

Внешнюю силу, приложенную к какой-либо точке системы, обозначим а внутреннюю А . Заметим, что внутренние и внешние силы могут включать в себя как активные силы, так и силы реакций связей. [c.281]

Внутренние силы не влияют явно на движение центра масс. Они могут влиять только неявно, через внешние силы. Следовательно, одними внутренними силами, без внешних, нельзя вывести из равновесия или изменить движение центра масс системы. Но внутренними силами для неизолированной механической системы можно создать движение отдельных частей системы и, следовательно, взаимодействие с внешними телами, вызывая этим внешние силы реакций связей или изменяя активные силы. Это может изменить движение центра масс или вывести его из равновесия.

[c.292]

В отличие от всех остальных сил, действующих на механическую систему и называемых активными силами, реакции внешних и внутренних связей называются пассивными. Модуль и направление каждой активной силы не зависит от других сил, приложенных к системе (например, силы тяжести и др.), модули же и направления реакций связей зависят от совокупности действующих на систему сил, а также и от движения системы.

[c.97]

Теорема живых сил. Прежде чем выводить другие следствия из общего уравнения динамики, удобно установить здесь еще одну о ц ую теорему о движении системы, формулировка которой не зависит от подразделения сил на внешние и внутренние или активные и реакции связей. [c.278]

Как известно из теоретической механики, опорные реакции балок определяют путем составления для всей балки и решения уравнений равновесия статики. Будем помнить, что при определении внутренних сил реакции связей учитываются наравне с активными внешними силами, действующими на балку.

[c.252]

Как внешние, так и внутренние силы могут быть в свою очередь или активными, или реакциями связей. Разделение сил на внешние и внутренние является условным и зависит от того, движение какой системы тел мы рассматриваем. Например, если рассматривать [c.331]

Дифференциальные уравнения движения системы. Рассмотрим систему, состоящую из п материальных точек. Выделим какую-нибудь точку системы с массой т — Обозначим равнодействующую всех приложенных к точке внешних сил (и активных и реакций связей) через Р1, а равнодействующую всех внутренних сил — через Р к. Если точка имеет при этом ускорение у, то по основному закону динамики [c.342]

Определение 1. В отличие от сил реакций связей заранее заданные силы к (внутренние или внешние) называют активными силами. [c.115]

Следует отметить, что внутренние силы при действии па систему внешних активных сил или сил реакций внешних связей могут косвенно влиять на изменение количества движения системы Р и момента количества движения К. Не изменяя непосредственно эти величины, внутренние силы могут изменять состояние системы (г, у). Изменение состояния системы приводит, вообще говоря, к изменению результирующей внешних

[c. 153]

Силы, действующие на тела такой системы, можно подразделить на две категории внешние—силы, приложенные к телам данной системы, но обусловленные наличием других тел, не входящих в эту систему, ц внутренние—силы взаимодействия между телами одной и той же системы. Такое подразделение относится как к активным силам, так и к реакциям связей [c.87]

Установив понятие работы силы на возможном перемещении, можно расширить классификацию связей. Рассматривая силы, приложенные к точкам системы, для каждой точки можно распределить приложенные к ней силы на два класса активные силы н реакции связей. Обозначим равнодействующую всех активных сил (внешних и внутренних), приложенных к точке В/, равнодействующую всех сил реакций связей равнодействующую всех сил Е , т. е.

[c.328]

В неизолированных механических системах внутренние силы, вызывая движение отдельных частей системы вследствие взаимодействия о внешними телами или окружающей материальной средой, могут вызвать внешние силы в виде сил реакций связей или изменения активных сил, которые могут изменить количество движения системы. [c.289]

В уравнениях (27) и (29) в число внешних и внутренних сил входят и активные силы и силы реакции связей. Но в случае стационарных связей без трения реакции таких связей не производят работы при любом перемещении системы. Поэтому в этом случае неизвестные реакции связей не входят ни в одно из уравнений (27) и (29). [c.640]

Действительно, если система находится в равновесии, то в равновесии находятся и все тела данной системы. Поэтому мы можем каждое тело освободить от наложенных на него внешних и внутренних связей, заменив их соответствующими реакциями, и рассматривать равновесие каждого тела, используя уже знакомые нам условия равновесия. При этом только надо иметь ввиду, что внутренние силы взаимодействия между телами системы (активные и реакции внутренних связей) по аксиоме о равенстве сил действия и противодействия обязательно равны по модулю и имеют противоположные направления. Так, освобождая тело А (рис. 219) от внутренней связи 17

[c. 259]

Реакции представляют собой силы, определяемые связями в данном случае это будут внешние силы, так как они не вызываются действием точек, принадлежащих телу. В связи с этим необходимо различать два рода внешних сил активные, или прямо приложенные силы, которые задают произвольно и заставляют действовать на тело, и силы связи, или реакции, возникающие автоматически как следствия первых. Внутренние силы, действующие между точками системы, представляют собою также силы связи, но они попарно исключаются и не входят в условия равновесия.

[c.238]

К общим теоремам предыдущего параграфа мы пришли, отправляясь от разделения сил, действующих на систему, на внешние и внутренние. Здесь мы применим другой критерий классификации (п. 3) и разделим эти силы на активные (или прямо приложенные) и реакции связей. Точнее, обозначим через f,- равнодействующую активных сил, приложенных к любой точке [c.266]

Отметим, что деления системы сил на внутренние и внешние силы и на активные силы и реакции связей не взаимосвязаны.

[c.89]

Общие замечания о теоремах и законах динамики. Рассмотрим движение системы материальных точек Pj = 1, 2,. .., N) в некоторой инерциальной системе координат. Пусть — масса точки а — ее радиус-вектор относительно начала координат. Если система несвободна, то ее можно рассматривать как свободную, если помимо активных сил, приложенных к точкам системы, учесть реакции связей. Если затем все силы, приложенные к системе, разбить на внешние и внутренние, то из аксиом Ньютона получим дифференциальные уравнения движения рассматриваемой механической системы в виде [c.156]

Представляется также интересным разделить реакции связей, подобно активным силам, на внутренние и внешние ( 171). Если внутренние связи идеальны, сумма их реакций равна нулю [c.303]

Если ввести понятия реактивных и активных переменных, причем первые характеризуют реакцию материала на внешние термомеханические воздействия, а вторые — внутренние силы, порожденные этими воздействиями, то каждая активная переменная связана с реактивными переменными с помощью определяющего уравнения. При этом также существует и обратная связь, т.е. каждая реактивная переменная зависит от активных переменных. В соответствии с принципом причинности любая реактивная переменная может зависеть от настоящих и прошлых значений активных переменных, но не от их значений в будущем. [c.182]

В теории механизмов, в зависимости от характера решаемых задач, применяют различные классификации сил. Согласно первой классификации действующие на механическую систему силы подразделяют на заданные (активные) и реакции связей. Согласно второй классификации действующие на систему силы делят на внешние и внутренние по отношению к этой системе. Эти две классификации сил известны из курса обнщй механики. Третья классификация является специфичной для теории механизмов. Согласно третьей классификации силы, действующие на механизм и развивающие мощность, подразделяют на силы движущие и силы сопротивления. [c.56]

Принцип Даламбера для системы материальных точек. Рассмотрим систему п материальных точек М, М ,. . ., Л/ , на которую наложены геометрические неосвобождающие связи (н. 1.1. гл. XVII), которые, вообще говоря, не будем предполагать стационарными и идеальными. Массы точек обозначим mi, m2,. .., т . Равнодействующую заданных активных сил (как внешних, так и внутренних), приложенных к v-й точке, обозначим Fv, а равноде11ствующую реакций связей, приложенных к v-й точке, через (v = l, 2,. … .., п) (рис. 20.4). Для каждой из точек системы, на основании второго закона Ньютона, будем иметь [c.363]

Действующие на механическую систему активные силы 1 реакции связей разделя-ют на внешние F% и внутренние Fi (индексы е и i от латинских exterior — внешний и interior — внутренний). Внешними называют силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы. Внутренними называют силы, с которыми точки или тела данной системы действуют друг на друга. Это разделение является условным и зависит от того, какая механическая система рассматривается. Например, если рассматривается движение всей Солнечной системы, то сила притяжения Земли к Солнцу будет внутренней если же рассматривается движение системы Земля — Луна, то для этой системы та же сила будет внешней. [c.263]

Рассмотрим теперь механическую систему, состоящую из п материальных точек. Выделим какую-нибудь из точек системы с массой wZfe. Под действием приложенных к ней внешних и внутренних сил и Fi (в которые входят и активные силы, и реакции связей) точка будет двигаться по отношению к инерциальной системе отсчета с некоторым ускорением сг . Введя для этой точки силу инерции —mtflf , получим согласно равенству (85), что [c.345]

Обозначим равнодействующие всех (и внешних, и внутренних) активных сил и реакций связей, действующихjia какую-нибудь точку системы 5ft, соответственно через FI и Тогд , поскольку каждая из точек системы находится в раэновесии, а сле- [c.361]

Силы, действующие в мате- Классификация сил. В динамике, как и в риальной системе, подраз- статике, приступая К решению каждои за-деляют на внутренние и дачи, МЫ должны В первую очередь опре-внешние или на активные и делить материальную точку, или абсолютно реакции связей твердое тело, или материальную систему, [c.255]

Представим равнодействующую силу, приложенную к каждо1[ точке системы, разложенной не на активную силу и реакцию связей, а па внутреннюю и внешнюю силы по отношению ко всей системе [c.344]

На элементы конструкции действуют внешние нагрузки активные и реактивные (реакции связей), — под действием которых возникают внутренние силы силы взашлсдейстЕ ия между частицами твердого тела, препятствующие ею деформации. Как всякую системук сил, внутренние силы, распределенные в сечении нагружен)яого бруса, можно привести центру тяжести сеяния, в результате получим главный вектор R и главный момент М (R) внутренних сил в сечении. Метод сечений позволяет определить внутренние силы, возникающие в поперечных сечениях бруса, через внеииние нагрузки. [c.4]

Обращаем внимание, что, говоря о внутренних силовых факторах, не рекомендуется употреблять глагол действуют, лучше говорить возникают. Выскажем некоторые соображения в защиту этой рекомендации. Известно, что существуют две основные системы построения курса сопротивления материалов. Согласно первой, продольные силы, изгибающие моменты и т. д. рассматриваются как внутренние силовые факторы, согласно второй — как равнодействуюнгие внешних сил, приложенных по одну сторону от проведенного сечения. Здесь, следуя программе для техникумов, методике, принятой ведущими кафедрами вузов, мы трактуем изгибающие моменты и прочие аналогичные величины как внутренние силовые факторы. При этом естественно говорить о их возникновении под действием внешних сил подобно тому, как возникают реакции связей абсолютно жестких тел. При таком подходе нелогично приписывать внутренним силовым факторам какую-либо активную роль, скажем, говорить, что изгибающий момент вызывает изгиб бруса.

Такой подход последовательно проведен во всей книге, и мы неоднократно подчеркиваем реактивный характер внутренних силовых факторов. Из сказанного не следует делать вывод о недопустимости иных трактовок, но принятая более логична. [c.56]

Изобразим систему вместе с действуюшими на нее внешними силами активными (Р = mig, Q = mag, G = m.g) и реакциями связей (Ni, Fi, R, Nj, Fj). Внутренние силы не показываем, так как [c.228]

Докажем необходимость и достаточность этого условия равновесия. Пусть система, на которую наложены идеальные голоно.ч-ные стационарные удерживающие связи, состоит из п точек. Обозначил через F/, равнодействующую приложенных к к-й точке активных сил, а через — равнодействующую реакций внешних и внутренних связей, наложенных на ту же точку. При равновесии системы каждая ее точка также находится в равновесии, поэтому для каждой точки можно записать условие равновесия в виде [c.267]

Система уравнений (14. 3) выражает принцип Даламбе-ра для системы материальных точек если к каждой точ ке движущейся механической системы условно приложить соответствующую силу инерции, то в любой момент движения действующие на эту точку активные силы [внешние и внутренние), силы реакций связей внешних и внутренних) и сила инерции образуют уравновешен ную систему сил. [c.281]

Оси координат и точки, относительно которых берутся моменты сил, выбираются так, чтобы не подлежащие определению неизвестные силы не входили в уравнения равновесия. Если из составленных уравнений для нерас-члененной системы определить искомые величины hj представляется возможным, то применяют метод расчленения системы на составные части. К каждой части прикладываются активные силы (внешние и внутренние), реакции отброшенных внешних и внутренних связей и силы инерции. Составляются уравнения принципа Да-ламбера для каждой части, и в результате их совместного решения находятся искомые величины. [c.284]

Чтобы избежать опасной путаницы, мы тотчас же условиися, что эта вторая классификация сил не зависит от первой. Для некоторых частных систем, как, например, для свободного твер дого тела, находящегося под действием силы тяжести и поверхностных растягивающих или сжимающих сил, обе классификации приводят к одному и тому же распределению сил в этом случае активные силы (вес и поверхностные силы) являются внешними, а реакции (силы связей твердого тела) — внутренними. Но достаточно подумать о связях, осуществляемых посредством соединенил системы, с внешними по отношению к ней телами (например, подвешенное или опертое твердое тело), а с другой стороны, о силах, происходящих не от связей, но возбуждаемых искусственными приспособлениями или возникающих в естественных физических условиях (например, ньютонианское притяжение между материальными элементами движущейся системы), чтобы видеть, что, вообще говоря, и активные силы, и силы реакции могут быть как внешними >шк и внутренними. [c.255]

Две указанные выше классификации сил, действующих на материальную систему, играют ва>1общих теорем и последующих конкретных приложений. Не будет поэтому лишним вспомнить, что аналогичные обстоятельства имели место в статике, где сначала, разделив силы на внешние и внутренние, мы пришли к основным условиям равновесия (т. I, гл. XII), приложимым в качествь необходимых к всевозможным типам материальных систем (например, к стержневым системам, нитям и т. д., гл. XIV) и, в частности, являющимся достаточными для равновесия твердого тела (гл. Х1П) затем в общей статике (гл. XV), отправляясь от разделения сил на активные силы и реакции и присоединяя ограничительные предпо—ложения о природе связей (отсутствие трения), мы пришли, примени принцип виртуальной работы, к исключению неизвестных реакций н условий равновесия. [c.256]

Мы получили таким образом теорему живых сил в дифференциал ной форме во время движения материальной системы с какими угодно связями и под действием каких угодно сил приращение, которое получает живая сила системы за какой-нибудь элементк времени, равно полной работе, совершаемой за тот же самый элемент времени всеми силами, действующими на систему (внешними и внутренними, активными и реакциями). [c.278]

В результате Л. Б. Левенсон приходит к ряду выводов. Проблема сил инерции существует, ибо ученые до сих пор не пришли к единому мнению об их сущности. Силы могут быть активными и реактивными к последним относятся силы трения, сопротивление среды, силы упругости и силы инерции. Своеобразие сил инерции заключается в следующем 1) по происхождению и действию сила инерции стоит особняком, не являясь ни внешней, ни внутренней (в узком понимании) силой 2) возникающие в одиночку (не парами) силы инерции должны быть уравновешены 3) при отсутствии физической связи, передающей ускорение, сила инерции, хотя и существует как кинематическая реакция материи, но проявить свое действие в ясном виде не может 4) при свободном движении материальной точки из-за полного отсутствия связей действие силы инерции также не может явно проявиться тогда ускоряющая сила действует непосредственно на каждую частицу тела, минуя связи, и сообщает всем частицам равные и параллельные ускорения. [c.49]

Связи, реакции связей и принцип освобождаемости в статике.

Теоретическая механика

Принцип освобождаемости.

Связи и реакции связей

Как уже упоминалось в предыдущих статьях, статика изучает условия, при которых тела и материальные точки находятся в состоянии равновесия. Казалось бы, благодаря аксиомам статики, описывающим основные свойства силового взаимодействия между телами, решение задач равновесия тел не должно представлять трудностей — неизвестные силы можно найти, зная, что они должны уравновешиваться известными силами, отсюда и ключ к решению.
Тем не менее, основная сложность при расчетах заключается в том, что силы — векторные величины, и для решения задач необходимо знать не только их скалярные размерности (модули), но и направление в пространстве, а также точки приложения. В результате получается, что каждая неизвестная сила содержит три вопроса: куда она направлена, где приложена, и какова ее величина?

Исключить некоторые неизвестные составляющие сил помогает анализ связей между телами. Как мы уже знаем, все тела и материальные точки подразделяются на свободные и связанные (несвободные). В статике чаще всего приходится решать задачи, в которых рассматривается условие равновесия связанных тел, т. е. имеющих некоторые (или полные) ограничения на перемещение в пространстве относительно других тел.
Эти ограничения называются связями.

Примерами связей, ограничивающих перемещение тела, может послужить поверхность или какая-либо опора, на которой лежит тело, жесткая заделка части тела в массив, исключающая любое его перемещение, а также гибкие и шарнирные связи, частично ограничивающие возможность тела перемещаться в пространстве.
Анализ таких связей позволяет понять, какие силовые факторы возникают в них при противодействии перемещению связанного тела. Эти силовые факторы называют силами реакции или реакциями связей (обычно их называют просто реакциями).
Силы, которыми тело воздействует (давит) на связи называют силами давления.
Следует отметить, что силы реакций и давлений приложены к различным телам, поэтому не представляют собой систему сил.

Силы, действующие на любое тело можно разделить на активные и реактивные.
Активные силы стремятся перемещать тело, к которому они приложены, в пространстве, а реактивные силы — препятствуют этому перемещению. Силы реакции связей относятся к реактивным силам.
Принципиальное отличие активных сил от реактивных заключается в том, что величина реактивных сил зависит от величины активных сил, но не наоборот. Активные силы часто называют нагрузками.

При решении большинства задач статики несвободное тело условно изображают как свободное с помощью так называемого принципа освобождаемости, который формулируется следующим образом: всякое несвободное (связанное) тело можно рассматривать как свободное, если отбросить связи и заменить их реакциями.

***

Типичные связи тел и их реакции

Рассмотрим наиболее часто встречающиеся связи, а также возникающие в них реакции при приложении нагрузок.

Идеально гладкая плоскость

Реакция идеально гладкой плоскости направлена перпендикулярно опорной плоскости в сторону тела, так как такая связь не дает телу перемещаться лишь в одном направлении — в сторону опорной плоскости, т. е. перпендикулярно ей (см. рисунок 1,а).
Если же тело находится на наклонной плоскости, то силу его тяжести G можно разложить на две составляющие, из которых одна будет направлена параллельно плоскости (Xa), другая — перпендикулярно ей (Ya). При этом первая сила будет стремиться передвигать тело по плоскости в сторону уклона, а вторая — прижимать его к плоскости (см. рисунок 1,б).
Реакция наклонной плоскости будет равна по модулю составляющей, перпендикулярной плоскости и направлена в сторону, противоположную этой составляющей, уравновешивая ее. Если тело касается плоскости одной точкой (например, шар или угол), то реакция будет приложена к этой точке тела.
В других случаях, когда тело касается плоскости некоторой поверхностью, имеет место взаимодействие посредством нагрузки, распределенной по этой поверхности (распределенной нагрузки).

Идеально гладкая поверхность

Идеально гладкая поверхность (отличается от плоскости криволинейностью) реагирует перпендикулярно касательной плоскости, т. е. по нормали к опорной поверхности в сторону тела, так как нормаль — единственное направление перемещения тела, которое не допускает данная связь (см. рисунок 1,в).

Закрепленная точка или ребро угла

В случае, если перемещение тела ограничивается закрепленной точкой или ребром угла, реакция связи направлена по нормали к поверхности идеально гладкого тела в сторону тела, так как нормаль к поверхности тела — единственное направление, движение в котором ограничено этим видом связи (см. рисунок 1,г).

Гибкая связь

Реакция гибкой связи (гибкая нить) не дает телу удаляться от точки подвеса и поэтому направлена вдоль связи от тела к точке подвеса, т. е. известны точка приложения реакции гибкой связи и ее направление. На рисунке 2 изображена гибкая связь, служащая связующим звеном между двумя стержнями и телом.

В конструкциях широкое распространение имеют связи, которые называются шарнирами. Шарнир представляет собой подвижное соединение двух тел (деталей), допускающее только вращение вокруг общей точки (шаровой шарнир) или вокруг общей оси (цилиндрический шарнир). Рассмотрим, какие реакции возникают при связывании тела с помощью шарниров.

Идеально гладкий цилиндрический шарнир

При связывании тела цилиндрическим шарниром возможно его перемещение вдоль оси шарнира и вращение относительно этой оси. Реакция цилиндрического шарнира расположена в плоскости, перпендикулярной его оси и пересекает эту ось. Направление вектора реакции шарнира на этой плоскости зависит от направления вектора нагрузки.
Примером цилиндрического шарнира может послужить обыкновенный подшипник качения.

Идеально гладкий шаровой шарнир

В этом случае заранее известно лишь то, что реакция проходит через центр шарнира, так как тело, связанное шаровым шарниром, может поворачиваться в любом направлении относительно оси шарнира, но не может совершать никаких линейных перемещений в пространстве, т. е. удаляться от центра шарнира или приближаться к нему.

Идеально гладкий подпятник

Подпятник можно рассматривать, как сочетание цилиндрического шарнира и опорной плоскости, поэтому реакция подпятника считается состоящей из двух составляющих: X_a и Y_a. При этом одна из реакций будет направлена вдоль нормали к опоре в сторону тела (как у опорной плоскости), другая — перпендикулярно оси подпятника (как у цилиндрического шарнира).
Полная реакция подпятника будет равна векторной сумме этих составляющих: R_a = X_a +Y_a.

Стержень, закрепленный шарнирно

Стержень, закрепленный двумя концами в идеально гладких шарнирах и нагруженный концами (рис. 2), реагирует только по линии, соединяющей оси шарниров, т. е. вдоль своей оси (согласно III аксиоме статики). При этом реакция стержня может быть направлена и к центру шарнира (точке крепления), и от него (в зависимости от направления нагрузки), поскольку этот вид связи удерживает тело на фиксированном расстоянии, не позволяя ему удаляться или приближаться. Этим стержень принципиально отличается от гибкой связи, у которой реакция всегда направлена от точки крепления в сторону связи (гибкая связь удерживает тело только от удаления, не запрещая ему приближаться к точке крепления).

Жесткая заделка

Этот вид связи полностью лишает тело возможности перемещаться в любом направлении и вращаться относительно какой-либо оси или точки.
При жесткой заделке тела (рис. 3) в опоре возникает не только реактивная сила R_A, но и реактивный момент М_A.
Жесткая заделка является «темной лошадкой» при вычислениях, поскольку изначально ни направление реакций, ни их величина неизвестны, особенно если нагрузка представлена системой сил. Тем не менее, используя разложение активных сил на составляющие, последовательно можно определить и реактивную силу R_A, и реактивный момент M_A, действующие в жесткой заделке.
В случае, если тело связано не только жесткой заделкой, но и другим видом связи, задача становится нерешимой обычными методами статики, поскольку неизвестных реакций больше, чем возможное количество уравнений равновесия.

Пример решения задачи по определению реакций жесткой заделки приведен на этой странице.

***

Понятие бруса и балки в технической механике

В статике нередко приходится решать задачи на условие равновесия элементов конструкций, называемых брусьями.
Брусом принято считать твердое тело, у которого длина значительное больше поперечных размеров. Осью бруса считается геометрическое место (множество) центров тяжести всех поперечных сечений этого бруса.
Брус с прямолинейной осью, положенный на опоры и изгибаемый приложенными к нему нагрузками, называют балкой.

***

Распределенные нагрузки

Главная страница

Дистанционное образование

Специальности

Учебные дисциплины

Олимпиады и тесты

2. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ

2.1. Свободное и несвободное тело. Активные и реактивные силы

Тело называется свободным, если под действием приложенных к нему сил может перемещаться в любом направлении (рис. 2.1, а).

Тело, свобода перемещения которого ограничена другими телами, называется несвободным (рис. 2.1, б).

Тела, ограничивающие свободу перемещения данного тела, называются его связями.

При действии данного тела на связь с ее стороны возникает противодействие. Сила, с которой связь действует на данное тело, называется реакцией связи (R).

Таким образом, все силы, действующие на данное тело, можно подразделить на активные и реактивные силы.

Активными называются известные по модулю и направлению силы, с которыми на данное тело действуют другие тела, не являющиеся его связями.

Реактивные силы – это реакции связей данного тела. Реакции связей возникают только в том случае, когда тело под действием активных сил давит на связи. При этом направление реакции связи противоположно направлению, по которому связь препятствует перемещению данного тела, и зависит от типа связи.

При решении задач статики часто используется принцип освобождаемости тел от связей. Согласно этому принципу несвободное тело (рис. 2.1, б) можно рассматривать как свободное, если связи заменить их реакциями (рис. 2.1, в).

2.2. Основные типы связей

1.Абсолютно гладкая плоскость (или поверхность), где силы трения пренебрежимо малы. Реакция R гладкой плоскости (или поверхности) направлена по нормали к поверхности (рис. 2.2, а – 2.2, в).

2.Ребро. Реакция ребра R направлена по нормали к поверхности тела, опирающегося на это ребро (рис. 2.2, г).

3.Гибкая связь (трос, канат, нить). Реакция нити Т на данное тело направлена вдоль нити (рис. 2.2, д). Гибкая связь может испытывать только растяжение. При этом растягивающее усилие (натяжение) нити неизменно на всех ее участках и равно реакциям нити на соединяемые ей тела. При растяжении реакции направлены от тел, соединяемых нитью (рис. 2.2, е). Если пренебречь силами трения, то натяжение нити на всех ее участках равно величине подвешенного к ней груза (Т = Р).

4.Тонкий невесомый (незагруженный) стержень с шарнирами по концам.

Шарнир – это устройство, допускающее поворот одного тела относительно другого. Реакция тонкого стержня N на данное тело направлена по прямой, соединяющей шарнирные концы стержня (рис. 2.3, а). В зависимости от направления сил, действующих со стороны шарниров, прямой невесомый

стержень АВ может испытывать растяжение или сжатие (рис. 2.3, б). Усилие стержня изображается его реакциями на шарниры: при растяжении – стрелками от шарниров, а при сжатии – стрелками к шарнирам.

5. Шарнирно-подвижная опора (рис. 2.4, а). Эта связь допускает поворот данного тела вокруг оси опорного шарнира и поступательное (линейное) перемещение тела параллельно опорной плоскости. Реакция связи R проходит через центр шарнира перпендикулярно опорной плоскости. Конструкция шарнира представляет собой подшипник (цилиндрический шарнир), наружная обойма которого крепится к опоре, а внутренний валик – к данному телу. Шарнирно-подвижная опора эквивалентна одной связи 4-го типа (рис. 2.4, б).

6. Шарнирно-неподвижная опора (рис. 2.4, в). Эта связь допускает только поворот данного тела вокруг оси опорного шарнира, препятствуя любому поступательному движению тела. Реакция связи R проходит через центр шарнира, но линия действия реакции может быть какой угодно в зависимости от сил, действующих на данное тело. Таким образом, определению подлежат как модуль R, так и угол α, определяющий направление реакции. Очень часто вместо R и α определяют составляющие Х и У реакции по взаимно перпендикулярным осям х и у, после чего, используя в условиях плоской задачи зависимости (1.1) и (1.2), определяют модуль и направление реакции

R = X + У = Хi + Уj

где Х, У – проекция R на оси х, у.

R = \/ Х2 + У2 , tg α = У / Х → α

Шарнирно-неподвижная опора эквивалентна двум связям 4-го типа (рис. 2.4, г).

7.Жестко защемляющая опора (заделка). Эта связь (рис. 2.4, д)

препятствует любому поступательному и вращательному движению данного

тела. Составляющими реакции заделки А являются горизонтальная Ха, вертикальная Уа составляющие и опорный момент Ма. Заделка эквивалентна трем связям 4-го типа, оси которых не должны пересекаться в данной точке

(рис. 2.4, е).

8.Шаровой шарнир (рис. 2.4, ж). Эта связь представляет собой шар, который может вращаться внутри сферической полости. Линия действия реакции R проходит как угодно в пространстве через центр шара. Модуль и направление реакции R можно определить через ее составляющие Х, У и Z по зависимостям (1.2) и (1.3).

Активные и реактивные силы в рычажном механизме захвата при контакте ведомого звена с твёрдым телом Текст научной статьи по специальности «Механика и машиностроение»

Преимущества измерителя массового расхода и плотности, построенного на описанном принципе, следующие: он может работать на потоке среды, осуществляет измерение на всём объёме (интегральным образом), обладает весьма малым гидравлическим сопротивлением.

Как видим, решение рассмотренной задачи представляет не только теоретический интерес, но и может быть использовано при построении измерительного прибора для измерения массового

расхода и плотности жидкости.

СПИСОК ЛИТЕРАТУРЫ

1. Майоров Е. В., Онищук В. А. Об инерционном способе одновременного измерения массового расхода жидкости и её плотности // Прикладная физика. — 2005. — №6. — С. 18.

2. Лойцянский Л. Г. Механика жидкости и газа: учебник для вузов. — 7-е изд., испр. — Москва : Дрофа, 2003.

REFERENCES

1. Mayorov E. V., Onishchuk V. A. Ob inertsionnom sposobe odnovremennogo izmereniya massovogo raskhoda zhidkosti I ee plotnosti [On the inertial method of simultaneous measurement of the mass flow rate of a liquid and its density] // Applied Physics, 2005, №6, P. 18.

2. Loytsyanskiy L. G. Mekhanika zhidkosti I gaza: uchebnik dlya vuzov [Fluid and gas mechanics: a textbook for universities]. 7th ed., Corr. Moscow: Drofa, 2003.

Жиляев Олег Валентинович, аспирант кафедры «Тепловая и топливная энергетика» УлГТУ, заместитель главного конструктора, руководитель Бюро новой продукции отдела главного конструктора Научно-Производственного Общества «Новые Технологии Эксплуатации Скважин», (ООО НПО «НТЭС») г. Бугульма (Республика Татарстан), [email protected].

Поступила 28.01.2019 г.

УДК 531.1; 531.8

В. К. МАНЖОСОВ, А. А. САМСОНОВ

АКТИВНЫЕ И РЕАКТИВНЫЕ СИЛЫ В РЫЧАЖНОМ МЕХАНИЗМЕ ЗАХВАТА ПРИ КОНТАКТЕ ВЕДОМОГО ЗВЕНА С ТВЁРДЫМ ТЕЛОМ

Статья посвящена передаче движения в рычажном механизме захвата. В технологических системах такие механизмы используются для подъёма и перемещения твёрдых цилиндрических тел. Силы трения в зоне контакта ведомого звена с цилиндрической поверхностью исключают возможность разрыва связи твёрдого тела и ведомого звена.

Определено соотношение силы на ведущем звене и возникающей нормальной реакции в зоне контакта ведомого звена с цилиндрической поверхностью. Определено влияние параметров механизма на соотношение этих сил. Определяется зона, в которой отношение сил достигает наименьших значений.

Ключевые слова: рычажный механизм, механизм захвата, передача движения, силы трения, угол передачи движения, условия равновесия.

Захваты рычажного типа составляют распространённую группу устройств, удерживающих объект транспортировки за счёт контактного взаимодействия ведомого звена с объектом [1, 2].

В работе [3] рассмотрена схема манипулятора для захвата и перемещения твёрдых цилиндрических тел. Исполнительный механизм (рис. 1), обеспечивающий захват, представляет собой рычажный механизм. Ведущее звено (ползун) исполнительного механизма перемещается поступательно, а ведомое звено (клешня) совершает вращательное движение в плоскости звена АВ = I (рис. 2) и клешни ОБС (обозначим эту плоскость как плоскость х-у).

Рис. 1. Механизм захвата

Рис. 2. Схема механизма в момент захвата

При захвате цилиндрических тел исполнительных механизмов как минимум три. Углы между плоскостями исполнительных механизмов определяются как ф = 2ж / п, где п — число исполнительных механизмов (п > 2).

Схема исполнительного механизма в момент контакта с объектом захвата представлена на рис. 2. При контакте точка С имеет координаты хС и ус = -к. Положение звена ОА в момент контакта определяется углом р . Расстояние от точки С до точек Б и О определяется отрезками БС= 1БС и ОС= 1С .

Положение отрезка ОС относительно вертикали определяется углом рк, положение отрезка БС относительно ОБ= 1Б определяется углом рБ .

При контакте с твёрдым телом в точке контакта (в точке С) повороту звена ОБС противодействует нормальная составляющая реакции — Я и сила трения Е = / ■ Я, где / — коэффициент трения.

Если при перемещении твёрдого тела захват удерживает его за счёт сил трения Е, то величина этих сил должна быть определена из условия надёжности захвата.

Рассекая звено АВ и используя аксиому связей, определим соотношение между движущей силой Р, действующей на ползун, и продольной силой N в поперечном сечении звена АВ. На рис. 3 представлена схема сил, действующих на ползун В и отсечённую часть звена АВ.

Рис. 3. Схема сил, действующих на ползун В и отсечённую часть звена АВ

Рис. 4. Схема сил, действующих на часть звена АВ и ведомое звено (клешню) ОБС

Из условия статического равновесия сил (полагая, что связи звеньев идеальные) следует, что

N cos р-P _ 0, N _ P / cos /3. (1)

На рис. 4 представлена схема сил, действующих на отсечённую часть звена АВ и ведомое звено (клешню) ОБСв момент контакта с твёрдым телом. Из условия статического равновесия сил (полагая, что связи звеньев за исключением в зоне контакта идеальные) следует, что

N cosa-lA — Rh — F ■ xc _ 0, F _ f ■ RN _ R(h + f’ Xc ), (2)

lA cosa

где a — угол давления.

Приравнивая (1) и (2), приходим к равенству

P _ R(h + f ■ xc ) p _ (h + f ■ xc ) cos 3 _ , R ~

cos 3

L cosa

L cos a

В зависимости от угла р и длин звеньев ОА = 1А , АВ = l определяются углы / и рА (рис. 2): 1А /sin/ = l/sinp, sin3 = -ysinp, 3 = arcsin(-ysinp), рА = я-(р + /). В зависимости от lD, хС и h определяются lC , ph, pDC , lDC, pD :

(3)

(4)

lc — ‘sj Xc + h

ph _ arc sin

cos pD _

V lc J

l2 +12 -12 2l l

, Pdc (P + Ph ), lDc _л112c + lD — 2lclD cos Pdc

(pD _ arc cos

Перейдём к относительным величинам: Тогда

l_l / 1а ; xc _ xc/ 1А ; h _ h / 1А ; 1d _ 1D / 1А ;

l2 + i2 — I2

1d^1dc lc

2l l ^1d1dc

l Dc lDc / la ; l c lc / la

■ n sinp .1d1dc

cosa

(5)

(6)

(7)

(8)

От угла (рА зависит величина угла передачи движения от звена АВ рычагу ОВ (обозначим его как у) и величина угла давления а = ж /2 — у:

гя-рА, если р<я/2-3; \р +3, если р<я/2-

рА, если р>я/2-3;

у_.

я-(р + 3), если р>я/2-3

(9)

Координата хС точки контакта зависит от поперечных размеров объекта захвата. я /2 .

Так как a _ я / 2 — у, то cos a _ sin у и равенство (8) можно представить в виде

P _ (h + f ■ Xc ) cos 3 R sin у

(10)

На рис. 5 представлены диаграммы, характеризующие изменение углов (рА, у и ß в зависимости от угла ( . Изменение угла ( рассматривается в диапазоне от 1 до 2 радиан при следующих параметрах механизма: l = 5; lD = 1,2; xC = 1; h = 1,2.

В рассматриваемом диапазоне параметров угол ß изменяется в весьма малых пределах от 0,17 до 0,2. В этой связи угол (А = ж — (( + ß) практически линейно зависит от угла ( .

Диаграмма угла передачи движения у имеет чётко выраженный максимум при ( = 1,37. Величина угла у при этом достигает значения у = 1,57 = ж/2 . На рис. 5 затенённая зона показывает область рационального диапазона угла (, при котором целесообразно обеспечивать контакт ведомого звена (клешни) с твёрдым телом. В этом диапазоне угол передачи движения у принимает значения от 1,5 до 1,57.

Обратимся к расчётной зависимости (10), определяющей соотношение движущей силы Р и возникающей в контактной зоне реакции R, значение которой определяет силу трения F = f • R,способной удержать твёрдое тело при захвате и его перемещении.

На рис. 6 представлена диаграмма соотношения сил P/R зависимости от угла (, при котором происходит контакт ведомого звена с твёрдым телом (коэффициент трения f = 0,2). Параметры механизма захвата приняты следующими: l = 5; lD = 1,2; xC = 1; h = 1,2.

а 2

а 1,5

£ 1

£ 0,5

1 = 5; 4 = 1,2;

<Ра = 1′ h =1 7

«X у

ß /

<P, рал

1 1,1 1J2 U 1,4 L5 1,6 1,7 1,8 1,9 2 Рис. 5. Изменение углов (A, у и ß в зависимости от угла (

1.7

1,65

1,Ь

ч Я 1,55

и Я К 1.5

а 1,45

о 1,4

1,35

1.3

Г =5: lD = хс =1; h = 1. 1 — /

£>:рад

1 1,1 и 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2 Рис. 6. Диаграмма соотношения сил Р/Лзависимости от угла р при коэффициенте трения / = 0,2

На диаграмме явно можно проследить диапазон минимальных соотношений сил P/R, который вновь попадает в область рациональных значений угла (, когда целесообразно обеспечить контакт ведомого звена (клешни) с твёрдым телом. При принятых параметрах минимальное соотношение сил P/R = 1,37. Это указывает на то, что даже в наиболее благоприятном случае значение движущей силы Р почти на 40 % превышает реакцию R в зоне контакта.

Анализируя зависимость (10), заметим, что для снижения соотношения P/R необходимо увеличивать угол ß и стремиться обеспечить значение угла у близким к ж /2. Целесообразно также стремиться к уменьшению h и xC .

СПИСОК ЛИТЕРАТУРЫ

1. Артоболевский И. И. Механизмы в современной технике. Т. 1. Рычажные механизмы. — Москва : Наука, 1970. — 608 с.

2. Mannaa A. R., Akyurt M., El-Kalay A. K. Six-link Gripperfor Cylindrical Objects // Journal of Islamic Academy of Sciences 3:1, pp. 6- 10, 1990.

3. Самсонов А. А. Манипуляторы для дистанционного перемещения грузов // Сб. материалов 52-й НТК УлГТУ. Ч. 1. — Ульяновск :УлГТУ, 2018. — С. 132 — 135.

REFERENCES

1. Аrtobolevskij I. I. Mekhanizmy v sovremennoj tekhnike. Mechanisms in modern technology. T. 1. Lever mechanisms. Moscow: Science, 1970, 608 p.

2. Mannaa A. R., Akyurt M., El-Kalay A. K. Six-link Gripperfor Cylindrical Objects // Journal of Islamic Academy of Sciences 3:1, pp. 6-10, 1990.

3. Samsonov А. А. Manipulyatory dlya distantsionnogo peremeshheniya gruzov [Manipulators for remote movement of goods] // Sb. materialov 52-j NTK UlGTU. [Materials of the 52nd NTK UlSTU]. CH. Part 1. Ulyanovsk: UlSTU, 2018, pр. 132-135.

Манжосов Владимир Кузьмич, доктор технических наук, профессор, профессор кафедры «Промышленное и гражданское строительство» Ульяновского государственного технического университета. Имеет статьи, монографии, изобретения в области динамики машин, моделирования процессов удара [e-mail: [email protected] ].

Самсонов Александр Анатольевич, аспирант кафедры «Промышленное и гражданское строительство» Ульяновского государственного технического университета. Имеет статьи и патенты в области создания механизмов различного технологического назначения [e-mail: [email protected]].

Поступила 11.02.2019 г.

Активные силы — Большая Энциклопедия Нефти и Газа, статья, страница 1

Активные силы

Cтраница 1

Активные силы, действующие на систему, в общем случае могут зависеть не только от положений и скоростей точек системы и времени, но и от некоторых параметров. [1]

Активные силы не зависят от связей, а значит, и от реакций связей, наложенных на твердое тело. [2]

Активные силы — понятие, связанное со вторым и третьим законами Ньютона. [4]

Активные силы, приложенные к каждой материальной точке движущейся системы и реакции связей, ограничивающих ее движение, уравновешиваются силами инерции. [5]

Активные силы можно также условно назвать заданными силами; это те из сил, приложенных к механической системе, которые сохраняются, если связи мгновенно исчезнут. Реакции связен называют иногда пассивными силами; они заранее неизвестны и зависят не только от тех материальных приспособлений, которые реализуют связи, но и от активных сил и от движения системы. [6]

Активные силы вызывают ускорение материальных тел и реакции Силы не могут вызывать ускорение и появляются при сил. [7]

Активные силы, действующие на катки в виде колес ( рис. 66), кроме силы тяжести Р обычно состоят из силы Q, приложенной к центру колеса параллельно общей касательной в точке А, и пары сил с моментом L, стремящейся катить колесо, называемое в этом случае ведомо-ведущим. Если L 0, а 2 0, то колесо называют ведомым; если L O, a 2 0, то ведущим. Ведомо-ведущими являются колеса локомотива, идущего вторым в составе поезда. [8]

Активные силы можно также условно назвать заданными силамщ это те из сил, приложенных к механической системе, которые сохраняются, если связи мгновенно исчезнут. [9]

Активные силы, например центробежная сила при криволинейном течении и гидростатическая подъемная сила в течении с переменной в вертикальном направлении плотностью, также очень сильно влияют на переход ламинарного течения в турбулентное. [10]

Активные силы, действующие на катки в виде колес ( рис. 66), кроме силы тяжести F обычно состоят из силы Q, приложенной к центру колеса параллельно общей касательной в точке А, и пары сил с моментом L, стремящейся катить колесо, называемое в этом случае ведомо-ведущим. Если L 0, a Q Q, то колесо называют ведомым; если L O, a Q-Q, то ведущим. Ведомо — ведущими являются колеса локомотива, идущего вторым в составе поезда. [11]

Активные силы вызывают деформацию. Реактивные силы препятствуют перемещению частиц металла при деформации. В процессе деформации тела приложенные к нему внешние силы вызывают в нем возникновение внутренних сил, стремящихся восстановить первоначальную форму и размеры тела. Это происходит вследствие изменения межатомных расстояний, следовательно, изменение величины силы взаимодействия приводит к нарушению межатомного равновесия. Внешние силы встречают противодействие внутренних сил. Эти внутренние силы вызывают напряжения в теле. Напряжением называют интенсивность внутренней силы, приходящуюся на единицу площади сечения. Напряжение на схемах изображают векторами — стрелками, показывающими направление действия сил. [13]

Активные силы принято называть нагрузками. По способу приложения нагрузки бывают объемные и поверхностные ( распределенные и сосредоточенные), по характеру изменения в процессе приложения — статические, динамические и повторно-переменные, по продолжительности действия — постоянные и временные. [14]

Активные силы в высокотемпературной области деформации вызывают знак, противоположный знаку деформаций, которые образуются в процессе наложения сварных швов. Приложением активных сил можно заметным образом уменьшить величину остаточной деформации, устранить ее совершенно и получить даже деформации знака, обратного знаку тех деформаций, которые получаются при сварке в ненагруженном состоянии. [15]

Страницы: 1 2 3 4

Активные реактивные силы — Большая Энциклопедия Нефти и Газа, статья, страница 1

Активные реактивные силы

Cтраница 1

Активные и реактивные силы являются внешними силами ( нагрузками), вызывающими деформацию изгиба в балке. [1]

Принцип Даламбера формулируется так: активные и реактивные силы, действующие на материальную точку, вместе с силами инерции образуют систему взаимно уравновешенных сил, удовлетворяющую всем условиям равновесия. [2]

Как было сказано выше, внешними нагрузками балки являются активные и реактивные силы и моменты. [3]

Решая задачу первым способом, мы учитывали только фактически действующие на тело активные и реактивные силы и составили шесть всеобщих уравнений движения ( 169) и ( 192), связывающих проекции этих сил с массами и с проекциями ускорений частиц тела. [4]

Для определения внутренних силовых факторов применим метод сечений, причем изображать балку будем только одной линией — осью, к которой приложены активные и реактивные силы. [5]

Пусть все активные и реактивные силы и массы механизма приведены к одному из его звеньев. [6]

Расчеты с учетом инерционных нагрузок ведутся известным из теоретической механики методом кинетостатики, основанном на принципе Даламбера. Согласно этому принципу все активные и реактивные силы, приложенные к телу, вместе с силами инерции образуют систему взаимно уравновешенных сил, удовлетворяющую всем условиям равновесия. Таким образом, задачи динамики и сопромата решаются методами статики. [7]

Страницы: 1

Силы действия и реагирования: закон и примеры — стенограмма видео и урока

Пары сил и третий закон Ньютона

Третий закон Ньютона гласит, что силы всегда действуют парами. Рассмотрим пример мальчика, играющего с игрушкой для собаки, и его иллюстрации. Мальчик действует на игрушку собаки, а игрушка собаки — на мальчика. Эти две силы создают пару взаимодействия .Силы всегда приходят парами, как в этом примере. Рассмотрим мальчика (A) как одну систему, а игрушку (B) как другую. Какие силы действуют на каждую из двух систем? Представьте себе мальчика, тянущего за игрушкой, а игрушку вытаскивают из мальчика. Вы можете видеть, что каждая система воздействует на другую. Две силы — F (A на B) и F (B на A) — это силы взаимодействия между ними. Обратите внимание на симметрию: A на B и B на A.

Силы F (A на B) и F (B на A) представляют собой пару взаимодействий , которая представляет собой набор двух сил, которые направлены в противоположных направлениях, имеют равные величины и действуют на разные объекты.Иногда пару взаимодействия называют парой действие-реакция. Это может означать, что одно вызывает другое; однако это не так. Например, сила, с которой мальчик тянет игрушку, не заставляет игрушку тянуть мальчика. Эти две силы либо существуют вместе, либо не существуют вовсе.

Не может быть единственной силы, действующей в одиночку. Силы приходят только в парах действие-противодействие. Тщательно продумайте, как двигать скейтборд ногой. Ваша ступня отталкивается от земли. Сила действует на землю.Однако вы двигаетесь, поэтому сила должна действовать и на вас. Почему вы переезжаете? Какая сила действует на вас? Вы двигаетесь, потому что сила воздействия вашей ноги на землю создает силу реакции земли на вашу ногу. Вы «чувствуете» землю, потому что чувствуете силу реакции, давящую на вашу ногу. Сила реакции — это то, что заставляет вас двигаться, потому что она действует на вас.

Третий закон движения Ньютона объясняет, что силы всегда действуют парами действие-противодействие.Третий закон гласит, что для каждой силы действия существует равная и противоположная сила противодействия. Представьте, что вы попадаете в бейсбольный мяч. Бита оказывает на мяч силу. Это сила действия. Мяч оказывает на биту одинаковую и противоположную силу. Это сила реакции. Такая пара взаимодействия — еще один пример третьего закона Ньютона. Бейсбол заставляет биту двигаться в одном направлении, а бита — в противоположном. Эти две силы создают пару взаимодействия на разных объектах, они равны по силе и противоположны по направлению.Сила (F) А (бита) на В (мяч) равна по величине и противоположна по направлению силе В на А: F (А на В) = — F (В на А).

Ньютон понял, что если один объект тянет за другой, второй объект также тянет назад первый объект. Если один объект толкает другой, второй толкает первый объект. Другими словами, на каждое действие одной силы есть противодействие другой силы.

Парные диаграммы действие-реакция

При сортировке сил действия и противодействия полезно рисовать диаграммы.Нарисуйте каждый объект отдельно от другого. Представьте каждую силу в виде стрелки в соответствующем направлении. Рекомендации в этой таблице могут помочь вам разобраться в силах действия и противодействия.

Рассмотрим ситуацию, когда вы держите книгу в руке. Вы можете нарисовать одну схему для себя и одну для книги. Есть ли пары взаимодействия? Вы можете использовать стрелки для обозначения силы и направления силы. В этом случае пара взаимодействия — это сила книги на руке и сила руки на книге.

Примеры действия-реакции

Мы уже рассмотрели некоторые примеры. Но каковы еще примеры действия-противодействия? Посмотрим на ракетный двигатель. Третий закон Ньютона объясняет, как работают ракетные двигатели. Горячие газы вытесняются из задней части ракеты. Это сила действия. Газы действуют на ракету с равной и противоположной силой. Это сила реакции. Реакция толкает ракету вверх и отрывает ее от земли.

Также подумайте, что происходит, когда дайвер прыгает на трамплин? Доска отскакивает и поднимает дайвера в воздух.Сила воздействия на доску со стороны дайвера вызывает силу реакции со стороны доски на дайвера. Сила дайвера на доске равна силе, действующей на доску, и противоположна ей. Подумайте о том, как сила трамплина влияет на работу дайвера. Чем больше сила приложена к трамплину, тем выше будет прыжок.

Наконец, подумайте о том, как команда экипажа использует третий закон движения Ньютона для перемещения лодки.Когда весло опускается в воду, вода оказывает одинаковое усилие на обе стороны весла. Однако, когда участники тянут весла, поверхность их плоской стороны отталкивается от воды. Вода отталкивает весла с равной и противоположной силой. Лодка движется в направлении, противоположном веслам, с силой, равной силе весла, когда они отталкиваются от воды. Лодка движется, потому что силы против нее неуравновешены. Как вы думаете, почему важно, чтобы все члены экипажа одновременно тянули весла? Что ж, если члены экипажа не работают вместе, их собственные силы будут уравновешивать друг друга, уменьшая общую несбалансированную силу, которую они пытаются достичь.

Вращающийся водяной спринклер — еще один пример сил действия и противодействия. Вода нагнетается из спринклера. Это действие. Реакция — это движение разбрызгивателей от воды. Вы чувствуете такую же реакцию, когда держите водяной шланг и быстро включаете воду. Возможно, вы видели, как пожарные изо всех сил пытаются контролировать пожарный шланг. Когда вода покидает шланг, его выталкивают назад. Эта реакция затрудняет обращение со шлангом.

Осьминоги и кальмары также используют третий закон движения Ньютона.Осьминог или кальмар передвигается, сначала втягивая воду в свое тело. Затем животное с силой выдавливает воду из своего тела через отверстие за головой. Сила вытесненной воды перемещает животное в противоположном направлении.

Вот последний пример, когда мы думаем о третьем законе Ньютона и о том, что силы действуют в противоположных направлениях; вы только что надули воздушный шар. Сначала держите его отверстием вниз и отпустите. В каком направлении движется воздушный шар? При открытии вниз воздушный шар движется вверх.Снова надуйте шар, держите его горизонтально и отпустите. В каком направлении движется воздушный шар? Воздушный шар будет двигаться горизонтально от конца, из которого выходит воздух. Как бы вы объяснили, почему оба шара не движутся в одном направлении? Направление движения противоположно направлению выходящего воздуха.

Итоги урока

Силы всегда действуют парами. Третий закон Ньютона гласит, что для каждой действующей силы существует равная и противоположная сила противодействия.Пары действие-реакция можно увидеть во всех сферах жизни, от бейсбола и скейтбординга до морских животных и ракетных кораблей. При различении силы действия и противодействия вы можете рассмотреть возможность рисования диаграммы, которая иллюстрирует объекты, на которые действует сила, и направление этих сил.

Третий закон движения Ньютона

Для каждой силы воздействия существует равная и противоположная сила реакции
Также называются парами действие-реакция
Парная диаграмма действие-реакция иногда полезна для определения силы действия и противодействия

Результаты обучения

Закончив, вы сможете:

Вспомнить третий закон движения Ньютона
Объясните взаимосвязь между силами действия и противодействия
Приведите пример пары действие-противодействие

Механика
ньютонов — Реактивная сила на двух объектах с центральными силами
У меня есть путаница с реактивными силами, в том, как они действуют, и я надеюсь подчеркнуть свое замешательство с некоторыми (очень) плохо нарисованными мной рисунками.
Насколько я понимаю (вероятно, неверно), реактивная сила третьего закона Ньютона — это вектор силы, равный по величине и противоположный по направлению приложенной силы. В случае объекта, совершающего круговое движение, ось ощущает внешнюю силу от вращающегося тела. Если я стреляю из пистолета, сила выстрела отталкивает меня (отсюда и удар ногой). У пушек есть колеса не зря. Насколько я понимаю, это показано на изображении, которое я вырезал, но на нем изображен человек, бьющий кого-то в лицо, и соответствующие силы в результате: Я не совсем уверен, совпадает ли $ F_ {face} $ с нормальной силой, но силы должны быть сбалансированы, так как после контакта кулак перестает двигаться и испытывает шок (точно так же, как удар по черепу может сломать тебе руку).Нормальная сила, или просто $ F_ {face} $ — это сила реакции от лица к лицу в результате самого удара. По крайней мере, так я считаю.
Это понимание реактивных сил причиняет мне боль сейчас, когда я рассматриваю следующий сценарий: два объекта чувствуют центральные силы в результате друг друга (пусть центральной силой будет гравитация).
На втором плохом рисунке у меня есть и $ A $, и $ B $, оказывающие друг на друга силу. $ A $ чувствует силу $ F_ {ab} $ (сила на $ A $ в результате $ B $), в то время как $ B $ ощущает $ F_ {ba} $ (сила на $ B $ в результате $ A $) .Пусть $ F_ {ab} = -F_ {ba} $.
Силы с буквой R впереди являются реактивными — и я построил их из ошибочной необходимости, которую я не могу строго опровергнуть. Если $ A $ тянет за $ B $, то по третьему закону Ньютона $ B $ должен тянуть за $ A $, точно так же, как лицо ударяет кулаком, как кулак ударяет по лицу. Это утверждение объясняет принудительное воздействие $ RF_ {ba} $ на $ A $, и та же ошибочная логика применяется к $ B $ и $ RF_ {ab} $. Может ли кто-нибудь выделить ключевые недоразумения, которые вызывают у меня этот странный ход мыслей?
Модель сил поясничного отдела позвоночника, предназначенная для анализа, с активными и…
Контекст 1
… при создании биомеханической модели, которая представляет силы, действующие на позвоночник, было сделано несколько предположений. Во время определенной физической нагрузки положение туловища будет изменено, скорее всего, в прогрессивном направлении или просто согнуто вперед на угол?, Что вызовет реакцию тела для стабилизации туловища. Этот ответ вызовет сжимающие силы в поясничном отделе позвоночника за счет сокращения мышц живота и спины, как показано на рисунке 2, вызывая повышение внутрибрюшного давления (ВБД), а также давления в мышцах спины (BMP), которое создается жесткостью сокращенных мышц спины. .BMP зависит от уровня сокращения мышц спины, и гипотетически целью является обеспечение механической поддержки. Обе силы давления зависят от размера области, на которую они действуют, они считаются сконцентрированными как результирующие силы в центре каждой области поясничного позвонка и ориентированы перпендикулярно оси позвоночника для простоты анализа. Кроме того, внутрибрюшная полость упрощена и показана эллиптической, что на самом деле, скорее всего, не так. Поясничный сегмент туловища, показанный на Рисунке 3, упрощен, с учётом сил, возникающих во время физического эксперимента.Внешние силы имеют отношение к результирующим силам, которые …
Контекст 2
… на поясничном отделе позвоночника и по величине напряжения, которое они создают, но в целях универсального использования этой модели их величина и направление не соответствуют не имеет первостепенного значения. Они включены в силы поперечного сечения наряду с силами массы верхней и нижней части тела (относительно площадей поперечного сечения). На рисунке 3 представлена модель сил поясничного сегмента позвоночника, изолированная от остального тела.F R, F S и M R — силы реакции на нижнем сечении поясничного отдела позвоночника, F C, F L1 и M L1 — активные силы на верхнем сечении поясничного отдела позвоночника, а G — массовая сила объема поясничного отдела позвоночника. IAP и BMP представляют собой результирующие силы для каждого позвоночного, вызванные ими. Вектор силы тяжести отмечен g. Если нижняя часть зафиксирована, как предполагалось, то F C, F L1 и M L1 состоят из всех внешних и мышечных сил, индуцированных в этой области. Предполагается, что динамические силы равны нулю, поскольку система должна сначала преодолеть статическое равновесие.Также предполагается, что нижняя часть тела зафиксирована. Диапазон движений поясничного отдела позвоночника 72 градуса при фиксированном тазе. Во время повседневной деятельности исправить таз невозможно, но это не входит в объем данного анализа. Уравнения статического равновесия для нашей модели в осевом и перпендикулярном направлениях дают два важных …
ReaxFF / AMBER — модель гибридного реактивного / нереактивного силового поля для моделирования молекулярной динамики
J Chem Theory Comput. Авторская рукопись; доступно в PMC 2021 25 мая.
Опубликовано в окончательной редакции как:
PMCID: PMC8145783
NIHMSID: NIHMS1703862
Али Рахнамун
Кафедра химии и кафедра биохимии и молекулярной биологии, Университет штата Мичиган, Ист-Лансинг, 48824-1322, Мичиган Соединенные Штаты;
Mehmet Cagri Kaymak
Департамент компьютерных наук и инженерии, Университет штата Мичиган, Ист-Лансинг, Мичиган 48824-1322, США
Мадушанка Манатунга
Департамент химии и факультет биохимии и молекулярной биологии, Университет штата Мичиган, Восточный Лансинг, Мичиган, 48824-1322, США;
Андреас В.Götz
Суперкомпьютерный центр Сан-Диего, Калифорнийский университет Сан-Диего, Ла-Хойя, Калифорния 92093-0505, США;
Адри К. Т. ван Дуин
Кафедра машиностроения, Государственный университет Пенсильвании, Юниверсити Парк, Пенсильвания 16802, США;
Kenneth M. Merz, Jr.
Кафедра химии и кафедра биохимии и молекулярной биологии, Университет штата Мичиган, Ист-Лансинг, Мичиган 48824-1322, США;
Хасан Метин Актулга
Департамент компьютерных наук и инженерии, Университет штата Мичиган, Ист-Лансинг, Мичиган 48824-1322, США;
Али Рахнамун, кафедра химии и кафедра биохимии и молекулярной биологии, Университет штата Мичиган, Ист-Лансинг, Мичиган 48824-1322, США;
Авторы, отвечающие за переписку: Кеннет М.Merz, Jr. — кафедра химии и кафедра биохимии и молекулярной биологии, Университет штата Мичиган, Ист-Лансинг, Мичиган 48824-1322, США; moc.liamg@1zremk, ude.usm@ekrjzrem, Хасан Метин Актулга — Департамент компьютерных наук и инженерии, Университет штата Мичиган, Ист-Лансинг, Мичиган 48824-1322, США; ude.usm@amh
Abstract
Комбинированные квантово-механические / молекулярно-механические (КМ / ММ) модели с использованием полуэмпирических методов и ab initio методов широко освещались в последние несколько десятилетий.Было показано, что эти методы способны обеспечить уникальное понимание целого ряда проблем, но они по-прежнему ограничены относительно короткими временными масштабами, особенно в моделях QM / MM, использующих методы ab initio . Промежуточный подход между моделью, основанной на КМ и классической механикой, может помочь заполнить этот временной промежуток и облегчить изучение ряда интересных проблем. Реактивные силовые поля представляют собой промежуточный подход, исследуемый в этой статье. Широко используемой реактивной моделью является ReaxFF, которая в значительной степени применяется к задачам материаловедения и обычно используется как автономная (т.е., вся система моделируется с помощью ReaxFF). Мы сообщаем о гибридном инструменте молекулярной динамики (MD) ReaxFF / AMBER, который представляет возможности ReaxFF для регистрации разрыва и образования связей в программном пакете AMBER MD. Этот инструмент позволяет нам изучать локальные реактивные события в больших системах за небольшую часть вычислительных затрат моделей QM / MM. Мы описываем реализацию ReaxFF / AMBER, проверяем эту реализацию, используя сольватированную в воде молекулу бензола, и сравниваем ее характеристики с рядом аналогичных подходов.Чтобы проиллюстрировать прогностические возможности ReaxFF / AMBER, мы провели исследование перегруппировки Клайзена в водном растворе. Впервые для ReaxFF мы смогли использовать потенциал средней силы AMBER (PMF) для проведения исследования PMF этой органической реакции. Возможность фиксировать локальные реакции в больших системах с использованием комбинированного ReaxFF / AMBER открывает ряд проблем, которые можно решить с помощью этой модели для решения как химических, так и биологических процессов.
Графический реферат
1.ВВЕДЕНИЕ
Точное моделирование химии относительно больших и сложных систем в достаточно длительных временных масштабах важно для инструментов вычислительного атомистического моделирования. Моделирование классической молекулярной механики (ММ) оказалось полезным для изучения сложных систем, в которых не происходит разрыва или образования связей. В таких методах эмпирические силовые поля (EFF), которые могут описывать взаимосвязь между геометрией и энергией системы с набором относительно простых потенциальных функций, использовались для описания многих систем вокруг их равновесной конфигурации.Однако методы, основанные на EFF, не могут моделировать химические реакции из-за жестких требований к связности таких методов. Методы квантовой механики (QM) могут смягчить ограничения методов на основе EFF, такие как образование или разрыв связей и флуктуации заряда из-за изменений геометрии. Однако модели QM обычно применяются к фрагментам областей, участвующих, скажем, в ферментативной реакции, что ограничивает возможность исследования влияния воздействия окружающей среды. Хотя методы, основанные на КМ, могут быть очень точными при прогнозировании событий химической реакции, они по-прежнему ограничиваются небольшими системами, моделируемыми в коротких временных масштабах.
Гибридные методы квантовой механики / молекулярной механики (QM / MM) были разработаны для объединения лучших характеристик моделей EFF и QM для решения ряда химических проблем. ^1,2 В методах QM / MM вся система делится на две отдельные зоны QM и MM. Зона QM — это химически активная область, которая обрабатывается рядом методов QM, а остальная часть системы — это зона MM, которая обрабатывается с помощью EFF. С момента появления метода QM / MM были реализованы различные подходы, и этот метод нашел широкое применение для работы со сложными системами в реалистичных средах из-за значительного снижения вычислительных затрат по сравнению с чистыми методами QM.^3–7 В пакете AMBER MD уже давно поддерживаются различные инструменты моделирования QM / MM. ^8,9 Некоторые методы QM, включая полуэмпирическое пренебрежение двухатомным перекрытием (NDDO) и плотно-функциональным плотным связыванием (DFTB), являются встроенными (т. Е. внутреннее ) и изначально поддерживаются в AMBER. ^10,11 Более продвинутые методы QM поддерживаются через интерфейс интеграции на основе файлов с внешними пакетами программного обеспечения QM. ^12,13
Несмотря на очень инновационные методы, алгоритмические улучшения и быстрые реализации, вычислительные затраты области QM по-прежнему остаются фактором, ограничивающим скорость при моделировании QM / MM.Поле реактивной силы (ReaxFF) — это потенциал, основанный на концепции длины связи / порядка связи, который объединяет методы QM и MM с точки зрения функциональности и вычислительных затрат. Важно отметить, что ReaxFF обеспечивает разумное приближение реактивных явлений при вычислительных затратах, сопоставимых с методами MM. В этой статье мы сообщаем о гибридном инструменте ReaxFF / AMBER MD, который представляет возможности ReaxFF для отслеживания разрыва и образования связей в программном пакете AMBER MD. Этот инструмент позволяет нам изучать локальные реактивные события в больших системах за небольшую часть вычислительных затрат моделей QM / MM.
Еще одна серьезная проблема с атомистическим моделированием состоит в том, что химические реакции через переходные состояния могут происходить в масштабе времени, который не может быть достигнут с помощью обычного молекулярно-динамического моделирования. Поэтому для определения переходного состояния химической реакции используются подходы, основанные на расширенных методах отбора проб, с использованием методов QM / MM. Зонтичный отбор проб ¹⁴ — один из наиболее известных усовершенствованных методов отбора проб, который можно легко использовать в новом инструменте ReaxFF / AMBER. Мы используем его здесь, чтобы наметить профиль реакции перегруппировки Клейзена в качестве валидационного исследования.
2. ПРЕДЫСТОРИЯ О REAXFF
ReaxFF — это классическая модель ММ по духу, которая явно моделирует химические реакции на основе концепции длины связи / порядка связи и динамического распределения зарядов. Подобно нереактивным моделям ММ, ReaxFF состоит из двух наборов терминов: связанных и несвязанных (ван-дер-ваальсовых и электростатических взаимодействий). Однако ReaxFF допускает образование и диссоциацию связей и, следовательно, имеет значительно отличающиеся условия связывания, чем классические потенциалы.
Чтобы проиллюстрировать философию метода, мы описываем определение энергии связи с использованием порядков связи для углерода и водорода (другие элементы также зависят от их конкретных свойств), в то время как структура и определение остальных терминов можно найти в оригинальном описании ReaxFF. ¹⁵ Тип одиночного атома в ReaxFF определяет каждый элемент, например, нет sp , sp ² или sp ³ гибридизированных атомов углерода, а есть только один тип атома углерода.Энергия связи ( E _связь, уравнение 1) описывается как функция сигмы (BOijσ), первая π (BOijπ) и второй π (BOijππ) ордера на облигации, а также соответствующие параметры D _e, p _{be 1} и p _{bc 2} параметров. Сами различные порядки связей (BOijσ, BOijπ, BOijππ) вычисляются с использованием попарного расстояния ( r _ij) между атомами i — j , идеальных расстояний связи (r0σ, r0π, r0ππ) для типы атомов i и j , а также параметры силового поля p _{bo [1–6]}, как показано в уравнении 2.Все три члена в уравнении 2 рассматриваются для связи между двумя атомами углерода, в то время как только первый член используется для связи σ , которая образуется между атомом углерода и атомом водорода. Однако представление на основе попарного расстояния даст небольшие порядки связи между 1 и 3 атомами, что приведет к завышению порядка связи между соответствующими атомами. Коррекция порядка облигаций ( BO _ij в уравнении 3) применяется для минимизации дальних порядков облигаций для таких ситуаций, где Δi ′ (уравнение 4) — отклонение нескорректированного суммирования порядков облигаций от валентности. состояние атома (например,g., углерод и водород имеют валентности четыре и один соответственно).
Ebond = −Deσ⋅BOijσ⋅exp [pbe1 (1- (BOijσ) pbc2)] — Deπ⋅BOijπ − Deππ⋅BOijππ
(1)
BOij ′ = BOijσ + BOijπ + BOijππ = exp [pbo1⋅ ( rijroσ) pbo2] + exp [pbo3⋅ (rijroπ) pbo4] + exp [pbo5⋅ (rijroππ) pbo6]
(2)
BOij = BOij′⋅f1 (Δi ′, Δj ′) ⋅f4 (Δi ′, BOij ′) ⋅f5 (Δj ′, BOij ′)
(3)
Δi ′ = — Vali + ∑j = 1соседей (i) BOij ′
(4)
Во время моделирования MD, порядки связи оцениваются на каждом временном шаге и используются для определения атомной связности в пределах заранее определенного отрезка расстояния (обычно 5 Å).Временной шаг 0,25 фс может использоваться для большинства симуляций, в то время как меньший временной шаг необходим для исследований при более высоких температурах (> 1500K). Кривые энергии непрерывны на протяжении всего процесса моделирования, даже в областях, связанных с образованием / разрывом связи, где благоприятные реакции могут происходить автоматически без каких-либо ограничений. Это обеспечивается включением других условий, связанных с порядком выпуска облигаций (см. Уравнение 5). Углы соединения ( E _val) и скручивания ( E _tor) оцениваются с использованием аналогичных соображений относительно порядка соединения.В потенциале порядка связи атомы часто не достигают своих оптимальных координационных чисел. Следовательно, ReaxFF требует дополнительных абстракций, таких как одиночная пара ( E _lp), коррекция избыточной / недостаточной координации ( E _более и E _менее), штраф за 3 тела ( E _pen) для систем с двумя двойными связями, разделяющими атом, член трехчастичного сопряжения ( E _coa), поправка на C ₂ ( E _C2), поправка на энергию тройной связи ( E _{тройной}) и 4-элементное спряжение ( E _{конъюнктура}).Возможности резюмируются ниже. Подробные выражения для каждого термина можно найти в литературе. ¹⁵
Эсистема = Ebond + Elp + Eover + Eunder + Eval + Epen + Ecoa + EC2 + Etriple + Etors + Econj + EH -bond + EvdWaals + ECoulomb
(5)
Чтобы предотвратить скачки энергии во время образования / диссоциации связи, в ReaxFF существуют несвязанные взаимодействия между каждой парой атомов (даже для 1–2, 1–3 взаимодействий). Электростатические взаимодействия представлены экранированным кулоновским членом, а взаимодействие Ван-дер-Ваальса использует экранированный потенциал Морзе для предотвращения нереалистичных значений на очень коротких расстояниях.Важным и дорогостоящим в вычислительном отношении предшественником электростатических взаимодействий является необходимость динамического определения частичных зарядов на каждом этапе MD, что достигается с помощью моделей заряда (таких как QEq ¹⁶ и EEM ¹⁷), которые требуют решения линейной системы. уравнений. Полученная формула является сложной, но очень гибкой и переносимой. Это позволило ReaxFF широко применять для решения широкого круга сложных задач. Первоначально разработан для углеводородов; ¹⁵ Метод ReaxFF широко использовался для исследования сложных систем в широком диапазоне приложений, включая биологические системы, ^18–22 материалы, ^23–29 катализаторы, ^30,31 горение и батареи.³²
В дополнение к исходной программе ReaxFF на основе Fortran, ¹⁵ ReaxFF также доступен в пакете Purdue Reactive Molecular Dynamics (PuReMD) с открытым исходным кодом ^33,34 и интегрирован в большой открытый исходный код. -масштабный атомно-молекулярный массово-параллельный симулятор (LAMMPS). ³⁵ Метод ReaxFF также доступен в других важных средах моделирования, включая программу Amsterdam Density Functional (ADF) ³⁶ и Materials Studio, выпущенную Biovia по лицензии (https: // www.3dsbiovia.com), а также Nanohub (http://www.nanohub.org).
3. ИНТЕГРАЦИЯ REAXFF / AMBER
Подобно методам QM / MM, в методе ReaxFF / AMBER атомы делятся на три категории: (i) атомы ReaxFF, которые включают все атомы в химически реактивной области и обрабатываются реализация ReaxFF, (ii) переходные атомы ReaxFF / MM, которые включают все атомы в пределах определенной границы области ReaxFF и обрабатываются совместно ReaxFF и AMBER, и (iii) атомы MM, которые включают все оставшиеся атомы и являются обрабатывается исключительно AMBER.Эти категории проиллюстрированы сферическими формами, но эти области, очевидно, могут иметь любую форму. Далее мы опишем реализацию метода ReaxFF / AMBER.
ReaxFF / AMBER регионов в реализации интеграции.
3.1. Реализация.
AMBER — это драйвер моделирования в интеграции ReaxFF / AMBER MD. После того, как AMBER классифицирует атомы по соответствующим группам, он отправляет всю необходимую информацию для атомов ReaxFF и ReaxFF / MM в программу ReaxFF.Инструмент ReaxFF / AMBER в настоящее время использует интерфейс внешней модели; то есть необходимые передачи данных между ReaxFF и AMBER выполняются с использованием файлового обмена данными. Поэтому после того, как AMBER завершает запись файлов обмена данными, он запускает программу ReaxFF как внешний двоичный файл и ожидает своих выходных файлов. Затем программа ReaxFF запускает непериодическое моделирование с нулевым шагом для расчета динамических зарядов, энергии и сил на атомах ReaxFF и ReaxFF / MM. По завершении он записывает эту информацию обратно в другой файл, который, наконец, считывается AMBER для завершения вычислений энергии и силы для областей ReaxFF / MM и MM.
При реализации интерфейса между программами ReaxFF и AMBER мы приняли следующую процедуру для успешной гибридной модели:
Рассчитаны динамические заряды на атомах ReaxFF под действием атомов ReaxFF / MM со статическими зарядами.
Все взаимодействия ReaxFF (как указано в уравнении 5 выше) между парами ReaxFF – ReaxFF рассчитываются без каких-либо изменений.
Электростатические взаимодействия между парами атомов ReaxFF (с динамическим зарядом) -ReaxFF / MM (со статическим зарядом) рассчитываются ReaxFF.
Ван-дер-Ваальсовы взаимодействия между парами атомов ReaxFF – ReaxFF / MM обрабатываются AMBER (например, с использованием потенциала Леннарда-Джонса).
Взаимодействия между парами MM-ReaxFF / MM и MM-MM обрабатываются AMBER как обычно.
Следует отметить, что у текущего инструмента ReaxFF / AMBER есть некоторые ограничения. Теперь можно изучать только системы с нековалентными связями между областями ReaxFF и ReaxFF / MM. Кроме того, на данный момент можно использовать только параллелизм с общей памятью.Тем не менее, как мы продемонстрируем ниже, текущая реализация служит доказательством осуществимости и преимуществ этого подхода.
3.2. Динамические заряды с использованием модифицированного метода выравнивания электроотрицательности (mEEM).
Поскольку мы позволяем статически заряженным ММ и атомам переходной области поляризовать атомы ReaxFF, модель динамического заряда, используемая ReaxFF, должна быть изменена. Как упоминалось ранее, ReaxFF может использовать метод выравнивания зарядов (QEq) или выравнивания электроотрицательности (EEM) для определения зарядов.Наша текущая реализация основана на EEM. Прежде чем описывать необходимые модификации, мы кратко обсудим модель заряда EEM, которая в настоящее время используется ReaxFF / AMBER.
Модель заряда EEM ²⁹ основана на принципе, согласно которому заряды должны распределяться по атомам, чтобы удовлетворять ограничениям как для суммарного заряда системы, так и для уравновешенной электроотрицательности атомов. Пусть заряды атомов равны q = ( q ₁, q ₂,…, q _n), а позиции будут R = ( r ₁, r ₂,…, r _n), где q _i ∈ R и r _i ∈
09 R На основе принципа выравнивания электроотрицательности Сандерсона, ³⁷, необходимо уравнять электроотрицательность всех атомов.
где ϵ _i — электроотрицательность атома i , а ϵ_ — средняя молекулярная электроотрицательность. Другое ограничение вынуждает сумму зарядов атомов быть равной данному чистому заряду системы.
Ограничения и параметризованные межатомные взаимодействия могут быть объединены в следующее линейное уравнение, в котором заряды q являются решением:
[h2n1nT0] [qϵ _] = [- χqnet]
Здесь χ — вектор атомных электроотрицательностей n на 1, а значения H _ij, то есть отдельные элементы n на n Матрица H , определяются как δ _ij η _i + (1 — δ _ij) F _{ij, F _{ij _ij — оператор дельты Кронекера, η _i — идемпотенциал, а F _ij определяется как}}
Fi, j = 1rij3 + γij − 33, rij≤rnonb 0, иначе
В приведенных выше уравнениях rij = ‖ri − rj‖ — это расстояние между атомами i и j , r _nonb — радиус отсечки, γij = γiγj — попарный экранирующий член , настроенный для типов элементов атомов i и j , чтобы избежать неограниченной электростатической энергии на малых расстояниях, а ϵ_ — диэлектрическая проницаемость среды.Было продемонстрировано, что модель EEM воспроизводит рассчитанные QM заряды Малликена. ³⁸
Чтобы учесть поляризационный эффект атомов переходной области на основной области ReaxFF, мы вводим атомы ReaxFF / AMBER как частицы с фиксированными зарядами в решатель EEM. Это делается путем модификации системы уравнений следующим образом. Предполагая, что имеется c атомов ReaxFF и t атомов переходной области, тогда H _core ∈ R ^{c × c} захватывает взаимодействия внутри основной области ReaxFF, а H _core-trans ∈ R ^{c × t} фиксирует воздействие атомов переходной области на атомы ReaxFF.
[Hcore Hcore-trans 1cHtrans-core Htrans 1t1cT1tT0] [qcore qtrans ϵ _] = [- χcore −χtrans qnet]
Поскольку прямое решение вышеупомянутой линейной системы масштабируется кубическим образом с числом общих атомов, обычно используются итерационные решатели для получения приближений к оптимизированным динамическим зарядам. В такой итерационной схеме мы развиваем только заряды на основных атомах, поскольку q _trans — фиксированные значения, заданные в силовом поле MM. Таким образом, строки, соответствующие атомам переходной области, можно не учитывать в указанной выше линейной системе, и мы получаем
[Hcore Hcore-trans 1c1cT1tT0] [qcore ϵ _] = [- χcore qnet]
Поскольку q _trans является фиксированным, его можно переставить как
[Hcore 1c1cT0] [qcore ϵ _] = [- χcore qnet] — [Hcore-trans 0tT] [qtrans]
Эти модификации гарантируют, что наличие фиксированных зарядов не замедлит этап уравновешивания зарядов, поскольку фиксированные заряды и динамические заряды разделены.См. Пример в разделе «Вспомогательная информация» (S1).
Вышеуказанных модификаций достаточно для запуска непериодических симуляций ReaxFF / MM, а также периодических граничных симуляций без дальнодействующих электростатических взаимодействий. При периодическом моделировании границ с электростатическими взаимодействиями на больших расстояниях AMBER использует подход Эвальда с сеткой частиц (PME), который вычисляет взаимодействия в пределах определенного расстояния отсечки напрямую и аппроксимирует остальные по сетке. ³⁹ Чтобы иметь возможность учитывать дальнодействующие взаимодействия в EEM, мы включили влияние точек сетки на атомы ReaxFF путем дальнейшего расширения матрицы EEM, то есть путем добавления столбца и строки, содержащих эффекты точки сетки.Эта схема не сохраняет энергию при моделировании NVE с периодическими границами, потому что ReaxFF использует конусообразные электростатические взаимодействия ⁴⁰, которые заставляют кулоновские эффекты медленно затухать до 0 при радиусе отсечки взаимодействия, который обычно устанавливается равным 10–12 Å (см. SI, Рисунок S1). Снижение кулоновских взаимодействий является встроенной функцией формулировки ReaxFF, и существующие наборы параметров ReaxFF были обучены с учетом этого принципа проектирования. Мы считаем, что путем переобучения параметров ReaxFF без сужающихся кулоновских ядер можно успешно включить периодическое моделирование границ с помощью PME, но это выходит за рамки данной статьи, поэтому мы оставляем это в качестве темы для дальнейшего изучения.
3.3. Проверка.
Для проверки полученной комбинации ReaxFF / AMBER мы провели эксперименты с системами бензол-в-воде, одна с периодическими граничными условиями, а другая без (). Бензол не реагирует с водой, но цель этих вычислительных экспериментов состояла в том, чтобы подтвердить, что метод ReaxFF / MM может обеспечить энергосбережение и произвести разумные динамические заряды.
(Слева) Бензол ReaxFF в капле воды TIP3P с общим количеством атомов 627, (справа) Бензол ReaxFF в резервуаре с водой TIP3P с общим количеством атомов 4398.
Для обоих симуляций (непериодического и периодического) системы сначала минимизируют энергию, а затем нагревают до 300 K с помощью термостата Берендсена в AMBER. Наконец, моделирование ReaxFF / MM NVE запускается с использованием временного шага 0,25 фс для проверки энергосбережения и заряда. Был выбран относительно короткий временной шаг, поскольку это рекомендуемая настройка для моделирования ReaxFF, особенно в присутствии атомов H. Для всех симуляций алгоритм SHAKE был отключен.
Как показано на, энергия сохраняется для обоих моделей.показывает заряды углерода и водорода для атомов Reax (обозначаемых как Reax-C и Reax-H, соответственно), а также среднее значение по всем атомам C и H на временном шаге (обозначается как Reax-C-Avg и Reax-H. -Avg соответственно). Как можно видеть, динамические заряды, создаваемые ReaxFF / MM под действием статически заряженных атомов переходной области, соответствуют зарядам углерода и водорода, указанным в силовом поле AMBER для бензола (обозначенном как AMBER-C и AMBER-H, соответственно. ).
Моделирование молекулы бензола в воде с использованием модели воды TIP3P и ансамбля NVE.Использовался шаг по времени 0,25 фс. (Синий) Непериодическое граничное условие с бесконечным обрезанием. (Красный) Периодическое граничное условие с отсечкой QM 10 Å (qmcut = 10 Å) и отключенным взаимодействием ReaxFF / PME (qm_pme = 0).
Динамические заряды ReaxFF и фиксированные заряды AMBER с моделированием ReaxFF / MM молекулы бензола в воде с периодическими граничными условиями с использованием параметров qmcut = 10 A и qm_pme = 0
3.4. Анализ производительности.
Как упоминалось ранее, мотивация метода ReaxFF / MM заключается в том, что он может значительно сократить время вычислений, которое потребовалось бы для сопоставимого моделирования QM / MM.Чтобы проиллюстрировать это, мы провели сравнительный анализ вычислительных затрат на отдельные модели уравновешивания аллилвинилового эфира (AVE), который состоит из 14 атомов, с использованием ReaxFF, PuReMD, SCC-DTFB, PM3, MM, метода Хартри – Фока (HF) и функционала плотности. теория (ДПФ) с использованием функционала B3LYP. В расчетах HF и DFT использовался базисный набор 6–31G *. Тестовое моделирование проводилось с использованием автономных программ ReaxFF, PuReMD, AMBER и программного пакета QUICK ⁴¹ в режиме последовательного выполнения на процессоре Intel Xeon E5–2670 v2, который работает на 2.50 ГГц. Ориентировочное время на шаги моделирования показано в.
Таблица 1.
Время последовательного выполнения в секундах на временной шаг и наносекундах в день для вычислений SCC-DFTB, PM3, ReaxFF, PuReMD, MM, HF и DFT ^{^a}
секунд / итерация (относительно MM)
(8,1) 9000 Re, 9000 Re, 9000 Re, реализация оригинальной реализации ReaxFF на Фортране. Для этих эталонных расчетов принимаются временные шаги 1 фс для MM, 0,5 фс для SCC-DFTB и PM3 и 0,25 фс для вычислений ReaxFF. Эти контрольные данные показывают, что метод ReaxFF может быть в ~ 2–5 раз быстрее, чем методы PM3 или SCC-DFTB, на 3 порядка быстрее, чем методы HF или DFT, и в ~ 18 раз медленнее, чем традиционные методы молекулярной механики.Следовательно, ReaxFF может предложить альтернативу расчетам QM / MM для обработки более крупных сложных систем в более длительных масштабах времени.
В настоящее время программное обеспечение ReaxFF / AMBER использует исходный код Fortran ReaxFF через интерфейс обмена данными на основе файлов. Мы проанализировали вычислительную производительность программного обеспечения ReaxFF / AMBER с помощью непериодического моделирования бензола в воде для 1000 шагов с использованием бесконечного ограничения электростатического взаимодействия. Разбивка по времени, показанная на, усреднена в ходе этого моделирования.Пожалуйста, обратитесь к разделу 3 SI, чтобы узнать о спецификациях аппаратного и программного обеспечения, использованного в этих вычислительных экспериментах.
Разбивка общего времени выполнения программного обеспечения ReaxFF / AMBER для моделирования бензола в воде на его основные компоненты. Общее время, затрачиваемое на один шаг, составляет 0,46 с.
Поскольку обмен данными между ReaxFF и AMBER основан на файлах, он требует записи и чтения файлов на каждом этапе моделирования. Также существуют дополнительные расходы, связанные с запуском программы ReaxFF как внешнего двоичного файла.Наконец, модификации автономной реализации ReaxFF минимальны, и по этой причине ReaxFF выделяет и инициализирует различные структуры данных на каждом временном шаге. Время, затрачиваемое на ввод-вывод и системные вызовы внешней программы, будет устранено путем введения обмена данными на основе массивов между соответствующими подпрограммами ReaxFF и AMBER. Кроме того, постоянно сохраняя структуры данных в памяти и повторно используя их на каждом временном шаге, мы могли бы сократить большую часть времени, затрачиваемого на выделение и инициализацию.Когда все эти потенциальные обновления будут учтены, программное обеспечение ReaxFF / AMBER будет значительно ускорено по сравнению с тем, что показано здесь, потому что только 10,9% общего времени тратится на необходимые вычисления ReaxFF (см.).
4. МОДЕЛИРОВАНИЕ КЛАЙЗЕНОВОЙ ПЕРЕОРРАНЖИРОВКИ С REAXFF / AMBER
Чтобы продемонстрировать возможности новой интеграции ReaxFF / AMBER, мы выполнили моделирование ReaxFF / MM классической перегруппировки Клейзена аллилвинилового эфира (AVE), растворенного в явной воде TIP3P модель ⁴², как показано на.Поскольку перегруппировка Клайзена является хорошо изученной реакцией, ^43,44 было выбрано для оценки химической точности нашего нового метода. В этих симуляциях растворитель обрабатывается AMBER с использованием водной модели TIP3P, а реагент AVE обрабатывается ReaxFF. Никакие ковалентные связи не пересекают границу ReaxFF / AMBER.
(a) Сольватация аллилвинилового эфира (AVE) в октаэдрической воде TIP3P с общим числом 4319 атомов. (б) Молекулярная структура AVE.
4.1. Оптимизация параметров ReaxFF.
Существующее силовое поле ReaxFF ⁴⁵ было протестировано для моделирования перегруппировки Клейзена. Первоначальные тесты показали, что система попала в локальный минимум после достижения переходного состояния (TS), и поэтому надлежащая перестройка Клайзена не могла быть обнаружена ().
Перегруппировка Клайзена AVE в вакууме с использованием оригинальных и обученных силовых полей ReaxFF. Исходное силовое поле приводит к попаданию в локальный минимум.
Чтобы решить эту проблему, были сгенерированы данные ab initio QM для перегруппировки Клайзена AVE в вакууме.Метод внутренней координаты реакции (IRC) был использован для получения данных QM из двух различных переходных состояний, подобных стулу и лодке. Все вычисления по оптимизации и IRC выполнялись с помощью пакета Gaussian 16. Для расчетов использовался функционал ⁴⁶ B3LYP и базис 6–31G *. Посредством расчетов IRC был зарегистрирован переход перегруппировки Клейзена для всех конфигураций, подобных стулу и лодке, а также изменения энергии. Сравнение этих данных QM с исходными результатами силового поля ReaxFF показано на рис.Эти начальные различия в энергии и неспособность исходного силового поля уловить перестройку Клейзена указали на необходимость тренировки силового поля по сгенерированным данным QM. Обучающие данные, используемые для оптимизации набора параметров ReaxFF, могут включать данные QM о зарядах, теплоте пластов (ккал / моль), геометрии с минимизированной энергией (в ангстремах или градусах), параметрах ячеек решетки (в ангстремах или градусах) и относительных энергиях (ккал. / моль). Все обучающие данные добавляются в обучающий набор, и силовое поле повторно параметризуется, чтобы минимизировать функцию ошибок:
ei = (xi, QM − xi, ReaxFFσi) 2
где x _{i, QM} и x i, _ReaxFF — значения QM и ReaxFF для i -й записи обучающего набора, соответственно, а σ _i — весовые параметры. которые определяют желаемую точность для отдельных элементов данных обучения.Параметры силового поля, которые должны быть настроены, определяются в отдельном входном файле. Функция обучения ReaxFF в автономном коде Fortran затем использует схему строкового поиска для оптимизации каждого параметра, настраиваемого по одному. Входные файлы для тренировки силового поля и параметры силового поля, полученные в результате этой процедуры оптимизации, предоставляются в SI.
(a) QM (B3LYP / 6–31G *) в сравнении с исходными результатами силового поля ReaxFF для перестройки Клейзена структур, подобных стулу и лодке.(b) QM (B3LYP / 6–31G *) против результатов тренированного силового поля ReaxFF для перестройки Клейзена структур, подобных стулу и лодке. Энергии относятся к энергии, оптимизированной для полностью открытой геометрии AVE, в качестве эталонной.
показывает результаты нашей подгонки к данным QM для переходных состояний, подобных стулу и лодке. Оценка нового силового поля после тренировки показала удовлетворительное поведение при фиксации перегруппировки Клейзена в вакууме (). Таким образом, это обновленное силовое поле ReaxFF использовалось для выполнения расчетов свободной энергии перегруппировки Клайзена AVE в присутствии явной воды TIP3P с использованием ReaxFF / AMBER.
4.2. Расчет свободной энергии с зонтичным отбором.
Драйвер MD в схеме интеграции ReaxFF / AMBER — AMBER. Следовательно, мы можем использовать все передовые методы отбора проб AMBER. Одной из таких функций является метод расчета свободной энергии зонтичной выборки. Используя недавно оптимизированный набор параметров, функция зонтичной выборки AMBER в сочетании с методом анализа взвешенной гистограммы (WHAM) была использована для определения потенциала средней силы (PMF) этой реакции с помощью ReaxFF / AMBER.Координатой реакции, выбранной для моделирования зонтичного отбора проб, было расстояние между двумя концевыми атомами углерода AVE, называемое расстоянием C ₁ –C ₅ ().
Перегруппировка Клайзена AVE при изменении расстояния C ₁ –C ₅ с 3,5 до 1,6 Å.
Серия гармонических потенциалов использовалась, чтобы ограничить координаты реакции определенными окнами. Расстояние C ₁ –C ₅ изменялось от 3,5 до 1,6 Å.Для областей около переходного состояния (1,7–2,4 Å) использовалось 1000 ккал / моль · Å ², чтобы получить достаточное количество отсчетов для каждого окна, а для областей, далеких от переходного состояния (1,6–1,7 Å и 2,4– 3,5 Å) использовалось более слабое ограничение (200–700 ккал / моль. ² Å). Для диапазона 1,6–3,0 Å были определены интервалы окон 0,02 Å, а для диапазона 3,0–3,5 Å были определены интервалы окон 0,1 Å. Всего для выборки было создано 81 окно, при изменении расстояния C ₁ –C ₅ от 3.От 5 до 1,6 Å. Все моделирование проводилось с использованием жесткой модели воды с трехточечным зарядом TIP3P. АВЭ сольватировали в октаэдрическом ящике молекул воды TIP3P радиусом 25 Å. Все моделирование проводилось с периодическими граничными условиями. Файлы топологии для AVE были созданы с использованием общего силового поля AMBER (GAFF). ⁴⁷ AMBER MM моделирование с использованием периодических граничных условий было выполнено с отсечкой 10 Å для несвязанных взаимодействий в реальном пространстве, а алгоритм Эвальда с сеткой частиц (PME) был включен для учета электростатики на больших расстояниях за пределами отсечки.
После минимизации 2000 шагов в каждом окне, мы выполнили уравновешивание NPT (постоянное количество атомов, постоянное давление и постоянная температура) в течение 25 пс, используя динамику Ланжевена постоянного давления с баростатом Берендсена при 300 К и 1 атм. Алгоритм встряхивания был включен для этих имитаций в области MM, и временной шаг 0,25 фс был выбран как для областей ReaxFF (без дрожания), так и для областей AMBER. Сбор данных для зонтичного отбора проб начинался после фазы уравновешивания в течение 5 пс в каждом окне.Зонтичная выборка заключалась в сборе данных одновременно из отдельных окон координаты реакции. Определяя правильные константы гармонического ограничения в каждом окне, мы позволили соседним окнам перекрываться и обеспечили достаточное количество окон, чтобы покрыть все пространство координат реакции. Выборка данных выполнялась каждые 0,0125 пс на этапе производства моделирования зонтичной выборки. Наконец, PMF был рассчитан путем объединения данных из каждого окна с использованием WHAM.
4.3. Результаты и их обсуждение.
Чтобы оценить потенциал изменения средней силы (PMF) как функцию координаты реакции, определенной для перегруппировки Клейзена, были использованы расчеты зонтичной выборки. Как уже упоминалось, моделирование в разных окнах должно было быть таким, чтобы мы могли наблюдать сходимость при выборке для завершения вычислений зонтичной выборки. Чтобы убедиться, что все окна правильно перекрываются перед выполнением вычислений WHAM, были сгенерированы гистограммы всех окон ().Этот график показывает, что имелось надлежащее перекрытие, и никаких явных пропусков не наблюдалось. Используя этот набор данных, мы использовали WHAM для построения PMF перегруппировки Клейзена.
Гистограмма C ₁ –C ₅ выборки расстояния из зонтичных окон выборки. Расстояние C ₁ –C ₅ изменялось от 3,5 до 1,6 Å. Для областей, далеких от переходного состояния (1,5–1,7 Å и 2,4–3,5 Å), использовалось более слабое ограничение (200–700 ккал / моль · Å ²), а для областей вблизи переходного состояния (1.7–2,4 Å) использовалось более сильное ограничение (1000 ккал / моль · Å ²). Для диапазона 1,6–3,0 Å были определены окна интервала 0,02 Å, а для окон 3,0–3,5 Å был определен интервал 0,1 Å.
PMF, полученная в результате расчетов зонтичной выборки, показана на. Вычисленную PMF можно использовать для оценки высоты барьера перегруппировки Клайзена и конфигурации переходного состояния. Из этих расчетов была получена высота барьера 34,8 ккал / моль. Мы также использовали реализацию метода самосогласованной функциональной плотности заряда (SCC-DFTB), который является полуэмпирическим методом, основанным на теории функционала плотности (DFT), ⁴⁸, а также полуэмпирическим пренебрежением двухатомным перекрытием (NDDO). Метод PM3 ⁴⁹ как часть поддержки QM / MM в программе AMBER 18 MD для выполнения вычислений перегруппировки Клейзена.Кроме того, был выполнен другой расчет PMF для зонтичного отбора проб QM / MM SCC-DFTB с использованием модели воды SPC / E для оценки влияния модели воды на это моделирование. Результаты всех этих расчетов PMF показаны на. Конфигурация перехода этих различных методов показана на рисунке S3. Интеграция ReaxFF / AMBER успешно отразила реакцию перегруппировки Клейзена.
PMF перегруппировки AVE Клейзена в периодической воде TIP3P с использованием комбинации ReaxFF / AMBER. Энергии относятся к энергии, оптимизированной для полностью открытой геометрии AVE, в качестве эталонной.
Первое кинетическое исследование термической перестройки AVE в газовой фазе, проведенное Шулером и Мерфи, показало, что энергия активации составляет 30,6 ккал / моль. ⁵⁰ Это согласуется с другими экспериментальными отчетами об экспериментальных энергиях активации переходов кресла. ^51–53 Сообщается, что эта высота барьера в водном растворителе ниже, чем в газовой фазе и неполярных растворителях. ⁵⁴ Длина связи в переходном состоянии 2,2–2,3 Å была получена с использованием различных методов моделирования.⁵⁵
5. ВЫВОДЫ
В этой работе был разработан интерфейс AMBER / ReaxFF, который предлагает возможность регистрации химических реакций в качестве альтернативы методам AMBER QM / MM. Основная цель этой разработки — получить подход к добавлению характеристики реактивности в моделирование классической нереакционной молекулярной динамики с уменьшенными вычислительными затратами по сравнению с методами QM / MM. Этот новый интерфейс будет полезным инструментом для моделирования больших биомолекулярных систем с локальными реактивными областями.Первоначальная реализация этого интерфейса на основе файлов была оценена путем расчета профиля реакции перегруппировки Клайзена AVE, сольватированной в модели воды TIP3P. Мы провели моделирование зонтичной выборки, создав серию конфигураций по расстоянию между двумя концевыми атомами углерода в AVE в качестве координаты реакции, выполнили моделирование смещения и извлекли PMF. Эти результаты показали способность интеграции ReaxFF / AMBER улавливать реакцию перегруппировки Клейзена, несмотря на небольшие неточности в высоте барьера реакции, которые могут быть улучшены путем более тщательной тренировки силового поля ReaxFF.
Данные тестирования времени показали, что основная часть времени вычислений была потрачена на ввод-вывод, инициализацию / синхронизацию в этой файловой версии интеграции. Поэтому мы разработаем реализацию этой интеграции на основе массивов, которая приведет к устранению накладных расходов на ввод-вывод и инициализацию / синхронизацию моделирования. Чтобы еще больше повысить скорость вычислений, мы интегрируем PuReMD, который является эффективной параллельной реализацией исходного ReaxFF на основе языка C.PuReMD содержит значительные улучшения производительности по сравнению с используемыми в настоящее время эталонными реализациями ReaxFF на основе Fortran, и он имеет реализации с общей памятью, распределенной памятью и графическим процессором, что позволит нам использовать преимущества современных массивно-параллельных архитектур. Производительность AMBER / ReaxFF (PuReMD) на основе массивов будет представлена в последующих работах.
БЛАГОДАРНОСТИ
Эта работа была частично поддержана грантом NIH (Премия № GM130641), грантом NSF CDS&E (Премия №1807622) и грант NSF OAC (1835144). В этой работе использовались вычислительные ресурсы, предоставленные Институтом кибер-исследований при Университете штата Мичиган.
Сноски
Дополнительная информация
Дополнительная информация доступна бесплатно по адресу https://pubs.acs.org/doi/10.1021/acs.jctc.0c00874.
Модифицированный пример EEM; включение дальнодействующих электростатических взаимодействий в ReaxFF; спецификации аппаратного и программного обеспечения, используемого в вычислительных экспериментах; QM Claisen перестановочные переходные конфигурации; Входные данные для тренировки силового поля Reax, используемые для моделирования перестройки AVE Claisen (PDF)
Полная контактная информация доступна по адресу: https: // pubs.acs.org/10.1021/acs.jctc.0c00874
Авторы заявляют об отсутствии конкурирующих финансовых интересов.
Информация для авторов
Али Рахнамун, Департамент химии и Департамент биохимии и молекулярной биологии, Университет штата Мичиган, Ист-Лансинг, Мичиган 48824-1322, США;
Мехмет Кагри Каймак, факультет компьютерных наук и инженерии, Университет штата Мичиган, Ист-Лансинг, Мичиган 48824-1322, США.
Мадушанка Манатунга, кафедра химии и кафедра биохимии и молекулярной биологии, Университет штата Мичиган, Ист-Лансинг, Мичиган 48824-1322, США;
Андреас В.Götz, Суперкомпьютерный центр Сан-Диего, Калифорнийский университет в Сан-Диего, Ла-Хойя, Калифорния 92093-0505, США;
Адри К. Т. ван Дуин, факультет машиностроения, Государственный университет Пенсильвании, Юниверсити-Парк, Пенсильвания 16802, США;
Кеннет М. Мерц младший, факультет химии и факультет биохимии и молекулярной биологии, Университет штата Мичиган, Ист-Лансинг, Мичиган 48824-1322, США;
Хасан Метин Актулга, факультет компьютерных наук и инженерии, Университет штата Мичиган, Ист-Лансинг, Мичиган 48824-1322, США;
ССЫЛКИ
(1) Warshel A; Левитт М Теоретические исследования ферментативных реакций: диэлектрическая, электростатическая и стерическая стабилизация иона карбония в реакции лизоцима.J. Mol. Биол 1976, 103, 227–249. [PubMed] [Google Scholar] (2) Лин Х; Truhlar DG QM / MM: что мы узнали, где мы находимся и куда мы идем дальше? Теор. Chem. Acc 2007, 117, 185. [Google Scholar] (3) Senn HM; Тиль В Методы QM / MM для биомолекулярных систем. Энгью. Chem., Int. Эд 2009, 48, 1198–1229. [PubMed] [Google Scholar] (4) Фриснер Р.А.; Гуаллар V Ab initio методы квантовой химии и смешанной квантовой механики / молекулярной механики (QM / MM) для изучения ферментативного катализа. Анну. Rev. Phys. Chem 2005, 56, 389–427.[PubMed] [Google Scholar] (5) Гуаллар V; Wallrapp FH Методы QM / MM: Заглянем внутрь биохимии гемовых белков. Биофиз. Chem 2010, 149, 1–11. [PubMed] [Google Scholar] (6) Magalhães RP; Fernandes HS; Sousa SF Моделирование ферментативных механизмов с помощью подходов QM / MM: текущее состояние и будущие проблемы. Isr. J. Chem 2020, 60, 655–666. [Google Scholar] (7) Лю X; Fang D; Ито С; Окамото Y; Овчинников В; Цуй Кью Моделирование свободной энергии QM / MM: последние достижения и проблемы. Мол. Simul 2016, 42, 1056–1078. [Бесплатная статья PMC] [PubMed] [Google Scholar] (8) Перлман Д.А. Дело DA; Колдуэлл JW; Росс WS; Cheatham TE; DeBolt S; Фергюсон Д; Seibel G; Коллман П. AMBER, пакет компьютерных программ для применения молекулярной механики, анализа нормальных режимов, молекулярной динамики и расчетов свободной энергии для моделирования структурных и энергетических свойств молекул.Comput. Phys. Сообщество 1995, 91, 1–41. [Google Scholar] (9) Дело DA; Cheatham TE 3rd; Darden T; Gohlke H; Луо Р; Merz KM Jr .; Онуфриев А; Simmerling C; Ван Б; Вудс RJ Программы биомолекулярного моделирования Amber. J. Comput. Chem 2005, 26, 1668–1688. [Бесплатная статья PMC] [PubMed] [Google Scholar] (10) Walker R; Кроули М; Случай D Реализация быстрого и точного потенциального метода QM / MM в AMBER. J. Comput. Chem 2008, 29, 1019–1031. [PubMed] [Google Scholar] (11) Сибра Г. d. М .; Walker RC; Эльстнер М; Дело DA; Ройтберг А.Е. Реализация метода SCC-DFTB для гибридного моделирования QM / MM в пакете Amber Molecular Dynamics.J. Phys. Chem. А 2007, 111, 5655–5664. [Бесплатная статья PMC] [PubMed] [Google Scholar] (12) Гётц А.В.; Кларк MA; Уокер RC Расширяемый интерфейс для моделирования молекулярной динамики QM / MM с AMBER. J. Comput. Chem 2014, 35, 95–108. [Бесплатная статья PMC] [PubMed] [Google Scholar] (13) Isborn CM; Götz AW; Кларк MA; Walker RC; Мартинес Т.Дж. Электронные спектры поглощения из молекулярной динамики MM и ab Initio QM / MM: влияние окружающей среды на спектр поглощения фотоактивного желтого белка. J. Chem. Теория вычислений 2012, 8, 5092–5106.[Бесплатная статья PMC] [PubMed] [Google Scholar] (14) Кестнер Дж. Отбор проб зонтиков. ПРОВОДА Comput. Мол. Наука 2011, 1, 932–942. [Google Scholar] (15) van Duin ACT; Dasgupta S; Lorant F; Годдард WA ReaxFF: реактивное силовое поле для углеводородов. J. Phys. Chem. А 2001, 105, 9396–9409. [Google Scholar] (16) Рапп AK; Годдард WA Уравновешивание заряда для моделирования молекулярной динамики. J. Phys. Chem 1991, 95, 3358–3363. [Google Scholar] (17) Мортье WJ; Гош СК; Шанкар С. Метод выравнивания электроотрицательности для расчета зарядов атомов в молекулах.Варенье. Chem. Soc 1986, 108, 4315–4320. [Google Scholar] (18) Samieegohar M; Sha F; Clayborne AZ; Вэй Т ReaxFF MD моделирование наночастиц золота с привитыми пептидами. Langmuir 2019, 35, 5029–5036. [PubMed] [Google Scholar] (19) Ян С; Чжао Т; Zou L; Ван Х; Чжан И Молекулярно-динамическое моделирование разрушения молекул ДНК в раковых клетках плазменными АФК на основе ReaxFF. Phys. Плазма 2019, 26, 083504. [Google Scholar] (20) Hubin PO; Jacquemin D; Leherte L; Vercauteren DP Параметризация реактивного силового поля ReaxFF для альдольной реакции, катализируемой пролином.J. Comput. Chem 2016, 37, 2564–2572. [PubMed] [Google Scholar] (21) Monti S; Jose J; Сахаджан А; Kalarikkal N; Томас С Структура и динамика наночастиц золота, украшенных конъюгатами хитозан-гентамицин: моделирование молекулярной динамики ReaxFF для выявления доставки лекарств. Phys. Chem. Chem. Физ 2019, 21, 13099–13108. [PubMed] [Google Scholar] (22) Trnka T; Тварошка I; Коча Я Автоматизированная тренировка реактивных силовых полей ReaxFF для энергетики ферментативных реакций. J. Chem. Теория вычислений 2018, 14, 291–302.[PubMed] [Google Scholar] (23) Рахнамун А; van Duin ACT Моделирование реактивной молекулярной динамики распада каптона, полиимида POSS, аморфного кремнезема и тефлона при ударе атомарного кислорода с использованием метода реактивного силового поля Reaxff. J. Phys. Chem. А 2014, 118, 2780–2787. [PubMed] [Google Scholar] (24) Raymand D; van Duin ACT; Baudin M; Херманссон К. Поле реактивной силы (ReaxFF) для оксида цинка. Серфинг. Наука 2008, 602, 1020–1031. [Google Scholar] (25) Chenoweth K; Cheung S; van Duin ACT; Годдард WA; Кобер Э.М. Моделирование термического разложения полимера поли (диметилсилоксана) с использованием реактивного силового поля ReaxFF.Варенье. Chem. Soc 2005, 127, 7192–7202. [PubMed] [Google Scholar] (26) Руссо М.Ф .; Li R; Mench M; van Duin ACT Молекулярно-динамическое моделирование реакций алюминий – вода с использованием реактивного силового поля ReaxFF. Int. J. Водородная энергия 2011, 36, 5828–5835. [Google Scholar] (27) Людвиг Дж. Vlachos DG; van Duin ACT; Годдард WA Динамика диссоциации водорода на ступенчатых поверхностях платины с использованием реактивного силового поля ReaxFF. J. Phys. Chem. B 2006, 110, 4274–4282. [PubMed] [Google Scholar] (28) Юн К.; Рахнамун А; Swett JL; Ибери V; Каллен Д.А.; Влассюк IV; Белянинов А; Джесси С; Пел X; Овчинникова О.С.; Rondinone AJ; Unocic RR; van Duin ACT Моделирование в атомном масштабе образования дефектов в графене при облучении ионами благородных газов.САУ Нано 2016, 10, 8376–8384. [PubMed] [Google Scholar] (29) Рахнамун А; van Duin ACT Исследование теплопроводности ледяных кластеров после ударного осаждения на поверхности кремнезема с использованием реактивного силового поля ReaxFF. Phys. Chem. Chem. Физ 2016, 18, 1587–1594. [PubMed] [Google Scholar] (30) Zou C; Ван Дуин А Исследование каталитической химии сложной поверхности железа с помощью метода реактивного силового поля ReaxFF. JOM 2012, 64, 1426–1437. [Google Scholar] (31) Шин Ю.К .; Kwak H; Васенков А.В.; Sengupta D; van Duin ACT Разработка реактивного силового поля ReaxFF для Fe / Cr / O / S и его применение для окисления бутана над покрытым пиритом катализатором Cr2O3.ACS Catal 2015, 5, 7226–7236. [Google Scholar] (32) Senftle TP; Hong S; Ислам ММ; Kylasa SB; Zheng Y; Шин Ю.К .; Юнкермайер С; Engel-Herbert R; Яник MJ; Aktulga HM; Verstraelen T; Грама А; van Duin ACT Реактивное силовое поле ReaxFF: разработка, приложения и направления на будущее. npj Comput. Матер 2016, 2, 15011. [Google Scholar] (33) Aktulga HM; Фогарти JC; Pandit SA; Грама А.Ю. Параллельная реактивная молекулярная динамика: численные методы и алгоритмические методы. Параллельные вычисления 2012, 38, 245–259.[Google Scholar] (34) Киласа С.Б .; Aktulga HM; Грама А.Ю. PuReMD-GPU: пакет моделирования реактивной молекулярной динамики для графических процессоров. J. Comput. Физ 2014, 272, 343–359. [Google Scholar] (35) Плимптон SJ; Томпсон А.П. Вычислительные аспекты многочастичных потенциалов. Миссис бык 2012, 37, 513–521. [Google Scholar] (36) Камат А.М.; van Duin ACT; Яковлев А Молекулярно-динамическое моделирование лазерно-индуцированного накала сажи с использованием расширенного реактивного силового поля ReaxFF. J. Phys. Chem. А 2010, 114, 12561–12572. [PubMed] [Google Scholar] (37) Сандерсон Р. Интерпретация длин облигаций и классификация облигаций.Наука 1951, 114, 670–672. [PubMed] [Google Scholar] (38) Bultinck P; Langenaeker W; Lahorte P; Де Профт Ф; Geerlings P; Waroquier M; Tollenaere J Метод выравнивания электроотрицательности I: параметризация и проверка расчетов атомных зарядов. J. Phys. Chem. А 2002, 106, 7887–7894. [Google Scholar] (39) Darden T; York D; Педерсен Л Сетка частиц Эвальда: метод N log (N) для сумм Эвальда в больших системах. J. Chem. Физ 1993, 98, 10089–10092. [Google Scholar] (40) Chenoweth K; van Duin ACT; Годдард WA ReaxFF Reactive Force Field для молекулярно-динамического моделирования окисления углеводородов.J. Phys. Chem. А 2008, 112, 1040–1053. [PubMed] [Google Scholar] (41) Manathunga M; Miao Y; Грязь; Götz AW; Мерц КМ Параллельная реализация методов функциональной теории плотности в программе вычислительного ядра квантового взаимодействия. J. Chem. Теория вычислений 2020, 16, 4315–4326. [PubMed] [Google Scholar] (42) Йоргенсен В.Л .; Чандрасекхар Дж; Madura JD; Impey RW; Klein ML Сравнение простых потенциальных функций для моделирования жидкой воды. J. Chem. Физ 1983, 79, 926–935. [Google Scholar] (43) Ганем Б. Механизм перестановки Клейзена: снова дежавю.Энгью. Chem., Int. Эд. Англ. 1996, 35, 936–945. [Google Scholar] (44) Гао Дж. Комбинированное исследование методом КМ / ММ перегруппировки Клейзена аллилвинилового эфира в водном растворе. Варенье. Chem. Soc 1994, 116, 1563–1564. [Google Scholar] (45) Zhang W; ван Дуин А Улучшение описания ReaxFF для слабых взаимодействий функционализированный углеводород / вода в конденсированной фазе. J. Phys. Chem. B 2018, 122. [PubMed] [Google Scholar] (46) Frisch MJ; Грузовые автомобили GW; Schlegel HB; Scuseria GE; Робб МА; Cheeseman JR; Scalmani G; Бароне V; Петерсон Г.А.; Nakatsuji H; Li X; Caricato M; Маренич А.В.; Bloino J; Янеско Б.Г.; Gomperts R; Mennucci B; Гратчиан HP; СП Ортис; Измайлов А.Ф .; Зонненберг JL; Уильямс-Янг Д; Ding F; Lipparini F; Egidi F; Гоингс J; Пэн Б; Петроне А; Хендерсон Т; Ranasinghe D; Закжевский В.Г .; Гао Дж; Rega N; Zheng G; Liang W; Hada M; Ehara M; Toyota K; Fukuda R; Hasegawa J; Ishida M; Накадзима Т; Honda Y; Китао О; Nakai H; Вревен Т; Throssell K; Монтгомери Дж. А. Мл.; Peralta JE; Ogliaro F; Bearpark MJ; Heyd JJ; Братья EN; Кудин К.Н.; Староверов В.Н.; Кейт Т.А.; Кобаяши Р; Normand J; Рагхавачари К; Rendell AP; Burant JC; Айенгар СС; Tomasi J; Cossi M; Millam JM; Klene M; Adamo C; Cammi R; Очтерски JW; Мартин Р.Л .; Morokuma K; Farkas O; Foresman JB; Fox DJ Гауссов 16 Gaussian, Inc .: Wallingford, CT, 2016. [Google Scholar] (47) Wang J; Wolf RM; Колдуэлл JW; Коллман PA; Дело DA Разработка и тестирование общего янтарного силового поля. J. Comput. Chem 2004, 25, 1157–1174.[PubMed] [Google Scholar] (48) Эльстнер М; Порезаг Д; Юнгникель G; Эльснер Дж; Haugk M; Frauenheim T; Сухай С; Seifert G Самосогласованный метод плотной связи с функционалом плотности заряда для моделирования свойств сложных материалов. Phys. Ред. B: Конденс. Matter Mater. Физ 1998, 58, 7260–7268. [Google Scholar] (49) Стюарт Дж.Дж. Оптимизация параметров для полуэмпирических методов V: Модификация аппроксимаций NDDO и применение до 70 элементов. J. Mol. Модель 2007, 13, 1173–1213. [Бесплатная статья PMC] [PubMed] [Google Scholar] (50) Schuler FW; Мерфи GW Кинетика перегруппировки винилаллилового эфира 1.Варенье. Chem. Soc 1950, 72, 3155–3159. [Google Scholar] (51) Gajewski JJ; Конрад Н.Д. Переменная структура переходного состояния в 3,3-сигматропных сдвигах от. альфа-вторичные изотопные эффекты дейтерия. Варенье. Chem. Soc 1979, 101, 6693–6704. [Google Scholar] (52) Уист О; Черный КА; Houk K Изотопные эффекты теории функционала плотности и энергии активации перегруппировок Коупа и Клейзена. Варенье. Chem. Soc 1994, 116, 10336–10337. [Google Scholar] (53) Hiersemann M; Nubbemeyer U Перегруппировка Клейзена: методы и приложения; Джон Вили и сыновья, 2007.[Google Scholar] (54) Zhang J; Ян Йи; Ян Л; Гао YQ Исследование динамики и кинетики химических реакций «в воде» путем расширенного отбора проб реактивных траекторий. J. Phys. Chem. B 2015, 119, 14505–14514. [PubMed] [Google Scholar] (55) Гость JM; Craw JS; Винсент Массачусетс; Hillier IH Влияние воды на перегруппировку Клайзена аллилвинилового эфира: теоретические методы, включая явную корреляцию растворителя и электронов. J. Chem. Soc., Перкин Пер. 2 1997, 71–74. [Google Scholar]
Лекция 4: Что такое сила?
Лекция 4: Что такое сила?
Что такое сила?
Единственная постоянная в мире — это действие гравитации на каждую и каждое строение, которое возводится.Основная функция всех структурных дизайн состоит в том, чтобы сделать здание стоящим. Понимание архитектоники поможет дать возможность дизайнеру включить эти проблемы в язык дизайна, который создаст значительно более четкое архитектурное выражение. Первичный для Это исследование представляет собой концепцию force . На самом деле сила очень абстрактна. Его можно определить, но он не может стать физически очевидным, пока не встретится сопротивление. Представьте себе глыбу льда высотой шесть футов, скользящую по не имеющей трения поверхность, проложенная внутри хоккейной площадки.Если человек упирается в стену и пытается остановить лед, она почувствует приложенную силу по глыбе льда. Она передает силу ледяной глыбы в сила, которая движется через ее тело в землю. Земля сопротивляется ей с силой разной величины, чтобы соответствовать ей, когда она прилагает все большие усилия. сила сопротивления, чтобы остановить глыбу льда. Если все эти силы будут переданы успешно, то слайд останавливается без силы и устойчивости отказ. Однако если хоть один из элементов этой хрупкой структурной системы провал……
Основным в изучении архитектоники является концепция сил. Если форма (его форма) или движение (поступательное движение / вращение) тела (структура, структурный элемент) была изменена, сила заставила изменять. Форма доски меняется, когда на нее стоит человек. Парусник перемещается, если ветер ударяет по парусу. Изменения формы и положения связаны с Силы обычно возникают при взаимодействии двух или более тел. Эти тела может быть полностью физическим (планка и человек) или более абстрактным (парус и ветер).Силы могут быть представлены графически или математически в виде векторов. количества. Величины вектора указывают величину и направление, как в отличие от Скалярных величин, которые указывают только величину.
Элементы силы
Учитывая единичное усилие , интересно знать все следующее:
1. Место применения
2. Звездная величина
3. Направление действий
4.Смысл
Точка приложения
Точка приложения — это точное место приложения силы к телу. Эта точка обычно описывается набором координат и представлен графически кончиком стрелки. Пункт приложения уникальна для каждой силы. Точка и сила не могут двигаться. Если несколько силы равной величины присутствуют в данной ситуации, силы уникальная основанная на открытии точка приложения, линия действия и их смысл.Может случиться так, что силы равной величины разделяют одну и ту же точку применения, в этом случае направление действия и смысл определяют их уникальность.
Величина
Величину силы принято выражать в фунтах (фунтах), кипы (килограммы; 1 кип = 1000 фунтов), ньютоны (Н) или килоньютоны (кН; 1 кН = 1000 Н)). Величину можно представить графически, нарисовав вектор для масштабирования. Точное определение величины этих векторов Суть метода Графическая статика .
Линия действия
Силу можно рассматривать как отрезок бесконечно длинной линии. Каждой силе ассоциируется с характеристической линией, которая называется линией действия. Справочная ось используется для описания ориентации этой строки. На рисунке показано, что линию действий можно описать в с точки зрения угла и наклона.Перевод происходит, когда сила пытается переместиться тело по его линии действия. (Бенджамин) Если линия действия сила не проходит через тело, тогда сила пытается вращаться тело.Это вводит понятие моментов, которые мы обсудим. скоро.
Смысл
Ощущение силы определяет направление (положительное или отрицательное), в котором сила движется по линии действия. Графически смысл может быть представлен стрелкой, указывающей в активном направлении. Это важно всегда следить за чувством силы и за тем, что условность использовалась для прикрепления данного знака остается неизменным. Смысл и направление могут быть либо письменным словесным описанием (т.е. вниз и вправо, вверх и влево, немного вверх и вправо) или более удобно выразить с точки зрения 360 градусов (т.е. 112 градусов, 273 градусов, 87,5 градусов). В в последнем случае единица начинается с нуля и увеличивается по часовой стрелке с направлением стрелки, пока не будет достигнуто 360.
Направление всегда относится к линии действия вектора, а направление смысл — это то, как вектор будет двигаться вдоль этой линии. в Например, направление и ощущение силы в 100 фунтов будет «вниз» и влево «или» 240 градусов.»
Сила 100 фунтов наносится на каменную колонну на схеме. Колонка испытает эта сила в каждой точке на линии действия силы. Как важность Фактически, сила также будет передана на землю, которая поддерживает колонка. Таким образом, земля под колонной по линии действия сила также будет испытывать нагрузку в 100 тысяч фунтов. Это иллюстрирует принцип . Проходимости . Точка приложения внешней силы, действующей на тело (конструкцию) может передаваться в любом месте по силовой линии действия без воздействия на другие внешние силы (реакции и нагрузки) действуя на это тело.Это означает, что НЕТ ЧИСТЫХ ИЗМЕНЕНИЙ в статике. воздействие на любое тело, если оно находится в равновесии. Это может быть дальше проиллюстрировано следующей диаграммой.
Виды сил (внешние, внутренние, реактивные)
Имея средства для описания сил, теперь мы можем взглянуть на типы сил, которые могут существовать в структурной системе. Силы или моменты, которые применяются непосредственно к конструкции, описываются как внешние . Реактивный Силы генерируются в местах, где два или более тела встречаются (соединения и опоры) и являются прямым результатом применения внешних силы.(3-й закон Ньютона: для каждого действия есть равное и противоположное реакция) Силы или моменты, которые развиваются в структуре в ответ к внешним силам описываются как внутренние .
Предположим, что балка поддерживается на концах. Нагрузка приложена к верхняя часть балки, направленная вниз. Этот груз мог быть человек, стоящий на балке. Нагрузка вызывает реакции, которые отжимаются в двух точках служба поддержки. Линия действия груза (человека) на балку также проходит через крюк, прикрепленный к нижней стороне балки.Теперь, если человек, стоявший на перекладине, спускался вниз и держался за крюк ровно ниже точки, где они раньше находились, чтобы линии действия были точно такие же, реакции на концах лучей не изменится. Это потому, что нагрузка человека все еще действует по той же линии действий. Пока нагрузка приложена в любой точке по линии действия внешние реакции не изменятся.
Вышеуказанная ферма нагружена силой, действующей в точке C.Этот нагрузка создает реакции на две опоры A и B. Нагрузка на ферму мог двигаться куда угодно по линии действия, а внешние реакции в A и B останутся прежними. Это означает, что если нагрузка была приложена в точках D, E, F или G реакции в точках A и B не изменятся. Обратите внимание, что Единственным предметом обсуждения в данный момент является тот факт, что внешние реакции не изменятся. Понятно, что внутренние силы будут меняться в значительной степени внутри фермы, поскольку сила перемещается по линии действия.Этот вопрос будет обсуждаться в следующей лекции.
Эта балка странной формы — еще один пример конструкции, которая нагружена в определенной точке, а именно E. Чтобы конструкция оставалась в покое должны быть какие-то реакции в точках A и B. B — реакция натяжения, поскольку это трос. Опять же, если нагрузка была приложена в точках C, D, E, F или G на этом твердом теле (конструкции) реакции в A и B останутся такими же.
ТОЛЬКО ВНЕШНИЕ силы (реакции) остаются неизменными.Некоторые из внутренних силы сопротивления в элементах конструкции изменяются по мере изменения нагрузки применяется в разных точках вдоль линии его действия. Это иллюстрирует одно важное различие между ВНУТРЕННИМИ и ВНЕШНИМИ силами.
Принцип прозрачности применим к любому телу (капли, воздушные шары, простые балки, кривые балки, фермы, оболочки и т. д.). Это не зависит от размер или форма тела.
Вопросы для размышления
Что происходит с реакциями в точках A и B, если смысл нагрузка будет обратной на обеих предыдущих диаграммах?
Проблемы
Краткое содержание изображения лекции
Дополнительное чтение
Schodek.стр. 30 — 35.
Авторские права © 1995,1996, Крис Х. Любкеман и Дональд Петинг
Авторские права © 1997, 1998 Крис Х. Любкеман
Неравновесная сила может стабилизировать двумерные активные нематики
Значение
Живые системы отличаются от мертвого вещества одним важным аспектом: они приводятся в движение внутренними двигателями. В анизотропных жидкостях широко распространенная теория активной материи предсказывает, что это обязательно приводит к нестабильности от состояния покоя к крупномасштабному и, в конечном итоге, некогерентному движению.Здесь мы бросаем вызов этой общей мудрости, пересматривая симметрии наиболее распространенной экспериментальной геометрии для активных систем. Мы обнаружили дополнительную связь между активностью и движением, которая может сделать активную систему даже более стабильной, чем ее пассивный аналог, при сохранении других отличительных черт неравновесной физики. Наши результаты бросают вызов общепринятым взглядам на активное вещество и проясняют интерпретацию множества экспериментов.
Abstract
Суспензии активно управляемых анизотропных объектов демонстрируют отчетливо неравновесное поведение, и современные теории предсказывают, что они неспособны поддерживать ориентационный порядок при высокой активности.Напротив, здесь мы показываем, что нематические суспензии на субстрате могут демонстрировать порядок при произвольно высокой активности из-за ранее не сообщаемой потенциально стабилизирующей активной силы. Более того, эта сила неизбежно возникает в теориях активных ориентируемых жидкостей при геометрическом ограничении. Образовавшаяся неравновесная упорядоченная фаза демонстрирует устойчивые гигантские флуктуации числа, которые не могут быть подавлены даже несжимаемым растворителем. Наши результаты применимы практически ко всем экспериментальным тестам, используемым для исследования активного нематического упорядочения самодвижущихся коллоидов, бактериальных суспензий и цитоскелета, и имеют поддающееся проверке значение при интерпретации их неравновесного поведения.
Живые системы преобразуют химическую энергию в движение, тем самым нарушая детальный баланс в микроскопическом масштабе. Макроскопически эти нарушения приводят к стрессам и токам, ответственным за внутриклеточные потоки, ведущие к движению клеток (1), коллективной миграции клеток во время эмбрионального развития (2) и стае птиц (3). Подобные неравновесные токи возникают в неживых системах, таких как хемотаксические коллоиды (4) и вибрирующие гранулированные стержни (5). Эти системы часто описываются активными гидродинамическими теориями, классом континуальных описаний, выведенных из теорий равновесия жидких кристаллов, но дополненных дополнительными «активными» силами, возникающими в результате микроскопического движения (6–8).Эти теории являются предпочтительными инструментами для изучения специфических неравновесных свойств в коллективном поведении жидких суспензий анизотропных активных единиц, таких как филаменты цитоскелета (9, 10) или бактерии (11).
Центральным вопросом активной гидродинамики является определение влияния активности на динамическую устойчивость и устойчивость к колебаниям различных типов ориентационного и поступательного порядка. Предыдущие исследования показали, что из-за взаимодействия активного напряжения и потока растворителя нематический порядок в несжимаемых активных суспензиях всегда нестабилен за пределами критического значения активности (7, 8, 12–14).Этот порог нестабильности исчезает в пределе бесконечного размера системы, что означает, что, в отличие от своих равновесных аналогов, эти системы в целом нестабильны. Однако в двухмерных экспериментальных реализациях эту нестабильность можно подавить трением жидкости о подложку. Тем не менее, современные теории предсказывают, что даже в этих условиях нестабильность всегда возникает при достаточно высокой активности (15), что может быть экспериментально реализовано путем увеличения плотности миозиновых моторов или бактерий или количества доступного для них топлива.
Еще одна отличительная черта активных систем — статистика флуктуаций их плотности. В равновесных системах вдали от критических точек и с взаимодействиями конечного радиуса действия область пространства, содержащая в среднем N частиц, будет подвергаться флуктуациям этого числа порядка N независимо от того, находится ли она в несжимаемом растворителе или нет. Напротив, активные гидродинамические теории систем без несжимаемости демонстрируют флуктуации порядка выше N из-за активных массовых токов, возникающих из-за флуктуаций ориентации (5, 7, 8, 16, 17).Хотя эти так называемые гигантские флуктуации числа явно наблюдались в условиях без растворителя, мало что известно об их форме в присутствии несжимаемого растворителя (18), а их наблюдение в биологических экспериментах было трудным и противоречивым (19).
Чтобы помочь интерпретировать богатое динамическое поведение типично квазидвумерных экспериментов с активными системами (10, 11, 19, 20), здесь мы теоретически изучаем упорядочение и флуктуации неполярной активной жидкости в контакте с подложкой.Пересматривая основы активных гидродинамических теорий в двух измерениях, мы сначала обнаруживаем, что контакт с подложкой допускает дополнительную активную силу с отчетливой угловой симметрией. Эта сила не сохраняет угловой момент, но существует даже в ахиральных системах. Вопреки распространенному мнению, повышенная активность при наличии этого члена может привести к стабилизации нематического упорядочения. Здесь мы сначала качественно обсудим геометрический смысл этой дополнительной силы и выведем ее форму из соображений симметрии в чисто двумерной системе.Далее мы покажем, что гигантские флуктуации числа в активной нематической фазе устойчивы к введению несжимаемого растворителя, а также этой активной силы. Наконец, мы показываем, что эта потенциально стабилизирующая активная сила возникает естественным образом из принятой модели трехмерной активной жидкости в условиях вертикального удержания, и утверждаем, что это доминирующая активная сила в перенормированной теории в присутствии шума. Наши результаты предлагают правдоподобные объяснения устойчивости порядка при высокой активности, а также систематики нестабильностей в бактериальных, живых жидких кристаллах и цитоскелетных системах.
Качественный аргумент
Хорошо известная дестабилизация активного нематика является результатом приложения частиц диполярного распределения силы любого знака к окружающему их растворителю. Как показано на рис. 1 A и B , диполярные распределения силы любого знака всегда дестабилизируют упорядоченное состояние. Суть нашего аргумента состоит в том, что в отличие от этих диполярных распределений, распределения сил с более высокой угловой симметрией в целом не дестабилизируют упорядоченную фазу.Чтобы убедиться в этом, рассмотрим квадратную форму с квадрупольным распределением силы, показанную на рис. 1 C , которая вытягивает жидкость перпендикулярно своим граням и выталкивает ее из углов. Нарушение идеально выровненного ряда частиц, проявляющих эту более симметричную плотность активной силы, приводит к сгруппировке их углов в одних местах, что усиливает их выталкивание жидкости и их распространение в других. В результате жидкость имеет тенденцию течь из расширенных областей в сгруппированные области, т. Е., в направлении, противоположном изображенному на фиг. 1 A , который толкает частицы обратно к идеально выровненному состоянию. Более того, четырехкратная симметрия частиц не позволяет им различать возмущения растяжения и изгиба. В результате их активность — если она правильного знака — всегда помогает стабилизировать выровненное состояние.
Рис. 1.
Активные силы влияют на стабильность ориентируемой жидкости. ( A , Top ) Нематический «съемник» всасывает окружающий растворитель вдоль его длинного направления (синие стрелки), чтобы отклонить его вдоль короткого направления (красные стрелки).( A , Bottom ) Таким образом, расширенная конфигурация приводит к потокам растворителя, показанным толстыми стрелками, которые увлекают частицы и, таким образом, подчеркивают исходное возмущение, вращая их, как показано тонкими стрелками. ( B ) «Толкатели» с противоположным силовым диполем, хотя и устойчивы к смещению, нестабильны в конфигурации изгиба. ( C ) Введенная здесь активная сила также присутствует в нематических активных системах, но связана с более высокими мультиполями распределений плотности силы.В показанном здесь примере результирующий поток последовательно стабилизирует упорядоченное состояние частиц. Мы показываем, что для систем на подложке эта активная стабилизация может преодолеть хорошо описанную дестабилизацию, связанную с дипольными членами.
Помимо этих схематических примеров, распределение сил в активном нематике обычно имеет вклад как диполярной, так и более высокой симметрии. Однако в активных системах, таких как взвешенные пленки и объемные трехмерные жидкости, где сохраняется импульс, все вклады с более высокой симметрией субдоминируют по сравнению с дипольными на больших масштабах.Здесь мы показываем, что это не так в 2D-системах на подложке, а также в 3D-жидкостях при вертикальном ограничении. В результате, в зависимости от ее величины и знака активная сила с более высокой угловой симметрией может привести к общей стабилизации активной жидкости, что противоречит широко распространенному мнению о том, что несжимаемые активные нематики всегда нестабильны при высокой активности.
Модель активной нематической суспензии на подложке
Теперь мы предлагаем формальное описание динамики локальной ориентации θ (r, t) и скорости v (r, t) нашей нематически упорядоченной 2D активной суспензии, а также концентрация c (r, t) его активных частиц., запишем линейные динамические уравнения, совместимые с симметриями системы в длинноволновом (гидродинамическом) пределе. Уравнение динамики углового поля: | λ | <1 означает перемешивание потока (как у бактерий). Здесь мы используем упрощенный функционал свободной энергии с одной константой Франка H = ∫d2rK2 (∇θ) 2 + g (c), [2] где K> 0 характеризует тенденцию частиц к выравниванию, а g (c) — произвольная функция концентрации.
Поле течения и активные силы.
Поток управляется силами, внутренними по отношению к жидкости, и наличие подложки диктует динамику Дарси, Γv = −∇Π + f p + f a, [3] где Γ можно рассматривать как коэффициент трения о подложку. Давление Π служит множителем Лагранжа, обеспечивающим выполнение условия несжимаемости ∇⋅v = 0 для суспензии в целом, при этом допуская колебания концентрации взвешенных частиц. Мы не рассматриваем случай сжимаемой среды, что не добавляет интереса к физике.+ 1 − λ2∂xδHδθŷ. [4] Помимо этих стандартных условий равновесия, плотность активной силы f a зависит от θ только через свой градиент из-за инвариантности вращения. Сочетание этого с инвариантностью отражения (x, y, θ) → (x, −y, −θ) нашей ахиральной системы диктует это до самого низкого порядка по градиентам fxa = — (ζ1Δμ + ζ2Δμ) ∂yθ [5a] fya = — ( ζ1Δμ − ζ2Δμ) ∂xθ, [5b] где ζ1 и ζ2 — две независимые, априори неизвестные феноменологические константы, а Δμ обозначает силу общей активности в системе, например, разность химических потенциалов между АТФ клеточного топлива и его продукты гидролиза.Мы интерпретируем два компонента fa на рис. 2, где fxa вызывает горизонтальный поток жидкости в расширенном нематике, в то время как fya управляет вертикальным потоком жидкости в изогнутом нематике. Активная сила, зависящая от градиентов c, также разрешена в fa, но не существенно меняет наше обсуждение ( SI Приложение, IA. Dynamics on the Substrate ). В то время как активная сила, пропорциональная ζ1, является стандартной в теориях активной жидкости, в настоящей работе вводится и исследуется влияние соленоидальной силы ζ2.
Рис. 2.
Две составляющие активной силы fa определяют устойчивость активного нематика по отношению к растяжению и изгибу. ( A ) Расширенное возмущение ∂yθ ≠ 0 (черные сегменты) индуцирует активную силу fxa = a∂yθ, которая стабилизирует систему качания потока, если a <0 (показано стрелками). ( B ) Возмущение изгиба ∂xθ ≠ 0 создает активную силу fya = b∂xθ, которая стабилизирует систему качания потока, если b> 0.
Эту силу можно понять простым языком, введя нематический директор n = (cos⁡θ, sin⁡θ).В системах с сохранением импульса активная сила может быть только дивергенцией симметричного напряжения, а именно fa = ζ1 Δμ∇⋅ (nn) = ζ1Δμ [n (∇⋅n) + n⋅∇n]. Сила ζ2 включает обмен угловым моментом с подложкой, и ее введение, таким образом, позволяет использовать активную силу с разными префакторами для членов n (∇⋅n) и n⋅∇n. Предлагаемая нами форма плотности активной силы также имеет ту же симметрию, что и общая флексоэлектрическая поляризация в нематических жидких кристаллах, тогда как ∇⋅ (nn) аналогична более ограниченному случаю, в котором величины поляризации для деформации изгиба и расширения равной силы одинаковы (21, 22).Поскольку локальная поляризация в системе из равновесия может быть связана с локальной плотностью силы, эта аналогия обеспечивает дополнительное эвристическое обоснование уравнения. 5 .
Динамика концентрации.
Эволюция концентрации c определяется уравнением сохранения ∂tc = −∇⋅ (Jp + Ja), где ток пассивных частиц имеет вид Jp = −Γc∇δH / δc. Как и в случае с fa, активный ток Ja состоит из двух различных θ-зависимых активных членов априори, но член, аналогичный ζ2, будучи ротором, выпадает из уравнения сохранения, давая ∂tc = Γc∇2δHδc + ζcΔμ∂x∂yθ , [6] где активный член ζcΔμ связывает флуктуации ориентации с флуктуациями концентрации и фигурирует в стандартных теориях активных нематиков (7, 16).+ sinϕŷ). Комбинируя уравнения. 1–6 и исключив давление путем проецирования в направлении, перпендикулярном q, мы обнаруживаем, что динамика диффузная в ведущем порядке по q: ∂tθq = −D (ϕ) q2θq, где зависящий от направления коэффициент ориентационной диффузии определяется выражением D (ϕ ) = ΓθK + Δμ2Γ (1 − λ⁡cos⁡2⁡ϕ) (- ζ1⁡cos⁡2⁡ϕ + ζ2). [7] Таким образом, система линейно устойчива при малых q тогда и только тогда, когда D (ϕ) является положительный для всех значений ϕ, т. е. если второй член в правой части уравнения. 7 не настолько велика, чтобы преодолеть стабилизирующий эффект релаксации директора через ΓθK.Теперь мы сосредоточимся на этом втором члене, который доминирует при высокой активности, т. Е. При большом Δμ. Случай систем с падающим потоком (| λ | <1), где (1 − λ⁡cos⁡2⁡ϕ) всегда положительно, легко интерпретировать, поскольку он управляется активной силой fa. Как показано на рис. 2, растяжение можно стабилизировать с помощью силы fxa, которая зависит от ∂yθ только через отрицательный коэффициент, тогда как для стабилизации изгиба требуется, чтобы fya зависела от ∂xθ через положительный коэффициент. Поскольку предыдущие исследования неявно предполагают ζ2 = 0, уравнение. 5 ясно показывает, что они навязывают равенство этих двух коэффициентов, подразумевая дестабилизацию либо изгиба, либо изгиба, в зависимости от его знака.Введение активной силы (ζ2 ≠ 0) теперь дает возможность этим коэффициентам иметь противоположные знаки. При ζ2> | ζ1 | это означает, что стабильность системы, то есть скорость положительной релаксации, увеличивается с увеличением активности, как показано на фиг. 3 A . Напротив, рис. 3 показывает, что и выравнивание потока (| λ |> 1), и ζ2 <| ζ1 | системы остаются в целом нестабильными при высокой активности.
Рис. 3.
Области стабильности упорядоченной фазы, обозначенные знаком D (ϕ) в уравнении. 7 как функция параметра выравнивания потока λ, отношения ζ1 / ζ2 двух активных сил и общей величины активности относительно пассивного трения Δμ̃ = ζ2Δμ / 2KΓΓθ. ( A ) При Δμ̃> 0 область линейной стабильности упорядоченной фазы (оттенки синего) сужается с увеличением активности, но центральный синий квадрат остается стабильным при произвольно высокой активности. ( B ) При Δμ̃ <0 стабильность отменяется для достаточно большой активности, а именно Δμ̃ <−1.
Гигантские колебания числа
Открыв возможность стабильного гомогенного нематика при высокой активности, мы теперь исследуем природу флуктуаций концентрации, возникающих в таком состоянии, когда к уравнениям добавляются несохраняющие и сохраняющие источники шума. 1 и 6 соответственно. Мы обнаружили, что гигантские флуктуации числа сохраняются, несмотря на дальнодействующие эффекты, связанные с несжимаемым полем скорости. Этот результат, который резко контрастирует со случаем несжимаемых активных полярных систем (23), можно увидеть без подробных расчетов, исследуя структуру уравнений. 6 и 7 . В самом деле, по сравнению со сжимаемыми нематическими системами, несжимаемость привносит только несингулярную анизотропию в скорость ориентационной релаксации (2). 7 , без изменения масштабирования с помощью волнового числа. Поскольку гигантские флуктуации числа зависят исключительно от масштабирования волнового числа скорости ориентационной релаксации, а не от ее анизотропии (16), они также должны присутствовать в нашей системе. В частности, простой подсчет мощности в рамках линеаризованной обработки демонстрирует, что из-за активного тока концентрации флуктуации концентрации δc = c − ⟨c⟩ масштабируются с q так же, как флуктуации ориентации. Следовательно, статический структурный фактор Sq≡∫r⟨δc (0) δc (r) ⟩exp (−iq⋅r) / ⟨c⟩ флуктуаций концентрации масштабируется как 1 / q2.Эквивалентно, в области, содержащей в среднем N частиц, SD в количестве линейно масштабируется с N в двух измерениях. Изменяется только форма прогнозируемой анизотропии Sq (приложение SI, IA. Dynamics on the Substrate ) по сравнению с тем, что указано в ссылке. 16, из-за фактора D (ϕ) в уравнении. 7 . Наши выводы остаются в силе даже после включения более общих разрешенных симметрией активных и пассивных членов (приложение SI, IA. Dynamics on the Substrate ).
Появление дополнительной активной силы в замкнутых активных нематиках
Чтобы дополнительно прояснить физическое происхождение нашей активной силы, мы рассматриваем динамику трехмерной активной подвески поперечного размера L, заключенной в масштабе длины h≪L в направлении z. и спроецируйте его на 2D плоскость xy.Для выполнения этой операции мы используем стандартное приближение смазки, корректное в пределах малых h / L (24, 25). Это приближение основано на разделении шкалы между градиентами и скоростями внутри и перпендикулярно плоскости xy, а именно ∂¯z≫ (∂¯x, ∂¯y) и v¯z≪ (v¯x, v¯y). , где чертой обозначены трехмерные переменные и операторы. Затем получают двумерные уравнения потока путем усреднения каждого члена в трехмерных уравнениях потока по толщине ограниченной жидкости. Мы проиллюстрируем эту процедуру путем усреднения трехмерной плотности вязкой силы ∇¯2v¯, найденной как в стандартном уравнении Навье – Стокса, так и в уравнении потока для полной трехмерной активной жидкости.Рассмотрим простой профиль Пуазейля v¯⊥ (x, y, z) = (4 / h3) z (h − z) v¯0 (x, y) для вертикальной структуры потока, где v¯⊥ = ( v¯x, v¯y) — это проекция трехмерного вектора скорости на плоскость xy, v¯0 (x, y) — его значение в средней плоскости, и где условие прилипания наложено на ограничивающие поверхности в точке z = 0 и z = h. Обозначая v (x, y) = (2/3) v¯0 (x, y) усредненную по z скорость, мы находим, что плотность вязкой силы, усредненная по толщине, имеет вид 1h∫0hη¯∇¯2v¯⊥dz = −12η ¯h3v + OhL2, [8] что дает начало левой части уравнения. 3 с Γ = 12η¯ / h3. Для нашего дальнейшего обсуждения важно отметить, что эта усредненная двумерная плотность вязкой силы имеет нулевой порядок по градиенту, несмотря на то, что ее трехмерный аналог пропорционален ∇¯2. Действительно, в процессе усреднения каждый вертикальный градиент ∂¯z эффективно заменяется коэффициентом, пропорциональным 1 / h, и горизонтальные градиенты выпадают, потому что они являются субдоминирующими в пределе h≪L. Хотя предварительный фактор уравнения. 8 предполагает профиль Пуазейля для потока, только числовой коэффициент в его правой части и, следовательно, определение Γ изменяются, если рассматриваются другие виды потоков.
В трехмерных активных жидкостях эта плотность вязкой силы уравновешивается дивергенцией активных напряжений. Эта дивергенция может быть выражена в терминах трехмерного нематического параметра порядка Q¯ (r¯, t) как ∇¯⋅Q¯S. [9] Здесь верхний индекс S обозначает симметричную часть тензора, а I¯ обозначает единичный тензор. В то время как два первых члена в правой части уравнения. 9 являются стандартными, последний термин не будет учитываться при обработке градиентного расширения неограниченной трехмерной жидкости.Действительно, в то время как первые имеют первый порядок по трехмерному градиенту ∇¯, вторые — третьего порядка. Однако, подобно усредненной по толщине плотности вязкой силы по формуле. 8 , его аналог, усредненный по толщине, дает начало членам более низкого (первого) порядка в горизонтальном градиенте, и поэтому им нельзя пренебрегать. Таким образом, этот член дает начало второй константе активности ζ2, обсуждавшейся в предыдущих разделах. Чтобы увидеть это более ясно, обратите внимание, что один из членов, возникающих из силы ∇¯j∇¯iQ¯⋅∇¯⋅Q¯jS, равен ∇¯2Q¯⋅∇¯⋅Q¯≈∂¯z2Q¯⋅∇¯⋅ Q¯.Чтобы усреднить этот и другие члены, мы дополняем стандартную процедуру, описанную для плотности вязкой силы, обработкой среднего поля, при которой среднее значение z произведения двух полей аппроксимируется произведением их индивидуальных средних значений z ( SI Приложение, II . Вывод эффективных двумерных уравнений движения из трехмерных уравнений для активных жидкостей, ограниченных в одном направлении ). Обозначая z-усредненную проекцию аполярного параметра порядка на плоскость xy как Q (x, t) = S2cos⁡2⁡θ sin⁡2⁡θsin⁡2⁡θ −cos2θ, [10] среднее значение дивергенции третий член в правой части уравнения. 9 вносит двумерную плотность силы формы Q⋅∇⋅Q в уравнение баланса сил, усредненных по толщине. Поскольку этот вклад имеет тот же порядок в 2D-градиенте, что и стандартная плотность активной силы ∇⋅ (ζ¯1ΔμQ), его необходимо сохранить в 2D-описании.
Выполнение этой процедуры усреднения для уравнения эволюции для параметра порядка трехмерного нематика, а также для уравнения баланса сил ( SI Приложение, II. Вывод эффективных двумерных уравнений движения из трехмерных уравнений для активных жидкостей, заключенных в одну Направление ), мы получаем усредненные по всей толщине двумерные динамические уравнения ∂tQ = −v⋅∇Q + ω⋅Q − Q⋅ω − λU − ΓθH, [11a] Γv = −∇Π − λ∇⋅H − 2 ∇⋅ (QH) A, −ζ1Δμ∇⋅Q − 2ζ2Δμ Q⋅∇⋅Q, [11b] где ζ1 = ζ¯1 и ζ2 = 9ζ¯2 / h3.Усредненная по толщине динамика поля концентрации описывается формулой. 6 . Эти уравнения сводятся к уравнениям. 1–5 в упорядоченной фазе, где S релаксирует за микроскопическое время до своего стационарного значения, которое мы установили на 1 без потери общности. В уравнении. 11 H — молекулярное поле, сопряженное с Q, верхний индекс A обозначает антисимметричную часть тензора, а ω и U — соответственно антисимметричная и симметричная части тензора ∇v. Давление Π накладывает несжимаемость, как в формуле. 3 . Уравнение 11 демонстрирует, что сила ∝ζ2, ранее введенная посредством общих аргументов симметрии, является естественной возникающей особенностью ограниченной трехмерной активной динамики. Обратите внимание, что, хотя мы включили только один член порядка ¯2 в уравнение. 9 для ясности, другие члены O (∇¯n≥2) также вносят вклад как в эту дополнительную активную силу ζ2, так и в обычную ζ1 при усреднении толщины и не вводят никаких качественно новых членов. В размерном отношении каждый дополнительный фактор of в трехмерной теории должен сопровождаться префактором порядка, масштабом, определяемым размером взвешенных частиц.Между тем, аналогично формуле. 8 каждый вертикально усредненный градиент дает коэффициент 1 / ч. Таким образом, мы ожидаем ζ2 / ζ1∼ (ℓ / h) 2. В результате в плотно замкнутых суспензиях с h∼ℓ коэффициенты ζ2 и ζ1 должны быть сравнимы по величине.
Доминирование и общность сверхактивной силы
Помимо этих микроскопических соображений, мы предсказываем, что сила ζ2 будет преобладать над старой силой ζ1 в перенормированной теории в присутствии шума. Действительно, согласно формулам.−∂xθŷ, в котором не учитывается фактор анизотропии cos⁡2⁡θ. Поскольку активные нематики имеют только квазидальний порядок, все анизотропные члены усредняют до нуля на больших масштабах из-за инвариантности вращения (17), что означает, что cos⁡2⁡θ⟩ убывает как степень размера системы с типично малым показателем . Следовательно, для больших систем изотропная активная сила ζ2 не исчезает с увеличением размера расходящейся системы ( SI Приложение, III. За пределами линейной теории: масштабирование активной силы с расстоянием ) и, таким образом, преобладает над силой ζ1.
В дополнение к своей роли в нематических и полярных системах, активная сила, введенная здесь, является ключом к характеристике активности в активных системах с более высокой симметрией, включая тетрактическую (5) и гексатическую (26, 27) фазы, как ожидается из схематического представления Рис.1 C . В этих системах симметрия требует, чтобы ζ1, ζc и λ в уравнениях. 1–6 все равны нулю, что означает, что наш член ζ2 является единственным возможным источником активных нестабильностей. Он возникает через антисимметричный участок активного напряжения, пропорциональный в двух измерениях θϵ в пределе θ≪1, где поле псевдоскалярных углов θ — это мода с нарушенной симметрией, а ϵ — двумерный тензор Леви – Чивиты.Хотя это не вызывает общей нестабильности, эти активные п-атомы на подложках, тем не менее, нестабильны при ζ2Δμ <−2ΓΓθK независимо от присутствия несжимаемого растворителя. Кроме того, вышеупомянутый характер чистого завитка члена ζ2 означает, что они не вносят вклад в массовые токи. Таким образом, активные тетратики и гексатики имеют нормальные (негиантные) колебания числа.
Динамика дефектов
Помимо анализа линейной устойчивости, активность ориентируемых жидкостей также изменяет динамику дефектов., и, следовательно, не может привести к неисправности движителя. Точно так же в системах с более высокой симметрией, где разрешен только член ζ2, дефекты, параметризованные как θ = ± nψ в полярных координатах (r, ψ) (с n = 1/4 для тетратиков и n = 1/6 для гексатиков), приводят только до изотропной плотности активной силы. Следовательно, баллистическое движение дефектов в таких системах с более высокой симметрией невозможно.
Экспериментальные последствия и обсуждение
Присутствие активного члена ζ2 имеет измеримые значения для текущих экспериментов с биологически активным веществом.Прежде всего, мы предсказываем существование устойчивых состояний при сколь угодно высоких значениях параметра активности Δμ. Это помогает рационализировать недавнее наблюдение высокоупорядоченных аполярных нематических фаз в ограниченных суспензиях бактерий Escherichia coli (19). Отсутствие бактериальной турбулентности в этих системах было бы загадкой при лечении с одним параметром активности ζ1. В самом деле, в экспериментах используется безупречный мутант, то есть система с сильно уменьшенным Γθ в уравнении. 7 , что должно способствовать нестабильности. Решение вполне может заключаться в нашем механизме, включающем второй параметр активности с возможно стабилизирующим эффектом.
Хотя это качественное предсказание помогает объяснить сохранение стабильных состояний в ситуациях с высокой активностью или низкой диссипацией, его недостаточно для определения того, является ли выровненное состояние в данном эксперименте стабильным благодаря нашему механизму или потому, что наибольшее экспериментально доступное Δμ равно просто слишком маленький.Чтобы различать эти две возможности, отметим, что в шумной среде стабилизирующее влияние активного члена ζ2 на коэффициент диффузии D (ϕ), указанный в формуле. 7 прямо отражается на величине угловых колебаний даже в стабильном выровненном состоянии. Учитывая интенсивность углового шума 2TΓθ, наша теория, таким образом, предсказывает, что равновременный коррелятор для угловых флуктуаций имеет вид θq (t) θ − q (t)⟩ = TΓθD (ϕ) q2. [12] В теории, включающей только старую версию ζ1 активный член, увеличение отношения Δμ / Γ (т.е.g., за счет увеличения количества АТФ, доступного в анализе цитоскелета) должно приводить к уменьшению этого коррелятора по одним направлениям ϕ и увеличению по другим. Напротив, при наличии механизма стабилизации, обсуждаемого здесь (т.е. при ζ2> | ζ1 |), этот коррелятор будет уменьшаться по всем направлениям ϕ, обеспечивая количественный тест на существование стабилизации ζ2.
Наш линейный анализ стабильности также помогает эвристически понять формирование паттернов в бактериальных и цитоскелетных активных жидкостях (10, 11, 31, 32).Анизотропия D (ϕ) в уравнении. 7 означает, что упорядоченная фаза дестабилизируется, когда она сначала становится отрицательной для любого угла ϕu. В этом случае, вероятно, образуются полосы с нормальным вектором, ориентированным вдоль ϕu, масштаб длины которых может быть получен простым расширением до четвертого порядка по волновому числу q двухмерного модового анализа, который привел к формуле. 7 . Результирующая динамика имеет вид ∂tδθq = — [D (ϕ) q2 + Kr (ϕ) q4] δθq, где возникает стабилизирующий коэффициент Kr (ϕ) = (K / 4Γ) (1 − λ⁡cos⁡2⁡ϕ) 2 просто из эластичности Фрэнка и, таким образом, учитывает модели с размером ≈Kr (ϕu) / | D (ϕu) | без использования ранее применявшихся специальных градиентных разложений высокого порядка (11, 32, 33).Более того, когда эффективная двумерная динамика — это динамика замкнутой трехмерной жидкости, как обсуждалось выше, Γ∝1 / h3, так что Kr доминирует над такими специальными членами с коэффициентом O (h / ℓ) 2, который может быть большим в зависимости от масштаб заключения.
Помимо этих приложений, эта теория порядка q4 может быть расширена для объяснения упорядочения и формирования структуры в новых «живых жидких кристаллах», а именно пассивных нематических жидких кристаллах с хорошо изученными физическими свойствами, перфузируемыми небольшими количествами бактерий.Из-за небольшого количества активных бактерий в них эти системы разделяют большую часть своих пассивных свойств с встраиваемыми, часто хорошо охарактеризованными жидкими кристаллами. Это открывает беспрецедентные возможности для количественной проверки наших и других теоретических прогнозов. Подробная связь между этими системами и текущим исследованием обсуждается в Приложении IV SI. Living Liquid Crystals , где мы вводим два связанных угловых поля для локального выравнивания пассивных жидкокристаллических частиц и активных бактериальных частиц.Наш подход учитывает активность без необходимости в ранее введенных специальных ориентационных связях, нарушающих симметрию Онзагера, между этими двумя угловыми полями (20) и приводит к критерию устойчивости, аналогичному критерию в формуле. 7 . Поскольку величина, аналогичная λ, может быть настроена количественно, изменяя пассивные свойства жидкого кристалла, наш прогноз стабильности можно напрямую проверить, и мы прогнозируем появление паттернов с аналогичным настраиваемым масштабом длины. Изменение встраиваемого жидкого кристалла, вязкости растворителя или масштаба удержания также должно позволить модификации параметров, аналогичных K, Γ и Γθ в уравнении. 7 и позволяют напрямую проверить, остается ли стабильная система переброски потока с большим положительным значением ζ2, когда Δμ / (KΓΓθ)> 2, как мы прогнозируем.
Наконец, наш подход предлагает объяснение недавнему наблюдению (34), что переход к управляемой активностью турбулентности в растяжимых системах микротрубочки-кинезин, заключенных в канал, контролируется соотношением сторон поперечного сечения этого канала. Усредняя динамику по направлению z в канале с прямоугольным поперечным сечением Ly × h, мы смотрим на флуктуации расширения с наибольшей длиной волны в направлении y, отмечая при этом, что растяжимые частицы подразумевают ζ¯1> 0, что стабилизирует флуктуации расширения.Предполагая дестабилизирующее ζ¯2 <0, мы прогнозируем, что система должна стать нестабильной при уменьшении h, а затем отношение ζ2 / ζ1∝1 / h3 увеличивается. Следовательно, мы предсказываем, что активная сила ζ2 играет дестабилизирующую роль в системах микротрубочка-кинезин.
Благодарности
Мы благодарим Олега Лаврентовича за указание на сходство между активной силой и флексоэлектрической поляризацией. S.R. и M.C.M. поблагодарить Институт теоретической физики им. Кавли (KITP) за гостеприимство во время завершения некоторых из этих работ.Эта работа поддержана Интеграционным грантом Марии Кюри PCIG12-GA-2012-334053, «Investissements d’Avenir» Laboratoire d’excellence Physique: Atomes Lumière Matière (LabEx PALM) (ANR-10-LABX-0039-PALM), Agence Nationale de la Recherche (ANR), грант ANR-15-CE13-0004-03, и стартовый грант Европейского исследовательского совета Groupement de Recherche 677532 (для ML). Группа М.Л. принадлежит к консорциуму CNRS Physique de la cellule au corrective Initiative d’excellence. S.R. благодарит за поддержку Национальную стипендию Дж. К. Боуза Совета по научным и инженерным исследованиям, Индия, и Траст-фонд образования и развития Tata.M.C.M. был поддержан наградами Национального научного фонда США NSF-DMR-1609208 и NSF-DGE-1068780, целевым грантом 342354 Фонда Саймонса и Программой Сиракуз для мягкой материи и живой материи. A.M., P.S., S.R. и M.C.M. также выражаем признательность за поддержку Института теоретической физики им. Кавли в рамках гранта NSF PHY11-25915. S.R. и M.C.M. также благодарим KITP за поддержку в рамках Grant PHY-1748958. J.L был поддержан младшим председателем Initiative d’Excellence Bordeaux.
Сноски
Автор: А.M., M.C.M., S.R. и M.L. спланированное исследование; A.M., P.S., J.S.L., S.R. и M.L. проведенное исследование; и A.M., P.S., M.C.M., J.S.L., S.R. и M.L. написал газету.
Авторы заявляют об отсутствии конфликта интересов.
Эта статья представляет собой прямое представление PNAS.
Эта статья содержит вспомогательную информацию на сайте www.pnas.org/lookup/suppl/doi:10.1073/pnas.1720607115/-/DCSupplemental.
Список сил реакции — 2017
Вы можете перечислить силы реакции на выбранных объектах для активного статического, нелинейного, испытания на падение и динамического исследования.Программное обеспечение перечисляет X-, Y-, Z-компоненты силы реакции и результирующую силу реакции на выбранных объектах, а также на всей модели.
Чтобы вывести список сил реакции, после выполнения анализа щелкните правой кнопкой мыши на «Результаты» и выберите «Список результирующих сил». В PropertyManager в разделе Параметры выберите Сила реакции.
Вы также можете щелкнуть (Simulation CommandManager).
Силы реакции не рассчитываются для твердых тел.
Сила реакции
Перечисляет компоненты X, Y, Z силы реакции и результирующую силу реакции на выбранных объектах и на всей модели.
метод временной шаг (fs) нс / день (относительно PuReMD)
SCC-DFTB 3.088 × 10 ⁻³ (39.8) 0,5 13,99 (0,2)
PM3 1,83 × 10 ⁻³ (23,6) 0,5 23,61 (0,4)
ReaxFF
ReaxFF 0,25 34,56 (0,6)
PuReMD 3,63 × 10 ⁻⁴ (4,7) 0,25 59,50 (1,0)
20 ММ 70006
20 мм 7 −5 (1,0) 1 1114.84 (18,7)
HF 1,833 (23 651,6)
DFT 2,762 (35 638,7)
График отклика Доступно только для нелинейных исследований, испытаний на падение и динамических исследований. Создает двухмерные графики хронологии для X-, Y-, Z-компонентов силы реакции и результирующей силы реакции для выбранных объектов и для всей модели.
Момент реакции
Перечисляет компоненты X, Y, Z момента реакции и результирующий момент реакции на выбранных объектах и на всей модели.
График отклика Доступно только для нелинейных исследований, испытаний на падение и динамических исследований. Создает двухмерные графики хронологии для X-, Y-, Z-компонентов момента реакции и результирующего момента реакции для выбранных объектов и для всей модели.
Параметры отображения
Показать равнодействующие силы Преобразует три вектора силы (компоненты X, Y и Z) в вектор результирующей силы.
No related posts.
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Copyright © 2019 БилдоМан - строй своими руками. | Карта сайта

метод	временной шаг (fs)	нс / день (относительно PuReMD)
SCC-DFTB	3.088 × 10 ⁻³ (39.8)	0,5	13,99 (0,2)
PM3	1,83 × 10 ⁻³ (23,6)	0,5	23,61 (0,4)
ReaxFF
ReaxFF	0,25	34,56 (0,6)
PuReMD	3,63 × 10 ⁻⁴ (4,7)	0,25	59,50 (1,0)
	20 ММ 70006
20 мм 7 −5 (1,0)	1	1114.84 (18,7)
HF	1,833 (23 651,6)
DFT	2,762 (35 638,7)