Частота импульсного тока формула: The page cannot be found

Категория: Разное -Добавлено от alexxlab

Содержание

Импульсные токи низкой частоты и низкого напряжения

ПЛАН

  1.  Виды импульсного тока.
  2.  Электросон.
  3.  Электродиагностика.
  4.  Электростимуляция.
  5.  ДДТ и СМТ.
  6.  Методика и техника.
  7.  Аппараты.
  8.  Показания и противопоказанияю

Ключевые моменты лекции

Импульсный ток – отдельные «порции» и толчки тока

СМТ – амплипульс

ДДТ – диадинамические токи

Ток Ледюка – частота импульсов 1-130 Гц,

продолжительности импульса 0,2 – 2 мс

Тетанизирующий ток – частота пульса – 100 Гц

Ток Лапика – частота импульсов 8100 Гц,

продолжительность 2-60 мс

Литература

Клячкин Л. М. Физиотерапия. – 1995 – 33-64 стр.

ЛЕКЦИЯ № 2

Тема: Импульсные токи низкой частоты и низкого напряжения

В современной физиотерапии следует считать весьма перспективным дальнейшее совершенствование импульсных ритмических воздействий при лечении различных патологических состояний, так как импульсное воздействия в определенном заданном режиме соответствуют физиологическим ритмам функционирующих органов и систем.

Импульсный ток – представляет собой отдельные «порции», «толчки» тока, имеющего одно направление при прохождении импульсов постоянного тока и меняющееся направлении при прохождении импульсов переменного тока.

Специфика импульсов постоянного тока заключается в том, что каждый отдельный импульс представляет собой более или менее быстро нарастающий и спадающий по напряжению постоянный ток со следующей за ним паузой.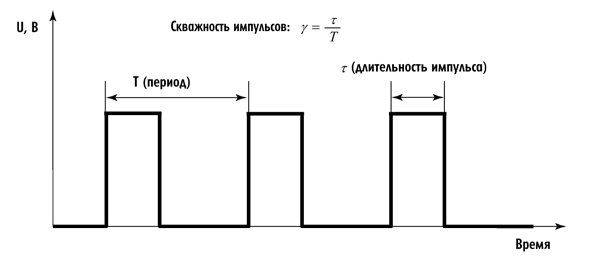 При прохождении каждого импульса постоянного тока в межэлектродном пространстве происходит перемещение внутритканевых, внутриклеточных ионов. При действии постоянного импульсного тока клетки возбуждаются. А во время пауз – возвращаются в состояние покоя. Физиологической реакцией на прохождение каждого импульса будет сокращение мышц под электродом.

Действие импульсного постоянного тока зависит от формы импульсов, их продолжительности, интенсивности (       тока) и частоты подачи импульсов (длительность пауз между импульсами).

Виды импульсных токов

По виду различают 3 вида импульсных токов.

  1.  Импульсный ток прямоугольной формы

                           (ток Ледюка)

                                              частота импульсов 1-130 Гц

продолжительность каждого импульса

0,2-2 мс

Этот ток усиливает процесс торможения в коре головного мозга, и его применяют для получения состояния, аналогичного физиологическому сну (э л е к т р о с о н).

2. Импульсный ток остроконечной формы

(тетанизирующий – тонизирующий?- сон)

Частота импульсов – 100 Гц

Этот ток вызывает сокращение мышц, и его применяют для упражнения мышц при ослабленной их функции (электростимуляция, электродиагностика, электроанальгезия).

3. Импульсный ток экспоненциальной формы

(ток Лапина)

Частота импульсов – 8-100 Гц

Продолжительность – 2-60 мс

Этот ток применяется для электрогимнастики, электродиагностики, электроаналгезии. Причем частота и длительность импульсов зависит от степени поражения мышцы.

Э Л Е К Т Р О С О Н

Электросон – это метод воздействия на центральную нервную систему импульсным током низкой и малой силы. Этот метод был предложен в 1943 году советскими учеными Ливенцевым, Гиляровским, Кирилловым.

Механизм действия

Механизм лечебного действия электросна представляет собой сложный процесс, включающий прямое и рефлекторное влияние импульсного тока в качестве слабого ритмического раздражения подкорковых образований и коры головного мозга.

Метод электросна вызывает сон, близкий естественному, физиологическому сну. Однако исследования последних лет говорят о том, что электросон, в отличие от физиологического, протекает с увеличением минутного объема дыхания с повышенным насыщением крови кислородом.

Электросон:

— снижает повышенное АД,

— способствует снижению эмоциональной активности,

— способствует нормализации функционального состояния системы свертывания и антисвертывания крови,

— усиливает вагусное влияние – как при обычном сне (при бронхиальной астме),

— снижает внутриглазное давление у больных глаукомойЮ

— действует болеутоляюще при болевых синдромах, связанных с язвенной болезнью, ожогами, при кардиалгии и др.,

— улучшает вегетативные функции,

— нормализует основной обмен,

— снижает уровень сахара в крови,

— способствует нормализации основных процессов высшей нервной деятельности,

— снимает утомление,

— повышает эффективность снотворных веществ при комбинированном лечении,

— улучшает кровоснабжение головного мозга,

— усиливает регуляторную роль ЦНС по отношению к другим органам и системам организма.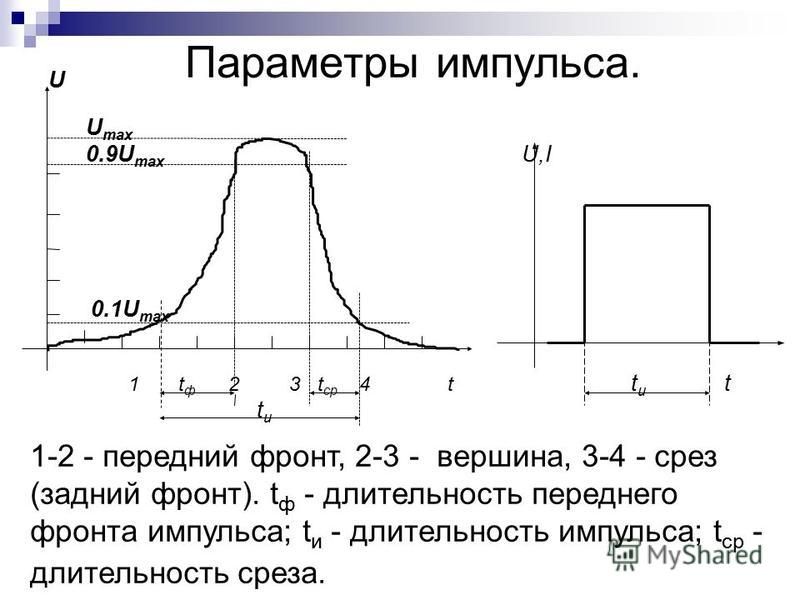

Методика и техника проведения электросна

При отпуске процедур электросна используется глазнично-затылочная методика расположения электродов. В набор электродов входят две пары электродов: глазничный и затылочный.

Перед процедурой в металлические чашечки электродов закладывают ватные тампоны, смоченные водой. Глазничный электрод накладывают на кожу век закрытых глаз, а второй – на кожу в области сосцевидных отростков позади ушных раковин. Оба электрода фиксируются с помощью ремешков к резиновой повязке, которая закреплена на голове: под подбородком, на затылке и темени. К электродам привязаны концы раздвоенного мягкого провода, с помощью которого затылочный электрод присоединяют к положительной клемме аппарата, а глазничный – отрицательной (катод).

Процедуры проводят в отдельной тихой, хорошо проветренной полузатемненной комнате. Больной должен раздеться и лечь в спокойной, непринужденной позе. После наложения электродов и присоединения к аппарату – включают ток.

Частота подачи импульсов в методе электросна зависит от: особенностей функционального состояния нервной системы больного, от тяжести и фазы заболевания, от возраста и других факторов. Поэтому при различных заболеваниях индивидуально подбирают такую частотную характеристику, при которой у больных наступает дремотное состояние, сонливость, сон. Силу тока регулируют в зависимости от ощущения больного (чувство ползания мурашек  под электродами, легкая вибрация в области век, слабые ритмичные толчки).

По окончании процедуры м\с включает аппарат, а больной может спать до самостоятельного пробуждения.

Продолжительность процедур колеблется от 30 мин до 1-2 часов – в зависимости от особенностей нервной системы больного и от характера заболевания. Процедуры проводят ежедневно. На курс лечения – 10-15 процедур – в зависимости от характера заболевания, переносимости процедур.

Аппараты: ЭС-1, ЭС-2, ЭС-3, ЭС-4Т.

Показания к назначению электросна

Заболевания со стороны нервной системы:

— неврозы,

— неврастения,

— галлюцинаторная форма шизофрении,

— отдаленные последствия травматической болезни головного мозга (посттравматические энцефалопатии),

— мигрень,

— атеросклероз сосудов головного мозга (начальный период),

— ишемическая болезнь сердца.

Заболевания со стороны внутренних органов:

— гипертоническая болезнь I-II ст.,

— гипотоническая болезнь,

— язвенная болезнь желудка и 12-перстной кишки,

— бронхиальная астма (легкий и средний период),

— экземы, дерматозы, нейродермиты,

— облитерирующий эндартериит,

— ревматическая хорея,

— токсикозы беременности.

Противопоказания

  1.  Непереносимость тока.
  2.  Воспалительные заболевания глаз.
  3.  Мокнущие дерматиты лица.
  4.  Истерия.
  5.  Арахноидит.
  6.  Тяжелые степени нарушения кровообращения.
  7.  Лихорадочные состояния.
  8.  Острый период инфаркта миокарда.
  9.  Острый период церебрального инсульта.
  10.   Отрицательное отношение больного к электрическому току.

ЭЛЕКТРОДИАГНОСТИКА

Электродиагностика – это исследование возбудимости нервно-мышечного аппарата путем электрического раздражения. В зависимости от функционального состояния нерва и мышцы их реакции на электрическое раздражение различны, поэтому по ним можно судить о характере и глубине поражения нервно-мышечного аппарата.

Исследование проводят на аппаратах КЭД-5, АСМ-3, УЭИ-1, Стимул-1 по двигательным точкам нервов и мышц. Двигательная точка нерва – это участок, где ствол нерва наиболее поверхностно расположен и доступен исследованию. Двигательная точка мышцы – это  проекция зоны внедрения и разветвления нерва в мышце. Наиболее типичное расположение двигательных точек дано в специальных таблицах Эрба.

Для правильной оценки данных, полученных при исследовании, необходимо исходить из нормальной реакции нервно-мышечного аппратаа на электрический ток.

Техника проведения диагностики

Чаще всего используется 1-полюсная методика при помощи пуговчатого электрода с кнопочным прерывателем и обычного пластинчатого электрода гидрофизической прокладки.

Электростимуляция – это метод, основанный на применении импульсного или прерывистого гальванического тока для вызывания ритмических сокращений мышц (то есть воздействие на нервно-мышечный аппарат).

В настоящее время электростимуляцию можно проводить на серийно выпускаемых аппаратах УЭИ-1, СНИМ-1, Амплипульс-3, Амплипульс-3Т.

Механизм действия электростимуляции

Электростимуляция регулирует мышечный тонус, улучшает кровообращение и обмен веществ в пораженных мышцах, поддерживает их сократительную способность и замедляет атрофию.

Показания для электростимуляции

  1.  Вялые параличи и парезы мышц лица, туловища, конечностей.
  2.  Атония гладкой мускулатуры внутренних органов.
  3.  Парезы и параличи мышц гортани.
  4.  Некоторые формы тугоухости.
  5.  Сексуальные неврозы.
  6.  Нарушения сердечного ритма и дыхания.
  7.  Парезы кишечника (недержание кала).
  8.  Недержание мочи (для стимуляции сфинктера мочевого пузыря).

Противопоказания

  1.  Воздействие на мышцы внутренних органов при желчно- и почечнокаменной болезни.
  2.  Склонность к кровотечению
  3.  Острые гнойные процессы органов брюшной полости.
  4.  Воздействие на мышцы при переломах костей до момента их консолидации.
  5.  Вывихи.
  6.  Трофические длительно не заживающие язвы конечностей.
  7.  Тромбофлебиты.
  8.  Первый месяц после операции наложения шва на нерв (при травме нерва).

Виды ДДТ

1. Одноактный непрерывный:       ОН – ощущение покалывания

под электродами,

вызывает сокращение мышц,

обладает раздражающим, возбуждающим действием.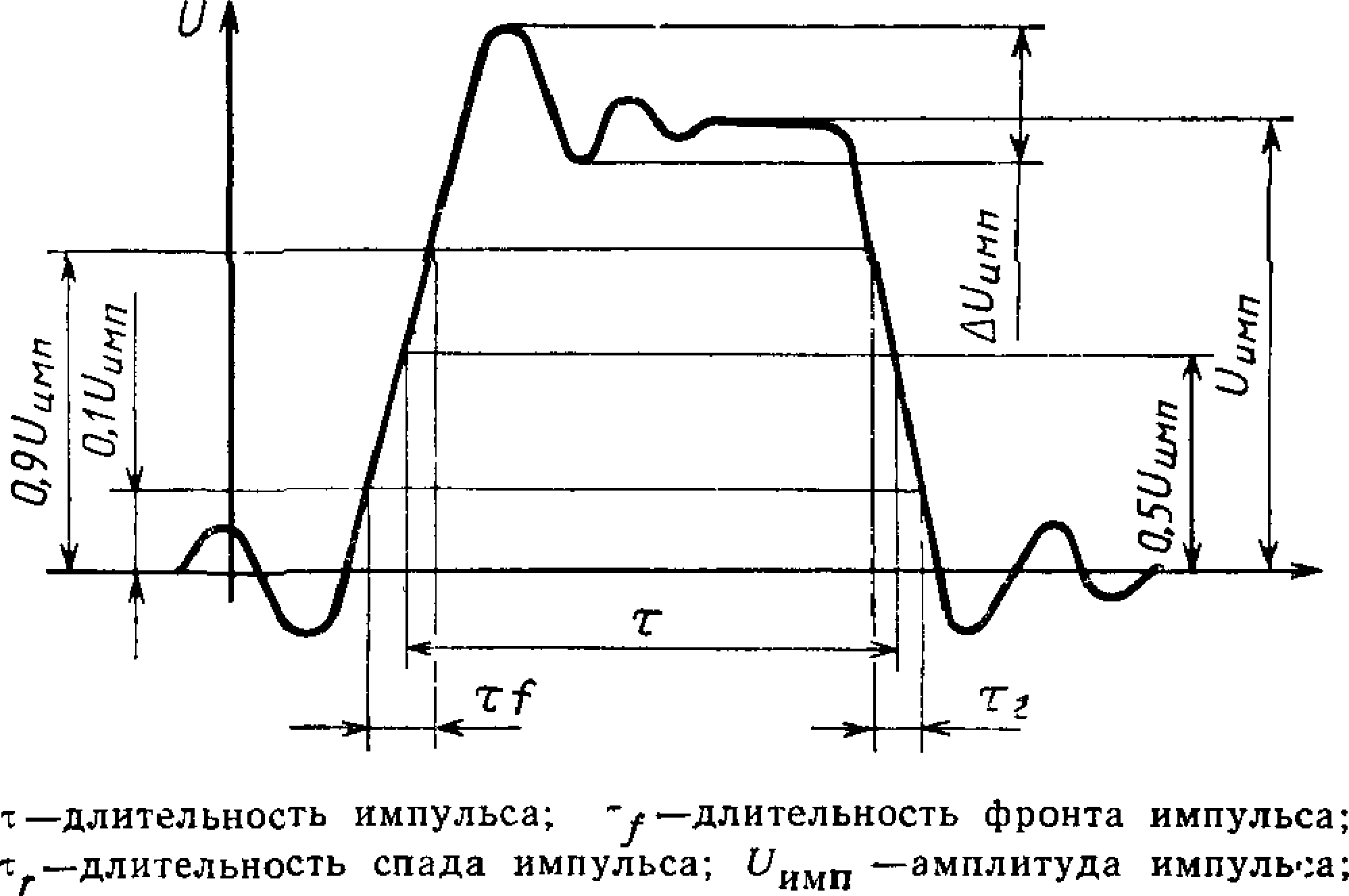

2. Двуактный непрерывный:         ДН – легкое покалывание, при

усилении – чувство вибрации,

анальгезирующий эффект,

тормозной.

3. Ритм синкопа                            – вызывает сокращение мышц с

последующим расслаблением

во время паузы (поэтому

применяется при электростимуляции).

4. Ток, модулированный короткими периодами:

К.П. – больной ощущает сильное, болезненное сокращение, своеобразная вибрация, массаж мышц, — усиление кровообращения,

сосуды расширяются,

повышается температура,

в месте воздействия,

рассасывающее действие,

активизируется обмен веществ.

5. Ток, модулированный длинными периодами:

больной ощущает сильное

длительное сокращение

мышц (3,5), и сменяется оно

нежной вибрацией (6,5).

Уменьшает эффект возбуждения, меняя тормозным болеутоляющим.

6. Однотактный волновой   – усиливает обезболивающий эффект.

7. Двутактный волновой      

Аппараты: СНИМ-1, Тонус-1, Модель – 717,  Диадинамик-1

Диадинамофорез.

Амплипульс-терапия (СМТ)

Воздействие СМ-токов, благодаря которым обеспечивается хорошая их проходимость через кожу, исключается раздражающее их действие их на кожу и ее рецепторы.

Аппараты: Амплипульс-3Т, А-4.

Различают следующие виды СМТ:

  1.  Исходный немодулируемый ток.
  2.  Ток «постоянная модуляция» ПМ (1р. р.)

(раздражающее)

  1.  Ток «посылки-паузы» «П-П» (2 р.р.)

(стимулирующее)

  1.  Ток модулированных и немодулированных колебаний ПН (3 р. р.)

(обезболивающее)

  1.  Ток перемежающейся частоты ПЧ (4 р.р.)

(обезболивающее).

СМТ обладают следующим действием:

  1.  болеутоляющим;
  2.  способствуют улучшению периферического кровообращения и функционального состояния нервно-мышечного аппарата.

Техника и методика отпуска процедур такая же, как и ДД-терапии.

Показания к назначению ДДТ и СМТ:

  1.  Ушибы мышц.
  2.  Растяжение связок.
  3.  Периартриты.
  4.  Заболевания периферической нервной системы с наличием болевого синдрома (радикулиты, невриты), особенно в остром периоде.
  5.  Облитерирующий эндартериит.
  6.  Парезы и паралич мышц конечностей, туловища, лица.
  7.  Дискинезия толстой кишки с преобладанием атонического компонента.

Противопоказания

  1.  Общие физиотерапевтические.
  2.  Острые воспалительные заболевания в полостях.
  3.  Инфекционные лихорадочные состояния.
  4.  Активный туберкулез в фазе интоксикации.
  5.  Недостаточность кровообращения 2-3 степени.
  6.  Беременности (область живота и поясницы).
  7.  Психоз.

Общее сопротивление электрической цепи, чему оно равно и как найти по формуле.

Как известно во всем нужна своя мера, которая позволяет делать точные системы, устройства, механизмы, схемы. Мера множественная, имеет свои конкретные величины. В сфере электротехники основными величинами являются напряжение, ток, сопротивление, мощность, частота (для переменного и импульсного тока). Величины между собой связаны определенными формулами. Самой важной формулой, наиболее используемой электриками, электронщиками является закон Ома ( I = U/R, то есть — сила тока равна напряжению деленному на сопротивление). Зная любые две величины из этой формулы всегда можно найти третью.

От сопротивления электрической цепи зависит силы тока при наличии определенного напряжения. Если меняется сопротивление в цепях схемы, то и меняться режимы ее работы в отдельных ее участках или во всей цепи. Знание величины сопротивления могут помочь выявить неисправность, узнать (вычислить из формулы) другие электрические величины в схеме, зависящие от этого сопротивления.

Теперь давайте посмотрим от чего зависит общее сопротивление электрической цепи. Общее — это сумма частных. Любая электрическая цепь и схема содержит в себе электрические компоненты, которые обладают внутренним сопротивлением. Даже обычный конденсатор (две пластины проводника, разделенные диэлектриком, что позволяет накапливать электрический заряд между этими пластинами, не пропуская постоянный ток), который, казалось бы, по сути своей его не должен иметь (точнее оно бесконечно большое) обладает реактивным сопротивлением.

Самая простая электрическая цепь состоит из источника питания и нагрузки. К примеру это будет обычная батарейка и маленькая лампочка накаливания. И батарейка и лампочка имеют свои сопротивления, которые суммируются, что определяет силу тока, текущему по этой простейшей цепи (при определенной величине напряжения). Допустим к нашей цепи мы добавим еще один элемент нагрузки (вторую такую же лампочку). Ее можно подключить к этой простейшей цепи двумя способами либо параллельно первой лампочки, либо же последовательно ей

При последовательном подключении сопротивление будет суммироваться:

При параллельном подключении общее сопротивление можно найти по таким формулам:

То есть, большинство схем будут иметь в себе либо параллельное подключение сопротивлений, либо последовательное или же смешанное. В случае сложной электрической цепи определение общего электрического сопротивления происходит по частям (группам), состоящим, опять же, из параллельных и последовательных подключений элементов, обладающими сопротивлением. Правильнее начинать с той части цепи, схемы, которая имеет наибольшую удаленность от двух конечных выводов, рассматриваемых как контакты общего сопротивления. На рисунке ниже приведен пример последовательности вычисления общего сопротивления сложной цепи, схемы.

Но ведь существуют электрические цепи, в которых общее сопротивление может постоянно меняться, к примеру схема стабилизированного регулятора частоты вращения постоянного электродвигателя, подключенная к самому двигателю. При изменении нагрузки на валу двигателя будет меняться его внутреннее сопротивление, следовательно меняться будет и режимы работы схемы (поддерживающая нужную частоту вращения вала). В таких цепях электрическое сопротивление является динамическим, изменяющемся. Можно лишь рассчитать усредненное сопротивление, которое не будет абсолютно точным.

Помимо этого, как было подмечено ранее, существует еще реактивное сопротивление, которое бывает у индуктивных и емкостных элементов цепи. Оно явно себя проявляет в схемах, что работают с переменным, импульсным током. Если в цепях постоянного тока конденсатор (стоящий последовательно) не будет проводить через себя ток, то в цепи переменного тока будет все иначе. Причем его реактивное сопротивление будет зависеть от частоты (при одной и той же емкости). Вот формулы для нахождения реактивного емкостного и индуктивного сопротивления:


P.S. общее сопротивление можно находить и через использование закона Ома, который гласит, что сопротивление равно напряжение деленное на силу тока. Следовательно, берем мультиметр, измеряем ток и напряжение в том месте цепи, где хотим узнать сопротивление. Воспользовавшись формулой Ома находим (определяем) электрическое сопротивление нужного участка цепи. Напомню, что при использовании закона ома нужно применять основные единицы измерения — ток в амперах, напряжение в вольтах, а сопротивление в омах.

Первая миля — научно-технический журнал — Первая миля

В.Горячев, к.т.н., главный специалист ЗАО «СпецЭлектронСистемы»,
А.Чуприн, главный конструктор ЗАО «СпецЭлектронСистемы» / [email protected],
М.Савин, начальник управления развития радиоэлектронных технологий, ЭКБ и специальных программ ФГУП «МНИИРИП»
УДК 621. 311.69, DOI: 10.22184/2070-8963.2019.85.8.62.67

В первой части статьи были приведены уточненная и упрощенная формулы для расчета критической индуктивности сглаживающих фильтров. Во второй части расчетные формулы сведены к табличному виду, позволяющему по исходным данным, таким как минимальное сопротивление нагрузки и период следования импульсов на входе фильтра, выбрать необходимую формулу.

Итак, в первой части статьи мы получили удобную и простую формулу для подсчета критической индуктивности Lкр, выраженную через заданные параметры: Rн.min, разброс напряжения по входу и по току нагрузки (27) [1]:

Lкр > Rн.min × T × (1 – 1/Кu)/КI. (1)
Рассмотрим наиболее часто встречаемые случаи, когда Кu = 2, то есть Uвх.max = 2 Uвх.min,
КI = 0,2, то есть Δ I = 0,2 Iн.max. Подставив указанные данные в формулу (27), находим:
Lкр > Rн.min × T × (1- 1/2)/0,2 = Rн.min × T/0,4 = 2,5 × Rн.min × T.
Пусть Кu = 2, КI = 0,1: Lкр > Rн.min × T × (1 – 1/2)/0,1 = Rн.min × T × 0,5/0,1 = 5Rн.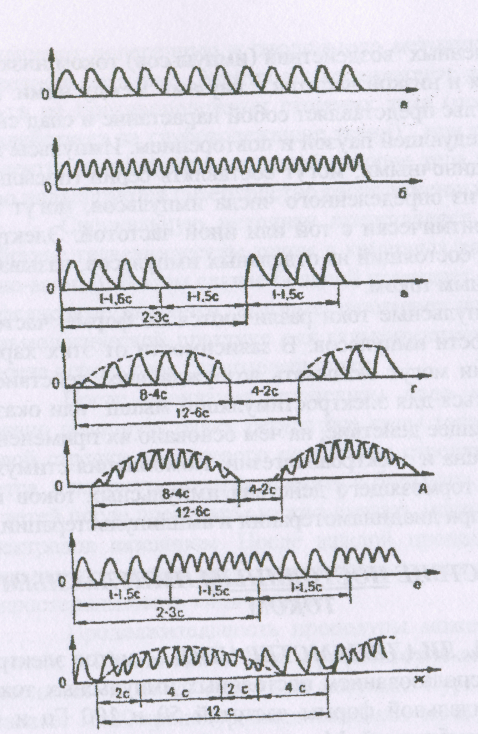 min × T.

Следовательно, для уменьшения в два раза тока пульсаций (Δ I = 0,1Iн.max) пришлось в два раза увеличить величину критической индуктивности.

В табл.1 приведены величины Lкр, посчитанные по формуле (1) для наиболее распространенных случаев из практики, когда Кu = 1,5 и 2; КI = 0,1, 0,2, 0,3.

Следует отметить, что полученные по упрощенной формуле (1) величины критической индуктивности будут занижены по сравнению с данными в соответствии с формулой (24) [1] примерно на 10%. Поэтому подсчитанную величину индуктивности необходимо увеличить на 10%, добавив к этому разброс параметров сердечника в части начальной магнитной проницаемости, а также учесть отрицательное влияние температуры и возможное уменьшение индуктивности за счет пикового тока. Итого расчетную индуктивность следует увеличить примерно на 30%.

Выше было отмечено, что критическая индуктивность Lкр находится при максимальном напряжении на входе ВИП, то есть при Uвх = Uвх.max. Это обусловлено тем, что именно в данном режиме коэффициент заполнения Кз имеет минимальное значение, и по этой причине нагрузка теперь уже более продолжительную часть времени будет потреблять энергию не от источника первичного питания, а от дросселя, то есть последний в этом случае будет обладать большей накопленной энергией и, следовательно, максимальной величиной критической индуктивности.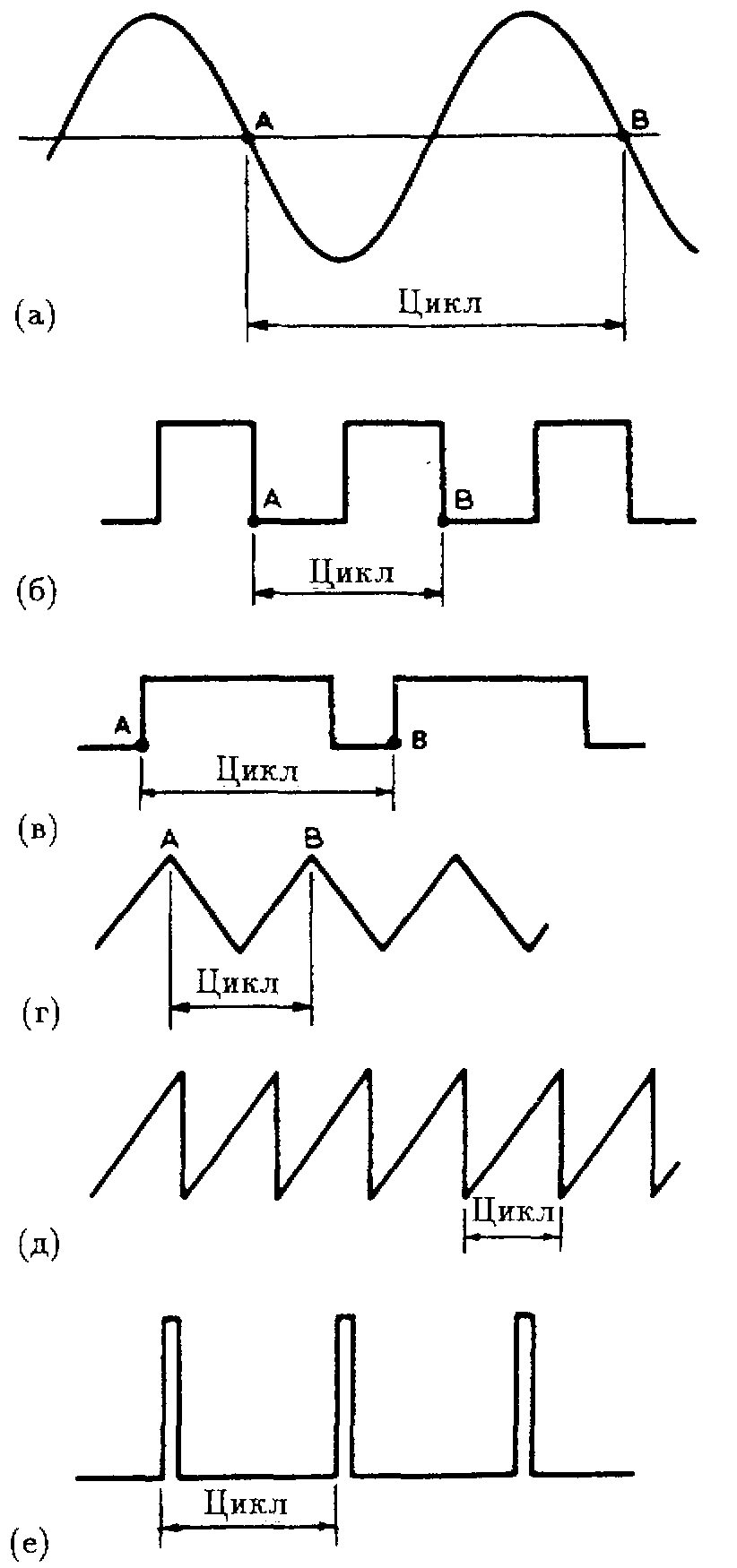

Сказанное означает, что при входом напряжении, меньшем чем Uвх.max, величина критической индуктивности будет иметь меньшее значение. Последнее однозначно вытекает из формулы (10, [1]). Действительно, при меньшем входном напряжении уменьшается величина напряжения на дросселе, то есть напряжение UL = Uвх L – Uвых (см. формулу 11 [1]).

Но при этом возрастает длительность импульса Δt = tи = tON, которая при уменьшении напряжения Uвх L стремится к постоянному значению Т, равному периоду следования импульсов на входе дросселя (параметр Кз = tи/Т стремится к единице). Учитывая, что напряжение UL = Uвх L – Uвых при уменьшении напряжения Uвх L стремится к нулю (напряжение UL будет равно нулю при Uвх L = Uвых), получим, что критическая индуктивность Lкр будет также стремиться к нулю, так как произведение нуля на постоянную величину дает в итоге ноль. Из этого следует, что только при максимальном напряжении на входе ВИП, то есть при Uвх = Uвх.max сглаживающий фильтр работает с индуктивностью, равной ее критической величине, то есть с L = Lкр. А во всем остальном диапазоне входных напряжений, начиная от Uвх = Uвх.min, и практически до напряжения, равного напряжению Uвх.max, сглаживающий фильтр работает в режиме, когда индуктивность дросселя превышает L = Lкр для каждого значения входного напряжения, меньшего по величине, чем Uвх.max. Например, если бы мы посчитали величину дросселя L = Lкр при Uвх = Uвх.min, то она получилась бы практически в два раза меньше, чем при напряжении на входе ВИП, равном напряжению Uвх.max. Хорошо это или плохо с точки зрения качества питания, формируемого вторичным источником питания (ВИП)?
Несомненно хорошо в том плане, что благодаря избыточной индуктивности, имеющей место при минимальном входном напряжении, то есть при Uвх = Uвх.min, у нас будет меньший уровень тока пульсаций ΔI, что следует из формулы (10) [1]. Действительно, из этой формулы можно записать
ΔI = ( UL× Δt)/L, (2)
где L = Lкр, найденное при Uвх = Uвх.max.

Поскольку величина индуктивности L постоянна и имеет максимальное значение, а при уменьшении входного напряжения произведение UL × Δt стремится к нулю (о чем говорилось выше), то и величина тока пульсаций станет меньше.

Но не совсем хорошо в том плане, что избыточная индуктивность при Uвх = Uвх.min может стать причиной ухудшения качества выходного напряжения в виде его кратковременного изменения при резких сбросах и набросах тока нагрузки (на выходном напряжении могут появиться кратковременные выбросы и провалы незначительной амплитуды). То есть все это должно быть учтено при организации обратной связи.

При расчете дросселя фильтра необходимо знать не только величину его критической индуктивности, но и максимальную величину пикового тока, необходимую при подсчете потерь в дросселе фильтра и для оценки возможности его вхождения в насыщение (см. ниже). Величину пикового тока определим из формулы:
Iпик = Iн.max + (ΔI/2), (2а)
где (ΔI/2) – амплитуда тока пульсации, которая равна минимальному току нагрузки, о чем упоминалось выше; Iн.max – максимально заданный ток нагрузки источника питания;
(ΔI) = КI × Iн.max – прирост тока дросселя за время открытого состояния полевого МОП-транзистора. То есть величина пикового тока зависит от коэффициента КI – чем он меньше, тем меньше пульсации тока. Отметим, что пульсации тока в дросселе должны быть обязательно линейными, поскольку именно в этом случае получают максимально высокий КПД. Причем чем меньше величина этих пульсаций, тем меньше пульсирующие токи протекают во всех элементах схемы ВИП и меньше уровень помех. Следовательно, последние меньше нагреваются, то есть они работают в более облегченном режиме, что повышает их надежность (увеличивается срок службы). И с этих позиций желательно иметь более высокую индуктивность дросселя. Насколько ее можно увеличить относительно критической индуктивности?

Известно, что форма тока в транзисторе имеет вид несимметричной трапеции (треугольник у трапеции с одной стороны). Увеличивая индуктивность дросселя, мы тем самым увеличиваем прямоугольность формы тока в транзисторе. А прямоугольная форма тока – это идеаль­ная и недостижимая для транзистора форма, при которой потери (I2 × R) в МОП-транзисторе минимальны.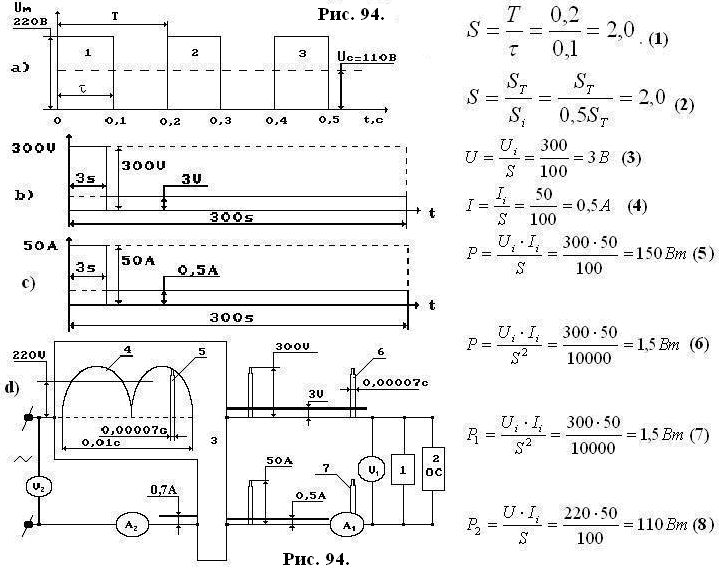 При этом форма трапеции зависит от коэффициен­та ее прямоугольности Кпр, который меняет­ся от Кпр = 0 до Кпр = 1 в зависимости от величины Lкр дросселя. Подсчитано, что для треугольного токового сигнала потери (I2 × R) составляют на 32% больше, чем для прямоугольного сигнала равной площади. Но важно отметить, что уже при Кпр > 0,6 дальнейшее увеличение коэффициента Кпр за счет увеличения величины индуктивности фильтра дает лишь незначительный вклад в снижение потерь, всего на 2%. Очевидно, что нет никакого практического смысла стремиться к идеальной прямоугольной форме тока за счет увеличения индуктивности дросселя, который при этом будет занимать много места. Поэтому практически достаточно иметь величину индуктивности всего лишь в два раза больше критической [9]. Таким образом, с точки зрения повышения КПД источника питания, более чем критическая индуктивность дросселя фильтра вполне оправдана. Однако чрезмерно большая индуктивность увеличивает инерционность системы ООС, то есть система в этом случае не способна реагировать на быстрые изменения тока нагрузки. Другими словами, сглажи­вающий Г-образный фильтр (СгФ) с индуктивностью дросселя фильтра Lф > 2Lкр может, например, применяться в импульсных ВИП, работающих практически на постоянную нагрузку с высоким требованием по КПД со стабилизацией выхода (или, что то же самое, нестабильность выхода) в пределах 5–7%, для которых высокие удельные показатели не являются определяющими. Поскольку в LC-фильтре потери незначительны (это в основном, потери в обмотке провода), он обладает малым внутренним сопротивлением. В последнем случае фильтр можно рассматривать как источник напряжения. А это означает, что он достаточно хорошо стабилизирует напряжение и без ООС при условии, что дроссель фильтра работает в режиме непрерывного тока и без резкого сброса тока нагрузки в заданных пределах.

В принципе, в СгФ конденсатор фильтра С1 не является обязательным элементом [8]. Если индуктивность дросселя принять бесконечно большой, то любое приращение тока в дросселе будет индуцировать в его обмотке бесконечно большую ЭДС самоиндукции, препятствующую изменению тока в дросселе. Следовательно, ток, как в дросселе, так и в нагрузке не может претерпевать изменений во времени [7]. Следует отметить, что ток дросселя и ток нагрузки – это не одно и то же. И, как отмечалось выше, ток нагрузки равен среднему току дросселя. Однако мы будем считать, что индуктивность дросселя больше Lкр, поэтому ток нагрузки приравниваем к току дросселя [6], то есть чем больше индуктивность дросселя по сравнению с критической, тем меньше амплитуда тока пульсации и, следовательно, тем более ток дросселя будет приближаться к току нагрузки.
Большинство ВИП проектируются для работы в режиме непрерывного тока (режим НТ), особенно при высоких мощностях. В этом случае упрощается фильтр и создается меньше помех. Однако применяются фильтры и с малой величиной Lкр, например, при Кi = 0,3. Преимущества такого дросселя: малые размеры, невысокая стоимость; ток дросселя может меняться более быстро при изменении тока нагрузки; вместе с большой емкостью С1 снижаются резкие броски и провалы при резких изменениях тока нагрузки, то есть улучшаются динамические показатели импульсных ВИП. Поэтому одним из эффективных способов улучшения динамических характеристик ВИП является увеличение частоты преобразования. Это приводит к увеличению быстродействия замкнутой системы автоматического регулирования выходного напряжения [5]. Таким образом, выбор величины индуктивности дросселя при его разработке не является тривиальной задачей, поскольку приходится учитывать много факторов. И здесь чаще всего необходим компромисс, так как, выигрывая в одном, мы проигрываем в другом: малые пульсации – большие габариты, невысокая динамика, высокий КПД, малый уровень помех; большие пульсации – малые габариты, улучшенная динамика, более высокий уровень помех, ухудшенная надежность, более высокие потери, пониженный КПД. Но в обоих случаях дроссель должен работать так, чтобы ток в нем имел геометрически правильную треугольную или пилообразную форму, которая, как уже упоминалось выше, именуется пульсацией тока, поскольку именно такая форма тока обеспечивает максимальный КПД.
Причем, с учетом пикового тока, дроссель не должен входить в насыщение, так как в противном случае форма тока будет искривлена, что является дополнительным источником помех. При нагрузке меньше Iн = Iн.min СгФ перейдет в режим прерывистого тока (режим ПТ). В этом случае во время паузы ток в дросселе прекратится раньше, чем поступит следующий импульс на вход дросселя, то есть тока в дросселе не будет, поскольку дроссель быстро разрядится (постоянная времени индуктивности дросселя уменьшится). И ток в нагрузку станет поступать только от конденсатора. Поскольку постоянная времени конденсатора увеличится (конденсатор будет медленнее разряжаться), напряжение на конденсаторе возрастет (при холостом ходе и без ООС напряжение на выходе ВИП будет стремиться к амплитудному значению входного напряжения, так как для конденсатора фильтра отсутствует цепь разряда). Но за счет ООС уменьшится длительность импульса, формируемого ШИМ, и напряжение на выходе придет в норму.
Однако СгФ уже не будет работать в соответствии с формулой (1). И для ВИП в целом это более напряженный режим, так как передаточная функция резко меняется; в работу полностью включается обратная связь, обеспечивающая устойчивость функционирования схемы с учетом фазового сдвига.

Теперь несколько слов о конденсаторе фильтра. Конденсатор С1 в схеме СгФ служит: для сглаживания пульсаций тока дросселя до требуемой величины; для минимизации амплитуд выбросов и провалов на выходе ВИП (то есть на самом конденсаторе фильтра С1), которые имеют место быть в СгФ при резких изменениях тока нагрузки.

В первом варианте ток пульсаций дросселя должен замыкаться через конденсатор фильтра С1, поскольку он изменяется во времени и поэтому для конденсатора его можно рассматривать как переменный ток. А это значит, что конденсатор должен обладать малым эквивалентным последовательным сопротивлением (ЭПС или ЕSR в английском обозначении), которое должно быть значительно меньше, чем минимальное сопротивление нагрузки Rн.min. В этом случае амплитуда пульсаций напряжения Uп на выходе ВИП будет определяться из выражения:
Uп ≈ ЭПС × (ΔI). (3)
Из (3) вытекает, что амплитуда пульсаций напряжения практически не зависит от величины емкости конденсатора фильтра С1, а в основном определяется качеством последнего, то есть его ЭПС. И чем меньше ЭПС конденсатора, тем меньше напряжение пульсаций Uп на нем. Последнее означает, что если, например, ЭПС конденсатора равно нулю, то и напряжение пульсаций теоретически будет равно нулю [3]. Однако практически их величина теперь будет ограничена емкостным сопротивлением конденсатора Хс = 1/2πfС на частоте импульсного сигнала на входе СгФ (f = 1/T), которая на высокой частоте заметно меньше, чем ЭПС. В частности, в работе [3] отмечается, что для алюминиевых электролитических конденсаторов имеет место сле­дующее равенство:
Rо  × Со ≈ 65 мкс
(более точно находится в пределах 50–80 мкс). (4)

Из него следует, что ЭПС тем меньше, чем больше емкость конденсатора, то есть более габаритные конденсаторы обладают меньшим ЭПС. И тогда по заданной величине пульсаций Uп и известной величине тока пульсаций ΔI можно определить величину ЭПС конденсатора:
ЭПС = Uп/ΔI. (5)
Уже по найденной величине ЭПС, применяя равенство (4), можно найти величину емкости конденсатора фильтра:
Со = 65/ЭПС(мкФ). (6)

Из равенства (4) следует, что чем меньше ЭПС, тем больше величина емкости конденсатора и тем больше накопится в нем энергии, которая потребуется при резких сбросах и набросах нагрузки. Однако такое равенство не соблюдается для керамических конденсаторов, которые находят наиболее широкое применение в бортовых ВИП. Как отмечается в работе [4], керамические конденсаторы менее склонны к этому компромиссу. А это означает, что для устранения тех же пульсаций потребуется керамический конденсатор меньшей емкости и меньших габаритов. В частности, практически идеальный конденсатор можно получить за счет параллельного соединения N > 2 однотипных конденсаторов с малым значением величины ЭПС и ЭПИ (эквивалентная последовательная индуктивность, ESL в английском варианте). Соединяя параллельно N конденсаторов емкостью Со, мы можем получить эквивалентный конденсатор емкостью N × Со, обладающий эквивалентной ЭПСэ = ЭПС/N и ЭПИэ = ЭПИ/N c частотными свойствами одного конденсатора емкостью Со (эквивалентный конденсатор будет обладать максимальной резонансной частотой, то есть частотой одного конденсатора малой емкости Со). Полученный таким образом конденсатор будет обладать требуемым ЭПС при сравнительно невысокой величине суммарной емкости, причем такой, которая справится с устранением пульсаций в соответствии с выражением (3). Но здесь, как отмечалось выше, необходимо иметь в виду, что в LC фильтре возможны выбросы и провалы напряжения при резких сбросах и набросах тока нагрузки. И теперь вступает в силу второе требование, которое необходимо учитывать при его выборе, а именно энергетическая составляющая конденсатора.

Величина емкости конденсатора, подсчитанная исходя из требований к пульсациям, не справится с задачей постоянства выходного напряжения при бросках тока нагрузки вследствие малой накопленной энергии, определяемой выражением:
Ес = СU2/2 . (7)
Причем величина этой энергии всегда постоян­на, тогда как энергия, накопленная в индуктивности, зависит от протекающего через дроссель пикового тока, то есть определяется формулой:
ЕL =L (Iпик)2/2, (8)
где Iпик – амплитуда пикового тока, определяемая выражением (2).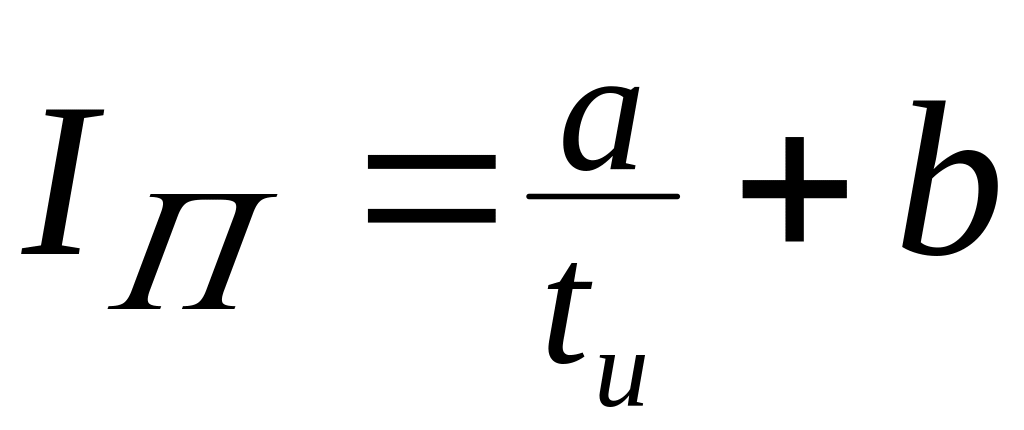

В результате при токе нагрузки Iн = Iн.min, то есть на границе режима НТ, энергия в дросселе будет минимальна, и вся ответственность за поддержание постоянного напряжения на выходе ВИП в этот момент придется на конденсатор. Последний, в отсутствии импульсов на входе фильтра (худший случай – половина периода следования импульсов), должен будет снабжать энергией нагрузку. А если в этот момент ток нагрузки от Iн = Iн.min изменится до величины Iн = Iн.max, то энергия, накопленная в конденсаторе, может оказаться равной энергии, потребляемой в этот момент нагрузкой (Ен), определяемой как:
ЕН = Рmax × (Т/2), (9)
где Рmax – максимальная выходная мощность ВИП.

Это приведет к просадке напряжения на выходе источника питания. Но чтобы напряжение Uвых оставалось в заданных пределах, необходимо, чтобы энергия в конденсаторе была как минимум в 15–20 раз выше энергии, потребляемой нагрузкой [2]. А для этого потребуется увеличить емкость конденсатора в 15–20 и более раз за счет параллельного подключения дополнительного конденсатора (принимая при этом во внимание, что емкость конденсатора зависит от ряда дестабилизирующих факторов, таких как температура, частота, напряжение). Более точно, все зависит от требований к стабилизации выходного напряжения, то есть к величине отклонения выходного напряжения (± ΔU) от номинала. Именно эта увеличенная емкость позволит сгладить выбросы напряжения при спаде тока нагрузки, поскольку ООС не сможет быстро отреагировать на эти изменения в силу своей инерцион­ности. В частности, при сбросе тока нагрузки до холостого хода можно считать, что вся энергия, накопленная в дросселе фильтра, передается в конденсатор. Последнее приведет к росту выходного напряжения.

И здесь к сказанному выше необходимо добавить следующее: в любых импульсных ВИП изменение выходного напряжения при скачках тока нагрузки будут тем меньше, чем больше емкость конденсатора фильтра [10].

При выборе величин LФ и СФ необходимо учитывать и такой фактор, как бросок тока при включении ВИП. Бросок будет тем меньше, чем больше коэффициент ρ (волновое сопротивление фильтра), определяемый из выражения:
ρ = ( LФ/СФ)0,5, (10)
то есть чем больше индуктивность дросселя фильтра LФ. Однако в этом случае возможен выброс напряжения на конденсаторе при резком сбросе тока нагрузки, о чем упоминалось выше.

Применительно к бортовым ВИП, для которых требуется высокая удельная мощность (малые габариты в единице объема) при достаточно высоком КПД (не менее 78%), наиболее компромиссное решение – это когда LФ = 1,3 Lкр, при ΔI = 0,2 Iн.max и КU = 2. И теперь, после всех перечисленных выше необходимых для разработчика замечаний, рассчитаем величину Lкр фильтра по следующим исходным данным: Uвх.min = 20 B; Uвх.max = 40 B; Uвых = 5 В; Т = 2 мкс; tпрос = 0,2 мкс; ΔI = 0,2 Iн.max; Iн.max = 2 А; Iн.min = 0,2 А.

Произведем расчет критической индуктивности по полной (уточненной) формуле, то есть по выражению (24) [1]:
Lкр ≥ Uвых × [(Т × (Uвх.max – Uвх.min) + (Uвх.min × tПРОС)] /
/ Uвх.max × (КI × Iн.max) = 5[2(40 – 20) +(20 × 0,2)]/40 × (0,2 × 2) =
= (5 × 40 + 4 × 5 )/16 = 13,75 мкГн.

Найдем величину Lкр по упрощенной формуле. Для этого обратимся к таблице, из которой по коэффициентам КU = 2 и КI = 0,2 находим формулу:
Lкр > 2,5 Rн.min × Т = 2,5 × 2,5 × 2 = 12,5 мкГн.

Таким образом, индуктивность, посчитанная по упрощенной формуле, оказалась меньше на 10% относительно индуктивности в соответствии с формулой (24) [1]. С учетом возможных отклонений индуктивность в 12,5 мкГн необходимо умножить на множитель 1,3. В итоге получим, что искомая критическая индуктивность Lкр = 12,5 × 1,3 = 16,25 мкГн.

ЛИТЕРАТУРА
Горячев В.И., Чуприн А.В. Расчет критической индуктивности дросселя сглаживающего фильтра. Часть1 // ПЕРВАЯ МИЛЯ. 2019. № 7. С. 60–65.
Горячев В.И., Чуприн А.В. Узел внутреннего напряжения питания в бортовых ВИП // ПЕРВАЯ МИЛЯ. 2016. № 4. С. 50–57.
Abraham I., Pressman Keith Billings, Taylor Morey. Switching power supply design. Third Edition.
Application Note 4266. An efficiency primer for switching – mode, DC-DC converter power supplies. 31.08.2015.
Сергеев Б.С. Схемотехника функциональных узлов источников вторичного электропитания. – М.: Радио Связь, 1992.
Семенов Б.Ю. Силовая электроника. – М.: Солон-Р, 1999.
Китаев В.Е., Бокуняев А.А., Колпаков М.Ф. Расчет источников электропитания устройств связи. – М.: Радио связь, 1993.
Захаров В.К., Лыпарь Ю.И. Электронные устройства автоматики и телемеханики. – Л.: Энергоатомиздат. Ленинградское отделение, 1984.
Силовые полупроводниковые приборы / Пер. с англ. под ред. В.В.Токарева. – Воронеж, 1995.
Источники вторичного электропитания. Справочное пособие / Под ред. Ю.И.Конева. – М.: Радио и связь, 1983.

Частота импульсов

— обзор

8.3.1 Модель интегральной частотно-импульсной модуляции

Модель IPFM используется для генерации серии событий, таких как серии повторений сердцебиения, и предполагает наличие непрерывного входного сигнала с особая физиологическая интерпретация. На рис. 8.3 представлена ​​блок-схема модели IPFM и показаны сигналы, которые могут появиться на разных этапах модели. В этой модели входной сигнал интегрируется до тех пор, пока не будет достигнут порог R , при котором событие генерируется в момент времени t k . Затем интегратор сбрасывается на ноль, процедура повторяется и так далее. Порог R определяет среднюю длину интервала между последовательными событиями. Входной сигнал, будучи положительным, представляет собой сумму двух величин, а именно, уровня постоянного тока m 0 и модулирующей функции m (t), составляющая постоянного тока которой равна нулю, а амплитуда ограничена таким образом. что ∣ м ( т ) | ≪ м 0 , чтобы входной сигнал всегда оставался положительным.Предполагая, что модель IPFM действительна, наша цель состоит в том, чтобы разработать метод, который может извлекать информацию о м (t) из наблюдаемых серий времен событий t k , , представленных сигналом

Рисунок 8.3. (a) Модель интегральной частотно-импульсной модуляции (IPFM), (b) входная функция m 0 + m ( t ), которая модулирует изменение длины интервала, (c) выход y ( t ) интегратора, предполагая пороговый уровень на R, и (d) результирующую серию событий при временах возникновения t 0 , t 1 ,…, t M .

(8.2) dEu (t) = Σk = 0Mδ (t − tk),

, где верхний индекс « u » означает, что события происходят неравномерно во времени (а позже также обозначают неравномерную выборку). Определение единичной импульсной функции δ ( t ) и выборки последовательности импульсов в (8.2) можно найти в большинстве учебников, охватывающих основы сигналов и систем, см., Например, [12].

С физиологической точки зрения выходной сигнал интегратора на рис. 8.3 можно рассматривать как заряд мембранного потенциала синоатриальной кардиостимулятора [13].Мембранный потенциал увеличивается до тех пор, пока не будет превышен определенный порог, а затем срабатывает потенциал действия, который в сочетании с эффектом многих других потенциалов действия инициирует новое сердцебиение. Входные данные интегратора состоят из м 0 , который определяет среднюю частоту сердечных сокращений, и модулирующего сигнала м ( t ), который описывает изменения частоты сердечных сокращений, модулируемые вегетативной активностью синусового канала. узел. Как правило, м (t) ограничена полосой, так что спектральные компоненты выше 0.В состоянии покоя можно пренебречь 4–0,5 Гц. Допущение ∣ м (t) │≪ м 0 включено, чтобы гарантировать, что ВСР мала по сравнению со средней частотой сердечных сокращений.

С математической точки зрения, ряд событий определяется следующим уравнением, которое является центральным для модели IPFM:

(8.3) ∫tk − 1tk (m0 + m (τ)) dτ = R, k = 1,…, М.

Функция модуляции м ( t ) определяет изменение длины интервала между двумя последовательными событиями, происходящими при t k — l и t k . Без какой-либо модуляции, т.е. для м ( t ) = 0, результирующий ряд событий является совершенно регулярным и имеет постоянную длину интервала, равную об / м 0 ; соответствующая немодулированная средняя частота повторения F I = 1 / T I определяется как

(8.4) FI = m0R.

Константа м 0 обычно устанавливается равной единице, подразумевая, что порог с обратной связью R определяет среднюю частоту повторения F I в герцах; также R идентично средней длине интервала RR T I ,

(8.5) R = 1FI = TI.

Следовательно, «частота сердечных сокращений» модели IPFM равна 60 событиям в минуту, когда T I выбрано равным 1 с.

Предполагая, что начальное событие происходит при t 0 = 0, интеграл в (8.3) альтернативно можно выразить как

(8.6) ∫0tk (1 + m (τ)) dτ = kTI, k = 0,…, M,

, где k — целое число, которое индексирует событие k th . Более того, вместо того, чтобы определять модель IPFM только для тех моментов времени t k , когда превышен порог T I , ее можно обобщить на функцию непрерывного времени, введя следующее определение [14] ,

(8.7) ∫0t (1 + m (τ)) dτ = κ (t) TI.

Здесь интегрирование до определенного времени t пропорционально непрерывной функции индексации k ( t ), значение которой при t k идентично целочисленному индексу события k, , т. е. k ( t k ) = k. Обобщение модели IPFM в (8.7) позже позволит разработать представление сердечного ритма, известное как сигнал сердечного ритма .

Поведение функции регулирования м ( т ) передает важную информацию о HRV. Однако предварительные сведения о м ( т ) отсутствуют, и, следовательно, м ( т ) необходимо оценивать по времени появления наблюдаемых рядов событий. При оценке эффективности различных методов, разработанных для представления сердечного ритма, обычно предполагается, что m ( t ) определяется как сумма синусоид P с амплитудами m p и частотами F p. ,

(8.8) m (t) = Σp = 1Pmpsin (2πFpt).

Модель множественных синусоид может учитывать ВСР, вызванную дыханием, изменениями артериального давления и другими физиологическими факторами. Обычно предполагается, что амплитуды м l ,…, м P в (8.8) намного меньше единицы. Естественно, модулирующей функции m ( t ) могут быть назначены другие структуры, чем предложенная в (8.8). Например, это может быть определено процессом AR с ограниченной полосой пропускания, спектральные пики которого соответствуют частотам F 1 ,…. FP, введено в модель кратных синусоид в (8.8) [14, 15].

Модель IPFM — важный инструмент для имитационных исследований и лучшего понимания механизмов, лежащих в основе ВСР [14, 16–21]. Тем не менее, следует помнить, что эта модель не обеспечивает точного описания синоатриальной активности; могут быть интересны более сложные модели [22–25]. Следует также отметить, что модель IPFM ни в коем случае не ограничивается исследованием ВСР, но была признана столь же полезной в других биомедицинских приложениях, где наблюдаются серии событий, например, в области нейрофизиологии [26 –28].

Как получить среднеквадратичное значение импульсных и прямоугольных сигналов — Освоение дизайна электроники

Среднеквадратичное значение пульсовой волны можно легко вычислить, начиная с определения среднеквадратичного значения. Форма импульса показана на рисунке 1. Отношение t1 / T — это скважность импульсного сигнала. Как показано в других статьях на этом веб-сайте (MasteringElectronicsDesign.com: Как получить среднеквадратичное значение трапецеидальной формы волны и MasteringElectronicsDesign.com: Как получить среднеквадратичное значение треугольной формы волны), определение среднеквадратичного значения является интегралом по периоду сигнала. как в уравнении (1).

Рисунок 1

(1)

Импульсная функция с переменной «время» является константой, которая представляет собой амплитуду сигнала между 0 и t1 и нулем от t1 до T, как в (2).

(2)

где с u1 (t) я отметил функцию формы сигнала на рисунке 1. После замены u1 (t) в уравнении (1) мы можем найти квадрат среднеквадратичного значения, как в следующем выражении.

(3)

Следовательно, среднеквадратичное значение импульсного сигнала составляет

(4)

Это выражение также можно найти в (5)

(5)

где с D я отметил скважность импульсного сигнала, D = t1 / T.

Что делать, если импульсный сигнал биполярный, как на рисунке 2?

Рисунок 2

В этом случае следует ожидать, что отрицательная часть сигнала также будет вносить вклад в энергию, подаваемую на нагрузку.Чтобы вычислить его среднеквадратичное значение, давайте разделим сигнал на две части: от 0 до t1 и от t1 до T, как в (6).

(6)

где с u11 (t) и u12 (t) я отметил два участка формы сигнала на рисунке 2.

Среднеквадратичное значение u11 (t) идентично значению, показанному в уравнении (3).

(7)

Аналогичным образом мы можем вычислить среднеквадратичное значение u12 (t):

(8)

Затем вычисляется общее среднеквадратичное значение формы биполярного импульса путем применения квадратного корня из суммы квадратов u11 RMS и u12 RMS .

(9)

После расчетов среднеквадратичное значение сигнала биполярного импульса составляет

(10)

Как видите, среднеквадратичное значение биполярного импульса не зависит от его рабочего цикла и равно его амплитуде.

Зная среднеквадратичное значение импульсного сигнала, мы можем легко вычислить среднеквадратичное значение периодического прямоугольного сигнала.Прямоугольная волна на рисунке 3 представляет собой импульсный сигнал с коэффициентом заполнения 50%. Его среднеквадратичное значение можно рассчитать по уравнению (5), где D = 1/2. Его среднеквадратичное значение приведено в (11).

Рисунок 3

(11)

>>> <<<

Представление сигналов во временной и частотной областях

Электрические сигналы имеют представление как во временной, так и в частотной области.Во временной области напряжение или ток выражаются как функция времени, как показано на рисунке 1. Большинство людей относительно комфортно относятся к представлениям сигналов во временной области. Сигналы, измеренные на осциллографе, отображаются во временной области, а цифровая информация часто передается с помощью напряжения как функции времени.

Рис. 1. Представление электрического сигнала во временной области.

Сигналы также могут быть представлены величиной и фазой как функцией частоты.Сигналы, которые периодически повторяются во времени, представлены спектром мощности, как показано на рисунке 2. Сигналы, которые ограничены по времени (т.е. ненулевые только в течение конечного времени), представлены энергетическим спектром, как показано на рисунке 3.

Рисунок 2. Спектр мощности периодического сигнала.

Рисунок 3. Энергетический спектр ограниченного по времени (переходного) сигнала.

Представления в частотной области особенно полезны при анализе линейных систем.Инженеры по ЭМС и целостности сигналов должны уметь работать с сигналами, представленными как во временной, так и в частотной областях. Источники сигналов и помехи часто определяются во временной области. Однако поведение системы и преобразования сигналов более удобны и интуитивно понятны при работе в частотной области.

Линейные системы

Теория линейных систем играет ключевую роль в инженерном анализе электрических и механических систем. Инженеры моделируют самые разные вещи, включая поведение схемы, распространение сигнала, связь и излучение, как линейные преобразования.Таким образом, важно точно понять, что мы подразумеваем под линейной системой, чтобы понять, как и когда использовать доступные нам мощные инструменты анализа линейных систем.

На рис. 4 показана система с одним входом, x (t) , и одним выходом, y (t) = H [x (t)] . Если вход, x 1 (t) дает выход y 1 (t) , а вход x 2 (t) дает выход y 2 (t) , то система является линейной тогда и только тогда, когда

ay1 (t) + by2 (t) = H [ax1 (t) + bx2 (t)] (1)

, где a и b — константы.Другими словами, масштабирование ввода константой приведет к выходу, масштабированному той же константой; а объединение (суммирование) двух входов даст выход, который представляет собой сумму выходов, произведенных отдельными входами.

Рисунок 4: Линейная система.

Контрольный вопрос

Какое из следующих уравнений описывает взаимосвязь между выходом y (t) и входом x (t) линейной системы?

  1. y = 5x
  2. y (t) = 0
  3. y = 8x + 3
  4. y = x 2
  5. y (t) = 5t x (t)
  6. y = грех x
  7. y (t) = 5 δ / δt [x (t)]

Из вышеперечисленных вариантов только a, b и g являются линейными преобразованиями системы. y = 0 — не очень интересная система, потому что ее выход всегда равен нулю, но она линейна. Простые производные и интегральные операторы являются линейными, поскольку они удовлетворяют условиям уравнения (1). Остальные варианты — нелинейные операции. Обратите внимание, что y = 8x + 3 — это уравнение прямой линии, но оно не описывает линейную систему, потому что оно имеет ненулевой выход, когда нет входа.

Анализ линейных систем в частотной области

Линейные системы обладают уникальным свойством: любой синусоидальный вход будет давать синусоидальный выходной сигнал с точно такой же частотой.Другими словами, если ввод имеет форму,

x (t) = Aincos (ω0t + φin). (2)

, то результат будет иметь вид

y (t) = Aoutcos (ω0t + φout). (3)

Как правило, величина и фаза синусоидального сигнала могут изменяться, но частота должна быть постоянной. Это дает нам очень мощный инструмент анализа для анализа линейных систем. Если мы представим входной сигнал как сумму его компонентов в частотной области, то мы можем выразить выходной сигнал как простое масштабирование величин и сдвиг фаз этих компонентов.

Фазорная нотация

Для облегчения анализа откликов линейной системы на синусоидальные входные сигналы удобно представлять сигналы в сокращенной форме, известной как обозначение вектора. Рассмотрим ввод формы

x (t) = Acos (ωt + φ). (4)

Это может быть представлено как,

x (t) = Re {Aej (ωt + φ)} = A⋅Re {ejωtejφ}. (5)

, где Re {•} указывает действительную часть комплексной величины. Признавая, что частота ω будет одинаковой во всей системе, нам не нужно специально писать термин e jωt , если мы помним, что он есть.То же самое относится к обозначению Re {•} . Это позволяет нам выразить синусоидальный сигнал просто через его величину и фазу как

x = Aejϕ или A∠ϕ. (6)

Выражение в (6) — это сигнал в (4), выраженный с использованием векторной записи. Обратите внимание, что мы должны знать частоту сигнала, чтобы перейти от векторной записи к представлению во временной области.

Контрольный вопрос

Запишите следующие сигналы в векторной записи:

  1. x (t) = 5 cos (wt) В
  2. y (t) = 5 sin (wt) ампер
  3. z (t) = 5t sin (wt) вольт

Первый сигнал, выраженный в векторных обозначениях, просто равен x = 5 вольт.Чтобы получить обозначение вектора для второго сигнала, мы понимаем, что sin (ωt) = cos (ωt + π / 2), поэтому y = 5e j (π / 2) . Третий сигнал не является синусоидой и поэтому не может быть выражен с помощью векторной записи.

Серия Фурье

Конечно, многие входы в линейные системы, которые мы хотели бы проанализировать, не являются синусоидальными. В этом случае желательно представить более произвольные формы сигналов в виде суммы синусоидальных частотных составляющих. Затем мы анализируем каждый компонент по отдельности и применяем концепцию суперпозиции для восстановления выходного сигнала.

Периодический сигнал может быть представлен как сумма его частотных компонентов путем вычисления его коэффициентов ряда Фурье. Можно записать периодический сигнал с периодом Т,

x (t) = ∑n = −∞∞cnejn2πf0t (7a)

где

cn = 1T∫t0t0 + Tx (t) e − jn2πf0tdt. (7b)

Если x (t) является сигналом области реального времени, коэффициенты c n и c -n являются комплексно сопряженными (т.е.), и мы можем переписать уравнение (7) в форме

x (t) = c0 + ∑n = 1∞ (cnejn2πf0t + cn ∗ e − jn2πf0t) = c0 + ∑n = 1∞ (| cn | ejn2πf0t + ϕn + | cn | e− (jn2πf0t + ϕn)) = c0 + ∑n = 1∞2 | cn | cos (n2πf0t + ϕn).(8)

В этой форме мы видим, что коэффициенты ряда Фурье состоят из постоянной составляющей c 0 и частот положительных гармоник nω 0 (n = 1,2,3,…). Это односторонний ряд Фурье, а коэффициенты соответствуют амплитудам частотных гармоник, которые можно измерить с помощью анализатора спектра.

Несколько периодических сигналов и их представления в частотной области показаны на рисунке 5. Представление периодического сигнала в частотной области представляет собой линейчатый спектр.Он может иметь ненулевые значения только при постоянном токе, основной частоте и гармониках основной гармоники. Поскольку периодические сигналы не имеют начала и конца, ненулевые периодические сигналы имеют бесконечную энергию, но обычно имеют конечную мощность. Полная мощность сигнала во временной области,

Ptotal = 1T∫t0t0 + Tx2 (t) dt. (9)

равно сумме мощностей в каждом компоненте частотной области,

Ptotal = ∑n = −∞∞ | cn | 2. (10)

Рисунок 5. Периодические сигналы во временной и частотной области.

Пример 1: Представление последовательности импульсов в частотной области

Определите представление в частотной области для последовательности импульсов, показанной на рисунке 6.

Рисунок 6: Последовательность импульсов.

Во временной области этот сигнал описывается следующей формулой:

x (t) = {1 vnT

Коэффициенты ряда Фурье затем вычисляются с использованием уравнения (7b) как,

cn = 1T∫0Tx (t) e − jn2πf0tdt = 1T∫0τ (A) e − jn2πt / Tdt = AT∫0τe − jn2πt / T dt = AτT [sin (nπτT) (nπτT)] e − j (nπτT) .(E2)

Обратите внимание, что при τ → 0 наш сигнал во временной области выглядит как последовательность импульсов, а амплитуды всех гармоник приближаются к одному и тому же значению. При τ → T / 2 сигнал становится прямоугольной формы, а величина гармоник становится равной

.

cn = A2 | sin (nπ2) (nπ2) || e − j (nπ2) | = {Anπn = ± 1, ± 3, ± 5 ⋯ 0n = ± 2, ± 4, ± 6 ⋯. (E3)

В этом случае амплитуда четных гармоник равна нулю, а нечетные гармоники линейно убывают с частотой (n).

Преобразование Фурье

Переходные сигналы (т.е. сигналы, которые начинаются и заканчиваются в определенное время) также могут быть представлены в частотной области с помощью преобразования Фурье. Представление преобразования Фурье переходного сигнала, x (t), задается как,

Икс (е) знак равно ∫ − ∞∞x (t) e − j2πf tdt. (11)

Обратное преобразование Фурье может использоваться для преобразования представления сигнала в частотной области обратно во временную область,

x (t) = 12π∫ − ∞∞X (f) ej2πf tdf. (12)

Некоторые переходные сигналы во временной области и их преобразования Фурье показаны на рисунке 7.

Рис. 7. Переходные сигналы во временной и частотной области.

Обратите внимание, что переходные сигналы имеют нулевую среднюю мощность (при усреднении за все время), но имеют конечную энергию. Полная энергия переходного сигнала во временной области определяется выражением

.

E = ∫ − ∞∞x2 (t) dt. (13)

Это должно равняться полной энергии в представлении сигнала в частотной области,

E знак равно ∫ − ∞∞ | X (f) | 2 df. (14)

Представление трапецеидального сигнала в частотной области

Давайте рассмотрим представление в частотной области периодического трапецеидального сигнала, показанного на рисунке 8.Изучение поведения этого сигнала помогает нам понять взаимосвязь между представлениями временной и частотной области в целом. Кроме того, сходство между трапецеидальной формой волны и обычным цифровым сигналом будет полезно, когда мы исследуем проблемы ЭМС или целостности сигнала в цифровых системах.

Рис. 8. Трапецеидальная форма волны.

Используя односторонний ряд Фурье, уравнения (7b) и (8), мы можем представить этот сигнал как сумму его частотных составляющих [1],

x (t) = c0 + ∑n = 1∞2 | cn | cos (n 2πf0 t + ϕn).(15)

где

2 | cn | = 2AτT | sin (nπτT) (nπτT) || sin (nπtrT) (nπtrT) |. (16)

Уравнение (16) можно вывести, отметив, что трапецеидальная форма волны на рисунке 7 может быть получена путем свертки последовательности импульсов на рисунке 9 с другой серией импульсов, импульсы которой имеют ширину t r и амплитуду A / t . r . Свертка во временной области эквивалентна умножению в частотной области, поэтому мы можем просто перемножить два представления этих последовательностей импульсов в частотной области, чтобы получить уравнение (16).

Каждый член, 2 | c n |, — амплитуда n-й гармоники. Если мы предположим, что t r << T, то заметим, что третий член примерно равен sin (малое число) small number≈1 для нижних гармоник. Если τ = T2 (т.е. коэффициент заполнения 50%), то числитель второго члена равен 1 для гармоник (n = 1,3,5,…) и 0 для четных гармоник (n = 2,4,6. ,…). В этом случае амплитуда нижних гармоник обратно пропорциональна n (т. Е. Амплитуда нижних гармоник уменьшается пропорционально частоте).На более высоких гармониках третий член также начинает уменьшаться пропорционально частоте, поэтому общая амплитуда верхних гармоник уменьшается в среднем со скоростью, пропорциональной квадрату частоты. Это частотное представление трапециевидного сигнала (τ = T2, tr≪T) и его огибающая показаны на рисунке 9.

Рисунок 9: Представление трапецеидального сигнала в частотной области

Пример 2: Гармоники трапециевидного сигнала

Форма сигнала, показанная на Рисунке 10 ниже, измерена на осциллографе в лаборатории.Время нарастания и спада составляет 0,8 нс.

а.) Какая основная частота?

b.) Рассчитайте амплитуды гармоник на частотах 50, 150, 250 и 1,55 ГГц.

Если время нарастания и спада увеличится до 1,6 наносекунды, то на сколько дБ снизятся гармоники на частотах 50, 150, 250 и 550 МГц?

Рис. 10. Трапецеидальная форма волны для Примера 2.

Учитывая, что период равен 20 нсек, основная частота легко определяется как f0 = 1T = 12 × 10-8 = 50 МГц.Поэтому нас просят определить амплитуды 1 -й , 3 -й , 5 -й и 11 -й гармоник. Применяя уравнение (16) для n = 1,3,5 и 11, получаем амплитуды этих гармоник,

2 | c1 | = 2 (1 v) 2 | sin (1π (10) 20) (1π (10) 20) || sin (1π (0.8) 20) (1π (0.8) 20) | = (1 v ) (0,64) (1,00) = 0,64 v2 | c3 | = 2 (1 v) 2 | sin (3π (10) 20) (3π (10) 20) || sin (3π (0,8) 20) (3π (0,8 ) 20) | = (1 v) (0,21) (0,98) = 0,21 v2 | c5 | = 2 (1 v) 2 | sin (5π (10) 20) (5π (10) 20) || sin (5π ( 0,8) 20) (5π (0,8) 20) | = (1 v) (0.13) (0,94) = 0,12 v2 | c11 | = 2 (1 v) 2 | sin (11π (10) 20) (11π (10) 20) || sin (11π (0,8) 20) (11π (0,8) 20 ) | = (1 v) (0,06) (0,71) = 0,04 v.

Ни одна из этих гармоник не зависит от времени нарастания. Они имеют практически ту же амплитуду, что и при нулевом времени нарастания. Однако увеличение времени нарастания до 1,6 нс существенно влияет на амплитуду верхних гармоник,

2 | c1 | = 2 (1 v) 2 | sin (1π (10) 20) (1π (10) 20) || sin (1π (1.6) 20) (1π (1.6) 20) | = (1 v ) (0,64) (. 99) = 0,63 v2 | c3 | = 2 (1 v) 2 | sin (3π (10) 20) (3π (10) 20) || sin (3π (1.6) 20) (3π (1,6) 20) | = (1 v) (0,21) (0,91) = 0,19 v2 | c5 | = 2 (1 v) 2 | sin (5π (10) 20) (5π (10) 20) || sin (5π (1,6) 20) (5π (1,6) 20) | = (1 v) (0,13) (0,76) = 0,10 v2 | c11 | = 2 (1 v) 2 | sin (11π (10 ) 20) (11π (10) 20) || sin (11π (1,6) 20) (11π (1,6) 20) | = (1 v) (0,06) (0,13) = 0,008 v.

Удвоение времени нарастания с 0,8 до 1,6 нс уменьшает первую гармонику всего на 20log (0,64,63) = 0,14 дБ. Третья гармоника уменьшается на 20log (0,21,19) = 0,87 дБ. Пятая гармоника уменьшается на 20log (.12.10) = 1,6 дБ, а одиннадцатая гармоника уменьшается на 20log (0.040.008) = 14 дБ.

Обратите внимание, что изменение времени нарастания может оказать существенное влияние на амплитуду верхних гармоник без значительного изменения представления сигнала во временной области. Проблемы, связанные с излучаемыми электромагнитными помехами или перекрестными помехами на верхних частотах гармоник цифрового сигнала, часто можно решить, увеличив время нарастания сигнала цифрового сигнала. Как правило, время нарастания, равное 10% длины в битах или более, по-прежнему дает очень хороший цифровой сигнал, в то же время значительно ограничивая амплитуду сигнала на частотах выше 10 -й гармоники.

Измерение частоты и рабочего цикла с помощью Arduino

Arduino имеет несколько приложений. Мы можем найти его применение во многих различных областях и областях. Его можно использовать в области измерений также для измерения электрических величин (таких как напряжение, ток, мощность и т. Д.) Или физических величин (таких как температура, влажность, сила света, влажность и т. Д.) Или значений электронных компонентов и т. Д.

В данной статье показано, как измерять частоту и скважность импульсов с помощью Arduino.Измерение частоты требуется во многих различных приложениях. В области связи измерение частоты является наиболее важным. Рабочий цикл также является важным параметром для измерения, потому что он дает% от ширины импульса, что означает время включения импульса. При управлении скоростью двигателя постоянного тока и управлении углом серводвигателя необходимо измерять ширину импульса. Также измеряется ширина импульса для проверки симметрии импульса в некоторых приложениях, таких как приемник цифрового сигнала, ретрансляторы и т. Д. Итак, давайте посмотрим, как мы можем использовать Arduino для измерения частоты и рабочего цикла импульсов.В данном проекте Arduino измеряет частоту, время включения, время выключения и рабочий цикл импульсов и отображает их на ЖК-дисплее 16×4

Описание:

Как показано на рисунке выше, в схеме всего два основных компонента (1) Плата разработки arduino UNO и (2) ЖК-дисплей 16×4

· Импульсы подаются непосредственно в качестве входа на цифровой контакт 7 Arduino

· Контакты Rs и En ЖК-дисплея подключены к цифровым контактам 9 и 8 соответственно платы Arduino .Вывод Rw подключен к земле

· Последние четыре вывода данных D4 — D7 подключены к выводам 10, 11, 12 и 13 Arduino.

· Анодный вывод светодиода задней подсветки (вывод 15) и вывод Vcc (2) ЖК-дисплея подается питание 5 В через плату Arduino

· Катод светодиода задней подсветки (вывод 16) и вывод Vss (1) подключены к земле

· Поток One1 K подключен к выводу Vee для изменения контрастности ЖК-дисплея

Работа схемы :

· Когда плата Arduino получает питание через USB, на ЖК-дисплее отображаются четыре параметра: « freq: Ton: Toff: Duty: » в каждой строке, как показано

· Теперь, когда появляются импульсы подается на вывод 7, Arduino сначала ожидает, пока импульс не станет высоким.Когда он становится высоким, он вычисляет период времени (в микросекундах), в течение которого пульс остается высоким. Это it Ton time

· Затем рассчитывается период времени (в микросекундах), в течение которого пульс остается низким. Это время Toff

· Затем он складывает эти два временных интервала, чтобы получить общее время — означает период

· Из общего времени arduino вычисляет частоту как

Частота = 1 / время

· И из Ton и Toff вычисляет нагрузку как

Duty = Ton / (Ton + Toff)

· Затем он отображает все четыре параметра на ЖК-дисплее

· Снова через 1 секунду он повторяет ту же процедуру

· Таким образом, он непрерывно измеряет изменение частоты и рабочего цикла импульса

Калькулятор максимального однозначного диапазона и частоты повторения импульсов радара • Электрические, радиочастотные и электронные калькуляторы • Онлайн-преобразователи единиц

1 — Время повторения импульсов (PRT), 2 — Несущая частота, 3 — Отраженный эхо-импульс от цели

Этот калькулятор определяет максимальную однозначную дальность действия простого импульсного радара на основе частоты повторения импульсов радара или повторения импульсов период.В радиолокационной системе эхо-сигналы от целей должны приниматься и обрабатываться до того, как передатчик отправит следующий импульс. Если время для возврата эхо-импульса от цели больше, чем время повторения импульсов (также называемое периодом повторения импульсов), возникает неоднозначность диапазона. Об этом мы поговорим позже.

Пример: Рассчитайте максимальную однозначную дальность действия радара на основе известной частоты повторения импульсов 2 кГц или частоты повторения импульсов 500 мкс.

Вход

Частота повторения импульсов

f PRF килогерц (кГц) мегагерц (МГц) гигагерц (ГГц)

или время повторения импульсов

нанометров нс) микросекунда (мкс) миллисекунда (мс) секунда (с)

Выход

Макс. однозначный диапазон

R макс. м миля Морская миля (международная)

Для расчета введите значения в в соответствующих полях выберите Британские или метрические единицы и нажмите или коснитесь кнопки Вычислить .

Частота повторения импульсов (PRF) радара определяет количество импульсов, передаваемых в секунду. Радар излучает импульс несущей частоты во время передачи, затем ожидает отраженного эхо-импульса в течение периода прослушивания, а затем излучает следующий импульс, как показано на рисунке выше. Время между передними фронтами переданных импульсов называется временем повторения импульсов (PRT). Он равен обратной величине PRF:

Очевидно, что радар не может послать другой импульс, не дожидаясь эхо-импульса, возвращенного от цели.Следовательно, максимальное расстояние измерения R max радара определяется не только уравнением радара, но также зависит от продолжительности времени приема. Эхо-сигналы, поступающие после периода приема, могут оставаться необнаруженными, если приемник не прослушивает в момент их прибытия, или они могут быть обнаружены в течение следующего периода времени приема, где они приведут к неправильному измерению (неоднозначное измерение дальности). Таким образом, неоднозначность диапазона возникает, когда время, необходимое для возврата эхо-импульса от цели, превышает период повторения импульсов.

Рассмотрим следующий пример. Радар передает первый импульс. Время возврата эхо-импульса от удаленной цели составляет 1,3 миллисекунды, а частота повторения импульсов радара f PRF = 1 кГц или период повторения импульсов T PRT = 1 мс. В этом случае эхо-импульс будет принят в течение следующего периода приема, а разница во времени между вторым переданным импульсом и эхо-импульсом составит всего 300 микросекунд. То есть цель окажется ближе, чем есть на самом деле.

Максимальный однозначный диапазон определяется следующим образом:

, где

c = 299 792 458 м / с — скорость света,

f PRF — частота повторения импульсов, а

T PRT — период повторения импульсов.

Это уравнение используется в нашем калькуляторе. Из этого уравнения мы можем видеть, что если мы увеличим период повторения импульсов (или уменьшим частоту повторения импульсов), максимальный однозначный диапазон будет увеличен.

Ранние поисковые радары, разработанные в 1940-х годах, имели частоту повторения импульсов всего в несколько сотен герц, что обеспечивало им однозначную дальность действия более 100 миль. В то же время, учитывая, что современные цели могут двигаться со скоростью до 20 Махов, перемещаясь около 7 км в секунду, возможно, что при периоде следования импульсов в несколько миллисекунд цель, особенно если она летит на малой высоте, улетит незамеченными. Более низкие частоты повторения импульсов создают другие проблемы, такие как неоднозначность скорости цели и плохое отображение цели на экране радара.Поэтому во многих случаях уменьшать это значение нежелательно. Следовательно, в современных радарах частота повторения импульсов может составлять от нескольких кГц до десятков или сотен килогерц, и они используют различные методы, например, смещение интервала между импульсами, чтобы можно было определить правильный диапазон.

Многорежимная РЛС управления огнем AN / APG-73 X-диапазона с активной фазированной антенной решеткой в ​​носовой части канадского истребителя CF-18 Hornet

Как и любой радар, обычно имеет уникальные параметры передаваемых сигналов в различных режимах работы, можно создавать библиотеки общих сигналов, которые могут использоваться различным оборудованием для обнаружения, анализа, идентификации, определения местоположения и регистрации всех враждебных действий, связанных с электромагнитным спектром, — от наблюдения или подготовки до нападения и до последнего. помолвка.Примером такой активности является блокировка РЛС управления огнем на истребителе или корабле.

ALR-67 Антенны приемника радиолокационного оповещения, установленные на многоцелевом истребителе F / A-18 Hornet

Современные приемные системы, используемые для сбора радиоэлектронной разведки, работают в полосе частот приблизительно от 0,2 до 20 ГГц. Обычно они позволяют автоматически обнаруживать несколько (несколько сотен) целей, идентифицировать, пеленговать, анализировать и контролировать все типы радиолокационных, навигационных и других сигналов.Для определения точного положения излучающего оборудования могут быть развернуты две и более станций с расстоянием между ними от 10 до 30 км. Их высокочувствительное оборудование позволяет принимать сигналы от целей не только в зоне прямой видимости, но и отраженные от тропосферы, обеспечивая рабочее расстояние до 600–800 км при охвате 360 °.

В отличие от разведывательных систем 1970-х и 1980-х годов, в которых операторам приходилось запоминать параметры нескольких сотен радаров, современные системы позволяют быстро и полностью автоматически анализировать и идентифицировать излучающее оборудование.Они также обеспечивают точную идентификацию сигналов неизвестных типов радиолокационного оборудования. Полученная информация в конечном итоге используется для наложения идентифицированных радаров и оборудования, в котором они установлены, на карту, отображаемую на большом дисплее.

Библиотеки общих сигналов и методов, используемых в ELINT, также используются в системах приемников радиолокационных предупреждений, предназначенных для обнаружения, анализа, определения режима работы и классификации радиоизлучений радиолокационных систем. Такие системы обычно устанавливаются на военные самолеты, а простые системы могут быть установлены на других объектах, таких как автомобили.Они могут выдавать предупреждение при обнаружении опасного радиолокационного сигнала. Приемник радиолокационной сигнализации имеет визуальный дисплей в кабине пилота и передает аудиосигналы пилоту. На дисплее отображаются обнаруженные радары и серьезность угроз.

Эту статью написал Анатолий Золотков. катодная защита обсадных труб нефтяных скважин, влияние параметров импульсной защиты на распределение потенциала было не очень ясным.Поэтому, в соответствии с текущей ситуацией на нефтяных месторождениях в Китае, была выбрана типичная структура характеристик пласта нефтяных скважин и создана модель катодной защиты импульсного тока для обсадных труб нефтяных скважин. На основе установленной модели было изучено влияние параметров импульсного тока (частоты и рабочего цикла) и анодного расстояния на эффект катодной защиты прямоугольного импульсного тока. Результаты показали, что лучший защитный эффект может быть получен путем выбора подходящего анодного расстояния, высокой частоты и умеренного рабочего цикла.

1. Введение

Повреждение обсадной трубы нефтяной скважины влияет не только на ее нормальную добычу, но и на нормальную работу соседних скважин, что приводит к нарушению нормальной добычи всего месторождения [1]. За рубежом для защиты обсадных колонн от коррозии широко применяется катодная защита [2]. Внешняя токовая катодная защита обсадных труб нефтяных скважин является стандартным методом сдерживания коррозии наружных стенок обсадных труб [3]. Эта технология является очень экономичным и эффективным методом предотвращения коррозии наружной стенки обсадной колонны [4].Катодная защита импульсным током успешно применялась для защиты обсадных труб кустовых скважин в 1968 г. [5]. Некоторыми исследователями доказано, что импульсная система катодной защиты обсадной трубы нефтяной скважины имеет более равномерную плотность тока, большую глубину защиты и лучший защитный эффект, чем система катодной защиты протекторного анода и система катодной защиты постоянного тока [6, 7]. Однако существует множество переменных электрических параметров импульсного тока, таких как частота, амплитуда, рабочий цикл и форма импульса, которые не оказывают явного влияния на эффект защиты.Кроме того, геологическая среда и стратиграфическая структура обсадной колонны сложны, и, следовательно, диэлектрические свойства тока катодной защиты, протекающего через обсадную колонну, различны. Таким образом, в настоящее время только несколько нефтяных месторождений используют эту технологию в небольших масштабах.

Результаты полевого применения показывают, что катодная защита импульсного тока имеет более равномерную плотность тока, более глубокое проникновение, меньший ток и более равномерное распределение потенциала на поверхности корпуса, что обеспечивает большую глубину защиты корпуса, чем традиционный катод постоянного тока [8 ].Например, в катодной защите постоянного тока обсадных труб глубоких скважин глубина защиты может достигать только около 1500 м. Если используется технология катодной защиты импульсным током, глубина защиты может быть увеличена до более чем 3000 метров [9]. Метвалли представил теоретическое исследование импульсных систем катодной защиты, чтобы показать, как они ведут себя в различных условиях эксплуатации, с помощью программного пакета 3D-полевого подхода. Эффективность катодной защиты импульсным током в пустынных и прибрежных районах сравнивалась в статье Метвалли.Метвалли дал много предложений по применению катодной защиты импульсным током. Однако предложения о применении импульсной катодной защиты для обсадных труб нефтяных скважин с многослойной структурой породы не поступало [10]. Джордж изучал скорость коррозии и срок службы анода трубопровода в установившемся режиме и в условиях импульсного выхода постоянного тока [11]. В настоящее время проектирование импульсной катодной защиты обсадных труб в нефтяных и газовых скважинах часто является эмпирическим или может достигнуть уровня только полуэмпирического и полутеоретического с помощью теории катодной защиты для магистральных трубопроводов.Хотя известно, что применение катодной защиты импульсного тока к обсадной колонне в добывающих скважинах может увеличить глубину защиты, часто неясно, как потенциал катодной защиты распределяется на разных глубинах и насколько глубоко можно защитить каждую скважину. Отсутствие достаточного понимания механизма защиты препятствует применению и продвижению этой технологии. В соответствии с текущей ситуацией на нефтяных месторождениях в Китае и типичными характеристиками пласта была создана модель катодной защиты импульсного тока для обсадной трубы нефтяной скважины, а также влияние волнового импульсного тока и других факторов на эффект катодной защиты прямоугольных импульсов. тока были изучены.

В соответствии с конструкцией обсадной трубы нефтяной скважины создана модель импульсной токовой катодной защиты внешней стенки обсадной колонны. Граничные условия использовались для решения дифференциальных уравнений в модели. Теоретически проанализированы потенциал катодной защиты и плотность тока на любой глубине на внешней поверхности корпуса. Кроме того, модель была применена к типичной структуре пластов в Китае. По характеристикам строения пласта соответственно получены методики расчета защитного потенциала обсадной колонны в каждом пласте.Проанализированы характеристики различных пластов, создана лабораторная модель обсадной колонны, проведены испытания катодной защиты импульсным током.

Влияние параметров импульсного тока (частоты и рабочего цикла) на потенциал защиты корпуса было проанализировано по результатам испытаний, и было получено правило влияния. С помощью этой экспериментальной модели было дополнительно проверено влияние анодного расстояния на потенциал защиты корпуса. Экспериментально обсуждалось влияние основных параметров импульсной токовой катодной защиты модели обсадной колонны нефтяной скважины.

Путем моделирования установленной тестовой модели обнаружено, что в такой многослойной геологической структуре обсадная труба нефтяной скважины может быть хорошо защищена, когда частота параметров импульсного источника питания составляет 3500 Гц, а рабочий цикл составляет 50%, и там оптимальное анодное расстояние. Это может оказаться большим подспорьем для инженеров-проектировщиков и инженеров, ответственных за проектирование и установку обсадных труб нефтяных скважин на месторождении.

2. Создание модели катодной защиты импульсным током для обсадной колонны
2.1. Теоретический анализ распределения потенциала катодной защиты корпуса

Принципиальная схема модели корпуса внешнего импульсного тока показана на рисунке 1. Ток катодной защиты на внешней поверхности корпуса может быть выражен следующим образом: где — небольшой участок на кожухе, E — потенциал кожуха малого участка, — переходное сопротивление, а I — ток кожуха маленького участка. Здесь потенциал земли равен нулю.


Кроме того, при протекании тока через участок будет падение напряжения из-за сопротивления самого трубопровода. Если средний ток, проходящий через участок трубопровода, равен I , а сопротивление на единицу длины трубопровода равно, то напряжение, генерируемое небольшим трубопроводом, можно выразить следующим уравнением:

Если производные формул (1) и (2) соответственно, и, где — коэффициент затухания, тогда

Общие решения приведенных выше дифференциальных уравнений следующие: где A 1 , B 1 , A 2 и B 2 — константы.

Граничные условия: если x = 0, то E = E 0 , I = I 0 ; если, то E = 0, I = 0.

Подставляя граничные условия в формулы (4) и (5), можно получить защитные распределения тока и напряжения корпуса:

Формула (7) показывает, что приложенный потенциал на пути обсадной колонны изменяется экспоненциально. Его характерно то, что потенциал вблизи точки слияния быстро уменьшается, и чем дальше от точки слияния, тем медленнее спад.Потенциал E зависит в основном от переходного сопротивления R T . По формулам (1) и (6) можно рассчитать защитный потенциал в любой точке обсадной колонны:

Формула (8) показывает, что скорость падения кривой приложенного потенциала обсадной колонны (градиент изменения потенциала) зависит от по коэффициенту затухания и переходному сопротивлению трубопровода R T . Если учесть влияние самопроизвольного потенциала трубопровода, защитный потенциал E оболочки можно выразить следующим образом: где U 0 — самопроизвольный потенциал трубопровода.

2.2. Возможное распределение катодной защиты в обсадной колонне

В инженерном применении пластовая структура, через которую проходит нефтяная обсадная колонна, является сложной, включая поверхностный слой почвы, водоносный горизонт, различные слои горных пород и нефтеносные слои. Нефтяные скважины в бассейне Шэньси-Ганьсу-Нинся с широким распространением и стабильной литологией в основном расположены на стыке Шэньси, Ганьсу и Нинся. Нижняя часть стратиграфической структуры представлена ​​преимущественно пурпурно-красным аргиллитом, а дно — желтым средне- и крупнозернистым полевошпатовым песчаником с огромной косой слоистостью.Аргиллиты и глинистые алевролиты с преобладанием пурпурно-красного цвета в середине впадины переслаиваются мелкозернистыми полевошпатовыми песчаниками с косой слоистостью. Верхняя часть — красный мелкозернистый и крупнозернистый полевошпатовый песчаник с крупной косой слоистостью, содержащий мелкий гравий и глинистый гравий. Принципиальная схема базовой модели конструкции показана на рисунке 2. На основе модели импульсного тока на рисунке 1 и формул (4) и (5), модель текущего поля системы катодной защиты импульсным током обсадной колонны, включая интерфейс внешней стенки. кожуха установлен.Модель изучает взаимосвязь между потенциалом защиты поверхности обсадной колонны и глубиной x на любой глубине по глубине скважины.


Согласно теоретическому анализу, приведенному в предыдущем разделе и на Рисунке 2, метод расчета потенциала защиты обсадной колонны в верхнем слое почвы выглядит следующим образом: где — потенциал верхнего слоя почвы, R Tx1 — удельное сопротивление. верхнего слоя почвы, — коэффициент затухания верхнего слоя почвы, L x 1 — глубина верхнего слоя почвы, и R X1 — сопротивление при x метрах от устья скважины в почвенный слой.

Потенциал защиты обсадной колонны первого слоя породы следующий: где — потенциал первого слоя породы, R Tx2 — удельное сопротивление первого слоя породы, — коэффициент затухания первого слоя породы, L x 2 — это глубина первого слоя породы, а R X 2 — сопротивление на расстоянии x метра от устья скважины в первом слое породы.

Потенциал защиты обсадной колонны второго пласта породы следующий: где — потенциал второго пласта породы, R Tx3 — удельное сопротивление второго пласта породы, — коэффициент затухания второго пласта породы, L x 3 — это глубина второго пласта породы, а R X3 — сопротивление на расстоянии x метра от устья скважины во втором слое породы.Используя данные удельного сопротивления и глубины слоев воды, породы, глины и нефти, можно получить закон защитного потенциала обсадной колонны в каждом слое. Следующие ниже эксперименты основаны на приведенном выше теоретическом анализе, а также на удельном сопротивлении и глубине каждого слоя, полученных из данных.

3. Эксперименты
3.1. Тестовая модель

На основе приведенной выше модели и удельного сопротивления пластового слоя была создана тестовая модель, как показано на Рисунке 3. Система катодной защиты для моделируемой обсадной колонны вертикальной нефтяной скважины была построена в корпусе 5 × 0.Желоб ПВХ 5 × 0,5 м. Испытательной средой была соленая вода, а катодом — сталь с углом 40 градусов. Катод располагался на 20 см ниже уровня жидкости в емкости по горизонтали. Глубина проникновения воды в анод была такой же, как у катода. Источник питания — самодельный импульсный. Потенциал катодной защиты регистрировался осциллографом.


Удельное сопротивление пласта модели на Рисунке 2 было рассчитано для защитного потенциала обсадной колонны в разумных пределах.В соответствии с формулами (10) — (12) и требованием потенциала катодной защиты удельное сопротивление каждого слоя можно рассчитать отдельно. Но удельное сопротивление формации сильно различается в каждом районе добычи нефти. На это также влияют плотность и пористость структуры пласта, содержание порового флюида и свойства жидкости. Sun et al. измеряли удельное сопротивление многослойной пластовой структуры в определенной области, а диапазон изменения удельного сопротивления составлял от 0 до 30 [12]. Чжан смоделировал влияние разного сопротивления разных слоев на потенциал катодной защиты [13].Ghimire et al. изучили изменение удельного сопротивления пласта вокруг ствола скважины [14]. Лю и др. изучили изменения сопротивления пласта нефтяных скважин в районе Чжидан, север Шэньси [15]. Они обнаружили, что среднее удельное сопротивление составляло 5,2, а удельное сопротивление не превышало 21 при использовании акустической разницы во времени для измерения удельного сопротивления формации. Анализируя данные в приведенной выше литературе, можно сделать вывод, что удельное сопротивление формации сильно различается, и трудно найти закон изменения сопротивления формации.

Нефтяные скважины в литературе [15] и модели стратиграфической структуры нефтяных скважин в статье расположены в бассейне Шэньси-Ганьсу-Нинся. Таким образом, согласно исследованиям Лю, удельное сопротивление каждого слоя в испытании на моделировании измеряется от 0 до 21. Учитывая требование потенциала катодной защиты, для разных пластов рассчитываются разные значения удельного сопротивления.

Согласно формуле (10) удельное сопротивление грунтового слоя рассчитывается следующим образом:

Когда известны граничные условия и удельное сопротивление обсадной колонны, удельное сопротивление грунтового слоя можно рассчитать, задав соответствующее значение защитного потенциал почвенного слоя.Таким же образом можно рассчитать удельное сопротивление первого слоя породы и второго слоя породы по формулам (11) и (12). Когда защитные потенциалы, и равны -0,85 В, граничное условие составляет 0,3 В, в модели 0,180 А, а удельное сопротивление корпуса равно, результаты расчетов показаны в таблице ниже.

В соответствии с удельным сопротивлением пласта в Таблице 1 рассчитывается сопротивление пласта в модели на Рисунке 3. Если предположить, что на Рисунке 3 сопротивление R X1 расположено в 180 метрах от устья скважины, сопротивление R X2 расположено в 1000 метрах от устья скважины, сопротивление R X3 расположено в 1500 метрах от устье скважины, а сопротивление расположено в 1800 метрах от устья скважины, согласно рисунку 2, эти сопротивления R X1 , R X2 , R X3 , и R X3 ‘ составляют сопротивления слоя почвы, первого слоя слоя породы, верхней части второго слоя слоя породы и нижней части второго слоя слоя породы, соответственно.В соответствии со структурой слоя на Рисунке 2 значения сопротивления R X1 , R X2 , R X3 , и рассчитываются как 896, 7942, 12183 и 15704 с использованием удельное сопротивление водоносного пласта 1 и удельное сопротивление в таблице 1. Таким образом, рассчитанные значения сопротивления были введены в имитационное испытание, показанное на рисунке 3. Эксперименты проводились в соответствии с рисунком 3, как показано на рисунке 4.


3.2. Процесс испытания

Процесс испытания включал в себя подготовку испытательных инструментов и оборудования, подготовку образца, загрузку образца, определение времени испытания, выбор параметров источника питания и т. Д. Этот эксперимент включал следующие процессы.

3.2.1. Подготовка испытательного оборудования

(1) В качестве источника питания был выбран самодельный импульсный источник питания. (2) Насыщенный электрод из сульфата меди был выбран в качестве электрода сравнения. (3) Графитовый анод был выбран в качестве анода.(4) Резервуар для коррозионных испытаний был адаптирован в соответствии с размером. Белый пластинчатый желоб из ПВХ размером 5 × 0,5 × 0,5 м был специально изготовлен для изоляции и предотвращения помех от паразитных токов. (5) Осциллограф TDS1002 использовался для контроля потенциала, амплитуды и частоты импульсной волны.

3.2.2. Подготовка образца

В качестве образца была выбрана сталь, соответствующая национальному стандарту, длиной 4,5 м. Перед испытанием образец был отполирован и удалена ржавчина. После полировки образец обезжиривали и сушили ацетоном.

3.2.3. Метод загрузки образцов

В этом эксперименте был выбран тип полки, и образцы были помещены на самодельную пластиковую полку из ПВХ. Для правильного размещения образца в нижней части лотка был установлен кронштейн. Образец помещался на кронштейн. В процессе испытания соблюдались следующие принципы: (1) Во время испытания образец был должным образом размещен и изолирован от металла в испытательной системе, и помехи от паразитных токов были предотвращены.2. Образец целиком проник в окружающую среду, глубина погружения составляла 20 см. Глубина погружения вспомогательного анода и электрода сравнения соответствовала глубине образца. (3) Во время испытания образец легко было взять и разместить.

3.2.4. Планируемое время испытаний

Согласно результатам соответствующих исследований, годовая скорость коррозии обсадных труб нефтяных скважин в пластовой структуре бассейна Шэньси-Ганьсу-Нинся варьируется от 0,1 мм / год до 1.0 мм / год. В таблице 2 показано время, необходимое для экспериментов по коррозии. Согласно данным табл. 2, время имитационного эксперимента составило 72–168 часов.

Оценка или прогноз скорости коррозии (мм / год) Время испытания (ч) Замена раствора или нет
24–72 №
1.0–0.1 72–168 №
0.1–0,01 168–336 Замена примерно раз в 7 дней
<0,01 336–720 Замена примерно раз в 7 дней
> 1,0 24–72
3.2.5. Выбор метода ортогональных испытаний

Чтобы исследовать защитный эффект обсадных труб нефтяных скважин при импульсном токе, шесть уровней частоты ( F ) и рабочего цикла ( P ) и три уровня рабочего цикла ( P ) были выбраны.В таблице 3 перечислены экспериментальные факторы и уровни.

902 F 1)
1 2 3 4 5 6
1500 Гц ( F 2) 2500 Гц ( F 3) 3500 Гц ( F 4) 4500 Гц ( F 5) 5500 Гц ( F 6)
Рабочий цикл ( P ) 20% ( P 1) 50% ( P 2) 70% ( P 3)
4.Результаты и обсуждение. по действию импульсного тока катодная защита проводилась по установленной модели. Согласно установленной модели катодной защиты импульсного тока обсадной колонны и удельного сопротивления различных пластов, можно рассчитать потенциал
E на глубине x .Здесь слой почвы с электродом сравнения 1 был установлен на высоте 180 метров, слой породы с электродом сравнения 2 на высоте 1000 метров, слой породы с электродом сравнения 3 на высоте 1500 метров и слой породы с электродом сравнения 4 на высоте 1800 метров. Были рассчитаны переходные сопротивления в каждом слое, соответственно, и резисторы были подключены к испытательному устройству для тестирования. Согласно критериям оценки эффекта катодной защиты, эффективная защита может быть достигнута, когда потенциал поляризации падает между -0.77 и −l.03 В.

4.1. Испытание катодной защиты постоянным током

На рисунке 5 представлена ​​диаграмма потенциалов катодной защиты постоянного тока. После 72 часов установки и работы системы моделирования для эксперимента был проведен сбор данных. Данные записывались каждые 60 минут, как показано на рисунке 5.


Результаты могут быть получены на основе анализа, приведенного на рисунке 5. Защитный эффект корпуса у электрода сравнения 1 лучше, а защитный потенциал находится в пределах потенциала катодной защиты.Однако защитные потенциалы на электродах сравнения на 2, 3 и 4 участках выходят за пределы диапазона потенциала катодной защиты и не защищены катодной защитой. Общая глубина защиты образца недостаточна.

4.2. Эксперимент с катодной защитой с импульсным током

Были записаны подробные данные о стабильном потенциале защиты прямоугольной формы при различных рабочих циклах, соответственно. Защитные потенциалы в четырех точках регистрировали в шести группах, каждая с интервалом в 1 час.Среднее значение было получено при анализе данных. На рисунках 6–8 представлены экспериментальные результаты при различных частотах и ​​рабочих циклах.




На рисунке 6 показан эффект катодной защиты от импульсного тока для ввода с рабочим циклом 20% на разных частотах. Анализируя рисунок 6, можно получить следующие результаты. Защитный потенциал на электроде сравнения 1 превышает диапазон защитного потенциала от 1500 Гц до 4500 Гц с максимальным значением -1.03 В и находится в состоянии повышенной защиты. На очень низких или очень высоких частотах, таких как 500 Гц или 5500 Гц, потенциал электрода сравнения 1 в меньшей степени превышает защитный потенциал. В диапазоне от 1500 Гц до 5500 Гц защитный потенциал на электроде сравнения 2 находится в пределах диапазона потенциала катодной защиты, а защитные потенциалы на электроде сравнения 3 и электроде сравнения 4 ниже диапазона потенциала катодной защиты без катодной защиты. При катодной защите постоянного тока защитные потенциалы на электроде сравнения 1 и электроде сравнения 2 находятся в диапазоне -0.От 77 В до 1,03 В, а защитные потенциалы на электроде сравнения 3 и электроде сравнения 4 ниже, чем потенциал катодной защиты, которые не были эффективно защищены. По сравнению с катодной защитой постоянного тока и катодной защитой от импульсного тока обнаружено, что с увеличением глубины корпуса потенциал защиты резко уменьшается, и тенденция катодной защиты постоянного тока становится более очевидной. Когда частота катодной защиты импульсного тока ниже 3500 Гц или ниже, значение потенциала катодной защиты импульсного тока ниже, чем у катодной защиты постоянного тока.Когда частота катодной защиты импульсного тока составляет от 3500 Гц до 5500 Гц или выше, значение потенциала катодной защиты импульсного тока выше, чем у катодной защиты постоянного тока.

На рисунке 7 показан эффект катодной защиты от импульсного тока для ввода с рабочим циклом 50% на различных частотах. Анализируя рисунок 7, можно получить следующие результаты. Когда частота составляет 2500 Гц или 3500 Гц, защитные потенциалы на электроде сравнения 1 и электроде сравнения 2 находятся в диапазоне защитных потенциалов, и они хорошо защищены.В диапазоне от 1500 Гц до 5500 Гц защитные потенциалы на электродах сравнения 3 и 4 все еще ниже, чем потенциал катодной защиты, но значение защитного потенциала выше, чем при 20% продолжительности рабочего цикла, что ближе к диапазону защитного потенциала. При катодной защите постоянного тока защитные потенциалы на электродах сравнения 1 и 2 находятся в диапазоне от -0,77 В до -1,03 В, а защитные потенциалы на электродах сравнения 3 и 4 ниже, чем потенциал катодной защиты, который не был эффективно использован. защищен.По сравнению с катодной защитой по постоянному току и катодной защитой от импульсного тока обнаружено, что катодная защита по постоянному току имеет тенденцию крутого спада на электроде сравнения 1 и электроде сравнения 2, чем катодная защита с импульсным током. Когда частота составляет 3500 Гц, защитный потенциал на электроде сравнения 3 находится в пределах диапазона потенциала катодной защиты, и катодная защита обеспечивается. На других частотах электрод сравнения 3 не имеет катодной защиты.Когда частота катодной защиты импульсного тока выше 500 Гц, значения потенциала катодной защиты импульсного тока на электроде сравнения 3 и электроде сравнения 4 выше, чем у катодной защиты постоянного тока.

На рисунке 8 показан эффект катодной защиты от импульсного тока для ввода с рабочим циклом 70% на разных частотах. Анализируя рисунок 8, можно получить следующие результаты. Защитный потенциал на электроде сравнения 1 находится в состоянии повышенной защиты из-за более высокого защитного потенциала.Защитный потенциал электрода сравнения 2 находится в диапазоне защитных потенциалов, и он эффективно защищен. Защитные потенциалы на электроде сравнения 3 и электроде сравнения 4 ниже, чем в диапазоне потенциалов катодной защиты, который не достигает катодной защиты. При катодной защите постоянного тока защитные потенциалы электрода сравнения 1 и электрода сравнения 2 находятся в диапазоне от -0,77 В до -1,03 В, а защитные потенциалы электрода сравнения 3 и электрода сравнения 4 ниже, чем потенциал катодной защиты, который не были эффективно защищены.Экспериментальные результаты катодной защиты по постоянному току и катодной защиты по импульсному току показывают, что потенциал защиты катодной защиты по импульсному току выше, чем у катодной защиты по постоянному току на разных частотах.

Путем объединения рисунков 6–8 была рассчитана разница данных. Набор различий был получен путем вычитания данных о потенциале катодной защиты на фиг. 7 из данных о потенциале катодной защиты на фиг. 6. Конкретный метод заключался в вычитании потенциала катодной защиты, измеренного в том же положении и на той же частоте.Результаты расчета представлены в таблице 4.

500 Гц 1500 Гц 2500 Гц 3500 Гц 4500 Гц 5500 Гц
4500 Гц		 5500 Гц
Электрод сравнения 1 мВ −11 −43 −15 −47 73 60
Электрод сравнения 2 мВ 22 41.6 71,7 75,9 52,6 8,9
Электрод сравнения 3 мВ 6,5 −5,8 20,7 49,4 48,2 14,9 0,6 30,1 43,3 55,1 7,1

Таким же образом, другой набор разностей был получен путем вычитания 8 потенциальных данных защиты от катодной защиты. данные о потенциале катодной защиты на Рисунке 7.Результаты расчетов представлены в Таблице 5.

500 Гц 1500 Гц 2500 Гц 3500 Гц 4500 Гц 5500 Гц
4500 Гц		 5500 Гц
Электрод сравнения 1 мВ 39 83 67 39 −3 17
Электрод сравнения 2 мВ 64.9 2 −33,1 25,8 −19,5 7,7
Электрод сравнения 3 мВ 32,8 21,6 −15,1 6126 −2 61 −2 61 −2 Электрод сравнения 4 мВ 13,3 8,5 −5,3 −49,4 −31,1 4

, 5 если рабочий цикл импульсного источника питания составляет 50%, разница между контрольным электродом 2, контрольным электродом 3 и контрольным электродом 4 положительна, поэтому защитный эффект лучше, чем при рабочем цикле 20%.Когда рабочий цикл импульсного источника питания составляет 70%, разница между электродом сравнения 2, электродом сравнения 3 и электродом сравнения 4 оказывается отрицательной. Следовательно, оптимальный параметр рабочего цикла составляет 50%. На рисунке 7 показано, что при частоте 3500 Гц потенциал катодной защиты является наибольшим у электрода сравнения 2, электрода сравнения 3 и электрода сравнения 4, поэтому оптимальная частота составляет 3500 Гц. Таким образом, можно видеть, что, когда рабочий цикл составляет 50%, а частота составляет 3500 Гц, эффект катодной защиты импульсного тока лучше, чем эффект катодной защиты постоянного тока, и эффект защиты является лучшим.Таким образом, можно сделать вывод, что защитный эффект лучше, когда частота подходит в середине, а рабочий цикл составляет 50% при испытании. Приведенные выше результаты моделирования служат эталоном для применения технологии катодной защиты импульсным током в реальной системе обсадных труб нефтяных скважин.

4.3. Влияние анодного расстояния на катодную защиту импульсного тока

В соответствии с оптимальными параметрами ( F = 3500 Гц), полученными в результате вышеуказанных испытаний моделирования, распределение потенциала катодной защиты для каждой точки измерения показано на рисунке 9.


На рисунке 9 показана кривая распределения потенциала на поверхности кожуха при разном анодном расстоянии D. Когда анодное расстояние D составляет 1 см, распределение точек на поверхности кожуха составляет от 698 до 1061 мВ. В верхней части корпуса (у электрода сравнения 1) начало проявляться явление чрезмерной защиты, в то время как нижняя часть (у электрода сравнения 3) еще не достигла эффективной защиты. При D 5 см диапазон распределения точек на поверхности кожуха составляет 705–1067 мВ.Верхняя часть корпуса (у электрода сравнения 1) все еще защищена, но это не очевидно. Нижняя часть (у электрода сравнения 4) все еще не эффективна, но она улучшается, когда D составляет 1 см. Когда D составляет 10 см, распределение точек на поверхности обсадной колонны составляет от 735 до 1014 мВ. В верхней части (у электрода сравнения 1) нет избыточной защиты. Нижняя часть (у электрода сравнения 4) кожуха по-прежнему не работает. Когда D составляет 20 см, точечное распределение на поверхности корпуса составляет от 666 до 1059 мВ.В верхней части трубки (у электрода сравнения 1) начало проявляться явление чрезмерной защиты, а в нижней части (у электрода сравнения 4) еще не достигнута эффективная защита.

Из анализа приведенных выше результатов мы можем сделать очень важный вывод: в этом эксперименте существует оптимальное анодное расстояние. Однако, только регулируя анодное расстояние, нельзя полностью защитить весь корпус; то есть из анализа экспериментальных данных, когда анодное расстояние составляет 10 см, защитный эффект всего кожуха лучше.Поэтому очень сложно добиться эффективной защиты всей линии, регулируя только значение D . В это время следует соответствующим образом отрегулировать параметры импульсного тока.

5. Выводы

При использовании импульсного тока для катодной защиты обсадных труб нефтяных скважин, распределенных в бассейне Шэньси-Ганьсу-Нинся, на основе приведенного выше теоретического анализа и экспериментов можно сделать следующие выводы: (1) Катод будет лучше защищен. когда параметры катодной защиты импульсного тока выбраны на более высокой частоте и умеренном рабочем цикле (2) Существует оптимальное значение анодного расстояния, благодаря которому система импульсной катодной защиты обеспечивает лучший защитный эффект

Доступность данных

данные, использованные для подтверждения выводов этого исследования, можно получить у соответствующего автора по запросу.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов.

Благодарности

Это исследование было выполнено при финансовой поддержке Координационного инновационного проекта науки и технологий провинции Шэньси (грант № 2013KTCL-04).

ГЛАВА-4

ГЛАВА-4

Глава 4

ЯМР СПЕКТРОСКОПИЯ

Сигнал ЯМР во временной области

Когда поперечная намагниченность вращается вокруг оси Z, она индуцирует ток в катушке с проволокой, расположенной вокруг оси X.График зависимости тока от времени дает синусоидальную волну. Эта волна, конечно, будет затухать с постоянной времени. Т 2 * из-за расфазировки спин-пакетов. Этот сигнал называется свободным индукционным затуханием (FID). Мы увидим в главе 5 как FID преобразуется в спектр частотной области.

Соглашение о частоте +/-

Векторы поперечной намагниченности, вращающиеся быстрее, чем вращающаяся система отсчета, называются вращающимися с положительной частотой относительно вращающейся системы координат (+).Векторы, вращающиеся медленнее, чем вращающаяся рамка, называются вращающимися с отрицательной частотой относительно вращающейся рамки. (-).

Последовательность 90-FID

Набор РЧ-импульсов, применяемых к образцу для получения определенной формы ЯМР-сигнала, называется последовательностью импульсов. В последовательности импульсов 90-FID чистая намагниченность поворачивается вниз в плоскость X’Y ‘с Импульс 90 °. Вектор суммарной намагниченности начинает прецессировать вокруг оси + Z.Величина вектора также убывает со временем.

Временная диаграмма — это многоосевой график некоторого аспекта последовательности импульсов в зависимости от времени. Временная диаграмма для последовательности импульсов из 90 FID имеет график зависимости РЧ-энергии от времени и другой график зависимости сигнала от времени.

Когда эта последовательность повторяется, например, когда требуется улучшение отношения сигнал-шум, амплитуда сигнала после преобразования Фурье (S) будет зависеть от T 1 и время между повторениями, называемое временем повторения (TR) последовательности.В приведенном ниже уравнении сигнала k — константа пропорциональности и — плотность спинов в образце.

S = к (1 — e -TR / T1 )

Последовательность спин-эхо

Другой часто используемой импульсной последовательностью является импульсная последовательность спинового эха. Здесь сначала к спиновой системе прикладывается импульс 90 °. Импульс 90 ° поворачивает намагниченность вниз в плоскость X’Y ‘. Поперечная намагниченность начинает сбрасываться по фазе.

В некоторый момент времени после импульса 90 ° применяется импульс 180 °. Этот импульс поворачивает намагниченность на 180 ° вокруг оси X ‘.

180 o Импульс заставляет намагниченность, по крайней мере, частично перефазировать и генерировать сигнал, называемый эхом.

На временной диаграмме показаны относительные положения двух радиочастотных импульсов и сигнала.

Уравнение сигнала для повторяющейся последовательности спин-эхо как функция времени повторения TR и времени эхо-сигнала (TE), определяемого как время между импульсом 90 o и максимальной амплитудой в эхо-сигнале, составляет

S = k & rho (1 — e -TR / T1 ) e -TE / T2

Это уравнение действительно только при TR >> TE.

Последовательность восстановления инверсии

Последовательность импульсов восстановления с инверсией также может использоваться для записи спектра ЯМР. В этой последовательности 180 ° сначала применяется импульс. Это поворачивает чистую намагниченность вниз к оси -Z. Намагниченность претерпевает релаксацию спиновой решетки и возвращается к своему положению равновесия вдоль оси + Z. Прежде чем он достигнет равновесия, применяется импульс под углом 90 °, который поворачивает продольную намагниченность в плоскости XY.В этом примере импульс 90 ° применяется вскоре после импульса 180 °. Как только намагниченность присутствует в плоскости XY, она вращается вокруг оси Z и меняет фазу, образуя FID.

Еще раз, на временной диаграмме показаны относительные положения двух радиочастотных импульсов и сигнала.

Сигнал как функция TI, когда последовательность не повторяется:

S = k ρ (1-2e -TI / T1 )

Следует отметить, что переход через нуль этой функции происходит для TI = T 1 ln 2.

Когда последовательность восстановления инверсии повторяется каждые TR секунд, для усреднения сигнала или визуализации, уравнение сигнала становится S = k ρ (1 — 2e -TI / T1 + e -TR / T1 ).

Химическая смена

Когда атом находится в магнитном поле, его электроны циркулируют вокруг направления приложенного магнитного поля. Эта циркуляция вызывает небольшое магнитное поле в ядре, которое противодействует приложенному извне полю.

Магнитное поле в ядре (эффективное поле), следовательно, обычно меньше приложенного поля на долю σ.

B = B o (1-σ)

Электронная плотность вокруг каждого ядра в молекуле варьируется в зависимости от типов ядер и связей в молекуле. Противоположное поле и, следовательно, эффективное поле в каждом ядре будут различаться. Это называется явлением химического сдвига.

Рассмотрим молекулу метанола.Резонансные частоты двух типов ядер в этом примере различаются. Эта разница будет зависеть от силы магнитного поля, B o , используется для проведения ЯМР-спектроскопии. Чем больше значение B o , тем больше разница частот. Эта взаимосвязь может затруднить сравнение спектров ЯМР, снятых на спектрометрах, работающих при разной напряженности поля. Термин химический сдвиг был разработан, чтобы избежать этой проблемы.

Химический сдвиг ядра — это разница между резонансной частотой ядра и стандартной, относительно стандарта. Это количество указывается в ppm и обозначается символом дельта, d.

δ = (ν — ν REF ) x10 6 / ν REF

В ЯМР-спектроскопии этим стандартом часто является тетраметилсилан, сокращенно ТМС. В организме нет ТМС, но есть два основных водородсодержащих вещества — вода и жир.Разница в химическом сдвиге между этими двумя типами водорода составляет примерно 3,5 ppm.

Проблемы

  1. С точки зрения 1 H ЯМР, человеческое тело состоит в основном из жировых водородов (-CH 2 -) и водных водородов (H 2 O). Разница резонансных частот между сигналом ЯМР от этих двух типов водорода составляет приблизительно 220 Гц на тепловизоре 1,5 Тесла. В чем разница химического сдвига?
  2. Значения водорода T 1 , T 2 и спиновой плотности для обычных тканей мозга перечислены в следующей таблице.
    Ткань T 1 (с) T 2 (мс) ρ *
    CSF 0,8 — 20 110-2000 70-230
    Белый 0,76 — 1,08 61-100 70-90
    Серый 1,09 — 2,15 61-109 85-125
    Менинги 0,5 — 2.2 50–165 5–44
    Мышцы 0,95 — 1,82 20-67 45-90
    Жир 0,2 — 0,75 53-94 50-100
    * На основе ρ = 111 для 12 мМ водного NiCl 2

    При каком значении TI сигнал от жира приблизительно равен нулю в последовательности восстановления с инверсией?

  3. При использовании последовательности импульсов 90-FID и образца, содержащего все ткани, о которых идет речь, номер два, какое значение TR будет гарантировать не менее 98% сигнала от всех тканей?
  4. Вы используете последовательность импульсов спин-эхо и образец жировой ткани в вопросе номер два.Если минимальное значение TE, которое вы можете получить, составляет 20 мс, сколько больше сигнала вы можете получить с последовательностью 90-FID?
  5. С точки зрения ЯМР 1 H, человеческое тело состоит в основном из жировых водородов (-CH 2 -) с химическим сдвигом ~ 1 PPM и водных водородов (H 2 O) с химическими веществами. сдвиг ~ 4,5 промилле. Какова разница в резонансной частоте сигнала ЯМР от этих двух типов водорода?
  6. Значения водорода T 1 , T 2 и спиновой плотности для обычных тканей мозга перечислены в следующей таблице.
    Ткань T 1 (с) T 2 (мс) ρ *
    CSF 0,8 — 20 110-2000 70-230
    Белый 0,76 — 1,08 61-100 70-90
    Серый 1,09 — 2,15 61-109 85-125
    Менинги 0,5 — 2.2 50–165 5–44
    Мышцы 0,95 — 1,82 20-67 45-90
    Жир 0,2 — 0,75 53-94 50-100
    * На основе ρ = 111 для 12 мМ водного NiCl 2

    При каких значениях TR и TE сигнал от белого вещества примерно равен сигналу от серого вещества в последовательности импульсов спинового эха?

  7. При использовании последовательности импульсов восстановления с инверсией и образца, содержащего все ткани, о которых идет речь, номер два, какое значение TI, превышающее 2 мс, будет гарантировать не менее 90% сигнала от всех тканей?
  8. Вы используете последовательность импульсов 90-FID и образец ткани мозга, о котором идет речь.Насколько меньше сигнала будет для жировой ткани при TR = 100 мс, чем при TR = 500 мс?
Перейдите к: [следующей главе | начало главы | предыдущая глава | крышка]

Авторские права © 1996-2019 J.

No related posts.

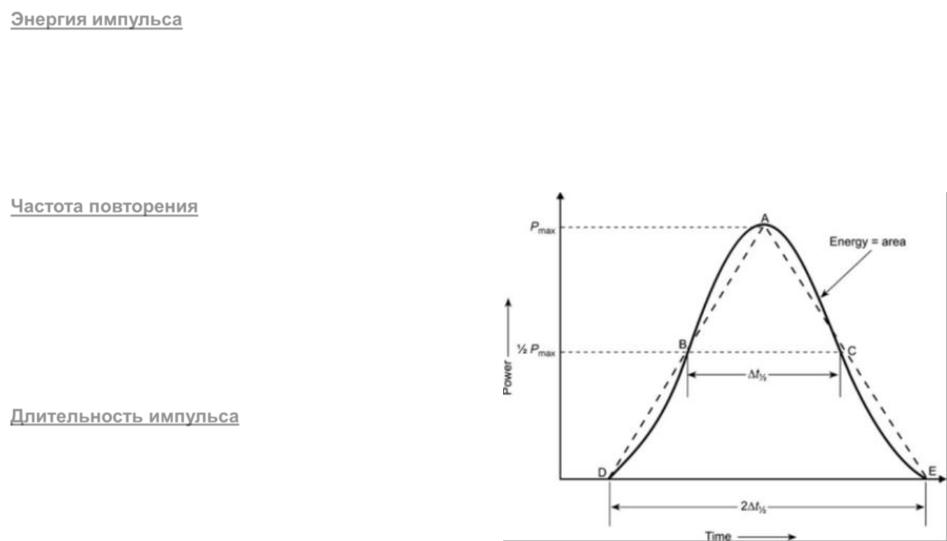
Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *