Частота вращения это в физике: Частота вращения (обращения) — БилдоМан

Содержание

HydroMuseum – Частота вращения

Частота вращения

Частота вращения—физическая величина, характеристика периодического процесса, равная числу полных циклов, совершённых за единицу времени. Стандартные обозначения в формулах — υ, f, ω или F. Единицей частоты в Международной системе единиц (СИ) в общем случае является Герц (Гц, Hz). Величина, обратная частоте, называется периодом.

Периодический сигнал характеризуется мгновенной частотой, являющейся скоростью изменения фазы, но тот же сигнал можно представить в виде суммы гармонических спектральных составляющих, имеющих свои частоты. Свойства мгновенной частоты и частоты спектральной составляющей различны, подробнее об этом можно прочитать, например, в книге Финка «Сигналы, помехи, ошибки».

В теоретической физике, а также в некоторых прикладных электрорадиотехнических расчётах удобно использовать дополнительную величину — циклическую (круговую, радиальную, угловую) частоту (обозначается

ω).

Циклическая частота связана с частотой колебаний соотношением ω=2πf. В математическом смысле циклическая частота — это первая производная полной фазы колебаний по времени. Единица циклической частоты — радиан в секунду (рад/с, rad/s) .

В механике при рассмотрении вращательного движения аналогом циклической частоты служит угловая скорость.

Частота дискретных событий (частота импульсов) — физическая величина, равная числу дискретных событий, происходящих за единицу времени. Единица частоты дискретных событий секунда в минус первой степени (с⁻¹

, s⁻¹), однако на практике для выражения частоты импульсов обычно используют герц.

Частота вращения — это физическая величина, равная числу полных оборотов за единицу времени. Единица частоты вращения — секунда в минус первой степени (с⁻¹, s⁻¹), оборот в секунду. Часто используются такие единицы, как оборот в минуту, оборот в час и т. д.

Другие величины, связанные с частотой

Ширина полосы частот — f_max − f_min
Частотный интервал — log(f_max/f_min)
Девиация частоты —Δf/2
Период — 1/f
Длина волны — υ/f
Угловая скорость (скорость вращения) — dφ/ dt; 2πF_BP

Метрологические аспекты

Измерения

Для измерения частоты применяются частотомеры разных видов, в том числе: для измерения частоты импульсов — электронно-счётные и конденсаторные, для определения частот спектральных составляющих — резонансные и гетеродинные частотомеры, а также анализаторы спектра.

Для воспроизведения частоты с заданной точностью используют различные меры — стандарты частоты (высокая точность), синтезаторы частот, генераторы сигналов и др.

Сравнивают частоты компаратором частоты или с помощью осциллографа по фигурам Лиссажу.

Эталоны

Государственный первичный эталон единиц времени, частоты и национальной шкалы времени ГЭТ 1-98 — находится во ВНИИФТРИ

Вторичный эталон единицы времени и частоты ВЭТ 1-10-82 — находится в СНИИМ (Новосибирск)

Частота вращения — это… Что такое Частота вращения?

Частота вращения

Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке

Угловая скорость (синяя стрелка) в одну единицу против часовой стрелки

Углова́я ско́рость — векторная величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли, просто «вручную» подсчитывая число оборотов за единицу времени.

Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью определяется формулой:

где — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) r от оси вращения можно считать так: v = rω. Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.

В случае плоского вращения, то есть когда все векторы скоростей точек тела лежат (всегда) в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.

Производная угловой скорости по времени есть угловое ускорение.
Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю).
Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчета, однако в разных инерциальных системах отсчета может различаться ось или центр вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
В случае движения одной единственной точки в трехмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:

, где — радиус-вектор точки (из начала координат), — скорость этой точки. — векторное произведение, — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.

При измерении угловой скорости в оборотах в секунду (об/с), модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц) (то есть в таких единицах ).

В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости связан с частотой вращения так:

Наконец, при использовании градусов в секунду связь с частотой вращения будет:

См. также

Wikimedia Foundation. 2010.

Частота сети
Частота сердечных сокращений

Смотреть что такое «Частота вращения» в других словарях:

частота вращения ВК — частота вращения ветроколеса Угол, проходимый лопастью ВК за единицу времени, измеренный в оборотах в единицу времени или в радианах. [ГОСТ Р 51237 98] Тематики ветроэнергетика Синонимы частота вращения ветроколеса EN rotation speed … Справочник технического переводчика
частота вращения — частота вращения … Справочник технического переводчика
Частота вращения — 3. 113 Частота вращения число оборотов в единицу времени. Источник: ГОСТ Р МЭК 1029 2 4 96: Машины переносные электрические. Частные тр … Словарь-справочник терминов нормативно-технической документации
частота вращения — sukimosi dažnis statusas T sritis automatika atitikmenys: angl. rotating speed; rotation frequency; rotational speed vok. Drehgeschwindigkeit, f; Rotationsgeschwindigkeit, f rus. скорость вращения, f; частота вращения, f pranc. fréquence de… … Automatikos terminų žodynas
частота вращения — sūkių dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Kūno sukimosi apie tam tikrą ašį dažnis, išreiškiamas sūkių skaičiumi per vienetinį laiko tarpą. atitikmenys: angl. rotating frequency; rotating speed; rotation frequency;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Частота вращения w — 69. Частота вращения w Угловая скорость вращения поворотной части крана в установившемся режиме движения. Определяется при наибольшем вылете с рабочим грузом при установке крана на горизонтальной площадке и скорости ветра не более 3 м/с на высоте … Словарь-справочник терминов нормативно-технической документации
частота вращения — sukimosi dažnis statusas T sritis fizika atitikmenys: angl. rotation frequency vok. Rotationsfrequenz, f; Umlauffrequenz, f rus. частота вращения, f pranc. fréquence de rotation, f … Fizikos terminų žodynas
ЧАСТОТА ВРАЩЕНИЯ — величина, равная отношению числа оборотов, совершённых телом, ко времени вращения. Обозначается обычно п. Единица Ч. в. (в СИ) с 1. Внесистемные единицы об/мин и об/с … Большой энциклопедический политехнический словарь
частота вращения — rotation frequency Число оборотов вращающегося звена в единицу времени. Шифр IFToMM: Раздел: СТРУКТУРА МЕХАНИЗМОВ … Теория механизмов и машин
частота вращения ротора (вала) ГТД в режиме сопровождения — частота вращения режима сопровождения Частота вращения ротора ГТД при запуске в момент отключения пускового устройства. [ГОСТ 23851 79] Тематики двигатели летательных аппаратов Синонимы частота вращения режима сопровождения … Справочник технического переводчика

Пульсация светового потока

На многие вещи, связанные с повседневной деятельностью человека, зачастую влияет качество света—это давно известный факт. Иногда мы даже не задумываемся о последствиях—процессы проходят на подсознательном уровне, почти как во сне. Как снизить нагрузку на мозг в четыре раза и увеличить эффективность труда, а также о других эффектах пульсации светового потока—подробнее в нашей статье.

В двух словах

Пульсация светового потока = эффект мерцания.

Снижение пульсаций источника света является важной составляющей в борьбе за качество света. В последнее время одним из заметных трендов на рынке LED-освещения становится гонка за нулевым значением коэффициента пульсации. Так ли это важно на самом деле, давайте разбираться

Подробнее о коэффициенте пульсации

Пульсация светового потока—это одна из основных характеристик источников искусственного освещения, отражающая частоту мерцания и качество света в целом. Характеризуется данный эффект специальным параметром—коэффициентом пульсации.

Для тех, кто любит формулы и ГОСТы

Коэффициент пульсации—это относительная величина и измеряется она в % от разности максимального и минимального значений освещенности в люксах, приведенная к усредненному значению освещенности за период.

В России ограничения по значениям Kп светильников регламентируются СНиП 23-05-95, ГОСТ 17677-82 и СанПиН 2.2.2/2.4.1340-03. В Европе и США подобных норм не существует. Основные ограничения, существующие в России:

Пульсации освещенности, частотой до 300 Гц, на рабочих местах не должны превышать 20%, в некоторых случаях (при работе с ПЭВМ) – 5%.
В местах временного пребывания (коридоры, лестницы, переходы и т.п.) уровень пульсации не нормируется.
Не нормируются пульсации освещенности, частота которых превышает 300 Гц.

Предыстория появления эффекта

Физика работы LED такова, что включение диода возможно только при определенном значении силы тока и его направлении. Для подключения светодиодных светильников в цепях переменного напряжения (бытовой сети) и управления их яркостью мы, как специалисты-светотехники, вынуждены применять специальные пускорегулирующие устройства—LED-драйверы и диммеры с широтно-импульсной модуляцией—ШИМ (о ней читайте в нашей следующей статье).

И здесь все просто—колебания тока на выходе таких устройств порождает колебания светового потока LED, именно поэтому применение пускорегулирующей аппаратуры в системах освещения порождают подобный специфический эффект.

В этом плане обычная лампа накаливания подвержена тем же самым воздействиям со стороны питающей сети. Однако, она более инертна по своим характеристикам, поэтому мерцания частотой в 50 Гц фактически отсутствуют.

Теперь немного о том, как пульсация света может влиять на самочувствие человека и чем она опасна.

О пороге восприятия частоты пульсаций света и их влияние на человека

В большинстве случаев человеческий глаз не фиксирует пульсацию источника искусственного света, поскольку существует определенный порог восприятия, связанный с особенностями нашего зрения и частотой самих пульсаций.

Многократными исследованиями доказано, что критическая частота восприятия пульсаций—300 Гц, при достижении этого значения человеческий мозг перестает воспринимать их как таковые. При частоте до 120 Гц мозг на подсознательном уровне воспринимает пульсацию как некий “месседж” и пытается его обработать. Считается, что таким образом, человек воспринимает до 4 частот мерцаний от различных источников света, что в значительной степени повышает “загруженность” его центрального вычислителя—головного мозга.

Можно выделить два вида влияний пульсации светового потока на человека: краткосрочные и долгосрочные, см. таблицу 1.

Таблица 1

Влияние пульсаций на человека

Краткосрочное влияние	Долгосрочное влияние
усталость органов зрения снижение внимания утомляемость организма замедление активности мозга тошнота и нарушение пищеварения нарушение циркадных ритмов	депрессия бессонница патология сердечно-сосудистой системы патология органов зрения патология ЖКТ эректильная дисфункция расстройство НС

Стробоскопический эффект — положительные и отрицательные стороны

Наиболее опасным последствием пульсации света можно назвать стробоскопический эффект на промышленных объектах, где присутствуют быстро движущиеся открытые механизмы и детали машин. Частота их вращения может совпасть с частотой мерцания света и может показаться, что механизм неподвижен, что зачастую является причиной серьезных травм и повреждений, см.рисунок ниже

Эффект мерцания источника света может быть зафиксирован при фото- и видеосъемке на коротких выдержках—тот эффект, о котором было рассказано в самом начале статьи. Данный неприятный момент может испортить не только несколько фотографий, но и испортить имидж студий и съемочных павильонов.

Световое оборудование для клубов и концертных площадок

Лазерные и диодные стробоскопы—это одни из самых распространенных световых девайсов, которые любят применять в клубах и на дискотеках. Интересный кратковременный световой эффект повышает настроение посетителям и является абсолютно безвредным для человека.

В заключение от Aledo

В последнее время нам все чаще приходится слышать о том, что на рынке появляются светильники с коэффициентом пульсации 1-2%—это результат борьбы производителей LED за конкурентные преимущества, о которых мы писали в самом начале статьи.

Наша позиция в этом вопросе такова: коэффициент пульсации источника света 20%—это абсолютно нормальное и допустимое значение, обозначенное в ГОСТе и СанПиНе. Конечно, существуют условия труда и быта человека, где необходимо максимальное снижение Kп (до 5% и ниже), но это весьма частные и редкие случаи. Мы всегда стараемся анализировать проект, исходим из реальных потребностей наших клиентов и предлагаем наиболее рациональные варианты для систем освещения.

Кстати, в шоуруме kaledoscop есть специальный прибор, который мы используем для тестирования наших решений и поставляемого оборудования,—пульсометр. Приезжайте к нам в гости, за чашкой кофе или чая, мы сможем показать на деле, что такое пульсация светового потока и какие решения существуют в России и мире для снижения подобного эффекта.

Равномерное движение по окружности. Скорость, ускорение

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: движение по окружности с постоянной по модулю скоростью, центростремительное ускорение.

Равномерное движение по окружности — это достаточно простой пример движения с вектором ускорения, зависящим от времени.

Пусть точка вращается по окружности радиуса . Скорость точки постоянна по модулю и равна . Скорость называется линейной скоростью точки.

Период обращения — это время одного полного оборота. Для периода имеем очевидную формулу:

. (1)

Частота обращения — это величина, обратная периоду:

Частота показывает, сколько полных оборотов точка совершает за секунду. Измеряется частота в об/с (обороты в секунду).

Пусть, например, . Это означает, что за время точка совершает один полный
оборот. Частота при этом получается равна: об/с; за секунду точка совершает 10 полных оборотов.

Угловая скорость.

Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат в центре окружности (рис. 1).

Рис. 1. Равномерное движение по окружности

Пусть — начальное положение точки; иными словами, при точка имела координаты . Пусть за время точка повернулась на угол и заняла положение .

Отношение угла поворота ко времени называется угловой скоростью вращения точки:

. (2)

Угол , как правило, измеряется в радианах, поэтому угловая скорость измеряется в рад/с. За время, равное периоду вращения, точка поворачивается на угол . Поэтому

. (3)

Сопоставляя формулы (1) и (3), получаем связь линейной и угловой скоростей:

. (4)

Закон движения.

Найдём теперь зависимость координат вращающейся точки от времени. Видим из рис. 1, что

Но из формулы (2) имеем: . Следовательно,

. (5)

Формулы (5) являются решением основной задачи механики для равномерного движения точки по окружности.

Центростремительное ускорение.

Теперь нас интересует ускорение вращающейся точки. Его можно найти, дважды продифференцировав соотношения (5):

С учётом формул (5) имеем:

(6)

Полученные формулы (6) можно записать в виде одного векторного равенства:

(7)

где — радиус-вектор вращающейся точки.

Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительным.

Кроме того, из формулы (7) мы получаем выражение для модуля центростремительного ускорения:

(8)

Выразим угловую скорость из (4)

и подставим в (8). Получим ещё одну формулу для центростремительного ускорения:

Вращательное движение

Страница 1 из 3

Существует большое количество расчетных задач, которые моделируют явления, происходящие в различных вращающихся агрегатах или около них. При постановке подобной численной задачи важно выбрать способ описания вращения в численной модели, который будет корректен с точки зрения физики и оптимален с точки зрения производительности вычислений. FlowVision позволяет задавать вращение различными способами: с помощью вращающейся локальной системы координат; с помощью подвижных тел; с помощью скользящих поверхностей. С целью помочь пользователю разобраться с постановкой такого типа задач, рассмотрены примеры задач разного типа, начиная с физико-математических основ.

1. Кинематика вращательного движения

1.1. Вращательное движение материальной точки

Вращательное движение материальной точки (м.т.) вокруг неподвижной оси – это движение материальной точки по окружности радиуса R, центр которой лежит на неподвижной относительно данной системы отсчета прямой (ось вращения), перпендикулярной плоскости, в которой лежит траектория точки.

Рис.1.

Вращательное движение тела вокруг неподвижной оси — движение тела, при котором все его точки, двигаясь в параллельных плоскостях, описывают окружности с центрами, лежащими на одной неподвижной прямой, называемой осью вращения. Тело, совершающее вращательное движение, имеет одну степень свободы, и его положение относительно данной системы отсчёта определяется углом поворота φ между неподвижной полуплоскостью и полуплоскостью, жёстко связанной с телом, проведёнными через ось вращения.

Рис.2.

1.2. Угол поворота

Угол φ считается положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси Az), и отрицательным, если по ходу часовой стрелки. Чтобы знать положение в любой момент времени, надо знать зависимость угла φ от времени t, т.е. φ=f(t).

1.3. Основные кинематические характеристики вращательного движения

Основными кинематическими характеристиками вращательного движения являются угловая скорость и угловое ускорение .
Угловая скорость и угловое ускорение величины векторные. Вектор угловой скорости направлен вдоль оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис.3). Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси. Аналогично углу поворота, когда вращение происходит против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси Az) ω>0, а когда по ходу часовой стрелки, то ω<0. Таким образом, знак ωопределяет направление вращения.
а) б) в)

Рис.3

1.4. Прочие кинематические характеристики

Скорость точки M на расстоянии R от оси (рис.2):

Тангенциальная составляющая ускорения точки M (рис.3б):

Нормальная составляющая ускорения точки M (рис.3б):

Полное ускорение точки M (рис.3б):

Формула Эйлера (рис.3в):

2. Силы инерции, действующие на материальную точку во вращающейся системе отсчета

2.

1. Материальная точка, покоящаяся во вращающейся системе отсчета

Если рассмотреть движение вращающейся точки M, то относительно неподвижной системы координат (СК) XYZ (рис.4а) силу, действующую на неё можно определить из второго закона Ньютона: . Относительно вращающейся системы координат X’Y’Z’ точка M неподвижна (рис.4б). Это обеспечивается тем, что равнодействующая сил уравновешивается инерциальной силой (центробежной): .

Рис.4 (а,б)

2.2. Материальная точка, движущаяся во вращающейся системе отсчета

Если же точка движется во вращающейся системе отсчета, то помимо центробежной силы на неё действует ещё одна сила инерции – сила Кориолиса (рис.5). Направление силы Кориолиса определяется правилом правого винта.

Рис. 5.

Таким образом, при переходе от основной неподвижной СК к локальной СК, которая является вращающейся системой отсчета, появляются дополнительные составляющие вектора силы, которые действуют на материальную точку: центробежная сила и сила Кориолиса .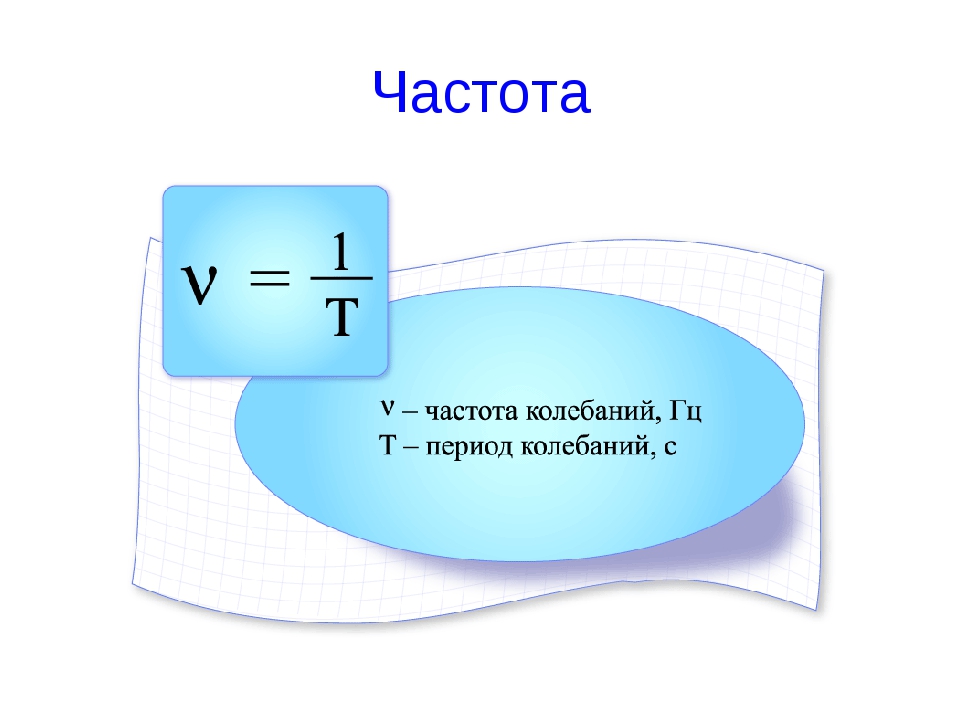

О Росстандарте

Федеральное агентство по техническому регулированию и метрологии входит в систему федеральных органов исполнительной власти Российской Федерации и находится в ведении Министерства промышленности и торговли Российской Федерации.

Ведомство образовано в соответствии с Указом Президента Российской Федерации от 20 мая 2004 г. № 649 «Вопросы структуры федеральных органов исполнительной власти».

Федеральное агентство по техническому регулированию и метрологии является федеральным органом исполнительной власти, осуществляющим функции по оказанию государственных услуг, управлению государственным имуществом в сфере технического регулирования и метрологии. До внесения изменений в законодательные акты Российской Федерации Федеральное агентство по техническому регулированию и метрологии осуществляет лицензирование деятельности по изготовлению и ремонту средств измерений, а также функции по государственному метрологическому контролю и надзору. Федеральное агентство осуществляет также контроль и надзор за соблюдением обязательных требований национальных стандартов и технических регламентов до принятия Правительством Российской Федерации решения о передаче этих функций другим федеральным органам исполнительной власти.

Федеральное агентство по техническому регулированию и метрологии ведет свою деятельность в соответствии с Положением, утвержденным постановлением Правительства Российской Федерации от 17 июня 2004 г. № 294.

Федеральное агентство по техническому регулированию и метрологии осуществляет свою деятельность непосредственно, через свои территориальные органы и через подведомственные организации.

Коллегиальным совещательным органом является Коллегия Федерального агентства по техническому регулированию и метрологии, совещательно-консультативным коллегиальным органом при Федеральном агентстве является Общественный совет.

Приказом Росстандарта от 2 декабря 2016 г. № 1860 (pdf , 0.41 Мб) утверждено Положение о Журнале (pdf , 0.02 Мб) «Вестник Федерального агентства по техническому регулированию и метрологии».

1.1.2. Долговечность | ZKL Group

Долговечность (ресурс) подшипника определяется количеством оборотов, совершаемых одним кольцом относительно второго до тех пор, пока не появятся первые признаки усталости материала одного из колец или тел качения.

Однако долговечность подшипников одного типа может значительно отличаться, поэтому для расчета долговечности согласно STN ISO 281 используется базовая долговечность, представляющая собой время эксплуатации, которого достигнет или превысит группа подшипников с надежностью 90%.

Формула базовой долговечности

Базовая долговечность подшипника математически определяется формулой, которая действительна для всех типов подшипников.

L₁₀ – базовая долговечность [10⁶ об]

C – базовая динамическая грузоподъемность 
(значения C_r, C_a приведены в табличной части) [кН]

P – эквивалентная динамическая нагрузка подшипника (формулы для расчета P_r, P_a  приведены в п. 1.1.3 и при каждой конструктивной группе подшипников) [кН]

p – показатель степени для шарикоподшипников p = 3 
для цилиндрических, игольчатых, сферических и конических роликоподшипников

В таблице 1 приведена зависимость долговечности L₁₀ в миллионах оборотов и соответствующее соотношение C/P. Если частота вращения не меняется, для расчета долговечности можно использовать видоизмененную формулу, которая определяет базовую долговечность в часах работы:

[h]

L_10h – базовая долговечность [ч]

n – частота вращения [мин^-1]

Зависимость соотношения C/P от базовой долговечности L_10h и частоты вращения n приведена для шарикоподшипников в таблице 2, а для цилиндрических, игольчатых, сферических и конических роликоподшипников – в таблице 3.

Для опор осей дорожных и рельсовых транспортных средств базовую долговечность можно выразить видоизмененной формулой в количестве пройденных километров.

L_10ч – базовая долговечность [10⁶км]

D – диаметр колеса [м]

Ориентировочные значения базовой долговечности

Если для данного варианта опоры не установлена заранее долговечность, можно ориентироваться на значения, приведенные в таблицах 4 и 5.

Формула скорректированной долговечности

Скорректированная долговечность – это базовая долговечность, при расчете которой, кроме нагрузки, учитывается влияние материала деталей подшипника, физико-механические и химические свойства смазки, а также температурный режим работы подшипника.

L_na – скорректированная долговечность для надежности (100-n) %

и условий работы, отличающихся от стандартных [10⁶ об]

a₁ — коэффициент надежности, если она отличается от 90%-й, см. таблицу 6

a₂₃ — коэффициент материала, смазки, технологии производства и условий эксплуатации, смотри рис. 1

L₁₀ – базовая долговечность [10⁶об]

Для базового определения значений коэффициента a₂₃ следует исходить из диаграммы на рисунке 1.

υ – кинематическая вязкость смазки при рабочей температуре подшипника [мм².с^-1]

υ ₁ – кинематическая вязкость для определенной частоты вращения и выбранного размера подшипника [мм². с^-1]

Значения для υ и υ ₁ определяем по диаграмме на рисунке 24 или 23.

В диаграмме на рис. 1, линия I относится к радиальным шарикоподшипникам, которые работают в очень чистой среде. В остальных случаях коэффициент a₂₃ принимается ниже в зависимости от чистоты среды, причем тенденция к снижению зависит от конструктивной группы подшипника и усиливается в следующем порядке:

— радиально-упорные шариковые подшипники

— конические роликовые подшипники

— цилиндрические роликовые подшипники

— двухрядные самоустанавливающиеся шариковые подшипники

— сферические роликовые подшипники

Линия II может использоваться при установлении коэффициента a₂₃ для сферических роликовых подшипников, которые работают в запыленной среде.

Калькулятор угловой скорости

Этот калькулятор угловой скорости представляет собой простой в использовании инструмент, который дает немедленный ответ на вопрос «Как найти угловую скорость?». В тексте вы найдете несколько формул угловой скорости, узнаете о различных единицах угловой скорости и, наконец, оцените угловую скорость Земли! Вы когда-нибудь задумывались, какова связь между угловой скоростью и угловой частотой или где применяется угловая скорость? Читайте дальше, чтобы узнать, и станьте экспертом в области кругового движения.

Что такое угловая скорость?

Угловая скорость описывает вращательное движение тел. Он измеряет, насколько быстро они перемещаются вокруг некоторого центра вращения. Мы можем думать о двух разных видах вращения. Первый описывает движение центра масс данного объекта вокруг определенной точки в пространстве , которую можно описать как начало координат. Некоторые примеры включают планеты, движущиеся вокруг Солнца, или автомобиль, съезжающий с шоссе.

Второй рассказывает о вращении тела вокруг собственного центра масс — спине (не путать с квантовым свойством частиц, также называемым спином). Вы наверняка видели, как баскетболист крутит мяч на пальце.

Как правило, можно сказать, что чем быстрее движение, тем выше угловая скорость. Чтобы определить некоторые конкретные значения, мы должны перейти к уравнениям угловой скорости, описанным в следующем разделе.

Формулы угловой скорости

В этом калькуляторе угловой скорости мы используем две разные формулы угловой скорости в зависимости от того, какие входные параметры у вас есть.

Первое уравнение угловой скорости аналогично уравнению для линейной скорости:

ω = (α₂ - α₁) / t = Δα / t ,

, где α₁ и α₂ — два значения углов на окружности, а Δα — их разность. t — время, за которое происходит изменение угла. Как видите, для нормальной скорости есть отношение изменения положения за период, а здесь мы используем угол вместо расстояния.

Вторая формула угловой скорости может быть получена из соотношения линейной скорости и радиуса с помощью векторного произведения, которое составляет:

v = ω × r .

Мы можем переписать это выражение, чтобы получить уравнение угловой скорости:

ω = r × v / | r | ² ,

, где все эти переменные являются векторами , а | r | обозначает абсолютное значение радиуса.Фактически угловая скорость — это псевдовектор, направление которого перпендикулярно плоскости вращательного движения.

Единицы угловой скорости

Существует несколько единиц угловой скорости, и те, которые используются в нашем калькуляторе угловой скорости, указаны ниже:

рад / с или радиан в секунду — определение, которое происходит прямо из первой формулы угловой скорости. Он сообщает, насколько велико вращение (или угол), через которое тело движется за заданное время,
об / мин или об / мин — единица, наиболее часто встречающаяся на практике.С его помощью вы можете описать, с какой скоростью вращается колесо или двигатель. Вы легко можете себе представить разницу между 10 и 100 об / мин .
Гц или герц — те же единицы измерения, которые используются для частоты, но редко используются в контексте угловой скорости. Это в некотором роде похоже на об / мин , говорящее нам, сколько полных оборотов совершается за заданное время. Разница в том, что раньше базовой единицей времени была минута, а здесь — секунда.

Естественно, все эти единицы угловой скорости конвертируются между собой с использованием следующих соотношений:

1 RMP = 0,10472 рад / с = 0,01667 Гц ,

или наоборот:

1 Гц = 6,283 рад / с = 60 об / мин .

Зависимость угловой скорости от угловой частоты

Посмотрите определение угловой частоты:

ω = 2 * π * f ,

, где f — частота.Как видим, обозначается той же буквой. Кроме того, единица угловой частоты — рад / с, , точно такая же, как и для угловой скорости. Так что может возникнуть вопрос: «В чем разница между угловой скоростью и угловой частотой?».

Ответ относительно прост. Соотношение между угловой частотой и угловой скоростью аналогично соотношению между , скоростью и скоростью . Первый — это величина второго, или, другими словами, угловая частота — это скаляр, а угловая скорость — это (псевдо) вектор.

Угловая частота обычно используется, когда говорят о гармоническом движении, примером которого является простой маятник. Как вы понимаете, движение должно быть представлено не стандартным вращением, а просто движением, которое периодически повторяет свое положение. Однако угловая скорость жестко связана с движением вокруг некоторой точки. Следовательно, мы можем сказать, что угловая частота является более общей величиной и может использоваться для описания широкого круга физических проблем, в то время как угловая скорость включает только вращательное движение.

Как найти угловую скорость Земли?

Как насчет того, чтобы использовать наш калькулятор угловой скорости? Оценим угловую скорость Земли! Во-первых, мы рассматриваем скорость вращения.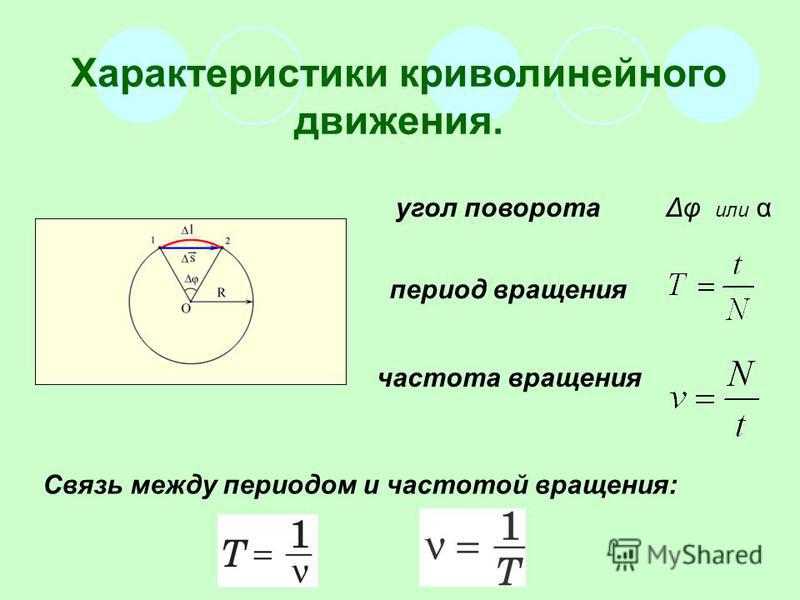 Мы знаем, что Земля совершает полный оборот относительно далеких звезд примерно за 23 ч 56 мин 4 с , что составляет примерно 23,934 ч . Полное вращение составляет угол 2π рад , поэтому результирующая угловая скорость равна:

ω₁ = 2π рад / 23.934 ч = 0,2625 рад / ч = 0,00007292 рад / с ,

или 7,292 * 10⁻⁵ рад / с (в экспоненциальном представлении).

Теперь, когда мы знаем угловую скорость вращения Земли, мы можем оценить ее линейную скорость на экваторе. Для этого нам нужен радиус Земли, который составляет примерно 6 371 км . Единственное, что нам нужно сделать, это вставить значения во вторую формулу угловой скорости:

v₁ = r₁ * ω₁ = 6,371 км * 7,292 * 10⁻⁵ рад / с = 0,4646 км / с = 464.6 м / с .

Чтобы вычислить линейную скорость относительно центра Земли, все, что вам нужно сделать, это умножить полученный результат на косинус широты вашего города. Кстати, вы когда-нибудь задумывались, почему ракеты обычно запускаются с космодрома, расположенного вблизи экватора, а не с полюсов? Ну, почти 500 м / с ускорение в начале — это значительная часть его конечной скорости. Таким образом, перемещение начальной точки как можно ближе к экватору снижает количество топлива, необходимого для разгона ракеты.

После этого мы можем еще раз спросить, как найти угловую скорость Земли, но на этот раз орбитальную. Все расчеты аналогичны, но нам нужно изменить время с 23,943 ч на один год, что составляет примерно 365,25 дней. Изменение угла такое же, полный оборот.

ω₂ = 2π рад / 23,934 h = 0,0000001991 рад / с = 1,991 * 10⁻⁷ рад / с ,

и линейная скорость Земли относительно Солнца (для среднего радиуса 1.496 * 10⁸ км ) составляет:

v₂ = 1,496 * 10⁸ км * 1,991 * 10⁻⁷ рад / с = 29,785 км / с .

Мы движемся довольно быстро, не так ли?

Физические величины, зависящие от угловой скорости

Существует множество физических величин, связанных с угловой скоростью, некоторые из которых перечислены ниже:

Угловое ускорение — описывает, как угловая скорость изменяется со временем. Чем больше разница угловых скоростей, тем больше значение углового ускорения.
Кинетическая энергия вращения — мера энергии при круговом движении. Как и в случае с кинетической энергией, зависимость (угловой) скорости квадратичная.
Центробежная сила — ее можно почувствовать в автомобиле, когда он поворачивает. Чем быстрее вы поворачиваете или чем он круче, тем выше становится центробежная сила, которую можно четко почувствовать.
Эффект Кориолиса — заставляет объекты поворачиваться, если они помещены на вращающееся тело (например,г. на Земле) вместо того, чтобы двигаться по прямой.
Система шкивов — это не физическая величина, точнее говоря, это интересное устройство, все дело в угловой скорости. Самая простая система состоит из двух шкивов, обычно с разной окружностью или радиусом. Они связаны ремнем, поэтому их линейные скорости идентичны , но поскольку они имеют разные размеры, их угловые скорости изменяются пропорционально . Зная это и имея двигатель с четко определенной скоростью вращения, мы можем с хорошей точностью установить угловую скорость выходного элемента, просто отрегулировав его размер.

Сохранение углового момента

Есть несколько фундаментальных правил, которые говорят нам о величинах, сохраняемых в изолированных системах. Самыми известными из них являются сохранение энергии и сохранение количества движения. Вместе с ними существует еще сохранения момента импульса .Если мы подумаем о двух моментах времени, правило можно записать как:

I₁ * ω₁ = I₂ * ω₂ ,

, где I₁ и I₂ — начальный и конечный массовые моменты инерции соответственно, величины, которые описывают распределение массы относительно центра тел.

Мы видим, что , если момент инерции увеличивается, угловая скорость уменьшается, и наоборот . Итак, каковы последствия этого явления? Представим, что вы фигурист. Когда вы вращаетесь, вы обладаете некоторой угловой скоростью. Если ваши руки широко раскрыты, момент инерции массы относительно велик . Затем вы приближаете руки к остальному телу. Как следствие, ваш момент инерции уменьшается на , поэтому из-за того, что общий угловой момент должен быть сохранен, ваша угловая скорость увеличивается на — это означает, что вы будете вращаться быстрее! Это не магия, а просто физика!

Если кататься на коньках не любишь, можно попробовать проверить правило на обычном вращающемся кресле.Просто помните, безопасность превыше всего! Убедитесь, что для этого эксперимента достаточно места. После этого просто начните вращаться и посмотрите, как изменяется ваша угловая скорость, когда вы двигаете руками вперед и назад. Кроме того, вы можете усилить эффект, используя гантели. В результате вы можете объединить упражнения и развлечения в одно целое!

Momentum Machine: физика и механика, наука

Ньютон обнаружил, что движущийся объект имеет тенденцию оставаться в движении по прямой линии и с постоянной скоростью, если на него не действует чистая сила. Сегодня мы называем это наблюдение законом сохранения количества движения. Импульс объекта — это произведение его массы и скорости.

Для вращающихся объектов существует эквивалентный закон. Вращающийся объект имеет тенденцию продолжать вращаться с постоянным угловым моментом , если на него не действует внешняя скручивающая сила. Определение углового момента более сложное, чем определение количества движения. Угловой момент — это произведение двух величин, известных как угловая скорость и момент инерции.Угловая скорость — это просто скорость, измеряемая в градусах или радианах в секунду, а не в метрах в секунду.

Момент инерции зависит как от массы объекта, так и от того, как эта масса распределяется. Чем дальше от оси вращения расположена масса, тем больше момент инерции. Таким образом, ваш момент инерции меньше, когда вы держите руки по бокам, и больше, когда вы вытягиваете руки прямо.

Если на движение вращающейся системы не влияет внешняя скручивающая сила, то угловой момент для этой системы сохраняется, а это означает, что угловой момент остается неизменным.

Человек, сидящий на вращающемся стуле или табурете, приближается к системе, в которой сохраняется угловой момент. Трение подшипников о штанге стула служит внешней скручивающей силой, но для таких стульев эта сила обычно довольно мала. Поскольку угловой момент сохраняется, произведение угловой скорости и момента инерции должно оставаться постоянным. Это означает, что если один из этих факторов увеличивается, другой должен уменьшаться, и наоборот. Если вы изначально вращаетесь с вытянутыми руками, то, когда вы втягиваете руки внутрь, ваш момент инерции уменьшается.Это означает, что ваша угловая скорость должна увеличиваться, и вы вращаетесь быстрее.

Сохранение углового момента объясняет, почему фигуристы начинают вращаться быстрее, когда они внезапно втягивают руки внутрь, или почему дайверы или гимнасты, которые уменьшают свой момент инерции, переходя в положение группировки , начинают переворачиваться или поворачиваться с большей скоростью.

Создайте сверхскоростную игрушку из бумаги

Что может вращаться 100 000 раз в минуту и генерировать силы, в 30 000 раз превышающие силу тяжести? Сюрприз! Этой игрушке тысячи лет, и ее называют вертолетом или жужжащей игрушкой.Вот как это работает:

Пожалуй, самое крутое в этой игрушке то, что ее действительно легко сделать — все, что вам нужно, это лист бумаги, скотч, гвоздь и веревка. Вторая интересная вещь заключается в том, что группа физиков и биоинженеров из Стэнфордского университета придумала, как превратить этот тип игрушки в машину, называемую центрифугой. Центрифуги быстро вращают материалы для разделения их компонентов по плотности. В этом случае бумажная центрифуга, которую они сделали, может отделять плазму, тромбоциты, лимфоциты и эритроциты от крови без электричества.Все это стоит менее 18 центов.

Интересно, как работает физика? Попробуйте сами сделать одну из этих игрушек.

Сделайте и используйте бумажную игрушку-жужжание:

Кредит: Ariel Zych

Просто вырежьте два круга из толстого картона и скрепите их скотчем. Вы можете использовать эту распечатку, чтобы делать круги. Проделайте два отверстия близко друг к другу в центре круга и проденьте трехфутовую веревку через каждое отверстие (это будет похоже на пуговицу с резьбой).Свяжите концы веревки вместе, чтобы образовалась петля, и свободно растяните петлю между двумя руками с бумажным диском в центре.

Чтобы заставить вашу игрушку вращаться, закрутите диск по кругу, чтобы скрутить веревку, затем быстро разведите руки в стороны и снова по направлению друг к другу, чтобы размотать, а затем перемотайте скрученные веревки. Потренируйтесь несколько раз, пока не научитесь быстро делать .

Кредит: Ариэль Зих

Как это работает?

Как вы, наверное, заметили, ваш диск на самом деле вращается в двух направлениях — в направлении «наматывания», при котором струна наматывается, когда вы сводите руки вместе, и в направлении «разматывания», при котором струна разматывается, когда вы разводите руки.Раскручивание витков струны прикладывает крутящий момент или вращающую силу к бумажному диску, заставляя диск вращаться. Диск набирает скорость по мере разматывания струны, и вы слышите «жужжащий» звук, когда он рассекает воздух. При достаточной скорости диск продолжит вращаться даже после того, как струна полностью размотана и больше не прикладывает крутящий момент (благодаря инерции!). Быстро перемещая руки вперед и назад, вы можете крутить, раскручивать и крутить струну снова и снова, создавая невероятную скорость вращения диска между каждым гребком.

Предоставлено: Ариэль Зих.

Как быстро вращается моя жужжащая игрушка?

Скорость вращения часто измеряется в оборотах в минуту (об / мин). Чтобы упростить оценку количества оборотов, которые диск делает за заданный период времени, мы предположим, что количество оборотов одинаково в любом направлении (разматывание или наматывание) и что они происходят примерно с одинаковой скоростью. По этой причине мы будем называть и «разматывающие», и «ветровые» удары просто «штрихами».”

Определите, сколько гребков вы можете делать в минуту.

Разматывайте и раскручивайте свою игрушку-гудок на максимальной скорости. Используйте таймер, чтобы подсчитать количество гребков за 10 секунд. Запишите это количество как «количество гребков за 10 секунд».
В минуте 60 секунд. Подсчитайте количество гребков, которое вы можете сделать за минуту, умножив количество гребков на предыдущем шаге на шесть. (Мы предполагаем, что вы будете делать одинаковое количество движений каждые 10 секунд.)

Определите, сколько оборотов приходится на один ход намотки.

С помощью маркера нарисуйте толстую линию на одной стороне вашей игрушки для жужжания.
Заводите и разматывайте игрушку-жужжание так же быстро, как на шаге 1. После того, как вы наберете полную скорость, вместо того, чтобы разводить руки, быстро хлопните в ладоши, чтобы диск не раскручивался. Вы должны были «запечатлеть» все повороты, которые ваша игрушка создала одним движением.
Используя леску на внешней стороне вашей игрушки-жужжалки, подсчитайте количество полных оборотов, которые делает ваша жужжалка, медленно позволяя ей раскручиваться, останавливаясь, когда она полностью разматывается.Это количество оборотов за ход.

Рассчитайте количество оборотов в минуту:

Умножьте количество движений в минуту на количество оборотов за один ход, чтобы получить количество оборотов в минуту. Это твоя скорость!

Измените свой дизайн:

На максимальную скорость вращения игрушечной игрушки могут влиять самые разные вещи, от типа используемой струны (например, леска, проволока, нить) до длины струны, радиуса диска, расстояния между отверстиями. центр и масса самого диска.Вы можете использовать эту распечатку, чтобы легко делать игрушки-жужжалки с разными радиусами.

Измените одну переменную вашего проекта и повторите шаги с 1 по 6. Затем измените другую переменную и повторите шаги еще раз. По мере того, как ваши проекты становятся более продвинутыми, вы можете закрепить отверстия в середине лентой.

Как превратить эту игрушку в центрифугу?

Как отмечалось выше, центрифуга — это устройство, которое вращает смеси достаточно быстро, чтобы разделить материалы внутри смеси по плотности.Центрифуги обычно используются для анализа биологических образцов, таких как кровь, моча или культуры клеток, для выделения патогенов и ДНК для диагностики заболеваний. Модифицировав игрушку-жужжку, чтобы она работала как центрифуга, М. Саад Бхамла и его коллеги из лаборатории Пракаша в Стэнфордском университете создали недорогой способ обработки образцов для диагностики заболеваний даже при отсутствии электричества. Он работает, помещая маленькие пузырьки с образцами крови между двумя бумажными дисками и вращая их скрученной нитью, точно так же, как вы это делали в этом упражнении.Создатели «paperfuge», как называют изобретение, смогли достичь своей конструкции скорости 125 000 оборотов в минуту. Это более 2000 оборотов в секунду!

Бумажная центрифуга. Предоставлено: Brandon Echter

. Узнайте больше об их конструкции и о том, как они использовали ее для успешной изоляции малярийных паразитов из образцов крови, прочитав их публикацию или посмотрев это видео о своей работе.

Равномерное круговое движение

Введение

Равномерное круговое движение — это движение объекта, движущегося с постоянной (равномерной) скоростью по круговой траектории.Помимо скорости, есть несколько других переменных, которые используются для характеристики движения. Это радиус движения r , угловая скорость ω , период T и частота вращения f . Период — это время, необходимое для того, чтобы объект совершил один оборот движения. Угловая скорость — это угловое смещение в секунду, и оно связано с частотой следующим образом: с ω в рад / с.Частота вращения — это количество оборотов в секунду и определяется по формуле: с f в Гц или сек ^-1. Скорость объекта является касательной к окружности с величиной v = rω . Ускорение , a направлено к центру круга (центростремительное) с величиной, определяемой следующим образом: с a м / с ². Чтобы объект массой м мог двигаться по окружности с постоянной скоростью, на объект должна действовать чистая центростремительная сила.Величина чистой силы F должна быть постоянной и связана с центростремительным ускорением вторым законом Ньютона: с F в N. Эта центростремительная сила может быть обеспечена за счет натяжения (как в этой лаборатории), трения (как для автомобиля, движущегося по кривой), нормальной силы (как в петлеобразных американских горках) или гравитации (как для движения спутника). В этом эксперименте вы будете измерять период объекта, совершающего равномерное круговое движение с фиксированным радиусом, но с различными значениями F .По периоду можно рассчитать угловую скорость. Используя эти известные значения и приведенные выше уравнения, вы можете найти эмпирическую массу вращающегося объекта и сравнить со значением массы, полученным путем непосредственного взвешивания его на весах.

Аппарат UCM

Аппарат UCM состоит из регулируемой вращающейся платформы . На расстоянии х от центра вращения находится узел боковой стойки , на котором висит объект массой м , называемый вращающейся массой (не путать со статической массой ).Вращающаяся масса прикреплена к пружине на центральной стойке с помощью струны и небольшого шкива. Когда платформа вращается, вращающаяся масса будет перемещаться по круговой траектории из-за силы, прилагаемой к ней струной (посредством натяжения пружины). Поскольку невозможно получить мгновенное считывание этой силы натяжения во время вращения платформы, косвенное измерение этой силы будет производиться с использованием веса статической массы, как показано и объяснено ниже.

Рисунок 1

Когда платформа не вращается, вращающаяся масса не свисает вертикально с боковой стойки, а, скорее, втягивается внутрь за счет натяжения струны и пружины. При проведении эксперимента вы будете регулировать скорость вращения платформы до тех пор, пока вращающаяся масса не будет висеть вертикально на радиусе r . Оранжевый индикаторный диск поможет вам определить, когда вращающаяся масса достигла этого положения.

Рисунок 2

Период вращения измеряется секундомером .Платформу можно вращать, поворачивая стержень с накаткой вручную.

Процедура

Выравнивание предмета

Если платформа неровная, это отрицательно скажется на ваших результатах. Студенты первой лаборатории недели должны были уже выровнять прибор. Будем надеяться, что с тех пор аппарат не перемещали, и его не нужно будет снова выравнивать. Проверьте, выровнено ли ваше устройство, включив двигатель регулировки скорости и наблюдая за оранжевым индикаторным диском, чтобы увидеть, качается ли он вверх и вниз при вращении платформы.Если ваше устройство необходимо выровнять, выполните следующие действия.

1
Чтобы примерно выровнять платформу, поместите пузырьковый уровень в середину платформы и отрегулируйте два регулировочных винта на основании устройства до тех пор, пока пузырь не будет отцентрирован.
2
Поместите дополнительную массу (~ 500 г) на тот же конец вращающейся платформы, что и вращающаяся масса. Если платформа неровная, тяжелый конец будет качаться в низкую сторону.
3
Отрегулируйте регулировочные винты на ножках основания до тех пор, пока конец платформы не будет качаться равномерно, когда ее осторожно поворачивают вручную.

Установка радиуса

1
Осторожно отсоедините вращающуюся массу от струн. Используйте весы, чтобы взвесить его, и запишите значение массы.
2
Подвесьте вращающуюся гирю к боковой стойке и подсоедините шнур от пружины к гири.Убедитесь, что эта струна проходит под (а не за) маленьким шкивом на центральной стойке.
3
Переместите кронштейн индикатора на центральной стойке в самое нижнее положение.
4
Вытяните вращающуюся массу от центральной стойки, пока оранжевый индикатор не окажется в центре кронштейна. Если струна, поддерживающая вращающуюся массу, не является вертикальной, когда индикатор выровнен с кронштейном, боковую стойку следует перемещать внутрь или наружу, пока струна не станет вертикальной.Используйте вертикальную линию на боковой стойке, чтобы облегчить это выравнивание. При затяжке боковой стойки, нажмите на платформу, чтобы убедиться, что она надежно удерживается в вертикальном положении, и избегайте чрезмерного затягивания и поломки пластикового винта с накатанной головкой!
5
Измерьте и запишите радиус, а также оценку погрешности на основе центровки.
6
Теперь ваш аппарат должен быть готов к работе в максимально широком диапазоне центростремительных сил.(Почему это важно?) Центростремительную силу можно изменять, перемещая опору пружины вверх и вниз, при этом другие части устройства остаются на месте. Этот диапазон движения по центральной стойке должно быть не менее 5 см, что соответствует диапазону натяжения пружины примерно 1,2 Н.

Установка величины центростремительной силы

В этой первой части процедуры вы будете использовать метод static (без вращения) для настройки устройства на известное значение центростремительной силы.

1
Присоедините зажимной шкив к концу платформы, ближайшему к вращающейся массе. Прикрепите веревку к вращающейся массе и навесьте известную массу (начиная с 20 г) над зажимным шкивом. Отрегулируйте прижимной шкив вверх или вниз по мере необходимости так, чтобы веревка между шкивом и вращающаяся масса расположена горизонтально. (Почему это важно?)
2
Запишите значение этой статической массы , которая будет определять центростремительную силу.
3
Отрегулируйте опору пружины по вертикали, пока оранжевый индикаторный диск не окажется по центру кронштейна индикатора. Теперь устройство должно быть выровнено, чтобы точно знать радиус движения вращающейся массы, когда платформа вращается.

На этом этапе остановитесь и проанализируйте все силы, действующие на вращающуюся массу. Каковы их масштабы и направления? Какие-то силы не совсем вертикальные или горизонтальные? Если да, то как это повлияет на ваши результаты?

Контрольно-пропускной пункт 1:
Прежде чем продолжить, попросите ТА проверить ваше устройство.

Измерение периода

1
Удалите статическую массу и струну из вращающейся массы. (Почему?)
2
Поверните устройство, равномерно поворачивая стержень с накаткой по часовой стрелке. Уделите минуту, чтобы прочувствовать поворот платформы с постоянной скоростью. Увеличивайте скорость до тех пор, пока оранжевый индикаторный диск не окажется по центру кронштейна индикатора на центральной стойке.Это указывает на то, что струна, поддерживающая вращающуюся массу, вертикальна и, следовательно, масса находится на желаемом радиусе.
3
Когда один партнер по лаборатории вращает платформу, другой должен использовать секундомер для измерения времени, необходимого для совершения одного оборота. Сделайте десять таких измерений.
4
Альтернативный метод измерения среднего периода заключается в использовании секундомера для измерения времени для N (например, 10) оборотов и деления на N, чтобы получить T .Сделайте это хотя бы для одного испытания и сравните со значением, полученным с помощью процедуры, приведенной на шаге 3. Какой метод, по вашему мнению, более точен?
5
Прежде чем продолжить, проверьте свои результаты для этой единственной точки данных и убедитесь, что ваше эмпирическое значение для вращающейся массы является разумным. Если ваш результат не имеет смысла, проанализируйте свою процедуру и исправьте все ошибки, прежде чем брать дополнительные данные.

КПП 2:
Перед тем, как продолжить, ваш технический специалист должен проверить ваши данные и результаты расчетов.

Изменение центростремительной силы

Повторите описанную выше процедуру как минимум с пятью различными статическими массами (и, следовательно, пятью различными силами), которые охватывают максимально широкий диапазон значений (обычно от 40 до 150 г).

Анализ

1
Вес статической массы, висящей на шкиве, равен центростремительной силе F , приложенной пружиной. Вычислите эту силу для каждого из пяти испытаний, умножив статическую массу на г , и запишите результаты.
2
Для каждой центростремительной силы F вычислите средний период вращения T и его стандартную ошибку.
3
Для каждого значения F рассчитайте ω ² и его неопределенность из
4
Постройте график ω ² и F (с планками ошибок) и выполните аппроксимацию методом наименьших квадратов.
5
Определите экспериментальное значение вращающейся массы, м , исходя из наклона вашего графика и уравнения центростремительной силы.Определите пересечение и линейного соответствия вашим данным. Это то, чего вы ожидаете?

Обсуждение

Сравните значение м , полученное при подборе кривой, с измеренными значениями вращающейся массы м и радиуса движения r . Есть согласие в пределах неопределенностей? Если вы проведете этот эксперимент осторожно, вы сможете получить результаты с ошибкой менее 3%. Сравните значение интерцепта y с ожидаемым значением.Они согласны? Почему для этого (и большинства других) экспериментов важно получить данные в самом широком диапазоне значений? Каковы потенциальные последствия близкого расположения точек данных? Объясните, как вы собираете данные с помощью этого устройства, чтобы проверить следующую гипотезу: для данного значения величины центростремительной силы F радиус движения r обратно пропорционален квадрату угловой скорости ω .

Линейная скорость в зависимости от скорости вращения: определения и уравнения

Уравнения

Каждому из двух типов скорости соответствует уравнение. Обычная линейная скорость рассчитывается по следующему уравнению:

Уравнение скорости

Скорость — это смещение (или изменение положения), деленное на время.Возьмите количество метров, которое переместился объект, и разделите его на время, которое потребовалось для перемещения.

Угловая скорость определяется следующим уравнением:

Уравнение угловой скорости

Угловая скорость — это угловое смещение (или изменение углового положения), деленное на время. Возьмите количество градусов, на которое повернулся объект, и разделите его на время, которое потребовалось для поворота.

Пример

Может быть, было бы проще, если бы мы рассмотрели пример.Скажем, мяч летит по воздуху и одновременно вращается. Мяч перемещается на 20 метров за 4 секунды, при этом за это время совершает 5 оборотов. Каковы линейная и угловая скорости мяча?

Хорошо, прежде всего мы должны записать то, что мы знаем. Мы знаем, что смещение составляет 20 метров, и мы знаем, что время составляет 4 секунды. Мы также можем вычислить угловое смещение, потому что знаем, сколько раз оно повернулось. Каждое полное вращение составляет 2 пи радиана, и оно поворачивается 5 раз.2-пи умножить на 5 — это то же самое, что и 10-пи. Таким образом, угловое смещение составляет 10 пи. Подставьте эти числа в два уравнения, и мы получим ответы: линейная скорость составляет 5 метров в секунду, а угловая скорость — 7,9 радиан в секунду.

Пример вопроса

Резюме урока

Линейная скорость — это скорость и направление объекта, движущегося по прямой линии, измеряемая в метрах в секунду. Скорость вращения — это скорость вращения объекта, измеряемая в радианах в секунду. Радианы — это альтернатива измерению углов в градусах. В круге 360 градусов; аналогично, в круге 2 пи радиана.

Вы можете рассчитать линейную скорость, разделив смещение (или изменение положения) на время, которое потребовалось для изменения положения. И вы можете рассчитать угловую скорость, разделив угловое смещение (или изменение углового положения) на время, которое потребовалось для изменения углового положения.

5.1: Основы вращения — Физика LibreTexts

До сих пор мы рассматривали движение, которое легко описывается в декартовых координатах, часто движущееся по прямым линиям. Такое движение случается часто, но есть и второй общий класс: вращательное движение. Неудивительно, что для описания вращательного движения полярные координаты (или их трехмерные аналоги цилиндрические и сферические координаты) намного удобнее, чем декартовы ¹.Например, если мы рассмотрим случай, когда диск вращается с постоянной скоростью вокруг своего центра, самый простой способ сделать это — указать, на сколько градусов (или радиан) точка на границе перемещается за секунду. Сравните это с линейным движением — оно определяется тем, на сколько метров вы продвигаетесь в линейном направлении в секунду, что является скоростью (с размером L / T). Изменение угла в секунду дает вам угловую скорость !, где вращение против часовой стрелки считается положительным.Угловая скорость имеет размерность 1 / T, поэтому это частота. Он измеряется в градусах в секунду или радианах в секунду. Если угол в определенный момент времени обозначен как \ (\ theta (t) \), то, очевидно, \ (\ omega = \ dot \ theta \), точно так же, как \ (v = \ dot x \) в линейном движении.

В трех измерениях \ (\ omega \) становится вектором, где величина по-прежнему является скоростью вращения, а направление дает вам направление вращения с помощью правила правой руки: вращение происходит в плоскости, перпендикулярной к !, и в направлении, в котором указывают пальцы правой руки, если ваш большой палец указывает на \ (\ omega \) (это дает \ (\ omega \) в положительном направлении \ (\ hat z \) для вращательного движения в плоскость xy).Вернемся на данный момент к 2D, назовем угловое положение \ (\ theta (t) \), затем

\ [\ omega = \ frac {\ mathrm {d} \ theta} {\ mathrm {d} t} = \ dot {\ theta} \]

Если мы хотим знать декартовы координаты позиции, мы можем просто использовать обычное преобразование полярных координат в декартовы и написать

\ [\ boldsymbol {r} (t) = r \ cos (\ omega t) \ hat {\ boldsymbol {x}} + r \ sin (\ omega t) \ hat {\ boldsymbol {y}} = r \ шляпа {\ boldsymbol {r}} \ label {r} \]

где \ (r \) — расстояние до начала координат.Обратите внимание, что \ (r \) указывает в направлении полярного единичного вектора \ (\ hat r \). Уравнение \ ref {r} дает нам интерпретацию \ (\ omega \) как частоты: если мы рассмотрим объект, совершающий равномерное вращение (т.е. постоянный радиус и постоянную скорость), в его направлениях x и y он колеблется с частотой \(\омега\). Пока наше движение остается чисто вращательным, радиальное расстояние r не меняется, и мы можем найти линейную скорость, взяв производную по времени от \ ref {r}:

\ [\ boldsymbol {v} (t) = \ dot {\ boldsymbol {r}} (t) = — \ omega r \ sin (\ omega t) \ hat {x} + \ omega r \ cos (\ omega t) \ hat {y} = \ omega r \ hat {\ boldsymbol {\ theta}} \]

, поэтому, в частности, у нас есть \ (v = \ omega r \).Обратите внимание, что и v, и \ (\ omega \) обозначают мгновенные скорости, а уравнение \ ref {r} справедливо только тогда, когда \ (\ omega \) является постоянным. Однако соотношение \ (v = \ omega r \) всегда выполняется. Чтобы убедиться в этом, выразите \ (\ theta \) в радианах, \ (\ theta = \ frac {s} {r} \), где s — это расстояние, пройденное в направлении вращения. {2} r \ hat {\ boldsymbol {r}} \ label {linaccl} \]

В разделе 5.2 ниже мы будем использовать уравнение \ ref {linaccl} в сочетании со вторым законом движения Ньютона для расчета чистой центростремительной силы, необходимой для поддержания постоянной скорости вращения. Конечно, угловая скорость \ (\ omega \) вовсе не обязательно должна быть постоянной. Если это не так, мы можем определить угловое ускорение, взяв его производную по времени:

\ [\ alpha = \ frac {\ mathrm {d} \ omega} {\ mathrm {d} t} = \ ddot {\ theta} \]

или в трех измерениях, где \ (\ omega \) — вектор:

\ [\ boldsymbol {\ alpha} = \ frac {\ mathrm {d} \ boldsymbol {\ omega}} {\ mathrm {d} t} \]

Обратите внимание, что когда \ (\ boldsymbol {\ alpha} \) параллельно \ (\ boldsymbol {\ omega} \), это просто представляет изменение скорости вращения (т.е.е., ускорение / замедление вращения), но когда это не так, это также означает изменение плоскости вращения. Как в двух, так и в трех измерениях изменение скорости вращения приводит к тому, что линейное ускорение имеет компонент в тангенциальном направлении в дополнение к радиальному ускорению (\ ref {linaccl}). Тангенциальная составляющая ускорения определяется производной линейной скорости:

\ [\ boldsymbol {a} _ {\ mathrm {t}} = \ frac {\ mathrm {d} \ boldsymbol {v}} {\ mathrm {d} t} = r \ frac {\ mathrm {d} \ boldsymbol {\ omega}} {\ mathrm {d} t} = r \ boldsymbol {\ alpha} \]

В двух измерениях \ (\ boldsymbol {a} _ {\ mathrm {t}} \) указывает вдоль направления \ (\ pm \ hat {\ boldsymbol {\ theta}} \).

Естественно, есть и более сложные возможности — также может изменяться радиус вращательного движения. Мы рассмотрим этот случай более подробно в главе 6, но сначала рассмотрим «чистые» вращения, когда расстояние до оси вращения фиксировано.

¹ Если вам нужно напомнить о полярных координатах или вы не знакомы с полярными базисными векторами, ознакомьтесь с приложением A.2.

Как вы измеряете скорость вращения галактики, принимая во внимание движение нашей галактики, солнечной системы, планеты и т. Д.?

Почти все измерения движения в астрономии используют закон физики, называемый эффектом Доплера. Это изменение длины волны (или частоты, цвета или высоты тона) волны, излучаемой движущимся источником, было впервые описано физиком Кристианом Допплером в 1842 году. Это знакомо большинству из нас: я уверен, что вы заметили, что Сирена машины скорой помощи меняет тон при прохождении мимо вас, переходя от более высокого (по мере движения к вам) на более низкий (по мере прохождения и удаления). Тот же эффект происходит со светом, излучаемым звездами и газом в галактиках.Со световыми волнами даже большие движения создают лишь крошечный сдвиг в цвете, но мы все равно можем измерить его с помощью инструмента, называемого спектрографом, который делит свет на составляющие его длины волн, позволяя астрономам выделять специфические особенности, вызванные атомами в звездах или газе. .

Одной из самых известных и распространенных из этих характеристик является водород-альфа (или Hα), который составляет ровно 656,28 нанометра (для неподвижного источника). Чтобы измерить скорость вращения галактики, мы наносим на карту линию, подобную Hα, через галактику и сравниваем ее со значением от источника в состоянии покоя.Если мы увидим, что на одной стороне галактики линия смещена в синюю сторону (движется к нам), а на другой стороне смещена в красную сторону (удаляется) относительно центрального красного смещения галактики, мы знаем, что галактика вращается, и величина сдвиг любой строки говорит нам, насколько. Обычно это делается с помощью спектроскопа с длинной щелью, который измеряет сдвиги в одной спектральной линии по всей галактике. Альтернативно, разрешенная спектроскопия целых галактик стала возможной в последние годы, поэтому теперь мы часто получаем полные спектральные карты.

Другой метод использует радиотелескоп для измерения 21-сантиметровой эмиссионной линии водорода, которая также показывает вращение галактики. Линия 21 см показывает нам, где находится водород в галактике, и когда этот водород либо вращается к нам, либо от нас относительно центрального красного смещения галактики, результирующий доплеровский сдвиг расширяет одиночную эмиссионную линию до линии с двумя пиками, каждый связан с движением в том или ином направлении.