Частотный отклик механических систем | Блог COMSOL
В продолжение статьи нашего корпоративного блога о демпфировании механических колебаний мы подробно расскажем про анализ гармонического отклика механических систем при учете демпфирования. Мы также продемонстрируем различные способы определения и анализа частотного отклика в программном пакете COMSOL Multiphysics®.
Что такое частотный отклик?
В общем смысле, частотный отклик системы показывает реакцию системы (в части некоторых свойств) на воздействие как функцию от частоты возбуждения. В контексте моделирования в COMSOL Multiphysics под частотным откликом, как правило, подразумевается линейный (или линеаризованный) отклик на гармоническое возбуждение. Для построения графика кривой частотного отклика необходимо провести частотный анализ для заданного набора частот (исследование в частотной области). В общем случае на такой кривой будут визуализированы различимые пики, положение которых определяется собственными резонансными частотами системы.
т.е. меньше, чем собственная частота колебаний демпфированной системы.
Фактически сдвиг по частоте получается в два раза больше. Может показаться парадоксальным то, что частота возбуждения, вызывающая максимальное усиление колебаний, не совпадает с частотой свободных колебаний. Это можно объяснить фазовым сдвигом между силой и смещением, который обусловлен демпфированием. Без демпфирования нагрузка и смещение синфазны ниже собственной частоты и сдвинуты на 180° по фазе выше собственной частоты (с быстрым переходом в её окрестности). Демпфирование обеспечивает более плавный переход фазового сдвига (см. график ниже). Вне зависимости от уровня демпфирования, фазовый сдвиг на собственной частоте колебаний недемпфированной системы всегда составляет 90°.
Зависимость фазового сдвига смещения как функция от частоты.
Несовпадение по фазе силы и смещения при демпфировании, оказывает влияние на процесс передачи энергии этой силой системе.
Описание демпфирования через коэффициент гистерезисных потерь
Повторим анализ для системы с одной степенью свободы с гистерезисными потерями. 2}{8}
2}{8}
\right )
Анализ, в результате которого можно получить соответствующее снижение частоты возбуждения, которое также меньше собственной частоты колебаний демпфированной системы, в данной статье не приведен.
Фазовый сдвиг между возбуждением и откликом при описании демпфирования через коэффициент гистерезисных потерь особенно интересен, поскольку он наблюдается даже при очень низких частотах возбуждения. Его асимптотическое значение — arctan(η).
Зависимость фазового сдвига смещения от частоты в случае введения демпфирования в систему через коэффициент гистерезисных потерь. Низкочастотные асимптоты обозначены пунктирными линиями.
Замечание о трении
В случае сопряжения эффекта демпфирования с эффектом трения между двумя поверхностями, отклик на гармоническое воздействие уже не будет являться гармоническим, ввиду наличия нелинейности в системе. При этом отклик может быть периодическим, но ангармоническим. Такие задачи уже невозможно решить с помощью методов анализа в частотной области, в которых предполагается линейность отношения внешнего воздействия и результата этого воздействия.
Моделирование частотного отклика в COMSOL Multiphysics®
Настройка исследования
После добавления физического интерфейса из группы Механика Конструкций в Мастере создания моделей становится доступно для выбора несколько типов исследования, четыре из которых можно использовать для вычисления частотного отклика:
- Frequency Domain
- Frequency Domain, Prestressed
- Frequency Domain, Modal
- Frequency Domain, Prestressed, Modal
Доступные типы исследования для интерфейса Solid Mechanics.
Два исследования из указанных выше реализуют прямое решение, а в двух других используется техника модальной суперпозиции. При использовании исследований группы Prestressed можно учитывать изменение жесткости конструкции, обусловленное стационарной предварительной нагрузкой. Методика суперпозиции мод идеально подходит для расчетов в частотной области, поскольку при этом реализуется простой выбор подходящих мод собственных колебаний на основе заданных частот.
В любом случае частотный анализ выполняется при условии, что в настройках исследования указаны значения частот, для которых требуется вычислить отклик. Зачастую бывает эффективно сгустить частотные точки около собственных частот конструкции (для получения лучшего разрешения).
Ввод частот для проведения частотного анализа.
Обратите внимание на то, что без демпфирования отклик на собственной резонансной частоте стремится к бесконечности. Другими словами, невозможно решить задачу о частотном отклике без демпфирования на частоте равной собственной или близкой к ней. Численный результат при этом будет представлять собой вырожденную или, по крайней мере, плохообусловленную системную матрицу.
Гармоническое возмущение или нет?
В узле
Опции задания настройки Linearity.
В принципе, любой анализ в частотной области можно рассматривать как небольшое возмущение, так что использование опции Linear perturbation (Линейное возмущение) не будет ошибочным. Однако, в наиболее распространенном случае колебания происходят относительно нулевого положения. При этом не так важно, рассматривается ли задача как Linear (линейная) или 
Нагрузка, заданная на грань и помеченная как Harmonic Perturbation.
Рассматриваемая настройка позволяет разграничить нагрузки, приводящие к предварительным напряжениям, и гармонические возбуждения, воздействующие поверх них.
При добавлении стандартного исследования в Frequency Domain (Исследование в частотной области) по умолчанию в Linearity не ставится вариант с учетом возмущений. Поэтому, в таком случае не следует использовать для нагрузок метку Harmonic Perturbation
Интерпретация полученных результатов
Результаты расчета в частотной области являются комплекснозначными, а их гармоническое изменение — неявное. {i \phi})
{i \phi})
Фазовый угол Φ представляет собой свойство, задаваемое в наборе данных исследовании, где его можно изменить.
Задание ненулевого фазового угла в наборе данных.
В большинстве случаев при проведении расчета в частотной области требуется установить зависимость амплитуды искомой величины v от частоты. Это означает, что анализировать следует не саму величину v, а её модуль abs(v). Их отличия показаны на следующем рисунке.
Пример графика частотного отклика. Обратите внимание на то, что график для «u» идентичен графику для «real(u)».
Для более детального анализ можно добавить на график мнимую часть и аргумент результирующей величины:
Пример графика частотного отклика с отображением фазы.
Для низких частот действительная часть близка к абсолютной величине. Вблизи собственной частоты мнимая часть, наоборот, вносит свой основной вклад. Это означает, что отклик не синфазен с возбуждающей нагрузкой.
А теперь посмотрим, что произойдет, если значение фазового угла в наборе данных будет изменено на 45°.
Частотный отклик при задании величины 45° для фазового угла в наборе данных.
Как и ожидалось, график амплитуды остается неизменным. При этом графики действительной и мнимой частей меняются, а кривая фазы сдвигается вверх на π/4. На самом деле, такой же график получился бы при добавлении фазового угла 45° к нагрузке.
Задание сдвига по фазе в нагрузке.
Вместо ввода фазового угла можно эквивалентным образом указать нагрузку напрямую, используя комплексный формализм:
Комплексное представление нагрузки, аналогичное варианту на изображении выше.
Возможность задать фазовый угол определенно очень важна для случая, когда нагрузки не совпадают по фазе. Например, вращающуюся несбалансированную массу можно описать традиционным способом, указав для нагрузки по оси y фазовый сдвиг на 90° относительно нагрузки по оси x.
Результаты исследования при учете гармонических возмущений
При использовании исследования, в котором учитываются гармонические возмущения (на фоне стационарной нагрузки), будет сформировано два набора результатов: решение для предварительного напряжения и решение для гармонического возмущения. В данном случае при настройке графиков или операций вычисления появится дополнительная настройка: Expression evaluated for.
Выбор способа расчета величины в рамках исследования, в котором учитываются гармонические возмущения.
Здесь можно выбрать для какого решения нужно вывести/рассчитать величину: для решения с расчетом гармонических возмущений, для решения с расчетом предварительного напряжения или для их сочетания. В случае выбора решения с расчетом гармонических возмущений также будет доступна еще одна дополнительная опция: чекбокс Compute differential.
Активация чекбокса Compute differential.
Последняя настройка влияет на обработку нелинейных выражений. 2 будет рассчитано как
2 будет рассчитано как 2*u0*u, где u0 — значение в точке линеаризации.
Преобразование данных из частотной во временную область
В некоторых ситуациях может потребоваться непосредственно визуализировать гармонический отклик, полученный в рамках расчета в частотной области, как функцию от времени. В частности, это может быть полезно при наличии нескольких возбуждающих нагрузок с разными частотами.
Отклик на возбуждение от двух нагрузок с разными частотами.
Провести конвертацию данных из частотной области во временную можно возможно посредством шага исследования Frequency to Time FFT (Быстрое преобразование Фурье из частотной области во временную область).
Последовательность исследований для перевода результатов из частотной области во временную.
Этот метод используется в следующих учебных моделях:
Заключение
Расчет в частотной области представляет собой мощное средство для анализа линейных систем, подверженных воздействию гармонического возбуждения. На самом деле, можно свести к исследованию в частотной области любую задачу с периодической формой возбуждающего сигнала нагрузки за счет конвертации его с использованием преобразования Фурье.
На самом деле, можно свести к исследованию в частотной области любую задачу с периодической формой возбуждающего сигнала нагрузки за счет конвертации его с использованием преобразования Фурье.
В Галерее приложений доступно множество примеров анализа частотного отклика механических систем, например:
Преобразователь частоты, Серия А300 — для общепромышленной нагрузки
Общепромышленная серия преобразователей частоты подходит для оборудования с тяжелым пуском и высокой нагрузкой (станки, экструдеры, куттеры, компрессоры, конвейеры, погружные насосы и мн. др.). Преобразователь частоты с высокоточным пусковым моментом при низких скоростях (пусковой вращающий момент: 0.5Hz/150% (векторное управление), 1Hz/150% (U/f)), встроенным ПИД-регулятором (см. инструкцию по настройке), функции полной защиты двигателя с возможностью изменять параметры настройки, съемным выносным пультом управления, повышенным перегрузочным моментом до 200%, автоматическим подъемом крутящего момента, функцией коррекции скольжения, автоматическим регулированием напряжения (AVR) и встроенным интерфейсом RS-485.
Преобразователь частоты серии А300 имеет съемный пульт управления и может использоваться удаленно, до 60 метров от частотного преобразователя по витой паре без переходников и дополнительных модулей, усилителей сигнала.
Внимание! Номинальный ток электродвигателя не должен превышать номинальный ток частотного преобразователя!
Преобразователь частоты вентиляторной нагрузки
Такие устройства предназначены для контролируемого изменения скорости вращения электродвигателя (управления электродвигателем), путём трансформации входного напряжения (220 или 380 Вольт) в импульсное выходное с частотой от 0 до 300 Герц. При этом на обмотках электродвигателя создаётся переменный синусоидальный ток с регулируемой амплитудой и частотой (основной принцип преобразователя частоты переменного тока).
Преобразователь частоты для насосов
Такие устройства предназначены для контролируемого изменения скорости вращения электродвигателя (управления электродвигателем), путём трансформации входного напряжения (220 или 380 Вольт) в импульсное выходное с частотой от 0 до 300 Герц. При этом на обмотках электродвигателя создаётся переменный синусоидальный ток с регулируемой амплитудой и частотой (основной принцип преобразователя частоты переменного тока).
При этом на обмотках электродвигателя создаётся переменный синусоидальный ток с регулируемой амплитудой и частотой (основной принцип преобразователя частоты переменного тока).
Частотный преобразователь взрывозащищенный ЧПВ | Компания EXC — производство и модернизация горно-шахтного оборудования
Конструкция ЧПВ
Конструкция и состав секции частотного преобразователя могут изменяться в зависимости от мощности подключаемого двигателя, номинального напряжения, характера нагрузки.
При небольшой мощности нагрузки (до 100кВт при напряжении 690В, например) преобразователю частоты достаточно принудительного воздушного охлаждения, организованного внутри оболочки.
Если нагрузка большей мощности, либо требуется работа в тяжелом режиме (запуск груженого конвейера), преобразователь частоты снабжается внутренним и внешним контурами охлаждения.
Преобразователи для вентиляторов местного проветривания
Отличительными особенностями данной серии являются воздушное охлаждение, компактные размеры, высокая степень адаптации к системам АГК шахт.
Частотные преобразователи для вентиляторов местного проветривания выполняют функции защиты электродвигателя и обслуживающего персонала, регулирования скорости вращения вентиляторов, передачи данных в систему аэрогазового контроля шахты, контроля целостности вентиляционных рукавов.
Cостав ЧПВ:
- преобразователь частоты;
- датчики скорости воздуха;
- искробезопасные источники питания;
- микроконтроллерные средства защиты;
- аппаратура управления и обмена информацией с системой АГК.
Конструктивные особенности ЧПВ
Преобразователь частоты находится внутри взрывозащитной оболочки, закреплен на выкатной раме для удобства его обслуживания. Для максимального отвода тепла организована принудительная протяжка воздуха от преобразователя частоты по специальному каналу охлаждения с оребрением.
Аппаратура управления расположена на быстросъемной панели, закрепленной на распашной двери, что облегчает доступ для обслуживания.
В комплекте с ЧПВ поставляются два взрывобезопасных датчика скорости. Один устанавливается на выходе вентиляционного рукава, а второй — около вентилятора.
Контроль производительности и регулирование оборотов вентилятора осуществляется в зависимости от показаний датчика, который установлен на выходе из вентиляционного рукава. Если разница показаний двух датчиков превышает задаваемый порог, то на дисплей выводится сообщение о повреждении вентиляционного рукава и наличии утечек воздуха.
Наличие контроллера управления с цифровыми интерфейсами позволяет интегрировать ЧПВ в системы аэрогазового контроля шахты, а также передавать данные о производительности и прочих параметрах вентилятора местного проветривания, объеме и скорости воздуха, подаваемого в тупиковый забой и осуществлять дистанционное управление ЧПВ и ВМП.
Волны
Частота
Частота — это мера того, как часто повторяющееся событие, такое как волна, происходит за определенный промежуток времени. Одно завершение повторяющегося узора называется циклом. Только движущиеся волны, меняющие свое положение во времени, обладают частотой. Частота — это один из способов определить, насколько быстро движется волна.
Одно завершение повторяющегося узора называется циклом. Только движущиеся волны, меняющие свое положение во времени, обладают частотой. Частота — это один из способов определить, насколько быстро движется волна.
Волны могут двигаться двумя способами. Частоты прогрессивных волн или тех, которые движутся вперед, показывают, насколько быстро волна движется вперед в единицах циклов в единицу времени.Частоты стоячих волн или тех, которые колеблются на месте, представляют собой скорость колебаний в единицах циклов в единицу времени.
| Определение Словарное определение частоты: Физика. a) количество периодов или регулярно происходящих событий любого данного вида в единицу времени, обычно одну секунду. б) количество циклов или завершенных чередований в единицу времени волны или колебания. Символ: f ; Сокр .: част. |
Единицы
Частота выражается в единицах циклов в единицу времени.
Хотя частота является мерой скорости движения, она не идентична скорости. Например, если мы думаем о машине, которая движется со скоростью 60 миль в час, мы имеем в виду именно это. Однако, если мы говорим, что волна имеет частоту 60 циклов в час, точки на волне могут перемещаться быстрее или медленнее в зависимости от длины волны.Сравнивая две волны одинаковой длины, более высокая частота ассоциируется с более быстрым движением. Сравнивая две волны с разной длиной волны, более высокая частота не всегда указывает на более быстрое движение, хотя может. Волны разных длин волн могут иметь одинаковую частоту. Для некоторых целей частота измерения более полезна, чем абсолютная скорость.
Единица, Герц
Единица Герц (Гц) используется для описания частоты в циклах в секунду. В предложении правильный формат записи этого отношения:
Один цикл представляет собой движение одной длины волны.
Номера радиосвязи
Часто можно услышать радиочастоты, указанные в мегагерцах (МГц) . .. (в разработке).
.. (в разработке).
Период волны
Частота волны также связана с другим измерением, называемым периодом волны (T). Период волны — это время, необходимое для прохождения одного цикла, и единицы всегда выражаются во времени. Чем быстрее движется волна, тем меньше период ее волны.
Вместо измерения в терминах фиксированной единицы времени, второй, период волны, использует фиксированное количество циклов, один цикл…
Как вы измеряете период волны?
Период волны можно определить, измерив, сколько времени требуется двум пикам, чтобы пройти определенную точку. Вы можете сделать это для океанских волн, стоя на пирсе и используя секундомер.
Строится …
Оптические частотные гребенки | NIST
Что делают оптические частотные гребенки?
Оптические частотные гребенки — это специализированные лазеры, которые действуют как линейка для света. Они измеряют точные частоты света — от невидимого инфракрасного и ультрафиолетового до видимого красного, желтого, зеленого и синего света — быстро и точно.
Они измеряют точные частоты света — от невидимого инфракрасного и ультрафиолетового до видимого красного, желтого, зеленого и синего света — быстро и точно.
Эти устройства, получившие Нобелевскую премию, заполняют важный технологический пробел. Оптические частотные гребенки позволяют ученым измерять и контролировать световые волны, как если бы они были радиоволнами. Благодаря оптическим частотным гребенкам технологии, использующие радио- и микроволновые частоты, такие как часы, компьютеры и средства связи, теперь легко подключаются к оптическим волнам, которые колеблются в 10 000 раз более высоких частот.
Оптические частотные гребенки появились в конце 1990-х годов как часть видения ученых NIST по созданию более совершенных оптических атомных часов. Сегодня ученые NIST находятся в авангарде разработки этих инструментов, и они нашли применение не только для хронометража.
На что способна расческа
Благодаря простому измерению гребенка оптических частот изменила науку. Так что же может расческа? Много — и возможности постоянно расширяются.
Так что же может расческа? Много — и возможности постоянно расширяются.Как используются гребенки оптических частот?
Хронометраж
Оптические частотные гребенки были революционными для атомных часов и хронометража.Оптические атомные часы отмечают ход времени, считая собственные колебания атомов, так же, как старые часы считают колебания маятника. Эти атомы колеблются примерно 500 000 миллиардов раз в секунду — это намного более высокая частота, чем стандартные атомные часы на основе микроволнового излучения. Современные электронные системы, которые используются для измерения частоты в атомных часах на основе микроволнового излучения, просто не могут считать оптические «тики».
Поскольку зубцы гребенки оптических частот равномерно расположены и точны, гребенка действует как шестеренки часов, принимая более быстрые оптические частоты и разделяя их на более низкочастотные микроволновые сигналы, используемые электроникой и современными атомными часами. Это позволяет ученым связать высокочастотные «тики» оптических атомных часов с более низкочастотными «тиканьями» микроволновых часов и электроникой, которые используются в современных компьютерах и системах связи.
Это позволяет ученым связать высокочастотные «тики» оптических атомных часов с более низкочастотными «тиканьями» микроволновых часов и электроникой, которые используются в современных компьютерах и системах связи.
Как частотные гребенки объединяют спектр ЭМП
Гребни оптических частот могут действовать как шестеренки в часах, позволяя ученым легко преобразовывать высокочастотные оптические частоты в низкочастотные микроволны и наоборот. Они даже могут помочь ученым переводить между разными оптическими частотами.Благодаря этим «шестерням», передающим точные сигналы между электроникой, приборами на базе микроволнового излучения и оптическими атомными часами, ученые могут использовать эти новые мощные часы для более быстрых и точных систем хронометража. Оптические атомные часы могут в конечном итоге изменить определение секунды.
Чтобы эти новые часы можно было использовать для национального и глобального хронометража, ученым необходимо иметь возможность сравнивать сигналы от часов на разных расстояниях. В этом также могут помочь оптические гребенки. NIST и JILA, совместный исследовательский институт NIST и CU Boulder, использовали лидар для передачи сигналов времени по воздуху, сравнивая два разных типа атомных часов.
В этом также могут помочь оптические гребенки. NIST и JILA, совместный исследовательский институт NIST и CU Boulder, использовали лидар для передачи сигналов времени по воздуху, сравнивая два разных типа атомных часов.
Улучшенные системы хронометража имеют решающее значение во многих технологических приложениях, от биржевой торговли до навигации. Спутники и приемники глобальной системы позиционирования (GPS) отправляют радиосигналы туда и обратно и используют синхронизацию этих сигналов для определения местоположения пользователя. GPS использует военное время, и эти часы периодически сверяют свое время с гражданскими часами, такими как оптические атомные часы NIST и им подобные по всему миру. Ученые надеются, что в будущем на навигационных спутниках будут установлены оптические атомные часы, которые сделают систему еще более точной и позволят GPS определять местоположение с точностью до сантиметра.
Оптические атомные часы также полезны в исследованиях квантовой физики. Разделив время на невероятно маленькие срезы, ученые могут использовать эти часы для измерения ранее необнаруживаемых изменений, таких как гравитационное красное смещение на малых расстояниях, влияние гравитации на течение времени.
Разделив время на невероятно маленькие срезы, ученые могут использовать эти часы для измерения ранее необнаруживаемых изменений, таких как гравитационное красное смещение на малых расстояниях, влияние гравитации на течение времени.
Стронциевые оптические атомные часы JILA стали возможны благодаря частотной гребенке.
Кредит: Группа Йе и Брэд Бэксли, JILA
Астрономия и космология
Усовершенствованные оптические атомные часы также позволяют ученым изучать природные константы за пределами нашей планеты.Например, с помощью оптических частотных гребенок ученые NIST используют эти улучшенные часы для поиска неуловимой темной материи.
Оптические частотные гребенки также помогают ученым искать экзопланеты вокруг далеких звезд. Отслеживая точные цвета света от этих звезд, они могут искать колебание в движении звезды, которое указывало бы на присутствие земной планеты, вращающейся вокруг звезды.![]()
Точное измерение расстояния
Оптические гребенки работают на больших расстояниях.В 2013 году NIST запатентовал лидар — систему обнаружения и определения расстояния, в которой используются оптические частотные гребенки для измерения расстояния до объекта путем анализа отраженного от него света.
Это уже используется в нескольких исследовательских приложениях. Лаборатория пожарных исследований NIST использовала частотные гребенки, чтобы «видеть» сквозь пламя и идентифицировать тающие объекты. Лидар на основе частотной гребенки также использовался для создания трехмерных карт. В конце концов, лидар, использующий оптические частотные гребенки, сможет удерживать спутники и другие космические инструменты в тесноте, действуя как единый инструмент.
Атмосфера и парниковые газы
Атомы и молекулы можно определить по тем частотам света, которые они поглощают. Поскольку гребенки оптических частот генерируют миллионы частот в виде коротких импульсов, их можно использовать для быстрого и эффективного изучения количества, структуры и динамики различных молекул и атомов.
У него много потенциальных применений, и он уже используется для изучения загрязнения. Используя оптические частотные гребенки, ученые из JILA изучили короткоживущие молекулы, которые связывают горение ископаемого топлива с загрязнением воздуха.Структуру и динамику больших и сложных молекул также можно исследовать с помощью частотных гребенок.
Ученые также работают над использованием оптических частотных гребенок для обнаружения следовых количеств различных молекул в газах. В 2019 году ученые и инженеры из NIST, Университета Колорадо в Боулдере и LongPath Technologies разработали портативную спектроскопическую систему с двумя гребенками для обнаружения мельчайших выбросов метана с нефтяных и газовых месторождений.
Иллюстрация, показывающая, как следовые газы обнаруживаются на нефтяных и газовых месторождениях с помощью мобильного двухчастотного гребенчатого лазерного спектрометра.Спектрометр расположен в центре круга, окруженного световозвращающими зеркалами. Лазерный свет от спектрометра (желтая линия) проходит через газовое облако, попадает в ретрорефлектор и возвращается прямо в исходную точку. Собранные данные используются для определения утечек газовых примесей (включая метан), а также мест утечек и уровней их выбросов.
Лазерный свет от спектрометра (желтая линия) проходит через газовое облако, попадает в ретрорефлектор и возвращается прямо в исходную точку. Собранные данные используются для определения утечек газовых примесей (включая метан), а также мест утечек и уровней их выбросов.
Кредит: Стефани Сайзмор и Ян Коддингтон / NIST
Медицинская диагностика
Оптическая частотная гребенка может найти применение и в медицине.Так же, как его можно использовать в приложениях химии, гребенку можно использовать для обнаружения следов молекулярных индикаторов болезни. Ученые из JILA экспериментируют с гребнями, чтобы создать алкотестеры, обнаруживающие болезни.
Как работают оптические частотные гребенки?
Частотные гребенки измеряют неизвестную оптическую частоту, измеряя частоту повторения непрерывной последовательности световых импульсов, которая находится в более широком, легко измеряемом радиочастотном диапазоне.
Свет включает в себя широкий спектр цветов, которые распространяются волнами.Каждый из этих цветов света — от невидимого инфракрасного и ультрафиолетового до красного, синего или желтого видимого света — имеет соответствующую частоту или количество пиков волны, которые проходят через фиксированную точку каждую секунду.
Радиоволны и микроволны также распространяются со скоростью света, но их пики намного дальше друг от друга, что позволяет современной электронике легко их подсчитывать и отслеживать.
Оптические частотные гребенки излучают непрерывную серию очень коротких, близко расположенных импульсов света, содержащих миллион различных цветов, от невидимого инфракрасного до видимого и ультрафиолетового спектра.
Благодаря технологии, называемой «синхронизация мод», все частоты в каждом импульсе начинаются синхронно, синхронно друг с другом.
Результат напоминает зубцы гребешка, разделяя каждую частоту на отдельный пик — отсюда и название устройства. Расстояние между зубцами очень маленькое и ровное, и они действуют как стрелки на линейке для измерения света, излучаемого звездами, атомами, другими лазерами и т. Д. С чрезвычайной точностью.
Расстояние между зубцами очень маленькое и ровное, и они действуют как стрелки на линейке для измерения света, излучаемого звездами, атомами, другими лазерами и т. Д. С чрезвычайной точностью.
Как были созданы гребенки оптических частот?
Хотя они могут показаться простыми, оптические частотные гребенки являются результатом десятилетий исследований и инноваций, в том числе значительного вклада NIST.
Физики раздумывали над идеей этого специализированного лазера с 1970-х годов, когда Теодор Хэнш из Института квантовой оптики Макса Планка в Германии предложил модель первой оптической частотной гребенки, когда он был в Стэнфордском университете. Ученые знали, что непрерывные лазеры могут генерировать свет только одного цвета, а импульсные лазеры могут генерировать несколько цветов. Чем короче импульс, тем больше частот может выдавать лазер.
Ученым нужно было знать расстояние между «зубцами» — отдельные частоты света — гребешка. Для этого требовались лазеры с синхронизацией мод. При синхронизации режима все цвета в каждом импульсе начинают совпадать по фазе друг с другом.
Для этого требовались лазеры с синхронизацией мод. При синхронизации режима все цвета в каждом импульсе начинают совпадать по фазе друг с другом.
В середине 1990-х годов лазеры, сделанные на кристаллах сапфира, легированного титаном, могли генерировать эти синхронизированные частоты в фемтосекундах — миллиардных долях миллиардной доли секунды.
Ученым также нужно было откалибровать гребенку, чтобы настроить ее на известную частоту. Калибровка гребенки определит частоту смещения или место начала «галочки» на гребне в абсолютном смысле.Хэнш понял, что лучший способ сделать это — заставить гребенку воспроизводить октаву частот, где самая высокая частота как минимум вдвое меньше самой низкой. Вмешательство частоты с ее двойником — так называемое «самообучение» — позволяет ученым точно определять каждую частоту.
Это было невозможно, пока группа ученых из Bell Laboratories не создала оптическое волокно толщиной с волос, которое могло бы передавать более октавный диапазон частот. Это было решающим достижением для оптических частотных гребенок и последним фрагментом головоломки.С помощью этого оптического волокна Ян Холл и его коллеги из JILA смогли разработать технику саморегулирования, в которой они нуждались в 1999 году. Они первыми сравнили работу нескольких фемтосекундных частотных гребенок, тем самым продемонстрировав воспроизводимость.
Это было решающим достижением для оптических частотных гребенок и последним фрагментом головоломки.С помощью этого оптического волокна Ян Холл и его коллеги из JILA смогли разработать технику саморегулирования, в которой они нуждались в 1999 году. Они первыми сравнили работу нескольких фемтосекундных частотных гребенок, тем самым продемонстрировав воспроизводимость.
Холл и его команда физиков из JILA, включая Стивена Кундиффа, Скотта Диддамса, Дэвида Джонса и Джун Йе, разработали несколько других методов, которые приблизили оптическую частотную гребенку к реальности. В конце 1990-х годов команда разработала систему калибровки для фемтосекундного лазера, создавая контролируемые, четко определенные импульсы, содержащие тысячи цветов.Они также улучшили стабилизацию лазера, сделав его устойчивым. В 2005 году Холл и Хэнш разделили часть Нобелевской премии по физике за их вклад в создание оптической частотной гребенки.
Что дальше с оптическими частотными гребенками?
С 1999 года ученые NIST и JILA быстро усовершенствовали гребенку и все еще находятся на переднем крае развития и инноваций в области оптических частотных гребенок.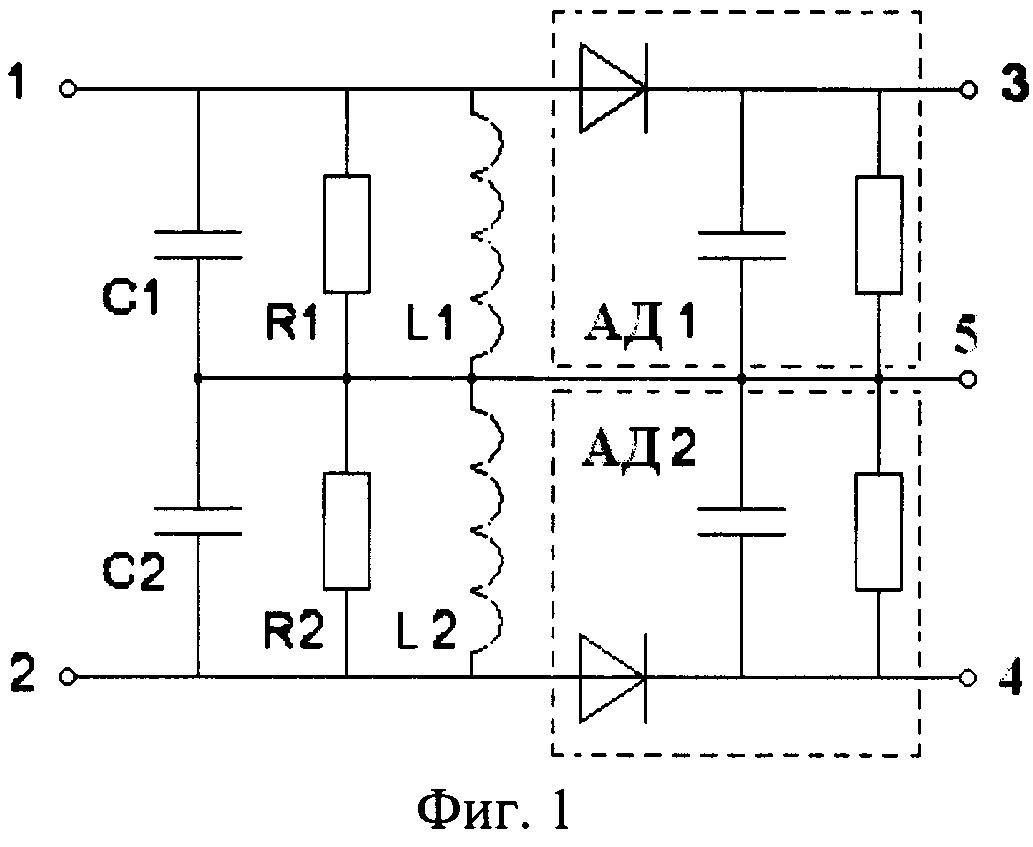 Современные оптические частотные гребенки охватывают более широкий диапазон электромагнитных частот, чем их более ранние аналоги, от глубокого инфракрасного до крайнего ультрафиолета.Однажды ультрафиолетовая расческа может быть использована для управления переходами в ядрах атомов, что откроет новые возможности для часов и спектроскопии для изучения наномира.
Современные оптические частотные гребенки охватывают более широкий диапазон электромагнитных частот, чем их более ранние аналоги, от глубокого инфракрасного до крайнего ультрафиолета.Однажды ультрафиолетовая расческа может быть использована для управления переходами в ядрах атомов, что откроет новые возможности для часов и спектроскопии для изучения наномира.
Экспериментальная установка для генерации набора стабильных частот в криогенно охлаждаемой гребенке частот лазерного микрорезонатора. Кольцевой микрорезонатор, достаточно маленький, чтобы поместиться на микрочипе, работает при очень низкой мощности лазера и изготовлен из полупроводникового арсенида алюминия-галлия.
Кредит: NIST
гребенчатые гребенки с волоконным лазером были следующим значительным достижением в области оптических гребенок.Ученые NIST и JILA внесли значительный вклад в создание и усовершенствование этих гребней. Эти гребенки, использующие обычные оптоволоконные компоненты телекоммуникаций, могут работать непрерывно и более компактны, чем оригинальные оптические гребенки. Это делает их «рабочими лошадками» для метрологии. В настоящее время они используются для многочисленных экспериментов (включая часы) в NIST и других лабораториях, а также в полевых приложениях, таких как лидары и аэрокосмическая промышленность. Также рассматриваются и проходят испытания частотные гребенки с волоконным лазером для выхода в космос.Ученые и инженеры NIST постоянно улучшают характеристики, мощность и долговечность гребенок с волоконным лазером для использования в новых приложениях и средах.
Это делает их «рабочими лошадками» для метрологии. В настоящее время они используются для многочисленных экспериментов (включая часы) в NIST и других лабораториях, а также в полевых приложениях, таких как лидары и аэрокосмическая промышленность. Также рассматриваются и проходят испытания частотные гребенки с волоконным лазером для выхода в космос.Ученые и инженеры NIST постоянно улучшают характеристики, мощность и долговечность гребенок с волоконным лазером для использования в новых приложениях и средах.
В то время как многие частотные гребни в настоящее время имеют размер обувной коробки и широко доступны для использования в лабораториях и за их пределами, ученые усердно работают над их уменьшением. Ученые работают над созданием гребенок оптических частот, настолько маленьких, что они могут поместиться на микрочипе.
Многие ученые надеются, что если частотные гребенки поместятся на микрочип, они смогут найти еще более широкое коммерческое применение.Микрочастицы могут улучшить системы связи, особенно в центрах обработки данных и других высокопроизводительных вычислительных системах. Спектроскопические возможности оптической частотной гребенки можно использовать в смартфонах и носимых устройствах для мониторинга здоровья.
Спектроскопические возможности оптической частотной гребенки можно использовать в смартфонах и носимых устройствах для мониторинга здоровья.
Однако эти приложения еще далеко. В настоящее время для работы микрогребням требуются инструменты, не входящие в состав микросхемы, такие как источники питания, усилители и лазеры накачки. Многие из этих компонентов были уменьшены в размерах, но объединить их все на одном кристалле очень сложно.Но, возможно, самое большое препятствие, которое необходимо преодолеть, — это сделать эти микрогребни саморегулирующимися, что необходимо для обеспечения точности гребней.
Исследования, направленные на преодоление этих препятствий, продвигаются вперед. Даже если полностью «гребешок на кристалле» никогда не будет реализован, микрогребни уже находят применение в исследованиях. С миниатюрными двухчастотными гребенками NIST уже разработал атомные часы в масштабе микросхемы. Ученые из NIST и их сотрудники будут продолжать исследовать огромный потенциал микрочастиц, гребенок волоконных лазеров и гребенок оптических частот.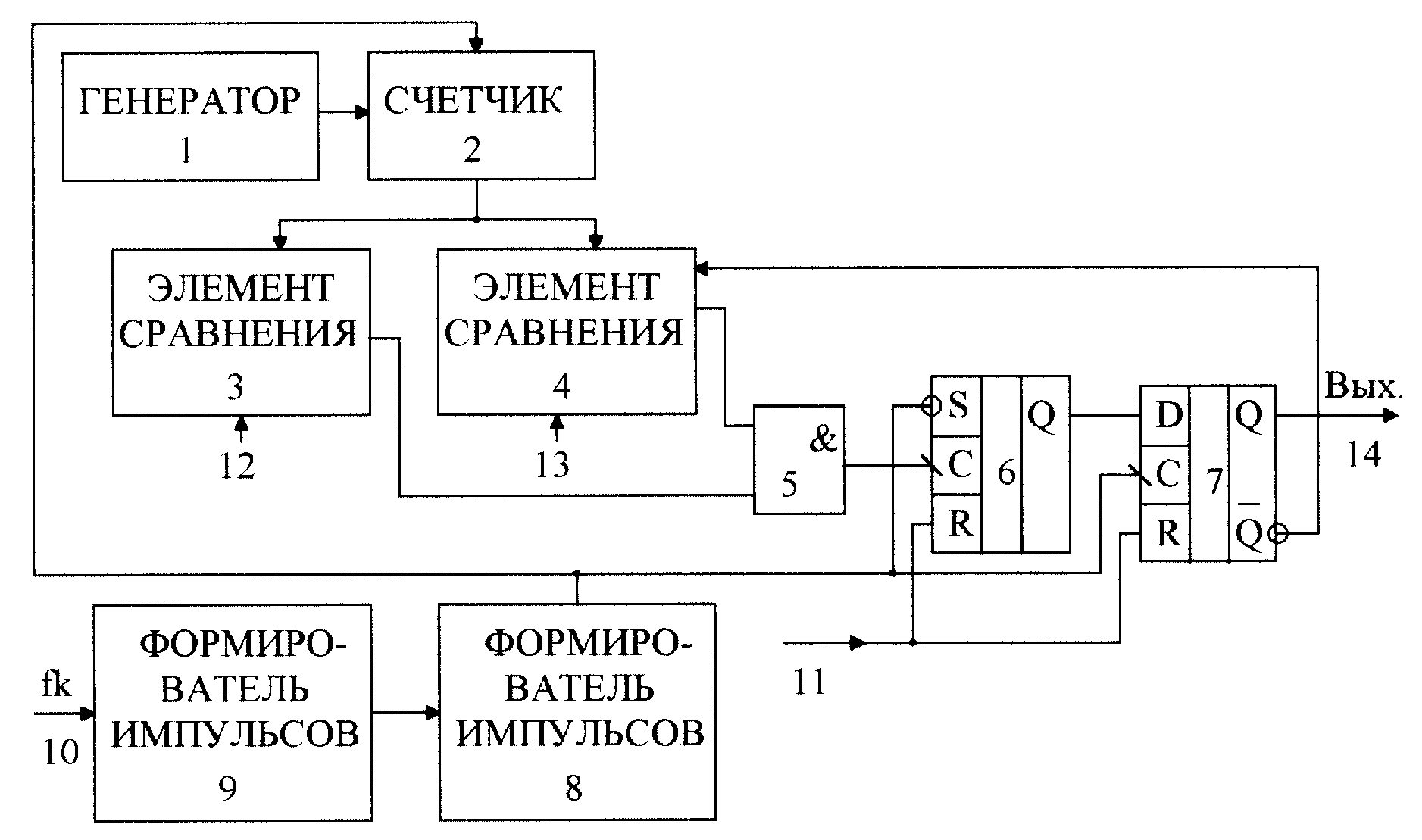
Последние новости
частот музыкальных нот, A4 = 440 Гц
частот музыкальных нот, A4 = 440 ГцЧастоты для равномерно темперированной гаммы, A
4 = 440 Гц Другие варианты настройки, A 4 =Скорость звука = 345 м / с = 1130 фут / с = 770 миль / час
Подробнее о скорости звука
(«Средняя С» — это C 4 )
| Примечание | Частота (Гц) | Длина волны (см) |
|---|---|---|
| С 0 | 16.35 | 2109,89 |
| C # 0 / D b 0 | 17,32 | 1991,47 |
| D 0 | 18,35 | 1879,69 |
| D # 0 / E b 0 | 19,45 | 1774. 20 20 |
| E 0 | 20.60 | 1674.62 |
| Факс 0 | 21,83 | 1580.63 |
| F # 0 / G b 0 | 23,12 | 1491.91 |
| G 0 | 24,50 | 1408.18 |
| G # 0 / A b 0 | 25,96 | 1329,14 |
| A 0 | 27.50 | 1254,55 |
| A # 0 / B b 0 | 29,14 | 1184,13 |
| B 0 | 30,87 | 1117,67 |
| С 1 | 32,70 | 1054. 94 94 |
| C # 1 / D b 1 | 34,65 | 995.73 |
| D 1 | 36,71 | 939,85 |
| D # 1 / E b 1 | 38,89 | 887.10 |
| E 1 | 41.20 | 837,31 |
| Ф. 1 | 43,65 | 790,31 |
| F # 1 / G b 1 | 46.25 | 745.96 |
| G 1 | 49.00 | 704.09 |
| G # 1 / A b 1 | 51,91 | 664,57 |
| A 1 | 55,00 | 627,27 |
| A # 1 / B b 1 | 58,27 | 592. 07 07 |
| B 1 | 61,74 | 558,84 |
| С 2 | 65,41 | 527,47 |
| C # 2 / D b 2 | 69,30 | 497,87 |
| D 2 | 73,42 | 469,92 |
| D # 2 / E b 2 | 77.78 | 443,55 |
| E 2 | 82,41 | 418,65 |
| Ф. 2 | 87,31 | 395,16 |
| F # 2 / G b 2 | 92,50 | 372,98 |
| G 2 | 98,00 | 352,04 |
| G # 2 / A b 2 | 103. 83 83 | 332,29 |
| A 2 | 110,00 | 313,64 |
| A # 2 / B b 2 | 116,54 | 296,03 |
| B 2 | 123,47 | 279,42 |
| С 3 | 130,81 | 263,74 |
| C # 3 / D b 3 | 138.59 | 248,93 |
| D 3 | 146,83 | 234,96 |
| D # 3 / E b 3 | 155,56 | 221,77 |
| E 3 | 164,81 | 209,33 |
Ф. 3 3 | 174,61 | 197,58 |
| F # 3 / G b 3 | 185.00 | 186,49 |
| G 3 | 196,00 | 176.02 |
| G # 3 / A b 3 | 207,65 | 166,14 |
| A 3 | 220,00 | 156,82 |
| A # 3 / B b 3 | 233,08 | 148.02 |
| B 3 | 246,94 | 139,71 |
| С 4 | 261,63 | 131,87 |
| C # 4 / D b 4 | 277,18 | 124,47 |
| D 4 | 293,66 | 117,48 |
| D # 4 / E b 4 | 311. 13 13 | 110,89 |
| E 4 | 329,63 | 104,66 |
| Ф. 4 | 349,23 | 98,79 |
| F # 4 / G b 4 | 369,99 | 93,24 |
| G 4 | 392,00 | 88.01 |
| G # 4 / A b 4 | 415.30 | 83,07 |
| A 4 | 440,00 | 78,41 |
| A # 4 / B b 4 | 466,16 | 74,01 |
| B 4 | 493,88 | 69,85 |
| С 5 | 523,25 | 65. 93 93 |
| C # 5 / D b 5 | 554.37 | 62,23 |
| D 5 | 587,33 | 58,74 |
| D # 5 / E b 5 | 622,25 | 55,44 |
| E 5 | 659,25 | 52,33 |
| Ф. 5 | 698,46 | 49,39 |
| F # 5 / G b 5 | 739.99 | 46,62 |
| G 5 | 783,99 | 44.01 |
| G # 5 / A b 5 | 830,61 | 41,54 |
| A 5 | 880,00 | 39. 20 20 |
| A # 5 / B b 5 | 932,33 | 37.00 |
| B 5 | 987,77 | 34,93 |
| С 6 | 1046,50 | 32,97 |
| C # 6 / D b 6 | 1108,73 | 31,12 |
| D 6 | 1174,66 | 29,37 |
| D # 6 / E b 6 | 1244.51 | 27,72 |
| E 6 | 1318,51 | 26,17 |
Ф. 6 6 | 1396,91 | 24,70 |
| F # 6 / G b 6 | 1479,98 | 23,31 |
| G 6 | 1567,98 | 22,00 |
| G # 6 / A b 6 | 1661.22 | 20,77 |
| A 6 | 1760,00 | 19.60 |
| A # 6 / B b 6 | 1864,66 | 18,50 |
| B 6 | 1975,53 | 17,46 |
| С 7 | 2093,00 | 16,48 |
| C # 7 / D b 7 | 2217.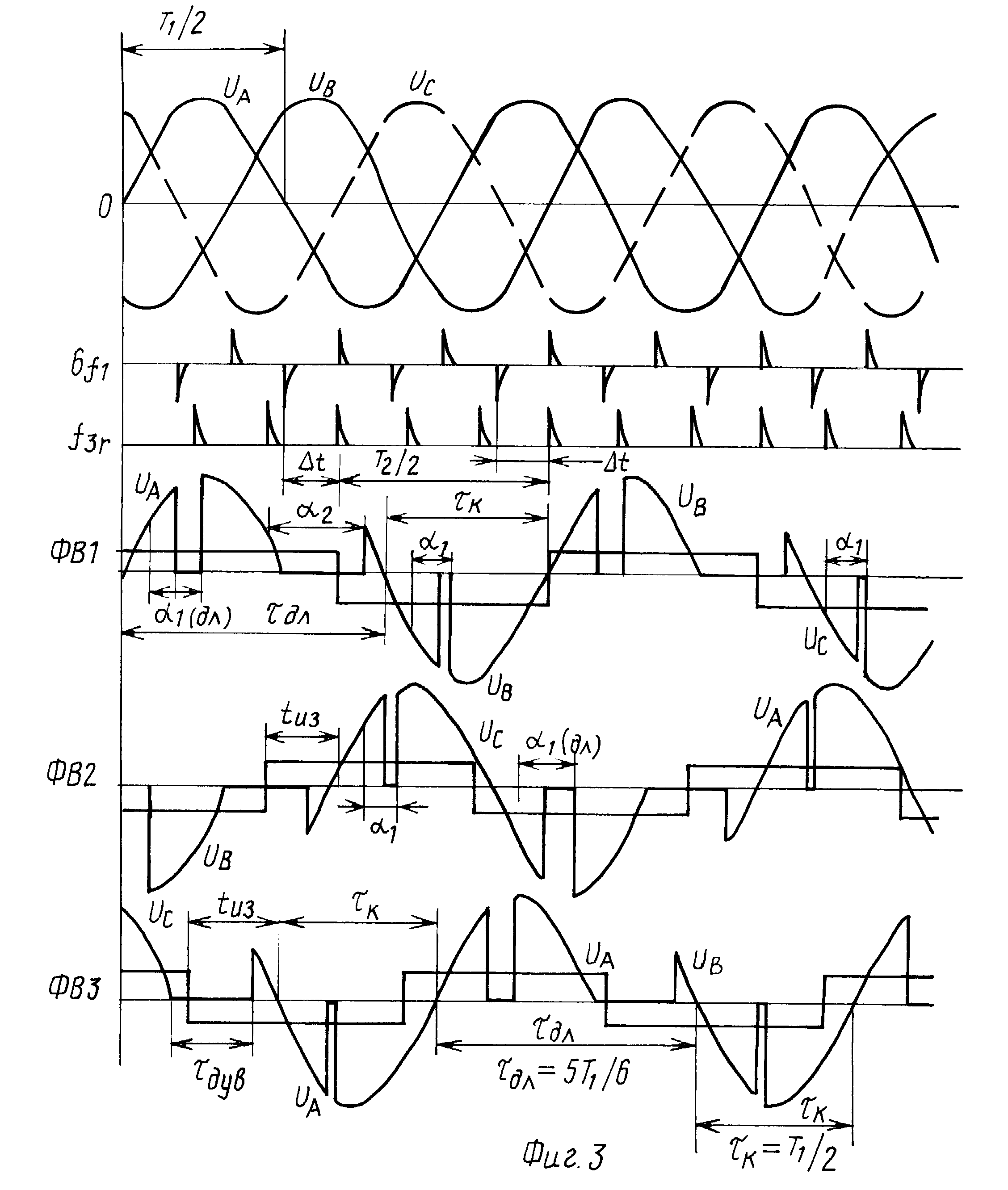 46 46 | 15,56 |
| D 7 | 2349,32 | 14,69 |
| D # 7 / E b 7 | 2489.02 | 13,86 |
| E 7 | 2637.02 | 13,08 |
| Ф. 7 | 2793,83 | 12,35 |
| F # 7 / G b 7 | 2959.96 | 11,66 |
| G 7 | 3135,96 | 11,00 |
| G # 7 / A b 7 | 3322,44 | 10,38 |
| A 7 | 3520,00 | 9,80 |
| A # 7 / B b 7 | 3729,31 | 9. 25 25 |
| B 7 | 3951.07 | 8,73 |
| С 8 | 4186.01 | 8,24 |
| C # 8 / D b 8 | 4434,92 | 7,78 |
| D 8 | 4698,63 | 7,34 |
| D # 8 / E b 8 | 4978.03 | 6.93 |
| E 8 | 5274.04 | 6.54 |
| Ф. 8 | 5587.65 | 6,17 |
| F # 8 / G b 8 | 5919. 91 91 | 5,83 |
| G 8 | 6271,93 | 5,50 |
| G # 8 / A b 8 | 6644.88 | 5,19 |
| A 8 | 7040,00 | 4,90 |
| A # 8 / B b 8 | 7458,62 | 4,63 |
| B 8 | 7902,13 | 4,37 |
(Чтобы преобразовать длину в см в дюймы, разделите на 2,54)
Дополнительная информация о шкале равномерного темперирования
Уравнения, используемые для этой таблицы
Вопросы / комментарии к: Suits @ mtu.edu
На этих страницах нет всплывающих окон или рекламы. Если вы их видите, значит, их добавляет треть
вечеринка без согласия автора.
Если вы их видите, значит, их добавляет треть
вечеринка без согласия автора.
To MTU Physics Home
Информация об авторских правах
Частота эмодзи — Юникод
АРХИВ
ЭТОТ РАЗДЕЛ СОДЕРЖИТ ДАННЫЕ EMOJI ЗА ПРЕДЫДУЩИЕ ГОДЫ
Как Консорциум Unicode выбирает, какие новые смайлы добавить в стандарт Unicode? Одним из важных факторов являются данные о том, как часто используются текущие смайлы.Шаблоны использования помогают принимать решения о будущих смайликах. Консорциум работает над сбором информации о том, как часто используются различные смайлы, и делает эти данные общедоступными.
Прокрутите вниз, чтобы увидеть список смайлов Unicode v12.0, упорядоченных в порядке их частоты использования.
Зачем измерять частоту использования эмодзи?
Свидетельство частоты — одно из многих соображений, принимаемых во внимание при рассмотрении предложений смайликов. Консорциум теперь готов помочь людям, предлагающим новые смайлы, опубликовать этот список текущих смайликов, ранжированных по тому, как часто они используются в целом. Это сводный рейтинг — в пределах определенного региона или на определенных платформах или программах порядок ранжирования частоты может быть другим. (Также обратите внимание, что не все браузеры и системы отображают все смайлы Unicode, что может повлиять на то, как этот список будет отображаться для вас.)
Консорциум теперь готов помочь людям, предлагающим новые смайлы, опубликовать этот список текущих смайликов, ранжированных по тому, как часто они используются в целом. Это сводный рейтинг — в пределах определенного региона или на определенных платформах или программах порядок ранжирования частоты может быть другим. (Также обратите внимание, что не все браузеры и системы отображают все смайлы Unicode, что может повлиять на то, как этот список будет отображаться для вас.)
Порядок ранжирования основан на средней частоте использования каждого смайлика в нескольких источниках.Варианты пола и оттенка кожи сведены в таблицу, таким образом, 👩🚀, 👩🏻🚀… 👩🏿🚀, 👨🚀, 👨🏻🚀… 👨🏿🚀… все собраны в один репрезентативный элемент, 👩 🚀, чтобы дать более четкое представление о том, как часто используется эта концепция. Обратите внимание, что новые смайлы, как правило, встречаются реже, поскольку их развертывание на всех устройствах часто требует времени. Смайлы разделены на группы на основе сравнения с частотой наиболее популярных смайлов: 😂. Каждая группа содержит смайлики, которые используются примерно в два раза чаще, чем в группе выше.Таким образом, элементы в группе 1 имеют менее ½ частоты, элементы в группе 2 имеют менее частоты и так далее. В группе 11 и выше частота ниже медианной (и менее 1/2048 частоты). Смайлы с очень низкой частотой содержат мало данных: строки 16 и 17 содержат лишь некоторые их образцы. Смайлы отображаются в порядке убывания в каждой группе. Эти данные могут быть обновлены в любое время по мере появления новой информации.
Каждая группа содержит смайлики, которые используются примерно в два раза чаще, чем в группе выше.Таким образом, элементы в группе 1 имеют менее ½ частоты, элементы в группе 2 имеют менее частоты и так далее. В группе 11 и выше частота ниже медианной (и менее 1/2048 частоты). Смайлы с очень низкой частотой содержат мало данных: строки 16 и 17 содержат лишь некоторые их образцы. Смайлы отображаются в порядке убывания в каждой группе. Эти данные могут быть обновлены в любое время по мере появления новой информации.
Распределение частот
J Pharmacol Pharmacother.2011 январь-март; 2 (1): 54–56.
S Manikandan
Помощник редактора, JPP
Помощник редактора, JPP
Адрес для корреспонденции: Маникандан С., Отдел фармакологии, Медицинский колледж и научно-исследовательский институт Индиры Ганди, Кадиркамам, Пудучерри, Индия. Электронная почта: moc.oohay@100nadnakinam Авторские права © Журнал фармакологии и фармакотерапии Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии наличия оригинала. работа правильно цитируется.
работа правильно цитируется.
ВВЕДЕНИЕ
Следующим шагом после завершения сбора данных является организация данных в осмысленной форме, чтобы можно было легко увидеть тенденцию, если таковая имеется, возникающую из данных. Один из распространенных методов организации данных — построение частотного распределения. Распределение частот — это организованная таблица / графическое представление количества людей в каждой категории по шкале измерения. [1] Это позволяет исследователю удобно просматривать все данные.Он показывает, являются ли наблюдения высокими или низкими, а также сосредоточены ли они в одной области или распределены по всему масштабу. Таким образом, частотное распределение представляет собой картину того, как отдельные наблюдения распределены в шкале измерений.
ОТОБРАЖЕНИЕ РАСПРЕДЕЛЕНИЯ ЧАСТОТ
Таблицы частот
Таблица частот (распределения) показывает различные категории измерений и количество наблюдений в каждой категории. Перед построением частотной таблицы следует иметь представление о диапазоне (минимальное и максимальное значения).Диапазон разделен на произвольные интервалы, называемые «интервалом классов». Если интервалов между классами будет слишком много, то не произойдет уменьшения объемности данных, также станут заметны незначительные отклонения. С другой стороны, если их очень мало, то форму самого распределения определить невозможно. Обычно достаточно 6–14 интервалов. [2]
Перед построением частотной таблицы следует иметь представление о диапазоне (минимальное и максимальное значения).Диапазон разделен на произвольные интервалы, называемые «интервалом классов». Если интервалов между классами будет слишком много, то не произойдет уменьшения объемности данных, также станут заметны незначительные отклонения. С другой стороны, если их очень мало, то форму самого распределения определить невозможно. Обычно достаточно 6–14 интервалов. [2]
Ширину класса можно определить, разделив диапазон наблюдений на количество классов. Ниже приведены некоторые рекомендации относительно ширины классов: [1]
Желательно иметь одинаковую ширину классов.Неравную ширину классов следует использовать только тогда, когда в данных существуют большие пробелы.
Интервалы классов должны быть взаимоисключающими и неперекрывающимися.
Следует избегать открытых классов на нижней и верхней стороне (например, <10,> 100).
Таблица распределения частоты пульса в состоянии покоя у здоровых людей приведена в таблице. . Он также дает совокупную и относительную частоту, что помогает легче интерпретировать данные.
. Он также дает совокупную и относительную частоту, что помогает легче интерпретировать данные.
Таблица 1
Распределение частоты пульса в состоянии покоя у здоровых добровольцев (N = 63)
| Импульс / мин | Частота | Накопленная частота | Относительная совокупная частота (%) | 56 |
|---|---|---|---|
| 56 | |||
| 2 | 2 | 3,17 | |
| 65–69 | 7 | 9 | 14,29 |
| 70–74 | 11 | 20 | 31.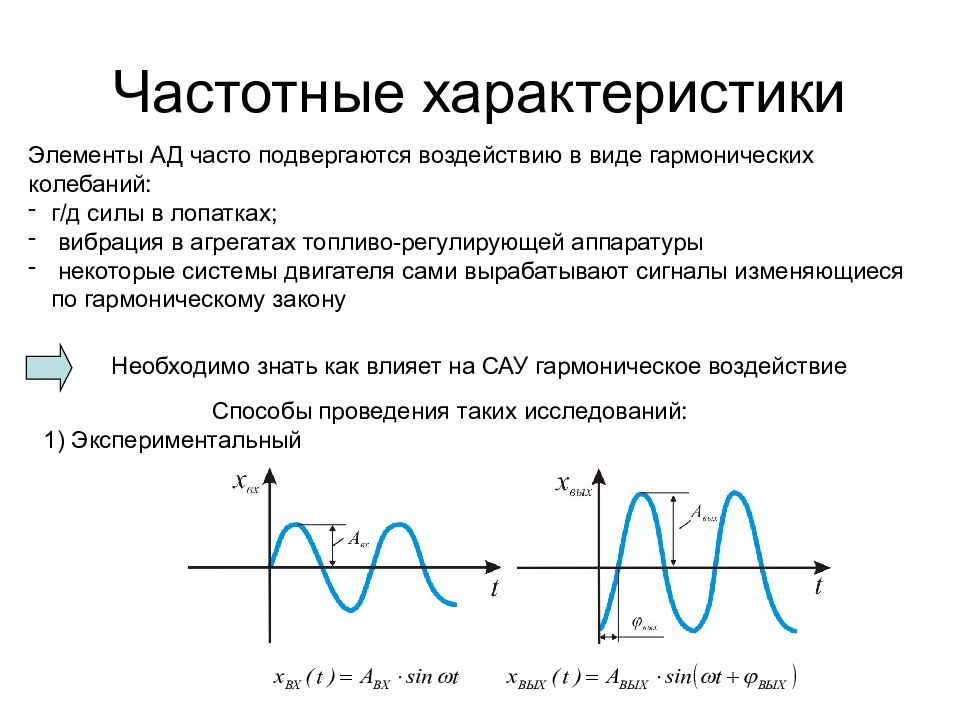 75 75 |
| 75–79 | 15 | 35 | 55,56 |
| 80–84 | 10 | 45 | 71,43 |
| 85–89 | 9 | 54 9001 | |
| 90–94 | 6 | 60 | 95,24 |
| 95–99 | 3 | 63 | 100 |
Графики распределения частот
График распределения частот представляет собой схематическое изображение информация в частотной таблице.
Гистограмма
Гистограмма — это графическое представление интересующей переменной по оси X и количества наблюдений (частоты) по оси Y . Проценты можно использовать, если целью является сравнение двух гистограмм с разным количеством субъектов. Гистограмма используется для отображения частоты, когда данные измеряются в интервале или шкале отношений. изображает гистограмму, построенную для данных, приведенных в.
Гистограмма частоты пульса в состоянии покоя у здоровых добровольцев (N = 63)
Столбиковая диаграмма и гистограмма могут выглядеть одинаково, но между ними есть три важных различия: [3,4]
На гистограмме есть нет промежутка между полосами, поскольку переменная непрерывна.На гистограмме будет промежуток между полосами.
Необязательно, чтобы все столбцы были одинаковой ширины на гистограмме (зависит от интервала классов), тогда как на столбчатой диаграмме они равны.
Площадь каждого столбца соответствует частоте на гистограмме, тогда как на столбчатой диаграмме это высота [].
Полигон частот
Многоугольник частот создается путем соединения всех средних точек верхних полос гистограммы прямой линией без отображения полос.Полигон частот упрощает сравнение двух частотных распределений. Когда общая частота велика, а интервалы классов узкие, многоугольник частот становится гладкой кривой, известной как частотная кривая. Многоугольник частот, иллюстрирующий данные в, показан на.
Полигон частот пульса в состоянии покоя у здоровых добровольцев (N = 63)
График в виде прямоугольников и усов
Этот график, впервые описанный Тьюки в 1977 году, также можно использовать для иллюстрации распределения данных.Имеется вертикальный или горизонтальный прямоугольник (прямоугольник), концы которого соответствуют верхнему и нижнему квартилям (75 -й и 25 -й процентиль соответственно). Таким образом, средние 50% наблюдений представлены прямоугольником. Длина поля указывает на изменчивость данных. Линия внутри рамки обозначает медианное значение (иногда обозначается знаком плюс). Положение медианы указывает, искажены данные или нет. Если медиана ближе к верхнему квартилю, то они искажены отрицательно, а если она близка к нижнему квартилю, то искажены положительно.
Положение медианы указывает, искажены данные или нет. Если медиана ближе к верхнему квартилю, то они искажены отрицательно, а если она близка к нижнему квартилю, то искажены положительно.
Линии за пределами квадрата с обеих сторон известны как усы []. Эти усы в 1,5 раза превышают длину коробки, то есть межквартильный размах (IQR). Конец усов называется внутренним забором, и любое значение за его пределами является выбросом. Если распределение симметрично, то усы одинаковой длины. Если данные с одной стороны скудны, соответствующий боковой ус будет коротким. Внешний забор (обычно не отмеченный) находится на расстоянии в три раза превышающем IQR по обе стороны коробки.Причина, по которой внутреннее и внешнее ограждение в 1,5 и 3 раза превышает IQR, соответственно, заключается в том, что 95% наблюдений находятся в пределах 1,5-кратного IQR, а 99% — в 3 раза больше IQR. [5]
Принципиальная диаграмма «прямоугольник и усы»
ХАРАКТЕРИСТИКИ РАСПРЕДЕЛЕНИЯ ЧАСТОТ
Есть четыре важных характеристики частотного распределения. [6] Это следующие:
[6] Это следующие:
Меры центральной тенденции и местоположения (среднее, медиана, мода)
Меры дисперсии (диапазон, дисперсия, стандартное отклонение)
Степень симметрии / асимметрии (асимметрия)
Плавность или выпуклость (эксцесс).
Подробно они будут рассмотрены в следующем выпуске.
Сноски
Источник поддержки: Нет
Конфликт интересов: Не заявлено
ССЫЛКИ
1. Gravetter FJ, Wallnau LB. 5-е изд. Бельмонт: Уодсворт — обучение Томсона; 2000. Статистика поведенческих наук. [Google Scholar] 2. Доусон Б., Трапп Р.Г. 4-е изд. Нью-Йорк: Макгроу Хилл; 2004. Фундаментальная и клиническая биостатистика. [Google Scholar] 3. Сундарам К.Р., Двиведи С.Н., Шринивас В.1-е изд. Нью-Дели: B.I Publications Pvt Ltd; 2010. Принципы и методы медицинской статистики. [Google Scholar] 4. Swinscow TDV, Кэмпбелл MJ. (Индийская) 10-е изд. Нью-Дели: Viva Books Private Limited; 2003. Статистика на первом месте, 10-е изд (индийское) [Google Scholar] 5. Норман Г.Р., Штрайнер Д.Л. 2-е изд. Гамильтон: B.C. Decker Inc; 2000. Биостатистика самое необходимое. [Google Scholar] 6. Сундар Рао PS, Ричард Дж. 4-е изд. Нью-Дели: Prentice Hall of India Pvt Ltd; 2006. Введение в биостатистику и методы исследования.[Google Scholar]
Статистика на первом месте, 10-е изд (индийское) [Google Scholar] 5. Норман Г.Р., Штрайнер Д.Л. 2-е изд. Гамильтон: B.C. Decker Inc; 2000. Биостатистика самое необходимое. [Google Scholar] 6. Сундар Рао PS, Ричард Дж. 4-е изд. Нью-Дели: Prentice Hall of India Pvt Ltd; 2006. Введение в биостатистику и методы исследования.[Google Scholar]Музей-студия в Гарлеме
Частота отражает текущий творческий момент среди 35 начинающих художников. Художники в возрасте от 25 до 46 лет, живущие и работающие в Соединенных Штатах, подвержены влиянию разных жанров: от народных сказок до хип-хопа, от незападной эстетики до абстрактной живописи, от дизайна татуировок до чернокожих спортсменов и т. Д. С более чем 85 новыми работами в различных медиа, включая живопись, рисунок, скульптуру, фотографию, видео, цифровую анимацию и смешанную технику, Frequency демонстрирует нетематический, нелинейный климат современного искусства сегодня.
Новаторская выставка Музея-студии Freestyle (2001) определила группу молодых художников, которые стали новым поколением индикаторов и задающих темп. Freestyle оказал огромное влияние на понимание современного искусства чернокожих и отношения к нему этого музея. Он привнес в общественное сознание понятие «пост-черный» — термин, придуманный директором музея-студии и главным хранителем Тельмой Голден. Он выявил поколение чернокожих художников, которые не стеснялись отказаться от ярлыка «черных художников» или противостоять ему, предпочитая, чтобы их воспринимали как людей со сложными исследованиями черноты в своей работе.Пост-чернокожее искусство стало важной позицией в этот переходный момент в стремлении определить текущие изменения в афроамериканском искусстве и в конечном итоге стало частью вечного переопределения черноты в современной культуре. Эта широко обсуждаемая идея обрела самостоятельную жизнь в общественной сфере не только в современном искусстве, но и в популярной культуре и культурных исследованиях.
Freestyle оказал огромное влияние на понимание современного искусства чернокожих и отношения к нему этого музея. Он привнес в общественное сознание понятие «пост-черный» — термин, придуманный директором музея-студии и главным хранителем Тельмой Голден. Он выявил поколение чернокожих художников, которые не стеснялись отказаться от ярлыка «черных художников» или противостоять ему, предпочитая, чтобы их воспринимали как людей со сложными исследованиями черноты в своей работе.Пост-чернокожее искусство стало важной позицией в этот переходный момент в стремлении определить текущие изменения в афроамериканском искусстве и в конечном итоге стало частью вечного переопределения черноты в современной культуре. Эта широко обсуждаемая идея обрела самостоятельную жизнь в общественной сфере не только в современном искусстве, но и в популярной культуре и культурных исследованиях.
Почти пять лет спустя Frequency (обычно ошибочно принимаемая за Freestyle II) продолжает эту традицию с новой группой художников. Куратор выставки Тельма Голден и бывший помощник куратора Кристин Ю. Ким, на этой выставке нет преобладающих тем, за исключением, возможно, подавляющего чувства индивидуальности. Как следует из названия, точек с частотой ассимилирует расходящиеся звуки, ситуации и явления. Использование изображений и материалов на этой выставке носит широкий и экспериментальный характер: стразы, песок, спички, ракушки каури, декорации ручной работы, присвоенные спортивные кадры, семейные снимки, найденные предметы 1950-х, 60-х и 70-х годов, а также современные и черные. исторические иконы, такие как Харриет Табман, Пол Робсон, нигерийский кардинал Фрэнсис Аринце, Джон Колтрейн и Террелл Оуэнс.В каждой работе аспекты американской культуры переосмысливаются и уточняются для новых целей.
Куратор выставки Тельма Голден и бывший помощник куратора Кристин Ю. Ким, на этой выставке нет преобладающих тем, за исключением, возможно, подавляющего чувства индивидуальности. Как следует из названия, точек с частотой ассимилирует расходящиеся звуки, ситуации и явления. Использование изображений и материалов на этой выставке носит широкий и экспериментальный характер: стразы, песок, спички, ракушки каури, декорации ручной работы, присвоенные спортивные кадры, семейные снимки, найденные предметы 1950-х, 60-х и 70-х годов, а также современные и черные. исторические иконы, такие как Харриет Табман, Пол Робсон, нигерийский кардинал Фрэнсис Аринце, Джон Колтрейн и Террелл Оуэнс.В каждой работе аспекты американской культуры переосмысливаются и уточняются для новых целей.
Частота продолжает роль Музея-студии как места для динамичного обмена идеями об искусстве и обществе. С момента своего открытия в 1968 году музей играет каталитическую роль в поддержке и представлении разнообразных работ известных и начинающих чернокожих художников.
Частота частично финансируется Фондом изобразительных искусств Энди Уорхола, Фондом семьи Питера Нортона и Фондом Горация У.Фонд Голдсмита.
Что такое частотная характеристика и как она влияет на мою музыку?
Если вы достаточно долго болтались в звуковых кругах, вы, вероятно, знаете термин «частотная характеристика». Это может возникнуть практически в любой дискуссии, начиная от наушников и динамиков и кончая ЦАП и усилителями, и даже акустикой помещения. Если вы знакомы с этим предметом или этот термин для вас впервые, вот все, что вам нужно знать о частотной характеристике.
Примечание редактора: эта статья была обновлена 30 июня 2021 г., чтобы уточнить некоторые формулировки.
Как следует из названия, мы имеем дело с частотой и тем, насколько хорошо конкретный компонент может воспроизводить все тона, которые мы слышим. Человеческий слух колеблется от очень низких частот всего 20 Гц до очень высоких частот около 20 кГц. Хотя индивидуальный слух будет варьироваться в зависимости от этих двух крайностей. В музыкальном смысле мы часто видим это разделение на басы, средние и высокие частоты.Это не фиксированные определения, но обычно низкие частоты соответствуют частотам от 20 до 300 Гц, средние частоты — от 300 Гц до 4 кГц, а высокие частоты считаются как все, что выше 4 кГц, очень грубо говоря.
Частотная характеристика описывает диапазон частот или музыкальных тонов, которые может воспроизводить компонент.
Частотная характеристика измеряет, воспроизводит ли и насколько хорошо конкретный аудиокомпонент все эти слышимые частоты, и вносит ли он какие-либо изменения в сигнал на своем пути.Например, какая самая низкая частота может воспроизводиться сабвуфером X. За исключением любых преднамеренных настроек эквалайзера, идеальная частота на выходе компонента должна быть равна входной, чтобы не изменять сигнал. Это часто называют «плоской» частотной характеристикой, когда синусоидальная волна фиксированного объема (измеряемая в децибелах) может проходить через систему и будет иметь одинаковую амплитуду на всех частотах на выходе.
Частотную характеристику часто можно представить как фильтр, который может усиливать или ослаблять входной сигнал для изменения звука.
Другими словами, идеальная частотная характеристика — это такая, при которой не регулируется громкость низких, средних или высоких частот из нашего источника. Для сравнения: если вы возились с настройками эквалайзера любого музыкального приложения, вы, возможно, видели не плоскую настройку эквалайзера, которая усиливает басы или срезает высокие частоты и т. Д. Так что, если компонент (например, драйвер наушников) не имеет плоская частотная характеристика, вы можете в конечном итоге услышать больше или меньше определенных частот, чем было в исходном сигнале. В крайних случаях это может испортить впечатление от прослушивания.
Проблемы с получением плоского ответа
Сравнение идеального (зеленый), вероятного неуловимого реального примера (желтый) и более слышимого (красный) частотных характеристик для динамиков.
К сожалению, со звуком то, что идеально, и то, что происходит на самом деле, редко идут рука об руку, и добиться идеально ровной частотной характеристики по всей цепочке аудиосигнала невероятно сложно. Чаще всего это проблема с драйверами наушников и динамиками, где механические свойства, электроника и акустика объединяются, создавая нелинейность, влияющую на звук.Например, согласование импеданса и емкостная связь между усилителями и динамиками, катушками индуктивности динамиков и драйверами и даже акустикой комнаты, в которой вы находитесь, могут повлиять на окончательную частотную характеристику.
В реальном мире вы часто будете видеть, что характеристики частотной характеристики указывают диапазон частот, например, 20 Гц — 20 кГц, за которым следует величина изменения частотной характеристики, указанная в децибелах, например +/- 6 дБ. Это просто говорит нам о максимальной величине усиления или среза в любой точке между заданными частотами, поэтому на самом деле ничего не говорит о том, как будет звучать продукт.
Каждый компонент в сигнальной цепи в идеале должен иметь ровную частотную характеристику, чтобы звук проходил без изменений. Но на самом деле многие компоненты не обеспечивают идеальной производительности.
Вообще говоря, для большинства людей плюс-минус 3 дБ считается нижним пределом того, что вы можете услышать, поэтому небольшие отклонения в 1 или 2 дБ здесь и здесь не о чем беспокоиться. Но несколько отклонений на 3 дБ или выше, скорее всего, вызовут заметные изменения в вашей музыке.Резонансные частоты, которые появляются в виде заметных изолированных горбов на частотной диаграмме, могут быть особенно проблематичными, поскольку некоторые музыкальные ноты и тона затем становятся преувеличенными или маскированными.
Следовательно, недостаточно посмотреть на частотную характеристику, например, 20 Гц-20 кГц +/- 3 дБ, лучше иметь возможность увидеть , где происходят эти колебания акцентов и как они распределяются. Более плавная частотная характеристика лучше, чем сильно изменяемая, идеальная цель — плоская.
В то время как компоненты динамика наушников могут иметь широкий диапазон частот, компоненты ЦАП и усилителя должны быть плоскими.
Когда дело доходит до ЦАП, выходной сигнал всегда должен быть почти полностью плоским на слышимых частотах, даже в современных недорогих конструкциях. Преобразование из цифрового в аналоговый в современном оборудовании представляет собой прямое преобразование выборки, прежде чем отфильтровать шум на частотах, выходящих далеко за пределы человеческого восприятия. На данном этапе нет никаких механических или акустических проблем, о которых стоит беспокоиться.
Схемы усилителянемного сложнее, но в целом: даже комбинация ЦАП / усилитель со средним значением должна иметь ровную частотную характеристику при питании всех, кроме динамиков / наушников с самым низким импедансом.
Анализ Фурье и ваша музыка
У музыкальных продюсеров есть своя работа, поскольку изменение акцента означает изменение качества звука в целом.
До сих пор мы имели дело с довольно простым для понимания аспектом частотной характеристики: нелинейный отклик изменяет способ звучания нашего источника.Однако это касается не только общих понятий, таких как низкие и высокие частоты, но также влияет на качество звука каждого инструмента в миксе. Чтобы разобраться в этом более тонком аспекте того, как нелинейная частотная характеристика может влиять на то, что мы слышим, нам нужно обратиться к анализу Фурье.
Вкратце, анализ Фурье и преобразование Фурье показывают, что сложная форма волны может быть выражена как сумма серии синусоидальных волн различной амплитуды. Таким образом, квадрат, треугольник или любая другая форма волны, которая появляется во временной области, может быть представлена множеством различных индивидуальных частот с разными амплитудами в частотной области.Сюда входят формы волны, которые создаются музыкальными инструментами, от резких ударов малого барабана до толстых прямоугольных электрогитар.
В музыкальных инструментах эти синусоидальные волны преимущественно связаны гармонически, располагаясь на нечетных и четных октавах (кратных частоте основной ноты) над основной нотой. Так, например, если вы играете естественную до на скрипке, она звучит на основной частоте 261 Гц плюс некоторая вторая гармоника на 522 Гц, третья на 783 Гц, четвертая на 1044 Гц и так далее с уменьшающимся количеством уровней.У других инструментов есть различное относительное гармоническое содержание, которое создает их уникальные звуки. На приведенной ниже диаграмме в качестве примера показаны различия частотных соотношений между звуком фортепиано и скрипки.
Гармоники могут быть тихими, но они не менее важны для вашей музыки.
ResearchGate
Почему это важно? Вернемся к частотной характеристике и фильтрации, и теперь мы можем видеть, что неплоская характеристика не только изменяет общее представление нашей музыки, но также может изменить способ звучания отдельных инструментов.Даже если на графике частотной характеристики нет серьезных проблем с низкими или высокими частотами, меньшие нелинейности на определенных частотах могут изменить наше восприятие определенных инструментов.
Некоторые общие правила эквализации заключаются в том, что уменьшение основной частоты инструмента дает менее мощный звук, а увеличение — добавляет «глубину». Точно так же уменьшение гармоник инструмента приводит к тусклым звукам, лишенным видимого пространства, тогда как усиление гармоник увеличивает присутствие, но в конечном итоге может звучать слишком резко.Сделав еще один шаг вперед, усиление и срезание различных частот инструментов может даже привести к маскировке или усилению звука других инструментов на дорожке. Таким образом, нелинейная частотная характеристика может свести на нет всю тяжелую работу, которую инженер вложил в тщательное микширование трека.
Почему важна частотная характеристика
Может, это и не кричащее, но Beyerdynamic DT 770 Studio чертовски металлический.
По традиционным стандартам HiFi точная аудиосистема — это аудиосистема, которая принимает входной сигнал и выводит его , не изменяя его вообще .Сюда входят компоненты, начиная от исходного аудиофайла и заканчивая цифровой обработкой, и такие компоненты, как ЦАП, вплоть до усилителя и динамиков. Частотная характеристика — лишь одна часть этого уравнения, но она существенно влияет на то, как звучит выходной сигнал, и, по совпадению, довольно легко измерить.
Связано: Амплитудно-частотная характеристика: Где живут звуки?
Амплитудно-частотная характеристика не сводится только к тому, слишком много низких, средних или высоких частот исходит из системы.Это также может более тонко повлиять на тон и баланс инструментов в треке, потенциально окрашивая и даже разрушая наше впечатление от прослушивания. Совершенно ровный, идеальный отклик не возможен для каждого компонента, но современные высокотехнологичные технологии, безусловно, могут приблизиться к тому, что человек никогда не сможет сказать.
Если наша цель — послушать музыку в как можно более чистом виде, то мы должны обратить внимание на частотную характеристику. Это также может быть удобным инструментом, если вы ищете способ эквалайзера использовать далеко не идеальное оборудование.