Что такое реактивный ток: О природе реактивной энергии / Хабр

О природе реактивной энергии / Хабр

Вокруг реактивной энергии сложилось немало легенд, активно способствовала развитию околонаучного фольклора любовь нашего человека к халяве и разнообразным теориям глобального заговора.

В рунете можно найти множество success story о том как простой мужичок из глубинки годами эксплуатирует халявную реактивную энергию (которую бытовой счетчик электроэнергии не регистрирует) и живет себе, не зная бед. Так же можно найти заметки людей, призывающих бросить бесполезное занятие поиска источника халявы в халявной реактивной энергии. Для того чтобы окончательно раставить точки над ‘i’ в этом вопросе, я решил написать этот пост, не мудрствуя лукаво.

Как известно, потребляемая от источника переменного тока энергия складывается из двух составляющих:

1. Активной энергии
2. Реактивной энергии

1. Активная энергия — та часть потребляемой энергии, которая целиком и безвозвратно преобразуется приемником в другие виды энергии

.

Пример: Протекая через резистор, ток совершает активную работу, что выражается в увеличении тепловой энергии резистора. Вне зависимости от фазы протекающего тока, резистор преобразует его энергию в тепловую. Резистору не важно в каком направлении течет по нему ток, важна лишь его величина: чем он больше, тем больше тепла высвободится на резисторе (количество выделенного тепла равно произведению квадрата тока и сопротивления резистора).

2. Реактивная энергия — та часть потребляемой энергии, которая в следующую четверть периода будет целиком отдана обратно источнику

.

Пример: Представим себе, что к источнику переменного тока подключен конденсатор. Начальный заряд на обкладках конденсатора равен нулю, начальная фаза напряжения источника так же равна нулю. Одно полное колебание состоит из четырех четвертьпериодов:

1. Напряжение источника растет от 0 до максимального мгновенного значения (при действующем значении U источника 230V оно равно 230 * 1,4142 = 325V) При этом конденсатор потребляет ток, необходимый для его полного заряда
2. Напряжение источника стремительно уменьшается (движется к нулю), при этом, напряжение на заряженном конденсаторе оказывается выше чем на источнике, что вызывает течение тока в обратную сторону (ведь ток течет от большего потенциала к меньшему) , то есть конденсатор разряжается, отдавая накопленную энергию обратно источнику!
3. Для следующих двух четвертьпериодов вышеописанная история повторяется с тем лишь различием, что токи заряда и разряда емкости потекут в противоположных направлениях.

   В случае включения вместо конденсатора катушки индуктивности, суть процесса не изменится.

   В этом и состоит главный фокус реактивной энергии — в момент ‘прилива’ мы заполняем свои цистерны, в момент отлива же, мы сливаем их содержимое обратно

   . Как можно заметить из этой простой аналогии, мы просто туда-сюда переливаем жидкость (или ток в электроцепях). Если же мы соблазнимся слить хоть немного жидкости ‘налево’ (включить последовательно с реактивным конденсатором активный резистор), то мы станем брать ‘несколько больше’ чем возвращать, а это ‘несколько больше’ уже является активной энергией по определению (ведь мы эту часть не возвращаем обратно, не так ли?), за которую как известно, приходится платить.

   Или иной пример: предположим, что мы берем у кредитора некоторую сумму денег взаймы и сразу же возвращаем ему взятый только что кредит. Если мы отдадим ровно столько, сколько взяли (чистая реактивность) — мы придем к исходному состоянию и никто никому не будет ничего должен.

   В случае же, если мы потратим часть кредита на какую ни будь покупку и вернем то, что осталось от кредита после совершения покупки (добавим в цепь активную нагрузку и часть энергии уйдет из системы) — мы будем все еще должны. Эта потраченная часть является активной составляющей взятого нами кредита.

   Теперь у вас может возникнуть один весьма резонный вопрос — если все так просто, и для того чтобы энергия считалась реактивной, ее просто нужно полностью вернуть обратно источнику, почему предприятия вынуждены платить за потребляемую

   (и полностью возвращаемую) реактивную энергию?

   Все дело в том, что в случае чисто реактивной нагрузки, момент максимально потребляемого тока (реактивного) приходится на момент минимального значения напряжения, и наоборот, в момент максимума напряжения на клеммах нагрузки, протекающий через нее ток равен нулю.

   Протекающий реактивный ток греет питающие проводники — но это активные потери, вызванные протеканием реактивного тока по проводникам с ограниченной проводимостью, что эквивалентно последовательно включенным с реактивной нагрузкой активным резистором.

   Так же, поскольку в момент максимума реактивного тока напряжение на полюсах реактивного элемента переходит через ноль, активная мощность подводимая к нему в этот момент (произведение тока и напряжения) равна нулю. Вывод — реактивный ток вызывает нагрев проводов, не совершая при этом никакой полезной работы. Следует заметить, что эти потери так-же является активными и будут засчитываться бытовым счетчиком активной энергии.

   Большие предприятия сопсобны генерировать достаточно большие реактивные токи, которые отрицательно сказываются на функционировании энергосистемы. По этой причине, для них проводится учет как активной, так и реактивной составляющей потребленной энергии. Для уменьшения генерации реактивных токов

   (вызывающих вполне реальные активные потери), на предприятиях размещают установки компенсации реактивной мощности.

Реактивная мощность

Применение переменного тока началось в конце XIX века. На замену небольшим и локальным системам постоянного тока пришла передача электрической энергии с использованием переменного тока, что потребовало расширения существующих локальных систем энергоснабжения. Кроме того, было необходимо и обеспечение передачи электроэнергии на дальние расстояния. Поэтому возникали различные проблемы с управлением напряжением и стабильностью, связанные в первую очередь с отсутствием баланса реактивной мощности в системах.

Для управления напряжениями стационарной системы применялись шунтирующие конденсаторы и шунтирующие реакторы. То есть применялась коммутируемая компенсация реактивной мощности. А динамическая компенсация реактивной мощности основывалась на вращающихся машинах, например синхронных компенсаторах.

Из истории мы знаем, что в середине 60-х годов 20 века появились первые статические компенсирующие устройства реактивной мощности, т.е. реакторы, управляемые постоянным током (ртутные вентили), и устройства, управляемые тиристорами (конденсаторы с тиристорным управлением, реакторы с тиристорным управлением). Они имели малое время отклика, низкие потери и практически не требовали технического обслуживания, что сняло многие ограничения, присущие вращающимся машинам и устройствам, управляемым постоянным током.

Так что же такое реактивная мощность? Обратимся к учебнику физики. Там написано совсем мало. Полная мощность делится на активную и реактивную. Активная составляющая мощности полезно используется, превращаясь в механическую, химическую, световую и другие энергии.

Реактивная же составляющая мощности не выполняет полезной работы, она служит лишь для создания магнитных полей в индуктивных приёмниках (электродвигатели, трансформаторы и т.п.), циркулируя всё время между источником и приёмником. Она может рассматриваться как характеристика скорости обмена энергией между генератором и магнитным полем приёмника электроэнергии.

Ну а физика процесса представляет собой следующее: переменный ток идёт по проводу в обе стороны, в идеале нагрузка должна полностью усвоить и переработать полученную энергию. При рассогласованиях между генератором и потребителем происходит одновременное протекание токов от генератора к нагрузке и от нагрузки к генератору (нагрузка возвращает запасённую ранее энергию).

Такие условия возможны только для переменного тока при наличии в цепи любого реактивного элемента, имеющего собственную индуктивность или ёмкость. Индуктивный реактивный элемент стремится сохранить неизменным протекающий через него ток, а ёмкостной — напряжение. Через идеальные резистивные и индуктивные элементы протекает максимальный ток при нулевом напряжении на элементе и, наоборот, максимальное напряжение оказывается приложенным к элементам, имеющим ёмкостной характер, при токе, протекающем через них, близком к нулю.
 

 

Для чего необходима компенсация реактивной мощности?

Основной нагрузкой в промышленных электросетях являются асинхронные электродвигатели и распределительные трансформаторы. Эта индуктивная нагрузка в процессе работы является источником реактивной электроэнергии (

реактивной мощности), которая совершает колебательные движения между нагрузкой и источником (генератором), не связана с выполнением полезной работы, а расходуется на создание электромагнитных полей и создает дополнительную нагрузку на силовые линии питания. Поэтому очень важен компенсатор реактивной мощности.

Реактивная мощность характеризуется задержкой (в индуктивных элементах ток по фазе отстает от напряжения) между синусоидами фаз напряжения и тока сети. Показателем потребления реактивной мощности является коэффициент мощности (КМ), численно равный косинусу угла (ф) между током и напряжением. КМ потребителя определяется как отношение потребляемой активной мощности к полной, действительно взятой из сети, т.е.: cos(ф) = P/S. Этим коэффициентом принято характеризовать уровень реактивной мощности двигателей, генераторов и сети предприятия в целом. Чем ближе значение cos(ф) к единице, тем меньше доля взятой из сети реактивной мощности.

Пример: при cos(ф) = 1 для передачи 500 KW в сети переменного тока 400 V необходим ток значением 722 А. Для передачи той же активной мощности при коэффициенте cos(ф) = 0,6 значение тока повышается до 1203 А.

Соответственно все оборудование питания сети, передачи и распределения энергии должны быть рассчитаны на большие нагрузки.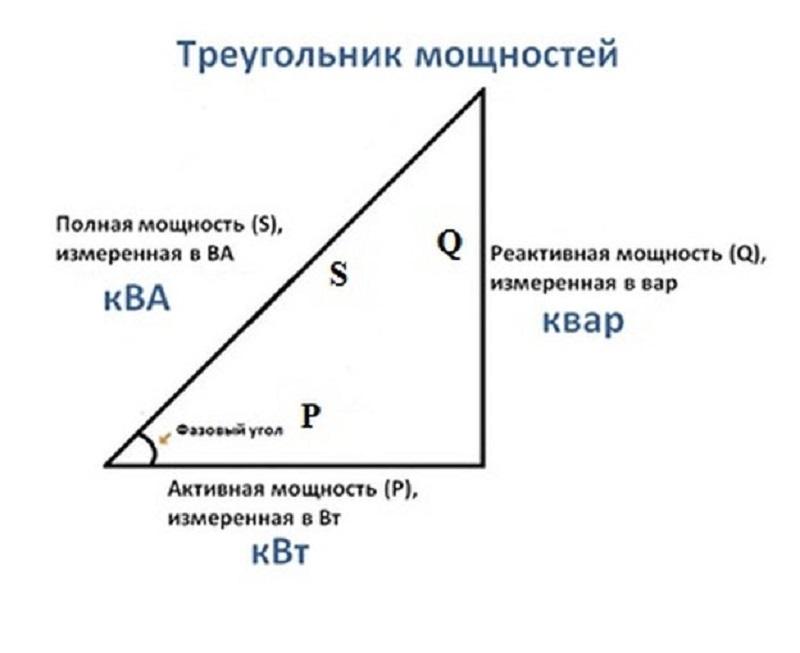 Кроме того, в результате больших нагрузок срок эксплуатации этого оборудования может соответственно снизиться. Дальнейшим фактором повышения затрат является возникающая из-за повышенного значения общего тока теплоотдача в кабелях и других распределительных устройствах, в трансформаторах и генераторах. Возьмем, к примеру, в нашем выше приведенном случае при cos(ф) = 1 мощность потерь равную 10 KW. При cos(ф) = 0,6 она повышается на 180% и составляет уже 28 KW. Таким образом, наличие реактивной мощности является паразитным фактором, неблагоприятным для сети в целом.

В результате этого:

• возникают дополнительные потери в проводниках вследствие увеличения тока;
• снижается пропускная способность распределительной сети;
• отклоняется напряжение сети от номинала (падение напряжения из-за увеличения реактивной составляющей тока питающей сети).

 

Все сказанное выше является основной причиной того, что предприятия электроснабжения требуют от потребителей снижения доли реактивной мощности в сети. Решением данной проблемы является компенсация реактивной мощности – важное и необходимое условие экономичного и надежного функционирования системы электроснабжения предприятия. Эту функцию выполняют устройства компенсации реактивной мощности КРМ-0,4 (УКМ-58) — конденсаторные установки, основными элементами которых являются конденсаторы.

Правильная компенсация позволяет:

• снизить общие расходы на электроэнергию;
• уменьшить нагрузку элементов распределительной сети (подводящих линий, трансформаторов и распределительных устройств), тем самым продлевая их срок службы;
• снизить тепловые потери тока и расходы на электроэнергию;
• снизить влияние высших гармоник;
• подавить сетевые помехи, снизить несимметрию фаз;
• добиться большей надежности и экономичности распределительных сетей.

Кроме того, в существующих сетях

• исключить генерацию реактивной энергии в сеть в часы минимальной нагрузки;
• снизить расходы на ремонт и обновление парка электрооборудования;
• увеличить пропускную способность системы электроснабжения потребителя, что позволит подключить дополнительные нагрузки без увеличения стоимости сетей;
• обеспечить получение информации о параметрах и состоянии сети.

А во вновь создаваемых сетях — уменьшить мощность подстанций и сечения кабельных линий, что снизит их стоимость.

 

Зачем компенсировать реактивную мощность?

Реактивная мощность и энергия ухудшают показатели работы энергосистемы, то есть загрузка реактивными токами генераторов электростанций увеличивает расход топлива; увеличиваются потери в подводящих сетях и приемниках; увеличивается падение напряжения в сетях.

Реактивный ток дополнительно нагружает линии электропередачи, что приводит к увеличению сечений проводов и кабелей и соответственно к увеличению капитальных затрат на внешние и внутриплощадочные сети.

Компенсация реактивной мощности, в настоящее время, является немаловажным фактором позволяющим решить вопрос энергосбережения практически на любом предприятии.

По оценкам отечественных и ведущих зарубежных специалистов, доля энергоресурсов, и в частности электроэнергии занимает величину порядка 30-40% в стоимости продукции. Это достаточно веский аргумент, чтобы руководителю со всей серьезностью подойти к анализу и аудиту энергопотребления и выработке методики компенсации реактивной мощности. Компенсация реактивной мощности – вот ключ к решению вопроса энергосбережения.

Основные потребители реактивной мощности:

• асинхронные электродвигатели, которые потребляют 40% всей мощности совместно с бытовыми и собственными нуждами;
• электрические печи 8%;
• преобразователи 10%;
• трансформаторы всех ступеней трансформации 35%;
• линии электропередач 7%.

 

В электрических машинах переменный магнитный поток связан с обмотками. Вследствие этого в обмотках при протекании переменного тока индуктируются реактивные э.д.с. обуславливающие сдвиг по фазе (fi) между напряжением и током. Этот сдвиг по фазе обычно увеличивается, а косинус фи уменьшается при малой нагрузке. Например, если косинус фи двигателей переменного тока при полной нагрузке составляет 0,75-0,80, то при малой нагрузке он уменьшится до 0,20-0,40.

Мало нагруженные трансформаторы также имеют низкий коэффициент мощности (косинус фи). Поэтому, применять компенсацию реактивной мощности, то результирующий косинус фи энергетической системы будет низок и ток нагрузки электрической, без компенсации реактивной мощности, будет увеличиваться при одной и той же потребляемой из сети активной мощности. Соответственно при компенсации реактивной мощности (применении автоматических конденсаторных установок КРМ) ток потребляемый из сети снижается, в зависимости от косинус фи на 30-50%, соответственно уменьшается нагрев проводящих проводов и старение изоляции.

Кроме этого, реактивная мощность наряду с активной мощностью учитывается поставщиком электроэнергии, а следовательно, подлежит оплате по действующим тарифам, поэтому составляет значительную часть счета за электроэнергию.

Наиболее действенным и эффективным способом снижения потребляемой из сети реактивной мощности является применение установок компенсации реактивной мощности (конденсаторных установок).

Использование конденсаторных установок для компенсации реактивной мощности позволяет:

• разгрузить питающие линии электропередачи, трансформаторы и распределительные устройства;
• снизить расходы на оплату электроэнергии
• при использовании определенного типа установок снизить уровень высших гармоник;
• подавить сетевые помехи, снизить несимметрию фаз;
• сделать распределительные сети более надежными и экономичными.

 

продольная и поперечная компенсация реактивной мощности

Преобразование энергии в электрической цепи. Мгновенная, активная, реактивная и полная мощности синусоидального тока. (Лекция №7)

Передача энергии w по электрической цепи (например, по линии электропередачи), рассеяние энергии, то есть переход электромагнитной энергии в тепловую, а также и другие виды преобразования энергии характеризуются интенсивностью, с которой протекает процесс, то есть тем, сколько энергии передается по линии в единицу времени, сколько энергии рассеивается в единицу времени. Интенсивность передачи или преобразования энергии называется мощностью р. Сказанному соответствует математическое определение:

.

(1)

Выражение для мгновенного значения мощности в электрических цепях имеет вид:

.

(2)

Приняв начальную фазу напряжения за нуль, а сдвиг фаз между напряжением и током за , получим:

.

(3)

Итак, мгновенная мощность имеет постоянную составляющую и гармоническую составляющую, угловая частота которой в 2 раза больше угловой частоты напряжения и тока.

Когда мгновенная мощность отрицательна, а это имеет место (см. рис. 1), когда u и i разных знаков, т.е. когда направления напряжения и тока в двухполюснике противоположны, энергия возвращается из двухполюсника источнику питания.

Такой возврат энергии источнику происходит за счет того, что энергия периодически запасается в магнитных и электрических полях соответственно индуктивных и емкостных элементов, входящих в состав двухполюсника. Энергия, отдаваемая источником двухполюснику в течение времени t равна .

Среднее за период значение мгновенной мощности называется активной мощностью .

Принимая во внимание, что , из (3) получим:

.

(4)

Активная мощность, потребляемая пассивным двухполюсником, не может быть отрицательной (иначе двухполюсник будет генерировать энергию), поэтому , т.е. на входе пассивного двухполюсника . Случай Р=0, теоретически возможен для двухполюсника, не имеющего активных сопротивлений, а содержащего только идеальные индуктивные и емкостные элементы.

1. Резистор (идеальное активное сопротивление).

Здесь напряжение и ток (см. рис. 2) совпадают по фазе , поэтому мощность всегда положительна, т.е. резистор потребляет активную мощность

2. Катушка индуктивности (идеальная индуктивность)

При идеальной индуктивности ток отстает от напряжения по фазе на . Поэтому в соответствии с (3) можно записать
.

Участок 1-2: энергия , запасаемая в магнитном поле катушки, нарастает.

Участок 2-3: энергия магнитного поля убывает, возвращаясь в источник.

3. Конденсатор (идеальная емкость)

Аналогичный характер имеют процессы и для идеальной емкости. Здесь . Поэтому из (3) вытекает, что . Таким образом, в катушке индуктивности и конденсаторе активная мощность не потребляется (Р=0), так как в них не происходит необратимого преобразования энергии в другие виды энергии. Здесь происходит только циркуляция энергии: электрическая энергия запасается в магнитном поле катушки или электрическом поле конденсатора на протяжении четверти периода, а на протяжении следующей четверти периода энергия вновь возвращается в сеть. В силу этого катушку индуктивности и конденсатор называют реактивными элементами, а их сопротивления Х_L и Х_С , в отличие от активного сопротивления R резистора, – реактивными.

Интенсивность обмена энергии принято характеризовать наибольшим значением скорости поступления энергии в магнитное поле катушки или электрическое поле конденсатора, которое называется реактивной мощностью.

В общем случае выражение для реактивной мощности имеет вид:

(5)

Она положительна при отстающем токе (индуктивная нагрузка- ) и отрицательна при опережающем токе (емкостная нагрузка- ). Единицу мощности в применении к измерению реактивной мощности называют вольт-ампер реактивный (ВАр).

В частности для катушки индуктивности имеем:

, так как .

.

Из последнего видно, что реактивная мощность для идеальной катушки индуктивности пропорциональна частоте и максимальному запасу энергии в катушке. Аналогично можно получить для идеального конденсатора:

.

Полная мощность

Помимо понятий активной и реактивной мощностей в электротехнике широко используется понятие полной мощности:

.

(6)

Активная, реактивная и полная мощности связаны следующим соотношением:

.

(7)

Отношение активной мощности к полной называют коэффициентом мощности. Из приведенных выше соотношений видно, что коэффициент мощности равен косинусу угла сдвига между током и напряжением. Итак,

.

(8)

Комплексная мощность

Активную, реактивную и полную мощности можно определить, пользуясь комплексными изображениями напряжения и тока. Пусть , а . Тогда комплекс полной мощности:

,

(9)

где — комплекс, сопряженный с комплексом .

.

Комплексной мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует (активно-индуктивная нагрузка), для которого имеем:

Применение статических конденсаторов для повышения cos

Как уже указывалось, реактивная мощность циркулирует между источником и потребителем. Реактивный ток, не совершая полезной работы, приводит к дополнительным потерям в силовом оборудовании и, следовательно, к завышению его установленной мощности. В этой связи понятно стремление к увеличению в силовых электрических цепях.

Следует указать, что подавляющее большинство потребителей (электродвигатели, электрические печи, другие различные устройства и приборы) как нагрузка носит активно-индуктивный характер.

Если параллельно такой нагрузке (см. рис. 5), включить конденсатор С, то общий ток , как видно из векторной диаграммы (рис. 6), приближается по фазе к напряжению, т.е. увеличивается, а общая величина тока (а следовательно, потери) уменьшается при постоянстве активной мощности . На этом основано применение конденсаторов для повышения .

Какую емкость С нужно взять, чтобы повысить коэффициент мощности от значения до значения ?

Разложим на активную и реактивную составляющие. Ток через конденсатор компенсирует часть реактивной составляющей тока нагрузки :

;

(10)

;

(11)

.

(12)

Из (11) и (12) с учетом (10) имеем

,

но , откуда необходимая для повышения емкость:

.

(13)

Баланс мощностей

Баланс мощностей является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи.

а) Постоянный ток

Для любой цепи постоянного тока выполняется соотношение:

(14)

Это уравнение представляет собой математическую форму записи баланса мощностей: суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи.

Следует указать, что в левой части (14) слагаемые имеют знак “+”, поскольку активная мощность рассеивается на резисторах. В правой части (14) сумма слагаемых больше нуля, но отдельные члены здесь могут иметь знак “-”, что говорит о том, что соответствующие источники работают в режиме потребителей энергии (например, заряд аккумулятора).

б) Переменный ток.

Из закона сохранения энергии следует, что сумма всех отдаваемых активных мощностей равна сумме всех потребляемых активных мощностей, т.е.

(15)

В ТОЭ доказывается (вследствие достаточной громоздкости вывода это доказательство опустим), что баланс соблюдается и для реактивных мощностей:

,

(16)

где знак “+” относится к индуктивным элементам , “-” – к емкостным .

Умножив (16) на “j” и сложив полученный результат с (15), придем к аналитическому выражению баланса мощностей в цепях синусоидального тока (без учета взаимной индуктивности):

или

.

Литература

1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

1. Что такое активная мощность?
2. Что такое реактивная мощность, с какими элементами она связана?
3. Что такое полная мощность?
4. Почему необходимо стремиться к повышению коэффициента мощности ?
5. Критерием чего служит баланс мощностей?
6. К источнику с напряжением подключена активно-индуктивная нагрузка, ток в которой . Определить активную, реактивную и полную мощности.

Ответ: Р=250 Вт; Q=433 ВАр; S=500 ВА.

7. В ветви, содержащей последовательно соединенные резистор R и катушку индуктивности L, ток I=2 A. Напряжение на зажимах ветви U=100 B, а потребляемая мощность Р=120 Вт. Определить сопротивления R и XL элементов ветви.

Ответ: R=30 Ом; XL=40 Ом.

8. Мощность, потребляемая цепью, состоящей из параллельно соединенных конденсатора и резистора, Р=90 Вт. Ток в неразветвленной части цепи I1=5 A, а в ветви с резистором I2=4 A. Определить сопротивления R и XC элементов цепи.

Ответ: R=10 Ом; XС=7,5 Ом.

Что такое реактивная мощность и её компенсация

17.08.2017

Что такое реактивная мощность и что с ней делать.

Асинхронные двигатели, трансформаторы, газоразрядные и люминесцентные лампы, индукционные и дуговые печи и т.д. в силу своих физических свойств вместе с активной энергией потребляют из сети также и реактивную энергию, которая необходима для создания электромагнитного поля. В отличие от активной энергии, реактивная не преобразуется в другие виды – механическую или тепловую – и не выполняет полезной работы, однако вызывает потери при ее передаче. На Рис.1 изображены направления протекания тока при работе с реактивными нагрузками.

Рис.1. Полная мощность.

Наличие в сети реактивной мощности (Q, Вар) характеризуется коэффициентом мощности (PF, cos ф) и является соотношением активной (P, Вт) к полной (S, ВА). Ниже можно увидеть зависимость полной мощности от ее составляющих как на векторной диаграмме, так и на более житейском уровне – бокале пива, где пиво является активной составляющей, а пена – реактивной. Никто же не хочет иметь бокал только с пеной?

Рис.2. Треугольник мощностей. Расчет коэффициента мощности.

При низких значениях коэффициента мощности в сети будет возникать ряд нежелательных явлений, которые могут привести к существенному уменьшению срока службы оборудования. Рекомендуется иметь cos ф не менее 0,9 (например, в Чехии за cos ф менее 0,95 штрафуют). Для этого разработан ряд мероприятий по регулированию баланса реактивной мощности в сети – компенсация реактивной мощности.

Компенсация реактивной мощности (КРМ).

Следует понимать, что реактивная мощность бывает двух характеров – индуктивная и емкостная. Нас интересует компенсация только первого типа, т.к. второй встречается редко. В нашем случае – сетях с индуктивной нагрузкой – для увеличения cos ф требуется устанавливать компенсационные конденсаторы. Но как это сделать?

Выбор способа компенсации предполагает определение места установки конденсаторов (зачастую в составе конденсаторной установки (далее КУ)). Существует три основных варианта:

• Индивидуальная компенсация

Размещение конденсаторов у устройств с низким cos ф и включение одновременно с последними.

• Групповая компенсация

Размещение конденсаторов у группы устройств (например, пожарных насосов).

• Централизованная компенсация

Предусматривает установку КУ на главном распределительном щите. Если предыдущие варианты могли быть как регулируемыми, так и нет, то этот, как правило, регулируемый.

Рис.3. Способы компенсации.

При правильном подборе КУ мероприятия по компенсации реактивной мощности позволяют:

• существенно уменьшить нагрузку на трансформаторах, а следовательно уменьшить их нагрев и увеличить срок службы

• при включении КУ в расчет при проектировании новых объектов, существенно уменьшить сечение проводников

• при включении КУ в уже существующие сети, разгрузить их, повышая пропускную способность без реконструкции

• снизить расходы на электроэнергию за счет снижения потери в проводниках

• повысить стабильность напряжения (все) и качество электроэнергии (при использовании ФКУ)

Где мы можем сэкономить видно невооруженным глазом, но для начала придется и потратиться.

Во-первых, необходимо заказать проект, который следует доверить проверенной организации. Которая в свою очередь проведет ряд измерений или сделает расчеты для новых объектов и исходя из них даст рекомендации по способу компенсации, типу КУ и их параметрам.

Во-вторых, следует выбрать организацию-сборщика, которая соберет, установит и настроит наши КУ.

Что может входить в состав КУ?

Рассмотрим максимально возможную комплектацию конденсаторной установки:

1. Вводное устройство – автоматический выключатель, разъединитель предохранительный или выключатель нагрузки (при наличии еще одного вводного устройства, например, в ГРЩ).

2. Защитные устройства ступеней – большинство производителей (например, ZEZ Silko) рекомендуют использовать плавкие вставки с характеристикой gG (см. таблицу ниже), но нередко можно встретить и защиту автоматическими выключателями.

3. Коммутационное устройство (для статической компенсации НН) – контактор с токоограничевающей приставкой (контакты предварительного включения с сопротивлениями). Важно выбрать качественного производителя, т.к. через контактор при включении ступени проходят огромные токи (до 200Iе), обусловленные зарядом конденсатора, например, Benedict-Jager или Eaton (Moeller).

4. Антирезонансные дроссели (реакторы) – используются для защиты от перегрузки токами конденсаторов при наличии в сети высших гармоник.

5. Компенсационные конденсаторы – главный компонент всей установки – емкостной элемент. Читать подробнее о применении, конструкции и монтаже низковольтных цилиндрических компенсационных конденсаторов в предыдущей статье.

6. Регулятор реактивной мощности – своего рода анализатор сети с функцией управления ступенями. В зависимости от модели разные регуляторы кроме основных параметров (U, I, P, cos ф, количество подключенных ступеней) контролируют и ряд дополнительных (нелинейные искажения, температура и т.д). Также могу быть и дополнительные функции, например, коммуникация или автонастройка.

* Рассмотрена только основная комплектация без оболочек и микроклимата, защиты вторичных цепей.

Номинальный ток 3-фазного конденсатора [A]	3-фазн. компенсационная мощность при 400 V [kvar]	Рекомендуемое сечение Cu проводников [mm2]	Номинальный ток предохранителя [A]
2,9	2	2,5	8
3,6	2,5	2,5	8
4,5	3,15	2,5	10
5,8	4	2,5	10
7,2	5	2,5	16
9	6,25	2,5	16
11,5	8	4	20
14,4	10	4	25
18,1	12,5	6	32
21,7	15	6	40
28,8	20	10	50
36,1	25	10	63
43,4	30	16	80
50,5	35	16	100
57,7	40	25	100
72,2	50	25	125
86,6	60	35	160
115,5	80	70	200
144,3	100	95	250

Таблица 1. Подбор предохранителей и проводников.

В заключение хочется напомнить, что неверно спроектированные, собранные и настроенные компенсационные установки или из материалов сомнительного происхождения имеют обыкновение громко выходить из строя.

Коммерческое предложение действительно на 01.03.2021 г.

Зачем нужен учет реактивной электроэнергии?

Реактивный ток возникает только в тех цепях, в которых присутствуют емкости и индуктивности. Обычно он расходуется на то, чтобы без пользы нагревать проводники в составе системы. Примером нагрузок такого типа являются двигатели различного вида, мобильные инструменты. Чтобы вести анализ подобных потерь, применяются счетчики Меркурий.

Тонкости процедуры

В первую очередь подобный учет необходим для того, чтобы уменьшить потери активной электроэнергии. Последние возникают по причине перетекания мощностей реактивного типа. Данная деятельность, для которой используются счетчики Меркурий 230, является реальной эксплуатационной технологией, помогающей беречь энергию в сетях.
Помимо этого, эффективный экономический анализ перетоков реактивного типа требуется также для того, чтобы обеспечить первоочередные стандартные условия качества тока. Здесь речь идет о напряжениях, которые возникают на границе балансовой принадлежности сетей специализированных организаций. Помимо этого, при помощи учета уменьшается аварийность оборудования в системе и у потребителей.
При использовании процедуры в комплексе с существующими методиками составления тарифов на активную энергию плата за перетоки будет являться стимулом экономического типа, предназначенным для снижения отрицательного воздействия мощностей потребителей на потери в основной и распределительной сетях.
Помимо этого, стоит упомянуть следующие причины, по которым необходим учет подобной энергии:

• Снижение нагрузки на трансформаторы силового типа. По этой причине увеличивается срок службы агрегатов.
• Устранение возможности штрафов за то, что снижается переток.
• Уменьшение нагрузок на кабели и провода. Помимо этого, можно применять жилы меньшего сечения.
• Снижение уровня высших гармоник, присутствующих в сети.
• Уменьшение потребления электрической энергии.

Обычно для данной цели применяются специализированные установки. Они позволяют обеспечить компенсацию реактивной мощности от 12 до 50% от оплаты услуг. Вышеприведенные нюансы помогут понять, для каких целей применяется учет реактивного тока.

Понятие о реактивных и активных мощностях и нагрузках

Главная цель при передаче электроэнергии – повышение эффективности работы сетей. Следовательно, необходимо уменьшение потерь. Основной причиной потерь является реактивная мощность, компенсация которой значительно повышает качество электроэнергии.

Батареи статических конденсаторов

Реактивная мощность вызывает ненужный нагрев проводов, перегружаются электроподстанции. Трансформаторная мощность и кабельные сечения вынужденно подвергаются завышениям, сетевое напряжение снижается.

Понятие о реактивной мощности

Для выяснения, что же такое реактивная мощность, надо определить другие возможные виды мощности. При существовании в контуре активной нагрузки (резистора) происходит потребление исключительно активной мощности, полностью расходуемой на энергопреобразование. Значит, можно сформулировать, что такое активная мощность, – та, при которой ток совершает эффективную работу.

На постоянном токе происходит потребление исключительно активной мощности, рассчитываемой соответственно формуле:

P = U x I.

Измеряется в ваттах (Вт).

В электроцепях с переменным током при наличии активной и реактивной нагрузки мощностной показатель суммируется из двух составных частей: активной и реактивной мощности.

Реактивная нагрузка бывает двух видов:

1. Емкостная (конденсаторы). Характеризуется фазовым опережением тока по сравнению с напряжением;
2. Индуктивная (катушки). Характеризуется фазовым отставанием тока по отношению к напряжению.

Емкостная и индуктивная нагрузка

Если рассмотреть контур с переменным током и подсоединенной активной нагрузкой (обогреватели, чайники, лампочки с накаливающейся спиралью), ток и напряжение будут синфазными, а полная мощность, взятая в определенную временную отсечку, вычисляется путем перемножения показателей напряжения и тока.

Однако когда схема содержит реактивные компоненты, показатели напряжения и тока не будут синфазными, а будут различаться на определенную величину, определяемую углом сдвига «φ». Пользуясь простым языком, говорится, что реактивная нагрузка возвращает столько энергии в электроцепь, сколько потребляет. В результате получится, что для активной мощности потребления показатель будет нулевой. Одновременно по цепи протекает реактивный ток, не выполняющий никакую эффективную работу. Следовательно, потребляется реактивная мощность.

Реактивная мощность – часть энергии, которая позволяет устанавливать электромагнитные поля, требуемые оборудованием переменного тока.

Расчет реактивной мощности ведется по формуле:

Q = U x I x sin φ.

В качестве единицы измерения реактивной мощности служит ВАр (вольтампер реактивный).

Выражение для активной мощности:

P = U x I x cos φ.

Треугольник мощностей

Взаимосвязь активной, реактивной и полной мощности для синусоидального тока переменных значений представляется геометрически тремя сторонами прямоугольного треугольника, называемого треугольником мощностей. Электроцепи переменного тока потребляют две разновидности энергии: активную мощность и реактивную. Кроме того, значение активной мощности никогда не является отрицательным, тогда как для реактивной энергии возможна либо положительная величина (при индуктивной нагрузке), либо отрицательная (при емкостной нагрузке).

Треугольник мощностей

Важно! Из треугольника мощностей видно, что всегда полезно снизить реактивную составляющую, чтобы повысить эффективность системы.

Полная мощность не находится как алгебраическая сумма активного и реактивного мощностного значения, это векторная сумма P и Q. Ее количественное значение вычисляется извлечением квадратного корня из суммы квадратов мощностных показателей: активного и реактивного. Измеряться полная мощность может в ВА (вольтампер) или производных от него: кВА, мВА.

Чтобы была рассчитана полная мощность, необходимо знать разность фаз между синусоидальными значениям U и I.

Коэффициент мощности

Пользуясь геометрически представленной векторной картиной, можно найти отношение сторон треугольника, соответствующих полезной и полной мощности, что будет равно косинусу фи или мощностному коэффициенту:

cos φ = P/S.

Данный коэффициент находит эффективность работы сети.

Количество потребляемых ватт – то же самое, что и количество потребляемых вольтампер при мощностном коэффициенте, равном 1 или 100%.

Важно! Полная мощность тем ближе к показателю активной, чем больше cos φ, или чем меньше угол сдвига синусоидальных величин тока и напряжения.

Если, к примеру, имеется катушка, для которой:

• Р = 80 Вт;
• Q = 130 ВАр;
• тогда S = 152,6 BA как среднеквадратичный показатель;
• cos φ = P/S = 0,52 или 52%

Можно сказать, что катушка требует 130 ВАр полной мощности для выполнения полезной работы 80 Вт.

Коррекция cos φ

Для коррекции cos φ применяется тот факт, что при емкостной и индуктивной нагрузке вектора реактивной энергии располагаются в противофазе. Так как большинство нагрузок является индуктивными, подключив емкость, можно добиться увеличения cos φ.

Принцип компенсации реактивной мощности

Главные потребители реактивной энергии:

1. Трансформаторы. Представляют собой обмотки, имеющие индуктивную связь и посредством магнитных полей преобразуюшие токи и напряжения. Эти аппараты являются основным элементом электросетей, передающих электроэнергию. Особенно увеличиваются потери при работе на холостом ходу и при низкой нагрузке. Широко используются трансформаторы в производстве и в быту;
2. Индукционные печи, в которых расплавляются металлы путем создания в них вихревых токов;
3. Асинхронные двигатели. Крупнейший потребитель реактивной энергии. Вращающий момент в них создается посредством переменного магнитного поля статора;
4. Преобразователи электроэнергии, такие как силовые выпрямители, используемые для питания контактной сети железнодорожного транспорта и другие.

Конденсаторные батареи подсоединяются на электроподстанциях для того, чтобы контролировать напряжение в пределах установленных уровней. Нагрузка меняется в течение дня с утренними и вечерними пиками, а также на протяжении недели, снижаясь в выходные, что изменяет показатели напряжения. Подключением и отключением конденсаторов варьируется его уровень. Это делается от руки и с помощью автоматики.

Как и где измеряют cos φ

Реактивная мощность проверяется по изменению cos φ специальным прибором – фазометром. Его шкала проградуирована в количественных значениях cos φ от нуля до единицы в индуктивном и емкостном секторе. Полностью скомпенсировать негативное влияние индуктивности не удастся, но возможно приближение к желаемому показателю – 0,95 в индуктивной зоне.

Фазометр

Фазометры применяются при работе с установками, способными повлиять на режим работы электросети через регулирование cos φ.

1. Так как при финансовых расчетах за потребленную энергию учитывается и ее реактивная составляющая, то на производствах устанавливаются автоматические компенсаторы на конденсаторах, емкость которых может меняться. В сетях, как правило, используются статические конденсаторы;
2. При регулировании cos φ у синхронных генераторов путем изменения возбуждающего тока необходимо его отслеживать визуально в ручных рабочих режимах;
3. Синхронные компенсаторы, представляющие собой синхронные двигатели, работающие без нагрузки, в режиме перевозбуждения выдают в сеть энергию, которая компенсирует индуктивную составляющую. Для регулирования возбуждающего тока наблюдают за показаниями cos φ по фазометру.

Синхронный компенсатор

Коррекция коэффициента мощности – одна из эффективнейших инвестиций для сокращения затрат на электроэнергию. Одновременно улучшается качество получаемой энергии.

Видео

Оцените статью:

Что такое реактивная мощность? — Определение из Техопедии

Другой способ объяснить это состоит в том, что реактивная мощность — это результирующая мощность в ваттах цепи переменного тока, когда форма волны тока не совпадает по фазе с формой волны напряжения, обычно на 90 градусов, если нагрузка является чисто реактивной, и является результатом емкостных или индуктивных нагрузок.

Фактическая работа выполняется только тогда, когда ток находится в фазе с напряжением, например, в резистивных нагрузках. Пример — включение лампы накаливания; в реактивной нагрузке энергия течет к нагрузке половину времени, тогда как в другой половине мощность течет от нее, что создает иллюзию, что нагрузка не рассеивает и не потребляет мощность.

Три вида мощности

Реактивная мощность — это один из трех типов мощности, присутствующих в нагруженных цепях.

Истинная мощность

Фактическая мощность в ваттах, рассеиваемая схемой

Реактивная мощность

Рассеиваемая мощность от индуктивных и емкостных нагрузок, измеренная в вольт-амперах, реактивная (VAR)

Полная мощность

Комбинация измерения реактивной и истинной мощности в вольт-амперах (ВА)

Реактивная мощность также называется «фантомной мощностью», потому что неясно, куда она идет.Общеизвестно, что реактивные нагрузки, такие как конденсаторы и катушки индуктивности, на самом деле не рассеивают мощность в том смысле, что она не используется для их питания, но измерение напряжения и тока вокруг них указывает на то, что они падают напряжение и потребляют ток.

Мощность, рассеиваемая при этом падении напряжения и потребляемом токе, представляет собой тепло или ненужную энергию и не выполняется как фактическая работа; поэтому инженеры искали способы уменьшить это. Из-за этого фантомного питания проводники и генераторы должны иметь соответствующие номиналы и размеры, чтобы выдерживать полный ток, включая потери, а не только ток, который выполняет фактическую работу.

Маятник часов

Некоторые эксперты в области энергетики говорят о реактивной мощности как о части движения конденсатора, которое напоминает движение маятника часов от зенита до надира. По этой аналогии, когда маятник качается вверх, переменный ток подает активную мощность на устройство назначения. По мере того, как маятник движется вниз, реактивная мощность возвращается в сеть для поглощения.

В таких определениях эксперты сказали бы, что реактивная энергия — это энергия, циркулирующая взад и вперед между источником и нагрузкой, в частности, что реактивная мощность «исчезает» обратно к источнику.В некотором смысле это связано с задержкой между током и напряжением. Помимо конденсаторов, статические компенсаторы VAr и синхронные конденсаторы могут использоваться для управления реактивной мощностью в системе.

Ключевым моментом является размещение оборудования реактивного тока рядом с силовыми нагрузками. Это уменьшает количество реактивного тока, который система доставки должна переносить на определенное расстояние.

Реактивная мощность в сети

Чтобы справиться с реалиями переменного тока и изменения путей передачи энергии, проектировщики принимают меры по контролю напряжения.Эксперты по энергетике отмечают, что даже 5% -ное изменение напряжения в данной системе может вызвать отключение электроэнергии и другие проблемы.

С этой целью многие элементы электрической системы, такие как трансформаторы, могут переключаться с передачи на поглощение реактивной мощности по фазам. Но те, кто близок к отрасли, подчеркивают, что это станет еще более важным, когда мы переведем части американской электросети на возобновляемые источники энергии.

Реактивная мощность и возобновляемые источники

Реактивная мощность также очень важна в контексте меняющихся энергосистем.

По многим важным причинам возобновляемые источники энергии, такие как солнце и ветер, заменяют традиционные источники энергии, такие как уголь и природный газ. Но это может иметь разветвления для электросети в целом.

«Всплеск возобновляемых источников энергии в сети без достаточной вращающейся массы может вызвать серьезные проблемы: отключение электроэнергии в определенных областях, чтобы привести спрос в соответствие с предложением; и отключение крупных электростанций от сети, чтобы предотвратить их перегрузку », — пишет Арчи Робб из Renewable Energy World, описывая принцип« инерции сети »и то, как это применимо к управлению реактивной мощностью в системе, которая переходит на возобновляемые источники энергии. строить.

Поскольку возобновляемые источники энергии поставляют энергию в сеть по-разному, возникнет потребность в микроуправлении активной мощностью и реактивной мощностью соответственно.

11.2: Истинная, реактивная и полная мощность

Реактивная мощность

Мы знаем, что реактивные нагрузки, такие как катушки индуктивности и конденсаторы, рассеивают нулевую мощность, но тот факт, что они падают напряжение и потребляют ток, создает обманчивое впечатление, будто они на самом деле рассеивают мощность. Эта «фантомная мощность» называется реактивной мощностью и измеряется в единицах, называемых вольт-ампер-реактивная (ВАР), а не в ваттах.Математическим обозначением реактивной мощности является (к сожалению) заглавная буква Q.

.

Истинная сила

Фактическая мощность, используемая или рассеиваемая в цепи, называется реальной мощностью и измеряется в ваттах (как всегда, обозначается заглавной буквой P).

Полная мощность

Комбинация реактивной мощности и истинной мощности называется кажущейся мощностью , и она является произведением напряжения и тока цепи без учета фазового угла.Полная мощность измеряется в единицах вольт-ампер, (ВА) и обозначается заглавной буквой S.

Расчет реактивной, истинной или полной мощности

Как правило, истинная мощность зависит от рассеивающих элементов схемы, обычно от сопротивления (R). Реактивная мощность — это функция реактивного сопротивления цепи (X). Полная мощность — это функция полного импеданса цепи (Z). Поскольку для расчета мощности мы имеем дело со скалярными величинами, любые комплексные начальные величины, такие как напряжение, ток и импеданс, должны быть представлены их полярными величинами , а не действительными или мнимыми прямоугольными составляющими.Например, если я вычисляю истинную мощность по току и сопротивлению, я должен использовать полярную величину для тока, а не просто «реальную» или «мнимую» часть тока. Если я вычисляю полную мощность по напряжению и импедансу, обе эти ранее комплексные величины должны быть уменьшены до их полярных величин для скалярной арифметики.

Существует несколько уравнений мощности, связывающих три типа мощности с сопротивлением, реактивным сопротивлением и импедансом (все с использованием скалярных величин):

Обратите внимание, что существует два уравнения для расчета истинной и реактивной мощности.Для расчета полной мощности доступны три уравнения, P = IE используется только для этой цели. Изучите следующие схемы и посмотрите, как эти три типа мощности взаимосвязаны: чисто резистивная нагрузка на рисунке ниже, чисто реактивная нагрузка на рисунке ниже и резистивная / реактивная нагрузка на рисунке ниже.

Только резистивная нагрузка

Истинная мощность, реактивная мощность и полная мощность для чисто резистивной нагрузки.

Только реактивная нагрузка

Истинная мощность, реактивная мощность и полная мощность для чисто реактивной нагрузки.

Активная / реактивная нагрузка

Истинная мощность, реактивная мощность и полная мощность для резистивной / реактивной нагрузки.

Треугольник власти

Эти три типа мощности — истинная, реактивная и кажущаяся — связаны друг с другом в тригонометрической форме. Мы называем это треугольником мощности : (рисунок ниже).

Треугольник мощности, связывающий кажущуюся мощность с реальной мощностью и реактивной мощностью.

Используя законы тригонометрии, мы можем найти длину любой стороны (количество любого типа мощности), учитывая длины двух других сторон или длину одной стороны и угол.

Отзыв

• Мощность, рассеиваемая нагрузкой, обозначается как истинная мощность . Истинная мощность обозначается буквой P и измеряется в ваттах (Вт).
• Мощность, просто потребляемая и возвращаемая нагрузкой из-за ее реактивных свойств, обозначается как реактивной мощности .Реактивная мощность обозначается буквой Q и измеряется в вольт-амперных реактивных единицах (ВАР).
• Полная мощность в цепи переменного тока, как рассеиваемая, так и поглощенная / возвращаемая, обозначается как кажущаяся мощность . Полная мощность обозначается буквой S и измеряется в вольт-амперах (ВА).
• Эти три типа власти тригонометрически связаны друг с другом. В прямоугольном треугольнике P = смежная длина, Q = противоположная длина и S = ​​длина гипотенузы.Противоположный угол равен фазовому углу импеданса (Z) цепи.

Анализ мощности переменного тока в реактивных цепях | Глава 3 — Питание в системах переменного тока

Мы уже знаем, что чисто реактивные компоненты (или чисто реактивные схемы) не рассеивают мощность. Мы также знаем, что чисто реактивный импеданс имеет угол + 90 ° или –90 °. Как связаны эти два факта? Что ж, рассмотрим следующий сюжет:

Рисунок 1.Графическое представление взаимосвязи между напряжением, током и мощностью.

Напряжение и ток сдвинуты по фазе на 90 °. Форма волны мощности показывает результат умножения тока и напряжения. Как видите, умножение двух синусоид с разностью фаз 90 ° дает синусоиду, которая является положительной для половины каждого цикла и отрицательной для половины каждого цикла. Это указывает на то, что мощность не рассеивается, потому что вся мощность, подаваемая в систему (в течение одной половины цикла переменного тока), возвращается к источнику (в течение другой половины цикла).

На Рисунке 1 форма волны напряжения достигает максимального значения раньше формы волны тока. Другими словами, напряжение опережает ток, а это значит, что график соответствует индуктивной цепи. График для емкостной цепи будет иметь текущее опережающее напряжение, но общий результат (в отношении мощности) будет таким же: среднее значение формы сигнала мощности будет равно нулю, что указывает на передачу энергии к источнику и от источника, но нет фактическое рассеивание мощности.

Ключевые концепции анализа мощности переменного тока

Это последняя страница в главе 1.Мы завершим эту главу обзором информации, которая будет особенно важна, если вы продолжите изучение синусоидальной мощности в главе 2. Важно развить полное понимание того, как реактивная схема взаимодействует с током и напряжением и как это влияет на мощность. Это действительно суть анализа мощности переменного тока, потому что чисто резистивные цепи очень просты, а индуктивность и емкость чрезвычайно распространены в реальных системах.

Амплитуда, частота, фаза

Синусоидальное напряжение и ток — это постоянно изменяющаяся величина, которая имеет амплитуду (которая связана с максимальным значением формы сигнала), частоту (измеряется в циклах в секунду или радианах в секунду) и фазу (которая определяет временное положение сигнал относительно другой формы сигнала).

Пиковое значение

по сравнению с RMS

Есть два способа задать амплитуду синусоидального сигнала. Пиковое значение (которое также можно было бы назвать амплитудой или величиной) соответствует наибольшему расстоянию между горизонтальной осью и любой точкой на кривой. Среднеквадратичная амплитуда равна пиковому значению, деленному на квадратный корень из 2; он часто используется, поскольку обеспечивает простой способ расчета средней рассеиваемой мощности в цепях переменного тока.

Фазоры

Синусоидальные токи и напряжения могут быть представлены в виде векторов, которые представляют собой комплексные числа, состоящие из величины и угла.Это можно использовать пиковое значение или среднеквадратичное значение амплитуда в качестве величины в фазоре, а угол фазора равно фазовый сдвиг относительно этого сигнала к «нулевой фазе» опорный сигналу.

Сопротивление, реактивное сопротивление и импеданс

Все эти три слова относятся к элементам схемы, препятствующим прохождению тока. Сопротивление приводит к рассеянию мощности, реактивное сопротивление приводит к сдвигу фаз между напряжением и током, а импеданс относится к любому противодействию току, будь то сопротивление, реактивное сопротивление или их комбинация.Когда схема содержит как резистивные, так и реактивные элементы, импеданс представляет собой комплексное число, в котором действительная часть соответствует сопротивлению, а мнимая часть соответствует реактивному сопротивлению. Цепь переменного тока, состоящая из импедансов и векторов, представляющих ток и напряжение, может быть проанализирована так, как если бы это была цепь постоянного тока, состоящая из сопротивлений и постоянных токов и напряжений.

Конденсаторы и индукторы

Это так называемые реактивные компоненты. У них есть только реактивное сопротивление; другими словами, их импеданс имеет только мнимую часть.Конденсаторы создают задержку напряжения относительно тока; таким образом, в емкостной цепи ток ведет к напряжению. Катушки индуктивности создают задержку тока относительно напряжения; таким образом, в индуктивной цепи напряжение ведет к току.

Активная и реактивная мощность

Конденсаторы и катушки индуктивности имеют важное значение для энергосистем. Создавая разность фаз между напряжением и током, эти компоненты приводят к реактивной мощности, которая относится к мощности, поставляемой источником, но не потребляемой нагрузкой.Вместо этого эта мощность соответствует энергии, которая временно накапливается реактивными элементами, а затем возвращается источнику. Активная мощность, напротив, рассеивается схемой нагрузки.

Коэффициент мощности

Эта величина передает информацию о пропорциях активной и реактивной мощности, необходимой для системы переменного тока. Более высокая доля реактивной мощности обычно считается нежелательной, поскольку это снижает эффективность передачи мощности переменного тока от источника к нагрузке.

РЕАКТИВНАЯ МОЩНОСТЬ — прикладное промышленное электричество

Рис. 6.1 Чисто резистивная цепь переменного тока: напряжение и ток резистора совпадают по фазе.

Если бы мы изобразили ток и напряжение для очень простой цепи переменного тока, состоящей из источника и резистора (рисунок выше), это выглядело бы примерно так: (рисунок ниже)

Рисунок 6.2 Напряжение и ток «синфазны» для резистивной цепи.

Поскольку резистор просто и прямо сопротивляется протеканию тока в любое время, форма волны падения напряжения на резисторе точно совпадает по фазе с формой волны тока через него.Мы можем посмотреть в любой момент времени вдоль горизонтальной оси графика и сравнить эти значения тока и напряжения друг с другом (любой «снимок», показывающий значения волны, упоминается как мгновенных значений , что означает значения в этот момент по времени). Когда мгновенное значение тока равно нулю, мгновенное напряжение на резисторе также равно нулю. Аналогичным образом, в тот момент, когда ток через резистор достигает своего положительного пика, напряжение на резисторе также находится на своем положительном пике, и так далее.В любой момент времени на волнах закон Ома верен для мгновенных значений напряжения и тока.

Мы также можем рассчитать мощность, рассеиваемую этим резистором, и нанести эти значения на тот же график: (рисунок ниже)

Рисунок 6.3 Мгновенная мощность переменного тока в чисто резистивной цепи всегда положительная.

Резисторы и индукторы

Катушки индуктивности ведут себя не так, как резисторы. В то время как резисторы просто противодействуют протеканию тока через них (снижая напряжение, прямо пропорциональное току), индукторы противодействуют изменениям тока через них, снижая напряжение, прямо пропорциональное скорости изменения тока.В соответствии с законом Ленца , это индуцированное напряжение всегда имеет такую ​​полярность, чтобы поддерживать ток на его текущем уровне. То есть, если ток увеличивается по величине, индуцированное напряжение будет «противодействовать» току; если ток уменьшается, полярность изменится на противоположную и «подтолкнет» ток, чтобы противодействовать уменьшению. Это противодействие текущему изменению называется реактивным сопротивлением , а не сопротивлением . Выражаясь математически, соотношение между падением напряжения на катушке индуктивности и скоростью изменения тока через катушку индуктивности выглядит следующим образом:

[латекс] e = L \ frac {d_i} {d_t} [/ латекс]

Переменный ток в простой индуктивной цепи

Выражение di / dt — это выражение из расчетов, означающее скорость изменения мгновенного тока (i) во времени в амперах в секунду.Индуктивность (L) измеряется в Генри, а мгновенное напряжение (е), конечно, выражается в вольтах. Иногда вы можете встретить скорость мгновенного напряжения, выраженную как «v» вместо «e» (v = L di / dt), но это означает то же самое. Чтобы показать, что происходит с переменным током, давайте проанализируем простую цепь индуктивности:

Рисунок 6.4 Чистая индуктивная цепь: ток индуктора отстает от напряжения индуктора на 90 °.

Если бы мы изобразили ток и напряжение для этой очень простой схемы, это выглядело бы примерно так:

Рисунок 6.5 Чистая индуктивная цепь, формы сигналов.

Помните, что падение напряжения на катушке индуктивности является реакцией на изменение тока через нее на . Следовательно, мгновенное напряжение равно нулю всякий раз, когда мгновенный ток достигает пика (нулевое изменение или наклон уровня на синусоидальной волне тока), а мгновенное напряжение находится на пике везде, где мгновенный ток имеет максимальное изменение (точки самый крутой наклон на текущей волне, где она пересекает нулевую линию).Это приводит к появлению волны напряжения, сдвинутой по фазе на 90 ° с волной тока. Глядя на график, кажется, что волна напряжения имеет «фору» по сравнению с волной тока; напряжение «опережает» ток, а ток «отстает» от напряжения.

Ток отстает от напряжения на 90 ° в чисто индуктивной цепи.

Все становится еще интереснее, когда мы строим график мощности для этой схемы:

Рисунок 6.6 В чисто индуктивной цепи мгновенная мощность может быть положительной или отрицательной.

Поскольку мгновенная мощность является произведением мгновенного напряжения и мгновенного тока (p = ie), мощность равна нулю, когда мгновенный ток или напряжение равно нулю. Если мгновенный ток и напряжение положительные (над линией), мощность положительная. Как и в примере с резистором, мощность также положительна, когда мгновенные ток и напряжение отрицательны (ниже линии). Однако, поскольку волны тока и напряжения сдвинуты по фазе на 90 °, бывают моменты, когда одна положительная, а другая отрицательная, что приводит к одинаково частым возникновению отрицательной мгновенной мощности .

Что такое отрицательная сила?

Но что означает отрицательная мощность ? Это означает, что катушка индуктивности возвращает мощность в цепь, а положительное значение мощности означает, что она поглощает мощность из цепи. Поскольку положительные и отрицательные циклы мощности равны по величине и продолжительности во времени, индуктор возвращает обратно в цепь столько же энергии, сколько потребляет в течение всего цикла. В практическом смысле это означает, что реактивное сопротивление катушки индуктивности рассеивает нулевую полезную энергию, в отличие от сопротивления резистора, который рассеивает энергию в виде тепла.Имейте в виду, это только для идеальных катушек индуктивности, у которых нет сопротивления провода.

Реактивное сопротивление в зависимости от сопротивления

Противодействие катушки индуктивности изменению тока приводит к противодействию переменному току в целом, который по определению всегда изменяется по мгновенной величине и направлению. Это противодействие переменному току аналогично сопротивлению, но отличается тем, что всегда приводит к сдвигу фаз между током и напряжением и рассеивает нулевую мощность. Из-за различий он имеет другое название: реактивное сопротивление .Реактивное сопротивление по переменному току выражается в омах, как и сопротивление, за исключением того, что его математический символ — X вместо R. Чтобы быть конкретным, реактивное сопротивление, связанное с катушкой индуктивности, обычно обозначается заглавной буквой X с буквой L в качестве нижнего индекса, например это: X _L .

Поскольку напряжение на катушках индуктивности падает пропорционально скорости изменения тока, они будут терять большее напряжение при более быстром изменении тока и меньшее напряжение при более медленном изменении тока. Это означает, что реактивное сопротивление в Ом для любой катушки индуктивности прямо пропорционально частоте переменного тока.Точная формула для определения реактивного сопротивления выглядит следующим образом:

[латекс] X_L = 2πfL [/ латекс]

Если мы подвергнем индуктор 10 мГн воздействию частот 60, 120 и 2500 Гц, он проявит реактивные сопротивления, указанные в таблице ниже.

Реактивное сопротивление индуктора 10 мГн:

Таблица 6.1 Реактивное сопротивление индуктора 10 мГн

Частота (Герцы)	Реактивное сопротивление (Ом)
60	3.7699
120	7,5398
2500	157.0796

В уравнении реактивного сопротивления термин «2πf» (все в правой части, кроме L) имеет особое значение. Это количество радианов в секунду, на которое «вращается» переменный ток, если вы представите себе один цикл переменного тока, представляющий вращение полного круга. радиан — это единица измерения угла: в одном полном круге 2π радиана, так же как в полном круге 360 °.Если генератор переменного тока является двухполюсным блоком, он будет производить один цикл на каждый полный оборот вала, что составляет каждые 2π радиан или 360 °. Если эту константу 2π умножить на частоту в Герцах (циклов в секунду), результатом будет число в радианах в секунду, известное как угловая скорость системы переменного тока.

Угловая скорость в системах переменного тока

Угловая скорость может быть представлена ​​выражением 2πf или ее собственным символом, строчной греческой буквой омега, которая похожа на нашу строчную римскую букву «w»: ω.Таким образом, формула реактивного сопротивления X _L = 2πfL также может быть записана как X _L = ωL.

Следует понимать, что эта «угловая скорость» является выражением того, насколько быстро колеблются колебания переменного тока, полный цикл равен 2π радиан. Это не обязательно отражает фактическую скорость вала генератора переменного тока. Если генератор имеет более двух полюсов, угловая скорость будет кратной скорости вала. По этой причине ω иногда выражается в единицах электрических радиан в секунду, а не в (простых) радианах в секунду, чтобы отличить его от механического движения.

Как бы мы ни выразили угловую скорость системы, очевидно, что она прямо пропорциональна реактивному сопротивлению в катушке индуктивности. По мере увеличения частоты (или скорости вала генератора переменного тока) в системе переменного тока катушка индуктивности будет оказывать большее сопротивление прохождению тока, и наоборот. Переменный ток в простой индуктивной цепи равен напряжению (в вольтах), деленному на индуктивное реактивное сопротивление (в омах), точно так же, как переменный или постоянный ток в простой резистивной цепи равен напряжению (в вольтах), деленному на сопротивление (в Ом).Пример схемы показан здесь:

Индуктивное сопротивление

(Индуктивное сопротивление индуктора 10 мГн при 60 Гц)

[латекс] X_L = 3,7600 Ом [/ латекс]

[латекс] I_ {X_ {L}} = \ frac {E} {X} [/ латекс]

[латекс] = \ frac {10 В} {3,7600 Ом} [/ латекс]

[латекс] \ mathbf {= 2.6526A} [/ латекс]

Фазовые углы

Однако мы должны помнить, что здесь напряжение и ток не совпадают по фазе. Как было показано ранее, напряжение имеет фазовый сдвиг + 90 ° по отношению к току.Если мы представим эти фазовые углы напряжения и тока математически в виде комплексных чисел, мы обнаружим, что сопротивление катушки индуктивности току также имеет фазовый угол:

[латекс] \ text {Opposition} = \ frac {\ text {Voltage}} {\ text {Current}} [/ latex]

[латекс] \ text {Opposition} = \ frac {10 V \ angle \ text {90 °}} {2.6526A \ angle \ text {90 °}} [/ латекс]

[латекс] \ begin {align} \ text {Opposition} = & 3.7699 \ Omega \ angle \ text {90 °} \\ \ text {или} & 0 + j3.7699 \ Omega \ end {align} [/ latex]

Математически мы говорим, что фазовый угол сопротивления катушки индуктивности току равен 90 °, что означает, что сопротивление катушки индуктивности току является положительной мнимой величиной. Этот фазовый угол реактивного противодействия току становится критически важным при анализе цепей, особенно для сложных цепей переменного тока, где реактивное сопротивление и сопротивление взаимодействуют. Будет полезно представить любое сопротивление компонента току в виде комплексных чисел, а не скалярных величин сопротивления и реактивного сопротивления.

• Индуктивное реактивное сопротивление — это противодействие, которое индуктор предлагает переменному току из-за сдвинутого по фазе накопления и высвобождения энергии в его магнитном поле. Реактивное сопротивление обозначается заглавной буквой «X» и измеряется в омах, как и сопротивление (R).
• Индуктивное реактивное сопротивление можно рассчитать по следующей формуле: X _L = 2πfL
• Угловая скорость цепи переменного тока — это еще один способ выразить ее частоту в единицах электрических радиан в секунду вместо циклов в секунду.Его символизирует строчная греческая буква «омега» или ω.
• Индуктивное реактивное сопротивление увеличивается с увеличением частоты. Другими словами, чем выше частота, тем сильнее она противодействует потоку электронов переменного тока.

Возьмем эту схему в качестве примера для работы:

Последовательный резистор цепи индуктивности: ток отстает от приложенного напряжения от 0 ° до 90 °.

Резистор будет обеспечивать сопротивление 5 Ом переменному току независимо от частоты, а катушка индуктивности — 3 Ом.Реактивное сопротивление 7699 Ом на переменный ток при 60 Гц.

Поскольку сопротивление резистора является действительным числом (5 Ом 0 ° или 5 + j0 Ом), а реактивное сопротивление катушки индуктивности — мнимым числом (3,7699 Ом ∠ 90 ° или 0 + j3,7699 Ом), совокупный эффект двух компонентов будет противодействовать току, равному комплексной сумме двух чисел.

Это комбинированное противодействие будет векторной комбинацией сопротивления и реактивного сопротивления. Чтобы кратко выразить это противопоставление, нам нужен более полный термин для обозначения сопротивления току, чем просто сопротивление или реактивное сопротивление.

Этот термин называется импедансом , его символ — Z, и он также выражается в единицах Ом, точно так же, как сопротивление и реактивное сопротивление. В приведенном выше примере полное сопротивление цепи составляет:

Сопротивление по закону Ома

Импеданс связан с напряжением и током, как и следовало ожидать, аналогично сопротивлению в законе Ома:

На самом деле, это гораздо более полная форма закона Ома, чем то, чему учили в электронике постоянного тока (E = IR), так же как импеданс является гораздо более полным выражением сопротивления потоку тока, чем сопротивление. Любое сопротивление и любое реактивное сопротивление по отдельности или в комбинации (последовательно / параллельно) могут и должны быть представлены как единый импеданс в цепи переменного тока.

Чтобы рассчитать ток в приведенной выше схеме, нам сначала нужно указать опорный фазовый угол для источника напряжения, который обычно принимается равным нулю. (Фазовые углы резистивного и индуктивного импеданса равны , всегда 0 ° и + 90 °, соответственно, независимо от заданных фазовых углов для напряжения или тока).

Как и в случае чисто индуктивной схемы, волна тока отстает от волны напряжения (источника), хотя на этот раз отставание не так велико: всего 37,016 ° по сравнению с полными 90 °, как в случае чисто индуктивного схема.

Ток отстает от напряжения в последовательной цепи L-R.

Для резистора и катушки индуктивности соотношение фаз между напряжением и током не изменилось.Напряжение на резисторе синфазно (сдвиг 0 °) с током через него, а напряжение на катушке индуктивности на + 90 ° не совпадает по фазе с током, проходящим через него. Мы можем проверить это математически:

Напряжение на резисторе имеет тот же фазовый угол, что и ток через него, что говорит нам о том, что E и I находятся в фазе (только для резистора).

Напряжение на катушке индуктивности имеет фазовый угол 52.984 °, в то время как ток через катушку индуктивности имеет фазовый угол -37,016 °, разница между ними составляет ровно 90 °. Это говорит нам о том, что E и I все еще не совпадают по фазе на 90 ° (только для катушки индуктивности).

Используйте закон Кирхгофа о напряжении

Мы также можем математически доказать, что эти комплексные значения в сумме составляют общее напряжение, как и предсказывает закон Кирхгофа:

Давайте возьмем те же компоненты для нашей схемы последовательного примера и подключим их параллельно:

Рисунок 6.7 Параллельная цепь R-L.

Поскольку источник питания имеет ту же частоту, что и схема последовательного примера, а резистор и катушка индуктивности имеют одинаковые значения сопротивления и индуктивности, соответственно, они также должны иметь одинаковые значения импеданса. Итак, мы можем начать нашу таблицу анализа с тех же «заданных» значений:

Таблица 6.2 Таблица анализа импеданса 1

Единственная разница в нашей методике анализа на этот раз состоит в том, что мы будем применять правила для параллельных цепей вместо правил для последовательных цепей.Принцип такой же, как и для DC. Мы знаем, что напряжение равномерно распределяется между всеми компонентами в параллельной цепи, поэтому мы можем передать значение общего напряжения (10 вольт ∠ 0 °) на все столбцы компонентов:

Таблица 6.3. Таблица анализа импеданса 2

Теперь мы можем применить закон Ома (I = E / Z) по вертикали к двум столбцам таблицы, рассчитав ток через резистор и ток через катушку индуктивности:

Таблица 6.4 Таблица анализа импеданса 3

Как и в случае цепей постоянного тока, токи ответвления в параллельной цепи переменного тока складываются в общий ток (Закон Кирхгофа по току все еще сохраняется для переменного тока, как и для постоянного тока):

Таблица 6.5 Таблица анализа импеданса 4

Наконец, общий импеданс можно рассчитать с помощью закона Ома (Z = E / I) по вертикали в столбце «Всего». Кстати, параллельный импеданс также можно рассчитать с помощью обратной формулы, идентичной той, которая используется при вычислении параллельных сопротивлений.

[латекс] \ tag {6.1} Z_ {parallel} = \ frac {1} {\ frac {1} {Z_1} + \ frac {1} {Z_2} + \ dots \ frac {1} {Z_n}} [ / латекс]

Единственная проблема с использованием этой формулы заключается в том, что она обычно требует большого количества нажатий клавиш калькулятора.И если вы полны решимости использовать формулу, подобную этой «от руки», будьте готовы к очень большому объему работы! Но, как и в случае с цепями постоянного тока, у нас часто есть несколько вариантов расчета величин в наших таблицах анализа, и этот пример ничем не отличается. Независимо от того, каким способом вы рассчитаете полное сопротивление (закон Ома или обратная формула), вы получите одно и то же значение:

Таблица 6.6 Таблица анализа импеданса 5

• Импедансом (Z) управляют так же, как и сопротивлением (R) при анализе параллельной цепи: параллельные импедансы уменьшаются, образуя общий импеданс, с использованием обратной формулы.Только обязательно выполняйте все вычисления в сложной (не скалярной) форме!

[латекс] Z_ {parallel} = \ frac {1} {(\ frac {1} {Z1} + \ frac {1} {Z2} +… \ Frac {1} {Zn})} [/ латекс]

• Закон Ома для цепей переменного тока:

[латекс] E = {I} {Z} [/ латекс]; [латекс] I = \ frac {E} {Z} [/ latex]; [латекс] Z = \ frac {E} {I} [/ latex]

• Когда резисторы и катушки индуктивности смешиваются вместе в параллельных цепях (так же, как в последовательных цепях), общий импеданс будет иметь фазовый угол где-то между 0 ° и + 90 °.Ток в цепи будет иметь фазовый угол от 0 ° до -90 °.
• Параллельные цепи переменного тока обладают теми же фундаментальными свойствами, что и параллельные цепи постоянного тока: напряжение равномерно по всей цепи, токи ответвления складываются, чтобы сформировать общий ток, а импедансы уменьшаются (по обратной формуле), чтобы сформировать общий импеданс.

В идеальном случае индуктор действует как чисто реактивное устройство. То есть его противодействие переменному току строго основано на индуктивной реакции на изменения тока, а не на трении электронов, как в случае с резистивными компонентами.Однако катушки индуктивности не так уж чисты в своем реактивном поведении. Начнем с того, что они сделаны из проволоки, и мы знаем, что все проволоки обладают некоторой измеримой величиной сопротивления (кроме сверхпроводящей проволоки). Это встроенное сопротивление действует так, как если бы оно было подключено последовательно с идеальной индуктивностью катушки, например:

Рисунок 6.8 Катушка индуктивности Эквивалентная схема реальной катушки индуктивности.

Следовательно, полное сопротивление любой реальной катушки индуктивности всегда будет представлять собой сложную комбинацию сопротивления и индуктивного реактивного сопротивления.

Эту проблему усугубляет то, что называется скин-эффектом , который представляет собой тенденцию переменного тока течь через внешние области поперечного сечения проводника, а не через середину. Когда электроны движутся в одном направлении (постоянный ток), они используют для движения всю площадь поперечного сечения проводника. С другой стороны, электроны, меняющие направление потока, стремятся избежать прохождения через самую середину проводника, ограничивая доступную эффективную площадь поперечного сечения. Скин-эффект становится более выраженным с увеличением частоты.

Кроме того, переменное магнитное поле индуктора, питаемого переменным током, может излучаться в космос как часть электромагнитной волны, особенно если переменный ток имеет высокую частоту. Эта излучаемая энергия не возвращается к катушке индуктивности и поэтому проявляется в виде сопротивления (рассеиваемой мощности) в цепи.

Помимо резистивных потерь в проводе и излучения, в индукторах с железным сердечником действуют и другие эффекты, которые проявляются как дополнительное сопротивление между выводами.Когда на индуктор подается переменный ток, создаваемые переменные магнитные поля имеют тенденцию индуцировать циркулирующие токи в железном сердечнике, известные как вихревые токи , . Эти электрические токи в железном сердечнике должны преодолевать электрическое сопротивление, обеспечиваемое железом, который не так хорош в качестве проводника, как медь. Вихретоковым потерям в первую очередь противодействуют, разделив железный сердечник на множество тонких листов (пластин), каждый из которых отделен от другого тонким слоем электроизоляционного лака.Поскольку поперечное сечение сердечника разделено на множество электрически изолированных участков, ток не может циркулировать в пределах этой площади поперечного сечения, и из-за этого не будет (или будет очень мало) резистивных потерь.

Как и следовало ожидать, потери на вихревые токи в металлических сердечниках индуктора проявляются в виде тепла. Эффект более выражен на высоких частотах и ​​может быть настолько сильным, что иногда его используют в производственных процессах для нагрева металлических предметов! Фактически, этот процесс «индукционного нагрева» часто используется при литье металлов высокой чистоты, когда металлические элементы и сплавы должны нагреваться в вакууме, чтобы избежать загрязнения воздухом, и, таким образом, стандартная технология нагрева сжиганием была бы бесполезной.Это «бесконтактная» технология, когда нагретое вещество не должно касаться катушки (катушек), создающей магнитное поле.

В высокочастотной среде вихревые токи могут возникать даже в поперечном сечении самого провода, что способствует возникновению дополнительных резистивных эффектов. Чтобы противодействовать этой тенденции, можно использовать специальный провод, сделанный из очень тонких, индивидуально изолированных жил, который называется Litz wire (сокращение от Litzendraht ). Изоляция, отделяющая жилы друг от друга, предотвращает циркуляцию вихревых токов по всей площади поперечного сечения провода.

Кроме того, любой магнитный гистерезис, который необходимо преодолевать при каждом изменении направления магнитного поля индуктора, представляет собой расход энергии, который проявляется как сопротивление в цепи. Некоторые материалы сердечника (например, феррит) особенно известны своим гистерезисным эффектом. Противодействовать этому эффекту лучше всего путем правильного выбора материала сердечника и ограничения пиковой напряженности магнитного поля, генерируемого в каждом цикле.

В целом паразитные резистивные свойства реального индуктора (сопротивление провода, радиационные потери, вихревые токи и гистерезисные потери) выражаются одним термином «эффективное сопротивление»:

Рисунок 6.9 Эквивалентная схема реального индуктора с потерями на скин-эффект, излучение, вихревые токи и гистерезис.

Стоит отметить, что скин-эффект и потери на излучение применимы к прямым отрезкам провода в цепи переменного тока так же хорошо, как и к спиральному проводу. Обычно их совокупный эффект слишком мал, чтобы его можно было заметить, но на радиочастотах они могут быть довольно большими. Например, антенна радиопередатчика спроектирована специально для рассеивания наибольшего количества энергии в виде электромагнитного излучения.

Конденсаторы Vs. Резисторы

Конденсаторы не ведут себя так же, как резисторы. В то время как резисторы пропускают через себя поток электронов, прямо пропорциональный падению напряжения, конденсаторы противодействуют изменениям напряжения, потребляя или подавая ток, когда они заряжаются или разряжаются до нового уровня напряжения. Поток электронов «через» конденсатор прямо пропорционален скорости изменения напряжения на конденсаторе. Это противодействие изменению напряжения является еще одной формой реактивного сопротивления , но оно прямо противоположно тому, которое демонстрируют индукторы.

Характеристики цепи конденсатора

Выражаясь математически, соотношение между током, протекающим через конденсатор, и скоростью изменения напряжения на конденсаторе выглядит следующим образом:

[латекс] i = C \ frac {d_e} {d_t} [/ латекс]

Выражение de / dt — это выражение из расчетов, означающее скорость изменения мгновенного напряжения (e) во времени в вольтах в секунду. Емкость (C) выражается в фарадах, а мгновенный ток (i), конечно, выражается в амперах.Иногда скорость мгновенного изменения напряжения с течением времени выражается как dv / dt вместо de / dt: вместо напряжения используется строчная буква «v» или «e», но это означает то же самое. Чтобы показать, что происходит с переменным током, давайте проанализируем простую схему конденсатора:

Рисунок 6.10 Чистая емкостная цепь: напряжение конденсатора отстает от тока конденсатора на 90 °

Если бы мы изобразили ток и напряжение для этой очень простой схемы, это выглядело бы примерно так:

Рисунок 6.11 Чистые формы сигналов емкостной цепи.

Помните, что ток через конденсатор — это реакция на изменение напряжения на нем на . Следовательно, мгновенный ток равен нулю всякий раз, когда мгновенное напряжение достигает пика (нулевое изменение или наклон уровня синусоидальной волны напряжения), а мгновенный ток находится на пике везде, где мгновенное напряжение находится на максимальном изменении (точки самый крутой наклон на волне напряжения, где она пересекает нулевую линию).Это приводит к появлению волны напряжения, которая на -90 ° не совпадает по фазе с волной тока. Глядя на график, кажется, что волна тока имеет «фору» по сравнению с волной напряжения; ток «опережает» напряжение, а напряжение «отстает» от тока.

Рисунок 6.12 Напряжение отстает от тока на 90 ° в чисто емкостной цепи.

Как вы могли догадаться, та же необычная волна мощности, которую мы видели в простой цепи индуктивности, присутствует и в простой цепи конденсатора:

Рисунок 6.13 В чисто емкостной цепи мгновенная мощность может быть положительной или отрицательной.

Как и в случае с простой схемой индуктора, сдвиг фазы на 90 градусов между напряжением и током приводит к появлению волны мощности, которая в равной степени чередуется между положительным и отрицательным. Это означает, что конденсатор не рассеивает мощность, поскольку он реагирует на изменения напряжения; он просто поочередно поглощает и высвобождает энергию.

Реактивное сопротивление конденсатора

Противодействие конденсатора изменению напряжения переводится в противодействие переменному напряжению в целом, которое по определению всегда изменяется по мгновенной величине и направлению.Для любой данной величины переменного напряжения на данной частоте конденсатор данного размера будет «проводить» определенную величину переменного тока. Так же, как ток через резистор является функцией напряжения на резисторе и сопротивления, предлагаемого резистором, переменный ток через конденсатор является функцией переменного напряжения на нем и реактивного сопротивления , обеспечиваемого конденсатором, . Как и в случае катушек индуктивности, реактивное сопротивление конденсатора выражается в омах и обозначается буквой X (или, если точнее, X _C ).

Поскольку конденсаторы «проводят» ток пропорционально скорости изменения напряжения, они будут пропускать больше тока при более быстром изменении напряжения (поскольку они заряжаются и разряжаются до тех же пиков напряжения за меньшее время) и меньший ток при более медленном изменении напряжения. . Это означает, что реактивное сопротивление в Ом для любого конденсатора равно , обратно пропорционально частоте переменного тока.

[латекс] X_C = \ frac {1} {2πfC} [/ латекс]

Реактивное сопротивление конденсатора 100 мкФ:

Частота (Герцы)	Реактивное сопротивление (Ом)
60	26.5258
120	13,2629
2500	0,6366

Обратите внимание, что отношение емкостного реактивного сопротивления к частоте прямо противоположно отношению индуктивного реактивного сопротивления. Емкостное реактивное сопротивление (в омах) уменьшается с увеличением частоты переменного тока. И наоборот, индуктивное реактивное сопротивление (в омах) увеличивается с увеличением частоты переменного тока. Индукторы противодействуют более быстрому изменению токов, производя большие падения напряжения; Конденсаторы противодействуют более быстрому изменению падений напряжения за счет увеличения тока.

Как и в случае катушек индуктивности, член 2πf в уравнении реактивного сопротивления может быть заменен строчной греческой буквой Омега (ω), которая обозначается как угловая скорость цепи переменного тока . Таким образом, уравнение X _C = 1 / (2πfC) также может быть записано как X _C = 1 / (ωC), где ω приведено в единицах радиан в секунду .

Переменный ток в простой емкостной цепи равен напряжению (в вольтах), деленному на емкостное реактивное сопротивление (в омах), точно так же, как переменный или постоянный ток в простой резистивной цепи равен напряжению (в вольтах), деленному на сопротивление (в Ом).Следующая схема иллюстрирует это математическое соотношение на примере:

Емкостное реактивное сопротивление.

[латекс] X_C = 26,5258 Ом [/ латекс]

[латекс] I = \ frac {E} {X} [/ латекс]

[латекс] I = \ frac {10} {26,5258 Ом} [/ латекс]

[латекс] I = 0,3770A [/ латекс]

Однако мы должны помнить, что здесь напряжение и ток не совпадают по фазе. Как было показано ранее, ток имеет фазовый сдвиг + 90 ° по отношению к напряжению.Если мы представим эти фазовые углы напряжения и тока математически, мы сможем вычислить фазовый угол реактивного сопротивления конденсатора току.

Напряжение в конденсаторе отстает от тока на 90 °.

Математически мы говорим, что фазовый угол сопротивления конденсатора току составляет -90 °, что означает, что сопротивление конденсатора току является отрицательной мнимой величиной. (См. Рисунок выше.) Этот фазовый угол реактивного противодействия току становится критически важным при анализе цепей, особенно для сложных цепей переменного тока, в которых взаимодействуют реактивное сопротивление и сопротивление.Будет полезно представить любое сопротивление компонента току в виде комплексных чисел, а не только скалярных величин сопротивления и реактивного сопротивления.

• Емкостное реактивное сопротивление — это противодействие, которое конденсатор предлагает переменному току из-за сдвинутого по фазе накопления и высвобождения энергии в его электрическом поле. Реактивное сопротивление обозначается заглавной буквой «X» и измеряется в омах, как и сопротивление (R).
• Емкостное реактивное сопротивление можно рассчитать по следующей формуле: XC = 1 / (2πfC)
• Емкостное реактивное сопротивление уменьшается с увеличением частоты.Другими словами, чем выше частота, тем меньше он противодействует (тем больше «проводит») переменному току.

Используя компоненты того же значения в нашей схеме последовательного примера, мы подключим их параллельно и посмотрим, что произойдет:

Рисунок 6.14 Параллельная цепь RC.

Резистор и конденсатор параллельно

Поскольку источник питания имеет ту же частоту, что и схема последовательного примера, а резистор и конденсатор имеют одинаковые значения сопротивления и емкости, соответственно, они также должны иметь одинаковые значения импеданса.Итак, мы можем начать нашу таблицу анализа с тех же «заданных» значений:

Таблица 6.7

Сейчас это параллельная схема, и мы знаем, что напряжение распределяется поровну между всеми компонентами, поэтому мы можем поместить цифру для общего напряжения (10 вольт ∠ 0 °) во все столбцы:

Таблица 6.8 Расчет

с использованием закона Ома

Теперь мы можем применить закон Ома (I = E / Z) по вертикали к двум столбцам таблицы, вычислив ток через резистор и ток через конденсатор:

Таблица 6.9

Так же, как и в цепях постоянного тока, токи ответвления в параллельной цепи переменного тока складываются в общий ток (снова Закон Кирхгофа):

Таблица 6.10.

Наконец, общий импеданс можно рассчитать с помощью закона Ома (Z = E / I) по вертикали в столбце «Всего». Как мы видели в главе об индуктивности переменного тока, параллельный импеданс также можно рассчитать, используя обратную формулу, идентичную той, которая используется при вычислении параллельных сопротивлений. Следует отметить, что это правило параллельного импеданса остается в силе независимо от типа импедансов, подключенных параллельно.Другими словами, не имеет значения, рассчитываем ли мы схему, состоящую из параллельных резисторов, параллельных катушек индуктивности, параллельных конденсаторов или какой-либо их комбинации: в форме импедансов (Z) все термины являются общими и могут применяться равномерно по той же формуле. И снова формула параллельного импеданса выглядит так:

[латекс] Z_ {parallel} = \ frac {1} {\ frac {1} {Z_1} + \ frac {1} {Z_2} + \ dots \ frac {1} {Z_n}} [/ латекс]

Единственным недостатком использования этого уравнения является значительный объем работы, необходимой для его вычисления, особенно без помощи калькулятора, способного манипулировать сложными величинами.Независимо от того, как мы рассчитываем полное сопротивление для нашей параллельной цепи (закон Ома или обратная формула), мы получим ту же цифру:

• Импедансом (Z) управляют так же, как и сопротивлением (R) при анализе параллельной цепи: параллельные импедансы уменьшаются, образуя общий импеданс, с использованием обратной формулы. Только не забудьте
  • выполнять все вычисления в комплексном (не скалярном) виде! ZTotal = 1 / (1 / Z1 + 1 / Z2 +.. 1 / Zn)
  • Закон Ома для цепей переменного тока: E = IZ; I = E / Z; Z = E / I
  • Когда резисторы и конденсаторы смешиваются вместе в параллельных цепях (так же, как в последовательных цепях), общий импеданс будет иметь фазовый угол где-то между 0 ° и -90 °.Ток в цепи будет иметь фазовый угол от 0 ° до + 90 °.
  • Параллельные цепи переменного тока обладают теми же фундаментальными свойствами, что и параллельные цепи постоянного тока: напряжение равномерно по всей цепи, токи ответвления складываются, чтобы сформировать общий ток, а импедансы уменьшаются (по обратной формуле), чтобы сформировать общий импеданс.

(Следующий раздел был адаптирован из: Уроки электрических цепей, Том II, Глава 5 — Реактивное сопротивление и импеданс — R, L и C)

Прежде чем мы начнем исследовать влияние резисторов, катушек индуктивности и конденсаторов, соединенных вместе в одних и тех же цепях переменного тока, давайте кратко рассмотрим некоторые основные термины и факты.

Сопротивление

Это по сути трение против потока тока. В той или иной степени он присутствует во всех проводниках (за исключением проводов super !), Особенно в резисторах. Когда переменный ток проходит через сопротивление, возникает падение напряжения, синфазное с током. Сопротивление математически обозначается буквой «R» и измеряется в омах (Ом).

Реактивное сопротивление

Это, по сути, инерция против тока.Он присутствует везде, где электрические или магнитные поля развиваются пропорционально приложенному напряжению или току, соответственно; но особенно в конденсаторах и катушках индуктивности. Когда переменный ток проходит через чистое реактивное сопротивление, возникает падение напряжения, которое на 90 ° не совпадает по фазе с током. Реактивное сопротивление математически обозначается буквой «X» и измеряется в омах (Ом).

Импеданс

Это исчерпывающее выражение любых форм противодействия протеканию тока, включая как сопротивление, так и реактивное сопротивление.Он присутствует во всех схемах и во всех компонентах. Когда переменный ток проходит через полное сопротивление, возникает падение напряжения, которое находится где-то между 0 ° и 90 ° не в фазе с током. Импеданс математически обозначается буквой «Z» и измеряется в единицах Ом (Ом) в сложной форме.

Идеальные резисторы обладают сопротивлением, но не реактивным сопротивлением. Идеальные катушки индуктивности и идеальные конденсаторы обладают реактивным сопротивлением, но не имеют сопротивления. Все компоненты обладают импедансом, и из-за этого универсального качества имеет смысл перевести все значения компонентов (сопротивление, индуктивность, емкость) в общие термины импеданса в качестве первого шага при анализе цепи переменного тока.

Рис. 6.15. Идеальный резистор, катушка индуктивности и конденсатор.

Фазовый угол импеданса для любого компонента — это фазовый сдвиг между напряжением на этом компоненте и током через этот компонент. Для идеального резистора падение напряжения и ток всегда находятся в фазе друг с другом, поэтому угол импеданса резистора считается равным 0 °. Для идеального индуктора падение напряжения всегда опережает ток на 90 °, поэтому фазовый угол импеданса индуктора равен + 90 °.Для идеального конденсатора падение напряжения всегда отстает от тока на 90 °, поэтому считается, что фазовый угол импеданса конденсатора составляет -90 °.

Импедансы в переменном токе ведут себя аналогично сопротивлениям в цепях постоянного тока: они добавляются последовательно и уменьшаются параллельно. Пересмотренная версия закона Ома, основанная на импедансе, а не на сопротивлении, выглядит так:

Закон Ома для цепи переменного тока

[латекс] \ begin {align} \ tag {6.2} \ text {E} & = {I} {Z} \\ \ text {I} & = \ frac {E} {Z} \\ \ text {Z } & = \ frac {E} {I} \ end {align} [/ latex]

Мы можем взять те же компоненты из последовательной схемы и переставить их в параллельную конфигурацию для простого примера схемы:

Рисунок 6.16 Пример параллельной схемы R, L и C.

Импеданс в параллельных компонентах

Тот факт, что эти компоненты подключены параллельно, а не последовательно, теперь абсолютно не влияет на их индивидуальные импедансы. Пока источник питания имеет ту же частоту, что и раньше, индуктивное и емкостное сопротивление вообще не изменится.

Рисунок 6.17 Пример параллельной цепи R, L и C с импедансами, заменяющими значения компонентов.

Со всеми значениями компонентов, выраженными как импедансы (Z), мы можем создать таблицу анализа и действовать, как в предыдущем примере задачи, за исключением того, что на этот раз следуя правилам параллельных цепей вместо последовательного.

Зная, что напряжение распределяется поровну между всеми компонентами в параллельной цепи, мы можем передать цифру для общего напряжения во все столбцы компонентов в таблице:

Значения компонентов в таблице 6.11 выражаются как изображение импеданса 2

Теперь мы можем применить закон Ома (I = E / Z) по вертикали в каждом столбце, чтобы определить ток через каждый компонент:

Таблица 6.12. Значения компонентов выражаются в виде изображения импеданса 3

Расчет полного тока и полного импеданса

Есть две стратегии для расчета полного тока и полного импеданса.Во-первых, мы могли вычислить общий импеданс из всех отдельных параллельных сопротивлений (Z _Total = 1 / (1 / Z _R + 1 / Z _L + 1 / Z _C ), а затем вычислить общий ток путем деления напряжения источника на полное сопротивление (I = E / Z).

Тем не менее, работа с уравнением параллельного импеданса с комплексными числами — непростая задача, учитывая все взаимные колебания (1 / Z). Это особенно верно, если вам не повезло, что у вас нет калькулятора, который обрабатывает комплексные числа, и вы вынуждены делать все это вручную (преобразовать отдельные импедансы в полярную форму, затем преобразовать их все в прямоугольную форму для сложения, а затем преобразовать обратно в полярную форму для окончательной инверсии, затем инвертировать).Второй способ рассчитать общий ток и полное сопротивление — сложить все токи ответвления, чтобы получить общий ток (полный ток в параллельной цепи — переменного или постоянного тока — равен сумме токов ответвления), а затем использовать закон Ома. для определения полного сопротивления по общему напряжению и общему току (Z = E / I).

Таблица 6.13 Расчет полного тока и полного импеданса

Любой из методов, выполненный должным образом, даст правильные ответы.

За заметным исключением расчетов мощности (P), все расчеты цепей переменного тока основаны на тех же общих принципах, что и расчеты для цепей постоянного тока.Единственное существенное отличие состоит в том, что в расчетах переменного тока используются комплексные величины, а в расчетах постоянного тока используются скалярные величины. Закон Ома, законы Кирхгофа и даже сетевые теоремы, изученные на постоянном токе, по-прежнему остаются верными для переменного тока, когда напряжение, ток и импеданс выражаются комплексными числами. Те же стратегии поиска и устранения неисправностей, которые применяются в цепях постоянного тока, применимы и для переменного тока, хотя с переменным током, безусловно, может быть труднее работать из-за фазовых углов, которые не регистрируются портативным мультиметром.

Power — это отдельная тема, которая будет рассмотрена в отдельной главе этой книги. Поскольку мощность в реактивной цепи одновременно поглощается и выделяется, а не просто рассеивается, как в случае с резисторами, ее математическая обработка требует более прямого применения тригонометрии для решения.

При анализе цепи переменного тока первым шагом в анализе является преобразование всех значений резисторов, катушек индуктивности и конденсаторов в импедансы (Z) в зависимости от частоты источника питания.После этого выполните те же шаги и стратегии, которые были изучены для анализа цепей постоянного тока, используя новую форму закона Ома: E = IZ; I = E / Z; и Z = E / I

Помните, что только вычисленные значения, выраженные в полярной форме , применимы непосредственно к эмпирическим измерениям напряжения и тока. Прямоугольные обозначения — это просто полезный инструмент для сложения и вычитания сложных величин. Полярная запись, где величина (длина вектора) напрямую связана с величиной измеренного напряжения или тока, а угол напрямую связан с фазовым сдвигом в градусах, является наиболее практичным способом выражения сложных величин для анализа схем.

Установление характеристик тока короткого замыкания для солнечного фотоэлектрического генератора с учетом прохождения низкого напряжения и требования подачи реактивного тока

Основные моменты

•

Установлены различные возможные характеристики тока короткого замыкания для фотоэлектрического генератора.

•

Разрешить споры о возможности использования реле максимального тока для приложений IBDG.

•

Определите подходящий тип средств управления RCI, чтобы удовлетворить требования к характеристикам реле максимального тока.

Аннотация

Исследования тока короткого замыкания часто требуются для определения правильных настроек реле максимального тока. Известно, что обычные синхронные генераторы демонстрируют высокую величину тока во время повреждения, что представляет собой идеальный сценарий для локализации повреждения с использованием экономичных реле максимального тока. С другой стороны, величина тока повреждения от возобновляемой генерации, такой как солнечная фотоэлектрическая (PV), намеренно ограничена из-за ограничений в силовых электронных компонентах.Таким образом, возникает спор относительно возможности использования реле максимального тока в приложениях распределенных генераторов на основе инверторов (IBDG). Эти споры в основном возникают из-за отсутствия твердого понимания характеристик тока короткого замыкания от IBDG. Проблема дополнительно усугубляется наличием множества возможных средств контроля тока повреждения, при которых различные характеристики тока повреждения могут быть получены от IBDG. В свете этой проблемы целью данной статьи является определение различных возможных характеристик тока повреждения IBDG, с особым вниманием к соответствию последним требованиям сетевых кодексов, таким как отключение низкого напряжения (LVRT) с подачей реактивного тока (RCI).Пять различных типов управления RCI анализируются следующим образом: управление переменным активным током, управление постоянной активной мощностью, управление постоянной реактивной мощностью, управление постоянным активным током и управление максимальным током. На основе установленных в этой статье характеристик тока короткого замыкания могут быть разрешены споры, касающиеся возможности использования реле максимального тока для приложений IBDG, и могут быть определены подходящие типы управления RCI, которые обеспечивают удовлетворительную работу реле максимального тока.

Ключевые слова

Распределенная генерация

Характеристика тока короткого замыкания

LVRT

Подача реактивного тока

Реле максимального тока

Защита

Рекомендуемые статьиЦитирующие статьи (0)

Полный текст

© 2018 Elsevier Ltd. Все права защищены.

Рекомендуемые статьи

Ссылки на статьи

Зачем снижать реактивную мощность? Больше мощности — меньше меди

Какие типы реактивной мощности бывают?

Индуктивная реактивная мощность

Двигатели, трансформаторы и устройства управления являются индуктивными нагрузками.При индуктивных нагрузках требуется питание для намагничивающих катушек. Эта мощность называется индуктивной реактивной мощностью. Мы называем векторную сумму активной мощности (P) и индуктивной реактивной мощности (Q1) полной мощностью (S1). В этом примере полная мощность носит индуктивный характер.

Емкостная реактивная мощность

Конденсаторы в электронном оборудовании и длинные кабели представляют собой емкостные нагрузки. При емкостных нагрузках для зарядки этой емкости требуется мощность. Эта мощность называется емкостной реактивной мощностью.Векторная сумма фактической мощности (P) и емкостной реактивной мощности (Q1) называется полной мощностью (S1). В этом примере полная мощность носит емкостной характер.

Степень, в которой энергия используется для индуктивной и емкостной реактивной мощности, обозначается значением cos-phi. В международном масштабе это называется коэффициентом смещения мощности (dPF). Это соотношение между фактической и полной мощностью основной составляющей (составляющей 50 Гц).

Гармоническая реактивная мощность

В современных установках все больше и больше нелинейных нагрузок.Примерами этого являются, например, выпрямители (блоки питания ноутбуков, серверы) и инверторы в современных ИБП и преобразователях частоты. Характерной чертой нелинейной нагрузки является то, что используемый ток больше не является синусоидальным. Мы также называем искажение тока, возникающее в результате этого гармонического искажения.

Дополнительная мощность, возникающая в результате гармонических искажений, — это то, что мы называем гармонической реактивной мощностью (Qh). Эта реактивная мощность не является ни индуктивной, ни емкостной. Вот почему мы наносим реактивную мощность гармоник на третью ось, так называемую ось z.Векторная сумма реальной мощности (P) и слепой мощности гармоник (Qh) снова называется полной мощностью (S).

Сочетание видов реактивной мощности

Практика показывает сочетание разных видов реактивной мощности. В приведенном ниже примере возникает гармоническая реактивная мощность, а преобладает индуктивная реактивная мощность.

Запомните:

Коэффициент смещения мощности (dPF или cos-phi) — это отношение фактической мощности в (кВт) к полной мощности основной составляющей 50 Гц.Если гармоники отсутствуют, общий коэффициент мощности (PF) равен коэффициенту мощности смещения (dPF).

Коэффициент мощности (PF) — это соотношение между фактической и полной мощностью при любых обстоятельствах.

Познакомьтесь со своим измерителем мощности — что такое реальная, полная и реактивная мощность

Первое — простой вопрос

Верно или нет? Мощность = Напряжение x Ток. Это утверждение верно для систем постоянного тока, но для систем переменного тока есть две основные сложности. Значение тока и напряжения постоянно меняется. Какое значение вы используете? Напряжение и ток могут не совпадать по фазе. Умножение тока и напряжения, когда они не совпадают по фазе, требует корректировки для компенсации фазы. Именно этот фазовый сдвиг заставляет нас определять реальную, полную и реактивную мощность. Этот фазовый сдвиг происходит, когда источник питания питает индуктивную или емкостную нагрузку ». Большинство нагрузок являются индуктивными (двигатели) или резистивными (нагреватели), поэтому сдвиг фаз обычно в одном направлении. Двигатель имеет обмотку. Обмотанный проводник по существу определяет индуктор. Таким образом, обмотка представляет собой сопротивление намотанного провода и индуктивность обмотки.

RMS или эффективное значение

Пиковые значения на кривых переменного напряжения или тока сохраняются лишь на короткое время. Они на самом деле не отражают способность напряжения и тока выполнять работу и поэтому не используются в расчетах мощности.Ученые используют статистический метод для определения эффективных значений. Это называется среднеквадратичным или среднеквадратичным значением. Результатом определения является следующее: Veff / rms = 0,707 x V пик. То же самое относится и к току. СОВЕТ: вы можете разумно предположить, что все напряжения и токи, сообщаемые измерителем мощности, представлены как среднеквадратические или эффективные значения, если не указано иное. . СОВЕТ: Большинство мультиметров сообщают среднеквадратичные значения

Полная мощность

Полная мощность — это мощность, передаваемая источником питания такой нагрузке, как двигатель.Практически во всех реальных ситуациях, когда используется переменный ток, вам необходимо подать на устройство больше мощности (кажущейся мощности), чем оно будет работать (реальная мощность). (Векторная) разница между ними представляет работу, проделанную для преодоления индуктивной и Возможности воздействия нагрузки. Полная мощность измеряется в единицах ВА — Вольт-амперы. На самом деле это ватты, но мы используем новое название единицы, чтобы избежать путаницы. Таким образом, когда вы видите VA на листе технических данных, вы можете сделать разумный вывод, что речь идет о полной мощности.Полная мощность рассчитывается: S (общий символ для полной мощности) = Veff / rms x Ieff / rms — однофазный расчет

Коэффициент мощности и фаза

Рассчитан коэффициент мощности: PF = косинус (фазовый угол в радианах) Коэффициент мощности не имеет инженерных единиц. Значение PF находится в диапазоне от -1 до 0 до 1 (запаздывание — без опережения) Нагрузки, которые представляют только Коэффициент мощности резистивной нагрузки (без емкости или индуктивности) равен 1. Индуктивные нагрузки Фаза тока отстает от номинального напряжения — Трансформаторы и двигатели (намотанные проводники) Емкостные нагрузки Токовые выводы Типичное напряжение — Скрытые кабели, конденсаторные батареи Нет ничего «плохого» в том, что коэффициент мощности не равен 1,0.

Реальная мощность и реактивная мощность

Думайте о реальной мощности как о полезной мощности — мере того, как много работы выполняется.Единицы измерения реальной мощности — ватты. Реальная мощность рассчитывается: P (реальная) = S (кажущаяся мощность) x pf Реактивная мощность — это (векторная) разница между полной и реальной мощностью. Энергия, используемая для производства реактивной мощности, сохраняется в магнитном / электрическом поле индуктивной нагрузки. В случае емкостной нагрузки магнитное / электрическое поле индуктивной нагрузки создает реактивную мощность. Реактивную мощность нельзя использовать для полезной работы. Реактивная мощность обозначается символом: Q Технические единицы реактивной мощности — VAR — вольт-амперы реактивной мощности.Это также ватты, но мы используем VAR, чтобы знать, что мы говорим о реактивной мощности.

Диаграмма: измерение RMS

Диаграмма: вперед / назад

THD — Общее гармоническое искажение (также называемое искажением)

Проще говоря, THD — это мера искажения, выраженная в%.Если устройству (любому активному устройству, но представьте себе выпрямители, приводы с регулируемой скоростью… как практические примеры) подается синусоидальная волна на входе, выход никогда не будет точным 100% воспроизведением входа. Серия гармоник исходной волны искажает исходную форму волны. THD% — это попытка «пронумеровать» степень искажения для сравнения. Число% является несколько спорным, поскольку некоторые гармоники являются более важными, чем другие, и нет никакого взвешивания.

THD (%) = 100 * SQRT [(V22 + V32 + V42 +… + Vn2)] / Vt Где V2, V3 — среднеквадратичные значения каждой гармоники напряжения, а Vt — общее среднеквадратичное выходное напряжение.

Провисание / вздутие или провал / скачок

Продолжительность 0,5 цикла и более. Провалы напряжения — это наиболее частые нарушения питания. Провалы напряжения могут исходить от электросети. В большинстве случаев провисания возникают внутри здания. Например, в бытовой электропроводке наиболее частой причиной провалов напряжения является пусковой ток, потребляемый двигателями холодильников и кондиционеров.Прогибы обычно не мешают лампам накаливания или флуоресцентному освещению. двигатели или обогреватели. Однако в некотором электронном оборудовании отсутствует достаточный внутренний накопитель энергии, и поэтому оно не может выдерживать провалы напряжения питания. Оборудование может преодолевать очень короткие глубокие провалы или более длинные, но более мелкие провалы.

Пониженное / повышенное напряжение

Перенапряжение — это увеличение действующего напряжения более чем на 110% в течение более одной минуты.Пониженное напряжение — это снижение эффективного напряжения до менее 90% в течение более одной минуты. Будьте осторожны с этим определением, потому что оно имеет тенденцию меняться от поставщика к поставщику.

Переходные напряжения / скачки / скачки

Относится к краткосрочным (менее 1 цикла) событиям. Низкочастотные переходные процессы часто называют «переходными процессами при переключении конденсаторов». Высокочастотные переходные процессы часто называют импульсами, пиками или скачками.Они могут быть вызваны включением разряженного конденсатора коррекции коэффициента мощности по линии. Высокочастотные переходные процессы вызваны молнией или отключением индуктивных нагрузок. Типичное время нарастания порядка микросекунды; типичные времена затухания составляют от десятков до сотен микросекунд. Часто затухание представляет собой экспоненциально затухающую форму звонка с частотой приблизительно 100 кГц. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт