Что такое действующее значение силы тока. Действующие значения силы тока и напряжения
Силу переменного тока (напряжения) можно охарактеризовать при помощи амплитуды. Однако амплитудное значение тока непросто измерить экспериментально. Силу переменного тока удобно связать с каким-либо действием, производимым током, не зависящим от его направления. Таковым является, например, тепловое действие тока. Поворот стрелки амперметра, измеряющего переменный ток, вызывается удлинением нити, которая нагревается при прохождении по ней тока.
Действующим илиэффективным значением переменного тока (напряжения) называется такое значение постоянного тока, при котором на активном сопротивлении выделяется за период такое же количество теплоты, как и при переменном токе.
Свяжем эффективное значение тока с его амплитудным значением. Для этого рассчитаем количество теплоты, выделяемое на активном сопротивлении переменным током за время, равное периоду колебаний. Напомним, что по закону Джоуля-Ленца количество теплоты, выделяющееся на участке цепи cсопротивлениемпри
. Переменный ток можно считать постоянным
только в течение очень малых промежутков
времени
Переменный ток можно считать постоянным
только в течение очень малых промежутков
времени
. Поделим период колебанийна очень большое число малых промежутков времени
. Количество теплоты
, выделяемое на сопротивленииза время
:
. Общее количество теплоты, выделяемое за период, найдется суммированием теплот, выделяемых за отдельные малые промежутки времени, или, другими словами, интегрированием:
.
Сила тока в цепи изменяется по синусоидальному закону
,
.
Опуская вычисления, связанные с интегрированием, запишем окончательный результат
.
Если бы по цепи шёл некоторый постоянный ток , то за время, равное, выделилось бы тепло
. По определению постоянный ток, оказывающий такое же тепловое действие, что и переменный, будет равен эффективному значению переменного тока
. Находим эффективное значение силы тока, приравнивая теплоты, выделяемые за период, в случаях постоянного и переменного токов
(4. 28)
28)
Очевидно, точно такое же соотношение связывает эффективное и амплитудное значения напряжения в цепи с синусоидальным переменным током:
(4.29)
Например, стандартное напряжение в сети 220 В – это эффективное напряжение. По формуле (4.29) легко посчитать, что амплитудное значение напряжения в этом случае будет равно 311 В.
4.4.5. Мощность в цепи переменного тока
Пусть на некотором участке цепи с переменным током сдвиг фаз между током и напряжением равен , т.е. сила тока и напряжение изменяются по законам:
,
.
Тогда мгновенное значение мощности, выделяемой на участке цепи,
Мощность изменяется со временем. Поэтому можно говорить лишь о ее среднем значении. Определим среднюю мощность, выделяемую в течение достаточно длительного промежутка времени (во много раз превосходящего период колебаний):
С использованием известной тригонометрической формулы
.
Величину
усреднять не нужно, так как она не зависит от времени, следовательно:
.
За длительное время значение косинуса много раз успевает измениться, принимая как отрицательные, так и положительные значения в пределах от (1) до 1. Понятно, что среднее во времени значение косинуса равно нулю
,
поэтому
(4.30)
Выражая амплитуды тока и напряжения через их эффективные значения по формулам (4.28) и (4.29), получим
. (4.31)
Мощность, выделяемая на участке цепи с переменным током, зависит от эффективных значений тока и напряжения и
и
. Если участок цепи содержит только индуктивность или только ёмкость, то
и
.
Объяснить среднее нулевое значение
мощности, выделяемой на индуктивности
и ёмкости можно следующим образом.
Индуктивность и ёмкость лишь заимствуют
энергию у генератора, а затем возвращают
её обратно. Конденсатор заряжается, а
затем разряжается. Сила тока в катушке
увеличивается, затем снова спадает до
нуля и т.
Если участок цепи содержит несколько элементов, то сдвига фаз может быть иным. Например, в случае участка цепи, изображенного на рис. 4.5, сдвиг фаз между током и напряжением определяется по формуле (4.27).
Пример 4.7. К генератору переменного синусоидального тока подключён резистор с сопротивлением. Во сколько раз изменится средняя мощность, расходуемая генератором, если к резистору подключить катушку с индуктивным сопротивлением
а) последовательно, б) параллельно (рис. 4.10)? Активным сопротивлением катушки пренебречь.
Решение. Когда к генератору подключено одно только активное сопротивление, расходуемая мощность
(см. формулу (4.30)).
формулу (4.30)).
Рассмотрим цепь на рис. 4.10, а. В примере 4.6 было определено амплитудное значение силы тока генератора:
. Из векторной диаграммы на рис. 4.11,а определяем сдвиг фаз между током и напряжением генератора
.
В результате средняя расходуемая генератором мощность
.
Ответ: при последовательном включении в цепь индуктивности средняя мощность, расходуемая генератором, уменьшится в 2 раза.
Рассмотрим цепь на рис. 4.10,б. В примере 4.6 было определено амплитудное значение силы тока генератора
. Из векторной диаграммы на рис. 4.11,б определяем сдвиг фаз между током и напряжением генератора
.
Тогда средняя мощность, расходуемая генератором
Ответ: при параллельном включении индуктивности средняя мощность, расходуемая генератором, не изменяется.
Как известно, переменная э.д.с. индукции вызывает в цепи переменный ток. При наибольшем значении э.д.с. сила тока будет иметь максимальное значение и наоборот.
Характеристикой переменного тока могут быть действия, которые не зависят от направления тока и могут быть такими же, как и при постоянном токе. К таким действиям можно отнести тепловое. К примеру, переменный ток протекает через проводник с заданным сопротивлением. Через определенный промежуток времени в этом проводнике выделится какое-то количество тепла. Можно подобрать такое значение силы постоянного тока, чтобы на этом же проводнике за то же время выделялось этим током такое же количество тепла, что и при переменном токе. Такое значение постоянного тока называется действующим значением силы переменного тока.
В данное время в мировой промышленной практике широко распространен трехфазный переменный ток , который имеет множество преимуществ перед однофазным током. Трехфазной называют такую систему, которая имеет три электрические цепи со своими переменными э.д.с. с одинаковыми амплитудами и частотой, но сдвинутые по фазе относительно друг друга на 120° или на 1/3 периода. Каждая такая цепь называется
Трехфазной называют такую систему, которая имеет три электрические цепи со своими переменными э.д.с. с одинаковыми амплитудами и частотой, но сдвинутые по фазе относительно друг друга на 120° или на 1/3 периода. Каждая такая цепь называется
Для получения трехфазной системы нужно взять три одинаковых генератора переменного однофазного тока, соединить их роторы между собой, чтобы они не меняли свое положение при вращении. Статорные обмотки этих генераторов должны быть повернуты относительно друг друга на 120° в сторону вращения ротора. Пример такой системы показан на рис. 3.4.б.
Согласно вышеперечисленным условиям, выясняется, что э.д.с., возникающая во втором генераторе, не будет успевать измениться, по сравнению с э.д.с. первого генератора, т. е. она будет опаздывать на 120°. Э.д.с. третьего генератора также будет опаздывать по отношению ко второму на 120°.
Однако такой способ получения переменного трехфазного тока весьма громоздкий и экономически невыгодный. Чтобы упростить задачу, нужно все статорные обмотки генераторов совместить в одном корпусе. Такой генератор получил название генератор трехфазного тока (рис. 3.4.а). Когда ротор начинает вращаться, в каждой обмотке возникает
Чтобы упростить задачу, нужно все статорные обмотки генераторов совместить в одном корпусе. Такой генератор получил название генератор трехфазного тока (рис. 3.4.а). Когда ротор начинает вращаться, в каждой обмотке возникает
а) б)
Рис. 3.4. Пример трехфазной системы переменного тока
а) генератор трёхфазного тока; б) с тремя генераторами;
изменяющаяся э.д.с. индукции. Из-за того что происходит сдвиг обмоток в пространстве, фазы колебаний в них также сдвигаются относительно друг друга на 120°.
Для того чтобы подсоединить трехфазный генератор переменного тока к цепи, нужно иметь 6 проводов. Для уменьшения количества проводов обмотки генератора и приемников нужно соединить между собой, образовав трехфазную систему. Данных соединений два: звезда и треугольник. При использовании и того и другого способа можно сэкономить электропроводку.
Соединение звездой
Обычно генератор трехфазного тока изображают в виде 3 статорных обмоток, которые располагаются друг к другу под углом 120°. Начала обмоток принято обозначать буквами А, В, С , а концы — X, Y, Z . В случае, когда концы статорных обмоток соединены в одну общую точку (нулевая точка генератора), способ соединения называется «звезда». В этом случае к началам обмоток присоединяются провода, называемые линейными (рис. 3.5 слева).
Начала обмоток принято обозначать буквами А, В, С , а концы — X, Y, Z . В случае, когда концы статорных обмоток соединены в одну общую точку (нулевая точка генератора), способ соединения называется «звезда». В этом случае к началам обмоток присоединяются провода, называемые линейными (рис. 3.5 слева).
Точно так же можно соединять и приемники (рис. 3.5., справа). В этом случае провод, который соединяет нулевую точку генератора и приемников, называется нулевой. Данная система трехфазного тока имеет два разных напряжения: между линейным и нулевым проводами или, что то же самое, между началом и концом любой обмотки статора. Такая величина называется фазным напряжением (Uл ). Поскольку цепь трехфазная, то линейное напряжение будет в v3 раз больше фазного, т. е.: Uл = v3Uф.
Соединение треугольником.
Рисунок 3.6. Пример соединения треугольником
При использовании данного способа соединения конец X первой обмотки генератора подключают к началу В второй его обмотки, конец Y второй обмотки — к началу С третьей обмотки, конец Z третьей обмотки — к началу А первой обмотки. Пример соединения показан на рис. 3.6. При данном способе соединения фазных обмоток и подключении трехфазного генератора к трехпроводной линии линейное напряжение по своему значению сравнивается с фазным: Uф = Uл
Пример соединения показан на рис. 3.6. При данном способе соединения фазных обмоток и подключении трехфазного генератора к трехпроводной линии линейное напряжение по своему значению сравнивается с фазным: Uф = Uл
Контрольные вопросы
1. Перечислите основные параметры, характеризующие переменный ток.
2. Дайте определение частоты и единицы её измерения.
3. Дайте определение амплитуды и единицы её измерения.
4. Дайте определение периода и единицы его измерения.
5. Отличие простейшего генератора трёхфазного тока от генератора однофазного тока.
6. Что такое фаза?
7. Что представляет собой ротор генератора трёхфазного тока?
8. Почему сдвинуты по фазе обмотки статора генератора трёхфазного тока?
9. Особенность симметричной системы трёх фаз.
10. Принцип соединения фазных обмоток трёхфазных генераторов и трансформаторов по схеме «звезда».
11. Принцип соединения фазных обмоток трёхфазных генераторов и трансформаторов по схеме «треугольник».
3.2. Виды сопротивлений в цепях переменного тока
В цепях переменного тока сопротивления разделяют на активные и реактивные.
В активных сопротивлениях , включенных в цепь переменного тока, электрическая энергия преобразуется в тепловую. Активным сопротивлением R обладают, например, провода электрических линий, обмотки электрических машин и т.д.
В реактивных сопротивлениях электрическая энергия, вырабатываемая источником, не расходуется. При включении реактивного сопротивления в цепь переменного тока возникает лишь обмен энергией между ним и источником электрической энергии. Реактивное сопротивление создают индуктивности и ёмкости.
Если не учитывать взаимное влияние отдельных элементов электрической цепи, то в общем случае электрическая цепь синусоидального тока может быть представлена тремя пассивными элементами: активным сопротивлением R, индуктивностью L и емкостью C.
Активное сопротивление в цепи переменного тока .
При включении в цепь переменного тока активного сопротивления, ток и напряжение совпадают по фазе (рис. 3.7) и изменяются по одному и тому же cинусоидальному закону: u=U m sinωt . Они одновременно достигают своих максимальных значений и одновременно проходят через нуль (рис. 3.7.б).
Для цепи переменного тока, содержащей только активное сопротивление, закон Ома имеет такую же форму, как и для цепи постоянного тока: I=U/R.
Электрическая мощность р в цепи с активным сопротивлением в любой момент времени равна произведению мгновенных значений силы тока i и напряжения u : p=ui .
Рисунок 3.7. Схема включения в цепь переменного тока активного сопротивления R (a), кривые тока i , напряжения u и мощности p (б) и векторная диаграмма.
Из графика видно, что изменение мощности происходит с двойной частотой по отношению к изменению тока и напряжения, т.е. один период изменения мощности соответствует половине периода изменения тока и напряжения. Все значения мощности положительные, это означает, что энергия передается от источника к потребителю.
Все значения мощности положительные, это означает, что энергия передается от источника к потребителю.
Средняя мощность Рcp , потребляемая активным сопротивлением, P=UI=I 2 R – это и есть активная мощность.
Под индуктивностью L будем понимать элемент электрической цепи (катушку индуктивности, потерями которой можно пренебречь), способный запасать энергию в своём магнитном поле, который не имеет активного сопротивления и ёмкостиС (рис.3.8).
При включении в цепь переменного тока индуктивности, изменяющийся ток непрерывно индуцирует в ней э.д.с. самоиндукции e L = LΔi/Δt, где Δi/Δt – скорость изменения тока.
Когда угол ωt равен 90° и 270° скорость изменения тока Δi/Δt =0, поэтому э.д.с. e L =0.
Скорость изменения тока будет наибольшей, когда угол ωt равен 0°, 180° и 360°. В эти минуты времени э.д.с. имеет наибольшее значение.
Кривая мощности представляет собой синусоиду, которая изменяется с двойной частотой по сравнению с частотой изменения тока и напряжения. Мощность имеет положительные и отрицательные значения, т.е. возникает непрерывный колебательный процесс обмена энергией между источником и индуктивностью.
Мощность имеет положительные и отрицательные значения, т.е. возникает непрерывный колебательный процесс обмена энергией между источником и индуктивностью.
Рисунок 3.8. Схема включения в цепь переменного тока индуктивности (а), кривые тока i , напряжения u , э.д.с. e L (б) и векторная диаграмма (в)
Э.д.с. самоиндукции согласно правилу Ленца направлена так, чтобы препятствовать изменению тока. В первую четверть периода, когда ток увеличивается, э.д.с. имеет отрицательное значение (направлена против тока).
Во вторую четверть периода, когда ток уменьшается, э.д.с. имеет положительное значение (совпадает по направлению с током).
В третью четверть периода ток меняет своё направление и увеличивается, поэтому э.д.с. направлена против тока и имеет положительное значение.
В четвёртую четверть периода ток уменьшается и э.д.с. самоиндукции стремится поддержать прежнее положение тока и имеет отрицательное значение. В результате ток отстает от напряжения по фазе на угол 90 О.
Сопротивление катушки или проводника переменному току, вызванное действием э.д.с. самоиндукции, называется индуктивным сопротивлением Х L [Ом]. Индуктивное сопротивление не зависит от материала катушки и от площади поперечного сечения проводника.
В цепях переменного тока катушки индуктивности соединяют последовательно и параллельно.
При последовательном соединении катушек эквивалентная индуктивностьLэ и эквивалентное индуктивное сопротивление X L э будут равны:
Lэ=L 1 +L 2 +… X L э=X L 1 +X L 2 +…
При параллельном соединении катушек:
1/Lэ=1/L 1 +1/L 2 +… 1/X L э=1/X L 1 +1/X L 2 +…
Контрольные вопросы
1. Какие виды сопротивления в цепях переменного тока Вы знаете?
2. Что значит активное сопротивление?
3. Что такое реактивное сопротивление?
4. Какие элементы цепи создают реактивное сопротивление?
5. Что такое активная мощность?
1. Дайте определение индуктивности.
2. Что происходит в первую четверть периода колебательного процесса обмена энергией между источником и индуктивностью?
3. Что происходит во вторую четверть периода колебательного процесса обмена энергией между источником и индуктивностью?
4. Дайте определение индуктивного сопротивления.
3.3. Конденсаторы. Ёмкость в цепи переменного тока
Конденсатор – устройство, способное накапливать электрические заряды.
Простейший конденсатор представляет собой две металлические пластины (электроды), разделенные диэлектриком.
Каждый конденсатор характеризуется номинальной емкостью и допустимым напряжением. Напряжение конденсатора указывают на корпусе, и превышать его нельзя. Конденсаторы различаются формой электродов (плоский), типом диэлектрика и ёмкостью (постоянной и переменной).
Cтраница 2
Действующим значением силы тока I называется сила постоянного тока, выделяющего в проводнике за то же время такое же количество теплоты, что и переменный ток.
Как видно из рисунка, в каждый момент времени величины напряжения и силы тока принимают различные значения. Поэтому, чтобы судить о величине силы тока и напряжения переменного тока, пользуются действующим значением силы тока и напряжения. Чтобы определить действующее значение силы переменного тока, его приравнивают к силе постоянного тока, которое выделило бы в проводнике такое же количество тепла, как и переменный ток.
Трансформатор, содержащий в первичной обмотке 300 витков, включен в сеть переменного тока с действующим напряжением 220 В. Вторичная цепь трансформатора питает нагрузку с активным сопротивлением 50 Ом. Найти действующее значение силы тока во вторичной цепи, если падение напряжения во вторичной обмотке трансформатора, содержащей 165 витков, равно 50 В.
Таким образом, при замене операции извлечения корня сравнением время, за которое интегрируемый сигнал с ГЛИН станет равен интегралу от квадрата измеренной силы тока, пропорционально действующему значению силы тока. До этого К2 был открыт в течение времени т и пропускал на счетчик СИ импульсы с генератора тактовых импульсов ГТИ. Число импульсов TV / гтит записанное в СЧ, пропорционально действующему значению силы тока. Это число хранится в / 77, а по окончании цикла измерения отображается на ЦИ.
До этого К2 был открыт в течение времени т и пропускал на счетчик СИ импульсы с генератора тактовых импульсов ГТИ. Число импульсов TV / гтит записанное в СЧ, пропорционально действующему значению силы тока. Это число хранится в / 77, а по окончании цикла измерения отображается на ЦИ.
Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения и средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.
Рх o jjFr В слУчае т — н — СУХОЙ лампы применяют способ термометра, подвешиваемого вблизи генераторной лампы, и отмечают его показание. Затем, разрывая цепь колебательного контура генератора, дают на сетку генераторной лампы положительный потенциал до тех пор, пока термометр не по. Беря в последнем случае величины 1а и Еа как исходные, определяем Рх из соотношения Рх1а Еа. Мощность в антенне определяется по ф-ле Рх — / /, где РЯ — мощность eW, ra — активное сопротивление антенны в Q и 1а — действующее значение силы тока в антенне в А. По скольку по современным международным нормам под мощностью передатчика принято понимать мощность в антенне, то упомянутая выше ф-ла определяет одновременно и мощность передатчика.
Мощность в антенне определяется по ф-ле Рх — / /, где РЯ — мощность eW, ra — активное сопротивление антенны в Q и 1а — действующее значение силы тока в антенне в А. По скольку по современным международным нормам под мощностью передатчика принято понимать мощность в антенне, то упомянутая выше ф-ла определяет одновременно и мощность передатчика.
Тепловые измерители имеют наиболее широкое практич. Действие тепловых измерителей состоит в удлинении тонкой проволоки при нагревании ее проходящим по ней переменным током высокой частоты. Сам по себе эффект ограничивает пределы применимости таких измерителей токами от нескольких тА до 1 — 3 А в зависимости от материала тонкой проволоки, примененной в измерителе. Применяются сплавы серебра с платиной, платины с иридием и др. Если сплав применяется в виде проволоки, то она имеет диаметр сотых долей мм. При ленте толщина составляет 0 01 мм, ширина 3 мм и длина 25 — 30 мм. Удлинение нити нагреваемым током пропорционально квадрату действующего значения силы тока. Перемещение по шкале измерителя стрелки, связанной с той же проволокой с помощью особой подвижной системы, обычно пропорционально квадратному корню из действующей силы тока. Из-за этого шкалы тепловых измерителей имеют неравномерные интервалы между делениями.
Перемещение по шкале измерителя стрелки, связанной с той же проволокой с помощью особой подвижной системы, обычно пропорционально квадратному корню из действующей силы тока. Из-за этого шкалы тепловых измерителей имеют неравномерные интервалы между делениями.
В данном случае колебания тока являются гармоническими (график колебаний — синусоида) и вынужденными, поскольку параметры колебаний (частота, амплитуда) определяются внешним источником — генератором. Некоторые электротехнические устройства (например, колебательный контур) способны генерировать свободные гармонические колебания электрического тока. По левой ветви рамки — от нас и, поскольку в этом случае через клемму а течет ток в направлении, обратном показанному на рис. 12.1, ее полярность — минус. Поскольку при данном положении рамки сила тока имеет наибольшее значение, фаза колебаний может быть г / 2 или 3 / 2ir, в зависимости от того, какое направление тока в рамке мы принимаем за положительное. Сравнивая формулу (12. 1) и заданную зависимость, нетрудно заметить, что 1т 10 А и ш 4тград / с. Далее, используя формулу (12.2), определяем частоту колебаний (отв. Используя закон Джоуля — Ленца (Q I2Rt), определяем действующее значение силы тока (отв.
1) и заданную зависимость, нетрудно заметить, что 1т 10 А и ш 4тград / с. Далее, используя формулу (12.2), определяем частоту колебаний (отв. Используя закон Джоуля — Ленца (Q I2Rt), определяем действующее значение силы тока (отв.
Действующие значения тока и напряжения формулы. Эффективное, действующее напряжение, сила тока
Как известно, переменная э.д.с. индукции вызывает в цепи переменный ток. При наибольшем значении э.д.с. сила тока будет иметь максимальное значение и наоборот. Это явление называется совпадением по фазе. Несмотря на то что значения силы тока могут колебаться от нуля и до определенного максимального значения, имеются приборы, с помощью которых можно замерить силу переменного тока.
Характеристикой переменного тока могут быть действия, которые не зависят от направления тока и могут быть такими же, как и при постоянном токе. К таким действиям можно отнести тепловое. К примеру, переменный ток протекает через проводник с заданным сопротивлением. Через определенный промежуток времени в этом проводнике выделится какое-то количество тепла. Можно подобрать такое значение силы постоянного тока, чтобы на этом же проводнике за то же время выделялось этим током такое же количество тепла, что и при переменном токе. Такое значение постоянного тока называется действующим значением силы переменного тока.
Через определенный промежуток времени в этом проводнике выделится какое-то количество тепла. Можно подобрать такое значение силы постоянного тока, чтобы на этом же проводнике за то же время выделялось этим током такое же количество тепла, что и при переменном токе. Такое значение постоянного тока называется действующим значением силы переменного тока.
В данное время в мировой промышленной практике широко распространен трехфазный переменный ток , который имеет множество преимуществ перед однофазным током. Трехфазной называют такую систему, которая имеет три электрические цепи со своими переменными э.д.с. с одинаковыми амплитудами и частотой, но сдвинутые по фазе относительно друг друга на 120° или на 1/3 периода. Каждая такая цепь называется фазой.
Для получения трехфазной системы нужно взять три одинаковых генератора переменного однофазного тока, соединить их роторы между собой, чтобы они не меняли свое положение при вращении. Статорные обмотки этих генераторов должны быть повернуты относительно друг друга на 120° в сторону вращения ротора. Пример такой системы показан на рис. 3.4.б.
Пример такой системы показан на рис. 3.4.б.
Согласно вышеперечисленным условиям, выясняется, что э.д.с., возникающая во втором генераторе, не будет успевать измениться, по сравнению с э.д.с. первого генератора, т. е. она будет опаздывать на 120°. Э.д.с. третьего генератора также будет опаздывать по отношению ко второму на 120°.
Однако такой способ получения переменного трехфазного тока весьма громоздкий и экономически невыгодный. Чтобы упростить задачу, нужно все статорные обмотки генераторов совместить в одном корпусе. Такой генератор получил название генератор трехфазного тока (рис. 3.4.а). Когда ротор начинает вращаться, в каждой обмотке возникает
а) б)
Рис. 3.4. Пример трехфазной системы переменного тока
а) генератор трёхфазного тока; б) с тремя генераторами;
изменяющаяся э.д.с. индукции. Из-за того что происходит сдвиг обмоток в пространстве, фазы колебаний в них также сдвигаются относительно друг друга на 120°.
Для того чтобы подсоединить трехфазный генератор переменного тока к цепи, нужно иметь 6 проводов. Для уменьшения количества проводов обмотки генератора и приемников нужно соединить между собой, образовав трехфазную систему. Данных соединений два: звезда и треугольник. При использовании и того и другого способа можно сэкономить электропроводку.
Для уменьшения количества проводов обмотки генератора и приемников нужно соединить между собой, образовав трехфазную систему. Данных соединений два: звезда и треугольник. При использовании и того и другого способа можно сэкономить электропроводку.
Соединение звездой
Обычно генератор трехфазного тока изображают в виде 3 статорных обмоток, которые располагаются друг к другу под углом 120°. Начала обмоток принято обозначать буквами А, В, С , а концы — X, Y, Z . В случае, когда концы статорных обмоток соединены в одну общую точку (нулевая точка генератора), способ соединения называется «звезда». В этом случае к началам обмоток присоединяются провода, называемые линейными (рис. 3.5 слева).
Точно так же можно соединять и приемники (рис. 3.5., справа). В этом случае провод, который соединяет нулевую точку генератора и приемников, называется нулевой. Данная система трехфазного тока имеет два разных напряжения: между линейным и нулевым проводами или, что то же самое, между началом и концом любой обмотки статора. Такая величина называется фазным напряжением (Uл ). Поскольку цепь трехфазная, то линейное напряжение будет в v3 раз больше фазного, т. е.: Uл = v3Uф.
Такая величина называется фазным напряжением (Uл ). Поскольку цепь трехфазная, то линейное напряжение будет в v3 раз больше фазного, т. е.: Uл = v3Uф.
Рассмотрим следующую цепь.
Она состоит из источника переменного напряжения, соединительных проводов и некоторой нагрузки. Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением.
Активное сопротивление
Сопротивление R называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону:
U = Um*cos(ω*t).
Мгновенное значение силы тока можем вычислить по закону Ома, оно будет пропорционально мгновенному значению напряжения.
I = u/R = Um*cos(ω*t)/R = Im*cos(ω*t).
Сделаем вывод: в проводнике с активным сопротивлением разность фаз между колебаниями напряжения и силы тока отсутствует. 2) = Um/√2.
2) = Um/√2.
Теперь подставим действующие значения силы тока и напряжения, в выражение Im = Um/R. Получим:
Данное выражение является законом Ома для участка цепи с резистором, по которому течет переменный ток. Как и в случае механических колебаний, в переменном токе нас мало будут интересовать значения силы тока, напряжении в какой-то отдельный момент времени. Гораздо важнее будет знать общие характеристики колебаний — такие, как амплитуда, частота, период, действующие значения силы тока и напряжения.
Кстати, стоит отметить, что вольтметры и амперметры, предназначенные для переменного тока, регистрируют именно действующие значения напряжения и силы тока.
Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока.
,
После подстановки значения тока i и последующих преобразований получим, что действующее значение переменного тока равно:
Аналогичные соотношения могут быть получены также для напряжения и ЭДС:
Большинство электроизмерительных приборов измеряют не мгновенные, а действующие значения токов и напряжений.
Учитывая, например, что действующее значение напряжения в нашей сети составляет 220В, можно определить амплитудное значение напряжения в сети: U m =U Ö2=311В. Соотношение между действующим и амплитудным значениями напряжений и токов важно учитывать, например, при проектировании устройств с применением полупроводниковых элементов.
Действующее значение переменного тока
Теория / ТОЭ / Лекция N 3. Представление синусоидальных величин с помощью векторов и комплексных чисел.
Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.
Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, — периодом Т.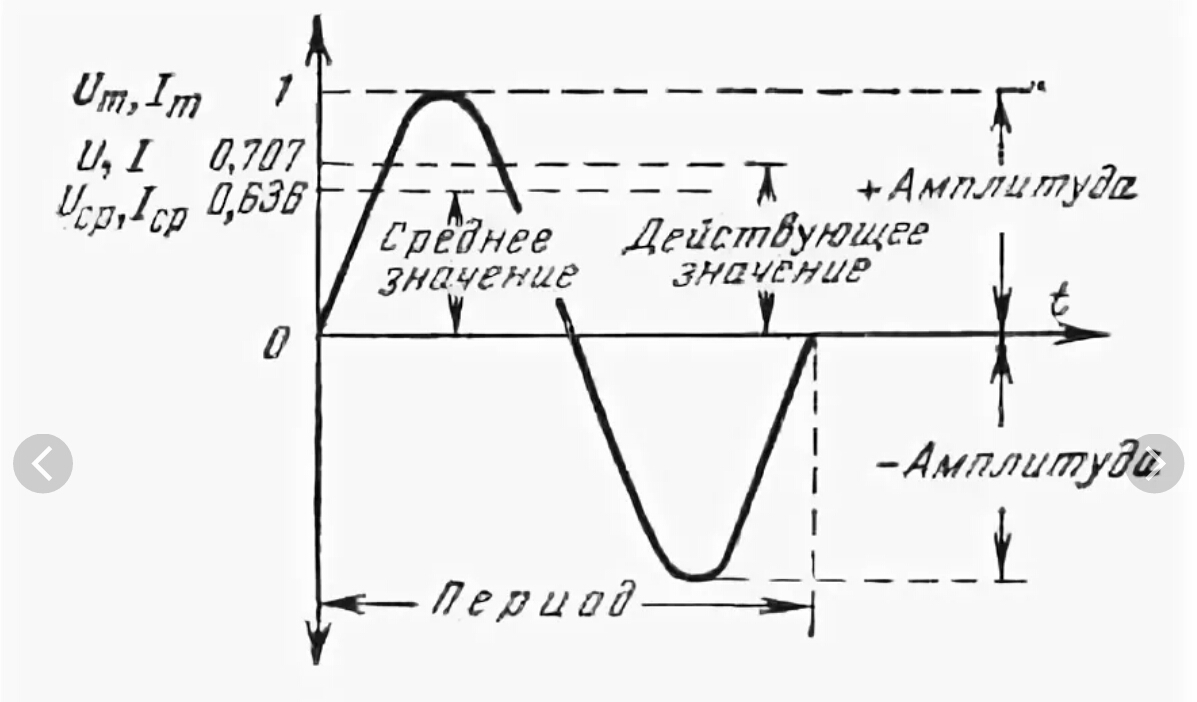 Для периодического тока имеем
Для периодического тока имеем
Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .
Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:
i — мгновенное значение тока ;
u – мгновенное значение напряжения ;
е — мгновенное значение ЭДС ;
р — мгновенное значение мощности .
Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m ).
Амплитуда тока;
Амплитуда напряжения;
Амплитуда ЭДС.
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:
, |
Аналогично определяются действующие значения ЭДС и напряжения.
Синусоидально изменяющийся ток
Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.
Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:
Значения аргументов синусоидальных функций и называются фазами синусоид, а значение фазы в начальный момент времени (t =0): и — начальной фазой ( ).
Величину , характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть , где f– частота.
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз .
Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:
Векторное изображение синусоидально изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное ) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е 1 и е 2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:
Каждый из этих токов синусоидален и может быть представлен уравнением
Результирующий ток также будет синусоидален:
Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt =0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .
Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt =0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
.
Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: .
Действующее и среднее значения переменного тока и напряжения.
Среднее или среднеарифметическое значение Fcp произвольной функции времени f (t )за интервал времени Т определяется по формуле:
Численно среднее значение Fср равно высоте прямоугольника, равновеликого по площади фигуре, ограниченной кривой f (t ), осью t и пределами интегрирования 0 – Т (рис. 35).
35).
Для синусоидальной функции среднее значение за полный период Т (или за целое число полных периодов) равно нулю, так как площади положительной и отрицательной полуволн этой функции равны. Для переменного синусоидального напряжения определяют среднее по модулю значение за полный период Т или среднее значение за половину периода (Т /2) между двумя нулевыми значениями (рис. 36) :
Ucp = Um∙ sinwt dt = 2R . Таким образом, количественные параметры электрической энергии на переменном токе (количество энергии, мощность) определяются действующими значениями напряжения U и тока I . По этой причине в электроэнергетике все теоретические расчеты и экспериментальные измерения принято выполнять для действующих значений токов и напряжений. В радиотехнике и в технике связи, наоборот, оперируют максимальными значениями этих функций.
Приведенные выше формулы для энергии и мощности переменного тока полностью совпадают с аналогичными формулами для постоянного тока. На этом основании можно утверждать, что энергетически постоянному току эквивалентно действующее значение переменного тока.
На этом основании можно утверждать, что энергетически постоянному току эквивалентно действующее значение переменного тока.
Что берется за действующее значение силы переменного тока и переменного напряжения
что берется за действующее значение силы переменного тока и переменного напряжения?
Боевое яйцо
Переменный ток, в широком смысле электрический ток, изменяющийся во времени. Обычно в технике под П. т. понимают периодический ток, в котором среднее значение за период силы тока и напряжения равно нулю.
Переменные токи и переменные напряжения постоянно изменяются по величине. В каждое другое мгновение у них другая величина. Возникает вопрос, как же их измерять? Для их измерения введено понятие действующее значение.
Действующим или эффективным значением переменного тока называют величину такого постоянного тока, который по своему тепловому действию равноценен данному переменному току.
Действующим или эффективным значением переменного напряжения называют величину такого постоянного напряжения, которое по своему тепловому действию равноценно данному переменному напряжению.
Все переменные токи и напряжения в технике измеряются в действующих значениях. Приборы измеряющие переменные величины показывают их действующее значение.
Вопрос: напряжение в электросети 220 В, что это значит?
Это значит, что источник постоянного напряжения с напряжением 220 В оказывает такое же тепловое действие как и электросеть.
Действующее значение тока или напряжения синусоидальной формы в 1,41 раз меньше амплитуды этого тока или напряжения.
Пример: Определить амплитуду напряжения электросети с напряжением 220 В.
Амплитуда равна 220 * 1,41=310,2 В.
Значения действующего напряжения и силы тока. Определение. Соотношение с амплитудой для разной формы. (10+)
Понятие эффективных (действующих) значений напряжения и силы тока
Когда мы говорим о переменных напряжении или силе тока, особенно сложной формы, то встает вопрос о том, как их измерять. Ведь напряжение постоянно меняется. Можно измерять амплитуду сигнала, то есть максимум модуля значения напряжения. Такой метод измерения нормально подходит для сигналов относительно гладкой формы, но наличие коротких всплесков портит картину. Еще одним критерием выбора способа измерения является то, для каких целей делается измерение. Так как в большинстве случаев интерес представляет мощность, которую может отдать тот или иной сигнал, то применяется действующее (эффективное) значение.
Такой метод измерения нормально подходит для сигналов относительно гладкой формы, но наличие коротких всплесков портит картину. Еще одним критерием выбора способа измерения является то, для каких целей делается измерение. Так как в большинстве случаев интерес представляет мощность, которую может отдать тот или иной сигнал, то применяется действующее (эффективное) значение.
Вашему вниманию подборка материалов: Действующее (эффективное) значение для сигналов стандартной формыСинусоидальный сигнал (синус, синусоида) [Действующее значение ] = [Амплитудное значение ] / [Квадратный корень из 2 ] Прямоугольный сигнал (меандр) [Действующее значение ] = [Амплитудное значение ] Треугольный сигнал [Действующее значение ] = [Амплитудное значение ] / [Квадратный корень из 3 ] Закон Ома и мощность для действующих значений напряжения и силы токаЭффективное значение напряжения измеряется в Вольтах, а силы тока в Амперах. Для эффективных значений верен закон Ома: = / [Сопротивление нагрузки, Ом ] [Рассеиваемая на омической нагрузке мощность, Вт ] = [Действующее значение силы тока, А ] * [Действующее значение напряжения, В ] К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости , чтобы быть в курсе. Если что-то непонятно, обязательно спросите! Еще статьи Микроконтроллеры — пример простейшей схемы, образец применения. Фузы (… Практика проектирования электронных схем. Самоучитель электроники…. Силовой мощный импульсный трансформатор, дроссель. Намотка. Изготовить… Силовой резонансный фильтр для получения синусоиды от инвертора… Бесперебойник своими руками. ИБП, UPS сделать самому. Синус, синусоида… Преобразователь однофазного напряжения в трехфазное. Принцип действия,… Электрическое напряжение. Амплитуда сигнала. Амплитудное. Вольт. Volt…. |
>> Активное сопротивление. Действующие значения силы тока и напряжения
§ 32 АКТИВНОЕ СОПРОТИВЛЕНИЕ. ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ СИЛЫ ТОКА И НАПРЯЖЕНИЯ
Перейдем к более детальному рассмотрению процессов, которые происходят в цепи, подключенной к источнику переменного напряжения.
Сила тока в цени с резистором. Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (рис. 4.10). Эту величину, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением.
В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряже ния (рис. 4.11), а амплитуда силы тока определяется равенством
Мощность в цепи с резистором. В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение изменяются сравнительно быстро. Поэтому при прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет быстро меняться со временем. Но этих быстрых изменений мы не замечаем.
Как правило, нам нужно бывает знать среднюю мощ ностъ тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого достаточно найчи среднюю мощность за один период. Под средней за период, мощностью переменного тока понимают отношение суммарной энергии , поступающей в цепь за период, к периоду.
Под средней за период, мощностью переменного тока понимают отношение суммарной энергии , поступающей в цепь за период, к периоду.
Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой
P = I 2 R. (4.18)
На протяжении очень малого интервала времени переменный ток можно считать практически постоянным.
Поэтому мгновенная моoность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой
P = i 2 R. (4.19)
Найдем среднее значение мощности за период. Для этого сначала преобразуем формулу (4.19), подставляя в нее выражение (4.16) для силы тока и используя известное из математики соотношение
График зависимости мгновенной мощности от времени изображен на рисунке 4.12, а. Согласно графику (рис. 4.12, б.), на протяжении одной восьмой периода, когда , мощность в любой момент времени больше, чем . Зато на протяжении следующей восьмой части периода, когда cos 2t
Средняя мощность равна, таким образом, первому члену в формуле (4. 20):
20):
Действующие значения силы тока и напряжения . Из формулы (4.21) видно, что величина есть среднее за период значение квадрата силы тока:
Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы неременного тока. Действующее зртачепие силы неременного тока обозначается через I:
Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты , что и при переменном токе за то же время.
Действующее значение переменного напряжения определяется аналогично действующему значению силы тока:
Заменяя в формуле (4.17) амплитудные значения силы тока и напряжения на их действующие значения, получаем
Это закон Ома для участка цепи переменного тока с резистором.
Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.
Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.
Кроме того, действующие значения удобнее мгновенных значений еще и потому, что именно они непосредственно определяют среднее значение мощности Р переменного тока:
P = I 2 R = UI.
Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.
1. Чему равна амплитуда напряжения в осветительных сетях переменного тока, рассчитанных на напряжение 220 В!
2. Что называют действующими значениями силы тока и напряжения!
Мякишев Г. Я., Физика. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 17-е изд. , перераб. и доп. — М. : Просвещение, 2008. — 399 с: ил.
, перераб. и доп. — М. : Просвещение, 2008. — 399 с: ил.
Библиотека с учебниками и книгами на скачку бесплатно онлайн , Физика и астрономия для 11 класса скачать , школьная программа по физике, планы конспектов уроков
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные урокиВконтакте
Одноклассники
Google+
ТОЭ Лекции — №13 Действующее значение переменного тока
Понятие действующего значения тока вводится в связи с необходимостью производства
измерений. Что измерять у переменного тока? Если бы мы имели дело только с синусоидами – кривыми одной
формы, то можно было бы измерять амплитуды. Но на практике встречаются самые разные кривые, и может
оказаться так, что два различных по форме тока имеют одинаковые амплитуды, хотя очевидно, что на
электрическую цепь они будут оказывать разное воздействие.
Что измерять у переменного тока? Если бы мы имели дело только с синусоидами – кривыми одной
формы, то можно было бы измерять амплитуды. Но на практике встречаются самые разные кривые, и может
оказаться так, что два различных по форме тока имеют одинаковые амплитуды, хотя очевидно, что на
электрическую цепь они будут оказывать разное воздействие.
Поэтому наиболее целесообразно оценивать величину тока по той работе, которую он совершает. При такой оценке действие переменного тока сравнивается с аналогичным действием постоянного тока. Например, если некоторый переменный ток выделяет на участке цепи такое же количество тепла, что и постоянный ток силой 10 ампер, то говорят, что величина этого переменного тока составляет 10 ампер. Это значение тока и называют действующим.
Итак, действующим значением переменного тока называется численное значение такого
постоянного тока, который за время, равное одному периоду, выделяет в сопротивлении такое же количество
тепла, что и ток переменный. .
.
Таким образом, для оценки величины переменного тока мы должны сделать следующее.
1.Определить количество теплоты, выделяющейся в сопротивлении R за время Т при протекании переменного тока i. Это количество теплоты равно:
2.Подобрать такой постоянный ток I, который за то же время Т в том же сопротивлении R выделяет такое же количество тепла. При постоянном токе оно равно: W=I2RT.
3. Приравнять W=W:
откуда
Последняя формула и определяет действующее значение переменного тока.
Пример 2.1. На вход некоторой цепи подается импульсное напряжение треугольной формы (рис. 13.1, а). Чему равно его действующее значение?
Решение
Пример 2.2. На рис. 13.1, б показана
кривая напряжения на выходе схемы однофазного однополупериодного выпрямления. Чему равно действующее
значение напряжения, если его амплитудное значение Um составляет 311 В?
Чему равно действующее
значение напряжения, если его амплитудное значение Um составляет 311 В?
Решение
Пример 2.3. Определить действующее значение синусоидального тока i=Imsin(ωt):
Решение
Рассмотренные примеры показывают, что действующее значение переменного тока зависит от его формы.
Действующие значения э. д. с., напряжения и силы переменного тока
При синусоидальном переменном токе средние значения напряжения и тока за период равны нулю и не могут служить его характеристиками. Однако среднее значение квадрата силы тока за период отлично от нуля. Следовательно, при включении в цепь переменного тока измерительного прибора, отклонение стрелки которого пропорционально квадрату силы тока, стрелка отклонится и установится на определенном делении шкалы. Каков смысл этого показания?
Вспомним, что количество выделенного в проводнике тепла изменяется пропорционально квадрату силы тока. Представим себе, что в цепь переменного тока включен тепловой амперметр, действие которого основано на выделении тепла электрическим током. Поскольку шкала такого амперметра градуируется на амперы для постоянного тока, можно заключить, что переменный ток по своему тепловому эффекту эквивалентен постоянному току, силу которого указывает на шкале прибора стрелка. Это позволяет ввести понятие эффективного значения силы переменного тока. Эффективным (или действующим) значением силы переменного тока называют силу такого постоянного тока I, который за один период переменного тока выделяет столько же тепла, сколько последний за то же время.
Представим себе, что в цепь переменного тока включен тепловой амперметр, действие которого основано на выделении тепла электрическим током. Поскольку шкала такого амперметра градуируется на амперы для постоянного тока, можно заключить, что переменный ток по своему тепловому эффекту эквивалентен постоянному току, силу которого указывает на шкале прибора стрелка. Это позволяет ввести понятие эффективного значения силы переменного тока. Эффективным (или действующим) значением силы переменного тока называют силу такого постоянного тока I, который за один период переменного тока выделяет столько же тепла, сколько последний за то же время.
Все амперметры, предназначенные для переменного тока, показывают эффективное значение силы тока. В курсе электротехники доказывается, что оно в √2 раз меньше амплитудного значения силы тока Iм, т. е.
Iм = Iм/√2 ≈ 0,707Iм. (26.5)
Так как деления на шкале вольтметра соответствуют произведению Iвrв, где при переменном токе Iв — эффективное значение тока, протекающего через вольтметр, а rв — сопротивление вольтметра, то U=Iвrв называют эффективным напряжением переменного тока, которое в √2 раз меньше Uм, т. е.
е.
U = Uм/√2 ≈ 0,7O7UM. (26.6)
Аналогично эффективное значение э. д. с. переменного тока Ɛ в √2 раз меньше его амплитудного значения Ɛм:
Ɛ = Ɛм/√2 ≈ 0,707Ɛм. (26.7)
Все вольтметры, предназначенные для переменного тока, показывают эффективные значения э. д. с. и напряжения.
действующее значение — Перевод на немецкий — примеры русский
На основании Вашего запроса эти примеры могут содержать грубую лексику.
На основании Вашего запроса эти примеры могут содержать разговорную лексику.
Предложить пример
Другие результаты
Тебя обвинят во вмешательстве в действующее расследование.
Du wirst dafür angeklagt werden, eine laufende Ermittlung zu stören. Сержант, это действующее федеральное расследование. .. это секретная информация.
.. это секретная информация.
А так же действующее завещание и доверенность.
Антон Хавелка открыл в 1876 году действующее и поныне кафе «Под пальмой».
Anton Hawelka eröffnete 1876 das heute noch bestehende Café Pod Palmą („Unter der Palme»).
После указанного периода все случаи незаконного ношения и хранения оружия подпадают под действующее законодательство Украины.
Nach dieser Frist fallen alle Fälle von illegalem Transport und Lagerung von Waffen wieder unter die Gesetze der Ukraine.
Понятие права включает в себя только положительное, действующее право.
Действующее наименование «Nottaway» было принято в начале двадцатого столетия.
Die heutige Schreibung Nottaway wurde zu Beginn des 20. Jahrhunderts festgelegt.Сила тяжести — это тоже силовое поле, действующее на тела, имеющие массу.
Die Schwerkraft ist auch ein Kraftfeld, das Einfluss auf Masse hat.Ни Европейская Комиссия, ни любое лицо, действующее от имени Комиссии, не несет ответственность за использованиенижеследующей информации.
Weder die Europäische Kommission noch Personen, die im Namen dieser Kommission handeln, sind für die etwaige Verwendungder nachstehenden Informationen verantwortlich.
Моя фабрика — самое старое действующее производство в Вуберне.
Meine Fabrik ist das älteste überlebende Unternehmen in Woburn.
Он просит ввести новое действующее лицо в пьесу — полицейского.
Er möchte, dass ein Polizist vorkommt.
Это действующее место преступления, сэр.
Я не собираюсь снова превращаться в действующее лицо в «Амнезии Корди».
Скажи им, что это действующее место преступления, пресс-конференция будет позже.
Sagen Sie ihnen, dass dies ein aktiver Tatort ist und es später eine Pressekonferenz geben wird. Katrin Schinköth-Haase (действующее лицо и певица) и Maria-Clara Thiele (действующее лицо и пианистка (Флюгель)) Валерия Моретти: Клара Шуман.
Действующее агентство было создано в качестве замены EBN при президенте Фернанду Колор ди Мелу и управляется компанией «Empresa Brasil de Comunicação» (EBC).
Die heutige Agentur wurde als EBN-Ersatz unter Präsident Fernando Collor de Mello geschaffen und untersteht der Verwaltung durch die Empresa Brasil de Comunicação (EBC).
Одно из этих умений, доступное с самого начала игры и действующее на протяжении всей игры, называется Пассивным.
Eine dieser Fähigkeiten ist bereits von Beginn an verfügbar und wirkt während des gesamten Spielgeschehens, genannt Passive.
ССНС был известен как «стратегически планирующее и тактически действующее ядро внепарламентской оппозиции» против «чрезвычайного законодательства».
Ab 1965 galt der SDS als strategisch planende und taktisch operierende Kerntruppe der Außerparlamentarischen Opposition (APO) gegen die Notstandsgesetze.Управление. Действующее правительство — вот что вывело Калифорнию из кошмара 1850 года.
funktionierende Regierung zu haben — das führte Kalifornien aus der Misere von 1850.Дьявол также довольно часто фигурирует как действующее лицо «Симпсонов».
Family Guy wird oft eine allzu auffällige Ähnlichkeit zu den Simpsons vorgeworfen.
| Метки: |
Что называют действующими значениями силы тока и напряжения.
 Эффективное, действующее напряжение, сила тока
Эффективное, действующее напряжение, сила тока
Переменный синусоидальный ток в течение периода имеет разные секундные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?
При расчетах цепей переменного тока, также при электронных измерениях неловко воспользоваться моментальными либо амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Не считая того, об электронном эффекте временами изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.
Более комфортным оказалось введение понятий так именуемых действующих значений тока и напряжения . В базу этих понятий положено термическое (либо механическое) действие тока, не зависящее от его направления.
— это значение неизменного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.
Для оценки деяния, производимого переменным током, мы сравним его деяния с термическим эффектом неизменного тока.
Мощность Р неизменного тока I , проходящего через сопротивление r , будет Р = Р 2 r .
Мощность переменного тока выразится как средний эффект моментальной мощности I 2 r за целый период либо среднее значение от (Im х sinωt ) 2 х r за то же время.
Пусть среднее значение t2 за период будет М. Приравнивая мощность неизменного тока и мощность при переменном токе, имеем: I 2 r = Mr, откуда I = √ M ,
Величина I именуется действующим значением переменного тока.
Среднее значение i2 при переменном токе определим последующим образом.
Построим синусоидальную кривую конфигурации тока. Возведя в квадрат каждое секундное значение тока, получим кривую зависимости Р от времени.
Обе половины этой кривой лежат выше горизонтальной оси, потому что отрицательные значения тока (-i ) во 2-ой половине периода, будучи построены в квадрат, дают положительные величины.
Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное с помощью высшей арифметики, будет равно 1/2I 2 m
. Как следует, М =
1/2I 2 m
Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное с помощью высшей арифметики, будет равно 1/2I 2 m
. Как следует, М =
1/2I 2 m
Потому что действующее значение I переменного тока равно I = √ M , то совсем I = Im / √ 2
Аналогично зависимость меж действующим и амплитудным значениями для напряжения U и Е имеет вид:
U = Um / √ 2 , E= Em / √ 2
Действующие значения переменных величин обозначаются строчными знаками без индексов (I , U, Е).
На основании произнесенного выше можно сказать, что действующее значение переменного тока равно такому неизменному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.
Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, демонстрируют действующие значения тока либо напряжения.
При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. {2}dt}}.}
{2}dt}}.}
Для синусоидального тока:
I = 1 2 ⋅ I m ≈ 0,707 ⋅ I m , {\displaystyle I={\frac {1}{\sqrt {2}}}\cdot I_{m}\approx 0{,}707\cdot I_{m},}
I m {\displaystyle I_{m}} — амплитудное значение тока.
Для тока треугольной и пилообразной формы:
I = 1 3 ⋅ I m ≈ 0,577 ⋅ I m . {\displaystyle I={\frac {1}{\sqrt {3}}}\cdot I_{m}\approx 0{,}577\cdot I_{m}.}
Аналогичным образом определяются действующие значения ЭДС и напряжения.
Дополнительные сведения
В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value — эффективное значение. Также применяется аббревиатура RMS (rms) — root mean square — среднеквадратичное (значение).
В электротехнике приборы электромагнитной, электродинамической и тепловой систем калибруются на действующее значение.
Источники
- «Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
- Курс физики.
 А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5 - «Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 — § 7.10
Ссылки
- Действующие значения тока и напряжения
- Среднеквадратичное значение
Мгновенные, максимальные, действующие и средние значения электрических величин переменного тока
Мгновенное и максимальное значения. Величину переменной электродвижущей силы, силы тока, напряжения и мощности в любой момент времени называют мгновенными значениями этих величин и обозначают соответственно строчными буквами (e, i, u, p ).
Максимальным значением (амплитудой) переменной э. д. с. (или напряжения или тока) называется та наибольшая величина, которой она достигает за один период. Максимальное значение электродвижущей силы обозначается Е m , напряжения — U m , тока — I m .
Действующим (или эффективным) значением переменного тока называется такая сила постоянного тока, которая, протекая через равное сопротивление и за одно и то же время, что и переменный ток, выделяет одинаковое количество тепла.
Для синусоидального переменного тока действующее значение меньше максимального в 1,41 раз, т. е. в раз.
Аналогично действующие значения переменной электродвижущей силы и напряжения меньше их максимальных значений тоже в 1,41 раза.
По величине измеренных действующих значений силы переменного тока, напряжения или электродвижущей силы можно вычислить их максимальные значения:
E m = E · 1,41; U m = U · 1,41; I m = I · 1,41;
Среднее значение = отношению количества эл энергии прошедшего через сечение проводника за половину периода к величине этого полупериода.
Под средним значением понимают среднеарифметическое ее значение за половину периода.
/ Среднее и действующие значения синусоидальных токов и напряжений
Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода. Среднее значение тока
т. е. среднее значение синусоидального тока составляет от амплитудного. Аналогично,
Аналогично,
Широко применяют понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным). Действующее значение тока
Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Аналогично,
Можно сопоставить тепловое действие синусоидального тока с тепловым действием постоянного тока, текущего то же время по тому же сопротивлению.
Количество теплоты, выделенное за один период синусоидальным током,
Выделенная за то же время постоянным током теплота равна Приравняем их:
Таким образом, действующее значение синусоидального тока численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.
Для установления эквивалентности переменного тока в отношении энергии и мощности, общности методов расчета, а также сокращения вычислительной работы изменяющиеся непрерывно во времени токи. ЭДС и напряжения заменяют эквивалентными неизменными во времени величинами. Действующим или эквивалентным значением называется такой неизменный во времени ток, при котором выделяется в резистивном элементе с активным сопротивлением r за период то же количество энергии, что и при действительном изменяющемся синусоидально токе.
ЭДС и напряжения заменяют эквивалентными неизменными во времени величинами. Действующим или эквивалентным значением называется такой неизменный во времени ток, при котором выделяется в резистивном элементе с активным сопротивлением r за период то же количество энергии, что и при действительном изменяющемся синусоидально токе.
Энергия за период, выделяющаяся в резистивном элементе при синусоидальном токе,
i 2r dt = | I m 2 sin2 ωt r dt. . | |||
При неизменном во времени токе энергия
W = I 2rT
Приравняв правые части
I m
0,707I m .
Таким образом, действующее значение тока меньше амплитудного в √2 раз.
Аналогично определяют действующие значения ЭДС и напряжения:
Е = E m / √2, U = U m / √2.
Действующему значению тока пропорциональна сила, действующая на ротор двигателя переменного тока, подвижную часть измерительного прибора и т. д. Когда говорят о значениях напряжения, ЭДС и тока в цепях переменного тока, имеют в виду их действующие значения. Шкалы измерительных приборов переменного тока отградуированы соответственно в действующих значениях тока и напряжения. Например, если прибор показывает 10 А, то это значит, что амплитуда тока
I m = √2I = 1,41 10 = 14,1 A,
и мгновенное значение тока
i = I m sin (ωt + ψ) = 14,1 sin (ωt + ψ).
При анализе и расчет выпрямительных устройств пользуются средними значениями тока, ЭДС и напряжения, под которыми понимают среднее арифметическое значение соответствующей величины за полпериода (среднее значение за период, как известно, равно нулю):
T 2 | ||||||||||
Е ср = | Е т sin ωt dt = | sin ωt d ωt = | |cos ωt | π 0 = | 0,637Е т . | ||||||
Аналогично можно найти средние значения тока и напряжения:
I ср = 2I т /π; U ср = 2U т /π.
Отношение действующего значения к среднему значению какой-либо периодически изменяющейся величины называется коэффициентом формы кривой. Для синусоидального тока
Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь? При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления. Действующее значение переменного тока — это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе. Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока. Мощность Р постоянного тока I, проходящего через сопротивление r, будет Р = Р2r. Мощность переменного тока выразится как средний эффект мгновенной мощности I2r за целый период или среднее значение от (Im х sinωt)2 х rза то же время. Пусть среднее значение t2 за период будет М. Величина I называется действующим значением переменного тока. Среднее значение i2 при переменном токе определим следующим образом. Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени. Действующее значение переменного тока Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i) во второй половине периода, будучи возведены в квадрат, дают положительные величины. Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно1/2I2m. Следовательно, М = 1/2I2m Так как действующее значение I переменного тока равно I = √M, то окончательно I = Im / √2 Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид: U = Um / √2,E= Em / √2 Действующие значения переменных величин обозначаются прописными буквами без индексов (I, U, Е). На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии. Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения. При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √2 раз. От этого расположение векторов на диаграмме не изменяется. |
Список параметров напряжения и силы электрического тока
В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока
Значения переменного напряжения (тока)
Мгновенное значение
Мгновенное значение — это значение сигнала в определённый момент времени, функцией которого является (u (t) , i (t) {\displaystyle u(t)~,\quad i(t)}).{2}(t)dt}}}
Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I {\displaystyle I} и U {\displaystyle U} совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.
Когда не оговаривают особо, то обычно имеют ввиду именно среднеквадратичные значения величины напряжения или силы тока.
В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.
Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом.
Среднее значение
Среднее значение (смещение) — постоянная составляющая напряжения или силы тока
U = 1 T ∫ 0 T u (t) d t , I = 1 T ∫ 0 T i (t) d t {\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}u(t)dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}i(t)dt}
В электротехнике используется редко, но сравнительно часто используется в радиотехнике (ток смещения и напряжение смещения).{T}\mid i(t)\mid dt}
На практике используется редко, однако большинство измерительных приборов переменного тока — магнитоэлектрической системы (т. е., в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку. В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.
Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.
Коэффициенты пересчёта значений
- Коэффициент формы кривой переменного напряжения (тока) — величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению. Для синусоидального напряжения (тока) равен π / 2 2 ≈ 1.11 {\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11} .
- Коэффициент амплитуды кривой переменного напряжения (тока) — величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) равен 2 {\displaystyle {\sqrt {2}}} .
Параметры постоянного тока
- Размах пульсации напряжения (тока) — величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени
- Коэффициент пульсации напряжения (тока) — величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
- Коэффициент пульсации напряжения (тока) по действующему значению — величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
- Коэффициент пульсации напряжения (тока) пo среднему значению — величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)
Литература и документация
Литература
- Справочник по радиоэлектронным устройствам : В 2-х т.; Под ред. Д. П. Линде — М.: Энергия, 1978
- Шульц Ю. Электроизмерительная техника: 1000 понятий для практиков: Справочник: Пер. с нем. М.:Энергоатомиздат, 1989
Нормативно-техническая документация
- ГОСТ 16465-70 Сигналы радиотехнические измерительные. Термины и определения
- ГОСТ 23875-88 Качество электрической энергии. Термины и определения
- ГОСТ 13109-97 Электрическая энергия. Совместимость технических средств. Нормы качества электрической энергии в системах электроснабжения общего назначения
Ссылки
- Электрические цепи постоянного тока
- Переменный ток. Изображение синусоидальных переменных
- Амплитудное, среднее, эффективное
- Периодические несинусоидальные ЭДС, токи и напряжения в электрических цепях
- Системы тока и номинальные напряжения электроустановок
- Электричество
- Проблемы высших гармоник в современных системах электропитания
Какой физический смысл имеет действующее значение напряжения и тока
Александр титов
Действующее значение силы ПЕРЕМЕННОГО тока — это такое значение величины ПОСТОЯННОГО тока, действие которого произведёт ту же самую работу (или тепловой эффект) , что и действие переменного тока за время одного периода его действия.2 = Im/2, откуда I = Im / корень из 2. Это и есть действующее значение тока.
То же самое с действующим значением напряжения и ЭДС.
Vitas latish
можно грубо сказать
— напряжение — потенциальная энергия…. расческа- волосы…. напряжение = свечение, искорки, подъем волос… .
— ток это работа, действие, сила.. . тепло, горение, движение выплеск кенетической энергии
Определение 1
Эффективным (действующим) называют значение переменного тока равное величине эквивалентного постоянного тока, который при прохождении через такое же сопротивление, что и переменный ток выделяет на нем то же количество тепла за одинаковые промежутки времени.
Количественная связь амплитуд силы и напряжения переменного тока и эффективных значений
Количество тепла, которое выделяется переменным током на сопротивлении $R$ за малый промежуток времени $dt$, равно:
Тогда за один период переменный ток выделяет тепла ($W$):
Обозначим через $I_{ef}$ силу постоянного тока, который на сопротивлении $R$ выделяет такое же количество тепла ($W$), как и переменный ток $I$ за время равное периоду колебаний переменного тока ($T$). Тогда выразим $W$ через постоянный ток и приравняем выражение к правой части уравнения (2), имеем:
Выразим из уравнения (3) силу эквивалентного постоянного тока, получим:
Если сила тока изменяется по синусоидальному закону:
подставим выражение (5) для переменного тока в формулу (4), тогда величина постоянного тока выразится как:
Следовательно, выражение (6) может быть преобразовано к виду:
где $I_{ef}$ называют эффективным значением силы тока. Аналогично записывают выражения для эффективных (действующих) значений напряжений:
Применение действующих значений тока и напряжения
Когда в электротехнике говорят о силе переменного тока и напряжении, то имеют в виду их эффективные значения. В частности, вольтметры и амперметры градуируют обычно на эффективные значения. Следовательно, максимальное значение напряжения в цепи переменного тока примерно в 1,5 раза больше того, что показывает вольтметр. Этот факт следует учесть при расчете изоляторов, исследовании проблем безопасности.
Эффективные значения используют для характеристики формы сигнала переменного тока (напряжения). Так, вводят коэффициент амплитуды ($k_a$). равный:
и коэффициент формы ($k_f$):
где $I_{sr\ v}=\frac{2}{\pi }\cdot I_m$ —средневыпрямленное значение силы тока.
Для синусоидального тока $k_a=\sqrt{2},\ k_f=\frac{\pi }{2\sqrt{2}}=1,11.$
Пример 1
Задание: Напряжение, которое показал вольтметр равно $U=220 В$. Какова амплитуда напряжения?
Решение:
Как было сказано, вольтметры и амперметры обычно градуируют на действующие значения напряжения (силу тока), следовательно, прибор показывает в наших обозначениях $U_{ef}=220\ В.$ В соответствии с известным соотношением:
найдем амплитудное значение напряжения, как:
Вычислим:
Ответ: $U_m\approx 310,2\ В.$
Пример 2
Задание: Как связана мощность переменного тока на сопротивлении $R$ и эффективные значения тока и напряжения?
Решение:
Среднее значение мощности переменного тока в цепи равно
\[\left\langle P\right\rangle =\frac{A_T}{T}=\frac{U_mI_mcos\varphi }{2}\left(2.2}_mR=\frac{U_mI_mcos \varphi}{2}\left(2.3\right),\]
где $I_m\ $- амплитуда силы тока, $U_m$ — амплитуда внешнего напряжения, $\varphi$ — разность фаз между силой тока и напряжением.
У постоянного тока мгновенная мощность совпадает со средней. Для $I_{ef}$=const можно положить $cos\varphi =1,\ $значит формулу (2.3) можно записать как:
если вместо амплитудных значений ($U_m\ и\ I_m$) использовать их эффективные (действующие) значения:
Следовательно, мощность тока можно записать как:
где $cos \varphi$ — коэффициент мощности. В технике этот коэффициент делают как можно большим. При малом $cos\varphi $ для того, чтобы в цепи выделялась необходимая мощность нужно пропускать большой ток, что ведет к росту потерь в подводящих проводах.
Такую же мощность (как в выражении (2.3)) развивает постоянный ток, сила которого представлена в формуле (2.5).
Ответ: $P_{tR}=U_{ef}I_{ef}cos\varphi .$
При расчете цепей переменного тока обычно пользуются понятием действующих (эффективных) значений переменного тока, напряжения и э. д. с.
Действующие значения тока, напряжения и э. д. с. обозначаются прописными буквами .
На шкалах измерительных приборов и технической документации также указываются действующие значения величин.
Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.
Количество тепла, выделенное переменным током в со противлении за бесконечно малый промежуток времени
а за период переменного тока Т
Приравняв Полученное выражение количеству тепла выделенному в том же сопротивлении постоянным током за то же время Т, получим:
Сократив общий множитель , получим действующее значение тока
Рис. 5-8. График переменного тока и квадрата тока.
На рис. 5-8 построена кривая мгновенных значений тока i и кривая квадратов мгновенных значений Площадь, ограниченная последней кривой и осью абсцисс, представляет собой в некотором масштабе величину, определяемую выражением Высота прямоугольника равновеликого площади, ограниченной кривой и осью абсцисс, равная среднему значению ординат кривой представляет собой квадрат действующего значения тока
Если ток изменяется по закону синуса, т. е.
Аналогично для действующих значений синусоидальных напряжений и э. д. с. можно написать:
Кроме действующего значения тока и напряжения, иногда пользуются еще понятием среднего значения тбка и напряжения.
Среднее значение синусоидального тока за период равно нулю, так как в течение первой половины периода определенное количество электричества Q проходит через поперечное сечение проводника в прямом направлении. В течение второй половины периода то же количество электричества проходит через сечение проводника в обратном направлении. Следовательно, количество электричества, прошедшее через сечение проводника за период, равно нулю, равно нулю и среднее за период значение синусоидального тока.
Поэтому среднее значение синусоидального тока вычисляют за полупериод, в течение которого ток остается положительным. Среднее значение тока равно отношению количества электричества, прошедшего через сечение проводника за половину периода, к продолжительности этого полупериода.
В механической системе вынужденные колебания возникают при действии на нее внешней периодической силы. Аналогично этому вынужденные электромагнитные колебания в электрической цепи происходят под действием внешней периодически изменяющейся ЭДС или внешнего изменяющегося напряжения.
Вынужденные электромагнитные колебания в электрической цепи представляют собой переменный электрический ток .
- Переменный электрический ток — это ток, сила и направление которого периодически меняются.
Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω по синусоидальному или косинусоидальному закону:
\(~u = U_m \cdot \sin \omega t\) или \(~u = U_m \cdot \cos \omega t\) ,
где u – мгновенное значение напряжения, U m – амплитуда напряжения, ω – циклическая частота колебаний. Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае
\(~i = I_m \cdot \sin (\omega t + \varphi_c)\) ,
где φ c – разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Исходя из этого можно дать еще такое определение:
- Переменный ток – это электрический ток, который изменяется с течением времени по гармоническому закону.
Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц.
Генератор переменного тока
Основная часть электроэнергии в мире в настоящее время вырабатывается генераторами переменного тока, создающими гармонические колебания.
- Генератором переменного тока называется электротехническое устройство, предназначенное для преобразования механической энергии в энергию переменного тока.
ЭДС индукции генератора изменяется по синусоидальному закону
\(e={\rm E}_{m} \cdot \sin \omega \cdot t,\)
где \({\rm E}_{m} =B\cdot S\cdot \omega\) — амплитудное (максимальное) значение ЭДС. При подключении к выводам рамки нагрузки сопротивлением R , через нее будет проходить переменный ток. По закону Ома для участка цепи сила тока в нагрузке
\(i=\dfrac{e}{R} =\dfrac{B \cdot S \cdot \omega }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\)
где \(I_{m} = \dfrac{B\cdot S\cdot \omega }{R}\) — амплитудное значение силы тока.
Основными частями генератора являются (рис. 1):
- индуктор — электромагнит или постоянный магнит, который создает магнитное поле;
- якорь — обмотка, в которой индуцируется переменная ЭДС;
- коллектор со щетками — устройство, посредством которого снимается с вращающихся частей или подается по ним ток.
Неподвижная часть генератора называется статором , а подвижная — ротором . В зависимости от конструкции генератора его якорь может быть как ротором, так и статором. При получении переменных токов большой мощности якорь обычно делают неподвижным, чтобы упростить схему передачи тока в промышленную сеть.
На современных гидроэлектростанциях вода вращает вал электрогенератора с частотой 1-2 оборота в секунду. Таким образом, если бы якорь генератора имел только одну рамку (обмотку), то получался бы переменный ток частотой 1-2 Гц. Поэтому, для получения переменного тока промышленной частоты 50 Гц якорь должен содержать несколько обмоток, позволяющих увеличить частоту вырабатываемого тока. Для паровых турбин, ротор которых вращается очень быстро, используют якорь с одной обмоткой. В этом случае частота вращения ротора совпадает с частотой переменного тока, т.е. ротор должен делать 50 об/с.
Мощные генераторы вырабатывают напряжение 15-20 кВ и обладают КПД 97-98 %.
Из истории . Первоначально Фарадей обнаружил лишь едва заметный ток в катушке при движении вблизи нее магнита. «Какая от этого польза?» — спросили его. Фарадей ответил: «Какая может быть польза от новорожденного?» Прошло немногим более половины столетия и, как сказал американский физик Р. Фейнман, «бесполезный новорожденный превратился в чудо-богатыря и изменил облик Земли так, как его гордый отец не мог себе и представить».
*Принцип действия
Принцип действия генератора переменного тока основан на явлении электромагнитной индукции.
Пусть проводящая рамка площадью S вращается с угловой скоростью ω вокруг оси, расположенной в ее плоскости перпендикулярно однородному магнитному полю индукцией \(\vec{B}\) (см. рис. 1).
При равномерном вращении рамки угол α между направлениями вектора индукции магнитного поля \(\vec{B}\) и нормали к плоскости рамки \(\vec{n}\) меняется со временем по линейному закону. Если в момент времени t = 0 угол α 0 = 0 (см. рис. 1), то
\(\alpha = \omega \cdot t = 2\pi \cdot \nu \cdot t,\)
где ω — угловая скорость вращения рамки, ν — частота ее вращения.
В этом случае магнитный поток, пронизывающий рамку будет изменяться следующим образом
\(\Phi \left(t\right)=B\cdot S\cdot \cos \alpha =B\cdot S\cdot \cos \omega \cdot t.\)
Тогда согласно закону Фарадея индуцируется ЭДС индукции
\(e=-\Phi «(t)=B\cdot S\cdot \omega \cdot \sin \omega \cdot t = {\rm E}_{m} \cdot \sin \omega \cdot t.\)
Подчеркнем, что ток в цепи проходит в одном направлении в течение полуоборота рамки, а затем меняет направление на противоположное, которое также остается неизменным в течение следующего полуоборота.
Действующие значения силы тока и напряжения
Пусть источник тока создает переменное гармоническое напряжение
\(u=U_{m} \cdot \sin \omega \cdot t.\;\;\;(1)\)
Согласно закону Ома, сила тока в участке цепи, содержащей только резистор сопротивлением R , подключенный к этому источнику, изменяется со временем также по синусоидальному закону:
\(i = \dfrac{u}{R} =\dfrac{U_{m} }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\;\;\; (2)\)
где \(I_m = \dfrac{U_{m}}{R}.\) Как видим, сила тока в такой цепи также меняется с течением времени по синусоидальному закону. Величины U m , I m называются амплитудными значениями напряжения и силы тока . Зависящие от времени значения напряжения u и силы тока i называют мгновенными .
Кроме этих величин используются еще одна характеристика переменного тока: действующие (эффективные) значения силы тока и напряжения .
- Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Обозначается буквой I .
- Действующим (эффективным) значением напряжения переменного тока называется напряжение такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Обозначается буквой U .{2}}{R}.\)
Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R , выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока, вследствие того, что их колебания совпадают по фазе.
Эффективное значение синусоидальной волны
Эффективное значение синусоидальной волныE max , E avg , I max и I avg — используемые значения в измерениях переменного тока. Другое используемое значение — ЭФФЕКТИВНОЕ значение переменного тока. Это значение переменное напряжение или ток, которые будут иметь такое же влияние на сопротивление, как и сопоставимое значение постоянного напряжения или тока будет иметь на том же сопротивлении.
В предыдущем обсуждении вам сказали, что когда ток течет через сопротивление, тепло выделяется. произведено.Когда через сопротивление протекает постоянный ток, количество электроэнергии преобразованная в тепло, равна I 2 R Вт. Однако, поскольку переменный ток при максимальном значении 1 ампер не поддерживает постоянное значение, переменный ток не будет выделять столько тепла в сопротивлении, сколько постоянный ток 1 ампер.
На Рисунке 1-15 сравнивается эффект нагрева 1 ампера постоянного тока с эффектом нагрева 1 ампер переменного тока.
Рисунок 1-15.- Нагревательный эффект переменного и постоянного тока.
Изучите виды A и B на рис. 1-15 и обратите внимание, что тепло (70,7 ° C), производимое 1 ампер переменного тока (то есть переменного тока с максимальным значением 1 ампер) составляет всего лишь 70,7% тепла (100 C) вырабатывается 1 ампером постоянного тока. Математически,
Следовательно, для действующего значения переменного тока (I eff ) = 0.707 X I макс. .
Скорость, с которой выделяется тепло в сопротивлении, является удобной основой для установление эффективного значения переменного тока, известное как «нагрев эффект «. Считается, что переменный ток имеет эффективное значение, равное единице. ампер, когда он выделяет тепло с заданным сопротивлением с той же скоростью, что и один ампер постоянный ток.
Вы можете вычислить эффективное значение синусоидального тока с достаточной степенью точности, принимая мгновенные значения тока через равные промежутки времени вдоль кривой и извлечение квадратного корня из средней суммы квадратов значений.
По этой причине эффективное значение часто называют «среднеквадратическим». (среднеквадратичное) значение. Таким образом,
Другими словами, эффективное или среднеквадратичное значение (I eff ) синусоидальной волны ток составляет 0,707 максимального значения тока (I max ). Таким образом, I eff = 0,707 X I макс. . Если известен I eff , вы можете найти I max по используя формулу I max = 1.414 X I эфф . Вы можете задаться вопросом, где постоянная 1,414 происходит от. Чтобы узнать это, еще раз изучите рисунок 1-15 и прочтите следующее. объяснение. Предположим, что постоянный ток на рисунке 1-15 (A) поддерживается на уровне 1 ампер, а температура резистора на уровне 100С. Также предположим, что переменный ток на рисунке 1-15 (B) увеличен. до тех пор, пока температура резистора не достигнет 100 C. На этом этапе обнаруживается, что максимальная Значение переменного тока 1,414 ампер требуется для того, чтобы иметь такой же нагревательный эффект, как и прямой Текущий.Следовательно, в цепи переменного тока максимальный требуемый ток в 1,414 раза больше эффективный ток. Вам важно помнить вышеупомянутые отношения и то, что эффективное значение (I eff ) любой синусоидальной волны тока всегда в 0,707 раза больше максимальное значение (I max ).
Поскольку переменный ток возникает из-за переменного напряжения, соотношение эффективное значение напряжения к максимальному значению напряжения такое же, как отношение эффективное значение тока до максимального значения тока.Другими словами, эффективное или среднеквадратичное значение (E eff ) синусоидального напряжения в 0,707 раз больше максимальное значение напряжения (E max ),
Когда значение переменного тока или напряжения указано в книге или на диаграмме, значение является эффективным, если не указано иное. Помните, что все измерители, если не указано иное, откалиброваны для индикации действующие значения тока и напряжения.
Проблема: известно, что в цепи имеется переменное напряжение 120 В и пиковое или максимальный ток 30 ампер. Каковы значения пикового напряжения и эффективного тока?
На рисунке 1-16 показано соотношение между различными значениями, используемыми для обозначения амплитуда синусоидальной волны. Просмотрите значения на рисунке, чтобы убедиться, что вы понимаете, что каждый значение указывает.
Рисунок 1-16. — Различные значения, используемые для обозначения амплитуды синусоидальной волны.
Q.32 Какая наиболее удобная основа для сравнения переменного и постоянного напряжения
а токи?
В.33 Какое значение переменного тока используется для сравнения с постоянным током?
В.34 Какова формула для определения действующего значения переменного тока?
В.35 Если пиковое значение синусоидальной волны составляет 1000 вольт, то каково эффективное (E eff )
ценить?
В.36 Если I eff = 4,25 ампера, что такое max ?
Пик vs.Среднее значение по сравнению с действующим напряжением
Термин «среднеквадратичное значение» означает «среднеквадратическое значение», также называемое эквивалентом переменного тока и постоянного напряжения.
Термин «среднеквадратичное значение» означает «среднеквадратическое значение», также называемое эффективным или тепловым значением переменного тока, эквивалентно напряжению постоянного тока, которое будет обеспечивать такое же количество тепловыделения в резисторе, как и напряжение переменного тока. если применяется к тому же резистору.
RMS не является «средним» напряжением, и его математическое отношение к пиковому напряжению зависит от типа формы сигнала. Среднеквадратичное значение — это квадратный корень из среднего (среднего) значения функции квадрата мгновенных значений.
Поскольку напряжение переменного тока повышается и понижается со временем, для получения заданного среднеквадратичного напряжения требуется большее напряжение переменного тока, чем для постоянного тока. Например, для достижения среднеквадратичного значения 120 В (0,707 x169) потребуется пиковое значение переменного тока 169 вольт.
В этом примере величина нагрева напряжения 169 переменного тока эквивалентна значению нагрева источника постоянного тока на 120 вольт.Большинство мультиметров, будь то вольтметры или амперметры, измеряют среднеквадратичное значение, принимая чисто синусоидальную форму волны.
Важные термины, которые следует запомнить
Пиковое напряжение (Vp)
Максимальное мгновенное значение функции, измеренное от нулевого уровня напряжения. Для формы волны, показанной выше, пиковая амплитуда и пиковое значение одинаковы, поскольку среднее значение функции равно нулю вольт.
Пиковое напряжение (В пик-пик)
Полное напряжение между положительным и отрицательным пиками формы волны; то есть сумма величин положительного и отрицательного пиков.
RMS Напряжение (Vrms)
Среднеквадратичное или эффективное значение сигнала.
Среднее напряжение (Vavg)
Уровень сигнала, определяемый условием, что площадь, ограниченная кривой выше этого уровня, в точности равна площади, ограниченной кривой ниже этого уровня.
Важные уравнения, которые следует запомнить
- Vp x 0,707 = Vrms
- Vrms = 1,11 x Vavg
- 1.414 x Vrms = Vp
- Vavg = 0,637 x Vp
Дополнительная литература / Источники
Комментарии
Войдите или зарегистрируйтесь, чтобы комментировать.Значения переменного тока
Есть три значения переменного тока, которые мгновенное, пиковое и эффективное (среднеквадратичное, RMS).
Мгновенное значение
Мгновенное значение напряжения или тока — это индуцированное напряжение или ток, протекающий в любой момент во время цикл.Синусоидальная волна представляет собой серию этих значения. Мгновенное значение напряжения меняется от нуля при 0 ° до максимума при 90 °, обратно до нуля при 180 °, максимум в обратном направлении на 270 °, и снова до нуля на 360 °. Любая точка на синусоиде считается мгновенным значением напряжения.
Пиковое значение
Пиковое значение — это наибольшее мгновенное значение. В наибольшее положительное значение возникает, когда синусоида напряжения составляет 90 °, а наибольшее отрицательное значение происходит при 270 °.Максимальное значение 1,41 раза эффективное значение. Это так называемые пиковые значения.
Эффективное значение
Действующее значение также известно как среднеквадратичное значение или среднеквадратичный, который относится к математическому процессу по которому выводится значение. Большинство вольтметров переменного тока при использовании будет отображать эффективное или среднеквадратичное значение. Действующее значение меньше максимального значения, равный 0,707 максимального значения.
Эффективное значение синусоиды на самом деле является мерой теплового эффекта синусоидальной волны.Фигура 10-107 показано, что происходит, когда резистор подключен к источнику переменного напряжения. В иллюстрации A, некоторое количество тепла выделяется мощность в резисторе. На рисунке B показано то же самое резистор теперь вставлен в источник постоянного напряжения. В значение источника постоянного напряжения теперь можно регулировать так что резистор рассеивает такое же количество тепла, как это было, когда он был в цепи переменного тока. RMS или эффективное значение синусоидальной волны равно постоянное напряжение, выделяющее такое же количество тепла как синусоидальное напряжение.
Пиковое значение синусоиды можно преобразовать в соответствующее среднеквадратичное значение, используя следующие отношение.
Может применяться как к напряжению, так и к току.
Алгебраическое преобразование формулы и решение для Vp также может определять пиковое напряжение. Результирующий формула:
Вп = 1,414 В среднекв.
Таким образом, значение 110 вольт дано для переменного тока. в дома поставлено всего 0.707 от максимального напряжения этого предложения. Максимальное напряжение примерно 155 вольт (110 1,41 = максимум 155 вольт).
При исследовании переменного тока используются любые значения для тока или напряжения принимаются действующие значения если не указано иное, и на практике только используются действующие значения напряжения и тока. Аналогично вольтметры и амперметры переменного тока измерить эффективное значение.
Что такое пиковое значение, среднее значение и среднеквадратичное значение? — определение и объяснение
Пиковое значение
Определение: Максимальное значение, достигаемое переменным количеством в течение одного цикла, называется его значением P eak .Он также известен как максимальное значение, амплитуда или пик. Синусоидальная переменная величина достигает пикового значения под углом 90 градусов, как показано на рисунке ниже.
Пиковые значения переменного напряжения и тока представлены E m и I m соответственно.
Среднее значение
Определение: Среднее значение всех мгновенных значений переменного напряжения и токов за один полный цикл называется средним значением .
Если мы рассмотрим симметричные волны, такие как синусоидальный ток или форма волны напряжения, положительный полупериод будет точно равен отрицательному полупериоду. Следовательно, среднее значение за полный цикл будет ноль .
Работа выполняется как по положительному, так и по отрицательному циклу, поэтому среднее значение определяется без учета знаков.
Итак, единственным положительным полупериодом считается определение среднего значения переменных величин синусоидальных волн.Давайте рассмотрим пример, чтобы понять это.
Разделите положительный полупериод на ( n ) количество равных частей, как показано на рисунке выше
Пусть i 1 , i 2 , i 3 …… .. i n — средние ординаты
Среднее значение тока I ср = среднее значение средних ординат
R.M.S значение
Определение: Постоянный ток, который при протекании через резистор с известным сопротивлением в течение определенного периода времени, в результате такое же количество тепла выделяется переменным током, когда он протекает через тот же резистор в течение того же периода времени. время называется р.M.S или действующее значение переменного тока.
Другими словами, значение R.M.S определяется как квадратный корень из средних квадратов мгновенных значений.
Пусть I будет переменным током, протекающим через резистор R в течение времени t секунд, который производит такое же количество тепла, как и постоянный ток (I eff ). База одного изменения делится на n равных частей, так что каждый интервал составляет t / n секунд, как показано на рисунке ниже.
Пусть i 1 , i 2 , i 3 , ………..in быть средними ординатами
Затем тепло произведено в
Так как Ieff рассматривается как эффективное значение этого тока, то общее количество тепла, произведенного этим током, будет
Теперь, приравняв уравнение (1) и (2), получим
I eff = квадратный корень из среднего квадратов мгновенных значений = R.M.S значение
Среднеквадратичное значение — это фактическое значение переменной величины, которая говорит нам о способности источника переменного тока передавать энергию.
Амперметр регистрирует среднеквадратичное значение переменного тока, а вольтметр записывает среднеквадратическое значение переменного напряжения. Бытовая однофазная сеть переменного тока составляет 230 В, 50 Гц, где 230 В — это среднеквадратичное значение переменного напряжения.
Значения напряжения и тока системы в цепи постоянного тока постоянны, поэтому нет проблем с оценкой их величин, но в системе переменного тока переменное напряжение и ток изменяются время от времени, и, следовательно, необходимо оценивать их величины.
Следующие три способа (пиковое значение, среднее значение и среднеквадратичное значение), приведенные выше, используются для выражения величины напряжения и тока.
Анализ генерации переменного тока: эффективные значения, фазовый угол и частота
Анализ процесса производства электроэнергии переменного тока и переменного тока, который мы используем практически во всех аспектах нашей жизни, необходим для лучшего понимания того, как мощность переменного тока используется в современных технологиях.
Эффективные значения
Выходное напряжение генератора переменного тока можно выразить двумя способами.Один — графически с использованием синусоидальной волны (рис. 3). Второй способ — алгебраически с помощью уравнения e = E max sin ωt, которое будет рассмотрено позже в тексте.
Рисунок 3: Синусоидальная волна напряжения
Когда напряжение вырабатывается генератором переменного тока, результирующий ток изменяется пропорционально напряжению. Когда катушка генератора вращается на 360 °, выходное напряжение проходит один полный цикл. За один цикл напряжение увеличивается от нуля до E в одном направлении, уменьшается до нуля, увеличивается до E max в противоположном направлении (отрицательное значение E max ), а затем снова уменьшается до нуля.Значение E max происходит при 90 ° и называется пиковым напряжением. Время, необходимое генератору для завершения одного цикла, называется периодом, а количество циклов в секунду называется частотой (измеряется в герцах).
Один из способов обозначения переменного напряжения или тока — это пиковое напряжение (E p ) или пиковый ток (I p ). Это максимальное напряжение или ток для синусоидального сигнала переменного тока.
Другое значение, значение размаха (E p-p или I p ), представляет собой величину напряжения или диапазон тока, охватываемого синусоидальной волной.Однако наиболее часто используемым значением переменного тока является эффективное значение. Эффективное значение переменного тока — это количество переменного тока, которое производит такой же нагревательный эффект, как и такое же количество постоянного тока.
Проще говоря, эффективное значение переменного тока в один ампер будет производить такое же количество тепла в проводнике за заданное время, что и один ампер постоянного тока. Эффект нагрева от данного переменного тока пропорционален квадрату тока. Эффективное значение переменного тока можно вычислить, возведя в квадрат все амплитуды синусоидальной волны за один период, взяв среднее из этих значений, а затем извлекая квадратный корень.Действующее значение, являющееся корнем из среднего (среднего) квадрата токов, известно как среднеквадратическое значение или среднеквадратичное значение. Чтобы понять значение эффективного тока, приложенного к синусоиде, см. Рисунок 4.
Значения I нанесены на верхнюю кривую, а соответствующие значения I 2 нанесены на нижнюю кривую. Кривая I 2 имеет вдвое большую частоту, чем I, и изменяется выше и ниже новой оси. Новая ось представляет собой среднее значение I 2 , а квадратный корень из этого значения представляет собой среднеквадратичное или эффективное значение тока.Среднее значение ½ I max 2 . Тогда среднеквадратичное значение
.Существует шесть основных уравнений, которые используются для преобразования значения переменного напряжения или тока в другое значение, как указано ниже.
- Среднее значение = пиковое значение x 0,637
- Эффективное значение (RMS) = пиковое значение x 0,707
- Пиковое значение = среднее значение x 1,57
- Эффективное значение (RMS) = среднее значение x 1,11
- Пиковое значение = эффективное значение (RMS) x 1.414
- Среднее значение = эффективное (RMS) x 0,9
Обычно встречающиеся значения тока (I) и напряжения (E) считаются действующими значениями; поэтому нижний индекс не используется.
Рисунок 4: Действующее значение тока
Еще одно полезное значение — это среднее значение амплитуды в течение положительной половины цикла.
Приведенное ниже уравнение представляет собой математическую связь между I av , I max и I.
I средн. = 0,637 I макс. = 0,9 I
Приведенное ниже уравнение представляет собой математическую связь между E ср. , E max и E.
E ср. = 0,637 E макс. = 0,9 E
Пример 1:
Пиковое значение напряжения в цепи переменного тока составляет 200 В. Каково среднеквадратичное значение напряжения?
E = 0,707E макс.
E = 0,707 x 200 = 141,4 В
Пример 2:
Пиковый ток в цепи переменного тока составляет 10 ампер.Какое среднее значение тока в цепи?
I средн. = 0,637 I макс.
I av = 0,637 x 10 = 6,37 ампер
Фазовый уголФазовый угол — это доля цикла в градусах, которая прошла с тех пор, как напряжение или ток прошли через заданное значение. Данное значение обычно равно нулю. Возвращаясь к рисунку 3, возьмите точку 1 как начальную точку или нулевую фазу. Фаза в точке 2 равна 30 °, точке 3 — 60 °, точке 4 — 90 ° и так далее, до точки 13, где фаза равна 360 ° или нулю.Более часто используется термин разность фаз.
Рисунок 5: Соотношение фаз
Разность фаз может использоваться для описания двух разных напряжений с одинаковой частотой, которые проходят через нулевые значения в одном направлении в разное время. На рисунке 5 углы вдоль оси указывают фазы напряжений e 1 и e 2 в любой момент времени.
При 120 ° e 1 проходит через нулевое значение, которое на 60 ° опережает e 2 (e 2 равно нулю при 180 °).Считается, что напряжение e 1 опережает e 2 на 60 электрических градусов, или можно сказать, что e 2 отстает от e 1 на 60 электрических градусов.
Разность фаз также используется для сравнения двух разных токов или тока и напряжения. Если разность фаз между двумя токами, двумя напряжениями или напряжением и током равна нулю, они считаются «синфазными». Если разность фаз отлична от нуля, говорят, что они «не совпадают по фазе».”
Расчет напряженияПриведенное ниже уравнение представляет собой математическое представление напряжения, связанного с любой конкретной ориентацией катушки (индуктора).
e = E макс sinθ
где
e = наведенная ЭДС
E max = максимальная наведенная ЭДС
θ = угол от точки отсчета (градусы или радианы)
Пример 1:
Какова наведенная ЭДС в катушке, создающей максимальную ЭДС 120 В, когда угол от точки отсчета составляет 45 °?
e = E макс. sinθ
e = 120 v Sin (45)
е = 84.84 В
Максимальное индуцированное напряжение также можно назвать пиковым напряжением E p . Если (t) — это время, за которое катушка поворачивается на угол (θ), то угловая скорость (ω) катушки равна θ / t и выражается в радианах / сек.
Уравнение ниже является математическим представлением угловой скорости.
θ = ωt
где
ω = угловая скорость (радиан / сек)
t = время поворота на угол от точки отсчета (с)
θ = угол от точки отсчета (радианы)
Используя законы замещения, можно выразить взаимосвязь между наведенным напряжением, максимальным наведенным напряжением и угловой скоростью.
Приведенное ниже уравнение представляет собой математическое представление взаимосвязи между индуцированным напряжением, максимальным напряжением и угловой скоростью, оно равно выходной мощности генератора переменного тока.
e = E макс sin (ωt)
, где
e = наведенная ЭДС (вольты)
E max = максимальная наведенная ЭДС (вольты)
ω = угловая скорость (радиан / сек)
t = время поворота на угол от точки отсчета (сек)
Максимальный наведенный ток рассчитывается аналогичным образом.Приведенное ниже уравнение представляет собой математическое представление зависимости между максимальным индуцированным током и угловой скоростью.
i = I макс sin (ωt)
где
I = индуцированный ток (AMPS)
я макс = максимальный наведенный ток (AMPS)
ω = угловая скорость (рад / сек) =
т время, чтобы повернуть на угол от опорного (сек)
Частота переменного напряжения или тока может быть напрямую связана с угловой скоростью вращающейся катушки.Единицы угловой скорости — радианы в секунду, а 2π радиан — полный оборот.
Радиан — это угол, образующий дугу, равную радиусу окружности. Один радиан равен 57,3 градуса. Один цикл синусоидальной волны генерируется, когда катушка вращается на 2π радиан.
Уравнение ниже представляет собой математическое соотношение между частотой (f) и угловой скоростью (ω) в цепи переменного тока.
ω = 2πf
где
ω = угловая скорость (радиан / сек)
f = частота (Гц)
Пример 1:
Частота цепи 120 В переменного тока составляет 60 Гц.Найдите следующее: 1. Угловая скорость 2. Угол от точки отсчета через 1 мс 3. Индуцированная ЭДС в этой точке
Решение:
1. ω = 2πf
ω = 2 (3,14) (60 Гц) = 376,8 радиан / сек
2. θ = ωt
θ = (376,8 радиан / сек) (0,001 сек) = 0,3768 радиан
3. e = E max sinθ
e = (120 В) (sin 0,3768 радиан)
e = (120 В) (0,3679)
e = 44,15 В
электрических цепей — Почему мы используем среднеквадратические значения (RMS), когда говорим о напряжении переменного тока
Попытки найти среднее значение AC напрямую дадут вам ответ ноль … Следовательно, используются значения RMS. Они помогают найти эффективное значение переменного тока (напряжения или тока).
Это RMS — математическая величина (используется во многих математических полях ), используемая для сравнения как переменного, так и постоянного тока (или напряжения). Другими словами (в качестве примера), среднеквадратичное значение переменного тока (тока) — это постоянный ток, который при пропускании через резистор в течение заданного периода времени будет производить такое же тепло, что и переменный ток при прохождении через такой же резистор за то же время.2/2 $, а затем определение квадратного корня $ I_0 / \ sqrt {2} $ даст RMS.
Это пример , время : (я думаю, вы не просили вычислить RMS)
Учтите, что обе лампы выдают одинаковый уровень яркости. Таким образом, они теряют одинаковое количество тепла (независимо от того, переменный или постоянный ток). Чтобы связать и то и другое, нам нечего использовать лучше, чем значение RMS. Постоянное напряжение лампы составляет 115 В, а переменное — 170 В.2} $$
Измерений амплитуды переменного тока | Базовая теория переменного тока
На данный момент мы знаем, что переменное напряжение меняется по полярности, а переменный ток — по направлению. Мы также знаем, что переменный ток может изменяться множеством различных способов, и, отслеживая изменение во времени, мы можем построить его в виде «формы волны».
Мы можем измерить скорость чередования, измерив время, необходимое для развития волны, прежде чем она повторится («период»), и выразить это как количество циклов в единицу времени или «частоту».В музыке частота такая же, как , высота звука , что является важным свойством, отличающим одну ноту от другой.
Однако мы сталкиваемся с проблемой измерения, если пытаемся выразить, насколько велика или мала величина переменного тока. С постоянным током, где величины напряжения и тока обычно стабильны, у нас нет проблем с выражением того, сколько напряжения или тока у нас есть в любой части цепи.
Но как дать единичное измерение величины чему-то, что постоянно меняется?
Способы выражения величины сигнала переменного тока
Один из способов выразить интенсивность или величину (также называемую амплитудой ) величины переменного тока — это измерить высоту его пика на графике формы сигнала.Это известно как значение пика или пика сигнала переменного тока: Рисунок ниже
Пиковое напряжение формы волны.
Другой способ — измерить общую высоту между противоположными вершинами. Это известно как значение размаха (P-P) сигнала переменного тока: Рисунок ниже
Размах напряжения формы волны.
К сожалению, любое из этих выражений амплитуды сигнала может ввести в заблуждение при сравнении двух разных типов волн.Например, прямоугольная волна с пиком 10 вольт, очевидно, представляет собой большее количество напряжения в течение большего количества времени, чем треугольная волна с пиком 10 вольт.
Эффекты этих двух напряжений переменного тока, питающих нагрузку, будут совершенно разными: Рисунок ниже
Прямоугольная волна дает больший эффект нагрева, чем такая же треугольная волна пикового напряжения.
Один из способов выразить амплитуду различных форм волны более эквивалентным способом — это математически усреднить значения всех точек на графике формы волны до единого совокупного числа.Это измерение амплитуды известно просто как среднее значение сигнала.
Если мы усредним все точки на осциллограмме алгебраически (то есть с учетом их знака , положительного или отрицательного), среднее значение для большинства сигналов технически равно нулю, потому что все положительные точки компенсируют все отрицательные точки по полный цикл: рисунок ниже
Среднее значение синусоиды равно нулю.
Это, конечно, будет верно для любой формы волны, имеющей участки равной площади выше и ниже «нулевой» линии графика.Однако, как практическая мера совокупного значения формы волны, «среднее» обычно определяется как математическое среднее абсолютных значений всех точек за цикл.
Другими словами, мы вычисляем практическое среднее значение сигнала, рассматривая все точки на волне как положительные величины, как если бы форма сигнала выглядела следующим образом: Рисунок ниже
Форма волны, измеренная измерителем «среднего отклика» переменного тока.
Нечувствительные к полярности движения механических счетчиков (счетчики, рассчитанные на одинаковую реакцию на положительные и отрицательные полупериоды переменного напряжения или тока) регистрируются пропорционально (практическому) среднему значению формы сигнала, потому что инерция стрелки относительно напряжения пружина естественным образом усредняет силу, создаваемую изменяющимися значениями напряжения / тока с течением времени.
И наоборот, чувствительные к полярности движения измерителя бесполезно вибрируют при воздействии переменного напряжения или тока, их стрелки быстро колеблются около нулевой отметки, указывая истинное (алгебраическое) среднее значение нуля для симметричной формы волны. Когда в этом тексте упоминается «среднее» значение формы сигнала, предполагается, что подразумевается «практическое» определение среднего значения, если не указано иное.
Другой метод получения совокупного значения амплитуды сигнала основан на способности формы сигнала выполнять полезную работу при приложении к сопротивлению нагрузки.К сожалению, измерение переменного тока, основанное на работе, выполняемой осциллограммой, не совпадает со «средним» значением этой формы сигнала, потому что мощность , рассеиваемая данной нагрузкой (работа, выполняемая за единицу времени), не прямо пропорциональна величине любого из них. напряжение или ток, приложенные к нему.
Напротив, мощность пропорциональна квадрату напряжения или тока, приложенного к сопротивлению (P = E 2 / R и P = I 2 R). Хотя математика такого измерения амплитуды может быть непростой, польза от этого есть.
Рассмотрим ленточную пилу и лобзик, две части современного деревообрабатывающего оборудования. Пилы обоих типов режут дерево тонким зубчатым металлическим диском с приводом от двигателя. Но в то время как ленточная пила использует непрерывное движение полотна для резки, лобзик использует возвратно-поступательное движение.
Сравнение переменного тока (AC) с постоянным током (DC) можно сравнить со сравнением этих двух типов пил: Рисунок ниже
Ленточная пила — аналог DC vs AC.
Проблема попытки описать изменяющиеся величины переменного напряжения или тока в одном совокупном измерении также присутствует в этой аналогии с пилой: как бы мы могли выразить скорость полотна лобзика? Полотно ленточной пилы движется с постоянной скоростью, подобно тому, как проталкивает постоянное напряжение или постоянный ток движется с постоянной величиной. С другой стороны, полотно лобзика движется вперед и назад, скорость его полотна постоянно меняется. Более того, возвратно-поступательное движение любых двух лобзиков может быть разного типа, в зависимости от механической конструкции пил.
Один лобзик может двигать лезвие синусоидально, а другой — треугольником. Оценка лобзика на основе его пиковой скорости будет вводить в заблуждение при сравнении одного лобзика с другим (или лобзика с ленточной пилой!). Несмотря на то, что эти разные пилы перемещают свои лезвия по-разному, они равны в одном отношении: все они режут древесину, и количественное сравнение этой общей функции может служить общей основой для оценки скорости лезвия.
Представьте себе лобзик и ленточную пилу бок о бок, оснащенные одинаковыми лезвиями (одинаковым шагом зубьев, углом и т. Д.), Одинаково способными резать одинаковую толщину одного и того же вида древесины с одинаковой скоростью. Можно сказать, что эти две пилы были эквивалентны или равны по своей режущей способности. Можно ли использовать это сравнение для определения «эквивалентной скорости полотна ленточной пилы» возвратно-поступательному движению полотна лобзика; связать эффективность лесозаготовки одного с другим?
Это общая идея, используемая для присвоения измерения «эквивалента постоянного тока» любому переменному напряжению или току: независимо от величины постоянного напряжения или тока, будет происходить такое же количество рассеивания тепловой энергии через равное сопротивление: Рисунок ниже
Среднеквадратичное напряжение вызывает такой же нагревательный эффект, как и такое же напряжение постоянного тока
Какое значение имеет среднеквадратичное значение (RMS) для переменного тока?
В двух приведенных выше схемах у нас одинаковое сопротивление нагрузки (2 Ом), рассеивающее одинаковое количество энергии в виде тепла (50 Вт), одна питается от переменного тока, а другая от постоянного тока.Поскольку изображенный выше источник переменного напряжения эквивалентен (с точки зрения мощности, подаваемой на нагрузку) 10-вольтовой батарее постоянного тока, мы бы назвали это «10-вольтовым» источником переменного тока.
Более конкретно, мы обозначим его значение напряжения как 10 вольт RMS . Квалификатор «RMS» означает Среднеквадратическое значение , алгоритм, используемый для получения значения эквивалента постоянного тока из точек на графике (по сути, процедура состоит из возведения в квадрат всех положительных и отрицательных точек на графике формы сигнала, усреднения этих квадратов значений. , а затем извлечение квадратного корня из этого среднего, чтобы получить окончательный ответ).
Иногда вместо «RMS» используются альтернативные термины эквивалент или эквивалент постоянного тока , но количество и принцип одинаковы.
Измерение амплитудыRMS — лучший способ связать величины переменного тока с величинами постоянного тока или другими величинами переменного тока с разной формой волны при измерении электрической мощности.
Из других соображений лучше всего использовать измерения от пика до пика. Например, при определении правильного размера провода (допустимой нагрузки) для передачи электроэнергии от источника к нагрузке лучше всего использовать измерение среднеквадратичного тока, поскольку основная проблема с током — это перегрев провода, который является функцией рассеивание мощности, вызванное током через сопротивление провода.
Однако при оценке изоляторов для работы в высоковольтных системах переменного тока измерения пикового напряжения являются наиболее подходящими, поскольку здесь основной проблемой является «пробой» изолятора, вызванный кратковременными скачками напряжения независимо от времени.
Инструменты, используемые для измерения амплитуды сигнала
Измерения размаха и пика лучше всего выполнять с помощью осциллографа, который может фиксировать пики формы сигнала с высокой степенью точности благодаря быстрому срабатыванию электронно-лучевой трубки в ответ на изменения напряжения.Для измерений RMS будут работать аналоговые измерительные приборы (D’Arsonval, Weston, железная лопасть, электродинамометр), если они были откалиброваны в значениях RMS.
Поскольку механическая инерция и демпфирующие эффекты движения электромеханического счетчика делают отклонение стрелки естественным образом пропорциональным среднему значению переменного тока, а не истинному среднеквадратичному значению, аналоговые счетчики должны быть специально откалиброваны (или неправильно откалиброваны, в зависимости от как вы на это смотрите), чтобы указать напряжение или ток в единицах RMS.
Точность этой калибровки зависит от предполагаемой формы волны, обычно синусоидальной.
Электронные счетчики, специально разработанные для измерения среднеквадратичных значений, лучше всего подходят для этой задачи. Некоторые производители инструментов разработали хитроумные методы определения среднеквадратичного значения любой формы волны. Один из таких производителей производит измерители True-RMS с крошечным резистивным нагревательным элементом, питаемым напряжением, пропорциональным измеряемому.
Эффект нагрева этого элемента сопротивления измеряется термически, чтобы получить истинное среднеквадратичное значение без каких-либо математических вычислений, только законы физики в действии в соответствии с определением среднеквадратичного значения.Точность этого типа измерения RMS не зависит от формы волны.
Взаимосвязь пика, размаха, среднего и RMS
Для «чистых» сигналов существуют простые коэффициенты преобразования для приравнивания пикового, разностного, среднего (практического, а не алгебраического) и среднеквадратичного значений друг к другу:
Коэффициенты преобразования для обычных сигналов.
В дополнение к измерениям RMS, среднего, пика (пика) и размаха сигнала переменного тока существуют соотношения, выражающие пропорциональность между некоторыми из этих основных измерений.Пик-фактор сигнала переменного тока, например, представляет собой отношение его пикового (пикового) значения, деленного на его среднеквадратичное значение.
Форм-фактор сигнала переменного тока — это отношение его среднеквадратичного значения к его среднему значению. Сигналы прямоугольной формы всегда имеют пик и коэффициент формы, равные 1, поскольку пик такой же, как среднеквадратичное и среднее значения. Синусоидальные сигналы имеют среднеквадратичное значение 0,707 (величина, обратная квадратному корню из 2) и форм-фактор 1,11 (0,707 / 0.636).
Сигналы треугольной и пилообразной формы имеют среднеквадратичное значение 0,577 (величина, обратная квадратному корню из 3) и форм-фактор 1,15 (0,577 / 0,5).
Имейте в виду, что константы преобразования, показанные здесь для пиковых, среднеквадратичных и средних амплитуд синусоидальных, прямоугольных и треугольных волн, справедливы только для чистых форм этих форм волны. Среднеквадратичные и средние значения искаженной формы волны не связаны одними и теми же отношениями: Рисунок ниже
Сигналы произвольной формы не имеют простого преобразования.
Это очень важная концепция, которую необходимо понимать при использовании аналогового движения измерителя Д’Арсонваля для измерения переменного напряжения или тока. Аналоговый механизм Д’Арсонваля, откалиброванный для индикации среднеквадратичной амплитуды синусоидальной волны, будет точным только при измерении чистых синусоидальных волн.
Если форма сигнала измеряемого напряжения или тока не является чистой синусоидой, показание измерителя не будет истинным среднеквадратичным значением формы сигнала, потому что степень отклонения стрелки в аналоговом перемещении измерителя Д’Арсонваля пропорционально среднему значению сигнала, а не среднеквадратичному значению.
Калибровка измерителяRMS получается путем «перекоса» диапазона измерителя так, чтобы он отображал небольшое кратное среднему значению, которое будет равно среднеквадратичному значению для определенной формы волны и только для определенной формы волны .
Поскольку форма синусоидальной волны является наиболее распространенной в электрических измерениях, она является формой волны, принятой для калибровки аналогового измерителя, а небольшое кратное, используемое при калибровке измерителя, составляет 1,1107 (форм-фактор: 0,707 / 0,636: отношение среднеквадратичных значений деленное на среднее значение для синусоидального сигнала).
Любая форма волны, кроме чистой синусоидальной волны, будет иметь другое соотношение среднеквадратичных и средних значений, и, следовательно, измеритель, откалиброванный для синусоидального напряжения или тока, не будет показывать истинное среднеквадратичное значение при считывании несинусоидальной волны. Помните, что это ограничение применяется только к простым аналоговым счетчикам переменного тока, не использующим технологию True-RMS.
ОБЗОР:
- Амплитуда сигнала переменного тока — это его высота, как показано на графике во времени.Измерение амплитуды может принимать форму пика, размаха, среднего или среднеквадратичного значения.
- Пиковая амплитуда — это высота сигнала переменного тока, измеренная от нулевой отметки до самой высокой положительной или самой низкой отрицательной точки на графике. Также известен как гребень амплитуда волны .
- Полная амплитуда — это общая высота сигнала переменного тока, измеренная от максимальных положительных до максимальных отрицательных пиков на графике. Часто обозначается как «П-П».
- Средняя амплитуда — это математическое «среднее» всех точек сигнала за период одного цикла. Технически, средняя амплитуда любой формы сигнала с участками равной площади выше и ниже «нулевой» линии на графике равна нулю. Однако в качестве практической меры амплитуды среднее значение сигнала часто вычисляется как математическое среднее значение абсолютных значений всех точек (принимая все отрицательные значения и считая их положительными). Для синусоиды среднее значение, вычисленное таким образом, приблизительно равно 0.637 пикового значения.
- «RMS» означает среднеквадратическое значение и является способом выражения величины переменного напряжения или тока в терминах, функционально эквивалентных постоянному току. Например, среднеквадратичное значение 10 вольт переменного тока — это величина напряжения, при которой через резистор заданного значения рассеивается такое же количество тепла, что и при источнике питания постоянного тока на 10 вольт. Также известен как «эквивалент» или «эквивалент постоянного тока» для переменного напряжения или тока. Для синусоидальной волны среднеквадратичное значение составляет примерно 0,707 от его пикового значения.
- Пик-фактор сигнала переменного тока — это отношение его пика (пик) к его среднеквадратичному значению.
- Форм-фактор сигнала переменного тока — это отношение его среднеквадратичного значения к его среднему значению.
- Аналоговые, электромеханические движения счетчика реагируют пропорционально среднему значению переменного напряжения или тока. Когда требуется индикация среднеквадратичного значения, калибровка измерителя должна быть соответственно «искажена». Это означает, что точность показаний RMS электромеханического измерителя зависит от чистоты формы волны: от того, точно ли она совпадает с формой волны, используемой при калибровке.
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
.
 …
…


 Теория синусоидального тока является ключом к пониманию теории других цепей.
Теория синусоидального тока является ключом к пониманию теории других цепей.
 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
 Они же визуально различаются, с этим не поспоришь. По частоте? Тоже да, но иногда это вызывает вопросы. Некоторые считают, что само определение частоты применимо исключительно для синусоидального сигнала и его нельзя использовать, например, для последовательности импульсов. Возможно, формально они и правы, но я не разделяю их точку зрения. А еще как еще можно? А, например, по деньгам! Неожиданно? Напрасно. Ток ведь стоит денег. Вернее, стоит денег работа тока. В конце концов ведь те самые киловатт·часы, за которые вы все платите каждый месяц по счетчику не что иное, как работа тока. А поскольку деньги вещь серьезная, то ради такого стоит и термин отдельный ввести. И для сравнения между собой токов различной формы по количеству работы ввели понятие действующего тока.
Они же визуально различаются, с этим не поспоришь. По частоте? Тоже да, но иногда это вызывает вопросы. Некоторые считают, что само определение частоты применимо исключительно для синусоидального сигнала и его нельзя использовать, например, для последовательности импульсов. Возможно, формально они и правы, но я не разделяю их точку зрения. А еще как еще можно? А, например, по деньгам! Неожиданно? Напрасно. Ток ведь стоит денег. Вернее, стоит денег работа тока. В конце концов ведь те самые киловатт·часы, за которые вы все платите каждый месяц по счетчику не что иное, как работа тока. А поскольку деньги вещь серьезная, то ради такого стоит и термин отдельный ввести. И для сравнения между собой токов различной формы по количеству работы ввели понятие действующего тока. Звучит очень хитро и, скорее всего, если вы читаете это определение в первый раз, то вряд ли вы его поймете. Это нормально. Когда я его в первый раз услышал в школе, я сам долго доходил, что же это значит. Поэтому сейчас я постараюсь разобрать это определение поподробнее, чтобы вы поняли, что за этой мудреной фразой скрывается быстрее, чем я в свое время.
Звучит очень хитро и, скорее всего, если вы читаете это определение в первый раз, то вряд ли вы его поймете. Это нормально. Когда я его в первый раз услышал в школе, я сам долго доходил, что же это значит. Поэтому сейчас я постараюсь разобрать это определение поподробнее, чтобы вы поняли, что за этой мудреной фразой скрывается быстрее, чем я в свое время. А теперь, внимание, господа, важный момент! Давайте мы заменим переменный ток на постоянный, причем выберем его такой величины (ну то есть столько ампер), чтобы на том же самом резисторе R за то же самое время Tпериод выделилось ровно такое же количество джоулей Q. Очевидно, мы должны как-то определить величину этого самого постоянного тока, эквивалентного переменному с энергетической точки зрения. И вот когда мы найдем эту величину, то она-то как раз и будет тем самым действующим значением переменного тока. А теперь, господа, вернитесь еще разок к тому мудреному формальному определению, которое я давал вначале. Сейчас оно стало лучше понятно, не так ли?
А теперь, внимание, господа, важный момент! Давайте мы заменим переменный ток на постоянный, причем выберем его такой величины (ну то есть столько ампер), чтобы на том же самом резисторе R за то же самое время Tпериод выделилось ровно такое же количество джоулей Q. Очевидно, мы должны как-то определить величину этого самого постоянного тока, эквивалентного переменному с энергетической точки зрения. И вот когда мы найдем эту величину, то она-то как раз и будет тем самым действующим значением переменного тока. А теперь, господа, вернитесь еще разок к тому мудреному формальному определению, которое я давал вначале. Сейчас оно стало лучше понятно, не так ли? Если по причине нелюбви к математике вам это кажется чем-то слишком мудреным, вы волне можете пропустить выкладки и посмотреть сразу результат. А у меня что-то сегодня настроение вспомнить молодость и аккуратненько разобраться со всеми этими интегральчиками
Если по причине нелюбви к математике вам это кажется чем-то слишком мудреным, вы волне можете пропустить выкладки и посмотреть сразу результат. А у меня что-то сегодня настроение вспомнить молодость и аккуратненько разобраться со всеми этими интегральчиками Полезнейшее свойство, кстати! Рекомендую его запомнить. Геометрически это тоже понятно: первая полуволна синуса идет выше оси абсцисс и интеграл от нее больше нуля, а вторая полуволна идет ниже оси абсцисс, поэтому его величина меньше нуля. А по модулю они равны между собой, поэтому их сложение (собственно, интеграл за весь период) даст в итоге нолик.
Полезнейшее свойство, кстати! Рекомендую его запомнить. Геометрически это тоже понятно: первая полуволна синуса идет выше оси абсцисс и интеграл от нее больше нуля, а вторая полуволна идет ниже оси абсцисс, поэтому его величина меньше нуля. А по модулю они равны между собой, поэтому их сложение (собственно, интеграл за весь период) даст в итоге нолик. Поэтому мы можем записать
Поэтому мы можем записать Действующее значения напряжения точно также в корень из двух раз меньше амплитуды.
Действующее значения напряжения точно также в корень из двух раз меньше амплитуды..doc_html_80280bebe3a5f2e5.gif) В розетках у нас, оказывается, синус с амплитудой аж 311 В, а не 220, как можно было подумать сначала. Что бы убрать все сомнения представлю вам картинку, как выглядит закон изменения напряжения в наших розетках (помним, что частота сети равна 50 Гц или, что тоже самое, период равен 20 мс). Этот закон представлен на рисунке 1.
В розетках у нас, оказывается, синус с амплитудой аж 311 В, а не 220, как можно было подумать сначала. Что бы убрать все сомнения представлю вам картинку, как выглядит закон изменения напряжения в наших розетках (помним, что частота сети равна 50 Гц или, что тоже самое, период равен 20 мс). Этот закон представлен на рисунке 1.
 А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
 Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.
Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I2r = Mr, откуда I = √M,
Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I2r = Mr, откуда I = √M,