Электричество и магнетизм
Рассмотрим снова контур с током, но не станем его помещать на этот раз во внешнее магнитное поле. Ток сам создает свое собственное поле В, которое пронизывает контур. Это поле, как следует из закона Био — Савара — Лапласа, пропорционально силе тока
Собственное магнитное поле контура с током обуславливает наличие магнитного потока Y через поверхность, опирающуюся на этот контур, который также будет пропорционален силе тока в контуре
Введем коэффициент пропорциональности L
|
|
(8.16) |
Коэффициент пропорциональности L называется индуктивностью контура.
|
Индуктивность контурачисленно равна магнитному потоку, собственного магнитного поля через поверхность, опирающуюся на контур, при условии протекания в контуре единичного тока. |
Индуктивность контура определяется формой и размерами контура, а также свойствами окружающей среды.
|
В системе СИ единицей измерения индуктивности является генри (Гн)
|
Если в проводящем контуре протекает переменный электрический ток, то магнитное поле этого тока также меняется с течением времени. Собственный магнитный поток, создаваемый этим полем, также является переменным. Изменение магнитного потока влечет за собой возникновение ЭДС электромагнитной индукции.
|
Явление возникновения ЭДС индукции в замкнутом проводящем контуре вследствие изменения тока, текущего в этом контуре, называется явлением самоиндукции. |
Видео 8.
Возникающая при этом ЭДС называется ЭДС самоиндукции. Явление самоиндукции является частным случаем электромагнитной индукции.
Явление самоиндукции является, в частности, причиной явления, которое называют «экстра токи замыкания и размыкания». Оно состоит в следующем. Собственное магнитное поле в цепи постоянного тока изменяется в моменты замыкания или размыкания цепи. Это означает, что в такие моменты в цепи должна возникать ЭДС самоиндукции. Направление токов самоиндукции следует из правила Ленца. При замыкании цепи ЭДС самоиндукции вызывает ток, препятствующий увеличению основного тока в цепи, что делает конечной скорость роста силы тока, а при размыкании ток самоиндукции, препятствуя его уменьшению, делает конечной скорость убывания тока. Если бы не ЭДС самоиндукции, то при замыкании цепи ток мгновенно нарастал бы до своего стационарного значения, а при размыкании цепи, мгновенно убывал бы до нуля.
Выведем формулу для ЭДС самоиндукции . Для этого надо продифференцировать полный магнитный поток, охватываемый проводящим контуром, по времени
Для этого надо продифференцировать полный магнитный поток, охватываемый проводящим контуром, по времени
|
|
(8.17) |
Если контур не меняет свою форму, и рядом с контуром нет ферромагнетиков, то его индуктивность от времени не зависит. Однако, даже при неизменной форме контура, при наличии ферромагнетиков, например, ферромагнитного сердечника, индуктивность контура зависит от силы тока в нём и, тем самым, от времени, если ток переменный. Таким образом, в присутствии ферромагнетиков
,
что необходимо учитывать при дифференцировании
Подставляя это выражение в (8.17), получаем для неподвижного контура всреде
|
|
(8. |
Если же индуктивность контура не зависит от силы тока в нём, то имеем
|
|
(8.19) |
Мы приходим к закону самоиндукции. В этом простейшем случае:
|
В отсутствие ферромагнетиков ЭДС самоиндукции в цепи прямопропорциональна скорости изменения силы тока в этой цепи. |
Будем считать катушку длинной, а магнитное поле внутри нее — однородным. Пропустим через соленоид ток I. Тогда магнитная индукциявнутри соленоида равна, как мы знаем (см. (6.20)), равна
где — магнитная проницаемость сердечника, a n — число витков на единицу длины. Полное число витков в катушке равно , где l — ее длина. Пусть S — площадь поперечного сечения соленоида. Полный магнитный поток (потокосцепление) определяется как
Полное число витков в катушке равно , где l — ее длина. Пусть S — площадь поперечного сечения соленоида. Полный магнитный поток (потокосцепление) определяется как
|
|
(8.20) |
где V — объем соленоида: V = Sl. Согласно определению индуктивности как коэффициента пропорциональности между и I, получаем величину индуктивности длинного соленоида (рис. 8.31)
|
|
(8.21) |
Рис. 8.31. Индуктивность соленоида
При замыкании или размыкании цепи (то есть в случаях, когда ток в цепи меняется по величине) в ней вследствие явления самоиндукции возникают дополнительные токи, которые по правилу Ленца всегда направлены так, чтобы воспрепятствовать причине их вызывающей, то есть чтобы воспрепятствовать нарастанию или убыванию тока в цепи. Следовательно, как уже было сказано,при замыкании цепи ЭДС самоиндукции будет замедлять скорость нарастания тока, а при размыкании, напротив, замедлять скорость уменьшения тока в ней.
Следовательно, как уже было сказано,при замыкании цепи ЭДС самоиндукции будет замедлять скорость нарастания тока, а при размыкании, напротив, замедлять скорость уменьшения тока в ней.
Самоиндукция. Индуктивность. Энергия магнитного поля тока
Самоиндукция. Индуктивность. Энергия магнитного поля тока
- Подробности
- Просмотров: 625
Самоиндукция
Каждый проводник, по которому протекает эл.ток, находится в собственном магнитном поле.
При изменении силы тока в проводнике меняется м.поле, т.е. изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока ведет в возникновению вихревого эл.поля и в цепи появляется ЭДС индукции.
Это явление называется самоиндукцией.
Самоиндукция — явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока.
Проявление явления самоиндукции
Замыкание цепи
При замыкании в эл. цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны).
цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны).
В результате Л1 загорается позже, чем Л2.
Размыкание цепи
При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке, возникает вихревое эл.поле, направленное как ток (стремящееся сохранить прежнюю силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи.
Вывод:
в электротехнике явление самоиндукции проявляется при замыкании цепи (электрический ток нарастает постепенно) и при размыкании цепи (электрический ток пропадает не сразу).
ИНДУКТИВНОСТЬ
От чего зависит ЭДС самоиндукции?
Электрический ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф ~ B), индукция пропорциональна силе тока в проводнике
(B ~ I), следовательно магнитный поток пропорционален силе тока (Ф ~ I).
ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника (размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.
Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.
Индуктивность — физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду.
Также индуктивность можно рассчитать по формуле:
где Ф — магнитный поток через контур, I — сила тока в контуре.
Единицы измерения индуктивности в системе СИ:
Индуктивность катушки зависит от:
числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды ( возможен сердечник).
ЭДС САМОИНДУКЦИИ
ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.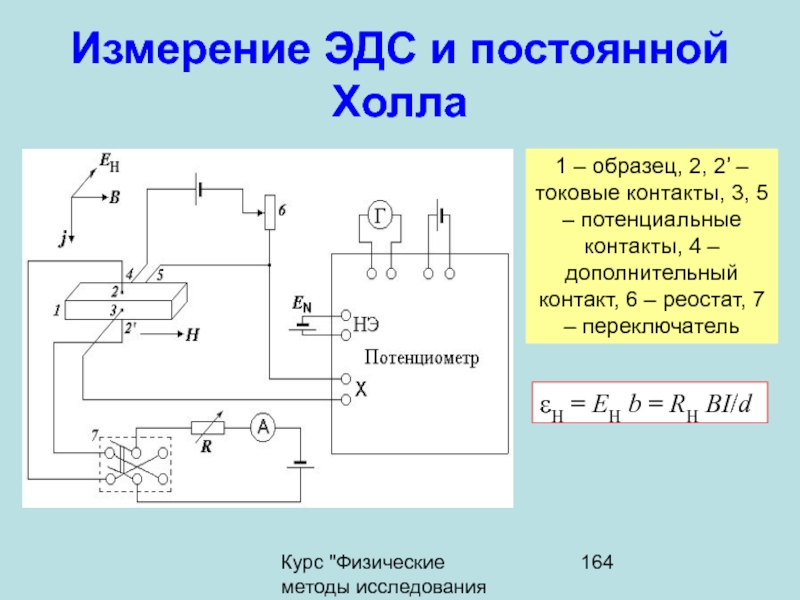
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА
Вокруг проводника с током существует магнитное поле, которое обладает энергией.
Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии.
В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля.
Энергия магнитного поля равна собственной энергии тока.
Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.
Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока.
Куда пропадает энергия магнитного поля после прекращения тока? — выделяется ( при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)
ВОПРОСЫ К ПРОВЕРОЧНОЙ РАБОТЕ
по теме «Электромагнитная индукция»
1. Перечислить 6 способов получения индукционного тока.
Перечислить 6 способов получения индукционного тока.
2. Явление электромагнитной индукции (определение).
3. Правило Ленца.
4. Магнитный поток ( определение, чертеж, формула, входящие величины, их ед. измерения).
5. Закон электромагнитной индукции (определение, формула).
6. Свойства вихревого электрического поля.
7. ЭДС индукции проводника, движущегося в однородном магнитном поле ( причина появления, чертеж, формула, входящие величины, их ед. измерения).
8. Самоиндукция (кратко проявление в электротехнике, определение).
9. ЭДС самоиндукции (ее действие и формула).
10. Индуктивность (определение, формулы, ед. измерения).
11. Энергия магнитного поля тока (формула, откуда появляется энергия м. поля тока, куда пропадает при прекращении тока).
Электромагнитное поле — Класс!ная физика
Взаимодействие токов. Магнитное поле. Вектор магнитной индукции. Сила Ампера —
Действие магнитного поля на движущийся заряд. Магнитные свойства вещества —
Явление электромагнитной индукции. Магнитный поток. Направление индукционного тока. Правило Ленца —
ЭДС электромагнитной индукции. Вихревое электрическое поле —
ЭДС индукции в движущихся проводниках
Магнитные свойства вещества —
Явление электромагнитной индукции. Магнитный поток. Направление индукционного тока. Правило Ленца —
ЭДС электромагнитной индукции. Вихревое электрическое поле —
ЭДС индукции в движущихся проводниках
—
Самоиндукция. Индуктивность. Энергия магнитного поля. Вопросы к пр/работе
Тест по физике на тему «Электромагнитная индукция»
Тест 11-1(электромагнитная индукция)
Вариант 1
1. Кто открыл явление электромагнитной индукции?
А. X. Эрстед. Б. Ш. Кулон. В. А. Вольта. Г. А. Ампер. Д. М. Фарадей. Е. Д. Максвелл.
2. Выводы катушки из медного провода присоединены к чувствительному гальванометру. В каком из перечисленных опытов гальванометр обнаружит возникновение ЭДС электромагнитной индукции в катушке?
В катушку вставляется постоянный магнит.
Из катушки вынимается постоянный магнит.
Постоянный магнит вращается вокруг своей продольной оси внутри катушки.

А. Только в случае 1. Б. Только в случае 2. В. Только в случае 3. Г. В случаях 1 и 2. Д. В случаях 1, 2 и 3.
3.Как называется физическая величина, равная произведению модуля В индукции магнитного поля на площадь S поверхности, пронизываемой магнитным полем, и косинус
угла а между вектором В индукции и нормалью п к этой поверхности?
А. Индуктивность. Б. Магнитный поток. В. Магнитная индукция. Г. Самоиндукция. Д. Энергия магнитного поля.
4. Каким из приведенных ниже выражений определяется ЭДС индукции в замкнутом контуре?
A. Б. В. Г. Д.
5. При вдвигании полосового магнита в металлическое кольцо и выдвигании из него в кольце возникает индукционный ток. Этот ток создает магнитное поле. Каким полюсом обращено магнитное поле тока в кольце к: 1) вдвигаемому северному полюсу магнита и 2) выдвигаемому северному полюсу магнита.
A. 1 — северным, 2 — северным. Б. 1 — южным, 2 — южным.
Б. 1 — южным, 2 — южным.
B. 1 — южным, 2 — северным. Г. 1 — северным, 2 — южным.
6. Как называется единица измерения магнитного потока?
А. Тесла. Б. Вебер. В. Гаусс. Г. Фарад. Д. Генри.
7. Единицей измерения какой физической величины является 1 Генри?
А. Индукции магнитного ноля. Б. Электроемкости. В. Самоиндукции. Г. Магнитного потока. Д. Индуктивности.
8. Каким выражением определяется связь магнитного по тока через контур с индуктивностью L контура и силой тока I в контуре?
A. LI. Б. . В. LI ‘ . Г. LI2. Д. .
9. Каким выражением определяется связь ЭДС самоиндукции с силой тока в катушке?
А. Б. В. LI. Г. . Д. LI ‘.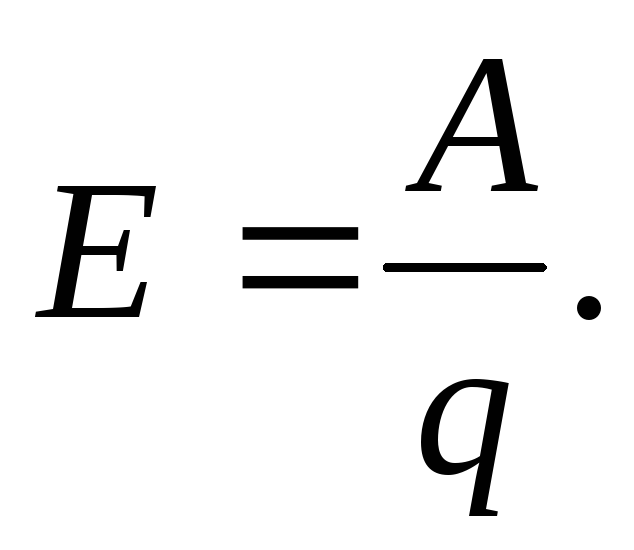
10. Ниже перечислены свойства различных полей. Какими из них обладает электростатическое поле?
Линии напряженности обязательно связаны с электрическими зарядами.
Линии напрялсенности не связаны с электрическими зарядами.
Поле обладает энергией.
Поле не обладает энергией.
Работа сил по перемещению электрического заряда по замкнутому пути может быть не равна нулю.
Работа сил по перемещению электрического заряда по любому замкнутому пути равна нулю.
А. 1, 4, 6. Б. 1, 3, 5. В. 1, 3, 6. Г. 2, 3, 5. Д. 2, 3, 6. Е. 2, 4, 6.
11. Контур площадью 1000 см2 находится в однородном магнитном поле с индукцией 0,5 Тл, угол между вектором В индукции и нормалью к поверхности контура 60°. Каков магнитный поток через контур?
А. 250 Вб. Б. 1000 Вб. В. 0,1 Вб. Г. 2,5 · 10-2 Вб. Д. 2,5 Вб.
В. 0,1 Вб. Г. 2,5 · 10-2 Вб. Д. 2,5 Вб.
12. Какая сила тока в контуре индуктивностью 5 мГн создает магнитный поток 2 · 10-2 Вб?
А. 4 мА. Б. 4 А. В. 250 А. Г. 250 мА. Д. 0,1 А. Е. 0,1 мА.
13. Магнитный поток через контур за 5 · 10-2 с равномерно уменьшился от 10 мВб до 0 мВб. Каково значение ЭДС в контуре в это время?
А. 5 · 10-4 В. Б. 0,1 В. В. 0,2 В. Г. 0,4 В. Д. 1 В. Е. 2 В.
14. Каково значение энергии магнитного поля катушки индуктивностью 5 Гн при силе тока в ней 400 мА?
А. 2 Дж. Б. 1 Дж. В. 0,8 Дж. Г. 0,4 Дж. Д. 1000 Дж. Е. 4·105 Дж.
15. Катушка, содержащая n витков провода, подключена к источнику постоянного тока с напряжением U на выходе. Каково максимальное значение ЭДС самоиндукции в катушке при увеличении напряжения на ее концах от 0 В до U В?
A, U В, Б.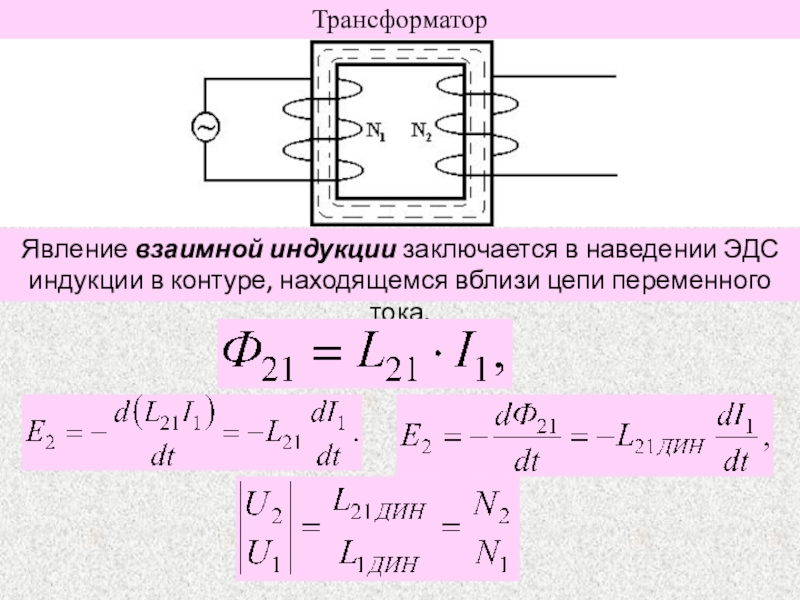 nU В. В. U/п В. Г. Может быть во много раз больше U, зависит от скорости изменения силы тока и от индуктивности катушки.
nU В. В. U/п В. Г. Может быть во много раз больше U, зависит от скорости изменения силы тока и от индуктивности катушки.
16. Две одинаковые лампы включены в цепь источника постоянного тока, первая последовательно с резистором, вторая последовательно с катушкой. В какой из ламп (рис. 1) сила тока при замыкании ключа К достигнет максимального значения позже другой?
А. В первой. Б. Во второй. В. В первой и второй одновременно. Г. В первой, если сопротивление резистора больше сопротивления катушки. Д. Во второй, если сопротивление катушки больше сопротивления резистора.
17. Катушка индуктивностью 2 Гн включена параллельно с резистором электрическим сопротивлением 900 Ом, сила тока в катушке 0,5 А, электрическое сопротивление катушки 100 Ом. Какой электрический заряд протечет в цепи катушки и резистора при отключении их от источника тока (рис. 2)?
А. 4000 Кл. Б. 1000 Кл. В. 250 Кл. Г. 1 • 10 -2 Кл. Д. 1,1 • 10-3 Кл. Е. 1 • 10-3 Кл.
Д. 1,1 • 10-3 Кл. Е. 1 • 10-3 Кл.
18. Самолет летит со скоростью 900 км/ч, модуль вертикальной составляющей вектора индукции магнитного поля Земли 4 • 105 Тл. Какова разность потенциалов между концами крыльев самолета, если размах крыльев равен 50 м?
А. 1,8 В. Б. 0,9 В. В. 0,5 В. Г. 0,25 В.
19. Какой должна быть сила тока в обмотке якоря электромотора для того, чтобы на участок обмотки из 20 витков длиной 10 см, расположенный перпендикулярно вектору индукции в магнитном поле с индукцией 1,5 Тл, действовала сила 120 Н?
А. 90 А. Б. 40 А. В. 0,9 А. Г. 0,4 А.
20. Какую силу нужно приложить к металлической перемычке для равномерного ее перемещения со скоростью 8 м/с по двум параллельным проводникам, расположенным на расстоянии 25 см друг от друга в однородном магнитном поле с индукцией 2 Тл? Вектор индукции перпендикулярен плоскости, в которой расположены рельсы. Проводники замкнуты резистором с электрическим сопротивлением 2 Ом.
А. 10000 Н. Б. 400 Н. В. 200 Н. Г. 4 Н. Д. 2 Н. Е. 1 Н.
Вариант 2
1. Как называется явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока через контур?
А. Электростатическая индукция. Б. Явление намагничивания. В. Сила Ампера. Г. Сила Лоренца. Д. Электролиз. Е. Электромагнитная индукция.
2. Выводы катушки из медного провода присоединены к чувствительному гальванометру. В каком из перечисленных опытов гальванометр обнаружит возникновение ЭДС электромагнитной индукции в катушке?
В катушку вставляется постоянный магнит.
Катушка надевается на магнит.
3)Катушка вращается вокруг магнита, находящегося
внутри нее.
А.В случаях 1, 2 и 3. Б. В случаях 1 и 2. В. Только в случае 1. Г. Только в случае 2. Д. Только в случае 3.
3. Каким из приведенных ниже выражений определяется магнитный поток?
A. BScosα. Б. . В. qvBsinα. Г. qvBI. Д. IBlsina.
4. Что выражает следующее утверждение: ЭДС индукции в замкнутом контуре пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром?
А. Закон электромагнитной индукции. Б. Правило Ленца. В. Закон Ома для полной цепи. Г. Явление самоиндукции. Д. Закон электролиза.
5. При вдвигании полосового магнита в металлическое кольцо и выдвигании из него в кольце возникает индукционный ток. Этот ток создает магнитное поле. Каким полюсом обращено магнитное поле тока в кольце к: 1) вдвигаемому южному полюсу магнита и 2) выдвигаемому южному полюсу магнита.
A. 1 — северным, 2 — северным. Б. 1 — южным, 2 — южным.
B. 1 — южным, 2 — северным. Г. 1 — северным, 2 — южным.
6. Единицей измерения какой физической величины является 1 Вебер?
А. Индукции магнитного поля. Б. Электроемкости. В. Самоиндукции. Г. Магнитного потока. Д. Индуктивности.
7. Как называется единица измерения индуктивности?
А. Тесла. Б. Вебер. В. Гаусс. Г. Фарад. Д. Генри.
8. Каким выражением определяется связь энергии магнитного потока в контуре с индуктивностью L контура и силой тока I в контуре?
А. . Б. . В. LI2, Г. LI ‘ . Д. LI.
9.Какая физическая величина х определяется выражением х= для катушки из п витков.
А. ЭДС индукции. Б. Магнитный поток. В. Индуктивность. Г. ЭДС самоиндукции. Д. Энергия магнитного поля. Е. Магнитная индукция.
10. Ниже перечислены свойства различных полей. Какими из них обладает вихревое индукционное электрическое поле?
Линии напряженности обязательно связаны с электрическими зарядами.
Линии напряженности не связаны с электрическими зарядами.
Поле обладает энергией.
Поле не обладает энергией.
Работа сил по перемещению электрического заряда по замкнутому пути может быть не равна нулю.
Работа сил по перемещению электрического заряда по любому замкнутому пути равна нулю.
А. 1, 4, 6. Б. 1, 3, 5. В. 1, 3, в. Г. 2, 3, 5. Д. 2, 3, 6. Е. 2, 4, 6.
11. Контур площадью 200 см2 находится в однородном магнитном поле с индукцией 0,5 Тл, угол между вектором В индукции и нормалью к поверхности контура 60°. Каков магнитный поток через контур?
А. 50 Вб. Б. 2 · 10-2 Вб. В. 5 · 10-3 Вб. Г. 200 Вб. Д. 5 Вб.
12. Ток 4 А создает в контуре магнитный поток 20 мВб. Какова индуктивность контура?
А. 5 Гн. Б. 5 мГн. В. 80 Гн. Г. 80 мГн. Д. 0,2 Гн. Е. 200 Гн.
13. Магнитный поток через контур за 0,5 с равномерно уменьшился от 10 мВб до 0 мВб. Каково значение ЭДС в контуре в это время?
А. 5 · 10-3 В. Б. 5 В. В. 10 В. Г. 20 В. Д. 0,02 В. Е. 0,01 В.
14. Каково значение энергии магнитного поля катушки индуктивностью 500 мГн при силе тока в ней 4 А?
А. 2 Дж. Б. 1 Дж. В. 8 Дж. Г. 4 Дж. Д. 1000 Дж. Е. 4000 Дж.
15. Катушка, содержащая п витков провода, подключена к источнику постоянного тока с напряжением U на выходе. Каково максимальное значение ЭДС самоиндукции в катушке при уменьшении напряжения на ее концах от U В до 0 В?
A. U В. Б. nU В. В. U/n В. Г. Может быть во много раз больше U, зависит от скорости изменения силы тока и от индуктивности катушки.
16. В электрической цепи, представленной на рисунке 1, четыре ключа 1, 2, 3 и 4 замкнуты. Размыкание какого из четырех даст лучшую возможность обнаружить явление самоиндукции?
А. 1. Б. 2. В. 3. Г. 4. Д. Любого из четырех.
17. Катушка индуктивностью 2 Гн включена параллельно с резистором электрическим сопротивлением 100 Ом, сила тока в катушке 0,5 А, электрическое сопротивление катушки 900 Ом. Какой электрический заряд протечет в цепи катушки и резистора при отключении их от источника тока (рис. 2)?
А. 4000 Кл. Б. 1000 Кл. В. 250 Кл. Г. 1 • 10-2 Кл. Д. 1,1 • 10-3 Кл. Е. 1 • 10-3 Кл.
18. Самолет летит со скоростью 1800 км/ч, модуль вертикальной составляющей вектора индукции магнитного поля Земли 4 • 10-5 Тл. Какова разность потенциалов между концами крыльев самолета, если размах крыльев равен 25 м?
А. 1,8 В. В. 0,5 В. В. 0,9 В. Г. 0,25 В.
19. Прямоугольная рамка площадью S с током I помещена в магнитном поле с индукцией В . Чему равен момент силы, действующей на рамку, если угол между вектором В и нормалью к рамке равен а?
A. IBS sin а. Б. IBS. В. IBS cos а. Г. I2BS sin а. Д. I2BS cos а.
20. По двум вертикальным рельсам, верхние концы которых замкнуты резистором электрическим сопротивлением R, начинает скользить проводящая перемычка массой т и длиной I. Система находится в магнитном поле. Вектор индукции перпендикулярен плоскости, в которой расположены рельсы. Найдите установившуюся скорость и движения перемычки. Сила трения пренебрежимо мала.
А. . В. В. . Г. . Д. .
Ответы:
Номер вопроса и ответ
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Вариант 1
Д
Г
Б
Б
Г
Б
Д
А
Д
В
Г
Б
В
Г
А
Б
Е
В
Б
Е
Вариант 2
Е
Б
А
А
В
Г
Д
Б
А
Г
В
Б
Д
Г
Г
А
Е
Б
В
А
Электромагнитная индукция
Магнитный поток. В однородном магнитном поле, модуль вектора индукции которого равен В, помещен плоский замкнутый контур площадью S. Нормаль n к плоскости контура составляет угол a с направлением вектора магнитной индукции В (см. рис. 1).
Магнитным потоком через поверхность называется величина Ф, определяемая соотношением:
Ф = В·S·cos a.
Единица измерения магнитного потока в систем СИ — 1 Вебер (1 Вб).
Электромагнитная индукция. Явление электромагнитной индукции обнаружено в 1831 г. Фарадеем. Оно выражает взаимосвязь электрических и магнитных явлений.
Рассмотрим некоторые экспериментальные факты:
постоянный магнит вставляют в катушку, замкнутую на гальванометр, или вынимают из нее. При движении магнита в контуре возникает электрический ток
Аналогичный результат будет иметь место в случае перемещения электромагнита, по которому пропускают постоянный ток, относительно первичной катушки или при изменении тока в неподвижной вторичной катушке.
рамку, замкнутую на гальванометр, помещают в однородное магнитное поле и вращают. В рамке возникает электрический ток. Если же рамка движется поступательно, не пересекая силовых линий, то ток в ней не возникает.
рамка движется в неоднородном магнитном поле. Число линий индукции, пересекающих рамку, изменяется. В рамке возникает электрический ток
Ток, возникающий в контуре при изменении магнитного потока, называют индукционным током.
Вы знаете, что условием существования электрического тока в замкнутом контуре является наличие электродвижущей силы, поддерживающей разность потенциалов. Следовательно, при изменении магнитного потока, пронизывающего замкнутый контур, в нем возникает ЭДС, которую называют ЭДС индукции (ei).
Явление возникновения ЭДС в контуре при изменении магнитного потока, пронизывающего контур, называется электромагнитной индукцией.
Если контур замкнут, то ЭДС индукции проявляется в возникновении электрического индукционного тока
I = ei/R , где R- сопротивление контура.
Если контур разомкнут, то на концах проводника возникает разность потенциалов, равная ei.
Направление индукционного тока в контуре определяется правилом Ленца:
Индукционный ток направлен так, чтобы своим магнитным полем противодействовать изменению магнитного потока, которым он вызван.
Направление индукционного тока определяется следующим образом:
1. установить направление внешнего магнитного поля В.
2. определить увеличивается или уменьшается поток вектора магнитной индукции внешнего поля.
3. по правилу Ленца указать направление вектора магнитной индукции индукционного тока Вi.
4. по правилу правого винта определить направление индукционного тока в контуре.
ЭДС индукции в движущемся проводнике. Пусть проводник длиной L перемещается со скоростью V в однородном магнитном поле, пересекая силовые линии. Вместе с проводником движутся заряды, находящиеся в проводнике. На движущийся в магнитном поле заряд действует сила Лоренца. Свободные электроны смещаются к одному концу проводника, а на другом остаются нескомпенсированные положительные заряды. Возникает разность потенциалов, которая и представляет собой ЭДС индукции ei. Ее величину можно определить, рассчитав работу, совершаемую силой Лоренца при перемещении заряда вдоль проводника:
ei = A/q = F·L/q.
Отсюда следует, что
ei = B·V·L·sin a.
Самоиндукция является частным случаем разнообразных проявлений электромагнитной индукции.
Рассмотрим контур, подключенный к источнику тока. По контуру протекает электрический ток I. Этот ток создает в окружающем пространстве магнитное поле. В результате контур пронизывается собственным магнитным потоком Ф. Очевидно, что собственный магнитный поток пропорционален току в контуре, создавшему магнитной поле:
Ф = L·I.
Коэффициент пропорциональности L называется индуктивностью контура. Индуктивность зависит от размеров, формы проводника, магнитных свойств среды. Единица измерения индуктивности в системе СИ — 1 Генри (Гн).
Если ток в контуре изменяется, то изменяется и собственный магнитный поток Фс. Изменение величины Фс приводит к возникновению в контуре ЭДС индукции. Данное явление называется самоиндукцией, а соответствующее значение — ЭДС самоиндукции eiс.
Из закона электромагнитной индукции следует, что
eiс = dФс/dt.
Если L = const, то eiс= — L·dI/dt.
Каким выражением определяется эдс самоиндукции. Явление самоиндукции
Самоиндукцией называется наведение ЭДС в проводнике при изменении электрического тока в этом проводнике.
Когда подается напряжение на катушку электромагнита, ток возрастает не сразу. Он увеличивается постепенно. Нарастание тока тормозится возникшим напряжением, противоположным приложенному. Это напряжение – электродвижущая сила (ЭДС) самоиндукции. Значение ЭДС постепенно уменьшается, и ток в электромагните возрастает до номинального значения.
Взаимодействие электрического и магнитного полей – причина самоиндукции
Электрическое и магнитное поля взаимосвязаны: электрический ток или меняющееся электрическое поле создает магнитное поле.
В свою очередь, меняющееся магнитное поле создает электрическое поле.
Рассмотрим процессы в проводящем контуре, когда в нем меняется электрический ток (например, его включают или выключают).
- В проводнике, помещенном в меняющееся магнитное поле, наводится ЭДС.
- Если в проводнике меняется величина электрического тока – возникает меняющееся магнитное поле.
- Меняющееся магнитное поле, созданное током в проводнике, наводит ЭДС самоиндукции в этом же проводнике.
Не во всех электрических цепях возникает эффект самоиндукции. Лампочка накаливания мгновенно вспыхивает при подаче тока, и мгновенно гаснет при его отключении, а в электромагните, на который подается и выключается постоянное напряжение, процессы растянуты во времени. У лампочки и электромагнита разная инерционность.
В механике мерой инерционности является масса: чтобы привести в движение массивный предмет, нужно прикладывать усилие в течение некоторого времени.
В электротехнике мерой инерционности является величина, названная индуктивностью. Она обозначается символом L . Единица измерения индуктивности – Генри (Гн), а также производные единицы: миллиГенри (мГн), микроГенри (мкГн) и так далее. Чем больше индуктивность цепи, тем дольше и мощнее протекают переходные процессы. Лампочка накаливания имеет очень малую индуктивность, а у электромагнита индуктивность большая.
В радиотехнике и электротехнике используются дроссели – детали, имеющие нормированные значения индуктивности.
На рисунке приведена схема опыта, демонстрирующего явление самоиндукции.
Катушка, намотанная на ферритовый сердечник, имеет значительную индуктивность. Источник питания – батарейка с номиналом полтора вольта. Пока тумблер находится во включенном состоянии, лампочка горит тускло, поскольку напряжения батарейки для нее недостаточно. После размыкания тумблера лампочка вспыхивает ярко и потом гаснет.
Почему лампочка вспыхивает после отключения напряжения питания? Через нее разряжается ЭДС самоиндукции, наведенная в катушке в момент выключения напряжения.
Но почему свет не просто продолжает гореть, а вспыхивает ярче, чем при включенном тумблере? ЭДС самоиндукции превышает номинальное напряжение батарейки. Рассмотрим, от чего зависит такой эффект.
От чего зависит ЭДС самоиндукции?
ЭДС самоиндукции, возникающая в электрической цепи, зависит от ее индуктивности и от скорости изменения тока в цепи.
Скорость изменения тока имеет важное значение. Если он мгновенно выключается, то есть скорость изменения очень большая, то и ЭДС самоиндукции велико. Наведенное напряжение разряжается через параллельные ветви цепи (в опыте с лампочкой – через лампочку).
Самоиндукция и переходные процессы в электрических цепях
Индуктивность электрической плитки или лампочки накаливания очень мала, и ток в этих электроприборах, при включении и выключении, возникает или исчезает практически мгновенно. Индуктивность электродвигателя велика, и он «выходит на режим» в течение нескольких минут.
Если выключить ток в большом электромагните с большим значением индукции, допустив высокую скорость уменьшения тока, то между контактами выключателя вспыхивает искра, а в случае большого тока может загореться вольтова дуга. Это опасное явление, поэтому в цепях с большой индуктивностью ток снижают постепенно, используя реостат (элемент с переменным электрическим сопротивлением).
Безопасное отключение электроэнергии – серьезна проблема. На все выключатели действуют «ударные нагрузки», возникающие из-за ЭДС самоиндукции при отключении тока, и выключатели «искрят». Для каждого типа выключателей указывается максимальное значение тока, которое можно коммутировать. Если ток превышает допустимое значение, в выключателе может вспыхнуть электрическая дуга.
На опасных производствах, в угольных шахтах, хранилищах нефтепродуктов простое искрение выключателей недопустимо. Здесь применяются взрывобезопасные выключатели, надежно защищенные герметичным пластмассовым корпусом. Цена таких выключателей в десятки раз выше, чем обычных – это необходимая плата за безопасность.
>> Самоиндукция. Индуктивность
§ 15 САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ
Самоиндукция . Если по катушке идет переменный ток, то магнитный поток, пронизывающий катушку, меняется. Поэтому в том же самом проводнике, по которому идет переменный ток, возникает ЭДС индукции. Это явление называют самоиндукцией .
При самоиндукции проводящий контур выполняет двойную роль: переменный ток в проводнике вызывает появление магнитного потока через поверхность, ограниченную контуром. А так как магнитный поток изменяется со временем, то появляется ЭДС индукции . По правилу Ленца в момент нарастания тока напряженность вихревого электрического поля направлена против тока. Следовательно, в этот момент вихревое поле препятствует нарастанию тока. Наоборот, в момент уменьшения тока вихревое поле поддерживает его.
Явление самоиндукции можно наблюдать в простых опытах. На рисунке 2.13 показана схема параллельного соединения двух одинаковых ламп. Одну из них подключают к источнику через резистор R, а другую — последовательно с катушкой L, снабженной железным сердечником.
При замыкании ключа первая лампа вспыхивает практически сразу, а вторая — с заметным запозданием. ЭДС самоиндукции в цепи этой лампы велика, и сила тока не сразу достигает своего максимального значения (рис. 2.14).
Появление ЭДС самоиндукции при размыкании можно наблюдать в опыте с цепью, схематически показанной на рисунке 2.15. При размыкании ключа в катушке L возникает ЭДС самоиндукции, поддерживающая первоначальный ток. в результате в момент размыкания через гальванометр идет ток (цветная стрелка), направленный против начального тока до размыкания (черная стрелка). Сила тока при размыкании цепи может превышать силу тока, проходящего через гальванометр при замкнутом ключе. Это означает, что ЭДС самоиндукции больше ЭДС батареи элементов.
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные урокиИзобретение относится к электротехнике, в частности к конструкциям индукционных генераторов тока, и может быть использовано в электромагнитных установках и электрических машинах, таких как двигатели, генераторы, трансформаторы, в частности, в качестве повышающего трансформатора. Технический результат состоит в повышении эдс на выходе за счет использования импульсных напряжений на вторичной обмотке и осуществления конструкции вторичной обмотки, которая бы позволяла производить непосредственный съем с генератора возникающего импульсного напряжения, и одновременно суммарной мощности первичной и вторичной обмоток. 6 з.п. ф-лы, 2 ил.
Рисунки к патенту РФ 2524387
Изобретение относится к электротехнике, в частности к конструкциям импульсных индукционных генераторов тока.
Назначением данного изобретения является использование импульсного генератора ЭДС самоиндукции для обеспечения импульсного энергопитания различных электромагнитных установок и электрических машин, что позволяет существенно расширить арсенал импульсных источников энергии. Из уровня техники известен «Индукционный синхронный генератор», Заявка RU 9811934 7, опубл. 10.09.2000, МПК H02K 21/14, использующий токи обмотки статора, на якоре которого токи пульсируют, и индуктор (ротор), выполненный защищенным от магнитного поля токов обмотки якоря статора. Позволяет расширить режимы работы генератора. Однако в генераторе присутствуют вращающиеся части, а следовательно, он обладает всеми недостатками таких генераторов, т.е. не решены проблемы, связанные с коммутацией электроэнергии. В предложенной конструкции невозможно получение требуемого высокого напряжения.
Известен «Генератор электрической энергии», заявка RU 9402533 5, опубл. 10.06.1996, МПК H02K 19/16, содержащий составные кольцевые обмотки с сердечником, индукционную катушку и обмотку возбуждения. Позволяет увеличить производительность генератора электрической энергии, уменьшить индуктивное сопротивление статорной обмотки, уменьшить затраты на механическую работу при преобразовании механической энергии в электрическую и повысить КПД. Однако генератор в силу особенностей конструкции не позволяет использовать ЭДС самоиндукции. В генераторе присутствуют вращающиеся части, а, следовательно, он обладает всеми недостатками таких генераторов, т.е. не решены проблемы, связанные с коммутацией электроэнергии.
Известна полезная модель «Комбинированная электромагнитная обмотка», патент RU 96443, опубл. 27.07.2010, МПК H01F 5/00, в которой имеется два или более проводника с выводами, и проводники разделены диэлектриком. Позволяет расширить режимы работы. Однако оба проводника применяются в качестве первичной обмотки, отсутствует вторичная обмотка высокого напряжения, что не позволяет обмотку использовать в трансформаторах высокого напряжения, а также не обеспечивает съем и использование ЭДС индукции от вторичной обмотки.
Наиболее близкой заявкой на изобретение является «Индуктивно-статический способ генерации электрической энергии и устройство для его осуществления», RU 2004124018, опубл. 27.01.2006, МПК H01F 1/00, в соответствии с которым имеется первичная и вторичная обмотки, образующие катушку индуктивности с переходом свободной магнитной энергии в индуктивно-зависимое состояние, и происходит наведение ЭДС индукции и получение уплотнения магнитных потоков, пропорциональное увеличению электрической мощности. Позволяет использовать вторичную обмотку с меньшей на величину уплотнения магнитных потоков индуктивностью, чем достигается пропорциональное уплотнение и увеличение электрической мощности генератора. В способе используют индукционный и, одновременно, статический способы генерации. Однако не предложена конструкция вторичной обмотки генератора, которая позволяет производить непосредственный съем с генератора возникающее импульсное напряжение и ток ЭДС самоиндукции.
Также наиболее близким решением является классическая электрическая схема для проведения опытов по демонстрации электромагнитной индукции при размыкании цепи. Эта схема (устройство) функционально является импульсным генератором ЭДС самоиндукции. В связи с вышесказанным, в качестве прототипа принимаем установку, показанную на чертеже — рис.424 стр.231, учебник: Курс физики, часть вторая, изд. «Наука», Москва 1970 г. Авторы: Л.С. Жданов, В.А. Маранджан.
Однако в классической схеме сердечник из электротехнической стали конструктивно не способен выполнять в устройстве одновременно две функции: электропроводящей обмотки и классического, как на рис.424 прототипа, магнитопровода, т.е сердечника (М) индукционной катушки. Прототип не позволяет производить непосредственный съем и использование ЭДС самоиндукции, возникающей в сердечнике классической индукционной катушки.
Задачей предложенного изобретения является использование импульсных напряжений и осуществление конструкции вторичной обмотки генератора, которая бы позволяла производить непосредственный съем с генератора возникающего импульсного напряжения.
Техническим результатом, который обеспечивает предложенное техническое решение, является существенное расширение арсенала средств для импульсного генерирования и преобразования электроэнергии. Заявленный технический результат обеспечен за счет того, что импульсный генератор ЭДС самоиндукции конструктивно исполнен в виде первичной и вторичной обмоток однофазного повышающего трансформатора в стандартном техническом исполнении (с учетом того, что вторичная обмотка является одновременно функционально электропроводником и магнитопроводом, то предлагается рассматривать представленную конструкцию как простейшую индукционную катушку с сердечником, конструктивно исполненным в виде спиральной катушки с возможностью съема с него ЭДС самоиндукции) и они снабжены двумя или более проводниками, которые разделены диэлектриком и каждый проводник имеет выводы. Генератор отличается тем, что первичная обмотка (проводник) низкого напряжения выполнена спирально-ленточной и имеет по меньшей мере 2 витка, намотанных плотно или с небольшим зазором, виток к витку, лента обмотки выполнена шириной от 120 до 200 мм и толщиной от 1 до 2 мм; вторичная обмотка (проводник) высокого напряжения также выполнена спирально-ленточной, лента обмотки выполнена из электротехнической стали, покрытой электроизоляцией, и имеет по меньшей мере 100 витков, намотанных плотно или с небольшим зазором, виток к витку, лента выполнена шириной от 120 до 200 мм и толщиной не более 0,1 мм. Первичная обмотка электрически соединена с аккумуляторной батареей низкого напряжения через ключ-прерыватель с образованием замкнутой электрической цепи, где вторичная обмотка является одновременно электропроводящей обмоткой и магнитопроводом. При этом витки первичной обмотки расположены снаружи витков вторичной обмотки таким образом, что обе обмотки образуют повышающий трансформатор, в котором вторичная обмотка является индукционной катушкой трансформатора высокого напряжения, обеспечивая электропроводность за счет ленты из электротехнической стали, изолированной внешним слоем изоляции и, одновременно, выполняет функцию сердечника для первичной обмотки, ЭДС снимают посредством проводников, электрически подсоединенных к концам ленты вторичной обмотки, и получают за счет периодического срабатывания ключа-прерывателя, причем обеспечивают за счет частоты срабатывания ключа-прерывателя расчетные импульсное напряжение и ток, возникающие во вторичной обмотке, по формуле
где — где L — индуктивность цепи или коэффициент пропорциональности между скоростью изменения силы тока в контуре и возникающей вследствие этого ЭДС самоиндукции,
— скорость изменения силы тока в электрической цепи
В частных случаях первичная обмотка может быть выполнена из медного или алюминиевого проводника, может иметь 3 витка и более, количество витков ограничено трансформаторным отношением: отношение количества витков вторичной обмотки к количеству витков первичной обмотки, что определяет коэффициент трансформации, т.е. насколько напряжение во вторичной обмотке больше, чем в первичной. Например, аккумуляторная батарея низкого напряжения может быть рассчитана на 12-24 вольт и она является источником постоянного тока. В частности, периодическое срабатывание ключа-прерывателя осуществляют с промышленной частотой переменного тока 50 Гц. При этом частоты могут быть любые технически возможные для осуществления, но лучше 50 Гц, так как ее проще преобразовать либо потреблять с помощью имеющихся стандартных преобразователей или электроприборов. Расчетная ЭДС самоиндукции во вторичной обмотке обеспечивается, в частности, геометрией контура и магнитными свойствами сердечника для первичной обмотки. Так она может быть выполнена с формой контура, который выполнен круглым с диаметром 150 мм и более, что зависит от коэффициента трансформации, который и определит диаметр вторичной обмотки в зависимости от применяемой толщины электротехнической стали, или круглой спиральной формой. Поскольку вторичная обмотка является обмоткой высокого напряжения и выполнена из электротехнической стали, то это значит, что ее магнитные свойства определены самим материалом (т.е собственно магнитными свойствами электротехнической стали).
Изобретение в наиболее обобщенном виде иллюстрируется чертежами. Конкретное конструктивное исполнение не ограничивается показанными на чертежах вариантами исполнения.
На Фиг.1 показана схема расположения первичной и вторичной обмоток и аккумуляторная батарея с ключом-прерывателем.
На Фиг.2 — показано сечение А-А по соединенным вторичной и первичной обмоткам.
Данное техническое решение иллюстрируется чертежом, который не охватывает всех возможных конструктивных вариантов исполнения представленной схемы подключения.
Устройство Импульсного генератора ЭДС самоиндукции показано на фиг.1 и фиг.2 (в разрезе), и это устройство конструктивно исполнено в виде однофазного повышающего трансформатора (а также конструктивно является простейшей индукционной катушкой), который состоит из первичной (1) спирально-ленточной обмотки (медный или алюминиевый проводник), 2-3 витка толщиной 1-2 мм, шириной 120 мм, подключенной к аккумуляторной батарее (2) низкого напряжения 12-24 в — источник постоянного тока через ключ-прерыватель (3), образующих замкнутую электрическую цепь.
Вторичная спирально-ленточная обмотка высокого напряжения (4) из электротехнической стали, покрытой электроизоляцией, имеет количество витков от 100 и более, толщина ленты 0,1 мм, ширина 120 мм.
Вторичная обмотка (4) из электротехнической стали выполняет в конструкции две функции одновременно: электропроводящей обмотки и магнитопровода.
В качестве электропроводника вторичная обмотка (4) является индукционной катушкой высокого напряжения повышающего трансформатора.
В качестве магнитопровода вторичная обмотка (4) является сердечником для первичной обмотки (2) классической индукционной катушки.
Первичная (1) и вторичной (4) обмотки однофазного повышающего трансформатора и снабжены двумя или более проводниками (5), проводники вторичной обмотки имеют вывод (6) — т.е. ЭДС снимают посредством проводников (5, 6), электрически подсоединенных к концам ленты вторичной обмотки, и получают за счет периодического срабатывания ключа-прерывателя (3). Причем токи, возникающие во вторичной обмотке, рассчитывают по формуле
где L — индуктивность цепи или коэффициент пропорциональности между скоростью изменения силы тока в контуре первичной обмотки (1) и возникающей вследствие этого ЭДС самоиндукции во вторичной обмотке (2),
— скорость изменения силы тока в электрической цепи первичной обмотки (1) за счет ключа-прерывателя (3).
Периодическое срабатывание ключа-прерывателя (3) осуществляют с промышленной частотой переменного тока 50 Гц. Расчетную ЭДС самоиндукции во вторичной обмотке (4) обеспечивают геометрией контура вторичной обмотки (4) и магнитными свойствами сердечника (4) для первичной обмотки (1).
Форма контура, полученного первичной (1) и вторичной (4) обмотками, в представленном варианте выполнена круглой диаметром 150 мм и более.
Устройство работает следующим образом.
При замыкании ключом (3) электрической цепи первичной обмотки (1) возникает магнитное поле, энергия которого запасается в магнитном поле вторичной обмотки (4).
Размыкание ключа (3) цепи первичной обмотки (1) образует убывающий ток, который по правилу Ленца стремится поддержать ЭДС наведенной индукции вторичной обмотки (4).
В результате запасенная в магнитном поле вторичной обмотки (4) энергия преобразуется в дополнительную энергию тока самоиндукции первичной обмотки (1), запитавшей электрическую цепь вторичной обмотки (4).
В зависимости от количества запасенной в цепи вторичной обмотки (4) магнитной энергии мощность тока самоиндукции может быть различной и определяется по известной формуле:
Таким образом, данным изобретением достигается технический результат, состоящий в том, что конструкция, материал и двойное функциональное назначение вторичной обмотки устройства позволяет снимать и эффективно использовать возникающую ЭДС самоиндукции.
Промышленная применимость предложенного технического решения подтверждается общими правилами физики. Так, эффект самоиндукции описан в учебнике (Л.С. Жданов, В.А. Маранджян, курс физики для средних специальных заведений, ч. 2 электричество, изд. Третье, стереотипное, главная редакция физико-математической литературы, М., 1970 г., стр.231,232,233). Самоиндукция возникает при размыкании цепи, она прямо пропорциональна скорости изменения силы тока в электрической цепи. В традиционных схемах явление самоиндукции всегда сопровождается возникновением искры, возникающей в месте разрыва цепи. Поскольку в предложенной конструкции нет разрыва электрической цепи во вторичной обмотке (4) благодаря ее конструкции, в зависимости от количества запасенной в этой цепи магнитной энергии, ток размыкания не осуществляет искрение, а переходит в генерированную мощность. Таким образом, в конструкции вторичной обмотки (4) при размыкании цепи постоянного тока в первичной обмотке (1) запасенная в магнитном поле этой цепи энергия превращается в энергию тока самоиндукции в цепи вторичной обмотки (4).
Поскольку электродвижущей силой (ЭДС) называют величину, равную работе сторонних сил, в нашем случае — это изменяющееся магнитное поле первичной катушки (1), отнесенной к единице положительного заряда, это и есть ЭДС, действующая в цепи или на ее участке, в нашем случае — это вторичная обмотка (4). Сторонние силы можно охарактеризовать работой, которую они совершают над перемещающимися по цепи зарядами, и размерность ЭДС совпадает с размерностью потенциала и измеряется в тех же единицах. Поэтому векторную величину Е еще называют напряженностью поля сторонних сил. Поле сторонних сил в нашем случае возникает за счет переменного магнитного поля в первичной обмотке (1). Таким образом, ЭДС, действующая в замкнутой цепи, может быть определена как циркуляция вектора напряженности поля сторонних сил, т.е. сторонних сил, возникающих в первичной обмотке (1) за счет прерывания электрического поля ключом-прерывателем (3). Данное правило обеспечивает возникновение ЭДС индукции во вторичной обмотке (4). Это физическое явление описано в в учебнике (И.В. Савельев, Курс физики, том 2, электричество, стр.84,85, изд. Второе стереотипное, изд. Наука, главная редакция физико-математической литературы, М., 1966 г.).
Кроме сторонних сил, на заряд действуют силы электростатического поля, которые возникают непосредственно во вторичной катушке (4).
Устройство также использует явление электромагнитной индукции, описанной в (Р.А. Мустафаев, В.Г. Кривцов, учебник, физика, в помощь поступающим в ВУЗы, изд. М., Высшая школа, 1989 г.).
Таким образом, используемая в предложенном изобретении конструкция генератора как устройство позволяет эффективно генерировать, снимать и использовать ЭДС самоиндукции. Таким образом, устройство может быть изготовлено промышленным способом и внедряться в качестве перспективного эффективного импульсного генератора ЭДС самоиндукции, который позволяет расширить арсенал технических средств для импульсного генерирования и преобразования электроэнергии.
ФОРМУЛА ИЗОБРЕТЕНИЯ
1. Импульсный генератор эдс самоиндукции, конструктивно исполненный в виде однофазного повышающего трансформатора, состоящего из первичной и вторичной обмоток и снабжен двумя или более проводниками, которые разделены диэлектриком, а проводник имеет выводы, отличающийся тем, что первичная обмотка низкого напряжения выполнена спирально-ленточной и имеет по меньшей мере два витка, намотанных плотно или на небольшом расстоянии друг от друга, лента обмотки выполнена шириной 120-200 мм и толщиной 1-2 мм; вторичная обмотка высокого напряжения также выполнена спирально-ленточной, лента обмотки выполнена из электротехнической стали, покрытой электроизоляцией, имеет по меньшей мере 100 витков, намотанных плотно или на небольшом расстоянии друг от друга, лента выполнена шириной 120-200 мм и толщиной не более 0,1 мм, первичная обмотка электрически соединена с аккумуляторной батареей низкого напряжения через ключ-прерыватель с образованием замкнутой электрической цепи, а вторичная обмотка является одновременно электропроводящей обмоткой и магнитопроводом, при этом витки первичной обмотки расположены снаружи витков вторичной обмотки таким образом, что обе обмотки образуют повышающий трансформатор, в котором вторичная обмотка является индукционной катушкой повышающего трансформатора, обеспечивая электропроводность за счет ленты из электротехнической стали, изолированной внешним слоем изоляции, и одновременно выполняет функцию сердечника для первичной обмотки, эдс снимают посредством проводников, электрически подсоединенных к концам ленты вторичной обмотки, и получают за счет периодического срабатывания ключа-прерывателя.
2. Импульсный генератор эдс самоиндукции по п.1, отличающийся тем, что первичная обмотка выполнена из медного или алюминиевого проводника.
3. Импульсный генератор эдс самоиндукции по п.1, отличающийся тем, что первичная обмотка имеет три витка.
4. Импульсный генератор эдс самоиндукции по п.1, отличающийся тем, что аккумуляторная батарея низкого напряжения рассчитана на 12-24 вольт и является источником постоянного тока.
5. Импульсный генератор эдс самоиндукции по п.1, отличающийся тем, что периодическое срабатывание ключа-прерывателя осуществляют с промышленной частотой переменного тока 50 Гц.
6. Импульсный генератор эдс самоиндукции по п.1, отличающийся тем, что расчетную эдс самоиндукции обеспечивают геометрией контура и магнитными свойствами сердечника для первичной обмотки.
7. Импульсный генератор эдс самоиндукции по п.1, отличающийся тем, что форма контура выполнена круглой диаметром 150 мм и более.
При замыкании выключателя в цепи, представленной на рисунке 1, возникнет электрический ток, направление которого показано одинарными стрелками. С появлением тока возникает магнитное поле, индукционные линии которого пересекают проводник и индуктируют в нем электродвижущую силу (ЭДС). Как было указано в статье «Явление электромагнитной индукции «, эта ЭДС называется ЭДС самоиндукции. Так как всякая индуктированная ЭДС по правилу Ленца направлена против причины, ее вызвавшей, а этой причиной будет ЭДС батареи элементов, то ЭДС самоиндукции катушки будет направлена против ЭДС батареи. Направление ЭДС самоиндукции на рисунке 1 показано двойными стрелками.
Таким образом, ток устанавливается в цепи не сразу. Только когда магнитный поток установится, пересечение проводника магнитными линиями прекратится и ЭДС самоиндукции исчезнет. Тогда в цепи будет протекать постоянный ток.
На рисунке 2 дано графическое изображение постоянного тока. По горизонтальной оси отложено время, по вертикальной оси — ток. Из рисунка видно, что если в первый момент времени ток равен 6 А, то в третий, седьмой и так далее моменты времени он также и будет равен 6 А.
На рисунке 3 показано, как устанавливается ток в цепи после включения. ЭДС самоиндукции, направленная в момент включения против ЭДС батареи элементов, ослабляет ток в цепи, и поэтому в момент включения ток равен нулю. Далее в первый момент времени ток равен 2 А, во второй момент времени — 4 А, в третий — 5 А, и только спустя некоторое время в цепи устанавливается ток 6 А.
| Рисунок 3. График нарастания тока в цепи с учетом ЭДС самоиндукции | Рисунок 4. ЭДС самоиндукции в момент размыкания цепи направлена одинаково с ЭДС источника напряжения |
При размыкании цепи (рисунок 4) исчезающий ток, направление которого показано одинарной стрелкой, будет уменьшать свое магнитное поле. Это поле, уменьшаясь от некоторой величины до нуля, будет вновь пересекать проводник и индуктировать в нем ЭДС самоиндукции.
При выключении электрической цепи с индуктивностью ЭДС самоиндукции будет направлена в ту же сторону, что и ЭДС источника напряжения. Направление ЭДС самоиндукции показано на рисунке 4 двойной стрелкой. В результате действия ЭДС самоиндукции ток в цепи исчезает не сразу.
Таким образом, ЭДС самоиндукции всегда направлена против причины, ее вызвавшей. Отмечая это ее свойство, говорят что ЭДС самоиндукции имеет реактивный характер.
Графически изменение тока в нашей цепи с учетом ЭДС самоиндукции при замыкании ее и при последующем размыкании в восьмой момент времени показано на рисунке 5.
| Рисунок 5. График нарастания и исчезновения тока в цепи с учетом ЭДС самоиндукции | Рисунок 6. Индукционные токи при размыкании цепи |
При размыкании цепей, содержащих большое количество витков и массивные стальные сердечники или, как говорят, обладающих большой индуктивностью, ЭДС самоиндукции может быть во много раз больше ЭДС источника напряжения. Тогда в момент размыкания воздушный промежуток между ножом и неподвижным зажимом рубильника будет пробит и появившаяся электрическая дуга будет плавить медные части рубильника, а при отсутствии кожуха на рубильнике может ожечь руки человека (рисунок 6).
В самой цепи ЭДС самоиндукции может пробить изоляцию витков катушек, электромагнитов и так далее. Во избежание этого в некоторых выключающих приспособлениях устраивают защиту от ЭДС самоиндукции в виде специального контакта, который замыкает накоротко обмотку электромагнита при выключении.
Следует учитывать, что ЭДС самоиндукции проявляет себя не только в моменты включения и выключения цепи, но также и при всяких изменениях тока.
Величина ЭДС самоиндукции зависит от скорости изменения тока в цепи. Так, например, если для одной и той же цепи в одном случае в течение 1 секунды ток в цепи изменился с 50 до 40 А (то есть на 10 А), а в другом случае с 50 до 20 А (то есть на 30 А), то во втором случае в цепи будет индуктироваться втрое большая ЭДС самоиндукции.
Величина ЭДС самоиндукции зависит от индуктивности самой цепи. Цепями с большой индуктивностью являются обмотки генераторов, электродвигателей, трансформаторов и индукционных катушек, обладающих стальными сердечниками. Меньшей индуктивностью обладают прямолинейные проводники. Короткие прямолинейные проводники, лампы накаливания и электронагревательные приборы (печи, плитки) индуктивностью практически не обладают и появления ЭДС самоиндукции в них почти не наблюдается.
Магнитный поток, пронизывающий контур и индуктирующий в нем ЭДС самоиндукции, пропорционален току, протекающему по контуру:
Ф = L × I ,
где L — коэффициент пропорциональности. Он называется индуктивностью. Определим размерность индуктивности:
Ом × сек иначе называется генри (Гн).
1 генри = 10 3 ; миллигенри (мГн) = 10 6 микрогенри (мкГн).
Индуктивность, кроме генри, измеряют в сантиметрах:
1 генри = 10 9 см.
Так, например, 1 км линии телеграфа обладает индуктивностью 0,002 Гн. Индуктивность обмоток больших электромагнитов достигает нескольких сотен генри.
Если ток в контуре изменился на Δi , то магнитный поток изменится на величину Δ Ф:
Δ Ф = L × Δ i .
Величина ЭДС самоиндукции, которая появится в контуре, будет равна (формула ЭДС самоиндукции):
При равномерном изменении тока по времени выражение будет постоянным и его можно заменить выражением . Тогда абсолютная величина ЭДС самоиндукции, возникающая в контуре, может быть найдена так:
На основании последней формулы можно дать определение единицы индуктивности — генри:
Проводник обладает индуктивностью 1 Гн, если при равномерном изменении тока на 1 А в 1 секунду в нем индуктируется ЭДС самоиндукции 1 В.
Как мы убедились выше, ЭДС самоиндукции возникает в цепи постоянного тока только в моменты его включения, выключения и при всяком его изменении. Если же величина тока в цепи неизменна, то магнитный поток проводника постоянен и ЭДС самоиндукции возникнуть не может (так как . В моменты изменения тока в цепи ЭДС самоиндукции мешает изменениям тока, то есть оказывает ему своеобразное сопротивление.
Часто на практике встречаются случаи, когда нужно изготовить катушку, не обладающую индуктивностью (добавочные сопротивления к электроизмерительным приборам, сопротивления штепсельных реостатов и тому подобные). В этом случае применяют бифилярную обмотку катушки (рисунок 7)
Значение слова самоиндукция
Самоиндукция
Частный случай явления индукции токов (см. Индукция), а именно индукция тока в проводнике, вызываемая изменением силы тока, протекающего по этому проводнику. Это явление было замечено Фарадеем в г., три года спустя после его знаменитого открытия индукции токов. Фарадей нашел, что всякое изменение силы тока в проводнике сопровождается возникновением особой электродвижущий силы, которая стремится возбудить в этом проводнике ток, противодействующий происходящему изменению главного тока. Так, при увеличении силы тока в проводнике появляется в нем электродвижущая сила , вследствие которой происходит замедление в возрастании силы тока; при уменьшении силы тока появляется электродвижущая сила, от которой ослабление тока становится также медленнее. Такая электродвижущая сила, возникающая в проводнике при изменении силы тока в нем, называется электродвижущей силой С., а ток, возбуждаемый ею, носит название экстратока. — С. наблюдается особенно хорошо, когда в цепи тока находится катушка, и еще лучше, когда внутри этой катушки помещен железный сердечник . В последнем случае при замыкании цепи ток появляется сначала слабый, а затем только в течение некоторого промежутка времени он, непрерывно возрастая, достигает своей наибольшей силы. При размыкании цепи С. усиливает искру, являющуюся в месте разрыва цепи, и может вызвать весьма сильное физиологическое действие на организм человека или животного, когда тело человека или животного введено в цепь тока. Закон, которому подчинено явление С., тот же, какой управляет вообще явлениями индукции токов. Самоиндукция происходит вследствие того, что при изменении силы тока изменяется магнитный поток , пронизывающий контур этого тока и возбуждающийся самим этим током. Электродвижущая сила С., являющаяся в какой-либо момент времени, равна скорости изменения силы этого магнитного потока, взятой с обратным знаком и соответствующей рассматриваемому моменту времени, или иначе — она равна взятому с обратным знаком и рассчитанному на единицу времени изменению числа линий магнитной индукции, пронизывающих контур данного тока и возбуждающихся этим же током (см. Магнитизм). Обозначая чрез i силу тока, мы можем силу магнитного потока, пронизывающего контур этого тока и возбуждаемого последним, выразить чрез Li . Величина L , зависящая от формы и размеров контура тока, от свойства окружающей среды и в некоторых случаях (когда проводник приготовлен из сильно магнитного металла) от магнитных свойств проводника, носит название коэффициента С. цепи. Согласно вышеприведенному закону, электродвижущая сила С. ε выражается через
ε = d (Li )/dt … (1)
и в случае, когда находящиеся в цепи проводники неизменны, т. е. сохраняют свои размеры и форму, а также магнитные свойства этих проводников остаются одинаковыми при различных силах тока и окружающая среда не подвергается никакому изменению, электродвижущая сила С. вычисляется по формуле
ε = —L(di /dt) … (2)
т. е. при данных условиях коэффициент С. имеет постоянную величину. Принимая во внимание закон Ома и формулу (2), мы получаем для силы тока i , являющегося в какой-либо цепи, которой сопротивление R и коэффициент С. L , от электродвижущей силы Е , выражение
i = [(Е — L)(di /dt)]/R … (3)
Отсюда при условии, что Е постоянна, т. е. что ток получается от источника, обладающего постоянной электродвижущей силой (элемент, гальваническая батарея или аккумуляторы), при помощи интегрального исчисления находим
i = (Е/R) … (4).
Здесь е обозначает основание Неперовых логарифмов, a t — время, протекшее от момента замыкания цепи до момента, для которого мы определяем силу i . Из формулы (4) видно, что ток достигает своей наибольшей силы Е/R только через бесконечно большое время, но на самом деле величина e -(R/L)t очень быстро становится ничтожно малой и притом тем быстрее, чем больше R и меньше L. Однако для большой величины L, как это будет в том случае, когда в цепи находится электромагнит , продолжительность установления тока может быть немалая. Она может измеряться даже минутами. Когда в цепи находится источник тока, которого электродвижущая сила изменяется гармонически n раз в единицу времени (в секунду), т. е. выражается через Е = Е 0 Sin2 π nt , то для получающегося при этом переменного тока теория дает (см. Переменный ток) формулу
i = Е 0 (Sin2 π nt — θ)/(√[R 2 +4 π 2 n 2 L 2 ]) … (5)
в которой tgθ = 2 π nL/R . Из формулы (5) видно, что в данном случае для опроделения силы тока необходимо знать, кроме величины электродвижущей силы и сопротивления цепи, еще и коэффициент С. цепи. При таком переменном токе кажущееся сопротивление, т. е. величина √(R 2 +4 π 2 n 2 L 2) при большой величине L может быть значительно больше R , т. е. того сопротивления, какое оказывает цепь току постоянному. Определение величины L производится в большей части случаев непосредственно путем опыта, так как теория дает возможность только для немногих проводников найти формулу для L. Так, напр., для очень длинной прямой катушки, состоящей из n оборотов, расположенных в одном слое, теоретически выводится формула
L = 4 π 2 (n 2 /l )S.
В этой формуле S обозначает поперечное сечение катушки. Для длинной прямой катушки, состоящей из n оборотов, расположенных в нескольких слоях, может быть применена формула
L =n 2 r 2 /(0,01844r + 0,035l + 0,031d )
в которой r обозначает средний радиус оборотов, l — длину катушки, d — толщину обмотки ее. Для цилиндрического проводника, приготовленного из немагнитного металла и имеющего длину l, а диаметр d , коэффициент С. вычисляется по формуле
L = 2l
когда ток распространяется равномерно по всей массе проводника, и по формуле
L = 2l
Когда ток ограничивается только поверхностным слоем проводника. Последняя формула особенно важна в теории вибратора Гертца (см. Гертца явления). Соответственно абсолютной электромагнитной (С. G. S.) системе единиц величина L выражается в сантиметрах. Практическая единица для коэффициентов С., называемая генри или также квадрантом, равняется 10 9 см.
Опытное сравнение коэффициентов С. двух проводников может быть произведено по способу, аналогичному способу сравнения сопротивлений проводников при помощи мостика Витстона. Составляется цепь по схеме мостика Витстона, при чем в две соседние ветви четырехугольника этой схемы помещаются сравниваемые проводники, в две другие ветви ящики сопротивлений [Образцы сопротивлений обыкновенно принимаются неиндуктивными, т. е полагают, что коэффициенты самоиндукции их равны 0. Вообще у проволоки, сложенной вдвое, можно считать коэффициент С. равным нулю, хотя это не вполне строго.], в диагональную ветвь помещается вторичная обмотка катушки Румкорфа, а в другую диагональную ветвь, т. е. в самый мостик, вводится телефон . Изменением сопротивлений в двух ветвях четырехугольника достигают наконец того, что телефон перестает издавать звуки. В этом случае должно быть L 1:L 2 = R 3:R 4 . Здесь L 1 и L 2 обозначают коэффициенты С. проводников, находящихся в ветвях 1 и 2, R 3 и R 4 — сопротивления ветвей 3 и 4. Об опытном определении абсолютной величины коэффициента С. см. в подробных курсах физики , напр. в соч. И. Боргмана «Основания учения об электрических и магнитных явлениях» (т. II).
И . Боргман.
Самоиндукцией называется наведение ЭДС в проводнике при изменении электрического тока в этом проводнике.
Когда подается напряжение на катушку электромагнита, ток возрастает не сразу. Он увеличивается постепенно. Нарастание тока тормозится возникшим напряжением, противоположным приложенному. Это напряжение – электродвижущая сила (ЭДС) самоиндукции. Значение ЭДС постепенно уменьшается, и ток в электромагните возрастает до номинального значения.
Взаимодействие электрического и магнитного полей – причина самоиндукции
Электрическое и магнитное поля взаимосвязаны: электрический ток или меняющееся электрическое поле создает магнитное поле.
В свою очередь, меняющееся магнитное поле создает электрическое поле.
Рассмотрим процессы в проводящем контуре, когда в нем меняется электрический ток (например, его включают или выключают).
- В проводнике, помещенном в меняющееся магнитное поле, наводится ЭДС.
- Если в проводнике меняется величина электрического тока – возникает меняющееся магнитное поле.
- Меняющееся магнитное поле, созданное током в проводнике, наводит ЭДС самоиндукции в этом же проводнике.
Не во всех электрических цепях возникает эффект самоиндукции. Лампочка накаливания мгновенно вспыхивает при подаче тока, и мгновенно гаснет при его отключении, а в электромагните, на который подается и выключается постоянное напряжение, процессы растянуты во времени. У лампочки и электромагнита разная инерционность.
В механике мерой инерционности является масса: чтобы привести в движение массивный предмет, нужно прикладывать усилие в течение некоторого времени.
В электротехнике мерой инерционности является величина, названная индуктивностью. Она обозначается символом L . Единица измерения индуктивности – Генри (Гн), а также производные единицы: миллиГенри (мГн), микроГенри (мкГн) и так далее. Чем больше индуктивность цепи, тем дольше и мощнее протекают переходные процессы. Лампочка накаливания имеет очень малую индуктивность, а у электромагнита индуктивность большая.
В радиотехнике и электротехнике используются дроссели – детали, имеющие нормированные значения индуктивности.
На рисунке приведена схема опыта, демонстрирующего явление самоиндукции.
Катушка, намотанная на ферритовый сердечник, имеет значительную индуктивность. Источник питания – батарейка с номиналом полтора вольта. Пока тумблер находится во включенном состоянии, лампочка горит тускло, поскольку напряжения батарейки для нее недостаточно. После размыкания тумблера лампочка вспыхивает ярко и потом гаснет.
Почему лампочка вспыхивает после отключения напряжения питания? Через нее разряжается ЭДС самоиндукции, наведенная в катушке в момент выключения напряжения.
Но почему свет не просто продолжает гореть, а вспыхивает ярче, чем при включенном тумблере? ЭДС самоиндукции превышает номинальное напряжение батарейки. Рассмотрим, от чего зависит такой эффект.
От чего зависит ЭДС самоиндукции?
ЭДС самоиндукции, возникающая в электрической цепи, зависит от ее индуктивности и от скорости изменения тока в цепи.
Скорость изменения тока имеет важное значение. Если он мгновенно выключается, то есть скорость изменения очень большая, то и ЭДС самоиндукции велико. Наведенное напряжение разряжается через параллельные ветви цепи (в опыте с лампочкой – через лампочку).
Самоиндукция и переходные процессы в электрических цепях
Индуктивность электрической плитки или лампочки накаливания очень мала, и ток в этих электроприборах, при включении и выключении, возникает или исчезает практически мгновенно. Индуктивность электродвигателя велика, и он «выходит на режим» в течение нескольких минут.
Если выключить ток в большом электромагните с большим значением индукции, допустив высокую скорость уменьшения тока, то между контактами выключателя вспыхивает искра, а в случае большого тока может загореться вольтова дуга. Это опасное явление, поэтому в цепях с большой индуктивностью ток снижают постепенно, используя реостат (элемент с переменным электрическим сопротивлением).
Безопасное отключение электроэнергии – серьезна проблема. На все выключатели действуют «ударные нагрузки», возникающие из-за ЭДС самоиндукции при отключении тока, и выключатели «искрят». Для каждого типа выключателей указывается максимальное значение тока, которое можно коммутировать. Если ток превышает допустимое значение, в выключателе может вспыхнуть электрическая дуга.
На опасных производствах, в угольных шахтах, хранилищах нефтепродуктов простое искрение выключателей недопустимо. Здесь применяются взрывобезопасные выключатели, надежно защищенные герметичным пластмассовым корпусом. Цена таких выключателей в десятки раз выше, чем обычных – это необходимая плата за безопасность.
(основные величины и закономерности)
Индукция магнитного поля – силовая характеристика магнитного поля. Характеризует влияние магнитного поля на движущиеся заряды и токи. Единица измерения – тесла,
.
Потоком вектора магнитной индукции (магнитным потоком) через площадку
(или магнитным потоком) называется произведение
, или
,
(8*)
где – единичный вектор – нормаль к этой площадке,– вектор магнитной индукции,
– угол между векторамии(рис. 1). (Магнитный поток можно трактовать, как количество линий магнитной индукции, которые пересекают поверхность). Единица измерения магнитного потока – вебер:
.
Явление электромагнитной индукции состоит в возникновении ЭДС в замкнутом проводящем контуре при изменении магнитного потока, который пронизывает этот контур. (Например, когда в замкнутый контур (без батарейки) вносят магнит, в контуре возникает ЭДС и ток, который называют индукционным).
Закон Фарадея : ЭДС индукции, которая возникает в замкнутом проводящем контуре, равняется скорости изменения магнитного потока:
.
(9*)
Эта ЭДС порождает индукционный ток. Знак „–” указывает на направление индукционного тока согласно правилу Ленца: при изменении магнитного потока, который пронизывает контур, в нём возникает индукционный ток такого направления, который своим магнитным полем противодействует первичному изменению магнитного потока . На рис. 2* магнитный поток, который пронизывает контур, благодаря внесению магнита, увеличивается. Поэтому индукционный ток должен иметь такое направление, чтобы его магнитное поле было противоположным полю магнита. Направление этого тока можно определить по правилу буравчика.
Если ток проходит по замкнутому контуру, он создает магнитное поле (и, следовательно, магнитный поток) через этот же контур. Когда ток в контуре меняется – меняется и магнитный поток через этот контур, поэтому должна возникать ЭДС индукции (самоиндукции). То есть явление самоиндукции состоит в возникновении ЭДС самоиндукции в замкнутом контуре при изменении тока в этом контуре . Когда по контуру течет ток , то созданный им магнитный поток будет пропорциональным силе тока:
, где коэффициент пропорциональностиназываютиндуктивностью контура. То есть индуктивность контура численно равняется магнитному потоку, который пронизывает контур при силе тока
|
(Индуктивность зависит от формы, размеров контура и среды, но не зависит от силы тока). Единица измерения индуктивности – генри:
.
Поскольку магнитный поток равняется
, то по закону Фарадея (9*) ЭДС самоиндукции
. Если индуктивностьпостоянная, то ее можно вынести за знак производной. Тогда ЭДС самоиндукции равняется
|
Знак „–” в этом выражении означает, что ток самоиндукции противодействует начальному изменению тока. (Например, когда ток в контуре увеличивается, ток самоиндукциипротивоположен начальному току. Когда токв контуре уменьшается, тонаправлен в ту же сторону, что и).
2. Индуктивность, емкость и активное сопротивление в цепи переменного тока
Рассмотрим контур, который включает в себя индуктивность , емкостьи активное сопротивление. Пусть в этот контур включен источник ЭДС, которая изменяется по гармоничному закону (синуса или косинуса) с амплитудойи циклической частотой
, где
– линейная частота. Выясним, как влияют,иотдельно и вместе на ток в этом цепи и какие падениянапряжения будут на этих элементах. Ток на всех элементах цепи будет одинаковым (ток неразрывный). Пусть он меняется по закону синуса
|
где – амплитудное значение силы тока (пока еще неизвестное).
2.1.Активное сопротивление в цепи переменного тока
Рассмотрим электрическую цепь, которая состоит только из источника переменного тока и активного сопротивления R . Падение напряжения на активном сопротивлении определяется из закона Ома и выражения (1)
. (2)
Величина
будет представлять собой амплитудное значение напряжения на активном сопротивлении. Сравнивая выражения (1) и (2) видим, что колебания напряжения и тока на активном сопротивлении происходит с одинаковой фазой (по закону синуса, рис.1). Заметим, что в цепи с активным сопротивлением происходит необратимый процесс преобразования электрической энергии в тепловую.
Раздел очень прост в использовании. В предложенное поле достаточно ввести нужное слово, и мы вам выдадим список его значений. Хочется отметить, что наш сайт предоставляет данные из разных источников – энциклопедического, толкового, словообразовательного словарей. Также здесь можно познакомиться с примерами употребления введенного вами слова.
Вопросы к слову самоиндукция в словаре кроссвордиста
Толковый словарь русского языка. Д.Н. Ушаков
самоиндукция
самоиндукции, ж. (физ.).
только ед. Явление состоящее в том, что когда в проводнике изменяется ток, то в нем появляется электродвижущая сила, препятствующая этому изменению. Катушка самоиндукции.
Прибор, обладающий индуктивностью.
Новый толково-словообразовательный словарь русского языка, Т. Ф. Ефремова.
самоиндукция
ж. Возбуждение электродвижущей силы в проводниках при изменении проходящего по ним тока и возбужденного этим током магнитного потока.
Энциклопедический словарь, 1998 г.
самоиндукция
возбуждение электродвижущей силы индукции (эдс) в электрической цепи при изменении электрического тока в этой цепи; частный случай электромагнитной индукции. Электродвижущая сила самоиндукции прямо пропорциональна скорости изменения тока; коэффициент пропорциональности называется индуктивностью.
Самоиндукция
возникновение эдс индукции в проводящем контуре при изменении в нём силы тока; частный случай индукции электромагнитной. При изменении тока в контуре меняется поток магнитной индукции через поверхность, ограниченную этим контуром, в результате чего в нём возбуждается эдс ≈ эдс С. Направление эдс С. определяется Ленца правилом, т. е. при увеличении тока в цепи эдс С. препятствует возрастанию тока, а при уменьшении тока ≈ его убыванию. Т. о., С. подобна явлению инерции в механике. Эдс С. el пропорциональна скорости изменения силы тока i и индуктивности L контура: el = ≈L di/dt.
В электрической цепи, содержащей постоянную эдс, при замыкании цепи сила тока за счёт эдс С. устанавливается не мгновенно, а через некоторый промежуток времени (см. Переходные процессы), а при размыкании цепи ток не прекращается мгновенно; возникающая при размыкании цепи эдс С. может во много раз превысить эдс источника. В цепи переменного тока вследствие С. сила тока в катушке, обладающей индуктивностью, отстаёт по фазе от напряжения на концах катушки на p/2 (см. Переменный ток).
Явление С. играет важную роль в электротехнике и радиотехнике. Благодаря С. происходит перезарядка конденсатора, соединённого последовательно с катушкой индуктивности (см. Колебательный контур), в результате в контуре возникают свободные электромагнитные колебания.
Лит.: Калашников С. Г., Электричество, М., 1970 (Общий курс физики, т. 2).
Г. Я. Мякишев.
Википедия
Самоиндукция
Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре при изменении протекающего через контур тока.
При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность , ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.
Это явление и называется самоиндукцией. (Понятие родственно понятию взаимоиндукции, являясь как бы его частным случаем).
Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию. Этим свойством ЭДС самоиндукции сходна с силой инерции.
Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока i :
$\mathcal E = -L \frac{di}{dt}$.
Коэффициент пропорциональности L называется коэффициентом самоиндукции или индуктивностью контура.
Примеры употребления слова самоиндукция в литературе.
Вы создаете модель не из стальных конструкций и бетонных оснований — вы делаете ее с помощью электрического тока, пропущенного через сопротивления, катушки самоиндукции и конденсаторы, Проходя через соответствующую электрическую схему, ток моделирует те же самые процессы, какие происходят и в реальной модели моста.
Никому и в голову не приходило, что явление самоиндукции , открытое Фарадеем, может иметь практическое применение, И тут на сцепе появляется таинственный незнакомец П.
Поймите, упрямый человек: если вы будете знать величину требуемой самоиндукции , то рассчитать форму индуктора можно будет без особых затруднений.
Формула ЭДС индукции, E
Закон Фарадея – Максвелла для электромагнитной индукции
Основной формулой, которая определяет ЭДС индукции, является закон Фарадея – Максвелла, больше известный как основной закон электромагнитной индукции (или закон Фарадея). Этот закон утверждает, что ЭДС индукции в контуре, находящемся в переменном магнитном поле, равна по величине и противоположна по знаку скорости изменения магнитного потока () через поверхность, которую ограничивает данный контур:
где – скорость изменения магнитного потока. Полная производная в законе (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) соответствует правилу Ленца. Формула (1) для ЭДС индукции записана для системы СИ.
В случае равномерного изменения магнитного потока формулу ЭДС индукции можно записать как:
Частные случаи формул ЭДС индукции
Если контур содержит N витков, которые соединяются последовательно, то ЭДС индукции вычисляют как:
где – потокосцепление.
При движении прямолинейного проводника в однородном магнитном поле в нем возникает ЭДС индукции, которая равна:
где v – скорость движения проводника; l – длина проводника; B – модуль вектора магнитной индукции поля; .
При вращении с постоянной скоростью в однородном магнитном поле плоского контура вокруг оси, которая лежит в плоскости контура в нем возникает ЭДС индукции, равная:
где S – площадь, которую ограничивает виток; – поток самоиндукции витка; — угловая скорость; () – угол поворота контура. Следует учесть, что формула (5) справедлива, если ось вращения составляет прямой угол с направлением вектора внешнего поля .
Если во вращающейся рамке имеется N витков и самоиндукцией рассматриваемой системы можно пренебречь, то:
В стационарном проводнике, который находится в переменном магнитном поле, ЭДС индукции находят по формуле:
Примеры решения задач по теме «ЭДС индукции»
Самоиндуктивность и индуктивность— University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Соотнесите скорость изменения тока с наведенной ЭДС, создаваемой этим током в той же цепи
- Вывести самоиндукцию цилиндрического соленоида
- Вывести самоиндукцию прямоугольного тороида
Взаимная индуктивность возникает, когда ток в одной цепи создает изменяющееся магнитное поле, которое индуцирует ЭДС в другой цепи.Но может ли магнитное поле повлиять на ток в исходной цепи, создавшей поле? Ответ положительный, и это явление называется самоиндукцией .
Катушки индуктивности
(рисунок) показывает некоторые силовые линии магнитного поля, возникающие из-за тока в кольцевой проволочной петле. Если ток постоянный, магнитный поток через контур также постоянен. Однако, если бы ток I изменялся со временем — скажем, сразу после замыкания переключателя S, — тогда соответственно изменился бы магнитный поток.Тогда закон Фарадея говорит нам, что в цепи будет индуцирована ЭДС, где
Поскольку магнитное поле, создаваемое токоведущим проводом, прямо пропорционально току, поток, создаваемый этим полем, также пропорционален току; то есть
Магнитное поле создается током I в контуре. Если бы I изменялись со временем, магнитный поток через петлю также изменился бы, и в петле была бы индуцирована ЭДС.
Это также можно записать как
, где постоянная пропорциональности L известна как самоиндукция проволочной петли.Если петля имеет N витков, это уравнение становится
По соглашению, положительное значение нормали к петле связано с током по правилу правой руки, поэтому на (Рисунок) нормаль направлена вниз. В соответствии с этим соглашением положительное значение на (Рисунок), поэтому L всегда имеет положительное значение .
Для контура с Н витков, поэтому наведенная ЭДС может быть записана в терминах самоиндукции как
При использовании этого уравнения для определения L проще всего игнорировать знаки и рассчитать L как
Поскольку самоиндукция связана с магнитным полем, создаваемым током, любая конфигурация проводников обладает самоиндукцией.Например, помимо проволочной петли, длинный прямой провод имеет самоиндукцию, как и коаксиальный кабель. Коаксиальный кабель чаще всего используется в индустрии кабельного телевидения, и его также можно найти для подключения к кабельному модему. Коаксиальные кабели используются из-за их способности передавать электрические сигналы с минимальными искажениями. Коаксиальные кабели имеют два длинных цилиндрических проводника, которые обладают током и самоиндукцией, что может иметь нежелательные эффекты.
Элемент схемы, используемый для обеспечения самоиндукции, известен как индуктор.Он представлен символом, показанным на (Рисунок), который напоминает катушку с проводом, основную форму индуктора. (Рисунок) показывает несколько типов индукторов, обычно используемых в схемах.
Символ, обозначающий катушку индуктивности в цепи.
Катушки индуктивности разнообразные. Независимо от того, заключены ли они в капсулу, как показанные три верхних, или намотаны в катушку, как самая нижняя, каждая из них представляет собой просто относительно длинную катушку с проволокой. (Источник: Windell Oskay)
В соответствии с законом Ленца отрицательный знак на (рис.) Указывает, что наведенная ЭДС на катушке индуктивности всегда имеет полярность, которая противостоит изменению тока.Например, если бы ток, протекающий от A, к B на (Рисунок) (a), увеличивался, наведенная ЭДС (представленная воображаемой батареей) имела бы указанную полярность, чтобы противодействовать увеличению. Если бы ток от A, до B, уменьшался, то наведенная ЭДС имела бы противоположную полярность, опять же, чтобы противодействовать изменению тока ((Рисунок) (b)). Наконец, если бы ток через катушку индуктивности был постоянным, в катушке не было бы индуцированной ЭДС.
Индуцированная ЭДС на катушке индуктивности всегда препятствует изменению тока. Это можно представить себе как воображаемую батарею, заставляющую течь ток, чтобы противодействовать изменению в (а) и усиливать изменение в (б).
Одно из распространенных применений индуктивности — это возможность светофора определять, когда автомобили ждут на перекрестке. Электрическая цепь с индуктором размещается на дороге под местом остановки ожидающего автомобиля.Кузов автомобиля увеличивает индуктивность, и схема изменяется, посылая сигнал на светофор, чтобы изменить цвет. Точно так же металлоискатели, используемые для безопасности аэропортов, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и как приемник. Импульсный сигнал от катушки передатчика вызывает сигнал в приемнике. На самоиндукцию цепи влияет любой металлический объект на пути ((Рисунок)). Металлоискатели можно настроить на чувствительность, а также они могут определять присутствие металла на человеке.
Знакомые ворота безопасности в аэропорту не только обнаруживают металлы, но также могут указывать их приблизительную высоту над полом. (кредит: «Alexbuirds» / Wikimedia Commons)
При вспышках фотокамер обнаруживаются большие наведенные напряжения. Во вспышках камеры используются аккумулятор, два индуктора, которые работают как трансформатор, и система переключения или осциллятор для создания больших напряжений. Вспомните из статьи «Колебания при колебаниях», что «колебание» определяется как колебание величины или повторяющиеся регулярные колебания величины между двумя крайними значениями вокруг среднего значения.Также вспомните (из «Электромагнитная индукция об электромагнитной индукции»), что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке. Система генератора делает это много раз, когда напряжение батареи повышается до более чем 1000 вольт. (Вы можете услышать пронзительный вой от трансформатора, когда конденсатор заряжается.) Конденсатор сохраняет высокое напряжение для последующего использования для питания вспышки.
Самоиндуктивность катушки Индуцированная ЭДС 2.0 В измеряется на катушке из 50 плотно намотанных витков, в то время как ток через нее равномерно увеличивается от 0,0 до 5,0 А за 0,10 с. а) Какова собственная индуктивность катушки? (б) Каков поток через каждый виток катушки при токе 5,0 А?
СтратегияОбе части этой проблемы предоставляют всю информацию, необходимую для решения самоиндукции в части (a) или потока через каждый виток катушки в части (b). Необходимые уравнения (рисунок) для части (a) и (рисунок) для части (b).
Решение
- Игнорируя отрицательный знак и используя величины, получаем, из (Рисунок),
- Из (рисунок), поток выражается в единицах тока так
Значение Самоиндукция и магнитный поток, вычисленные в частях (a) и (b), являются типичными значениями для катушек, используемых в современных устройствах. Если ток не меняется во времени, поток не изменяется во времени, поэтому ЭДС не индуцируется.
Проверьте свое понимание Ток течет через катушку индуктивности на (Рисунок) от B до A вместо A к B , как показано.Увеличивается или уменьшается ток, чтобы создать ЭДС, показанную на диаграмме (а)? На диаграмме (б)?
а. уменьшение; б. увеличение; Поскольку ток течет в противоположном направлении диаграммы, чтобы получить положительную ЭДС в левой части диаграммы (а), нам нужно уменьшить ток влево, что создает усиленную ЭДС, где положительный конец находится слева. Чтобы получить положительную ЭДС в правой части диаграммы (b), нам нужно увеличить ток слева, что создает усиленную ЭДС там, где положительный конец находится справа.
Проверьте свое понимание Изменяющийся ток индуцирует ЭДС 10 В на катушке индуктивности 0,25 Гн. С какой скоростью меняется ток?
Хороший подход к расчету самоиндукции катушки индуктивности состоит из следующих шагов:
Стратегия решения проблем: самоиндуктивность
- Предположим, через катушку индуктивности протекает ток I .
- Определите магнитное поле, создаваемое током.Если есть соответствующая симметрия, вы можете сделать это с помощью закона Ампера.
- Получить магнитный поток,
- При известном магнитном потоке самоиндуктивность может быть определена по формуле (Рисунок),.
Чтобы продемонстрировать эту процедуру, мы теперь вычисляем самоиндуктивности двух катушек индуктивности.
Цилиндрический соленоид
Рассмотрим длинный цилиндрический соленоид длиной l , площадью поперечного сечения A, и N, витков провода.Мы предполагаем, что длина соленоида настолько больше, чем его диаметр, что мы можем считать, что магнитное поле распространяется по всей внутренней части соленоида, то есть мы игнорируем концевые эффекты в соленоиде. При токе –, протекающем через катушки, магнитное поле, создаваемое внутри соленоида, составляет
., поэтому магнитный поток на один виток равен
Используя (рисунок), находим для самоиндукции соленоида
Если — количество витков на единицу длины соленоида, то можно записать (рисунок) как
где — объем соленоида.Обратите внимание, что самоиндукция длинного соленоида зависит только от его физических свойств (таких как количество витков провода на единицу длины и объема), а не от магнитного поля или тока. Это верно для индукторов в целом.
САМ ИНДУКЦИЯ | |||
| Собственная индукция — это явление, при котором изменение электрического тока в Катушка создает наведенную ЭДС в самой катушке. | |||
| МАТЕМАТИЧЕСКАЯ ПРЕДСТАВИТЕЛЬСТВО: | |||
| Собственная наведенная ЭДС в катушке прямо пропорциональна скорости изменения электрический ток в катушке. | |||
ЭМФ а DI / Dt или ЭДС = -L DI / Dt Где, L = собственная индуктивность катушки. | |||
| САМ ИНДУКТИВНОСТЬ | |||
| Собственная индуктивность катушки определяется как отношение самоиндуцированной ЭДС к скорость изменения тока в катушке. | |||
Я индуктивность = ЭДС / DI / Dt | |||
Обозначается на L, и это зависит от физических характеристик катушки. Единица себя индуктивность — Генри. | |||
| ГЕНРИ | |||
| Для последняя информация, бесплатные компьютерные курсы и важные заметки посетите: www.citycollegiate.com | |||
Я индуктивность катушки составляет один генри, если изменение тока на один ампер на второй через него вырабатывает в нем ЭДС в один вольт. 1 генри = 1 вольт / 1 ампер / сек | |||
ПОЯСНЕНИЕ САМОИНДУКЦИИ | |||
Рассмотреть катушка, подключенная к батарее через реостат, как показано на рисунке.В ток через катушку создает магнитный поток, который связывается с сама катушка. Если мы изменим сопротивление в цепи, ток через катушка изменяется, и магнитный поток, проходящий через катушку, также изменяется. Этот изменение магнитного потока указывает на наличие ЭДС в самой катушке. Такая ЭДС называется самоиндуцированная ЭДС и это явление называется самоиндукцией. | |||
| Для последняя информация, бесплатные компьютерные курсы и важные заметки посетите: www.citycollegiate.com | |||
23,9 Индуктивность — Физика колледжа: OpenStax
Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы так, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшими потерями энергии в другие формы. Есть ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется , индуктивность .
Взаимная индуктивность — это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе. См. Рис. 1, где простые катушки индуцируют ЭДС друг в друге.
Рис. 1. Эти катушки могут наводить ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2.(Обратите внимание, что « E 2 индуцированная» представляет наведенную ЭДС в катушке 2.)Во многих случаях, когда геометрия устройств является фиксированной, магнитный поток изменяется путем изменения тока. Поэтому мы концентрируемся на скорости изменения тока, [latex] \ boldsymbol {\ Delta I / \ Delta t} [/ latex], как на причине индукции. Изменение текущего [латекса] \ boldsymbol {I_1} [/ latex] в одном устройстве, катушка 1 на рисунке, вызывает [латекс] \ boldsymbol {\ textbf {emf} _2} [/ latex] в другом.Мы выражаем это в форме уравнения как
[латекс] \ boldsymbol {\ textbf {emf} _2 = -M} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta I_1} {\ Delta t}} [/ latex],
, где [латекс] \ boldsymbol {M} [/ latex] определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность [латекс] \ boldsymbol {M} [/ latex], тем эффективнее связь. Например, катушки на рисунке 1 имеют небольшой [латекс] \ boldsymbol {M} [/ latex] по сравнению с катушками трансформатора в главе 23.7 Рисунок 3. Единицы измерения [латекс] \ boldsymbol {M} [/ latex]: [латекс] \ boldsymbol {(\ textbf {V} \ cdot \; \ textbf {s}) / \ textbf {A} = \ Omega \ cdot \; \ textbf {s}} [/ latex], который назван henry (H) в честь Джозефа Генри. То есть [латекс] \ boldsymbol {1 \; \ textbf {H} = 1 \ Omega \ cdot \; \ textbf {s}} [/ latex].
Природа здесь симметрична. Если мы изменим ток [латекс] \ boldsymbol {I_2} [/ latex] в катушке 2, мы индуцируем [латекс] \ boldsymbol {\ textbf {emf} _1} [/ latex] в катушке 1, что равно
[латекс] \ boldsymbol {\ textbf {emf} _1 = -M} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta I_2} {\ Delta t}} [/ latex],
, где [latex] \ boldsymbol {M} [/ latex] — то же самое, что и для обратного процесса.Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью [латекс] \ boldsymbol {M} [/ latex] .
Большая взаимная индуктивность [латекс] \ boldsymbol {M} [/ latex] может быть желательной, а может и нежелательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность [латекс] \ boldsymbol {M} [/ latex] — это перемотать катушки, чтобы нейтрализовать создаваемое магнитное поле.(См. Рисунок 2.)
Рис. 2. Нагревательные катушки электрической сушилки для одежды могут быть намотаны противотоком, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по отношению к корпусу сушилки.Самоиндукция , действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению.Большинство устройств имеют фиксированную геометрию, поэтому изменение потока происходит полностью из-за изменения тока [latex] \ boldsymbol {\ Delta I} [/ latex] через устройство. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается
[латекс] \ boldsymbol {\ textbf {emf} = -L} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta I} {\ Delta t}} [/ латекс],
где [латекс] \ boldsymbol {L} [/ latex] — это самоиндукция устройства. Устройство, которое демонстрирует значительную самоиндукцию, называется дросселем и обозначено символом на Рисунке 3.
Рис. 3.Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция [латекс] \ boldsymbol {L} [/ latex] устройства, тем сильнее его сопротивление любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой [латекс] \ boldsymbol {L} [/ latex] и не позволяет току быстро меняться. Чтобы избежать этого эффекта, необходимо получить небольшой [латекс] \ boldsymbol {L} [/ latex], например, за счет встречной намотки катушек, как на рисунке 2.
Катушка индуктивностиA 1 Гн — это большая катушка индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с [latex] \ boldsymbol {L = 1.0 \; \ textbf {H}} [/ latex], через которое протекает ток 10 A. Что произойдет, если мы попытаемся быстро отключить ток, возможно, всего за 1,0 мс? ЭДС, заданная как [latex] \ boldsymbol {\ textbf {emf} = -L (\ Delta I / \ Delta t)} [/ latex], будет препятствовать изменению. Таким образом, ЭДС будет индуцирована [latex] \ boldsymbol {\ textbf {emf} = -L (\ Delta I / \ Delta t) = (1.0 \; \ textbf {H}) [(10 \; \ textbf { A}) / (1.0 \; \ textbf {ms})] = 10 000 \; \ textbf {V}} [/ latex]. Положительный знак означает, что это большое напряжение направлено в том же направлении, что и ток, но противодействует его уменьшению. Такие большие ЭДС могут вызвать дуги, повредить коммутационное оборудование, и поэтому может потребоваться более медленное изменение тока.
Есть применение для такого большого наведенного напряжения. Во вспышках камеры используются батарея, два индуктора, которые работают как трансформатор, и система переключения или генератор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи повышается до более чем тысячи вольт. (Вы можете услышать пронзительный вой от трансформатора, когда конденсатор заряжается.) Конденсатор сохраняет высокое напряжение для последующего использования для питания вспышки. (См. Рисунок 4.)
Рис. 4. Благодаря быстрому переключению катушки индуктивности можно использовать батареи 1,5 В для индукции ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, в насадке для вспышки камеры.Можно рассчитать [латекс] \ boldsymbol {L} [/ latex] для индуктора, учитывая его геометрию (размер и форму) и зная создаваемое магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Итак, в этом тексте индуктивность [латекс] \ boldsymbol {L} [/ латекс] обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности.Начнем с того, что наведенная ЭДС определяется законом индукции Фарадея как [latex] \ boldsymbol {\ textbf {emf} = -N (\ Delta \ phi / \ Delta t)} [/ latex] и по определению собственной индуктивности, как [латекс] \ boldsymbol {\ textbf {emf} = — L (\ Delta I / \ Delta t)} [/ latex]. Приравнивая эти доходности к
[латекс] \ boldsymbol {\ textbf {emf} = -N} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta \ phi} {\ Delta t}} [/ latex] [латекс] \ boldsymbol { = -L} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta I} {\ Delta t}} [/ latex].
Решение для [latex] \ boldsymbol {L} [/ latex] дает
[латекс] \ boldsymbol {L = N} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta \ phi} {\ Delta I}} [/ латекс].
Это уравнение для самоиндукции [latex] \ boldsymbol {L} [/ latex] устройства всегда верно. Это означает, что самоиндукция [латекс] \ boldsymbol {L} [/ латекс] зависит от того, насколько эффективен ток для создания магнитного потока; чем эффективнее, тем лучше [латекс] \ boldsymbol {\ Delta \ phi \ Delta I} [/ latex].
Давайте воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь [латекс] \ boldsymbol {A} [/ latex] соленоида фиксирована, изменение магнитного потока составляет [латекс] \ boldsymbol {\ Delta \ phi = \ Delta (BA) = A \ Delta B} [/ латекс].Чтобы найти [латекс] \ boldsymbol {\ Delta B} [/ latex], отметим, что магнитное поле соленоида задается как [латекс] \ boldsymbol {B = \ mu _0 nI = \ mu 0 \ frac {NI} {\ ell}} [/ латекс]. (Здесь [latex] \ boldsymbol {n = N / \ ell} [/ latex], где [latex] \ boldsymbol {N} [/ latex] — количество витков, а [latex] \ boldsymbol {\ ell} [/ latex] — длина соленоида.) Изменяется только текущий, так что [latex] \ boldsymbol {\ Delta \ phi = A \ Delta B = \ mu_0 NA \ frac {\ Delta I} {\ ell}} [/ latex] . Замена [latex] \ boldsymbol {\ Delta \ phi} [/ latex] на [latex] \ boldsymbol {L = N \ frac {\ Delta \ phi} {\ Delta I}} [/ latex] дает
[латекс] \ boldsymbol {L = N} [/ latex] [латекс] \ boldsymbol {\ frac {\ Delta \ phi} {\ Delta I}} [/ latex] [латекс] \ boldsymbol {= N} [/ латекс] [латекс] \ boldsymbol {\ frac {\ mu_0 NA \ frac {\ Delta I} {\ ell}} {\ Delta I}} [/ латекс].2A} {\ ell}} [/ latex] [латекс] \ boldsymbol {(\ textbf {соленоид})}. [/ Latex]
Это самоиндукция соленоида с площадью поперечного сечения [латекс] \ boldsymbol {A} [/ latex] и длиной [латекс] \ boldsymbol {\ ell} [/ latex]. Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, в соответствии с его определением.
Пример 1: Расчет самоиндукции соленоида среднего размера
Рассчитайте самоиндукцию соленоида длиной 10,0 см и диаметром 4,00 см, который имеет 200 катушек.2)} {0.100 \; \ textbf {m}} \\ [1em] & \ boldsymbol {0.632 \; \ textbf {mH}} \ end {array} [/ latex].
Обсуждение
Этот соленоид среднего размера. Его индуктивность около миллигенри также считается умеренной.
Одно из распространенных применений индуктивности используется в светофорах, которые могут определить, когда автомобили ждут на перекрестке. Электрическая цепь с индуктором размещается на дороге под местом остановки ожидающей машины. Кузов автомобиля увеличивает индуктивность, и схема изменяется, посылая сигнал на светофор, чтобы изменить цвет.Точно так же металлоискатели, используемые для безопасности аэропортов, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и как приемник. Импульсный сигнал в катушке передатчика вызывает сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать приблизительное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, которая была обнаружена на «бомбардировщике в нижнем белье.”) См. Рисунок 5.
Рис. 5 Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (Источник: Alexbuirds, Wikimedia Commons)23,9 Индуктивность — Физика колледжа, главы 1-17
Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы так, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшими потерями энергии в другие формы.Есть ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ — да, и эта физическая величина называется индуктивностью.
Взаимная индуктивность — это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе. См. [Ссылка], где простые катушки индуцируют ЭДС друг в друге.
Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность M указывает на эффективность связи между ними.Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2. (Обратите внимание, что «E2E2 размер 12 {E rSub {size 8 {2}}} {}индуцированный» представляет наведенную ЭДС в катушке 2.)
Во многих случаях, когда геометрия устройств фиксирована, магнитный поток изменяется за счет изменения тока. Поэтому мы концентрируемся на скорости изменения тока, ΔI / ΔtΔI / Δt размер 12 {ΔI} {}, как на причине индукции. Изменение тока I1I1 размером 12 {I rSub {размер 8 {1}}} {} в одном устройстве, катушка 1 на рисунке, вызывает ЭДС 2-го размера 12 {«ЭДС» rSub {размер 8 {2}}} { } в другом.Мы выражаем это в форме уравнения как
ЭДС2 = −MΔI1Δt, ЭДС2 = −MΔI1Δt, размер 12 {«ЭДС» rSub {размер 8 {2}} = — M {{ΔI rSub {размер 8 {1}}} больше {Δt}}} {}
, где размер MM 12 {M} {} определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность MM размером 12 {M} {}, тем эффективнее связь. Например, катушки в [link] имеют небольшой размер MM 12 {M} {} по сравнению с катушками трансформатора в [link].Единицы измерения для MM размера 12 {M} {}: (Вс) / A = Ом⋅с (В⋅с) / A = Ом⋅с размер 12 {(В cdot s) «/ A» =% OMEGA cdot s } {}, которого назвали генри (H) в честь Джозефа Генри. То есть 1 H = 1Ω⋅s1 H = 1Ω⋅s размер 12 {1`H = 1`% OMEGA cdot s} {}.
Природа здесь симметрична. Если мы изменим ток I2I2 размером 12 {I rSub {размер 8 {2}}} {} в катушке 2, мы индуцируем ЭДС 1 размера 12 {«ЭДС» rSub {размер 8 {1}}} {} в катушке 1, что дает
ЭДС1 = −MΔI2Δt, ЭДС1 = −MΔI2Δt, размер 12 {«ЭДС» rSub {размер 8 {1}} = — M {{ΔI rSub {размер 8 {2}}} больше {Δt}}} {}
, где размер MM 12 {M} {} такой же, как и для обратного процесса.Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью MM размером 12 {M} {} .
Большая взаимная индуктивность MM размером 12 {M} {} может быть желательной или нежелательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность MM размера 12 {M} {} состоит в том, чтобы намотать катушки против ветра, чтобы нейтрализовать создаваемое магнитное поле.(См. [Ссылку].)
Нагревательные катушки электрической сушилки для одежды могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по отношению к корпусу сушилки.Самоиндуктивность, действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению.Большинство устройств имеют фиксированную геометрию, и поэтому изменение магнитного потока полностью связано с изменением тока ΔIΔI размером 12 {ΔI} {} через устройство. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается
ЭДС = −LΔIΔt, ЭДС = −LΔIΔt, размер 12 {«ЭДС» = — L {{ΔI} сверх {Δt}}} {}
, где LL размер 12 {L} {} — это собственная индуктивность устройства. Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначено символом в [ссылка].Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция LL, размер 12 {L} {} устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой размер LL 12 {L} {} и не позволяет току быстро изменяться. Чтобы избежать этого эффекта, необходимо добиться небольшого размера LL 12 {L} {}, например, за счет встречной намотки катушек, как в [ссылка].
Катушка индуктивностиA 1 Гн — это большая катушка индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с L = 1,0 HL = 1,0 H размером 12 {L = 1 “.” 0`H} {}, через который протекает ток 10 А. Что произойдет, если мы попытаемся быстро отключить ток, возможно, всего за 1,0 мс? ЭДС, заданная как emf = −L (ΔI / Δt) emf = −L (ΔI / Δt) размер 12 {«emf» = — L (ΔI / Δt)} {}, будет препятствовать изменению. Таким образом, ЭДС будет индуцирована равной ЭДС = −L (ΔI / Δt) = (1.0 H) [(10 A) / (1.0 мс)] = 10,000 Vemf = −L (ΔI / Δt) = (1.0 H) [(10 A) / (1,0 мс)] = 10 000 В.Положительный знак означает, что это большое напряжение направлено в том же направлении, что и ток, но противодействует его уменьшению. Такие большие ЭДС могут вызвать дуги, повредить коммутационное оборудование, и поэтому может потребоваться более медленное изменение тока.
Есть применение для такого большого наведенного напряжения. Во вспышках камеры используются батарея, два индуктора, которые работают как трансформатор, и система переключения или генератор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи повышается до более чем тысячи вольт. (Вы можете услышать пронзительный вой от трансформатора, когда конденсатор заряжается.) Конденсатор сохраняет высокое напряжение для последующего использования для питания вспышки. (См. [Ссылку].)
Благодаря быстрому переключению катушки индуктивности можно использовать батареи 1,5 В для индукции ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, в насадке для вспышки камеры.Можно рассчитать LL размер 12 {L} {} для катушки индуктивности, учитывая ее геометрию (размер и форму) и зная создаваемое ею магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Таким образом, в этом тексте индуктивность LL размером 12 {L} {} обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности.Начнем с того, что наведенная ЭДС определяется законом индукции Фарадея как ЭДС = −N (ΔΦ / Δt) ЭДС = −N (ΔΦ / Δt) размер 12 {«ЭДС» = — N (ΔΦ / Δt)} {} и, по определению самоиндукции, как ЭДС = −L (ΔI / Δt) ЭДС = −L (ΔI / Δt) размер 12 {«ЭДС» = — L (ΔI / Δt)} {}. Приравнивая эти доходности к
эдс = −NΔΦΔt = −LΔIΔt.emf = −NΔΦΔt = −LΔIΔt. размер 12 {«ЭДС» = — N {{ΔΦ} над {Δt}} = — L {{ΔI} над {Δt}}} {}
Решение для размера LL 12 {L} {} дает
L = NΔΦΔI.L = NΔΦΔI. размер 12 {L = N {{ΔΦ} более {ΔI}}} {}
Это уравнение для самоиндукции LL устройства размером 12 {L} {} всегда верно.Это означает, что величина собственной индуктивности LL 12 {L} {} зависит от того, насколько эффективен ток для создания магнитного потока; чем эффективнее, тем больше ΔΦΔΦ размер 12 {ΔΦ} {} / ΔIΔI размер 12 {ΔI} {}.
Давайте воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь AA соленоида фиксирована, изменение магнитного потока составляет
ΔΦ = Δ (BA) = AΔBΔΦ = Δ (BA) = AΔB.
Чтобы найти
ΔBΔB, заметим, что магнитное поле соленоида определяется выражением B = μ0nI = μ0NIℓB = μ0nI = μ0NIℓ размер 12 {B = μ rSub {размер 8 {0}} ital «nI» = μ rSub {size 8 {0}} {{ital «NI»} over {ℓ}}} {}.(Здесь n = N / ℓn = N / ℓ размер 12 {n = N / ℓ} {}, где
NN — количество катушек, а
ℓℓ — длина соленоида.) Меняется только ток, так что ΔΦ = AΔB = μ0NAΔIℓΔΦ = AΔB = μ0NAΔIℓ размер 12 {ΔΦ = AΔB = μ rSub {size 8 {0}} ital «NA» {{ΔI} over {ℓ}}} {}. Подставляя
ΔΦΔΦ в L = NΔΦΔIL = NΔΦΔI, размер 12 {L = N {{ΔΦ} над {ΔI}}} {} дает
L = NΔΦΔI = Nμ0NAΔIℓΔI.L = NΔΦΔI = Nμ0NAΔIℓΔI. размер 12 {L = N {{ΔΦ} над {ΔI}} = N {{μ rSub {размер 8 {0}} итал «NA» {{ΔI} над {ℓ}}} над {ΔI}}} {}
Это упрощается до
L = μ0N2Aℓ (соленоид).L = μ0N2Aℓ (соленоид). размер 12 {L = {{μ rSub {размер 8 {0}} N rSup {размер 8 {2}} A} больше {ℓ}}} {}
Это самоиндукция соленоида с площадью поперечного сечения AA и длиной
. Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, в соответствии с его определением.
Расчет самоиндукции соленоида среднего размера
Рассчитайте самоиндукцию соленоида длиной 10,0 см и диаметром 4,00 см, который имеет 200 катушек.
Стратегия
Это простое применение L = μ0N2AℓL = μ0N2Aℓ размера 12 {L = {{μ rSub {размер 8 {0}} N rSup {размер 8 {2}} A} над {ℓ}}} {}, поскольку все величины в уравнении, за исключением размера LL 12 {L} {}, известны.
Решение
Используйте следующее выражение для самоиндукции соленоида:
L = μ0N2Aℓ.L = μ0N2Aℓ. размер 12 {L = {{μ rSub {размер 8 {0}} N rSup {размер 8 {2}} A} больше {ℓ}}} {}
Площадь поперечного сечения в этом примере A = πr2 = (3.14…) (0,0200 м) 2 = 1,26 × 10−3м2A = πr2 = (3,14…) (0,0200 м) 2 = 1,26 × 10−3м2 размер 12 {A = πr rSup {размер 8 {2}} = (3 “ . »« 14 »«. »«. »«. ») (0«. »« 0200 »` m) rSup {size 8 {2}} = 1 «.» «26» умножить на «10» rSup {размер 8 {- 3}} `m rSup {размер 8 {2}}} {}, NN принимается равным 200, а длина ℓℓ равна 0,100 м. Мы знаем, что проницаемость свободного пространства равна μ0 = 4π × 10−7T⋅m / Aμ0 = 4π × 10−7T⋅m / A. Подставляя их в выражение для
LL, получаем
L = (4π × 10−7 Тм / А) (200) 2 (1,26 × 10−3 м2) 0,100 м = 0,632 мГн. L = (4π × 10−7 Тм / А) (200) 2 (1.26 × 10−3 м2) 0,100 м = 0,632 мГн.
Обсуждение
Этот соленоид среднего размера. Его индуктивность около миллигенри также считается умеренной.
Одно из распространенных применений индуктивности используется в светофорах, которые могут определить, когда автомобили ждут на перекрестке. Электрическая цепь с индуктором размещается на дороге под местом остановки ожидающей машины. Кузов автомобиля увеличивает индуктивность, и схема изменяется, посылая сигнал на светофор, чтобы изменить цвет.Точно так же металлоискатели, используемые для безопасности аэропортов, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и как приемник. Импульсный сигнал в катушке передатчика вызывает сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать приблизительное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, которая была обнаружена на «бомбардировщике в нижнем белье.») См. [Ссылка].
Привычные ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (Источник: Alexbuirds, Wikimedia Commons)Самоиндуктивность
— определение, формула, единицы измерения и часто задаваемые вопросы
Давайте рассмотрим волшебство концепции самоиндукции.
Рассмотрим катушку и пропустим через нее ток, не только ток, но и изменяющийся ток.
Теперь из-за изменения тока в нем индуцируется дополнительный ток, т.е.е. индуцированный ток.
Итак, вы знаете, что означает этот наведенный ток?
Ну, индуцированный ток нематериален, и это свойство катушки генерировать его из-за изменяющегося тока, подаваемого нами через батарею.
Не все ли так просто?
Однако наше внимание уделяется самоиндукции, поэтому давайте вернемся к рассмотрению этой волшебной концепции.
Итак, что вы наблюдали в этом явлении и почему оно волшебное?
Итак, волшебство заключается в следующем: при пропускании тока в катушку она индуцирует внутри себя ток, известный как самоиндуцированный.Вот почему это явление известно как самоиндукция.
Собственная индуктивность катушки
Рассмотрим катушку и пропустим через нее ток. Подача тока является первичным током, и здесь мы рассмотрим два случая, а именно:
Подача тока, которая увеличивается, и
Подача тока уменьшается.
Случай a: Рассмотрим катушку, в которой первичный (подаваемый) ток увеличивается в направлении, показанном ниже на диаграмме.
(изображение будет загружено в ближайшее время)
Как вы знаете, возрастающий (изменяющийся) ток сам по себе генерирует индуцированный ток, то есть самоиндуцированный ток, но он течет в направлении, противоположном направлению тока ток поставлен. Направление этого самоиндуцированного тока показано на диаграмме ниже.
(изображение будет загружено в ближайшее время)
Этот индуцированный ток препятствует любому изменению (или увеличению тока) того тока, из-за которого он возникает.
Теперь возьмем другой случай:
Случай b: Рассмотрим катушку, в которой ток уменьшается. Здесь происходит следующее: этот индуцированный ток способствует изменению (или уменьшению) приложенного тока.
Это означает, что индуцированный ток течет в направлении приложенного тока и способствует его увеличению.
(изображение будет загружено в ближайшее время)
Мы поняли, что индуцированный ток противодействует увеличению тока и поддерживает уменьшение тока.
(изображение скоро будет загружено)
Что такое самоиндуктивность?
Рассмотрим круг, в котором изменяющийся ток создает магнитное поле (B).
Направление этого поля можно определить, согнув пальцы правой руки, и мы получим направление B, которое указывает внутрь, что можно увидеть в виде крестиков на диаграмме ниже:
(изображение будет загружу скоро)
Теперь при увеличении тока силовые линии магнитного поля тоже увеличиваются. Это означает B α i.
Из-за увеличения B также увеличивается поток (ΦB).
Как только поток увеличивается, тогда, согласно закону индукции Фарадея, в этой катушке возникает наведенная ЭДС.
По закону Ленца,
Эта наведенная ЭДС представляет собой разность потенциалов между двумя точками в этой катушке, из-за которой генерируется наведенный ток. Этот индуцированный ток уменьшит первичный ток. Его направление наружу, то есть противоположно направлению B.
Этот ток создает свой поток, который противодействует потоку (ΦB), из-за которого он был создан.
Итак, это явление самоиндукции.
Формула самоиндуктивности
Рассмотрим катушку с током, имеющую N витков, как показано ниже:
(изображение будет загружено в ближайшее время)
Если поток через одну катушку равен Φ, то для N количества витков катушек, это будет:
ΦT (общий поток) = NΦ, и
ΦT α i
После удаления знака пропорциональности получим
ΦT = Li ⇒ L = \ [\ frac {N \ Phi T} {i} \]
Где L — коэффициент самоиндукции.
Здесь L — постоянная, не зависящая от Φ и i. Скорее это зависит от следующего:
Геометрия,
Форма и
Размер индуктора (катушки).
Это означает, что индуктивность не изменяется при увеличении или уменьшении при изменении Φ и i.
Единица самоиндукции
Единица самоиндукции — Вебер / Ампер или Генри «H».
Размер самоиндукции составляет [ML 2 T -2 A -2 ].
Определение коэффициента самоиндукции
По закону Фарадея ЭДС, \ [e = — \ frac {\ Phi T} {dt} \]
Итак, \ [e = | — L \ frac {di} {dt} | \ Rightarrow L = \ frac {e} {| \ frac {di} {dt} |} \]
Если значение изменения тока или di / dt составляет 1 ампер / секунду, то L = e. Это определение коэффициента самоиндукции.
Мы знаем, что индуктивность — это свойство электрического проводника, благодаря которому изменение тока вызывает ЭДС.
Самоиндукция и взаимная индукция
S.№ | Самоиндукция | Взаимная индукция |
1. Определение | Если скорость тока вызывает ЭДС или напряжение в той же катушке, то этот тип индукции является самоиндукция. | Если скорость изменения тока вызывает наведенную ЭДС в соседней катушке, то это взаимная индукция. |
2. Формула | \ [e = — L \ frac {di} {dt} \] и \ [L = \ frac {e} {| di / dt |} \] Для N числа витков в катушке, \ [L = \ frac {N \ Phi T} {i} \] | Если ток течет в первичной катушке, то коэффициент взаимной индукции, \ [ M = \ frac {N_ {2} \ Phi_ {12}} {i_ {1}} \] Если ток течет во вторичной катушке, то \ [M = \ frac {N_ {1} \ Phi_ { 21}} {i_ {2}} \] |
Взаимное | Определение самоиндуктивности | Формула
При изменении магнитного потока, связанного с катушкой (или проводником), в катушке индуцируется ЭДС.Эту ЭДС можно вызвать двумя способами:
- Путем вращения катушки в стационарном магнитном поле или вращением магнитного поля в стационарной катушке (как в генераторах переменного и постоянного тока). ЭДС, наведенная таким образом, называется динамически индуцированной ЭДС. Это так называется потому, что в этом случае движется либо магнитное поле, либо катушка.
- Магнитное поле и катушка неподвижны. Но поток, связанный с катушкой, изменяется путем изменения тока, создающего этот поток (как в трансформаторах).Наведенная таким образом ЭДС называется статически индуцированной ЭДС. Это так называется, потому что магнитное поле и катушка в этом случае неподвижны. Статически индуцированная ЭДС может быть подразделена на следующие две категории:
- Самоиндуцированная ЭДС
- Взаимно индуцированная ЭДС
Самоиндуцированная ЭДС
ЭДС, индуцированная в катушке из-за изменения магнитного потока, создаваемого ею при соединении с собственными витками, известна как самоиндуцированная ЭДС.
Рассмотрим катушку, имеющую N витков на железном сердечнике, подключенном к батарее, как показано на рисунке. Ток I протекает через катушку, он создает магнитный поток φ. Этот поток также связан со своими поворотами. Если ток, протекающий через катушку, изменяется путем изменения переменного сопротивления R, это изменяет магнитную связь с катушкой, и, следовательно, в катушке индуцируется ЭДС.
ЭДС, индуцированная таким образом, называется самоиндуцированной ЭДС. Направление наведенной ЭДС таково, что она противодействует изменению тока i.е. причина, которая его порождает (закон Ленца).
Величина самоиндуцированной ЭДС прямо пропорциональна скорости изменения потока, связанного с катушкой (закон Фарадея). Но скорость изменения магнитного потока, связанного с катушкой, прямо пропорциональна скорости изменения тока в катушке.
Следовательно, самоиндуцированная ЭДС, e α — d I / dt
Или e = — L (d I / dt) ………. (I)
Где L — константа пропорциональности и известна как коэффициент самоиндукции или самоиндукции или индуктивности катушки.
Свойство катушки противодействовать любому изменению тока, протекающего через нее, известно как самоиндукция или индуктивность катушки.
Собственная индуктивность, L = (N 2 µ o µ r a) ÷ l
, где N = количество витков катушек,
a = площадь поперечного сечения магнитопровода,
l = длина магнитной цепи.
Катушка достигает этого свойства из-за самоиндуцированной ЭДС в катушке , когда ток, протекающий через нее, изменяется.
Как показано на рисунке, если ток в катушке увеличивается (за счет изменения сопротивления реостата), самоиндуцированная ЭДС устанавливается в таком направлении, чтобы противодействовать нарастанию тока, т.е. -индуцированная ЭДС противоположна приложенному напряжению.
Аналогично, если ток в катушке уменьшается, самоиндуцированная ЭДС устанавливается в таком направлении, чтобы противодействовать падению тока, то есть направление самоиндуцированной ЭДС находится в том же направлении , что и направление приложенное напряжение.
Можно отметить, что самоиндукция не предотвращает изменение тока, так как дополнительная энергия выдается аккумулятором для преодоления этого противодействия. Однако задерживает изменение тока через катушку .
Можно отметить, что наличие индуктивности в цепи проявляется только при изменении тока в цепи.
Например, если устойчивый (прямой) поток через катушку, имеющую индуктивность (в силу ее геометрических и магнитных свойств), не будет проявлять ее присутствие.
Однако, когда переменный (непрерывно изменяющийся) ток течет через ту же катушку, он будет эффективно проявлять свое присутствие.
Единица индуктивности — Генри (Гн).
Если в уравнении (i) выше, e = 1 В и d I / dt = 1 А / секунду, то L = 1 Гн.
Следовательно, катушка (или цепь), как говорят, имеет индуктивность один Генри, если в нем индуцируется ЭДС в 1 вольт при изменении тока через него со скоростью один ампер в секунду.
Из приведенного выше выражения ясно, что индуктивность обратно пропорциональна сопротивлению магнитной цепи.Следовательно, катушка, намотанная на магнитопровод (с низким сопротивлением), имеет большую индуктивность, чем эквивалентная катушка с воздушным сердечником.
Взаимно индуцированная ЭДС
ЭДС, индуцированная в катушке из-за изменения магнитного потока, создаваемого другой катушкой, называется взаимно индуцированной ЭДС.
Рассмотрим катушку X, имеющую N 1 витков, и катушку Y, имеющую N 2 витков, намотанных на железный стержень. Когда эти катушки подключены по схеме, как показано на рисунке, ток течет через катушку X и создает магнитный поток φ 1 .
Часть этого потока также связана с катушкой Y. Если ток, протекающий через катушку X, изменяется путем изменения переменного сопротивления R, он изменяет поток, связывающий с другой катушкой Y, и, следовательно, в катушке Y индуцируется ЭДС.
ЭДС, индуцированная таким образом, известна как взаимно индуцированная ЭДС. Направление взаимно индуцированной ЭДС таково, что она противодействует изменению тока в катушке X, то есть причине, которая его вызывает (закон Ленца).
Математически взаимно индуцированная ЭДС, e m α — d I 1 / dt
или e m = — M (d I 1 / dt)
Где M — константа пропорциональности, известная как коэффициент взаимной индуктивности или взаимной индуктивности катушки.
Взаимная индуктивность между двумя катушками может быть определена как свойство второй катушки, благодаря которому она противодействует изменению тока в первой катушке. Выражения для взаимной индуктивности:
M = (N 1 N 2 µ o µ r1 a 1 ) ÷ l 1
M = (N 1 N 2 µ o µ r2 a 2 ) ÷ l 2
где, N 1 , N 2 = количество витков витков,
a 1 , a 2 = площади поперечного сечения магнитных цепей,
l 1 , l 2 = длины магнитных цепей.
Коэффициент сцепления
Доля магнитного потока, создаваемого током в первой катушке, которая связана со второй катушкой, называется коэффициентом связи (k) между двумя катушками.
Коэффициент связи, k = M ÷ √ (L 1 L 2 )
где M = взаимная индуктивность между двумя катушками,
L 1 = собственная индуктивность первой катушки,
L 2 = Самоиндукция второй катушки.
Значение k равно единице, если поток, создаваемый одной катушкой, полностью связан с другой. Из-за эффекта рассеяния потока значение k всегда меньше единицы. Величина взаимной индуктивности зависит от значения коэффициента связи (k). Его значение максимально при k = 1.
Электромагнетизм | Все сообщения
© http://www.yourelectricalguide.com/ Определение и формула самоиндукции.
6.9 Индуктивность | Texas Gateway
Катушки индуктивности
Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока.До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы так, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшими потерями энергии в другие формы. Есть ли полезная физическая величина, связанная с эффективностью для данного устройства? Ответ — да, и эта физическая величина называется индуктивностью.
Взаимная индуктивность — это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе.См. Рис. 6.39, где простые катушки индуцируют ЭДС друг в друге.
Рис. 6.39. Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2. (Обратите внимание, что E2E2 , наведенная , представляет наведенную ЭДС в катушке 2.)Во многих случаях, когда геометрия устройств фиксирована, магнитный поток изменяется изменяющимся током.Поэтому мы концентрируемся на скорости изменения тока, ΔI / Δt, ΔI / Δt, размер 12 {ΔI} {} как причина индукции. Изменение тока I1I1 размером 12 {I rSub {размер 8 {1}}} {} в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС размером 12 {«ЭДС» rSub {размер 8 {2}}} { } в другом. Мы выражаем это в форме уравнения как
6.34 ЭДС2 = −MΔI1Δt, ЭДС2 = −MΔI1Δt, размер 12 {«ЭДС» rSub {размер 8 {2}} = — M {{ΔI rSub {размер 8 {1}}} над { Δt}}} {}, где размер MM 12 {M} {} определяется как взаимная индуктивность между двумя устройствами.Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность M, M, размер 12 {M} {}, тем эффективнее связь. Например, катушки на рисунке 6.39 имеют небольшой размер MM 12 {M} {} по сравнению с катушками трансформатора на рисунке 6.28. Единицы измерения для MM: (V⋅s) / A = Ω⋅s, (V⋅s) / A = Ω⋅s, что называется a Генри (H), после Джозефа Генри. То есть 1 H = 1Ω⋅s, 1 H = 1Ω⋅s.
Природа здесь симметрична. Если мы изменим ток I2I2 размером 12 {I rSub {размер 8 {2}}} {} в катушке 2, мы индуцируем ЭДС 1 размера 12 {«emf» rSub {size 8 {1}}} {} в катушке 1, что дает
6.35 emf1 = −MΔI2Δt, emf1 = −MΔI2Δt, размер 12 {«emf» rSub {size 8 {1}} = — M {{ΔI rSub {size 8 {2}}} over {Δt}}} {}, где размер MM 12 {M} {} такой же, как и для обратного процесса. Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью M.M. размер 12 {M} {}
Большая взаимная индуктивность MM размером 12 {M} {} может быть желательной или нежелательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика.Один из способов уменьшить взаимную индуктивность MM размера 12 {M} {} состоит в том, чтобы намотать катушки против ветра, чтобы нейтрализовать создаваемое магнитное поле. (См. Рисунок 6.40.)
Рис. 6.40. Нагревательные змеевики электрической сушилки для одежды могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по сравнению с корпусом сушилки.
Самоиндукция, действие закона индукции Фарадея устройства на самого себя, также существует.Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению. Большинство устройств имеют фиксированную геометрию, и поэтому изменение магнитного потока полностью связано с изменением тока ΔIΔI размером 12 {ΔI} {} через устройство. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается
6.36 ЭДС = −LΔIΔt, ЭДС = −LΔIΔt, размер 12 {«ЭДС» = — L {{ΔI} над {Δt}}} {}, где LL, размер 12 {L} {} — это собственная индуктивность устройства. Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначено символом на рисунке 6.41.
Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция LL, размер 12 {L} {} устройства, тем сильнее оно сопротивляется любому изменению тока через него.Например, большая катушка с множеством витков и железным сердечником имеет большой размер LL 12 {L} {} и не позволяет току быстро изменяться. Чтобы избежать этого эффекта, необходимо добиться небольшого размера LL 12 {L} {}, например, за счет встречной намотки катушек, как показано на рисунке 6.40.
Катушка индуктивности 1 Гн — это большая катушка индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с L = 1.0 HL = 1.0 H размером 12 {L = 1 «.» 0`H} {}, через который протекает ток 10 А. Что произойдет, если мы попытаемся быстро отключить ток, возможно, всего за 1,0 мс? ЭДС, заданная eemf = −L (ΔI / Δt), будет выступать против изменения.Таким образом, ЭДС будет индуцирована eemf = −L (ΔI / Δt) = (1,0 H) [(10 A) / (1,0 мс)] = 10 000 В. . Положительный знак означает, что это большое напряжение направлено в том же направлении, что и ток, но противодействует его уменьшению. Такие большие ЭДС могут вызвать дуги, повредить коммутационное оборудование, и поэтому может потребоваться более медленное изменение тока.
Есть применение для такого большого наведенного напряжения. Во вспышках камеры используются батарея, два индуктора, которые работают как трансформатор, и система переключения или генератор для создания больших напряжений.(Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи повышается до более чем тысячи вольт. (Вы можете услышать пронзительный вой от трансформатора, когда конденсатор заряжается.) Конденсатор сохраняет высокое напряжение для последующего использования для питания вспышки. (См. Рисунок 6.42.)
Рисунок 6.42 Быстрое переключение катушки индуктивности, 1.Батареи на 5 В можно использовать для наведения ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, в насадке для вспышки камеры.
Можно рассчитать размер LL 12 {L} {} для катушки индуктивности, учитывая ее геометрию (размер и форму) и зная создаваемое ею магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Итак, в этом тексте индуктивность LL размером 12 {L} {} обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму.Поучительно вывести уравнение для его индуктивности. Начнем с того, что заметим, что индуцированная ЭДС определяется законом индукции Фарадея как eemf = −N (ΔΦ / Δt) и, по определению самоиндукции, как eemf = −L (ΔI / Δt). Приравнивая эти доходности к
6.37 ЭДС = −NΔΦΔt = −LΔIΔt.emf = −NΔΦΔt = −LΔIΔt. размер 12 {«emf» = — N {{ΔΦ} свыше {Δt}} = — L {{ΔI} более {Δt}}} {}Решение для размера LL 12 {L} {} дает
6.38 L = NΔΦΔI.L = NΔΦΔI. размер 12 {L = N {{ΔΦ} больше {ΔI}}} {}Это уравнение для самоиндукции LL устройства размером 12 {L} {} всегда верно.Это означает, что величина собственной индуктивности LL 12 {L} {} зависит от того, насколько эффективен ток для создания магнитного потока; чем эффективнее, тем больше ΔΔΦ / ΔI является.
Давайте воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь AA соленоида фиксирована, изменение магнитного потока равно ΔΦ = Δ (BA) = AΔB.ΔΦ = Δ (BA) = AΔB. Найти ΔB, ΔB, заметим, что магнитное поле соленоида определяется выражением B = μ0nI = μ0NIℓ.B = μ0nI = μ0NIℓ. Размер 12 {B = μ rSub {размер 8 {0}} ital «nI» = μ rSub { размер 8 {0}} {{ital «NI»} больше {ℓ}}} {} (Здесь nn = N / ℓ, куда NN — количество витков и ℓℓ — длина соленоида.) Изменяется только ток, так что ΔΦ = AΔB = μ0NAΔIℓ.ΔΦ = AΔB = μ0NAΔIℓ.размер 12 {ΔΦ = AΔB = μ rSub {размер 8 {0}} ital «NA» {{ΔI} over {ℓ}}} {} Подстановка ΔΦΔΦ в L = NΔΦΔIL = NΔΦΔI размер 12 {L = N {{ΔΦ} над {ΔI}}} {} дает
6,39 L = NΔΦΔI = Nμ0NAΔIℓΔI.L = NΔΦΔI = Nμ0NAΔIℓΔI. размер 12 {L = N {{ΔΦ} над {ΔI}} = N {{μ rSub {размер 8 {0}} итал «NA» {{ΔI} над {ℓ}}} над {ΔI}}} {}Это упрощается до
6.40 L = μ0N2Aℓ (соленоид) .L = μ0N2Aℓ (соленоид). размер 12 {L = {{μ rSub {размер 8 {0}} N rSup {размер 8 {2}} A} больше {ℓ}}} {}Это самоиндукция соленоида с площадью поперечного сечения AA и длина ℓ, ℓ, Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, в соответствии с его определением.
Пример 6.7 Расчет самоиндукции соленоида среднего размера
Рассчитайте самоиндукцию соленоида длиной 10,0 см и диаметром 4,00 см, который имеет 200 катушек.
Стратегия
Это прямое применение L = μ0N2Aℓ, L = μ0N2Aℓ, размер 12 {L = {{μ rSub {размер 8 {0}} N rSup {размер 8 {2}} A} над {ℓ}}} {} поскольку все величины в уравнении, кроме размера LL 12 {L} {}, известны.
Решение
Используйте следующее выражение для самоиндукции соленоида:
6.41 L = μ0N2AℓL = μ0N2Aℓ размер 12 {L = {{μ rSub {размер 8 {0}} N rSup {размер 8 {2}} A} больше {ℓ}}} {}Площадь поперечного сечения в этом примере равна A = πr2 = (3,14…) (0,0200 м) 2 = 1,26 · 10−3 м2, A = πr2 = (3,14…) (0,0200 м) 2 = 1,26 · 10−3 м2, NN отводится быть 200, а длина ℓℓ — 0,100 м. Мы знаем, что проницаемость свободного пространства равна μ0 = 4π × 10−7T⋅m / A.μ0 = 4π × 10−7T⋅m / A. Подставляя их в выражение для LL дает
6,42 L = (4π × 10−7 Tm / A) (200) 2 (1,26 × 10−3 м2) 0,100 м = 0,632 мH.L = (4π × 10−7 Tm / A) (200) 2 (1,26 × 10−3 м2) 0,100 м = 0,632 мГн.Обсуждение
Этот соленоид среднего размера. Его индуктивность около миллигенри также считается умеренной.
Одно из распространенных применений индуктивности используется в светофорах, которые могут определить, когда автомобили ждут на перекрестке.
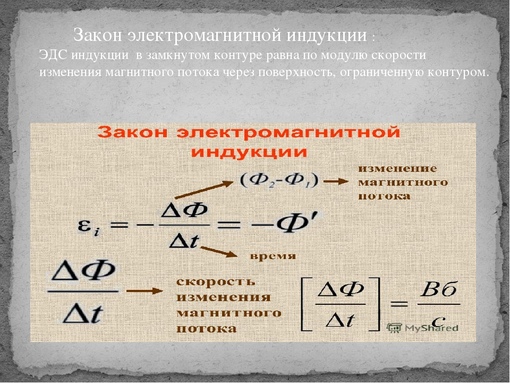
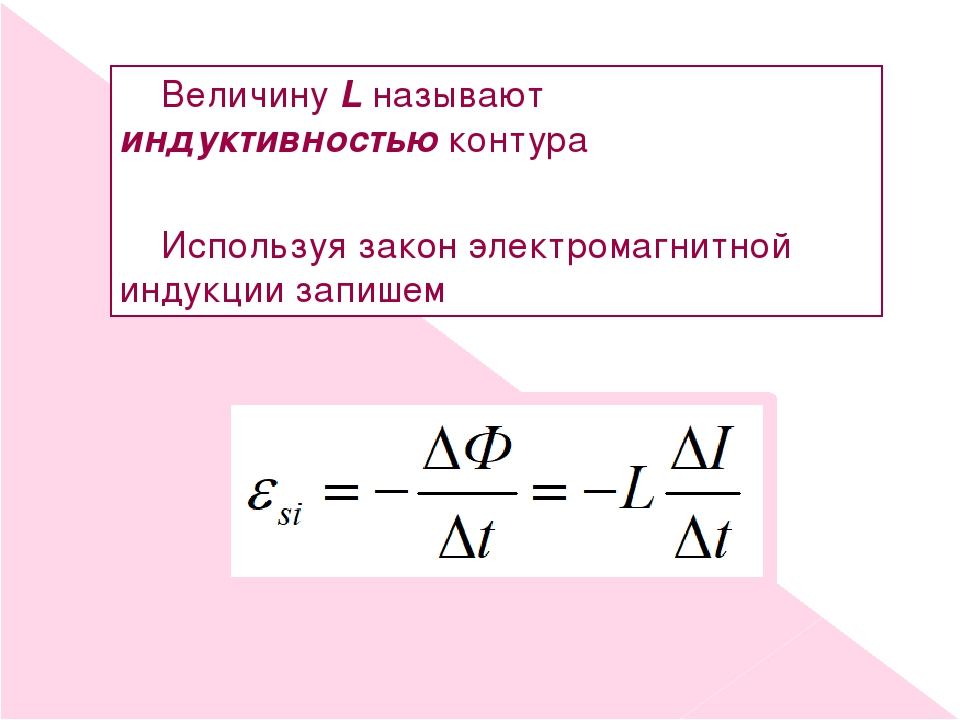 18)
18)