Эффективное напряжение это – , , — БилдоМан — всё о строительстве и ремонте

Содержание

Эффективное напряжение Википедия

В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока

Значения переменного напряжения (тока)

Далее для определенности будем говорить большей частью о параметрах напряжения, хотя они справедливы и для токов.

Мгновенное значение

Мгновенное значение — это значение сигнала в определённый момент времени, функцией которого является ( u(t) ,i(t){\displaystyle u(t)~,\quad i(t)} ). Мгновенные значения медленно изменяющегося сигнала можно определить с помощью малоинерционного вольтметра постоянного тока, самописца или шлейфового осциллографа, для периодических быстротекущих процессов используется электронно-лучевой или цифровой осциллограф.

Амплитудное значение

Амплитудное (пиковое) значение, иногда называемое просто «амплитуда» — наибольшее мгновенное значение напряжения или силы тока за период (без учёта знака):

UM=max(|u(t)|) ,IM=max(|i(t)|){\displaystyle U_{M}=\max(|u(t)|)~,\qquad I_{M}=\max(|i(t)|)}

Пиковое значение напряжения измеряется с помощью импульсного вольтметра или осциллографа.

Среднеквадратичное значение

Среднеквадратичное значение (устар. действующее, эффективное) — корень квадратный из среднего значения квадрата напряжения или тока.

U=1T∫0Tu2(t)dt ,I=1T∫0Ti2(t)dt{\displaystyle U={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}u^{2}(t)dt}}~,\qquad I={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}i^{2}(t)dt}}}

Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I{\displaystyle I} и U{\displaystyle U} совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.

Когда не оговаривают особо, то обычно имеют в виду именно среднеквадратичные значения величины напряжения или силы тока.

В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.

Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом.

Среднее значение

Среднее значение (смещение) — постоянная составляющая напряжения или силы тока

U=1T∫0Tu(t)dt ,I=1T∫0Ti(t)dt{\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}u(t)dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}i(t)dt}

В электротехнике используется редко, но сравнительно часто используется в радиотехнике (ток смещения и напряжение смещения). Геометрически это разность площадей под и над осью времени, делённая на период. Для синусоидального сигнала смещение равно нулю.

Средневыпрямленное значение

Средневыпрямленное значение — среднее значение модуля сигнала

U=1T∫0T∣u(t)∣dt ,I=1T∫0T∣i(t)∣dt{\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}\mid u(t)\mid dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}\mid i(t)\mid dt}

На практике используется редко, однако большинство измерительных приборов переменного тока — магнитоэлектрической системы (т. е., в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку. В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.

Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.

Коэффициенты пересчёта значений

Коэффициент формы кривой переменного напряжения (тока) — величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению. Для синусоидального напряжения (тока) равен π/22≈1.11{\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11}.

Коэффициент амплитуды кривой переменного напряжения (тока) — величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) равен 2{\displaystyle {\sqrt {2}}}.

Параметры постоянного тока

Размах пульсации напряжения (тока) — величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени

Коэффициент пульсации напряжения (тока) — величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
- Коэффициент пульсации напряжения (тока) по действующему значению — величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
- Коэффициент пульсации напряжения (тока) пo среднему значению — величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей

Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)

Литература и документация

Литература

Нормативно-техническая документация

Ссылки

См. также

wikiredia.ru

Эффективное напряжение — это… Что такое Эффективное напряжение?

Мощность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

Эффективная мощность, мощность двигателя, отдаваемая рабочей машине непосредственно или через силовую передачу. Различают полезную, полную и номинальную Э. м. двигателя. Полезной называют Э. м. двигателя за вычетом затрат мощности на приведение в действие вспомогательных агрегатов или механизмов, необходимых для его работы, но имеющих отдельный привод (не от двигателя непосредственно). Полная Э. м. — мощность двигателя без вычета указанных затрат. Номинальная Э. м., или просто номинальная мощность, — Э. м., гарантированная заводом-изготовителем для определённых условий работы. В зависимости от типа и назначения двигателя устанавливаются Э. м., регламентируемые стандартами или техническими условиями (например, наибольшая мощность судового реверсивного двигателя при определённой частоте вращения коленчатого вала в случае заднего хода судна — так называемая мощность заднего хода, наибольшая мощность авиационного двигателя при минимальном удельном расходе топлива — так называемая крейсерская мощность и т. п.). Э. м. зависит от форсирования (интенсификации) рабочего процесса, размеров и механического кпд двигателя.

[1]

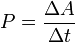$P = \frac{\Delta A}{\Delta t} \,\!$ — средняя мощность

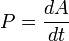$P = \frac{dA}{dt} \,\!$ — мгновенная мощность

Так как работа является мерой изменения энергии, мощность можно определить также как скорость изменения энергии системы.

Единицы измерения

В системе СИ единицей измерения мощности является ватт, равный одному джоулю, делённому на секунду.

Другой распространённой единицей измерения мощности является лошадиная сила.

Соотношения между единицами мощности
Единицы	Вт	кВт	МВт	кгс·м/с	эрг/с	л. с.
1 ватт	1	10^-3	10^-6	0,102	10⁷	1,36·10^-3
1 киловатт	10³	1	10^-3	102	10¹⁰	1,36
1 мегаватт	10⁶	10³	1	102·10³	10¹³	1,36·10³
1 килограмм-сила-метр в секунду	9,81	9,81·10^-3	9,81·10^-6	1	9,81·10⁷	1,33·10^-2
1 эрг в секунду	10^-7	10^-10	10^-13	1,02·10^-8	1	1,36·10^-10
1 лошадиная сила^[2]	735,5	735,5·10^-3	735,5·10^-6	75	7,355·10⁹	1

Мощность в механике

Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:

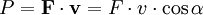$P = \mathbf F \cdot \mathbf v = F \cdot v \cdot \cos\alpha$

F — сила, v — скорость, α — угол между вектором скорости и силы.

Частный случай мощности при вращательном движении:

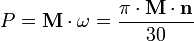$P = \mathbf M \cdot \mathbf \omega = \frac {\mathbf \pi \cdot \mathbf M \cdot \mathbf n} {30}$

M — момент, 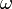$\mathbf \omega$ — угловая скорость, 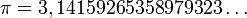$~\pi=3,14159265358979323\dots$ — число пи, n — частота вращения (об/мин).

Электрическая мощность

Электри́ческая мо́щность

— физическая величина, характеризующая скорость передачи или преобразования электрической энергии.

S=P+jQ

S — Полная мощность, ВА

P — Активная мощность, Вт

Q — Реактивная мощность, ВАр

Приборы для измерения мощности

Примечания

↑ Большая Советская энциклопедия
↑ «метрическая лошадиная сила»

См. также

Ссылки

Wikimedia Foundation. 2010.

dic.academic.ru

Kvant. Эффективное напряжение — PhysBook

Ланге В. Эффективное напряжение в сети переменного тока //Квант. — 2001. — № 3. — С. 40-41.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Перспективность использования электрической энергии в технике и быту стала очевидной еще в начале XIX века, а в конце его началась настоящая война между сторонниками постоянного и переменного тока. В ней, однако, не было ни победителей, ни побежденных, так как для одних целей оказывается необходимым постоянный ток (например, при электролизе), в других случаях целесообразнее использовать переменный (в особенности, при передаче электроэнергии на большие расстояния). Уместно напомнить, что сейчас существуют простые установки, позволяющие легко преобразовывать один вид тока в другой.

В соответствии с названием, в сетях постоянного тока напряжение остается неизменным, а в сетях

переменного тока оно со временем меняется. Обычно изменение напряжения происходит по синусоидальному закону $~U = U_0 \sin \omega t$, где ω — циклическая частота, связанная с периодом Т соотношением $~\omega = \frac{2\pi}{T}$, a U₀ — амплитудное значение напряжения. Графически характер изменения напряжения со временем показан на рисунке 1,а.

Рис. 1

Предположим, что необходимо рассчитать мощность Р, которую будет потреблять из сети переменного тока с амплитудным напряжением U₀ электрическая печь, имеющая сопротивление R. Как известно, такие расчеты выполняются с помощью закона Джоуля-Ленца:

$~P = I^2 R$ ,

или в нашем случае

$~P = \frac{U^2}{R}$ .

Однако в рассматриваемой цепи напряжение меняется и по знаку, и по величине. Как учесть эти два обстоятельства?

Начнем с ответа на более простой первый вопрос. В законе Джоуля-Ленца фигурирует квадрат напряжения, а поскольку (+U)² = (-U)² , тепловыделение не зависит от знака разности потенциалов (или, что то же, от направления тока). Стало быть, и в сети переменного тока электрическая печь будет исправно выполнять свое назначение.

Попробуем теперь ответить на вопрос, какое напряжение надо подставить в формулу закона Джоуля-Ленца, чтобы получить правильное значение мощности в случае переменного тока. Для этого рассчитаем количество теплоты, выделяемое переменным током за время, равное периоду. И сделаем это следующим образом.

Поскольку теплоотдача определяется квадратом напряжения, легко понять, что тепловыделение имеет период $~\frac T2$ (рис. 1,б). Более того, достаточно рассмотреть интервал от 0 до $~\frac T4$, так как выделенная на рисунке фигура, если учесть ее зеркальные отражения, повторяется именно с таким периодом. На этом интервале фаза колебаний меняется от φ₁ = 0 до $~\varphi_2 = \frac{\pi}{4}$.

Запишем выражение для мощности электропечи в некоторый момент времени t:

$~P(t) = \frac{U^2}{R} = \frac{U^2_0}{R} \sin^2 \omega t$ .

Ее среднее значение <Р> в интервале времени от 0 до $~\frac T4$ представим в виде

\(~

= <\frac{U^2_0}{R} \sin^2 \omega t> = \frac{U^2_0}{R} <\sin^2 \omega t>\) .</center>

В угловых скобках остался зависящий от времени сомножитель, обозначаемый далее буквой y. Для расчета его среднего значения воспользуемся рисунком 2, отметив на оси абсцисс точки E₁, Е и E₂, соответствующие фазам $~\frac{\pi}{4} — \alpha$, $~\frac{\pi}{4}$ и $~\frac{\pi}{4} + \alpha$, где α — произвольный угол, удовлетворяющий условию $~0 < \alpha < \frac{\pi}{4}$. Ясно, что

<center>$~E_1C_1 = \sin^2 \left( \frac{\pi}{4} — \alpha \right) = \cos^2 \left( \frac{\pi}{2} — \left( \frac{\pi}{4} — \alpha \right)\right) = \cos^2 \left( \frac{\pi}{4} + \alpha \right) = 1 — \sin^2 \left( \frac{\pi}{4} + \alpha \right) = 1 — C_2E_2$ .</center>

Таким образом, кривая 0С₁СС₂В делит прямоугольник 0DBA на две равные части, каждая площадью

Чтобы найти среднее значение $~\sin^2 \omega t$ за время изменения фазы от 0 до $~\frac{\pi}{2}$, нужно площадь криволинейной фигуры 0СВА разделить на ее основание:

После этого находим среднее значение мощности за время от t₁ = 0 до $~t_2 = \frac T4$ :

Поскольку такой же результат можно получить для каждого из последующих интервалов длительностью $~\frac T4$ правая часть формулы дает мощность плитки сопротивлением R, включенной в сеть переменного тока с амплитудным значением напряжения U₀.

Пусть эта же плитка включена в сеть постоянного тока с таким напряжением U_ef, что ее мощность осталась прежней. Тогда, приравнивая мощность плитки в сети постоянного тока

правой части предыдущего выражения, после несложного преобразования получим

Напряжение в сети постоянного тока, где плитка дает такой же тепловой эффект, как и в сети переменного тока с амплитудным значением напряжения, в $~\sqrt 2$ большим, называется эффективным (или действующим) напряжением в сети переменного тока. В обычной городской еети амплитудное напряжение составляет приблизительно 310 В. Тогда для эффективного напряжения получается хорошо знакомое число 220 В.

Заметим, что аналогичное соотношение связывает эффективное и амплитудное значения и для силы тока в сети переменного тока.

www.physbook.ru

Эффективное значение напряжения

Действующее значение переменного тока

Действующее (эффективное) значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.

В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение переменного тока.

Иначе говоря, действующее значение переменного тока можно определить по формуле:

I = 1 T ∫ 0 T i 2 d t . {\displaystyle I={\sqrt {{\frac {1}{T}}\int _{0}^{T}i^{2}dt}}.}

Для синусоидального тока:

I = 1 2 ⋅ I m ≈ 0,707 ⋅ I m , {\displaystyle I={\frac {1}{\sqrt {2}}}\cdot I_{m}\approx 0{,}707\cdot I_{m},}

где

I m {\displaystyle I_{m}} — амплитудное значение тока.

Для тока треугольной и пилообразной формы:

I = 1 3 ⋅ I m ≈ 0,577 ⋅ I m . {\displaystyle I={\frac {1}{\sqrt {3}}}\cdot I_{m}\approx 0{,}577\cdot I_{m}.}

Аналогичным образом определяются действующие значения ЭДС и напряжения.

Дополнительные сведения

В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value — эффективное значение. Также применяется аббревиатура RMS (rms) — root mean square — среднеквадратичное (значение).

В электротехнике приборы электромагнитной, электродинамической и тепловой систем калибруются на действующее значение.

Источники

«Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
Курс физики. А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
«Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 — § 7.10

Ссылки

Действующие значения тока и напряжения
Среднеквадратичное значение

Это заготовка статьи по физике. Вы можете помочь проекту, дополнив её.

ru.wikipedia.org⁫>

Список параметров напряжения и силы электрического тока

Значения переменного напряжения (тока)

Мгновенное значение

Мгновенное значение — это значение сигнала в определённый момент времени, функцией которого является ( u ( t ) , i ( t ) {\displaystyle u(t)~,\quad i(t)} ). Мгновенные значения медленно изменяющегося сигнала можно определить с помощью малоинерционного вольтметра постоянного тока, самописца или шлейфового осциллографа, для периодических быстротекущих процессов используется электронно-лучевой или цифровой осциллограф.

Амплитудное значение

Амплитудное (пиковое) значение, иногда называемое просто «амплитуда» — наибольшее мгновенное значение напряжения или силы тока за период (без учёта знака):

U M = max ( | u ( t ) | ) , I M = max ( | i ( t ) | ) {\displaystyle U_{M}=\max(|u(t)|)~,\qquad I_{M}=\max(|i(t)|)}

Пиковое значение напряжения измеряется с помощью импульсного вольтметра или осциллографа.

Среднеквадратичное значение

U = 1 T ∫ 0 T u 2 ( t ) d t , I = 1 T ∫ 0 T i 2 ( t ) d t {\displaystyle U={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}u^{2}(t)dt}}~,\qquad I={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}i^{2}(t)dt}}}

Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I {\displaystyle I} и U {\displaystyle U} совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.

Когда не оговаривают особо, то обычно имеют ввиду именно среднеквадратичные значения величины напряжения или силы тока.

zna4enie.ru

Эффективное напряжение — это… Что такое Эффективное напряжение?

Эффективное напряжение

Эффективное напряжение — напряжение, действующее в скелете грунта, определяемое как разность между полным напряжением в образце грунта и давлением в поровой жидкости.

3.1 эффективное напряжение: Напряжение, действующее в скелете грунта, определяемое как разность между полным напряжением в образце грунта и поровым давлением.

Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.

Эффективное кодирование символов цифрового сигнала данных
Эффективное осевое усилие, действующее на штуцер, Н

Смотреть что такое «Эффективное напряжение» в других словарях:

эффективное напряжение — efektinė įtampa statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. effective voltage vok. effektive Spannung, f rus. действующее напряжение, n; эффективное… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
эффективное напряжение — efektinė įtampa statusas T sritis fizika atitikmenys: angl. effective voltage vok. effektive Spannung, f rus. действующее напряжение, n; эффективное напряжение, n pranc. tension efficace, f … Fizikos terminų žodynas
эффективное напряжение — efektyvusis įtempis statusas T sritis fizika atitikmenys: angl. effective stress vok. effektive Spannung, f rus. эффективное напряжение, n pranc. contrainte effective, f … Fizikos terminų žodynas
Эффективное напряжение — Мощность физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени. Эффективная мощность, мощность двигателя, отдаваемая рабочей машине непосредственно или через силовую передачу.… … Википедия
эффективное напряжение шума интегральной микросхемы — эффективное напряжение шума Отношение шума на выходе, выраженного в эффективных значениях напряжения в заданной полосе частот, к коэффициенту усиления интегральной микросхемы. Обозначение Uш.эфф Uneff [ГОСТ 19480 89] Тематики микросхемы Синонимы… … Справочник технического переводчика
(эффективное) напряжение прикосновения — ((effective) touch voltage): Напряжение между проводящими частями при одновременном прикосновении к ним человека или животного. 826 11 07 [195 05 02] Источник: ГОСТ Р МЭК 60050 826 2009: Установки электрические. Термины и определения … Словарь-справочник терминов нормативно-технической документации
напряжение прикосновения — Напряжение, появляющееся на теле человека при одновременном прикосновении к двум точкам проводников или проводящих частей, входящих в электрическую цепь, в том числе при повреждении изоляции. [ГОСТ Р 50669 94] напряжение прикосновения Напряжение… … Справочник технического переводчика
Напряжение электронагревательной секции рабочее — Рабочее напряжение электронагревательной секции номинальное эффективное напряжение, при котором предусмотрена эксплуатация электронагревательной секции… Источник: ГОСТ Р 50571.25 2001. Электроустановки зданий. Часть 7. Требования к специальным… … Официальная терминология
эффективное поле зрения ФЭПП — Телесный угол, определяемый соотношением где Uc напряжение фотосигнала ФЭПП; допускается замена параметра Uc на Ic, Iф; θ угол между направлением падающего излучения и нормалью к фоточувствительному элементу; φ азимутальный угол.… … Справочник технического переводчика
напряжение — 3.10 напряжение: Отношение растягивающего усилия к площади поперечного сечения звена при его номинальных размерах. Источник: ГОСТ 30188 97: Цепи грузоподъемные калиброванные высокопрочные. Технические условия … Словарь-справочник терминов нормативно-технической документации

normative_reference_dictionary.academic.ru

эффективное напряжение — это… Что такое эффективное напряжение?

эффективное напряжение: net voltage

эффективное наполнение
эффективное обозначение

Смотреть что такое «эффективное напряжение» в других словарях:

Эффективное напряжение — напряжение, действующее в скелете грунта, определяемое как разность между полным напряжением в образце грунта и давлением в поровой жидкости. Источник: ГОСТ 12248 96: Грунты. Методы лабораторного определения характеристик прочности и… … Словарь-справочник терминов нормативно-технической документации
эффективное напряжение — efektinė įtampa statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. effective voltage vok. effektive Spannung, f rus. действующее напряжение, n; эффективное… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
эффективное напряжение — efektinė įtampa statusas T sritis fizika atitikmenys: angl. effective voltage vok. effektive Spannung, f rus. действующее напряжение, n; эффективное напряжение, n pranc. tension efficace, f … Fizikos terminų žodynas
эффективное напряжение — efektyvusis įtempis statusas T sritis fizika atitikmenys: angl. effective stress vok. effektive Spannung, f rus. эффективное напряжение, n pranc. contrainte effective, f … Fizikos terminų žodynas
Эффективное напряжение — Мощность физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени. Эффективная мощность, мощность двигателя, отдаваемая рабочей машине непосредственно или через силовую передачу.… … Википедия
эффективное напряжение шума интегральной микросхемы — эффективное напряжение шума Отношение шума на выходе, выраженного в эффективных значениях напряжения в заданной полосе частот, к коэффициенту усиления интегральной микросхемы. Обозначение Uш.эфф Uneff [ГОСТ 19480 89] Тематики микросхемы Синонимы… … Справочник технического переводчика
(эффективное) напряжение прикосновения — ((effective) touch voltage): Напряжение между проводящими частями при одновременном прикосновении к ним человека или животного. 826 11 07 [195 05 02] Источник: ГОСТ Р МЭК 60050 826 2009: Установки электрические. Термины и определения … Словарь-справочник терминов нормативно-технической документации
напряжение прикосновения — Напряжение, появляющееся на теле человека при одновременном прикосновении к двум точкам проводников или проводящих частей, входящих в электрическую цепь, в том числе при повреждении изоляции. [ГОСТ Р 50669 94] напряжение прикосновения Напряжение… … Справочник технического переводчика
Напряжение электронагревательной секции рабочее — Рабочее напряжение электронагревательной секции номинальное эффективное напряжение, при котором предусмотрена эксплуатация электронагревательной секции… Источник: ГОСТ Р 50571.25 2001. Электроустановки зданий. Часть 7. Требования к специальным… … Официальная терминология
эффективное поле зрения ФЭПП — Телесный угол, определяемый соотношением где Uc напряжение фотосигнала ФЭПП; допускается замена параметра Uc на Ic, Iф; θ угол между направлением падающего излучения и нормалью к фоточувствительному элементу; φ азимутальный угол.… … Справочник технического переводчика
напряжение — 3.10 напряжение: Отношение растягивающего усилия к площади поперечного сечения звена при его номинальных размерах. Источник: ГОСТ 30188 97: Цепи грузоподъемные калиброванные высокопрочные. Технические условия … Словарь-справочник терминов нормативно-технической документации

dic.academic.ru

Действующее напряжение Википедия

Значения переменного напряжения (тока)

Мгновенное значение

Амплитудное значение

Амплитудное (пиковое) значение, иногда называемое просто «амплитуда» — наибольшее мгновенное значение напряжения или силы тока за период (без учёта знака):

UM=max(|u(t)|) ,IM=max(|i(t)|){\displaystyle U_{M}=\max(|u(t)|)~,\qquad I_{M}=\max(|i(t)|)}

Пиковое значение напряжения измеряется с помощью импульсного вольтметра или осциллографа.

Среднеквадратичное значение

U=1T∫0Tu2(t)dt ,I=1T∫0Ti2(t)dt{\displaystyle U={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}u^{2}(t)dt}}~,\qquad I={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}i^{2}(t)dt}}}

Среднее значение

Среднее значение (смещение) — постоянная составляющая напряжения или силы тока

U=1T∫0Tu(t)dt ,I=1T∫0Ti(t)dt{\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}u(t)dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}i(t)dt}

Средневыпрямленное значение

Средневыпрямленное значение — среднее значение модуля сигнала

U=1T∫0T∣u(t)∣dt ,I=1T∫0T∣i(t)∣dt{\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}\mid u(t)\mid dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}\mid i(t)\mid dt}

Коэффициенты пересчёта значений

Коэффициент формы кривой переменного напряжения (тока) — величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению. Для синусоидального напряжения (тока) равен π/22≈1.11{\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11}.

Коэффициент амплитуды кривой переменного напряжения (тока) — величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) равен 2{\displaystyle {\sqrt {2}}}.

Параметры постоянного тока

Размах пульсации напряжения (тока) — величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени

Коэффициент пульсации напряжения (тока) — величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
- Коэффициент пульсации напряжения (тока) по действующему значению — величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
- Коэффициент пульсации напряжения (тока) пo среднему значению — величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей

Эффективное напряжение Википедия

Значения переменного напряжения (тока)

Мгновенное значение

Амплитудное значение

Среднеквадратичное значение

Среднее значение

Средневыпрямленное значение

Коэффициенты пересчёта значений

Параметры постоянного тока

Литература и документация

Литература

Нормативно-техническая документация

Ссылки

См. также

Эффективное напряжение — это… Что такое Эффективное напряжение?

Единицы измерения

Мощность в механике

Электрическая мощность

Приборы для измерения мощности

Примечания

См. также

Ссылки

Kvant. Эффективное напряжение — PhysBook

Эффективное значение напряжения

Действующее значение переменного тока

Дополнительные сведения

Источники

Ссылки

Список параметров напряжения и силы электрического тока

Значения переменного напряжения (тока)

Мгновенное значение

Амплитудное значение

Среднеквадратичное значение

Эффективное напряжение — это… Что такое Эффективное напряжение?

Смотреть что такое «Эффективное напряжение» в других словарях:

эффективное напряжение — это… Что такое эффективное напряжение?

Смотреть что такое «эффективное напряжение» в других словарях:

Действующее напряжение Википедия

Значения переменного напряжения (тока)

Мгновенное значение

Амплитудное значение

Среднеквадратичное значение

Среднее значение

Средневыпрямленное значение

Коэффициенты пересчёта значений

Параметры постоянного тока

Литература и документация

Литература

Нормативно-техническая документация

Ссылки

См. также

Добавить комментарий Отменить ответ