Сопротивления в цепи переменного тока
Сопротивления в цепи переменного тока
Категория:
Сварка металлов
Сопротивления в цепи переменного тока
В цепях переменного тока различают активное, индуктивное и емкостное сопротивления.
Под активным сопротивлением R понимается сопротивление проводника, измеренное при црохождении по нему переменного тока. Сопротивление проводника, измеренное при постоянном токе, называется омическим. В одной и той же электрической цепи активное сопротивление больше омического. При низких частотах переменного тока разница между активным и омическим сопротивлением проводника мала и ее можно не учитывать. В цепи переменного тока с активным сопротивлением (идеальный частный случай) напряжение и вызванный им ток совпадают по фазе, т. е. кривые напряжения и тока одновременно проходят через нулевые и амплитудные значения. На векторной диаграмме этой цепи векторы напряжения и тока совпадают по направлению.
В любой электрической цепи переменного тока вокруг проводников с током возникает магнитное поле, следовательно электрическая цепь всегда обладает индуктивностью. Если переменное напряжение приложить к катушке индуктивности, ток в цепи будет меньше в сравнении с тем током, который бы протекал при наличии одного активного сопротивления катушки. ЭДС самоиндукции катушки противодействует периодическим изменениям переменного тока, т. е. в катушке возникает дополнительное препятствие (кроме активного сопротивления) прохождению по ней переменного тока. Противодействие катушки индуктивности переменному току, измеряемое в омах, условно назвали индуктивным сопротивлением. Индуктивное сопротивление пропорционально индуктивности цепи и частоте переменного тока. Коэффициент обусловлен круговым движением, связанным с периодом синусоидальной волны тока (напряжения).
Индуктивное сопротивление XL при постоянном токе равно нулю. По этой причине недопустима ошибочная подача постоянного напряжения на электрические машины и аппараты переменного тока — в этом случае в их обмотках возникает очень большой постоянный ток, разрушающий их своим тепловым действием.
Рис. 1. Взаимоиндукция
Рис. 8. Совпадение (а) и сдвиг (б) по фазе синусоидальных напряжений и токов
Индуктивность электрической цепи вызывает сдвиг по фазе между приложенным переменным напряжением и током, вызванным этим напряжением. В цепи с чистой индуктивностью (идеальный частный случай) ток отстает на четверть периода (90°) от приложенного напряжения.
Электрический ток возникает под действием электрического поля, поэтому всякая электрическая цепь обладает некоторой емкостью С. Способность накапливать электрические заряды с одновременным повышением потенциала до определенного уровня называется электрической емкостью. Для получения необходимых емкостей применяют электрические конденсаторы. В некоторых случаях влияние емкостей на режим цепи незначительно и его можно не учитывать.
Если к электрической цепи, замкнутой на емкость, приложить постоянное напряжение, то ток возникает только в момент включения и прекращается, когда емкость заряжается до напряжения источника. Переменное напряжение, приложенное к этой же цепи, изменяется периодически и вместе с ним периодически изменяется заряд емкости. Переменный ток создает переменный ток заряда и разряда. Конденсаторы различной емкости вызывают в цепи разные токи заряда и разряда. Конденсатор можно рассматривать как некоторое сопротивление переменному току, т: е. включенный в цепь переменного тока он вносит в нее дополнительное емкостное сопротивление, измеряемое в омах. Чем больше переменный ток, тем меньше емкостное сопротивление конденсатора . Емкостное сопротивление цепи обратно пропорционально емкости конденсатора и частоте переменного тока.
Переменное напряжение, приложенное к этой же цепи, изменяется периодически и вместе с ним периодически изменяется заряд емкости. Переменный ток создает переменный ток заряда и разряда. Конденсаторы различной емкости вызывают в цепи разные токи заряда и разряда. Конденсатор можно рассматривать как некоторое сопротивление переменному току, т: е. включенный в цепь переменного тока он вносит в нее дополнительное емкостное сопротивление, измеряемое в омах. Чем больше переменный ток, тем меньше емкостное сопротивление конденсатора . Емкостное сопротивление цепи обратно пропорционально емкости конденсатора и частоте переменного тока.
Таким образом, индуктивность и емкость вносят дополнительные сопротивления в цепь переменного тока и вызывают сдвиг по фазе между приложенным напряжением и током, возникающим под действием этого напряжения. Причем индуктивность и емкость вызывают фазовые сдвиги противоположного направления, т. е. как бы компенсируют друг друга.
Индуктивное XL и емкостное Хс сопротивления являются условными величинами, их возникновение обусловлено реакцией цепи на изменения тока и напряжения в ней, поэтому оба эти сопротивления называются реактивными.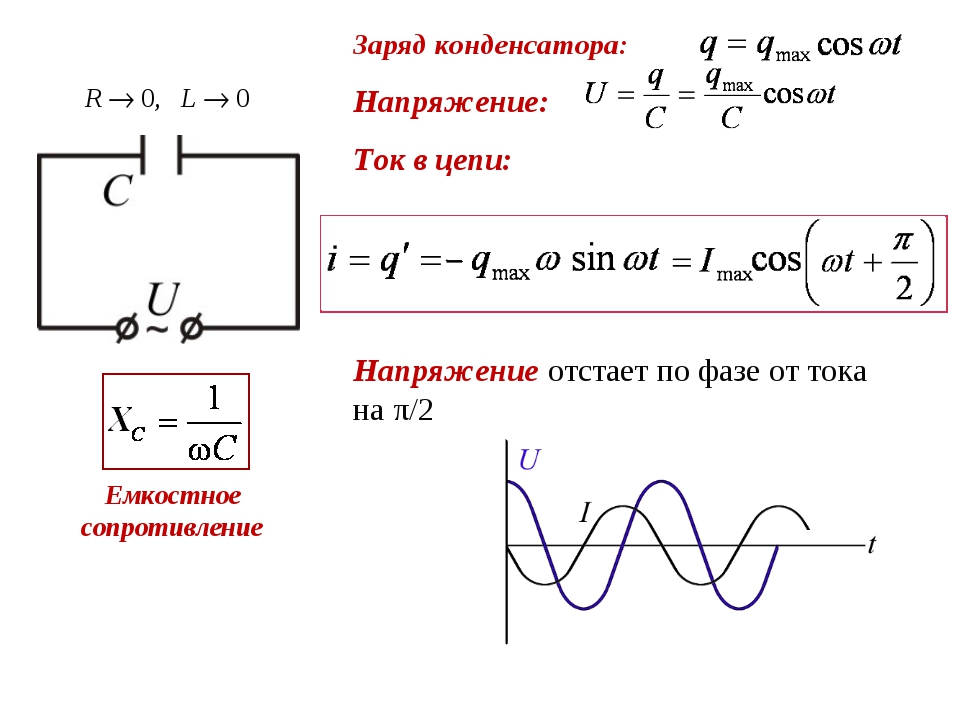
Реклама:
Читать далее:
Мощности в цепях переменного тока
Статьи по теме:
Цепь тока переменного — Энциклопедия по машиностроению XXL
Цепи тока переменного однофазного 224 —постоянного — Определения и соотношения 219— 222 [c.1004]Цепи тока переменного однофазного и трехфазного 112—114 [c.795]
Цепь тока переменного 308—310
[c. 575]
575]
ЦЕПИ ОДНОФАЗНОГО ПЕРЕМЕННОГО ТОКА [c.112]
Во всех этих примерах речь идет об использовании переменного электрического тока. Переменный электрический ток в энергетических электрических цепях является результатом возбуждения в них вынужденных электромагнитных колебаний. Эти вынужденные колебания создаются генераторами переменного тока, работающими на электростанциях.
Если с помощью контактных колец и скользящих по ним щеток соединить концы витка с электрической цепью, то под действием этой ЭДС индукции в электрической цепи возникнут вынужденные гармонические колебания силы тока — переменный ток. [c.237]
При подключении нагрузки к 1 онцам вторичной катушки во вторичной цепи возникает переменный ТОК. Мощность тока в [c.246]
Схема электронного мостика такова, что в измерительной цепи протекает переменный ток.
Цепи электрические переменного тока I (1-я)-519 [c.335]
Цепи однофазного переменного тока [c.224]
В зарубежных вариантах приборов при поданном напряжении =12 в непосредственно измеряют силу идущего по цепи тока и по ней оценивают состояние пленки. Соответствующая электрическая схема представлена на рис. 12-11. Для измерений используется только переменный ток.
В магнитометре используется дифференциальный феррозонд с разомкнутыми сердечниками и продольным возбуждением. Он содержит два параллельных друг другу одинаковых прямоугольного сечения сердечника 1 (рис. 55) толщиной 0,02, шириной 1,5 и длиной 7 мм, изготовленных из отожженного пермаллоя. Сердечники наложены на основания (подложки) толщиной 0,55, шириной 1,9 и длиной 10 мм. Поверх них намотаны в один слой обмотки возбуждения 2, включенные последовательно и образующие цепь возбуждения сердечников. Эту цепь питают переменным синусоидальным током If. Обмотки 2 соединены таким
Эту цепь питают переменным синусоидальным током If. Обмотки 2 соединены таким
Кондуктометры состоят из чувствительного элемента (датчика) и измерительного преобразователя, соединенных в общую электрическую цепь. К электродам чувствительного элемента прикладывается низкое переменное напряжение. Протекающий при этом в электрической цепи ток зависит от сопротивления жидкости, заполняющей чувствительный элемент. Этот ток измеряется преобразователем со шкалой, отградуированной в единицах удельной электрической проводимости. [c.571]
Плавное регулирование сварочного тока в трансформаторе с дросселем осуществляется изменением индуктивного сопротивления последнего за счет изменения воздушного зазора в его магнитной цепи. Иногда применяется дополнительное ступенчатое витковое регулирование первичной или вторичной обмотки трансформатора. Индуктивное сопротивление дросселя можно регулировать не только механическим, но и электрическим путем.
В вибровозбудителях малой мощности иногда используют постоянно намагниченный магнитопровод, что эквивалентно подмагничиванию постоянным током. В вибрационных стендах применяют также вибровозбудители с конденсатором, включенным в цепь обмотки переменного тока это позволяет использовать резонансные эффекты в электрических цепях [10].
Если емкость включена в задающую цепь генератора переменного напряжения, то можно измерять не токи или напряжения, а временные параметры — частоту или длительность. В классическом генераторе с индуктивностью период колебаний пропорционален У С, а е резистивно-емкостном генераторе он линейно зависит от С. Этот метод обладает большой гибкостью, так как всегда можио выбрать оптимальный вид выходного сигнала. Например, при включении преобразователя е переменным зазором в цепь резистивно-емкостного генератора частота колебаний
[c.200]
В классическом генераторе с индуктивностью период колебаний пропорционален У С, а е резистивно-емкостном генераторе он линейно зависит от С. Этот метод обладает большой гибкостью, так как всегда можио выбрать оптимальный вид выходного сигнала. Например, при включении преобразователя е переменным зазором в цепь резистивно-емкостного генератора частота колебаний
[c.200]
Для маркировки конденсаторов постоянной емкости применяют букву К (конденсатор постоянной емкости) и цифры, определяющие вид диэлектрика. В табл. 6.1 приведены сокращенные обозначения и типы некоторых конденсаторов в табл. 6.2 — сведения о некоторых типах конденсаторов, предназначенных для работы в цепях постоянного, переменного и пульсирующего токов. [14]. [c.274]
Технические данные конденсаторов для работы в цепях постоянного, переменного и пульсирующего токов [c.275]
Что покажут миллиамперметры магнитоэлектрической и выпрямительной (с двухполупериодным выпрямителем) систем, включенные в цепь с переменным током прямоугольной формы и с амплитудой 10 мА
[c.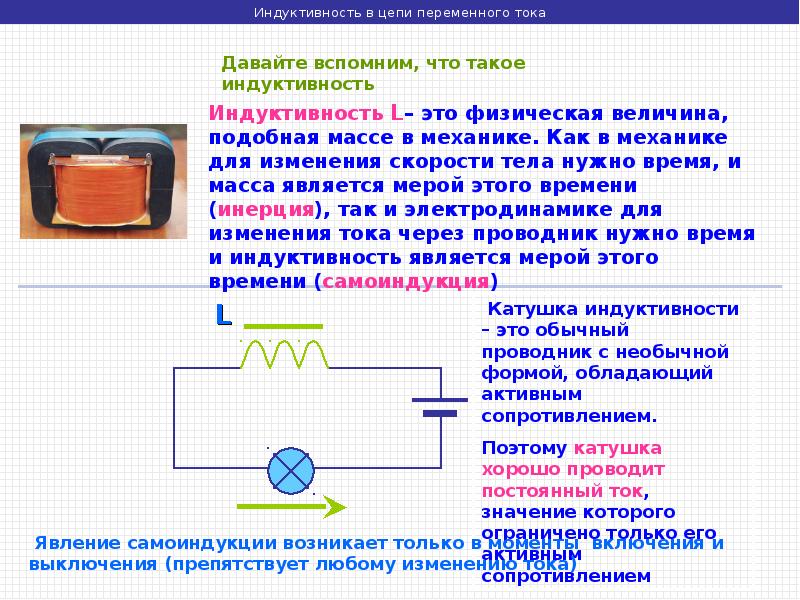 140]
140]
Уровень случайных помех. Кроме частных случайных погрешностей, обусловленных нерегулярными колебаниями воздействий влияющих факторов, уровень помех, ограничивающих возможность измерения малых сигналов, вызывается также тепловыми шумами в активных резистивных элементах и уровнем случайных пульсаций тока в измерительных цепях, индуцированных переменными электромагнитными полями. Снижение уровня электромагнитных помех достигается соответствующим экранированием измерительных цепей. Однако уровень шумов радиоэлектронной аппаратуры не всегда удается снизить до требуемой величины, и минимальное его значение приходится учитывать при определении динамического диапазона измерений. [c.80]
Напряженке цепи тока, В переменного постоянного Частота, Гц [c.96]
Примечания 1. Номинальное напряжение цепи управления переменного тока 127, 220 В. [c.186]
Величина Xl зависит от воздушного зазора между якорем и ярмом и вызвана действующими в цепи с переменным током
[c. 180]
180]
В положении п е р е к р ы ш и (III и IV положения ручки крана машиниста) постоянный ток от зажима генератора управления ГУ (см. рис. 124) через контакты контроллера КМ, контакт ТР4 возбуждает катушку ОР реле отпуска и его контакт 0Р4 через контакт KPI замыкает цепь питания катушки сильноточного реле К. Контакты 0Р1, 0Р2 размыкают цепь питания переменным током линейных проводов и замыкают цепь их питания постоянным током через контакт Kt сильноточного реле. Катушка контрольного реле КР питается постоянным током. При переключении с источника переменного на источник постоянного тока якорь контрольного реле остается в притянутом положении в результате замедления на отпадание под влиянием конденсатора Сз. Через контакты КР2 контрольного реле и 0Р5 реле отпуска лампа П сигнализатора питается постоянным током. В рельсы и на корпус подвижного состава идет ток плюсовой полярности, а в линейный провод Л 1—минусовой. При этом возбуждаются катушки вентилей ОВ электровоздухораспределителей, протеканию же тока через катушки вентилей торможения ТВ препятствуют селеновые выпрямители ВС, пропускающие ток только в одном направлении. [c.188]
[c.188]
Реле трансмиттера коммутирует цепь первичной обмотки кодового трансформатора КТ р. При замыкании контакта реле в рельсовую цепь подается переменный ток (импульс), при размыкании контакта подача тока прекращается (интервал). [c.261]
Напомним, что постоянным называется электрический ток, который не изменяется при прохождении по цепи ни по величине, ни по направлению. Постоянный ток получают от аккумулятора или электрического генератора постоянного тока. Переменным называется [c.65]
Рассмотрим элемент, состоящий из цинкового и медного электродов, погруженных в растворы ZnSOi и USO4, соответственно (элемент Даниэля). Пусть внешняя цепь включает переменное сопротивление R, вольтметр V и амперметр А (рис. 4.1). Разность потенциалов (э. д. с.) между цинковым и медным электродами в отсутствие тока близка к 1 В. Если теперь, подобрав соответствующее сопротивление R, обеспечить протекание во внешней цепи небольшого тока, то измеряемая разность потенциалов станет меньше 1 В вследствие поляризации обоих электродов. По мере роста тока напряжение падает. Наконец, при коротком замыкании разность потенциалов между медным и цинковым электродами приближается к нулю. Влияние силы тока в цепи на напряжение элемента Даниэля можно графически изобразить с помощью поляризационной диаграммы, представляющей собой зависимость потенциалов Е медного и цинкового электродов от полного тока I (рис. 4.2). Способ определения этих потенциалов будет пояснен в разделе 4.3. Символами Ezn и Еси обозначены так называемые потенциалы разомкнутого элемента, отвечающие отсутствию тока в цепи. Поляризации цинкового электрода отвечает кривая аЪс, медного — кривая def. При силе тока, равной / , поляризация цинка в вольтах определяется как разность между [c.47]
В литературе наш пример с часами был впервые рассмотрен в Ele trote hn. Zeit hrift за 1904 г. в связи с актуальной в то время проблемой колебаний синхронных машин . Два синхронных генератора переменного тока, включенные параллельно и работающие на одну и ту же цепь тока, испытывают в случае резонанса нежелательные колебания числа оборотов и тока. Эти колебания являются по существу увеличенным отображением колебаний наших часов, а также и рассмотренных здесь явлений связи и резонанса симпатических маятников. [c.157]
РПИБ-М Регулирование электрической активной мощности в трехфазных цепях переменного тока Переменный, частота 50 Гц 2 Первичный прибор с дифференциально — трансформаторным датчиком производства завода Манометр и датчиком трансформатора тока ДТТ-58 производства МЗТА Вместо указанного прибора с дифференциально — трансформаторным датчиком могут применяться Первичные приборы с ферродинамиче-скими, индукционными или реостатными датчиками [c.771]
Вибровозбудителн с конденсатором в цепи обмотки переменного тока могут-возбуждать вибрацию с частотой qdijp, где q, р — целые числа [10]. Динамика вибровозбудителей постоянного тока с механическими или электронными прерывате- лями охватывается теорией электромеханических систем с прерывателем (см. т. 2). [c.264]
В также деформируется, а магнитная проницаемость рамки меняется, что изменяет и индуктивность катушки, которая, как и в предыдущем случае, может быть включена в цепь моста переменного тока. При высокой чувствительности эти тензометры обладают нестабильностью в работе, связанной с остаточным изменением свойств пермалоя при деформации. [c.355]
Переменный ток в термогенераторах можно получать с помощью периодического нагревания и охлаждения спаев ТЭЭЛ. Разработаны различные конструкции подобных ТЭГ. А. X. Черкасским была предложена идея такого ТЭГ переменного тока. В одном из вариантов предусматривалось применение вращающихся батарей ТЭЭЛ с соответствующими коллекторами для получения постоянного или переменного тока [5]. Устройство, основанное на использовании теплового потока, периодически обтекающего горячие спаи ТЭЭЛ, исследовалось также в США [6]. Принципиальная схема одного из таких ТЭГ показана на рис. 3.4. Тонкие пленки полупроводников д- и р-типов образуют термоэлектрическую цепь, которая вплетена в диэлектрик таким образом, что горячие спаи находятся на одной стороне, а холодные — на другой. Если такой ТЭГ вращается или источники тепла и холода движутся вокруг ТЭГ, спаи периодически нагреваются и охлаждаются и в цепи возникает переменный ток. [c.43]
При питании анодной цепи постоянным током определенного напряжения проводимость лампы сохраняется и после снятия пальца с проводящего слоя колбы, а реле, включенное в анодную или катодную цепь, остается возбужденным до снятия напряжения, приложенного к анодной цепи. Таким образом, лампа может быть использована как элемент памяти. Если анодная цепь питается переменным или выпрямленным однополупе-риодным током, то лампа и включенное в анодную [c.31]
На железных дорогах прошел испытания однопроводный ЭПТ, в котором в качестве второго провода используется корпус подвижного состава, а контроль электрических цепей осуществляется переменным током с помощью концевого блока, включаемого на хвостовом вагоне. [c.207]
Для электроакустических трактов высокого качества наибольшее распространение в настоящее время получил конденсаторный (электростатический) микрофон. Принципиально он работает следующим образом (рис. 5.8, д). Жестко натянутая мембрана I под воздействием звукового давления южет колебаться относительно неподвижного электрода 2, являясь вместе с ним обкладками электрического конденсатора. Этот к9нденсатор включается в электрическую цепь последовательно с ист очником постоянного тока Е и активным. нагрузочным сопротивленцем Я. При колебаниях мембраны емкость конденсатора меняется с частотой воздействующего на мембрану звукового давления, в связи с чем в электрической цепи появляется переменный ток той же частоты и на нагрузочном сопротивлении возникает падение напряжения, являющееся выходным сигналом микрофона. Выходное напряжение микрофона [c.70]
Аппаратура с магнитоупругими (магнитострикционными) тензодатчиками [18], [26]. Используется изменение импеданца цепи, питаемой переменным током 10—50 кги,, в связи с изменением магнитной 11роницаемости датчика при деформации. [c.493]
Сопротивление цепи переменного тока емкостное
Соотношение неопределенностей Гейзенберга 430 Сопротивление цепи переменного тока емкостное 310 [c.574]Для исследования состояния поверхности металлических образцов и процессов адсорбции на ней, а также свойств окисных и защитных изоляционных пленок на поверхности металла применяют емкостно-омический метод (рис. 358). Емкость и сопротивление исследуемого электрода определяют компенсационным методом — подбором соответствующих величин емкости и сопротивления Rs на мостике переменного тока с осциллографом в качестве нуль—инструмента. В электрохимических исследованиях этот метод сочетают с поляризационным методом, измеряя импеданс (полное активное и реактивное сопротивление цепи переменного тока) при различных значениях потенциала исследуемого электрода (см. 166). [c.465]
Найдите емкостное сопротивление конденсатора электроемкостью 10 мкФ в цепи переменного тока с частотой 50 Гц. [c.296]
| Фиг. 7. Цепь переменного тока, содер жащая последовательно включенные активное, индуктивное и емкостное сопротивления. |
Активное, индуктивное и емкостное сопротивления в цепи переменного тока [c.36]
В цепях переменного тока различают активное, индуктивное и емкостное сопротивления. [c.12]
Емкость в цепи переменного тока проводит ток (в отличие от постоянного ). Сопротивление, которое оказывает емкость переменному току, называют емкостным. [c.146]
Одним из перспективных и в настоящее время активно развиваемых способов возбуждения мощных СОг-ла-зеров являются также самостоятельные ВЧ-разряды и разряды переменного тока. Схема электродного варианта газоразрядной камеры и достигнутые характеристики лазеров с возбуждением разрядом переменного тока приведены в табл. 4.5 (схема 5). Разрядный ток протекает между большим количеством равномерно расположенных по плате электродов, в цепи каждого из которых включена балластная емкость. Безэлектродный вариант Вч-разряда иллюстрируется в табл. 4.5 (схема 6). Электрический ток поддерживается между охлаждаемыми диэлектрическими профилированными электродами, внутри которых расположены токоподводы. Роль распределенного балластного емкостного сопротивления играет при этом диэлектрическое покрытие. [c.142]
В такой схеме все напряжение практически ложится на емкостные плечи, так как их сопротивление переменному току l/w много больше сопротивлений, включенных в другие плечи. Поэтому, несмотря на наличие высокого напряжения можно безопасно производить уравновешивание моста изменением R3 и j. Для защиты цепи в случае пробоя образца предусмотрены разрядники. Индикатором равновесия моста обычно служит вибрационный гальванометр, зачастую вклю- [c.507]
В цепи с чисто емкостным сопротивлением (идеальный частный случай) переменный синусоидальный ток опережает приложенное напряжение на четверть периода (90°). [c.13]
В качестве источников тока при сварке переменным током обычно используют стандартные сварочные трансформаторы с дросселями типа РСТЭ-24, РСТЭ-34, СТАН-0, СТАН-1 и другие. При аргонодуговой сварке на переменном токе происходит некоторое выпрямление тока. Это ухудшает технологические свойства дуги и механические свойства сварных соединений, а также ухудшает условия эксплуатации сварочного трансформатора. Предупредить выпрямление тока можно включением в сварочную цепь индуктивного и емкостного сопротивления, В качестве 18 [c.18]
При активном сопротивлении электрическая энергия расходуется на образование теплоты. Реактивное сопротивление может быть индуктивным (х ), образующим магнитное поле, или емкостным (хс), образующим электрическое поле. Полное сопротивление цепи для переменного тока [c.121]
Ранее были рассмотрены случаи, когда кроме к выходу выпрямителя были подключены L или С. Часто в цепь выпрямленного тока для снижения переменной составляющей напряжения на потребителе / н (фильтрации) включают индуктивные и емкостные реактивные сопротивления (см. рис. 2.12, а). При таком включении выпрямитель работает на смешанную нагрузку. На рис. 2.20 приведены две широко распространенные схемы фильтров Г-образного (рис. 2.20, а) и П-образного (рис. 2.20, б). Для получения малых пульсаций напряжения на нагрузочном сопротивлении в этих схемах применяются дроссели большой индуктивности L и конденсаторы большой емкости и Сц так что [c.93]
При прохождении постоянного тока электрическая цепь оказывает ему только омическое сопротивление. Переменный ток может встретить в цепи, кроме омического (называемого в этом случае активным), еще индуктивное и емкостное (так называемые реактив- [c.137]
Емкостное сопротивление конденсатора и индуктивное сопротивление катушки зависят от частоты (I) приложенного напряжения. Поэтому при постоянной амплитуде U колебаний напряжения амплитуда 1 , колебаний силы тока в цепи зависит от частоты (1) переменного напряжения. [c.244]
Применение тиристорной схемы управления позволяег простыми средствами бесступенчато регулировать обороты электродвигателя. Диоды Д7—Д10 в цепи управления тиристоров Д5 и Д6 установлены для предотвращения возникновения импульса обратной полярности на управляющем электроде. Резисторы R1 и R2 включены для выравнивания углов зажигания тиристоров. Сдвиг фазы управляющего напряжения относительно напряжения питания тиристоров осуществляется с помощью фазовращателя, который представляет собой цепь переменного тока, содержащую активное, индуктивное и емкостное сопротивления. При изменении сопротивлений резисторов R3 и R4 фаза управляющего напряжения тиристоров сдвигается в идеальном случае от О до 180°, практически л[c.332]
Большая часть примеров а книге приведена для цепей постоянного тока, поскольку наличие иидуктпвпого и емкостного сопротивлений в цепях переменного тока значительно усложняет все расчеты и снижает наглядность таких примеров. Кроме того, на электровозах переменного тока большая часть цепей выполнена на постоянном токе. [c.221]
П. переменного тока. При компенсации на переменном токе необходимо, чтобы непосредственно сравниваемые эдс были равны по величине и имели одинаковые 1) частоту, 2) форму кривой и 3) фазу. Выполнения первых двух условий достигают, питая потенциометр через соответствующий трансформатор от того же генератора, напряжение к-рого нужно измерить. Для выполнения третьего условия необходим регулятор фаз (П. сист. Дрисдаля) или особый трансформатор без железа (комплексный П. системы Гартмана и Брауна). В виду отсутствия эталона переменной эдс для установления силы рабочего тока в П. переменного тока служат электродинамические амперметры, поэтому точность измерения величины напряжения не превосходит точности этого амперметра (0,5%). П. переменного тока применяются при всех точных измерениях в цепях переменного тока при калибровке амперметров и вольтметров, при точном измерении емкостного и индуктивного сопротивления цепи, при определении угла сдвига фаз между токами в отдельных участках цепи. Измерение угла при помощи регулятора фаз м. б. произведено с точностью не более 0,5°, с помощью комплексного П.—до 0,25°, но измерение последним величины эдс имеет погрешность 0,5 [c.241]
Если в электрической цепи, изображенной на рис. IV.2.7, отсутствует индуктивность (i/ =0) и то такая цепь переменного тока называется цепью с емкостным сопротивлением х . В такой цепн колебания силы тока опережают колебания внешней э.д.с. по фазе на я/2 (рис. IV.2.10) [c.310]
ЭТОМ охранный электрод образца соединяется с заземленным экраном, а высоковольтный — с указанной вершиной (рис. 3-2). В два другие плеча включаТотся переменный резистор R3 и постоянный резистор R4, шунтированный конденсатором переменной емкости С4. В такой схеме вее напряжение практически приходится на емкостные плечи, так как их сопротивление переменному току 1/(ц)С) много больше сопротивлений резисторов, включенных в другие плечи. Поэтому, несмотря на наличие высокого напряжения, можно безопасно уравновешивать мост изменением параметров R3 и С4. Для защиты цепи в случае пробоя образца предусмотрены разрядники. Индикатором равновесия моста обычно служит вибрационный гальванометр (см. ниже), зачастую включенный через усилитель. [c.51]
Действующие значения напряжения и тока. Соотношения между амплитудными и действующими значениями. Активное и реактивное сопротивления. Индуктивное и емкостное сопротивления. Примеры индуктивных и емкостных сопротивлений в электротехнике. Полное сопротивление цепи. Последовательное и параллельное соединение активных, индуктивных и емкостных сопротивлений. Закон Ома для цейи переменного тока. Мощность переменного тока. Активная и реактивная мощность. Полная мощность переменного тока. Коэффициент мощности. [c.318]
Наиболее часто значения С и tg б на частоте 50 Гц определяют при помощи мостов переменного тока. Предел измерения моста по емкости должен быть не менее емкости образца, а по tg б превышать примерно в 2 раза tg 6 образца. Принципиальная схема такого моста показана на рис. 29.23, а. Мост питается через повышающий трансформатор, позволяющий получать напряжение на мосте до 10 кВ. В два плеча, примыкающие к высоковольтной>. вершине, включают испытуемый образец Сх и. высоковольтный конденсатор Со, охранный электрод образца соединяют с заземленным экраном моста. В такой схеме все напряжение питания практически приходится на емкостные плечи, так как их сопротивление переменному току много больше сопротивлений других плеч. Это позвояет безопасно уравновешивать мост изменением j и Да. Для защиты цепи в случае пробоя образца предусмотрены разрядники. [c.370]
Емкостное и индуктивное сопротивления называют реактивными, оказывающими противодействие переменному току электрической цепи. В этих со- 2 I I противлениях потерь элек- [c.98]
В случае использования постоянного магнитного поля электромагнитные расходомеры практически безыинерционны, однако при этом возникает поляризация электродов. С целью исключения этого нежелательного явления используются электромагниты, питаемые переменным током промышленной или повышенной частоты. Возможности измерения переменных расходов в этом случае ограничены. Значительное повышение частоты магнитного возбуждения затрудняется индуктивной связью питающей и измерительной цепей, емкостным сопротивлением преобразователя и линии связи. В трубопроводах круглого сечения наведенная э. д. с. зависит от распределения скорости по сечению и, следовательно, от числа Ке. Если рабочий участок канала преобразователя расходомера имеет прямоугольную форму, две противоположные стенки которого являются усредняющими электродами, то показания расходомера не зависят от распределения скорости по поперечному сечению [148] и, следовательно, не зависят от вязкости, плотности и других физических свойств потока. Расходомеры могут применяться и в тех случаях, когда жидкости содержат газовые пузыри, взвешенные частицы и твердые включения при условии, что эти включения не создают осадка на электродах, изолирующего их от жидкости. Во всех этих случаях [c.373]
Если к электрической цепи, замкнутой на емкость, приложить постоянное напряжение, то ток возникает только в момент включения и прекращается, когда емкость заряжается до напряжения источника. Переменное напряжение, приложенное к этой же цепи, изменяется периодически и вместе с ним периодически изменяется заряд емкости. Переменный ток создает переменный ток заряда и разряда (рис. 9). Конденсаторы различной емкости вызывают в цепи разные токи заряда и разряда. Конденсатор можно рассматривать как некоторое сопротивление переменному току, т. е. включенный в цепь переменного тоха он вносит в нее дополнительное емкостное сопротивление, измеряемое в омах. Чем бо.пьше переменный ток, тем меньше емкостное сопротивление конденсатора Л с- Емкостное сопротивление цепи обратно пропорционально [c.13]
На выемной панели блока размещены элементы электрической схемы (рис. 6.19) реле. При подаче напряжения питания 36 В на делитель частоты ДЧ и 230 В на конденсаторы фильтра С2 напряжение частотой 25 Гц, получаемое от делителя частоты ДЧ, прикладывается между землей и тремя фазами переменного тока 230 В через выпрямитель УОЗ-б, реле К, килоомметр РК, заграждающий фильтр Ы—СЗ и емкостный фильтр С2. При снижении сопротивления изоляции сети или появлении отключающей утечки на стороне переменного или выпрямленного тока зарядного устройства или на зажимах заряжаемой батареи ток, протекающий по оперативной цепи, возрастает, и реле К срабатывает. Оно размыкает свои контакты в цепи отключающей катушки выключателя, к которому подключено зарядное устройство, и замыкает другие контакты в цепи сигнального устройства. [c.231]
Эти устройства осуществляют автоматический контроль изоляции постоянным оперативным током. В качестве постороннего источника энергии применяется понижаюгций трансформатор с выпрямителем. В измерительной цепи т аких схем, кроме постоянного оперативного тока постороннего ист очника энергии, проходит переменный ток, вызванный напряжением контролируемой сети. Для его ослабления применяют фильтрующие сопротивления (емкостные или индуктивные). [c.73]
В поле электромагнита 1 с обмоткой возбуждения 2 находится подвижная система 3, состоящая из трех коаксиально намотанных катущек а, d и Ь. Катушки and включены навстречу друг другу. Последовательно с катушкой а включается измеряемая емкость 4, последовательно с катушкой d включается образцовая емкость 5. Эти две параллельные цепи присоединены через предохранительное сопротивление 6 к обмотке 7 электромагнита I. Обмотка 7 является вторичной обмоткой трансформатора, первичную обмотку которого представляет обмотка 2. Ток в обмотке 2 является индуктивным, токи в катушках and — емкостными вследствие трансформации они сдвинуты на 180° так, что ток питания в обмотке 2 и ток, проходящий через подвижную систему 3, находятся в фазе, благодаря чему создается значительный вращающий момент. Так как катушки and включены навстречу друг другу, то прибор измеряет разность токов, протекающих через измеряемую емкость 4 и через емкость 5, служащую для сравнения. Противодействующий момент, прилагаемый к подвижной системе 3, с которой скреплена стрелка /, получается электрическим способом, за счет тока, индуцированного в обмотке в подвижной системе 3. Источником этого тока является переменное поле электромагнита I. Противодействующий момент, вызываемый этим током, находится в такой же зависимости от величины тока 2, как и момент, обусловленный наличием токов в катушках and. Установка стрелки f на нуль производится перемещением якоря И катушки самоиндукции 9 посредством винта 10. Катушка 9 и сопротивление 8 включены в цепь обмотки катушки Ь. [c.797]
Получила распространение также переносная пробойноиспытательная установка ПИУ-1 (рис. 6-18), позволяющая получать постоянное напряжение 1. .. 5 /се. В установке не предусмотрено плавное повышение напряжения, и это приходится осуществлять с помощью дополнительного устройства, включаемого между сетью и зажимами питания установки (потенциометр, лабораторный автотрансформатор и др.). Повысительный трансформатор Т имеет четыре секции для получения напряжений 1, 2, 3 и 5 /се включение секций производится при помощи контакторов К , Kz, и К . Каждый контактор имеет две пары контактов при нажатии кнопки вначале замыкаются верхние контакты в цепи вторичной обмотки трансформатора, а затем — нижние контакты в цепи первичной обмотки. Кроме того, предусмотрен контактор Кь с надписью включение , обеспечивающий безопасность работы с установкой первичная обмотка трансформатора будет включена только в нажатом положении этой кнопки. Одновременно, когда нажимают на кнопку, размыкается цепь с сопротивлением = 6 ком, которое шунтирует зажимы высокого напряжения в нерабочем положении. Таким образом, для получения высокого напряжения необходимо одновременно включить контактор Кб и один из контакторов Ki — К . Переменное напряжение на вторичной обмотке выпрямляется при помощи кенотрона Л для сглаживания пульсаций служит емкостный фильтр ( l и Са). Вольтметр постоянного тока включен через 180 [c.180]
Параметрический (варакториый) диод является полупроводниковым прибором, который используется как элемент цепи с переменным реактивным сопротивлением (емкостным). По своей структуре параметрические диоды разделяются на диоды с р-п переходом и контактами металл — полупроводник (диоды с барьером Шотки). Наиболее перспективными являются последние. Изменение реактивного сопротивления обусловлено тем, что емкость р-п перехода или барьерная емкость контакта металл — полупроводник изменяются под воздействием приложенного напряжения. Это позволяет использовать параметрические диоды для модуляции или пере1слючения СВЧ сигналов генерирования гармоник управляющего сигнала усиления СВЧ колебаний преобразования частоты одного из двух подводимых сигналов. Параметрические диоды используются в режиме обратного смещения. Малый обратный ток параметрического диода в рабочем режиме позволяет получить очень малый коэффициент шума параметрических усилителей на этих диодах. [c.93]
Урок 43-2 (продолжение) Переменный ток
Рассмотрим по отдельности случаи подключения внешнего источника переменного тока к резистру с сопротивлением R, конденсатору емкости C и катушки индуктивности L. Во всех трех случаях напряжения на резисторе, конденсаторе и катушке равны напряжению источника переменного тока.
1. Резистор в цепи переменного тока
Сопротивление R называют активным, потому что цепь с таким сопротивлением поглощает энергию.
Активное сопротивление — устройство, в котором энергия электрического тока необратимо преобразуется в другие виды энергии (внутреннюю, механическую)
Пусть напряжение в цепи меняется по закону: u = Umcos ωt ,
тогда сила тока меняется по закону: i = u/R = IRcosωt
u – мгновенное значение напряжения;
i – мгновенное значение силы тока;
IR — амплитуда тока, протекающего через резистор.
Связь между амплитудами тока и напряжения на резисторе выражается соотношением RIR = UR
Колебания силы тока совпадают по фазе с колебаниями напряжения. (т.е. фазовый сдвиг между током и напряжением на резисторе равен нулю).
2. Конденсатор в цепи переменного тока
При включении конденсатора в цепь постоянного напряжения сила тока равна нулю, а при включении конденсатора в цепь переменного напряжения сила тока не равна нулю. Следовательно, конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока.
Соотношение между амплитудами тока IC и напряжения
UC:
Ток опережает по фазе напряжение на угол π/2.
3. Катушка в цепи переменного тока
В катушке, включенной в цепь переменного напряжения, сила тока меньше силы тока в цепи постоянного напряжения для той же катушки. Следовательно, катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи постоянного напряжения.
Соотношение между амплитудами тока IL и напряжения UL:
ωLIL = UL
Ток отстает по фазе от напряжения на угол π/2.
Теперь можно построить векторную диаграмму для последовательного RLC-контура, в котором происходят вынужденные колебания на частоте ω. Поскольку ток, протекающий через последовательно соединенные участки цепи, один и тот же, векторную диаграмму удобно строить относительно вектора, изображающего колебания тока в цепи. Амплитуду тока обозначим через I0. Фаза тока принимается равной нулю. Это вполне допустимо, так как физический интерес представляют не абсолютные значения фаз, а относительные фазовые сдвиги.
Векторная диаграмма на рисунке построена для случая, когда или В этом случае напряжение внешнего источника опережает по фазе ток, текущий в цепи, на некоторый угол φ.
Векторная диаграмма для последовательной RLC-цепи
Из рисунка видно, что
откуда следует
Из выражения для I0 видно, что амплитуда тока принимает максимальное значение при условии
или
Явление возрастания амплитуды колебаний тока при совпадении частоты ω внешнего источника с собственной частотой ω0 электрической цепи называется электрическим резонансом. При резонансе
Сдвиг фаз φ между приложенным напряжением и током в цепи при резонансе обращается в нуль. Резонанс в последовательной RLC-цепи называется резонансом напряжений. Аналогичным образом с помощью векторной диаграммы можно исследовать явление резонанса при параллельном соединении элементов R, L и C (так называемый резонанс токов).
При последовательном резонансе (ω = ω0) амплитуды UC и UL напряжений на конденсаторе и катушке резко возрастают:
Рисунок иллюстрирует явление резонанса в последовательном электрическом контуре. На рисунке графически изображена зависимость отношения амплитуды UC напряжения на конденсаторе к амплитуде 0 напряжения источника от его частоты ω. Кривые на рисунке называются резонансными кривыми.
Поведение конденсатора в цепи переменного тока
Если говорить строго, то через конденсатор не проходит ни постоянный, ни переменный ток, так как между обкладками находится изолятор, в котором свободные электрические заряды двигаться не могут.
Включение конденсатора в цепь постоянного тока равносильно разрыву этой цепи. Что же касается переменного тока, то он будет протекать по цепи, в которую включен конденсатор, благодаря периодическому заряду и разряду этого конденсатора. Действительно, когда происходит заряд конденсатора, то электрические заряды, например электроны, на одной обкладке накапливаются, а с другой обкладки уходят. При этом они, конечно, двигаются по соединительным проводам, подключенным к обкладкам конденсатора. Такое же движение зарядов, только в противоположном направлении, происходит и при разряде конденсатора.
Если включить конденсатор в цепь переменного тока, то он будет периодически заряжаться то в одной полярности, то в противоположной. Это значит, что электроны будут накапливаться то на одной, то на другой обкладке, и каждый раз при заряде и разряде свободные электроны будут двигаться по цепи, в которую включен конденсатор, не попадая, однако, в изолятор, включенный между обкладками. А поскольку под действием переменного напряжения в цепи конденсатора двигаются заряды, то мы считаем, что конденсатор пропускает переменный ток, хотя и в этом случае заряды не проходят через изолятор.
Конденсатор влияет на величину переменного тока в цепи, и поэтому (по аналогии с законом Ома) его часто рассматривают как сопротивление. Это так называемое емкостное сопротивление обозначается буквой хс и так же, как и обычное сопротивление, измеряется в омах. Величина хс зависит от частоты переменного тока и от емкости С конденсатора: с уменьшением емкости конденсатора, так же как и с уменьшением частоты переменного тока, емкостное сопротивление конденсатора увеличивается (рис. 80, 81, лист 87). Эту зависимость удобно записать в виде простой формулы:
Смысл этой формулы весьма прост: чем меньше емкость С, тем меньше зарядов будет двигаться к обкладкам при каждом заряде и разряде конденсатора; чем меньше частота переменного тока, тем реже будет заряжаться и разряжаться конденсатор. Отсюда следует, что с уменьшением f и С уменьшается ток в цепи, или, иными словами, растет сопротивление конденсатора.
Этот вывод имеет огромное практическое значение. Так, например, если нам понадобится включить в цепь конденсатор с очень маленьким емкостным сопротивлением, то емкость этого конденсатора нужно будет выбирать с учетом частоты переменного тока в цепи. Для высоких частот можно будет взять конденсатор небольшой емкости, а вот для низких частот емкость конденсатора придется взять большой. Это хорошо иллюстрируется простым примером. На частоте 100 кгц конденсатор емкостью 100 пф обладает емкостным сопротивлением хс=16 ком. При уменьшении частоты в 1000 раз, то есть на частоте 100 гц, сопротивление конденсатора возрастет в 1000 раз и станет равным 16 000 ком (16 Мом). Для того чтобы при уменьшении частоты емкостное сопротивление не изменилось, нужно увеличить емкость конденсатора. Сопротивление 16 ком на частоте 100 гц будет иметь конденсатор емкостью 100 000 пф (0,1 мкф).
Из приведенной выше формулы следует также, что уменьшение емкости конденсатора связи Ссв (лист 85) приведет к росту сопротивления этого конденсатора, а следовательно, к уменьшению тока в цепи антенны. Поэтому емкость Ссв нельзя брать слишком малой.
Сказанное можно пояснить еще иначе. Конденсатор связи и колебательный контур Lк Ск можно рассматривать как делитель напряжения, к которому приложена э. д. с, действующая между зажимами А («антенна») и З («земля»). Мы не будем пока говорить о том, чему равно сопротивление колебательного контура — даже без этого ясно: чем больше емкостное сопротивление конденсатора связи, тем меньшая часть э. д. с. будет действовать на нижней части делителя — на контуре и подключенной к нему цепи детектор — телефон.
Конденсатор в цепи переменного тока
Соберем цепь с конденсатором, в какой генератор переменного тока делает синусоидальное напряжение. Разберем поочередно, что произойдет в цепи, когда мы замкнем ключ. Исходным будем считать тот момент, когда напряжение генератора равно нулю.
В первую четверть периода напряжение на зажимах генератора будет возрастать, начиная от нуля, и конденсатор начнет заряжаться. В цепи появится ток, но в 1-ый момент заряда конденсатора, невзирая на то, что напряжение на его пластинках только-только появилось и еще сильно мало, ток в цепи (ток заряда) будет большим. По мере же роста заряда конденсатора ток в цепи убывает и доходит до нуля в момент, когда конденсатор стопроцентно зарядится. При всем этом напряжение на пластинках конденсатора, строго следуя за напряжением генератора, становится к этому моменту наибольшим, но оборотного знака, т. е. ориентировано навстречу напряжению генератора.Рис. 1. Изменение тока и напряжения в цепи с емкостью
Таким макаром, ток с большей силой устремляется в свободный от заряда конденсатор, но здесь же начинает убывать по мере наполнения зарядами пластинок конденсатора и падает до нуля, стопроцентно зарядив его.
Сравним это явление с тем, что происходит с потоком воды в трубе, соединяющей два сообщающихся сосуда (рис. 2),один из которых заполнен, а другой пустой. Стоит только выдвинуть заслонку, преграждающую путь воде, как вода сразу из левого сосуда под огромным напором устремится по трубе в пустой правый сосуд. Но тотчас же напор воды в трубе начнет равномерно слабеть, вследствие выравнивания уровней в сосудах, и свалится до нуля. Течение воды закончится.
Рис. 2. Изменение напора воды в трубе, соединяющей сообщающиеся сосуды, сходно с конфигурацией тока в цепи во время заряда конденсатора
Подобно этому и ток поначалу устремляется в незаряженный конденсатор, а потом равномерно слабеет по мере его заряда.
С началом 2-ой четверти периода, когда напряжение генератора начнет поначалу медлительно, а потом все резвее и резвее убывать, заряженный конденсатор будет разряжаться на генератор, что вызовет в цепи ток разряда. По мере убывания напряжения генератора конденсатор все в большей и большей степени разряжается и ток разряда в цепи растет. Направление тока разряда в этой четверти периода обратно направлению тока заряда в первой четверти периода. Соответственно этому кривая тока, пройдя нулевое значение, размещается уже сейчас ниже оси времени.
К концу первого полупериода напряжение на генераторе, также и на конденсаторе стремительно приближается к нулю, а ток в цепи медлительно добивается собственного наибольшего значения. Вспомнив, что величина тока в цепи тем больше, чем больше величина переносимого по цепи заряда, станет ясным, почему ток добивается максимума тогда, когда напряжение на пластинках конденсатора, а как следует, и заряд конденсатора стремительно убывают.
С началом третьей четверти периода конденсатор вновь начинает заряжаться, но полярность его пластинок, так же как и полярность генератора, меняется «а оборотную, а ток, продолжая течь в том же направлении, начинает по мере заряда конденсатора убывать, В конце третьей четверти периода, когда напряжения на генераторе и конденсаторе добиваются собственного максимума, ток становится равным нулю.
В последнюю четверть периода напряжение, уменьшаясь, падает до нуля, а ток, изменив свое направление в цепи, добивается наибольшей величины. На этом и завершается период, за которым начинается последующий, в точности повторяющий предшествующий, и т. д.
Итак, под действием переменного напряжения генератора два раза за период происходят заряд конденсатора (1-ая и 3-я четверти периода) и два раза его разряд (2-ая и 4-ая четверти периода). Но потому что чередующиеся один за одним заряды и разряды конденсатора сопровождаются всякий раз прохождением по цепи зарядного и разрядного токов, то мы можем заключить, что по цепи с емкостью проходит переменный ток.
Убедиться в этом можно на последующем ординарном опыте. Подключите к сети переменного тока через лампочку электронного освещения мощностью 25 Вт конденсатор емкостью 4—6 мкф. Лампочка зажгется и не погаснет до того времени, пока не будет разорвана цепь. Это гласит о том, что по цепи с емкостью проходил переменный ток. Но проходил он, естественно, не через диэлектрик конденсатора, а в каждый момент времени представлял собой либо ток заряда либо ток разряда конденсатора.
Диэлектрик же, как нам понятно, поляризуется под действием электронного поля, возникающего в нем при заряде конденсатора, и поляризация его исчезает, когда конденсатор разряжается.
При всем этом диэлектрик с возникающим в нем током смещения служит для переменного тока собственного рода продолжением цепи, а для неизменного разрывает цепь. Но ток смещения появляется исключительно в границах диэлектрика конденсатора, и потому сквозного переноса зарядов по цепи не происходит.
Сопротивление, оказываемое конденсатором переменному току, находится в зависимости от величины емкости конденсатора и от частоты тока.
Чем больше емкость конденсатора, тем больший заряд переносится по цепи за время заряда и разряда конденсатора, а как следует, и тем больший будет ток в цепи. Повышение же тока в цепи свидетельствует о том, что уменьшилось ее сопротивление.
Как следует, с повышением емкости миниатюризируется сопротивление цепи переменному току.
Повышение частоты тока наращивает величину переносимого по цепи заряда, потому что заряд (а равно и разряд) конденсатора должен произойти резвее, чем при низкой частоте. В то же время повышение величины переносимого в единицу времени заряда равносильно повышению тока в цепи, а как следует, уменьшению ее сопротивления.
Если же мы любым методом будем равномерно уменьшать частоту переменного тока и сведем ток к неизменному, то сопротивление конденсатора, включенного в цепь, будет равномерно возрастать и станет нескончаемо огромным (разрыв цепи) к моменту возникновения в цепи неизменного тока.
Как следует, с повышением частоты миниатюризируется сопротивление конденсатора переменному току.
Подобно тому как сопротивление катушки переменному току именуют индуктивным, сопротивление конденсатора принято именовать емкостным.
Таким макаром, емкостное сопротивление тем больше, чем меньше емкость цепи и частота питающего ее тока.
Емкостное сопротивление обозначается через Хс и измеряется в омах.
Зависимость емкостного сопротивления от частоты тока и емкости цепи определяется формулой Хс = 1/ωС, где ω — радиальная частота, равная произведению 2πf, С—емкость цепи в фарадах.
Емкостное сопротивление, как и индуктивное, является реактивным по собственному нраву, потому что конденсатор не потребляет энергии источника тока.
Формула закона Ома для цепи с емкостью имеет вид I = U/Xc, где I и U — действующие значения тока и напряжения; Хс — емкостное сопротивление цепи.
Свойство конденсаторов оказывать огромное сопротивление токам низкой частоты и просто пропускать токи высочайшей частоты обширно употребляется в схемах аппаратуры связи.
При помощи конденсаторов, к примеру, достигается нужное для работы схем разделение неизменных токов и токов низкой частоты от токов высочайшей частоты.
Если необходимо преградить путь току низкой частоты в высокочастотную часть схемы, поочередно врубается конденсатор маленький емкости. Он оказывает огромное сопротивление низкочастотному току и в то же время просто пропускает ток высочайшей частоты.
Если же нужно не допустить ток высочайшей частоты, к примеру, в цепь питания радиостанции, то употребляется конденсатор большой емкости, включаемый параллельно источнику тока. Ток высочайшей частоты в данном случае проходит через конденсатор, минуя цепь питания радиостанции.
Активное сопротивление и конденсатор в цепи переменного тока
На практике нередко встречаются случаи, когда в цепи поочередно с емкостью включено активное сопротивление. Общее сопротивление цепи в данном случае определяется по формуле
Как следует, полное сопротивление цепи, состоящей из активного и емкостного сопротивлений, переменному току равно корню квадратному из суммы квадратов активного и емкостного сопротивлений этой цепи.
Закон Ома остается справедливым и для этой цепи I = U/Z.
На рис. 3 приведены кривые, характеризующие фазовые соотношения меж током и напряжением в цепи, содержащей емкостное и активное сопротивления.
Рис. 3. Ток, напряжение и мощность в цепи с конденсатором и активным сопротивлением
Как видно из рисунка, ток в данном случае опережает напряжение уже не на четверть периода, а меньше, потому что активное сопротивление нарушило чисто емкостный (реактивный) нрав цепи, о чем свидетельствует уменьшенный сдвиг фаз. Сейчас уже напряжение на зажимах цепи обусловится как сумма 2-ух слагающих: реактивной слагающей напряжения uс, идущей на преодоление емкостного сопротивления цепи, и активной слагающей напряжения преодолевающей активное ее сопротивление.
Чем больше будет активное сопротивление цепи, тем наименьший сдвиг фаз получится меж током и напряжением.
Кривая конфигурации мощности в цепи (см. рис. 3) два раза за период заполучила отрицательный символ, что является, как нам уже понятно, следствием реактивного нрава цепи. Чем наименее реактивная цепь, тем меньше сдвиг фаз меж током и напряжением и тем огромную мощность источника тока эта цепь потребляет.
|
Иногда возникает задача понизить переменное напряжение сети 220 вольт до некоторого заданного значения, причем применение понижающего трансформатора (в таком случае) не всегда бывает целесообразным. Скажем, низкочастотный понижающий трансформатор, выполненный традиционно на трансформаторном железе, способный преобразовать мощность 200 Ватт, весит больше килограмма, не говоря о высокой стоимости. Следовательно в некоторых случаях можно применить гасящий резистор, который ограничит ток, однако при этом на самом гасящем резисторе выделится мощность в виде тепла, а это не всегда является приемлемым. Например, если нужно запитать 200 Ваттную лампу только на половину ее наминала, потребовалось бы рассеять мощность в 100 Ватт на гасящем резисторе, а это крайне сомнительное решение. Весьма удобной альтернативой, для данного примера, может служить применение гасящего конденсатора, емкостью около14мкф, (такой можно собрать из трех металлопленочных типа К73-17 по 4,7мкф, рассчитанных на 250в, а лучше – на 400в) это позволит получить нужный ток без необходимости рассеивать значительную мощность в виде тепла. Рассмотрим физическую сторону этого решения. Как известно, конденсатор, включенный в цепь переменного тока, является реактивным элементом, обладающим емкостным сопротивлением, связанным с частотой переменного тока в цепи, а также с собственной емкостью. Чем больше емкость конденсатора и чем выше частота переменного напряжения в цепи, тем больший ток проходит через конденсатор, значит емкостное сопротивление конденсатора обратно пропорционально его емкости, а также частоте переменного тока, в цепи, куда он включен.
А поскольку и то
Получим значение тока лампы равное 0,91 А. Теперь можно найти требуемое значение емкости гасящего конденсатора, она будет равна 15,2 мкФ. Следует отметить, что этот расчет верен для чисто активной нагрузки, когда имеет место эффективное значение. При использовании же выпрямителя, необходимо учесть, что эффективное значение тока будет немного меньше в силу действия пульсаций. Также следует помнить, что в качестве гасящих конденсаторов, полярные конденсаторы применять ни в коем случае нельзя. |
Лучшее сочетание вакуумных и полупроводниковых характеристик — однотактный гибридный усилитель звука. Мы не создаём иллюзий, |
Электрические конденсаторы в цепях переменного тока
В этом месяце мы обсудим функции конденсатора в цепи переменного тока, включая заряд и разряд, приложения и соединения в силовых цепях, а также безопасность конденсаторов.
Электрический конденсатор — это электрическое устройство, которое накапливает электричество или электрическую энергию и улучшает коэффициент мощности цепи переменного тока. Он состоит из трех основных частей.Две обычно представляют собой металлические пластины, разделенные и изолированные третьей частью, известной как диэлектрик. Заряд конденсатора зависит от размера и расстояния между проводящими пластинами, а также от типа изолирующей или диэлектрической среды между пластинами.
Все конденсаторы, независимо от типа, обозначаются по их зарядной емкости. Для цепей электроприборов, таких как двигатели и разрядное освещение высокой интенсивности, конденсаторы обозначаются фарадом, единицей электрической емкости, названной в честь британского ученого Майкла Фарадея.В распределительной сети конденсаторы обозначаются в киловольт-амперах реактивной мощности, или кВАр, для простоты применения. Измерители потребления измеряют потребность в коэффициенте мощности в кВАр. Если нагрузка двигателя потребителя вызывает индуктивное напряжение 700 кВАр на линии, это можно исправить, подключив к линии емкостное напряжение 700 кВАр. Это не так просто, но идею вы поняли.
Зарядка и разрядка конденсатора в цепи переменного тока
Конденсатор немного похож на батарею. Хотя они работают совершенно по-разному, конденсаторы и аккумуляторы хранят электрическую энергию.Вы знаете, что батарея имеет две клеммы. Внутри батареи химические реакции производят электроны на одном выводе и поглощают электроны на другом. Конденсатор — гораздо более простое устройство, и он не может производить новые электроны — он только хранит их.
Например, когда вы видите в небе молнию, вы видите огромный конденсатор. Одна пластина — это облако, другая пластина — это земля, а молния — это заряд, высвобождающийся между этими двумя пластинами. Очевидно, что в таком большом конденсаторе вы можете удерживать огромное количество заряда.
Применения в цепях питания
Конденсаторы должны применяться аккуратно и правильно. Как указывалось ранее, конденсатор предназначен для улучшения коэффициента мощности схемы. Конденсатор только корректирует коэффициент мощности конденсатора обратно в систему. Конденсаторы не влияют на коэффициент мощности между конденсатором и реактивной нагрузкой, вызывая коэффициент мощности. Неправильно установленные конденсаторы могут обеспечивать больший реактивный ток, чем требуется нагрузке, что приводит к опережающему коэффициенту мощности и увеличению потерь вместо уменьшения.Именно поэтому конденсаторы находятся после тщательного изучения системы квалифицированными инженерами.
Соединения в цепях питания
Установка одного конденсатора или батареи конденсаторов является простой процедурой после определения правильного размера и места установки. Во многих отношениях конденсатор установить намного проще, чем трансформатор, потому что нет вторичных вводов, а конденсатор представляет собой герметичный блок. У одних агрегатов по две втулки, у других — по одной.
Распределительные конденсаторы с двумя изолированными вводами обычно подключаются между фазами, но могут быть соединены фазой с землей. Конденсаторы с одним изолированным вводом обычно соединяются фазой с изолированным вводом, а корпус — с землей. В подстанциях конденсаторы распределительного напряжения подключаются параллельно, разделяя фазные напряжения передачи. Они установлены на изолированном каркасе, который является частью межсоединения, работающего при фазном напряжении передачи. Любой, кто работает с любым конденсатором, должен хорошо знать, как он подключен и при каком напряжении работает.
Вам также следует знать о конденсаторах постоянной и переключаемой емкости. Эти термины просто относятся к способу подачи питания на конденсатор. Если он зафиксирован, проходной изолятор, подключенный к источнику, попадает непосредственно в плавкий вырез. Этот выключатель — единственное средство включения или выключения конденсатора. В случае переключаемого конденсатора проходной изолятор, подключенный к источнику, идет к переключающему устройству, включенному последовательно между плавким предохранителем и конденсатором. Назначение этого переключающего устройства — позволить конденсатору работать в то время, когда это больше всего необходимо.Существует множество типов элементов управления, которые определяют, должен ли конденсатор быть включен или выключен в зависимости от требований системы. Ниже приведены примеры средств управления и то, для чего они чаще всего используются:
• Контроль времени используется в областях, где известно, что нагрузка возникает с определенными интервалами либо из-за промышленного использования, либо из-за требований жилых помещений.
• Текущее управление используется в областях, где нагрузка клиента является прерывистой и не всегда присутствует в одно и то же время дня.
• Контроль температуры используется в тех областях, где сезонные изменения увеличивают индуктивную нагрузку на систему (например,г., кондиционер). В основном доступны два основных контроля температуры: включение при 85 градусах и выключение при 65 градусах или включение при 90 градусах и выключение при 70 градусах.
• Контроль напряжения используется в областях, где нагрузка вызывает падение напряжения в системе, которое можно легко контролировать. Регуляторы напряжения также часто используются вместе с регуляторами времени, тока и температуры.
• Ручное управление используется для более простого отключения переключаемого банка, который часто используется для сезонной нагрузки.
Безопасность конденсаторов
Хотя конденсаторы являются простыми устройствами, они чрезвычайно опасны после отключения от обслуживания, поскольку могут сохранять заряд.Они должны быть построены с резисторами утечки, которые снижают их напряжение до менее 50 вольт через пять минут. Однако никогда не принимайте ничего как должное. Обязательно подождите пять минут после отсоединения, а затем закоротите втулки перемычкой с помощью рукоятки для дробовика. Перед началом работы с любым конденсатором, установленным на опоре, всегда выполняйте эти процедуры, потому что конденсатор может удерживать заряд без каких-либо признаков того, что он это делает.
При выводе конденсаторов из эксплуатации нельзя выделить следующие шаги:
• Отключите от источника.
• Подождите пять минут, чтобы разрядился заряд.
• Замкните накоротко вводы или, в случае конденсаторов с одним выводом, короткое замыкание между вводом и корпусом.
• Сохраняйте соединение короткого замыкания на месте до тех пор, пока конденсатор не будет подключен для обслуживания.
Об авторе: Джон Мортон, CUSP, начал свою карьеру в электротехнической промышленности в 1970 году в качестве земледельца в компании Houston Lighting and Power, ныне известной как CenterPoint Energy. В 1997 году он принял должность инструктора по вопросам электротехники и связи в отделе распространения знаний Техасского университета A&M, а в 2004 году он занял свою нынешнюю должность директора по безопасности и обучению в Willbros T&D Services в Техасе.
Конденсаторы переменного тока— определение, функция и вывод через конденсатор переменного тока
Эта статья дает четкое представление об электрических цепях при использовании переменного напряжения на конденсаторе. В этой схеме мы соединили конденсатор и переменное напряжение V, обозначенное символом «~».
[Изображение будет скоро загружено]
Напряжение в цепи создает разность потенциалов на ее выводах, которая изменяется синусоидально.
Выражение для разности потенциалов v или переменного напряжения приведено ниже:
v = vmsinωt
Где
vm = амплитуда колеблющейся разности потенциалов
ω = угловая частота
Мы можем вычислить ток, имеющийся в резисторе текущего напряжения, с использованием правила петли Кирхгофа.
Вот выражение правила петли Кирхгофа:
\ [\ sum \] v (t) = 0
На приведенной выше диаграмме поясняется источник переменного напряжения, приложенного к конденсатору.
Емкость в цепи переменного тока и емкостное реактивное сопротивление
На приведенном выше рисунке мы можем записать выражение для конденсатора:
v = \ [\ frac {q} {C} \]
Как упоминалось ранее относительно v, мы можно переписать выражение как:
vmsinωt = \ [\ frac {q} {C} \]
Мы можем вычислить количество тока в цепи, используя это соотношение:
i = \ [\ frac { dq} {dt} \]
⇒ i = \ [\ frac {d (v_ {m} Csinωt)} {dt} \] = ωCvmcos ωt
⇒ i = \ [i_ {m} sin (ωt + \ frac {π} {2}) \]
В приведенном выше выражении используется соотношение Cosωt = \ [sin (ωt + \ frac {π} {2}) \]
Кроме того, мы можем переписать амплитуда тока как:
im = ωCvm
Или, мы можем выразить это как
im = \ [\ frac {v_ {m}} {\ frac {1} {ω_ {C}}} \]
В этом выражении \ [\ frac {1} {ω_ {C}} \] можно принять как эквивалент сопротивления устройства.
Вот почему термин для этого выражения называется емкостным сопротивлением. XC — это символ, используемый для обозначения сопротивления.
XC = \ [\ frac {1} {ω_ {C}} \]
Кроме того, мы можем вычислить амплитуду тока в цепи, используя следующее соотношение:
im = \ [\ frac {v_ {m}} {X_ {C}} \]
Как конденсатор работает в цепи переменного тока?
В электрической цепи конденсатор напрямую связан с напряжением питания переменного тока. Когда происходит изменение напряжения питания (напряжение увеличивается или уменьшается), конденсатор заряжается или разряжается вслед за изменением напряжения.
Когда ток проходит по цепи, он будет следовать в одном направлении, а затем в другом, не позволяя действительному току проходить через конденсатор.
Однако в цепи постоянного тока сценарий другой. Когда ток протекает через конденсатор, подключенный к цепи постоянного тока, пластина конденсатора имеет как положительный, так и отрицательный заряд.
Цепи конденсатора переменного тока
[Изображение будет скоро загружено]
Когда конденсатор подключен к цепи переменного тока, он будет последовательно заряжаться и разряжаться со скоростью, рассчитанной по частоте источника питания.В цепях переменного тока емкость зависит от частоты, поскольку конденсатор постоянно заряжается и разряжается.
Какова роль конденсатора в цепях переменного и постоянного тока?
1. Роль конденсатора в цепи постоянного тока
В цепи постоянного тока (постоянного тока) конденсатор заряжается медленнее. Конденсатор заряжается до напряжения питания, но препятствует дальнейшему прохождению через него тока. Он блокирует ток, поскольку диэлектрик конденсатора является непроводящим и является изолятором.
2. Роль конденсатора в цепи переменного тока
Когда конденсатор используется в цепи переменного тока, он заряжается и разряжается для изменения напряжения питания. Согласно записи, ток становится прямо пропорциональным максимальной величине напряжения на пластинах.
Конденсаторы, включенные в цепь переменного тока, блокируют источник питания, когда они полностью заряжены. Когда в цепи присутствует источник переменного тока, конденсаторы будут попеременно заряжаться и разряжаться со скоростью, определяемой частотой питания.
Функция конденсатора в цепи переменного тока
Мы знаем, что конденсаторы используются для хранения энергии на своих проводящих пластинах в виде электрического заряда.
Конденсаторы используются для повышения напряжения выше входного. Это помогает в плавных колебаниях тока.
Что наиболее важно, конденсаторы используются в схемах выпрямителя для выравнивания колебаний тока.
Конденсаторы также используются для блокировки статического напряжения постоянного тока и позволяют сигналам переменного тока проходить из одной области схемы в другую.Эти типы конденсаторов известны как конденсаторы связи.
Чтобы устранить любой сигнал переменного тока в точке смещения постоянного тока, используются развязывающие конденсаторы.
Пусковой момент можно улучшить за счет конденсаторов. Также конденсаторы хороши для использования в однофазной сети.
Кроме того, конденсаторы используются для повышения коэффициента мощности в энергосистемах.
Переменный ток через конденсаторное происхождение
Мы можем назвать пару проводников конденсатором, разделенными некоторой средой.Когда мы соединяем конденсатор с цепью переменного тока, мы можем найти ток, протекающий через него.
Когда мы подключаем лампу в эту цепь, она светится, что показывает прохождение тока в цепи переменного тока. Мы пришли к выводу, что конденсатор является проводником в цепи переменного тока, но работает как изолятор в цепи постоянного тока.
[Изображение будет скоро загружено]
Phys 3041 Notes — D
Phys 3041 Notes — DPhys 3041 Заметки
© 1997 Джонатан Карты.Эти примечания не могут быть распространены или дублированы в какой-либо форме, печатной или электронной, без разрешения. Разрешается устанавливать электронные гипертекстовые ссылки только на эти оригинальные документы.Анализ цепей переменного тока
Цепи переменного тока (переменного тока) — это цепи, в которых напряжения и токи зависят от времени. Они намного богаче по возможностям, чем цепи постоянного тока, и мы рассмотрим здесь цепи переменного тока, содержащие резисторы. конденсаторы и катушки индуктивности. Наш анализ этих схем будет использовать комплексные числа для представления зависящих от времени токов и напряжений.Этот подход заставляет анализ этих цепей следовать линиям, очень похожим на те, что были разработаны для цепей постоянного тока.
Резисторы в цепях переменного тока
Простая цепь переменного тока, которую мы могли бы построить, представляла бы собой зависящий от времени источник напряжения, подключенный к одному резистору. Источник напряжения обеспечивает простое синусоидальное напряжение: В o cos (wt) .V o называется амплитудой сигнала, а w — угловой частотой.Период сигнала T — это время, необходимое для одного полного цикла. Частота f — это количество циклов, выполняемых за одну секунду (циклов в секунду), а единицей измерения является герц (1 Гц = 1 цикл в секунду). Частота просто обратна периоду.
Ток, протекающий в цепи, следует из прямого применения закона Ома и меняет направление через резистор. В этой схеме напряжение и ток «синфазны», оба достигают максимума и минимума одновременно.
Величина переменного напряжения часто характеризуется двумя другими показателями: размахом напряжения, В pp = 2 В o , и среднеквадратичным (среднеквадратичным) напряжением. Среднеквадратичное значение напряжения — это значение, сообщаемое большинством мультиметров при измерении сигналов переменного тока, и такие фразы, как «110 В переменного тока», которые появляются рядом со шнуром питания на бытовых и лабораторных приборах, обычно означают 110 В действующее значение . Для синусоидального напряжения , В действующее значение = В o /2 -1/2 =.707 В или .
Обычно среднеквадратичное значение находится путем возведения напряжения в квадрат, вычисления среднего значения В 2 ( t ) и последующего извлечения квадратного корня.
Среднеквадратичное значение напряжения используется для вычисления средней мощности, рассеиваемой на резисторе. Мгновенная мощность теперь задается P (t) = V (t) I (t) ,
в то время как средняя мощность вычисляется за один полный цикл. С I (t) = V (t) / R , мы имеем P (t) = V 2 (t) / R , и нахождение средней мощности сводится к вычислению среднего квадрата напряжения, показанного выше.Средняя мощность тогда всего
= < V 2 > / R = V среднеквадратичное значение 2 / R .
Конденсаторы
Конденсаторы — это устройства для хранения заряда. Удобная модель конденсатора — это пара параллельных металлических пластин, каждая из которых имеет площадь A и расстояние между ними d . Емкость этой системы представляет собой отношение заряда, накопленного на пластинах (+ Q и -Q), к разнице напряжений, В, , между пластинами:C = Q / V ,
или емкость можно представить как коэффициент пропорциональности между напряжением и накопленным зарядом:
Q = C V .
Мы будем часто использовать последний в нашем анализе цепей с конденсаторами. Емкость системы параллельных пластин пропорциональна площади пластин (чем больше площадь, тем больше накопленный заряд при фиксированном напряжении) и обратно пропорциональна расстоянию между пластинами. (Электрическое поле между пластинами однородно, поэтому для фиксированного заряда меньшее расстояние означает меньшее напряжение: вспомните, что здесь В = E d .) В большинстве случаев емкость увеличивают за счет добавления диэлектрического материала (легко поляризуемого изолятора) между пластинами.Затем емкость увеличивается в раз, равном диэлектрической проницаемости материала.
В цепи постоянного тока (не зависящей от времени) конденсаторы не играют никакой роли, кроме переходной при первом включении питания. После зарядки с ними больше ничего не происходит. Электрические заряды не проходят через конденсатор. Материал между пластинами является изолирующим, и добавление заряда к одной пластине просто отталкивает идентичный заряд от лицевой пластины, оставляя на ней противоположный заряд.Когда конденсатор заряжен, он действует как бесконечное сопротивление. Только когда приложенные напряжения и результирующие токи меняются со временем, конденсаторы могут играть важную роль в работе схемы. Мы рассмотрим переходную характеристику конденсаторов позже.
Рассмотрим конденсатор, подключенный к источнику переменного напряжения.
Поскольку напряжение зависит от времени, заряд на пластинах также должен изменяться со временем:
Q (t) = C V (t) .
Если заряд добавляется или вычитается из пластины, должен быть ток, в данном случае обеспечиваемый источником напряжения:
I = dQ / dt = C dV / dt .
Это поведение сильно отличается от поведения резисторов. Ток пропорционален
к скорости изменения напряжения. Чем быстрее изменяется напряжение, тем больше должен быть ток, чтобы обеспечить Q = CV . Для простого синусоидального приложенного напряжения, В (t) = В o cos (wt) , результирующий ток определяется как:
I (t) = -wCV o sin (wt) = wCV o cos (вес + 90) .
Это показывает фазовый сдвиг между напряжением и током в одну четверть цикла.
Когда приложенное напряжение достигает экстремума, ток, протекающий по цепи, равен нулю. И наоборот, всякий раз, когда напряжение проходит через ноль, ток либо максимальный, либо минимальный. В этом случае считается, что ток опережает напряжение: ток достигает максимума на четверть цикла раньше, чем напряжение. (Альтернативное описание напряжения, опережающего ток на 3/4 цикла, одинаково верно, но обычно для определения того, кто впереди, а кто отстает, выбирается меньший из двух углов.)
Эту разность фаз между током и напряжением можно эффективно обработать с помощью комплексных чисел. Для этого реальное управляющее напряжение ( В (t) = V o cos (wt) ) заменяется комплексным управляющим напряжением, полученным путем сложения мнимого члена:
В (t) = V o. cos (wt) + i V o sin (wt) = V o e iwt .
Эта форма имеет два существенных преимущества: мы восстановим нечто похожее на закон Ома; а фазовые сдвиги, которые происходят в более сложных схемах, включающих резисторы и катушки индуктивности вместе с конденсаторами, будут очень естественно выпадать из-за обработки напряжений и токов как комплексных чисел во время вычислений.Все, что нам нужно сделать, это не забыть взять реальную часть наших сложных результатов, чтобы получить реальные результаты.
Применять это к простому источнику переменного напряжения и одиночному конденсатору несложно.
Q (t) = CV o e iwt
I (t) = dQ / dt = C dV / dt
I (t) = iwCV o e iwt
I (t) = iwC V (t).
Обратите внимание, что в этой форме ток теперь пропорционален приложенному напряжению.Это аналог закона Ома для резисторов. Аналогом сопротивления называется импеданс конденсатора:
Z c = V (t) / I (t) = 1 / iwC .
Импеданс — это мнимое число. i содержит информацию о разности фаз 90, — между током и напряжением для конденсаторов. Чтобы найти реальный ток, мы просто расширяем V ( t ) до V o cos (wt) + i V o sin (wt) и умножаем все:
I (t ) = iwCV o cos (wt) + i 2 wCV o sin (wt)
I (t) = -wCV o sin (wt) + iwCV o cos (wt)
и берем только действительную часть результата:
I (t) = -wCV o sin (wt) ,
это именно то, что мы получали раньше.Для такой простой схемы, как эта, использование сложных представлений для напряжения и тока может показаться чрезмерно сложным, но этот метод окупается возможностью обрабатывать более сложные схемы очень простыми методами.
Обратите внимание, что сопротивление конденсатора зависит от частоты. Импеданс очень велик на низких частотах, и для данной амплитуды V o для управляющего напряжения результирующая амплитуда тока I o будет небольшой.Предельный случай этой ситуации — w = 0 — цепь постоянного тока — где емкость имеет бесконечный импеданс или эффективное сопротивление и ток не течет. Другая крайность возникает на высоких частотах, где полное сопротивление уменьшается до нуля: конденсатор действует как «короткое замыкание» на высоких частотах, где переменный ток может протекать с незначительным падением напряжения на конденсаторе. Величину этого импеданса часто называют реактивным сопротивлением конденсатора: X c = 1 / wC .С помощью идеи сопротивления, обобщенного на импеданс, правила последовательного и параллельного сопротивлений могут быть расширены для обработки общих, комплексных импедансов (резистивные действительные импедансы резисторов в сочетании с реактивными воображаемыми импедансами конденсаторов, а затем и катушек индуктивности) по тем же правилам. Обобщения правил Кирхгофа можно затем применить и к цепям переменного тока. Полезным применением этих методов являются RC-цепи, которые можно использовать для выборочного ослабления сигналов на некоторых частотах, позволяя при этом сигналы на других частотах проходить через них практически без изменений.Рассмотрим такие RC-фильтры.
A. C. Цепи, содержащие сопротивление и емкость
Пусть переменный ток Цепи содержат сопротивление R Ом последовательно с конденсатором емкостью C фарад. Эта схема изображена на рис. 32 (а).
Пусть, I = среднеквадратичное значение. значение тока, протекающего по цепи,
В R = среднеквадратичное значение напряжение на сопротивлении
= IR — фаза с I,
В С = г.РС. напряжение на конденсаторе
= IX C с отставанием I на 90 °,
И v = среднеквадратичное значение. напряжение, приложенное ко всей цепи, представляет собой векторную сумму V R и V C .
Векторная диаграмма схемы представлена на рис. 32 (с). На этой диаграмме ток опережает приложенное напряжение (или напряжение отстает от тока) на угол θ, так что,
тангенс угла θ = X C / R
Это также показано на волновой диаграмме на рис.32 (б).
На векторной диаграмме V R , V C и V образовали прямоугольный треугольник, в котором V R представляет собой прилегающую сторону или основание, V C представляет противоположную сторону или перпендикуляр, а V представляет собой гипотенузу.
— это противодействие протеканию тока, обеспечиваемое совместно сопротивлением и емкостным реактивным сопротивлением цепи, и называется импедансом цепи. Обозначается буквой Z и выражается в омах.Таким образом,
Импеданс цепи,
Ток, протекающий по цепи,
I = V / Z ампер и
Напряжение, приложенное к цепи,
В = IZ вольт.
Мощность, потребляемая цепью :
Поскольку средняя мощность, потребляемая конденсатором, равна нулю, мощность, потребляемая всей цепью, равна мощности, поглощаемой только сопротивлением. Опять же, напряжение на сопротивлении составляет V R вольт, а ток, протекающий через него, равен I ампер.Следовательно,
мощность, потребляемая цепью = мощность, поглощаемая сопротивлением,
или P = V R I Вт.
Но В R = ИК вольт.
. . . P = IR x I = I 2 R Вт.
Из векторной диаграммы:
cos θ = В R / В
или, V R = V cos θ вольт.
Следовательно, P = Vcos θ x I
= VI cos θ ватт.
cos θ — коэффициент мощности цепи.Поскольку ток опережает приложенное напряжение, фазовый угол θ является опережающим углом, а коэффициент мощности cos θ является опережающим коэффициентом мощности.
Из векторной диаграммы:
cos θ = V R / V = IR / IZ = R / Z впереди.
Емкостное реактивное сопротивление— Как найти последовательные и параллельные конденсаторы
Найдите емкостное реактивное сопротивление цепи с последовательными или параллельными конденсаторами, используя этот простой двухэтапный процесс.
Шаг 1. Найдите общую емкость цепи
Предположим, у нас есть три конденсатора, 12 Ф, 20 Ф и 30 Ф, подключенных к источнику с частотой 60 Гц.Каково полное емкостное реактивное сопротивление (X C ) при последовательном или параллельном подключении?
1А. Для конденсаторов серии
Когда конденсаторы соединены последовательно, общая емкость меньше, чем любая из отдельных емкостей последовательных конденсаторов. Если два или более конденсатора соединены последовательно, общий эффект будет таким, как у одного (эквивалентного) конденсатора, имеющего суммарное расстояние между пластинами отдельных конденсаторов.
Конденсаторы серииПример:
1/12 = 0,083, 1/20 = 0,050, 1/30 = 0,033
0,083 + 0,050 + 0,033 = 0,166
1 / 0,163 = 6,02 мкФ
Примечание: математические расчеты упрощены для целей иллюстрации. Для более точных чисел воспользуйтесь калькулятором.
1Б. Для параллельных конденсаторов
При параллельном подключении конденсаторов общая емкость складывается из емкостей отдельных конденсаторов.Если два или более конденсатора соединены параллельно, общий эффект будет таким, как у одного эквивалентного конденсатора, имеющего сумму площадей пластин отдельных конденсаторов.
Параллельные конденсаторы Пример:
12 + 20 + 30 = 62 мкФ
Шаг 2: Найдите емкостное реактивное сопротивление
Как и сопротивление, реактивное сопротивление измеряется в Ом, но ему присваивается символ X, чтобы отличить его от чисто резистивного значения R, и поскольку рассматриваемый компонент является конденсатором, реактивное сопротивление конденсатора называется емкостным реактивным сопротивлением (X C ) который измеряется в Ом.
Поскольку конденсаторы заряжаются и разряжаются пропорционально скорости изменения напряжения на них, чем быстрее изменяется напряжение, тем больше тока протекает. Точно так же, чем медленнее изменяется напряжение, тем меньше будет протекать ток. Это означает, что реактивное сопротивление конденсатора переменного тока «обратно пропорционально» частоте источника питания.
X C — емкостное реактивное сопротивление в омах, f — частота в герцах, а C — емкость переменного тока в фарадах. Очень важно преобразовать наш пример из микрофарад в фарады, чтобы получить правильный результат!
1 мкФ = 0,000001 F
Серия 60 Гц Пример:
6,02 мкФ = 0,000006 Ф (упрощенно)
2 х 3,14 х 60 х 0,000006 = 0,0022608
1 / 0,0022608 = 442,32 Ом
Параллельный 60 Гц Пример:
62 мкФ = 0,000062 F
2 х 3.14 х 60 х 0,000062 = 0,0233616
1 / 0,0233616 = 42,805 Ом
Теперь посмотрим, что произойдет при изменении частоты на 400 Гц :
Серия 400 Гц Пример:
2 х 3,14 х 400 х 0,000006 = 0,015072
1 / 0,015072 = 66,34 Ом
Параллельный 400 Гц Пример:
2 х 3,14 х 400 х 0,000062 = 0,155744
1 / 0,155744 = 6,42 Ом
Полезные ссылки
Лаборатория 4 — Зарядка и разрядка конденсатора
Введение
Конденсаторы — это устройства, которые могут накапливать электрический заряд и энергию.Конденсаторы имеют несколько применений, например, в качестве фильтров в источниках питания постоянного тока и в качестве аккумуляторов энергии для импульсных лазеров. Конденсаторы пропускают переменный ток, но не постоянный, поэтому они используются для блокировки постоянной составляющей сигнала, чтобы можно было измерить переменную составляющую. Физика плазмы использует способность конденсаторов накапливать энергию. В физике плазмы часто требуются короткие импульсы энергии при чрезвычайно высоких напряжениях и токах. Конденсатор можно медленно заряжать до необходимого напряжения, а затем быстро разряжать для обеспечения необходимой энергии.Можно даже зарядить несколько конденсаторов до определенного напряжения, а затем разрядить их таким образом, чтобы получить от системы большее напряжение (но не больше энергии), чем было вложено. В этом эксперименте используется схема RC , которая является одной из простейших схем, в которой используется конденсатор. Вы изучите эту схему и способы изменения ее эффективной емкости, комбинируя конденсаторы последовательно и параллельно.Обсуждение принципов
Конденсатор состоит из двух проводов, разделенных небольшим расстоянием.Когда проводники подключены к зарядному устройству (например, к батарее), заряд передается от одного проводника к другому до тех пор, пока разность потенциалов между проводниками из-за их равного, но противоположного заряда не станет равной разности потенциалов между клеммами. зарядного устройства. Количество заряда, накопленного на любом проводнике, прямо пропорционально напряжению, а константа пропорциональности известна как емкость . Это записывается алгебраически как Заряд C измеряется в единицах кулонов (C), напряжениеΔV
в вольт (В) и емкость C в единицах фарад (F). Конденсаторы — физические устройства; Емкость является собственностью устройства.Зарядка и разрядка
В простой RC-цепи резистор и конденсатор соединены последовательно с батареей и переключателем. См. Рис.1.Рисунок 1 : Простая RC-цепь
Когда переключатель находится в положении 1, как показано на рис. 1 (а), заряд на проводниках через некоторое время достигает максимального значения. Когда переключатель переведен в положение 2, как на рис.1 (b), аккумулятор больше не является частью цепи и, следовательно, заряд конденсатора не может быть восполнен. В результате конденсатор разряжается через резистор. Если мы хотим исследовать зарядку и разрядку конденсатора, нас интересует, что происходит сразу, после того, как переключатель перемещается в положение 1 или положение 2, а не дальнейшее поведение схемы в ее установившемся состоянии. Для схемы, показанной на рис. 1 (а), уравнение петли Кирхгофа можно записать как Решение уравнения.(2) является(3)
Q = Q fQ f
представляет собой окончательный заряд на конденсаторе, который накапливается через бесконечный промежуток времени, R — сопротивление цепи, а C — емкость конденсатора. Из этого выражения вы можете видеть, что заряд растет экспоненциально во время процесса зарядки.См. Рис. 2 (а). Когда переключатель перемещается в положение 2, для схемы, показанной на рис. 1 (b), уравнение петли Кирхгофа теперь имеет вид Решение уравнения. (4) является(5)
Q = Q 0 e (−t / RC)
гдеQ 0
представляет начальный заряд на конденсаторе в начале разряда, т. е. приt = 0.
Из этого выражения видно, что заряд экспоненциально затухает при разряде конденсатора, и что для полной разрядки требуется бесконечное количество времени.См. Рис. 2 (b).Рисунок 2 : График изменения во времени
Постоянная времени
τ ПроизведениеRC
(имеющее единицы времени) имеет особое значение; это называется постоянной времени цепи. Постоянная времени — это время, необходимое для повышения заряда зарядного конденсатора до 63% от его конечного значения. Другими словами, когдаt = RC,
(6)
Q = Q f(7)
1 — е −1 = 0.632.
Другой способ описать постоянную времени — сказать, что это количество секунд, необходимое для того, чтобы заряд на разряжающемся конденсаторе упал до 36,8%(e -1 = 0,368)
от его начального значения. Мы можем использовать определение(I = dQ / dt)
тока через резистор и уравнение. (3) Q = Q fQ = Q 0 e (−t / RC)
, чтобы получить выражение для тока во время процессов зарядки и разрядки.(8)
зарядка: I = + I 0 e −t / RC
(9)
разгрузка: I = −I 0 e −t / RC
где в формуле. (8)зарядка: I = + I 0 e −t / RC
и уравнение. (9)разряд: I = −I 0 e −t / RC
— максимальный ток в цепи в момент времени t = 0. Тогда разность потенциалов на резисторе будет выражена следующим образом.(10)
зарядка: ΔV = + ΔV f e −t / RC
(11)
нагнетание: ΔV = — ΔV 0 e −t / RC
Обратите внимание, что во время процесса разряда ток будет течь через резистор в противоположном направлении. Следовательно, I иΔV
в уравнении. (9)разряда: I = −I 0 e −t / RC
и уравнение. (11)разряд: ΔV = — ΔV 0 e −t / RC
отрицательны.Это напряжение как функция времени показано на рис.3.Рисунок 3 : Напряжение на резисторе как функция времени
Полезно описывать зарядку и разрядку в терминах разности потенциалов между проводниками (т.е. «напряжение на конденсаторе»), поскольку напряжение на конденсаторе можно измерить непосредственно в лаборатории. Используя соотношениеQ = C ΔV,
Ур. (3) Q = Q fQ = Q 0 e (−t / RC)
, которые описывают зарядку и разрядку конденсатора, можно переписать в терминах напряжения. Просто разделите оба уравнения наC,
, и отношения станут следующими.(12)
зарядка: ΔV = ΔV f(13)
нагнетание: ΔV = ΔV 0 e (−t / RC)
Обратите внимание, что эти два уравнения похожи по форме на формулу.(3) Q = Q fQ = Q 0 e (−t / RC)
. График зависимости напряжения на конденсаторе от времени показан на рисунке 4 ниже.Рисунок 4 : Напряжение на конденсаторе как функция времени
Переставив уравнение. (12) зарядка: ΔV = ΔV f(15)
−ln−ln ((ΔV f — ΔV) / ΔV f )
от времени даст прямолинейный график с наклоном 1/ RC . Точно так же для процесса разряда формула. 13разрядка: ΔV = ΔV 0 e (−t / RC)
можно переписать, чтобы получить Возьмите натуральный логарифм (ln) от обеих частей этого выражения и умножьте на –1, чтобы получить(17)
−ln−ln (ΔV) / ΔV 0 )
от времени даст прямолинейный график с наклоном 1/ RC .Использование прямоугольной волны для имитации роли переключателя
В этом эксперименте вместо переключателя мы будем использовать генератор сигналов, который может генерировать периодические волновые формы различной формы, такие как синусоидальная волна, треугольная волна и прямоугольная волна. Также можно регулировать как частоту, так и амплитуду формы волны. Здесь мы будем использовать генератор сигналов для создания изменяющегося во времени напряжения прямоугольной формы на конденсаторе, аналогичного показанному на рис.5.Рисунок 5 : Прямоугольная волна с периодом Τ
Выходное напряжение генератора сигналов изменяется назад и вперед от постоянного положительного значения до постоянного нуля вольт через равные интервалы времени t . ВремяT = 2t
— это период прямоугольной волны. В течение первой половины цикла, когда напряжение положительное, это похоже на то, что переключатель находится в положении 1. Во второй половине цикла, когда напряжение равно нулю, это то же самое, что переключатель находится в положении 2. .Таким образом, прямоугольная волна, представляющая собой напряжение постоянного тока, которое периодически включается и выключается, служит одновременно аккумулятором и переключателем в схеме, показанной на рис.1. Генератор сигналов позволяет выполнять это переключение многократно, и можно оптимизировать сбор данных, регулируя частоту повторения. Эта частота будет зависеть от постоянной времени RC-цепи. Когда время t больше постоянной времени τ RC-цепи, у конденсатора будет достаточно времени для зарядки и разрядки, и напряжение на конденсаторе будет таким, как показано на рис.4.Цель
В этом эксперименте (смоделированный компьютером) осциллограф будет использоваться для отслеживания разности потенциалов и, таким образом, косвенно, заряда конденсатора. Измерения напряжения будут использоваться двумя разными способами для вычисления постоянной времени цепи. Наконец, конденсаторы будут подключены параллельно, чтобы проверить их эквивалентную емкость.Оборудование
- Печатная плата PASCO
- Сигнальный интерфейс с выходной мощностью
- Соединительные провода
- Программное обеспечение Capstone
Процедура
Распечатайте лист для этой лабораторной работы.Этот лист понадобится вам для записи ваших данных.Настройка RC-цепи
Печатная плата RLC, которую вы будете использовать, среди других элементов состоит из трех резисторов и двух конденсаторов. См. Рис. 6 ниже. Теоретически вы можете использовать разные комбинации резисторов и конденсаторов. В этом эксперименте вы будете использовать резисторы 33 и 100 Ом и два конденсатора.Рисунок 6 : Печатная плата RLC
1
Подключите крайнюю правую выходную клемму сигнального интерфейса к резистору 33 Ом в точке 2.2
Чтобы обойти индуктор, подключите провод от точки 8 к точке 9.3
Подключите точку 6 ко второй выходной клемме сигнального интерфейса, чтобы замкнуть цепь.4
Подключите пробник напряжения к аналоговому каналу A.5
Чтобы измерить напряжение на конденсаторе, подключите черный провод датчика напряжения к точке 6, а красный провод — к точке 9. Убедитесь, что земля интерфейса (вывод «-») подключена к той же стороне конденсатора, что и земля генератора сигналов (выход мощности).Подключение вашей схемы должно выглядеть так, как показано на рис.7.Рисунок 7 : Принципиальная схема
Контрольная точка 1:
Попросите своего технического специалиста проверить соединения вашей цепи.
Процедура A: Постоянная времени контура
В этом эксперименте мы будем использовать компьютер для эмуляции осциллографа.6
Откройте файл Capstone, связанный с этой лабораторной работой.Отобразится экран, аналогичный показанному на рис. 8.Рисунок 8 : Начальный экран файла Capstone
7
Настройте генератор сигналов на создание положительной прямоугольной волны, выбрав положительную прямоугольную волну в окне генератора сигналов, как показано на рисунке 9 ниже.Рисунок 9 : Окно генератора сигналов
8
Если это еще не установлено при открытии файла Capstone, настройте генератор сигналов на создание прямоугольной волны амплитудой 5 В с частотой 20 Гц и установите смещение напряжения на 5 В.9
Включите генератор сигналов, щелкнув ON в окне генератора сигналов.10
Чтобы контролировать сигнал, нажмите кнопку START в главном окне. Потребуется отрегулировать шкалы времени и напряжения, чтобы получить кривую сигнала, подобную показанной на рис. 10. Это позволит вам наблюдать, как напряжение на конденсаторе изменяется как функция времени. Для этого установите курсор на любое значение вдоль оси, которую вы хотите увеличить, и переместите курсор влево-вправо или вверх-вниз по мере необходимости.При правильном увеличении у вас будет только одна длина волны на графике, как на кривой на рис.10.Рисунок 10 : Трасса сигнала
Если в любой момент вы захотите удалить записанный набор данных, нажмите кнопку Delete Last Run под графиком.11
Нажмите кнопку Показать координаты из кнопок над графиком. См. Рис.11.Рисунок 11 : Показать координаты
Когда активна функция отображения координат, показания напряжения и времени отображаются, куда бы вы их ни перетащили, как на рис.11. Используя этот инструмент, определите и запишите время начала (то есть, когда кривая начиналась от 0 вольт) на рабочем листе.12
Вычислите 63,2% максимального напряжения,ΔV f ,
(которое должно быть 5 В), настройку амплитуды генератора сигналов. Используя Показать координаты , определите и запишите время начала (то есть, когда кривая начиналась вверх с 0 вольт) на рабочем листе.13
По этим двум значениям времени определите и запишите время, необходимое для перехода сигнала от Δ В = 0 до Δ В = 0.632ΔV f .
Это ваше экспериментальное значение для RC .14
В рабочем листе введите принятые значения сопротивления и емкости, которые напечатаны на печатной плате.15
Вычислите экспериментальное значение емкости, используя свое экспериментальное значение для RC и принятое значение R . Запишите это на листе.16
Вычислите ошибку в процентах, используя два значения емкости.См. Приложение Б. Checkpoint 2:
Попросите вашего технического специалиста проверить ваши данные и расчеты, прежде чем продолжить.
Процедура B: Расчет емкости графическими методами
17
Запишите максимальное напряжение на листе.18
Из записанных данных найдите с помощью интеллектуального инструмента моменты времени, при которых Δ В, = 1, 2, 3 и 4 В на восходящей части кривой.Запишите эту информацию в Таблицу данных 1 на рабочем листе. Примечание : Возможно, вам придется сильно увеличить масштаб, чтобы получить необходимую точность при использовании интеллектуального инструмента.19
Выполните необходимые вычисления, чтобы заполнить Таблицу данных 1.20
Используя Excel, постройте график−ln ((ΔV f — ΔV) / ΔV f )
в зависимости от времени. См. Приложение G.21
Используйте параметр линии тренда в Excel, чтобы нарисовать линию, наиболее подходящую для ваших данных, определить наклон линии и записать это значение на листе.См. Приложение H.22
По значению крутизны определите постоянную времени и емкость. Запишите эти значения на листе.23
Вычислите ошибку в процентах между этим значением емкости и принятым значением. Контрольная точка 3:
Попросите своего технического специалиста проверить ваши данные, график и расчеты, прежде чем продолжить.
Процедура C: Измерение эффективной емкости
Емкость увеличивается непосредственно при параллельном подключении конденсаторов и в обратном порядке при последовательном подключении.Это противоположно правилу для резисторов. Для конденсаторов, подключенных параллельно, эффективная емкость определяется выражением(18)
C eff = C 1 + C 2 + C 3 +. . .
а для конденсаторов, включенных последовательно, эффективная емкость равна24
Подключите второй конденсатор (330 мкМ Ф) параллельно конденсатору, используемому в процедуре A, подключив провод от точки 6 к точке 7.25
Переключите резистор на резистор 10 Ом, переместив соединение из точки 2 в точку 1.26
Запишите другой набор данных, щелкнув START в главном окне. После того, как вы записали второй набор данных, вы можете захотеть отобразить только эти данные на графике и удалить набор данных 1. Для этого удалите первый прогон (см. Примечание к шагу 10). На графике вы будете видеть только одну длину волны.27
В этой части эксперимента вы будете рассматривать разрядную часть кривой. Теперь начальное напряжениеΔV 0
будет наивысшим значением пика перед тем, как график начнет спадать.Запишите это значение на листе.28
Из записанных данных найдите с помощью интеллектуального инструмента моменты времени, при которых Δ В, = 1, 2, 3 и 4 В на спадающей части кривой. ( Примечание : вам может потребоваться сильно увеличить масштаб, чтобы получить необходимую точность при использовании интеллектуального инструмента). Запишите эту информацию в таблицу данных 2 на рабочем листе.29
Выполните необходимые вычисления, чтобы заполнить Таблицу данных 2.30
Используя Excel, постройте график зависимости−ln (ΔV) / ΔV 0 )
от времени.31
Используйте параметр линии тренда в Excel, чтобы нарисовать линию, наиболее подходящую для ваших данных, определить наклон линии и записать это значение на листе.32
По значению наклона определите постоянную времени и запишите это значение в рабочий лист.33
ВычислитеC eff ,
эффективную емкость параллельной комбинации, используя принятое значение для R .34
Сравните это экспериментальное значение с тем, что вы получили из уравнения.18C eff = C 1 + C 2 + C 3 +. . .
и принятые значения емкости путем вычисления ошибки в процентах между двумя значениями. Контрольная точка 4:
Попросите своего технического специалиста проверить ваши данные и расчеты, прежде чем продолжить.
Copyright © 2012 Advanced Instructional Systems, Inc. и Государственный университет Северной Каролины | Кредиты
Импеданс в цепях переменного тока — Видео и стенограмма урока
Импеданс и резисторы
Понятие сопротивления, которое мы обсуждали в другом уроке, также применимо к цепям переменного тока, но оно немного отличается.В цепях переменного тока сопротивление изменяется в зависимости от того, в какой части синусоидальной кривой вы находитесь в данный момент. Чтобы отразить это, мы используем другой термин: импеданс. Импеданс — это сопротивление компонента в цепи переменного тока. Это то, что вы получите, если воспользуетесь среднеквадратичными значениями тока и напряжения в законе Ома. Мы просто заменяем R сопротивления на Z для импеданса.
I = V / R становится…
Irms = Vrms / Z
Импеданс, как и сопротивление, измеряется в Ом.
Решение проблем с использованием комбинаций резисторов, конденсаторов или катушек индуктивности может быть затруднено в цепях переменного тока и требует использования комплексных чисел.
Реактивное сопротивление конденсаторов и индукторов
Как будто у нас не хватило названий для одного и того же, вот еще одно: реактивное сопротивление . Говоря конкретно о конденсаторах и катушках индуктивности, их «импеданс» обычно называют «реактивным сопротивлением». Для катушки индуктивности это называется индуктивным реактивным сопротивлением и используется символ XL, а для конденсатора это называется емкостным реактивным сопротивлением и используется символ XC.И снова это можно вернуть в обычное уравнение закона Ома, заменив сопротивление R.
I = V / R становится…
Irms = Vrms / XL (индуктивное реактивное сопротивление)
или
Irms = Vrms / XC (емкостное реактивное сопротивление)
Это уравнение, которое мы можем использовать для расчета емкостного реактивного сопротивления, где C — емкость конденсатора, измеренная в Фарадах, а f — частота источника переменного тока — количество раз, когда он меняет направление в секунду. — измеряется в Герцах.
XC = 1/2 * pi * f * C
И это уравнение для индуктивного реактивного сопротивления, где L — индуктивность катушки индуктивности, измеренная в Генри, а f — снова частота источника переменного тока, измеренная в Фарады.
XL = 2 * pi * f * L
Пример расчета
Итак, например, предположим, что у вас есть цепь переменного тока, которая содержит индуктор 5 Генри на основном источнике питания на 120 вольт. И вас просят вычислить среднеквадратичное значение тока, протекающего по цепи, если частота переменного тока составляет 60 Гц.
Ну, прежде всего, мы должны записать то, что мы знаем. Индуктивность L составляет 5 Генри. Напряжение, В, составляет 120 вольт. А частота f равна 60 Гц.
Нас просят вычислить действующее значение тока Irms. Основываясь на законе Ома, Irms равно Vrms, деленному на R. Но поскольку это цепь переменного тока, это действительно Vrms, деленное на Z (импеданс), и поскольку мы говорим об индукторе, мы должны снова заменить это, сделав это Vrms, разделенное на XL.
Irms = Vrms / XL
Мы знаем, что Vrms равно 120 вольт, поэтому нам просто нужно вычислить XL.К счастью, у нас есть уравнение для этого: XL равен 2 * pi * f * L. Итак, 2 умножить на пи, умножить на частоту 60 Гц, умножить на индуктивность (5 Генри). Введите все это в калькулятор, и вы получите индуктивное реактивное сопротивление (XL) 1885 Ом.
Наконец, подставьте ЭТО число в уравнение закона Ома, 120, разделенное на 1885, дает нам ток 0,064 ампера.
Вот и все, готово.
Краткое содержание урока
Большинство электрических цепей в доме являются цепями переменного тока. Переменный ток — это то место, где вместо тока, протекающего только в одном направлении по цепи, он очень быстро переключает направление. В цепи переменного тока ток, напряжение и мощность изменяются синусоидально — в виде синусоидальной кривой. Поскольку ток и напряжение всегда меняются, мы используем то, что называется среднеквадратичным (или среднеквадратичным) током и среднеквадратичным напряжением. Вы можете рассчитать эти числа, используя следующие уравнения:
Irms = I0 / квадратный корень из 2
Vrms = V0 / квадратный корень из 2
V0 — пиковое или максимальное напряжение, измеренное в вольтах, а I0 — пиковый или максимальный ток. измеряется в амперах.
В цепях переменного тока мы не используем термин «сопротивление». Вместо этого мы называем это импедансом: Импеданс — это просто сопротивление компонента в цепи переменного тока. Это то, что вы получите, если воспользуетесь среднеквадратичными значениями тока и напряжения в законе Ома. Мы просто заменяем R сопротивления на Z для импеданса.
I = V / R становится…
Irms = Vrms / Z
Когда у нас есть конденсаторы или катушки индуктивности в цепи, мы снова заменяем Z на импеданс. Мы называем сопротивление конденсатора или катушки индуктивности реактивным сопротивлением. Реактивное сопротивление — это просто импеданс конденсатора или катушки индуктивности. Для катушки индуктивности это называется индуктивным реактивным сопротивлением и используется символ XL, а для конденсатора это называется емкостным реактивным сопротивлением и используется символ XC. Еще раз, это можно вернуть в обычное уравнение закона Ома, заменив сопротивление R.
I = V / R становится…
Irms = Vrms / XL для индуктивного реактивного сопротивления
или
Irms = Vrms / XC для емкостное реактивное сопротивление
У нас также есть уравнение для расчета емкостного реактивного сопротивления и уравнение для расчета индуктивного реактивного сопротивления.В этих уравнениях C — это емкость конденсатора, измеренная в фарадах, L — индуктивность индуктора, измеренная в Генри, а f — частота источника переменного тока — количество раз, когда он меняет направление в секунду, измеряется в Герц.
XC = 1/2 * pi * f * C
XL = 2 * pi * f * L
Результаты обучения
После этого урока вы сможете:
- Описать, как работают цепи переменного тока
- Напомним синусоидальный характер цепей переменного тока
- Объясните, что такое импеданс и как его рассчитать
- Определите уравнения для расчета емкостного и индуктивного реактивного сопротивления