Энергетическая освещенность формула – — — БилдоМан

Содержание

Энергетическая освещённость Википедия

Облучённость Ee{\displaystyle E_{e}} — физическая величина, одна из энергетических фотометрических величин^[1]. Характеризует поверхностную плотность мощности излучения, падающего на поверхность. Количественно равна отношению потока излучения dΦe{\displaystyle d\Phi _{e}}, падающего на малый участок поверхности, к площади этого участка dS{\displaystyle dS}^[1]^[2]:

Ee=dΦedS.{\displaystyle E_{e}={\frac {d\Phi _{e}}{dS}}.}

Численно облучённость равна модулю составляющей вектора Пойнтинга, перпендикулярной поверхности, усредненной за время, существенно превосходящее период электромагнитных колебаний.

Единица измерения в Международной системе единиц (СИ): Вт·м⁻².

Если поверхность освещается точечным источником^[3], то для её облучённости выполняется:

Ee=Ier2cos⁡θ,{\displaystyle E_{e}={\frac {I_{e}}{r^{2}}}\cos \theta ,}

где Ie{\displaystyle I_{e}} — сила излучения источника в направлении интересующей точки поверхности, r{\displaystyle r} — расстояние между этой точкой и источником, а θ{\displaystyle \theta } — угол, который нормаль к поверхности образует с направлением на источник.

Другое, используемое в литературе, но не предусмотренное ГОСТом^[1] наименование облучённости, — энергетическая освещённость.

Спектральная плотность облучённости

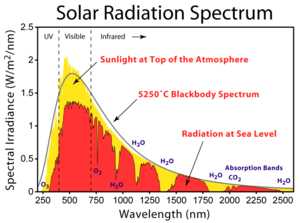Спектры облучённости, создаваемой солнечным излучением над атмосферой Земли и на уровне моря.

Спектральная плотность облучённости Ee,λ{\displaystyle E_{e,\lambda }} — отношение величины облученности dEe,{\displaystyle dE_{e},} приходящейся на малый спектральный интервал dλ,{\displaystyle d\lambda ,} к ширине этого интервала:

Ee,λ(λ)=dEedλ.{\displaystyle E_{e,\lambda }(\lambda )={\frac {dE_{e}}{d\lambda }}.}

Единицей измерения Ee,λ{\displaystyle E_{e,\lambda }} в системе СИ является Вт·м⁻³. Поскольку длины волн принято измерять в нанометрах, то на практике используется Вт·м⁻²·нм⁻¹.

Зависимость спектральной плотности облучённости от длины волны излучения называют спектром облучённости. На рисунке представлены спектры облучённости, создаваемой солнечным излучением за пределами земной атмосферы и на уровне моря. Там же для сравнения приведен спектр излучения абсолютно черного тела нагретого до температуры 5250 °С (~ 5525 К). Видно, что облучённость на поверхности Земли заметно ниже, чем в космосе, из-за поглощения излучения газами, составляющими атмосферу.

Световой аналог

В системе световых фотометрических величин аналогом облучённости является освещённость Ev{\displaystyle E_{v}}. По отношению к облучённости освещённость является редуцированной фотометрической величиной, получаемой с использованием значений относительной спектральной световой эффективности монохроматического излучения для дневного зрения V(λ){\displaystyle V(\lambda )}

[4]:

Ev=Km⋅∫380 nm780 nmEe,λ(λ)V(λ)dλ,{\displaystyle E_{v}=K_{m}\cdot \int \limits _{380~nm}^{780~nm}E_{e,\lambda }(\lambda )V(\lambda )d\lambda ,}

где Km{\displaystyle K_{m}} — максимальная световая эффективность излучения^[5], равная в системе СИ 683 лм/Вт^[6]. Её численное значение следует непосредственно из определения канделы.

Энергетические фотометрические величины СИ

Сведения о других основных энергетических фотометрических величинах приведены в таблице. Обозначения величин даны по ГОСТ 26148—84^[1].

Энергетические фотометрические величины СИ

Здесь dS1{\displaystyle dS_{1}} — площадь элемента поверхности источника, dS2{\displaystyle dS_{2}} — площадь элемента поверхности приёмника, ε{\displaystyle \varepsilon } — угол между нормалью к элементу поверхности источника и направлением наблюдения.

Примечания

wikiredia.ru

Энергетическая освещенность

Министерство образования Российской Федерации

Волгоградский государственный технический университет

Кафедра «Техническая эксплуатация и ремонт автомобилей»

СЕМЕСТРОВАЯ РАБОТА

по дисциплине «Основы научных исследований»

Тема: «Энергетическая освещенность»

Вариант: 74

Студент: Литвинов Александр Владимирович

Группа: АТ-312

Направление: 5521 «Эксплуатация транспортных средств»

Преподаватель: Зотов Николай Михайлович

Дата сдачи на проверку: ___________

Роспись студента: ___________

Волгоград 2003

СОДЕРЖАНИЕ:

1. Характеристика энергетической освещенности ….…………………. 3

2. Способы, датчики и приборы, используемые для измерения энергетической освещенности и их принципы работы……….……..…………6

3. Примеры измерения энергетической освещенности при производстве, испытании, диагностировании, техническом обслуживании и ремонте автомобилей или их элементов ….…..……………..……………12

Список литературы………………………………………………………..13

1. Характеристика энергетической освещенности

До относительно недавнего времени (начало XX века) глаз человека был единственным известным приемником излучения. Поэтому мера излучения определялась только реакцией глаза, т. е. световым потоком.

Однако в настоящее время положение существенно изменилось. Хорошо известны и во многих случаях подробно изучены излучения в ультрафиолетовой и в инфракрасной областях спектра; часто говорят также о рентгеновском и гамма-излучениях, энергия которых в большинстве случаев относительно мала. В связи с этим появилась потребность в оценке общей мощности излучения не только со зрительной (визуальной), но и с физической точки зрения, и наряду со световым потоком все большую роль начинает играть поток излучения, который иногда называют также лучистым потоком. Под потоком излучения (лучистым потоком) понимается общая мощность, передаваемая электромагнитными колебаниями, независимо от длины волны или частоты излучений, входящих в состав рассматриваемого потока. Поток принято обозначать буквой Ф и измерять в ваттах.

Как естественное следствие того, что поток излучения становится одной из основ радиационной энергетики, возникает потребность во всех видах его производных, применяемых для характеристики разных случаев его пространственного распределения.

Угловая плотность лучистого потока называется силой излучения и определяется выражением:

, где dФ – лучистый поток, распространяющийся в данном направлении внутри элементарного телесного угла dΩ, содержащего это направление. Телесный угол есть мера множества прилегающих друг к другу направлений в пространстве (рис. 1). Он измеряется площадью, которую на поверхности сферы единичного радиуса вырезает коническая поверхность, содержащая все эти направления и имеющая вершину в центре сферы, или, что то же самое, отношением площади, вырезаемой на поверхности сферы произвольного радиуса к квадрату радиуса: ,

где

– вырезаемая конической поверхностью площадь; l – радиус сферы. В данной работе рассматривается энергетическая освещенность (облученность), характеризующая уровень облучения поверхности, на которую падает поток излучения, и распределение потока вдоль поверхности (рис. 2). Таким образом, это величина, определяющая поверхностную плотность потока: ,

где dA – элемент облучаемой поверхности; dФ – падающий на этот элемент поток.

Очевидно, что если поток распределяется на поверхности равномерно, то:

где Ф – поток, падающий на всю поверхность.

Единица измерения облученности – ватт на квадратный метр. Для примера облученность солнечной энергией при высоком Солнце и чистой атмосфере (у земной поверхности длины волн λ = 0,3 — 4 мкм) в Белоруссии составляет для перпендикулярной лучам площадки 1 кВт/м² , а для горизонтальной 0,8 кВт/м² . Значение облученности может находиться в очень широких пределах.

Если поверхность dA облучается точечным источником (любой источник может считаться точечным при достаточно больших расстояниях по сравнению с размерами источников) и расположена под углом θ к оси телесного угла dΩ, то для облученности получим формулу (рис. 3):

Если поверхность нормальна к направлению распространения излучения, то:

Эту зависимость часто называют законом обратных квадратов.

Для характеристики общей насыщенности пространства энергией излучения вводится понятие пространственной облученности .

Для раскрытия понятия пространственной облученности введем понятие лучистости. Лучистостью B называется сила излучения с единицы площади проекции испускающей поверхности на плоскость, перпендикулярную к направлению излучения. Лучистость определяет поверхностно-угловое распределение лучистого потока в пространстве.

Пусть точка О находится в пространстве, где излучение распространяется во всевозможных направлениях (рис. 4). Опишем вокруг данной точки малую сферу с экваториальным сечением, площадь которого равна единице. Допустим, что элемент пространства, окружающего сферу, видимый из точки О под телесным углом имеет лучистость B. Лучистый поток через сферу, создаваемый этим элементом пространства, равен: ,

а полный лучистый поток через рассматриваемую «единичную» сферу от всего пространства определится интегрированием этого выражения в пределах полного телесного угла 4π:

Лучистый поток, падающий со всех сторон на сферу с экваториальным сечением, равным единице площади, и называют пространственной облученностью E

0 . Таким образом, пространственная облученность:

Если лучистость В постоянна по всему пространству, то:

В случае, когда излучение падает в данную точку пространства только из полусферы, обладающей постоянной лучистостью:

Размерность пространственной облученности одинакова с размерностью обычной облученности на плоскости: Вт/м² .

Насыщенность пространства энергией излучения может быть определена еще при помощи среднесферической облученности E_4π , которая определяется выражением:

и представляет собой среднюю облученность по поверхности элементарно малой сферы с центром в данной точке пространства.

Необходимо подчеркнуть, что среднесферическая облученность представляет собой чис

mirznanii.com

📌 ЭНЕРГЕТИЧЕСКАЯ ОСВЕЩЁННОСТЬ — это… 🎓 Что такое ЭНЕРГЕТИЧЕСКАЯ ОСВЕЩЁННОСТЬ?

ЭНЕРГЕТИЧЕСКАЯ ОСВЕЩЁННОСТЬ

ЭНЕРГЕТИЧЕСКАЯ ОСВЕЩЁННОСТЬ: (облучённость), поверхностная плотность лучистого потока; равна отношению потока излучения к площади облучаемой поверхности. Единица измерения Э. о.— Вт/м2. В системе световых величин аналогом Э. о. явл. освещённость.

ЭНЕРГЕТИЧЕСКАЯ ОСВЕЩЁННОСТЬ

(облучённость)- поверхностная плотность лучистого потока; равна отношению потока излучения к площади облучаемой поверхности. Единица измерения Э. о.- Вт/м

2. В системе световых величин аналогом Э. о. является освещённость.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.

ЭНАНТИОМОРФИЗМ
ЭНЕРГЕТИЧЕСКАЯ СИЛА СВЕТА

Смотреть что такое «ЭНЕРГЕТИЧЕСКАЯ ОСВЕЩЁННОСТЬ» в других словарях:

энергетическая освещённость — energinė apšvieta statusas T sritis fizika atitikmenys: angl. irradiance vok. Bestrahlungsstärke, f rus. энергетическая освещённость, f pranc. éclairement énergétique, m; irradiance, f … Fizikos terminų žodynas
энергетическая освещённость — отношение потока излучения к площади облучаемой поверхности. Единица измерения энергетической освещённости Вт/м2. В системе световых величин аналогом является освещённость. * * * ЭНЕРГЕТИЧЕСКАЯ ОСВЕЩЕННОСТЬ ЭНЕРГЕТИЧЕСКАЯ ОСВЕЩЕННОСТЬ, поток… … Энциклопедический словарь
ЭНЕРГЕТИЧЕСКАЯ ОСВЕЩЁННОСТЬ — то же, что облучённость. В системе световых величин аналогом Э. о. является освещённость … Естествознание. Энциклопедический словарь
Энергетическая освещённость поверхности
— отношение потока излучения, падающего на площадку приёмника излучения, к её площади. , [Вт/м2] Энергетическая освещённость поверхности поверхностная плотность падающего потока излучения. Единица измерения освещённости называется люксом … Википедия
энергетическая освещённость суммарного излучения — visuminė energinė apšvieta statusas T sritis fizika atitikmenys: angl. total irradiance vok. Gesamtbestrahlungsstärke, f rus. энергетическая освещённость суммарного излучения, f pranc. irradiance totale, f … Fizikos terminų žodynas
ОСВЕЩЁННОСТЬ ЭНЕРГЕТИЧЕСКАЯ — облучённость, величина Ее, равная отношению потока излучения, падающего на поверхность к площади освещаемой поверхности: Ее dФе/dS, где dФе поток излучения, падающего на малый элемент поверхности площадью dS. Единица О. э. (в СИ) Вт/м2 … Большой энциклопедический политехнический словарь
Освещённость энергетическая — в точке поверхности, отношение потока излучения (См. Поток излучения), падающего на малый элемент поверхности, содержащий рассматриваемую точку, к площади этого элемента. Употребляются синонимы: «облученность», а в метеорологии и… … Большая советская энциклопедия
Энергетическая светимость — Размерность M·T 3 Единицы измерения СИ Вт·м 2 СГС … Википедия
Энергетическая фотометрическая величина — Энергетическая фотометрическая величина фотометрическая величина, количественно выражаемая в единицах энергии или мощности и производных от них[1]. Энергетические величины характеризуют свет безотносительно к свойствам человеческого зрения … Википедия
Энергетическая экспозиция — количество облучения, доза Не, отношение энергии dQe падающего на элемент облучаемой поверхности к площади dA этого элемента. Эквивалентное определение: Э. э. есть произведение освещенности энергетической (См. Освещённость энергетическая) … Большая советская энциклопедия

dic.academic.ru

3.2.4 Освещенность поверхности, е

Освещенностью поверхности называют величину

Е = (3.8)

где:

∆Φ — световой поток, падающей на поверхность площади

∆S, рисунок 3.3. Если ∆Φ = 1лм,

∆S = 1м, освещенность = 1люксу, (лк).

То есть, 1лк = 1лм : 1м².

Рисунок 3.3

3.2.5 Закон освещенности

Элементарные преобразования [5, с.48] позволяют установить взаимосвязь освещенности Е поверхности с расстоянием R и углом падения света j на поверхность, рисунок 3.3, в виде:

. (3.9)

Формула (3.9) носит название закона освещенности.

3.2.6 Светимость излучающей поверхности, м

До сих пор, мы рассматривали точечные источники света. Всякий реальный источник имеет конечные размеры. Пусть светящаяся площадка площади DS, рисунок 3.4, излучает свет в полусферу, которой соответствует телесный угол DW = 2πср. Обозначим через DΦ_ПС световой поток, излучаемый площадью DS в полусферу.

Величина , лм/м² называется светимостью излучающей площадиDS.

Согласно рисунка 3.4 светимость М численно равна световому потоку, излучаемому с единицы площади светящейся поверхности в телесный угол 2π стерадиан.

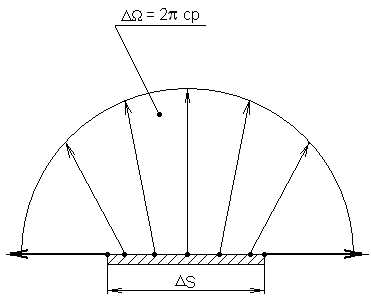
Рисунок 3.4

3.2.7 Яркость светящейся поверхности, l

Пусть светящаяся поверхность площади DS излучает световой поток DΦ в телесный угол DΩ, ось симметрии которого составляет угол Θ с нормалью к излучающей поверхности, рисунок 3.5.

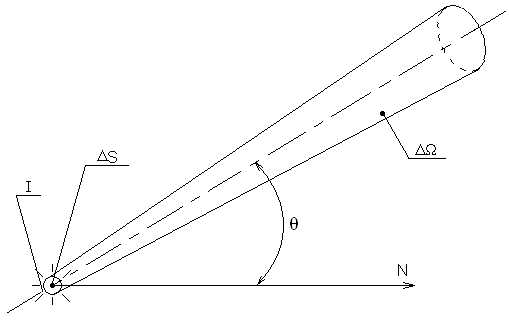
Рисунок 3.5

Величина

, (3.10)

согласно [5, c.52], называется яркостью светящейся поверхности.

3.2.8 Закон Ламберта

В 1760 году немецким ученым Ламбертом было по казано, что, если площадь DS не только излучает свет, но еще идеально равномерно рассеивает его по всем направлениям, яркость излучения L не зависит от угла Θ, входящего в (3.10).

Согласно закона Ламберта

L_L = const, (3.11)

для любых Θ, входящих в (3,10).

Элементарные преобразования, [5, с.52], показывают, что для Ламбертовского источника, взаимосвязь между светимостью излучающей поверхности М_L и ее яркостью L_L имеет вид:

М_L = L_L × π (3.12)

3.2.9 Световая экспозиция, нс

Световой экспозицией H_С называется произведение освещенности поверхности Е на время t, в течение которого производится облучение поверхности. По определению,

H_С = Е × t, (лк × с) (3.13)

В заключение раздела 3.2 мы приводим в таблице 3.2 основные фотометрические характеристики, аналитические выражения для них и размерности в “S I“.

Таблица 3.2 Перечень основных фотометрических характеристик.

Наименование фотометрических величин	Аналитическое выражение	Размерность в “SI“
Сила света	I_С	Кандела, (кд)
Световой поток	DΦ = I ×DΩ	Люмен, (лм)
Освещенность поверхности		Люкс, (лк), (люмен на квадратный метр), (лм/м).
Светимость излучающей поверхности		Люмен на квадратный метр, (лм/м)
Яркость светящейся поверхности		Кандела на квадратный метр, (кд/м)

3.3 Энергетические характеристики оптического излучения [15, с. 15]

3.3.1 Энергетическая экспозиция, Н_Э

Величина, равная отношению энергии излучения DW, падающего на поверхность, к площади этой поверхности DS:

, (3.14)

3.3.2 Поток излучения, Ф_Э

Величина, равная отношению энергии излучения DW, переносимой излучением, к времени переноса этого излучения Dt

Ф_Э = , (Вт), (3.15)

называется потоком излучения.

3.3.3 Энергетическая светимость Є (интегральная излучательная способность)

Интегральная излучательная способность равна отношению потока излучения Ф_Э к площади DS_И, с которой этот поток испускается:

Є = ,(3.16)

3.3.4 Облученность поверхности, Є_О

Величина, равная отношению потока излучения Ф_Э к площади DS_П, на которую этот поток падает и поглощается

Є₀ = . (3.17)

Библиография

Игнатов А.Н. Основы оптоэлектроники. Ч.1. Излучающие и фото-приемные приборы. – Новосибирск, 1988.
Игнатов А.Н. Основы оптоэлектроники. Ч.2. Жидкокристаллические и электролюминесцентные индикаторные приборы. – Новосибирск, 1989.
Селиванов Л.В. Основы оптики. Часть I. – Новосибирск.: СибГАТИ, 1995г. – 54с
Селиванов Л.В. Основы оптики. Часть II. – Новосибирск.: СибГАТИ, 1995г. – 56с.
Селиванов Л.В. Основы оптики. Часть V. – Новосибирск.: СибГАТИ, 1997г. – 56с.
Селиванов Л.В. Основы оптики. Часть IV. – Новосибирск.: СибГАТИ, 1997г. – 63с.
Goss F., Hanchen H. Ann. Phys. Ser. 6, I. – Leipzig, 1947 – 333s.
Хансперджер Р. Интегральная оптики. Перевод с английского. – М.: МИР, 1985г. – 380с.
Мальке Г., Гессинг П. Волоконно-оптические кабели. Перевод с английского. – Новосибирск: ИЗДАТЕЛЬ, 1997г. – 264с.
Чео П.К. Волоконная оптика. Перевод с английского. – М.: Энергоатомиздат, 1988г. – 279с.
Гауэр Д. Оптические системы связи. Перевод с английского. – М.: Радио и связь, 1989г. – с.
Мэзон У. Физическая акустика, т.3, ч.Б. Перевод с английского. – М.: МИР, 1968г. – 320с.
Селиванов Л.В. Основы оптики. Часть III. – Новосибирск: СибГАТИ, 1995г. – 44с.
Ландсберг Г.С. Оптика. – М.: НАУКА, 1976г. – 926с.
Физические величины. Справочник / под редакцией Григрьевой И.С., Мейлихов Е.З. – М.: Энергоатомиздат, 1991г. – 1232с.

studfiles.net

Энергетическая освещенность формула. Световой поток. Подробнее об освещенности

Для открытой местности и помещения, а также приведем величины светового потока при разных обстоятельствах.

Свеча и прялка

До широко распространенной электрификации источником света были солнце, луна, костер и свеча. Ученые уже в пятнадцатом веке умели создавать систему линз для усиления освещенности, но большинство людей работали и жили при свечах.

Некоторым было жалко тратить деньги на восковые источники света, или этот способ продлить день был просто недоступен. Тогда использовали альтернативные варианты топлива — масло, жир животных, дерево. Например, русские крестьянки средней полосы всю жизнь ткали лен при свете лучины. Читатель может спросить: «Почему это надо было делать ночью?» Ведь коэффициент естественной освещенности днем гораздо выше. Дело в том, что в светлое время суток у крестьянок было множество других забот. Кроме того, процесс ткачества весьма кропотлив и требует спокойствия. Женщинам было важно, чтобы никто не наступал на полотно, чтобы дети не путали нитки, а мужчины не отвлекали.

Но при такой жизни есть одна опасность: световой поток (формулу мы приведем чуть ниже) от лучины очень низкий. Глаза перенапрягались, и женщины быстро теряли зрение.

Освещение и обучение

Когда первоклассники идут в школу первого сентября, они с волнением ожидают чудес. Их захватывают линейка, цветы, красивая форма. Они интересуются, какой будет их учительница, с кем они будут сидеть за одной партой. И эти ощущения человек запоминает на всю жизнь.

Но взрослые, когда отправляют детей в школу, должны подумать о более прозаических вещах, нежели восторг или разочарование. Родителей и учителей заботит удобство парты, размер классной комнаты, качество мела и формула освещенности помещения. Эти показатели имеют нормы для детей всех возрастов. Поэтому школьники должны быть благодарны за то, что люди заранее продумали не только учебную программу, но и материальную сторону вопроса.

Освещение и работа

Недаром в школах проводятся проверки, в которых применяется формула расчета освещенности комнат для занятий. Дети десять или одиннадцать лет только и делают, что читают и пишут. Потом они вечером выполняют домашнее задание, снова не расставаясь с ручками, тетрадками и учебниками. После чего современные подростки еще и утыкаются в разнообразные экраны. В итоге вся жизнь школьника сопряжена с нагрузкой на зрение. Но школа — только начало жизненного пути. Дальше всех этих людей ждет вуз и труд.

Каждый вид работ требует своего светового потока. Формула расчета всегда учитывает, что человек делает по 8 часов в сутки. Например, часовщик или ювелир должен рассматривать мельчайшие детали и оттенки цветов. Поэтому рабочее место людей этой профессии требует больших и ярких ламп. А ботанику, который изучает растения тропического леса, наоборот, необходимо постоянно пребывать в полумраке. Орхидеи и бромелии привыкли к тому, что верхний ярус деревьев отбирает почти весь солнечный свет.

Формула

Подходим непосредственно к формуле освещенности. Ее математическое выражение выглядит так:

E υ = dΦ υ / dσ.

Рассмотрим выражение поближе. Очевидно, что E υ — это и есть освещенность, тогда Φ υ — это световой поток, а σ — малая единица площади, на которую поток падает. Видно, что Е — величина интегральная. Это значит, что рассматриваются очень небольшие отрезки и кусочки. То есть ученые суммируют освещенность всех этих маленьких участков, чтобы получить конечный результат. Единица освещенности — люкс. Физический смысл одного люкса — это такой световой поток, для которого на один квадратный метр приходится один люмен. Люмен, в свою очередь, — это весьма конкретная величина. Она обозначает световой поток, который излучает точечный изотропный источник (следовательно, Сила света этого источника равна одной канделе в телесный угол один стерадиан. Единица освещенности сложная величина, которая включает понятие «кандела». Физический смысл последнего определения таков: сила света в известном направлении от источника, который испускает монохроматическое излучение частотой 540·10 12 Гц (длина волны лежит в видимой области спектра), причем энергетическая сила света равна 1/683 Вт/ср.

Понятия, связанные с освещенностью

Конечно, все эти понятия на первый взгляд похожи на сферического коня в вакууме. Таких источников не существует в природе. И внимательный читатель непременно задаст себе вопрос: «Зачем это нужно?» Но у физиков есть необходимость сравнивать. Следовательно, им приходится вводить некие нормы, на которые надо ориентироваться. Формула освещенности проста, но многое может быть непонятно. Раскроем это подробнее.

Индекс «υ»

Индекс υ означает, что величина не совсем фотометрическая. И связано это с тем, что человеческие возможности ограничены. Например, глаз воспринимает только видимый спектр электромагнитного излучения. Причем центральную часть этой шкалы (относится к зеленому цвету) люди видят гораздо лучше, чем краевые области (красный и фиолетовый). То есть фактически человек не воспринимает 100% фотонов желтого или голубого цвета. При этом существуют приборы, лишенные такой погрешности. Редуцированные величины, которыми оперирует формула освещенности (световой поток, например) и которые обозначаются греческой буквой «υ», имеют поправку на человеческое зрение.

Генератор монохроматического излучения

В самой основе, как уже было сказано выше, лежит количество фотонов с определенной длиной волны, которые испускаются в определенном направлении за единицу времени. Даже самый монохроматический лазер имеет некоторое распределение по длинам волн. И уж точно он должен на чем-то держаться. Значит, фотоны испускаются не во всех направлениях. Но в формуле фигурирует такое понятие, как «точечный источник света». Это очередная модель, призванная унифицировать некоторую величину. И ни один объект вселенной не может так называться. Итак, точечный источник света — это генератор фотонов, который излучает равное количество квантов электромагнитного поля во всех направлениях, его размер равен математической точке. Однако есть одна хитрость, она может сделать реальный объект точечным источником: если расстояние, на которое долетают фотоны, очень велико по сравнению с размерами генератора. Таким образом, наша центральна звезда Солнце — это диск, а вот далекие звезды — это точки.

Беседка, колодец, парк

Наверняка внимательный читатель замечал следующее: в яркий солнечный день открытая местность кажется освещенной гораздо сильнее, чем закрытая с одной стороны поляна или лужайка. Поэтому берег моря так манит: там всегда солнечно и тепло. А вот даже большая поляна в лесу — более темная и холодная. И неглубокий колодец освещен плохо в самый яркий день. Это потому, что если человек видит только часть небосвода, до его глаза долетает меньше фотонов. Коэффициент естественной освещенности так и вычисляется, как соотношение потока света от всего небосвода к видимому участку.

Круг, овал, угол

Все эти понятия имеют отношение к геометрии. Но сейчас речь пойдет о явлении, которое непосредственно относится к формуле освещенности и, следовательно, к физике. До этого момента предполагалось, что свет падает на поверхность перпендикулярно, строго вниз. Это, конечно же, тоже приближение. При соблюдении данного условия удаление от источника света означает падение освещенности пропорционально квадрату расстояния. Таким образом, звезды, которые человек видит невооруженным глазом на небе, либо расположены не так далеко от нас (все они относятся к галактике Млечный Путь), либо очень яркие. Но если свет падает на поверхность под углом, все иначе.

Представьте себе фонарик. Он дает круглое пятно света, когда направлен строго перпендикулярно стене. Если его наклонить, то пятно изменит форму на овал. Как известно из геометрии, у овала площадь больше. А раз фонарик все тот же, значит, и сила света та же, но она как бы «размазана» на большую площадь. Сила света зависит от по закону косинуса.

Весна, зима, осень

Заголовок звучит как название красивого фильма. Но наличие сезонов напрямую зависит от угла, под которым падает свет в своей наивысшей точке на поверхность планеты. И в данный момент речь идет не только о Земле. Сезоны существует на любом объекте солнечной системы, ось вращения которого наклонена по отношению к эклиптике (например, на Марсе). Читатель, наверное, уже догадался: чем больше угол наклона, тем меньше фотонов приходится на квадратный километр поверхности в секунду. Значит, тем холоднее будет сезон. В момент наибольшего отклонения планеты в полушарии царит зима, в момент наименьшего — лето.

Ц

realartist.ru

Основные фотометрические единицы (световой поток, сила света, освещенность, светимость и яркость)

Основные фотометрические единицы (световой поток, сила света, освещенность, светимость и яркость)

Фотометрия — раздел оптики, занимающийся вопросами измерения интенсивности света и его источников. В фотометрии используются следующие величины:

1) энергетические — характеризуют энергетические параметры оптического излучения безотносительно к его действию на приемники излучения;

2) световые — характеризуют физиологические действия света и оцениваются по воздействию на глаз (исходят из так называемой средней чувствительности глаза) или другие приемники излучения.

Энергетический поток— энергия, переносимая волной за время 1 с; единица — ватт, Вт.

Энергетическая освещенность— отношение энергетического потока ΔФ_Э к площади облучаемой им поверхности ΔQ:

единица — ватт на квадратный метр, Вт/м².

Энергетическая сила света— отношение энергетического потока ΔФ_Э к

телесному углу ΔΩ, в котором распределено это излучение:

;

единица – ватт на стерадиан, Вт/ср.

Энергетическая светимость – отношение энергетического потока ΔФ_э к площади излучающей поверхности источника ΔQ_И:

;

единица – Вт/м².

Энергетическая яркость— отношение энергетической силы света ΔI_Э, к площади проекции ΔQ_П излучающей поверхности источника на плоскость, перпендикулярную направлению наблюдения:

единица — Вт/(м² ср).

Световой поток— энергия, оцениваемая по зрительному воздействию на глаз человека; единица — люмен, лм (1 лм равен световому потоку монохроматического излучения с длиной волны 555 нм, энергетический поток которого равен 1/683 Вт).

Освещенность— отношение светового потока ΔФ к площади ΔΩ облучаемой им поверхности:

единица — люкс, лк.

Сила света— отношение светового потока ΔФ к телесному углу ΔΩ:

Единица – кандела, кд (одна из основных единиц в СИ). Кандела равна силе света в заданном направлении от источника излучения частотой 540∙10¹² Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср.

Светимость – отношение светового потока ΔФ к площади излучаемой поверхности ΔQ_И источника:

;

Единица лм/м².

Яркость – отношение силы света ΔI к площади проекции ΔQ_П поверхности источника на плоскость, перпендикулярную направлению наблюдения:

;

Единица – кд/м².

Освещенность Е_Т, создаваемая точечным источником, рассчитывается по формуле:

где I – сила света, r – расстояние между источником и облучаемой им поверхностью, φ – угол между нормалью к поверхности и направлением распространения волн.

Что такое луч света?

Светово́й луч в геометрической оптике — линия, вдоль которой переносится световая энергия. Менее чётко, но более наглядно, можно назвать световым лучом пучок света малого поперечного размера.

Понятие светового луча является краеугольным приближением геометрической оптики. В этом определении подразумевается, что направление потока лучистой энергии (ход светового луча) не зависит от поперечных размеров пучка света. В силу того, что свет представляет собой волновое явление, имеет место дифракция, и в результате узкий пучок света распространяется не в каком-то одном направлении, а имеет конечное угловое распределение.

Однако в тех случаях, когда характерные поперечные размеры пучков света достаточно велики по сравнению с длиной волны, можно пренебречь расходимостью пучка света и считать, что он распространяется в одном единственном направлении: вдоль светового луча.

Закон независимости действия световых пучков.

Световой поток можно разбить на отдельные световые пучки, выделяя их,

например, при помощи диафрагм. Действие этих выделенных световых пучков

оказывается независимым, т.е. эффект, производимый отдельным пучком, не

зависит от того, действуют ли одновременно другие пучки или они устранены.

Закон преломления света.

На границе двух сред свет меняет направление своего распространения. Часть световой энергии возвращается в первую среду, т.е. происходит отражение света. Если вторая среда прозрачна, то часть света при определенных условиях может пройти через границу сред, также меняя при этом, как правило, направление своего распространения. Это явление называетсяпреломлением света. Вследствие преломления наблюдается кажущееся изменение размеров, формы и расположения предметов. В этом нас могут убедить простые наблюдения. Установим наклонно карандаш в стакане с водой. Часть карандаша, находящаяся в воде, кажется сдвинутой в сторону и увеличенной в диаметре.

Подобные явления объясняются изменением напрвления лучей на границе двух сред. Луч, распространяющийся в первой среде и достигающий границы, называетсяпадающим лучом, называемыйa. Он составляет с перпендикуляром к границе, проведенным через точку падения, уголуглом падения. Луч, прошедший во вторую среду, называютпреломленным лучом, который этот луч образует с тем же перпендикуляром, называютb. Уголуглом преломления.

Закон преломления, установленный экспериментально в XVII веке, формулируется следующим образом: Падающий луч, преломленный луч и перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух данных сред.

Sin a / sin b = n

Закон отражения света.

Закон отражения света определяет взаимное расположение падающего луча, отраженного луча и перпендикуляра к поверхности, восстановленного в точке падения.

Очевидно, что этот закон будет выполняться и в том случае, если свет будет распространяться в обратном направлении.a равен углу падения gЭтот закон справедлив для волн любой природы и формулируется так: падающий луч, отраженный луч и перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости; угол отражения Обратимостьхода световых лучей является их важным свойством.

Т.е Луч падающий, отраженный и перпендикуляр в точке падения лежат в одной плоскости. Угол падения равен углу отражения.

Что такое интерференция?

Явление интерференции свидетельствует о том, что свет — это волна.

Интерференциейсветовых волн называется сложение двух когерентных волн, вследствие которого наблюдается усиление или ослабление результирующих световых колебаний в различных точках пространства.

Интерференция света — это явление наложения когерентных световых волн, в результате которого происходит перераспределение световой энергии в пространстве.

В точках пространства, куда когерентные волны приходят в фазе, они усиливают друг друга; в точках, куда они попадают в противофазе, происходит ослабление света. На экране наблюдается характерная интерференционная картина в виде чередования темных и светлых полос — максимумов и минимумов освещенности, если падающий свет монохроматический. Заметим, что сказанное имеет место лишь тогда, когда направления колебаний светового вектора обеих волн совпадают.

В случае максимума интенсивности интерференционной картины в оптической разности хода двух когерентных волн укладывается целое число длин волн (в вакууме)

Принцип Гюйгенса – Френеля.

Согласно принципу Гюйгенса-Френеля световая волна, возбуждаемая каким-либо источником S может быть представлена как результат суперпозиции когерентных вторичных волн. Каждый элемент волновой поверхности S (рис.) служит источником вторичной сферической волны, амплитуда которой пропорциональна величине элемента dS.

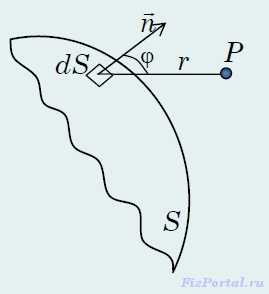
Амплитуда этой вторичной волны убывает с расстоянием r от источника вторичной волны до точки наблюдения по закону 1/r. Следовательно, от каждого участка dS волновой поверхности в точку наблюдения Р приходит элементарное колебание:

где (ωt + α₀) − фаза колебания в месте расположения волновой поверхности S, k − волновое число, r − расстояние от элемента поверхности dS до точки P, в которую приходит колебание. Множитель а₀ определяется амплитудой светового колебания в месте наложения элемента dS. Коэффициент K зависит от угла φ между нормалью к площадке dS и направлением на точку Р. При φ = 0 этот коэффициент максимален, а при φ/2 он равен нулю.
Результирующее колебание в точке Р представляет собой суперпозицию колебаний (1), взятых для всей поверхности S:

Эта формула является аналитическим выражением принципа Гюйгенса-Френеля.

Виды поляризованного света.

Под поляризацией света понимают пространственное соотношение между направлением распространения света и направлением колебания электрического вектора. Световая волна образуется в результате наложения большого количества волновых цугов, испускаемых отдельными возбужденными атомами источника света. Направления колебаний векторов и у отдельных цугов – самые разнообразные. Поэтому в результирующей световой волне направление колебаний суммарного светового вектора хаотически изменяется. Такой свет называется естественным . Свет, у которого направления колебаний векторов и упорядочены, называется поляризованным .

Свет называется линейно поляризованным (плоско поляризованным), если колебания электрического (светового) вектора происходят вдоль одного направления.

Плоскость, проходящая через вектор и направление луча, называется плоскостью поляризации.

Свет, состоящий из естественной и поляризованной составляющих, называется частично поляризованным.

При сложении двух световых волн одинаковой частоты, линейно поляризованных во взаимно перпендикулярных плоскостях, результирующий вектор может поворачиваться по мере распространения волны (происходит сложение взаимно перпендикулярных колебаний одинаковой частоты). Свет, у которого конец вектора , вращаясь вдоль направления луча, описывает эллипс называется эллиптически поляризованным, если – окружность, то поляризованным по кругу.

Закон Малюса.

Если два поляроида поставлены на пути лучей так, что их плоскости пропускания параллельны друг другу, то колебания электромагнитного поля световой волны, пропущенные первым из них (поляризатором Р), будут пропущены и вторым (анализатором А). Наоборот, при взаимно перпендикулярном расположении плоскостей пропускания скрещенных поляроидов колебания, пропущенные одним из них, будут задержаны вторым. Таким образом пропускание света парой поляроидов зависит от угла между их плоскостями пропускания (рис. 5 а).

Из рисунка 5 б) видно, что амплитудные значения напряженности светового вектора связаны между собой:

Е_А = Е_р cos α. (1)

А так как интенсивность света I ~ E² , то

I = I₀ • cos² α, (2)

где I_о — интенсивность поляризованного света, падающего на анализатор, I — интенсивность поляризованного света, прошедшего через анализатор.

Формула (2) является выражением закона Малюса: интенсивность света I, выходящего из анализатора, пропорциональна квадрату косинуса угла α между направлением плоскостей пропускания вектора Е поляризатора и анализатора.

Для прозрачных поляроидов поляризатор Р пропускает 50% интенсивности естественного света, тогда закон Малюса можно также записать для естественного света

. (3)

Закон Кирхгофа.

Закон Кирхгофа.Между спектральной плотностью энергетической светимости и спектральной поглощательной способностью существует определенная связь, установленная Кирхгофом и сформулированная им следующим образом: отношение спектральной плотности энергетической светимости к спектральной поглощательной способности не зависит от природы тела и является для всех тел одной и той же функцией частоты и температуры: . Это равенство называется законом Кирхгофа. Спектральная плотность энергетической светимости и спектральная поглощательная способность могут меняться от тела к телу, но их отношение одинаково для всех тел. Если тело сильнее поглощает какие-либо лучи, то оно будет эти лучи сильнее и испускать (не отражать, а испускать).

Закон Кирхгофа справедлив для всех тел, в том числе и для абсолютно черного тела, для которого . Следовательно, для такого тела . Таким образом, универсальная функция Кирхгофа есть не что иное, как спектральная плотность энергетической светимости абсолютно черного тела.

Закон Стефана-Больцмана.

Закон Стефана — Больцмана — закон излучения абсолютно чёрного тела. Определяет зависимостьмощности излучения абсолютно чёрного тела от его температуры. Формулировка закона:

Мощность излучения абсолютно чёрного тела прямопропорциональна площади поверхности и четвёртой степенитемпературы тела: P = SεσT⁴,

где ε — степень черноты (для всех веществ ε < 1, для абсолютно черного тела ε = 1). При помощи законаПланка для излучения, постоянную σ можно определелить как

где — постоянная Планка, k — постоянная Больцмана, c — скорость света.

Численное значение Дж · с^-1 · м^-2 · К^-4.

Закон открыт независимо Й. Стефаном и Л. Больцманом в предположении пропорциональности плотностиэнергии излучения и его давления p = ρ / 3. В 1880 г. подтверждён Лео Гретцем.

Важно отметить, что закон говорит только об общей излучаемой энергии. Распределение энергии поспектру излучения описывается формулой Планка, в соответствии с которой в спектре имеетсяединственный максимум, положение которого определяется законом Вина.

Применение закона к расчёту эффективной температуры поверхности Земли даёт оценочное значение, равное 249 К или −24 °C.

Законы Вина.

В 1893 г. немецкий физик В.Вин теоретически рассмотрел термодинамический процесс сжатия излучения, заключенного в полости с идеально зеркальными стенками, и пришел к выводу, что испускательная способность абсолютно черного тела прямо пропорциональна кубу частоты и является функцией отношения ν/T:

, (16.12)

где α – постоянная величина, F — некоторая функция, конкретный вид которой термодинамическими методами установить невозможно.

Переходя в этой формуле Вина от частоты к длине волны, получим:

. (16.13)

Как видно, в выражение для излучательной способности температура входит лишь в виде произведенияλT. Уже это обстоятельство позволило предсказать некоторые особенности функции . В частности, эта функция достигает максимума при определенной длине волныλ_m, которая при изменении температуры тела изменяется так, чтобы выполнялось условие: λ_mT = const.

Таким образом, В. Вин сформулировал закон теплового излучения, согласно которому длина волны λ_m, на которую приходится максимум излучательной способности абсолютно черного тела, обратно пропорциональна его абсолютной температуре. Этот закон можно записать в виде

, (16.14)

где — постоянная Вина.

Закон Вина называют законом смещения, подчеркивая тем самым, что при повышении температуры абсолютно черного тела положение максимума его излучательной способности смещается в область коротких длин волн. Результаты экспериментов, приведенные на рис. 16.4, подтверждают этот вывод не только качественно, но и количественно, строго в соответствии с формулой (16.14).

С ростом температуры любого тела длина волны, вблизи которой тело излучает больше всего энергии, также смещается в сторону коротких длин волн. Это смещение, однако, уже не описывается простой формулой (16.14), которую для излучения реальных тел можно использовать только в качестве оценочной, т.е. формула (16.14) остается в силе только при больших частотах и низких температурах.

Кроме закона смещения (16.14) Вин получил выражение для максимального значения излучательной способности АЧТ. Эту зависимость называют вторым законом Вина, согласно которому максимальное значение испускательной способности АЧТпрямо пропорционально абсолютной температуре в пятой степени:

, (16.15)

где . Однако, получить теоретическое выражение для универсальной функции Кирхгофа, хорошо описывающее экспериментальные результаты во всем диапазоне длин волн излучения тела, Вину не удалось.

Формула Бальмера.

Спектры излучения изолированных атомов, например, атомов разреженного одноатомного газа или паров металла, состоят из отдельных спектральных линий и носят название линейчатых. Относительная простота линейчатых спектров объясняется тем, что электроны, входящие в состав таких атомов, находятся под действием только внутриатомных сил и практически не испытывают возмущающего действия со стороны окружающих удаленных атомов. Изучение линейчатых спектров показывает, что в расположении линий, образующих спектр, наблюдаются определённые закономерности: линии располагаются не беспорядочно, а группируются сериями. Впервые это было обнаружено Бальмером (1885 г.) для атома водорода. Сериальные закономерности в атомных спектрах присущи не только атому водорода, но и другим атомам и свидетельствуют о проявлении квантовых свойств излучающих атомных систем. Для атома водорода эти закономерности могут быть выражены с помощью соотношения (обобщенная формула Бальмера)

Сериальные формулы свидетельствуют о существовании физических закономерностей в спектре атома водорода, объяснить которые с помощью классической физики невозможно.

Постулаты Бора.

Основу теории Бора составили три постулата и классическая механика Ньютона. На основании того, что атомные спектры представляют собой набор отдельных линий, соответствующих дискретному набору частот , , …., Бор сделал вывод, что атомы не могут обладать энергией, способной изменяться непрерывно, и сформулировал следующие постулаты:

1. Постулат стационарных состояний. В атоме существуют стационарные (не изменяющиеся со временем) состояния, характеризующиеся определенными дискретными значениями энергии, в которых он не излучает и не поглощает энергию.

2. Постулат квантования орбит. В стационарных состояниях атома электрон может двигаться лишь по таким орбитам, для которых момент импульса электрона имеет дискретные значения, удовлетворяющие условию:

где n = 1,2,3 … , скорость электрона поn-ой орбите радиуса , – постоянная Планка.

3. Постулат частот. При переходе электрона из одного стационарного состояния в другое стационарное состояние излучается (поглощается) один фотон с энергией, равной разности энергий соответствующих стационарных состояний и :

При происходит излучение энергии, при — поглощение энергии. Набор возможных квантовых переходов и определяет линейчатый спектр атома:

Строение ядра.

Строение атомного ядра.

Атом – это мельчайшая частица химического элемента, сохраняющая все его свойства. По своей структуре атом представляет сложную систему, состоящую из находящегося в центре атома положительно заряженного ядра очень малого размера (10^-13 см) и отрицательно заряженных электронов, вращающихся вокруг ядра на различных орбитах. Отрицательный заряд электронов равен положительному заряду ядра, при этом в целом оказывается электрически нейтральным.

Атомные ядра состоят из нуклонов – ядерных протонов (Z – число протонов) и ядерных нейтронов (N – число нейтронов). « Ядерные» протоны и нейтроны отличаются от частиц в свободном состоянии. Например, свободный нейтрон, в отличие от связанного в ядре, нестабилен и превращается в протон и электрон.

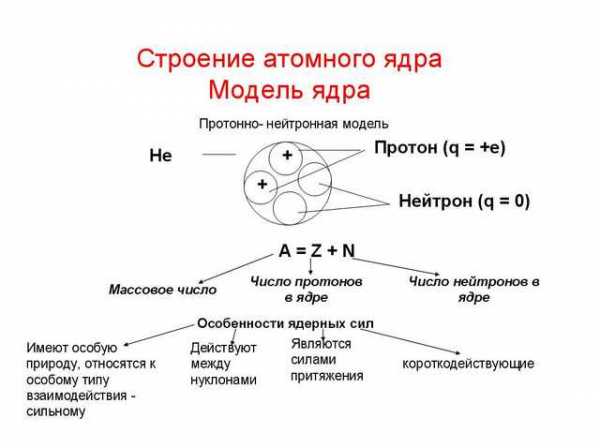
Протон – элементарная частица любого атома, он имеет положительный заряд, равный заряду электрона. Число электронов в оболочке атома определяется числом протонов в ядре.

Нейтрон – другой вид ядерных частиц всех элементов. Его нет лишь в ядре легкого водорода, состоящего из одного протона. Он не имеет заряда, электрически нейтрален. В атомном ядре нейтроны являются стабильными, а в свободном состоянии они неустойчивы. Число нейтронов в ядрах атомов одного и того же элемента может колебаться, поэтому число нейтронов в ядре не характеризует элемент.

Нуклоны (протоны + нейтроны) удерживаются внутри атомного ядра ядерными силами притяжения. Ядерные силы в 100 раз сильнее электромагнитных сил и поэтому удерживает внутри ядра одноименно заряженные протоны. Ядерные силы проявляются только на очень малых расстояниях (10^-13см), они составляют потенциальную энергию связи ядра, которая при некоторых превращениях частично освобождается, переходит в кинетическую энергию.