Физический смысл магнитной индукции:
⇐ ПредыдущаяСтр 7 из 11Следующая ⇒Индукция магнитного поля численно равна максимальной силе, с которой данное поле действует на проводник длиной 1 метр с силой тока 1 Ампер.

Направление индукции магнитного поля –
от Южного к Северному полюсу свободно установившейся магнитной стрелки.
 Магнитный поток
Магнитный поток
Нарисуем замкнутый контур, n – нормаль к его плоскости.
Поместим контур в магнитное поле с индукцией В.
Магнитный поток- это скалярная физическая величина, равная произведению модуля вектора индукции магнитного поля на площадь контура и на косинус угла между вектором индукции и нормалью к площади контура

Единица измерения магнитного потока – Вебер
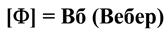
Вб = Тл*м2
Явление электромагнитной индукции
Явление электромагнитной индукции было открыто выдающимся английским физиком М. Фарадеем в 1831 г. Фарадей наблюдал возникновение электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока
Вопрос Фарадея:: если током можно намагнитить железо, то не может ли магнит вызвать появление тока?
Явление ЭМИ состоит в том, что при любом изменении магнитного потока, пронизывающего замкнутый контур, в контуре возникает ЭДС индукции. Если контур проводящий, то в нем будет протекать ток, который называется индукционным. Если контур из диэлектрика, то он поляризуется.
Сторонние силы действуют внутри источника тока и вызывают разделение зарядов, т. е. движение электронов от + к – источника. Имеют неэлектрическую природу.
ЭДС индукции возникает только в тот интервал времени, когда
Изменение магнитного потока через контур:
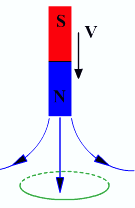
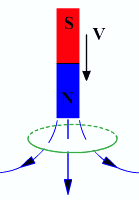 .
.
Закон электромагнитной индукции (закон Фарадея)
ЭДС индукции
По закону ЭМИ изменение магнитного потока приводит к появлению ЭДС, которая называется ЭДС индукции.
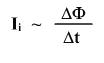
 По закону Ома для полной цепи сила тока равна отношению ЭДС к полному сопротивлению цепи
По закону Ома для полной цепи сила тока равна отношению ЭДС к полному сопротивлению цепи
следовательно, ЭДС индукции пропорциональна скорости изменения магнитного потока
 |
Закон электромагнитной индукции (Фарадея):
 |
Понятие об электромагнитной теории Максвелла. Вихревое электрическое поле. Правило Ленца. Самоиндукция. Индуктивность.
Направление индукционного тока.
Правило Ленца (1883 г)индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
 Опыт Ленца
Опыт Ленца
Описание опыта:замкнутое кольцо отталкивается от магнита, если его вдвигают в кольцо, и притягивается, если магнит выдвигают.
Движение кольца обусловлено магнитным полем индукционного тока.
Применение правила Ленца
Пример Магнит движется вправо (вдвигается в контур)
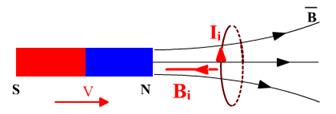 |
1. Определить направление силовых линий внешнего поля B.
2. Определить, увеличивается или уменьшается магнитный поток через
контур.
3. Определить направление индукционного магнитного поля Bi
Если магнитный поток увеличивается, Bi направлено против B, компенсируя это увеличение. Если магнитный поток уменьшается, Bi направлено одинаково с B, компенсируя это уменьшение.
- По правилу буравчика определить направление индукционного тока.
Вихревое электрическое поле
Причина появления ЭДС индукции в замкнутом контуре при изменении магнитного потока заключается в возникновении вихревого электрического поля в любой области пространства, где существует переменное магнитное поле. – гипотеза Максвелла. Силовые линии вихревого поля замкнуты.
Перечислим свойства известных нам полей
1. Электростатическое, возникает везде, где есть эл. заряды. Силовые линии начинаются и заканчиваются на зарядах. Потенциальное, т.е. работа по замкнутому контуру равна нулю. напряженность, потенциал.
2. Поле тока – магнитное, вихревое, работа по замкнутому контуру не равна нулю. Ток течет в сторону убывания потенциала. Поле действует только на движущиеся заряды
3. Вихревое электрическое поле. Действует на любые заряды. Работа по замкнутому контуру равна ЭДС индукции. ЭДС индукции определяется законом Фарадея.
 Самоиндукция. Индуктивность
Самоиндукция. Индуктивность
Самоиндукция является важным частным случаем
электромагнитной индукции, когда изменяющийся
магнитный поток, вызывающий ЭДС индукции,
создается током в самом контуре.
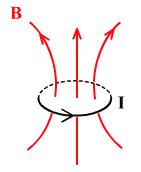
возникает магнитное поле. Силовые линии этого поля
пронизывают все окружающее пространство, в том числе, пересекают площадь самого контура.
Магнитный поток, который вызван током в этом самом контуре, называется собственным магнитным потоком.
Поскольку магнитный поток пропорционален индукции магнитного поля, собственный магнитный поток пропорционален силе тока в контуре
 | |||
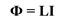 |
Следовательно, можно ввести коэффициент пропорциональности
Коэффициент пропорциональности L между собственным магнитным потоком в контуре и силой тока в нем называется индуктивностью контура.
Индуктивность проводника зависит от размеров, формы проводника, магнитных свойств среды.
Единица измерения индуктивности называется Генри
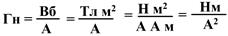 |
infopedia.su
Магнитная индукция, магнитный поток: определение, формулы, смысл
 Магнитная индукция (обозначается символом В) – главная характеристика магнитного поля (векторная величина ), которая определяет силу воздействия на перемещающийся электрический заряд (ток) в магнитном поле, направленной в перпендикулярном направлении скорости движения.
Магнитная индукция (обозначается символом В) – главная характеристика магнитного поля (векторная величина ), которая определяет силу воздействия на перемещающийся электрический заряд (ток) в магнитном поле, направленной в перпендикулярном направлении скорости движения.
Магнитная индукция определяется способностью влиять на объект с помощью магнитного поля. Эта способность проявляется при перемещении постоянного магнита в катушке, в результате чего в катушке индуцируется (возникает) ток, при этом магнитный поток в катушке также увеличивается.
Физический смысл магнитной индукции
Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка состоит из металла). В кристаллической решетке металла расположены электрические заряды — электроны. Если на металл не оказывать ни какое магнитное воздействие, то заряды (электроны) находятся в покое и никуда не движутся.
Если же металл попадает под действие переменного магнитного поля (из-за перемещения постоянного магнита внутри катушки — именно перемещения), то заряды начинают двигаться под действием этого магнитного поля.
В результате чего в металле возникает электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости перемещения одного относительно другого.
При помещении металлической катушки в магнитное поле заряженные частицы металлический решетки (в кашутке) поворачиваются на определенный угол и размещаются вдоль силовых линий магнитного поля.
Чем выше сила магнитного поля, тем больше количество частиц поворачиваются и тем более однородным будет являться их расположение.
Магнитные поля, ориентированные в одном направлении не нейтрализуют друг друга, а складываются, формируя единое поле.
Формула магнитной индукции
где, В — вектор магнитной индукции, F — максимальная сила действующая на проводник с током, I — сила тока в проводнике, l — длина проводника.


Магнитный поток
Магнитный поток это скалярная величина, которая характеризует действие магнитной индукции на некий металлический контур.
Магнитная индукция определяется числом силовых линий, проходящих через 1 см2 сечения металла.
Магнитометры, используемые для ее измерения, называют теслометрами.
Единицей измерения магнитной индукции в системе СИ является Тесла (Тл).
После прекращения движение электронов в катушке сердечник, если он выполнен из мягкого железа, теряет магнитные качества. Если он изготовлен из стали, то он имеет способность некоторое время сохранять свои магнитные свойства.

pue8.ru
Физический смысл
В
вакууме (или в отсутствие среды, способной
к магнитной поляризации, а также в
случаях, когда последняя пренебрежима)
напряжённость магнитного поля совпадает
с вектором магнитной индукции с точностью
до коэффициента, равного 1 в СГС и μ0 в СИ. В магнетиках (магнитных средах) напряжённость
магнитного поля имеет физический смысл
«внешнего» поля, то есть совпадает
(быть может, в зависимости от принятых
единиц измерения, с точностью до
постоянного коэффициента, как например
в системе
74 Виды магнетиков Диамагнетики имеют магнитную проницаемость чуть меньше 1. Отличаются тем, что выталкиваются из области магнитного поля. Парамагнетики имеют магнитную проницаемость чуть более 1. Подавляющее количество материалов являются диа- и пара- магнетиками. Ферромагнетики обладают исключительно большой магнитной проницаемостью, доходящей до миллиона. По мере усиления поля проявляется явление гистерезиса, когда при увеличении напряженности и при последующем уменьшении напряженности значения В(Н) не совпадают друг с другом. В литературе различают несколько определений магнитной проницаемости. Начальная магнитная проницаемость mн — значение магнитной проницаемости при малой напряженности поля. Максимальная магнитная проницаемость mmax — максимальное значение магнитной проницаемости, которое достигается обычно в средних магнитных полях. Из других основных терминов, характеризующих магнитные материалы, отметим следующие. Намагниченность насыщения — максимальная намагниченность, которая достигается в сильных полях, когда все магнитные моменты доменов ориентированы вдоль магнитного поля. Петля гистерезиса — зависимость индукции от напряженности магнитного поля при изменении поля по циклу: подъем до определенного значения — уменьшение, переход через нуль, после достижения того же значения с обратным знаком — рост и т.п. Максимальная петля гистерезиса — достигающая максимальной намагниченности насыщения. Остаточная индукция Bост — индукция магнитного поля на обратном ходе петли гистерезиса при нулевой напряженности магнитного поля. Коэрцитивная сила Нс — напряженность поля на обратном ходе петли гистерезиса при которой достигается нулевая индукция.
75
Магнитные моменты атомов |
Магнитный момент Элементарные
частицы обладают внутренним
квантовомеханическим свойством
известным как спин.
Оно аналогичноугловому
моментуобъекта вращающегося вокруг
собственногоцентра
масс, хотя строго говоря, эти частицы
являются точечными и нельзя говорить
об их вращении. Спин измеряют в единицах
приведённойпланковской
постоянной( Магнитное поле, создаваемоемагнитным моментоматома, определяется этими различными формами углового момента, как и в классической физике вращающиеся заряженные объекты создают магнитное поле. Однако, наиболее значительный вклад происходит от спина. Благодаря свойству электрона, как и всех фермионов, подчинятьсяправилу запрета Паули, по которому два электрона не могут находиться в одном и том жеквантовом состоянии, связанные электроны спариваются друг с другом, и один из электронов находится в состоянии со спином вверх, а другой — с противоположной проекцией спина — состояние со спином вниз. Таким образом магнитные моменты электронов сокращаются, уменьшая полный магнитный дипольный момент системы до нуля в некоторых атомах с чётным числом электронов.[32] В ферромагнитныхэлементах, таких как железо, нечётное число электронов приводит к появлению неспаренного электрона и к ненулевому полному магнитному моменту. Орбитали соседнихатомов перекрываются, и наименьшее энергетическое состояние достигается, когда все спины неспаренных электронов принимают одну ориентацию, процесс известный как обменное взаимодействие. Когдамагнитные моменты ферромагнитных атомов выравниваются, материал может создавать измеримое макроскопическое магнитное поле. Парамагнитные материалысостоят изатомов , магнитные моменты которых разориентированы в отсутствии магнитного поля, но магнитные моменты отдельных атомов выравниваются при приложении магнитного поля.[32][33] Ядро атома тоже может обладать ненулевым полным спином. Обычно при термодинамическом равновесииспины ядер ориентированы случайным образом. Однако, для некоторых элементов (таких какксенон-129) возможно поляризовать значительную часть ядерных спинов для создания состояния с сонаправленными спинами —состояния называемогогиперполяризацией. Это состояние имеет важное прикладное значение вмагнитно-резонансной томографии.[34][35] |
76 Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии.
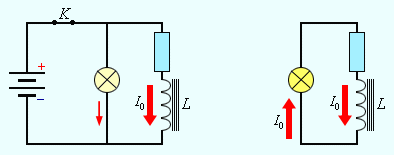
Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы. Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки. Энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, равна Wм = LI2/ 2 Формула очень похожа на формулу для кинетической энергии, роль массы m выполняет индуктивность L, а скорости v соответствуетсила тока I.
77Дивергенция
(расхождение вектора) – это алгебраическая
скалярная величина, характеризующая
источники поля в рассматриваемой точке
поля или указывающая на отсутствие
источников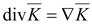 Численно дивергенцию в
данной точке определяют как предел, к
которому стремится отношение потока
вектора через замкнутую поверхность
к объему, ограниченному этой поверхностью,
при стремлении этого объема к нулю
Численно дивергенцию в
данной точке определяют как предел, к
которому стремится отношение потока
вектора через замкнутую поверхность
к объему, ограниченному этой поверхностью,
при стремлении этого объема к нулю .(14.14)
Дивергенция вектора магнитной индукции
.(14.14)
Дивергенция вектора магнитной индукции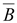 всегда
равна нулю, так как линии вектора
всегда
равна нулю, так как линии вектора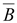 замкнуты
(не имеют начала и конца).
В декартовой системе координат
замкнуты
(не имеют начала и конца).
В декартовой системе координат (14.15).
(14.15).
Теорема о циркуляции магнитного поля займёмся
вычислением циркуляции вектора
магнитной индукции Обратим
внимание на то, что модуль вектора
магнитной индукции в нашем случае
одинаков во всех точках силовой линии
и, следовательно, контура L: Циркуляция положительна, когда направление обхода контура связано с направлением тока правилом буравчика (рис. 9.10.a). В противном случае циркуляция отрицательна |
studfile.net
Магнитная индукция
2
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ — существует вокруг электрического заряда, материально. Основное свойство электрического поля: действие с силой на эл.заряд, внесенный в него. Электростатическое поле— поле неподвижного эл.заряда, не меняется со временем. Напряженность электрического поля. — количественная характеристика эл. поля. — это отношение силы, с которой поле действует на внесенный точечный заряд к величине этого заряда. — не зависит от величины внесенного заряда, а характеризует электрическое поле!
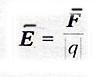
Направление вектора напряженности совпадает с направлением вектора силы, действующей на положительный заряд, и противоположно направлению силы, действующий на отрицательный заряд.
Напряженность поля точечного заряда:
 где
q0 — заряд, создающий электрическое
поле.
В любой точке поля напряженность
направлена всегда вдоль прямой,
соединяющей эту точку и q0.
где
q0 — заряд, создающий электрическое
поле.
В любой точке поля напряженность
направлена всегда вдоль прямой,
соединяющей эту точку и q0.
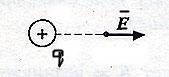
3
ПРИНЦИП СУПЕРПОЗИЦИИ ( НАЛОЖЕНИЯ ) ПОЛЕЙ

Если в данной точке пространства различные электрически заряженные частицы 1, 2, 3… и т.д. создают электрические поля с напряженностью Е1, Е2, Е3 … и т.д., то результирующая напряженность в данной точке поля равна геометрической сумме напряженностей.
Силовые линии эл. поля — непрерывные линии, касательными к которым являются векторы напряженности эл.поля в этих точках. Однородное эл.поле — напряженность поля одинакова во всех точках этого поля. Свойства силовых линий: не замкнуты (идут от + заряда к _ ), непрерывны, не пересекаются, их густота говорит о напряженности поля (чем гуще линии, тем больше напряженность).
Графически надо уметь показать эл.поля: точечного заряда, двух точечных зарядов, обкладок конденсатора ( в учебнике есть).
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ заряженного шара.
Есть заряженный проводящий шар радиусом R.
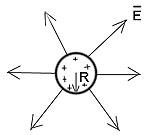
— заряд равномерно рапределен лишь по поверхности шара! Напряженность эл. поля снаружи:
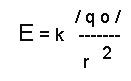
Напряженность внутри шара: Е = 0
12
ЭЛЕКТРОЕМКОСТЬ — характеризует способность двух проводников накапливать электрический заряд. — не зависит от q и U. — зависит от геометрических размеров проводников, их формы, взаимного расположения, электрических свойств среды между проводниками.

 Единицы
измерения в СИ: ( Ф — фарад )
Единицы
измерения в СИ: ( Ф — фарад )
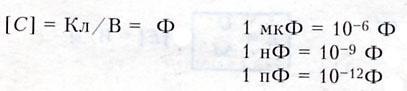
КОНДЕНСАТОРЫ
— электротехническое устройство, накапливающее заряд ( два проводника, разделенных слоем диэлектрика ).
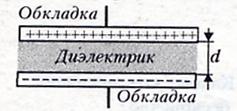 где
d много меньше размеров проводника. Обозначение
на электрических схемах:
где
d много меньше размеров проводника. Обозначение
на электрических схемах:
 Все
электрическое поле сосредоточено внутри
конденсатора.
Заряд конденсатора —
это абсолютное значение заряда одной
из обкладок конденсатора.
Все
электрическое поле сосредоточено внутри
конденсатора.
Заряд конденсатора —
это абсолютное значение заряда одной
из обкладок конденсатора.
Виды конденсаторов: 1. по виду диэлектрика: воздушные, слюдяные, керамические, электролитические 2. по форме обкладок: плоские, сферические. 3. по величине емкости: постоянные, переменные (подстроечные).
Электроемкость плоского конденсатора
 где
S — площадь пластины (обкладки) конденсатора
d
— расстояние между пластинами
eо —
электрическая постоянная
e —
диэлектрическая проницаемость диэлектрика
где
S — площадь пластины (обкладки) конденсатора
d
— расстояние между пластинами
eо —
электрическая постоянная
e —
диэлектрическая проницаемость диэлектрика
Включение конденсаторов в электрическую цепь
параллельное

последовательное

Тогда общая электроемкость (С):
при параллельном включении
. при
последовательном включении
при
последовательном включении
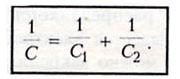
ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА
Конденсатор — это система заряженных тел и обладает энергией. Энергия любого конденсатора:

 где
С — емкость конденсатора
q — заряд
конденсатора
U — напряжение на обкладках
конденсатора
Энергия конденсатора
равна работе, которую совершит
электрическое поле при сближении пластин
конденсатора вплотную,
или равна
работе по разделению положительных и
отрицательных зарядов , необходимой
при зарядке конденсатора.
где
С — емкость конденсатора
q — заряд
конденсатора
U — напряжение на обкладках
конденсатора
Энергия конденсатора
равна работе, которую совершит
электрическое поле при сближении пластин
конденсатора вплотную,
или равна
работе по разделению положительных и
отрицательных зарядов , необходимой
при зарядке конденсатора.
ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ КОНДЕНСАТОРА
Энергия
конденсатора приблизительно равна
квадрату напряженности эл. поля внутри
конденсатора.
Плотность энергии эл.
поля конденсатора: 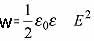
14
Электри́ческий ток — направленное (упорядоченное) движение заряженных частиц[1][2][3]. Такими частицами могут являться: в металлах —электроны, в электролитах — ионы (катионы и анионы), в газах — ионы и электроны, в вакууме при определенных условиях — электроны, вполупроводниках — электроны и дырки (электронно-дырочная проводимость). Иногда электрическим током называют также ток смещения, возникающий в результате изменения во времени электрического поля].
Сила
тока — физическая
величина 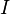 ,
равная отношению количества
заряда
,
равная отношению количества
заряда 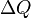 ,
прошедшего через некоторую поверхность
за время
,
прошедшего через некоторую поверхность
за время 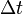 ,
к величине этого промежутка времени[1]:
,
к величине этого промежутка времени[1]:
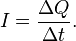
В качестве рассматриваемой поверхности часто используется поперечное сечение проводника.
Сила тока в Международной системе единиц (СИ) измеряется в амперах (русское обозначение: А; международное: A), ампер является одной из семиосновных единиц СИ. 1 А = 1 Кл/с.
По закону
Ома сила
тока  для
участка цепи прямо пропорциональна
приложенному напряжению
для
участка цепи прямо пропорциональна
приложенному напряжению  к
участку цепи и обратно
пропорциональнасопротивлению
к
участку цепи и обратно
пропорциональнасопротивлению  проводника этого
участка цепи:
проводника этого
участка цепи:
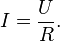
Носителями
заряда, движение которых, приводит к
возникновению тока, являются заряженные
частицы, в роли которых обычно
выступаютэлектроны, ионы или дырки.
Сила тока зависит от заряда 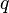 этих
частиц, их концентрации
этих
частиц, их концентрации 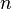 ,
средней скорости упорядоченного движения
частиц
,
средней скорости упорядоченного движения
частиц  ,
а также площади
,
а также площади 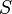 и
формы поверхности, через которую течёт
ток.
и
формы поверхности, через которую течёт
ток.
Если 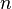 и
и 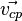 постоянны
по объёму проводника, а интересующая
поверхность плоская, то выражение для
силы тока можно представить в виде
постоянны
по объёму проводника, а интересующая
поверхность плоская, то выражение для
силы тока можно представить в виде
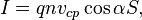
где  —
угол между скоростью частиц
и вектором
нормали к
поверхности.
—
угол между скоростью частиц
и вектором
нормали к
поверхности.
В
более общем случае, когда сформулированные
выше ограничения не выполняются,
аналогичное выражение можно записать
только для силы тока 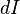 ,
протекающего через малый элемент
поверхности площадью
,
протекающего через малый элемент
поверхности площадью 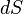 :
:

Тогда выражение для силы тока, протекающего через всю поверхность, записывается в виде интеграла по поверхности

В металлах заряд переносят электроны, соответственно в этом случае выражение для силы тока имеет вид

где e — элементарный электрический заряд.
Вектор  называют плотностью
электрического тока.
Как следует из сказанного выше, его
величина равна силе тока, протекающей
через малый элемент поверхности единичной
площади, расположенный перпендикулярно
скорости
называют плотностью
электрического тока.
Как следует из сказанного выше, его
величина равна силе тока, протекающей
через малый элемент поверхности единичной
площади, расположенный перпендикулярно
скорости 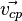 ,
а направление совпадает с направлением
упорядоченного движения заряженных
частиц[2].
,
а направление совпадает с направлением
упорядоченного движения заряженных
частиц[2].
Для измерения силы тока используют специальный прибор — амперметр (для приборов, предназначенных для измерения малых токов, также используются названия миллиамперметр, микроамперметр, гальванометр). Его включают в разрыв цепи в том месте, где нужно измерить силу тока. Основные методы измерения силы тока: магнитоэлектрический, электромагнитный и косвенный (путём измерения вольтметром напряжения на известном сопротивлении).
В случае переменного тока различают мгновенную силу тока, амплитудную (пиковую) силу тока и эффективную силу тока (равную силе постоянного тока, который выделяет такую же мощность).
Пло́тность то́ка — векторная физическая величина, имеющая смысл силы тока, протекающего через элемент поверхности единичной площади[1]. Например, при равномерном распределении плотности тока и всюду ортогональности её плоскости сечения, через которое вычисляется или измеряется ток, величина вектора плотности тока:

где I — сила тока через поперечное сечение проводника площадью S (также см.рисунок).
Иногда речь может идти о скалярной[2] плотности тока, в таких случаях под ней подразумевается именно та величина j, которая приведена в формуле.
В общем случае:
 ,
,
где 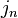 —
нормальная (ортогональная) составляющая
вектора плотности тока по отношению к
элементу поверхности площадью
—
нормальная (ортогональная) составляющая
вектора плотности тока по отношению к
элементу поверхности площадью  ;
вектор
;
вектор  —
специально вводимый вектор элемента
поверхности, ортогональный элементарной
площадке и имеющий абсолютную величину,
равную её площади, позволяющий записать
подынтегральное выражение как обычное
скалярное произведение.
—
специально вводимый вектор элемента
поверхности, ортогональный элементарной
площадке и имеющий абсолютную величину,
равную её площади, позволяющий записать
подынтегральное выражение как обычное
скалярное произведение.
Как видим из этого определения, сила тока есть поток вектора плотности тока через некую заданную фиксированную поверхность.
В
простейшем предположении, что все
носители тока (заряженные частицы)
двигаются с одинаковым вектором
скорости 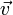 и
имеют одинаковые заряды
и
имеют одинаковые заряды 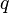 (такое
предположение может иногда быть
приближенно верным; оно позволяет лучше
всего понять физический смысл плотности
тока), а концентрация их
(такое
предположение может иногда быть
приближенно верным; оно позволяет лучше
всего понять физический смысл плотности
тока), а концентрация их 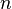 ,
,

или
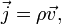
где  —
плотность заряда этих носителей.
—
плотность заряда этих носителей.
Направление
вектора 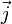 соответствует
направлению вектора скорости
соответствует
направлению вектора скорости 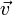 ,
с которой движутся заряды,
создающие ток, если q положительно.
,
с которой движутся заряды,
создающие ток, если q положительно.
В
реальности даже носители одного типа
движутся вообще говоря и как правило с
различными скоростями. Тогда под 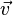 следует
понимать среднюю скорость.
следует
понимать среднюю скорость.
В сложных системах (с различными типами носителей заряда, например, в плазме или электролитах)

то
есть вектор плотности тока есть сумма
плотностей тока по всем типам подвижных
носителей; где  — концентрация
частиц каждого
типа,
— концентрация
частиц каждого
типа, 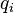 —
заряд частицы данного типа,
—
заряд частицы данного типа, 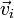 —
вектор средней скорости частиц этого
типа.
—
вектор средней скорости частиц этого
типа.
Выражение для общего случая может быть записано также через сумму по всем индивидуальным частицам:
15
Зако́н О́ма — эмпирический физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.
В
своей оригинальной форме он был записан
его автором в виде :  ,
,
Здесь X —
показания гальванометра,
т.е в современных обозначениях сила
тока I, a —
величина, характеризующая свойства
источника тока, постоянная в широких
пределах и не зависящая от величины
тока, то есть в современной терминологии
электродвижущая сила (ЭДС)  , l —
величина, определяемая длиной соединяющих
проводов, чему в современных представлениях
соответствует сопротивление внешней
цепи R и,
наконец, b параметр,
характеризующий свойства всей установки,
в котором сейчас можно усмотреть учёт
внутреннего сопротивления источника
тока r[1].
, l —
величина, определяемая длиной соединяющих
проводов, чему в современных представлениях
соответствует сопротивление внешней
цепи R и,
наконец, b параметр,
характеризующий свойства всей установки,
в котором сейчас можно усмотреть учёт
внутреннего сопротивления источника
тока r[1].
В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает
Закон Ома для полной цепи:
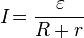 ,
(2)
,
(2)
где:
 — ЭДС источника
напряжения,
— ЭДС источника
напряжения, — сила
тока в
цепи,
— сила
тока в
цепи, — сопротивление всех
внешних элементов цепи,
— сопротивление всех
внешних элементов цепи, — внутреннее
сопротивление источника
напряжения.
— внутреннее
сопротивление источника
напряжения.
Из закона Ома для полной цепи вытекают следствия:
При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.
Часто[2] выражение:
 (3)
(3)
(где 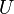 есть напряжение или падение
напряжения,
или, что то же, разность
потенциалов между
началом и концом участка проводника)
тоже называют «Законом Ома».
есть напряжение или падение
напряжения,
или, что то же, разность
потенциалов между
началом и концом участка проводника)
тоже называют «Законом Ома».
Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:
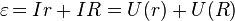 (4)
(4)
То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.
К другой записи формулы (3), а именно:
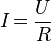 (5)
(5)
применима другая формулировка:
| Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи. |
|
Выражение (5) можно переписать в виде:
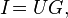 (6)
(6)
где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо[3], в Международной системе единиц (СИ) единицей измерения проводимости является си́менс (русское обозначение: См; международное: S), величина которого равна обратному ому.
ЗАКОН ДЖОУЛЯ -ЛЕНЦА
При прохождениии тока по проводнику проводник нагревается, и происходит теплообмен с окружающей средой, т.е. проводник отдает теплоту окружающим его телам.
Количество теплоты, выделяемое проводником с током в окружающую среду, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.
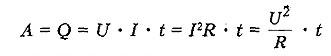
По закону сохранения энергии количество теплоты, выделяемое проводником численно равно работе, которую совершает протекающий по проводнику ток за это же время.
В системе СИ:
[Q] = 1 Дж
19
МАГНИТНОЕ ПОЛЕ
— это особый вид материи, посредством которой осуществляется взаимодействие между движущимися электрически заряженными частицами.
СВОЙСТВА ( стационарного) МАГНИТНОГО ПОЛЯ
Постоянное (или стационарное) магнитное поле — это магнитное поле, неизменяющееся во времени .
1. Магнитное поле создается движущимися заряженными частицами и телами, проводниками с током, постоянными магнитами.
2. Магнитное поле действует на движущиеся заряженные частицы и тела, на проводники с током, на постоянные магниты, на рамку с током.
3. Магнитное поле вихревое, т.е. не имеет источника.
— это силовая характеристика магнитного поля.
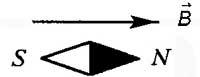
Вектор магнитной индукции направлен всегда так, как сориентирована свободно вращающаяся магнитная стрелка в магнитном поле.
Единица измерения магнитной индукции в системе СИ:

Направление линий магнитной индукции
— определяется по правилу буравчика или по правилу правой руки.
Правило буравчика ( в основном для прямого проводника с током):
Если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока.
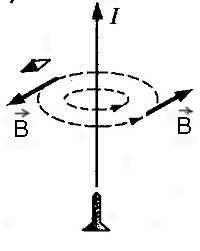
Правило правой руки ( в основном для определения направления магнитных линий внутри соленоида):
Если обхватить соленоид ладонью правой руки так, чтобы четыре пальца были направлены вдоль тока в витках, то отставленный большой палец покажет направление линий магнитного поля внутри соленоида.

Существуют другие возможные варианты применения правил буравчика и правой руки.
Сила ампера
— это сила, с которой магнитное поле действует на проводник с током.
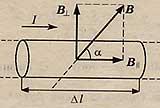

Модуль силы Ампера равен произведению силы тока в проводнике на модуль вектора магнитной индуции, длину проводника и синус угла между вектором магнитной индукции и направлением тока в проводнике.
Сила Ампера максимальна, если вектор магнитной индукции перпендикулярен проводнику.
Если вектор магнитной индукции параллелен проводнику, то магнитное поле не оказывает никакого действия на проводник с током, т.е. сила Ампера равна нулю.
Направление силы Ампера определяется по правилу левой руки:
Если левую руку расположить так, чтобы перпендикулярная проводнику составляющая вектора магнитной индукции входила в ладонь, а 4 вытянутых пальца были направлены по направлению тока, то отогнутый на 90 градусов большой палец покажет направление силы, действующий на проводник с током.
Примеры:
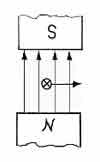 или
или 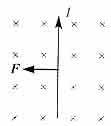
Действие магнитного поля на рамку с током
Однородное магнитное поле ориентирует рамку (т.е. создается вращающий момент и рамка поворачивается в положение, когда вектор магнитной индукции перпендикулярен плоскости рамки).
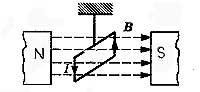
Неоднородное магнитное поле ориентирует + притягивает или отталкивает рамку с током. Так, в магнитном поле прямого проводника с током (оно неоднородно) рамка с током ориентируется вдоль радиуса магнитной линии и притягивается или отталкивается от прямого проводника с током в зависимости от направления токов.
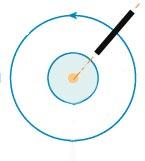
22
Магнитный момент витка с током это физическая величина, как и любой другой магнитный момент, характеризует магнитные свойства данной системы. В нашем случае систему представляет круговой виток с током. Этот ток создает магнитное поле, которое взаимодействует с внешним магнитным полем. Это может быть как поле земли, так и поле постоянного или электромагнита.
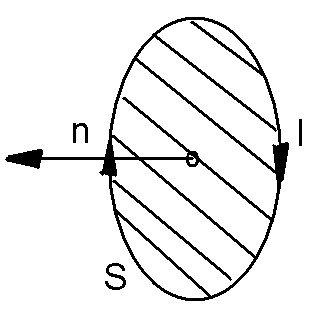
Рисунок — 1 круговой виток с током
Круговой виток с током можно представить в виде короткого магнита. Причем этот магнит будет направлен перпендикулярно плоскости витка. Расположение полюсов такого магнита определяется с помощью правила буравчика. Согласно которому северный плюс будет находиться за плоскостью витка, если ток в нем будет двигаться по часовой стрелке.
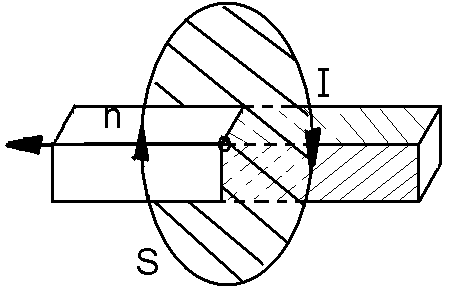
Рисунок— 2 Воображаемый полосовой магнит на оси витка
На этот магнит, то есть на наш круговой виток с током, как и на любой другой магнит, будет воздействовать внешнее магнитное поле. Если это поле будет однородным, то возникнет вращающий момент, который будет стремиться развернуть виток. Поле буде поворачивать виток так чтобы его ось расположилась вдоль поля. При этом силовые линии самого витка, как маленького магнита, должны совпасть по направлению с внешним полем.
Если же внешнее поле будет не однородным, то к вращающему моменту добавится и поступательное движение. Это движение возникнет вследствие того что участки поля с большей индукцией будут притягивать наш магнит в виде витка больше чем участки с меньшей индукцией. И виток начнет двигаться в сторону поля с большей индукцией.
Величину магнитного момента кругового витка с током можно определить по формуле.
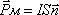
studfile.net
связь магнитного потока и ВМИ
Один из параметров магнитного поля – его силовая характеристика. Она обозначает, с какой силой поле влияет на движущиеся в нём заряженные частицы. Это значение из разряда векторных величин, носит название магнитная индукция B→.
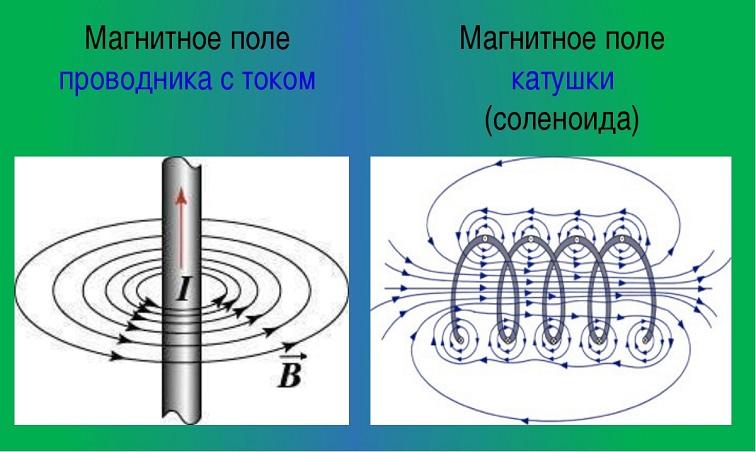
Индукция B→ проводника с током и соленоида
Физический смысл магнитной индукции (МИ)
Возможность действовать на предмет магнитным полем (МП) определяет сущность настоящей индукции. Она появляется в момент перемещения в катушке индуктивности магнита постоянной природы. Результатом такого движения является появление тока, с одновременным увеличением магнитного потока. Поскольку обмотка у катушки металлическая, а структура металла – кристаллическая решётка, то можно объяснить физические свойства этого явления.
Электроны, находящиеся в этой решётке, при отсутствии магнитного воздействия находятся в покое. Движения никакого нет. Оно начинается в тот момент, когда электроны попадают под воздействие переменного МП (поле изменяется при перемещении постоянного магнита).
Значение возникающего в катушке тока зависит от диаметра жилы и количества витков, физических характеристик магнита и скорости его движения.
Единица размерности в системе Си рассматриваемой характеристики – тесла. Она обозначается буквами Тл.
Важно! Электроны в решётке, после попадания катушки в МП, разворачиваются под некоторым углом и выстраиваются вдоль силовых линий МП. Количество ориентированных частиц и однородность их размещения зависимы от величины поля.
Вектор – это вектор индукции магнитного поля (градиентный параметр МП).
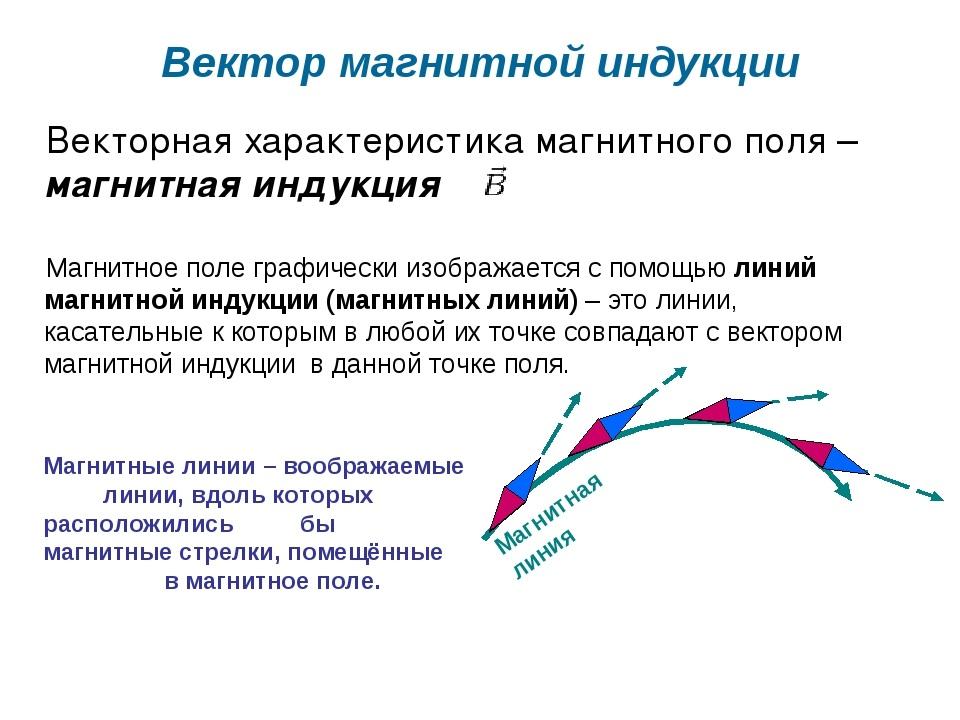
Вектор магнитной индукции
Направление вектора МИ
Направление магнитных полей может указать стрелка магнита, помещаемая в эти поля. Она будет крутиться до тех пор, пока не остановится. Северный конец стрелки покажет, куда ориентирован B→ орт того или иного поля.
Таким же образом ведёт себя рамка с током, имеющая возможность без помех ориентироваться в МП. Направленность вектора индукции указывает ориентацию нормали к такому замкнутому электромагнитному контуру.
Внимание! Здесь используют правило буравчика (правого винта). Если винт вращать так, как направлен ток в рамке, то поступательное продвижение винта совпадёт с направлением положительной нормали.
В некоторых случаях, чтобы найти направление, применяют правило правой руки.

Определение направления B→
Наглядное отображение линий МИ
Линию, к которой можно провести касательную, совпадающую с B→, называют линией магнитной индукции (МИ). С помощью таких линий можно визуально отобразить магнитное поле. Это сомкнутые контурные чёрточки, которые охватывают токи. Их густота всегда пропорциональна величине B→ в конкретной точке МП.
Информация. Когда имеют дело с МП прямого движения заряженных частиц, то эти линии изображаются в виде концентрических окружностей. Они имеют свой центр, расположенный на прямой линии с током, и находятся в плоскостях, расположенных под прямым углом к нему.
С направлением магнитных линий также можно определиться, пользуясь правилом буравчика.

Графическое обозначение линий МИ
Модуль вектора магнитной индукции
Чтобы определить величину вектора МИ, нужно узнать его модуль. Как определяется модуль вектора магнитной индукции (градиент)? Это можно понять на примере небольшой модели. Если поместить в поле подковообразного магнита горизонтально подвешенный проводник, то МП магнита будет действовать только на участок, расположенный в междуполюсном промежутке. Сила F→, действующая на этот участок, будет направлена под прямым углом к линиям индукции и самому проводнику. Она достигает своего максимума, когда орт МИ располагается перпендикулярно проводнику.
Значение модуля B→ будет равно отношению максимального значения этой силы F→ к произведению длины отрезка ∆L на силу движения зарядов (I), а именно:
B = Fm/I*∆L.
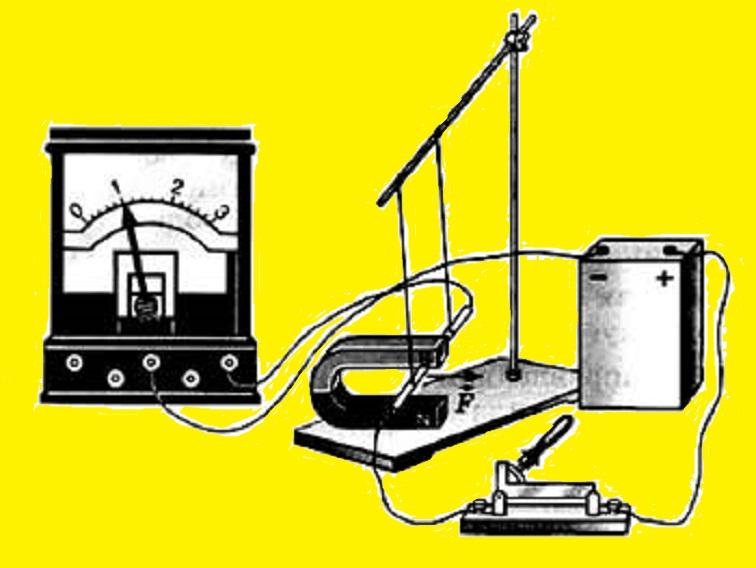
Электрическая модель для определения модуля B→
Основные формулы для вычисления вектора МИ
Вектор магнитной индукции, формула которого B = Fm/I*∆L, можно находить, применяя другие математические вычисления.
Закон Био-Савара-Лапласа
Описывает правила нахождения B→ магнитного поля, которое создаёт постоянный электроток. Это экспериментально установленная закономерность. Био и Савар в 1820 году выявили её на практике, Лапласу удалось сформулировать. Этот закон является основополагающим в магнитостатике. При практическом опыте рассматривался неподвижный провод с малым сечением, через который пропускали электроток. Для изучения выбирался малый участок провода, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.
Интересно. Лаплас Пьер Симон предложил считать током даже движение одного электрона и на этом утверждении, с помощью данного закона, доказал возможность определения МП продвигающегося точечного заряда.
Согласно этому физическому правилу, каждый сегмент dl проводника, по которому протекает электрический ток I, образовывает в пространстве вокруг себя на промежутке r и под углом α магнитное поле dB:
dB = µ0 *I*dl*sin α /4*π*r2,
где:
- dB – магнитная индукция, Тл;
- µ0 = 4 π*10-7 – магнитная постоянная, Гн/м;
- I – сила тока, А;
- dl – отрезок проводника, м;
- r – расстояние до точки нахождения магнитной индукции, м;
- α – угол, образованный r и вектором dl.
Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП нужного тока. Оно будет равно векторной сумме.
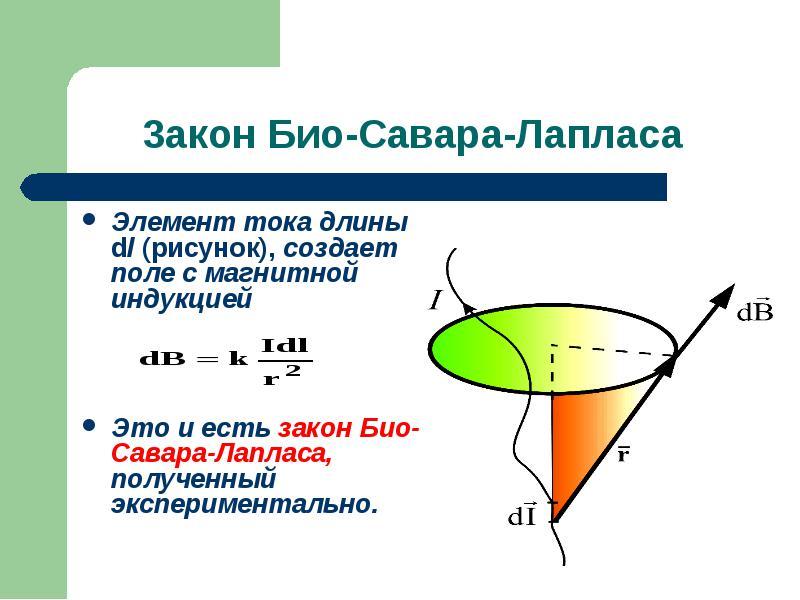
Закон Био-Савара-Лапласа
Существуют формулы, описывающие этот закон для отдельных случаев МП:
- поля прямого перемещения электронов;
- поля кругового движения заряженных частиц.
Формула для МП первого типа имеет вид:
В = µ* µ0*2*I/4*π*r.
Для кругового движения она выглядит так:
В = µ*µ0*I/4*π*r.
В этих формулах µ – это магнитная проницаемость среды (относительная).
Рассматриваемый закон вытекает из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, где электрическое поле постоянно, как раз рассматривают Био и Савар.
Принцип суперпозиции
Для МП существует принцип, согласно которому общий вектор магнитной индукции в определённой точке равен векторной сумме всех векторов МИ, созданных разными токами в данной точке:
B→= B1→+ B2→+ B3→… + Bn→
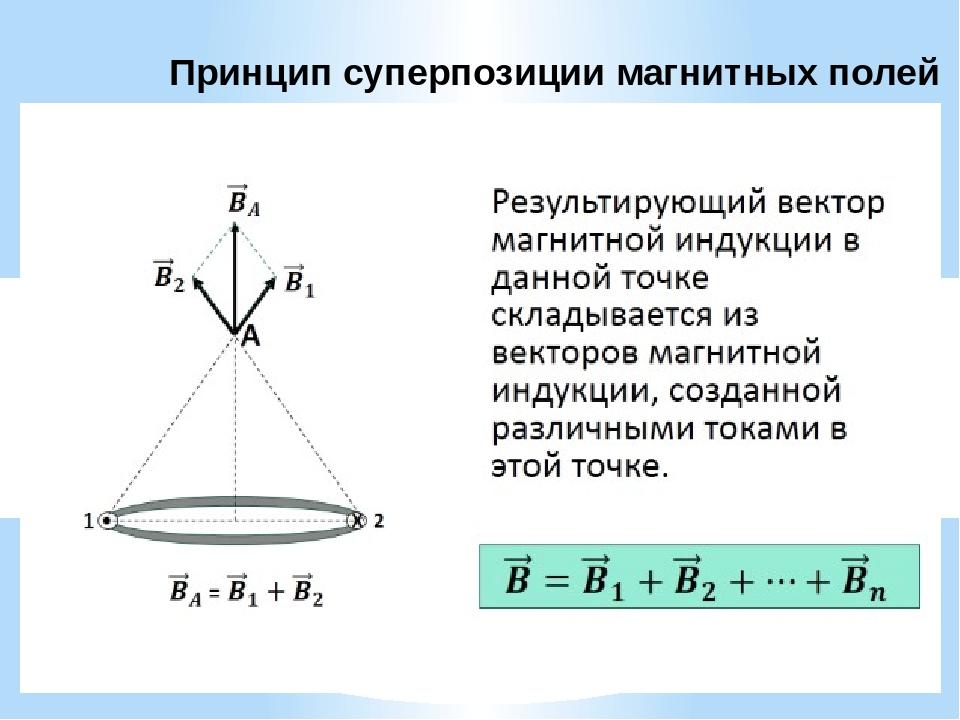
Принцип суперпозиции
Теорема о циркуляции
Изначально в 1826 году Андре Ампер сформулировал данную теорему. Он разобрал случай с постоянными электрическими полями, его теорема применима к магнитостатике. Теорема гласит: циркуляция МП постоянного электричества по любому контуру соразмерна сумме сил всех токов, которые пронизывают этот контур.
Стоит знать! Тридцать пять лет спустя Д. Максвелл обобщил это утверждение, проведя параллели с гидродинамикой.
Другое название теоремы – закон Ампера, описывающий циркуляцию МП.
Математически теорема записывается следующим образом.

Математическая формула теоремы о циркуляции
где:
- B→– вектор магнитной индукции;
- j→ – плотность движения электронов.
Это интегральная форма записи теоремы. Здесь в левой части интегрируют по некоторому замкнутому контуру, в правой части – по натянутой поверхности на полученный контур.
Магнитный поток
Одна из физических величин, характеризующих уровень МП, пересекающего любую поверхность, – магнитный поток. Обозначается буквой φ и имеет единицу измерения вебер (Вб). Эта единица характерна для системы СИ. В СГС магнитный поток измеряется в максвеллах (Мкс):
108 Мкс = 1 Вб.
Магнитный поток φ определяет величину МП, пронизывающую определённую поверхность. Поток φ зависит от угла, под которым поле пронизывает поверхность, и силы поля.
Формула для расчёта имеет вид:
φ = |B*S| = B*S*cosα,
где:
- В – скалярная величина градиента магнитной индукции;
- S – площадь пересекаемой поверхности;
- α – угол, образованный потоком Ф и перпендикуляром к поверхности (нормалью).
Внимание! Поток Ф будет наибольшим, когда B→ совпадёт с нормалью по направлению (угол α = 00). Аналогично Ф = 0, когда он проходит параллельно нормали (угол α = 900).
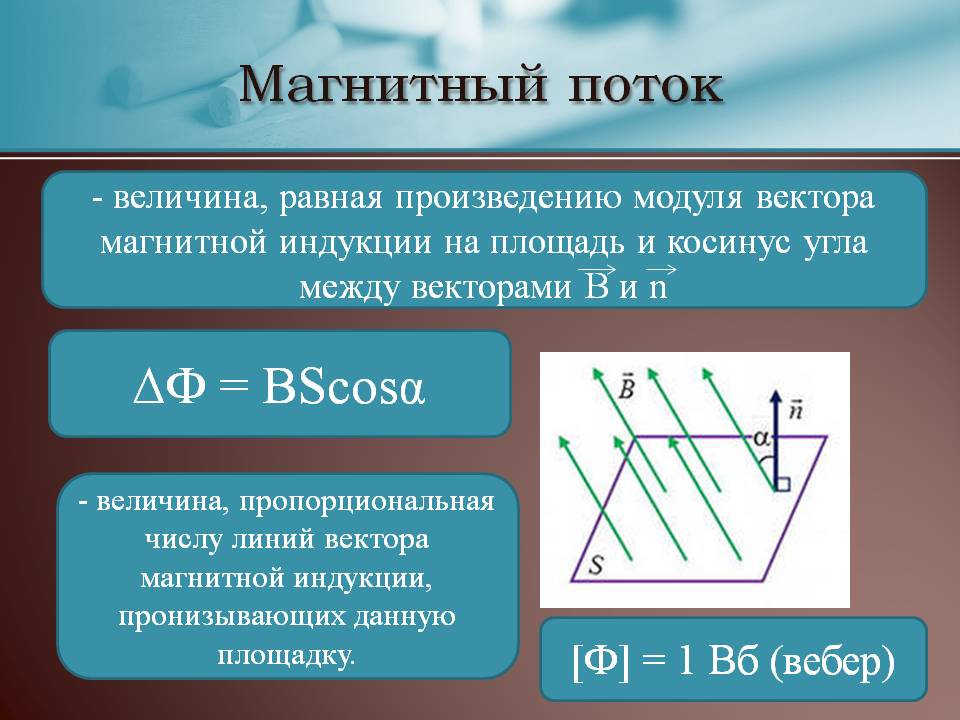
Магнитный поток
Вектор магнитной индукции, или магнитная индукция, указывает направление поля. Применяя простые методы: правило буравчика, свободно ориентирующуюся магнитную стрелку или контур с током в магнитном поле, можно определить направление действия этого поля.
Видео
amperof.ru
Теорема о циркуляции вектора магнитной индукции в стационарном случае. Вихревой характер магнитного поля.
Теорема о циркуляции вектора магнитной индукции поля постоянных токов в вакууме может быть доказана на основе закона Био-Савара, что, в общем случае, достаточно сложно.
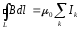 — циркуляция вектора
магнитной индукции по любому замкнутому
контуру равна произведению магнитной
постоянной на алгебраическую сумму
токов охватываемых этим контуром.
— циркуляция вектора
магнитной индукции по любому замкнутому
контуру равна произведению магнитной
постоянной на алгебраическую сумму
токов охватываемых этим контуром.
Ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта
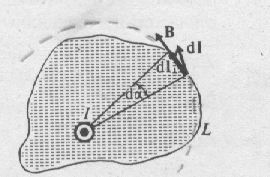
РИС.76 РИС.77
Если ток распределен
по объему, в котором расположен контур,
то полный ток охваченный контуром 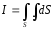 ,
где интеграл берется по произвольной
поверхности натянутой на контур,
плотность тока соответствует токе
расположения площадки
,
где интеграл берется по произвольной
поверхности натянутой на контур,
плотность тока соответствует токе
расположения площадки .
В этом случае теорема о циркуляции:
.
В этом случае теорема о циркуляции:

Теорема о циркуляции позволяет достаточно просто рассчитать индукцию магнитного по известному распределению токов, если можно выбрать контур, вдоль которого модуль вектора магнитной индукции и направление постоянно.
Поле внутри соленоида тем более однородно, чем больше длина соленоида по сравнению с его диаметром. Для «бесконечного» соленоида снаружи вблизи его поверхности магнитного поля нет и можно выбрать контур, лишь часть которого совпадает с линией магнитной индукции
Ток охватываемый
контуром  ,
гдеN
– число витков с током, охваченных
контуром. Тогда:
,
гдеN
– число витков с током, охваченных
контуром. Тогда: 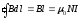
Следовательно, индукцию магнитного поля внутри «бесконечного» соленоида можно рассчитать по формуле
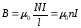 ,
где n
– число витков соленоида на единицу
длины.
,
где n
– число витков соленоида на единицу
длины.
Факт, что циркуляция вектора магнитной индукции по замкнутому контуру не равна нулю, означает, что, в отличие от электростатического, магнитное поле – не потенциально.
Используем теорему
Стокса 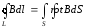 и сравним это выражение с записью теоремы
о циркуляции вектора магнитной индукции
в случае непрерывного распределения
тока в некотором объеме.
и сравним это выражение с записью теоремы
о циркуляции вектора магнитной индукции
в случае непрерывного распределения
тока в некотором объеме.
 — дифференциальная
(локальная) форма теоремы о циркуляции.
Математическая констатация того факта,
что линии вектора магнитной индукции
замкнуты вокруг вектора плотности тока
по правилу правого буравчика и поэтому
магнитное поле называют вихревым
или соленоидальным.
— дифференциальная
(локальная) форма теоремы о циркуляции.
Математическая констатация того факта,
что линии вектора магнитной индукции
замкнуты вокруг вектора плотности тока
по правилу правого буравчика и поэтому
магнитное поле называют вихревым
или соленоидальным.
Используем, что  или с помощью определителя:
или с помощью определителя:
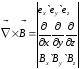 ,
, 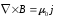 .
.
Электростатическое поле при наличии диэлектриков. Поляризация. Связанные и свободные заряды. Электростатическая теорема Гаусса при наличии диэлектриков.
Свободные заряды – заряды, способные под влиянием электрического поля перемещаться на макроскопические расстояния и переносить ток (электроны в металлах, ионы в газах и электролитах) и заряды, нанесенные извне на поверхность диэлектрика и нарушающие их нейтральность.
Заряды, входящие в состав нейтральных молекул диэлектриков, ионы, закрепленные в твердых диэлектриках вокруг определенных положений равновесия, называются связанными.
Проводники — вещества, у которых есть свободные заряды.
Диэлектрики (изоляторы) — вещества, у которых отсутствуют свободные заряды. Они не проводят электрический постоянный ток.
1) Поведение диэлектриков в электрическом поле
Существует три типа поляризации в диэлектрике:
Неполярные диэлектрики
В отсутствии
внешнего электрического поля молекулы
не обладают электрическим моментом —
H2,
N2,
O2,
CO2,
CH4.
Если наложить электрическое поле 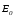 ,
то молекула поляризуется (Рис. 33), у нее
появляется электрический момент
,
то молекула поляризуется (Рис. 33), у нее
появляется электрический момент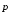 (центры положительного и отрицательного
зарядов смещаются друг относительно
друга).
(центры положительного и отрицательного
зарядов смещаются друг относительно
друга).
 Рис.
33
Рис.
33
Момент молекулы 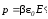 прямо пропорционален напряженности
поля, действующей на молекулу.
прямо пропорционален напряженности
поля, действующей на молекулу.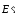 отличается от поля
отличается от поля внутри диэлектрика
внутри диэлектрика .
.
Величина  характеризует
поляризуемость молекулы. Молекулярная
диэлектрическая восприимчивость
определяется внутренними свойствами
молекулы и несущественно зависит от
характеризует
поляризуемость молекулы. Молекулярная
диэлектрическая восприимчивость
определяется внутренними свойствами
молекулы и несущественно зависит от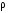 иT.
иT.
Данный вид
поляризации (сдвиг положительных зарядов
в направлении внешнего поля  ,
а отрицательных противоположно и
преобретение диэлектрического дипольного
момента) —электронная
поляризация смещения.
,
а отрицательных противоположно и
преобретение диэлектрического дипольного
момента) —электронная
поляризация смещения.
Полярные диэлектрики (CO, N2O, SO2 ,H2O и другие)
В отсутствии
внешнего электрического поля каждая
молекула имеет определенный дипольный
момент 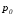 .
Вследствие теплового движения в
отсутствии поля молекулы, молекулы
располагаются хаотически. Векторная
сумма всех дипольных моментов
.
Вследствие теплового движения в
отсутствии поля молекулы, молекулы
располагаются хаотически. Векторная
сумма всех дипольных моментов (Рис. 34, а). При наложении внешнего поля
(Рис. 34, а). При наложении внешнего поля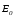 на каждый диполь действуют силы,
стремящиеся повернуть (ориентировать)
его параллельно
на каждый диполь действуют силы,
стремящиеся повернуть (ориентировать)
его параллельно (Рис. 34,б).
(Рис. 34,б).
Рис. 34,а Рис. 34,б
Возникает частичное
упорядочивание в расположении диполей,
и оно тем большее, чем сильнее  и нижеT.
Такой тип поляризации называется ориентированной
или дипольной поляризацией.
и нижеT.
Такой тип поляризации называется ориентированной
или дипольной поляризацией.
В)Твердые диэлектрики (ионные кристаллы)
Для твердых диэлектриков существует еще один механизм поляризации — поляризация ионного смещения (NaCl, KCl, …).
Кристаллическая решетка — две подрешетки с положительными и отрицательными ионами, сдвинутые по отношению друг к другу. Под влиянием внешнего поля решетки смещаются по отношению друг к другу (так как на каждую из подрешеток действуют различные по модулю и направлению силы).
2) Поляризованность
Для количественной
характеристики поляризации диэлектрика
вводят физическую величину — поляризованность 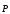 ,
равную векторной сумме электрических
моментов всех молекул, заключенных в
единице объема
,
равную векторной сумме электрических
моментов всех молекул, заключенных в
единице объема
 ,
, 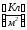 (35)
(35)
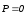 —диэлектрическая
неполяризованность.
—диэлектрическая
неполяризованность.
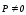 —диэлектрическая
поляризованность.
—диэлектрическая
поляризованность.
Поляризованность зависит от напряженности внешнего поля. В общем случае:
 ,
(i,j,k
– по
осям)
,
(i,j,k
– по
осям)
 —диэлектрическая
восприимчивость вещества.
—диэлектрическая
восприимчивость вещества.
Матричная запись 
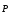 —зависит от высших
степеней
—зависит от высших
степеней 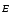 ,
следовательно, нелинейный диэлектрик
(в сильных
,
следовательно, нелинейный диэлектрик
(в сильных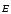 )
)
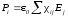 —линейный
диэлектрик
—линейный
диэлектрик
а) Диэлектрик
называется анизотропным, если его свойства различны по направлениям.
Девятикомпонентный тензор 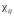 полностью характеризует свойства такого
диэлектрика.
полностью характеризует свойства такого
диэлектрика.
б) Диэлектрик
называется линейным изотропным,
если его свойства по всем направлениям
одинаковы. Они характеризуются одной
скалярной величиной 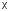 .
.
 (36)
(36)
Величина  .
Например у воды
.
Например у воды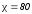 ,
у спирта
,
у спирта ,
а у сегнетоэлектриков достигает
нескольких тысяч.
,
а у сегнетоэлектриков достигает
нескольких тысяч.
в)
Существуют, однако, и диэлектрики, для
которых эта формула не применима. Это
некоторые ионные кристаллы и электреты,
а также сегнетоэлектрики. У
сегнетоэлектриков связь между 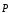 и
и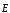 нелинейная и
зависит от предшествующих значений
нелинейная и
зависит от предшествующих значений 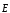 (это явление называютгистерезисом).
(это явление называютгистерезисом).
Неполярные диэлектрики

Рис. 35, а Рис. 35,б
 ,
следовательно,
,
следовательно, 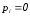 ,
а значит
,
а значит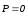
1) Разряженные газы  (внешнее
поле
(внешнее
поле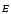 << поля внутри
атома и молекулы, поэтому смещение
заряда внутри молекулы мало и
<< поля внутри
атома и молекулы, поэтому смещение
заряда внутри молекулы мало и 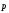 линейно зависит от
линейно зависит от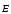 )
)
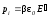 ,
следовательно,
,
следовательно, 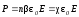 ,
гдеn
– концентрация молекул.
,
гдеn
– концентрация молекул. 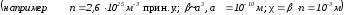
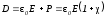
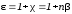 —относительная
диэлектрическая проницаемость. Для
изотропных диэлектриков это скалярная
величина, для анизотропных —
девятикомпонентный тензор.
—относительная
диэлектрическая проницаемость. Для
изотропных диэлектриков это скалярная
величина, для анизотропных —
девятикомпонентный тензор.
 ,
(39)
,
(39)
где ρ – плотность, т.е. ε не зависит от температуры (лишь при высоких температурах молекулы переходят в возбужденное состояние – диссоциируются при этом ε(Т)).
 —для линейного
изотропного диэлектрика.
—для линейного
изотропного диэлектрика.
2) Плотные газы (неразряженные и неполярные жидкости):
Формула 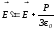
(где
(где  поляризованность вещества) получена
для кристалла с кубической решеткой
Лоренцем и справедлива для плотных
газов поостренных из точечных неполярных
молекул.
поляризованность вещества) получена
для кристалла с кубической решеткой
Лоренцем и справедлива для плотных
газов поостренных из точечных неполярных
молекул. учитывает
действие всех зарядов за исключением
рассматриваемых.
учитывает
действие всех зарядов за исключением
рассматриваемых.
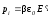
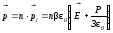

Полярные диэлектрики (HCl, H2O, CO, HI, спирты, эфир и др.)
Рис. 36, а Рис. 36, б
1)
Когда 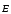 = 0, то
= 0, то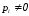 ,
но вследствие хаотического теплового
движения
,
но вследствие хаотического теплового
движения ,
следовательно
,
следовательно .
.
2) 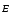 ≠ 0. Поле частично ориентирует молекулы
≠ 0. Поле частично ориентирует молекулы
Здесь 
среднее значение проекции дипольного
момента молекул на направление поля
среднее значение проекции дипольного
момента молекул на направление поля  .
.
а)
В случае неоднородной
поляризации связанные заряды появляются не только
на поверхности, но и внутри. Причем, если
диэлектрика взять замкнутую поверхность
S,
то поток вектора 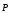 равен заряду поляризованному (связанному)
равен заряду поляризованному (связанному) внутри
объемаV,
ограниченной этой поверхностью – теорема
Гаусса для вектора
внутри
объемаV,
ограниченной этой поверхностью – теорема
Гаусса для вектора 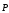 .
.

Так при наличии диэлектрика поле  определяется всеми зарядамисвязанными и свободными,
значит теорема
Гаусса для вектора
определяется всеми зарядамисвязанными и свободными,
значит теорема
Гаусса для вектора 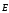 :
:
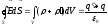 (46)
(46)
где q и q‘ — сторонние и связанные заряды, охватываемые поверхностью S.
Это
затруднение, однако, можно обойти, если
выразить заряд q‘ через
поток вектора  потеорема
Гаусса для вектора
потеорема
Гаусса для вектора 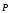 .
.
 (47)
(47)
Эту формулу иногда называют электростатическая теорема Гаусса при наличии диэлектриков. Она справедлива при любом расположении диэлектриков и граничных поверхностей : часть или весь объем может быть заполнен различными диэлектриками, поверхность S может проходить в вакууме или пересекать диэлектрик.
studfile.net
александр леготкин -магнитное поле-
Тип урока: урок изучения нового материала.
Вид урока: лекция с элементами эвристической беседы и демонстрационным экспериментом.
Цели:
• ввести понятие силы Ампера, выявить, от каких факторов зависит величина силы Ампера;
• научить учащихся определять направление действия силы Ампера с помощью мнемонического правила «левой руки» ;
• определить физический смысл модуля вектора магнитной индукции.
Ответьте на вопросы:
- Что понимают под магнитным полем?
- Как направлены линии магнитной индукции?
- Как, зная направление линий магнитной индукции, определить направление вектора индукции в данной точке поля?
- Дайте определение понятия линий магнитной индукции.
- Чем, согласно гипотезе Ампера вызван земной магнетизм?
Сила Ампера .
Магнитное поле действует не только на движущиеся заряженные частицы, но и на токи. В наиболее простом случае прямолинейного тока I сила, действующая со стороны однородного магнитного поля с индукцией В, направленного так, что линии индукции составляют угол a с направлением тока, равна FA = IBlsin a, где l — длина участка проводника с током. Эту силу называют силой Ампера.
Опыт показывает, что сила Ампера перпендикулярна плоскости, в кокоторой лежит проводник и вектор В. Направление силы Ампера можно
определить по правилу левой руки.
Правило левой руки: если левую руку расположить так, что четыре вытянутых пальца указывают на направление тока в проводнике, а вектор магнитной индукции входит в ладонь, то отогнутый на 90 градусов большой палец покажет направление силы, действующей на отрезок проводника.
FAmax = IBl – максимальная сила, действующая на отрезок проводника, расположенный перпендикулярно вектору магнитной индукции.
Модуль вектора магнитной индукции численно равен максимальной силе, действующей на отрезок проводника длиной 1 метр при силе тока в нем 1 Ампер.
Единица магнитной индукции – тесла (1 Тл): 1 Тл = 1 Н / (А*м)
mpf-pro.narod.ru

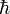 ),
тогда электроны, протоны и нейтроны
имеют спин равный ½
),
тогда электроны, протоны и нейтроны
имеют спин равный ½ .
В атоме электроны обращаются вокругядраи обладаюторбитальным
угловым моментомпомимо спина, в
то время как ядро само по себе имеет
угловой момент благодаря ядерному
спину.[31]
.
В атоме электроны обращаются вокругядраи обладаюторбитальным
угловым моментомпомимо спина, в
то время как ядро само по себе имеет
угловой момент благодаря ядерному
спину.[31] по
замкнутому контуру. Начнём с простого
контура. Пусть для начала контур
совпадает с силовой линией магнитного
поля прямолинейного тока (рис. 9.7.). По
определению, циркуляция вектора по
замкнутому контуру равна следующему
интегралу:
по
замкнутому контуру. Начнём с простого
контура. Пусть для начала контур
совпадает с силовой линией магнитного
поля прямолинейного тока (рис. 9.7.). По
определению, циркуляция вектора по
замкнутому контуру равна следующему
интегралу: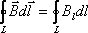
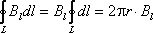 .
(9.15)
Согласно (9.8),
.
(9.15)
Согласно (9.8),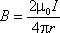 .
Поэтому циркуляцию вектора
.
Поэтому циркуляцию вектора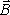 (9.15)
можно записать так:
(9.15)
можно записать так: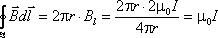 Вывод.
В рассмотренном частном случаециркуляция
вектора магнитной индукции по
замкнутому контуру пропорциональна
току, охватываемому этим контуром.
Вывод.
В рассмотренном частном случаециркуляция
вектора магнитной индукции по
замкнутому контуру пропорциональна
току, охватываемому этим контуром. — ЭДС источника
напряжения,
— ЭДС источника
напряжения,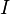 — сила
тока в
цепи,
— сила
тока в
цепи,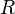 — сопротивление всех
внешних элементов цепи,
— сопротивление всех
внешних элементов цепи, — внутреннее
сопротивление источника
напряжения.
— внутреннее
сопротивление источника
напряжения.
