Амплитуда силы тока в контуре формула
ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ.
СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ.
Электромагнитные колебания – взаимосвязанные колебания электрического и магнитного полей.
Электромагнитные колебания появляются в различных электрических цепях. При этом колеблются величина заряда, напряжение, сила тока, напряженность электрического поля, индукция магнитного поля и другие электродинамические величины.
Свободные электромагнитные колебания возникают в электромагнитной системе после выведения ее из состояния равновесия, например, сообщением конденсатору заряда или изменением тока в участке цепи.
Это затухающие колебания, так как сообщенная системе энергия расходуется на нагревание и другие процессы.
Вынужденные электромагнитные колебания – незатухающие колебания в цепи, вызванные внешней периодически изменяющейся синусоидальной ЭДС.
Электромагнитные колебания описываются теми же законами, что и механические, хотя физическая природа этих колебаний совершенно различна.
Электрические колебания – частный случай электромагнитных, когда рассматривают колебания только электрических величин. В этом случае говорят о переменных токе, напряжении, мощности и т.д.
Колебательный контур – электрическая цепь, состоящая из последовательно соединенных конденсатора емкостью C, катушки индуктивностью L и резистора сопротивлением R.
Состояние устойчивого равновесия колебательного контура характеризуется минимальной энергией электрического поля (конденсатор не заряжен) и магнитного поля (ток через катушку отсутствует).
Величины, выражающие свойства самой системы (параметры системы): L и m, 1/C и k
величины, характеризующие состояние системы:
величины, выражающие скорость изменения состояния системы: u = x'(t) и i = q'(t) .
ХАРАКТЕРИСТИКИ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ
Можно показать, что уравнение свободных колебаний для зарядаq = q(t) конденсатора в контуре имеет вид
где q» – вторая производная заряда по времени. Величина
Величина
является циклической частотой. Такими же уравнениями описываются колебания тока, напряжения и других электрических и магнитных величин.
Одним из решений уравнения (1) является гармоническая функция
Период колебаний в контуре дается формулой (Томсона):
Величина φ = ώt + φ, стоящая под знаком синуса или косинуса, является фазой колебания.
Фаза определяет состояние колеблющейся системы в любой момент времени t.
Ток в цепи равен производной заряда по времени, его можно выразить
Чтобы нагляднее выразить сдвиг фаз, перейдем от косинуса к синусу
ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
1. Гармоническая ЭДС возникает, например, в рамке, которая вращается с постоянной угловой скоростью в однородном магнитном поле с индукцией В. Магнитный поток Ф , пронизывающий рамку с площадью S ,
где- угол между нормалью к рамке и вектором магнитной индукции .
По закону электромагнитной индукции Фарадея ЭДС индукции равна
где – скорость изменения потока магнитной индукции.
Гармонически изменяющийся магнитный поток вызывает синусоидальную ЭДС индукции
где – амплитудное значение ЭДС индукции.
2. Если к контуру подключить источник внешней гармонической ЭДС
то в нем возникнут вынужденные колебания, происходящие с циклической частотой ώ, совпадающей с частотой источника.
При этом вынужденные колебания совершают заряд q, разность потенциалов u , сила тока i и другие физические величины. Это незатухающие колебания, так как к контуру подводится энергия от источника, которая компенсирует потери. Гармонически изменяющиеся в цепи ток, напряжение и другие величины называют переменными. Они, очевидно, изменяются по величине и направлению. Токи и напряжения, изменяющиеся только по величине, называют пульсирующими.
В промышленных цепях переменного тока России принята частота 50 Гц.
Для подсчета количества теплоты Q, выделяющейся при прохождении переменного тока по проводнику с активным сопротивлением R, нельзя использовать максимальное значение мощности, так как оно достигается только в отдельные моменты времени. Необходимо использовать среднюю за период мощность – отношение суммарной энергии W, поступающей в цепь за период, к величине периода:
Необходимо использовать среднюю за период мощность – отношение суммарной энергии W, поступающей в цепь за период, к величине периода:
Поэтому количество теплоты, выделится за время Т:
Действующее значение I силы переменного тока равно силе такого постоянного тока, который за время, равное периоду T, выделяет такое же количество теплоты, что и переменный ток:
Отсюда действующее значение тока
Аналогично действующее значение напряжения
Трансформатор – устройство, увеличивающее или уменьшающее напряжение в несколько раз практически без потерь энергии.
Трансформатор состоит из стального сердечника, собранного из отдельных пластин, на котором крепятся две катушки с проволочными обмотками. Первичная обмотка подключается к источнику переменного напряжения, а к вторичной присоединяют устройства, потребляющие электроэнергию.
называют коэффициентом трансформации. Для понижающего трансформатора К > 1, для повышающего
Пример. Заряд на пластинах конденсатора колебательного контура изменяется с течением времени в соответствии с уравнением . Найдите период и частоту колебаний в контуре,циклическую частоту, амплитуду колебаний заряда и амплитуду колебаний силы тока. Запишите уравнение , выражающее зависимость силы тока от времени.
Заряд на пластинах конденсатора колебательного контура изменяется с течением времени в соответствии с уравнением . Найдите период и частоту колебаний в контуре,циклическую частоту, амплитуду колебаний заряда и амплитуду колебаний силы тока. Запишите уравнение , выражающее зависимость силы тока от времени.
Из уравнения следует, что . Период определим по формуле циклической частоты
Зависимость силы тока от времени имеет вид:
Амплитуда силы тока.
Ответ: заряд совершает колебания с периодом 0,02 с и частотой 50 Гц, которой соответствует циклическая частота 100 рад/с, амплитуда колебаний силы тока равна 510 3 А, ток изменяется по закону:
i=-5000 sin100t
Основным устройством, определяющим рабочую частоту любого генератора переменного тока, является колебательный контур. Колебательный контур (рис.1) состоит из катушки индуктивности L (рассмотрим идеальный случай, когда катушка не обладает омическим сопротивлением) и конденсатора C и называется замкнутым.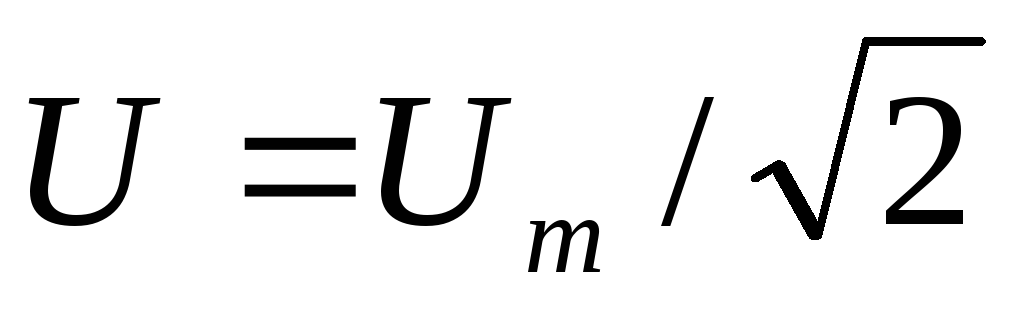 Характеристикой катушки является индуктивность, она обозначается L и измеряется в Генри (Гн), конденсатор характеризуют емкостью C, которую измеряют в фарадах (Ф).
Характеристикой катушки является индуктивность, она обозначается L и измеряется в Генри (Гн), конденсатор характеризуют емкостью C, которую измеряют в фарадах (Ф).
Пусть в начальный момент времени конденсатор заряжен так (рис.1), что на одной из его обкладок имеется заряд +Q, а на другой – заряд –Q. При этом между пластинами конденсатора образуется электрическое поле, обладающее энергией
, (1)
где – амплитудное (максимальное) напряжение или разность потенциалов на обкладках конденсатора.
После замыкания контура конденсатор начинает разряжаться и по цепи пойдет электрический ток (рис.2), величина которого увеличивается от нуля до максимального значения . Так как в цепи протекает переменный по величине ток, то в катушке индуцируется ЭДС самоиндукции, которая препятствует разрядке конденсатора. Поэтому процесс разрядки конденсатора происходит не мгновенно, а постепенно. В каждый момент времени разность потенциалов на обкладках конденсатора
(2)
(где – заряд конденсатора в данный момент времени) равна разности потенциалов на катушке, т. е. равна ЭДС самоиндукции
е. равна ЭДС самоиндукции
. (3)
| Рис.1 | Рис.2 |
Когда конденсатор полностью разрядится и , сила тока в катушке достигнет максимального значения (рис.3). Индукция магнитного поля катушки в этот момент также максимальна, а энергия магнитного поля будет равна
. (4)
Затем сила тока начинает уменьшаться, а заряд будет накапливаться на пластинах конденсатора (рис.4). Когда сила тока уменьшится до нуля, заряд конденсатора достигнет максимального значения Q, но обкладка, прежде заряженная положительно, теперь будет заряжена отрицательно (рис. 5). Затем конденсатор вновь начинает разряжаться, причем ток в цепи потечет в противоположном направлении.
Так процесс перетекания заряда с одной обкладки конденсатора на другую через катушку индуктивности повторяется снова и снова. Говорят, что в контуре происходят электромагнитные колебания. Этот процесс связан не только с колебаниями величины заряда и напряжения на конденсаторе, силы тока в катушке, но и перекачкой энергии из электрического поля в магнитное и обратно.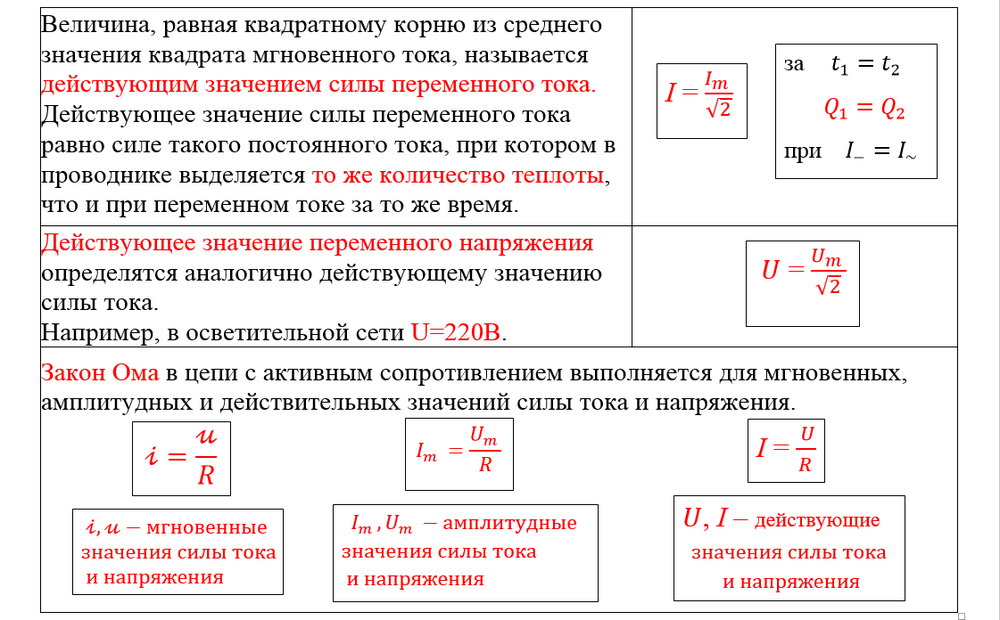
| Рис.3 | Рис.4 |
Перезарядка конденсатора до максимального напряжения произойдет только в том случае, когда в колебательном контуре нет потерь энергии. Такой контур называется идеальным.
В реальных контурах имеют место следующие потери энергии:
1) тепловые потери, т.к. R ¹ 0;
2) потери в диэлектрике конденсатора;
3) гистерезисные потери в сердечнике катушке;
4) потери на излучение и др. Если пренебречь этими потерями энергии, то можно написать, что , т.е.
. (5)
Колебания, происходящие в идеальном колебательном контуре, в котором выполняется это условие, называются свободными, или собственными, колебаниями контура.
В этом случае напряжение U (и заряд Q) на конденсаторе изменяется по гармоническому закону:
, (6)
где n – собственная частота колебательного контура, w = 2pn – собственная (круговая) частота колебательного контура. Частота электромагнитных колебаний в контуре определяется как
Частота электромагнитных колебаний в контуре определяется как
или . (7)
Период T – время, в течение которого совершается одно полное колебание напряжения на конденсаторе и тока в контуре, определяется формулой Томсона
. (8)
Сила тока в контуре также изменяется по гармоническому закону, но отстает от напряжения по фазе на . Поэтому зависимость силы тока в цепи от времени будет иметь вид
. (9)
На рис.6 представлены графики изменения напряжения U на конденсаторе и тока I в катушке для идеального колебательного контура.
В реальном контуре энергия с каждым колебанием будет убывать. Амплитуды напряжения на конденсаторе и тока в контуре будут убывать, такие колебания называются затухающими. В задающих генераторах их применять нельзя, т.к. прибор будет работать в лучшем случае в импульсном режиме.
| Рис.5 | Рис.6 |
Для получения незатухающих колебаний необходимо компенсировать потери энергии при самых разнообразных рабочих частотах приборов, в том числе и применяемых в медицине.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 10034 – | 7811 – или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
07.06.2019
5 июня Что порешать по физике
30 мая Решения вчерашних ЕГЭ по математике
Колебания напряжения на конденсаторе в цепи переменного тока описываются уравнением где все величины выражены в СИ. Емкость конденсатора равна Найдите амплитуду силы тока. (Ответ дать в амперах.)
Общий вид зависимости напряжения на конденсаторе в колебательном контуре: где — амплитудное значение напряжения. Сравнивая с находим, что Значение максимального заряда на обкладках конденсатора равно Амплитуда колебаний силы тока связана с частотой колебаний и максимальным значением заряда конденсатора соотношением Отсюда находим
Позвольте предложить, на мой взгляд, более простой способ решения. Известно, что в цепи переменного тока, в которой есть конденсатор, выполняется зависимость Im=Um/Xc, где под током и напряжением имеются ввиду их амплитудные значения, а Хс – емкостное сопротивление конденсатора, равное Хс=1/w*C. Подставляя 2-ую формулу в первую, окончательно имеем: Im=Um*w*C. Подставляя значения величин из условия, получаем значение амплитуды силы тока, которое совпадает с вашим.
Известно, что в цепи переменного тока, в которой есть конденсатор, выполняется зависимость Im=Um/Xc, где под током и напряжением имеются ввиду их амплитудные значения, а Хс – емкостное сопротивление конденсатора, равное Хс=1/w*C. Подставляя 2-ую формулу в первую, окончательно имеем: Im=Um*w*C. Подставляя значения величин из условия, получаем значение амплитуды силы тока, которое совпадает с вашим.
P. S. Мой способ решения кажется мне более разумным по той причине, что обе формулы даны в учебнике по физике, в отличие от последней формулы в предложенном вами способе решения.
Спасибо. Хороший вариант.
Но использованная в конце формула, конечно же, дается в школьном курсе. Ведь насколько я знаю, в этот момент в школьной физике уже начинают использовать производные. Формула следует из закона изменения заряда со временем при гармонических колебаниях и из того, что ток — это производная от заряда
Переменное напряжение и его значения — Help for engineer
Переменное напряжение и его значения
Все мы знаем, что дома в розетках у нас напряжение 220В. Но не каждый знает, какое именно это напряжение. Давайте же разберемся с этой ситуацией.
Но не каждый знает, какое именно это напряжение. Давайте же разберемся с этой ситуацией.
Для упрощения рассматриваемого примера будем считать, что вид напряжения – синусоида, то есть переменное напряжение (с определенной периодичностью меняет значение с положительного на отрицательное).
Рисунок 1 – Вид переменного напряжения
На рисунке 1 изображен вид идеального синусоидального напряжения одного периода Т. Есть несколько значений напряжения, о которых обычно говорят и используют, рассмотрим:
| Амплитудное значение напряжения (Um) – это максимальное, мгновенное значение напряжения, то есть амплитуда синусоиды. |
Теперь правильнее будет говорить о токе.
Действующее значение переменного тока — это величина постоянного тока, который может выполнить ту же самую работу (нагрев). |
Действующее значение напряжения (U) обозначают латинской буквой без индекса, в литературе может еще использоваться термин – эффективное значение напряжения.
Для периодически изменяющегося сигнала за период Т, величина действующего напряжения находится:
Приведем формулу к простому виду, приняв за изменяющийся сигнал синусоиду. Между рассмотренными выше двумя параметрами существует зависимость, которая выражается формулой:
То есть амплитудное значение в 1,414 раза больше действующего.
Вернемся к домашним розеткам с напряжением 220В. Это действующее значение напряжения, которое можно измерить тестером. Определим его амплитудное значение напряжения:
Среднее значение синусоидального тока, напряжения будет равно нулю. Поэтому если говорят о среднем значении переменного тока, то подразумевают рассматривание его в пол периода.
Недостаточно прав для комментирования
Переменный ток. 2 — материалы для подготовки к ЕГЭ по Физике
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания, колебательный контур, резонанс.Давайте начнём с одного математического приёма, чтобы не отвлекаться потом на его объяснение. Это — тригонометрический метод введения вспомогательного угла. Он наверняка вам известен, но всё же повторить его не помешает.
Речь идёт о преобразовании выражения . Вынесем за скобки «амплитудный множитель» :
Зачем нужно такое вынесение за скобки? Оказывается, в скобках при синусе и косинусе образовались замечательные множители! Сумма квадратов этих множителей равна единице:
Значит, эти множители являются соответственно косинусом и синусом некоторого угла :
(1)
В результате получаем:
Остаётся заметить, что в скобках стоит синус суммы, так что мы приходим к окончательному выражению:
(2)
При этом для «начальной фазы» имеем из (1) простую формулу:
(3)
Теперь мы готовы рассмотреть вынужденные колебания, происходящие в колебательном контуре с активным сопротивлением. К источнику переменного напряжения последовательно подключены: резистор сопротивлением , катушка индуктивности и конденсатор ёмкости (рис. 1).
К источнику переменного напряжения последовательно подключены: резистор сопротивлением , катушка индуктивности и конденсатор ёмкости (рис. 1).
Рис. 1. Колебательный контур с резистором
Так как элементы соединены последовательно, сила тока в них одинакова в любой момент времени (вспомните условие квазистационарности!). Поэтому нам будет удобно начать не с напряжения источника, как раньше, а с силы тока, и считать, что ток в цепи колеблется по закону синуса: .
А теперь вспоминаем материал предыдущего листка.
1. Пусть — мгновенное значение напряжения на резисторе. Оно связано с силой тока обычным законом Ома:
(4)
2. Напряжение на конденсаторе отстаёт по фазе от тока на ; это значит, что фаза напряжения равна . Амплитуда напряжения равна:
Таким образом,
(5)
3. Напряжение на катушке , наоборот, опережает по фазе силу тока на . Амплитуда:
В результате получаем:
(6)
Напряжение источника равно сумме напряжений на резисторе, катушке и конденсаторе:
Подставляя сюда выражения (4)–(6), получим:
(7)
Вот теперь нам и понадобится метод вспомогательного угла. Выражение во внешних скобках имеет для этого подходящий вид: . Пользуясь выражениями (2) и (3), получим:
Выражение во внешних скобках имеет для этого подходящий вид: . Пользуясь выражениями (2) и (3), получим:
(8)
где
(9)
Угол является сдвигом фаз между напряжением источника и силой тока в цепи: фаза напряжения больше фазы тока на величину . Амплитуда напряжения:
(10)
Получив все эти результаты, мы их несколько переиначим и приведём в соответствие с тем, что было в предыдущем листке.
Начнём с напряжения источника. Предположим, как и ранее, что оно меняется по закону синуса:
Как мы сейчас выяснили, фаза тока меньше фазы напряжения на величину :
При этом амплитуда силы тока находится из формулы (10):
(11)
Выражение (11) имеет вид закона Ома:
где
(12)
Величина — это полное сопротивление цепи. Такое сопротивление оказывает наш колебательный контур переменному току.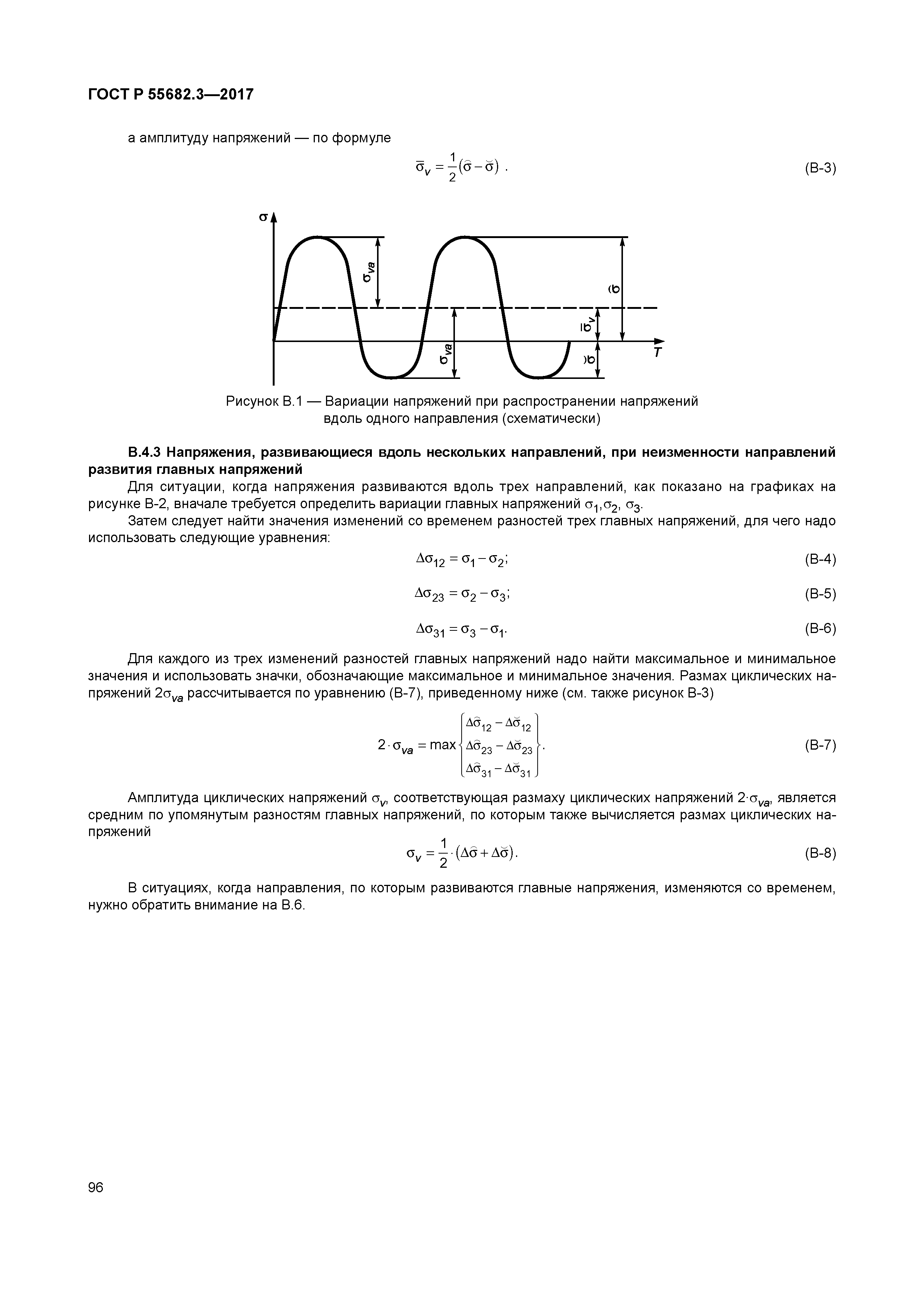
Закон Ома в данном случае выполнен лишь для
Резонанс в колебательном контуре
Как видно из выражения (11), амплитуда силы тока в контуре зависит от частоты колебаний. Построим график этой зависимости — так называемую резонансную кривую (рис. 2).
Рис. 2. Резонансная кривая
При имеем . Математическая причина стремления тока к нулю — неограниченное возрастание ёмкостного сопротивления , в результате чего полное сопротивление также стремится к бесконечности.
Физическая причина очевидна: ток малой частоты — это почти постоянный ток, а для постоянного тока конденсатор является разрывом цепи.
При опять-таки имеем : график асимптотически приближается к оси .
Теперь это происходит за счёт неограниченного роста индуктивного сопротивления . Физическая причина также ясна: при быстром изменении тока в катушке возникает большая ЭДС самоиндукции, препятствующая его увеличению.
Физическая причина также ясна: при быстром изменении тока в катушке возникает большая ЭДС самоиндукции, препятствующая его увеличению.
При некоторой частоте амплитуда силы тока достигает максимума: наступает резонанс. Из (11) нетрудно видеть, что величина принимает максимальное значение
(13)
и происходит это при выполнении равенства
Отсюда находим :
Это хорошо знакомая нам частота собственных колебаний в контуре с нулевым активным сопротивлением. Она же, как видим, является резонансной частотой нашего контура.
Из (13) мы видим, что резонансное значение амплитуды тока тем больше, чем меньше активное сопротивление . На рис. 3 представлены три резонансные кривые. Верхняя кривая отвечает достаточно малому сопротивлению , средняя кривая — большему сопротивлению, нижняя кривая — ещё большему сопротивлению.
Рис. 3. Резонансные кривые при различных
Таким образом, резонансный пик тем острее, чем меньше активное сопротивление контура.
При резонансе в контуре происходят любопытные вещи.
1. Амплитуды напряжений на конденсаторе и катушке равны друг другу. Действительно:
При малых значениях эти амплитуды могут значительно превосходить амплитуду напряжения источника! Это, кстати, является наглядной демонстрацией одного важного факта:
Хотя сумма мгновенных значений напряжения на элементах контура равна мгновенному значению напряжению источника, сумма амплитуд напряжений на отдельных элементах может и не быть равной амплитуде напряжения источника
2. Равен нулю сдвиг фаз между током в контуре и напряжением источника: . Математически мы это видим из соотношения (9): при получается .
Физическую причину синфазности тока и напряжения понять также не сложно. Дело в том, что напряжения и на конденсаторе и катушке колеблются в противофазе (т. е. разность фаз между ними равна ), а их амплитуды при резонансе равны. Стало быть, они отличаются только знаком: , и в сумме дают нуль. Получается, что (словно бы в цепи имелся один только резистор), а колебания напряжения и тока на резисторе происходят синфазно.
е. разность фаз между ними равна ), а их амплитуды при резонансе равны. Стало быть, они отличаются только знаком: , и в сумме дают нуль. Получается, что (словно бы в цепи имелся один только резистор), а колебания напряжения и тока на резисторе происходят синфазно.
Резонанс играет важнейшую роль в радиосвязи. Когда осуществляется приём радиосигнала, радиоволны различных частот возбуждают в контуре колебания. Но амплитуды колебаний будут малы для сигналов тех радиостанций, частоты которых отличаются от собственной частоты контура. Контур выделяет лишь ту радиоволну, частота которой равна его собственной частоте; именно эти колебания будут иметь значительную амплитуду.
Поэтому, когда мы настраиваем приёмник на какую-то радиостанцию, мы меняем собственную частоту контура (как правило, путём изменения ёмкости конденсатора), пока не наступит резонанс с искомой радиоволной.
Referat. Переменный ток — PhysBook
Переменный ток
Как известно, сила тока в любой момент времени пропорциональна ЭДС источника тока (закон Ома для полной цепи). Если ЭДС источника не изменяется со временем и остаются неизменными параметры цепи, то через некоторое время после замыкания цепи изменения силы тока прекращаются, в цепи течет постоянный ток.
Если ЭДС источника не изменяется со временем и остаются неизменными параметры цепи, то через некоторое время после замыкания цепи изменения силы тока прекращаются, в цепи течет постоянный ток.
Однако в современной технике широко применяются не только источники постоянного тока, но и различные генераторы электрического тока, в которых ЭДС периодически изменяется. При подключении в электрическую цепь генератора переменной ЭДС в цепи возникают вынужденные электромагнитные колебания или переменный ток.
Переменный ток – это периодические изменения силы тока и напряжения в электрической цепи, происходящие под действием переменной ЭДС от внешнего источника
или
Переменный ток – это электрический ток, который изменяется с течением времени по гармоническому закону.
Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω по синусоидальному или косинусоидальному закону:
\(~u = U_m \cdot \sin \omega t\) или \(~u = U_m \cdot \cos \omega t\) ,где u – мгновенное значение напряжения, Um – амплитуда напряжения, ω – циклическая частота колебаний.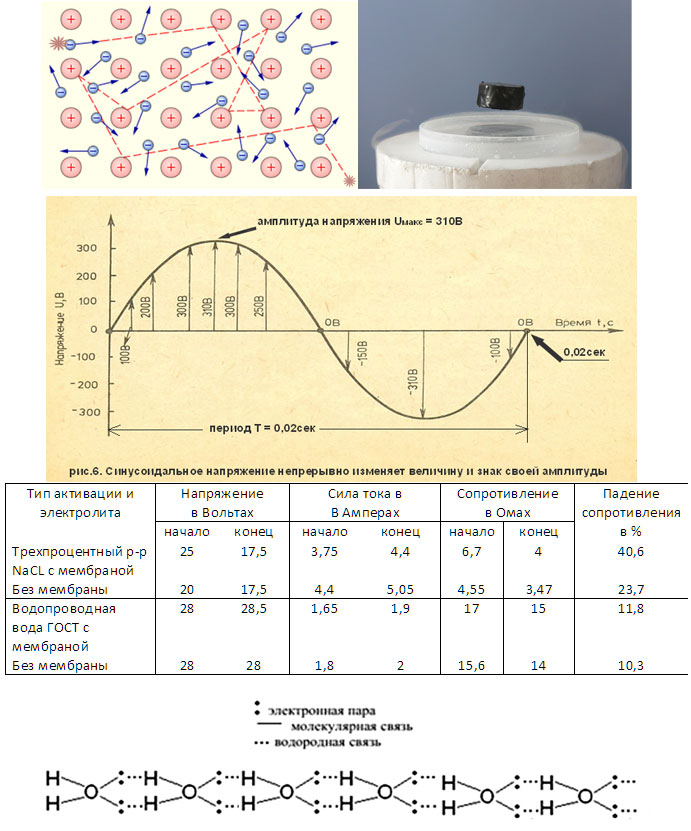 Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае
Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае
где φc – разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц.
Резистор в цепи переменного тока
Пусть цепь состоит из проводников с малой индуктивностью и большим сопротивлением R (из резисторов). Например, такой цепью может быть нить накаливания электрической лампы и подводящие провода. Величину R, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением. В цепи переменного тока могут быть и другие сопротивления, зависящие от индуктивности цепи и ее емкости. Сопротивление R называется активным потому, что, только на нем выделяется энергия, т.е.
Например, такой цепью может быть нить накаливания электрической лампы и подводящие провода. Величину R, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением. В цепи переменного тока могут быть и другие сопротивления, зависящие от индуктивности цепи и ее емкости. Сопротивление R называется активным потому, что, только на нем выделяется энергия, т.е.
Сопротивление элемента электрической цепи (резистора), в котором происходит превращение электрической энергии во внутреннюю энергию, называют активным сопротивлением.
Итак, в цепи имеется резистор, активное сопротивление которого R, а катушка индуктивности и конденсатор отсутствуют (рис. 1).
Рис. 1
Пусть напряжение на концах цепи меняется по гармоническому закону
\(~u = U_m \cdot \sin \omega t\) .Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому можно считать, что мгновенное значение силы тока определяется законом Ома:
Поэтому можно считать, что мгновенное значение силы тока определяется законом Ома:
Следовательно, в проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения (рис. 2), а амплитуда силы тока равна амплитуде напряжения, деленной на сопротивление:
Рис. 2
При небольших значениях частоты переменного тока активное сопротивление проводника не зависит от частоты и практически совпадает с его электрическим сопротивлением в цепи постоянного тока.
Катушка в цепи переменного тока
Индуктивность влияет на силу переменного тока в цепи. Это можно обнаружить с помощью простого опыта. Составим цепь из катушки большой индуктивности и лампы накаливания (рис. 3). С помощью переключателя можно присоединять эту цепь либо к источнику постоянного напряжения, либо к источнику переменного напряжения. При этом постоянное напряжение и действующее значение переменного напряжения должны быть одинаковы. Опыт показывает, что лампа светится ярче при постоянном напряжении. Следовательно, действующее значение силы тока в рассматриваемой цепи меньше силы постоянного тока.
Опыт показывает, что лампа светится ярче при постоянном напряжении. Следовательно, действующее значение силы тока в рассматриваемой цепи меньше силы постоянного тока.
Рис. 3
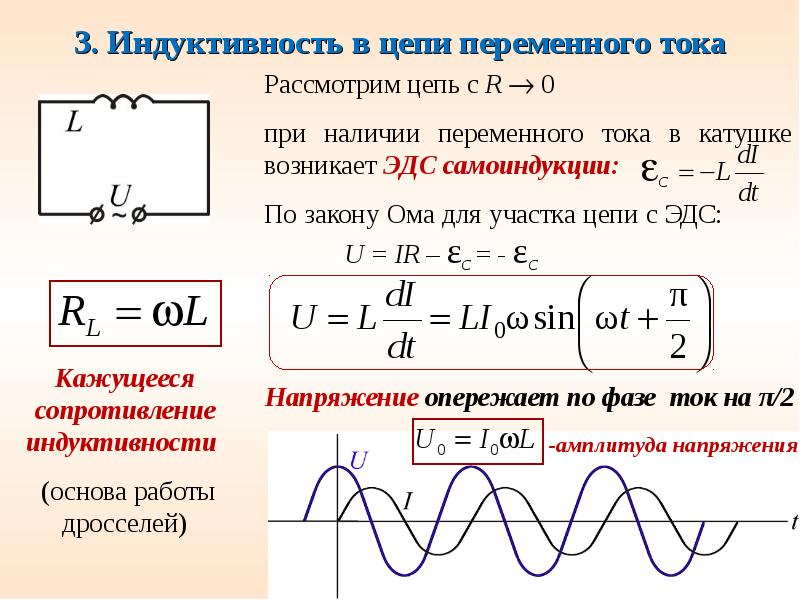
Объясняется это самоиндукцией. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь по прошествии некоторого времени сила тока достигает наибольшего (установившегося) значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет успевать достигать тех установившихся значений, которые она приобрела бы с течением времени при постоянном напряжении, равном максимальному значению переменного напряжения. Следовательно, максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью L цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения.
Докажем это математически. Пусть в цепь переменного тока включена идеальная катушка с электрическим сопротивлением провода, равным нулю (рис. 4). При изменениях силы тока по гармоническому закону
Пусть в цепь переменного тока включена идеальная катушка с электрическим сопротивлением провода, равным нулю (рис. 4). При изменениях силы тока по гармоническому закону
в катушке возникает ЭДС самоиндукции
\(~e = -L \cdot i’ = I_m \cdot L \cdot \omega \cdot \sin \omega t\) ,где L – индуктивность катушки, ω – циклическая частота переменного тока.
Рис. 4
Так как электрическое сопротивление катушки равно нулю, то ЭДС самоиндукции в ней в любой момент времени равна по модулю и противоположна по знаку напряжению на концах катушки, созданному внешним генератором:
\(~u = -e = -I_m \cdot L \cdot \omega \cdot \sin \omega t\) .Следовательно, при изменении силы тока в катушке по гармоническому закону напряжение на ее концах изменяется тоже по гармоническому закону, но со сдвигом фазы:
\(~u = I_m \cdot L \cdot \omega \cdot \cos (\omega t + \frac{\pi}{2})\) .Следовательно, колебания напряжения на катушке индуктивности опережают колебания силы тока на π/2, или, что то же самое, колебания силы тока отстают по фазе от колебаний напряжения на π/2.
В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю (рис. 5). В момент, когда напряжение становится равным нулю, сила тока максимальна по модулю.
Рис. 5
Произведение \(I_m \cdot L \cdot \omega\) является амплитудой колебаний напряжения на катушке:
\(~U_m = I_m \cdot L \cdot \omega\) .Отношение амплитуды колебаний напряжения на катушке к амплитуде колебаний силы тока в ней называется индуктивным сопротивлением (обозначается XL):
\(~X_L = \frac{U_m}{I_m} = L \cdot \omega\) .Связь амплитуды колебаний напряжения на концах катушки с амплитудой колебаний силы тока в ней совпадает по форме с выражением закона Ома для участка цепи постоянного тока:
\(~I_m = \frac{U_m}{X_L}\) .В отличие от электрического сопротивления проводника в цепи посто-янного тока, индуктивное сопротивление не является постоянной величиной, характеризующей данную катушку. Оно прямо пропорционально частоте переменного тока. Поэтому амплитуда колебаний силы тока в катушке при постоянном значении амплитуды колебаний напряжения должна убывать обратно пропорционально частоте. Постоянный ток вообще «не замечает» индуктивности катушки. При ω = 0 индуктивное сопротивление равно нулю (XL = 0).
Поэтому амплитуда колебаний силы тока в катушке при постоянном значении амплитуды колебаний напряжения должна убывать обратно пропорционально частоте. Постоянный ток вообще «не замечает» индуктивности катушки. При ω = 0 индуктивное сопротивление равно нулю (XL = 0).
Зависимость амплитуды колебаний силы тока в катушке от частоты приложенного напряжения можно наблюдать в опыте с генератором пере-менного напряжения, частоту которого можно изменять. Опыт показывает, что увеличение в два раза частоты переменного напряжения приводит к уменьшению в два раза амплитуды колебаний силы тока через катушку.
Конденсатор в цепи переменного тока
Рассмотрим процессы, протекающие в электрической цепи переменного тока с конденсатором. Если подключить конденсатор к источнику постоянного тока, то в цепи возникнет кратковременный импульс тока, который зарядит конденсатор до напряжения источника, а затем ток прекратится. Если заряженный конденсатор отключить от источника постоянного тока и соединить его обкладки с выводами лампы накаливания, то конденсатор будет разряжаться, при этом наблюдается кратковременная вспышка лампы.
При включении конденсатора в цепь переменного тока процесс его зарядки длится четверть периода. После достижения амплитудного значения напряжение между обкладками конденсатора уменьшается и конденсатор в течение четверти периода разряжается. В следующую четверть периода конденсатор вновь заряжается, но полярность напряжения на его обкладках изменяется на противоположную и т.д. Процессы зарядки и разрядки конденсатора чередуются с периодом, равным периоду колебаний приложенного переменного напряжения.
Как и в цепи постоянного тока, через диэлектрик, разделяющий обкладки конденсатора, электрические заряды не проходят. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора по проводам, соединенным с его выводами, течет переменный ток. Лампа накаливания, включенная последовательно с конденсатором в цепь переменного тока (рис. 6), кажется горящей непрерывно, так как человеческий глаз при высокой частоте колебаний силы тока не замечает периодического ослабления свечения нити лампы.
Рис. 6
Установим связь между амплитудой колебаний напряжения на обкладках конденсатора и амплитудой колебаний силы тока. При изменениях напряжения на обкладках конденсатора по гармоническому закону
\(~u = U_m \cdot \cos \omega t\) ,заряд на его обкладках изменяется по закону:
\(~q = C \cdot u = U_m \cdot C \cdot \cos \omega t\) .Электрический ток в цепи возникает в результате изменения заряда конденсатора: i = q’. Поэтому колебания силы тока в цепи происходят по закону:
\(~i = -U_m \cdot \omega \cdot C \cdot \sin \omega t = U_m \cdot \omega \cdot C \cdot \cos (\omega t + \frac{\pi}{2})\) .Следовательно, колебания напряжения на обкладках конденсатора в цепи переменного тока отстают по фазе от колебаний силы тока на π/2 или колебания силы тока опережают по фазе колебания напряжения на π/2 (рис. 7). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того как напряжение достигает максимума, сила тока становится равной нулю и т. д.
д.
Рис. 7
Произведение \(U_m \cdot \omega \cdot C\) является амплитудой колебаний силы тока:
\(~I_m = U_m \cdot \omega \cdot C\) .Отношение амплитуды колебаний напряжения на конденсаторе к амплитуде колебаний силы тока называют емкостным сопротивлением конденсатора (обозначается ХC):
\(~X_C = \frac{U_m}{I_m} = \frac{1}{\omega \cdot C}\) .Связь между амплитудным значением силы тока и амплитудным значением напряжения по форме совпадает с выражением закона Ома для участка цепи постоянного тока, в котором вместо электрического сопротивления фигурирует емкостное сопротивление конденсатора:
\(~I_m = \frac{U_m}{X_C}\) .Емкостное сопротивление конденсатора, как и индуктивное сопротивление катушки, не является постоянной величиной. Оно обратно пропорционально частоте переменного тока. Поэтому амплитуда колебаний силы тока в цепи конденсатора при постоянной амплитуде колебаний напряжения на конденсаторе возрастает прямо пропорционально частоте.
Закон Ома для электрической цепи переменного тока
Рассмотрим электрическую цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки (рис. 8). Если к выводам этой электрической цепи приложить электрическое напряжение, изменяющееся по гармоническому закону с частотой ω и амплитудой Um, то в цепи возникнут вынужденные колебания силы тока с той же частотой и некоторой амплитудой Im. Установим связь между амплитудами колебаний силы тока и напряжения.
Рис. 8
В любой момент времени сумма мгновенных значений напряжений на последовательно включенных элементах цепи равна мгновенному значению приложенного напряжения:
\(~u = u_R + u_L + u_C\) . (1)Во всех последовательно включенных элементах цепи изменения силы тока происходят практически одновременно, так как электромагнитные взаимодействия распространяются со скоростью света. Поэтому можно считать, что колебания силы тока во всех элементах последовательной цепи происходят по закону:
\(~i = I_m \cdot \cos \omega t\) .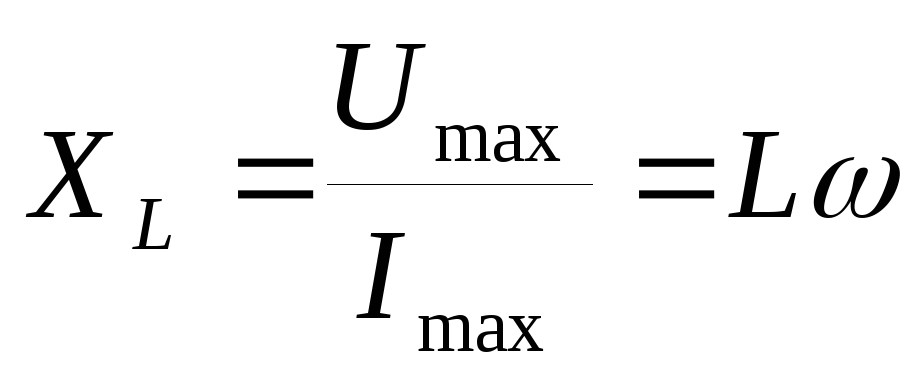 (2)
(2)Колебания напряжения на резисторе совпадают по фазе с колебаниями силы тока, колебания напряжения на конденсаторе отстают по фазе на π/2 от колебаний силы тока, а колебания напряжения на катушке опережают по фазе колебания силы тока на π/2. Поэтому уравнение (1) можно записать так:
\(~u = U_{Rm} \cdot \cos \omega t + U_{Lm} \cdot \cos (\omega t + \frac{\pi}{2}) + U_{Cm} \cdot \cos (\omega t — \frac{\pi}{2})\) , (3)где URm, UCm и ULm – амплитуды колебаний напряжения на резисторе, конденсаторе и катушке.
Амплитуду колебаний напряжения в цепи переменного тока можно выразить через амплитудные значения напряжения на отдельных ее элементах, воспользовавшись методом векторных диаграмм.
При построении векторной диаграммы необходимо учитывать, что колебания напряжения на резисторе совпадают по фазе с колебаниями силы тока, поэтому вектор, изображающий амплитуду напряжения URm, совпадает по направлению с вектором, изображающим амплитуду силы тока Im. Колебания напряжения на конденсаторе отстают по фазе на π/2 от колебаний силы тока, поэтому вектор \(~\vec U_{Cm}\) отстает от вектора \(~\vec I_{m}\) на угол 90°. Колебания напряжения на катушке опережают колебания силы тока по фазе на π/2, поэтому вектор \(~\vec U_{Lm}\) опережает вектор \(~\vec I_{m}\) на угол 90° (рис. 9).
Колебания напряжения на конденсаторе отстают по фазе на π/2 от колебаний силы тока, поэтому вектор \(~\vec U_{Cm}\) отстает от вектора \(~\vec I_{m}\) на угол 90°. Колебания напряжения на катушке опережают колебания силы тока по фазе на π/2, поэтому вектор \(~\vec U_{Lm}\) опережает вектор \(~\vec I_{m}\) на угол 90° (рис. 9).
Рис. 9
На векторной диаграмме мгновенные значения напряжения на резисторе, конденсаторе и катушке определяются проекциями на горизонтальную ось векторов \(~\vec U_{Rm}\) , \(~\vec U_{Cm}\) и \(~\vec U_{Lm}\) , вращающихся с одинаковой угловой скоростью ω против часовой стрелки. Мгновенное значение напряжения во всей цепи равно сумме мгновенных напряжений uR, uC и uL на отдельных элементах цепи, т. е. сумме проекций векторов \(~\vec U_{Rm}\) , \(~\vec U_{Cm}\) и \(~\vec U_{Lm}\) на горизонтальную ось. Так как сумма проекций векторов на произвольную ось равна проекции суммы этих векторов на ту же ось, то амплитуду полного напряжения можно найти как модуль суммы векторов:
\(~\vec U_m = \vec U_{Rm} + \vec U_{Cm} + \vec U_{Lm}\) . 2}} = \frac{R}{Z}\) . (9)
2}} = \frac{R}{Z}\) . (9)Величина cos φ играет важную роль при вычислении мощности в электрической цепи переменного тока.
Мощность в цепи переменного тока
Мощность в цепи постоянного тока определяется произведением напряжения на силу тока:
\(~P = U \cdot I\) .Физический смысл этой формулы прост: так как напряжение U численно равно работе электрического поля по перемещению единичного заряда, то произведение U∙I характеризует работу по перемещению заряда за единицу времени, протекающего через поперечное сечение проводника, т.е. является мощностью. Мощность электрического тока на данном участке цепи положительна, если энергия поступает к этому участку из остальной сети, и отрицательна, если энергия с этого участка возвращается в сеть. На протяжении очень малого интервала времени переменный ток можно считать неизменным. Поэтому мгновенная мощность в цепи переменного тока определяется такой же формулой:
\(~p = u \cdot i\) .Пусть напряжение на концах цепи меняется по гармоническому закону
\(~u = U_m \cdot \cos \omega t\)(с тем же успехом, разумеется, вместо \(~u = U_m \cdot \cos \omega t\) можно было бы записать \(~u = U_m \cdot \sin \omega t\)), то и сила тока будет меняться со временем гармонически с той же частотой, но в общем случае будет сдвинута по фазе относительно напряжения:
\(~i = I_m \cdot \cos (\omega t + \varphi_c)\) ,где φc – сдвиг фаз между силой тока и напряжением. Поэтому для мгновенной мощности можно записать:
Поэтому для мгновенной мощности можно записать:
При этом мощность меняется со временем как по модулю, так и по знаку. В течение одной части периода энергия поступает к данному участку цепи (р > 0), но в течение другой части периода некоторая доля энергии вновь возвращается в сеть (р < 0). Как правило, во всех случаях нам надо знать среднюю мощность на участке цепи за достаточно большой промежуток времени, включающий много периодов. Для этого достаточно определить среднюю мощность за один период.
Чтобы найти среднюю мощность за период, преобразуем полученную формулу таким образом, чтобы выделить в ней член, не зависящий от времени. С этой целью воспользуемся известной формулой для произведения двух косинусов:
\(~\cos \alpha \cdot \cos \beta = \frac{\cos (\alpha — \beta) + \cos (\alpha + \beta)}{2}\) .В рассматриваемом случае α = ω∙t и β = ω∙t + φc. 2\) .
2\) .
Действующим значением силы тока называют величину, в \(~\sqrt{2}\) раз меньшую ее амплитудного значения:
\(~I = \frac{I_m}{\sqrt{2}}\) .Действующее значение силы тока равно силе такого постоянного тока, при котором средняя мощность, выделяющаяся в проводнике в цепи переменного тока, равна мощности, выделяющейся в том же проводнике в цепи постоянного тока.
Аналогично можно доказать, что
действующее значение переменного напряжения в \(~\sqrt{2}\) раз меньше его амплитудного значения:
\(~U = \frac{U_m}{\sqrt{2}}\) .Заметим, что обычно электрическая аппаратура в цепях переменного тока показывает действующие значения измеряемых величин. Переходя к действующим значениям силы тока и напряжения, уравнение (10) можно переписать:
\(~P = \frac{U_m}{\sqrt{2}} \cdot \frac{I_m}{\sqrt{2}} \cos \varphi_c = U \cdot I \cos \varphi_c\) . (10)Таким образом, мощность переменного тока на участке цепи определяется именно действующими значениями силы тока и напряжения. Она зависит также от сдвига фаз φc между напряжением и током. Множитель cos φc в формуле называется коэффициентом мощности.
Она зависит также от сдвига фаз φc между напряжением и током. Множитель cos φc в формуле называется коэффициентом мощности.
В случае, когда φc = ± π/2 , энергия, поступающая к участку цепи за период, равна нулю, хотя в цепи и существует ток. Так будет, в частности, если цепь содержит только катушку индуктивности или только конденсатор. Как же средняя мощность может оказаться равной нулю при наличии тока в цепи? Это поясняют приведенные на рисунке 10 графики изменения со временем мгновенных значений напряжения, силы тока и мощности при φc = — π/2 (чисто индуктивное сопротивление участка цепи). График зависимости мгновенной мощности от времени можно получить, перемножая значения силы тока и напряжения в каждый момент времени. Из этого графика видно, что в течение одной четверти периода мощность положительна и энергия поступает к данному участку цепи; но в течение следующей четверти периода мощность отрицательна, и данный участок отдает без потерь обратно в сеть полученную ранее энергию. Поступающая в течение четверти периода энергия запасается в магнитном поле тока, а затем без потерь возвращается в сеть.
Поступающая в течение четверти периода энергия запасается в магнитном поле тока, а затем без потерь возвращается в сеть.
Рис. 10
Лишь при наличии проводника с активным сопротивлением в цепи, не содержащей движущихся проводников, электромагнитная энергия превращается во внутреннюю энергию проводника, который нагревается. Обратного превращения внутренней энергии в электромагнитную на участке с активным сопротивлением уже не происходит.
При проектировании цепей переменного тока нужно добиваться, чтобы cos φc не был мал. Иначе значительная часть энергии будет циркулировать по проводам от генератора к потребителям и обратно. Так как провода обладают активным сопротивлением, то при этом энергия расходуется на нагревание проводов.
Неблагоприятные условия для потребления энергии возникают при включении в сеть электродвигателей, так как их обмотка имеет малое активное сопротивление и большую индуктивность. Для увеличения cos φc в сетях питания предприятий с большим числом электродвигателей включают специальные компенсирующие конденсаторы. Нужно также следить, чтобы электродвигатели не работали вхолостую или с недогрузкой. Это уменьшает коэффициент мощности всей цепи. Повышение cos φc является важной народнохозяйственной задачей, так как позволяет с максимальной отдачей использовать генераторы электростанций и снизить потери энергии. Это достигается правильным проектированием электрических цепей. Запрещается использовать устройства с cos φc < 0,85.
Нужно также следить, чтобы электродвигатели не работали вхолостую или с недогрузкой. Это уменьшает коэффициент мощности всей цепи. Повышение cos φc является важной народнохозяйственной задачей, так как позволяет с максимальной отдачей использовать генераторы электростанций и снизить потери энергии. Это достигается правильным проектированием электрических цепей. Запрещается использовать устройства с cos φc < 0,85.
Литература
- Мякишев Г.Я., Синяков А.З. Физика: Колебания и волны. 11 кл.: Учеб. для углубленного изучения физики. – М.: Дрофа, 2002. – 288 с.
- Физика: Учеб. пособие для 11 кл. шк. и классов с углубл. изуч. физики / А.Т. Глазунов, О.Ф. Кабардин, А.Н. Малинин и др.; Под ред. А.А. Пинского. – М.: Просвещение, 1995.– 432 с.
Метод комплексных амплитуд | Викитроника вики
Метод расчёта линейных в установившемся режиме в отношении гармонических сигналов.
Этот метод использует обобщения понятий сопротивления, напряжения, силы тока (и прочих) до комплексных величин, являющихся функцией частоты.
Амплитуда и фаза[править | править код]
Гармоническую функцию можно выразить формулой:
где
- — амплитуда,
- — циклическая частота,
- — начальная фаза.
Для электрических систем функция может описывать напряжение (приведено для примера), силу тока, магнитный поток, заряд, а также в приложении к электрическим средам — проекции электрического поля, плотности тока и т. п.
Эти два параметра можно представить в виде вектора на плоскости, где амплитуда — длина, а фаза — угол, отсчитанный по традиции от положительного направления оси абсцисс против часовой стрелки.
Изменение сигнала по времени можно представить вращением вектора вокруг начала координат против часовой стрелки с угловой скоростью ω, и тогда проекция вектора на ось x или у будет описывать гармоническую функцию:
Линейные преобразования гармонических функций[править | править код]
Любое линейное преобразование может увеличивать или уменьшать амплитуду на постоянное число раз и изменять фазу на постоянный угол, или добавлять и при том не меняет частоту. Так что возможно рассматривать поведение системы на определённой частоте, оперируя только амплитудой и фазой.
Так что возможно рассматривать поведение системы на определённой частоте, оперируя только амплитудой и фазой.
В геометрическом представлении сложение двух сигналов будет представляться в виде сложения двух векторов, усиление (или ослабление) — изменением длины, а сдвиг фазы — поворотом (изменением направления). Проекции векторов на оси координат также имеют важное значение. Гармонический сигнал с произвольной амплитудой и фазой можно представить как сумму двух сигналов — сигнала с нулевой фазой и сигнала с фазой (90°). Координаты по x и y при этом будут означать амплитуду этих компонентов.
Активное и реактивное сопротивление[править | править код]
Напряжение и ток на резисторе подчиняются закону Ома, и таким образом имеют одно значение фазы, а отношение их амплитудных значений равно сопротивлению.
Если же пропустить гармонический сигнал через конденсатор или катушку индуктивности, то амплитуды напряжения и тока также будут находиться в некотором соотношении, но разница в фазе будет составлять 90° для индуктивности и −90° для конденсатора.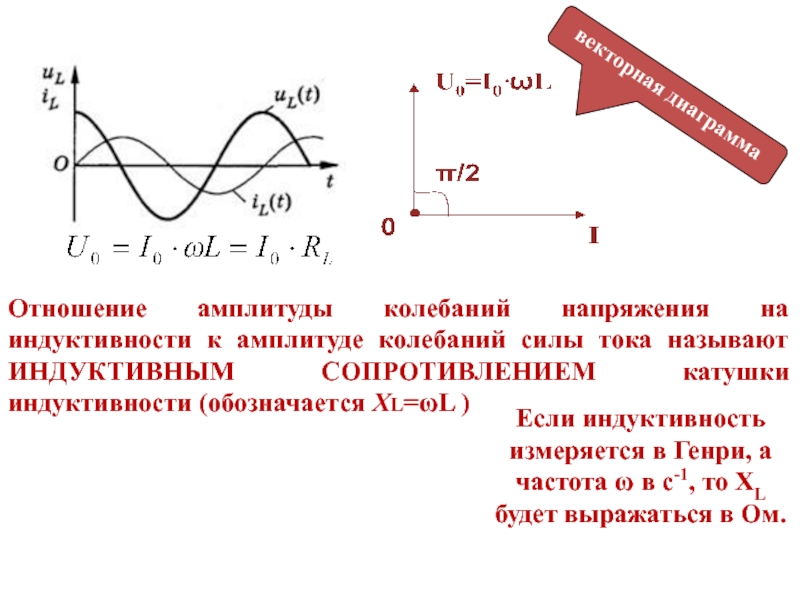 Это значит, что амплитуды тока и напряжения через них можно выразить в виде формулы:
Это значит, что амплитуды тока и напряжения через них можно выразить в виде формулы:
где величина, называемая реактивным сопротивлением. При этом для положительного сдвига фазы принимается положительным, а для отрицательного — отрицательным, что позволяет единообразно описывать индуктивность и ёмкость (сигналы с фазами +90° и −90° находятся в противофазе, то есть находятся в отрицательном соотношении). Значение реактивного сопротивления для индуктивности и ёмкости выражается формулами:
Геометрическую интерпретацию легко перенести на интерпретацию в комплексных числах, считая амплитуду модулем комплексного числа, а фазу — аргументом. Такое число называется комплексной амплитудой, и обозначается символом циркумфлекса («крышки») над символом амплитуды.
Разложение по координатам будет соответствовать действительной и мнимой части комплексной амплитуды. Сигнал таким образом можно выразить через комплексную амплитуду следующим образом:
В такой системе сложение сигналов представимо сложением комплексных чисел.
Как изменение амплитуды сигнала, так и сдвиг фазы при этом представимы одной операцией, причём коэффициент передачи (усиления / ослабления) выражается модулем множителя, а сдвиг — его аргументом.
Расширение электротехнических законов на комплексные амплитуды[править | править код]
Закон Ома выражает соотношение напряжения (для простоты будем рассматривать закон Ома для участка цепи, в случае закона Ома для полной цепи всё аналогично до замены напряжения на ЭДС) и тока в цепи. Коэффициентом соответствия здесь служит сопротивление:
Аналогом сопротивления в методе комплексных амплитуд является импеданс (). Таким образом закон Ома будет выглядеть так:
Это позволяет единообразно описывать поведение как активного сопротивления, так и реактивного (конденсаторы, индуктивности) и производить с ними операции аналогично операциям с активным сопротивлением.
Амплитуда цикла напряжений — Энциклопедия по машиностроению XXL
Амплитуда цикла напряжений 254 [c. 356]
356]Неровности, являясь концентраторами напряжений, снижают сопротивление усталости деталей, особенно при наличии резких переходов, выточек и т. п. Так, при уменьшении параметра шероховатости поверхности впадины нарезанной или шлифованной резьбы болтов от = 1,0 мкм до Ra == 0,1 мкм допускаемая предельная амплитуда цикла напряжений увеличивается на 20—50 %, причем в большей степени для болтов из высокопрочных легированных термически обработанных сталей и в меньшей —для болтов из низколегированных и углеродистых сталей, что объясняется большей чувствительностью ле/ ированных сталей к концентрации напряжений. [c.195]
Формула (15.8) получена без учета дополнительных факторов, влияющих на значения максимальных напряжений, например концентрации напряжений, состояния поверхности, размеров детали. Эти факторы мало влияют на прочность при постоянных напряжениях, поэтому их влияние относят к амплитуде цикла напряжения.
 С учетом перечисленных факторов формула (15.5) имеет вид
[c.156]
С учетом перечисленных факторов формула (15.5) имеет вид
[c.156]Здесь а а и х — амплитуды циклов напряжений при изгибе (см. рис. 1.3, а) и кручении (см. рис. 1.3,6) с заменой на и на [c.26]
Предельные амплитуды циклов напряжений для образцов из алюминиевых сплавов с концентратором напряжений [c.12]
Уменьшение амплитуды цикла напряжений, действующих в детали или образце, может быть простейшим объяснением явления остановки развития усталостной трещины. При этом не имеет значения причина, вызывающая такое уменьшение переход на более низкий уровень рабочей нагрузки при мягком режиме нагружения или уменьшение жесткости детали, работающей в цикле с заданной амплитудой деформации. Важно только, чтобы это уменьшение действующих напряже- [c.30]
Оа=190 МПа на базе испытаний 10 циклов и обнаружения поверхностных усталостных трещин производили повторное нагружение этих образцов с более высокими амплитудами цикла напряжений.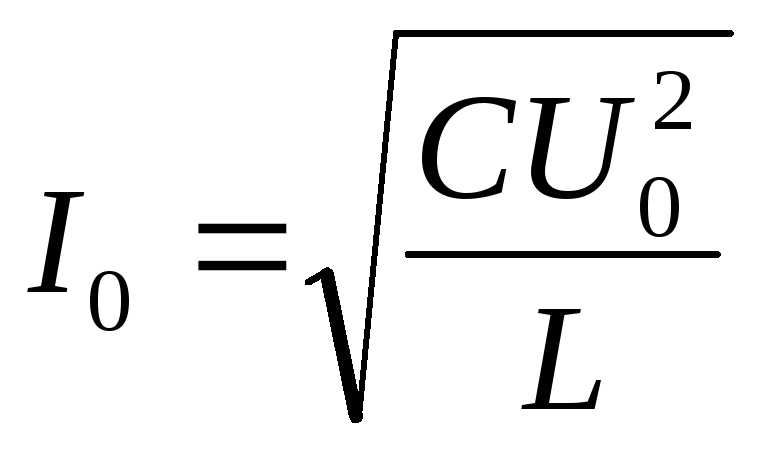 Как показывают результаты этих опытов (см. табл. 3, образцы 1—4), повторное нагружение с амплитудой цикла напряжений 195 МПа не приводит к поломке образцов и росту имеющихся поверхностных трещин. Образцы, нагруженные повторно с амплитудой цикла 200 и 210 МПа, сломались только после 4,5-10 и 2,3-10 циклов нагружения соответственно. Образец, выдержавший без разрушения по I циклов повторного нагружения с амплитудой напряжения 190, 195 и 200 МПа, разрушился только при амплитуде 205 МПа. Следовательно, можно считать доказанным, что для исследуемой стали преодоление трещиной упрочненной зоны у ее вершины возможно только при увеличении уровня циклических напряжений.
[c.35]
Как показывают результаты этих опытов (см. табл. 3, образцы 1—4), повторное нагружение с амплитудой цикла напряжений 195 МПа не приводит к поломке образцов и росту имеющихся поверхностных трещин. Образцы, нагруженные повторно с амплитудой цикла 200 и 210 МПа, сломались только после 4,5-10 и 2,3-10 циклов нагружения соответственно. Образец, выдержавший без разрушения по I циклов повторного нагружения с амплитудой напряжения 190, 195 и 200 МПа, разрушился только при амплитуде 205 МПа. Следовательно, можно считать доказанным, что для исследуемой стали преодоление трещиной упрочненной зоны у ее вершины возможно только при увеличении уровня циклических напряжений.
[c.35]
Н. Фрост показал, что минимальная амплитуда цикла напряжений, которая может вызвать рост уже имеющейся усталостной трещины, зависит от ее размера. Если размер трещины мал по сравнению с габаритами образца или детали, справедливо следующее эмпирическое соотношение [c.110]
Качественно аналогичные результаты были получены при исследованиях перехода на более высокий уровень амплитуды цикла напряжений для образцов с нераспространяющимися усталостными трещинами, причиной возникновения которых было поверхностное упрочнение вершины концентратора напряжений. [c.136]
[c.136]
Теоретическая разработка вопроса о влиянии остаточных напряжений, возникающих при поверхностном пластическом деформировании, на сопротивление усталости была сделана И. В. Кудрявцевым. Показано, что относительный предел выносливости, измененный под воздействием остаточных напряжений, может быть определен с учетом интенсивности амплитуды цикла напряжений, а также относительных средних напряжений цикла и остаточных напряжений, действующих в тех же плоскостях, что и главные напряжения повторного нагружения. Свойства материала учитываются поправочным коэффициентом, меняющимся от нуля (для пластических материалов) до 0,4 (для хрупких материалов). [c.140]
Испытывались на чистый изгиб с вращением до разрушения гладкие образцы диаметром 9 и 14 мм с дефектом, нанесенным сверлом диаметром 0,3 мм на глубину 0,3 мм. Гладкие образцы испытывались при амплитудах цикла напряжений, равных 260, 240, 220, 200 и 180 МПа, при которых было испытано 16, 18, 10,6 и 7 образцов соответственно. Образцы с дефектом испытывали при амплитудах 260,
[c.30]
Образцы с дефектом испытывали при амплитудах 260,
[c.30]
Уравнения (15) и (17) дают возможность привести значения у к одному уровню амплитуды цикла напряжений в соответствии с формулой [c.33]
Повышение предельной амплитуды цикла напряжений 1 (2-я) — 444 [c.20]
Это отношение называется коэфициентом асимметрии цикла или коэфициентом амплитуды. Цикл характеризуется также амплитудой цикла напряжений [c.71]
Волнистость и шероховатость нарушают герметичность ответственных соединений. Неровности, являясь концентраторами напряжений, снижают усталостную прочность деталей, особенно при наличии резких переходов, выточек и т. п. Так, при уменьшении шероховатости нарезанной или шлифованной резьбы болтов с 7 до 10-го класса чистоты предельная амплитуда цикла напряжений увеличивается на 20—50%, [c.356]В табл. 6.2 приведен пример вычисления выборочного среднего и дисперсии логарифма числа циклов до разрушения образцов из сплава В95 при амплитуде цикла напряжений Оа = 285 МПа по данным табл.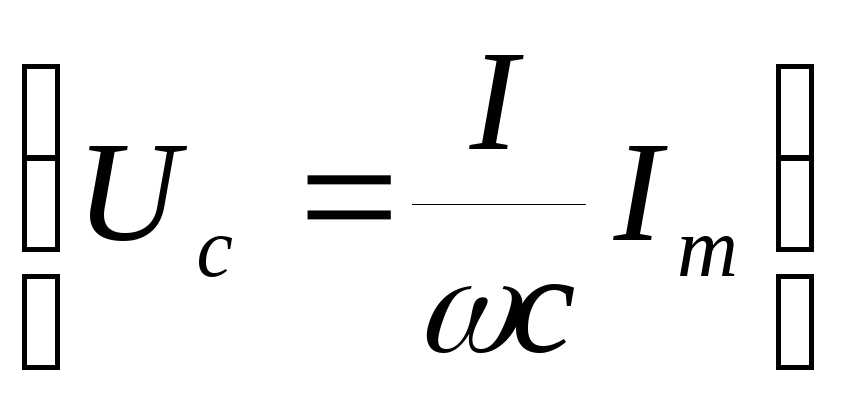 6.1.
[c.140]
6.1.
[c.140]
Значения долговечности образцов нз сплава ВЙБ при амплитуде цикла напряжений — 210 МПа [c.142]
Функцию (й (х) для учета изменения условной дисперсии величины у = g N по формуле (5.68) подбирают на основании анализа опытных данных. С этой целью строят график зависимости выборочной дисперсии величины у = lg N от амплитуды цикла напряжений Оа и аппроксимируют степенной функцией [c.147]
Статистический анализ результатов испытаний па усталость, не учитывающий переменность дисперсии логарифма числа циклов до разрушения с изменением уровня амплитуды цикла напряжений, не дает достоверных кривых усталости для низких значений вероятностей разрушения и практически не отражается на медианной кривой усталости [24]. [c.153]
По результатам испытаний на усталость На 4—6 уровнях амплитуды цикла напряжений строят семейство кривых эмпирической функции распределения долговечности на вероятностной сетке. Подобные кривые для образцов из сплава В95 по данным табл. 6.1 приведены на рис. 6.3.
[c.154]
Подобные кривые для образцов из сплава В95 по данным табл. 6.1 приведены на рис. 6.3.
[c.154]
По построенной таким образом априорной кривой усталости объекта будущих испытаний на усталость устанавливают уровни амплитуд цикла напряжений, входящих в формулы (6.40) и (6.42). Верхний уровень выбирают с учетом требования на протяженность кривой усталости в зону низкой долговечности, однако при этом напряжении медиана числа циклов до разрушения не должна быть ниже 5-10 + + 10 циклов, т. е. долговечность при испытании должна определяться областью многоцикловой усталости. [c.160]
Остальные уровни амплитуд цикла напряжений ири испытании выбирают в диапазоне между максимальным и минимальным уровнями через равные интервалы. [c.160]
Начинать испытания следует с промежуточных уровней и ири необходимости производить их корректировку. Для уточнения предела неограниченной выносливости объектов, имеющих горизонтальный участок на кривой усталости, ири амплитуде цикла напряжений 0,95—1,05 величины предела выносливости необходимо испытать до базовой долговечности дополнительную группу образцов объемом 10—20 % от п, но не менее трех. [c.160]
[c.160]
При построении семейства кривых усталости для достаточно широкого диапазона вероятностей разрушения (0,01 амплитуды напряжений. Минимальный уровень амплитуды выбирают с таким расчетом, чтобы до базового числа циклов разрушилось 5—15 % объектов, испытуемых на этом уровне амплитуды цикла напряжений. На следующем (в порядке возрастания) уровне должно разрушаться около 40—60 % объектов испытаний, т. е. этот уровень примерно соответствует медиане предела выносливости для принятого базового числа циклов. [c.163]
Один из современных подходов к объяснению эффекта прекращения роста усталостной трещины при уменьшении амплитуды цикла напряжений основан на явлении так называемого закрытия трещины. Он состоит в следующем. Изменение скорости роста трещины, связанное с изменением амплитуды напряжений, зависит от амплитуды коэффициента интенсивности напряжений ЛК. Однако величина АК, определенная по полному размаху напряжений, не является действительной, определяющей рост трещины, поскольку трещина не остается открытой на протяжении всего цикла нагружения [20]. Возникновение зоны пластической деформации у вершины трещины при максимальном растягивающем напряжении знакопостоянного цикла ведет к образованию остаточных напряжений сжатия, которые при разгрузке могут закрыть трещину [14]. При знакопеременном цикле напряжений трещина закрывается при действии сжимающих напряжений цикла, однако и в этом случае эффект возникновения зоны пластической деформации у вершины трещины приводит к более раннему ее закрытию. Истинная скорость распространения усталостной трещины зависит от так называемого эффективного размаха коэффициента интенсивности напряжений АКпф, определяемого по части цикла нагружения, в которой трещина находится в открытом состоянии.
[c.31]
Возникновение зоны пластической деформации у вершины трещины при максимальном растягивающем напряжении знакопостоянного цикла ведет к образованию остаточных напряжений сжатия, которые при разгрузке могут закрыть трещину [14]. При знакопеременном цикле напряжений трещина закрывается при действии сжимающих напряжений цикла, однако и в этом случае эффект возникновения зоны пластической деформации у вершины трещины приводит к более раннему ее закрытию. Истинная скорость распространения усталостной трещины зависит от так называемого эффективного размаха коэффициента интенсивности напряжений АКпф, определяемого по части цикла нагружения, в которой трещина находится в открытом состоянии.
[c.31]
Критическое условие распространения трещины до излома ири вторичном напряжении ниже исходного предела выносливости определяется уравнением о»/ = С, где /г = 3 С = 4-10 . Однако большинство исследованных трещин, начав развиваться ири вторичном нагружении ниже предела выносливости, затем снова останавливались.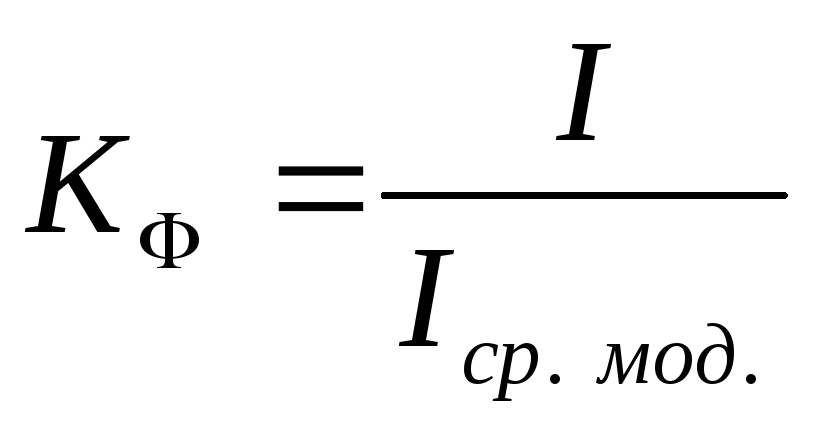 Длина такой нераснространяющей-ся трещины зависит от длины исходной усталостной трещины амплитуды цикла напряжений на уровне выше предела вьшос-. ливости, ири котором была выращена исходная трещина, и амплитуды цикла напряжений на уровне ниже предела выносливости, при котором происходили испытания образцов с исходной трещиной. Зависимости длины нераспространяющихся усталостных трещин при различных сочетаниях первого и второго уровней амплитуд цикла напряжений приведены на рис. 49.
[c.116]
Длина такой нераснространяющей-ся трещины зависит от длины исходной усталостной трещины амплитуды цикла напряжений на уровне выше предела вьшос-. ливости, ири котором была выращена исходная трещина, и амплитуды цикла напряжений на уровне ниже предела выносливости, при котором происходили испытания образцов с исходной трещиной. Зависимости длины нераспространяющихся усталостных трещин при различных сочетаниях первого и второго уровней амплитуд цикла напряжений приведены на рис. 49.
[c.116]
При одной и той же длине I2 исходной усталостной трещины, выращенной при различных первичных амплитудах цикла напряжений аь длина нерасиространяющейся трещины, получающейся при одной и той же вторичной амплитуде цикла на-напряжений 02, тем больше, чем выше первичная амплитуда напряжений а (рис. 49, а). Длина li нерасиространяющейся усталостной трещины, возникающей в образцах с одинаковыми исходными трещинами длиной I2, выращенными при одной и той же первичной амплитуде напряжений oi, тем меньше, чем ниже амплитуда вторичного напряжения аг (рис 49,6). Кроме того, длина I2 исходной трещины, выращенной при одной и той же первичной амплитуде напряжений oi, с которой начинается рост трещины при вторичной амплитуде напряжений 02, тем больше, чем меньше значение 02-
[c.117]
Кроме того, длина I2 исходной трещины, выращенной при одной и той же первичной амплитуде напряжений oi, с которой начинается рост трещины при вторичной амплитуде напряжений 02, тем больше, чем меньше значение 02-
[c.117]
Полученные зависимости можно объяснить следующим образом. При одной и той же длине исходной усталостной трещины, выращенной при различных напряжениях оь размер поврежденной зоны (зоны пластической деформации) у вершины такой трещины тем больше, чем выше напряженке Оь При одном и том же уровне вторичных напряжений ог трещина распространяется тем легче, чем больше зона пластической деформации у вершины исходной трещины. При этом выход треи1,ины из этой поврежденной зоны в неповрежденную затруднен, а для некоторого уровня вторичных напряжений не-возмо кен. Отсюда получается зависимость длины 1 нераспро-страняющейся усталостной трещины от амплитуды цикла напряжений О] выращивания исходной трещины. [c.118]
Глубина нераспространяющейся усталостной трещины увеличивается с ростом уровня амплитуды или максимальных напряжений цикла нагрузки, причем тем интенсивнее, чем больше коэффициент асимметрии цикла нагружения. Детали с усталостными трещинами одного размера могут выдерживать без разрушения тем более высокие амплитуды цикла напряжений,, чем больше среднее напряжение цикла смещено в сторону сжатия. На рис. 56 приведены зависимости глубины нераспро-страняющнхся усталостных трещин, возникших в призматических образцах (40×40 мм) с концентратором напряжений из стали 45 при асимметричном цикле нагружения с различными напряжениями сжатия. Увеличение среднего сжимающего напряжения снижает рост размера нераспространяющейся усталостной трещины.
[c.136]
Детали с усталостными трещинами одного размера могут выдерживать без разрушения тем более высокие амплитуды цикла напряжений,, чем больше среднее напряжение цикла смещено в сторону сжатия. На рис. 56 приведены зависимости глубины нераспро-страняющнхся усталостных трещин, возникших в призматических образцах (40×40 мм) с концентратором напряжений из стали 45 при асимметричном цикле нагружения с различными напряжениями сжатия. Увеличение среднего сжимающего напряжения снижает рост размера нераспространяющейся усталостной трещины.
[c.136]
| Фиг. 80. Предельные значения амплитуды цикла напряжений (j ) для болтов М10 — МЗО, изготовленных из стали с = 45—55 кгШм. |
 Таким образом получается цензурированная справа выборка. В табл. 6.1 приведены ряды распределения цензурированных выборок, образовавшихся при амплитудах цикла напряжений Од = 210 МПа и Оа = 190 МПа. Оценку математического о кидания, среднего квадратического отклонения, границы доверительных интервалов для этих числовых характеристик находят по формулам (2.26), (2.27), (2.45) и (2.54).
[c.141]
Таким образом получается цензурированная справа выборка. В табл. 6.1 приведены ряды распределения цензурированных выборок, образовавшихся при амплитудах цикла напряжений Од = 210 МПа и Оа = 190 МПа. Оценку математического о кидания, среднего квадратического отклонения, границы доверительных интервалов для этих числовых характеристик находят по формулам (2.26), (2.27), (2.45) и (2.54).
[c.141]При асимметричном цикле нагружения с постоянным значением среднего напряжения (Ощ = onst) в формулах (6.40) и (6.42) следует заменить величину a i на оценку медианы предельной амплитуды цикла напряжений для принятой базы (Р а)з а величину на относительную среднюю квадратическую ошибку определения медианы предельной амплитуды [c.157]
Эффективность планирования испытаний на усталость в значительной степени вависит от степени достоверности предварительного построения медианной кривой усталости по справочной информации, на основании которой назначают уровни амплитуд цикла напряжений для испытания элементов на усталость, а также предварительно оценивают величину медианы предела ограниченной выносливости, входящую в формулы (6.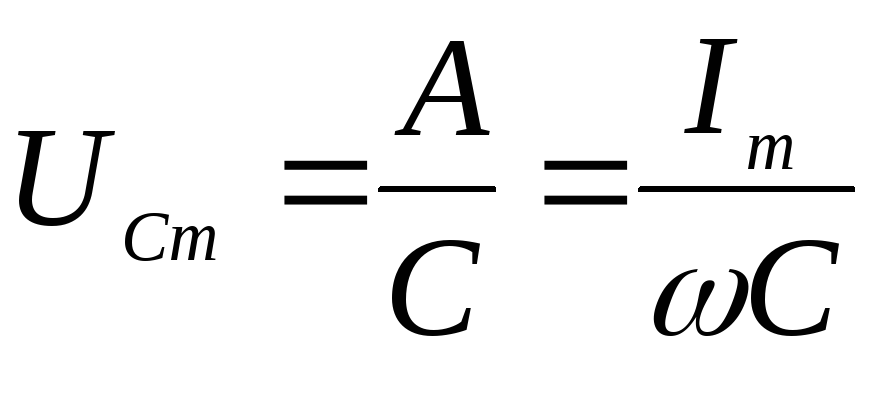 40) и (6.42).
[c.157]
40) и (6.42).
[c.157]
Нижний уровень амплитуды цикла напряжений для объектов испытаний, имеющих горизонтальный 5щасток на кривой усталости, выбирают равным расчетному значению предельной амплитуды ио формуле (6.52). Для элементов из магниевых, алюминиевых, титановых и других сп.чавов, у которых отсутствует горизонтальный участок на кривой усталости, нижний уровень амплитуды цикла напряжений выбирают из диапазона 1,0—1,2 от оценки предельной амплитуды для принятой базы испытания ио формуле (6.46). В случае выбора левой границы указанного диапазона отпадет необходимость экстраполяции кривой усталости в область базовой долговечности, что нри принятом уровне ошибки определения предела выносливости приводит к снижению общего числа испытуемых объектов и к увеличению машинного времени испытаний на нижнем уровне напряжений. И наоборот, выбор правой границы диапазона для нижнего уровня амплитуды цикла вызовет потребность экстраполяции кривой, что при заданном уровне ошибки приведет к увеличению числа объектов испытаний и снижению машинного времени, которое в основном определяется временем испытания на нижнем уровне напряжения.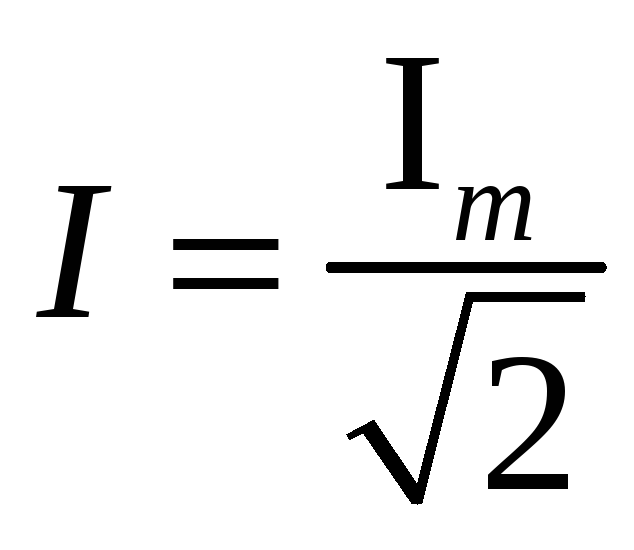 [c.160]
[c.160]
По формуле (6.41) вычисляем значения средней нз планируемых амплитуд цикла напряжений при нспытанни [c.161]
Задаемся тремя уровнями амплитуд цикла напряжений при нспытанни. Верхний урп Beifb Од, = 300 МПа. что соответствует долговечности 7.5-10 циклов по априорной крив… усталости, НИ5КНИЙ уровень принимаем равным оценке предела выносливости о — 185 МПл, средний уровень = 240 МПа. [c.162]
Закон Ома для полной цепи переменного тока. | |
Если в цепи переменного тока имеются нагрузки разных типов, то закон Ома выполняется только для максимальных (амплитудных) и действующих значений тока и напряжения. В этом случае: — полное сопротивление переменному току. | |
Учитывая, что отношение напряжения к силе тока – это сопротивление, и подставляя конкретные выражения для соответствующих сопротивлений, получим: . | |
Сдвиг фаз в цепи переменного тока определяется характером нагрузки: или . |
|
Мощность в цепи переменного тока. | |
Активной мощностью переменного тока называется средняя за период мощность необратимых преобразований в цепи переменного тока (преобразование энергии электрического тока во внутреннюю энергию): | |
или, переходя к действующим значениям, . | |
Величина наз. коэффициентом мощности. При малом коэффициенте мощности потребляется лишь малая часть мощности, вырабатываемой генератором. Остальная часть мощности периодически перекачивается от генератора к потребителю и обратно и рассеивается в линиях электропередач. | коэффициент мощности |
Резонанс в электрической цепи. | |
Резонанс в электрической цепи — явление резкого возрастания амплитуды вынужденных колебаний тока при приближении частоты внешнего напряжения (эдс) и собственной частоты колебательного контура. |
|
Из выражения для полного сопротивления переменному току видим, что сопротивление будет минимальным (сила тока при заданном напряжении – максимальной) при условии или .
| |
Следовательно, — т.е. частота изменения внешнего напряжения равна собственной частоте колебаний в контуре. | |
Амплитуды колебаний напряжения на индуктивности и емкости будут равны
и — т.е. они равны по величине и противоположны по фазе (напряжение на индуктивности опережает по фазе напряжение на емкости на p). |
|
Следовательно, . |
|
Полное падение напряжения в контуре равно падению напряжения на активном сопротивлении. Амплитуда установившихся колебаний тока будет определяться уравнением . В этом и состоит смысл явления резонанса. |
|
При этом если величина , то напряжения на емкостной и индуктивной нагрузках могут оказаться много больше внешнего напряжения (эдс генератора)! | |
На рисунке представлена зависимость тока в колебательном контуре от частоты при значениях R, где R1<R2<R3. | |
В параллельном контуре при малых активных сопротивлениях R1 и R2 токи в параллельных ветвях противоположны по фазе. Тогда, согласно правилу Кирхгофа . | |
В случае резонанса . Резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные емкостное и индуктивное сопротивления при приближении частоты внешнего напряжения к собственной частоте колебательного контура наз. резонансом токов. |
|
Применение: одно из основных применений резонанса в электрической цепи – настройка радио и телевизионных приемников на частоту передающей станции. Необходимо учитывать резонансные явления, когда в цепи, не рассчитанной на работу в условиях резонанса, возникают чрезмерно большие токи или напряжения (расплавление проводов, пробой изоляции и т. |
|
Как рассчитать амплитуду тока
Обновлено 13 декабря 2020 г.
Автор: Allison Boley
При движении электронов создается ток. Фактически, ток измеряет это движение; в частности, это заряд, который движется, деленный на время, необходимое для движения (или, если вы использовали исчисления, это производная заряда по времени). Иногда ток постоянный, как в простой цепи. В других случаях ток изменяется с течением времени, например, в цепи RLC (цепи с резистором, катушкой индуктивности и конденсатором).Какой бы ни была ваша схема, вы можете рассчитать амплитуду тока либо из уравнения, либо напрямую измерив свойства цепи.
TL; DR (слишком долго; не читал)
Уравнение тока в цепи с конденсатором или катушкой индуктивности: I = Asin (Bt + C) или I = Acos (Bt + C), где A , B и C — константы.
Расчет амплитуды по закону Ома
Уравнение для тока простой цепи — это закон Ома:
I = \ frac {V} {R}
где I — ток, V — напряжение, а R — сопротивление. В этом случае амплитуда тока остается неизменной и равна I.
В этом случае амплитуда тока остается неизменной и равна I.
Расчет изменяющихся токов
Уравнение тока в цепи с конденсатором или индуктором должно иметь вид:
I = A \ sin {(Bt + C)}
I = A \ cos {(Bt + C)}
где A, B и C — константы.
У вас может быть другое уравнение, которое включает много переменных. В таком случае найдите ток, который должен дать уравнение в одной из вышеуказанных форм.Независимо от того, выражено ли уравнение через синус или косинус, коэффициент A — это амплитуда тока. (B — угловая частота, а C — фазовый сдвиг.)
Расчет амплитуды по цепи
Настройте схему по своему усмотрению и подключите ее параллельно к осциллографу. Вы должны увидеть на осциллографе синусоидальную кривую; сигнал представляет собой напряжение в цепи.
Измерение напряжения с помощью осциллографа
Подсчитайте количество вертикальных линий сетки, называемых делениями, на осциллографе от центра волны до ее пика. Теперь проверьте настройку «вольт на деление» на осциллографе. Умножьте эту настройку на количество делений, чтобы определить напряжение на пике. Например, если ваш пик находится на 4 деления выше центра графика, а осциллограф установлен на 5 В на деление, то ваше пиковое напряжение составляет 20 вольт. Это пиковое напряжение и есть амплитуда напряжения.
Теперь проверьте настройку «вольт на деление» на осциллографе. Умножьте эту настройку на количество делений, чтобы определить напряжение на пике. Например, если ваш пик находится на 4 деления выше центра графика, а осциллограф установлен на 5 В на деление, то ваше пиковое напряжение составляет 20 вольт. Это пиковое напряжение и есть амплитуда напряжения.
Найдите угловую частоту волны. Сначала подсчитайте количество горизонтальных линий / делений сетки, которые волна занимает, чтобы завершить один период.Проверьте настройку «секунд на деление» на осциллографе и умножьте это значение на количество делений, чтобы определить период времени волны. Например, если период равен 5 делениям, а осциллограф установлен на 1 мс на деление, то ваш период равен 5 мсек, или 0,005 с.
Возьмите обратную величину периода и умножьте полученный ответ на 2π (π≈3,1416). Это ваша угловая частота.
Преобразование измерения напряжения в ток
Преобразование амплитуды напряжения в амплитуду тока.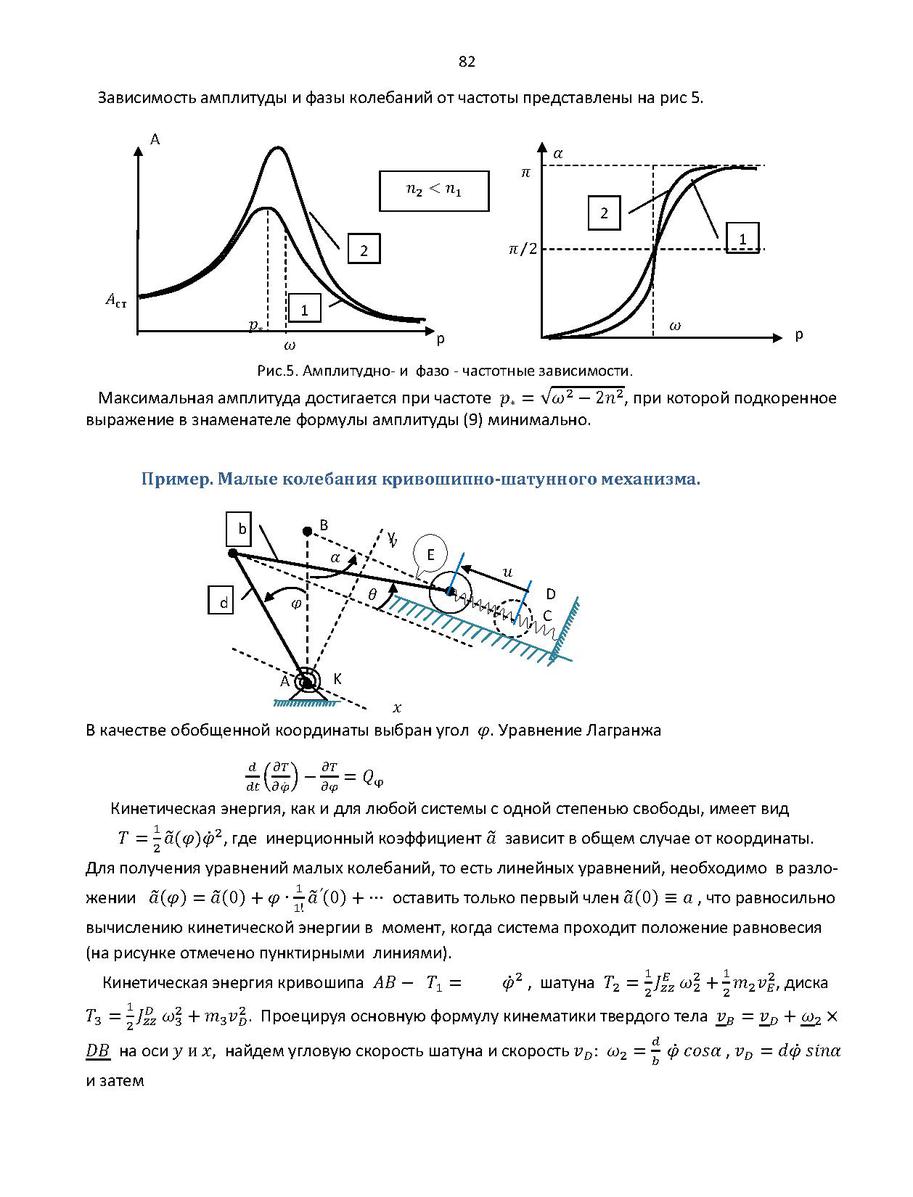 Уравнение, которое вы используете для преобразования, будет зависеть от того, какие компоненты у вас есть в вашей цепи. Если у вас есть только генератор и конденсатор, умножьте напряжение на угловую частоту и емкость. Если у вас есть только генератор и индуктор, разделите напряжение на угловую частоту и индуктивность. Более сложные схемы требуют более сложных уравнений.
Уравнение, которое вы используете для преобразования, будет зависеть от того, какие компоненты у вас есть в вашей цепи. Если у вас есть только генератор и конденсатор, умножьте напряжение на угловую частоту и емкость. Если у вас есть только генератор и индуктор, разделите напряжение на угловую частоту и индуктивность. Более сложные схемы требуют более сложных уравнений.
Измерение синусоидальной волны
- • Знайте измерения, связанные с синусоидальными волнами
- • а.Пиковое значение.
- • б. Амплитуда.
- • ок. Пиковое значение.
- • d. Периодическое время.
- • e. Средняя стоимость.
- • ф. Среднеквадратичное значение.
Рис 1.2.1 Характеристики синусоидальной волны
Форма волны — это график, показывающий изменение, обычно напряжения или тока, во времени. Горизонтальная ось показывает течение времени слева направо. Вертикальная ось показывает измеренную величину (это напряжение на рис.1.2.1).
Вертикальная ось показывает измеренную величину (это напряжение на рис.1.2.1).
Шесть наиболее важных характеристик синусоидальной волны:
ПИК ДО ПИК значения.
МГНОВЕННОЕ значение.
АМПЛИТУДА.
Пиковое значение.
ПЕРИОДИЧЕСКОЕ ВРЕМЯ.
СРЕДНЕЕ значение.
RMS значение.
Эти характеристики показаны на рис. 1.2.1
Пиковое значение
Значение PEAK TO PEAK — это расстояние по вертикали между вершиной и основанием волны. Он будет измеряться в вольтах на осциллограмме напряжения и может быть обозначен как V PP или V PK − PK .В форме волны тока он будет обозначен как I PP или I PK-PK , поскольку I (не C) используется для представления тока.
Мгновенное значение
Это значение (напряжение или ток) волны в любой конкретный момент. часто выбирается, чтобы совпасть с каким-то другим событием. Например. Мгновенное значение синусоидальной волны на четвертой части цикла будет равно пиковому значению. См. Точку X на рис. 1.2.1.
См. Точку X на рис. 1.2.1.
Амплитуда
АМПЛИТУДА синусоидальной волны — это максимальное расстояние по вертикали, достигнутое в любом направлении от центральной линии волны.Поскольку синусоидальная волна симметрична относительно своей центральной линии, амплитуда волны составляет половину от максимального значения, как показано на рисунке 1.2.2.
Пиковое значение
Пиковое значение волны представляет собой наибольшее значение волновые достигает выше опорного значения. Обычно используемое эталонное значение — ноль. В форме волны напряжения пиковое значение может быть обозначено как V PK или V MAX (I PK или I MAX в форме кривой тока).
Если измеряемая синусоида симметрична по обе стороны от нуля вольт (или от нуля ампер), это означает, что уровень постоянного или постоянного тока волны равен нулю вольт, тогда пиковое значение должно быть таким же, как амплитуда, то есть половина от максимального до максимального значения.
Рис. 1.2.2 Определение максимального значения V
PKОднако это не всегда так, если также присутствует составляющая постоянного тока, отличная от нуля вольт, синусоидальная волна будет симметричной относительно этого уровня, а не нуля. Нижняя осциллограмма на рис. 1.2.2 показывает, что пиковое значение теперь может быть даже больше, чем пиковое значение (однако амплитуда волны остается той же, и это разница между пиковым значением и «центральной линией»). «формы волны).
Периодическое время и частота
ПЕРИОДИЧЕСКОЕ ВРЕМЯ (обозначается символом T) — это время в секундах, миллисекундах и т. Д., Принятое для одного полного цикла волны. Его можно использовать для определения ЧАСТОТЫ волны по формуле T = 1 / ƒ
. Таким образом, если периодичность волны составляет 20 мс (или 1/50 секунды), то должно быть 50 полных циклов волны за одну секунду. Частота 50 Гц. Обратите внимание, что при использовании этой формулы, если периодическое время указывается в секундах, тогда частота будет в Гц.
Рис 1.2.3 Среднее значение синусоиды
Среднее значение
СРЕДНЕЕ значение. Обычно это означает среднее значение только половины периода волны. Если взять среднее значение полного цикла, оно, конечно, будет равно нулю, поскольку в синусоиде, симметричной относительно нуля, есть равные отклонения выше и ниже нулевой линии.
При использовании только половины цикла, как показано на рис. 1.2.3, среднее значение (напряжение или ток) всегда составляет 0,637 от пикового значения волны.
В AV = В PK x 0,637
или
I AV = I PK X 0,637
Среднее значение — это значение, которое обычно определяет напряжение или ток, показываемые на измерительном приборе. Однако есть некоторые измерители, которые будут считывать значение RMS, они называются «измерителями True RMS».
Среднеквадратичное значение.
Среднеквадратичное значение или ROOT MEAN SQUARED — это значение эквивалентного постоянного (неизменяемого) напряжения или тока, которые будут обеспечивать такую же энергию в цепи, как измеренная синусоидальная волна. То есть, если синусоидальная волна переменного тока имеет среднеквадратичное значение 240 вольт, она будет обеспечивать такую же энергию для схемы, что и источник постоянного тока на 240 вольт.
То есть, если синусоидальная волна переменного тока имеет среднеквадратичное значение 240 вольт, она будет обеспечивать такую же энергию для схемы, что и источник постоянного тока на 240 вольт.
Можно показать, что среднеквадратичное значение синусоидальной волны составляет 0,707 пикового значения.
В RMS = V PK x 0,707 и I RMS = I PK x 0,707
Кроме того, пиковое значение синусоиды равно 1,414 x среднеквадратичное значение.
Форм-фактор
Если V AV (0,637) умножить на 1.11 ответ — 0,707, что является среднеквадратичным значением. Это различие называется форм-фактором волны, и соотношение 1,11 справедливо только для идеальной синусоидальной волны. Если волна имеет другую форму, изменится либо среднеквадратичное значение, либо среднее значение (или оба), а также отношения между ними. Это важно при измерении переменного напряжения с помощью измерителя, поскольку это среднее значение, которое фактически измеряет большинство измерителей. Однако они отображают среднеквадратичное значение, просто умножая напряжение на 1,11.Следовательно, если измеряемая волна переменного тока не является идеальной синусоидальной волной, показания будут немного неправильными. Однако, если вы заплатите достаточно денег, вы можете купить истинный измеритель RMS, который фактически вычисляет значение RMS несинусоидальных волн.
Однако они отображают среднеквадратичное значение, просто умножая напряжение на 1,11.Следовательно, если измеряемая волна переменного тока не является идеальной синусоидальной волной, показания будут немного неправильными. Однако, если вы заплатите достаточно денег, вы можете купить истинный измеритель RMS, который фактически вычисляет значение RMS несинусоидальных волн.
Электроснабжение (Линия)
Чтобы продемонстрировать некоторые из этих характеристик при использовании, рассмотрим очень распространенную синусоидальную волну, напряжение сети или форму сигнала линии, которая во многих частях мира составляет номинальное напряжение 230 В.
Электрооборудование, подключаемое к сети, всегда имеет этикетку с информацией о том, к какому источнику питания может быть подключено оборудование.Эти метки очень разные по внешнему виду, но часто есть изображение синусоидальной волны, показывающей, что переменный ток. необходимо использовать поставку. Заявленное напряжение будет 230 В (или 120 В в США) или диапазон напряжений, включая эти значения. Эти напряжения фактически относятся к среднеквадратичному значению синусоидальной волны сети. На этикетке также указано, что частота источника питания составляет 50 Гц в Европе или 60 Гц в США.
Эти напряжения фактически относятся к среднеквадратичному значению синусоидальной волны сети. На этикетке также указано, что частота источника питания составляет 50 Гц в Европе или 60 Гц в США.
Из этого небольшого количества информации можно определить другие значения:
а.Пиковое напряжение формы волны, как В PK = В RMS x 1,414
г. СРЕДНЕЕ значение сигнала, как V AV = V PK x 0,637
г. Значение PEAK TO PEAK формы волны. Это в два раза больше АМПЛИТУДЫ, которая (поскольку форма сигнала сети симметрична относительно нуля вольт) совпадает с величиной V PK .
Поскольку V PK уже известен из. следует, что V PP = V PK x 2
г.ПЕРИОДИЧЕСКОЕ ВРЕМЯ, равное T = 1 / ƒ
. Цепьпеременного тока — напряжение, ток и мощность
В цепи переменного тока переменный ток генерируется источником синусоидального напряжения
Напряжение
Токи в цепях с резистивной нагрузкой pure , емкостной или индуктивной нагрузкой .
Мгновенное напряжение в синусоидальной цепи переменного тока может быть выражено в форме во временной области как
u (t) = U max cos (ω t + θ) (1)
где
u (t) = напряжение в цепи в момент времени t (В)
U max = максимальное напряжение при амплитуде синусоидальной волны (В)
t = время (с)
ω = 2 π f
= угловая частота синусоидальной волны (рад / с)
f = частота (Гц, 1 / с)
θ = фазовый сдвиг синусоидальной волны (рад)
Мгновенное напряжение в качестве альтернативы может быть выражено в частотной области (или векторном) как
U = U (jω) = U max e jθ (1а)
где
U (jω) = U = комплексное напряжение (В)
Вектор — это комплексное число, выраженное в полярной форме, состоящее из величины, равной пиковой амплитуде синусоидального сигнала, и фазы.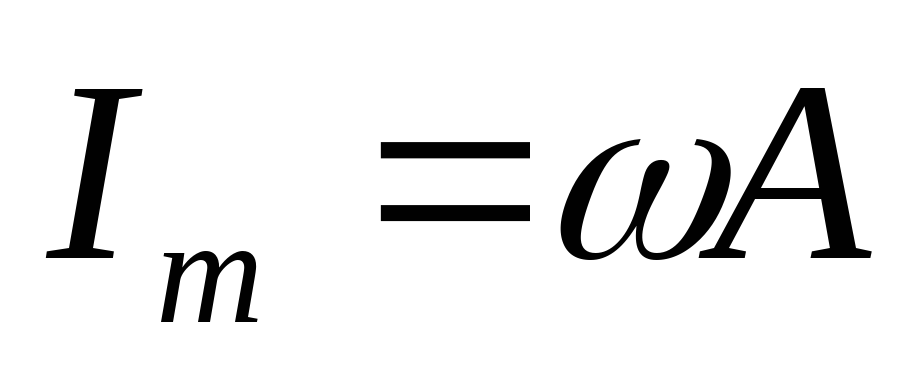 угол, равный фазовому сдвигу синусоидального сигнала относительно косинусоидального сигнала.
угол, равный фазовому сдвигу синусоидального сигнала относительно косинусоидального сигнала.
Обратите внимание, что конкретная угловая частота — ω — явно не используется в выражении вектора.
Ток
Мгновенный ток можно выразить в форме во временной области как
i (t) = I m cos (ω t + θ) (2)
где
i (t) = ток в момент времени t (A)
I max = максимальный ток при амплитуде синусоидальной волны (A)
Токи в цепях с чистые резистивные нагрузки , емкостные индуктивные нагрузки или показаны на рисунке выше.Ток в «реальной» цепи с резистивной, индуктивной и емкостной нагрузкой показан на рисунке ниже.
Мгновенный ток в цепи переменного тока альтернативно можно выразить в частотной области (или векторной) форме как
I = I (jω) = I max e jθ (2a)
, где
I = I (jω) = комплексный ток (A)
Частота
Обратите внимание, что частота большинства систем переменного тока является фиксированной, например, 60 Гц в Северной Америке и 50 Гц в большей части остального мира.
Угловая частота для Северной Америки
ω = 2 π 60
= 377 рад / с
Угловая частота для большей части остального мира
ω = 2 π 50
= 314 рад / с
Активная нагрузка
Напряжение на резистивной нагрузке в системе переменного тока может быть выражено как
U = RI (4)
где
R = сопротивление (Ом)Для резистивной нагрузки в цепи переменного тока напряжение составляет в фазе с током.
Индуктивная нагрузка
Напряжение на индуктивной нагрузке в системе переменного тока может быть выражено как
U = j ω LI (5)
, где
L = индуктивность (Генри)
Для индуктивной нагрузки ток в цепи переменного тока составляет π / 2 (90 o ) фаза после напряжения (или напряжение перед током).
Емкостная нагрузка
Напряжение индуктивной нагрузки в системе переменного тока можно выразить как
U = 1 / (j ω C) I (6)
где
C = емкость (фарад)
Для емкостной нагрузки ток в цепи переменного тока опережает напряжение на π / 2 (90 o ) фаза .
В реальной электрической цепи присутствует смесь резистивных, емкостных и индуктивных нагрузок с фазовым сдвигом напряжение / ток в диапазоне — π / 2 <= φ <= π / 2 , как показано на рисунок ниже.
Ток в «реальной» цепи со смесью резистивных, индуктивных и емкостных нагрузок. φ — фазовый угол между током и напряжением.
Импеданс
Закон Ома для сложного переменного тока может быть выражен как
U z = I z Z (7)
, где
U z = падение напряжения на нагрузке (вольт, В)
I z = ток через нагрузку (ампер, А)
Z = полное сопротивление нагрузки (Ом, Ом)
Полное сопротивление в цепи переменного тока можно рассматривать как комплексное сопротивление. Импеданс действует как частотно-зависимый резистор, где сопротивление является функцией частоты синусоидального возбуждения.
Импеданс действует как частотно-зависимый резистор, где сопротивление является функцией частоты синусоидального возбуждения.
Импедансы в серии
Результирующий импеданс для последовательных сопротивлений может быть выражен как
Z = Z 1 + Z 2 (7b)
Сопротивление параллельно
Результирующее полное сопротивление для параллельных сопротивлений может быть выражено как
1 / Z = 1 / Z 1 + 1 / Z 2 (7c)
Полная проводимость
Полная проводимость — это инвертированный импеданс
Y = 1 / Z (8)
, где
Y = полная проводимость (1 / Ом)
RMS или эффективное напряжение
RMS значение — это эффективное значение синусоидального напряжения или тока.
RMS — среднеквадратичное значение — или эффективное напряжение может быть выражено как
U действующее значение = U eff
= U max / (2) 1/2
= 0,707 U макс. (9)
(9)
где
U среднеквадратичное значение = U eff
= действующее напряжение (В)
9007 макс. = максимальное напряжение (амплитуда) источника синусоидального напряжения (В)
RMS — среднеквадратическое значение — или эффективный ток может быть выражен как
I rms = I eff
= I max / (2) 1/2
= 0.707 I макс (10)
где
I действующее значение = I eff
= действующее значение тока (A)
9009 = максимальный ток (амплитуда) источника синусоидального напряжения (A)
Вольтметры и амперметры переменного тока показывают среднеквадратичное значение напряжения или тока — или 0,707 максимальных пиковых значений. Максимальные пиковые значения равны 1.В 41 раз больше значений вольтметра.
Максимальные пиковые значения равны 1.В 41 раз больше значений вольтметра.
Пример
- для системы 230 В U действующее значение = 230 В и U макс = 324 В
- для системы 120 В U среднеквадратичное значение = 120 В и U max = 169 В
Трехфазное напряжение переменного тока — от линии к линии и от линии к нейтрали
В трехфазной системе переменного тока напряжение может подаваться между линиями и нейтралью (фазный потенциал) или между линиями (линейный потенциал).Результирующие напряжения для двух общих систем — европейской системы 400/230 В и североамериканской системы 208/120 В указаны для одного периода на рисунках ниже.
400/230 В пер. L3 и L2 — L3
— это трехфазные линейные потенциалы — линейных потенциалов Величина линейных потенциалов равна 3 1/2 (1. 73) величина фазового потенциала.
73) величина фазового потенциала.
U действующее значение, линия = 1,73 U действующее значение, фаза (11)
208 В / 120 В переменного тока
печать 208/120 В Трехфазная диаграмма
Мощность
Активно — или реально, или истинно — мощность, которая выполняет фактическую работу в цепи — может быть рассчитана как
P = U действующее значение I действующее значение cos φ (12)
, где
P = активная активная мощность (Вт)
φ = фазовый угол между током и напряжением (рад, градусы)
Cos φ также называется коэффициентом мощности.
Реактивную мощность в цепи можно рассчитать как
Q = U действующее значение I среднеквадратичное значение sin φ (13)
Q = реактивная мощность (ВАР)
AC, DC и электрические сигналы
AC, DC и электрические сигналы | Клуб электроникиAC | DC | Свойства сигнала | RMS
Следующая страница: Осциллографы (CRO)
См. Также: Диоды | Блоки питания
Также: Диоды | Блоки питания
AC означает переменный ток, а DC означает постоянный ток.Переменный и постоянный ток также используются при обозначении напряжений и электрических сигналов. которые не токи! Например: источник питания 12 В переменного тока имеет переменное напряжение. (что сделает поток переменного тока).
Электрический сигнал — это напряжение или ток, передающий информацию, обычно это означает напряжение. Этот термин может использоваться для любого напряжения или тока в цепи.
Переменный ток (AC)
Переменный ток (AC) течет в одну сторону, затем в другую, постоянно меняя направление.
Напряжение переменного тока постоянно меняется с положительного (+) на отрицательное (-).
Скорость изменения направления называется частотой переменного тока и измеряется в герц (Гц) , то есть количество циклов вперед-назад в секунду .
Электросеть в Великобритании имеет частоту 50 Гц.
Подробнее о свойствах сигнала см. Ниже.
Источник переменного тока подходит для питания некоторых устройств, таких как лампы и обогреватели, но почти все электронные схемы требуют постоянного источника постоянного тока (см. ниже).
Переменный ток от источника питания
Эта форма называется синусоидой .
Этот треугольный сигнал является переменным током, потому что он меняет
между положительным (+) и отрицательным (-).
Постоянный ток (DC)
Постоянный ток (DC) всегда течет в одном направлении, но может увеличиваться и уменьшаться.
Напряжение постоянного тока всегда положительное (или всегда отрицательное), но оно может увеличиваться и уменьшаться.
Для электронных схем обычно требуется постоянный источник питания постоянного тока , который имеет одно значение.
или источник питания smooth DC , который имеет лишь небольшую вариацию, называемую пульсацией .
Элементы, батареи и регулируемые источники питания обеспечивают устойчивый постоянный ток , который идеально подходит для электронных схем.
Блоки питания содержат трансформатор, преобразующий от сети переменного тока к безопасному низковольтному переменному току. Затем переменный ток преобразуется в постоянный ток мостовой выпрямитель, но выход изменяет постоянный ток , что не подходит для электронных схем.
Некоторые источники питания включают конденсатор для обеспечения smooth DC , который подходит для менее чувствительных электронных схем, в том числе большинство проектов на этом сайте.
Лампы, обогреватели и двигатели будут работать от любого источника постоянного тока.
Дополнительную информацию см. На странице источников питания.
Источники питания также описаны на веб-сайте Electronics in Meccano.
Постоянный ток
от батареи или регулируемого источника питания,
идеально подходит для электронных схем.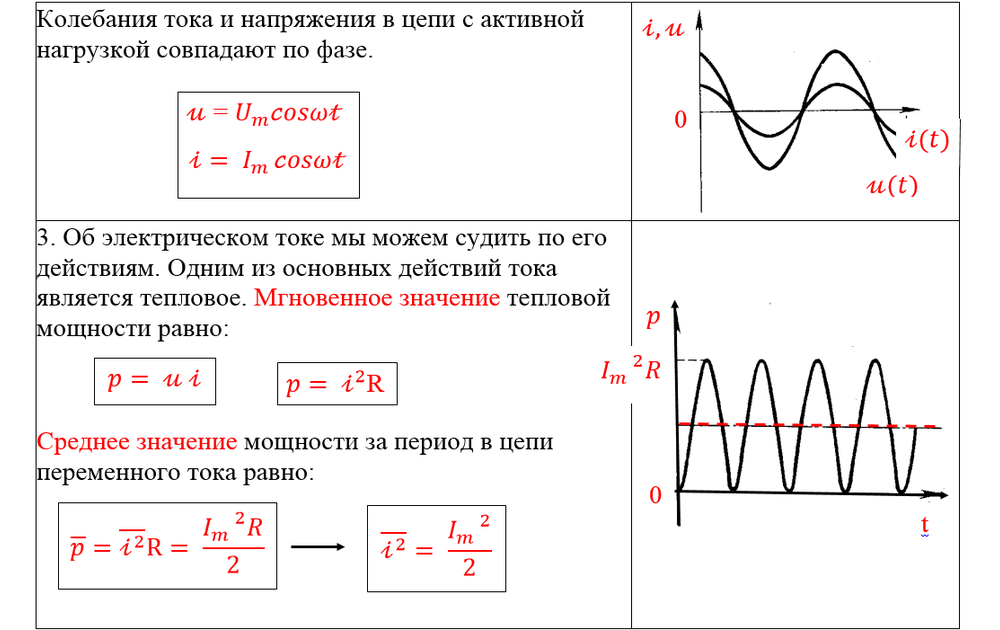
Smooth DC
от сглаженного источника питания,
подходит для некоторой электроники.
Изменение постоянного тока
от источника питания без сглаживания,
это не подходит для электроники.
Свойства электрических сигналов
Электрический сигнал — это напряжение или ток, передающий информацию, обычно это означает напряжение. Этот термин может использоваться для любого напряжения или тока в цепи.
График «напряжение-время» ниже показывает различные свойства электрического сигнала. Помимо свойств, отмеченных на графике, есть частота количество циклов в секунду.
На диаграмме показана синусоида , но свойства применимы к любому сигналу с постоянно повторяющейся формой.
- Амплитуда — максимальное напряжение, достигаемое сигналом.
Измеряется в В , В .

- Пиковое напряжение — другое название амплитуды.
- Пиковое напряжение в два раза больше пикового напряжения (амплитуды). При считывании осциллограммы обычно измеряют пиковое напряжение.
- Период времени — это время, необходимое сигналу для завершения одного цикла.
Он измеряется в секундах (с) , но периоды времени обычно короткие, поэтому часто используются миллисекунды (мс) и микросекунды (мкс).
1 мс = 0,001 с и 1 мкс = 0,000001 с. - Частота — это количество циклов в секунду.Он измеряется в герцах (Гц) , но частоты имеют тенденцию быть высокими, поэтому часто используются килогерцы (кГц) и мегагерцы (МГц).
1 кГц = 1000 Гц и 1 МГц = 1000000 Гц.
Периодичность и период
Частота и период времени противоположны друг другу:
| частота = | 1 |
| период времени |
и
| период времени = | 1 |
| частота |
Электросеть в Великобритании имеет частоту 50 Гц поэтому он имеет период времени 1 / 50 = 0. 02s = 20 мс .
02s = 20 мс .
Не хватает денег на проекты в области электроники? Продайте свой старый iPhone, iPad, MacBook или другое устройство Apple: macback.co.uk
Среднеквадратические значения (RMS)
Значение переменного напряжения непрерывно изменяется от нуля до положительного пика через от нуля до отрицательного пика и снова обратно к нулю. Очевидно, что в большинстве случаев оно меньше пикового напряжения, так что это не лучшая мера его реального эффекта.
Вместо этого мы используем среднеквадратичное напряжение (В RMS ) что равно 0.7 пикового напряжения (В пик ):
и
Эти уравнения также применимы к , текущий .
Важно отметить, что эти уравнения верны только для синусоидальных волн (наиболее распространенного типа переменного тока), потому что Коэффициенты 0,7 и 1,4 — это разные значения для других форм.
Действующее значение — эффективное значение переменного напряжения
или текущий. Это эквивалентное постоянное значение постоянного тока, которое дает такой же эффект.
Это эквивалентное постоянное значение постоянного тока, которое дает такой же эффект.
Например, лампа, подключенная к источнику питания 6V RMS AC , будет гореть с той же яркостью. при подключении к источнику постоянного тока 6 В постоянного тока . Тем не менее, лампа будет тусклее, если подключена к сети с пиковым напряжением 6 В переменного тока . питание, потому что его среднеквадратичное значение составляет всего 4,2 В (это эквивалентно постоянному 4,2 В постоянного тока).
Возможно, вам будет полезно думать о среднеквадратичном значении как о среднем значении, но, пожалуйста, помните что это не совсем средний показатель! Фактически, среднее напряжение (или ток) типичного сигнала переменного тока равен нулю, потому что положительная и отрицательная части полностью компенсируются.
Что показывают измерители переменного тока, это среднеквадратичное или пиковое напряжение?
Вольтметры и амперметры переменного тока показывают значение RMS напряжения или тока.
Что на самом деле означает «6 В переменного тока», это среднеквадратичное или пиковое напряжение?
Если имеется в виду пиковое значение, оно должно быть четко указано, в противном случае предположим, что это значение RMS . В повседневном использовании напряжение переменного тока (и токи) всегда задается как среднеквадратичных значений , потому что это позволяет провести разумное сравнение с постоянными напряжениями (и токами) постоянного тока, например, от батареи.
Например, «питание 6 В переменного тока» означает 6 В RMS, пиковое напряжение составляет 8,4 В. Электроснабжение Великобритании 230 В переменного тока, это означает 230 В RMS, поэтому пиковое напряжение сети составляет около 320 В.
Так что же на самом деле означает среднеквадратичное значение (RMS)?
Сначала возведите все значения в квадрат, затем найдите среднее (среднее) этих квадратичных значений по
полный цикл и найдите квадратный корень из этого среднего. Это значение RMS.
Смущенный? Не обращайте внимания на математику (она выглядит сложнее, чем есть на самом деле), просто примите
что среднеквадратичные значения напряжения и тока являются гораздо более полезной величиной, чем пиковые значения.
Это значение RMS.
Смущенный? Не обращайте внимания на математику (она выглядит сложнее, чем есть на самом деле), просто примите
что среднеквадратичные значения напряжения и тока являются гораздо более полезной величиной, чем пиковые значения.
Следующая страница: Осциллографы (CRO) | Исследование
Политика конфиденциальности и файлы cookie
Этот сайт не собирает личную информацию.
Если вы отправите электронное письмо, ваш адрес электронной почты и любая личная информация будет
используется только для ответа на ваше сообщение, оно не будет передано никому.
На этом веб-сайте отображается реклама, если вы нажмете на
рекламодатель может знать, что вы пришли с этого сайта, и я могу быть вознагражден.
Рекламодателям не передается никакая личная информация.Этот веб-сайт использует некоторые файлы cookie, которые классифицируются как «строго необходимые», они необходимы для работы веб-сайта и не могут быть отклонены, но они не содержат никакой личной информации. Этот веб-сайт использует службу Google AdSense, которая использует файлы cookie для показа рекламы на основе использования вами веб-сайтов.
(включая этот), как объяснил Google.
Чтобы узнать, как удалить файлы cookie и управлять ими в своем браузере, пожалуйста
посетите AboutCookies.org.
Этот веб-сайт использует службу Google AdSense, которая использует файлы cookie для показа рекламы на основе использования вами веб-сайтов.
(включая этот), как объяснил Google.
Чтобы узнать, как удалить файлы cookie и управлять ими в своем браузере, пожалуйста
посетите AboutCookies.org.
electronicsclub.info © Джон Хьюс 2021 г.
Веб-сайт размещен на Tsohost
Что такое амплитуда? Амплитуда смещения частицы как рассчитать амплитуду пик звуковой волны амплитуда волны звуковой сигнал градиент звукового давления вычислить амплитуду в зависимости от напряжения определение условия скорости звуковых частиц вопрос вычислить амплитуду максимальное смещение равновесие точное определение шкала децибел градиент давления звуковой волны среднеквадратичное значение звукового поля удлинение колебание пик струны до пика удлинения продольные волны давления длина волны период частота
Что такое амплитуда? Амплитуда смещения частицы как рассчитать амплитуду пик звуковой волны амплитуда волны звуковой сигнал градиент звукового давления вычислить амплитуду в зависимости от напряжения определение условия скорости звуковых частиц вопрос вычислить амплитуду максимальное смещение равновесие точное определение шкала децибел градиент давления звуковой волны среднеквадратичное значение звукового поля удлинение колебание пика струны до максимального удлинения продольные волны давления длина волны период частота — sengpielaudio Sengpiel Berlin| Определение амплитуды: 1.  Максимальная степень вибрации или смещения синусоидального (!) Колебания, измеренная от
положение равновесия. Амплитуда — это максимальное абсолютное значение периодически изменяющейся
количество. Максимальная степень вибрации или смещения синусоидального (!) Колебания, измеренная от
положение равновесия. Амплитуда — это максимальное абсолютное значение периодически изменяющейся
количество. 2. Максимальное отличие переменного электрического тока или потенциала от среднего значения. Термин «амплитуда» используется для обозначения величины колебания, поэтому амплитуда синусоиды « y = A × sin (ω × t) » составляет | А | , где | А | — это абсолютное значение A . Амплитуда — это переменная, характеризующая синусоидальные колебания. Это дает отклонение физическая величина от нейтрального положения (нулевой точки) до положительного или отрицательного значения. Амплитуда выражается физической величиной — например, напряжением, звуковым давлением и т. Д. Амплитуды выражаются либо как мгновенные значения, либо в основном как пиковые значения. Амплитуда — это колебание или смещение волны от ее среднего значения.  Со звуковыми волнами это
степень смещения частиц воздуха, и эта амплитуда звука или амплитуда звука равна
воспринимается как громкость звука. Со звуковыми волнами это
степень смещения частиц воздуха, и эта амплитуда звука или амплитуда звука равна
воспринимается как громкость звука. Из «Британской энциклопедии»: для поперечной волны, например волны на натянутой струне, амплитуда измеряется максимальным смещением любой точки струны от ее положения когда струна в покое. Для продольной волны, такой как звуковая волна, амплитуда измеряется максимальное смещение частицы из положения равновесия.Когда амплитуда волна неуклонно уменьшается, потому что ее энергия «теряется» (превращается в тепло), это называется затухает. Звуковые волны в воздухе — это продольные волны давления. |
Бросить камень в пруд
Обычно говорят об «амплитуде», как если бы была определенная амплитуда.
как смещение или удлинение от нулевой оси (базовая линия или равновесие).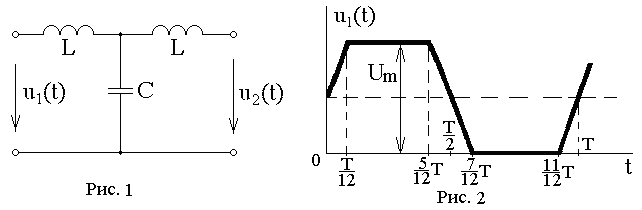 Амплитуда может быть словом, описывающим волну. Это означает, что максимальная сумма волна отклоняется от базовой линии или равновесия. Смещение обычно используется для описывают движущиеся частицы, например, насколько далеко они переместились от заданной точки. Длина волны в продольной волне относится к расстоянию между двумя последовательные сжатия или между двумя последовательными разрежениями. Определение: амплитуда — это максимальное отклонение от равновесия.Для продольной волны, которая представляет собой волну давления, это будет максимальное увеличение (или уменьшение) давления от равновесного давления, которое является причиной, когда сжатие (или разрежение) проходит точку. Амплитуда — это расстояние от положения равновесия среды до сжатие или разрежение. Пиковое значение синусоидальных сигналов переменного тока называется амплитудой, начиная с нулевая линия. Амплитуда обычно относится к размеру скалярного или векторного поля.  |
Длина волны и Расстояние — Период и Время
| Амплитуда A не имеет ничего общего с частотой, длина волны, период времени и скорость звука. |
| Мы часто слышим вопрос: насколько велика амплитуда? В нашем случае это
« амплитуда звука «.Обычно мы спрашиваем, как будто есть «один» амплитуда звуковых волн в воздухе. Восприятие громкости звука
определяется амплитудой звуковых волн — чем выше
амплитуда, тем громче звук или шум. Какая амплитуда звука (амплитуда звука)? В приведенной выше ссылке «Величины звукового поля плоской волны» мы находим: амплитуду смещения частицы ξ или амплитуду смещения амплитуду звукового давления p или амплитуду давления амплитуда скорости звуковой частицы v , или амплитуда скорости частицы амплитуда градиента давления Δ p , или амплитуда градиента давления. 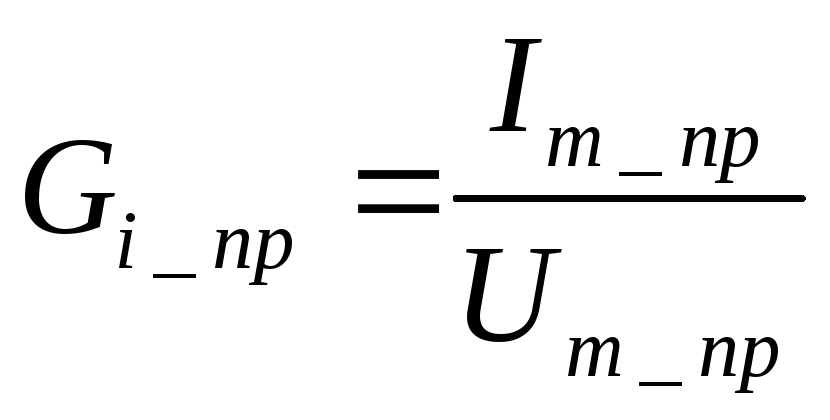 Каждый раз, когда мы добавляем 6 дБ, фактически амплитуда сигнала удваивается. Все эти термины представляют собой величины звукового поля. Есть проблемы с величинами звуковой энергии (мощность), когда мы используем термин амплитуда. Избегайте применения амплитуды слова на уровнях мощности или количества энергии. Количество звукового поля не является звуковой энергией или количество звуковой мощности. Кроме того, подумайте об амплитуде колебаний струны. Максимальная величина отклонения волны называется амплитудой. Гармоническое движение: Смещение = A × sin (2 × π × f × t ), что означает: A = амплитуда (пик), f = частота, t = время. Скорость звуковых частиц v не следует путать со скоростью звука c или скорость звука, все измеряются в м / с: |
| Амплитуда как смещение частицы ξ = v / (2 π × f ) = p / (2 π × Z ) Амплитуда звука давления = давление p = ξ × 2 π × Z = v × Z Z = ρ × c Удельное акустическое сопротивление воздуха при 20C составляет Z = 413 N · с / м Амплитуда звукового давления — это максимальное значение звукового давления.  Поскольку звуковое давление p является периодической величиной, оно определяется как эффективное. звуковое давление p RMS (среднеквадратичное значение). |
| Изменение амплитуды не имеет никакого отношения к изменение высоты тона (частоты) и наоборот. |
Сложение амплитуд (и уровней)
| Амплитуды, коррелированные Сумма напряжений, когерентная (0 °) 1 + 1 = 2 | Амплитуды, некоррелированные Сумма мощностей, некогерентная (90 °) √ (1² + 1²) = 1.414 … |
Интенсивность звука пропорциональна амплитуде (звук
давление) в квадрате; I ~ p ², поэтому
амплитуда (звуковое давление) пропорциональна корню квадратному из интенсивности звука; стр. ~ √ I . ~ √ I . |
Что такое амплитуда?
http://www.indiana.edu/~emusic/acoustics/amplitude.htm
| http: // uk.answers.yahoo.com/question/index?qid=20111025210805AAIaFhX Вопрос с ответами.yahoo: Звук … Что такое амплитуда? Мне интересно, что создает амплитуду звука волна? Я понимаю, что в представлении поперечной волны амплитуда — это максимальное значение волновая функция, но как это перевести в продольные волны? Это имеет смысл для меня чем короче или больше расстояние между воздушным карманом высокого или низкого давления, разница между звуком более высокой или низкой частоты, но если рассматривать как частоту определяет высоту звука и скорость звука постоянна (в зависимости от среды), что что обеспечивает более мягкий или громкий звук? Я читал, что интенсивность или энергия звука волны — это то, что делает его громче или тише, но если звук распространяется с той же скоростью, что Свойство волны, распространяющейся по воздуху, имеет в виду термин интенсивность или энергия? |
Ответ ответов. Yahoo: Yahoo: «Звук … Что такое амплитуда?» Это действительно хороший вопрос, потому что есть проблема с определением слово амплидуде. Амплитуда — это величина изменения колебательной переменной при каждом колебании.
в колебательной системе. Например, звуковые волны в воздухе — это колебания в
атмосферного давления и их амплитуды пропорциональны изменению
давление за одно колебание. Если переменная совершает регулярные колебания и
график системы построен с осциллирующей переменной в качестве вертикальной оси и
время по горизонтальной оси, амплитуда визуально представлена вертикальной
расстояние между экстремумами кривой и равновесным значением. |
| Ответ ответов.Yahoo: Громкость зависит от звукового давления, частоты, полосы пропускания и продолжительности. Громкость — это качество звука, которое в первую очередь является психологическим коррелятом физическая сила (амплитуда). Это субъективная мера, которую часто путают с объективные измерения силы звука, такие как размеры звукового поля, например звук давление или уровень звукового давления SPL в децибелах, а также величины звуковой энергии, например интенсивность звука или звуковая мощность; см .  : : «Громкость — Википедия»: http: // en.wikipedia.org/wiki/Loudness Cheers ebs PS: Не забывайте, что наши барабанные перепонки эффективно двигаются «звуковым давлением»; см .: «Звуковое давление и звуковая мощность — Следствие и причина»: http://www.sengpielaudio.com/SoundPressureAndSoundPower.pdf Мы измеряем звук с помощью измерителя SPL (SPL = уровень звукового давления). |
| Примечание. Время, частота и фаза тесно связаны. Высота амплитуды не влияет на эти параметры. Амплитуда А не имеет ничего общего с частотой, длиной волны, продолжительность времени и скорость звука. |
среднеквадратичное напряжение , пиковое напряжение и размах напряжения
Параметры формы синусоидального сигнала «переменного тока 117 В и 230 В (среднеквадратичное значение)» приведены в таблице ниже.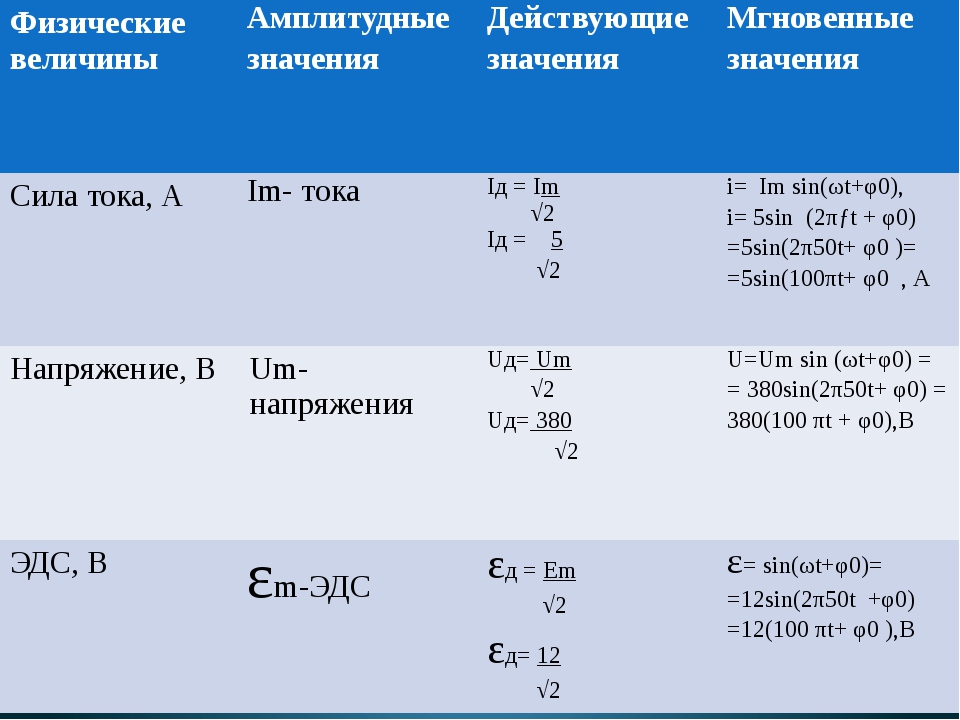 |
| Среднее напряжение | действующее напряжение ( В среднеквадратичное значение ) | Пиковое напряжение ( В p ) = ( Û ) | Пиковое напряжение ( В pp ) |
| 0 вольт | 117 В = В RMS = ~ В | 165 В = √2 × В RMS = 0,5 × В pp | 330 В = 2 × √2 × В RMS = 2 × В p |
| 0 вольт | 230 В = В RMS = ~ В | 325 В = √2 × В RMS = 0,5 × В pp | 650 В = 2 × √2 × В RMS = 2 × В p |
| Значение В RMS переменного напряжения В (t) = В 0 × f (t) определяется так, чтобы эффективная мощность постоянного тока соответствует В RMS 2 / R = V RMS × I RMS омическому сопротивлению средней резистивной мощности этого переменного напряжения до того же сопротивления. |
| Пик-фактор означает отношение пикового напряжения к среднеквадратичному напряжению. Если нам понадобится для расчета аттенюатора (расчет затухания) рассчитываем делитель напряжения . |
Преобразователи напряжения
| В СКЗ = ~ В | В стр. | В стр. | |
| Среднее значение напряжения В среднеквадратичное значение = | – | 0.7071 × В стр | 0,3535 × V pp |
| Пиковое напряжение В p = | 1,414 × В RMS | – | 0,5000 × В стр. |
| Пиковое напряжение В pp = | 2,828 × В RMS | 2.000 × V p | – |
Нечеткие уравнения в книгах
| Звуковые волны — это продольные волны в воздухе, которые мы воспринимаем. как вибрация: амплитуда звукового давления, интенсивность звука, звук энергия, тональность, импульсивность, резкость, громкость, громкость, раздражение, шероховатость, хрупкость, эхо-содержание, четкость, разборчивость, информативность. |
Прямоугольные напряжения — Vpk, Vpk-pk, Vavg, Vrms
При построении графика зависимости напряжения (В) от фазы (θ) прямоугольная волна выглядит так, как показано на рисунке справа. Форма волны повторяется каждые 2π радиан (360 °) и симметрична относительно оси напряжения. (при отсутствии смещения постоянного тока). Напряжение и ток, демонстрирующие циклическое поведение, называются переменными; то есть переменного тока (AC). Здесь показан один полный цикл. Основное уравнение для прямоугольной волны выглядит следующим образом:Есть несколько способов, которыми амплитуда прямоугольная волна обозначается как пиковое напряжение (V pk или V p ), размах напряжения (V pp или V p-p ) или V pkpk или V pk-pk ), среднего напряжения (V av или V avg ) и среднеквадратичного напряжения (V rms ).Пиковое напряжение и размах напряжения очевидны, глядя на приведенный выше график. Среднеквадратичное и среднее напряжение не так очевидны.
См. Также Синусоидальные напряжения и Страница напряжения треугольной волны.
Среднеквадратичное напряжение (В действующее значение )
Как следует из названия, В действующее значение рассчитывается путем извлечения квадратного корня из среднего квадрата напряжения в правильно выбранном интервале. На случай, если симметричные формы волны, такие как прямоугольная волна, четверть цикла точно представляет все четыре четверти цикла формы волны.Следовательно, это приемлемо для выбора цикла первой четверти, который идет от 0 радиан (0 °) до π / 2 радианы (90 °).
В среднеквадратичное значение — значение, отображаемое подавляющим большинством вольтметров переменного тока. Это значение, которое при применении сопротивление, производит такое же количество тепла, что и напряжение постоянного тока той же величины. Например, приложено 1 В через резистор 1 Ом выделяет 1 Вт тепла. Прямоугольная волна 1 В RMS , приложенная к резистору 1 Ом, также выделяет 1 Вт тепла.Это 1 V среднеквадратичное значение прямоугольная волна имеет пиковое напряжение 1 В и размах напряжения 2 В.
С момента получения полного вывода формул
для среднеквадратичного ( В, ) напряжения затруднительно, здесь это сделано за вас.
Среднее напряжение (В средн. )
Как следует из названия, В среднеквадратичное значение рассчитывается путем взятия среднего значения напряжения в правильно выбранном интервале.В этом случае Для симметричных сигналов, таких как прямоугольная волна, четверть цикла точно представляет все четыре четверти цикла формы волны. Следовательно, Допустимо выбрать цикл первой четверти, который идет от 0 радиан (0 °) до π / 2 радианы (90 °).
Как и в случае формулы V rms , здесь также приводится полный вывод для формулы V avg .
Итак, V avg = V pk
* Понятия не имею, почему мы пишем «Sinewave», а не «Trianglewave» и «Squarewave».»
Импеданс
ИмпедансЗакон Ома описывает взаимосвязь между ток и напряжение в цепях, которые находятся в равновесии, т. е. когда ток и напряжение не меняются. Когда у нас есть ситуация, когда изменяется ток (часто называемая цепью переменного тока) факторы должны быть приняты во внимание.
Реактивное сопротивлениеЕсть устройства, которые против любых изменений в текущий поток.Их не замечают, пока не изменится напряжение, но когда это происходит, эти устройства проявляют удивительные свойства, впитывая ток и возвращение его позже, так что вычисления закона Ома выйти не так. Свойство противоположного изменения называется реактивным сопротивлением. Он также измеряется в омах.
КонденсаторыЕсли сделать бутерброд из двух металлических пластин и кусок стекла, вы сделали конденсатор.Если вы примените положительное напряжение на одну пластину и отрицательное напряжение на другую, некоторое время будет протекать ток, потому что стекло может хранить электроны. Со временем это прекратится, поскольку стекло впитает столько электроны как можно. На этом этапе мы говорим, что конденсатор полностью заряжен. заряжен, и вольтметр, подключенный между двумя пластинами, покажет значение близко к тому, что изначально давало ток. Если затем соединить две металлические пластины вместе, ток будет течь. в противоположном направлении по мере разряда конденсатора.
На протяжении всего этого обработать. Начиная с разряженной стадии ток течет сильно сначала, но замедляется, поскольку напряжение на конденсаторе приближается к зарядному напряжению. Аналогично, при разряде ток сначала течет сильно, затем сужается по мере приближения заряда нуль. Любое сопротивление между источником заряда и разряженным конденсатор будет ограничивать начальный зарядный ток — поскольку конденсатор заряжает напряжение на резисторе снижается (это разница между источником напряжения и возрастающим напряжением пластина конденсатора.) Резистор подчиняется закону Ома, поэтому ток в конденсатор (и, очевидно, с другой стороны) истощается в Показанная здесь постепенная кривая:
Ток заряда конденсатора
Это означает, что напряжение на конденсаторе изменения кривой тоже:
Напряжение на конденсаторе во время его зарядки.
Время, необходимое для этого, определяется по сопротивлению ток должен проходить, а размер и материал конденсатора.Поскольку в конце он меняется очень медленно, невозможно определить время, когда конденсатор заряжен на 100%. В на самом деле это никогда не происходит. «Постоянная времени» определяется как время, необходимое для достижения 63% полной зарядки. Значение для измерения размер конденсатора (называемый емкостью) определяется формула
Емкость измеряется в фарадах, а единица измерения Фарадный конденсатор, включенный последовательно с резистором на один Ом, имеет постоянную времени одной секунды.В реальной жизни мы имеем дело с большими сопротивлениями и довольно короткое время, поэтому конденсаторы в большинстве схем имеют номинал диапазон микрофарад. (Это 10-6 фарад.)
Если вы соедините два конденсатора параллельно, вы сделайте конденсатор большего размера, и их значения сложатся:
Если они соединены последовательно, вы получите это:
переменного тока и конденсатор
А теперь представьте зарядку и разрядку конденсатор очень быстро — мы могли бы сделать это с помощью тонального генератора вместо батареи в качестве источника напряжения.
Если начать с высокой частоты и посмотреть ток через цепь, это почти как если бы конденсатор там вообще не было! Это потому, что ток самый высокий в начале цикл заряда, и если источник тока сильно меняет направление быстрее, чем постоянная времени, это всегда в начале цикла зарядки. При уменьшении частоты амплитуда тока уменьшается — до точка, где нет ничего, кроме легкой ряби на устойчивой ценность.
Следует отметить еще одну важную вещь здесь: ток на 90 ° не совпадает по фазе с напряжением, текущее лидерство.
Как видите, у нас есть ситуация, когда Закон Ома не раскрывает всей истории. Ток через конденсатор зависит от частоты сигнала. Частота зависимым противодействием току является реактивное сопротивление, которое указано в формулы буквой X. Емкостное реактивное сопротивление находится с помощью формула:
X — реактивное сопротивление в Ом.
F — частота в герцах.
C — емкость в фарадах.
Так как частотный член находится внизу дроби, вы можете видеть, что при падении частоты реактивное сопротивление Продолжается. Другими словами, конденсаторы препятствуют низкой частоте сигналы.
Объединение емкостного реактивного сопротивления и сопротивление
Чтобы закон Ома работал для изменения токов, мы переопределяем его как
I = E / Z
Где Z представляет собой импеданс , противостояние всему текущему, меняется или нет.Импеданс последовательно подключенные резистор и конденсатор находится по формуле:
Импеданс резистора и конденсатора в параллельный немного сложнее:
Простой фильтр
А резистор и конденсатор можно объединить в сделайте схему делителя переменного тока или фильтра.
Когда частота низкая, полное сопротивление конденсатор высокий, поэтому большая часть тока будет проходить через резистор.По мере увеличения частоты отводится больше тока. через конденсатор, меньше на остальную часть цепи. Таким образом ответ низкий. Если вы поменяли местами конденсатор и резистор, у вас будет схема высоких частот.
Частота среза определяется как частота, при которой сопротивление резистора равно реактивное сопротивление конденсатора. В этот момент сигнал составляет 0,707 раза. исходная амплитуда или уменьшенная на 3 дБ. Выше частоты среза, сигнал падает на 6 дБ на октаву.Ниже этой точки (в полоса пропускания) сигнал не изменяется. Чтобы найти отсечку частота:
Катушки индуктивности
Конденсаторы— не единственные гаджеты, у которых есть реактивное сопротивление. Если вы возьмете какой-нибудь провод и плотно намотаете, значит, вы сделали индуктор. Вот что происходит:
Когда ток проходит через индуктора L создается магнитное поле. Не появляется внезапно он нарастает.Магнитное поле, движущееся мимо провода, создает ток, и растущее поле движется. В этом случае он движется провести провода самой катушки таким образом, чтобы противостоять входящий ток, поэтому текущий поток задерживается следующим образом:
Текущий потокЗнакомо? Это такая же кривая, как конденсатор, за исключением того, что ток через катушку индуктивности строится как напряжение на конденсаторе. (И да, напряжение на катушке индуктивности начинается с высокого уровня и падает, как ток в конденсатор.) Что я на самом деле Интересно в индукторах то, что после источника тока удаляется, коллапсирующее магнитное поле поддерживает ток в течение немного.
Во многих отношениях индуктор противоположен конденсатор. Имеет постоянную времени:
Где L — индуктивность в единицах называется Генрис. Индуктивность для катушек индуктивности последовательно и параллельно следует форме для резисторов, по крайней мере, если катушки индуктивности не достаточно близко друг к другу, чтобы взаимодействовать магнитно.
Реактивное сопротивление катушки индуктивности:
Так как частота просто умножается на индуктивности, индукторы препятствуют высокочастотным сигналам. Когда вы применяете синусоидальной волны на катушку индуктивности, ток отстает от напряжения на 90 °.
Можно делать фильтры с резисторами и индукторы, но они не распространены в аудио, потому что индукторы подходящего размера довольно большие. Их используют в радио- и видеосхемах много.
Катушки индуктивности и конденсаторы комбинированный
Когда вы размещаете индуктор последовательно с конденсатор, получится интересный эффект. Сопротивление найдено по:
Импеданс — это абсолютное значение разница реактивных сопротивлений конденсатора и катушки индуктивности. Поскольку частота сигнала используется для вычисления обеих частей реактивного сопротивления, но одна возрастает с частотой, а один падает, кривая импеданса выглядит как это:
Существует магическая частота, называемая резонансная частота, где течет много тока, но выше и ниже резонанса ток меньше.Если конденсатор и индуктивности включены параллельно, эта формула дает полное сопротивление:
График частоты текущих стихов выглядит так это:
Что здесь происходит? Ну на низком частот индуктор пропускает почти все (помните, индуктор — это просто провод для постоянного тока), а конденсатор все блокирует. При повышении частоты катушка индуктивности тормозит, но конденсатор перенимать.Когда импедансы обоих совпадают, ток отсутствует. течь. Как это возможно?
Это из-за смены фаз: ток через конденсатор на 90 ° опережает напряжение, а ток через индуктор находится на 90 ° сзади. Когда цепь находится в резонанс, два компенсируются. В реальных схемах последовательное сопротивление имеет тенденцию к уменьшению пиков. Это называется демпфированием, и отношение индуктивное сопротивление к сопротивлению известно как Q (для качества фактор).
Трансформаторы
Как я уже говорил, вы не видите много индукторы в аудиосхемах, в первую очередь из-за размера, но также потому что они не очень точны по сравнению с конденсаторами. Существует одна жизненно важная функция, которую могут выполнять только индукторы:
Если две катушки индуктивности расположены близко друг к другу, ток протекание в одном из них вызовет ток в другом. Такое расположение называется трансформатором.Что касается звука, есть три полезных особенности трансформаторов:
- Правая часть (вторичная) цепи полностью изолирован от левого (первичного). Это означает любой стабильное напряжение (или смещение постоянного тока) от источника не появляется при конечный результат.
- Если во вторичной обмотке больше витков катушки, чем в первичной, напряжение, развиваемое на вторичный будет пропорционально выше.Это не может быть бесплатно — ток во вторичной обмотке будет пропорционально меньше. В другом словами, мощность (напряжение, умноженное на ток) постоянна.
- Если провода от истока к трансформатор длинный, есть вероятность, что паразитные токи будут индуцированы от внешних источников (радиосигналы, гудящие поля и прочий хлам). Поскольку эти токи будут иметь одинаковое направление в обоих проводах, они не будут развивать напряжение на первичной обмотке, поэтому нет шума ток появится во вторичном.
Итак, используем трансформаторы для изоляции шума подавление и изменение напряжения сигналов переменного тока (чаще всего для регулировки питание от сети на что-то полезное для аудиосистемы.
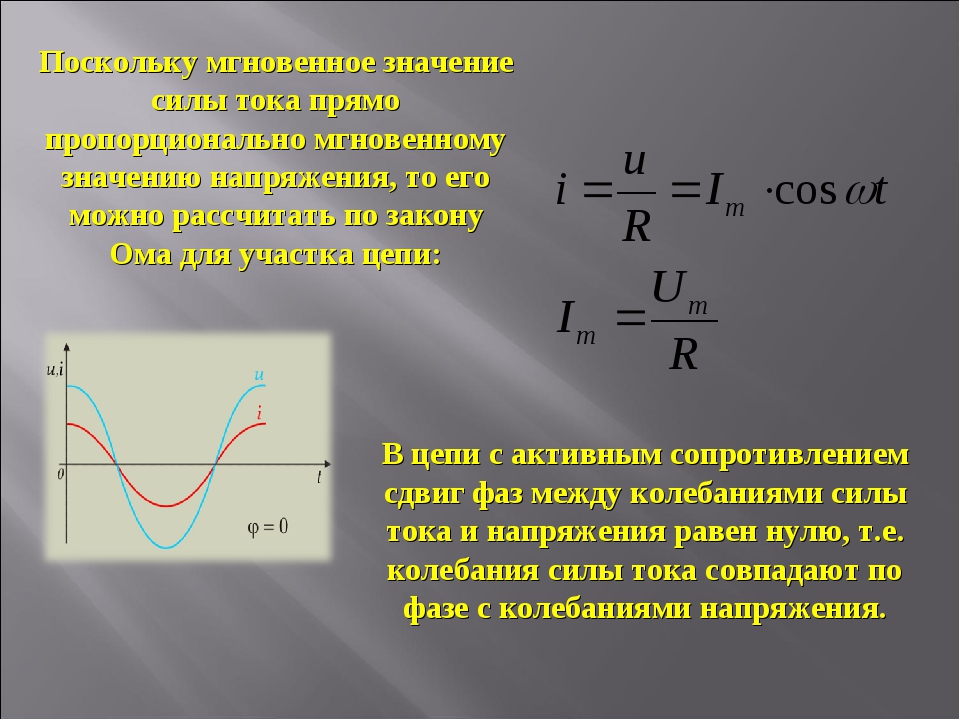

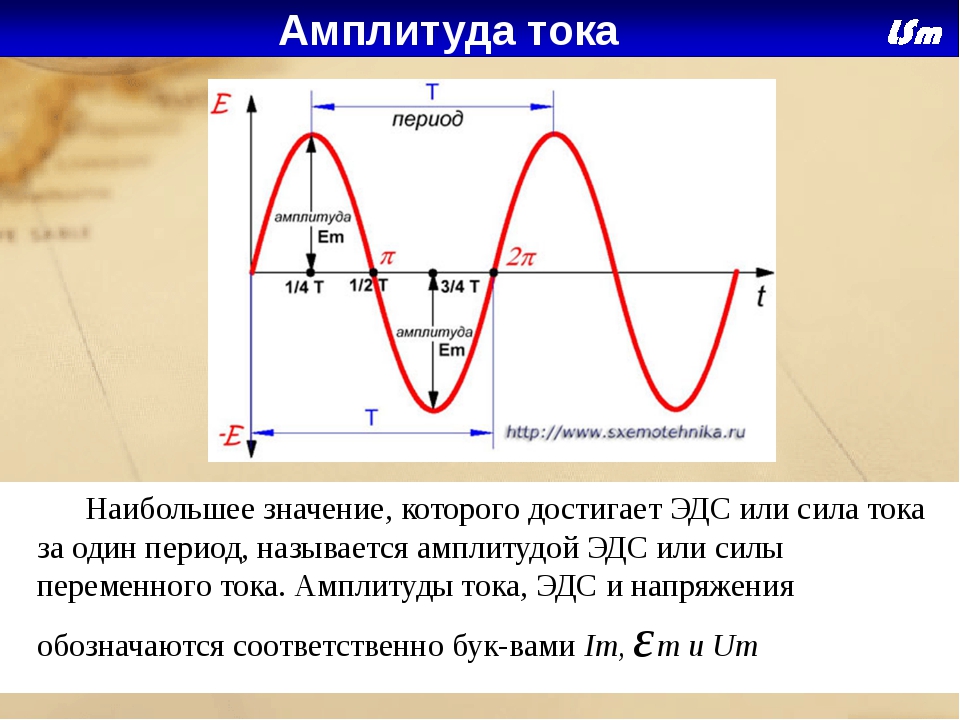

 д.).
д.).