Формула амплитуды напряжения – амплитудное значение напряжение | Электрознайка. Домашний Электромастер.

амплитудное значение напряжение | Электрознайка. Домашний Электромастер.

Действующее значение синусоидального
переменного напряжения – тока.

data-ad-client=»ca-pub-5076466341839286″
data-ad-slot=»1404500382″>
♦Переменный электрический ток в нашей бытовой электросети представляет собой синусоиду, как на рисунке 1.

Напряжение меняет свою величину от 0 до + Umax и от 0 до — Umax .  Полный цикл этих изменений называется периодом.
Период измеряется в секундах и обозначается буквой   Т.
Количество периодов переменного тока за 1 секунду, есть частота  f.
Частота переменного тока f измеряется в герцах .

f = 1 / T.

Например.
Частота в нашей электрической сети 50 Гц.  Период этих колебаний будет равен:

T = 1 / f = 1 / 50 = 0,02 сек.

Наибольшее значение изменяющегося переменного напряжения – тока называется амплитудным значением или амплитудой.

Umax = Ua и Imax = Ia

За один период напряжение принимает эти значения два раза: + Ua  и  — Ua .

♦ Если подключить в цепь переменного напряжения какую-нибудь активную нагрузку, например паяльник, в цепи потечет переменный электрический ток, так же принимающий значения +Ia и — Ia, и повторяющий форму синусоиды.
На нагрузке выделяется электрическая мощность в виде тепла. Неважно какой ток течет в цепи — переменный или постоянный. Выделение тепла не зависит от направления тока в цепи.
Выделенное тепло будет равно той энергии, которую затрачивает электрический ток при прохождении по сопротивлению нагрузки.

Введено понятие действующего значения переменного напряжения Uд и тока Iд.

Действующее значение переменного тока — это такое значение величины постоянного тока, который проходя по сопротивлению нагрузки за тот же промежуток времени, выделит такое же количество тепла, что и переменный ток.

♦ Переменный ток оказывает такое же тепловое действие, как и постоянный ток, если амплитуда синусоидального переменного тока превышает величину постоянного тока в 1,41 раз.
Следовательно действующее (или эффективное) значение переменного тока будет равно:

Iд = Ia / 1,41 = 0,707 Ia. – действующее значение переменного тока

Uд = Ua / 1,41 = 0,707 Ua — действующее значение переменного напряжения

На все эти теоретические размышления можно посмотреть иначе!

   ♦Имеем синусоиду переменного напряжения длительностью в 1 период как на рисунке 1.
После выпрямительных диодов оно принимает вид как на рисунке 2.

Нижняя половинка синусоиды перевернута вверх, чтобы удобнее было представить процесс преобразования.

    ♦На рисунке приняты обозначения:

Um = Ua = 1 — амплитудное значение величины переменного напряжения. Значение  

Ua примем за единицу.

Из формулы приведенной выше Uд = 1 / 1,41 = 0,707 — действующее напряжение равно 0,707 от амплитудного значения        Ua = 1.
Заштрихованная часть синусоиды обозначает затраченную на нагревание паяльника электрическую энергию. В промежутках между половинками синусоид ток по цепи не протекает, а следовательно и не выделяется электрическая мощность.
♦Проведем линию, обозначающую Uд = 0,707.
Она отсекает верхнюю часть половинок синусоид.
Если эти отсеченные вершинки синусоиды уложить в провалы между полупериодами, получится полностью заполненная

площадь соответствующая значениям постоянного напряжения U и тока I.
Получается, что мощность синусоидального переменного тока с амплитудными значениями Ua и Ia равна мощности действующего значения Uд и Iд переменного тока и равна мощности постоянного тока со значениями U и I.
Одна и та же электрическая мощность, выраженная в трех видах.

P = Ua х Ia = Uд х Iд = U х I

♦ Электрические приборы для измерения переменного напряжения и тока отградуированы на отображение действующих значений Uд и Iд.
В нашей бытовой электросети действующее, эффективное, напряжение переменного тока Uд равно 220 вольт

.
Максимальное, амплитудное значение напряжения в сети равно:
Um = Ua = Uд х 1,41 = 220 х 1,41 = 310,2 вольт.

Процесс поэтапного преобразования переменного напряжения в пульсирующее напряжение, а затем в постоянное напряжение, наблюдается в схемах выпрямителей.

data-ad-client=»ca-pub-5076466341839286″
data-ad-slot=»1404500382″>

domasniyelektromaster.ru

Прописные истины для новичков. — Начинающим — Теория

Как рассчитать шунт для амперметра?
Почему, я намотал вторичную обмотку на 12 вольт, а блок питания у меня выдаёт 16 вольт?.

Как измерить, какую мощность выдаёт усилитель низкой частоты?
Такие вопросы порой часто возникают от новичков радиолюбителей. Кратко напомним им, чем нужно руководствоваться в своей практической деятельности.

Закон Ома.

Основным законом, которым руководствуются радиолюбители — является Закон Ома..
Георг Симон ОМ
Georg Simon Ohm,  1787–1854
Немецкий физик. Родился в Эрлангене 16 марта в 1787 году (по другим источникам он родился в 1789-м). Окончил местный университет. Преподавал математику и естественные науки. В академических кругах его признали достаточно поздно. В 1849 году стал профессором Мюнхенского университета, хотя уже в 1827 году он опубликовал закон, который теперь носит его имя. Помимо электричества занимался акустикой и изучением человеческого слуха.

Георг Ом экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, на который не действуют сторонние силы), пропорционально напряжению U на концах проводника.
I = U/R, где R — электрическое сопротивление проводника.
Уравнение это выражает закон Ома для участка цепи (не содержащего источника тока). Формулировка этого закона следующая:
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорционально его сопротивлению.
Единица электрического сопротивления системы СИ называется Ом в честь этого выдающегося ученого. Сопротивление проводника в 1 Ом будет в том случае, если при протекающем по нему токе в 1 Ампер, падение напряжения на нём будет 1 Вольт.
Так же при прохождении тока по проводнику, на нём выделяется мощность(он нагревается), и чем больше протекающий по нему ток, тем больше выделяемая на нём мощность.
Как Вы должны знать  U — это работа, выполняемая при перемещении одного кулона, а ток I — количество кулонов, проходящих за 1 сек. Поэтому произведение тока на напряжение показывает полную работу, выполненную за 1 сек, то есть электрическую мощность или мощность электрического тока в Ваттах.
Вывод: поскольку электрическая мощность «P» в одинаковой степени зависит от тока «I» и от напряжения «U», то, следовательно, одну и ту же электрическую мощность можно получить либо при большом токе и малом напряжении, или же, наоборот, при большом напряжении и малом токе.
Из всего этого вытекают следующие формулы для расчётов тока, напряжения, сопротивления, мощности.
Величины, проставляемые в этих формулах; напряжение в вольтах, сопротивление в омах, ток в амперах, мощность в ваттах.

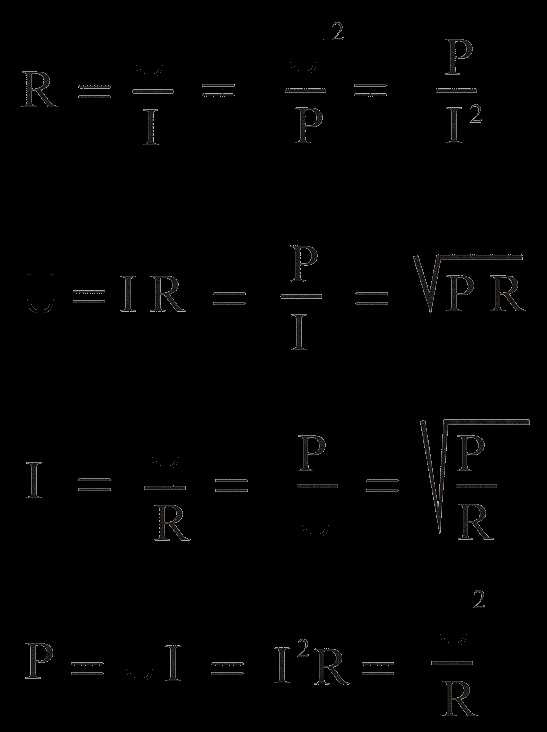
Последняя формула определяет мощность тока и выведена на основании практических опытов, проделанных в 1841 году Д. П. Джоулем и независимо от него в 1842 году, опытами Э. Х. Ленца. Называется Законом Джоуля — Ленца. Звучит так;

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка.

Для определения всех этих величин, есть очень интересная диаграмма (таблица), где отражены все эти формулы.
В центре искомые величины, а в секторах с соответствующими цветами — варианты решений в зависимости от известных величин.

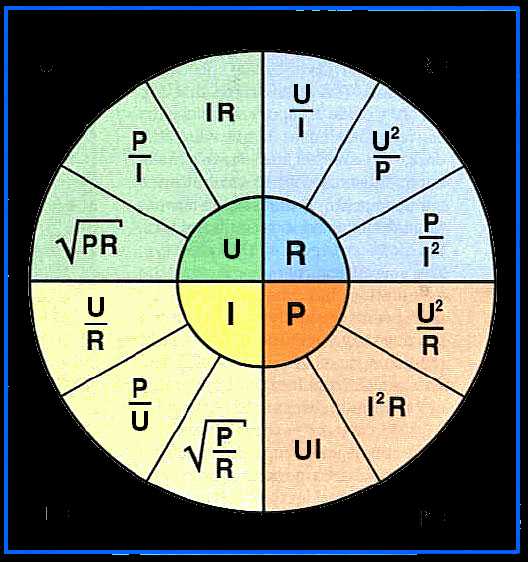
Имеется ещё более упрощённая диаграмма для определения величин, исходя из закона Ома. Называется в простонародье — треугольник Ома.

Выглядит она следующим образом:

В этом треугольнике Ома, нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления.
Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:

,

• — ЭДС цепи,
• I — сила тока в цепи,
• R — сопротивление всех элементов цепи,
• r — внутреннее сопротивление источника питания.

Закон Ома для полной цепи звучит так — Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.

Электрические измерения.

Нарисуем простейшую электрическую цепь, состоящую из батареи «В» и нагрузки «R», и рассмотрим, как необходимо измерять протекающий по цепи ток, и напряжение на нагрузке.

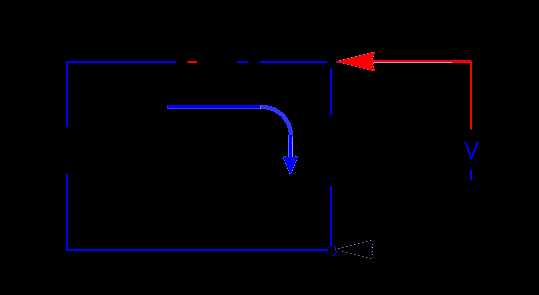
Что бы измерить протекающий в цепи ток, необходимо в разрыв источника питания и нагрузки включить измерительный прибор (амперметр).
Для того, что бы на измеряемую цепь было как можно меньше влияний и для повышения точности измерения, амперметры изготавливают с очень малым внутренним сопротивлением, то есть если включить амперметр в разрыв проверяемой цепи, то он практически не добавит к измеряемой цепи дополнительного сопротивления, и протекающий по цепи ток практически не изменится, или уменьшится на очень незначительную величину не оказывающую значительного влияния на конечный результат измерения.
Поэтому категорически нельзя измерять «ток приходящий на нагрузку» путём подключения амперметра параллельно нагрузке, или непосредственно у источника питания (без нагрузки) и таким образом попытаться замерить выходной ток выдаваемый источником питания или осветительной сетью.
Это равносильно тому, что подключить параллельно нагрузке или источнику питания обычный провод. Попросту сказать — закоротить цепь.
Если источник питания обладает хорошей мощностью — будет очень сильный Б А Х !!! Последствия могут быть самыми разными, от выхода из строя измерительного прибора (амперметра), что обычно и случается, и до выбитых пробок (АЗС) в квартире и обесточивания помещения и возможного поражения током.

Для измерения напряжения на нагрузке необходимо, что бы подключаемый к ней вольтметр не шунтировал нагрузку и не оказывал заметного влияния на результат измерения. Для этого вольтметры изготавливают с очень высоким входным сопротивлением и их наоборот подключают параллельно измеряемой цепи. Благодаря высокому входному сопротивлению вольтметра — сопротивление измеряемой цепи практически не изменяется, или изменяется очень не значительно, не оказывая заметного влияния на результат измерения.

На рисунке выше показан порядок включения амперметра и вольтметра для измерения напряжения на нагрузке и протекающего через неё тока. Так же указана полярность подключения измерительных приборов в измеряемую цепь.

Постоянный и переменный ток.

Кратко напомню — постоянный ток (DC), это такой ток, который в течении определённого промежутка времени не изменяет своей величины и направления.
Переменный ток (AC) — это ток, который в течении определённого промежутка времени периодически изменяется как по величине, так и по направлению.

На рисунке выше, на графиках изображены диаграммы постоянного (а), и переменного (б) тока.
Промежуток времени, на протяжении которого совершается полный цикл изменения тока, называется периодом. Период обозначается буквой Т и измеряется в секундах.
Промежуток времени, на протяжении которого совершается половина полного цикла изменения тока, называется полупериодом. Следовательно, период изменения тока (ЭДС или напряжения) состоит из двух полупериодов. Совершенно очевидно, что все периоды одного и того же переменного тока равны между собой.
В течение одного периода своего изменения,ток дважды достигает максимального значения.
Максимальное значение переменного тока (ЭДС или напряжения) называется его амплитудой или амплитудным значением тока.

Действующее (эффективное) и амплитудное значение переменного синусоидального тока (напряжения).

Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Возникает вопрос, как же его измерять? Для его измерения и введено понятие — «Действующее (или эффективное) значение» переменного тока.

Что же такое действующее (или эффективное) и амплитудное значение переменного тока?
Как Вам попроще объяснить, чтобы было понятно.
Действующее (эффективное) значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время, выделяет такое же количество энергии.
То есть если к какой либо активной нагрузке (нагревательный элемент, лампа накаливания, резистор и т.д.) подключить переменный ток, который за определённый промежуток времени (например 10 секунд) выделит на активной нагрузке то-же количество энергии, тепла на нагревательном элементе, резисторе, или разогреет спираль лампы накаливания до точно такой же светоотдачи, что и постоянный ток какой-то определённой величины за тот же промежуток времени (тоже 10 секунд) — то тогда действующее (эффективное) значение такого переменного тока будет равняться величине постоянного тока.

Все электроизмерительные приборы (амперметры, вольтметры), отградуированы для измерения действующего значения синусоидального тока или напряжения.

Что такое «Амплитудное значение» переменного тока?
Если объяснять попроще, то это самое максимальное значение (величина) синусоидального тока на самом пике (максимуме) синусоиды.
Амплитудное значение переменного тока можно измерить электронно — лучевым осциллографом, так как все осциллографы откалиброваны на измерение амплитудных значений.

Поскольку действующее значение переменного синусоидального тока пропорционально квадратному корню из площади, то оно получается в 1,41 раза меньше его амплитудного значения.
Проще говоря — если измерить величину переменного тока (напряжения) электроизмерительными приборами, отградуированными для измерения переменного синусоидального тока (напряжения), то есть например замерить величину переменного напряжения на вторичной обмотке трансформатора, — то амплитудное значение напряжения на этой обмотке будет соответственно в 1,41 раз больше замеренного.
Это справедливо только для переменного синусоидального тока (напряжения).

Все конденсаторы в выпрямительных фильтрах соответственно заряжаются до величины амплитудного значения.

Можно посчитать, что при действующем напряжении сети 220 В, амплитудное его значение будет составлять 310 вольт (220 помножить на 1,41).

Отсюда вытекает, что если собрать выпрямитель переменного действующего напряжения 220 вольт, то конденсаторы фильтра необходимо применять на рабочее напряжение не менее чем на 350 вольт, так как они заряжаются до амплитудного (максимального) значения переменного напряжения, а ещё лучше не менее 400 вольт, для обеспечения надёжности работы выпрямителя.

Для действующего значения переменного синусоидального напряжения (тока) — справедливы формулы для расчётов сопротивлений, мощности, действующих токов и напряжений — приведённые выше в Законе Ома для постоянного тока.

Ответим на вопросы в начале статьи;

Как рассчитать шунт для амперметра?
Большинство отечественных измерительных головок для амперметров, рассчитываются на полное отклонение при подведении к ним напряжения в 75 мВ (0,075 вольта). У них на шкале имеется надпись «НШ — 75 мВ», или «Наружный шунт 75 мв», или что-то подобное.
Нам стало известно две величины, а именно — необходимый нам ток полного отклонения и напряжение полного отклонения измерительной головки.
Например, нам нужно рассчитать шунт на 20 ампер. По Закону Ома 0,075 делим на 20 = 0,00375 Ом.
Изготовить такой шунт можно из медной проволоки, посмотрев её удельное сопротивление по таблице ЗДЕСЬ . Только необходимо брать проволоку, диаметром желательно не менее 1,5 мм, так как шунт при большом токе будет греться, и показания прибора будет изменяться (при нагреве проволоки увеличится её внутреннее сопротивление).

Почему из 12 вольт переменного напряжения, стало около 16 вольт постоянного — надеюсь Вам стало понятно. У переменного напряжения 12 вольт (действующее его значение) — амплитудное значение будет в 1,41 раз больше, то есть 16,92 вольта, минус около вольта падение напряжения на диодах. В итоге получается около 16 вольт — до которых и заряжаются электролитические конденсаторы фильтра.

Как правильно измерить мощность УНЧ?
Давайте для начала вспомним теорию.
Выходная мощность усилителей НЧ измеряется на синусоидальном сигнале. У идеального двухтактного выходного каскада, максимальное амплитудное значение синусоидального сигнала на выходе может приблизиться к величине равной половине напряжения источника питания.
У каскада по мостовой схеме, выходное напряжение может приблизиться к величине напряжения источника питания.
Говоря другими словами, у автомобильной магнитолы при напряжении питания 13,5 вольт, для двухтактного выходного каскада максимальное выходное напряжение (синус) будет 6,5 вольт, а его действующее значение 4,6 вольта, для мостовой схемы соответственно 13 В. и 9,2 вольта.
Возьмём минимальную нагрузку для этих усилителей 2 Ома, соответственно максимальная выходная мощность (исходя из Закона Джоуля — Ленца) для первой магнитолы, которую она выдаст теоретически — будет 10,6 ватта, для второй — 42,3 ватта (это для нагрузки 2 Ома). На практике не более 10 и не более 40, или и того меньше. Для 4-х Ом соответственно ещё в два раза меньше. Я не говорю уже об искажениях, здесь мы просто измеряем максимальную выходную мощность.

В бытовых условиях измерять выходной сигнала усилителя (при подаче на вход синусоидального сигнала), лучше обычными «цешками» или бытовыми «цифровиками», так как они сразу измеряют действующее значение синусоидального сигнала. На выход усилителя лучше включать при замерах эквивалент нагрузки, то есть сопротивления с мощностью рассеивания, не менее максимально расчётной мощности усилителя, и с сопротивлением, равному сопротивлению предполагаемой нагрузки (это, что-бы не раздражать себя и соседей звуками во время замеров). Дальше, зная максимальное выходное напряжение и сопротивление нагрузки, рассчитываем мощность по вышеприведённым формулам, то есть напряжение в квадрате делённое на сопротивление нагрузки.
Так, что если Вы в магазине увидите подобный аппарат, и продавец Вас будет уверять, что на канал он выдаёт по 60-80 ватт — это развод, рекламный ход и т.д., если только для питания этого усилителя не применяется повышающий преобразователь.

 

vprl.ru

Электрическое напряжение — Википедия

У этого термина существуют и другие значения, см. Напряжение.

Электри́ческое напряже́ние между точками A и B электрической цепи или электрического поля — физическая величина, значение которой равно работе эффективного электрического поля (включающего сторонние поля), совершаемой при переносе единичного пробного электрического заряда из точки A в точку B^[1][2].

При этом считается, что перенос пробного заряда не изменяет распределения зарядов на источниках поля (по определению пробного заряда). Напряжение в общем случае формируется из вкладов двух работ: работы электрических сил AABel{\displaystyle A_{AB}^{el}} и работы сторонних сил AABex{\displaystyle A_{AB}^{ex}}. Если на участке цепи не действуют сторонние силы (то есть AABex=0{\displaystyle A_{AB}^{ex}=0}), работа по перемещению включает только работу потенциального электрического поля AABel{\displaystyle A_{AB}^{el}} (которая не зависит от пути, по которому перемещается заряд), и электрическое напряжение UAB{\displaystyle U_{AB}} между точками A и B совпадает с разностью потенциалов между этими точками (поскольку φA−φB=AABel/q{\displaystyle \varphi _{A}-\varphi _{B}=A_{AB}^{el}/q}). В общем случае напряжение UAB{\displaystyle U_{AB}} между точками A и B отличается от разницы потенциалов между этими точками^[3] на работу сторонних сил по перемещению единичного положительного заряда. Эту работу называют электродвижущей силой EAB{\displaystyle {\mathcal {E}}_{AB}} на данном участке цепи: EAB=AABex/q.{\displaystyle {\mathcal {E}}_{AB}=A_{AB}^{ex}/q.}

UAB=φA−φB+EAB.{\displaystyle U_{AB}=\varphi _{A}-\varphi _{B}+{\mathcal {E}}_{AB}.}

Определение электрического напряжения можно записать в другой форме. Для этого нужно представить работу AABef{\displaystyle A_{AB}^{ef}} как интеграл вдоль траектории L, проложенной из точки A в точку B.

UAB=∫LE→efdl→{\displaystyle U_{AB}=\int \limits _{L}{\vec {E}}_{ef}d{\vec {l}}} — интеграл от проекции эффективной напряжённости поля E→ef{\displaystyle {\vec {E}}_{ef}} (включающего сторонние поля) на касательную к траектории L, направление которой в каждой точке траектории совпадает с направлением вектора dl→{\displaystyle d{\vec {l}}} в данной точке. В электростатическом поле, когда сторонних сил нет, значение этого интеграла не зависит от пути интегрирования и совпадает с разностью потенциалов.

Размерность электрического напряжения в Международной системе величин (англ. International System of Quantities, ISQ), на которой основана Международная система единиц (СИ), — L²MT^-3I^-1. Единицей измерения напряжения в СИ является вольт (русское обозначение: В; международное: V).

Понятие напряжение ввёл Георг Ом в работе 1827 года, в которой предлагалась гидродинамическая модель электрического тока для объяснения открытого им в 1826 году эмпирического закона Ома: U=IR{\displaystyle U\!=IR}.

Напряжение в цепи постоянного тока между точками A и B — работа, которую совершает электрическое поле при переносе пробного положительного заряда из точки A в точку B.

Для описания цепей переменного тока применяются следующие напряжения:

• мгновенное напряжение;
• амплитудное значение напряжения;
• среднее значение напряжения;
• среднеквадратическое значение напряжения;
• средневыпрямленное значение напряжения.

Мгновенное напряжение есть разность потенциалов между двумя точками, измеренная в данный момент времени. Зависит от времени (является функцией времени):

u=u(t).{\displaystyle u=u(t).}

Амплитудное значение напряжения есть максимальное по модулю значение мгновенного напряжения за весь период колебаний:

UM=max(|u(t)|).{\displaystyle U_{M}=\max(|u(t)|).}

Для гармонических (синусоидальных) колебаний напряжения мгновенное значение напряжения выражается как:

u(t)=UMsin⁡(ωt+ϕ).{\displaystyle u(t)=U_{M}\sin(\omega t+\phi ).}

Для сети переменного синусоидального напряжения со среднеквадратическим значением 220 В амплитудное напряжение равно приблизительно 311,127 В.

Амплитудное напряжение можно измерить с помощью осциллографа.

Среднее значение напряжения (постоянная составляющая напряжения) есть напряжение, определяемое за весь период колебаний, как:

Um=1T∫0Tu(t)dt.{\displaystyle U_{m}={\frac {1}{T}}\int _{0}^{T}u(t)dt.}

Для синусоиды среднее значение напряжения равно нулю.

Среднеквадратическое значение напряжения (устаревшие наименования: действующее, эффективное) есть напряжение, определяемое за весь период колебаний, как:

Uq=1T∫0Tu2(t)dt.{\displaystyle U_{q}={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}u^{2}(t)dt}}.}

Среднеквадратическое значение напряжения наиболее удобно для практических расчётов, так как на линейной активной нагрузке оно совершает ту же работу (например, лампа накаливания имеет ту же яркость свечения, нагревательный элемент выделяет столько же тепла), что и равное ему постоянное напряжение.

Для синусоидального напряжения справедливо равенство:

Uq=12UM≈0,707UM;UM=2Uq≈1,414Uq.{\displaystyle U_{q}={1 \over {\sqrt {2}}}U_{M}\approx 0,707U_{M};\qquad U_{M}={\sqrt {2}}U_{q}\approx 1,414U_{q}.}

В технике и быту при использовании переменного тока под термином «напряжение» имеется в виду именно среднеквадратическое значение напряжения, и все вольтметры проградуированы, исходя из его определения. Однако конструктивно большинство приборов фактически измеряют не среднеквадратическое, а средневыпрямленное (см. ниже) значение напряжения, поэтому для несинусоидального сигнала их показания могут отличаться от истинного значения.

Средневыпрямленное значение напряжения есть среднее значение модуля напряжения:

Um=1T∫0T|u(t)|dt.{\displaystyle U_{m}={\frac {1}{T}}\int \limits _{0}^{T}|u(t)|dt.}

Для синусоидального напряжения справедливо равенство:

Um=2πUM(≈0,637UM)=22πUq(≈0,9Uq).{\displaystyle U_{m}={2 \over \pi }U_{M}(\approx 0,637U_{M})={2{\sqrt {2}} \over \pi }U_{q}(\approx 0,9U_{q}).}

На практике используется редко, однако большинство вольтметров переменного тока (те, в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала и проградуирована по среднеквадратическим значениям.

В цепях трёхфазного тока различают фазное и линейное напряжения. Под фазным напряжением понимают среднеквадратичное значение напряжения на каждой из фаз нагрузки относительно нейтрали, а под линейным — напряжение между подводящими фазными проводами. При соединении нагрузки в треугольник фазное напряжение равно линейному, а при соединении в звезду (при симметричной нагрузке или при глухозаземлённой нейтрали) линейное напряжение в 3{\displaystyle {\sqrt {3}}} раз больше фазного.

На практике напряжение трёхфазной сети обозначают дробью, в числителе которой стоит фазное при соединении в звезду (или, что то же самое, потенциал каждой из линий относительно земли), а в знаменателе — линейное напряжение. Так, в России наиболее распространены сети с напряжением 220/380 В; также иногда используются сети 127/220 В и 380/660 В.

Объект	Тип напряжения	Значение (на вводе потребителя)	Значение (на выходе источника)
Электрокардиограмма	Импульсное	1—2 мВ	—
Телевизионная антенна	Переменное высокочастотное	1—100 мВ	—
Гальванический цинковый элемент типа АА («пальчиковый»)	Постоянное	1,5 В	—
Литиевый гальванический элемент	Постоянное	3—3,5 В (в исполнении пальчикового элемента, на примере Varta Professional Lithium, AA)	—
Логические сигналы компьютерных компонентов	Импульсное	3,3 В; 5 В	—
Батарейка типа 6F22 («Крона»)	Постоянное	9 В	—
Силовое питание компьютерных компонентов	Постоянное	5 В, 12 В	—
Электрооборудование автомобилей	Постоянное	12/24 В	—
Блок питания ноутбука и жидкокристаллических мониторов	Постоянное	19 В	—
Сеть «безопасного» пониженного напряжения для работы в опасных условиях	Переменное	36—42 В	—
Напряжение наиболее стабильного горения свечи Яблочкова	Постоянное	55 В	—
Напряжение в телефонной линии (при опущенной трубке)	Постоянное	60 В	—
Напряжение в электросети Японии	Переменное трёхфазное	100/172 В	—
Напряжение в домашних электросетях США	Переменное трёхфазное	120 В / 240 В (сплит-фаза)	—
Напряжение в бытовых электросетях России	Переменное трёхфазное	220/380 В	230/400 В
Разряд электрического ската	Постоянное	до 200—250 В	—
Контактная сеть трамвая и троллейбуса	Постоянное	550 В	600 В
Разряд электрического угря	Постоянное	до 650 В	—
Контактная сеть метрополитена	Постоянное	750 В	825 В
Контактная сеть электрифицированной железной дороги (Россия, постоянный ток)	Постоянное	3 кВ	3,3 кВ
Распределительная воздушная линия электропередачи небольшой мощности	Переменное трёхфазное	6—20 кВ	6,6—22 кВ
Генераторы электростанций, мощные электродвигатели	Переменное трёхфазное	10—35 кВ	—
На аноде кинескопа	Постоянное	7—30 кВ	—
Статическое электричество	Постоянное	1—100 кВ	—
На свече зажигания автомобиля	Импульсное	10—25 кВ	—
Контактная сеть электрифицированной железной дороги (Россия, переменный ток)	Переменное	25 кВ	27,5 кВ
Пробой воздуха на расстоянии 1 см		10—20 кВ	—
Катушка Румкорфа	Импульсное	до 50 кВ	—
Пробой слоя трансформаторного масла толщиной 1 см		100—200 кВ	—
Воздушная линия электропередачи большой мощности	Переменное трёхфазное	35 кВ, 110 кВ, 220 кВ, 330 кВ	38 кВ, 120 кВ, 240 кВ, 360 кВ
Электрофорная машина	Постоянное	50—500 кВ	—
Воздушная линия электропередачи сверхвысокого напряжения (межсистемные)	Переменное трёхфазное	500 кВ, 750 кВ, 1150 кВ	545 кВ, 800 кВ, 1250 кВ
Трансформатор Тесла	Импульсное высокочастотное	до нескольких МВ	—
Генератор Ван де Граафа	Постоянное	до 7 МВ	—
Грозовое облако	Постоянное	От 2 до 10 ГВ	—

ru.wikipedia.org

Список параметров напряжения и силы электрического тока — Википедия

В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока

Значения переменного напряжения (тока)[править | править код]

Далее для определенности будем говорить большей частью о параметрах напряжения, хотя они справедливы и для токов.

Мгновенное значение[править | править код]

Мгновенное значение — это значение сигнала в определённый момент времени, функцией которого является (  u(t) ,i(t){\displaystyle u(t)~,\quad i(t)}    ). Мгновенные значения медленно изменяющегося сигнала можно определить с помощью малоинерционного вольтметра постоянного тока, самописца или шлейфового осциллографа, для периодических быстротекущих процессов используется электронно-лучевой или цифровой осциллограф.

Амплитудное значение[править | править код]

• Амплитудное (пиковое) значение, иногда называемое просто «амплитуда» — наибольшее мгновенное значение напряжения или силы тока за период (без учёта знака):

UM=max(|u(t)|) ,IM=max(|i(t)|){\displaystyle U_{M}=\max(|u(t)|)~,\qquad I_{M}=\max(|i(t)|)}

Пиковое значение напряжения измеряется с помощью импульсного вольтметра или осциллографа.

Среднеквадратичное значение[править | править код]

Среднеквадратичное значение (устар. действующее, эффективное) — корень квадратный из среднего значения квадрата напряжения или тока.

U=1T∫0Tu2(t)dt ,I=1T∫0Ti2(t)dt{\displaystyle U={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}u^{2}(t)dt}}~,\qquad I={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}i^{2}(t)dt}}}

Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I{\displaystyle I} и U{\displaystyle U} совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.

Когда не оговаривают особо, то обычно имеют в виду именно среднеквадратичные значения величины напряжения или силы тока.

В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.

Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом.

Среднее значение[править | править код]

Среднее значение (смещение) — постоянная составляющая напряжения или силы тока

U=1T∫0Tu(t)dt ,I=1T∫0Ti(t)dt{\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}u(t)dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}i(t)dt}

В электротехнике используется редко, но сравнительно часто используется в радиотехнике (ток смещения и напряжение смещения). Геометрически это разность площадей под и над осью времени, делённая на период. Для синусоидального сигнала смещение равно нулю.

Средневыпрямленное значение[править | править код]

Средневыпрямленное значение — среднее значение модуля сигнала

U=1T∫0T∣u(t)∣dt ,I=1T∫0T∣i(t)∣dt{\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}\mid u(t)\mid dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}\mid i(t)\mid dt}

На практике используется редко, однако большинство измерительных приборов переменного тока — магнитоэлектрической системы (т. е., в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку. В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.

Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.

• Коэффициент формы кривой переменного напряжения (тока) — величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению. Для синусоидального напряжения (тока) равен π/22≈1.11{\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11}.

• Коэффициент амплитуды кривой переменного напряжения (тока) — величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) равен 2{\displaystyle {\sqrt {2}}}.

• Размах пульсации напряжения (тока) — величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени

• Коэффициент пульсации напряжения (тока) — величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
  • Коэффициент пульсации напряжения (тока) по действующему значению — величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
  • Коэффициент пульсации напряжения (тока) пo среднему значению — величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей

Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)

Литература[править | править код]

Нормативно-техническая документация[править | править код]

ru.wikipedia.org

Параметры переменного напряжения | Практическая электроника

Как вы помните из предыдущей статьи, переменное напряжение – это напряжение, которое меняется со временем. Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами.

Среднее значение напряжения

Среднее значение переменного напряжения Uср – это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.

среднее значение напряжения за период

Например,чему равняется среднее значение напряжения за эти два полупериода? В данном случае ноль вольт. Почему так? Площади S1 и S2 равны. Но все дело в том, что площадь S2 берется со знаком “минус”. А так как площади равны, то в сумме они дают ноль: S1+(-S2)=S1-S2=0. Для бесконечного по времени синусоидального сигнала среднее значение напряжения также равняется нулю.

То же самое касается и других сигналов, например, двухполярного меандра. Меандр – это прямоугольный сигнал, у которого длительности паузы и импульса равны. В этом случае его среднее напряжение также будет равняться нулю.

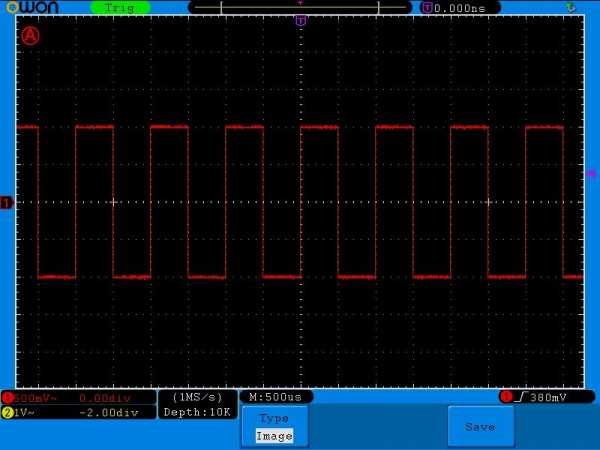меандр

Средневыпрямленное значение напряжения

Чаще всего используют средневыпрямленное значение напряжения Uср. выпр. То есть площадь сигнала, которая “пробивает пол” берут не с отрицательным знаком, а с положительным.

средневыпрямленное значение напряжения будет уже равняться не нулю, а S1+S2=2S1=2S2. Здесь мы суммируем площади, независимо от того, с каким они знаком.

На практике средневыпрямленное значение напряжения получить легко, использовав диодный мост. После выпрямления синусоидального сигнала, график будет выглядеть вот так:

выпрямленное переменное напряжение после диодного моста

Для того, чтобы примерно узнать, чему равняется средневыпрямленное напряжение, достаточно узнать максимальную амплитуду синусоидального сигнала Umax и сосчитать ее по формуле:

Среднеквадратичное значение напряжения

Чаще всего используют среднеквадратичное значение напряжения или его еще по-другому называют действующим. В литературе обозначается просто буквой U. Чтобы его вычислить, тут уже  простым графиком не отделаешься. Среднеквадратичное значение –  это значение постоянного напряжения, который, проходя через  нагрузку (скажем, лампу накаливания), выделяет за тот же промежуток времени такое же количество мощности, какое выделит в этой нагрузке переменное напряжение. В английском языке среднеквадратичное напряжение  обозначается так: RMS (rms) – root mean square.

Связь между амплитудным и среднеквадратическим значением устанавливается через коэффициент амплитуды K_a:

Вот некоторые значения коэффициента амплитуды K_a для некоторых сигналов переменного напряжения:

Более точные значения 1,41 и 1,73 – это √2 и √3 соответственно.

Как измерить среднеквадратичное значение напряжения

Для правильного замера среднеквадратического значения напряжения у нас должен быть мультиметр с логотипом T-RMS. RMS – как вы уже знаете – это среднеквадратическое значение. А что за буква “T” впереди? Думаю, вы помните, как раньше была мода на одно словечко: “тру”. “Она вся такая тру…”, “Ты тру или не тру?” и тд. Тру (true) – с англ. правильный, верный.

Так вот, T-RMS  расшифровывается как True RMS –  “правильное среднеквадратическое значение”. Мои токоизмерительные клещи могут замерять этот параметр без труда, так как на них есть логотип “T-RMS”.

мультиметр с True RMS

Проведем небольшой опыт. Давайте соберем вот такую схемку:

Выставим на моем китайском генераторе частоты треугольный сигнал с частотой, ну скажем, 100 Герц

генератор частоты

А вот осциллограмма этого сигнала. Внизу, в красной рамке, можно посмотреть его параметры

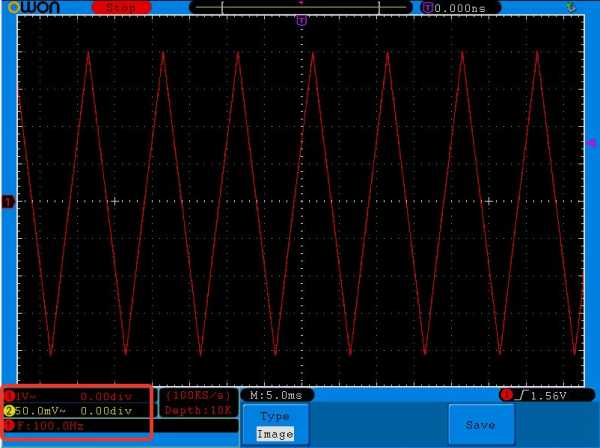треугольный сигнал

И теперь вопрос: чему будет равно среднеквадратическое напряжение этого сигнала?

Так как один квадратик у нас равняется 1 Вольт (мы это видим внизу осциллограммы в красной рамке), то получается, что амплитуда Umax этого треугольного сигнала равняется 4 Вольта. Для того, чтобы рассчитать среднеквадратическое напряжение, мы воспользуемся формулой:

Итак, смотрим нашу табличку и находим интересующий нас сигнал:

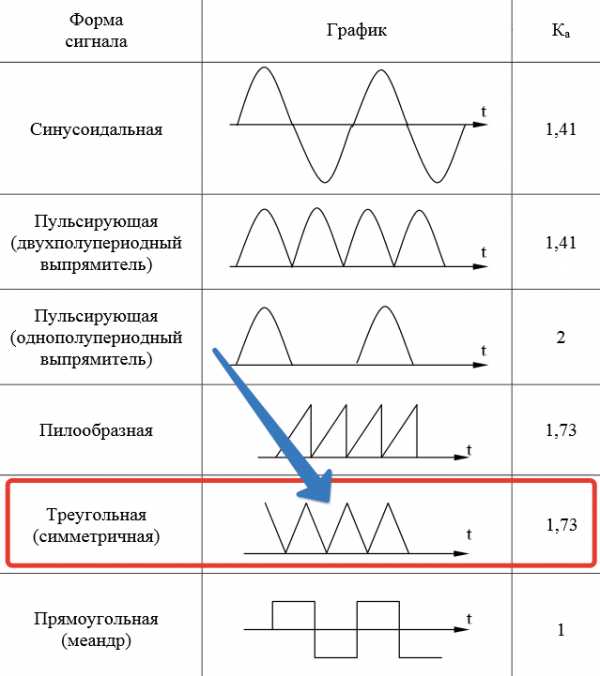
Для нас не важно, пробивает ли сигнал “пол” или нет, главное, чтобы сохранялась форма сигнала. Видим, что наш коэффициент амплитуды K_a= 1,73.

Подставляем его в формулу и вычисляем среднеквадратическое значение нашего треугольного сигнала

Проверяем нашим прибором, так ли оно на самом деле?

Супер! И в правду Тrue RMS.

Замеряем это же самое напряжение с помощью моего китайского мультиметра

Он меня обманул :-(. Он умеет измерять только среднеквадратическое значение синусоидального сигнала, а у нас сигнал треугольный.

Самый интересный сигнал в плане расчетов – это двуполярный меандр, ну тот есть тот, который “пробивает пол”.

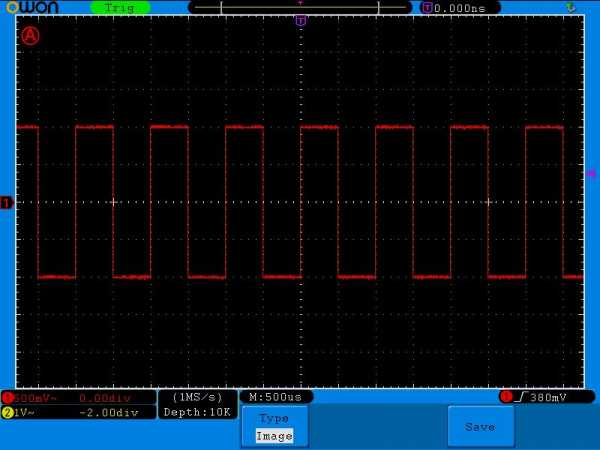
Его амплитудное Umax, средневыпрямленное Uср.выпр. и среднеквадратичное напряжение U равняется одному и тому же значению. В данном случае это 1 Вольт.

Вот вам небольшая картинка, чтобы не путаться

среднее, среднеквадратичное и пиковое значения напряжения

• Сред.  – средневыпрямленное значение сигнала. Это и есть площадь под кривой
• СКЗ – среднеквадратичное напряжение. Как мы видим, для синусоидальных сигналов, оно будет больше, чем средневыпрямленное.
• Пик. – амплитудное значение сигнала
• Пик-пик. – размах или двойная амплитаду. Или иначе, амплитуда от пика до пика.

Так что же все-таки показывает мультиметр при измерении переменного напряжения? Показывает он НЕ амплитудное, НЕ среднее  и НЕ среднее выпрямленное напряжение, а среднее квадратическое, то есть действующее напряжение! Об этом всегда помним.

www.ruselectronic.com

Действующее значение переменного тока — Википедия

Материал из Википедии — свободной энциклопедии

Действующее (эффективное) значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.

В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение переменного тока. Иначе говоря, действующее значение переменного тока можно определить по формуле:

I=1T∫0Ti2dt.{\displaystyle I={\sqrt {{\frac {1}{T}}\int _{0}^{T}i^{2}dt}}.}

Действующее значение в типичных случаях[править | править код]

Приведены формулы для электрического тока. Аналогичным образом определяются действующие значения ЭДС и напряжения.

Синусоида[править | править код]

Для синусоидального тока:

I=12⋅Im≈0,707⋅Im,{\displaystyle I={\frac {1}{\sqrt {2}}}\cdot I_{m}\approx 0{,}707\cdot I_{m},}

где

Im{\displaystyle I_{m}} — амплитудное значение тока.

Прямоугольная форма[править | править код]

Для тока, имеющего форму однополярного прямоугольного импульса, действующее значение тока зависит от скважности:

I=ImD,{\displaystyle I=I_{m}{\sqrt {D}},}

где

D{\displaystyle D} — коэффициент заполнения (величина, обратная скважности).

В частности, для тока, имеющего форму однополярного меандра (коэффициент заполнения 0,5):

I=Im0,5≈0,707⋅Im.{\displaystyle I=I_{m}{\sqrt {0,5}}\approx 0,707\cdot I_{m}.}

Для тока, имеющего форму двухполярного меандра:

I=Im.{\displaystyle I=I_{m}.}

Треугольная форма[править | править код]

Для тока треугольной и пилообразной формы (независимо от того, меняется ли направление тока):

I=13⋅Im≈0,577⋅Im.{\displaystyle I={\frac {1}{\sqrt {3}}}\cdot I_{m}\approx 0{,}577\cdot I_{m}.}

Трапециевидная форма[править | править код]

Для тока трапециевидной формы действующее значение можно определить разбив период на отрезки положительного фронта, действия максимального значения и отрицательного фронта:

I=Imt1+3t2+t33T,{\displaystyle I=I_{m}{\sqrt {\frac {t_{1}+3t_{2}+t_{3}}{3T}}},}

где

t1{\displaystyle t_{1}} — длительность положительного фронта;

t2{\displaystyle t_{2}} — длительность действия максимального значения;

t3{\displaystyle t_{3}} — длительность отрицательного фронта;

T{\displaystyle T} — длительность полного периода.

Дугообразная форма[править | править код]

Для тока имеющего форму дуги (половины окружности):

I=Im23≈0,816⋅Im.{\displaystyle I=I_{m}{\sqrt {\frac {2}{3}}}\approx 0{,}816\cdot I_{m}.}

В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value — эффективное значение. Также применяется аббревиатура RMS или rms — root mean square — среднеквадратичное (значение).

Электроизмерительные приборы (амперметры, вольтметры) для измерения в цепях переменного тока обычно градуируются так, чтобы их показания соответствовали действующему значению синусоидального тока или напряжения. При измерении несинусоидальных токов и напряжений приборы различных систем могут давать разные показания^[1].

• «Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
• Курс физики. А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
• «Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 — § 7.10

ru.wikipedia.org

Переменный ток — Википедия

     Синусоидальный

Переме́нный ток — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным^[1].

Хотя переменный ток часто переводят на английский как alternating current, эти термины не эквивалентны. Термин alternating current (AC) в узком смысле означает синусоидальный ток, в широком смысле — периодический знакопеременный ток (то есть периодический двунаправленный ток). Условное обозначение на электроприборах: ∼{\displaystyle \thicksim } или ≈{\displaystyle \thickapprox } (знак синусоиды), или латинскими буквами AC{\displaystyle AC}.

Так как переменный ток в общем случае меняется в электрической цепи не только по величине, но и по направлению, то одно из направлений переменного тока в цепи считают условно положительным, а другое, противоположное первому, условно отрицательным. В соответствии с этим и величину мгновенного значения переменного тока в первом случае считают положительной, а во втором случае — отрицательной.

Переменный ток — величина алгебраическая, знак его определяется тем, в каком направлении в рассматриваемый момент времени протекает ток в цепи — в положительном или отрицательном.

Величина переменного тока, соответствующая данному моменту времени, называется мгновенным значением переменного тока.

Максимальное мгновенное значение переменного тока, которое он достигает в процессе своего изменения, называется амплитудой тока Im{\displaystyle I_{m}}.

График зависимости переменного тока от времени называется развёрнутой диаграммой переменного тока.

Развёрнутая диаграмма переменного синусоидального тока

На рисунке приведена развёрнутая диаграмма переменного тока, изменяющегося с течением времени по величине и направлению. На горизонтальной оси 0t{\displaystyle 0t} отложены в определённом масштабе отрезки времени, а по вертикальной оси — величины тока, вверх — от начальной точки 0{\displaystyle 0} — положительные, вниз — отрицательные. Часть развёрнутой диаграммы тока, расположенная выше оси времени 0t{\displaystyle 0t}, характеризует изменение положительных величин во времени, а часть, расположенная ниже оси времени 0t{\displaystyle 0t}, — изменение отрицательных величин.

В начальный момент времени t=0{\displaystyle t=0} ток равен нулю (i=0){\displaystyle (i=0)}. Затем он с течением времени растёт в положительном направлении, в момент времени t=T4{\displaystyle t={\frac {T}{4}}} достигает максимального значения, после чего убывает по величине и в момент времени t=T2{\displaystyle t={\frac {T}{2}}} становится равным нулю. Затем, пройдя через нулевое значение, ток меняет свой знак на противоположный, то есть становится отрицательным, затем растёт по абсолютной величине, затем достигает максимума при t=34T{\displaystyle t={\frac {3}{4}}T}, после чего убывает и при t=T{\displaystyle t=T} становится равным нулю.

Развёрнутая диаграмма периодического переменного тока

Периодическим переменным током называется такой электрический ток, который через равные промежутки времени повторяет полный цикл своих изменений, возвращаясь к своей исходной величине.

На представленной диаграмме мы видим, что через равные промежутки времени T{\displaystyle T} график тока воспроизводится полностью без каких-либо изменений.

Время T{\displaystyle T}, в течение которого переменный периодический ток совершает полный цикл своих изменений, возвращаясь к своей исходной величине, называется периодом переменного тока.

Величина, обратная периоду, называется частотой переменного тока:

f=1T{\displaystyle f={\frac {1}{T}}}, где

f{\displaystyle f} — частота переменного тока;

T{\displaystyle T} — период переменного тока.

Если выразить время T{\displaystyle T} в секундах (sec), то будем иметь:

f=1T[1sec]{\displaystyle f={\frac {1}{T}}\left[{\frac {1}{sec}}\right]}, то есть размерность частоты переменного тока выражается в 1/с.

Частота переменного тока численно равна числу периодов в секунду.

За единицу измерения частоты переменного тока принят 1 герц (1 гц, 1 Гц, 1 Hz).

Герц — единица Международной системы единиц (СИ), названа в честь Генриха Герца. Через основные единицы СИ герц выражается следующим образом: 1 Гц = 1 с⁻¹. Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.

Частота переменного тока равна одному герцу, если период тока равен одной секунде (один полный цикл за одну секунду).

Стандарты частоты[править | править код]

В большинстве стран в электротехнике применяются частоты 50 или 60 Гц (60 Гц — этот вариант принят в США и Канаде). В некоторых странах, например, в Японии, используются оба стандарта (см. Промышленная частота переменного тока).

Частота 16 ⅔ Гц до сих пор используется в некоторых европейских железнодорожных сетях (Австрия, Германия, Норвегия, Швеция и Швейцария), частота 25 Гц — на старых железнодорожных линиях США. (См. Электрификация железных дорог переменным током пониженной частоты).

В авиации и военной технике для снижения массы устройств или с целью повышения частоты вращения электродвигателей переменного тока применяется частота 400 Гц.

Число оборотов ротора n[1min]{\displaystyle n\left[{\frac {1}{min}}\right]} синхронного электродвигателя определяется по формуле:

n=60fp{\displaystyle n={\frac {60f}{p}}}, где

f{\displaystyle f} — частота переменного тока;

p{\displaystyle p} — число пар полюсов.

Так как минимальное число пар полюсов равно единице, тогда синхронный электродвигатель, работающий на переменном токе частотой 50 герц разовьёт 3 000 оборотов в минуту, а электродвигатель, работающий на переменном токе частотой 400 герц, разовьёт 24 000 оборотов в минуту. Частота вращения ротора асинхронного электродвигателя меньше, чем частота питающего его тока и зависит от нагрузки. Скольжение — разность между частотой вращения вращающегося магнитного поля и частотой вращения ротора.

В технике связи применяются частоты более высокие, и в частности в радиотехнике — порядка миллионов и миллиардов герц.

Синусоидальным током называется периодический переменный ток, который с течением времени изменяется по гармоническому закону синуса.

Синусоидальный ток — элементарный, то есть его невозможно разложить на другие более простые переменные токи^[2].

Переменный синусоидальный ток выражается формулой:

i=Imsin⁡ωt{\displaystyle i=I_{m}\sin \omega t}, где

Im{\displaystyle I_{m}} — амплитуда синусоидального тока;

ωt{\displaystyle \omega t} — некоторый угол, называемый фазой синусоидального тока.

Фаза синусоидального тока ωt{\displaystyle \omega t} изменяется пропорционально времени t{\displaystyle t}.

Множитель ω{\displaystyle \omega }, входящий в выражение фазы ωt{\displaystyle \omega t} — величина постоянная, называемая угловой частотой переменного тока (круговой частотой переменного тока).

Угловая частота ω{\displaystyle \omega } синусоидального тока зависит от частоты f{\displaystyle f} этого тока и определяется формулой:

ω=2πf=2πT{\displaystyle \omega =2\pi f={\frac {2\pi }{T}}}, где

ω{\displaystyle \omega } — угловая (круговая) частота синусоидального тока;

f{\displaystyle f} — частота синусоидального тока;

T{\displaystyle T} — период синусоидального тока;

2π{\displaystyle 2\pi } — центральный угол окружности, выраженный в радианах.

Исходя из формулы ω=2πf=2πT{\displaystyle \omega =2\pi f={\frac {2\pi }{T}}}, можно определить размерность угловой (круговой) частоты:

[ω]=[2πT]=[1sec]{\displaystyle \left[\omega \right]=\left[{2\pi \over T}\right]=\left[{1 \over sec}\right]}, где

sec{\displaystyle sec} — время в секундах,

2π{\displaystyle 2\pi } — угол в радианах, является безразмерной величиной.

Фаза ωt{\displaystyle \omega t} синусоидального тока измеряется радианами.

1 радиан = 57,29° = 57°17′, угол 90° = π2{\displaystyle \pi \over 2} радиан, угол 180° = π{\displaystyle \pi } радиан, угол 270° = 3π2{\displaystyle 3\pi \over 2} радиан, угол 360° = 2π{\displaystyle 2\pi } радиан,
где π=3,14{\displaystyle \pi =3,14} радиан; π{\displaystyle \pi } — число «Пи», ° — угловой градус и ′ — угловая минута.

---

Формула i=Imsin⁡ωt{\displaystyle i=I_{m}\sin \omega t} описывает случай, когда наблюдение за изменением переменного синусоидального тока начинается с момента времени t=0{\displaystyle t=0}. Если начальный момент времени не равен нулю, тогда формула для определения мгновенного значения переменного синусоидального тока принимает следующий вид:

i=Imsin⁡(ωt+ψ){\displaystyle i=I_{m}\sin(\omega t+\psi )}, где

(ωt+ψ){\displaystyle (\omega t+\psi )} — фаза переменного синусоидального тока;

ψ{\displaystyle \psi } — угол, называемый начальной фазой переменного синусоидального тока.

Если в формуле i=Imsin⁡(ωt+ψ){\displaystyle i=I_{m}\sin(\omega t+\psi )} принять t=0{\displaystyle t=0}, то будем иметь

ωt=0{\displaystyle \omega t=0}, ωt+ψ=ψ{\displaystyle \omega t+\psi =\psi } и it=0=Imsin⁡ψ{\displaystyle i_{t=0}=I_{m}\sin \psi }.

Начальная фаза — это фаза синусоидального тока в момент времени t=0{\displaystyle t=0}.

Начальная фаза переменного синусоидального тока может быть положительной (ψ>0){\displaystyle (\psi >0)} или отрицательной (ψ<0){\displaystyle (\psi <0)} величиной. При ψ>0{\displaystyle \psi >0} мгновенное значение синусоидального тока в момент времени t=0{\displaystyle t=0} положительно, при ψ<0{\displaystyle \psi <0} — отрицательно.

Если начальная фаза ψ=π2{\displaystyle \psi ={\frac {\pi }{2}}}, то ток определяется по формуле i=Imsin⁡(ωt+π2){\displaystyle i=I_{m}\sin(\omega t+{\frac {\pi }{2}})}. Мгновенное значение его в момент времени t=0{\displaystyle t=0} равно

it=0=Imsin⁡π2=Im{\displaystyle i_{t=0}=I_{m}\sin {\frac {\pi }{2}}=I_{m}}, то есть равно положительной амплитуде тока.

Если начальная фаза ψ=−π2{\displaystyle \psi =-{\frac {\pi }{2}}}, то ток определяется по формуле i=Imsin⁡(ωt−π2){\displaystyle i=I_{m}\sin(\omega t-{\frac {\pi }{2}})}. Мгновенное значение его в момент времени t=0{\displaystyle t=0} равно

it=0=Imsin⁡(−π2)=−Im{\displaystyle i_{t=0}=I_{m}\sin(-{\frac {\pi }{2}})=-I_{m}}, то есть равно отрицательной амплитуде тока.

Два синусоидальных тока совпадают по фазе друг с другом

Синусоидальные токи сдвинуты по фазе на угол π2{\displaystyle {\frac {\pi }{2}}}

ru.wikipedia.org