| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа. / / Движение по окружности. Уравнение движения по окружности. Угловая скорость. Нормальное = центростремительное ускорение. Период, частота обращения (вращения). Связь линейной и угловой скорости Поделиться:
| |||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | ||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www. | |||||
1.1.8 Движение тела по окружности. Угловая и линейная скорости точки. Центростремительное ускорение точки
Видеоурок: Движение по окружности
Лекция: Движение тела по окружности. Угловая и линейная скорости точки. Центростремительное ускорение точки
Траектория движения — окружность.
Так как скорость — векторная величина, то она зависит не только от модуля значения, но и от направления. Поэтому движение тела по окружности можно назвать равноускоренным. Даже если тело будет двигаться с постоянной по величине скоростью, её направление будет постоянно изменяться.
Любое криволинейное движение можно свести к нескольким движениям по окружности.
Примером данного движения является бег по стадиону, ход стрелки часов, прогулка на корде лошади и другое.Основные характеристики движения1. Линейная скорость
Мгновенная скорость (линейная) — на протяжении всего движения меняет свое направление вдоль касательной к траектории.
Так как траектория движения точки — окружность, то в качестве пути в числителе находится формула длины перемещения.
Поэтому формула мгновенной скорости приобретает следующий вид, где Т — период:
2. Центростремительное ускорение
Направлено перпендикулярно к линейной скорости на протяжении всего движения.
Центростремительное ускорение определяется по формуле:
3. Период вращения
Период вращения — это величина, определяющая время, за которое тело делает одно полное вращение.
Период — это скалярная величина. Основной единицей периода является [Т]=1с.
Период определяется по формуле:
где N — количество оборотов, t — время, за которое они были совершены.
4. Частота вращения
Определяет, насколько часто совершаются обороты в единицу времени.
Частота — скалярная величина. Измеряется в [n] = 1с-1.
Частота определяется по формуле:
5. Угловое перемещение
Угловое перемещение — величина, которая определяется углом поворота радиуса, соединяющего центр описываемой окружности, с точкой, где находится тело, относительно начального его положения.
Данная величина может измеряться в градусной или радианной мере углов.
6. Угловая скорость
Это значение, которое определяет, насколько изменяется угловое перемещение со временем.
Измеряется в 1 рад/с.Определяется по формуле:где
— угловая скорость материальной точки, 1/с
— угол поворота радиус — вектора, рад- промежуток времени, с
Угловое перемещение связано с линейной скоростью и центростремительным ускорением следующей формулой:
Расчетные формулы основных параметров асинхронных двигателей
В таблице 1 представлены расчетные формулы для определения основных параметров асинхронных двигателей.
В данной таблице собраны все формулы, которые касаются расчета параметров асинхронных двигателей.
Используя формулы из данной таблицы, вам больше не придется искать нужную формулу в различных справочниках.
Таблица 1 — Расчетные формулы для определения основных параметров асинхронных двигателей
| Наименование величин | Формулы | Принятые обозначения |
|---|---|---|
| Потребляемая активная мощность из сети, кВт | U1, I1 – линейные значения напряжения, В и тока двигателя, А; cosϕ – коэффициент мощности; | |
| Потребляемая реактивная мощность, квар | ||
| Полезная мощность на валу, кВт | Ƞ — КПД двигателя; | |
| Потребляемый двигателем ток, А | ||
| Вращающий момент двигателя, кГм | nном. | |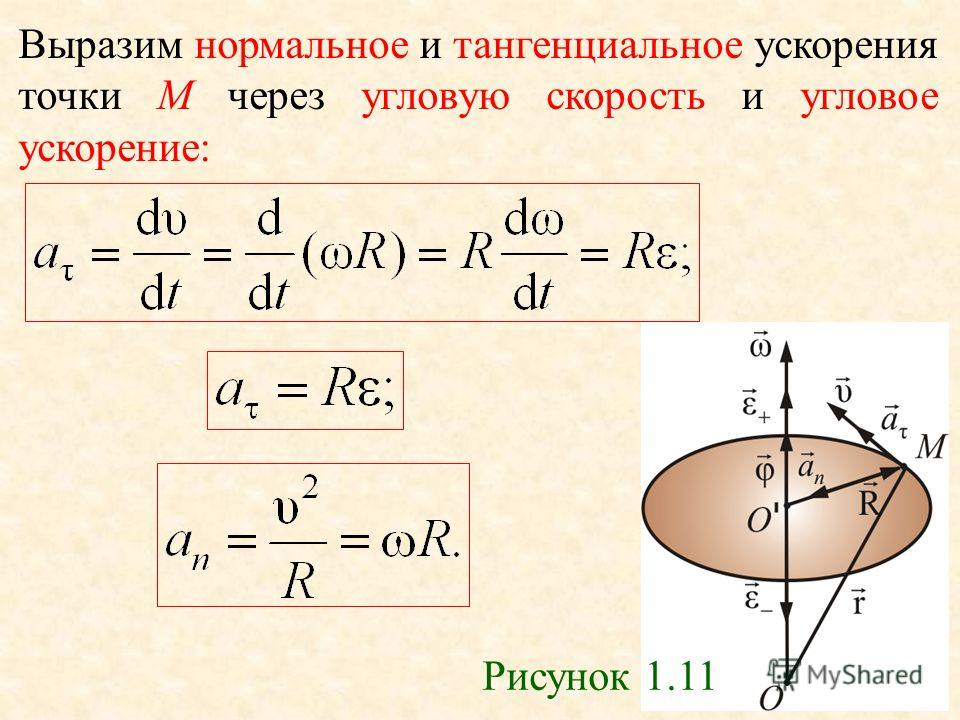
| Синхронная скорость вращения магнитного поля, об/мин | f1 – частота питающего тока, Гц; р – число пар полюсов машины; | |
| Скольжение двигателя | ||
| Скорость вращения ротора при нагрузке, об/мин | ||
| ЭДС обмоток статора и ротора, В | kоб.1, kоб.2 – обмоточные коэффициенты статора и ротора, равные произведению коэффициентов укорочения kу шага и распределения обмотки kw; | |
| Коэффициенты трансформации по напряжению и по току | w1, w2 – числа витков обмоток статора и ротора; m1, m2 – числа фаз в обмотках статора и ротора.  У двигателей с фазным ротором.m2 = 3 у двигателей с короткозамкнутым ротором; m2 = z2, т.е. числу пазов в роторе. | |
| Параметры схемы замещения | zк, rк, хк – полное, активное и индуктивное сопротивления при КЗ двигателя, Ом; ∆Рк – суммарные потери в меди статора и ротора двигателя, Вт; r1, x1 – активное и индуктивное сопротивления обмотки статора, Ом; r2’, x2’ – активные и индуктивные сопротивления ротора, приведенные к обмотке статора, Ом; | |
| Ток холостого хода, А | Iном. – номинальный ток двигателя, А | |
| Критическое скольжение | sinϕ – коэффициент реактивной мощности; kм – коэффициент перегрузочной способности; | |
| Уравнение вращающего момента | Sном. – скольжение при номинальной нагрузке | |
| Скольжение двигателя s2 при введении добавочного сопротивления в ротор | ||
| КПД двигателя при введении добавочного сопротивления в ротор | ||
| Критический максимальный момент, развиваемый в двигательном (+) и генераторном (-) режимах, кГм | U1ф – фазное напряжение, В | |
| Уравнение вращающего момента при добавочном сопротивлении в цепи ротора |
Литература:
1. Справочная книга электрика. В.И. Григорьева, 2004 г.
Всего наилучшего! До новых встреч на сайте Raschet.info.
активное сопротивление двигателя, полное сопротивление двигателя, реактивное сопротивление двигателя, ток двигателяПоделиться в социальных сетях
Благодарность:
Если вы нашли ответ на свой вопрос и у вас есть желание отблагодарить автора статьи за его труд, можете воспользоваться платформой для перевода средств «WebMoney Funding» и «PayPal».
Данный проект поддерживается и развивается исключительно на средства от добровольных пожертвований.
Проявив лояльность к сайту, Вы можете перечислить любую сумму денег, тем самым вы поможете улучшить данный сайт, повысить регулярность появления новых интересных статей и оплатить регулярные расходы, такие как: оплата хостинга, доменного имени, SSL-сертификата, зарплата нашим авторам.
Угловая скорость — это… Что такое Угловая скорость?
Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке Угловая скорость (синяя стрелка) в одну единицу против часовой стрелкиУглова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
- ,
а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.
Единица измерения угловой скорости, принятая в системах СИ и СГС — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли просто «вручную», подсчитывая число оборотов за единицу времени.
Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью , определяется формулой:
где — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) от оси вращения можно считать так: Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.
- В случае плоского вращения, то есть когда все векторы скоростей точек тела лежат (всегда) в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
- Производная угловой скорости по времени есть угловое ускорение.
- Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю).
- Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчета, однако в разных инерциальных системах отсчета может различаться ось или центр вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
- В случае движения одной единственной точки в трехмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:
- , где — радиус-вектор точки (из начала координат), — скорость этой точки. — векторное произведение, — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.
- При измерении угловой скорости в оборотах в секунду (об/с), модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц), то есть в таких единицах . В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости связан с частотой вращения так: . Наконец, при использовании градусов в секунду связь с частотой вращения будет: .
Связь с конечным поворотом в пространстве
- Пусть поворот, изменяющийся во времени, задан величиной угла и ортом оси конечного поворота в пространстве . Тогда угловая скорость, соответствующая этому повороту, равна
- .
- .
- Если для описания поворота используется кватернион, выражаемый через угол и орт оси поворота как , то угловая скорость находится из выражения .
- .
См. также
Литература
- Лурье А. И. Аналитическая механика\\ А. И. Лурье. — М.: ГИФМЛ, 1961. — С. 100-136
И. Лурье. — М.: ГИФМЛ, 1961. — С. 100-136Период вращения тела по окружности. Равномерное движение по окружности. Угловая скорость и угловое ускорение
>>Физика: Период и частота обращения
Равномерное движение по окружности характеризуют периодом и частотой обращения.
Период обращения — это время, за которое совершается один оборот.
Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой Т и определяется по формуле:
Итак, чтобы найти период обращения, надо время, за которое совершено п оборотов, разделить на число оборотов .
Другой характеристикой равномерного движения по окружности является частота обращения.
Частота обращения — это число оборотов, совершаемых за 1 с. Если, например, за время t = 2 с тело совершило n = 10 оборотов, то легко сообразить, что за 1 с оно успевало совершить 5 оборотов.
Это число и выражает частоту обращения. Обозначается она греческой буквой V (читается: ню) и определяется по формуле:
Итак, чтобы найти частоту обращения, надо число оборотов разделить на время, в течение которого они произошли.
За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с -1 (читается: секунда в минус первой степени). Раньше эту единицу называли «оборот в секунду», но теперь это название считается устаревшим.
Сравнивая формулы (6.1) и (6.2), можно заметить, что период и частота — величины взаимно обратные. Поэтому
Формулы (6.1) и (6.3) позволяют найти период обращения Т, если известны число n и время оборотов t или частота обращения V . Однако его можно найти и в том случае, когда ни одна из этих величин неизвестна. Вместо них достаточно знать скорость тела V и радиус окружности r, по которой оно движется.
Для вывода новой формулы вспомним, что период обращения — это время, за которое тело совершает один оборот, т.
е. проходит путь, равный длине окружности (l окр = 2 П r, где П ≈3,14- число «пи», известное из курса математики). Но мы знаем, что при равномерном движении время находится делением пройденного пути на скорость движения. Таким образом,
Итак, чтобы найти период обращения тела, надо длину окружности, по которой оно движется, разделить на скорость его движения.
??? 1. Что такое период обращения? 2. Как можно найти период обращения, зная время и число оборотов? 3. Что такое частота обращения ? 4. Как обозначается единица частоты? 5. Как можно найти частоту обращения, зная время и число оборотов? 6. Как связаны между собой период и частота обращения? 7. Как можно найти период обращения, зная радиус окружности и скорость движения тела?
Отослано читателями из интернет-сайтов
Сборник конспектов уроков по физике, рефераты на тему из школьной программы. Календарно тематическое планирование. физика 8 класс онлайн, книги и учебники по физике.
Школьнику подготовиться к уроку.
Расстояние и время, которое уходит на преодоление этого расстояния, связывает физическое понятие — скорость.
И у человека, как правило, не вызывает вопросов определение этой величины. Все понимают, что двигаться на автомобиле со скоростью 100 км/ч — значит за один час проехать 100 километров.
А как быть, если тело вращается? Например, обычный бытовой вентилятор делает с десяток оборотов в секунду. И в то же время скорость вращения лопастей такова, что их запросто можно остановить рукой без вреда для себя. Земля вокруг своей звезды — Солнца — делает один оборот за целый год, а это более 30 миллионов секунд, но скорость её движения по околозвёздной орбите составляет около 30 километров за одну секунду!
Как же связать привычную скорость с быстротой вращения, как выглядит формула угловой скорости?
Понятие угловой скорости
Понятие угловой скорости используется в изучении законов вращения. Оно применяется ко всем вращающимся телам. Будь то вращение некоторой массы вокруг другой, как в случае с Землёй и Солнцем, или же вращение самого тела вокруг полярной оси (суточное вращение нашей планеты).
Отличие угловой скорости от линейной в том, что она фиксирует изменение угла, а не расстояния в единицу времени. В физике угловую скорость принято обозначать буквой греческого алфавита «омега» — ω.
Классическая формула угловой скорости вращения рассматривается так.
Представим, что вокруг некоторого центра А вращается физическое тело с постоянной скоростью. Его положение в пространстве относительно центра определяется углом φ. В некоторый момент времени t1 рассматриваемое тело находится в точке В. Угол отклонения тела от начального φ1.
Затем тело перемещается в точку С. Оно находится там в момент времени t2. Время, понадобившееся для данного перемещения:
Меняется и положение тела в пространстве. Теперь угол отклонения равен φ2. Изменение угла за период времени ∆t составило:
∆φ = φ2 — φ1.
Теперь формула угловой скорости формулируется следующим образом: угловая скорость определяется как отношение изменения угла ∆φ за время ∆t.
Единицы измерения угловой скорости
Скорость движения тела линейная измеряется в разных величинах.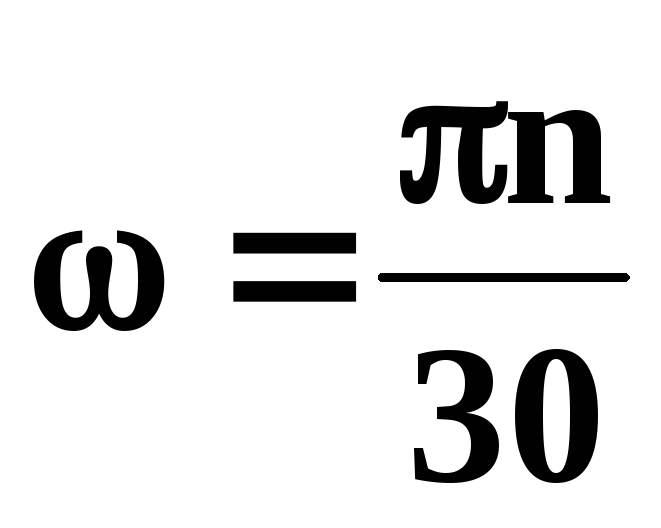
Движение автотранспорта по дорогам привычно указывают в километрах в час, морские суда делают узлы — морские мили в час. Если же рассматривать движение космических тел, то тут чаще всего фигурируют километры в секунду.
Угловая скорость в зависимости от величины и от предмета, который вращается, также измеряется в разных единицах.
Радианы в секунду (рад/с) — классическое мерило скорости в международной системе единиц (СИ). Показывают — на сколько радиан (в одном полном обороте 2 ∙ 3,14 радиан) успевает повернуться тело за одну секунду.
Обороты в минуту (об/мин) — самая распространённая единица для обозначения скоростей вращения в технике. Валы двигателей как электрических, так и автомобильных выдают именно (достаточно посмотреть на тахометр в своём автомобиле) обороты в минуту.
Обороты в секунду (об/с) — используется реже, прежде всего в образовательных целях.
Период обращения
Иногда для определения скорости вращения удобнее пользоваться другим понятием.
Периодом обращения принято называть время, за которое некое тело делает оборот 360° (полный круг) вокруг центра вращения. Формула угловой скорости, выраженная через период обращения, принимает вид:
Выражать периодом обращения быстроту вращения тел оправдано в случаях, когда тело вращается относительно медленно. Вернёмся к рассмотрению движения нашей планеты вокруг светила.
Формула угловой скорости позволяет вычислить её, зная период обращения:
ω = 2П/31536000 = 0,000000199238499086111 рад/с.
Глядя на полученный результат, можно понять, почему, рассматривая вращение небесных тел, удобнее пользоваться именно периодом обращения. Человек видит перед собой понятные цифры и наглядно представляет себе их масштаб.
Связь угловой и линейной скоростей
В некоторых задачах должны быть определены линейная и угловая скорость. Формула трансформации проста: линейная скорость тела равняется произведению угловой скорости на радиус вращения. Как это показано на рисунке.
«Работает» выражение и в обратном порядке, с его помощью определяется и угловая скорость. Формула через скорость линейную получается путём несложных арифметических манипуляций.
Обычно, когда говорят о перемещении, мы представляем себе объект, который движется по прямой. Скорость такого движения принято называть линейной, и расчёт ее средней величины выполняется просто: достаточно найти отношение пройденного расстояния к времени, за которое оно было телом преодолено. Если же объект перемещается по окружности, то в этом случае уже определяется не линейная, а Что это за величина и как ее рассчитывают? Об этом как раз и пойдет разговор в данной статье.
Угловая скорость: понятие и формула
Когда движется по окружности, быстроту ее перемещения можно характеризовать величиной угла поворота радиуса, который соединяет движущийся объект с центром данной окружности. Понятно, что эта величина в зависимости от времени постоянно меняется. Быстрота, с которой этот процесс происходит, и есть не что иное, как угловая скорость.
Другими словами, это отношение величины отклонения радиус-вектора объекта к промежутку времени, которое потребовалось объекту на совершение такого поворота. Формула угловой скорости (1) может быть записана в таком виде:
w = φ / t, где:
φ — угол поворота радиуса,
t — период времени вращения.
Единицы измерения величины
В международной системе общепринятых единиц (СИ) для характеристики поворотов принято использовать радианы. Поэтому 1 рад/с — основная единица, которая используется в расчетах угловой скорости. В то же время никто не запрещает применять градусы (напомним, что один радиан равен 180/пи, или 57˚18’). Также угловая скорость может выражаться в числе оборотов за минуту или за секунду. Если перемещение по окружности происходит равномерно, то данная величина может быть найдена по формуле (2):
где n — частота вращения.
В противном случае подобно тому, как это делают для обычной скорости, рассчитывают среднюю, или мгновенную угловую скорость. Следует отметить, что рассматриваемая величина является векторной. Для определения ее направления обычно используют которое часто применяется в физике. Вектор угловой скорости направлен в ту же сторону, в которую происходит винта с правой резьбой. Другими словами, он устремлен вдоль оси, вокруг которой вращается тело, в ту сторону, откуда вращение видно происходящим против движения часовой стрелки.
Примеры расчета
Предположим, требуется определить, чему равна линейная и угловая скорость колеса, если известно, что его диаметр равен одному метру, а угол вращения изменяется в соответствии с законом φ=7t. Воспользуемся нашей первой формулой:
w = φ / t = 7t / t = 7 с -1 .
Это и будет искомая угловая скорость. Теперь перейдем к поиску привычной нам быстроты перемещения. Как известно, v = s / t. Учитывая, что s в нашем случае — это колеса (l =2π*r), а 2π — один полный оборот, получается следующее:
v = 2π*r / t = w * r = 7 * 0.5 = 3.5 м/с
Вот еще одна задачка на эту тему. Известно, что на экваторе равен 6370 километров. Требуется определить линейную и угловую быстроту движения точек, находящихся на этой параллели, которое возникает в результате вращения нашей планеты вокруг своей оси. В данном случае нам понадобится вторая формула:
w = 2π*n = 2*3,14 *(1/(24*3600)) = 7,268 *10 -5 рад/с.
Осталось выяснить, чему равна линейная скорость: v = w*r = 7,268 *10 -5 *6370 * 1000 = 463 м/с.
Движение тела по окружности с постоянной по модулю скоростью — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги.
Положение тела на окружности определяется радиусом-вектором \(~\vec r\), проведенным из центра окружности. Модуль радиуса-вектора равен радиусу окружности R (рис. 1).
За время Δt тело, двигаясь из точки А в точку В , совершает перемещение \(~\Delta \vec r\), равное хорде АВ , и проходит путь, равный длине дуги l .
Радиус-вектор поворачивается на угол Δφ . Угол выражают в радианах.
Скорость \(~\vec \upsilon\) движения тела по траектории (окружности) направлена по касательной к траектории. Она называется линейной скоростью . Модуль линейной скорости равен отношению длины дуги окружности l к промежутку времени Δt за который эта дуга пройдена:
\(~\upsilon = \frac{l}{\Delta t}.\)
Скалярная физическая величина, численно равная отношению угла поворота радиуса-вектора к промежутку времени, за который этот поворот произошел, называется угловой скоростью :
\(~\omega = \frac{\Delta \varphi}{\Delta t}.\)
В СИ единицей угловой скорости является радиан в секунду (рад/с).
При равномерном движении по окружности угловая скорость и модуль линейной скорости — величины постоянные: ω = const; υ = const.
Положение тела можно определить, если известен модуль радиуса-вектора \(~\vec r\) и угол φ , который он составляет с осью Ox (угловая координата). Если в начальный момент времени t 0 = 0 угловая координата равна φ 0 , а в момент времени t она равна φ , то угол поворота Δφ радиуса-вектора за время \(~\Delta t = t — t_0 = t\) равен \(~\Delta \varphi = \varphi — \varphi_0\). Тогда из последней формулы можно получить кинематическое уравнение движения материальной точки по окружности :
\(~\varphi = \varphi_0 + \omega t.\)
Оно позволяет определить положение тела в любой момент времени t . Учитывая, что \(~\Delta \varphi = \frac{l}{R}\), получаем\[~\omega = \frac{l}{R \Delta t} = \frac{\upsilon}{R} \Rightarrow\]
\(~\upsilon = \omega R\) — формула связи между линейной и угловой скоростью.
Промежуток времени Τ , в течение которого тело совершает один полный оборот, называется периодом вращения :
\(~T = \frac{\Delta t}{N},\)
где N — число оборотов, совершенных телом за время Δt .
За время Δt = Τ тело проходит путь \(~l = 2 \pi R\). Следовательно,
\(~\upsilon = \frac{2 \pi R}{T}; \ \omega = \frac{2 \pi}{T} .\)
Величина ν , обратная периоду, показывающая, сколько оборотов совершает тело за единицу времени, называется частотой вращения :
\(~\nu = \frac{1}{T} = \frac{N}{\Delta t}.\)
Следовательно,
\(~\upsilon = 2 \pi \nu R; \ \omega = 2 \pi \nu .\)
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 18-19.
Движение по окружности – частный случай криволинейного движения. Скорость тела в любой точке криволинейной траектории направлена по касательной к ней (рис.2.1). Скорость как вектор при этом может изменяться и по модулю (величине) и по направлению. Если модуль скоростиостается неизменным, то говорят оравномерном криволинейном движении.
Пусть тело движется по окружности с постоянной по величине скоростью из точки 1 в точку 2.
При этом тело пройдет путь, равный длине дуги ℓ 12 между точками 1 и 2 за времяt. За это же времяtрадиус- векторR, проведенный из центра окружности 0 к точке, повернется на угол Δφ.
Вектор скорости в точке 2 отличается от вектора скорости в точке 1 по направлению на величину ΔV:
;
Для характеристики изменения вектора скорости на величину δv введем ускорение:
(2.4)
Вектор в любой точке траектории направлен по радиусуRкцентру окружности перпендикулярно к вектору скоростиV 2 . Поэтому ускорение, характеризующее при криволинейном движении изменение скоростипо направлению, называютцентростремительным или нормальным . Таким образом, движение точки по окружности с постоянной по модулю скоростью являетсяускоренным .
Если скорость изменяется не только по направлению, но и по модулю (величине), то кроме нормального ускорениявводят еще икасательное (тангенциальное) ускорение, которое характеризует изменение скорости по величине:
или
Направлен вектор по касательной в любой точке траектории (т.е. совпадает с направлением вектора). Угол между векторамииравен 90 0 .
Полное ускорение точки, движущейся по криволинейной траектории, определяется как векторная сумма (рис.2.1.).
.
Модуль вектора
.
Угловая скорость и угловое ускорение
При движении материальной точки по окружности радиус-векторR, проведенный из центра окружности О к точке, поворачивается на угол Δφ (рис.2.1). Для характеристики вращения вводятся понятия угловой скорости ω и углового ускорения ε.
Угол φ можно измерять в радианах. 1 рад равен углу, который опирается на дугу ℓ, равную радиусуRокружности, т.е.
илиℓ 12 = R φ (2.5.)
Продифференцируем уравнение (2.5.)
(2.6.)
Величина dℓ/dt=V мгн. Величину ω =dφ/dtназываютугловой скоростью (измеряется в рад/с). Получим связь между линейной и угловой скоростями:
Величина
ω векторная. Направление вектораопределяетсяправилом винта (буравчика) :
оно совпадает с направлением перемещения
винта, ориентированного вдоль оси
вращения точки или тела и вращаемого в
направлении поворота тела (рис.2.2), т.е.
.
Угловым ускорением называется векторная величина производная от угловой скорости (мгновенное угловое ускорение)
, (2.8.)
Вектор совпадает с осью вращения и направлен в туже сторону, что и вектор, если вращение ускоренное, и в противоположную, если вращение замедленное.
Число оборотов n тела в единицу времени называют частотой вращения .
Время Т одного полного оборота тела называют периодом вращения . При этом R опишет угол Δφ=2π радиан
С учетом сказанного
, (2.9)
Уравнение (2.8) можно записать следующим образом:
(2.10)
Тогда тангенциальная составляющая ускорения
а =R(2.11)
Нормальное ускорение а n можно выразить следующим образом:
с учетом (2.7) и (2.9)
(2.12)
Тогда полное ускорение .
Для вращательного движения с постоянным угловым ускорением можно записать уравнение кинематики по аналогии с уравнением (2.1) – (2.3) для поступательного движения:
,
.
Движение по окружности | fizmatuski.narod.ru
Движение по окружности
Движение по окружности – частный случай криволинейного движения.
При движении по окружности движение может быть:
- С постоянной по величине скоростью V=const
- С одинаково изменяющейся по величине скоростью Δ V= const
- С неодинаково изменяющейся по величине скоростью, ΔV разное, изменяется не одинаково.
!!! Но при этом во всех 3-х случаях V изменяется по направлению (всегда). Движение по окружности – это периодически повторяющееся движение.
Основными характеристиками такого движения являются:
— период – это время 1 полного оборота (t – все время, N – число оборотов за время t)
— частота – число оборотов за 1с. (Гц)
l = 2πR – путь за 1 поворот (длина окружности) (м)
L = 2πRN – путь за N оборотов (м).
1.Рассмотрим движение с постоянной по величине скоростью. По определению, скорость это путь, пройденнфй телом за единицу времени:
— это путевая скорость движения тела по окружности. Зная значения величин, входящих в эту формулу, получим формулы скорости, которые выражают зависимость от основных характеристик движения по окружности:
ω = 2πn – циклическая частота или угловая скорость (число оборотов за 2π секунды), измеряется в (Гц = рад/с).
(Гц)
Аналогия: тело со V тело проходит путь L, со скоростью ω проходит угловой путь φ (поворачивается на угол).
Угловое расстояние: φ = ωt или φ = 2πN
— ускорение, которое показываем изменение направления скорости ( но не величины) т.к. всегда перпендикулярна и направлена к центру окружности, то это ускорение называется центростремительным:
— формула, определяющая центростремительное ускорение. Подставляя вместо скорости её формулы, получим расчётные формулы для центростремительного ускорения:
— формулы для вычисления центростремительного ускорения через основные характеристики.
Рассмотрим частные случаи движения тел по окружности:
1. Движение по одному кругу, но по окружностям разного радиуса:
Если т.А и т.В двигаются синхронно то они вместе совершают 1 оборот, значит Т1 = Т2 (периоды их оборотов одинаковы), а из этого следует
ременная связь или зубчатая связь
=> n1 = n2 => ω1 = ω2, Зная связь между линейной и угловой скоростями, между ускорением и угловой скоростью, получим выражения:
2. Рассмотрим случай, когда два тела совершают круговые движения, но связаны ременной или зубчатой передачей
В этом случае скорости движения двух тел равны (нет провисания ремня ): V1 = V2
Зная формулы, связывающие линейную скорость с периодом вращения и с ускорением, получим:
2. Более сложный случай, когда скорость изменяется по величине.
— это средняя путевая скорость движения тела по окружности, где её изменение по величине характеризуется тангенциальным ускорением: ат , изменение скорости по направлению характеризуется центростремительным ускорением ац , которое в каждой точке разное, так как разной будет скорость движения по величине: . Эти два ускорения взаимно перпендикулярны т.к. ац направлено к центру окружности, а ат — по касательной ( если разгон, то по направлению скорости, если торможение, то в противоположную сторону).Так как тангенциальное ускорение не изменяется, а центростремительное изменяется, то будет изменяться и общее ускорение
Изменение скорости приведёт к изменению связанных с ним характеристик: периода, частоты и угловой скорости вращения.
Вернуться к конспектам урока
Асинхронные электродвигатели (страница 2)
1. Определить угловую скорость вращении ротора асинхронного электродвигателя, если обмотка статора четырехполюсная, частота напряжения сети, к которой присоединен электродвигатель, 50 Гц и скольжение ротора равно 3,5%.
Решение:
Частота токов, проходящих в обмотках статора, равна частоте напряжения сети:
Кроме того, известно, что обмотка статора четырехполюсная, т. е. число пар полюсов р = 2.
Скорость вращения магнитного потока, вызываемого трехфазной системой токов, проходящих в обмотках статора, зависит от частоты этих токов и числа пар полюсов обмотки р, так как , откуда число оборотов в минуту вращающегося синхронно магнитного потока
Угловая скорость вращения
Вращение ротора асинхронного электродвигателя возможно лишь при наличии отставания ротора от вращающегося магнитного потока. Величина, характеризующая это отставание, называется скольжением:
где — скорость вращения магнитного потока;
— скорость вращения ротора.
Подставив числовые значения, получим
откуда
Угловая скорость вращения ротора
2. На щитке асинхронного электродвигателя значится: 730 об/мин, 50 Гц.
Определить скольжение ротора, вращающегося с указанной скоростью, и число пар полюсов обмотки статора. Каким было скольжение ротора в первые мгновения пуска?
Решение:
В табл. 13 синхронных скоростей вращения при частоте 50 Гц ближайшей скоростью вращения (по отношению к скорости ) является скорость .
Следовательно, скольжение ротора
Число пар полюсов обмотки статора
Число полюсов
В момент пуска ротор неподвижен . Поэтому скольжение при пуске
Такое значение имеет скольжение ротора в момент пуска любого асинхронного электродвигателя.
Таблица 13
р пар полюсов | 1 | 2 | 3 | 4 | 5 |
n, об/мин | 3000 | 1500 | 1000 | 750 | 600 |
3. В разрыв провода линии, соединяющей контактные кольца ротора асинхронного электродвигателя с трехфазным реостатом, введен магнитоэлектрический амперметр, шкала которого имеет нулевое значение посередине (рис. 80). Разомкнув рубильник, шунтировавший амперметр во время разбега ротора, не поднимая щеток, наблюдали за отклонениями амперметра: оказалось, что за полминуты указательная стрелка прибора совершила 60 полных колебаний.
Определить скорость вращения ротора в течение указанного промежутка времени, если обмотка статора шестиполюсная и частота напряжения сети 50 Гц.
Решение:
Полное колебание указательной стрелки соответствует полному периоду тока в обмотке ротора. Если 60 полных колебаний (периодов) произошло за полминуты, то число полных колебаний (периодов) в секунду равно двум. Следовательно,
Магнитный поток в асинхронном электродвигателе вращается относительно ротора со скоростью, равной разности скоростей:
причем частота тока в роторе
Подставив числовые значения, получим
При шестиполюсной обмотке статора и частоте токов в цепи статора скорость вращения магнитного потока
Подставим в выражение для величины
откуда скорость вращения ротора
Скольжение ротора
4. Когда трехфазный асинхронный двигатель с фазным ротором присоединили к сети с линейным напряжением 220 В, напряжение между контактными кольцами при разомкнутой обмотке ротора составило 90 В.
Определить коэффициент трансформации, рассматривая этот электродвигатель как трансформатор в режиме холостого хода, если обмотки статора и ротора соединены звездой.
Решение:
Фазное напряжение на обмотке статора при схеме соединения звездой в раз меньше линейного напряжения. Следовательно,
Фазное напряжение на обмотке ротора
Коэффициент трансформации фазных напряжений
5. Асинхронный электродвигатель с короткозамкнутым ротором характеризуется отношением вращающих моментов соответственно при пуске и при номинальном режиме .
Можно ли осуществить пуск двигателя в случае полной его нагрузки на валу и понижения напряжения в сети на 5 и 10%? К сети присоединен статор.
Решение:
Вращающий момент асинхронного двигателя прямо пропорционален квадрату напряжения в сети:
Следовательно, если напряжение в сети понизится на 5% и составит , то вращающий момент
Отношение
Так как пусковой момент при номинальном напряжении , то при понижении напряжения в сети на 5% пусковой момент
Таким образом, пуск при этих условиях позволит электродвигателю развить вращающий момент больше номинального.
Если напряжение в сети понизится на 10% и составит , то вращающий момент
Пусковой момент при указанном понижении напряжения
Обозначим через долю, которую составляет пусковой вращающий момент от вращающего момента при номинальном напряжении. Тогда для возможности пуска электродвигателя при номинальной нагрузке должно быть выполнено равенство
Поэтому при пуске электродвигателя напряжение сети может составлять от номинального напряжения долю
Таким образом, при заданной кратности пускового момента от номинального понижение напряжения в сети может происходить на и пуск может быть осуществлен при номинальной нагрузке на валу электродвигателя.
6. Асинхронный электродвигатель с короткозамкнутым ротором типа А51-4 имеет следующие номинальные данные: ; кратность вращающих моментов .
Определить вращающие моменты: номинальный , максимальный и пусковой .
Решение:
Номинальный вращающий момент можно определить из основного соотношения
Вращающий момент измерен в и мощность Р — в Вт. При этом
Если подставить сюда в качестве Р мощность, измеренную в киловаттах, то число будет в 1000 раз меньше.
Таким образом, при тех же единицах измерения вращающего момента получим
Подставим величины номинального режима:
Используя известные кратности моментов, максимальный вращающий момент
пусковой вращающий момент
7. Асинхронный электродвигатель развивает номинальную мощность при номинальной скорости вращения ротора , имея перегрузочную способность 2,1.
Выразить зависимость между вращающим, моментом и скольжением ротора S электродвигателя.
Решение:
Номинальный вращающий момент
Перегрузочная способность l = 2,1 представляет собой отношение максимального вращающего момента к номинальному вращающему моменту . Следовательно,
Номинальному вращающему моменту соответствует и номинальное скольжение
где в качестве подставлена ближайшая большая (по отношению к ) синхронная скорость вращения магнитного потока статора.
Зависимость между вращающим моментом и скольжением ротора s в асинхронном двигателе выражается формулой
где означает критическое скольжение, а и s соответствуют одному и тому же режиму работы. Если в левую часть подставить , то в качестве s следует подставить . Тогда можно определить критическое скольжение , при котором имеет место момент . В этом случае получается квадратное уравнение, из которого берут большее значение корня.
Так как
Разделив на 0,238 левую и правую части равенства и сосредоточив все члены в одной стороне, получим
Корни полученного квадратного уравнения
Далее берется только больший из корней (при положительном знаке перед корнем):
Подставив в формулу, выражающую зависимость между вращающим моментом и скольжением ротора s, численные значения , получим требуемую зависимость
Угловая скорость Земли — Вселенная сегодня
[/ caption]
Планета Земля совершает три движения: она вращается вокруг своей оси, что дает нам день и ночь; он вращается вокруг Солнца, давая нам времена года, и проходит через Млечный Путь вместе с остальной частью Солнечной системы. В каждом случае ученые пытались рассчитать не только время, необходимое для этого, но и соответствующие относительные скорости. Когда речь идет о вращении Земли вокруг своей оси, этот процесс занимает 23 часа 56 минут 4 часа.09 секунд этот процесс известен как звездные сутки, а скорость, с которой он движется, известна как угловая скорость Земли. Это в равной степени относится к Земле, вращающейся вокруг оси Солнца и центра Галактики Млечный Путь.
В физике угловая скорость — это векторная величина, которая определяет угловую скорость объекта и ось, вокруг которой объект вращается. Единица измерения угловой скорости в системе СИ — радианы в секунду, хотя она может быть измерена в других единицах, таких как градусы в секунду, обороты в секунду и т. Д.и обычно обозначается символом омега (ω, реже Ω). Радиан по определению — это единица измерения, которая связывает радиус дуги, длину дуги и угол, образованный дугой. Полный радиан равен 360 градусам, следовательно, мы знаем, что Земля совершает два радиана при полном вращении вокруг оси. Однако иногда ее также называют скоростью вращения, и ее величина — скорость вращения — обычно измеряется в циклах или оборотах в единицу времени (например, оборотов в минуту).Кроме того, когда объект вращается вокруг оси, каждая точка объекта имеет одинаковую угловую скорость.
Математически средняя угловая скорость объекта может быть представлена следующим уравнением: ω среднее = Δθ / Δt, где ω — радианы / обороты в секунду (в среднем), Δ — изменение количества, θ — скорость, а t — время. При вычислении угловой скорости Земли, когда она совершает полный оборот вокруг своей оси (солнечные сутки), это уравнение представляется как: ω avg = 2πrad / 1day (86400 секунд), что соответствует умеренным угловым значениям. скорость 7.2921159 × 10 -5 радиан / сек. В случае солнечного года, где ω ср. = 2πрад / 1 год (3,2 × 10 7 секунд), мы видим, что угловая скорость составляет 2,0 × 10 -7 рад / с.
Мы написали много статей об угловой скорости Земли для Universe Today. Вот статья об угловой скорости, а вот статья о том, почему Земля вращается.
Если вам нужна дополнительная информация об угловой скорости Земли, ознакомьтесь со следующими статьями:
Угловая скорость Земли
Вращение Земли
Мы также записали серию Astronomy Cast, посвященную планете Земля.Послушайте, Эпизод 51: Земля.
Источники:
http://en.wikipedia.org/wiki/Angular_velocity
http://hyperphysics.phy-astr.gsu.edu/hbase/rotq.html
http://hypertextbook.com/facts/2002/ JasonAtkins.shtml
http://en.wikipedia.org/wiki/Earth%27s_rotation#Rotation_period
http://www.livephysics.com/tables-of-physical-data/mechanical/angular-speed-of-earth. html
Как это:
Нравится Загрузка …
Основы углового ускорения и вращательного момента инерции
Угловое ускорение и момент инерции в конструкции машиныКак поставщик гибких приводных муфт и предохранительных муфт с шариковой фиксацией нас часто просят оказать небольшую помощь в расчете крутящих моментов, особенно для клиентов, желающих модернизировать существующее оборудование. 2).Уравнение ниже определяет скорость изменения угловой скорости.
ω = угловая скорость в стандартной системе СИ, радиан в секунду (рад / сек), 1 радиан = 57,3 градуса
t = время разгона в секундах
π = 3,1416
n = скорость привода в оборотах в минуту об / мин
В следующем примере угловая скорость будет рассчитана для ускорения от 0 до 60 об / мин за одну секунду. Обратите внимание, что 2π радиан в секунду = 60 об / мин.
Этот расчет очень полезен при проектировании машин, поскольку угловое ускорение, умноженное на крутящий момент инерции, равняется крутящему моменту. Имейте в виду, что точный момент инерции может быть трудно вычислить на основе сложной геометрии реальных приводных линий, а другие переменные, такие как трение, не учитываются в следующем расчете. Тем не менее, он по-прежнему очень полезен при приближении требований к крутящему моменту или установлении базовых минимальных значений для определения размеров компонентов.
Дж = момент инерции в кг ∙ м 2
T = крутящий момент в Н ∙ м
N = сила в Ньютонах
кг = масса в килограммах
м = радиус плеча рычага в метрах
В последнем примере ниже мы будем использовать угловое ускорение, которое мы нашли выше, для расчета крутящего момента на маховике с радиусом 1 метр и массой 1000 кг.
Как мы видим, если бы маховик с радиусом 1 метр и массой 1000 кг разогнался до 60 об / мин за одну секунду, для этого потребовалось бы 3141.59 Ньютон-метров входного крутящего момента.
Надеюсь, этот обзор по вычислению углового ускорения оказался для вас полезным. Если у вас есть вопросы, касающиеся выбора размеров и применения муфт вала или предохранительных муфт, обращайтесь в наш технический отдел.
Как рассчитать формулу угловой скорости
Формула угловой скорости: В физике угловая скорость относится к тому, насколько быстро объект вращается или вращается относительно другой точки, т.е.е. насколько быстро угловое положение или ориентация объекта меняется со временем. Есть два типа угловой скорости: орбитальная угловая скорость и угловая скорость вращения. Угловая скорость вращения означает, насколько быстро твердое тело вращается относительно центра вращения.
Орбитальная угловая скорость относится к тому, насколько быстро точечный объект вращается вокруг фиксированного начала координат, то есть скорость изменения его углового положения относительно начала координат во времени. Как правило, угловая скорость измеряется в углах в единицу времени, т.е.грамм. радиан в секунду. Единица измерения угловой скорости в системе СИ выражается в радианах / сек, причем радиан имеет безразмерное значение, равное единице, поэтому единицы измерения угловой скорости в системе СИ представлены как 1 / сек . Угловая скорость обычно обозначается символом омега ( ω , иногда Ω ). По соглашению, положительная угловая скорость означает вращение против часовой стрелки, а отрицательная — по часовой стрелке.
Например, геостационарный спутник совершает один оборот в день над экватором, или 360 градусов за 24 часа, и имеет угловую скорость ω = 360/24 = 15 градусов в час, или 2π / 24 ≈ 0.26 радиан в час. Если угол измеряется в радианах, линейная скорость равна радиусу, умноженному на угловую скорость, {\ displaystyle v = r \ omega}. Таким образом, с радиусом орбиты 42000 км от центра Земли скорость спутника в космосе составляет v = 42000 × 0,26 ≈ 11000 км / ч. Угловая скорость положительна, поскольку спутник движется на восток вместе с вращением Земли (против часовой стрелки над северным полюсом).
Как рассчитать формулу угловой скоростиВ трех измерениях угловая скорость представляет собой псевдовектор, величина которого измеряет скорость, с которой объект вращается или вращается, а ее направление указывает перпендикулярно плоскости мгновенного вращения или углового смещения.Ориентация угловой скорости условно задается правилом правой руки.
Формула для угловой скорости
В простейшем случае кругового движения по радиусу {\ displaystyle r} с положением, заданным угловым смещением {\ displaystyle \ phi (t)} от оси x, орбитальная угловая скорость — это скорость изменения угла с относительно времени: {\ displaystyle \ omega = {\ tfrac {d \ phi} {dt}}}. Если {\ displaystyle \ phi} измеряется в радианах, расстояние от оси x вокруг круга до частицы равно {\ displaystyle \ ell = r \ phi}, а линейная скорость равна {\ displaystyle v (t) = {\ tfrac {d \ ell} {dt}} = r \ omega (t)}, так что {\ displaystyle \ omega = {\ tfrac {v} {r}}}.
В общем случае частицы, движущейся в плоскости, орбитальная угловая скорость — это скорость, с которой вектор положения относительно выбранного начала координат «выметает» угол. На диаграмме показан вектор положения {\ displaystyle \ mathbf {r}} от начала координат {\ displaystyle O} до частицы {\ displaystyle P} с его полярными координатами {\ displaystyle (r, \ phi)}. (Все переменные являются функциями времени {\ displaystyle t}.) Частица имеет линейное разделение скорости как {\ displaystyle \ mathbf {v} = \ mathbf {v} _ {\ |} + \ mathbf {v} _ {\ perp }} с радиальным компонентом {\ displaystyle \ mathbf {v} _ {\ |}}, параллельным радиусу, и поперечно-радиальным (или тангенциальным) компонентом {\ displaystyle \ mathbf {v} _ {\ perp}} перпендикулярно радиусу.Когда нет радиальной составляющей, частица движется вокруг начала координат по окружности; но когда нет поперечно-радиального компонента, он движется по прямой от начала координат. Поскольку при радиальном движении угол остается неизменным, только поперечно-радиальная составляющая линейной скорости вносит вклад в угловую скорость.
Угловая скорость ω — это скорость изменения углового положения относительно времени, которая может быть вычислена из поперечной радиальной скорости как:
- {\ displaystyle \ omega = {\ frac {d \ phi} {dt}} = {\ frac {v _ {\ perp}} {r}}.}
Здесь поперечная радиальная скорость {\ displaystyle v _ {\ perp}} является величиной со знаком {\ displaystyle \ mathbf {v} _ {\ perp}}, положительной для движения против часовой стрелки, отрицательной для движения по часовой стрелке. Если взять полярные координаты для линейной скорости {\ displaystyle \ mathbf {v}}, получаем величину {\ displaystyle v} (линейную скорость) и угол {\ displaystyle \ theta} относительно радиус-вектора; в этих терминах {\ displaystyle v _ {\ perp} = v \ sin (\ theta)}, так что
- {\ displaystyle \ omega = {\ frac {v \ sin (\ theta)} {r}}.{\ perp} = (- y, x)}.
В двух измерениях угловая скорость — это число со знаком плюс или минус, указывающее ориентацию, но не указывающее в направлении. Знак обычно считается положительным, если радиус-вектор вращается против часовой стрелки, и отрицательным, если по часовой стрелке. Тогда угловая скорость может быть названа псевдоскалярной, числовой величиной, которая меняет знак при инверсии четности, такой как инвертирование одной оси или переключение двух осей.
Читайте также: Формула трехчлена идеального квадрата
Как рассчитать угловую скорость на основе числа оборотов в минуту?
оборотов в минуту можно преобразовать в угловую скорость в градусах в секунду, умножив оборотов в минуту на 6, так как один оборот составляет 360 градусов и 60 секунд в минуту.Если об / мин равно 1 об / мин , угловая скорость в градусах в секунду будет 6 градусов в секунду, так как 6, умноженное на 1, равно 6.
Какова формула угловой скорости?
Чтобы получить нашу вторую формулу для угловой скорости , мы понимаем, что тета дается в радианах, а определение радианной меры дает theta = s / r. Таким образом, мы можем подставить theta = s / r в нашу первую формулу для угловой скорости .Это дает w = (s / r) / t.
Обороты — это то же самое, что и угловая скорость?
Угловая скорость равна скорости вращения . Что-то крутится. Это сокращение от Оборотов в минуту. Другими связанными единицами измерения, выражающими то же свойство , являются градусы в секунду и радианы в секунду.
Формула средней угловой скорости
Во-первых, когда вы говорите об «угловом» чем-либо, будь то скорость или какая-либо другая физическая величина, осознайте, что, поскольку вы имеете дело с углами, вы говорите о путешествии по кругам или их частям.Вы можете вспомнить из геометрии или тригонометрии, что длина окружности равна его диаметру, умноженному на константу пи, или πd . (Значение пи составляет примерно 3,14159.) Это чаще всего выражается в терминах радиуса круга r , который составляет половину диаметра, что составляет длину окружности 2πr .
Кроме того, вы, вероятно, где-то по пути узнали, что круг состоит из 360 градусов (360 °). Если вы переместитесь на расстояние S по окружности, то угловое смещение θ будет равно S / r.Таким образом, один полный оборот дает 2πr / r, что оставляет 2π. Это означает, что углы меньше 360 ° могут быть выражены в единицах пи или, другими словами, в радианах.
Взяв всю эту информацию вместе, вы можете выразить углы или части круга в единицах, отличных от градусов:
1 радиан = (360 ° / 2π) = 57,3 °,
В то время как линейная скорость выражается в длине в единицу времени, угловая скорость измеряется в радианах в единицу времени, обычно в секунду.
Если вы знаете, что частица движется по круговой траектории со скоростью v на расстоянии r от центра круга, причем направление v всегда перпендикулярно радиусу круга, тогда угловую скорость можно записать
, где ω — греческая буква омега. Единицы угловой скорости — радианы в секунду; вы также можете рассматривать эту единицу как «обратные секунды», потому что v / r дает м / с, деленные на м, или с -1 , что означает, что радианы технически являются безразмерной величиной.
Формула центростремительного ускорения, угловая скорость
Формула углового ускорения выводится так же, как и формула угловой скорости: это просто линейное ускорение в направлении, перпендикулярном радиусу окружности (эквивалентно, его ускорение по касательной к круговой траектории в любой точке) делится на радиус круга или части круга, который составляет:
, потому что для кругового движения t = ωr / t = v / t.
α , как вы, наверное, знаете, это греческая буква «альфа». Индекс «t» здесь означает «касательную».
Как ни странно, однако, вращательное движение имеет другой вид ускорения, называемый центростремительным («центростремительным») ускорением. Это дается выражением:
Это ускорение направлено к точке, вокруг которой вращается рассматриваемый объект. Это может показаться странным, поскольку объект не приближается к этой центральной точке, так как радиус r фиксирован.Думайте о центростремительном ускорении как о свободном падении, при котором нет опасности столкновения объекта с землей, потому что сила, притягивающая объект к нему (обычно сила тяжести), точно компенсируется тангенциальным (линейным) ускорением, описываемым первым уравнением в эта секция. Если бы a c не было равно a t , объект либо улетел бы в космос, либо вскоре врезался бы в середину круга.
Читайте также: Средняя и мгновенная скорость изменения
Формула угловой скорости Физика
Прежде чем мы перейдем к угловой скорости, мы сначала рассмотрим линейную скорость. Линейная скорость применяется к объекту или частице, движущимся по прямой линии. Это скорость изменения положения объекта во времени.
Линейная скорость может быть рассчитана по формуле v = s / t , где v = линейная скорость, s = пройденное расстояние и t = время, необходимое для преодоления расстояния. Например, если я проехал 120 миль за 2 часа, то для расчета моей линейной скорости я бы вставил с = 120 миль и t = 2 часа в мою формулу линейной скорости, чтобы получить v = 120 / 2 = 60 миль в час.Один из наиболее распространенных примеров линейной скорости — это ваша скорость при движении по дороге. Ваш спидометр показывает вашу скорость или показатель в милях в час. Это скорость изменения вашего положения относительно времени, другими словами, ваша скорость — это ваша линейная скорость.
Перед тем, как перейти к угловой скорости, нам нужно рассмотреть еще одну вещь — радианы. Когда мы имеем дело с угловой скоростью, мы используем радианную меру угла, поэтому важно, чтобы мы были знакомы с радианной мерой.Техническое определение радиан. Измерение — это длина дуги, образуемой углом, деленная на радиус круга, частью которого является угол, где «подтянутый» означает, что она должна быть противоположной углу и продолжаться от одной точки на круг к другому, оба отмечены углом. Это говорит нам, что угол тета = с / r радиан, где с = длина дуги, соответствующей тета, и r = радиус круга, частью которого является тета.
Формула угловой скорости в линейную скорость Поскольку большинству из нас удобно измерять углы в градусах, удобно, что мы можем легко преобразовать градус в радиан, умножив градус на пи / 180. Например, угол 45 градусов имеет мера в радианах 45 (пи / 180), которая равна пи / 4 радиана.
Читайте также: Формула линейной интерполяции
Скорость вращения — обзор
3.1 Влияние крутящего момента и скорости вращения
Крутящий момент и скорость вращения шестерни не влияют на распределение нагрузки MEP, но оба они влияют на коэффициент трения и, следовательно, на эффективность.На рис. 2 представлены результаты исследований от S1 до S5, в которых крутящий момент изменялся от 100 до 800 Н · м, а скорость вращения шестерни от 2000 до 10000 об / мин.
Рис. 2. Результаты исследований от S1 до S5
Третий переменный параметр, различающийся в каждом исследовании, был представлен как параметр семейства поверхностей на рис. 2. Можно заметить, что эффективность практически нечувствительна к вариациям. крутящего момента и скорости. Фактически, все поверхности на диаграммах рис. 2 очень похожи на плоскости, параллельные горизонтальной координатной плоскости.
Напротив, на эффективность сильно влияют другие параметры, представленные на рис. 2 (семейство параметров поверхностей). Фактически, эффективность значительно увеличивается с увеличением количества зубьев на шестерне и колесе (обратите внимание, что в этом исследовании более высокое передаточное число означает большее количество зубьев колеса) и угла давления; и уменьшается с увеличением динамической вязкости и шероховатости.
Аналогичные результаты получены из исследования S6, представленного на рис. 3, в котором параметром семейств поверхностей является крутящий момент.Поскольку крутящий момент мало влияет на эффективность, все поверхности расположены очень близко друг к другу. На рис. 3а показано, как эффективность увеличивается с увеличением количества зубьев на шестерне и колесе. Рисунки 3b и 3c показывают, что КПД также растет с увеличением отношения контактов.
Рис. 3. Результаты исследования S6, параметр семейства: M t
Обратите внимание (рис. 3b), что в этом случае КПД не растет с увеличением числа зубьев шестерни. Это связано с тем, что для сохранения неизменного коэффициента контакта число зубьев колеса должно уменьшаться по мере увеличения числа зубьев шестерни, и оба эффекта компенсируют друг друга.Это причина, по которой эффективность уменьшается с увеличением количества зубьев на шестерне при относительно низких значениях отношения контакта и относительно большом количестве зубьев шестерни, как показано на рис. 3b.
Интересные результаты могут быть получены при рассмотрении зависимых вариаций крутящего момента и скорости вращения для сохранения неизменной передаваемой мощности. На рисунке 4 представлены результаты исследований S7-S9, в которых передаваемая мощность является параметром семейств кривых. Из всех диаграмм видно, что на КПД не влияет (или очень мало) крутящий момент, но явно зависит от мощности, возрастающей вместе с ней.Очевидно, что эффективность снижается с увеличением динамической вязкости и шероховатости (рис. 4a и 4b) и увеличивается с увеличением количества зубьев на шестерне и соотношением контактов (рис. 4c и 4e). В этом случае эффективность уменьшается с увеличением передаточного числа, поскольку в условиях исследования 9 более высокое передаточное число означает меньшее количество зубьев шестерни.
Рис. 4. Результаты исследований S7 — S9, параметр семейства: P
Угловое движение — мощность и крутящий момент
- Работа является результатом силы, действующей на некотором расстоянии.Работа измеряется в джоулях (Нм) или фут-фунтах.
- Крутящий момент — это сила вращения, создаваемая коленчатым валом двигателя. Чем больший крутящий момент производит двигатель, тем выше его способность выполнять работу. Поскольку крутящий момент является вектором, действующим в определенном направлении, он обычно измеряется в единицах Н · м или фунт-фут.
- Мощность — это скорость выполнения работы — работа за определенный промежуток времени. Мощность измеряется в ваттах (Дж / с) или в лошадиных силах.
Мощность и крутящий момент тела при угловом движении
Мощность вращающегося тела может быть выражена как
P = T ω
= T 2 π n об / с
= T π n об / мин /30 (1)
где
P = мощность (Вт)
T = крутящий момент или момент (Нм)
ω = угловая скорость (рад / с)
π = 3.14 …
n об / с = оборотов в секунду (об / с, 1 / с)
n об / мин = оборотов в минуту (об / мин, 1 / мин)
- 1 рад = 360 o /2 π = ~ 57,29578 .. o
Примечание! — объект, такой как электродвигатель, может иметь активный момент без вращения, но без вращения ( ω = 0 ) не вырабатывается энергия.
В британских единицах
P = T n об / мин /5252 (1b)
где
P = мощность (л.с.)
T = крутящий момент (фут-фунт
f )Пример — крутящий момент, создаваемый вращающимся двигателем
Электродвигатель работает со скоростью 3600 об / мин с измеренной потребляемой мощностью 2000 Вт .Крутящий момент, создаваемый двигателем (без потерь), можно рассчитать, переставив (1) на
T = 30 P / (π n об / мин )
= 30 (2000 Вт) / (π ( 3600 об / мин))
= 5,3 Нм
Калькулятор крутящего момента
P — мощность (Вт)
n м — обороты (об / мин)
Загрузить и распечатать Двигатель — крутящий момент и График мощности и частоты вращения
Крутящий момент тела при угловом движении
T = I α (2)
, где
I = момент инерции (кг · м 2 , фунт f футов с 2 )
α = угловое ускорение (рад / с 2 )
Скорость вращения в машинах переменного тока
Скорость вращения
Вращающееся магнитное поле в предыдущем примере может быть мыслится как два вращающихся магнитных полюса, северный полюс и южный полюс.Как осциллограмма тока питания перемещается на 180 градусов, двухполюсное поле перемещается на 180 градусов, а положение северного и южного полюсов поменялось местами. Когда текущий сигнал переместился через 360 градусов 2-полюсное поле переместилось на 360 градусов.
Нет причин ограничивать количество полюсов в машине двумя. Если количество катушки увеличены, катушки можно расположить так, чтобы схема намотки повторялась более одного раза по окружности воздушного зазора.Это проиллюстрировано на изображении ниже, на котором показана диаграмма ММЖ для одной фазы. Уменьшая угол между положительной и отрицательной сторонами катушки и повторяя расположение катушек, мы получаем 4 магнитных полюса, а не 2.
Математически фундаментальная МДС для каждой фазы, которая организована для создания полюсов \ (p \), задается следующим образом:
\ [ \ begin {выровнено} \ mathcal {F_A} & = Ni_A \ frac {2} {\ pi} \ sin \ left [\ frac {p} {2} \ left (\ theta \ right) \ right] \\ \ mathcal {F_B} & = Ni_B \ frac {2} {\ pi} \ sin \ left [\ frac {p} {2} \ left (\ theta — \ frac {2 \ pi} {3} \ right) \ Правильно] \\ \ mathcal {F_C} & = Ni_C \ frac {2} {\ pi} \ sin \ left [\ frac {p} {2} \ left (\ theta + \ frac {2 \ pi} {3} \ right) \ Правильно] \ end {выровнен} \]
Важно отметить, что в приведенном выше уравнении N — это количество витков в одной катушке.Член \ (p / 2 \) указывает, что основной mmf повторяет \ (p / 2 \) раз по окружности машины \ (p \) должно быть четным числом, поскольку физически у нас не может быть нечетного числа полюсов. Предполагая синусоидальное питание со сбалансированным трехфазным набором, анализ для двухполюсного поля можно повторить, чтобы найти новые функции, описывающие ММФ в терминах пространства (тета) и времени (t)
\ [ \ mathcal {F} _ {tot} = \ frac {3 \ hat {I} N} {\ pi} \ cos \ left [\ omega t — \ frac {p} {2} \ theta \ right] \]
Рассматривая эту формулировку, важно понимать, что \ (\ omega \) — это электрическая частота, а \ (\ theta \) — это механическое угловое положение в машине.Чтобы избежать путаницы, важно определить электрические частоты и фазовые углы \ (\ omega_e, \, \ theta_e \), а также механическую скорость и угловое положение \ (\ omega_m, \, \ theta_m \).
Рассматривая диаграмму выше, можно увидеть, что электромагнитный период 4-полюсной диаграммы равен \ (\ pi \) механическим радианам. Взаимосвязь между электрическими и механическими углами и скоростями / частотой имеет важное значение и определяется по формуле:
\ [ \ begin {выровнено} \ theta_e & = \ frac {p} {2} \ theta_m \\ \ omega_e & = \ frac {p} {2} \ omega_m \ end {выровнен} \]
Используя эти обозначения, мы можем описать МДС с помощью электрических или механических величин, или даже их комбинации.
\ [ \ begin {align} \ mathcal {F} _ {tot} & = \ frac {3 \ hat {I} N} {\ pi} \ cos \ left [\ omega_e t — \ frac {p} {2} \ theta_m \ right] \\ \ mathcal {F} _ {tot} & = \ frac {3 \ hat {I} N} {\ pi} \ cos \ left [\ omega_e t — \ theta_e \ right] \\ \ mathcal {F} _ {tot} & = \ frac {3 \ hat {I} N} {\ pi} \ cos \ left [\ frac {p} {2} \ left (\ omega_m t — \ theta_m \ right ) \Правильно] \ end {align} \]
Наконец, в электрической машине может быть множество различных механических скоростей. Механическая скорость вращения магнитного поля из-за основного электрического тока \ (f_e \) очень важна, и ей дано отличное название, синхронная скорость, \ (\ omega_s \).Синхронная скорость в радианах в секунду определяется как:
.\ [ \ omega_s = \ frac {4 \ pi f_e} {p} \]
Обычно для описания скорости вращения используются единицы числа оборотов в минуту (об / мин). Описана скорость в об / мин. с использованием символа \ (n \) и связано с радианами в секунду с помощью
\ [ \ begin {выровнено} n & = \ frac {60} {2 \ pi} \ omega_m \\ n & = \ frac {30} {\ pi} \ omega_m \ end {выровнен} \]
, следовательно,
\ [ n_s = \ frac {120 f_e} {p} \]
Угловая и линейная скоростьи об / мин
Purplemath
По некоторым причинам учебники часто обращаются к вопросам угловой скорости, линейной скорости и оборотов в минуту (об / мин) вскоре после объяснения секторов круга, их площади и длины дуги.
Длина дуги — это расстояние до части окружности; и линейное расстояние, которое преодолевает, скажем, велосипед, связано с радиусом шин велосипеда. Если вы отметите одну точку на передней шине велосипеда (скажем, точку напротив клапана шины) и посчитаете, сколько раз колесо вращается, вы можете найти количество окружностей окружности, на которые переместилась отмеченная точка.
MathHelp.com
Если вы «раскрутите» эти окружности, чтобы получить прямую линию, то вы найдете расстояние, которое проехал велосипед. Я думаю, что именно такая взаимосвязь между различными показателями и является причиной того, что эта тема часто возникает на данном этапе исследования.
Во-первых, нам нужна техническая терминология и определения.
«Угловая скорость» — это показатель поворота в единицу времени. Он сообщает вам размер угла, под которым что-то вращается за данный промежуток времени. Например, если колесо вращается шестьдесят раз за одну минуту, то его угловая скорость составляет 120π радиан в минуту. Затем угловая скорость измеряется в радианах в секунду, греческая строчная омега (ω) часто используется в качестве названия.
«Линейная скорость» — это мера расстояния в единицу времени. Например, если колесо в предыдущем примере имеет радиус 47 сантиметров, то каждый проход по окружности составляет 94π см, или около 295 см. Поскольку колесо совершает шестьдесят таких оборотов за одну минуту, общая пройденная длина составляет 60 × 94 & pi = 5640π см, или около 177 метров, за одну минуту. (Это примерно 10,6 км / ч, или около 6,7 миль / ч.)
«Число оборотов в минуту», обычно сокращенно обозначаемое как «об / мин», является мерой вращения за единицу времени, но единица времени — всегда одна минута.И вместо того, чтобы указывать угол поворота, он просто дает количество поворотов. Когда вы смотрите на тахометр на приборной панели автомобиля, вы смотрите на текущие обороты двигателя автомобиля. В приведенном выше примере частота вращения будет просто «60».
«Частота» f — это мера вращения (или вибрации) за единицу времени, но единицей времени всегда является одна секунда. Единицей измерения частот является «герц», который обозначается как Гц.
Взаимосвязь между частотой f (в Гц), об / мин и угловой скоростью ω (в радианах) показана ниже (все элементы в любой строке эквивалентны):
Однако вы можете обнаружить, что «угловая скорость» используется как взаимозаменяемые (но только неофициально, не учеными) с оборотами в минуту или частотой.Кроме того, некоторые (например, физики) считают, что «угловая скорость» является векторной величиной, а ω — скалярной величиной, называемой «угловой частотой».
Пожалуйста, не запоминайте эти потенциальные слияния и не беспокойтесь о том, какими могут быть «векторы» или «скаляры». Я говорю вам об этом, чтобы предупредить вас, что вы должны уделять очень пристальное внимание тому, как ваш конкретный учебник и ваш конкретный преподаватель определяют различные термины для этого конкретного класса.И знайте, что на следующем уроке термины и определения могут быть другими.
Колесо имеет диаметр 100 сантиметров. Если колесо поддерживает тележку, движущуюся со скоростью 45 километров в час, то какова частота вращения колеса с точностью до целого числа оборотов в минуту?
«Об / мин» — это количество оборотов колеса в минуту.Чтобы выяснить, сколько раз это колесо вращается за одну минуту, мне нужно найти (линейное или прямое) расстояние, пройденное (за минуту) при движении со скоростью 45 км / ч. Затем мне нужно будет найти длину окружности колеса и разделить общее поминутное (линейное) расстояние на это «разовое» расстояние. Количество окружностей, которые умещаются в пределах общего расстояния, — это количество оборотов колеса за этот период времени.
Сначала я переведу (линейную) скорость тележки из км / ч в «сантиметры в минуту», используя то, что я узнал о преобразовании единиц.(Почему «сантиметры в минуту»? Потому что я ищу «обороты в минуту», поэтому минуты — лучшая единица времени, чем часы. Кроме того, диаметр дан в сантиметрах, так что это лучшая единица длины, чем километры. )
Таким образом, расстояние, пройденное за одну минуту, составляет 75 000 сантиметров. Диаметр колеса — 100 см, поэтому радиус — 50 см, а длина окружности — 100π см. Сколько из этих окружностей (или оборотов колеса) умещается внутри 75 000 см? Другими словами, если бы я снял протектор этого колеса с тележки и разложил его ровно, то получилось бы расстояние 100π см.Сколько из этих длин укладывается на все расстояние, пройденное за одну минуту? Чтобы узнать, сколько из (этого) помещается в такое количество (этого), я должен разделить (это) на (это), поэтому:
Затем, округляя до ближайшего целого числа оборотов (то есть округляя ответ до целого числа), мой ответ:
Примечание. Эта скорость не такая высокая, как может показаться: чуть меньше четырех оборотов в секунду. Вы можете сделать это на своем велосипеде, не вспотев.Вот еще одно примечание: источник, из которого я получил свою схему для вышеупомянутого упражнения, использовал «угловую скорость» и «ω» для «числа оборотов в минуту». Да, в учебнике алгебры использовались неправильные единицы измерения.
В предыдущем упражнении была указана скорость автомобиля и информация о колесе. Отсюда мы нашли количество оборотов в минуту. Мы можем пойти и другим путем; мы можем начать с числа оборотов в минуту (плюс информацию о колесе) и найти скорость транспортного средства.
Велосипедное колесо имеет диаметр 78 см. Если колесо вращается со скоростью 120 оборотов в минуту, какова линейная скорость велосипеда в километрах в час? Ответ округлите до одного десятичного знака.
Линейная скорость — это расстояние по прямой, которое велосипед проходит за определенный период времени.Они дали мне количество оборотов колеса в минуту. Фиксированная точка на шине (скажем, камешек на протекторе шины) перемещает длину окружности за каждый оборот. Раскручивая это расстояние по земле, велосипед будет перемещаться по земле на одинаковое расстояние, по одной окружности за раз, за каждый оборот. Итак, в этом вопросе меня просят найти длину окружности, а затем использовать ее, чтобы найти общее расстояние, пройденное за минуту.
Так как диаметр равен 78 см, то окружность равна C = 78π см.Разматывая путь шины до прямой линии на земле, это означает, что велосипед перемещается на 78π см вперед за каждый оборот шины. Таких оборотов в минуту 120, итого:
(78π см / об) × (120 об / мин) = 9,360π см / мин
Теперь мне нужно преобразовать это из сантиметров в минуту в километры в час:
Велосипед движется со скоростью около 17,6 км / ч.
… или около одиннадцати миль в час.
Предположим, что орбита Земли круглая с радиусом 93 000 000 миль, и пусть «один год» равен 365,25 дням. В этих условиях найдите линейную скорость Земли в милях в секунду. Ответ округлите до одного десятичного знака.
Скорость — это (линейное или эквивалентное прямолинейное) расстояние, пройденное за одну секунду, деленное на одну секунду.Они дали мне информацию за год, так что я начну с этого. Окружность круга с r = 93000000 миль будет линейным расстоянием, которое Земля преодолеет за один год.
C = 2π (93000000 миль) / год = 186000000π миль / год
Это количество миль, пройденных за один год, но мне нужно количество миль, пройденных за одну секунду. В сутках двадцать четыре часа, в часе шестьдесят минут и в минуте шестьдесят секунд, поэтому общее количество секунд в этом году составляет:
Тогда линейная скорость, представляющая собой общее линейное расстояние, деленное на общее время и выраженное в единицах скорости, равна:
Тогда, округленная до одного десятичного знака, линейная скорость Земли равна:
«Эй!» Я слышу, как ты плачешь.»Когда мы собираемся использовать угловые меры для чего-нибудь?» Хотя многие («большинство»?) Упражнений в вашей книге, вероятно, будут похожи на приведенные выше, иногда вы можете столкнуться с фактическими радианами и градусами.
Поезд движется со скоростью 10 миль в час по кривой радиусом 3000 футов. На какой угол повернется поезд за одну минуту? Округлить до ближайшего целого числа градусов.
«Кривая радиуса 3000 футов» означает, что, если бы я попытался плотно подогнать круг внутри кривой, наилучшим образом подошел бы круг с радиусом r = 3000 футов.Другими словами, я могу использовать факты круга, чтобы ответить на этот вопрос.
Поскольку радиус кривой выражен в футах и мне нужно найти угол, пройденный за одну минуту, я начну с преобразования скорости миль в час в футы в секунду:
(10 миль / час) (5280 фут / миль) (1 час / 60 мин) = 880 фут / мин
Длина изогнутого пути, который проходит поезд, также является частью окружности круга.Итак, эти 880 футов — это длина дуги, и теперь мне нужно найти предполагаемый угол (подразумеваемого) сектора круга:
Но это значение в радианах (потому что это то, что использует формула длины дуги), и мне нужно, чтобы мой ответ был в градусах, поэтому мне нужно преобразовать:
Поезд поворачивает на угол примерно:
Представьте, что вы стоите в центре этого воображаемого круга (то есть на расстоянии трех тысяч футов от поворота, более чем в полумиле) и наблюдаете, как поезд движется по повороту.Если вы протянете руку на расстоянии вытянутой руки, сожмете кулак и, крепко прижав средние пальцы большим пальцем вниз, приподнимите мизинец и указательный пальцы, расстояние между ними составит около пятнадцати градусов. Поезд вряд ли продвинется дальше. Если бы вы держали кулак на расстоянии вытянутой руки и вытягивали мизинец и большой палец, расстояние было бы около двадцати пяти градусов.