Как измерить косинус фи
Для измерения косинус фи лучше всего иметь специальные приборы, предназначенные для непосредственного его измерения — фазометры.
Фазометр — электроизмерительный прибор, предназначенный для измерения углов сдвига фаз между двумя изменяющимися периодически электрическими колебаниями.
Если таких приборов нет, то измерять коэффициент мощности можно косвенным методом . Например, в однофазной сети косинус фи можно определить по показаниям амперметра, вольтметра и ваттметра:
cos фи = P / (U х I), где Р, U, I — показания приборов.
в цепи трехфазного тока cos фи = P w / ( √ 3 х Uл х Iл)
где Pw — мощность всей системы, Uл, Iл — линейные напряжение и ток, измеренные вольтметром и амперметром.
В симметричной трехфазной цепи значение косинус фи можно определить из показаний двух ваттметров P w 1 и P w 2 по формуле
Общая относительная погрешность рассмотренных методов равна сумме относительных погрешностей каждого прибора, поэтому точность косвенных методов невелика.
Численное значение косинус фи зависит от характера нагрузки. Если нагрузкой являются лампы накаливания и нагревательные приборы, то косинус фи = 1, если нагрузка содержит еще и асинхронные электродвигатели, то косинус фи
Поэтому на практике в электрических сетях определяют так называемый средневзвешенный коэффициент мощности за какое-то определенное время, допустим, за сутки или месяц. Для этого в конце рассматриваемого периода снимают показания счетчиков активной и реактивной энергии Wa и Wv и определяют средневзвешенное значение коэффициента мощности по формуле
Это значение средневзвешенного коэффициента мощности желательно иметь в электрических сетях равным 0,92 — 0,95.
Использование фазометра для измерения коэффициента мощности
Измерить непосредственно фазовый сдвиг между напряжением и током нагрузки можно при помощи специальных измерительных приборов — фазометров .
Наибольшее распространение получили фазометры электродинамической системы , в которых неподвижная катушка включена последовательно с нагрузкой, а подвижные катушки — параллельно нагрузке, так, что ток одной из них отстает от напряжения на угол β1. Для этого последовательно с катушкой включена активно-индуктивная нагрузка, а ток другой опережает напряжение на некоторый угол β2 , для чего включена активно-емкостная нагрузка, причем β1 + β2 = 90 о
Для этого последовательно с катушкой включена активно-индуктивная нагрузка, а ток другой опережает напряжение на некоторый угол β2 , для чего включена активно-емкостная нагрузка, причем β1 + β2 = 90 о
Рис. 1. Схема включения фазометра (а) и векторная диаграмма напряжений и токов (б).
Угол отклонения стрелки такого прибора зависит только от значения косинуса фи.
Для измерения фазового сдвига между двумя напряжениями часто применяют цифровые фазометры . В цифровых фазометрах прямого преобразования для измерения фазового сдвига его преобразуют в интервал времени и измеряют последний. Исследуемые напряжения подают на два входа прибора, на цифровом отсчетном устройстве прибора снимают показания числа импульсов, поступающих на счетчик прибора за один период исследуемых напряжений, которое соответствует фазовому сдвигу в градусах (или в долях градуса).
Из щитовых приборов, предназначенных для измерения, наиболее простой фазометр типа Д31, который может работать в однофазных сетях переменного тока с частотой 50, 500, 1000, 2400, 8000 Гц. Класс точности 2,5. Пределы измерений косинуса фи от 0,5 емкостного фазового сдвига до 1 и от 1 до 0,5 индуктивного фазового сдвига. Фазометры включают через измерительные трансформаторы тока с вторичным током 5 А и измерительные трансформаторы напряжения с вторичным напряжением 100 В.
Класс точности 2,5. Пределы измерений косинуса фи от 0,5 емкостного фазового сдвига до 1 и от 1 до 0,5 индуктивного фазового сдвига. Фазометры включают через измерительные трансформаторы тока с вторичным током 5 А и измерительные трансформаторы напряжения с вторичным напряжением 100 В.
Для измерения косинуса фи в трехфазной сети при симметричной нагрузке можно применять щитовые фазометры типа Д301. Класс их точности 1,5. Последовательные цепи включают на ток 5 А непосредственно, а также через трансформатор тока, параллельные цепи включают непосредственно на 127, 220, 380 В, а также через измерительные трансформаторы напряжения.
Для измерения косинус фи лучше всего иметь специальные приборы, предназначенные для непосредственного его измерения — фазометры.
Фазометр — электроизмерительный прибор, предназначенный для измерения углов сдвига фаз между двумя изменяющимися периодически электрическими колебаниями.
Если таких приборов нет, то измерять коэффициент мощности можно косвенным методом .
cos фи = P / (U х I), где Р, U, I — показания приборов.
в цепи трехфазного тока cos фи = P w / ( √ 3 х Uл х Iл)
где Pw — мощность всей системы, Uл, Iл — линейные напряжение и ток, измеренные вольтметром и амперметром.
В симметричной трехфазной цепи значение косинус фи можно определить из показаний двух ваттметров P w 1 и P w 2 по формуле
Общая относительная погрешность рассмотренных методов равна сумме относительных погрешностей каждого прибора, поэтому точность косвенных методов невелика.
Численное значение косинус фи зависит от характера нагрузки. Если нагрузкой являются лампы накаливания и нагревательные приборы, то косинус фи = 1, если нагрузка содержит еще и асинхронные электродвигатели, то косинус фи
Поэтому на практике в электрических сетях определяют так называемый средневзвешенный коэффициент мощности за какое-то определенное время, допустим, за сутки или месяц. Для этого в конце рассматриваемого периода снимают показания счетчиков активной и реактивной энергии Wa и Wv и определяют средневзвешенное значение коэффициента мощности по формуле
Для этого в конце рассматриваемого периода снимают показания счетчиков активной и реактивной энергии Wa и Wv и определяют средневзвешенное значение коэффициента мощности по формуле
Это значение средневзвешенного коэффициента мощности желательно иметь в электрических сетях равным 0,92 — 0,95.
Использование фазометра для измерения коэффициента мощности
Измерить непосредственно фазовый сдвиг между напряжением и током нагрузки можно при помощи специальных измерительных приборов — фазометров .
Наибольшее распространение получили фазометры электродинамической системы , в которых неподвижная катушка включена последовательно с нагрузкой, а подвижные катушки — параллельно нагрузке, так, что ток одной из них отстает от напряжения на угол β1. Для этого последовательно с катушкой включена активно-индуктивная нагрузка, а ток другой опережает напряжение на некоторый угол β2 , для чего включена активно-емкостная нагрузка, причем β1 + β2 = 90 о
Рис. 1. Схема включения фазометра (а) и векторная диаграмма напряжений и токов (б).
1. Схема включения фазометра (а) и векторная диаграмма напряжений и токов (б).
Угол отклонения стрелки такого прибора зависит только от значения косинуса фи.
Для измерения фазового сдвига между двумя напряжениями часто применяют цифровые фазометры . В цифровых фазометрах прямого преобразования для измерения фазового сдвига его преобразуют в интервал времени и измеряют последний. Исследуемые напряжения подают на два входа прибора, на цифровом отсчетном устройстве прибора снимают показания числа импульсов, поступающих на счетчик прибора за один период исследуемых напряжений, которое соответствует фазовому сдвигу в градусах (или в долях градуса).
Из щитовых приборов, предназначенных для измерения, наиболее простой фазометр типа Д31, который может работать в однофазных сетях переменного тока с частотой 50, 500, 1000, 2400, 8000 Гц. Класс точности 2,5. Пределы измерений косинуса фи от 0,5 емкостного фазового сдвига до 1 и от 1 до 0,5 индуктивного фазового сдвига. Фазометры включают через измерительные трансформаторы тока с вторичным током 5 А и измерительные трансформаторы напряжения с вторичным напряжением 100 В.
Для измерения косинуса фи в трехфазной сети при симметричной нагрузке можно применять щитовые фазометры типа Д301. Класс их точности 1,5. Последовательные цепи включают на ток 5 А непосредственно, а также через трансформатор тока, параллельные цепи включают непосредственно на 127, 220, 380 В, а также через измерительные трансформаторы напряжения.
Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей и мощности искажения (собирательное название — неактивная мощность). Следует отличать понятие «коэффициент мощности» от понятия «косинус фи», который равен косинусу сдвига фазы переменного тока, протекающего через нагрузку, относительно приложенного к ней напряжения. Второе понятие используют в случае синусоидальных тока и напряжения, и только в этом случае оба понятия эквивалентны.
Содержание
Определение и физический смысл [ править | править код ]
Коэффициент мощности равен отношению потребляемой электроприёмником активной мощности к полной мощности. Активная мощность расходуется на совершение работы. В случае синусоидальных тока и напряжения полная мощность представляет собой геометрическую сумму активной и реактивной мощностей. Иными словами, она равна корню квадратному из суммы квадратов активной и реактивной мощностей. В общем случае полную мощность можно определить как произведение действующих (среднеквадратических) значений тока и напряжения в цепи. В качестве единицы измерения полной мощности принято использовать вольт-ампер (В∙А) вместо ватта (Вт).
Активная мощность расходуется на совершение работы. В случае синусоидальных тока и напряжения полная мощность представляет собой геометрическую сумму активной и реактивной мощностей. Иными словами, она равна корню квадратному из суммы квадратов активной и реактивной мощностей. В общем случае полную мощность можно определить как произведение действующих (среднеквадратических) значений тока и напряжения в цепи. В качестве единицы измерения полной мощности принято использовать вольт-ампер (В∙А) вместо ватта (Вт).
В электроэнергетике для коэффициента мощности приняты обозначения cos φ <displaystyle operatorname varphi > (где φ <displaystyle varphi > — сдвиг фаз между силой тока и напряжением) либо λ <displaystyle lambda > . Когда для обозначения коэффициента мощности используется λ <displaystyle lambda > , его величину обычно выражают в процентах.
Согласно неравенству Коши—Буняковского, активная мощность, равная среднему значению произведения тока и напряжения, всегда не превышает произведение соответствующих среднеквадратических значений. Поэтому коэффициент мощности принимает значения от нуля до единицы (или от 0 до 100 %).
Поэтому коэффициент мощности принимает значения от нуля до единицы (или от 0 до 100 %).
Коэффициент мощности математически можно интерпретировать как косинус угла между векторами тока и напряжения (в общем случае бесконечномерных). Поэтому в случае синусоидальных напряжения и тока величина коэффициента мощности совпадает с косинусом угла, на который отстоят соответствующие фазы.
В случае синусоидального напряжения, но несинусоидального тока, если нагрузка не имеет реактивной составляющей, коэффициент мощности равен доле мощности первой гармоники тока в полной мощности, потребляемой нагрузкой.
При наличии реактивной составляющей в нагрузке кроме значения коэффициента мощности иногда также указывают характер нагрузки: активно-ёмкостный или активно-индуктивный. В этом случае коэффициент мощности соответственно называют опережающим или отстающим.
Прикладной смысл [ править | править код ]
Можно показать, что если к источнику синусоидального напряжения (например, розетка
230 В, 50 Гц) подключить нагрузку, в которой ток опережает или отстаёт по фазе на некоторый угол от напряжения, то на внутреннем активном сопротивлении источника выделяется повышенная мощность. На практике это означает, что при работе на нагрузку с реактивной составляющей от электростанции требуется больше отвода тепла, чем при работе на активную нагрузку; избыток передаваемой энергии выделяется в виде тепла в проводах, и в масштабах, например, предприятия потери могут быть довольно значительными.
На практике это означает, что при работе на нагрузку с реактивной составляющей от электростанции требуется больше отвода тепла, чем при работе на активную нагрузку; избыток передаваемой энергии выделяется в виде тепла в проводах, и в масштабах, например, предприятия потери могут быть довольно значительными.
Не следует путать коэффициент мощности и коэффициент полезного действия (КПД) нагрузки. Коэффициент мощности практически не влияет на энергопотребление самого устройства, включённого в сеть, но влияет на потери энергии в идущих к нему проводах, а также в местах выработки или преобразования энергии (например, на подстанциях). Т.е. счётчик электроэнергии в квартире практически не будет реагировать на коэффициент мощности устройств, поскольку оплате подлежит лишь электроэнергия, совершающая работу (активная составляющая нагрузки). В то же время от КПД непосредственно зависит потребляемая электроприбором активная мощность. Например, компактная люминесцентная («энергосберегающая») лампа потребляет примерно в 1,5 раза больше энергии, чем аналогичная по яркости светодиодная лампа. Это связано с более высоким КПД последней. Однако независимо от этого каждая из этих ламп может иметь как низкий, так и высокий коэффициент мощности, который определяется используемыми схемотехническими решениями.
Это связано с более высоким КПД последней. Однако независимо от этого каждая из этих ламп может иметь как низкий, так и высокий коэффициент мощности, который определяется используемыми схемотехническими решениями.
Математические расчёты [ править | править код ]
Коэффициент мощности необходимо учитывать при проектировании электросетей. Низкий коэффициент мощности ведёт к увеличению доли потерь электроэнергии в электрической сети в общих потерях. Если его снижение вызвано нелинейным, и особенно импульсным характером нагрузки, это дополнительно приводит к искажениям формы напряжения в сети. Чтобы увеличить коэффициент мощности, используют компенсирующие устройства. Неверно рассчитанный коэффициент мощности может привести к избыточному потреблению электроэнергии и снижению КПД электрооборудования, питающегося от данной сети.
Для расчётов в случае гармонических переменных U <displaystyle U> (напряжение) и I <displaystyle I> (сила тока) используются следующие математические формулы:
- χ = P S <displaystyle chi =<frac
>>
Здесь P <displaystyle P> — активная мощность, S <displaystyle S> — полная мощность, Q <displaystyle Q> — реактивная мощность, T — мощность искажения.
Типовые оценки качества электропотребления [ править | править код ]
При одной и той же активной мощности нагрузки мощность, бесполезно рассеиваемая на проводах, обратно пропорциональна квадрату коэффициента мощности. Таким образом, чем меньше коэффициент мощности, тем ниже качество потребления электроэнергии. Для повышения качества электропотребления применяются различные способы коррекции коэффициента мощности, то есть его повышения до значения, близкого к единице.
| Значение коэффициента мощности | Высокое | Хорошее | Удовлетворительное | Низкое | Неудовлетворительное |
|---|---|---|---|---|---|
| cos φ <displaystyle operatorname varphi > | 0,95…1 | 0,8…0,95 | 0,65…0,8 | 0,5…0,65 | 0…0,5 |
| λ <displaystyle lambda > | 95…100 % | 80…95 % | 65…80 % | 50…65 % | 0…50 % |
Например, большинство старых светильников с люминесцентными лампами для зажигания и поддержания горения используют электромагнитные балласты (ЭмПРА), характеризующиеся низким значением коэффициента мощности, то есть неэффективным электропотреблением. Многие компактные люминесцентные («энергосберегающие») лампы, имеющие ЭПРА, тоже характеризуются низким коэффициентом мощности (0,5. 0,65). Но аналогичные изделия известных производителей, как и большинство современных светильников, содержат схемы коррекции коэффициента мощности, и для них значение cos φ <displaystyle operatorname varphi > близко к 1, то есть к идеальному значению.
Многие компактные люминесцентные («энергосберегающие») лампы, имеющие ЭПРА, тоже характеризуются низким коэффициентом мощности (0,5. 0,65). Но аналогичные изделия известных производителей, как и большинство современных светильников, содержат схемы коррекции коэффициента мощности, и для них значение cos φ <displaystyle operatorname varphi > близко к 1, то есть к идеальному значению.
Несинусоидальность [ править | править код ]
Низкое качество потребителей электроэнергии, связанное с наличием в нагрузке мощности искажения, то есть нелинейная нагрузка (особенно при импульсном её характере), приводит к искажению синусоидальной формы питающего напряжения. Несинусоидальность — вид нелинейных искажений напряжения в электрической сети, который связан с появлением в составе напряжения гармоник с частотами, многократно превышающими основную частоту сети. Высшие гармоники напряжения оказывают отрицательное влияние на работу системы электроснабжения, вызывая дополнительные активные потери в трансформаторах, электрических машинах и сетях; повышенную аварийность в кабельных сетях.
Источниками высших гармоник тока и напряжения являются электроприёмники с нелинейными нагрузками. Например, мощные выпрямители переменного тока, применяемые в металлургической промышленности и на железнодорожном транспорте, газоразрядные лампы, импульсные источники питания и др.
Коррекция коэффициента мощности [ править | править код ]
Коррекция коэффициента мощности (англ. power factor correction (PFC)) — процесс приведения потребления конечного устройства, обладающего низким коэффициентом мощности при питании от силовой сети переменного тока, к состоянию, при котором коэффициент мощности соответствует принятым стандартам.
К ухудшению коэффициента мощности (изменению потребляемого тока непропорционально приложенному напряжению) приводят нерезистивные нагрузки: реактивная и нелинейная. Реактивные нагрузки корректируются внешними реактивностями, именно для них определена величина cos φ <displaystyle cos varphi > . Коррекция нелинейной нагрузки технически реализуется в виде той или иной дополнительной схемы на входе устройства.
Данная процедура необходима для равномерного использования мощности фазы и исключения перегрузки нейтрального провода трёхфазной сети. Так, она обязательна для импульсных источников питания мощностью в 100 и более ватт [ источник не указан 3122 дня ] . Компенсация обеспечивает отсутствие всплесков тока потребления на вершине синусоиды питающего напряжения и равномерную нагрузку на силовую линию.
Реле контроля нагрузки, контроля мощности и cos φ
Реле контроля нагрузки позволяют контролировать различные варианты сбоя в работе промышленного оборудования, имеющего своим основным элементов двигатель или насос. Для этого реле контроля подключается в цепь питания электродвигателя, измеряет активную мощность или коэффициент мощности (cos φ) и осуществляет управляющее воздействие при выходе контролируемых значений за предустановленные пороги срабатывания.
Реле контроля мощности и коэффициента мощности cos φ не контролируют параметры цепи питания, как реле контроля фаз.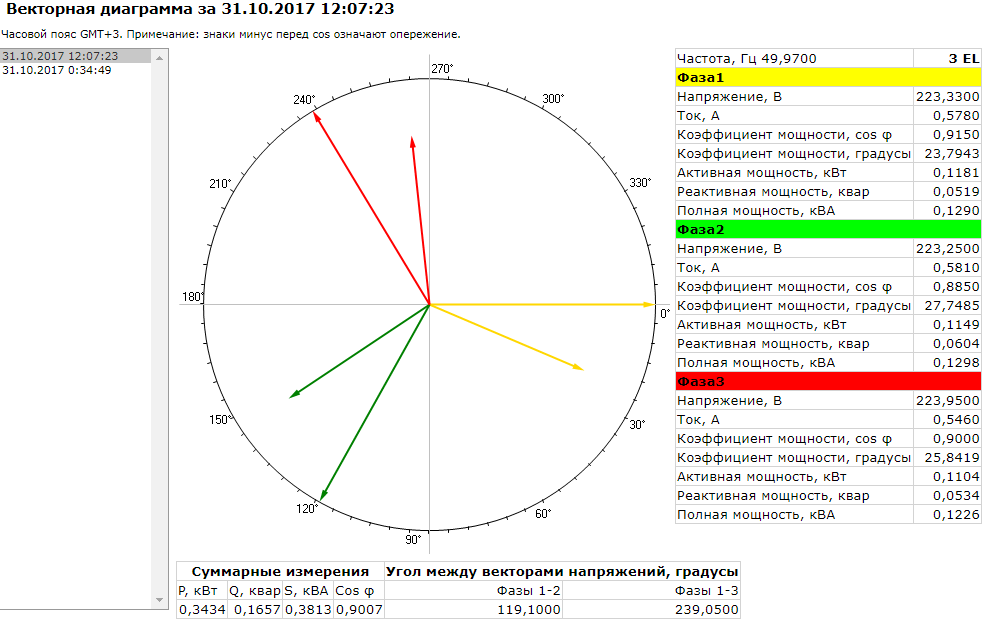 Для вычисления активной мощности или коэффициента мощности необходимо измерить величину напряжения и ток по одной из фаз цепи питания электродвигателя, это может быть однофазная или трехфазная нагрузка. Выводы о работе и состоянии двигателя, делаются на основе контроля за показаниями изменения потребляемой мощности во время работы с помощью реле.
Для вычисления активной мощности или коэффициента мощности необходимо измерить величину напряжения и ток по одной из фаз цепи питания электродвигателя, это может быть однофазная или трехфазная нагрузка. Выводы о работе и состоянии двигателя, делаются на основе контроля за показаниями изменения потребляемой мощности во время работы с помощью реле.
- Реле активной мощности — реле контроля потребляемой активной мощности однофазными и трехфазными нагрузками в сетях переменного тока, позволяют уверенно контролировать как ситуацию перегрузки, так и ситуацию недогрузки.
- Реле коэффициента мощности — реле контролирующее фазовое смещение между током и напряжением и анализирует cos-φ, что позволяет уверенно определять только ситуацию недогрузки или перегрузки, при существенном изменении коэффициента мощности в этом случае.
- Реле контроля тока позволяют уверенно определять только ситуацию перегрузки, во время скачка тока.

Измерить коэффициент мощности можно косвенными методами.
В однофазной сети косинус фи можно определить по показаниям амперметра, вольтметра и ваттметра по формуле:
cos φ = P / (U х I),где
Р, U, I — показания приборов.
в цепи трехфазного тока
cos φ = Pw / (√3 х Uл х Iл)
где Pw — мощность всей системы, Uл, Iл — линейные напряжение и ток, измеренные вольтметром и амперметром.
В симметричной трехфазной цепи значение косинус фи можно определить из показаний двух ваттметров Pw1 и Pw2 по формуле:
Общая относительная погрешность рассмотренных методов равна сумме относительных погрешностей каждого прибора, поэтому точность косвенных методов невелика.
Численное значение косинус фи зависит от характера нагрузки. Если нагрузкой являются лампы накаливания и нагревательные приборы, то косинус фи = 1, если нагрузка содержит еще и асинхронные электродвигатели, то косинус фи < 1. При изменении нагрузки электродвигателя его косинус фи существенно изменяется (от 0,1 на холостом ходу до 0,86 — 0,87 при номинальной нагрузке), изменяется и косинус фи сетей.
Если нагрузкой являются лампы накаливания и нагревательные приборы, то косинус фи = 1, если нагрузка содержит еще и асинхронные электродвигатели, то косинус фи < 1. При изменении нагрузки электродвигателя его косинус фи существенно изменяется (от 0,1 на холостом ходу до 0,86 — 0,87 при номинальной нагрузке), изменяется и косинус фи сетей.
Поэтому на практике в электрических сетях определяют так называемый средневзвешенный коэффициент мощности за какое-то определенное время, допустим, за сутки или месяц. Для этого в конце рассматриваемого периода снимают показания счетчиков активной и реактивной энергии Wa и Wv и определяют средневзвешенное значение коэффициента мощности по формуле:
Это значение средневзвешенного коэффициента мощности желательно иметь в электрических сетях равным 0,92 — 0,95.
Для измерения cos φ (косинуса фи) используют фазометры, позволяющие измерить непосредственно фазовый сдвиг между напряжением и током нагрузки.
Фазометр — электроизмерительный прибор, предназначенный для измерения углов сдвига фаз между двумя изменяющимися периодически электрическими колебаниями.
Электродинамические фазометры в которых неподвижная катушка включена последовательно с нагрузкой, а подвижные катушки — параллельно нагрузке, так, что ток одной из них отстает от напряжения на угол β1. Для этого последовательно с катушкой включена активно-индуктивная нагрузка, а ток другой опережает напряжение на некоторый угол β2, для чего включена активно-емкостная нагрузка, причем β1 + β2 = 90о
Угол отклонения стрелки такого прибора зависит только от значения косинуса фи.
Цифровые фазометры для измерения фазового сдвига между двумя напряжениями.
В цифровых фазометрах прямого преобразования для измерения фазового сдвига его преобразуют в интервал времени и измеряют последним. Исследуемые напряжения подают на два входа прибора, на цифровом отсчетном устройстве прибора снимают показания числа импульсов, поступающих на счетчик прибора за один период исследуемых напряжений, которое соответствует фазовому сдвигу в градусах (или в долях градуса).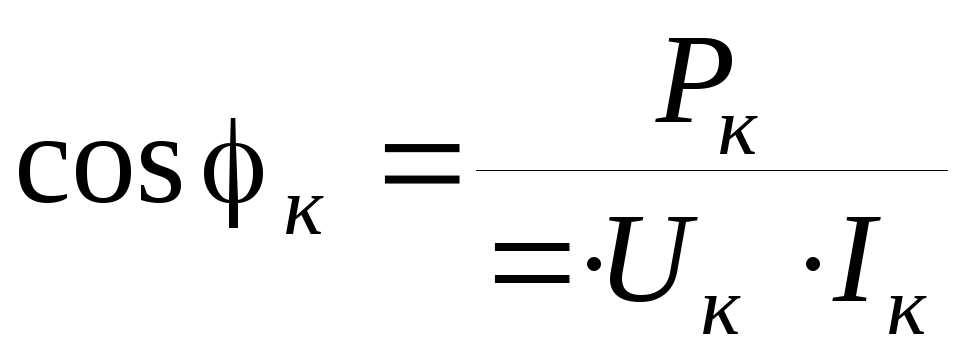
Из щитовых приборов, предназначенных для измерения, наиболее простой фазометр типа Д31, который может работать в однофазных сетях переменного тока с частотой 50, 500, 1000, 2400, 8000 Гц. Класс точности 2,5. Пределы измерений косинуса фи от 0,5 емкостного фазового сдвига до 1 и от 1 до 0,5 индуктивного фазового сдвига. Фазометры включают через измерительные трансформаторы тока с вторичным током 5 А и измерительные трансформаторы напряжения с вторичным напряжением 100 В.
Для измерения косинуса фи в трехфазной сети при симметричной нагрузке можно применять щитовые фазометры типа Д301. Класс их точности 1,5. Последовательные цепи включают на ток 5 А непосредственно, а также через трансформатор тока, параллельные цепи включают непосредственно на 127, 220, 380 В, а также через измерительные трансформаторы напряжения.
Диапазоны измерения параметров реле:
Для двигателей небольшой мощности измерение параметров можно проводить напрямую в следующих диапазонах:
- диапазон измерения тока до 10А, двигатель до ~4.
 7кВт
7кВт - диапазон измерения тока до 12А, двигатель до ~5.7кВт
- диапазон измерения тока до 16А, двигатель до ~7,5кВт
для расширения диапазона измерения используются трансформаторы тока.
Как измерить коэффициент мощности | Онлайн журнал электрика
Для измерения косинуса фи идеальнее всего иметь особые приборы, созданные для конкретного его измерения — фазометры.
Фазометр — это электроизмерительный прибор, созданный для измерения углов сдвига фаз между 2-мя изменяющимися временами электронными колебаниями.
Если таких устройств нет, то определять коэффициент мощности можно косвенным способом. К примеру, в однофазной сети косинус фи можно найти по свидетельствам амперметра, вольтметра и ваттметра:
cos фи = P / (U х I), где Р, U, I — показания устройств.
в цепи трехфазного тока cos фи = Pw / (√3 х Uл х Iл)
где Pw — мощность всей системы, Uл, Iл — линейные напряжение и ток, измеренные вольтметром и амперметром.
В симметричной трехфазной цепи значение косинус фи можно найти из показаний 2-ух ваттметров Pw1 и Pw2 по формуле:
Общая относительная погрешность рассмотренных способов равна сумме относительных погрешностей каждого прибора, потому точность косвенных способов невелика.
Численное значение косинус фи находится в зависимости от типа нагрузки. Если нагрузкой являются лампы накаливания и нагревательные приборы, то косинус фи = 1, если нагрузка содержит к тому же асинхронные электродвигатели, то косинус фи < 1. При изменении нагрузки электродвигателя его косинус фи значительно меняется (от 0,1 на холостом ходу до 0,86 — 0,87 при номинальной нагрузке), меняется и косинус фи сетей.
Потому на практике в электрических сетях определяют так называемый средневзвешенный коэффициент мощности за какое-то определенное время, допустим, за день либо месяц. Для этого в конце рассматриваемого периода снимают показания счетчиков активной и реактивной энергии Wa и Wv и определяют средневзвешенное значение коэффициента мощности по формуле:
Это значение средневзвешенного коэффициента мощности лучше иметь в электронных сетях равным 0,92 — 0,95.
Внедрение фазометра для измерения коэффициента мощности
Измерить конкретно фазовый сдвиг между напряжением и током нагрузки можно с помощью особых измерительных устройств — фазометров.
Наибольшее распространение получили фазометры электродинамической системы, в которых неподвижная катушка включена поочередно с нагрузкой, а подвижные катушки — параллельно нагрузке, так, что ток какой-то из них отстает от напряжения на угол β1. Для этого поочередно с катушкой включена активно-индуктивная нагрузка, а ток другой опережает напряжение на некий угол β2, зачем включена активно-емкостная нагрузка, при этом β1 + β2 = 90о
Рис. 1. Схема включения фазометра (а) и векторная диаграмма напряжений и токов (б).
Угол отличия стрелки такового прибора зависит только от значения косинуса фи.
Для измерения фазового сдвига между 2-мя напряжениями нередко используют цифровые фазометры. В цифровых фазометрах прямого преобразования для измерения фазового сдвига его конвертируют в интервал времени и определяют последний. Исследуемые напряжения подают на два входа прибора, на цифровом отсчетном устройстве прибора снимают показания числа импульсов, поступающих на счетчик прибора за один период исследуемых напряжений, которое соответствует фазовому сдвигу в градусах (либо в толиках градуса).
Исследуемые напряжения подают на два входа прибора, на цифровом отсчетном устройстве прибора снимают показания числа импульсов, поступающих на счетчик прибора за один период исследуемых напряжений, которое соответствует фазовому сдвигу в градусах (либо в толиках градуса).
Из щитовых устройств, созданных для измерения, более обычный фазометр типа Д31, который может работать в однофазных сетях переменного тока с частотой 50, 500, 1000, 2400, 8000 Гц. Класс точности 2,5. Пределы измерений косинуса фи от 0,5 емкостного фазового сдвига до 1 и от 1 до 0,5 индуктивного фазового сдвига. Фазометры включают через измерительные трансформаторы тока с вторичным током 5 А и измерительные трансформаторы напряжения с вторичным напряжением 100 В.
Для измерения косинуса фи в трехфазной сети при симметричной нагрузке можно использовать щитовые фазометры типа Д301. Класс их точности 1,5. Поочередные цепи включают на ток 5 А конкретно, также через трансформатор тока, параллельные цепи включают конкретно на 127, 220, 380 В, также через измерительные трансформаторы напряжения.
Читайте также: закон об инвалидах 181 фз действующий на 2019-2020 год (льготы)
Измерение Cos φ методом одного амперметра Текст научной статьи по специальности «Электротехника, электронная техника, информационные технологии»
в
ДОЦЕНТ Р. А. ВОРОНОВ.
¡ИЗМЕРЕНИЕ Cos? МЕТОДОМ ОДНОГО АМПЕРМЕТРА.
1.
Применяемые на практике методы измерения угла сдвига фаз 9 >и коэффициента мощности Соэср требуют включения различных .приборов, встречающихся сравнительно редко. Чаще всего производятся измерения по ваттметрам, вольтметру и амперметру, коэффициент же мощности вычисляется по уравнению
Cos 9 =
V.J
для однофазного тока и
р
Cos?
1/» a vj
для трехфазного с симметричной нагрузкой.
Реже используют показания двух ваттметров, включенных по -схеме Арона, с вычислением по уравнению
Л + Р2
с дальнейшим переходом к Cos ср. Еще реже (из-за дефицитности м дороговизны приборов) используются непосредственные отсчеты но фазометрам.
Помимо необходимости иметь точные приборы, часто отсутствующие там, где требуется произвести измерение Cos ср, их необходимо еще включать в сеть. При этом, для включения ампермет-ровых обмоток приборов, требуется производить рассечку проводов, что в большинстве случаев, может быть выполнено только при выключенной сети.
В настоящее время, в связи с повсеместно проводимыми обследованиями установок с целью улучшения Cos?, измерения последнего получают чрезвычайно большое значение. В виду массовости таковых измерений и, часто, невозможностью выключать установки для присоединения приборов, производство измерений обычными способами сильно затруднено. необходимо иметь такой способ измерения Cos <р, который использовал бы именно эти амперметры. Кроме того, из-за возможности расхождения в показаниях приборов* количество амперметров, необходимых для одного измерения, должно быть минимальным.
необходимо иметь такой способ измерения Cos <р, который использовал бы именно эти амперметры. Кроме того, из-за возможности расхождения в показаниях приборов* количество амперметров, необходимых для одного измерения, должно быть минимальным.
В настоящей статье дается описание нового метода измерения* Cos? в цепях трехфазного тока, имеющего чрезвычайную простоту и требующего только одного самого простого амперметра. Этот амперметр может быть даже очень неправильным, лишь бы только-его ошибки были приблизительно пропорциональны показанию.
При простоте применения этого метода измерений и достаточна точных результатах, можно предполагать, что он получит большое распространение в тех случаях, где не требуется большой точности.
2.
Предположим, что сеть трехфазного тока, изображенная на чертеже Í, имеет симметричные фазовые напряжения, что соответствует равенству линейных напряжений. Рас-£ полагая на диаграмме (черт. 2) вектор фазового напряжения первой фазы вертикально* силу тока Jx этой фазы, показываемую амперметром, можно представить в виде комплекса
Рас-£ полагая на диаграмме (черт. 2) вектор фазового напряжения первой фазы вертикально* силу тока Jx этой фазы, показываемую амперметром, можно представить в виде комплекса
J\ Л . Cos Ср — J Jx . Sin CP,
Л » • * *
» М М | « i ,
% * W ы
1
Чер. 1.
где у — угол сдвига тока по отношению к фазовому напряжению, взятый положительным для индуктивной нагрузки.
Если теперь между проводами этой фазы и соседней (например, отстающей 2-й фазы) вставить
Чер. 2,
дополнительное омическое сопротивление R0> то показания амперметра изменятся, т. Vs-Vi
Vs-Vi
т. е направленное в ту же сторону, как и напряжение Vl2 (против часовой стрелки), то вектор силы тока J0 будет иметь прямопро-тивоположное направление, но для нахождения тока J-¿ необходимо взять уже разность токов, а не сумму. Результат от этого, конечно, не изменится.
Эт ф =
(с)
откуда
Соб <р =
(Ф
Последние два уравнеьия (с) и (с!) могут служить для нахождения угла сдвига и коэффициента мощности. При этом, кроме трех показаний основного амперметра, необходимо знать еще и силу тока в сопротивлении или величину последнего и линейное напряжение, вычисляя ток
Вследствие необходимости брать отсчеты по двум приборам, могущим иметь ошибки разных знаков, точность результата получается не слишком большой. о — А АЛ~АА~\~ А Л А А Л+АЛ
о — А АЛ~АА~\~ А Л А А Л+АЛ
или
Вводя обозначения
Л + Л + А =2 А
(Л++У|) — (Л А + Л А+А А) = &
(е)
получаем биквадратное уравнение
Д — 2 Л+ £2 = О,
рарешая которое имеем
= +
(О
по которому, зная три показания основного амперметра, легко вычислить значение тока в сопротивлении. Необходимо отметить, что остальные значения для силы тока, получаемые как корни уравнения четвертой степени, соответствуют расположению векторов, не могущему быть в действительной цепи
Полученные два значения, отличающиеся только знаком, соответствуют емкостному и индуктивному сдвигу с равными коэффициентами мощности. В с числить значения Бтср и Со в у непредстав-
В с числить значения Бтср и Со в у непредстав-
ляет никакого затруднения, но при производстве большого числа измерений оказывается слишком длинным и утомительным.
4.
Для упрощения работы можно, вместо вычислений, воспользоваться графическим построением, вытекающим из векторной диаграммы. Вынося вектора токов на отдельный чертеж, легко видеть (черт. 3), что их взаимное расположение получается вполне определенным.
Черт. 3.
Вектора трех токов Л;Л и i3 оказываются расположенными так, что их концы находятся на равностороннем треугольнике ABC, стороны которого равны силе тока У0 в сопротивлении R0i а сторона ВС располагается перпендикулярно к вектору напряжения.
Исходя из этого расположения, можно предложить следующий ход построения векторной диаграммы. Выбирая произвольное направление, откладываем на нем (черт. 4) три отрезка ОАх; ОВх и ОСи равные в масштабе полученным отсчетам но амперметру Уь J2 и У3. Через две из полученных точек (лучше самую ближнюю к точке О и самую дальнюю от нее) проводим вспомогательные окружности с центром в точке О. На чертеже 4 такие дуги проведены для точек Ах и С(.
Равносторонний треугольник должен быть такого размера, чтобы своими вершинами он мог попасть на две проведенных дуги и в точку Вх. Проводя из последней еще одну засечку радиусом Вх С, несколько большим, чем длина отрезки Ах Си получаем равнобедренный треугольник АВХ С. Изменяя длину взятого радиуса ВА, под* бираем его так, чтобы расстояние АС получилось равным с ним по величине. Такое соотношение легко получить после двух-трех пробных засечек.
Полученный таким подбором треугольник АВХ С будет равносторонним и будет соответствовать треугольнику ABC чертежа 3. Проводя из точки О прямую ОА и опуская перпендикуляр OD на сторону ВС построенного треугольника (или на ее продолжение), получаем искомый угол сдвига фаз, как угол между прямыми ОА и OD. Опуская еще из точки А перпендикуляр АЕ на прямую OD, получим также коэффициент мощности из соотношения отрезков
r ОЕ
Cos ф =—
т О А
Стороны построенного треугольника АВХ С определяют в масштабе силу тока в сопротивлении R0. При построении этого треугольника, засечка из точки В может быть произведена и по другую сторону оси, что повлияет только на направления угла сдвига (емкостный или индуктивный), а не на его величину и значение Cos 9. Эти два расположения соответствуют двум значениям тока У0, получаемого из уравнения (f) и отличающихся только знаком. Зная, какая в сети имеется нагрузка, легко сообразить, какое расположение выбрать в каждом случае.
Если не знают, какая нагрузка имеется в сети, но известно чередование фаз, то можно пользоваться правилом, вытекающим из
Черт. 4.
чертежа 2 и уравнений (а) и (Ь). Для индуктивной нагрузки больший ток будет получаться при вставлении сопротивления R0 в опережающую фазу, а при емкостной—в отстающую. Это же правило можно использовать для определения чередования фаз.
Построение треугольника ABC по длинам отрезков ОД, ОВ и ОС без подбора засечками, повидимому, является неразрешимой задачей.
Быстрее всего коэффициент мощности можно получить, если воспользоваться специально для этого построенной номограммой, приведенной на чертеже 5. Беря по амперметру три отсчета Л; Л и /3, вычисляем отношения
* Л .>Ь. При емкостной
нагрузке эти соотношения получаются обратными, что дает возможность использовать эту же часть номограммы, но с перестановкой значений Ъ и с местами.
Для построения номограммы, разделим уравнения (а) и (Ь) на Принимая во внимание обозначения, введенные выше, получаем после их подстановки
или
= 1 Л2 ■ Г2 = 1+Л2-
■2aCos(cp + 30°) (h)
Cos(cp — 30°)
Задаваясь различными значениями а и Соб<р и вычисляя соответствующие значения Ъ и с, получаем возможность построить всю
номограмму по токам. Зычисленые значения Ь и с для различных коэффициентов мощности приведены в таблице, в конце статьи.
6.
При производстве измерений, на точность результата имеют влияние точность амперметра, несимметрия линейных напряжений сети и дополнительные падения напряжения, вызываемые приключаемым
0.1 0.2 0.3 04 0.5 0.6 0.7 0 8 0,9 о.эч
0.99
* сопротивлением. Разберем, какие можно ожидать в этих случаях отличия получаемого значения Совср от действительной его величины.
Неточность амперметра, при производстве всех отсчетов по одному прибору, будет только тогда оказывать влияние, когда
ошибка не пропорциональна показанию. Так как в большинстве случаев, если и нет такой пропорциональности целиком, но все же все ошибки имеются одного знака, то они будут частично сглаживать друг друга и влиять на окончательный результат сравнительно мало. Проверка ряда технических приборов переменного тока различных фирм и учет получающихся ошибок в величинах отношений
¿ = А и
. Л Л
показал, что наибольшие отклонения между ними не превосходят 1—1,5°/0. Рассматривая номограмму видим, что такая ошибка при а = (0,3—0,5) соответствует отклонению в значениях Соэ<р в худшем случае на следующие величины:
ОД+0,03 0,5 + 0,04 0,8 + 0,03 1,0 + 0,00
При применении точных амперметров лабораторного или контрольного типов, расхождение в значениях не превосходит 0,5—0,8°/0, а отклонения в результатах снижаются примерно вдвое.
7.
Выясним теперь вопрос о том, как влияет несимметрия в линейных напряжениях.
Если эта несимметрия выразилась в том, что одно из линейных напряжений, имеющееся между теми фазами, в которых нет амперметра (т. е. фазы 2 и 3), увеличилось или уменьшилось, а остальные два напряжения остались неизменными, то это скажется на диаграмме чертежа 3 только в изменении углов между отрезками АВ и АС и вектором напряжения ОУ. При несимметрии в 5% эти углы, вместо 30° будут иметь значения
1,05 V
агсБШ = агсвт 0,525 = 31° 40′
при возрастании третьего напряжения, или
0,95 V
агсэт —-у— — агсвт 0,475 == 28° 22′
при его уменьшении.
Полагая, что при измерении было включено сопротивление из расчета
Л
и что нагрузка имела сдвиг фаз равный ср=.60°, найдем по уравнениям (К), с изменением в них углов 30° на полученный выше, значения для b и с
£2=l-f0,52-{-2 • 0,52 . Cos(60°4-31° 40′) = 1,221 с2 = 14-0,524-2 . 0,52 . Cos(60° — 31° 40′) — 2,130 или ¿ = 1,105 с =.1,459
Рассматривая эти значения, как полученные из опыта, находим по номограмме, что им соответствует Cos у — 0,47, вместо действительного значения Cos 60° = 0,5.
% Подробным же образом для уменьшения напряжения, т. е. для угла 28° 22′ вместо 30°, получим значение Coscp= 0,53. Таким образом,отклонение в получаемом значении коэффициента мощности может для данных условий достигать примерно 0,03 в ту и другую сторону.
Указанный случай при сдвиге в 60° и искажении .напряжения между 2-й и 3-й фазами, будет иметь наибольшее отклонение в значениях Cos ср. При других углах сдвига фаз и других несимметриях напряжений, это отклонение будет меньше. Наименьшим оно получится при ваттной нагрузке. В этом случае при искажении напряжения между 2-й и 3-й фазой ошибки в
эн
V) О
о
о
0.5
Черт. 6.
Cosy
1.0
результате не будет совсем при искажении же напряжения между 1-й фазой (в которой вставлен амперметр) и одной из двух других, ошибка может достигать только 0,01.
Производя подобные вычисления для
всех возможных случаев, несимметрии напряжений, получаем кривую наибольших отклонений результата для 5°/0 несимметрии напряжений и отношения а=0,5, построенную на черт 6. о.1 ставлены на чертеже 7, из
которого видим, что с Черт* 7″ увеличением отношения
а возможная ошибка быстро возрастает.
0.05
Применение в качестве сопротивления R0 реостата из металлических ламп накаливания уменьшает ошибку, в виду увеличения его сопротивления при увеличении папряжения.
8.
Для выяснения влияния дополнительного падения напряжения в подводящих проводах, получающегося в связи с включением сопротивления R0i проведем примерный расчет для одной из нагрузок.
Для этого расчета возьмем цепь с фазовым напряжением нагрузки 120 V (линейное 208 1/) и нагрузку, потребляющую 12 Л при индуктивном сдвиге в 60°. (Cos <р = 0,5). Сопротивление проводов примем только омическим с таким расчетом, чтобы напряжение источника тока (сети) было не более 125 V (падение напряжения около 4°/о).
Сопротивление фазы нагрузки будет равно
V
Ън = — (Cos ср -J-/Sin <р)
J
а сопротивление проводов Rnp
120
12
(0,50,866) = 5+у 8,66
■Yes-
(8,66)2 — 5 = 0,78 ома Л
Для того, чтобы значения отношения а = необходимо иметь ток
J\
было близко к 0,5,
/0 = 0,5 • J\ = 6 ампер
или сопротивление
Яо =
208
34,7 = 35 ом.A 7
«ъ uvj;
Черт. 8.
Вся схема включения представится в виде приведенной на черт. 8.
Заменяя треугольник, образуемый сопротивлениями нагрузки и сопротивлением на эквивалентную ему звезду, и складывая полученные сопротивления с остальными, получаем простую звезду с сопротивлениями отдельных фаз.
¿ = ¿3 = 6,41+74,52 ¿2 = 5,464-7 10,71
или
« 1Х = 1Ъ — 7УЫ ома = 12,01 ома Найдя теперь проводимости отдельных фаз
Г1 = Г3 = 0,104 —/0,0735
Г2 = 0,378—у 0,0742
вычисляем потенциал нулевой точки эквивалентной звезды нагрузки по отношению нулевой точки сети. = 144,8 У и = 101,5 V
деля на сопротивления фаз, находим силы тока в проводах
Л = 16,9 А; Л = 12,1 А; У3 = 12,93 А
легко видеть, что ток соответствует току, проходящему через амперметр при вставлении сопротивления Я0 в опережающую фазу (т. е, отсчету /3), атокУ3— при вставлении сопротивления в отстающую фазу (т. е, отсчету /2) * * —
Помня, что при работе без сопротивления нагрузка потребляла 12 ампер (т. е. /1 = 12Л), находим отношения
е = .Ж=,,41 — 08
12 12
По этим значениям по номограмме получаем значение Cos ср = 0,46. отличающееся от действительного (Cos ср = 0,5) в сторону уменьшения на 0,04.
Производя подобные же расчеты для других условий, легко видеть, что это отклонение от истинной вдличины будет больше при меньшем коэффициенте мощности или большей силе тока в дополнительном сопротивлении. При Coscp=l ошибки не будет совсем, при Coscp = 0 она достигнет почти 0,1. Индуктивность проводов несколько улучшает результат при индуктивной же нагрузке, но ухудшает при емкостной. При увеличении падения напряжения в проводах ошибка возрастает почти пропорционально таковому (немного медленнее). Наличие нулевого провода почти не отражается на получающейся ошибке.
Для случаев нормальной работы сетей и нагрузок, подобные подсчеты показали, что ошибка обычно не превосходит значения
A Cos ср <; 0,1 (1 — Cos ср) в сторону уменьшения результата.
9.
Проверяя применение этого способа к измерению коэффициентов мощности асинхронных моторов в различных условиях их работы и сравнивая получаемые результаты с показаниями фазометра, оказалось, что ошибка ни разу не превысила значения 0,05, будучи обычно равными 0,02—0,03. В большинстве случаев из за падения напряжения в проводах, эта ошибка была в сторону уменьшения результата и только при нескольких измерениях она оказалась в сторону увеличения (вероятно, из-за несимметрии напряжений). Так как измерения производились примерно при таких же условиях, какие обычно имеются в промышленных установках, можно считать, что и там больших расхождений получаться не будет.
Таким образом данный способ применим в тех случаях, когда не требуется знать точной величины коэффициента мощности, а достаточно иметь его с отклонением до 0,05 в ту или другую сторону. Необходимость включения реостата R0 ставит предел применения этого способа для мощностей не свыше 30—40 KVA в сетях с напряжением до 380 вольт.
10.
Данный способ измерения может быть изменен, включая вместо омического сопротивления R0y индуктивные или емкостные. В этом случае в диаграмме чертежа 4 угол между отрезками ВС и OD должен быть не 90°, а другой, в соответствии с включаемым сопротивлением. Обозначая угол сдвига для последнего через ср0, получаем
/ CDO = 90 + ср0
Уравнения (с), (d), (/), (g) и (/г) получают другое, еще более сложное выражение, номограмма же чертежа 5 дает значения
Cos (ср + ср0)
При включении одной емкости, уравнения (с) дает значение Cos ср, а уравнение (d) — Sincp, номограмма же чертежа 5 значения Sincp, но в тех пределах, как она построена действительна только для емкостной нагрузки.
Замена омического сопротивления на емкость может иметь некоторые значения при измерении Coscp в высоковольтных сетях.
Вместо амперметра можно использовать щипцы Диттца, производя ими измерения в различных местах цепи. В этом случае легко измерить также и /0, а, следовательно, воспользоваться уравнениями {с) и (d).
В настоящее время разрабатывается конструкция щипцов и амперметров, которые дали бы возможность производить такие измерения для любых мощностей и напряжений, при чем таковые измерения смогут быть распространены и на однофазный ток.
В заключение необходимо отметить, что при применении описанного способа к цепям трехфазного тока с несимметричной нагрузкой фаз, получаемые значения Cos ср будут относиться к той фазе, в которой имелся амперметр и будут соответствовать углу сдвига между током в проводе и фазовым напряжением сети, считая таковые симметричными.
Таблица значений, необходимых для построения номограммы чертежа 5.
Сое <р а Ь и с 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8
0,0 с 1.054 1.113 1.179 1.249 1.323 1.400 1.480 1.562
Ъ 0.954 0.917 0.889 0.872 0.866 0.872 0.889 0.917
0,1 с 1.063 1.128 1.200 1.276 1.356 1.437 1.520 1.608
Ь 0.963 0.936 0.918 0.912 0.916 0.933 0.957 0.992
0,2 с 1.071 1.143 1.220 1.300 1.384 1.470 1.556 1.644
Ь 0.973 0.956 0.947 0.852 0.965 0.988 1.023 1.064
0,3 с 1.078 1.157 1.238 1.322 1.410 1.499 1.588 1.680
Ъ 0.982 0.976 0.979 0.993 1.017 1.049 1.089 1.138
0,4 с 1.085 1.168 1.254 1.342 1.432 1.521 1.617 1.711
Ь 0.993 0.998 1.011 1.034 1.067 1.108 1.154 1,208
0,5 с 1.089 1.178 1.269 1.361 1.454 1.549 1.644 1.739
Ь 1.004 1.020 1.044 1.077 1.119 1.167 1.220 1.318
0,6 с 1.093 1.187 1.281 1.377 1.474 1.571 1.668 1.763
Ь 1.016 1.043 1.078 1.121 1.170 1.226 1.287 1.352
0,7 с 1.097 1.193 1.291 1.389 1.488 1.586 1.683 1.785
Ъ 1.029 1.068 1.113 1 166 1.224 1.288 1.359 1.428
0,8 с 1.099 1.198 1.298 1.397 1.497 1.597 1.698 1.798
Ь 1.043 1.094 1.151 1.214 1.282 1.352 1.428 1.508
0,9 с 1.099 1.199 1.299 1.398 1.498 1.598 1.698 1.798
Ъ 1.058 1.125 1.193 1.267 1.344 1.425 1.510 1.593
0,97 с 1.097 1.194 1.291 1.389 1.489 1.587 1.683 1.783
Ь 1.074 1.152 1.234 1.317 1.403 1.491 1.5*0 1.672
1,0 с — Ь 1.089 1.178 1.269 1.361 1.454 1.549 1.644 1.739
Измерение коэффициента мощности — КиберПедия
Для измерения cos φ обычно применяют приборы для непосредственного его измерения — фазометры.
Фазометр — электроизмерительный прибор, предназначенный для измерения углов сдвига фаз между двумя изменяющимися периодически электрическими колебаниями.
Если таких приборов нет, то измерять коэффициент мощности можно косвенным методом. Например, в однофазной сети косинус фи можно определить по показаниям амперметра, вольтметра и ваттметра:
cos φ = P / (U х I), где Р, U, I — показания приборов.
в цепи трехфазного тока cos φ = Pw / (√3 х Uл х Iл)
где Pw — мощность всей системы, Uл, Iл — линейные напряжение и ток, измеренные вольтметром и амперметром.
В симметричной трехфазной цепи значение косинус фи можно определить из показаний двух ваттметров Pw1 и Pw2 по формуле
Общая относительная погрешность рассмотренных методов равна сумме относительных погрешностей каждого прибора, поэтому точность косвенных методов невелика.
Численное значение косинус фи зависит от характера нагрузки. Если нагрузка чисто активная (лампы накаливания, нагревательные приборы), то cos φ = 1, если нагрузка содержит еще и асинхронные электродвигатели, то cos φ < 1. При изменении нагрузки электродвигателя его cos φ существенно изменяется (от 0,1 на холостом ходу до 0,86 — 0,87 при номинальной нагрузке), изменяется и косинус фи сетей.
Поэтому на практике в электрических сетях определяют так называемый средневзвешенный коэффициент мощности за какое-то определенное время, допустим, за сутки или месяц. Для этого в конце рассматриваемого периода снимают показания счетчиков активной и реактивной энергии Wa и Wv и определяют средневзвешенное значение коэффициента мощности по формуле
Это значение средневзвешенного коэффициента мощности желательно иметь в электрических сетях равным 0,92 — 0,95.
Измерение частоты и фазы
Согласно ПУЭ измерение частоты должно производиться:
1) на каждой секции шин генераторного напряжения;
2) на каждом генераторе блочной тепловой или атомной электростанции;
3) на каждой системе (секции) шин высшего напряжения электростанции;
4) в узлах возможного деления энергосистемы на несинхронно работающие части.
Регистрация частоты или ее отклонения от заданного значения должна производиться:
1) на электростанциях мощностью 200 МВт и более;
2) на электростанциях мощностью 6 МВт и более, работающих изолированно.
Абсолютная погрешность регистрирующих частотомеров на электростанциях, участвующих в регулировании мощности, должна быть не более ± 0,1 Гц.
Частота — одна из важнейших характеристик периодического процесса; определяется числом полных циклов (периодов) изменения сигнала в единицу времени.
Период — наименьший интервал времени, удовлетворяющий уравнению и(t) = и(t + Т). Мгновенная угловая частота определяется через производную во времени от фазы напряжения сигнала, т. е. ω(t) = dψ/dt. Так как фаза у гармонического сигнала растет во времени по линейному закону, то частота f — постоянная величина, т. е. f = 1/[(2π)( dψ/dt)] = ω(t) /(2 π ).
Частотомеры — приборы, измеряющие частоту.
Частота электрических сигналов измеряется методами непосредственной оценки и сравнения.
Измерение частоты методом непосредственной оценки производится цифровыми электронно-счетными частотомерами. Измерение частоты сигналов методом сравнения осуществляется с помощью осциллографа, частотомеров гетеродинных, построенных на биениях, и др. Цифровые частотомеры предназначаются для точных измерений частоты гармонических и импульсных сигналов; используются для измерения отношения частот, периода, длительности импульсов, интервалов времени.
Пример. Частотомер ЦД2120.2 — для измерения и индикации частоты и для коммутации цепей нагрузок при выходе измеряемой частоты за заданную уставку.
Область применения — на предприятиях энергетической промышленности для контроля качества вырабатываемой электроэнергии; на предприятиях — энергопотребителях.
Технические характеристики:
· Диапазон измерения от 45 до 55 Гц при номинальной частоте измерения 50 Гц и дискретности измерения частоты 0,005 Гц.
· Входное напряжение цепи измерения (220 +44, -110) В; (100 +20, -50) В; (0,2 ± 0,1) В.
· Предел допускаемого значения основной погрешности 0,015 % во всем диапазоне измерения.
· Быстродействие — десять периодов измеряемой частоты.
· Питание частотомера осуществляется от источника переменного тока напряжением (200 ± 33) В или (100 ± 15) В и частотой (50 ± 5) Гц.
· Мощность, потребляемая частотомером, не более 10 ВА.
· количество коммутируемых цепей — 7;
· параметры коммутируемых цепей — напряжение постоянного и переменного тока (220±33) В, мощность до 10 ВА.
· Частотомер ЦД2120.2 имеет выход на внешний разъем результатов измерения частоты в двоично-десятичном коде 8-4-2-1 с ценой единицы наименьшего разряда кода 0,01 Гц, а также сигнала «конец измерения».
· Подключение внешних проводов выполнено под винт, что повышает защиту от случайных касаний токоведущих частей клемм.
· Условия эксплуатации:
· температура окружающего воздуха от 5 до 50 °С;
· относительная влажность 90 % при 20 °С.
· Габаритные размеры частотомера не более 80 х 160 х 250 мм.
· Масса частотомера не более 2 кг.
Фаза характеризует состояние гармонического сигнала в рассматриваемый момент времени. Для синусоидальной функции
u(t) = Umох sin (ωt + ψ) фаза гармонического сигнала (ωt + ψ) является линейной функцией времени.
Сдвиг по фазе у представляет собой модуль разности начальных фаз двух сигналов u(t)1 =Umох1 sin (ωt + ψ1) и u(t)2 = Umох2 sin (ωt + ψ2) одинаковой частоты:
φ = ψ1 + ψ2
Методы измерения сдвига по фазе зависят от диапазона частот, уровня, формы сигнала и требуемой точности измерения. Как правило, применяют методы непосредственной оценки и сравнения.
Фазометры — приборы, измеряющие сдвиг по фазе в радианах или градусах.
К фазометрам непосредственной оценки относят: аналоговые электромеханические фазометры с логометрическими механизмами; аналоговые электронные фазометры с преобразованием фазового сдвига в пропорциональный ток; цифровые фазометры.
Измерение сдвига по фазе методом сравнения производится с помощью осциллографа. В широком диапазоне частот в маломощных цепях при грубых измерениях сдвиг по фазе измеряют с помощью осциллографа, а при более точных измерениях — методом сравнения, используя осциллограф в качестве индикатора равенства фаз.
На промышленной частоте при измерении сдвига по фазе применяют логометрические фазометры, использование которых рекомендуется при больших уровнях синусоидального сигнала и сопряжено с большим потреблением энергии и невысокой точностью. При точных измерениях сдвига по фазе используют аналоговые и цифровые электронные фазометры.
Сдвиг по фазе между напряжением U и током I на промышленной частоте измеряется вольтметром, амперметром и ваттметром и определяется по формуле φ = аrссоs [Р/(UI)].
Наибольшее распространение получили фазометры электродинамической системы, в которых неподвижная катушка включена последовательно с нагрузкой, а подвижные катушки — параллельно нагрузке, так, что ток одной из них отстает от напряжения на угол β1. Для этого последовательно с катушкой включена активно-индуктивная нагрузка, а ток другой опережает напряжение на некоторый угол β2, для чего включена активно-емкостная нагрузка, причем β1 + β2 = 90о
Угол отклонения стрелки такого прибора зависит только от значения косинуса фи.
Для измерения фазового сдвига между двумя напряжениями часто применяют цифровые фазометры. В цифровых фазометрах прямого преобразования для измерения фазового сдвига его преобразуют в интервал времени и измеряют последний. Исследуемые напряжения подают на два входа прибора, на цифровом отсчетном устройстве прибора снимают показания числа импульсов, поступающих на счетчик прибора за один период исследуемых напряжений, которое соответствует фазовому сдвигу в градусах (или в долях градуса).
Из щитовых приборов, предназначенных для измерения, наиболее щитовой фазометр типа Д301, который может работать в однофазных сетях переменного тока с частотой 50, 500, 1000, 2400, 8000 Гц. Класс точности 2,5. Пределы измерений косинуса фи емкостного фазового сдвига от 0,5 до 1 и от 1 до 0,5 индуктивного фазового сдвига.
Последовательные цепи включают на ток 5 А непосредственно, а также через трансформатор тока, параллельные цепи включают непосредственно на 127, 220, 380 В, а также через измерительные трансформаторы напряжения
Цифровые измерения
Как считать электрическую мощность?
Чтобы обеспечить нормальное функционирование электрической проводки, необходимо ещё на этапе проектирования правильно рассчитать мощность, подобрать кабель подходящего сечения. От этого зависит не только срок эксплуатации системы, но и пожаробезопасность сооружения. Если выбрать сечение ошибочно или неправильно рассчитать мощность, можно столкнуться с такими опасными последствиями, как возгорание электропроводки, короткие замыкания, пожар и пр. При выборе оборудования и кабельно-проводниковой продукции важно учитывать разные критерии, среди которых напряжение, сила тока, особенности эксплуатации сети.
Формула расчёта
В уже функционирующей сети измерить мощность электрического тока можно при помощи специального оборудования. Что же делать на этапе проектирования? Ведь самой цепи ещё нет. В этом случае применяется расчётный метод.
Существует два вида мощности: активная и реактивная. Активная превращается в полезную энергию безвозвратно, считается полезной. Реактивная предусматривает затрату определенного (расчетного согласно установленного оборудования и типа оборудования) количества энергии.
В нашем случае реактивная мощность нам не интересна, и мы не будем ее рассчитывать!
В цепях переменного тока, ток и напряжения сдвигаются относительно друг друга.
Этот сдвиг на угол cos обозначается буквой φ (фи).
При расчёте мощности электрической мощности следует учитывать тип сети:
P=U*I*cosφ — для однофазной;
P=√3*U*I*cosφ — для трехфазной.
U – это напряжение сети,
I – сила тока,
cosφ – коэффициент мощности.
cosφ – коэффициент мощности, это паспортная величина оборудования, если не известно о типе оборудования (например, квартиры), то cosφ – расчетный и берется из инструкции по проектированию (СП 256.1325800.2016)
Зависимость коэффициента мощности
Чтобы рассчитать полную (Обращаем внимание, что имеется ввиду установленная, т.е. полная мощность) мощность, необходимо определить суммарную мощность всей техники и оборудования, которые будут эксплуатироваться, и подключаться к данной электрической сети. Это можно узнать путём суммирования мощностей приборов (этот показатель указан в паспорте товара).
При определении коэффициента мощности учитывается характер нагрузки. К примеру, для нагревательного оборудования он близится к 1. Важно учитывать, что любая активная нагрузка предполагает незначительную реактивную составляющую, поэтому коэффициент мощности будет равен не 1, а 0,95. Для более мощных приборов – 0,8. Напряжение для однофазных цепей принимается 220 В, для трехфазных – 380 В.
Пример решения контрольной по электротехнике
Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.
На рисунке, изображён магнитопровод с воздушным зазором. Материал сердечника — электротехническая сталь. Размеры сердечника по средней магнитной линии в мм : ℓ1=280 мм ; ℓ2=330 мм ; ℓ3=370 мм ; ℓ0=2 мм. Толщина сердечника 50 мм. В сердечнике требуется создать магнитный поток Ф=0,0048 Вб. Определить ток, который должен проходить по обмотке катушки, если она имеет w=800 витков. Вычислить, также ток катушки, для создания заданного магнитного потока, если в сердечнике будет отсутствовать воздушный зазор.
Дано : ℓ1=280 мм ; ℓ2=330 мм ; ℓ3=370 мм ; ℓ0=2 мм ; d=50 мм ; w=800 ; Ф=0,0048 Вб.
Найти : I
Решение.
1. Начертим схему замещения магнитной цепи.
Цепь содержит три участка : первый состоит из одного участка – электротехнической стали ; второй из одного участка – электротехнической стали ; третий из двух участков — электротехнической стали и воздушного зазора.
Найдём длины и площади сечения участков.
Первый участок : S1=0.05×0.1=5×10-3 м2 ; ℓ1=280 мм=0,28 м
Второй участок : S2=0.05×0.08=4×10-3 м2 ; ℓ2=330 мм=0,33 м ;
Третий участок : S3=0.05×0.08=4×10-3 м2 ; ℓ3=370 мм=0,37 м.
2. Составим для магнитной цепи уравнения по законам Кирхгофа.
По второму закону Кирхгофа составляем одно уравнение.
Ф(Rм1+Rм2+Rм3+R0)=F (1)
Найдём магнитные индукции на каждом участке : B1=Ф/S1=0.0048/0.005=0.96 Тл ;
B2=B3=B0=Ф/S2=Ф/S3=0.0048/0.004=1.2 Тл
Найдём напряжённости магнитного поля на каждом участке : на участках из электротехнической стали напряжённость поля находим по кривой намагничивания
h2=600 А/м ; h3=h4=1400 А/м.
Напряжённость магнитного поля находим по формуле : H0=B0/μ0=1.2/(4π×10-7)=9.6×105 А/м
(где μ0=4π×10-7 Гн/м – магнитная постоянная).
Запишем уравнение (1) :
F=Iw=h2ℓ1+h3ℓ2+h4ℓ3+H0ℓ0=600×0.28+1400×0.33+1400×0.37+9.6×105×0.002=3068 А
Откуда находим ток, который должен проходить по обмотке : I=3068/800=3.8 А
Найдём ток в обмотке катушки, необходимый для создания магнитного потока Ф=0,0048 Вб, если воздушный зазор отсутсвует.
F=Iw=h2ℓ1+h3ℓ2+h4(ℓ3+ℓ0)=600×0.28+1400×(0.33+0.37+0.002)=1150.8
Откуда ток катушки : I=1150.8/800=1.4 А
Ответ : 1) I=3.8 A ; 2) I=1.4 A.
Задача 7.
К переменному напряжению U=150 В частотой f=50 Гц подключены последовательно соединённые резистор и конденсатор. По цепи проходит ток I=3 А, при этом на резисторе возникает падение напряжения Ua=90 В. Начертить схему цепи. Определить полное сопротивление цепи z, сопротивление резистора R, сопротивление XC и ёмкость С конденсатора, коэффициент мощности cosφ, напряжение UC на ёмкостном сопротивлении. Построить в масштабе mu=20 В/см векторную диаграмму напряжений, отложив горизонтально вектор тока.
Дано : U=150 В ; f=50 Гц ; I=3 А ; Ua=90 В.
Найти : z , R , XC , C , cosφ , UC.
Решение.
Находим полное сопротивление цепи : z=U/I=150/3=50 Ом.
Сопротивление резистора : R=Ua/I=90/3=30 Ом.
Находим сопротивление XC : XC==40 Ом.
Находим ёмкость конденсатора : C=1/(2πfXC)=1/(2×50×3.14×40)=79.6×10-6 Ф=79,6 мкФ.
Находим коэффициент мощности цепи : cosφ=R/z=30/50=0.6
Находим напряжение на ёмкости : UC=IXC=3×40=120 В.
Для построения векторной диаграммы, найдём длины векторов : ℓUa=Ua/mu=90/20=4.5 см ;
ℓUc=UC/mu=120/20=6 см.
Построение векторной диаграммы начинаем с построения вектора тока I, который откладываем горизонтально. Вектор напряжения Ua откладываем параллельно вектору тока I. От конца вектора Ua откладываем вектор напряжения UC перпендикулярно вектору тока I, в сторону его опережения. Геометрическая сумма векторов Ua и UC даёт вектор U.
Схема цепи и векторная диаграмма построены на рисунке.
Ответ : z=50 Ом ; R=30 Ом ; XC=40 Ом ; C=79,6 мкФ ; cosφ=0.6 ; UC=120 В.
Задача 13.
Последовательно с катушкой, активное сопротивление которой R=5 Ом и индуктивное XL=
=26 Ом, включен конденсатор, ёмкостное сопротивление которого XC=14 Ом. Ток в цепи I=12 А, частота f=50 Гц. Начертить схему цепи. Определить полное сопротивление цепи z ; коэффициент мощности cosφ и напряжение на зажимах цепи U. Вычислить индуктивность катушки L0, при которой в цепи наступает резонанс напряжений. Для режима резонанса напряжений определить полное сопротивление цепи z0 ; ток I0 ; падение напряжения на активном Ua0 и ёмкостном UC0 сопротивлениях ; коэффициент мощности цепи cosφ0 ; полную S, активную P и реактивную Q мощности цепи. Построить в масштабе mu=50 В/см векторную диаграмму напряжений для режима резонанса, отложив горизонтально вектор тока.
Дано : R=5 Ом ; XL=260 Ом ; XC=14 Ом ; I=12 A ; f=50 Гц.
Найти : z ; cosφ ; U ; L0 ; z0 ; I0 ; Ua0 ; UC0 ; cosφ0 ; S ; P ; Q.
Решение.
Схема цепи приведена на рисунке.
Полное сопротивление цепи : z==13 Ом
Коэффициент мощности цепи : cosφ=R/z=5/13=0,38
Напряжение, приложенное к цепи : U=Iz=12×13=156 В
Найдём индуктивность катушки, которую нужно включить в сеть с конденсатором, чтобы в цепи возник резонанс напряжений. Условие резонанса :
XL0=XC=14 Ом
Индуктивность катушки : L0=XL0/(2πf)=14/(2×3.14×50)=0.045 Гн=45 мГн.
Полное сопротивление цепи в режиме резонанса напряжений равно активному сопротивлению : z0=R=5 Ом.
Ток в цепи в режиме резонанса напряжений : I0=U/z0=156/5=31,2 А.
Падение напряжения на активном сопротивлении в режиме резонанса напряжений : Ua0=I0R=31.2×5=156 В.
Падение напряжения на ёмкостном сопротивлении в режиме резонанса напряжений :
UC0=I0XC=31.2×14=436.8 В.
Коэффициент мощности цепи в режиме резонанса напряжений : cosφ0=R/z0=5/5=1
Активная P, реактивная Q и полная S мощности цепи в резонансе напряжений :
P=I02R=31.22×5=4867.2 Вт ; Q=0 ; S=P=4867.2 В∙А.
Для построения векторной диаграммы найдём длины векторов : ℓUa=156/50=3.1 см ;
ℓUc0=436.8/50=8.7 см.
Построение векторной диаграммы начинаем с построения вектора тока I, который откладываем горизонтально. Вектор напряжения Ua0 откладываем параллельно вектору тока I. От конца вектора Ua0 откладываем вектор напряжение UC0 перпендикулярно вектору тока I в сторону отставания от него. От конца вектора UC0 откладываем вектор напряжения UL0 перпендикулярно вектору тока I в сторону его опережения (по модулю вектора UC0 и UL0 равны).
Геометрическая сумма векторов Ua0 , UC0 и UL0 даёт вектор напряжения U, приложенного к цепи (U=Ua0).
Ответ : z=13 Ом ; cosφ=0.38 ; U=156 В ; L0=45 мГн ; z0=5 Ом ; I0=31.2 A ; Ua0=156 В ; UC0=
=436.8 В ; cosφ0=1 ; P=4867.2 Вт ; Q=0 ; S=4867.2 В∙А.
№ 19
Цепь переменного тока состоит из двух параллельных ветвей. В первую ветвь включены последовательно активное и индуктивное сопротивления : R1=12 Ом ; XL=9 Ом. Вторая ветвь состоит из последовательно соединённых активного и ёмкостного сопротивлений : R2=12 Ом ; XC=16 Ом. Напряжение на зажимах цепи U=220 В. Начертить схему цепи. Определить токи I1 , I2 в параллельных ветвях и ток I в неразветвленной части цепи ; коэффициент мощности всей цепи ; активную P , реактивную Q и полную S мощности цепи. Задачу решить методом разложения токов на активные и реактивные составляющие. Построить векторную диаграмму токов в масштабе mi=2 А/см. Вычислить активную g и реактивную bc проводимости второй ветви.
Дано : R1=12 Ом ; XL=9 Ом ; R2=12 Ом ; XC=16 Ом ; U=220 В.
Найти : I1 , I2 , I , cosφ , P , Q , S , g2 , bc.
Решение.
Схема цепи изображена на рисунке.
Находим полные сопротивления параллельных ветвей.
Z1==15 Ом ; Z2= =20 Ом.
Находим токи в параллельных ветвях : I1=U/Z1=220/15=14.7 A ; I2=U/Z2=220/20=11 A
Найдём углы сдвига фаз между токами I1 и I2 и напряжением U.
φ1=arctg[XL/R1]=arctg[9/12]=37°
φ2=arctg[-XC/R2]=arctg[-16/12]=-53°
Находим активные составляющие токов I1, I2 и I.
Ia1=I1cosφ1=14.7×cos(37°)=11.7 A ; Ia2=I2cosφ2=11×cos(-53°)=6.6 A ;
Ia=Ia1+Ia2=11.7+6.6=18.3 A
Находим реактивные составляющие токов I1 , I2 и I.
Ip1=I1sinφ1=14.7×sin(37°)=8.84 A ; Ip2=I2sinφ2=11×sin(-53°)=-8.78 A
Ip=Ip1+Ip2=8.84-8.78=0,06 А
Полный ток в неразветвленной части цепи : I==18.3 A.
Найдём коэффициент мощности цепи : cosφ=Ia/I=18.3/18.3=1
В цепи имеет место резонанс токов.
Найдём активную P, реактивную Q и полную S мощности цепи.
P=I12R1+I22R2=14.72×12+112×12=4045.08 Вт
Q=I12XL-I22XC=14.72×9-112×16=8.8 вар
S=UI=220×18.3=4026 В∙А , или S==4045 В∙А.
Вычислим активную g2 и реактивную bc составляющие второй ветви.
g2=R2/Z22=12/202=0.05 сим ; bc=-XC/Z22=-16/202=-0.04 сим.
Для построения векторной диаграммы найдём длины векторов :
ℓIa1=Ia1/mI=11.7/2=5.9 см ; ℓIp1=Ip1/mI=8.84/2=4.4 см ; ℓI1=I1/mI=14.7/2=7.4 см ;
ℓIa2=Ia2/mI=6.6/2=3.3 см ; ℓIp2=Ip2/mI=8.78/2=4.4 см ; ℓI2=I2/mI=11/2=5.5 см.
ℓIa=Ia/mI=18.3/2=9.2 см ; ℓIp=Ip/mI=0.06/2=0.03 см ; ℓI=I/mI=18.3/2=9.2 см.
Построение векторной диаграммы начинаем с построения вектора напряжения U , который откладываем горизонтально. Вектор тока Ia1 откладываем параллельно вектору напряжения U. От конца вектора Ia1 откладываем вектор тока Ip1 перпендикулярно вектору U в сторону отставания от него. Геометрическая сумма векторов Ia1 и Ip1 дают вектор I1. Вектор тока Ia2 откладываем параллельно вектору напряжения U. От конца вектора Ia2 откладываем вектор тока Ip2 перпендикулярно вектору напряжения U в сторону его опережения. Геометрическая сумма векторов Ia2 и Ip2 дают вектор I2. Вектор I строим как геометрическая сумма векторов I1 и I2 , или как геометрическую сумму векторов Ia и Ip.
Ответ : I1=14.7 A ; I2=11 A ; I=18.3 A ; cosφ=1 ; P=4045 Вт ; Q=8.8 вар ; S=4045 В∙А ; g2=0.05 сим ; bc=-0.04 сим.
№ 21
Три одинаковых приёмника с сопротивлениями ZA=ZB=ZC=12+j16 Ом, соединены звездой и питаются от трёхфазной сети с линейным напряжением Uл=220 В. Начертить схему цепи. Определить фазное напряжение Uф ; фазные Iф и линейные Iл токи ; полную S , активную P и реактивную Q мощности ; коэффициент мощности cosφ трёхфазного потребителя. Построить в масштабе mu=40 В/см , mI=2 А/см векторную диаграмму напряжений и токов.
Дано : ZA=ZB=ZC=12+j16 Ом ; Uл=220 В
Найти : Uф , Iф , Iл , S , P , Q , cosφ.
Решение.
Так как приёмник симметричный, то полное сопротивление фаз :
Z=ZA=ZB=ZC===20 Ом.
Фазное напряжение : Uф=Uл/=220/=127 В
Так как приёмник соединён звездой, то фазные и линейные токи равны :
Iф=Iл=Uф/Z=127/20=6.35 А.
Коэффициент мощности цепи : cosφ=R/Z=12/20=0.6 ; угол сдвига фаз между током Iф и напряжением Uф : φ=arccos(0.6)=53°
Активная мощность цепи : P=3Iф2R=3×6.352×12=1452 Вт.
Реактивная мощность цепи : Q=3Iф2X=3×6.352×16=1935 вар
Полная мощность цепи : S==2419 В∙А.
Для построения векторной диаграммы найдём длины векторов :
ℓUф=Uф/mu=127/40=3.2 см ; ℓIф=Iф/mI=6.35/2=3.2 см.
Построение диаграммы начинаем с построения векторов фазных напряжений UA, UB и UC , которые откладываем под углом 120° относительно друг – друга, предварительно отложив вектор UA вдоль вещественной оси.
Вектора фазных токов откладываем под углом φ=53° от соответствующих фазных напряжений. Соединив концы векторов фазных напряжений, получим треугольник линейных напряжений.
Ответ : Uф=127 В ; Iф=6,35 А ; S=2419 В∙А ; P=1452 Вт ; Q=1935 вар ; cosφ=0.6.
№ 30
Конденсатор С=30 мкФ, соединённый последовательно с резистором R=0.5 МОм, заряжается от сети с постоянным напряжением U=220 В. Определить постоянную времени цепи τ и значение разрядного тока и напряжения в конденсаторе для моментов времени t=0, τ, 2τ, 3τ, 4τ, 5τ. Начертить схему цепи. Построить в масштабе кривые iзар=f(t) ; uc=f(t).
Дано : С=30 мкФ ; R=0.5 МОм ; U=220 В.
Найти : τ ; iзар=f(t) ; uc=f(t).
Решение.
Постоянная времени цепи : τ=RC=0.5×106×30×10-6=15 c
Напряжение на конденсаторе при заряде : uc=U(1-e-t/τ)=220(1-e-t/τ) В
Вычислим значение напряжения на конденсаторе в моменты времени : t=0, τ, 2τ, 3τ, 4τ, 5τ. Вычисления сведём в таблицу.
|
t, c |
0 |
τ |
2τ |
3τ |
4τ |
5τ |
|
e-t/τ |
1 |
0.37 |
0.14 |
0.05 |
0.02 |
0.01 |
|
uc , В |
0 |
138.6 |
189.2 |
209 |
215.6 |
217.8 |
По результатам расчёта строим кривую : uc=f(t).
Ток переходного режима, или зарядный ток : i=Ie-t/τ===440e-t/τ мкА
Вычислим значение зарядного тока в моменты времени : t=0, τ,2τ, 3τ, 4τ, 5τ.
Вычисления сведём в таблицу.
|
t, c |
0 |
τ |
2τ |
3τ |
4τ |
5τ |
|
e-t/τ |
1 |
0,37 |
0,14 |
0,05 |
0,02 |
0,01 |
|
I, мкA |
440 |
162,8 |
61,6 |
22 |
8,8 |
4,4 |
По результатам расчёта строим кривую : i=440e-t/τ мкА.
Ответ : τ=15 с ; uc=220(1-e-t/τ) В ; i=440e-t/τ мкА.
Как рассчитать трехфазную мощность
Обновлено 12 ноября 2018 г.
Ли Джонсон
Трехфазная мощность — широко используемый метод производства и передачи электроэнергии, но вычисления, которые вам нужно выполнить, немного сложнее чем для однофазных систем. Тем не менее, при работе с уравнениями трехфазной мощности вам не нужно ничего делать, поэтому вы сможете легко решить любую поставленную вам задачу трехфазного питания.Главное, что вам нужно сделать, это найти ток с учетом мощности в цепи или наоборот.
TL; DR (слишком долго; не читал)
Выполните расчет трехфазной мощности по формуле:
P = √3 × pf × I × V
Где pf — коэффициент мощности, I — ток, В, — напряжение, а P — мощность.
Однофазное и трехфазное питание
Однофазное и трехфазное питание — это термины, описывающие электричество переменного тока (AC).Ток в системах переменного тока постоянно изменяется по амплитуде (т. Е. По размеру) и направлению, и это изменение обычно принимает форму синусоидальной волны. Это означает, что он плавно изменяется с серией пиков и спадов, описываемых синусоидальной функцией. В однофазных системах такая волна всего одна.
Двухфазные системы разделяют его на две части. Каждая секция тока сдвинута по фазе с другой на половину цикла. Таким образом, когда одна из волн, описывающих первую часть переменного тока, находится на пике, другая — на минимальном значении.
Однако двухфазное питание встречается нечасто. Трехфазные системы используют тот же принцип разделения тока на противофазные составляющие, но с тремя вместо двух. Три части тока сдвинуты по фазе на треть цикла каждая. Это создает более сложную схему, чем двухфазное питание, но они одинаково компенсируют друг друга. Каждая часть тока равна по размеру, но противоположна направлению двух других частей, вместе взятых.
Формула трехфазной мощности
Наиболее важные уравнения трехфазной мощности связывают мощность ( P в ваттах) с током ( I в амперах) и зависят от напряжения ( В ).В уравнении также присутствует «коэффициент мощности» ( pf ), который учитывает разницу между реальной мощностью (которая выполняет полезную работу) и полной мощностью (которая подается в схему). Большинство типов расчетов трехфазной мощности выполняется с использованием этого уравнения:
P = √3 × pf × I × V
Здесь просто указано, что мощность является квадратным корнем из трех (около 1,732), умноженным на коэффициент мощности (обычно от 0,85 до 1, см. Ресурсы), ток и напряжение.Не позволяйте символам пугать вас, используя это уравнение; Как только вы включите все необходимые составляющие в уравнение, им будет легко пользоваться.
Преобразование кВт в амперы
Допустим, у вас есть напряжение, общая мощность в киловаттах (кВт) и коэффициент мощности, и вы хотите узнать ток (в амперах) в цепи. Изменив приведенную выше формулу расчета мощности, получим:
I = P / (√3 × pf × V)
Если ваша мощность выражена в киловаттах (т.е.е., тысячи ватт) лучше всего либо преобразовать его в ватты (умножив на 1000), либо сохранить в киловаттах, убедитесь, что ваше напряжение указано в киловольтах (кВ = вольт ÷ 1000). Например, если у вас коэффициент мощности 0,85, мощность 1,5 кВт и напряжение 230 В, просто укажите мощность как 1500 Вт и вычислите:
I = P / (√3 × pf × V)
= 1500 Вт / √3 × 0,85 × 230 В
Эквивалентно, мы могли бы работать с кВ (учитывая, что 230 В = 0,23 кВ), и найти то же самое:
I = P / (√3 × pf × V)
= 1.5 кВт / √3 × 0,85 × 0,23 кВ
Преобразование ампер в кВт
Для обратного процесса используйте форму приведенного выше уравнения:
P = √3 × pf × I × V
Просто умножьте свои известные значения, чтобы найти ответ. Например, для I = 50 A, V = 250 V и pf = 0,9 это дает:
P = √3 × pf × I × V
= √3 × 0,9 × 50 A × 250 В
Поскольку это большое число, преобразуйте его в кВт, используя (значение в ваттах) / 1000 = (значение в киловаттах).
19,486 Вт / 1000 = 19,486 кВт
Выработка трехфазной мощности в трехфазных цепях
Питание в трехфазных цепях
Трехфазное питание в основном используется для выработки, передачи и распределения электроэнергии из-за их превосходства. Он более экономичен по сравнению с однофазным питанием и требует для питания трех токоведущих проводов. Мощность в однофазной системе или цепи определяется соотношением, показанным ниже:
Где,
В — напряжение однофазное, т.е.е. V фаза
I — ток однофазного тока, т.е. I фаза и
Cosϕ — коэффициент мощности цепи.
В комплекте:
В трехфазных цепях (сбалансированная нагрузка) мощность определяется как сумма различных мощностей в трехфазной системе. т.е.
Мощность в соединениях звездой в трехфазных цепях задается как
Фазное и линейное напряжение при соединении звездой представлено, как показано ниже:
Следовательно, уравнение (1) можно записать как:
Мощность при соединении треугольником в трехфазных цепях определяется уравнением, показанным ниже:
При соединении треугольником соотношение между фазным и линейным напряжением и фазой и линейным током определяется как:
Следовательно, уравнение (3) можно записать как
Таким образом, общая мощность в 3-фазной сбалансированной системе нагрузки, независимо от их соединений, независимо от того, подключена ли система звездой или треугольником, мощность определяется соотношением:
√3 V L I L Cosϕ
Единицы измерения — киловатт (кВт) или ватт (Вт).
Полная мощность определяется как
Единица измерения полной мощности — киловольт-ампер (кВА) или вольт-ампер (ВА).
Аналогично, Реактивная мощность определяется уравнением:
Единицы измерения — реактивные киловольт-амперы (кВАр) или вольт-амперные реактивные (ВАР).
Генерация трехфазных ЭДС в трехфазной цепи
В трехфазной системе есть три равных напряжения или ЭДС одной частоты, имеющих разность фаз 120 градусов.Эти напряжения могут создаваться трехфазным генератором переменного тока с тремя одинаковыми обмотками, электрически смещенными друг от друга на 120 градусов.
Когда эти обмотки остаются неподвижными, а магнитное поле вращается, как показано на рисунке A ниже, или когда обмотки остаются неподвижными, а магнитное поле вращается, как показано ниже на рисунке B, в каждой обмотке индуцируется ЭДС. Величина и частота этих ЭДС одинаковы, но смещены друг от друга на угол 120 градусов.
Рассмотрим три идентичные катушки a 1 a 2 , b 1 b 2 и c 1 c 2 , как показано на рисунке выше. На этом рисунке a 1 , b 1 и c 1 — это начальные клеммы, а a 2 , b 2 и c 2 — конечные клеммы трех катушек. Между пусковыми клеммами a 1 , b 1 и c 1 должна поддерживаться разность фаз в 120 градусов.
Теперь пусть три катушки установлены на одной оси, и они вращаются, либо удерживая катушку в неподвижном состоянии и перемещая магнитное поле, либо наоборот, против часовой стрелки со скоростью (ω) радиан в секунду. В трех катушках индуцируются три ЭДС соответственно.
Рассматривая фигуру C, анализ их величин и направлений представлен следующим образом:
ЭДС, индуцированная в катушке a 1 a 2 , равна нулю и увеличивается в положительном направлении, как показано формой волны на рисунке C выше, представленной как e a1a2 .
Катушка b 1 b 2 электрически на 120 градусов позади катушки a 1 a 2 . ЭДС, индуцированная в этой катушке, является отрицательной и становится максимально отрицательной, как показано волной e b1b2 .
Точно так же катушка c 1 c 2 находится на 120 градусов электрически позади катушки b 1 b 2 , или мы также можем сказать, что катушка c 1 c 2 находится на 240 градусов позади катушки катушка а 1 а 2 .ЭДС, индуцированная в катушке, является положительной и уменьшается, как показано на рисунке C, представленном формой волны e c1c2 .
Фазорная диаграмма
ЭДС, индуцированные в трех катушках в трехфазных цепях, имеют одинаковую величину и частоту и смещены на угол 120 градусов друг от друга, как показано ниже на векторной диаграмме:
Эти ЭДС трехфазных цепей можно выразить в виде различных уравнений, приведенных ниже:
Это все о генерации трехфазного питания в трехфазных цепях.
| Cos Phi
Конденсаторы коррекции коэффициента мощностииспользуются с целью улучшения коэффициента мощности в сетях низкого напряжения. В наших конденсаторах используется технология MKP, состоящая из пленки из металлизированного полипропилена (PP), которая имеет чрезвычайно низкий коэффициент потерь. Диэлектрическая система самовосстанавливающаяся и не имеет жидкой пропитки. Элементы конденсатора заключены в цилиндрические алюминиевые корпуса и заполнены гелем на основе растительного масла, который является нетоксичным, биоразлагаемым и экологически чистым.
Конденсаторы имеют защиту от избыточного давления для отключения от источника питания в случае внутреннего отказа и по окончании срока службы.
Разъединитель избыточного давления
Трехфазные конденсаторы соединены треугольником. Трехфазные конденсаторы, соединенные треугольником, более безопасны для электрической среды, чем другие (например, соединенные звездой). Они не только обеспечивают емкостное сопротивление каждой фазе, но и не допускают дисбаланса напряжений.
Если конденсаторный элемент выйдет из строя по какой-либо причине в одной фазе, он перейдет от закрытого треугольника к конфигурации открытого треугольника. В этом случае напряжение на каждой фазе остается неизменным. Отказ конденсаторной ячейки будет означать только падение кВАр в цепи. Другими словами, трехфазный конденсатор, подключенный по схеме треугольника 30 кВАр, с вышедшим из строя элементом обеспечит 20 кВАр электрической системе вместо 30 кВАр.
Конденсаторы, соединенные треугольником, также способны до некоторой степени циркулировать гармонические токи в схеме треугольника, тем самым помогая уменьшить гармоники в электрической системе.
Конденсаторы можно устанавливать в любом положении. Крепление осуществляется с помощью шпильки M12 снизу, которая также может использоваться для заземления — максимальный момент затяжки 5 Нм. Подключение к клемме осуществляется винтами M5 с максимальным крутящим моментом 2 Нм. Соединительные кабели должны позволять верху конденсатора подниматься на 20 мм для обеспечения правильной работы разъединителя избыточного давления. Для расширения верхняя часть конденсатора должна быть свободной без фиксирующего зажима. При необходимости фиксирующие зажимы можно установить только на нижней части конденсатора ниже паза.
| Общие технические условия Номинальное напряжение: 230, 480, 600, 690 Частота: 50/60 Гц Стандарты: IEC 60831-1 + 2, EN 60831-1 + 2, UL 810, ГОСТ 1282-88, VDE 0560 46 + 47 Максимальное перенапряжение: UN + 10% (до 8 часов ежедневно) UN + 15% (до 30 минут в день) UN + 20% (до 5 минут) UN + 30% (до 1 минуты) Максимальный ток: 1.5 — 2,0 * В Допуск емкости: -5 / + 10% Тестовое напряжение, клемма / клемма: 2,15 * UN, AC, 2 с Тестовое напряжение: клемма / корпус: UN UN> 500 В: 2 x UN + 2000 В переменного тока, 10 с Пусковой ток: Макс 400 x IN Срок службы: 150 000-200 000 (в зависимости от напряжения и температуры) Степень защиты: IP 20, (по запросу IP54) Допустимая относительная влажность: 95% Макс. Над уровнем моря: 4000 м Монтаж: Шпилька M12 снизу, любое положение Корпус: Алюминий Диэлектрик: МКП — металлизированная ПП пленка Пропитка: Сухого типа, инертный газ N2 Разрядные резисторы : в комплекте — 50 В, 1 минута или 75 В, 3 минуты |
Связанные
Конденсаторы, соединенные треугольником и звездой
Блоки статической коррекции коэффициента мощности (статья)
Блоки коррекции статического коэффициента мощности
Банки коррекции коэффициента мощности с автоматическим переключением
Понимание преимуществ трехфазного распределения электроэнергии
Большинство из нас мало думают об электричестве — до тех пор, пока мы не получим счет или не произойдет перерыв в обслуживании.Но операторы центров обработки данных хорошо осведомлены о стоимости, стабильности и надежности электроэнергии, и это вызывает повышенный интерес к трехфазным распределительным устройствам (PDU).
Стандартная розетка в США подает переменный ток частотой 60 Гц. Шестьдесят раз в секунду ток, протекающий по цепи, меняет направление на противоположное. Изобразите синусоидальную волну: максимальная амплитуда волны представляет пиковое положительное напряжение, а минимальная амплитуда представляет максимальное отрицательное напряжение. Дважды за цикл волна проходит через нулевую ось, что означает отсутствие подачи напряжения.
Это нормально для тостеров, микроволновых печей и другой бытовой техники, а также для ПК, стоящего на вашем столе. Однако переменный ток с частотой 60 Гц не очень эффективен или непостоянен, когда речь идет о питании оборудования центра обработки данных.
Почему мы используем трехфазное питание?
Трехфазное питание передает три переменных тока через одну и ту же цепь, каждый из которых равномерно разделен по фазовому углу.Другими словами, каждую треть цикла одна из волн достигает пикового напряжения, а мощность, подаваемая цепью, остается постоянной.
В электрической сети используется трехфазная система распределения энергии, поскольку она позволяет передавать более высокую передачу при более низкой силе тока. Это позволяет использовать медную проволоку большего сечения (более тонкую), что значительно снижает затраты на материалы и рабочую силу.
Те же преимущества проявляются и в центре обработки данных. Трехфазная цепь обеспечивает большую удельную мощность, чем однофазная, при той же силе тока, что позволяет уменьшить размер проводки и снизить затраты. Кроме того, трехфазное питание упрощает балансировку нагрузок, сводит к минимуму токи гармоник и необходимость в больших нейтральных проводах. Он также оптимизирует использование электрической мощности для повышения энергоэффективности.
Альтернативно-фазный стоечный БРП PRO2 от Server Technology распределяет фазы по розеткам, а не по отдельным банкам.Это позволяет использовать более короткие кабели, что улучшает воздушный поток, упрощает балансировку нагрузки и повышает эффективность.
PDU использует технологию розеток высокой плотности (HDOT) серверной технологии, которая подходит для 42 розеток C13 в устройстве с сетевым управлением 42U. PDU HDOT более чем на 20 процентов меньше сопоставимых устройств, использующих стандартные розетки, что позволяет максимально увеличить доступное пространство в задней части стойки. Конструкция HDOT также обеспечивает собственное удержание шнура с силой отрыва более 12 фунтов, уменьшая или устраняя необходимость во вспомогательных устройствах фиксации шнура.
С увеличением плотности розеток увеличивается мощность и потенциально повышается теплоотдача. Блоки распределения питания HDOT изготавливаются из жаропрочных материалов с классом воспламеняемости UL94 V-0, что делает их подходящими для самых суровых условий центров обработки данных.
Измерение мощности на каждую розетку (POPS) обеспечивает высокоточное измерение тока, напряжения, активной мощности, полной мощности, коэффициента мощности и пик-фактора на каждой розетке. POPS также может подавать сигналы тревоги и предупреждения, когда ток, мощность и коэффициент мощности достигают низких и высоких значений.Четырехэтапный процесс настройки
Server Technology удобен для пользователя и графически помогает клиентам выбрать напряжение, силу тока, фазу, тип вилки, ориентацию входного кабеля, конфигурацию розетки, возможности подключения и цвет. Кроме того, компания разработала быстродействующий производственный процесс, который обеспечивает короткие сроки изготовления индивидуальных PDU с точной комбинацией розеток в тех местах, где они нужны заказчику.
Специалисты по питанию центров обработки данных Rahi могут помочь вам определить, могут ли трехфазные блоки распределения питания принести пользу вашему предприятию, и спроектировать решение, точно соответствующее вашим требованиям.Свяжитесь с нами сегодня, чтобы получить бесплатную консультацию.
Как понять треугольник мощности в трехфазной системе переменного тока
| Рис. 1. Треугольник мощности |
Треугольник мощности в системе переменного тока
1. Реальная мощность (P) — Реальная мощность выражается в ваттах (Вт).
- В электрическом нагревательном оборудовании это фактическая мощность, которая преобразуется непосредственно в тепло.Что касается электрических машин, это мощность, которая непосредственно преобразуется в механическую энергию.
- Эта мощность в основном потребляется катушкой индуктивности и конденсатором.
- Полная мощность — это мощность, фактически потребляемая сетью, работающей в системе переменного тока.(1-)
, также известен как угол коэффициента мощности
Для некоторых соображений коэффициент мощности можно проанализировать как эффективность системы. Три типа коэффициента мощности
- Коэффициент мощности с запаздыванием — когда напряжение отстает от тока при распространении двух переменных волн. Это происходит при индуктивных нагрузках.
- Опережающий коэффициент мощности — когда ток опережает напряжение при распространении двух переменных волн.Это происходит при емкостных нагрузках.
- Unity Power Factor — когда волны напряжения и тока одновременно поступают в координату x. Это происходит в чисто резистивных нагрузках или когда емкостная нагрузка равна индуктивной нагрузке в системе.
| Рис. 2. Распространение волн напряжения и тока во временной координате |
- P = 3 VpIp cos Θ или √3 VL IL cos Θ <формула 4> для активной мощности 3 фазы
- Q = 3 VpIp sin Θ или √3 VL IL sin Θ <формула 5> для реактивной мощности, 3 фазы
- S = 3 VpIp или √3 VL IL <формула 6> для полной мощности, 3 фазы
Пример:
Две отдельные трехфазные электрические системы выдают одинаковую мощность в 10 000 Вт.Система №1 имеет коэффициент мощности 0,60, а другая (система №2) имеет коэффициент мощности 0,85. Определить ток, потребляемый каждой системой? (в двух системах используются одинаковые линейные напряжения, 440 вольт)
Решение:
Система № 1,
- P = √3 VL IL cos Θ; cos Θ = коэффициент мощности = 0,6
- IL = 10 000 / (√3 * 440 * .6)
- IL = 21,87 Ампер
Система № 2,
- P = √3 VL IL cos Θ; cos Θ = коэффициент мощности = 0.85
- IL = 10 000 / (√3 * 440 * 0,85)
- IL = 15,44 Ампер
В приведенном выше примере две сети выдают одинаковое количество полезной мощности, но другая сеть более эффективна по сравнению с другими. Это из-за коэффициента мощности.
Таким образом, мы можем сказать, что две сети могут выдавать одинаковую полезную мощность (WATTS), но различаются потребляемой полной мощностью — одна высокая, а другая низкая.
3-фазные выходы> Конфигурация> Анализ мощности> Электрические измерения> Модули> Настройка
Чтобы отобразить все каналы, перейдите во вторую вкладку (Настройка) в разделе модуля редактирования и выберите список каналов в раскрывающемся меню.
ПРИМЕЧАНИЕ: Следующее описание и примеры действительны для всех типов 3-фазных систем: 3-фазная звезда, 3-фазный Aron, 3-фазный треугольник и 3-фазный V.
Dewesoft автоматически создает следующие основные выходные каналы
Выбор текущих каналов = отключен
Выбор расчета линейных напряжений = отключено
К «Используемым» аналоговым каналам добавляются напряжение (U_Ln_h2 и U_Ln_rms) и частотные каналы. Выбор текущих каналов = отключено
Выбор расчета линейных напряжений = включен
К основным каналам (см. Слева) добавлены выделенные каналы -> каналы напряжения между линиями.
Выбор текущих каналов = включен
Выбор расчета линейных напряжений = отключено
К основным каналам добавлены токовый и силовой каналы.
Когда вы сравниваете каналы на приведенном выше рисунке с созданными каналами для однофазных выходов, вы можете видеть, что для трехфазных систем добавляются только каналы того же типа для второй — L2 и третьей — L3 фазной линии.
ПРИМЕЧАНИЕ: каналов гармоник h2 создаются в любом случае для: каналов напряжения и тока (U и I), каналов мощности (P, Q, S, phi, cos phi).
Выходные каналы гармоник -> установлен флажок Гармоники
Для получения информации о настройках этой опции и выходных каналах см. -> Однофазные выходы.
ПРИМЕЧАНИЕ: Дополнительно к каналам однофазных гармоник создаются только выходные каналы того же типа для второй линии фазы L2 и третьей фазы L3.
каналов вывода THD -> опция THD отмечена
Для получения информации о настройках этой опции и выходных каналах см. -> Однофазные выходы.
ПРИМЕЧАНИЕ: Дополнительно к однофазным каналам THD создаются только выходные каналы того же типа для второй — L2 и третьей — L3-фазной линии.
Симметричные компоненты -> опция Симметричные компоненты отмечена
Мы можем вычислить симметричные компоненты, установив следующий флажок.
Симметричные компоненты доступны только в трехфазных системах и сообщают нам о дисбалансе сети.
Каналы вывода значений периода -> отмечена опция значений периода
Для получения информации о настройках этой опции и выходных каналах см. -> Однофазные выходы.
ПРИМЕЧАНИЕ: Дополнительно к каналам значений периода одной фазы создаются только выходные каналы того же типа для второй — L2 и третьей — L3 линии фазы.
Waveforms -> Waveforms опция отмечена
Если мы измеряем линейные напряжения, мы можем рассчитать формы сигналов для линейных напряжений, выбрав следующую опцию:
Каналы вывода мерцания -> параметр мерцания отмечен
Для получения информации о настройках этой опции и выходных каналах см. -> Однофазные выходы.
ПРИМЕЧАНИЕ: Дополнительно к однофазным каналам фликера создаются только выходные каналы того же типа для второй — L2 и третьей — L3 линии фазы.
Основы измерения электроэнергии
Основные измерения электрической мощностиПонимание выработки электроэнергии, потерь мощности и различных типов измеряемой мощности может быть пугающим. Ниже приведен обзор основных измерений электрической и механической мощности.
Электрический ток, напряжение и сопротивлениеЛюбое обсуждение электричества неизбежно приводит к электрическому току, напряжению и сопротивлению.Эти концепции показаны ниже на рисунке 1. Электрический ток — это сам поток электричества, который измеряется в единицах, называемых амперами (A). Напряжение — это сила, которая заставляет электричество течь, и измеряется в единицах, называемых вольтами (В или U). Сопротивление выражает сложность, с которой течет электричество, и измеряется в единицах, называемых омами (Ом).
На рисунке ниже эти взаимосвязи показаны в виде электрических цепей. В электрической цепи электрический ток проходит через различные типы нагрузки, включая сопротивление, индуктивность и емкость, от положительной полярности источников питания, таких как батареи, а затем возвращается к отрицательной полярности источника питания.Нагрузка — это термин, который обычно используется для обозначения чего-то, что получает электричество от источника питания и действительно работает (обеспечивает свет, в случае лампочки).
Рисунок 1 — Основные элементы электрической схемы Мощность
Электрическая энергия может быть преобразована в другие формы энергии и использована. Например, его можно преобразовать в тепло в электронагревателе, в крутящий момент в двигателе или в свет люминесцентной или ртутной лампы. В таких примерах работа, которую электричество выполняет за определенный период (или затраченная электрическая энергия), называется электрической мощностью.Единица измерения электрической мощности — ватт (Вт). 1 ватт эквивалентен 1 джоуля работы, выполняемой за 1 секунду.
В электрических системах напряжение — это сила, необходимая для перемещения электронов. Ток — это скорость потока заряда в секунду через материал, к которому приложено определенное напряжение. Умножив напряжение на соответствующий ток, можно определить мощность.
Постоянный ток (DC) МощностьПостоянный ток, или DC, относится к системам питания, в которых используется одна полярность напряжения и тока, однако амплитуда может изменяться (циклическая или случайная).
Рисунок 2 — Базовая схема, показывающая напряжение и ток с источником постоянного напряжения Закон Ома
При расчетах электрических цепей используется ряд формул, но именно закон Ома показывает наиболее фундаментальную взаимосвязь: взаимосвязь между электрическим током, напряжением и сопротивлением. Закон Ома гласит, что электрический ток течет пропорционально напряжению. Ниже показана формула для выражения отношения между током (I) и напряжением (U).
По этой формуле ток (I) уменьшается при увеличении значения R и, наоборот, ток (I) увеличивается при уменьшении значения R. R здесь представляет сопротивление (или электрическое сопротивление). Другими словами, мы видим, что по мере увеличения или уменьшения сопротивления (R) ток течет с большей или меньшей легкостью. Эту формулу можно переписать, как показано ниже. Если известны два значения: ток, напряжение и сопротивление, вы можете получить оставшееся значение.
Мощность постоянного тока (DC) P (W) определяется умножением приложенного напряжения (U) на ток I (A), как показано выше.В приведенном ниже примере количество электроэнергии, определяемое предыдущим уравнением, извлекается из источника питания и потребляется сопротивлением R (в омах) каждую секунду. По закону Ома формулу можно переписать следующим образом:
Электрические цепи постоянного тока поддерживают постоянный ток и напряжение без циклических изменений ни в одном из них. Таким образом, получить мощность постоянного тока (P) с полученной формой волны, приведенной ниже, несложно.
Электропитание переменного токаЭлектропитание, обычно используемое в Японии, работает от 100 В переменного тока.Эти 100 В представляют собой напряжение, выраженное как среднеквадратичное значение (СКЗ).
100 В от настенных розеток воспринимаются как чистые синусоидальные волны, как показано на рисунке ниже. Мы можем видеть, что полярность меняется циклически, и что напряжения постоянно колеблются. Волны переменного напряжения имеют чистые синусоидальные волны, как график на рисунке 3, а также множество других волн, таких как искаженные волны, такие как обычные формы, такие как треугольная и прямоугольная волна. Чтобы определить размер этих волн переменного тока и напряжения, нам нужны значения, соответствующие одному стандарту.Поэтому используется среднеквадратичное значение (среднеквадратичное значение), которое было получено на основе постоянного тока и напряжения.
Рисунок 3 — Циклы изменения полярности переменного напряжения синусоидальной, треугольной и прямоугольной формы Среднеквадратичное значение (СКЗ)
Среднеквадратичное значение обычно используется при выражении значений переменного тока и напряжения и измеряется в единицах амплитуды и единицах. В приведенном выше примере 100 В — это напряжение, выраженное как среднеквадратичное значение (СКЗ).
Простое среднее значение синусоиды равно нулю, поэтому требуется другое уравнение.Вот почему используется среднеквадратичное значение (среднеквадратичное значение), которое было установлено на основе постоянного тока и напряжения. Он основан на объеме работы, выполняемой определенным количеством постоянного тока и напряжения, и выражает — используя те же значения, что и постоянный ток и напряжение — величину переменного тока и напряжения, которые выполняют такой же объем работы.
Если теплотворная способность при подаче напряжения постоянного тока на резистор такая же, как теплотворная способность при подаче переменного тока другой формы волны, действующее значение этого напряжения переменного тока будет таким же, как и для напряжения постоянного тока.
Например, теплотворная способность при приложении постоянного напряжения 100 В к резистору 10 Ом такая же, как теплотворная способность при подаче переменного тока 100 В на тот же резистор. Концепция среднеквадратичного значения для электрического тока такая же.
Рисунок 4 — Равная теплотворная способность между сигналами постоянного и переменного тока
Теплотворная способность — это объем выполненной работы, поэтому по следующей формуле мощность рассчитывается как теплотворная способность.
В качестве примера на следующей диаграмме показаны колебания мощности в зависимости от времени, когда на резистор 10 Ом подается постоянный ток 1 А и переменный ток 1 Ампер.
Рисунок 5 — Зависимость мощности от времени при постоянном и переменном токе
Поскольку при постоянном токе нет колебаний значения тока, значение мощности остается постоянным 10 Вт. Однако, поскольку значение тока постоянно колеблется при переменном токе, значение мощности колеблется со временем. То, что эти два типа мощности (теплотворная способность) равны, равносильно утверждению, что средние значения Pdc и P1 — Pn равны. Это выражается формулой ниже.
Здесь резистор (R) постоянный, поэтому им можно пренебречь. Следующее выражает результирующую взаимосвязь между постоянным током и переменным током.
Делая интервал между I1 и In как можно меньшим в этой формуле, в конечном итоге Irms дает квадратный корень из площади части, заключенной в форме волны, деленной на время. Это выражается формулой ниже.
Важно знать, что постоянный ток 1 А выполняет ту же работу, что и переменный среднеквадратичный ток 1 Ампер.При постоянном и установившемся постоянном токе вы можете получить значение мощности, просто умножив ток на напряжение.
Однако переменный ток не так прост, как постоянный, из-за разницы фаз между током и напряжением. Ниже приведены три типа питания переменного тока. Обычно мощность и потребляемая мощность относятся к активной мощности.
Электропитание в системах переменного токаКак и в случае постоянного тока, значение мощности (мгновенное значение мощности) для переменного тока в определенный момент времени может быть получено путем умножения напряжения и тока для этого момента времени.
При переменном токе, поскольку и ток, и напряжение периодически меняются, значения мощности также постоянно меняются. Это показано на следующей диаграмме.
В качестве энергии в секунду мощность может быть получена из среднего значения мгновенной энергии, то есть площади участка, заключенного в форме волны, по времени. Формула выглядит следующим образом:
Например, если к резистору приложен ток 1 Ампер и напряжение 100 Ом, как показано ниже, мощность станет 100 Вт при вычислении по приведенной выше формуле.
При подаче тока и напряжения на резистор результирующие формы сигналов показаны на Рисунке 6 ниже.
Рисунок 6 — Отсутствие разности фаз в чисто резистивной нагрузке
Считается, что ток и напряжение находятся «в фазе» по полярности и времени, когда формы сигнала тока и напряжения проходят через нуль. Ток и напряжение всегда совпадают по фазе, когда нагрузка состоит только из сопротивления.
Когда нагрузка имеет катушку в дополнение к сопротивлению, происходит фазовый сдвиг между сигналом напряжения и тока.Это отставание называется разностью фаз, как показано на рисунке 7.
Рисунок 7 — Разности фаз, характерные для индуктивной и емкостной нагрузки
Разность фаз обычно выражается как Φ (фи), а единица измерения — радианы, но часто указывается в градусах. В приведенном ниже примере точка A начинается из точки P и совершает один оборот по окружности круга O. Расстояние между точкой A и прямой линией, проходящей через центр O и точку P (красная линия) как ось Y и ∠AOP (φ), поскольку ось X дает синусоидальную волну ниже.
Рисунок 8 — Синусоидальная волна с фазой
На рис. 9 показаны кривые тока и напряжения, сдвинутые по фазе на 60 °. При рассмотрении положения на окружности напряжения (u) и тока (i) в соответствии с приведенным выше примером, ∠uoi постоянна в каждый момент времени. Угол этого ∠uoi указывает величину разности фаз между напряжением (u) и током (i).
Рисунок 9 — Синусоидальные волны напряжения и тока с разностью фаз
Три типа нагрузки цепи переменного тока показаны на рисунке 10.Как показано ниже, разность фаз между током и напряжением зависит от типа нагрузки.
Рисунок 10 — Фазовое и векторное представление цепей переменного тока с резистивной, индуктивной или емкостной нагрузкой
Для фаз ток может отставать от напряжения или опережать. Ток отстает на 90 °, когда нагрузка состоит только из индуктивности, и опережает на 90 °, когда только емкость. Когда существуют все три типа, разность фаз колеблется в соответствии с соотношением размеров каждого компонента.Затем давайте посмотрим на мощность, когда есть разность фаз между током и напряжением.
Электропитание переменного тока с разностью фазКогда существует разность фаз между током и напряжением, происходит мгновенное изменение энергии, как показано на рисунке 11.
Когда ток или напряжение равны 0, мгновенная мощность становится равной 0. Когда полярности тока и напряжения меняются в промежутках между ними, мгновенная мощность становится отрицательной. Мощность — это среднее значение мгновенной энергии, поэтому мощность становится меньше, чем когда ток и напряжение совпадают по фазе (пунктирная линия).
Рисунок 11 — Мгновенная энергия, когда напряжение и ток имеют разность фаз Треугольник мощности и коэффициент мощности
Цепи переменного тока, содержащие емкость, индуктивность или и то, и другое, содержат активную и реактивную мощность. Треугольник мощности, показанный на рисунке 12, помогает проиллюстрировать потребление энергии в индуктивной или емкостной цепи. Треугольник мощности представляет собой прямоугольный треугольник, показывающий соотношение четырех основных элементов, активной мощности, реактивной мощности, полной мощности и коэффициента мощности.
Рисунок 12 — Треугольник мощности показывает соотношение активной и реактивной мощности. Активная мощность
Активная мощность (P) — это истинная мощность, которую устройство потребляет и выполняет реальную работу в электрической цепи. Активная мощность рассчитывается ниже в ваттах (Вт).
Реактивная мощностьРеактивная мощность (Q) — это мощность, которая не потребляется устройством и передается между источником питания и нагрузкой.Реактивная мощность, которую иногда называют мощностью без мощности, забирает мощность из цепи из-за фазового сдвига, создаваемого емкостными и / или индуктивными компонентами. Этот фазовый сдвиг уменьшает количество активной мощности для выполнения работы и усложняет расчет мощности. Реактивная мощность рассчитывается ниже и измеряется в вольт-амперах реактивной мощности (ВАр). В цепи постоянного тока нет реактивной мощности.
Полная мощностьПолная мощность (S) — это гипотенуза треугольника мощности, состоящая из векторного сложения активной мощности (P) и реактивной мощности (Q).Расчет полной мощности представляет собой умножение среднеквадратичного значения напряжения на действующий ток с единицей измерения вольт-ампер (ВА).
Коэффициент мощностиПри определении коэффициента мощности для синусоидальных волн коэффициент мощности равен косинусу угла между напряжением и током (Cos Φ). Это определяется как коэффициент мощности «смещения» и подходит только для синусоидальных волн. Для всех других форм сигналов (несинусоидальных волн) коэффициент мощности определяется как мощность в ваттах, деленная на полную мощность в амперах напряжения.Это называется «истинным» коэффициентом мощности и может использоваться для всех форм сигналов, как синусоидальных, так и несинусоидальных, с использованием квалификатора λ (лямбда).
Коэффициент мощности (λ) увеличивается или уменьшается в зависимости от величины разности фаз (φ). Рисунок 13 иллюстрирует это явление.
Рисунок 13 — Коэффициент мощности при различных разностях фаз
Для идеальных синусоидальных волн ток и напряжение совпадают по фазе, полная мощность и активная мощность становятся равными, а коэффициент мощности равен 1.Коэффициент мощности уменьшается с увеличением разности фаз; коэффициент мощности составляет 0,5 (активная мощность равна 1/2 полной мощности) при разности фаз 60 ° и 0 при разности фаз 90 °. Коэффициент мощности 0 означает, что ток течет к нагрузке, но она не работает.
Векторное отображение переменного токаВременной сдвиг между напряжением и током называется разностью фаз, а Φ — фазовым углом. Смещение по времени в основном вызвано нагрузкой, на которую подается питание.Как правило, разность фаз равна нулю, когда нагрузка является чисто резистивной. Ток отстает от напряжения, когда нагрузка индуктивна. Когда нагрузка емкостная, ток опережает напряжение.
Рисунок 14 — Сдвиг фаз между напряжением и током при чисто индуктивной или емкостной нагрузке
Векторный дисплей используется для четкого отображения зависимости величины и фазы между напряжением и током. Положительный фазовый угол представлен углом против часовой стрелки по отношению к вертикальной оси.
Рисунок 15. Векторная диаграмма показывает соотношение амплитуды и фазы между напряжением и током
Системы питания переменного тока
Питаниепеременного тока может быть однофазным или многофазным. Однофазное электричество используется для питания обычных бытовых и офисных электроприборов, но для распределения электроэнергии и подачи электричества непосредственно на оборудование более высокой мощности почти повсеместно используются трехфазные системы переменного тока.
Однофазные электрические схемыСуществуют две распространенные схемы подключения для однофазных цепей.Наиболее распространена однофазная двухпроводная схема. Другой — однофазная трехпроводная схема, обычно встречающаяся в бытовых приборах.
Однофазная 2-проводная система (1P2W)Обеспечивает однофазное питание переменного тока по двум проводам. Самая простая система, она используется при подключении источников питания ко многим электрическим устройствам, например, бытовой электронике. При подключении ваттметра к однофазной двухпроводной системе необходимо учесть несколько моментов перед подключением.
Рисунок 16. Различные схемы подключения однофазной двухпроводной системы Влияние паразитной емкости
При измерении однофазного устройства влияние паразитной емкости на точность измерения можно минимизировать, подключив токовый входной терминал прибора к стороне, которая ближе всего к потенциалу земли источника питания.
Рисунок 17 — Схема подключения для минимизации паразитной емкости
Влияние измеренных амплитуд напряжения и тока
Когда измеряемый ток относительно велик, подключите клемму измерения напряжения между клеммой измерения тока и нагрузкой.Когда измеренный ток относительно невелик, подключите клемму измерения тока между клеммой измерения напряжения и нагрузкой.
Рисунок 18 — Схема подключения при относительно большом измеряемом токе Двухфазная трехпроводная система (1P3W)
Обеспечивает однофазное питание переменного тока по трехпроводным проводам. Однофазная трехпроводная система является наиболее распространенной системой распределения электроэнергии. Электроэнергия, подаваемая в большинство домохозяйств, поставляется с использованием этой системы.В следующем примере требуются два ваттметра для измерения двух напряжений (U1, U2) и двух токов (I1, I2).
Рисунок 19 — Трехпроводная система с разделением фаз Трехфазные электрические схемы
В отличие от однофазных систем, по проводам трехфазного источника питания проходит переменный ток той же частоты и амплитуды напряжения относительно общего эталона, но с разностью фаз в одну треть периода. Трехфазные системы имеют преимущества перед однофазными, что делает их пригодными для передачи энергии и в таких приложениях, как асинхронные двигатели.
Характеристики трехфазных систем- Ток и напряжение на каждой фазе имеют разность фаз 120 ° в сбалансированной системе.
- Напряжение линии — это напряжение, измеренное между любыми двумя линиями в трехфазной цепи.
- Фазное напряжение — это напряжение, измеренное на нагрузке в фазе .
- Линейный ток — это ток через любую одну линию между трехфазным источником и нагрузкой.
- Фазный ток — это ток через любой компонент трехфазного источника или нагрузки.
- При соединении треугольником линейное напряжение совпадает с фазным напряжением. Для синусоидальных волн линейный ток в √3 раз больше фазного тока.
- При соединении звездой линейное напряжение в √3 раз больше фазного напряжения, а токи одинаковы.
- Трехфазные источники питания могут передавать в три раза больше мощности, используя всего в 1,5 раза больше проводов, чем однофазные источники питания (т. Е. Три вместо двух). Таким образом, соотношение емкости к материалу проводника увеличивается вдвое.
- Трехфазные системы также могут создавать вращающееся магнитное поле с заданным направлением и постоянной величиной, что упрощает конструкцию электродвигателей.
До сих пор мы обсуждали, что источник питания и нагрузка соединены двумя проводниками. Это известно как однофазная двухпроводная система. При питании от переменного тока существует однофазное и трехфазное питание, доступны следующие системы электропитания. Трехфазное питание может использоваться в трех- или четырехпроводной конфигурации в звездообразном или треугольном режиме.
Диаграммы на Рисунке 20 показывают источник и нагрузку в конфигурации треугольником или звездой (WYE).
Рисунок 20 — Конфигурации трехфазного треугольника и звезды (WYE) Теорема Блонделя
При обсуждении измерения мощности с помощью ваттметров часто ссылаются на теорему Блонделя при определении правильного метода подключения ваттметров и количества требуемых для наиболее точного измерения.Теорема утверждает, что мощность, подаваемая в систему из N проводников, равна алгебраической сумме мощности, измеренной N ваттметрами. Кроме того, если общая точка находится на одном из проводов, счетчик этого проводника может быть удален, и потребуется только N-1 счетчик.
Трехфазное соединение звездой (3P4W)Измерение относительно просто, если объектом измерения является трехфазная 4-проводная система. Как показано на схеме ниже, трехфазный 4-проводный включает в себя подключение ваттметров к каждой фазе на основе нейтрального проводника.Получите мощность для каждой фазы, измерив напряжение (фазное напряжение) и ток (фазный ток) для каждой фазы с помощью разных ваттметров. Суммирование даст значение мощности трехфазного переменного тока. Для измерения трехфазной 4-проводной мощности требуется три ваттметра.
Рисунок 21 — Трехфазное соединение звездой (3P4W)
Полная мощность, активная мощность и реактивная мощность для трехфазной мощности — это сумма каждой фазы.
Трехфазный дельта-двухваттметр (3P3W)Измерение в трехфазной трехпроводной системе немного сложнее, поскольку нейтральный проводник, который использовался в качестве основы для трехфазной четырехпроводной системы, отсутствует и фазное напряжение невозможно измерить.Измерение в трехфазной трехпроводной системе включает получение значения мощности трехфазного переменного тока с использованием метода, называемого методом 2-ваттметра.
Применяя теорему Блонделя и используя метод двух ваттметров, мы можем получить значения мощности трехфазного переменного тока. Схема подключения метода двух ваттметров и векторная карта показаны ниже.
Вывод теоремы Блонделя приводится ниже.
Приведенный выше расчет показывает, что мы можем получить значения мощности трехфазного переменного тока из значений мощности в двух линиях и значений тока в двух фазах.Поскольку этот метод требует контроля только двух значений тока и двух напряжений вместо трех, установка и конфигурация проводки упрощаются. Он также может точно измерять мощность в сбалансированной или несбалансированной системе. Его гибкость и низкая стоимость установки делают его подходящим для производственных испытаний, при которых требуется измерить только мощность или несколько других параметров.
Другими словами, для измерения трехфазной мощности мощность может быть получена путем измерения мощности для каждой фазы и вычисления общей мощности.Для метода двух ваттметров уравнение показано ниже.
Трехфазное соединение треугольником (3V3A)Существует еще один метод измерения при трехфазной трехпроводной системе: измерение трех напряжений и трех токов (3V3A). Как и метод двух ваттметров, этот метод измеряет ток фазы T и линейное напряжение между R и S. Ниже представлена схема подключения.
Рисунок 22 — Трехфазное соединение треугольником (3V3A)
Поскольку метод трех напряжений и трех токов (3V3A) измеряет ток фазы T, он позволяет увидеть баланс тока между фазами, что было невозможно при использовании метода двух ваттметров.Для инженерно-исследовательских и опытно-конструкторских работ трехфазный
Трехпроводный методс использованием трех ваттметров лучше всего, поскольку он предоставляет дополнительную информацию, которая может использоваться для балансировки нагрузки и определения истинного коэффициента мощности. В этом методе используются все три напряжения и все три тока. Измеряются все три напряжения (R — T, S — T, R — S).
Векторный дисплей измерений трехфазного переменного токаМы будем использовать трехфазную систему Y «звезда», чтобы проиллюстрировать концепцию трехфазного векторного дисплея.В звездообразной системе напряжения и токи каждой фазы смещены на 120 °. Нейтральная точка Y-системы находится в центре, где все напряжения и токи теоретически равны нулю.
При измерениях в звездообразной системе, где присутствует физический нейтральный провод; напряжения будут измеряться относительно этой нейтральной точки, это называется «фазным напряжением». При проведении измерений в звездной системе, где физический нейтральный провод отсутствует; напряжения будут измеряться относительно друг друга, это называется «линейное напряжение» или «соединение треугольником».Соединение по схеме «треугольник» образует равносторонний треугольник с интервалом между напряжениями 60 градусов, в отличие от соединения по схеме «звезда», где напряжения изменяются на 120 градусов. Величина линейных напряжений в √3 раз выше фазных напряжений. Токи в звездной системе всегда измеряются последовательно относительно нейтральной точки, при этом угловые измерения относительно векторов напряжения обозначаются Φ. Рисунок 23 иллюстрирует взаимосвязь между измерениями напряжений при соединении треугольником и звездой с помощью векторной диаграммы.
Рисунок 23 — Векторная диаграмма измерений трехфазного треугольника и звезды. Измерение трехфазного коэффициента мощности
Общий коэффициент мощности для трехфазной цепи определяется путем суммирования общего ватта, деленного на общее измерение в ВА.
Используя метод двух ваттметров, сумма общих ватт (W1 + W2) делится на измерения VA. Однако, если нагрузка несимметрична (фазные токи разные), это может привести к ошибке при вычислении коэффициента мощности, поскольку в расчете используются только два измерения ВА.Два VA усредняются, потому что предполагается, что они равны; однако, если это не так, будет получен ошибочный результат. Поэтому для несимметричных нагрузок лучше всего использовать метод трех ваттметров, так как он обеспечит правильный расчет коэффициента мощности как для сбалансированных, так и для несбалансированных нагрузок.
При использовании метода трех ваттметров в приведенном выше расчете коэффициента мощности используются все три измерения ВА.
ГармоникиГармоники относятся ко всем синусоидальным волнам, частота которых является целым кратным основной волны (обычно это синусоидальный сигнал линии электропередачи с частотой 50 Гц или 60 Гц или от 0 до 2 кГц для вращающихся машин).Гармоники — это искажение формы нормального электрического тока, обычно передаваемого нелинейными нагрузками. В отличие от линейных нагрузок, где потребляемый ток пропорционален и следует форме волны входного напряжения, нелинейные нагрузки, такие как двигатели с регулируемой скоростью, потребляют ток короткими резкими импульсами. Когда основная волна и последующие гармонические составляющие объединяются, формы волны искажаются, и возникает интерференция.
Рисунок 24 — Искаженные формы сигналов состоят из нескольких гармонических составляющих Гармоники
необходимо контролировать, поскольку они могут вызвать необычный шум, вибрацию, нагрев или неправильную работу устройств и сократить их срок службы.Внутренние и международные стандарты, такие как IEC61000-3, существуют для контроля гармоник. Поэтому инженерам необходимо обнаруживать гармоники и оценивать их влияние на компоненты, системы и подсистемы в приложении. Размер и разность фаз следует измерять не только для основной частоты, но и для каждой более высокочастотной составляющей. Высокоточные анализаторы мощности могут измерять гармоники до 500-го порядка.
Для вращающихся машин основные амплитуды являются единственными составляющими, которые эффективно способствуют вращению оси. Все остальные гармонические составляющие приводят к потерям в виде тепла и вибрации.
Измерение гармоникИспользуя режим измерения гармоник, можно измерить размер и разность фаз для каждой основной частоты, а также гармоники для каждого градуса, включенного в ток, напряжение и мощность. Например, в случае основной частоты (основной составляющей) 50 Гц третья составляющая составляет 150 Гц, пятая составляющая 250 Гц и так далее, и возможно измерение до 500-й составляющей на частоте 2,5 кГц.
Рисунок 25. Сумма нечетных гармонических составляющих в искаженный сигнал
Для отображения результатов измерения гармоник анализатор мощности может отображать размер каждого градуса, как показано на рисунке 26 ниже, или отображать такие параметры, как размер, соотношение содержания и фаза в списке.
Рисунок 26 — Гистограмма, показывающая зависимость энергии гармоник от порядка Заключение
При измерении мощности необходимо учитывать множество факторов, включая входную мощность, КПД инвертора, КПД, гармоники и коэффициент мощности. Эти измерения включают сложные уравнения, поэтому большинство компаний используют анализаторы мощности для автоматического получения результатов.
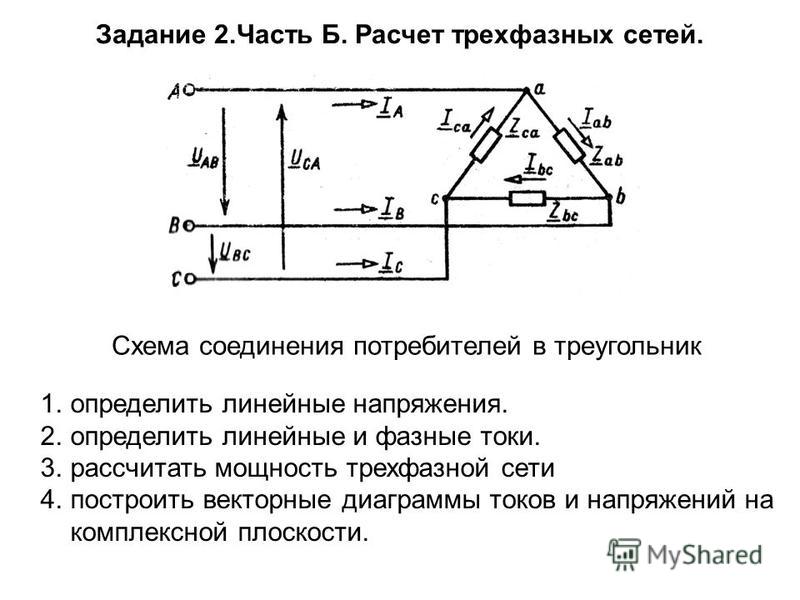
 7кВт
7кВт