\(\cos\)\(\frac{π}{3}\)\(=\)\(\frac{1}{2}\)
\(\cos2=-0,416…\)
Содержание:
Аргумент и значение
Косинус острого угла
Косинус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к гипотенузе.
Пример:
1) Пусть дан угол и нужно определить косинус этого угла.
2) Достроим на этом угле любой прямоугольный треугольник.
3) Измерив, нужные стороны, можем вычислить косинус.
Косинус острого угла больше \(0\) и меньше \(1\)
Если при решении задачи косинус острого угла получился больше 1 или отрицательным, то значит где-то в решении есть ошибка.
Косинус числа
Числовая окружность позволяет определить косинус любого числа, но обычно находят косинус чисел как-то связанных с Пи: \(\frac{π}{2}\), \(\frac{3π}{4}\), \(-2π\).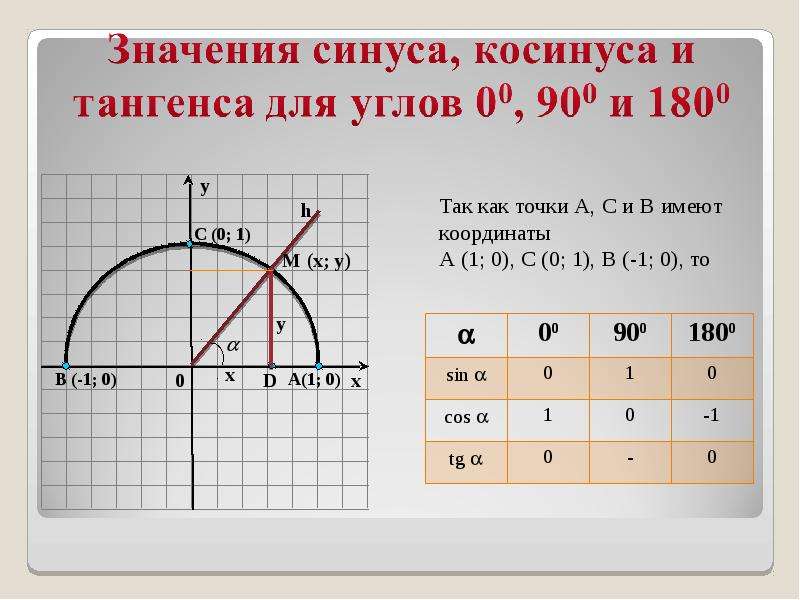
Например, для числа \(\frac{π}{6}\) — косинус будет равен \(\frac{\sqrt{3}}{2}\). А для числа \(-\)\(\frac{3π}{4}\) он будет равен \(-\)\(\frac{\sqrt{2}}{2}\) (приблизительно \(-0,71\)).
Косинус для других часто встречающихся в практике чисел смотри в тригонометрической таблице.
Значение косинуса всегда лежит в пределах от \(-1\) до \(1\). При этом вычислен косинус может быть для абсолютно любого угла и числа.
Косинус любого угла
Благодаря числовой окружности можно определять косинус не только острого угла, но и тупого, отрицательного, и даже большего, чем \(360°\) (полный оборот). Как это делать — проще один раз увидеть, чем \(100\) раз услышать, поэтому смотрите картинку.
Теперь пояснение: пусть нужно определить косинус угла КОА с градусной мерой в \(150°\). Совмещаем точку О с центром окружности, а сторону ОК – с осью \(x\).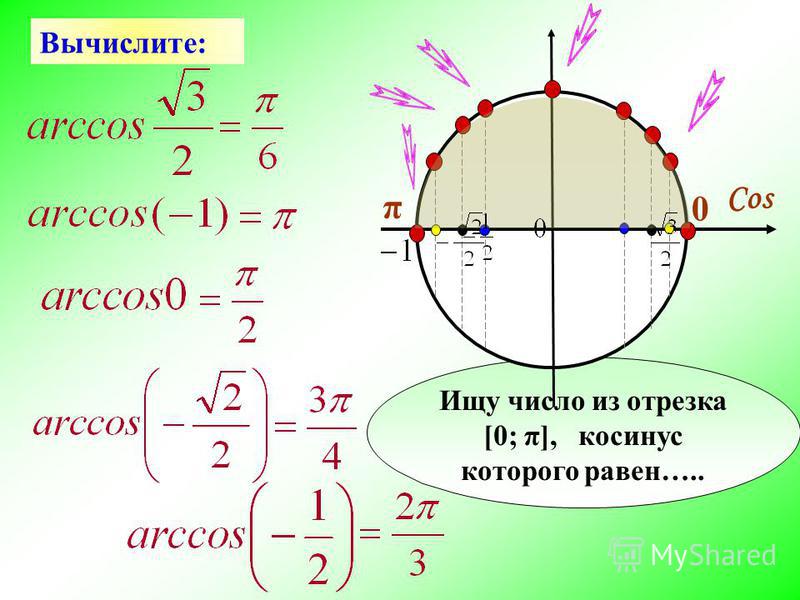
После этого откладываем \(150°\) против часовой стрелки. Тогда ордината точки А покажет нам косинус этого угла.
Если же нас интересует угол с градусной мерой, например, в \(-60°\) (угол КОВ), делаем также, но \(60°\) откладываем по часовой стрелке.
И, наконец, угол больше \(360°\) (угол КОС) — всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол \(405°\) отложен как \(360° + 45°\).
Несложно догадаться, что для откладывания угла, например, в \(960°\), надо сделать уже два оборота (\(360°+360°+240°\)), а для угла в \(2640°\) — целых семь.
Стоит запомнить, что:
Косинус прямого угла равен нулю. Косинус тупого угла — отрицателен.
Знаки косинуса по четвертям
С помощью оси косинусов (то есть, оси абсцисс, выделенной на рисунке красным цветом) легко определить знаки косинусов по четвертям числовой (тригонометрической) окружности:
— там, где значения на оси от \(0\) до \(1\), косинус будет иметь знак плюс (I и IV четверти – зеленая область),
2x}\)— котангенсом и синусом того же угла (или числа): формулой \(ctgx=\)\(\frac{\cos{x}}{\sinx}\)
Другие наиболее часто применяемые формулы смотри здесь.
Функция \(y=\cos{x}\)
Если отложить по оси \(x\) углы в радианах, а по оси \(y\) — соответствующие этим углам значения косинуса, мы получим следующий график:
График данной функции
— область определения – любое значение икса: \(D(\cos{x} )=R\)
— область значений – от \(-1\) до \(1\) включительно: \(E(\cos{x} )=[-1;1]\)
— четная: \(\cos(-x)=\cos{x}\)
— периодическая с периодом \(2π\): \(\cos(x+2π)=\cos{x}\)
— точки пересечения с осями координат:
ось абсцисс: \((\)\(\frac{π}{2}\)\(+πn\),\(;0)\), где \(n ϵ Z\)
ось ординат: \((0;1)\)
— промежутки знакопостоянства:
функция положительна на интервалах: \((-\)\(\frac{π}{2}\)\(+2πn;\) \(\frac{π}{2}\)\(+2πn)\), где \(n ϵ Z\)
— промежутки возрастания и убывания:
функция возрастает на интервалах: \((π+2πn;2π+2πn)\), где \(n ϵ Z\)
функция убывает на интервалах: \((2πn;π+2πn)\), где \(n ϵ Z\)
— максимумы и минимумы функции:
функция имеет максимальное значение \(y=1\) в точках \(x=2πn\), где \(n ϵ Z\)
функция имеет минимальное значение \(y=-1\) в точках \(x=π+2πn\), где \(n ϵ Z\).
Смотрите также:
Синус
Тангенс
Котангенс
Решение уравнения \(\cosx=a\)
|
Пожалуйста активируйте JavaScript в настройках браузера.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
./../communityhost.ru/includes/layouts/bb/styles/grey/box/sub_headline_bg.gif»>
Если кто помнит тригонометрию, может синус через тангенс выразить. Там со знаками легче определиться.
08.2008
./../communityhost.ru/includes/layouts/bb/styles/grey/box/sub_headline_bg.gif»>
./../communityhost.ru/includes/layouts/bb/styles/grey/box/sub_headline_bg.gif»>
./../communityhost.ru/includes/layouts/bb/styles/grey/box/sub_headline_bg.gif»>
ТТ подключены «Полярниками» к источнику.
./../communityhost.ru/includes/layouts/bb/styles/grey/box/sub_headline_bg.gif»>
./../communityhost.ru/includes/layouts/bb/styles/grey/box/sub_headline_bg.gif»>
Опять что-то с чем-то в первом квадранте (P+,Q+(ind) и P и Q потербляются из сети) cos должен быть положительным. Или здесь опять вопрос о том, что считать положительной мощностью, что отрицательной?
08.2008
./../communityhost.ru/includes/layouts/bb/styles/grey/box/sub_headline_bg.gif»>
./../communityhost.ru/includes/layouts/bb/styles/grey/box/sub_headline_bg.gif»>
Без плюсов и минусов. А в описаниях счётчиков были нарисованы те самые квадранты и подробненько написано, где направление какой мощности к шинам, где от шин
gif»>
Синус, косинус и тангенс угла — урок. Геометрия, 9 класс.
В системе координат построим полуокружность радиуса \(1\) с центром в начале координат.
Как уже известно, в прямоугольном треугольнике синус острого угла определяется как отношение противолежащего катета к гипотенузе, а косинус острого угла определяется как отношение прилежащего катета к гипотенузе.
В треугольнике \(AOX\):
sinα=AXAO;cosα=OXAO.
Так как радиус полуокружности \(R = AO = 1\), то sinα=AX;cosα=OX.
Длина отрезка \(AX\) равна величине координаты \(y\) точки \(A\), а длина отрезка \(OX\) равна величине координаты \(x\) точки \(A\):
Acosα;sinα.
Следовательно, для углов 0°≤α≤180° видно, что −1≤cosα≤1;0≤sinα≤1.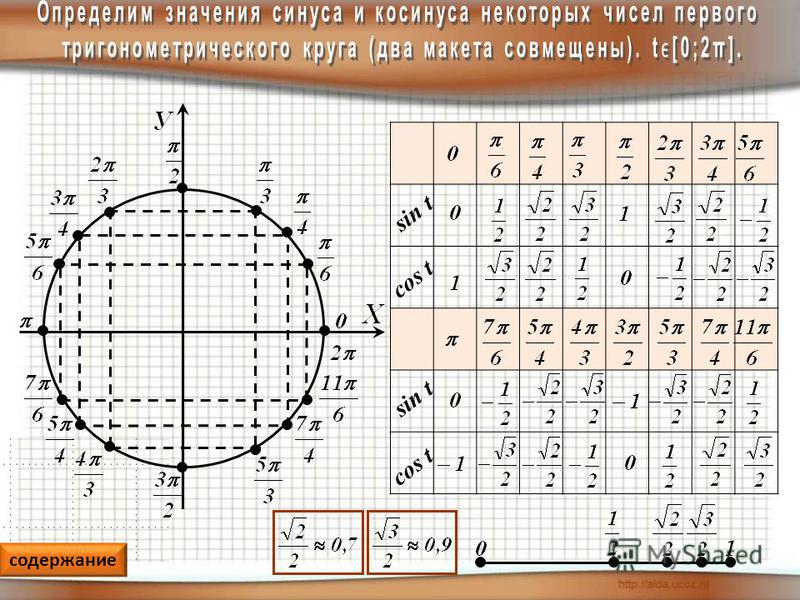
В прямоугольном треугольнике тангенс острого угла равен отношению противолежащего катета к прилежащему катету, а значит,
tgα=AXOX=sinαcosα.
Используя единичную полуокружность и рассмотренную информацию, определим синус, косинус и тангенс для 0°;90°;180°.
sin0°=0;cos0°=1;tg0°=0;sin90°=1;cos90°=0;tg90° не существует;sin180°=0;cos180°=−1;tg180°=0.
Рассмотрим оба острых угла в треугольнике \(AOX\). Если вместе они образуют 90°, то оба выразим через α.
Если sinα=AXAO;cosα=OXAO, то sin90°−α=OXAO;cos90°−α=AXAO.
Видим, что справедливы равенства:
cos90°−α=sinα;sin90°−α=cosα.
Рассмотрим тупой угол, который также выразим через α.
Справедливы следующие равенства:
sin180°−α=sinα;cos180°−α=−cosα.
Эти формулы называются формулами приведения:
cos90°−α=sinα;sin90°−α=cosα.
sin180°−α=sinα;cos180°−α=−cosα.
Если в треугольнике \(AOX\) применить теорему Пифагора, получаем AX2+OX2=1.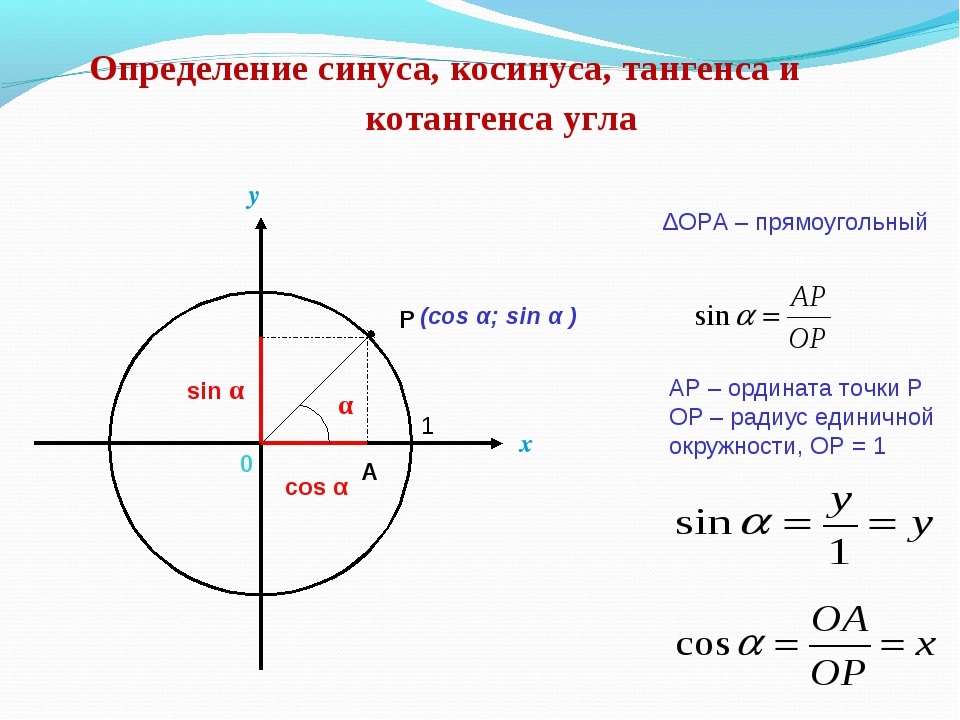
Заменив отрезки соответственно синусом и косинусом, мы напишем
Главное тригонометрическое тождество
sin2α+cos2α=1.
Это тождество позволяет вычислить величину синуса угла, если дан косинус
(как уже отмечено, синус для углов 0°≤α≤180° только 0 или положительный):
sin2α+cos2α=1;sin2α=1−cos2α;sinα=1−cos2α
— или величину косинуса угла, если дан синус:
sin2α+cos2α=1;cos2α=1−sin2α;cosα=±1−sin2α.
Для острых углов косинус положительный, а для тупых углов берём отрицательное значение.
Косинус двойного угла
В тригонометрии многие формулы легче вывести, чем вызубрить. Косинус двойного угла — замечательная формула! Она позволяет получить формулы понижения степени и формулы половинного угла.
Итак, нам нужны косинус двойного угла и тригонометрическая единица:
Они даже похожи: в формуле косинуса двойного угла — разность квадратов косинуса и синуса, а в тригонометрической единице — их сумма.
Если из тригонометрической единицы выразить косинус:
и подставить его в косинус двойного угла, то получим:
Это — еще одна формула косинуса двойного угла:
Эта формула — ключ к получению формулы понижения степени:
Итак, формула понижения степени синуса:
Если в ней угол альфа заменить на половинный угол альфа пополам, а двойной угол два альфа — на угол альфа, то получим формулу половинного угла для синуса:
Теперь из тригонометрической единицы выразим синус:
Подставим это выражение в формулу косинуса двойного угла:
Получили еще одну формулу косинуса двойного угла:
Эта формула — ключ к нахождению формулы понижения степени косинуса и половинного угла для косинуса.
Таким образом, формула понижения степени косинуса:
Если в ней заменить α на α/2, а 2α — на α, то получим формулу половинного аргумента для косинуса:
Так как тангенс — отношение синуса к косинусу то формула для тангенса:
Котангенс — отношение косинуса к синусу.
Поэтому формула для котангенса:
Конечно, в процессе упрощения тригонометрических выражений формулы половинного угла или понижения степени нет смысла каждый раз выводить. Гораздо проще перед собой положить листик с формулами. И упрощение продвинется быстрее, и зрительная память включится на запоминание.
Но несколько раз вывести эти формулы все же стоит. Тогда вы будете абсолютно уверены в том, что на экзамене, когда нет возможности воспользоваться шпаргалкой, вы без труда их получите, если возникнет необходимость.
Тригонометрические и геометрические преобразования, sin(A + B), sin(A
Коэффициенты для суммы углов
Как демонстрируют различные примеры, иногда нам нужны значения углов, отличных от 0, 30, 45, 60 и 90 градусов. В этой главе вы должны научиться двум вещам:
1. sin(A + B) не является равным sinA + sinB. В этом случае не срабатывает простое раскрытие скобок, как в алгебре.
2. Формулу, по которой вычисляется sin(A + B).
Во-первых, покажем, что раскрытие скобок не «срабатывает». Пусть A = 30 градусов и B = 45 градусов. Sin30 равен 0.5. Sin45 равен 0.7071. Складывая, получим 1.2071.
Вы знаете, что ни синус, ни косинус не может быть больше 1. Почему? Потому что в дробях, по которым они вычисляются, гипотенуза выступает в качестве знаменателя. Самое большее значение мы получим, если числитель равен знаменателю. Синус или косинус не может быть больше 1, и поэтому значение 1,2071 не верно.
Нахождение синуса, косинуса или тангенса полного угла (A + B)
Нахождение sin(A + B)
Самый простой способ найти sin (A + B) — используя геометрическое построение, показанное на рисунке. Большой угол (A + B), состоит из двух маленьких, А и В. Рисунок (1) показывает, что противоположная сторона состоит из двух частей.
Нижняя часть, разделенная линией между углами (2), есть синус А. Линия между двумя углами, разделенная гипотенузой (3), есть косинус B. Умножаем их. Средняя линия и в числителе, и в
знаменателе, поэтому они сокращаются, оставляя нижнюю часть противоположной стороны над гипотенузой (4).
Обратите внимание на маленький прямоугольный треугольник (5). Затененный угол есть A, потому что линия на его верхней части параллельна линии в основании. Подобные прямоугольные треугольники с углом А показывают, что верхний угол, отмеченный А также равен оригинальному углу А. Верхняя часть противоположной (6) над длинной, заштрихованный треугольник является соs А. Противоположный над основной гипотенузой (7) есть синус. Поскольку стороны с пометкой «противоположные» (7) и в числителе и знаменателе, когда cos и sin перемножаются, cosAsinB есть верхняя часть оригинального противоположного — для (A + B) — разделенные основной гипотенузой (8).
Теперь, сложим это все вместе (9). Sin(A + B) есть две части противоположного — все разделенные гипотенузой (9). Записывая это в тригонометрическую форму: sin(A + B) = sin A cos B + cos A sin B.
Нахождение cos(A + B)
Очень похожая конструкция находит формулу для косинуса угла созданного двумя углами, сложенными вместе.
Используя ту же самую конструкцию (1), обратите внимание, что смежная сторона является полной линией основания (для соs A), c частью, которая вычитается справа. Каждая часть должна использовать тот же знаменатель, гипотенузу (A + B) треугольника.
Полная линия основания, разделенная линией между углами A и E есть cosA (2). Эта разделяющая линия, деленная гипотенузой (A + B) треугольника, есть cos B (3). Поэтому, полная линия основания, деленная гипотенузой есть произведение cosAcosB (4).
Теперь, небольшая часть, которая должна быть вычтена. Заштрихованная часть (5) представляет sinA, который умножается заштрихованной частью (6) есть sin E, который есть другой частью и , которая нам нужна (7). Вычитание дает соs (А + В) (8), поэтому формула, которая нам нужна:
cos(A + B) = cos A cos B — sin A sin B
Нахождение tan(A + B)
Полный геометрический вывод формулы для tg (A + B) является сложным. Проще всего вывести его из двух формул, которые мы уже сделали. В любом угле, тангенс равен синус, деленному на косинус. Используя тот факт, tan (A + B) = sin(A + B)/соs(A + B). Это выражение можно расширить к виду:
tan(A + B) = [sin A cos B + cos A sin B]/[cos A cos B — sin A sin B]
Разделив верхнюю и нижнюю часть на cos A cos B, что превращает все члены в тангенсы, получаем:
tan(A + B) = [tan A + tan B]/[1 — tan A tan B]
Коэффициенты для 75 градусов
Покажем коэффициенты синуса, косинуса и тангенса, подставляя в формулу суммы, и потом упрощая результат к своей простейшей форме, прежде чем находить суммы. После внесения основных замен в каждом конкретном случае, примерная работа в заштрихованной части, чтобы показать, как результат сводится к простейшей форме для оценки.
Если вы используете ваш карманный калькулятор для оценки, скорей всего, не имеет значения или вы упрщаете выражения сначала или просто пропускаете его! Все зависит от калькулятора: некоторые вычисля.т разницу, некоторые нет!
Коэффициенты углов, больших, чем 90 градусов
До сих пор рассматривалось соотношение острых углов (между 0 и 90 градусами). Другие треугольники с тупым углом (более 90 градусов) и до 180 градусов могут появиться в последующих задачах. Для упрощения классификации углов по размеру, они делятся на сектора (квадранты).
Квадрант есть четвертой частью круга. Так как круг делится на 360 градусов, квадранты имеют по 90 градусов. 0-90 градусов это первый квадрант, 90-180 — второй, 180-270 — третий и 270-360 — четвертый.
Используя линии, обозначающие границы квадранта, 0 или 360 это горизонталь направо, 90 — вертикально вверх, 180 — горизонталь слева и 270 сверху вниз. Теперь, используем этот метод для построения графиков.
Большие углы определяется вектором вращения, начиная с нуля и вращением против часовой стрелки. Горизонтальные элементы х: положительные справа, отрицательные слева. Вертикальные элементы у: положительные вверх, отрицательные вниз. Вращающийся вектор является р. Таким образом, синус угла есть y/r, косинус х/r, и тангенс у/х. Вектор r — всегда положителен. Таким образом, знак отношения может быть вычислен для различных секторов.
Здесь приведены знаки для трех отношений в четырех квадрантах.
Кроме того, как эквивалентный угол в первой четверти «переключается» когда вектор переходит из одного квадранта в другой. В первой четверти, стороны определены в соотношениях для синуса, косинуса и тангенса. При перемещении к большим углам в остальных секторах, противоположная сторона всегда есть вертикальная (у). То, что называется смежное, всегда есть горизонталью (х). Гипотенуза это всегда вращающийся вектор (r). Вы можете видеть картину как изменяются тригонометрические соотношения для углов.
Отношения в четырех квадрантах
Отношения для различных углов
Теперь у вас есть два пути получить формулы для различных углов. Во-первых, используя геометрическую конструкцию, такую, которая, например, была использована для суммы углов, реверсивную так, что (A — B) есть угол B вычитающийся из угла A.
В рассуждениях, аналогичных тем, которые были использованы для суммы углов, здесь представлены несколько сокращенные формулы для синуса и косинуса:
sin(A — B) = sin A cos B — cos A sin B
and
cos(A — B) = cos A cos B + sin A sin B
Геометрическая конструкция
Формулы суммы и разницы
Второй способ нахождения формулы для разницы углов использует уже полученную формулу суммы, но делает B отрицательным. Из нашего исследования знаков для различных секторов, отрицательные углы с 1-го квадранта будут в 4 квадранте. Проводя эту подстановку, получим тот же результат, который был получен геометрически в предыдущем разделе.
Поиск формулы тангенса проходит тем же методом, или заменой синуса и косинуса в формулах или более непосредственно, превращая tg(-B) = — tg B. В любом случае вы получите:
tan(A — B) = [tan A — tan B]/[1 + tan A tan B]
Отношения с помощью четырех секторов
Вы можете вывести несколько отношений с формулами суммы и разности. Вы уже сделали соотношение для 75 градусов. Теперь можно выполнить то же для 15 градусов. Эти формулы дают соотношения для углов в 15 градусов интервалы через четыре квадранта. Построив их на 360 градусов, вы можете увидеть, как эти три соотношения изменяются, когда вектор проходит через четыре квадранта.
«Волна» синуса и косинуса колеблется вверх и вниз между +1 и -1. Обратите внимание, что «волны» смещены на 90 градусов друг относительно друга. Этот факт станет важным позже.
Кривая тангенса начинается, как синусоида, но вскоре она стремится достичь бесконечности на 90 градусах. Двигаясь » вне видимости» в положительном направлении, она «приходит» с отрицательного направления с другой стороны на 90 градусах. Проходя через точку в 180 градусов, функция тангенса повторяет то, что она «делала» проходя 0 или 360 градусов. На 270 градусах она повторяет то же, было на 90 градусах.
Пифагор в тригонометрии
Формула часто может быть упрощена, так как были найдены выводы формулы тангенса от формул синуса и косинуса, а также изменение ее членов одного отношения к другому отношению, использeущеuj другие члены. При этом, теорема Пифагора, выраженная в тригонометрическом соотношении, очень удобна.
Предположим, что прямоугольный треугольник имеет гипотенузу длиной 1. Тогда одна из сторон будет иметь длину sinA, а другая — cosA. Отсюда, согласно теореме Пифагора: cos2 A + sin2 A = 1. Это выражение всегда истинно для любого значения A.
Немного о том, как это было записано. Cos2 A означает (cos A)2. Если вы написали это как cos A2, уравнение будет означать что-то другое. A есть число в нескольких угловых значениях, которое представляет угол. A2 было бы то же самое число, возведенное в квадрат. Его значение зависело бы от использованного числового значения, поэтому это не очень хороший член для использования. Это означает квадрат синуса ли косинуса, не сам угол. Формула Пифагора может быть выражена иначе. Например, две другие формы:
cos2 A = 1 — sin2 A, и sin2 = 1 — cos2 A.
Умножение углов
Формулы сумм, вместе с теоремой Пифагора, используются для углов, которые в 2, 3 или больше раз кратны любым оригинальным углам. Здесь приводятся формулы для 2А и 3А.
Формула суммы работает, когда оба угла одинаковые или различны: sin(A + B) или sin(A + A). Однако, sin(A + A) в действительности sin 2A. Поэтому, sin 2A есть sin A cos A + cos A sin A. Оба члена выражения есть одним и тем же произведением, записанным в разном порядке, так что это выражение может быть упрощено до sin 2A = 2 sin A cos A.
Подобным образом, cos 2A = cos A cos A — sin A sin A, что также может быть записано как: cos 2A = cos2 A — sin2 A. Используя теорему Пифагора, изменяем это к виду: cos 2A = 2cos2 A — 1. Наконец, tg 2A = 2 tg A/[1 — tg2 A].
Теперь тройной угол (3А) используется, чтобы показать, как получены следующие кратные углы. В основном, это так же просто, как запись 3A = 2 + A и повторного применения формулы суммы. Но тогда, чтобы получить в результате формулу в работающем виде, необходимо заменить часть 2А, на выражения с простым углом А.
На рисунках внизу вы можете видеть, что с каждым разом вычисления становятся сложнее.
УМНОЖЕНИЕ УГЛОВ Производные от формул суммы
УМНОЖЕНИЕ УГЛОВ Соотношения для 3A
Свойства равнобедренного треугольника
Вы уже видели, что прямоугольный треугольник является полезным строительным блоком для других фигур. Равнобедренный треугольник имеет несколько различных видов использования. Дело в том, что его использование основывается на том, что равнобедренный треугольник имеет две равные стороны и два равные углы между основанием и боковыми равными сторонами. Перпендикуляр из третьего угла на третью сторону делит ее пополам. Таким образом весь треугольник делится на два равных прямоугольных треугольника.
Любой треугольник, за исключением прямоугольного треугольника, можно разделить на три прилегающих равнобедренных треугольника, разделив каждую сторону на две равные части и построить перпендикуляры из точек разделения. Там, где любые два из этих перпендикуляров встречаются, если линии тянутся к углам исходного треугольника, три линии должны быть равны, потому что две из них образуют стороны равностороннего треугольника. Таким образом, перпендикуляр с третьей стороны исходного треугольника должен также встретиться в одной точке.
Это утверждение справедливо, как мы покажем здесь, независимо от того, является ли исходный треугольник острым или тупым. Разница с тупым прямоугольным треугольником в том, что место встречи перпендикуляров лежит снаружи исходного треугольника, а не внутри.
Что происходит в прямоугольном треугольнике? Перпендикуляры от средней точки гипотенузы другой стороны будут делить пополам эти две стороны — вы получаете два из трех! Место встречи находится гипотенузе.
Углы в окружности
Основное свойство окружности это то, что ее центр находится на одинаковом расстоянии от любой точки окружности. Это расстояние есть радиусом окружности.
Если вы нарисуете любой треугольник внутри круга, перпендикуляры из средней точки его сторон встретятся в центре окружности а радиусы из углов треугольника делят его на три равнобедренных треугольника
Теперь, если вы назовете равные пары углов в каждом равнобедренном треугольнике A, A, B, B, C, C, вы обнаружите, что исходный треугольник имеет один угол A+B, один угол B+C, и один угол A+ C. Три угла в сумме дают 2A + 2B + 2С, а это как известно равно 180 градусов.
В любом равнобедренном треугольнике угол при вершине равен 180 градусов минус удвоенный угол при основании. Поэтому, согласно предыдущего пункта, 180 — 2A должен быть такой же, как и 2B + 2С, например.
Рассмотрим угол правый нижний угол, опирающийся на окружность. Угол в центре равен 2B + 2С. Углом, опирающийся на окружность равен B + C. Вы видите, что для любого сегмента круга, угол в центре всегда в два раза больше угла, опирающегося на окружность.
Утверждение выше приводит к интересным фактам об углах в окружностях. Вместо определения углов со стороной треугольника, используют дугу (часть окружности) круга. Часть окружности, которая определяется углом в центре называется хордой окружности.
Угол в центре в два раза больше чем угол на окружности
Любой угол, касающийся окружности, используя хорду как ограничение угла, равен половине угла в центре. Таким образом, все углы в круге, с основанием на той же хорде, должны быть равны. Предположим, что хорда имеет угол 120 градусов. Угол на окружности будет равен 60 градусам.
Особый случай представляет собой полукруг (точный полукруг). Угол в центре представляет собой прямую линию (180 градусов). Каждый угол в полукруге равен 90 градусам (прямой угол). Любой треугольник в полукруге является прямоугольным треугольником.
Определения
Выше мы часто использовали углы, которые дополняют углы до прямого угла (90 градусов) или до двух прямых углов (180 градусов). Когда два угла образовывают угол 180 градусов (два прямых угла), они называются дополнительными. Если два угла добавить до 90 градусов (один прямой угол), их называют комплементарными
Вопросы и задачи
1. Синус угла А равен 0,8 и синус угла B равен 0.6. Из различных зависимостей, полученных до сих пор, найдите следующее: тангенс А, тангенс B, синус (A + B), косинус (A + B), синус (A — B), косинус (A — B), тангенс (А + B) и тангенс (A — B) без использования таблиц или тригонометрических клавиш калькулятора.
2.На экваторе Земля имеет радиус 4000 км. Углы вокруг экватора измеряется в меридианах долготы, с линией с севера на юг проходящей через Гринвич (Англия), в качестве нулевого отсчета. Два места используются для наблюдения за луной: первое это Кения, на экваторе 37,5 к востоку от Гринвича, а другой является Суматра, на экваторе к востоку 100,5. Как далеко друг от друга эти два места, если расстояние измерять мнимой прямой, проходящей через Землю?
3.Если бы наблюдения были сделаны горизонтально от точки наблюдения в вопросе 2 (к востоку от первой, к западу от второй), под каким углом была бы линия пересечения наблюдений?
4.В определенное время, точно синхронизированное в обоих местах, наблюдается спутник. В Кении, высота линии визирования с центром на спутнике составляет 58 градусов выше горизонтали на восток. На Суматре, высота составляет 58 градусов выше горизонтали на запад. Как далеко находится спутник? Используйте расстояние между точками рассчитанное в вопросе 2.
5. Косинус определенного угла в два раза больше синуса того же угла. Чему равен тангенс этого угла? Не используйте таблицы или калькулятор для ответа на этот вопрос.
6. Синус определенного угла равен именно 0.28. Найдите косинус и тангенс этого угла. Не используйте таблицы или калькулятор для ответа на этот вопрос.
7. Синус определенного угла равен 0.6. Найдите синус углов, больших чем заданный в два и три раза.
8. Найдите синус и косинус угла, большего ровно в два раза чем угол из вопроса 7.
9. Используя 15 градусов, как единичный угол, и формулы для отношения 2А и 3А найдите значения синусов 30 и 45 градусов.
10. Используя 30 градусов, как единичный угол, найти значения синусов 60 и 90 градусов.
11. Используя 45 градусов, как единичный угол, найдите значения тангенсов 60 и 90 градусов.
12. Используя 60 градусов, как единичный угол, найдите значения косинусов 120 и 180 градусов.
13. Используя 90 градусов, как единичный угол, найдите значения косинусов 180 и 270 градусов.
14. Используя формулы тангенса для умножения углов и таблицы, найдите тангенсы утроенных углов в 29, 31, 59 и 61 градусов. Посчитайте изменения знака между утроенным углом 29 и 31 градусов и между 59 и 61 градусов.
15. Синус угла составляет 0,96. Найдите синус и косинус удвоенного угла.
16. Задача сводится к алгебраической выражению вида 8cos2 A + cos A = 3. Решите для косинуса А, и укажите, в каком квадранте будет угол, представляющий каждое решение придет. Приведите приближенные значения из таблицы или используя калькулятор.
Урок геометрии по теме «Синус, косинус, тангенс и котангенс угла». 9-й класс
Цели:
- cистематизировать знания по теме синус, косинус, тангенс и котангенс острого угла;
- eметь применять формулы приведения для решения алгебраических и тригонометрических задач;
- hазвивать тригонометрический аппарат для решения алгебраических и тригонометрических задач.
Оформление: чертежи единичной полуокружности, прямоугольного треугольника, таблица значений тригонометрических функций.
Подготовка:
- готовые чертежи и таблицы;
- презентация “Своя игра”.
ХОД УРОКА
I.. Актуализация знаний учащихся.
1. Как выражается sinα, cosα, tgα и ctgα острого угла прямоугольного треугольника?
2. Выясните, принадлежат ли единичной окружности точки:
А(-;), В(-; 2), С(- ;), D(; - ).
3. Выясните, какие точки лежат в I и во II четвертях: М(; - ), N (; ), Р (; ), S (- ; ).
4. Найдите значения sinα, tgα и ctgα, если cosα=- .
II. Систематизация знаний учащихся.
На прямоугольной системе координат построим полуокружность радиуса, равного 1 – единичная полуокружность. Возьмем точку М(х; у), принадлежащую этой полуокружности.
Sinα – это ордината точки, т. е. sinα=у.
Cosα – это абсцисса точки, т. е. cosα=х.
Так как координаты (х; у) точек единичной полуокружности заключены в промежутках 0<у<1 и -1<х<1, то для любого α справедливы следующие неравенства: 0< sinα <1 и -1< cosα <1.
(Приложение 1)
Рассмотрим треугольник АВС – прямоугольный. <А=α. Тангенсом острого угла α называется отношение противолежащего катета к прилежащему катету, т.е. tgα==
Аналогично, выражаем котангенс острого угла α. Мы вводили определение, хотя в учебнике оно не рассматривалось. Котангенсом острого угла α называется отношение прилежащего катета к противолежащему катету, т.е. ctgα==
Основное тригонометрическое тождество:
sin2α+cos2α=1
tgα=
ctgα=.
Справедливы следующие тождества:
sin(900-α)=сosα sin(900+α)=сosα
cos(900-α)= sinα cos(900+α)=-sinα
sin(1800-α)=sinα cos(1800-α)= — cosα — это формулы приведения.
А теперь вспомним значения sinα, cosα, tgα и ctgα для табличных углов (Приложение 2).
III. Решение задач.
В приложении 3 дан чертеж: полуокружность с обозначениями дуг вида 150n и точек 0, ±1, ±0,5, ± на оси абсцисс и полуоси ординат. По чертежу определите:
- Может ли синус быть числом отрицательным?
- Может ли косинус быть числом положительным?
- В каких пределах может изменяться косинус?
- В каких пределах может изменяться синус?
- Чему равен синус 1500?
- Каким может быть тангенс в I и во II четвертях?
- Найдите sinα, tgα и ctgα, если cosα=-.
- Найдите tgα и ctgα, если sinα= и 900<α<1800.
- Вычислите sinα, cosα, tgα и ctgα, если α=1350 и α=1200.
IV. Рефлексия.
Приложение 4 – “Своя игра”.
V. Подведение итогов. Домашнее задание.
- Вычислите sinα, cosα, tgα и ctgα, если α=1500.
- Найдите cosα, tgα и ctgα, если sinα=
Тригонометрические тождества и преобразования
Для решения некоторых задач будет полезной таблица тригонометрических тождеств, которая позволит гораздо проще совершать преобразования функций:Простейшие тригонометрические тождества
Частное от деления синуса угла альфа на косинус того же угла равно тангенсу этого угла (Формула 1). См. также доказательство правильности преобразования простейших тригонометрических тождеств.
Частное от деления косинуса угла альфа на синус того же угла равно котангенсу этого же угла (Формула 2)
Секанс угла равен единице, деленной на косинус этого же самого угла (Формула 3)
Сумма квадратов синуса и косинуса одного и того же угла равна единице (Формула 4). см. также доказательство суммы квадратов косинуса и синуса.
Сумма единицы и тангенса угла равна отношению единицы к квадрату косинуса этого угла (Формула 5)
Единица плюс котангенс угла равна частному от деления единицы на синус квадрат этого угла (Формула 6)
Произведение тангенса на котангенс одного и того же угла равно единице (Формула 7).
Преобразование отрицательных углов тригонометрических функций (четность и нечетность)
Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.
Как видно, косинус и секанс является четной функцией, синус, тангенс и котангенс — нечетные функции.
Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа).
Косинус «минус альфа» даст тоже самое значение, что и косинус угла альфа.
Тангенс минус альфа равен минус тангенс альфа.
Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)
Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами:
Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла) в одинарный происходит по следующим правилам:
Синус двойного угла равен удвоенному произведению синуса на косинус одинарного угла
Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла
Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица
Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла
Тангенс двойного угла равен дроби, числитель которой — удвоенный тангенс одинарного угла, а знаменатель равен единице минус тангенс квадрат одинарного угла.
Котангенс двойного угла равен дроби, числитель которой — квадрат котангенса одинарного угла минус единица, а знаменатель равен удвоенному котангенсу одинарного угла
Формулы универсальной тригонометрической подстановки
Указанные ниже формулы преобразования могут пригодиться, когда нужно аргумент тригонометрической функции ( sin α, cos α, tg α) разделить на два и привести выражение к значению половины угла. Из значения α получаем α/2 .Данные формулы называются формулами универсальной тригонометрической подстановки. Их ценность заключается в том, что тригонометрическое выражение с их помощью сводится к выражению тангенса половины угла, вне зависимости от того, какие тригонометрические функции (sin cos tg ctg) были в выражении изначально. После этого уравнение с тангенсом половины угла решить гораздо проще.
Тригонометрические тождества преобразования половины угла
Указанные ниже формулы тригонометрического преобразования половинной величины угла к его целому значению.Значение аргумента тригонометрической функции α/2 приводится к значению аргумента тригонометрической функции α.
Тригонометрические формулы сложения углов
cos (α — β) = cos α · cos β + sin α · sin β
sin (α + β) = sin α · cos β + sin β · cos α
sin (α — β) = sin α · cos β — sin β · cos α
cos (α + β) = cos α · cos β — sin α · sin β
Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:
Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.
Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.
Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.
Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.
Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.
Формулы преобразования суммы или разности тригонометрических функций
Выражения, представляющие собой сумму вида sin α + sin β можно преобразовать с помощью следующих формул:Формулы тройного угла — преобразование sin3α cos3α tg3α в sinα cosα tgα
Иногда необходимо преобразовать тройную величину угла так, чтобы аргументом тригонометрической функции вместо 3α стал угол α.В этом случае можно воспользоваться формулами (тождествами) преобразования тройного угла:
Формулы преобразования произведения тригонометрических функций
Если возникает необходимость преобразовать произведение синусов разных углов косинусов разных углов или даже произведения синуса на косинус, то можно воспользоваться следующими тригонометрическими тождествами:В этом случае произведение функций синуса, косинуса или тангенса разных углов будет преобразовано в сумму или разность.
Формулы приведения тригонометрических функций
Пользоваться таблицей приведения нужно следующим образом. В строке выбираем функцию, которая нас интересует. В столбце — угол. Например, синус угла (α+90) на пересечении первой строки и первого столбца выясняем, что sin (α+90) = cos α .
См. также Полный список формул приведения тригонометрических функций.
| Угол |
α + 90 α + π/2 |
α + 180 α + π |
α + 270 α + 3π/2 |
90 — α π/2- α |
180 — α π- α |
270 — α 3π/2- α |
360 — α 2π- α |
| sin | cos α | -sin α | -cos α | cos α | sin α | -cos α | -sin α |
| cos | -sin α | -cos α | sin α | sin α | -cos α | -sin α | cos α |
| tg | -ctg α | tg α | -ctg α | ctg α | -tg α | ctg α | -tg α |
| ctg | -tg α | ctg α | -tg α | tg α | -ctg α | tg α | -ctg α |
Как найти отрицательный косинус
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
5. Знаки тригонометрических функций
М. Борна
Углы более 90 °
Интерактивный график
Не пропустите интерактивный графический апплет ниже, который показывает значение тригонометрических соотношений для углов `> 90 ^ @`.2`. Тогда коэффициенты следующие:
`sin θ = y / r` `cos θ = x / r` `tan θ = y / x` | `csc θ = r / y` `сек θ = r / x` `детская кроватка θ = x / y` |
Чем это отличается от определений, которые мы уже встречали в разделе 2, «Синус, косинус, тангенс и взаимные отношения»? Единственная разница в том, что теперь x или y (или оба) могут быть отрицательными , потому что теперь наш угол может быть в любом квадранте.Отсюда следует, что тригонометрические отношения могут оказаться отрицательными или положительными. В предыдущем разделе задействованные углы всегда были меньше 90 °, поэтому все 6 отношений были положительными.
Обратите внимание, что r всегда положительно.
Пример 1
Давайте посмотрим, как определяются тригонометрические соотношения на конкретном примере. 2) `= sqrt (4 + 9) = sqrt13`
Для этого примера мы определяем тригонометрические отношения для θ в следующим образом:
`sin theta = y / r = 3 / sqrt13 = 0.83205``cos theta = x / r = (- 2) / sqrt13 = -0,55470`
`tan theta = y / x = 3 / -2 = -1,5`
`csc theta = r / y = sqrt13 / 3 = 1.2019``sec theta = r / x = sqrt13 / -2 = -1,80278`
`детская кроватка theta = x / y = (- 2) / 3 = -0,6667`
Четыре квадранта — положительный или отрицательный?
Обратите внимание на пример выше, что наш угол находился во втором квадранте. Также обратите внимание, что во втором квадранте значение y положительно.Поскольку r всегда положительно, то y / r всегда будет положительным в квадранте II. Таким образом, мы заключаем, что sin theta всегда будет положительным во втором квадранте.
Также обратите внимание (в случае cos theta), что x было отрицательным. Во втором квадранте x всегда отрицательно. Так что cos theta тоже всегда будет отрицательным.
Для случая tan theta y положительно, а x отрицательно, поэтому y / x всегда будет отрицательным.
Рассматривая другие квадранты, мы видим закономерность.
В квадранте II sin theta положительны, cos theta и tan theta отрицательны.
В квадранте III tan theta положительна (и x , и y отрицательны, поэтому y / x положительно), sin theta и cos theta отрицательны.
В квадранте IV cos theta положительна, sin theta и tan theta отрицательны.
Конечно, обратные отношения csc theta, sec theta и cot theta следуют той же схеме:
В квадранте II , csc theta положительна, sec theta и cot theta отрицательна.
В квадранте III , cot theta положительны, csc theta и sec theta отрицательны.
В квадранте IV , sec theta положительны, csc theta и cot theta отрицательны.
Нам не нужно запоминать взаимные значения наизусть, но рекомендуется запомнить, где положительные значения sin theta, cos theta и tan theta.
Мы используем эту диаграмму, чтобы запомнить, какие отношения положительны в каждый квадрант. Мы можем запомнить это, используя:
A ll S tations T o C entral.
Это означает : В первом квадранте (I) все соотношения положительные.
Во втором квадранте (II) синус (и cosec) положительный.
В третьем квадранте (III) tan (и котан) находятся положительный.
В четвертом квадранте (IV) cos (и сек) находятся положительный.
Они просто следуют из знака (+ или -) x или y для каждого квадранта, как мы видели выше.
Эти знаки важны, когда мы находим угол от заданное соотношение.
Интерактивный график
Вот интерактивный график, на котором вы можете изучить концепции тригонометрических соотношений.
Перетащите точку P по кривой во все 4 квадранта и обратите внимание на соотношения sin, cos и tan. этот результат.Обратите внимание, в частности, на положительные соотношения. в каждом квадранте.
Также обратите внимание, что «sin theta» — это , определенный как «y / r», «cos theta» определяется как «x / r», а «tan theta» определяется как «y / x».
Отсюда положительные и отрицательные значения, и это просто расширение отношений, которые мы узнали ранее, когда тета была ограничена значением менее 90 °.
Авторские права © www.intmath.com
Примеры 2
Какой знак (+ или -) у следующего?
а.2) `= sqrt (9 + 16)` = sqrt25 = 5`
Так
`грех \ θ = у / г = -4 / 5`
`cos \ θ = x / r = -3 / 5`
`тангенс \ θ = у / х = (-4) / (- 3) = 4 / 3`
А для обратных отношений:
`csc \ θ = r / y = -5 / 4`
`сек \ θ = r / x = -5 / 3`
`детская кроватка \ θ = x / y = 3 / 4`
Синус, косинус и тангенс в четырех квадрантах
Синус, косинус и тангенс
Три основных функции в тригонометрии — это синус, косинус и тангенс.
Их легко посчитать:
Разделите длину одной стороны прямоугольного треугольника
на другую сторону
… но надо знать с какой стороны!
Для угла θ функции рассчитываются следующим образом:
Функция синуса: | sin ( θ ) = Противоположно / Гипотенуза |
Функция косинуса: | cos ( θ ) = Соседний / Гипотенуза |
Функция касания: | tan ( θ ) = напротив / рядом |
Пример: Что такое синус 35 °?
Используя этот треугольник (длины до одного десятичного знака): sin (35 °) = Противоположно / Гипотенуза = 2.8 / 4,9 = 0,57 … |
Декартовы координаты
Используя декартовы координаты, мы отмечаем точку на графике цифрой , насколько далеко вдоль и насколько далеко она находится до :
Точка (12,5) находится на 12 единиц вдоль и на 5 единиц вверх.
Четыре квадранта
Когда мы включаем отрицательных значений , оси x и y делят пространство на 4 части:
Квадранты I, II, III и IV
(пронумерованы против часовой стрелки)
- В Квадранте I и x, и y положительны,
- в квадранте II x отрицательно (y все еще положительно),
- в Квадранте III и x, и y отрицательны, а
- в квадранте IV x снова положительно, а y отрицательно.
Как это:
| Квадрант | X (горизонтально) | Y (вертикально) | Пример |
|---|---|---|---|
| I | Положительно | Положительно | (3,2) |
| II | Отрицательный | Положительно | (-5,4) |
| III | Отрицательный | Отрицательный | (-2, -1) |
| IV | Положительно | Отрицательный | (4, −3) |
Пример: точка «C» (−2, −1) расположена на 2 единицы в отрицательном направлении и на 1 единицу вниз (т.е.е. отрицательное направление).
И x, и y отрицательны, поэтому эта точка находится в «Квадранте III»
Опорный угол
Углы могут быть больше 90º
Но мы можем вернуть их ниже 90º, используя ось x в качестве ориентира.
Думайте, что «ссылка» означает «ссылаться x»
Самый простой метод — сделать набросок!
Пример: 160º
Начните с положительной оси x и поверните на 160º
Затем найдите угол к ближайшей части оси x, в данном случае
20º
Базовый угол для 160º равен 20º
Здесь мы видим четыре примера с исходным углом 30º:
Вместо эскиза можно использовать эти правила:
| Квадрант | Опорный угол |
| I | θ |
| II | 180º — θ |
| III | θ — 180º |
| IV | 360º — θ |
Синус, косинус и тангенс в Четыре квадранта
Теперь давайте посмотрим на детали прямоугольного треугольника 30 ° в каждом из 4-х квадрантов.
В квадранте I все нормально, синус, косинус и тангенс положительны:
Пример: синус, косинус и тангенс 30 °
Синус | грех (30 °) = 1/2 = 0,5 |
Косинус | cos (30 °) = 1,732 / 2 = 0,866 |
Касательная | тангенса угла (30 °) = 1/1.732 = 0,577 |
Но в квадранте II направление x отрицательно, , а косинус и тангенс становятся отрицательными:
Пример: синус, косинус и тангенс 150 °
Синус | грех (150 °) = 1/2 = 0,5 |
Косинус | cos (150 °) = -1.732/2 = -0,866 |
Касательная | тангенса угла (150 °) = 1 / -1,732 = -0,577 |
В квадранте III синус и косинус отрицательны:
Пример: синус, косинус и тангенс 210 °
Синус | sin (210 °) = -1/2 = -0.5 |
Косинус | cos (210 °) = -1,732 / 2 = -0,866 |
Касательная | тангенса угла (210 °) = -1 / -1,732 = 0,577 |
Примечание: касательная положительная , потому что деление отрицательного на отрицательное дает положительный результат.
В квадранте IV синус и тангенс отрицательны:
Пример: синус, косинус и тангенс 330 °
Синус | sin (330 °) = -1/2 = -0.5 |
Косинус | cos (330 °) = 1,732 / 2 = 0,866 |
Касательная | тангенса угла (330 °) = -1 / 1,732 = -0,577 |
Есть выкройка! Посмотрите, когда синус-косинус и касательная положительны …
- Все три положительные в квадранте I
- Только синус положительный в Квадранте II
- Только касательная положительна в Квадранте III
- Только косинус положительный в квадранте IV
Это можно показать еще проще:
На этом графике также отображается «ASTC».
Некоторым людям нравится запоминать четыре буквы ASTC одной из этих:
- Все студенты изучают химию
- Все учащиеся проходят исчисление
- Все глупые коты Тома
- Все станции до центра
- A dd S угар T o C оферта
Может, ты придумаешь что-нибудь свое. Или просто помните ASTC.
Обратный Sin, Cos и Tan
Что такое обратный синус 0.5?
sin -1 (0,5) =?
Другими словами, когда y равно 0,5 на графике ниже, каков угол?
Есть много углов , где y = 0,5
Проблема: калькулятор выдаст вам только одно из этих значений …
… но всегда есть два значения от 0 ° до 360 °
(и бесконечно много больше):
| | Первое значение | Второе значение |
| Синус | θ | 180º — θ |
| Косинус | θ | 360º — θ |
| Касательная | θ | θ + 180º |
Теперь мы можем решить уравнения для под любым углом!
Пример: Решить sin θ = 0.5
Получаем первое решение из калькулятора = sin -1 (0,5) = 30º (находится в квадранте I)
Следующее решение: 180º — 30º = 150º (Квадрант II)
Пример: Решить cos θ = -0,85
Получаем первое решение из калькулятора = cos -1 (-0,85) = 148,2º (Квадрант II)
Другое решение: 360º — 148,2º = 211,8º (Квадрант III)
Нам может потребоваться привести наш угол между 0º и 360º, добавив или вычтя 360º
Пример: Решить tan θ = -1.3
Мы получаем первое решение из калькулятора = tan -1 (−1,3) = −52,4º
Это меньше 0º, поэтому мы прибавляем 360º: −52,4º + 360º = 307,6º (Квадрант IV)
Другое решение: −52,4º + 180º = 127,6º (Квадрант II)
3914, 3915, 3916, 3917, 3918, 3919, 3920, 3921, 3922, 3923
Отрицательные углы в тригонометрии — стенограмма видео и урока
Идентификаторы отрицательного угла
Идентификаторы отрицательного угла — это тригонометрические идентификаторы, которые показывают отношения между тригонометрическими функциями, когда мы берем тригонометрическую функцию отрицательного угла.Эти идентификаторы выглядят следующим образом:
- sin (- x ) = -sin ( x )
- cos (- x ) = cos ( x )
- загар (- x ) = -тан ( x )
- csc (- x ) = -csc ( x )
- сек (- x ) = сек ( x )
- детская кроватка (- x ) = детская кроватка ( x )
Хорошая новость в том, что эти тождества с отрицательным углом довольно легко запомнить.Вы можете видеть, что функция косинуса и функция секанса — единственные в списке, которые не меняют знак. Для всех остальных тригонометрических функций в списке отрицательный угол изменит знак функции. Довольно просто, правда?
Хорошо, теперь, когда мы знаем эти личности, мы можем увидеть, что случилось с вами и вашим коллегой. Обратите внимание на тождество с отрицательным углом, включающее функцию косинуса. У нас есть cos (- x ) = cos ( x ). Это говорит нам, что cos (-30) = cos (30).Ага! Неудивительно, что вы и ваш коллега получили одинаковый результат. Вам нужно будет решить, какой угол использовать при соединении балок, используя другие критерии.
Мы видим, что использование тождеств с отрицательным углом может иметь место в окружающем нас мире. Давайте рассмотрим еще несколько примеров, чтобы лучше познакомиться с этими идентичностями.
Пример 1
На этот раз предположим, что вы занимаетесь скрапбукингом и хотите, чтобы фотография определенным образом умещалась на странице.Вы собираетесь создать угол x с фотографией и плотной бумагой, такой, что sec ( x ) = 2. Вы обнаружите, что когда вы работаете с углом, который имеет размер 60 градусов, у вас есть:
Вы пробуете этот угол, и он выглядит не совсем правильно, поэтому вы хотите знать, есть ли другой угол, который удовлетворяет вашим критериям. Введите тождества с отрицательным углом! Согласно тождествам с отрицательным углом, sec (- x ) = sec ( x ).Следовательно, должно быть так, что sec (-60) = sec (60) = 2. Вы вздыхаете с облегчением и пытаетесь использовать угол с мерой -60 градусов. Выглядит идеально!
Пример 2
Рассмотрим еще один пример. Допустим, вы сидите на уроке тригонометрии, и инструктор объясняет вам значение sin (45).
Исходя из этого, ваш инструктор хочет, чтобы вы нашли значение sin (-45). У меня отличные новости! Мы можем использовать наши тождества с отрицательным углом, чтобы найти это.Тождество отрицательного угла, включающее функцию синуса, дает sin (- x ) = -sin ( x ). Нам дано, что sin (45) = √2 / 2. Следовательно, -sin (45) = -√2 / 2.
Наконец, по тождеству отрицательного угла, мы имеем, что, поскольку -sin (45) = -√ 2/2 и sin (- x ) = -sin ( x ), должно быть так, что sin (-45) = -√2 / 2.
Резюме урока
Тригонометрические тождества дают отношения между различными вариациями тригонометрических функций.Отождествления с отрицательным углом показывают взаимосвязь между тригонометрическими функциями, когда мы берем тригонометрическую функцию отрицательного угла. Эти тождества с отрицательным углом заключаются в следующем.
- sin (- x ) = -sin ( x )
- cos (- x ) = cos ( x )
- загар (- x ) = -тан ( x )
- csc (- x ) = -csc ( x )
- сек (- x ) = сек ( x )
- детская кроватка (- x ) = детская кроватка ( x )
Мы можем использовать эти идентичности во многих различных областях, таких как тригонометрия, строительство, строительство, астрономия и физика.По мере того, как вы продвигаетесь к изучению тригонометрии, вы обнаружите, что эти идентичности неоценимы.
Тригонометрических идентичностей — Задача 2
Я хочу поговорить о тождествах с противоположным углом. Сначала давайте рассмотрим эти определения: функция — это даже если f of -x равно f of x, функция add is f of -x равна -1/2 от x. Что это обозначает?
Это говорит о том, что если вы выбираете противоположные входы, вы получаете одинаковый выход.Вот что значит быть четной функцией, а нечетная функция — это функция, в которой противоположные входы дают противоположные выходы. Итак, мы увидим, что на самом деле все триггерные функции либо четные, либо нечетные, вот что мы собираемся показать.
Итак, давайте посмотрим на единичный круг. Вот единичный круг с углом тета, начерченный на нем, и это точка p (x, y), и вы знаете, что x дает мне косинус теты, а y дает мне синус теты. Итак, я хочу узнать, каков косинус отрицательной теты.И я нарисовал отрицательную тэту.
Отрицательная тета будет отражением положительной теты поперек оси x, поэтому координаты этой точки q, которая является отражением точки p, будут одинаковыми для x и противоположными для y. А это означает, что косинус отрицательной теты в точности совпадает с косинусом теты. Итак, мы только что доказали, что косинус четный.
А что насчет синуса? Значения y противоположны, поэтому синус отрицательной теты равен минус y, а y — синус теты. Синус — это не функция.
А что насчет касательной? Касательная, помните, что тета-тэта идентична тета-синусу по сравнению с тета-косинусом. Касательная к отрицательной тэте будет синусом отрицательной тэты по сравнению с косинусом отрицательной тэты. Теперь синус отрицательной тэты противоположен синусу тэты, а косинус отрицательной тэты — косинус тэта, позвольте мне записать это. Отрицательный синус тета косинус тета и вот он. Это ровно минус касательная тета.
Итак, касательная не является функцией. Как я уже сказал, все триггерные функции либо четные, либо нечетные, косинус четный, синус нечетный, а тангенциальный — нечетные, это будут действительно важные тождества позже.
Идентичности отрицательного угла единичного круга
Отрицательные углы, как и мятежные подростки, противоречат друг другу. «Мне не нужно тебя слушать, папа. Мне не нужно идти против часовой стрелки, если я не хочу. Боже!»
Не то чтобы мы что-то имели против непослушных подростков; у нас есть несколько историй из нашей юности, от которых у тебя волосы дыбом встают дыбом, ya whippersnapper. Однако такая противоположность делает отрицательные углы предсказуемыми.
Уловка для работы с непослушными углами
Косинус играет круто.Положительный, отрицательный: косинусу все равно, он просто будет продолжать делать то, что хочет. А Сине терпеть не может, когда ему говорят, что делать. Если вы попытаетесь дать команду синусоиде, когда в миксе есть отрицательный угол, синус будет делать прямо противоположное тому, что вы сказали.
См.? Исходный угол (A) отображается красным цветом, а отрицательный угол (-A) — синим. Отношения между A и -A являются идентичностями отрицательного угла (броское название, верно?):
cos (-A) = cos A
sin (-A) = — (sin A)
Математики называют косинусом четная функция и синус нечетная функция на основе этих идентификаторов.Мы бы назвали их Джо и Ларри, но это не очень наглядно.
Четные функции таковы, что f (- x ) = f ( x ), что означает, что ввод отрицательного значения вместо этого возвращает положительное значение. Однако нечетные функции возвращают значение, противоположное положительному; f (- x ) = — f ( x ).
Если мы хотим узнать синус или косинус отрицательного угла, мы можем выразить его через положительный угол.Это работает для любого угла любого размера в любом квадранте, в любое время и в любом месте. Если мы скажем «любой» еще раз, у нас может закончиться «любой». И это было бы не весело.
Пример задачи
Что такое синус и косинус?
Почему ты всегда должен быть таким негативным? Давайте перевернем этот хмурый взгляд вверх ногами.
Давайте начнем операцию «Больше не грустное лицо», вычислив синус и косинус положительного числа
Фаза 1 завершена; инверсия хмурого взгляда составляет 20%.расположен в четвертом квадранте, поэтому x супер-улыбается, а y внизу на свалках. Это означает, что:
Мы достигли 70% изменения плохого настроения. Однако не путайте это с настоящим счастьем. Мы нашли синус и косинус для положительных значений, но мы хотели их найти для.
Пришло время развернуть наше секретное оружие, идентификацию отрицательного угла.
Помните, что косинус холодный; он был, пока угол был положительным, поэтому он остается таким, пока он отрицательный.Синус — отдельная история.
Мы сделали это. Мы достигли максимального удовольствия. Так. счастливый.
Самая легкая ошибка, которую можно сделать с отрицательными углами, — это остановиться слишком рано и фактически не применять тождества отрицательных углов. Вы можете сказать, забыли ли вы, по ноющей печали в вашем сердце.