Последовательное и параллельное соединение конденсаторов
Соединение конденсаторов в электрической цепи может быть последовательным, параллельным и последовательно-пареллельным (смешанным).
Если провести аналогию между соединением конденсаторов и соединением резисторов , то стоит отметить, что формулы расчета общей емкости и общего сопротивления идентичны, только между разными типами соединений:
Формула Cобщ при параллельном соединении конденсаторов = формула Rобщ при последовательном соединении резисторов.
Формула Cобщ при последовательном соединении конденсаторов = формула Rобщ при параллельном соединении резисторов.
- Cобщ — общая емкость
- Rобщ — общее сопротивление
Параллельное соединение конденсаторов
Параллельное соединение конденсаторов В результате к одной точке может быть присоединено несколько конденсаторов.
В результате к одной точке может быть присоединено несколько конденсаторов.
При параллельном соединении формируется один большой конденсатор с площадью обкладок, равной сумме площадей обкладок всех отдельных компонентов. Поскольку емкость конденсаторов прямо пропорциональна площади обкладок, общая емкость Собщ при параллельном соединении равняется сумме емкостей всех конденсаторов в цепи.
Параллельное соединение конденсаторов
Напряжение при параллельном соединении
На все параллельно соединенные конденсаторы падает одинаковое напряжение. Так происходит, потому что существует всего лишь две точки, между которыми может быть разность потенциалов (напряжение). Другими словами, можно сказать что при параллельном соединении все конденсаторы подключены к одному источнику напряжения.
Падение напряжения при параллельном соединении
Ток при параллельном соединении
Ток конденсатора во время переходного периода зависит от его емкости и изменения напряжения:
- ic — ток конденсатора
- C — Емкость конденсатора
- ΔVC/Δt – Скорость изменения напряжения
При параллельном соединении через каждый конденсатор потечет одельный ток, в зависимости от емкости конденсатора:
Ток при параллельном соединении
Последовательное соединение конденсаторов
Последовательное соединение конденсаторов – это соединение двух или более конденсаторов
в форме цепи, в которой каждый отдельный конденсатор соединяется с другим
отдельным конденсатором только в одной точке.
Последовательное соединение конденсаторов
Ток при последовательном соединении
Ток (iC), заряжающий последовательную цепь конденсаторов, будет одинаковым для всех конденсаторов, поскольку у него есть только один возможный путь прохождения:
Вследствие того что через все последовательно соединенные конденсаторы течет одинаковый ток, количество накопленого электрического заряда для каждого конденсатора будет одинаковым, независимо от его емкости. Так происходит, потому что электрический заряд, накапливаемый на обкладке любого конденсатора, должен прийти с обкладки примыкающего конденсатора.
Таким образом, последовательно соединенные конденсаторы имеют одинаковый электрический заряд:
Посмотрим на последовательную цепь из трех конденсаторов на рисунке выше. Правая обкладка первого конденсатора
С1 соединяется с левой второго конденсатора С2, у которого правая обкладка соединяется с левой третьего конденсатора С3.
В итогое эффективная площадь обкладок уменьшается до площади обкладок самого маленького конденсатора. Это объясняется тем, что как только обкладки наименшей площади заполнятся электрическим зарядом, данный конденсатор перестанет пропускать ток. В результате ток прекратиться во всей цепи, и процесс зарядки остальных конденсаторов также прекратится.
При последовательном соединении общее расстояние между обкладками увеличивается до суммы расстояний между обкладками всех конденсаторов.
Таким образом, последовательная цепь формирует один большой конденсатор с площадью обкладок элемента с наименьшей емкостью, и расстоянием между обкладками, равному сумме всех расстояний в цепи.
Площадь и расстояние между обкладками при последовательном соединении
Падение напряжения и общая емкость при последовательном соединении
На каждый отдельный конденсатор в последовательной цепи падает разное напряжение.
Применим закон Кирхгофа для напряжения в последовательной цепи из трех конденсаторов:
Падение напряжения при последовательном соединении
Емкость конденсатора прямо пропорциональна его заряду и обратно пропорциональна его напряжению — C = Q/V. Как уже упоминалось выше, последовательно соединенные конденсаторы имеют одинаковый электрический заряд — Qобщ = Q1 = Q2 = Q3.
Следовательно:
Разделив все выражение на Qобщ мы получим
Из данного уравнения можно легко вывести формулу общей емкости для любого частного случая последовательного соединения.
Например, общая емкость для трех конденсаторов:
Общая емкость для двух конденсаторов:
Смешанное соединение конденсаторов
Если в цепи есть и последовательное и параллельное соединение, то такую цепь называют смешанной
или последовательно-параллельной.
Смешанное соединение конденсаторов
Общая емкость смешанного соединения конденсаторов
Чтобы посчитать общую емкость смешанного соединения конденсаторов, следуют такому же алгоритму, как и при расчете общего сопротивления смешанного соединения резисторов.
- Цепь разбивают на участки с только пареллельным или только последовательным соединением
- Вычисляют общую емкость для каждого отдельного участка.
- Вычисляют общую емкость для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 2:
Преобразование смешанного соединения в параллельное
Зачем все это нужно?
Вполне справедливым может оказаться вопрос, для чего надо соединять конденсаторы
последовательно, если общая емкость будет меньше? Скорее всего, первым что приходит
в голову — это чтобы получить новый эквивалентный конденсатор с меньшей емкостью. Но в производстве микросхем вряд ли будут делать подобное, поскольку, во -первых,
обычно нужно экономить место на печатной плате, а во-вторых, нет смысла тратить деньги
на два компонента или больше, если можно купить один с требуемой емкостью.
Но в производстве микросхем вряд ли будут делать подобное, поскольку, во -первых,
обычно нужно экономить место на печатной плате, а во-вторых, нет смысла тратить деньги
на два компонента или больше, если можно купить один с требуемой емкостью.
Но если в параллельном или последовательном соединении конденсаторов еще есть хоть какая-то логика, то кому вообще нужно смешанное?
Дело в том, что емкостью, то есть способностью накапливать электрический заряд, обладает любое тело в природе, даже человеческое. Если мы говорим о электрической цепи, то все ее элементы на практике обладают емкостью, и их можно представить как конденсаторы. Часто такую емкость еще называют паразитической, потому как она создает разного рода помехи.
Например, у нас есть какая-то электронная цепь с множеством различных компонентов,
которая принимает сигнал, обрабатывает его определенным образом и выдает на выход результат.
Ток и напряжения при последовательном соединении резистивного, индуктивного и емкостного элементов
Пусть в ветви (рис. 3.8), состоящей из последовательно соединенных элементов r, L и С, т. е. в последовательном контуре или rLC-цепи, известен ток
Выясним, каковы напряжения на отдельных элементах и на входе.
На основании второго закона Кирхгофа
Постоянная интегрирования в выражении для принята равной нулю, так как в установившемся режиме, как уже указывалось, напряжение на любом участке цепи синусоидальное.
Из полученных выражений для видно, что напряжение на сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает ток по фазе на угол π/2, а напряжение на емкости отстает по фазе от тока на угол π/2.
На рис. 3.9 показаны кривые мгновенных значений тока и напряжений в случае, если амплитуда напряжения на индуктивности больше амплитуды напряжения на емкости . Синусоида совпадает по фазе с синусоидой тока, а синусоиды сдвинуты относительно синусоиды тока на угол π/2 соответственно влево (опережение) и вправо (отставание). Таким образом, напряжения на индуктивности и на емкости сдвинуты относительно друг друга по фазе на угол π (находятся в противофазе).
Ординаты кривой напряжения
согласно (3.13) равны алгебраической сумме ординат кривых .
Определение напряжения н сводится к вычислению амплитуды Um и начальной фазы , которые могут быть найдены непосредственным суммированием трех синусоидальных функций времени с последующими тригонометрическими преобразованиями. Однако, как указывалось, проще всего задача решается комплексным методом.
Запишем комплексный ток и комплексные напряжения на основании выражений для их мгновенных значений:
В выражениях для учтено, что
Сопоставив выражения для мгновенных напряжений (3. 15), (3.16) с комплексными напряжениями (3.19), (3.20), можно установить простое правило перехода от производной и интеграла синусоидальной функции времени к изображающим их комплексным величинам: синусоидальная функция заменяется изображающей ее комплексной величиной, дифференцирование заменяется умножением на jw, а интегрирование — делением на jw.
15), (3.16) с комплексными напряжениями (3.19), (3.20), можно установить простое правило перехода от производной и интеграла синусоидальной функции времени к изображающим их комплексным величинам: синусоидальная функция заменяется изображающей ее комплексной величиной, дифференцирование заменяется умножением на jw, а интегрирование — делением на jw.
Сумме синусоидальных напряжений (3.13) соответствует сумма изображающих их векторов или комплексных действующих напряжений:
Это соотношение представляет собой уравнение по второму закону Кирхгофа, записанное в комплексной или векторной форме; оно представлено на векторной диаграмме (рис. 3.10). Напряжение совпадает по фазе с током i, поэтому вектор направлен одинаково с вектором I. Напряжение опережает по фазе i на π/2, поэтому вектор сдвинут относительно вектора I на угол π/2 «вперед» (против направления движения часовой стрелки). Напряжение отстает по фазе от i на π/2, поэтому вектор сдвинут относительно вектора I на угол π/2 «назад» (по направлению движения часовой стрелки).
Соображения о взаимном расположении векторов напряжения и тока непосредственно следует и из записи выражений комплексных напряжений .
Вектор (3.18) получается умножением I на действительную величину r. Аргумент комплексной величины rI такой же, как и комплексного тока I, поэтому направление вектора совпадает с направлением вектора I. Вектор (3.19) получается умножением I на . Умножение тока I на действительную величину не изменяет аргумента, а умножение на увеличивает аргумент на π/2. Следовательно, вектор повернут относительно вектора I на угол π/2 «вперед». Вектор (3.20) получается делением I на . Деление комплексной величины на не изменяет аргумента, а деление на j, равносильно умножению на уменьшает аргумент на π/2. Следовательно, вектор повернут относительно вектора I на угол π/2 «назад».
Так как умножение и деление вектора на j приводят к повороту вектора на π/2 соответственно «вперед» и «назад», то множитель j часто называют оператором поворота на π/2.
Сложив векторы , получим вектор U. Его длина определяет действующее напряжение , а положение относительно координатных осей — начальную фазу .
Его длина определяет действующее напряжение , а положение относительно координатных осей — начальную фазу .
Решим ту же задачу аналитически. Теперь уравнение (3.22) будем рассматривать как соотношение между комплексными числами. Подставив в него значения комплексных напряжений, получим
Это соотношение между комплексным напряжением и током называют законом Ома в комплексной форме. Записав комплексные величины в показательной форме, получим
Так как то
Таким образом, амплитуда и начальная фаза напряжения на выводах контура определены и можно записать выражение для мгновенного напряжения:
В заключение отметим, что уравнение для комплексных токов и напряжений и векторные диаграммы взаимно связаны. Уравнения можно рассматривать как запись геометрических суммирований векторов, выполняемых на векторной диаграмме, и, наоборот, векторную диаграмму можно рассматривать как графическое представление соотношений между комплексными величинами в уравнении.
Как меняется напряжение при последовательном соединении. Соединение резисторов
Ток в электроцепи проходит по проводникам от источника напряжения к нагрузке, то есть к лампам, приборам. В большинстве случаев в качестве проводника используются медные провода. В цепи может быть предусмотрено несколько элементов с разными сопротивлениями. В схеме приборов проводники могут быть соединены параллельно или последовательно, также могут быть смешанные типы.
Элемент схемы с сопротивлением называется резистором, напряжение данного элемента является разницей потенциалов между концами резистора. Параллельное и последовательное электрическое соединение проводников характеризуется единым принципом функционирования, согласно которому ток протекает от плюса к минусу, соответственно потенциал уменьшается. На электросхемах сопротивление проводки берется за 0, поскольку оно ничтожно низкое.
Параллельное соединение предполагает, что элементы цепы подсоединены к источнику параллельно и включаются одновременно. Последовательное соединение означает, что проводники сопротивления подключаются в строгой последовательности друг за другом.
Последовательное соединение означает, что проводники сопротивления подключаются в строгой последовательности друг за другом.
При просчете используется метод идеализации, что существенно упрощает понимание. Фактически в электрических цепях потенциал постепенно снижается в процессе перемещения по проводке и элементам, которые входят в параллельное или последовательное соединение.
Последовательное соединение проводников
Схема последовательного соединения подразумевает, что они включаются в определенной последовательности один за другим. Причем сила тока во всех из них равна. Данные элементы создают на участке суммарное напряжение. Заряды не накапливаются в узлах электроцепи, поскольку в противном случае наблюдалось бы изменение напряжения и силы тока. При постоянном напряжении ток определяется значением сопротивления цепи, поэтому при последовательной схеме сопротивление меняется в случае изменения одной нагрузки.
Недостатком такой схемы является тот факт, что в случае выхода из строя одного элемента остальные также утрачивают возможность функционировать, поскольку цепь разрывается. Примером может служить гирлянда, которая не работает в случае перегорания одной лампочки. Это является ключевым отличием от параллельного соединения, в котором элементы могут функционировать по отдельности.
Примером может служить гирлянда, которая не работает в случае перегорания одной лампочки. Это является ключевым отличием от параллельного соединения, в котором элементы могут функционировать по отдельности.
Последовательная схема предполагает, что по причине одноуровневого подключения проводников их сопротивление в любой точки сети равно. Общее сопротивление равняется сумме уменьшения напряжений отдельных элементов сети.
При данном типе соединения начало одного проводника подсоединяется к концу другого. Ключевая особенность соединения состоит в том, что все проводники находятся на одном проводе без разветвлений, и через каждый из них протекает один электроток. Однако общее напряжение равно сумме напряжений на каждом. Также можно рассмотреть соединение с другой точки зрения – все проводники заменяются одним эквивалентным резистором, и ток на нем совпадает с общим током, который проходит через все резисторы. Эквивалентное совокупное напряжение является суммой значений напряжения по каждому резистору.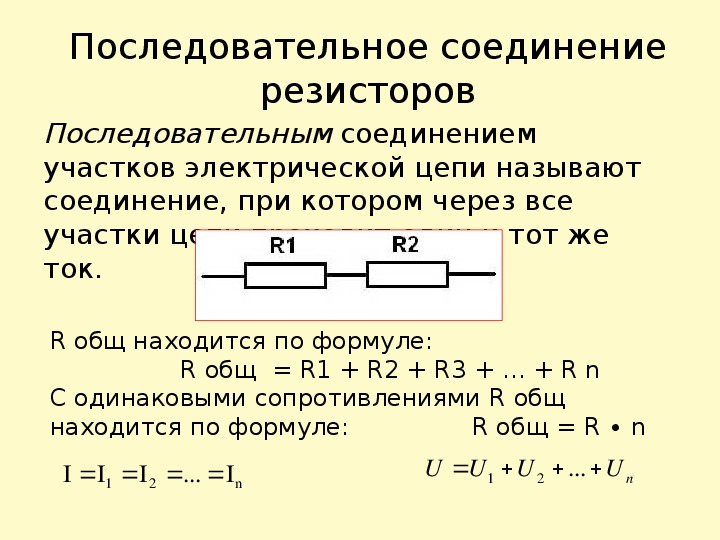 Так проявляется разность потенциалов на резисторе.
Так проявляется разность потенциалов на резисторе.
Использование последовательного подключения целесообразно, когда требуется специально включать и выключать определенное устройство. К примеру, электрозвонок может звенеть только в момент, когда присутствует соединение с источником напряжения и кнопкой. Первое правило гласит, что если тока нет хотя бы на одном из элементов цепи, то и на остальных его не будет. Соответственно при наличии тока в одном проводнике он есть и в остальных. Другим примером может служить фонарик на батарейках, который светит только при наличии батарейки, исправной лампочки и нажатой кнопки.
В некоторых случаях последовательная схема нецелесообразна. В квартире, где система освещения состоит из множества светильников, бра, люстр, не стоит организовывать схему такого типа, поскольку нет необходимости включать и выключать освещение во всех комнатах одновременно. С этой целью лучше использовать параллельное соединение, чтобы иметь возможность включения света в отдельно взятых комнатах.
Параллельное соединение проводников
В параллельной схеме проводники представляют собой набор резисторов, одни концы которых собираются в один узел, а другие – во второй узел. Предполагается, что напряжение в параллельном типе соединения одинаковое на всех участках цепи. Параллельные участки электроцепи носят название ветвей и проходят между двумя соединительными узлами, на них имеется одинаковое напряжение. Такое напряжение равно значению на каждом проводнике. Сумма показателей, обратных сопротивлениям ветвей, является обратной и по отношению к сопротивлению отдельного участка цепи параллельной схемы.
При параллельном и последовательном соединениях отличается система расчета сопротивлений отдельных проводников. В случае параллельной схемы ток уходит по ветвям, что способствует повышению проводимости цепи и уменьшает совокупное сопротивление. При параллельном подключении нескольких резисторов с аналогичными значениями совокупное сопротивление такой электроцепи будет меньше одного резистора число раз, равное числу .
В каждой ветви предусмотрено по одному резистору, и электроток при достижении точки разветвления делится и расходится к каждому резистору, его итоговое значение равно сумме токов на всех сопротивлениях. Все резисторы заменяются одним эквивалентным резистором. Применяя закон Ома, становится понятным значение сопротивления – при параллельной схеме суммируются значения, обратные сопротивлениям на резисторах.
При данной схеме значение тока обратно пропорционально значению сопротивления. Токи в резисторах не взаимосвязаны, поэтому при отключении одного из них это никоим образом не отразится на остальных. По этой причине такая схема используется во множестве устройств.
Рассматривая возможности применения параллельной схемы в быту, целесообразно отметить систему освещения квартиры. Все лампы и люстры должны быть соединены параллельно, в таком случае включение и отключение одного из них никак не влияет на работу остальных ламп. Таким образом, добавляя выключатель каждой лампочки в ветвь цепи, можно включать и отключать соответствующий светильник по необходимости. Все остальные лампы работают независимо.
Все остальные лампы работают независимо.
Все электроприборы объединяются параллельно в электросеть с напряжением 220 В, затем они подключаются к . То есть все приборы подключаются независимо от подключения прочих устройств.
Законы последовательного и параллельного соединения проводников
Для детального понимания на практике обоих типов соединений, приведем формулы, объясняющие законы данных типов соединений. Расчет мощности при параллельном и последовательном типе соединения отличается.
При последовательной схеме имеется одинаковая сила тока во всех проводниках:
Согласно закону Ома, данные типы соединений проводников в разных случаях объясняются иначе. Так, в случае последовательной схемы, напряжения равны друг другу:
U1 = IR1, U2 = IR2.
Помимо этого, общее напряжение равно сумме напряжений отдельно взятых проводников:
U = U1 + U2 = I(R1 + R2) = IR.
Полное сопротивление электроцепи рассчитывается как сумма активных сопротивлений всех проводников, вне зависимости от их числа.
В случае параллельной схемы совокупное напряжение цепи аналогично напряжению отдельных элементов:
А совокупная сила электротока рассчитывается как сумма токов, которые имеются по всем проводникам, расположенным параллельно:
Чтобы обеспечить максимальную эффективность электрических сетей, необходимо понимать суть обоих типов соединений и применять их целесообразно, используя законы и рассчитывая рациональность практической реализации.
Смешанное соединение проводников
Последовательная и параллельная схема соединения сопротивления могут сочетаться в одной электросхеме при необходимости. К примеру, допускается подключение параллельных резисторов по последовательной или их группе, такое тип считается комбинированным или смешанным.
В таком случае совокупное сопротивление рассчитывается посредством получения сумм значений для параллельного соединения в системе и для последовательного. Сначала необходимо рассчитывать эквивалентные сопротивления резисторов в последовательной схеме, а затем элементов параллельного. Последовательное соединение считается приоритетным, причем схемы такого комбинированного типа часто используются в бытовой технике и приборах.
Последовательное соединение считается приоритетным, причем схемы такого комбинированного типа часто используются в бытовой технике и приборах.
Итак, рассматривая типы подключений проводников в электроцепях и основываясь на законах их функционирования, можно полностью понять суть организации схем большинства бытовых электроприборов. При параллельном и последовательном соединениях расчет показателей сопротивления и силы тока отличается. Зная принципы расчета и формулы, можно грамотно использовать каждый тип организации цепей для подключения элементов оптимальным способом и с максимальной эффективностью.
Практически каждому, кто занимался электрикой, приходилось решать вопрос параллельного и последовательного соединения элементов схемы. Некоторые решают проблемы параллельного и последовательного соединения проводников методом «тыка», для многих «несгораемая» гирлянда является необъяснимой, но привычной аксиомой. Тем не менее, все эти и многие другие подобные вопросы легко решаются методом, предложенным еще в самом начале XIX века немецким физиком Георгом Омом. Законы, открытые им, действуют и поныне, а понять их сможет практически каждый.
Законы, открытые им, действуют и поныне, а понять их сможет практически каждый.
Основные электрические величины цепи
Для того чтобы выяснить, как то или иное соединение проводников повлияет на характеристики схемы, необходимо определиться с величинами, которые характеризуют любую электрическую цепь. Вот основные из них:
Взаимная зависимость электрических величин
Теперь необходимо определиться , как все вышеперечисленные величины зависят одна от другой. Правила зависимости несложны и сводятся к двум основным формулам:
Здесь I – ток в цепи в амперах, U – напряжение, подводимое к цепи в вольтах, R – сопротивление цепи в омах, P – электрическая мощность цепи в ваттах.
Предположим, перед нами простейшая электрическая цепь, состоящая из источника питания с напряжением U и проводника с сопротивлением R (нагрузки).
Поскольку цепь замкнута, через нее течет ток I. Какой величины он будет? Исходя из вышеприведенной формулы 1, для его вычисления нам нужно знать напряжение, развиваемое источником питания, и сопротивление нагрузки. Если мы возьмем, к примеру, паяльник с сопротивлением спирали 100 Ом и подключим его к осветительной розетке с напряжением 220 В, то ток через паяльник будет составлять:
Если мы возьмем, к примеру, паяльник с сопротивлением спирали 100 Ом и подключим его к осветительной розетке с напряжением 220 В, то ток через паяльник будет составлять:
220 / 100 = 2,2 А.
Какова мощность этого паяльника ? Воспользуемся формулой 2:
2,2 * 220 = 484 Вт.
Хороший получился паяльник, мощный, скорее всего, двуручный. Точно так же, оперируя этими двумя формулами и преобразуя их, можно узнать ток через мощность и напряжение, напряжение через ток и сопротивление и т.д. Сколько, к примеру, потребляет лампочка мощностью 60 Вт в вашей настольной лампе:
60 / 220 = 0,27 А или 270 мА.
Сопротивление спирали лампы в рабочем режиме:
220 / 0,27 = 815 Ом.
Схемы с несколькими проводниками
Все рассмотренные выше случаи являются простыми – один источник, одна нагрузка. Но на практике нагрузок может быть несколько, и соединены они бывают тоже по-разному. Существует три типа соединения нагрузки:
- Параллельное.

- Последовательное.
- Смешанное.
Параллельное соединение проводников
В люстре 3 лампы, каждая по 60 Вт. Сколько потребляет люстра? Верно, 180 Вт. Быстренько подсчитываем сначала ток через люстру:
180 / 220 = 0,818 А.
А затем и ее сопротивление:
220 / 0,818 = 269 Ом.
Перед этим мы вычисляли сопротивление одной лампы (815 Ом) и ток через нее (270 мА). Сопротивление же люстры оказалось втрое ниже, а ток — втрое выше. А теперь пора взглянуть на схему трехрожкового светильника.
Все лампы в нем соединены параллельно и подключены к сети. Получается, при параллельном соединении трех ламп общее сопротивление нагрузки уменьшилось втрое? В нашем случае — да, но он частный – все лампы имеют одинаковые сопротивление и мощность. Если каждая из нагрузок будет иметь свое сопротивление, то для подсчета общего значения простого деления на количество нагрузок мало. Но и тут есть выход из положения – достаточно воспользоваться вот этой формулой:
1/Rобщ. = 1/R1 + 1/R2 + … 1/Rn.
= 1/R1 + 1/R2 + … 1/Rn.
Для удобства использования формулу можно легко преобразовать:
Rобщ. = (R1*R2*… Rn) / (R1+R2+ … Rn).
Здесь Rобщ . – общее сопротивление цепи при параллельном включении нагрузки. R1 … Rn – сопротивления каждой нагрузки.
Почему увеличился ток, когда вы включили параллельно три лампы вместо одной, понять несложно – ведь он зависит от напряжения (оно осталось неизменным), деленного на сопротивление (оно уменьшилось). Очевидно, что и мощность при параллельном соединении увеличится пропорционально увеличению тока.
Последовательное соединение
Теперь настала пора выяснить, как изменятся параметры цепи, если проводники (в нашем случае лампы) соединить последовательно.
Расчет сопротивления при последовательном соединении проводников исключительно прост:
Rобщ. = R1 + R2.
Те же три шестидесятиваттные лампы, соединенные последовательно, составят уже 2445 Ом (см. расчеты выше). Какими будут последствия увеличения сопротивления цепи? Согласно формулам 1 и 2 становится вполне понятно, что мощность и сила тока при последовательном соединении проводников упадет. Но почему теперь все лампы горят тускло? Это одно из самых интересных свойств последовательного подключения проводников, которое очень широко используется. Взглянем на гирлянду из трех знакомых нам, но последовательно соединенных ламп.
Но почему теперь все лампы горят тускло? Это одно из самых интересных свойств последовательного подключения проводников, которое очень широко используется. Взглянем на гирлянду из трех знакомых нам, но последовательно соединенных ламп.
Общее напряжение, приложенное ко всей цепи, так и осталось 220 В. Но оно поделилось между каждой из ламп пропорционально их сопротивлению! Поскольку лампы у нас одинаковой мощности и сопротивления, то напряжение поделилось поровну: U1 = U2 = U3 = U/3. То есть на каждую из ламп подается теперь втрое меньшее напряжение, вот почему они светятся так тускло. Возьмете больше ламп – яркость их упадет еще больше. Как рассчитать падение напряжения на каждой из ламп, если все они имеют различные сопротивления? Для этого достаточно четырех формул, приведенных выше. Алгоритм расчета будет следующим:
- Измеряете сопротивление каждой из ламп.
- Рассчитываете общее сопротивление цепи.
- По общим напряжению и сопротивлению рассчитываете ток в цепи.

- По общему току и сопротивлению ламп вычисляете падение напряжения на каждой из них.
Хотите закрепить полученные знания ? Решите простую задачу, не заглядывая в ответ в конце:
В вашем распоряжении есть 15 однотипных миниатюрных лампочек, рассчитанных на напряжение 13,5 В. Можно ли из них сделать елочную гирлянду, подключаемую к обычной розетке, и если можно, то как?
Смешанное соединение
С параллельным и последовательным соединением проводников вы, конечно, без труда разобрались. Но как быть, если перед вами оказалась примерно такая схема?
Смешанное соединение проводников
Как определить общее сопротивление цепи? Для этого вам понадобится разбить схему на несколько участков. Вышеприведенная конструкция достаточно проста и участков будет два — R1 и R2,R3. Сначала вы рассчитываете общее сопротивление параллельно соединенных элементов R2,R3 и находите Rобщ.23. Затем вычисляете общее сопротивление всей цепи, состоящей из R1 и Rобщ. 23, соединенных последовательно:
23, соединенных последовательно:
- Rобщ.23 = (R2*R3) / (R2+R3).
- Rцепи = R1 + Rобщ.23.
Задача решена, все очень просто. А теперь вопрос несколько сложнее.
Сложное смешанное соединение сопротивлений
Как быть тут? Точно так же, просто нужно проявить некоторую фантазию. Резисторы R2, R4, R5 соединены последовательно. Рассчитываем их общее сопротивление:
Rобщ.245 = R2+R4+R5.
Теперь параллельно к Rобщ.245 подключаем R3:
Rобщ.2345 = (R3* Rобщ.245) / (R3+ Rобщ.245).
Rцепи = R1+ Rобщ.2345+R6.
Вот и все!
Ответ на задачу о елочной гирлянде
Лампы имеют рабочее напряжение всего 13.5 В, а в розетке 220 В, поэтому их нужно включать последовательно.
Поскольку лампы однотипные, напряжение сети разделится между ними поровну и на каждой лампочке окажется 220 / 15 = 14,6 В. Лампы рассчитаны на напряжение 13,5 В, поэтому такая гирлянда хоть и заработает, но очень быстро перегорит. Чтобы реализовать задумку, вам понадобится минимум 220 / 13,5 = 17, а лучше 18-19 лампочек.
Как подключить в кукольном домике несколько светильников
Когда вы задумываетесь о том как сделать освещение в кукольном домике или румбоксе, где не один, а несколько светильников, то встает вопрос о том, как их подключить, объединить в сеть. Существует два типа подключения: последовательное и параллельное, о которых мы слышали со школьной скамьи. Их и рассмотрим в этой статье.
Я постараюсь описать всё простым доступным языком, чтобы всё было понятно даже самым-самым гуманитариям, не знакомым с электрическими премудростями.
Примечание : в этой статье рассмотрим только цепь с лампочками накаливания. Освещение диодами более сложное и будет рассмотрено в другой статье.
Для понимания каждая схема будет сопровождена рисунком и рядом с чертежом электрической монтажной схемой.
Сначала рассмотрим условные обозначения на электрических схемах.
| Название элемента | Символ на схеме | Изображение |
| батарейка/ элемент питания | ||
| выключатель | ||
| провод | ||
| пересечение проводов (без соединения) | ||
| соединение проводов (пайкой, скруткой) | ||
| лампа накаливания | ||
| неисправная лампа | ||
| неработающая лампа | ||
| горящая лампа |
Как уже было сказано, существуют два основных типа подключения: последовательное и параллельное. Есть ещё третье, смешанное: последовательно-параллельное, объединяющее то и другое. Начнем с последовательного, как более простого.
Есть ещё третье, смешанное: последовательно-параллельное, объединяющее то и другое. Начнем с последовательного, как более простого.
Последовательное подключение
Выглядит оно вот так.
Лампочки располагаются одна за другой, как в хороводе держась за руки. По этому принципу были сделаны старые советские гирлянды.
Достоинства — простота соединения.
Недостатки — если перегорела хоть одна лампочка, то не будет работать вся цепь.
Надо будет перебирать, проверять каждую лампочку, чтобы найти неисправную. Это может быть утомительным при большом количестве лампочек. Так же лампочки должны быть одного типа: напряжение, мощность.
При этом типе подключения напряжения лампочек складываются. Напряжение обозначается буквой U , измеряется в вольтах V . Напряжение источника питания должно быть равно сумме напряжений всех лампочек в цепи.
Пример №1 : вы хотите подключить в последовательную цепь 3 лампочки напряжением 1,5V. Напряжение источника питания, необходимое для работы такой цепи 1,5+1,5+1,5=4,5V.
Напряжение источника питания, необходимое для работы такой цепи 1,5+1,5+1,5=4,5V.
У обычных пальчиковых батареек напряжение 1,5V. Чтобы из них получить напряжение 4,5V их тоже нужно соединить в последовательную цепь, их напряжения сложатся.
Подробнее о том, как выбрать источник питания написано в этой статье
Пример №2: вы хотите подключить к источнику питания 12V лампочки по 6V. 6+6=12v. Можно подключить 2 таких лампочки.
Пример №3: вы хотите соединить в цепь 2 лампочки по 3V. 3+3=6V. Необходим источник питания на 6 V.
Подведем итог: последовательное подключение просто в изготовлении, нужны лампочки одного типа. Недостатки: при выходе из строя одной лампочки не горят все. Включить и выключить цепь можно только целиком.
Исходя из этого, для освещения кукольного домика целесообразно соединять последовательно не более 2-3 лампочек. Например, в бра. Чтобы соединить большее количество лампочек, необходимо использовать другой тип подключения — параллельное.
Читайте так же статьи по теме:
- Обзор миниатюрных ламп накаливания
- Диоды или лампы накаливания
Параллельное подключение лампочек
Вот так выглядит параллельное подключение лампочек.
В этом типе подключения у всех лампочек и источника питания одинаковые напряжения. То есть при источнике питания 12v каждая из лампочек должна иметь тоже напряжение 12V. А количество лампочек может быть различным. А если у вас, допустим, есть лампочки 6V, то и источник питания нужно брать 6V.
При выходе из строя одной лампочки другие продолжают гореть.
Лампочки можно включать независимо друг от друга. Для этого к каждой нужно поставить свой выключатель.
По этому принципу подключены электроприборы в наших городских квартирах. У всех приборов одно напряжение 220V, включать и выключать их можно независимо друг от друга, мощность электроприборов может быть разной.
Вывод : при множестве светильников в кукольном домике оптимально параллельное подключение, хотя оно чуть сложнее, чем последовательное.
Рассмотрим ещё один вид подключения, соединяющий в себе последовательное и параллельное.
Комбинированное подключение
Пример комбинированного подключения.
Три последовательные цепи, соединенные параллельно
А вот другой вариант:
Три параллельные цепи, соединенные последовательно.
Участки такой цепи, соединенные последовательно, ведут себя как последовательное соединение. А параллельные участки — как параллельное соединение.
Пример
При такой схеме перегорание одной лампочки выведет из строя весь участок, соединенный последовательно, а две другие последовательные цеписохранят работоспособность.
Соответственно, и включать-выключать участки можно независимо друг от друга. Для этого каждой последовательной цепи нужно поставить свой выключатель.
Но нельзя включить одну-единственную лампочку.
При параллельно-последовательном подключении при выходе из строя одной лампочки цепь будет вести себя так:
А при нарушении на последовательном участке вот так:
Пример:
Есть 6 лампочек по 3V, соединенные в 3 последовательные цепи по 2 лампочки. Цепи в свою очередь соединены параллельно. Разбиваем на 3 последовательных участка и просчитываем этот участок.
Цепи в свою очередь соединены параллельно. Разбиваем на 3 последовательных участка и просчитываем этот участок.
На последовательном участке напряжения лампочек складываются, 3v+3V=6V. У каждой последовательной цепи напряжение 6V. Поскольку цепи соединены параллельно, то их напряжение не складывается, а значит нам нужен источник питания на 6V.
Пример
У нас 6 лампочек по 6V. Лампочки соединены по 3 штуки в параллельную цепь, а цепи в свою очередь — последовательно. Разбиваем систему на три параллельных цепи.
В одной параллельной цепи напряжение у каждой лампочки 6V, поскольку напряжение не складывается, то и у всей цепи напряжение 6V. А сами цепи соединены уже последовательно и их напряжения уже складываются. Получается 6V+6V=12V. Значит, нужен источник питания 12V.
Пример
Для кукольных домиков можно использовать такое смешанное подключение.
Допустим, в каждой комнате по одному светильнику, все светильники подключены параллельно. Но в самих светильниках разное количество лампочек: в двух — по одной лампочке, есть двухрожковое бра из двух лампочек и трехрожковая люстра. В люстре и бра лампочки соединены последовательно.
У каждого светильника свой выключатель. Источник питания 12V напряжения. Одиночные лампочки, соединенные параллельно, должны иметь напряжение 12V. А у тех, что соединены последовательно напряжение складывается на участке цепи
. Соответственно, для участка бра из двух лампочек 12V (общее напряжение)делим на 2 (количество лампочек), получим 6V (напряжение одной лампочки).
Для участка люстры 12V:3=4V (напряжение одной лампочки люстры).
Больше трех лампочек в одном светильнике соединять последовательно не стоит.
Теперь вы изучили все хитрости подключения лампочек накаливания разными способами. И, думаю, что не составит труда сделать освещение в кукольном домике со многими лампочками, любой сложности. Если же что-то для вас ещё представляет сложности, прочитайте статью о простейшем способе сделать свет в кукольном домике, самые базовые принципы. Удачи!
Причем это могут быть не только проводники, но и конденсаторы. Здесь важно не запутаться в том, как выглядит каждое из них на схеме. А уже потом применять конкретные формулы. Их, кстати, нужно помнить наизусть.
Как различить эти два соединения?
Внимательно посмотрите на схему. Если провода представить как дорогу, то машины на ней будут играть роль резисторов. На прямой дороге без каких-либо разветвлений машины едут одна за другой, в цепочку. Так же выглядит и последовательное соединение проводников. Дорога в этом случае может иметь неограниченное количество поворотов, но ни одного перекрестка. Как бы ни виляла дорога (провода), машины (резисторы) всегда будут расположены друг за другом, по одной цепочке.
Совсем другое дело, если рассматривается параллельное соединение. Тогда резисторы можно сравнить со спортсменами на старте. Они стоят каждый на своей дорожке, но направление движения у них одинаковое, и финиш в одном месте. Так же и резисторы — у каждого из них свой провод, но все они соединены в некоторой точке.
Формулы для силы тока
О ней всегда идет речь в теме «Электричество». Параллельное и последовательное соединение по-разному влияют на величину в резисторах. Для них выведены формулы, которые можно запомнить. Но достаточно просто запомнить смысл, который в них вкладывается.
Так, ток при последовательном соединении проводников всегда одинаков. То есть в каждом из них значение силы тока не отличается. Провести аналогию можно, если сравнить провод с трубой. В ней вода течет всегда одинаково. И все препятствия на ее пути будут сметаться с одной и той же силой. Так же с силой тока. Поэтому формула общей силы тока в цепи с последовательным соединением резисторов выглядит так:
I общ = I 1 = I 2
Здесь буквой I обозначена сила тока. Это общепринятое обозначение, поэтому его нужно запомнить.
Ток при параллельном соединении уже не будет постоянной величиной. При той же аналогии с трубой получается, что вода разделится на два потока, если у основной трубы будет ответвление. То же явление наблюдается с током, когда на его пути появляется разветвление проводов. Формула общей силы тока при :
I общ = I 1 + I 2
Если разветвление составлено из проводов, которых больше двух, то в приведенной формуле на такое же количество станет больше слагаемых.
Формулы для напряжения
Когда рассматривается схема, в которой выполнено соединение проводников последовательно, то напряжение на всем участке определяется суммой этих величин на каждом конкретном резисторе. Сравнить эту ситуацию можно с тарелками. Удержать одну из них легко получится одному человеку, вторую рядом он тоже сможет взять, но уже с трудом. Держать в руках три тарелки рядом друг с другом одному человеку уже не удастся, потребуется помощь второго. И так далее. Усилия людей складываются.
Формула для общего напряжения участка цепи с последовательным соединением проводников выглядит так:
U общ = U 1 + U 2 , где U — обозначение, принятое для
Другая ситуация складывается, если рассматривается Когда тарелки ставятся друг на друга, их по-прежнему может удержать один человек. Поэтому складывать ничего не приходится. Такая же аналогия наблюдается при параллельном соединении проводников. Напряжение на каждом из них одинаковое и равно тому, которое на всех них сразу. Формула общего напряжения такая:
U общ = U 1 = U 2
Формулы для электрического сопротивления
Их уже можно не запоминать, а знать формулу закона Ома и из нее выводить нужную. Из указанного закона следует, что напряжение равно произведению силы тока и сопротивления. То есть U = I * R, где R — сопротивление.
Тогда формула, с которой нужно будет работать, зависит от того, как выполнено соединение проводников:
- последовательно, значит, нужно равенство для напряжения — I общ * R общ = I 1 * R 1 + I 2 * R 2;
- параллельно необходимо пользоваться формулой для силы тока — U общ / R общ = U 1 / R 1 + U 2 / R 2 .
Далее следуют простые преобразования, которые основываются на том, что в первом равенстве все силы тока имеют одинаковое значение, а во втором — напряжения равны. Значит, их можно сократить. То есть получаются такие выражения:
- R общ = R 1 + R 2 (для последовательного соединения проводников).
- 1 / R общ = 1 / R 1 + 1 / R 2 (при параллельном соединении).
При увеличении числа резисторов, которые включены в сеть, изменяется количество слагаемых в этих выражениях.
Стоит отметить, что параллельное и последовательное соединение проводников по-разному влияют на общее сопротивление. Первое из них уменьшает сопротивление участка цепи. Причем оно оказывается меньше самого маленького из использованных резисторов. При последовательном соединении все логично: значения складываются, поэтому общее число всегда будет самым большим.
Работа тока
Предыдущие три величины составляют законы параллельного соединения и последовательного расположения проводников в цепи. Поэтому их знать нужно обязательно. Про работу и мощность необходимо просто запомнить базовую формулу. Она записывается так: А = I * U * t , где А — работа тока, t — время его прохождения по проводнику.
Для того чтобы определить общую работу при последовательном соединении нужно заменить в исходном выражении напряжение. Получится равенство: А = I * (U 1 + U 2) * t, раскрыв скобки в котором получится, что работа на всем участке равна их сумме на каждом конкретном потребителе тока.
Аналогично идет рассуждение, если рассматривается схема параллельного соединения. Только заменять полагается силу тока. Но результат будет тот же: А = А 1 + А 2 .
Мощность тока
При выведении формулы для мощности (обозначение «Р») участка цепи опять нужно пользоваться одной формулой: Р = U * I. После подобных рассуждений получается, что параллельное и последовательное соединение описываются такой формулой для мощности: Р = Р 1 + Р 2 .
То есть, как бы ни были составлены схемы, общая мощность будет складываться из тех, которые задействованы в работе. Именно этим объясняется тот факт, что нельзя включать в сеть квартиры одновременно много мощных приборов. Она просто не выдержит такой нагрузки.
Как влияет соединение проводников на ремонт новогодней гирлянды?
Сразу же после того, как перегорит одна из лампочек, станет ясно, как они были соединены. При последовательном соединении не будет светиться ни одна из них. Это объясняется тем, что пришедшая в негодность лампа создает разрыв в цепи. Поэтому нужно проверить все, чтобы определить, какая перегорела, заменить ее — и гирлянда станет работать.
Если в ней используется параллельное соединение, то она не перестает работать при неисправности одной из лампочек. Ведь цепь не будет полностью разорвана, а только одна параллельная часть. Чтобы отремонтировать такую гирлянду, не нужно проверять все элементы цепи, а только те, которые не светятся.
Что происходит с цепью, если в нее включены не резисторы, а конденсаторы?
При их последовательном соединении наблюдается такая ситуация: заряды от плюсов источника питания поступают только на внешние обкладки крайних конденсаторов. Те, что находятся между ними, просто передают этот заряд по цепочке. Этим объясняется то, что на всех обкладках появляются одинаковые заряды, но имеющие разные знаки. Поэтому электрический заряд каждого конденсатора, соединенного последовательно, можно записать такой формулой:
q общ = q 1 = q 2 .
Для того чтобы определить напряжение на каждом конденсаторе, потребуется знание формулы: U = q / С. В ней С — емкость конденсатора.
Общее напряжение подчиняется тому же закону, который справедлив для резисторов. Поэтому, заменив в формуле емкости напряжение на сумму, мы получим, что общую емкость приборов нужно вычислять по формуле:
С = q / (U 1 + U 2).
Упростить эту формулу можно, перевернув дроби и заменив отношение напряжения к заряду емкостью. Получается такое равенство: 1 / С = 1 / С 1 + 1 / С 2 .
Несколько по-другому выглядит ситуация, когда соединение конденсаторов — параллельное. Тогда общий заряд определяется суммой всех зарядов, которые накапливаются на обкладках всех приборов. А значение напряжения по-прежнему определяется по общим законам. Поэтому формула для общей емкости параллельно соединенных конденсаторов выглядит так:
С = (q 1 + q 2) / U.
То есть эта величина считается, как сумма каждого из использованных в соединении приборов:
С = С 1 + С 2.
Как определить общее сопротивление произвольного соединения проводников?
То есть такого, в котором последовательные участки сменяют параллельные, и наоборот. Для них по-прежнему справедливы все описанные законы. Только применять их нужно поэтапно.
Сперва полагается мысленно развернуть схему. Если представить ее сложно, то нужно нарисовать то, что получается. Объяснение станет понятнее, если рассмотреть его на конкретном примере (см. рисунок).
Ее удобно начать рисовать с точек Б и В. Их необходимо поставить на некотором удалении друг от друга и от краев листа. Слева к точке Б подходит один провод, а вправо направлены уже два. Точка В, напротив, слева имеет два ответвления, а после нее расположен один провод.
Теперь необходимо заполнить пространство между этими точками. По верхнему проводу нужно расположить три резистора с коэффициентами 2, 3 и 4, а снизу пойдет тот, у которого индекс равен 5. Первые три соединены последовательно. С пятым резистором они параллельны.
Оставшиеся два резистора (первый и шестой) включены последовательно с рассмотренным участком БВ. Поэтому рисунок можно просто дополнить двумя прямоугольниками по обе стороны от выбранных точек. Осталось применить формулы для расчета сопротивления:
- сначала ту, которая приведена для последовательного соединения;
- потом для параллельного;
- и снова для последовательного.
Подобным образом можно развернуть любую, даже очень сложную схему.
Задача на последовательное соединение проводников
Условие. В цепи друг за другом подсоединены две лампы и резистор. Общее напряжение равно 110 В, а сила тока 12 А. Чему равно сопротивление резистора, если каждая лампа рассчитана на напряжение в 40 В?
Решение. Поскольку рассматривается последовательное соединение, формулы его законов известны. Нужно только правильно их применить. Начать с того, чтобы выяснить значение напряжения, которое приходится на резистор. Для этого из общего нужно вычесть два раза напряжение одной лампы. Получается 30 В.
Теперь, когда известны две величины, U и I (вторая из них дана в условии, так как общий ток равен току в каждом последовательном потребителе), можно сосчитать сопротивление резистора по закону Ома. Оно оказывается равным 2,5 Ом.
Ответ. Сопротивление резистора равно 2,5 Ом.
Задача на параллельное и последовательное
Условие. Имеются три конденсатора с емкостями 20, 25 и 30 мкФ. Определите их общую емкость при последовательном и параллельном соединении.
Решение. Проще начать с В этой ситуации все три значения нужно просто сложить. Таким образом, общая емкость оказывается равной 75 мкФ.
Несколько сложнее расчеты будут при последовательном соединении этих конденсаторов. Ведь сначала нужно найти отношения единицы к каждой из этих емкостей, а потом сложить их друг с другом. Получается, что единица, деленная на общую емкость, равна 37/300. Тогда искомая величина получается приблизительно 8 мкФ.
Ответ. Общая емкость при последовательном соединении 8 мкФ, при параллельном — 75 мкФ.
При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.
Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.
Последовательное соединение
Последовательное соединение – это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.
При последовательном соединении сопротивления элементов суммируются.
Параллельное соединение
Параллельное соединение – это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.
При параллельном соединении эквивалентное сопротивление находится как:
В случае двух параллельно соединенных резисторов
В случае трех параллельно подключенных резисторов:
Смешанное соединение
Смешанное соединение – соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.
Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R 3 . Следует понимать, что после преобразования эквивалентное сопротивление R 1 R 2 и резистор R 3 , соединены последовательно.
Итак, остается самое интересное и самое сложное соединение проводников.
Мостовая схема
Мостовая схема соединения представлена на рисунке ниже.
Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.
И находят сопротивления R 1 , R 2 и R 3 .
Ток в последовательной цепи. Задача на параллельное и последовательное. Основные электрические величины цепи
Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.
Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.
Графическое обозначение схемы параллельного соеднинения
На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).
В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.
Формула для расчета параллельного соединения сопротивлений
При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:
В частном случае при подключении параллельно двух сопротивлений:
Эквивалентное сопротивление цепи определяется по формуле:
В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:
Формулы для частного рассчета вытекают из основной формулы.
Формула для расчета параллельного соединения емкостей (конденсаторов)
При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:
Формула для расчета параллельного соединения индуктивностей
При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:
Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.
Пример свертывания параллельного сопротивления
Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.
Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.
Ток при параллельном соединении
При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.
Напряжение при параллельном соединении
При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.
Применение параллельного соединения
1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.
2. Делитель токов.
Подробности Категория: Статьи Создано: 06.09.2017 19:48Как подключить в кукольном домике несколько светильников
Когда вы задумываетесь о том как сделать освещение в кукольном домике или румбоксе, где не один, а несколько светильников, то встает вопрос о том, как их подключить, объединить в сеть. Существует два типа подключения: последовательное и параллельное, о которых мы слышали со школьной скамьи. Их и рассмотрим в этой статье.
Я постараюсь описать всё простым доступным языком, чтобы всё было понятно даже самым-самым гуманитариям, не знакомым с электрическими премудростями.
Примечание : в этой статье рассмотрим только цепь с лампочками накаливания. Освещение диодами более сложное и будет рассмотрено в другой статье.
Для понимания каждая схема будет сопровождена рисунком и рядом с чертежом электрической монтажной схемой.
Сначала рассмотрим условные обозначения на электрических схемах.
| Название элемента | Символ на схеме | Изображение |
| батарейка/ элемент питания | ||
| выключатель | ||
| провод | ||
| пересечение проводов (без соединения) | ||
| соединение проводов (пайкой, скруткой) | ||
| лампа накаливания | ||
| неисправная лампа | ||
| неработающая лампа | ||
| горящая лампа |
Как уже было сказано, существуют два основных типа подключения: последовательное и параллельное. Есть ещё третье, смешанное: последовательно-параллельное, объединяющее то и другое. Начнем с последовательного, как более простого.
Последовательное подключение
Выглядит оно вот так.
Лампочки располагаются одна за другой, как в хороводе держась за руки. По этому принципу были сделаны старые советские гирлянды.
Достоинства — простота соединения.
Недостатки — если перегорела хоть одна лампочка, то не будет работать вся цепь.
Надо будет перебирать, проверять каждую лампочку, чтобы найти неисправную. Это может быть утомительным при большом количестве лампочек. Так же лампочки должны быть одного типа: напряжение, мощность.
При этом типе подключения напряжения лампочек складываются. Напряжение обозначается буквой U , измеряется в вольтах V . Напряжение источника питания должно быть равно сумме напряжений всех лампочек в цепи.
Пример №1 : вы хотите подключить в последовательную цепь 3 лампочки напряжением 1,5V. Напряжение источника питания, необходимое для работы такой цепи 1,5+1,5+1,5=4,5V.
У обычных пальчиковых батареек напряжение 1,5V. Чтобы из них получить напряжение 4,5V их тоже нужно соединить в последовательную цепь, их напряжения сложатся.
Подробнее о том, как выбрать источник питания написано в этой статье
Пример №2: вы хотите подключить к источнику питания 12V лампочки по 6V. 6+6=12v. Можно подключить 2 таких лампочки.
Пример №3: вы хотите соединить в цепь 2 лампочки по 3V. 3+3=6V. Необходим источник питания на 6 V.
Подведем итог: последовательное подключение просто в изготовлении, нужны лампочки одного типа. Недостатки: при выходе из строя одной лампочки не горят все. Включить и выключить цепь можно только целиком.
Исходя из этого, для освещения кукольного домика целесообразно соединять последовательно не более 2-3 лампочек. Например, в бра. Чтобы соединить большее количество лампочек, необходимо использовать другой тип подключения — параллельное.
Читайте так же статьи по теме:
- Обзор миниатюрных ламп накаливания
- Диоды или лампы накаливания
Параллельное подключение лампочек
Вот так выглядит параллельное подключение лампочек.
В этом типе подключения у всех лампочек и источника питания одинаковые напряжения. То есть при источнике питания 12v каждая из лампочек должна иметь тоже напряжение 12V. А количество лампочек может быть различным. А если у вас, допустим, есть лампочки 6V, то и источник питания нужно брать 6V.
При выходе из строя одной лампочки другие продолжают гореть.
Лампочки можно включать независимо друг от друга. Для этого к каждой нужно поставить свой выключатель.
По этому принципу подключены электроприборы в наших городских квартирах. У всех приборов одно напряжение 220V, включать и выключать их можно независимо друг от друга, мощность электроприборов может быть разной.
Вывод : при множестве светильников в кукольном домике оптимально параллельное подключение, хотя оно чуть сложнее, чем последовательное.
Рассмотрим ещё один вид подключения, соединяющий в себе последовательное и параллельное.
Комбинированное подключение
Пример комбинированного подключения.
Три последовательные цепи, соединенные параллельно
А вот другой вариант:
Три параллельные цепи, соединенные последовательно.
Участки такой цепи, соединенные последовательно, ведут себя как последовательное соединение. А параллельные участки — как параллельное соединение.
Пример
При такой схеме перегорание одной лампочки выведет из строя весь участок, соединенный последовательно, а две другие последовательные цеписохранят работоспособность.
Соответственно, и включать-выключать участки можно независимо друг от друга. Для этого каждой последовательной цепи нужно поставить свой выключатель.
Но нельзя включить одну-единственную лампочку.
При параллельно-последовательном подключении при выходе из строя одной лампочки цепь будет вести себя так:
А при нарушении на последовательном участке вот так:
Пример:
Есть 6 лампочек по 3V, соединенные в 3 последовательные цепи по 2 лампочки. Цепи в свою очередь соединены параллельно. Разбиваем на 3 последовательных участка и просчитываем этот участок.
На последовательном участке напряжения лампочек складываются, 3v+3V=6V. У каждой последовательной цепи напряжение 6V. Поскольку цепи соединены параллельно, то их напряжение не складывается, а значит нам нужен источник питания на 6V.
Пример
У нас 6 лампочек по 6V. Лампочки соединены по 3 штуки в параллельную цепь, а цепи в свою очередь — последовательно. Разбиваем систему на три параллельных цепи.
В одной параллельной цепи напряжение у каждой лампочки 6V, поскольку напряжение не складывается, то и у всей цепи напряжение 6V. А сами цепи соединены уже последовательно и их напряжения уже складываются. Получается 6V+6V=12V. Значит, нужен источник питания 12V.
Пример
Для кукольных домиков можно использовать такое смешанное подключение.
Допустим, в каждой комнате по одному светильнику, все светильники подключены параллельно. Но в самих светильниках разное количество лампочек: в двух — по одной лампочке, есть двухрожковое бра из двух лампочек и трехрожковая люстра. В люстре и бра лампочки соединены последовательно.
У каждого светильника свой выключатель. Источник питания 12V напряжения. Одиночные лампочки, соединенные параллельно, должны иметь напряжение 12V. А у тех, что соединены последовательно напряжение складывается на участке цепи
. Соответственно, для участка бра из двух лампочек 12V (общее напряжение)делим на 2 (количество лампочек), получим 6V (напряжение одной лампочки).
Для участка люстры 12V:3=4V (напряжение одной лампочки люстры).
Больше трех лампочек в одном светильнике соединять последовательно не стоит.
Теперь вы изучили все хитрости подключения лампочек накаливания разными способами. И, думаю, что не составит труда сделать освещение в кукольном домике со многими лампочками, любой сложности. Если же что-то для вас ещё представляет сложности, прочитайте статью о простейшем способе сделать свет в кукольном домике, самые базовые принципы. Удачи!
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Во многих электрических схемах мы можем обнаружить последовательное и . Разработчик схем может, например, объединить несколько резисторов со стандартными значениями (E-серии), чтобы получить необходимое сопротивление.
Последовательное соединении резисторов — это такое соединение, при котором ток, протекающий через каждый резистор одинаков, поскольку имеется только одно направление для протекания тока. В тоже время падение напряжения будет пропорционально сопротивлению каждого резистора в последовательной цепи.
Последовательное соединение резисторов
Пример № 1
Используя закон Ома, необходимо вычислить эквивалентное сопротивление серии последовательно соединенных резисторов (R1. R2, R3), а так же падение напряжения и мощность для каждого резистора:
Все данные могут быть получены с помощью закона Ома и для лучшего понимания представлены в виде следующей таблицы:
Пример № 2
а) без подключенного резистора R3
б) с подключенным резистором R3
Как вы можете видеть, выходное напряжение U без нагрузочного резистора R3, составляет 6 вольт, но то же выходное напряжение при подключении R3 становится всего лишь 4 В. Таким образом, нагрузка, подключенная к делителю напряжения, провоцирует дополнительное падение напряжение. Данный эффект снижения напряжения может быть компенсирован с помощью установленного вместо постоянного резистора, с помощью которого можно скорректировать напряжение на нагрузке.
Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных последовательно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или несколько резисторов соединены вместе (вывод одного соединяется с выводом другого резистора) — то это последовательное соединение резисторов. Ток, протекающий через резисторы имеет одно и тоже значение, но падение напряжения на них не одно и то же. Оно определяется сопротивлением каждого резистора, которое рассчитывается по закону Ома (U = I * R).
Ток в электроцепи проходит по проводникам от источника напряжения к нагрузке, то есть к лампам, приборам. В большинстве случаев в качестве проводника используются медные провода. В цепи может быть предусмотрено несколько элементов с разными сопротивлениями. В схеме приборов проводники могут быть соединены параллельно или последовательно, также могут быть смешанные типы.
Элемент схемы с сопротивлением называется резистором, напряжение данного элемента является разницей потенциалов между концами резистора. Параллельное и последовательное электрическое соединение проводников характеризуется единым принципом функционирования, согласно которому ток протекает от плюса к минусу, соответственно потенциал уменьшается. На электросхемах сопротивление проводки берется за 0, поскольку оно ничтожно низкое.
Параллельное соединение предполагает, что элементы цепы подсоединены к источнику параллельно и включаются одновременно. Последовательное соединение означает, что проводники сопротивления подключаются в строгой последовательности друг за другом.
При просчете используется метод идеализации, что существенно упрощает понимание. Фактически в электрических цепях потенциал постепенно снижается в процессе перемещения по проводке и элементам, которые входят в параллельное или последовательное соединение.
Последовательное соединение проводников
Схема последовательного соединения подразумевает, что они включаются в определенной последовательности один за другим. Причем сила тока во всех из них равна. Данные элементы создают на участке суммарное напряжение. Заряды не накапливаются в узлах электроцепи, поскольку в противном случае наблюдалось бы изменение напряжения и силы тока. При постоянном напряжении ток определяется значением сопротивления цепи, поэтому при последовательной схеме сопротивление меняется в случае изменения одной нагрузки.
Недостатком такой схемы является тот факт, что в случае выхода из строя одного элемента остальные также утрачивают возможность функционировать, поскольку цепь разрывается. Примером может служить гирлянда, которая не работает в случае перегорания одной лампочки. Это является ключевым отличием от параллельного соединения, в котором элементы могут функционировать по отдельности.
Последовательная схема предполагает, что по причине одноуровневого подключения проводников их сопротивление в любой точки сети равно. Общее сопротивление равняется сумме уменьшения напряжений отдельных элементов сети.
При данном типе соединения начало одного проводника подсоединяется к концу другого. Ключевая особенность соединения состоит в том, что все проводники находятся на одном проводе без разветвлений, и через каждый из них протекает один электроток. Однако общее напряжение равно сумме напряжений на каждом. Также можно рассмотреть соединение с другой точки зрения – все проводники заменяются одним эквивалентным резистором, и ток на нем совпадает с общим током, который проходит через все резисторы. Эквивалентное совокупное напряжение является суммой значений напряжения по каждому резистору. Так проявляется разность потенциалов на резисторе.
Использование последовательного подключения целесообразно, когда требуется специально включать и выключать определенное устройство. К примеру, электрозвонок может звенеть только в момент, когда присутствует соединение с источником напряжения и кнопкой. Первое правило гласит, что если тока нет хотя бы на одном из элементов цепи, то и на остальных его не будет. Соответственно при наличии тока в одном проводнике он есть и в остальных. Другим примером может служить фонарик на батарейках, который светит только при наличии батарейки, исправной лампочки и нажатой кнопки.
В некоторых случаях последовательная схема нецелесообразна. В квартире, где система освещения состоит из множества светильников, бра, люстр, не стоит организовывать схему такого типа, поскольку нет необходимости включать и выключать освещение во всех комнатах одновременно. С этой целью лучше использовать параллельное соединение, чтобы иметь возможность включения света в отдельно взятых комнатах.
Параллельное соединение проводников
В параллельной схеме проводники представляют собой набор резисторов, одни концы которых собираются в один узел, а другие – во второй узел. Предполагается, что напряжение в параллельном типе соединения одинаковое на всех участках цепи. Параллельные участки электроцепи носят название ветвей и проходят между двумя соединительными узлами, на них имеется одинаковое напряжение. Такое напряжение равно значению на каждом проводнике. Сумма показателей, обратных сопротивлениям ветвей, является обратной и по отношению к сопротивлению отдельного участка цепи параллельной схемы.
При параллельном и последовательном соединениях отличается система расчета сопротивлений отдельных проводников. В случае параллельной схемы ток уходит по ветвям, что способствует повышению проводимости цепи и уменьшает совокупное сопротивление. При параллельном подключении нескольких резисторов с аналогичными значениями совокупное сопротивление такой электроцепи будет меньше одного резистора число раз, равное числу .
В каждой ветви предусмотрено по одному резистору, и электроток при достижении точки разветвления делится и расходится к каждому резистору, его итоговое значение равно сумме токов на всех сопротивлениях. Все резисторы заменяются одним эквивалентным резистором. Применяя закон Ома, становится понятным значение сопротивления – при параллельной схеме суммируются значения, обратные сопротивлениям на резисторах.
При данной схеме значение тока обратно пропорционально значению сопротивления. Токи в резисторах не взаимосвязаны, поэтому при отключении одного из них это никоим образом не отразится на остальных. По этой причине такая схема используется во множестве устройств.
Рассматривая возможности применения параллельной схемы в быту, целесообразно отметить систему освещения квартиры. Все лампы и люстры должны быть соединены параллельно, в таком случае включение и отключение одного из них никак не влияет на работу остальных ламп. Таким образом, добавляя выключатель каждой лампочки в ветвь цепи, можно включать и отключать соответствующий светильник по необходимости. Все остальные лампы работают независимо.
Все электроприборы объединяются параллельно в электросеть с напряжением 220 В, затем они подключаются к . То есть все приборы подключаются независимо от подключения прочих устройств.
Законы последовательного и параллельного соединения проводников
Для детального понимания на практике обоих типов соединений, приведем формулы, объясняющие законы данных типов соединений. Расчет мощности при параллельном и последовательном типе соединения отличается.
При последовательной схеме имеется одинаковая сила тока во всех проводниках:
Согласно закону Ома, данные типы соединений проводников в разных случаях объясняются иначе. Так, в случае последовательной схемы, напряжения равны друг другу:
U1 = IR1, U2 = IR2.
Помимо этого, общее напряжение равно сумме напряжений отдельно взятых проводников:
U = U1 + U2 = I(R1 + R2) = IR.
Полное сопротивление электроцепи рассчитывается как сумма активных сопротивлений всех проводников, вне зависимости от их числа.
В случае параллельной схемы совокупное напряжение цепи аналогично напряжению отдельных элементов:
А совокупная сила электротока рассчитывается как сумма токов, которые имеются по всем проводникам, расположенным параллельно:
Чтобы обеспечить максимальную эффективность электрических сетей, необходимо понимать суть обоих типов соединений и применять их целесообразно, используя законы и рассчитывая рациональность практической реализации.
Смешанное соединение проводников
Последовательная и параллельная схема соединения сопротивления могут сочетаться в одной электросхеме при необходимости. К примеру, допускается подключение параллельных резисторов по последовательной или их группе, такое тип считается комбинированным или смешанным.
В таком случае совокупное сопротивление рассчитывается посредством получения сумм значений для параллельного соединения в системе и для последовательного. Сначала необходимо рассчитывать эквивалентные сопротивления резисторов в последовательной схеме, а затем элементов параллельного. Последовательное соединение считается приоритетным, причем схемы такого комбинированного типа часто используются в бытовой технике и приборах.
Итак, рассматривая типы подключений проводников в электроцепях и основываясь на законах их функционирования, можно полностью понять суть организации схем большинства бытовых электроприборов. При параллельном и последовательном соединениях расчет показателей сопротивления и силы тока отличается. Зная принципы расчета и формулы, можно грамотно использовать каждый тип организации цепей для подключения элементов оптимальным способом и с максимальной эффективностью.
При последовательном соединении сопротивление равно. Параллельное соединение сопротивлениий (резисторов)
Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Последовательное соединение резисторов . При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:
E = IR 1 + IR 2 + IR 3 = I(R 1 + R 2 + R 3) = IR эк (19)
где R
эк
= R 1 + R 2 + R 3 .
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U 1 =IR 1 ; U 2 = IR 2 , U 3 = IR з и в данном случае E = U, то длярассматриваемой цепи
U = U 1 + U 2 +U 3 (20)
Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:
U 1: U 2: U 3 = R 1: R 2: R 3 (21)
т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:
При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов . При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :
G эк = G 1 + G 2 +G 3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Смешанное соединение резисторов . Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле
R 123 =R 12 R 3 /(R 12 +R 3)=(R 1 +R 2)R 3 /(R 1 +R 2 +R 3).
При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
R эк = R 123 + R 4 = (R 1 + R 2) R 3 / (R 1 + R 2 + R 3) + R 4
Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.
1. При последовательном соединении проводников
1. Сила тока во всех проводниках одинакова :
I 1 = I 2 = I
2. Общее напряжение U на обоих проводниках равно сумме напряжений U 1 и U 2 на каждом проводнике :
U = U 1 + U 2
3. По закону Ома, напряжения U 1 и U 2 на проводниках равны U 1 = IR 1 , U 2 = IR 2 а общее напряжение U = IR где R – электрическое сопротивление всей цепи, тогда IR = IR 1 + I R 2. Отсюда следует
R = R 1 + R 2
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
2. При параллельном соединении проводников
1. Напряжения U 1 и U 2 на обоих проводниках одинаковы
U 1 = U 2 = U
2. Сумма токов I 1 + I 2 , протекающих по обоим проводникам, равна току в неразветвленной цепи :
I = I 1 + I 2
Этот результат следует из того, что в точках разветвления токов (узлы A и B ) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд I Δt , а утекает от узла за то же время заряд I 1 Δt + I 2 Δt . Следовательно, I = I 1 + I 2 .
3. Записывая на основании закона Ома
где R – электрическое сопротивление всей цепи, получим
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рисунке приведен пример такой сложной цепи и указана последовательность вычислений. Сопротивления всех проводников указаны в омах (Ом).
На пракутике одного источника тока в цепи бывает недостаточно, и тогда источники тока тоже соединяют между собой для питания цепи. Соединение источников в батарею может быть последовательным и параллельным.
При последовательном соединении два соседних источника соединяются разноименными полюсами.
Т.е., для последовательного соединения аккумуляторов, к ″плюсу″ электрической схемы подключают положительную клемму первого аккумулятора. К его отрицательной клемме подключают положительную клемму второго аккумулятора и т.д. Отрицательную клемму последнего аккумулятора подключают к ″минусу″ электрической схемы.
Получившаяся при последовательном соединении аккумуляторная батарея имеет ту же емкость, что и у одиночного аккумулятора, а напряжение такой аккумуляторной батареи равно сумме напряжений входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые напряжения, то напряжение батареи равно напряжению одного аккумулятора, умноженному на количество аккумуляторов в аккумуляторной батарее.
1. ЭДС батареи равна сумме ЭДС отдельных источников ε= ε 1 + ε 2 + ε 3
2 . Общее сопротивление батареи источников равно сумме внутренних сопротивлений отдельных источников r батареи = r 1 + r 2 + r 3
Если в батарею соединены n одинаковых источников, то ЭДС батареи ε= nε 1, а сопротивление r батареи = nr 1
3.
При параллельном соединении соединяют между собой все положительные и все отрицательные полюсы двух или n источников.
Т.е., при параллельном соединении, аккумуляторы соединяют так, чтобы положительные клеммы всех аккумуляторов были подключены к одной точке электрической схемы (″плюсу″), а отрицательные клеммы всех аккумуляторов были подключены к другой точке схемы (″минусу″).
Параллельно соединяют только источники с одинаковой ЭДС . Получившаяся при параллельном соединении аккумуляторная батарея имеет то же напряжение, что и у одиночного аккумулятора, а емкость такой аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые емкости, то емкость аккумуляторной батареи равна емкости одного аккумулятора, умноженной на количество аккумуляторов в батарее.
1. ЭДС батареи одинаковых источников равна ЭДС одного источника. ε= ε 1 = ε 2 = ε 3
2. Сопротивление батареи меньше, чем сопротивление одного источника r батареи = r 1 /n
3. Сила тока в такой цепи по закону Ома
Электрическая энергия, накопленная в аккумуляторной батарее равна сумме энергий отдельных аккумуляторов (произведению энергий отдельных аккумуляторов, если аккумуляторы одинаковые), независимо от того, как соединены аккумуляторы — параллельно или последовательно.
Внутреннее сопротивление аккумуляторов, изготовленных по одной технологии, примерно обратно пропорционально емкости аккумулятора. Поэтому т.к.при параллельном соединении емкость аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов, т.е увеличивается, то внутреннее сопротивление уменьшается.
Параллельным соединением сопротивлений называется такое соединение, когда начала сопротивлений соединены в одну общую точку, а концы — в другую.
Для параллельного соединения сопротивлений характерны следующие свойства:
Напряжения на зажимах всех сопротивлений одинаковы:
U 1 = U 2 =U 3 =U ;
Проводимость всех параллельно соединённых сопротивлений равна сумме проводимостей отдельных сопротивлений:
1/R = 1/R 1 + 1/R 2 + 1/R 3 = R 1 R 2 + R 1 R 3 + R 2 R 3 /R 1 R 2 R 3 ,
где R — эквивалентное (равнодействующее) сопротивление трёх сопротивлений (в данном случае R 1 , R 2 и R 3 ) .
Чтобы получить сопротивление такой цепи, надо перевернуть дробь, определяющую величину её проводимости. Следовательно, сопротивление параллельного разветвления из трёх резисторов:
R = R 1 R 2 R 3 /R 1 R 2 + R 2 R 3 + R 1 R 3 .
Эквивалентным сопротивлением называется такое сопротивление, которым можно заменить несколько сопротивлений (включенных параллельно или последовательно), не изменяя величины тока в цепи.
Чтобы найти эквивалентное сопротивление при параллельном соединении, необходимо сложить проводимости всех отдельных участков, т.е. найти общую проводимость. Величина, обратная общей проводимости, и является общим сопротивлением.
При параллельном соединении эквивалентная проводимость равна сумме проводимостей отдельных ветвей, следовательно, эквивалентное сопротивление в этом случае всегда меньше наименьшего из параллельно включенных сопротивлений.
На практике могут быть случаи, когда цепь состоит из более, чем трёх параллельных ветвей. Все полученные соотношения остаются справедливыми и для цепей, состоящих из любого числа параллельно соединённых резисторов.
Найдём эквивалентное сопротивление двух параллельно включенных сопротивлений R 1 и R 2 (см. рис.). Проводимость первой ветви равна 1/R 1 , проводимость второй ветви — 1/R 2 . Общая проводимость:
1/R = 1/R 1 + 1/R 2 .
Приведём к общему знаменателю:
1/R = R 2 + R 1 /R 1 R 2 ,
отсюда эквивалентное сопротивление
R = R 1 R 2 /R 1 + R 2 .
Эта формула и служит для расчётов общего сопротивления цепи, состоящей из двух параллельно включенных сопротивлений.
Таким образом, эквивалентное сопротивление двух параллельно включенных сопротивлений равно произведению этих сопротивлений, делённому на их сумму.
При параллельном соединении n равных сопротивлений R 1 эквивалентное сопротивление их будет в n раз меньше, т.е.
R = R 1 /n .
На схеме, изображённой на последнем рисунке, включено пять сопротивлений R 1 по 30 Ом каждое. Следовательно, общее сопротивление R будет
R = R 1 /5 = 30/5 = 6 Ом.
Можно сказать, что сумма токов, подходящих к узловой точке А (на первом рисунке), равна сумме токов, от неё отходящих:
I = I 1 + I 2 + I 3 .
Рассмотрим, как происходит разветвление тока в цепях с сопротивлениями R 1 и R 2 (второй рисунок). Так как напряжение на зажимах этих сопротивлений одинаково, то
U = I 1 R 1 и U = I 2 R 2 .
Левые части этих равенств одинаковы, следовательно, равны и правые части:
I 1 R 1 = I 2 R 2 ,
или
I 1 /I 2 = R 2 /R 1 ,
Т.е. ток при параллельном соединении сопротивлений разветвляется обратно пропорционально сопротивлениям ветвей (или прямо пропорционально их проводимостям). Чем больше сопротивление ветви, тем меньше ток в ней, и наоборот.
Таким образом, из нескольких одинаковых резисторов можно получить общий резистор с бОльшей мощностью рассеивания.
При параллельном соединении неодинаковых резисторов в наиболее высокоомном резисторе выделяется наибольшая мощность.
Пример 1. Имеются два сопротивления, включенных параллельно. Сопротивление R 1 = 25 Ом, а R 2 = 50 Ом. Определить общее сопротивление цепи R общ .
Решение. R общ = R 1 R 2 /R 1 + R 2 = 25 . 50 / 25 + 50 ≈ 16, 6 Ом.
Пример 2. В ламповом усилителе имеются три лампы, нити накала которых включены параллельно. Ток накала первой лампы I 1 = 1 ампер, второй I 2 = 1, 5 ампера и третьей I 3 = 2, 5 ампера. Определить общий ток цепи накала ламп усилителя I общ .
Решение. I общ = I 1 + I 2 + I 3 = 1 + 1, 5 + 2, 5 = 5 ампер.
Параллельное соединение резисторов часто встречается в радиотехнической аппаратуре. Два или более резисторов включается параллельно в тех случаях, когда ток в цепи слишком большой и может вызвать чрезмерный нагрев резистора.
Примером параллельного соединения потребителей электрической энергии может служить включение электрических ламп обычной осветительной сети, которые соединяются параллельно. Достоинство параллельного соединения потребителей заключается в том, что выключение одного из них не влияет на работу других.
Сопротивление при последовательном соединении резисторов равно сумме всех резисторов
Часто надо посчитать общее сопротивление при последовательном соединении резисторов. Внешний участок электрической цепи часто образуется не одним приемником с определенным сопротивлением, а несколькими, соединенными последовательно, параллельно или смешанно.
Если несколько сопротивлений электрической цепи соединены, как указано на рисунке ниже, одно за другим без разветвлений и по ним проходит один и тот же ток, то такое соединение называется последовательным соединением сопротивлений.
Последовательное соединение сопротивлений показано на рисунке.
По закону Ома напряжения на отдельных участках цепи (сопротивлениях) или падения напряжения
U1 = IR1;
U2 = IR2;
U3 = IR3;
U4 = IR4.
Так как ток во всех участках имеет одинаковое значение, то напряжения на участках пропорциональны их сопротивлениям, т. е.
U1 : U2 = R1 : R2;
U2 : U3 = R2 : R3;
U3 : U4 = R3 : R4.
Мощности отдельных участков соответственно равны:
P1 = U1I;
P2 = U2I;
P3 = U3I;
P4 = U4I,
а мощность всей цепи, по закону сохранения энергии равная сумме мощностей отдельных участков,
P = P1 + P2 + P3 + P3 = I(U1 + U2 + U3 + U4) = IU,
откуда следует, что напряжение на зажимах цепи U равно сумме напряжений на отдельных участках:
U = U1 + U2 + U3 + U4
Разделив правую и левую части этого выражения на ток, получим:
U : I = U1 : I + U2 : I + U3 : I + U4 : I
или
R = R1 + R2 + R3 + R4
где R — общее сопротивление при последовательном соединении в цепи, т. е. такое равноценное (эквивалентное) сопротивление, заменяя которым все сопротивления цепи (R1, R2, R3 и R4) при неизменном напряжении на ее зажимах, получим то же самое значение тока.
Или
Общее сопротивление при последовательном соединении проводников (сопротивлений) равно сумме всех сопротивлений в цепи.
Например:
Последовательно с постоянным сопротивлением, имеющей сопротивление R1 = 2 ком (2000 ом), включен реостат R2 (переменное сопротивление), сопротивление которого можно изменять от 0 до 10 ком (10000 ом). Определить, в каких пределах можно регулировать ток в цепи при напряжении, подведенным к этой цепи, равным 120 В.
При последовательном соединении сопротивление равно:
R = R1 + R2
При сопротивлении реостата, равным нулю:
I = U : ( R1 + R2 ) = 120 : (2000 + 0) = 0,06 а
При введенном реостате на максимальное значение
I = U : ( R1 + R2 ) = 120 : (2000 + 10000) = 0,01 а
Таким образом, ток можно регулировать в пределах от 0,01 а до 0,06 а.
Общее напряжение в цепи. Последовательное и параллельное соединение сопротивлений
В предыдущем конспекте был установлено, что сила тока в проводнике зависит от напряжения на его концах. Если в опыте менять проводники, оставляя напряжение на них неизменным, то можно показать, что при постоянном напряжении на концах проводника сила тока обратно пропорциональна его сопротивлению. Объединив зависимость силы тока от напряжения и его зависимость от сопротивления проводника, можно записать: I = U/R . Этот закон, установленный экспериментально, называется закон Ома (для участка цепи).
Закон Ома для участка цепи : сила тока в проводнике прямо пропорциональна приложенному к его концам напряжению и обратно пропорциональна сопротивлению проводника. Прежде всего закон всегда верен для твёрдых и жидких металлических проводников. А также для некоторых других веществ (как правило, твёрдых или жидких).
Потребители электрической энергии (лампочки, резисторы и пр.) могут по-разному соединяться друг с другом в электрической цепи. Д ва основных типа соединения проводников : последовательное и параллельное. А также есть еще два соединения, которые являются редкими: смешанное и мостовое.
Последовательное соединение проводниковПри последовательном соединении проводников конец одного проводника соединится с началом другого проводника, а его конец — с началом третьего и т.д. Например, соединение электрических лампочек в ёлочной гирлянде. При последовательном соединении проводников ток проходит через все лампочки. При этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд. То есть заряд не скапливается ни в какой части проводника.
Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова: I 1 = I 2 = I .
Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений : R 1 + R 2 = R . Потому что при последовательном соединении проводников их общая длина увеличивается. Она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.
По закону Ома напряжение на каждом проводнике равно: U 1 = I* R 1 , U 2 = I*R 2 . В таком случае общее напряжение равно U = I ( R 1 + R 2) . Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике : U = U 1 + U 2 .
Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.
Для последовательного соединения проводников справедливы законы :1) сила тока во всех проводниках одинакова; 2) напряжение на всём соединении равно сумме напряжений на отдельных проводниках; 3) сопротивление всего соединения равно сумме сопротивлений отдельных проводников.
Параллельное соединение проводниковПримером параллельного соединения проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.
При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи. А вторым концом к другой точке цепи. Вольтметр, подключенный к этим точкам, покажет напряжение и на проводнике 1, и на проводнике 2. В таком случае напряжение на концах всех параллельно соединённых проводников одно и то же: U 1 = U 2 = U .
При параллельном соединении проводников электрическая цепь разветвляется. Поэтому часть общего заряда проходит через один проводник, а часть — через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: I = I 1 + I 2 .
В соответствии с законом Ома I = U/R, I 1 = U 1 /R 1 , I 2 = U 2 /R 2 . Отсюда следует: U/R = U 1 /R 1 + U 2 /R 2 , U = U 1 = U 2 , 1/R = 1/R 1 + 1/R 2 Величина, обратная общему сопротивлению параллельно соединенных проводников, равна сумме величин, обратных сопротивлению каждого проводника.
При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление г , то их общее сопротивление равно: R = г/2 . Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения. В результате уменьшается сопротивление.
Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно. Они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них. А также соответствие суммарной силы тока предельно допустимой силе тока.
Для параллельного соединения проводников справедливы законы:1) напряжение на всех проводниках одинаково; 2) сила тока в месте соединения проводников равна сумме токов в отдельных проводниках; 3) величина, обратная сопротивлению всего соединения, равна сумме величин, обратных сопротивлениям отдельных проводников.
На уроке рассматривается параллельное соединение проводников. Изображается схема такого соединения, показывается выражение для вычисления силы тока в такой цепи. Также вводится понятие эквивалентного сопротивления, находится его значение для случая параллельного соединения.
Соединения проводников бывают различные. Они могут быть параллельными, последовательными и смешанными. На данном уроке мы рассмотрим параллельное соединение проводников и понятие эквивалентного сопротивления.
Параллельным соединением проводников называется такое соединение, при котором начала и концы проводников соединяются вместе. На схеме такое соединение обозначается следующим образом (рис. 1):
Рис. 1. Параллельное соединение трех резисторов
На рисунке изображены три резистора (прибор, основанный на сопротивлении проводника) с сопротивлениями R1, R2, R3. Как видим, начала этих проводников соединены в точке А, концы — в точке Б, а расположены они параллельно друг другу. Также в цепи может быть большее количество параллельно соединенных проводников.
Теперь рассмотрим следующую схему (рис. 2):
Рис. 2. Схема для исследования силы тока при параллельном соединении проводников
В качестве элементов цепи мы взяли две лампы (1а, 1б). Они также имеют свое сопротивление, поэтому мы их можем рассматривать наравне с резисторами. Эти две лампы соединены параллельно, соединяются они в точках А и Б. К каждой лампе подсоединен свой амперметр: соответственно, А 1 и А 2 . Также есть амперметр А 3 , который измеряет силу тока во всей цепи. В цепь еще входит источник питания (3) и ключ (4).
Замкнув ключ, мы будем следить за показаниями амперметров. Амперметр А 1 покажет силу тока, равную I 1 , в лампе 1а, амперметр А 2 — cилу тока, равную I 2 , в лампе 1б. Что же касается амперметра А 3 , то он покажет силу тока, равную сумме токов в каждой отдельной взятой цепи, соединенных параллельно: I = I 1 + I 2 . То есть, если сложить показания амперметров А 1 и А 2 , то получим показания амперметра А 3 .
Стоит обратить внимание, что если одна из ламп перегорит, то вторая будет продолжать работать. При этом весь ток будет проходить через эту вторую лампу. Это очень удобно. Так, например, электроприборы в наших домах включаются в цепь параллельно. И если один из них выходит из строя, то остальные остаются в рабочем состоянии.
Рис. 3. Схема для нахождения эквивалентного сопротивления при параллельном соединении
На схеме рис. 3 мы оставили один амперметр (2), но добавили в электрическую цепь вольтметр (5) для измерения напряжения. Точки А и Б являются общими и для первой (1а), и для второй лампы (1б), а значит, вольтметр измеряет напряжение на каждой из этих ламп (U 1 и U 2) и во всей цепи (U). Тогда U = U 1 = U 2 .
Эквивалентным сопротивлением называется сопротивление, которое может заменить все элементы, входящие в данную цепь. Посмотрим, чему же оно будет равно при параллельном соединении. Из закона Ома можно получить, что:
В данной формуле R — эквивалентное сопротивление, R 1 и R 2 — сопротивление каждой лампочки, U = U 1 = U 2 — напряжение, которое показывает вольтметр (5). При этом мы используем то, что сумма токов в каждой отдельной цепи равна общей силе тока (I = I 1 + I 2). Отсюда можно получить формулу для эквивалентного сопротивления:
Если в цепи будет больше элементов, соединенных параллельно, то и слагаемых будет больше. Тогда придется вспомнить, как работать с простыми дробями.
Стоить отметить, что при параллельном соединении эквивалентное сопротивление будет достаточно малым. Соответственно, сила тока будет достаточно большой. Это стоит учитывать при включении в розетки большого количества электрических приборов. Ведь тогда сила тока возрастет, что может привести к перегреванию проводов и пожарам.
На следующем уроке мы рассмотрим другой тип соединения проводников — последовательное.
Список литературы
- Генденштейн Л.Э, Кайдалов А.Б., Кожевников В.Б. Физика 8 / Под ред. Орлова В.А., Ройзена И.И. — М.: Мнемозина.
- Перышкин А.В. Физика 8. — М.: Дрофа, 2010.
- Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. — М.: Просвещение.
- Физика ().
- Сверхзадача ().
- Интернет-портал Nado5.ru ().
Домашнее задание
- Стр. 114-117: вопросы № 1-6. Перышкин А.В. Физика 8. — М.: Дрофа, 2010.
- Могут ли быть параллельно соединены более трех проводников?
- Что случится, если одна из двух ламп, которые соединены параллельно, перегорит?
- Если к любой цепи параллельно подключить еще один проводник, всегда ли её эквивалентное сопротивление будет уменьшаться?
При одновременном включении нескольких приемников электроэнергии в одну и ту же сеть, эти приемники можно легко рассматривать просто как элементы единой цепи, каждый из которых обладает собственным сопротивлением.
В ряде случаев такой подход оказывается вполне приемлемым: лампы накаливания, электрические обогреватели и т. п. — можно воспринимать как резисторы. То есть приборы можно заменить на их сопротивления, и легко произвести расчет параметров цепи.
Способ соединения приемников электроэнергии может быть одним из следующих: последовательный, параллельный или смешанный тип соединения.
Последовательное соединение
Когда несколько приемников (резисторов) соединяются в последовательную цепь, то есть второй вывод первого присоединяется к первому выводу второго, второй вывод второго соединяется с первым выводом третьего, второй вывод третьего с первым выводом четвертого и т. д., то при подключении такой цепи к источнику питания, через все элементы цепи потечет ток I одной и той же величины. Данную мысль поясняет приведенный рисунок.
Заменив приборы на их сопротивления, рисунок преобразуем в схему, тогда сопротивления с R1 по R4, соединенные последовательно, примут каждый на себя определенные напряжения, которые в сумме дадут значение ЭДС на зажимах источника питания. Для простоты здесь и далее изобразим источник в виде гальванического элемента.
Выразив падения напряжений через ток и через сопротивления, получим выражение для эквивалентного сопротивления последовательной цепи приемников: общее сопротивление последовательного соединения резисторов всегда равно алгебраической сумме всех сопротивлений, составляющих эту цепь. А поскольку напряжения на каждом из участков цепи можно найти из закона Ома (U = I*R, U1 = I*R1, U2 = I*R2 и т. д.) и E = U, то для нашей схемы получаем:
Напряжение на клеммах источника питания равно сумме падений напряжений на каждом из соединенных последовательно приемников, составляющих цепь.
Так как ток через всю цепь течет одного и того же значения, то справедливым будет утверждение, что напряжения на последовательно соединенных приемниках (резисторах) соотносятся между собой пропорционально сопротивлениям. И чем выше будет сопротивление, тем выше окажется и напряжение, приложенное к приемнику.
Для последовательного соединения резисторов в количестве n штук, обладающих одинаковыми сопротивлениями Rk, эквивалентное общее сопротивление цепи целиком будет в n раз больше каждого из этих сопротивлений: R = n*Rk. Соответственно и напряжения, приложенные к каждому из резисторов цепи будут между собой равны, и окажутся в n раз меньше напряжения, приложенного ко всей цепи: Uk = U/n.
Для последовательного соединения приемников электроэнергии характерны следующие свойства: если изменить сопротивление одного из приемников цепи, то напряжения на остальных приемниках цепи при этом изменятся; при обрыве одного из приемников ток прекратится во всей цепи, во всех остальных приемниках.
В силу этих особенностей последовательное соединение встречается редко, и используют его лишь там, где напряжение сети выше номинального напряжения приемников, в отсутствие альтернатив.
К примеру напряжением 220 вольт можно запитать две последовательно соединенные лампы равной мощности, каждая из которых рассчитана на напряжение 110 вольт. Ежели данные лампы при одинаковом номинальном напряжении питания будут обладать различной номинальной мощностью, то одна из них будет перегружена и скорее всего мгновенно перегорит.
Параллельное соединение
Параллельное соединение приемников предполагает включение каждого из них между парой точек электрической цепи с тем, чтобы они образовывали параллельные ветви, каждая из которых питается напряжением источника. Для наглядности опять заменим приемники их электрическими сопротивлениями, чтобы получить схему, по которой удобно вести расчет параметров.
Как уже было сказано, в случае параллельного соединения каждый из резисторов испытывает действие одного и того же напряжения. И в соответствии с законом Ома имеем: I1=U/R1, I2=U/R2, I3=U/R3.
Здесь I — ток источника. Первый закон Кирхгофа для данной цепи позволяет записать выражение для тока в неразветвленной ее части: I = I1+I2+I3.
Отсюда общее сопротивление для параллельного соединения между собой элементов цепи можно найти из формулы:
Величина обратная сопротивлению называется проводимостью G, и формулу для проводимости цепи, состоящей из нескольких параллельно соединенных элементов, также можно записать: G = G1 + G2 + G3. Проводимость цепи в случае параллельного соединения образующих ее резисторов равна алгебраической сумме проводимостей этих резисторов. Следовательно, при добавлении в цепь параллельных приемников (резисторов) суммарное сопротивление цепи уменьшится, а суммарная проводимость соответственно возрастет.
Токи в цепи состоящей из параллельно соединенных приемников, распределяются между ними прямо пропорционально их проводимостям, то есть обратно пропорционально их сопротивлениям. Здесь можно привести аналогию из гидравлики, где поток воды распределяется по трубам в соответствии с их сечениями, тогда большее сечение аналогично меньшему сопротивлению, то есть большей проводимости.
Если цепь состоит из нескольких (n) одинаковых резисторов, соединенных параллельно, то общее сопротивление цепи будет ниже в n раз, чем сопротивление одного из резисторов, а ток через каждый из резисторов будет меньше в n раз, чем общий ток: R = R1/n; I1 = I/n.
Цепь, состоящая из параллельно соединенных приемников, подключенная к источнику питания, отличается тем, что каждый из приемников находится под напряжением источника питания.
Для идеального источника электроэнергии справедливо утверждение: при подключении или отключении параллельно источнику резисторов, токи в остальных подключенных резисторах не изменятся, то есть при выходе из строя одного или нескольких приемников параллельной цепи, остальные будут продолжать работать в прежнем режиме.
В силу данных особенностей параллельное соединение обладает значительным преимуществом перед последовательным, и по этой причине именно соединение параллельное наиболее распространено в электрических сетях. Например, все электроприборы в наших домах предназначены для параллельного подключения к бытовой сети, и если отключить один, то остальным это ничуть не навредит.
Сравнение последовательных и параллельных цепей
Под смешанным соединением приемников понимают такое их соединение, когда часть или несколько из них соединены между собой последовательно, а другая часть или несколько — параллельно. При этом вся цепь может быть образована из разных соединений таких частей между собой. Для примера рассмотрим схему:
Три последовательно соединенных резистора подключены к источнику питания, параллельно одному из них подключены еще два, а третий — параллельно всей цепи. Для нахождения полного сопротивления цепи идут путем последовательных преобразований: сложную цепь последовательно приводят к простому виду, последовательно вычисляя сопротивление каждого звена, и так находят общее эквивалентное сопротивление.
Для нашего примера. Сначала находят общее сопротивление двух резисторов R4 и R5, соединенных последовательно, затем сопротивление параллельного соединения их с R2, потом прибавляют к полученному значению R1 и R3, и после — вычисляют значение сопротивления всей цепи, включая параллельную ветвь R6.
Различные способы соединения приемников электроэнергии применяют на практике для различных целей, чтобы решать конкретные поставленные задачи. Например, смешанное соединение можно встретить в схемах плавного заряда в мощных блоках питания, где нагрузка (конденсаторы после диодного моста) сначала получает питание последовательно через резистор, затем резистор шунтируется контактами реле, и нагрузка оказывается подключенной к диодному мосту параллельно.
Андрей Повный
Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Последовательное соединение резисторов . При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:
E = IR 1 + IR 2 + IR 3 = I(R 1 + R 2 + R 3) = IR эк (19)
где R
эк
= R 1 + R 2 + R 3 .
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U 1 =IR 1 ; U 2 = IR 2 , U 3 = IR з и в данном случае E = U, то длярассматриваемой цепи
U = U 1 + U 2 +U 3 (20)
Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:
U 1: U 2: U 3 = R 1: R 2: R 3 (21)
т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:
При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов . При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :
G эк = G 1 + G 2 +G 3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Смешанное соединение резисторов . Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле
R 123 =R 12 R 3 /(R 12 +R 3)=(R 1 +R 2)R 3 /(R 1 +R 2 +R 3).
При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
R эк = R 123 + R 4 = (R 1 + R 2) R 3 / (R 1 + R 2 + R 3) + R 4
Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.
Практически каждому, кто занимался электрикой, приходилось решать вопрос параллельного и последовательного соединения элементов схемы. Некоторые решают проблемы параллельного и последовательного соединения проводников методом «тыка», для многих «несгораемая» гирлянда является необъяснимой, но привычной аксиомой. Тем не менее, все эти и многие другие подобные вопросы легко решаются методом, предложенным еще в самом начале XIX века немецким физиком Георгом Омом. Законы, открытые им, действуют и поныне, а понять их сможет практически каждый.
Основные электрические величины цепи
Для того чтобы выяснить, как то или иное соединение проводников повлияет на характеристики схемы, необходимо определиться с величинами, которые характеризуют любую электрическую цепь. Вот основные из них:
Взаимная зависимость электрических величин
Теперь необходимо определиться , как все вышеперечисленные величины зависят одна от другой. Правила зависимости несложны и сводятся к двум основным формулам:
Здесь I – ток в цепи в амперах, U – напряжение, подводимое к цепи в вольтах, R – сопротивление цепи в омах, P – электрическая мощность цепи в ваттах.
Предположим, перед нами простейшая электрическая цепь, состоящая из источника питания с напряжением U и проводника с сопротивлением R (нагрузки).
Поскольку цепь замкнута, через нее течет ток I. Какой величины он будет? Исходя из вышеприведенной формулы 1, для его вычисления нам нужно знать напряжение, развиваемое источником питания, и сопротивление нагрузки. Если мы возьмем, к примеру, паяльник с сопротивлением спирали 100 Ом и подключим его к осветительной розетке с напряжением 220 В, то ток через паяльник будет составлять:
220 / 100 = 2,2 А.
Какова мощность этого паяльника ? Воспользуемся формулой 2:
2,2 * 220 = 484 Вт.
Хороший получился паяльник, мощный, скорее всего, двуручный. Точно так же, оперируя этими двумя формулами и преобразуя их, можно узнать ток через мощность и напряжение, напряжение через ток и сопротивление и т.д. Сколько, к примеру, потребляет лампочка мощностью 60 Вт в вашей настольной лампе:
60 / 220 = 0,27 А или 270 мА.
Сопротивление спирали лампы в рабочем режиме:
220 / 0,27 = 815 Ом.
Схемы с несколькими проводниками
Все рассмотренные выше случаи являются простыми – один источник, одна нагрузка. Но на практике нагрузок может быть несколько, и соединены они бывают тоже по-разному. Существует три типа соединения нагрузки:
- Параллельное.
- Последовательное.
- Смешанное.
Параллельное соединение проводников
В люстре 3 лампы, каждая по 60 Вт. Сколько потребляет люстра? Верно, 180 Вт. Быстренько подсчитываем сначала ток через люстру:
180 / 220 = 0,818 А.
А затем и ее сопротивление:
220 / 0,818 = 269 Ом.
Перед этим мы вычисляли сопротивление одной лампы (815 Ом) и ток через нее (270 мА). Сопротивление же люстры оказалось втрое ниже, а ток — втрое выше. А теперь пора взглянуть на схему трехрожкового светильника.
Все лампы в нем соединены параллельно и подключены к сети. Получается, при параллельном соединении трех ламп общее сопротивление нагрузки уменьшилось втрое? В нашем случае — да, но он частный – все лампы имеют одинаковые сопротивление и мощность. Если каждая из нагрузок будет иметь свое сопротивление, то для подсчета общего значения простого деления на количество нагрузок мало. Но и тут есть выход из положения – достаточно воспользоваться вот этой формулой:
1/Rобщ. = 1/R1 + 1/R2 + … 1/Rn.
Для удобства использования формулу можно легко преобразовать:
Rобщ. = (R1*R2*… Rn) / (R1+R2+ … Rn).
Здесь Rобщ . – общее сопротивление цепи при параллельном включении нагрузки. R1 … Rn – сопротивления каждой нагрузки.
Почему увеличился ток, когда вы включили параллельно три лампы вместо одной, понять несложно – ведь он зависит от напряжения (оно осталось неизменным), деленного на сопротивление (оно уменьшилось). Очевидно, что и мощность при параллельном соединении увеличится пропорционально увеличению тока.
Последовательное соединение
Теперь настала пора выяснить, как изменятся параметры цепи, если проводники (в нашем случае лампы) соединить последовательно.
Расчет сопротивления при последовательном соединении проводников исключительно прост:
Rобщ. = R1 + R2.
Те же три шестидесятиваттные лампы, соединенные последовательно, составят уже 2445 Ом (см. расчеты выше). Какими будут последствия увеличения сопротивления цепи? Согласно формулам 1 и 2 становится вполне понятно, что мощность и сила тока при последовательном соединении проводников упадет. Но почему теперь все лампы горят тускло? Это одно из самых интересных свойств последовательного подключения проводников, которое очень широко используется. Взглянем на гирлянду из трех знакомых нам, но последовательно соединенных ламп.
Общее напряжение, приложенное ко всей цепи, так и осталось 220 В. Но оно поделилось между каждой из ламп пропорционально их сопротивлению! Поскольку лампы у нас одинаковой мощности и сопротивления, то напряжение поделилось поровну: U1 = U2 = U3 = U/3. То есть на каждую из ламп подается теперь втрое меньшее напряжение, вот почему они светятся так тускло. Возьмете больше ламп – яркость их упадет еще больше. Как рассчитать падение напряжения на каждой из ламп, если все они имеют различные сопротивления? Для этого достаточно четырех формул, приведенных выше. Алгоритм расчета будет следующим:
- Измеряете сопротивление каждой из ламп.
- Рассчитываете общее сопротивление цепи.
- По общим напряжению и сопротивлению рассчитываете ток в цепи.
- По общему току и сопротивлению ламп вычисляете падение напряжения на каждой из них.
Хотите закрепить полученные знания ? Решите простую задачу, не заглядывая в ответ в конце:
В вашем распоряжении есть 15 однотипных миниатюрных лампочек, рассчитанных на напряжение 13,5 В. Можно ли из них сделать елочную гирлянду, подключаемую к обычной розетке, и если можно, то как?
Смешанное соединение
С параллельным и последовательным соединением проводников вы, конечно, без труда разобрались. Но как быть, если перед вами оказалась примерно такая схема?
Смешанное соединение проводников
Как определить общее сопротивление цепи? Для этого вам понадобится разбить схему на несколько участков. Вышеприведенная конструкция достаточно проста и участков будет два — R1 и R2,R3. Сначала вы рассчитываете общее сопротивление параллельно соединенных элементов R2,R3 и находите Rобщ.23. Затем вычисляете общее сопротивление всей цепи, состоящей из R1 и Rобщ.23, соединенных последовательно:
- Rобщ.23 = (R2*R3) / (R2+R3).
- Rцепи = R1 + Rобщ.23.
Задача решена, все очень просто. А теперь вопрос несколько сложнее.
Сложное смешанное соединение сопротивлений
Как быть тут? Точно так же, просто нужно проявить некоторую фантазию. Резисторы R2, R4, R5 соединены последовательно. Рассчитываем их общее сопротивление:
Rобщ.245 = R2+R4+R5.
Теперь параллельно к Rобщ.245 подключаем R3:
Rобщ.2345 = (R3* Rобщ.245) / (R3+ Rобщ.245).
Rцепи = R1+ Rобщ.2345+R6.
Вот и все!
Ответ на задачу о елочной гирлянде
Лампы имеют рабочее напряжение всего 13.5 В, а в розетке 220 В, поэтому их нужно включать последовательно.
Поскольку лампы однотипные, напряжение сети разделится между ними поровну и на каждой лампочке окажется 220 / 15 = 14,6 В. Лампы рассчитаны на напряжение 13,5 В, поэтому такая гирлянда хоть и заработает, но очень быстро перегорит. Чтобы реализовать задумку, вам понадобится минимум 220 / 13,5 = 17, а лучше 18-19 лампочек.
Напряжение в последовательной цепи
Напряжение в последовательной цепи
Напряжение, падающее на резисторе в цепи, состоящей из одного резистора и источника напряжения, представляет собой полное напряжение в цепи и равно приложенному напряжению. Общее напряжение в последовательной цепи, состоящей из более чем одного резистора, также равно приложенному напряжению, но состоит из суммы падений напряжения отдельных резисторов.В любой последовательной схеме сумма падений напряжения на резисторе должна равняться напряжению источника. Это утверждение может быть подтверждено исследованием схемы, показанной на рисунке 3-17. В этой цепи потенциал источника (E T ) в 20 вольт падает на последовательную цепь, состоящую из двух резисторов сопротивлением 5 Ом. Общее сопротивление цепи (R T ) равно сумме двух отдельных сопротивлений или 10 Ом. Используя закон Ома, ток в цепи можно рассчитать следующим образом:
Рисунок 3-17.- Расчет отдельных падений напряжения в последовательной цепи.
Поскольку известно, что сопротивление каждого резистора составляет 5 Ом, а ток через резисторы составляет 2 ампера, падение напряжения на резисторах может быть рассчитано. Таким образом, напряжение (E 1 ) на R 1 составляет:
Осмотрев цепь, вы можете увидеть, что R 2 имеет такое же омическое значение, что и R 1 , и пропускает тот же ток. Падение напряжения на R 2 , следовательно, также равно 10 вольт.Если сложить эти два падения по 10 вольт, общее падение составит 20 вольт, что в точности равно приложенному напряжению. Для последовательной схемы тогда:
E T = E 1 = E 2 + E 3 =. . . E n
Пример: последовательная цепь состоит из трех резисторов, имеющих номиналы 20 Ом, 30 Ом и 50 Ом соответственно. Найдите приложенное напряжение, если ток через резистор 30 Ом равен 2 ампера. (Аббревиатура amp обычно используется для обозначения ампер.)
Для решения проблемы сначала рисуется электрическая схема и маркируется (рис. 3-18).
Рисунок 3-18. — Решение для приложенного напряжения в последовательной цепи.
Подстановка:
ПРИМЕЧАНИЕ. При использовании закона Ома величины для уравнения ДОЛЖНЫ быть взяты из ОДНОЙ части схемы. В приведенном выше примере напряжение на R 2 было вычислено с использованием тока через R 2 и сопротивления R 2 .
Величина падения напряжения на резисторе определяется приложенным напряжением и пропорционально сопротивлению цепи. Падения напряжения, возникающие в последовательной цепи, прямо пропорциональны сопротивлениям. Это результат того, что через каждый резистор протекает одинаковый ток — чем больше сопротивление резистора, тем больше падение напряжения на нем.
Последовательная цепь, состоящая из трех резисторов, имеет ток 3 ампера. Если R 1 = 20 Ом, R 2 = 60 Ом и R 3 = 80 Ом, каковы (а) полное сопротивление и (б) напряжение источника цепи?
Какое напряжение падает на каждом резисторе цепи, описанной в вопросе 17?
Если бы ток был увеличен до 4 ампер, каким было бы падение напряжения на каждом резисторе в цепи, описанной в вопросе 17?
Что нужно сделать со схемой, описанной в вопросе 17, чтобы увеличить ток до 4 ампер?
Отдел цепей и напряжений серии Отдел цепей и напряжений серииПример 1: Найдите полное эквивалентное сопротивление в следующей цепи
Пример 2: Для следующей цепи:
- Найдите общее сопротивление
- Найдите текущий i
- Найдите напряжение на резисторе 10 Ом
Решение
|
Пример 3: Для следующей цепи:
- Найдите общее значение сопротивления R T
- Найдите текущий i
- Найдите напряжение на отдельных резисторах
- Проверить закон напряжения Кирхгофа
Пример 4: Для следующей цепи:
- Найти V 1
- Найти V 2
- Проверить закон напряжения Кирхгофа вокруг замкнутого контура
Отдел напряжения :
В следующей схеме ток, проходящий через все последовательно включенные резисторы, равен Чтобы найти падение напряжения v i на резисторе R i , мы используем ток и значение резистора .Правая часть уравнения дает нам уравнение деления напряжения. |
Примеры:
Пример 5: Для следующей схемы
- Найдите общее значение сопротивления R T
- Найдите текущий i
- Найдите напряжение на резисторах
- Проверить закон напряжения Кирхгофа
Пример 6: Найдите ток для следующей цепи
Практические задачи :
(Щелкните изображение, чтобы просмотреть решение)
Задача 1: Найдите следующую схему.
Посмотреть решение
Решение: Применить закон Кирхгофа о напряжении |
Задача 2: Рассчитайте напряжения для следующей цепи.
Посмотреть решение
Решение: текущее, Применение закона Кирхгофа: |
Проблема 3: Найдите приложенное напряжение к следующей цепи, используя предоставленную информацию
Посмотреть решение
Проблема 4: Найдите значение резистора R , используя предоставленную информацию
Посмотреть решение
Задача 5 : Найти V x
Посмотреть решение
Упражнения:
ТОПОЛОГИЯ ЦЕПЕЙ И ЗАКОНЫ — Прикладное промышленное электричество
На этой странице мы изложим три принципа, которые вы должны понимать в отношении последовательных цепей:
Ток : величина тока одинакова для любого компонента в последовательной цепи.
Сопротивление : Общее сопротивление любой последовательной цепи равно сумме отдельных сопротивлений.
Напряжение : напряжение питания в последовательной цепи равно сумме отдельных падений напряжения.
Давайте взглянем на несколько примеров последовательных цепей, демонстрирующих эти принципы. Начнем с последовательной схемы, состоящей из трех резисторов и одной батареи:
Рисунок 3.1Первый принцип, который нужно понять о последовательных схемах, заключается в следующем:
Величина тока в последовательной цепи одинакова для любого компонента в цепи.
Общий ток серии
[латекс] \ tag {3.1} I_ {Total} = I_1 = I_2 = … = I_n [/ latex]
Это связано с тем, что в последовательной цепи существует только один путь прохождения тока. Поскольку электрический заряд проходит через проводники, как шарики в трубке, скорость потока (скорость мрамора) в любой точке цепи (трубки) в любой конкретный момент времени должна быть одинаковой.
По расположению 9-вольтовой батареи мы можем сказать, что ток в этой цепи будет течь по часовой стрелке от точки 1 к 2, к 3 к 4 и обратно к 1.Однако у нас есть один источник напряжения и три сопротивления. Как мы можем использовать здесь закон Ома?
Важная оговорка к закону Ома заключается в том, что все величины (напряжение, ток, сопротивление и мощность) должны относиться друг к другу в терминах одних и тех же двух точек в цепи. Мы можем увидеть эту концепцию в действии на примере схемы с одним резистором ниже.
Использование закона Ома в простой цепи с одним резисторомВ схеме с одной батареей и одним резистором мы можем легко вычислить любое количество, потому что все они относятся к одним и тем же двум точкам в цепи:
[латекс] I \: = \ frac {E} {R} [/ латекс]
[латекс] I \: = \ frac {9V} {3k \ Omega} [/ латекс]
[латекс] \ pmb {I = 3 мА} [/ латекс]
Поскольку точки 1 и 2 соединены вместе проводом с незначительным сопротивлением, как и точки 3 и 4, мы можем сказать, что точка 1 электрически является общей с точкой 2, а точка 3 электрически общей с точкой 4.Поскольку мы знаем, что между точками 1 и 4 (непосредственно через батарею) имеется электродвижущая сила 9 В, и поскольку точка 2 является общей для точки 1, а точка 3 — общей для точки 4, мы также должны иметь 9 В между точками 2. и 3 (прямо через резистор).
Следовательно, мы можем применить закон Ома ( I = E / R) к току через резистор, потому что мы знаем напряжение (E) на резисторе и сопротивление (R) этого резистора. Все термины (E, I, R) относятся к одним и тем же двум точкам в цепи, к одному и тому же резистору, поэтому мы можем безоговорочно использовать формулу закона Ома.
Использование закона Ома в схемах с несколькими резисторамиВ схемах, содержащих более одного резистора, мы должны соблюдать осторожность при применении закона Ома. В приведенном ниже примере схемы с тремя резисторами мы знаем, что у нас есть 9 вольт между точками 1 и 4, что является величиной электродвижущей силы, управляющей током через последовательную комбинацию R 1 , R 2 и R . 3 . Однако мы не можем взять значение 9 вольт и разделить его на 3 кОм, 10 кОм или 5 кОм, чтобы попытаться найти значение тока, потому что мы не знаем, сколько напряжения присутствует на любом из этих резисторов по отдельности.
Цифра 9 вольт — это всего величина для всей цепи, тогда как цифры 3к, 10к и 5кОм представляют собой отдельные величины для отдельных резисторов. Если бы мы включили цифру для общего напряжения в уравнение закона Ома с цифрой для отдельного сопротивления, результат не будет точно соответствовать какой-либо величине в реальной цепи.
Для R 1 закон Ома будет связывать величину напряжения на R 1 с током через R 1 , учитывая сопротивление R 1 , 3 кОм:
[латекс] I_ {R1} \: = \ frac {E_ {R1}} {R_1} [/ latex] или [латекс] E_ {R1} = I_ {R1} {(R_1)} [/ latex]
Но, поскольку мы не знаем напряжение на R 1 (только полное напряжение, подаваемое батареей на комбинацию из трех последовательно соединенных резисторов), и мы не знаем ток через R 1 , мы можем ‘ t делать какие-либо расчеты по любой из формул.То же самое касается R 2 и R 3 : мы можем применять уравнения закона Ома тогда и только тогда, когда все члены представляют свои соответствующие количества между одними и теми же двумя точками в цепи.
Итак, что мы можем сделать? Нам известно напряжение источника (9 вольт), приложенное к последовательной комбинации R 1 , R 2 и R 3 , и мы знаем сопротивление каждого резистора, но поскольку эти величины не входят в В том же контексте мы не можем использовать закон Ома для определения тока в цепи.Если бы мы только знали, что такое полное сопротивление для цепи: тогда мы могли бы вычислить общий ток с нашим значением для общего напряжения ( I = E / R ).
Объединение нескольких резисторов в эквивалентный общий резисторЭто подводит нас ко второму принципу последовательной схемы:
Общее сопротивление любой последовательной цепи равно сумме отдельных сопротивлений.
[латекс] \ tag {3.2} R_ {total} = R_1 + R_2 + … + R_n [/ латекс]
Это должно иметь интуитивный смысл: чем больше последовательно подключенных резисторов, через которые должен протекать ток, тем труднее будет протекать ток.
В примере задачи у нас были последовательно подключены резисторы 3 кОм, 10 кОм и 5 кОм, что дало нам общее сопротивление 18 кОм:
[латекс] R_ {total} = R_1 + R_2 + R_3 [/ латекс]
[латекс] R_ {total} = 3 \ text {k} \ Omega + 10 \ text {k} \ Omega + 5 \ text {k} \ Omega [/ latex]
[латекс] \ pmb {R_ {total} = 18 \ text {k} \ Omega} [/ latex]
По сути, мы вычислили эквивалентное сопротивление 1 R, 2 R и 3 R вместе.Зная это, мы могли бы перерисовать схему с одним эквивалентным резистором, представляющим последовательную комбинацию R 1 , R 2 и R 3 :
. Расчет тока цепи с использованием закона ОмаТеперь у нас есть вся необходимая информация для расчета тока цепи, потому что у нас есть напряжение между точками 1 и 4 (9 вольт) и сопротивление между точками 1 и 4 (18 кОм):
[латекс] I_ {total} \: = \ frac {E_ {total}} {R_ {total}} [/ латекс]
[латекс] \: = \ frac {9V} {18k \ Omega} [/ латекс]
[латекс] \ pmb {I_ {total} = 500 мкА} [/ латекс]
Расчет напряжений компонентов по закону ОмаЗная, что ток одинаков во всех компонентах последовательной цепи (и мы только что определили ток через батарею), мы можем вернуться к нашей исходной принципиальной схеме и отметить ток через каждый компонент:
Теперь, когда мы знаем величину тока, протекающего через каждый резистор, мы можем использовать закон Ома для определения падения напряжения на каждом из них (применяя закон Ома в его надлежащем контексте):
[латекс] E_ {R1} = I_ {R1} {R_1} [/ латекс]
[латекс] = (500 мкА) {(3кОм)} [/ латекс]
[латекс] \ pmb {E_ {R1} = 1.5V} [/ латекс]
[латекс] E_ {R2} = I_ {R2} {R_2} [/ латекс]
[латекс] = (500 мкА) {(10 кОм)} [/ латекс]
[латекс] \ pmb {E_ {R2} = 5V} [/ латекс]
[латекс] E_ {R3} = I_ {R3} {R_3} [/ латекс]
[латекс] = (500 мкА) {(5 кОм)} [/ латекс]
[латекс] \ pmb {E_ {R3} = 2.5V} [/ латекс]
Обратите внимание на падение напряжения на каждом резисторе, и как сумма падений напряжения (1,5 + 5 + 2,5) равна напряжению батареи (источника питания): 9 вольт.
Это третий принцип последовательных цепей:
Напряжение питания в последовательной цепи равно сумме отдельных падений напряжения.
Общее последовательное напряжение
[латекс] E_ {total} = E_1 + E_2 + … E_n \ tag {3.3} [/ latex]
Анализ простых последовательных цепей с помощью «табличного метода» и закона ОмаОднако метод, который мы только что использовали для анализа этой простой последовательной схемы, можно упростить для лучшего понимания.Используя таблицу для перечисления всех напряжений, токов и сопротивлений в цепи, становится очень легко увидеть, какие из этих величин могут быть правильно связаны в любом уравнении закона Ома:
Таблица 3.1
Правило для такой таблицы — применять закон Ома только к значениям в каждом вертикальном столбце. Например, E R1 только с I R1 и R 1 ; E R2 только с I R2 и R 2 ; и т.д. Вы начинаете свой анализ с заполнения тех элементов таблицы, которые даны вам с самого начала:
Как видно из расположения данных, мы не можем подать 9 вольт ET (полное напряжение) ни на одно из сопротивлений (R 1 , R 2 или R 3 ) в любая формула закона Ома, потому что они находятся в разных столбцах. Напряжение батареи 9 В составляет , а не , приложенное непосредственно к R 1 , R 2 или R 3 . Однако мы можем использовать наши «правила» для последовательных цепей, чтобы заполнить пустые места в горизонтальном ряду. В этом случае мы можем использовать правило ряда сопротивлений для определения общего сопротивления из суммы отдельных сопротивлений:
Теперь, введя значение общего сопротивления в крайний правый столбец («Общее»), мы можем применить закон Ома I = E / R к общему напряжению и общему сопротивлению, чтобы получить общий ток 500 мкА. :
Затем, зная, что ток распределяется поровну между всеми компонентами последовательной цепи (еще одно «правило» последовательной схемы), мы можем заполнить токи для каждого резистора из только что рассчитанного значения тока:
Наконец, мы можем использовать закон Ома для определения падения напряжения на каждом резисторе, по столбцу за раз:
Таблица 3.6Таким образом, последовательная цепь определяется как имеющая только один путь, по которому может течь ток. Из этого определения следуют три правила последовательных цепей: все компоненты имеют одинаковый ток; сопротивления складываются, чтобы равняться большему общему сопротивлению; а падение напряжения в сумме дает большее общее напряжение. Все эти правила находят корень в определении последовательной цепи. Если вы полностью понимаете это определение, то правила — не что иное, как сноски к определению.
- Компоненты в последовательной цепи имеют одинаковый ток:
[латекс] I_ {Всего} = I_1 = I_2 = I_3 =… = I_n [/ latex]
- Общее сопротивление в последовательной цепи равно сумме отдельных сопротивлений:
[латекс] R_ {Всего} = R_1 + R_2 + … + R_n [/ латекс]
- Общее напряжение в последовательной цепи равно сумме отдельных падений напряжения:
[латекс] E_ {Всего} = E_1 + E_2 + … + E_n [/ латекс]
В этом разделе мы изложим три принципа, которые вы должны понимать в отношении параллельных цепей:
Напряжение: Напряжение одинаково на всех компонентах параллельной цепи.
Ток: Полный ток цепи равен сумме токов отдельных ответвлений.
Сопротивление: Отдельные сопротивления уменьшите , чтобы равняться меньшему общему сопротивлению, вместо добавьте , чтобы получить общее.
Давайте взглянем на несколько примеров параллельных цепей, демонстрирующих эти принципы.
Начнем с параллельной схемы, состоящей из трех резисторов и одной батареи:
Рисунок 3.5 Напряжение в параллельных цепяхПервый принцип для понимания параллельных цепей заключается в том, что напряжение одинаково на всех компонентах в цепи . Это связано с тем, что в параллельной цепи есть только два набора электрически общих точек, и напряжение, измеренное между наборами общих точек, всегда должно быть одинаковым в любой момент времени.
[латекс] E_ {Total} = E_1 = E_2 = … = E_n \ tag {3.4} [/ latex]
Следовательно, в приведенной выше схеме напряжение на R 1 равно напряжению на R 2 , которое равно напряжению на R 3 , которое равно напряжению на батарее.
Это равенство напряжений можно представить в другой таблице для наших начальных значений:
Таблица 3.7 Применение закона Ома для простых параллельных схемКак и в случае с последовательными цепями, применимо то же предостережение для закона Ома: значения напряжения, тока и сопротивления должны быть в одном контексте, чтобы вычисления работали правильно.
Однако в приведенном выше примере схемы мы можем немедленно применить закон Ома к каждому резистору, чтобы найти его ток, потому что мы знаем напряжение на каждом резисторе (9 вольт) и сопротивление каждого резистора:
[латекс] I_ {R1} \: = \ frac {E_ {R1}} {R_1} [/ латекс]
[латекс] \: = \ frac {(9V)} {(10kΩ)} [/ latex]
[латекс] \ pmb {I_ {R1} \: = 0.9mA} [/ латекс]
[латекс] I_ {R2} \: = \ frac {E_ {R2}} {R_2} [/ латекс]
[латекс] \: = \ frac {(9V)} {(2kΩ)} [/ латекс]
[латекс] \ pmb {I_ {R2} \: = 4,5 мА} [/ латекс]
[латекс] I_ {R3} \: = \ frac {E_ {R3}} {R_3} [/ латекс]
[латекс] \: = \ frac {(9V)} {(1kΩ)} [/ latex]
[латекс] \ pmb {I_ {R3} = 9mA} [/ латекс]
Таблица 3.8На данный момент мы все еще не знаем, каков полный ток или полное сопротивление для этой параллельной цепи, поэтому мы не можем применить закон Ома к крайнему правому столбцу («Всего»). Однако, если мы внимательно подумаем о том, что происходит, должно стать очевидным, что общий ток должен равняться сумме всех токов отдельных резисторов («ответвлений»):
Рис. 3.6По мере того, как полный ток выходит из положительного (+) вывода аккумуляторной батареи в точке 1 и проходит по цепи, часть потока разделяется в точке 2, чтобы пройти через R 1 , еще часть разделяется в точке 3, чтобы уйти. через 2 рандов, а оставшаяся часть идет через 3 рандов.Подобно реке, разветвляющейся на несколько более мелких ручьев, общий расход всех потоков должен равняться расходу всей реки.
То же самое происходит, когда токи через R 1 , R 2 и R 3 соединяются, чтобы течь обратно к отрицательной клемме батареи (-) к точке 8: поток тока из точки 7 до точки 8 должно равняться сумме токов (ответвлений) через R 1 , R 2 и R 3 .
Это второй принцип параллельных цепей: полный ток цепи равен сумме токов отдельных ветвей .
Используя этот принцип, мы можем заполнить место ИТ в нашей таблице суммой I R1 , I R2 и I R3 :
Таблица 3.9 Как рассчитать полное сопротивление в параллельных цепяхНаконец, применив закон Ома к крайнему правому столбцу («Всего»), мы можем вычислить полное сопротивление цепи:
Таблица 3.10 Уравнение сопротивления в параллельных цепяхОбратите внимание на кое-что очень важное.Общее сопротивление цепи составляет всего 625 Ом: на меньше , чем у любого из отдельных резисторов. В последовательной цепи, где общее сопротивление было суммой отдельных сопротивлений, общее сопротивление должно было быть на больше, чем на , чем у любого из резисторов по отдельности.
Здесь, в параллельной цепи, наоборот: мы говорим, что отдельные сопротивления уменьшают , а не добавляют , чтобы получить общее .
Этот принцип завершает нашу триаду «правил» для параллельных цепей, точно так же, как было обнаружено, что у последовательных цепей есть три правила для напряжения, тока и сопротивления.
Математически соотношение между общим сопротивлением и отдельными сопротивлениями в параллельной цепи выглядит следующим образом:
Уравнение сопротивления в параллельных цепях[латекс] R_ {total} = \ frac {1} {\ frac {1} {R_1} + \ frac {1} {R_2} + … + \ frac {1} {R_n}} \ tag {3.5 } [/ латекс]
Три правила параллельных цепейТаким образом, параллельная цепь определяется как цепь, в которой все компоненты подключены между одним и тем же набором электрически общих точек.Другими словами, все компоненты подключены друг к другу через клеммы.
Из этого определения следуют три правила параллельных цепей:
Все компоненты имеют одинаковое напряжение.
Сопротивления уменьшаются до меньшего общего сопротивления.
Токи ответвления в сумме равняются большему общему току.
Как и в случае с последовательными цепями, все эти правила находят корень в определении параллельной цепи. Если вы полностью понимаете это определение, то правила — не что иное, как сноски к определению.
- Компоненты в параллельной цепи имеют одинаковое напряжение:
[латекс] E_ {Всего} = E_1 = E_2 = … = E_n [/ латекс]
- Общее сопротивление в параллельной цепи на меньше , чем любое из отдельных сопротивлений:
[латекс] R_ {Total} = \ frac {1} {\ frac {1} {R_1} + \ frac {1} {R_2} + … + \ frac {1} {R_n}} [/ латекс]
- Полный ток в параллельной цепи равен сумме токов отдельных ответвлений:
[латекс] I_ {Всего} = I_1 + I_2 +.2R} [/ латекс]
Этим легко управлять, добавив еще одну строку в нашу знакомую таблицу напряжений, токов и сопротивлений:
Таблица 3.11 Мощностьдля любого конкретного столбца таблицы может быть найдена с помощью соответствующего уравнения закона Ома ( соответствует в зависимости от того, какие цифры представлены для E, I и R в этом столбце).
Интересное правило для общей мощности по сравнению с индивидуальной мощностью состоит в том, что оно является аддитивным для любой конфигурации цепи : последовательной, параллельной, последовательной / параллельной или другой.Мощность — это мера скорости работы, и поскольку рассеиваемая мощность должна равняться полной мощности, подаваемой источником (источниками) (согласно Закону сохранения энергии в физике), конфигурация схемы не влияет на математику.
- Мощность складывается в любая конфигурация резистивной цепи :
[латекс] P_ {Всего} = P_1 + P_2 + … + P_n [/ латекс]
Напоминания при использовании закона ОмаОдна из наиболее распространенных ошибок, которые делают начинающие студенты-электронщики при применении законов Ома, — это смешивание контекстов напряжения, тока и сопротивления.Другими словами, ученик может ошибочно использовать значение I (ток) через один резистор и значение E (напряжение) через набор соединенных между собой резисторов, полагая, что они придут к сопротивлению этого резистора.
Не так! Запомните это важное правило: переменные, используемые в уравнениях закона Ома, должны быть общими для одних и тех же двух точек в рассматриваемой цепи. Я не могу переоценить это правило. Это особенно важно в последовательно-параллельных комбинированных схемах, где соседние компоненты могут иметь разные значения как для падения напряжения , так и для тока .
При использовании закона Ома для вычисления переменной, относящейся к отдельному компоненту, убедитесь, что напряжение, на которое вы ссылаетесь, относится только к этому единственному компоненту, а ток, который вы ссылаетесь, проходит исключительно через этот единственный компонент, а сопротивление, на которое вы ссылаетесь, равно исключительно для этого единственного компонента. Аналогичным образом, при вычислении переменной, относящейся к набору компонентов в цепи, убедитесь, что значения напряжения, тока и сопротивления относятся только к этому полному набору компонентов!
Хороший способ запомнить это — обратить пристальное внимание на две точки , завершающие анализируемый компонент или набор компонентов, убедившись, что рассматриваемое напряжение проходит через эти две точки, и что рассматриваемый ток является потоком электрический заряд от одной из этих точек до другой, что рассматриваемое сопротивление эквивалентно одному резистору между этими двумя точками, и что рассматриваемая мощность — это полная мощность, рассеиваемая всеми компонентами между этими двумя точками .
Примечания к «Табличному» методу анализа цепей«Табличный» метод, представленный как для последовательных, так и для параллельных цепей в этой главе, является хорошим способом сохранить контекст закона Ома правильным для любой конфигурации цепи. В таблице, подобной приведенной ниже, вам разрешено применять уравнение закона Ома только для значений одного вертикального столбца за раз:
Таблица 3.12Получение значений по горизонтали по столбцам допустимо в соответствии с принципами последовательных и параллельных цепей:
Таблица 3.13 Таблица 3.14«Табличный» метод не только упрощает управление всеми соответствующими величинами, но также облегчает перекрестную проверку ответов, упрощая поиск исходных неизвестных переменных другими методами или работая в обратном направлении для решения исходных данные значения из ваших решений. Например, если вы только что решили для всех неизвестных напряжений, токов и сопротивлений в цепи, вы можете проверить свою работу, добавив строку внизу для расчета мощности на каждом резисторе, чтобы посмотреть, добавляются ли все отдельные значения мощности. до полной мощности.Если нет, значит, вы где-то ошиблись! Хотя в этой технике «перекрестной проверки» вашей работы нет ничего нового, использование таблицы для упорядочивания всех данных для перекрестной проверки (-ий) приводит к минимуму путаницы.
- Примените закон Ома к вертикальным столбцам в таблице.
- Применить правила последовательного / параллельного горизонтального ряда в таблице.
- Проверьте свои расчеты, работая «в обратном направлении», чтобы попытаться прийти к первоначально заданным значениям (из ваших первых рассчитанных ответов), или решая количество с использованием более чем одного метода (из разных заданных значений).
Принцип, известный как Закон напряжения Кирхгофа (открытый в 1847 году немецким физиком Густавом Р. Кирхгофом), можно сформулировать так:
«Алгебраическая сумма всех напряжений в контуре должна равняться нулю»
[латекс] E_ {T} = E_1 + E_2 + … + E_n = 0 [/ латекс]
Под алгебраическим я имею в виду учет знаков (полярностей), а также величин.Под петлей я имею в виду любой путь, прослеживаемый от одной точки в цепи до других точек в этой цепи и, наконец, обратно в исходную точку.
Демонстрация закона напряжения Кирхгофа в последовательной цепиДавайте еще раз посмотрим на нашу примерную последовательную схему, на этот раз пронумеровав точки в цепи для опорного напряжения:
Рисунок 3.7Если бы мы подключили вольтметр между точками 2 и 1, красный измерительный провод к точке 2 и черный измерительный провод к точке 1, измеритель зарегистрировал бы +45 вольт.Обычно знак «+» не отображается, а скорее подразумевается для положительных показаний на дисплеях цифровых счетчиков. Однако для этого урока очень важна полярность показаний напряжения, поэтому я буду явно показывать положительные числа: E 2-1 = + 45V
Когда напряжение указывается с двойным нижним индексом (символы «2-1» в обозначении «E 2-1 »), это означает напряжение в первой точке (2), измеренное относительно второй точки. (1). Напряжение, указанное как «E cd », будет означать напряжение, указанное цифровым измерителем с красным измерительным проводом в точке «c» и черным измерительным проводом в точке «d»: напряжение в точке «c» относительно «D».
Рис. 3.8.Если бы мы взяли тот же вольтметр и измерили падение напряжения на каждом резисторе, обходя цепь по часовой стрелке с красным измерительным проводом нашего измерителя на точке впереди и черным измерительным проводом на точке сзади, получим следующие показания:
[латекс] E_ {3-2} = -10V [/ латекс]
[латекс] E_ {4-3} = -20 В [/ латекс]
[латекс] E_ {1-4} = -15 В [/ латекс]
Рисунок 3.9Мы уже должны быть знакомы с общим принципом для последовательных цепей, согласно которому отдельные падения напряжения в сумме составляют общее приложенное напряжение, но измерение падения напряжения таким образом и внимание к полярности (математическому знаку) показаний показывает другое. аспект этого принципа: все измеренные напряжения в сумме равны нулю:
В приведенном выше примере петля образована следующими точками в следующем порядке: 1-2-3-4-1.Не имеет значения, с какой точки мы начинаем или в каком направлении идем при отслеживании петли; сумма напряжений по-прежнему будет равна нулю. Чтобы продемонстрировать это, мы можем подсчитать напряжения в контуре 3-2-1-4-3 той же цепи:
Это может иметь больше смысла, если мы перерисуем наш пример последовательной схемы так, чтобы все компоненты были представлены в виде прямой линии:
Рисунок 3.10Это все та же последовательная схема, только компоненты расположены в другой форме.Обратите внимание на полярность падения напряжения на резисторе по отношению к батарее: напряжение батареи отрицательное слева и положительное справа, тогда как все падения напряжения на резисторе ориентированы в другую сторону: положительное слева и отрицательное справа. Это потому, что резисторы сопротивляются потоку электрического заряда, проталкиваемого батареей. Другими словами, «толкание», оказываемое резисторами против потока электрического заряда , должно быть в направлении, противоположном источнику электродвижущей силы.
Здесь мы видим, что цифровой вольтметр покажет на каждом компоненте в этой цепи, черный провод слева и красный провод справа, как показано горизонтально:
Рисунок 3.11Если бы мы взяли тот же вольтметр и считали напряжение по комбинациям компонентов, начиная с единственного R 1 слева и продвигаясь по всей цепочке компонентов, мы увидим, как напряжения складываются алгебраически (до нуля):
Рисунок 3.12Тот факт, что последовательные напряжения складываются, не должен быть загадкой, но мы заметили, что полярность этих напряжений сильно влияет на то, как складываются цифры. При считывании напряжения на R 1 —R 2 и R 1 —R 2 —R 3 (я использую символ «двойное тире» «-» для обозначения серии соединение между резисторами R 1 , R 2 и R 3 ), мы видим, как измеряемые напряжения последовательно увеличиваются (хотя и отрицательные) величины, потому что полярности отдельных падений напряжения имеют одинаковую ориентацию (положительный слева , отрицательный справа).Сумма падений напряжения на R 1 , R 2 и R 3 равна 45 вольт, что соответствует выходу батареи, за исключением того, что полярность батареи противоположна падению напряжения на резисторе (отрицательный слева, положительный справа), поэтому мы получаем 0 вольт, измеренный на всей цепочке компонентов.
То, что мы должны получить ровно 0 вольт на всей струне, тоже не должно быть тайной. Глядя на схему, мы видим, что крайний левый угол струны (левая сторона R 1 : точка номер 2) напрямую соединен с крайним правым уголком струны (правая сторона батареи: точка номер 2), так как необходимо для завершения схемы.Поскольку эти две точки соединены напрямую, они являются электрически общими , друг с другом. И, как таковое, напряжение между этими двумя электрически общими точками должно быть равным нулю.
Демонстрация закона напряжения Кирхгофа в параллельной цепиЗакон Кирхгофа о напряжении (иногда для краткости обозначаемый как KVL ) будет работать для любой конфигурации цепи вообще, а не только для простой серии. Обратите внимание, как это работает для этой параллельной цепи:
Рисунок 3.13В параллельной схеме напряжение на каждом резисторе такое же, как и напряжение питания: 6 вольт. Суммируя напряжения вокруг контура 2-3-4-5-6-7-2, получаем:
Обратите внимание, как я обозначил конечное (суммарное) напряжение как E 2-2 . Поскольку мы начали нашу пошаговую последовательность в точке 2 и закончили в точке 2, алгебраическая сумма этих напряжений будет такой же, как напряжение, измеренное между той же точкой (E 2-2 ), которое, конечно, должно быть равно нулю. .
Действие закона Кирхгофа о напряжении независимо от топологии цепиТот факт, что эта цепь является параллельной, а не последовательной, не имеет ничего общего с правомерностью закона Кирхгофа о напряжении. В этом отношении схема может быть «черным ящиком» — конфигурация ее компонентов полностью скрыта от нашего взгляда, с набором открытых клемм для измерения напряжения между ними — и KVL все равно останется верным:
Рисунок 3.14.Попробуйте выполнить любой порядок шагов от любого терминала на приведенной выше диаграмме, вернувшись к исходному терминалу, и вы обнаружите, что алгебраическая сумма напряжений всегда равна нулю.
Более того, «петля», которую мы отслеживаем для KVL, даже не обязательно должна быть реальным током в прямом смысле этого слова. Все, что нам нужно сделать, чтобы соответствовать KVL, — это начинать и заканчивать в одной и той же точке цепи, подсчитывая падения напряжения и полярности при переходе между следующей и последней точкой. Рассмотрим этот абсурдный пример, отслеживая «петлю» 2-3-6-3-2 в той же параллельной цепи резистора:
Рисунок 3.15 Использование закона напряжения Кирхгофа в сложной цепиKVL можно использовать для определения неизвестного напряжения в сложной цепи, где известны все другие напряжения вокруг определенного «контура».В качестве примера возьмем следующую сложную схему (фактически две последовательные цепи, соединенные одним проводом внизу):
Рисунок 3.16Чтобы упростить задачу, я опустил значения сопротивления и просто указал падение напряжения на каждом резисторе. Две последовательные цепи имеют общий провод между собой (провод 7-8-9-10), что позволяет измерять напряжение между двумя цепями.
Если бы мы хотели определить напряжение между точками 4 и 3, мы могли бы составить уравнение KVL с напряжением между этими точками как неизвестным:
[латекс] E_ {4-3} + E_ {9-4} + E_ {8-9} + E_ {3-8} = 0 [/ латекс]
[латекс] E_ {4-3} + 12 В + 0 В + 20 В = 0 В [/ латекс]
[латекс] E_ {4-3} + 32V = 0 [/ латекс]
[латекс] \ pmb {E_ {4-3} = -32V} [/ латекс]
Рисунок 3.17 Рисунок 3.18 Рисунок 3.19 Рисунок 3.20Обходя контур 3-4-9-8-3, мы записываем значения падения напряжения так, как их регистрировал бы цифровой вольтметр, измеряя с помощью красного измерительного провода на острие впереди и черного измерительного провода на точка позади, когда мы продвигаемся по петле. Следовательно, напряжение от точки 9 до точки 4 является положительным (+) 12 вольт, потому что «красный провод» находится в точке 9, а «черный провод» — в точке 4. Напряжение от точки 3 до точки 8 является положительным. (+) 20 вольт, потому что «красный провод» находится в точке 3, а «черный провод» — в точке 8.Напряжение от точки 8 до точки 9, конечно, равно нулю, потому что эти две точки электрически общие.
Наш окончательный ответ для напряжения от точки 4 до точки 3 — отрицательное (-) 32 вольта, что говорит нам, что точка 3 на самом деле положительна по отношению к точке 4, именно то, что цифровой вольтметр показал бы красным проводом в точке 4. и черный отрыв в точке 3:
Рис. 3.21.Другими словами, первоначальное размещение наших «выводов счетчика» в этой проблеме KVL было «задом наперед».«Если бы мы сгенерировали наше уравнение KVL, начиная с E 3-4 вместо E 4-3 , шагая по той же петле с противоположной ориентацией измерительных проводов, окончательный ответ был бы E 3-4 = + 32 вольта:
Рис. 3.22Важно понимать, что ни один из подходов не является «неправильным». В обоих случаях мы приходим к правильной оценке напряжения между двумя точками 3 и 4: точка 3 положительна по отношению к точке 4, а напряжение между ними составляет 32 вольта.
- Закон Кирхгофа о напряжении (KVL): «Алгебраическая сумма всех напряжений в контуре должна равняться нулю»
Закон Кирхгофа о течениях, часто сокращаемый до KCL, гласит, что «алгебраическая сумма всех токов, входящих и выходящих из узла, должна равняться нулю».
Этот закон используется для описания того, как заряд входит и покидает точку соединения или узел на проводе.
Вооружившись этой информацией, давайте теперь рассмотрим пример применения закона на практике, почему он важен и как он был разработан.
Обзор параллельной цепиДавайте внимательнее рассмотрим эту последнюю параллельную схему примера:
Рисунок 3.23 Таблица 3.15Решение для всех значений напряжения и тока в этой цепи:
На данный момент мы знаем значение тока каждой ветви и полного тока в цепи. Мы знаем, что полный ток в параллельной цепи должен равняться сумме токов ответвления, но в этой цепи происходит нечто большее, чем просто это.Взглянув на токи в каждой точке соединения проводов (узле) в цепи, мы должны увидеть кое-что еще:
Рисунок 3.24 3.7. 3 тока на входе и выходе из узлаВ каждом узле положительной «шины» (провода 1-2-3-4) у нас есть разделение тока от основного потока к каждому последующему резистору ответвления. В каждом узле на отрицательной «шине» (провод 8-7-6-5) у нас есть ток, сливающийся вместе, чтобы сформировать основной поток от каждого последовательного резистора ответвления.Этот факт должен быть довольно очевиден, если вы подумаете об аналогии контура водопровода с каждым ответвлением, действующим как тройник, разделением или слиянием потока воды с основным трубопроводом, когда он движется от выхода водяного насоса к обратному каналу. резервуар или отстойник.
Если мы внимательно рассмотрим один конкретный узел «тройник», такой как узел 6, мы увидим, что ток, входящий в узел, равен по величине току, выходящему из узла:
Рисунок 3.25Сверху и справа у нас есть два тока, входящие в соединение проводов, обозначенное как узел 6.Слева у нас есть единственный ток, выходящий из узла, равный по величине сумме двух входящих токов. Обратимся к аналогии с водопроводом: пока в трубопроводе нет утечек, поток, поступающий в фитинг, должен также выходить из фитинга. Это верно для любого узла («подгонки»), независимо от того, сколько потоков входит или выходит. Математически мы можем выразить это общее соотношение как таковое: [латекс] I_ {существующий} = I_ {ввод} [/ латекс]
Действующий закон Кирхгофаг.Кирхгоф решил выразить его в несколько иной форме (хотя и математически эквивалентной), назвав его Текущий закон Кирхгофа (KCL):
[латекс] I_ {ввод} = -I_ {существующий} = 0 [/ латекс]
Текущий закон Кирхгофа, кратко изложенный в одной фразе, гласит:
«Алгебраическая сумма всех токов, входящих и выходящих из узла, должна равняться нулю»
[латекс] I_ {T} = I_1 + I_2 + … + I_n = 0 [/ латекс]
То есть, если мы присвоим каждому току математический знак (полярность), обозначающий, входят ли они (+) или выходят (-) из узла, мы можем сложить их вместе, чтобы получить гарантированно нулевое значение.
Взяв наш пример узла (номер 6), мы можем определить величину тока, выходящего слева, задав уравнение KCL с этим током в качестве неизвестного значения:
[латекс] I_2 + I_3 + I_ {2 + 3} = 0 [/ латекс]
[латекс] 2 мА + 3 мА + I_ {2 + 3} = 0 [/ латекс]
[латекс] \ text {… решение для I …} [/ латекс]
[латекс] I = -2 мА-3 мА [/ латекс]
[латекс] \ pmb {I = -5mA} [/ латекс]
Отрицательный знак (-) на значении 5 миллиампер говорит нам, что ток равен на выходе из узла , в отличие от токов 2 миллиампер и 3 миллиампер, которые оба должны быть положительными (и, следовательно, входит в узел). .Независимо от того, обозначает ли отрицательное или положительное значение текущий вход или выход, совершенно произвольно, если они являются противоположными знаками для противоположных направлений и мы остаемся последовательными в наших обозначениях, KCL будет работать.
Вместе законы напряжения и тока Кирхгофа представляют собой замечательную пару инструментов, полезных при анализе электрических цепей. Их полезность станет еще более очевидной в следующей главе («Сетевой анализ»), но достаточно сказать, что эти законы заслуживают того, чтобы их запомнил изучающий электронику не меньше, чем закон Ома.
- Текущий закон Кирхгофа (KCL): «Алгебраическая сумма всех токов, входящих и выходящих из узла, должна равняться нулю»
Ток и напряжение
- Изучив этот раздел, вы сможете:
- Опишите распределение электрических потенциалов (напряжений) и токов в электрических цепях.
- • Последовательные резистивные цепи.
- • Параллельные резистивные цепи.
- Рассчитайте распределение напряжений в резистивном делителе потенциала.
Ток и напряжение в резисторных цепях
В поисках неизвестного
Помимо определения сопротивления, закон Ома может использоваться для расчета напряжений и токов в резисторных цепях. Перед тем, как попробовать это, было бы неплохо взглянуть на некоторые основные факты о сетях резисторов.
Рис.4.0.1 Простая последовательная схема
Рис.4.0.2 Простая параллельная схема
В простой цепи СЕРИИ , показанной на рис. 4.0.1, одинаковый ток течет через все компоненты. Однако каждый компонент будет иметь разное НАПРЯЖЕНИЕ (p.d.) на нем. Сумма этих отдельных напряжений (V R1 + V R2 + V R3 и т. Д.) В последовательной цепи равна напряжению питания (ЭДС).
Однако в простой ПАРАЛЛЕЛЬНОЙ ЦЕПИ , показанной на рис. 4.0.2, одинаковое напряжение присутствует на всех компонентах, но через каждый компонент может протекать разный ТОК. Сумма этих отдельных составляющих токов в параллельной цепи равна току питания. (I S = I R1 + I R2 + I R3 и т. Д.)
Правило разделителя потенциала
Рис. 4.0.3 Делитель потенциала
Если два или более резистора соединены последовательно через потенциал (например,грамм. Напряжение питания), напряжение на каждом резисторе будет пропорционально сопротивлению этого резистора. V R1 ∝ R 1 и V R2 ∝ R 2 и т. Д.
Чтобы рассчитать напряжение на любом резисторе в делителе потенциала, умножьте напряжение питания (E) на пропорцию этого резистора к общему сопротивлению всех резисторов.
Например, если R 2 вдвое превышает значение R 1 , то на R 2 будет в два раза больше напряжения, чем на R 1 .Следовательно, напряжение на R 1 будет составлять одну треть напряжения питания (E), а напряжение на R 2 будет составлять две трети напряжения питания (E). Таким образом, если напряжение питания и значения резистора известны, тогда напряжение на каждом резисторе может быть вычислено с помощью ПРОПОРЦИИ, и как только напряжение на каждом резисторе известно, можно рассчитать напряжение в любой точке цепи.
Используя эти несколько фактов, можно получить огромное количество информации о токах и напряжениях в цепи, если известны значения сопротивлений цепи.Попробуйте сами с помощью нашей викторины на странице «Сетевые расчеты модуля» 4.6 «Резисторы и схемы».
Подключение источников питания параллельно или последовательно для увеличения выходной мощности
В некоторых приложениях использования одного источника питания может быть недостаточно для обеспечения мощности, необходимой для нагрузки. Причины использования нескольких источников питания могут включать избыточную работу для повышения надежности или увеличения выходной мощности. При обеспечении комбинированного питания необходимо следить за тем, чтобы все источники питания передавали его сбалансированным образом.
Источники питания, подключенные для резервирования
Резервные источники питания — это топология, в которой выходы нескольких источников питания соединены для повышения надежности системы, но не для увеличения выходной мощности. Резервные конфигурации обычно предназначены для получения выходного тока только от основных источников питания и для получения тока от резервных источников питания в случае отказа одного из основных источников питания. Поскольку отбор тока нагрузки создает нагрузку на компоненты в источнике питания, высокая надежность в системе достигается, когда ток не потребляется от резервных источников до тех пор, пока не возникнет проблема с одним из основных источников питания.
- Источники питания A и B аналогичны; Vout и максимальный Iout одинаковые
- Напряжение нагрузки равно напряжению питания
- Максимальный ток нагрузки равен максимальному выходному току одного источника
- Электронный переключатель подключает один из выходов питания к нагрузке
Источники питания с параллельными выходами
Обычная топология, используемая для увеличения выходной мощности, заключается в параллельном подключении выходов двух или более источников питания.В этой конфигурации каждый источник питания обеспечивает необходимое напряжение нагрузки, а параллельное подключение источников увеличивает доступный ток нагрузки и, следовательно, доступную мощность нагрузки.
Эту топологию можно успешно реализовать, но есть много соображений для обеспечения эффективности конфигурации. Для параллельных конфигураций предпочтительны источники питания с внутренними цепями, поскольку внутренние цепи улучшают эффективность распределения тока. Если источники питания, используемые в приложении для распределения тока, не имеют внутренних цепей распределения, необходимо использовать внешние методы, которые могут быть менее эффективными.
Основная проблема заключается в том, насколько равномерно ток нагрузки распределяется между источниками питания. Распределение тока нагрузки зависит как от конструкции источников питания, так и от конструкции внешней цепи и проводников, используемых для параллельного подключения выходов источников питания. Практически всегда при параллельном подключении используются одинаковые блоки питания из-за проблем, связанных с эффективной настройкой блоков питания. Однако можно настроить источники питания параллельно с согласованными выходными напряжениями и несовпадающими максимальными выходными токами.
Более подробное обсуждение параллельного подключения источников питания можно найти в нашем техническом документе Current Sharing with Power Supplies.
- Источники питания A и B должны иметь одинаковый Vout; Максимум Iout может быть разным
- Напряжение нагрузки равно напряжению питания
- Максимальный ток нагрузки равен сумме максимального выходного тока обоих источников
- Цепи контроля тока уравновешивают ток нагрузки между источниками питания
Источники питания с последовательными выходами
Другой вариант увеличения мощности, подаваемой на нагрузку, — это соединение выходов нескольких источников питания последовательно, а не параллельно.Некоторые из преимуществ использования последовательной топологии включают в себя: почти идеальное использование подачи питания между источниками, отсутствие необходимости в конфигурации или совместном использовании цепей, а также устойчивость к большому разнообразию конструкций приложений. Как упоминалось ранее, при параллельном подключении выходов источников питания каждый источник обеспечивает необходимое напряжение, а ток нагрузки распределяется между источниками. Для сравнения, когда выходы источников питания соединены последовательно, каждый источник обеспечивает требуемый ток нагрузки, а выходное напряжение, подаваемое на нагрузку, будет представлять собой комбинацию последовательно включенных источников.
Следует отметить, что когда блоки питания сконфигурированы с последовательным подключением выходов, источники питания не обязательно должны иметь аналогичные выходные характеристики. Ток нагрузки будет ограничен наименьшим допустимым током нагрузки любого из источников в конфигурации, а напряжение нагрузки будет суммой выходных напряжений всех источников в цепочке.
Есть несколько ограничений, налагаемых на источники питания, когда они используются в конфигурации с последовательным выходом.Одним из ограничений является то, что выход источников питания должен быть спроектирован так, чтобы выдерживать смещение напряжения из-за последовательной конфигурации. Это напряжение смещения обычно не является проблемой, но выходные напряжения источников питания с заземлением не могут быть суммированы на выходах других источников. Второе ограничение заключается в том, что выход источника питания может подвергаться обратному напряжению, если выход неактивен, когда активны остальные выходы в цепочке. Проблема обратного напряжения может быть легко решена путем размещения диода с обратным смещением на выходе каждого источника питания.Номинальное напряжение пробоя диода должно быть больше, чем выходное напряжение отдельного источника питания, а номинальный ток диода должен быть больше, чем максимальный номинальный выходной ток любого источника питания в последовательной цепочке.
- Источники питания A и B могут иметь разные максимальные значения Vout и Iout
- Напряжение нагрузки равно сумме выходных напряжений питания
- Максимальный ток нагрузки равен наименьшему из максимального выходного тока любого источника
- Диоды обратного смещения защищают выходы источников питания
Сводка
Источники питания, подключенные параллельно:
- Плохое использование мощности из-за допуска управления разделением тока между источниками
- Требуется специальная цепь для управления разделением тока между источниками
- Чувствительность к проектированию и изготовлению проводов, соединяющих источники питания параллельно
- Наиболее простая конструкция с аналогичными блоками питания
Источники питания, подключенные последовательно:
- Эффективное использование мощности ограничено только точностью выходного напряжения каждого источника
- Нет необходимости в цепях для управления распределением напряжения или тока между источниками
- Отсутствие чувствительности к конструкции или конструкции проводников, соединяющих источники питания в серии
- Простая конструкция с любой комбинацией источников питания
Хотя общий метод, используемый для увеличения мощности нагрузки, подаваемой от источников питания, заключается в параллельном подключении выходов, другим решением может быть последовательное соединение выходов нескольких источников питания.У поставщиков блоков питания, таких как CUI, есть технический персонал, который может помочь настроить приемлемое решение для этих и других проблем применения блоков питания.
Категории: Основы , Выбор продукта
Вам также может понравиться
У вас есть комментарии к этому сообщению или темам, которые вы хотели бы, чтобы мы освещали в будущем?
Отправьте нам письмо по адресу powerblog @ cui.ком
| Analog Devices
Некоторые файлы cookie необходимы для безопасного входа в систему, но другие необязательны для функциональной деятельности. Сбор наших данных используется для улучшения наших продуктов и услуг. Мы рекомендуем вам принять наши файлы cookie, чтобы обеспечить максимальную производительность и функциональность нашего сайта. Для получения дополнительной информации вы можете просмотреть сведения о файлах cookie.Узнайте больше о нашей политике конфиденциальности.
Принять и продолжить Принять и продолжитьФайлы cookie, которые мы используем, можно разделить на следующие категории:
- Строго необходимые файлы cookie:
- Это файлы cookie, которые необходимы для работы analog.com или определенных предлагаемых функций. Они либо служат единственной цели передачи данных по сети, либо строго необходимы для предоставления онлайн-услуг, явно запрошенных вами.
- Аналитические / рабочие файлы cookie:
- Эти файлы cookie позволяют нам выполнять веб-аналитику или другие формы измерения аудитории, такие как распознавание и подсчет количества посетителей и наблюдение за тем, как посетители перемещаются по нашему веб-сайту.Это помогает нам улучшить работу веб-сайта, например, за счет того, что пользователи легко находят то, что ищут.
- Функциональные файлы cookie:
- Эти файлы cookie используются для распознавания вас, когда вы возвращаетесь на наш веб-сайт. Это позволяет нам персонализировать наш контент для вас, приветствовать вас по имени и запоминать ваши предпочтения (например, ваш выбор языка или региона). Потеря информации в этих файлах cookie может сделать наши службы менее функциональными, но не помешает работе веб-сайта.
- Целевые / профилирующие файлы cookie:
- Эти файлы cookie записывают ваше посещение нашего веб-сайта и / или использование вами услуг, страницы, которые вы посетили, и ссылки, по которым вы переходили. Мы будем использовать эту информацию, чтобы сделать веб-сайт и отображаемую на нем рекламу более соответствующими вашим интересам. Мы также можем передавать эту информацию третьим лицам с этой целью.
Объяснение цепей постоянного тока — сопротивление, напряжение и потребляемая мощность
(Последнее обновление: 12 сентября 2021 г.) Цепи серии DC:Цепи серии DC — В этой статье мы рассмотрим цепи серии DC.Мы рассмотрим напряжение, ток, сопротивление и потребляемую мощность. Я все объясню с помощью очень простых принципиальных схем. Чтобы было понятно и понятно, я также поделюсь с вами результатами моделирования. Я буду использовать Proteus для моделирования.
Независимо от того, какую сложную схему вы выберете, вы всегда найдете электронные компоненты, соединенные последовательно или параллельно, вы также найдете параллельные и последовательные цепи одновременно. Для простоты я буду придерживаться только последовательной схемы.Если вы новичок в электронике и хотите узнать о схемах серии DC, эта статья для вас.
Вы можете подумать, почему нам нужно начинать с цепей постоянного тока? Ответ заключается в том, что как новичок вы можете проводить некоторые базовые эксперименты с использованием светодиодов, вам может потребоваться построить схему делителя напряжения и т. Д. Итак, после прочтения этой статьи вы сможете выполнять базовые вычисления, а также сможете использовать эти знания в некоторых практических проектах.
Ссылки для покупок на Amazon:Супер стартовый набор для начинающих
Двухканальный цифровой осциллограф / 200 МГц
Переменная поставка:
Цифровой мультиметр:
Комплект паяльника: «лучший»
Переносной сверлильный станок для печатных плат:
* Обратите внимание: это партнерские ссылки.Я могу получить комиссию, если вы купите компоненты по этим ссылкам. Буду признателен за вашу поддержку!
Сопротивление в последовательных цепях:Вы уже знаете основное определение резистора, резистор — это пассивный электронный компонент, который используется для ограничения протекания тока. У резистора нет полярности, поэтому не имеет значения, каким образом вы подключаете резистор. Итак, в любом случае, если мы поместим два резистора в линию, то есть одна ножка резистора соединена с другой ножкой резистора 2 и , это приведет к последовательной цепи.
В последовательных цепях общее сопротивление определяется простым сложением всех сопротивлений. Мы помечаем каждый резистор заглавной буквой R и нумеруем их как R1, R2, R3 и т. Д. Причина, по которой мы назначаем разные номера, заключается в том, что мы можем легко различить и легко указать на конкретный резистор. Как бы то ни было, общее сопротивление показано заглавной буквой R и нижним индексом T, который представляет общее сопротивление или полное сопротивление. Чтобы вычислить общее сопротивление последовательной цепи очень просто, мы просто складываем значения сопротивления каждого резистора.
Начнем с одного резистора R1 = 100 Ом. Два вывода резистора R1 соединены с плюсом батареи 5 В и контактами GND. Если я спрошу вас, каково полное сопротивление? Уверен, ваш ответ будет 100 Ом. Вы знаете, что на самом деле сопротивление немного выше, знаете почему? Потому что у проводов, которые мы используем, есть некоторое сопротивление, которое также добавляется. Но это значение обычно слишком мало для проводов небольшой длины, и мы обычно пренебрегаем этим сопротивлением. Так что, во всяком случае, если вы подключите еще один резистор в серии.
Теперь общее сопротивление будет R t = R1 + R2 = 100 + 10 = 110 Ом. Теперь вы можете продолжать добавлять резисторы последовательно. Все, что вам нужно, это сложить все сопротивления, чтобы найти общее сопротивление, это очень просто.
Помимо резисторов, вы также можете последовательно подключать другие электронные компоненты, вы можете подключать батареи последовательно для увеличения напряжения, вы можете подключать конденсаторы последовательно, вы можете подключать резистор последовательно со светодиодом, вы можете создавать цепь RLC , так далее.В последовательной цепи ток имеет только один путь, поэтому во всей последовательной цепи ток останется неизменным. Позвольте мне объяснить это с помощью схемы, приведенной ниже.
Три резистора R1, R2 и R3 соединены последовательно с батареей 5 В. Каждый резистор составляет 10 кОм. Поскольку все эти резисторы соединены последовательно, через все резисторы будет проходить одинаковый ток. Кстати, в этих схемах я использую поток электронов от отрицательного к положительному. Возможно, вы привыкли видеть обычный ток, который меняется от положительного к отрицательному.Электронный поток — это то, что на самом деле происходит. Обычной была исходная теория, но ее все еще преподают, потому что ее легко понять, просто помните о тех двух, на которых мы используем. Итак, вернемся к теме. Итак, в последовательной цепи будет течь такой же ток. Давайте проверим это, добавив амперметры. Амперметр — это устройство, которое используется для измерения тока. Амперметр следует подключать последовательно, а вольтметр — параллельно. Не забывайте об этом.
Это та же схема, но на этот раз я добавил последовательно амперметры.Вы можете видеть, что через все резисторы течет один и тот же ток. Вы также можете подтвердить это расчетами.
Мы знаем из закона Ома
В = ИК
В = 5 В
Общее сопротивление = R1 + R2 + R3 = 10K + 10K + 10K = 30K Ом
Общее сопротивление R т = 30 кОм
I =?
Итак,
Ток «I» = V / R
Ток = 5 / 30К
Ток = 0,17 мА
На этот раз я сделал небольшое изменение, то есть изменил номинал резистора R2, теперь он равен 1 кОм.Поскольку общее сопротивление изменилось, значение тока также изменилось, но вы можете видеть все тот же ток, протекающий через последовательную цепь. Давайте решим очень практичный пример, он вам всегда понадобится.
Серийный ток Цепей:Я уверен, что вы уже знакомы с тем фактом, что ток — это поток электронов. Здесь я собираюсь привести вам очень популярный пример: поток электроники подобен воде, которая течет по трубе, поэтому чем выше ток, тем больше электронов течет.Единица измерения тока — ампер, а сокращенно — амперы. Устройство под названием Амперметр используется для измерения тока, о котором я уже говорил. Я уже объяснял метод измерения тока с помощью цифрового мультиметра. Измеритель напряжения очень прост в использовании, нам нужно только подключить измерительные щупы мультиметра параллельно с компонентом или устройством, на котором нам нужно измерить напряжение. Предположим, вы хотите измерить напряжение батареи, все, что вам нужно, это подключить положительный измерительный провод вольтметра к положительной клемме батареи, а измерительный провод GND мультиметра — с клеммой GND аккумулятора, и вы выполните показание напряжения на дисплее мультиметра.Если амперметр подключен последовательно, то ток, протекающий по цепи, будет проходить через амперметр. Это также добавит сопротивление цепи, но обычно оно слишком мало и им обычно пренебрегают.
Мультиметрыдействительно хороши, поскольку они используются для измерения напряжения, сопротивления, целостности цепи, короткого замыкания и т. Д. Поэтому я настоятельно рекомендую вам купить его как можно скорее. Я предоставил ссылку для покупки на Amazon. Теперь мы рассмотрим несколько практических примеров.
Токоограничивающий резистор:Вы очень хорошо знаете, изучая электронику, самый первый эксперимент, с которого мы начинаем, — это зажечь светодиод «Light Emitting Diode».Думаешь, это легко? Что ж, поверьте мне, я видел, как сотни парней вычисляли неправильное значение, и в итоге они сжигали светодиод. Сначала вам нужно узнать о характеристиках светодиода, таких как ток и напряжение, которые ему нужны. Если у вас есть светодиод 5V и источник напряжения также 5 вольт, тогда нет необходимости в каких-либо расчетах, вы можете пойти дальше и соединить положительную ножку светодиода с положительной клеммой батареи и клеммой GND светодиода. с клеммой заземления аккумуляторной батареи.
Это простейшая ситуация, когда номинальные напряжения точно такие же.У вас есть светодиод на 5 В и батарея на 5 В или светодиод на 12 В и батарея на 12 В. Это очень простые ситуации.
Что делать, если напряжение светодиода отличается от напряжения батареи? Допустим, у нас есть светодиод со следующими характеристиками.
Напряжение светодиода = 2,5 В
Светодиодный ток = 10 мА
Нет сомнений в том, что этот светодиод выйдет из строя в кратчайшие сроки. Теперь у вас есть варианты, чтобы успешно зажечь этот светодиод. Вы можете уменьшить напряжение источника, или вам нужно будет использовать что-то, что снизит избыточное напряжение.Теперь самый простой способ — вы можете подключить резистор последовательно со светодиодом. Как вы можете видеть на следующей схеме, светодиод D1 соединен последовательно с резистором R1, и его значение неизвестно. Теперь нам нужно найти его ценность.
То, что мы уже знаем, есть;
Напряжение аккумуляторной батареи или напряжение источника составляет 5 вольт.
Ток светодиода составляет 10 мА, а
Напряжение светодиода составляет 2,5 В.
Итак, используя закон Ома, мы можем найти номинал резистора.Как известно
В = ИК
R = V / I
R = (5 В — 2,5 В) / 10 мА
Поскольку светодиод падает на 2,5 В, нам нужно вычесть это напряжение из напряжения батареи.
R = 200 Ом
Значит, номинал резистора должен быть не менее 200 Ом. На рынке доступны не все номиналы резисторов, поэтому вы можете выбрать резистор следующего более высокого номинала. Обычно я использую резистор на 330 Ом. Никогда не используйте резистор, значение которого меньше расчетного, иначе светодиод нагреется и срок службы сократится.Для лучшей производительности используйте резистор немного большего номинала. Как вы можете видеть на схеме ниже.
Вы можете видеть, что ток немного уменьшился, теперь он составляет 7,52 мА, и он останется холодным.
Теперь, допустим, у вас есть тот же светодиод, но на этот раз источник напряжения 12 вольт. Проделаем те же расчеты.
R = (12 В — 2,5 В) / 10 мА
На этот раз вы можете видеть, что я вычитал 2,5 вольта из 12 вольт, так как наша батарея 12 вольт.
R = 950 Ом
Если вы хотите включить 2.Для светодиода 5В вам понадобится резистор на 950 Ом. Как я сказал ранее, не все резисторы доступны на рынке, поэтому выберите резистор следующего большего номинала, который составляет 1000 Ом или 1 кОм. Вы можете легко найти этот резистор на рынке.
Теперь вы можете ясно видеть, что ток довольно близок к 10 мА, значение немного ниже 10 мА, и это потому, что мы немного используем резистор большего номинала, который просто идеален. Теперь, используя тот же метод, вы можете зажечь любой светодиод от любого источника напряжения.Вы уже знаете, что сопротивление противостоит приложенному напряжению, и сопротивление измеряется единицей Ом Ом.
Если вы используете резистор меньшего номинала, вы повредите светодиод. Если вы используете рассчитанный резистор или немного выше, он будет работать отлично, а если вы используете гораздо большее значение, светодиод не будет светиться. Потому что все напряжение будет падать на резисторе.
Напряжение в серии Цепей:Поток электронов возникает из-за напряжения, которое является толкающей силой, и это похоже на давление в трубе, теперь, по здравому смыслу, чем выше давление, тем больше воды будет течь.То же самое относится и к напряжению: чем больше напряжение вы приложите, тем больше электронов будет течь. Вы можете проверить это, подключив источник переменного напряжения со светодиодом или небольшой двигатель постоянного тока. Возьмем, к примеру, светодиод. Предположим, мы используем тот же светодиод на 2,5 В и 10 мА.
Первоначально, когда нет напряжения или нулевого напряжения, светодиод не горит, так как нет толкающей силы и нет потока электронов, или вы можете сказать, что нет потока тока. Но когда я начну увеличивать напряжение, наступит момент, когда светодиод начнет светиться.На изображении ниже вы можете видеть, что светодиод горит, но он довольно тусклый.
Еще я увеличил напряжение и он стал светиться ярче.
Теперь, если вы продолжите увеличивать напряжение, оно будет становиться все ярче и ярче, и наступит время, когда светодиод перегорит. Каждое электронное устройство или компонент имеет номинальные значения напряжения и тока, которые вы не должны пересекать. Прежде чем подавать напряжение, сначала проверьте характеристики напряжения и тока, которые вы можете найти в таблицах данных.
В отличие от тока, напряжение в последовательной цепи отличается. Когда напряжение подается на резисторы, включенные последовательно, напряжение делится между всеми резисторами в цепи. Их также называют схемами делителя напряжения. Давайте посмотрим на следующую схему.
Два резистора одинакового номинала R1 = 10K и R2 = 10K соединены последовательно с источником напряжения 12В. Когда резисторы одинакового номинала подключаются последовательно, напряжение делится поровну.
Теперь изменим значение R2 на 1 кОм.
Теперь вы можете видеть, что падение напряжения на резисторе R2 уменьшилось до 1,09 В. Таким образом вы можете увеличить количество резисторов, для практики вы можете использовать резисторы разного номинала и считывать напряжение на каждом резисторе. Вы можете использовать формулу деления напряжения для вычисления значений. Таким образом, независимо от того, сколько резисторов подключено последовательно, общее падение напряжения на всех резисторах будет точно таким же, как у источника напряжения.Вы также можете прочитать мою статью о KVL «Закон напряжения Кирхгофа» и KCL «Текущий закон Кирхгофа».
Приведу очень практический пример. Я довольно давно использую это в разных проектах на базе Arduino.
Резистор последовательно с кнопкой:В схеме ниже вы можете увидеть резистор 10 кОм, подключенный последовательно с кнопкой. Оба подключены к источнику 5 В. Посередине подключен вольтметр. Эта конфигурация резистора обычно известна как резистор подтягивания.Как вы можете видеть изначально, кнопка открыта, и вы можете видеть, что напряжение на вольтметре составляет 5 вольт.
Итак, напряжение между резистором и кнопкой составляет 5 вольт, вы можете взять провод из середины и подключить его к контакту ввода-вывода Arduino. На контакте будет 5 вольт.
При нажатии кнопки напряжение падает до 0 вольт. Теперь вы можете использовать эту кнопку как датчик. Когда кнопка открыта, он дает 5 В для Arduino, а когда кнопка закрыта, он дает ноль.В зависимости от сигналов 5v и 0 вы можете выполнять различные задачи с помощью Arduino.
Потребляемая мощность в последовательных цепях:Мы можем использовать следующие формулы для измерения энергопотребления.
Мощность (Вт) = (Напряжение) 2 / Сопротивление или
Мощность (Вт) = Напряжение x Ток
Как резистор может потреблять энергию?Допустим, резистор соединен с батареей. Вы можете подумать, считается ли резистор нагрузкой, потребляющей ток?
Если это все, что подключено к клеммам аккумулятора, то ответ — да.Резистор — это нагрузка на батарею, и, следовательно, течет ток. Резистор «потребляет» мощность (не ток), и эта мощность является произведением напряжения на резисторе на протекающий ток. Текущий расход определяется из уравнения I = V / R.
Мы не говорим потребляемый, потому что один и тот же ток течет по всей цепи, как кровь по кровеносной системе. Энергия или мощность, необходимая для проталкивания тока через резистор, исходит от батареи и в итоге нагревается в резисторе.По той же аналогии, что и кислород в кровотоке (я признаю, что это не лучшая аналогия). Резисторы «ограничивают ток», «рассеивают» мощность и «потребляют» энергию.
Интересным примером могут быть светодиоды на 1 вольт и источник питания на 12 вольт. используйте один резистор и, скажем, 10 светодиодов рассчитают падение напряжения, необходимое для резистора в этом примере. 10 светодиодов на 1 вольт означают, что последовательно включенные светодиоды снизят напряжение на 10 вольт.
Значит, резистор должен только упасть с 12 до 10 или 2 вольт.Кроме того, если бы каждый светодиод был 20 мА, для последовательной проводки потребовалось бы, чтобы резистор пропускал 2 В и 20 мА; резистор потребляет 40 мВт, поэтому подойдет резистор на 1/4 Вт.
, если вы использовали 10 светодиодов на 1 В и 10 резисторов, по одному на светодиод. Тогда резистор должен будет упасть с 12 до 1, и все равно будет достаточно 20 мА. Мощность каждого резистора должна составлять 224 мВт, и вам лучше всего использовать резистор на 1/2 Вт.
Но, поскольку у вас их 10, и каждый из них потребляет 224 мВт мощности, общее количество резисторов будет потреблять 2.24 Вт мощности.
Статьи по теме:Что такое резистор, разные типы резисторов и их применение
Последовательные и параллельные резисторы — примеры
Фоторезистор с Raspberry Pi
Углеродный резистор против металлопленочного резистора
Цветовая маркировка резистора
Нравится:
Нравится Загрузка .

