Определите емкость конденсатора 50 гц: Определите емкость конденсатора,сопротивление которого в цепи переменного тока частотой 50Гц

Определите ёмкость конденсатора, сопротивление которого в цепи переменного тока частотой 50 Гц равно 800 Ом. Помогите, пжлст.

Коэффициент трансформации

k = U1/U2 = 300/300000 = 1/1000

С другой стороны

k = U1/U2 = n1/n2

Отсюда находим n2 = n1*U2/U1 = 10*300000/300 = 1000 витков

Повтори то, что я пишу и хорошо поймешь: 
1 Открыть психрометрическую таблицу 2) Найти  разницу сухого и влажного 20-14=6   3) На пересечении таблицы сухой(20) и разница(6) найти 51 процент. Это и есть ответ. Абсолютную находят по таблице зависимости давления и плотности насыщенного пара от температуры По таблице при 20 плотность 17,3 г/см3 Значит абсолютная влажность 17,3 г

Так как вес равен 600н а формула веса mg ,g равен 10н на кг, то 600н делить на 10н на кг будет 60кг

7 месяцев назад

№ 2
Дано:
q = 2 нКл = 2*10⁻⁹ Кл
F = 0,4 мН = 0,4*10⁻³ Н
___________
E — ?

E = F/q = 0,4*10⁻³/2*10⁻⁹ = 200 000 Н/Кл    или   200 кН/Кл

№1
q = 4 мКл = 4*10⁻³ Кл
W = 1,6 Дж
__________
C — ?

W = q²/(2*C)
С = q² / (2*W) = (4*10⁻³)²/(2*1,6) = 5*10⁻⁶ Ф     или    5 мкФ

№ 3

Сила тяжести пылинки
F = m*g
Сила, действующая на пылинку со стороны электрического поля:
F =q*E

Приравниваем:
m*g = q*E
m = q*E/g = 1,6*10⁻¹¹*6*10³/10 = 9,6*10⁻⁹ кг

2 месяца назад

Ну если прям без взвешивания то надо знать прям знать массу гаек по размерам а так без взвешивания никак ты не узнаешь массу

10 месяцев назад

Однофазные цепи переменного тока (страница 2)

Решение:
Полное сопротивление схемы

Полная мощность на входе схемы

Потери мощности в обмотке катушки

Активная мощность схемы

Коэффициент мощности схемы

Из таблиц тригонометрических величин .
Активное сопротивление схемы

сопротивление дуги

Индуктивное сопротивление цепи представлено индуктивным сопротивлением катушки:

Эту же величину можно определить из треугольника сопротивлении (рис. 25, масштаб )

Искомая индуктивность катушки

Если бы вместо катушки был включен реостат, то сопротивление схемы имело бы ту же величину 6 Ом, но было бы чисто активным:

откуда

Потери мощности в катушке

Потери мощности в реостате

Отсюда ясно, что к. п. д. схемы выше при «погашении» избытка напряжения индуктивной катушкой. Действительно, к. п. д. при наличии катушки

к. п. д. при наличии реостата

Не следует забывать, что «погашение» избытка напряжения катушкой (или конденсатором) ухудшает коэффициент мощности (в данном примере при наличии катушки и при наличии реостата).

22. Последовательно с катушкой, параметры которой и L=15,92 мГн, включен реостат сопротивлением, .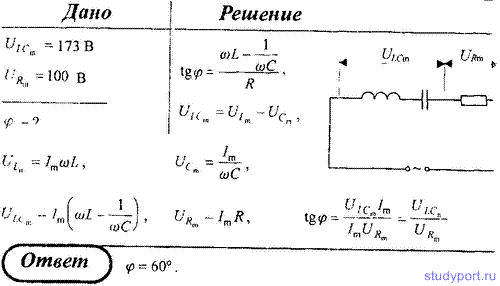 Цепь включена на напряжение U=130 В при частоте f=50 Гц.
Определить ток в цепи; напряжение на катушке и реостате; коэффициент мощности цепи и катушки.

Решение:
Индуктивное сопротивление катушки

Полное сопротивление катушки

Активное сопротивление цепи, состоящей из последовательно соединенных катушки и реостата,

Полное сопротивление цепи

На основании закона Ома ток в цепи

Напряжение на катушке

Напряжение на реостате

Арифметическая сумма много больше приложенного напряжения U=130 В. Коэффициент мощности цепи

Коэффициент мощности катушки

Следовательно, реостат увеличивает коэффициент мощности и сопротивление цепи, но уменьшает ток, увеличивает потребление энергии схемой.
Действительно, активная мощность катушки

активная мощность реостата

Так как цепь неразветвленная и ток один, то с него целесообразно начать построение векторной диаграммы (рис. 26).
Напряжение на реостате, представляющем собой чисто активное сопротивление, совпадает по фазе с током; на диаграмме вектор этого напряжения совпадает по направлению с вектором тока. Из конца вектора в сторону опережения вектора тока I, под углом в сторону, противоположную вращению стрелки часов, откладываем вектор напряжения на катушке . Векторы построены так с целью сложения по правилу многоугольника.

23. Неразветвленная цепь составлена из двух катушек: у первой катушки индуктивность и сопротивление , у второй катушки индуктивность и сопротивление .
Определить ток в цепи и напряжения на каждой катушке, а также построить в масштабе векторную диаграмму, если частота f=50 Гц и приложенное напряжение U=12,6 В.

Решение:
Индуктивное сопротивление первой катушки

т. е. оно численно равно активному сопротивлению , что обусловливает отставание тока по фазе от напряжения на 1/8 периода (на 45°).
Действительно, тангенс угла сдвига фаз

Индуктивное сопротивление второй катушки

Так как ее активное сопротивление то тангенс угла сдвига фаз

Построим в масштабе треугольник сопротивлений для рассматриваемой цепи. Для этого зададимся масштабом сопротивлений . Тогда на диаграмме сопротивление 1,57 Ом будет изображено отрезком 15,7 мм, сопротивление 2,7 Ом — отрезком 27 мм и т. д. На рис. 27 отрезок, изображающий активное сопротивление , отложен в горизонтальном направлении, а отрезок, изображающий индуктивное сопротивление , — в вертикальном направлении под прямым углом к .

Полное сопротивление первой катушки является гипотенузой прямоугольного треугольника. Из вершины с этого треугольника в горизонтальном направлении отложен отрезок, изображающий сопротивление , и под прямым углом к нему вверх — отрезок, изображающий сопротивление . Гипотенуза се прямоугольного треугольника означает полное сопротивление второй катушки.
Из рис. 27 видно, что отрезок ае, изображающий полное сопротивление z неразветвленной цепи из двух катушек, не равен сумме отрезков ас и се, т. е. . Чтобы определить полное сопротивление z рассматриваемой цепи, следует сложить отдельно активные (, отрезок аf) и индуктивные (, отрезок ef) сопротивления катушек.
Гипотенуза ае, означающая полное сопротивление z цепи, определяется по теореме Пифагора:

Ток в цепи определяется по закону Ома:

Напряжение на первой катушке

Напряжение на второй катушке

Строим векторную диаграмму (рис. 28), приняв масштабы:
а) для тока ; тогда вектор тока изобразится отрезком длиной 25 мм;
б) для напряжения ; при этом вектор напряжения будет иметь длину 55,2 мм, вектор напряжения — длину 71 мм, а вектор приложенного напряжения — длину 126 мм.
Начало вектора совмещено с концом вектора для возможности сложения векторов напряжений но правилу многоугольника (напряжение, приложенное к неразветвленной цепи катушек, равно геометрической сумме напряжений отдельных катушек).

 

StudyPort.Ru — Механические и электромагнитные колебания

Страница 1 из 6

4. Колебания и волны

1. Гармонические колебания величины s описываются уравнением s = 0,02 cos (6πt + π/3), м.

Определите: 1) амплитуду колебаний; 2) циклическую частоту; 3) частоту колебаний; 4) период колебаний.

2. Запишите уравнение гармонического колебательного движения точки, совершающей колебания с амплитудой A = 8 см, если за t = 1 мин совершается n = 120 колебаний и начальная фаза колебаний равна 45°.

3. Материальная точка совершает гармонические колебания с амплитудой A = 4 см и периодом T = 2 с. Напишите уравнение движения точки, если ее движение начинается из положения x₀ = 2 см.

4. Точка совершает гармонические колебания с периодом T = 6 с и начальной фазой, равной нулю. Определите, за какое время, считая от начала движения, точка сместится от положения равновесия на половину амплитуды.

5. Напишите уравнение гармонического колебания точки, если его амплитуда A = 15 см, максимальная скорость колеблющейся точки v_max = 30 см/с, начальная фаза φ = 10°.

6. Точка совершает гармонические колебания по закону x = 3 cos (πt/2 + π/8), м. Определите: 1) период T колебаний: 2) максимальную скорость V_max точки; 3) максимальное ускорение a_max точки.

7. Точка совершает гармонические колебания с амплитудой A = 10 см и периодом T = 5 с. Определите для точки: 1) максимальную скорость; 2) максимальное ускорение.

8. Скорость материальной точки, совершающей гармонические колебания, задается уравнением v(t) = -6 sin 2 πt, м/с. Запишите зависимость смещения этой точки от времени.

9. Материальная точка совершает колебания согласно уравнению x = A sin ωt. В какой-то момент времени смещение точки x₁ = 15 см. При возрастании фазы колебания в два раза смещение x₂ оказалось равным 24 см. Определите амплитуду A колебания.

10. Материальная точка совершает гармонические колебания согласно уравнению x = 0,02 cos (πt + π/2), м. Определите: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу колебаний; 4) максимальную скорость точки; 5) максимальное ускорение точки; 6) через сколько времени после начала отсчета точка будет проходить через положение равновесия.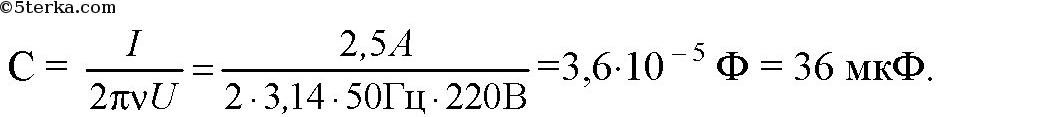

11. Определите максимальные значения скорости и ускорения точки, совершающей гармонические колебания с амплитудой A = 3 см и периодом T = 4 с.

12. Материальная точка, совершающая гармонические колебания с частотой ν = 1 Гц, в момент времени t = 0 проходит положение, определяемое координатой х₀ = 5 см, со скоростью v₀ = -15 см/с. Определите амплитуду колебаний.

13. Тело массой m = 10 г совершает гармонические колебания по закону х = 0,1 cos(4πt + π/4), м. Определите максимальные значения: 1) возвращающей силы; 2) кинетической энергии.

14. Материальная точка массой m = 50 г совершает гармонические колебания согласно уравнению x = 0,1 cos 3πt/2, м. Определите: 1) возвращающую силу F для момента времени t = 0,5 с; 2) полную энергию Е точки.

15. Материальная точка массой m = 20 г совершает гармонические колебания по закону x = 0,1 cos(4πt + π/4), м. Определите полную энергию Е этой точки.

16.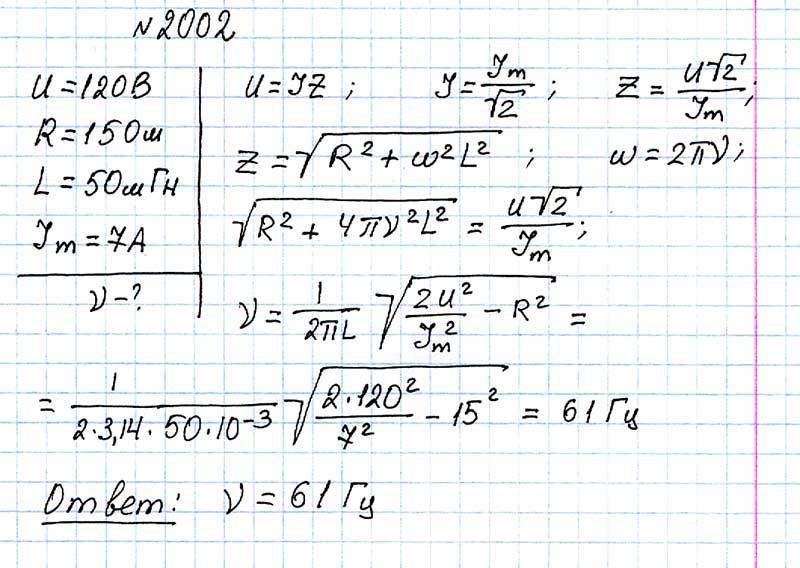 Полная энергия E гармонически колеблющейся точки равна 10 мкДж, а максимальная сила F_max, действующая на точку, равна -0,5 мН. Напишите уравнение движения этой точки, если период T колебаний равен 4 с, а начальная фаза φ = π/6.

17. Определите отношение кинетической энергии T точки, совершающей гармонические колебания, к ее потенциальной энергии П, если известна фаза колебания.

18. Определите полную энергию материальной точки массой m, колеблющейся по закону x = A cos(ω₀t + φ).

19. Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой A = 8 см. Определите жесткость k пружины, если известно, что максимальная кинетическая энергия T_max груза составляет 0,8 Дж.

20. Материальная точка колеблется согласно уравнению х = A cos ωt, где A = 5 см и ω = π/12 с

-1. Когда возвращающая сила F в первый раз достигает значения -12 мН, потенциальная энергия П точки оказывается равной 0,15 мДж. Определите: 1) этот момент времени t; 2) соответствующую этому моменту фазу ωt.

цепь переменного тока содержащая емкость индуктивность и сопротивление



цепь переменного тока содержащая емкость индуктивность и сопротивление

38)

ЦЕПЬ ПЕРЕМЕННОГО ТОКА, СОДЕРЖАЩАЯ ЕМКОСТЬ

Если в цепь постоянного, тока включить конденсатор (идеаль­ный — без потерь), то в течение очень короткого времени после включения по цепи потечет зарядный ток. После того как конден­сатор зарядится до напряжения, равного напряжению источника, кратковременный ток в цепи прекратится. Следовательно, для постоянного тока конденсатор представляет собой разрыв цепи, или, иными словами, бесконечно большое сопротивление.

Если же конденсатор включить в цепь переменного тока, то он будет заряжаться попеременно то в одном, то в другом направлении.

При этом в цепи будет проходить переменный ток. Рассмотрим это явление подробнее.

В момент включения напряжение на конденсаторе равно нулю. В течение первой четверти периода, когда напряжение сети будет возрастать (рис. 143), конденсатор будет заряжаться.

По мере накопления зарядов на обкладках конденсатора напря­жение конденсатора увеличивается. Когда напряжение сети к концу первой четверти периода достигнет максимального значения  Um, напряжение конденсатора также станет равным Um, заряд конден­сатора прекращается и ток в цепи становится равным нулю. Ток в цепи конденсатора можно определить по формуле

где ∆q — количество электричества, протекающее по цепи за время ∆t.

 Из электростатики известно:

где   С — емкость конденсатора;

u — напряжение сети;

uc — напряжение конденсатора. Окончательно для тока имеем

Из последнего выражения видно, что, когда  ∆u/∆t   максимально (положения a, в, d),  i также максимально.

 

Когда  ∆u/∆t   = 0 (положения   б, г на рис. 143), то i также равно нулю.

Во вторую четверть периода напряжение сети будет уменьшать­ся, и конденсатор начнет разряжаться. Ток в цепи меняет свое направление на обратное.

В следующую половину периода напряжение сети меняет свое направление и наступает перезаряд конденсатора и затем снова его разряд.

Из рис. 143 видно, что ток I в цепи с емкостью в своих изменениях опережает по фазе напряжение конденсатора на 1/4 периода, или 90°.

Сравнивая векторные диаграммы цепей с индуктивностью и емкостью, мы видим, что индуктивность и емкость на фазу тока влияют прямо противоположно.

Пользуясь высшей математикой, можно доказать, что ток в цепи с емкостью пропорционален напряжению Uc, приложенному к конденсатору, угловой частоте w и величине емкости конденсатора  C:

Обозначим

Величина Хс называется емкостным сопротивле­нием, или реактивным сопротивлением ем­кости, и измеряется в омах. Выражение закона Ома для цепи переменного тока, содержащей емкость, имеет вид

Та часть напряжения сети, которая приложена к конденсатору, называется емкостным падением напряжения (или   реактивной   слагающей   напряжения)   и   обозначается   Uc:

Емкостное сопротивление Хс, так же как индуктивное сопро­тивление xL, зависит от частоты переменного тока.

Но если с увеличением частоты индуктивное сопротивление увеличивается, то емкостное сопротивление, наоборот, будет умень­шаться.

Пример 6. Определить сопротивление конденсатора емкостью 5 мкф при частоте 50 гц:

при частоте 400 гц:

 

На рис. 144 показана кривая мгновенной мощности в цепи с емкостью. Из чертежа видно, что в первую четверть периода цепь с емкостью забирает из сети энергию, которая запасается в электрическом поле конденсатора.

Энергию, запасаемую конденсатором к моменту, когда напряже­ние на нем равно максимальному значению, можно определить по известной формуле CU2м/2.

В следующую четверть периода конденсатор разряжается на сеть, отдавая ей ранее запасенную в нем энергию.

За вторую половину периода явление колебаний энергии пов­торяется. Таким образом, в цепи с емкостью происходит лишь обмен энергией между сетью и конденсатором без ее потерь.

Поэтому средняя за период мощность, или активная мощность, цепи с емкостью равна нулю, как и в цепи с индуктивностью.

Из графика, изображенного на рис. 144, видно, что мгновенная мощность в цепи с емкостью два раза в течение каждого периода (когда wt = 45°, 135° и т. д.) достигает максимального значения, равного

 

Этой величиной принято характеризовать количественно про­цесс обмена энергии между источником и электрическим полем конденсатора. Ее также называют реактивной мощностью и обозначают буквой Q.

Учитывая,, что в рассматриваемой цепи U = IХc, получим сле­дующее выражение для реактивной мощности:

В сеть переменного тока напряжением 220

№ 1995
Конденсатор и электрическая лампочка включены последовательно в цепь переменного тока напряжением 440 В и частотой 50 Гц. Какую емкость должен иметь конденсатор для того, чтобы через лампочку протекал ток 0,5 А и падение напряжения на ней было 110 В?

№ 2002
В сеть переменного тока с напряжением 120 В последовательно включены проводник с активным сопротивлением 15 Ом и катушка индуктивностью 50 мГн. Найти частоту тока, если амплитуда тока в сети равна 7 А.

№ 2009
В цепь переменного тока напряжением 220 В и частотой 50 Гц включены последовательно емкость 35,4 мкФ, сопротивление 100 Ом и индуктивность 0,7 Гн. Найти ток в цепи и падения напряжения на емкости, сопротивлении и катушке.

Reshak.ru — сборник решебников для учеников старших классов. Здесь можно найти решебники, ГДЗ, переводы текстов по школьной программе. Практически весь материал, собранный на сайте — сделанный для людей. Все решебники выполнены качественно, с приятной навигацией. Вы сможете скачать гдз, решебник английского, улучшить ваши школьные оценки, повысить знания, получить намного больше свободного времени.

Главная задача сайта: помогать школьникам в решении домашнего задания. Кроме того, весь материал гдз совершенствуется, добавляются новые сборники решений.

Информация

© adminreshak.ru

Если можно, расписать полностью. 1. В сеть переменного тока напряжением 220 В включена
катушка индуктивностью 50 мГн. а) чему равна частота переменного тока, если сила тока в цепи 1,75 А? Активным сопротивлением катушки пренебречь.
б) определите ёмкость конденсатора, который нужно включить в данную цепь, чтобы в ней наступил резонанс.
в) определить резонансную частоту в цепи, если последовательно с имеющимся конденсатором включить такой же конденсатор.

2. Первичная обмотка понижающего трансформатора содержит 10000 витков и включена в сеть переменного тока напряжением 380 В.
а) чему равно напряжение во вторичной обмотке, если она состоит из 1000 витков?
б) сопротивление вторичной обмотки трансформатора 1 ом, сила тока 3 А. Чему равно напряжение на нагрузке, подключенной к вторичной обмотке трансформатора?
в) чему равен КПД трансформатора?
Заранее премного благодарна

Урок 9. конденсатор и катушка индуктивности в цепи переменного электрического тока — Физика — 11 класс

Физика, 11 класс

Урок 9. Конденсатор и катушка индуктивности в цепи переменного электрического тока

Перечень вопросов, рассматриваемых на уроке:

Процессы, происходящие в цепи переменного электрического тока при наличии конденсатора и катушки индуктивности;

Устройство и принцип действия генератора переменного тока и трансформатора;

Автоколебания;

Проблемы передачи электроэнергии и способы повышения эффективности её использования.

Глоссарий по теме

Автоколебания – незатухающие колебания в системе, поддерживаемые за счет постоянного источника энергии.

Электрические машины преобразующие механическую энергию в электрическую называются генераторами.

Трансформатор – устройство, применяемое для повышения или понижения переменного напряжения.

Коэффициент трансформации – величина равная отношению напряжений в первичной и вторичной обмотках трансформатора.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 86 – 95.

Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2014. – С. 128 – 132.

Степанова. Г.Н. Сборник задач по физике. 10-11 класс. М., Просвещение 1999 г.

Е.А. Марон, А.Е. Марон. Контрольные работы по физике. М., Просвещение, 2004

Основное содержание урока

Переменный ток, которым мы пользуемся, вырабатывается с помощью генераторов переменного тока на электростанциях. Для передачи произведенной электроэнергии строятся линии электропередачи. В каждом населенном пункте имеются трансформаторы. Какую роль играют трансформаторы при передаче электроэнергии? Об этом мы поговорим на данном уроке.

В июле 1832 года Фарадей получил анонимное письмо, в котором автор описывал устройство созданного им генератора постоянного тока. Ознакомившись с содержанием письма Фарадей тут же отослал его в редакцию научного журнала. Автор этого письма не назвал себя, его фамилия осталась неизвестной.

Электрические машины преобразующие механическую энергию в электрическую называются генераторами. Впоследствии генераторы постоянного тока непрерывно совершенствовались. Потом, когда начали использовать переменный ток они уступили место генераторам переменного тока. Переменный ток в основном вырабатывается генераторами переменного тока. Простой моделью генератора может служить прямоугольная рамка, вращающаяся в магнитном поле. При вращении рамки, магнитный поток пронизывающий площадь поверхности, ограниченную рамкой, меняется по гармоническому закону:

N- число витков.

Возникает ЭДС индукции который меняется по гармоническому закону.

ЭДС индукции в рамке равна:

Если с помощью контактных колец и скользящих по ним щёток соединить концы рамки с электрической цепью, то в цепи возникнет переменный ток.

В современной энергетике для производства электроэнергии используются электромеханические индукционные генераторы. Принцип действия таких генераторов основан на явлении электромагнитной индукции. Основными частями генератора являются статор и ротор. Неподвижная часть генератора называется статором, а вращающаяся – ротором.

Постоянный ток не может идти по цепи содержащей конденсатор, т. к. цепь оказывается разомкнутой. При включении конденсатора в цепь переменного тока конденсатор будет периодически заряжаться и разряжаться с частотой равной частоте приложенного напряжения. В результате периодически меняющихся процессов зарядки и разрядки конденсатора в цепи течет переменный ток. Лампа накаливания, включенная в цепь переменного тока последовательно с конденсатором кажется горящей непрерывно, т.к. при высокой частоте колебаний силы тока человеческий глаз не способен заметить периодического ослабления нити накала. Конденсатор оказывает сопротивление прохождению тока. Это сопротивление называют ёмкостным.

Величину Х_C, обратную произведению циклической частоты на электрическую ёмкость конденсатора называют ёмкостным сопротивлением.

Ёмкостное сопротивление не является постоянной величиной. Мы видим, что конденсатор оказывает бесконечно большое сопротивление постоянному току. Чем больше ёмкость конденсатора и частота колебаний, тем больше ток перезарядки. При наличии в цепи переменного тока конденсатора колебания силы тока опережают по фазе колебания напряжения конденсаторе на 90º. Сдвиг фазы колебаний силы тока на 90º относительно фазы колебания напряжения на конденсаторе приводит к тому, что мощность переменного тока в течение одной четверти периода имеет положительный знак, а в течение второй четверти – отрицательный. Поэтому среднее значение мощности за период равно нулю.

Индуктивность в цепи, так же, как и ёмкость, влияет на силу переменного тока. Объясняется это явлением самоиндукции. В любом проводнике, по которому протекает переменный ток, возникает ЭДС самоиндукции. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при этом вихревое электрическое поле тормозит движение электронов. Лишь спустя некоторое время сила тока достигает максимального значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет успевать достигать тех значений, которые она приобрела бы при постоянном напряжении. Следовательно, максимальное значение силы переменного тока ограничивается индуктивностью цепи и его частотой колебаний.

Величину Х_L, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.

Если частота равна нулю, то индуктивное сопротивление тоже равно нулю. Поэтому постоянный ток как бы не «замечает» катушку индуктивности в цепи.

Колебания напряжения на катушке опережают по фазе колебания силы тока на 90º.

Сдвиг фазы колебаний приводит к тому, что средняя мощность за период колебаний равна нулю.

Генератор на транзисторе используется для создания высокочастотных электромагнитных колебаний.

Для потребления электрической энергии нужно доставить его от источника к потребителю. Для этого строят линии электропередачи. При передаче электроэнергии на расстояние возникают потери энергии вследствие нагревания проводов. Тепловые потери можно определить используя закон Джоуля – Ленца:

Из этой формулы следует, что для уменьшения потерь энергиинужно уменьшить сопротивление или повысить напряжение. Уменьшения сопротивления проводов ЛЭП требует увеличения их площади поперечного сечения, что приведет к увеличению массы проводов. Увеличение массы проводов связано с большими расходами на укрепление столбов линии электропередачи, для их удержания и на производство металла для них. Наиболее эффективным является увеличение напряжения.

Для изменения напряжения в сети используют трансформаторы. Трансформатор был изобретен в 1876 году Яблочковым и в 1882 году усовершенствован Усагиным. Простейший трансформатор состоит из двух катушек, надетых на общий замкнутый стальной сердечник. Эти катушки называются обмотками трансформатора. Обмотка трансформатора, подключаемая к источнику переменного напряжения, называют первичной, а другая к которой присоединяют нагрузку – вторичной. Действие трансформатора основано на явлении электромагнитной индукции. При прохождении переменного тока по первичной обмотке в трансформаторе возникает переменное магнитное поле. Это поле пронизывает обе обмотки и в них возникает вихревое электрическое поле, которое действуя на заряженные частицы во вторичной обмотке способствует возникновению в ней переменного напряжения.

Величина равная отношению напряжений в первичной и вторичной обмотках трансформатора называют коэффициентом трансформации. Его обозначают буквой «k».

k– коэффициент трансформации.

U₁ и_{U2 – напряжения на первичной и на вторичной обмотке.}

N₁ и _{N2— число витков на первичной и на вторичной обмотке.}

Если k < 1 — трансформатор повышающий,

k > 1 — трансформатор понижающий.

КПД трансформатора равен отношению мощности в нагрузке к мощности, подаваемой из сети на первичную обмотку:

Для передачи электроэнергии на расстояние напряжение повышают с помощью трансформатора, а для потребления — понижают. В массивных проводниках при изменении магнитного поля возникают индукционные токи (токи Фуко), которые нагревают проводник. Чтобы эти индукционные токи не нагревали сердечник трансформатора его делают не сплошным, а из отдельных пластин, скрепленных вместе.

Закон Ома гласит: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.

Из формулы закона Ома для переменного тока мы видим, что при постоянной амплитуде напряжения, амплитуда силы тока зависит от частоты. Амплитуда силы тока будет максимальной, если полное сопротивление минимально. Полное сопротивление цепи минимально при равенстве индуктивного и ёмкостного сопротивления. В этом заключается условие возникновения резонанса в электрической цепи.

Резонанс в электрической цепи – это явление резкого возрастания амплитуды колебаний силы тока в контуре при совпадении частоты вынужденных колебаний с частотой собственных колебаний контура.

 Явление резонанса широко используется в радиотехнике, в схемах настройки радиоприемников. Меняя электроемкость конденсатора в колебательном контуре можно настроить его на нужную волну, т.е. выделить частоту на которой работает передающая станция

Разбор тренировочных заданий

1. Каково амплитудное значение ЭДС, возникающей в рамке из 50 витков, если она вращается с циклической частотой 180 рад/с в магнитном поле индукцией 0,4 Тл? Площадь рамки 0,02 м².

Дано:

N=50

ω=180 рад/с

B=0,4 Тл

S=0,02 м²

_________

Ԑ_m=?

Решение:

Ответ: 72 В.

2. Катушка с индуктивностью 0,08 Гн присоединена к источнику переменного тока частотой 1000 Гц. При этом вольтметр показывает 100 В. Определить амплитуду тока в цепи. Ответ округлить до десятых.

Дано:

L=0,08 Гн

ν= 1000 Гц

U=100 В

__________

I_m=?

Решение:

Напишем закон Ома для переменного тока

Т.к. Х_C и R равны нулю, то

Учитывая, что , получаем:

Найдем амплитудное значение напряжения:

Подставим числовые данные в формулу для расчета амплитуды силы тока:

Ответ: I_m = 0,3 А.

Контрольная работа по физике Переменный ток 11 класс

Контрольная работа по физике Переменный ток 11 класс с ответами. Контрольная работа включает 4 варианта, в каждом варианте по 7 заданий.

1 вариант

1. Конденсатор емкостью 250 мкФ включается в сеть пе­ременного тока. Определите емкостное сопротивление конденсатора при частоте 50 Гц.

2. Чему равен период собственных колебаний в колеба­тельном контуре, если индуктивность катушки равна 2,5 мГн, а емкость конденсатора 1,5 мкФ?

3. Напряжение меняется с течением времени по закону u = 40sin(10πt + π/6) В. Определите амплитуду, действующее значение, круговую частоту колебаний и началь­ную фазу колебаний напряжения.

4. Сколько оборотов в минуту должна совершать рамка из 20 витков проволоки размером 0,2 х 0,4 м в магнитном поле с индукцией 1 Тл, чтобы амплитуда ЭДС равнялась 500 В?

5. Напряжение в цепи изменяется по закону u = U_msin^2π/_Tt, причем амплитуда напряжения 200 В, а период 60 мс. Какое значение принимает напряжение через 10 мс?

6. Катушка индуктивностью 75 мГн последовательно с конденсатором включена в сеть переменного тока с на­пряжением 50 В и частотой 50 Гц. Чему равна емкость конденсатора при резонансе в полученной сети?

7. В колебательном контуре конденсатору сообщили за­ряд 1 мКл, после чего в контуре возникли затухающие электромагнитные колебания. Какое количество теплоты выделится к моменту, когда максимальное напряжение на конденсаторе станет меньше начального максималь­ного значения в 4 раза? Емкость конденсатора равна 10 мкФ.

2 вариант

1. Катушка с индуктивностью 35 мГн включается в сеть переменного тока. Определите индуктивное сопротивле­ние катушки при частоте 60 Гц.

2. Определите частоту собственных колебаний в колеба­тельном контуре, состоящем из конденсатора емкостью 2,2 мкФ и катушки с индуктивностью 0,65 мГн.

3. ЭДС индукции, возникающая в рамке при вращении в однородном магнитном поле, изменяется по закону е = 12sin100πt В. Определите амплитуду ЭДС, действую­щее значение ЭДС, круговую частоту колебаний и на­чальную фазу колебаний.

4. Конденсатор емкостью 800 мкФ включен в сеть пере­менного тока с частотой 50 Гц с помощью проводов, со­противление которых 3 Ом. Какова сила тока в конденса­торе, если напряжение в сети 120 В?

5. В цепь переменного тока с частотой 50 Гц включено ак­тивное сопротивление 5 Ом. Амперметр показывает силу тока 10 А. Определите мгновенное значение напряжения через 1/300 с, если колебания силы тока происходят по закону косинуса.

6. В колебательном контуре индуктивность катушки рав­на 0,2 Гн, а амплитуда колебаний силы тока 40 мА. Найдите энергию электрического поля конденсатора и магнитного поля катушки в момент, когда мгновенное значение силы тока в 2 раза меньше амплитудного значения.

7. Переменный ток возбуждается в рамке, имеющей 200 витков. Площадь одного витка 300 см² Индукция маг­нитного поля 1,5 ⋅ 10^-2 Тл. Определите ЭДС индукции че­рез 0,01 с после начала движения рамки из нейтрального положения. Амплитуда ЭДС равна 7,2 В.

3 вариант

1. Определите емкость конденсатора, сопротивление ко­торого в цепи переменного тока частотой 50 Гц равно 800 Ом.

2. В рамке, равномерно вращающейся в однородном маг­нитном поле, индуцируется ток, мгновенное значение ко­торого выражается формулой i = 3sin157t А. Определите амплитуду, действующее значение, круговую частоту ко­лебаний и начальную фазу колебаний силы тока.

3. Рассчитайте период собственных колебаний в колебательном контуре при емкости конденсатора 2 мкФ и ин­дуктивности катушки 0,5 мГн.

4. Рамка площадью 150 см², содержащая 50 витков про­волоки, равномерно вращается со скоростью 120 об/мин в однородном магнитном поле с магнитной индукцией 0,8 Тл. Найдите амплитуду ЭДС индукции в рамке.

5. Амплитуда напряжения в колебательном контуре 100 В, частота колебаний 5 МГц. Через какое время на­пряжение будет 71 В?

6. Конденсатор емкостью 10 мкФ зарядили до напряже­ния 400 В и подключили к катушке. После этого возник­ли затухающие электрические колебания. Какое количе­ство теплоты выделится в контуре за время, в течение ко­торого амплитуда колебаний уменьшится вдвое?

7. Электроплитка сопротивлением 50 Ом включена в сеть переменного тока с частотой 50 Гц и напряжением 220 В. Запишите уравнения, выражающие зависимость напряжения и силы тока от времени для электроплитки. Чему равно мгновенное значение силы тока и напряже­ния через 1/100 с, если колебания происходят по закону синуса?

4 вариант

1. Какой индуктивности катушку надо включить в коле­бательный контур, чтобы при емкости конденсатора 2 мкФ получить частоту 1 кГц?

2. Сила тока в электрической цепи изменяется по закону i = 3cos(100πt + π/3) А. Определите амплитуду силы то­ка, действующее значение силы тока, круговую частоту колебаний и начальную фазу колебаний.

3. Рассчитайте сопротивление конденсатора емкостью 250 мкФ, включенного в цепь переменного тока с часто­той 200 Гц.

4. Индуктивность колебательного контура равна 0,01 Гн, а емкость 1 мкФ. Конденсатор зарядили до разности по­тенциалов 200 В. Какой наибольший ток возникает в контуре в процессе электромагнитных колебаний?

5. Конденсатор и катушка соединены последовательно. Емкостное сопротивление конденсатора 5 кОм. Какой должна быть индуктивность катушки, чтобы резонанс наступил в цепи при частоте колебаний силы тока 20 кГц?

6. В колебательном контуре с индуктивностью 0,4 Гн и емкостью 20 мкФ амплитудное значение силы тока равно 0,1 А. Каким будет напряжение в момент, когда энергия электрического и энергия магнитного полей будут рав­ны? Колебания считать незатухающими.

7. В цепь переменного тока с частотой 400 Гц включена катушка индуктивностью 0,1 Гн. Определите, какой ем­кости конденсатор надо включить в эту цепь, чтобы осу­ществился резонанс.

Ответы на контрольную работа по физике Переменный ток 11 класс
1 вариант
1. 12,7 Ом
2. 0,38 мс
3. 40 В; 28,4 В; 10π рад/с; π/6 рад
4. ≈ 3000 об/мин
5. 100 В
6. 135 мкФ
7. 0,047 Дж
2 вариант
1. 13,2 Ом
2. 4233 Гц
3. 12 В; 8,5 В; 100π рад/с; 0
4. 24 А
5. 35,5 В
6. 120 мкДж; 40 мкДж
7. 5,04 В
3 вариант
1. 4 мкФ
2. 3 А; 2,14 А; 157 рад/с; 0
3. 0,2 мс
4. 7,5 В
5. 25 нс
6. 0,6 Дж
7. u = 310 х sin 100pt; 0; 0
4 вариант
1. 12,7 мГн
2. 3 А; 2,13 А; 100π рад/ с; π/3 рад
3. 3,2 Ом
4. 2 А
5. 0,04 Гн
6. 10 В
7. 1,6 мкФ

Калькулятор расчета конденсатора однофазного двигателя

Однофазный двигатель Вычислитель конденсатора:

Введите входное напряжение, мощность двигателя в ваттах, КПД в процентах, частоту, затем нажмите кнопку расчета, вы получите необходимое значение емкости.

Формула для расчета конденсатора однофазного двигателя:

Изначально однофазный двигатель требует небольшого толчка ротора для вращения ротора с номинальной частотой вращения. Выбор правильного конденсатора для однофазного двигателя действительно сложен, он может привести к запуску двигателя или нет.

Однофазная емкость C _(мкФ) в микрофарадах равна произведению мощности P _(Вт) в ваттах и ​​КПД η, умноженного на 1000, на произведение напряжения V _(В) в квадрате вольт и частота F _(Гц) . Формула для расчета емкости конденсатора

C _(мкФ) = (P _(W) x η x 1000) / (V _(V) x V _(V) x f)

Посмотрите на формулу, требуемое значение емкости прямо пропорционально мощности двигателя.Следовательно, при увеличении размера двигателя размер емкости также будет увеличиваться.

Расчет номинального напряжения конденсатора:

Номинальное напряжение конденсатора равно произведению напряжения, измеренного на обоих концах основной обмотки, в вольтах, на корень из единицы и отношение витков n квадрат.

В _(К) = Vp √ (1 + n ² )

n равно отношению витков основной / вспомогательной обмотки. Вышеприведенная формула используется для определения приблизительного напряжения на конденсаторе.

Пример 1:

Рассчитайте необходимое значение номинальной емкости для однофазного, 220 В, 1 л.с., 50 Гц, 80% двигателя.

1 л.с. = 746 Вт.

Воспользуйтесь нашей формулой расчета емкости.

C _(мкФ) = 746 x 80 x 1000 / (220 x 220 x 50) = 24,66 мкФ.

Следовательно, двигателю мощностью 1 л.с. требуется емкость 24,66 мкФ для плавного пуска двигателя. Но на рынке можно получить 25 мкФ.

Диапазон напряжения конденсатора должен составлять 440 В мин.

Пример 2:

Таким же образом возьмем другой пример:

Рассчитайте пусковую емкость для однофазного вентилятора 70 Вт, 220 В, 50 Гц, КПД 85%.

C _(мкФ) = 70 x 80 x 1000 / (230 x 230 x 50) = 2,459 мкФ. ок. 2,5 мкФ.

Следовательно, вы можете проверить наш расчет с вашим вентилятором.

Диапазон напряжения конденсатора должен составлять 440 В мин.

Amazon.com: Superior Electric AMT-CMC7004 CMC7004 40MFD +/- 5% 50 Гц / 60 Гц 450 В переменного тока, рабочий конденсатор цилиндрового двигателя (CBB60), красный: Industrial & Scientific

Amazon’s Choice выделяет высоко оцененные продукты по хорошей цене, доступные для немедленной отправки.

Амазонки Выбор в промышленных электрических конденсаторах от Superior Electric

---

Прейскурантная цена:	15,74 $ Подробности
Цена:	14 долларов.90 + Депозит без импортных сборов и $ 18,15 за доставку в Российскую Федерацию Подробности
Вы экономите:	0,84 доллара США (5%)

Доступно по более низкой цене у других продавцов, которые могут не предлагать бесплатную доставку Prime.

• Убедитесь, что это подходит введя номер вашей модели.
• Емкость: 40 MFD ± 5%
• Номинальное напряжение: 450 В переменного тока
• Номинальная частота: 50/60 Гц
• Форма / Корпус: Круглый / Фенольный | Диаметр: 1,80 дюйма | Длина: 3,80 дюйма
• Температура окружающей среды: 25/70/21 | Цвет: белый | Контакты: 2

› См. Дополнительные сведения о продукте

Реактивное сопротивление, индуктивное и емкостное | Физика

Цели обучения

К концу этого раздела вы сможете:

• Зависимость напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
• Рассчитайте индуктивное и емкостное сопротивление.
• Рассчитывайте ток и / или напряжение в простых индуктивных, емкостных и резистивных цепях.

Многие цепи также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы исследуем, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.

Индукторы и индуктивное сопротивление

Предположим, индуктор подключен непосредственно к источнику переменного напряжения, как показано на рисунке 1.Разумно предположить, что сопротивление пренебрежимо мало, поскольку на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на схему. Также показан график зависимости напряжения и тока от времени.

Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, имеющей незначительное сопротивление. (б) График зависимости тока и напряжения на катушке индуктивности от времени.

График на Рисунке 1 (b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и повышается до своего пика после напряжения, которое им управляет, точно так же, как это было в случае, когда напряжение постоянного тока было включено в предыдущем разделе.Когда напряжение становится отрицательным в точке а, ток начинает уменьшаться; оно становится нулевым в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова вслед за напряжением. Напряжение становится положительным в точке c и начинает делать ток менее отрицательным. В точке d ток проходит через ноль, когда напряжение достигает своего положительного пика, чтобы начать следующий цикл. Кратко это поведение можно описать следующим образом:

Напряжение переменного тока в индукторе

Когда на катушку индуктивности подается синусоидальное напряжение, оно опережает ток на одну четверть цикла или на фазовый угол 90º.

Ток отстает от напряжения, поскольку индукторы препятствуют изменению тока. При изменении тока возникает обратная ЭДС В = — L (Δ I / Δ t ). Это считается эффективным сопротивлением катушки индуктивности переменному току. Среднеквадратичный ток I через катушку индуктивности L определяется версией закона Ома:

[латекс] I = \ frac {V} {{X} _ {L}} \\ [/ latex],

, где В, — среднеквадратичное значение напряжения на катушке индуктивности, а X _L определяется как

.

[латекс] {X} _ {L} = 2 \ pi {fL} \\ [/ латекс],

с f частота источника переменного напряжения в герцах (анализ схемы с использованием правила петли Кирхгофа и вычислений фактически дает это выражение). X _L называется индуктивным реактивным сопротивлением , потому что катушка индуктивности препятствует прохождению тока. X _L имеет единицы измерения Ом (1 Гн = 1 Ом с, так что частота, умноженная на индуктивность, имеет единицы (циклы / с) (Ом ⋅ с) = Ом)), что соответствует его роли в качестве эффективное сопротивление. Имеет смысл, что X _L пропорционально L , поскольку чем больше индукция, тем больше его сопротивление изменению.Также разумно, что X _L пропорционально частоте f , поскольку большая частота означает большее изменение тока. То есть Δ I / Δ t является большим для больших частот (большие f , маленькие Δ t ). Чем больше изменение, тем больше сопротивление катушки индуктивности.

Пример 1. Расчет индуктивного сопротивления, а затем тока

(a) Рассчитайте индуктивное сопротивление 3.Индуктор 00 мГн при подаче переменного напряжения 60,0 Гц и 10,0 кГц. (b) Каков среднеквадратичный ток на каждой частоте, если приложенное действующее напряжение составляет 120 В?

Стратегия

Индуктивное реактивное сопротивление находится непосредственно из выражения X _L = 2πf L . Как только X _L найден на каждой частоте, закон Ома, как указано в уравнении I = V / X _L , можно использовать для определения тока на каждой частоте.

Решение для (а)

Ввод частоты и индуктивности в уравнение X _L = 2πf L дает

X _L = 2πf L = 6,28 (60,0 / с) (3,00 мГн) = 1,13 Ом при 60 Гц.

Аналогично, на 10 кГц,

X _L = 2πf L = 6,28 (1,00 × 10 ⁴ / с) (3,00 мГн) = 188 Ом при 10 кГц.

Решение для (b)

Среднеквадратичное значение тока теперь определяется с использованием версии закона Ома в уравнении I = В / X _L , при условии, что приложенное действующее напряжение составляет 120 В.Для первой частоты это дает

[латекс] I = \ frac {V} {{X} _ {L}} = \ frac {120 \ text {V}} {1.13 \ text {} \ Omega} = 106 \ text {A at} 60 \ текст {Hz} \\ [/ latex].

Аналогично, на 10 кГц,

[латекс] I = \ frac {V} {{X} _ {L}} = \ frac {120 \ text {V}} {188 \ text {} \ Omega} = 0,637 \ text {A at} 10 \ текст {кГц} \\ [/ latex].

Обсуждение

Катушка индуктивности по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток невелик, что соответствует тому, как катушка индуктивности препятствует быстрому изменению.Таким образом, наиболее затруднены высокие частоты. Индукторы могут использоваться для фильтрации высоких частот; например, большую катушку индуктивности можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выводимый из ваших динамиков или высокочастотные всплески мощности на ваш компьютер.

Обратите внимание, что, хотя сопротивлением в рассматриваемой цепи можно пренебречь, переменный ток не очень велик, потому что индуктивное реактивное сопротивление препятствует его протеканию.С переменным током нет времени, чтобы ток стал слишком большим.

Конденсаторы и емкостное сопротивление

Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рисунке 2. Сопротивление такой цепи можно сделать настолько малым, что оно окажет незначительное влияние по сравнению с конденсатором, поэтому мы можем предположить, что сопротивление незначительно. Напряжение на конденсаторе и ток показаны на рисунке как функции времени.

Рисунок 2.(а) Источник переменного напряжения, включенный последовательно с конденсатором С, имеющим незначительное сопротивление. (б) График зависимости тока и напряжения на конденсаторе от времени.

График на Рисунке 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке а конденсатор полностью разряжен (на нем Q = 0 ) и напряжение на нем равно нулю.Ток остается отрицательным между точками a и b, вызывая обратное напряжение на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и доводя напряжение до нуля в точке c, что позволяет току достичь своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение соответствует тому, что делает ток, на четверть цикла:

Напряжение переменного тока в конденсаторе

Когда на конденсатор подается синусоидальное напряжение, оно следует за током на одну четверть цикла или на фазовый угол 90º.

Конденсатор влияет на ток, имея возможность полностью его отключить, когда он полностью заряжен. Поскольку применяется переменное напряжение, возникает среднеквадратичный ток, но он ограничивается конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичный ток I в цепи, содержащей только конденсатор C , определяется другой версией закона Ома как

.

[латекс] I = \ frac {V} {{X} _ {C}} \\ [/ latex],

, где В, — среднеквадратичное значение напряжения, и определено X _C (Как и в случае с X _L , это выражение для X _C является результатом анализа цепи используя правила и исчисление Кирхгофа) равным

[латекс] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex],

, где X _C называется емкостным реактивным сопротивлением , потому что конденсатор препятствует прохождению тока. X _C имеет единицы измерения Ом (проверка оставлена ​​в качестве упражнения для читателя). X _C обратно пропорциональна емкости C ; Чем больше конденсатор, тем больший заряд он может накапливать и тем больше может протекать ток. Она также обратно пропорциональна частоте f ; чем выше частота, тем меньше времени остается для полной зарядки конденсатора и, следовательно, меньше препятствует току.

Пример 2. Расчет емкостного реактивного сопротивления, а затем тока

(a) Рассчитайте емкостное реактивное сопротивление конденсатора 5,00 мФ при приложении переменного напряжения 60,0 Гц и 10,0 кГц. (b) Каков среднеквадратичный ток, если приложенное действующее напряжение составляет 120 В?

Стратегия

Емкостное реактивное сопротивление находится непосредственно из выражения в [latex] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex]. Как только X _C найден на каждой частоте, закон Ома сформулирован как I = V / X _C может использоваться для определения тока на каждой частоте.

Решение для (а)

Ввод частоты и емкости в [латекс] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex], дает

[латекс] \ begin {array} {lll} {X} _ {C} & = & \ frac {1} {2 \ pi fC} \\ & = & \ frac {1} {6.28 \ left (60.0 / \ text {s} \ right) \ left (5.00 \ text {} \ mu \ text {F} \ right)} = 531 \ text {} \ Omega \ text {at} 60 \ text {Hz} \ end {массив }\\[/латекс].

Аналогично, на 10 кГц,

[латекс] \ begin {array} {lll} {X} _ {C} & = & \ frac {1} {2 \ pi fC} = \ frac {1} {6.{4} / \ text {s} \ right) \ left (5,00 \ mu \ text {F} \ right)} \\ & = & 3,18 \ text {} \ Omega \ text {at} 10 \ text {кГц} \ end {array} \\ [/ latex].

Решение для (b)

Среднеквадратичное значение тока теперь определяется с использованием версии закона Ома в I = В / X _C , учитывая приложенное действующее напряжение 120 В. Для первой частоты это дает

[латекс] I = \ frac {V} {{X} _ {C}} = \ frac {120 \ text {V}} {531 \ text {} \ Omega} = 0,226 \ text {A at} 60 \ текст {Hz} \\ [/ latex].

Аналогично, на 10 кГц,

[латекс] I = \ frac {V} {{X} _ {C}} = \ frac {120 \ text {V}} {3.18 \ text {} \ Omega} = 3.37 \ text {A at} 10 \ текст {Hz} \\ [/ latex].

Обсуждение

Конденсатор очень по-разному реагирует на двух разных частотах, а индуктор реагирует прямо противоположным образом. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы одобряют изменения, тогда как индукторы противодействуют изменениям. Конденсаторы больше всего препятствуют низким частотам, так как низкая частота позволяет им успеть зарядиться и остановить ток.Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно с системой воспроизведения звука, избавляет ее от гула 60 Гц.

Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с напряжением переменного тока, приложенным к конденсатору, присутствует среднеквадратичный ток. Это связано с тем, что напряжение постоянно меняет направление, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), X _C стремится к бесконечности, и ток равен нулю, когда конденсатор заряжен.На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет незначительное реактивное сопротивление и не препятствует току (он действует как простой провод). Конденсаторы оказывают противоположное влияние на цепи переменного тока, чем индукторы .

Резисторы в цепи переменного тока

В качестве напоминания рассмотрим Рисунок 3, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток равны точно в фазах в резисторе.Отсутствует частотная зависимость поведения простого сопротивления в цепи:

Рис. 3. (a) Источник переменного напряжения, включенный последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе.

Напряжение переменного тока в резисторе

Когда на резистор подается синусоидальное напряжение, напряжение точно совпадает по фазе с током — они имеют фазовый угол 0 °.

Сводка раздела

• Для катушек индуктивности в цепях переменного тока мы обнаруживаем, что когда на индуктор подается синусоидальное напряжение, напряжение опережает ток на одну четверть цикла или на фазовый угол 90 °.
• Противодействие катушки индуктивности изменению тока выражается как сопротивление переменному току.
• Закон Ома для катушки индуктивности

  [латекс] I = \ frac {V} {{X} _ {L}} \\ [/ latex],

  , где В, — среднеквадратичное значение напряжения на катушке индуктивности.

• X _L определяется как индуктивное реактивное сопротивление, определяемое по формуле

  [латекс] {X} _ {L} = 2 \ pi fL \\ [/ латекс],

  с f частота источника переменного напряжения в герцах.

• Индуктивное реактивное сопротивление X _L выражается в единицах Ом и имеет наибольшее значение на высоких частотах.
• Для конденсаторов мы обнаруживаем, что когда на конденсатор подается синусоидальное напряжение, напряжение следует за током на одну четверть цикла или на фазовый угол 90º.
• Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току; Закон Ома для конденсатора

  [латекс] I = \ frac {V} {{X} _ {C}} \\ [/ latex],

  , где В, — среднеквадратичное значение напряжения на конденсаторе.

• X _C определяется как емкостное реактивное сопротивление, определяемое по формуле

  [латекс] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex].

• X _C имеет единицы измерения Ом и имеет наибольшее значение на низких частотах.

Концептуальные вопросы

1. Пресбиакузис — это возрастная потеря слуха, которая постепенно влияет на высокие частоты. Усилитель слухового аппарата предназначен для равномерного усиления всех частот. Чтобы отрегулировать его мощность на пресбиакузис, включите ли вы конденсатор последовательно или параллельно динамику слухового аппарата? Объяснять.

2. Будете ли вы использовать большую индуктивность или большую емкость последовательно с системой для фильтрации низких частот, таких как гул 100 Гц в звуковой системе? Объяснять.

3. Высокочастотный шум в сети переменного тока может повредить компьютеры. Использует ли съемный блок, предназначенный для предотвращения этого повреждения, большую индуктивность или большую емкость (последовательно с компьютером) для фильтрации таких высоких частот? Объяснять.

4. Зависит ли индуктивность от тока, частоты или и того, и другого? А как насчет индуктивного сопротивления?

5. Объясните, почему конденсатор на Рисунке 4 (а) действует как фильтр низких частот между двумя цепями, тогда как конденсатор на Рисунке 4 (b) действует как фильтр высоких частот.

Рисунок 4. Конденсаторы и катушки индуктивности. Конденсатор с высокой и низкой частотой.

6. Если конденсаторы на Рисунке 4 заменить катушками индуктивности, что будет действовать как фильтр низких частот, а какой — как фильтр высоких частот?

Задачи и упражнения

1. На какой частоте индуктор 30,0 мГн будет иметь реактивное сопротивление 100 Ом?

2. Какое значение индуктивности следует использовать, если требуется реактивное сопротивление 20,0 кОм при частоте 500 Гц?

3.Какую емкость следует использовать для получения реактивного сопротивления 2,00 МОм при 60,0 Гц?

4. На какой частоте конденсатор 80,0 мФ будет иметь реактивное сопротивление 0,250 Ом?

5. (a) Найдите ток через катушку индуктивности 0,500 Гн, подключенную к источнику переменного тока 60,0 Гц, 480 В. (б) Каким будет ток на частоте 100 кГц?

6. (a) Какой ток протекает, когда источник переменного тока 60,0 Гц, 480 В подключен к конденсатору 0,250 мкФ? (b) Каким будет ток на частоте 25,0 кГц?

7. А 20.Источник 0 кГц, 16,0 В, подключенный к катушке индуктивности, вырабатывает ток 2,00 А. Что такое индуктивность?

8. Источник 20,0 Гц, 16,0 В вырабатывает ток 2,00 мА при подключении к конденсатору. Какая емкость?

9. (a) Катушка индуктивности, предназначенная для фильтрации высокочастотного шума от энергии, подаваемой на персональный компьютер, включается последовательно с компьютером. Какая минимальная индуктивность должна обеспечивать реактивное сопротивление 2,00 кОм для шума 15,0 кГц? (б) Каково его реактивное сопротивление при 60?0 Гц?

10. Конденсатор на рисунке 4 (а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. (а) Какая емкость необходима для создания реактивного сопротивления 100 кОм при частоте 120 Гц? (б) Каким было бы его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите значение ваших ответов на (a) и (b).

11. Конденсатор на Рисунке 4 (b) будет фильтровать высокочастотные сигналы, замыкая их на землю / землю. (a) Какая емкость необходима для получения реактивного сопротивления [латекса] \ text {10.0 м \ Omega} [/ latex] для сигнала 5,00 кГц? (б) Каким будет его реактивное сопротивление при 3,00 Гц? (c) Обсудите значение ваших ответов на (a) и (b).

12. Необоснованные результаты При регистрации напряжений, обусловленных мозговой активностью (ЭЭГ), сигнал 10,0 мВ с частотой 0,500 Гц подается на конденсатор, создавая ток 100 мА. Сопротивление незначительное. а) Какая емкость? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка ответственны?

13. Создайте свою проблему Рассмотрите возможность использования индуктора последовательно с компьютером, работающим от электричества 60 Гц. Постройте задачу, в которой вы вычисляете относительное снижение напряжения входящего высокочастотного шума по сравнению с напряжением 60 Гц. Среди вещей, которые следует учитывать, — допустимое последовательное реактивное сопротивление катушки индуктивности для мощности 60 Гц и вероятные частоты шума, проходящего через линии электропередач.

Глоссарий

индуктивное сопротивление:

противодействие катушки индуктивности изменению тока; рассчитывается по X _L = 2π fL

емкостное реактивное сопротивление:

сопротивление конденсатора изменению тока; рассчитывается по [latex] {X} _ {C} = \ frac {1} {2 \ pi fC} \\ [/ latex]

Избранные решения проблем и упражнения

1.531 Гц

3. 1,33 нФ

5. (а) 2,55 А (б) 1,53 мА

7. 63,7 мкГн

9. (а) 21,2 мГн (б) 8,00 Ом

Как найти размер конденсатора в кВАр и фарад для коррекции коэффициента мощности

Как найти значение емкости конденсатора нужного размера в кВАр и микрофарадах для коррекции коэффициента мощности — 3 метода

Поскольку мы получили много электронных писем и сообщений от аудитории для составьте пошаговое руководство, в котором показано, как рассчитать надлежащий размер конденсаторной батареи в кВАр и микрофарадах для коррекции коэффициента мощности и улучшения как в однофазных, так и в трехфазных цепях.

В этой статье будет показано, как найти конденсаторную батарею подходящего размера как в микрофарадах, так и в кВАр, чтобы улучшить существующие «т.е. отставание «P.F от целевого», т. е. желаемый », поскольку скорректированный коэффициент мощности имеет множество преимуществ. Ниже мы показали три различных метода с решенными примерами для определения точного значения емкости конденсатора для коррекции коэффициента мощности.

Теперь давайте начнем и рассмотрим следующие примеры…

Как рассчитать значение конденсатора в кВАр?

Пример: 1

Трехфазный асинхронный двигатель мощностью 5 кВт имеет P.F (коэффициент мощности) 0,75 отстает. Какой размер конденсатора в кВАр требуется для повышения коэффициента мощности до 0,90?

Решение № 1 (простой метод с использованием табличного умножителя)

Потребляемая мощность двигателя = 5 кВт

Из таблицы множитель для улучшения коэффициента мощности с 0,75 до 0,90 составляет 0,398

Требуемый кВАр конденсатора для повышения коэффициента мощности с 0,75 до 0,90

Требуемый конденсатор, кВАр = кВт x Таблица 1, множитель 0,75 и 0,90

= 5 кВт x 0,398

= 1.99 кВАр

И номинал конденсаторов, подключенных в каждой фазе

= 1,99 кВАр / 3

= 0,663 кВАр

Решение № 2 (классический метод расчета)

Мощность двигателя = P = 5 кВт

Исходный коэффициент мощности = Cosθ ₁ = 0,75

Конечный коэффициент мощности = Cosθ ₂ = 0,90

θ ₁ = Cos ^-1 = (0,75) = 41 ° 0,41; Tan θ ₁ = Tan (41 ° .41) = 0,8819

θ ₂ = Cos ^-1 = (0.90) = 25 ° 0,84; Tan θ ₂ = Tan (25 ° .50) = 0,4843

Требуемый конденсатор, кВАр для улучшения коэффициента мощности с 0,75 до 0,90

Требуемый конденсатор, кВАр = P (Tan θ ₁ — Tan θ ₂ )

= 5 кВт (0,8819 — 0,4843)

= 1,99 кВАр

И номинал конденсаторов, подключенных в каждой фазе

1,99 кВАр / 3 = 0,663 кВАр

Примечание: Таблицы размеров конденсатора в кВАр и микрофарад

Следующие таблицы (приведенные в конце этого поста) были подготовлены для упрощения расчета кВАр для улучшения коэффициента мощности.Размер конденсатора в кВАр — это мощность в кВт, умноженная на коэффициент в таблице для улучшения существующего коэффициента мощности до предлагаемого коэффициента мощности. Ознакомьтесь с другими решенными примерами ниже.

Пример 2:

Генератор выдает нагрузку 650 кВт при коэффициенте мощности 0,65. Какой размер конденсатора в кВАр требуется, чтобы повысить коэффициент мощности (P.F) до единицы (1)? И сколько еще кВт может выдать генератор при той же нагрузке в кВА, когда коэффициент мощности улучшится.

Решение № 1 (Простой метод таблицы с использованием Таблица Несколько )

Подача кВт = 650 кВт

Из таблицы 1, множитель для улучшения коэффициента мощности с 0.65 к единице (1) составляет 1,169

Требуемый конденсатор кВАр для улучшения коэффициента мощности с 0,65 до единицы (1).

Требуемый конденсатор, кВАр = кВт x Таблица 1, множитель 0,65 и 1,0

= 650 кВт x 1,169

= 759,85 кВАр

Мы знаем, что P.F = Cosθ = кВт / кВА. . .or

кВА = кВт / Cosθ

= 650 / 0,65 = 1000 кВА

Когда коэффициент мощности повышается до единицы (1)

Количество кВт = кВА x Cosθ

= 1000 x 1 = 1000 кВт

Следовательно увеличенная мощность от генератора

1000кВт — 650кВт = 350кВт

Решение № 2 (классический метод расчета)

Подача кВт = 650 кВт

Оригинал P.F = Cosθ ₁ = 0,65

Конечная P.F = Cosθ ₂ = 1

θ ₁ = Cos ^-1 = (0,65) = 49 ° 0,45; Tan θ ₁ = Tan (41 ° .24) = 1,169

θ ₂ = Cos ^-1 = (1) = 0 °; Tan θ ₂ = Tan (0 °) = 0

Требуемый конденсатор, кВАр для улучшения коэффициента мощности с 0,75 до 0,90

Требуемый конденсатор, кВАр = P (Tan θ ₁ — Tan θ ₂ )

= 650 кВт ( 1.169–0)

= 759.85 кВАр

Как рассчитать емкость конденсатора в микрофарадах и кВАр?

Следующие методы показывают, что определяет необходимое значение емкости конденсаторной батареи как в кВАр, так и в микрофарадах . Кроме того, решенные примеры также показывают, что как преобразовать емкость конденсатора в микрофарадах в кВАр и кВАр в микрофарады для P.F. Таким образом, конденсаторная батарея нужного размера может быть установлена ​​параллельно каждой стороне фазовой нагрузки для получения заданного коэффициента мощности.

Пример: 3

Однофазный двигатель с напряжением 500 вольт 60 c / с потребляет ток полной нагрузки 50 ампер с запаздыванием по коэффициенту мощности 0,86. Коэффициент мощности двигателя необходимо повысить до 0,94, подключив к нему батарею конденсаторов. Рассчитать требуемую емкость конденсатора как в кВАр, так и в мк-фарадах?

Решение:

(1) Найти требуемую емкость емкости в кВАр для улучшения коэффициента мощности с 0,86 до 0,94 (два метода)

Решение № 1 (метод таблицы)

Двигатель Вход = P = V x I x Cosθ

= 500 В x 50 А x 0.86

= 21,5 кВт

Из таблицы, множитель для улучшения коэффициента мощности с 0,86 до 0,94 составляет 0,230

Требуемый конденсатор, кВАр для повышения коэффициента мощности с 0,86 до 0,94

Требуемый конденсатор, кВАр = кВт x табличный множитель 0,86 и 0,94

= 21,5 кВт x 0,230

= 4,9 кВАр

Решение № 2 (метод расчета)

Вход двигателя = P = V x I x Cosθ

= 500 В x 50 A x 0.86

= 21,5 кВт

Фактический или существующий коэффициент мощности = Cosθ ₁ = 0,86

Требуемый или целевой коэффициент мощности = Cosθ ₂ = 0,94

θ ₁ = Cos ^-1 = (0,86) = 30,68 °; Tan θ ₁ = Tan (30,68 °) = 0,593

θ ₂ = Cos ^-1 = (0,95) = 19,94 °; Tan θ ₂ = Tan (19,94 °) = 0,363

Требуемый конденсатор, кВАр для улучшения коэффициента мощности с 0,86 до 0,95

Требуемый конденсатор, кВАр = P в кВт (Tan θ ₁ — Tan θ ₂ )

= 21.5 кВт (0,593 — 0,363)

= 4,954 кВАр

(2) Найти требуемую емкость емкости в фарадах для повышения коэффициента мощности с 0,86 до 0,97 (два метода)

Решение № 1 (метод таблицы)

Мы уже рассчитали требуемую емкость конденсатора в кВАр, поэтому мы можем легко преобразовать ее в фарады с помощью этой простой формулы

Требуемая емкость конденсатора в фарадах / микрофарадах

• C = кВАр / (2π x f x В ² ) в Фараде
• C = кВАр x 10 ⁹ / (2π x f x В ² ) в Микрофараде

Ввод значений в формулу выше

= (4.954 кВАр) / (2 x π x 60 Гц x 500 ² В)

= 52,56 мкФ

Решение № 2 (метод расчета)

кВАр = 4,954… (i)

Мы знаем что;

I _C = V / X _C

Тогда как X _C = 1 / 2π x f x C

I _C = V / (1 / 2π x f x C)

I _C = V x 2π x f x C

= (500V) x 2π x (60 Гц) x C

I _C = 188495.5 x C

And,

kVAR = (V x I _C ) / 1000… [kVAR = (V x I) / 1000]

= 500V x 188495,5 x C

I _C = 94247750 x C… (ii)

Приравнивая уравнения (i) и (ii), мы получаем

94247750 x C = 4,954 кВАр x C

C = 4,954 кВАр / 94247750

C = 78,2 мкФ

Пример 4

Какое значение емкости должно быть подключено параллельно с потребляемой мощностью 1 кВт при 70% отстающем коэффициенте мощности от источника 208 В, 60 Гц, чтобы поднять общий коэффициент мощности до 91%.

Решение:

Вы можете использовать метод таблицы или метод простого расчета, чтобы найти требуемое значение емкости в фарадах или кВАр для увеличения коэффициента мощности с 0,71 до 0,97. Итак, в этом случае мы использовали метод таблицы.

P = 1000 Вт

Фактический коэффициент мощности = Cosθ ₁ = 0,71

Требуемый коэффициент мощности = Cosθ ₂ = 0,97

Из таблицы, множитель для улучшения коэффициента мощности с 0,71 до 0,97 составляет 0,741

Требуемый конденсатор kVAR до улучшить П.F от 0,71 до 0,97

Требуемый конденсатор кВАр = кВт x табличный множитель 0,71 и 0,97

= 1 кВт x 0,741

= 741 ВАр или 0,741 кВАр (требуемое значение емкости в кВАр)

Ток в конденсаторе =

I _C = Q _C / V

= 741 кВАр / 208 В

= 3,56 A

И

X _C = V / I _C

= 208 В / 3,76 = 58,42 Ом

C = 1 / (2π x f x X _C )

C = 1 (2π x 60 Гц x 58.42 Ом)

C = 45,4 мкФ (требуемое значение емкости в фарадах)

Конденсатор кВАр в мкФарад и мкфарад в кВАр Преобразование

Следующие формулы используются для расчета и преобразования конденсатора кВАр в Фарад и наоборот.

Требуемый конденсатор в кВАр

Конденсатор преобразовывает фарады и микрофарады в вар, кВАр и мВАр.

• VAR = C x 2π x f x V ² x 10 ^-6 … VAR
• VAR = C в мкФ x f x В ² / (159.155 x 10 ³ )… в Вар
• кВАр = C x 2π x f x В ² x 10 ^-9 … в кВАр
• кВА = C в мкФ x f x V ² ÷ (159,155 x 10 ⁶ )… в кВАр
• MVAR = C x 2π x f x В ² x 10 ^-12 … в МВАр
• МВАр = C в мкФ x f x В ² ÷ (159.155 x 10 ⁹ )… в МВАр

Требуемый конденсатор в фарадах / микрофарадах.

Конденсатор преобразователя, кВАр в фарадах и микрофарадах

• C = кВАр x 10 ³ / 2π x f x В ² … в Фарадах
• x 48 Q в кВАр / f x В ² … в Фарадах
• C = кВАр x 10 ⁹ / (2π x f x В ² ) … в микрофарадах
• C = 159.155 x 10 ⁶ x Q в кВАр / f x В ² … в микрофарадах

Где:

Полезно знать:

Ниже приведены важные электрические формулы используется при расчете улучшения коэффициента мощности.

Активная мощность (P) в ваттах:

• кВт = кВА x Cosθ
• кВт = л.с. x 0,746 или (л.с. x 0,746) / КПД… (л.с. = мощность двигателя в лошадиных силах)
• кВт = √ (кВА ² — кВАр ² )
• кВт = P = V x I Cosθ… (однофазный)
• кВт = P = √3x V x I Cosθ… (трехфазный межфазный)
• кВт = P = 3x V x I Cosθ… (трехфазная фаза)

Полная мощность (S) в ВА:

• кВА = √ (кВт ² + кВАр ² )
• кВА = кВт / Cosθ

Реактивная мощность (Q) в ВА:

• кВАр = √ (кВА ² — кВт ² )
• кВАр = C x (2π x f x В ² )

Коэффициент мощности (от 0.1 к 1)

• Коэффициент мощности = Cosθ = P / VI… (однофазный)
• Коэффициент мощности = Cosθ = P / (√3x V x I)… (трехфазный межфазный)
• Коэффициент мощности = Cosθ = P / (3x V x I)… (трехфазная линия на нейтраль)
• Коэффициент мощности = Cosθ = кВт / кВА… (как однофазный, так и трехфазный)
• Коэффициент мощности = Cosθ = R / Z… (сопротивление / Импеданс)

И

• X _C = 1 / (2π x f x C)… (X _C = емкостное реактивное сопротивление)
• I _C = V / X _C … (I = V / R)

Связанные сообщения:

Калькуляторы для определения размеров конденсаторных батарей и коррекции коэффициента мощности

Если два вышеупомянутых метода кажутся немного сложными (что, по крайней мере, не должно), вы можете использовать следующие Онлайн калькуляторы коэффициента мощности кВАр и микрофарад, сделанные нашей командой для вас.

Таблица размеров конденсаторов и таблица для коррекции коэффициента мощности

Следующая диаграмма коррекции коэффициента мощности может использоваться, чтобы легко найти правильный размер батареи конденсаторов для желаемого улучшения коэффициента мощности. Например, если вам нужно улучшить существующий коэффициент мощности с 0,6 до 0,98, просто посмотрите на множитель для обоих цифр в таблице, равный 1,030. Умножьте это число на существующую активную мощность в кВт. Вы можете найти реальную мощность, умножив напряжение на ток и существующий отстающий коэффициент мощности i.е. P в ваттах = напряжение в вольтах x ток в амперах x Cosθ ₁ . Таким простым способом вы найдете необходимое значение емкости в кВАр, которое необходимо для получения желаемого коэффициента мощности.

Таблица — от 0,01 до 0,25 Таблица — от 0,26 до 0,50 Таблица — от 0,51 до 0,75 Таблица — от 0,76 до 1,0

Вот вся таблица, если вам нужно ее скачать в качестве справочной.

Вся таблица — от 0,10 до 1,0 (Щелкните изображение, чтобы увеличить)

Связанные сообщения

Все, что вам нужно знать о конденсаторе MFD

Конденсатор — это электрический компонент, отвечающий за изменение тока в одной или нескольких обмотках в одной -фазный асинхронный двигатель, работающий на переменном токе.Основная цель использования конденсатора — создание магнитного поля.

Вы можете получить два разных типа конденсаторов двигателя: пусковые конденсаторы и рабочие конденсаторы. Пусковой конденсатор — единственная операция во время фазы запуска двигателя, а затем отключается от цепи.

С другой стороны, рабочий конденсатор непрерывно работает для регулировки сдвига фазы или тока в двигателе или обмотке машины. Цель состоит в том, чтобы оптимизировать эффективность, производительность и крутящий момент двигателя.Вы можете найти конденсатор двигателя в кондиционере, спа-насосе, больших вентиляторах, воротах с электроприводом и т. Д.

Что такое конденсаторы MFD

Огромное количество конденсаторов имеют маркировку mFD или MFD, указанную после их значение емкости. Вы сможете увидеть его как МФД, а также как µF, что означает микрофарад.

Итак, возникает вопрос, являются ли mFD и µF одним и тем же? Простой ответ — они принадлежат к одной шкале измерения, т.е.е., mFD означает «миллифарад», тогда как µF означает «микрофарад». В основном компании-производители старых конденсаторов используют mFD вместо конденсаторов µF.

Причина в том, что в те времена было обычной практикой маркировать конденсаторы как mFD или MFD. Причина, скорее всего, заключалась в том, что машины не могли напечатать символ µ на ​​корпусе двигателя.

Также возможно, что у производителя просто были свои причины оставить свои конденсаторы, известные как конденсаторы MFD.

Вы можете измерить конденсатор с помощью номиналов MFD. MFD или микрофарад — это техническая терминология, используемая для описания уровня емкости конденсатора. Следовательно, чем выше номиналы MFD конденсатора, тем больше электрического тока может выдерживать ваш конденсатор.

Стандартный конденсатор может иметь диапазон MFD от 5 до 80 MFD. Если вы ищете конденсатор MFD, но не можете его найти, вы всегда можете получить мкФ. Оба они работают одинаково; единственное отличие — это единица измерения, в которой указывается уровень емкости

Четыре конденсатора MFD Факты, которые вы должны знать

Вот пять фактов о конденсаторах MFD, с которыми вы должны ознакомиться.

• Конденсаторы MFD могут хранить только разные заряды. Они не могут увеличить получаемое вами напряжение. Однако они могут только повысить напряжение в цепи. Вы можете увидеть, что через конденсатор проходит более высокое напряжение по сравнению с фактическим линейным напряжением, но это из-за ЭДС. Обратная ЭДС — это, по сути, противодействующая электродвижущая сила, создаваемая двигателем, а не конденсатором.
• Чем выше уровень емкости, тем больше ток на пусковой обмотке.
• Всегда соблюдайте номинальное напряжение на конденсаторе, поскольку оно показывает, с каким напряжением может выдержать ваш конденсатор.Например, если указано 370 В, вы можете заменить его на более высокую емкость 440 В. Однако, если ваш конденсатор уже на 440 В, вы не можете заменить его на более низкую емкость 370 В.
• Вы всегда можете проверить свой конденсатор, пока устройство находится в рабочем состоянии. Вы можете просто измерить ток пусковой обмотки, выходящей из конденсатора. Просто умножьте ампер на 2652 в случае мощности 60 Гц и на 3183 при питании 50 Гц. Теперь разделите полученное число на напряжение на конденсаторе.

Заключение

Теперь, когда вы знаете, что означает конденсатор MFD, вы никогда не почувствуете себя сбитым с толку от номинальных характеристик. Будь то мкФ или МФД, вам нужно только преобразовать микрофарады в миллифарады и наоборот. Обращайтесь к нам с любыми вопросами или проблемами MFD относительно вашего следующего проекта.

Емкостное реактивное сопротивление — обзор

X

Символ реактивного сопротивления.

X _C

Символ емкостного реактивного сопротивления.

X _L

Символ индуктивного реактивного сопротивления.

Демодуляция X и Z

Система демодуляции цветного ТВ, в которой два повторно вставленных сигнала поднесущей 3,58 МГц отличаются примерно на 60 °, а не на обычные 90 °. Напряжения R-Y, B-Y и G-Y выводятся из демодулированных сигналов, и эти напряжения управляют тремя пушками кинескопа. Важным преимуществом этой системы является то, что схема приемника проще, чем требуется при I- и Q-демодуляции.

Ось X

1. Референтная ось в кристалле кварца. 2. Горизонтальная ось в системе прямоугольных координат. 3. Направление по горизонтали или слева направо в двумерной системе координат. X-X означает одно направление, в котором следует метод пошагового повторения.

Диапазон X

Радиочастотный диапазон от 5200 до 11000 МГц с длинами волн от 5,77 до 2,75 см.

X-образный стержень

Прямоугольный кристаллический стержень, обычно вырезанный из Z-образного сечения, вытянутый параллельно X и с его краями, параллельными X, Y и Z.

X-конденсатор

Конденсатор для подавления радиопомех, предназначенный для приложений, в которых отказ конденсатора не приведет к опасности поражения электрическим током.

Х-образный кристалл

Кристалл, вырезанный так, что его основные поверхности перпендикулярны электрической оси (X) исходного кристалла кварца.

ксенон

Инертный газ, используемый в некоторых тиратронах и других газовых трубках.

ксеноновая импульсная лампа

Источник некогерентного белого света высокой интенсивности; он работает, разряжая конденсатор через трубку с газом ксеноном. Такое устройство часто используется в качестве источника излучения накачки для различных лазеров с оптическим возбуждением.

ксерографический принтер

Устройство для печати оптического изображения на бумаге; светлые и темные области представлены электростатически заряженными и незаряженными участками на бумаге.Порошковые чернила, присыпанные пылью на бумаге, прилипают к заряженным участкам и впоследствии растворяются в бумаге под воздействием тепла.

ксерографическая запись

Запись, полученная с помощью ксерографии.

ксерография

1. Эта ветвь электростатической электрофотографии, в которой изображения формируются на фотопроводящей изолирующей среде с помощью инфракрасного, видимого или ультрафиолетового излучения. Затем среду присыпают порошком, который прилипает только к электростатически заряженному изображению.Затем применяется тепло, чтобы сплавить порошок в постоянное изображение. 2. Процесс печати электростатической электрофотографии, в котором используется светопроводящая изолирующая среда в сочетании с инфракрасным, видимым или ультрафиолетовым излучением для создания структур скрытого электростатического заряда для достижения наблюдаемой записи.

xeroprinting

Эта ветвь электростатической электрофотографии, в которой узор из изоляционного материала на проводящей среде используется для формирования структур электростатического заряда для использования при копировании.

ксерорадиография

Процесс печати электростатической электрофотографии, в котором используется светопроводящая изолирующая среда в сочетании с рентгеновскими или гамма-лучами для создания структур скрытого электростатического заряда для получения наблюдаемого рисунка.

ксерорадиографическое оборудование

Оборудование, использующее принципы электростатики и фотопроводимости для записи рентгеновских изображений на сенсибилизированной пластине через короткое время после экспонирования.

xfmr

Сокращенное обозначение трансформатора.

xistor

Сокращенное обозначение транзистора.

Разъем XLR

Экранированный трехжильный микрофонный штекер или розетка с фиксатором для разблокировки пальцем для предотвращения случайного извлечения. Стандартный разъем для профессиональных пользователей микрофонов.

xmitter

Сокращенное обозначение передатчика.Также сокращенно trans или xmtr.

xmsn

Сокращенное обозначение передачи.

xmtr

Аббревиатура передатчика. Также сокращенно транс или xmitter.

X-off

Передатчик выключен.

X-on

Датчик включен.

X-частица

Частица, имеющая такой же отрицательный заряд, что и электрон, но масса между электроном и протоном.Он создается космическим излучением, падающим на молекулы газа или фактически составляющим часть космических лучей.

Рентгеновский аппарат

Рентгеновская трубка и принадлежности к ней, включая рентгеновский аппарат.

Рентгеновская кристаллография

1. Использование рентгеновских лучей для изучения расположения атомов в кристалле. 2. Изучение структуры кристаллических материалов с использованием взаимодействия рентгеновских лучей и электронной плотности кристалла (дифракции).

Устройство для обнаружения рентгеновских лучей

Устройство, обнаруживающее неоднородности поверхности и объема твердых тел с помощью рентгеновских лучей.

Камера для дифракции рентгеновских лучей

Камера, которая направляет пучок рентгеновских лучей на образец неизвестного материала и позволяет полученным дифрагированным лучам воздействовать на полосу пленки.

Картина дифракции рентгеновских лучей

Картина, полученная на пленке, экспонированной в камере для дифракции рентгеновских лучей.Он состоит из частей кругов с разным расстоянием между ними в зависимости от исследуемого материала.

Рентгеновский гониометр

Прибор, который определяет положение электрических осей кристалла кварца путем отражения рентгеновских лучей от атомных плоскостей кристалла.

Рентгеновские лучи

Также называются рентгеновскими лучами. Проникающее излучение, подобное свету, но имеющее гораздо более короткие длины волн (от 10 ^–7 до 10 ^–10 см).Обычно они генерируются при бомбардировке металлической мишени потоком высокоскоростных электронов.

Рентгеновский спектрограф

Прибор, который используется для построения диаграмм дифракции рентгеновских лучей, такой как рентгеновский спектрометр с фотографическими или другими регистрирующими устройствами.

Рентгеновский спектрометр

1. Прибор для получения спектра рентгеновского излучения и измерения длин волн его компонентов. 2. Прибор, предназначенный для получения рентгеновского спектра материала в качестве помощи в его идентификации.Этот метод особенно полезен, когда материал не может быть физически разрушен.

Спектр рентгеновского излучения

Расположение пучка рентгеновских лучей в порядке длины волны.

Рентгеновский толщиномер

Бесконтактный толщиномер, используемый для измерения и индикации толщины движущегося холоднокатаного стального листа в процессе прокатки. Рентгеновский луч, направленный через лист, поглощается пропорционально толщине материала и его атомному номеру, и измерение количества поглощения дает непрерывное указание толщины листа.

Рентгеновская трубка

Вакуумная трубка, в которой рентгеновские лучи производятся путем бомбардировки мишени высокоскоростными электронами, ускоренными электростатическим полем.

Мишень для рентгеновской трубки

Также известен как антикатод. Электрод или электродная секция, на которую фокусируется электронный луч и излучает рентгеновские лучи.

xso

Аббревиатура для кварцевого стабилизатора.

xtal

Аббревиатура кристалла.

X-волна

Одна из двух составляющих, на которые магнитное поле Земли делит радиоволну в ионосфере. Другой компонент — обыкновенная, или О-, волна.

Кристалл XY-огранки

Кристалл, ограненный таким образом, что его характеристики находятся между кристаллами X- и Y-огранки.

Плоттер XY

1.Устройство, используемое вместе с компьютером для нанесения координатных точек в виде графика. 2. Компьютерное устройство вывода, которое реагирует на цифровые сигналы предварительно записанных и / или обработанных данных путем распечатки линейных сегментов. Эти данные, которые могут включать буквенно-цифровые символы, диаграммы, таблицы или рисунки, загружаются из памяти компьютера со скоростью, достаточной для работы плоттера. XY-плоттер нельзя использовать для прямой записи аналоговых сигналов без дигитайзеров.

Регистратор XY

1.Регистратор, который отслеживает на графике отношения между двумя переменными, ни одна из которых не является временем. Иногда диаграмма перемещается, и одна из переменных контролируется так, что взаимосвязь увеличивается пропорционально времени. 2. Регистратор, в котором два сигнала одновременно записываются одним пером, которое приводится в движение в одном направлении (ось X) одним сигналом, а в другом направлении (ось Y) — вторым сигналом. 3. Регистратор данных, который используется для записи изменения одного параметра по отношению к другому.Например, изменение давления в зависимости от температуры. Для этих записывающих устройств доступен широкий спектр преобразователей для преобразования физических параметров в электрические сигналы, используемые в самописце. Датчики давления, термопары, тензодатчики и акселерометры — вот несколько примеров. 4. Тип регистратора, который реагирует на поступающие аналоговые сигналы по мере их появления. Сигналы печатаются на графике заранее определенного размера, который может охватывать тестовые периоды от нескольких секунд до целого года. XY-рекордер записывает непрерывные линии.Кроме того, скорость отклика прибора важна для точности записи.

Переключатель XY

Переключатель с дистанционным управлением, расположенный так, что дворники перемещаются вперед и назад по горизонтали.

Решения NCERT для физики класса 12 Глава 7 Переменный ток — Бюллетень Toppers

Бесплатные решения NCERT для класса 12 по физике Глава 7 Переменный ток решены опытными преподавателями в соответствии с руководящими принципами книги NCERT (CBSE) и представлены вам бюллетенем Toppers.Эти вопросы с упражнениями на переменный ток с решениями для класса 12 по физике охватывают все вопросы главы 12 по переменному току и помогут вам пересмотреть полный учебный план и получить дополнительные оценки в соответствии с рекомендациями Совета CBSE из последней книги NCERT для класса 12 по физике. Вы можете прочитать и загрузить NCERT Book Solution, чтобы лучше понять все темы и концепции.
7.1 — ВВЕДЕНИЕ
7.2 — НАПРЯЖЕНИЕ ПЕРЕМЕННОГО ТОКА НА РЕЗИСТОРЕ
7.3 — ПРЕДСТАВЛЕНИЕ ПЕРЕМЕННОГО ТОКА И НАПРЯЖЕНИЯ ВРАЩАЮЩИМИ ВЕКТОРАМИ — ФАЗОРЫ
7.4 — НАПРЯЖЕНИЕ ПЕРЕМЕННОГО ТОКА НА ИНДУКТОРЕ
7,5 — НАПРЯЖЕНИЕ ПЕРЕМЕННОГО ТОКА НА КОНДЕНСАТОР
7.6 — НАПРЯЖЕНИЕ ПЕРЕМЕННОГО ТОКА НА ЦЕПЬ LCR СЕРИИ
7.6.1 — Диаграмма типа
7.6.2 — Аналитическое решение
7.6.3 — Резонанс
7.8 — КОЛЕБАНИЯ LC
7.9 — ТРАНСФОРМАТОРЫ.

Решения NCERT переменного тока — класс 12, физика

Упражнение: ответы на вопросы по номеру страницы: 266
В1: резистор 100 Ом подключается к источнику переменного тока 220 В, 50 Гц.
(a) Какое действующее значение тока в цепи?
(b) Какая чистая мощность потребляется за полный цикл?
Ответ:
Сопротивление резистора, R = 100 Ом
Напряжение питания, В = 220 В
Частота, v = 50 Гц
(a) Действующее значение тока в цепи определяется как:

(b) Чистая мощность, потребляемая за полный цикл, определяется как:
P = VI
= 220 × 2,2 = 484 Вт

---

Q2: (a) Пиковое напряжение источника переменного тока составляет 300 В.Какое среднеквадратичное напряжение?
(b) Действующее значение тока в цепи переменного тока составляет 10 А. Что такое пиковый ток?
Ответ:
(a) Пиковое напряжение источника переменного тока, В ₀ = 300 В
Действующее значение напряжения определяется как:

(b) Термическое значение тока определяется как:
I = 10 A
Теперь пиковый ток определяется как:

---

Q3: Катушка индуктивности 44 мГн подключена к источнику переменного тока 220 В, 50 Гц. Определите действующее значение тока в цепи.
Ответ :
Индуктивность индуктора, L = 44 мГн = 44 × 10 ^-3 H
Напряжение питания, В = 220 В
Частота, v = 50 Гц
Угловая частота, ω = 2πv
Индуктивное реактивное сопротивление, X _L = ωL
Действующее значение тока определяется как:

Следовательно, действующее значение тока в цепи составляет 15,92 А.

---

Q4: Конденсатор емкостью 60 мкФ подключен к источнику переменного тока 110 В, 60 Гц. Определите действующее значение тока в цепи.
Ответ:
Емкость конденсатора, C = 60 мкФ = 60 × 10-6 Ф
Напряжение питания, V = 110 В
Частота, v = 60 Гц
Угловая частота, ω = 2πv
Емкостное реактивное сопротивление

Rms значение тока задается как:

Следовательно, действующее значение тока составляет 2,49 А.

---

Q5: В упражнениях 7.3 и 7.4, какова чистая мощность, потребляемая каждой цепью за полный цикл. Поясните свой ответ.
Ответ:
В индуктивной цепи
действующее значение тока, I = 15.92 A
Действующее значение напряжения, V = 220 В
Следовательно, потребляемая полезная мощность может быть получена по соотношению,
P = VI cos Φ
Где
Φ = разность фаз между V и I
Для чисто индуктивной цепи , разность фаз между переменным напряжением и током составляет 90 °, т.е. Φ = 90 °.
Следовательно, P = 0, т. Е. Полезная мощность равна нулю.
В емкостной цепи,
действующее значение тока, I = 2,49 А
действующее значение напряжения, V = 110 В
Следовательно, потребляемая полезная мощность может быть получена как:
P = VI Cos Φ
Для чисто емкостной цепи , разность фаз между переменным напряжением и током составляет 90 ° i.е., Φ = 90 °.
Следовательно, P = 0, т. Е. Полезная мощность равна нулю.

---

Q6: Получите резонансную частоту ωr последовательного контура LCR с L = 2,0 Гн, C = 32 мкФ и R = 10 Ом. Какое значение Q у этой схемы?
Ответ:
Индуктивность, L = 2,0 Гн
Емкость, C = 32 мкФ = 32 × 10 ^-6 F
Сопротивление, R = 10 Ом
Резонансная частота задается соотношением,

Теперь, Q -значение схемы дается как:

Следовательно, Q-Value этой схемы равно 25.

---

Q7: Заряженный конденсатор 30 мкФ подключен к катушке индуктивности 27 мГн. Какая угловая частота свободных колебаний контура?
Ответ:
Емкость, C = 30 мкФ = 30 × 10 ^-6 F
Индуктивность, L = 27 мГн = 27 × 10 ^-3 H
Угловая частота задается как:

Следовательно, угловая частота свободных колебаний контура 1,11 × 10 ³ рад / с.

---

Q8: Предположим, начальный заряд конденсатора в упражнении 7.7 составляет 6 мКл. Какая общая энергия изначально хранится в цепи? Какова общая энергия в более позднее время?
Ответ:
Емкость конденсатора, C = 30 мкФ = 30 × 10 ^-6 F
Индуктивность индуктора, L = 27 мГн = 27 × 10 ^-3 H
Заряд конденсатора, Q = 6 мКл = 6 × 10 ^-3 C
Общая энергия, запасенная в конденсаторе, может быть рассчитана по соотношению

Общая энергия в более позднее время останется прежней, поскольку энергия распределяется между конденсатором и катушкой индуктивности.

---

Q9: Последовательная цепь LCR с R = 20 Ом, L = 1,5 Гн и C = 35 мкФ подключена к источнику переменного тока переменной частоты 200 В. Когда частота источника питания равна собственной частоте цепи, какова средняя мощность, передаваемая в цепь за один полный цикл?
Ответ:
В резонансе частота источника питания равна собственной частоте данной цепи LCR.
Сопротивление, R = 20 Ом
Индуктивность, L = 1,5 Гн
Емкость, C = 35 мкФ = 30 × 10 ^-6 F
Напряжение питания переменного тока в цепи LCR, V = 200 В
Полное сопротивление цепи дано по соотношению,

При резонансе,
.’. Z = R = 20 Ом
Ток в цепи можно рассчитать как:

Следовательно, средняя мощность, передаваемая в цепь за один полный цикл = VI
= 200 × 10 = 2000 Вт.

---

Q10: Радиостанция может настраиваться на частотный диапазон части диапазона MW вещания: (от 800 кГц до 1200 кГц). Если его LC-цепь имеет эффективную индуктивность 200 мкГн, каков должен быть диапазон его переменного конденсатора?
[Подсказка: для настройки собственная частота, то есть частота свободных колебаний LC-контура, должна быть равна частоте радиоволны.]
Ответ:
Диапазон частоты (v) радио составляет от 800 кГц до 1200 кГц.
Нижняя частота настройки, v ₁ = 800 кГц = 800 × 10 ³ Гц
Верхняя частота настройки, v ₂ = 1200 кГц = 1200 × 10 ³ Гц
Эффективная индуктивность контура L = 200 мкГн = 200 × 10 ^-6 H
Емкость переменного конденсатора для v ₁ задается как:
C ₁
Где,
ω ₁ = Угловая частота для конденсатора C ₁


Емкость переменной конденсатор для v ₂ ,
C ₂
Где,
ω ₂ = угловая частота для конденсатора C ₂


Следовательно, диапазон переменного конденсатора составляет от 88.От 04 пФ до 198,1 пФ.

---

Q11: На рисунке 7.21 показана последовательная цепь LCR, подключенная к источнику переменной частоты 230 В. L = 5,0 Гн, C = 80 мкФ, R = 40 Ом

(a) Определите частоту источника, которая приводит контур в резонанс.
(b) Определите полное сопротивление цепи и амплитуду тока на резонансной частоте.
(c) Определите среднеквадратичное падение потенциала на трех элементах цепи. Покажите, что падение потенциала на ЖК-комбинации равно нулю на резонансной частоте.
Ответ:
Индуктивность индуктора, L = 5,0 Гн
Емкость конденсатора, C = 80 мкГн = 80 × 10 ^-6 F
Сопротивление резистора, R = 40 Ом
Потенциал переменной источник напряжения, V = 230 В
(a) Резонансная угловая частота задается как:

Следовательно, цепь войдет в резонанс для частоты источника 50 рад / с.
(b) Импеданс контура определяется соотношением,

При резонансе,

Амплитуда тока на резонансной частоте задается как:
Где
В ₀ = Пиковое напряжение

Следовательно, в резонансе полное сопротивление цепи составляет 40 Ом, а амплитуда тока равна 8.13 А.
(c) Среднеквадратичное падение потенциала на катушке индуктивности,
(В _L ) среднеквадратичное значение = I × ωRL
Где
I = действующее значение тока

Падение потенциала на конденсаторе,

Падение потенциала на резистор,
(VR) rms = IR
= 230/40 × 40 = 230 В
Падение потенциала на комбинации LC,

В резонансе,
мкВ _LC = 0
Следовательно, доказано, что потенциал падение через комбинацию LC равно нулю на резонансной частоте.

---

Q12: LC-цепь содержит катушку индуктивности 20 мГн и конденсатор 50 мкФ с начальным зарядом 10 мКл. Сопротивлением цепи можно пренебречь. Пусть момент замыкания цепи равен t = 0.
(a) Какая общая энергия сохраняется изначально? Сохраняется ли он при колебаниях ЖК?
(б) Какова собственная частота цепи?
(c) В какой момент накопленная энергия
(i) полностью электрическая (т.е.е., хранится в конденсаторе)? (ii) полностью магнитные (т.е. хранящиеся в индукторе)?
(d) В какое время общая энергия распределяется поровну между катушкой индуктивности и конденсатором?
(e) Если в цепь вставлен резистор, сколько энергии в конечном итоге рассеивается в виде тепла?
Ответ:
Индуктивность индуктора, L = 20 мГн = 20 × 10 ^-3 Гн
Емкость конденсатора, C = 50 мкФ = 50 × 10 ^-6 Ф
Начальный заряд конденсатора , Q = 10 мКл = 10 × 10 ^-3 C
(a) Полная энергия, изначально запасенная в цепи, определяется как:

Следовательно, общая энергия, запасенная в цепи LC, будет сохранена, потому что нет резистор, включенный в цепь.
(b) Собственная частота контура определяется соотношением,

Собственная угловая частота,


Следовательно, собственная частота контура составляет 10 ³ рад / с.
(c) (i) Для периода времени (T), общий заряд конденсатора в момент времени t,
Для накопленной энергии является электрической, мы можем записать Q ‘= Q.
Следовательно, можно сделать вывод, что энергия хранящийся в конденсаторе полностью электрический в момент времени t =
(ii) Магнитная энергия является максимальной, когда электрическая энергия Q ‘равна 0.
Следовательно, можно сделать вывод, что энергия, запасенная в конденсаторе, является полностью магнитной в момент времени,
(d) Q ¹ = Заряд конденсатора, когда общая энергия равномерно распределяется между конденсатором и катушкой индуктивности в момент времени t .
Когда общая энергия равномерно распределяется между катушкой индуктивности и конденсатором, энергия, запасенная в конденсаторе, = 1/2 (максимальная энергия).

Следовательно, общая энергия поровну распределяется между индуктором и емкостью в определенный момент времени,
(e) Если в цепь вставлен резистор, тогда общая начальная энергия рассеивается в виде тепловой энергии в цепи.Сопротивление гасит колебания ЖК.

---

Q13: Катушка с индуктивностью 0,50 Гн и сопротивлением 100 Ом подключена к источнику переменного тока 240 В, 50 Гц.
(а) Каков максимальный ток в катушке?
(b) Какова временная задержка между максимумом напряжения и максимумом тока?
Ответ:
Индуктивность индуктора, L = 0,50 Гн
Сопротивление резистора, R = 100 Ом
Потенциал напряжения питания, V = 240 В
Частота питания, v = 50 Гц
( a) Пиковое напряжение определяется как:

Угловая частота источника питания,
ω = 2 πv
= 2π × 50 = 100 π рад / с
Максимальный ток в цепи определяется как:

(b) Уравнение для напряжения имеет вид:
V = V ₀ cos ωt
Уравнение для тока имеет вид:
I = I ₀ cos (ωt — Φ)
Где
Φ = разность фаз между напряжением и током
В момент времени t = 0.
В = В ₀ (напряжение максимальное)
Для ωt — Φ = 0, т. Е. В момент времени t = Φ / ω
I = I ₀ (ток максимальный)
Следовательно, временной лаг между максимальным напряжением а максимальный ток равен Φ / ω.
Теперь фазовый угол Φ определяется соотношением

Следовательно, задержка между максимальным напряжением и максимальным током составляет 3,2 мс.

---

Q14: Получите ответы (a) — (b) в упражнении 7.13, если цепь подключена к высокочастотному источнику питания (240 В, 10 кГц).Поэтому объясните утверждение, что на очень высокой частоте индуктор в цепи почти равен разомкнутой цепи. Как катушка индуктивности ведет себя в цепи постоянного тока после установившегося режима?
Ответ:
Индуктивность индуктора, L = 0,5 Гц
Сопротивление резистора, R = 100 Ом
Потенциал питающих напряжений, V = 240 В
Частота питающего напряжения, v = 10 кГц = 10 ⁴ Гц
Угловая частота, ω = 2πv = 2π × 10 ⁴ рад / с
(a) Пиковое напряжение,
Максимальный ток,

(b) Для разности фаз Φ имеем соотношение:

Можно заметить, что I ₀ в этом случае очень мало.Следовательно, на высоких частотах индуктор составляет разомкнутую цепь.
В цепи постоянного тока после достижения установившегося состояния ω = 0. Следовательно, индуктор L ведет себя как чисто проводящий объект.

---

Q15: Конденсатор емкостью 100 мкФ, подключенный последовательно с сопротивлением 40 Ом, подключен к источнику питания 110 В, 60 Гц.
(а) Каков максимальный ток в цепи?
(b) Какова временная задержка между максимумом тока и максимумом напряжения?
Ответ:
Емкость конденсатора, C = 100 мкФ = 100 × 10 ^-6 F
Сопротивление резистора, R = 40 Ом
Напряжение питания, В = 110 В
(а) Частота колебаний, v = 60 Гц
Угловая частота, ω = 2πv = 2π x 60 рад / с
Для RC-цепи мы имеем соотношение для импеданса как:

Пиковое напряжение, В ₀ =
Дан максимальный ток как:

(b) В конденсаторной цепи напряжение отстает от тока на фазовый угол Φ.Этот угол задается соотношением:

Следовательно, время задержки между максимальным током и максимальным напряжением составляет 1,55 мс.

---

Q16: Получите ответы на (a) и (b) в упражнении 7.15, если цепь подключена к источнику питания 110 В, 12 кГц? Поэтому объясните утверждение, что конденсатор является проводником на очень высоких частотах. Сравните это поведение с поведением конденсатора в цепи постоянного тока после установившегося режима.
Ответ:
Емкость конденсатора, C = 100 мкФ = 100 × 10 ^-6 F
Сопротивление резистора, R = 40 Ом
Напряжение питания, В = 110 В
Частота питания, В = 12 кГц = 12 × 10 ³ Гц
Угловая частота, ω = 2 πv = 2 × π × 12 × 10 ³ 03
= 24π × 10 ³ рад / с
Пиковое напряжение,
Максимальный ток,

Для RC-цепи напряжение отстает от тока на фазовый угол Φ, определяемый как:

Следовательно, Φ стремится к нулю на высоких частотах.На высокой частоте конденсатор C действует как проводник.
В цепи постоянного тока после достижения установившегося состояния ω = 0. Следовательно, конденсатор C составляет разомкнутую цепь.

---

Q17: Поддержание частоты источника равной резонансной частоте последовательной цепи LCR, если три элемента, L, C и R расположены параллельно, показывают, что общий ток в параллельной цепи LCR минимален на этой частоте . Получите текущее действующее значение в каждой ветви цепи для элементов и источника, указанных в упражнении 7.11 для этой частоты.
Ответ:
Катушка индуктивности (L), конденсатор (C) и резистор (R) подключены параллельно друг другу в цепи, где
L = 5,0 Гн
C = 80 мкФ = 80 × 10 ^-6 F
R = 40 Ом
Потенциал источника напряжения, V = 230 В
Импеданс (Z) данной параллельной цепи LCR задается как:

Где
ω = угловая частота
При резонансе,

Следовательно, величина Z максимальна при 50 рад / с.В результате общий ток минимален.
Среднеквадратичный ток, протекающий через катушку индуктивности L, определяется как:

Среднеквадратичный ток, протекающий через конденсатор C, определяется как:

Среднеквадратичный ток, протекающий через резистор R, определяется как:

---

Q18: Цепь, содержащая последовательно соединенные катушку индуктивности 80 мГн и конденсатор емкостью 60 мкФ, подключена к источнику питания 230 В, 50 Гц. Сопротивлением цепи можно пренебречь.
(a) Получите текущую амплитуду и среднеквадратичные значения.
(b) Получите среднеквадратичные значения перепадов потенциала на каждом элементе.
(c) Какая средняя мощность передается на катушку индуктивности?
(d) Какая средняя мощность передается конденсатору?
(e) Какова общая средняя мощность, потребляемая цепью? [«Среднее» означает «усредненное за один цикл».]
Ответ:
Индуктивность, L = 80 мГн = 80 × 10 Гн
Емкость, C = 60 мкФ = 60 × 10 ^-6 F
Напряжение питания , V = 230 В
Частота, v = 50 Гц
Угловая частота, ω = 2πv = 100 π рад / с
Пиковое напряжение, В ₀ =
(a) Максимальный ток определяется как:

Отрицательный Знак появляется, потому что ωL <1 / ωC
Амплитуда максимального тока,
Следовательно, действующее значение тока,
(b) Разность потенциалов на катушке индуктивности,
В _L = I × ωL
= 8.22 × 100 π × 80 × 10 ^-3
= 206,61 В
Разность потенциалов на конденсаторе,

(c) Средняя мощность, потребляемая катушкой индуктивности, равна нулю, поскольку фактическое напряжение опережает ток на π / 2.
(d) Средняя мощность, потребляемая конденсатором, равна нулю, поскольку напряжение отстает от тока на π / 2.
(e) Общая потребляемая мощность (усредненная за один цикл) равна нулю.

---

Q19: Предположим, что цепь в упражнении 7.18 имеет сопротивление 15 Ом.Получите среднюю мощность, передаваемую каждому элементу цепи, и общую потребляемую мощность.
Ответ:
Средняя мощность, передаваемая на резистор = 788,44 Вт
Средняя мощность, передаваемая на конденсатор = 0 Вт
Полная мощность, потребляемая цепью = 788,44 Вт
Индуктивность индуктора, L = 80 мГн = 80 × 10 ^-3 H
Емкость конденсатора, C = 60 мкФ = 60 × 10 ^-6 F
Сопротивление резистора, R = 15 Ом
Потенциал питания, V = 230 В
Частота сигнала, v = 50 Гц
Угловая частота сигнала, ω = 2πv = 2π × (50) = 100π рад / с
Элементы соединены последовательно друг с другом.Следовательно, полное сопротивление цепи определяется как:

Ток, протекающий в цепи,
Средняя мощность, передаваемая на сопротивление, определяется как:
PR = I ² R
= (7,25) ² × 15 = 788,44 Вт
Средняя мощность, передаваемая на конденсатор, PC = Средняя мощность, передаваемая на катушку индуктивности, PL = 0
Общая мощность, потребляемая цепью:
= PR + PC + PL
= 788,44 + 0 + 0 = 788,44 Вт
Следовательно, общая мощность, потребляемая схема 788,44 Вт.

---

Q20: Последовательная цепь LCR с L = 0.12 H, C = 480 нФ, R = 23 Ω подключен к источнику переменного тока 230 В.
(a) Какова частота источника, при которой амплитуда тока максимальна. Получите это максимальное значение.
(b) Какова частота источника, при которой средняя мощность, потребляемая цепью, является максимальной. Получите значение этой максимальной мощности.
(c) Для каких частот источника мощность передается в цепь вдвое меньшей мощности на резонансной частоте? Какова текущая амплитуда на этих частотах?
(г) Какова добротность данной схемы?
Ответ:
Индуктивность, L = 0.12 H
Емкость, C = 480 нФ = 480 × 10 ^-9 F
Сопротивление, R = 23 Ом
Напряжение питания, В = 230 В
Пиковое напряжение определяется как:
В ₀ = = 325,22 В
(a) Ток, протекающий в цепи, определяется соотношением,

Где,
I ₀ = максимум при резонансе
При резонансе мы имеем

Где
ω _R = угловая частота резонанса

∴Резонансная частота,
А, максимальный ток
(b) Максимальная средняя мощность, потребляемая цепью, определяется как:

Следовательно, резонансная частота (V _R ) равна 663.48 Гц
(c) Мощность, передаваемая в цепь, составляет половину мощности на резонансной частоте.
Частоты, при которых передаваемая мощность равна половине, =

Где,

Следовательно, изменение частоты,
∴
И,
Следовательно, на частотах 648,22 Гц и 678,74 Гц передаваемая мощность составляет половину.
На этих частотах амплитуда тока может быть задана как:

(d) Добротность данной цепи может быть получена с помощью соотношения,

Следовательно, добротность данной схемы равна 21.74.

---

Q21: Получите резонансную частоту и добротность последовательной цепи LCR с L = 3,0 Гн, C = 27 мкФ и R = 7,4 Ом. Желательно улучшить резкость резонанса схемы за счет уменьшения ее «полной ширины на половине максимума» в 2 раза. Предложите подходящий способ.
Ответ:
Индуктивность, L = 3,0 Гн
Емкость, C = 27 мкФ = 27 × 10 ^-6 F
Сопротивление, R = 7,4 Ом
При резонансе угловая частота источника для данной серии LCR Схема задается как:

Q-фактор серии:

Чтобы улучшить резкость резонанса за счет уменьшения его «полной ширины на половине максимума» в 2 раза без изменения, нам нужно уменьшить R до половины i.э.,
Сопротивление =

---

Q22: Ответьте на следующие вопросы:
(a) В любой цепи переменного тока приложенное мгновенное напряжение равно алгебраической сумме мгновенных напряжений на последовательных элементах цепи? Верно ли то же самое для среднеквадратичного напряжения?
(б) Конденсатор используется в первичной цепи индукционной катушки.
(c) Сигнал приложенного напряжения состоит из суперпозиции постоянного и переменного напряжения высокой частоты.Схема состоит из последовательно соединенных катушек индуктивности и конденсатора. Покажите, что сигнал постоянного тока появится на C, а сигнал переменного тока — на L.
(d) Дроссельная катушка, соединенная последовательно с лампой, подключена к линии постоянного тока. Видно, что лампа ярко светит. Установка железного сердечника в дроссель не приводит к изменению яркости лампы. Предскажите соответствующие наблюдения, если подключение к сети переменного тока.
(e) Зачем нужна дроссельная катушка при использовании люминесцентных ламп с сетью переменного тока? Почему нельзя использовать обычный резистор вместо дроссельной катушки?
Ответ:
(а) Да; утверждение неверно для среднеквадратичного напряжения
Это правда, что в любой цепи переменного тока приложенное напряжение равно средней сумме мгновенных напряжений на последовательных элементах схемы.Однако это неверно для среднеквадратичного напряжения, поскольку напряжения на разных элементах могут не совпадать по фазе.
(b) Высокое индуцированное напряжение используется для зарядки конденсатора.
Конденсатор используется в первичной цепи индукционной катушки. Это связано с тем, что при разрыве цепи высокое индуцированное напряжение используется для зарядки конденсатора, чтобы избежать искр.
(c) Сигнал постоянного тока появится на конденсаторе C, потому что для сигналов постоянного тока импеданс катушки индуктивности (L) пренебрежимо мал, в то время как сопротивление конденсатора (C) очень велико (почти бесконечно).Следовательно, сигнал постоянного тока появляется через C. Для сигнала переменного тока высокой частоты импеданс L высокий, а сопротивление C очень низкое. Следовательно, через L. появляется сигнал высокой частоты переменного тока.
(d) Если в дроссельную катушку вставить железный сердечник (который включен последовательно с лампой, подключенной к линии переменного тока), лампа будет тускло светиться. Это связано с тем, что дроссельная катушка и железный сердечник увеличивают сопротивление цепи.
(e) Дроссельная катушка необходима при использовании люминесцентных ламп с сетью переменного тока, поскольку она снижает напряжение на лампе без больших потерь энергии.Обычный резистор нельзя использовать вместо дроссельной катушки для этой цели, потому что он тратит энергию в виде тепла.

---

Q23: Линия электропередачи подает входную мощность 2300 В на понижающий трансформатор с первичной обмоткой на 4000 витков. Какое должно быть количество витков во вторичной обмотке, чтобы получить выходную мощность 230 В?
Ответ:
Входное напряжение, В ₁ = 2300
Число витков первичной обмотки, n ₁ = 4000
Выходное напряжение, В ₂ = 230 В
Число витков вторичной обмотки = n ₂
Напряжение связано с количеством витков следующим образом:

Следовательно, во второй обмотке 400 витков.

---

Q24: На гидроэлектростанции напор воды находится на высоте 300 м, а доступный расход воды составляет 100 м3 с ^-1 . Если КПД турбогенератора составляет 60%, оцените доступную электроэнергию от станции (g = 9,8 м · с ^-2 ).
Ответ:
Высота водяного напора, h = 300 м
Объем расхода воды в секунду, V = 100 м ³ / с
КПД турбогенератора, n = 60% = 0,6
Ускорение от гравитация, g = 9.8 м / с ²
Плотность воды, ρ = 10 ³ кг / м ³
Электроэнергия, получаемая от завода = η x hρgV
= 0,6 x 300 x 10 ³ x 9,8 x 100
= 176,4 x 10 ⁶ Вт
= 176,4 МВт

---

Q25: Небольшой городок с потребностью в 800 кВт электроэнергии при 220 В расположен в 15 км от электростанции, вырабатывающей мощность 440 В. Сопротивление двухпроводной линии электропередачи составляет 0,5 Ом на км. Город получает электроэнергию от линии через понижающий трансформатор 4000-220 В на подстанции в городе.
(a) Оцените потери мощности в линии в виде тепла.
(b) Какую мощность должна обеспечивать установка, если предположить, что потери мощности из-за утечки незначительны?
(c) Охарактеризуйте повышающий трансформатор на заводе.
Ответ:
Общая необходимая электрическая мощность, P = 800 кВт = 800 × 10 ³ Вт
Напряжение питания, В = 220 В
Напряжение, при котором электростанция вырабатывает энергию, В ‘= 440 В
Расстояние между город и электростанция, d = 15 км
Сопротивление двухпроводных линий электропередачи = 0.5 Ом / км
Суммарное сопротивление проводов, R = (15 + 15) 0,5 = 15 Ом
В подстанции используется понижающий трансформатор номиналом 4000 — 220 В.
Входное напряжение, В ₁ = 4000 В
Выходное напряжение, В ₂ = 220 В
Действующее значение тока в проводных линиях определяется как:

(a) Потери мощности в линии = I ₂ R
= (200) ² × 15
= 600 × 10 ³ Вт
= 600 кВт
(b) Предполагая, что потеря мощности незначительна из-за утечки тока:
Полная мощность, поставляемая станцией = 800 кВт + 600 кВт
= 1400 кВт
(c) Падение напряжения в линии электропередачи = IR = 200 × 15 = 3000 В
Следовательно, общее напряжение, передаваемое от установки = 3000 + 4000
= 7000 В
Также , вырабатываемая мощность составляет 440 В.
Следовательно, номинал повышающего трансформатора, находящегося на электростанции, составляет 440 В — 7000 В.

---

Q26: Проделайте то же упражнение, что и выше, с заменой более раннего трансформатора на понижающий трансформатор на 40000-220 В (как и раньше, пренебрегайте потерями утечки, хотя это уже может быть не очень хорошим предположением из-за очень задействована передача высокого напряжения). Следовательно, объясните, почему предпочтительна передача высокого напряжения?
Ответ:
Номинал понижающего трансформатора 40000 В — 220 В.
Входное напряжение, В ₁ = 40000 В
Выходное напряжение, В ₂ = 220 В
Общая необходимая электрическая мощность, P = 800 кВт = 800 × 103 Вт
Потенциал источника, В = 220 В
Напряжение, при котором Электростанция вырабатывает электроэнергию, V ‘= 440 В
Расстояние между городом и электростанцией, d = 15 км
Сопротивление двухпроводных линий, передающих мощность = 0,5 Ом / км
Полное сопротивление проводных линий, R = (15 + 15) 0,5 = 15 Ом
P = V ₁ I
Действующий ток в проводной линии определяется как:
I = P / V ₁


(a) Потери мощности в линии = I ² R
= (20) ² × 15
= 6 кВт
(b) Предполагая, что потеря мощности незначительна из-за утечки тока.

No related posts.