Основы цифровой электроники.
Введение в цифровую электронику
С самой глубокой древности, от начала цивилизации люди испытывали потребность в счёте. Ученые считают, что сначала возникли понятия характеризующие количество и лишь потом, возникли слова, обозначавшие качественные характеристики предметов. Постепенно возникли и сформировались различные системы счёта. Наиболее широкое распространение и в древности, и в настоящее время получила десятеричная система исчисления. Это объясняется просто: у человека на руках десять пальцев, то есть руки это счёты с ограниченными возможностями, но которые всегда с собой.
Систем исчисления существует много, в принципе любое число может быть основанием системы, но не все они удобны и применяются на практике. Широко распространены шестидесятеричная система, она применяется при счёте времени: 60 сек.= 1 мин. 60 мин.= 1 час и двенадцатеричная, когда счёт ведётся дюжинами и эта же система является денежной системой принятой в Великобритании.
Нас интересует самая простая и самая распространённая в наше время двоичная (бинарная) система исчисления. Все компьютеры от персональных, до суперкомпьютеров
А началось всё ещё в XVII веке, когда талантливый математик Лейбниц впервые описал двоичную систему исчисления, которую, как считают, он позаимствовал из древних китайских математических трактатов. В середине IXX века математик Д. Буль написал и опубликовал работу, которая выводила уравнения алгебры на основе понятий формальной логики. Базовых понятия было всего два: высказывание
И наконец, в 30-е годы XX века Клод Шеннон защитил интересную диссертацию. Её темой было использование реле и переключателей для создания примитивного вычислителя-сумматора. Все принципы работы были реализованы на действиях двоичной арифметики и Булевой алгебры. По сути, на этой диссертации основана вся цифровая техника, то есть она послужила тем зёрнышком, из которого выросло и продолжает расти огромное дерево цифровой электроники.
Двоичная система исчисления.
В ней используются всего две цифры: «1» и «
Поначалу это может показаться неудобным, так как числа получаются слишком длинными, но учитывая скорость работы современных процессоров и число операций в секунду, которая у сверхмощных компьютеров может достигать фантастических величин достигающих 20 000 терафлоп, то разрядность представляемых чисел не играет практически никакой роли. 1 терафлоп это 1 триллион операций в секунду.

Перевод чисел из десятичной системы в двоичную систему осуществляется последовательным делением числа на 2. Первое деление даёт младший разряд, а последнее деление даёт старший разряд числа. Если число делится без остатка, пишем «0», а с остатком пишем «1». 201310 = 111110111012, что означает, текущий год по основанию 10 равен указанному числу по основанию 2. Для обратного преобразования достаточно суммировать веса разрядов представляющие собой степени числа 2. Число разряда начинается с 0, затем 1, 2,3…10. Для данного примера получим: 1024+512+256+128+64+16+8+4+1=2013. Пропущены второй и шестой разряды, где стоят нули, то есть 2 и 32.
Двоичное число легко представить в виде последовательности прямоугольных импульсов.
На рисунке показано напряжение питания +5,0V. На таком напряжении питания работают интегральные микросхемы транзисторно-транзисторной логики (ТТЛ) с малой степенью интеграции, которые в своё время пользовались огромной популярностью у радиолюбителей. Их используют и сейчас в несложных самоделках. Это микросхемы серий К155, К133 и микросхемы высокого быстродействия и более высокой частоты КР1533 и К555. В них использовались диоды Шоттки.
Уровень логической единицы не обязательно должен быть уровнем +5,0V, как показано на рисунке. Логическая единица могла находиться в интервале от + 2,4V до +5V, а логический ноль в интервале от 0V до +0,4V. Если на выходе микросхемы при проверке её осциллографом на выходе оказывалось напряжение в интервале от +0,4 до +2,4, то такое состояние называли «
- а) неисправна данная микросхема;
- в) эту микросхему подсаживает следующая за ней микросхема.
Поскольку микросхемы бывают с разным напряжением питания, то и уровни логического нуля и логической единицы будут иметь другие значения. Логику, где логическая единица положительна, принято называть позитивной логикой. Есть схемы, где логическая единица равна нулю, а логический ноль это импульс отрицательной полярности.
Теперь, когда вы знакомы с основой цифровой электроники, не поленитесь узнать, что такое базовые логические элементы и RS-триггер.
Главная » Цифровая электроника » Текущая страница
Также Вам будет интересно узнать:
go-radio.ru
Цифровая электроника для начинающих
Это продолжение «Необычная электроника для начинающих. Введение»
Твоё путешествие в мир электроники мы начнем с погружения в цифровую электронику. Во-первых, потому что это верхушка пирамиды электронного мира, во-вторых, базовые понятия цифровой электроники просты и понятны.
Задумывался ли ты о том, какой феноменальный прорыв в науке и технике произошел благодаря электронике и цифровой электронике в частности? Если нет, тогда возьми свой смартфон и внимательно на него посмотри. Такая простая с виду конструкция — результат огромной работы и феноменальных достижений современной электроники. Создание такой техники стало возможным благодаря простой идее о том, что любую информацию можно представить в виде чисел. Таким образом, независимо от того, с какой информацией работает устройство, глубоко внутри оно занимается обработкой чисел.
Тебе наверняка знакомы римские и арабские цифры. В римской системе числа представляются в виде комбинации букв I, V, X, L, C, D, M, а в арабской с помощью комбинации символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Но существуют и другие формы представления числа. Одна из них — это двоичная форма. Или, как её чаще называют, двоичная система счисления. В такой системе счисления любое число представляет собой последовательность только из «0» и «1».
| Арабские | Римские | Двоичные |
| 0 | — | 00 |
| 1 | I | 01 |
| 2 | II | 10 |
| 3 | III | 11 |
Математики c инженерами хорошо потрудились, и сегодня любая информация может быть представлена в виде комбинации нулей и единиц: сигнал с датчика движения, музыка, видео, фото, температура, и даже вот этот текст, который ты сейчас читаешь, на самом деле в недрах твоего устройства имеет вид последовательности из нулей и единиц.
Независимо от того, с какой информацией работает цифровое устройство, глубоко внутри оно занимается обработкой чисел.

Почему именно «0» и «1», а не «0», «1» и «2», к примеру? На самом деле были вполне успешные попытки создать цифровую технику, которая использует не двоичную, а троичную систему исчисления («0», «1» и «2»), но двоичная все же победила.
Возможно, победа досталась ей, потому что СССР развалился, а может потому, что «0» и «1» легче представить в виде электрических сигналов. А значит, цифровые устройства на основе двоичной системы исчисления проще и дешевле производить. Подробнее о двоичных числах я расскажу позже.
Структура цифрового устройства
Почти в каждом цифровом устройстве встречаются типовые элементы, из комбинации которых оно состоит. Какие-то элементы совсем простые, какие-то более сложные, а какие-то совсем сложные. В любительской практике чаще всего встречаются: триггеры, таймеры, счетчики, регистры, микроконтроллеры, компараторы и др.
Давай выберем что-нибудь из этого списка и посмотрим, как оно устроено. Пусть это будет микроконтроллер (МК)! Ладно, признаюсь. Микроконтроллер я выбрал неспроста. Дело в том, что именно появление микропроцессоров произвело настоящую революцию в электронике и выдвинуло её развитие на новый уровень.
МК является наиболее многочисленным и популярным видом микропроцессоров в мире. Особенным его делает то, что микроконтроллер представляет собой микро-PC — целый компьютер в одной микросхеме. Представь себе компьютер размером, например, с копейку. Вот это и есть МК.
Микроконтроллеры используются повсеместно: в современных телевизорах, холодильниках, планшетах, охранных системах. Везде, где требуется чем-то управлять, микроконтроллер может найти своё место. А всё благодаря тому, что, как и любой микропроцессор, МК можно программировать. В итоге один и тот же вид микросхем можно использовать в сотнях различных устройств.
В наше время наибольшей популярностью пользуются, к примеру, микроконтроллеры AVR, PIC, ARM. Каждая из компаний, что выпускает перечисленные виды МК, производит десятки, если не сотни, разновидностей микроконтроллеров, предназначенных под все мыслимые и немыслимые задачи.
Как работает микроконтроллер
Несмотря на всю сложность конструкции настоящего микроконтроллера, рассказать, как он функционирует можно всего одним предложением: «В память микроконтроллера записывается текст программы, МК считывает команды из этой программы и выполняет их», — вот и всё.

Конечно, МК не может выполнить какие угодно команды. У него есть базовый набор команд, которые он понимает и знает как выполнить. Комбинируя эти команды, можно получить практически любую программу, с помощью которой устройство будет
mp16.ru
мир электроники — Основы цифровой техники
Категория
Рано или поздно любому радиолюбителю приходится слышать или сталкиваться с такими фразами как логический ноль или логическая единица, триггеры, счетчики и так далее…
Все эти понятия относятся к целому разделу электронных устройств под общим понятием цифровые или логические устройства.
Почему их назвали цифровыми?
Большинство устройств- усилители, например, или блоки питания работают по принципу аналогового сигнала: амплитуда напряжений может изменяться, иметь различные полярности, разную частоту, может изменять свою форму и так далее.
Цифровые устройства работают несколько иначе: там либо есть сигнал, либо его нету.
Самый простейший пример: выключать с лампочкой. Пусть это и не совсем удачное сравнение но там всего-лишь два положения: либо горит, либо не горит. Причем при этом не учитывается ни мощность электролампочки, ни цвет, ни яркость, ни напряжение питания, просто: или да, или нет.
Так вот: на цифровых устройствах так-же учитывается всего-лишь два состояния: есть напряжение на выходе (входе)- значит логическая единица, нет напряжения- значит логический ноль.
Однако это еще не все: все эти самые цифровые устройства (о которых и пойдет речь в данном разделе) умеют работать еще и по некой логике: они могут, например, менять свое логическое состояние лишь при определенных условиях.
Например: у нас есть две лампочки с выключателями, но при этом они между собою взаимосвязаны условием- гореть может лишь одна. То есть: если одна включена, то другую включить невозможно.
Немного подумав можно даже и схему было-бы накидать чтобы такое устройство сделать, но это нам сейчас не надо- скажу только лишь что это устройство имеет название ИЛИ (ну то есть понятно: или один выход, или другой и не в коем случае ни вместе).
Ну и, конечно же, так как здесь у нас присутствуют цифры, то существует даже определенная алгебра для расчета цифровых устройств!
Ну так вот: именно таким цифровым (или логическим) устройствам мы и займемся в этом разделе.
Итак:
Логические элементы
простая логика
триггеры
счетчики
Триггер Шмитта
Цифровые микросхемы и работа с ними
Теория цифровой техники
Логические числа, представление логических чисел
Алгебра логических элементов
Минимизация логических функций
Интегрирующие и дифференцирующие цепи
Триггеры на логических элементах
Шифраторы и Дешифраторы
Мультиплексор и Демультиплексор
Регистры
Оперативные запоминающие устройства
Постоянное запоминающее устройство
Сумматор
Арифметико-логические устройства
Устройства умножения и деления
ЦАП: Цифро- аналоговый преобразователь
АЦП: Аналогово-цифровой преобразователь
Цифровой фильтр с временной реализацией
Цифровой фильтр с частотной реализацией
DRAM, DIMM, SIMM, SDRAM, ESDRAM, DRDRAM, RIMM
Ну и под конец: часть материалов (в основном теория) взята с сайта http://naf-st.ru/
radio-uchebnik.ru
Цифровая электроника.
Просто о цифровой электронике
На страницах раздела Цифровая электроника рассказывается о базовых принципах, на которых строится одна из самых развитых отраслей электроники.
Здесь Вы узнаете, что такое триггер, регистр, дешифратор, микроконтроллер…, а также познакомитесь с базовыми логическими элементами и не только. Для более наглядного изучения основ цифровой техники приводятся эксперименты с реальными цифровыми микросхемами, которые найдутся в запаснике любого начинающего радиолюбителя.
Цифровая электроника начинается с «0» и «1». Именно двоичная система исчисления и алгебра логики послужила тем фундаментом, на котором была выстроена цифровая подвижная радиосвязь, компьютеры и компьютерные сети, вычислительные системы и робототехника.
Для начала увлекательного пути в мире цифровой электроники, советуем познакомиться с базовыми логическими элементами…
Элементы цифровой электроники
Основы цифровой электроники.
С чего начинается цифровая электроника? С процессоров? С логических микросхем? С программируемой логики? Нет. Цифровая электроника начинается с двоичной системы исчисления. Это тот фундамент, на котором держится вся цифровая техника. Это статья является вводной частью в мир цифровой электроники.
Базовые логические элементы
Основу цифровой электроники составляют базовые логические элементы И, ИЛИ, НЕ. Как обозначаются на схеме логические элементы? Как они работают? Об этом вы узнаете из статьи «Базовые логические элементы».
Интегральные микросхемы. Начало пути.
Как и в освоении космоса, так и в радиоэлектронике между СССР и странами капиталистического мира шла постоянная гонка. Кто быстрее возьмёт новый рубеж? Как в космосе, так и в электронике мы взяли прекрасный старт, но потом резко затормозили и стали аутсайдерами. Микросхемы ТТЛ это более или менее удачный ответ Западу.
На вакуумных электронных лампах мы уверенно держали марку, на транзисторах споткнулись, а на интегральных схемах полностью потеряли темп. И когда на Западе уже занимались новыми разработками БИС и СБИС, у нас ещё широко применялись микросхемы малой степени интеграции.
Эксперименты с RS-триггером
Практическая статья о том, как можно собрать простейший RS-триггер на базе микросхем транзисторно-транзисторной логики (ТТЛ). Одна из схем триггера выполнена на базе логических элементов 2И-НЕ микросхемы К155ЛА3, а вторая на базе микросхемы с двумя D-триггерами КМ555ТМ2.
JK-триггер.
Что такое JK-триггер? В чём особенность данного типа триггеров? Об этом вы узнаете из этой статьи.
Что такое регистр? Регистр сдвига.
Что такое регистр? Возможно, вы уже слышали этот термин цифровой электроники, но мало себе представляли, какую функцию выполняет регистр в цифровых схемах. Более подробно о назначении, устройстве и применении регистров вы узнаете из предложенной статьи.
Шифраторы и дешифраторы.
Шифраторы и дешифраторы активно применяются в цифровой электронике. Для чего они нужны и как работают? Об этом вы узнаете из предложенной статьи. Показан пример работы дешифратора и светодиодного семисегментного индикатора – «восьмёрки».
Самоделки на логических микросхемах
Бегущие огни на светодиодах.
В статье представлена схема бегущих огней на светодиодах, которая реализована на микросхемах ТТЛ (155 серия). Подробно объясняется работа устройства и назначение микросхем.
go-radio.ru
Самостоятельное изучение схемотехники. Основные понятия. Часть 1 / Habr
Изучение цифровой схемотехники нужно начинать с теории автоматов. В этой статье можно найти некоторые элементарные вещи, которые помогут не потеряться в дальнейших статьях. Я постарался сделать статью легкочитабельной и уверен, что неподготовленный читатель сможет в ней легко разобраться.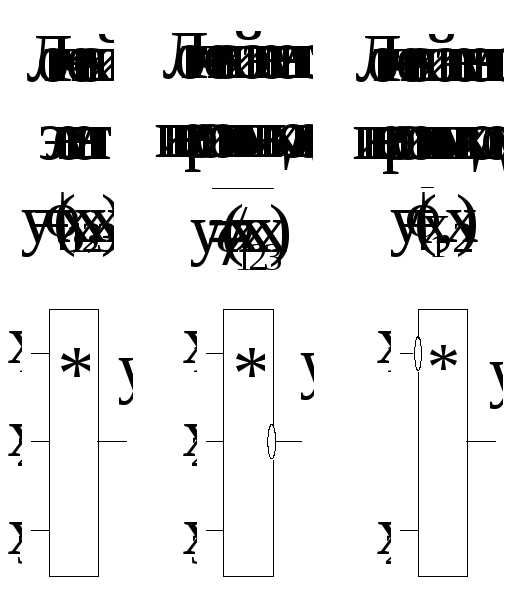
Сигнал — материальный носитель информации, используемый для передачи сообщений по системе связи. Сигнал, в отличие от сообщения, может генерироваться, но его приём не обязателен (сообщение должно быть принято принимающей стороной, иначе оно не является сообщением, а всего лишь сигналом).
В статье рассматривается цифровой дискретный сигнал. Это такой сигнал, который имеет несколько уровней. Очевидно, что двоичный сигнал имеет два уровня — и их принимают за 0 и 1. Когда высокий уровень обозначается единицей, а низкий нулем — такая логика называется позитивной, иначе негативной.
Цифровой сигнал можно представить в виде временной диаграммы.
В природе дискретных сигналов не существует, по этому их заменяют аналоговыми. Аналоговый сигнал не может перейти из 0 в 1 мгновенно, по этому такой сигнал обладает фронтом и срезом.
Если рисовать упрощенно то это выглядит так:
1 — низкий уровень сигнала, 2 — высокий уровень сигнала, 3 — нарастание сигнала (фронт), 4 — спад сигнала (срез)
Сигналы можно преобразовывать. Для этого на практике используются логические элементы, а чтобы это записать формально используются логические функции. Вот основные:
Отрицание — инвертирует сигнал.
На схемах обозначается так:
Логическое ИЛИ (логическое сложение, дизъюнкция)
На схеме:
Логическое И (логическое умножение, конъюнкция)
На схеме:
Последние два могут иметь отрицание на выходе (И-НЕ, ИЛИ-НЕ). Значения их логических функций инвертируются, а на схеме выход рисуется кружочком.
Сводная таблица логических функций двух аргументов выглядит так:

Работа с логическими функциями основывается на законах алгебры логики, основы которых изложены в прикрепленном файле. Так же там есть задания для самоконтроля и контрольные вопросы по теме.
Логической схемой называется совокупность логических электронных элементов, соединенных между собой таким образом, чтобы выполнялся заданный закон функционирования схемы, иначе говоря, — выполнялась заданная логическая функция.
По зависимости выходного сигнала от входного все электронные логические схемы можно условно разбить на:
Схемы первого рода, т.е. комбинационные схемы, выходной сигнал которых зависит только от состояния входных сигналов в каждый момент времени;
Схемы второго рода или накапливающие схемы (схемы последовательностные), содержащие накапливающие схемы (элементы с памятью), выходной сигнал которых зависит как от входных сигналов, так и от состояния схемы в предыдущие моменты времени.
По количеству входов и выходов схемы бывают: с одним входом и одним выходом, с несколькими входами и одним выходом, с одним входом и несколькими выходами, с несколькими входами и выходами.
По способу осуществления синхронизации схемы бывают с внешней синхронизацией (синхронные автоматы), с внутренней синхронизацией (асинхронные автоматы являются их частным случаем).
Практически любой компьютер состоит из комбинации схем первого и второго рода разной сложности. Таким образом, основой любого цифрового автомата, обрабатывающего цифровую информацию, являются электронные элементы двух типов: логические или комбинационные и запоминающие. Логические элементы выполняют простейшие логические операции над цифровой информацией, а запоминающие служат для ее хранения. Как известно, логическая операция состоит в преобразовании по определенным правилам входной цифровой информации в выходную.
Можно считать, что элементарные логические функции являются логическими операторами упомянутых электронных элементов, т.е. схем. Каждая такая схема обозначается определенным графическим символом. (Они были представлены выше — Элементы И, ИЛИ, НЕ, ИЛИ-НЕ, И-НЕ)
В качестве примера ниже представлена схема электрическая функциональная логического преобразователя (комбинационного автомата), реализующего логическую функцию в элементном базисе из логических элементов И, ИЛИ, НЕ.
Для закрепления предлагаю, самостоятельно синтезировать логическую схему, реализующую следующие логические функции:
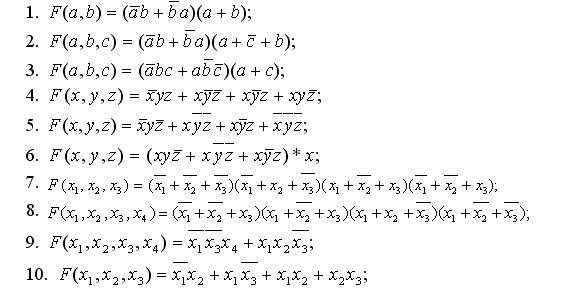
Сделать это можно к примеру в Electronic workbench.
Вот для примера первое выполненное задание:
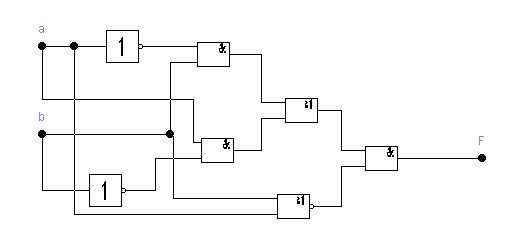
И файл ewb 5.12.
Hint: Для того чтобы включить условные обозначения в соответствии с отечественными ГОСТ-ами в файл настроек EWB.INI нужно добавить строку DIN = ON
На этом первая часть статьи заканчивается. Надеюсь, что она была не слишком утомительной. Все вышеописанное необходимо для понимания принципов работы с сигналами в электрических схемах. В следующей статье будут рассмотрены способы минимизации логических функций, понятие абстрактного автомата и пример синтеза RS-триггера.
habr.com
9. Логические основы цифровой техники
Содержание
9.2. Минимизация логических функций с помощью алгебраических преобразований 3
10. Основные параметры цифровых схем 5
11. Элемент И-НЕ в ДТЛ 5
12. Элемент И-НЕ в ТТЛ 6
13. ТТЛ со сложным инвертором 7
14. Логические элементы с тремя устойчивыми состояниями 8
15. Логические элементы с открытым коллектором 9
16. Режим неиспользуемых входов цифровых микросхем 10
17. Функциональные узлы комбинационного типа 12
17.1. Шифратор. Построение на логических элементах 13
17.2. Дешифратор. Построение на логических элементах 14
17.5. Мультиплексор 17
19
Рис. 22. Условное обозначение мультиплексора 4-1 19
17.6. Демультиплексор 19
17.7. Наращивание размерности мультиплексора 20
17.8. Полусумматор. Синтез полного сумматора из полусумматоров 21
Синтез полного сумматора на логических элементах 22
Сумматор параллельного действия с последовательным переносом 23
Параллельный сумматор с параллельным переносом 24
17.9. Цифровые компараторы 25
, 26
, 26
. 26
9.2. Минимизация логических функций с помощью алгебраических преобразований
10. Основные параметры цифровых схем
11. Элемент И-НЕ в ДТЛ
12. Элемент И-НЕ в ТТЛ
13. ТТЛ со сложным инвертором
14. Логические элементы с тремя устойчивыми состояниями
15. Логические элементы с открытым коллектором
16. Режим неиспользуемых входов цифровых микросхем
17. Функциональные узлы комбинационного типа
17.1. Шифратор. Построение на логических элементах
17.2. Дешифратор. Построение на логических элементах
17.3. Наращивание размерности дешифратора
17.4. Воспроизведение произвольных логических функций с помощью дешифратора
17.5. Мультиплексор
17.6. Демультиплексор
17.7. Наращивание размерности мультиплексора
17.8. Полусумматор. Синтез полного сумматора из полусумматоров
17.9. Цифровые компараторы
17.10. Преобразователь кода для семисегментной индикации
17.11. Асинхронный RS-триггер с прямыми входами
17.12. Асинхронный RS-триггер с инверсными входами
17.13. Асинхронный JK-триггер
17.14. Счётный Т-триггер
17.15. Синхронные триггеры на логических элементах
17.16. Синхронный RS-триггер
17.17. Синхронные JK- и Т-триггеры
17.18. Синхронный триггер задержки (D-триггер)
17.19. Синхронные триггеры со статическим и с динамическим управлением
17.20. Синхронные MS-триггеры
17.21. Итоговая классификация триггеров
9.1. Основные законы и следствия Булевой алгебры
Для описания логических операций используется математический аппарат, получивший название алгебры логики, или Булевой алгебры.
В алгебре логики рассматриваются переменные, которые могут принимать только два значения: 1 и 0.
Основные логические функции:
Логическое отрицание НЕ (инверсия). Обозначается в виде черточки над аргументом:
 .
В качестве примера цепи, реализующей
функцию НЕ, можно привести размыкающий
контакт реле. При срабатывании реле
цепь, в которую входит такой контакт,
будет размыкаться.
.
В качестве примера цепи, реализующей
функцию НЕ, можно привести размыкающий
контакт реле. При срабатывании реле
цепь, в которую входит такой контакт,
будет размыкаться.Логическое умножение И (конъюнкция). Символически обозначается: или
В качестве примера электрической цепи, реализующей функцию И, можно привести соединение последовательно замыкающих контактов нескольких реле. Цепь в этом случае будет замкнута тогда и только тогда, когда сработают все реле.
Логическое сложение ИЛИ (дизъюнкция). Операция обозначается выражениями: либо
В качестве примера электрической цепи, реализующей функцию ИЛИ, можно привести параллельное соединение замыкающих контактов нескольких реле. Цепь, в которую входят эти контакты, будет замкнута, если сработает хотя бы один контакт.
Основные законы алгебры логики:
переместительный:
, ;
сочетательный:
, ;
распределительный:
, ;
закон поглощения:
, ;
закон склеивания:
, ;
закон отрицания или правило де Моргана:
, .
Правило де Моргана справедливо для любого числа переменных:
Для алгебра логики справедливы следующие соотношения:
;
;
;
;
;
.
9.2. Минимизация логических функций с помощью алгебраических преобразований
Минимизация логических функций применяется при синтезе комбинационных логических цепей (КЛЦ). КЛЦ — это такие цепи, выходные сигналы которых не зависят от предыстории и однозначно определяются сигналами, поступающими на их входы в рассматриваемый момент времени.
Синтез КЛЦ проводят в следующей последовательности:
Составляется таблица истинности. Эта таблица показывает, чему равен выходной сигнал цепи при различных комбинациях входных сигналов.
Исходя из таблицы истинности, записывается логическая функция.
Логическая функция минимизируется и преобразуется к удобному виду для реализации на логических ячейках заданного типа.
Рассмотрим работу мажоритарной ячейки на 3 входа. Строим таблицу истинности:
Таблица 5
Таблица истинности
№ | X1 | Х2 | Х3 | F |
0 | 0 | 0 | 0 | 0 |
1 | 0 | 0 | 1 | 0 |
2 | 0 | 1 | 0 | 0 |
3 | 0 | 1 | 1 | 1 |
4 | 1 | 0 | 0 | 0 |
5 | 1 | 0 | 1 | 1 |
6 | 1 | 1 | 0 | 1 |
7 | 1 | 1 | 1 | 1 |
Построим схему по полученному выражению:
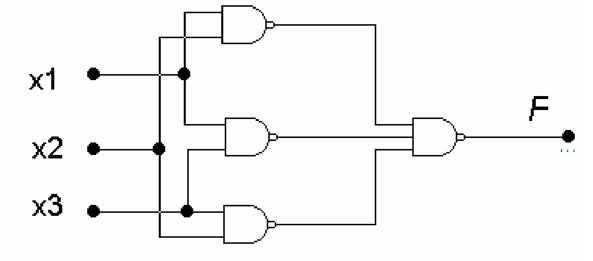
Рис. 6. Реализация мажоритарной ячейки на 3 входа по минимизированному выражению
Основные параметры цифровых схем
Основными параметрами цифровых интегральных схем является быстродействие, потребляемая мощность, коэффициент объединения по входу, коэффициент разветвления по выходу, устойчивость против внешних воздействий, помехоустойчивость, степень интеграции, надежность, пороговое напряжение.
Элемент И-НЕ в ДТЛ
Цифровые схемы могут быть построены по-разному, но в их основе, как правило, лежат схемы, выполняющие функции И-НЕ либо ИЛИ-НЕ. Поэтому интегральные схемы содержат обычно схемы И либо ИЛИ, выполненные на резисторах, диодах или транзисторах, и транзисторные инверторы. Транзисторный инвертор может быть простейшим — на одном транзисторе, включённом по схеме с общим эмиттером, или сложным — многотранзисторным с каскадным включением транзисторов в выходном каскаде.
Разберём работу схемы И-НЕ с ДТЛ, работающую от положительных сигналов (рисунок 7). Схема состоит из двух частей. В первой входные переменные подаются на диодный элемент И. Вторая часть выполнена на транзисторе и представляет собой инвертор. Таким образом в схеме последовательно выполняется логическая операция И-НЕ. Диоды VD3, VD4 называются смещающими диодами и предназначены для надёжного закрывания транзистора.
ДТЛ-элементы обладают большим быстродействием, большим коэффициентом объединения по входу, высокой помехозащищённостью и широко используются в системах цифровой техники. Отсутствие конденсаторов и высокоомных резисторов делает их удобными для микроэлектронного исполнения. Однако, ТТЛ-элементы получили в настоящее время большее распространение. В первую очередь это связано с тем, серьёзным недостатком ДТЛ является большое количество диодов, каждый из которых необходимо тщательно изолировать, что увеличивает площадь микросхемы.
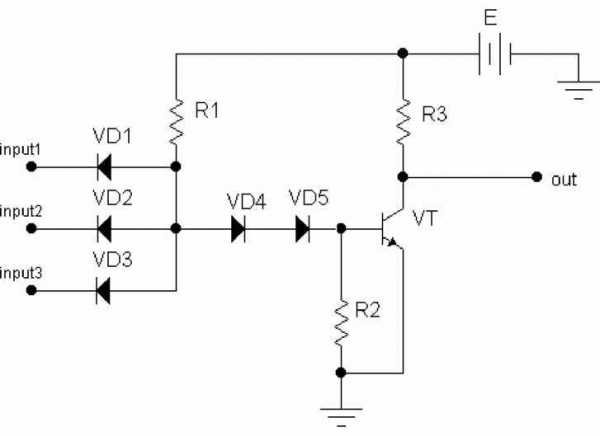
Рис. 7. Элемент И-НЕ в ДТЛ
studfile.net
Логические основы компьютерной техники.
Джордж Буль разработал логическую систему, названную булевой алгеброй, на основе которой построена вся современная вычислительная техника. В основе логики лежит понятие «булева примитива». Булева алгебра и ее система булевых примитивов может быть реализована на электронных схемах, которые и реализуют булевы выражения. Такие схемы называются логическими элементами, и всего их восемь (а базовых их всего три: логический элемент «И», «ИЛИ», «НЕ»). Элемент воспринимает один или несколько входных битов, обрабатывает их определенным образом и формирует выходной бит. Выходной бит элемента предсказуем, потому, что элемент действует в соответствии с конкретным логическим выражением. Восемь элементов называются: буфер, инвертор, элемент И (AND), элемент ИЛИ (OR), элемент исключающее ИЛИ (XOR), элемент НЕ-И (NAND), элемент НЕ-ИЛИ (NOR) и элемент исключающее НЕ-ИЛИ (ENOR). Их входы и выходы обычно выведены на контакты реальных микросхем. Из этих элементов специалисты-системотехники строят схемы состоящие из миллионов таких элементов. Проверяя входы и выходы такой микросхемы, состоящей из логических элементов, всегда можно убедиться в ее работоспособности.
В настоящее время очень сложные части схем компьютеров (из элементов «И», «ИЛИ», «НЕ») формируются в сверхбольших микросхемах (чипах), которые объединяют в комплекты (чипсеты). Чипсет может быть создан для реализации системной платы компьютера, видеоакселератора, звуковой карты, электроники жесткого диска и т. д., но на различных платах, как правило, всегда присутствует небольшое количество микросхем малой и средней степени интеграции элементов. Материал данного раздела необходим для оценки работоспособности микросхем малой и средней степени интеграции элементов при поиске неисправности в электронных схемах компьютеров, и для понимания работы цифровых схем компьютеров.
Логические элементы.
Буфер (повторитель)
Буфер (повторитель) представляет собой просто усилительный каскад. В логическом смысле усиление является аналоговой функцией, а не цифровой, но буферы часто требуются и в цифровых схемах. Например, биты адреса при выходе из процессора оказываются довольно слабыми по нагрузочной способности, и их нельзя подавать в шину адреса без усиления по току. Поэтому на каждой линии адреса имеется буфер, который усиливает ток передаваемого бита. Имеются буферы и на каждой линии шины данных компьютера (практически здесь есть два буфера по одному для каждого направления). Буферы обеспечивают надежную работу шин адреса и данных. Логика работы буфера заключается в следующем. При подаче на вход буфера логического состояния такое же состояние появляется и на выходе буфера. Если на вход подается Н-уровень (высокий уровень напряжения, например 2,4 вольта), на выходе также действует Н-уровень, а при подаче на вход L-уровня (низкий уровень напряжения, например, 0.2 вольта) на выходе будет L-уровень. На электрических принципиальных схемах буфер обозначается треугольником; вход подается на сторону треугольника, а выход снимается с противолежащей вершины. Логическое состояние при подаче на любой из буферов быстро проходит на выход и усиливается по току. На прохождение сигнала от входа к выходу требуется определенное время, которое называется временем задержки распространения.
|
|
|
Рис. 1. Буфер (усилитель) |
Инверторы
Инвертор или элемент «НЕ» (NOT) обозначается на схемах как треугольник с небольшим кружком на выходной вершине (рис.2). Выходное логическое состояние при прохождении инвертора изменяется на противоположное (Н-уровень изменяется на L-уровень и наоборот). Инверторы, как показывает их обозначение, усиливают ток логического состояния, а их внутренняя схема инвертирует входное состояние.
|
|
|
Рис.2. |
|
Рис. 3. Выход «открытый коллектор» означает, что в микросхеме нет нагрузочного резистора и должен использоваться внешний резистор. Такая схема увеличивает нагрузочную способность. |
Элементы «И» (AND)
Элемент AND реализует функцию логического «И». В компьютере при объединении по «И» нескольких битов образуется результирующий бит. Он имеет L-уровень за исключением ситуации, когда все входные биты имеют Н-уровень. Если хотя бы один из входных битов имеет L-уровень, выходной бит будет иметь L-уровень. Только когда все входы имеют Н-уровень, на выходе появится Н-уровень.
На рис. 4 показана таблица истинности элемента AND с двумя входами. При большем числе входов результат будет аналогичным. Имеется только одна комбинация входов, когда на выходе появляется Н-уровень. Обозначение элемента AND приведено на рис. 4, причем все выходы независимо от их числа подаются на плоскую сторону, а выход снимается с закругленной вершины. Элемент AND напоминает некоторый ключ, который включает и выключает схему, подсоединенную к его выходу. Обычно на одном или нескольких входах элемента AND действуют Н-уровни, поэтому на выходе имеется L-уровень, что соответствует выключенному состоянию. При включении схемы на все входы элемента AND подаются Н-уровни. Элемент AND изменяет выход с L-уровня на Н-уровень и включает схему, подсоединенную к выходу. Таблицы истинности позволяют полностью проверить работу этого элемента. Когда в элементе AND (см. рис. 4) хотя бы один из входов имеет L-уровень, на выходе должен действовать L-уровень. Только когда на обоих входах есть Н-уровни, выход должен иметь L-уровень. При проверке входов и выхода с помощью логического пробника, тестера или осциллографа они должны соответствовать таблице истинности. Если выход не верен, то микросхема неисправна.
|
|
|
Рис. 4. В таблице истинности показаны два входа и один выход |
Элементы «ИЛИ» (OR)
Логическое «ИЛИ» показывает еще один способ обработки битов. Если элемент AND дает на выходе Н-уровень только при наличии Н-уровней на всех входах, то элемент OR имеет на выходе L-уровень только при наличии L-уровней на всех входах. Элемент OR также может иметь несколько входов. Когда любой из них имеет Н-уровень, на выходе будет действовать Н-уровень. Только при наличии L-уровней на всех входах выход имеет L-уровень.
Обозначение элемента OR (рис. 5) напоминает обозначение элемента AND, только выход показывается острым, а не закругленным. Обычно плоская часть для входов закруглена. Для проверки правильности работы элемента OR используется таблица истинности.
|
|
|
Рис. 5. На таблице истинности показаны два входа и один выход, но число входов может быть больше. |
Элементы NOT, AND и OR реализуют основные логические функции вычислительной техники, а остальные элементы являются их комбинациями. При объединении элементов NOT и AND получается элемент «НЕ-ИЛИ» (NAND), а при объединении элементов NOT и OR получается элемент «НЕ-ИЛИ» (NOR). Элемент исключающее «ИЛИ» (EOR) образуется при соединении нескольких элементов NAND. Элемент исключающее «НЕ-ИЛИ» получается при добавлении элемента NOT к элементу EOR. Такие элементы, образованные из трех основных элементов, выпускаются как отдельные микросхемы. При поиске неисправности их следует считать особыми элементами и привлекать для тестирования их таблицы истинности.
Элементы «НЕ-И» (NAND)
По таблице истинности элемента NAND (рис. 6) видно, что его выходы аналогичны выходам элемента AND, но инвертированы. Элемент AND формирует на выходе Н-уровень только при наличии Н-уровней на всех входах, а на выходе элемента NAND действует L-уровень только при наличии Н-уровней на всех входах. В любой другой ситуации на выходе элемента NAND имеется Н-уровень.
|
|
|
Рис. 6. Таблица истинности элемента NAND |
Элемент NAND — это просто элемент AND с добавленным инвертором. Из элементов NAND состоят все ТТЛ-микросхемы, т.е. он является основным логическим элементом. Только на элементах NAND можно реализовать любой другой логический элемент или регистр. ТТЛ-микросхема состоит из биполярных транзисторов, диодов и резисторов. Имеются ТТЛ-транзисторы с несколькими эмиттерами, обычные транзисторы с одним эмиттером, р-n-переходы, действующие как диоды, и крошечные интегральные резисторы. Базовый элемент NAND состоит из пяти частей (рис. 7): один элемент AND, один элемент NOT и три буфера (элементы YES). Элемент AND выполнен на многоэмиттерном транзисторе с соответствующим числом входов (эмиттеров). Он формирует Н-уровень при наличии Н-уровней на всех входах. Выход элемент AND подается на инвертор NOT, который инвертирует и усиливает сигнал.
Затем сигнал разделяется на два тракта. По одному тракту сигнал проходит через помехоустойчивый буфер, а затем через второй буфер, предназначенный для усиления Н-уровня сигнала. По второму тракту усиливается L-уровень сигнала. Выходные буферы объединяются и обеспечивают общий выход. Отметим, что при любом уровне, выходной сигнал оказывается усиленным.
|
|
|
Рис. 7. Элемент NAND |
Элементы «НЕ-ИЛИ» (NOR)
Таблица истинности элемента NOR на рис. 8 показывает, что на выходе элемента NOR имеется Н-уровень только при наличии L-уровней на всех входах; в противном случае на выходе действует L-уровень. Выход является инвертированным выходом элемента OR. Элемент NOR, является объединением элемента OR и инвертора. Есть много разновидностей таких логических элементов, которые можно использовать при проектировании цифровых устройств.
|
Рис. 8. Обозначение элемента NOR и его таблица истинности |
Элементы «исключающее ИЛИ» (EOR).
На первый взгляд, обозначение элемента EOR (рис. 9) похоже на обозначение элемента OR, однако, при ближайшем рассмотрении, обнаруживается различие: на входе имеется вторая изогнутая линия. Входы подаются на внешнюю линию.
|
|
|
Рис. 9. Обозначение элемента EOR |
Таблица истинности элемента EOR, для первых трех комбинаций, совпадает с таблицей истинности элемента OR, но в четвертой комбинации имеется различие. В элементе OR при наличии Н-уровней на двух входах выход также должен иметь Н-уровень, а в элементе EOR в этой ситуации на выходе образуется L-уровень. Различие между элементами OR и EOR только в этой комбинации. Если поразмыслить, то выходы элемента OR не строго соответствуют логике. По определению элемента OR, если один или второй вход имеют Н-уровень, то выход должен иметь Н-уровень. Это истинно для входных комбинаций LL, LH и HL. В комбинации LL ни один из входов не имеет Н-уровня, поэтому на выходе L-уровень. В комбинациях LH и HL один из входов имеет Н-уровень, поэтому на выходе должен быть Н-уровень. Однако в последней комбинации НН оба входа имеют Н-уровень, а не первый или второй, а на выходе элемента OR сохраняется Н-уровень, что противоречит логике. Здесь скрыто определенное противоречие элемента OR. Элемент EOR подчиняется логике. Четыре входных комбинации двухвходового элемента EOR логически повторяют элемент OR за исключением комбинации НН. Когда на обоих входах элемента EOR имеются Н-уровни, выход в соответствии с логикой имеет L-уровень. Элемент EOR формирует на выходе Н-уровень, только в том случае, когда один или второй из входов имеют Н-уровень, но не тогда, когда оба они имеют Н-уровень. Отметим, что иногда элемент EOR называют XOR.
Элементы «исключающее НЕ-ИЛИ» (ENOR)
Элемент ENOR представляет собой элемент EOR с добавленным инвертором, который на схемах обозначается аналогично элементу EOR, но с кружком на выходе элемента (рис. 10). Таблица истинности показывает, что выход элемента ENOR является инвертированным выходом элемента DOR. При проверке составного элемента ENOR удобнее игнорировать функцию ENOR и проверять оба элемента отдельно. Например, следует проверить оба входа элемента EOR и его выход. Если выходной сигнал не соответствует ожидаемому, элемент неисправен. Если выход правилен, следует проверить вход и выход инвертора. Неправильный вход или выход могут локализовать неисправность.
|
|
|
Рис. 10. Таблица истинности элемента ENOR |
Элементы ENOR и другие можно образовать, используя другие микросхемы. Например, на рис. 10 показано, как образовать элемент ENOR из пяти элементов NAND.
Альтернативные обозначения
Обозначения элементов NOT, AND, NAND и NOR на схемах распознаются довольно легко. Для этих элементов имеются альтернативные обозначения, приведенные на рис. 11. Элемент AND можно показать как элемент OR с кружками инверсии на входах и выходе. Такое обозначение означает, что схема выполняет функцию AND, но при этом она вначале инвертирует входы, затем объединяет их по ИЛИ и инвертирует выход. Окончательный результат представляет объединение входных сигналов по И.
Альтернативное обозначение элемента OR состоит из элемента AND с кружками инверсии на входах и выходе. Можно встретить элемент NOR в виде элемента AND с инвертированными входами, а элемент NAND — как элемент OR с инвертированными входами. У инвертора кружок инверсии может находиться на входе, а не на выходе. У элемента AND один из четырех входов может иметь кружок инверсии. На схемах можно встретить разнообразные обозначения, правильными являются базовые. Вы должны уметь проследить, как бит проходит от одного элемента к другому. В исправных микросхемах он должен подчиняться таблицам истинности. Напряжение (логический уровень, состояние) бита изменяется в соответствии с логической функцией того элемента, через который он проходит.
|
|
|
Рис.11. Элемент NOR с кружками NOT на входах действует как элемент AND |
Элемент NAND с «кружками» NOT на входах действует как элемент OR. Элемент AND с «кружками» NOT на входах действует как элемент NOR. Элемент OR с «кружками» NOT на входах действует как элемент NAND.
Построение схем из элементов
Напомним, что элементы NOT, AND и OR реализованы из микроскопических транзисторов, диодов, резисторов и конденсаторов, размещенных на кристалле кремния. Из этих базовых элементов образуются элементы NAND, NOR, EOR и ENOR. Для усиления сигналов применяются буферы. Рассмотренные элементы, за исключением буферов, при работе компьютера просто включаются и выключаются в предсказуемой последовательности. Следующий этап заключается в построении из элементов более сложных схем: триггеров, защелок, регистров сдвига, счетчиков, сумматоров, шифраторов, дешифраторов, мультиплексоров и др.
Триггер можно построить на двух биполярных транзисторах, двух полевых транзисторах и других приборах. Напомним, что триггер это схема, которая может хранить Н- или L-уровень. Он хранит логический бит, когда один из двух элементов включен, а другой выключен. Триггер изменяет состояние, когда внешний сигнал заставляет измениться состояния элементов. Другими словами, выключенный элемент включается, а включенный выключается. Поведение триггера обычно описывает таблица истинности. Взаимодействие элементов и триггеров обеспечивает цифровую обработку.
Защелка тоже предназначена для хранения бита. Типичной защелкой служит D-триггер (буква D означает Data - данные). Защелка, как и триггер, может хранить Н- или L-уровень. Группа на восьми D-триггеров может хранить байт данных.
В компьютерах часто применяется микросхема мультиплексора, которая представляет собой набор логических элементов для управления передачами битов по линиям шины. Например, 16 бит необходимо подавать в два приема по восемь битов на одни и те же адресные входы. Именно такую задачу и решает мультиплексор.
Дешифратор, например, имеет три входа данных и формирует из них восемь выходных сигналов. Три входных бита образуют восемь комбинаций LLL, LLH, LHL, LHH, HLL, HLH, HHL и ННН. Каждая из этих комбинаций дешифруется внутренними элементами и выбирает одну из восьми выходных линий. У дешифратора имеется также три входа разрешения, упрощающих применение микросхемы.
При объединении логических элементов и триггеров можно построить совершенно новые цифровые схемы, одной из которых является счетчик. Если, например, к двум элементам AND добавить триггер, то получается схема, которая может считать. Конечно, она не сможет считать большие числа, но способна сосчитать двоичные нули и единицы, которые кодируются двумя уровнями. Триггер и два элемента AND образуют двоичный счетчик. Счетчик может формировать также арифметический перенос. Один триггер является одноразрядным счетчиком (он может находиться в двух состояниях: нуль или единица). Если триггер находится в состоянии единица и на вход поступает сигнал «I», то триггер обнуляется и на выходе триггера появляется сигнал «I». Таким образом, реализуется перенос в старший разряд при сложении единицы разряда двоичных чисел. При необходимости считать более единицы нужно просто увеличить число разрядов.
Кроме проведения счета триггеры и логические элементы могут действовать как регистры сдвига. Регистр сдвига — это группа триггеров, которые могут сдвигать свое содержимое на один бит вправо или влево по импульсу управления.
al-tm.ru
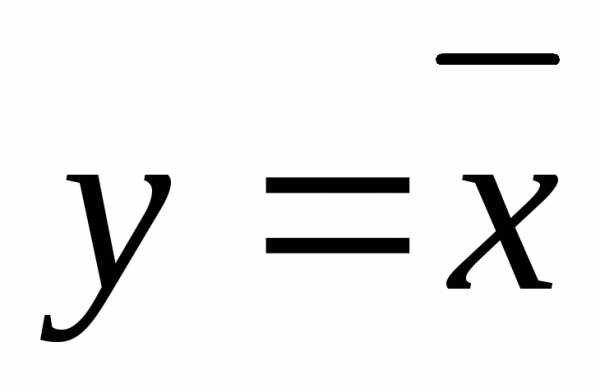 .
В качестве примера цепи, реализующей
функцию НЕ, можно привести размыкающий
контакт реле. При срабатывании реле
цепь, в которую входит такой контакт,
будет размыкаться.
.
В качестве примера цепи, реализующей
функцию НЕ, можно привести размыкающий
контакт реле. При срабатывании реле
цепь, в которую входит такой контакт,
будет размыкаться.