Основы цифровой техники – .

Цифровая электроника для начинающих

Это продолжение «Необычная электроника для начинающих. Введение»

Твоё путешествие в мир электроники мы начнем с погружения в цифровую электронику. Во-первых, потому что это верхушка пирамиды электронного мира, во-вторых, базовые понятия цифровой электроники просты и понятны. 

Задумывался ли ты о том, какой феноменальный прорыв в науке и технике произошел благодаря электронике и цифровой электронике в частности? Если нет, тогда возьми свой смартфон и внимательно на него посмотри. Такая простая с виду конструкция — результат огромной работы и феноменальных достижений современной электроники. Создание такой техники стало возможным благодаря простой идее о том, что любую информацию можно представить в виде чисел. Таким образом, независимо от того, с какой информацией работает устройство, глубоко внутри оно занимается обработкой чисел.

Тебе наверняка знакомы римские и арабские цифры. В римской системе числа представляются в виде комбинации букв I, V, X, L, C, D, M, а в арабской с помощью комбинации символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Но существуют и другие формы представления числа. Одна из них — это двоичная форма. Или, как её чаще называют, двоичная система счисления. В такой системе счисления любое число представляет собой последовательность только из «0» и «1».

Арабские	Римские	Двоичные
0	—	00
1	I	01
2	II	10
3	III	11

Математики c инженерами хорошо потрудились, и сегодня любая информация может быть представлена в виде комбинации нулей и единиц: сигнал с датчика движения, музыка, видео, фото, температура, и даже вот этот текст, который ты сейчас читаешь, на самом деле в недрах твоего устройства имеет вид последовательности из нулей и единиц. 

Независимо от того, с какой информацией работает цифровое устройство, глубоко внутри оно занимается обработкой чисел.

Почему именно «0» и «1», а не «0», «1» и «2», к примеру? На самом деле были вполне успешные попытки создать цифровую технику, которая использует не двоичную, а троичную систему исчисления («0», «1» и «2»), но двоичная все же победила.

Возможно, победа досталась ей, потому что СССР развалился, а может потому, что «0» и «1» легче представить в виде электрических сигналов. А значит, цифровые устройства на основе двоичной системы исчисления проще и дешевле производить. Подробнее о двоичных числах я расскажу позже. 

Структура цифрового устройства

Почти в каждом цифровом устройстве встречаются типовые элементы, из комбинации которых оно состоит. Какие-то элементы совсем простые, какие-то более сложные, а какие-то совсем сложные. В любительской практике чаще всего встречаются: триггеры, таймеры, счетчики, регистры, микроконтроллеры, компараторы и др.

Давай выберем что-нибудь из этого списка и посмотрим, как оно устроено. Пусть это будет микроконтроллер (МК)! Ладно, признаюсь. Микроконтроллер я выбрал неспроста. Дело в том, что именно появление микропроцессоров произвело настоящую революцию в электронике и выдвинуло её развитие на новый уровень. 

МК является наиболее многочисленным и популярным видом микропроцессоров в мире. Особенным его делает то, что микроконтроллер представляет собой микро-PC — целый компьютер в одной микросхеме. Представь себе компьютер размером, например, с копейку. Вот это и есть МК. 

Микроконтроллеры используются повсеместно: в современных телевизорах, холодильниках, планшетах, охранных системах. Везде, где требуется чем-то управлять, микроконтроллер может найти своё место. А всё благодаря тому, что, как и любой микропроцессор, МК можно программировать. В итоге один и тот же вид микросхем можно использовать в сотнях различных устройств. 

В наше время наибольшей популярностью пользуются, к примеру, микроконтроллеры AVR, PIC, ARM. Каждая из компаний, что выпускает перечисленные виды МК, производит десятки, если не сотни, разновидностей микроконтроллеров, предназначенных под все мыслимые и немыслимые задачи. 

Как работает микроконтроллер

Несмотря на всю сложность конструкции настоящего микроконтроллера, рассказать, как он функционирует можно всего одним предложением: «В память микроконтроллера записывается текст программы, МК считывает команды из этой программы и выполняет их», — вот и всё.

 

Конечно, МК не может выполнить какие угодно команды. У него есть базовый набор команд, которые он понимает и знает как выполнить. Комбинируя эти команды, можно получить практически любую программу, с помощью которой устройство будет делать именно то, что от него хотят.

В с

mp16.ru

3.Арифметические основы цифровой техники.

Глава 1 Арифметические основы цифровой техники

В цифровых устройствах приходится иметь дело с различными видами информации. Достаточно часто информация может представлять собой числа. Числа могут быть представлены в различных системах счисления. Форма записи в них чисел существенно различается между собой.

3.1 Системы счисления

Начнем с определения системы счисления. Система счисления — это совокупность правил записи чисел цифровыми знаками. Системы счисления бывают позиционные и непозиционные. В настоящее время и в технике и в быту широко используются как позиционные, так и непозиционные системы счисления. Рассмотрим сначала примеры непозиционных систем счисления.

В качестве классического примера непозиционной системы счисления обычно приводят римскую форму записи чисел. Там не менее это не единственная непозиционная система счисления, используемая в настоящее время.

Сейчас, как и в глубокой древности, для записи числа используются так называемые “палочки”. Эта форма записи чисел наиболее понятна и требует для записи числа всего один символ. Число образуется суммой этих “палочек”. Однако при записи больших чисел возникают неудобства. Число получается громоздким и его трудно читать.

В следующем варианте непозиционной системы счисления стали использовать несколько символов (цифр). Каждая цифра обозначает различное количеств единиц. Конечное число точно так же как и в предыдущем варианте образуется суммой цифр. Наиболее яркий вариант использования такой системы счисления — это денежные отношения. Мы с ними сталкиваемся каждый день. Здесь никому не приходит в голову, что сумма, которую мы выкладываем за продукты, может зависеть от того, в каком порядке мы расположим монеты на столе! Номинал монеты или банкноты не зависит от того, в каком порядке она была вынута из кошелька. Это классический пример непозиционной системы счисления.

Однако чем большее число требуется представить в такой системе счисления, тем большее количество цифр требуется для этого. Позиционные системы счисления были придуманы относительно недавно для того, чтобы сэкономить количество цифр, используемое для записи чисел.

Значение цифры в позиционной системе счисления зависит от её позиции в записываемом числе. В позиционной системе счисления появляются два очень важных понятия — основание системы счисления и вес цифры. Дело в том, что в позиционной системе счисления число представляется в виде формулы разложения:

A_p=a_npⁿ+a_n-1p^n-1+…+a₂p² +a₁p¹+a₀p⁰+a_-1p^-1+a_-2p ^-2+…+a_-kp^-k

где p — основание системы счисления p_i — вес единицы данного разряда a

i — цифры, разрешённые в данной системе счисления.

При этом количество цифр в системе счисления зависит от основания. Количество цифр равно основанию системы счисления. В двоичной системе счисления две цифры, в десятичной – десять, а в шестнадцатеричной – шестнадцать. Число в любой позиционной системе счисления записываются в виде последовательности цифр:

A=a_na_n-1…a₂a₁a₀,a_-1a_-2 …a_-k,

где ai – цифры данной системы счисления, а цифра, соответствующая единицам определяется по положению десятичной запятой (или десятичной точки в англоязычных странах). Каждая цифра, использованная в записи числа, называется разрядом.

Какие же системы счисления применяются в настоящее время? Первый ответ, который я ожидаю – это десятичная система счисления. А ещё? Да, да не удивляйтесь! Мы широко используем и другие системы счисления! Достаточно посмотреть себе на левую руку. Там мы увидим часы. Сколько минут помещается в часе? Шестьдесят! Сколько секунд помещается в минуте? Шестьдесят! Налицо признаки шестидесятеричной системы счисления. Это наследование древней вавилонской системы счисления, которую вместе с компасом и часами европейцы заимствовали от арабов.

А еще примеры? Да сколько угодно! Картушка компаса делится на восемь румбов. Чем не восьмеричная система счисления? А давно ли в России отказались от полушек (четверть копейки) или грошей (половина копейки)? А следующее значение монеты – две копейки! Чем не двоичная система счисления?

Рассмотрим подробнее системы счисления, наиболее часто используемые в цифровой технике.

studfiles.net

мир электроники — Основы цифровой техники

Категория

Рано или поздно любому радиолюбителю приходится слышать или сталкиваться с такими фразами как логический ноль или логическая единица, триггеры, счетчики и так далее…
Все эти понятия относятся к целому разделу электронных устройств под общим понятием цифровые или логические устройства.

Почему их назвали цифровыми?
Большинство устройств- усилители, например, или блоки питания работают по принципу аналогового сигнала: амплитуда напряжений может изменяться, иметь различные полярности, разную частоту, может изменять свою форму и так далее.

Цифровые устройства работают несколько иначе: там либо есть сигнал, либо его нету.
Самый простейший пример: выключать с лампочкой. Пусть это и не совсем удачное сравнение но там всего-лишь два положения: либо горит, либо не горит. Причем при этом не учитывается ни мощность электролампочки, ни цвет, ни яркость, ни напряжение питания, просто:  или да, или нет.

Так вот: на цифровых устройствах так-же учитывается всего-лишь два состояния: есть напряжение на выходе (входе)- значит логическая единица, нет напряжения- значит логический ноль.

Однако это еще не все: все эти самые цифровые устройства (о которых и пойдет речь в данном разделе) умеют работать еще и по некой логике: они могут, например, менять свое логическое состояние лишь при определенных условиях.
Например: у нас есть две лампочки с выключателями, но при этом они между собою взаимосвязаны условием- гореть может лишь одна. То есть: если одна включена, то другую включить невозможно.
Немного подумав можно даже и схему было-бы накидать чтобы такое устройство сделать, но это нам сейчас не надо- скажу только лишь что это устройство имеет название ИЛИ (ну то есть понятно: или один выход, или другой и не в коем случае ни вместе).

Ну и, конечно же, так как здесь у нас присутствуют цифры, то существует даже определенная алгебра для расчета цифровых устройств!

Ну так вот: именно таким цифровым (или логическим) устройствам мы и займемся в этом разделе.
Итак:

Логические элементы

простая логика
триггеры
счетчики
Триггер Шмитта
Цифровые микросхемы и работа с ними

Теория цифровой техники

Логические числа, представление логических чисел
Алгебра логических элементов
Минимизация логических функций
Интегрирующие и дифференцирующие цепи
Триггеры на логических элементах
Шифраторы и Дешифраторы
Мультиплексор и Демультиплексор
Регистры
Оперативные запоминающие устройства
Постоянное запоминающее устройство
Сумматор
Арифметико-логические устройства
Устройства умножения и деления
ЦАП: Цифро- аналоговый преобразователь
АЦП: Аналогово-цифровой преобразователь
Цифровой фильтр с временной реализацией
Цифровой фильтр с частотной реализацией
DRAM, DIMM, SIMM, SDRAM, ESDRAM, DRDRAM, RIMM

Ну и под конец: часть материалов (в основном теория) взята с сайта http://naf-st.ru/

radio-uchebnik.ru

9. Логические основы цифровой техники

Содержание

9.2. Минимизация логических функций с помощью алгебраических преобразований 3

10. Основные параметры цифровых схем 5

11. Элемент И-НЕ в ДТЛ 5

12. Элемент И-НЕ в ТТЛ 6

13. ТТЛ со сложным инвертором 7

14. Логические элементы с тремя устойчивыми состояниями 8

15. Логические элементы с открытым коллектором 9

16. Режим неиспользуемых входов цифровых микросхем 10

17. Функциональные узлы комбинационного типа 12

17.1. Шифратор. Построение на логических элементах 13

17.2. Дешифратор. Построение на логических элементах 14

17.5. Мультиплексор 17

19

Рис. 22. Условное обозначение мультиплексора 4-1 19

17.6. Демультиплексор 19

17.7. Наращивание размерности мультиплексора 20

17.8. Полусумматор. Синтез полного сумматора из полусумматоров 21

Синтез полного сумматора на логических элементах 22

Сумматор параллельного действия с последовательным переносом 23

Параллельный сумматор с параллельным переносом 24

17.9. Цифровые компараторы 25

, 26

, 26

. 26

9.2. Минимизация логических функций с помощью алгебраических преобразований

10. Основные параметры цифровых схем

11. Элемент И-НЕ в ДТЛ

12. Элемент И-НЕ в ТТЛ

13. ТТЛ со сложным инвертором

14. Логические элементы с тремя устойчивыми состояниями

15. Логические элементы с открытым коллектором

16. Режим неиспользуемых входов цифровых микросхем

17. Функциональные узлы комбинационного типа

17.1. Шифратор. Построение на логических элементах

17.2. Дешифратор. Построение на логических элементах

17.3. Наращивание размерности дешифратора

17.4. Воспроизведение произвольных логических функций с помощью дешифратора

17.5. Мультиплексор

17.6. Демультиплексор

17.7. Наращивание размерности мультиплексора

17.8. Полусумматор. Синтез полного сумматора из полусумматоров

17.9. Цифровые компараторы

17.10. Преобразователь кода для семисегментной индикации

17.11. Асинхронный RS-триггер с прямыми входами

17.12. Асинхронный RS-триггер с инверсными входами

17.13. Асинхронный JK-триггер

17.14. Счётный Т-триггер

17.15. Синхронные триггеры на логических элементах

17.16. Синхронный RS-триггер

17.17. Синхронные JK- и Т-триггеры

17.18. Синхронный триггер задержки (D-триггер)

17.19. Синхронные триггеры со статическим и с динамическим управлением

17.20. Синхронные MS-триггеры

17.21. Итоговая классификация триггеров

9.1. Основные законы и следствия Булевой алгебры

Для описания логических операций используется математический аппарат, получивший название алгебры логики, или Булевой алгебры.

В алгебре логики рассматриваются переменные, которые могут принимать только два значения: 1 и 0.

Основные логические функции:

1. Логическое отрицание НЕ (инверсия). Обозначается в виде черточки над аргументом: . В качестве примера цепи, реализующей функцию НЕ, можно привести размыкающий контакт реле. При срабатывании реле цепь, в которую входит такой контакт, будет размыкаться.

2. Логическое умножение И (конъюнкция). Символически обозначается: или

В качестве примера электрической цепи, реализующей функцию И, можно привести соединение последовательно замыкающих контактов нескольких реле. Цепь в этом случае будет замкнута тогда и только тогда, когда сработают все реле.

3. Логическое сложение ИЛИ (дизъюнкция). Операция обозначается выражениями: либо

В качестве примера электрической цепи, реализующей функцию ИЛИ, можно привести параллельное соединение замыкающих контактов нескольких реле. Цепь, в которую входят эти контакты, будет замкнута, если сработает хотя бы один контакт.

Основные законы алгебры логики:

1. переместительный:

, ;

2. сочетательный:

, ;

3. распределительный:

, ;

4. закон поглощения:

, ;

5. закон склеивания:

, ;

6. закон отрицания или правило де Моргана:

, .

Правило де Моргана справедливо для любого числа переменных:

Для алгебра логики справедливы следующие соотношения:

1. ;

2. ;

3. ;

4. ;

5. ;

6. .

9.2. Минимизация логических функций с помощью алгебраических преобразований

Минимизация логических функций применяется при синтезе комбинационных логических цепей (КЛЦ). КЛЦ — это такие цепи, выходные сигналы которых не зависят от предыстории и однозначно определяются сигналами, поступающими на их входы в рассматриваемый момент времени.

Синтез КЛЦ проводят в следующей последовательности:

1. Составляется таблица истинности. Эта таблица показывает, чему равен выходной сигнал цепи при различных комбинациях входных сигналов.

2. Исходя из таблицы истинности, записывается логическая функция.

3. Логическая функция минимизируется и преобразуется к удобному виду для реализации на логических ячейках заданного типа.

Рассмотрим работу мажоритарной ячейки на 3 входа. Строим таблицу истинности:

Таблица 5

Таблица истинности

№	X1	Х2	Х3	F
0	0	0	0	0
1	0	0	1	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	0
5	1	0	1	1
6	1	1	0	1
7	1	1	1	1

Построим схему по полученному выражению:

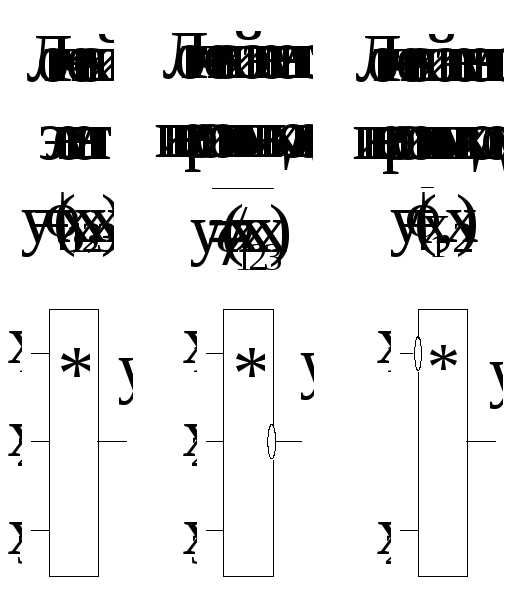
Рис. 6. Реализация мажоритарной ячейки на 3 входа по минимизированному выражению

10. Основные параметры цифровых схем

Основными параметрами цифровых интегральных схем является быстродействие, потребляемая мощность, коэффициент объединения по входу, коэффициент разветвления по выходу, устойчивость против внешних воздействий, помехоустойчивость, степень интеграции, надежность, пороговое напряжение.

10. Элемент И-НЕ в ДТЛ

Цифровые схемы могут быть построены по-разному, но в их основе, как правило, лежат схемы, выполняющие функции И-НЕ либо ИЛИ-НЕ. Поэтому интегральные схемы содержат обычно схемы И либо ИЛИ, выполненные на резисторах, диодах или транзисторах, и транзисторные инверторы. Транзисторный инвертор может быть простейшим — на одном транзисторе, включённом по схеме с общим эмиттером, или сложным — многотранзисторным с каскадным включением транзисторов в выходном каскаде.

Разберём работу схемы И-НЕ с ДТЛ, работающую от положительных сигналов (рисунок 7). Схема состоит из двух частей. В первой входные переменные подаются на диодный элемент И. Вторая часть выполнена на транзисторе и представляет собой инвертор. Таким образом в схеме последовательно выполняется логическая операция И-НЕ. Диоды VD3, VD4 называются смещающими диодами и предназначены для надёжного закрывания транзистора.

ДТЛ-элементы обладают большим быстродействием, большим коэффициентом объединения по входу, высокой помехозащищённостью и широко используются в системах цифровой техники. Отсутствие конденсаторов и высокоомных резисторов делает их удобными для микроэлектронного исполнения. Однако, ТТЛ-элементы получили в настоящее время большее распространение. В первую очередь это связано с тем, серьёзным недостатком ДТЛ является большое количество диодов, каждый из которых необходимо тщательно изолировать, что увеличивает площадь микросхемы.

Рис. 7. Элемент И-НЕ в ДТЛ

studfiles.net

9. Основы цифровой техники

9.1. Общие сведения о цифровой обработке сигналов

Основная задачи радиоэлектроники – приём, передача, обработка и хранение информации. Для решения этих задач в настоящее время наряду с аналоговыми методами обработки сигналов широко используется цифровая обработка сигналов. По сравнению с обработкой аналоговых сигналов обработка цифровых сигналов имеет ряд особенностей и дает ряд преимуществ: помехозащищенность, уплотнение канала за счет временного разделения, методов кодирования, защищенность канала от несанкционированного доступа. Основные процессы при цифровой обработке сигналов поясняет структурная схема, представленная на рис.9.1.

Рис. 9.1 Структурная схема системы цифровой обработки сигналов

Цифровая форма сигналов естественным образом используется для обработки информации в вычислительной технике. Она оказывается удобной (рациональной) при обработке сигналов измерительных приборов, сигналов управления. В цифровых устройствах информация представляется в виде цифровых кодов. Для записи цифровых кодов используется позиционная система счисления. Для устройств цифровой техники удобной является двоичная система счисления. Ей соответствуют два устойчивых состояния электронных приборов: открыт, закрыт.

9.2. Цифровое представление информации. Цифровые коды

С изобретением письменности человек использует буквы, цифры и другие знаки для фиксации информации, т.е. в процессе письма информация кодируется символами по принятым правилам грамматики. При передаче информации радиоэлектронными средствами также важную роль играют коды. Впервые коды получили широкое распространение при передаче информации с помощью телеграфа (азбука Морзе).

В цифровой технике для представления информации используется позиционная система счисления. В позиционной системе счисления число Z, содержащее, в общем виде, целую и дробную части, записывается последовательностью цифр, которую можно представить как сумму

, (9.1)

где n – число разрядов целой части, a_k – значащая цифра k – го разряда, q – основание системы счисления, m – число разрядов дробной части.

В цифровой электронике широко применяется двоичная система счисления с основанием q=2, в которой значащая цифра каждого разряда a_k принимает только два значения – 0 и 1 (содержит информацию объемом в 1 бит). Последовательность значащих цифр в (9.1), если упустить знаки суммирования и разряды основанияq, есть () — разрядный цифровой двоичный код из 0 и 1. В компьютерной технике кроме двоичного кода используют еще восьмеричный код – группы из 3 битов двоичного кода, и шестнадцатеричный код – группы из 4 битов (см. табл. 9.1).

Таблица 9.1

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111	0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17	0 1 2 3 4 5 6 7 8 9 A B C D E F

При вводе и выводе информации в компьютерах буквенно-цифровые символы кодируются в виде групп двоичных цифр из 7 битов (используется так называемый 7-ми разрядный буквенно-цифровой код ASCII). В приборах с цифровой индикацией таких, например, как вольтметры, частотомеры, часы и т.п. оперируют с десятичными цифрами, представленными двоично-десятичным кодом. В двоично-десятичном коде каждая десятичная цифра представляется группой из 4 двоичных цифр: . Здесь множители, представленные степенями основания (2³=8, 2²=4, 2¹=2, 2⁰=1) называются весами. Если веса расположены по возрастанию, то код называется регулярным двоично-десятичным кодом. Если веса расположить “нерегулярно”, получим другой код. Связывая веса сложным образом, можно создать секретный код , который можно будет расшифровать только зная “ключ” кода. Ниже (табл. 9.2) для примера приведено несколько двоично-десятичных кодов.

Таблица 9.2

Деся- тичное число	Регулярный двоично- десятичный код	Код Эйкена	Код Грея	Код с избытком 3
0 1 2 3 4 5 6 7 8 9	0000 0001 0010 0011 0100 0101 0110 0111 1000 1001	0000 0001 0010 0011 1000 1011 1100 1101 1110 1111	0000 0001 0011 0010 0110 0111 0101 0100 1100 1101	0011 0100 0101 0110 0111 1000 1001 1010 1011 1100

studfiles.net

2. Основы цифровой техники

А2 = 0,1010 × 210 ,

где m = 0,1010, q = 2, p = 10;

б) числа с фиксированной запятой представляются в виде единого целого, причем положение запятой в используемой разрядной сетке жестко фиксировано. Обычно числа с фиксированной запятой даются в виде правильной дроби.

Цифровые системы с плавающей запятой сложнее, так как требуют дополнительных операций как над мантиссами, так и над порядками.

Для представления знака числа используется дополнительный знаковый разряд Z, который обычно располагается перед числовыми разрядами:

Z = 0 — для положительных чисел,

Z = 1 — для отрицательных чисел.

Арифметические операции над двоичными числами могут производиться по тем же правилам, что и над десятичными:

	2						0010
	3						0011
	5						0101

Однако с целью упрощения цифровых систем для выполнения вычитания, умножения, деления обычно применяются специальные алгоритмы.

Операцию вычитания реализуют с помощью операции сложения,

представляя вычитаемое в обратном коде. А2 — обратный код двоичного числа А2 , который получается заменой всех 0 на 1, и

наоборот. (Обратный код числа А2 называется также дополнением до 1, так как для цифр в каждом разряде числа справедливо

выражение a j + a j = 1. ) Вычитаемое, включая его знаковый разряд, представляется в обратном коде и складывается с уменьшаемым вместе с его знаковым разрядом. Если в знаковом разряде образуется перенос, то эта 1 прибавляется к младшему разряду суммы:

studfiles.net

Глава 10. Основы цифровой электроники

10.1 Представление информации в цифровой системе

Основу построения современной вычислительной техники составляют так называемые цифровые схемы, реализующие различные арифметические и логические операции. В отличие от традиционной арифметики и логики в цифровых схемах оперируют двоичными представлениями цифр, чисел, логических функций и их аргументов. Инструментом для построения цифровых схем служит Булева алгебра, которая применительно к цифровой технике называется также алгеброй логики.

Двоичные представления переменных характеризуются тем, что они принимают только два значения, которые обычно называют нулем и единицей и обозначают символами 0 и 1 соответственно. Таким образом, для двоичной переменной X_i можно записать X_i= {0,1}. В алгебре логики существуют три основные операции:

— логическое умножение (конъюнкция) с обозначением y=x₁x₂=x₁x₂=x₁x₂;

— логическое сложение (дизъюнкция) с обозначением у = х₁ х₂ = х₁+х₂;

— инверсия с обозначением .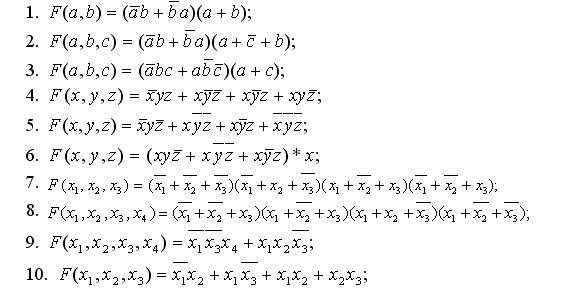

Правила определения значений логических функций удобно определять через так называемые таблицы истинности, в которых устанавливаются соответствия между двоичными значениями аргументов и функций.

Например, таблицы истинности 10.110.3 определяют значения логических функций умножения, сложения и инверсии для всех возможных значений переменных.

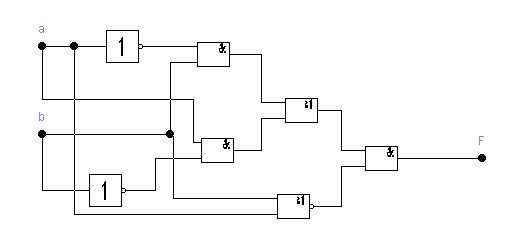
Аналогично можно определить результаты выполнения арифметических операций выполняемых при двоичном представлении чисел.

Например, в таблице 10.4 показано, как формируется результат сложения S двух двоичных чисел х₁ и х₂ с учетом переноса Р в старший разряд числа.

Таблица 10.4. Реализация операции двоичного сложения

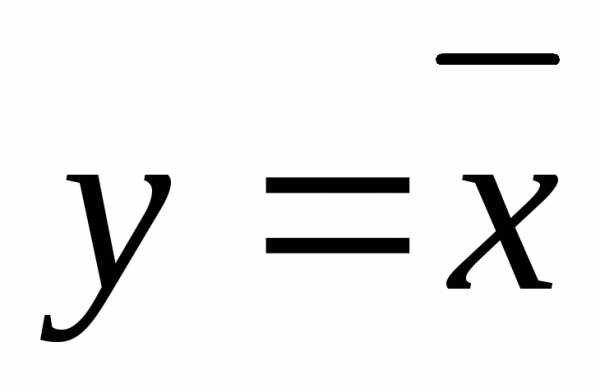
Другим способом определения результатов логических и арифметических операций является их соответствующее аналитическое представление в виде формул, например в форме такого выражения:

y = х₁х₂х₃ + х₂х₄ + х₁х₂х₅ +…

Подробно с вопросами теории и практических применений булевой алгебры и двоичной арифметики, составляющих основу построения современных цифровых систем, можно ознакомиться в соответствующей литературе. Здесь мы подробнее остановимся на вопросах реализации электронных элементов и узлов, составляющих техническую основу построения цифровой техники.

Учитывая, что двоичные переменные имеют только два дискретных значения, в качестве соответствующих схемотехнических решений можно использовать схемы, имеющие два легко различимых рабочих состояния.

Простейшим способом реализации логической переменной, является обычный ключ, изображенный на рисунке 10.1.

Рис.10.1. Представление логической переменной в виде ключа

Можно условиться, что разомкнутый ключ эквивалентен логическому нулю, а замкнутый – логической единице. Легко убедится, что в этом случае два последовательно соединенных ключа будут реализовывать логическую функцию И, а два параллельно соединенных ключа – логическую функцию ИЛИ.

Другой возможностью представления логических переменных, которая и используется в современной цифровой технике, является электрическое напряжение, имеющее два хорошо различимых уровня: высокий и низкий, так как это реализовано, например, в транзисторных ключевых схемах, рассмотренных в предыдущем разделе.

Этим уровням ставятся в соответствие двоичные переменные ноль и единица (0, 1). При этом при использовании положительной логики логическому нулю ставится в соответствие низкий уровень напряжений, а логической единице – высокий. При использовании отрицательной логики применяется противоположный способ задания нуля и единицы.

Основные логические функции, их модификации и комбинации, а так же арифметические операции реализуются через соответствующие наборы стандартных электронных схем. При этом для реализации одной и той же функции существует и используется достаточно большое число различных электронных схем. Поэтому с целью упрощения документации, решения задач анализа и синтеза цифровых схем используют специальные условные изображения цифровых элементов, которые обозначают только выполняемую логическую функцию, но не раскрывают внутреннее строение схемы.

На рис.10.2 показан общий принцип обозначения элементов, каждый из которых состоит из прямоугольного поля, в котором размещается указатель функции выполняемой логическим элементом (*). Справа от поля логического элемента обычно указываются его выходы, слева – входы.

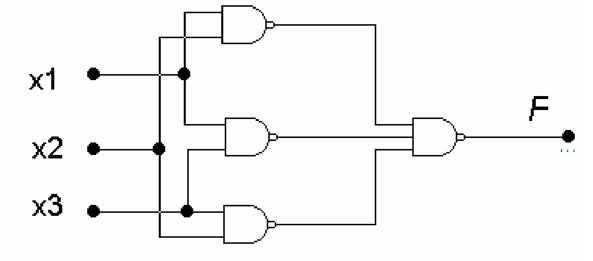
Рис.10.2. Общий принцип обозначения логических элементов

На рис. 10.3 показаны варианты изображения элементов, реализующих конкретные наборы логических функций.

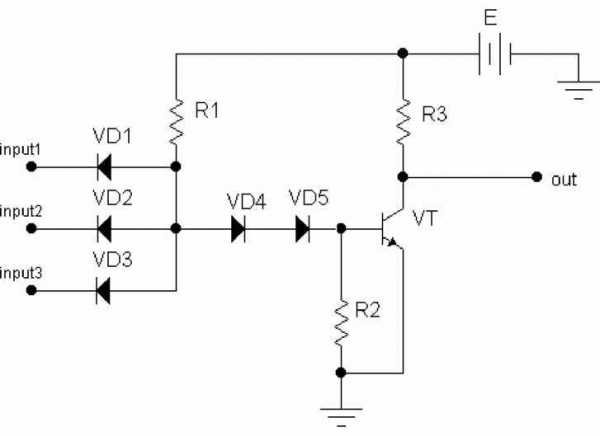
Рис.10.3. Варианты изображений логических элементов

Поскольку в цифровой технике напряжение как физическая величина рассматривается редко, (в основном при проектировании схем элементов и при решении вопросов согласования) входные и выходные сигналы обозначаются символами U только при необходимости, а в основном они описываются обозначением логических переменных x, y, z и т.д.

studfiles.net