Построение векторных диаграмм
Наверняка при решении задач по электротехнике многие сталкивались с некоторыми сложностями в построении векторных диаграмм. Начнем с определения векторной диаграммы.
Векторная диаграмма — это изображение синусоидально изменяющихся величин в виде векторов на плоскости.
Векторные диаграммы применяют потому, что сложение и вычитание синусоидальных величин, неизбежные при расчете цепей переменного тока, наиболее просто выполняются в векторной форме. Кроме того векторные диаграммы отличаются простотой и наглядностью.
Построение векторной диаграммы выполняется в прямоугольной плоскости. Чтобы построить диаграмму нужно провести вектор длиною равный амплитудному значению искомой величины, под углом сдвига относительно другой величины. Возможно, вы не сразу поймете смысл сказанного, для этого нужно изучить пример.
В качестве примера рассмотрим построение векторной диаграммы для цепи, состоящей из последовательно подключенных конденсатора, резистора и катушки. Напряжение на катушке
Катушка носит индуктивный характер, а значит, в ней напряжение опережает ток по фазе на 90°.
Конденсатор носит емкостной характер, значит, ток в нем опережает по фазе напряжение на 90°.
Резистор обладает только активным сопротивлением, и напряжение в нем совпадает по фазе с током.
Итак, для начала отложим вектор тока в масштабе. Масштаб для тока у нас будет 1 А/см.

Теперь отложим вектор напряжения на катушке, масштаб для напряжения возьмем 5 В/см, получается, что нужно отложить шесть клеток вверх, так как напряжение в катушке опережает ток. Для наглядности обозначим синим цветом.

Далее мы будем откладывать вектор активного сопротивления, так как напряжение в одной фазе с током, то мы его откладываем из конца вектора UL параллельно вектору тока

Следующим шагом отложим вектор напряжения на конденсаторе, так как оно запаздывает на 90°, мы его отложим вертикально вниз, из конца вектора UR. Обозначим желтым цветом.

И последним этапом мы отложим вектор общего напряжения, из начала координат в конец вектора UC

Общее напряжение получилось равным 2,23 В, причем характер цепи емкостной, так как напряжение отстает от тока.
Аналогичным образом выполняется построение векторной диаграммы токов.
Читайте также последовательная RLС-цепь
правила построения диаграмм, онлайн построение
Цифровое представление динамических процессов затрудняет восприятие, усложняет расчет выходных параметров после изменения условий на входе или в результате выполненной обработки. Векторная диаграмма токов и напряжений помогает успешно решать обозначенные задачи. Ознакомление с теорией и практическими примерами поможет освоить данную технологию.
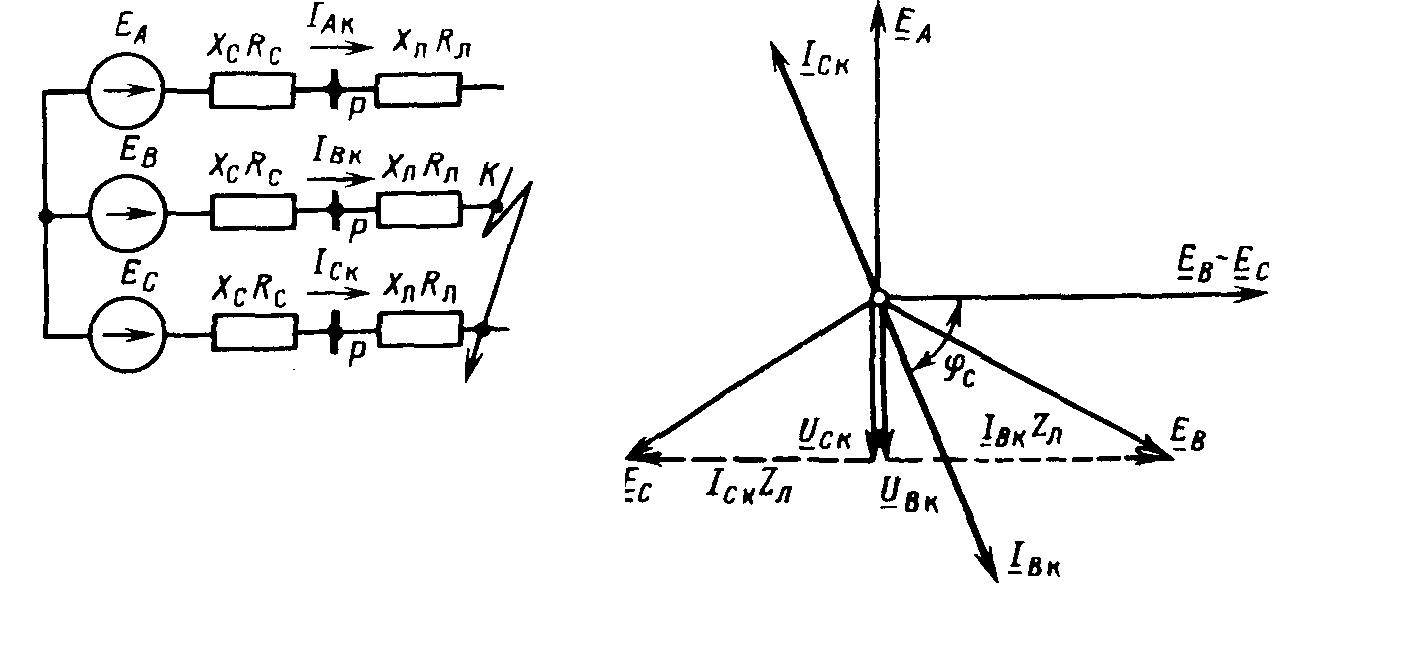
Диаграмма, поясняющая процесс короткого замыкания в трехфазной цепи счетчика электроэнергии
Разновидности векторных диаграмм
Для корректного отображения переменных величин, которые определяют функциональность радиотехнических устройств, хорошо подходит векторная графика. Подразумевается соответствующее изменение основных параметров сигнала по стандартной синусоидальной (косинусоидальной) кривой. Для наглядного представления процесса гармоническое колебание представляют, как проекцию вектора на координатную ось.
С применением типовых формул несложно рассчитать длину, которая получится равной амплитуде в определенный момент времени. Угол наклона будет показывать фазу. Суммарные влияния и соответствующие изменения векторов подчиняются обычным правилам геометрии.
Различают качественные и точные диаграммы. Первые применяют для учета взаимных связей. Они помогают сделать предварительную оценку либо используются для полноценной замены вычислений. Другие создают с учетом полученных результатов, которые определяют размеры и направленность отдельных векторов.
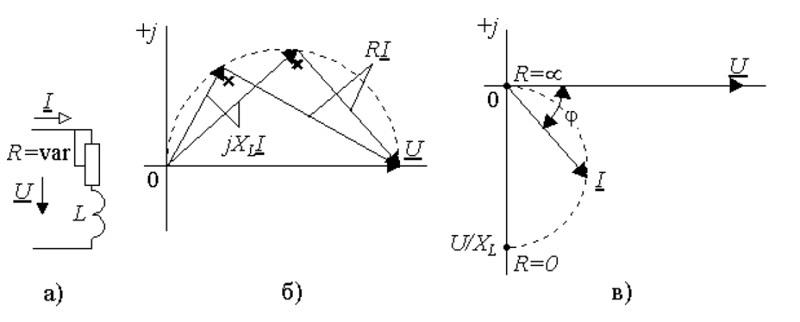
Круговая диаграмма
Допустим, что надо изучить изменение параметров тока в цепи при разных значениях сопротивления резистора в диапазоне от нуля до бесконечности. В этой схеме напряжение на выходе (U) будет равно сумме значений (UR и UL) на каждом из элементов. Индуктивный характер второй величины подразумевает перпендикулярное взаимное расположение, что хорошо видно на части рисунка б). Образованные треугольники отлично вписываются в сегмент окружности 180 градусов. Эта кривая соответствует всем возможным точкам, через которые проходит конец вектора UR при соответствующем изменении электрического сопротивления. Вторая диаграмма в) демонстрирует отставание тока по фазе на угол 90°.
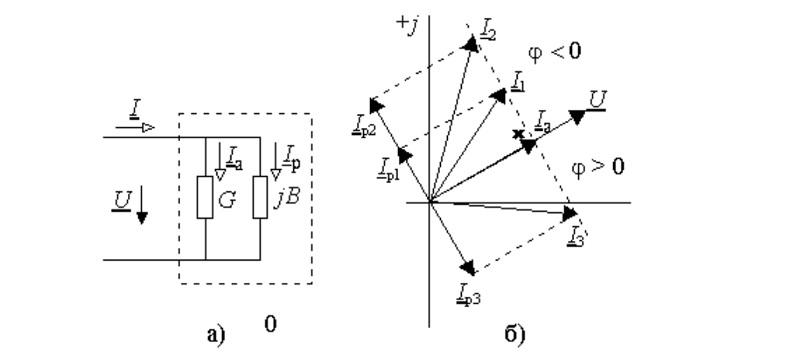
Линейная диаграмма
Здесь изображен двухполюсный элемент с активной и реактивной составляющими проводимости (G и jB, соответственно). Аналогичными параметрами обладает классический колебательный контур, созданный с применением параллельной схемы. Отмеченные выше параметры можно изобразить векторами, которые расположены постоянно под углом 90°. Изменение реактивной компоненты сопровождается перемещением вектора тока (I1…I3). Образованная линия располагается перпендикулярно U и на расстоянии Ia от нулевой точки оси координат.
Векторные диаграммы и комплексное представление
- А – длина;
- W – угловая скорость;
- f0 – начальный угол.
Значение действительной части равно A*cos*(w*t+f0). Это выражение описывает типичное гармоническое колебание с базовыми характеристиками.
Примеры применения
В следующих разделах приведены описания задач, которые решают с помощью представленной методики. Следует подчеркнуть, что применение комплексных чисел пригодно для сложных расчетов с высокой точностью. Однако на практике достаточно часто сравнительно простой векторной графики с наглядным отображением исходной информации на одном рисунке.
Механика, гармонический осциллятор
Таким термином обозначают устройство, которое можно вывести из равновесного состояния. После этого система возвращается в сторону исходного положения, причем сила (F) соответствующего воздействия зависит от дальности первичного перемещения (d) прямо пропорционально. Величину ее можно уточнить с помощью постоянного корректирующего коэффициента (k). Отмеченные определения связаны формулой F=-d*k
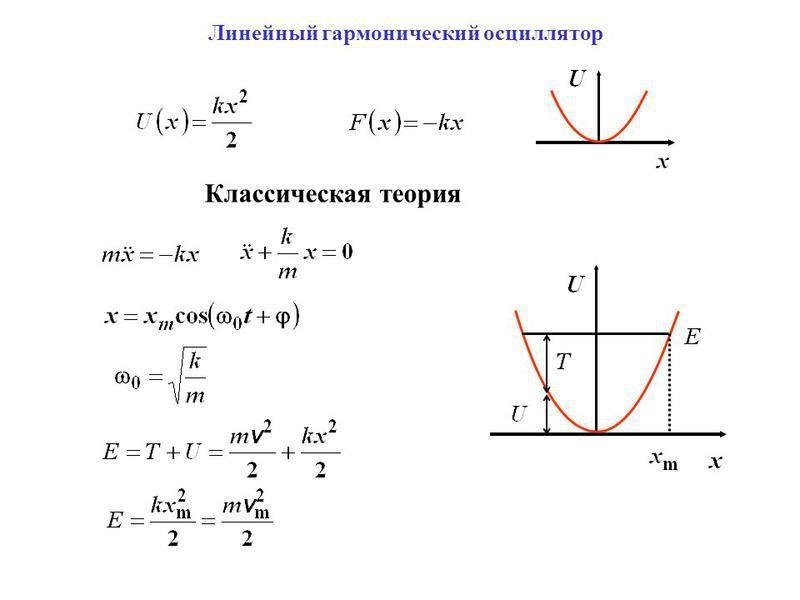
Формулы для расчета основных параметров гармонического осциллятора
К сведению. Аналогичные процессы происходят в системах иной природы. Пример – создание аналога на основе электротехнического колебательного контура (последовательного или параллельного). Формулы остаются теми же с заменой соответствующих параметров.
Свободные гармонические колебания без затухания
Продолжая изучение темы на примерах механических процессов, можно отметить возможность построения двухмерной схемы. Скорость в этом случае на оси Х отображается так же, как и в одномерном варианте. Однако здесь можно учесть дополнительно фактор ускорения, которое направляют под углом 90° к предыдущему вектору.
Гармонический осциллятор с затуханием и внешней вынуждающей силой
В этом случае также можно воспользоваться для изучения взаимного влияния дополнительных факторов векторной графикой. Как и в предыдущем примере, скорость и другие величины представляют в двухмерном виде. Чтобы правильно моделировать процесс, проверяют суммарное воздействие внешних сил. Его направляют к центру системы (точке равновесия). С применением геометрических формул вычисляют амплитуду механических колебаний после начального воздействия с учетом коэффициента затухания и других значимых факторов.
Расчет электрических цепей
Векторную графику применяют для сравнительно несложных цепей, которые созданы из набора элементов линейной категории: конденсаторы, резисторы, катушки индуктивности. Для более сложных схем пользуются методикой расчета «Комплексных амплитуд», в которой реактивные компоненты определяют с помощью импедансов.
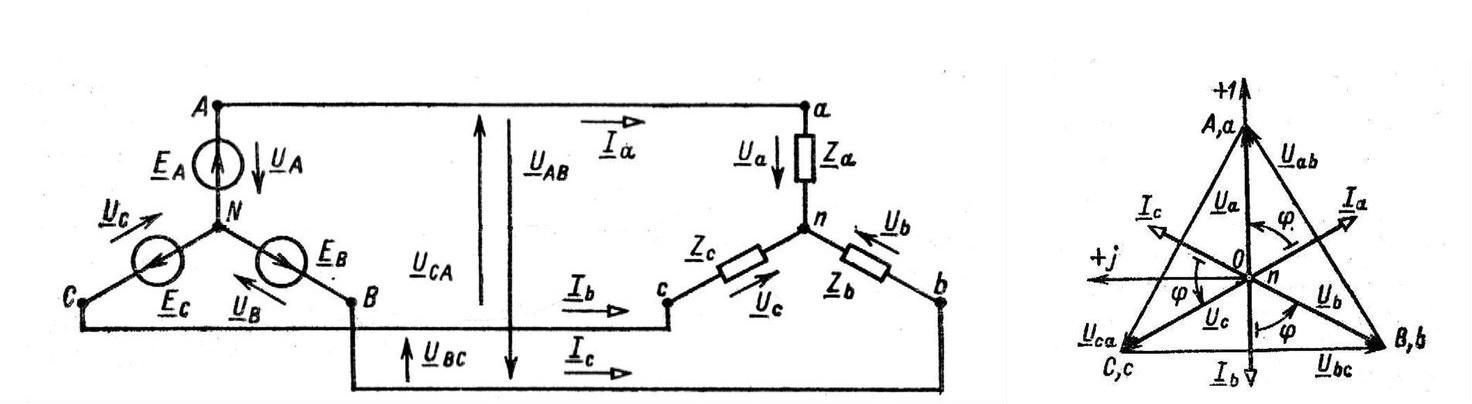
Векторная диаграмма для схемы соединений без нейтрального провода – звезда
Векторная диаграмма в данном случае выполняет функцию вспомогательного чертежа, который упрощает решение геометрических задач. Для катушек и конденсаторов, чтобы не пользоваться комплексным исчислением, вводят специальный термин – реактивное сопротивление. При синусоидальном токе изменение напряжения на индуктивном элементе описывается формулой U=-L*w*I0sin(w*t+f0).
Несложно увидеть подобие с классическим законом Ома. Однако в данном примере изменяется фаза. По этому параметру на конденсаторе напряжение отстает от тока на 90°. В индуктивности – обратное распределение. Эти особенности учитывают при размещении векторов на рисунке. В формуле учитывается частота, которая оказывает влияние на величину этого элемента.
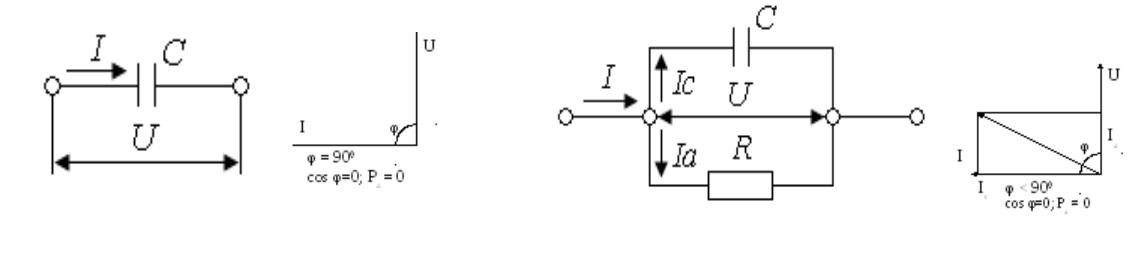
Схемы и векторные диаграммы для идеального элемента и диэлектрика с потерями
Преобразование Фурье
Векторные технологии применяют для анализа спектров радиосигналов в определенном диапазоне. Несмотря на простоту методики, она вполне подходит для получения достаточно точных результатов.
Сложение двух синусоидальных колебаний
В ходе изучения таких источников сигналов рекомендуется работать со сравнительно небольшой разницей частот. Это поможет создать график в удобном для пользователя масштабе.
Фурье-образ прямоугольного сигнала
В этом примере оперируют суммой синусоидальных сигналов. Последовательное сложение векторов образует многоугольник, вращающийся вокруг единой точки. Для правильных расчетов следует учитывать отличия непрерывного и дискретного распределения спектра.
Дифракция
Для этого случая пользуются тем же отображением отдельных синусоид в виде векторов, как и в предыдущем примере. Суммарное значение также вписывается в окружность.
Построение векторной диаграммы напряжений и токов
Для изучения технологии выберем однофазный источник синусоидального напряжения (U). Ток изменяется по формуле I=Im*cos w*t. Подключенная цепь содержит последовательно подключенные компоненты со следующими значениями:
- резистор: Ur=Im*R*cos w*t;
- конденсатор: Uc=Im*Rc*cos (w*t-π/2), Rc=1/w*C;
- катушка: UL= Im*RL*cos(w*t+π/2), RL=w*L.
При прохождении по цепи переменного тока на реактивных элементах будет соответствующий сдвиг фаз. Чтобы построить вектора правильно, рассчитывают амплитуды и учитывают изменение направлений. Ниже приведена последовательность создания графики вручную.
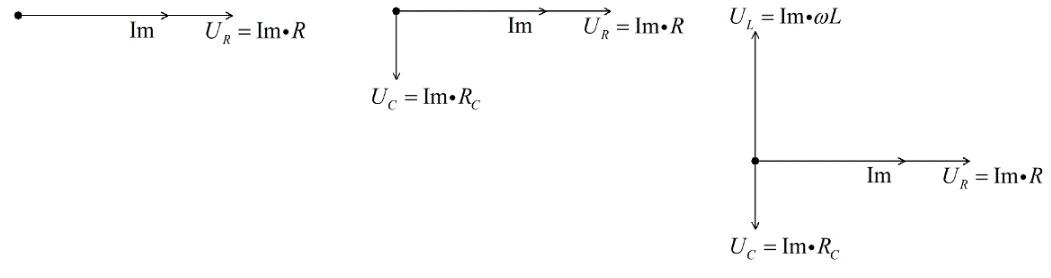
Диаграмма напряжений и токов на отдельных элементах
Далее с применением элементарных правил геометрии проверяют взаимное влияние векторов.
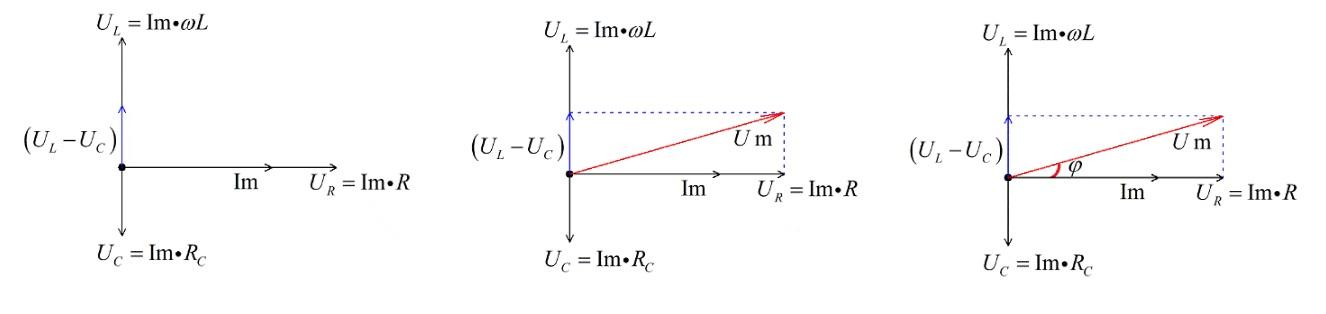
Решение векторного уравнения
На первом рисунке приведен результат сложения двух векторов при условии, когда Uc меньше UL. Добавив значение на сопротивление, получим результирующее напряжение Um. На третьей иллюстрации отмечен общий фазовый сдвиг.
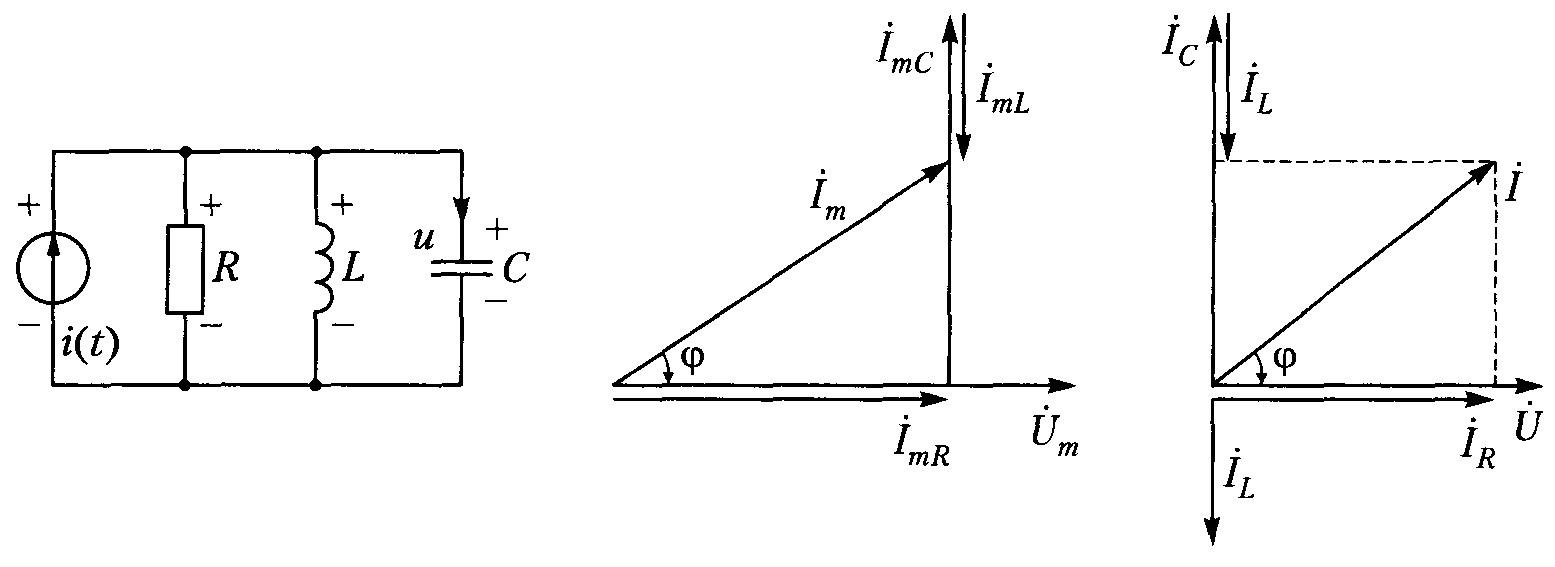
Векторное отображение процессов в параллельном колебательном контуре, резонанс напряжений
В топографической диаграмме начало координат совмещают с так называемой точкой «нулевого потенциала». Такое решение упрощает изучение отдельных участков сложных схем.
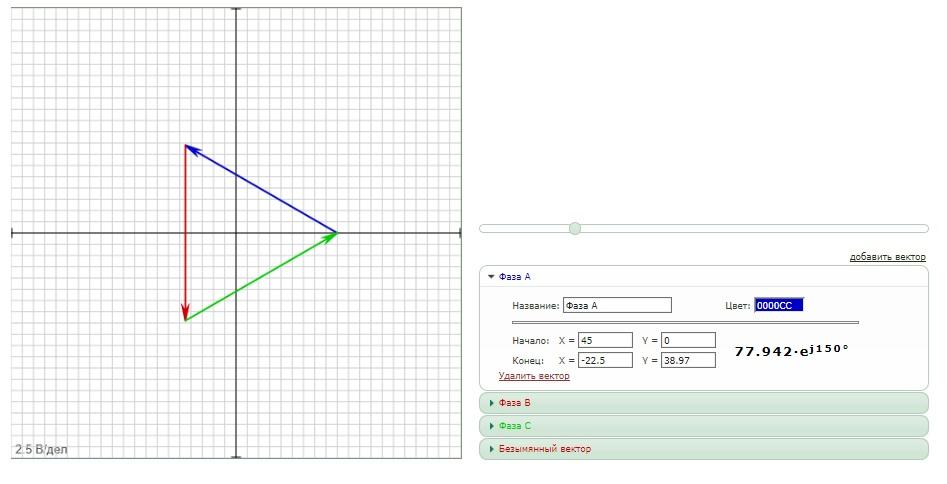
Специализированный редактор онлайн
В интернете можно найти программу для построения векторных диаграмм в режиме online.
Видео
Векторные диаграммы. Построение векторных диаграмм

При расчете электрических цепей переменного тока пользуются весьма простым и наглядным способом графического изображения синусоидальных величин при помощи вращающихся векторов.
Обоснование векторной диаграммы
Предположим, что ток задан уравнением
i = Imsin(ωt +Ψ)
Проведем две взаимно перпендикулярные оси и из точки пересечения осей проведем вектор Im, длина которого в определённом масштабе Mi выражает амплитуду тока Im:
Im = Im/Mi

Направление вектора выберем так, чтобы с положительным направлением горизонтальной оси вектор составлял угол, равный начальной фазе Ψ (рис. 12.10).
Проекция этого вектора на вертикальную ось определяет мгновенный ток в начальный момент времени: i0 = ImsinΨ.
Представим себе, что вектор Im вращается против движения часовой стрелки с угловой скоростью, равной угловой частоте ω. Его положение в любой момент времени определяется углом ωt +Ψ ,
Тогда мгновенный ток для произвольного момента времени t можно определить проекцией вектора Im на вертикальную ось в этот момент времени.
Следующая статья сложение и вычитания векторов векторной диаграммы.
Например, для t = t1
i1 = Imsin(ωt1 +Ψ)
в общем случае
i = Imsin(ωt +Ψ)
Получили такое же уравнение, каким был задан переменный ток, что свидетельствует о возможности изображения тока вращающимся вектором при нанесении его на чертеж в начальном положении.
Построение векторной диаграммы
Вращая вектор Im‘ против движения часовой стрелки, в прямоугольной системе координат построим график изменения проекции его на вертикальную ось в пределах одного оборота (одного периода). Получим известный уже график синусоидальной функции, соответствующий заданному уравнению.
При построении векторов положительные углы отсчитывают от положительного направления горизонтальной оси против вращения часовой стрелки, а отрицательные — по ее движению.
В процессе расчета электрической цепи определяется ряд синусоидальных величин. Все их можно изобразить на одном чертеже при помощи вращающихся векторов, привязав к одной паре взаимно перпендикулярных осей.
Совокупность векторов, изображающих на одном чертеже несколько синусоидальных величин одинаковой частоты в начальный момент времени, называется векторной диаграммой.
Например, напряжение и ток в электрической цепи выражаются уравнениями:
u = 125 sin(ωt + 30°)
i = 12 sin(ωt — 20°).
Векторная диаграмма такой цепи изображена на рис. 12.11. Если выбрать масштабы напряжения и тока
Mu = 50 В/см; Mi = 4 А/см;
то
Um = Um/Mu = 125/50 = 2,5 см; Im = Im = im/Mi = 12/4 = 3 см.

Векторная диаграмма содержит векторы синусоидальных величин одинаковой частоты, поэтому они вращаются с одинаковой частотой и их взаимное расположение не меняется.
Начало отсчета времени выбирают произвольно, поэтому один из векторов диаграммы можно направить произвольно; остальные же нужно располагать с учетом сдвига фаз по отношению к первому или предыдущему вектору.
Сложение и вычитание векторов
Главным достоинством векторных — это возможность простого сложения и вычитания двух величин. Например: требуется сложить, два тока, заданных уравнениями

Сложим два заданных тока i1 и i2 по известному правилу сложения векторов (рис. 12.12, а). Для этого изобразим токи в виде векторов из общего начала 0. Результирующий вектор найдем как диагональ параллелограмма, построенного на слагаемых векторах:
Im = Im1 + Im2
Сложение векторов, особенно трех и более, удобнее вести в таком порядке: один вектор остается на месте, другие переносятся параллель
но самим себе так, чтобы начало последующего вектора совпало с концом предыдущего.
Вектор Im, проведенный из начала первого вектора в конец последнего, представляет собой сумму всех векторов (рис. 12.12, б).
Вычитание одного вектора из другого выполняют сложением прямого вектора (уменьшаемого) и обратного (вычитаемого) (рис. 12.13):

При сложении синусоидальных величин в отдельных случаях можно применить аналитическое решение: применительно к рис. 12.12, а — по теореме косинусов; к рис. 12.14, а — сложение модулей векторов; б — вычитание модулей векторов, в — по теореме Пифагора.
Векторные диаграммы электрических цепей | FaultAn.ru
При исследовании электрических цепей и моделировании часто пользуются векторными диаграммами токов и напряжений. Под векторной диаграммой понимается совокупность векторов, изображающих синусоидальные функции времени [1].
Воспользуйтесь программой расчёта электрических цепей для построения векторных диаграмм онлайн.
Представление синусоидальных функций в виде комплексных чисел
Векторная диаграмма – это удобный инструмент представления синусоидальных функций времени, коими являются, к примеру, напряжения и токи электрической цепи переменного тока.
Рассмотрим, например, произвольный ток, представленный в виде синусоидальной функции
i(t) = 10 sin(ωt + 30°).
Данный синусоидальный сигнал можно представить в виде комплексной величины
I = 10∠30°.
Для формирования комплексного числа используются модуль и фаза синусоидального сигнала.
Закон Ома в комплексной форме
Известно [1], что напряжение U на сопротивлении Z связано с током I, протекающим через это сопротивление, согласно закону Ома:
U = Z ∙ I.
Кроме того, известны соотношения, определяющие активное сопротивление резистора, индуктивное сопротивление катушки и ёмкостное сопротивление конденсатора:
ZR = R, ZL = jXL, ZC = −jXC,
где XL = ωL, XC = 1/(ωC), R – сопротивление резистора, L – индуктивность катушки, C – ёмкость конденсатора, ω = 2pf – циклическая частота, f – частота сети, j – мнимая единица.
Векторная диаграмма при последовательном соединении элементов
Для построения векторных диаграмм сперва составляют уравнения по законам Кирхгофа для рассматриваемой электрической цепи.
Рассмотрим электрическую цепь, представленную на рис. 1, и нарисуем для неё векторную диаграмму напряжений. Обозначим падение напряжение на элементах.
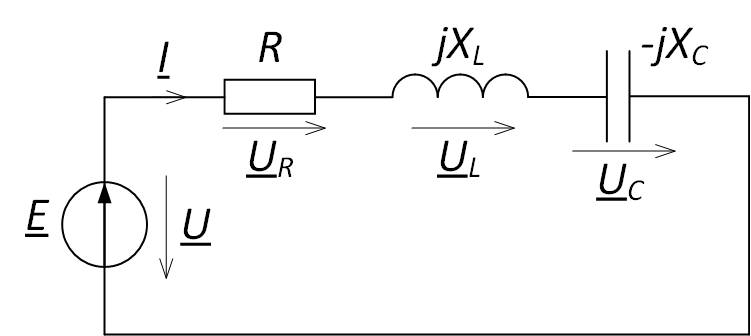 Рис. 1. Последовательное соединение элементов цепи
Рис. 1. Последовательное соединение элементов цепи
Составим уравнение для данной цепи по второму закону Кирхгофа:
UR + UL + UC = E.
По закону Ома падение напряжений на элементах определяется по следующим выражениям:
UR = I ∙ R,
UL = I ∙ jXL,
UC = −I ∙ jXC.
Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости. Обычно вектора токов и напряжений отображаются в своих масштабах: отдельно для напряжений и отдельно для токов.
Из курса математики известно, что j = 1∠90°, −j = 1∠−90°. Отсюда при построении векторной диаграммы умножение какого-либо вектора на мнимую единицу j приводит к повороту этого вектора на 90 градусов против часовой стрелки, а умножение на −j приводит к повороту этого вектора на 90 градусов по часовой стрелке.
При построении векторной диаграммы напряжений на комплексной плоскости сперва отобразим вектор тока I, после чего относительного него будем отображать вектора падений напряжений (рис. 2) с учётом приведённых выше соотношений для мнимой единицы.
Падение напряжения на резисторе UR совпадает по направлению с током I (т.к. UR = I ∙ R, а R – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Падение напряжения на индуктивном сопротивлении опережает вектор тока на 90° (т.к. UL = I ∙ jXL, а умножение на j приводит повороту этого вектора на 90° против часовой стрелки). Падение напряжения на ёмкостном сопротивлении отстаёт от вектора тока на 90° (т.к. UC = −I ∙ jXC, а умножение на −j приводит повороту этого вектора на 90° по часовой стрелке).
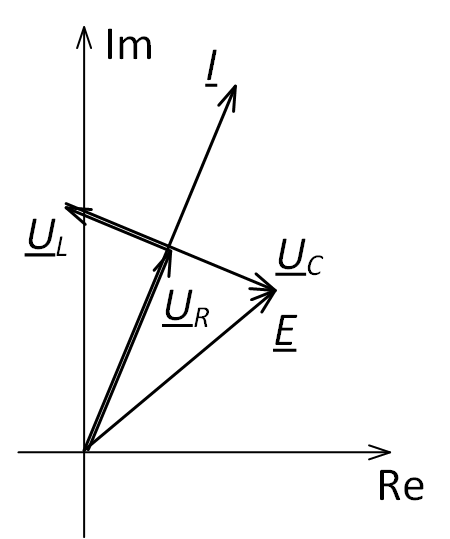
Рис. 2. Векторная диаграмма напряжений при последовательном соединении элементов цепи
Следует обратить внимание, что на одной векторной диаграмме изображают только векторы тех величин, у которых частота совпадает!
Векторная диаграмма при параллельном соединении элементов
Рассмотрим электрическую цепь, представленную на рис. 3, и нарисуем для неё векторную диаграмму токов. Обозначим направление токов в ветвях.
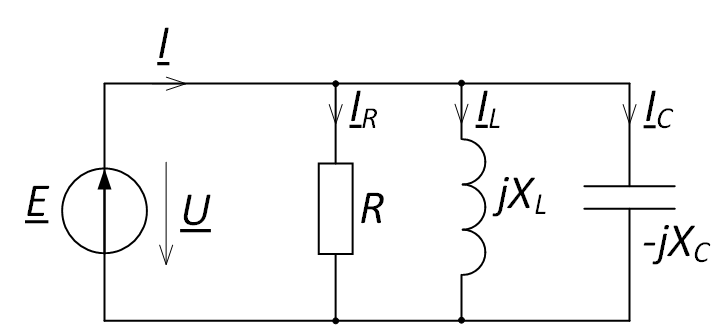
Рис. 3. Параллельное соединение элементов цепи
Составим уравнение для данной цепи по первому закону Кирхгофа:
I – IR – IL – IC = 0,
откуда
I = IR + IL + IC.
Определим по закону Ома токи в ветвях по следующим выражениям, учитывая, что 1 / j = −j:
IR = E / R,
IL = E / (jXL) = −j ∙ E / XL,
IC = E / (−jXC) = j ∙ E / XC,
Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости.
При построении векторной диаграммы токов на комплексной плоскости сперва отобразим вектор ЭДС E, после чего относительного него будем отображать вектора токов токов (рис. 4) с учётом приведённых выше соотношений для мнимой единицы.
Ток в резисторе IR совпадает по направлению с ЭДС E (т.к. IR = E / R, а R – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Ток в индуктивном сопротивлении отстаёт от вектора ЭДС на 90° (т.к. IL = −j ∙ E / XL, а умножение на −j приводит повороту этого вектора на 90° по часовой стрелки). Ток в ёмкостном сопротивлении опережает вектор ЭДС на 90° (т.к. IC = j ∙ E / XC, а умножение на j приводит повороту этого вектора на 90° против часовой стрелки). Результирующий вектор тока определяется после геометрического сложения всех векторов по правилу параллелограмма.

Рис. 4. Векторная диаграмма токов при параллельном соединении элементов цепи
Для произвольной цепи алгоритм построения векторных диаграмм аналогичен вышеизложенному с учётом протекаемых в ветвях токов и прикладываемых напряжений.
Обращаем ваше внимание, что на сайте представлен инструмент для построения векторных диаграмм онлайн для трёхфазных цепей.
Список использованной литературы
- Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.
Если вам нравится наш контент, помогите в развитии сайта.
Рекомендуемые записи
Построение векторных диаграмм | FaultAn.ru
Задание исходных данных
Для построения векторной диаграммы необходимо задать напряжения и токи в полярной форме. Для этого предусмотрены соответствующие поля (рис. 1). Угол напряжений и токов задаётся в градусах.

Рис. 1. Задание исходных данных
Для построения векторной диаграммы только для токов либо только для напряжений, необходимо выбрать соответствующие параметры чекбоксов (рис. 2).

Рис. 2. Выбор данных для отображения
После задания всех параметров необходимо нажать кнопку «Построить», в результате чего будет отображена векторная диаграмма для заданных величин (рис. 3). Все величины отображаются в относительных единицах. За базисную величину для напряжений и для токов берутся максимальное из трёх заданных напряжений и токов соответственно.
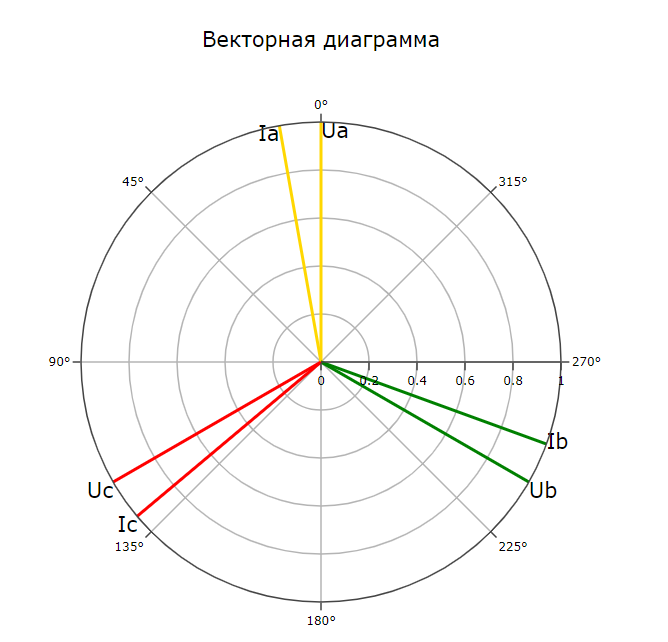
Рис. 3. Векторная диаграмма
Выбор базового вектора
При построении векторной диаграммы доступен выбор базового вектора (рис. 4). При выборе вектора базовым его угол принимается равным 0°, а углы остальных векторов отсчитываются относительно него.

Рис. 4. Выбор базового вектора
В выпадающем списке появляются только те данные, которые выбраны для отображения чекбоксами (рис. 2). Более подробно про выбор базового вектора можете прочитать здесь.
Инструменты
Для векторной диаграммы доступны инструменты для анализа: увеличение/уменьшение графика, отображение значений. Полученные результаты можно экспортировать в рисунок в формате png.
Векторная диаграмма токов и напряжений: график, обозначения, виды
 Использование векторных диаграмм при анализе, расчете цепей переменного тока делает возможным рассмотреть более доступно и наглядно происходящие процессы, а также в некоторых случаях значительно упростить выполняемые расчеты.
Использование векторных диаграмм при анализе, расчете цепей переменного тока делает возможным рассмотреть более доступно и наглядно происходящие процессы, а также в некоторых случаях значительно упростить выполняемые расчеты.
Векторной диаграммой принято называть геометрическое представление изменяющихся по синусоидальному (либо косинусоидальному) закону направленных отрезков — векторов, отображающих параметры и величины действующих синусоидальных токов, напряжений либо их амплитудных величин.
Широкое применение векторные диаграммы нашли в электротехнике, теории колебаний, акустике, оптике и т.д.
Различают 2-х вида векторных диаграмм:
- точные;
- качественные.
Интересное видео о векторных диаграммах смотрите ниже:
Точные изображаются по результатам численных расчетов при условии соответствия масштабов действующих значений. При их построении можно геометрически определить фазы и амплитудные значения искомых величин.
Качественные диаграммы изображаются с учетом взаимных соотношений между электрическими величинами, без указания численных характеристик.
Они являются одним из основных средств анализа электрических цепей, позволяя наглядно иллюстрировать и качественно контролировать ход решения задачи и легко установить квадрант, в котором располагается искомый вектор.
 Для удобства при построении диаграмм анализируют неподвижные векторы для определенного момента времени, который выбирается таким образом, чтобы диаграмма имела удобный для понимания вид. Ось OХ соответствует величинам действительных чисел, ось OY — оси мнимых чисел (мнимая единица). Синусоида отображает движение конца проекции на ось OY. Каждому напряжению и току соответствует собственный вектор на плоскости в полярных координатах. Его длина отображает амплитудное значение величины тока, при этом угол равен фазе.
Для удобства при построении диаграмм анализируют неподвижные векторы для определенного момента времени, который выбирается таким образом, чтобы диаграмма имела удобный для понимания вид. Ось OХ соответствует величинам действительных чисел, ось OY — оси мнимых чисел (мнимая единица). Синусоида отображает движение конца проекции на ось OY. Каждому напряжению и току соответствует собственный вектор на плоскости в полярных координатах. Его длина отображает амплитудное значение величины тока, при этом угол равен фазе.
Векторы, изображаемые на такой диаграмме, характеризуются равновеликой угловой частотой ω. В виду чего при вращении их взаимное расположение не изменяется.
Ещё одно полезное видео о векторных диаграммах:
Поэтому при изображении векторных диаграмм один вектор можно направить произвольным образом (например, по оси ОХ).
А остальные — изображать по отношению к исходному под различными углами, соответственно равными углам сдвига фаз.
Таким образом, векторная диаграмма дает отчетливое представление об опережении либо отставании различных электрических величин.
Допустим у нас есть ток, величина которого изменяется по некоторому закону:
i = Im sin (ω t + φ).
С начала координат 0 под углом φ проведем вектор Im, величина которого соответствует Im. Его направление выбирается так, чтобы с положительным направлением оси OX вектор составлял угол — соответствующий фазе φ.
Проекция вектора на вертикальную ось и определяет значение мгновенного тока в начальный момент времени.
В основном векторные диаграммы изображают для действующих значений, а не амплитудных. Векторы действующих значений количественно отличаются от амплитудных значений — масштабом, поскольку:
I = Im /√2.

Основным преимуществом векторных диаграмм называют возможность простого и быстрого сложения и вычитания 2-х параметров при расчете электроцепей.
Построение векторной диаграммы напряжений. Катушка. Конденсатор. Сопротивление. Сдвиг фаз.
Достаточно сложным и чаще всего не изучаемым аспектом темы переменный ток является метод построения векторных диаграмм. Анализируя вынужденные электромагнитные колебания, мы уже обсудили сдвиг тока и напряжения на реактивных сопротивлениях (катушка индуктивности и конденсатор) по сравнению с активным сопротивлением (резистор). Тогда одним из задаваемых вопросов задачи является вопрос о направлении суммарного тока или напряжения в данный конкретный момент времени. Для ответа на этот вопрос и используется метод построения векторных диаграмм.
Векторная диаграмма — это изображение гармонически изменяющихся величин (текущего тока и напряжения) в виде векторов на плоскости.
Рис. 1. Векторная диаграмма
Построение векторных диаграмм происходит в прямоугольной декартовой системе координат. Построение начинается с проведения вектора, численно равного амплитудному значению тока в цепи. Данный вектор сонаправим в осью ОХ (рис. 1.1).
Т.к. напряжение на активном сопротивлении находится в одной фазе с током, то вектор амплитуды напряжения сонаправлен с вектором тока (рис. 1.2. красный).
На катушке напряжение опережает ток, поэтому отложим вектор амплитуды напряжения на катушке () вверх под углом относительно вектора тока (рис. 1.2. синий).
На конденсаторе напряжение отстаёт от тока, поэтому отложим вектор амплитуды напряжения на конденсаторе () вниз под углом относительно вектора тока (рис. 1.2. зелёный).
Угол , используемый в логике построений, используется в случае идеальности контура и катушки.
Для построения общего вектора напряжения достаточно векторно сложить напряжения:
(1)
Проще всего сначала найти вектор-сумму (т.к. они расположены вдоль одной прямой). В нашем случае, эти вектора разнонаправлены, найдём (рис. 1.3. жёлтый).
И последнее, осталось сложить получившийся вектор с вектором для получения значения полного напряжения в цепи (рис. 1.4. оранжевый). Для получения модуля вектора воспользуемся теоремой Пифагора, т.к. вектора находятся под прямым углом. Тогда:
(2)
Угол — угол между вектором силы тока и полного напряжения называется сдвигом фаз между колебаниями силы тока и напряжения. Данный параметр можно найти и исходя из параметров системы:
(3)
Вывод: задачи на данную тематику касаются поиска сдвига фаз между колебаниями силы тока и напряжения через график (рис. 1.4) или через соотношение (3), а также поиска полного напряжения в цепи также через график (рис. 1.4) или через соотношение (2).
Поделиться ссылкой:
Векторный график СводкаВекторный график — это многомерный график, используемый в таких отраслях, как метеорология, авиация, исследования и строительство, который иллюстрирует модели потоков (например, ветра, воды, магнитных полей и т. Д.). И направление, и величина представлены на векторном графике. Origin включает два типа векторных графиков:
Требуется минимальная исходная версия: Origin 2015 SR0 Что вы узнаетеИз этого туториала Вы узнаете, как:
ступеней Этот учебник связан с Вектор XYAMXYAM означает X, Y, угол и величину. Векторы начнутся из точки (X, Y) и повернутся на указанный угол. В следующем примере для создания векторного графика используется режим данных XYAM.
Вектор XYXYДругой режим организации данных — XYXY; где первые X, Y — начальная точка вектора, а последние X, Y — конечная точка. Чтобы создать такой векторный график, активируйте рабочую книгу Book9E в папке 2D Vector , выделите в ней все четыре столбца данных и выберите Plot: Specialized: Vector XYXY из главного меню. При необходимости удалите заголовки осей. |
построить векторную диаграмму — это … Что такое построить векторную диаграмму?
График вектора ветра выпадений — Диаграмма вектора ветра, основанная на структуре ветра от поверхности Земли до самой большой высоты, представляющей интерес… Военный словарь
участок Боде -; аппроксимации прямой линии обозначены полюсом Боде; фаза изменяется от 90 ° на низких частотах (из-за вклада числителя, который составляет 90 ° на всех частотах) до 0 ° на высоких частотах (где фазовый вклад…… Wikipedia
Математическая диаграмма — Эта статья об общих диаграммах в математике.Для диаграмм в теоретико-категорийном смысле см. Диаграмма (теория категорий). Элементы Евклида, мс. из Люнебурга, 1200 г. н.э. Математические диаграммы — это диаграммы в области математики,…… Wikipedia
Список редакторов векторной графики — Ниже приводится список редакторов векторной графики. Бесплатное / открытое программное обеспечение; Dia: Dia — это программа для создания диаграмм на основе gtk +, выпущенная под лицензией GPL. Dia может экспортировать графику в несколько форматов.; Inkscape: векторная графика…… Wikipedia
Механизм очага — Механизм очага землетрясения описывает неупругую деформацию в области очага, которая генерирует сейсмические волны.В случае события, связанного с разломом, это относится к ориентации сдвинутой плоскости разлома и вектору сдвига…… Wikipedia
Delta-v — Для использования в других целях, см. Delta v (значения). В астродинамике Δv или дельта v (буквально изменение скорости) — это скаляр, который принимает единицы скорости. Это мера количества усилий, необходимых для перехода от одной траектории к другой… Wikipedia
Треугольник ветра — Треугольник ветра представляет собой графическое представление взаимосвязи между движением воздушного судна и ветром.Он широко используется в навигации с точным счислением. Треугольник ветра — это векторная диаграмма с тремя векторами. * Вектор воздуха представляет…… Wikipedia
HSL и HSV — Рис. 1. HSL (a – d) и HSV (e – h). Выше (a, e): вырезать 3D-модели каждого из них. Ниже: двухмерные графики, показывающие сразу два из трех параметров модели, при этом другой остается постоянным: цилиндрические оболочки (b, f) постоянного насыщения, в данном случае…… Wikipedia
Комплексное число — Комплексное число может быть визуально представлено как пара чисел, образующих вектор на диаграмме, называемой диаграммой Аргана, представляющей комплексную плоскость.Re — действительная ось, Im — мнимая ось, а i — квадратный корень из –1. Комплекс…… Википедия
Аттрактор Ресслера — Аттрактор Ресслера (pronEng | ˈrɒslɚFact | date = декабрь 2007 г.) является аттрактором для системы Ресслера, системы трех нелинейных обыкновенных дифференциальных уравнений. Эти дифференциальные уравнения определяют динамическую систему с непрерывным временем, которая…… Wikipedia
Список математических статей (P) — NOTOC PP = NP проблема P адический анализ P адическое число P адический порядок P компактная группа P группа P² неприводимая P матрица P лапласиана P rep P значение P вектор P y метод Pacific Journal of Mathematics Алгоритм слияния пакетов Матрица упакованного хранения Упаковка…… Wikipedia
Создание, изменение и доступ к элементам вектора
Из этой статьи вы узнаете о векторах в программировании R. Вы научитесь создавать их, получать доступ к их элементам с помощью различных методов и изменять их в своей программе.
Вектор — это базовая структура данных в R. Она содержит элементы того же типа. Типы данных могут быть логическими, целочисленными, двойными, символьными, сложными или необработанными.
Тип вектора можно проверить с помощью функции typeof () .
Еще одно важное свойство вектора — это его длина.Это количество элементов в векторе, которое можно проверить с помощью функции length () .
Как создать вектор в R?
Векторы обычно создаются с помощью функции c () .

Поскольку вектор должен иметь элементы одного типа, эта функция попытается привести элементы к одному и тому же типу, если они различны.
Принуждение — это от низшего к высшему типу от логического к целому числу до двойного к символьному.
> х <- с (1, 5, 4, 9, 0)
> typeof (x)
[1] "двойной"
> длина (x)
[1] 5
> x <- c (1; 5.4; ИСТИНА; "привет")
> х
[1] «1» «5.4» «ИСТИНА» «привет»
> typeof (x)
[1] "персонаж" Если мы хотим создать вектор последовательных чисел, очень полезен оператор : .
Пример 1: Создание вектора с помощью оператора
> x <- 1: 7; Икс
[1] 1 2 3 4 5 6 7
> у <- 2: -2; Y
[1] 2 1 0 -1 -2 Более сложные последовательности могут быть созданы с помощью функции seq () , например, определение количества точек в интервале или размера шага.
Пример 2: Создание вектора с помощью функции seq ()
> seq (1, 3, by = 0.2) # указать размер шага [1] 1,0 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 3,0 > seq (1, 5, length.out = 4) # указать длину вектора [1] 1.000000 2.333333 3.666667 5.000000
Как получить доступ к элементам вектора?
Доступ к элементам вектора можно получить с помощью векторной индексации. Вектор, используемый для индексации, может быть логическим, целочисленным или символьным вектором.
Использование целочисленного вектора в качестве индекса
Векторный индекс в R начинается с 1, в отличие от большинства языков программирования, где индекс начинается с 0.
Мы можем использовать вектор целых чисел в качестве индекса для доступа к определенным элементам.
Мы также можем использовать отрицательные целые числа для возврата всех элементов, кроме указанных.
Но мы не можем смешивать положительные и отрицательные целые числа, в то время как индексирование и действительные числа, если они используются, усекаются до целых.
> х
[1] 0 2 4 6 8 10
> x [3] # доступ к 3-му элементу
[1] 4
> x [c (2, 4)] # доступ ко 2-му и 4-му элементам
[1] 2 6
> x [-1] # доступ ко всем, кроме 1-го элемента
[1] 2 4 6 8 10
> x [c (2, -4)] # нельзя смешивать положительные и отрицательные целые числа
Ошибка в x [c (2, -4)]: только 0 могут быть смешаны с отрицательными индексами
> х [c (2.4, 3.54)] # действительные числа обрезаются до целых
[1] 2 4
Использование логического вектора в качестве индекса
Когда мы используем логический вектор для индексации, возвращается позиция, в которой логический вектор равен ИСТИНА .
Эта полезная функция помогает нам фильтровать вектор, как показано ниже.
> x [c (ИСТИНА, ЛОЖЬ, ЛОЖЬ, ИСТИНА)]
[1] -3 3
> x [x <0] # векторов фильтрации на основе условий
[1] -3 -1
> х [х> 0]
[1] 3
В приведенном выше примере выражение x> 0 даст логический вектор (FALSE, FALSE, FALSE, TRUE) , который затем используется для индексации.
Использование вектора символов в качестве индекса
Этот тип индексации полезен при работе с именованными векторами. Мы можем назвать каждый элемент вектора.
> x <- c («первый» = 3, «второй» = 0, «третий» = 9)
> имена (х)
[1] «первый» «второй» «третий»
> x ["секунда"]
второй
0
> x [c («первый», «третий»)]
первая треть
3 9
Как изменить вектор в R?
Мы можем изменить вектор с помощью оператора присваивания.
Мы можем использовать описанные выше методы для доступа к определенным элементам и их изменения.
Если мы хотим усечь элементы, мы можем использовать переназначения.
> х
[1] -3 -2 -1 0 1 2
> х [2] <- 0; x # изменить 2-й элемент
[1] -3 0 -1 0 1 2
> х [х <0] <- 5; x # изменять элементы меньше 0
[1] 5 0 5 0 1 2
> х <- х [1: 4]; x # усечь x до первых 4 элементов
[1] 5 0 5 0
Как удалить вектор?
Мы можем удалить вектор, просто присвоив ему NULL .
> х
[1] -3 -2 -1 0 1 2
> x <- NULL
> х
НОЛЬ
> х [4]
НОЛЬ
,Скачать программу для построения векторных диаграмм бесплатно для Windows
Программа построения векторных диаграмм
в Software InformerИнструмент для моделирования сложных многослойных диэлектрических устройств, MOS- и MIM-устройств.
Эта программа есть... Диаграммы энергетических диапазонов и ... Нарисовать диаграмму диапазонов для МОП ... Показать движение диаграммы диапазонов
21 Gadwin Systems, Inc. 49 коммерческий
создавать блок-схемы, бизнес, технические схемы.
11 MeeSoft 7458 Freeware
Diagram Designer - это графический редактор для редактирования графических данных.
94 Корпорация MetaProducts 4 Freeware
Net Activity Diagram (NAD) - это приложение Windows 9x / NT / 2000 / ME / XP, которое контролирует ваш компьютер Int ....
1 Программное обеспечение Effexis 66 условно-бесплатная
Создает потоки вызовов и диаграммы последовательности UML из текстовых входных данных.
Подробнее Программа построения векторных диаграмм
Программа построения векторных диаграмм, введение
14 Vector Magic, Inc. 9898 условно-бесплатная
Vector Magic - это утилита, конвертирующая растровые изображения в векторы.
14 Принципиальная электрическая схема 1689 Открытый источник
Он помогает создавать электронные схемы и экспортировать их в виде изображений.
4 Программное обеспечение Efofex 645 условно-бесплатная
Декартовы диаграммы, поляры, параметрика, поля наклона, объемы вращения.
2 EDrawSoft 644 условно-бесплатная
Создавайте диаграммы в ручном режиме или используя бесплатные шаблоны.
6 Программное обеспечение NCH 8250 Freeware
Создавайте визуальные представления процессов, организаций и интеллект-карт.
5 Джозеф А. Хувальдт 105 Freeware
Программа для извлечения информации из сканированных графиков.
Дополнительные заголовки, содержащие программу построения векторных диаграмм
17 Тодд Томпсон +829 Freeware
TriPlot - это программа построения трилинейных диаграмм для исследователей и студентов.
3 Программное обеспечение Тодда А. Томпсона 199 Freeware
Это программа построения диаграмм направленной розы для исследователей и студентов.
93 MetaSoft Pty Ltd 388 условно-бесплатная
VDraw4 - это профессиональная программа для визуализации векторных диаграмм и данных.
Земляные работы 17 коммерческий
Исключительно умная программа для представления и построения графиков скважин.
Zetaware условно-бесплатная
С помощью этого инструмента легко использовать троичную программу построения графиков!
2 Стивен Фолкман 2 Freeware
ES-Plot - программа построения графиков для инженеров и ученых.
1 EDrawSoft 132 условно-бесплатная
Мощная, но простая в использовании программа для рисования диаграмм UML.
1 G R Freeth 92 Freeware
PolarPlot - это программа для построения полярной диаграммы антенны.
Векторная студия 50 условно-бесплатная
Vector Studio - это простая в использовании программа для рисования векторных изображений.
1 Владимир Галушко 243 условно-бесплатная
3DField - это программа для построения контурных поверхностей и трехмерных данных.
MathSoft Engineering & Education, Inc.
Halliburton Energy Services 5
Wainfo Technologies 1
,