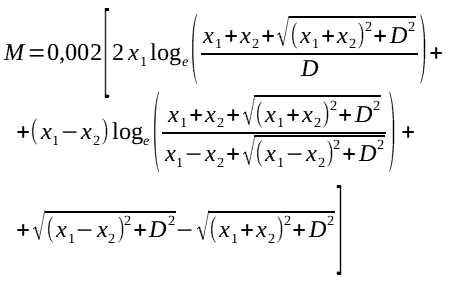Расчет многослойной катушки индуктивности онлайн – On-line калькуляторы, расчет многослойной катушки индуктивности

Онлайн калькулятор расчета многослойной катушки индуктивности

На практике нередко случаются ситуации, когда при выходе со строя катушки индуктивности, ее необходимо восстановить – намотать новую проволоку взамен старой. При этом вам уже известны геометрические параметры катушки, но требуется узнать, сколько сделать витков, слоев, их толщину и длину необходимого для этого провода. Стоит отметить, что при намотке витки должны ложиться вплотную без зазора.

Для расчета индуктивности многослойной катушки используется такая формула:

Где,

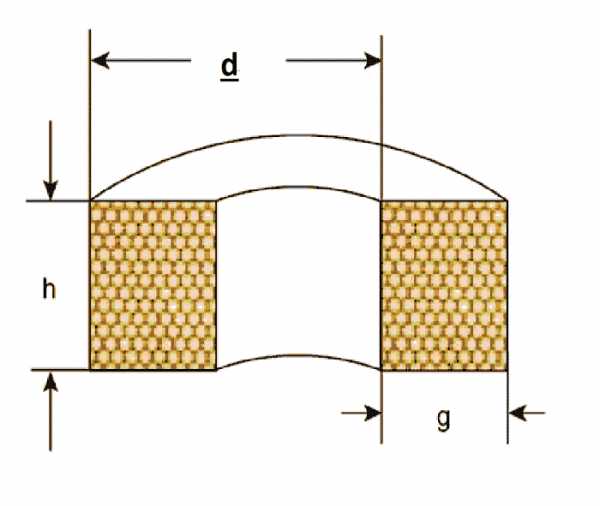
• d – сумма диаметра каркаса и толщины намотки только с одной стороны;
• n – количество витков;
• g – толщина намотанной проволоки;
• h – высота намотанной проволоки;

Из этой формулы, зная величину индуктивности, можно вывести толщину намотки:

Для определения количества витков необходимо воспользоваться формулой:

Где,

• d­_пр – диаметр провода
• h – высота катушки;
• g – толщина намотки.

Расчет количества витков

Длину одного витка можно определить следующим образом:

l_вит = π * d_вит

Где π – это константа, а d_{вит_}— это диаметр витка.

Тогда, зная общее число витков и принимая, что d – это усредненное значение диаметра для всех витков, длина всего провода будет определяться по формуле:

L_w = n * π * d

Через сопротивление провода можно определить его диаметр, для чего понадобится выразить сопротивление через геометрические параметры устройства.

R = ρ * ( L_w / S ),

где ρ – удельное сопротивление металла, из которого изготовлен проводник, а S – площадь проводника, которая определяется по формуле:

Подставив значение площади и длины провода, получим такое выражение для определения сопротивления:

Из значения сопротивления можно вывести формулу для определения диаметра провода, подставив предварительно формулу для вычисления количества витков:

 

После получения величины диаметра провода, можно определить количество витков, которое подставляется с остальными данными в первую формулу для расчета индуктивности.

Число слоев можно определить, разделив толщину намотки на диаметр провода:

N = g / d_пр

Посредством вышеприведенных вычислений можно определить все параметры многослойной катушки индуктивности, которые помогут вам изготовить устройство с нужными параметрами. Также, чтобы облегчить вычисления вы можете воспользоваться нашим онлайн калькулятором ниже.

www.asutpp.ru

Расчет параметров катушки | Онлайн калькулятор

Катушка индуктивности представляет собой электрическую сборную конструкцию, которая может изготавливаться в следующих исполнениях:

1. В виде намотанной на каркас обмотки из провода определенного диаметра.
2. Как витая бескаркасная спираль, предварительно сформированная на твердой основе, а затем снятая с нее.
3. Катушка, намотанная многослойным проводом в специальной матерчатой изоляции.

Особенностью этого электротехнического компонента является наличие у него значительной по величине индуктивности при относительно малой емкостной составляющей и низком активном сопротивлении. Это приводит к тому, что при протекании переменного тока она проявляет себя как элемент, обладающий большой инерционностью.

Обратите внимание: Благодаря этой особенности катушки текущий по ней ток отстает от приложенного напряжения на определенный угол (90 градусов). У профессионалов это явление получило название «отставание по фазе».

Для того, чтобы получить точные значения индуктивности катушки заданной формы, следует ввести ее основные параметры в онлайн-калькулятор. В нем автоматически рассчитывается такой важный показатель, как число витков в данном изделии. После ввода данных в специальную форму вы мгновенно получите искомое значение.

 

Наш онлайн-калькулятор производит автоматизированный расчет значений катушки индуктивности без сердечника с использованием метода эллиптических интегралов Максвелла. Калькулятор предусматривает расчет значений как однослойных обмоток, так и многослойных.

А вот формула индуктивности:

где,

• L – индуктивность;
• D – диаметр витка;
• N – число витков;
• h – длина намотки;
• g – количество слоев

Преимущества расчета значений параметров катушки с помощью онлайн-калькулятора очевиден.

 

( 1 оценка, среднее 1 из 5 )

Понравилась статья? Поделиться с друзьями:

fishkielektrika.ru

Калькулятор индуктивности однослойной катушки, Электротехнические и радиотехнические калькуляторы, Конвертер величин

Однослойная катушка индуктивности: D_c — диаметр оправки или каркаса катушки, D — диаметр катушки, p — шаг намотки катушки, d — диаметр провода без изоляции и d_i — диаметр провода с изоляцией.

Калькулятор определяет индуктивность однослойной катушки.

Пример: рассчитать индуктивность однослойной катушки без сердечника, состоящей из 10 витков на цилиндрическом каркасе диаметром 2 см; длина катушки 1 см.

Входные данные

Диаметр каркаса или оправки катушки

Dмиллиметр (мм)сантиметр (см)дюйм

Количество витков

N

Длина катушки

lмиллиметр (мм)сантиметр (см)дюйм

Выходные данные

Индуктивность катушки

L мГн

Введите диаметр каркаса катушки, число витков и длину катушки, выберите единицы и нажмите кнопку Рассчитать.

Пример: рассчитать число витков и длину намотки катушки 10 мкГн, намотанной эмалированным проводом 0,65 мм (диаметр с изоляцией 0,7 мм) на оправке 2 см.

Входные данные

Требуемая индуктивность

Lгенри (Гн)миллигенри (мГн)микрогенри (мкГн)наногенри (нГн)пикогенри (пГн)

Диаметр каркаса или оправки катушки

Dмиллиметр (мм)сантиметр (см)метр (м)дюйм

Диаметр провода без изоляции

dмиллиметр (мм)сантиметр (см)метр (м)дюймАмериканский калибр проводов

Диаметр изолированного провода

d_iмиллиметр (мм)сантиметр (см)метр (м)дюйм

Выходные данные

Длина намотки

l мм

Количество витков

L

На рисунке выше показана однослойная катушка индуктивности: D_c — диаметр катушки, D — диаметр оправки или каркаса катушки, p — шаг намотки катушки, d — диаметр провода без изоляции и d_i — диаметр провода с изоляцией

Для расчета индуктивности L_S применяется приведенная ниже формула из статьи Р. Уивера (R. Weaver) Численные методы расчета индуктивности:

Здесь

D — диаметр оправки или каркаса катушки в см,

l — длина катушки в см,

N — число витков и

L — индуктивность в мкГн.

Эта формула справедлива только для соленоида, намотанного плоским проводом. Это означает, что катушка намотана очень тонкой лентой без зазора между соседними витками. Она является хорошим приближением для катушек с большим количеством витков, намотанных проводом круглого сечения с минимальным зазором между витками. Американский физик Эдвард Беннетт Роса (Edward Bennett Rosa, 1873–1921) работавший в Национального бюро стандартов США (NBS, сейчас называется Национальное бюро стандартов и технологий (NIST) разработал так называемые корректирующие коэффициенты для приведенной выше формулы в форме (см. формула 10.1 в статье Дэвида Найта, David W. Knight):

Здесь L_S — индуктивность плоской спирали, описанная выше, и

где k_s — безразмерный корректирующий коэффициент, учитывающий разницу между самоиндукцией витка из круглого провода и витка из плоской ленты; k_m — безразмерный корректирующий коэффициент, учитывающий разницу в полной взаимоиндукции витков из круглого провода по сравнению с витками из плоской ленты; D_c — диаметр катушки в см, измеренный между центрами проводов и N — число витков.

Величина коэффициента Роса k_m определяется по формуле 10.18 в упомянутой выше статье Дэвида Найта:

Коэффициент Роса k_s, учитывающий различие в самоиндукции, определяется по формуле 10.4 в статье Д. Найта:

Здесь p — шаг намотки (расстояние между витками, измеренное по центрам проводов) и d — диаметр провода. Отметим, что отношение p/d всегда больше единицы, так как толщина изоляции провода конечна, а минимально возможное расстояние между двумя соседними витками с очень тонкой изоляцией, расположенными без зазора, равна диаметру провода d.

Факторы, влияющие на индуктивность катушки

На индуктивность катушки влияют несколько факторов.

• Количество витков. Катушка с большим количеством витков имеет бóльшую индуктивность по сравнению с катушкой с меньшим количеством витков.
• Длина намотки. Две катушки с одинаковым количеством витков, но разной длиной намотки имеют разную индуктивность. Более длинная катушка имеет меньшую индуктивность. Это связано с тем, что магнитное поле менее компактной катушки более слабое и оно не может хорошо концентрироваться в растянутой катушке.
• Диаметр катушки. Две плотно намотанные катушки с одинаковым количеством витков и разными диаметрами имеют разную индуктивность. Катушка с бóльшим диаметром имеет бóльшую индуктивность.
• Сердечник. Для увеличения индуктивности в катушку часто вставляется сердечник из материала с высокой магнитной проницаемостью. Сердечники с более высокой магнитной проницаемостью позволяют получить более высокую индуктивность. Сердечники, изготовленные из магнитной керамики — феррита, часто используются в катушках и трансформаторах различных электронных устройств, так как у них очень низкие потери на вихревые токи.

Упрощенная эквивалентная схема реальной катушки индуктивности: R_w — сопротивление обмотки и ее выводов; L — индуктивность идеальной катушки; R_l — сопротивление вследствие потерь в сердечнике; и C_w — паразитная емкость катушки и ее выводов.

Эквивалентная схема реальной катушки индуктивности

В этом калькуляторе мы рассматривали идеальную катушку индуктивности. В то же время, в реальной жизни таких катушке не бывает. Катушки обычно конструируются с минимальными размерами таким образом, чтобы они помещались в миниатюрное устройство. Любую реальную катушку индуктивности можно представить в виде идеальной индуктивности, к которой параллельно подключены емкость и сопротивление, а еще одно сопротивление подключено последовательно. Параллельное сопротивление учитывает потери на гистерезис и вихревые токи в магнитном сердечнике. Это параллельное сопротивление зависит от материала сердечника, рабочей частоты и магнитного потока в сердечнике.

Паразитная емкость появляется в связи с тем, что витки катушки находятся близко друг к другу. Любые два витка провода можно рассмотреть как две обкладки маленького конденсатора. Витки разделяются изолятором, таким как воздух, изоляционный лак, лента или иной изоляционный материал. Относительная диэлектрическая проницаемость материалов, используемых для изоляции, увеличивает емкость обмотки. Чем выше эта проницаемость, тем выше емкость. В некоторых случаях дополнительная емкость может появиться также между катушкой и противовесом, если катушка расположена над ним. На высоких частотах реактивное сопротивление паразитной емкости может быть весьма высоким и игнорировать его нельзя. Для уменьшения паразитной емкости используются различные методы намотки катушек.

Для уменьшения паразитной емкости катушки с высокой добротностью для радиопередатчиков наматывают так, чтобы было достаточно большое расстояние между витками

Если индуктивность большая, то сопротивление обмотки (R_w на схеме) игнорировать уже нельзя. Тем не менее, оно мало по сравнению с реактивным сопротивлением больших катушке на высоких частотах. Однако, на низких частотах и на постоянном токе это сопротивление необходимо учитывать, так как в этих условиях через катушку могут протекать значительные токи.

Катушки индуктивности и обмотки в различных устройствах

www.translatorscafe.com

Бесплатная программа расчёта катушек индуктивности Coil32 — Софт для радиолюбителя — Программы

 

Катушки индуктивности практически используются почти в любой радио-аппаратуре, и довольно часто перед радиолюбителями возникает вопрос:
Как рассчитать индуктивность той, или иной катушки? Конечно можно рассчитать индуктивность по определённым формулам, но это требует времени, которого радиолюбителям всегда не хватает.

Бесплатная программа Coil32, автором которой является Кустарев Валерий, позволяет быстро рассчитать индуктивность практически любой катушки.

В программе учитываются наиболее распространенные варианты каркасов катушек. Можно рассчитать бескаркасную катушку в виде одиночного витка, на каркасах различной формы, на ферритовых кольцах и в броневых сердечниках, а также плоскую печатную катушку с круглой и квадратной формой витков. Для рассчитанной катушки, так же можно сразу рассчитать и ёмкость конденсатора в колебательном контуре.

Программа бесплатна и свободна для использования и распространения. В последней версии Coil32 v11.6.1.890 доступны расчёты:

• Одиночный круглый виток
• Однослойная виток к витку
  В качестве начальных параметров при расчете катушки можно выбрать два варианта:
  1. Известны диаметр каркаса и диаметр провода, длина намотки вычисляется.
  2. Известны диаметр каркаса и длина намотки, диаметр провода вычисляется
• Однослойная катушка с шагом
• Катушка с не круглой формой витков
• Многослойная катушка
  В качестве начальных параметров при расчете катушки можно выбрать два варианта:
  1. Известны диаметр каркаса, длина намотки и диаметр провода. Вычисляется число витков, попутно определяется толщина катушки, ее омическое сопротивление постоянному току и приблизительная длина провода для намотки («сколько надо отрезать»).
  2. Известны диаметр каркаса, длина намотки и предельное омическое сопротивление катушки. Вычисляется число витков, попутно определяется толщина катушки, нужный минимальный диаметр провода  и приблизительная длина провода для намотки.
• Тороидальная однослойная катушка
• Катушка на ферритовом кольце
• Катушка в броневом сердечнике
  (Ферритовом и карбонильном)
• Тонкопленочная катушка
  (Плоская катушка на печатной плате с круглой и квадратной формой витков и в виде одиночного прямого проводника)

Для расчета дополнительных видов индуктивности, которых нет в общем списке программы под заголовком «Выберите форму катушки» — имеется набор дополнительных плагинов «Plugins». Список плагинов и их краткое описание отображены на рисунке ниже.

 

 

В чем преимущества данной программы перед аналогами?

• Программа рассчитывает индуктивность различных типов катушек под имеющийся каркас.
• Результаты расчетов выводятся в текстовое поле справа, откуда их можно сохранить в файл. Можно открыть этот файл в «MS Word» и распечатать.
• Есть возможность рассчитать добротность для радиочастотных однослойных катушек индуктивности.
• Можно рассчитать основные параметры колебательного контура для однослойной катушки
• Можно рассчитать длину провода для намотки однослойной, многослойной катушки и катушки на ферритовом кольце.
• Для расчёта катушек в броневых сердечниках, есть возможность выбора одного из нескольких стандартных сердечников, что позволяет рассчитать катушку в несколько кликов.
• Для плоских катушек на печатной плате программа подскажет оптимальные размеры для достижения наивысшей добротности.
• Программа имеет мультиязычный интерфейс (20 языков) и дополнительные наборы скинов, которые можно скачать и установить из меню «Настройки».

Программа распространяется бесплатно в стиле «Portable» и не имеет установщика. Для работы с программой — скачайте архив, распакуйте его в любое удобное для Вас место и запустите файл Coil32.exe. При постоянной работе с программой, желательно создать для нее специальную папку и вынести ярлык Coil32.exe на рабочий стол.

Скачать Coil32.
 

 

 

 

vprl.ru

Калькулятор расчета индуктивности катушки с воздушным сердечником

Катушка индуктивности является неотъемлемым элементом большинства современных приборов. При этом она используется для различных целей в работе электрических цепей. В случае необходимости замены можно использовать как заводскую, так и изготовленную самостоятельно катушку. Но при этом необходимо учитывать ее основной параметр – индуктивность. Для того чтобы рассчитать индуктивность катушки без сердечника можно воспользоваться универсальной формулой:

где μ­­₀ – магнитная проницаемость вакуума,  μ – магнитная проницаемость сердечника (можно взять из таблицы 1), N – число витков, S – площадь сечения катушки,

l – длина намотки. Такой способ является универсальным и может использоваться, как для полых катушек, так и для имеющих сердечник.

Таблица 1

Материал	— µ —  (Гн/м)
Воздух	1.25663753*10−6
Алюминий	1.256665*10−6
Аустенитная нержавеющая сталь	1.260*10−6  — 8.8*10−6
Вакуум (µ0)	4π*10−7
Вода	1.256627*10−6
Водород	1.2566371*10−6
Висмут	1.25643*10−6
Дерево	1.25663760*10−6
Железо (чистота 99.8%)	6.3*10−3
Железо (99.95% чистое Fe отожженное в водороде)	2.5*10−1
Железо-кобальтовые сплавы	2.3*10−2
Медь	1.256629*10−6
Никель-цинковый феррит — магнит	2.0*10−5 – 8.0*10−4
Мартенситная нержавеющая сталь (отожженная)	9.42*10−4 — 1.19*10−3
Мартенситная нержавеющая сталь (закаленная)	5.0*10−5 — 1.2*10−4
NANOPERM® — магнитомягкий нанокристаллический сплав	1.0*10−1
Неодимовый магнит	1.32*10−6
Никель	1.26*10−4 — 7.54*10−4
Пермаллой (сплав 80% никеля и 20% железа)	1.0*10−2
Платина	1.256970*10−6
Сарфир	1.2566368*10−6
Сверхпроводники	0
Углеродистая сталь	1.26*10−4
Ферритная нержавеющая сталь (отожженная)	1.26*10−3 — 2.26*10−3
Фторопласт 4, Ф-4,   Teflon	1.2567*10−6

Если рассматривать частный вариант – катушку с воздушным сердечником, то для расчета ее индуктивности можно использовать формулу:

Где D – диаметр катушки, n – количество витков, а l – длина ее намотки.

Такой способ расчета будет справедливым для катушек, имеющих однослойную структуру, набираемых в один уровень. В случае если катушка наматывается в несколько слоев, то их толщина вносит дополнительные изменения в расчет. При этом формула расчета преобразится к виду:

Где D – диаметр катушки, n – количество витков, h – высота самой катушки, g – толщина слоя намотки.

Для упрощения процесса расчета индуктивности катушки без сердечника можно воспользоваться онлайн калькулятором. Здесь вы указываете ее основные параметры – диаметр, длину и количество витков, после чего нажать кнопку «Рассчитать» и вы получите значение индуктивности без лишних вычислений и затрат времени.

www.asutpp.ru

справка, Расчет многослойной катушки на прямоугольном каркасе

Подробности

Опубликовано: 20 февраля 2016

Просмотров: 3890

 

Столкнувшись с трудностями при расчете многослойной катушки на круглом каркасе, мы отказались от простой эмпирической формулы Вилера и пошли по пути усложнения модели катушки и алгоритма расчета. В случае с многослойной катушкой на прямоугольном каркасе, которая довольно часто используется, совершенно очевидно, что следует пойти аналогичным путем. При этом катушку можно представить как набор соосных прямоугольных рамок и рассчитывать общую индуктивность катушки как сумму их собственных и взаимных индуктивностей.

Но мы можем пойти дальше и представить катушку как набор линейных проводов. Каждый виток представляет из себя набор из четырех таких отрезков. Причем взаимно-перпендикулярные отрезки  не взаимодействуют между собой и их взаимная индуктивность равна нулю. Пользуясь тем, что прямоугольник — симметричная фигура, мы можем провести вычисления только для двух его сторон. Удвоив результат вычислений, мы получим общую индуктивность катушки. На следующем рисунке изображены два параллельных отрезка провода неодинаковой длины для наглядности и понимания формул расчета.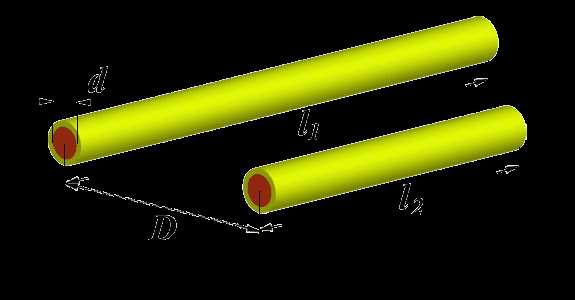
Для таких расчетов нам необходимо знать следующее…

1. Формулу собственной индуктивности отрезка провода:

   [1]

   где:
   • L — индуктивность [мкГн]
   • l = l₁ или l = l₂ — длина проводника [мм];
   • r = d/2 — радиус проводника [мм];
   
   Более известна формула, которая является упрощением вышеприведенной, но мы ее не используем, как менее точную:

   [2]

2. Формулу взаимной индуктивности двух отрезков провода неодинаковой длины:

   [3]

   где:
   • M — величина взаимоиндукции [мкГн];
   • x₁ = l₁/2 — половина длины первого проводника [мм];
   • x₂ = l₂/2 — половина длины второго проводника [мм];
   • D — расстояние между центрами проводников [мм];
   
   Формула верна для проводников центры которых лежат на одной оси, что у нашей катушки, в принципе, имеет место.

---

Катушка рассчитывается численным методом «виртуальной намотки». При добавлении нового витка, рассчитывается собственная индуктивность всех его отрезков, а также возможная взаимоиндукция со всеми другими отрезками с учетом взаимного направления тока в них. В общей сумме мы получаем собственную индуктивность многослойной катушки. Попутно рассчитывается длина провода, необходимая для намотки и его сопротивление постоянному току. Кроме плагина multi_rectangular к программе Coil32 для Windows, который доступен для загрузки из меню программы и рассчитывает такую катушку индуктивности, вы можете воспользоваться онлайн калькулятором многослойной катушки на прямоугольном каркасе.

Реальный виток имеет скругленные углы, а не представляет из себя идеальный прямоугольник. Это обстоятельство, а также ограниченная точность исходных формул, не позволяют достичь высокой точности расчетов. Погрешность расчета составляет около ±5% от величины индуктивности. Имеется ввиду, что намотка плотная, без зазоров и межслойных прокладок. Несмотря на невысокую точность, этот численный алгоритм позволяет рассчитать произвольную многослойную катушку на прямоугольном каркасе не прибегая к поиску сложных эмпирических формул, всегда имеющих ограничения по геометрии намотки. С помощью данного алгоритма, например, мы можем без труда рассчитать индуктивность многовитковой прямоугольной рамки большого диаметра.

Ссылки по теме:

1. The self and mutual inductances of linear conductors. (E. B. Rosa 1908) — формулы индуктивности и взаимоиндукции линейных проводников, формула [1] в статье соответствует фомуле 9 на стр.305. Формула собственной индуктивности линейного отрезка провода.
2. American National Bureau of Standarts circular C74 — формула [3] в статье соотвествует формуле 182 на стр.273 с исправлениями. Формула взаимоиндукции двух симметрично расположенных линейных проводников неодинаковой длины.

Добавить комментарий

coil32.ru

Coil32 — Расчет конической катушки Тесла

Подробности

Опубликовано: 26 августа 2013

Обновлено: 06 мая 2018

Просмотров: 11001

Для работы калькулятора необходимо включить JavaScript в вашем браузере!

Расчет конической катушки Тесла:

Хотя я, мягко говоря, не разделяю всевозможные метафизические теории энтузиастов катушек Тесла и ловцов «свободной энергии эфира», это не основание отказываться от реализации расчетов таких катушек, в частности конической катушки, которая часто используется в подобных устройствах. Коническую катушку можно рассчитать по следующим оригинальным эмпирическим формулам Харольда Вилера, которые применял сам Тесла:

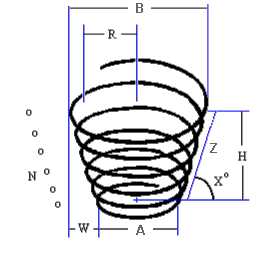
• N — число витков катушки
• A — Диаметр основания конуса
• B — Диаметр верхней части конуса
• H — Высота конуса
• W = (B — A)/2 — Эффективная ширина
• Z — Длина катушки (по гипотенузе!) Z = √(W² + H²)
• X — Угол конуса (sin(X) = H/Z; cos(X) = W/Z)
• R = A/2 + W/2 — Средний радиус катушки
• L₁ = R²*N²/(9*R+10*H) — Вертикальный компонент индуктивности
• L₂ = R²*N²/(8*R+11*W) — Горизонтальный компонент индуктивности
• L = √[(L₁*Sin(X))² + (L₂*cos(X))²] — Итоговая индуктивность катушки

Индуктивность в микрогенри, размеры в дюймах. Однако наш калькулятор рассчитывает коническую катушку численным алгоритмом по формуле Максвелла [1]. Этот метод расчета более точный и он также используется в калькуляторах многослойной катушки и спиральной катушки Тесла. Калькулятор обновлен 01.05.2018, не забудьте обновить кэш браузера.

---

Калькулятор конической катушки Тесла

ВВЕСТИ ДАННЫЕ:

---

Добавить комментарий

coil32.ru