Угловую скорость можно выразить через частоту: Линейная скорость через угловую, теория и онлайн калькуляторы — БилдоМан

Содержание

Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями

Подробности: Просмотров: 640

«Физика — 10 класс»

Угловая скорость.

Каждая точка тела, вращающегося вокруг неподвижной оси, проходящей через точку О, движется по окружности, и различные точки проходят за время Δt разные пути. Так, АА₁ > ВВ₁ (рис. 1.62), поэтому модуль скорости точки А больше, чем модуль скорости точки В. Но радиус-векторы, определяющие положение точек А и В, поворачиваются за время Δt на один и тот же угол Δφ.

Угол φ — угол между осью ОХ и радиус-вектором определяющим положение точки А (см. рис. 1.62).

Пусть тело вращается равномерно, т. е. за любые равные промежутки времени радиус-векторы поворачиваются на одинаковые углы.

Чем больше угол поворота радиус-вектора, определяющего положение какой-то точки твёрдого тела, за определённый промежуток времени, тем быстрее вращается тело и тем больше его угловая скорость.

Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела υφ к промежутку времени υt, за который этот поворот произошёл.

Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению

Угловая скорость в СИ выражается в радианах в секунду (рад/с). Например, угловая скорость вращения Земли вокруг оси 0,0000727 рад/с, а точильного диска — около 140 рад/с.

Угловую скорость можно связать с частотой вращения.

Частота вращения — число полных оборотов за единицу времени (в СИ за 1 с).

Если тело совершает ν (греческая буква «ню») оборотов за 1 с, то время одного оборота равно 1/ν секунд.

Время, за которое тело совершает один полный оборот, называют периодом вращения и обозначают буквой Т.

Таким образом, связь между частотой и периодом вращения можно представить в виде

Полному обороту тела соответствует угол Δφ = 2π. Поэтому согласно формуле (1.26)

Если при равномерном вращении угловая скорость известна и в начальный момент времени t

0 = 0 угол φ₀ = 0, то угол поворота радиус-вектора за время t согласно уравнению (1.26)

φ = ωt.

Если φ₀ ≠ 0, то φ — φ₀ = ωt, или φ = φ₀ ± ωt.

Радиан равен центральному углу, опирающемуся на дугу, длина которой равна радиусу окружности, 1 рад = 57°17’48». В радианной мере угол равен отношению длины дуги окружности к её радиусу: φ = l/R.

Угловая скорость принимает положительные значения, если угол между радиус-вектором, определяющим положение одной из точек твёрдого тела, и осью ОХ увеличивается (рис. 1.63, а), и отрицательные, когда он уменьшается (рис. 1.63, б).

Тем самым мы можем найти положение точек вращающегося тела в любой момент времени.

Связь между линейной и угловой скоростями.

Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть её отличие от угловой скорости.

Мы уже отмечали, что при вращении абсолютно твёрдого тела разные его точки имеют неодинаковые линейные скорости, но угловая скорость для всех точек одинакова.

Установим связь между линейной скоростью любой точки вращающегося тела и его угловой скоростью. Точка, лежащая на окружности радиусом R, за один оборот пройдёт путь 2πR. Поскольку время одного оборота тела есть период Т, то модуль линейной скорости точки можно найти так:

Так как ω = 2πν, то

Из этой формулы видно, что, чем дальше расположена точка тела от оси вращения, тем больше её линейная скорость. Для точек земного экватора υ = 463 м/с, а для точек на широте Санкт-Петербурга υ = 233 м/с. На полюсах Земли υ = 0.

Модуль центростремительного ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности:

Следовательно,

а_цс = ω²R.

Запишем все возможные расчётные формулы для центростремительного ускорения:

Мы рассмотрели два простейших движения абсолютно твёрдого тела — поступательное и вращательное. Однако любое сложное движение абсолютно твёрдого тела можно представить как сумму двух независимых движений: поступательного и вращательного.

На основании закона независимости движений можно описать сложное движение абсолютно твёрдого тела.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Кинематика — Физика, учебник для 10 класса — Класс!ная физика

Физика и познание мира — Что такое механика — Механическое движение. Система отсчёта — Способы описания движения — Траектория. Путь. Перемещение — Равномерное прямолинейное движение. Скорость. Уравнение движения — Примеры решения задач по теме «Равномерное прямолинейное движение» — Сложение скоростей — Примеры решения задач по теме «Сложение скоростей» — Мгновенная и средняя скорости — Ускорение — Движение с постоянным ускорением — Определение кинематических характеристик движения с помощью графиков — Примеры решения задач по теме «Движение с постоянным ускорением» — Движение с постоянным ускорением свободного падения — Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» — Равномерное движение точки по окружности — Кинематика абсолютно твёрдого тела.

Поступательное и вращательное движение — Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями — Примеры решения задач по теме «Кинематика твёрдого тела»

Теоретична механіка кінематика — Методические указания

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ

“ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ”

Ю.М. Андрєєв, Г.О. Аніщенко, А.О. Ларін

ТЕОРЕТИЧНА МЕХАНІКА. КІНЕМАТИКА

ЗК-2 — ПОСТУПАЛЬНИЙ ТА ОБЕРТАЛЬНИЙ РУХ

ХАРКІВ 2004

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ

“ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ”

Ю. М. Андрєєв, Г.О. Аніщенко, А.О. Ларін

ТЕОРЕТИЧНА МЕХАНІКА. КІНЕМАТИКА

ЗК-2 — ПОСТУПАЛЬНИЙ ТА ОБЕРТАЛЬНИЙ РУХ

Контрольні завдання та методичні вказівки

щодо їх виконання для студентів заочної форми навчання

Затверджено

редакційно-видавничою

радою університету,

протокол № 1 от 27.02.04

ХАРКІВ НТУ „ХПИ” 2004

ББК 22.21

УДК 531 : 534

Рецензент В.М. Адашевський, канд. техн. наук, професор кафедри теоретичної механіки НТУ «ХПІ».

Теоретична механіка. Кінематика. ЗК-2 — Поступальний та обертальний рух. Контрольні завдання та методичні вказівки щодо їх виконання для студентів заочної форми навчання / Андрєєв Ю.

М., Аніщенко Г.О., Ларін А.О. – Харків: НТУ “ХПІ”, 2004.-24 с. –Рос. мовою

Методичні вказівки містять контрольні завдання для самостійної роботи студентів при вивченні теоретичної механіки. У стислому вигляді подані теоретичні основи кінематики поступального та обертального руху навколо нерухомої осі твердих тіл, зокрема перетворення цих рухів. Запропоновано питання для самоконтролю. Наведено приклади із розв’язанням типових задач.

Призначено для студентів заочної форми навчання усіх спеціальностей.

Методические указания содержат контрольные задания для самостоятельной работы студентов при изучении теоретической механики. В кратком виде представлены теоретические основы кинематики поступательного и вращательного движения вокруг неподвижной оси твердых тел, включая преобразования этих движений. Предложены вопросы для самоконтроля. Приведены примеры с решением типовых задач.

Предназначено для студентов заочной формы обучения всех специальностей.

Іл.35. Табл. 2. Бібліогр. 9 найм.

ББК 22.21

Ю.М.Андрєєв, Г.О.Аніщенко, А.О.Ларін, 2004 р.

 НТУ «ХПІ», 2004 р.

ВВЕДЕНИЕ

Кинематика является важным разделом курса теоретической механики, в котором изучается движение материальных тел в пространстве с геометрической точки зрения. При этом их инерционные характеристики и действующие на них силы, определяющие это движение, во внимание не принимаются. Поступательное и вращательное вокруг неподвижной оси (далее, часто, просто вращательное) движения твердого тела являются простейшими. Это базовые ключевые понятия кинематики твердого тела. Они широко распространены в технике. Основные понятия кинематики простейших движений, способы определения их кинематических характеристик имеют не только самостоятельное значение. Они используются при изучении более сложных видов движения твердого тела, в теории сложного движения точек и тел. В различных механизмах, приборах и устройствах применяется преобразование простейших движений: поступательного в поступательное, вращательного во вращательное, поступательного во вращательное, и наоборот.

Настоящие методические указания предназначены для самостоятельной работы студентов, изучающих курс теоретической механики. Указания содержат краткие теоретические сведения по кинематике поступательного движения и вращательного движения твердого тела вокруг неподвижной оси, рассматриваются частные случаи вращательного движения. Предложены вопросы для самоконтроля, примеры решения типовых задач на законы вращательного движения и на преобразования простейших движений. Приведены варианты контрольных заданий, список рекомендованной литературы.

1. ЦЕЛЬ И ФОРМУЛИРОВКА ЗАДАНИЯ

Цель задания – развитие и закрепление у студентов практических навыков решения задач на законы вращательного движения твердого тела и на преобразование простейших движений.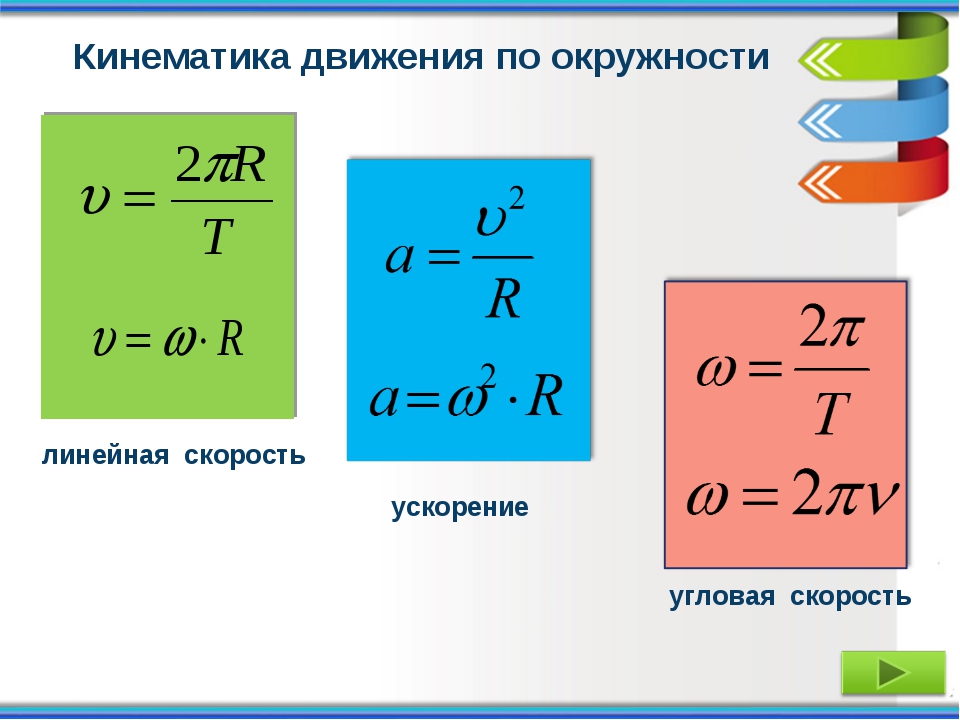

Задание включает задачи двух типов. В задачах первого типа необходимо исследовать кинематику равномерного и равнопеременного вращения твердого тела вокруг неподвижной оси. В задачах второго типа необходимо определить кинематические характеристики преобразованных движений, скорости и ускорения точек.

Для изучения темы и выполнения контрольного задания необходимо:

внимательно прочитать соответствующий раздел в учебнике, выбранном из списка рекомендуемой литературы; ознакомиться с теоретическими сведениями и методическими рекомендациями настоящих указаний; составить краткий конспект, записав основные определения, теоремы и формулы;
ответить на контрольные вопросы;
разобрать решение типовых задач на примерах, приведенных в настоящих указаниях;
самостоятельно выполнить индивидуальные контрольные задания в соответствии с предложенным преподавателем вариантом (например, вариант 5. ЗК-2 означает: 5 – порядковый номер контрольного задания, З – задание для студента заочной формы обучения, К – раздел «Кинематика», 2 – номер темы раздела).
оформить решенные задачи в виде контрольной работы в отдельной тетради;
зарегистрировать выполненное контрольное задание в установленные сроки в деканате заочного обучения у методиста.

2. Теоретические положения

2.1. Поступательное движение твердого тела

Поступательным движением твердого тела называется такое движение, при котором прямая, соединяющая любые две точки этого тела, остается параллельной своему начальному положению. Из определения поступательного движения следует, что скорости и ускорения всех точек тела одинаковы. Поэтому тело при поступательном движении можно считать точкой и задавать его движение с помощью координат любой его точки, например, А, в функции времени

(1)

Так как для описания положения тела в пространстве надо задать три параметра (декартовые координаты одной из его точек), говорят, что тело при поступательном движении в пространстве имеет три степени свободы. Поскольку скорости и ускорения всех точек твердого тела при поступательном движении одинаковы, можно пользоваться терминами «скорость тела», «ускорение тела», подразумевая скорость и ускорение любой его точки. При координатном способе задания движения скорость и ускорение тела определяются проекциями на координатные оси, вычисляемые, соответственно, как первая и вторая производные от соответствующих координат по времени:

(2)

(3)

Модули скорости и ускорения определяются по формулам

(4)

2.2. Вращение твердого тела вокруг неподвижной оси

2.2.1. Задание вращательного движения. Угловая скорость и угловое ускорение. Рассмотрим теперь движение твердого тела, при котором какие-либо две его точки остаются неподвижными. Через эти точки проходит прямая, все точки которой также будут неподвижными. Она называется осью вращения. Все точки тела, не лежащие на оси вращения, описывают окружности в плоскостях, перпендикулярных оси, и с центрами, расположенными на оси. В этом случае рассматриваемое тело имеет одну степень свободы, а его движение определяется одним параметром – углом поворота вокруг оси вращения Oz. При этом принято считать угол поворота  положительным, если поворот тела, наблюдаемый с положительного направления оси, виден происходящим против хода часовой стрелки. Таким образом, для задания вращательного движения достаточно задать положение оси вращения и функцию изменения угла поворота от времени

. (5)

Основными кинематическими характеристиками вращательного движения являются угловая скорость и угловое ускорение. Эти величины — векторные и откладываются по оси вращения. Направление вектора угловой скорости определяется направлением вращения, т.е. этот вектор откладывается в ту сторону, смотря с которой вращение видно происходящим против хода часовой стрелки.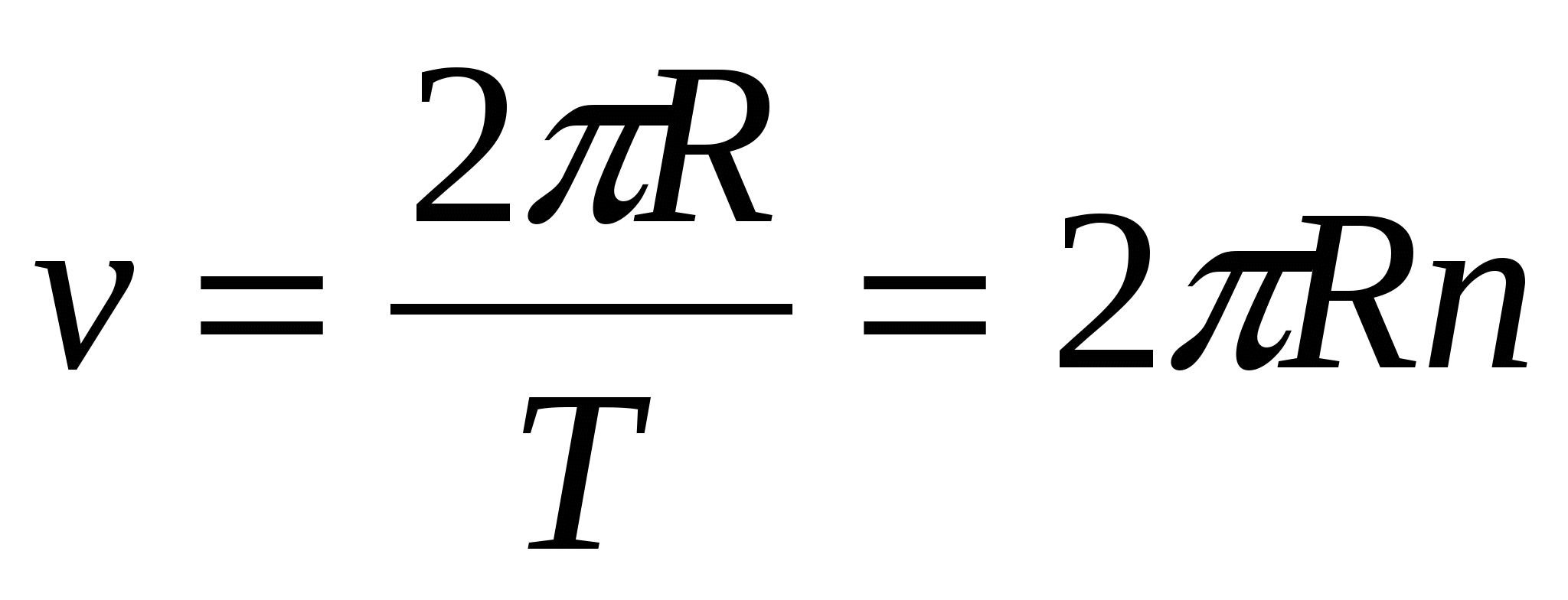 Вектор углового ускорения совпадает с направлением вектора угловой скорости при ускоренном вращении и противоположен ему – при замедленном (см. рис. 1).

Алгебраические значения угловой скорости и углового ускорения определяются, соответственно, как первая и вторая производные от угла поворота тела по времени

(6)

(7)

По существу, алгебраические значения угловой скорости и углового ускорения являются проекциями векторов угловой скорости и углового ускорения на ось вращения, и по их знакам можно также определять направления векторов. Сами векторы можно выразить через орт оси z и проекции и :

Таким образом, угловая скорость тела, вращающегося вокруг неподвижной оси, есть механическая величина, определяющая быстроту изменения во времени угла поворота тела.

Угловое ускорение тела есть механическая величина, определяющая быстроту изменения во времени угловой скорости тела.

Измеряется угловая скорость в рад/с, а угловое ускорение в рад/с². В инженерной практике для характеристики быстроты вращения используется внесистемная единица – обороты в минуту (об/мин), которая обозначается обычно буквой n. Перевод оборотов в минуту в радианы в секунду осуществляется по формуле

(8)

2.2.2. Определение скорости и ускорения точки тела при вращательном движении. Определить скорость точки A вращающегося тела можно, продифференцировав по времени радиус-вектор этой точки , проведенный из любой точки на оси вращения (т. О на рис. 2). Тогда из правила дифференцирования вектора постоянного модуля получим формулу Эйлера:

_₍₉₎

Из формулы (9) следует, что скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению вектора угловой скорости тела на радиус-вектор этой точки. Определим модуль скорости точки:

(10)

Рисунок 2 Рисунок 3

Для определения ускорения точки вращающегося тела продифференцируем по времени выражение (9). Тогда из правила дифференцирования векторного произведения получим:

. (11)

Из формулы (11) следует, что ускорение любой точки твердого тела, вращающегося вокруг неподвижной оси, представляет собой геометрическую сумму двух взаимно перпендикулярных составляющих – вращательного и осестремительного ускорений (рис. 3). Вращательное или касательное ускорение точки направлено по касательной к ее траектории (окружности радиуса h) и имеет значение

. (12)

Осестремительное или нормальное ускорение точки направлено к оси вращения по нормали к траектории движения точки и равно

(13)

Модуль полного ускорения точки A равен

(14)

Угол β, образованный векторами полного и осестремительного ускорений, определяется из формулы

₍₁₅₎

Преобразования простейших движений твердого тела

Рисунок 4 Рисунок 5 Рисунок 6

Рисунок 7 Рисунок 8

Простейшими движениями твердого тела являются поступательное и вращательное. В механизмах часто осуществляется преобразование вращательного движения в поступательное и наоборот. Рассмотрим определение угловой скорости барабана 2 при заданной скорости груза 1, подвешенного на нити, намотанной на барабан (рис. 4). Скорости всех точек нити, на которой висит груз, одинаковы (нить считается нерастяжимой), скорость точки схода нити с барабана колеса равна скорости груза. Но с этой точкой соприкасается точка, принадлежащая колесу, совершающему вращательное движение, и имеющая ту же скорость. Это позволяет определить угловую скорость колеса. При этом будем полагать, что положительному движению груза соответствует положительное вращение колеса. Запишем теперь алгебраическое значение угловой скорости 1-го колеса

. (16)

Аналогично можно определить скорость груза по заданной угловой скорости колеса:

(17)

При передаче вращения от одного тела к другому используются зубчатые или фрикционные зацепления (рис. 5 и 6), а также цепные или ременные передачи (рис. 7 и 8). В первом случае колеса 1 и 2 имеют общую точку, поэтому скорости точек, находящихся на их ободьях, одинаковы, т.е.

. (18)

При записи алгебраического значения угловой скорости 2-го колеса учтем, что внешнее зацепление (рис. 5) меняет направление вращения на противоположное

(19)

а внутреннее зацепление (рис. 6) направление вращения не меняет

(20)

Одинаковы модули скоростей и для точек на шкивах ременной передачи. Здесь также направление вращения может либо изменяться на противоположное при передаче движения (рис. 7), либо нет (рис. 8). Угловая скорость при этом определяется соответственно по формулам (19) и (20).

2.4. Равномерное и равнопеременное вращения

Вращение называется равномерным, если в процессе движения угловая скорость остается постоянной по модулю и по направлению, то есть, если . Домножив правую и левую часть этого равенства на dt, и проинтегрировав левую часть полученного равенства в пределах от до , а правую от 0 до t, получим закон равномерного вращения:

. (21)

Вращение называется равнопеременным, если угловое ускорение тела в процессе движения остается постоянным по модулю и направлению, то есть, если . Чтобы найти закон изменения угловой скорости в этом случае, проинтегрируем левую часть равенства в пределах от до , а правую часть от 0 до t:

(22)

Так как , то , и, интегрируя это выражение при изменении угла поворота от до и времени – от 0 до t, получим закон равнопеременного вращения:

(23)

2.5. Вопросы для самоконтроля

1. Какое движение твердого тела называется вращательным?

2. Чем определяется положение твердого тела при вращательном движении?

3. Что характеризует угловая скорость тела и как она определяется?

4. Что характеризует угловое ускорение и как оно определяется?

5. В каких единицах измеряется угловая скорость и угловое ускорение?

6. Что такое частота вращения и как она связана с угловой скоростью тела?

7. Какое вращение называется равномерным? Запишите выражения для угла поворота и угловой скорости при равномерном вращении.

8. Какое вращение называется равномерным? Запишите выражения для угла поворота и угловой скорости при равномерном вращении.

9. Запишите формулу Эйлера для определения вектора скорости точки? Как вычисляется модуль скорости точки?

10. Приведите выражения для вектора ускорения точки и его составляющих: вращательного и осестремительного ускорений.

11. Как определяются модули составляющих ускорения точки? Чему равен модуль ускорения точки?

12. Что такое преобразованием простейших движений твердого тела?

3. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

И ВАРИАНТЫ КОНТРОЛЬНЫХ ЗАДАНИЙ

3.1. Законы равномерного и равнопеременного вращения твердого тела вокруг неподвижной оси

Пример №1. С момента включения электродвигателя его ротор начинает вращаться равноускоренно и по истечении времени t₁ секунд приобретает угловую скорость, соответствующую n = 1200 об/мин, сделав при этом N = 80 оборотов. Определить угловое ускорение ротора и время t₁.

Решение.

Так как ротор вращается равноускоренно, его угловая скорость и угол поворота определяются выражениями

Движение начинается из состояния покоя, поэтому начальная угловая скорость ротора ; примем также, что и его начальный угол поворота равен нулю, то есть . Тогда . Подставляя значение из первого уравнения во второе, получим . Тогда из первого уравнения .

В момент t₁ угловая скорость ротора равна

рад/с,

а угол поворота составляет

рад.

Подставляя эти значения в полученные формулы, получаем

Пример №2. Вал, делающий n = 90 об/мин, после выключения электродвигателя начинает вращаться равнозамедленно и останавливается через t₁= 40 с. Определить, сколько оборотов сделал вал за это время.

Решение.

Вал вращается равноускоренно, поэтому его угловая скорость и угол поворота определяются выражениями

Начальный угол поворота вала примем равным нулю . Начальной угловой скоростью при замедленном вращении будет та, которую вал имел до выключения двигателя, то есть

В момент остановки двигателя при t = t₁ угловая скорость вала равна нулю: . Поэтому

Обозначим число оборотов, сделанных валом за время t₁,_{через N.
Тогда угол поворота за время t₁ можно вычислить по формуле:}

или .

Откуда найдем оборотов.

3.2. Варианты контрольных заданий

1. Вал паровой турбины начинает вращаться равноускоренно из состояния покоя. Определить угловое ускорение вала, если за первые две минуты он совершил 5400 оборотов.

Ответ: = 1,5 рад/с²= 4,71 рад/с².

2. Вал вращается, совершая n = 60 об/мин. С некоторого момента времени он начинает вращаться равнозамедленно и, совершив N = 180 оборотов, остановился. Определить угловое ускорение вала и время, прошедшее до его остановки.

Ответ : = – рад/с²; t = 360 с.

3. Вал начинает вращаться из состояния покоя с угловым ускорением  = 4 рад/с². Через какое время вал сделает 128 оборотов.

Ответ: t = 20 с.

4. В период разгона диск вращается вокруг своей оси по закону (рад). Определить угловую скорость и угловое ускорение маховика в тот момент времени, корда он сделает 27 оборотов.

Ответ:  = 27 рад/сек;  = 9 рад/сек².

5. Колесо из состояния покоя начинает вращаться равноускоренно и через t=3с делает 900 об/мин. Определить угловое ускорение и число оборотов N, сделанных колесом за указанное время.

Ответ:  = 31,4 рад/с²; N = 22,5 об.

6. Шкив электродвигателя делает 1500 об/мин. Через t₀=2 мин ток был выключен и шкив, вращаясь равнозамедленно, через t = 6 сек остановился. Определить полное число оборотов N.

Ответ: N = 3075 об.

7. После выключения тока шкив, вращаясь равнозамедленно (= рад/с²) через 20 с остановился. Определить начальную угловую скорость ₀ шкива и число оборотов N за указанное время.

Ответ: ₀ = 20  рад/с; N=100 об.

8. Маховое колесо диаметром d = 3 м, вращаясь равноускоренно в течении t =4 мин, сделало N=400 оборотов. Определить окружную скорость точек на ободе колеса по истечении 4 минут.

Ответ: v = 31,4 м/с.

9. Маховое колесо диаметром d = 3 м через 5 минут после начала равноускоренного вращения делает 180 об/мин. Определить окружную скорость, вращательное и осестремительное ускорения точек на ободе колеса по истечению 5 минут.

Ответ: v = 28,26 м/с; а_вр= 0,094 м/с²; а_ос= 532,42 м/с².

10. Вращение колеса диаметром d = 0,4 м определяется уравнением  = 180t–15t² (рад). Определить окружную скорость, вращательное и осестремительное ускорения точек на ободе колеса и угловую скорость вначале движения.

Ответ: v = 36 м/сек; а_вр= – 6 м/сек²; а_ос= 6480 м/сек²; ₀= 180 рад/сек.

11. Диск вращается по закону = 4–2t³ (рад). Определить его угловую скорость и угловое ускорение, а также характер движения (ускоренное или замедленное).

Ответ: = – 6t²(рад/с),  = –12t (рад/с²). Движение замедленное.

12. Диск радиусом R = 2,5 см вращается равноускоренно. Известно, что через t₁= 2с после начала движения скорость точки А на его ободе оказалась равной 10 см/с, а при t₂= 4 с – вдвое большей .Определить вращательное и осестремительное ускорения точки в указанные моменты времени.

Ответ: а₁^вр = 5 см/с²; а₁^ос= 40 см/с²; а₂^вр = 5 см/с²; а₂^ос= 160 см/с².

13. Диск вращается по закону = 0,14πt²–2 (рад). Определить для t = 2,5 с его угловую скорость и угловое ускорение, а также характер движения (ускоренное или замедленное).

Ответ:  = 2,2 рад/с;  = 0,88 рад/с². Движение ускоренное.

14. Диск радиусом R = 0,5 м вращается равнозамедленно. Известно, что точка М, принадлежащая ободу диска, прошла в своем движении до остановки диска путь S = 6,4 м, имея в начальный момент времени скорость υ₀= 0,8 м/с. Определить угловую скорость, угловое ускорение диска, а также вращательное и осестремительное ускорения точки М в начальный момент времени.

Ответ:  = 1,6 рад/с;  = 0,1 рад/с². а^вр = 0,05 м/с²; а^ос= 1,28 м/с².

15. Точка А, принадлежащая ободу вращающегося диска радиусом R = 90 см, имеет в начальный момент времени скорость υ₀=120 см/с, через время t = 10 мин её скорость стала равной υ = 150 см/с. Определить для этого момента времени вращательное и осестремительное ускорения точки, если движение равноускоренное.

Ответ: а^вр = 0,05 см/с²; а^ос= 250 см/с².

16. Диск радиусом R =1,25 м вращается по закону  = 0,2πt² (рад). Определить его угловую скорость, а также вращательное и осестремительное ускорения т. М после того, как диск совершит 1 оборот.

Ответ:  = 3,97 рад/с; а^вр = 0,50 м/с²; а^ос= 6,317 м/с².

17. Угловая скорость, соответствующая n =3600 об/мин, с которой вращается ротор турбины, за 12 с увеличилась в 2 раза. Определить, сколько оборотов сделал за это время ротор, считая вращение равноускоренным.

Ответ: N = 1080 оборотов.

18. Колесо радиусом R = 80 см начинает вращаться равноускоренно из состояния покоя. После того, как оно совершило N = 750 оборотов, скорость точки на его ободе оказалась равной 200 м/с. Определить время, за которое достигнута указанная скорость.

Ответ: t = 37,7 с.

19. Точка М обода маховика радиусом R = 1,5 м движется по закону S= (м). Определить угловую скорость, угловое ускорение маховика, а также модули составляющих ускорения точки М в момент, когда её скорость υ = 9π (м/с), а также число оборотов, которое совершит маховик к этому времени.

Ответ:  = 6π рад/с;  = 2π/3 рад/с²; а^вр = 3,14 м/с²; а^ос= 533 м/с²; N = 50/3 об.

20. Диск начинает равноускоренно вращаться из состояния покоя и за время
t = 10с совершает N = 20 оборотов. Определить ускорение точки диска, отстоящей от оси на расстоянии ОМ = 0,2 м, в момент времени t₁ = 5с.

Ответ: а = 2,563 м/с².

21. Диск радиусом R = 0,15 м в момент времени, когда скорость точки М на его ободе υ = 0,48 м/с, начинает вращаться равнозамедленно. До полной остановки диска точка М прошла путь S = 0,4 м. Определить в указанный момент времени её ускорение, а также угловую скорость и угловое ускорение диска.

Ответ:  = 3,2 рад/с; = 1,92 рад/с²; а =0,56 м/с²;

22. Диск радиусом R = 1 м, вращаясь с постоянным ускорением, за время t = π/4 (с), повернулся на угол 90^о, при этом скорость его некоторой точки А оказалась равной 4 м/с. Определить угол между вектором скорости и вектором ускорения точки А в указанный момент времени, а также ускорение точки.

Ответ: = 72^о20; а_А =1 6,8 м/с².

23. Диск начинает равноускоренно вращаться с угловым ускорением  =16 рад/с² из состояния покоя. Определить, в какой момент времени ускорение т. А будет составлять с радиусом угол 45^о, а также число оборотов, которое совершит диск за это время.

Ответ: t₁ = 0,25 с; t₂= 3,96 с.

24. Ротор вентилятора, вращающегося с угловой скоростью  = 20 рад/с, после выключения сделал 60 оборотов до остановки. Определить угловое ускорение ротора и время движения, считая его равнозамедленным, до остановки.

Ответ: ₀ = 0,53 рад/с²; t = 37,7 с.

3.3. Преобразование простейших движений твердого тела

Пример №1. Рассмотрим пример решения задания для механизма, кинематическая схема которого приведена на рис. 9. Ведущим звеном является груз и задан закон изменения его вертикальной координаты x(t)=30+10t²(см), радиусы колес R₁= R₃= 10 см, R₂= 30 см, r₂= 20 см. Определить модули скорости v и ускорения a точки М для момента времени t₁= 1c.

Рисунок 9

Решение

1. Обозначим и покажем на рис. 10 точки механизма, через которые передается движение от одного (ведущего) звена к другому (ведомому). Это точки А, В, D₁, D₂.

Рисунок 10 Рисунок 11

2. Решение задачи начнем с определения скорости груза. Поскольку груз совершает поступательное движение, его можно считать точкой, движение которой задано координатным способом. При этом груз движется только вдоль оси x. Проекция скорости груза на эту ось определяется как производная от координаты x по времени. . При t = 1 с v_x=20 см/с. Поскольку знак проекции скорости на ось x положительный, вектор скорости груза направлен вниз, т.е. в положительном направлении оси x.

3. Скорости всех точек нити, на которой висит груз, одинаковы (нить считается нерастяжимой), скорость точки схода нити с барабана колеса 1 равна скорости груза. Но с этой точкой соприкасается точка, принадлежащая также и колесу 1, совершающему вращательное движение вокруг неподвижной оси. Это позволяет определить угловую скорость 1-го колеса. При этом будем полагать, что положительному движению груза соответствует положительное вращение колеса. Запишем теперь алгебраическое значение угловой скорости 1-го колеса

. При t=1с ₁_z=2 рад/с.

4. Колеса 1 и 2 находятся в зацеплении и имеют общую точку В (см. рис.10). Поэтому скорости точек колес, находящихся на их ободьях, одинаковы. При записи алгебраического значения угловой скорости 2-го колеса учтем, что внешнее зацепление меняет направление вращения на противоположное При t = 1с ₂_z=1 рад/с.

5. Одинаковы скорости и для точек D₁ и D₂ , расположенных на шкивах ременной передачи. Однако здесь направление вращения не изменяется, поэтому При t = 1 с

6. Определим теперь скорость точки M 3-го колеса в момент времени t = 1с. Величина скорости определяется как произведение модуля угловой скорости на расстояние от точки M до оси вращения, которое равно радиусу. Направление вектора скорости покажем перпендикулярно радиусу, соединяющему точку с осью вращения, в соответствии с направлением вращения (см. рис. 11).

7. Для определения ускорения точки M необходимо знать угловое ускорение 3-го колеса. Алгебраическое значение углового ускорения определим как производную по времени от алгебраического значения угловой скорости. Алгебраические значения угловой скорости и углового ускорения имеют одинаковые знаки, следовательно, вращательное движение является ускоренным.

8. Ускорение точки M определяется как геометрическая сумма векторов вращательного и осестремительного ускорений, модули которых вычислим по формулам.

Тогда полное ускорение точки M

;

Покажем векторы ускорений на рис. 11. Движение 3-го колеса ускоренное, поэтому вращательное ускорение точки M направлено в ту же сторону, что и ее скорость. Осестремительное ускорение всегда направлено к оси вращения.

Если в условии будет задан не закон движения груза x(t), а зависимость угла поворота 1-го колеса от времени, например, ₁(t) = 3+t ²(рад), изменения в решении задачи коснутся только начального этапа. Алгебраическое значение угловой скорости 1-го колеса определим как производную от его угла поворота по времени.

Дальнейшее решение задачи не отличается от приведенного примера.

3.4. Варианты заданий

Расчетные схемы заданий представлены таблице 1, а числовые исходные данные — в таблице 2. В одних вариантах ведущим звеном является груз и задан закон изменения его вертикальной координаты x(t), а в других – одно из колес и задан закон изменения его угла поворота (t).

Таблица 1 — Расчетные схемы для задания ЗК-2 по кинематике простейших движений твердого тела

Продолжение таблицы 1

Таблица 2 — Исходные данные для задания ЗК-2 по кинематике простейших

движений твердого тела

Номер варианта	Уравнение движения ведущего звена	R₁, см	R₂, см	r₂, см	R₃, см	r₃, см	Момент времени, с
1	_₌₃_+t²	10	50	30	15	–	0,5
2	_x₌₂₊₃_t²	–	40	30	50	40	1
3	_₌₃_+t²	10	40	15	30	–	1
4	_x=₄_t²	–	20	15	40	20	0,5
5	_₌₁_+t²	10	30	10	15	–	0,5
6	_x=₄_t²	–	10	–	20	10	0,5
7	_₌₄₊₂_t²	20	50	40	30	–	1
8	_x=t²	–	20	–	40	30	1
9	_x=₂_t²	–	20	10	50	20	1
10	_₌₂₊₂_t²	10	40	20	15	–	0,5
11	_x=₅_+t²	–	40	20	30	–	0,5
12	_₌_t²₊₂	15	40	20	10	–	1
13	_X₌₃_t²_+t	–	30	15	50	30	1
14	_X₌₁₀_+t²	–	20	10	30	20	1
15	_₌₃_t²₊₂	10	30	–	15	25	2
16	_X₌₅_t²₊₅	–	40	30	50	40	1
17	_₌₄_t²₊₂	10	30	20	10	–	1
18	_x=₆_t²	–	20	10	50	20	2
19	_₌₄_t²_–₂	15	30	10	40	–	2
20	_x=₄_+t²	–	20	10	60	–	1
21	_X₌₅_t²_–₄	–	40	–	40	20	1
22	_₌₃₊₂_t²	30	60	–	30	20	2
23	_x=₄_+t²	–	10	–	80	40	1
24	_x=₃_+t²	–	10	–	30	15	1

СПИСОК ЛИТЕРАТУРЫ

1. Тарг С.М. Краткий курс теоретической механики. – М.: Высшая школа, 1998. – 416с.

2. Павловський М.А. Теоретична механіка: Підручник. – К.: Техніка, 2002. – 512 с.

3. Попов М.В. Теоретическая механика: Краткий курс: Учебник для втузов. – М.: Наука. Гл. ред. физ.-мат. лит. 1986. – 336 с.

4. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах: в 3-х т. Т.1. Статика и кінематика. – М.: Наука, 1990. – 672с.

5. Яблонский А.А., Никифорова В.М. Курс теоретической механики. Учебник для технических вузов. – Издательство «Лань», 2001. – 768с.

6. Сборник заданий для курсовых работ по теоретической механике: Учеб. пособие для техн. вузов /Яблонский А.А., Норейко С.С., Вольфсон С.А. и др.; Под ред. А.А. Яблонского. – Изд. 4-е, перераб. и доп. — М.: Высш. шк., 1985. – 367 с.

7. Практическое руководство по теоретической механике для студентов-иностранцев. Раздел «Кинематика» /Янушевская В.Ф., Анищенко Г.О. – Харьков: ХГПУ, 2000. – 48с.

8. Анищенко Г.О., Морачковский О.К. Кінематика: Конспект лекцій по теоретической механике. – Харьков: НТУ «ХПИ», 2002. – 64с.

9. Дистанционный курс http://dl.kpi.kharkov.ua/techn/tu16/default.asp?rus

СОДЕРЖАНИЕ

	Введение	3
1.	Цель и формулировка задания	4
2.	Теоретические положения	5
2.1	Поступательное движение твердого тела	5
2.2	Вращательное движение твердого тела вокруг неподвижной оси	6
2.3	Преобразование простейших движений	8
2.4	Равномерное и равнопеременное вращения	9
2.5	Вопросы для самоконтроля	10
3	Примеры решения задач и варианты контрольных заданий	11
3.1	Законы равномерного и равнопеременного вращения твердого тела вокруг неподвижной оси	11
3.2	Варианты заданий	12
3.3	Преобразование простейших движений твердого тела	15
3.4	Варианты заданий	18
	Список литературы	22

Навчальне видання

Теоретична механіка. Кінематика

ЗК-2 — Поступальний та обертальний рух

Контрольні завдання та методичні вказівки

щодо їх виконання для студентів заочної форми навчання

усіх спеціальностей

АНДРЄЄВ Юрій Михайлович

АНІЩЕНКО Галина Оттівна

ЛАРІН Андрій Олексійович

Відповідальний за випуск О.К. Морачковський

Роботу до видання рекомендував С.К. Шелковий

В авторський редакції

План 2004 р., поз. 66 /

Підп. до друку . .04 . Формат 60×84 1/16. Папір офсетний.

Друк – ризографія. Гарнітура Times New Roman. Ум. друк. арк. 1,4

Обл.-вид. арк. 1,6. Тираж 300 прим. Зам № . Ціна договірна.

______________________________________________________________________________

Видавничий центр НТУ „ХПІ”. 61002, Харків, вул. Фрунзе, 21.

Свідоцтво про державну реєстрацію ДК № 116 від 10.07.2000 р.

________________________________________________________

Друкарня НТУ „ХПІ”. 61002, Харків, вул. Фрунзе, 21.

Средняя угловая скорость начального звена

Для стационарного движения должна быть задана средняя угловая скорость начального звена в предположении, что требуемое соотношение между движущими силами и силами сопротивления поддерживается автоматическим регулятором. [c.497]

СРЕДНЯЯ УГЛОВАЯ СКОРОСТЬ НАЧАЛЬНОГО ЗВЕНА [c.509]

Определение момента инерции маховика при силах, зависящих от положений звеньев. Одной из кинематических характеристик установившегося движения является коэффициент неравномерности движения механизма б, под которым понимается отношение разности максимального и минимального значений угловой скорости начального звена к ее среднему значению за один период установившегося движения [c.94]

Под скоростью машины понимается угловая скорость начального звена. Первый период на тахограмма соответствует времени разбега (пуска) машины, при этом скорость возрастает от нуля до установившегося значения. Второй период — установившийся режим, при котором скорость колеблется относительно среднего значения, т. е. является периодической функцией времени. Третий период — выбег — соответствует времени торможения, скорость падает от установившегося значения до нуля. [c.94]

Графическим интегрированием определяем плои адь диаграммы Л1с == Мс (ф) (рис. 19.12, а) и находим среднее значение момента Л1о.ср сил сопротивления. Если приближенно принять, что средняя угловая скорость Шср начального звена соответствует равенству средних моментов сил движущих и сил сопротивления [c.394]

Различают несколько средних угловых скоростей вращения начального звена механизма. [c.509]

Момент инерции маховика и его масса завися от его местоположения в кинематической цепи механизма. Чем выше частота вращения вала, на котором установлен маховик, тем меньше его размеры при вычисленном моменте инерции /f I группы звеньев, обеспечивающем движение начального звена с номинальной средней угловой скоростью и заданным коэффициентом [c.149]

На рис. 7.13 показаны сечение (заштрихованное) витка червяка средней плоскостью зацепления, начальные цилиндры 1 — червяка и 2—червячного колеса, имеющие соответственно радиусы и Га, начальная плоскость 3 и оси вращения /-/червяка и//-//колеса. Направления угловых скоростей звеньев червячной пары показаны дуговыми стрелками 1 и соа. [c.266]

Из этих уравнений получим для стационарных режимов колебаний значения амплитуды Яо и начальной фазы колебаний координаты о звена 1 и уравнение для определения среднего значения Qo установившейся угловой скорости ротора двигателя [c.95]

Скорость скольжения шкива — Формула для определения 438 —угловая средняя начального звена 510 [c.584]

Требуется определить момент инерции маховика при заданной средней угловой скорости начального звена из условия, что максимальный момент, развиваемый двигателем, должен быть меньше опрокидывающего момента Мопр, по достижении которого ротор двигателя переходит на неустойчивую часть характеристики Ь — Ь и останавливается, или, иначе, из условия штш>(йопр, где соонр — угловая скорость при Мопр. [c.96]

При небольшом отклонении угловой скорости от среднего значения ее и плавном ходе кривой действительных угловых скоростей средняя арифметическая угловая скорость отличается от йстинной средней скорости меньше, чем средняя планиметрическая скорость. На этом основании в большинстве расчетов среднюю арифметическую скорость отождествляют с истинной средней угловой скоростью начального звена. [c.510]

И угловые скорости начального звена. Тогда по аналогии с равенствами (19.1)—(19.3) будем иметь для действительной средней угловой скорости ( j p) выражение [c.376]

При установившемся движении угловая скорость начального звена или постоянная, или колеблется относительно среднего значения, причем эти колебания скорости являются периодическими и могут быть уменьшены путем установки маховика. Условием установившегося движения является равенство рабог сил движущих и сил сопротивления (по модулю) за каждый цикл движения. Если это условие нарушается вследствие уменьше1 ия или увеличения сил сопротивления, то скорость движения соответственно увеличивается или уменьшается. Для многих машин это изменение скорости недопустимо, и тогда возникает задача поддержания величины скорости на заданном уровне. С этой целью применяют регуляторы скорости, основанные на том, что при изменении скорости автоматически изменяется величина движущей силы, и условие установившегося движения сохраняется для любого значения силы сопротивления. [c.308]

Истинной средней угловой скоростью вращения называют угловую скорость равномерного вращательного движения, при котором начальное звено опишет угол, равный углу поворота за время, равное периоду Т, в действительном неравномерном двкженки. Исходя из этого определения, можно истинную среднюю угловую скорость выразить следующим равенством [c.509]

Это и есть искомое расчётное уравнение для определе1ШЯ момента инерции маховика. Оно даёт несколько преувеличенные значения, так как в нём не принят в расчёт приведённый момент инерции других звеньев поэтому истинное значение 8 надо ожидать несколько меньшим против заданного, что говорит в пользу такого расчёта. Если бы была необходимость получить это истинное значение 8 , то мы должны были бы по диаграмме моментов построить полностью диаграмму угловой скорости, подсчитывая не только указанные выше площадки а, б,. .., но и промежуточные, а с другой стороны, подсчитывая и соответствующие приведённые моменты инерции. Однако такая диаграмма могла бы быть построена лишь при условии, что известна угловая скорость в каком-либо положении. Вместо этого мы знаем только среднее её значение. Путём нескольких пробных построений можно было бы подойти достаточно близко к выполнению двух условий известной средней скорости и равенства начальной и конечной скоростей. Однако такая точность не имеет практического значения, а потому ограничиваемся приведённым выше приближённым расчётом. [c.424]

Силы инерции определяют по ускорениям центров тяжести звеньев при условии, что начальное звено (кривошип) вращается с постоянной угловой скоростью, в то время как в реальной машине вследствие действия переменных сил кривошип вращается неравно-Л5ерно. Поэтому определенная из кинетостатического расчета уравновешивающая сила может отличаться от действительно приложен-1ЮЙ внешней силы (силы сопротивления или движущей силы), однако их средние значения при постоянном числе оборотов кривошипа в единицу времени будут одинаковы. Разность между вычисленной уравновешивающей силой и приложенной внешней силой определяет добавочные силы инерции звеньев, возникающие при неравномерном вращении кривошипа. [c.377]

Несоответствие между приведенными к начальному звену моментами движущих сил и сил сопротивления и изменение приведенного момента инерции механизма вызывают при установившемся движении машины периодическое изменение угловой скорости. Для одних [у ашин это изменение не имеет никакого значения и колебания угловой скорости могут быть значительными, для других машин требуется высокая равномерность вращения, при которой отклонения угловой скорости от среднего значения ее невелики. [c.510]

скорость вращения

Угловая скорость — Википедия

Линейную скорость (совпадающую с модулем вектора скорости) точки на определённом расстоянии (радиусе) от оси вращения можно считать так: =.

Единицы измерения скорости вращения (угловой скорости …

Конвертер единиц скорости вращения (угловой скорости). Мгновенный перевод из нужной единицы во все остальные.

Суточное вращение Земли — Википедия

Линейная скорость вращения Земли (на экваторе) — 465,1013 м/с (1674,365 км/ч). Линейная скорость вращения на широте 60° в два раза меньше, чем на экваторе.

Как управлять скоростью вращения кулера на ПК или ноутбуке

Скорость вращения вентилятора – это не случайный показатель. Он устанавливается материнской платой , которая получает информацию от BIOS.

Суточное вращение Земли — Википедия

Единицы измерения скорости вращения (угловой скорости …

Настройка скорости вращения кулера на ноутбуке — ВсёПросто

Изменить скорость вращения кулера с ее помощью достаточно легко, для этого нужно: Установить и запустить приложение. Перейти в расширенные настройки, затем в раздел «Fan».

Изменить скорость вращения кулера на Корпусе, CPU и GPU

Изменить скорость вращения кулера на ЦП и корпусе через bios. Это самый оптимальный вариант, так как ни одна сторонняя программа мне не помогла, чтобы изменить скорость вращения кулера на центральном процессоре и …

Как управлять скоростью вращения кулера на ПК или ноутбуке

Выбор правильной скорости вращения фрезы

Значит скорость вращения одного деления будет равна 4 000 об/мин. Если ваш фрезер не имеет контроля скорости, вам не повезло. В магазинах доступны

Скорость вращения Земли

Скорость вращения Земли вокруг оси – 1675 км/ч. Получается, что каждую секунду вы смещаетесь практически на 0.5 км. Можно провести вычисление самостоятельно. Земная окружность на экваторе …

Обороты болгарки: скорость вращения диска в минуту УШМ …

Скорость вращения диска УШМ варьируется в диапазоне от 2800 до 11000 об/мин. Скорость рассчитана так, чтобы линейная скорость диска не была больше 80

Предельная частота вращения подшипника. — Подшипники в …

Допустимая частота вращения подшипника при жидкой и пластичной смазке. Как увеличить максимальную скорость вращения подшипника.

BIOS: регулировка скорости вращения вентиляторов — Советы …

С помощью данной опции можно установить скорость вращения дополнительных вентиляторов, когда температура внутри системного блока не превышает допустимых значений.

1.9.2 Угловая и линейная скорости вращения — Физика по …

Угловая скорость выражается в радианах в секунду (рад/с). Например, угловая скорость вращения Земли вокруг оси равна 0,0000727 рад/с, а точильного диска — около 140 рад/с 1. Угловую скорость можно выразить через частоту …

. тело движется по окружности радиусом 3м со скоростью 12 …

Тело движется по окружности радиусом 3м со скоростью 12 м/с. Чему равна частота вращения?, получи быстрый ответ на вопрос у нас ответил 1 человек — Знания Орг.

«С какой скоростью движется планета Земля вокруг …

11 мая 2020 Александр Мынов ответил: Со скоростью один оборот за сутки)))) Угловая скорость вращения Земли вокруг собственной оси: Линейная скорость вращения Земли (на экваторе) — 465,1013 м/с (1674,365 км/ч).

Центрифуга скорость вращения — Справочник химика 21

Центрифуга скорость вращения Центрифуги делятся по характеру процесса — на машины периодического и непрерывного действия (автоматические), но расположению ротора — на горизонтальные и вертикальные, в зависимости …

Скорость вращения Земли

Скорость вращения шпинделя жесткого диска. Максимальная

Скорость вращения шпинделя задается при создании жесткого диска, и превысить ее невозможно. Жесткие диски с 5400 оборотов в минуту устанавливаются в ноутбуки по умолчанию, так как отвечают …

. тело движется по окружности радиусом 3м со скоростью 12 …

Центрифуга скорость вращения — Справочник химика 21

Скольжение и скорость вращения ротора — ОБЩАЯ

Скорость вращения магнитного поля относительно ротора, т.е. разность ( и, — п 2), называют скольжением. Обычно скольжение выражают в долях скорости вращения поля и

Обороты болгарки: скорость вращения диска в минуту УШМ …

Регулирование скорости вращения асинхронного двигателя …

Скорость вращения двигателя можно регулировать также изменением частоты питающего тока, но этот способ практически не применяется ввиду отсутствия простых и

Предельная частота вращения подшипника. — Подшипники в …

«С какой скоростью движется планета Земля вокруг …

BIOS: регулировка скорости вращения вентиляторов — Советы …

Как настроить скорость вращения кулеров на компьютере …

Как настроить скорость вращения кулера на компьютере Осуществить настройку можно как программно (правками в BIOS, установкой приложения SpeedFan), так и физически (подключив вентиляторы через …

С какой скоростью вращается Земля вокруг своей оси? ⚛ физика

Линейная скорость в зависимости от широты. Но это на экваторе. Ближе к полюсам, как я уже говорил, значение будет ниже. Так как радиус вращения будет снижаться.

Как изменить скорость вращения кулера процессора

Скорость вращения кулера на процессе изменяется с помощью программных и аппаратных средств. Таким образом регулируется эффективность охлаждения и уровень шума.

Скорости вращения шнека

ω – угловая скорость вращения шнека, рад/сек; R – радиус скважины, м; n – скорость вращения шнека, об/мин. Критической называется скорость вращения шнека при которой силы Т

Оборотов в минуту (rpm — Скорость вращения), частота

Оборотов в минуту (rpm — Скорость вращения), частота Введите число Оборотов в минуту (rpm) , которое вы хотите преобразовать в текстовое поле, чтобы увидеть результаты в таблице.

Скорость вращения шпинделя жесткого диска. Максимальная

Скорости вращения шнека

Роторы скорость вращения — Справочник химика 21

Роторы скорость вращения Подшипники для центробежных насосов со скоростью вращения ротора свыше 1000 об мин заливают баббитом Б-83, имеющим следующий состав 10—12% сурьмы, 5,5—6,5% меди, 83% олова.

Как изменить скорость вращения кулера процессора

С какой скоростью вращается Земля вокруг своей оси? ⚛ физика

Предельная частота вращения подшипника. — Подшипники в …

Обороты болгарки: скорость вращения диска в минуту УШМ …

Как настроить скорость вращения кулеров на компьютере …

Технологии управления скоростью вращения вентиляторов …

Соответственно и скорость вращения вентилятора, равно как и уровень создаваемого им шума, будет изменяться в зависимости от температуры процессора (рис. 7). Рис. 7.

Скорость вращения галактик — Allbest

Скорость вращения галактики как скорость вращения различных компонентов галактики вокруг её центра. Особенности движения газа и звёзд. Распределение звезд, анализ их поля скоростей как информация о движении в …

Скорость вращения — — Энциклопедия по машиностроению

Скорость резания, т. е. окружная скорость вращения фрезы, м/мин, С помощью гитары скоростей 9 устанавливают частоту вращения шпинделя в минуту. Гитара деления (обкатки) ii служит для сообщения заготовке окружной …

Регулировка оборотов кулера процессора и видеокарты

Астронет > Вращение солнца

Вращение солнца Вращение солнца изучено гораздо лучше, чем у других звезд; угловая скорость вращения меняется как по широте, так и по глубине вследствие медленно происходящей циркуляции вещества в основном во …

Равномерное движение по окружности | Физика для всех

Равномерное движение по окружности – это простейший пример криволинейного движения. Например, по окружности движется конец стрелки часов по циферблату. Скорость движения тела по окружности носит название линейная скорость.

При равномерном движении тела по окружности модуль скорости тела с течением времени не изменяется, то есть v = const, а изменяется только направление вектора скорости Тангенциальное ускорение в этом случае отсутствует (a_r = 0), а изменение вектора скорости по направлению характеризуется величиной, которая называется центростремительное ускорение (нормальное ускорение) a_n или а_ЦС. В каждой точке траектории вектор центростремительного ускорения направлен к центру окружности по радиусу.

Модуль центростремительного ускорения равен

a_ЦС=v² / R

Где v – линейная скорость, R – радиус окружности

Рис. 1.22. Движение тела по окружности.

Когда описывается движение тела по окружности, используется угол поворота радиуса – угол φ, на который за время t поворачивается радиус, проведённый из центра окружности до точки, в которой в этот момент находится движущееся тело. Угол поворота измеряется в радианах. Радиан равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу окружности (рис. 1.23). То есть если l = R, то

1 радиан= l / R

Так как длина окружности равна

l = 2πR

то

360^о = 2πR / R = 2π рад.

Следовательно

1 рад. = 57,2958^о = 57^о18’

Угловая скорость равномерного движения тела по окружности – это величина ω, равная отношению угла поворота радиуса φ к промежутку времени, в течение которого совершён этот поворот:

ω = φ / t

Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной скорости определяется отношением длины пройденного пути l к промежутку времени t:

v= l / t

Линейная скорость при равномерном движении по окружности направлена по касательной в данной точке окружности. При движении точки длина l дуги окружности, пройденной точкой, связана с углом поворота φ выражением

l = Rφ

где R – радиус окружности.

Тогда в случае равномерного движения точки линейная и угловая скорости связаны соотношением:

v = l / t = Rφ / t = Rω или v = Rω

Рис. 1.23. Радиан.

Период обращения – это промежуток времени Т, в течение которого тело (точка) совершает один оборот по окружности.Частота обращения – это величина, обратная периоду обращения – число оборотов в единицу времени (в секунду). Частота обращения обозначается буквой n.

n = 1 / T

За один период угол поворота φ точки равен 2π рад, поэтому 2π = ωT, откуда

T = 2π / ω

То есть угловая скорость равна

ω = 2π / T = 2πn

Центростремительное ускорение можно выразить через период Т и частоту обращения n:

a_ЦС = (4π²R) / T² = 4π²Rn²

Периодические движения и определение весов

В физике угловая частота ω (также обозначаемая терминами угловая скорость , радиальная частота , круговая частота , орбитальная частота и радианная частота ) является скалярной мерой скорости вращения. Угловая частота (или угловая скорость) — это величина вектора угловой скорости .Термин вектор угловой частоты иногда используется как синоним векторной величины угловой скорости. ^[1]

Поскольку один оборот (или колебание) равен 2π радиан, угловая скорость ω может быть выражена как функция времени, которое требуется системе для прохождения одного цикла.

где

ω — угловая частота или угловая скорость (измеряется в радианах в секунду),

T — период (измеряется в секундах) и является обратной величиной частоты (измеряется в колебаниях в секунду).

f — обычная частота (измеряется в герцах) (иногда обозначается ν),

v — тангенциальная скорость точки относительно оси вращения (измеряется в метрах в секунду),

r — радиус вращения (в метрах).

If часто полезно учитывать время, которое требуется колебательной системе, чтобы сделать один полный оборот или пройти через одну длину волны, или вернуться в исходную точку (для маятника или пружины) для различных физических систем, колебания которых имеют характеристику частота.. Например, в стабильной атмосфере период колебаний воздушной посылки относительно ее исходного местоположения будет связан с частотой Бранта-Вайсаллы,

, который относится к параметру статической устойчивости:

Частота Бранта-Вайсаллы просто констатирует очевидное — для стабильной посылки, чем больше вертикальное смещение относительно ее исходного положения и чем стабильнее посылка, тем быстрее воздушная посылка будет «пытаться» вернуться в свое исходное положение.Благодаря своему собственному импульсу он выйдет за исходное положение и затем будет колебаться вокруг него.

Для погодных систем синоптического масштаба период колебаний связан с параметром Кориолиса. Определение того, относится ли характерный период к одному или другому, можно сделать на основе радиуса деформации Россби.

Радиус деформации Россби можно использовать в качестве масштабного коэффициента, чтобы определить, какие упрощения можно сделать в управляющих уравнениях движения.Для условий средних широт радиус деформации Россби составляет примерно 1000 км или около того … это означает, что физические циркуляционные системы должны быть по крайней мере этого размера, чтобы геострофическое приближение было действительным, а период колебаний связан с ускорениями Кориолиса. Для физических систем с радиусом менее 1000 км или около того кориолисовы ускорения относительно не важны, а другие факторы, такие как колебания вокруг вертикальной плоскости в статически стабильной атмосфере, являются наиболее важными.

Решение этих уравнений для периода систем синоптического масштаба дает период примерно в 1 день или более для систем синоптического масштаба (то есть время, которое требуется воздушной подушке, чтобы пройти через систему) и 10 минут или около того для систем микромасштаб. Таким образом, мезомасштаб можно рассматривать как состоящий из атмосферных движений, колебания которых можно охарактеризовать между этими пределами.

Угловое смещение, скорость, ускорение

Мы живем в мире, который определяется тремя пространственными измерениями и одним измерение времени.Объекты перемещаются в этом домене двумя способами. Объект переводит, или меняет адрес , с одного указать на другое. И объект вращается , или меняет свою ориентацию . В общем, движение объекта включает в себя как перемещение во всех трех направлениях, так и вращение на вокруг три основных оси.

На этой странице мы будем рассматривать только вращение твердого объекта вокруг одна ось.Вращение объекта аналогично переводу в номере переменных, которые мы должны учитывать, но обозначения очень сбивают с толку, потому что он традиционно описывался с использованием греческих символов. На слайде в вверху страницы мы использовали традиционные греческие обозначения. Чтобы упростить соблюдение статьи 508, мы просто укажем названия переменных. здесь в тексте, а не использовать символьный шрифт. Theta — это символ, который выглядит как 0 с горизонтальной линией, проходящей через него. Phi — это символ, который выглядит как 0 с вертикальной линией, проходящей через него. Омега — это символ, который выглядит как фигурный w . Альфа — это символ, похожий на перекрещенную ленту.

Поскольку объект вращается вокруг оси вращения самым простым способом для описания движения использовать полярные координаты. Мы можем указать угловую ориентацию объекта на в любое время t , указав угол theta , на который объект повернулся от некоторой опорной линии.Изначально наш объект находится в ориентации «0», заданной углом тета 0 в момент времени t0 . Мы нарисовали красную линию на диске с указанием исходной ориентации. Объект вращается до тех пор, пока time t1 , а красная линия поворачивается на угол theta 1 . Мы можем определить угловое смещение — фи как разница угла между условием «0» и условием «1».

фи = тета 1 — тета 0

Угловое смещение — это векторная величина, означающая, что угловое смещение имеет размер и направление, связанные с ним.Направление важно для более поздних математических процессов, но определение немного сбивает с толку. Как объект вращается из точки «0» в точку «1», вращается вокруг оси, поэтому направление угловое смещение измеряется по оси. Положительное значение направления оси определяется правилом правой руки . Вытяните правую руку, как если бы пожать кому-нибудь руку. Согните пальцы с основанием в точке «0» и наконечниками, идущими в точку «1».Ваш большой палец указывает перпендикулярно плоскости вращения в положительном направлении по оси вращения.

Угловое смещение измеряется в единицах радиан . Два радиана пи равны 360 градусов. Угловое перемещение не является длиной (не измеряется в метрах или футах), поэтому угловое смещение отличается чем линейное перемещение. Поскольку твердый объект вращается вокруг оси вращения, все точек объекта испытывают такое же угловое смещение, но точки дальше от оси перемещаются дальше, чем точки ближе к оси.На слайде мы рассматриваем две точки; один расположен на радиусе ra на краю диска, а другой расположен в радиусе rb , что меньше ra . Как объект вращается за счет углового смещения phi , точка на краю диска перемещает расстояние на по круговой траектории. Точка руб. также движется в круговой путь, но расстояние сб короче, чем расстояние сб .В основном, длина кругового пути с равна радиус r умноженный на угловое смещение phi , выраженное в радианах.

для углового перемещения phi ,

s = phi * r

ra> rb

sa> sb

Угловая скорость — омега объекта изменение угла во времени.Средняя угловая скорость — это угловое смещение, разделенное по временному интервалу:

омега = (тета 1 — тета 0) / (t1 — t0)

Это средняя угловая скорость за промежуток времени от t0 до t1 , но объект может ускоряться и замедляться в течение определенного промежутка времени. В любой момент объект может иметь угловую скорость, отличную от средней.Если мы сократим разница во времени вплоть до очень небольшого (дифференциального) размера, мы можем определить мгновенная угловая скорость — это дифференциальное изменение угла, деленное на дифференциальное изменение во времени;

омега = д тета / дт

где символ d / dt — это дифференциал от исчисления. Угловая скорость равна векторная величина и имеет как величину, так и направление. Направление такое же, как и направление углового смещения, от которого мы определили угловая скорость.

Угловая скорость измеряется в радианах в секунду , или оборотов в секунду или оборотов в минуту (об / мин). Угловая скорость разная чем линейная скорость, которая измеряется длиной за время (футы в секунду или метры в секунду). Все точки объекта вращаются с одинаковой угловой скоростью, но находятся дальше от ось вращения движется с тангенциальной скоростью , отличной от , чем точки ближе к оси вращения.Тангенциальная скорость измеряется по круговой траектории. с , что мы рассматривали ранее. Касательная скорость В равна угловой скорость омега в раз больше радиуса r :

для углового перемещения phi ,

V = омега * г

ra> rb

Va> Vb

Когда мы изначально укажите вращение нашего объекта с theta 0, и т0 , мы также должны указать начальную мгновенную угловую скорость omega 0 .Аналогично в конечной позиции theta 1, и t1 , угловая скорость меняется на угловую скорость omega 1 .

Среднее угловое ускорение — альфа объекта — это изменение угловой скорости во времени.

альфа = (омега 1 — омега 0) / (t1 — t0)

Как и в случае с угловой скоростью, это только средняя угловая скорость. ускорение.В любой момент объект может иметь угловое ускорение, отличное от среднего. Если мы сократим разница во времени вплоть до очень небольшого (дифференциального) размера, мы можем определить мгновенное угловое ускорение должно быть изменением дифференциала в угловая скорость, деленная на дифференциальное изменение во времени:

альфа = d омега / dt

Точно так же, как силы производят линейные ускорения, a крутящий момент производит угловые ускорения.Если мы можем определить крутящие моменты на объекте и то, как крутящие моменты меняются со временем, мы можем использовать уравнения, представленные на этом слайде, для определения углового ускорения, угловая скорость и угловое смещение объекта как функция времени. Авиационные инженеры используют эту информацию для прогнозирования вращения самолета в полете, которые становятся важными для устойчивости и управление самолетом.

Деятельность:

Экскурсии с гидом

Навигация..

Руководство для начинающих Домашняя страница

Угловая скорость: определение, формула и примеры — стенограмма видео и урока

Радианы

Перед тем, как перейти к угловой скорости, нам нужно рассмотреть еще одну вещь, а именно радианы. Когда мы имеем дело с угловой скоростью, мы используем радианную меру угла, поэтому важно, чтобы мы были знакомы с радианной мерой. Техническое определение радиан. Измерение — это длина дуги, образуемой углом, деленная на радиус круга, частью которого является угол, где подразумеваемый означает, что она должна быть противоположной углу и продолжаться от одной точки на круг к другому, оба отмечены углом.Это говорит нам о том, что угол тета = с, / r радиан, где с, = длина дуги, соответствующей тета, а r = радиус окружности, частью которой является тета.

**Радианная мера угла**

Поскольку большинство из нас привыкли к градусному измерению углов, удобно, что мы можем легко преобразовать градус в радиан, умножив градус на пи / 180.Например, угол в 45 градусов имеет радиан 45 (пи / 180), что равно пи / 4 радиана.

Угловая скорость

Угловая скорость встречается реже, чем линейная скорость, поскольку применяется только к объектам, движущимся по круговой траектории. Например, гоночная машина на круговой трассе, шар рулетки на колесе рулетки или колесо обозрения — все они имеют угловую скорость.

**Примеры угловой скорости**

Угловая скорость объекта — это угловое смещение объекта во времени.Когда объект движется по круговой траектории, центральный угол, соответствующий положению объекта на круге, изменяется. Угловая скорость, представленная как w , представляет собой скорость изменения этого угла во времени.

**Угловая скорость**

Например, колесо обозрения может вращать пи / 6 радиан каждую минуту. Следовательно, угловая скорость колеса обозрения будет равна пи / 6 радиан в минуту.

Формулы угловой скорости

Существует трех формул , которые мы можем использовать для определения угловой скорости.

Вариант 1

Первое вытекает прямо из определения. Угловая скорость — это скорость изменения позиционного угла объекта относительно времени, поэтому w = theta / t , где w = угловая скорость, theta = позиционный угол и t = время.

Например, если гоночный автомобиль движется по круговой трассе и проходит 1 круг, или 2pi радиана за 4 минуты, то мы можем найти угловую скорость автомобиля, подставив theta = 2pi радиан и t = 4 минуты в наша формула, чтобы получить w = 2pi / 4 = pi / 2 радиан в минуту.Угловая скорость автомобиля составляет пи / 2 радиана в минуту.

Вариант 2

Чтобы получить нашу вторую формулу для угловой скорости, мы понимаем, что тета выражается в радианах, а определение радианной меры дает theta = с / r . Таким образом, мы можем подставить theta = s / r в нашу первую формулу угловой скорости. Это дает w = ( s / r ) / t . Упрощение дает w = s / ( r t ), где s = длина дуги, r = радиус и t = время.

Например, если колесо рулетки имеет радиус 10 дюймов, а шарик проходит 7 дюймов по круговой траектории за 2 секунды, то мы можем найти угловую скорость шара, вставив s = 7 дюймов, r = 10 дюймов, и t = 2 секунды в w = s / ( r t ), чтобы получить w = 7 / (10 * 2) = 0,35 радиана в секунду. Угловая скорость мяча составляет 0,35 радиана в секунду.

Вариант 3

Последняя формула основана на признании того, что мы можем переписать нашу вторую формулу угловой скорости как w = s / ( r t ) = ( s / t ) (1/ r ).Напомним, что с / t — это наша линейная скорость, поэтому мы можем переписать эту формулу как w = v (1/ r ) = v / r , где v = linear скорость и r = радиус окружности.

Например, если гоночный автомобиль движется по круговой трассе со скоростью 110 миль в час, а радиус гоночной трассы составляет 0,2 мили, то мы можем найти угловую скорость автомобиля, подключив v = 110 миль в час и р = 0.2 мили в нашу формулу, чтобы получить w = 110 / 0,2 = 550 радиан в час.

Резюме урока

Мы рассмотрели линейной скорости, , скорость изменения положения объекта, движущегося по прямой линии, относительно времени и радиан, мера угла (тета = с / r , где s = длина дуги и r = радиус). Мы видели, что оба они играют важную роль в угловой скорости. Угловая скорость — это угловое смещение во времени объекта или частицы, которые движутся по круговой траектории.У нас есть три формулы, которые мы используем для определения угловой скорости, и они отображаются на экране.

**Формулы угловой скорости**

Эти формулы и определения снабдили нас всем необходимым для эффективной и действенной работы с угловой скоростью.

Определение угловой частоты в физике.

Примеры угловой частоты в следующих разделах:

Период и частота
- Обратите внимание, что период и частота являются обратными друг другу.
- Часто периодическое движение лучше всего выражается в терминах угловых частоты , представленных греческой буквой ω (омега).
- Угловой частота относится к угловому смещению в единицу времени (например, при вращении) или скорости изменения фазы синусоидальной формы волны (например, в колебаниях и волнах), или скорости изменения аргумента синусоидальной функции.
- Угловая частота часто выражается в радианах в секунду (напомним, что в круге 2π радиана).
- Синусоидальные волны различных частот ; нижние волны имеют более высокие частоты , чем те, что выше.
Фазоры
- Фазоры используются для анализа электрических систем в синусоидальном установившемся состоянии и с однородной угловой частотой .
- В физике фазовый вектор или фазор — это представление синусоидальной функции, амплитуда (A), частота (ω) и фаза (θ) не зависят от времени, как показано на диаграмме на.
- , показанный на рисунке ниже, представляет собой косинусоидальный сигнал с амплитудой A, частотой , и фазой θ.
- Амплитуда A характеризует размах сигнала 2A от пика до пика, угловая частота частота ω характеризует период T = 2π / ω между переходами от отрицательного к положительному нулю (или положительным пикам или отрицательным пикам) и фаза θ характеризует время τ = −θ / ω, когда сигнал достигает своего первого пика.
- В синусоидальном установившемся состоянии каждое напряжение и ток (или сила и скорость) в системе синусоидальны с угловой частотой ω.
Управляемые колебания и резонанс
- \ omega $ — частота привода для синусоидального приводного механизма.
- F_0 $, управляющая частота $ \!
- \ omega $, незатухающий угловой частота $ \!
- Для конкретной управляющей частоты частота называется резонансной, или резонансной частотой $ \!
- Установившееся изменение амплитуды с частотой и затухание управляемого простого генератора гармоник.
Угловое ускорение, Альфа
- Угловое ускорение — это скорость изменения угловой скорости , математически выраженная как $ \ alpha = \ Delta \ omega / \ Delta t $.
- Угловое ускорение — это скорость изменения угловой скорости .
- Угловое ускорение определяется как скорость изменения угловой скорости .
- В форме уравнения угловое ускорение выражается следующим образом:
- Единицами измерения углового ускорения являются (рад / с) / с или рад / с2.
Волновая природа материи вызывает квантование
- Если струна была свободна и ни к чему не прикреплена, мы знаем, что она могла бы колебаться на любой управляемой частоте .
- Как только струна становится «связанной системой» с определенными граничными ограничениями, она допускает волны только с дискретным набором частот .
- Угловой момент равен $ L = m_e v r $, поэтому мы получаем квантование углового момента :
Постоянное угловое ускорение
- Постоянное угловое ускорение описывает отношения между угловой скоростью , углом поворота и временем.
- Просто используя нашу интуицию, мы можем начать видеть взаимосвязь таких величин вращения, как θ (угол поворота), ω (угловая скорость , скорость) и α ( угловое ускорение, ).
- Аналогичным образом кинематика вращательного движения описывает отношения между углом поворота, угловой скоростью , угловым ускорением и временем.
- Как и в линейной кинематике, где мы предположили, что a является постоянным, здесь мы предполагаем, что угловое ускорение α является постоянной величиной, и можем использовать соотношение: $ a = r \ alpha $, где r — радиус кривой.Точно так же у нас есть следующие отношения между линейными и угловыми значениями : $ v = r \ omega \\ x = r \ theta $
- Свяжите угол поворота, угловую скорость , и угловое ускорение , с их эквивалентами в линейной кинематике
Вращательные столкновения
- В замкнутой системе угловой момент сохраняется так же, как и линейный импульс.
- Для объектов с вращательной составляющей существует угловой момент .
- Угловой момент математически определяется как L = Iω или L = rxp.
- Объект, который имеет большую угловую скорость ω (), такой как центрифуга, также имеет довольно большой угловой момент .
- После столкновения стрела прилипает к цилиндру качения, и система имеет чистый угловой момент , равный исходному угловому моменту стрелки до столкновения.
Сохранение углового момента
- Закон сохранения углового момента гласит, что, когда на объект не действует внешний крутящий момент, никакого изменения углового момента не произойдет.
- Сохраняющаяся величина, которую мы исследуем, называется угловым моментом .
- Обозначение для углового момента — буква L.
- Если изменение углового момента ΔL равно нулю, то угловой момент постоянен; следовательно,
- (I: инерция вращения, $ \ omega $: угловая скорость )
Эффект Зеемана и ядерный спин
- Эффект Зеемана — это расщепление атомных уровней на основе значения полного углового момента в направлении магнитного поля $ m_J $.
- $ {\ bf I} $ — это полный угловой момент протона, и этот полный угловой момент системы равен $ {\ bf F} = {\ bf J} + {\ bf I} $.
- Расщепление между этими двумя состояниями соответствует частоте , равной 1420 ~ МГц или $ \ lambda = 21 $ ~ см.
- Есть два отдельных эффекта: взаимодействие магнитного момента ядра с магнитным моментом, индуцированным электронным орбитальным угловым моментом , и взаимодействие между двумя магнитными моментами.
- , где $ r $ — расстояние между электроном и ядром, а $ {\ bf l} $ — орбитальный угловой момент электрона.
Транспорт энергии
- ЭМИ также несет как импульс, так и угловой момент .
- Квантовая природа света становится более очевидной на высоких частотах (или высокой энергии фотонов).
- Такие фотоны ведут себя больше как частицы, чем фотоны с более низкой частотой .
- ЭМ волны с более высокими частотами несут больше энергии.
- Поскольку $ v \ propto f $, мы находим, что более высокие частоты подразумевают большую скорость.

Период и частота — AP Physics 1

Пояснение:

Чтобы решить эту проблему, мы можем начать с сохранения энергии:

Постановка задачи говорит нам, что цилиндр изначально находится в состоянии покоя, поэтому мы можем исключить начальную кинетическую энергию.Если мы предположим, что высота цилиндра при достижении периода 0,2 с имеет высоту 0, мы можем исключить конечную потенциальную энергию. Следовательно, получаем:

Расширяя эти члены и убедившись, что у нас есть линейная и вращательная составляющие кинетической энергии, мы получаем уравнение (1):

Прежде чем двигаться дальше, мы знаем, что нам нужно будет вычислить что-то, что мы можем использовать для определения периода цилиндра. Мы знаем, что период — это то, сколько времени требуется цилиндру, чтобы совершить один полный оборот.Думая практически, мы можем использовать окружность цилиндра и линейную скорость для определения периода:

Используя переменные, получаем уравнение:

Преобразуя конечную скорость, мы получаем уравнение (2):

Теперь мы знаем, что период зависит от конечной линейной скорости. Вернемся к этому уравнению. Теперь мы можем вернуться к уравнению (1) и начать подставлять выражения для неизвестных переменных слева направо.Первая неизвестная переменная — это начальная высота. Однако мы можем использовать пройденное расстояние цилиндра и угол наклона:

Изменяя исходную высоту, мы получаем уравнение (3):

Далее следующий неизвестный член — конечная скорость. Мы можем заменить уравнение (2), которое мы уже получили:

Далее следующий неизвестный член — момент инерции. Используя выражение для цилиндра, получаем уравнение (4):

Двигаясь дальше, последний неизвестный член — это конечная скорость вращения.Мы можем использовать соотношение между этим и линейной скоростью:

Теперь подставляя уравнение (2), мы получаем уравнение (5):

Теперь мы можем подставить уравнения 2, 3, 4 и 5 в уравнение (1):

Исключив массу из обеих частей уравнения и расширив каждый член:

Объединение терминов справа:

Перестановка по длине:

Проверьте свои подразделения и убедитесь, что у вас остались секунды, прежде чем двигаться дальше!

Мы знаем значения для каждой переменной, так что пора подключиться и подумать:

Вычислитель частоты вращения с заданной угловой частотой

Частота вращения при заданной угловой частоте Формула

rotational_frequency = Угловая скорость / (2 * пи)
ν _гниль = ω / (2 * пи)

Как мы получаем частоту вращения, если задана угловая частота?

Угловая скорость (ω) — это скорость изменения углового смещения во времени.Где частота вращения (f) — это количество оборотов в единицу времени. За один оборот имеем угловое смещение, равное 2 * пи радиан. Таким образом, частота вращения и угловая скорость могут быть связаны, поскольку частота вращения равна угловой скорости, деленной на 2 * pi {т. Е. f = ω / (2 * пи)}.

Как рассчитать частоту вращения по угловой частоте?

Калькулятор частоты вращения с заданной угловой частотой использует rotational_frequency = Angular Velocity / (2 * pi) для расчета частоты вращения. Формула частоты вращения с заданной угловой частотой определяется как количество оборотов в единицу времени.За один оборот имеем угловое смещение, равное 2 * пи радиан. Таким образом, частота вращения (f) и угловая скорость (ω) могут быть связаны, поскольку частота вращения равна угловой скорости, деленной на 2 * pi {т. Е. f = ω / (2 * пи)}. Частота вращения и обозначена символом ν _rot .

Как рассчитать частоту вращения по заданной угловой частоте с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для вычисления частоты вращения при заданной угловой частоте, введите угловую скорость (ω) и нажмите кнопку вычисления.Вот как вычисление частоты вращения с учетом угловой частоты может быть объяснено с заданными входными значениями -> 3,183099 = 20 / (2 * pi) .

Тангенциальная скорость: определение, формула и уравнение

Тангенциальная скорость — это составляющая движения вдоль края окружности, измеренная в любой произвольный момент времени. Тангенциальная скорость описывает движение объекта по краю этой окружности, направление которого в любой заданной точке окружности всегда вдоль касательной к этой точке.

Тангенциальная скорость измеряется в любой точке, касательной к вращающемуся колесу. Таким образом, угловая скорость ω связана с тангенциальной скоростью Vt формулой: Vt = ω r. Здесь r — радиус колеса. Тангенциальная скорость — это составляющая движения по краю круга, измеренная в любой произвольный момент времени. Как следует из названия, тангенциальная скорость описывает движение объекта по краю этого круга, направление которого в любой заданной точке круга всегда вдоль касательной к этой точке.

Спрыгивать с движущегося автобуса опасно, поэтому осознанное решение совершить прыжок вызывает чувство трепета. Прыжок с края крутящейся карусели — это ее 9-летняя версия, если только у вас нет брата или сестры, который добровольно пинает вас в стиле «Это спарта» и отправляет в небытие.

Помимо того, что я обычно отклоняюсь от того, что важно, и излишне делясь тем, что я считаю травмами, изменяющими мою жизнь, у меня было еще кое-что, известное как тангенциальная скорость .Ага! Вот о чем эта статья!

Что такое касательная?

Касательная — это линия, которая касается функции только в одной точке. Термин функция здесь используется для обозначения любой нелинейной кривой. Он представляет собой уравнение — взаимосвязь между координатами «x» и «y» на двухмерном графике.

Например, рассмотрим кривую, с которой мы больше всего знакомы — старый добрый круг. Круг определяется уравнением

. Это означает, что для постоянного радиуса «r» определенные значения «x» и «y» очерчивают великолепную дугу, которая, как конец игры Snake , встречает свой собственный конец.

Визуализация обведения круга с центром в исходной точке.

Однако для простоты я специально рассмотрел уравнение, описывающее ортодоксальную окружность, центр которой лежит в начале координат — опорной точке или координатах (0,0), а радиус r — это расстояние. от начала до края этого круга.

Как следует из названия, тангенциальная скорость описывает движение объекта по краю этой окружности, направление которого в любой заданной точке окружности всегда вдоль касательной к этой точке.Однако концепция не ограничивается только равномерным круговым движением; это также относится ко всем с нелинейным перемещением . Если объект движется из точки A в точку B по нелинейной кривой, то красные стрелки представляют тангенциальную скорость

в различных точках этой траектории.

А пока остановимся на круге.

Формула тангенциальной скорости

Сначала мы вычисляем угловое смещение «q», которое представляет собой отношение длины дуги «s», которую объект описывает на этой окружности, к ее радиусу «r».Это угловая часть под тенью дуги, между двумя линиями, исходящими из центра и соединенными с ее концами. Измеряется в радианах.

Скорость изменения углового смещения объекта называется его угловой скоростью. Он обозначается буквой «w», а его стандартная единица измерения — радианы в секунду (рад / с). Она отличается от линейной скорости, поскольку имеет дело только с объектами, движущимися по кругу. По сути, он измеряет скорость, с которой изменяется угловое смещение.

Вычисление линейной или тангенциальной скорости при равномерном круговом движении.

Линейная составляющая угловой скорости известна как линейная скорость, которая представляет собой скорость изменения линейного смещения объекта на . Линейное смещение — это указанная выше дуга, то есть длина дуги. Скорость изменения произведения радиуса «r» и углового смещения «q» представляет собой линейную скорость объекта. Радиус исключается из операции, так как он постоянный. Мы понимаем, что скорость — это произведение угловой скорости объекта и радиуса круга, который он отслеживает.

Линейная скорость объекта , движущегося по окружности, измеренная в произвольный момент времени, и есть его тангенциальная скорость!

Другой способ определить линейную скорость — это период времени. Если период времени — это время, необходимое объекту для того, чтобы один раз обойти круг, то скорость, с которой он это делает, равна ‘s / t’ (расстояние / время).

Связь между линейной или тангенциальной скоростью «v» и периодом времени «T».

Величина, обратная «T», известна как частота и обозначается буквой «f».Это количество циклов, выполняемых за секунду. Произведение 2pf известно как угловая частота и обозначается буквой «w», что помогает нам прийти к ранее полученному результату.

Совместное произведение

Крайне важно знать, что тангенциальная скорость — это вектор, то есть у нее есть размер и направление. Векторы обозначены стрелкой над их стандартным символом. Хотя их направление постоянно меняется, их общая ценность остается неизменной. Каждый вектор представляет собой крест или векторное произведение двух векторов, которое является произведением их величин и синуса угла между ними.Результирующий вектор имеет направление, перпендикулярное обоим задействованным векторам.

Почему значение тангенциальной скорости безразлично к ее непрерывно меняющемуся направлению и тангенциальным скоростям с одинаковой величиной, но разными направлениями на произвольных краях окружности.

Два вектора, произведение которых нам требуется, — это радиус «r» и угловая скорость «w». Правило правой руки гласит, что если вы удерживаете ось правой рукой и вращаете пальцы в направлении движения вращающегося тела, то ваш большой палец будет указывать в направлении угловой скорости , явно подразумевает, что

и перпендикулярны друг другу.И поскольку синус 90 равен единице, результирующий перпендикулярный вектор этих величин в любой точке на окружности всегда будет оставаться неизменным.

Интересно, что объекты внутри или на круге имеют одинаковую угловую скорость, но разные тангенциальные скорости. Это связано с его зависимостью от радиуса, как видно из его формулы. Следовательно, люди на краю карусели будут улетать с большей скоростью, чем те, кто сидит в ней глубже.

Почему объекты приобретают большую линейную скорость по мере удаления от центра круга.

Важность тангенциальной скорости

Касательная скорость может наблюдаться во многих случаях, включая любое нелинейное движение, такое как резкий скачок из поворота или отклонение спутника или самой Земли от его круговой орбиты. Круговое движение спутника или нашей Земли происходит в оккультной зоне , где центростремительная сила, тянущая его внутрь, компенсируется линейной скоростью, толкающей его прямо вперед.

Земля перемещается в космос из-за своей линейной или тангенциальной скорости.

Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями

Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями

Теоретична механіка кінематика — Методические указания

ББК 22.21

ББК 22.21

СПИСОК ЛИТЕРАТУРЫ

Средняя угловая скорость начального звена

скорость вращения

Угловая скорость — Википедия

Единицы измерения скорости вращения (угловой скорости …

Суточное вращение Земли — Википедия

Как управлять скоростью вращения кулера на ПК или ноутбуке

Суточное вращение Земли — Википедия

Единицы измерения скорости вращения (угловой скорости …

Настройка скорости вращения кулера на ноутбуке — ВсёПросто

Изменить скорость вращения кулера на Корпусе, CPU и GPU

Как управлять скоростью вращения кулера на ПК или ноутбуке

Выбор правильной скорости вращения фрезы

Скорость вращения Земли

Обороты болгарки: скорость вращения диска в минуту УШМ …

Предельная частота вращения подшипника. — Подшипники в …

BIOS: регулировка скорости вращения вентиляторов — Советы …

1.9.2 Угловая и линейная скорости вращения — Физика по …

. тело движется по окружности радиусом 3м со скоростью 12 …

«С какой скоростью движется планета Земля вокруг …

Центрифуга скорость вращения — Справочник химика 21

Скорость вращения Земли

Скорость вращения шпинделя жесткого диска. Максимальная

. тело движется по окружности радиусом 3м со скоростью 12 …

Центрифуга скорость вращения — Справочник химика 21

Скольжение и скорость вращения ротора — ОБЩАЯ

Обороты болгарки: скорость вращения диска в минуту УШМ …

Регулирование скорости вращения асинхронного двигателя …

Предельная частота вращения подшипника. — Подшипники в …

«С какой скоростью движется планета Земля вокруг …

BIOS: регулировка скорости вращения вентиляторов — Советы …

Как настроить скорость вращения кулеров на компьютере …

С какой скоростью вращается Земля вокруг своей оси? ⚛ физика

Как изменить скорость вращения кулера процессора

Скорости вращения шнека

Оборотов в минуту (rpm — Скорость вращения), частота

Скорость вращения шпинделя жесткого диска. Максимальная

Скорости вращения шнека

Роторы скорость вращения — Справочник химика 21

Как изменить скорость вращения кулера процессора

С какой скоростью вращается Земля вокруг своей оси? ⚛ физика

Предельная частота вращения подшипника. — Подшипники в …

Обороты болгарки: скорость вращения диска в минуту УШМ …

Как настроить скорость вращения кулеров на компьютере …

Технологии управления скоростью вращения вентиляторов …

Скорость вращения галактик — Allbest

Скорость вращения — — Энциклопедия по машиностроению

Регулировка оборотов кулера процессора и видеокарты

Астронет > Вращение солнца

Равномерное движение по окружности | Физика для всех

Периодические движения и определение весов

Угловое смещение, скорость, ускорение

Угловая скорость: определение, формула и примеры — стенограмма видео и урока

Радианы

Угловая скорость

Формулы угловой скорости

Резюме урока

Определение угловой частоты в физике.

Примеры угловой частоты в следующих разделах:

Период и частота

Фазоры

Управляемые колебания и резонанс

Угловое ускорение, Альфа

Волновая природа материи вызывает квантование

Постоянное угловое ускорение

Вращательные столкновения

Сохранение углового момента

Эффект Зеемана и ядерный спин

Транспорт энергии

Период и частота — AP Physics 1

Вычислитель частоты вращения с заданной угловой частотой

Частота вращения при заданной угловой частоте Формула

Как мы получаем частоту вращения, если задана угловая частота?

Как рассчитать частоту вращения по угловой частоте?

Тангенциальная скорость: определение, формула и уравнение