Логические элементы
 В данной статье расскажем что такое логические элементы, рассмотрим самые простые логические элементы.
В данной статье расскажем что такое логические элементы, рассмотрим самые простые логические элементы.
Любое цифровое устройство — персональный компьютер, или современная система автоматики состоит из цифровых интегральных микросхем (ИМС), которые выполняют определённые сложные функции. Но для выполнения одной сложной функции необходимо выполнить несколько простейших функций. Например, сложение двух двоичных чисел размером в один байт происходит внутри цифровой микросхемы называемой «процессор» и выполняется в несколько этапов большим количеством логических элементов находящихся внутри процессора. Двоичные числа сначала запоминаются в буферной памяти процессора, потом переписываются в специальные «главные» регистры процессора, после выполняется их сложение, запоминание результата в другом регистре, и лишь после результат сложения выводится через буферную память из процессора на другие устройства компьютера.
Процессор состоит из функциональных узлов: интерфейсов ввода-вывода, ячеек памяти – буферных регистров и «аккумуляторов», сумматоров, регистров сдвига и т.д. Эти функциональные узлы состоят из простейших логических элементов, которые, в свою очередь состоят из полупроводниковых транзисторов, диодов и резисторов. При конструировании простых триггерных и других электронных импульсных схем, сложные процессоры не применить, а использовать транзисторные каскады – «прошлый век». Тут и приходят на помощь – логические элементы.
Логические элементы, это простейшие «кубики», составные части цифровой микросхемы, выполняющие определённые логические функции. При этом, цифровая микросхема может содержать в себе от одного, до нескольких единиц, десятков, …и до нескольких сотен тысяч логических элементов в зависимости от степени интеграции. Для того, чтобы разобраться,
Начнём с того, что единица цифровой информации это «один бит». Он может принимать два логических состояния – логический ноль «0», когда напряжение равно нулю (низкий уровень), и состояние логической единицы «1», когда напряжение равно напряжению питания микросхемы (высокий уровень).
Поскольку простейший логический элемент это электронное устройство, то это означает, что у него есть входы (входные выводы) и выходы (выходные выводы). И входов и выходов может быть один, а может быть и больше.
Для того, чтобы понять принципы работы простейших логических элементов используется «таблица истинности». Кроме того, для понимания принципов работы логических элементов, входы, в зависимости от их количества обозначают: Х1, Х2, … ХN, а выходы: Y1, Y2, … YN.
Функции, выполняемые простейшими логическими элементами, имеют названия. Как правило, впереди функции ставится цифра, обозначающая количество входов. Простейшие логические элементы всегда имеют лишь один выход.
Рассмотрим простейшие логические элементы
— «НЕ» (NOT)
У элемента «НЕ» всегда один вход и один выход. По таблице истинности следует, что при наличии на входе элемента логического нуля, на выходе будет логическая единица. И наоборот, при наличии на входе логической единицы, на выходе будет логический ноль. Цифра «1» внутри прямоугольника обозначает функцию «ИЛИ», её принято рисовать и внутри прямоугольника элемента «НЕ», но это ровным счётом ничего абсолютно не значит.
Обозначение D1.1 означает, что D — цифровой логический элемент, 1 (первая) — номер микросхемы в общей схеме, 1 (вторая) — номер элемента в микросхеме. Точно также расшифровываются и другие логические элементы.
Часто, чтобы отличить цифровые микросхемы от аналоговых микросхем, применяют обозначения из двух букв: DD – цифровая микросхема, DA – аналоговая микросхема. В последующем, мы не будем заострять внимание на это обозначение, а вернёмся лишь тогда, когда это будет необходимым.
Самой распространённой микросхемой «транзисторно-транзисторной логики» (ТТЛ), выполняющей функцию «НЕ», является интегральная микросхема (ИМС) К155ЛН1, внутри которой имеется шесть элементов «НЕ». Нумерация выводов этой микросхемы показана справа.
— «И» (AND) – функция сложения (если на всех входах единица, то на выходе будет единица, в противном случае, если хотя бы на одном входе ноль, то и на выходе всегда будет ноль). В алгебре-логике элемент «И» называют «конъюнктор». Графическое обозначение элемента «2И» и его таблица истинности представлены слева.
Название элемента «2И» обозначает, что у него два входа, и он выполняет функцию «И». На схеме внутри прямоугольника микросхемы рисуется значок «&», что на английском языке означает «AND» (в переводе на русский — И).
По таблице истинности следует, что на выходе элемента «И» будет логическая единица только в одном случае — когда на обоих входах будет логическая единица. Если хотя бы на одном входе ноль, то и на выходе будет ноль.
Самой распространённой микросхемой «транзисторно-транзисторной логики» (ТТЛ), выполняющей функцию «2И», является интегральная микросхема (ИМС) К155ЛИ1, внутри которой имеется четыре элемента «2И». Нумерация выводов этой микросхемы показана справа.
Для того, чтобы вам было понятнее что такое «2И», «3И», «4И», и т.д., приведу графическое обозначение и таблицу истинности элемента «3И».
По таблице истинности следует, что на выходе элемента «3И» будет логическая единица только в том случае — когда на всех трёх входах будет логическая единица. Если хотя бы на одном входе будет логический ноль, то и на выходе элемента также будет логический ноль. Самой распространённой микросхемой ТТЛ, выполняющей функцию «3И», является микросхема К555ЛИ3, внутри которой имеется три элемента «3И».
— «И-НЕ» (NAND) – функция сложения с отрицанием (если на всех входах единица, то на выходе будет ноль, в противном случае на выходе всегда будет единица). Графическое обозначение элемента «2И-НЕ» и его таблица истинности приведены слева.
По таблице истинности следует, что на выходе элемента «2И-НЕ» будет логический ноль только в том случае, если на обоих входах будет логическая единица. Если хотя бы на одном входе ноль, то на выходе будет единица.
Самой распространённой микросхемой ТТЛ, выполняющей функцию «2И-НЕ», является ИМС К155ЛА3, а микросхемами КМОП (комплементарный металлооксидный полупроводник) – ИМС К561ЛА7 и К176ЛА7, внутри которых имеется четыре элемента «2И-НЕ». Нумерация выводов этих микросхем показана справа.
Сравнив таблицы истинности элемента «2И-НЕ» и элемента «2И» можно догадаться об эквивалентности схем:
Добавив к элементу «2И» элемент «НЕ» мы получили элемент «2И-НЕ». Так можно собрать схему, если нам необходим элемент «2И-НЕ», а у нас в распоряжении имеются только элементы «2И» и «НЕ».
И наоборот:
Добавив к элементу «2И-НЕ» элемент «НЕ» мы получили элемент «2И». Так можно собрать схему, если нам необходим элемент «2И», а у нас в распоряжении имеются только элементы «2И-НЕ» и «НЕ».
Аналогичным образом, путём соединения входов элемента «2И-НЕ» мы можем получить элемент «НЕ»:
Обратите внимание, что было введено новое в обозначении элементов – дефис, разделяющий правую и левую часть в названии «2И-НЕ». Этот дефис непременный атрибут при инверсии на выходе (функции «НЕ»).
— «ИЛИ» (OR) – функция выбора (если хотя бы на одном из входов – единица, то на выходе – единица, в противном случае на выходе всегда будет ноль). В алгебре-логике, элемент «ИЛИ» называют «дизъюнктор». Графическое обозначение элемента «2ИЛИ» и его таблица истинности приведены слева.
Самой распространённой микросхемой ТТЛ, выполняющей функцию «2ИЛИ», является ИМС К155ЛЛ1, внутри которой имеется четыре элемента «2ИЛИ». Нумерация выводов этой микросхемы показана справа.
Предположим, что нам в схеме необходим элемент, выполняющий функцию «2ИЛИ», но у нас есть в распоряжении только элементы «НЕ» и «2И-НЕ», тогда можно собрать схему, которая будет выполнять функцию «2ИЛИ»:
— «ИЛИ-НЕ» (NOR) – функция выбора (если хотя бы на одном из входов – единица, то на выходе – ноль, в противном случае на выходе всегда будет единица). Как вы поняли, элемент «ИЛИ-НЕ» выполняет функцию «ИЛИ», а потом инвертирует его функцией «НЕ».
Графическое обозначение элемента «2ИЛИ-НЕ» и его таблица истинности приведена слева.
Самой распространённой микросхемой ТТЛ, выполняющей функцию «2ИЛИ-НЕ», является ИМС К155ЛЕ1, а микросхемами КМОП – К561ЛЕ5 и К176ЛЕ5, внутри которых имеется четыре элемента «2ИЛИ-НЕ». Нумерация выводов этих микросхем показана справа.
Предположим, что нам в схеме необходим элемент, выполняющий функцию «2ИЛИ-НЕ», но у нас есть в распоряжении только элементы «НЕ» и «2И-НЕ», тогда можно собрать следующую схему, которая будет выполнять функцию «2ИЛИ-НЕ»:
По аналогии с элементом «2И-НЕ», путём соединения входов элемента «2ИЛИ-НЕ» мы можем получить элемент «НЕ»:
— «Исключающее ИЛИ» (XOR) — функция неравенства двух входов (если на обоих входах элемента одинаковые сигналы, то на выходе – ноль, в противном случае на выходе всегда будет единица). Операция, которую он выполняет, часто называют «сложение по модулю 2».
Графическое обозначение элемента «Исключающее ИЛИ» и его таблица истинности приведены слева.
Самой распространённой микросхемой ТТЛ, выполняющей функцию «Исключающее ИЛИ», является ИМС К155ЛП5, а микросхемами КМОП – К561ЛП2 и К176ЛП2, внутри которых имеется четыре элемента «Исключающее ИЛИ». Нумерация выводов этих микросхем показана справа.
Предположим, что нам в схеме необходим элемент, выполняющий функцию «Исключающее ИЛИ», но у нас есть в распоряжении только элементы «2И-НЕ», тогда можно собрать следующую схему, которая будет выполнять функцию «Исключающее ИЛИ»:
В цифровой схемотехнике процессоров главная функция — «Суммирование двоичных чисел», поэтому сложный логический элемент – «Сумматор» является неотъемлемой частью арифметико-логического устройства любого, без исключения процессора. Составной частью сумматора является набор логических элементов, выполняющих функцию «Исключающее ИЛИ с переносом остатка». Что это такое? В соответствии с наукой «Информатика», результатом сложения двух двоичных чисел, две единицы одного разряда дают ноль, при этом формируется «единица переноса» в следующий старший разряд, который участвует в операции суммирования в старшем разряде. Для этого в схему добавляется ещё один вывод «переноса» — «Р».
Графическое обозначение элемента «Исключающее ИЛИ с переносом» и его таблица истинности представлена слева.
Такая функция сложения одноразрядных чисел в простых устройствах обычно не используется, и как правило, интегрирована в состав одной микросхемы – сумматора, с минимальным количеством разрядов – четыре, для сложения четырехбитных чисел. По причине слабого спроса, промышленность таких логических элементов не выпускает. Поэтому, в случае необходимости, функцию «Исключающее ИЛИ с переносом» можно собрать по следующей схеме из элементов «2И-НЕ» и «2ИЛИ-НЕ», которая активно применяется как внутри простых сумматоров, так и во всех сложных процессорах (в том числе Pentium, Intel-Core, AMD и других, которые появятся в будущем):
Вышеперечисленные логические элементы выполняют статические функции, а на основе них строятся более сложные статические и динамические элементы (устройства): триггеры, регистры, счётчики, шифраторы, дешифраторы, сумматоры, мультиплексоры.
meanders.ru
Схемная реализация логических элементов И-ИЛИ-НЕ и других
Для выполнения логических операций и решать логические задачи с помощью средств электроники были изобретены логические элементы. Их создают с помощью диодов, транзисторов и комбинированных элементов (диодно-транзисторные). Такая логика получила название диодной логики (ДЛ), транзисторной (ТЛ) и диодно–транзисторной (ДТЛ). Используют как полевые, так и биполярные транзисторы. В последнем случае предпочтение отдается устройствам типа n-p-n, так как они обладают большим быстродействием.
Логический элемент «ИЛИ»
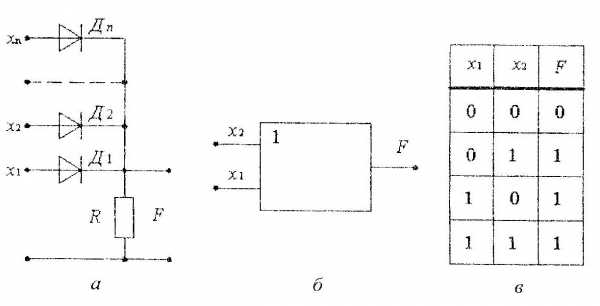
Схема логического элемента «ИЛИ» представлена на рисунке 1 а. На каждый из входов может подаваться сигнал в виде какого-то напряжения (единица) или его отсутствия (ноль). На резисторе R появиться напряжение даже при его появлении на каком – либо из диодов.
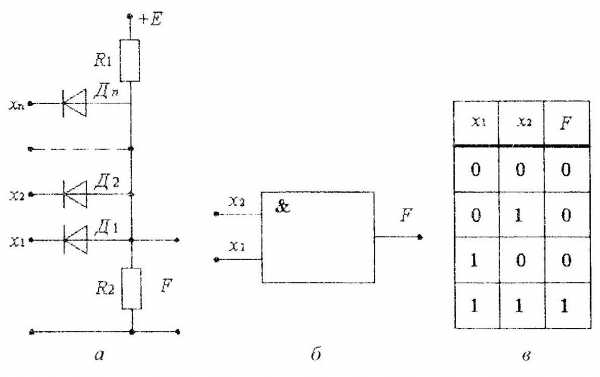 Рис. 1
Рис. 1Элементы или могут иметь несколько логических входов. Если используются не все входы, то те входы которые не используются следует соединять с землей (заземлять), чтобы избежать появления посторонних сигналов.
На рисунке 1б показано обозначение на электрической схеме элемента, а на 1в таблица истинности.
Логический элемент «И»
Схема элемента приведена на рис. 2. Если хотя – бы к одному из входов будет сигнал равный нулю, то через диод будет протекать ток. Падение напряжения на диоде стремится к нулю, соответственно на выходе тоже будет ноль. На выходе сможет появится сигнал только при условии, что все диоды будут закрыты, то есть на всех входах будет сигнал. Рассчитаем уровень сигнала на выходе устройства:
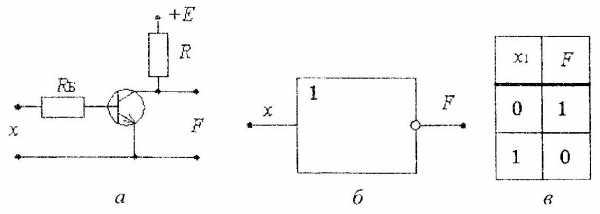 Рис.2
Рис.2на рис. 2 б – обозначение на схеме, в – таблица истинности.
Логический элемент «НЕ»
В логическом элементе «НЕ» используют транзистор (рис.3 а). при наличии положительного напряжения на входе х=1 транзистор открывается и напряжение его коллектора стремится к нулю. Если х=0 то положительного сигнала на базе нет, транзистор закрыт, ток не проходит через коллектор и на резисторе R нет падения напряжения, соответственно на коллекторе появится сигнал Е. условное обозначение и таблица истинности приведены на рис. 3 б,в.
 Рис.3
Рис.3Логический элемент «ИЛИ-НЕ»
При создании различных схем на логических элементах часто применяют элементы комбинированные. В таких элементах совмещены несколько функций. Принципиальная схема показана на рис. 4 а.
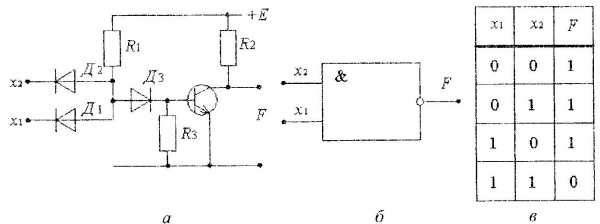 Рис.4
Рис.4Здесь диоды Д1 и Д2 выполняют роль элемента «ИЛИ», а транзистор играет роль инвертора. Обозначение элемента на схеме и его таблица истинности рис. 4б и в соответственно.
Логический элемент «И-НЕ»
Показана схема на рис. 5 а. Здесь диод Д3 выполняет роль так сказать фильтра во избежание искажения сигнала. Если на вход х1 или х2 не подан сигнал (х1=0 или х2=0), то через диод Д1 или Д2 будет протекать ток. Падение на нем не равно нулю и может оказаться достаточным для открытия транзистора. Последствием чего может стать ложное срабатывание и на выходе вместо единицы мы получим ноль. А если в цепь включить Д3, то на нем упадет значительная часть напряжения открытого на входе диода, и на базу транзистора практически ничего не приходит. Поэтому он будет закрыт, а на выходе будет единица, что и требуется при наличии нуля на каком либо из входов. На рис. 5б и в показаны таблица истинности и схемное обозначение данного устройства.
 Рис.5
Рис.5Логические элементы получили широчайшее применение в электронике и микропроцессорной технике. Многие системы управления строятся с использованием именно этих устройств.
elenergi.ru
5. Логические элементы цифровых устройств
Логические элементы — это электронные устройства, предназначенные для обработки информации представленной в виде двоичных кодов, отобpажаемыx напpяжeниeм (сигналом) выcoкого и низкого уpовня. Логические элементы реализyют логические функции И, ИЛИ, НЕ и их комбинации. Указанные логические операции выполняются с помощью электронных схем, входящих в состав микросхем. Из логических элементов И, ИЛИ, НЕ, можно сконстpуировать цифровое электронное устройство любой сложности.
Логические элементы могут выполнять логические функции в режимах положительной и отрицательной логики. В режиме положительной логики логической единице соответствует высокий уровень напряжения, а логическому нулю — низкий уровень напряжения. В режиме отрицательной логики наоборот логической единице соответствует низкий уровень напряжения, а логическому нулю — высокий.
Если в режиме положительной логики логический элемент, реализует операцию И, то в режиме отрицательной логики выполняет операцию ИЛИ, и наоборот. И если в режиме положительной логики — И-НЕ, то в режиме отрицательной логики — ИЛИ-НЕ.
Условное графическое обозначение логического элемента представляет собой прямоугольник, внутри которого ставится изображение указателя функции. Входы изображают линиями с левой стороны прямоугольника, выходы элемента — с правой стороны. При необходимости разрешается располагать входы сверху, а выходы снизу. У логических элементов И, ИЛИ может быть любое начиная с двух количество входов и один выход. У элемента НЕ один вход и один выход. Если вход обозначен окружностью, то это значит, что функция выполняется для сигнала низкого уровня (отрицательная логика). Если окружностью обозначен выход, то элемент производит логическое отрицание (инверсию) результата операции, указанной внутри прямоугольника.
Все цифровые устройства делятся на комбинационные и на последовательностные. В комбинационных устройствах выходные сигналы в данный момент времени однозначно определяются входными сигналами в тот же момент. Выходные сигналы последовательностного устройства (цифрового автомата) в данный момент времени определяются не только логическими переменными на его входах, но еще зависят и от предыдущего состояния этого устройства. Логические элементы И, ИЛИ, НЕ и их комбинации являются комбинационными устройствами. К последовательностным устройствам относятся триггеры, регистры, счетчики.
Логический элемент И (рис. 1) выполняет операцию логического умножения (конъюнкцию). Такую операцию обозначают символом /\ или значком умножения (·). Если все входные переменные равны 1, то и функция Y=X1·X2 принимает значение логической 1. Если хотя бы одна переменная равна 0, то и выходная функция будет равна 0.
Таблица 1 | ||||
Y=X1·X2 | X1 | X2 | Y | |
0 | 0 | 0 | ||
0 | 1 | 0 | ||
1 | 0 | 0 | ||
Рис. 1 | 1 | 1 | 1 |
Наиболее наглядно логическая функция характеризуется таблицей, называемой таблицей истинности (Табл. 1). Талица истинности содержит всевозможные комбинации входных переменных Х и соответствующие им значения функции Y. Количество комбинаций составляет 2n, где n – число аргументов.
Логичеcкий элeмент ИЛИ (рис. 2) выполняет операцию логического сложения (дизъюнкцию). Обозначают эту операцию символом \/ или знаком сложения (+). Функция Y=X1\/X2 принимает значение логической 1, если хотя бы одна переменная равна 1. (Табл. 2).
Таблица 2 | ||||
Y=X1\/X2 | X1 | X2 | Y | |
0 | 0 | 0 | ||
0 | 1 | 1 | ||
1 | 0 | 1 | ||
Рис. 2 | 1 | 1 | 1 |
Логический элемент НЕ (инвертор) выполняет операцию логического отрицания (инверсию). При логическом отрицании функция Y принимает значение противоположное входной переменной Х (Табл. 3). Эту операцию обозначают .
Таблица 3 | |||
Y= | X1 | Y | |
0 | 1 | ||
Рис. 3 | 1 | 0 |
Кроме указанных выше логических элементов, на практике широко используются элементы И-НЕ, ИЛИ-НЕ, Исключающее ИЛИ.
Логичеcкий элемeнт И-НЕ (рис. 4) выполняет операцию логического умнoжения над входными переменными, а затем инвертирует полученный результат и выдаёт его на выход.
Таблица 4 | ||||
X1 | X2 | Y | ||
0 | 0 | 1 | ||
0 | 1 | 1 | ||
1 | 0 | 1 | ||
Рис. 4 | 1 | 1 | 0 |
Логический элемент ИЛИ-НЕ (рис. 5) выполняет операцию логического сложения над входными переменными, а затем инвертирует полученный результат и выдаёт его на выход.
Таблица 5 | ||||
X1 | X2 | Y | ||
0 | 0 | 1 | ||
0 | 1 | 0 | ||
1 | 0 | 0 | ||
Рис. 5 | 1 | 1 | 0 |
Логический элемент Исключающее ИЛИ представлен на рис. 6. Логическая функция Исключающее ИЛИ (функция «неравнозначность» или сумма по модулю два) записывается в виде и принимает значение 1 при X1≠X2, и значение 0 при X1=X2=0 или X1=X2=1 (Табл. 6).
Таблица 6 | ||||
Y=X1X2 | X1 | X2 | Y | |
0 | 0 | 0 | ||
0 | 1 | 1 | ||
1 | 0 | 1 | ||
Рис. 6 | 1 | 1 | 0 |
Любой из выше перечисленных элементов можно заменить устройством, собранным только из базовых двухвходовых элементов ИЛИ-НЕ или И-НЕ. Например: операция НЕ (рис. 7, а) приX1 = X2 = X; операция И (рис. 7, б) .
Рис. 7
Интегральные логические элементы выпускаются в стандартных корпусах с 14 или 16 выводами. Один вывод используется для подключения источника питания, еще один является общим для источников сигналов и питания. Оставшиеся 12 (14) выводов используют как входы и выходы логических элементов. В одном корпусе может находится несколько самостоятельных логических элементов. На рисунке 8 показаны условные графические обозначения и цоколевка (нумерация выводов) некоторых микросхем.
К155ЛЕ1 К155ЛА3 К155ЛП5
Рис. 8
Базовый элемент транзисторно-транзисторной логики (ТТЛ). На рисунке 9 показана схема логического элемента И-НЕ ТТЛ с простым однотранзисторным ключом.
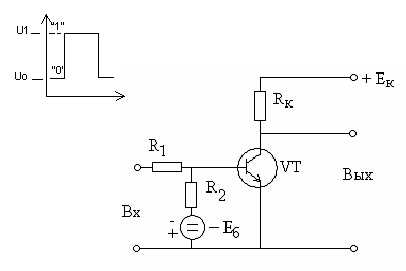 Рис.
9
Рис.
9
Простейший логический элемент ТTЛ строится на базе многоэмиттерного транзистор VT1. Пpинцип дейcтвия такого транзистора тот же, что и у обычного биполяpного транзистора. Oтличие заключается в том, что инжекция носителей заряда в базу осуществляется через несколько самостoятельных эмиттерных р—n-переходов. При поступлении на входы логической единицы U1вх, запираются все эмиттерные переxоды VT1. Ток, текущий через резистор Rб, замкнется через открытые р-n—переходы: коллектoрный VT1 и эмиттерный VT2. Этoт ток откpоет транзиcтор VT2, и напряжение на его выходе станет близким к нулю, т. е. Y=U0вых. Если хотя бы на один вход (или на все входы) VT1 будет подан сигнал логического нуля U0вх, то ток, текyщий по Rб, замкнeтся через откpытый эмиттерный переход VT1. Пpи этoм входной ток VT2 будет близoк к нулю, и выходной транзистоp окажется запеpтым, т. е. Y=U1вых. Таким образом, рассмотренная схема осуществляет логическую операцию И-НЕ.
Контрольные вопросы.
Что называется логическим элементом?
Чем различаются положительная и отрицательная логики?
Что называется таблицей истинности?
Каким символом обозначают логическое умножение?
Как на схемах изображают логический элемент И?
При каких входных переменных на выходе логического элемента И формируется логическая 1?
Каким символом обозначают логическое сложение?
Как на схемах изображают логический элемент ИЛИ?
При каких входных переменных на выходе логического элемента ИЛИ формируется логическая 1?
Как на схемах изображают логический элемент НЕ?
Как на схемах изображают логический элемент И-НЕ?
При каких входных переменных на выходе логического элемента И-НЕ формируется логическая 1?
Как на схемах изображают логический элемент ИЛИ-НЕ?
При каких входных переменных на выходе логического элемента ИЛИ-НЕ формируется логическая 1?
Как на схемах изображают логический элемент Исключающее ИЛИ?
При каких входных переменных на выходе логического элемента Исключающее ИЛИ формируется логическая 1?
Как из элемента ИЛИ-НЕ получить элемент НЕ?
Как из элемента И-НЕ получить элемент НЕ?
Опишите принцип действия базового элемента ТТЛ.
studfiles.net
3 Базовые логические элементы — Сайт el-utmiit!
И, ИЛИ, НЕ и их комбинации
ИЛИ – логическое сложение (дизъюнкция) – OR;
И – логическое умножение (конъюнкция) – AND;
НЕ – логическое отрицание (инверсия) – NOT.
Логические элементы являются «кирпичиками» для построения различных узлов цифровой схемотехники. Например, слева схема мультиплексора, справа цифрового компаратора.
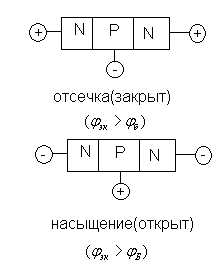
Примем за основу позитивную логику, где высокий уровень будет «1», а низкий уровень примем за «0». Чтобы можно было более наглядно рассмотреть выполнение логических операций, существуют таблицы истинности для каждой логической функции. Сразу нетрудно понять, что выполнение логических функций «и» и «или» подразумевают количество входных сигналов не менее двух, но их может быть и больше.
Простейшие логические схемы
Реализацию логических выражений можно осуществить с помощью простых электронных схем, на входы которых поступают электрические входные сигналы, а на выходе формируется выходной сигнал, который соответствует логической функции.
1. Логический элемент И. Представляет собой схему, в которой сигнал 1 на выходе появляется только тогда, когда на входе А и входе В совпадают сигналы 1. Простейший логический элемент И может быть реализован на последовательно включённых контактах реле, управляемых с помощью кнопок.
Релейно-контактная схема элемента И
Условное обозначение логического элемента И с двумя входами показано ниже. На выходе логического элемента И сигнал 1 появится только тогда, когда на всех входах совпадут сигналы 1.
Условное графическое изображение логического элемента И
2. Логический элемент ИЛИ. Представляет собой схему, на выходе которой появляется сигнал 1, если на входе А или входе В или на обоих входах присутствует сигнал 1. Простейший логический элемент ИЛИ может быть реализован на параллельно включённых контактах реле, управляемых с помощью кнопок.
Релейно-контактная схема элемента ИЛИ
Условное обозначение логического элемента ИЛИ с двумя входами показано ниже. На выходе логического элемента ИЛИ сигнал 1 появится в случае появления хотя бы на одном из входов сигнала 1.
Условное графическое изображение логического элемента ИЛИ
3. Логический элемент НЕ. Представляет собой схему, на выходе А которой появляется сигнал 1 при отсутствии на входе А сигнала 1. Простейший логический элемент НЕ реализован на реле с нормально замкнутыми контактами.
Релейно-контактная схема элемента НЕ
Условное обозначение логического элемента НЕ показано ниже. На выходе логического элемента НЕ сигнал 1 появится в случае отсутствия сигнала 1 на входе
Условное графическое изображение логического элемента НЕ
Логические элементы И, ИЛИ и не предназначены для выполнения трёх основных операций цифровой логики над дискретными сигналами. С помощью этих элементов можно реализовать логические операции любой сложности. Поэтому эти элементы называются основными.
Примеры применения логических элементов
Генераторы импульсов
Преобразователи формы сигналов
Перевод чисел из десятичной системы в двоичную систему осуществляется последовательным делением числа на 2. Первое деление даёт младший разряд, а последнее деление даёт старший разряд числа. Если число делится без остатка, пишем «0», а с остатком пишем «1». 201310 = 111110111012, что означает, текущий год по основанию 10 равен указанному числу по основанию 2. Для обратного преобразования достаточно суммировать веса разрядов представляющие собой степени числа 2. Число разряда начинается с 0, затем 1, 2,3…10. Для данного примера получим: 1024+512+256+128+64+16+8+4+1=2013. Пропущены второй и шестой разряды, где стоят нули, то есть 2 и 32.
Двоичное число легко представить в виде последовательности прямоугольных импульсов.
На рисунке показано напряжение питания +5,0V. На таком напряжении питания работают интегральные микросхемы транзисторно-транзисторной логики (ТТЛ) с малой степенью интеграции, которые в своё время пользовались огромной популярностью у радиолюбителей. Их используют и сейчас в несложных самоделках. Это микросхемы серий К155, К133 и микросхемы высокого быстродействия и более высокой частоты КР1533 и К555. В них использовались диоды Шоттки.
Уровень логической единицы не обязательно должен быть уровнем +5,0V, как показано на рисунке. Логическая единица могла находиться в интервале от + 2,4V до +5V, а логический ноль в интервале от 0V до +0,4V. Если на выходе микросхемы при проверке еёосциллографом на выходе оказывалось напряжение в интервале от +0,4 до +2,4, то такое состояние называли «серый» уровень. Он означал:
- а) неисправна данная микросхема;
- в) эту микросхему подсаживает следующая за ней микросхема.
Поскольку микросхемы бывают с разным напряжением питания, то и уровни логического нуля и логической единицы будут иметь другие значения. Логику, где логическая единица положительна, принято называть позитивной логикой. Есть схемы, где логическая единица равна нулю, а логический ноль это импульс отрицательной полярности.
Примеры применения логических элементов для выбора числового значения при котором необходимо включить исполнительное устройство.
Данная схема включает светодиод на 5 и 7
Ниже приведена схема счета до 5.
На выходе получаем код 0110 — это число 6, и этот код сбрасывает счетчик в ноль, но на индикаторе мы видим счет от 0 до 5.
Перевод чисел. Используем бесконечный ряд и пишем числа справа налево
Переведем число 57 из десятичной в двоичную.
Подставляем единички к тем числам, сумма которых даст 57
128 64 32 16 8 4 2 1
0 0 1 1 1 0 0 1
128*0+64*0+ 32*1+16*1+8*1+4*0+2*0+1 = 57
Получили двоичный код числа 57 это 111001
el-utmiit.jimdo.com
Основные логические элементы и схемы их построения
Логические основы работы компьютера
Знания из области математической логики можно использовать для конструирования электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого-то предмета нашего мира, условно называемых “ложь” и “истина”. Таким предметом, имеющим два фиксированных состояния, может быть электрический ток.
Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, обозначаемые условно 0, если “отсутствует” электрический сигнал, и 1, если “имеется” электрический сигнал.
Базовые логические элементы реализуют три основные логические операции: «И», «ИЛИ», «НЕ».
Логический элемент «НЕ» (инвертор)
Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.
У этого элемента один вход и один выход. На функциональных схемах он обозначается:
Говорят также, что элемент «НЕ» инвертирует значение входной двоичной переменной.
Проверь соответствие логического элемента “НЕ” логическому элементу “НЕ”. Воспользуйся тренажером Логические элементы.xlsx
Логический элемент «И» (конъюнктор)
Логический элемент «И» (конъюнктор) выдает на выходе значение логического произведения входных сигналов.
Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
Сигнал на выходе конъюнктора появляется тогда и только тогда, когда поданы сигналы на все входы. На элементарном уровне конъюнкцию можно представить себе в виде последовательно соединенных выключателей. Известным примером последовательного соединения проводников является елочная гирлянда: она горит, когда все лампочки исправны. Если же хотя бы одна из лампочек перегорела, то гирлянда не работает.
Проверь соответствие логического элемента “И” логическому элементу “И”. Воспользуйся тренажером Логические элементы.xlsx
Логический элемент «ИЛИ» (дизъюнктор)
Логический элемент «ИЛИ» (дизъюнктор) выдает на выходе значение логической суммы входных сигналов. Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
Сигнал на выходе дизъюнктора не появляется тогда и только тогда, когда на все входы не поданы сигналы.
На элементарном уровне дизъюнкцию можно представить себе в виде параллельно соединенных выключателей.
Примером параллельного соединения проводников является многорожковая люстра: она не работает только в том случае, если перегорели все лампочки сразу.
Проверь соответствие логического элемента “ИЛИ” логическому элементу “ИЛИ”. Воспользуйся тренажером Логические элементы.xlsx
Пример 1.
Составьте логическую схему для логического выражения: F=A \/ B /\ A.
1. Две переменные – А и В.
2. Две логические операции: 1-/\, 2-\/.
3. Строим схему:
Пример 2.
Постройте логическую схему, соответствующую логическому выражению F=А/\В\/ ¬(В\/А). Вычислить значения выражения для А=1,В=0.
1. Переменных две: А и В; 1 4 3 2
2. Логических операций три: /\ и две \/; А/\В\/ ¬ (В\/ А).
3. Схему строим слева направо в соответствии с порядком логических операций:
4. Вычислим значение выражения: F=1 /\ 0 \/ ¬(0 \/ 1)=0
mir-logiki.ru
7.2. Логические элементы
Логические операции реализуются с использованием электрических схем, которые называются логическими элементами. Они изготавливаются в виде интегральных микросхем в большинстве своем на базе диодов и транзисторов, либо только транзисторов. В связи с этим различают два типа логических элементов: ДТЛ (диодно-транзисторная логика) и ТТЛ (транзисторно-транзисторная логика). На рис. 7.2 представлены схемные обозначения элементов, выполняющих простейшие логические операции. При этом элементы “ИЛИ” и “И” – двухвходовые, т.е. выполняющие операции с двумя входными переменными. Однако промышленностью выпускаются логические элементы “ИЛИ” и “И” с большим числом входных клемм.
Рисунок 7.2. Схемное обозначение логических элементов
На рис. 7.3 приведена
схема на диодах, с помощью которой
реализуется операция логического
сложения. Действительно, при отсутствии
на входах этой схемы сигналов (x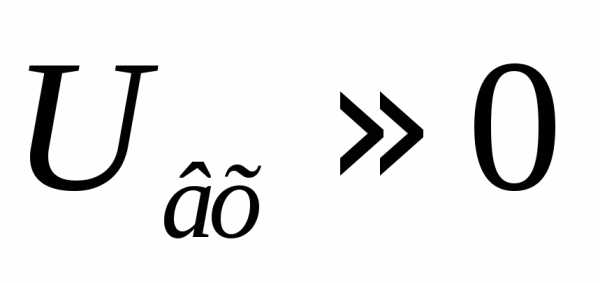 = 0, гдеi
= 1, 2, …
n)все диоды будут находиться в закрытом
состоянии и на резисторе падение
напряжения равно нулю(F
= 0).При
подаче хотя бы на один вход схемы сигнала
положительной полярности диод,
установленный на этом входе, перейдет
в открытое состояние. Через него и
последовательно включенный с ним
резисторRбудет протекать ток, падение напряжения
на резисторе будет отличаться от нуля.F
= 1.
= 0, гдеi
= 1, 2, …
n)все диоды будут находиться в закрытом
состоянии и на резисторе падение
напряжения равно нулю(F
= 0).При
подаче хотя бы на один вход схемы сигнала
положительной полярности диод,
установленный на этом входе, перейдет
в открытое состояние. Через него и
последовательно включенный с ним
резисторRбудет протекать ток, падение напряжения
на резисторе будет отличаться от нуля.F
= 1.

Рисунок 7.3. Реализация Рисунок 7.4. Реализация логической логической операции операции «И» на диодах
«ИЛИ» на диодах
Нетрудно также
показать, что схема на рис. 7.4 обеспечивает
выполнение операции “И”. Через резистор
R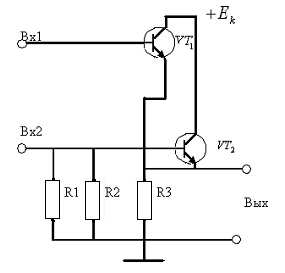 будет протекать ток, и с этого резистора
будет сниматься напряжение, равноеUвых = ER
будет протекать ток, и с этого резистора
будет сниматься напряжение, равноеUвых = ER /(R
/(R + R
+ R ),
т.е. F
= 1, когда катоды всех диодов будут
под положительным потенциалом, превышающим
величинуUвых (x
),
т.е. F
= 1, когда катоды всех диодов будут
под положительным потенциалом, превышающим
величинуUвых (x = 1), а, следовательно, все диоды будут
закрыты. Если хотя бы на одном входе
схемы сигнал отсутствует, соответствующий
диод будет открыт, и через него будет
протекать ток в обход резистораR
= 1), а, следовательно, все диоды будут
закрыты. Если хотя бы на одном входе
схемы сигнал отсутствует, соответствующий
диод будет открыт, и через него будет
протекать ток в обход резистораR ,
поскольку его сопротивление выбирается
много больше сопротивления открытого
диода. Падение напряжения на резистореR
,
поскольку его сопротивление выбирается
много больше сопротивления открытого
диода. Падение напряжения на резистореR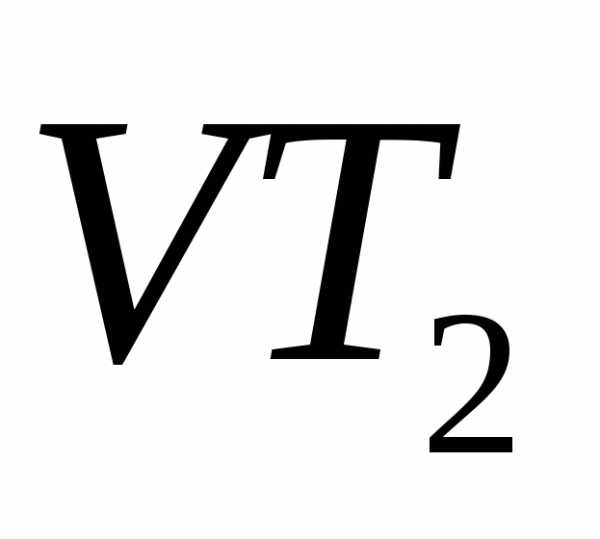 в данном случае будет равно нулю.F
= 0.
в данном случае будет равно нулю.F
= 0.
Операция “НЕ” может быть реализована на биполярном транзисторе типа n—p—n, включенного по параллельному варианту построения ключевой схемы (рис. 4.2.а). Как было показано в разделе 4.1, при подаче на вход схемы сигнала положительной полярности определенного уровня(x = 1) транзистор будет находиться в открытом состоянии, т.е. в точке “б” на рис. 4.4,б. Этому режиму транзистора соответствует очень малая величина напряжения коллектор-эмиттер, ΔUКЭ ОТК, которая является выходом схемы, F = 0. При отсутствии на входе сигнала(x = 0)транзистор будет закрыт (точка «а» на рис. 4.4,в), и с выхода схемы снимается напряжение, практически равное+Е, т.е. F = 1.
Следует отметить, что напряжение на выходе схем рис.7.3 и 7.4, равное нулю, обеспечиваются лишь при идеальном шунтировании резистора, с которого снимается выходное напряжение открытыми диодами. При реализации логической операции «НЕ» из-за наличия остаточного напряжения на открытом транзисторе выходное напряжение также отличается от нуля. Таким образом, в реальных логических элементах логическим нулем, фактически, является не нулевое, а малая величина напряжения. В связи с этим в справочных данных обычно вместо «0» указывается «н» (низкий уровень напряжения) и соответственно вместо «1» указывается «в» (высокий уровень напряжения).
Логические элементы выпускаются промышленностью в виде серий. Элементы каждой серии, выполняющие различные операции, могут сопрягаться в сложную схему логического устройства. Элементы серии создаются на базе основного элемента, который обычно выполняет операции “ИЛИ-НЕ” или “И-НЕ”. Математическая форма представления этих операций имеет вид:
F = иF = .
Схемы, реализующие операции “ИЛИ-НЕ” и “И-НЕ”, могут быть получены при последовательном соединении двух схем, выполняющих операции соответственно “ИЛИ”-“НЕ” и “И”-“НЕ”, что показано на рис. 7.5,а и 7.6,а для случая двухвходовых элементов. Схемные обозначения элементов “ИЛИ-НЕ” и “И-НЕ” представлены на рис. 7.5,б и 7.6,б, а таблицы истинности – в табл. 7.4 и 7.5.
Рисунок 7.5. Логическая операция «ИЛИ-НЕ»:
а – принцип реализации операции,
б — схемное обозначение логического элемента
Рисунок 7.6. Логическая операция «И-НЕ»:
а – принцип реализации операции,
б — схемное обозначение логического элемента

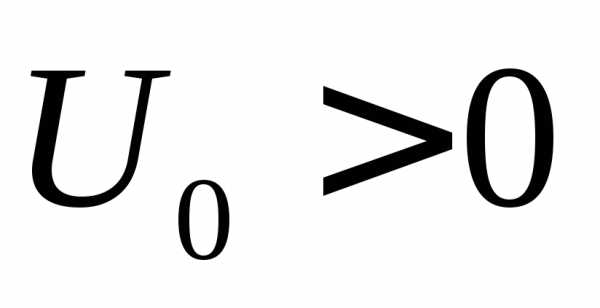
Рисунок 7.7. Реализация логической операции «И-НЕ»
на транзисторах
На рис. 7.7 представлена
схема на транзисторах, реализующая
логическую операцию “И-НЕ”. Особенностью
этой схемы является использование
многоэмиттерного транзистора Т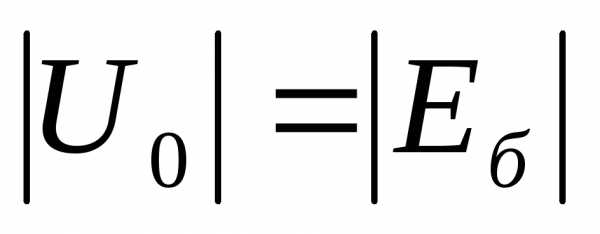 ,
которым заменяется диодная часть
элемента “И-НЕ”, выполняющего операцию
“И”. В многоэмиттерном транзисторе
эмиттерный слой состоит из нескольких
областей при общих базовом и коллекторном
слоях. Принцип работы схемы рис. 7.7
следующий. Если на все эмиттерные входы
транзистораТ
,
которым заменяется диодная часть
элемента “И-НЕ”, выполняющего операцию
“И”. В многоэмиттерном транзисторе
эмиттерный слой состоит из нескольких
областей при общих базовом и коллекторном
слоях. Принцип работы схемы рис. 7.7
следующий. Если на все эмиттерные входы
транзистораТ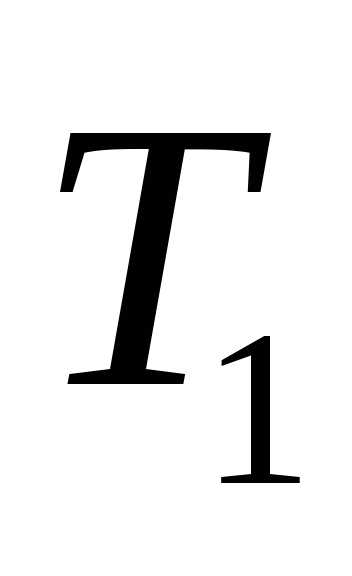 будет подано положительное напряжение,
равноеЕ
будет подано положительное напряжение,
равноеЕ (т.е.
всеx
(т.е.
всеx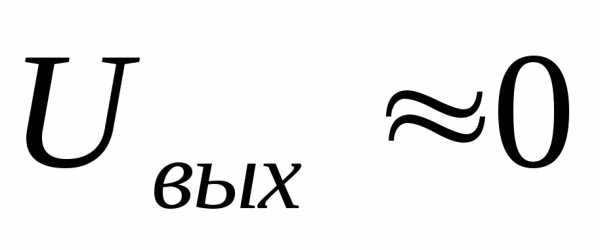 = 1), все
эмиттерные переходы транзистора будут
закрыты, а его ток базы будет протекать
через открытый коллекторный переход,
обусловливая протекание коллекторного
тока, который одновременно является
базовым током транзистораТ
= 1), все
эмиттерные переходы транзистора будут
закрыты, а его ток базы будет протекать
через открытый коллекторный переход,
обусловливая протекание коллекторного
тока, который одновременно является
базовым током транзистораТ .
ТранзисторТ
.
ТранзисторТ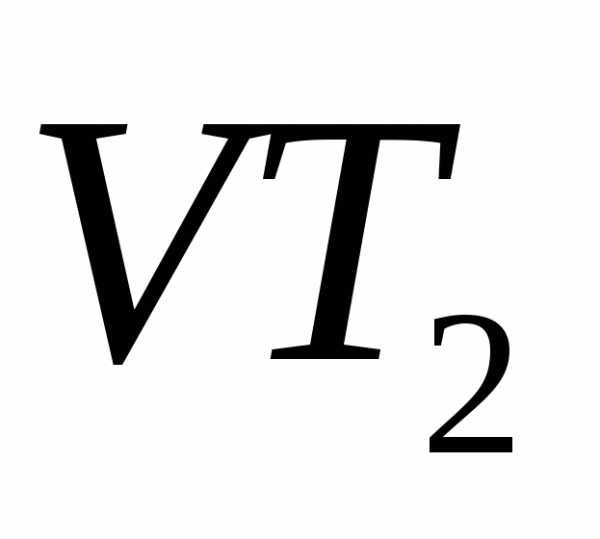 ,
который выполняет операцию логического
отрицания, в этом случае будет находиться
в открытом состоянии, и на его выходе
напряжение будет практически отсутствовать(F
= 0). При отсутствии хотя бы на одном
эмиттерном входе транзистораТ
,
который выполняет операцию логического
отрицания, в этом случае будет находиться
в открытом состоянии, и на его выходе
напряжение будет практически отсутствовать(F
= 0). При отсутствии хотя бы на одном
эмиттерном входе транзистораТ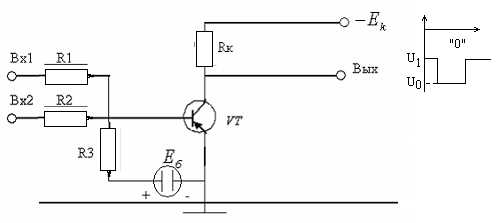 сигнала положительной полярности, ток,
протекающий через резисторRи через соответствующий открытый
эмиттерный переход, будет замыкаться
по цепи этого эмиттерного входа. Базовый
ток транзистораТ
сигнала положительной полярности, ток,
протекающий через резисторRи через соответствующий открытый
эмиттерный переход, будет замыкаться
по цепи этого эмиттерного входа. Базовый
ток транзистораТ будет равен нулю, поскольку суммарное
сопротивление коллекторного перехода
транзистораТ
будет равен нулю, поскольку суммарное
сопротивление коллекторного перехода
транзистораТ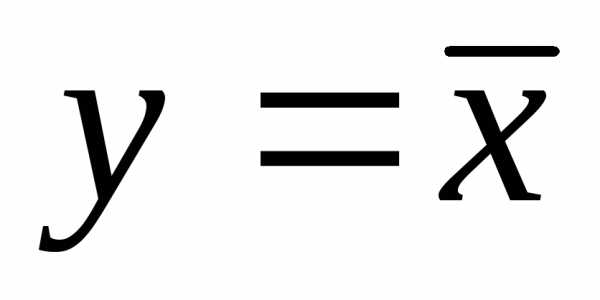 и базового слоя транзистораТ
и базового слоя транзистораТ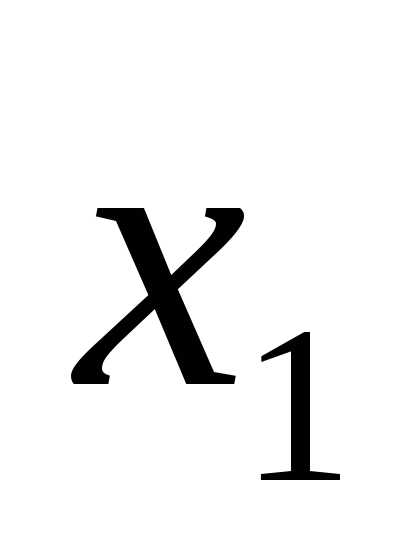 оказывается довольно большим по сравнению
с сопротивлением открытого эмиттерного
перехода транзистораТ
оказывается довольно большим по сравнению
с сопротивлением открытого эмиттерного
перехода транзистораТ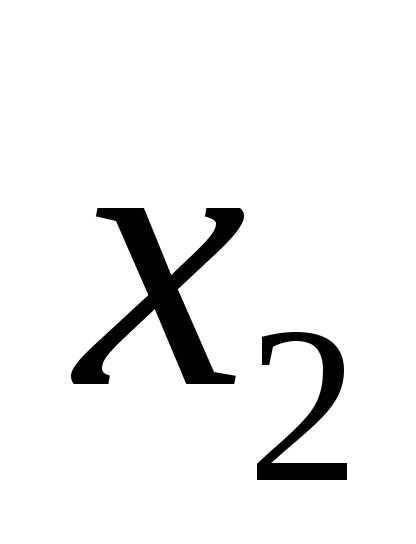 .
ТранзисторТ
.
ТранзисторТ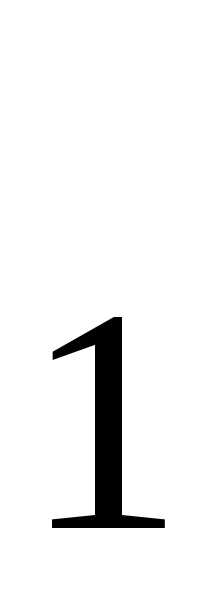 поэтому будет находиться в закрытом
состоянии, и на его выходе напряжение
будет близко к величине+Е
поэтому будет находиться в закрытом
состоянии, и на его выходе напряжение
будет близко к величине+Е ,
т.е.F
= 1.
,
т.е.F
= 1.
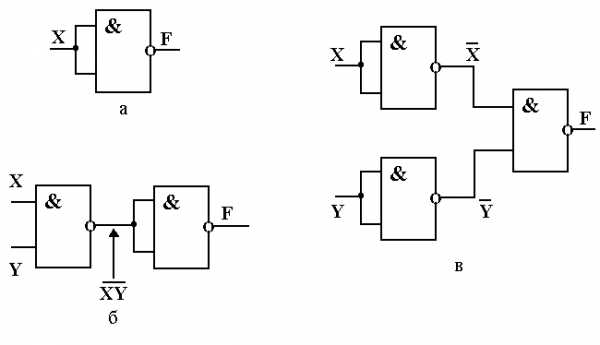
Рисунок 7.8. Схемы реализации логических операций на элементах «И-НЕ»
а – операции «НЕ», б – операции «И», в — операции «ИЛИ»
Логические элементы «ИЛИ-НЕ» и «И-НЕ» называют базовыми, поскольку схемы, составленные только из этих элементов одного типа, позволяют реализовывать простейшие логические операции. Это нетрудно доказать с использованием формул алгебры логики, например, на схемах, составленных из элементов «И-НЕ», которые приведены на рис. 7.8.
На вход элемента схемы рис. 7.8,а подаются две одинаковых переменных x. Поэтому согласно тождествам (7.11) и (7.1)
F
=  =
=  +
+  =
=  .
.
Таким образом, схема рис. 7.8,а выполняет операцию “НЕ”.
В качестве выходного каскада схемы рис. 7.8,б используется элемент “И-НЕ”, включенный по схеме рис. 7.8,а. Он инвертирует информацию, поступающую с входа первого элемента. Если учесть тождество (7.9), то
F
=  =xy.
=xy.
Следовательно, схема рис. 7.8,б выполняет операцию “И”.
Информация,
поступающая на каждый входной элемент
схемы рис. 7.8,в, инвертируется, т.е.  и
и  .
Тогда последовательное использование
тождеств (7.11) и (7.9) позволяет показать,
что эта схема реализует операцию
логического сложения “ИЛИ”
.
Тогда последовательное использование
тождеств (7.11) и (7.9) позволяет показать,
что эта схема реализует операцию
логического сложения “ИЛИ”
F
= 
 =
= +
+ = x + y.
= x + y.
К основным показателям логических элементов, в первую очередь, относят быстродействие, потребляемую мощность и помехоустойчивость. Быстродействие характеризуется временем задержки реакции выходного сигнала при изменении сигнала на входе элемента. Время задержки логических элементов обычно составляет 0,01 – 0,3 мкс. Их потребляемая мощность обычно находится в пределах от 1 мкВт до 250 мВт и связана с быстродействием: потребляющие большую мощность элементы имеют более высокое быстродействие. При работе логических элементов в составе аппаратуры возможны случаи ложного срабатывания под действием напряжений помех, попадающих на вход микросхемы. Мерой невосприимчивости элементов к помехам является помехоустойчивость, которая зависит от структуры микросхемы, режима работы в ней транзисторов, величины питающего напряжения.
studfiles.net
РадиоКот :: Логические элементы
РадиоКот >Обучалка >Цифровая техника >Основы цифровой техники >Логические элементы
Абсолютно все цифровые микросхемы состоят из одних и тех же логических элементов – «кирпичиков» любого цифрового узла. Вот о них мы и поговорим сейчас.
Логический элемент – это такая схемка, у которой несколько входов и один выход. Каждому состоянию сигналов на входах, соответствует определенный сигнал на выходе.
Итак, какие бывают элементы?
Смотрим:
Элемент «И» (AND)
Иначе его называют «конъюнктор».
Для того, чтобы понять как он работает, нужно нарисовать таблицу, в которой будут перечислены состояния на выходе при любой комбинации входных сигналов. Такая таблица называется « таблица истинности ». Таблицы истинности широко применяются в цифровой технике для описания работы логических схем.
Вот так выглядит элемент «И» и его таблица истинности:
Поскольку вам придется общаться как с русской, так и с буржуйской тех. документацией, я буду приводить условные графические обозначения (УГО) элементов и по нашим и по не нашим стандартам.
Смотрим таблицу истинности, и проясняем в мозгу принцип. Понять его не сложно: единица на выходе элемента «И» возникает только тогда, когда на оба входа поданы единицы. Это объясняет название элемента: единицы должны быть И на одном, И на другом входе.
Если посмотреть чуток иначе, то можно сказать так: на выходе элемента «И» будет ноль в том случае, если хотя бы на один из его входов подан ноль. Запоминаем. Идем дальше.
Элемент «ИЛИ» (OR)
По другому, его зовут «дизъюнктор».
Любуемся:
Опять же, название говорит само за себя.
На выходе возникает единица, когда на один ИЛИ на другой ИЛИ на оба сразу входа подана единица. Этот элемент можно назвать также элементом «И» для негативной логики: ноль на его выходе бывает только в том случае, если и на один и на второй вход поданы нули.
Едем дальше. Дальше у нас очень простенький, но очень необходимый элемент.
Элемент «НЕ» (NOT)
Чаще, его называют «инвертор».
Надо чего-нибудь говорить по поводу его работы?
Ну тогда поехали дальше. Следующие два элемента получаются путем установки инвертора на выход элементов «И» и «ИЛИ».
Элемент «И-НЕ» (NAND)
Элемент И-НЕ работает точно так же как «И», только выходной сигнал полностью противоположен. Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» — единица. И наоборот. Э то легко понять по эквивалентной схеме элемента:
Элемент «ИЛИ-НЕ» (NOR)
Та же история – элемент «ИЛИ» с инвертором на выходе.
Следующий товарищ устроен несколько хитрее:
Элемент «Исключающее ИЛИ» (XOR)
Он вот такой:
Операция, которую он выполняет, часто называют «сложение по модулю 2». На самом деле, на этих элементах строятся цифровые сумматоры.
Смотрим таблицу истинности. Когда на выходе единицы? Правильно: когда на входах разные сигналы. На одном – 1, на другом – 0. Вот такой он хитрый.
Эквивалентная схема примерно такая:
Ее запоминать не обязательно.
Собственно, это и есть основные логические элементы. На их основе строятся абсолютно любые цифровые микросхемы. Даже ваш любимый Пентиум 4.
Далее мы позанудствуем о том, как синтезировать цифровую схему, имея ее таблицу истинности. Это совсем несложно, а знать надо, ибо пригодится (еще как пригодится) нам в дальнейшем.
Ну и напоследок – несколько микросхем, внутри которых содержатся цифровые элементы. Около выводов элементов обозначены номера соответствующих ног микросхемы. Все микросхемы, перечисленные здесь, имеют 14 ног. Питание подается на ножки 7 (-) и 14 (+). Напряжение питания – смотри в таблице в предыдущем параграфе.
<<—Вспомним пройденное—-Поехали дальше—>>
Как вам эта статья? | Заработало ли это устройство у вас? |
www.radiokot.ru