Алгебра Буля — это… Что такое Алгебра Буля?
алгебра буля — исторически первый раздел математической логики, разработанный ирландским логиком и математиком Дж. Булем в середине XIX в. Буль применил алгебраические методы для решения логических задач и сформулировал на языке алгебры некоторые… … Словарь терминов логики
АЛГЕБРА ЛОГИКИ — система алгебраич. методов решения логич. задач, а также совокупность задач, решаемых такими методами. А. л. в узком смысле слова алгебраич. (табличное, матричное) построение классич. логики высказываний, в котором рассматриваются… … Философская энциклопедия
алгебра логики — АЛГЕБРА ЛОГИКИ исторически первая форма математической (символической) логики, сложившаяся к последней трети 19 в. К ее созданию привела аналогия между решением алгебраических уравнений и выводом следствий из посылок, а также то, что… … Энциклопедия эпистемологии и философии науки
АЛГЕБРА
Алгебра логики — раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности), и логические операции над ними. А. л. возникла в середине 19 в. в трудах Дж. Буля (См. Буль) и развивалась… … Большая советская энциклопедия
АЛГЕБРА ЛОГИКИ — раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логич. значений (истинности пли ложности), и логич. операций над ними. А. л. возникла в сер. 19 в. в трудах Дж. Буля (см. [1], [2]) и развилась затем в работах Ч … Математическая энциклопедия
БУЛЕВА АЛГЕБРА — БУЛЕВА АЛГЕБРА, область математики, содержащая правила обращения с множествами, а также с логическими утверждениями типа «и», «или». Например, в Булевой алгебре выражение ху означает «х и у», а х+у это «х или у». Данный принцип широко применяется … Научно-технический энциклопедический словарь
БУЛЕВА АЛГЕБРА — булева решетк а, частично упорядоченное множество специального вида. Б. а. наз. дистрибутивная решетка (дистрибутивная структура), имеющая наибольший элемент 1 единицу Б. а., наименьший элемент 0 нуль Б. а. и содержащая вместе с каждым своим… … Математическая энциклопедия
Булева алгебра — (араб.) – система алгебраических операций с символами, названная в честь Д. Буля, одного из её создателей. Также называется калькуляцией (лат. calсulatio – счёт, подсчёт). Интересно, что Д. Буль рассматривал свою работу как представление основных … Энциклопедический словарь по психологии и педагогике
БУЛЕВА АЛГЕБРА — Названная по имени ее создателя, английского математика Джорджа Буля, система операций с символами, которая использует алгебраические процедуры, но независимо от определенных математических интерпретаций. Булева логика, или калькуляция (как она… … Толковый словарь по психологии
dal.academic.ru
Джордж Буль Отец булевой алгебры. Архитекторы компьютерного мира
Джордж Буль
Отец булевой алгебры
Чистая математика была открыта Булем в работе, которую он назвал «Законы мышления».
Бертран Рассел
Джордж Буль
Все механизмы, шестеренки, вакуумные лампы и печатные платы — все это еще не компьютер.
Важны также разработки Паскаля и Лейбница, о которых мы вам уже рассказали, и Бэббиджа, о достижениях которого мы расскажем в следующей главе. Эти разработки требовали первоначальной теории логики для того, чтобы, в конечном счете, вдохнуть жизнь в машины, которые «думают».
Расширив общий метод Лейбница, сформулированный на 188 лет раньше, в котором все истинные причины были сведены к виду вычислений, английский математик Д. Буль в 1854 году заложил основу того, что мы сегодня знаем как математическую логику, опубликовав работу «Исследование законов мышления».
В этой работе, изданной, когда ему было 39 лет, Буль свел логику к чрезвычайно простому типу алгебры, алгебры логики высказываний, которая представляла собой систему символов и правил, применяемую к различным объектам (числам, буквам, предложениям).
Его теория логики, основанная на трех основных действиях — AND (и), OR (или), NOT (не), — должна была стать в XX веке основой для разработки переключающих телефонных линий и проекта ЭВМ. Так же, как и идеями Лейбница, булевой алгеброй пренебрегали в течение многих лет после того, как она была создана.
Важность работы, признанной логиком де Морганом, современником Буля, заключалась в следующем: «Символические процессы алгебры, созданные как инструменты числового вычисления, компетентно выражают каждый закон мысли и обладают грамматикой и словарем всего того, что содержит систему логики. Мы это и не предполагали, пока это не было доказано в „Законах мышления“».
Джордж Буль родился 2 ноября 1815 года в Линкольне (Англия), в семье бедного башмачника. Хотя он был современником Ч. Бэббиджа, но происходил не из привилегированного класса, как Бэббидж.
Выходец из слоя общества, дети которого фактически были лишены посещения университета, Джордж должен был заниматься самостоятельно.
Хотя промышленная революция уже произошла в Англии, знание древних языков было показателем уровня образования джентльмена. Конечно, никакой латинский или греческий не преподавали в школе, которую посещал Буль. Буль сам изучил греческий и латинский, пользуясь поддержкой малообразованного отца, и в возрасте 12 лет сумел перевести оду Хорейса на английский язык. Ничего не понимая в качестве техники перевода, гордый отец Буля все-таки напечатал его в местной газете. Некоторые специалисты заявляли, что 12-летний мальчик не мог сделать такой перевод, другие отмечали серьезные технические дефекты перевода. Решив совершенствовать свои знания латинского и греческого, Буль провел следующие два года в серьезном изучении этих языков, и снова без чьей-либо помощи.
Хотя этих знаний было недостаточно, чтобы превратиться в истинного джентльмена, такая тяжелая работа дисциплинировала его и способствовала классическому стилю созревавшей булевой прозы.
Известно, что его отец оставил школу после трех лет обучения, и в то же время удивительно, что Буль получил раннее математическое образование от своего отца, который был самоучкой в этой области.
В возрасте 16 лет для Буля стало необходимостью начать трудовую жизнь, чтобы помочь своим родителям. Получив работу «младшего учителя», или ассистента учителя в начальной школе, Буль должен был провести 4 года, преподавая в двух различных школах.
Всегда думая о перспективе занимаемого места в жизни, Буль начал рассматривать несколько путей, открытых для него. Его первоначальное преподавание было всегда на уровне, однако он не считал это профессией, хотя она и была почетна. Буль стал священнослужителем.
Когда он не преподавал, то проводил время в серьезном изучении французского, немецкого и итальянского языков, в подготовке к церковной жизни. Неудачи, бедность его семейства еще раз разрушили планы Буля; родители убеждали его отказаться от религиозной жизни ввиду их ухудшающегося финансового положения.
Отзывчивый, как всегда, к советам родителей, Буль решил открыть собственную школу. Ему было 20 лет. Преподавая, Буль считал себя также студентом и приступил к изучению полного курса высшей математики. Он проштудировал «Математические начала» Ньютона, «Аналитическую механику» Лагранжа, труды Лапласа и других авторов.
Свои математические исследования Буль начал с разработки операторных методов анализа и теории дифференциальных уравнений, а затем подобно де Моргану, с которым к этому времени подружился, занялся математической логикой.
В своей первой основной работе «Математический анализ логики, являющийся опытом исчисления дедуктивного рассуждения» 1847 года Буль отчетливо показал так называемое количественное истолкование объектов логики и необходимость нового подхода к решению проблем логики.
Этот подход требовал изменения и расширения символического языка алгебры: выбора символики, операций и законов, определяющих эти операции и отражающих специфику объектов исследования, — т. е. по существу создания нового исчисления. Буль писал: «Те, кто знаком с настоящим состоянием символической алгебры, отдают себе отчет в том, что обоснованность процессов анализа зависит не от интерпретации используемых символов, а только от законов их комбинирования. Каждая интерпретация, сохраняющая предложенные отношения, равно допустима, и подобный процесс анализа может, таким образом, при одной интерпретации представлять решение вопроса, связанного со свойствами чисел, при другой — решение геометрической задачи и при третьей — решение проблемы динамики или статики. Необходимо подчеркнуть фундаментальность этого принципа».
С публикацией «Математического анализа…» взгляды и блестящая интуиция этого тихого, простого человека стали ясны его друзьям — математикам, которые советовали ему поступить в Кембридж, для получения общепринятого математического образования.
Буль неохотно отверг эти предложения, потому что его родные полностью существовали на его заработок. Не жалуясь на особенности своего обучения от случая к случаю, Буль, наконец, получил небольшой перерыв в 1849 году, когда его назначили профессором математики в недавно открытом Королевском колледже.
Это назначение позволило ему посвятить больше времени «Законам мышления…» — второй его основной работе, которую он непрерывно оттачивал и усовершенствовал в течение еще 5 лет, до публикации в 1854 году.
Как писал Буль в первом параграфе книги: «Цель данного трактата:
? исследовать фундаментальные законы тех действий разума, с помощью которых выполняются рассуждения;
? выразить их в символическом языке исчислений и на этой основе создать науку логики и построить метод;
? сделать этот метод непосредственно основой общего метода для выражения теории вероятностей;
? наконец, получить различные элементы истины;
? оценить в рамках решения этих вопросов некоторое вероятное сообщение».
И далее: «Теперь фактически исследования следующих страниц показывают логику, в практическом аспекте, как систему процессов, проведенных при помощи символов, имеющих определенную интерпретацию и подчиненных законам, основанным на этой единственной интерпретации. Но в то же самое время они показывают эти законы как идентичные по форме с законами общих символов алгебры, с одним единственным дополнением, viz».
Другими словами, в общей алгебре не выполняется, например: что каждый х тождественно равен своему квадрату — но это истина в булевой алгебре. Согласно Булю, х2 = х для любого х в его системе. В числовой системе это уравнение имеет единственное решение «О» и «1». В этом заключается важность двоичной системы для современных компьютеров, логические части которых эффективно реализуют двоичные операции.
Кроме логики, булева алгебра имеет два других важных применения. Булева алгебра применяется в натуральной алгебре. Принимая также во внимание идею «количества элементов» в множестве, булева алгебра стала основой для теории вероятностей.
Несмотря на большое значение булевой алгебры во многих других областях математики, необычайная работа Буля в течение многих лет считалась странностью. Как и Бэббидж, Буль был человеком, опередившим свое время. Это произошло раньше, чем Альфред Уайтхед и Бертран Рассел опубликовали свой трехтомник «Принципы математики» (1910–1913), в котором рассматривались вопросы формальной логики.
Заслуживает внимания и то, что на достижения Буля частично опирались математические открытия, к тому времени появившиеся в Англии, в том числе и идеи Бэббиджа. Математики обратили внимание на идею Бэббиджа о математических операциях и величинах, использующихся в них. Идея стала возможной благодаря группе британских специалистов в области алгебры, к которым принадлежал и Буль.
Буль продемонстрировал, что логика может сводиться к очень простым алгебраическим системам, после чего для Бэббиджа и его последователей стало возможным создание механических устройств, которые могли решать необходимые логические задачи.
Через год после опубликования «Законов мышления…» Буль женился на Мэри Эверест, племяннице профессора греческого языка Королевского колледжа. Счастливый брак длился в течение девяти лет, вплоть до безвременной кончины Джорджа Буля. 8 декабря 1864 года, в возрасте 49 лет, почитаемый и известный, он умер от воспаления легких.
Буль был человеком последовательным и дисциплинированным, тем не менее, он широко демонстрировал собственное видение мира в своих утверждениях. Это мощное сочетание интеллекта и интуиции в Джордже Буле воплотилось в различных математических идеях. В заключение очерка об отце булевой алгебры хотелось бы коротко рассказать о семье Буля.
Как уже упоминалось, жена Буля была племянницей Джорджа Эвереста, в 1841 году завершившего в Индии грандиозные по масштабам работы.
В честь его заслуг высочайшая вершина мира Джомолунгма в Гималаях одно время даже именовалась Эверестом. Сама Мэри, в отличие от жен многих других математиков, понимала научные идеи своего мужа и своим вниманием и участием подвигала его на продолжение исследований. После его смерти она написала несколько сочинений и в последнем из них — «Философия и развлечения алгебры», — опубликованном в 1909 году, пропагандировала математические идеи Джорджа.
У четы Булей было пять дочерей. Старшая, Мэри, вышла замуж за Ч. Хинтона — математика, изобретателя и писателя-фантаста — автора широко известной повести «Случай в Флатландии», где описаны некие существа, живущие в плоском двухмерном мире. Из многочисленного потомства Хинтонов трое внуков стали учеными: Говард — энтомологом, а Вильям и Джоан — физиками. Последняя была одной из немногих женщин-физиков, принимавших участие в работе над атомным проектом в США.
Вторая дочь Булей, Маргарет, вошла в историю как мать крупнейшего английского механика и математика, иностранного члена Академии наук СССР Джеффри Тэйлора. Третья, Алисия, специализировалась в исследовании многомерных пространств и получила почетную ученую степень в Гронингенском университете. Четвертая, Люси, стала первой в Англии женщиной-профессором, возглавившей кафедру химии.
Но наиболее известной из всех дочерей Булей стала младшая, Этель Лилиан, вышедшая замуж за ученого — эмигранта из Польши Войнича. Войдя в революционную эмигрантскую среду, она написала прославивший ее на весь мир роман «Овод». За ним последовало еще несколько романов и музыкальных произведений, а также перевод на английский язык стихотворений Тараса Шевченко. Войнич скончалась в Нью-Йорке в возрасте 95 лет, немного не дожив до столетия со дня смерти своего знаменитого отца математика Джорджа Буля.
Поделитесь на страничкеСледующая глава >
history.wikireading.ru
Алгебра Буля — это… Что такое Алгебра Буля?
алгебра буля — исторически первый раздел математической логики, разработанный ирландским логиком и математиком Дж. Булем в середине XIX в. Буль применил алгебраические методы для решения логических задач и сформулировал на языке алгебры некоторые… … Словарь терминов логики
АЛГЕБРА ЛОГИКИ — система алгебраич. методов решения логич. задач, а также совокупность задач, решаемых такими методами. А. л. в узком смысле слова алгебраич. (табличное, матричное) построение классич. логики высказываний, в котором рассматриваются… … Философская энциклопедия
алгебра логики — АЛГЕБРА ЛОГИКИ исторически первая форма математической (символической) логики, сложившаяся к последней трети 19 в. К ее созданию привела аналогия между решением алгебраических уравнений и выводом следствий из посылок, а также то, что… … Энциклопедия эпистемологии и философии науки
АЛГЕБРА — часть математики, посвященная изучению алгебраических операций. Исторический очерк. Простейшие алгебраич. операции арифметич. действия над натуральными и положительными рациональными числами встречаются в самых ранних математич. текстах,… … Математическая энциклопедия
Алгебра логики — раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности), и логические операции над ними. А. л. возникла в середине 19 в. в трудах Дж. Буля (См. Буль) и развивалась… … Большая советская энциклопедия
АЛГЕБРА ЛОГИКИ — раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логич. значений (истинности пли ложности), и логич. операций над ними. А. л. возникла в сер. 19 в. в трудах Дж. Буля (см. [1], [2]) и развилась затем в работах Ч … Математическая энциклопедия
БУЛЕВА АЛГЕБРА — БУЛЕВА АЛГЕБРА, область математики, содержащая правила обращения с множествами, а также с логическими утверждениями типа «и», «или». Например, в Булевой алгебре выражение ху означает «х и у», а х+у это «х или у». Данный принцип широко применяется … Научно-технический энциклопедический словарь
БУЛЕВА АЛГЕБРА — булева решетк а, частично упорядоченное множество специального вида. Б. а. наз. дистрибутивная решетка (дистрибутивная структура), имеющая наибольший элемент 1 единицу Б. а., наименьший элемент 0 нуль Б. а. и содержащая вместе с каждым своим… … Математическая энциклопедия
Булева алгебра — (араб.) – система алгебраических операций с символами, названная в честь Д. Буля, одного из её создателей. Также называется калькуляцией (лат. calсulatio – счёт, подсчёт). Интересно, что Д. Буль рассматривал свою работу как представление основных … Энциклопедический словарь по психологии и педагогике
БУЛЕВА АЛГЕБРА — Названная по имени ее создателя, английского математика Джорджа Буля, система операций с символами, которая использует алгебраические процедуры, но независимо от определенных математических интерпретаций. Булева логика, или калькуляция (как она… … Толковый словарь по психологии
dic.academic.ru
Что такое Булева алгебра? Есть примеры (см)?
Я тоже хочу ответить на этот специфический вопрос, связанный с открытием основателем математической логики Д.Булем алгебры, названной в его честь. Булеву алгебру можно использовать в курсе математической логики как модель изучаемого классического исчисления высказываний. Кто изучал это, тот знает, что в этом случае 0 называют ложью, 1 — истиной. Выражения, которые содержат булевы операции и переменные, — это и есть высказывательные формы.
Остановимся на необходимых определениях логики высказываний, которые продемонстрируем на примерах.
Высказывание — это повествовательное предложение, относительно которого можно сказать истинно оно или ложно.
Например,
А: Москва — столица России — высказывание, причем истинное.
В: 2+2=5 — это ложное высказывание.
2+2 — это не высказывание, т.к. относительно его нельзя сказать истинно оно или ложно.
Нас интересуют не все логические операции, а только конъюнкция (логическое умножение), дизъюнкция (логическое сложение) и отрицание.
Конъюнкцией двух высказываний называется новое высказывание, обозначаемое А /\ В, истинное тогда и только тогда, когда оба высказывания истинны.
Дизъюнкцией двух высказываний называется сложное высказывание, обозначаемое А \/ В, ложное тогда и только тогда, когда оба высказывания ложны.
Отрицанием высказывания А называется высказывание, обозначаемое /А (не А), ложное тогда и только тогда, когда само высказывание истинно.
Составим конъюнкцию, дизъюнкцию высказываний А и В (см. выше) и отрицание высказывания А.
А /\ В: Москва-столица России и 2+2=5 (соответствует союз и) — конъюнкция ложная (см. третью строку таблицы истинности для нее — 1,2,4 столбцы).
А \/ В: Москва — столица России или 2+2=5 (соответствует союз или) — дизъюнкция истинная (см. третью строку таблицы истинности для нее — 1,2,5 столбцы).
/А: Неверно, что Москва — столица России (можно и так: Москва — не столица России ) (соответствует частица не) — отрицание ложное (см. третью строку таблицы истинности для отрицания — 1,2,3 столбцы).
Ниже приведена сводная таблица истинности, которая составлена для всех пяти операций (имеются еще 2 операции: импликация и эквиваленция, см. шестой и седьмой столбцы), но в определении булевой алгебры они не участвуют).
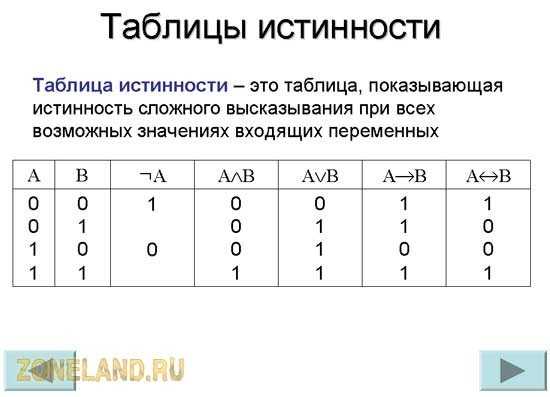
А теперь дадим точное определение булевой алгебры (см. здесь).
Булевой алгеброй называется непустое множество A с двумя бинарными операциями /\ (аналог конъюнкции), \/ (аналог дизъюнкции), унарной операцией /(аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для любых элементов из А a, b и c из множества A верны следующие аксиомы:
a /\ (b /\ c) = (a /\ b) /\ c a \/ (b \/ c) = (a \/ b) \/ c ассоциативность
a /\ b = b /\ a a \/ b = b \/ a коммутативность
a /\ (a \/ b) = a a \/ (a /\ b) = a законы поглощения
a /\ (b \/ c) = (a /\ b) \/ (a /\ c) a \/ (b /\ c) = (a \/ b) /\ (a \/ c) дистрибутивность одной операции относительно другой
a \/ / a = 1 a /\ /a = 0 дополнительность
Замечание: бинарная операция связывает два элемента, унарная — один элемент.
Несколько слов об авторе, в честь кого названа эта алгебра.
Отмечу, что булева алгебра широко применяется на практике. Для интересующихся предлагаю посмотреть вот этот красочный материал., в котором показано, что
А также рассмотрена алгебра лотки.
www.bolshoyvopros.ru
Алгебра высказываний (булева алгебра) — Информатика, информационные технологии
Основные понятия
Основное понятие булевой алгебры — выказывание. Под простым высказыванием понимается предложение, о котором можно сказать, истинно оно или ложно (третьего не дано). Высказывания обозначаются латинскими буквами и могут принимать одно из двух значений: ЛОЖЬ (обозначим 0 ) или ИСТИНА (обозначим 3). Например, содержание высказывания А: «дважды два равно четырем» истинно А = 1, а высказывание В: «три больше пяти» всегда есть ЛОЖЬ. В дальнейшем нас не будет интересовать содержательная часть высказываний, а только их истинность. Два высказывания А и В называются равносильными, если они имеют одинаковые значения истинности, записывается А = В.
Логические операции
Сложное высказывание можно построить из простых с помощью логических операций: отрицания, конъюнкции, дизъюнкции, импликации и логических выражений, представляющих собой комбинации логических операций. Рассмотрим их подробней.
Операцией отрицания А называют высказывание (или , говорят не А), которое истинно тогда, когда А ложно, и ложно тогда, когда А истинно. Например, если событие А состоит в том, что «завтра будет снег», то «завтра НЕ будет снега», истинность одного утверждения автоматически означает ложность второго. Отрицание — унарная (т.е. для одного операнда) логическая операция. Ей соответствует языковая конструкция, использующая частицу НЕ,
Это правило можно записать в виде следующей таблицы:
Такая таблица называется таблицей истинности.
Конъюнкцией (логическим умножением) двух высказываний А и В является новое высказывание С, которое истинно только тогда, когда истинны оба высказывания, записывается (при этом говорят С равно А и В). Примером такой операции может быть следующая: пусть высказывание А состоит в том, что «высота шкафа меньше высоты двери», событие В «ширина шкафа меньше ширины двери», событие С «шкаф можно внести в дверь, если ширина шкафа меньше ширины двери И высота шкафа меньше высоты двери», т.е. данная операция применяется, если два высказывания связываются союзом И.
Таблица истинности этой операции, как следует из определения, имеет вид
Дизъюнкцией (логическим сложением) двух высказываний А и В является новое высказывание С, которое истинно, если истинно хотя бы одно высказывание. Записывается (при этом говорят:
С равно А ИЛИ В). Пример такой операции следующий: пусть высказывание А состоит в том, что «студент может добираться домой на автобусе», событие В «студент может добираться домой на троллейбусе», событие С «студент добрался домой на автобусе ИЛИ троллейбусе», т.е. данная операция применяется, если два высказывания связываются союзом ИЛИ.
Таблица истинности такой операции следующая:
Импликацией двух высказываний А (А называется посылкой) и В (В называется заключением) является новое высказывание С, которое ложно только тогда, когда посылка истинна, а заключение ложно, записывается (при этом говорят, из А следует В). Примером такой операции может быть любое рассуждение типа: если произошло событие А, то произойдет событие В, «если идет дождь, то на небе тучи». Очевидно, операция не симметрична, т.е. из не всегда истинно, в нашем примере «если на небе тучи, то идет дождь» не всегда истинно.
Таблица истинности импликации следующая:
Эквиваленцией двух высказываний А и В является новое высказывание С, которое .истинно только тогда, когда оба высказывания имеют одинаковые значения истинности, записывается
Примером такой операции может быть любое высказывание типа: событие А равносильно событию В.
Таблица истинности:
Логические Выражения. Порядок логических операций
С помощью логических операций из простых высказываний (логических переменных и констант) можно построить логические выражения, которые также называются булевскими функциями. Например.
Чтобы избежать большого количества скобок в булевских функциях, принято следующее соглашение о старшинстве операций.
Первыми выполняются операции в скобках, затем операции в следующем порядке: отрицание, конъюнкция и дизъюнкция слева направо, импликация, эквиваленция.
Зависимости между логическими операциями
Операции не являются независимыми; одни из них могут быть выражены через другие. Можно доказать с помощью таблиц истинности следующие равносильности:
Одну и ту же зависимость между логическими переменными можно выразить различными формулами. Поэтому важно иметь возможность приводить формулы с помощью эквивалентных преобразований к некоторому стандартному виду. Существует несколько стандартных форм, к которым приводятся логические выражения с помощью эквивалентных преобразований (формул 1—23).
Первая из них — дизъюнктивная нормальная форма (ДНФ), имеет вид , где каждое из составляющих есть конъюнкция простых высказываний и их отрицаний, например:
Вторая- конъюнктивная нормальная форма (КНФ), имеет вид
где каждое из составляющих есть дизъюнкция простых высказываний и их отрицаний, например:
Табличное и алгебраическое задание булевских функций
Задать булевскую функцию можно, определяя ее значения для всех наборов значений аргументов. Каждый аргумент может иметь два значения: 0 и 1, следовательно, n аргументов могут принимать 2n различных наборов. Пусть, например, булевская функция имеет три аргумента: X,, Х2, Х3 Общее число наборов 23 = 8; зададим таблицу истинности функции, указав для каждого набора значение функции.
Для составления алгебраической формы по результатам таблицы сделаем следующее. В комбинациях, где функция принимает значение 1, единицу заменим именем функции, а нуль — именем с отрицанием (т.е. комбинации 0 0 1 поставим в соответствие выражение ), все элементы соединим знаками дизъюнкции, для рассматриваемого примера получим
Как нетрудно заметить, построенная функция удовлетворяет заданной таблице истинности. Функция представляет дизъюнктивную нормальную форму. Кроме того, заметим, что в каждую группу дизъюнкций входят все аргументы функции. Такая ДНФ называется совершенной, а каждая группа дизъюнкций называется коституентой единицы.
Аналогично, для комбинаций, где функция принимает значение нуля, можно построить алгебраическую форму
,
которая также удовлетворяет заданной таблице истинности и представляет собой конъюнктивную нормальную форму, в данном случае совершенную. Каждая конъюнкция называется конституентой нуля.
В главе 2 будет показано, как, основываясь на булевой алгебре, создаются цифровые устройства.
1.6.2. Элементы теории множеств
Множеством называется любое объединение определенных вполне различимых объектов; их может и не быть вообще. Можно говорить о множестве точек на отрезке [0,1], множестве студентов в группе, множестве снежных дней в июле на экваторе, т.е. множество образуют любые объекты, объединенные по любому признаку. Объекты, составляющие множество, называются элементами множества. Множество, не имеющее ни одного элемента, называется пустым, оно обозначается 0. Множество, состоящее из конечного числа элементов, называется конечным, в противном случае — бесконечным.
Задать множество можно перечислением его элементов. Например, множество образованное из п элементов ар а2, …, ап, обозначается А = {а,, а2, …, ап}; пишется а е А (говорится «элемент а при надлежит множеству А»), если а является элементом множества А, в противном случае
Задать множество можно также, указав общее свойство для всех его и только его элементов. Например, множество точек равноудаленных от концов отрезка.
Два множества считаются равными, если состоят из одних и тех же элементов; записывается этот факт А = В.
Множество А1 называется подмножеством А (записываете ),
если все элементы множества А, являются элементами А,
Для множеств определены следующие операции: объединение, пересечение, дополнение.
Объединением множеств А и В (записывается ) называется
множество, состоящее из элементов как одного, так и второго множества. Например, А и В — множества точек, принадлежащих некоторым двум кругам, имеющим общие точки, тогда объединением будет фигура, состоящая из общих точек.
Пересечением множеств А и В (записывается ) называется
множество, состоящее из элементов, принадлежащих как одному, так и второму множеству одновременно.
Дополнением множества А до В называется множество, состоящее из элементов множества В, не принадлежащих А. Дополнение обозначается (рис. 1.7).
Рис. 1.7. Операции надмножествами
16.3, Элементы теории графов
Основные понятия
Граф задается парой множеств: множества Е, называемого множеством вершин, и множества II, называемого множеством ребер. Ребро есть пара, где ,
указывающая, между какими двумя вершинами проведено ребро. Говорят, что ребро инцидентно вершинам е., е. Если порядок ребер не имеет значения, т.е. , то ребро называется неориентированным или просто ребром, если же порядок имеет значение, то ребро называется ориентированным ребром или дугой. Вершина еi. — называется началом дуги, еj. — конец дуги. Граф, содержащий хотя бы одну дугу, называется ориентированным графом или орграфом
Граф называется конечным, если множество Е вершин
конечно.
Граф •, у которого любые две вершины соединены ребром,
называется полным. Если хотя бы две вершины соединены несколькими ребрами, то такой граф называется мультиграфом. Две вершины называются смежными, если они соединены ребром. Число ребер, инцидентных данной вершине е., называется локальной степенью этой вершины p(ei) Число ребер r графа G(Е,U) определяется выражением
, где n — количество вершин в графе. Рассмотрим граф,
изображенный на рис. 1.8.
Рис. 1.8. Ориентированный граф
Множество вершин графа состоит из пяти элементов: Е = {1, 2, 3, 4, 5}, а множество ребер U = {(1, 2), (1, 4), (1, 5), (2, 3), (3, 4), {5, 3)}. Ребро (5, 3) — является ориентированным ребром или дугой. Число ребер в графе определяется по значению локальных степеней для каждой вершины:
Важным в теории графов является понятие части графа G(Е,U), который обозначается
Множества вершин и ребер части графа являются подмножествами вершин и ребер исходного графа
Статьи к прочтению:
Начала Булевой алгебры
Похожие статьи:
Операции (высказывания) алгебры логики
Основные понятия алгебры логики. Логические основы ЭВМ Двоичная система счисления — позиционная система счисления с основанием 2. В этой системе…
Системы функций алгебры логики
Рассмотрим теорему Жегалкина, которая играет важную роль в алгебре логики. Теорема Жегалкина. Любая булева функция может быть представлена многочленом…
csaa.ru
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математическая логика. Булева алгебра = алгебра логики. / / Булевы = логические функции. Основные законы математической логики = законы Булевой алгебры. Формы представления булевых = логических функций. Поделиться:
| ||||||||||||||||||||||||||
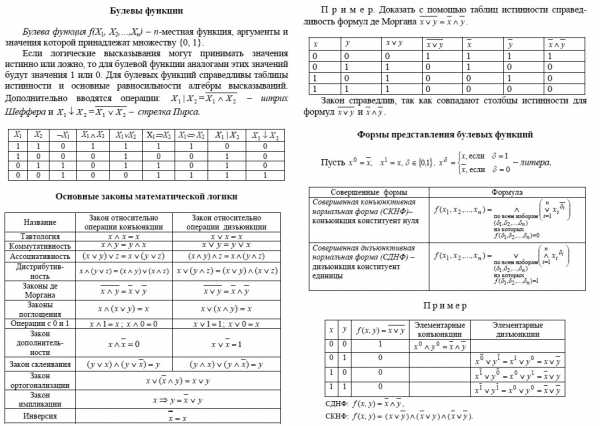*Бабичева, Болдовская, Справочник по математике. СибАДИ, 2010. (классная книга)
dpva.ru