Частота и угловая скорость: Формула расчета частоты вращений

Угловая скорость и ускорение. Определения и формулы для расчета.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющаяся приращением угла поворота тела за промежуток времени.

Обозначение: ω (омега).

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

• если известно количество оборотов n за единицу времени t:
  
• если задан угол поворота φ за единицу времени:
  

Размерности:

• Количество оборотов за единицу времени [об/мин], [c^-1].
• Угол поворота за единицу времени [рад/с].

Быстрота изменения угла φ (перемещения из положения П₁ в положение П₂) – это и есть угловая скорость:

ω=dφ/dt=φ’, рад/с; с^-1    (2.3)

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω=1,5 с^-1=9,42 рад/с.

Приняв k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Угловое ускорение

Изменение угловой скорости характеризуется угловым ускорением:

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает, а при отрицательном вращение замедляется.

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

ω=n2π/60=nπ/30 рад/с; с^-1.

Формула угловой скорости в физике

Определение и формула угловой скорости

Определение

Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.

Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.

Перемещение при вращении характеризуют при помощи угла поворота . Часто используют вектор элементарного поворота , который равен по величине элементарному углу поворота тела замаленький отрезок времени dtи направлен по мгновенной оси вращения в сторону, откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами. Углы вращения на конечные величины векторами не являются.

Определение

Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой . Математически определение угловой скорости записывают так:

Угловая скорость — векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).

Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости), так и за счет поворота оси вращения в пространстве ( при этом изменяет направление).

Равномерное вращение

Если тело за равные промежутки времени поворачивается на один и тот же угол, то такое вращение называют равномерным. При этом модуль угловой скорости находят как:

где – угол поворота, t – время, за которое этот поворот совершён.

Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот ). Угловая скорость связана с периодом обращения как:

С числом оборотов в единицу времени () угловая скорость связана формулой:

Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения, но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно с данной мгновенной величиной скорости.

Формула, связывающая линейную и угловую скорости

Линейная скорость точки А (рис.1), которая расположена на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением:

где – перпендикулярная к оси вращения компонента радиус-вектора точки (рис.1). Вектор проводят от точки, находящейся на оси вращения к рассматриваемой точке.

Единицы измерения угловой скорости

Основной единицей измерения угловой скорости в системе СИ является: []=рад/с

В СГС: []=рад/с

Примеры решения задач

Пример

Задание. Движение тела с неподвижной осью задано уравнением , в рад, t в сек. Начало вращения при t=0 c. Положительным считают углы указанные направлением стрелки (рис.2). В каком направлении ( относительно часовой стрелки поворачивается тело) в момент времени t=0,5 c.

Решение. Для нахождения модуля угловой скорости применим формулу:

Используем заданную в условии задачи функцию , возьмем производную от нее по времени, получим функцию :

Вычислим, чему будет равна угловая скорость в заданный момент времени (при t=0,5 c):

Ответ. В заданный момент времени тело имеет угловую скорость равную нулю, следовательно, она останавливается.

Что такое угловая скорость и как ее рассчитывают?

Обычно, когда говорят о перемещении, мы представляем себе объект, который движется по прямой. Скорость такого движения принято называть линейной, и расчёт ее средней величины выполняется просто: достаточно найти отношение пройденного расстояния к времени, за которое оно было телом преодолено. Если же объект перемещается по окружности, то в этом случае уже определяется не линейная, а угловая скорость. Что это за величина и как ее рассчитывают? Об этом как раз и пойдет разговор в данной статье.

Угловая скорость: понятие и формула

Когда материальная точка движется по окружности, быстроту ее перемещения можно характеризовать величиной угла поворота радиуса, который соединяет движущийся объект с центром данной окружности. Понятно, что эта величина в зависимости от времени постоянно меняется. Быстрота, с которой этот процесс происходит, и есть не что иное, как угловая скорость. Другими словами, это отношение величины отклонения радиус-вектора объекта к промежутку времени, которое потребовалось объекту на совершение такого поворота. Формула угловой скорости (1) может быть записана в таком виде:

w = φ / t, где:

φ – угол поворота радиуса,

t – период времени вращения.

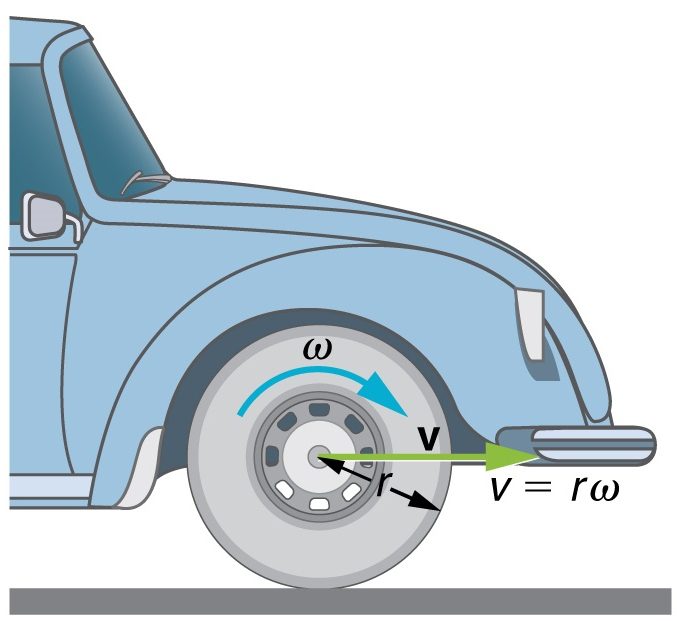
Единицы измерения величины

В международной системе общепринятых единиц (СИ) для характеристики поворотов принято использовать радианы. Поэтому 1 рад/с – основная единица, которая используется в расчетах угловой скорости. В то же время никто не запрещает применять градусы (напомним, что один радиан равен 180/пи, или 57˚18’). Также угловая скорость может выражаться в числе оборотов за минуту или за секунду. Если перемещение по окружности происходит равномерно, то данная величина может быть найдена по формуле (2):

w = 2π*n,

где n – частота вращения.

В противном случае подобно тому, как это делают для обычной скорости, рассчитывают среднюю, или мгновенную угловую скорость. Следует отметить, что рассматриваемая величина является векторной. Для определения ее направления обычно используют правило буравчика, которое часто применяется в физике. Вектор угловой скорости направлен в ту же сторону, в которую происходит поступательное движение винта с правой резьбой. Другими словами, он устремлен вдоль оси, вокруг которой вращается тело, в ту сторону, откуда вращение видно происходящим против движения часовой стрелки.

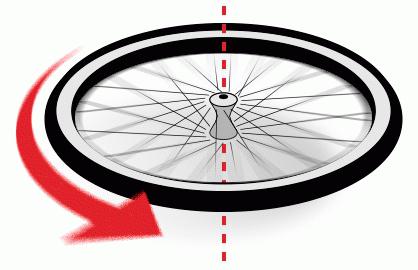
Примеры расчета

Предположим, требуется определить, чему равна линейная и угловая скорость колеса, если известно, что его диаметр равен одному метру, а угол вращения изменяется в соответствии с законом φ=7t. Воспользуемся нашей первой формулой:

w = φ / t = 7t / t = 7 с^-1.

Это и будет искомая угловая скорость. Теперь перейдем к поиску привычной нам быстроты перемещения. Как известно, v = s / t. Учитывая, что s в нашем случае – это длина окружности колеса (l =2π*r), а 2π — один полный оборот, получается следующее:

v = 2π*r / t = w * r = 7 * 0.5 = 3.5 м/с

Вот еще одна задачка на эту тему. Известно, что радиус Земли на экваторе равен 6370 километров. Требуется определить линейную и угловую быстроту движения точек, находящихся на этой параллели, которое возникает в результате вращения нашей планеты вокруг своей оси. В данном случае нам понадобится вторая формула:

w = 2π*n = 2*3,14 *(1/(24*3600)) = 7,268 *10^-5 рад/с.

Осталось выяснить, чему равна линейная скорость: v = w*r = 7,268 *10^-5 *6370 * 1000 = 463 м/с.

Равномерное движение по окружности. Скорость, ускорение

 

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: движение по окружности с постоянной по модулю скоростью, центростремительное ускорение.

Равномерное движение по окружности — это достаточно простой пример движения с вектором ускорения, зависящим от времени.

Пусть точка вращается по окружности радиуса . Скорость точки постоянна по модулю и равна . Скорость называется линейной скоростью точки.

Период обращения — это время одного полного оборота. Для периода имеем очевидную формулу:

. (1)

Частота обращения — это величина, обратная периоду:

.

Частота показывает, сколько полных оборотов точка совершает за секунду. Измеряется частота в об/с (обороты в секунду).

Пусть, например, . Это означает, что за время точка совершает один полный
оборот. Частота при этом получается равна: об/с; за секунду точка совершает 10 полных оборотов.

 

Угловая скорость.

 

Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат в центре окружности (рис. 1).

Рис. 1. Равномерное движение по окружности

 

Пусть — начальное положение точки; иными словами, при точка имела координаты . Пусть за время точка повернулась на угол и заняла положение .

Отношение угла поворота ко времени называется угловой скоростью вращения точки:

. (2)

Угол , как правило, измеряется в радианах, поэтому угловая скорость измеряется в рад/с. За время, равное периоду вращения, точка поворачивается на угол . Поэтому

. (3)

Сопоставляя формулы (1) и (3), получаем связь линейной и угловой скоростей:

. (4)

 

Закон движения.

 

Найдём теперь зависимость координат вращающейся точки от времени. Видим из рис. 1, что

.

Но из формулы (2) имеем: . Следовательно,

. (5)

Формулы (5) являются решением основной задачи механики для равномерного движения точки по окружности.

 

Центростремительное ускорение.

 

Теперь нас интересует ускорение вращающейся точки. Его можно найти, дважды продифференцировав соотношения (5):

С учётом формул (5) имеем:

(6)

Полученные формулы (6) можно записать в виде одного векторного равенства:

(7)

где — радиус-вектор вращающейся точки.

Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1). Поэтому ускорение точки, равномерно движущейся по окружности, называется

центростремительным.

Кроме того, из формулы (7) мы получаем выражение для модуля центростремительного ускорения:

(8)

Выразим угловую скорость из (4)

и подставим в (8). Получим ещё одну формулу для центростремительного ускорения:

.

 

Угловая скорость — это… Что такое Угловая скорость?

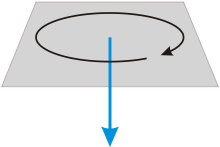Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке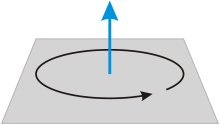 Угловая скорость (синяя стрелка) в одну единицу против часовой стрелки

Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

,

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Единица измерения угловой скорости, принятая в системах СИ и СГС — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли просто «вручную», подсчитывая число оборотов за единицу времени.

Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью , определяется формулой:

где  — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) от оси вращения можно считать так: Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.

• В случае плоского вращения, то есть когда все векторы скоростей точек тела лежат (всегда) в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
• Производная угловой скорости по времени есть угловое ускорение.
• Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю).
• Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчета, однако в разных инерциальных системах отсчета может различаться ось или центр вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
• В случае движения одной единственной точки в трехмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:

, где  — радиус-вектор точки (из начала координат),  — скорость этой точки.  — векторное произведение,  — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.

• При измерении угловой скорости в оборотах в секунду (об/с), модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц), то есть в таких единицах . В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости связан с частотой вращения так: . Наконец, при использовании градусов в секунду связь с частотой вращения будет: .

Связь с конечным поворотом в пространстве

• Пусть поворот, изменяющийся во времени, задан величиной угла и ортом оси конечного поворота в пространстве . Тогда угловая скорость, соответствующая этому повороту, равна

.

.

• Если для описания поворота используется кватернион, выражаемый через угол и орт оси поворота как , то угловая скорость находится из выражения .

.

См. также

Литература

• Лурье А. И. Аналитическая механика\\ А. И. Лурье. — М.: ГИФМЛ, 1961. — С. 100-136

Равномерное движение тела по окружности – FIZI4KA

1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.

При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности. Под телом в данном случае имеют в виду материальную точку.

2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности ​\( T \)​ — время, в течение которого тело совершает один полный оборот. Единица периода — ​\( [\,T\,] \)​ = 1 с.

Частота обращения ​\( (n) \)​ — число полных оборотов тела за одну секунду: ​\( n=N/t \)​. Единица частоты обращения — \( [\,n\,] \) = 1 с^-1 = 1 Гц (герц). Один герц — это такая частота, при которой тело совершает один оборот за одну секунду.

Связь между частотой и периодом обращения выражается формулой: ​\( n=1/T \)​.

Пусть некоторое тело, движущееся по окружности, за время ​\( t \)​ переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол ​\( \varphi \)​.

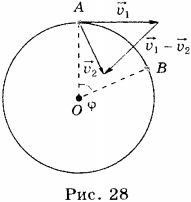
Быстроту обращения тела характеризуют угловая и линейная скорости.

Угловая скорость ​\( \omega \)​ — физическая величина, равная отношению угла поворота \( \varphi \) радиуса-вектора к промежутку времени, за которое этот поворот произошел: ​\( \omega=\varphi/t \)​. Единица угловой скорости — радиан в секунду, т.е. ​\( [\,\omega\,] \)​ = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен ​\( 2\pi \)​. Поэтому ​\( \omega=2\pi/T \)​.

Линейная скорость тела ​\( v \)​ — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.

Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: ​\( \vec{v}=l/t \)​. За один оборот точка проходит путь, равный длине окружности. Поэтому ​\( \vec{v}=2\pi\!R/T \)​. Связь между линейной и угловой скоростью выражается формулой: ​\( v=\omega R \)​.

Из этого равенства следует, что чем дальше от центра окружности расположена точка вращающегося тела, тем больше её линейная скорость.

4. Ускорение тела равно отношению изменения его скорости ко времени, за которое оно произошло. При движении тела по окружности изменяется направление скорости, следовательно, разность скоростей не равна нулю, т.е. тело движется с ускорением. Оно определяется по формуле: ​\( \vec{a}=\frac{\Delta\vec{v}}{t} \)​ и направлено так же, как вектор изменения скорости. Это ускорение называется центростремительным ускорением.

Центростремительное ускорение при равномерном движении тела по окружности — физическая величина, равная отношению квадрата линейной скорости к радиусу окружности: ​\( a=\frac{v^2}{R} \)​. Так как ​\( v=\omega R \)​, то ​\( a=\omega^2R \)​.

При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. При равномерном движении тела по окружности

1) изменяется только модуль его скорости
2) изменяется только направление его скорости
3) изменяются и модуль, и направление его скорости
4) не изменяется ни модуль, ни направление его скорости

2. Линейная скорость точки 1, находящейся на расстоянии ​\( R_1 \)​ от центра вращающегося колеса, равна ​\( v_1 \)​. Чему равна скорость ​\( v_2 \)​ точки 2, находящейся от центра на расстоянии ​\( R_2=4R_1 \)​?

1) ​\( v_2=v_1 \)​
2) ​\( v_2=2v_1 \)​
3) ​\( v_2=0,25v_1 \)​
4) ​\( v_2=4v_1 \)​

3. Период обращения точки по окружности можно вычислить по формуле:

1) ​\( T=2\pi\!Rv \)​
2) \( T=2\pi\!R/v \)​
3) \( T=2\pi v \)​
4) \( T=2\pi/v \)​

4. Угловая скорость вращения колеса автомобиля вычисляется по формуле:

1) ​\( \omega=a^2R \)​
2) \( \omega=vR^2 \)​
3) \( \omega=vR \)
4) \( \omega=v/R \)​

5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?

1) увеличилась в 2 раза
2) уменьшилась в 2 раза
3) увеличилась в 4 раза
4) не изменилась

6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?

1) не изменилось
2) уменьшилось в 16 раз
3) уменьшилось в 4 раза
4) уменьшилось в 2 раза

7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?

1) увеличилось в 9 раз
2) уменьшилось в 9 раз
3) уменьшилось в 3 раза
4) увеличилось в 3 раза

8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?

1) 200 000 с
2) 3300 с
3) 3·10^-4 с
4) 5·10^-6 с

9. Чему равна частота вращения точки обода колеса, если период обращения составляет 0,05 с?

1) 0,05 Гц
2) 2 Гц
3) 20 Гц
4) 200 Гц

10. Линейная скорость точки обода велосипедного колеса радиусом 35 см равна 5 м/с. Чему равен период обращения колеса?

1) 14 с
2) 7 с
3) 0,07 с
4) 0,44 с

11. Установите соответствие между физическими величинами в левом столбце и формулами для их вычисления в правом столбце. В таблице под номером физической
величины левого столбца запишите соответствующий номер выбранной вами формулы из правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) линейная скорость
Б) угловая скорость
В) частота обращения

ФОРМУЛА
1) ​\( 1/T \)​
2) ​\( v^2/R \)​
3) ​\( v/R \)​
4) ​\( \omega R \)​
5) ​\( 1/n \)​

12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце.
В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) угловая скорость
Б) линейная скорость
B) центростремительное ускорение

ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) увеличилась
2) уменьшилась
3) не изменилась

Часть 2

13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?

Ответы

Равномерное движение тела по окружности

5 (100%) 1 vote

Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями

Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями

Подробности

Просмотров: 386

«Физика — 10 класс»

Угловая скорость.

Каждая точка тела, вращающегося вокруг неподвижной оси, проходящей через точку О, движется по окружности, и различные точки проходят за время Δt разные пути. Так, АА₁ > ВВ₁ (рис. 1.62), поэтому модуль скорости точки А больше, чем модуль скорости точки В. Но радиус-векторы, определяющие положение точек А и В, поворачиваются за время Δt на один и тот же угол Δφ.

Угол φ — угол между осью ОХ и радиус-вектором определяющим положение точки А (см. рис. 1.62).

Пусть тело вращается равномерно, т. е. за любые равные промежутки времени радиус-векторы поворачиваются на одинаковые углы.

Чем больше угол поворота радиус-вектора, определяющего положение какой-то точки твёрдого тела, за определённый промежуток времени, тем быстрее вращается тело и тем больше его угловая скорость.

Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела υφ к промежутку времени υt, за который этот поворот произошёл.

Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению

Угловая скорость в СИ выражается в радианах в секунду (рад/с). Например, угловая скорость вращения Земли вокруг оси 0,0000727 рад/с, а точильного диска — около 140 рад/с.

Угловую скорость можно связать с частотой вращения.

Частота вращения — число полных оборотов за единицу времени (в СИ за 1 с).

Если тело совершает ν (греческая буква «ню») оборотов за 1 с, то время одного оборота равно 1/ν секунд.

Время, за которое тело совершает один полный оборот, называют периодом вращения и обозначают буквой Т.

Таким образом, связь между частотой и периодом вращения можно представить в виде

Полному обороту тела соответствует угол Δφ = 2π. Поэтому согласно формуле (1.26)

Если при равномерном вращении угловая скорость известна и в начальный момент времени t₀ = 0 угол φ₀ = 0, то угол поворота радиус-вектора за время t согласно уравнению (1.26)

φ = ωt.

Если φ₀ ≠ 0, то φ — φ₀ = ωt, или φ = φ₀ ± ωt.

Радиан равен центральному углу, опирающемуся на дугу, длина которой равна радиусу окружности, 1 рад = 57°17’48». В радианной мере угол равен отношению длины дуги окружности к её радиусу: φ = l/R.

Угловая скорость принимает положительные значения, если угол между радиус-вектором, определяющим положение одной из точек твёрдого тела, и осью ОХ увеличивается (рис. 1.63, а), и отрицательные, когда он уменьшается (рис. 1.63, б).

Тем самым мы можем найти положение точек вращающегося тела в любой момент времени.

Связь между линейной и угловой скоростями.

Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть её отличие от угловой скорости.

Мы уже отмечали, что при вращении абсолютно твёрдого тела разные его точки имеют неодинаковые линейные скорости, но угловая скорость для всех точек одинакова.

Установим связь между линейной скоростью любой точки вращающегося тела и его угловой скоростью. Точка, лежащая на окружности радиусом R, за один оборот пройдёт путь 2πR. Поскольку время одного оборота тела есть период Т, то модуль линейной скорости точки можно найти так:

Так как ω = 2πν, то

Из этой формулы видно, что, чем дальше расположена точка тела от оси вращения, тем больше её линейная скорость. Для точек земного экватора υ = 463 м/с, а для точек на широте Санкт-Петербурга υ = 233 м/с. На полюсах Земли υ = 0.

Модуль центростремительного ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности:

Следовательно,

а_цс = ω²R.

Запишем все возможные расчётные формулы для центростремительного ускорения:

Мы рассмотрели два простейших движения абсолютно твёрдого тела — поступательное и вращательное. Однако любое сложное движение абсолютно твёрдого тела можно представить как сумму двух независимых движений: поступательного и вращательного.

На основании закона независимости движений можно описать сложное движение абсолютно твёрдого тела.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Кинематика — Физика, учебник для 10 класса — Класс!ная физика

Физика и познание мира — Что такое механика — Механическое движение. Система отсчёта — Способы описания движения — Траектория. Путь. Перемещение — Равномерное прямолинейное движение. Скорость. Уравнение движения — Примеры решения задач по теме «Равномерное прямолинейное движение» — Сложение скоростей — Примеры решения задач по теме «Сложение скоростей» — Мгновенная и средняя скорости — Ускорение — Движение с постоянным ускорением — Определение кинематических характеристик движения с помощью графиков — Примеры решения задач по теме «Движение с постоянным ускорением» — Движение с постоянным ускорением свободного падения — Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» — Равномерное движение точки по окружности — Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение — Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями — Примеры решения задач по теме «Кинематика твёрдого тела»

Калькулятор угловой скорости

Как найти угловую скорость Земли?

Как насчет того, чтобы использовать наш калькулятор угловой скорости? Оценим угловую скорость Земли! Во-первых, мы рассматриваем скорость вращения. Мы знаем, что Земля совершает полный оборот относительно далеких звезд примерно за 23 ч 56 мин 4 с , что составляет примерно 23,934 ч . Полное вращение составляет угол 2π рад , поэтому результирующая угловая скорость равна:

ω₁ = 2π рад / 23.934 ч = 0,2625 рад / ч = 0,00007292 рад / с ,

или 7,292 * 10⁻⁵ рад / с (в экспоненциальном представлении).

Теперь, когда мы знаем угловую скорость вращения Земли, мы можем оценить ее линейную скорость на экваторе. Для этого нам нужен радиус Земли, который составляет примерно 6,371 км . Единственное, что нам нужно сделать, это вставить значения во вторую формулу угловой скорости:

v₁ = r₁ * ω₁ = 6,371 км * 7,292 * 10⁻⁵ рад / с = 0,4646 км / с = 464.6 м / с .

Чтобы вычислить линейную скорость относительно центра Земли, все, что вам нужно сделать, это умножить полученный результат на косинус широты вашего города. Кстати, вы когда-нибудь задумывались, почему ракеты обычно запускаются с космодромов, расположенных вблизи экватора, а не с полюсов? Ну, почти 500 м / с ускорение в начале — это значительная часть его конечной скорости. Таким образом, перемещение стартовой точки как можно ближе к экватору уменьшает количество топлива, необходимого для разгона ракеты.

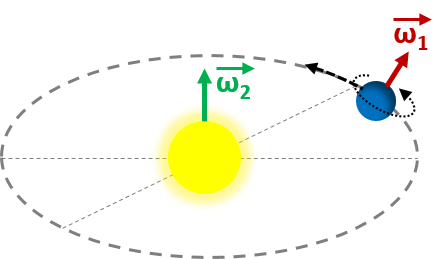
После этого мы можем еще раз спросить, как найти угловую скорость Земли, но на этот раз орбитальную. Все расчеты аналогичны, но мы должны изменить время с 23,943 ч на один год, что составляет примерно 365,25 дней. Изменение угла такое же, полный оборот.

ω₂ = 2π рад / 23,934 h = 0,0000001991 рад / с = 1,991 * 10⁻⁷ рад / с ,

и линейная скорость Земли относительно Солнца (для среднего радиуса 1.496 * 10⁸ км ) составляет:

v₂ = 1,496 * 10⁸ км * 1,991 * 10⁻⁷ рад / с = 29,785 км / с .

Мы движемся довольно быстро, не так ли?

.

Чем угловая частота отличается от угловой скорости? Я имею в виду, что мы можем интуитивно сказать, что такое угловая скорость, но каково интуитивное объяснение угловой частоты ??

Физика

Наука

• Анатомия и физиология
• Астрономия
• Астрофизика
• Биология
• Химия
• наука о планете Земля
• Наука об окружающей среде
• Органическая химия
• Физика

Математика

• Алгебра
• Исчисление
• Геометрия
• Предалгебра
• Precalculus
• Статистика
• Тригонометрия

Гуманитарные науки

.

единиц угловой скорости и частоты — MATLAB и Simulink

единиц для угловой скорости и Частота

Единицы угловой скорости, например рад / с , град / с, , и об / мин , также может использоваться для частота измерения циклических процессов.Это соответствует частоте, определяемой как обороты в секунду в механическом контексте или циклов в второй в электрическом контексте, и позволяет вам писать частотно-зависимые уравнения без требуется преобразование 2 * pi фактор.Однако в системе единиц СИ единица измерения частоты — герцы (Гц), определяемые как 1 / с .

Программа Simscape ™ определяет единицу измерения герц. ( Гц ) как 1 / с , в соответствии с системой единиц СИ. это определение хорошо работает, когда частота относится к невращательный периодический сигнал, такой как частота источника ШИМ.Для циклических процессов однако блочные уравнения должны содержать 2 * pi коэффициент преобразования, в преобразовать числовое значение, указанное в Гц , или с ^-1 , угловой частоте.

В результате единицы частоты (на основе Гц ) и единиц угловой скорости (на основе об / мин ) напрямую не кабриолет, и используя один вместо другого может привести к неожиданным переводным коэффициентам применяется к числовым значениям блоком уравнения.Например, напряжение переменного тока Исходный блок явно умножает значение, которое вы указываете для его Частота параметр по 2 * pi , чтобы преобразовать его в угловой частота до вычисления синуса функция.

Выпадающие списки предлагаемых единиц в блоке диалоги отражают это различие. Например, если блок имеет частоту параметр с единицей измерения по умолчанию Гц , выпадающий список для этого параметр содержит только единицы, непосредственно конвертируемые до Гц (например, кГц , МГц, и ГГц ) и не содержит единицы угловой скорости.И наоборот, если вы определите настраиваемый блок, в котором Частота параметр имеет по умолчанию об / мин , его раскрывающийся список предлагаемых единиц будет включать град / с и рад / с , но не будет содержать Гц, кГц , МГц или ГГц .

Когда вы вводите единичное выражение в поле со списком единиц параметров (вместо выбора значение из раскрывающегося списка), менеджер единиц Simscape считает единицы измерения частота и угловая скорость должны быть соразмерными. Например, если единицей параметра по умолчанию является Гц , печатать умеете не только 1 / с , но и выражения например град / с и рад / с .Это поведение в соответствии с реализацией Simscape угловых единиц (см. Угловые единицы). Это Вы обязаны убедиться, что введенное вами выражение правильно работает с блокировать уравнения и отражает ваш дизайн намерение.

Примечание

До выпуска R2013a определение единицы для Гц было об / с . Для информация о том, как обновить устаревшие модели и пользовательские библиотеки Simscape, написанные на R2012b или ранее см. соображения совместимости в Определение единицы измерения Гц теперь соответствует SI в примечаниях к версии R2013a.

.

Угловая частота — Простая английская Википедия, бесплатная энциклопедия

По физике угловая частота. ω. (также называется угловой скоростью , радиальной частотой и радианной частотой) — это мера скорости вращения. Высокая угловая частота означает, что что-то вращается очень быстро. Угловая частота — это величина вектора угловой скорости , которая также известна как вектор угловой частоты . ω → {\ displaystyle {\ vec {\ omega}}} .

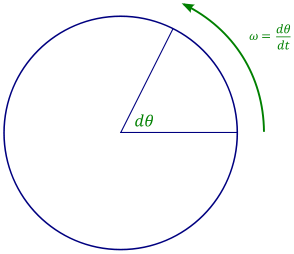Угловая частота — это мера того, насколько быстро объект вращается.

Это полезно во многих областях математики и естествознания, так как позволяет понять многие свойства физических объектов в нашем мире. В единицах СИ угловая частота измеряется в радианах в секунду с размерами t ^-1 , поскольку радианы безразмерны.

Угловая частота часто выражается в радианах в секунду ( т — 1 {\ displaystyle t ^ {- 1}} ), так как с ним легче работать.Таким образом, угловая частота определяется выражением

  
    
      
        ω
        знак равно
        
          
            
              2
              π
            
            Т
          
        
        знак равно
        2
        π
        ж
      
    
    {\ displaystyle \ omega = {\ frac {2 \ pi} {T}} = 2 \ pi f}
  
 
 

где Т {\ displaystyle T} — время (период) одного оборота (оборота) и ж {\ displaystyle f} это частота.

Если колесо поворачивается на угол θ {\ displaystyle \ theta} вовремя т {\ displaystyle t} тогда угловая частота в любой момент определяется выражением

  
    
      
        ω
        знак равно
        
          
            
              d
              θ
            
            
              d
              т
            
          
        
      
    
    {\ displaystyle \ omega = {\ frac {d \ theta} {dt}}}
  
   
 

Если скорость вращения постоянна, это становится,

  
    
      
        ω
        знак равно
        
          
            θ
            т
          
        
      
    
    {\ displaystyle \ omega = {\ frac {\ theta} {t}}}
  
 
 

и так похоже на скорость.

Для объектов, движущихся по кругу, угловая частота также может быть задана как (в радианах),

  
    
      
        ω
        знак равно
        
          
            v
            р
          
        
      
    
    {\ displaystyle \ omega = {\ frac {v} {r}}}
  
 
 

где v {\ displaystyle v} это скорость и р {\ displaystyle r} это расстояние от середины круга.

Угловая частота важна для определения того, может ли объект оставаться над землей против силы тяжести или же волчок может стоять. Это также важно для создания частоты подачи электроэнергии в сеть и уменьшения нагрева из-за трения в двигателях.

спутников [изменить | изменить источник]

Объекты притягиваются к земле под действием силы тяжести. Чтобы противостоять этому, спутник должен лететь достаточно быстро, чтобы не коснуться земли. Чтобы силы равнялись друг другу,

  
    
      
        
          
            
              грамм
              M
              м
            
            
              р
              
                2
              
            
          
        
        знак равно
        м
        
          ω
          
            2
          
        
        р
      
    
    {\ displaystyle {\ frac {GMm} {r ^ {2}}} = m \ omega ^ {2} r}
  
 
 

где M {\ displaystyle M} масса большего тела и грамм {\ displaystyle G} — гравитационная постоянная.Чтобы получился круг, угловая частота должна быть равна,

  
    
      
        
          ω
          
            c
            я
            р
            c
            л
            е
          
        
        знак равно
        
          
            
              
                грамм
                M
              
              
                р
                
                  3
                
              
            
          
        
      
    
    {\ displaystyle \ omega _ {круг} = {\ sqrt {\ frac {GM} {r ^ {3}}}}}
  
 
 

, что ведет к одному из законов Иоганна Кеплера.

Сетевое питание [изменить | изменить источник]

Генераторы на электростанциях вращаются с определенной частотой. Скорость, с которой они вращаются, дает нам частоту, с которой работают наши источники электроэнергии. Их можно замедлить с помощью больших тормозов или больших тяжелых колес, которые не позволяют генераторам вращаться слишком быстро.

Примеры измерения угловой частоты включают [изменить | изменить источник]

.