Вращательное движение
Страница 1 из 3
Существует большое количество расчетных задач, которые моделируют явления, происходящие в различных вращающихся агрегатах или около них. При постановке подобной численной задачи важно выбрать способ описания вращения в численной модели, который будет корректен с точки зрения физики и оптимален с точки зрения производительности вычислений. FlowVision позволяет задавать вращение различными способами: с помощью вращающейся локальной системы координат; с помощью подвижных тел; с помощью скользящих поверхностей. С целью помочь пользователю разобраться с постановкой такого типа задач, рассмотрены примеры задач разного типа, начиная с физико-математических основ.
1. Кинематика вращательного движения
1.1. Вращательное движение материальной точки
Вращательное движение материальной точки (м.т.) вокруг неподвижной оси – это движение материальной точки по окружности радиуса R, центр которой лежит на неподвижной относительно данной системы отсчета прямой (ось вращения), перпендикулярной плоскости, в которой лежит траектория точки.
Рис.1.
Вращательное движение тела вокруг неподвижной оси — движение тела, при котором все его точки, двигаясь в параллельных плоскостях, описывают окружности с центрами, лежащими на одной неподвижной прямой, называемой осью вращения. Тело, совершающее вращательное движение, имеет одну степень свободы, и его положение относительно данной системы отсчёта определяется углом поворота φ между неподвижной полуплоскостью и полуплоскостью, жёстко связанной с телом, проведёнными через ось вращения.
Рис.2.
1.2. Угол поворота
Угол φ считается положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси Az), и отрицательным, если по ходу часовой стрелки.
1.3. Основные кинематические характеристики вращательного движения
Основными кинематическими характеристиками вращательного движения являются угловая скорость и угловое ускорение .
Угловая скорость и угловое ускорение величины векторные. Вектор угловой скорости направлен вдоль оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис.3). Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси. Аналогично углу поворота, когда вращение происходит против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси Az) ω>0, а когда по ходу часовой стрелки, то ω<0. Таким образом, знак ωопределяет направление вращения.
Рис.3
1.4. Прочие кинематические характеристики
Скорость точки M на расстоянии R от оси (рис.2):
Тангенциальная составляющая ускорения точки M (рис.3б):
Нормальная составляющая ускорения точки M (рис.3б):
Полное ускорение точки M (рис.3б):
Формула Эйлера (рис.3в):
2. Силы инерции, действующие на материальную точку во вращающейся системе отсчета
2.1. Материальная точка, покоящаяся во вращающейся системе отсчета
Если рассмотреть движение вращающейся точки M, то относительно неподвижной системы координат (СК) XYZ (рис.4а) силу, действующую на неё можно определить из второго закона Ньютона: . Относительно вращающейся системы координат X’Y’Z’ точка M неподвижна (рис.4б). Это обеспечивается тем, что равнодействующая сил уравновешивается инерциальной силой (центробежной): .
Рис.4 (а,б)
2.2. Материальная точка, движущаяся во вращающейся системе отсчета
Если же точка движется во вращающейся системе отсчета, то помимо центробежной силы на неё действует ещё одна сила инерции – сила Кориолиса (рис.
5). Направление силы Кориолиса определяется правилом правого винта.
Рис. 5.
Таким образом, при переходе от основной неподвижной СК к локальной СК, которая является вращающейся системой отсчета, появляются дополнительные составляющие вектора силы, которые действуют на материальную точку: центробежная сила и сила Кориолиса .
Вращательное движение твердого тела — Теория и решение задач
Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П0 и П, одна из которых неподвижна, а другая жестко связана с телом.
φ=φ(t) – уравнение вращательного движения твердого тела.
Рис. 1.3
За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z.
Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.
Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:
В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2π⋅n, где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим
Вектор угловой скорости
где k – единичный вектор оси вращения.
Угловое ускорение – мера изменения угловой скорости:
Вектор углового ускорения – производная вектора угловой скорости по времени (рис.
1.4)
Рис. 1.4
- Если ε >0 и ω >0 (рисунок 1.4), то угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов
- При ε <0 и ω <0 – тело вращается ускоренно в отрицательную сторону. Направление векторов ω и ε совпадают, оба они направлены в отрицательную сторону оси вращения Oz.
- Если ε <0 и ω >0, то имеем замедленное вращение в положительную сторону. Векторы ω и ε направлены в противоположные стороны.
- Если ε >0 при
ω <0, то имеем замедленное вращение в отрицательную сторону. Векторы ω и ε направлены в противоположные стороны. - Если угловая скорость ω=const, то вращательное движение называется равномерным. Уравнение равномерного вращения
φ=φ0+ωt
- Если угловое ускорение ε=const, то вращательное движение называется равнопеременным.
Уравнение равнопеременного вращения и уравнение, выражающее угловую скорость в любой момент времениω=ω0+εt
представляют совокупность основных формул вращательного равнопеременного движения тела.
Вращательное движение | Физика
Расскажу вам о вращательном движении.
На первый взгляд может даже показаться, что вращательное движение нарушает законы механики.
В чем же нарушение и каких законов? Ну, скажем, закон инерции. Ведь всякое тело, если на него не действуют уравновешенные силы, должно или покоиться, или двигаться равномерно и прямолинейно. Но вот я даю боковой толчок этому глобусу, и он начинает вращаться. Если бы не трение, он, вероятно, вращался бы вечно, как вращается земной шар, никем не подталкиваемый. Как же быть с первым законом Ньютона? Или есть два закона инерции: одни для прямолинейного, а другой для вращательного движения?
Не торопитесь, мы сейчас выясним, в чем тут дело, и убедимся, что беспокоиться за законы Ньютона не приходится.
Вращательное движение отличается от поступательного. Однако есть в них и много общего, и весьма полезно сопоставить эти два вида движения. Много путаницы в головах учащихся происходит оттого, что в курсе физики средней школы не строго разграничивают механику материальной точки и механику материального тела. Скажите, вы помните, что называется поступательным движением?
– Конечно. Движение тела, при котором все его точки движутся одинаково.
– А как вы это понимаете?
– Я понимаю это так, что все точки тела в каждый момент времени имеют одинаковую по модулю и направлению скорость. Все точки описывают одинаковые траектории.
– Вот именно. Поэтому и можно рассматривать поступательное движение тела как движение одной точки, вернее, заменить движение тела движением его центра масс. Если на такое тело (материальную точку) не действуют другие тела, т. е. если оно не испытывает на себе действия неуравновешенных сил, то оно покоится или движется равномерно и прямолинейно.
Вращение тела характеризуют угловой скоростью, показывающей, на какой угол оно повернется за единицу времени. В технике угловую скорость часто выражают числом оборотов в минуту. Если угловая скорость постоянна, то мы говорим, что тело вращается равномерно. Если угловая скорость равномерно возрастает, то вращение называют равноускоренным. Сходство законов поступательного и вращательного движения поразительное. Только буквенные обозначения различны, а формулы получаются совершенно одинаковые. Вот первая параллель:
Все задачи по кинематике как вращательного, так и поступательного движения решаются по этим формулам аналогично.
– Это все понятно. Но как же быть с законом Ньютона?
– Не торопитесь, слушайте дальше. Рассмотрим движение одной материальной точки. Если хотите, вы можете представить себе ее как маленький тяжелый шарик. Можно сделать так, чтобы он двигался по окружности? (Катим маленький шарик от шарикоподшипника по столу.)
– Конечно, нет, он катится по прямой.
Можно, конечно, вести шарик по окружности, поддерживая его все время пальцами. Но стоит только убрать руку, как он будет продолжать движение по прямой линии.
– Итак, материальная точка может двигаться по окружности только под действием силы. Я вел шарик рукой, можно было бы привязать к нему веревочку или катить его внутри желобка. Как только прекратится действие силы, шарик начнет двигаться прямолинейно и равномерно.
В твердом теле не одна точка, а множество. Как вы думаете, они (точки) свободны или связаны?
– На них действует сила сцепления.
– Верно. Они-то и удерживают точки на круговой орбите. Не будь этих сил, материальные точки вращающегося тела разлетелись бы, как грязь слетает с вращающихся колес.
Есть еще одно сходство между поступательным и вращательным движением. При поступательном движении все точки тела движутся в данный момент времени с одинаковой линейной скоростью v. Если тело вращается, тоо все точки вращающегося тела движутся с одинаковой угловой скоростью ω.
Например, угловые скорости всех точек вращающейся спицы AB (рис. 59) одинаковы, а линейные различны.
На уроке физики вам говорили. Что равномерное движение точки по окружность есть в то же время движение с ускорением. Это ускорение называется центростремительным ускорением. Оно не характеризует изменение скорости по модулю, а характеризует только изменение направления скорости. Тут нелегко разобраться.
Я бы отстаивал определение равномерного вращательного движения только по угловой скорости. Тогда те параллельные формулы, о которых я говорил, будут всем понятны. Да и в технике, когда речь идет о равномерном вращении маховика или ротора электрического генератора или двигателя, подразумевают постоянной угловую скорость. Постоянное число оборотов якоря генератора обеспечивает постоянное напряжение в сети; постоянное число оборотов маховика обеспечивает плавный ход машины и экономичность ее работы. Это постоянство стараются поддержать, регулируя работу машины.
Теперь проведем параллель динамическую. По второму закону Ньютона ускорение, получаемое телом, вычисляется из формулы a = F/m. При вращении тела изменение угловой скорости будет зависеть от силы. Теперь скажите, все ли равно, где приложить силу при завинчивании, скажем, гайки: к концу рукоятки гаечного ключа или к самой гайке?
Вращающее действие силы, или момент силы, – вот что здесь важно, вот что является аналогом силы поступательного движения. Параллель найдена: силе в поступательном движении соответствует момент силы во вращательном движении. Так продолжим нашу сравнительную табличку.
– Я еще не написал формулу второго закона Ньютона, потому что об этом законе следует сказать подробнее. В формулу закона Ньютона входит масса m. Что она характеризует?
– Инертность тела.
– Правильно. Теперь подумайте, характеризует ли масса инертность вращающегося тела?
– Инертность вращающегося тела характеризуется не массой, а особой величиной, называемой моментом инерции, в которую входит как составная часть и масса. Момент инерции обозначается буквой I. Он зависит от массы тела и распределения этой массы, т. е. от формы тела. Тела различной формы имеют различные моменты инерции.
Простейший случай — движение материальной точки по окружности. Момент инерции такой точки равен произведению массы точки на квадрат расстояние ее от оси вращения, т. е. I = mr2. Если массу отнести от оси вращения на расстояние, вдвое большее, то инертность этой массы, или устойчивость вращательного движения, будет больше в четыре раза. Вот почему маховые колеса делают большими. Но слишком увеличивать радиус нельзя. С увеличением радиуса колеса увеличивается линейная скорость точек обода колеса: v = ωr. Учитывая, что центростремительное ускорение есть a = v2/r, получаем отсюда: a = ω2r. Это означает, что с увеличением радиуса колеса растет центростремительное ускорение точек его обода. Создающая это ускорение сила сцепления молекул может оказаться недостаточной для удержания их на круговом пути, и тогда колесо разрушится.
Каждое тело можно представить состоящим из множества точек. Для вычисления момента инерции тела надо суммировать моменты инерции отдельных точек. Эта задача вам пока не под силу. Скажу только, что для диска и сплошного цилиндра, вращающихся вокруг собственной оси, I = ½ mr2. В телах такой формы разные точки тела находятся на разных расстояниях от оси вращения, начиная от 0 и до r. Момент инерции тонкого круглого кольца (есть сходство с ободом маховика) I = mr2. Обо всем этом вы узнаете из курса теоретической механики, когда будете учиться в техникуме или институте. Сейчас же вы должны понять, что во вращательном движении роль массы играет момент инерции и закон динамики вращательного движения, аналогичный второму закону Ньютона, примет вид: M = Iα. Теперь мы можем закончить сравнительную таблицу, включив в нее формулы для основного уравнения динамики, импульса и кинетической энергии:
Основные определения и формулы
Скорость резания V (м/мин) – это окружная скорость перемещения режущих кромок фрезы. Эта величина определяет эффективность обработки и лежит в рекомендованных для каждого инструментального материала пределах. За один оборот фрезы точка режущей кромки, находящаяся на окружности фрезы диаметра D (мм), сможет пройти путь, равный длине окружности, то есть πD. Для того чтобы определить длину пути, пройденного точкой за одну минуту, нужно умножить длину пути за один оборот на частоту вращения фрезы, то есть πDN (мм/мин). Таким образом, формула для определения скорости резания будет следующей:
V = πDN/1000 (мм/мин).
Частота вращения шпинделя N (об/мин) равняется числу оборотов фрезы в минуту. Вычисляется в соответствии с рекомендованной для данного типа обработки скоростью резания:
N = 1000V/nD (об/мин).
При фрезеровании различают минутную подачу, подачу на зуб и подачу наоборот фрезы.
Подача на зуб Fz (мм/зуб) – величина перемещения фрезы или рабочего стола с заготовкой за время поворота фрезы на один зуб.
Подача на оборот Fo (мм/об) – величина перемещения фрезы или рабочего стола с заготовкой за один оборот фрезы. Подача на оборот равняется произведению подачи на зуб на число зубьев фрезы Z:
Fo = FzZ (мм/об).
Минутной подачей Fm (мм/мин) называется величина относительного перемещения фрезы или рабочего стола с заготовкой за одну минуту. Минутная подача равняется произведению подачи на оборот на частоту вращения фрезы:
Fm = FoN = FzZN (мм/мин).
Глубиной фрезерования h (мм) называется расстояние между обработанной и необработанной поверхностями, измеряемое вдоль оси фрезы.
Шириной фрезерования b (мм) называется величина срезаемого припуска, измеренная в радиальном направлении, или ширина контакта заготовки и инструмента.
Производительность снятия материала Q (см3) – это объем удаляемого материала в единицу времени, определяемый глубиной, шириной обработки и величиной подачи.
Q = (h × b × Fm)/1000.
Вращательное движение
Содержание:
Вращательное движение
- Когда тело вращается, две его точки(или связанные с ними точки) остаются неподвижными,а линия, проходящая через них, называется осью вращения. Примером вращательного движения может быть вращающаяся шестерня, вращение карусели и т.д. При удержании
плоскости Р через ось вращения она плотно соединяется с корпусом, и тогда при вращении корпуса эта плоскость займет новое положение(рис. 11.3). Начальное положение плоскости P и ее новое положение R{угол в настоящее время называется
углом поворота тела, и если плоскость R вращается против часовой стрелки, то Людмила Фирмаль
помимо оси вращения для полного определения движения тела, измеренного в радианах, мы должны также знать угол поворота<p как угол поворота тела.
/: Ф=/(/). (11.4) Это уравнение называется законом вращательного движения тела. Отношение угла поворота тела<p к соответствующему времени D / называется вектором средней угловой скорости данного времени, обозначаемым буквой «cf».
Предел средней угловой скорости с тенденцией от D/до нуля называется угловой скоростью, обозначаемой Ю.: Вектор угловой скорости всегда направлен вдоль оси вращения, и при рассмотрении от края вектора y до его начальной точки вращение тела происходит против часовой стрелки, а вектор Co положителен(рис. 11.4, а),
- если направление совпадает с осью z или отрицательно (рис. 11.4, Б), если не то же самое. В системе СИ угловая скорость измеряется радианами, деленными на секунды (рад/с). В машиностроении, на самом деле, это равномерное вращение Используйте число оборотов n в минуту, которое связано с равной 100º скорости угловой скорости: co=2l/g / 60=ll / 30 (рад/с) (11,6) Или p=Zoso/l (об / мин). (11.7) В общем случае угловая скорость не постоянна, а зависит от времени со=/(/),
(11.8) То есть для того, чтобы охарактеризовать вращение, необходимо знать скорость изменения угловой скорости. А также ускорение точки, характеризующее скорость изменения величины и угловой скорости, равной первой производной угловой скорости во времени, называется модулем углового ускорения тела.: dco d2f Вектор углового ускорения направлен вдоль оси вращения, и по мере вращения тела модуль угловой скорости может уменьшаться или увеличиваться. В первом случае вращение замедляется,а во втором-ускоряется. В ускоренном движении направление вектора ускорения совпадает с направлением вектора скорости,
а в замедленном движении векторы скорости и ускорения направлены в разные стороны. В системе СИ Людмила Фирмаль
угловое ускорение измеряется в радианах, деленных на секунды 101квадрат (рад / С2). Векторы угловой скорости и углового ускорения являются скользящими, то есть их можно приложить к любой точке оси вращения.
Равномерным вращением тела называют такое движение, при котором угловая скорость вращения тела остается постоянной. Если угловое ускорение тела постоянно,то это вращение называется равной переменной. Закон равномерного и эквивалентного переменного вращения получается таким же образом, как и аналогичный закон движения точки, поэтому при равномерном движении (аналогично формуле (10.3) F=To+ » o (11.Y) где fo-начальный угол поворота, а COO-постоянная угловая скорость тела. Замена S, s0, t’O на CP, F0, co » e в уравнении (10.9) дает закон равного
вариационного движения F=Fo4 «» o e / 2 / 2. (11.11) Где wo-начальная угловая скорость. В любой момент времени угловая скорость определяется выражением, аналогичным выражению (10.8): со=<О0+е/. (11.12) Если скорость и ускорение одинаково направлены в одном направлении при переменном вращении, то вращение равномерно ускоряется, и соответственно, если направление скорости и ускорения не совпадают, то вращение одинаково ускоряется. Например. После отключения двигателя его вал вращался на равном расстоянии до полной остановки в течение 10 секунд. За это время он сделал 60 поворотов. Определите угловое ускорение и угловую
скорость вала при остановке двигателя. Решение. Установите угол поворота вала во время выключения двигателя на f=60•2l=120L. Затем, согласно формуле (11.11)、 F=120L=so0 * 10+e-50. Из соотношения (11.13) (11.12), in<o=0 (t=1 0C), in (OO=-e-10. Подставляя эту формулу в Формулу (11.13), получим угловое ускорение е=-2.4 л. Тогда угловая скорость wc== — e-10=-(-2,4 л) 10=24л при выключении двигателя. Число оборотов вала в минуту p-Zoso/l=30-24L / l-=720rpm.
Смотрите также:
Решение задач по технической механике
Скорость вращения — видео по физике от Brightstorm
Скорость, с которой объект вращается или вращается, называется скоростью вращения . В отличие от линейной скорости, она определяется количеством вращений объекта за период времени.
Формула для скорости вращения: Скорость вращения = обороты / время , но линейная скорость = расстояние / время .
Хорошо, давайте поговорим о скорости вращения, скорость вращения действительно состоит из двух компонентов.Одна из них — это линейная скорость, которую также называют тангенциальной скоростью, и это, по сути, расстояние, на котором объект движется с течением времени, нормально. Если он движется по круговой орбите, если мы выпустим его с этой орбиты, он продолжит движение по касательной от этой точки с определенной скоростью, нормально. Другая скорость объекта — это скорость вращения, скорость вращения — это количество оборотов за раз. Итак, давайте рассмотрим пример, вас часто спрашивают: допустим, у нас есть 2 точки на записи, и рекорд вращается с определенной скоростью, например, 33 оборота в минуту, хорошо.Что ж, если мы сравним скорость этих двух объектов, она будет очень разной, если мы говорим о тангенциальной, линейной или тангенциальной скорости относительно скорости вращения. Итак, если мы посмотрим на них обоих, они оба имеют скорость вращения 33 оборота в минуту.
Но если мы посмотрим на скорость, с которой они движутся на записи, на линейную скорость, мы увидим, что линейная скорость на самом деле связана с радиальным расстоянием в зависимости от скорости вращения. Итак, если я скажу, что a равно x, а b равно 2x с точки зрения нашего радиального расстояния, расстояния с точки зрения радиуса от центра справа, мы увидим, что b будет двигаться намного быстрее, чем a.Вот почему 2 объекта могут иметь одинаковую скорость вращения, но очень разные линейные скорости.
Формула линейной скорости (вращающийся объект)
Линейная скорость точки на вращающемся объекте зависит от ее расстояния от центра вращения. Угловая скорость — это угол, под которым объект движется за определенный промежуток времени.
Угловая скорость измеряется в радианах в секунду (рад / с). В полном круге 2π радиана. На расстоянии r от центра вращения точка на объекте имеет линейную скорость, равную угловой скорости, умноженной на расстояние r.Единицы измерения линейной скорости — метры в секунду, м / с.
линейная скорость = угловая скорость x радиус вращения
v = ωr
v = линейная скорость (м / с)
ω = угловая скорость (радиан / с)
r = радиус вращения (м)
Формула линейной скорости (вращающийся объект) Вопросы:
1) Электродрель включена и вращается со скоростью 10,0 оборотов в секунду (об / с). Диаметр сверла 4,00 мм. Какова линейная скорость точки на поверхности сверла в метрах в секунду?
Ответ: Первый шаг — найти угловую скорость сверла.Число оборотов в секунду необходимо перевести в радианы в секунду. В полном круге 2π радиана.
ω = 10,0 об / с
Расстояние между центром вращения и точкой на поверхности сверла равно радиусу. Диаметр сверла указан в миллиметрах. Радиус в метрах:
∴r = 0,002 м
Используя формулу v = ωr, линейная скорость точки на поверхности бурового долота равна
v = ωr
∴v = (62.8 радиан / с) (0,002 м)
Линейная скорость точки на поверхности сверла составляет приблизительно 0,126 м / с. Радианы — это единица измерения «заполнитель», поэтому они не включаются при записи решенного значения для линейной скорости.
2) Еще вопрос.
Датчик, подключенный к автомобильному колесу, измеряет линейную скорость. Датчик находится на 0,080 м от центра вращения. В этом положении датчик показывает, что линейная скорость колеса равна 8.00 м / с. Если радиус колеса 0,220 м, какова линейная скорость на внешней кромке колеса?
Ответ: Линейная скорость различается на разных расстояниях от центра вращения, но угловая скорость одинакова везде на колесе. Чтобы решить эту проблему, сначала найдите угловую скорость, используя линейную скорость в положении датчика, 0,080 м.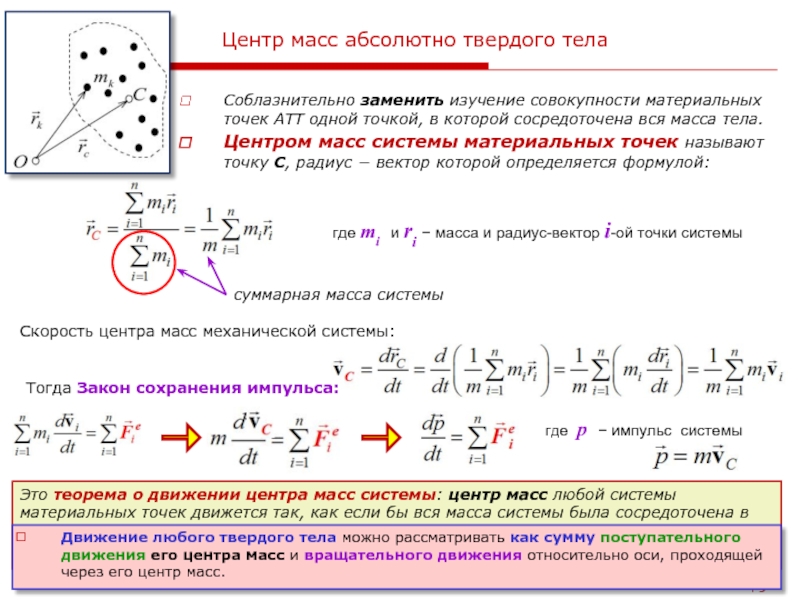
Формулу v = ωr можно переписать, чтобы найти угловую скорость ω:
Это также угловая скорость на внешней кромке колеса, где радиус r = 0.220 м. Формулу v = ωr можно снова использовать для определения линейной скорости на этом радиусе:
v = ωr
v = (100 рад / с) (0,220 м)
∴v = 22,0 м / с
Линейная скорость автомобильного колеса по внешнему краю составляет 22,0 м / с.
Как преобразовать обороты в минуту в линейную скорость
Обновлено 14 февраля 2020 г.
Ли Джонсон
Проверено: Lana Bandoim, B.S.
Вращательное движение — одна из самых важных вещей, которую нужно понимать при изучении классической физики, а преобразование скорости вращения в линейную скорость является ключевой задачей во многих задачах.
Сам расчет довольно прост, но сложен, если угловая скорость (то есть изменение углового положения в единицу времени) выражается в нестандартной форме, например, в оборотах в минуту (об / мин). Однако преобразовать число оборотов в минуту в скорость по-прежнему достаточно просто после преобразования числа оборотов в минуту в более стандартную меру угловой скорости.
Об / мин Формула и объяснение
Об / мин — это количество полных оборотов в минуту .Например, если колесо вращается так, что оно совершает один полный оборот в секунду, за 60 секунд оно совершит 60 оборотов, и поэтому оно будет вращаться со скоростью 60 об / мин. Формула RPM, которую вы можете использовать для определения скорости вращения в любой ситуации:
\ text {RPM} = \ frac {\ text {Число оборотов}} {\ text {время в минутах}}
Из этой формулы, вы можете рассчитать обороты в любой ситуации, даже если вы записывали количество оборотов меньше (или больше) минуты.Например, если колесо совершает 30 оборотов за 45 секунд (т.е. 0,75 минуты), результат будет: 30 ÷ 0,75 = 40 об / мин.
отоб / мин до угловой скорости
В большинстве ситуаций в физике вместо об / мин используется угловая скорость ( ω ), которая, по сути, представляет собой угловое изменение положения объекта в секунду, измеряемое в радианах в секунду.
Это гораздо более полезный формат, когда вы конвертируете число оборотов в минуту в линейную скорость, потому что существует простая связь между угловой скоростью и линейной скоростью, которая не существует в явной форме для числа оборотов в минуту.Учитывая, что полный оборот составляет 2π радиан, RPM действительно говорит вам «количество 2π радиан оборотов в минуту».
Используя это, легко увидеть, как преобразовать между об / мин и угловой скоростью: сначала преобразовать из минуты в секунду, а затем преобразовать количество оборотов в значение в радианах. Вам нужна формула:
ω = \ frac {\ text {RPM}} {60 \ text {секунда / минута}} × 2π \ text {rad / rev}
Проще говоря, вы делите на 60, чтобы преобразовать в оборотов в секунду, затем вы умножаете это на 2π, чтобы превратить это в значение в радианах в секунду, которое является искомой угловой скоростью .Например, если колесо в предыдущем разделе движется со скоростью 40 об / мин, вы преобразуете его в угловую скорость следующим образом:
\ begin {align} ω & = \ frac {40 \ text {RPM}} {60 \ text {second / минута}} × 2π \ text {rad / rev} \\ & = 4.19 \ text {rad / s} \ end {align}
Угловая скорость в скорость
С этого момента преобразование из об / мин в линейную скорость осуществляется простой. Вам нужна формула:
v = ωr
Где ω — угловая скорость, вычисленная на предыдущем шаге, а r — радиус круговой траектории движения, и вы умножаете их вместе, чтобы найти линейная скорость.Например, при вращении колеса со скоростью 40 об / мин, то есть 4,19 рад / с, принимая радиус 15 см = 0,15 м, скорость будет:
\ begin {align} v & = 4,19 \ text {rad / s} × 0,15 \ text {m} \\ & = 0,63 \ text {m / s} \ end {align}
Есть несколько дополнительных моментов, которые следует учитывать при выполнении этих вычислений. Во-первых, направление линейной скорости, которое вы вычисляете, всегда по касательной к точке на окружности, для которой вы рассчитываете.
Например, если вы раскачиваете йо-йо по гигантскому кругу, но струна порвалась, йо-йо улетел бы в любом направлении, в котором оно двигалось, в момент , когда струна порвалась.Во-вторых, очень важно думать о единицах измерения при расчете оборотов. Единицы расстояния, которые вы используете для радиуса, будут такими же, как единицы расстояния в вашей конечной скорости, поэтому лучше придерживаться метров или футов, даже если число для радиуса оказывается очень маленьким.
Вращательное движение | Блог Гэри Гарбера
До сих пор в этом семестре нашего изучения классической механики мы изучали поступательное движение. Теперь мы приступим к изучению вращательного движения.
У каждой концепции, которую мы изучили до сих пор, есть ротационный аналог.
В начале года мы обсуждали, как объект может претерпеть смещение x . Мы также могли повернуть объект на угол θ.
Аналогично, скорость объекта или скорость изменения положения
имеет аналог вращения, скорость вращения, скорость изменения угла
ω = Δθ / Δt
Существует также угловое ускорение, которое представляет собой скорость изменения угловой скорости.Мы можем изучить крутящий момент, который представляет собой силу вращения. Момент инерции (или инерции вращения) — это тенденция объекта оставаться в состоянии покоя или оставаться в состоянии вращательного движения. Основываясь на этом, угловой момент — это инерция вращения в состоянии вращательного движения. У нас также может быть кинетическая энергия вращения!
Если мы предположим, что объект непрерывно вращается, то другой способ взглянуть на вращательное движение — это исследовать период вращения, T . Измеряемый в единицах времени ( миллисекунд, секунды, часы, годы, эоны …), период — это время, необходимое для одного полного оборота.Мы также могли бы описать, как часто объект вращается. Частота объекта f обратно пропорциональна периоду вращения.
T = 1 / f
и
ф = 1 / т
Метрическая единица измерения частоты — герцы ( Гц, ), где 1 Гц = 1 циклов в секунду . Вы, вероятно, знакомы с термином Герц по частотам на шкале радиоприемника, например, WBUR 90,9 МГц или WBZ 1030 кГц .
Пример
Представьте себе маленького мальчика, который пытается вызвать головокружение, быстро вращаясь.Если он вращается с частотой 0,8 Гц, сколько времени ему потребуется, чтобы сделать 1 оборот?
f = 0,8 Гц
T = 1 / f = 1 / 0,8 Гц = 1 / 0,8 циклов в секунду = 1,25 секунд
Другая традиционная единица измерения частоты — оборотов в минуту или оборотов в минуту . Вы можете увидеть это на старомодном проигрывателе, который мог вращаться со скоростью 33 или 45 об / мин на .
А пока рассмотрим двух маленьких человечков LEGO, стоящих на проигрывателе.Когда проигрыватель поворачивается, мы можем описать движение маленьких человечков LEGO с точки зрения их линейной скорости (метры в секунду) или их скорости вращения. Если мы установим проигрыватель на 45 об / мин, то оба LEGO-человечка будут иметь одинаковую скорость вращения. Однако у них разные линейные или тангенциальные скорости. Мы используем слово тангенциальный, потому что, если человек LEGO поскользнется и упадет, его собственная инерция заставит его отлететь от проигрывателя по линии, касающейся его кругового движения!
Мы можем рассчитать линейную скорость для каждого человека, используя уравнение
v = 2πr / т
где r — радиус круга, а T — период вращения.Помните, что скорость — это расстояние во времени. В этом случае расстояние за один период вращения оказывается длиной окружности.
Если мужчины расположены на нашем проигрывателе на расстоянии 10 см и 4 см от центральной оси:
Пример
f = 45 об / мин
r = 12 см
Сначала вычисляем период.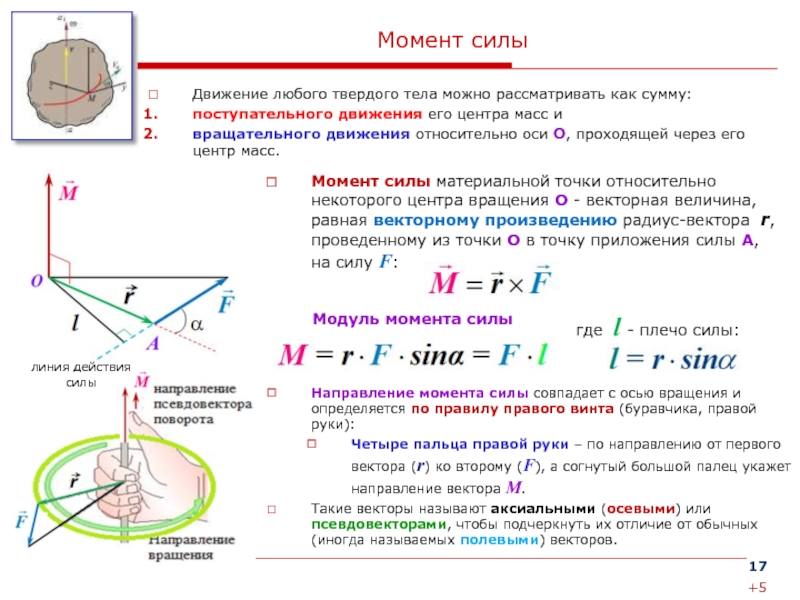
С 45 об / мин = 0,75 об / сек
Таким образом, период вращения равен 1.33 секунд .
Таким образом, скорость будет
v = 2πr / T = 2π (10 см ) / 1,33 с = 47 см / с
У маленького человечка, стоящего в радиусе 4 см, у него гораздо меньшая линейная скорость, хотя и такая же скорость вращения
v = 2πr / T = 2π (4 см ) / 1,33 с = 19 см / с
Существует тонкая разница между скоростью вращения и скоростью вращения, которую мы представим позже.
Мы можем определить взаимосвязь между линейной скоростью и угловой скоростью с помощью следующего уравнения
v = ω r
Обратите внимание, что ω, угловая скорость, была определена ранее как изменение угла в единицу времени.
ω = Δθ / Δt
При рассмотрении приведенного выше уравнения возникает интересный вопрос относительно единиц измерения угловой скорости. До сих пор мы использовали такие термины, как обороты в минуту или обороты в секунду. Но революцию можно было бы определить как ПОЛНЫЙ поворот на 360 °.
Вы, наверное, изучали единицы измерения углов в градусах. Но когда мы обсуждаем угловую скорость, мы обычно не говорим об целом числе оборотов. Таким образом, мы могли бы использовать такие единицы измерения, как градусы в секунду. Однако градус не является метрической единицей вращения. Стандартная единица измерения — радиан.
2π радиан = 360 °
Если мы посмотрим на изображение единичного круга, мы увидим преобразование между радианами и градусами. Это действительно одно и то же, просто разные единицы.
В каком-то смысле единственная разница между частотой и угловой скоростью заключается в единицах. Угловая скорость измеряется в радиан в секунду , а частота измеряется в герцах или оборотов в секунду . Таким образом, мы могли бы выразить алгебраическую связь между этими двумя терминами как
2πf = ω
Используя это, мы могли бы фактически найти угловую скорость нашего проигрывателя, который вращается со скоростью 45 об / мин .
ω = 2πf = 2π (0.75 об / с ) = 4,7 рад / с
Пример
Давайте еще раз посмотрим на человечков LEGO на проигрывателе. Используя соотношение между линейной скоростью и угловой скоростью, находим
v = ω r
v = 4,7 радиан / сек x 10 см = 47 см / сек
и для человека ближе к центру
v = 4,7 радиан / сек x 4 см = 19 см / сек
Важно отметить, что линейная скорость увеличивается как с угловой скоростью, так и с радиусом
КАЛЬКУЛЯТОР СКОРОСТИ ВРАЩЕНИЯ
3 августа 2018 г. · Скорость вращения ω можно оценить, учитывая изменение углового смещения θ со временем t.ω = θ t На практике это может быть немного сложно, поэтому для измерения скорости вращения, скажем, вала двигателя, мы визуально подсчитываем количество оборотов в минуту. Как я могу рассчитать скорость вращения? + Пример Онлайн-калькулятор угловой и линейной скорости, а также числа оборотов в системе, которая движется по круговой траектории с постоянной скоростью. Этот калькулятор преобразует количество оборотов в минуту (об / мин) точки P, вращающейся на расстоянии R от центра вращения O,… Калькулятор угловой, линейной скорости и оборотов Онлайн-калькулятор удельной скорости насоса.Калькулятор ниже может использоваться для расчета удельной скорости: n — частота вращения вала насоса (об / мин) q — расход (м 3 / ч, л / с, л / мин, м 3 / мин, галлонов США в минуту, британских галлонов в минуту) ч = подъем головы (м, фут) Примечание! Сравнивая насосы и документацию на них — помните об используемых агрегатах. Насосы особой скорости Ускорение, необходимое для удержания объекта на круговой траектории, равно ω²r, где ω — угловая скорость (= линейная скорость / r). Это центростремительное ускорение направлено к центру вращения, а соответствующая сила задается уравнением Ньютона F = M⋅a.Центробежная сила («фиктивная») уравновешивает эту силу. CalcTool: Калькулятор центробежной силы Смотрите больше видео на http://www.
brightstorm.com/science/physics ПОДПИСАТЬСЯ НА ВСЕ НАШИ ВИДЕО! Https: //www.youtube.com/subscription_center? Add_user = brightstorm2. Скорость вращения
Июл 01, 2016 · 5 000 за доказательство того, что Земля — это земной шар и код водного видообразования для расчета темной материи окончательный калькулятор балки калькулятор палеолода для ротационного SD в LaudeScience Update The Radio News Feature Of Aaas The Ultimate Balics CalculatorThe Ultimate Balics КалькуляторГлава 3Глава 3Решенное имя Eiel Salato Physics 4a Тест 4… Калькулятор скорости вращения Земли
Детализировано понятие тангенциальной скорости, а также указана формула для ее расчета.Отсутствие «радиана» в единицах измерения. При вычислении тангенциальной скорости как произведения радиуса геометрического места и угловой скорости произведение радиуса на угловое смещение в радианах дает общее расстояние по дуге. Как рассчитать тангенциальную скорость
Калькулятор тангенциальной скорости. Приведенный ниже онлайн-калькулятор тангенциальной скорости — это онлайн-инструмент, который поможет вам определить скорость вращающегося колеса или любого круглого объекта. Если вы знаете значение радиуса объекта, вы можете легко рассчитать тангенциальную скорость с помощью нашего онлайн-инструмента.Калькулятор тангенциальной скорости
Этот калькулятор предназначен для предоставления информации о движении колеса и шины на транспортном средстве на основе введенных данных. Введите скорость автомобиля. Выберите размер обода из раскрывающегося списка или вручную введите размер диаметра обода (не ширину). Затем выберите размер корпуса шины, перпендикулярное расстояние от внешнего вертикального края шины. Калькулятор движения колес и шин
Из числа оборотов в минуту можно найти угловую скорость — один оборот изменяет угол на радианы, таким образом, в минуту это радианы, а в секунду это радианы.Радианы в секунду — это угловая скорость. Линейная скорость тривиальна, 1 радиан соответствует дуге с… Онлайн-калькулятор: Угловая скорость и линейная скорость
13 февраля 2018 г.
· В дополнение к скорости вращения Земли вокруг своей оси, планета также движется со скоростью около 66 660 миль в час (107 278,87 км / ч) в… Скорость Земли
Калькулятор скорости, частоты и полюсов двигателя переменного тока getcalc.com — это онлайн-инструмент для электротехники, позволяющий рассчитать необходимую скорость вращения, частоту сети и количество полюсов для проектирования синхронного двигателя переменного тока.Определение и формулы. Синхронный двигатель — это электрический механизм, имеющий магнитные поля статора и ротора. В электротехнике расширение. Калькулятор скорости, частоты и полюсов двигателя переменного тока
Просмотр калькулятора. об / мин = максимальная безопасная скорость вращения, об / мин. d = малый диаметр, дюйм l = длина без опоры, дюйм K = коэффициент безопасности (задается пользователем от 1,25 до 3 общих) `F_s` = коэффициент конечной фиксации = 0,32 без фиксированных = 1,00 с опорными опорами = 1,55 с фиксированными опорами = 2,24 фиксированный-фиксированный. Загрузка столбца `P_s = (P_mF_l) / K` Просмотр калькулятора Формула Калькуляторы
Если вы знаете какие-либо 3 значения (размеры шкивов или число оборотов в минуту) и вам нужно вычислить 4-е, введите 3 известных значения и нажмите «Рассчитать», чтобы найти недостающее значение.Например, если ваш маленький шкив имеет диаметр 80 мм и вращается со скоростью 1000 об / мин, и вам нужно найти второй размер шкива, чтобы вращать его со скоростью 400 об / мин, введите шкив 1 80, шкив 1 об / мин 1000, шкив 2 об / мин 400 и нажмите «Рассчитать». чтобы найти второй диаметр шкива. Калькулятор шкивов. Обороты, длина ремня, скорость, анимированные диаграммы
18 ноября 2018 г. · Вопрос: рассчитайте скорость и крутящий момент выходного вала для простой зубчатой передачи. Где количество зубьев на ведущей и ведомой шестернях — 40 и 20 соответственно. Шестерня привода вращается со скоростью 100 об / мин и крутящим моментом 10 Нм.Количество зубьев ведущей шестерни (T1) = 40. Количество зубьев ведомой шестерни (T2) = 20.
Скорость ведущей шестерни (n1) = 100 об / мин. Зубчатая передача: расчет передаточного числа, крутящего момента и скорости.
Определение линейной скорости. Линейная скорость чаще всего определяется как тангенциальная скорость вращающегося объекта. Пример линейной скорости. Давайте посмотрим на пример проблемы. Во-первых, нам нужно измерить радиус вращения. В этом примере мы скажем, что радиус равен 50 м. Далее мы должны определить угловую скорость. Калькулятор линейной скорости
Наш калькулятор скорости наконечника предназначен для наиболее частого использования уравнения скорости наконечника.Скорость наконечника — расчет скорости наконечника на основе известного диаметра лезвия и числа оборотов в минуту. RPM — расчет оборотов, необходимых для достижения желаемой скорости наконечника с известным диаметром лезвия. Увеличение масштаба — согласование скорости наконечника одного миксера со скоростью второго диспергатора с разными размерами лопастей. Определение и формула скорости конца рабочего колеса
09 февраля 2021 г. · Соответственно, скорость вращения — это количество полных оборотов, которые объект делает за единицу времени. Он выражается в радианах в секунду (рад / с) или в оборотах в минуту (об / мин).Мы не будем больше останавливаться на этой теме, потому что это не является целью данного калькулятора скорости и расстояния. Калькулятор скорости Расчет удельной скорости насоса. Конкретная скорость используется для представления формы насоса. Конкретная скорость насоса может быть рассчитана на основе скорости вращения вала… Калькулятор удельной скорости насоса
Рассчитайте скорость в минуту, разделив скорость колеса на количество оборотов шины на милю. Например, если скорость колеса составляет 300 об / мин, шина в примере движется со скоростью 0.446 миль в минуту. Умножьте скорость в милях в минуту на 60, чтобы преобразовать скорость в мили в час (миль в час). В нашем примере шина с диаметром 30 дюймов вращается при 300 об / мин.
Как рассчитать скорость на основе скорости колеса и шины.
Рассчитайте идеальную скорость вращения (n) Скорость вращения привода (n) указывается в оборотах в минуту [об / мин]. Требуемая скорость вращения определяется из скорости резания V в метрах в минуту [м / мин] или в метрах в секунду [м / с] и диаметра инструмента d x π (3.14). Калькулятор скорости вращения PFERD
Калькулятор угловой скоростиУгловая скорость объекта или частицы — это скорость, с которой они вращаются вокруг выбранной центральной точки, или, другими словами: какое угловое расстояние покрывает объект вокруг чего-либо за период времени, и измеряется в углах на единицу. время. Стандартное измерение — в радианах в секунду, хотя на практике часто используются градусы в секунду, обороты в минуту (об / мин) и другие единицы, и наш калькулятор поддерживает большинство из них в качестве единиц вывода.Вектор угловой скорости всегда направлен перпендикулярно…
. можно вычислить. Физика водяного колеса
Скорость шпинделя — это частота вращения шпинделя станка, измеряемая в оборотах в минуту (об / мин). Предпочтительная скорость определяется путем движения назад от желаемой поверхностной скорости (sfm или м / мин) с учетом диаметра (заготовки или фрезы). Шпиндель может удерживать: Материал (как в патроне токарного станка). Сверло. Скорости и корма
01 апреля 2019 г. · Полное вращение — это угол 2π рад, поэтому результирующая угловая скорость будет: ω₁ = 2π рад / 23.934 ч = 0,2625 рад / ч = 0,00007292 рад / с, или 7,292 * 10⁻⁵ рад / с (в научном представлении). Калькулятор угловой скорости
Рассчитайте скорость вращения асинхронного двигателя. FAQ № FAQ02018. Связанное содержание. Основное содержание. Вопрос. Мы используем инвертор для контроля скорости. Как мы можем рассчитать скорость вращения асинхронного двигателя? Отвечать. Обычно скорость (N) асинхронного двигателя выражается следующей формулой: Преобразователь частоты: вычислить скорость вращения.Воспользуйтесь этим калькулятором скорости, а также множеством других калькуляторов, которые Roton предлагает в ваше распоряжение. Калькулятор скорости — Roton Products, Inc. Магазин продуктов Калькулятор скорости
Если скорость вращения указана в об / мин, а расстояние (r) выражено в сантиметрах, RCF может быть вычислена. Калькулятор ниже преобразует силу перегрузки (RCF) из числа оборотов в минуту (об / мин) или наоборот для получения более точных результатов экспериментов и контроля качества, требующих центрифугирования.Калькулятор G Force (RCF в об / мин)
Калькулятор крутящего момента, мощности, вращения и скорости; Вольт, Ампер, Калькулятор мощности; Калькулятор крутящего момента, мощности, скорости вращения. Крутящий момент {{data.Torque}} Скорость вращения {{data.Speed}} Мощность {{data.Power}} Вычислить Очистить все. Распечатать Получить как PDF. См. «Другие калькуляторы». См. «Поршневые насосы на складе». Калькулятор крутящего момента, мощности, скорости вращения
В физике одним из основных участников игры с линейной силой является работа; в форме уравнения работа равна силе, умноженной на расстояние, или W = Fs.
Работа имеет вахтовый аналог. Чтобы связать линейную силу, действующую на определенном расстоянии, с идеей вращательной работы, вы связываете силу с крутящим моментом (его угловой эквивалент), а расстояние с […] Как рассчитать вращательную работу
Синхронная скорость: это скорость вращения магнитного поля. В синхронном двигателе ротор вращается с синхронной скоростью. Однако в асинхронной машине (большинство электрических двигателей переменного тока асинхронные) скорость вращения немного ниже синхронной.Калькулятор скорости вращения электродвигателя (об / мин)
Нам нужно всего два значения, чтобы вычислить скорость вращения Земли на ее экваторе (0 градусов широты). Первое значение — это экваториальный радиус Земли, который можно легко получить из текстов по астрономии или в Интернете: R eq = 6 371,14 км. Второе значение — это звездный период вращения Земли. Расчет скорости вращения Земли
На расстоянии r от центра вращения точка на объекте имеет линейную скорость, равную угловой скорости, умноженной на расстояние r.Единицы измерения линейной скорости — метры в секунду, м / с. линейная скорость = угловая скорость x радиус вращения Формула линейной скорости (вращающийся объект)
09.09.2018 г. · Радиус от центра вращения. Угловая скорость или «скорость вращения». Тангенциальная скорость или «ободная скорость». Центростремительное ускорение или «уровень гравитации». Эти четыре параметра взаимозависимы: указание значений для любых двух из них также определяет значения двух других. Калькулятор назначает приоритет каждому параметру.SpinCalc
Обработка. . . Скорость кругового движения
Введите либо линейную скорость (скорость по прямой), либо угловую скорость (скорость вращения) в соответствующее синее поле, затем введите радиус вращения. Расчет дает соответствующую угловую или линейную скорость, а также центробежную силу. CalcTool: Линейный <
Скорость, с которой объект вращается или вращается, называется скоростью вращения. В отличие от линейной скорости, она определяется количеством вращений объекта за период времени.
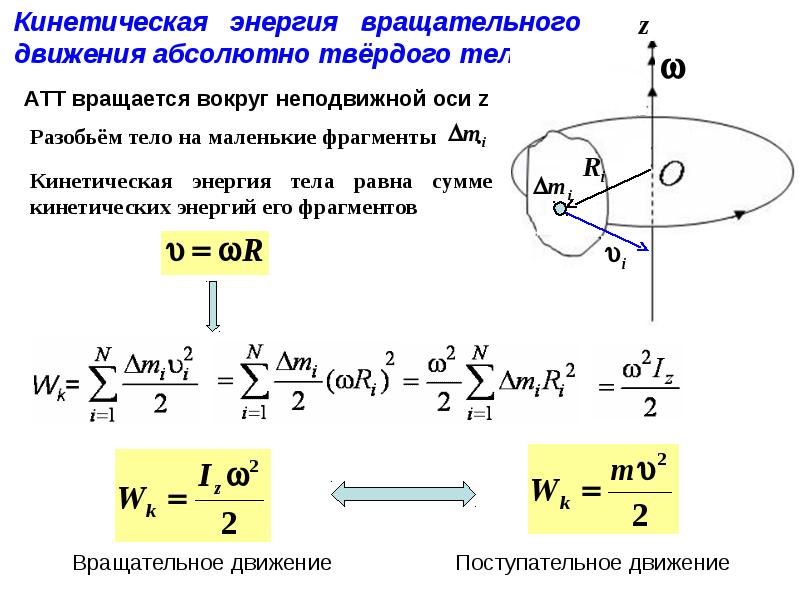Формула для скорости вращения: Скорость вращения = обороты / время, а линейная скорость = расстояние / время. Скорость вращения
Формула угловой скорости используется для расчета расстояния, которое тело преодолевает с точки зрения оборотов или оборотов к затраченному времени. Скорость — это то, насколько медленно или быстро движется объект. Угловая скорость — это скорость объекта во вращательном движении. Формула угловой скорости с решенными примерами
Похожие темы . Динамика — Движение — скорость и ускорение, силы и моменты; Связанные документы .Conn-Rod Mechanism — шатунный механизм; Сохранение импульса — импульс тела определяется как произведение его массы и скорости — вычислитель отдачи; Электродвигатели — крутящий момент в зависимости от мощности и оборотов в минуту — Скорость электродвигателей — выходная мощность и крутящий момент Угловое движение
Скорость вращения (или скорость вращения) объекта, вращающегося вокруг оси, — это количество оборотов объекта, деленное на время, выраженное в оборотах в минуту (об / мин), циклах в секунду (cps), радианах в секунду (рад / с ), так далее.Обозначение скорости вращения -. Скорость вращения
По этой формуле вы можете рассчитать число оборотов в минуту в любой ситуации, даже если вы записывали количество оборотов меньше (или больше) минуты. Например, если колесо совершает 30 оборотов за 45 секунд (т.е. 0,75 минуты), результат будет: 30 ÷ 0,75 = 40 об / мин. Число оборотов в минуту в угловую скорость Как преобразовать число оборотов в минуту в линейную скорость
Привет, я хотел бы рассчитать скорость вращения ветряной турбины мощностью 20 кВт и средней скоростью ветра 9 м / с.Я хочу знать, есть ли формула или указанный диапазон. Как я могу рассчитать скорость вращения ветряной турбины?
Обработка. . . Скорость вращения на широте
Калькулятор скорости вала Высокоскоростная обработка принесла производителям большие преимущества и будет продолжать приносить им пользу. Однако, когда так много говорят о высоких скоростях шпинделя, возникает соблазн модернизировать его для достижения максимально возможной скорости вала, но есть еще кое-что, что нужно… ENGINEERING.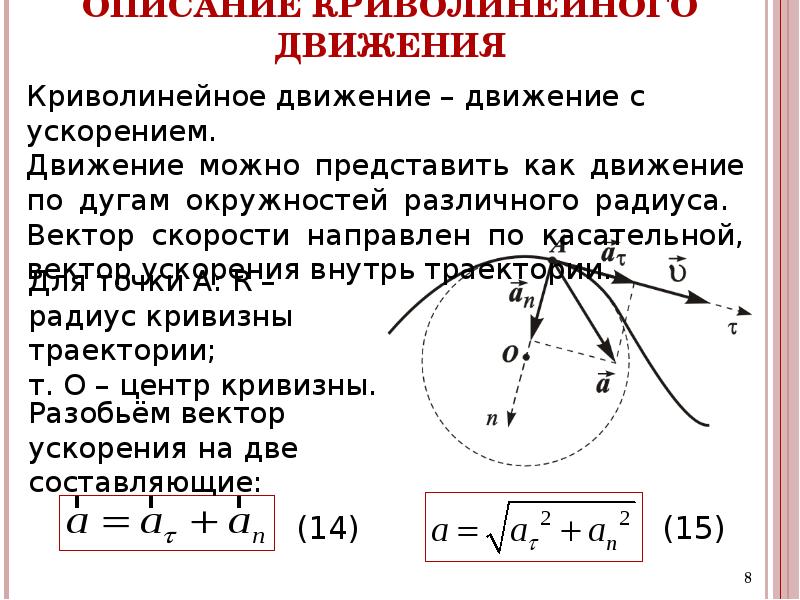
com
Частота вращения шпинделя при заданной скорости резания. Калькулятор использует частоту вращения шпинделя = скорость резания / (2 * pi * мгновенный радиус резания) для расчета частоты вращения шпинделя. Частота вращения шпинделя при заданной скорости резания равна метод определения требуемой частоты вращения шпинделя обрабатывающего инструмента, такой, чтобы.Частота вращения шпинделя при скорости резания.
Формула скорости вращения шпинделя рассчитывает рекомендуемую скорость вращения инструмента или детали, участвующей в обработке. Калькуляторы обработки
Калькулятор. Вычислите скорость, расстояние или время по формуле d = st, расстояние равно скорости, умноженной на время. Калькулятор Speed Distance Time Calculator может найти неизвестное значение sdt с двумя известными значениями. Время можно вводить или рассчитывать в секундах (с), минутах (мин), часах (час) или часах и минутах и секундах (чч: мм: сс).Калькулятор скорости, дистанции, времениОсновы углового ускорения и вращательного момента инерции
Угловое ускорение и момент инерции в конструкции машинКак поставщик гибких приводных муфт и предохранительных муфт с шариковой фиксацией нас часто просят оказать небольшую помощь в расчете крутящих моментов, особенно для клиентов, желающих модернизировать существующее оборудование. Чтобы помочь в процессе оценки крутящих моментов, мы рассмотрим один из основных расчетов, используемых для оценки крутящего момента, необходимого для ускорения вращающейся массы до определенной скорости в течение заданного времени.2). Уравнение ниже определяет скорость изменения угловой скорости.
ω = угловая скорость в стандартной системе СИ, радиан в секунду (рад / сек), 1 радиан = 57,3 градуса
t = время разгона в секундах
π = 3,1416
n = скорость привода в оборотах в минуту об / мин
В следующем примере угловая скорость будет рассчитана для ускорения от 0 до 60 об / мин за одну секунду.
Обратите внимание, что 2π радиан в секунду = 60 об / мин.
Этот расчет очень полезен при проектировании машин, поскольку угловое ускорение, умноженное на крутящий момент инерции, равняется крутящему моменту. Имейте в виду, что точный момент инерции может быть трудно вычислить на основе сложной геометрии реальных приводных линий, а другие переменные, такие как трение, не учитываются в следующем расчете. Тем не менее, он по-прежнему очень полезен при приближении требований к крутящему моменту или установлении базовых минимальных значений для определения размеров компонентов.
Дж = момент инерции в кг ∙ м 2
T = крутящий момент в Н ∙ м
Н = сила в Ньютонах
кг = масса в килограммах
м = радиус плеча рычага в метрах
В последнем примере ниже мы будем использовать угловое ускорение, которое мы нашли выше, для расчета крутящего момента на маховике с радиусом 1 метр и массой 1000 кг.
Как мы видим, если бы маховик с радиусом 1 метр и массой 1000 кг был разогнан до 60 об / мин за одну секунду, это потребовало бы 3141.59 Ньютон-метров входного крутящего момента.
Надеюсь, этот обзор по вычислению углового ускорения оказался для вас полезным. Если у вас есть вопросы, касающиеся выбора размеров и применения муфт валов или предохранительных муфт, обращайтесь в наш технический отдел.
Как рассчитать скорость: концы лопастей и др.
Эрозия передней кромки является основной причиной износа лопастей ветряных турбин.Когда ротор турбины вращается в воздухе, он сталкивается с пылью, грязью, насекомыми, градом и т. Д. Это не кажется большим, если не учитывать, что кончик лезвия может вращаться со скоростью более 100 миль в час. Как только лезвие изнашивается, вода может проникнуть внутрь, замерзнуть и в конечном итоге разрушить аэродинамику конструкции.
Чтобы оценить скорость лопасти, используйте эти уравнения для вычисления скорости вершины, а затем другую любопытную информацию о динамике ротора.
Скорость, S , это просто изменение расстояния с течением времени.Мили в час или мили в час в Северной Америке — самая распространенная единица измерения. Уравнение выглядит так:
S = д / т
Чтобы найти скорость наконечника, нам нужны диаметр ротора и частота вращения. Предположим, что диаметр ротора составляет 100 м, а скорость вращения (ω) составляет 15 об / мин, об / мин.
Расстояние в данном случае — это длина окружности ротора C , которая находится по формуле:
C = π D
Где D = диаметр в метрах, м
Итак, наш 100-метровый ротор описывает окружность:
C = π x 100 м
= 314 м, следовательно,
S = 314 м x 15 оборотов в минуту
= 4,710 м / мин
Поиск Google говорит, что нужно преобразовать м / мин в миль / ч, умножить на 0.0372 [миль / ч / м / мин].
Следовательно,
S миль / ч = 4710 м / мин x 0,0372
= 175 миль / ч.
Это довольно быстро. Многие легкие самолеты не могут достичь такой скорости. Таким образом, полное уравнение для конечной скорости миль в час с диаметром ротора в метрах , м, поскольку это наиболее распространенная единица для описания диаметров ротора, будет
.S миль / ч = π D ω x 0,0372 (1)
Теперь давайте спросим: как далеко от центра находится отметка 100 миль в час?
Ответ заключается в решении уравнения (1) для диаметра D и установке S = 100 миль в час, например:
D = S миль / ч / (π ω x 0.0372)
= 100 миль / ч / (3,14 x 15 об / мин x 0,0372)
= отметка диаметра 57 м
Или 28,5 м при измерении от центра ступицы до точки на лопасти.