Энергия сферического конденсатора: 30. Энергия электростатического поля

30. Энергия электростатического поля

1. Энергия системы зарядов.

, так как,

, так какпри.

—энергия системы зарядов.

Опред.—плотность энергии электростатического поля.

Вопр.казалось бы, зависимость отподынтегральной функцииточно такая же, как. Почему же занулив первый интеграл, мы не зануляем второй?

Отв. Первый интеграл берется по бесконечно удаленной от системы зарядов поверхности, где и поле, и потенциал равны 0, а второй – по всему пространству от -до +, в том числе и по областям, где поле данной системы отлично от 0.

, здесьпервое слагаемое – энергия электростатического поля в вакууме, а второе – энергия поляризованного диэлектрика.

Вопр.Что является носителем энергии: заряды или поле?

Отв.В рамках электростатики ответить нельзя, из электродинамики следует, что носителем энергии является поле.

.

2. Энергия заряженного проводника.

, так как заряды только на поверхности и.

а) Энергия заряженного металлического шара

Другой способ расчета энергии:

или

— энергия электростатического поля Земли.

б) Энергия шара, заряд которого равномерно распределен по его объему:

это может быть косвенным свидетельством того, что носителем энергии являетсяполе, ане заряд, так как в 2а и 2б случаях заряд один и тот же.

3. Энергия заряженного конденсатора.

1). Энергия различных видов конденсаторов.

а) Плоский конденсатор.

Плотность энергии плоского конденсатора:

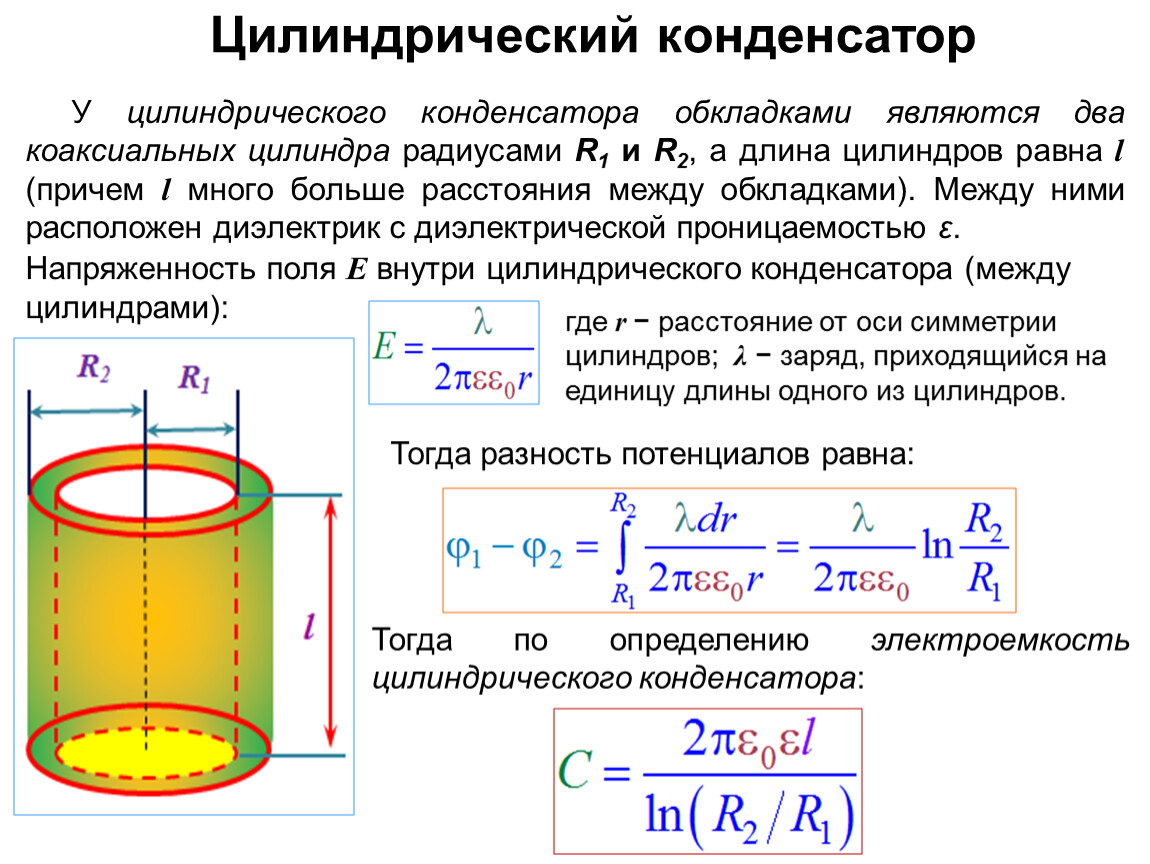
б) Цилиндрический конденсатор.

Плотность энергии цилиндрического конденсатора:

зависит от)

— энергия цилиндрического конденсатора.

в) Сферический конденсатор.

Плотность энергии сферического конденсатора:

—энергия сферического конденсатора.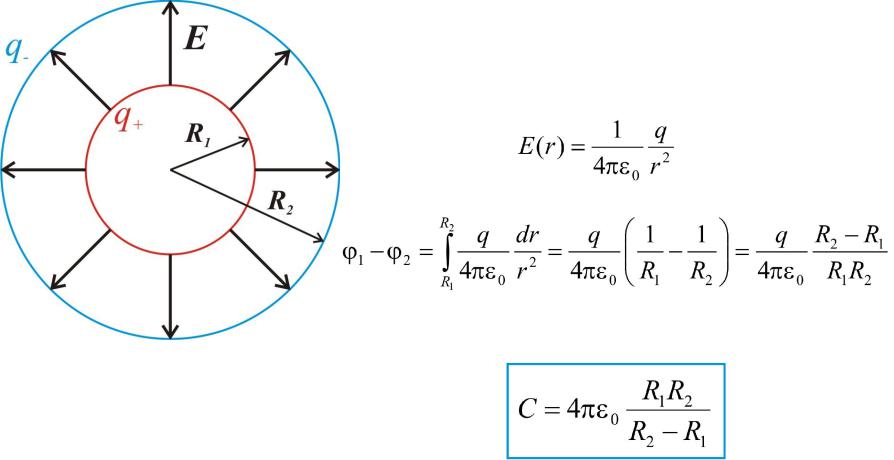

2). Влияние диэлектрика на плотность энергии заряженного конденсатора.

Рассмотрим 4 различных варианта половинного заполнения плоского конденсатора

диэлектриком.

а) Напряжение на пластинах конденсатора

Из граничных условий:

То есть при заполнении половины конденсатора диэлектриком

на пластины должен натечь дополнительный заряд.

;

Интересно сравнить среднюю плотность энергии конденсатора после его заполнения диэлектриком с первоначальной:

,

где , то есть средняя плотность энергии в конденсаторе возрастает за счет работы источника по сообщению дополнительного заряда пластинам конденсатора.

;, где

Из полученного соотношения следует, что емкость заполненного таким образом конденсатора также, как и энергия, возрастает в раз.

Эквивалентная схема соответствует параллельному соединению конденсаторов с половинной площадью пластин:

, то есть емкость действительно возрастает враз.

б) Напряжение на пластинах конденсатора .

В данном случае из граничных условий:

;.

Сравним среднюю плотность энергии до и после заполнения половины конденсатора диэлектриком:

, где.

, поэтому, то есть и в этом случае энергия возрастает за счет работы источника по переносу дополнительного заряда на обкладки.

Эквивалентная схема:

, то есть емкость возрастает враз.

в) Заряд на пластинах конденсатора.

Так как зависит только от геометрии ии не зависит от, как и в случае а).

, так каквозрастает а, тоубывает,

и , следовательно,

Проверим это:

, то есть напряжение на конденсаторе уменьшается.

;.

, то есть энергия уменьшается за счет работы по поляризации диэлектрика, а в случаях а) и б) эту работу брал на себя источник. При этом в данном случае зарядперераспределяется по пластинам неравномерно, но так, чтобы, при этом плотность заряда больше в присутствии диэлектрика.

г) Заряд на пластинах конденсатора.

, где, а

Средняя плотность энергии убывает вследствие поляризации диэлектрика.

3). Силы притяжения между обкладками плоского конденсатора.

Если горизонтально расположенный заряженный конденсатор опустить в диэлектрик, то диэлектрик будет втягиваться в конденсатор. С микроскопической точки зрения диэлектрик втягивается в заряженный конденсатор, так как у краев пластин поле меньше, чем внутри дипольный момент диэлектрика втягивается в область сильного поля, и это происходит до тех пор, пока электростатические силы не уравновешиваются весом дополнительного столба жидкости у края пластин, а энергетически: пока выигрыш в электростатической энергии не будет скомпенсирован увеличением потенциальной энергии.

Выясним, чему равны силы притяжения между обкладками плоского конденсатора,

заполненного диэлектриком.

— поле от одной обкладки.

— сила, действующая на вторую обкладку со стороны первой.

Это не есть истинная сила, действующая на обкладку, так как если существует диэлектрик, то появляются силы электрострикции – механические силы внутри диэлектрика и на поверхности раздела диэлектрика и тела, связанные с деформацией диэлектрика в электрическом поле.

В данном случае диэлектрик стремится втянуться в поле и раздвинуть пластины возникает дополнительное давление внутри конденсатора, которое ослабляет силу электростатического притяжения враз. Этот же вывод получается из энергетических соображений. Найдем работу по перемещению одной из пластин вдоль оси

, т.к..

;

Рассмотрим случай (так как привозникает дополнительная работа источника). В этом случае следует пользоваться выражением для энергии:

Тогда каждая пластина испытывает в присутствии диэлектрика дополнительное давление:

При горизонтальном расположении конденсатора электростатические силы уравновешиваются весом столба диэлектрика высотой :

Замечание.

Если диэлектрик – твердый, то сила взаимодействия между пластинами

, так как в этом случае дополнительного внутреннего давления со стороны диэлектрика пластины конденсатора не испытывают.

4. Энергия системы заряженных проводников.

1)

Рассмотрим 2 заряженных проводника и их влияние друг на друга. В отсутствии второго проводника заряд по первому проводнику распределяется иначе, чем в его присутствии.

— связывает заряд на первом проводнике с потенциалом второго.

В силу равноправия проводников

,

где первое слагаемое – энергия первого проводника, второе – энергия взаимодействия первого проводника со вторым, третье – энергия второго проводника.

2) Если проводников три, то

3) Если проводников , то

принцип суперпозиции для энергии не работает, так как энергия заключена в поле.

3.6. Примеры решения задач к разделу 3

Пример 1.
Плоский конденсатор заряжен и отключен от источника. Определите силу притяжения пластин конденсатора.
Ответ: отключенный конденсатор — электрически замкнутая система (Q = const), поэтому , где .

Пример 2.
Вычислите силу взаимодействия обкладок сферического конденсатора, если он заполнен диэлектриком с проницаемостью = 6, а радиусы

R₁ и R₂ равны соответственно 6 и 8 см. Конденсатор подключен к источнику с разностью потенциалов

Решение

Потенциальная энергия сферического конденсатора , подставляя выражение для емкости конденсатора получаем . Сила, действующая, например, на внешнюю обкладку составит

; F = 3 ·10^-3 Н.

Пример 3.
Цилиндрический конденсатор с радиусами обкладок соответственно R₁ = 10 и R₂ = 15 см, заполненный диэлектриком с проницаемостью = 4, подключен к источнику с разностью потенциалов = 3·10

2 В. Определите силу взаимодействия обкладок на единицу h = 1 м длины конденсатора.

Решение

Погонная энергия заряженного цилиндрического конденсатора есть

.

Сила взаимодействия обкладок ; F = 4,1 10^-4 Н / м.

Пример 4.
Потенциал наэлектризованного металлического шара и напряженность ЭСП на расстоянии а = 5 см от его поверхности составляют = 1,2·10⁴

В; Е = 6·10⁴ В / м. Определите энергию W шара.

Решение

Для определения энергии необходимо найти радиуса R шара и заряд Q на его поверхности. Находим их из известных соотношений: и . Тогда ; W = 4·10^-4 Дж.

Пример 5.
1) Сферическую тонкостенную оболочку радиуса R₁, равномерно заряженную по поверхности зарядом Q, расширили до радиуса R₂. Определите работу А₁₂, совершенную при расширении силами ЭСП.
Ответ: .
2) В центре сферической тонкостенной оболочки, по поверхности которой равномерно распределен заряд Q = 5 мкКл, расположен точечный заряд Q₀ = 1,5 мкКл. Определите работу сил ЭСП при расширении оболочки, т.е. при увеличении ее радиуса от R₁ = 50 мм до R₂ = 0,1 м.
Ответ: ; А₁₂ = 1,8 Дж.

Пример 6.
Система проводников состоит из двух концентрических тонкостенных металлических оболочек радиусов R₁ и R₂ и зарядами на оболочках соответственно Q₁ и Q₂. Определите полную энергию W системы.

Решение

Полная энергия системы двух сфер есть сумма их собственных энергий и потенциальной энергии взаимодействия , каждое из слагаемых есть:

; ; .
.

Пример 7.
1) У плоского конденсатора с площадью пластин S и расстоянием d между ними одна из пластин заземлена. Конденсатор заряжен и отключен от источника. Определите энергию 2-ой обкладки в ЭСП первой.

Решение

Потенциал ЭСП, создаваемого 1-ой (заземленной) обкладкой в месте расположения элементарных зарядов на 2-ой обкладке, равен . Потенциальная энергия элементарных зарядов на 2-ой обкладке в ЭСП первой составит

.

2) Плоский конденсатор с пластинами площадью S = 0,02 м2 каждая и расстоянием между ними d = 0,5 см заполнен диэлектриком с = 4. Конденсатор заряжается до разности потенциалов = 0,1 кВ после чего отключается от источника. Какую работу необходимо затратить, чтобы удалить диэлектрик из конденсатора?

Решение

Энергия конденсатора с диэлектриком , после извлечения диэлектрика . Искомая работа есть

; А = 2·10^-8 Дж.

3) Пусть имеется плоский воздушный конденсатор с площадью обкладок S. Какую работу А₁₂ против сил ЭСП надо совершить, чтобы медленно увеличить расстояние между обкладками от d₁ до d₂, если при этом поддерживать неизменными заряд Q на обкладках.

Решение

Работа внешних сил расходуется на изменение внутренней энергии конденсатора. Здесь существенно, что по условию Q = const, поэтому энергию удобно вычислять по формуле , тогда .

Пример 8.
1) Максимальная электроемкость конденсатора настройки в радиоэлектронном устройстве равна 100 пФ (1 пФ = 1·10^-12 Ф). Путем поворота подвижных пластин электроемкость конденсатора может быть уменьшена до 10 пФ. Предположим, что конденсатор подключен к источнику с разностью потенциалов = 0,3 кВ, когда его емкость максимальна.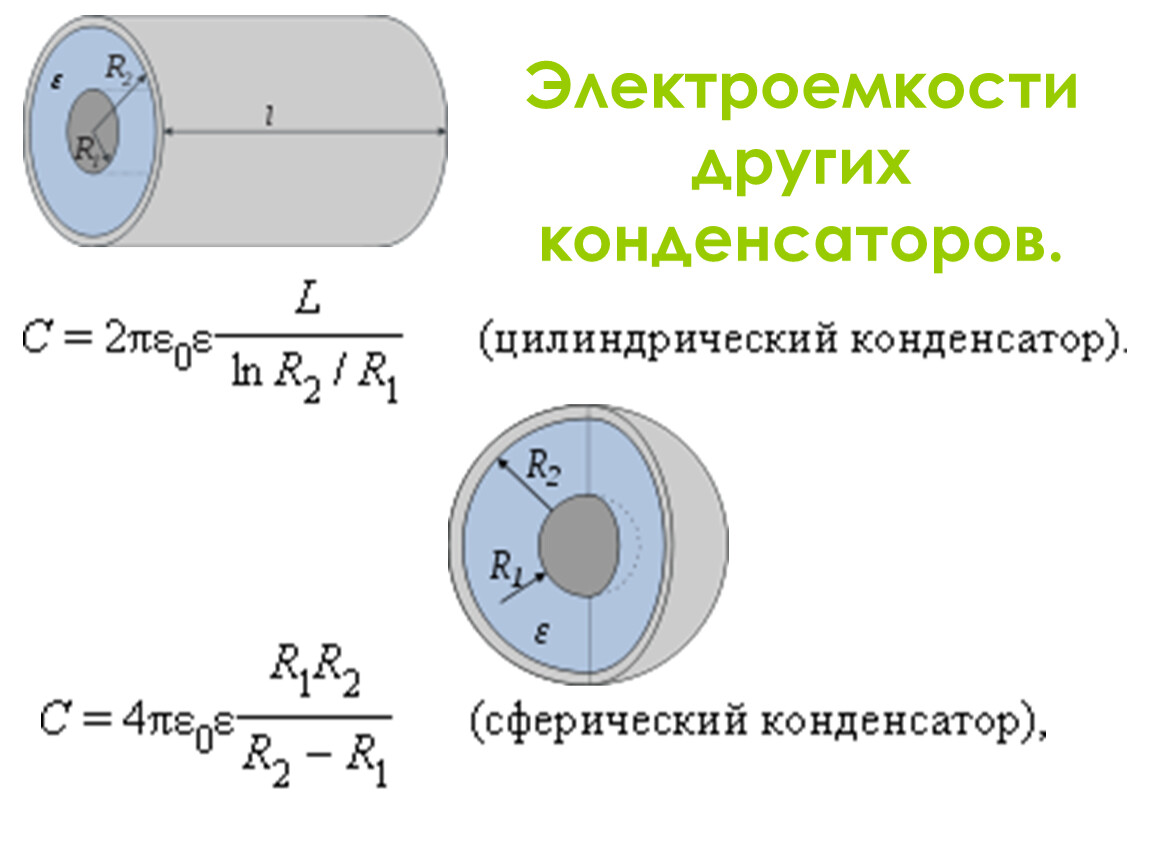 Затем ручка настройки поворачивается, и электроемкость конденсатора становится минимальной. Какая работа совершается при повороте ручки настройки?

Решение

Энергия заряженного конденсатора с электроемкостью С равна . Искомая работа (здесь внешней силы) равна разности энергий конденсатора после и до поворота ручки настройки, т. е. ; А = -4,1·10^-6 Дж.
2) Максимальная электроемкость плоского конденсатора переменной электроемкости С₁ = 400 пФ, минимальная — С₂ = 2 пФ. Изменение электроемкости в этих пределах достигается поворотом рукоятки ротора на 180⁰, при этом подвижные пластины остаются параллельными неподвижным. Момент сил трения в подшипниках ротора М = 5,00 10^-6 Н м. Какую работу надо совершить, чтобы изменить электроемкость конденсатора от максимальной до минимальной, если конденсатор подключен к источнику с разностью потенциалов = 100 В?
Ответ: ; А=13,8 10^-6 Дж.

Пример 9.
Пластины плоского многопластинчатого конденсатора площадью S = 20 см² каждая разделены слюдяным диэлектриком ( = 6) толщиной d = 5 10^-5 м. При разности потенциалов на конденсаторе = 0,33 кВ энергия ЭСП в нем W = 7,7·10^-4 Дж. Определите электроемкость конденсатора и число N пластин.
Ответ: ; С=3,21·10^-8 Ф; ; ; N = 17.

Пример 10.
Число удаленных друг от друга ртутных капелек N = 100, радиусом r = 1 мм каждая заряжены до одинакового потенциала = 9 В. Капельки соединяются в одну большую радиуса R. Определите изменение W электростатической составляющей энергии капель.

Решение

Заряд на каждой капельке , и энергия всех удаленных друг от друга капелек . После слияния капель в одну заряды и объемы складываются, поэтому и , откуда .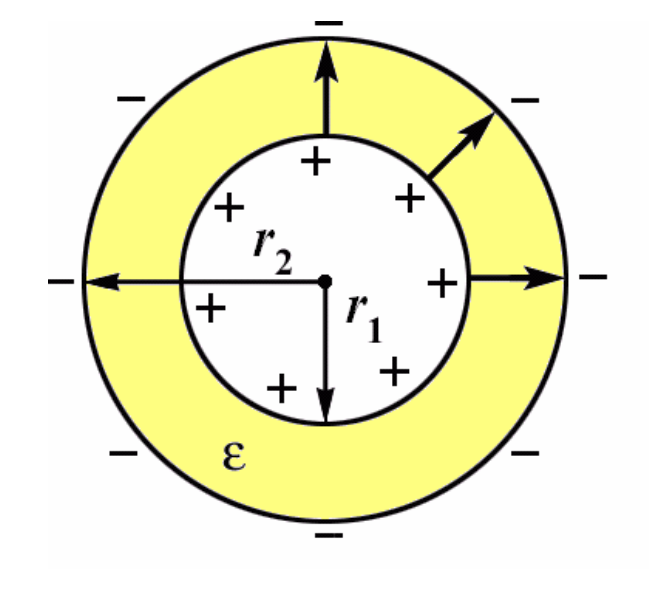
Энергия большой капли составит . Изменение энергии ; = 8,2·10^-9 Дж.

Пример 11.
1) Заряды на обкладках двух конденсаторов с электроемкостями С₁ и С₂ равны соответственно Q₁ и Q₂. Конденсаторы соединяют параллельно одноименными обкладками. Проанализируйте ситуацию и покажите, что при соединении конденсаторов энергия батареи уменьшается. Укажите на возможные «каналы» потери энергии. На основе полученного результата проанализируйте, возможна ли ситуация, при которой энергия не теряется.

Решение

Энергия конденсаторов до их соединения равна При параллельном соединении электроемкости конденсаторов складываются, поэтому энергия ЭСП батареи составит Изменение энергии при этом составит
Уменьшение энергии произошло за счет ее излучения во внешнее пространство и превращения во внутреннюю энергию соединительных проводов (при перераспределении зарядов). Потери энергии не происходит, если Q₁C₂ = Q₂C₁. Иначе, это отвечает условию
2) Конденсатор с электроемкостью С₁ = 1 мкФ, заряженный до разности потенциалов = 0,3 кВ, подключили параллельно к незаряженному конденсатору электроемкостью С₂ = 2 мкФ. Вычислите изменение энергии системы конденсаторов после соединения их в батарею и установления в ней равновесия.

Решение

После соединения конденсаторов в батарею ее электроемкость увеличится до значения С = (С₁ + С₂), но заряд останется неизменным. Следовательно, изменение энергии составит
3) Два конденсатора с электроемкостями С₁ = 6 и С₂ = 4 мкФ соединены последовательно и вся батарея заряжена до разности потенциалов = 1·10⁴ В. Затем конденсаторы отключаются от источника и соединяются в новую батарею параллельно одноименными обкладками. Определите изменение энергии батареи.

Решение

При последовательном соединении энергия . После параллельного соединения конденсаторов заряд на батарее , а ее электроемкость станет , поэтому энергия .
Изменение энергии:

; = — 5 Дж.

Пример 12.
Точечный заряд Q = 3,0 мкКл находится в центре сферического слоя из диэлектрика с проницаемостью = 3,0. Внутренний радиус R₁ cлоя составляет 0,25 см, внешний R₂ = 0,5 м. Вычислите энергию W ЭСП в таком слое.

Решение

В тонком сферическом слое толщиной dr и радиуса содержится энергия

Интегрируем далее это выражение по r в пределах от R₁ до R₂, получаем

; W = 27 мДж.

Пример 13.
Металлическому шару радиуса R₁ сообщен заряд Q. Шар окружен сферическим диэлектрическим слоем из материала с проницаемостью ; наружный радиус слоя R₂. Вся система находится в неограниченной однородной среде с проницаемостью . Определите энергию ЭСП заряженного шара. Определите энергетическую массу m ЭСП, заключенного в слое.

Решение

Разбиваем мысленно все пространство вокруг шара на сферические слои радиусов r, толщиной dr, объемом . Энергия ЭСП, заключенного в таком слое, составит , где есть объемная плотность энергии ЭСП.
Используя результаты исследования структуры напряженности E(r) такой системы и после интегрирования, получаем .
Для массы m ЭСП в слое согласно формуле Эйнштейна , имеем , где с₀ = 3,0·10⁸ м / с — скорость электромагнитных волн в вакууме. Поучительны цифровые оценки: если Q = 2·10^-6 Кл, R₁ = 0,1 м, R₂ = 0,2 м, = 2, то m = 1·10^-18 кг. Это намного больше, чем массы покоящихся электрона, протона, и др.

Пример 14.
Вычислите энергию W_p ЭСП между двумя эквипотенциальными поверхностями на расстояниях R₁ = 5 и R₂ = 10 см от весьма тонкого металлического провода длиной h = 1 м, линейная плотность заряда которого = 5·10^-8 Кл / м.

Решение

Предполагаем здесь проводник достаточно длинным, поэтому краевыми эффектами пренебрегаем. В тонком воображаемом цилиндрическом слое радиуса r и толщиной dr, расположенном соосно с проводником, ЭСП обладает элементарной энергией . Интегрируя эти элементарные энергии в пределах от R₁ до R₂, получаем ; W_p = 1,6·10^-5 Дж.

Электрическая емкость проводника. Конденсатор. Емкость плоского конденсатора. Соединение конденсаторов. Энергия, накопленная в конденсаторе. Энергия электрического поля. Плотность энергии электрического поля. Потенциаль

Электроемкостью (емкостью) C уединенного изолированного проводника называется физическая величина, равная отношению изменения заряда проводника q к изменению его потенциала f: C = Dq/Df.

Электроемкость уединенного проводника зависит только от его формы и размеров, а также от окружающей его диэлектрической среды (e). Единица измерения емкости в системе СИ называется Фарадой. Фарада (Ф) — это емкость такого уединенного проводника, потенциал которого повышается на 1 Вольт при сообщении ему заряда в 1 Кулон. 1 Ф = 1 Кл/1 В.

Конденсатором называют систему двух разноименно заряженных проводников, разделенных диэлектриком (например, воздухом). Свойство конденсаторов накапливать и сохранять электрические заряды и связанное с ними электрическое поле характеризуется величиной, называемой электроемкостью конденсатора. Электроемкость конденсатора равна отношению заряда одной из пластин Q к напряжению между ними U: C = Q/U.

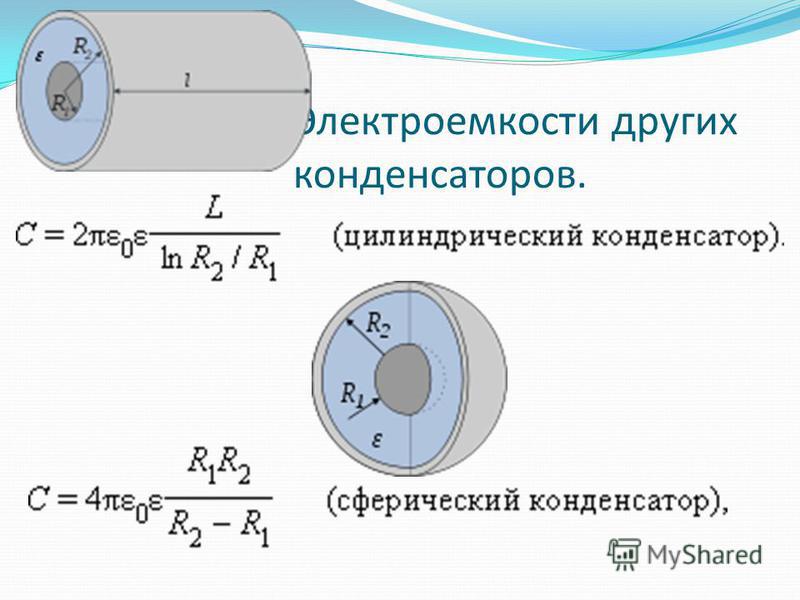
В зависимости от формы обкладок, конденсаторы бывают плоскими, сферическими и цилиндрическими. Формулы для расчета емкостей этих конденсаторов приведены в таблице.

Соединение конденсаторов в батареи. На практике конденсаторы часто соединяют в батареи — последовательно или параллельно.

При параллельном соединении напряжение на всех обкладках одинаковое U1 = U2 = U3 = U = e, а емкость батареи равняется сумме емкостей отдельных конденсаторов C = C1 + C2 + C3.

При последовательном соединении заряд на обкладках всех конденсаторов одинаков Q1 = Q2 = Q3, а напряжение батареи равняется сумме напряжений отдельных конденсаторов U = U1 + U2 + U3.

Емкость всей системы последовательно соединенных конденсаторов рассчитывается из соотношения: 1/C = U/Q = 1/C1 + 1/C2 + 1/C3.

Емкость батареи последовательно соединенных конденсаторов всегда меньше, чем емкость каждого из этих конденсаторов в отдельности.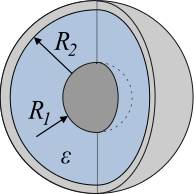 Энергия электростатического поля. Энергия заряженного плоского конденсатора Eк равна работе A, которая была затрачена при его зарядке, или совершается при его разрядке. A = CU2/2 = Q2/2С = QU/2 = Eк. Поскольку напряжение на конденсаторе может быть рассчитано из соотношения: U = E*d, где E — напряженность поля между обкладками конденсатора, d — расстояние между пластинами конденсатора, то энергия заряженного конденсатора равна: Eк = CU2/2 = ee0S/2d*E2*d2 = ee0S*d*E2/2 = ee0V*E2/2, где V — объем пространства между обкладками конденсатора. Энергия заряженного конденсатора сосредоточена в его электрическом поле.

Тип конденсатора	Формула для расчета емкости	Примечания	Схематическое изображение
Плоский конденсатор		S — площадь пластины; d — расстояние между пластинами.
Сферический конденсатор	C = 4pee0R1R2/(R2 — R1)	R2 и R1 — радиусы внешней и внутренней обкладок.
Цилиндрический конденсатор	C = 2pee0h/ln(R2/R1)	h — высота цилиндров.

Как и любая система заряженных тел, конденсатор обладает энергией. Вычислить энергию заряженного плоского конденсатора с однородным полем внутри него несложно. Энергия заряженного конденсатора. Для того чтобы зарядить конденсатор, нужно совершить работу по разделению положительных и отрицательных зарядов. Согласно закону сохранения энергии эта работа равна энергии конденсатора. В том, что заряженный конденсатор обладает энергией, можно убедиться, если разрядить его через цепь, содержащую лампу накаливания, рассчитанную на напряжение в несколько вольт (рис.14.37 ). При разрядке конденсатора лампа вспыхивает. Энергия конденсатора превращается в тепло и энергию света.

Выведем формулу для энергии плоского конденсатора. Напряженность поля, созданного зарядом одной из пластин, равна Е/2 , где Е -напряженность поля в конденсаторе. 2. Применение конденсаторов . Зависимость электроемкости конденсатора от расстояния между его пластинами используется при создании одного из типов клавиатур компьютера. На тыльной стороне каждой клавиши располагается одна пластина конденсатора, а на плате, расположенной под клавишами, — другая. Нажатие клавиши изменяет емкость конденсатора. Электронная схема, подключенная к этому конденсатору, преобразует сигнал в соответствующий код, передаваемый в компьютер. Энергия конденсатора обычно не очень велика — не более сотен джоулей. К тому же она не сохраняется долго из-за неизбежной утечки заряда. Поэтому заряженные конденсаторы не могут заменить, например, аккумуляторы в качестве источников электрической энергии. Но это совсем не означает, что конденсаторы как накопители энергии не получили практического применения. Они имеют одно важное свойство: конденсаторы могут накапливать энергию более или менее длительное время, а при разрядке через цепь с малым сопротивлением они отдают энергию почти мгновенно.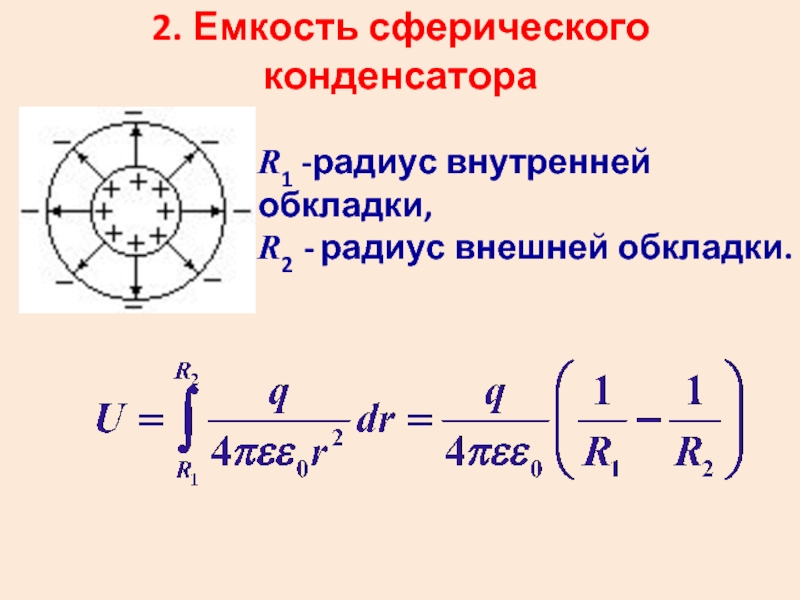 Именно это свойство широко используют на практике. Лампа-вспышка, применяемая в фотографии , питается электрическим током разряда конденсатора, заряжаемого предварительно специальной батареей. Возбуждение квантовых источников света — лазеров осуществляется с помощью газоразрядной трубки, вспышка которой происходит при разрядке батареи конденсаторов большой электроемкости. Однако основное применение конденсаторы находят в радиотехнике. Энергия конденсатора пропорциональна его электроемкости и квадрату напряжения между пластинами. Вся эта энергия сосредоточена в электрическом поле. Энергия поля пропорциональна квадрату напряженности поля.

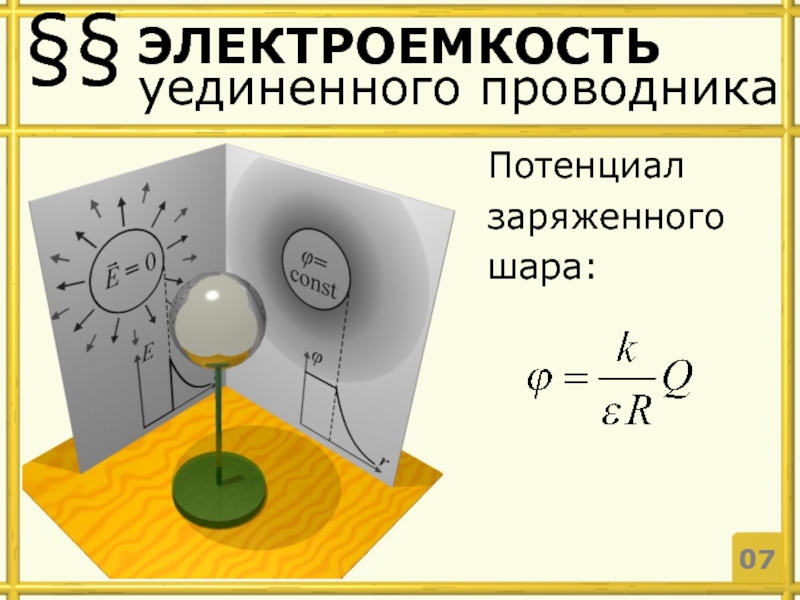
Имеется уединенный проводник. Ему сообщен заряд Q. Вычислим электрический потенциал в точке М.

Если на проводник поместить заряд Q·b, то

Потенциал в каждой точке поля возрастает прямо пропорционально заряду проводника, т.е. φ ~ Q.

, (2)

где с – электрическая ёмкость (ёмкость)

Или можно показать: ΔQ=cΔφ

(3)

Физический смысл емкости.

Отметим, что все предыдущее справедливо, если при этом не меняются формы и размеры проводника, а также внешние условия (среда, расположение окружающих предметов).

СИ :

IV.Конденсаторы.Вычисление емкости конденсаторов.

Конденсатором называется система двух (или более) проводников, имеющих такую форму и расположение относительно друг друга, что поле, создаваемое такой системой, локализовано в ограниченной области пространства.

Примеры конденсаторов :

Проводники, образующие конденсатор, называются обкладками .

Чтобы зарядить конденсатор, нужно присоединить его обкладки к источнику напряжения или одну обкладку соединить с Землей, а другую («+») с клеммой источника.

Емкостью конденсатора С называется величина, измеряемая отношением зарядаQна одной пластине к разности потенциалов между пластинами:

(4)

Примеры вычисления емкости конденсаторов .

1. Плоский конденсатор.

(5)

2. Сферический конденсатор.

(6)

Положим: r 1 –r 2 =d;d

Следствие:

если зазор мал, то С пл = С сф

если r 1 >>r 2 , то С сф = 4πεε 0 r→C сф = С шара

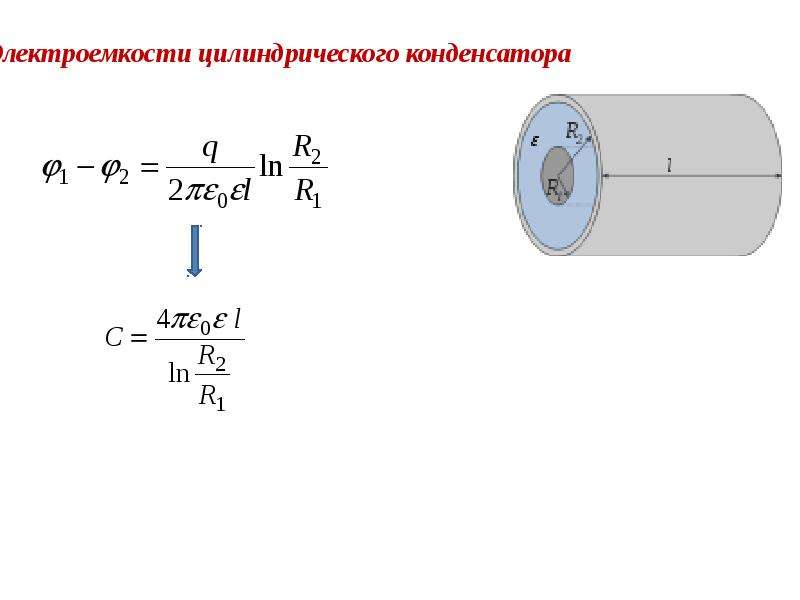
3. Цилиндрический конденсатор.

(7)

Если напряжение U на конденсаторе сделать слишком большим, то происходит разряд через слой диэлектрика – пробой. Поэтому каждый конденсатор характеризуется не только своей емкостью С, но и максимальным рабочим напряжениемU max =U пр.

Располагая разными по ёмкости конденсаторами, можно получить желаемую емкость, путем соединения конденсаторов:

а) последовательное:	б) параллельное:		в) смешенное
		Q = Q 1 + Q 2 + … + Q n CU = C 1 U + C 2 U + … +C n U C = C 1 + C 2 + … +C n

V.

Энергия заряженного конденсатора.Энергия электрического поля.

Для многих вопросов теории и практики необходимо определять электрическую энергию заряженного проводника. (Определяем через работу разряда проводника).

Пусть имеется проводник с зарядом Qи начальным потенциалом φ 0 . Тогда элементарная работа при переходе элементарного зарядаdQс проводника на землю равна:

dA=φ·dQ, где

 – мгновенное значение потенциала, но

dQ= –Cdφ(“–“ – означает уменьшение потенциала).

dA = –Cφ·dφ

Найденная работа совершилась за счет убыли потенциальной энергии и численно равна энергии заряженного проводника W:

Энергия заряженного конденсатора:

Формула для энергии заряженного тела по существу определяет и энергию электрического поля созданного заряженным телом:

(8)

Объемная плотность энергии электростатического поля – физическая величина, численно равная отношению потенциальной энергии поля в единице объема.

(9)

При создании схем во время занятия любительской радиоэлектроникой приходится оперировать значительным количеством терминологии. И одной из самых важных составляющих являются конденсаторы. Сами по себе они не очень интересны, главнее для нас — их функции. Вот, к примеру, электрическая энергия конденсатора. Что это? Она обусловлена тем, что электрическое поле, которое находится между обкладками конденсатора, само обладает энергией. Так, его напряженность является пропорциональной подаваемому напряжению. Давайте рассмотрим более детально и с рядом формул.

Энергия заряженного конденсатора

Обкладки конденсатора имеют электроемкость (Э). На них же расположено два электрических заряда: -з и +з. Тогда напряжение (Н), что существует между обкладками, будет равным:

Всё составляющие этого уравнения были рассмотрены выше, и если вы запутались, перечитайте, пока не сможете понять. Без этого будет невозможно продолжить ознакомление с материалом статьи, чтобы он усвоился. Данные знания необходимы, чтобы понять, как функционирует энергия поля конденсатора.

Но устройство со временем разряжается. Что с этим делать? Когда происходит процесс разрядки, то напряжение, существующее между его обкладками, будет убывать прямо пропорционально заряду от начального значения до нуля. В формульном выражении данное уравнение будет выглядеть таким образом:

Но у нас ещё есть работа А, которая совершается электрическим полем во время разрядки конденсатора. В формульном представлении всё выглядит следующим образом:

• А=з*Н ср =(з*Н)/2=(Э*Н 2)/2

Но вместе с этим возникает вопрос: чему будет равна потенциальная энергия конденсатора с данной электроемкостью Э, который заряжен до значения Н? Ответ на этот вопрос нам может дать такое уравнение:

• ПЭ=А=(Э*Н 2)/2=з 2 /(2*Э)=(з*Н)/2

Тут вам следует понять, что энергия конденсатора зависит от электрического поля, что существует между его обкладками, и оно же является её обладателем. А из этого можно сделать вывод, что она также пропорциональна квадрату напряженности. Чтобы запомнить, чему равна энергия заряженного конденсатора, можно выучить ещё одно школьное правило. Или даже точней будет сказать — освежить свою память им. Энергия конденсатора равняется работе, которая совершается электрическим полем во время сближения пластин устройства вплотную. Она также равна труду, что делается для разделения отрицательных и положительных зарядов, что необходим для последующей зарядки прибора. Это изучается в качестве примера в курсе школьной физики.

Электроемкость

В рамках предыдущего раздела статьи упоминалось такое слово. Учитывая его важность, при разборе ситуации с конденсатором можно разобраться с тем, что понимают под данным словом. Итак, электроемкость:

1. Используется в качестве характеристики способности накапливать электрический заряд конденсатором.
2. Является зависимой от целого ряда параметров:
   1. От геометрических размеров конденсатора.
   2. От его формы.
   3. От расположения в схеме.
   4. От свойств электрической среды, в которой собственно и находится конденсатор.
3. Не зависит от значений заряда и напряжения.

Электроемкость измеряется в Фарадах (на практике ещё добавляется приставка микро-, поскольку объем конденсатора обычно невелик).

Энергия поля и формула

Она примерно равняется квадрату напряженности электрического поля внутри конденсатора.

Плотность энергии измеряется по формуле:

Что можно дополнительно сказать по этому? Данный эффект суммируется с другими и может составлять электрическое поле всего устройства, частью которого является конденсатор.

Заключение

Итак, в рамках статьи была рассмотрена энергия конденсатора, а также поле, которое создаётся ею. Необходимо также учитывать, что другие детали электротехнических схем тоже обладают определённой энергией и могут позитивно сказываться на степени заряженности данного устройства. Если конденсатор находится за гранями схем и не используется ими, но находится вблизи, то он постепенно будет заряжаться. Правдивость этого факта очень легко проверить в домашних условиях, если есть необходимая измерительная техника. Для этого необходимо сам конденсатор поместить около телевизора, устройства радио или компьютера и записывать значение заряженности, которое будет показывать измерительная аппаратура. Благодаря этому свойству энергия конденсатора может меняться даже при отсутствии прямого видимого подключения к источнику питания.

Электрическая емкость проводника.

Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд . В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.

Конденсатор. Емкость плоского конденсатора.

Соединение конденсаторов.

Параллельное соединение конденсаторов
Обкладки конденсаторов соединяют попарно, т.е. в системе остается два изолированных проводника, которые и представляют собой обкладки нового конденсатора
Вывод: При параллельном соединении конденсаторов а) заряды складываются, б) напряжения одинаковые, в) емкости складываются. Т.о., общая емкость больше емкости любого из параллельно соединенных конденсаторов
Производят только одно соединение, а две оставшиеся обкладки — одна от конденсатора С 1 другая от конденсатора С 2 — играют роль обкладок нового конденсатора.
Вывод: При последовательном соединении конденсаторов а) напряжения складываются, б) заряды одинаковы, в) складываются величины, обратные емкости. Т.о., общая емкость меньше емкости любого из последовательно соединенных конденсаторов.

Энергия, накопленная в конденсаторе.

При заряде конденсатора внешний источник расходует энергию на разделение зарядов на положительные и отрицательные. Которые будут находиться на обкладках конденсатора. Следовательно, исходя из закона сохранения энергии, она никуда не пропадает, а остается в конденсаторе. Энергия в конденсаторе запасается в виде силы взаимодействия положительных и отрицательных зарядов находящихся на его обкладках. То есть в виде электрического поля. Которое сосредоточено между пластинами. Это взаимодействие стремится притянуть одну обкладку к другой, поскольку, как известно разноименные заряды притягиваются.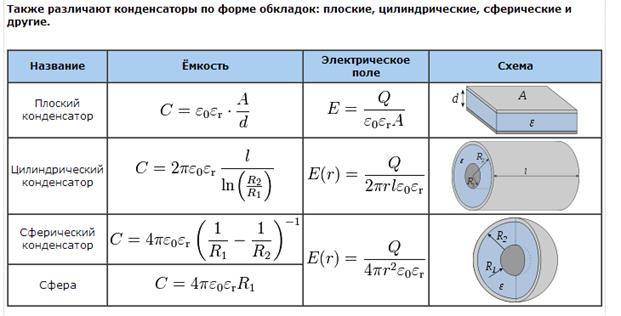

Как известно из механики F=mg , аналогично в электрике F=qE , роль массы играет заряд, а роль сили притяжения напряжённость поля.

Работа по перемещению заряда в электрическом поле выглядит так:A=qEd1-qEd2=qEd

C другой же стороны работа также равна разнице потенциальных энергий A=W1-W2=W.

Таким образом используя эти два выражения можно сделать вывод что потенциальная энергия накопленная в конденсаторе равна:

Формула 1 — Энергия заряженного конденсатора

Не трудно заметить, что формула очень похожа на потенциальную энергию из механики W=mgh .

Если провести аналогию с механикой: Представим камень, находящийся на крыше здания. Здесь взаимодействует масса земли с массой камня посредством силы тяжести, а здание высотой h противодействует силе гравитации. Если здание убрать камень упадет, следовательно, потенциальная энергия перейдет в кинетическую.

В электростатике же есть два разноименных заряда стремящихся притянутся друг к другу им противодействует диэлектрик толщиной d находящийся между обкладками. Если обкладки замкнуть между собой то потенциальная энергия заряда перейдет в кинетическую то есть в тепло.

В электротехнике формула для энергии в таком виде не применяется. Ее удобно выразить через емкость конденсатора и напряжение, до которого он заряжен.

Так как заряд конденсатора определяется зарядом одной из его пластин то напряжённость поля, создаваемая ею, будет равна E/2 . Поскольку общее поле складывается из полей создаваемых обеими обкладками заряжении одинаково, но с противоположным знаком.

Темы кодификатора ЕГЭ : электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.

Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах .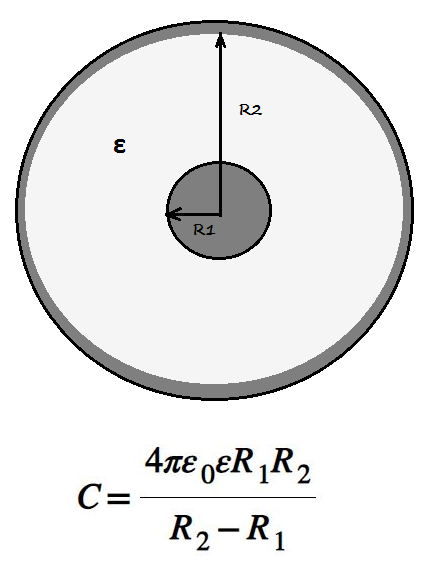

Но прежде введём понятие электрической ёмкости .

Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым .

Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду . Коэффициент пропорциональности принято обозначать , так что

Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:

(1)

Например, потенциал уединённого шара в вакууме равен:

где — заряд шара, — его радиус. Отсюда ёмкость шара:

(2)

Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в раз:

Соответственно, ёмкость шара в раз увеличивается:

(3)

Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.

Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.

В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В . Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.

Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.

Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным км.

МкФ.

Как видите, Ф — это очень большая ёмкость.

Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной .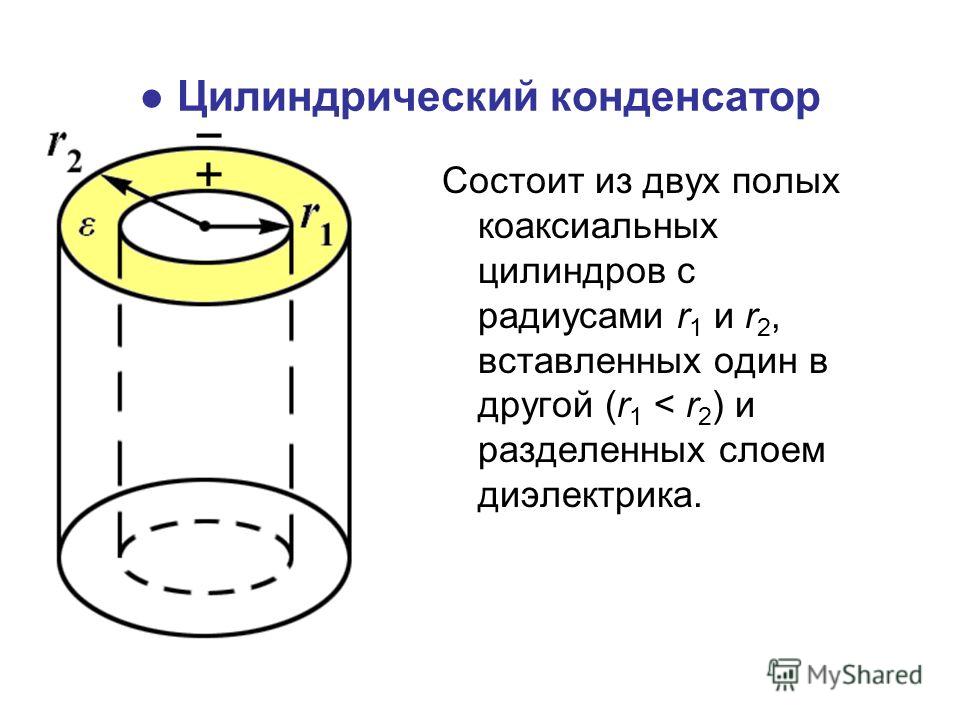 В самом деле, выразим из формулы (2) :

Следовательно, диэлектрическая постоянная может измеряться в Ф/м:

Ф.

Так легче запомнить, не правда ли?

Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.

Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.

Наиболее простым и важным примером такой системы является плоский конденсатор . Он состоит из двух параллельных металлических пластин (называемых обкладками ), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.

Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух

Пусть заряды обкладок равны и . Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина — заряд положительной обкладки — называется зарядом конденсатора .

Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.

Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:

Здесь — напряжённость поля положительной обкладки, — напряженность поля отрицательной обкладки, — поверхностная плотность зарядов на обкладке:

На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.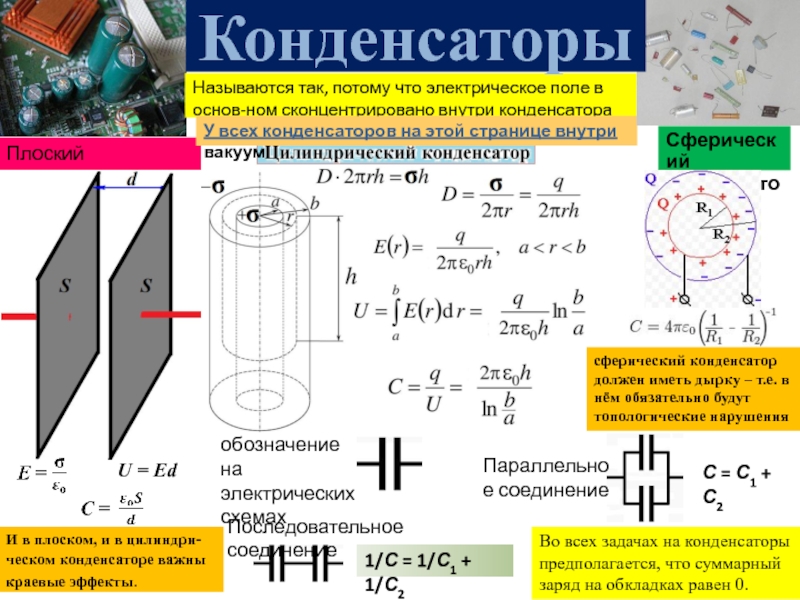

Рис. 1. Электрическое поле плоского конденсатора

Согласно принципу суперпозиции, для результирующего поля имеем:

Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):

Внутри конденсатора поле удваивается:

(4)

Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:

Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4) . Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.

Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты : поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.

Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов между обкладками равна произведению на (вспомните связь напряжения и напряжённости в однородном поле!):

(5)

Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:

(6)

Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6) , таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.

Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора :

(7)

Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?

Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:

(8)

Соответственно, напряжение на конденсаторе:

(9)

Отсюда ёмкость плоского конденсатора с диэлектриком :

(10)

Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.

Важное следствие формулы (10) : заполнение конденсатора диэлектриком увеличивает его ёмкость .

Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.

Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке.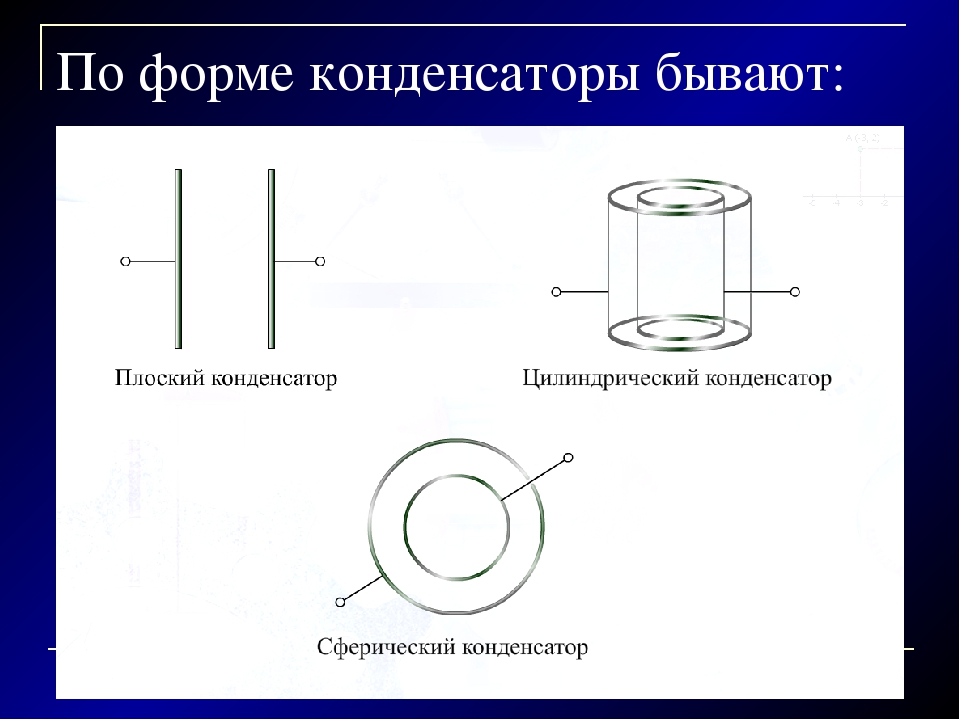 Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.

Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.

Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок .

Возьмём на второй обкладке настолько маленькую площадку, что заряд этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой

где — напряжённость поля первой обкладки:

Следовательно,

Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).

Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил , с которыми притягиваются к первой обкладке всевозможные маленькие заряды второй обкладки. При этом суммировании постоянный множитель вынесется за скобку, а в скобке просуммируются все и дадут . В результате получим:

(11)

Предположим теперь, что расстояние между обкладками изменилось от начальной величины до конечной величины . Сила притяжения пластин совершает при этом работу:

Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины > , то работа силы притяжения получается отрицательной, как и должно быть.

С учётом формул (11) и (7) имеем:

Это можно переписать следующим образом:

(12)

Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины . Это как раз и означает, что — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора .

Используя соотношение , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):

(13)

(14)

Особенно полезными являются формулы (12) и (14) .

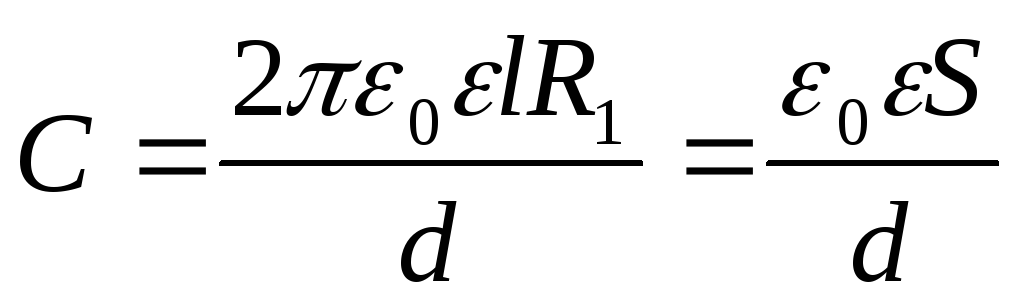
Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в раз, и вместо (11) получим:

При вычислении работы силы , как нетрудно видеть, величина войдёт в ёмкость , и формулы (12) — (14) останутся неизменными . Ёмкость конденсатора в них теперь будет выражаться по формуле (10) .

Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.

Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.

Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:

Но — объём конденсатора. Получаем:

(15)

Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля , сосредоточенного в некотором объёме .

Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.

Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.

Величина — энергия единицы объёма поля — называется объёмной плотностью энергии . Из формулы (15) получим:

(16)

В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.

Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15) и (16) будем иметь:

(17)

(18)

Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.

Занятие 13. Конденсаторы. Энергия электрического поля

СОДЕРЖАНИЕ ТЕОРИИ

1. Электроемкость уединенного проводника, металлической сферы, плоского конденсатора .

2. Сферические и цилиндрические конденсаторы.

3. Слоистые конденсаторы.

4. Последовательное и параллельное соединения конденсаторов.

5. Энергия заряженного уединенного проводника, конденсатора.

6. Энергия электрического поля.

7. Объемная плотность энергии электрического поля.

 

ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ

Электроемкость уединенного проводника

Потенциал уединенного проводника и его заряд связаны соотношением

где С – электроемкость уединенного проводника.

Электроемкость уединенной проводящей сферы радиусом R, находящейся в безграничной среде с диэлектрической проницаемостью e,

Электроемкость конденсатора

Напряжение на обкладках конденсатора связано с зарядом соотношением

где C – электроемкость конденсатора.

Электроемкость плоского конденсатора

где S – площадь каждой пластины; d – расстояние между пластинами;
e – диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.

Электроемкость сферического конденсатора (две концентрические сферы радиусами R₁ и R₂ (R₂>R₁), пространство между которыми заполнено диэлектриком с проницаемостью e,

Электроемкость цилиндрического конденсатора (два коаксиальных цилиндра радиусами r и R и длиной L, пространство между которыми заполнено диэлектриком с проницаемостью e)

 

Электроемкость системы конденсаторов

При параллельном соединении конденсаторов

где n – число конденсаторов в системе. При таком соединении

а общий заряд на обкладках

При последовательном соединении того же числа конденсаторов

причем при таком соединении

где U_i – напряжение на каждом конденсаторе, а заряд на обкладках одинаков

4. Энергия заряженного проводника:

Энергия уединенного заряженного проводника может быть найдена по одной из следующих формул

Энергия заряженного конденсатора

Энергия заряженного кондесатора может быть рассчитана из следующих соотношений:

В случае плоского конденсатора энергия

где S – площадь каждой пластины конденсатора; s – поверхностная плотность сторонних зарядов на пластинах; U – разность потенциалов между пластинами; e – диэлектрическая проницаемость диэлектрика, заполняющего конденсатор; E – результирующая напряженность поля в диэлектрике; d – расстояние между пластинами.

Объемная плотность энергии электрического поля

Величина

,

где D – электрическое смещение, называется объемной плотностью энергии электрического поля.

Объемная плотность энергии w связана с энергией W соотношением

dW=wdV,

где dV – элемент объема в системе координат, определяемой исходной симметрией поля.

Сила притяжения пластин плоского кондесатора

рассчитывается из соотношения

СПРАВОЧНЫЙ МАТЕРИАЛ

Относительная диэлектрическая проницаемость стекла – 6.

Относительная диэлектрическая проницаемость эбонита – 2,6.

Относительная диэлектрическая проницаемость парафина – 2.

 

ВОПРОСЫ И УПРАЖНЕНИЯ

1. Что называется электроемкостью уединенного проводника? От чего она зависит?

2. В каких единицах измеряется электроемкость?

3. Что представляет собой конденсатор?

4. Напишите выражения для электроемкости плоского, цилиндрического и сферического конденсаторов.

5. Как изменится емкость плоского конденсатора, если между его пластинами поместить: а) слой металла, заполняющего половину пространства между пластинами; б) той же толщины слой диэлектрика?

6. Для чего применяются соединения конденсаторов в батареи? Чему равняется электроемкость параллельно, последовательно соединенных конденсаторов?

7. Напишите выражения для энергии уединенного заряженного проводника, заряженного конденсатора.

8. Получите выражение для емкости плоского конденсатора.

9. Получите выражение для емкости уединенного металлического шара, помещенного в безграничный однородный диэлектрик.

10. Получите выражение для емкости сферического конденсатора, цилиндрического конденсатора.

11. Что является носителем энергии – заряды или поле? Напишите выражения для энергии и объемной плотности энергии электрического поля.

12. Получите выражение для силы притяжения пластин плоского конденсатора.

ЗАДАЧИ ГРУППЫ А

1.(9.77) Найти электроемкость земного шара. Считать радиус земного шара R=6400 км. На сколько изменится потенциал земного шара, если ему сообщить заряд q=1 Кл?

Ответ: C=710 мкФ; Dj=1400 В.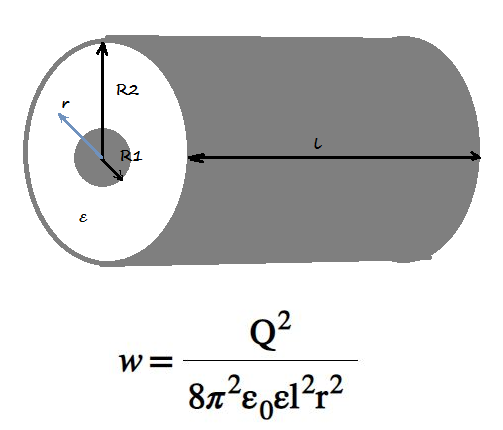

2.(9.79) Восемь заряженных шарообразных водяных капель радиусом r=1мм и зарядом q=0,1 нКл сливаются в одну общую каплю. Найти потенциал образовавшейся шаровой капли.

Ответ: j=3,6 кВ.

3.(9.92) Радиус центральной жилы коаксиального кабеля r=1,5 см, радиус оболочки R=3,5 см. Между центральной жилой и оболочкой приложена разность потенциалов Dj=2,3 кВ. Найти напряженность Е электрического поля на расстоянии d=2 см от оси кабеля.

Ответ: E=136 кВ/м.

4.(9.93) Вакуумный цилиндрический конденсатор имеет радиус внутреннего цилиндра r=1,5 см, радиус внешнего цилиндра R=3,5 см. Между цилиндрами приложена разность потенциалов Dj=2,3 кВ. Какую скорость u получит электрон под действием поля этого конденсатора, перемещаясь без начальной скорости с расстояния r₁=2,5 см до расстояния r₂=2 см от оси цилиндра?

Ответ: u=1,45.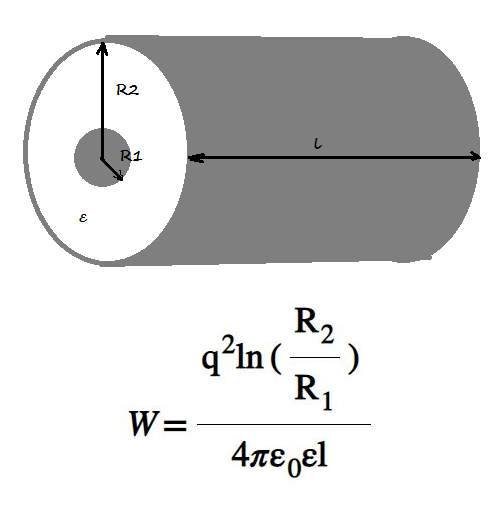 10⁷ м/с.

5.(9.96) Каким будет потенциал шара радиусом r=3 см, если: а) сообщить ему заряд q=1 нКл; б) окружить его концентрической металлической сферой радиусом R=4 см, соединенной с землей?

Ответ: a) j=300 В; б) j=75 В.

6.(9.98) Радиус внутреннего шара воздушного сферического конденсатора r=1 см, радиус внешнего шара R=4 см. Между шарами приложена разность потенциалов Dj=3 кВ. Найти напряженность Е электрического поля на расстоянии r₁=3 см от центра шаров.

Ответ: E=44,4 кВ/м.

7.(9.101) Два конденсатора зарядили до разности потенциалов U₁=300 В и U₂=100 В и соединили между собой одноименными обкладками. Измеренная при этом разность потенциалов между обкладками конденсаторов оказалась равна 250 В. Найти отношение емкостей С₁/ С₂.

Ответ: C₁/C₂=3.

8.(9.109) Два металлических шарика первый с зарядом q₁=10 нКл и радиусом r=3 см и второй с потенциалом j₂=9 кВ и радиусом R=2 см соединили проволочкой, емкостью которой можно пренебречь. Найти: а) потенциал j₁ первого шарика до разряда; б) заряд q₂ второго шарика до разряда; в) энергии W₁, W₂ каждого шарика до разряда; г) заряд и потенциал первого шарика после разряда; д) заряд и потенциал второго шарика после разряда; е) энергию W соединенных проводником шариков; ж) работу A разряда.

Ответ: а) j₁=3 кВ; б) q₂=20 нКл; в) W₁=15 мкДж,W₂=90 мкДж; г) =18 нКл, =5,4 кВ; д) =12 нКл, =5,4 кВ; е) W=81 мкДж; ж) A=24 мкДж.

9.(9.110) Заряженный шар А радиусом r=2 см приводится в соприкосновение с незаряженным шаром В, радиус которого R=3 см. После того как шары разъединили, энергия шара В оказалась равной 0,4 Дж. Какой заряд q был на шаре А до соприкосновения с шаром В?

Ответ:q=2,7 мкКл.

10.(9.116) Площадь пластин плоского воздушного конденсатора равна S=0,01 м², расстояние между ними d=2 см. К пластинам приложена разность потенциалов Dj=3 кВ. Какова будет напряженность E поля конденсатора, если, не отключая источника напряжения, пластины раздвинуть до расстояния b=5 см? Найти энергии W₁,W₂ конденсатора до и после раздвижения пластин.

Ответ: E=60 кВ/м; W₁=20 мкДж; W₂=8 мкДж.

ЗАДАЧИ ГРУППЫ Б

1.(3.53) Два конденсатора емкостью C₁=3 мкФ и C₂=6 мкФ соединены между собой и присоединены к батарее с ЭДС 120 В. Определить заряды q₁,q₂ каждого конденсатора и разность потенциалов между его обкладками U₁ и U₂, если конденсаторы соединены: а) параллельно; б) последовательно.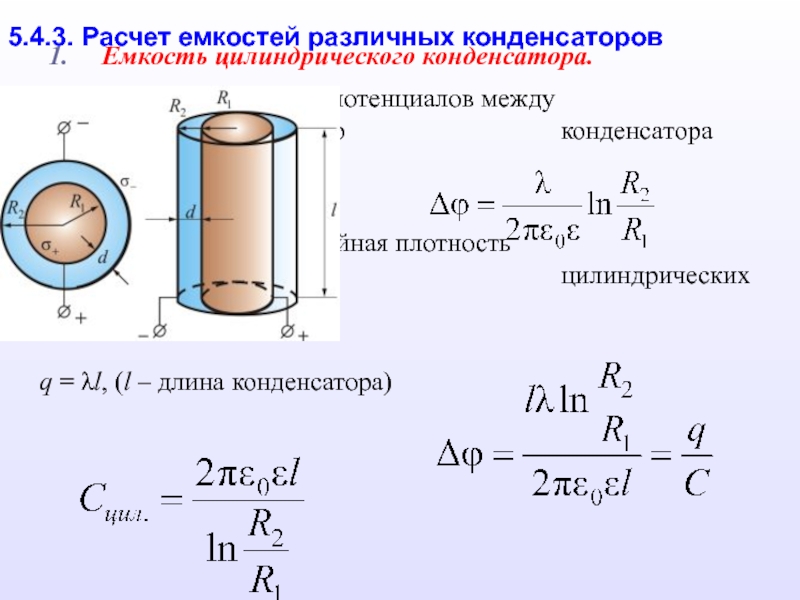

Ответ: 1) U₁=U₂=120 В, q₁=0,36 мКл, q₂=0,72 мКл;

2) q₁=q₂=0,24 мКл; U₁=80 В, U₂=40 В.

2.(3.55) Сила притяжения между пластинами плоского конденсатора F=5×10^-2 Н.Площадь каждой пластины S=200 см². Определить объемную плотность энергии w поля конденсатора.

Ответ: w=2,5 Дж/м³.

3.(3.58) Два металлических шара радиусом r=2 см и R=6 см соединены проводником, емкостью которого можно пренебречь. Шарам сообщили заряд Q=1 нКл. Найти поверхностную плотность заряда, установившуюся на шарах.

Ответ: s₁=50 нКл/м², s₂=17 нКл/м².

4.(3.59) Два плоских конденсатора емкостью C₁=0,5 мкФ и С₂=2 мкФ зарядили до разности потенциалов Dj₁=200 и Dj₂=300 В соответственно и соединили параллельно одноименными обкладками.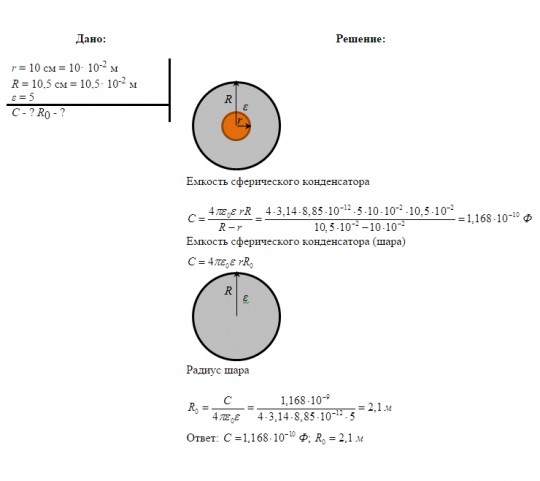 Найти изменение общей энергии DW конденсаторов.

Ответ: DW=0,002 Дж.

5.(3.62) Два конденсатора емкостью C₁=2 мкФ и С₂=4 мкФ соединены последовательно. Разность потенциалов между крайними точками батареи конденсаторов равна Dj=20 В. Определить заряды q₁,q₂ и разность потенциалов Dj₁,Dj₂ на обкладках каждого конденсатора.

Ответ: q₁=q₂=26,7 мкКл; Dj₁=13,3 В; Dj₂=6,7 В.

6.(3.66) Плоский воздушный конденсатор заряжен до разности потенциалов Dj₁=100 В и отключен от источника. После этого в конденсатор параллельно обкладкам на равном расстоянии от них поместили металлический лист толщиной b=2 мм. Найти разность потенциалов между обкладками Dj₂ после внесения листа, если площади обкладок и металлического листа одинаковы. Расстояние между обкладками конденсатора d=6 мм.

Ответ: Dj=66,7В.

7.(3.68) Два одинаковых плоских конденсатора соединены последовательно. Определить, на сколько изменится напряжение DU на одном из конденсаторов, если в другой внести диэлектрик из стекла, полностью заполняющий объем конденсатора. Диэлектрическая проницаемость стекла равна e=6. Конденсаторы присоединены к источнику напряжения U=100 В.

Ответ: DU=35,7 В.

8.(3.70) Два плоских воздушных одинаковых конденсатора соединены последовательно в батарею, которая подключена к источнику с ЭДС 12 В. Определить напряжение на конденсаторах U₁,U₂, если, отключив батарею от источника, один из конденсаторов погрузить в масло. Диэлектрическая проницаемость масла равна 5.

Ответ: U₁=6 В; U₂=1,2 В.

9.(3.71) Плоский воздушный конденсатор состоит из двух круглых пластин радиусом R=10 см каждая. Расстояние между ними d=1 см. Конденсатор зарядили до разности потенциалов Dj=1200 В и отключили от источника напряжения. Какую работу A нужно совершить, чтобы раздвинуть пластины до расстояния b=3,5 см между ними?

Ответ: A=50 мкДж.

10.(3.77) Между пластинами плоского конденсатора находится точечный заряд q=30 нКл. Поле конденсатора действует на него с силой F=10 мН. Определить силу f взаимного притяжения пластин, если площадь каждой пластины S=100 см².

Ответ: f=4,9 мН.

ЗАДАЧИ ГРУППЫ С

1. Найти объемную плотность энергии w электрического поля на расстоянии r=2 см от бесконечно длинной нити, однородно заряженной с линейной плотностью t=4,2×·10^-7 Кл/м.

Ответ: Дж/м³.

2. Найти объемную плотность энергии w электрического поля в точке, находящейся на расстоянии l=2 см от поверхности заряженного шара радиусом R=1 см, если поверхностная плотность заряда на шаре s=1,7×·10^-5 Кл/м².

Ответ: Дж/м³.

3. Внутри плоского конденсатора находится параллельная обкладкам пластинка, толщина которой равна 0,6 зазора между обкладками. Емкость конденсатора без пластинки С=20 нФ. Конденсатор сначала подключили к источнику постоянного напряжения U=200 В, затем отключили и после этого медленно извлекли пластинку из зазора. Найти работу A, затраченную на извлечение пластинки, если пластинка: а) металлическая; б) стеклянная.

Ответ: а) A=1,5 мДж, б) A=0,8 мДж.

4. Первоначально заряд q=100 пКл распределяется однородно по объему шара радиусом R=1 см. Затем, вследствие взаимного отталкивания, заряды переходят на поверхность шара. Какую работу А совершают при этом электрические силы над зарядом?

Ответ: нДж.

5. Шаровое облако ионизированных частиц расширяется, сохраняя однородное распределение заряда.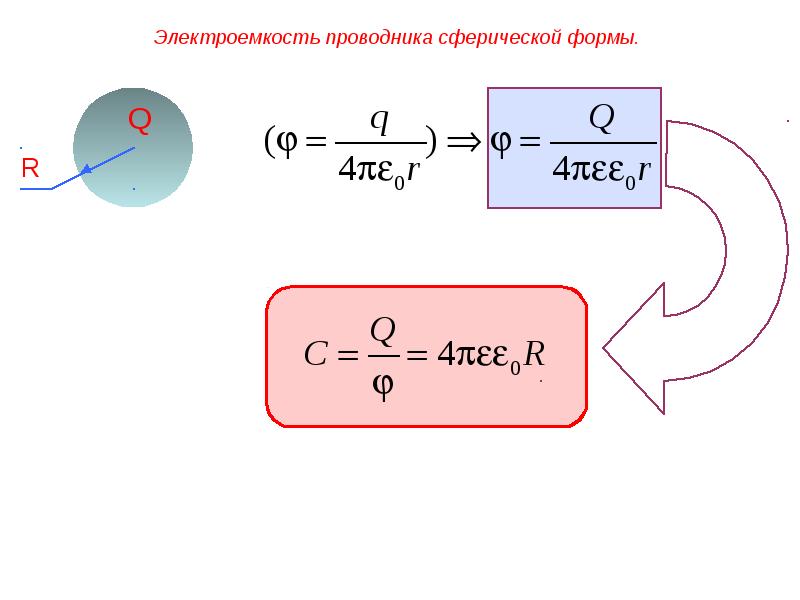 Изменится ли отношение энергии электрического поля внутри шара и за его пределами W₁/W₂? Диэлектрическая проницаемость всюду равна единице.

Ответ: Не изменится. W₁/W₂=1/5.

6. Заряд q равномерно распределен по объему шара радиусом R. Определить энергию W₁, заключенную внутри шара, и энергию W₂, заключенную в окружающем шар пространстве.

Ответ:

7. Цилиндрический конденсатор заполнен двумя цилиндрическими слоями диэлектриков, проницаемости которых e₁ и e₂. Внутренние радиусы слоев равны соответственно R₁, и а>R₁. Радиусы обкладок конденсатора R₁ и R₂ , причем R₂>R₁ , высота конденсатора l. Найти: а) емкость конденсатора С; б) энергию поля каждого из слоев W₁, W₂; в) полную энергию W поля конденсатора, если конденсатору сообщен заряд q.

Ответ: а)

б) в)

8. Сферический конденсатор заполнен двумя сферическими слоями диэлектриков с проницаемостями e₁ и e₂. Диэлектрики разграничивает сфера радиусом а. Радиусы обкладок конденсатора R₁ и R₂, причем R₂>R₁. Найти: а) емкость этого конденсатора С; б) энергию поля каждого из слоев W₁, W₂ и полную энергию поля конденсатора W, если ему сообщен заряд q.

Ответ: а)

б)

 

9. Бесконечно длинный цилиндр радиусом R однородно заряжен с объемной плотностью r. Найти энергию W_l , приходящуюся на единицу длины цилиндра, запасенную внутри.

Ответ:

10. Определить емкость уединенного шарового проводника радиусом R₁, окруженного прилегающим к нему концентрическим слоем однородного диэлектрика с относительной диэлектрической проницаемостью e и наружным радиусом R₂.

Ответ:

---

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

Глава 20. Конденсаторы

Для накопления разноименных электрических зарядов служит устройство, которое называется конденсатором. Конденсатор — система двух изолированных друг от друга проводников (которые часто называют обкладками конденсатора), один из которых заряжен положительным, второй — таким же по величине, но отрицательным зарядом. Если эти проводники представляют собой плоские параллельные пластинки, расположенные на небольшом рас-стоянии друг от друга, то конденсатор называется плоским.

Для характеристики способности конденсатора накапливать заряд вводится понятие электроемкости (часто говорят просто емкости). Емкостью конденсатора называется отношение заряда конденсатора к той разности потенциалов , которая возникает между обкладками при их заряжении зарядами и (эту разность потенциалов проводников часто называют электрическим напряжением между обкладками и обозначают буквой ):

(20.1)

Поскольку величины и (или ) в формуле (20.1) зависимы, то емкость (20.1) не зависит от и , а является характеристикой геометрии системы проводников. Действительно, при сообщении проводникам зарядов и проводники приобретут потенциалы, разность которых будет пропорциональна заряду . Поэтому в отношении (20.1) заряд сокращается.

Выведем формулу для емкости плоского конденсатора (эта формула входит в программу школьного курса физики). При заряжении параллельных пластин, расположенных на небольшом расстоянии друг от друга, зарядами и , в пространстве между ними возникает однородное электрическое поле с напряженностью (см. гл. 18):

(20.2)

Разность потенциалов между пластинами равна

(20.3)

где — площадь пластин, — расстояние между ними. Отсюда, вычисляя отношение заряда к разности потенциалов (20.3), находим емкость плоского конденсатора

(20.4)

Если все пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью , то поле (20.2) и разность потенциалов (20.3) убывает в раз, а емкость конденсатора в раз взрастает

(20.5)

Для конденсаторов, соединенных в батареи, вводится понятие эквивалентной емкости, как емкости одного конденсатора, который при заряжении его тем же зарядом, что и батарея дает ту же разность потенциалов, что и батарея конденсаторов. Приведем формулы для эквивалентной емкости, а также для заряда и электрического напряжения на каждом конденсаторе при последовательном и параллельном их соединении.

Последовательное соединение (см. рисунок). При сообщении левой пластине левого конденсатора заряда , а правой пластине правого заряда , на внутренних пластинах благодаря поляризации будут индуцироваться заряды (см. рисунок; значения индуцированных зарядов приведены под пластинами). Можно доказать, что в результате поляризации каждый конденсатор будет заряжен такими же зарядами и , как и заряды крайних пластин, напряжение на всей батарее конденсаторов равно сумме напряжений на каждом, а обратная эквивалентная емкость батареи — сумме обратных емкостей всех конденсаторов

(20.6)

Параллельное соединение (см. рисунок). В этом случае если сообщить левому проводнику заряд , правому сообщить заряд , заряд распределится между конденсаторами, вообще говоря, не одинаково, но по закону сохранения заряда .

Поскольку правые пластины всех конденсаторов соединены между собой, левые — тоже, то они представляют собой единые проводники, и, следовательно, разность потенциалов между пластинами каждого конденсатора будет одинакова: . Можно доказать, что при таком соединении конденсаторов эквивалентная емкость батареи равна сумме емкостей отдельных конденсаторов

(20.7)

Заряженный конденсатор обладает определенной энергией. Если конденсатор емкости заряжен зарядом , то энергия этого конденсатора (можно говорить энергия электрического поля конденсатора) равна

(20.8)

С помощью определения электрической емкости (20.1) можно переписать формулу (20.8) еще в двух формах:

(20.9)

Рассмотрим в рамках этого минимума сведений о конденсаторах типичные задачи ЕГЭ по физике, которые были предложены в первой части книги.

Электроемкость конденсатора — его геометрическая характеристика, которая при неизменной геометрии не зависит от заряда конденсатора (задача 20.1.1 — ответ 3). Аналогично не меняется емкость конденсатора при увеличении напряжения на конденсаторе (задача 20.1.2 — ответ 3).

Связь между единицами измерений (задача 20.1.3) следует из определения емкости (20.1). Единица электрической емкости в международной системе единиц измерений СИ называется Фарада. 1 Фарада — это емкость такого конденсатора, между пластинами которого возникает напряжение 1 В при зарядах пластин 1 Кл и -1 Кл (ответ 4).

Поскольку электрическое поле в плоском конденсаторе однородно, то напряженность поля в конденсаторе и напряжение между пластинами связаны соотношением (см. формулу (18.9)) , где — расстояние между пластинами. Отсюда находим напряженность поля между обкладками плоского конденсатора в задаче 20.1.4

(ответ 4).

Согласно определению электрической емкости имеем в задаче 20.1.5

(ответ 2).

Из формулы (20.4) для емкости плоского конденсатора заключаем, что при увеличении площади его пластин в 3 раза (задача 20.1.6) его емкость увеличивается в 3 раза (ответ 1).

При уменьшении в раз расстояния между пластинами емкость плоского конденсатора возрастет в раз. Поэтому новое напряжение на конденсаторе (задача 20.1.7) можно найти из следующей цепочки формул

где и — новый заряд конденсатора (ответ 3).

Так как конденсатор в задаче 20.1.8 подключен к источнику, то между его пластинами поддерживается постоянное напряжение независимо от расстояния между ними. Поэтому заряд конденсатора изменяется при раздвигании пластин так же, как изменяется его емкость. А поскольку при увеличении расстояния между пластинами вдвое емкость конденсатора уменьшается вдвое (см. формулу (20.4)), то вдвое уменьшается и заряд конденсатора (ответ 2).

В задаче 20.1.9 конденсатор отключен от источника в процессе сближения пластин. Поэтому не меняется их заряд. А поскольку напряженность электрического поля между пластинами определяется соотношением (20.2)

то напряженность электрического поля между пластинами также не изменяется (ответ 3). Этот же результат можно получить и через определение емкости с учетом того, что

произведение от расстояния между пластинами не зависит (см. формулу (20.4)).

Из формул (20.8), (20.9) видим, что только одно из приведенных в качестве ответов к задаче 20.1.10 соотношений (а именно — 2) определяет энергию конденсатора.

При последовательном соединении конденсаторов (задача 20.2.1) одинаковыми будут их заряды независимо от значений их электрических емкостей (ответ 2). При параллельном соединении конденсаторов (задача 20.2.2) одинаковыми будут напряжения на каждом из них (ответ 3).

Поскольку конденсатор в задаче 20.2.3 отключен от источ-ника напряжения, его заряд не меняется в процессе раздвигания пластин. Поэтому для исследования изменения энергии конденсатора удобно воспользоваться формулой (20.8)

(1)

Так как при увеличении расстояния между пластинами в раз электрическая емкость конденсатора уменьшается в раз, то согласно формуле (1) энергия конденсатора увеличится в раз (ответ 1).

В задаче 20.2.4 не изменяется напряжение на конденсаторе. Поэтому воспользуемся первой из формул (20.9)

Из этой формулы заключаем, что при увеличении в раз расстояния между пластинами энергия конденсатора уменьшится в раз — ответ 2. (Разница с предыдущей задачей связана с тем, что здесь кроме внешних сил, совершающих работу при раздвигании пластин, совершает работу источник напряжения.)

В задаче 20.2.5 изменяют расстояние между пластинами (и, следовательно, емкость) и заряд конденсатора. Поэтому удобно воспользоваться формулой (20.8)

Из этой формулы заключаем, что при увеличении расстояния между пластинами в 2 раза и увеличении заряда конденсатора в 2 раза его энергия возрастет в 8 раз (ответ 4).

Поскольку в задаче 20.2.6 конденсаторы соединены последовательно, емкость батареи конденсаторов можно найти по формуле (20.6), откуда находим емкость батареи конденсаторов (ответ 2).

В задаче 20.2.7 конденсаторы соединены параллельно, поэтому емкость батареи конденсаторов можно найти по формуле (20.7): (ответ 2).

Основной вопрос, на который нужно ответить в задаче 20.2.8, это как соединены конденсаторы? Последовательно, параллельно, по-другому? Попробуем по-другому расположить в пространстве и изменить длину соединительных проводов, чтобы схема стала более понятной. Очевидно, что можно соединить вершину 1 и вершину 3 («уменьшив» длину провода 1-3), а также вершины 2 и 4. При этом средний конденсатор разворачивается в пространстве, и схема приобретает вид, показанный на рисунке, откуда видно, что конденсаторы соединены параллельно. Поэтому (ответ 1).

Когда в заряженный плоский конденсатор вставляют металлическую пластинку (задача 20.2.9), параллельную обкладкам конденсатора, напряженность электрического поля внутри пластинки становится равным нулю, вне пластинки между обкладками конденсатора остается таким же, каким оно было в отсутствие пластинки , где — заряд конденсатора, — площадь его пластин. Поэтому напряжение между обкладками конденсатора определяется соотношением:

где — расстояние между обкладками конденсатора, — толщина пластинки. Отсюда находим емкость рассматриваемого конденсатора

(ответ 4).

Чтобы найти емкость сферического конденсатора (задача 20.2.10) сообщим его обкладкам заряды и , найдем напряжение между обкладками, вычислим отношение заряда к напряжению. Разность потенциалов двух концентрических сфер, заряженных зарядами и (напряжение между обкладками сферического конденсатора), определена в задаче 19.2.5., откуда находим электрическую емкость сферического конденсатора (ответ 3):

Сферический конденсатор — Большая Энциклопедия Нефти и Газа, статья, страница 3

Сферический конденсатор

Cтраница 3

В случае цилиндрического и сферического конденсатора поле в пространстве между его обкладками возбуждается единственно лишь зарядом внутренней обкладки. Поэтому, согласно с результатами решения задачи 6 ( стр.  [31]

В случае цилиндрического и сферического конденсатора поле в пространстве между его обкладками возбуждается единственно лишь зарядом внутренней обкладки.  [32]

Найти емкость С сферического конденсатора, состоящего из двух концентрических сфер с радиусами г — 10 см и Я 10 5 см. Пространство между сферами заполнено маслом. Какой радиус R0 должен иметь шар, помещенный в масло, чтобы иметь такую же емкость.  [33]

Найти емкость С сферического конденсатора, состоящего из двух концентрических сфер с радиусами г 10см и R 10 5 см. Пространство между сферами заполнено маслом. Какой радиус До должен иметь шар, помещенный в масло, чтобы иметь такую же емкость.  [34]

Пространство между обкладками сферического конденсатора частично заполнено диэлектриком, расположенным внутри телесного угла Q с вершиной в центре обкладок.  [35]

Заземленная внешняя обкладка сферического конденсатора имеет малую толщину. В ней проделано небольшое отверстие, через которое проходит изолированный провод, соединяющий внутреннюю обкладку конденсатора с третьим проводником, находящимся на большом расстоянии от конденсатора.  [36]

Особенно хороша модель сферического конденсатора в применении к цвиттерионным ПАВ. В их молекулах противоположные заряды удалены друг от друга, а в мицеллах образуется четкий сферический конденсатор с энергией, близкой к таковой для ионных мицелл.  [37]

Пространство между обкладками сферического конденсатора радиусов а и Ь наполнено воздухом. На внутрсвнюю сферу наносится слой краски постоянной толщины t и диэлектрической проницаемости К.  [38]

Вывести выражение для емкости сферического конденсатора с двумя слоями диэлектрика, если радиусы обкладок Rl и RZ, радиус граничной сферической поверхности R %, и диэлектрические проницаемости слоев е, и еа.  [39]

Электростатическое поле между обкладками сферического конденсатора обладает центральной симметрией. Поэтому его применяют при весьма точных лабораторных исследованиях.  [40]

При изучении фотографических явлений употребляется сферический конденсатор, состоящий из центрального катода — металлического шарика диаметром 1 5 см — к анода — внутренней поверхности посеребренной изнутри сферической колбы диаметром 11 см. Воздух из колбы откачивается.  [41]

При изучении фотоэлектрических явлений употребляется сферический конденсатор, состоящий из центрального катода — металлического шарика диаметром 1 5 см — и анода — внутренней поверхности посеребренной изнутри сферической колбы диаметром 11 см. Воздух из колбы откачивается.  [42]

По форме проводящих поверхностей различают плоские, цилиндрические и сферические конденсаторы.  [43]

Таким образом, в поле сферического конденсатора при определенных условиях происходят пространственная фокусировка электронного пучка и разложение его по энергии. Поле можно использовать для построения анализатора, способного определять не только энергию электронов, выходящих из точечного источника, но и позволяющего проводить энергетическое излучение полых конических электронных пучков.  [44]

Страницы:      1    2    3    4

Формула емкости конденсатора через напряжение. Зарядка конденсатора от источника постоянной эдс

По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.

Формула заряда конденсатора

где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.

Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.

Заряд на пластинах плоского конденсатора равен:

где – электрическая постоянная; – площадь каждой (или наименьшей) пластины; – расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.

Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:

где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.

Заряд на обкладках сферического конденсатора найдем как:

Заряд конденсатора связан с энергией поля (W) внутри него:

Из формулы (6) следует, что заряд можно выразить как:

Рассмотрим последовательное соединение из N конденсаторов (рис. 1).

Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.

При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.

Примеры решения задач по теме «Заряд конденсатора»

ru.solverbook.com

Формула емкости конденсатора, С

Если q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками, то величина C, равная:

называется емкостью конденсатора. Это постоянная величина, которая зависит то размеров и устройства конденсатора.

Рассмотрим два одинаковых конденсатора, разница между которым заключается только в том, что между обкладками одного вакуум (или часто говорят воздух), между обкладками другого находится диэлектрик. В таком случае при равных зарядах на конденсаторах разность потенциалов воздушного конденсатора будет в раз меньше, чем между обкладками второго. Значит емкость конденсатора с диэлектриком (C) в раз больше, чем воздушного ():

где – диэлектрическая проницаемость диэлектрика.

За единицу емкости конденсатора принимают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ). Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) служит фарад (Ф).

Формула электрической емкости плоского конденсатора

Поле между обкладками плоского конденсатора обычно считают однородным. Его однородность нарушается только около краев. При вычислении емкости плоского конденсатора этими краевыми эффектами часто пренебрегают. Это следует делать, если расстояние между пластинами мало в сравнении с их линейными размерами. Для расчета емкости плоского конденсатора применяют формулу:

Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого , соответствующая диэлектрическая проницаемость i-го слоя , равна:

Формула электрической емкости цилиндрического конденсатора

Цилиндрический конденсатор представляется собой две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость цилиндрического конденсатора вычисляется как:

Формула электрической емкости сферического конденсатора

Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком. Емкость такого конденсатора находят как:

где – радиусы обкладок конденсатора.

Примеры решения задач по теме «Емкость конденсатора»

ru.solverbook.com

Ёмкость конденсатора — Все формулы

Электрическая ёмкость — характеристика проводника (конденсатора), мера его способности накапливать электрический заряд.

Конденсатор состоит из двух проводников (обкладок), которые разделены диэлектриком. На емкость конденсатора не должны влиять окружающие тела, поэтому проводникам придают такую форму, чтобы поле, которое создается накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) две концентрические сферы; 3) два коаксиальных цилиндра. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, сферические и цилиндрические.

Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками

Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.

Конденсаторы можно классифицировать по следующим признакам и свойствам:

1) по назначению — конденсаторы постоянной и переменной емкости;

2) по форме обкладок различают конденсаторы плоские, сферические, цилиндрические и др.;

3) по типу диэлектрика — воздушные, бумажные, слюдяные, керамические, электролитические и т.д.

Так же есть:

Энергия конденсатора:

Ёмкость цилиндрического конденсатора:

Ёмкость плоского конденсатора:

Емкость сферического конденсатора:

В формуле мы использовали:

Электрическая ёмкость (ёмкость конденсатора)

Потенциал проводника (Напряжение)

Потенциал

Относительная диэлектрическая проницаемость

Электрическая постоянная

Площадь одной обкладки

Расстояние между обкладками

xn--b1agsdjmeuf9e.xn--p1ai

Заряд конденсатора, теория и примеры задач

Определение и заряд конденсатора

Возможность конденсатора накопить электрический заряд зависит от главной характеристики конденсатора – емкости (C).

По своему назначению конденсатор можно уподобить батарейке. Однако существует принципиальное отличие в принципах работы этих элементов. Отличаются, также максимальные емкости и скорости зарядки и разряда конденсатора и батарейки.

Если к конденсатору присоединить источник напряжения (рис.1), то на одной из пластин конденсатора станут накапливаться отрицательные заряды (электроны), на другой положительные частицы (положительные ионы). Между обкладками конденсатора находится диэлектрик, вследствие этого, заряды не могут перебраться на противоположную пластину. Однако заметим, что электроны двигаются от источника тока до пластины конденсатора.

При первоначальном соединении конденсатора и источника тока на обкладках конденсатора много свободного места. Это означает, что сопротивление току этот момент времени минимально, сам ток максимален. В ходе зарядки конденсатора сила тока в цепи постепенно падает, до того момента пока не закончится свободное место на обкладках. При полной зарядке конденсатора ток в цепи прекратится.

Время, которое затрачивается на зарядку конденсатора от нулевого заряда (максимального тока) до полностью заряженного конденсатора (минимальная или нулевая сила тока) называют переходным периодом заряда конденсатора. На практике процесс зарядки конденсатора считают законченным, если сила тока уменьшилась до 1% от начальной величины.

Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:

Примеры решения задач

ru.solverbook.com

Формула электроемкости конденсатора

Обкладки должны иметь такую форму и быть расположены так относительно друг друга, что поле, которое создается данной системой, было максимально сосредоточено в ограниченной области пространства, между обкладками.

Назначение конденсатора в том, чтобы накапливать и отдавать в электрической цепи заряд.

Основной характеристикой конденсатора является электрическая емкость (C). Электрическая емкость конденсатора – это взаимная емкость принадлежащих ему обкладок:

q – величина заряда на обкладке; – разность потенциалов между обкладками.

Электрическая ёмкость конденсатора зависит от диэлектрической проницаемости диэлектрика, который заполняет пространство между его обкладками. Если пространство между обкладками одного конденсатора заполнено диэлектриком с проницаемостью равной , а у второго конденсатора воздух между пластинами, то емкость конденсатора с диэлектриком (C) в раз больше, чем емкость воздушного конденсатора ():

Формула электроемкости основных типов конденсаторов

При расчете электроемкости плоского конденсатора нарушением однородности поля около краёв обкладок обычно пренебрегают. Это становится возможным, если расстояние между пластинами существенно меньше, чем линейные размеры обкладок. В таком случае электрическую емкость плоского конденсатора вычисляют при помощи формулы:

где – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.

Если плоский конденсатор между обкладками имеет N слоев диэлектрика, при этом толщина каждого слоя равна , а диэлектрическая проницаемость , то его электрическую емкость рассчитывают при помощи формулы:

Цилиндрический конденсатор составляют две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполнено диэлектриком. При этом емкость цилиндрического конденсатора находят как:

где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.

У сферического конденсатора обкладками служат две концентрические сферические проводящие поверхности, пространство обкладками заполняет диэлектрик. Емкость сферического конденсатора вычисляют как:

где – радиусы обкладок конденсатора. Если , то можно считать, что , тогда, мы имеем:

так как – площадь поверхности сферы, и если обозначить , то получим формулу для емкости плоского конденсатора (3). Если расстояние между обкладками сферического и цилиндрического конденсаторов малы (в сравнении с их радиусами), то в приближенных расчетах используют формулу емкости для плоского конденсатора.

Электрическую емкость для линии из двух проводов находят как:

где d – расстояние между осями проводов; R – радиус проводов; l – длина линии.

Формулы для вычисления электрической емкости соединений конденсаторов

Если конденсаторы соединены параллельно, то суммарная емкость батареи (C) находится как сумма емкостей отдельных конденсаторов ():

При последовательном соединении конденсаторов емкость батареи вычисляют как:

Если последовательно соединены N конденсаторов, с емкостями то емкость батареи найдем как:

Сопротивление конденсатора

Если конденсатор включен в цепь с постоянного тока, то сопротивление конденсатора можно считать бесконечно большим.

При включении конденсатора в цепь переменного тока, его сопротивление носит название емкостного, и вычисляют его с помощью формулы:

где – частота переменного тока; – угловая частота тока; C – емкость конденсатора.

Энергия поля конденсатора

Электрическое поле локализованное между пластинами конденсатора обладает энергией, которую можно вычислить при помощи формулы:

где –энергия поля конденсатора; q – заряд конденсатора; C – емкость конденсатора; – разность потенциалов между обкладками конденсатора.

Энергия поля плоского конденсатора:

Примеры решения задач по теме «Электроемкость конденсатора»

ru.solverbook.com

Как найти заряд конденсатора 🚩 как определить величину заряда 🚩 Естественные науки

В обычном (без плагинов и модов) варианте Minecraft такого понятия, как конденсатор, не существует. Вернее, устройство, выполняющее его функции, имеется, но название у него совершенно другое — компаратор. Некоторая путаница в этом плане произошла еще в период разработки такого прибора. Сперва — в ноябре 2012-го — представители Mojang (компании-создателя игры) объявили о скором появлении в геймплее конденсатора. Однако через месяц они высказались уже о том, что как такового этого прибора не будет, а вместо него в игре будет компаратор.

Подобное устройство существует для проверки заполненности расположенных позади него контейнеров. Таковыми могут быть сундуки (в том числе в виде ловушек), варочные стойки, раздатчики, выбрасыватели, печи, загрузочные воронки и т.п.

Помимо этого, его часто используют для сравнения двух сигналов редстоуна между собою — он выдает результат в соответствии с тем, как было запрограммировано в данной цепи, и с тем, какой режим выбран для самого механизма. В частности, компаратор может разрешить зажигание факела, если первый сигнал больше либо равен другому.

Также порой конденсатор-компаратор устанавливают рядом с проигрывателем, подключая его входом к последнему. Когда в звуковоспроизводящем устройстве проигрывается какая-либо пластинка, вышеупомянутый прибор будет выдавать сигнал, равный по силе порядковому номеру диска.

Скрафтить такой компаратор несложно, если имеется достаточно трудно добываемый ресурс — адский кварц. Его надо поставить в центральный слот верстака, над ним и по бокам от него установить три красных факела, а в нижнем ряду — такое же количество каменных блоков.

В большом количестве модов попадаются конденсаторы, имеющие самое разное предназначение. К примеру, в Galacticraft, где у геймеров есть возможность слетать на многие планеты для ознакомления с тамошними реалиями, появляется рецепт крафта кислородного конденсатора. Он служит для создания механизмов вроде коллектора и накопителя газа для дыхания, а также рамки воздушного шлюза. Для его изготовления четыре стальных пластины размещаются по углам верстака, в центре — оловянная канистра, а под нею — воздуховод. Остальные три ячейки занимают пластины из олова.

В JurassiCraft существует конденсатор потока — некий телепорт, позволяющий переместиться в удивительный игровой мир, кишащий динозаврами. Для создания такого прибора нужно поместить в два крайних вертикальных ряда шесть железных слитков, а в средний — два алмаза и между ними единицу пыли редстоуна. Дабы устройство заработало, надо поставить его на свинью либо вагонетку, а затем щелкнуть по нему правой клавишей мыши, быстро запрыгнув туда. При этом требуется поддержание высокой скорости устройства.

С модом Industrial Craft2 у игрока появляется возможность создавать как минимум два вида тепловых конденсаторов — красный и лазуритовый. Они служат исключительно для охлаждения ядерного реактора и для накопления его энергии и хороши для циклических сооружений такого типа. Остужаются они сами, соответственно, красной пылью или лазуритом.

Красный теплоконденсатор делается из семи единиц пыли редстоуна — их надо установить в виде буквы П и расставить под ними теплоотвод и теплообменник. Крафтинг же лазуритового устройства чуть посложнее. Для его создания четыре единицы пыли редстоуна расставляются по углам станка, в центр пойдет блок лазурита, по бокам от него — два красных тепловых конденсатора, сверху — теплоотвод реактора, а снизу — его же теплообменник.

В ThaumCraft, где сделан акцент на настоящем чародействе, конденсаторы тоже используются. Например, один из них — кристаллический — существует для аккумуляции и отдачи магии. Причем, что интересно, создавать его и многие другие вещи разрешено лишь после изучения особого элемента геймплея — исследования, проводимого за специальным столом и с определенными приборами.

Делается такой конденсатор из восьми тусклых осколков, в центр которых на верстаке помещается мистический деревянный блок. К сожалению, подобный прибор — равно как и его составляющие — просуществовал лишь до ThaumCraft 3, а в четвертой версии мода был упразднен.

www.kakprosto.ru

Соединение конденсаторов: формулы

Содержание:

1. Последовательное соединение
2. Онлайн калькулятор
3. Смешанное соединение
4. Параллельное соединение
5. Видео

В электронных и радиотехнических схемах широкое распространение получило параллельное и последовательное соединение конденсаторов. В первом случае соединение осуществляется без каких-либо общих узлов, а во втором варианте все элементы объединяются в два узла и не связаны с другими узлами, если это заранее не предусмотрено схемой.

Последовательное соединение

При последовательном соединении два и более конденсаторов соединяются в общую цепь таким образом, что каждый предыдущий конденсатор соединяется с последующим лишь в одной общей точке. Ток (i), осуществляющий зарядку последовательной цепи конденсаторов будет иметь одинаковое значение для каждого элемента, поскольку он проходит только по единственно возможному пути. Это положение подтверждается формулой: i = ic1 = ic2 = ic3 = ic4.

В связи с одинаковым значением тока, протекающего через конденсаторы с последовательным соединением, величина заряда, накопленного каждым из них, будет одинаковой, независимо от емкости. Такое становится возможным, поскольку заряд, приходящий с обкладки предыдущего конденсатора, накапливается на обкладке последующего элемента цепи. Поэтому величина заряда у последовательно соединенных конденсаторов будет выглядеть следующим образом: Qобщ= Q1 = Q2 = Q3.

Если рассмотреть три конденсатора С1, С2 и С3, соединенные в последовательную цепь, то выясняется, что средний конденсатор С2 при постоянном токе оказывается электрически изолированным от общей цепи. В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами. Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов.

Общее расстояние между обкладками при последовательном соединении представляет собой сумму расстояний между обкладками каждого элемента. В результате соединения в последовательную цепь, формируется единый большой конденсатор, площадь обкладок которого соответствует обкладкам элемента с минимальной емкостью. Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.

Падение напряжения на каждый конденсатор будет разным, в зависимости от емкости. Данное положение определяется формулой: С = Q/V, в которой емкость обратно пропорциональна напряжению. Таким образом, с уменьшением емкости конденсатора на него падает более высокое напряжение. Суммарная емкость всех конденсаторов вычисляется по формуле: 1/Cобщ = 1/C1 + 1/C2 + 1/C3.

Главная особенность такой схемы заключается в прохождении электрической энергии только в одном направлении. Поэтому в каждом конденсаторе значение тока будет одинаковым. Каждый накопитель в последовательной цепи накапливает равное количество энергии, независимо от емкости. То есть емкость может воспроизводиться за счет энергии, присутствующей в соседнем накопителе.

Онлайн калькулятор, для расчета емкости конденсаторов соединенных последовательно в электрической цепи.

Смешанное соединение

Параллельное соединение конденсаторов

Параллельным считается такое соединение, при котором конденсаторы соединяются между собой двумя контактами. Таким образом в одной точке может соединяться сразу несколько элементов.

Данный вид соединения позволяет сформировать единый конденсатор с большими размерами, площадь обкладок которого будет равна сумме площадей обкладок каждого, отдельно взятого конденсатора. В связи с тем, что емкость конденсаторов находится в прямой пропорциональной зависимости с площадью обкладок, общая емкость составить суммарное количество всех емкостей конденсаторов, соединенных параллельно. То есть, Собщ = С1 + С2 + С3.

Поскольку разность потенциалов возникает лишь в двух точках, то на все конденсаторы, соединенные параллельно, будет падать одинаковое напряжение. Сила тока в каждом из них будет отличаться, в зависимости от емкости и значения напряжения. Таким образом, последовательное и параллельное соединение, применяемое в различных схемах, позволяет выполнять регулировку различных параметров на тех или иных участках. За счет этого получаются необходимые результаты работы всей системы в целом.

electric-220.ru

Во всех электронных устройствах используются конденсаторы. При их конструировании или изготовлении своими руками параметры устройств рассчитываются по специальным формулам.

Расчёт конденсаторов

Один из главных параметров таких устройств – ёмкость. Рассчитать её можно по следующей формуле:

• C – ёмкость,
• q – заряд одной из обкладок элемента,
• U – разность потенциалов между обкладками.

В электротехнике вместо понятия «разность потенциалов между обкладками» используется «напряжение на конденсаторе».

Ёмкость элемента не зависит от конструкции и размеров устройства, а только от напряжения на нём и заряда обкладок. Но эти параметры могут изменяться в зависимости от расстояния между ними и материала диэлектрика. Это учитывается в формуле:

С=Co*ε, где:

• С – реальная ёмкость,
• Со – идеальная, при условии, что между пластинами вакуум или воздух,
• ε – диэлектрическая проницаемость материала между ними.

Например, если в качестве диэлектрика используется слюда, «ε» которой 6, то ёмкость такого устройства в 6 раз больше, чем воздушного, а при изменении количества диэлектрика меняются параметры конструкции. На этом принципе основана работа ёмкостного датчика положения.

Единицей ёмкости в системе СИ является 1 фарад (F). Это большая величина, поэтому чаще применяются микрофарады (1000000mkF=1F) и пикофарады (1000000pF=1mkF).

Расчет плоской конструкции

• ε – диэлектрическая проницаемость изолирующего материала,
• d – расстояние между пластинами.

Расчет конструкции цилиндрической формы

Цилиндрический конденсатор – это две соосные трубки различного диаметра, вставленные друг в друга. Между ними находится диэлектрик. При радиусе цилиндров, близком друг к другу и намного большем, чем расстояние между ними, цилиндрической формой можно пренебречь и свести расчёт к формуле, аналогичной той, по которой рассчитывается плоский конденсатор.

Вычисляются параметры такого устройства по формуле:

C=(2π*l*R*ε)/d, где:

• l – длина устройства,
• R – радиус цилиндра,
• ε – диэлектрическая проницаемость изолятора,
• d – его толщина.

Расчёт сферической конструкции

Есть устройства, обкладки которых представляют собой два шара, вложенные друг в друга. Формула ёмкости такого прибора:

C=(4π*l*R1*R2*ε)/(R2-R1), где:

• R1 – радиус внутренней сферы,
• R2 – радиус внешней сферы,
• ε – диэлектрическая проницаемость.

Ёмкость одиночного проводника

Кроме конденсаторов, способностью накапливать заряд обладают отдельные проводники. Одиночным проводником считается такой проводник, который бесконечно далёк от других проводников. Параметры заряженного элемента рассчитывается по формуле:

• Q – заряд,
• φ – потенциал проводника.

Объём заряда определяется размером и формой устройства, а также окружающей средой. Материал прибора значения не имеет.

Способы соединения элементов

Не всегда есть в наличии элементы с необходимыми параметрами. Приходится соединять их различными способами.

Параллельное соединение

Это такое соединение деталей, при котором к одной клемме или контакту присоединяются первые обкладки каждого конденсатора. При этом вторые обкладки присоединяются к другой клемме.

При таком соединении напряжение на контактах всех элементов будет одинаковым. Заряд каждого из них происходит независимо от остальных, поэтому общая ёмкость равна сумме всех величин. Её находят по формуле:

где C1-Cn – параметры деталей, участвующих в параллельном соединении.

Важно! Конденсаторы имеют предельное допустимое напряжение, превышение которого приведёт к выходу элемента из строя. При параллельном соединении устройств с различным допустимым напряжением этот параметр получившейся сборки равен элементу с наименьшим значением.

Последовательное соединение

Это такое соединение, при котором к клемме присоединяется только одна пластина первого элемента. Вторая пластина присоединяется к первой пластине второго элемента, вторая пластина второго – к первой пластине третьего и так далее. Ко второй клемме присоединяется только вторая обкладка последнего элемента.

При таком соединении заряд на обкладках конденсатора в каждом приборе будет равен остальным, однако напряжение на них будет разным: для зарядки устройств большей ёмкости тем же зарядом требуется меньшая разность потенциалов. Поэтому вся цепочка представляет собой одну конструкцию, разность потенциалов которой равна сумме напряжений на всех элементах, а заряд конденсатора равен сумме зарядов.

Последовательное соединение увеличивает допустимое напряжение и уменьшает общую ёмкость, которая меньше самого меньшего элемента.

Рассчитываются эти параметры следующим образом:

• Допустимое напряжение:

Uобщ=U1+U2+U3+…Un, где U1-Un – напряжение на конденсаторе;

• Общая ёмкость:

1/Собщ=1/С1+1/С2+1/С3+…1/Сn, где С1-Сn – параметры каждого устройства.

Интересно. Если в цепи только два элемента, то можно воспользоваться упрощённой формулой: Собщ=(С1*С2)/(С1+С2).

Смешанное соединение

Это такое соединение, в котором есть детали, соединённые последовательно, и есть соединённые параллельно. Параметры всей цепи рассчитывается в следующей последовательности:

1. определяются группы элементов, соединённые параллельно;
2. для каждой группы в отдельности рассчитывается эквивалентные значения;
3. рядом с каждой группой параллельно соединённых деталей пишутся получившиеся величины;
4. получившаяся схема эквивалентна последовательной схеме и рассчитывается по соответствующим формулам.

Знание формул, по которым можно найти емкость при изготовлении конденсаторов или их соединении необходимо при конструировании электронных схем.

Видео

Содержание:

Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.

В чем измеряется емкость конденсатора

Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.

Для измерения емкости применяется единица — фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q — заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.

Для расчетов используется формула:
в которой ε 0 = 8,854187817 х 10 -12 ф/м представляет собой постоянную величину. Прочие величины: ε — является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S — означает площадь обкладки, а d — зазор между обкладками.

Формула энергии конденсатора

С емкостью самым тесным образом связана другая величина, известная как . После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.

В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.

Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.

Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде:W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: W эл = CU 2 /2.

Формула заряда конденсатора

Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: U c = E.

Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.

В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).

Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома I зар = Е/R i , поскольку к сопротивлению Ri приложена вся ЭДС генератора.

Формула тока утечки конденсатора

Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.

Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора — способность получать и сохранять заряд электрического тока.

Основная формула для расчета выглядит следующим образом: I ут = U/R d , где I ут, — это ток утечки, U — напряжение, прилагаемое к конденсатору, а R d — сопротивление изоляции.

§ 6. Заряд и разряд конденсатора

Чтобы зарядить конденсатор, надо, чтобы свободные электроны перешли из одной обкладки на другую. Переход электронов с одной обкладки конденсатора на другую происходит под действием напряжения источника по проводам, соединяющим этот источник с обкладками конденсатора.

В момент включения конденсатора зарядов на его обкладках нет и напряжение на нем равно нулю μ с =0. Поэтому зарядный ток определяется внутренним сопротивлением источника r в и имеет наибольшую величину:

I З max =E/ r в.

По мере накопления зарядов на обкладках конденсатора напряжение на нем увеличивается и падение напряжения на внутреннем сопротивлении источника будет равно разности ЭДС источника и напряжения на конденсаторе (Е- μ с). следовательно, зарядный ток

i з =(Е- μ с)/ r в.

Таким образом, с увеличением напряжения на конденсаторе ток заряда снизится и при μ с =Е становится равным нулю. Процесс изменения напряжения на конденсаторе и тока заряда во времени изображен на рис. 1. В самом начале заряда напряжение на конденсаторе резко возрастает, так как зарядный ток имеет наибольшее значение и накопление зарядов на обкладках конденсатора происходит интенсивно. По мере повышения напряжения на конденсаторе зарядный ток уменьшается и накопление зарядов на обкладках замедляется. Продолжительность заряда конденсатора зависит от его емкости и сопротивления цепи, увеличение которых приводит к возрастанию продолжительности заряда. С увеличением емкости конденсатора, возрастает количество зарядов, накапливаемых на его пластинах, а если увеличить сопротивление цепи уменьшится и зарядный ток, а это замедляет процесс накопления зарядов на этих обкладках.

Если обкладки заряженного конденсатора подключить к какому-либо сопротивлению R , то за счет напряжения на конденсаторе будет протекать разрядный ток конденсатора. При разряде конденсатора электронысодной пластины (при их избытке) будут переходить на другую (при их недостатке) и будет продолжается до тех пор, пока потенциалы обкладок не выравняются, т. е. напряжение на конденсаторе станет равным нулю. Изменение напряжения в процессе разряда конденсатора изображено на рис. 2. Ток разряда конденсатора пропорционален напряжению на конденсаторе (i р =μ с /R ), и его изменение во времени подобно изменению напряжения.

В начальный момент разряда напряжение на конденсаторе наибольшее (μ с =Е) и разрядный ток максимальный (I р max =E /R ), так что разряд происходит быстро. При понижении напряжения, ток разряда снижается и процесс перехода зарядов с одной обкладки на другую затормаживается.

Время процесса разряда конденсатора зависит от сопротивления цепи и емкости конденсатора, причем возрастание как сопротивления, так и емкости увеличивает продолжительность разряда. С увеличением сопротивления разрядный ток снижается, замедляется процесс переноски зарядов с одной на другую обкладок; с увеличением емкости конденсатора повышается заряд на обкладках.

Таким образом, в цепи, содержащей конденсатор, ток проходит только в процессе его заряда и разряда, т. е. когда напряжение на обкладках претерпевает изменение во времени. При постоянстве напряжения ток через конденсатор не проходит, т. е. конденсатор не пропускает постоянный ток, так как между его обкладками помещен диэлектрик и в результате этого цепь разомкнута.

При зарядке конденсатора, последний способен накапливать электрическую энергию, потребляя ее от энергоисточника. Накопленная энергия сохраняется определенное время. При разряде конденсатора эта энергия переходит к разрядному резистору, нагревая его, т. е. энергию электрического поля превращается в тепловую. Чем выше емкость конденсатора и напряжение на его обкладках, тем будет больше энергии, запасенной на нем. Энергия электрического поля конденсатора определяется следующим выражением

W=CU 2 /2.

Если конденсатор емкостью 100 мкФ заряжен до напряжения 200 В, то энергия, запасенная в электрическом поле конденсатора, W =100· 10 -6 · 200 2 /2=2 Дж.

Вам понадобится

• — знание емкости или геометрических и физических параметров конденсатора;
• — знание энергии или заряда на конденсаторе.

Инструкция

Найдите напряжение между пластинами конденсатора, если известна текущая величина накопленной им энергии, а также его емкость. Энергия, запасенная конденсатором, может быть вычислена по формуле W=(C∙U²)/2, где C — емкость, а U — напряжение между пластинами. Таким образом, значение напряжения может быть получено как корень из удвоенного значения энергии, деленного на емкость. То есть, оно будет равно: U=√(2∙W/C).

Энергия, запасенная конденсатором, также может быть вычислена на основании значения содержащегося в нем заряда (количества ) и напряжения между обкладками. Формула, задающая соответствие между этими параметрами, имеет вид: W=q∙U/2 (где q — заряд). Следовательно, зная энергию и , можно вычислить напряжение между его пластинами по формуле: U=2∙W/q.

Поскольку заряд на конденсаторе пропорционален как приложенному к его пластинам напряжению, так и емкости устройства (он определяется формулой q=C∙U), то, зная заряд и емкость, можно найти и напряжение. Соответственно, для проведения расчета используйте формулу: U=q/C.

Для получения значения напряжения на конденсаторе с известными геометрическими и параметрами, сначала рассчитайте его емкость. Для простого плоского конденсатора, состоящего из двух проводящих пластин, разделенных , расстояние между которыми пренебрежимо мало по сравнению с их размерами, емкость может быть вычислена по формуле: C=(ε∙ε0∙S)/d.-12 Ф/м), ε — относительная диэлектрическая проницаемость пространства между пластинами (ее можно узнать из физических справочников). Вычислив емкость, рассчитайте напряжение одним из методов, приведенных в шагах 1-3.

Обратите внимание

Для получения корректных результатов при вычислении напряжений между обкладками конденсаторов, перед проведением расчетов приводите значения всех параметров в систему СИ.

Для того чтобы знать, можно ли использовать в том или ином месте схемы конденсатор, следует определить его . Способ нахождения этого параметра зависит от того, каким образом он обозначен на конденсаторе и обозначен ли вообще.

Вам понадобится

• Измеритель емкости

Инструкция

На крупных конденсаторах емкость обычно обозначена открытым текстом: 0,25 мкФ или 15 uF. В этом случае, способ ее определения тривиален.

На менее крупных конденсаторах (в том , SMD) емкость двумя или тремя цифрами. В первом случае, она обозначена в пикофарадах. Во втором случае, первые две цифры емкость , а третья — в каких единицах она выражена:1 — десятки пикофарад;
2 — сотни пикофарад;
3 — нанофарады;
4 — десятки нанофарад;
5 — доли микрофарады.

Существует также система обозначения емкости, использующая сочетания латинских букв и цифр. Буквы обозначают следующие цифры:A — 10;
B — 11;
C — 12;
D — 13;
E — 15;
F — 16;
G — 18;
H — 20;
J — 22;
K — 24;
L — 27;
M — 30;
N — 33;
P — 36;
Q — 39;
R — 43;
S — 47;
T — 51;
U — 56;
V — 62;
W — 68;
X — 75;
Y — 82;
Z — 91.Полученное число следует умножить на число 10, предварительно возведенное в степень, равную цифре, следующей после . Результат будет выражен в пикофарадах.

Встречаются конденсаторы, емкость на которых не обозначена вообще. Вы наверняка встречали их, в , в стартерах ламп дневного . В этом случае, измерить емкость можно только специальным прибором. Они цифровыми и мостовыми.В любом случае, если конденсатор впаян в то или иное устройство, его следует обесточить, разрядить в нем конденсаторы фильтра и сам конденсатор, емкость которого следует измерить, и лишь после этого выпаять его. Затем его необходимо подключить к прибору.На цифровом измерителе сначала выбирают самый грубый предел, затем переключают его до тех пор, пока он не покажет перегрузку. После этого переключатель переводят на один предел назад и читают показания, а по положению переключателя определяют, в каких единицах они выражены.На мостовом измерителе, последовательно переключая , на каждом из них прокручивают регулятор из одного конца шкалы в другой, пока звук из динамика не исчезнет. Добившись исчезновения , по шкале регулятора считывают результат, а единицы, в которых он выражен, также определяют по положению переключателя.Затем конденсатор устанавливают обратно в устройство.

Обратите внимание

Никогда не подключайте к измерителю заряженные конденсаторы.

Источники:

• Справочник по системам обозначения емкости

Найти значение электрического заряда можно двумя способами. Первый – измерить силу взаимодействия неизвестного заряда с известным и с помощью закона Кулона рассчитать его значение. Второй – внести заряд в известное электрическое поле и измерить силу, с которой оно действует на него. Для измерения заряда протекающего через поперечное сечение проводника за определенное время измерьте силу тока и умножьте ее на значение времени.

Вам понадобится

• чувствительный динамометр, секундомер, амперметр, измеритель электростатического поля, воздушный конденсатор.

Инструкция

Измерение заряда при его с известным зарядомЕсли известен одного тела, поднесите к нему неизвестный заряд и измерьте между ними в метрах. Заряды начнут взаимодействовать. С помощью динамометра измерьте силу их взаимодействия. Рассчитайте значение неизвестного заряда — для этого квадрат измеренного расстояния умножьте на значение силы и поделите на известный заряд.9)). Если заряды отталкиваются, то они одноименные, если же притягиваются – разноименные.

Измерение значения заряда , внесенного в электрическое полеИзмерьте значение постоянного электрического поля специальным прибором (измеритель электрического поля). Если такого прибора нет, возьмите воздушный конденсатор, зарядите его, измерьте напряжение на его обкладках и поделите не расстояние между пластинами – это и будет значение электрического поля внутри конденсатора в вольтах на метр. Внесите в поле неизвестный заряд. С помощью чувствительного динамометра измерьте силу, которая на него действует. Измерение проводите в . Поделите значение силы на напряженность электрического поля. Результатом будет значение заряда в Кулонах (q=F/Е).

Измерение заряда , протекающего через поперечное проводникаСоберите электрическую цепь с проводниками и последовательно подключите к ней амперметр. Замкните ее на источник тока и измерьте силу тока с помощью амперметра в амперах. Одновременно секундомером засеките , в которого в цепи был электрический ток. Умножив значение силы тока на полученное время, узнайте заряд, через поперечное сечение каждого за это время (q=I t). При измерениях следите, чтобы проводники не перегревались и не произошло короткое замыкание.

Конденсатором называется устройство, способное накапливать электрические заряды. Количество накапливаемой электрической энергии в конденсаторе характеризуется его емкостью . Она измеряется в фарадах. Считается, что емкость в один фарад соответствует конденсатору, заряженному электрическим зарядом в один кулон при разности потенциалов на его обкладках в один вольт.

Инструкция

Определите емкость плоского конденсатора по формуле С = S e e0/d, где S — площадь поверхности одной пластины, d — между пластинами, e — относительная диэлектрическая проницаемость , заполняющей пространство между пластинами (в вакууме она равна ), e0 — электрическая постоянная, равная 8,854187817 10(-12) Ф/м.Исходя из приведенной формулы, величина емкости будет зависеть от площади проводников, между ними и от материала диэлектрика. В качестве диэлектрика может применяться или слюда.

Вычислите емкость сферического конденсатора по формуле С = (4П e0 R²)/d, где П — число «пи», R — радиус сферы, d — величина зазора между его сферами.Величина емкости сферического конденсатора прямо пропорциональна концентрической сферы и обратно пропорциональна расстоянию между сферами.

Рассчитайте емкость цилиндрического конденсатора по формуле С = (2П e e0 L R1)/(R2-R1), где L — длина конденсатора , П — число «пи», R1 и R2 — радиусы его цилиндрических обкладок.

Если конденсаторы в цепи соединены параллельно, рассчитайте их общую емкость по формуле С = С1+С2+…+Сn, где С1, С2,…Сn – емкости параллельно соединенных конденсаторов.

Вычислите общую емкость последовательно соединенных конденсаторов по формуле 1/С = 1/С1+1/С2+…+1/Сn, где С1, С2,…Сn — емкости последовательно соединенных конденсаторов.

Обратите внимание

На любом конденсаторе обязательно должна быть нанесена маркировка, которая может быть буквенно-цифровая или цветовая. Маркировка отражает его параметры.

Источники:

• Цветовая маркировка резисторов, конденсаторов и индуктивностей

Емкость – величина, в системе СИ выражаемая в фарадах. Хотя используются, фактически, лишь производные от нее – микрофарады, пикофарады и так далее. Что касается электроемкости плоского конденсатора, она зависит от зазора меж обкладок и их площади, от вида диэлектрика, в данном зазоре расположенного.

Инструкция

В том случае, если обкладки конденсатора имеют одинаковую площадь и имеют расположение строго одна над другой, рассчитайте площадь одной из обкладок – любой. Если же одна из них относительно другой смещена либо они разные , нужно рассчитывать площадь области, в которой обкладки друг дружку перекрывают.

При этом используются общепринятые формулы, рассчитывать площади таких геометрических фигур, как круг (S=π(R^2)), прямоугольника (S=ab), его частного случая – квадрата (S=a^2) – и других.(-12) Ф/м и является, по сути, диэлектрической проницаемостью вакуума.

Физика для науки и техники II

5.6 Сферический конденсатор от Office of Academic Technologies на Vimeo.

5.06 Сферический конденсатор

Сферический конденсатор состоит из двух концентрических сферических проводящих пластин. Скажем, это представляет собой внешнюю сферическую поверхность или сферическую проводящую пластину, а эта представляет собой внутреннюю сферическую поверхность. Давайте снова зарядим эти поверхности так, чтобы соединить внутреннюю поверхность с положительной клеммой источника питания батареи, а внешнюю поверхность с отрицательной клеммой источника питания.При этом внутренняя поверхность будет заряжена положительно до некоторого количества кулонов плюс q, а внешняя поверхность будет заряжена отрицательно до некоторого количества кулонов минус q. Затем дайте нам некоторые размеры, скажем, внутренний радиус равен a, а внешний радиус равен b. Таким образом, зарядив конденсатор, мы завершили первый шаг по вычислению емкости этого сферического конденсатора.

На втором этапе мы рассчитаем электрическое поле между пластинами; поэтому выбираем произвольную точку между пластинами.Так как геометрия является сферической геометрией, мы выберем сферическую гауссовскую поверхность так, чтобы она проходила через интересующую точку. Допустим, эта точка находится на расстоянии r от центра сферического конденсатора. Закон Гаусса гласит, что интеграл от E dot dA по этой замкнутой поверхности s равен q, заключенному в ноль эпсилона, который является чистым зарядом внутри области, окруженной гауссовой поверхностью.

Итак, электрическое поле, после того как мы зарядим эти пластины, будет исходить от положительно заряженной пластины и входить в отрицательно заряженную пластину, поэтому оно будет направлено радиально наружу, заполняя область между этими двумя заряженными пластинами. .Следовательно, электрическое поле будет направлено радиально наружу от положительной пластины к отрицательной. Вектор площади поверхности, который представляет собой вектор увеличивающейся площади поверхности, перпендикулярен этой дополнительной поверхности на этой гауссовой сфере. Следовательно, это тоже будет в радиальном направлении наружу и перпендикулярно поверхности, как эта, так что угол между E и dA в каждой точке вдоль этой поверхности будет равен нулю градусов.

E dA Косинус нуля будет явной формой этого скалярного произведения, интегрированного по этой замкнутой поверхности, равно q, заключенного в ноль эпсилона.Косинус нуля равен 1, и пока мы находимся на поверхности этой гауссовой сферы, мы будем находиться на таком же расстоянии от источника заряда, который она окружает. Так что это будет постоянным на этой поверхности. Мы можем вынести его за пределы интеграла, что, таким образом, даст нам E, умноженное на интеграл от dA по этой гауссовой сфере.

Это будет равно q, заключенному в ноль Epsilon. Интеграл dA, опять же, добавляя все эти инкрементальные поверхности вдоль этой гауссовой сферической поверхности, в конечном итоге даст нам площадь поверхности этой сферы, которая равна 4 Pi, умноженному на квадрат радиуса, r в квадрате.Суммарный заряд, заключенный внутри области, окруженной этой сферой, представляет собой общий заряд, распределенный вдоль этой внутренней сферы, потому что он полностью охватывает эту сферу. Таким образом, это будет количество заряда вдоль внутренней сферы, равное q. У нас будет q над нулем Эпсилона.

Решение для электрического поля, отсюда между пластинами, окажется q больше 4 Пи эпсилон ноль r в квадрате. Если вы посмотрите на это выражение, мы увидим, что оно идентично электрическому полю точечного заряда.Как вы помните, мы упоминали, что сферическое распределение заряда, будь то сплошная сфера или сферическая оболочка, ведет себя как точечный заряд для всех внешних областей. Итак, эта точка p, представляющая интерес здесь, является внешней точкой для этого сферического распределения. Следовательно, он ведет себя как точечный заряд, как будто весь заряд q сконцентрирован в его центре, так что в конечном итоге электрическое поле равно q на 4 Пи эпсилон ноль r в квадрате.

Теперь, как только мы определим величину электрического поля, которое направлено радиально наружу, мы можем продолжить и вычислить или применить третий шаг, который заключается в том, что разность потенциалов между пластинами равна интегралу от положительной пластины к отрицательной в точке E. дл.Опять же, как и в случае с цилиндрическим конденсатором, мы собираемся выбрать путь в этом случае, чтобы вычислить этот интеграл по пути, в радиальном направлении. А так как наше электрическое поле направлено радиально наружу, мы выберем путь для получения интеграла также и в радиальном направлении, и поэтому dl будет равно dr для этого пути радиально наружу.

Другими словами, вектор инкрементного смещения dl будет заменен вектором инкрементного смещения в радиальном направлении. Тогда разность потенциалов между пластинами становится величиной E, которая равна q на 4 Pi Epsilon ноль r в квадрате.Величина dl будет равна величине dr, умноженной на косинус угла между этими двумя векторами.

Опять же, мы выбираем этот путь так, чтобы он совпадал с вектором электрического поля, так что угол между этими двумя векторами станет нулевым. Косинус нуля равен 1. Здесь q и 4 Пи Эпсилон ноль, они постоянны, поэтому мы можем взять его за пределы интеграла, и это оставляет нам разность потенциалов между пластинами этого конденсатора как q над 4 Пи Эпсилон нулевой интеграл. из dr над r в квадрате.Теперь интеграл берется от положительной пластины к отрицательной. Для этой области, если мы посмотрим на изменение радиального направления, мы начнем от внутреннего радиуса до внешнего радиуса, поэтому границы интеграла будут идти от a до b.

Далее, разность потенциалов будет равна q на протяжении 4 Пи. Нулевой интеграл эпсилона от dr по квадрату равен минус 1 по r, который будет оцениваться в точках a и b. Подставляя границы, разность потенциалов будет равна q на 4 Pi Epsilon ноль, и у нас будет минус 1 над b минусом, а еще один минус будет исходить от функции, сделает эту 1 положительной над a.Если у вас есть общий знаменатель, мы можем записать это выражение как q над 4 Пи Эпсилон ноль b минус a над ab. Это разность потенциалов между пластинами сферического конденсатора.

В последнем шаге говорится, что емкость рассчитывается по ее определению, которое представляет собой отношение величины заряда в конденсаторе к разности потенциалов между пластинами конденсатора, которая тогда будет равна — для разности потенциалов — мы имеем q больше 4 Пи ноль Эпсилона, умноженное на b минус a больше ab.

Заряды прекратятся, и емкость сферического конденсатора окажется равной 4 Pi Epsilon, умноженному на ноль ab над b минус a. Как и в предыдущих случаях, для параллельного конденсатора и цилиндрического конденсатора, здесь мы снова видим, что емкость напрямую зависит от физических свойств конденсатора. В данном случае для сферического конденсатора внутренний и внешний радиус конденсатора.

Здесь мы рассмотрим частный случай. Если вы рассматриваете заряженный цилиндр, мы всегда можем рассматривать этот цилиндр как конденсатор, так что его внешняя пластина расположена на бесконечности.Другими словами, мы можем сказать, что пусть a равно R, а b стремится к бесконечности. Итак, мы переносим внешнюю сферу на бесконечность и говорим о заряженной изолированной сфере. Этот случай соответствует заряженной изолированной сфере. Тогда мы можем выразить это выражение, емкость, как ноль 4 Pi Epsilon. И давайте, скажем, заменим a на большое R, оставим на мгновение b как b и запишем знаменатель в скобках b. Итак, возьмите b снаружи, 1 минус, замените a на R, R над b.

Буквы «b» в числителе и знаменателе сократятся, и по мере того, как b стремится к бесконечности, R над b будет приближаться к нулю, так что емкость изолированной заряженной сферы окажется равной 4 Pi Epsilon ноль, принимая R над b до нуля.Мы закончим просто буквой r, что указывает на то, что емкость изолированной заряженной сферы равна 4 Пи эпсилону, умноженному на ноль радиуса этой сферы.

Сферический конденсатор имеет внутреннюю сферу радиуса R1 с зарядом + Q и внешнюю концентрическую сферическую оболочку радиуса R2 с зарядом -Q. а) Найдите электрическое поле и плотность энергии в любой точке i

Вопрос:

Сферический конденсатор имеет внутреннюю сферу радиуса {eq} R_1 {/ eq} с зарядом + Q и внешней концентрической сферической оболочкой радиуса {eq} R_2 {/ eq} с зарядом -Q.2 {/ eq} dr между проводниками?

c) Интегрируйте ваш результат в части (b), чтобы найти общую энергию, запасенную в конденсаторе, и сравните ваш результат с результатом, полученным из U = (1/2) QV.

Конденсаторы

Конденсатор — это просто комбинация двух проводников, расположенных близко друг к другу. Обычно заряды на двух поверхностях конденсаторов равны и противоположны. Разность потенциалов двух пластин \ поверхностей называется потенциалом конденсатора.

Давайте возьмем конденсатор, заряд положительной пластины равен q и будет разностью потенциалов между его пластинами, тогда

{экв} Q \ propto V \\ Q = CV {/ eq} Где C называется емкостью.

Ответ и объяснение: 1

Учитывая

Внутренний и внешний радиус сферы равны {eq} R_1 и R_2. 2 (R_2-R_1)} {8 \ pi \ epsilon_0 (R_1R_2)} {/ eq}

по сравнению с

{eq} U = \ dfrac {QV} {2} {/ eq}

Разность потенциалов между внутренней и внешней поверхностью равна V

{eq} v = \ dfrac {Q (R_2-R_1)} {4 \ pi \ epsilon_0 (R_1R_2)} {/ eq}

Электрическая потенциальная энергия | Формула | Определение | Сферическая, цилиндрическая параллельная

Формула электрического потенциала и энергии электрического потенциала

Есть определение энергии электрического потенциала с формулой для 9-го, 10-го, 11-го, 12-го классов

• Что такое уравнение электрической потенциальной энергии?
• Как увеличить электрическую потенциальную энергию?
• Что подразумевается под электрическим потенциалом?

Определение электрической потенциальной энергии:

Потенциал точки в электрическом поле — это потенциальная энергия (из-за электрического поля), которой обладает единичный заряд в этой точке.

В = = \ dfrac {U} {Q} [J.C ^-2 или Вольт-В]

Где

• В — Электрический потенциал в рассматриваемой точке.
• U / q = потенциальная энергия единичного заряда.
• E = — град В

Напряженность электрического поля (E — вектор с составляющей).
E_x = — \ frac {\ partial V} {\ partial x}; E_y = — \ frac {\ partial V} {\ partial y}; E_z = — \ frac {\ partial V} {\ partial z} Емкость изолированного проводника Определение:

C = q / V = ​​постоянная

1. В ^-1 — Фарад — Ф

• C = емкость изолированного проводника зависит только от формы и размеров проводника.
• q — Заряд на проводнике.
• В — потенциал на проводе.

Емкость сферического изолированного проводника радиуса R составляет:

C = 4 \ pi \ in_0 R

Определение конденсатора с формулой: — конденсатор представляет собой систему из двух проводников с изоляцией между ними. У проводников одинаковые и противоположные заряды.

C = \ dfrac {Q} {треугольникV}

Где

C — Емкость конденсатора зависит только от геометрии конденсатора и материала между проводниками.

∆V = разность потенциалов между проводниками.

q — Абсолютное значение заряда на каждом проводе.

Конденсатор сферический: —

C = 4 \ пи \ дюйм R1R2 / R1-R2

Где

R ₁ и R ₂ — радиусы внутренней и внешней сферы.

ɛ — Абсолютная диэлектрическая проницаемость материала между проводниками.

Цилиндрический конденсатор Formula

: —

С =

Где, R ₁ и R ₂ — внутренний и внешний радиусы цилиндров.

L — Длина цилиндра.

Плоский конденсатор: —

C = ∈A / d

Где,

A = площадь поверхности одной из пластин.

d = расстояние между пластинами.

Конденсатор в серии Formula

:

q = q ₁ = q ₂ = q ₃ = ……… ..

В = В ₁ + В ₂ + В ₃ + …………

\ dfrac {1} {C} = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3} +…

Параллельный конденсатор:

q = q ₁ + q ₂ + q ₃ + …….

V = V ₁ = V ₂ = V ₃ = …….

C = C ₁ + C ₂ + C ₃ + …… ..

Где, q ₁ , V ₁ и C ₁ — соответственно заряд, разность потенциалов и емкость эквивалентного конденсатора в системе конденсаторов, включенных последовательно или параллельно.

N.B Формула определения

: — Конденсатор, эквивалентный количеству последовательно соединенных конденсаторов, имеет меньшую емкость, чем наименьшая емкость отдельных конденсаторов.2} {C}

U = общая энергия, запасенная в конденсаторе.

q, V и C — соответственно заряд, разность потенциалов между пластинами и емкость конденсатора.

Конденсатор

А образован двумя концентрическими сферическими проводниками. оболочки разделены вакуумом. Внутренняя сфера …

Сферический конденсатор образован двумя концентрическими сферическими проводящие оболочки разделены вакуумом. …

Сферический конденсатор образован двумя концентрическими сферическими проводящие оболочки разделены вакуумом.Внутренняя сфера имеет радиус rarar_a = 12,0 см, а внешняя сфера имеет радиус rbrbr_b = 14,8 см. Разность потенциалов 120 В применяется к конденсатор. а. Какая емкость конденсатора? Используйте ϵ0ϵ0epsilon_0 = 8,85 × 10-12 Ф / мФ / м для диэлектрической проницаемости свободного Космос. б. Какова величина E1 электрического поля E в…

Константы Часть A bo Конденсатор образован двумя концентрическими сферическими проводящими оболочками, разделенными …

Константы Часть A bo Конденсатор образован двумя концентрическими сферическими проводящими оболочками, разделенными вакуумом.Внутренняя сфера имеет радиус 11,0 см, а внешняя сфера — 14,5 см. На конденсатор подается разность потенциалов 100 В. Какова плотность энергии при ra 11,1 см ,. только за пределами внутренней сферы? ινα Αφ 6.25 10 5 Дж / м u Отправить предыдущие ответы Запросить ответ x Неверно; Попробуйте снова; Осталась одна попытка Часть B Что такое …

Емкость и электрическое поле сферического конденсатора.

Сферический конденсатор образован двумя концентрическими сферическими проводящими оболочками, разделенными вакуумом.Внутренняя сфера имеет радиус = 12,3, а внешняя сфера имеет радиус = 14,9. К конденсатору приложена разность потенциалов 120. Какова емкость конденсатора? Используйте = 8,85 × 10−12 для диэлектрической проницаемости свободного пространства. Какова величина электрического поля на радиусе 12,8, сразу за внутренней сферой? величина 14,6, как раз внутри внешнего …

Глава 24 # 36

Конденсатор образован двумя концентрическими сферическими проводящими оболочками, разделенными вакуумом.Внутренняя сфера имеет радиус 12,0, а внешняя сфера — 14,0. К конденсатору приложена разность потенциалов 150. Какова плотность энергии при = 12,1, сразу за пределами внутренней сферы? Какова плотность энергии при = 13,9, только внутри внешней сферы?

Шаг 2: сферический конденсатор

Сферический конденсатор образован двумя концентрическими сферическими проводящими оболочками, разделенными воздухом, как показано на рисунке. Внутренняя сфера имеет радиус a = 5 см, а внешняя — b = 10 см.Конденсатор заряжается до разности потенциалов. A. Какова емкость конденсатора? B. Какой заряд собирается на внешней поверхности? C. Какая энергия хранится в конденсаторе? D. какова средняя плотность (запасенная энергия на единицу объема) в конденсаторе?

Разность потенциалов и энергия электрического поля сферического конденсатора.

Сферический конденсатор образован двумя концентрическими сферическими проводящими оболочками, разделенными вакуумом. Внутренняя сфера имеет радиус 10.0 сантиметров, а расстояние между сферами составляет 1,50 сантиметра. Величина заряда на каждой сфере составляет 3,30 нанокулонов. Какова величина разности потенциалов между двумя сферами? Какая энергия электрического поля хранится в конденсаторе?

Концентрический сферический конденсатор заряжен до -Q на внешнем сфере и + Q на …

Концентрический сферический конденсатор заряжен до -Q на внешнем сфера и + Q на внутренней сфере.Внутренняя сфера твердая, с радиус = a, а внешняя сфера полая с радиусом = b. Между две сферы — это вакуум. а) Найдите разность потенциалов между r = a и r = b и, таким образом, найти емкость этой системы напрямую. б) Предполагая, что внешняя оболочка заземлена (т. е. при нулевом потенциале) использовать, чтобы найти емкость. c) Используя плотность энергии в …

Конденсатор состоит из концентрических проводящих сфер. Внутренняя сфера имеет радиус a, внешняя…

Конденсатор состоит из концентрических проводящих сфер. Внутренняя сфера имеет радиус a, внешняя сфера (тонкостенная оболочка) имеет радиус b. 1. Покажите, что емкость равна ab / k (b — a), когда пространство между внутренней и внешней сферами пусто. Начни с результата из закона Гаусса для поля вне однородного сферического заряда распределение (вывести потенциальную разницу между сферы). 2. Какова емкость, если a = 0,1 м и b = 0,103 …

Конденсатор состоит из двух концентрических проводящих цилиндрических оболочек.Радиус внутреннего цилиндрического …

Конденсатор состоит из двух концентрических проводящих цилиндрических оболочек. Радиус внутренней цилиндрической оболочки составляет 2,37 х 103 м, а внешней оболочки — 2,47 х 103 м. Когда цилиндры несут равные и противоположные заряды величиной 2,0 x 10-10 Кл, электрическое поле между пластинами имеет среднюю величину 3,8 x 104 В / м и направлено радиально наружу от внутренней оболочки к внешней оболочке. Определите (а) величину…

Конденсатор состоит из двух цилиндрических проводников. снаряды. Внутренняя оболочка имеет радиус A, …

Конденсатор состоит из двух цилиндрических проводников. снаряды. Внутренняя оболочка имеет радиус А, центрируется внутри внешняя оболочка и имеет положительную плотность поверхностного заряда + 3с. Внешняя оболочка имеет радиус B = 3A и отрицательный плотность поверхностного заряда -с. Предположим, что длина проводники? бесконечно? длинный по сравнению с радиусом B так что вы можете игнорировать все краевые эффекты.Пусть r будет вектор, направленный от центра конденсатора к любому …

Видео с вопросом: Анализ свойств сферического конденсатора

Стенограмма видео

Землю можно рассматривать как сферический конденсатор с двумя пластинами, где отрицательная пластина — это поверхность Земли, а положительная пластина — это дно ионосферы, которое находится на высоте примерно 70 километров.Разность потенциалов между поверхностью Земли и ионосферой составляет около 350000 вольт. Рассчитайте емкость этой системы. Найдите общий заряд этого конденсатора. Найдите энергию, хранящуюся в этой системе.

В этой задаче, состоящей из трех частей, мы хотим решить емкость системы, которую мы назовем 𝐶. Мы также хотим знать заряд конденсатора, который мы назовем, а также энергию, запасенную в системе, которую мы назовем.

В постановке задачи говорится, что мы должны рассматривать Землю как сферический конденсатор, где поверхность Земли является внутренней частью сферического конденсатора, а ионосфера, расположенная на расстоянии 70 километров над поверхностью Земли, является внешним слоем конденсатора.Итак, представьте отрицательные заряды на поверхности Земли и положительные заряды в ионосферном слое. Мы обозначили радиус Земли sub и радиус от центра Земли до ионосферы sub.

Давайте начнем с поиска этих значений и определения этих двух радиусов. Если мы посмотрим на радиус Земли в метрах, он будет примерно 6,37 умножить на 10 до шестого. Итак, это 𝑟 sub. 𝑟 sub 𝑖, как нам сказали, это плюс 70 километров. Если мы запишем оба этих члена в метрах, когда мы сложим их вместе, мы обнаружим, что sub равно 6.44 раза по 10 до шестого метра. Это внешний радиус нашего сферического конденсатора.

В первой части мы хотим найти емкость нашего конденсатора. Для сферического конденсатора это значение равно четырем 𝜋 умноженным на ε нулю, диэлектрической проницаемости свободного пространства, деленной на единицу по внутреннему радиусу сферического конденсатора минус единицу по внешнему радиусу. ε naught — постоянная величина. Предположим, что от 8,85 умножить на 10 до отрицательных 12 фарад на метр.

Используя наши переменные, емкость нашего конденсатора равна четырем 𝜋 ε ноль по отношению к единице, деленной на sub 𝑒 минус единица, деленная на sub.Поскольку мы знаем все значения, указанные в этом уравнении, мы можем подключить его сейчас и решить для 𝐶. Когда мы это сделаем, а затем введем эти значения в наш калькулятор, мы обнаружим, что 𝐶 равно 0,065 фарада. Это емкость этого сферического конденсатора, расположенного на Земле.

Затем мы хотим найти заряд 𝑄 на этом конденсаторе. Для начала вспомним общее уравнение для емкости. Емкость 𝐶 равна заряду, деленному на напряжение. И мы можем вспомнить из постановки задачи, что разность потенциалов, которая существует с обеих сторон этого сферического конденсатора 𝑉, составляет 350000 вольт.

𝐶 равно 𝑄 над 𝑉 означает, что 𝑄 равно 𝐶 умноженным на, или в нашем случае 0,065 фарад умножить на 350000 вольт, что, когда мы вычисляем это значение, приблизительно равно 23000 кулонам или 23 кг кулонам. Это заряд сферического конденсатора.

Теперь мы готовы решить вопрос об энергии 𝑢, хранящейся в этой системе. В общем, энергия, запасенная в конденсаторе, равна половине заряда 𝑄, хранящегося в конденсаторе, в квадрате деленного на его емкость. Таким образом, 𝑢 равно половине 𝑄 в квадрате над 𝐶.И мы решили как 𝑄, так и 𝐶 в предыдущей части этой проблемы. Таким образом, мы можем подключить их, чтобы найти 𝑢.

Когда мы это сделаем, соблюдая осторожность при использовании единиц кулонов для нашего заряда 𝑄, и введем эти значения на нашем калькуляторе, мы обнаружим, что 𝑢 до двух значащих цифр равняется 4,0 умножить на 10 до девятых джоулей или 4,0 гигаджоулей. Вот сколько энергии хранится в этом сферическом конденсаторе.

РЕШЕНИЕ: Сферический конденсатор образован двумя концентрическими сферическими проводящими оболочками, разделенными вакуумом.Внутренний…

Стенограмма видео

В данной задаче нам был предоставлен сферический конденсатор Ач, который используется для хирургических шоу, как показано здесь. Один выход и одного достаточно. Да, радио выключено. Даны эти две оболочки. Что касается внутреннего, то он хорошо идет на пять сантиметров или мы можем видеть 12,5 на 10 тарелок минус два метра или внешний. Это внутреннее, и это четыре из одного. Это 14 пунктов на каждый сантиметр или 14 пунктов на 10 номиналов тарелки минус два метра.Прежде всего, вы найдете емкость такой емкости, используя выражение для Абсалона, не младенец, рожденный в минус B или один B минус e. И когда я выставлю эти значения, емкость такого конденсатора окажется равной 59,4, и теперь потенциал в том месте, которое показывает, был задан как 1 20 единиц мира. Итак, теперь мы найдем накопитель заряда в таком конденсаторе, который позволяет нам заглянуть внутрь себя. Так что будет 89,4 в 10 декабря минус попугай в 1 20 войну. Итак, магазин зарядов оказывается одним сжиганием 074 на 10 тарелок без этого, вы знаете.Нет, нам нужно найти электрические поля в точках росы. Во-первых, острие очень близко к внутренней оболочке. Я не знаю, что у него было что-то вроде одной, а вторая точка очень близка к внешней оболочке и имеет смысл. Вам и из этих расстояний дается попка в нашем меню Ну 0,6 сантиметра а у нас 14 27 сантиметров. Мы должны определить плотность энергии у этих покупателей обуви. Итак, чтобы найти плотность энергии на данный момент, мы найдем напряженности электрического поля в этих двух точках, которые найдут электрическую напряженность, будут использовать выражение, когда опрос абсолютно не вами по нашему квадрату.Таким образом, даже если в тендере будет девять судов, девять в двух кварталах 1,74 в 10 дней, если часть минус состояние разделить скважиной 0,6 на 10 блюдо четыре минус два. Получается, что всего квадрата и этого электричества будет шесть. Жилье оно длилось восемь световых метров. Точно так же мы найдем электрическое поле после второй точки девять и выдадим девять. 1,74 на буксире. Возьмите номинальную величину минус h и разделите на 14,72. Полосная планка минус два, весь квадрат И эта электрическая выходит 4473 мира на метр.Итак, теперь, в первой части проблемной недели и находим новую плотность энергии в первой точке, которая оказывается ее молчаливой, стандартным выражением является не квадрат e. Итак, вот, ага. В 28,854 на буксире 10 тарелок по номиналу минус 12. Квадрат E означает, что это 60 единиц пота, и эта плотность энергии оказывается равной 1,64 в 10 штук по номиналу минус четыре камня. Но метр к. Во второй части задачи мы должны найти плотность энергии второй точки. Так что вы могли быть прощены задницей половине человека и не есть в другом месте.Итак, эта половина в 8,84 на 10. Блюдо для минус 4473 с целым потом, и оказывается, что это так. Направьте бой на буксире. 10. Блюдо номинальное минус пять Жюлей для вязальщицы. Если взять паралимпийский потенциал или снова плотность энергии, то у игроков везде одинаковое значение. Но, используя эти два ответа, очевидно, что никакая плотность энергии здесь не безумие, ах, это очень женский конденсатор. Благодарить.

Емкость сферического проводника

Емкость сферического проводника

Емкость — это способность накапливать электрическую энергию.Почти все вещи, включая вас, могут накапливать электрическую энергию и, следовательно, иметь емкость. Когда вы трете ногами ковер, заряженные частицы, называемые электронами, могут переноситься с ковра на вас. Емкость сферического проводника прямо пропорциональна его радиусу.

Сферический конденсатор — это емкость для сферических или цилиндрических проводников, которая может быть получена путем оценки разности напряжений между проводниками при заданном заряде каждого из них. Это своего рода конденсатор, который имеет одну или несколько тонких полых сферических пластин / проводников.Сферические конденсаторы могут быть различных типов, а именно: изолированный сферический конденсатор, концентрические сферические конденсаторы с двумя сферами и т. Д. Это зависит от внутреннего и внешнего радиуса каждой сферы.

Предположим, что центр сферического проводника A радиуса r (м), помещенного в вакуум или в воздух, равен O и содержит заряд + Q [рисунок]. Пусть емкость шара равна C, а его поверхностный потенциал равен V. Теперь, согласно определению емкости,

C = Q / V или V = Q / C…….…. (1)

Мы знаем, что заряды равномерно распределяются по всей поверхности проводника. Таким образом, будет казаться, что все силовые линии исходят из центра сферы. Даже если мы рассмотрим количество заряда Q в центре сферы O, силовые линии будут выходить аналогичным образом. Таким образом, в случае заряженного сферического проводника можно считать, что все заряды сосредоточены в центре.

Потенциал на поверхности сферического проводника,

V = 1 / 4πε ₀ x Q / r……… (2)

Из уравнений (1) и (2) получаем,

Q / C = 1 / 4πε ₀ x Q / r

, поэтому C = 4πε ₀ r…….(3)

(1) Для среды с диэлектрической проницаемостью ε _r , потенциал на сфере, V = Q / 4πε ₀ r

, поэтому C = Q / V = ​​4πε ₀ ε _r r……… (4)

Здесь ε ₀ = 8,854 x 10 ^-12 Кулон ² / Ньютон-метр ² (C ² / Нм ² ).

(2) «Емкость проводника 1 Фарад» означает, что для увеличения его потенциала на 1 вольт требуется 1 кулон заряда, а емкость проводника равна емкости сферического проводника в вакууме. или в воздухе радиусом 9 x 10 ⁹ м.

(3) Из уравнения (3), единица ε ₀ Фарад / метр (Ф / м).

Рабочее упражнение: Из двух металлических сфер одного радиуса одна полая, а другая сплошная.