Период и частота обращения | Физика
Равномерное движение по окружности характеризуют периодом и частотой обращения.
Период обращения — это время, за которое совершается один оборот.
Если, например, за время t=4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой T и определяется по формуле
Итак, чтобы найти период обращения, надо время, за которое совершено n оборотов, разделить на число оборотов.
Другой характеристикой равномерного движения по окружности является частота обращения.
Частота обращения — это число оборотов, совершаемых за 1 с. Если, например, за время t = 2 с тело совершило n = 10 оборотов, то легко сообразить, что за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой ν (читается: ню) и определяется по формуле
Итак, чтобы найти частоту обращения, надо число оборотов разделить на время, в течение которого они произошли.
За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с-1 (читается: секунда в минус первой степени). Раньше эту единицу называли «оборот в секунду», но теперь это название считается устаревшим.
Сравнивая формулы (6.1) и (6.2), можно заметить, что период и частота — величины взаимно обратные. Поэтому
Формулы (6.1) и (6.3) позволяют найти период обращения T, если известны число n и время оборотов t или частота обращения ν. Однако его можно найти и в том случае, когда ни одна из этих величин неизвестна. Вместо них достаточно знать скорость тела v и радиус окружности r, по которой оно движется. Для вывода новой формулы вспомним, что период обращения — это время, за которое тело совершает один оборот, т. е. проходит путь, равный длине окружности (l Таким образом,
Таким образом,
Итак, чтобы найти период обращения тела, надо длину окружности, по которой оно движется, разделить на скорость его движения.
Видео, не по теме но интересно
1. Что такое период обращения? 2. Как можно найти период обращения, зная время и число оборотов? 3. Что такое частота обращения? 4. Как обозначается единица частоты? 5. Как можно найти частоту обращения, зная время и число оборотов? 6. Как связаны между собой период и частота обращения? 7. Как можно найти период обращения, зная радиус окружности и скорость движения тела?
Кинематика — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Система СИ
К оглавлению…
Основные единицы измерения величин в системе СИ таковы:
- единица измерения длины — метр (1 м),
- времени — секунда (1 с),
- массы — килограмм (1 кг),
- количества вещества — моль (1 моль),
- температуры — кельвин (1 К),
- силы электрического тока — ампер (1 А),
- Справочно: силы света — кандела (1 кд, фактически не используется при решении школьных задач).

При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее.
Таблица дольных и кратных приставок в физике:
Путь и перемещение
К оглавлению…
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
где: v – скорость тела,
Средняя скорость
К оглавлению…
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:
где: Lполн – весь путь, который прошло тело, tполн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
- И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
К оглавлению. ..
..
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
где: v0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t).
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:
В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Аналогичные формулы получаются для остальных координатных осей. Формула для тормозного пути тела:
Свободное падение по вертикали
К оглавлению…
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Просто надо во всех формулах вместо индекса «х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Горизонтальный бросок
К оглавлению…
При горизонтальном броске с начальной скоростью v0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом полная скорость тела может быть найдена по формулам:
При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:
Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:
Угол между горизонтом и скоростью тела легко найти из соотношения:
Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали. Тогда этот угол будет находиться из соотношения:
Тогда этот угол будет находиться из соотношения:
Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:
Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:
При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:
Бросок под углом к горизонту (с земли на землю)
К оглавлению…
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т. е. тело бросали, например, с земли на землю):
е. тело бросали, например, с земли на землю):
Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:
Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
К оглавлению…
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны. Классический закон сложения скоростей:
Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
К оглавлению…
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.
Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:
Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:
В обеих формулах: N – количество оборотов за время t. Как видно из вышеприведенных формул, период и частота величины взаимообратные:
Как видно из вышеприведенных формул, период и частота величины взаимообратные:
При равномерном вращении скорость тела будет определяется следующим образом:
где: l – длина окружности или путь, пройденный телом за время равное периоду T. При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt. Очевидно, что за время равное периоду T тело пройдет угол равный 2π, следовательно при равномерном движении по окружности выполняются формулы:
Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:
Связь между модулем линейной скорости v и угловой скоростью ω:
При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
Модуль центростремительного ускорения связан с линейной v и угловой ω скоростями соотношениями:
Обратите внимание, что если тела (точки) находятся на вращающемся диске, шаре, стержне и так далее, одним словом на одном и том же вращающемся объекте, то у всех тел одинаковые период вращения, угловая скорость и частота.
Физика. Период и частота | Частная школа. 9 класс
Конспект по физике для 9 класса «Период и частота». Что такое период обращения. Что такое частота обращения. Как вычислить скорость и ускорение тела, движущегося по окружности, если известны его период и частота обращения.
Конспекты по физике Учебник физики Тесты по физике
Период и частота
Измерить скорость тела, движущегося по окружности, не всегда просто. Однако её можно вычислить, используя такие понятия, как период и частота обращения.
Однако её можно вычислить, используя такие понятия, как период и частота обращения.
ПЕРИОД
Когда тело движется по окружности с постоянной по модулю скоростью, через определённые промежутки времени движение повторяется снова и снова. Примером этому может служить движение на обычной детской карусели.
Время, в течение которого тело совершает один полный оборот, называют периодом обращения. Период обращения принято обозначать буквой Т. Единица этой физической величины в СИ — секунда.
С понятием периода обращения вы уже знакомились при изучении географии. Например, период обращения Земли вокруг своей оси составляет 23 ч 56 мин 4 с, а период обращения Земли вокруг Солнца — 1,00004 земных года. Самый короткий период обращения вокруг Солнца в нашей Солнечной системе имеет планета Меркурий. Её период обращения составляет 0,24085 земных лет. Интересно, что самая большая планета Солнечной системы — Юпитер — имеет самый короткий период обращения вокруг своей оси — всего 9 ч 50 мин. В 226 000 000 лет оценивается период обращения Солнечной системы вокруг ядра Галактики.
В 226 000 000 лет оценивается период обращения Солнечной системы вокруг ядра Галактики.
ЧАСТОТА
Число оборотов в единицу времени, которое совершает тело при движении по окружности, называют частотой обращения. Частоту обращения обозначают греческой буквой ν.
Если, катаясь на карусели в парке, мы совершаем один оборот за 20 с, то период обращения в этом случае Т = 20 с. Как определить частоту обращения при этом движении? Сколько оборотов совершает карусель за 1 с?
Очевидно, ν = 1/Т = 1/20 1/с, т. е. за 1 с карусель совершает одну двадцатую часть своего полного оборота.
Таким образом, частота обращения является величиной, обратной периоду обращения:
Именно поэтому единица этой физической величины обратна секунде, т. е. 1/с, или с-1.
СВЯЗЬ МОДУЛЯ СКОРОСТИ С ПЕРИОДОМ И ЧАСТОТОЙ ОБРАЩЕНИЯ
Чтобы определить модуль скорости тела, движущегося по окружности, достаточно знать радиус окружности R и период или частоту обращения. Действительно, один полный оборот тело совершает за время, равное периоду обращения Т. Путь, пройденный телом, в этом случае равен длине окружности: l = 2πR. Тогда можно записать:
Действительно, один полный оборот тело совершает за время, равное периоду обращения Т. Путь, пройденный телом, в этом случае равен длине окружности: l = 2πR. Тогда можно записать:
или с учётом формулы (1):
С учётом формул (2) и (3) можно найти центростремительное ускорение тела, выразив скорость через период или частоту обращения:
Часто мгновенную скорость движения по окружности называют линейной скоростью.
Модуль скорости движения тела по окружности рассчитывается по формуле:
Умение описывать движение тела по окружности чрезвычайно важно, так как движение по криволинейной траектории можно приближённо представить как движение по дугам окружностей различных радиусов.
РЕШЕНИЕ ЗАДАЧ
Задача 1.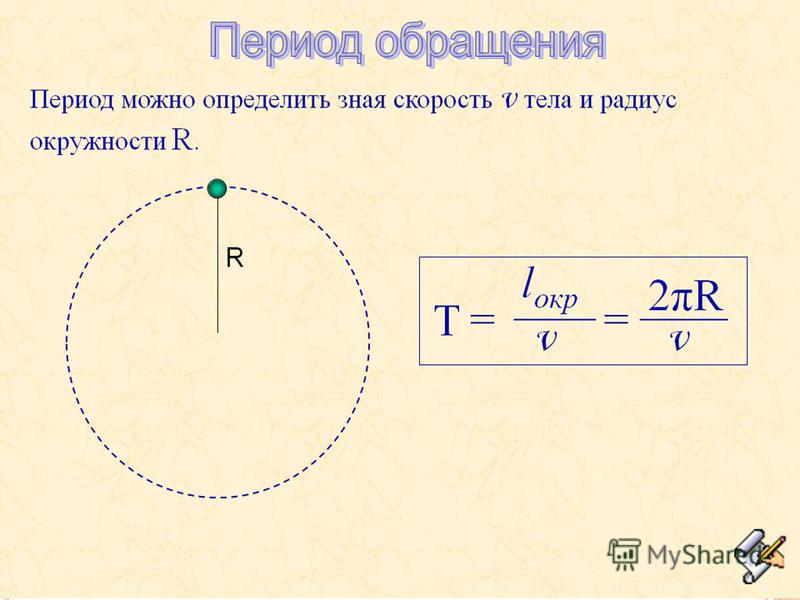 { – 3}}\; с \approx 1,2\; мс\]
{ – 3}}\; с \approx 1,2\; мс\]
Ответ: 1,2 мс.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Урок 5. поступательное движение. вращательное движение твердого тела — Физика — 10 класс
Физика, 10 класс
Урок 05. Поступательное движение. Вращательное движение твёрдого тела
Перечень вопросов, рассматриваемых на уроке:
- Поступательное и вращательное движение абсолютно твердого тела.
- Характеристики вращательного движения абсолютно твердого тела.
Глоссарий по теме
1. Абсолютно твердое тело – это тело, расстояние между любыми двумя точками которого остается постоянным при его движении.
2. Поступательным называется такое движение абсолютно твердого тела, при котором любой отрезок, соединяющий любые две точки тела, остается параллельным самому себе. Одинаковыми остаются при поступательном движении перемещение, траектория, путь, скорость, ускорение.
3. Вращением твердого тела вокруг неподвижной оси называется такое движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой перпендикулярной плоскостям этих окружностей. Сама эта прямая есть ось вращения.
4. Угол поворота – угол, на который поворачивается радиус-вектор, соединяющий центр окружности с точкой вращающегося тела.
5. Угловая скорость — отношение угла поворота φ к промежутку времени, в течение которого совершен этот поворот при равномерном движении.
6. Линейная скорость – отношение длины дуги окружности пройденной точкой тела к промежутку времени, в течение которого этот поворот совершен.
7. Период — промежуток времени, за который тело делает один полный оборот.
8. Частота обращения тела – число оборотов за единицу времени
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М.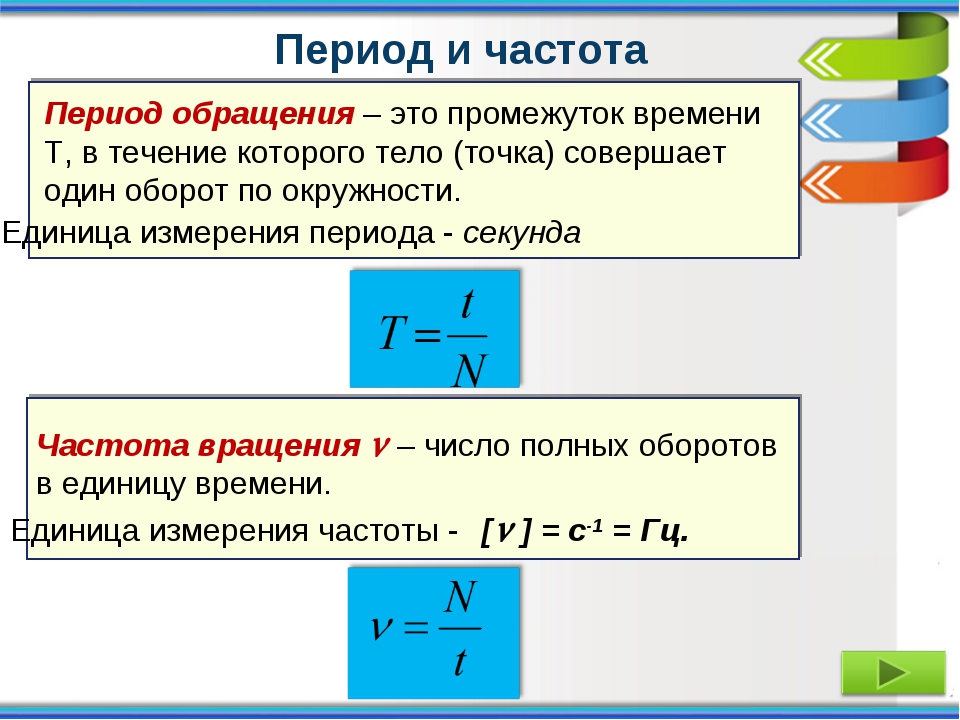 : Просвещение, 2016. – С. 57-61
: Просвещение, 2016. – С. 57-61
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.-С.20-22
Открытые электронные ресурсы:
http://kvant.mccme.ru/1986/11/kinematika_vrashchatelnogo_dvi.htm
Теоретический материал для самостоятельного изучения
1. Вы знаете, что в физике для упрощения исследования реальных ситуаций часто используются модели. Одной из механических моделей, используемых при описании движения и взаимодействия тел, является абсолютно твёрдое тело- тело, расстояние между любыми двумя точками которого остаётся постоянным при его движении.
2. Поступательным называется такое движение абсолютно твёрдого тела, при котором любой отрезок, соединяющий любые две точки тела, остаётся параллельным самому себе. Примером поступательного движения может служить свободное падение тел, движение лифта, поезда на прямолинейном участке дороги. При поступательном движении все точки тела описывают одинаковые траектории, совершают одинаковые перемещения, проходят одинаковые пути, в каждый момент времени имеют равные скорости и ускорения.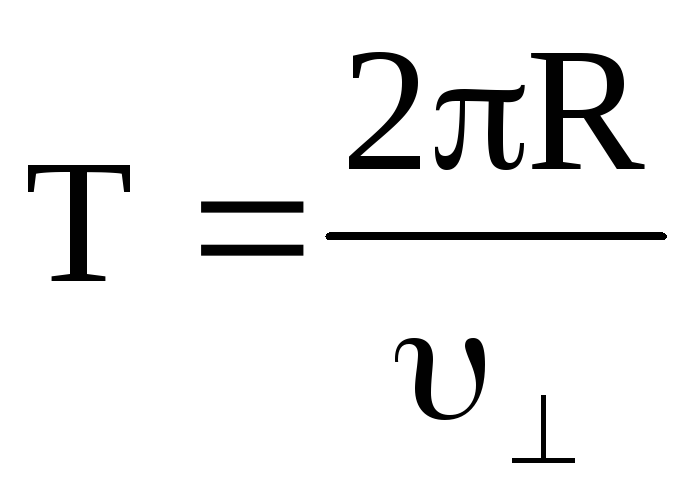
Для описания поступательного движения абсолютно твёрдого тела достаточно написать уравнение движения одной из его точек.
3. Вращательным движением абсолютно твёрдого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, называемой осью вращения. При этом плоскости, которым принадлежат эти окружности, перпендикулярны оси вращения.
Вращательное движение позволяет осуществить непрерывный процесс работы с использованием больших скоростей. Вращающиеся механизмы более компактны и более экономичны, так как потери энергии на преодоление сил трения качения меньше, чем на преодоление сил трения скольжения. Поэтому в современной технике вращательное движение рабочих частей машин всё более вытесняет возвратно-поступательное. Например, вместо ножовочной пилы в технике используют вращающуюся дисковую пилу, поршневые насосы в большинстве случаев вытесняются центробежными.
4. Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела ∆φ к промежутку времени ∆t, за которое этот поворот произошёл.
Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению запишем формулу угловой скорости;
При равномерном вращательном движении угловая скорость у всех точек вращающегося тела одинаковая. Поэтому угловая скорость, так же как и угол поворота, является характеристикой движения всего вращающегося тела, а не только отдельных его частей.
Примером вращательного движения, близкого к равномерному, может служить вращение Земли вокруг своей оси.
Угловая скорость в СИ выражается в радианах в секунду (рад/с).
Один радиан – это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности.
Угловая скорость положительна, если угол между радиусом вектором, определяющим положение одной из точек твердого тела, и осью ОХ увеличивается, и отрицательным, когда он уменьшается
5. Число полных оборотов за единицу времени называют частотой обращения.
Число полных оборотов за единицу времени называют частотой обращения.
Частоту обозначают греческой буквой «ню». Единица измерения частоты является секунда в минус первой степени
Время, за которое тело совершает один полный оборот, называют периодом обращения и обозначают буквой Т.
7. Связь между линейной и угловой скоростями:
8. Связь между ускорением и угловой скоростью:
Итак, мы рассмотрели два простейших движения абсолютно твердого тела – поступательное и вращательное. В жизни мы чаще встречаем сложное движение абсолютно твердого тела, однако, в этом случае любое сложное движение можно представить как сумму двух независимых движений: поступательного и вращательного.
Примеры и разбор типового тренировочного задания
- Ротор мощной паровой турбины делает 100 оборотов за 2 с. Определите угловую скорость.
Дано:
N=100 об.
t = 2 c
Найти: ω.
Решение:
2. Два шкива, соединенные друг с другом ремнем, вращаются вокруг неподвижных осей (см.рис). Больший шкив радиусом 20см делает 50 оборотов за 10 секунд, а частота вращения меньшего шкива 2400 оборотов в минуту. Чему равен радиус меньшего шкива? Шкивы вращаются без проскальзывания.
Дано:
Найти —
Решение:
Из условия задачи ученик видит что, шкивы соединены ремнем, следовательно, линейные скорости их равны:
но частота вращения разная.
Сокращает на 2π обе части.
Отсюда имеем:
и так, как в условии известно , то можем записать:
Отсюда находим радиус второго шкива:
Вторая неизвестная величина
Запишем формулу периода обращения для большего шкива:
так как по условию задачи нам известно число оборотов за 10 секунд.
Подставим в формулу (1) и получим конечную формулу:
Вращательное движение вокруг неподвижной оси — еще один частный случай движения твердого тела.Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, называемой осью вращения, при этом плоскости, которым принадлежат эти окружности, перпендикулярны оси вращения (рис.2.4). В технике такой вид движения встречается очень часто: например, вращение валов двигателей и генераторов, турбин и пропеллеров самолетов. Угловая скорость. Каждая точка вращающегося вокруг оси тела, проходящей через точку О, движется по окружности, и различные точки проходят за время разные пути. Так, , поэтому модуль скорости точки А больше, чем у точки В (рис.2.5). Но радиусы окружностей поворачиваются за время на один и тот же угол . Угол — угол между осью ОХ и радиус-вектором , определяющим положение точки А (см.  рис.2.5). рис.2.5).Пусть тело вращается равномерно, т. е. за любые равные промежутки времени поворачивается на одинаковые углы. Быстрота вращения тела зависит от угла поворота радиус-вектора, определяющего положение одной из точек твердого тела за данный промежуток времени; она характеризуется угловой скоростью. Например, если одно тело за каждую секунду поворачивается на угол , а другое — на угол , то мы говорим, что первое тело вращается быстрее второго в 2 раза. Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела к промежутку времени , за который этот поворот произошел. Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению Угловая скорость выражается в радианах в секунду (рад/с). Например, угловая скорость вращения Земли вокруг оси равна 0,0000727 рад/с, а точильного диска — около 140 рад/с1. Угловую скорость можно выразить через частоту вращения, т.  е. число полных оборотов за 1с. Если тело совершает (греческая буква «ню») оборотов за 1с, то время одного оборота равно секунд. Это время называют периодом вращения и обозначают буквой T. Таким образом, связь между частотой и периодом вращения можно представить в виде: е. число полных оборотов за 1с. Если тело совершает (греческая буква «ню») оборотов за 1с, то время одного оборота равно секунд. Это время называют периодом вращения и обозначают буквой T. Таким образом, связь между частотой и периодом вращения можно представить в виде:Полному обороту тела соответствует угол . Поэтому согласно формуле (2.1) Если при равномерном вращении угловая скорость известна и в начальный момент времени угол поворота , то угол поворота тела за время t согласно уравнению (2.1) равен: Если , то , или . Угловая скорость принимает положительные значения, если угол между радиус-вектором, определяющим положение одной из точек твердого тела, и осью ОХ увеличивается, и отрицательные, когда он уменьшается. Тем самым мы можем описать положение точек вращающегося тела в любой момент времени. Связь между линейной и угловой скоростями. Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть ее отличие от угловой скорости.  Мы уже отмечали, что при вращении твердого тела разные его точки имеют неодинаковые линейные скорости, но угловая скорость для всех точек одинакова. Между линейной скоростью любой точки вращающегося тела и его угловой скоростью существует связь. Установим ее. Точка, лежащая на окружности радиусом R, за один оборот пройдет путь . Поскольку время одного оборота тела есть период T, то модуль линейной скорости точки можно найти так: Так как , то Из этой формулы видно, что, чем дальше расположена точка тела от оси вращения, тем больше ее линейная скорость. Для точек земного экватора , а для точек на широте Санкт-Петербурга . На полюсах Земли . Модуль ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности: Следовательно, Чем дальше расположена точка твердого тела от оси вращения, тем большее по модулю ускорение она имеет. Итак, мы научились полностью описывать движение абсолютно твердого тела, вращающегося равномерно вокруг неподвижной оси, так как, пользуясь формулами , можем находить положение, модули скорости и ускорения любой точки тела в произвольный момент времени. 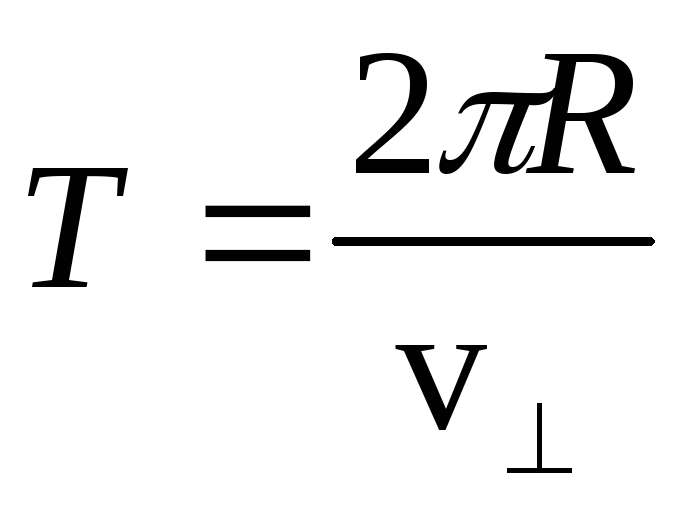 Знаем мы и направления и , a также форму траекторий точек. Знаем мы и направления и , a также форму траекторий точек. |
7.2: Классическая механика
Область классической механики включает изучение тел в движении, особенно физические законы, касающиеся тел, находящихся под воздействием сил. Большинство механических аспектов проектирования роботов тесно связано с концепциями из этой области. В данном блоке описываются несколько ключевых применяемых концепций классической механики.
СКОРОСТЬ — это мера того, насколько быстро перемещается объект. Обозначает изменение положения во времени (проще говоря, какое расстояние способен преодолеть объект за заданный период времени). Данная мера представлена в единицах расстояния, взятых в единицу времени, например, в количестве миль в час или футов в секунду.
ЧАСТОТА ВРАЩЕНИЯ – Скорость может также выражаться во вращении, то есть насколько быстро объект движется по кругу. Измеряется в единицах углового перемещения во времени (то есть в градусах в секунду), или в циклах вращения в единицу времени (например, в оборотах в минуту). Когда измерения представлены в оборотах в минуту (RPM), речь идет о частоте вращения. Есть речь идет об об/мин автомобильного двигателя, это означает, что измеряется скорость вращения двигателя.
Когда измерения представлены в оборотах в минуту (RPM), речь идет о частоте вращения. Есть речь идет об об/мин автомобильного двигателя, это означает, что измеряется скорость вращения двигателя.
УСКОРЕНИЕ – Изменение скорости во времени представляет собой ускорение. Чем больше ускорение, тем быстрее изменяется скорость. Если автомобиль развивает скорость от 0 до 60 миль в час за две секунды, в этом случае ускорение больше, чем когда он развивает скорость от 0 до 40 миль в час за тот же период времени. Ускорение — это мера изменения скорости. Отсутствие изменения означает отсутствие ускорения. Если объект движется с постоянной скоростью — ускорение отсутствует.
СИЛА — Ускорение является следствием воздействия сил, которые провоцируют изменение в движении, направлении или форме. Если вы нажимаете на объект, это означает, что вы прикладываете к нему силу. Робот ускоряется под воздействием силы, которую его колеса прикладывают к полу. Сила измеряется в фунтах или ньютонах.
Например, масса объекта воздействует на объект как сила вследствие гравитации (ускорение объекта в направлении центра Земли).
КРУТЯЩИЙ МОМЕНТ – Сила, направленная по кругу (вращение объекта), называется крутящим моментом. Крутящий момент — это вращающая сила. Если к объекту приложен крутящий момент, на границе первого возникает линейная сила. В примере с колесом, катящемся по земле, крутящий момент, приложенный к оси колеса, создает линейную силу на границе покрышки в точке ее контакта с поверхностью земли. Так и определяется крутящий момент — как линейная сила на границе круга. Крутящий момент определяется величиной силы, умноженной на расстояние от центра вращения (Сила х Расстояние = Крутящий момент). Крутящий момент измеряется в единицах силы, умноженной на расстояние, например, фунто-дюймах или ньютон-метрах.
В примере с колесом, катящемся по земле, если известен крутящий момент, приложенный к оси с закрепленным на ней колесом, мы можем рассчитать количество силы, прикладываемой колесом к поверхности. В этом случае, радиус колеса является расстоянием силы от центра вращения.
В этом случае, радиус колеса является расстоянием силы от центра вращения.
Сила = Крутящий момент/Радиус колеса
В примере с рукой робота, удерживающей объект, мы можем рассчитать крутящий момент, требуемый для поднятия объекта. Если объект обладает массой, равной 1 ньютону, а рука имеет длину 0,25 метра (объект располагается на расстоянии 0,25 метра от центра вращения), тогда
Крутящий момент = Сила х Расстояние = 1 ньютон х 0,25 метра = 0,25 ньютон-метров.
Это означает, что для удержания объекта в неподвижном положении, необходимо применить крутящий момент, равный 0,25 ньютон-метров. Чтобы переместить объект вверх, роботу необходимо приложить к нему крутящий момент, значение которого будет превышать 0,25 ньютон-метров, так как необходимо преодолеть силу гравитации. Чем больше крутящий момент робота, тем больше силы он прикладывает к объекту, тем больше ускорение объекта, и тем быстрее рука поднимет объект.
Пример 7.2
Пример 7.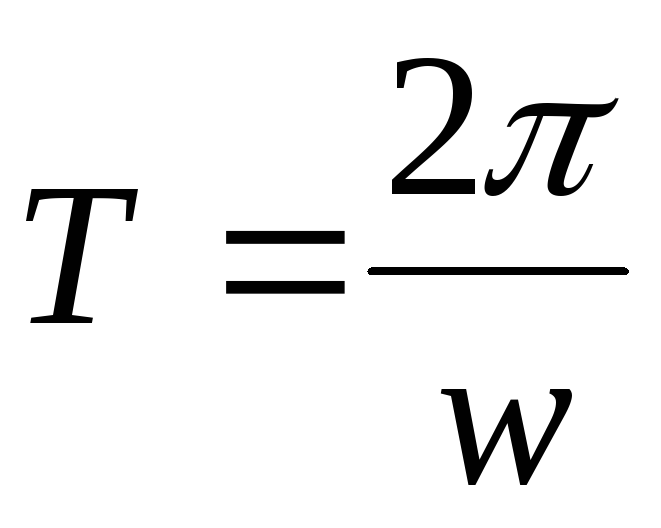 3
3
Для данных примеров, мы можем рассчитать крутящий момент, необходимый для подъем этих объектов.
Пример 7.2 — Крутящий момент = Сила х Расстояние = 1 ньютон х 0,125 метра = 0,125 ньютон-метров.
Для данного примера, длина рука равна половине длины руки из Примера 1, поэтому значение требуемого крутящего момента также в два раза меньше. Значение длины руки пропорционально значению требуемого крутящего момента. При равных исходных характеристиках объекта, чем короче рука, тем меньший крутящий момент необходим для подъема.
Пример 7.3 — Крутящий момент = Сила * Расстояние = 1 ньютон х 0,5 метра = 0,5 ньютон-метров.
Для данного примера, длина рука равна удвоенной длине руки из Примера 1, поэтому значение требуемого крутящего момента также в два раза больше.
Еще одна точка зрения относительно ограниченного крутящего момента в соединении руки робота заключается в следующем: более короткая рука сможет поднять объект большей массы, чем более длинная рука; однако, для первой доступная высота подъема объекта будет меньше, чем для второй.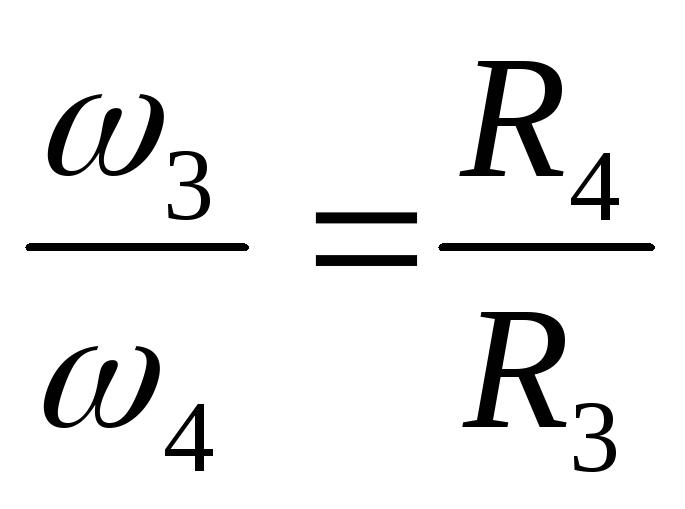
Пример 7.4
Пример 7.5
Эти примеры иллюстрируют руку робота, поднимающую объекты разной массы. Какова взаимосвязь с требуемым количеством крутящего момента?
Пример 4 — Крутящий момент = Сила х Расстояние = ½ ньютона х 0,25 метра = 0,125 ньютон-метров.
Пример 5 — Крутящий момент = Сила х Расстояние = 2 ньютона х 0,25 метра = 0,5 ньютон-метров.
Эти примеры иллюстрируют уменьшение значения требуемого крутящего момента по мере снижения массы объекта. Масса пропорциональна крутящему моменту, необходимому для ее подъема. Чем тяжелее объект, тем больше крутящий момент, требуемый для его подъема.
Проектировщики роботов должны обратить внимание на ключевые взаимосвязи между значениями крутящего момента, длины руки и массы объекта.
РАБОТА – Мера силы, приложенной на расстоянии, называется работой. Например, для удерживания объекта необходимо 10 фунтов силы. Далее, чтобы поднять этот объект на высоту 10 дюймов, требуется определенное количество работы. Количество работы, требуемое для подъема объекта на высоту 20 дюймов, удваивается. Работа также понимается как изменение энергии.
Количество работы, требуемое для подъема объекта на высоту 20 дюймов, удваивается. Работа также понимается как изменение энергии.
МОЩНОСТЬ — Большинство людей полагает, что мощность является термином из области электрики, но мощность также относится и к механике.
Мощность — это количество работы в единицу времени. Насколько быстро кто-то может выполнить работу?
В робототехнике принято понимать мощность как ограничение, так как соревновательные робототехнические системы имеют ограничения в части выходной мощности. Если роботу требуется поднять массу в 2 ньютона (прилагая 2 ньютона силы), скорость подъема будет ограничиваться количеством выходной мощности робота. Если робот способен произвести достаточное количество мощности, он сможет быстро поднять объект. Если он способен произвести лишь малое количество энергии, подъем объекта будет производиться медленно (либо не будет производиться вообще!).
Мощность определяется как Сила, умноженная на Скорость (насколько быстро выполняется толчок при постоянной скорости), и обычно выражается в Ваттах.
Мощность [Ватты] = Сила [Ньютоны] х Скорость [Метры в секунду]
1 Ватт = 1 (Ньютон х Метр) / Секунда
Как это применяется в соревновательной робототехнике? К проектам роботов применяются определенные ограничения. Проектировщики соревновательных роботов, использующие систему проектирования VEX Robotics Design, также должны учитывать физические ограничения, связанные с применением электромоторов. Электромотор обладает ограниченной мощностью, поэтому он может производить только определенное количество работы с заданной скоростью.
Примечание: все перспективные концепции имеют базовое описание. Более глубоко обсуждать эти физические свойства учащиеся будут в процессе обучения в ВУЗах, если выберут область STEM в качестве направления обучения.
Математика движения спутников
Движение объектов подчиняется законам Ньютона. Те же простые законы, которые управляют движением объектов на Земле, также распространяются на небес , чтобы управлять движением планет, лун и других спутников. Математика, описывающая движение спутника, аналогична математике, представленной для кругового движения в Уроке 1. В этой части Урока 4 мы будем иметь дело с разнообразием математических уравнений, описывающих движение спутников.
Математика, описывающая движение спутника, аналогична математике, представленной для кругового движения в Уроке 1. В этой части Урока 4 мы будем иметь дело с разнообразием математических уравнений, описывающих движение спутников.
Уравнение орбитальной скорости
Рассмотрим спутник с массой M sat , вращающийся вокруг центрального тела с массой M Central . Центральным телом может быть планета, солнце или другая большая масса, способная вызвать достаточное ускорение менее массивного соседнего объекта. Если спутник движется по кругу, то чистая центростремительная сила, действующая на этот орбитальный спутник, определяется соотношением
F net = (M sat • v 2 ) / RЭта чистая центростремительная сила является результатом силы тяжести, которая притягивает спутник к центральному телу, и может быть представлена как
F грав = (G • M sat • M Central ) / R 2 Поскольку F grav = F net , приведенные выше выражения для центростремительной силы и гравитационной силы могут быть установлены равными друг другу. Таким образом,
Таким образом,
Обратите внимание, что масса спутника присутствует в обеих частях уравнения; таким образом, его можно отменить, разделив на M sat . Затем обе части уравнения можно умножить на R , оставив следующее уравнение.
v 2 = (G • M Центральный ) / RВзяв квадратный корень из каждой стороны, получаем следующее уравнение для скорости спутника, движущегося вокруг центрального тела при круговом движении
, где G — 6.673 x 10 -11 Н • м 2 / кг 2 , M центральный — масса центрального тела, вокруг которого вращается спутник, а R — радиус орбиты спутника. .
Уравнение ускорения Аналогичные рассуждения можно использовать для определения уравнения ускорения нашего спутника, которое выражается через массы и радиус орбиты. Величина ускорения спутника равна ускорению свободного падения спутника в любом месте, по которому он вращается.В Уроке 3 уравнение ускорения свободного падения было дано как
Величина ускорения спутника равна ускорению свободного падения спутника в любом месте, по которому он вращается.В Уроке 3 уравнение ускорения свободного падения было дано как
Таким образом, ускорение спутника при круговом движении вокруг некоторого центрального тела определяется следующим уравнением
, где G составляет 6,673 x 10 -11 Н • м 2 / кг 2 , M центральный — это масса центрального тела, вокруг которого вращается спутник, а R — это масса центрального тела, вокруг которого вращается спутник. средний радиус орбиты спутника.
Уравнение периода обращения Последнее уравнение, которое полезно при описании движения спутников, — это форма Ньютона третьего закона Кеплера. Поскольку логика построения уравнения была представлена в другом месте, здесь будет представлено только уравнение. Период спутника ( T ) и среднее расстояние от центрального тела ( R ) связаны следующим уравнением:
Период спутника ( T ) и среднее расстояние от центрального тела ( R ) связаны следующим уравнением:
, где T — период спутника, R — средний радиус орбиты спутника (расстояние от центра центральной планеты), а G — 6.673 x 10 -11 Н • м 2 / кг 2 .
Во всех трех уравнениях очевидна важная концепция — период, скорость и ускорение орбитального спутника не зависят от массы спутника.
Ни одно из этих трех уравнений не содержит в себе переменной M спутник . Период, скорость и ускорение спутника зависят только от радиуса орбиты и массы центрального тела, на орбите которого находится спутник.Так же, как и в случае движения снарядов по Земле, масса снаряда не влияет на ускорение к Земле и скорость в любой момент. Когда сопротивление воздуха незначительно и присутствует только сила тяжести, масса движущегося объекта не играет роли. Так обстоит дело с орбитальными спутниками.
Так обстоит дело с орбитальными спутниками.
Чтобы проиллюстрировать полезность приведенных выше уравнений, рассмотрим следующие практические задачи.
| Практическая задача № 1 Спутник желает облететь Землю на высоте 100 км (приблизительно 60 миль) над поверхностью Земли. Определите скорость, ускорение и период обращения спутника. (Дано: M земля = 5,98 x 10 24 кг, R земля = 6,37 x 10 6 м) |
Как и большинство проблем в физике, эта проблема начинается с определения известной и неизвестной информации и выбора соответствующего уравнения, способного разрешить неизвестное.Для этой проблемы известные и неизвестные перечислены ниже.
| Выдано / Известно: R = R земля + высота = 6,47 x 10 6 м M земля = 5. G = 6,673 x 10 -11 Н · м 2 / кг 2 | Неизвестный: v = ??? а = ??? Т = ??? |
Обратите внимание, что радиус орбиты спутника можно найти, зная радиус Земли и высоту спутника над Землей.Как показано на диаграмме справа, радиус орбиты спутника равен сумме радиуса Земли и высоты над землей. Эти две величины можно сложить, чтобы получить радиус орбиты. В этой задаче 100 км необходимо сначала преобразовать в 100 000 м, а затем добавить к радиусу Земли. Уравнения, необходимые для определения неизвестного, перечислены выше. Начнем с определения орбитальной скорости спутника с помощью следующего уравнения:
v = SQRT [(G • M Центральный ) / R]Замена и решение следующие:
v = КОРЕНЬ [(6.673 x 10 -11 Н м 2 / кг 2 ) • (5,98 x 10 24 кг) / (6,47 x 10 6 м)]v = 7,85 x 10 3 м / с
Ускорение можно найти с помощью одного из следующих уравнений:
| (1) a = (G • M центральный ) / R 2 | (2) a = v 2 / R |
Уравнение (1) было получено выше. Уравнение (2) — это общее уравнение кругового движения. Для расчета ускорения можно использовать любое уравнение. Здесь будет продемонстрировано использование уравнения (1).
Уравнение (2) — это общее уравнение кругового движения. Для расчета ускорения можно использовать любое уравнение. Здесь будет продемонстрировано использование уравнения (1).
a = (6,673 x 10 -11 Н · м 2 / кг 2 ) • (5,98 x 10 24 кг) / (6,47 x 10 6 м) 2
a = 9,53 м / с 2
Обратите внимание, что это ускорение немного меньше, чем 9.8 м / с 2 ожидаемое значение на поверхности земли. Как обсуждалось в Уроке 3, увеличение расстояния от центра Земли снижает значение g.
Наконец, период можно рассчитать с помощью следующего уравнения:
Уравнение можно переписать к следующему виду
T = SQRT [(4 • pi 2 • R 3 ) / (G * M центральный )]Замена и решение следующие:
T = КОРЕНЬ [(4 • (3.1415) 2 • (6,47 x 10 6 м) 3 ) / (6,673 x 10 -11 Н м 2 / кг 2 ) • (5,98×10 24 кг)]T = 5176 с = 1,44 часа
| Практическая задача № 2 Период Луны составляет примерно 27,2 дня (2,35 x 10 6 с). |
Как и практическая задача № 2, эта проблема начинается с определения известных и неизвестных значений. Они показаны ниже.
| Выдано / Известно: T = 2,35 x 10 6 с M Земля = 5,98 x 10 24 кг G = 6.673 x 10 -11 Н м 2 / кг 2 | Неизвестный: R = ??? v = ??? |
Радиус орбиты можно рассчитать по следующей формуле:
Уравнение можно переписать к следующему виду
R 3 = [(T 2 • G • M центральный ) / (4 • pi 2 )]Замена и решение следующие:
R 3 = [((2. 35×10 6 с) 2 • (6,673 x 10 -11 Н м 2 / кг 2 ) • (5,98×10 24 кг)) / (4 • (3,1415) 2 ) ]
35×10 6 с) 2 • (6,673 x 10 -11 Н м 2 / кг 2 ) • (5,98×10 24 кг)) / (4 • (3,1415) 2 ) ]R 3 = 5,58 x 10 25 м 3
Взяв кубический корень из 5,58 x 10 25 м 3 , радиус можно определить следующим образом:
R = 3,82 x 10 8 мОрбитальная скорость спутника может быть вычислена по любому из следующих уравнений:
| (1) v = SQRT [(G • M Central ) / R] | (2) v = (2 • pi • R) / T |
Уравнение (1) было получено выше.Уравнение (2) — это общее уравнение кругового движения. Любое уравнение можно использовать для расчета орбитальной скорости; здесь будет продемонстрировано использование уравнения (1). Подстановка значений в это уравнение и решение следующие:
v = SQRT [(6,673 x 10 -11 Н · м 2 / кг 2 ) * (5,98×10 24 кг) / (3,82 x 10 8 м)]v = 1,02 x 10 3 м / с
| Практическая задача № 3 Геостационарный спутник — это спутник, который вращается вокруг Земли с периодом обращения 24 часа, что соответствует периоду вращения Земли. |
Как и в предыдущей задаче, решение начинается с идентификации известных и неизвестных значений. Это показано ниже.
| Выдано / Известно: T = 86400 с M земля = 5.98×10 24 кг R земля = 6,37 x 10 6 м G = 6.673 x 10 -11 Н м 2 / кг 2 | Неизвестный: ч = ??? |
Неизвестным в этой задаче является высота ( h ) спутника над поверхностью земли. Но уравнения с переменной h нет. Затем решение включает в себя сначала определение радиуса орбиты и использование этого значения R и R земли для определения высоты спутника над Землей.Как показано на диаграмме справа, радиус орбиты спутника равен сумме радиуса Земли и высоты над землей. Радиус орбиты можно найти с помощью следующего уравнения:
Но уравнения с переменной h нет. Затем решение включает в себя сначала определение радиуса орбиты и использование этого значения R и R земли для определения высоты спутника над Землей.Как показано на диаграмме справа, радиус орбиты спутника равен сумме радиуса Земли и высоты над землей. Радиус орбиты можно найти с помощью следующего уравнения:
Уравнение можно переписать к следующему виду
R 3 = [(T 2 * G * M центральный ) / (4 * pi 2 )]Замена и решение следующие:
R 3 = [((86400 с) 2 • (6.673 x 10 -11 Н · м 2 / кг 2 ) • (5,98×10 24 кг)) / (4 • (3,1415) 2 )]R 3 = 7,54 x 10 22 м 3
Взяв кубический корень из 7,54 x 10 22 м 3 , можно определить радиус
R = 4,23 x 10 7 м Радиус орбиты указывает расстояние, на котором спутник находится от центра Земли. Теперь, когда радиус орбиты найден, можно вычислить высоту над Землей. Поскольку поверхность Земли находится на расстоянии 6,37 x 10 6 м от ее центра (это радиус Земли), высота спутника должна составлять
Теперь, когда радиус орбиты найден, можно вычислить высоту над Землей. Поскольку поверхность Земли находится на расстоянии 6,37 x 10 6 м от ее центра (это радиус Земли), высота спутника должна составлять
над поверхностью земли. Таким образом, высота спутника составляет 3,59 x 10 7 м .
На орбите Земли вращаются сотни искусственных спутников.Список геостационарных спутников можно найти на http://www.satsig.net/sslist.htm. Используйте виджет Информация о спутнике ниже, чтобы изучить различные свойства — скорость, высоту, орбитальную траекторию и т. Д. — любого существующего спутника. Просто введите имя (правильно) спутника и нажмите кнопку Получить информацию . Проверьте свое понимание 1. Спутник вращается вокруг Земли.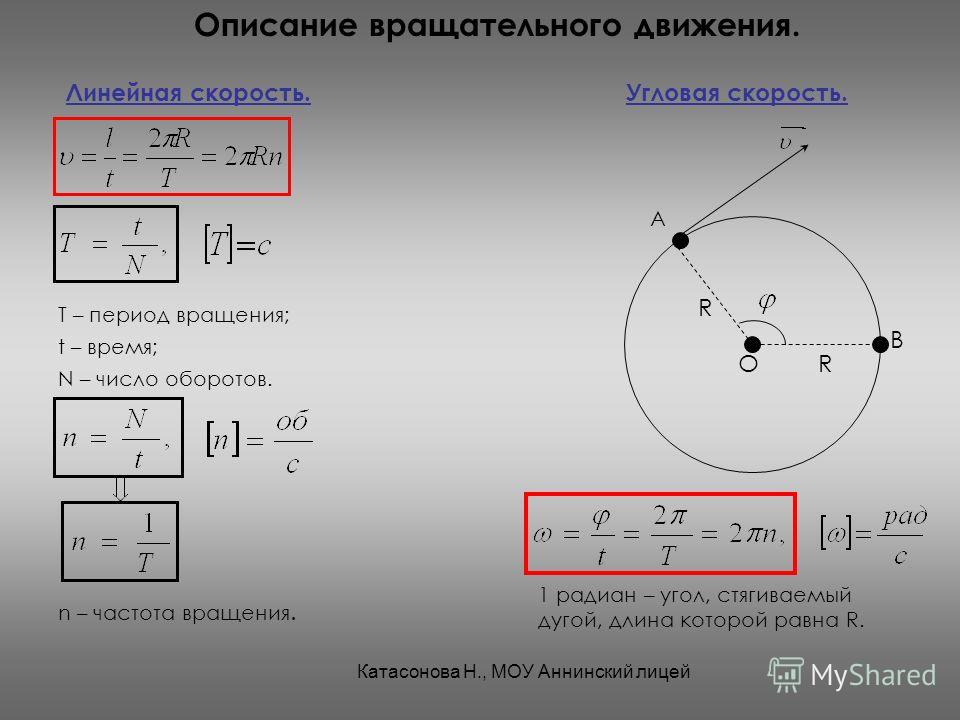 Какие из следующих переменных повлияют на скорость спутника?
Какие из следующих переменных повлияют на скорость спутника?
а. масса спутникаг. высота над поверхностью земли
г. масса земли
2. Используйте информацию ниже и соотношение выше, чтобы вычислить отношение T 2 / R 3 для планет вокруг Солнца, Луны вокруг Земли и спутников Сатурна вокруг планеты Сатурн.Значение G составляет 6,673 x 10 -11 Н • м 2 / кг 2 .
| солнце | M = 2,0 x 10 30 кг |
| земной шар | M = 6,0 x 10 24 кг |
| Сатурн | M = 5,7 x 10 26 кг |
а.T 2 / R 3 для планет около Солнцаг. T 2 / R 3 для Луны около Земли
г. T 2 / R 3 для спутников около Сатурна
3. Один из спутников Сатурна называется Мимас. Среднее орбитальное расстояние Mimas составляет 1,87 x 10 8 м. Средний орбитальный период Мимаса составляет примерно 23 часа (8.28×10 4 с). Используйте эту информацию, чтобы оценить массу планеты Сатурн.
Один из спутников Сатурна называется Мимас. Среднее орбитальное расстояние Mimas составляет 1,87 x 10 8 м. Средний орбитальный период Мимаса составляет примерно 23 часа (8.28×10 4 с). Используйте эту информацию, чтобы оценить массу планеты Сатурн.
4. Рассмотрим спутник, который находится на низкой орбите вокруг Земли на высоте 220 км над поверхностью Земли. Определите орбитальную скорость этого спутника. Используйте информацию, приведенную ниже.
| G = 6,673 x 10 -11 Нм 2 / кг 2 M земля = 5.98 x 10 24 кг R земля = 6,37 x 10 6 м |
5. Предположим, что космический шаттл находится на орбите Земли на высоте 400 км над ее поверхностью. Используйте информацию, приведенную в предыдущем вопросе, чтобы определить орбитальную скорость и период обращения космического корабля «Шаттл».
Используйте информацию, приведенную в предыдущем вопросе, чтобы определить орбитальную скорость и период обращения космического корабля «Шаттл».
Период вращения
Период вращения Период вращенияПериод вращения объекта Солнечной системы равен длине время, которое требуется этому объекту, чтобы один раз обернуться вокруг своей оси.За Например, Земле требуется 24 часа, чтобы один раз обернуться вокруг своей оси. Его период вращения — 24 часа или сутки.
Сначала давайте рассмотрим, как найти период вращения объект, будь то планета, апельсин или баскетбол.
Один из способов — найти ориентир или объект на поверхности и измерить
время, необходимое для того, чтобы объект повернулся и вернулся в
то же место. (К сожалению, не на всех планетах есть отметка «проштампована» на
их. Вам нужно будет найти что-то, что можно использовать в качестве ориентира или поверхности
функция позже. )
)
Прежде чем вы начнете исследовать настоящие планеты, давайте попрактикуемся с что-то более простое, например, баскетбол.
Примеры:
1. Если планета повернется на полпути (180 градусов) за 12 часов, как долго потребуется, чтобы полностью повернуть (360 градусов)?
Решение:
Известный поворот = 180 градусов
Полный оборот = 360 градусов
Известное время = 12 часов
Время полного вращения =?
360 градусов / 180 градусов = время полного вращения / 12 часов
Постоянное вращение = 360 градусов / 180 градусов x 12 часов = 24 часы
2.Часто планету не видно во время всего ее вращения. (В Солнце встает утром и закрывает нам вид на планеты; в планета ускользает за облака или за горизонт; и т. д.) Рассмотрим следующий пример.
Мы знаем, что поверхностный элемент вращающегося объекта покрывает 20
градусов за 4 часа. Каков период его вращения? (Решать
для решения этой проблемы вам нужно будет использовать некоторые соотношения. )
)
Решение:
Известный поворот = 20 градусов
Полный оборот = 360 градусов
Известное время = 4 часа
Время полного вращения =?
20 градусов / 360 градусов = 4 часа / Время полного вращения
Полное вращение = (360 градусов) (4 часа) / 20 градусов = 72 часы
Похоже, теперь вы понимаете, что такое период вращения, и готовы работать со скоростями вращения (или угловыми скоростями, как они иногда называются.)
Дом
Расстояние
Масс
Размеры и объем
Период вращения
Угловая скорость
формул — синодический и сидерический периоды
Одним из многих инструментов, используемых в астрономии, являются формулы, используемые для определения орбитального движения. Есть две основные формы орбиты:
- звездный период
- Синодический период
Сидерический период, на что указывает точность
звездное время, это реальная мера полного
орбита относительно
звезды (так как
звезды
неподвижный — или, по крайней мере, движущийся очень медленно). Синодический период — это чередование
планета так что это
кажется, находится в том же месте в
ночное небо.
Синодический период — это чередование
планета так что это
кажется, находится в том же месте в
ночное небо.
У нас есть две формулы, которые позволят нам определить звездный период вращения другого 8 планеты в наших Солнечная система с помощью синодического период (просто наблюдением).
Для планеты Венера и Меркурий, мы бы использовали:
Для Марс, Юпитер, Сатурн, Уран, Нептун и Мы бы использовали Плутон:
P = сидерический период в обоих
уравнения
S = синодический период в обоих уравнениях
E = орбита Земли в обоих уравнениях.
Поскольку вращение Земли составляет 1 год, E = 1 в обоих уравнениях.
Вот пример, основанный на справочный текст:
Найти сидерический период Юпитер:
P = сидерический период
E = 1
S = 1.092 года (наблюдаемый синодический период)
Вернуться к началу
Как рассчитать оборот планеты вокруг Солнца
Обновлено 16 декабря 2020 г.
Крис Дезиел
Сотрудничество немецкого астронома Иоганна Кеплера (1571–1630) и датского астронома Тихо Браге (1546 г.) — 1601), что привело к первой математической формулировке движения планет в западной науке.Сотрудничество создало три закона движения планет Кеплера, которые сэр Исаак Ньютон (1643-1727) использовал для разработки теории гравитации.
Первые два закона легко понять. Определение первого закона Кеплера состоит в том, что планеты движутся по эллиптическим орбитам вокруг Солнца, а второй закон гласит, что линия, соединяющая планету с Солнцем, сметает равные области в равное время по всей орбите планеты. Третий закон немного сложнее, и его вы используете, когда хотите вычислить период планеты или время, необходимое для обращения вокруг Солнца.Это год планеты.
Уравнение третьего закона Кеплера
На словах третий закон Кеплера состоит в том, что квадрат периода вращения любой планеты вокруг Солнца пропорционален кубу большой полуоси ее орбиты. 3
3
Где k — константа пропорциональности.
Это известно как закон периодов. Вы могли бы считать это «формулой периода планеты». Константа k равна 4π 2 / GM , где G — гравитационная постоянная. M — это масса Солнца, но более правильная формулировка будет использовать объединенную массу Солнца и рассматриваемой планеты ( M s + M p ). Однако масса Солнца настолько больше, чем масса любой планеты, что M s + M p по существу всегда одно и то же, поэтому безопасно просто использовать солнечную массу, М .
Расчет периода планеты
Математическая формулировка третьего закона Кеплера дает вам способ вычислить периоды планет в терминах земного периода или, альтернативно, длины их лет в единицах земного года. Для этого полезно выразить расстояние ( d ) в астрономических единицах (AU). 3} \ end {выравнивание}
3} \ end {выравнивание}
Вставьте расстояние планеты от Солнца на d (в AU), нажмите числа, и вы получите продолжительность его года в земных годах.3} = 11.86 \ text {Земные годы}
Расчет орбитального эксцентриситета
Величина, на которую орбита планеты отличается от круговой, называется эксцентриситетом. Эксцентриситет — это десятичная дробь от 0 до 1, где 0 обозначает круговую орбиту, а 1 обозначает такую вытянутую орбиту, что она напоминает прямую линию.
Солнце находится в одной из фокальных точек каждой планетной орбиты, и в процессе обращения каждая планета имеет афелий ( a ), или точку наибольшего сближения, и перигелий ( p ), или точка наибольшего расстояния.Формула для орбитального эксцентриситета ( E ):
E = \ frac {ap} {a + p}
При эксцентриситете 0,007 орбита Венеры наиболее близка к круговой, а орбита Меркурия — с эксцентриситетом. 0,21, самый дальний. Эксцентриситет земной орбиты 0,017.
Эксцентриситет земной орбиты 0,017.
| Оценка периода вращения Солнца Оценка скорости вращения Солнца Как вы можете использовать данные о солнечных пятнах, чтобы определить, сколько времени это займет чтобы Солнце однажды повернулось? Чтобы оценить скорость вращения Солнца, предположим, что Солнце — это плоский диск, точно такой, как он изображен на вашем копии или эскизы. Для этого упражнения вы можете использовать калькулятор.  С помощью (метрической) линейки измерьте, насколько далеко от левого края
Диск Солнца Георгий есть. С помощью (метрической) линейки измерьте, насколько далеко от левого края
Диск Солнца Георгий есть. Солнца, а это значит, что Джорджу потребуется 4 * 7 = 28 дней, чтобы пройти все
наоборот (при условии, что он сможет продержаться так долго). Солнца, а это значит, что Джорджу потребуется 4 * 7 = 28 дней, чтобы пройти все
наоборот (при условии, что он сможет продержаться так долго).28 дней = 7 дней * (24 см / 6 см) Если вы выбрали другое место или группу, как вы думаете, ваш ответ скорость вращения Солнца была бы такой же? Попытайтесь узнать, выполнив расчет для групп выше или ниже широты (то есть группы, которые находятся ближе или дальше от Солнца полюса). Вы только что оценили скорость вращения Солнца. Ваши данные будут более точными, если вы воспользуетесь Упражнение угловой скорости . Кому посмотрите, насколько близка ваша оценка , а также посмотрите анимация вращения Солнца.  Вернуться к активности вращения солнечных пятен |
Кривая вращения Млечного Пути
Дополнительная информация с www.Astronomynotes.com
Теперь, когда у нас есть представление о размере, звездном населении и общее представление о Млечном Пути как о галактике, давайте рассмотрим еще одно свойство, которое мы можем определить для Млечного Пути: его массу. В большинстве случаев, когда мы намереваемся вычислить массу астрономического объекта, мы возвращаемся к версии третьего закона Кеплера Ньютона:
P2 = (4π 2 x a3) / G (m1 + m2) Солнце вращается вокруг центра Галактики, поэтому, в принципе, если мы можем измерить расстояние Солнца от Центра Галактики и его период обращения, это означает, что мы можем оценить сумма масс Солнца и Галактики (по крайней мере, та часть Галактики, которая находится внутри орбиты Солнца).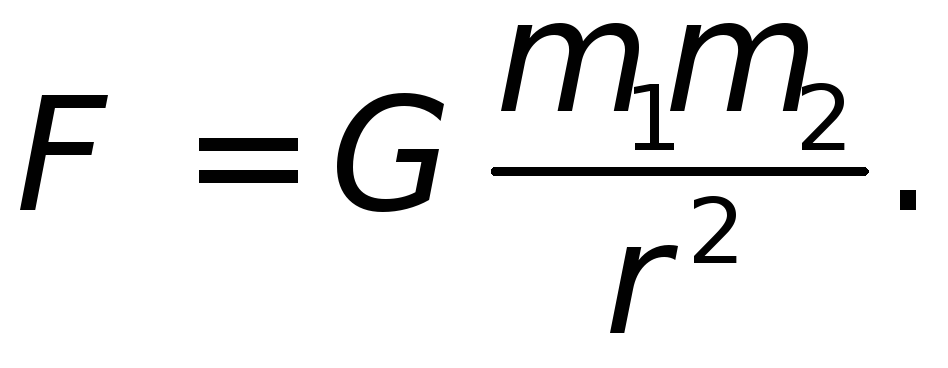 Поскольку мы ожидаем, что масса Галактики намного превысит массу Солнца, мы можем принять вычисленное нами значение за массу Галактики. Итак, каков ответ? Насколько массивна наша галактика?
Поскольку мы ожидаем, что масса Галактики намного превысит массу Солнца, мы можем принять вычисленное нами значение за массу Галактики. Итак, каков ответ? Насколько массивна наша галактика?
Расстояние от Солнца до центра Галактики можно измерить с помощью нескольких различных методов, но это измерение сложно. Исследователи по-прежнему расходятся во мнениях относительно точного значения, но оно составляет примерно 8 кпк (то есть 8000 парсеков). Есть связанное с этим, но тоже сложное измерение, и это скорость Солнца по отношению к Центру Галактики.Это примерно 200 км / сек, что позволяет нам оценить период обращения Солнца вокруг Галактического центра следующим образом:
- Предположим, что Солнце движется по круговой орбите с радиусом 8000 парсеков.
- Вычислите длину окружности орбиты Солнца: c = 2πr = (2π) * (8000 пк) * (3,1 x 1013 км / пк) = 1,6 x 1018 км.
- Вычислите период орбиты, взяв длину окружности и разделив ее на скорость: P = 1,6 x 1018 км / 200 км / сек = 8.
 0 x 1015 сек ≈ 250 миллионов лет.
0 x 1015 сек ≈ 250 миллионов лет.
Если вы возьмете большую полуось орбиты Солнца равной 8 килопарсек, а период обращения 250 миллионов лет, вы можете определить, что масса Млечного Пути по отношению к орбите Солнца составляет примерно 10 11 масс Солнца, или в 100 миллиардов раз больше массы Солнца.
Теперь сравним и сопоставим движения планет в Солнечной системе и движения звезд в Галактике. То, что мы сделали выше, чтобы вычислить период орбиты Солнца, заключалось в использовании уравнения:
орбитальный период (P) = окружность орбиты (2πr) / орбитальная скорость (v) Мы можем изменить это уравнение и вычислить орбитальную скорость для любого объекта с учетом его периода и большой полуоси.Если мы применим это к планетам в Солнечной системе, вы обнаружите, что по мере удаления от Солнца орбитальная скорость объекта уменьшается. Ниже представлен двухмерный график, который я создал для орбитальных скоростей планет (и Плутона) как функции их расстояния от Солнца. Каждая точка помечена первой буквой названия объекта (например, V = Венера). Этот тип графика (орбитальная скорость как функция расстояния от центра) называется кривой вращения .
Каждая точка помечена первой буквой названия объекта (например, V = Венера). Этот тип графика (орбитальная скорость как функция расстояния от центра) называется кривой вращения .
Рис. 8.16: График орбитальных скоростей планет Солнечной системы, показывающий, как они уменьшаются быстрее, чем линейно для объектов, более удаленных от Солнца.
Кредит: Крис Пальма
Поведение планет Солнечной системы, показанное на этом графике, часто называют Кеплеровским вращением . Ясно, что Галактика Млечный Путь сложнее Солнечной системы. Есть по крайней мере 100 миллиардов объектов, газовых облаков и пыли, и в центре нет ни одной доминирующей массы.Однако астрономы ожидали, что по мере того, как вы удаляетесь от центра Галактики, скорости звезд должны уменьшаться подобно кеплеровскому вращению, наблюдаемому у планет Солнечной системы. Однако астрономы заметили, что существует значительная разница между прогнозируемой формой кривой вращения Млечного Пути и тем, что фактически измеряется.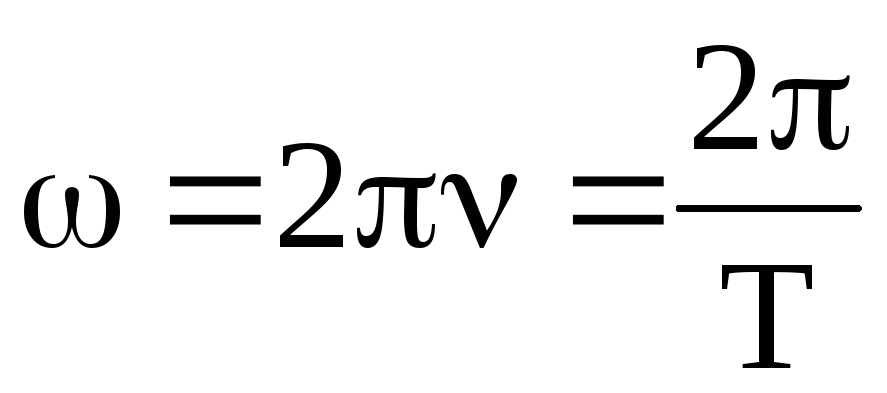 См. Изображение ниже.
См. Изображение ниже.
Рис. 8.17: Кривая вращения типичной спиральной галактики: предсказанная ( A ) и наблюдаемая ( B ).Расхождение кривых связано с темной материей.
Сплошная линия, обозначенная буквой B, представляет собой схематическую кривую вращения, подобную той, которая измеряется для Млечного Пути. Пунктирная линия, обозначенная A, представляет собой прогнозируемую кривую вращения, отображающую кеплеровское вращение. Кривая вращения B говорит нам о том, что наша модель Млечного Пути пока что-то упускает. Чтобы объекты, далекие от центра Галактики, двигались быстрее, чем предполагалось, должна существовать значительная дополнительная масса вдали от центра Галактики, оказывающая гравитационное притяжение на эти звезды.Это означает, что Млечный Путь должен включать в себя очень массивный компонент, намного превышающий размер видимого диска Галактики. Мы не видим никаких компонентов в видимом свете или любой другой части электромагнитного спектра, поэтому этот массивный ореол должен быть темным.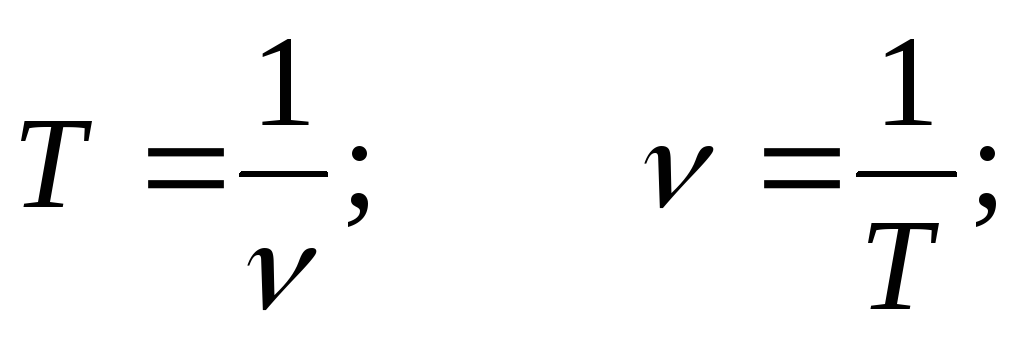 Сегодня мы называем это «гало темной материи» Галактики, и мы обсудим темную материю больше в нашем уроке по космологии.
Сегодня мы называем это «гало темной материи» Галактики, и мы обсудим темную материю больше в нашем уроке по космологии.
Возвращаясь к изображению Млечного Пути, которое мы изучали ранее, гало из проволочного каркаса на самом деле означает размер гало темной материи.На изображении ниже сравните масштаб диска с масштабом ореола темной материи.
Рис. 8.18: Схематическая диаграмма гало темной материи Млечного Пути, полученная из Partiview / Digital Universe Atlas, представленная каркасной сферой, которая полностью охватывает тонкий диск Млечного Пути и намного больше его.
Период и частота — AP Physics 1
Пояснение:Чтобы решить эту проблему, мы можем начать с сохранения энергии:
Постановка задачи говорит нам, что цилиндр изначально находится в состоянии покоя, поэтому мы можем исключить начальную кинетическую энергию.Если мы предположим, что высота цилиндра при достижении периода 0,2 с имеет высоту 0, мы можем исключить конечную потенциальную энергию. Следовательно, получаем:
Следовательно, получаем:
Расширяя эти члены и убедившись, что у нас есть линейная и вращательная составляющие кинетической энергии, мы получаем уравнение (1):
Прежде чем двигаться дальше, мы знаем, что нам нужно будет вычислить что-то, что мы можем использовать для определения периода цилиндра. Мы знаем, что период — это время, за которое цилиндр совершает один полный оборот.Думая практически, мы можем использовать окружность цилиндра и линейную скорость для определения периода:
Используя переменные, получаем уравнение:
Преобразуя конечную скорость, мы получаем уравнение (2):
Теперь мы знаем, что период зависит от конечной линейной скорости. Вернемся к этому уравнению. Теперь мы можем вернуться к уравнению (1) и начать подстановку в выражения для неизвестных переменных, двигаясь слева направо.Первая неизвестная переменная — это начальная высота. Однако мы можем использовать пройденное расстояние цилиндра и угол наклона:
Изменяя начальную высоту, мы получаем уравнение (3):
Далее следующий неизвестный член — конечная скорость. Мы можем заменить уравнение (2), которое мы уже получили:
Мы можем заменить уравнение (2), которое мы уже получили:
Далее следующий неизвестный член — момент инерции. Используя выражение для цилиндра, получаем уравнение (4):
Двигаясь дальше, последний неизвестный член — это конечная скорость вращения.Мы можем использовать соотношение между этим и линейной скоростью:
Теперь подставляя уравнение (2), мы получаем уравнение (5):
Теперь мы можем заменить уравнения 2, 3, 4 и 5 в уравнение (1):
Исключив массу из обеих частей уравнения и расширив каждый член:
Объединение терминов справа:
Изменение длины:
Проверьте свои подразделения и убедитесь, что у вас остались секунды, прежде чем двигаться дальше!
Мы знаем значения для каждой переменной, так что пора подключиться и подумать:
.

 9.2 Угловая и линейная скорости вращения
9.2 Угловая и линейная скорости вращения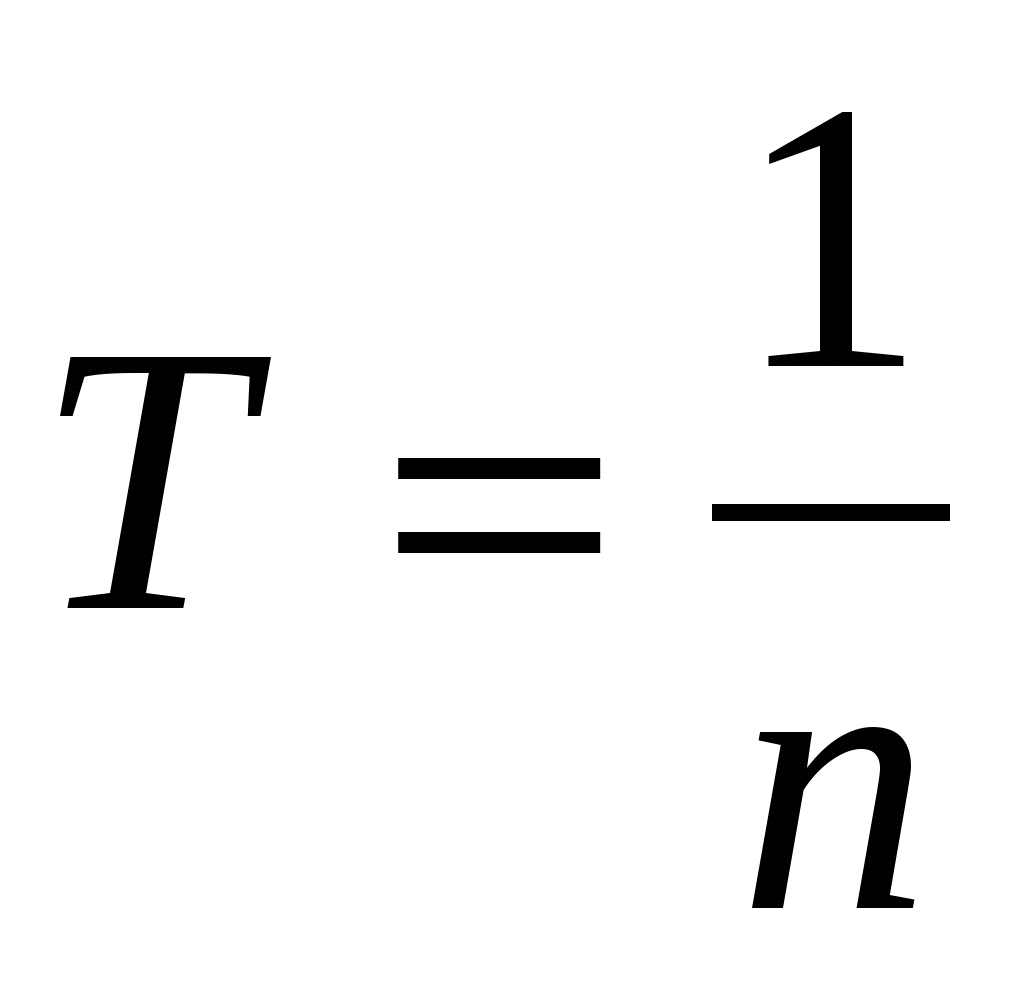 98×10 24 кг
98×10 24 кг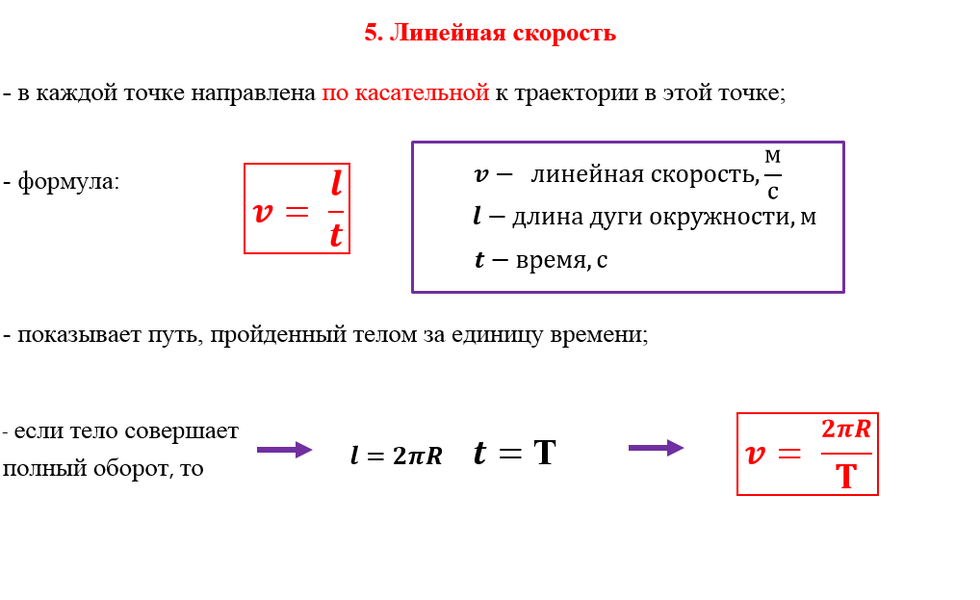 Определите радиус орбиты Луны и орбитальную скорость Луны.(Дано: M земля = 5,98 x 10 24 кг, R земля = 6,37 x 10 6 м)
Определите радиус орбиты Луны и орбитальную скорость Луны.(Дано: M земля = 5,98 x 10 24 кг, R земля = 6,37 x 10 6 м)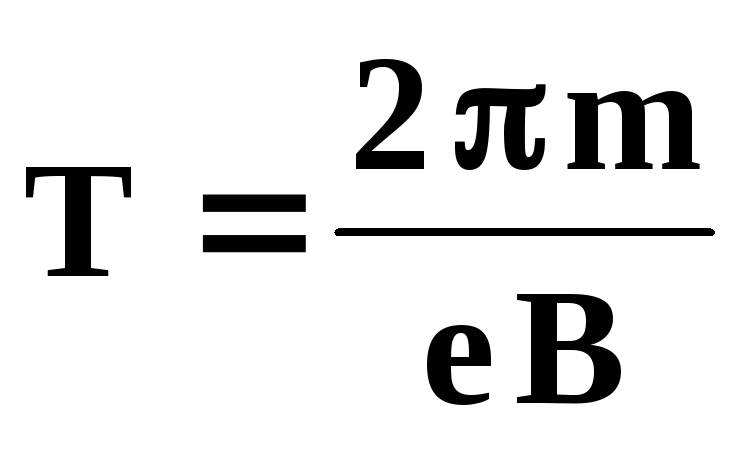 Особый класс геостационарных спутников — геостационарные спутники. Геостационарный спутник вращается вокруг Земли за 24 часа по орбитальной траектории, параллельной воображаемой плоскости, проведенной через экватор Земли. Такой спутник оказывается постоянно закрепленным над тем же местом на Земле. Если геостационарный спутник желает облететь Землю за 24 часа (86400 с), то на какой высоте над земной поверхностью он должен быть расположен? (Дано: M земля = 5,98×10 24 кг, R земля = 6.37 x 10 6 м)
Особый класс геостационарных спутников — геостационарные спутники. Геостационарный спутник вращается вокруг Земли за 24 часа по орбитальной траектории, параллельной воображаемой плоскости, проведенной через экватор Земли. Такой спутник оказывается постоянно закрепленным над тем же местом на Земле. Если геостационарный спутник желает облететь Землю за 24 часа (86400 с), то на какой высоте над земной поверхностью он должен быть расположен? (Дано: M земля = 5,98×10 24 кг, R земля = 6.37 x 10 6 м) 0 x 1015 сек ≈ 250 миллионов лет.
0 x 1015 сек ≈ 250 миллионов лет.