Как найти сопротивление проводника формула: Удельное сопротивление. Реостаты — урок. Физика, 8 класс.

Удельное сопротивление. Реостаты — урок. Физика, 8 класс.

Для рассмотрения характеристик электрических параметров рассмотрим назначение приборов:

1. сила тока в цепи определяется амперметров, который подключается последовательно с соблюдением полярности;
2. напряжение на участке цепи измеряется вольтметром, который подключается параллельно к тому участку или прибору, на котором нужно узнать разность потенциалов или напряжения;
3. на деревянной изолирующей подставке — устройство, имеющее провода с различными значениями сопротивления;
4. значение тока можно регулировать реостатом.

  

Рис. \(1\). Цепь с возможностью выбора проводника

 

Определим физические параметры (величины), влияющие на значение сопротивления проводника.

Эксперимент \(1\). Физическая величина — длина (прямая пропорциональность).

Эксперимент \(2\). Физическая величина — площадь поперечного сечения (обратная пропорциональность).

Эксперимент \(3\).

Материал проводника, физическая величина — удельное сопротивление проводника (прямая пропорциональность).

Примечание: «эксперимент» следует понимать как включение в электрическую цепь проводников с конкретными одинаковыми и различающимися физическими параметрами и сравнение значений сопротивлений данных проводников.

 

Впервые зависимость сопротивления проводника от вещества, из которого он изготовлен, и от длины проводника обнаружил немецкий физик Георг Ом. Он установил:

Сопротивление проводника напрямую зависит от его длины и материала,  но обратным образом зависит от площади поперечного сечения проводника.

 

Обрати внимание!

Из этого можно сделать вывод: чем длиннее проводник, тем больше его электрическое сопротивление.
Сопротивление проводника обратно пропорционально площади его поперечного сечения, т.е. чем толще проводник, тем его сопротивление меньше, и, наоборот, чем тоньше проводник, тем его сопротивление больше.

Чтобы лучше понять эту зависимость, представьте себе две пары сообщающихся сосудов, причём у одной пары сосудов соединяющая трубка тонкая, а у другой — толстая. Ясно, что при заполнении водой одного из сосудов (каждой пары) переход её в другой сосуд по толстой трубке произойдёт гораздо быстрее, чем по тонкой, т.е. толстая трубка окажет меньшее сопротивление течению воды. Точно так же и электрическому току легче пройти по толстому проводнику, чем по тонкому, т.е. первый оказывает ему меньшее сопротивление, чем второй.

 

Удельное сопротивление проводника зависит от строения вещества. Электроны при движении внутри металлов взаимодействуют с атомами (ионами), находящимися в узлах кристаллической решётки. Чем выше температура вещества, тем сильнее колеблются атомы и тем больше удельное сопротивление проводников.

Удельное электрическое сопротивление — физическая величина \(\rho\), характеризующая свойство материала оказывать сопротивление прохождению электрического тока:

ρ=R⋅Sl, где удельное сопротивление проводника обозначается греческой буквой \(\rho\) (ро), \(l\) — длина проводника, \(S\) — площадь его поперечного сечения.

Определим единицу удельного сопротивления. Воспользуемся формулой ρ=R⋅Sl.

Как известно, единицей электрического сопротивления является \(1\) Ом, единицей площади поперечного сечения проводника — \(1\) м², а единицей длины проводника — \(1\) м. Подставляя в формулу, получаем:

1 Ом ⋅1м21 м=1 Ом ⋅1 м, т.е. единицей удельного сопротивления будет Ом⋅м.

 

На практике (например, в магазине при продаже проводов) площадь поперечного сечения проводника измеряют в квадратных миллиметрах, В этом случае единицей удельного сопротивления будет:

1 Ом ⋅1мм21 м, т.е. Ом⋅мм2м.

В таблице приведены значения удельного сопротивления некоторых веществ при \(20\) °С.

 

Удельное сопротивление увеличивается пропорционально температуре.

При нагревании колебания ионов металлов в узлах металлической решётки увеличиваются, поэтому свободного пространства для передвижения электронов становится меньше. Электроны чаще отбрасываются назад, поэтому значение тока уменьшается, а значение сопротивления увеличивается.

 

Обрати внимание!

Из всех металлов наименьшим удельным сопротивлением обладают серебро и медь. А это значит, что медь и серебро лучше остальных проводят электрический ток.

При проводке электрических цепей, например, в квартирах не используют серебро, т.к. это дорого. Зато используют медь и алюминий, так как эти вещества обладают малым удельным сопротивлением.
Порой необходимы приборы, сопротивление которых должно быть большим. В этом случаем необходимо использовать вещество или сплав с большим удельным сопротивлением. Например, нихром.

Полиэтилен, дерево, стекло и многие другие материалы отличаются очень большим удельным сопротивлением. Поэтому они не проводят электрический ток. Такие материалы называют диэлектриками или изоляторами.

 

Очень часто нам приходится изменять силу тока в цепи. Иногда мы ее увеличиваем, иногда уменьшаем. Водитель трамвая или троллейбуса изменяет силу тока в электродвигателе, тем самым увеличивая или уменьшая скорость транспорта.  

Реостат — это резистор, значение сопротивления которого можно менять.

Реостаты используют в цепи для изменения значений силы тока и напряжения.

Реостат на рисунке состоит из провода с большим удельным сопротивлением (никелин, нихром), по которому передвигается подвижный контакт \(C\) по длине провода, плавно изменяя сопротивление реостата. Сопротивление такого реостата пропорционально длине провода между подвижным контактом \(C\) и неподвижным \(A\). Чем длиннее провод, тем больше сопротивление участка цепи и меньше сила тока. С помощью вольтметра и амперметра можно проследить эту зависимость.

 

Рис. \(2\). Реостат с подвижным контактом

 

На школьных лабораторных занятиях используют переменное сопротивление — ползунковый реостат.

 

 

Рис. \(3\). Ползунковый реостат

 

Он состоит из изолирующего керамического цилиндра, на который намотан провод с большим удельным сопротивлением. Витки проволоки должны быть изолированы друг от друга, поэтому либо проволоку обрабатывают графитом, либо оставляют на проволоке слой окалины.

Сверху над проволочной обмоткой закреплен металлический стержень, по которому  перемещается ползунок. Контакты ползунка плотно прижаты в виткам и при движении изолирующий слой графиты или окалины стирается, и тогда электрический ток может проходить от витков проволоки к ползунку, через него подводиться к стержню, имеющему на конце зажим \(1\).

Для соединения реостата в цепь используют зажим \(1\) и зажим \(2\). Ток, поступая через зажим \(2\), идёт по никелиновой проволоке и через ползунок подаётся на зажим \(1\). Перемещая ползунок от \(2\) к \(1\), можно увеличивать длину провода, в котором течёт ток, а значит, и сопротивление реостата.

В электрических схемах реостат изображается следующим образом:

 

Как и любой электрический прибор, реостат имеет допустимое значение силы тока, свыше которого прибор может перегореть. Маркировка реостата содержит диапазон его сопротивления и максимальное допустимое значение силы тока.

Обрати внимание!

Сопротивление реостата нужно учитывать в параметрах электрической цепи. При минимальных значениях сопротивления ток в цепи может вывести из строя амперметр.

Существуют реостаты, в которых переключатель подключается на проводники заданной длины и сопротивления: каждая спираль реостата имеет определённое сопротивление. Поэтому плавно изменять силу тока с помощью такого прибора не получится.

 

 

Рис. \(4\). Реостат с переключением

 

Повторим формулы

Сопротивление проводника: R=ρ⋅lS

 

Из этой формулы можно выразить и другие величины:

 

l=R⋅Sρ, S=ρ⋅lR, ρ=R⋅Sl.

Источники:

Рис. 1. © Якласс
Рис. 4. Бесплатно для коммерческого использования. Лицензия CC. Дата обращения 12.08.2021. https://search.creativecommons.org/photos/486dcbf0-ee87-4eaa-99fa-10019c67dae4

Формула сопротивления в физике

Содержание:

Определение и формула сопротивления

Определение

Скалярную физическую величину, (обычно обозначаемую R) равную:

$$R=\int_{1}^{2} \rho \frac{d l}{S}(1)$$

называют сопротивлением участка цепи между сечениями 1 и 2. В выражении (1) имеем $\rho$ – удельное сопротивление проводника, S – площадь поперечного сечения проводника, dl — элемент длины проводника.

Если проводник является однородным ($\rho$=const) и имеет форму цилиндра (S=const), то формула (1) может быть представлена как:

$$R=\rho \frac{l}{S}(2)$$

где l – длина участка рассматриваемого проводника.

Надо отметить, что удельное сопротивление проводника ($\rho$) – это сопротивление проводника единичной длины с поперечным сечением равным единице. Или иначе говорят, что удельное сопротивление вещества – это сопротивление куба с ребром 1 м изготовленного из рассматриваемого вещества, которое выражено в Ом, при токе, который параллелен ребру куба. Величина обратная удельному сопротивлению:

$$\sigma=\frac{1}{\rho}(3)$$

называется удельной проводимостью. Измеряется удельное сопротивление в системе СИ в [$\rho$]=Ом•м. Эта характеристика проводника зависит от температуры, в простейшем случае эта зависимость может быть линейна:

$$\rho=\rho_{0}(1+\alpha t)(4)$$

где $\rho_{0}$ – удельное сопротивление проводника при температуре равной 0C, t — температура в градусах Цельсия, $\alpha=\frac{1}{\rho} \frac{d \rho}{d T}$ – температурный коэффициент сопротивления, который показывает относительное приращение сопротивления при увеличении температуры на один градус, $\alpha$ может быть положительным и отрицательным. {-2}}=100$$

Ответ. n=100

Читать дальше: Формула внутренней энергии.

Формула сопротивления тока. Как найти электрическое сопротивление по закону Ома.

В сфере электрики и электроники такая вещь (и понятие) как сопротивление встречается повсеместно. Хоть может и показаться, что электрическое сопротивление это плохо, так как она препятствует свободному течению электрических зарядов по проводникам, но это не совсем так. Возможно вы уже сталкивались с тем, что во всем нужна своя мера. Любой вид энергии (в нашем случае электрической, электромагнитной) в той или иной системе нуждается в своем определенном количестве. Если энергии становится больше или меньше нужной меры, то как правило возникают различные нарушения правильной ее работы. Так что сопротивление в определенных случаях это даже очень хорошо.

Ну, а какая есть формула сопротивления тока? Основополагающей формулой, по которой можно найти электрическое сопротивление является та, которая исходит из обычного закона Ома.

Сама формула электрического сопротивления выражается так — сопротивление это отношение напряжения к силе тока. То есть, чтобы найти электрическое сопротивление нужно напряжение (разность потенциалов) разделить на силу тока. Все очень просто. Единицей измерения электрического сопротивления является «Ом» (названная в честь своего ученого открывателя). Напряжение измеряется в вольтах, а сила тока в амперах. В итоге мы имеем, 1 Ом равен 1 вольт деленный на 1 ампер. Используется и другие более крупные единицы измерения сопротивления — это килоомы (1 кОм = 1000 Ом), мегаомы (1 мОм = 1000 кОм = 1000 000 Ом).

Но всеже есть одно НО! Формулу нахождения сопротивления по закону Ома можно применять для постоянного и переменного тока лишь при наличии именно активного сопротивления (обычные резисторы, нагреватели, лампы накаливания и т.д.). Для случая реактивного сопротивления используется немного другая формула сопротивления тока. Она учитывает кроме напряжения и силы тока еще частоту, индуктивность, ёмкость.

Помимо этих формул еще можно привести такую, которая показывает зависимость сопротивления от вида и размеров проводника. Формула сопротивления тока уже будет содержать такие понятия как сечение проводника, его длина, удельное сопротивления (зависящее от конкретного материала).

А что собственно представляет собой это самое электрическое сопротивление? Думаю не лишним будет пояснить это. Итак, из физики нам известно, что любой проводник имеет так называемую кристаллическую решетку, состоящую из атомов и молекул, соединенных достаточно жесткими связями, что формирует устойчивую, фиксированную структуру. Атомы имеют ядро (состоящее из протонов и нейтронов), у которого положительный заряд. Вокруг ядра вращаются более мелкие частицы, называемые электронами, имеющими отрицательный электрический заряд.

Так вот, те электроны, что удалены от ядра дальше всего могут достаточно легко отрываться от своего атома и переходить к соседнему. При определенных условиях, а именно при подключении внешнего источника питания (а конкретнее внешнего электромагнитного поля) эти свободные электроны могут уже перемещаться упорядоченно в одном направлении. что порождает электрический ток. Но при своем движении электроны постоянно сталкиваются с другими атомами, что находятся на их пути. Вот именно это и является фактором электрического сопротивления. Следовательно предположить, что чем длиннее и тоньше будет проводник, тем больше препятствий будет на пути движения электронов, тем больше будет электрическое сопротивление. Ну, а еще одни проводники, в силу особенностей своей кристаллической решетки, будут иметь большее сопротивление, а другие — меньшее.

Напряжение можно еще сравнить с давлением (по аналогии с водой в трубах, к примеру), электрический ток это упорядоченное движение заряженных частиц, то есть в прямом смысле «поток зарядов (их количество, которое движется в одном направлении)». Вот и получается, что чем больше мы имеем (видим) напряжение на определенном участке электрической цепи (давление воды в водопроводе), при определенном потоке электронов, тем значит больше будет электрическое сопротивление, которое оказывается на движение этого самого потока электрических зарядов, внутри проводника. Все логично.

P.S. Если хорошо уметь представлять те физические процессы, что происходят внутри электрических схем, цепей, будет намного проще понять их изначальную суть. После этого любая формула становится более понятной, с точки зрения зависимости определенных физических величин. Это уже не просто набор каких-то знаков, это конкретная зависимость единиц измерения, что строго отображают в теории то, что работает на практике (в схемах, электрических устройствах и т.д.).

Расчёт сопротивления проводников и реостаты: формулы

 

Электрическое сопротивление проводника происходит из-за взаимодействия электрона с ионами кристаллической решетки.

Сопротивление проводника зависит от:

• — его длины,
• — площади поперечного сечения
• — от вещества из которого он изготовлен,

а также сопротивление прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения и зависит от вещества проводника. 19) имеют очень большое удельное сопротивление и почти не проводят электрический ток, их  используют для изоляторов.

Реостаты

Реостат — прибор, который используется для регулирования силы тока в цепи.

Самый простой реостат — проволока с большим удельным сопротивлением , такая как никелиновая или нихромовая.

Виды реостатов:

Ползунковый реостат — еще один вид реостатов , в котором  стальная проволока намотана на керамический цилиндр.Проволока покрыта тонким слоем окалины , которая не проводит электрический ток , поэтому ее витки изолированы друг от друга.Над обмоткой — металлический стержень по которому перемещается ползунок .

Он прижат к виткам обмотки.От трения ползунка о витки слой окалины стирается и электрический ток в цепи проходит от витков проволоки к ползунку, потом в стержень.Когда реостат подключили в цепь , можно передвигать ползунок , таким образом увеличивать или уменьшать сопротивление реостата.

Жидкостный реостат — представляет бак с электролитом, в который погружаются металлические пластины.  

Проволочный реостат — cостоит из проволоки из материала в котором высокое удельное сопротивление, натянутый на раму. 

Нельзя превышать силу тока реостата, потому что обмотка реостата может перегореть.

Реостат мы часто применяем в повседневной жизни, например, регулируя громкость телевизора и радио, увеличивая и уменьшая скорость езды на машине. 

Нужна помощь в учебе?

Предыдущая тема: Закон Ома для участка цепи: формулировка и формула, применение
Следующая тема:&nbsp&nbsp&nbspПоследовательное и параллельное соединение проводников

Физика 8 класс. Электрическое сопротивление. Удельное сопротивление :: Класс!ная физика

Физика 8 класс. ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ

Электрическое сопротивление ( R ) — это физическая величина, численно равная отношению
напряжения на концах проводника к силе тока, проходящего через проводник.
Величину сопротивления для участка цепи можно определить из формулы закона Ома для участка цепи.

Однако, сопротивление проводника не зависит от силы тока в цепи и напряжения, а определяется только формой, размерами и материалом проводника.

где l — длина проводника ( м ), S — площадь поперечного сечения (кв.м ),
r ( ро) — удельное сопротивление (Ом м ).

Удельное сопротивление

— показывает, чему равно сопротивление проводника, выполненного из данного вещества,
длиной в 1м и с поперечным сечением 1 м кв.

Единица измерения удельного сопротивления в системе СИ: 1 Ом м

Однако, на практике толщина проводов значительно меньше 1 м кв,
поэтому чаще используют внесистемную единицу измерения удельного сопротивления:

Единица измерения сопротивления в системе в СИ:

[R] = 1 Ом

Сопротивление проводника равно 1 Ом, если при разности потенциалов на его концах в 1 В,
по нему протекает ток силой 1 А.

___

Причиной наличия сопротивления у проводника является взаимодействие движущихся электронов с ионами кристалической решетки проводника. Из-за различия в строении криталической решетки у проводников, выполненных из различных веществ, сопротивления их отличаются друг от друга.

ЗАПОМНИ !

Существует физическая величина обратная сопротивлению — электрическая проводимость.

R — это сопротивление проводника,
1/R — это электрическая проводимость проводника
___

Величины проводимости проводников и изоляторов различаются в большое число раз,
измеряемое единицей с двадцатью двумя нулями!

ЗНАЕШЬ ЛИ ТЫ ?

… что сопротивления кожи человека обычно изменяется от 1 кОм ( для влажной кожи )
до 500 кОм ( для сухой кожи ). Сопротивление других тканей тела равно от 100 до 500 Ом.

Устали? — Отдыхаем!

Как найти сопротивление тока. Сопротивление тока: формула

Одним из физических свойств вещества является способность проводить электрический ток. Электропроводимость (сопротивление проводника) зависит от некоторых факторов: длины электрической цепи, особенностей строения, наличия свободных электронов, температуры, тока, напряжения, материала и площади поперечного сечения.

Протекание электрического тока через проводник приводит к направленному движению свободных электронов. Наличие свободных электронов зависит от самого вещества и берется из таблицы Д. И. Менделеева, а именно из электронной конфигурации элемента. Электроны начинают ударяться о кристаллическую решетку элемента и передают энергию последней. В этом случае возникает тепловой эффект при действии тока на проводник.

При этом взаимодействии они замедляются, но затем под действием электрического поля, которое их ускоряет, начинают двигаться с той же скоростью.

Электроны сталкиваются огромное количество раз. Этот процесс и называется сопротивлением проводника.

Следовательно, электрическим сопротивлением проводника считается физическая величина, характеризующая отношение напряжения к силе тока.

Что такое электрическое сопротивление: величина, указывающая на свойство физического тела преобразовывать энергию электрическую в тепловую, благодаря взаимодействию энергии электронов с кристаллической решеткой вещества. По характеру проводимости различаются:

1. Проводники (способны проводить электрический ток, так как присутствуют свободные электроны).
2. Полупроводники (могут проводить электрический ток, но при определенных условиях).
3. Диэлектрики или изоляторы (обладают огромным сопротивлением, отсутствуют свободные электроны, что делает их неспособными проводить ток).

Обозначается эта характеристика буквой R и измеряется в Омах (Ом) . Применение этих групп веществ является очень значимым для разработки электрических принципиальных схем приборов.

Для полного понимания зависимости R от чего-либо нужно обратить особое внимание на расчет этой величины.

Расчет электрической проводимости

Для расчета R проводника применяется закон Ома, который гласит: сила тока (I) прямо пропорциональна напряжению (U) и обратно пропорциональна сопротивлению.

Формула нахождения характеристики проводимости материала R (следствие из закона Ома для участка цепи): R = U / I.

Для полного участка цепи эта формула принимает следующий вид: R = (U / I) — Rвн, где Rвн — внутреннее R источника питания.

Способность проводника к пропусканию электрического тока зависит от многих факторов: напряжения, тока, длины, площади поперечного сечения и материала проводника, а также от температуры окружающей среды.

В электротехнике для произведения расчетов и изготовления резисторов учитывается и геометрическая составляющая проводника.

От чего зависит сопротивление: от длины проводника — l, удельного сопротивления — p и от площади сечения (с радиусом r) — S = Пи * r * r.

Формула R проводника: R = p * l / S.

Из формулы видно, от чего зависит удельное сопротивление проводника: R, l, S. Нет необходимости его таким способом рассчитывать, потому что есть способ намного лучше. Удельное сопротивление можно найти в соответствующих справочниках для каждого типа проводника (p — это физическая величина равная R материала длиною в 1 метр и площадью сечения равной 1 м².

Однако этой формулы мало для точного расчета резистора, поэтому используют зависимость от температуры.

Влияние температуры окружающей среды

Доказано, что каждое вещество обладает удельным сопротивлением, зависящим от температуры.

Для демонстрации это можно произвести следующий опыт. Возьмите спираль из нихрома или любого проводника (обозначена на схеме в виде резистора), источник питания и обычный амперметр (его можно заменить на лампу накаливания). Соберите цепь согласно схеме 1.

Схема 1 — Электрическая цепь для проведения опыта

Необходимо запитать потребитель и внимательно следить за показаниями амперметра.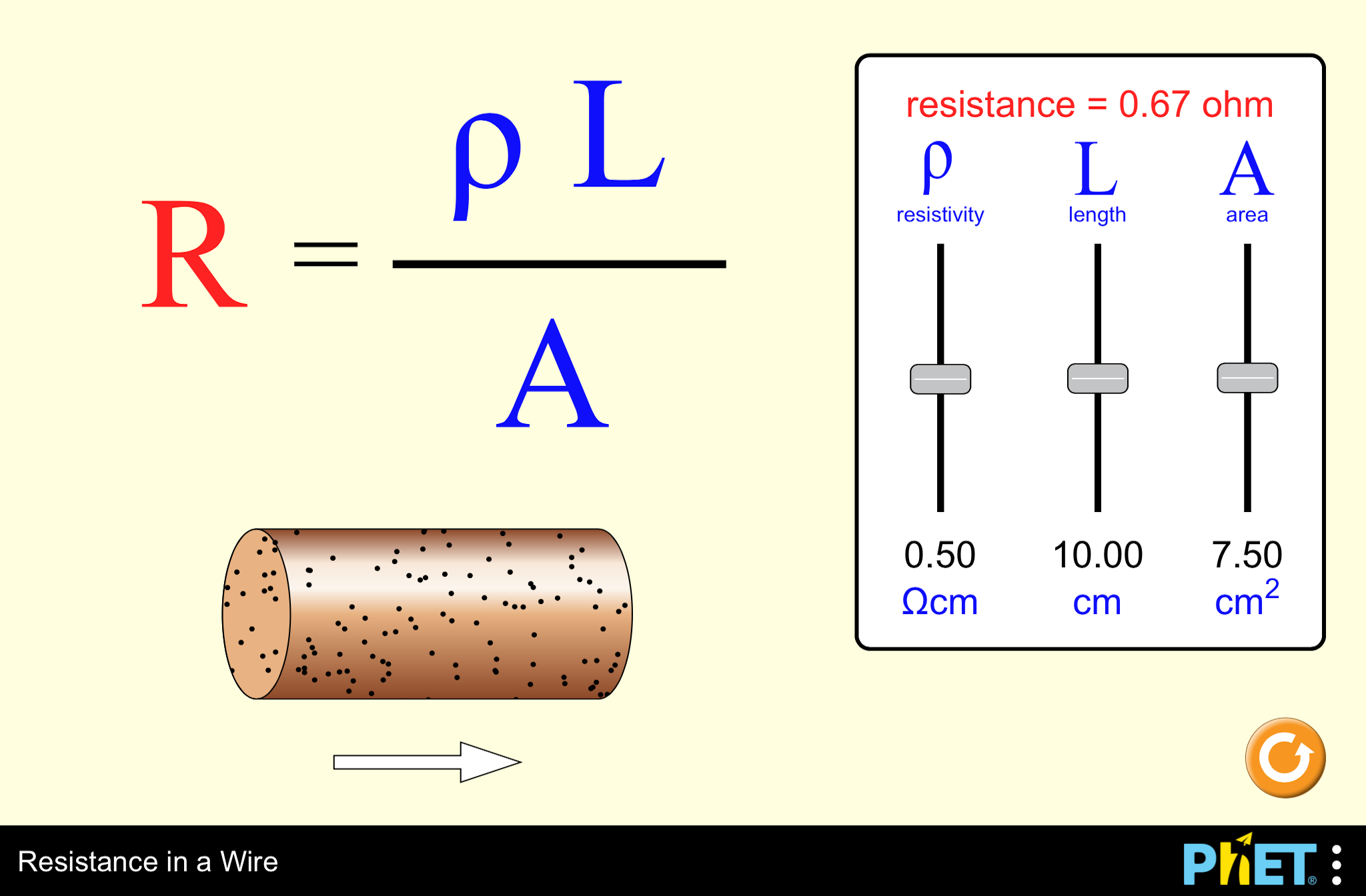 Далее следует нагревать R, не отключая, и показания амперметра начнут падать при росте температуры. Прослеживается зависимость по закону Ома для участка цепи: I = U / R. В данном случае внутренним сопротивлением источника питания можно пренебречь: это не отразится на демонстрации зависимости R от температуры. Отсюда следует, что зависимость R от температуры присутствует.

Физический смысл роста значения R обусловлен влиянием температуры на амплитуду колебаний (увеличение) ионов в кристаллической решетке. В результате этого электроны чаще сталкиваются и это вызывает рост R.

Согласно формуле: R = p * l / S, находим показатель, который зависит от температуры (S и l — не зависят от температуры). Остается p проводника. Исходя из это получается формула зависимости от температуры: (R — Ro) / R = a * t, где Ro при температуре 0 градусов по Цельсию, t — температура окружающей среды и a — коэффициент пропорциональности (температурный коэффициент).

Для металлов «a» всегда больше нуля, а для растворов электролитов температурный коэффициент меньше 0.

Формула нахождения p, применяемая при расчетах: p = (1 + a * t) * po, где ро — удельное значение сопротивления, взятое из справочника для конкретного проводника. В этом случае температурный коэффициент можно считать постоянным. Зависимость мощности (P) от R вытекает из формулы мощности: P = U * I = U * U / R = I * I * R. Удельное значение сопротивления еще зависит и от деформаций материала, при котором нарушается кристаллическая решетка.

При обработке металла в холодной среде при некотором давлении происходит пластическая деформация. При этом кристаллическая решетка искажается и растет R течения электронов. В этом случае удельное сопротивление также увеличивается. Этот процесс является обратимым и называется рекристаллическим отжигом, благодаря которому часть дефектов уменьшается.

При действии на металл сил растяжения и сжатия последний подвергается деформациям, которые называются упругими. Удельное сопротивление уменьшается при сжатии, так как происходит уменьшение амплитуды тепловых колебаний. Направленным заряженным частицам становится легче двигаться . При растяжении удельное сопротивление увеличивается из-за роста амплитуды тепловых колебаний.

Еще одним фактором, влияющим на проводимость, является вид тока, проходящего по проводнику.

Сопротивление в сетях с переменным током ведет себя несколько иначе, ведь закон Ома применим только для схем с постоянным напряжением. Следовательно, расчеты следует производить иначе.

Полное сопротивление обозначается буквой Z и состоит из алгебраической суммы активного, емкостного и индуктивного сопротивлений.

При подключении активного R в цепь переменного тока под воздействием разницы потенциалов начинает течь ток синусоидального вида. В этом случае формула выглядит: Iм = Uм / R, где Iм и Uм — амплитудные значения силы тока и напряжения. Формула сопротивления принимает следующий вид: Iм = Uм / ((1 + a * t) * po * l / 2 * Пи * r * r).

Емкостное сопротивление (Xc) обусловлено наличием в схемах конденсаторов. Необходимо отметить, что через конденсаторы проходит переменный ток и, следовательно, он выступает в роли проводника с емкостью.

Вычисляется Xc следующим образом: Xc = 1 / (w * C), где w — угловая частота и C — емкость конденсатора или группы конденсаторов. Угловая частота определяется следующим образом:

1. Измеряется частота переменного тока (как правило, 50 Гц).
2. Умножается на 6,283.

Индуктивное сопротивление (Xl) — подразумевает наличие индуктивности в схеме (дроссель, реле, контур, трансформатор и так далее). Рассчитывается следующим образом: Xl = wL, где L — индуктивность и w — угловая частота. Для расчета индуктивности необходимо воспользоваться специализированными онлайн-калькуляторами или справочником по физике. Итак, все величины рассчитаны по формулам и остается всего лишь записать Z: Z * Z = R * R + (Xc — Xl) * (Xc — Xl).

Для определения окончательного значения необходимо извлечь квадратный корень из выражения: R * R + (Xc — Xl) * (Xc — Xl). Из формул следует, что частота переменного тока играет большую роль, например, в схеме одного и того же исполнения при повышении частоты увеличивается и ее Z. Необходимо добавить, что в цепях с переменным напряжением Z зависит от таких показателей:

1. Длины проводника.
2. Площади сечения — S.
3. Температуры.
4. Типа материала.
5. Емкости.
6. Индуктивности.
7. Частоты.

Следовательно и закон Ома для участка цепи имеет совершенно другой вид: I = U / Z . Меняется и закон для полной цепи.

Расчеты сопротивлений требуют определенного количества времени, поэтому для измерений их величин применяются специальные электроизмерительные приборы, которые называются омметрами. Измерительный прибор состоит из стрелочного индикатора, к которому последовательно включен источник питания.

Измеряют R все комбинированные приборы , такие как тестеры и мультиметры. Обособленные приборы для измерения только этой характеристики применяются крайне редко (мегаомметр для проверки изоляции силового кабеля).

Прибор применяется для прозвонки электрических цепей на предмет повреждения и исправности радиодеталей, а также для прозвонки изоляции кабелей.

При измерении R необходимо полностью обесточить участок цепи во избежание выхода прибора из строя. Для это необходимо предпринять следующие меры предосторожности:

В дорогих мультиметрах есть функция прозвонки цепи, дублируемая звуковым сигналом, благодаря чему нет необходимости смотреть на табло прибора.

Таким образом, электрическое сопротивление играет важную роль в электротехнике. Оно зависит в постоянных цепях от температуры, силы тока, длины, типа материала и площади поперечного сечения проводника . В цепях переменного тока эта зависимость дополняется такими величинами, как частота, емкость и индуктивность. Благодаря этой зависимости существует возможность изменять характеристики электричества: напряжение и силу тока. Для измерений величины сопротивления применяются омметры, которые используются также и при выявлении неполадок проводки, прозвонки различных цепей и радиодеталей.

Одной из основных характеристик электрической цепи является сила тока. Она измеряется в амперах и определяет нагрузку на токопроводящие провода, шины или дорожки плат. Эта величина отражает количество электричества, которое протекло в проводнике за единицу времени. Определить её можно несколькими способами в зависимости от известных вам данных. Соответственно студенты и начинающие электрики из-за этого часто сталкиваются с проблемами при решении учебных заданий или практических ситуаций. В этой статье мы и расскажем, как найти силу тока через мощность и напряжение или сопротивление.

Если известна мощность и напряжение

Допустим вам нужно найти силу тока в цепи, при этом вам известны только напряжение и потребляемая мощность. Тогда чтобы её определить без сопротивления воспользуйтесь формулой:

После несложных мы получаем формулу для вычислений

Следует отметить, что такое выражение справедливо для цепей постоянного тока. Но при расчётах, например, для электродвигателя учитывают его полную мощность или косинус Фи. Тогда для трёхфазного двигателя его можно рассчитать так:

Находим P с учетом КПД, обычно он лежит в пределах 0,75-0,88:

Р1 = Р2/η

Здесь P2 – активная полезная мощность на валу, η – КПД, оба этих параметра обычно указывают на шильдике.

Находим полную мощность с учетом cosФ (он также указывается на шильдике):

S = P1/cosφ

Определяем потребляемый ток по формуле:

Iном = S/(1,73·U)

Здесь 1,73 – корень из 3 (используется для расчетов трёхфазной цепи), U – напряжение, зависит от включения двигателя (треугольник или звезда) и количества вольт в сети (220, 380, 660 и т.д.). Хотя в нашей стране чаще всего встречается 380В.

Если известно напряжение или мощность и сопротивление

Но встречаются задачи, когда вам известно напряжение на участке цепи и величина нагрузки, тогда чтобы найти силу тока без мощности воспользуйтесь , с его помощью проводим расчёт силы тока через сопротивление и напряжение.

Но иногда случается так, что нужно определить силу тока без напряжения, то есть когда вам известна только мощность цепи и её сопротивление. В этом случае:

При этом согласно тому же закону Ома:

P=I 2 *R

Значит расчёт проводим по формуле:

I 2 =P/R

Или возьмем выражение в правой части выражения под корень:

I=(P/R) 1/2

Если известно ЭДС, внутреннее сопротивление и нагрузка

Ко студенческим задачам с подвохом можно отнести случаи, когда вам дают величину ЭДС и внутреннее сопротивление источника питания. В этом случае вы можете определить силу тока в схеме по закону Ома для полной цепи:

I=E/(R+r)

Здесь E – ЭДС, r – внутреннее сопротивление источника питания, R – нагрузки.

Закон Джоуля-Ленца

Еще одним заданием, которое может ввести в ступор даже более-менее опытного студента – это определить силу тока, если известно время, сопротивление и количество выделенного тепла проводником. Для этого вспомним .

Его формула выглядит так:

Q=I 2 Rt

Тогда расчет проводите так:

I 2 =QRt

Или внесите правую часть уравнения под корень:

I=(Q/Rt) 1/2

Несколько примеров

В качестве заключения предлагаем закрепить полученную информацию на нескольких примерах задач, в которых нужно найти силу тока.

Из условия ясно, что нужно привести два варианта ответа для каждого из вариантов соединений. Тогда чтобы найти ток при последовательном соединении, сначала складывают сопротивления схемы, чтобы получить общее.

I=U/R=12/3=4 Ампера

При параллельном соединении двух элементов Rобщее можно рассчитать так:

Rобщ=(R1*R2)/(R1+R2)=1*2/3=2/3=0,67

Тогда дальнейшие вычисления можно проводить так:

В первую очередь нужно найти R общее параллельно соединенных R2 и R3, по той же формуле, что мы использовали выше.

В своей работе электрик часто сталкивается с вычислением различных величин и преобразований. Так для корректного подбора кабеля приходится подбирать нужное сечение. Логика выбора сечения основана на зависимости сопротивления от длины линии и площади сечения проводника. В этой статье мы рассмотрим, как выполняется расчет сопротивления провода по его геометрическим размерам.

Формула для расчета

Любые вычисления начинаются с формулы. Основной формулой для расчета сопротивления проводника является:

R=(ρ*l)/S

Где R – сопротивление в Омах, ρ – удельное сопротивление, l – длина в м, S – площадь поперечного сечения провода в мм 2 .

Эта формула подходит для расчета сопротивления провода по сечению и длине. Из неё следует, что в зависимости от длины изменяется сопротивление, чем длиннее – тем больше. И от площади сечения – наоборот, чем толще провод (большое сечение), тем меньше сопротивление. Однако непонятной остаётся величина, обозначенная буквой ρ (Ро).

Удельное сопротивление

Удельное сопротивление – это табличная величина, для каждого металла она своя. Она нужна для расчета и зависит от кристаллической решетки металла и структуры атомов.

Из таблицы видно, что самое меньшее сопротивление у серебра, для медного кабеля оно равняется 0,017 Ом*мм 2 /м. Такая размерность говорит нам, сколько приходится Ом при сечении в 1 миллиметр квадратный и длине в 1 метр.

Кстати, серебряное покрытие используется в контактах коммутационных аппаратов, автоматических выключателей, реле и прочего. Это снижает , повышает срок службы и уменьшает . При этом в контактах измерительной и точной аппаратуры используют позолоченные контакты из-за того, что они слабо окисляются или вообще не окисляются.

У алюминия, который часто использовался в электропроводке раньше, сопротивление в 1,8 раза больше чем у меди, равняется 2,82*10 -8 Ом*мм 2 /м. Чем больше сопротивление проводника, тем сильнее он греется. Поэтому при одинаковом сечении алюминиевый кабель может передать меньший ток, чем медный, это и стало основной причиной почему все современные электрики используют . У нихрома, который используется в нагревательных приборах оно в 100 раз больше чем у меди 1,1*10 -6 Ом*мм 2 /м.

Расчет по диаметру

На практике часто бывает так, что площадь поперечного сечения жилы не известна. Без этого значения ничего рассчитать не получится. Чтобы узнать её, нужно измерить диаметр. Если жила тонка, можно взять гвоздь или любой другой стержень, намотать на него 10 витков провода, обычной линейкой измерить длину получившейся спирали и разделить на 10, так вы узнаете диаметр.

Ну, или просто замерить штангенциркулем. Расчет сечения выполняется по формуле:

Обязательны ли расчеты?

Как мы уже сказали, сечение провода выбирают исходя из предполагаемого тока и сопротивления металла, из которого изготовлены жилы. Логика выбора заключается в следующем: сечение подбирают таким способом, чтобы сопротивление при заданной длине не приводило к значительным просадкам напряжения. Чтобы не проводить ряд расчетов, для коротких линий (до 10-20 метров) есть достаточно точные таблицы:

В этой таблице указаны типовые значения сечения медных и алюминиевых жил и номинальные токи через них. Для удобства указана мощность нагрузки, которую выдержит эта линия. Обратите внимание на разницу в токах и мощности при напряжении 380В, естественно, что это предполагается трёхфазная электросеть.

Расчет сопротивления провода сводится к использованию пары формул, при этом вы можете скачать готовые калькуляторы из Плэй Маркета для своего смартфона, например, «Electrodroid» или «Мобильный электрик». Эти знания пригодятся для расчетов нагревательных приборов, кабельных линий, предохранителей и даже популярных на сегодняшний день спиралей для электронных сигарет.

Материалы

Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному (в смысле отсутствия сторонних сил) металлическому проводнику, пропорциональна падению напряжения V на проводнике:

Напомним, что в случае однородного проводника напряжение U совпадает с разностью потенциалов (см. (33.6)).

Обозначенная в формуле (34.1) буквой R величина называется электрическим сопротивлением проводника. Единицей сопротивления служит равный сопротивлению такого проводника, в котором при напряжении в 1 В течет ток силой 1 А.

Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника

где l — длина проводника, S — площадь его поперечного сечения, — зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением вещества. Если то R численно равно . В СИ измеряется в ом-метрах (Ом-м).

Найдем связь между векторами j и Е в одной и той же точке проводника. В изотропном проводнике упорядоченное движение носителей тока происходит в направлении вектора Е.

Поэтому на правления векторов j и Е совпадают Выделим мысленно в окрестности некоторой точки элементарный цилиндрический объем с образующими, параллельными векторам j и Е (рис. 34.1). Через поперечное сечение цилиндра течет ток силой . Напряжение, приложенное к цилиндру, равно , где Е — напряженность поля в данном месте. Наконец, сопротивление цилиндра, согласно формуле (34.2), равно . Подставив эти значения в формулу (34.1), придем к соотношению

Воспользовавшись тем, что векторы j и Е имеют одинаковое направление, можно написать

Эта формула выражает закон Ома в дифференциальной форме.

Фигурирующая в (34.3) обратная величина называется удельной электрической проводимостью материала. Единица, обратная ому, называется сименсом (См). Соответственно единицей о является сименс на метр (См/м).

Допустим для простоты, что в проводнике имеются носители лишь одного знака. Согласно формуле (31.5) плотность тока в этом случае равна

Сравнение этого выражения с формулой (34.3) приводит к выводу, что скорость упорядоченного движения носителей тока пропорциональна напряженности поля Е, т. е. силе, сообщающей носителям упорядоченное движение. Пропорциональность скорости приложенной к телу силе наблюдается в тех случаях, когда кроме силы, вызвавшей движение, на тело действует сила сопротивления среды. Эта сила вызывается взаимодействием носителей тока с частицами, из которых построено вещество проводника. Наличие силы сопротивления упорядоченному движению носителей тока обусловливает электрическое сопротивление проводника.

Способность вещества проводить электрический ток характеризуется его удельным сопротивлением либо удельной проводимостью .

Их величина определяется химической природой вещества и условиями, в частности температурой, при которых оно находится.

Для большинства металлов при температурах, близких к комнатной, изменяется пропорционально абсолютной температуре Т:

При низких температурах наблюдаются отступления от этой закономерности (рис. 34.2). В большинстве случаев зависимость от Т следует кривой. Величина остаточного сопротивления рост в сильной степени зависит от чистоты материала и наличия остаточных механических напряжений в образце. Поэтому после отжига рост заметно уменьшается. У абсолютно чистого металла с идеально правильной кристаллической решеткой при абсолютном нуле

У большой группы металлов и сплавов при температуре порядка нескольких кельвинов сопротивление скачков обращается в нуль (кривая 2 на рис. 34.2). Впервые это явление, названное сверхпроводимостью, было обнаружено в 1911 г. Камерлинг-Оннесом для ртути. В дальнейшем сверхпроводимость была обнаружена у свинца, олова, цинка, алюминия и других металлов, а также у ряда сплавов. Для каждого сверхпроводника имеется своя критическая температура Т при которой он переходит в сверхпроводящее состояние. При действии на сверхпроводник магнитного поля сверхпроводящее состояние нарушается. Величина критического поля разрушающего сверхпроводимость, равна нулю при и растет с понижением температуры.

Полное теоретическое объяснение сверхпроводимости было дано академиком Н. Н. Боголюбовым и независимо от него Дж. Бардином, Л. Купером и Дж. Шриффером (см. § 56 тома 3).

Зависимость электрического сопротивления от температуры положена в основу термометров сопротивления. Такой термометр представляет собой металлическую (обычно платиновую) проволочку, намотанную на фарфоровый или слюдяной каркас. Проградуированный по постоянным температурным точкам термометр сопротивления позволяет измерять с погрешностью порядка несколько сотых градуса как низкие, так и высокие температуры. В последнее время все большее применение находят термометры сопротивления из полупроводников.

Мы начинаем публикацию материалов новой рубрики “” и в сегодняшней статье речь пойдет о фундаментальных понятиях, без которых не проходит обсуждение ни одного электронного устройства или схемы. Как вы уже догадались, я имею ввиду ток, напряжение и сопротивление 😉 Кроме того, мы не обойдем стороной закон, который определяет взаимосвязь этих величин, но не буду забегать вперед, давайте двигаться постепенно.

Итак, давайте начнем с понятия напряжения .

Напряжение.

По определению напряжение – это энергия (или работа), которая затрачивается на перемещение единичного положительного заряда из точки с низким потенциалом в точку с высоким потенциалом (т. е. первая точка имеет более отрицательный потенциал по сравнению со второй). Из курса физики мы помним, что потенциал электростатического поля – это скалярная величина, равная отношению потен­циальной энергии заряда в поле к этому заряду. Давайте рассмотрим небольшой пример:

В пространстве действует постоянное электрическое поле, напряженность которого равна E . Рассмотрим две точки, расположенные на расстоянии d друг от друга. Так вот напряжение между двумя точками представляет из себя ни что иное, как разность потенциалов в этих точках:

В то же время не забываем про связь напряженности электростатического поля и разности потенциалов между двумя точками:

И в итоге получаем формулу, связывающую напряжение и напряженность:

В электронике, при рассмотрении различных схем, напряжение все-таки принято считать как разность потенциалов между точками. Соответственно, становится понятно, что напряжение в цепи – это понятие, связанное с двумя точками цепи. То есть говорить, к примеру, “напряжение в резисторе” – не совсем корректно. А если говорят о напряжении в какой-то точке, то подразумевают разность потенциалов между этой точкой и “землей” . Вот так плавно мы вышли к еще одному важнейшему понятию при изучении электроники, а именно к понятию “земля” 🙂 Так вот “землей” в электрических цепях чаще всего принято считать точку нулевого потенциала (то есть потенциал этой точки равен 0).

Давайте еще пару слов скажем о единицах, которые помогают охарактеризовать величину напряжения . Единицей измерения является Вольт (В) . Глядя на определение понятия напряжения мы можем легко понять, что для перемещения заряда величиной 1 Кулон между точками, имеющими разность потенциалов 1 Вольт , необходимо совершить работу, равную 1 Джоулю . С этим вроде бы все понятно и можно двигаться дальше 😉

А на очереди у нас еще одно понятие, а именно ток .

Ток, сила тока в цепи.

Что же такое электрический ток ?

Давайте подумаем, что будет происходить если под действие электрического поля попадут заряженные частицы, например, электроны…Рассмотрим проводник, к которому приложено определенное напряжение :

Из направления напряженности электрического поля (E ) мы можем сделать вывод о том, что title=»Rendered by QuickLaTeX.com»> (вектор напряженности всегда направлен в сторону уменьшения потенциала). На каждый электрон начинает действовать сила:

Где e – это заряд электрона.

И поскольку электрон является отрицательно заряженной частицей, то вектор силы будет направлен в сторону противоположную направлению вектора напряженности поля. Таким образом, под действием силы частицы наряду с хаотическим движением приобретают и направленное (вектор скорости V на рисунке). В результате и возникает электрический ток 🙂

Ток – это упорядоченное движение заряженных частиц под воздействием электрического поля.

Важным нюансом является то, что принято считать, что ток протекает от точки с более положительным потенциалом к точке с более отрицательным потенциалом, несмотря на то, что электрон перемещается в противоположном направлении.

Носителями заряда могут выступать не только электроны. Например, в электролитах и ионизированных газах протекание тока в первую очередь связано с перемещением ионов, которые являются положительно заряженными частицами. Соответственно, направление вектора силы, действующей на них (а заодно и вектора скорости) будет совпадать с направлением вектора E . И в этом случае противоречия не возникнет, ведь ток будет протекать именно в том направлении, в котором движутся частицы 🙂

Для того, чтобы оценить ток в цепи придумали такую величину как сила тока. Итак, сила тока (I ) – это величина, которая характеризует скорость перемещения электрического заряда в точке. Единицей измерения силы тока является Ампер . Сила тока в проводнике равна 1 Амперу , если за 1 секунду через поперечное сечение проводника проходит заряд 1 Кулон .

Мы уже рассмотрели понятия силы тока и напряжения , теперь давайте разберемся каким образом эти величины связаны. И для этого нам предстоит изучить, что же из себя представляет сопротивление проводника .

Сопротивление проводника/цепи.

Термин “сопротивление ” уже говорит сам за себя 😉

Итак, сопротивление – физическая величина, характеризующая свойства проводника препятствовать (сопротивляться ) прохождению электрического тока.

Рассмотрим медный проводник длиной l с площадью поперечного сечения, равной S :

Сопротивление проводника зависит от нескольких факторов:

Удельное сопротивление – это табличная величина.

Формула, с помощью которой можно вычислить сопротивление проводника выглядит следующим образом:

Для нашего случая будет равно 0,0175 (Ом * кв. мм / м) – удельное сопротивление меди. Пусть длина проводника составляет 0.5 м , а площадь поперечного сечения равна 0.2 кв. мм . Тогда:

Как вы уже поняли из примера, единицей измерения сопротивления является Ом 😉

С сопротивлением проводника все ясно, настало время изучить взаимосвязь напряжения, силы тока и сопротивления цепи .

И тут на помощь нам приходит основополагающий закон всей электроники – закон Ома:

Сила тока в цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению рассматриваемого участка цепи.

Рассмотрим простейшую электрическую цепь:

Как следует из закона Ома напряжение и сила тока в цепи связаны следующим образом:

Пусть напряжение составляет 10 В, а сопротивление цепи равно 200 Ом. Тогда сила тока в цепи вычисляется следующим образом:

Как видите, все несложно 🙂

Пожалуй на этом мы и закончим сегодняшнюю статью, спасибо за внимание и до скорых встреч! 🙂

Facebook

Twitter

Вконтакте

Одноклассники

Google+

Как вычислить сопротивление проводника формула. Расчет сопротивлений проводов

Электричество само по себе невидимо, хотя от этого его опасность ничуть не меньше. Даже наоборот: как раз потому и опаснее. Ведь если бы мы его видели, как видим, например, воду, льющуюся из крана, то наверняка бы избежали множества неприятностей.

Вода. Вот она, водопроводная труба, и вот закрытый кран. Ничего не течет, не капает. Но мы точно знаем: внутри вода. И если система исправно работает, то вода эта там находится под давлением. 2, 3 атмосферы, или сколько там? Неважно. Но давление там есть, иначе система бы не работала. Где-то гудят насосы, гонят воду в систему, создают это самое давление.

А вот наш провод электрический. Где-то далеко, на другом конце тоже гудят генераторы, вырабатывают электричество. И в проводе от этого тоже давление… Нет-нет, не давление, конечно, тут в этом проводе напряжение . Оно тоже измеряется, но в своих единицах: в вольтах.

Давит в трубах на стенки вода, никуда не двигаясь, ждет, когда найдется выход, чтобы ринуться туда мощным потоком. И в проводе молча ждет напряжение, когда замкнется выключатель, чтобы потоки электронов двинулись выполнять свое предназначение.

И вот открылся кран, потекла струя воды. По всей трубе течет, двигаясь от насоса к расходному крану. А как только замкнулись контакты выключателя, в проводах потекли электроны. Что это за движение? Это ток . Электроны текут . И это движение, этот ток тоже имеет свою единицу измерения: ампер.

И еще есть сопротивление . Для воды это, образно говоря, размер отверстия в выпускном кране. Чем больше отверстие, тем меньше сопротивление движению воды. В проводах почти также: чем больше сопротивление провода, тем меньше ток.

Вот, как-то так, если образно представлять себе основные характеристики электричества. А с точки зрения науки все строго: существует так называемый закон Ома. Гласит он следующим образом: I = U/R .
I — сила тока. Измеряется в амперах.
U — напряжение. Измеряется в вольтах.
R — сопротивление. Измеряется в омах.

Есть еще одно понятие — мощность, W. С ним тоже просто: W = U*I . Измеряется в ваттах.

Собственно, это вся необходимая и достаточная для нас теория. Из этих четырех единиц измерения в соответствии с вышеприведенными двумя формулами можно вывести некоторое множество других:

№	Задача	Формула	Пример
1	Узнать силу тока, если известны напряжение и сопротивление.	I = U/R	I = 220 в / 500 ом = 0.44 а.
2	Узнать мощность, если известны ток и напряжение.	W = U*I	W = 220 в * 0.44 а = 96.8 вт.
3	Узнать сопротивление, если известны напряжение и ток.	R = U/I	R = 220 в / 0.44 а = 500 ом.
4	Узнать напряжение, если известны ток и сопротивление.	U = I*R	U = 0.44 а * 500 ом = 220 в.
5	Узнать мощность, если известны ток и сопротивление.	W = I 2 *R	W = 0.44 а * 0.44 а * 500 ом = 96.8 вт.
6	Узнать мощность, если известны напряжение и сопротивление.	W = U 2 /R	W = 220 в * 220 в / 500 ом = 96.8 вт.
7	Узнать силу тока, если известны мощность и напряжение.	I = W/U	I = 96.8 вт / 220 в = 0,44 а.
8	Узнать напряжение, если известны мощность и ток.	U = W/I	U = 96.8 вт / 0.44 а = 220 в.
9	Узнать сопротивление, если известны мощность и напряжение.	R = U 2 /W	R = 220 в * 220 в / 96.8 вт = 500 ом.
10	Узнать сопротивление, если известны мощность и ток.	R = W/I 2	R = 96.8 вт / (0,44 а * 0,44 а) = 500 ом.

Ты скажешь: — Зачем мне это все надо? Формулы, цифры… Я ж не собираюсь заниматься расчетами.

А я так отвечу: — Перечитай предыдущую статью . Как можно быть уверенным, не зная простейших истин и расчетов? Хотя, собственно, в бытовом практическом плане наиболее интересна только формула 7, где определяется сила тока при известных напряжении и мощности. Как правило, эти 2 величины известны, а результат (сила тока) безусловно необходим для определения допустимого сечения провода и для выбора защиты .

Есть еще одно обстоятельство, о котором следует упомянуть в контексте этой статьи. В электроэнергетике используется так называемый «переменный» ток. То есть, те самые электроны движутся в проводах не всегда в одном направлении, они постоянно меняют его: вперед-назад-вперед-назад… И эта смена направления движения — 100 раз в секунду.

Погоди, но ведь везде говорится, что частота 50 герц! Да, именно так и есть. Частота измеряется в количестве периодов за секунду, но в каждом периоде ток меняет свое направление дважды. Иначе сказать, в одном периоде две вершины, которые характеризуют максимальное значение тока (положительное и отрицательное), и именно в этих вершинах происходит смена направления.

Не будем вдаваться в подробности более глубоко, но все же: почему именно переменный, а не постоянный ток?

Вся проблема в передаче электроэнергии на большие расстояния. Тут как раз вступает в силу неумолимый закон Ома. При больших нагрузках, если напряжение 220 вольт, сила тока может быть очень большой. Для передачи электроэнергии с таким током потребуются провода очень большого сечения.

Выход здесь только один: поднять напряжение. Седьмая формула говорит: I = W/U . Совершенно очевидно, что если мы будем подавать напряжение не 220 вольт, а 220 тысяч вольт, то сила тока уменьшится в тысячу раз. А это значит, что сечение проводов можно взять намного меньше.

Поиск по сайту.
Вы можете изменить поисковую фразу.

Элементы электрической цепи можно соединить двумя способами. Последовательное соединение подразумевает подключение элементов друг к другу, а при параллельном соединении элементы являются частью параллельных ветвей. Способ соединения резисторов определяет метод вычисления общего сопротивления цепи.

Шаги

Последовательное соединение

Определите, является ли цепь последовательной. Последовательное соединение представляет собой единую цепь без каких-либо разветвлений. Резисторы или другие элементы расположены друг за другом.

Сложите сопротивления отдельных элементов. Сопротивление последовательной цепи равно сумме сопротивлений всех элементов, входящих в эту цепь. Сила тока в любых частях последовательной цепи одна и та же, поэтому сопротивления просто складываются.

• Например, последовательная цепь состоит из трех резисторов с сопротивлениями 2 Ом, 5 Ом и 7 Ом. Общее сопротивление цепи: 2 + 5 + 7 = 14 Ом.

Если сопротивление каждого элемента цепи не известно, воспользуйтесь законом Ома: V = IR, где V – напряжение, I – сила тока, R – сопротивление. Сначала найдите силу тока и общее напряжение.

Подставьте известные значения в формулу, описывающую закон Ома. Перепишите формулу V = IR так, чтобы обособить сопротивление: R = V/I. Подставьте известные значения в эту формулу, чтобы вычислить общее сопротивление.

• Например, напряжение источника тока равно 12 В, а сила тока равна 8 А. Общее сопротивление последовательной цепи: R O = 12 В / 8 А = 1,5 Ом.

Параллельное соединение

1. Определите, является ли цепь параллельной. Параллельная цепь на некотором участке разветвляется на несколько ветвей, которые затем снова соединяются. Ток течет по каждой ветви цепи.

   Вычислите общее сопротивление на основе сопротивления каждой ветви. Каждый резистор уменьшает силу тока, проходящего через одну ветвь, поэтому она оказывает небольшое влияние на общее сопротивление цепи. Формула для вычисления общего сопротивления: , где R 1 – сопротивление первой ветви, R 2 – сопротивление второй ветви и так далее до последней ветви R n .

   • Например, параллельная цепь состоит из трех ветвей, сопротивления которых равны 10 Ом, 2 Ом и 1 Ом.
     Воспользуйтесь формулой 1 R O = 1 10 + 1 2 + 1 1 {\displaystyle {\frac {1}{R_{O}}}={\frac {1}{10}}+{\frac {1}{2}}+{\frac {1}{1}}} , чтобы вычислить R O
     Приведите дроби к общему знаменателю : 1 R O = 1 10 + 5 10 + 10 10 {\displaystyle {\frac {1}{R_{O}}}={\frac {1}{10}}+{\frac {5}{10}}+{\frac {10}{10}}}
     1 R O = 1 + 5 + 10 10 = 16 10 = 1 , 6 {\displaystyle {\frac {1}{R_{O}}}={\frac {1+5+10}{10}}={\frac {16}{10}}=1,6}
     Умножьте обе части на R O: 1 = 1,6R O
     R O = 1 / 1,6 = 0,625 Ом.

2. Вычислите сопротивление по известной силе тока и напряжению. Сделайте это, если сопротивление каждого элемента цепи не известно.

   Подставьте известные значения в формулу закона Ома. Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I.

   • Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: R O = 9 В / 3 А = 3 Ом.

3. Поищите ветви с нулевым сопротивлением. Если у ветви параллельной цепи вообще нет сопротивления, то весь ток будет течь через такую ветвь. В этом случае общее сопротивление цепи равно 0 Ом.

Комбинированное соединение

1. Разбейте комбинированную цепь на последовательную и параллельную. Комбинированная цепь включает элементы, которые соединены как последовательно, так и параллельно. Посмотрите на схему цепи и подумайте, как разбить ее на участки с последовательным и параллельным соединением элементов. Обведите каждый участок, чтобы упростить задачу по вычислению общего сопротивления.

   • Например, цепь включает резистор, сопротивление которого равно 1 Ом, и резистор, сопротивление которого равно 1,5 Ом. За вторым резистором схема разветвляется на две параллельные ветви – одна ветвь включает резистор с сопротивлением 5 Ом, а вторая – с сопротивлением 3 Ом. Обведите две параллельные ветви, чтобы выделить их на схеме цепи.

2. Найдите сопротивление параллельной цепи. Для этого воспользуйтесь формулой для вычисления общего сопротивления параллельной цепи: 1 R O = 1 R 1 + 1 R 2 + 1 R 3 + . . . 1 R n {\displaystyle {\frac {1}{R_{O}}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+{\frac {1}{R_{3}}}+…{\frac {1}{R_{n}}}} .

   • В нашем примере параллельная цепь включает две ветви, сопротивления которых равны R 1 = 5 Ом и R 2 = 3 Ом.
     1 R p a r = 1 5 + 1 3 {\displaystyle {\frac {1}{R_{par}}}={\frac {1}{5}}+{\frac {1}{3}}}
     1 R p a r = 3 15 + 5 15 = 3 + 5 15 = 8 15 {\displaystyle {\frac {1}{R_{par}}}={\frac {3}{15}}+{\frac {5}{15}}={\frac {3+5}{15}}={\frac {8}{15}}}
     R p a r = 15 8 = 1 , 875 {\displaystyle R_{par}={\frac {15}{8}}=1,875} Ом.

3. Упростите цепь. После того как вы нашли общее сопротивление параллельной цепи, ее можно заменить одним элементом, сопротивление которого равно вычисленному значению.

   • В нашем примере избавьтесь от двух параллельных ветвей и замените их одним резистором с сопротивлением 1,875 Ом.

4. Сложите сопротивления резисторов, соединенных последовательно. Заменив параллельную цепь одним элементом, вы получили последовательную цепь. Общее сопротивление последовательной цепи равно сумме сопротивлений всех элементов, которые включены в эту цепь.

   • После упрощения цепи она состоит из трех резисторов со следующими сопротивлениями: 1 Ом, 1,5 Ом и 1,875 Ом. Все три резистора соединены последовательно: R O = 1 + 1 , 5 + 1 , 875 = 4 , 375 {\displaystyle R_{O}=1+1,5+1,875=4,375} Ом.

Среди прочих показателей, характеризующих электрическую цепь, проводник, стоит выделить электрическое сопротивление. Оно определяет способность атомов материала препятствовать направленному прохождению электронов. Помощь в определении данной величины может оказать как специализированный прибор – омметр, так и математические расчеты на основании знаний о взаимосвязях между величинами и физическими свойствами материала. Измерение показателя производится в Омах (Ом), обозначением служит символ R.

Закон Ома – математический подход при определении сопротивления

Соотношение, установленное Георгом Омом, определяет взаимосвязь между напряжением, силой тока, сопротивлением, основанную на математическом взаимоотношении понятий. Справедливость линейной взаимосвязи – R = U/I (отношение напряжения к силе тока) – отмечается не во всех случаях.
Единица измерения [R] = B/A = Ом. 1 Ом – сопротивление материала, по которому идет ток в 1 ампер при напряжении в 1 вольт.

Эмпирическая формула расчета сопротивления

Объективные данные о проводимости материала следуют из его физических характеристик, определяющих как его собственно свойства, так и реакции на внешние влияния. Исходя из этого проводимость зависит от:

• Размера.
• Геометрии.
• Температуры.

Атомы проводящего материала сталкиваются с направленными электронами, препятствуя их дальнейшему продвижению. При высокой концентрации последних атомы не способны им противостоять и проводимость оказывается высокой. Большие значения сопротивления характерны для диэлектриков, которые отличаются практически нулевой проводимостью.

Одной из определяющих характеристик каждого проводника является его удельное сопротивление – ρ. Оно определяет зависимость сопротивления от материала проводника и воздействий извне. Это фиксированная (в пределах одного материала) величина, которая представляет данные проводника следующих размеров – длина 1 м (ℓ), площадь сечения 1 кв.м. Поэтому взаимосвязь между данными величинами выражается соотношением: R = ρ* ℓ/S:

• Проводимость материала падает по мере увеличения его длины.
• Увеличение площади сечения проводника влечет за собой снижение его сопротивления. Такая закономерность обусловлена уменьшением плотности электронов, а, следовательно, и контакт частиц материала с ними становится более редким.
• Рост температуры материала стимулирует рост сопротивления, в то время как падение температуры влечет за собой его снижение.

Расчет площади сечения целесообразно производить согласно формуле S = πd 2 / 4. В определении длины поможет рулетка.

Взаимосвязь c мощностью (P)

Исходя из формулы закона Ома, U = I*R и P = I*U. Следовательно, P = I 2 *R и P = U 2 /R.
Зная величину силы тока и мощность, сопротивление можно определить как: R = P/I 2 .
Зная величину напряжения и мощности, сопротивление легко вычислить по формуле: R = U 2 /P.

Сопротивление материала и величины других сопутствующих характеристик могут быть получены с применением специальных измерительных приборов или на основании установленных математических закономерностей.

В природе существует два основных вида материалов, проводящие ток и не проводящие (диэлектрики). Отличаются эти материалы наличием условий для перемещения в них электрического тока (электронов).

Из токопроводящих материалов (медь, алюминий, графит, и многие другие), делают электрические проводники, в них электроны не связаны и могут свободно перемещаться.

В диэлектриках электроны привязаны к атомам намертво, поэтому ток в них течь не может. Из них делают изоляцию для проводов, детали электроприборов.

Для того чтобы электроны начали перемещаться в проводнике (по участку цепи пошел ток), им нужно создать условия. Для этого в начале участка цепи должен быть избыток электронов, а в конце – недостаток. Для создания таких условий используют источники напряжения – аккумуляторы, батарейки, электростанции.

В 1827 году Георг Симон Ом открыл закон силы электрического тока. Его именем назвали Закон и единицу измерения величины сопротивления. Смысл закона в следующем.

Чем толще труба и больше давление воды в водопроводе (с увеличением диаметра трубы уменьшается сопротивление воде) – тем больше потечет воды. Если представить, что вода это электроны (электрический ток), то, чем толще провод и больше напряжение (с увеличением сечения провода уменьшается сопротивление току) – тем больший ток будет протекать по участку цепи.

Сила тока, протекающая по электрической цепи, прямо пропорциональна приложенному напряжению и обратно пропорциональна величине сопротивления цепи.

Где I – сила тока, измеряется в амперах и обозначается буквой А ; U В ; R – сопротивление, измеряется в омах и обозначается Oм .

Если известны напряжение питания U и сопротивление электроприбора R , то с помощью выше приведенной формулы, воспользовавшись онлайн калькулятором, легко определить силу протекающего по цепи тока I .

С помощью закона Ома рассчитываются электрические параметры электропроводки, нагревательных элементов, всех радиоэлементов современной электронной аппаратуры, будь то компьютер, телевизор или сотовый телефон.

Применение закона Ома на практике

На практике часто приходится определять не силу тока I , а величину сопротивления R . Преобразовав формулу Закона Ома, можно рассчитать величину сопротивления R , зная протекающий ток I и величину напряжения U .

Величину сопротивления может понадобится рассчитать, например, при изготовлении блока нагрузок для проверки блока питания компьютера. На корпусе блока питания компьютера обычно есть табличка, в которой приведен максимальный ток нагрузки по каждому напряжению. Достаточно в поля калькулятора ввести данные величины напряжения и максимальный ток нагрузки и в результате вычисления получим величину сопротивления нагрузки для данного напряжения. Например, для напряжения +5 В при максимальной величине тока 20 А, сопротивление нагрузки составит 0,25 Ом.

Формула Закона Джоуля-Ленца

Величину резистора для изготовления блока нагрузки для блока питания компьютера мы рассчитали, но нужно еще определить какой резистор должен быть мощности? Тут поможет другой закон физики, который, независимо друг от друга открыли одновременно два ученых физика. В 1841 году Джеймс Джоуль, а в 1842 году Эмиль Ленц. Этот закон и назвали в их честь – Закон Джоуля-Ленца .

Потребляемая нагрузкой мощность прямо пропорциональна приложенной величине напряжения и протекающей силе тока. Другими словами, при изменении величины напряжения и тока будет пропорционально будет изменяться и потребляемая мощность.

где P – мощность, измеряется в ваттах и обозначается Вт ; U – напряжение, измеряется в вольтах и обозначается буквой В ; I – сила ток, измеряется в амперах и обозначается буквой А .

Зная напряжения питания и силу тока, потребляемую электроприбором, можно по формуле определить, какую он потребляет мощность. Достаточно ввести данные в окошки ниже приведенного онлайн калькулятора.

Закон Джоуля-Ленца позволяет также узнать силу тока, потребляемую электроприбором зная его мощность и напряжение питания. Величина потребляемого тока необходима, например, для выбора сечения провода при прокладке электропроводки или для расчета номинала .

Например, рассчитаем потребляемый ток стиральной машины. По паспорту потребляемая мощность составляет 2200 Вт, напряжение в бытовой электросети составляет 220 В. Подставляем данные в окошки калькулятора, получаем, что стиральная машина потребляет ток величиной 10 А.

Еще один пример, Вы решили в автомобиле установить дополнительную фару или усилитель звука. Зная потребляемую мощность устанавливаемого электроприбора легко рассчитать потребляемый ток и правильно подобрать сечение провода для подключения к электропроводке автомобиля. Допустим, дополнительная фара потребляет мощность 100 Вт (мощность установленной в фару лампочки), бортовое напряжение сети автомобиля 12 В. Подставляем значения мощности и напряжения в окошки калькулятора, получаем, что величина потребляемого тока составит 8,33 А.

Разобравшись всего в двух простейших формулах, Вы легко сможете рассчитать текущие по проводам токи, потребляемую мощность любых электроприборов – практически начнете разбираться в основах электротехники.

Преобразованные формулы Закона Ома и Джоуля-Ленца

Встретил в Интернете картинку в виде круглой таблички, в которой удачно размещены формулы Закона Ома и Джоуля-Ленца и варианты математического преобразования формул. Табличка представляет собой несвязанные между собой четыре сектора и очень удобна для практического применения

По таблице легко выбрать формулу для расчета требуемого параметра электрической цепи по двум другим известным. Например, нужно определить ток потребления изделием по известной мощности и напряжению питающей сети. По таблице в секторе тока видим, что для расчета подойдет формула I=P/U.

А если понадобится определить напряжение питающей сети U по величине потребляемой мощности P и величине тока I, то можно воспользоваться формулой левого нижнего сектора, подойдет формула U=P/I.

Подставляемые в формулы величины должны быть выражены в амперах, вольтах, ваттах или Омах.

Электрическое сопротивление — физическая величина, которая показывает, какое препятствие создается току при его прохождении по проводнику . Единицами измерения служат Омы, в честь Георга Ома. В своем законе он вывел формулу для нахождения сопротивления, которая приведена ниже.

Рассмотрим сопротивление проводников на примере металлов. Металлы имеют внутреннее строение в виде кристаллической решетки. Эта решетка имеет строгую упорядоченность, а её узлами являются положительно заряженные ионы. Носителями заряда в металле выступают “свободные” электроны, которые не принадлежат определенному атому, а хаотично перемещаются между узлами решетки. Из квантовой физики известно, что движение электронов в металле это распространение электромагнитной волны в твердом теле. То есть электрон в проводнике движется со скоростью света (практически), и доказано, что он проявляет свойства не только как частица, но еще и как волна. А сопротивление металла возникает в результате рассеяния электромагнитных волн (то есть электронов) на тепловых колебаниях решетки и её дефектах. При столкновении электронов с узлами кристаллической решетки часть энергии передается узлам, вследствие чего выделяется энергия. Эту энергию можно вычислить при постоянном токе , благодаря закону Джоуля-Ленца – Q=I 2 Rt. Как видите чем больше сопротивление, тем больше энергии выделяется.

Удельное сопротивление

Существует такое важное понятие как удельное сопротивление, это тоже самое сопротивление, только в единице длины. У каждого металла оно свое, например у меди оно равно 0,0175 Ом*мм2/м, у алюминия 0,0271 Ом*мм2/м. Это значит, брусок из меди длиной 1 м и площадью поперечного сечения 1 мм2 будет иметь сопротивление 0,0175 Ом, а такой же брусок, но из алюминия будет иметь сопротивление 0,0271 Ом. Выходит что электропроводность меди выше чем у алюминия. У каждого металла удельное сопротивление свое, а рассчитать сопротивление всего проводника можно по формуле

где p – удельное сопротивление металла, l – длина проводника, s – площадь поперечного сечения.

Значения удельных сопротивлений приведены в таблице удельных сопротивлений металлов (20°C)

Вещество	p , Ом*мм 2 /2	α,10 -3 1/K
Алюминий	0.0271
Вольфрам	0.055
Железо	0.098
Золото	0.023
Латунь	0.025-0.06
Манганин	0.42-0.48	0,002-0,05
Медь	0.0175
Никель
Константан	0.44-0.52	0.02
Нихром		0.15
Серебро	0.016
Цинк	0.059

Кроме удельного сопротивления в таблице есть значения ТКС, об этом коэффициенте чуть позже.

Зависимость удельного сопротивления от деформаций

При холодной обработке металлов давлением, металл испытывает пластическую деформацию. При пластической деформации кристаллическая решетка искажается, количество дефектов становится больше. С увеличением дефектов кристаллической решетки, сопротивление течению электронов по проводнику растет, следовательно, удельное сопротивление металла увеличивается. К примеру, проволоку изготавливают методом протяжки, это значит, что металл испытывает пластическую деформацию, в результате чего, удельное сопротивление растет. На практике для уменьшения сопротивления применяют рекристаллизационный отжиг, это сложный технологический процесс, после которого кристаллическая решетка как бы, “расправляется” и количество дефектов уменьшается, следовательно, и сопротивление металла тоже.

При растяжении или сжатии, металл испытывает упругую деформацию. При упругой деформации вызванной растяжением, амплитуды тепловых колебаний узлов кристаллической решетки увеличиваются, следовательно, электроны испытывают большие затруднения, и в связи с этим, увеличивается удельное сопротивление. При упругой деформации вызванной сжатием, амплитуды тепловых колебаний узлов уменьшаются, следовательно, электронам проще двигаться, и удельное сопротивление уменьшается.

Влияние температуры на удельное сопротивление

Как мы уже выяснили выше, причиной сопротивления в металле являются узлы кристаллической решетки и их колебания. Так вот, при увеличении температуры, тепловые колебания узлов увеличиваются, а значит, удельное сопротивление также увеличивается. Существует такая величина как температурный коэффициент сопротивления (ТКС), который показывает насколько увеличивается, или уменьшается удельное сопротивление металла при нагреве или охлаждении. Например, температурный коэффициент меди при 20 градусах по цельсию равен 4.1 · 10 − 3 1/градус. Это означает что при нагреве, к примеру, медной проволоки на 1 градус цельсия, её удельное сопротивление увеличится на 4.1 · 10 − 3 Ом. Удельное сопротивление при изменении температуры можно вычислить по формуле

где r это удельное сопротивление после нагрева, r 0 – удельное сопротивление до нагрева, a – температурный коэффициент сопротивления, t 2 – температура до нагрева, t 1 — температура после нагрева.

Подставив наши значения, мы получим: r=0,0175*(1+0.0041*(154-20))=0,0271 Ом*мм 2 /м. Как видите наш брусок из меди длиной 1 м и площадью поперечного сечения 1 мм 2 , после нагрева до 154 градусов, имел бы сопротивление, как у такого же бруска, только из алюминия и при температуре равной 20 градусов цельсия.

Свойство изменения сопротивления при изменении температуры, используется в термометрах сопротивления. Эти приборы могут измерять температуру основываясь на показаниях сопротивления. У термометров сопротивления высокая точность измерений, но малые диапазоны температур.

На практике, свойства проводников препятствовать прохождению тока используются очень широко. Примером может служить лампа накаливания, где нить из вольфрама, нагревается за счет высокого сопротивления металла, большой длины и узкого сечения. Или любой нагревательный прибор, где спираль разогревается благодаря высокому сопротивлению. В электротехнике, элемент главным свойством которого является сопротивление, называется – резистор . Резистор применяется практически в любой электрической схеме.

Видео с вопросом: Расчет сопротивления проводника

Стенограмма видеозаписи

Диаметр алюминиевой проволоки 10 миллиметров. Найдите сопротивление такого провода длиной 0,56 км, используемого для передачи энергии. Используйте значение удельного сопротивления алюминия 2,65 умноженное на 10 до отрицательной восьмой омметра.

Мы можем начать с рисования эскиза описываемого провода. Хотя эскиз нарисован не в масштабе, он дает нам представление о размерах алюминиевой проволоки.Наряду с размерами, нам сообщили, что этот провод имеет удельное сопротивление, обозначенное греческой буквой, от 2,65 умноженное на 10 до отрицательной восьмой омметра. Учитывая все это, мы хотим найти сопротивление этого провода.

Для этого существует математическая связь между сопротивлением и удельным сопротивлением, которую мы хотим вспомнить. Сопротивление 𝑟 провода равно его удельному сопротивлению, умноженному на его длину, деленную на его площадь поперечного сечения. И в нашем случае, поскольку наша площадь поперечного сечения круглая, мы также можем вспомнить площадь круга с точки зрения его диаметра, эта площадь равна 𝜋, деленному на четыре раза квадрат его диаметра.

Наша задача состоит в том, чтобы использовать это соотношение и предоставленную информацию для определения 𝑟, где 𝑟 — сопротивление алюминиевой проволоки. Мы можем начать с того, что подставим в это уравнение заданное значение удельного сопротивления 𝜚, а также длину провода в метрах. Обратите внимание, что мы пересчитали километры. Как только эти значения для 𝜚 и 𝐿 входят в наше уравнение, наша последняя задача — ввести выражение для площади поперечного сечения этого провода.

Глядя на наше уравнение для площади круга, мы видим, что оно выражается в диаметре, что и указано в формулировке задачи.Но в настоящее время наш диаметр выражается в миллиметрах, и мы хотим преобразовать его в метры, чтобы они соответствовали единицам в остальной части этого выражения для 𝑟. Поэтому вместо 10 миллиметров мы запишем диаметр как 10 в отрицательной трети метра. И эта величина возводится в квадрат и умножается на на четыре, чтобы найти площадь поперечного сечения.

Прежде чем вычислить значение, обратите внимание, что происходит с единицами измерения в этом выражении. В частности, единицы измерения сокращаются от числителя и знаменателя, и мы остаемся с единицами измерения сопротивления — омами.Эта доля составляет 0,19 Ом. Вот сопротивление этого длинного узкого провода.

Сопротивление

Одним из первых, кто измерил сопротивление проводников, был Георг Ом. Он приложил постоянное напряжение к проводнику и измерил величину тока, протекавшего через него. Сопротивление проводника — это напряжение, деленное на ток.Сегодня мы называем единицу сопротивления ом, а устройства, которые измеряют его таким же образом, как ом, называется омметр.

На рисунке выше только полоса медного цвета имеет значительное сопротивление.Предполагается, что тонкие черные провода и большие серые пластины являются идеальными проводниками. На практике им просто нужно иметь ничтожно малое сопротивление по сравнению с медью. цветная полоса.

Серые таблички на двух концах полосы служат для демонстрации важности позволить току легко течь в любую точку на конце бар.Если тонкий черный провод коснется стержня в какой-то точке или небольшом участке, тогда приведенные ниже расчеты сопротивления могут оказаться недействительными.

Когда Ом впервые опубликовал свои результаты в 1820-х годах, его высмеяли и заставили ушел в отставку с должности в университете и не мог найти постоянную работу. Но многие ученые смогли воспроизвести его результаты и нашел его выводы весьма полезными.В 1841 г. он был признан с медалью Копли (что примерно эквивалентно Нобелевской премии). К 1852 г. он был назначен на кафедру физики в Мюнхенском университете, который он продержался до своей смерти два года спустя.

Ом не просто измерил сопротивление проводников, а придумал математическая формула, позволяющая рассчитать их сопротивление на основе по их форме и составу.Он, вероятно, не знал, что его расчеты действительны только для постоянного или очень медленно меняющегося напряжения. Сегодня мы назовем сопротивление Ом рассчитанным и наблюдаемым сопротивлением постоянному току, и часто используют символ Р _DC .

Примерно через 60 лет после того, как Ом опубликовал свою работу, Гораций Лэмб использовал математические анализ, чтобы показать, что переменный ток имеет тенденцию течь у поверхности проводников.На высоких частотах переменного тока будет использоваться только тонкая полоска проводника, чтобы проводить ток. Сегодня мы знаем это как скин-эффект. Это может значительно увеличить сопротивление по сравнению с предсказанным Омом, а также вызывает изменение сопротивления в зависимости от частоты.

Расчет сопротивления объектов произвольной формы может быть сложной задачей, что может потребовать численного анализа (компьютерные программы).Однако там некоторые важные частные случаи, когда достаточно легко вычислить сопротивление постоянному току. Например, когда проводник достаточно длинный и узкая и сохраняет постоянную площадь поперечного сечения, тогда ее сопротивление легко найти.

9.4: Сопротивление и сопротивление — Physics LibreTexts

Что движет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, розетки и т. Д., Которые необходимы для поддержания тока.Все такие устройства создают разность потенциалов и называются источниками напряжения. Когда источник напряжения подключен к проводнику, он прикладывает разность потенциалов В, , которая создает электрическое поле. Электрическое поле, в свою очередь, воздействует на свободные заряды, вызывая ток. Величина тока зависит не только от величины напряжения, но и от характеристик материала, через который протекает ток. Материал может сопротивляться потоку зарядов, и мера того, насколько материал сопротивляется потоку зарядов, известна как удельное сопротивление .Это удельное сопротивление грубо аналогично трению между двумя материалами, которые сопротивляются движению.

Удельное сопротивление

Когда к проводнику прикладывается напряжение, создается электрическое поле \ (\ vec {E} \), и заряды в проводнике ощущают силу, создаваемую электрическим полем. Полученная плотность тока \ (\ vec {J} \) зависит от электрического поля и свойств материала. 2} {V / m} = \ dfrac {A} {V \ cdot m}.{-1} \).

Электропроводность — это внутреннее свойство материала. Другим неотъемлемым свойством материала является удельное сопротивление или электрическое сопротивление . Удельное сопротивление материала — это мера того, насколько сильно материал противостоит прохождению электрического тока. Символ удельного сопротивления — строчная греческая буква ро, \ (\ rho \), а удельное сопротивление — величина, обратная удельной электропроводности:

.

\ [\ rho = \ dfrac {1} {\ sigma}. \]

Единицей измерения удельного сопротивления в системе СИ является ом-метр \ ((\ Omega \ cdot m \).Мы можем определить удельное сопротивление через электрическое поле и плотность тока.

\ [\ rho = \ dfrac {E} {J}. \]

Чем больше удельное сопротивление, тем большее поле необходимо для создания заданной плотности тока. Чем ниже удельное сопротивление, тем больше плотность тока, создаваемого данным электрическим полем.{-1}\)ConductorsSemiconductors [1]Insulators»>

Материалы, перечисленные в таблице, разделены на категории проводников, полупроводников и изоляторов на основе широких групп удельного сопротивления. У проводников наименьшее удельное сопротивление, а у изоляторов наибольшее; полупроводники имеют промежуточное удельное сопротивление. Проводники имеют разную, но большую плотность свободных зарядов, тогда как большинство зарядов в изоляторах связаны с атомами и не могут двигаться. Полупроводники являются промежуточными, имеют гораздо меньше свободных зарядов, чем проводники, но обладают свойствами, из-за которых количество свободных зарядов сильно зависит от типа и количества примесей в полупроводнике.Эти уникальные свойства полупроводников находят применение в современной электронике, о чем мы поговорим в следующих главах.

Пример \ (\ PageIndex {1} \): плотность тока, сопротивление и электрическое поле для токоведущего провода

Рассчитайте плотность тока, сопротивление и электрическое поле 5-метрового медного провода диаметром 2,053 мм (калибр 12), по которому проходит ток \ (I — 10 \, мА \).

Стратегия

Мы можем рассчитать плотность тока, сначала найдя площадь поперечного сечения провода, которая равна \ (A = 3.{-5} \ dfrac {V} {m}. \ End {align *} \]

Значение

Исходя из этих результатов, неудивительно, что медь используется для проводов, проводящих ток, потому что сопротивление довольно мало. Обратите внимание, что плотность тока и электрическое поле не зависят от длины провода, но напряжение зависит от длины.

Упражнение \ (\ PageIndex {1} \)

Медные провода обычно используются для удлинителей и домашней электропроводки по нескольким причинам.2} \). Третья важная характеристика — пластичность. Пластичность — это мера способности материала вытягиваться в проволоку и мера гибкости материала, а медь обладает высокой пластичностью. Подводя итог, можно сказать, что проводник является подходящим кандидатом для изготовления проволоки, по крайней мере, с тремя важными характеристиками: низким удельным сопротивлением, высокой прочностью на разрыв и высокой пластичностью. Какие еще материалы используются для электромонтажа и в чем преимущества и недостатки?

Ответ

Серебро, золото и алюминий используются для изготовления проволоки.Все четыре материала обладают высокой проводимостью, серебро — самой высокой. Все четыре элемента легко сворачиваются в проволоку и обладают высоким пределом прочности на разрыв, хотя и не таким высоким, как медь. Очевидным недостатком золота и серебра является их стоимость, но серебряные и золотые провода используются для специальных применений, таких как провода для динамиков. Золото не окисляется, улучшая связи между компонентами. У алюминиевых проводов есть свои недостатки. Алюминий имеет более высокое удельное сопротивление, чем медь, поэтому требуется больший диаметр, чтобы соответствовать сопротивлению на длину медных проводов, но алюминий дешевле, чем медь, поэтому это не является серьезным недостатком.Алюминиевая проволока не обладает такой высокой пластичностью и прочностью на разрыв, как медная, но пластичность и прочность на разрыв находятся в допустимых пределах. Есть несколько проблем, которые необходимо решить при использовании алюминия, и следует соблюдать осторожность при выполнении соединений. Алюминий имеет более высокий коэффициент теплового расширения, чем медь, что может привести к ослаблению соединений и возможной опасности возгорания. Окисление алюминия не проводит и может вызвать проблемы. При использовании алюминиевых проводов необходимо использовать специальные методы, а компоненты, такие как электрические розетки, должны быть рассчитаны на прием алюминиевых проводов.

ФЭТ

Просмотрите это интерактивное моделирование, чтобы увидеть, как площадь поперечного сечения, длина и удельное сопротивление провода влияют на сопротивление проводника. Отрегулируйте переменные с помощью ползунков и посмотрите, станет ли сопротивление меньше или больше.

Температурная зависимость удельного сопротивления

Вернувшись к таблице \ (\ PageIndex {1} \), вы увидите столбец с надписью «Температурный коэффициент». Удельное сопротивление некоторых материалов сильно зависит от температуры.В некоторых материалах, таких как медь, удельное сопротивление увеличивается с повышением температуры. Фактически, в большинстве проводящих металлов удельное сопротивление увеличивается с повышением температуры. Повышение температуры вызывает повышенные колебания атомов в решетчатой ​​структуре металлов, которые препятствуют движению электронов. В других материалах, таких как углерод, удельное сопротивление уменьшается с повышением температуры. Во многих материалах зависимость является приблизительно линейной и может быть смоделирована с помощью линейного уравнения:

\ [\ rho \ приблизительно \ rho_0 [1 + \ alpha (T — T_0)], \]

, где \ (\ rho \) — удельное сопротивление материала при температуре Тл , \ (\ alpha \) — температурный коэффициент материала, а \ (\ rho_0 \) — удельное сопротивление при \ (T_0 \) , обычно принимается как \ (T_0 = 20.oC \).

Обратите внимание, что температурный коэффициент \ (\ alpha \) отрицателен для полупроводников, перечисленных в таблице \ (\ PageIndex {1} \), что означает, что их удельное сопротивление уменьшается с увеличением температуры. Они становятся лучшими проводниками при более высоких температурах, потому что повышенное тепловое перемешивание увеличивает количество свободных зарядов, доступных для переноса тока. Это свойство уменьшения \ (\ rho \) с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках.

Сопротивление

Теперь рассмотрим сопротивление провода или компонента. Сопротивление — это мера того, насколько сложно пропустить ток через провод или компонент. Сопротивление зависит от удельного сопротивления. Удельное сопротивление является характеристикой материала, используемого для изготовления провода или другого электрического компонента, тогда как сопротивление является характеристикой провода или компонента.

Чтобы рассчитать сопротивление, рассмотрите участок проводящего провода с площадью поперечного сечения A , длиной L и удельным сопротивлением \ (\ rho \).Батарея подключается к проводнику, обеспечивая разность потенциалов \ (\ Delta V \) на нем (рисунок \ (\ PageIndex {1} \)). Разность потенциалов создает электрическое поле, которое пропорционально плотности тока, согласно \ (\ vec {E} = \ rho \ vec {J} \).

Рисунок \ (\ PageIndex {1} \): потенциал, обеспечиваемый батареей, прикладывается к сегменту проводника с площадью поперечного сечения \ (A \) и длиной \ (L \).

Величина электрического поля на отрезке проводника равна напряжению, деленному на длину, \ (E = V / L \), а величина плотности тока равна току, деленному на поперечную площадь сечения \ (J = I / A \).Используя эту информацию и вспоминая, что электрическое поле пропорционально удельному сопротивлению и плотности тока, мы можем видеть, что напряжение пропорционально току:

\ [\ begin {align *} E & = \ rho J \\ [4pt] \ dfrac {V} {L} & = \ rho \ dfrac {I} {A} \\ [4pt] V & = \ left (\ rho \ dfrac {L} {A} \ right) I. \ end {align *} \]

Определение: Сопротивление

Отношение напряжения к току определяется как сопротивление \ (R \):

\ [R \ Equiv \ dfrac {V} {I}.\]

Сопротивление цилиндрического сегмента проводника равно удельному сопротивлению материала, умноженному на длину, разделенную на площадь:

\ [R \ Equiv \ dfrac {V} {I} = \ rho \ dfrac {L} {A}. \]

Единицей измерения сопротивления является ом, \ (\ Omega \). Для заданного напряжения чем выше сопротивление, тем ниже ток.

Резисторы

Обычным компонентом электронных схем является резистор. Резистор можно использовать для уменьшения протекания тока или обеспечения падения напряжения.На рисунке \ (\ PageIndex {2} \) показаны символы, используемые для резистора в принципиальных схемах цепи. Два обычно используемых стандарта для принципиальных схем предоставлены Американским национальным институтом стандартов (ANSI, произносится как «AN-см.») И Международной электротехнической комиссией (IEC). Обе системы обычно используются. Мы используем стандарт ANSI в этом тексте для его визуального распознавания, но отметим, что для более крупных и сложных схем стандарт IEC может иметь более четкое представление, что упрощает чтение.

Рисунок \ (\ PageIndex {2} \): символы резистора, используемые в принципиальных схемах. (а) символ ANSI; (b) символ IEC.

Зависимость сопротивления от материала и формы

Резистор можно смоделировать как цилиндр с площадью поперечного сечения A и длиной L , сделанный из материала с удельным сопротивлением \ (\ rho \) (рисунок \ (\ PageIndex {3} \)) . Сопротивление резистора \ (R = \ rho \ dfrac {L} {A} \)

Рисунок \ (\ PageIndex {3} \): Модель резистора в виде однородного цилиндра длиной L и площадью поперечного сечения A .Его сопротивление потоку тока аналогично сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление. Чем больше его площадь поперечного сечения A , тем меньше его сопротивление.

Чаще всего для изготовления резистора используется углерод. Углеродная дорожка намотана на керамический сердечник, к нему прикреплены два медных вывода. Второй тип резистора — это металлопленочный резистор, который также имеет керамический сердечник. Дорожка сделана из материала оксида металла, который имеет полупроводниковые свойства, аналогичные углеродным.Опять же, в концы резистора вставляются медные провода. Затем резистор окрашивается и маркируется для идентификации. Резистор имеет четыре цветные полосы, как показано на рисунке \ (\ PageIndex {4} \).

Рисунок \ (\ PageIndex {4} \): Многие резисторы напоминают рисунок, показанный выше. Четыре полосы используются для идентификации резистора. Первые две цветные полосы представляют собой первые две цифры сопротивления резистора. Третий цвет — множитель. Четвертый цвет обозначает допуск резистора.{-5} \, \ Omega \), а сверхпроводники вообще не имеют сопротивления при низких температурах. Как мы видели, сопротивление связано с формой объекта и материалом, из которого он состоит.

Сопротивление объекта также зависит от температуры, поскольку \ (R_0 \) прямо пропорционально \ (\ rho \). Для цилиндра мы знаем \ (R = \ rho \ dfrac {L} {A} \), поэтому, если L и A не сильно изменяются с температурой, R имеет ту же температурную зависимость, что и \ ( \ rho \).(Исследование коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, поэтому влияние температуры на L и A примерно на два порядка меньше, чем на \ (\ rho \).) Таким образом,

\ [R = R_0 (1 + \ alpha \ Delta T) \ label {Tdep} \]

— это температурная зависимость сопротивления объекта, где \ (R_0 \) — исходное сопротивление (обычно принимаемое равным \ (T = 20,00 ° C \), а R — сопротивление после изменения температуры \ (\ Дельта Т \).oC \).

Многие термометры основаны на влиянии температуры на сопротивление (Рисунок \ (\ PageIndex {5} \)). Один из наиболее распространенных термометров основан на термисторе, полупроводниковом кристалле с сильной температурной зависимостью, сопротивление которого измеряется для определения его температуры. Устройство небольшое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается.

Рисунок \ (\ PageIndex {5} \): Эти знакомые термометры основаны на автоматическом измерении сопротивления термистора в зависимости от температуры.oC) \ right) \\ [5pt] & = 4.8 \, \ Omega \ end {align *} \]

Значение

Обратите внимание, что сопротивление изменяется более чем в 10 раз, когда нить накала нагревается до высокой температуры, а ток через нить накала зависит от сопротивления нити и приложенного напряжения. Если нить накаливания используется в лампе накаливания, начальный ток через нить накала при первом включении лампы будет выше, чем ток после того, как нить накаливания достигнет рабочей температуры.

Упражнение \ (\ PageIndex {2} \)

Тензодатчик — это электрическое устройство для измерения деформации, как показано ниже. Он состоит из гибкой изолирующей основы, поддерживающей рисунок из проводящей фольги. Сопротивление фольги изменяется по мере растяжения основы. Как меняется сопротивление тензодатчика? Влияет ли тензодатчик на изменение температуры?

Ответ

Рисунок фольги растягивается по мере растяжения основы, а дорожки фольги становятся длиннее и тоньше.Поскольку сопротивление рассчитывается как \ (R = \ rho \ dfrac {L} {A} \), сопротивление увеличивается по мере того, как дорожки из фольги растягиваются. При изменении температуры меняется и удельное сопротивление дорожек фольги, изменяя сопротивление. Один из способов борьбы с этим — использовать два тензодатчика, один используется в качестве эталона, а другой — для измерения деформации. Два тензодатчика поддерживаются при постоянной температуре

Сопротивление коаксиального кабеля

Длинные кабели иногда могут действовать как антенны, улавливая электронные шумы, которые являются сигналами от другого оборудования и приборов.Коаксиальные кабели используются во многих случаях, когда требуется устранение этого шума. Например, их можно найти дома через кабельное телевидение или другие аудиовизуальные соединения. Коаксиальные кабели состоят из внутреннего проводника с радиусом \ (r_i \), окруженного вторым внешним концентрическим проводником с радиусом \ (r_0 \) (рисунок \ (\ PageIndex {6} \)). Пространство между ними обычно заполнено изолятором, например полиэтиленовым пластиком. Между двумя проводниками возникает небольшой ток радиальной утечки.Определите сопротивление коаксиального кабеля длиной L .

Рисунок \ (\ PageIndex {6} \): Коаксиальные кабели состоят из двух концентрических проводников, разделенных изоляцией. Они часто используются в кабельном телевидении или других аудиовизуальных средствах связи.

Стратегия

Мы не можем использовать уравнение \ (R = \ rho \ dfrac {L} {A} \) напрямую. Вместо этого мы смотрим на концентрические цилиндрические оболочки толщиной dr и интегрируем.

Решение

Сначала мы находим выражение для \ (dR \), а затем интегрируем от \ (r_i \) до \ (r_0 \),

\ [\ begin {align *} dR & = \ dfrac {\ rho} {A} dr \\ [5pt] & = \ dfrac {\ rho} {2 \ pi r L} dr, \ end {align *} \]

Объединение обеих сторон

\ [\ begin {align *} R & = \ int_ {r_i} ^ {r_0} dR \\ [5pt] & = \ int_ {r_i} ^ {r_0} \ dfrac {\ rho} {2 \ pi r L } dr \\ [5pt] & = \ dfrac {\ rho} {2 \ pi L} \ int_ {r_i} ^ {r_0} \ dfrac {1} {r} dr \\ [5pt] & = \ dfrac {\ rho} {2 \ pi L} \ ln \ dfrac {r_0} {r_i}.\ end {align *} \]

Значение

Сопротивление коаксиального кабеля зависит от его длины, внутреннего и внешнего радиусов, а также удельного сопротивления материала, разделяющего два проводника. Поскольку это сопротивление не бесконечно, между двумя проводниками возникает небольшой ток утечки. Этот ток утечки приводит к ослаблению (или ослаблению) сигнала, передаваемого по кабелю.

Упражнение \ (\ PageIndex {3} \)

Сопротивление между двумя проводниками коаксиального кабеля зависит от удельного сопротивления материала, разделяющего два проводника, длины кабеля и внутреннего и внешнего радиуса двух проводников.Если вы разрабатываете коаксиальный кабель, как сопротивление между двумя проводниками зависит от этих переменных?

Ответ

Чем больше длина, тем меньше сопротивление. Чем больше удельное сопротивление, тем выше сопротивление. Чем больше разница между внешним радиусом и внутренним радиусом, то есть чем больше соотношение между ними, тем больше сопротивление. Если вы пытаетесь максимизировать сопротивление, выбор значений для этих переменных будет зависеть от приложения.Например, если кабель должен быть гибким, выбор материалов может быть ограничен.

Phet: Цепь батарейного резистора

Просмотрите это моделирование, чтобы увидеть, как приложенное напряжение и сопротивление материала, через который протекает ток, влияют на ток через материал. Вы можете визуализировать столкновения электронов и атомов материала, влияющие на температуру материала.

Авторы и авторство

• Сэмюэл Дж.Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

Сопротивление проводника — Energy Education

Рис. 1. Нить накаливания загорается из-за сопротивления проводящего провода. ^[1]

Сопротивление проводника — это свойство проводника при определенной температуре, и оно определяется как величина сопротивления протеканию электрического тока через проводящую среду. ^[2] Сопротивление проводника зависит от площади поперечного сечения проводника, длины проводника и его удельного сопротивления. Важно отметить, что электрическая проводимость и удельное сопротивление обратно пропорциональны, а это означает, что чем больше проводимость, тем меньше сопротивление.

Сопротивление проводника можно рассчитать при температуре 20 ° C с помощью: ^[3]

[математика] \ R = \ frac {\ rho L} {A} [/ математика]

где:

• [math] R [/ math] — сопротивление в омах (Ом)
• [math] \ rho [/ math] — удельное сопротивление материала в омметрах (Ом · м)
• [math] L [/ math] — длина проводника в метрах (м)
• [math] A [/ math] — площадь поперечного сечения проводника в метрах в квадрате (м ² )

Эта формула говорит нам, что сопротивление проводника прямо пропорционально [математике] \ rho [ / math] и [math] L [/ math], и обратно пропорционально [math] A [/ math].Поскольку сопротивление некоторого проводника, например отрезка провода, зависит от столкновений внутри самого провода, сопротивление зависит от температуры. С повышением температуры сопротивление провода увеличивается, так как столкновения внутри провода увеличиваются и «замедляют» протекание тока. Величина изменения определяется температурным коэффициентом. ^[4] Положительный температурный коэффициент приводит к увеличению сопротивления с повышением температуры, тогда как отрицательный температурный коэффициент приводит к уменьшению сопротивления с повышением температуры.Поскольку проводники обычно демонстрируют повышенное удельное сопротивление с повышением температуры, они имеют положительный температурный коэффициент. Наиболее распространенные типы резисторов — это переменные резисторы и постоянные резисторы.

Используя сопротивление проводника, можно создать свет в лампе накаливания. В лампочке накаливания есть проволочная нить определенной длины и ширины, обеспечивающая определенное сопротивление. Если это сопротивление правильное, ток, протекающий через провод, замедляется ровно настолько, без остановки из-за слишком большого сопротивления, что нить накала нагревается до точки, в которой она начинает светиться. ^[5]

Подробнее о сопротивлении проводника см. HyperPhysics.

PhET: Сопротивление в проводе

Университет Колорадо любезно разрешил нам использовать следующую симуляцию Фета. Изучите моделирование, чтобы увидеть, как изменяется сопротивление проводника в зависимости от геометрии и удельного сопротивления:

Для дальнейшего чтения

Для получения дополнительной информации см. Соответствующие страницы ниже:

Список литературы

Что такое удельное сопротивление — формулы и единицы »Электроника

Удельное электрическое сопротивление является ключевым параметром для любого материала, используемого в электрических цепях, электронных компонентах и ​​многих других предметах.

---

Учебное пособие по сопротивлению Включает:
Что такое сопротивление Закон Ома Омические и неомические проводники Сопротивление лампы накаливания Удельное сопротивление Таблица удельного сопротивления для распространенных материалов Температурный коэффициент сопротивления Электрическая проводимость Последовательные и параллельные резисторы Таблица параллельных резисторов

---

Удельное сопротивление — это мера сопротивления определенного размера материала определенного размера электрической проводимости.

Удельное сопротивление также может называться удельным электрическим сопротивлением или объемным сопротивлением, хотя эти термины используются менее широко.

Хотя материалы сопротивляются прохождению электрического тока, некоторые из них проводят его лучше, чем другие.

Удельное сопротивление — это показатель, позволяющий сравнивать то, как различные материалы допускают или препятствуют протеканию тока.

Чтобы значения удельного сопротивления были значимыми, для удельного сопротивления используются определенные единицы, и существуют формулы для его расчета и соотнесения с сопротивлением в Ом для данного размера материала.

Материалы, которые легко проводят электрический ток, называются проводниками и имеют низкое удельное сопротивление.Те, которые плохо проводят электричество, называются изоляторами, и эти материалы обладают высоким удельным сопротивлением.

Удельное сопротивление различных материалов играет важную роль при выборе материалов, используемых для электрических проводов во многих электронных компонентах, включая резисторы, интегральные схемы и многое другое.

Определение и единицы удельного сопротивления

Удельное электрическое сопротивление образца материала может быть также известно как его удельное электрическое сопротивление.Это мера того, насколько сильно материал противостоит прохождению электрического тока.

Определение удельного сопротивления:

Удельное сопротивление вещества — это сопротивление куба этого вещества, имеющего края единичной длины, при том понимании, что ток течет перпендикулярно противоположным граням и равномерно распределяется по ним.

Удельное электрическое сопротивление — это электрическое сопротивление на единицу длины и на единицу площади поперечного сечения при заданной температуре.

Единицей измерения удельного электрического сопротивления в системе СИ является ом · метр (Ом · м). Обычно обозначается греческой буквой ρ, ро.

Хотя обычно используется единица измерения удельного сопротивления в системе СИ, омметр, иногда значения могут быть выражены в омах сантиметрах, Ом⋅см. 2

Из уравнений видно, что сопротивление можно изменять, изменяя множество различных параметров.

Например, поддерживая постоянное удельное сопротивление материала, сопротивление образца можно увеличить, увеличив длину или уменьшив площадь поперечного сечения. Из уравнений удельного сопротивления также видно, что увеличение удельного сопротивления материала приведет к увеличению сопротивления при тех же размерах. Аналогичным образом уменьшение удельного сопротивления приведет к уменьшению сопротивления.

Уровни удельного сопротивления материалов

Материалы делятся на разные категории в зависимости от их уровня или удельного сопротивления.-8

Полупроводники

Переменная *

Сверхпроводники

0

* Уровень проводимости полупроводников зависит от уровня легирования. Без легирования они выглядят почти как изоляторы, но с легированием доступны носители заряда, и сопротивление резко падает.Аналогично для электролитов уровень удельного сопротивления варьируется в широких пределах.

Определение удельного сопротивления гласит, что удельное сопротивление вещества — это сопротивление куба этого вещества, имеющего края единичной длины, при том понимании, что ток течет перпендикулярно противоположным граням и равномерно распределяется по ним.

Удельное сопротивление обычно измеряется в Омметрах. Это означает, что удельное сопротивление измеряется для куба материала размером метр в каждом направлении.

Практическое значение удельного сопротивления

Удельное сопротивление материалов важно, поскольку оно позволяет использовать правильные материалы в нужных местах в электрических и электронных компонентах.

Материалы, используемые в качестве проводников, например в электрических и общих соединительных проводах, должны иметь низкий уровень удельного сопротивления. Это означает, что для данной площади поперечного сечения сопротивление провода будет низким. Выбор правильного материала зависит от знания его свойств, одним из которых является его удельное сопротивление.

Например, медь является хорошим проводником, поскольку она обеспечивает низкий уровень удельного сопротивления, ее стоимость не слишком высока, а также она обеспечивает другие физические характеристики, которые полезны во многих электрических и электронных приложениях. Удельное сопротивление меди составляет около 1,7 x 10 ^-8 Ом · м (или 17 нОм), хотя цифры могут незначительно отличаться в зависимости от марки меди

.

Такие материалы, как медь и даже алюминий, обладают низким удельным сопротивлением, что делает их идеальными для использования в качестве электрических проводов и кабелей, причем медь часто является фаворитом.Серебро и золото имеют очень низкие значения удельного сопротивления, но, поскольку они значительно дороже, они не получили широкого распространения. Тем не менее, серебро иногда используется для обшивки проводов там, где необходимо его низкое удельное сопротивление, а золотое покрытие используется для сопрягаемых поверхностей многих электронных разъемов, чтобы обеспечить наилучшие контакты. Золото также хорошо подходит для электрических разъемов, поскольку оно не тускнеет и не окисляется, как другие металлы.

На соединительных контактах многоходового разъема для печатной платы нанесено золотое покрытие для уменьшения контактного сопротивления и предотвращения потускнения.

В качестве изоляторов, проводящих как можно меньший ток, требуются другие материалы.Удельное сопротивление изолятора будет на много порядков выше. Одним из примеров является воздух, и у него очень высокий показатель удельного сопротивления, превышающий 1,5 x 10 ¹⁴ , что, как можно видеть, очень, очень много выше, чем удельное сопротивление меди.

Удельное электрическое сопротивление играет важную роль во многих других электронных компонентах. В резисторах, например, удельное сопротивление различных материалов играет ключевую роль в обеспечении правильного сопротивления резисторов.

Удельное сопротивление также играет ключевую роль в других электронных компонентах.Для интегральных схем очень важно удельное сопротивление материалов в микросхеме. Некоторые области должны иметь очень низкое сопротивление и иметь возможность соединять различные области ИС внутри, тогда как другие материалы должны изолировать разные области. Опять же, для этого важно сопротивление.

Удельное сопротивление играет ключевую роль во многих областях электронных компонентов, а также многих электрических деталей.

Удельное электрическое сопротивление является ключевым параметром для материалов, которые будут использоваться в электрических и электронных системах.Эти вещества с высоким электрическим сопротивлением называются изоляторами и могут использоваться для этой цели. Они с низким уровнем удельного электрического сопротивления являются хорошими проводниками и могут использоваться во множестве приложений, от проводов до электрических соединений и многого другого.

Дополнительные концепции и руководства по основам электроники:
Voltage Текущий Мощность Сопротивление Емкость Индуктивность Трансформеры Децибел, дБ Законы Кирхгофа Q, добротность РЧ шум
Вернуться в меню «Основные понятия электроники».. .

Сопротивление в проводниках

• Изучив этот раздел, вы сможете:
• • Рассчитайте размеры проводника.
• • Опишите влияние длины и площади поперечного сечения на сопротивление проводника.

Как размеры проводника влияют на его сопротивление

Проводник — это любой материал, который пропускает через него электрический ток.Способность любого проводника в электрической цепи пропускать ток оценивается по его электрическому СОПРОТИВЛЕНИЮ. Сопротивление — это способность противодействовать прохождению электрического тока. Напряжение — это электрическая сила, которая заставляет ток течь через проводник, но чем больше значение сопротивления любого проводника, тем меньше тока будет течь для любого конкретного значения приложенного напряжения. Сопротивление проводника в основном зависит от трех факторов:

Рис. 1.3.1 Расчет размеров проводника

1.ДЛИНА проводника.

2. ПЛОЩАДЬ ПОПЕРЕЧНЯ кондуктора.

3. МАТЕРИАЛ, из которого изготовлен проводник.

Поскольку сопротивление больше в более длинных проводниках, чем в более коротких, то:

СОПРОТИВЛЕНИЕ (R) ПРОПОРЦИОНАЛЬНО ДЛЯ ДЛИНЫ (L)

и записывается как R ∝ L (∝ означает пропорционально …)

Следовательно, чем длиннее проводник, тем больше сопротивление и, следовательно, меньше тока.

Также, поскольку сопротивление меньше в проводниках с большой площадью поперечного сечения:

СОПРОТИВЛЕНИЕ (R) ОБРАТНО ПРОПОРЦИОНАЛЬНО ПОПЕРЕЧНОЙ ПЛОЩАДИ (A)

, который записывается как R ∝ 1 / A (или R ∝ A ^-1 ).

Чем больше площадь поперечного сечения, тем больше тока может протекать по проводнику, поэтому тем ниже значение сопротивления проводника.

Круглые проводники

Если проводник имеет круглое поперечное сечение, площадь круга можно определить по формуле:

π r ² Где π = 3,142 и r — радиус окружности.

Если поперечное сечение проводника квадратное или прямоугольное, площадь поперечного сечения проводника все же можно определить, просто умножив ширину на высоту.Большинство проводников, используемых в кабелях и т. Д., Конечно, имеют круглое поперечное сечение.

Материал, из которого изготовлен проводник, также влияет на его сопротивление на величину, зависящую от СОПРОТИВЛЕНИЯ материала, описанного в Модуле 1.4 резисторов и схем.

Расчет кода

| EC&M

В прошлом месяце мы рассмотрели, как NEC решает проблему падения напряжения, обсудив шесть примечаний к мелкому оттиску (FPN) и несколько конкретных правил. В этом месяце мы рассмотрим примеры, демонстрирующие, как рассчитать падение напряжения на проводниках, используя закон Ома или формулу падения напряжения (VD).

Метод закона Ома: только однофазный. Вы можете определить падение напряжения в проводниках цепи, умножив ток в цепи на общее сопротивление проводов цепи: VD = I x R. «I» равно нагрузке в амперах, а «R» равно сопротивлению сопротивление проводника указано в таблице 8 главы 9 для цепей постоянного тока или в таблице 9 главы 9 для цепей переменного тока. Примечание. Вы не можете использовать метод закона Ома для трехфазных цепей.

Однофазный, 120 В Пример: Какое падение напряжения на двух?12 проводов, питающих нагрузку 16 А, 120 В, расположенных на расстоянии 100 футов от источника питания (200 футов провода)?

(а) 3,2 В
(б) 6,4 В
(в) 9,6 В
(г) 12,8 В

Ответ: (б) 6.4V

Падение напряжения = I x R, где «I» равно 16 А и

«R» равно 0,4 Ом [Глава 9, Таблица 9: (2 Ом / 1000 футов) 2200 футов 42200 футов]

Следовательно, падение напряжения = 16A x 0,4 Ом или

Падение напряжения = 6,4 В, (6,4 В / 120 В = падение напряжения 5,3%) и

Рабочее напряжение = 120В — 6.4 В или

Рабочее напряжение = 113,6 В

VD Формульный метод. Если вы уже установили проводники цепи, определите падение напряжения на проводниках по одной из следующих формул:

VD = 2 x K x Q x I x D / CM (однофазный) или
VD = 1,732 x K x Q x I x D / CM (3-фазный), где «VD» = падение напряжения: мы выражаем падение напряжения на проводниках схемы в вольтах.

«K» = постоянная постоянного тока: это постоянная, представляющая сопротивление постоянному току для проводника круглого сечения 1000 мил и длиной 1000 футов при рабочей температуре 75 ° C.Постоянное значение постоянного тока, которое вы должны использовать для меди, составляет 12,9 Ом и 21,2 Ом для алюминиевых проводов. Константа «K» подходит для цепей переменного тока, где проводники не превышают № 1/0.

«Q» = Коэффициент регулировки переменного тока: Вы должны отрегулировать цепи переменного тока № 2/0 и выше для эффектов самоиндукции (скин-эффекта). Вы можете найти поправочный коэффициент «Q», разделив сопротивление переменному току, как указано в главе 9, таблица 9, на сопротивление постоянному току, как указано в главе 9, таблица 8.

«I» = Амперы: нагрузка в амперах при 100%, а не 125% для двигателей или постоянных нагрузок.

«D» = Расстояние: расстояние, на котором находится нагрузка от источника питания, а не общая длина проводников цепи.

«CM» = Круглые милы: Круговые милы проводника цепи, как указано в главе 9, таблица 8.

Однофазный пример: Каково падение напряжения на проводе № 6, который питает однофазную нагрузку 44 А, 240 В, расположенную на расстоянии 160 футов от щитка?

(а) 4.25В
(б) 6.9В
(в) 3%
(г) 5%

Ответ: (б) 6.9В

VD = 2 x K x I x D / CM, где
K = 12,9 Ом (медь),
I = 44A,
D = 160 футов и
CM = 26240 круглых милов (глава 9, таблица 8)

Следовательно, VD = 2 провода x 12,9 Ом x 44A x 160 футов / 26240 круглых мил, или
В = 46,9 В, (6,9 В / 240 В = падение напряжения 2,9%), и
Рабочее напряжение = 240 В — 6,9 В или
Рабочее напряжение = 233,1 В

Пример трехфазного тока: Предположим, у вас есть трехфазная нагрузка 208 В, 36 кВА (100 А), расположенная в 80 футах от щитовой панели и подключенная к разъему No.1 алюминиевый проводник. Какое падение напряжения в проводниках до отключения оборудования?

(а) 3,5В
(б) 7В
(в) 3%
(г) 5%

Ответ: (а) 3,5 В

VD = 1,732 x K x I x D / CM, где
K = 21,2 Ом (алюминий),
I = 100A,
D = 80 футов и
CM = 83690 круглых милов (глава 9, таблица 8)

Следовательно, VD = 1,732 x 21,2 Ом x 100A x 80 футов / 83690 круглых мил или
VD = 3,5 В (3,5 В / 208 В = 1,7%), а рабочее напряжение
= 208 В — 3.