Какие из четырех резисторов в электрической цепи, изображённой на рисунке 10.4 соединенных
2. Выберите верное утверждение A) Диффузия наблюдается в твердых веществах и газообразных Б) Диффузия наблюдается в твердых веществах. жидких и газооб … разных В) Диффузия наблюдается в жидких и газообразных веществах Г) Диффузия наблюдается только в газообразных веществах
1, Почему изменяется внутренния энергия мышки? Мышки дролеат не только от холода, но и для того, чтобы согреться. При дрогании скелетных мышц тепла В … делается не так уж много, но биохимические реакции выделения тепла резко ускоряются. Подромит мышка, постучит зубами и запустит на полную мощность свою Отопительную систему,
чему равно перемещение машины тна участке 0-10 с?
4. Выберите правильный вариант записи чисел 0,025 м и 75000 м с использованием приставок.A) 25 см, 75 ммB) 25 мм, 75 кмC) 0,25 мм, 75 кмD) 0,25 км, 75 … ммПомогите пожалуйста это СООООЧ!!!!
спортивный диск с радиусом 10 см после броска спортсмена летит со скоростью 25м/с.
Тело изменяет свою скорость так, как показано нарисунке. Определить скорость второго тела, если оно,двигаясь равномерно, за две секунды прошло тот же … путь,что и первое тело за то же время.
Как без всяких весов убедиться, что массы близнецов-братьев Мити и Вити одинаковы?физика 7 класс
срочно помогите я на соре даю 40 баллов кто напишет фигню тому баночень срочно зделать виде рисунка
какова кинетическая энергия 5-тонного грузовика, движущегося со скоростью 75 км / ч? Сколько тепла будет потеряно из-за трения в тормозных накладках, … когда автомобиль остановится?
4. уравнение координаты материальной точки имеет вид x=2+15t-7t².A) Опишите характер Движения точки. В) с каким ускорением движется тело?С) какова нач
… альная скорость телаD) укажите начальную координату телаЕ) Запишете уравнение пути.F) Найдите координату тела через 2 с. даю 20 баллов!! помогите
даю 20 баллов!! помогите
Учебник 1 и Шаг 5 на резисторы для Платы Intel® Galileo
Видя номера на экране может получить немного скучно. Давайте сделать еще один шаг вперед и сопоставить данные микрофона со светодиодом.
Как обсуждалось ранее, количество тока, протекающего через цепь, важно понять. Мы будем использовать резистор, чтобы ограничить поток тока в вашей цепи, чтобы гарантировать, что светодиод не получает больше электроэнергии, чем он должен работать.
При более внимательном рассмотрении светодиода, вы заметите, что он имеет только две точки с разной длиной, называют анод (положительный) и катод (отрицательный). Электричество течет через анод (длинная нога, положительный заряд), в светодиод, чтобы осветить его, а затем обратно вниз к катоду (короткая нога, отрицательный заряд), где он заземлен.
Расчет значений резистора
Это закон Ома.
(Операционное напряжение — передний напряжение) / ток (в амперах)
Он используется для расчета сопротивления в цепи и представлен в «Ohms» с помощью символа O.
- Операционное напряжение.
- Передние напряжение.
- Ток.
- Сопротивление. Количество сопротивления, необходимого для регулирования тока в цепи
Наш светодиод использует ток 20mA (миллиампер), чтобы быть приведенв в действие достаточно, чтобы не сгореть. Усилитель (ампер) представляет собой единицу измерения, используемую для электрического тока.
Как спецификации для основных светодиодов государств, и, как и большинство распространенных светодиодов, он имеет типичный передний напряжение 2,0 V и номинальной передний ток 20mA.
20мА 0,02 усилителя
| СОВЕТ, при расчете тока, где документация описывает значение в миллиампер, разделите его на 1000, чтобы использовать его для закона Ома. |
Как и большинство Arduinos, плата Intel® Galileo питается от 5 V (операционное напряжение). Поскольку светодиоду нужно только 2 V (переднего напряжения), чтобы питаться, мы можем получить разницу между ними и заполнить значения формулы.
Поскольку светодиоду нужно только 2 V (переднего напряжения), чтобы питаться, мы можем получить разницу между ними и заполнить значения формулы.
(Операционное напряжение — передний напряжение) / ток — значение резистора
(5 V — 2 V) / 0,02 усилители ?
3 / 0,02 й 150
Нам нужно 150 ohm резистор или больше, чтобы завершить эту схему.
Выбор правильного резистора
Для того, чтобы наш светодиод, чтобы иметь нужное количество тока течет к ним, мы должны увеличить сопротивление, так что меньше текущих потоков.
Это займет 150 ohms или больше, чтобы обеспечить надлежащий поток тока происходит, когда схема работает. Поскольку написание значений на резисторе довольно сложно, инженеры создали цветовую диаграмму, соответствующую значениям резистора. Это упрощает выбор правильного резистора.
Совет овечий совет, на которой мы используем пакет резисторов, имеет диаграмму, которая указывает на цвета, используемые для каждого значения резистора. Если вы используете другой резистор (например, 5 или 6 полос), ваши цвета будут меняться. Для более поздних резисторов группы, пожалуйста, обратитесь к спецификации производителя. Если вы используете другой резистор (например, 5 или 6 полос), ваши цвета будут меняться. Для более поздних резисторов группы, пожалуйста, обратитесь к спецификации производителя. |
Каждая цифра в значении сопротивления соответствует другому цвету. Мы используем 4-диапазонный цветовой код для наших резисторов.
Так как у нас нет резистора ровно для 150 ohm в пакете резистора, который мы используем, мы будем использовать резистор 220 ohm, который использует следующий цветовой код
- 2 Красный
- 2 Красный
- 0 Коричневый
Совет овечий совет, третья полоса может быть сложно понять. Так как наше значение составляет 220 на 4 полоса резистора, мы используем следующую формулу, Мы видим в нашей 4-диапазонный график резистора (в задней части пакета резистора), что 10 и коричневый, что дает нам группу красного, красного, коричневого цвета. |
Закон ома — формулировка простыми словами, определение,
Сопротивление
Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.
- Сопротивление — физическая величина, которая показывает способность проводника пропускать электрический ток. Чем выше сопротивление, тем ниже эта способность.
Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.
Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.
Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.
Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала.
Знайте!
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
- Удельное сопротивление проводника — это физическая величина, которая показывает способность материала пропускать электрический ток. Это табличная величина, она зависит только от материала.
Таблица удельных сопротивлений различных материалов
Удельное сопротивление ρ, Ом*мм2/м | Удельное сопротивление ρ, Ом*мм2/м |
Алюминий | 0,028 |
Бронза | 0,095 — 0,1 |
Висмут | 1,2 |
Вольфрам | 0,05 |
Железо | 0,1 |
Золото | 0,023 |
Иридий | 0,0474 |
Константан ( сплав Ni-Cu + Mn) | 0,5 |
Латунь | 0,025 — 0,108 |
Магний | 0,045 |
Манганин (сплав меди марганца и никеля — приборный) | 0,43 — 0,51 |
Медь | 0,0175 |
Молибден | 0,059 |
Нейзильбер (сплав меди цинка и никеля) | 0,2 |
Натрий | 0,047 |
Никелин ( сплав меди и никеля) | 0,42 |
Никель | 0,087 |
Нихром ( сплав никеля хрома железы и марганца) | 1,05 — 1,4 |
Олово | 0,12 |
Платина | 0. |
Ртуть | 0,94 |
Свинец | 0,22 |
Серебро | 0,015 |
Сталь | 0,103 — 0,137 |
Титан | 0,6 |
Хромаль | 1,3 — 1,5 |
Цинк | 0,054 |
Чугун | 0,5-1,0 |
Резистор
Все реальные проводники имеют сопротивление, но его стараются сделать незначительным. В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.
Из-за того, что проводник у нас «кругом-бегом-такой-идеальный», чаще всего за сопротивление в цепи отвечает резистор. Это устройство, которое нагружает цепь сопротивлением.
Это устройство, которое нагружает цепь сопротивлением.
Вот так резистор изображается на схемах:
В школьном курсе физики используют Европейское обозначение, поэтому запоминаем только его. Американское обозначение можно встретить, например, в программе Micro-Cap, в которой инженеры моделируют схемы.
Вот так резистор выглядит в естественной среде обитания:
Полосочки на нем показывают его сопротивление.
На сайте компании Ekits, которая занимается продажей электронных модулей, можно выбрать цвет резистора и узнать значение его сопротивления:
Источник: сайт компании Ekits
О том, зачем дополнительно нагружать сопротивлением цепь, мы поговорим в этой же статье чуть позже.
Реостат
Есть такие выключатели, которые крутишь, а они делают свет ярче-тусклее. В такой выключатель спрятан резистор с переменным сопротивлением — реостат.
Закон Ома для участка цепи
С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит. Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.
Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. Эти реакции выделяют энергию, которая потом передается электрической цепи.
У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «-».
У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.
Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.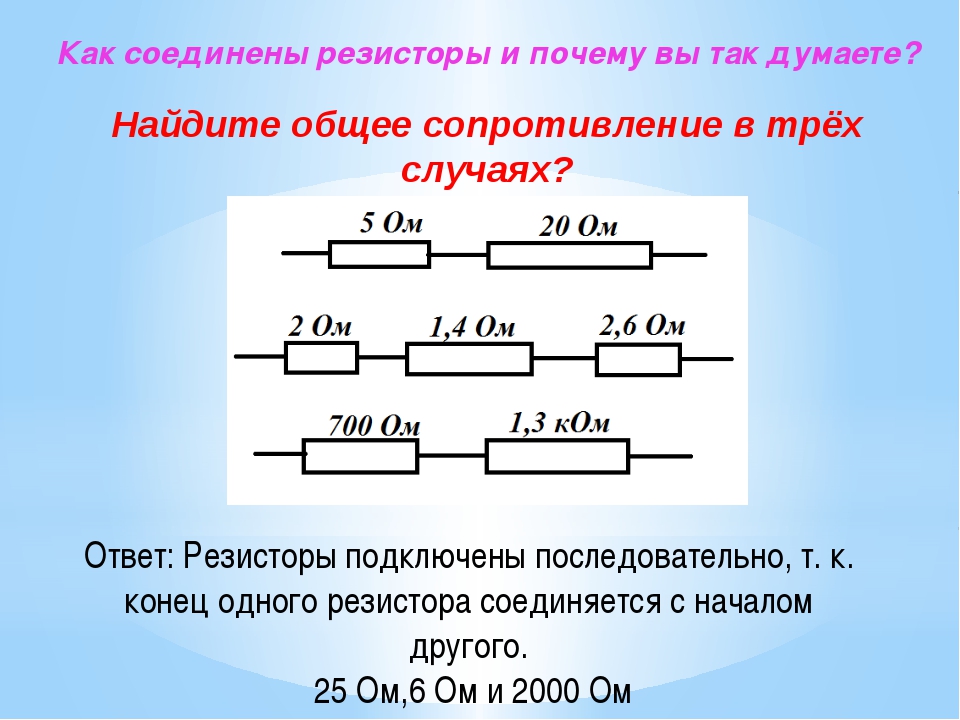
Математически его можно описать вот так:
Закон Ома для участка цепи I — сила тока [A] U — напряжение [В] R — сопротивление [Ом] |
Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее.
Сила тока измеряется в Амперах, а подробнее о ней вы можете прочитать в нашей статье 😇
Давайте решим несколько задач на Закон Ома для участка цепи.
Задача раз
Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а сопротивление нити накаливания равно 880 Ом. 2/м
2/м
Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.
Таблица удельных сопротивлений различных материалов
Удельное сопротивление ρ, Ом*мм2/м | Удельное сопротивление ρ, Ом*мм2/м |
Алюминий | 0,028 |
Бронза | 0,095 — 0,1 |
Висмут | 1,2 |
Вольфрам | 0,05 |
Железо | 0,1 |
Золото | 0,023 |
Иридий | 0,0474 |
Константан ( сплав Ni-Cu + Mn) | 0,5 |
Латунь | 0,025 — 0,108 |
Магний | 0,045 |
Манганин (сплав меди марганца и никеля — приборный) | 0,43 — 0,51 |
Медь | 0,0175 |
Молибден | 0,059 |
Нейзильбер (сплав меди цинка и никеля) | 0,2 |
Натрий | 0,047 |
Никелин ( сплав меди и никеля) | 0,42 |
Никель | 0,087 |
Нихром ( сплав никеля хрома железы и марганца) | 1,05 — 1,4 |
Олово | 0,12 |
Платина | 0. |
Ртуть | 0,94 |
Свинец | 0,22 |
Серебро | 0,015 |
Сталь | 0,103 — 0,137 |
Титан | 0,6 |
Хромаль | 1,3 — 1,5 |
Цинк | 0,054 |
Чугун | 0,5-1,0 |
Ответ: нить накаливания сделана из константана.
Закон Ома для полной цепи
Мы разобрались с законом Ома для участка цепи. А теперь давайте узнаем, что происходит, если цепь полная: у нее есть источник, проводники, резисторы и другие элементы.
В таком случае вводится Закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Так, стоп. Слишком много незнакомых слов — разбираемся по-порядку.
Что такое ЭДС и откуда она берется
ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.
- ЭДС — это сила, которая движет заряженные частицы в цепи. Она берется из источника тока. Например, из батарейки.
Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь. Именно эта энергия заставляет частицы двигаться по проводнику.
Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.
В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:
Закон Ома для полной цепи I = ε/(R + r) I — сила тока [A] ε — ЭДС [В] R — сопротивление [Ом] r — внутреннее сопротивление источника [Ом] |
Любой источник не идеален.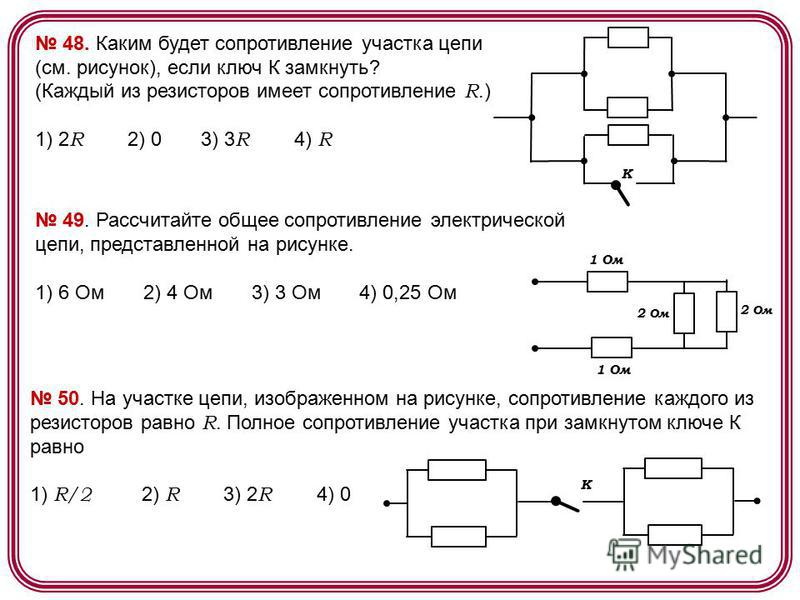 В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.
В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.
Решим задачу на полную цепь.
Задачка
Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом
Решение:
Возьмем закон Ома для полной цепи:
I = ε/(R + r)
Подставим значения:
I = 4/(3+1) = 1 A
Ответ: сила тока в цепи равна 1 А.
Когда «сопротивление бесполезно»
Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.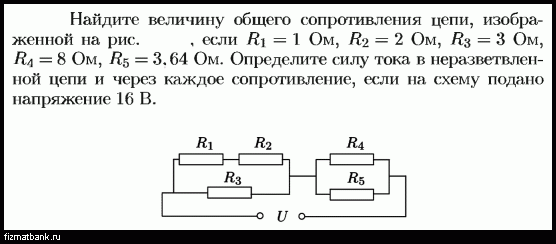
А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.
Ток идет по пути наименьшего сопротивления.
Теперь давайте посмотрим на закон Ома для участка цепи еще раз.
Закон Ома для участка цепи I = U/R I — сила тока [A] U — напряжение [В] R — сопротивление [Ом] |
Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.
То есть:
I = U/0 = ∞
Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.
Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.
Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.
Параллельное и последовательное соединение
Все это время речь шла о цепях с одним резистором. Рассмотрим, что происходит, если их больше.
Последовательное соединение | Параллельное соединение | |
Схема | Резисторы следуют друг за другом | Между резисторами есть два узла Узел — это соединение трех и более проводников |
Сила тока | Сила тока одинакова на всех резисторах I = I1 = I2 | Сила тока, входящего в узел, равна сумме сил токов, выходящих из него I = I1 + I2 |
Напряжение | Общее напряжение цепи складывается из напряжений на каждом резисторе U = U1 + U2 | Напряжение одинаково на всех резисторах U = U1 = U2 |
Сопротивление | Общее сопротивление цепи складывается из сопротивлений каждого резистора R = R1 + R2 | Общее сопротивление для бесконечного количества параллельно соединенных резисторов 1/R = 1/R1 + 1/R2 + … + 1/Rn Общее сопротивление для двух параллельно соединенных резисторов R = (R1 * R2)/R1 + R2 Общее сопротивление бесконечного количества параллельно соединенных одинаковых резисторов R = R1/n |
Зачем нужны эти соединения, если можно сразу взять резистор нужного номинала? Начнем с того, что все электронные компоненты изготавливаются по ГОСТу. Параллельное соединение также используют, как «запасной аэродром»: когда на конечный результат общее сопротивление сильно не повлияет, но в случае отказа одного из резисторов, будет работать другой. Признаемся честно: схемы, которые обычно дают в задачах (миллион параллельно соединенных резисторов, к ним еще последовательный, а к этому последовательному еще миллион параллельных) — в жизни не встречаются. Но навык расчета таких схем впоследствии упрощает подсчет схем реальных, потому что так вы невооруженным глазом отличаете последовательное соединение от параллельного. |
Решим несколько задач на последовательное и параллельное соединение.
Задачка раз
Найти общее сопротивление цепи.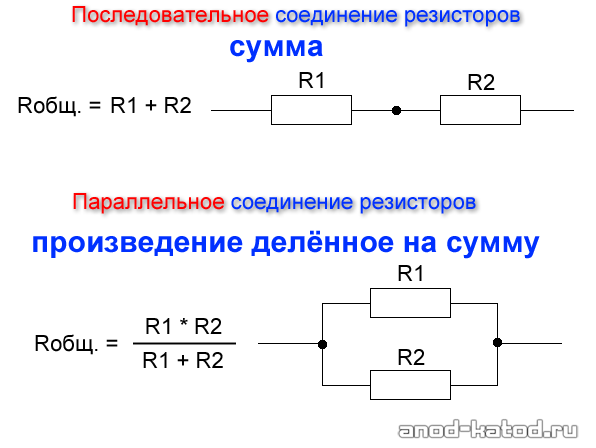
R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом, R4 = 4 Ом.
Решение:
Общее сопротивление при последовательном соединении рассчитывается по формуле:
R = R1 + R2 + R3 + R4 = 1 + 2 + 3 + 4 = 10 Ом
Ответ: общее сопротивление цепи равно 10 Ом
Задачка два
Найти общее сопротивление цепи.
R1 = 4 Ом, R2 = 2 Ом
Решение:
Общее сопротивление при параллельном соединении рассчитывается по формуле:
R = (R1 * R2)/R1 + R2 = 4*2/4+2 = 4/3 = 1 ⅓ Ом
Ответ: общее сопротивление цепи равно 1 ⅓ Ом
Задачка три
Найти общее сопротивление цепи, состоящей из резистора и двух ламп.
R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом
Решение:
Сначала обозначим, что лампы с точки зрения элемента электрической цепи не отличаются от резисторов.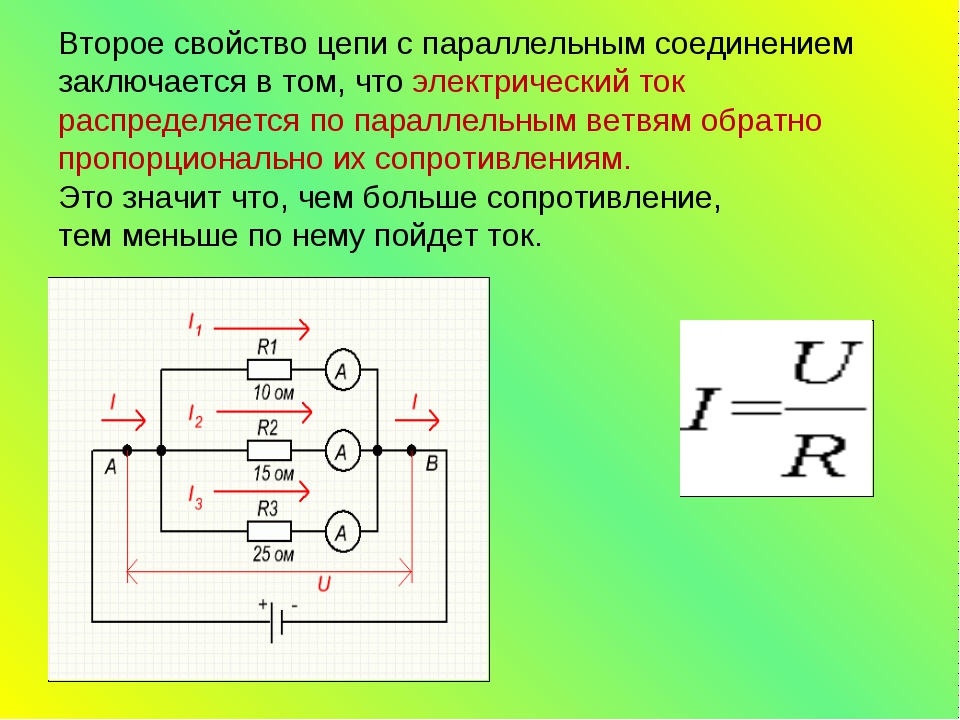 То есть у них тоже есть сопротивление, и они также влияют на цепь.
То есть у них тоже есть сопротивление, и они также влияют на цепь.
В данном случае соединение является смешанным. Лампы соеденены параллельно, а последовательно к ним подключен резистор.
Сначала посчитаем общее сопротивление для ламп. Общее сопротивление при параллельном соединении рассчитывается по формуле:
Rламп = (R2 * R3)/R2 + R3 = 2*3/2+3 = 6/5 = 1,2 Ом
Общее сопротивление при последовательном соединении рассчитывается по формуле:
R = R1 + Rламп = 1 + 1,2 = 2,2 Ом
Ответ: общее сопротивление цепи равно 2,2 Ом.
Наконец-то, последняя и самая сложная задача! В ней собрали все самое серьезное из этой статьи 💪.
Задачка четыре со звездочкой
К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. 2)/2R = R/2 = 10/2 = 5 Ом
2)/2R = R/2 = 10/2 = 5 Ом
И общее сопротивление цепи равно:
R = Rлампы + Rрезисторов = 5 + 5 = 10 Ом
Выразим внутреннее сопротивление источника из закона Ома для полной цепи.
I = ε/(R + r)
R + r = ε/I
r = ε/I — R
Подставим значения:
r = 12/0,5 — 10 = 14 Ом
Ответ: внутреннее сопротивление источника равно 14 Ом.
Участок цепи состоит из четырех резисторов. Резисторы R1 = 2 Ом
Участок цепи состоит из четырех резисторов. Резисторы R1 = 2 Ом и R2 = 3 Ом соединены параллельно. Последовательно с ними соединены резисторы R3 = 3 Ом и R4 = 0,8 Ом. К концам участка приложено напряжение U = 20 В. Найдите силу тока в каждом из четырех резисторов.
Участок цепи состоит из четырех резисторов. Резисторы R1 = 2 Ом и R2 = 3 Ом соединены параллельно. Последовательно с ними соединены резисторы R3 = 3 Ом и R4 = 0,8 Ом. К концам участка приложено напряжение U = 20 В. Найдите силу тока в каждом из четырех резисторов.
Решение
Закон Ома
I=U/R
Последовательное соединение проводников
Uобщ=U1+U2
Iобщ=I1=I2
Rобщ=R1+R2
Параллельное соединение проводников
Uобщ=U1=U2
Iобщ=I1+I2
Rобщ=(R1*R2)/(R1+R2)
Приведем к эквивалентным сопротивлениям:
Rэкв1=(R1*R2)/(R1+R2)=(2*3)/(2+3)=1,2 Ом
Rэкв2=R3+R4=3+0,8=3,8 Ом
Rэкв3=Rэкв1+Rэкв2=1,2+3,8=5 Ом
I=U/R=20/5=4 A
Тогда значит на R3 и R4 ток I=4 А, т. Е. I3=I4=4 А
Проверим
Uобщ=U1+U2=I*Rэкв1+I*Rэкв2=4*1.2+4*3.8=20 В
Далее
U1=I*Rэкв1=4*1,2=4,8 В
I1=U1/R1=4,8/2=2,4 A
I2=U1/R2=4,8/3=1,6 A
Проверим баланс токов:
I1+I2=I3=4 ->2.4+1.6=4=4->4=4=4
Проверим баланс напряжений
4,8+4*3,8=20->20=20
Ответ:
I1= 2,4 А
I2 = 1,6 А
I3=I4= 4 А
Так как при последовательном соединении сила тока на любом участке одинакова, значит достаточно найти общую силу тока в цепи. Для этого сначала найдем общее сопротивление двух параллельно соединенных резисторов:
\( R_{1,2}=\frac{R_1\cdot{R_2}}{R_1+R_2}=\frac{2\cdot{3}}{2+3}=1,2 \)Ом
Теперь найдем общее сопротивление всей цепи, учитывая, что оно равно сумме сопротивлений, теперь уже трех последовательно соединенных проводников:
\( R=R_{1,2}+R_3+R_4=1,2+3+0,8=5 \)Ом
А теперь поделив общее напряжение цепи на общее сопротивление и получим общую силу тока:
\( I=\frac{U}{R}=\frac{20}{5}=4 \)А
Такая сила тока будет и на 3 и 4 резисторах, а также в цепи из 1 и 2 резисторов.
Зная общее сопротивление и общую силу тока этих двух резисторов, найдем их общее напряжение:
\( U_{1,2}=R_{1,2}\cdot{I}=1,2\cdot4=4,8 \)В
Остается это напряжение поделить поочередно на сопротивления 1 и 2 резисторов и узнаем силу тока на них:
а) \( I_1=\frac{U_{1,2}}{R_1)}=\frac{4,8}{2}=2,4 \)А
б)\( I_2=\frac{U_{1,2}}{R_2}=\frac{4,8}{3}=1,6 \)А
Ответ:\( I_1=2,4A;I_2=1,6A;I_3=I_4=4A \)
Куб собран из одинаковых резисторов имеющих сопротивление. Сопротивление куба
Размер: px
Начинать показ со страницы:
Транскрипт1 9 класс 1. Минимальный путь Автомобиль, едущий со скоростью υ, в некоторый момент начинает движение с таким постоянным ускорением, что за время τ пройденный им путь s оказывается минимальным. Определите этот путь s. 2. Отражение в полете В баллистической лаборатории при проведении эксперимента по изучению упругого отражения от движущихся препятствий u производился выстрел маленьким шариком из небольшой υ катапульты, установленной на горизонтальной поверхности. Одновременно из точки, в которую по расчетам должен был S упасть шарик, с постоянной скоростью начинала движение навстречу массивная вертикальная стенка (см. рисунок). После упругого отражения от стенки, шарик падал на некотором расстоянии от катапульты. Затем эксперимент повторяли, изменяя только скорость движения стенки. Оказалось, что в двух экспериментах удар шарика о стенку произошел на одной и той же высоте h. Определите эту высоту, если известно, что время полета шарика до отражения в первом случае составило t1 = 1 с, а во втором t2 = 2 c. На какую максимальную высоту H поднимался шарик за весь полет? Чему равна начальная скорость шарика υ, если расстояние между местами его падения на горизонтальную поверхность в первом и втором экспериментах составило L = 9 м? Определите скорости равномерного движения стенки u1 и u2 в этих экспериментах и начальное расстояние S между стенкой и катапультой. Считайте g = 1 м/с 2. Примечание. В системе отсчёта, связанной со стенкой, модули скорости шарика до и после столкновения одинаковы, а угол отражения шарика равен углу падения. 3. Трехцилиндровый Тело, склеенное из трех соосных цилиндров разного поперечного сечения и разной высоты, погружают в некоторую жидкость и снимают зависимость силы Архимеда F, действующей на тело, от глубины h его погружения. Известно, что площадь сечения самого узкого (не факт, что самого нижнего) цилиндра S = 1 см 2. Постройте график зависимости F(h) и с его помощью определите высоту каждого из цилиндров, площади сечения двух других цилиндров и плотность жидкости. В процессе эксперимента ось вращения цилиндров оставалась вертикальной, g = 1 м/с 2. h, см F а, Н,3,9 1,8 2,4 3,6 4,2 4,8 6, 7,2 7,3 7,5 7,6 7,7 7,8 7,9 7,9
2 4. Два в кубе Куб собран из одинаковых резисторов, имеющих сопротивления R. Два резистора заменены на идеальные перемычки, как указано на рисунке. Найдите общее сопротивление получившейся системы между контактами A и B. Какие резисторы из оставшихся можно убрать, чтобы это не изменило общее сопротивление системы? Если известно, что через большинство резисторов в цепи течет ток I = 2 А, вычислите силу тока в проводе, подсоединенном к узлу A (или В)? Вычислите силу тока, текущего через идеальную перемычку AA? 5. Ледяное пятно Определите, какая максимальная масса mп водяного пара, взятого при температуре 1 С, может потребоваться для нагревания льда, находящегося в калориметре, до температуры плавления (без плавления). Точная масса льда и его начальная температура не известны, но эти значения могут лежать в выделенной на -3 m/m диаграмме области. Удельная теплота -4 парообразования L = 2,3 МДж/кг, удельная теплота плавления льда λ = 34 кдж/кг, удельная теплоемкость воды с = 4 2 Дж/(кг С), удельная теплоемкость льда с1 = 2 1 Дж/(кг С). Масса льда m на диаграмме приведена в условных единицах, показывающих, во сколько раз масса льда меньше, чем m = 1 кг. Теплоемкостью калориметра и потерями тепла пренебречь t, С
3 1 класс 1. Время мощности В результате проведенного эксперимента получена зависимость мощности N постоянной горизонтальной силы от времени t ее действия на изначально покоящийся на гладком горизонтальном столе брусок массы m = 2 кг. Некоторые измерения могли оказаться не очень точными. определите мощность силы в момент времени τ = 6 с; найдите значение силы F. N, Вт 1,4 2,8 4,5 5, 6, 1,4 14,7 16,6 18,3 t, с 1, 1,5 2, 2,5 3,2 5, 7,2 8,4 9, 2. В лунке Стержень АВ касается уступа K полусферической лунки радиуса R. Точка А движется равномерно со скоростью υ по поверхности лунки, начиная из нижней точки N, к точке M. Найти зависимость модуля скорости u конца стержня В от угла α, который стержень составляет с горизонтом. Длина стержня АВ равна 2R. 3. Вода со льдом В калориметре смешали некоторое количество воды и льда. Их точные массы и начальные температуры неизвестны, но эти значения лежат в выделенных на диаграмме заштрихованных областях. Найдите максимальное количество теплоты, которое могло быть передано водой льду, если после установления теплового равновесия масса льда не изменилась. Определите возможную массу содержимого калориметра в этом случае. Удельная теплота плавления льда λ = 34 кдж/кг, удельная теплоемкость воды с = 42 Дж/(кг С), удельная теплоемкость льда с1 = 21 Дж/(кг С). Массы воды и льда на диаграмме приведены в условных единицах, показывающих во сколько раз их массы меньше чем m = 1 кг. Теплоемкостью калориметра и потерями теплоты пренебречь t, С 1 m /m
4 4. Три в кубе Куб собран из одинаковых резисторов сопротивлением R. Три резистора заменили на идеальные перемычки, как указано на рисунке. Найдите общее сопротивление получившейся системы между контактами A и B. Какие резисторы из оставшихся можно убрать так, что это не изменит общее сопротивление системы? Если известно, что сила тока, текущего через большинство резисторов электрической цепи, равна, вычислите силу тока в проводе, подсоединенном к узлу A (или В)? I 2A Вычислите силу тока, текущего через идеальную перемычку AA? 5. Транспортёр на боку По шероховатому горизонтальному полу движется лежащий на боку ленточный транспортёр так, что плоскость ленты вертикальна. Скорость ленты транспортёра равна υ. Транспортёр перемещается по полу с постоянной скоростью u перпендикулярно основным участкам его ленты. За некоторое время транспортёр сместился на расстояние s. Его новое положение показано на рисунке. Транспортёр толкает по полу брусок, имеющий форму прямоугольного параллелепипеда. На рисунке дан вид сверху на эту систему. Пренебрегая прогибом ленты и считая движение бруска установившимся, найдите смещение бруска за время s/u. Определите работу по перемещению бруска, совершаемую транспортёром за это время. Коэффициент трения между бруском и полом равен μ1, а между бруском и лентой μ2.
5 11 класс 1. Мощность в пространстве На изначально покоящийся на гладком горизонтальном столе брусок массы m = 2 кг, начали действовать постоянной горизонтальной силой F. В результате была получена зависимость мощности N от перемещения s бруска. Некоторые измерения могли оказаться не очень точными. В каких координатных осях экспериментальная зависимость мощности от перемещения линейна? Определите мощность силы в точке с координатой s = 1 см. Найдите значение силы F. N, Вт,28,4,57,75 1,2 1,1 1,23 1,26 1,5 s, см 1, 2, 4, 7, «Тёмная материя» Скопления звёзд образуют бесстолкновительные системы галактики, в которых звёзды равномерно движутся по круговым орбитам вокруг оси симметрии системы. Галактика NGC 2885 состоит из скопления звёзд в виде шара (ядра радиусом rя = 4 кпк) и тонкого кольца, внутренний радиус которого совпадает с радиусом ядра, а внешний равен 15 rя. Кольцо состоит из звёзд с пренебрежимо малой по сравнению с ядром массой. В ядре звёзды распределены равномерно. Было установлено, что линейная скорость движения звёзд в кольце не зависит от расстояния до центра галактики: от внешнего края кольца вплоть до края ядра скорость звёзд υ = 24 км/с. Такое явление может быть объяснено наличием несветящейся массы («тёмной материи»), распределенной сферически симметрично относительно центра галактики вне её ядра. 1) Определите массу Mя ядра галактики. 2) Определите среднюю плотность ρя вещества ядра галактики. 3) Найдите зависимость плотности «тёмной материи» ρт(r) от расстояния до центра галактики. 4) Вычислите отношение массы «тёмной материи», влияющей на движение звёзд в диске, к массе ядра. Примечание: 1 кпк = 1 килопарсек = 3, м, гравитационная постоянная γ = 6, Н м 2 кг 2.
6 3. Четыре в кубе Куб собран из одинаковых резисторов, имеющих сопротивления R. Четыре резистора заменены на идеальные перемычки, как указано на рисунке. Найдите общее сопротивление получившейся системы между контактами A и B. Через какие резисторы сила текущего тока максимальна, а через какие и минимальна? Найдите эти значения силы тока, если сила тока, входящего в узел А равна I = 1,2 А? Какова сила тока, текущего через идеальную перемычку AA`? 4. Ромб. Циклический процесс, совершаемый над идеальным газом, на (p, V) плоскости представляет собой ромб (см. качественный рисунок). Вершины (1) и (3) лежат на одной изобаре, а вершины (2) и (4) на одной изохоре. За цикл газ совершил работу А. Насколько отличается количество теплоты Q12, подведённой к газу на участке 1-2, от количества теплоты Q 3,4 участке 3-4?, отведённой от газа на 5. Колебаниям нет! В электрической цепи (см. рис.), состоящей из резистора сопротивлением R, катушки индуктивностью L, на конденсаторе емкостью C находится заряд Q. В некоторый момент времени замыкают ключ К и одновременно начинают изменять емкость конденсатора так, что идеальный вольтметр показывает постоянное напряжение. 1) Как зависит от времени емкость конденсатора C(t) при изменении t от до t 1 C L? 2) Какую работу за время t1 совершили внешние силы? Считайте, что t 1 L / R C L. Подсказка. Количество теплоты, выделившейся на резисторе за время t1, равно t1 2 2 Q WR I () t Rdt. 3C
11 класс 1 Мощность в пространстве На изначально покоящийся на гладком горизонтальном столе брусок массы m = кг, начали действовать постоянной горизонтальной силой F В результате была получена зависимость
Региональный этап всероссийской олимпиады школьников по физике января 16 г 11 класс 1 Мощность в пространстве На изначально покоящийся на гладком горизонтальном столе брусок массы m = кг, начали действовать
Региональный этап всероссийской олимпиады школьников по физике. января 6 г. 9 класс. Минимальный путь Автомобиль, едущий со скоростью υ, в некоторый момент начинает движение с таким постоянным ускорением,
1 класс 1. Время мощности В результате проведенного эксперимента получена зависимость мощности N постоянной горизонтальной силы от времени t ее действия на изначально покоящийся на гладком горизонтальном
11 класс 1. Плотность кислорода Найти плотность кислорода при давлении param1 кпа и температуре param2 К. Газ считать идеальным. param1 50 150 200 300 400 param2 300 350 400 450 500 2. Мощность в цепи
7 класс 1. Моток медной проволоки имеет массу 360 г. Найдите длину проволоки в мотке, если площадь поперечного сечения проволоки 0,126 мм 2, а 1 см 3 меди имеет массу 8,94 г. Ответ выразите в метрах и
И. В. Яковлев Материалы по физике MathUs.ru Открытая олимпиада Физтех-лицея 2015 Физика, 11 класс 1. На тонком прозрачном горизонтальном столе лежит тонкая собирающая линза с фокусным расстоянием F = 70
Первый (отборочный) этап академического соревнования Олимпиады школьников «Шаг в будущее» по общеобразовательному предмету «Физика», Осень 05 г. Вариант З А Д А Ч А. Первую половину времени тело движется
9 класс Школьник Петя Иванов из имеющихся в его распоряжении шести проволок собрал схему, изображённую на рис. 1. Найти сопротивление цепи между точками А и D, если сопротивления проволок AB и BD равны
11 класс. 1 тур 1. Задача 1 Цилиндрическая шайба, скользившая по гладкому льду со скоростью, испытала лобовое упругое соударение с покоившейся цилиндрической шайбой другой массы. После соударения первая
Межрегиональная предметная олимпиада Казанского федерального университета по предмету «Физика» 9 класс. Вариант 1. 2014-2015 учебный год, интернет-тур 1. (1 балл) Мальчик Петя первую половину пути от школы
И. В. Яковлев Материалы по физике MathUs.ru Олимпиада «Физтех» по физике 11 класс, онлайн-этап, 2013/14 год 1. Камень, брошенный с крыши сарая почти вертикально вверх со скоростью 15 м/с, упал на землю
Банк заданий по физике 1 класс МЕХАНИКА Равномерное и равноускоренное прямолинейное движение 1 На рисунке приведён график зависимости координаты тела от времени при его прямолинейном движении по оси x.
Олимпиада имени Дж. Кл. Максвелла Региональный этап января 6 года 7 класс. Где тут плотность? В лаборатории провели измерtния массы и объема пяти тел, изготовленных из четырех материалов: березы, ρ Б =,7
Параграфы 88-93 повторить выполнить упражнение 12. Выполнить тест Вариант 3679536 1. Задание 1 На рисунке изображены графики зависимости модуля скорости движения четырёх автомобилей от времени. Один из
Минская городская олимпиада ФИЗИКА 2002 год 11 класс. 1. Ротор модели электродвигателя представляет собой прямоугольную рамку площадью S, содержащую n витков проволоки, закрепленную на массивном основании,
Министерство образования и науки Пермского края Физика Задания муниципального этапа всероссийской олимпиады школьников в Пермском крае 2017/2018 учебный год МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ПРОВЕДЕНИЮ МУНИЦИПАЛЬНОГО
МОСКОВСКАЯ ОЛИМПИАДА ШКОЛЬНИКОВ ПО ФИЗИКЕ 2016 2017 уч. г. НУЛЕВОЙ ТУР, ЗАОЧНОЕ ЗАДАНИЕ. 11 КЛАСС В прилагаемом файле приведено ноябрьское заочное задание для 11-го класса. Подготовьте несколько листов
10 класс. Вариант 1. 1. (1 балл) Частота вращения воздушного винта легкомоторного самолёта 1500 об/мин. Сколько оборотов успеет сделать винт на пути 90 км при скорости полёта 180 км/ч. 1) 750 2) 3000 3)
Физика. При расчетах принять: м Ускорение свободного падения g 10 с Универсальная газовая постоянная Дж R 8,31 моль К Постоянная Авогадро N A 6, 0 10 моль 3 1 Постоянная Планка h 34 6,63 10 Дж с 1 Ф Электрическая
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ НЭ БАУМАНА ЗАКЛЮЧИТЕЛЬНЫЙ ЭТАП ОЛИМПИАДЫ «ШАГ В БУДУЩЕЕ» ПО КОМПЛЕКСУ ПРЕДМЕТОВ «ТЕХНИКА И ТЕХНОЛОГИЯ» ВАРИАНТ 8 З А Д А Ч А Из пункта А, находящегося
Курчатов 2018, физика, отборочный этап 11 класс Гидростатика Задача 1.1 Куб со стороной a = 10 см плавает в ртути, погрузившись на 1/4 своего объёма. Поверх ртути постепенно доливают воду до тех пор, пока
Заключительный (очный) этап Всесибирской олимпиады по физике Задачи 9 кл. (29 марта 2009 г.) 2R m 3R 1. Массивная однородная цепь с грузом массы m на одном конце перекинута через блок радиуса R и находится
В прилагаемом файле приведено ноябрьское заочное задание для 11-го класса. Подготовьте несколько листов в клетку, на которых от руки напишите развёрнутые решения прилагаемых задач. Сфотографируйте страницы
Первый (отборочный) этап академического соревнования Олимпиады школьников «Шаг в будущее» по общеобразовательному предмету «Физика», осень 016 г. Вариант 1 1. Диск катится без проскальзывания по горизонтальной
Динамика твердого тела. 1. Тонкий однородный стержень АВ массы m = 1,0 кг движется поступательно с ускорением а = 2,0 м/с 2 под действием сил F 1 и F 2. Расстояние b = 20 см, сила F 2 = 5,0 Н. Найти длину
9Ф Раздел 1. Понятия, определения Вставьте недостающие слова: 1.1 Тело можно считать материальной точкой только тогда, когда 1.2 Если в любой момент времени все точки тела движутся одинаково, то такое
И. В. Яковлев Материалы по физике MathUs.ru Открытая олимпиада Физтех-лицея 2015 Физика, 9 класс 1. Масса до краёв заполненной пробирки с водой M 1 = 160 г. После того как в неё поместили кусочек металла
И. В. Яковлев Материалы по физике MathUs.ru Гравитация Задача 1. (МФТИ, 1987) С какой скоростью должен был бы лететь самолёт вдоль экватора, чтобы сила давления сидящих пассажиров на кресла самолёта уменьшилась
Итоговый годовой тест по физике 10 класс 1 вариант Часть А A1. По кольцевой автомобильной дороге длиной L = 15 км в одном направлении едут грузовой автомобиль и мотоцикл со скоростями соответственно V1
ОЛИМПИАДА ШКОЛЬНИКОВ «ШАГ В БУДУЩЕЕ» Комплекс предметов «ТЕХНИКА И ТЕХНОЛОГИИ» МАТЕРИАЛЫ ОЛИМПИАДНЫХ ЗАДАНИЙ 008-009 ГОД I. Научно-образовательное соревнование ЗАДАНИЯ ПО МАТЕМАТИКЕ Решить систему уравнений
Занятие 11 Итоговый 2. Механика. Задача 1 На рисунке представлен график зависимости пути S велосипедиста от времени t. Определите интервал времени после начала движения, когда велосипедист двигался со
Класс 11 Билет 11-01 Шифр 1. Систему из трех брусков, находящихся на горизонтальном столе, приводят в движение, прикладывая горизонтальную силу F (см. рис.). Коэффициент трения между столом и брусками
Физика, 9 класс (10 класс- 1 полугодие) Вариант 1 1 По графику зависимости модуля скорости от времени, представленному на рисунке, определите модуль ускорения прямолинейно движущегося тела в момент времени
Отложенные задания (25) В области пространства, где находится частица с массой 1 мг и зарядом 2 10 11 Кл, создано однородное горизонтальное электрическое поле. Какова напряжённость этого поля, если из
Минская областная олимпиада школьников по физике 2000 год 11 класс. 1. Две шайбы массами m и 2m, связанные невесомой нитью длиной l лежат на гладкой горизонтальной поверхности так, что нить полностью растянута.
9 класс Задача. Падение сосульки. С крыши дома оторвалась сосулька и за t=0.2 с пролетела мимо окна, высота которого h =.5 м. С какой высоты h x, относительно верхнего края окна она оторвалась? Размерами
И. В. Яковлев Материалы по физике MathUs.ru Открытая олимпиада Физтех-лицея 2015 Физика, 10 класс 1. Герметичный сосуд разделён на два отсека с теплоизолирующей перегородкой, в которой сделано небольшое
10 класс. Вариант 1 1. Тело соскальзывает с наклонной плоскости с углом наклона =30 о. На первых k=1/3 пути коэффициент трения 1 05,. Определите коэффициент трения на оставшемся отрезке пути, если у основания
Вариант 2805281 1. Мальчик съезжает на санках равноускоренно со снежной горки. Скорость санок в конце спуска 10 м/с. Ускорение равно 1 м/с 2, начальная скорость равна нулю. Какова длина горки? (Ответ дайте
Тульский государственный университет. Олимпиада по физике февраля 6 г.. Цилиндр радиуса R = см зажат между двумя горизонтальными поверхностями, которые движутся в разные стороны со скоростями v = 4 м/с
ВСЕРОССИЙСКЯ ОЛИМПИД ШКОЛЬНИКОВ ПО ФИЗИКЕ. 017 018 уч. г. МУНИЦИПЛЬНЫЙ ЭТП. 10 КЛСС 1. Два шарика брошены одновременно навстречу друг другу с одинаковыми начальными скоростями: один с поверхности земли
Административная работа за 1 полугодие Вариант 1. Часть 1 А1. На графике приведена зависимость скорости прямолинейно движущегося тела от времени. Определите модуль ускорения тела. 1) 10 м/с 2 2) 5 м/с
Первый (отборочный) этап академического соревнования Олимпиады школьников «Шаг в будущее» по образовательному предмету «физика», осень 05 г Вариант 5 З А Д А Ч А Тело совершает два последовательных, одинаковых
Олимпиадные задания 2014/2015 уч.г. 9 класс Вариант 1 1. Кубик плотности ρ 1 удерживается в равновесии невесомой пружиной под наклонной стенкой, угол наклона которой равен α, в жидкости плотности ρ 2 >ρ
216 год Класс 9 Билет 9-1 1 Два груза массами m и, находящиеся на гладком горизонтальном столе, связаны нитью и соединены с грузом массой 3m другой нитью, перекинутой через невесомый блок (см рис) Трением
Типовой вариант академического соревнования Олимпиады школьников «Шаг в будущее» по общеобразовательному предмету «Физика» З А Д А Ч А 1. Точка движется вдоль оси х по закону скорости точки при t = 1 c.
Задание 1 Цилиндрический сосуд, в который налита жидкость, закрыли герметичной крышкой и начали двигать вертикально вниз с ускорением 2,5 g. Определите давление жидкости на крышку сосуда, если в неподвижном
2.1. В калориметре находился лед при температуре t 1 = -5 С. Какой была масса m 1 льда, если после добавления в калориметр т 2 = 4 кг воды, имеющей температуру t 2 = 20 С, и установления теплового равновесия
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ НЭ БАУМАНА ЗАКЛЮЧИТЕЛЬНЫЙ ЭТАП ОЛИМПИАДЫ «ШАГ В БУДУЩЕЕ» ПО КОМПЛЕКСУ ПРЕДМЕТОВ «ТЕХНИКА И ТЕХНОЛОГИЯ» ВАРИАНТ 5 З А Д А Ч А Из пункта А, находящегося
Билет N 5 Билет N 4 Вопрос N 1 На тело массой m 2,0 кг начинает действовать горизонтальная сила, модуль которой линейно зависит от времени: F t, где 0.7 Н/с. Коэффициент трения k 0,1. Определить момент
Установление соответствия, часть 2 1. русок, находящийся на шероховатой горизонтальной поверхности, начинает двигаться равноускоренно под действием силы В системе отсчета, связанной с горизонтальной поверхностью,
Комплексная олимпиада школьников «Академика» Olym[email protected] 1. Начальная скорость камня, брошенного под некоторым углом к горизонту, равна 10 м/с, а спустя время 0,5 с скорость камня равна 7 м/с. На
Задание 1 Выберите, какова ориентация изображения предмета «b» в плоском зеркале «а» (см. рис.). a 45 0 b а б в г д Задание 2 Телу массы m и удельной теплоемкости c передали количество теплоты Q. Температура
Билет N 5 Билет N 4 Вопрос N 1 Два бруска с массами m 1 = 10,0 кг и m 2 = 8,0 кг, связанные легкой нерастяжимой нитью, скользят по наклонной плоскости с углом наклона = 30. Определите ускорение системы.
Республиканская Предметная Олимпиада Районный (Городской) этап Физика Имя Фамилия Школа 1 Длительность экзамена составляет 180 минут 4 неправильных ответа забирают балы за 1 правильный ответ 3 Каждый вопрос
Белорусская республиканская олимпиада по физике (Гомель, 1998 г.) 9 класс 9.1 Для исследования упругих свойств резины резиновая ленточка была подвешена вертикально, и к ее нижнему краю прикреплялись различные
Часть 1 Ответами к заданиям 1 4 являются цифра, число или последовательность цифр. Запишите ответ в поле ответа в тексте работы, а затем перенесите в БЛАНК ОТВЕТОВ 1 справа от номера соответствующего задания,
Задания В2 по физике 1. Пружинный маятник вывели из положения равновесия и отпустили без начальной скорости. Как изменяются в течение первой четверти периода колебаний груза маятника следующие физические
Олимпиада «Физтех» по физике 9 Класс Билет — Шифр (заполняется секретарём) 3. Пушка установлена на плоском склоне горы, образующем угол с горизонтом. При выстреле «вверх» по склону снаряд падает на склон
Олимпиада «Физтех» по физике 8 Класс Билет — Шифр (заполняется секретарём) Систему из трех брусков, находящихся на горизонтальном столе, приводят в движение, прикладывая горизонтальную силу (см рис) Коэффициент
1 Кинематика 1 Материальная точка движется вдоль оси x так, что времени координата точки x(0) B Найдите x (t) V x At В начальный момент Материальная точка движется вдоль оси x так, что ax A x В начальный
Занятие 7 Законы сохранения Задача 1 На рисунке изображены графики изменения скоростей двух взаимодействующих тележек разной массы (одна тележка догоняет и толкает другую). Какую информацию о тележках
Объяснение явлений 1. На рисунке представлен схематичный вид графика изменения кинетической энергии тела с течением времени. Выберите два верных утверждения, описывающих движение в соответствии с данным
И. В. Яковлев Материалы по физике MthUs.ru Электромагнитная индукция Задача 1. Проволочное кольцо радиусом r находится в однородном магнитном поле, линии которого перпендикулярны плоскости кольца. Индукция
9 класс. Вариант 1. Тело бросили с башни горизонтально. Через t = с его скорость увеличилась в k=3 раза. С какой скоростью V0 бросили тело? Скорость тела изменяется в зависимости от времени как Для заданного
7 класс 1. Сколько раз за сутки часовая и минутная стрелки часов лежат на одной прямой линии? 2. Масса пустой канистры 200 г, а канистры, заполненной керосином, 5 кг. Сколько литров керосина в канистре?
И. В. Яковлев Материалы по физике MathUs.ru Содержание Сила трения 1 Всероссийская олимпиада школьников по физике………………. 1 2 Московская физическая олимпиада……………………… 3 3 МФТИ
Итоги муниципального этапа всероссийской олимпиады школьников по физике 2012-2013 учебный год Анализ результатов муниципального этапа олимпиады 1 задание. 9 класс Экспериментатор Глюк с балкона наблюдает
Инструкция к заданиям #1_45: В этих заданиях заданы вопросы и приведены пять предполагаемых ответов, только один из которых правильный. Найдите соответствующий данному заданию номер в листе ответов, отыщите
Решения и критерии оценивания Задача 1 Деревянный цилиндр плавает в цилиндрическом сосуде с водой, как показано на рис. 1, выступая на a = 60 мм над уровнем жидкости, который равен h 1 = 300 мм. На верхнюю
ЛИЦЕЙ 1580 (ПРИ МГТУ ИМ.Н.Э.БАУМАНА) КАФЕДРА «ОСНОВЫ ФИЗИКИ», 11КЛАСС, 3 СЕМЕСТР 2018-2019 УЧЕБНЫЙ ГОД Вариант 0 Задача 1. Топкое прополочное кольцо площади S = 100 см. 2 -, имеющее сопротивление R = 0,01
Транскрипт1 Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год. Часть I.Расчёт сопротивлений Закон Ома. Сопротивление. Последовательное и параллельное соединение.симметричные схемы. Мостики. Преобразование звезда-треугольник. Цепи с перемычками. Бесконечные цепочки и сетки.. Определите эквивалентное сопротивление проволочных структур, представленных на рисунке. Сопротивление каждого звена структуры, т.е. проволочки между узлами вне зависимости от длины равно. а) б) в) г) д) е) ё) 2. Nточек соединены друг с другом одинаковыми проводниками с сопротивлением каждый. Определить эквивалентное сопротивление схемы между двумя соседними точками. 3. В мосте Уитстона сопротивления подбирают таким образом, что чувствительный гальванометр показывает нуль. а) Считая сопротивления, 2 и r известными, определите величину сопротивления rx. б)если поменять местами батарею и гальванометр, то снова получится мостовая схема. Сохранится ли баланс в новой схеме? 4. Найдите эквивалентное сопротивление участка цепи. а) 2 б) 2 в) Определите эквивалентное сопротивление участка цепи,содержащего перемычки с пренебрежимо малым сопротивлением. а) б) Электрическая цепь составлена из семи последовательно соединенных резисторов = ком, 2 = 2 ком, 3 = 3 ком, 4 = 4 ком, 5 = 5 ком, 6 = 6 ком, 7 = 7 ком и четырех перемычек. На вход подается напряжение U = 53,2 В. Укажите резисторы, через которые протекают минимальный и максимальный токи, и определите значения этих токов.
2 Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год. 7. Цепь, состоящая из трех резисторов и четырех одинаковых перемычек (две нижние соединены параллельно), подключена к источнику с напряжением U = 0 В. Считая известными = 3 Ом,определите силу тока в перемычке В. Сопротивление перемычек гораздо меньше сопротивления резисторов. U 2 В 8. Куб собран из одинаковых резисторов, имеющих сопротивления. Два резистора заменены на идеальные перемычки, как указано на рисунке. Найдите общее сопротивление получившейся системы между контактами и B. Какие резисторы из оставшихся можно убрать, и это не изменит общее сопротивление системы? Если известно, что через большинство резисторов в схеме течет ток I = 2, какой общий ток входит в систему в узле? Какой ток течет через идеальную перемычку `? ` K M C L В В` 9. Определите сопротивление проволочной сетки между указанными выводами. Рамка, выделенная толстой линией, имеет пренебрежимо малое сопротивление. Сопротивлениекаждого из остальных звеньев сетки равно. 0. Определите эквивалентное сопротивление полубесконечных цепочек резисторов, представленных на рисунке. 2 2 а) б) в) Определите эквивалентное сопротивление бесконечноразветвляющейся цепочки, состоящей из резисторов с сопротивлением. 2. Бесконечная сетка с квадратными ячейками изготовлена из проволоки. Сопротивление каждого ребра сетки равно. На рисунке C середина ребра B. Известно, что при подключении омметра между точками и B он показывает сопротивление /2. Какое сопротивление покажет омметр, подключенный между точками и C? 3. Определите сопротивление бесконечных плоских сеток с сопротивлением одной стороны ячейки, измеренное между узлами и В. а) б) в) В В В 4. Определите сопротивление бесконечной объемной кубической сетки с сопротивлением одной стороны ячейки, измеренное между соседними узлами и В.
3 Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год. 5. Пустотелый металлический шар имеет радиус r = 0 см и толщину стенок d = мм. Он изготовлен из меди, за исключением полоски на «экваторе» шириной a = 2 мм, которая выполнена из алюминия. Когда на «полюса» шара было подано напряжение U = 0, мв, через него пошел ток I = 5,2. Опыт повторили с другим шаром, у которого вместо алюминиевой полоски была железная. Какой ток пойдет через этот шар? Удельное сопротивление алюминия 0,03 Ом мм 2 /м, железа 0,0 Ом мм 2 /м. 6. Кольцо радиуса r = 0 см изготовлено из проволоки сечением S = 5 мм 2. Материал проволоки неоднороден и его удельное сопротивление зависит от угла φ так, как показано на графике. Сопротивление между всевозможными парами точек кольца измеряют омметром. Какое максимальное сопротивление может быть получено при таких измерениях?
4 Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год. Измерения силы тока и напряжения. мперметр, вольтметр и омметр. Часть II.Измерительные приборы. Определите неизвестные параметры электрической цепи. (Приборы считать идеальными). U 0 2 а) U 0 = 24 B = 2 I -? U v-? б) 2 U I 4 = = 2 2 = 3 3 = 2 4 = 20 5 = 0 U-? I 6 =? 2. Определите показание амперметра в изображенной на рисунке цепи. Напряжение источника U =,5 В, сопротивление каждого резистора = ком. 3. На участке цепи, схема которого приведена на рисунке, включены резисторы с сопротивлениями = 6 Ом, 2 = 3 Ом, 3 = 5 Ом, 4 = 8 Ом. Показания первого амперметра I = 0,. Найдите показания второго амперметра. 4. По известным показаниям приборов определите неизвестные. Сопротивления амперметров считать гораздо меньшим, чем сопротивление резисторов. Приборы одинаковые. 6 а) б) в) В 5 B 5 2 3В г) д) B Как будут изменяться показания идеальных приборов при перемещении ползунка реостата/потенциометра в направлении, указанном стрелкой или при размыкании ключа? 3 а) б) в) г) Ɛ,r Ɛ,r 6. Схема собрана из некоторого количества различающихся между собой резисторов, реостата, идеальных батарейки, вольтметра и амперметра. Ползунок реостата сдвигают, немного увеличивая его сопротивление. В какую сторону изменятся показания вольтметра и амперметра?
5 Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год. 7. Определите показания вольтметра, подключенного между двумя узлами фрагмента электрической цепи, если показания амперметров и 3 равны I = 2, I3 = 9 соответственно, а сопротивление резисторов = 0 Ом. I2 I3 I 8. Электрическая цепь в форме тетраэдра содержит четыре одинаковых резистора, идеальный источник постоянного напряжения и идеальный амперметр, который показывает силу тока I = 2. Если заменить амперметр идеальным вольтметром, он покажет напряжение U = 2 В. Определите напряжение U0 источника и сопротивление одного резистора. 9. Электрическая цепь представляет собой сетку, состоящую из одинаковых звеньев, имеющих одинаковые сопротивления. Одно из звеньев заменено на идеальный вольтметр. На схему подано напряжение U0 = 9,7 В. Найдите показание вольтметра. U0 0. Электрическая цепь представляет собой сетку, состоящую из одинаковых звеньев, имеющих одинаковые сопротивления. Одно из звеньев заменено на идеальный вольтметр. На схему подано напряжение U0 = 73 В. Найдите показание вольтметра. U0. Экспериментатор из нескольких одинаковых резисторов и одинаковых вольтметров собрал схему, изображенную на рисунке. Чему будет равна сумма показаний всех вольтметров, если на контакты В подать напряжение U = 6 В. Сопротивление вольтметров гораздо больше сопротивления резисторов. 2. Участок схемы состоит из неизвестных сопротивлений. Как, имея источник, идеальные амперметр и вольтметр, соединительные провода с нулевым сопротивлением, измерить сопротивление, подключенного к точкам и B, не разрывая ни одного контакта в схеме? W C K В N D C L E D F G 3. Знаток физики собрал схему из трех одинаковых резисторов, подключил ее к источнику постоянного напряжения (который можно считать идеальным) и измерил вольтметром напряжение сначала между точками и D, а потом между точками и B. У него получилось U = 3 В и U2 = 0,9 В соответственно. Тогда знаток физики соединил точки и C проводом (сопротивлением которого можно пренебречь) и измерил напряжение между точками B и D. Что он получил? 4. Схема, приведенная на рисунке, содержит 50 разных амперметров и 50 одинаковых вольтметров. Показания первого вольтметра U = 9,6 В, первого амперметра I = 9,5 м, второго амперметра I2 = 9,2 м. Определите по этим данным сумму показаний всех вольтметров. 5. Если к батарее подключен только первый вольтметр, то он показывает 4 В. Если подключен только второй — то он показывает 4,5 В. Если к батарее подключены последовательно оба этих вольтметра, то вместе они показывают 5 В. Какими будут показания этих двух вольтметров, если их подключить к этой же батарее параллельно? 2 B
6 Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год. 6. Электрическая цепь состоит из двух одинаковых вольтметров, и двух амперметров. Их показания U = 0 В, U2 = 20 В, I = 50 м, I2 = 70 м соответственно. Определите сопротивление резистора, получив ответ в общем виде. 7. Электрическая цепь состоит из батарейки, шести резисторов, значения сопротивлений которых = Ом, 2 = 2 Ом, 3 = 3 Ом, 4 = 4 Ом, и трех одинаковых амперметров, внутреннее сопротивление r которых мало. Вычислите показания амперметров, если напряжение батарейки U = 99 В. 8. Найдите показания одинаковых вольтметров. Сопротивления вольтметров гораздо больше сопротивлений резисторов = 0 Ом. Напряжение на входе U = 4,5 В. 9. К батарее с ЭДС Ɛ = 9 В и неизвестным внутренним сопротивлением подключены последовательно амперметр и вольтметр. Сопротивления приборов неизвестны. Если параллельно вольтметру включено сопротивление (его величина тоже неизвестна), то показание амперметра вдвое увеличивается, а показание вольтметра вдвое уменьшается. Каким стало показание вольтметра после подключения сопротивления? 20. Определите показания одинаковых омметров в схемах, представленных на рисунке.сопротивление каждого из резисторов в схемах равно. а) б) в) 2. Электрическая цепь представляет собой сетку, состоящую из одинаковых звеньев, имеющих одинаковые сопротивления. Два из звеньев заменены на одинаковые омметры. Найдите показания омметров. 22. Определите сумму показаний омметров в схеме, представленной на рисунке. Ɛ,r Ɛ 2,r Из одинаковых омметров собрали цепь, изображённую на рисунке. Один из приборов показывает сопротивление = 2000 Ом. Определите сумму показаний двух оставшихся омметров. 24. Построить график зависимости показаний правого омметра в зависимости от сопротивления реостата, которое может изменяться в пределах от 0 до 2. Собственное сопротивление омметра. Омметры считать одинаковыми. 0-2
7 Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год. Часть III.Источники напряжения. Нелинейные элементы Закон Джоуля-Ленца. Источники напряжения. Электродвижущая сила источника тока. Закон Ома для полной цепи. Соединения источников тока. Нелинейные элементы.. Схема, изображенная на рисунке, собрана из одинаковых лампочек и подключена к источнику напряжения. Расположите лампочки в порядке возрастания яркости. 2. К регулируемому источнику напряжения подключена схема из четырех резисторов, как показано на рисунке. мперметр показывает ток 2,5. На двух резисторах выделяется мощность 50 Вт, на других двух 200 Вт. Ключ K замыкают, а напряжение источника изменяют так, чтобы амперметр опять показывал 2,5. Какие мощности будут выделяться на резисторах после этого? 3. Цепочка из двух последовательно соединённых резисторов подключена к источнику постоянного напряжения U = 2 В. Сопротивление одного из них = 4 Ом. При каком значении сопротивления 2 второго резистора тепловая мощность, выделяющаяся на нём, будет максимальна? Найти эту максимальную мощность. 4. Имеются одинаковые резисторы, имеющие форму правильного цилиндра. Боковая поверхность каждого резистора хорошо теплоизолирована, и при его нагревании теплоотдача происходит только через торцы. Один из резисторов подсоединили к идеальной батарее. При этом он нагрелся до температуры t = 38 C. Потом к этой батарее последовательно подключили три таких резистора, плотно совместив их торцы и обеспечив хороший электрический контакт. До какой температуры нагреются резисторы? Комнатная температура t0 = 20 C. Мощность теплоотдачи пропорциональна разности температур резистора и окружающей среды. Сопротивление резисторов при нагревании не изменяется. 5. Цилиндрический проводник радиуса r состоит из двух однородных участков с удельными сопротивлениями ρ и ρ2 и соединяющего их неоднородного участка длины L. Какая тепловая мощность выделяется в неоднородном участке, если напряжение на ρ ρ 2 2r единицу длины проводника с удельным сопротивлением ρ равно u и L удельное сопротивление неоднородного участка линейно меняется от ρ до ρ2? 6. К идеальному источнику тока подключен резистор сопротивлением. Напряжение источника равно U. Оказалось, что температура резистора T зависит от времени t как T = T0 + αt (T0 и α известные константы). Резистор имеет массу m и изготовлен из вещества с удельной теплоемкостью c. Чему равна тепловая мощность, отдаваемая резистором в окружающую среду? 7. Сопротивление резистора линейно растет с температурой, а мощность теплоотдачи с его поверхности прямо пропорциональна разности температур резистора и окружающей среды. Если пропускать через резистор очень малый ток, его сопротивление равно 0. Когда величина тока, протекающего через резистор, приближается к I0, резистор быстро разогревается и плавится. Какое напряжение будет на резисторе, если через него пропустить ток I0/2? 8. К резистору, сопротивление которого зависит от температуры по закону (t) = 0 (+ αt), где t температура в С, αи 0 — неизвестные коэффициенты, подключают источник тока. Через некоторое время источник отключают от резистора. График зависимости температуры резистора от времени показан на рисунке. Мощность теплоотдачи резистора в окружающую среду пропорциональна разности температур резистора и окружающей среды: P = βt,гдеβ неизвестный коэффициент. Считая, что температура резистора одинакова во всех его точках, найдитеα.
8 Сейчас не удается отобразить рисунок. Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год. 9. Найдите ЭДС и внутреннее сопротивление эквивалентного источника (Ɛэ = φ φb) Ɛ Ɛ 2 а) б) в) 2r r B 2 r B Ɛ Ɛ r г) д) r е) 2Ɛ B B Ɛ Ɛ r Ɛ 2 Ɛ r B Ɛ r 2Ɛ Ɛ B r 0. Имеется цепь, содержащая N = 000 одинаковых источников тока с ЭДС Ɛ и внутренним сопротивлением r каждый. Между точками иb(на дуге СВ) находится m источников тока. Найдите разность потенциалов между точками и B. Какой будет эта разность потенциалов, если элементы будут обращены друг к другу одноименными полюсами?. Экспериментатор собрал электрическую цепь, состоящую из разных батареек с пренебрежимо малыми внутренними сопротивлениями и одинаковых плавких предохранителей, сопротивление которых тоже очень мало, и нарисовал ее схему (предохранители на схеме обозначены черными прямоугольниками). Экспериментатор помнит, что в тот день при проведении опыта все предохранители остались целыми. Напряжения некоторых батареек известны. Восстановите неизвестные значения напряжений. 2. На рисунке приведены идеализированные вольтамперные характеристики диода и резистора. Постройте вольтамперную характеристику участка цепи, содержащего диод и резистор, соединенные: а) параллельно; б) последовательно. I0 0 I U0 2U0 D U 3. На рисунке приведены идеализированные вольтамперные характеристики диода и резистора. Постройте вольтамперную характеристику участка цепи, содержащего диод и два резистора. -0,4-0,2 3,0 2,0,0 0 -,0 I, D 0,2 0,4 0,6 U, В а) б) 4. На рисунке приведены вольтамперные характеристики резистора и участка цепи, состоящего из резистора и нелинейного элемента, соединенных: а) последовательно; б) параллельно. -0,4-0,2 3,0 2,0,0 0 I, Σ 0,2 0,4 0,6 U, В Постройте вольтамперную характеристику нелинейного элемента. -,0 0,5 5. Определите, через какой нелинейный элемент пойдёт больший ток, 2 0,4 если его подключить к источнику с U0 = 0,5 В и r = Ом. 3 0,3 0,2 I, 0, 0 0, 0,2 0,3 0,4 0,5 0,6 U,В
9 Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год. 6. Найдите величину тока, идущего через диод, в цепи, представленной на рисунке.напряжение идеального источника U и сопротивление известны. 4 U 2 7. В одно из плеч моста включён нелинейныйэлементx,для которого зависимость силы тока Ix от приложенного напряжения Ux дается формулой:ix = Ux 3, где = 0,25 /В 3. Найти мощность Nx,выделяющуюсяна нелинейном элементе в условиях, когда ток через гальванометр Г отсутствует. Сопротивления остальных плеч моста = 2 Ом, 2 = 4 Ом и 3 = Ом. 8. Когда в настольную лампу вставили лампочку, на которой рассеивается мощность W = 60 Вт, то оказалось, что на соединительных проводах лампы рассеивается мощность W2 = 0 мвт. Какая мощность будет рассеиваться на соединительных проводах, если поставить лампочку мощностью W3 = 00 Вт? Напряжение в сети в обоих случаях считать равным U = 220 В. 9. Сопротивление элемента X меняется в зависимости от напряжения на нем. Если напряжение U Uкр сопротивление равно 2. Из трех элементов X собирают схему, показанную на рисунке. Найдите зависимость тока через схему от напряжения на ней. 20. Напряжение источника, подключенного к цепи, состоящей из одинаковых резисторов сопротивлением = Ом и нелинейного элемента, можно изменять. Зависимость показаний амперметра от напряжения источника задана на графике. Положительное направление тока задано на схеме электрической цепи. Восстановите по этим данным вольтамперную характеристику нелинейного элемента. 2. Электрическая цепь, схема которой представлена на рисунке, содержит три одинаковых резистора = 2 = 3 = и три одинаковых диода D, D2, D3. Вольтамперная характеристика диода представлена на графике. Определите силу тока через амперметр I в зависимости от напряжения UВ между точками и В. мперметр идеальный. Постройте график зависимости I от UB, указав значения тока и напряжения в характерных точках. 22. В вашем распоряжении имеется неограниченное количество резисторов произвольного сопротивления и диодов. Диоды пропускают ток только в одном направлении, при этом падение напряжения на них равно В (см. рис. а). Какую схему нужно собрать, чтобы она имела такую зависимость тока от напряжения, как показано на рис. б? Постарайтесь использовать как можно меньше элементов. Контрольная работа. Постоянный ток. на 0 Ом (на одном из параллельно соединённых резисторов) 2. 3/30
10 3. 0/ м 5. 4 м Фонд «Талант и успех». Образовательный центр «Сириус». Направление «Наука». прельская физическая смена. 207 год.
Электричество. Постоянный ток. Кирхгоф Задача 1. Электрическая цепь (см. рисунок) состоит из двух одинаковых вольтметров и двух амперметров. Их показания: U 1 = 10.0 В, U 2 = 10.5 В, I 1 = 50 ма, I 2 =
И. В. Яковлев Материалы по физике MathUs.ru Содержание Электрические цепи 1 Всероссийская олимпиада школьников по физике………………. 1 2 Московская физическая олимпиада………………………
Мастер-класс «Электродинамика. Постоянный ток. Работа и мощность тока». 1. По проводнику течёт постоянный электрический ток. Величина заряда, проходящего через проводник, возрастает с течением времени
1 Постоянный электрический ток Справочные сведения. ОПРЕДЕЛЕНИЕ СИЛЫ ТОКА Пусть через некоторую поверхность, площадь которой S, перпендикулярно ей, за время проходит заряд q. Тогда силой тока называется
Вариант 1 Начальный уровень 1. На рисунке изображен график зависимости силы тока в проводнике от напряжения на его концах. Чему равно сопротивление проводника? А. 8 Ом. Б. 0,125 Ом. В. 16 Ом. Г. 2 Ом.
С1.1. На фотографии изображена электрическая цепь, состоящая из резистора, реостата, ключа, цифровых вольтметра, подключенного к батарее, и амперметра. Используя законы постоянного тока, объясните, как
На рисунке показана цепь постоянного тока. Внутренним сопротивлением источника тока можно пренебречь. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать (
Задание 12. 1. На рисунке изображена схема электрической цепи, состоящей из трёх резисторов и двух ключей К1 и К2. К точкам А и В приложено постоянное напряжение. Максимальное количество теплоты, выделяемое
И. В. Яковлев Материалы по физике MathUs.ru Нелинейные элементы Вольт-амперная характеристика нелинейного элемента электрической цепи является нелинейной функцией. Задача 1. (Всеросс., 1993, финал, 9)
И. В. Яковлев Материалы по физике MathUs.ru Вычисление сопротивлений Задача 1. («Курчатов»016, 8) В лаборатории есть два куска медной проволоки одинакового поперечного сечения. Сопротивление этих кусков,
189 1) В каждом узле цепи сумма втекающих токов равна сумме вытекающих токов, иными словами, алгебраическая сумма всех токов в каждом узле равна нулю. 2) В любом замкнутом контуре, произвольно выбранном
Вариант 1 1. Сила тока в проводнике равномерно нарастает от 0 до 3 А в течение 10 с. Определить заряд, прошедший в проводнике за это время. Ответ: 15Кл. 2. Три батареи аккумуляторов с ЭДС 12 В, 5 В и 10
1. Сила тока в проводнике равномерно нарастает от 0 до 3 А в течение 10 с. Определить заряд, прошедший в проводнике за это время. Ответ: 15Кл. 2. Три батареи аккумуляторов с ЭДС 12 В, 5 В и 10 В и одинаковыми
Уральский федеральный университет имени первого Президента России Б.Н. Ельцина Специализированный учебно-научный центр Летняя школа 2019 Физика Разбор задач и критерии проверки Задача 1.Найти сопротивление
Занятие 19 Постоянный ток. Соединения проводников Задача 1 Перенос вещества происходит в случае прохождения электрического тока через: 1) Металлы и полупроводники 2) Полупроводники и электролиты 3) Газы
В схеме на рисунке сопротивление резистора и полное сопротивление реостата равны R, ЭДС батарейки равна E, её внутреннее сопротивление ничтожно (r = 0). Как ведут себя (увеличиваются, уменьшаются, остаются
Отложенные задания (69) Общее сопротивление участка цепи, изображенного на рисунке, равно 9 Ом. Сопротивления резисторов R 1 и R 2 равны. Чему равно сопротивление каждого резистора? 1) 81 Ом 2) 18 Ом 3)
И. В. Яковлев Материалы по физике MthUs.ru Правила Кирхгофа В статье «ЭДС. Закон Ома для полной цепи» мы вывели закон Ома для неоднородного участка цепи (то есть участка, содержащего источник тока): ϕ
С1.1. На рисунке приведена электрическая цепь, состоящая из гальванического элемента, реостата, трансформатора, амперметра и вольтметра. В начальный момент времени ползунок реостата установлен посередине
Физика 8.1-8.2. Примерный банк заданий Часть 1. Постоянный ток 1. На рисунке приведён участок электрической цепи, по которому течёт ток. В каком из проводников сила тока наименьшая? 1) 1 2) 2 3) 3 4) 4
«ЗАКОНЫ ПОСТОЯННОГО ТОКА». Электрическим током называют упорядоченное направленное движение заряженных частиц. Для существования тока необходимы два условия: Наличие свободных зарядов; Наличие внешнего
Средний уровень Решите устно Задания по теме «Расчет электрических цепей» 8 класс 5.. Резисторы с сопротивлением 5 Ом и 0 Ом соединены один раз последовательно, другой — параллельно. В каком случае их
ЛАБОРАТОРНАЯ РАБОТА 5 ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ПРОВОДНИКОВ Цель работы: изучение методов измерения сопротивлений, изучение законов электрического тока в цепях с последовательным и параллельным соединением
И. В. Яковлев Материалы по физике MathUs.ru Самоиндукция Пусть через катушку протекает электрический ток I, изменяющийся со временем. Переменное магнитное поле тока I порождает вихревое электрическое поле,
Задания 15 по физике 1. Электрическая цепь состоит из источника постоянного напряжения с ЭДС = 40 В и внутренним сопротивлением r=2 Ом, резистора с переменным сопротивлением и амперметра. На каком из приведенных
Иркутский государственный технический университет Кафедра общеобразовательных дисциплин ФИЗИКА Лабораторная работа 3.3. «Определение неизвестных сопротивлений при помощи мостовой схемы» доц. Щепин В.И.
Измерение мощности и работы тока в электрической лампе. Цель работы: Научиться определять мощность и работу тока в лампе. Оборудование: Источник тока, ключ, амперметр, вольтметр, лампа, секундомер. Ход
ФИЗИК, 11 класс, УМК 2 Вариант 1, Октябрь 2012 Краевая диагностическая работа по ФИЗИКЕ Вариант 1 Часть 1 При выполнении заданий 1 7 в бланке ответов 1 под номером выполняемого задания поставьте знак «х»
Постоянный электрический ток. Сила тока Постоянный электрический ток. Напряжение Закон Ома для участка цепи Электрическое сопротивление. Удельное сопротивление вещества Электродвижущая сила. Внутреннее
И. В. Яковлев Материалы по физике MathUs.ru Мощность тока Задача 1. («Курчатов», 2017, 8) С помощью электромотора груз массой 50 кг поднимают вверх. При этом груз движется с постоянной скоростью 3,5 см/с.
Юльметов А. Р. Постоянный электрический ток. Электрические измерения Методические указания к выполнению лабораторных работ Оглавление P3.2.4.1. Амперметр как омическое сопротивление в цепи………….
Pdf — файл pitf.ftf.nstu.ru => Преподаватели => Суханов И.И. Лабораторная работа 11 Изучение работы источника постоянного тока Цель работы для цепи «источник тока с нагрузкой» экспериментально получить
Тест по физике 1 вариант A1. Если при неизменном напряжении на концах проводника увеличить сопротивление проводника в 2 раза, то сила тока в проводнике 1) не изменится 3) уменьшится в 2 раза 2) увеличится
И. В. Яковлев Материалы по физике MathUs.ru Содержание Электрические цепи 1 Всероссийская олимпиада школьников по физике………………. 1 2 Московская олимпиада школьников по физике………………..
Московский физико-технический институт Эквивалентные преобразования электрических цепей. Методическое пособие по подготовке к олимпиадам. Составитель: Паркевич Егор Вадимович Москва 2014 Введение. В электротехнике
И. В. Яковлев Материалы по физике MathUs.ru Мощность тока Задача 1. Резисторы с сопротивлениями 2R и 3R соединены последовательно и подключены к источнику постоянного напряжения U. Найдите мощность, выделяющуюся
ПОСТОЯННЫЙ ТОК 2008 Цепь состоит из источника тока с ЭДС 4,5В и внутренним сопротивлением r=,5oм и проводников сопротивлением =4,5 Oм и 2= Oм Работа, совершенная током в проводнике за 20 мин, равна r ε
И. В. Яковлев Материалы по физике MathUs.ru Вычисление сопротивлений Задача 1. (МОШ, 2014, 9 10) Имеются 10 резисторов сопротивлением 1 ком. Нарисуйте схему электрической цепи, сопротивление которой как
Государственное высшее учебное заведение «ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра физики ОТЧЁТ по лабораторной работе 49 ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПОЛЕЗНОЙ МОЩНОСТИ И КОЭФФИЦИЕНТА ПОЛЕЗНОГО
Незаряженные стеклянные кубики 1 и 2 сблизили вплотную и поместили в электрическое поле положительно заряженного шара, как показано в верхней части рисунка. Затем кубики раздвинули и уже потом убрали заряженный
I вариант Тест по теме «Постоянный электрический ток». 1. Для возникновения тока в проводнике необходимо, чтобы… А — на его свободные заряды в определенном направлении действовала сила. Б — на его свободные
Задача 1 Демонстрационный вариант отборочного этапа Электроника 9 класс Как изменится сила взаимодействия между двумя точечными зарядами, если увеличить расстояние между ними в 2 раза? 1 уменьшится в 2
Нурушева Марина Борисовна старший преподаватель кафедры физики 023 НИЯУ МИФИ Электрический ток Электрический ток это направленное (упорядоченное) движение заряженных частиц. Условия существования электрического
Министерство образования Республики Беларусь Учреждение образования «МОГИЛЕВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРОДОВОЛЬСТВИЯ» Кафедра физики ИЗУЧЕНИЕ ЗАКОНОВ ПОСТОЯННОГО ТОКА. ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ МОСТИКОМ
Федеральное агентство по образованию РФ Ухтинский государственный технический университет 4 Измерение сопротивления на постоянном токе Методические указания к лабораторной работе для студентов всех специальностей
Министерство образования Российской Федерации ГОУ ВПО УГТУ-УПИ Кафедра физики ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ ПО ФИЗИКЕ ТЕМА: ЗАКОНЫ ПОСТОЯННОГО ТОКА МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ
ЛАБОРАТОРНАЯ РАБОТА 3 Изучение электропроводности металлов Теоретическое введение Электропроводность металлов Если на концах проводника поддерживается постоянная разность потенциалов, то внутри проводника
1 вариант 1. Определите силу тока и падение напряжения на проводнике R1 электрической цепи, изображенной на рисунке 121, если R1 = 2 Ом, R2 = 4 Ом, R3 = 6 Ом, ЭДС аккумулятора Ε = 4 В, его внутреннее сопротивление
Работа электрического тока, мощность, закон Джоуля Ленца 1. Чему равно время прохождения тока силой 5 А по проводнику, если при напряжении на его концах 120 В в проводнике выделяется количество теплоты,
Объяснение явлений 1. На рис. 1 приведена схема установки, с помощью которой исследовалась зависимость напряжения на реостате от величины протекающего тока при движении ползунка реостата справа налево.
Сила тока и заряд.. Сила тока в лампочке от карманного фонаря I = 0,3 А. Сколько электронов N проходит через поперечное сечение нити накала за время t = 0, c?.3. Какой заряд q пройдет по проводнику сопротивлением
Лабораторная работа Измерение сопротивления проводников мостиком Уитстона Оборудование: реохорд, набор неизвестных сопротивлений, гальванометр, источник постоянного тока, два ключа, магазин сопротивлений.
Лабораторная работа 3.3 ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ МОЩНОСТИ И КПД ИСТОЧНИКА ПОСТОЯННОГО ТОКА ОТ ВНЕШНЕЙ НАГРУЗКИ 3.3.. Цель работы Целью работы является знакомство с компьютерным моделированием цепей постоянного
Физика. 8 класс. Демонстрационный вариант 2 (90 минут) 1 Диагностическая тематическая работа 2 по подготовке к ОГЭ по ФИЗИКЕ по теме «Постоянный ток» Инструкция по выполнению работы На выполнение диагностической
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ
Электродинамика 1. При подключении резистора с неизвестным сопротивлением к источнику тока с ЭДС 10 В и внутренним сопротивлением 1 Ом напряжение на выходе источника тока равно 8 В. Чему равна сила тока
Решение задач по теме «Электродинамика» Захарова В.Т., учитель физики МАОУ СОШ 37 Задание 14. Пять одинаковых резисторов с сопротивлением 1 Ом соединены в электрическую цепь, через которую течёт ток I
Цель работы: познакомиться с одним из методов измерения электрического сопротивления резисторов. Проверить правила сложения сопротивлений при различных способах соединения резисторов. Задача: собрать схему
ПОДГОТОВКА к ОГЭ ЧАСТЬ 1 ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ 1.Два точечных заряда будут притягиваются друг к другу, если заряды 1.одинаковы по знаку и любые по модулю 2.одинаковы по знаку и обязательно одинаковы по
Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа 4» г. Сергиев Посад Лабораторная работа «Измерение ЭДС и внутреннего сопротивления источника тока» 10 «А» класс
Тест по физике Законы электрического тока 8 класс 1 вариант 1. В каких единицах измеряют силу тока? 1) В кулонах (Кл) 2) В амперах (А) 3) В омах (Ом) 4) В вольтах (В) 2. Известно, что через поперечное
Тема 12. Постоянный электрический ток 1. Электрический ток и сила тока Имеющиеся в веществе свободные носители заряда (электроны и/или ионы) в обычном состоянии движутся хаотично. Если создать внешнее
При выполнении заданий 1 7 в поле ответа запишите одну цифру, которая соответствует номеру правильного ответа. 1 На рисунке изображены два одинаковых электрометра, шары которых имеют заряды противоположных
65 7. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК 7. Электрический ток, сила и плотность тока Электрическим током называется упорядоченное (направленное) движение электрических зарядов. Сила тока скалярная физическая
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра «Общая физика и физика нефтегазового производства»
Отложенные задания (25) В области пространства, где находится частица с массой 1 мг и зарядом 2 10 11 Кл, создано однородное горизонтальное электрическое поле. Какова напряжённость этого поля, если из
Лабораторная работа 1 Измерение выталкивающей силы научиться измерять выталкивающую силу, действующую на тела разной формы, погруженные в воду. Приборы и материалы: тела цилиндрической, кубической и неправильной
Цели: обучающая : систематизировать знания и умения учащихся решать задачи ан расчет эквивалентных сопротивлений с помощью моделей, каркасов и т.д.
Развивающая: развитие навыков логического мышления абстрактного мышления, умений заменять схемы эквивалентности, упрощать расчет схем.
Воспитательная: воспитание чувства ответственности, самостоятельности, необходимости навыков приобретенных на уроке в будущем
Оборудование: проволочный каркас куба, тетраэдера, сетки бесконечной цепочки сопротивлений.
ХОД УРОКА
Актуализация:
1. Учитель: “Вспомним последовательное соединение сопротивлений”.
Учащиеся на доске зарисовывают схему.
и записывают
U об =U 1 +U 2
Y об =Y 1 =Y 2
Учитель: вспомним параллельное соединение сопротивлений.
Учащийся на доске зарисовывает элементарную схему:
Y об =Y 1 =Y 2
; для для n равных
Учитель: А теперь будем решать задачи на расчет эквивалентного сопротивления участок цепи представлен в виде геометрической фигуры, либо металлической сетки.
Задача № 1
Проволочный каркас в виде куба, рёбра которого представляют равные сопротивления R. Рассчитать эквивалентное сопротивление между точками А и В. Чтобы рассчитать эквивалентное сопротивление данного каркаса необходимо заменить эквивалентной схемой. Точки 1, 2, 3 имеют одинаковый потенциал, их можно соединить в один узел. А точки (вершины) куба 4, 5, 6 можно соединить в другой узел по той же причине. Учащиеся имеют на каждой парте такую модель. После выполнения описанных действий зарисовывают эквивалентную схему.
На участке АС эквивалентное сопротивление ; на СD ; на DB ; и окончательно для последовательного соединения сопротивлений имеем:
По тому же принципу потенциалы точек А и 6 равны, В и 3 равны. Учащиеся совмещают эти точки на своей модели и получают эквивалентную схему:
Расчёт эквивалентного сопротивления такой цепи прост
Задача № 3
Эта же модель куба, с включением в цепь между точками 2 и В. Учащиеся соединяют точки с равными потенциалами 1 и 3; 6 и 4. Тогда схема будет выглядеть так:
Точки 1,3 и 6,4 имеют равные потенциалы, и ток по сопротивлениям между этими точками не потечёт и схема упрощается до вида; эквивалентное сопротивление которой рассчитывается так:
Задача № 4
Равносторонняя треугольная пирамида, ребро которой имеет сопротивление R. Рассчитать эквивалентное сопротивление при включении в цепь.
Точки 3 и 4 имеют равный потенциал, поэтому по ребру 3,4 ток не потечёт. Учащиеся убирают его.
Тогда схема будет выглядеть так:
Эквивалентное сопротивление рассчитывается так:
Задача № 5
Металлическая сетка с сопротивлением звена равном R. Рассчитать эквивалентное сопротивление между точками 1 и 2.
В точке 0 можно звенья отделить, тогда схема будет иметь вид:
— сопротивление одной половины симметричной по 1-2 точкам. Параллельно ей такая же ветвь, поэтому
Задача № 6
Звезда состоит из 5-и равносторонних треугольников, сопротивление каждого.
Резисторы и сопротивление— AP Physics 2
Пояснение:Поскольку все резисторы подключены параллельно, все они будут испытывать одинаковое падение напряжения, равное напряжению батареи. Кроме того, поскольку каждый резистор имеет одинаковое сопротивление, ток, протекающий через четыре резистора, будет одинаковым.
Ток, протекающий через каждый резистор, можно показать по закону Ома:
Также, полный ток цепи можно найти, отметив:
Кроме того, общее сопротивление можно рассчитать, если учесть, что параллельные резисторы складываются обратно пропорционально.
Поскольку все резисторы одинаковые, можно отметить, что:
Подключаем к предыдущему уравнению, мы видим, что:
Таким образом, если четыре резистора соединены параллельно, общий ток в цепи равен. А поскольку общий ток равномерно распределяется между четырьмя резисторами, мы видим, что:
Теперь, если мы рассмотрим случай с пятью резисторами, соединенными параллельно, мы увидим, что общее сопротивление составляет:
Следовательно, общий ток в цепи при параллельном добавлении пятого резистора составляет:
И еще раз, поскольку каждый из пяти резисторов подключен параллельно, общий ток будет равномерно разделен между ними, что даст:
Таким образом, мы видим, что ток через каждый резистор одинаков как до, так и после добавления пятого резистора.
Подводя итог, можно сказать, что падение напряжения на каждом резисторе одинаково, поскольку они подключены параллельно. Кроме того, поскольку каждый резистор имеет одинаковое сопротивление, ток через каждый из них одинаков. Добавление пятого резистора параллельно уменьшило общее сопротивление цепи и увеличило общий ток, протекающий по цепи. Но поскольку этот новый, больший ток равномерно распределяется между всеми резисторами, включая новый, который был добавлен, ток через каждый из резисторов не изменяется.
Резисторыв схемах — Практика — Физический гипертекст
Давайте начнем процесс с комбинирования резисторов. В этой схеме четыре последовательных пары.
| R с = 3 Ом + 1 Ом R с = 4 Ом R с = 4 Ом + 2 Ом R с = 6 Ом |
| R с = 2 Ом + 3 Ом R с = 5 Ом R с = 1 Ом + 4 Ом R с = 5 Ом |
Эти пары образуют две параллельные цепи, одну слева и одну справа.
| ||||||||
|
| ||||||||
|
Каждый набор из четырех резисторов включен последовательно с другим.
| R с = 2,4 Ом + 0,6 Ом R с = 3 Ом |
| R с = 2,5 Ом + 0,5 Ом R с = 3 Ом |
Левая и правая половины цепи параллельны друг другу и батарее.
| |||||||||||
|
Теперь, когда у нас есть эффективное сопротивление всей цепи, давайте определим ток от источника питания, используя закон Ома.
| I всего = | В всего | + | 24 В | = 16 А |
| R всего | 1,5 Ом |
А теперь пройдемся по трассе (не буквально, конечно). На каждом соединении ток будет делиться: больше по пути с меньшим сопротивлением и меньше по пути с большим сопротивлением. Поскольку заряд не протекает нигде в полной цепи, ток будет одинаковым для всех элементов, последовательно соединенных друг с другом.
Левая и правая половины схемы идентичны по общему сопротивлению, что означает, что ток будет равномерно делиться между ними.
| 8 A для резистора 0,6 Ом на слева . |
| 8 A для резистора 0,5 Ом на правом . |
С каждой стороны ток снова делится на две параллельные ветви.
| Ветви на левый имеют сопротивления в соотношении… | ||||||||
| ||||||||
| что означает, что токи разделятся в соотношении… | ||||||||
| для резисторов 1 Ом и 3 Ом на слева . | ||||||||
| для резисторов 2 Ом и 4 Ом на слева . |
| Ветви на правом идентичны, поэтому ток разделяется на две равные половины. |
| ☟ |
| ☟ |
| ☟ |
| ☟ |
| ☟ |
| для резисторов 2 Ом и 3 Ом на правой стороне . |
| для резисторов 1 Ом и 4 Ом на правой стороне . |
11,2 Закон Ома | Электрические цепи
11,2 Закон Ома (ESBQ6)
temp textТри основные величины для электрических цепей: ток, напряжение (потенциал разница) и сопротивление . Резюме:
Электрический ток, \ (I \), определяется как скорость прохождения заряда через цепь.
Разность потенциалов или напряжение \ (В \) — это количество энергии на единицу заряда, необходимое для перемещения этого заряд между двумя точками в цепи.
Сопротивление, \ (R \), является мерой того, насколько «трудно» протолкнуть ток через элемент схемы.
Теперь посмотрим, как эти три величины связаны друг с другом в электрических цепях.
Георг обнаружил важную взаимосвязь между током, напряжением и сопротивлением в цепи. Симона Ома и называется он законом Ома .
- Закон Ома
Величина электрического тока, протекающего через металлический проводник при постоянной температуре в цепи, равна пропорциональна напряжению на проводнике и может быть описана как
\ (I = \ frac {V} {R} \)где \ (I \) — ток через проводник, \ (V \) — напряжение через проводник, а \ (R \) сопротивление проводника.Другими словами, при постоянной температуре сопротивление проводник постоянен, независимо от приложенного к нему напряжения или проходящего через него тока.
Закон Ома говорит нам, что если проводник имеет постоянную температуру, ток, протекающий через проводник прямо пропорционален напряжению на нем. Это означает, что если мы нанесем напряжение на По оси X графика и тока по оси Y графика мы получим прямую.
Наклон прямолинейного графика связан с сопротивлением проводника как \ [\ frac {I} {V} = \ frac {1} {R} \] Это можно изменить с точки зрения постоянного сопротивления как: \ [R = \ frac {V} {I} \]
временный текстЗакон Ома
Цель
Для определения взаимосвязи между током, протекающим через резистор, и потенциалом разность (напряжение) на одном и том же резисторе.
Аппарат
4 ячейки, 4 резистора, амперметр, вольтметр, соединительные провода
Метод
Этот эксперимент состоит из двух частей. В первой части мы будем изменять приложенное напряжение на резисторе. и измерить результирующий ток в цепи. Во второй части мы будем варьировать ток в цепи и измерьте полученное напряжение на резисторе.После получения обоих наборов измерений, мы рассмотрим взаимосвязь между током и напряжением на резистор.
Изменение напряжения:
Установите схему в соответствии со схемой 1), начиная с одной ячейки.
Нарисуйте следующую таблицу в своем лабораторном журнале.
Количество ячеек
Напряжение, В (\ (\ text {V} \))
Ток, I (\ (\ text {A} \))
\ (\ text {1} \)
\ (\ text {2} \)
\ (\ text {3} \)
\ (\ text {4} \)
Попросите учителя проверить электрическую цепь перед включением питания.
Измерьте напряжение на резисторе с помощью вольтметра, а ток в схему с помощью амперметра.
Добавьте в схему еще одну ячейку \ (\ text {1,5} \) \ (\ text {V} \) и повторите измерения.
Повторяйте, пока не получите четыре ячейки и не заполните таблицу.
Изменение тока:
Установите схему в соответствии со схемой 2), начиная только с 1 резистора в схема.
Нарисуйте следующую таблицу в своем лабораторном журнале.
Напряжение, В (\ (\ text {V} \))
Ток, I (\ (\ text {A} \))
Попросите учителя проверить вашу схему перед включением питания.
Измерьте ток и напряжение на единственном резисторе.
Теперь добавьте еще один резистор последовательно в цепь и измерьте ток и напряжение снова только на исходном резисторе. Продолжайте добавлять резисторы, пока не получите четыре последовательно, но не забывайте измерять напряжение только на исходном резистор каждый раз.Введите измеренные вами значения в таблицу.
Анализ и результаты
Используя данные, записанные в первой таблице, постройте график зависимости тока от напряжения. С напряжение — это переменная, которую мы изменяем напрямую, это независимая переменная. и будет нанесен на ось \ (x \).Текущий является зависимой переменной и должен быть отложено по оси \ (y \).
Используя данные, записанные во второй таблице, постройте график зависимости напряжения от тока. В этом в случае, если независимая переменная — это ток, который должен быть нанесен на ось \ (x \), и напряжение является зависимой переменной и должно быть отложено по оси \ (y \).
Выводы
Изучите график, который вы построили из первой таблицы. Что происходит с током через резистор при увеличении напряжения на нем? т.е. увеличивается или уменьшается?
Изучите график, который вы построили на основе второй таблицы. Что происходит с напряжением на резистор при увеличении тока через резистор? я.е. Увеличивается или уменьшается?
Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.
Вопросы и обсуждение
- Для каждого из ваших графиков вычислите градиент и по нему определите сопротивление оригинальный резистор. Получаете ли вы одно и то же значение, когда рассчитываете его для каждого из ваших графиков?
Как бы вы смогли найти сопротивление неизвестного резистора, используя только мощность? питание, вольтметр и известный резистор \ (R_0 \)?
Закон Ома
Учебное упражнение 11.1Постройте график напряжения (по оси X) и тока (по оси Y).
Какой тип графика вы получите (прямолинейный, парабола, другая кривая)
прямая линия
Рассчитайте градиент графика.
Градиент графика (\ (m \)) — это изменение тока, деленное на изменение напряжение:
\ begin {align *} m & = \ frac {\ Delta I} {\ Delta V} \\ & = \ frac {(\ text {1,6}) — (\ text {0,4})} {(\ text {12}) — (\ text {3})} \\ & = \ текст {0,13} \ end {выровнять *}Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.
Да. График с прямой линией получается, когда мы строим график зависимости напряжения от тока.
Как бы вы смогли найти сопротивление неизвестного резистора, используя только мощность? питание, вольтметр и известный резистор \ (R_ {0} \)?
Вы начинаете с подключения известного резистора в цепь с источником питания.Теперь ваша очередь Считайте напряжение источника питания и запишите это.
Затем вы последовательно подключаете два резистора. Теперь вы можете проводить измерения напряжения. для каждого из резисторов.
Итак, мы можем найти напряжения для двух резисторов. Теперь отметим, что:
\ [V = IR \]Итак, используя это и тот факт, что для резисторов, включенных последовательно, ток такой же везде в цепи мы можем найти неизвестное сопротивление.
\ begin {align *} V_ {0} & = IR_ {0} \\ I & = \ frac {V_ {0}} {R_ {0}} \\ V_ {U} & = IR_ {U} \\ I & = \ frac {V_ {U}} {R_ {U}} \\ \ frac {V_ {U}} {R_ {U}} & = \ frac {V_ {0}} {R_ {0}} \\ \ поэтому R_ {U} & = \ frac {V_ {U} R_ {0}} {V_ {0}} \ end {выровнять *}Омические и неомические проводники (ESBQ7)
Проводники, подчиняющиеся закону Ома, имеют постоянное сопротивление при изменении напряжения на них или ток через них увеличивается.Эти проводники называются омическими проводниками . График ток в зависимости от напряжения на этих проводниках будет прямолинейным. Некоторые примеры омических жилы — резисторы цепи и нихромовая проволока.
Как вы видели, когда мы говорим о законе Ома, есть упоминание о постоянной температуре . Этот происходит потому, что сопротивление некоторых проводников изменяется при изменении их температуры. Эти типы проводники называются неомическими проводниками , потому что они не подчиняются закону Ома.Лампочка распространенный пример неомического проводника. Другими примерами неомических проводников являются диоды и транзисторы.
В лампочке сопротивление нити накала резко возрастает по мере того, как она нагревается из комнаты. температура до рабочей температуры. Если мы увеличим напряжение питания в реальной цепи лампы, в результате увеличение тока вызывает повышение температуры нити, что увеличивает ее сопротивление.Это эффективно ограничивает увеличение тока. В этом случае напряжение и ток не изменяются. подчиняться закону Ома.
Явление изменения сопротивления при изменении температуры присуще почти всем металлам, из которых сделано большинство проводов. Для большинства приложений эти изменения сопротивления достаточно малы, чтобы их можно было игнорируется. При применении металлических ламп накаливания, температура которых сильно повышается (примерно до \ (\ text {1 000} \) \ (\ text {℃} \), и начиная с комнатной температуры) изменение довольно велико.
Как правило, для неомических проводов график зависимости напряжения от тока не будет прямолинейным, указывает на то, что сопротивление не является постоянным для всех значений напряжения и тока.
Включен рекомендуемый эксперимент для неформальной оценки. В этом эксперименте учащиеся получат данные о токе и напряжении для резистора и лампочки и определяют, какой из них подчиняется закону Ома. Вы будете нужны лампочки, резисторы, соединительные провода, источник питания, амперметр и вольтметр.Учащимся следует обнаружите, что резистор подчиняется закону Ома, а лампочка — нет.
Проводники омические и неомические
Цель
Чтобы определить, подчиняются ли два элемента схемы (резистор и лампочка) закону Ома
Аппарат
4 ячейки, резистор, лампочка, соединительные провода, вольтметр, амперметр
Метод
Две схемы, показанные на схемах выше, одинаковы, за исключением того, что в первой резистор, а во втором — лампочка.Настройте обе схемы, указанные выше, начиная с 1 клетка. Для каждой цепи:
Измерьте напряжение на элементе схемы (резисторе или лампочке) с помощью вольтметр.
Измерить ток в цепи с помощью амперметра.
Добавьте еще одну ячейку и повторяйте измерения, пока в вашей цепи не будет 4 ячейки.
Результаты
Нарисуйте в своей книге две таблицы, которые выглядят следующим образом. У вас должна быть одна таблица для измерения первой цепи с резистором и еще одна таблица для второй схемы измерения с помощью лампочки.
Количество ячеек | Напряжение, В (\ (\ text {V} \)) | Ток, I (\ (\ text {A} \)) |
\ (\ text {1} \) | ||
\ (\ text {2} \) | ||
\ (\ text {3} \) | ||
\ (\ text {4} \) |
Анализ
Используя данные в ваших таблицах, нарисуйте два графика \ (I \) (\ (y \) — ось) vs.\ (V \) (\ (x \) — ось), одна для резистора и один для лампочки.
Вопросы и обсуждение
Внимательно изучите свои графики и ответьте на следующие вопросы:
Как должен выглядеть график зависимости \ (I \) от \ (V \) для проводника, подчиняющегося закону Ома?
Один или оба ваших графика выглядят так?
Какой можно сделать вывод о том, подчиняются ли резистор и / или лампочка резистору Ома? Закон?
Имеет ли лампочка омический или неомический провод?
Использование закона Ома (ESBQ8)
Теперь мы готовы посмотреть, как закон Ома используется для анализа схем.
Рассмотрим схему с ячейкой и омическим резистором R. Если сопротивление резистора равно \ (\ text {5} \) \ (\ text {Ω} \) и напряжение на резисторе \ (\ text {5} \) \ (\ text {V} \), тогда мы можем использовать сопротивление Ома. Закон для расчета тока, протекающего через резистор. Наша первая задача — нарисовать схему диаграмма. При решении любой проблемы с электрическими цепями очень важно составить схему схему перед выполнением любых расчетов.Принципиальная схема этой проблемы выглядит следующим образом:
Уравнение закона Ома: \ [R = \ frac {V} {I} \]
, который можно преобразовать в: \ [I = \ frac {V} {R} \]
Ток, протекающий через резистор:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {5} \ text {V}} {\ text {5} \ Omega} \\ & = \ текст {1} \ текст {А} \ end {align *}
временный текстРабочий пример 1: Закон Ома
Изучите принципиальную схему ниже:
Сопротивление резистора равно \ (\ text {10} \) \ (\ text {Ω} \), а ток, проходящий через резистор — \ (\ text {4} \) \ (\ text {A} \).Какова разность потенциалов (напряжение) на резистор?
Определите, как подойти к проблеме
Нам задают сопротивление резистора и ток, проходящий через него, и просят рассчитать напряжение на нем. Мы можем применить закон Ома к этой проблеме, используя: \ [R = \ frac {V} {I}. \]
Решить проблему
Измените приведенное выше уравнение и замените известные значения на \ (R \) и \ (I \), чтобы найти \ (V \).\ begin {align *} R & = \ frac {V} {I} \\ R \ times I & = \ frac {V} {I} \ times I \\ V & = I \ раз R \\ & = \ текст {10} \ times \ text {4} \\ & = \ текст {40} \ текст {V} \ end {align *}
Напишите окончательный ответ
Напряжение на резисторе равно \ (\ text {40} \) \ (\ text {V} \).
Закон Ома
Учебное упражнение 11.2Рассчитайте сопротивление резистора с разностью потенциалов \ (\ text {8} \) \ (\ text {V} \) через него, когда через него протекает ток \ (\ text {2} \) \ (\ text {A} \). Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора составляет:
. \ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {8} {2} \\ & = \ текст {4} \ текст {Ω} \ end {выровнять *}Какой ток будет проходить через резистор \ (\ text {6} \) \ (\ text {Ω} \) при наличии разность потенциалов \ (\ text {18} \) \ (\ text {V} \) на концах? Нарисуйте схему диаграмму перед расчетом.
Сопротивление неизвестного резистора составляет:
. \ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {18} {6} \\ & = \ текст {3} \ текст {А} \ end {выровнять *}Какое напряжение на резисторе \ (\ text {10} \) \ (\ text {Ω} \), когда ток \ (\ text {1,5} \) \ (\ text {A} \) течет через него? Нарисуйте принципиальную схему перед выполнением расчет.
Сопротивление неизвестного резистора составляет:
. \ begin {align *} V & = I \ cdot R \\ & = (\ текст {1,5}) (10) \\ & = \ текст {15} \ текст {V} \ end {выровнять *}Резисторы последовательно и параллельно (ESBQ9)
В 10 классе вы узнали о резисторах и познакомились со схемами, в которых резисторы подключены в последовательно и параллельно.В последовательной цепи есть один путь, по которому течет ток. Параллельно В цепи есть несколько путей, по которым течет ток.
Когда в цепи более одного резистора, мы обычно можем рассчитать общую суммарную сопротивление всех резисторов. Это известно как сопротивление , эквивалентное .
Эквивалентное последовательное сопротивление
В цепи, в которой резисторы включены последовательно, эквивалентное сопротивление равно сумме сопротивлений всех резисторов.
- Эквивалентное сопротивление в последовательной цепи,
Для последовательно подключенных n резисторов эквивалентное сопротивление составляет:
. \ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + \ ldots + R_ {n} \]
Применим это к следующей схеме.
Резисторы включены последовательно, следовательно:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {3} \ text {Ω} + \ text {10} \ text {Ω} + \ text {5} \ text {Ω} \\ & = \ текст {18} \ текст {Ω} \ end {выровнять *}Эквивалентное параллельное сопротивление
В цепи, в которой резисторы включены параллельно, эквивалентное сопротивление определяется следующее определение.
- Эквивалентное сопротивление в параллельной цепи
Для параллельных резисторов \ (n \) эквивалентное сопротивление составляет:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ ldots + \ frac {1} {R_ {n}} \]
Применим эту формулу к следующей схеме.
Какое полное (эквивалентное) сопротивление в цепи?
\ begin {align *} \ frac {1} {R_ {p}} & = \ left (\ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}) } \Правильно) \\ & = \ left (\ frac {1} {\ text {10} \ text {Ω}} + \ frac {1} {\ text {2} \ text {Ω}} + \ frac {1} {\ text {1} \ text {Ω}} \ right) \\ & = \ left (\ frac {\ text {1} \ text {Ω} + \ text {5} \ text {Ω} + \ text {10} \ text { Ω}} {\ text {10} \ text {Ω}} \ right) \\ & = \ left (\ frac {\ text {16} \ text {Ω}} {\ text {10} \ text {Ω}} \ right) \\ R_ {p} & = \ text {0,625} \ text {Ω} \ end {выровнять *}Последовательное и параллельное сопротивление
Учебное упражнение 11.3Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) соединены последовательно. Рассчитать эквивалентное сопротивление.
Поскольку резисторы включены последовательно, мы можем использовать:
\ [R_ {s} = R_ {1} + R_ {2} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {10} \ text {kΩ} + \ text {10} \ text {kΩ} \\ & = \ текст {20} \ текст {кОм} \ end {выровнять *}Два резистора соединены последовательно.Эквивалентное сопротивление \ (\ text {100} \) \ (\ текст {Ω} \). Если один резистор \ (\ text {10} \) \ (\ text {Ω} \), вычислите номинал второго резистора.
Поскольку резисторы включены последовательно, мы можем использовать:
\ [R_ {s} = R_ {1} + R_ {2} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ R_ {2} & = R_ {s} — R_ {1} \\ & = \ text {100} \ text {Ω} — \ text {10} \ text {Ω} \\ & = \ текст {90} \ текст {Ω} \ end {выровнять *}Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) подключены параллельно.Рассчитать эквивалентное сопротивление.
Поскольку резисторы включены параллельно, мы можем использовать:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {100}} + \ frac {1} {\ text {10}} \\ & = \ frac {1 + 10} {\ text {100}} \\ & = \ frac {11} {\ text {100}} \\ R_ {p} & = \ text {9,09} \ text {kΩ} \ end {выровнять *}Два резистора подключены параллельно.Эквивалентное сопротивление \ (\ text {3,75} \) \ (\ текст {Ω} \). Если один резистор имеет сопротивление \ (\ text {10} \) \ (\ text {Ω} \), какое сопротивление у второго резистора?
Поскольку резисторы включены параллельно, мы можем использовать:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ \ frac {1} {R_ {2}} & = \ frac {1} {R_ {p}} — \ frac {1} {R_ {1}} \\ & = \ frac {1} {\ text {3,75}} — \ frac {1} {\ text {10}} \\ & = \ frac {\ text {10} — \ text {3,75}} {\ text {37,5}} \\ & = \ frac {\ text {6,25}} {\ text {37,5}} \\ R_ {2} & = \ текст {6} \ текст {Ω} \ end {выровнять *}Рассчитайте эквивалентное сопротивление в каждой из следующих цепей:
a) Резисторы включены параллельно, поэтому мы используем:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {3}} + \ frac {1} {\ text {2}} \\ & = \ frac {\ text {2} + \ text {3}} {\ text {6}} \\ & = \ frac {\ text {5}} {\ text {6}} \\ R & = \ текст {1,2} \ текст {Ω} \ end {выровнять *}b) Резисторы включены параллельно, поэтому мы используем:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \\ & = \ frac {1} {\ text {2}} + \ frac {1} {\ text {3}} + \ frac {1} {\ text {4}} + \ frac {1} {\ text { 1}} \\ & = \ frac {\ text {6} + \ text {4} + \ text {3} + \ text {12}} {\ text {12}} \\ & = \ frac {\ text {25}} {\ text {12}} \\ R & = \ text {0,48} \ text {Ω} \ end {выровнять *}c) Резисторы включены последовательно, поэтому мы используем:
\ [R_ {s} = R_ {1} + R_ {2} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} \\ & = \ текст {5} \ текст {Ω} \ end {выровнять *}d) Резисторы включены последовательно, поэтому мы используем:
\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + R_ {4} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} + \ text {4} \ text {Ω} + \ текст {1} \ текст {Ω} \\ & = \ текст {10} \ текст {Ω} \ end {выровнять *}Использование закона Ома в последовательных и параллельных цепях (ESBQB)
Используя определения эквивалентного сопротивления для резисторов, включенных последовательно или параллельно, мы можем проанализировать некоторые схемы с этими настройками.
Последовательные цепи
Рассмотрим схему, состоящую из трех резисторов и одного одиночная ячейка соединена последовательно.
Первый принцип, который нужно понять в отношении последовательных цепей, заключается в том, что величина тока одинакова. через любой компонент в цепи. Это потому, что существует только один путь для движения электронов. в последовательной цепи. По способу подключения батареи мы можем сказать, в каком направлении ток будет течь.Мы знаем, что ток по условию течет от положительного к отрицательному. Общепринятый ток в этой цепи будет течь по часовой стрелке от точки A к B, от C к D и обратно к А.
Мы знаем, что в последовательной цепи ток должен быть одинаковым во всех компонентах. Итак, мы можем написать:
\ [I = I_ {1} = I_ {2} = I_ {3}. \]Мы также знаем, что полное напряжение цепи должно быть равно сумме напряжений по всем три резистора.Итак, мы можем написать:
\ [V = V_ {1} + V_ {2} + V_ {3} \]Используя эту информацию и то, что мы знаем о вычислении эквивалентного сопротивления резисторов в серии, мы можем подойти к некоторым проблемам схемы.
Рабочий пример 2: Закон Ома, последовательная цепь
Вычислите ток (I) в этой цепи, если оба резистора имеют омическую природу.
Определите, что требуется
Нам необходимо рассчитать ток, протекающий в цепи.
Определите, как подойти к проблеме
Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома. Однако есть два резисторы в цепи и нам нужно найти общее сопротивление.
Найти полное сопротивление в цепи
Поскольку резисторы включены последовательно, общее (эквивалентное) сопротивление R составляет:
\ [R = R_ {1} + R_ {2} \]Следовательно,
\ begin {align *} R & = \ текст {2} + \ текст {4} \\ & = \ текст {6} \ текст {Ω} \ end {выровнять *}Применить закон Ома
\ begin {align *} R & = \ frac {V} {I} \\ R \ times \ frac {I} {R} & = \ frac {V} {I} \ times \ frac {I} {R} \\ I & = \ frac {V} {R} \\ & = \ frac {12} {6} \\ & = \ текст {2} \ текст {А} \ end {align *}
Напишите окончательный ответ
В цепи протекает ток \ (\ text {2} \) \ (\ text {A} \).
Рабочий пример 3: Закон Ома, последовательная цепь
Два омических резистора (\ (R_ {1} \) и \ (R_ {2} \)) соединены последовательно с ячейкой. Найди сопротивление \ (R_ {2} \), учитывая, что ток, протекающий через \ (R_ {1} \) и \ (R_ {2} \), равен \ (\ text {0,25} \) \ (\ text {A} \) и что напряжение на ячейке равно \ (\ text {1,5} \) \ (\ текст {V} \).\ (R_ {1} \) = \ (\ text {1} \) \ (\ text {Ω} \).
Нарисуйте схему и введите все известные значения.
Определите, как подойти к проблеме.
Мы можем использовать закон Ома, чтобы найти полное сопротивление R в цепи, а затем вычислить неизвестное сопротивление с использованием:
\ [R = R_ {1} + R_ {2} \], потому что он находится в последовательной цепи.
Найдите полное сопротивление
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {\ text {1,5}} {\ text {0,25}} \\ & = \ текст {6} \ текст {Ω} \ end {выровнять *}Найдите неизвестное сопротивление
Мы знаем, что:
\ [R = \ text {6} \ text {Ω} \]и что
\ [R_ {1} = \ text {1} \ text {Ω} \]С
\ [R = R_ {1} + R_ {2} \] \ [R_ {2} = R — R_ {1} \]Следовательно,
\ [R_ {1} = \ text {5} \ text {Ω} \]Рабочий пример 4: Закон Ома, последовательная цепь
Для следующей схемы рассчитайте:
падение напряжения \ (V_1 \), \ (V_2 \) и \ (V_3 \) на резисторах \ (R_1 \), \ (R_2 \), и \ (R_3 \)
сопротивление \ (R_3 \).
Определите, как подойти к проблеме
Нам даны напряжение на ячейке и ток в цепи, а также сопротивления двух из трех резисторов. Мы можем использовать закон Ома для расчета напряжения падение через известные резисторы. Поскольку резисторы включены в последовательную цепь, напряжение равно \ (V = V_1 + V_2 + V_3 \), и мы можем вычислить \ (V_3 \).Теперь мы можем использовать эту информацию для найти напряжение на неизвестном резисторе \ (R_3 \).
Рассчитать падение напряжения на \ (R_1 \)
Используя закон Ома: \ begin {align *} R_1 & = \ frac {V_1} {I} \\ I \ cdot R_1 & = I \ cdot \ frac {V_1} {I} \\ V_1 & = {I} \ cdot {R_1} \\ & = 2 \ cdot 1 \\ V_1 & = \ текст {2} \ текст {V} \ end {align *}
Рассчитать падение напряжения на \ (R_2 \)
Снова используя закон Ома: \ begin {align *} R_2 & = \ frac {V_2} {I} \\ I \ cdot R_2 & = I \ cdot \ frac {V_2} {I} \\ V_2 & = {I} \ cdot {R_2} \\ & = 2 \ cdot 3 \\ V_2 & = \ текст {6} \ текст {V} \ end {align *}
Рассчитать падение напряжения на \ (R_3 \)
Так как падение напряжения на всех резисторах вместе должно быть таким же, как и падение напряжения через ячейку в последовательной цепи, мы можем найти \ (V_3 \), используя: \ begin {align *} V & = V_1 + V_2 + V_3 \\ V_3 & = V — V_1 — V_2 \\ & = 18-2-6 \\ V_3 & = \ текст {10} \ текст {V} \ end {align *}
Найдите сопротивление \ (R_3 \)
Нам известны напряжение на \ (R_3 \) и ток через него, поэтому мы можем использовать закон Ома, чтобы рассчитать значение сопротивления: \ begin {align *} R_3 & = \ frac {V_3} {I} \\ & = \ frac {10} {2} \\ R_3 & = \ text {5} \ Omega \ end {align *}
Напишите окончательный ответ
\ (V_1 = \ text {2} \ text {V} \)
\ (V_2 = \ text {6} \ text {V} \)
\ (V_3 = \ text {10} \ text {V} \)
\ (R_1 = \ text {5} \ Omega \)
временный текстПараллельные цепи
Рассмотрим схему, состоящую из одной ячейки и трех резисторов, соединенных параллельно.
Первый принцип, который нужно понять в отношении параллельных цепей, заключается в том, что напряжение одинаково на всех компонентах в цепи. Это потому, что есть только два набора электрически общие точки в параллельной цепи и напряжение, измеренное между наборами общих точек всегда должны быть одинаковыми в любой момент времени. Итак, для показанной схемы верно следующее:
\ [V = V_ {1} = V_ {2} = V_ {3}.\]Второй принцип параллельной схемы состоит в том, что все токи, проходящие через каждый резистор, должны складываться. до полного тока в цепи:
\ [I = I_ {1} + I_ {2} + I_ {3}. \]Используя эти принципы и наши знания о том, как рассчитать эквивалентное сопротивление параллельной резисторов, теперь мы можем подойти к некоторым схемам, связанным с параллельными резисторами.
Рабочий пример 5: Закон Ома, параллельная цепь
Вычислите ток (I) в этой цепи, если оба резистора имеют омическую природу.
Определите, что требуется
Нам необходимо рассчитать ток, протекающий в цепи.
Определите, как подойти к проблеме
Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома. Однако есть два резисторы в цепи и нам нужно найти общее сопротивление.
Найдите эквивалентное сопротивление в цепи
Поскольку резисторы включены параллельно, общее (эквивалентное) сопротивление R составляет:
\ [\ frac {1} {R} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}}. \] \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\ & = \ frac {1} {2} + \ frac {1} {4} \\ & = \ frac {2 + 1} {4} \\ & = \ frac {3} {4} \\ \ text {Следовательно,} R & = \ text {1,33} \ Omega \ end {выровнять *}Применить закон Ома
\ begin {align *} R & = \ frac {V} {I} \\ R \ cdot \ frac {I} {R} & = \ frac {V} {I} \ cdot \ frac {I} {R} \\ I & = \ frac {V} {R} \\ I & = V \ cdot \ frac {1} {R} \\ & = (12) \ left (\ frac {3} {4} \ right) \\ & = \ текст {9} \ текст {А} \ end {выровнять *}Напишите окончательный ответ
В цепи протекает ток \ (\ text {9} \) \ (\ text {A} \).
Рабочий пример 6: Закон Ома, параллельная цепь
Два омических резистора (\ (R_1 \) и \ (R_2 \)) подключены параллельно ячейке. Найди сопротивление \ (R_2 \), учитывая, что ток, протекающий через ячейку, равен \ (\ text {4,8} \) \ (\ text {A} \) и что напряжение на ячейке равно \ (\ text {9} \) \ (\ text {V} \).
Определите, что требуется
Нам нужно рассчитать сопротивление \ (R_2 \).
Определите, как подойти к проблеме
Так как резисторы омические и нам даны напряжение на ячейке и ток через ячейку мы можем использовать закон Ома, чтобы найти эквивалентное сопротивление в цепи. \ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {9} {\ text {4,8}} \\ & = \ text {1,875} \ \ Omega \ end {align *}
Рассчитайте значение для \ (R_2 \)
Поскольку мы знаем эквивалентное сопротивление и сопротивление \ (R_1 \), мы можем использовать формулу для резисторов, включенных параллельно, найти сопротивление \ (R_2 \).\ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \ end {выровнять *} Переставляем решение для \ (R_2 \): \ begin {align *} \ frac {1} {R_2} & = \ frac {1} {R} — \ frac {1} {R_1} \\ & = \ frac {1} {\ text {1,875}} — \ frac {1} {3} \\ & = \ текст {0,2} \\ R_2 & = \ frac {1} {\ text {0,2}} \\ & = \ текст {5} \ \ Omega \ end {align *}
Напишите окончательный ответ
Сопротивление \ (R_2 \) равно \ (\ text {5} \) \ (\ Omega \)
temp textРабочий пример 7: Закон Ома, параллельная цепь
Ячейка 18 В подключена к двум параллельным резисторам \ (\ text {4} \) \ (\ Omega \) и \ (\ text {12} \) \ (\ Omega \) соответственно.Рассчитайте ток через ячейку и через каждый из резисторов.
Сначала нарисуйте схему, прежде чем производить какие-либо вычисления
Определите, как подойти к проблеме
Нам нужно определить ток через ячейку и каждый из параллельных резисторов. У нас есть была задана разность потенциалов на ячейке и сопротивления резисторов, поэтому мы можем использовать закон Ома для вычисления силы тока.
Рассчитать ток через ячейку
Чтобы рассчитать ток через ячейку, нам сначала нужно определить эквивалент сопротивление остальной части цепи. Резисторы включены параллельно и поэтому: \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\ & = \ frac {1} {4} + \ frac {1} {12} \\ & = \ frac {3 + 1} {12} \\ & = \ frac {4} {12} \\ R & = \ frac {12} {4} = \ text {3} \ \ Omega \ end {выровнять *} Теперь, используя закон Ома, чтобы найти ток через ячейку: \ begin {align *} R & = \ frac {V} {I} \\ I & = \ frac {V} {R} \\ & = \ frac {18} {3} \\ I & = \ text {6} \ text {A} \ end {align *}
Теперь определите ток через один из параллельных резисторов
Мы знаем, что для чисто параллельной схемы напряжение на ячейке такое же, как напряжение на каждом из параллельных резисторов.Для этой схемы: \ begin {align *} V & = V_1 = V_2 = \ text {18} \ text {V} \ end {выровнять *} Начнем с расчета тока через \ (R_1 \) по закону Ома: \ begin {align *} R_1 & = \ frac {V_1} {I_1} \\ I_1 & = \ frac {V_1} {R_1} \\ & = \ frac {18} {4} \\ I_1 & = \ text {4,5} \ text {A} \ end {align *}
Рассчитайте ток через другой параллельный резистор
Мы можем снова использовать закон Ома, чтобы найти ток в \ (R_2 \): \ begin {align *} R_2 & = \ frac {V_2} {I_2} \\ I_2 & = \ frac {V_2} {R_2} \\ & = \ frac {18} {12} \\ I_2 & = \ text {1,5} \ text {A} \ end {выровнять *} Альтернативный метод вычисления \ (I_2 \) заключался бы в использовании того факта, что токи через каждый из параллельных резисторов должны составлять суммарный ток через клетка: \ begin {align *} I & = I_1 + I_2 \\ I_2 & = I — I_1 \\ & = 6 — 4.5 \\ I_2 & = \ text {1,5} \ text {A} \ end {align *}
Напишите окончательный ответ
Ток через ячейку равен \ (\ text {6} \) \ (\ text {A} \).
Ток через резистор \ (\ text {4} \) \ (\ Omega \) равен \ (\ text {4,5} \) \ (\ text {A} \).
Ток через резистор \ (\ text {12} \) \ (\ Omega \) равен \ (\ text {1,5} \) \ (\ text {A} \).
Закон Ома в последовательной и параллельной цепях
Учебное упражнение 11.4Рассчитать номинал неизвестного резистора в цепи:
Сначала мы используем закон Ома для расчета полного последовательного сопротивления:
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {9} {1} \\ & = \ текст {9} \ текст {Ω} \ end {выровнять *}Теперь мы можем найти неизвестное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\ R_ {4} & = R_ {s} — R_ {1} — R_ {2} — R_ {3} \\ & = 9 — 3 — 3 — 1 \\ & = \ текст {2} \ текст {Ω} \ end {выровнять *}Рассчитайте значение тока в следующей цепи:
Сначала находим общее сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {1} + \ text {2,5} + \ text {1,5} \\ & = \ текст {5} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать текущую:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {9} {5} \\ & = \ текст {1,8} \ текст {А} \ end {выровнять *}Три резистора с сопротивлением \ (\ text {1} \) \ (\ text {Ω} \), \ (\ text {5} \) \ (\ text {Ω} \) и \ (\ text {10} \) \ (\ text {Ω} \) соответственно соединены в серия с \ (\ text {12} \) \ (\ text {V} \) батареей.Рассчитайте значение тока в схема.
Рисуем принципиальную схему:
Теперь мы находим общее сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ текст {1} + \ текст {5} + \ текст {10} \\ & = \ текст {16} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать текущую:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {12} {16} \\ & = \ текст {0,75} \ текст {A} \ end {выровнять *}Рассчитайте ток через ячейку, если оба резистора омические по своей природе.
Сначала находим общее сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {1}} + \ frac {1} {\ text {3}} \\ & = \ frac {3 + 1} {\ text {3}} \\ & = \ frac {4} {\ text {3}} \\ & = \ текст {0,75} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать текущую:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {9} {\ text {0,75}} \\ & = \ текст {12} \ текст {А} \ end {выровнять *}Рассчитайте номинал неизвестного резистора \ (R_ {4} \) в цепи:
Сначала находим общее сопротивление:
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {24} {\ text {2}} \\ & = \ текст {12} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать неизвестное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \\ \ frac {1} {R_ {4}} & = \ frac {1} {R_ {p}} — \ frac {1} {R_ {1}} — \ frac {1} {R_ {2}} — \ frac {1} {R_ {3}} \\ & = \ frac {1} {\ text {12}} — \ frac {1} {\ text {120}} — \ frac {1} {\ text {40}} — \ frac {1} {\ text {60}} \\ & = \ frac {10 — 1 — 3 — 2} {\ text {120}} \\ & = \ frac {4} {\ text {120}} \\ & = \ текст {30} \ текст {Ω} \ end {выровнять *}значение тока через аккумулятор
Рисуем принципиальную схему:
Чтобы вычислить значение тока через аккумулятор, нам сначала нужно вычислить эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {\ text {1}} + \ frac {1} {\ text {5}} + \ frac {1} {\ text {10}} \\ & = \ frac {10 + 2 + 1} {\ text {10}} \\ & = \ frac {13} {\ text {10}} \\ & = \ текст {0,77} \ текст {Ω} \ end {выровнять *}Теперь можем посчитать ток через батарею:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {0,77}} \\ & = \ текст {26} \ текст {А} \ end {выровнять *}значение тока в каждом из трех резисторов.
Для параллельной схемы напряжение на ячейке такое же, как и напряжение на каждой резисторов. Для этой схемы:
\ [V = V_ {1} = V_ {2} = V_ {3} = \ text {20} \ text {V} \]Теперь мы можем рассчитать ток через каждый резистор. Начнем с \ (R_ {1} \):
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {1}} \\ & = \ текст {20} \ текст {А} \ end {выровнять *}Затем мы вычисляем ток через \ (R_ {2} \):
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {5}} \\ & = \ текст {4} \ текст {А} \ end {выровнять *}И наконец вычисляем ток через \ (R_ {3} \):
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {10}} \\ & = \ текст {2} \ текст {А} \ end {выровнять *}Вы можете проверить, что они в сумме составляют общий ток.
Последовательные и параллельные сети резисторов (ESBQC)
Теперь, когда вы знаете, как работать с простыми последовательными и параллельными цепями, вы готовы к работе со схемами. которые объединяют эти две схемы, например, следующую схему:
Рисунок 11.1: Пример последовательно-параллельной сети. Пунктирными прямоугольниками обозначены параллельные участки цепи.Проработать такие схемы относительно легко, потому что вы используете все, что у вас уже есть. узнал о последовательных и параллельных цепях. Единственная разница в том, что вы делаете это поэтапно. На рисунке 11.1 схема состоит из двух параллельных частей. которые затем последовательно с ячейкой. Чтобы вычислить эквивалентное сопротивление для схемы, вы начнете с вычислить общее сопротивление каждой из параллельных частей, а затем сложить эти сопротивления в серии. {- 1} \\ & = \ текст {5} \, \ Omega \ end {align *}
Теперь вы можете рассматривать схему как простую последовательную схему следующим образом:
Следовательно, эквивалентное сопротивление: \ begin {align *} R & = R_ {p1} + R_ {p2} \\ & = 5 + 5 \\ & = 10 \, \ Omega \ end {align *}
Эквивалентное сопротивление схемы на Рисунке 11.1 — это \ (\ текст {10} \) \ (\ текст {Ω} \).
временный текстПоследовательные и параллельные сети
Учебное упражнение 11.5Начнем с определения эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {4} + \ frac {1} {2} \\ & = \ frac {3} {4} \\ R_ {p} & = \ text {1,33} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\ begin {align *} R_ {s} & = R_ {3} + R_ {p} \\ & = \ текст {2} + \ текст {1,33} \\ & = \ текст {3,33} \ текст {Ω} \ end {выровнять *}Начнем с определения эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {1} + \ frac {1} {2} \\ & = \ frac {3} {2} \\ R_ {p} & = \ text {0,67} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с тремя последовательно включенными резисторами, поэтому мы можем рассчитать эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {3} + R_ {4} + R_ {p} \\ & = \ текст {4} + \ текст {6} + \ текст {0,67} \\ & = \ текст {10,67} \ текст {Ω} \ end {выровнять *}Начнем с определения эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {3} + \ frac {1} {5} + \ frac {1} {1} \\ & = \ frac {23} {15} \\ R_ {p} & = \ text {0,652} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\ begin {align *} R_ {s} & = R_ {4} + R_ {p} \\ & = \ текст {2} + \ текст {0,652} \\ & = \ текст {2,652} \ текст {Ω} \ end {выровнять *}ток \ (I \) через ячейку.
Чтобы найти ток \ (I \), нам сначала нужно найти эквивалентное сопротивление. Мы начинаем путем вычисления эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {3} + \ frac {1} {5} + \ frac {1} {1} \\ & = \ frac {23} {15} \\ R_ {p} & = \ text {0,652} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\ begin {align *} R_ {s} & = R_ {4} + R_ {p} \\ & = \ текст {2} + \ текст {0,652} \\ & = \ текст {2,652} \ текст {Ω} \ end {выровнять *}Итак, ток через ячейку:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {12}} {\ text {2,652}} \\ & = \ текст {4,52} \ текст {А} \ end {выровнять *}ток через резистор \ (\ text {5} \) \ (\ text {Ω} \).
Ток через параллельную комбинацию резисторов равен \ (\ text {4,52} \) \ (\ текст {A} \). (Сила тока одинакова при последовательной комбинации резисторов и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение через параллельную комбинацию резисторов (не забудьте использовать эквивалентное параллельное сопротивление, а не эквивалент сопротивление цепи):
\ begin {align *} V & = I \ cdot R \\ & = (\ text {4,52}) (\ text {0,652}) \\ & = \ текст {2,95} \ текст {V} \ end {выровнять *}Поскольку напряжение на каждом резисторе в параллельной комбинации одинаковое, это также является напряжением на резисторе \ (\ text {5} \) \ (\ text {Ω} \).
Итак, теперь мы можем рассчитать ток через резистор:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {2,95}} {\ text {5}} \\ & = \ текст {0,59} \ текст {A} \ end {выровнять *}Если ток, протекающий через ячейку, равен \ (\ text {2} \) \ (\ text {A} \), и все резисторы являются омическими, рассчитайте напряжение на ячейке и на каждом из резисторов \ (R_1 \), \ (R_2 \) и \ (R_3 \) соответственно.
Чтобы найти напряжение, нам сначала нужно найти эквивалентное сопротивление. Мы начинаем с расчет эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {2} + \ frac {1} {4} \\ & = \ frac {3} {4} \\ R_ {p} & = \ text {1,33} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {p} \\ & = \ text {4,66} + \ text {1,33} \\ & = \ текст {5,99} \ текст {Ω} \ end {выровнять *}Итак, напряжение на ячейке:
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {5,99}) \\ & = \ текст {12} \ текст {V} \ end {выровнять *}Ток через параллельную комбинацию резисторов равен \ (\ text {2} \) \ (\ text {A} \).(Ток одинаков при последовательной комбинации резисторов, и мы можем рассмотреть весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение на каждом из резисторов. Начнем с поиска напряжение на \ (R_ {1} \):
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {4,66}) \\ & = \ текст {9,32} \ текст {V} \ end {выровнять *}Теперь находим напряжение на параллельной комбинации:
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {1,33}) \\ & = \ текст {2,66} \ текст {V} \ end {выровнять *}Поскольку напряжение на каждом резисторе в параллельной комбинации одинаковое, это также напряжение на резисторах \ (R_ {2} \) и \ (R_ {3} \).
ток через ячейку
Чтобы найти ток, нам сначала нужно найти эквивалентное сопротивление. Мы начинаем с расчет эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {1} + \ frac {1} {1} \\ & = 2 \\ R_ {p} & = \ text {0,5} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {4} + R_ {p} \\ & = \ text {2} + \ text {1,5} + \ text {0,5} \\ & = \ текст {4} \ текст {Ω} \ end {выровнять *}Итак, ток через ячейку:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {10}} {\ text {4}} \\ & = \ текст {2,5} \ текст {А} \ end {выровнять *}падение напряжения на \ (R_4 \)
Ток через все резисторы равен \ (\ text {2,5} \) \ (\ text {A} \).(Текущий то же самое через последовательные комбинации резисторов, и мы можем рассмотреть все параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение через \ (R_ {4} \):
\ begin {align *} V & = I \ cdot R \\ & = (\ text {2,5}) (\ text {1,5}) \\ & = \ текст {3,75} \ текст {V} \ end {выровнять *}ток через \ (R_2 \)
Ток через все резисторы равен \ (\ text {2,5} \) \ (\ text {A} \).(Текущий то же самое через последовательные комбинации резисторов, и мы можем рассмотреть все параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти ток через \ (R_ {2} \).
Сначала нам нужно найти напряжение на параллельной комбинации:
\ begin {align *} V & = I \ cdot R \\ & = (\ text {2,5}) (\ text {0,5}) \\ & = \ текст {1,25} \ текст {V} \ end {выровнять *}Теперь мы можем найти ток через \ (R_ {2} \), используя тот факт, что напряжение то же самое на каждом резисторе в параллельной комбинации:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {1,25}} {\ text {1}} \\ & = \ текст {1,25} \ текст {А} \ end {выровнять *}Схема моста Уитстона
Электрические цепи используются в авиакосмической технике, от систем управления полетом до приборов в кабине и двигателей системы управления, чтобы аэродинамическая труба приборостроение и эксплуатация.Самая простая схема состоит из одного резистора . и источник электрического потенциала или напряжения . Электроны проходят через схема, вырабатывающая ток электричества. Сопротивление, напряжение и ток связаны друг с другом соотношением Закон Ома. Обычно в практической схеме используется более одного резистора. При анализе схем с несколько резисторов, мы должны определить, подвержены ли резисторы какое-то напряжение или такой же ток.Несколько резисторов в параллельная цепь подвергаются одинаковому напряжению. Несколько резисторов в последовательная цепь подвергаются одинаковому току. На этой странице мы обсуждаем схема моста Уитстона , которая является важная схема, которая используется в оборудовании аэродинамической трубы
Если обозначить сопротивление R , ток i и напряжение В , то закон Ома гласит, что для каждого резистора в цепи:
V = i Rя = V / R
На рисунке изображена схема, состоящая из источника питания и четырех резисторов. соединены в квадрат.Резисторы соединены между собой в узлах которые помечены от a до c. Схема содержит потенциометр с маркировкой G , который определяет разность напряжений между узлами c и b . Значение потенциометра отображается в комната управления. Если рассматривать каждый резистор отдельно, каждый резистор имеет свой ток ( i1 , i2 , i3 и i4 ), сопротивление ( R1 , R2 , R3 и R4 ), и напряжение ( V1 , V2 , V3 и V4 ), которые связаны с каждым другое — по закону Ома.На практике резисторы фактически будут сопротивлением, обеспечиваемым тензодатчик в аэродинамической трубе система баланса сил.
Резисторы R1 и R3 подключены в ряд через узел б . Следовательно такой же ток протекает через R1 и R3 .
я (1-3) = я1 = я3а значение i (1-3) можно определить по закону Ома:
я (1-3) = V / (R1 + R3)Аналогично резисторы R2 и R4 соединены последовательно и одинаковый ток i (2-4) протекает через эти резисторы.Сила тока определяется по формуле:
я (2-4) = V / (R2 + R4)Изменение напряжения от узлов a к узлу b определяется по формуле:
Vb — Va = i (1-3) R1 = V R1 / (R1 + R3)Точно так же изменение напряжения от узла a к узлу c определяется по формуле:
Vc — Va = i (2-4) R2 = V R2 / (R2 + R4)Потенциометр G измеряет разницу напряжений между узлами b и c .
G = Vc — Vb = (Vc — Va) — (Vb — Va)G = V [{R2 / (R2 + R4)} — {R1 / (R1 + R3)}]
G / V = [(R2 R3) — (R1 R4)] / [(R1 + R3) (R2 + R4)]
Это последнее уравнение объясняет, как схему моста Уитстона можно использовать для исключить температурную погрешность при использовании тензодатчика для определения силы ветра модель туннеля. К модели подключаются два тензодатчика, а выход из датчики помещены в мост Уитстона как R1 и R2.Равные «балластные» резисторы бывают размещены в R3 и R4. Если датчик подвергается При повышении температуры сопротивление в R1 и R2 увеличивается на одинаковую величину. Но поскольку потенциометр измеряет разницу в сопротивлении между R1 и R2, чтение остается прежним.
Навигация ..
- Руководство для начинающих Домашняя страница
10.2 Последовательные и параллельные резисторы — University Physics Volume 2
Учебные цели
К концу этого раздела вы сможете:
- Определите термин эквивалентное сопротивление
- Рассчитайте эквивалентное сопротивление резисторов, включенных последовательно
- Рассчитайте эквивалентное сопротивление резисторов, включенных параллельно
В статье «Ток и сопротивление» мы описали термин «сопротивление» и объяснили основную конструкцию резистора.По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где V = IR. V = IR. В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи.
Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение (рисунок 10.11). В последовательной схеме выходной ток первого резистора течет на вход второго резистора; следовательно, ток в каждом резисторе одинаков. В параллельной схеме все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными, в зависимости от резистора.Сумма отдельных токов равна току, протекающему по параллельным соединениям.
Фигура 10.11 (а) При последовательном соединении резисторов ток одинаков в каждом резисторе. (b) При параллельном соединении резисторов напряжение на каждом резисторе одинаковое.
Резисторы серии
Считается, что резисторывключены последовательно, если ток течет через резисторы последовательно. Рассмотрим рисунок 10.12, на котором показаны три последовательно включенных резистора с приложенным напряжением, равным Vab.Vab. Поскольку заряды проходят только по одному пути, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме отдельных сопротивлений.
Фигура 10,12 (а) Три резистора, подключенные последовательно к источнику напряжения. (b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.
На рисунке 10.12 ток, идущий от источника напряжения, протекает через каждый резистор, поэтому ток через каждый резистор одинаков.Ток в цепи зависит от напряжения, подаваемого источником напряжения, и сопротивления резисторов. Для каждого резистора происходит падение потенциала, равное потере электрической потенциальной энергии при прохождении тока через каждый резистор. Согласно закону Ома падение потенциала В на резисторе при протекании через него тока рассчитывается по формуле V = IR, V = IR, где I — ток в амперах (A), а R — это сопротивление в Ом (Ом).(Ω). Поскольку энергия сохраняется, а напряжение равно потенциальной энергии на заряд, сумма напряжения, приложенного к цепи источником, и падения потенциала на отдельных резисторах вокруг контура должны быть равны нулю:
Это уравнение часто называют законом петли Кирхгофа, который мы рассмотрим более подробно позже в этой главе. На рисунке 10.12 сумма падения потенциала каждого резистора и напряжения, подаваемого источником напряжения, должна равняться нулю:
V-V1-V2-V3 = 0, V = V1 + V2 + V3, = IR1 + IR2 + IR3, I = VR1 + R2 + R3 = VRS.V-V1-V2-V3 = 0, V = V1 + V2 + V3, = IR1 + IR2 + IR3, I = VR1 + R2 + R3 = VRS.Поскольку ток через каждый компонент одинаков, равенство можно упростить до эквивалентного сопротивления, которое представляет собой просто сумму сопротивлений отдельных резисторов.
Любое количество резисторов может быть подключено последовательно. Если резисторы N соединены последовательно, эквивалентное сопротивление равно
. RS = R1 + R2 + R3 + ⋯ + RN − 1 + RN = ∑i = 1NRi. RS = R1 + R2 + R3 + ⋯ + RN − 1 + RN = ∑i = 1NRi.10.2
Одним из результатов включения компонентов в последовательную цепь является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты.Например, если несколько ламп подключены последовательно и одна лампа перегорела, все остальные лампы погаснут.
Пример 10.2
Эквивалентное сопротивление, ток и мощность в последовательной цепи
Батарея с напряжением на клеммах 9 В подключена к цепи, состоящей из четырех последовательно соединенных резисторов 20 Ом 20 Ом и одного резистора 10 Ом 10 Ом (рисунок 10.13). Предположим, что батарея имеет незначительное внутреннее сопротивление. (а) Рассчитайте эквивалентное сопротивление цепи. (б) Рассчитайте ток через каждый резистор.(c) Рассчитайте падение потенциала на каждом резисторе. (d) Определите общую мощность, рассеиваемую резисторами, и мощность, потребляемую батареей.Фигура 10,13 Простая последовательная схема с пятью резисторами.
Стратегия
В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений. Ток в цепи можно найти из закона Ома и равен напряжению, деленному на эквивалентное сопротивление. Падение потенциала на каждом резисторе можно найти с помощью закона Ома.Мощность, рассеиваемая каждым резистором, может быть найдена с помощью P = I2RP = I2R, а общая мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором. Мощность, подаваемая батареей, может быть найдена с помощью P = IεP = Iε.Решение
- Эквивалентное сопротивление — это алгебраическая сумма сопротивлений: RS = R1 + R2 + R3 + R4 + R5 = 20 Ом + 20 Ом + 20 Ом + 20 Ом + 10 Ом = 90 Ом. RS = R1 + R2 + R3 + R4 + R5 = 20 Ом + 20 Ом + 20 Ом + 20 Ом + 10 Ом = 90 Ом.
- Ток в цепи одинаков для каждого резистора в последовательной цепи и равен приложенному напряжению, деленному на эквивалентное сопротивление: I = VRS = 9V90Ω = 0.1A.I = VRS = 9V90Ω = 0,1A.
- Падение потенциала на каждом резисторе можно найти с помощью закона Ома: V1 = V2 = V3 = V4 = (0,1 А) 20 Ом = 2 В, V5 = (0,1 А) 10 Ом = 1 В, V1 + V2 + V3 + V4 + V5 = 9 В. V1 = V2 = V3 = V4 = (0,1 А) 20 Ом = 2 В, V5 = (0,1 А) 10 Ом = 1 В, V1 + V2 + V3 + V4 + V5 = 9 В. Обратите внимание, что сумма падений потенциала на каждом резисторе равна напряжению, подаваемому батареей.
- Мощность, рассеиваемая резистором, равна P = I2RP = I2R, а мощность, отдаваемая батареей, равна P = IεP = Iε: P1 = P2 = P3 = P4 = (0,1 A) 2 (20 Ом) = 0,2 Вт, P5 = (0.1A) 2 (10 Ом) = 0,1 Вт, Pdissipated = 0,2 Вт + 0,2 Вт + 0,2 Вт + 0,2 Вт + 0,1 Вт = 0,9 Вт, Psource = Iε = (0,1 A) (9 В) = 0,9 Вт. P1 = P2 = P3 = P4 = (0,1 A) 2 (20 Ом) = 0,2 Вт, P5 = (0,1 A) 2 (10 Ом) = 0,1 Вт, Pdissipated = 0,2 Вт + 0,2 Вт + 0,2 Вт + 0,2 Вт + 0,1 Вт = 0,9 Вт, Psource = Iε = (0,1 А) (9 В) = 0,9 Вт.
Значение
Есть несколько причин, по которым мы могли бы использовать несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи. Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов.Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной.Проверьте свое понимание 10.2
Проверьте свое понимание Некоторые гирлянды миниатюрных праздничных огней замыкаются на короткое замыкание при перегорании лампочки. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи. «Короткое замыкание» похоже на протягивание куска проволоки через компонент. Луковицы обычно сгруппированы в серии по девять луковиц.Если перегорает слишком много лампочек, в конце концов открываются шунты. Что вызывает это?
Кратко обозначим основные характеристики последовательно соединенных резисторов:
- Сопротивления серии
- суммируются, чтобы получить эквивалентное сопротивление: RS = R1 + R2 + R3 + ⋯ + RN − 1 + RN = ∑i = 1NRi. RS = R1 + R2 + R3 + ⋯ + RN − 1 + RN = ∑i = 1NRi.
- Через каждый резистор последовательно протекает один и тот же ток.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его. Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.
Параллельные резисторы
На рисунке 10.14 показаны резисторы, включенные параллельно, подключенные к источнику напряжения. Резисторы включены параллельно, когда один конец всех резисторов соединен непрерывным проводом с незначительным сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с незначительным сопротивлением. Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома I = V / R, I = V / R, где напряжение на каждом резисторе постоянно.Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.
Фигура 10,14 (а) Два резистора, подключенных параллельно источнику напряжения. (b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.
Ток, протекающий от источника напряжения на рисунке 10.14 зависит от напряжения, подаваемого источником напряжения, и эквивалентного сопротивления цепи. В этом случае ток течет от источника напряжения и попадает в переход или узел, где цепь разделяется, протекая через резисторы R1R1 и R2R2. По мере прохождения зарядов от батареи часть заряда проходит через резистор R1R1, а часть — через резистор R2.R2. Сумма токов, протекающих в переходе, должна быть равна сумме токов, текущих из перехода:
∑Iin = ∑Iout.∑Iin = ∑Iout.Это уравнение называется правилом соединения Кирхгофа и будет подробно обсуждено в следующем разделе. На рисунке 10.14 правило соединения дает I = I1 + I2I = I1 + I2. В этой схеме есть два контура, что приводит к уравнениям V = I1R1V = I1R1 и I1R1 = I2R2I1R1 = I2R2. Обратите внимание, что напряжение на резисторах, включенных параллельно, одинаковое (V = V1 = V2) (V = V1 = V2), а ток — аддитивный:
I = I1 + I2 = V1R1 + V2R2 = VR1 + VR2 = V (1R1 + 1R2) = VRPRP = (1R1 + 1R2) −1.I = I1 + I2 = V1R1 + V2R2 = VR1 + VR2 = V (1R1 + 1R2 ) = VRPRP = (1R1 + 1R2) −1.Обобщая на любое количество резисторов N , эквивалентное сопротивление RPRP параллельного соединения связано с отдельными сопротивлениями соотношением
RP = (1R1 + 1R2 + 1R3 + ⋯ + 1RN − 1 + 1RN) −1 = (∑i = 1N1Ri) −1.RP = (1R1 + 1R2 + 1R3 + ⋯ + 1RN − 1 + 1RN) −1 = (∑i = 1N1Ri) −1.10,3
Это соотношение приводит к эквивалентному сопротивлению RPRP, которое меньше наименьшего из отдельных сопротивлений. Когда резисторы подключены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
Пример 10,3
Анализ параллельной цепи
Три резистора R1 = 1,00 Ом, R2 = 2,00 Ом, R1 = 1,00 Ом, R2 = 2,00 Ом и R3 = 2,00 Ом, R3 = 2,00 Ом подключены параллельно. Параллельное соединение подключается к источнику напряжения V = 3.00VV = 3.00V. а) Какое эквивалентное сопротивление? (б) Найдите ток, подаваемый источником в параллельную цепь. (c) Рассчитайте токи в каждом резисторе и покажите, что в сумме они равны выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором.(e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.Стратегия
(a) Общее сопротивление для параллельной комбинации резисторов находится как RP = (∑i1Ri) −1RP = (∑i1Ri) −1.(Обратите внимание, что в этих вычислениях каждый промежуточный ответ отображается с дополнительной цифрой.)
(b) Ток, подаваемый источником, можно найти из закона Ома, заменив полное сопротивление I = VRP.I = VRP на RPRP.
(c) Отдельные токи легко вычислить по закону Ома (Ii = ViRi) (Ii = ViRi), поскольку каждый резистор получает полное напряжение.Полный ток складывается из отдельных токов: I = ∑iIi.I = ∑iIi.
(d) Мощность, рассеиваемую каждым резистором, можно найти с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны. Давайте использовать Pi = V2 / Ri, Pi = V2 / Ri, так как каждый резистор получает полное напряжение.
(e) Полная мощность также может быть рассчитана несколькими способами, используя P = IVP = IV.
Решение
- Общее сопротивление для параллельной комбинации резисторов находится по формуле 10.3. Ввод известных значений дает RP = (1R1 + 1R2 + 1R3) -1 = (11,00 Ом + 12,00 Ом + 12,00 Ом) -1 = 0,50 Ом. RP = (1R1 + 1R2 + 1R3) -1 = (11,00 Ом + 12,00 Ом + 12,00 Ом) -1 = 0,50 Ом. Общее сопротивление с правильным количеством значащих цифр составляет RP = 0,50 Ом. RP = 0,50 Ом. Как и предполагалось, RPRP меньше минимального индивидуального сопротивления.
- Полный ток можно найти из закона Ома, заменив полное сопротивление RPRP. Это дает I = VRP = 3,00 В 0,50 Ом = 6,00 А. I = VRP = 3,00 В 0,50 Ом = 6,00 А. Сила тока I для каждого устройства намного больше, чем для тех же устройств, соединенных последовательно (см. Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
- Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом, I1 = VR1 = 3,00 В 1,00 Ом = 3,00 А. I1 = VR1 = 3,00 В 1,00 Ом = 3,00 А. Сходным образом, I2 = VR2 = 3,00 В 2,00 Ом = 1,50 A I2 = VR2 = 3,00 В 2,00 Ом = 1,50 A а также I3 = VR3 = 3,00 В 2,00 Ом = 1,50 А. I3 = VR3 = 3,00 В 2,00 Ом = 1,50 А. Полный ток — это сумма отдельных токов: I1 + I2 + I3 = 6,00 А. I1 + I2 + I3 = 6,00 А.
- Мощность, рассеиваемую каждым резистором, можно найти с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны.Давайте использовать P = V2 / R, P = V2 / R, так как каждый резистор получает полное напряжение. Таким образом, P1 = V2R1 = (3,00 В) 21,00 Ом = 9,00 Вт. P1 = V2R1 = (3,00 В) 21,00 Ом = 9,00 Вт. Сходным образом, P2 = V2R2 = (3,00 В) 22,00 Ом = 4,50 Вт P2 = V2R2 = (3,00 В) 22,00 Ом = 4,50 Вт а также P3 = V2R3 = (3,00 В) 22,00 Ом = 4,50 Вт. P3 = V2R3 = (3,00 В) 22,00 Ом = 4,50 Вт.
- Общую мощность также можно рассчитать несколькими способами. Выбор P = IVP = IV и ввод общих текущих урожаев. P = IV = (6,00 A) (3,00 В) = 18,00 Вт. P = IV = (6,00 A) (3,00 В) = 18,00 Вт.
Значение
Общая мощность, рассеиваемая резисторами, также равна 18.00 Вт: P1 + P2 + P3 = 9,00 Вт + 4,50 Вт + 4,50 Вт = 18,00 Вт. P1 + P2 + P3 = 9,00 Вт + 4,50 Вт + 4,50 Вт = 18,00 Вт.Обратите внимание, что общая мощность, рассеиваемая резисторами, равна мощности, подаваемой источником.
Проверьте свое понимание 10,3
Проверьте свое понимание Рассмотрим одну и ту же разность потенциалов (V = 3,00 В) (V = 3,00 В), приложенную к одним и тем же трем последовательно соединенным резисторам. Будет ли эквивалентное сопротивление последовательной цепи больше, меньше или равно трем резисторам, включенным параллельно? Будет ли ток в последовательной цепи выше, ниже или равен току, обеспечиваемому тем же напряжением, приложенным к параллельной цепи? Как мощность, рассеиваемая последовательно подключенными резисторами, будет сравниваться с мощностью, рассеиваемой параллельно резисторами?
Проверьте свое понимание 10.4
Проверьте свое понимание Как бы вы использовали реку и два водопада для моделирования параллельной конфигурации двух резисторов? Как разрушается эта аналогия?
Суммируем основные характеристики резисторов параллельно:
- Эквивалентное сопротивление находится из RP = (1R1 + 1R2 + 1R3 + ⋯ + 1RN − 1 + 1RN) −1 = (∑i = 1N1Ri) −1, RP = (1R1 + 1R2 + 1R3 + ⋯ + 1RN − 1 + 1RN) −1 = (∑i = 1N1Ri) −1, и меньше любого отдельного сопротивления в комбинации.
- Падение потенциала на каждом параллельном резисторе одинаковое.
- Параллельные резисторы не получают суммарный ток каждый; они делят это. Ток, поступающий в параллельную комбинацию резисторов, равен сумме токов, протекающих через каждый резистор, включенный параллельно.
В этой главе мы представили эквивалентное сопротивление резисторов, соединенных последовательно, и резисторов, соединенных параллельно. Вы можете вспомнить, что в разделе «Емкость» мы ввели эквивалентную емкость конденсаторов, соединенных последовательно и параллельно. Цепи часто содержат как конденсаторы, так и резисторы.В таблице 10.1 приведены уравнения, используемые для эквивалентного сопротивления и эквивалентной емкости для последовательного и параллельного соединения.
| Комбинация серий | Параллельная комбинация | |
|---|---|---|
| Эквивалентная емкость | 1CS = 1C1 + 1C2 + 1C3 + ⋯ 1CS = 1C1 + 1C2 + 1C3 + ⋯ | CP = C1 + C2 + C3 + ⋯ CP = C1 + C2 + C3 + ⋯ |
| Эквивалентное сопротивление | RS = R1 + R2 + R3 + ⋯ = ∑i = 1NRiRS = R1 + R2 + R3 + ⋯ = ∑i = 1NRi | 1RP = 1R1 + 1R2 + 1R3 + ⋯ 1RP = 1R1 + 1R2 + 1R3 + ⋯ |
Стол 10.1 Сводка по эквивалентному сопротивлению и емкости в последовательной и параллельной комбинациях
Сочетания последовательного и параллельного
Более сложные соединения резисторов часто представляют собой просто комбинации последовательного и параллельного соединения. Такие комбинации обычны, особенно если учесть сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного подключения можно уменьшить до одного эквивалентного сопротивления, используя методику, показанную на рисунке 10.15. Различные части могут быть идентифицированы как последовательные или параллельные соединения, уменьшенные до их эквивалентных сопротивлений, а затем уменьшенные до тех пор, пока не останется единственное эквивалентное сопротивление. Процесс занимает больше времени, чем труден. Здесь мы отмечаем эквивалентное сопротивление как Req.Req.
Фигура 10,15 (а) Исходная схема из четырех резисторов. (b) Шаг 1: резисторы R3R3 и R4R4 включены последовательно, эквивалентное сопротивление R34 = 10 Ом, R34 = 10 Ом. (c) Шаг 2: сокращенная схема показывает, что резисторы R2R2 и R34R34 включены параллельно, с эквивалентным сопротивлением R234 = 5 Ом.R234 = 5 Ом. (d) Шаг 3: Уменьшенная схема показывает, что R1R1 и R234R234 соединены последовательно с эквивалентным сопротивлением R1234 = 12 Ом, R1234 = 12 Ом, что является эквивалентным сопротивлением Req.Req. (e) Уменьшенная схема с источником напряжения V = 24VV = 24V с эквивалентным сопротивлением Req = 12 Ом, Req = 12 Ом. Это приводит к току I = 2AI = 2A от источника напряжения.Обратите внимание, что резисторы R3R3 и R4R4 включены последовательно. Их можно объединить в одно эквивалентное сопротивление. Один из методов отслеживания процесса — включить резисторы в индексы.Здесь эквивалентное сопротивление R3R3 и R4R4 равно
. R34 = R3 + R4 = 6 Ом + 4 Ом = 10 Ом. R34 = R3 + R4 = 6 Ом + 4 Ом = 10 Ом.Теперь схема сокращается до трех резисторов, показанных на Рисунке 10.15 (c). Теперь мы видим, что резисторы R2R2 и R34R34 образуют параллельную цепь. Эти два резистора можно уменьшить до эквивалентного сопротивления:
. R234 = (1R2 + 1R34) -1 = (110 Ом + 110 Ом) -1 = 5 Ом. R234 = (1R2 + 1R34) -1 = (110 Ом + 110 Ом) -1 = 5 Ом.Этот шаг процесса сокращает схему до двух резисторов, показанных на Рисунке 10.15 (d).Здесь схема сводится к двум резисторам, которые в данном случае включены последовательно. Эти два резистора можно уменьшить до эквивалентного сопротивления, которое является эквивалентным сопротивлением цепи:
Req = R1234 = R1 + R234 = 7 Ом + 5 Ом = 12 Ом. Req = R1234 = R1 + R234 = 7 Ом + 5 Ом = 12 Ом.Основная цель этого анализа схемы достигнута, и теперь схема сводится к одному резистору и одному источнику напряжения.
Теперь мы можем проанализировать схему. Ток, обеспечиваемый источником напряжения, составляет I = VReq = 24V12Ω = 2A.I = VReq = 24 В 12 Ом = 2 А. Этот ток проходит через резистор R1R1 и обозначается как I1.I1. Падение потенциала на R1R1 можно найти с помощью закона Ома:
V1 = I1R1 = (2A) (7Ω) = 14V. V1 = I1R1 = (2A) (7Ω) = 14V.Глядя на рисунок 10.15 (c), это оставляет 24V-14V = 10V24V-14V = 10V, которые будут отброшены через параллельную комбинацию R2R2 и R34.R34. Ток через R2R2 можно найти с помощью закона Ома:
I2 = V2R2 = 10V10Ω = 1A.I2 = V2R2 = 10V10Ω = 1A.Резисторы R3R3 и R4R4 включены последовательно, поэтому токи I3I3 и I4I4 равны
. I3 = I4 = I − I2 = 2A − 1A = 1A.I3 = I4 = I − I2 = 2A − 1A = 1A.Используя закон Ома, мы можем найти падение потенциала на двух последних резисторах. Потенциал падения равен V3 = I3R3 = 6VV3 = I3R3 = 6V и V4 = I4R4 = 4V.V4 = I4R4 = 4V. Окончательный анализ заключается в рассмотрении мощности, подаваемой источником напряжения, и мощности, рассеиваемой резисторами. Мощность, рассеиваемая резисторами
P1 = I12R1 = (2A) 2 (7Ω) = 28W, P2 = I22R2 = (1A) 2 (10Ω) = 10W, P3 = I32R3 = (1A) 2 (6Ω) = 6W, P4 = I42R4 = (1A) 2 (4 Ом) = 4 Вт, рассеиваемая мощность = P1 + P2 + P3 + P4 = 48 Вт. P1 = I12R1 = (2A) 2 (7 Ом) = 28 Вт, P2 = I22R2 = (1A) 2 (10 Ом) = 10 Вт, P3 = I32R3 = (1A) 2 (6Ω) = 6W, P4 = I42R4 = (1A) 2 (4Ω) = 4W, Pdissipated = P1 + P2 + P3 + P4 = 48W.Полная энергия постоянна в любом процессе. Следовательно, мощность, подаваемая источником напряжения, равна Ps = IV = (2A) (24V) = 48W. Ps = IV = (2A) (24V) = 48W. Анализ мощности, подаваемой в схему, и мощности, рассеиваемой резисторами, является хорошей проверкой достоверности анализа; они должны быть равны.
Пример 10,4
Объединение последовательных и параллельных цепей
На рисунке 10.16 показаны резисторы, подключенные последовательно и параллельно. Мы можем считать R1R1 сопротивлением проводов, ведущих к R2R2 и R3.R3. (а) Найдите эквивалентное сопротивление цепи. (b) Какое падение потенциала V1V1 на резисторе R1R1? (c) Найдите ток I2I2 через резистор R2R2. (d) Какая мощность рассеивается R2R2? Фигура 10,16 Эти три резистора подключены к источнику напряжения, так что R2R2 и R3R3 параллельны друг другу, и эта комбинация включена последовательно с R1.R1.Стратегия
(a) Чтобы найти эквивалентное сопротивление, сначала найдите эквивалентное сопротивление параллельного соединения R2R2 и R3.R3. Затем используйте этот результат, чтобы найти эквивалентное сопротивление последовательного соединения с R1.R1.(b) Ток через R1R1 можно найти с помощью закона Ома и приложенного напряжения. Ток через R1R1 равен току от батареи. Падение потенциала V1V1 на резисторе R1R1 (которое представляет собой сопротивление в соединительных проводах) можно найти с помощью закона Ома.
(c) Ток через R2R2 можно найти с помощью закона Ома I2 = V2R2.I2 = V2R2. Напряжение на R2R2 можно найти, используя V2 = V-V1.V2 = V − V1.
(d) Используя закон Ома (V2 = I2R2) (V2 = I2R2), мощность, рассеиваемую резистором, также можно найти, используя P2 = I22R2 = V22R2P2 = I22R2 = V22R2.
Решение
- Чтобы найти эквивалентное сопротивление цепи, обратите внимание, что параллельное соединение R2R2 и R3R3 последовательно с R1R1, поэтому эквивалентное сопротивление равно Req = R1 + (1R2 + 1R3) -1 = 1,00 Ом + (16,00 Ом + 113,00 Ом) -1 = 5,10 Ом. Треб = R1 + (1R2 + 1R3) -1 = 1,00 Ом + (16,00 Ом + 113,00 Ом) -1 = 5,10 Ом. Общее сопротивление этой комбинации занимает промежуточное положение между значениями чистой серии и чистой параллели (20.0 Ом 20,0 Ом и 0,804 Ом 0,804 Ом соответственно).
- Ток через R1R1 равен току, подаваемому батареей: I1 = I = VReq = 12,0 В 5,10 Ом = 2,35 А. I1 = I = VReq = 12,0 В 5,10 Ом = 2,35 А. Напряжение на R1R1 равно V1 = I1R1 = (2.35A) (1Ω) = 2.35V. V1 = I1R1 = (2.35A) (1Ω) = 2.35V. Напряжение, приложенное к R2R2 и R3R3, меньше напряжения, подаваемого батареей, на величину V1.V1. Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных R2R2 и R3R3.
- Чтобы найти ток через R2R2, мы должны сначала найти приложенное к нему напряжение.Напряжение на двух параллельных резисторах одинаковое: V2 = V3 = V-V1 = 12,0 В-2,35 В = 9,65 В. V2 = V3 = V-V1 = 12,0 В-2,35 В = 9,65 В. Теперь мы можем найти ток I2I2 через сопротивление R2R2, используя закон Ома: I2 = V2R2 = 9,65 В 6,00 Ом = 1,61 А. I2 = V2R2 = 9,65 В 6,00 Ом = 1,61 А. Ток меньше 2,00 А, который протекал через R2R2, когда он был подключен параллельно к батарее в предыдущем примере параллельной цепи.
- Мощность, рассеиваемая R2R2, определяется выражением P2 = I22R2 = (1,61 A) 2 (6,00 Ом) = 15,5 Вт P2 = I22R2 = (1,61 A) 2 (6.00 Ом) = 15,5 Вт.
Значение
Анализ сложных схем часто можно упростить, сведя схему к источнику напряжения и эквивалентному сопротивлению. Даже если вся схема не может быть сведена к одному источнику напряжения и одному эквивалентному сопротивлению, части схемы могут быть уменьшены, что значительно упрощает анализ.Проверьте свое понимание 10,5
Проверьте свое понимание Рассмотрите электрические цепи в вашем доме.Приведите по крайней мере два примера схем, которые должны использовать комбинацию последовательных и параллельных схем для эффективной работы.
Практическое применение
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным и может проявляться из-за тепла, выделяемого в шнуре.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Что происходит в этих сильноточных ситуациях, показано на Рисунке 10.17. Устройство, представленное R3R3, имеет очень низкое сопротивление, поэтому при его включении протекает большой ток.Этот увеличенный ток вызывает большее падение IR в проводах, представленных R1R1, уменьшая напряжение на лампе (то есть R2R2), которое затем заметно гаснет.
Фигура 10,17 Почему гаснет свет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение IR в проводах и снижает напряжение на свету.
Стратегия решения проблем
Последовательные и параллельные резисторы
- Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения.Этот шаг включает список известных значений проблемы, поскольку они отмечены на вашей принципиальной схеме.
- Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
- Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно. Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные.Есть один список для серий, а другой — для параллелей.
- Проверьте, являются ли ответы разумными и последовательными.
Пример 10,5
Объединение последовательных и параллельных цепей
Два резистора, соединенных последовательно (R1, R2) (R1, R2), подключены к двум резисторам, включенным параллельно (R3, R4) (R3, R4). Последовательно-параллельная комбинация подключается к батарее. Каждый резистор имеет сопротивление 10,00 Ом. Провода, соединяющие резисторы и аккумулятор, имеют незначительное сопротивление.Через резистор R1.R1 проходит ток 2,00 А. Какое напряжение подается от источника напряжения?Стратегия
Используйте шаги предыдущей стратегии решения проблем, чтобы найти решение для этого примера.Решение
- Нарисуйте четкую принципиальную схему (рисунок 10.18).
Фигура 10,18 Чтобы найти неизвестное напряжение, мы должны сначала найти эквивалентное сопротивление цепи.
- Неизвестно напряжение аккумулятора.Чтобы определить напряжение, подаваемое батареей, необходимо найти эквивалентное сопротивление.
- В этой схеме мы уже знаем, что резисторы R1R1 и R2R2 включены последовательно, а резисторы R3R3 и R4R4 — параллельно. Эквивалентное сопротивление параллельной конфигурации резисторов R3R3 и R4R4 последовательно с последовательной конфигурацией резисторов R1R1 и R2R2.
- Напряжение, подаваемое батареей, можно найти, умножив ток от батареи на эквивалентное сопротивление цепи.Ток от аккумулятора равен току через R1R1 и равен 2,00 А. Нам нужно найти эквивалентное сопротивление, уменьшив цепь. Чтобы уменьшить схему, сначала рассмотрите два резистора, включенных параллельно. Эквивалентное сопротивление: R34 = (110,00 Ом + 110,00 Ом) -1 = 5,00 Ом. R34 = (110,00 Ом + 110,00 Ом) -1 = 5,00 Ом. Эта параллельная комбинация включена последовательно с двумя другими резисторами, поэтому эквивалентное сопротивление цепи равно Req = R1 + R2 + R34 = 25,00 Ом, Req = R1 + R2 + R34 = 25,00 Ом. Таким образом, напряжение, подаваемое батареей, равно V = IReq = 2.00A (25,00 Ом) = 50,00 В. V = IReq = 2,00 A (25,00 Ом) = 50,00 В.
- Один из способов проверить соответствие ваших результатов — это рассчитать мощность, подаваемую батареей, и мощность, рассеиваемую резисторами. Мощность, подаваемая батареей, составляет Pbatt = IV = 100,00 Вт. Pbatt = IV = 100,00 Вт.
Поскольку они включены последовательно, ток через R2R2 равен току через R1.R1. Поскольку R3 = R4R3 = R4, ток через каждый из них будет 1,00 Ампер. Мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором: Р = I12R1 + I22R2 + I32R3 + I42R4 = 40.00W + 40.00W + 10.00W + 10.00W = 100.00W.P = I12R1 + I22R2 + I32R3 + I42R4 = 40.00W + 40.00W + 10.00W + 10.00W = 100.00W. Поскольку мощность, рассеиваемая резисторами, равна мощности, потребляемой батареей, наше решение кажется последовательным.
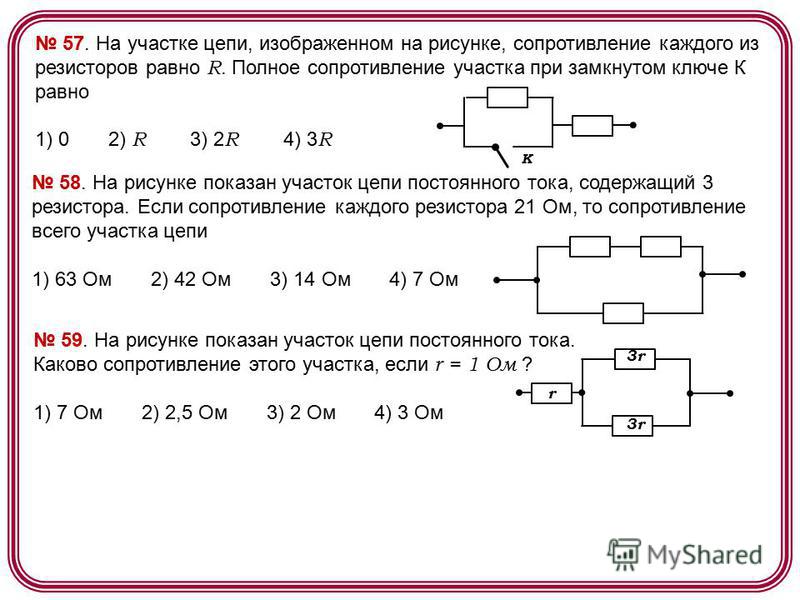
 107
107 107
107 То есть есть определенные значения резисторов, от которых нельзя отойти при производстве. Это значит, что не всегда есть резистор нужного номинала и его нужно соорудить из других резисторов.
То есть есть определенные значения резисторов, от которых нельзя отойти при производстве. Это значит, что не всегда есть резистор нужного номинала и его нужно соорудить из других резисторов.