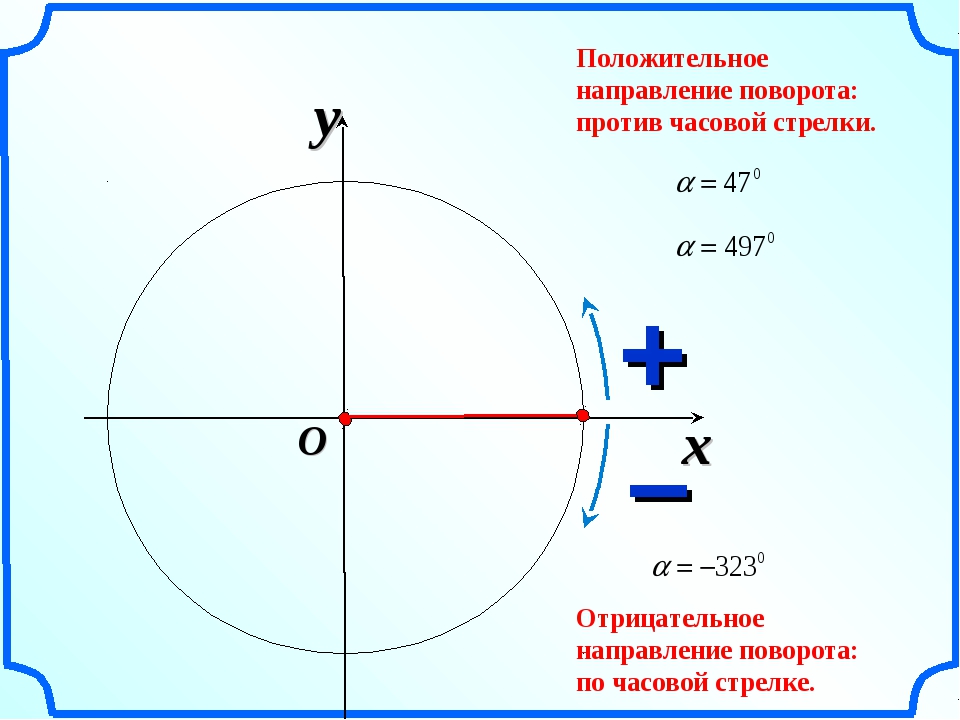
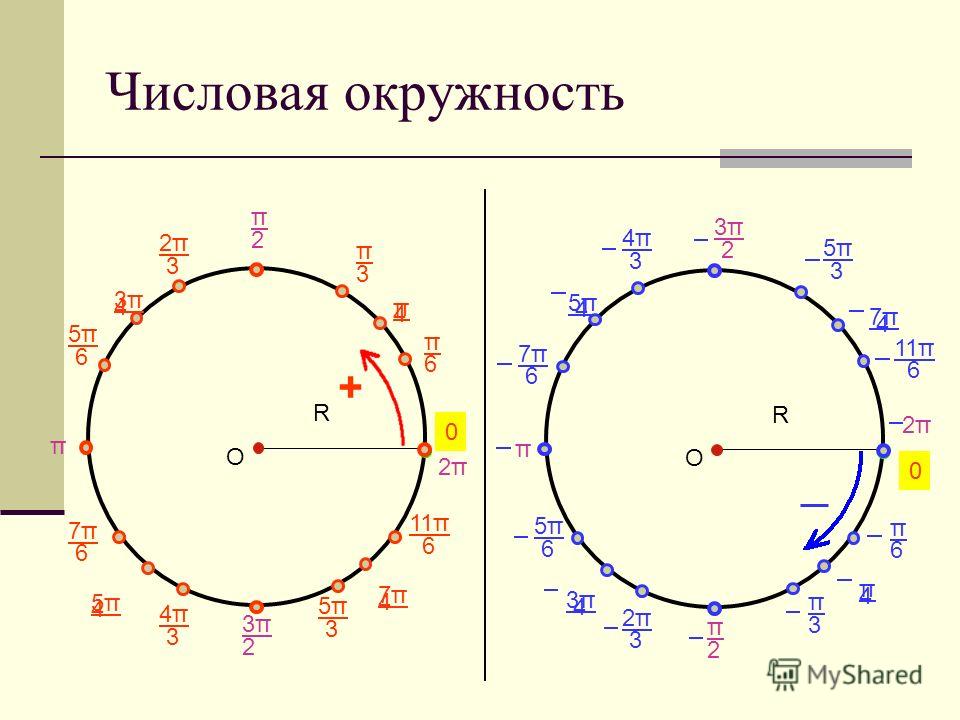
| Базовыми точками на числовой окружности для угла 60° и всех отстоящих от него на углы, кратные прямому (углы \(\frac{\pi}{3}+\frac{\pi k}{2}\)), будут четыре точки: 60°, 150°, 240°, 330° \(\left(\frac{\pi}{3},\ \frac{5\pi}{6},\ \frac{4\pi}{3},\ \frac{11\pi}{6}\right)\). {\circ}}=\sqrt{1-\frac14}=\frac{\sqrt{3}}{2}. $$ Все исследуемые точки на числовой окружности будут иметь пару координат из чисел \(\frac12\ \text{и}\ \frac{\sqrt{3}}{2}\) в разном порядке и с разными знаками. Чтобы различать их «на глаз», заметим, что \(\frac{\sqrt{3}}{2}\approx 0,87\gt\frac12\). Т.е, отрезок короче будет равен по модулю \(\frac12\), а длиннее \(\frac{\sqrt{3}}{2}\). {\circ}}=\sqrt{1-\frac14}=\frac{\sqrt{3}}{2}. $$ Все исследуемые точки на числовой окружности будут иметь пару координат из чисел \(\frac12\ \text{и}\ \frac{\sqrt{3}}{2}\) в разном порядке и с разными знаками. Чтобы различать их «на глаз», заметим, что \(\frac{\sqrt{3}}{2}\approx 0,87\gt\frac12\). Т.е, отрезок короче будет равен по модулю \(\frac12\), а длиннее \(\frac{\sqrt{3}}{2}\).| α | 60° | 150° | 240° | 330° | | π/3 | 5π/6 | 4π/3 | 11π/6 | | x | cosα | \(\frac12\) | \(-\frac{\sqrt{3}}{2}\) | \(-\frac12\) | \(\frac{\sqrt{3}}{2}\) | | y | sinα | \(\frac{\sqrt{3}}{2}\) | \(\frac12\) | \(-\frac{\sqrt{3}}{2}\) | \(-\frac12\) |
п.9. ПримерыПример 1.
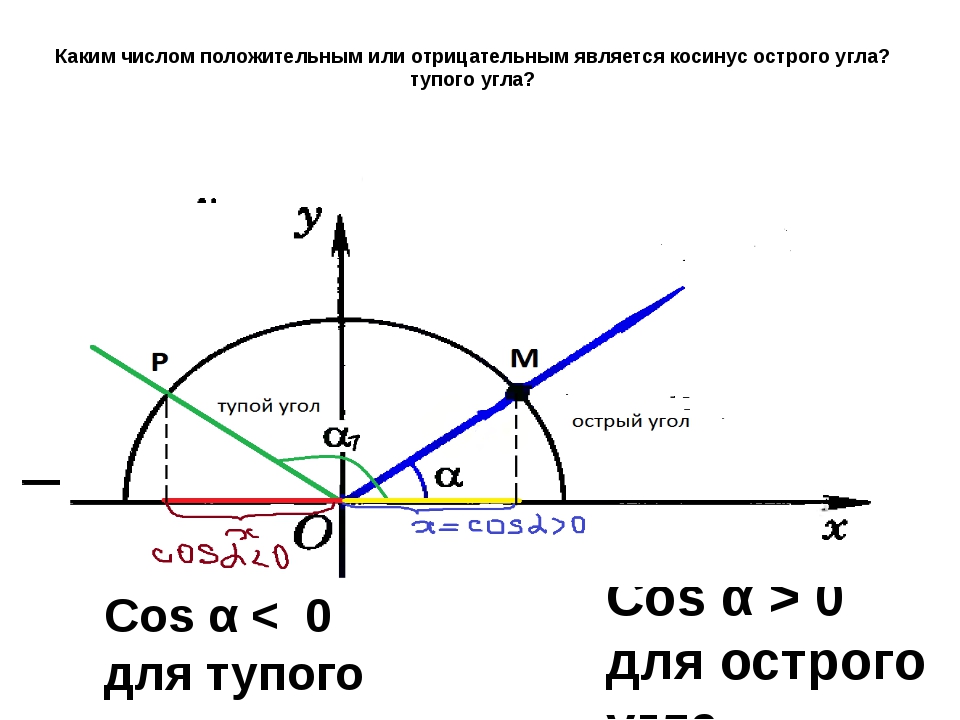
а) Найдите косинус угла α, если известно, что \(sin\alpha=0,8,\ \frac\pi2 \lt \alpha \lt \pi\)
Угол находится во второй четверти, значит, косинус отрицательный:
\(cos\alpha=-\sqrt{1-sin^2\alpha}=-\sqrt{1-0,8^2}=-\sqrt{0,36}=-0,6\) б) Найдите синус угла, если известно, что \(cos\alpha=\frac{5}{13},\ -\frac\pi2 \lt \alpha \lt 0\)
Угол находится в четвертой четверти, значит синус отрицательный:
\(sin\alpha=-\sqrt{1-cos^2\alpha}=-\sqrt{1-\frac{5}{13}^2}=-\sqrt{\frac{144}{169}}=-\frac{12}{13}\) Пример 2. Сравните числа Сравните числа
а) sin10° и sin320°
Угол 10° находится в 1-й четверти, sin10° > 0
Угол 320° находится в 4-й четверти, sin320° < 0
Получаем: sin320° < 0 < sin10°
sin10° > sin320°. б) cos115° и sin85°
Угол 85° находится в 1-й четверти, sin85° > 0
Угол 115° находится во 2-й четверти, cos115° < 0
Получаем: cos115° < 0 < sin85°
cos115° < sin85°. в) \(sin\frac{8\pi}{7}\) и \(cos\frac{11\pi}{25}\)
\(\pi\lt \frac{8\pi}{7}\lt \frac{3\pi}{2}\Rightarrow\) угол \(\frac{8\pi}{7}\) находится в 3-й четверти, \(sin\frac{8\pi}{7}\lt 0\)
\(0\lt \frac{11\pi}{25}\lt \frac{\pi}{2}\Rightarrow\) угол \(\frac{11\pi}{25}\) находится в 1-й четверти, \(cos\frac{11\pi}{25}\gt 0\)
Получаем: \(sin\frac{8\pi}{7} \lt 0\lt cos\frac{11\pi}{25}\)
\(sin\frac{8\pi}{7}\lt cos\frac{11\pi}{25}\) Пример 3. Заданы точки на числовой окружности. Найдите их координаты \begin{gather*} a)\ M\left(\frac{5\pi}{6}\right)\\ \frac{5\pi}{6}=5\cdot \frac\pi6=5\cdot30^{\circ}=150^{\circ} \end{gather*}
Косинус – длинный отрицательный \((-\frac{\sqrt{3}}{2})\)
Синус – короткий положительный \(\left(\frac12\right)\) \begin{gather*} x=cos\frac{5\pi}{6}=-\frac{\sqrt{3}}{2}\\ y=sin\frac{5\pi}{6}=\frac12 \end{gather*} | \begin{gather*} б)\ M\left(-\frac{2\pi}{3}\right)\\ -\frac{2\pi}{3}=-2\cdot \frac\pi3=-2\cdot 60^{\circ}=-120^{\circ} \end{gather*}
Косинус – короткий отрицательный \(\left(-\frac12\right)\)
Синус – длинный отрицательный \((-\frac{\sqrt{3}}{2})\) \begin{gather*} x=cos\left(-\frac{2\pi}{3}\right)=-\frac12\\ y=sin\left(-\frac{2\pi}{3}\right)=-\frac{\sqrt{3}}{2} \end{gather*} | | \begin{gather*} в)\ M\left(\frac{5\pi}{2}\right)\\ \frac{5\pi}{2}=\left(2+\frac12\right)\pi=2\pi+\frac\pi2\rightarrow\frac\pi2=90^{\circ} \end{gather*} \begin{gather*} x=cos\frac{5\pi}{2}=cos\frac\pi2=0\\ y=sin\frac{5\pi}{2}=sin\frac\pi2=1 \end{gather*} | \begin{gather*} г)\ M\left(-\frac{16\pi}{3}\right)\\ -\frac{16\pi}{3}=\frac{-18+2}{3}\pi=-6\pi+\frac{2\pi}{3}\rightarrow\frac{2\pi}{3}= 120^{\circ} \end{gather*}
Косинус – короткий отрицательный \(\left(-\frac12\right)\)
Синус – длинный положительный \(\left(\frac{\sqrt{3}}{2}\right)\) \begin{gather*} x=cos\left(-\frac{16\pi}{3}\right)=cos\frac{2\pi}{3}=-\frac12\\ y=sin\left(-\frac{16\pi}{3}\right)=sin\frac{2\pi}{3}=\frac{\sqrt{3}}{2} \end{gather*} |
Пример 4. Найти sint,cost для данных t. Найти sint,cost для данных t. \(a)\ t=\frac{13\pi}{4}\) | Отнимем полный оборот: \(\frac{13\pi}{4}-2\pi=\frac{13-8}{4}\pi=\frac{5\pi}{4}\)
Угол кратный \(\frac\pi4\), его синус и косинус по модулю равны \(\frac{\sqrt{2}}{2}\), знаки определяются расположением угла.
\(\pi\lt\frac{5\pi}{4}\lt\frac{3\pi}{2}\Rightarrow\) угол находится в 3-й четверти, синус и косинус отрицательные.
Получаем: \begin{gather*} sin\frac{13\pi}{4}=sin\frac{5\pi}{4}=-\frac{\sqrt{2}}{2}\\ cos\frac{13\pi}{4}=cos\frac{5\pi}{4}=-\frac{\sqrt{2}}{2} \end{gather*} |
\(б)\ t=\frac{11\pi}{2}\) | Отнимем 2 полных оборота: \(\frac{11\pi}{2}-2\cdot 2\pi=\frac{11-8}{2}\pi=\frac{3\pi}{2}\)
Угол кратный \(\frac\pi2\), находится на оси Y, в нижней точке числовой окружности.
Получаем: \begin{gather*} sin\frac{11\pi}{2}=sin\frac{3\pi}{2}=-1\\ cos\frac{11\pi}{2}=cos\frac{3\pi}{2}=0 \end{gather*} |
\(в)\ t=\frac{17\pi}{6}\) | Отнимем полный оборот: \(\frac{17\pi}{6}-2\pi=\frac{17-12}{6}\pi=\frac{5\pi}{6}\)
Угол типа \(\frac\pi6\), в котором синус и косинус – это пара из \(\frac12\) и \(\frac{\sqrt{3}}{2}\), фактическое значение определяется по чертежу, исходя из того, что \(\frac{\sqrt{3}}{2}\approx 0,87\gt\frac12\). Знаки определяются по расположению угла в четверти: \(\frac\pi2\lt\frac{5\pi}{6}\lt\pi\Rightarrow\) угол находится во 2-й четверти. Знаки определяются по расположению угла в четверти: \(\frac\pi2\lt\frac{5\pi}{6}\lt\pi\Rightarrow\) угол находится во 2-й четверти.
Из чертежа получаем:
Косинус – длинный отрицательный
Синус – короткий положительный
Таким образом: \begin{gather*} sin\frac{17\pi}{6}=sin\frac{5\pi}{6}=\frac12\\ cos\frac{17\pi}{6}=cos\frac{5\pi}{6}=-\frac{\sqrt{3}}{2} \end{gather*} |
\(г)\ t=-\frac{4\pi}{3}\) | Добавим полный оборот: \(-\frac{4\pi}{3}+2\pi=\frac{-4+6}{3}\pi=\frac{2\pi}{3}\)
Угол типа \(\frac\pi3\), в котором синус и косинус – это пара из \(\frac12\) и \(\frac{\sqrt{3}}{2}\), фактическое значение определяется по чертежу, исходя из того, что \(\frac{\sqrt{3}}{2}\approx 0,87\gt\frac12\). Знаки определяются по расположению угла в четверти: \(\frac\pi2\lt\frac{2\pi}{3}\lt\pi\Rightarrow\) угол находится во 2-й четверти.
Из чертежа получаем:
Косинус – короткий отрицательный
Синус – длинный положительный
Таким образом: \begin{gather*} sin\left(-\frac{4\pi}{3}\right)=sin\frac{2\pi}{3}=\frac{\sqrt{3}}{2}\\ cos\left(-\frac{4\pi}{3}\right)=cos\frac{2\pi}{3}=-\frac12 \end{gather*} |
cosx меньше aРассмотрим решение тригонометрических неравенств вида cosx меньше a (cosx<a) на единичной окружности. Снова применяем ассоциацию косинус-колобок. Оба кругленькие, оба начинаются с ко-. Колобку, в силу особенности его фигуры, удобнее двигаться влево-вправо, а не вверх-вниз. Влево-вправо на координатной плоскости — движение по оси ox. Значит, косинус — это x. То есть абсцисса, координата x точки на окружности. Геометрически cosx=a в точках пересечения единичной окружности и прямой x=a (прямая, параллельная оси ox). Соответственно, точки окружности, находящиеся правее этой прямой, соответствуют значениям косинуса, большим a, а cosx меньше a — левее этой прямой. Прямая и окружность могут пересекаться, не пересекаться и касаться. От их взаимного расположения зависит решение тригонометрического неравенства cosx меньше a. 1) cosx<a, при 0<a<1. Первая точка пересечения прямой и окружности находится, как обычно, — это arccos a. Поскольку нам нужны значения, в которых cos x меньше a, из первой точки ко второй мы идем по верхнему пути, против часовой стрелки. При таком направлении обхода угол увеличивается. Вторую точку получили, немного не дойдя до 2п. На сколько не дошли? На тот же угол, который соответствует arccos a. Раз не дошли, то это число вычитаем из 2п. Поэтому вторая точка пересечения прямой с окружностью есть 2п-arccos a. Итак, решением неравенства cos x меньше a является промежуток (arccos a; 2п-arccos a). Поскольку период косинуса равен 2п, к каждому из концов промежутка прибавляем 2пn, где n -целое число (то есть n принадлежит Z). Получаем окончательный вариант ответа: (arccos a+2пn; 2п-arccos a+2пn). Для нестрогого неравенства точки закрашиваем и ставим квадратные скобки. При таком направлении обхода угол увеличивается. Вторую точку получили, немного не дойдя до 2п. На сколько не дошли? На тот же угол, который соответствует arccos a. Раз не дошли, то это число вычитаем из 2п. Поэтому вторая точка пересечения прямой с окружностью есть 2п-arccos a. Итак, решением неравенства cos x меньше a является промежуток (arccos a; 2п-arccos a). Поскольку период косинуса равен 2п, к каждому из концов промежутка прибавляем 2пn, где n -целое число (то есть n принадлежит Z). Получаем окончательный вариант ответа: (arccos a+2пn; 2п-arccos a+2пn). Для нестрогого неравенства точки закрашиваем и ставим квадратные скобки. 2) cos x меньше -a, при 0<a<1. Решение неравенства аналогично первому случаю. Отличие — нужно вычислить арккосинус отрицательного числа (чуть позже я расскажу, как легко запомнить значения arccos (-a) с помощью ассоциации). А пока что arccos (-a)= п-arccos a. Ко второй точке здесь тоже идем против часовой стрелки, то есть значение угла увеличивается. Не доходим до 2п на величину arccos(-a), отсюда вторая точка есть 2п-arccos(-a). Чтобы учесть все решения неравенства, к концам промежутка прибавляем 2пn. Если неравенство нестрогое, точки закрашиваем и включаем в ответ (с квадратной скобкой). Не доходим до 2п на величину arccos(-a), отсюда вторая точка есть 2п-arccos(-a). Чтобы учесть все решения неравенства, к концам промежутка прибавляем 2пn. Если неравенство нестрогое, точки закрашиваем и включаем в ответ (с квадратной скобкой). 3) cosx<0 То есть ищем, где косинус отрицательный. В качестве первой точки промежутка, на котором косинус принимает отрицательные значения, берем п/2, вторая точка — 3п/2. Чтобы учесть все промежутки, на которых косинус отрицательный, прибавляем к концам промежутка 2пn. Таким образом, решение тригонометрического неравенства cosx<0 есть промежуток (п/2+2пn; 3п/2+2пn), где n — целое число. Если неравенство нестрогое, то есть ищем неотрицательные значения косинуса, точки закрашиваем, скобки берем квадратные. 4) cosx<1 В этом случае окружность и прямая x=a касаются в одной точке — в нуле. Таким образом, за исключением этой точки, окружность расположена левее прямой. Значит, cosx меньше 1 в любой точке, кроме точек вида 0+2пn. Чтобы записать решение тригонометрического неравенства cosx<1 в виде интервала, в качестве второго конца промежутка берем 2п и к обоим концам прибавляем 2пn. Получаем (2пn; 2п+2пn). Значит, cosx меньше 1 в любой точке, кроме точек вида 0+2пn. Чтобы записать решение тригонометрического неравенства cosx<1 в виде интервала, в качестве второго конца промежутка берем 2п и к обоим концам прибавляем 2пn. Получаем (2пn; 2п+2пn). 5) cosx<a, при a>1. В этом случае окружность целиком лежит левее прямой x=a и любое значение x удовлетворяет условию неравенства. Таким образом, в этом случае косинус меньше a на промежутке (-∞;+∞). 6) cosx<-a, при a>1. При таких a окружность целиком расположена правее прямой x=-a и нет ни одного x, удовлетворяющего требованию cosx меньше -a. Поэтому решений нет. В этом случае точку пересечения окружности и прямой исключать из решения не нужно, значит, x — любое число и решением является вся числовая прямая: (-∞;+∞). Единственным решением этого тригонометрического неравенства является точка п. С учетом периодичности косинуса, решением является множество точек вида п+2пn, где n — целое число. И в заключении — пример решения тригонометрического неравенства вида cosx меньше a: cosx<-1/2: Таблица косинусов, полная таблица косинусов для студентовСодержание: Таблица косинусов — наровне с
таблицей синусов
изучается в самом начале тригонометрии (И вместе с таблицей синусов является основным материалом тригонометрии). Без понимания данного материала и без знания хотя бы части таблицы косинусов будет очень сложно изучать тригонометрию и
применять тригонометричекие формулы.
Даже в университетском курсе часто используется тригонометрия, при решении интегралов и производных. Пользуйте таблицей косинусов на здоровье.
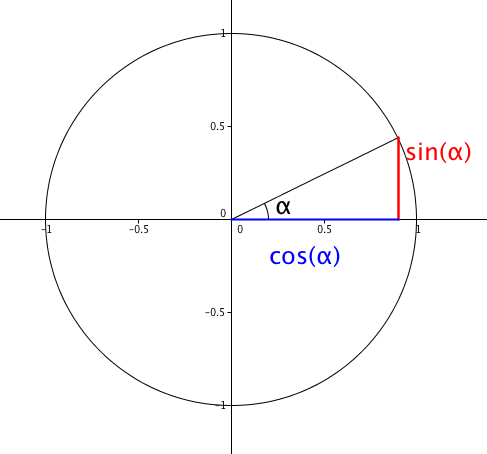
Таблица косинусов 0° — 180°
| | Cos(61°) | 0.4848 | | Cos(62°) | 0.4695 | | Cos(63°) | 0.454 | | Cos(64°) | 0.4384 | | Cos(65°) | 0.4226 | | Cos(66°) | 0.4067 | | Cos(67°) | 0.3907 | | Cos(68°) | 0.3746 | | Cos(69°) | 0.3584 | | Cos(70°) | 0.342 | | Cos(71°) | 0.3256 | | Cos(72°) | 0.309 | | Cos(73°) | 0.2924 | | Cos(74°) | 0.2756 | | Cos(75°) | 0.2588 | | Cos(76°) | 0. 2419 2419 | | Cos(77°) | 0.225 | | Cos(78°) | 0.2079 | | Cos(79°) | 0.1908 | | Cos(80°) | 0.1736 | | Cos(81°) | 0.1564 | | Cos(82°) | 0.1392 | | Cos(83°) | 0.1219 | | Cos(84°) | 0.1045 | | Cos(85°) | 0.0872 | | Cos(86°) | 0.0698 | | Cos(87°) | 0.0523 | | Cos(88°) | 0.0349 | | Cos(89°) | 0.0175 | | Cos(90°) | 0 | | Cos(91°) | -0.0175 | | Cos(92°) | -0.0349 | | Cos(93°) | -0.0523 | | Cos(94°) | -0.0698 | | Cos(95°) | -0.0872 | | Cos(96°) | -0.1045 | | Cos(97°) | -0.1219 | | Cos(98°) | -0.1392 | | Cos(99°) | -0.1564 | | Cos(100°) | -0. 1736 1736 | | Cos(101°) | -0.1908 | | Cos(102°) | -0.2079 | | Cos(103°) | -0.225 | | Cos(104°) | -0.2419 | | Cos(105°) | -0.2588 | | Cos(106°) | -0.2756 | | Cos(107°) | -0.2924 | | Cos(108°) | -0.309 | | Cos(109°) | -0.3256 | | Cos(110°) | -0.342 | | Cos(111°) | -0.3584 | | Cos(112°) | -0.3746 | | Cos(113°) | -0.3907 | | Cos(114°) | -0.4067 | | Cos(115°) | -0.4226 | | Cos(116°) | -0.4384 | | Cos(117°) | -0.454 | | Cos(118°) | -0.4695 | | Cos(119°) | -0.4848 | | Cos(120°) | -0.5 |
| | Cos(121°) | -0.515 | | Cos(122°) | -0. 5299 5299 | | Cos(123°) | -0.5446 | | Cos(124°) | -0.5592 | | Cos(125°) | -0.5736 | | Cos(126°) | -0.5878 | | Cos(127°) | -0.6018 | | Cos(128°) | -0.6157 | | Cos(129°) | -0.6293 | | Cos(130°) | -0.6428 | | Cos(131°) | -0.6561 | | Cos(132°) | -0.6691 | | Cos(133°) | -0.682 | | Cos(134°) | -0.6947 | | Cos(135°) | -0.7071 | | Cos(136°) | -0.7193 | | Cos(137°) | -0.7314 | | Cos(138°) | -0.7431 | | Cos(139°) | -0.7547 | | Cos(140°) | -0.766 | | Cos(141°) | -0.7771 | | Cos(142°) | -0.788 | | Cos(143°) | -0.7986 | | Cos(144°) | -0.809 | | Cos(145°) | -0. 8192 8192 | | Cos(146°) | -0.829 | | Cos(147°) | -0.8387 | | Cos(148°) | -0.848 | | Cos(149°) | -0.8572 | | Cos(150°) | -0.866 | | Cos(151°) | -0.8746 | | Cos(152°) | -0.8829 | | Cos(153°) | -0.891 | | Cos(154°) | -0.8988 | | Cos(155°) | -0.9063 | | Cos(156°) | -0.9135 | | Cos(157°) | -0.9205 | | Cos(158°) | -0.9272 | | Cos(159°) | -0.9336 | | Cos(160°) | -0.9397 | | Cos(161°) | -0.9455 | | Cos(162°) | -0.9511 | | Cos(163°) | -0.9563 | | Cos(164°) | -0.9613 | | Cos(165°) | -0.9659 | | Cos(166°) | -0.9703 | | Cos(167°) | -0.9744 | | Cos(168°) | -0. 9781 9781 | | Cos(169°) | -0.9816 | | Cos(170°) | -0.9848 | | Cos(171°) | -0.9877 | | Cos(172°) | -0.9903 | | Cos(173°) | -0.9925 | | Cos(174°) | -0.9945 | | Cos(175°) | -0.9962 | | Cos(176°) | -0.9976 | | Cos(177°) | -0.9986 | | Cos(178°) | -0.9994 | | Cos(179°) | -0.9998 | | Cos(180°) | -1 |
|
Таблица косинусов 180° — 360°
| Cos(181°) | -0.9998 | | Cos(182°) | -0.9994 | | Cos(183°) | -0.9986 | | Cos(184°) | -0.9976 | | Cos(185°) | -0.9962 | | Cos(186°) | -0.9945 | | Cos(187°) | -0.9925 | | Cos(188°) | -0. 9903 9903 | | Cos(189°) | -0.9877 | | Cos(190°) | -0.9848 | | Cos(191°) | -0.9816 | | Cos(192°) | -0.9781 | | Cos(193°) | -0.9744 | | Cos(194°) | -0.9703 | | Cos(195°) | -0.9659 | | Cos(196°) | -0.9613 | | Cos(197°) | -0.9563 | | Cos(198°) | -0.9511 | | Cos(199°) | -0.9455 | | Cos(200°) | -0.9397 | | Cos(201°) | -0.9336 | | Cos(202°) | -0.9272 | | Cos(203°) | -0.9205 | | Cos(204°) | -0.9135 | | Cos(205°) | -0.9063 | | Cos(206°) | -0.8988 | | Cos(207°) | -0.891 | | Cos(208°) | -0.8829 | | Cos(209°) | -0.8746 | | Cos(210°) | -0.866 | | Cos(211°) | -0. 8572 8572 | | Cos(212°) | -0.848 | | Cos(213°) | -0.8387 | | Cos(214°) | -0.829 | | Cos(215°) | -0.8192 | | Cos(216°) | -0.809 | | Cos(217°) | -0.7986 | | Cos(218°) | -0.788 | | Cos(219°) | -0.7771 | | Cos(220°) | -0.766 | | Cos(221°) | -0.7547 | | Cos(222°) | -0.7431 | | Cos(223°) | -0.7314 | | Cos(224°) | -0.7193 | | Cos(225°) | -0.7071 | | Cos(226°) | -0.6947 | | Cos(227°) | -0.682 | | Cos(228°) | -0.6691 | | Cos(229°) | -0.6561 | | Cos(230°) | -0.6428 | | Cos(231°) | -0.6293 | | Cos(232°) | -0.6157 | | Cos(233°) | -0.6018 | | Cos(234°) | -0. 5878 5878 | | Cos(235°) | -0.5736 | | Cos(236°) | -0.5592 | | Cos(237°) | -0.5446 | | Cos(238°) | -0.5299 | | Cos(239°) | -0.515 | | Cos(240°) | -0.5 |
| | Cos(241°) | -0.4848 | | Cos(242°) | -0.4695 | | Cos(243°) | -0.454 | | Cos(244°) | -0.4384 | | Cos(245°) | -0.4226 | | Cos(246°) | -0.4067 | | Cos(247°) | -0.3907 | | Cos(248°) | -0.3746 | | Cos(249°) | -0.3584 | | Cos(250°) | -0.342 | | Cos(251°) | -0.3256 | | Cos(252°) | -0.309 | | Cos(253°) | -0.2924 | | Cos(254°) | -0.2756 | | Cos(255°) | -0.2588 | | Cos(256°) | -0. 2419 2419 | | Cos(257°) | -0.225 | | Cos(258°) | -0.2079 | | Cos(259°) | -0.1908 | | Cos(260°) | -0.1736 | | Cos(261°) | -0.1564 | | Cos(262°) | -0.1392 | | Cos(263°) | -0.1219 | | Cos(264°) | -0.1045 | | Cos(265°) | -0.0872 | | Cos(266°) | -0.0698 | | Cos(267°) | -0.0523 | | Cos(268°) | -0.0349 | | Cos(269°) | -0.0175 | | Cos(270°) | -0 | | Cos(271°) | 0.0175 | | Cos(272°) | 0.0349 | | Cos(273°) | 0.0523 | | Cos(274°) | 0.0698 | | Cos(275°) | 0.0872 | | Cos(276°) | 0.1045 | | Cos(277°) | 0.1219 | | Cos(278°) | 0.1392 | | Cos(279°) | 0. 1564 1564 | | Cos(280°) | 0.1736 | | Cos(281°) | 0.1908 | | Cos(282°) | 0.2079 | | Cos(283°) | 0.225 | | Cos(284°) | 0.2419 | | Cos(285°) | 0.2588 | | Cos(286°) | 0.2756 | | Cos(287°) | 0.2924 | | Cos(288°) | 0.309 | | Cos(289°) | 0.3256 | | Cos(290°) | 0.342 | | Cos(291°) | 0.3584 | | Cos(292°) | 0.3746 | | Cos(293°) | 0.3907 | | Cos(294°) | 0.4067 | | Cos(295°) | 0.4226 | | Cos(296°) | 0.4384 | | Cos(297°) | 0.454 | | Cos(298°) | 0.4695 | | Cos(299°) | 0.4848 | | Cos(300°) | 0.5 |
| | Cos(301°) | 0.515 | | Cos(302°) | 0. 5299 5299 | | Cos(303°) | 0.5446 | | Cos(304°) | 0.5592 | | Cos(305°) | 0.5736 | | Cos(306°) | 0.5878 | | Cos(307°) | 0.6018 | | Cos(308°) | 0.6157 | | Cos(309°) | 0.6293 | | Cos(310°) | 0.6428 | | Cos(311°) | 0.6561 | | Cos(312°) | 0.6691 | | Cos(313°) | 0.682 | | Cos(314°) | 0.6947 | | Cos(315°) | 0.7071 | | Cos(316°) | 0.7193 | | Cos(317°) | 0.7314 | | Cos(318°) | 0.7431 | | Cos(319°) | 0.7547 | | Cos(320°) | 0.766 | | Cos(321°) | 0.7771 | | Cos(322°) | 0.788 | | Cos(323°) | 0.7986 | | Cos(324°) | 0.809 | | Cos(325°) | 0. 8192 8192 | | Cos(326°) | 0.829 | | Cos(327°) | 0.8387 | | Cos(328°) | 0.848 | | Cos(329°) | 0.8572 | | Cos(330°) | 0.866 | | Cos(331°) | 0.8746 | | Cos(332°) | 0.8829 | | Cos(333°) | 0.891 | | Cos(334°) | 0.8988 | | Cos(335°) | 0.9063 | | Cos(336°) | 0.9135 | | Cos(337°) | 0.9205 | | Cos(338°) | 0.9272 | | Cos(339°) | 0.9336 | | Cos(340°) | 0.9397 | | Cos(341°) | 0.9455 | | Cos(342°) | 0.9511 | | Cos(343°) | 0.9563 | | Cos(344°) | 0.9613 | | Cos(345°) | 0.9659 | | Cos(346°) | 0.9703 | | Cos(347°) | 0.9744 | | Cos(348°) | 0. 9781 9781 | | Cos(349°) | 0.9816 | | Cos(350°) | 0.9848 | | Cos(351°) | 0.9877 | | Cos(352°) | 0.9903 | | Cos(353°) | 0.9925 | | Cos(354°) | 0.9945 | | Cos(355°) | 0.9962 | | Cos(356°) | 0.9976 | | Cos(357°) | 0.9986 | | Cos(358°) | 0.9994 | | Cos(359°) | 0.9998 | | Cos(360°) | 1 |
|
На нашем сайте в основном автоматические находятся программы для решения задач по математике, но также
мы собрали много теоретического материала по математике и в частности по тригонометрии. Здесь Вы можете найти
таблицы тригонометрических функций:
таблицу косинусов,
таблицу синусов,
таблицу котангенсов и
таблицу тангенсов.
Также для улучшения понимания материала по тригонометрии мы добавили
тригонометрические формулы, чтобы
вызывало меньше затруднений решение тригонометрических задач по математике. Пользуйтесь нашим сайтом и таблицей косинусов на здоровье. Пользуйтесь нашим сайтом и таблицей косинусов на здоровье. Слишком сложно? Таблица косинусов, таблица значений косинусов не по зубам? Тебе ответит эксперт через 10 минут! Функция COSВ этой статье описаны синтаксис формулы и использование функции COS в Microsoft Excel.
Описание
Возвращает косинус заданного угла.
Синтаксис
COS(число)
Аргументы функции COS описаны ниже.
Замечания
Если угол задан в градусах, умножьте его на ПИ()/180 или воспользуйтесь функцией РАДИАНЫ, чтобы преобразовать его в радианы.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула
|
Описание
|
Результат
|
|
=COS(1,047)
|
Косинус 1,047 радиан
|
0,5001711
|
|
=COS(60*ПИ()/180)
|
Косинус 60 градусов
|
0,5
|
|
=COS(РАДИАНЫ(60))
|
Косинус 60 градусов
|
0,5
|
Отрицательный cos fi
Пожалуйста активируйте JavaScript в настройках браузера.
| Форум посвящен вопросам релейной защиты и автоматики. Обмену опытом эксплуатации РЗА. Общению релейщиков ЕЭС России. |
|
|
| gif»>
|
VLAX
+6
Сообщения: 299
Регистрация: 14.08.2008
|
|
|
Когда возможен? Только при генерировании активной энергии или есть еще варианты? Анализатор сети выдает:
P=8
Capasitive Q=0,8
Inductive Q=0 cos fi = -0,99 Вопрос почему минус. .. ..
|
|
|
|
|
|
|
zloi
+20
Сообщения: 234
Регистрация: 17. 07.2008 07.2008
|
|
|
VLAX>Когда возможен? Только при генерировании активной энергии или есть еще варианты? VLAX>Анализатор сети выдает:
VLAX>P=8
VLAX>Capasitive Q=0,8
VLAX>Inductive Q=0 VLAX>cos fi = -0,99 VLAX>Вопрос почему минус… Ёмкостная нагрузка ?
| | В театре абсурда ты главный герой… |
|
|
|
|
|
| ./../communityhost.ru/includes/layouts/bb/styles/grey/box/sub_headline_bg.gif»>
falcon
+92
Сообщения: 2133
Регистрация: 20.04.2007
Откуда: НАШ НОВЫЙ ФОРУМ: http://rzia.ru
|
|
|
VLAX>Когда возможен? Только при генерировании активной энергии или есть еще варианты? VLAX>Анализатор сети выдает:
VLAX>P=8
VLAX>Capasitive Q=0,8
VLAX>Inductive Q=0 VLAX>cos fi = -0,99 VLAX>Вопрос почему минус. .. .. Математика в анализаторе неправильная, потому и минус.
Правильная математика считает так:
—————
P=8
= 8 Q=-0.8i
= -0,8i S=P+Q
= 8-0,8i = 8,04*exp(-5,71°i) ф=arg(S)
= -0,0997 cos(ф)
= 0,995 |
|
|
|
|
|
|
Модераторы форумов
grsl
+101
Сообщения: 4577
Регистрация: 04. 03.2008 03.2008
Откуда: http://rzia.ru/
|
|
Анализатор показывает то что к нему подключено.
Емкостную нагрузку, как и сказал коллега zloi.
Вы находитесь во четвёртом квадранте, выдача активной мощности и потребление реактивной мощности.
Может что не нагрузка емкостная, а если то генератор в работе близком к кос1 то реактивные потери повышающего транса беруться из сети.второй вариант, что неверное подключение цепей напряжения. Ну и совсем так по теме, вопрос, какой cos показывает, есть два в анализаторах PF и DPF
| Новый Форум «Советы Бывалого Релейщика»
http://rzia.ru/ |
|
|
|
|
|
| ./../communityhost.ru/includes/layouts/bb/styles/grey/box/sub_headline_bg.gif»>
nkulesh
+15
Сообщения: 250
Регистрация: 11.11.2009
Откуда: Зея
|
|
Что такое «анализатор сети»? Род ВАФа?
Ёмкостное, индуктивное … это ведь относительно. Зависит от того, что принимать за положительное направление, ну, это к Ветхому завету восходит (никого из верующих не хотел задеть). Ну и от схемы самого включения зависит, обсуждали уже. Ну и от схемы самого включения зависит, обсуждали уже.
|
|
|
|
|
|
|
Саня
+3
Сообщения: 148
Регистрация: 08. 04.2008 04.2008
Откуда: Минск
|
|
VLAX>Когда возможен? Только при генерировании активной энергии или есть еще варианты?
Схему подключения с полярностью обмоток ТТ, ТН и прибора в студию.
|
|
|
|
|
| ru/includes/layouts/bb/styles/grey/box/sub_headline_bg.gif»>
|
|
|
|
Модераторы форумов
grsl
+101
Сообщения: 4577
Регистрация: 04.03.2008
Откуда: http://rzia.ru/
|
|
|
nkulesh>Что такое «анализатор сети»? Род ВАФа? Измерительный прибор. замеряют до сотен всяких параметров, определяют «качество» электроэнергии. замеряют до сотен всяких параметров, определяют «качество» электроэнергии.
Кроме стандартных, показывают гармоники по каждой фазе токов и нпаряжений, всякие лимиты по токам, напряжениям, крест-фактор, флики и…..обычо современые с большим объёмом памяти.
| Новый Форум «Советы Бывалого Релейщика»
http://rzia.ru/ |
|
|
|
|
|
| ./../communityhost.ru/includes/layouts/bb/styles/grey/box/sub_headline_bg.gif»>
|
|
|
|
scorp
+29
Сообщения: 1508
Регистрация: 06.04.2007
Откуда: заМКАДье
|
|
grsl>Анализатор показывает то что к нему подключено.
grsl>Емкостную нагрузку, как и сказал коллега zloi.
grsl>Вы находитесь во четвёртом квадранте, выдача активной мощности и потребление реактивной мощности.
grsl>Может что не нагрузка емкостная, а если то генератор в работе близком к кос1 то реактивные потери повышающего транса беруться из сети.grsl>второй вариант, что неверное подключение цепей напряжения. grsl>Ну и совсем так по теме, вопрос, какой cos показывает, есть два в анализаторах PF и DPF С «+» релейщики считают выдача в линию,ОП наооборот.
4 квадрант — это прием Р и выдача Q
|
|
|
|
|
| ./../communityhost.ru/includes/layouts/bb/styles/grey/box/sub_headline_bg.gif»>
Модераторы форумов
grsl
+101
Сообщения: 4577
Регистрация: 04.03.2008
Откуда: http://rzia.ru/
|
|
Спасибо scorp, я уже раз поправил нумерацию квадранта :-))), написал вначале второй.
| Новый Форум «Советы Бывалого Релейщика»
http://rzia. ru/ ru/ |
|
|
|
|
|
|
|
VLAX
+6
Сообщения: 299
Регистрация: 14. 08.2008 08.2008
|
|
В том то и дело, что какая-то хрень с этим анализатором. Посколько косинус функция четная, то при углах от меньше 90 по модулю он положителен.
Нагрузка — активно-емкостная, т.е P+ и Q-, потребляет из сети активную и отдает реактивную мощность. Соединено все правильно.grsl>Ну и совсем так по теме, вопрос, какой cos показывает, есть два в анализаторах PF и DPF
Встречный вопрос, что такое DPF? falcon>>>…
А есть причины для подобной математики, может где то приняты другие обозначения?
|
|
|
|
|
| ./../communityhost.ru/includes/layouts/bb/styles/grey/box/sub_headline_bg.gif»>
|
|
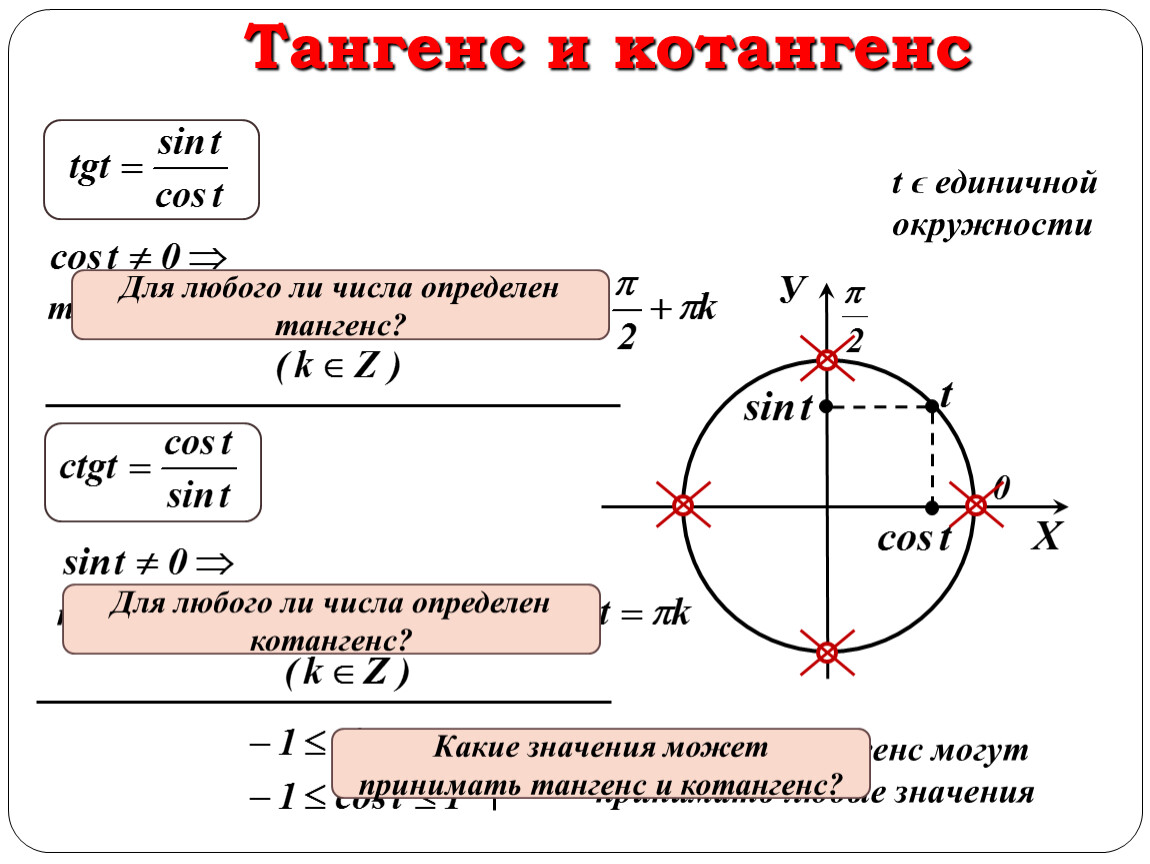
Тригонометрия за 5 минут! Тригонометрические функции и тригонометрический круг простыми словами | Клуб любителей математикиОфициальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах». Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:
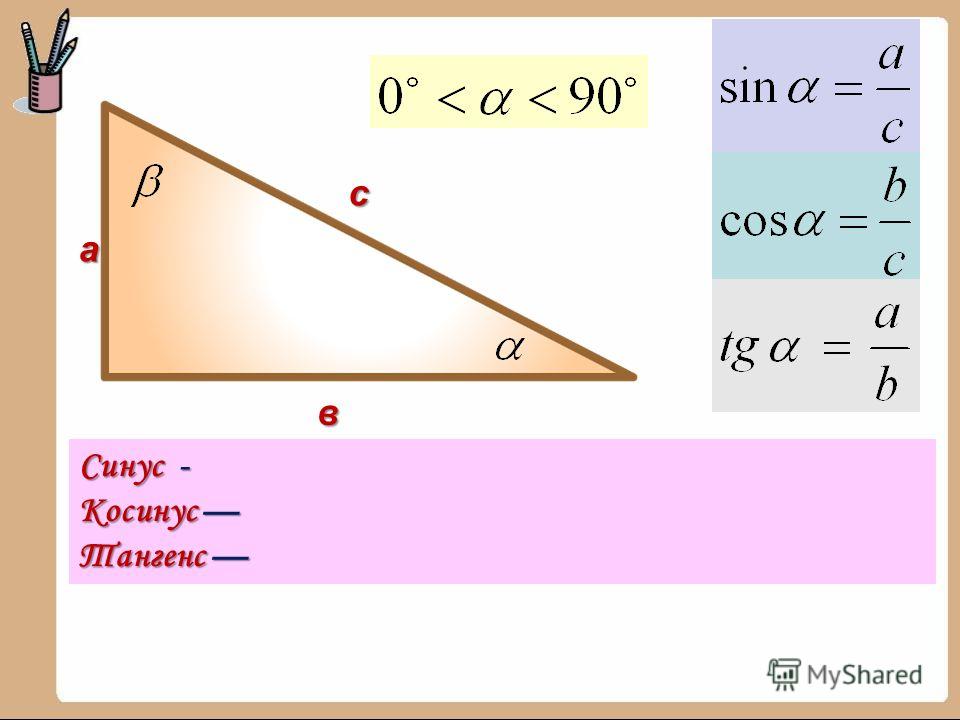
- Синус угла – отношение противолежащего катета к гипотенузе;
- Косинус угла – отношение прилежащего катета к гипотенузе;
- Тангенс угла – отношение противолежащего катета к прилежащему;
- Котангенс угла – отношение прилежащего катета к противолежащему.

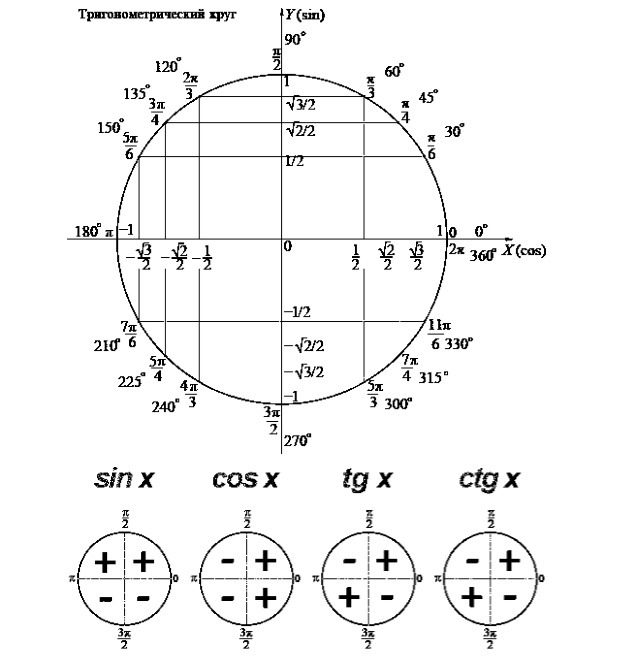
Или в виде формул: Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1). Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла. Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB. Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°. Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный. Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов. Значения тригонометрических функций
для первой четверти круга (0° – 90°)| |
0° |
30° |
45° |
60° |
90° |
|---|
sin |
0 |
|
|
|
1 |
cos |
1 |
|
|
|
0 |
tg |
0 |
|
1 |
√3 |
– |
ctg |
– |
√3 |
1 |
|
0 |
Принцип повтора знаков тригонометрических функцийУгол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону. Отрицательный угол считается угол, откладываемый в противоположную сторону. В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ. Например, значения тригонометрических функций для углов 270° и -90° равны. Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно. Тригонометрический кругУглы в радианахДля математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2πr. Следовательно 360° в радианах равно 2π, а 180° равно π радиан. Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π. Например, для угла 90° будет · π = πЧтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.
|
Онлайн тренажер
для запоминания значений тригонометрических функций для разных углов
|
Простые тригонометрические тождестваИспользуя вышеописанные формулы: тангенс угла выражается через отношение синуса к косинусу: Соответственно котангенс выражается аналогично: Также можно заметить, что произведение тангенса на котангес равно единице:
tg(a) · ctg(a) = · =- sin(a) · cos(a)
- cos(a) · sin(a)
= 1
Иными словами, тангенс угла обратно пропорционален котангенсу угла и наоборот:
tg(a) · ctg(a) = 1
;
tg(a) = ;
сtg(a) =
Используя теорему Пифагора в треугольнике, что сумма квадратов катетов равно квадрату гипотенузы
r2 = s2 + c2 = (sin(a) · r)2 + (cos(a) · r)2;
r2 · (sin(a)2 + cos(a)2) = r2 Сократим обе части на r2, получим:
sin2a + cos2a = 1
Разделив обе части на квадрат синуса или квадрат косинуса, получим еще два основных тригонометрических тождества: Обратный синус, косинус, тангенс Быстрый ответ: Для прямоугольного треугольника: Синус , функция sin принимает угол θ и дает отношение против гипотенузы Функция обратного синуса sin -1 принимает отношение против гипотенузы и дает угол θ Косинус и тангенс следуют аналогичной идее. Пример (длины до одного десятичного знака): sin (35 °) = Противоположно / Гипотенуза = 2,8 / 4,9 = 0,57 … sin -1 (противоположно / гипотенуза) = sin -1 (0,57 …) = 35 ° А теперь подробнее: Синус, косинус и тангенс — все основаны на прямоугольном треугольнике Они очень похожи по функциям…
поэтому мы посмотрим на синусоидальную функцию , а затем на обратный синус , чтобы понять, что это такое. Синусоидальная функция Синус угла θ равен: - длина стороны Противоположный угол θ
- делится на длину гипотенузы
Или проще: sin ( θ ) = Противоположно / Гипотенуза Пример: Что такое синус 35 °? | Используя этот треугольник (длины до одного десятичного знака): sin (35 °) = Противоположно / Гипотенуза
= 2. 8 / 4,9 8 / 4,9
= 0,57 … |
Функция синуса может помочь нам решить такие задачи: Пример: используйте синусоидальную функцию , чтобы найти «d» Мы знаем - Угол наклона кабеля к морскому дну составляет 39 °.
- Длина кабеля 30 м.
И мы хотим знать «d» (расстояние вниз). Начать с: sin 39 ° = противоположно / гипотенуза sin 39 ° = d / 30 Поменять местами стороны: d / 30 = sin 39 ° С помощью калькулятора найдите sin 39 °: d / 30 = 0.6293… Умножаем обе стороны на 30: d = 0,6293… x 30 d = 18,88 с точностью до 2 знаков после запятой Глубина «d» составляет 18,88 м Функция обратной синусоиды Но иногда нам нужно найти угол . . Вот где появляется «обратный синус». Он отвечает на вопрос «какой угол имеет синус, равный противоположному / гипотенузе?» Символ для обратного синуса — sin -1 , или иногда arcsin . Пример: найти угол «a» Мы знаем - Расстояние вниз 18,88 м.
- Длина кабеля 30 м.
И мы хотим узнать угол «а» Начать с: sin a ° = противоположно / гипотенуза sin a ° = 18,88 / 30 Вычислить 18,88 / 30: sin a ° = 0,6293 … Какой угол имеет синус, равный 0.6293 …?
Обратный синус нам расскажет. Обратный синус: a ° = sin −1 (0,6293 …) С помощью калькулятора найдите sin −1 (0,6293 …): a ° = 39,0 ° (с точностью до 1 знака после запятой) Угол «а» равен 39,0 ° Они как вперед, так и назад! - sin берет угол и дает нам соотношение «противоположно / гипотенуза»
- sin -1 берет отношение «противоположность / гипотенуза» и дает нам угол .
Пример: Функция синуса: sin ( 30 ° ) = 0,5 Обратный синус: sin −1 ( 0,5 ) = 30 ° Калькулятор | На калькуляторе вы нажимаете одну из следующих кнопок (в зависимости от марки вашего калькулятора):
либо «2ndF sin», либо «shift sin». |
На вашем калькуляторе попробуйте использовать sin, а затем sin -1 , чтобы увидеть, что произойдет Больше чем один угол! Обратный синус показывает только один угол … но есть и другие ракурсы, которые могут сработать. Пример: вот два угла, где противоположность / гипотенуза = 0,5
На самом деле существует бесконечно много углов , потому что вы можете продолжать складывать (или вычитать) 360 °: Помните об этом, потому что бывают случаи, когда вам действительно нужен один из других углов! Сводка Синус угла θ равен: sin ( θ ) = Противоположно / Гипотенуза и обратный синус: sin -1 (противоположно / гипотенуза) = θ А как насчет «кос» и «загар». ..? ..? Идея точно такая же, но с другим соотношением сторон. Косинус Косинус угла θ равен: cos ( θ ) = Соседний / Гипотенуза И обратный косинус равен: cos -1 (Соседний / Гипотенуза) = θ Пример: найти величину угла a ° cos a ° = Соседний / Гипотенуза cos a ° = 6,750 / 8,100 = 0.8333 … a ° = cos -1 (0,8333 …) = 33,6 ° (с точностью до 1 знака после запятой) Касательная Тангенс угла θ составляет: tan ( θ ) = напротив / рядом Таким образом, обратный тангенс равен: tan -1 (напротив / рядом) = θ Пример: Найдите размер угла x ° tan x ° = напротив / рядом tan x ° = 300/400 = 0.75 x ° = tan -1 (0,75) = 36,9 ° (с точностью до 1 десятичного знака) Другие названия Иногда sin -1 называется asin или arcsin
Аналогично cos -1 называется acos или arccos
И tan -1 называется atan или arctan Примеры: - arcsin (y) совпадает с sin -1 (y)
- атан (θ) совпадает с tan -1 (θ)
- и др.

Графики И, наконец, вот графики синуса, обратного синуса, косинуса и обратного косинуса:
Синус
Обратный синус
Косинус
Обратный косинус Вы что-нибудь заметили в графиках? - Они как-то похожи, правда?
- Но обратный синус и обратный косинус не «продолжаются вечно», как синус и косинус …
Давайте посмотрим на примере косинуса. Вот Косинус и Обратный косинус , нанесенные на тот же график:
Косинус и обратный косинус Зеркальные отражения (примерно по диагонали) Но почему обратный косинус обрезается сверху и снизу (точки на самом деле не являются частью функции) …? Потому что, чтобы быть функцией, она может дать только один ответ
, когда мы спрашиваем «что такое cos -1 (x)?» Один ответ или бесконечно много ответов Но мы видели ранее, что существует бесконечно много ответов , и пунктирная линия на графике показывает это. Так что да, — это бесконечно много ответов … … но представьте, что вы вводите 0,5 в свой калькулятор, нажимаете cos -1 , и это дает вам нескончаемый список возможных ответов … Итак, у нас есть правило, что функция может дать только один ответ . Итак, отсекая это таким образом, мы получаем только один ответ, но мы должны помнить, что могут быть другие ответы . Касательная и обратная касательная А вот и функция касательной и арктангенс.Вы видите, какие они зеркальные изображения (примерно по диагонали) …?
Касательная
Обратный тангенс Обратный косинус и обратный синус Обратный косинус и обратный синус Стандартные триггерные функции являются периодическими, то есть они повторяются. Следовательно, одно и то же выходное значение появляется для нескольких входных значений функции. Это делает невозможным построение обратных функций.Для решения уравнений, включающих триггерные функции, обязательно наличие обратных функций. Таким образом, математики должны ограничить функцию триггера, чтобы создать эти инверсии. Это делает невозможным построение обратных функций.Для решения уравнений, включающих триггерные функции, обязательно наличие обратных функций. Таким образом, математики должны ограничить функцию триггера, чтобы создать эти инверсии. Чтобы определить обратную функцию, исходная функция должна быть взаимно однозначно . Для существования взаимно однозначного соответствия (1) каждое значение в домене должно соответствовать ровно одному значению в диапазоне, и (2) каждое значение в диапазоне должно соответствовать ровно одному значению в домене.Первое ограничение распространяется на все функции; второй нет. Например, синусоидальная функция не удовлетворяет второму ограничению, поскольку одно и то же значение в диапазоне соответствует многим значениям в домене (см. Рисунок 1). Рисунок 1
Функция синуса не является взаимно однозначной. Чтобы определить обратные функции для синуса и косинуса, области этих функций ограничены. Ограничение, которое накладывается на значения области значений функции косинуса, составляет 0 ≤ x ≤ π (см. Рисунок 2).Эта ограниченная функция называется косинусом. Обратите внимание на заглавную букву «C» в косинусе. Ограничение, которое накладывается на значения области значений функции косинуса, составляет 0 ≤ x ≤ π (см. Рисунок 2).Эта ограниченная функция называется косинусом. Обратите внимание на заглавную букву «C» в косинусе. Рисунок 2
График функции ограниченного косинуса. Функция обратного косинуса определяется как функция, обратная ограниченной функции косинуса Cos −1 (cos x ) = x ≤ x ≤ π. Следовательно, Рисунок 3
График функции обратного косинуса. Тождества для косинуса и обратного косинуса: Развитие функции обратного синуса аналогично развитию функции косинуса. Ограничение, которое накладывается на значения домена синусоидальной функции, составляет . Эта ограниченная функция называется синусоидальной (см. Рисунок 4). Обратите внимание на заглавную букву «S» в слове «синус». Рисунок 4
График ограниченной синусоидальной функции. Функция обратного синуса (см. Рисунок 5) определяется как функция, обратная ограниченной функции синуса y = Sin x , Рисунок 5
График функции обратной синусоиды. Следовательно, Идентичности для синуса и обратного синуса: Графики функций y = Cos x и y = Cos −1 x являются отражениями друг друга относительно линии y = x . Графики функций y = Sin x и y = Sin −1 x также являются отражениями друг друга относительно линии y = x (см. Рисунок 6). Рисунок 6
Симметрия обратных синуса и косинуса. Пример 1: Используя рисунок 7, найдите точное значение Cos −1 . Рисунок 7
Чертеж для примера 1. Таким образом, y = 5π / 6 или y = 150 °. Пример 2: Используя рисунок 8, найдите точное значение Sin −1 . Рисунок 8
Рисунок для примера 2. Таким образом, y = π / 4 или y = 45 °. Пример 3: Найдите точное значение cos (Cos −1 0,62). Используйте тождество косинус-обратный косинус:
Математических слов: обратный косинус Обратный
Косинус
cos -1
Cos -1
arccos
Arccos функция, обратная косинусу. Основная идея : Найти cos -1 (½),
мы спрашиваем «что
угол имеет косинус, равный ½? »
ответ 60 °. В результате мы говорим cos -1 (½)
= 60 °.
В радианах это cos -1 (½).
= π / 3. В результате мы говорим cos -1 (½)
= 60 °.
В радианах это cos -1 (½).
= π / 3. Подробнее : На самом деле существует много углов, у которых косинус равен ½.
Мы действительно спрашиваем, «какой самый простой, самый основной угол, который имеет
косинус равен ½? »Как и прежде,
ответ 60 °.Таким образом, cos -1 (½)
= 60 ° или cos -1 (½) = π / 3. Подробности : Что такое cos -1 (–½)?
Мы выбираем 120 °, –120 °, 240 °,
или под другим углом?
Ответ — 120 °.
Обратным косинусом выбираем угол в верхней половине блока.
круг. Таким образом, cos -1 (–½)
= 120 ° или
cos -1 (–½) = 2π / 3. В
другими словами, диапазон cos -1 равен
ограничивается [0, 180 °] или [0, π]. Примечание: arccos означает «арккосинус»,
или радианная мера дуги на окружности, соответствующая
заданное значение косинуса. Техническое примечание : Поскольку ни одна из шести триггерных функций не синусоида,
косинус, тангенс, косеканс, секанс и котангенс взаимно однозначны,
их инверсии не являются функциями.
Каждая триггерная функция может иметь свой
домен ограничен, однако, чтобы сделать его обратным функцией.Некоторые математики пишут эти ограниченные триггерные функции и их
переворачивается с заглавной буквы (например, Cos или Cos -1 ).
Однако большинство математиков не следуют этой практике. Этот
веб-сайт не делает различий между заглавными и не заглавными буквами
триггерные функции. См.
также обратный
тригонометрия, обратная
триггерные функции, интервальное обозначение Arccos (x) | функция обратного косинуса Arccos (x), cos -1 (x), функция обратного косинуса. Определение Arccos Арккосинус x определяется как функция, обратная косинусу x, когда -1≤x≤1. Когда косинус y равен x: cos y = x Тогда арккосинус x равен функции обратного косинуса x, которая равна y: arccos x = cos -1 x = y (Здесь cos -1 x означает обратный косинус и не означает косинус в степени -1). Пример arccos 1 = cos -1 1 = 0 рад = 0 ° График arccos Правила Arccos | Название правила | Правило |
|---|
| Косинус арккозина | cos (arccos x ) = x | | Арккосинус косинуса | arccos (cos x ) = x + 2 k π,
когда k ∈ℤ
( k целое число) | | Arccos отрицательного аргумента | arccos (- x ) = π — arccos x =
180 ° — arccos x | | Дополнительные уголки | arccos x = π / 2 — arcsin x = 90 ° — arcsin x | | Сумма Arccos | arccos ( α ) + arccos ( β ) =
arccos ( αβ — √ (1- α 2 ) (1- β 2 )) | | Разница Arccos | arccos ( α ) — arccos ( β ) =
arccos ( αβ + √ (1- α 2 ) (1- β 2 )) | | Arccos греха x | arccos (sin x ) = — x — (2 k +0. 5) π 5) π | | Синус арккосинуса | | | Касательная к арккосинусу | | | Производная арккозина | | | Неопределенный интеграл арккосинуса | |
Стол Arccos | x | arccos (x) (рад) | arccos (x) (°) |
|---|
| -1 | π | 180 ° | | -√3 / 2 | 5π / 6 | 150 ° | | -√2 / 2 | 3π / 4 | 135 ° | | -1/2 | 2π / 3 | 120 ° | | 0 | π / 2 | 90 ° | | 1/2 | π / 3 | 60 ° | | √2 / 2 | π / 4 | 45 ° | | √3 / 2 | π / 6 | 30 ° | | 1 | 0 | 0 ° |
См. Также Также 1.2. Функции косинуса и синуса Функции косинуса и синуса Мы начали наше изучение тригонометрии с изучения единичной окружности, того, как обернуть числовую линию вокруг единичной окружности и как построить дуги на единичной окружности. Теперь мы можем использовать эти идеи для определения двух основных круговых или тригонометрических функций. Эти круговые функции позволят нам моделировать периодические явления, такие как приливы, количество солнечного света в течение дней в году, орбиты планет и многие другие. Рисунок \ (\ PageIndex {1} \): Круговые функции Может показаться, что единичный круг — довольно простой объект и малоинтересный, но математики почти всегда могут найти что-то интересное даже в таких простых объектах. Например, мы определяем две основные круговые функции, косинус и синус в терминах единичной окружности следующим образом. На рисунке \ (\ PageIndex {1} \) показана дуга длины \ (t \) на единичной окружности. Эта дуга начинается в точке \ ((1, 0) \) и заканчивается в ее конечной точке \ (P (t) \).Затем мы определяем косинус и синус дуги \ (t \) как координаты \ (x \) и \ (y \) точки \ (P \), так что \ (P (t) = (\ cos (t), sin (t)) \) (косинус обозначается как \ (\ cos \), а синус — как \ (\ sin \)). Значения косинуса и синуса определяются дугой \ (t \), а косинус и синус — это функций дуги \ (t \). Поскольку дуга лежит на единичной окружности, мы называем косинус и синус круговыми функциями . Важной частью тригонометрии является изучение косинуса и синуса, а также периодических явлений, которые эти функции могут моделировать.Это одна из причин, по которой круговые функции также называются тригонометрическими функциями , . Эта дуга начинается в точке \ ((1, 0) \) и заканчивается в ее конечной точке \ (P (t) \).Затем мы определяем косинус и синус дуги \ (t \) как координаты \ (x \) и \ (y \) точки \ (P \), так что \ (P (t) = (\ cos (t), sin (t)) \) (косинус обозначается как \ (\ cos \), а синус — как \ (\ sin \)). Значения косинуса и синуса определяются дугой \ (t \), а косинус и синус — это функций дуги \ (t \). Поскольку дуга лежит на единичной окружности, мы называем косинус и синус круговыми функциями . Важной частью тригонометрии является изучение косинуса и синуса, а также периодических явлений, которые эти функции могут моделировать.Это одна из причин, по которой круговые функции также называются тригонометрическими функциями , . Примечание Согласно веб-сайту «Самые ранние известные варианты использования некоторых математических слов» по адресу jeff560.tripod.com/mathword.html, слово синус происходит от санскрита через арабский и латинский языки. Хотя отчеты о фактическом происхождении различаются, похоже, что санскритское произведение «jya» (аккорд) было переведено на арабский язык как «jiba», но затем было переведено на латинский как «jaib» (залив), что стало «синусом» (залив или кривая).Затем это слово было переведено на английский язык, чтобы стать нашим «синусом». Слово косинус началось с Платона из Тиволи, который использовал выражение «chorda резидуи». Хотя латинское слово chorda было лучшим переводом санскритско-арабского слова синус, чем слово синус, это слово уже использовалось. Таким образом, «остаточная хорда» превратилась в «косинус». Хотя отчеты о фактическом происхождении различаются, похоже, что санскритское произведение «jya» (аккорд) было переведено на арабский язык как «jiba», но затем было переведено на латинский как «jaib» (залив), что стало «синусом» (залив или кривая).Затем это слово было переведено на английский язык, чтобы стать нашим «синусом». Слово косинус началось с Платона из Тиволи, который использовал выражение «chorda резидуи». Хотя латинское слово chorda было лучшим переводом санскритско-арабского слова синус, чем слово синус, это слово уже использовалось. Таким образом, «остаточная хорда» превратилась в «косинус». Примечание В математике мы всегда создаем формальные определения для обычно используемых объектов. Определения критически важны, потому что с согласованными определениями у всех будет общее понимание того, что означают эти термины.Без такого общего понимания возникла бы большая путаница, поскольку разные люди имеют разные значения разных терминов. Столь тщательные и точные определения необходимы для разработки математических свойств этих объектов. 2 = 1 \) (с положительным направлением против часовой стрелки) с начальной точкой \ ( (1, 0) \) и конечной точки \ ((x, y) \), затем косинус для \ (t \), обозначаемый \ (\ cos (t) \), и синус для t, обозначаемые \ (\ sin (t) \), определяются как \ [\ cos (t) = x \] и \ [\ sin (t) = y.\] 2 = 1 \) (с положительным направлением против часовой стрелки) с начальной точкой \ ( (1, 0) \) и конечной точки \ ((x, y) \), затем косинус для \ (t \), обозначаемый \ (\ cos (t) \), и синус для t, обозначаемые \ (\ sin (t) \), определяются как \ [\ cos (t) = x \] и \ [\ sin (t) = y.\] Рисунок 1.6 иллюстрирует эти определения для дуги, конечная точка которой находится в первом квадранте. В настоящее время невозможно определить точные значения функций косинуса и синуса для конкретных значений \ (t \). Однако это можно сделать, если конечная точка дуги длины \ (t \) лежит на оси \ (x \) или на оси \ (y \). Например, поскольку окружность единичной окружности равна \ (2 \ pi \), у дуги длины \ (t = \ pi \) будет конечная точка на полпути по окружности от точки \ ((1, 0) \).То есть конечная точка находится в \ ((1, 0) \). Следовательно, \ [\ cos (\ pi) = -1 \] и \ [\ sin (\ pi) = 0. \] Упражнение \ (\ PageIndex {1} \) Определите точные значения каждого из следующего: - \ (\ cos (\ dfrac {\ pi} {2}) \) и \ (\ sin (\ dfrac {\ pi} {2}) \).
 - \ (\ cos (\ dfrac {3 \ pi} {2}) \) и \ (\ sin (\ dfrac {3 \ pi} {2}) \).
- \ (\ cos (0) \) и \ (sin (0) \).
- \ (\ cos (- \ dfrac {\ pi} {2}) \) и \ (\ sin (- \ dfrac {\ pi} {2}) \).
- \ (\ cos (2 \ pi) \) и \ (\ sin (2 \ pi) \).
- \ (cos (- \ pi) \) и \ (\ sin (- \ pi) \).
Важное примечание: поскольку косинус и синус являются функциями дуги, длина которой является действительным числом t, вход t определяет выход косинуса и синуса. В результате необходимо указать входное значение при работе с косинусом и синусом. Другими словами, мы ВСЕГДА пишем \ (\ cos (t) \), где \ (t \) — ввод действительного числа, и НИКОГДА не просто \ (\ cos \). Повторюсь, косинус и синус являются функциями, поэтому мы ДОЛЖНЫ указать вход для этих функций. - Ответ
- \ [\ cos (\ dfrac {\ pi} {2}) = 0 \] \ [\ sin (\ dfrac {\ pi} {2}) = 1 \]
- \ [\ cos (\ dfrac {3 \ pi} {2}) = 0 \] \ [\ sin (\ dfrac {3 \ pi} {2}) = -1 \]
- \ [\ cos (0) = 1 \] \ [\ sin (0) = 1 \]
- \ [\ cos (- \ dfrac {\ pi} {2}) = 0 \] \ [\ sin (- \ dfrac {\ pi} {2}) = -1 \]
- \ [\ cos (2 \ pi) = 0 \] \ [\ sin (2 \ pi) = 1 \]
- \ [\ cos (- \ pi) = -1 \] \ [\ sin (- \ pi) = 0 \]
Упражнение \ (\ PageIndex {2} \) В этом упражнении мы будем использовать апплет Geogebra, который называется Конечными точками дуг на единичной окружности. Веб-адрес этого апплета — Веб-адрес этого апплета — . http://gvsu.edu/s/JY Для этого апплета мы контролируем значение ввода \ (t \) с помощью ползунка для \ (t \). Значения \ (t \) варьируются от \ (- 20 \) до \ (20 \) с шагом \ (0,5 \). Для заданного значения \ (t \) рисуется дуга длиной \ (t \), и отображаются координаты конечной точки этой дуги. Используйте этот апплет, чтобы найти приблизительные значения для каждого из следующих значений: - \ (\ cos (1) \) и \ (\ sin (1) \)
- \ (\ cos (2) \) и \ (\ sin (2) \)
- \ (\ cos (-4) \) и \ (\ sin (-4) \)
- \ (\ cos (5.5) \) и \ (\ sin (5.5) \)
- \ (\ cos (15) \) и \ (\ sin (15) \)
- \ (\ cos (-15) \) и \ (\ sin (-15) \)
- Ответ
- \ [\ cos (1) \ приблизительно 0,5403, \ sin (1) \ приблизительно 0,8415 \]
- \ [\ cos (2) \ приблизительно -0,4161, \ sin (2) \ приблизительно 0,9093 \]
- \ [\ cos (-4) \ приблизительно -0,6536, \ sin (-4) \ приблизительно 0,7568 \]
- \ [\ cos (5.
 5) \ приблизительно 0,7807, \ sin (5.5) \ приблизительно -0,7055 \] 5) \ приблизительно 0,7807, \ sin (5.5) \ приблизительно -0,7055 \] - \ [\ cos (15) \ приблизительно -0.7597, \ sin (15) \ приблизительно 0,6503 \]
- \ [\ cos (-15) \ приблизительно -0,7597, \ sin (-15) \ приблизительно 0,6503 \]
Некоторые свойства функций косинуса и синуса Функции косинуса и синуса называются круговыми функциями , потому что их значения определяются координатами точек на единичной окружности. Для каждого действительного числа \ (t \) существует соответствующая дуга, начинающаяся в точке \ ((1, 0) \) (направленной) длины \ (t \), лежащей на единичной окружности.Координаты конечной точки этой дуги определяют значения \ (\ cos (t \) и \ (\ sin (t \). В предыдущих курсах математики мы узнали, что область действия функции — это набор всех входных данных, которые дают определенный выход. Мы также узнали, что диапазон функции — это набор всех возможных выходов функции. Упражнение \ (\ PageIndex {3} \) - Какова область определения функции косинуса? Почему?
- Что такое область синусоидальной функции? Почему?
- Какую самую большую координату \ (x \) может иметь точка на единичной окружности? Какую наименьшую координату \ (x \) может иметь точка на единичной окружности? Что это говорит нам о диапазоне функции косинуса? Почему?
- Какую самую большую координату \ (y \) может иметь точка на единичной окружности? Какую наименьшую координату \ (y \) может иметь точка на единичной окружности? Что это говорит нам о диапазоне синусоидальной функции? Почему?
- Ответ
- Так как мы можем обернуть любое число на единичный круг, мы всегда можем найти конечную точку дуги, которая соответствует любому числу.Таким образом, определен косинус любого действительного числа, а область определения функции косинуса — это набор всех действительных чисел.
 - По той же причине, что и для функции косинуса, область определения функции синуса — это набор всех действительных чисел.
- На единичном круге наибольшая координата x, которую может иметь точка, равна 1, а наименьшая x-координата, которую может иметь точка, равна 1. Поскольку выходом функции косинуса является координата x точки на единичной окружности, диапазон функции косинуса — отрезок \ ([- 1, 1] \).Это означает \ (- 1 \ leq \ cos (t) \ leq 1 \) для любого действительного числа \ (t \).
- На единичной окружности наибольшая координата y, которую может иметь точка, равна 1, а наименьшая координата y, которую может иметь точка, равна 1. Поскольку выходом синусоидальной функции является координата y точки на единичной окружности, диапазон функции синуса — отрезок \ ([- 1, 1] \). Это означает \ (- 1 \ leq \ sin (t) \ leq 1 \) для любого действительного числа \ (t \).
Хотя мы, возможно, не сможем вычислить точные значения для многих входных данных для функций косинуса и синуса, мы можем использовать наши знания о системе координат и ее квадрантах, чтобы определить, являются ли определенные значения косинуса и синуса положительными или отрицательными. Идея состоит в том, что знаки координат точки \ (P (x, y) \), нанесенной на координатный план, определяются квадрантом, в котором находится точка (если только она не лежит на одной из осей). Рисунок \ (\ PageIndex {2} \) суммирует эти результаты для знаков значений функций косинуса и синуса. В левом столбце таблицы указано положение конечной точки дуги, определяемой действительным числом \ (t \). Идея состоит в том, что знаки координат точки \ (P (x, y) \), нанесенной на координатный план, определяются квадрантом, в котором находится точка (если только она не лежит на одной из осей). Рисунок \ (\ PageIndex {2} \) суммирует эти результаты для знаков значений функций косинуса и синуса. В левом столбце таблицы указано положение конечной точки дуги, определяемой действительным числом \ (t \). Рисунок \ (\ PageIndex {2} \): знаки функций косинуса и синуса| Квадрант | \ (\ cos (t) \) | \ (\ sin (t) \) |
|---|
| QI | положительный | положительный | | QII | отрицательный | положительный | | III квартал | отрицательный | отрицательный | | QIV | положительный | отрицательный | Теперь нам нужно определить, в каком квадранте находится конечная точка дуги, определяемой действительным числом t. Мы можем сделать это, еще раз используя тот факт, что длина окружности единичной окружности равна \ (2 \ pi \), и когда мы перемещаемся по единичной окружности из точки .1; 0 / в положительном (против часовой стрелки) направлении, мы будем пересекать одну из координатных осей каждые четверть оборота. Например, если \ (0 0 \) и \ (\ sin (t)> 0 \). Мы можем сделать это, еще раз используя тот факт, что длина окружности единичной окружности равна \ (2 \ pi \), и когда мы перемещаемся по единичной окружности из точки .1; 0 / в положительном (против часовой стрелки) направлении, мы будем пересекать одну из координатных осей каждые четверть оборота. Например, если \ (0 0 \) и \ (\ sin (t)> 0 \). Упражнение \ (\ PageIndex {4} \) - Если \ (\ dfrac {\ pi} {2}
- Если \ (\ pi
- Если \ (\ dfrac {3 \ pi} {2}
- Если \ (\ dfrac {5 \ pi} {2}
- Для каких значений \ (t \) (между \ (0 \) и \ (2 \ pi \)) положительно \ (\ cos (t) \)? Почему?
- Для каких значений \ (t \) (между \ (0 \) и \ (2 \ pi \)) положительно \ (\ sin (t) \)? Почему?
- Для каких значений \ (t \) (между \ (0 \) и \ (2 \ pi \)) \ (\ cos (t) \) отрицательно? Почему?
- Для каких значений \ (t \) (между \ (0 \) и \ (2 \ pi \)) \ (\ sin (t) \) отрицательно? Почему?
- Ответ
- Если \ (\ dfrac {\ pi} {2} 0 \).
 - Если \ (\ pi
- Если \ (\ dfrac {3 \ pi} {2} 0 \) и \ (\ sin (t) <0 \).
- Если \ (\ dfrac {5 \ pi} {2} 0 \) и \ (\ sin (t)> 0 \).
- Обратите внимание, что \ (\ cos (t) = 0 \) в \ (t = \ dfrac {\ pi} {2} \) и \ (t = \ dfrac {3 \ pi} {2} \). Поскольку \ (\ cos (t) \) является координатой x конечной точки дуги \ (t \), предыдущий ответ показывает, что \ (\ cos (t) \) положительно, когда \ (t \) находится в одном из интервалов \ ([0, \ dfrac {\ pi} {2}) \) или \ ((\ dfrac {3 \ pi} {2}, 2 \ pi] \).
- Обратите внимание, что \ (\ sin (t) = 0 \) при \ (t = 0 \) и \ (t = \ pi \). Поскольку \ (\ sin (t) \) является координатой x конечной точки дуги \ (t \), предыдущий ответ показывает, что \ (\ sin (t) \) положительно, когда \ (t \) находится в одном из интервалов \ ((0, \ pi) \).
 - Обратите внимание, что \ (\ cos (t) = 0 \) в \ (t = \ dfrac {\ pi} {2} \) и \ (t = \ dfrac {3 \ pi} {2} \). Поскольку \ (\ cos (t) \) — координата x конечной точки дуги \ (t \), предыдущий ответ показывает, что \ (\ cos (t) \) положительно, когда \ (t \) находится в интервале \ ((\ dfrac {\ pi} {2}, \ dfrac {3 \ pi} {2}) \).
- Обратите внимание, что \ (\ sin (t) = 0 \) при \ (t = \ pi \) и \ (t = 2 \ pi \). Поскольку \ (\ sin (t) \) является координатой x конечной точки дуги \ (t \), предыдущий ответ показывает, что \ (\ sin (t) \) положительно, когда \ (t \) находится в одном из интервалов \ ([0, \ dfrac {\ pi} {2}) \) или \ ((\ pi, 2 \ pi) \).
Упражнение \ (\ PageIndex {5} \) Используйте результаты, представленные на рисунке \ (\ PageIndex {2} \), чтобы определить, являются ли следующие величины положительными, отрицательными или нулевыми. (Не используйте калькулятор.) - \ (\ cos (\ dfrac {\ pi} {5}) \)
- \ (\ sin (\ dfrac {\ pi} {5}) \)
- \ (\ cos (\ dfrac {5 \ pi} {8}) \)
- \ (\ sin (\ dfrac {5 \ pi} {8}) \)
- \ (\ cos (\ dfrac {-9 \ pi} {16}) \)
- \ (\ sin (\ dfrac {-9 \ pi} {16}) \)
- \ (\ cos (\ dfrac {-25 \ pi} {12}) \)
- \ (\ sin (\ dfrac {-25 \ pi} {12}) \)
- Ответ
- Поскольку \ (0 <\ dfrac {\ pi} {5} <\ dfrac {\ pi} {2} \), конечная точка дуги \ (\ dfrac {\ pi} {5} \) находится в первый квадрант.
 Следовательно, \ (\ cos (\ dfrac {\ pi} {5}) \) положительно. Следовательно, \ (\ cos (\ dfrac {\ pi} {5}) \) положительно. - Используя информацию о \ (t \) в (1), \ (\ sin (\ dfrac {\ pi} {5}) \) положительно.
- Мы можем записать \ (\ dfrac {\ pi} {2} \) как \ (\ dfrac {4 \ pi} {8} \) и \ (\ pi \) как \ (\ dfrac {8 \ pi} { 8} \), поэтому \ (\ dfrac {\ pi} {2} \ <\ dfrac {5 \ pi} {8} <\ pi \). Это поместит конечную точку дуги \ (\ dfrac {5 \ pi} {8} \) во второй квадрант. Следовательно, \ (\ cos (\ dfrac {5 \ pi} {8}) \) отрицательно.
- Используя информацию о \ (t \) в (3), \ (\ sin (\ dfrac {5 \ pi} {8}) \) отрицательно.
- Мы можем записать \ (- \ dfrac {\ pi} {2} \) как \ (\ dfrac {-8 \ pi} {16} \) и \ (- \ pi \) как \ (\ dfrac {-16 \ pi} {16} \), поэтому \ (- \ pi <\ dfrac {-9 \ pi} {16} <- \ dfrac {\ pi} {2} \). Это помещает конечную точку дуги \ (\ dfrac {-9 \ pi} {16} \) в третий квадрант. Следовательно, (\ cos (\ dfrac {-9 \ pi} {16}) \) отрицательно.
- Используя информацию о \ (t \) в (5), (\ sin (\ dfrac {-9 \ pi} {16}) \) отрицательно.
 2 = (a + b) (a — b) \] 2 = (a + b) (a — b) \] \ [a + b = b + a \] \ [x (y + z) = xy + xz \] , где подразумевается, что все переменные представляют собой действительные числа.2) \). Идентичность Пифагора позволяет нам определить значение \ (\ cos (t) \) или \ (\ sin (t) \), если мы знаем значение другого и квадрант, в котором конечная точка дуги \ (t \) ложь. Это проиллюстрировано в следующем примере. Пример \ (\ PageIndex {1} \) Предположим, что \ (\ cos (t) = \ dfrac {2} {5} \) и конечная точка дуги \ ((t) \) лежит в четвертом квадранте. 5 Используйте эту информацию, чтобы определить значение \ (\ грех (т) \). Решение Основным инструментом, который мы будем использовать, является пифагорова идентичность, но имейте в виду, что конечной точкой дуги \ (t \) является точка \ ((\ cos (t), \ sin (t)) \).2 (t) = \ dfrac {21} {25} \] Это означает, что \ (\ sin (t) = \ pm \ sqrt {\ dfrac {21} {25}} \), и поскольку конечная точка дуги \ ((t) \) находится в четвертом квадранте, мы знайте, что \ (\ sin (t) <0 \). Следовательно, \ (\ sin (t) = — \ sqrt {\ dfrac {21} {25}} \). Поскольку \ (\ sqrt {25} = 5 \), мы можем написать Следовательно, \ (\ sin (t) = — \ sqrt {\ dfrac {21} {25}} \). Поскольку \ (\ sqrt {25} = 5 \), мы можем написать \ [\ sin (t) = — \ sqrt {\ dfrac {21} {25}} = — \ dfrac {\ sqrt {21}} {5}. \] Упражнение \ (\ PageIndex {7} \) - Если \ (\ cos (t) = \ dfrac {1} {2} \) и конечная точка дуги \ (t \) находится в четвертом квадранте, определите значение \ (\ sin (t) \).{2} (t) = \ dfrac {3} {4} \]
\ [\ sin (t) = \ pm \ dfrac {\ sqrt {3}} {4} \] Обратите внимание, что мы не можем определить знак \ (\ sin (t) \), используя только пифагорейскую идентичность. Нам нужна дополнительная информация о дуге \ (t \). В этом случае нам дано, что конечная точка дуги \ (t \) находится в четвертом квадранте, и, следовательно, \ (\ sin (t) <0 \). Следовательно, \ [\ sin (t) = — \ sqrt {\ dfrac {3} {4}} = — \ dfrac {\ sqrt {3}} {2} \] 2. Поскольку \ (\ sin (t) = — \ dfrac {2} {3} \), мы можем использовать тождество Пифагора, чтобы получить \ [\ cos ^ {2} (t) + (- \ dfrac {2} {3}) ^ {2} = 1] \ [\ cos ^ {2} (t) + \ dfrac {4} {9} = 1 \] \ [\ cos ^ {2} (t) = \ dfrac {5} {9} \] \ [\ sin (t) = \ pm \ dfrac {\ sqrt {5}} {9} \] Еще раз, нам нужна информация о дуге \ (t \), чтобы определить знак \ (\ cos (t) \). 2 = 1 \) (с положительным направлением против часовой стрелки) с начальной точкой \ ((1, 0) \) и конечная точка \ ((x, y) \), тогда \ (\ cos (t) = x \) и \ (\ sin (t) = y \). 2 = 1 \) (с положительным направлением против часовой стрелки) с начальной точкой \ ((1, 0) \) и конечная точка \ ((x, y) \), тогда \ (\ cos (t) = x \) и \ (\ sin (t) = y \). - Знаки \ (\ cos (t) \) и \ (\ sin (t) \) определяются квадрантом, в котором находится конечная точка дуги \ (t \).
| Квадрант | \ (\ cos (t) \) | \ (\ sin (t) \) |
|---|
| QI | положительный | положительный | | QII | отрицательный | положительный | | III квартал | отрицательный | отрицательный | | QIV | положительный | отрицательный |
- Одно из наиболее важных тождеств в тригонометрии, называемое тождеством Пифагора, выводится из уравнения для единичной окружности и гласит:
Для каждого действительного числа \ (t \), \ [\ cos ^ 2 (t) + \ sin ^ 2 (t) = 1. \ nonumber \] \ nonumber \] Что такое обратный косинус? Здравствуйте, и добро пожаловать в это видео о функциях обратного триггера ! Чтобы понять, что такое обратные тригонометрические функции, давайте сначала рассмотрим, что такое обычные тригонометрические функции. Помните, что общие три триггерные функции — это синус , косинус и тангенс . Эти триггерные функции используются для связывания сторон треугольника и углов между собой. Например, мы могли бы использовать касательную в задаче, где нам нужно найти длину недостающей стороны треугольника. Если мы вспомним SOH-CAH-TOA, мы увидим, что в этом треугольнике используется TOA, что означает: \ (\ tan {\ Theta} = \ frac {напротив} {смежный} \). Если мы подставим значения для нашего треугольника, мы получим: \ (\ tan {30} = \ frac {3} {x} \). Само по себе преобразование для получения x дает: \ (x = \ frac {3} {tan 30} \). Что затем упрощается до: \ (x \ приблизительно 5,20 \). Но что, если нам дан треугольник, размеры сторон которого мы знаем, но мы хотим знать величину угла, например: Если мы подставим его в наше уравнение TOA, мы получим: \ (tan x = \ frac {7} {18} \).{\ circ} \). Я хочу, чтобы вы попробовали еще один, но на этот раз сделайте это самостоятельно. После того, как я покажу вам проблему, поставьте видео на паузу и решите ее. Затем, когда вы закончите, посмотрите, совпадает ли ваш ответ с моим. Решите для x . В этой задаче нам даны наши смежные стороны и стороны гипотенузы, и мы ищем угол между ними. Это означает, что мы собираемся использовать CAH. Если мы составим наше уравнение, оно будет выглядеть так: \ (\ cos {x} = \ frac {9} {22} \).{\ circ} \) . Помните, что обратные триггерные функции — полная противоположность триггерных функций. Триггерные функции используются для определения отношения сторон треугольника к углу, а обратные триггерные функции помогают определить, что это за угловая мера при заданном соотношении сторон. Надеюсь, этот обзор обратных триггерных функций был вам полезен. Спасибо за просмотр и удачной учебы! Исчисление I — Производные обратных триггерных функций Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана. Раздел 3-7: Производные обратных триггерных функций В этом разделе мы рассмотрим производные обратных триггерных функций. Чтобы вывести производные обратных триггерных функций, нам понадобится формула из последнего раздела, относящаяся к производным обратных функций. Если \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) являются обратными функциями, тогда Чтобы вывести производные обратных триггерных функций, нам понадобится формула из последнего раздела, относящаяся к производным обратных функций. Если \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) являются обратными функциями, тогда \ [g ‘\ left (x \ right) = \ frac {1} {{f’ \ left ({g \ left (x \ right)} \ right)}} \] Напомним также, что две функции являются обратными, если \ (f \ left ({g \ left (x \ right)} \ right) = x \) и \ (g \ left ({f \ left (x \ right)} \ справа) = х \). Здесь мы подробно рассмотрим обратный синус, обратный косинус и арктангенс, а остальные три оставим вам, если хотите.{- 1}} x \ hspace {0,5 дюйма} \ Leftrightarrow \ hspace {0,5 дюйма} \ sin y = x \ hspace {0,25 дюйма} {\ mbox {for}} \, \, \, \, \, \, \, \, \, — \ frac {\ pi} {2} \ le y \ le \ frac {\ pi} {2} \] Итак, оценка обратной триггерной функции — это то же самое, что вопрос, какой угол (, т.е. \ (y \)) мы подключили к синусоидальной функции, чтобы получить \ (x \). Приведенные выше ограничения на \ (y \) необходимы для того, чтобы убедиться, что мы получаем непротиворечивый ответ на основе обратного синуса. Мы знаем, что на самом деле существует бесконечное количество углов, которые будут работать, и нам нужно постоянное значение, когда мы работаем с обратным синусом.{- 1}} \ left ({\ frac {1} {2}} \ right) \)
Показать решение Приведенные выше ограничения на \ (y \) необходимы для того, чтобы убедиться, что мы получаем непротиворечивый ответ на основе обратного синуса. Мы знаем, что на самом деле существует бесконечное количество углов, которые будут работать, и нам нужно постоянное значение, когда мы работаем с обратным синусом.{- 1}} \ left ({\ frac {1} {2}} \ right) \)
Показать решение Итак, мы действительно спрашиваем, какой угол \ (y \) решает следующее уравнение. \ [\ sin \ left (y \ right) = \ frac {1} {2} \], и мы ограничены значениями \ (y \) выше. Из единичного круга мы можем быстро увидеть, что \ (y = \ frac {\ pi} {6} \). У нас есть следующая взаимосвязь между функцией обратной синусоиды и функцией синуса.{- 1}} x \ hspace {0,5 дюйма} \ Leftrightarrow \ hspace {0,5 дюйма} \ cos y = x \ hspace {0,25 дюйма} {\ mbox {for}} \, \, \, \, \, \, \, \, \, 0 \ le y \ le \ pi \] Как и в случае с обратным синусом, у нас есть ограничение на углы \ (y \), которые мы получаем из функции обратного косинуса. {- 1}} x} \ right) = x \ hspace {0.{- 1}} x \ hspace {0,5 дюйма} \ Leftrightarrow \ hspace {0,5 дюйма} \ tan y = x \ hspace {0,25 дюйма} {\ mbox {for}} \, \, \, \, \, \, \, \, \, — \ frac {\ pi} {2} {- 1}} x} \ right) = x \ hspace {0.{- 1}} x \ hspace {0,5 дюйма} \ Leftrightarrow \ hspace {0,5 дюйма} \ tan y = x \ hspace {0,25 дюйма} {\ mbox {for}} \, \, \, \, \, \, \, \, \, — \ frac {\ pi} {2} Опять же, у нас есть ограничение на \ (y \), но обратите внимание, что мы не можем позволить \ (y \) быть одной из двух конечных точек в ограничение, указанное выше, поскольку касательная даже не определена в этих двух точках. Чтобы убедиться, что этот диапазон будет охватывать все возможные значения касательной, сделайте быстрый набросок функции касательной, и мы увидим, что в этом диапазоне мы действительно покрываем все возможные значения тангенса.{- 1}} 1 \).
Показать решение Здесь мы спрашиваем, \ [\ загар у = 1 \] где \ (y \) удовлетворяет указанным выше ограничениям. Из единичной окружности видно, что \ (y = \ frac {\ pi} {4} \). Поскольку нет ограничений на \ (x \), мы можем запросить пределы функции обратной касательной, когда \ (x \) стремится к плюсовой или минус бесконечности.
|
 Установленный период — 2 π ;
Установленный период — 2 π ;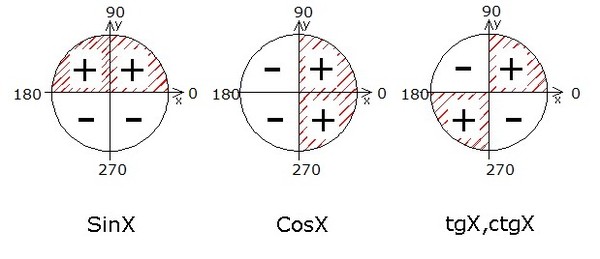
 Он находится в области вычисления: d ( \tg x) = \frac { R } { \frac { \pi }{ 2 } + \pi _{n}(n \in Z) } . Основной период – Т = π. Нулевой показатель достигается при х=πn, n ϵ Z. Экстремумы отсутствуют.
Он находится в области вычисления: d ( \tg x) = \frac { R } { \frac { \pi }{ 2 } + \pi _{n}(n \in Z) } . Основной период – Т = π. Нулевой показатель достигается при х=πn, n ϵ Z. Экстремумы отсутствуют. Установленный период — 2 π ;
Установленный период — 2 π ; 2\alpha=1 $$
2\alpha=1 $$ 2=\frac12 \overset{m\gt 0}{\Rightarrow} m=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2} $$ Все исследуемые точки на числовой окружности будут иметь пару координат \(\frac{\sqrt{2}}{2}\ \text{и}\ \frac{\sqrt{2}}{2}\), только с разными знаками.
2=\frac12 \overset{m\gt 0}{\Rightarrow} m=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2} $$ Все исследуемые точки на числовой окружности будут иметь пару координат \(\frac{\sqrt{2}}{2}\ \text{и}\ \frac{\sqrt{2}}{2}\), только с разными знаками.

 Сравните числа
Сравните числа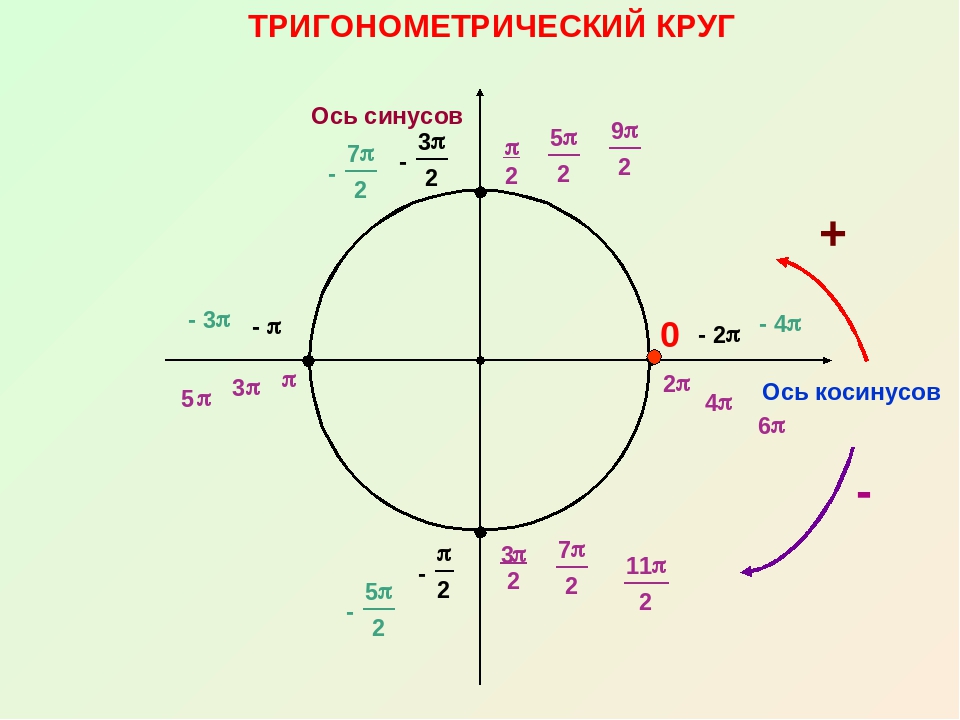 Найти sint,cost для данных t.
Найти sint,cost для данных t. Знаки определяются по расположению угла в четверти: \(\frac\pi2\lt\frac{5\pi}{6}\lt\pi\Rightarrow\) угол находится во 2-й четверти.
Знаки определяются по расположению угла в четверти: \(\frac\pi2\lt\frac{5\pi}{6}\lt\pi\Rightarrow\) угол находится во 2-й четверти.
 При таком направлении обхода угол увеличивается. Вторую точку получили, немного не дойдя до 2п. На сколько не дошли? На тот же угол, который соответствует arccos a. Раз не дошли, то это число вычитаем из 2п. Поэтому вторая точка пересечения прямой с окружностью есть 2п-arccos a. Итак, решением неравенства cos x меньше a является промежуток (arccos a; 2п-arccos a). Поскольку период косинуса равен 2п, к каждому из концов промежутка прибавляем 2пn, где n -целое число (то есть n принадлежит Z). Получаем окончательный вариант ответа: (arccos a+2пn; 2п-arccos a+2пn). Для нестрогого неравенства точки закрашиваем и ставим квадратные скобки.
При таком направлении обхода угол увеличивается. Вторую точку получили, немного не дойдя до 2п. На сколько не дошли? На тот же угол, который соответствует arccos a. Раз не дошли, то это число вычитаем из 2п. Поэтому вторая точка пересечения прямой с окружностью есть 2п-arccos a. Итак, решением неравенства cos x меньше a является промежуток (arccos a; 2п-arccos a). Поскольку период косинуса равен 2п, к каждому из концов промежутка прибавляем 2пn, где n -целое число (то есть n принадлежит Z). Получаем окончательный вариант ответа: (arccos a+2пn; 2п-arccos a+2пn). Для нестрогого неравенства точки закрашиваем и ставим квадратные скобки. Не доходим до 2п на величину arccos(-a), отсюда вторая точка есть 2п-arccos(-a). Чтобы учесть все решения неравенства, к концам промежутка прибавляем 2пn. Если неравенство нестрогое, точки закрашиваем и включаем в ответ (с квадратной скобкой).
Не доходим до 2п на величину arccos(-a), отсюда вторая точка есть 2п-arccos(-a). Чтобы учесть все решения неравенства, к концам промежутка прибавляем 2пn. Если неравенство нестрогое, точки закрашиваем и включаем в ответ (с квадратной скобкой).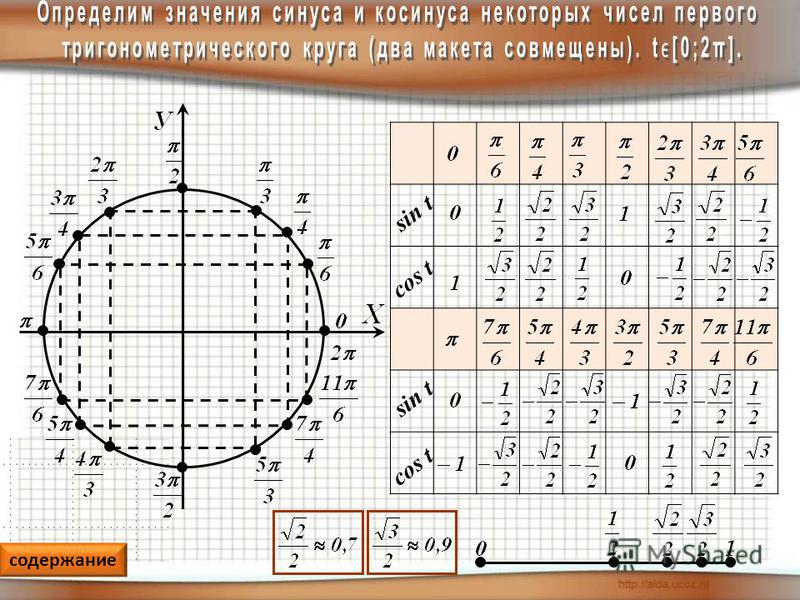 Значит, cosx меньше 1 в любой точке, кроме точек вида 0+2пn. Чтобы записать решение тригонометрического неравенства cosx<1 в виде интервала, в качестве второго конца промежутка берем 2п и к обоим концам прибавляем 2пn. Получаем (2пn; 2п+2пn).
Значит, cosx меньше 1 в любой точке, кроме точек вида 0+2пn. Чтобы записать решение тригонометрического неравенства cosx<1 в виде интервала, в качестве второго конца промежутка берем 2п и к обоим концам прибавляем 2пn. Получаем (2пn; 2п+2пn).
 9962
9962
 6018
6018 2419
2419 1736
1736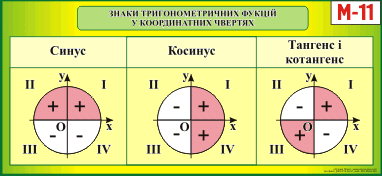 5299
5299 8192
8192 9781
9781 9903
9903 8572
8572 5878
5878 2419
2419 1564
1564 5299
5299 8192
8192 9781
9781 Пользуйтесь нашим сайтом и таблицей косинусов на здоровье.
Пользуйтесь нашим сайтом и таблицей косинусов на здоровье. При необходимости измените ширину столбцов, чтобы видеть все данные.
При необходимости измените ширину столбцов, чтобы видеть все данные.
 ..
..
 07.2008
07.2008 ..
.. 03.2008
03.2008 Ну и от схемы самого включения зависит, обсуждали уже.
Ну и от схемы самого включения зависит, обсуждали уже.
 04.2008
04.2008 замеряют до сотен всяких параметров, определяют «качество» электроэнергии.
замеряют до сотен всяких параметров, определяют «качество» электроэнергии.
 ru/
ru/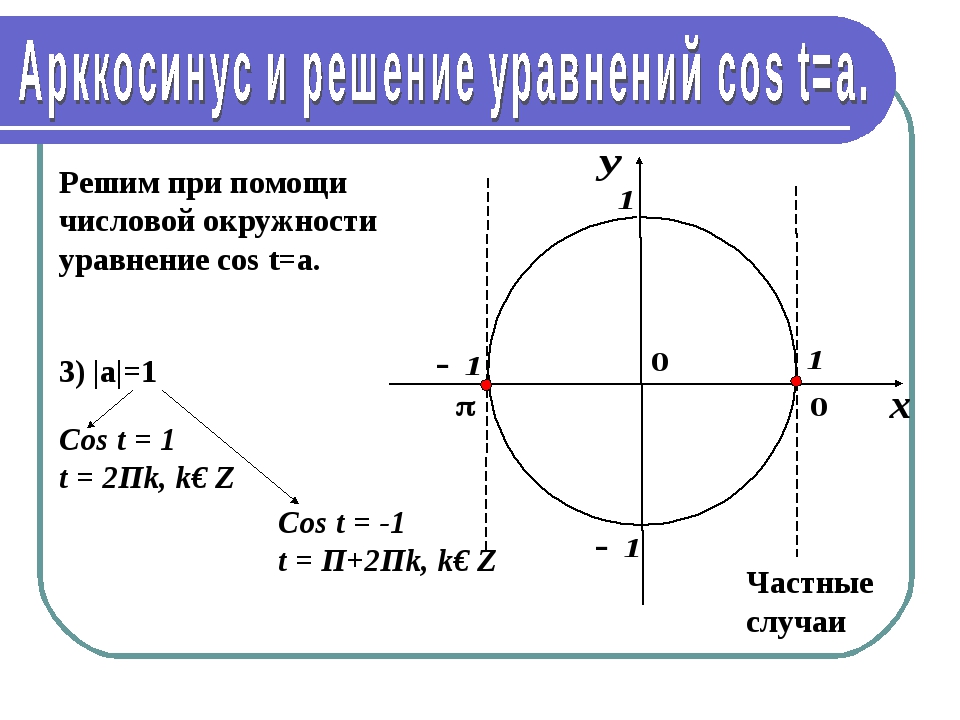 08.2008
08.2008
 Отрицательный угол считается угол, откладываемый в противоположную сторону.
Отрицательный угол считается угол, откладываемый в противоположную сторону.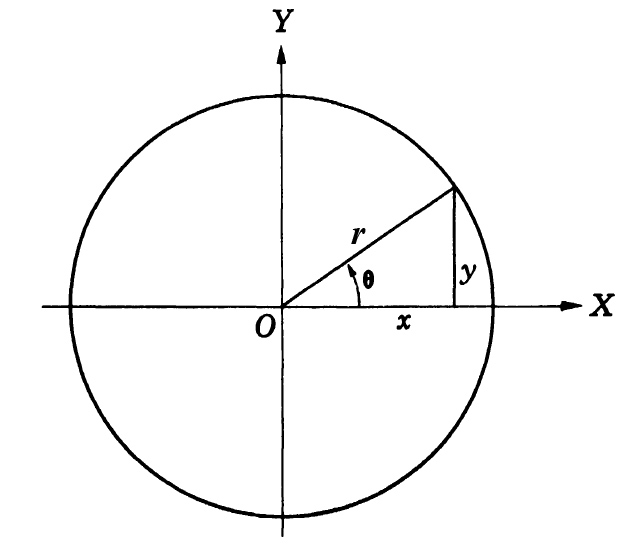

 8 / 4,9
8 / 4,9 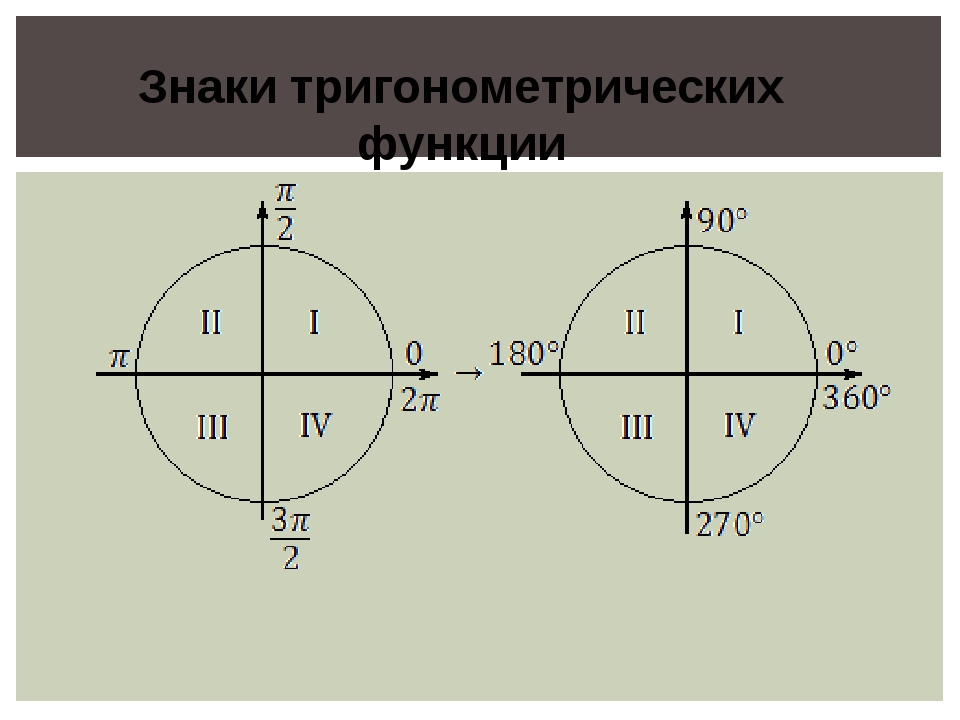

 ..?
..?
 Это делает невозможным построение обратных функций.Для решения уравнений, включающих триггерные функции, обязательно наличие обратных функций. Таким образом, математики должны ограничить функцию триггера, чтобы создать эти инверсии.
Это делает невозможным построение обратных функций.Для решения уравнений, включающих триггерные функции, обязательно наличие обратных функций. Таким образом, математики должны ограничить функцию триггера, чтобы создать эти инверсии. Ограничение, которое накладывается на значения области значений функции косинуса, составляет 0 ≤ x ≤ π (см. Рисунок 2).Эта ограниченная функция называется косинусом. Обратите внимание на заглавную букву «C» в косинусе.
Ограничение, которое накладывается на значения области значений функции косинуса, составляет 0 ≤ x ≤ π (см. Рисунок 2).Эта ограниченная функция называется косинусом. Обратите внимание на заглавную букву «C» в косинусе.
 В результате мы говорим cos -1 (½)
= 60 °.
В радианах это cos -1 (½).
= π / 3.
В результате мы говорим cos -1 (½)
= 60 °.
В радианах это cos -1 (½).
= π / 3.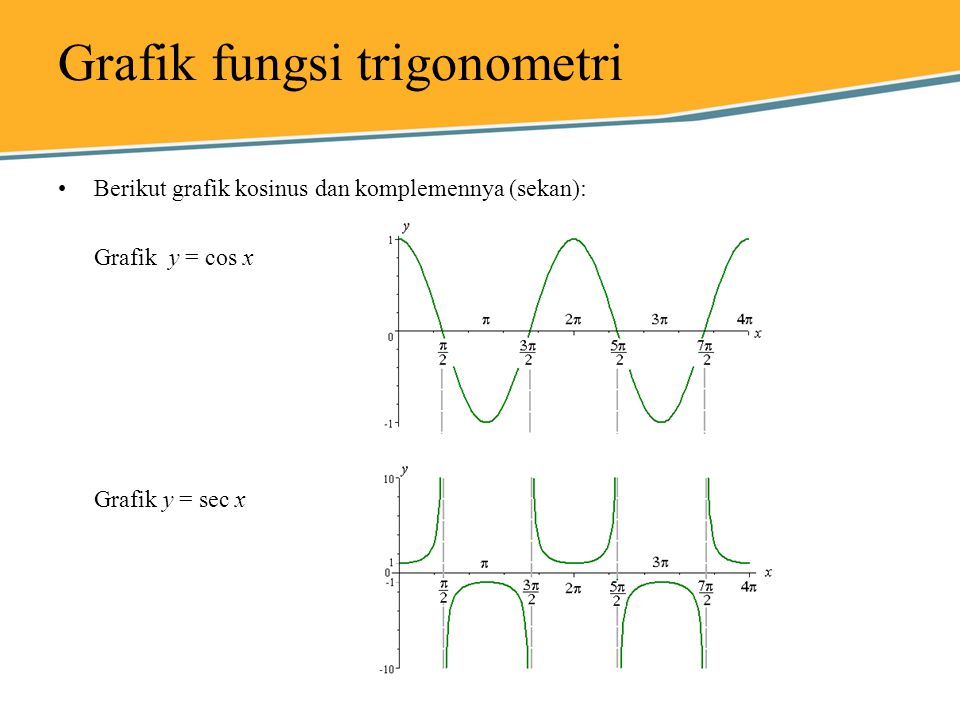
 5) π
5) π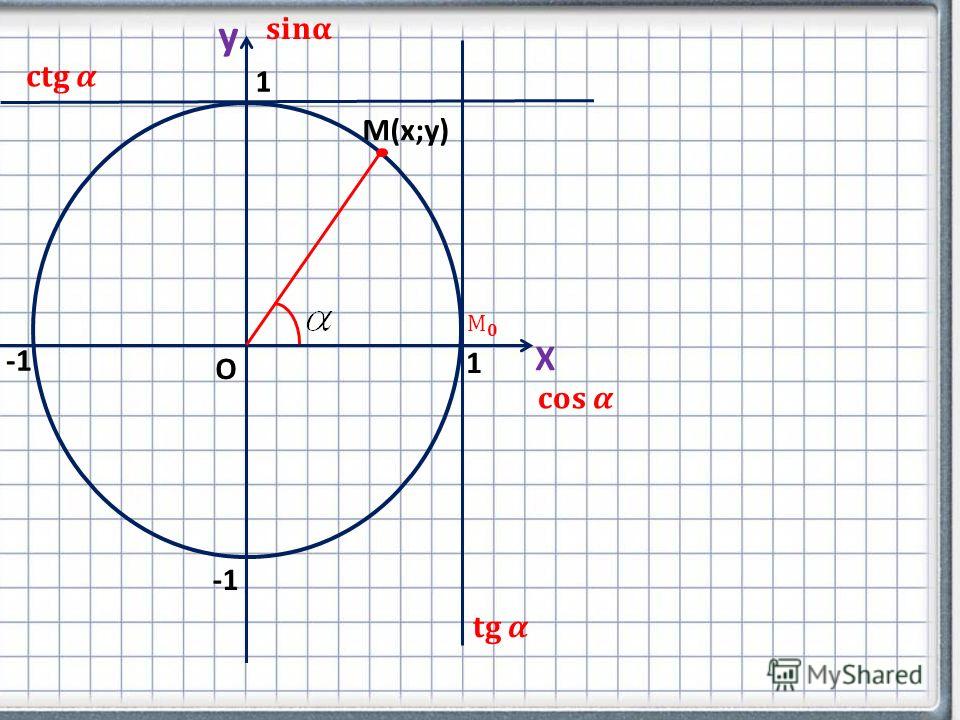 Также
Также Эта дуга начинается в точке \ ((1, 0) \) и заканчивается в ее конечной точке \ (P (t) \).Затем мы определяем косинус и синус дуги \ (t \) как координаты \ (x \) и \ (y \) точки \ (P \), так что \ (P (t) = (\ cos (t), sin (t)) \) (косинус обозначается как \ (\ cos \), а синус — как \ (\ sin \)). Значения косинуса и синуса определяются дугой \ (t \), а косинус и синус — это функций дуги \ (t \). Поскольку дуга лежит на единичной окружности, мы называем косинус и синус круговыми функциями . Важной частью тригонометрии является изучение косинуса и синуса, а также периодических явлений, которые эти функции могут моделировать.Это одна из причин, по которой круговые функции также называются тригонометрическими функциями , .
Эта дуга начинается в точке \ ((1, 0) \) и заканчивается в ее конечной точке \ (P (t) \).Затем мы определяем косинус и синус дуги \ (t \) как координаты \ (x \) и \ (y \) точки \ (P \), так что \ (P (t) = (\ cos (t), sin (t)) \) (косинус обозначается как \ (\ cos \), а синус — как \ (\ sin \)). Значения косинуса и синуса определяются дугой \ (t \), а косинус и синус — это функций дуги \ (t \). Поскольку дуга лежит на единичной окружности, мы называем косинус и синус круговыми функциями . Важной частью тригонометрии является изучение косинуса и синуса, а также периодических явлений, которые эти функции могут моделировать.Это одна из причин, по которой круговые функции также называются тригонометрическими функциями , .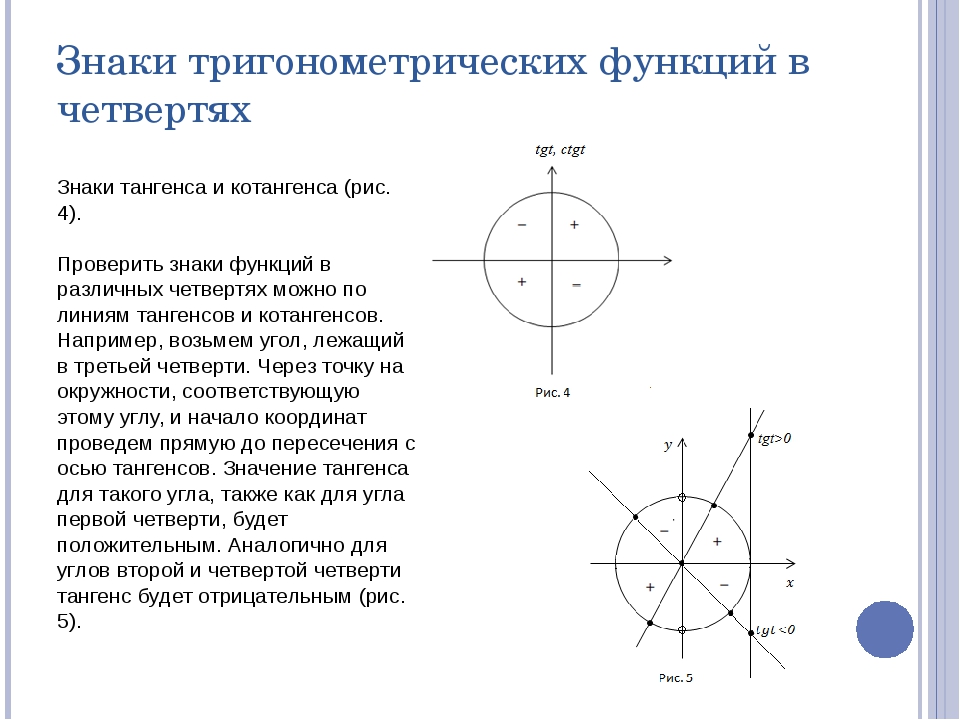 Хотя отчеты о фактическом происхождении различаются, похоже, что санскритское произведение «jya» (аккорд) было переведено на арабский язык как «jiba», но затем было переведено на латинский как «jaib» (залив), что стало «синусом» (залив или кривая).Затем это слово было переведено на английский язык, чтобы стать нашим «синусом». Слово косинус началось с Платона из Тиволи, который использовал выражение «chorda резидуи». Хотя латинское слово chorda было лучшим переводом санскритско-арабского слова синус, чем слово синус, это слово уже использовалось. Таким образом, «остаточная хорда» превратилась в «косинус».
Хотя отчеты о фактическом происхождении различаются, похоже, что санскритское произведение «jya» (аккорд) было переведено на арабский язык как «jiba», но затем было переведено на латинский как «jaib» (залив), что стало «синусом» (залив или кривая).Затем это слово было переведено на английский язык, чтобы стать нашим «синусом». Слово косинус началось с Платона из Тиволи, который использовал выражение «chorda резидуи». Хотя латинское слово chorda было лучшим переводом санскритско-арабского слова синус, чем слово синус, это слово уже использовалось. Таким образом, «остаточная хорда» превратилась в «косинус».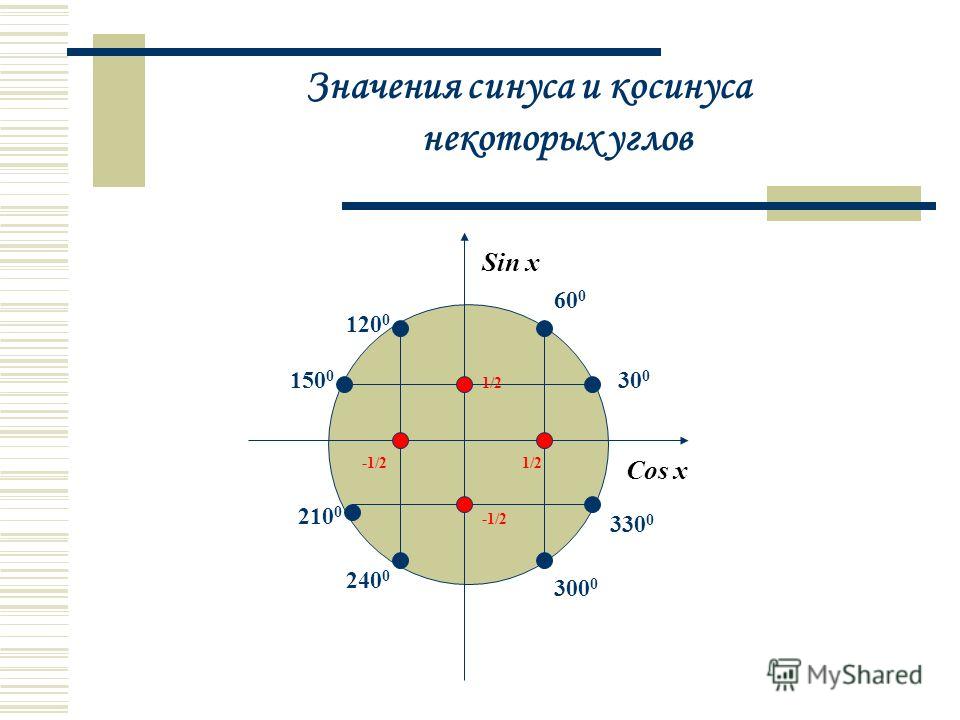 2 = 1 \) (с положительным направлением против часовой стрелки) с начальной точкой \ ( (1, 0) \) и конечной точки \ ((x, y) \), затем косинус для \ (t \), обозначаемый \ (\ cos (t) \), и синус для t, обозначаемые \ (\ sin (t) \), определяются как \ [\ cos (t) = x \] и \ [\ sin (t) = y.\]
2 = 1 \) (с положительным направлением против часовой стрелки) с начальной точкой \ ( (1, 0) \) и конечной точки \ ((x, y) \), затем косинус для \ (t \), обозначаемый \ (\ cos (t) \), и синус для t, обозначаемые \ (\ sin (t) \), определяются как \ [\ cos (t) = x \] и \ [\ sin (t) = y.\]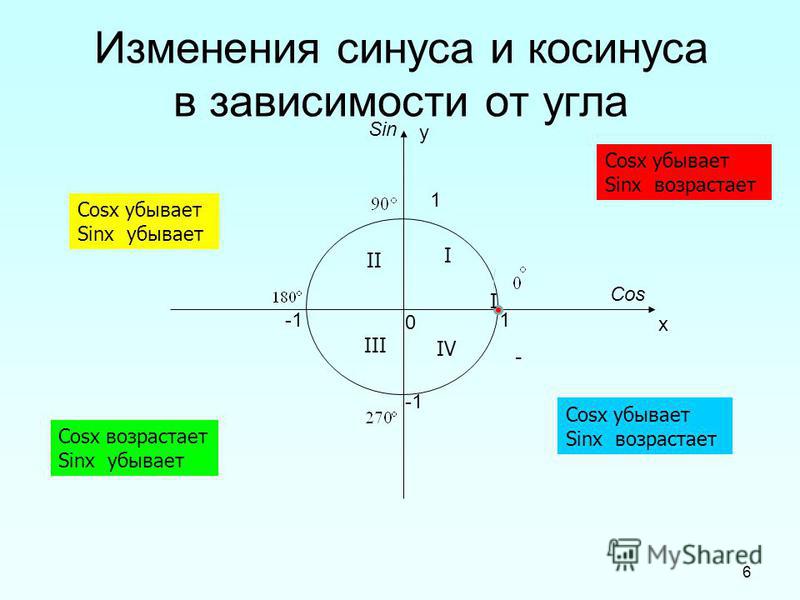
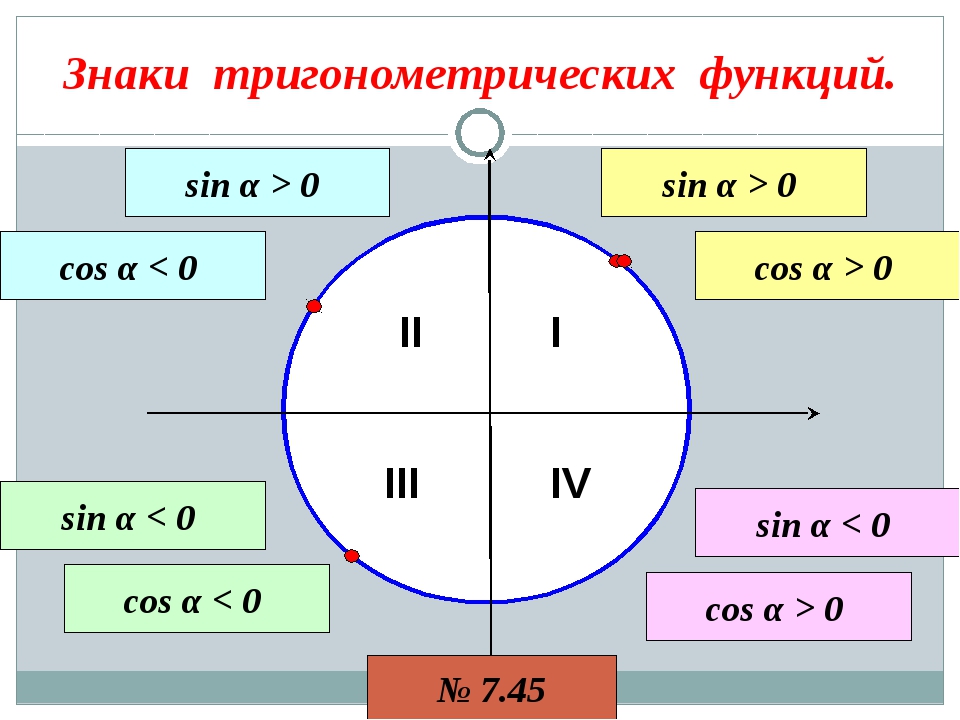 Веб-адрес этого апплета —
Веб-адрес этого апплета —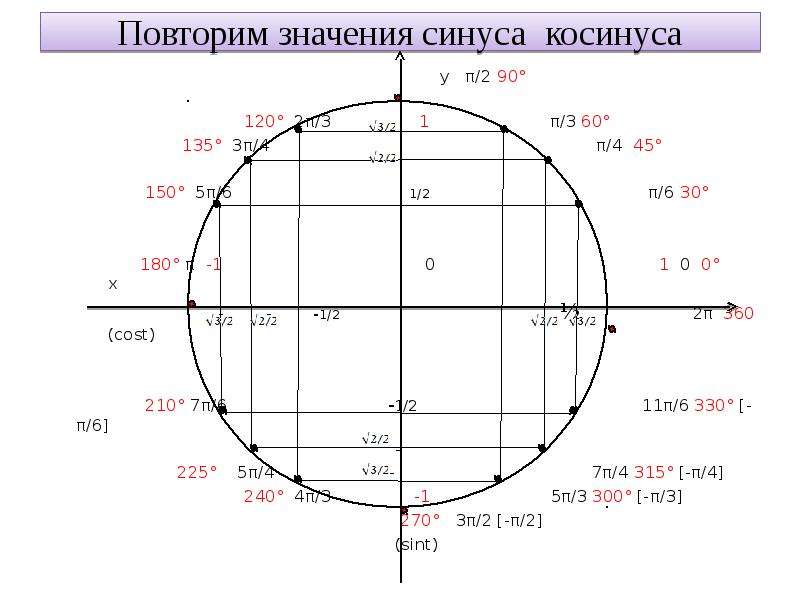 5) \ приблизительно 0,7807, \ sin (5.5) \ приблизительно -0,7055 \]
5) \ приблизительно 0,7807, \ sin (5.5) \ приблизительно -0,7055 \]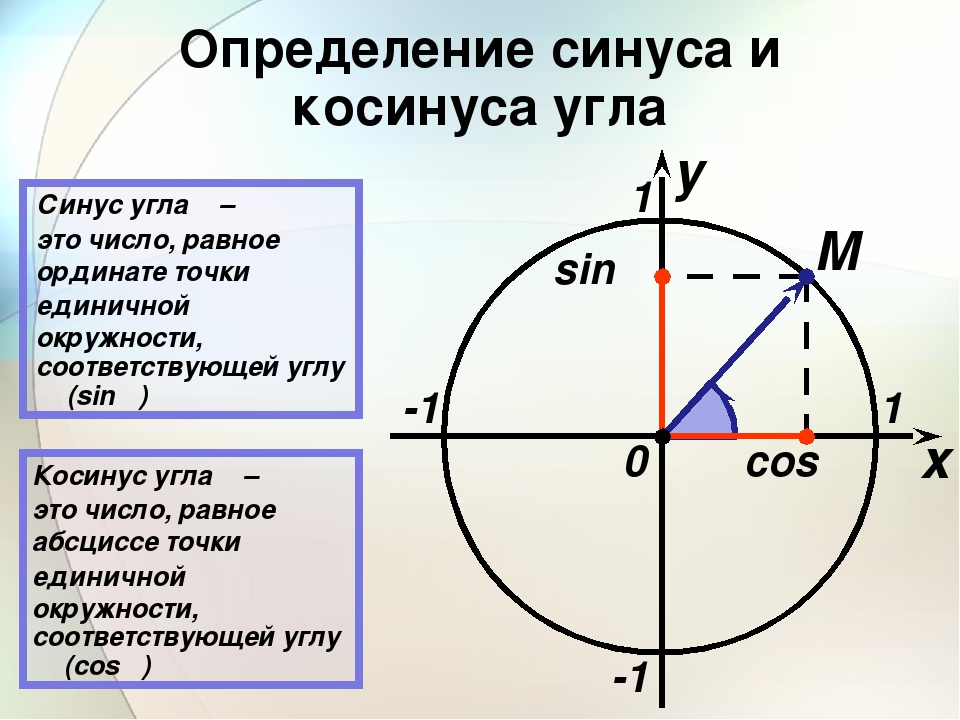
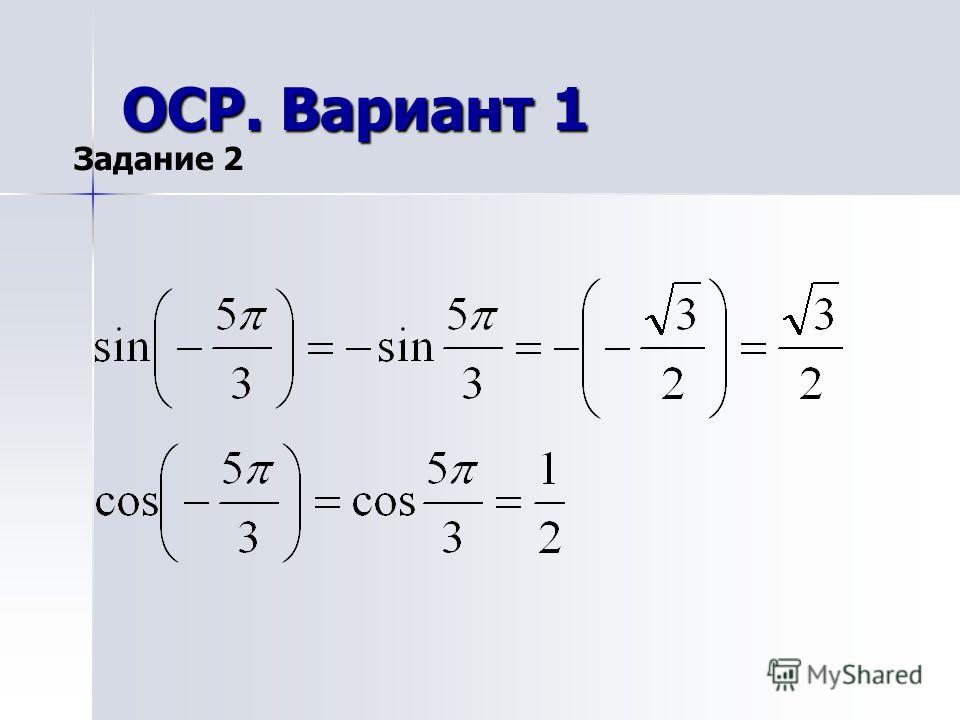
 Идея состоит в том, что знаки координат точки \ (P (x, y) \), нанесенной на координатный план, определяются квадрантом, в котором находится точка (если только она не лежит на одной из осей). Рисунок \ (\ PageIndex {2} \) суммирует эти результаты для знаков значений функций косинуса и синуса. В левом столбце таблицы указано положение конечной точки дуги, определяемой действительным числом \ (t \).
Идея состоит в том, что знаки координат точки \ (P (x, y) \), нанесенной на координатный план, определяются квадрантом, в котором находится точка (если только она не лежит на одной из осей). Рисунок \ (\ PageIndex {2} \) суммирует эти результаты для знаков значений функций косинуса и синуса. В левом столбце таблицы указано положение конечной точки дуги, определяемой действительным числом \ (t \). Мы можем сделать это, еще раз используя тот факт, что длина окружности единичной окружности равна \ (2 \ pi \), и когда мы перемещаемся по единичной окружности из точки .1; 0 / в положительном (против часовой стрелки) направлении, мы будем пересекать одну из координатных осей каждые четверть оборота. Например, если \ (0
Мы можем сделать это, еще раз используя тот факт, что длина окружности единичной окружности равна \ (2 \ pi \), и когда мы перемещаемся по единичной окружности из точки .1; 0 / в положительном (против часовой стрелки) направлении, мы будем пересекать одну из координатных осей каждые четверть оборота. Например, если \ (0

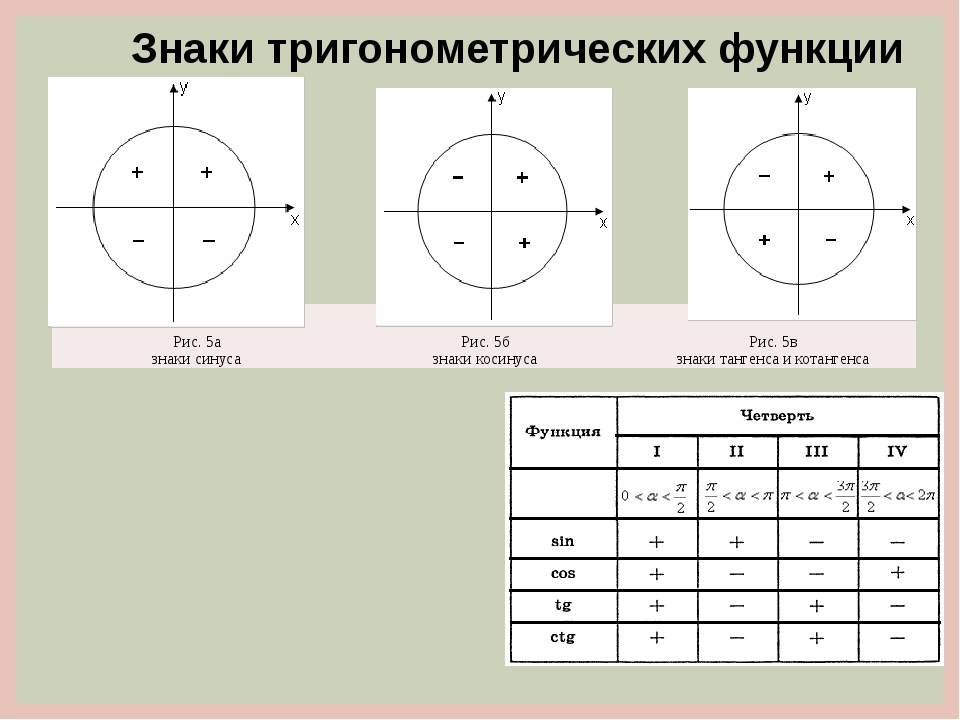 Следовательно, \ (\ cos (\ dfrac {\ pi} {5}) \) положительно.
Следовательно, \ (\ cos (\ dfrac {\ pi} {5}) \) положительно.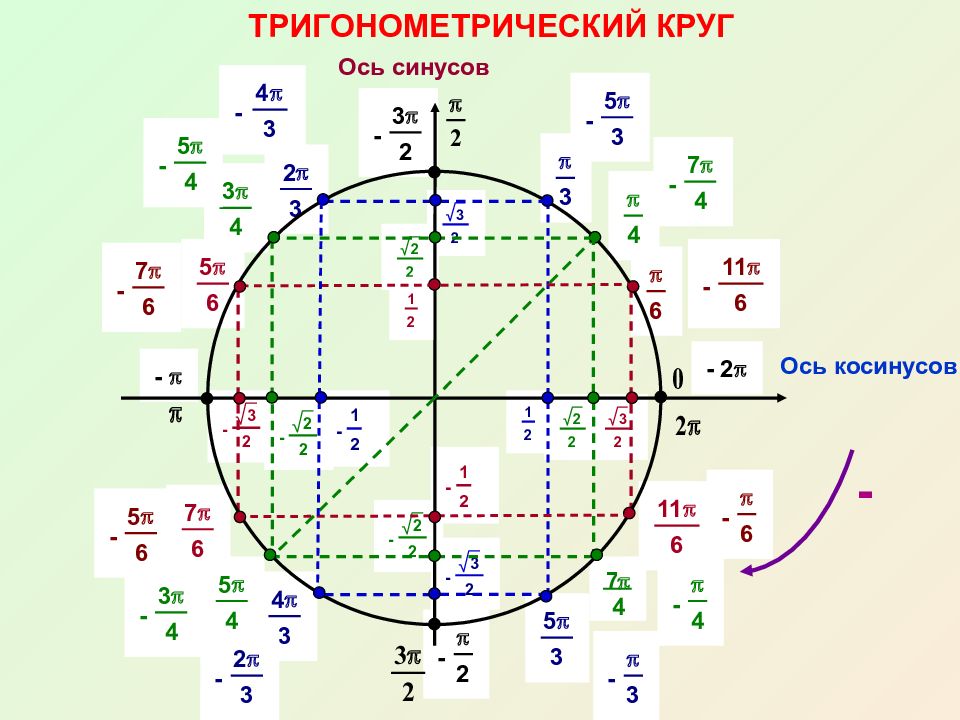 2 = (a + b) (a — b) \]
2 = (a + b) (a — b) \]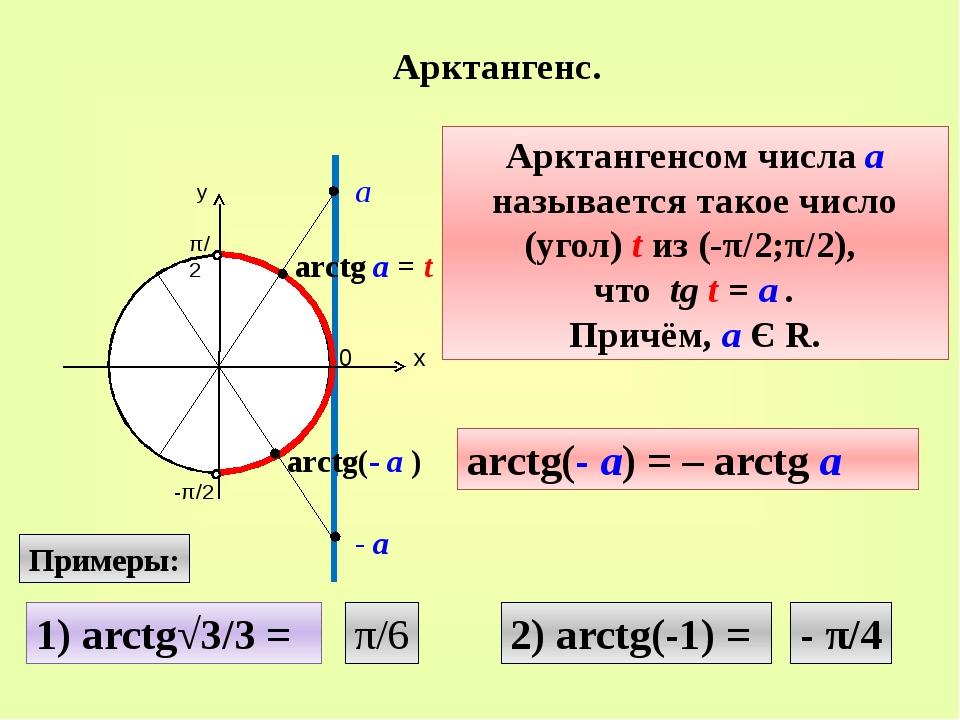 Следовательно, \ (\ sin (t) = — \ sqrt {\ dfrac {21} {25}} \). Поскольку \ (\ sqrt {25} = 5 \), мы можем написать
Следовательно, \ (\ sin (t) = — \ sqrt {\ dfrac {21} {25}} \). Поскольку \ (\ sqrt {25} = 5 \), мы можем написать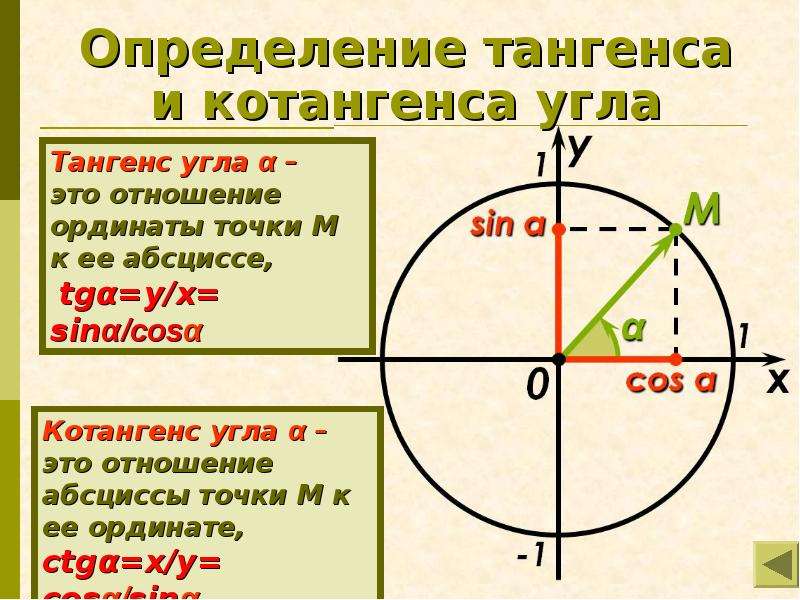 2 = 1 \) (с положительным направлением против часовой стрелки) с начальной точкой \ ((1, 0) \) и конечная точка \ ((x, y) \), тогда \ (\ cos (t) = x \) и \ (\ sin (t) = y \).
2 = 1 \) (с положительным направлением против часовой стрелки) с начальной точкой \ ((1, 0) \) и конечная точка \ ((x, y) \), тогда \ (\ cos (t) = x \) и \ (\ sin (t) = y \).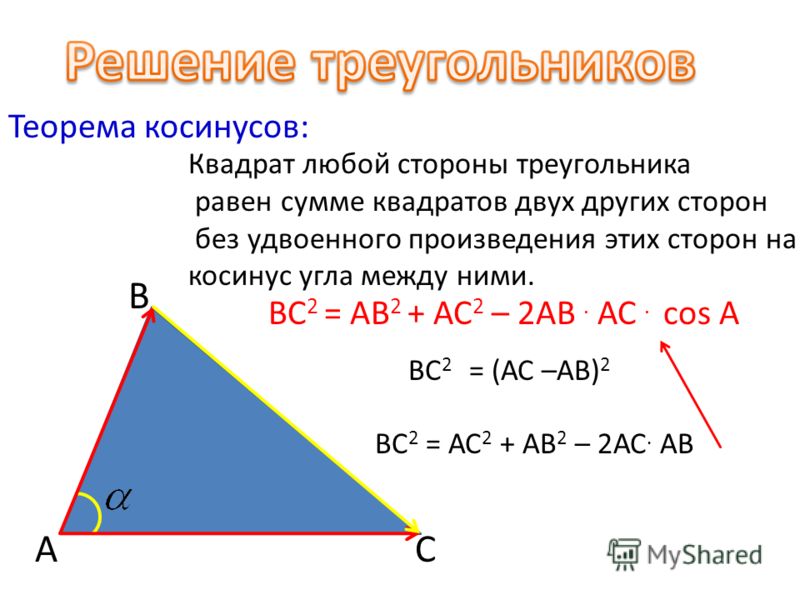 \ nonumber \]
\ nonumber \]
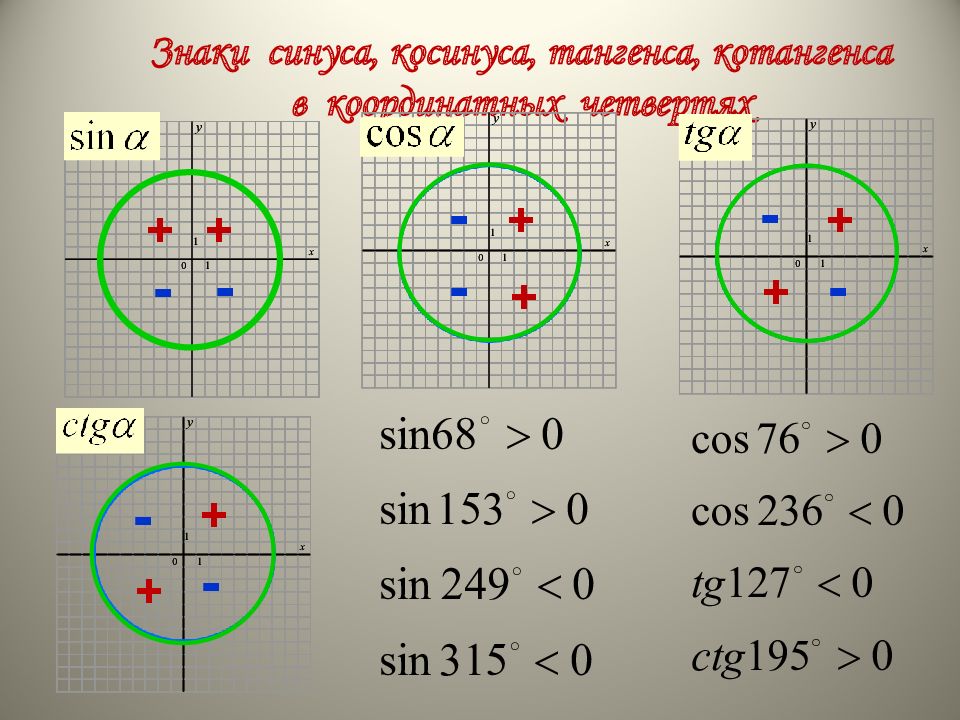
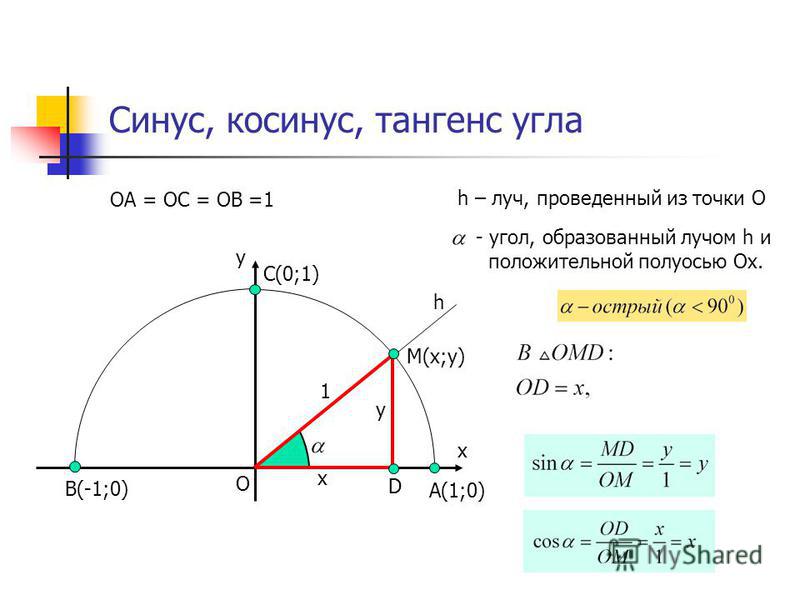 Чтобы вывести производные обратных триггерных функций, нам понадобится формула из последнего раздела, относящаяся к производным обратных функций. Если \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) являются обратными функциями, тогда
Чтобы вывести производные обратных триггерных функций, нам понадобится формула из последнего раздела, относящаяся к производным обратных функций. Если \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) являются обратными функциями, тогда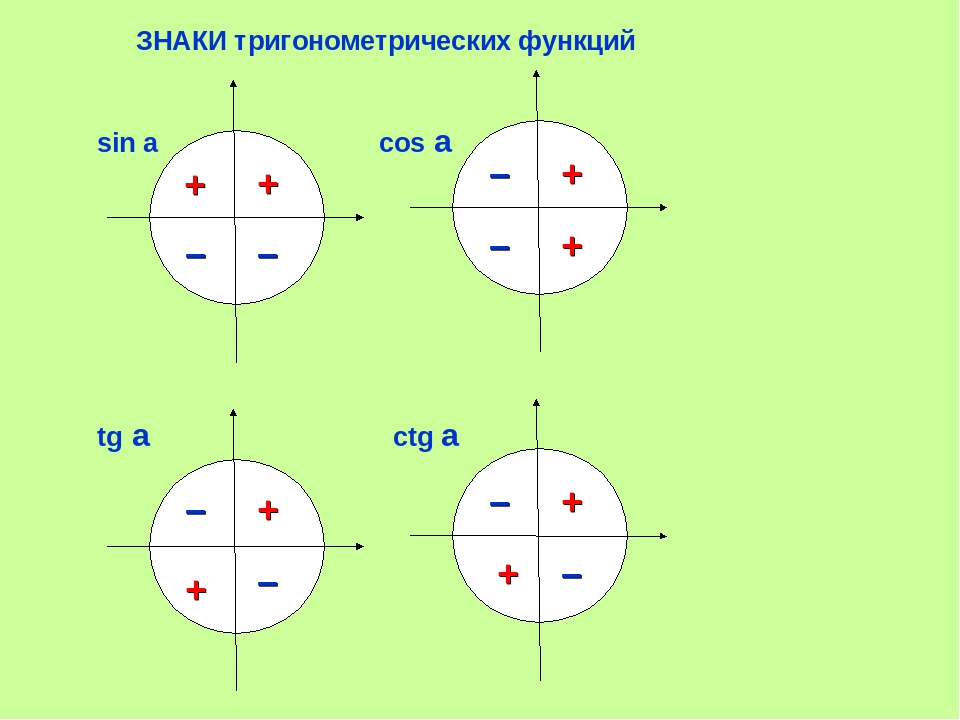 Приведенные выше ограничения на \ (y \) необходимы для того, чтобы убедиться, что мы получаем непротиворечивый ответ на основе обратного синуса. Мы знаем, что на самом деле существует бесконечное количество углов, которые будут работать, и нам нужно постоянное значение, когда мы работаем с обратным синусом.{- 1}} \ left ({\ frac {1} {2}} \ right) \)
Показать решение
Приведенные выше ограничения на \ (y \) необходимы для того, чтобы убедиться, что мы получаем непротиворечивый ответ на основе обратного синуса. Мы знаем, что на самом деле существует бесконечное количество углов, которые будут работать, и нам нужно постоянное значение, когда мы работаем с обратным синусом.{- 1}} \ left ({\ frac {1} {2}} \ right) \)
Показать решение {- 1}} x} \ right) = x \ hspace {0.{- 1}} x \ hspace {0,5 дюйма} \ Leftrightarrow \ hspace {0,5 дюйма} \ tan y = x \ hspace {0,25 дюйма} {\ mbox {for}} \, \, \, \, \, \, \, \, \, — \ frac {\ pi} {2}
{- 1}} x} \ right) = x \ hspace {0.{- 1}} x \ hspace {0,5 дюйма} \ Leftrightarrow \ hspace {0,5 дюйма} \ tan y = x \ hspace {0,25 дюйма} {\ mbox {for}} \, \, \, \, \, \, \, \, \, — \ frac {\ pi} {2}