Конденсатор и RC цепочка | Электроника для всех
Если соединить резистор и конденсатор, то получится пожалуй одна из самых полезных и универсальных цепей.
О многочисленных способах применения которой я сегодня и решил рассказать. Но вначале про каждый элемент в отдельности:
Резистор — его задача ограничивать ток. Это статичный элемент, чье сопротивление не меняется, про тепловые погрешности сейчас не говорим — они не слишком велики. Ток через резистор определяется законом ома — I=U/R, где U напряжение на выводах резистора, R — его сопротивление.
Конденсатор штука поинтересней. У него есть интересное свойство — когда он разряжен то ведет себя почти как короткое замыкание — ток через него течет без ограничений, устремляясь в бесконечность. А напряжение на нем стремится к нулю. Когда же он заряжен, то становится как обрыв и ток через него течь перестает, а напряжение на нем становится равным заряжающему источнику. Получается интересная зависимость — есть ток, нет напряжения, есть напряжение — нет тока.
Чтобы визуализировать себе этот процесс, представь ган… эмм.. воздушный шарик который наполняется водой. Поток воды — это ток. Давление воды на упругие стенки — эквивалент напряжения. Теперь смотри, когда шарик пуст — вода втекает свободно, большой ток, а давления еще почти нет — напряжение мало. Потом, когда шарик наполнится и начнет сопротивляться давлению, за счет упругости стенок, то скорость потока замедлится, а потом и вовсе остановится — силы сравнялись, конденсатор зарядился. Есть напряжение натянутых стенок, но нет тока!
Теперь, если снять или уменьшить внешнее давление, убрать источник питания, то вода под действием упругости хлынет обратно. Также и ток из конденсатора потечет обратно если цепь будет замкнута, а напряжение источника ниже чем напряжение в конденсаторе.
Емкость конденсатора. Что это?
Теоретически, в любой идеальный конденсатор можно закачать заряд бесконечного размера. Просто наш шарик сильней растянется и стенки создадут большее давление, бесконечно большое давление.
Просто наш шарик сильней растянется и стенки создадут большее давление, бесконечно большое давление.
Представь два стакана с бесконечно высокими стенками. Один узкий, как пробирка, другой широкий, как тазик. Уровень воды в них — это напряжение. Площадь дна — емкость. И в тот и в другой можно набузолить один и тот же литр воды — равный заряд. Но в пробирке уровень подскочит на несколько метров, А в тазике будет плескаться у самого дна. Также и в конденсаторах с малой и большой емкостью.
Залить то можно сколько угодно, но напряжение будет разным.
Плюс в реале у конденсаторов есть пробивное напряжение, после которого он перестает быть конденсатором, а превращается в годный проводник 🙂
А как быстро заряжается конденсатор?
В идеальных условиях, когда у нас бесконечно мощный источник напряжения с нулевым внутренним сопротивлением, идеальные сверхпроводящие провода и абсолютно безупречный конденсатор — этот процесс будет происходить мгновенно, с временем равным 0, равно как и разряд.
Но в реальности всегда существуют сопротивления, явные — вроде банального резистора или неявные, такие как сопротивление проводов или внутреннее сопротивление источника напряжения.
А у этого закона есть пара характерных величин:
- Т — постоянная времени, это время при котором величина достигнет 63% от своего максимума. 63% тут взялись не случайно, тут прямая завязка на такую формулу VALUET=max—1/e*max.
- 3T — а при троекратной постоянной значение достигнет 95% своего максимума.
Постоянная времени для RC цепи Т=R*C
Чем меньше сопротивление и меньше емкость, тем быстрей конденсатор заряжается. Если сопротивление равно нулю, то и время заряда равно нулю.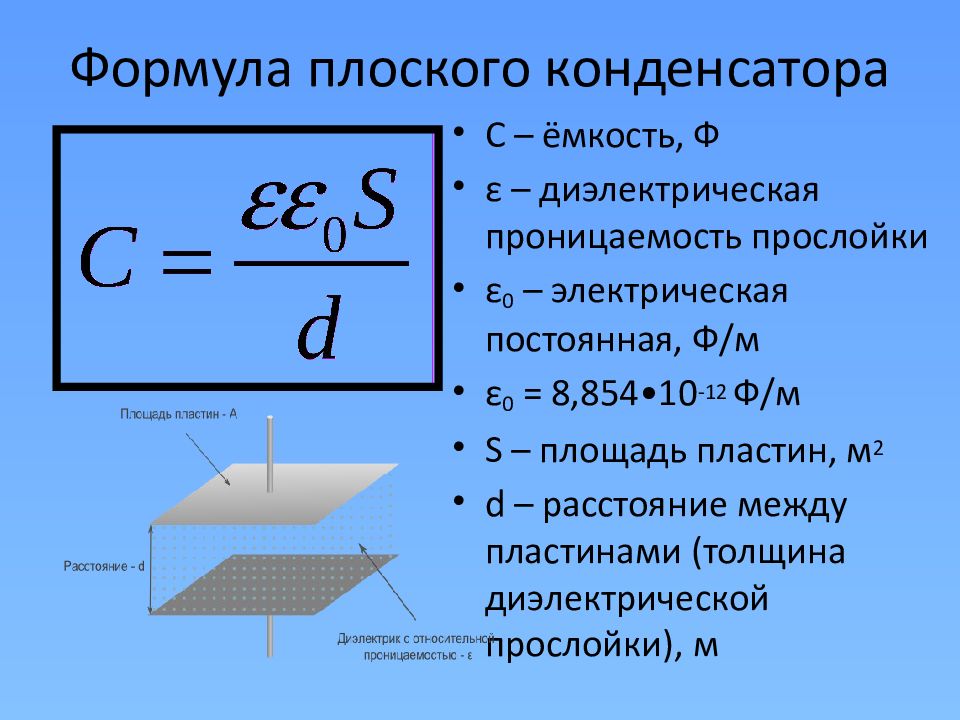
Рассчитаем за сколько зарядится на 95% конденсатор емкостью 1uF через резистор в 1кОм:
T= C*R = 10-6 * 103 = 0.001c
3T = 0.003c через такое время напряжение на конденсаторе достигнет 95% от напряжения источника.
Разряд пойдет по тому же закону, только вверх ногами. Т.е. через Твремени в на конденсаторе остаенется всего лишь 100% — 63% = 37% от первоначального напряжения, а через 3T и того меньше — жалкие 5%.
Ну с подачей и снятием напряжения все ясно. А если напряжение подали, а потом еще ступенчато подняли, а разряжали также ступеньками? Ситуация тут практически не изменится — поднялось напряжение, конденсатор дозарядился до него по тому же закону, с той же постоянной времени — через время 3Т его напряжение будет на 95% от нового максимума.
Чуть понизилось — подразрядился и через время 3Т напряжение на нем будет на 5% выше нового минимума.
Да что я тебе говорю, лучше показать. Сварганил тут в мультисиме хитровыдрюченный генератор ступечнатого сигнала и подал на интегрирующую RC цепочку:
Видишь как колбасится 🙂 Обрати внимание, что и заряд и разряд, вне зависимости от высоты ступеньки, всегда одной длительности!!!
А до какой величины конденсатор можно зарядить?
В теории до бесконечности, этакий шарик с бесконечно тянущимися стенками. В реале же шарик рано или поздно лопнет, а конденсатор пробьет и закоротит. Вот поэтому у всех конденсаторов есть важный параметр — предельное напряжение. На электролитах его часто пишут сбоку, а на керамических его надо смотреть в справочниках. Но там оно обычно от 50 вольт. В общем, выбирая кондер надо следить, чтобы его предельное напряжение было не ниже того которое в цепи. Добавлю что при расчете конденсатора на переменное напряжение следует выбирать предельное напряжение в 1.4 раза выше. Т.к. на переменном напряжении указывают действующее значение, а мгновенное значение в своем максимуме превышает его в 1.4 раза.
В реале же шарик рано или поздно лопнет, а конденсатор пробьет и закоротит. Вот поэтому у всех конденсаторов есть важный параметр — предельное напряжение. На электролитах его часто пишут сбоку, а на керамических его надо смотреть в справочниках. Но там оно обычно от 50 вольт. В общем, выбирая кондер надо следить, чтобы его предельное напряжение было не ниже того которое в цепи. Добавлю что при расчете конденсатора на переменное напряжение следует выбирать предельное напряжение в 1.4 раза выше. Т.к. на переменном напряжении указывают действующее значение, а мгновенное значение в своем максимуме превышает его в 1.4 раза.
Что следует из вышеперечисленного? А то что если на конденсатор подать постоянное напряжение, то он просто зарядится и все. На этом веселье закончится.
А если подать переменное? То очевидно, что он будет то заряжаться, то разряжаться, а в цепи будет туда и обратно гулять ток. Движуха! Ток есть!
Выходит, несмотря на физический обрыв цепи между обкладками, через конденсатор легко протекает переменный ток, а вот постоянному слабо.
Что нам это дает? А то что конденсатор может служить своего рода сепаратором, для разделения переменного тока и постоянного на соответствующие составляющие.
Любой изменяющийся во времени сигнал можно представить как сумму двух составляющих — переменной и постоянной.
Например, у классической синусоиды есть только переменная часть, а постоянная равна нулю. У постоянного же тока наоборот. А если у нас сдвинутая синусоида? Или постоянная с помехами?
Переменная и постоянная составляющие сигнала легко разделяются!
Чуть выше я тебе показал как конденсатор дозаряжается и подразряжается при изменениях напряжения. Так что переменная составляющая сквозь кондер пройдет на ура, т.к. только она заставляет конденсатор активно менять свой заряд. Постоянная же как была так и останется и застрянет на конденсаторе.
Но чтобы конденсатор эффективно разделял переменную составляющую от постоянной частота переменной составляющей должна быть не ниже чем 1/T
Возможны два вида включения RC цепочки:
Интегрирующая и дифференцирующая.
Фильтр низких частот без изменений пропускает постоянную составляющую (т.к. ее частота равна нулю, ниже некуда) и подавляет все что выше чем 1/T. Постоянная составляющая проходит напрямую, а переменная составляющая через конденсатор гасится на землю.
Такой фильтр еще называют интегрирующей цепочкой потому, что сигнал на выходе как бы интегрируется. Помнишь что такое интеграл? Площадь под кривой! Вот тут она и получается на выходе.
Как здесь вычисляется постоянная составляющая? А с виду и не скажешь, но надо помнить, что
Фильтр высоких частот работает наоборот. Он не пускает постоянную составляющую (т.к. ее частота слишком низка — 0) — ведь конденсатор для нее равносилен обрыву, а вот переменная пролазит через кондер без проблем.
А дифференцирующей цепью ее называют потому, что на выходе у нас получается дифференциал входной функции, который есть не что иное как скорость изменения этой функции.
- На участке 1 происходит заряд конденсатора, а значит через него идет ток и на резисторе будет падение напряжения.
- На участке 2 происходит резкое увеличение скорости заряда, а значит и ток резко возрастет, а за ним и падение напряжения на резисторе.
- На участке 3 конденсатор просто удерживает уже имеющийся потенциал. Ток через него не идет, а значит на резисторе напряжение тоже равно нулю.
- Ну и на 4м участке конденсатор начал разряжаться, т.к. входной сигнал стал ниже чем его напряжение. Ток пошел в обратную сторону и на резисторе уже отрицательное падение напряжения.
А если подать на вход прямоугольнй импульс, с очень крутыми фронтами и сделать емкость конденсатора помельче, то увидим вот такие иголки:
Вверху идет осциллограма того что на входе, внизу то что на выходе дифференциальной цепи.
Как видишь, тут мощные всплески на фронтах. Оно и понятно, в этом месте функция меняется резко, а значит производная (скорость изменения) этой функции велика, на пологих участках сигнал константа и его производная, скорость изменения, равна нулю — на графике ноль.
А если загнать в дифференциатор пилу, то на выходе получим…
прямоугольник. Ну, а чо? Правильно — производная от линейной функции есть константа, наклон этой функции определяет знак константы.
Короче, если у тебя сейчас идет курс матана, то можешь забить на богомерзкий Mathcad, отвратный Maple, выбросить из головы матричную ересь Матлаба и, достав из загашников горсть аналоговой рассыпухи, спаять себе истинно ТРУЪ аналоговый компьютер 🙂 Препод будет в шоке 🙂
Правда на одних только резисторах кондерах интеграторы и диффернциаторы обычно не делают, тут юзают операционные усилители. Можешь пока погуглить на предмет этих штуковин, любопытная вещь 🙂
Можешь пока погуглить на предмет этих штуковин, любопытная вещь 🙂
А вот тут я подал обычный приямоугольный сигнал на два фильтра высоких и низких частот. А выходы с них на осциллограф:
И вот что получилось на осциллографе:
Вот, чуть покрупней один участок:
| > |
Как видишь, на одном срезало постоянную составляющую, на другом переменную.
Ладно, что то мы отвлеклись от темы.
Как еще можно применить RC цепь?
Да способов много. Часто ее используют не только в качестве фильтров, но и как формирователи импульсов. Например, на сбросе контроллера AVR, если надо чтобы МК стартанул не сразу после включения питания, а с некоторой выдержкой:
При старте кондер разряжен, ток через него вваливат на полную, а напряжение на нем мизерное — на входе RESET сигнал сброса. Но вскоре конденсатор зарядится и через время Т его напряжение будет уже на уровне логической единицы и на RESET перестанет подаваться сигнал сброса — МК стартанет.
Но вскоре конденсатор зарядится и через время Т его напряжение будет уже на уровне логической единицы и на RESET перестанет подаваться сигнал сброса — МК стартанет.
А для AT89C51 надо с точностью наоборот RESET организовать — вначале подать единицу, а потом ноль. Тут ситуация обратная — пока кондер не заряжен, то ток через него течет большой, Uc — падение напряжения на нем мизерное Uc=0. А значит на RESET подается напряжение немногим меньше напряжения питания Uпит-Uc=Uпит.
Но когда кондер зарядится и напряжение на нем достигнет напряжения питания (Uпит=Uс), то на выводе RESET уже будет Uпит-Uc=0
Аналоговые измерения
Но фиг сними с цепочками сброса, куда прикольней использовать возможность RC цепи для замера аналоговых величин микроконтроллерами в которых нет АЦП.
Тут используется тот факт, что напряжение на конденсаторе растет строго по одному и тому же закону — экспоненте. В зависимости от кондера, резистора и питающего напряжения. А значит его можно использовать как опорное напряжение с заранее известными параметрами.
Работает просто, мы подаем напряжение с конденсатора на аналоговый компаратор, а на второй вход компаратора заводим измеряемое напряжение. И когда хотим замерить напряжение, то просто вначале дергаем вывод вниз, чтобы разрядить конденсатор. Потом возвращем его в режим Hi-Z, cбрасываем и запускаем таймер. А дальше кондер начинает заряжаться через резистор и как только компаратор доложит, что напряжение с RC догнало измеряемое, то останавливаем таймер.
Зная по какому закону от времени идет возрастание опорного напряжения RC цепи, а также зная сколько натикал таймер, мы можем довольно точно узнать чему было равно измеряемое напряжение на момент сработки компаратора. Причем, тут не обязательно считать экспоненты. На начальном этапе зарядки кондера можно предположить, что зависимость там линейная. Или, если хочется большей точности, аппроксимировать экспоненту кусочно линейными функциями, а по русски — отрисовать ее примерную форму несколькими прямыми или сварганить таблицу зависимости величины от времени, короче, способов вагон просто.
Если надо заиметь аналоговую крутилку, а АЦП нету, то можно даже компаратор не юзать. Дрыгать ножкой на которой висит конденсатор и давать ему заряжаться через перменный резистор.
По изменению Т, которая, напомню T=R*C и зная что у нас С = const, можно вычислить значение R. Причем, опять же необязательно подключать тут математический аппарат, в большинстве случаев достаточно сделать замер в каких-нибудь условных попугаях, вроде тиков таймера. А можно пойти другим путем, не менять резистор, а менять емкость, например, подсоединяя к ней емкость своего тела… что получится? Правильно — сенсорные кнопки!
Если что то непонятно, то не парься скоро напишу статью про то как прикрутить к микроконтроллеру аналоговую фиговину не используя АЦП. Там подробно все разжую.
Теперь, думаю, ты понял за что я так люблю RC цепочки и почему на моей отладочной плате PinBoard их несколько и с разными параметрами 🙂
Как рассчитать емкость гасящего конденсатора простого блока питания.
 . Обзоры товаров из Китая. Блок питания с гасящим конденсатором представляет собой простейший вариант запитать какое нибудь маломощное устройство.
. Обзоры товаров из Китая. Блок питания с гасящим конденсатором представляет собой простейший вариант запитать какое нибудь маломощное устройство.При всей своей простоте он имеет и два минуса:
1. Он гальванически связан с сетью! потому такие БП используются там, где нет вероятности прикосновения к контактам.
2. Такой Бп имеет не очень большой выходной ток. При увеличении выходного тока надо увеличивать емкость гасящего конденсатора и его габариты становятся существенными.
Внимание, будьте очень аккуратны, не прикасайтесь к контактам этого БП когда он включен.
Простейшая схема данного БП выглядит так:
Как можно увидеть из схемы, последовательно с сетью стоит конденсатор. Он то и является балластом,, на котором гасится часть напряжения.
Конденсатор не пропускает постоянный ток, но так как в сети переменный и конденсатор в итоге постоянно перезаряжется, то и получается, что в таком случае ток на выходе есть. Причем сила тока напрямую зависит от емкости конденсатора.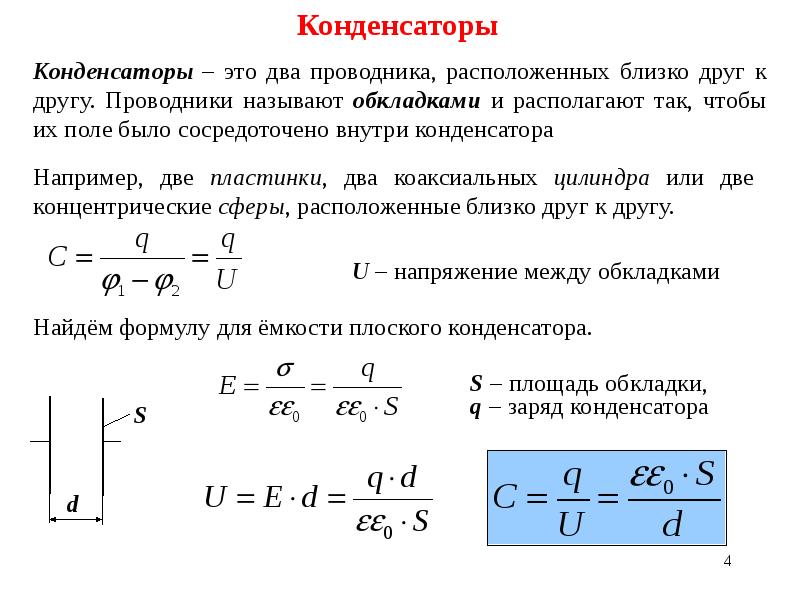
Собственно потому для расчета емкости конденсатора необходимо знать как минимум выходной ток нашего будущего БП, причем надо учесть и потребление стабилизатора, обычно это несколько мА.
И так. Есть две формулы, сложная и простая.
Сложная — подходит для расчета при произвольном выходном напряжении.
Простая — подходит в ситуациях, когда выходное напряжение не более 10% от входного.
I — выходной ток нашего БП
Uвх — напряжение сети, например 220 Вольт
Uвых — напряжение на выходе БП (или до стабилизаторе если такой есть), например 12 Вольт.
С — собственно искомая емкость.
Например я хочу сделать БП с выходным током до 150мА. Пример схемы приведен выше, вариант применения — радиопульт с питанием 5 Вольт + реле на 12 Вольт.
Подставляем наши 0.15 Ампера и получаем емкость 2.18мкФ, можно взять ближайший номинал из стандартных — 2,2мкФ, ну или «по импортному» — 225.
Все как бы вроде хорошо, схема простая, но есть несколько минусов, которые надо исключить:
1. Бросок тока при включении может сжечь диодный мост.
Бросок тока при включении может сжечь диодный мост.
2. При выходе из строя конденсатора может быть КЗ
3. Если оставить как есть, то вполне можно получить разряд от входного конденсатора, так как на нем может долго присутствовать напряжение даже после отключения БП от сети.
4. При снятии нагрузки напряжение на конденсаторе до стабилизатора поднимется до довольно большого значения.
Решения:
1. Резистор R1 последовательно с конденсатором
2. Предохранитель 0.5 Ампера.
3. Резистор R2 параллельно конденсатору.
4. Супрессор на 12 Вольт параллельно конденсатору после диодного моста. Я не рекомендую здесь использовать стабилитроны, супрессоры рассчитаны на большую мощность рассеивания и схема будет работать надежнее.
На схеме красным цветом я выделил новые компоненты, синим — небольшое дополнение в виде светодиода.
Но гасящие конденсаторы используют часто и в дешевых светодиодных лампах. Это плохо, так как у таких ламп меньше надежность и часто высокие пульсации света.
Ниже упрощенный вариант схемы такой лампы.
Попробуем рассчитать емкость для такого применения, но так как напряжение на выходе будет явно больше чем 1/10 от входного, то применим первую формулу.
В качестве выходного напряжения я заложил 48 Вольт, 16 светодиодов по 3 Вольта на каждом. Конечно это все условно, но близко к реальности.
Ток — 20мА, типичный максимальный ток для большинства индикаторных светодиодов.
У меня вышло, что необходим конденсатор емкостью 0.298 мкФ. Ближайший из распространенных номиналов — 0.27 или 0.33мкФ. Первый встречается гораздо реже, а второй уже будет давать превышение тока, потому можно составить конденсатор из двух параллельных, например по 0.15мкФ. При параллельном включении емкость складывается.
С емкостью разобрались, осталось еще пара моментов:
1. Напряжение конденсатора
2. Тип конденсатора.
С напряжением все просто, можно применить конденсатор на 400 Вольт, но надежнее на 630, хоть они и имеют больше размер.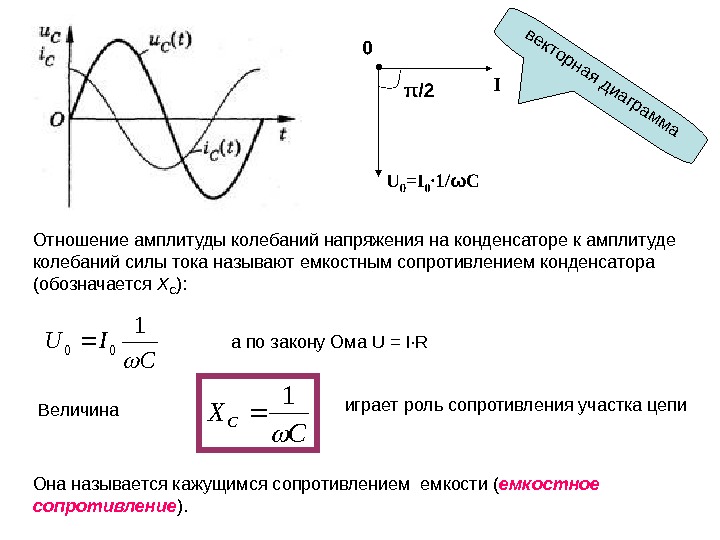
С типом чуть сложнее. Для такого применения лучше использовать конденсаторы, которые изначально предназначены для такого использования, например К73-17, CL21, X2
На фото конденсатор CL21
А это более надежный вариант, не смотрите что на нем указано 280 Вольт, у него это значение переменного действующего напряжения и он будет работать надежнее, чем К73-17 или CL21.
Такие конденсаторы могут выглядеть и так
А вот теперь можно еще раз внимательно посмотреть, что надо для того, чтобы собрать такой «простой» блок питания и решить, нужен ли он.
В некоторых ситуациях да, он поможет, но он имеет кучу минусов, потому на мой взгляд лучше применить просто небольшой импульсный блок питания, который уже имеет стабилизированное выходное напряжение, гальваническую изоляцию и больший выходной ток.
Как пример таких блоков питания я могу дать ссылку на подробный обзор четырех вариантов, с тестами, схемами и осмотров.
Но можно поступить еще лучше. Сейчас получили распространение монолитные блоки питания. По сути кубик, в котором находится миниатюрный БП
Сейчас получили распространение монолитные блоки питания. По сути кубик, в котором находится миниатюрный БП
Например HLK-PM01 производства Hi-link, стоимостью около двух долларов за штуку.
Или их китайский аналог TSP-05 производства Tenstar robot. Они немного дешевле, 1.93 доллара за штуку.
Практика показала, что качество у них сопоставимое.
Как я писал выше, они представляют из себя импульсный Бп в модульном исполнении. БП в пластмассовом корпусе залитый эпоксидной смолой.
Выпускаются на разные напряжения и способны поддерживать его на довольно стабильном уровне.
Внутренности поближе, на фото вариант от Hi-link
На этом вроде все. Надеюсь, что статья была полезна, постараюсь и в будущем находить интересные темы. Также интересны пожелания, что хотелось бы видеть в рубрике — Начинающим.
Онлайн калькулятор расчета запасаемой энергии в конденсаторе
Конструктивно конденсатор представляет собой емкостной элемент, состоящий из двух параллельно расположенных пластин, пространство между которыми заполнено диэлектриком.
Принцип работы конденсатора заключается в способности накапливать определенную величину заряда на пластинах и отдавать их обратно в сеть при прохождении через него переменного тока. Для цепи постоянного тока конденсатор представляет собой разрыв, но пластины все равно способны накапливать заряд. Основным параметром конденсатора является емкость, выражающаяся в Фарадах и способность накапливать заряд, выражаемая величиной энергии в Джоулях.
Если емкость конденсатора указывается на корпусе элемента и является его паспортным значением, то количество запасаемой энергии можно определить путем вычислений. Наиболее простым способом вычисления является использования онлайн калькулятора.
Для этого выполните такую последовательность действий:
- Внесите в первую графу калькулятора значение напряжения на конденсаторе в Вольтах;
- Укажите во втором поле величину емкости элемента в микрофарадах;
- Внесите значения сопротивления конденсатора и нажмите кнопку «Рассчитать».

В результате онлайн калькулятор расчета запасаемой энергии в конденсаторе выдаст значение заряда и времени, расходуемого на полный заряд емкостного элемента, подключенного к цепи.
Расчет величины заряда, накапливаемого в конденсаторе, и времени, необходимого для накопления этого заряда производится по таким формулам:
Где,
- W – это количество запасаемой энергии в конденсаторе;
- U – величина напряжения, приложенного к конденсатору;
- C – емкость конденсатора.
Для определения времени, затрачиваемого на накопление этого количества запасаемой энергии, в калькуляторе используется формула: Tзар = R*C
Где
- Tзар — период времени, необходимый для накопления заряда, зависящий от параметров элемента;
- R – величина омического сопротивления конденсатора;
- C – емкость конденсатора.
Расчет электролитического конденсатора в сетевом выпрямителе
Расчет электролитического конденсатора в сетевом выпрямителеРасчет сглаживающего конденсатора в сетевом выпрямителе.

Входной выпрямитель является неотъемлемым элементом большинства преобразователей, питающихся от переменного сетевого напряжения. После диодного моста напряжение на конденсаторе будет иметь вид пилы, верхняя точка которой равна амплитудному напряжению сети (минус падение напряжения на диодах моста, что несущественно для устройств, питающихся от 220В), а нижняя зависит от емкости конденсатора и тока потребления нагрузки выпрямителя. В этой статье приведен пример расчета емкости сглаживающего конденсатора выпрямителя. Более полная информация приведена в статье А.И. Колпакова.
В качестве примера приведен расчет конденсатора для реального преобразователя, разработка которого была доведена до практического воплощения, Pвых=1200Вт (выходное напряжение 60В, ток 20А, КПД около 90%)
Исходные данные для расчета:
Uвх = 220В (напряжение сети)
f = 50Гц (частота сетевого напряжения)
Задаваемые параметры:
Umin =260В (минимальное напряжение — задается минимальное значение пилообразного напряжения на конденсаторе)
Iнагр = 5. 13А (ток потребления
нагрузки выпрямителя, если известна мощность нагрузки, то ток
можно вычислить как I=Pвх/Uмин,
в моем случае Pвх=Pвых/КПД, т.е
I=(1200/0.9)/260=5.13А )
13А (ток потребления
нагрузки выпрямителя, если известна мощность нагрузки, то ток
можно вычислить как I=Pвх/Uмин,
в моем случае Pвх=Pвых/КПД, т.е
I=(1200/0.9)/260=5.13А )
Вычисляется время заряда конденсатора (в течение которого ток потребляется от сети). Так как напряжение изменяется по синусоидальному закону, используем для расчета формулу тригонометрии:
t(зар) = (arccos(Umin/Umax))/(2*pi*f)
Для синусоиды Umax = Uвх*1.41=220*1.41= 310 В (амплитудное сетевое напряжение), т.е.
t(зар) = (arccos(260/310))/(2*3.141*50) = 0.00183 c
Вычисляется время разряда конденсатора:
t(раз) = T-t(зар)
в двухполупериодном выпрямителе T = (1/f)/2 = 1/50/2=0.01с (частота сети в двухполупериодном выпрямителе удваивается)
t(раз) = 0.
 01-0.00183 =
0.0082 с
01-0.00183 =
0.0082 сНаходится емкость конденсатора, на которой за время t(раз) при токе нагрузки Iнагр напряжение с Umax уменьшится до Umin:
C = Iнагр*dt/dU,
в нашем случае dt это t(раз), а dU является разница (Umax-Umin)
C = 5.13*0.0082/(310-260) = 0.00084Ф = 840 мкФ
Находим пиковый зарядный ток:
Ipic = C*dU/dt,
где dU = Umax-Umin, а dt — это время заряда конденсатора, т.е. t(зар)
Ipic = 0.00084*(310-260)/0.00183 = 23А
Находим среднеквадратичное значение импульсного тока через конденсатор по формуле:
Irms = √(I(зар)²+I(разр)²),
где I(зар)-среднеквадратичный ток через конденсатор на цикле заряда, а I(разр) — среднеквадратичный ток через конденсатор на цикле разряда.

Считаем, что ток заряда конденсатора имеет треугольную форму, тогда
I(зар) = Ipic*√((t(зар)/T)/3) = 23*√((0.00183/0.01)/3) = 5.7A
На интервале разряда через конденсатор течет ток нагрузки, поэтому
I(разр) = Iнагр*t(раз)/T = 5.13*0.0082/0.01 = 4.2А
Итак, Irms = √(5.7²+4.2²) = 7.1А
Полученное Irms используется при выборе конденсатора (для электролитических конденсаторов обычно указывается допустимое значение импульсного тока для частоты 100Гц). Если у выбранного конденсатора допустимое значение импульсного тока меньше, необходимо набирать конденсаторы с меньшей емкостью и соединять в параллель исходя из условия: суммарная емкость не меньше рассчитанной, а ток, приходящийся на каждый из конденсаторов (ток по конденсаторам с одинаковой емкостью разделится равномерно), не более допустимого.

Расхождение теоретического расчета с практикой.
В заключение скажу, насколько вышеизложенная теория разошлась с практикой, и решайте сами, стоит ли применять эту методику.
Суммарная реальная емкость конденсаторов в моем преобразователе составила 1020мкФ, при этом измеренные осциллографом параметры были следующие:
Umin равнялось примерно 265-275В (близко к расчетному)
t(зар) составляло около 3мс (приличная погрешность — по расчету 1.8мс, а учитывая, что емкость выше расчетной, должно быть еще меньше)
Ipic составило 21А (близко к расчетному)
Расчет заряда и разряда конденсатора через сопротивление
| Полученные характеристики ЗАРЯДА конденсатора через сопротивление |
Заряд конденсатора емкостью \(C\) от источника тока через наружное сопротивление \(R\) происходит в соответствии с формулой
\(U_t=U_0(1-e^{-\frac{t}{T}})\)
при этом мгновенный зарядный ток:
\(i_t=\cfrac{U_0}{R}e^{-\frac{t}{T}}\)
где \(t\) — рассматриваемый момент времени в секундах от момента начала заряда;
\(U_t\) — напряжение на обкладках конденсатора момент времени t в Вольтах;
\(U_0\) — напряжение источника, от которого производится заряд конденсатора в Вольтах
\(e=2. {-\cfrac{t}{T}}\)
{-\cfrac{t}{T}}\)
где \(U_t\) — напряжение между обкладками конденсатора через \(t\) секунд после начала разряда,\(i_t\)— ток в цепи (внешней или внутренней) конденсатора существующей через \(t\) секунд после начала разряда.
Процессы заряда и разряда конденсаторов рассматриваются обычно в зависимости от постоянной времени цепи \(RC\). Постоянная времени практически указывает, через какой промежуток времени (в секундах) напряжение разряжаемого конденсатора уменьшается в \(e=2.718\) раз, от рассматриваемого напряжения. При заряде конденсатора постоянная времени указывает время (в секундах), в течение которого напряжение на обкладках повышается на 63% от разницы между имевшимся напряжением и напряжением источника тока заряда.
В связи с тем что заряд и разряд до полных значений конечных напряжений длятся неопределенно долгий срок, часто удобнее считать режим заряда законченным при доведении напряжения на обкладках до 99% от заряжающего напряжения (или до 1% от первоначальной величины напряжения при разряде).
| Полученные характеристики РАЗРЯДА конденсатора через сопротивление |
Определим время заряда конденсатора ёмкостью 1микроФарад, до 5 Вольт, если сопротивление цепи 1 килоОм.
Напряжение внешнего источника питания 12 Вольт, а на обкладках конденсатора напряжение, в момент подключения источника питания, составляло 1 Вольт.
Что бы сразу хотелось бы заметить. Как видно из задачи у нас есть остаточное напряжение на конденсаторе в размере 1 Вольт, которое надо учитывать в расчетах времени заряда.
Данные, которые мы будем вводить следующие:
U0=12-1 =11В
Ut=5-1=4В
R=1кОм
С=1мкФ
пишем запрос fiz U0=11В;Ut=4В;R=1кОм;C=1мкФ;key=zaryad
и получаем ответ
U0 = 11 Вольт
Ut = 4 Вольт
R = 1 килоОм
C = 1 микрофарад
T = 1 миллисекунда
tt = 0.4519851237 милисекунда
То есть решение = 451.98 мкс
Теперь давайте проверим наши расчеты. Если бы конденсатор был бы в момент подключения источника питания полностью разряжен
Если бы конденсатор был бы в момент подключения источника питания полностью разряжен
То при условии зарядки его до 1 Вольта наш запрос был бы таким
fiz U0=12В;Ut=1В;R=1кОм;C=1мкФ;key=zaryad
и время заряда было бы tt = 87.011377 микросекунда
а при зарядки до 5 Вольт был бы таким
fiz U0=12В;Ut=5В;R=1кОм;C=1мкФ;key=zaryad
и время заряда было бы tt = 538.9965007 микросекунда
То время заряда конденсатора с 1В до 5 Вольт составило бы 538.9965007 микросекунда минус 87.011377 микросекунда = 451.98 мкс
Что несомненно говорит о правильности наших расчетов по изначальным условиям.
- Гармонический состав импульса прямоугольной формы >>
Калькулятор резистивно-емкостной цепи • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
Данный калькулятор позволяет рассчитывать максимальный ток Imax в начале заряда конденсатора, максимальную энергию Emax и максимальный заряд конденсатора Qmax, когда он полностью заряжен при данном напряжении, а также постоянную времени RC-цепи.
Пример. Рассчитать постоянную времени, максимальную энергию, максимальный ток и максимальный заряд для цепи, состоящей из последовательно соединенных резистора 2 кОм и конденсатора 5 мкФ. Цепь подключена к источнику постоянного напряжения 10 V. Обратите внимание: напряжение не нужно для расчета постоянной времени RC-цепи.
Входные данные
Напряжение V
микровольт (мкВ)милливольт (мВ)вольт (В)киловольт (кВ)мегавольт (МВ)
Емкость C
фарад (Ф)микрофарад (мкФ)нанофарад (нФ)пикофарад (пФ)
Сопротивление R
миллиом (мОм)ом (Ом)килоом (кОм)мегаом (МОм)
Выходные данные
Постоянная времени
τ с
Макс. энергия
E Дж
Макс. ток
I А
Макс заряд
Q Кл
Введите величины в поля для ввода, выберите единицы измерения и нажмите кнопку Рассчитать.
Постоянная времени определяется по формуле
где τ — постоянная времени в секундах, R — сопротивление в омах и C — емкость в фарадах. Постоянная времени RC-цепи определяется как время, которое требуется, чтобы конденсатор зарядился до 63,2% его максимально возможного заряда при условии, что начальный заряд нулевой. Отметим, что конденсатор зарядится до 63,2% за время τ и почти полностью (до 99,3%) зарядится за время 5τ.
Постоянная времени RC-цепи определяется как время, которое требуется, чтобы конденсатор зарядился до 63,2% его максимально возможного заряда при условии, что начальный заряд нулевой. Отметим, что конденсатор зарядится до 63,2% за время τ и почти полностью (до 99,3%) зарядится за время 5τ.
Энергия E, которую хранит полностью заряженный до напряжения V конденсатор, при условии, что время заряда T ≫ τ, определяется формулой
где C — емкость в фарадах и V — напряжение в вольтах.
Максимальный ток I определяется по закону Ома:
Максимальный заряд Q определяется по формуле
где C — емкость в фарадах и V — напряжение в вольтах.
Фильтрующие электролитические конденсаторы на системной плате компьютера
Применение
Частотный разделитель ADSL — это фильтр нижних частот и три соединителя в корпусе
Конденсаторы часто используются в различных электрических и электронных устройствах и системах. Вероятно, вы не найдете ни одно электронное устройство, в котором не содержится хотя бы один конденсатор. Конденсаторы используются для хранения энергии, обеспечения импульсов энергии, для фильтрации питающего напряжения, для коррекции коэффициента мощности, для развязки по постоянному току, в электронных частотных фильтрах, для фильтрации шумов, для запуска электродвигателей, для хранения информации, для настройки колебательных контуров, в различных датчиках, в емкостных экранах мобильных телефонов… Этот список можно продолжать до бесконечности.
Вероятно, вы не найдете ни одно электронное устройство, в котором не содержится хотя бы один конденсатор. Конденсаторы используются для хранения энергии, обеспечения импульсов энергии, для фильтрации питающего напряжения, для коррекции коэффициента мощности, для развязки по постоянному току, в электронных частотных фильтрах, для фильтрации шумов, для запуска электродвигателей, для хранения информации, для настройки колебательных контуров, в различных датчиках, в емкостных экранах мобильных телефонов… Этот список можно продолжать до бесконечности.
Резистивно-емкостные (RC) цепи обычно используются в качестве простых фильтров нижних и верхних частот, а также простейших интегрирующих и дифференцирующих цепей.
Резистивно-емкостные фильтры нижних частот
Пример двухкаскадного RC-фильтра нижних частот с неинвертирующим операционным усилителем с единичным коэффициентом передачи, который используется в качестве буфера между двумя каскадами фильтра
Фильтры нижних частот пропускают только низкочастотные сигналы и подавляют высокочастотные сигналы. Частота среза определяется компонентами фильтра.
Частота среза определяется компонентами фильтра.
Такие фильтры широко используются в электронике. Например, их используют в сабвуферах для того, чтобы не подавать на них звуки высоких частот, которые они не могут воспроизводить. Фильтры нижних частот используются также в радиопередатчиках для блокировки нежелательных высокочастотных составляющих в передаваемом сигнале. У тех, кто пользуется ADSL подключением к Интернету, всегда установлены частотные разделители с такими фильтрами нижних частот, которые предотвращают возникновение помех в аналоговых устройствах (телефонах) от сигналов DSL и воздействия помех от аналоговых устройств на оборудование DSL, подключенное к обычной телефонной линии.
Фильтры нижних частот используются для обработки сигналов перед их аналого-цифровым преобразованием. Такие фильтры улучшают качество аналоговых сигналов при их дискретизации и необходимы для подавления высокочастотных компонентов сигнала выше частоты Найквиста таким образом, чтобы он удовлетворял требованиям теоремы Котельникова для данной частоты дискретизации, то есть максимальная частота не должна быть выше половины частоты выборки.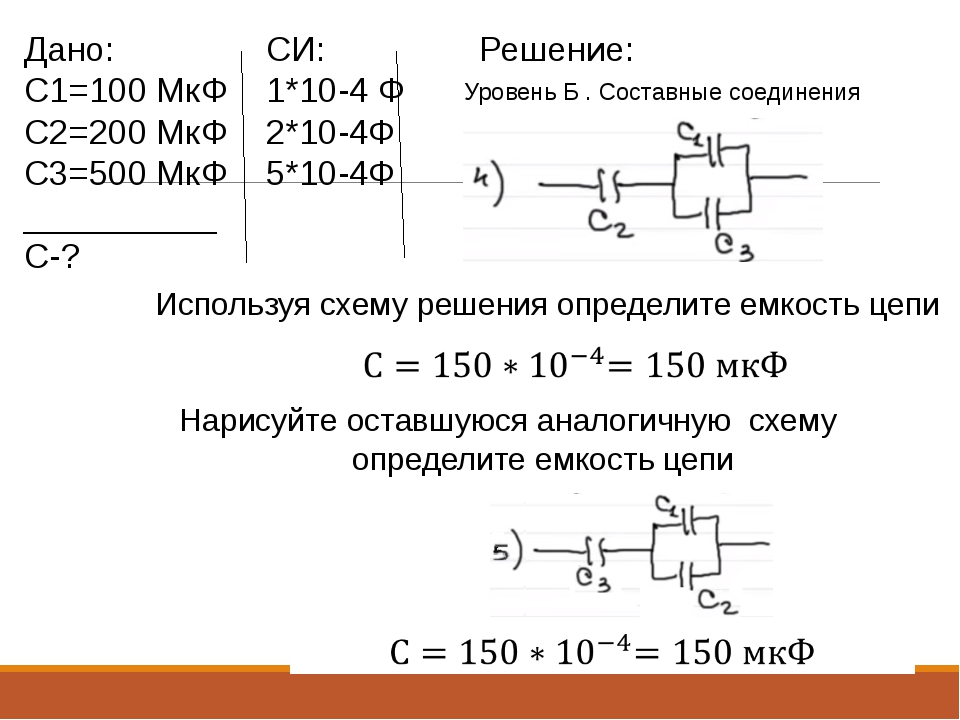
На верхнем рисунке показан простой фильтр нижних частот. В нем используются только пассивные компоненты, поэтому он называется пассивным фильтром нижних частот (ФНЧ). В более сложных пассивных ФНЧ используются также катушки индуктивности.
В отличие от пассивных фильтров нижних частот, в активных фильтрах используются усилительные устройства, например, транзисторы или операционные усилители. В пассивные фильтрах также часто имеются операционные усилители, применяемые для развязки. В зависимости от количества конденсаторов и катушек индуктивности, влияющих на крутизну частотной характеристики фильтра, они обычно называются «фильтрами первого порядка», «второго порядка» и так далее. Фильтр, состоящий только из одного резистора и одного конденсатора, называется фильтром первого порядка.
Простой пассивный RC-фильтр верхних частот
RC-фильтры верхних частот
Фильтры верхних частот пропускают только высокочастотные составляющие сигналов и ослабляют низкочастотные составляющие. Фильтры верхних частот используются, например, в разделительных фильтрах звуковых частот (кроссоверах) для подавления низкочастотных составляющих в сигналах, подаваемых на высокочастотные динамики («пищалки»), которые не могут воспроизводить такие сигналы и к тому же обладают малой мощностью по сравнению с мощностью низкочастотных сигналов.
Активный фильтр верхних частот с операционным усилителем
Фильтры верхних частот часто используются для блокировки постоянной составляющей сигналов в тех случаях, когда она нежелательна. Например, в профессиональных микрофонах очень часто используется «фантомное» питание постоянным напряжением, которое подается по микрофонному кабелю. В то же время микрофон записывает переменные сигналы, такие как человеческий голос или музыка. Постоянное напряжение не должно появляться на выходе микрофона и не должно поступать на вход микрофонного усилителя, поэтому для его блокировки используется фильтр верхних частот.
Простой полосовой фильтр, собранный из двух каскадов — фильтра нижних частот (C2, R2) и фильтра высоких частот (C1, R1)
Если фильтр нижних частот и фильтр верхних частот стоят друг за другом, они образуют полосовой фильтр, который пропускает частоты только в определенной полосе частот и не пропускает частоты за пределами этой полосы. Такие фильтры широко используются в радиоприемниках и радиопередатчиках. В приемниках полосовые фильтры используются только для селективного пропускания и усиления сигналов радиостанции в требуемой узкой полосе частот. При этом сигналы других радиостанций за пределами этой полосы подавляются. Передатчики могут передавать радиосигналы только в определенном разрешенном для них диапазоне частот. Поэтому в них используются полосовые фильтры для ограничения полосы передаваемого сигнала таким образом, что он вписывался в допустимые пределы.
Емкостной делитель напряжения ⋆ diodov.net
Простейший емкостной делитель напряжения состоит из двух последовательно соединенных конденсаторов и используется для снижения величины U на отдельных элементах электрической цепи.
Делитель постоянного напряжения на конденсаторах чаще всего применяют многоуровневых инверторов напряжения, широко используемых как на электроподвижном составе, так и в других направлениях силовой электроники.
Главная сложность практического применения такой схемы (и всех подобных схем) заключается в невозможности обеспечения равномерного разряда конденсаторов, вследствие чего напряжения на них будет распределяться не поровну. Чем сильнее разряжен один конденсатор по сравнению с другим (иди с другими), тем большая разница в U будет на них, что наглядно отображает формула:
По этой причине подобные схемы крайне нестабильно работают и обязательно предусматривают узлов подзарядки конденсаторов с целью выравнивания напряжения на последних.
Емкостной делитель напряжения в цепи переменного токаВ радиоэлектронике в большей степени находят применение емкостные делители переменного напряжения.
Конденсатор, как и катушка индуктивности, относится к реактивному элементу, то есть потребляет реактивную мощность от источника переменного тока, в отличие от резистора, который является активным элементов и потребляет исключительно активную мощность.
Реактивный элементЗдесь следует кратко пояснить разницу между активной и реактивной мощностями. Активная мощность выполняет полезную работу и реализуется только в том случае, когда ток и напряжение направлены в одном направлении и не отстают друг от друга, то есть находятся в одной фазе, что имеет место только на резисторе. На конденсаторе ток отстает от напряжения на угол φ = 90°. В результате чего ток напряжение находятся в противофазе, поэтому когда ток имеет максимальное значение напряжение равно нулю, а произведение этих двух величин дают мощность, которая в таком случае равна нулю, так как один из множителей равен нулю. Следовательно, мощность не потребляется.
Аналогичные процессы протекают и в цепи с катушкой индуктивности. Разница лишь в том, что на индуктивности i отстает от u на угол φ = 90°.
Реактивная мощность проявляется только в цепях переменного тока. Она составляет часть полной мощности и определяется по формуле:
Реактивная мощность в отличие от активной, не потребляется нагрузкой, а циркулирует между источником питания и нагрузкой. Поэтому конденсатора и катушка индуктивности являются реактивными элементами, не потребляющими активную мощность и по этой причине они практически не нагреваются.
Расчет сопротивления делителя напряжения на конденсаторах заключается в определении необходимых значений сопротивлений.
Сопротивление конденсатора XC является величиной не постоянной и зависит от частоты переменного тока f и емкости C:
Как видно из формулы, сопротивление снижается с увеличением частоты и емкости. Для постоянного тока, частота которого равна нулю, сопротивление стремится к бесконечности, поэтому, рассматриваемая далее схема емкостного делителя напряжения не применяется постоянном токе.
Для снижения величины uвых, например в два раза, емкости C1 и C2 должны быть равны. Универсальные формулами для определения выходных uвых1 и uвых2 в зависимости от входного и емкостей C1 и C2 имеют вид, аналогичный для резисторных делителей:
Поскольку частота переменного тока для всех конденсаторов одинакова, то формулу можно упростить:
Индуктивный делитель напряженияВ качестве делителей переменного напряжения также, но гораздо реже, применяют катушки индуктивности, которые относятся к реактивным элементам. Однако, в отличие от конденсаторов, которые являются накопителями электрического поля, катушки индуктивности накапливают магнитное поле.
Индуктивное сопротивление зависит от индуктивности L и частоты переменного тока f. С ростом этих параметров сопротивление катушки переменному току возрастает.
XL = 2πfL.
Упрощенный вариант формулы:
Как вы наверняка уже заметили, чтобы рассчитать емкостной делитель напряжения достаточно знать емкости конденсаторов, а индуктивный делитель – индуктивности.
Еще статьи по данной теме
Простые формулы конденсатора накопления энергии
У вас есть конденсатор, или вам нужно его выбрать, вы хотите вычислить некоторые вещи о нем с точки зрения его использования для хранения / доставки энергии (в отличие от фильтрации), вы хотели бы просто знать немного больше, чем онлайн-калькулятор, но не намного больше, потому что математика причиняет боль вашему мозгу. Эта страница для вас.
ln () (натуральный логарифм) часто встречается в уравнениях, натуральный логарифм — это обратное преобразование e в степень чего-либо (то есть ln (e x ) = x), в электронных таблицах это функция » ln () «, в коде (например, C / C ++ [Arduino!]), это обычно функция» log () «.
Все формулы предполагают «идеальный» конденсатор, без учета ESR или других неидеальных характеристик. Достаточно хорошо, чтобы попасть в бейсбольный стадион.
Вы можете изменить поля в каждом разделе, чтобы выполнить свой собственный расчет.
Помните, что ваше напряжение питания для зарядки конденсатора не должно превышать максимальное номинальное напряжение ваших конденсаторов (говоря в общих чертах).
У меня есть неизвестный конденсатор, известный резистор и секундомер, рассчитываю емкость.
C = (0 — секунды) / R / ln (1- (VCharged / VSupply))
Где секунды — это количество секунд, за которые взимается плата; R — резистор в Ом; VCharged — напряжение конденсатора в секундах; VSupply — это напряжение питания.
Вам не нужно заряжать конденсатор полностью, чтобы измерить его, если вы начинаете с разряда, рассчитываете период зарядки и записываете напряжение, которое вы достигли за этот период, вы можете выполнить расчет — но чем дольше (медленнее) вы заряжаете тем более точным будет ваш результат, потому что ваши ошибки и т. д. будут менее значимыми.Когда самая маленькая цифра на вашем счетчике, измеряющая напряжение конденсатора, изменяется один раз в секунду, это было бы разумным временем для остановки. Имейте в виду также, что конденсаторы имеют заведомо большой допуск (+/- 30% вполне нормально для некоторых типов конденсаторов).
Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.
Сколько ампер-часов (Ач) в этом конденсаторе?
Ач = (C * (VCharged — VDepleted)) / 3600
Где VCharged — это напряжение заряда конденсатора, VDepleted — это опустошенное напряжение, а C — это емкость.
Здесь вы можете увидеть, что если вы используете конденсатор для замены батареи, вам действительно нужно подключить его к преобразователю постоянного / постоянного тока с подходящим диапазоном входного напряжения, чтобы вы могли разрядить свой конденсатор до очень низкого напряжения, взяв наш В приведенном выше примере, если бы вместо напряжения отключения 3,3 В у нас было напряжение отключения 0,5 В, мы получили бы 10 мАч вместо жалких 2,5 мАч.
Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.
Пример
Конденсатор 10F, который был заряжен до 4,2В, разряжен до 3,3В, сколько там мАч?
(10 * (4,2 — 3,3)) / 3600 = 0,0025 Ач = 2,5 мАч
Сколько ватт-часов (Втч) в этом конденсаторе?
Вт · ч = (VCharged 2 — VDepleted 2 ) / (7200 / C)
Здесь вы можете видеть, что если вы используете конденсатор для замены батареи, вам действительно нужно подключить его к повышающему преобразователю с подходящим диапазоном входного напряжения, чтобы вы могли разрядить свой конденсатор до очень низкого напряжения, взяв наш пример выше. , если вместо 3.Напряжение отключения 3 В, у нас было напряжение отключения 0,5 В, мы получили бы 0,024 Вт-ч вместо мизерных 0,009 Вт-ч
Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.
Пример
Конденсатор 10F, который был заряжен до 4,2 В, разряжается до 3,3 В, сколько в нем Wh?
((4,2 2 ) — (3,3 2 )) / (7200/10) = 0,009375 Вт · ч
Сколько времени потребуется, чтобы зарядить этот конденсатор постоянным сопротивлением?
Секунды = 0 — (R * C * ln (1 — (VCharged / VSupply)))
Где VCharged — это напряжение, измеренное на конденсаторе, а VSupply — это напряжение источника питания, C — емкость в Фарадах, а R — резистор в Ом.
VCharged должно быть ниже, чем VSupply — помните, что по мере того, как конденсатор заряжается больше, его сопротивление зарядке увеличивается, оно никогда не может достичь того же напряжения, что и напряжение питания, даже если оно на неизмеримо меньше, оно всегда меньше.
Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.
Сколько времени потребуется, чтобы разрядить этот конденсатор через постоянное сопротивление?
Секунды = 0 — (R * C * ln (VDepleted / VCharged))
Где VCharged — начальное напряжение конденсатора, VDepleted — конечное напряжение, которое вы определите как разряженное, R — сопротивление, C — емкость.
VDepleted должно быть больше нуля — помните, что ваша реальная схема, вероятно, не может много сделать с чем-либо, даже отдаленно близким к нулю.
Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.
Сколько времени потребуется, чтобы зарядить / разрядить этот конденсатор постоянным током?
секунд = (C * (VCharged — VDepleted)) / Amps
Где C в фарадах, VCharged — это начальное напряжение на конденсаторе, VDepleted — это напряжение завершения разряда, а Amps — это ток в амперах.Для постоянного тока формула одинакова, независимо от того, разряжаете ли вы или заряжаете, разница в напряжении имеет значение, сколько напряжения должно нарастать или падать.
Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.
Пример
Конденсатор 10Ф разряжается с 5В до 4В при постоянном токе 500мА, сколько времени это занимает?
(10 * (5-4)) / 0,5 = 20 секунд (калькулятор)
Сколько времени потребуется, чтобы зарядить / разрядить этот конденсатор постоянной мощностью (Вт)?
Секунды = 0.5 * C * ((VCharged 2 — VDepleted 2 ) / Вт)
Где C — в фарадах, VS — это начальное напряжение на конденсаторе, VC — это напряжение завершения разряда, а P — мощность разряда в ваттах.
Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.
Пример
Конденсатор 10Ф разряжается с 5В до 4В при постоянной мощности 2Вт, сколько времени это занимает?
0.5 * 10 * ((5 2 -4 2 ) / 2) = 22,5 секунды
У меня есть аккумулятор / элемент на несколько ампер-часов. Сколько емкости мне нужно для непосредственной замены?
C = (Ач * 3600) / (VCharged — VDepleted)
Наивно мы можем предположить, что VCharged совпадает с номинальным напряжением вашей батареи, а VDepleted равно нулю, или, точнее говоря, VCharged — это максимальный заряд для вашей батареи, а VDepleted — это минимальное напряжение, которое может использовать ваша цепь.
Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.
Пример
Щелочной элемент емкостью 1250 мАч с полным напряжением 1,5 В и пустым напряжением 0,8 В должен быть заменен конденсатором, какого размера он должен быть?
(1,25 * 3600) / (1,5 — 0,8) = 6428 F
Очевидно, что это непрактично, поэтому см. Следующий раздел …
Если у меня есть батарея / элемент на несколько ампер-часов, какой емкости мне нужно заменить, если я использую преобразователь постоянного тока в постоянный?
C = 7200 / ((VCharged 2 — VDepleted 2 ) / ((Ah * VBattery) / 0.75))
Где Ah — это емкость батареи в Ач, VBattery — номинальное напряжение батареи, 0,75 — (наихудший случай) КПД преобразователя постоянного / постоянного тока, VCharged — это заряженное напряжение конденсатора, VDepleted — это наименьшее напряжение конденсатора вашего постоянного / постоянного тока. Преобразователь постоянного тока справится.
Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.
Пример
Щелочной элемент емкостью 1250 мАч с номинальным напряжением 1.5 В следует заменить конденсатором (батареей), который будет заряжаться до 10,8 В и приводится в действие понижающим преобразователем, который принимает входное напряжение до 1,6 В.
7200 / ((10,8 2 -1,6 2 ) / ((1,25 * 1,5) / 0,75)) = 157F
Я хочу рисовать x ампер в течение t секунд, какая емкость мне нужна?
C = (Амперы * секунды) / (VCharged — VDepleted)
Где C — требуемая емкость, Amps — это требуемый ток, VCharged — это начальное напряжение, до которого вы заряжали конденсатор, а VDepleted — это минимальное напряжение, которое вы будете принимать.Помните, как только вы потребляете ток из конденсатора, его напряжение падает, вот как это работает, поэтому вы не можете просто сказать: «Я хочу 1 ампер при X вольт», вы должны сказать, что я нарисую усилитель и может сделать это между этим и этим напряжением.
Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.
Пример
Вы хотите потреблять 500 мА от конденсатора, заряженного до 12 В, в течение 5 секунд, и после этого конденсатор будет измерять 9 В. Какого размера должен быть конденсатор?
(0.5 * 5) / (12 — 9) = 0,83F
Я хочу получать x Вт в течение t секунд, какая емкость мне нужна?
C = (секунды * 2) / ((VCharged 2 — VDepleted 2 ) / Watts)
Где C — емкость, Watts — мощность в ваттах, VCharged — это начальное напряжение, до которого вы заряжали конденсатор, а VDepleted — это минимальное напряжение, которое вы будете принимать. Помните, как только вы потребляете ток из конденсатора, его напряжение падает, вот как это работает, поэтому вы не можете просто сказать: «Я хочу 1 Вт при X Вольт», вы должны сказать, что я возьму ватт и может сделать это между этим и этим напряжением.
Вы можете использовать поля в примере, чтобы выполнить свои собственные вычисления, измените числа, чтобы увидеть, как себя ведут.
Пример
Вы хотите подавать 10 Вт в течение 5 секунд от конденсатора, первоначально заряженного до 12 В, а затем измеряя 9 В, какого размера должен быть конденсатор?
(5 * 2) / ((12 2 — 9 2 ) / 10) = 1,6F
Как вы пришли к этой формуле?
В представленной формуле нет ничего особенного. Хорошим справочником для упрощения работы является этот документ от ELNA, производителя суперконденсаторов, он охватывает основные уравнения для постоянного тока, мощности и разряда через сопротивление.
Electronics-Tutorials.ws обеспечивает разряд с постоянным сопротивлением, и заряд с постоянным сопротивлением также задается в виде Vc = Vs (1-e -t / RC ), которым можно управлять для определения t (см. Видео ниже) .
Это видео от Пола Уэсли Льюиса помогло моему лишенному математики мозгу научиться управлять манипуляциями.
Следующие ниже онлайн-калькуляторы были полезны при подтверждении моей работы Must Calculate, Circuits.dk, bitluni.net (ВНИМАНИЕ, расчет Wh на сайте bitluni неверен, если у вас минимальное напряжение> 0)
На основе этих уравнений и ресурсов получены следующие данные.
Вывод для ампер-часов
Начните с данной формулы для разряда при постоянном токе, установите t = 3600 секунд и решите, чтобы I было любым током, необходимым для разрядки конденсатора за это время и, следовательно, ампер-часов
секунд = (C * (VCharged — VDepleted)) / I
3600 = (C * (VCharged — VDepleted)) / I
I * 3600 = (C * (VCharged — VDepleted))
I = (C * (VCharged — VDepleted)) / 3600
(I = Ач)
Вывод для ватт-часов
Это выводится из формулы для разряда постоянной мощности, где t = 3600 секунд, вычисленных для P, равного любым ваттам, необходимым для разрядки конденсатора за это время и, следовательно, ватт-часам.
секунд = 0,5 * C * ((VCharged 2 — VDepleted 2 ) / P)
3600 = ((VCharged 2 — VDepleted 2 ) / P) * C * 0,5
3600 / 0,5 = ((VCharged 2 — VDepleted 2 ) / P) * C
7200 = ((VCharged 2 — VDepleted 2 ) / P) * C
7200 / C = (VCharged 2 — VDepleted 2 ) / P
P * (7200 / C) = (VCharged 2 — VDepleted 2 )
P = (VCharged 2 — VDepleted 2 ) / (7200 / C)
(P = Wh)
Вывод для эквивалентности батареи в ампер-часах
Это просто решение уравнения ампер-часов для емкости
Ач = (C * (VCharged — VDepleted)) / 3600
Ач * 3600 = C * (VCharged — VDepleted)
(Ач * 3600) / (VCharged — VDepleted) = C
Расчет эквивалентности батареи в ампер-часах с преобразователем постоянного тока
Мы используем полученное выше уравнение ватт-часов, заменяя ватт-часы заданными ампер-часами и эквивалентным напряжением батареи, скорректированным с коэффициентом полезного действия 75% для повышающего преобразователя.
Вт · ч = (VCharged 2 — VDepleted 2 ) / (7200 / C)
((Ач * VBattery) / 0,75) = (VCharged 2 — VDepleted 2 ) / (7200 / C)
7200 / C = (VCharged 2 — VDepleted 2 ) / (Ah * VBattery)
7200 = C * ((VCharged 2 — VDepleted 2 ) / (Ah * VBattery))
7200 / ((VCharged 2 — VDepleted 2 ) / (Ah * VBattery)) = C
Вывод для рисования ампер X для секунд T
Простое решение данного уравнения постоянного тока, решение для C
секунд = (C * (VCharged — VDepleted)) / I
секунд * I = C * (VCharged — VDepleted)
(секунды * I) / (VCharged — VDepleted) = C
Вывод для рисования X Вт для T секунд
Простое решение данного уравнения постоянной мощности, решение для C
секунд = 0.5 * C * ((VCharged 2 — VDepleted 2 ) / P)
секунд = C * ((VCharged 2 — VDepleted 2 ) / P) * 0,5
секунд * 2 = C * ((VCharged 2 — VDepleted 2 ) / P)
(секунды * 2) / ((VCharged 2 — VDepleted 2 ) / P) = C
Dynamics Track Конденсатор Цепи Wave Tank Оптическая скамья | Конденсатор с параллельными пластинами Заряд конденсаторов, разделение пластин и напряжение Конденсатор используется для хранения электрического заряда. Чем большее напряжение (электрическое давление) вы прикладываете к конденсатору, тем больше заряда нагнетается в конденсатор. Кроме того, чем большей емкостью обладает конденсатор, тем больший заряд будет вызван данным напряжением.Это соотношение описывается формулой q = CV, где q — накопленный заряд, C — емкость, а V — приложенное напряжение. Глядя на эту формулу, можно спросить, что бы произошло, если бы заряд оставался постоянным, а емкость изменялась. Ответ, разумеется, таков, что напряжение изменится! Это то, что вы будете делать в этой лаборатории. Лабораторный конденсатор Конденсатор с параллельными пластинами — это устройство, используемое для изучения конденсаторов.Это сводит к минимуму функцию конденсатора. Конденсаторы в реальном мире обычно скручены по спирали в небольших корпусах, поэтому конденсатор с параллельными пластинами значительно упрощает привязку функции к устройству. Этот конденсатор работает, накапливая противоположные заряды на параллельных пластинах, когда напряжение подается с одной пластины на другую. Количество заряда, который перемещается в пластины, зависит от емкости и приложенного напряжения в соответствии с формулой Q = CV, где Q — заряд в кулонах, C — емкость в фарадах, а V — разность потенциалов между пластинами в вольт. Конденсаторы накапливают энергию Если напряжение подается на конденсатор, а затем отключается, заряд, накопленный в конденсаторе, сохраняется до тех пор, пока конденсатор каким-либо образом не разрядится. Между пластинами возникает электрическое поле, которое позволяет конденсатору накапливать энергию. Это один из полезных аспектов конденсаторов, способность накапливать энергию в электрическом поле, чтобы ее можно было использовать позже. От чего зависит емкость? Количество заряда, которое может храниться на один приложенный вольт, определяется площадью поверхности пластин и расстоянием между ними.Чем больше пластины и чем ближе они расположены, тем больше заряда может храниться на каждый вольт разности потенциалов между пластинами. Заряд, накопленный на приложенный вольт, представляет собой емкость, измеряемую в фарадах. Может ли изменение емкости заряженного конденсатора изменить его напряжение? Лабораторный конденсатор можно регулировать, поэтому мы можем провести интересный эксперимент с емкостью и напряжением. Если конденсатор имеет постоянный заряд, изменение емкости должно вызвать изменение напряжения.Раздвигание пластин приведет к уменьшению емкости, поэтому напряжение должно увеличиться. Как можно математически определить емкость нашего конденсатора? C = ε 0 А / сут Где C — емкость в Фарадах, ε 0 — постоянная диэлектрической проницаемости свободного пространства (8,85×10 -12), A — площадь пластин в квадратных метрах, а d — расстояние между пластинами в метрах. Фарада — это очень большая величина емкости, поэтому мы будем использовать метрические префиксы для получения более удобных чисел. Емкость обычно измеряется в микрофарадах (мкФ), что составляет 1,0×10 -6F или пикофарадах (пФ), что составляет 1,0×10 -12F. 1.0F = 1,000,000 мкФ = 1,000,000,000,000 пФ! Будьте очень внимательны с расчетами! Этот расчет даст вам приблизительное значение емкости лабораторного конденсатора. Однако есть и другие факторы, которые вносят ошибки в реальные измерения емкости и напряжения.Вам нужно внимательно учитывать эти факторы. Лабораторное оборудование: Для получения хороших результатов эта лабораторная деятельность требует специального оборудования. Вам нужен хороший стабилизированный источник питания, чтобы напряжение, подаваемое на конденсатор, было одинаковым при каждом испытании. Вам также понадобится очень точный способ измерения напряжения между пластинами без резистивной нагрузки на конденсатор. Количество накопленного заряда очень мало, поэтому обычный вольтметр не подойдет.Мельчайший заряд, накопленный в конденсаторе, просто разрядится через измеритель, делая любые измерения бесполезными. Вы будете использовать специальный прибор для измерения напряжения, называемый электрометром, который измеряет напряжение без разряда конденсатора. Одна из проблем электрометра заключается в том, что он имеет некоторую собственную емкость. Поскольку эта емкость параллельна емкости конденсатора, встроенная емкость выводов должна быть добавлена к емкости конденсатора. Назначение: Целью данной лабораторной работы является исследование взаимосвязи между разделением пластин и напряжением в конденсаторе с параллельными пластинами, который поддерживается постоянным зарядом. Оборудование:
Осторожно: Это хрупкое оборудование. Все должно сочетаться с легчайшими прикосновениями. Ничего не заставляйте! Ваша первая задача — предсказать, что произойдет с напряжением конденсатора, когда вы зарядите его источником 10 В, а затем раздвинете пластины (что уменьшит емкость). Вы сделаете это в следующем разделе. Теоретические расчеты: Сначала необходимо рассчитать теоретическую емкость для каждого расстояния между пластинами. Мы сделаем первое, а потом вы сможете сделать все остальное! Самая сложная часть этого — правильно настроить юниты. Проще всего сложить все в метрах для расчетов:
В следующих разделах вы проведете реальный эксперимент для проверки (или, возможно, не проверки!) Ваших теоретических расчетов. Процедура настройки переменного конденсатора (если лаборатория уже настроена, переходите к следующему разделу!)
Сбор экспериментальных данных
Анализ данных:
|
Расчет спада напряжения конденсатора
Следующий калькулятор вычисляет спад напряжения на трехфазных батареях конденсаторов, соединенных звездой, после отключения от источника питания. Расчет предполагает, что напряжение в системе составляет 110% от номинального, и что конденсаторная батарея была отключена при пиковом напряжении.
На основе этих данных рассчитывается требуемый номинал разрядного резистора для удовлетворения отраслевых стандартных требований к разрядке для силовых конденсаторов среднего напряжения на 50 В за 300 секунд (Стандарт IEEE 18-2012, Стандарт для шунтирующих силовых конденсаторов).
Номинал нестандартного резистора также может быть исследован и нанесен на кривую разряда рядом со стандартной кривой разряда.
Calculator-1
Известные переменные: Конденсаторная батарея, трехфазная кВАр, напряжение и частота системы
Формулы и переменные
Где:
| В пик = Пиковое напряжение на конденсаторах перед отключением (кВ) |
| В LL = Линейная номинальная мощность конденсатора (кВ) |
| C = Емкость конденсаторного каскада на фазу (µФ на фазу) ) |
| f = Номинальная частота конденсатора |
| KVAR = Трехфазная мощность KVAR конденсаторного каскада (кВАр) |
| R = Сопротивление разрядного резистора (МОм) | В | В = Начальное напряжение конденсатора сразу после отключения (кВ) |
| t = Время после отключения конденсатора (сек) |
| В (t) = Напряжение через некоторое время (t) после того, как конденсатор был отключен отключено (сек) |
Интерес…
Конденсаторы в отключенном состоянии накапливают энергию, а также улавливают напряжение. Это напряжение может быть опасным, если при техническом обслуживании контактируют с выводами конденсатора. В результате, статья 460.28 (A) NEC и большинство других национальных стандартов гласит:
Должны быть предусмотрены средства для снижения остаточного напряжения конденсатора до 50 В или менее в течение 5 минут после отключения конденсатора от источника питания.
Производители силовых конденсаторов среднего напряжения встраивают в свои конденсаторы разрядные резисторы в соответствии с этими стандартами.Приведенный выше калькулятор вычисляет номинал резистора, кривую разряда или затухания, номинальную мощность резистора и энергию разряда конденсатора.
В некоторых приложениях требуется более быстрый разряд по напряжению. Более быстрый разряд достигается за счет уменьшения сопротивления резистора. При этом требования к номинальной мощности резистора увеличиваются. Обычно резисторы конденсаторов могут быть такого размера, чтобы позволить конденсаторам разряжаться не менее чем за 2 минуты.
Заряд конденсатораи постоянная времени, онлайн-калькулятор
Онлайн-калькулятор для расчета постоянной времени и напряжения зарядки
Онлайн калькулятор
На этой странице вы можете рассчитать зарядное напряжение конденсатора. в цепи ПДУ (проход нижних частот) в определенный момент времени.
Помимо номиналов резистора и конденсатора, приложенное входное напряжение и время даны для расчета.
Результат показывает напряжение зарядки в указанное время и постоянную времени τ (тау) RC-цепи. Конденсатор через время 5 τ ок. Заряжено 99,33%. Это означает, что в заданные моменты времени, значительно превышающие 5 τ входное напряжение всегда близко к напряжению зарядки.{- \ frac {t} {τ}} \ right) \)
\ (\ Displaystyle τ = R · С \)
Legende
\ (\ Displaystyle R \)
Резистор (& Ом;)
\ (\ Displaystyle С \)
Конденсатор (F)
\ (\ Displaystyle т \)
Постоянная времени (сек)
\ (\ Displaystyle U_0 \)
Приложенное напряжение (В)
\ (\ Displaystyle U_C \)
Напряжение заряда на конденсаторе (В)
|
Последовательные и параллельные конденсаторы
: что это такое, формула, напряжение (со схемами)
Когда вы изучаете физику электроники и хорошо разбираетесь в основах, таких как значение таких ключевых терминов, как напряжение , ток и сопротивление , наряду с важными уравнениями, такими как закон Ома — изучение того, как работают различные компоненты схемы, является следующим шагом к овладению предметом.
Конденсатор — один из наиболее важных компонентов для понимания, поскольку они широко используются практически во всех областях электроники. От конденсаторов связи и развязки до конденсаторов, которые заставляют работать вспышку камеры или играть ключевую роль в выпрямителях, необходимых для преобразования переменного тока в постоянный, трудно переоценить широкий спектр применения конденсаторов. Вот почему так важно знать, как рассчитать емкость и общую емкость конденсаторов различной конфигурации.
Что такое конденсатор?
Конденсатор — это простой электрический компонент, состоящий из двух или более проводящих пластин, которые удерживаются параллельно друг другу и разделены воздухом или изолирующим слоем. Две пластины обладают способностью накапливать электрический заряд, когда они подключены к источнику питания: одна пластина вырабатывает положительный заряд, а другая — отрицательный.
По сути, конденсатор похож на небольшую батарею, создающую разность потенциалов (т.е.например, напряжение) между двумя пластинами, разделенными изолирующим разделителем, называемым диэлектриком (который может быть выполнен из многих материалов, но часто из керамики, стекла, вощеной бумаги или слюды), который предотвращает протекание тока от одной пластины. пластину к другой, тем самым сохраняя накопленный заряд.
Для данного конденсатора, если он подключен к батарее (или другому источнику напряжения) с напряжением В, , он будет хранить электрический заряд Q . Эта способность более четко определяется «емкостью» конденсатора.
Что такое емкость?
Имея это в виду, значение емкости является мерой способности конденсатора накапливать энергию в виде заряда. В физике и электронике емкость обозначается символом C и определяется как:
C = \ frac {Q} {V}
Где Q — это заряд, накопленный в пластинах, а В — это разность потенциалов подключенного к ним источника напряжения. Короче говоря, емкость — это мера отношения заряда к напряжению, и поэтому единицами емкости являются кулоны заряда / вольт разности потенциалов.Конденсатор с более высокой емкостью сохраняет больше заряда при заданном значении напряжения.
Концепция емкости настолько важна, что физики присвоили ей уникальную единицу, названную фарад (в честь британского физика Майкла Фарадея), где 1 F = 1 C / V. Немного похоже на кулон для заряда, фарад — это довольно большая величина емкости, при этом большинство значений емкости конденсаторов находятся в диапазоне от пикофарада (пФ = 10 −12 Ф) до микрофарада (мкФ = 10 −6 ). F).
Эквивалентная емкость последовательных конденсаторов
В последовательной схеме все компоненты расположены на одном и том же пути вокруг контура, и таким же образом последовательно соединенные конденсаторы соединяются один за другим на едином пути вокруг схемы. . Общая емкость для ряда конденсаторов, включенных последовательно, может быть выражена как емкость одного эквивалентного конденсатора.
Формула для этого может быть получена из основного выражения для емкости из предыдущего раздела, переставленного следующим образом:
V = \ frac {Q} {C}
Поскольку закон Кирхгофа утверждает, что сумма напряжений падение напряжения вокруг полного контура цепи должно быть равно напряжению от источника питания, для количества конденсаторов n напряжения должны складываться следующим образом:
V_ {tot} = V_1 + V_2 + V_3 + … В_н
Где В до — полное напряжение от источника питания, а В 1 , В 2 , В 3 и так же падение напряжения на первом конденсаторе, втором конденсаторе, третьем конденсаторе и так далее.В сочетании с предыдущим уравнением это приводит к:
\ frac {Q_ {tot}} {C_ {tot}} = \ frac {Q_1} {C_1} + \ frac {Q_2} {C_2} + \ frac {Q_3 } {C_3} +… \ frac {Q_n} {C_n}
Где нижние индексы имеют то же значение, что и раньше. Однако заряд на каждой из пластин конденсатора (т.е. значения Q ) исходит от соседней пластины (т.е. положительный заряд на одной стороне пластины 1 должен соответствовать отрицательному заряду на ближайшей стороне пластины 2. и так далее), поэтому вы можете написать:
Q_ {tot} = Q_1 = Q_2 = Q_3 = Q_n
Таким образом, начисления аннулируются, в результате чего остается:
\ frac {1} {C_ {tot}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} +… \ frac {1} {C_n}
Поскольку емкость комбинации равна эквивалентной емкости одиночный конденсатор, это можно записать так:
\ frac {1} {C_ {eq}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} +… \ frac {1} {C_n}
для любого количества конденсаторов n .{−6} \ text {F} \\ & = 1.41 \ text {мкФ} \ end {align}
Эквивалентная емкость параллельных конденсаторов
Для параллельных конденсаторов аналогичный результат получается из Q = VC, тот факт, что падение напряжения на всех конденсаторах, подключенных параллельно (или на любых компонентах в параллельной цепи), одинаковое, и тот факт, что заряд на одном эквивалентном конденсаторе будет общим зарядом всех отдельных конденсаторов в параллельной комбинации . Результатом является более простое выражение для общей емкости или эквивалентной емкости:
C_ {eq} = C_1 + C_2 + C_3 +… C_n
, где снова n — общее количество конденсаторов.{−5} \ text {F} \\ & = 15 \ text {мкФ} \ end {align}
Комбинации конденсаторов: проблема первая
Нахождение эквивалентной емкости для комбинаций конденсаторов, расположенных последовательно и расположенных parallel просто подразумевает применение этих двух формул по очереди. Например, представьте комбинацию конденсаторов с двумя последовательно включенными конденсаторами: C 1 = 3 × 10 −3 F и C 2 = 1 × 10 −3 F. , и еще один конденсатор параллельно с C 3 = 8 × 10 −3 F.{−3} \ text {F} \ end {align}
Комбинации конденсаторов: Проблема Два
Для другой комбинации конденсаторов, три при параллельном подключении (со значениями C 1 = 3 мкФ, C 2 = 8 мкФ и C 3 = 12 мкФ) и один с последовательным подключением (с C 4 = 20 мкФ):
Подход в основном такой же, как и в последнем примере, за исключением того, что сначала вы обрабатываете параллельные конденсаторы.{−1}} \\ & = 10.7 \ text {мкФ} \ end {align}
Обратите внимание, что, поскольку все отдельные емкости были в микрофарадах, весь расчет может быть выполнен в микрофарадах без преобразования — если вы помните при цитировании ваших окончательных ответов!
Уравнение i-v конденсатора в действии
Конденсатор — один из идеальных элементов схемы. Давайте представим уравнение конденсатора $ i $ — $ v $, чтобы посмотреть, что произойдет с напряжением, если мы включим ток.
Автор Вилли Макаллистер.
Содержание
Куда мы направляемся
Постоянный ток, протекающий через конденсатор, создает напряжение с прямым нарастанием. Такое поведение предсказывается интегральной формой уравнения конденсатора $ i $ — $ v $.
Обычное уравнение конденсатора $ i $ — $ v $ — это $ i $ как функция $ v $ в производной форме,
$ i = \ text C \, \ dfrac {dv} {dt}
$$ \ text C $ — это емкость , , физическое свойство конденсатора.{\, T} i \, dt + v_0 $
$ v_0 $ — напряжение на конденсаторе в начале интеграла при $ t = 0 $.
Обозначение времени немного сложно,
Little $ t $ — непрерывная временная переменная внутри интеграла.
Big $ T $ — момент, когда вы хотите узнать напряжение на конденсаторе. $ T $ — верхний предел интеграла.
обозначение в исчислении: $ di / dt $$ i = \ text C \, \ dfrac {dv} {dt}
$$ d $ — это расчетное обозначение «дифференциала» или «крошечного изменения…».{\, T} i \, dt + v_0 $
Замкнутый $ \ int $ — еще один символ из исчисления. Это знак интеграла. По своему значению он аналогичен символу суммирования Sigma $ \ Sigma $. Интеграция противоположна производной.
В уравнении конденсатора знак интеграла означает, что вы складываете последовательность продуктов $ (i \ times dt) $ или (current $ \ times $ за крошечный интервал времени). Когда вы видите верхний и нижний пределы на символе интеграла, это означает, что это определенный интеграл . Это означает интегрировать в определенном диапазоне $ t $.{\, T} i \, dt + v_0 $
Текущий импульс имеет резкие изменения, поэтому мы собираемся решить для $ v (t) $ тремя отдельными порциями: до, во время и после текущего импульса.
Перед пульсом
Перед текущим импульсом $ (t <0) $ ток не течет, поэтому на $ \ text C $ не накапливается заряд. Следовательно, $ v _ {(t <0)} = 0 $. Нам даже не пришлось использовать это уравнение.
Во время пульса
В любое время во время импульса тока $ (0 \ lt t \ lt 3 \, \ text {ms}) $ ток течет, заряд накапливается на $ \ text C $ и напряжение растет.{\, T} i \, dt + v_0 $
Обратите внимание на временные переменные. Little $ t $ — это непрерывное время, интегрируемая переменная. Big $ T $ — это время, которое может накапливаться. Определенное интегральное время развертки $ t $ от $ 0 $ до некоторого времени накопления, big $ T $. Чтобы найти напряжение в конце импульса, мы устанавливаем большой $ T $ равным $ 3 \, \ text {ms} $.
$ i $ постоянно (верхняя часть импульса плоская) в течение этого времени, поэтому мы можем вывести его за пределы интеграла. Мы сказали, что конденсатор начался с заряда $ 0 $, поэтому $ v_0 $ равен нулю, и мы можем не учитывать его.{-6} \, \ text F} = 2000 \, \ text {вольт / секунду} $
Для любой длительности импульса напряжение равно
$ v (T) = 2000 \, \ text {volts / s} \, \ cdot T $
Ширина нашего импульса составляет $ T = 3 \, \ text {ms} $, поэтому напряжение на конденсаторе возрастает до
.$ v _ {(T = 3 \, \ text {ms})} = 2000 \, \ text {volts / sec} \, \ cdot \, 0.003 \, \ text {sec} = 6 \, \ text {volts } $
При постоянном токе $ 2 \, \ text {mA} $ напряжение на конденсаторе растет по прямой линии с наклоном $ 2000 \, \ text {volts / sec} $.Напряжение начинается с $ 0 \, \ text V $ и повышается до $ 6 \, \ text {volts} $ после $ 3 \, \ text {ms} $.
После пульса
Эта деталь довольно интересна, если вы не задумывались о ней раньше. После импульса ток падает до $ 0 $. Это означает, что заряд перестает накапливаться на конденсаторе. Это может показаться странным, но поскольку заряд не перемещается, накопившемуся на конденсаторе заряду некуда деваться, поэтому он остается на конденсаторе. Это означает, что нам следует ожидать, что напряжение на конденсаторе останется прежним.{\, T} 0 \, dt + 6 $
Интеграл равен $ 0 $, и мы получаем
.$ v (T) = 6 \, \ text V \ quad $ для любого значения $ T $.
Как только ток прекращается, заряд остается неизменным, поэтому напряжение на конденсаторе остается постоянным на уровне $ 6 \, \ text V $. Он остается там навсегда.
Общий ответ
Объединение трех частей вместе дает нам $ v (t) $ на нижнем графике,
Эта конфигурация схемы (источник тока, управляющий конденсатором) имеет прозвище.Он называется интегратором , потому что он накапливает или интегрирует заряд с течением времени. Он часто используется для создания напряжения в форме пилообразного сигнала.
Имитационная модель
Найдите ток и напряжение с помощью этой имитационной модели. Откройте ссылку и щелкните TRAN в верхней строке меню, чтобы выполнить имитацию переходных процессов. Источник тока моделируется как одиночный ИМПУЛЬС. (Дважды щелкните текущий источник, чтобы увидеть, как он определен.) Элементы управления масштабированием находятся в левой части окна светло-серым цветом.
Задача дизайна
Вот еще одна имитационная модель с источником тока, определенным иначе, как форма волны PWL (кусочно-линейная). Время и ток вводятся в виде списка пар [время, ток], разделенных запятыми, например: -1 с, 0,0 с, 0,1 нс, 2 мс, 3 мс, 2 мс, 3 мс, 0,5 с, 0.
Посмотрите, можете ли вы изменить форму волны тока, чтобы напряжение конденсатора упало до $ 0 \ text V $ в другом $ 3 \, \ text {ms} $. Вы собираетесь купить что-то вроде этого:
показать ответДважды щелкните текущий источник и введите его в PWL «список чередующихся значений времени и значений, разделенных запятыми».
-1 с, 0,0 с, 0,1 нс, 2 м, 3 мс, 2 м, 3 мс, -2 м, 6 мс, -2 м, 6 мс, 0,10 с, 0
Источник тока заряжает конденсатор на $ 3 \, \ text {ms} $, и напряжение нарастает. Затем он меняет направление, чтобы снять плату еще за $ 3 \, \ text {ms} $. Напряжение — это еще один рост, на этот раз с отрицательной крутизной, так как заряд удален.
Сводка
Если вы подаете постоянный ток в конденсатор, он создает напряжение, имеющее форму прямой кривой. Мы использовали интегральную форму уравнения конденсатора $ i $ — $ v $, чтобы предсказать это.
Подход к решению этой схемы является хорошим примером того, как инженеры делят проблему на мелкие кусочки, решают каждую простую часть и собирают полный ответ. Когда вы сталкиваетесь с такой сложной проблемой, как эта, первым вашим инстинктом должно быть: «Как я могу разрубить это на части?»
Расчет напряжения на зарядно-разрядном конденсаторе
Здесь выводится выражение для получения мгновенного напряжения на зарядном конденсаторе как функции времени, то есть V (t).
Рассмотрим конденсатор, подключенный последовательно с резистором к источнику постоянного постоянного тока через переключатель S.
«C» — это значение емкости, а « R» — значение сопротивления . ‘V’ — это напряжение источника постоянного тока, а « v » — мгновенное напряжение на конденсаторе.
Когда переключатель «S» замкнут, ток течет через конденсатор, и он заряжается до напряжения V от значения 0.По мере зарядки конденсатора напряжение на конденсаторе увеличивается, а ток в цепи постепенно уменьшается. Для незаряженного конденсатора ток в цепи будет максимальным в момент переключения. И зарядные токи достигают примерно нулевого значения, когда потенциал на конденсаторе становится равным напряжению источника «V».
Этапы вывода уравнения заряда конденсатора,
Исходя из закона напряжения, напряжение источника будет равно общему падению напряжения в цепи.
Следовательно,
Перепишите уравнение для выполнения функции интегрирования,
RHS упрощение,
При интегрировании получаем,
Поскольку мы рассматриваем незаряженный конденсатор (нулевое начальное напряжение), значение постоянной «K» может быть получено путем подстановки начальных условий времени и напряжения. В момент замыкания переключателя начальное условие — время t = 0, а напряжение на конденсаторе — v = 0.
Таким образом, мы получаем logV = k для t = 0 и v = 0.
Принимая экспоненту с обеих сторон,
Из приведенного выше выражения ясно, что мгновенное напряжение будет результатом таких факторов, как емкость, сопротивление последовательно с конденсатором, время и значение приложенного напряжения.
По мере увеличения значения постоянной RC значение экспоненциальной функции также увеличивается. То есть скорость нарастания напряжения на конденсаторе будет меньше со временем.Это показывает, что время зарядки конденсатора увеличивается с увеличением постоянной времени RC.
По мере увеличения значения времени «t» этот член уменьшается, и это означает, что напряжение на конденсаторе почти достигает значения насыщения.
Заряд
q и зарядный ток i конденсатораВыражение для напряжения на зарядном конденсаторе получается как,
ν = V (1- e -t / RC ) → уравнение (1).
В — напряжение источника
ν — мгновенное напряжение
C — емкость
R — сопротивление
t — время
Напряжение заряженного конденсатора, В = Q / C .
Q — Максимальный заряд
Мгновенное напряжение, v = q / C .
q — мгновенный заряд
q / C = Q / C (1- e -t / RC )
q = Q (1- e -t / RC )
Зарядный ток
Для конденсатора поток зарядного тока постепенно уменьшается до нуля по экспоненциальной функции затухания по времени.
Из закона напряжения,
ν = V (1-e -t / RC )
ν = V — V e -t / RC
V — ν = V e -t / RC → уравнение (2)
Напряжение источника, V = падение напряжения на резисторе (IR) + напряжение на конденсаторе ( ν ).
V = i R + ν
В — ν = i R
Подставьте V — ν = i R в уравнение 2.
Следовательно, i R = V e -t / RC
i = (V / R) e -t / RC
Поскольку V — это напряжение источника, а R — сопротивление, В / R будет максимальным значением тока, который может протекать по цепи.
В / R = Imax
i = Imax e -t / RC
Вывод уравнения разряда конденсатора
Для разряжающегося конденсатора напряжение на конденсаторе В разряжается до нуля.
Применяя закон Кирхгофа, В равно падению напряжения на резисторе R.
Ток i через резистор переписывается, как указано выше, и подставляется в уравнение 1.
Интегрируя и переставляя приведенное выше уравнение, мы получаем
Применение экспоненциальной функции,
Мгновенное напряжение на разряжающемся конденсаторе v = V e -t / RC
Мгновенный заряд, q = Q e -t / RC
Мгновенный ток, i = — Imax e -t / RC
Из приведенных выше уравнений ясно, что напряжение, ток и заряд конденсатора экспоненциально затухают во время разряда.Ток разряда имеет отрицательный знак, поскольку его направление противоположно току заряда.
.
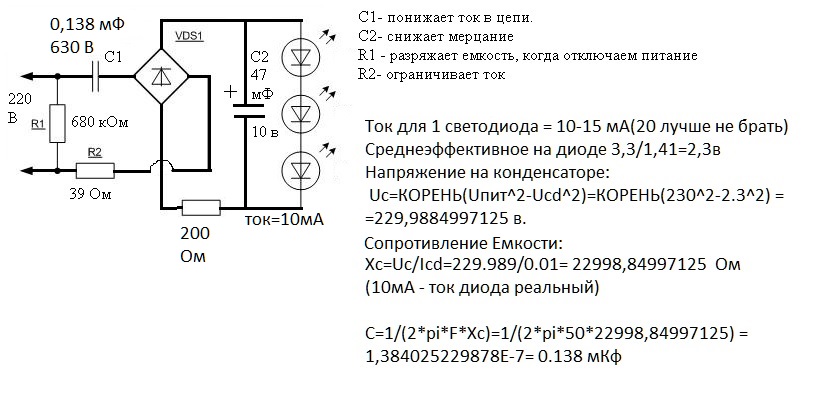 01-0.00183 =
0.0082 с
01-0.00183 =
0.0082 с
