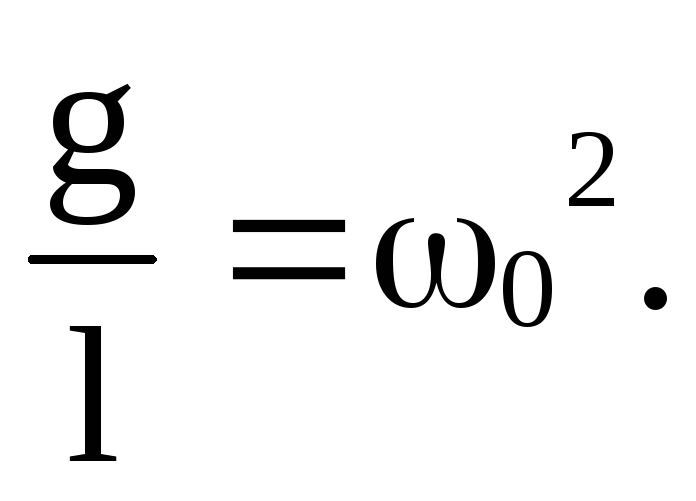Глава 7. Вращательное движение. Кинематика и динамика
Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел
(7.1) |
В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан — безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7.
(7.2) |
Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.
Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим
(7.3) |
Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.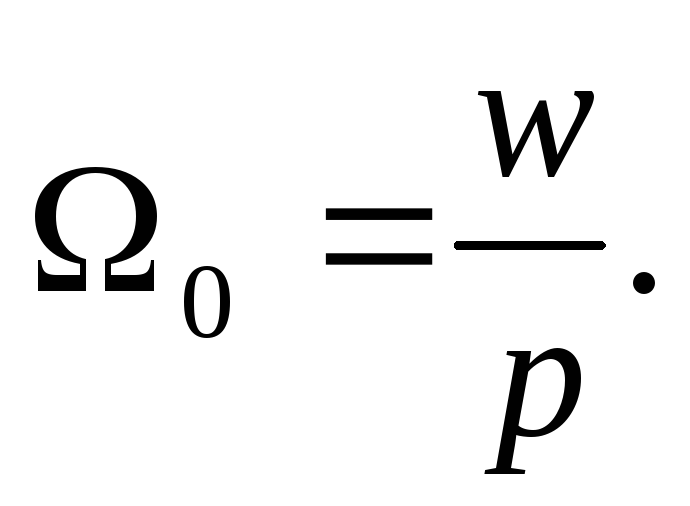
Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна
(7.4) |
Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах
(7.5) |
Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине
Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине
(7.6) |
Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.
Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.
Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»).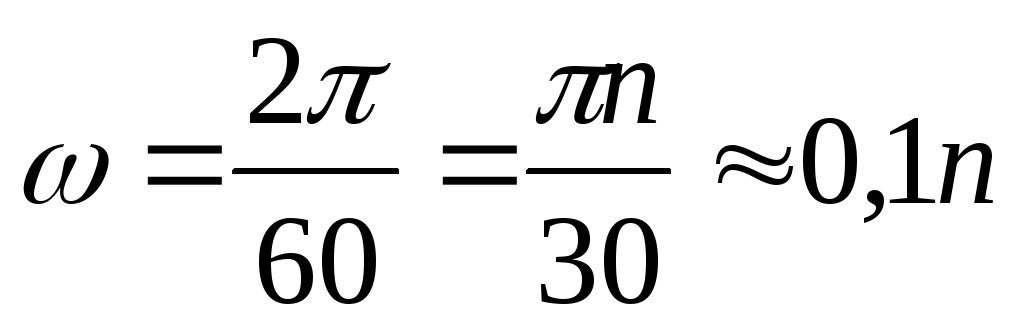
Для нахождения линейной скорости конца секундной стрелки часов (задача 7.1.2) используем связь угловой и линейной скоростей (7.5). Имеем
(правильный ответ – 2).
Применяя определение угловой скорости к колесу (задача 7.1.3), получаем
(правильный ответ 1).
Из формулы (7.2) имеем
(задача 7.1.4 – правильный ответ 4).
Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.1.5), из формулы (7.5) находим квадрат угловой скорости диска
А теперь по формуле (7. 5) для второй точки получаем
5) для второй точки получаем
(ответ 2).
Поскольку скорость автомобиля в
Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно
(ответ 4).
Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (задача 7.1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи –
 Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).
Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).
Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с2, получим для равнодействующей =2 Н (ответ 2).
Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из задачи 7.2.1
(ответ 1).
Для сравнения центростремительных ускорений материальных точек в задаче 7. 2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем
2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем
(ответ 3).
Для сравнения центростремительных ускорений тел в задаче 7.2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим
(7.5) |
Поэтому
(ответ 1).
Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)
где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем
Учитывая, что , получаем
(ответ 2).
Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7.2.5), центростремительное ускорение сообщается силой трения
Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства
(ответ 4).
В задаче 7. 2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем
2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем
(ответ 3).
В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает
(1) |
На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем
Подставляя в эту формулу силу из формулы (1), находим (ответ 2).
В задаче 7.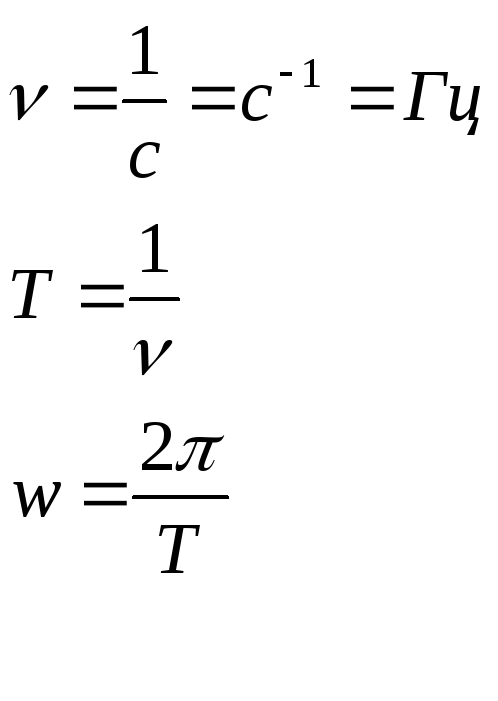 2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем
2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем
где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим
(ответ 3).
Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):
где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно
(задача 7. 2.9 – ответ 1).
2.9 – ответ 1).
Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7.2.10 – ответ 2).
Число оборотов в минуту — Revolutions per minute
«rpm» перенаправляется сюда. Для использования в других целях, см rpm (значения) .| Число оборотов в минуту | |
|---|---|
| Единица | Скорость вращения |
| Символ | об / мин или об / мин |
| Конверсии | |
| 1 об / мин в … | … равно … |
| SI угловая скорость | 2π / 60 рад / с ≈ 0,1047198 рад / с |
| Частота SI | 1 / 60 Гц ≈ 0,01666667 Гц |
| Производная частота вращения SI | 1 / 60 с −1 , 1 / 60 / с |
| Производная скорость вращения SI | 1 мин −1 , 1 / мин |
Число оборотов в минуту (сокращенно оборотов в минуту , оборотов в минуту , об / мин , г / мин , или с обозначением мин -1 ) это число витков в одной минуты .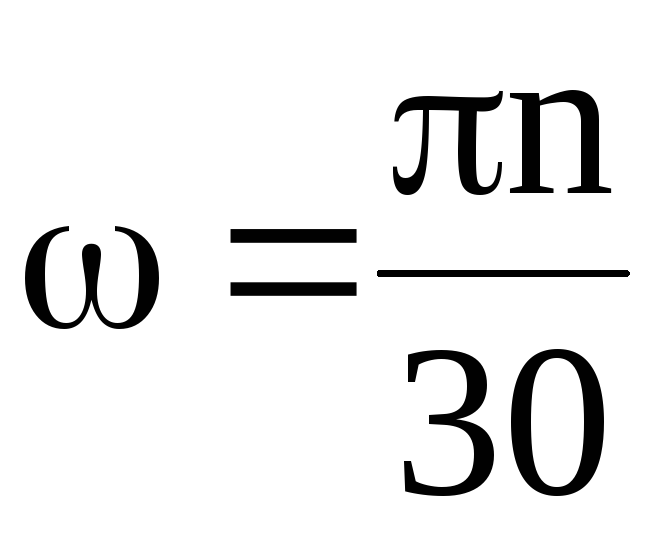 Это единица скорости вращения или частоты от вращения вокруг неподвижной оси .
Это единица скорости вращения или частоты от вращения вокруг неподвижной оси .
Международная система единиц
Согласно Международной системе единиц (СИ), об / мин не является единицей. Это потому, что слово « революция» — это скорее семантическая аннотация , чем единица. Вместо этого примечание делается в виде нижнего индекса знака формулы, если это необходимо. Из измеренной физической величины , формула знак должен быть е для (вращательной) частоты и со или Q , для угловой скорости . Соответствующая базовая производная единица СИ — с -1 или Гц . При измерении угловой скорости используется единица радиан в секунду .
|
Хотя они имеют одинаковые размеры (с -1 ), герц (Гц) и радиан в секунду (рад / с) — это две разные единицы, представляющие две разные, но пропорциональные величины ISQ : частота и угловая частота (угловая скорость, величина угловой скорости). ). Преобразование между частотой f (измеренной в герцах) и угловой скоростью ω (измеренной в радианах в секунду):
). Преобразование между частотой f (измеренной в герцах) и угловой скоростью ω (измеренной в радианах в секунду):
- ω знак равно 2 π ж , ж знак равно ω 2 π . {\ displaystyle \ omega = 2 \ pi f \ ,, \ qquad f = {\ frac {\ omega} {2 \ pi}} \ ,.}
Таким образом, диск, вращающийся со скоростью 60 об / мин, считается вращающимся со скоростью 2 π рад / с или 1 Гц, где первый измеряет угловую скорость, а второй отражает количество оборотов в секунду.
Если не-СИ единица об / мин считается единицей частоты, то 1 об / мин = 1 / 60 Гц . Если вместо этого считается, что это единица измерения угловой скорости, а слово «вращение» означает 2 π радиан , то 1 об / мин = 2 π / 60 рад / с .
Примеры
- На многих типах носителей для записи дисков скорость вращения носителя под считывающей головкой является стандартной и выражается в об / мин. Фонограф (граммофонные) записи , например, как правило , вращаются непрерывно в 16 2 / 3 , 33 1 ⁄ 3 , 45 или 78 об / мин (0,28, 0,55, 0,75 или 1,3 Гц соответственно).

- Современные стоматологические буры с воздушной турбиной могут вращаться со скоростью до 800 000 об / мин (13,3 кГц).
- Вторая рука обычных аналоговых вращается на 1 тактовых оборотов в минуту.
- Проигрыватели аудио CD читают свои диски с точной постоянной скоростью (4,3218 Мбит / с необработанных физических данных для 1,4112 Мбит / с (176,4 кБ / с) пригодных для использования аудиоданных) и, следовательно, должны изменять скорость вращения диска от 8 Гц (480 об / мин) при считывании по самому внутреннему краю до 3,5 Гц (210 об / мин) по внешнему краю.
- DVD- плееры также обычно читают диски с постоянной линейной скоростью. Скорость вращения диска варьируется от 25,5 Гц (1530 об / мин) при чтении по внутреннему краю до 10,5 Гц (630 об / мин) по внешнему краю.
- А стиральной машины барабанного «сек может вращаться со скоростью от 500 до 2000 оборотов в минуту (8-33 Гц) во время отжиме.
- Турбина для выработки электроэнергии ( с двухполюсным генератором переменного тока ) вращается со скоростью 3000 об / мин (50 Гц) или 3600 об / мин (60 Гц), в зависимости от страны — см.
 Вилки и розетки переменного тока .
Вилки и розетки переменного тока . - Современные автомобильные двигатели обычно работают со скоростью около 2 000–3 000 об / мин (33–50 Гц) в крейсерском режиме с минимальной скоростью (холостой ход) около 750–900 об / мин (12,5–15 Гц) и верхним пределом от 4500 до 10 000 об / мин ( 75–166 Гц) для дорожного автомобиля или почти (иногда выше) 20 000 об / мин для гоночных двигателей, например, в автомобилях Формулы 1 (в течение сезона 2006 года с двигателем 2.4 LN / A V8 ; в настоящее время ограничено 15 000 об / мин, с 1,6 л V6 турбо — гибридные конфигурации двигателя). Выхлопа из V8 автомобилей F1 имеют гораздо более высокую высоту , чем I4 двигатель , потому что каждый из цилиндров в течение четырехтактный двигатель срабатывает один раз на каждые два оборота коленчатого вала . Таким образом, восьмицилиндровый двигатель, вращающийся 300 раз в секунду, будет иметь частоту выхлопа 1200 Гц.
- Поршневой авиационный двигатель обычно вращается со скоростью от 2000 до 3000 об / мин (30–50 Гц).

- Компьютерные жесткие диски обычно вращаются со скоростью 5400 или 7200 об / мин (90 или 120 Гц), что является наиболее распространенной скоростью для дисков ATA или SATA в потребительских моделях. Высокопроизводительные диски (используемые в файловых серверах и игровых ПК для энтузиастов) вращаются со скоростью 10 000 или 15 000 об / мин (160 или 250 Гц), обычно с интерфейсами SATA, SCSI или Fibre Channel более высокого уровня и меньшими пластинами, чтобы обеспечить эти более высокие скорости, сокращение емкостью памяти и максимальной скоростью вращения по внешнему краю окупаются гораздо меньшим временем доступа и средней скоростью передачи благодаря высокой скорости отжима. До недавнего времени можно было найти недорогие и энергоэффективные накопители для ноутбуков со скоростью вращения шпинделя 4200 или даже 3600 об / мин (70 и 60 Гц), но они потеряли популярность из-за их более низкой производительности, повышения энергоэффективности в более быстрых моделях.
 и использование твердотельных накопителей в тонких и сверхпортативных ноутбуках. Подобно носителям CD и DVD, количество данных, которые можно сохранить или прочитать для каждого поворота диска, больше на внешнем крае, чем возле шпинделя; однако жесткие диски поддерживают постоянную скорость вращения, поэтому эффективная скорость передачи данных выше на краю (обычно это «начало» диска, в отличие от CD или DVD).
и использование твердотельных накопителей в тонких и сверхпортативных ноутбуках. Подобно носителям CD и DVD, количество данных, которые можно сохранить или прочитать для каждого поворота диска, больше на внешнем крае, чем возле шпинделя; однако жесткие диски поддерживают постоянную скорость вращения, поэтому эффективная скорость передачи данных выше на краю (обычно это «начало» диска, в отличие от CD или DVD). - Приводы гибких дисков обычно работали с постоянной скоростью 300 или иногда 360 об / мин (относительно медленные 5 или 6 Гц) с постоянной плотностью данных на оборот, что было просто и недорого реализовать, хотя и неэффективно. Некоторые конструкции, такие как те, которые использовались на старых компьютерах Apple (Lisa, ранний Macintosh, позже II), были более сложными и использовали переменные скорости вращения и плотность хранения на дорожку (при постоянной скорости чтения / записи) для хранения большего количества данных на диске; например, между 394 об / мин (с 12 секторами на дорожку) и 590 об / мин (8 секторов) с диском Mac с двойной плотностью 800 КБ при постоянной 39,4 КБ / с (макс.
 ) — по сравнению с 300 об / мин, 720 КБ и 23 КБ / с (макс.) для дисков двойной плотности в других машинах.
) — по сравнению с 300 об / мин, 720 КБ и 23 КБ / с (макс.) для дисков двойной плотности в других машинах. - Циппе типа центрифуги для обогащения урана вращается со скоростью 90000 оборотов в минуту (1500 Гц) или быстрее.
- Газотурбинные двигатели вращаются со скоростью десятки тысяч оборотов в минуту. Турбины авиамоделей JetCat способны развивать скорость более 100 000 об / мин (1700 Гц), а самая быстрая — 165 000 об / мин (2750 Гц).
- Система накопления энергии с маховиком работает в диапазоне 60 000–200 000 об / мин (1–3 кГц) с использованием пассивно магнитного маховика, левитирующего в вакууме. Материал маховика выбирается не из самого плотного, но из такого, который измельчается наиболее безопасно, при поверхностных скоростях, примерно в 7 раз превышающих скорость звука.
- Типичный компьютерный вентилятор диаметром 80 мм и 30 куб. Футов в минуту будет вращаться со скоростью 2600–3000 об / мин (43–50 Гц) при питании от источника постоянного тока 12 В.

- Миллисекундный пульсар может иметь вблизи 50000 оборотов в минуту (833 Гц).
- Турбокомпрессора может достигать 290000 оборотов в минуту (4,8 кГц), в то время как 80,000-200,000 оборотов в минуту (1-3 кГц) является общим.
- Нагнетателя может вращаться со скоростью от или на уровне 50,000-65,000 оборотов в минуту (833-1083 Гц)
- Молекулярная микробиология — молекулярные двигатели. Было измерено, что скорость вращения бактериальных жгутиков составляет 10 200 об / мин (170 Гц) для Salmonella typhimurium , 16 200 об / мин (270 Гц) для Escherichia coli и до 102 000 об / мин (1700 Гц) для полярного жгутика Vibrio alginolyticus , что позволяет использовать последнее. Организм перемещается в смоделированных естественных условиях с максимальной скоростью 540 мм / ч.
Смотрите также
Рекомендации
<img src=»https://en.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>Мощность момент — Энциклопедия журнала «За рулем»
Может ли бульдозер обогнать «формулу 1»? Может, но только на очень короткой дистанцииЧасто эксперты автомобильных изданий, рассказывая о выдающейся динамике машины, в первую очередь превозносит огромный крутящий момент двигателя, оставляя мощности роль второго плана. Мол, благодаря именно моменту машина ровно и напористо разгоняется в широком диапазоне оборотов и скоростей. Особенно востребовано это качество на высших передачах, – ведь тяговые силы и ускорения на них в любом случае не столь велики, как на первой или второй передаче. А для безаварийного движения в потоке транспорта возможность быстро прибавить скорость зачастую играет судьбоносную роль. Ездить на таком автомобиле даже психологически легче. И все же, когда нужно быстрей разогнаться, что важней – мощность или крутящий момент?
Мол, благодаря именно моменту машина ровно и напористо разгоняется в широком диапазоне оборотов и скоростей. Особенно востребовано это качество на высших передачах, – ведь тяговые силы и ускорения на них в любом случае не столь велики, как на первой или второй передаче. А для безаварийного движения в потоке транспорта возможность быстро прибавить скорость зачастую играет судьбоносную роль. Ездить на таком автомобиле даже психологически легче. И все же, когда нужно быстрей разогнаться, что важней – мощность или крутящий момент?
Сразу отметим: чаще всего эти два параметра «конфликтуют»… в головах журналистов, охотно повторяющих признанные публикой «истины» без какого-либо их анализа. На самом же деле смешно рассматривать мощность в отрыве от крутящего момента и наоборот. Первая показывает энергию, ежесекундно вырабатываемую двигателем, тогда как крутящий момент – всего лишь силовой фактор, показывающий, как нагружен при работе коленчатый вал. Крутящий момент может существовать и сам по себе, без мощности.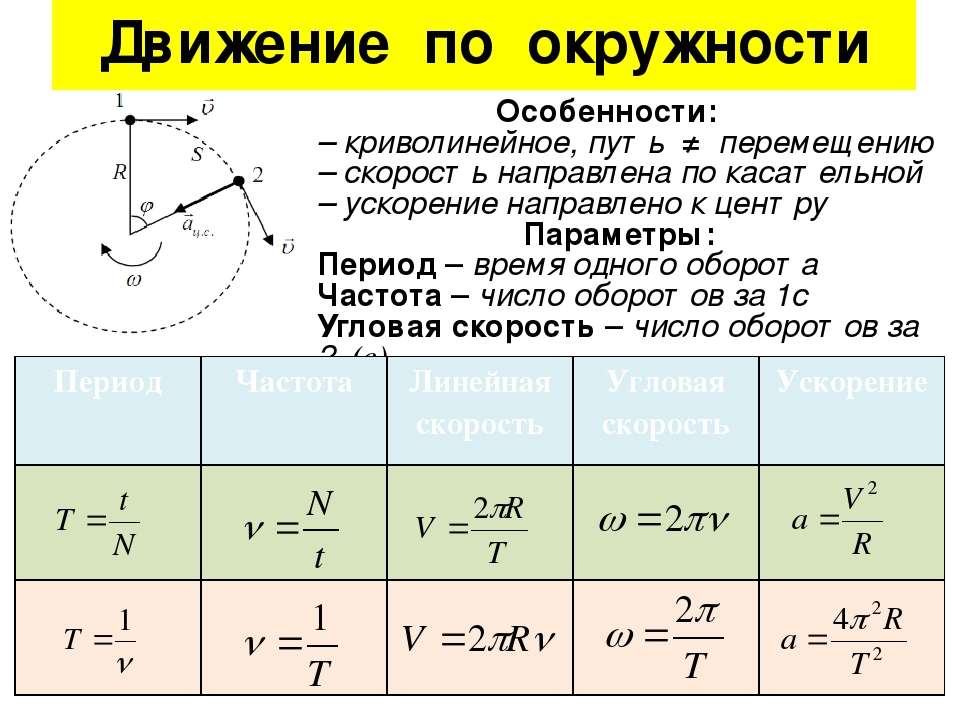 Например, при неожиданной остановке перегруженного двигателя на крутом подъеме, в песке, при буксировке тяжелого прицепа в какой-то миг момент еще есть, а движения уже нет. А в некоторых механизмах можно обнаружить и длительно действующий на какой-нибудь вал момент, удерживающий его от поворота. Например, в рулевом механизме, когда мы лишь удерживаем управляемые колеса в нужных положениях, тогда как дорога пытается их нарушить. А самый типичный пример: пытаясь открутить «прикипевший» болт, ключ удлинили метровой трубой, – а болт ни с места. Момент огромный, а работа не идет. А коли нет работы – то нет и мощности.
Например, при неожиданной остановке перегруженного двигателя на крутом подъеме, в песке, при буксировке тяжелого прицепа в какой-то миг момент еще есть, а движения уже нет. А в некоторых механизмах можно обнаружить и длительно действующий на какой-нибудь вал момент, удерживающий его от поворота. Например, в рулевом механизме, когда мы лишь удерживаем управляемые колеса в нужных положениях, тогда как дорога пытается их нарушить. А самый типичный пример: пытаясь открутить «прикипевший» болт, ключ удлинили метровой трубой, – а болт ни с места. Момент огромный, а работа не идет. А коли нет работы – то нет и мощности.
Тут впору вспомнить школьную физику. Нарисуйте круг радиуса R – это будет сечение вала – и приложите к нему «касательную» силу F. Крутящий момент этой силы М = F • R. За один оборот вала сила F пройдет путь 2πR – и выполнит работу: А = F • R • 2π = М • 2π. А работа за n оборотов: А = М • 2π • n. Если n – число оборотов в минуту, то работа за одну секунду – то есть, мощность – составит N = М • 2πn /60.
Выражение 2π n /60 = 0,1047 n = ω – угловая скорость вала. Итак, N = М • 0,1047 n (Формула [1]).
Но мы имеем дело не только с вращающимися деталями, но и движущимися линейно. В этом случае в формуле (1) момент М заменим силой F, а угловую скорость ω – линейной v. Получим: N = F • v (Формула [2]).
Эти формулы равноправны. Замерив, например, тяговую силу колес, умножим на достигнутую машиной скорость – и найдем затрачиваемую мощность. Но если крутящий момент на ведущей оси умножить на угловую скорость колес, получим то же самое.
Итак, мощность – это работа (или энергия) израсходованная или произведенная за 1 секунду. Конечно, о «законе сохранения энергии» знает каждый. Говоря по пионерски, она «не возникает из ничего», но и не исчезает, не оставив следа. Так, лишь около четверти тепловой энергии, получаемой двигателем от сгорания топлива, превращается в механическую, соответствующая мощность (эффективная) тратится на движение машины. Большая же часть полученной в цилиндрах двигателя теплоты идет на «обогрев» окружающего нас мира.
Большая же часть полученной в цилиндрах двигателя теплоты идет на «обогрев» окружающего нас мира.
Эффективная мощность тоже доходит до ведущих колес не вся – до 15 % ее может рассеять в виде тепла трение в узлах и агрегатах трансмиссии. Но для нас важней другое: если при открытом дросселе (или при полной подаче топлива в дизель) двигатель выдает на колеса сколько-то киловатт, то это – его «потолок». Никакими простыми механизмами вроде коробок передач, редукторов и т. п. превысить эту величину невозможно – этого «закон сохранения» не допустит.
Итак, крутящий момент – это удобный для нас «инструмент», связывающий процессы в двигателе с трансмиссией машины и ведущими колесами. Но не более того! Ракетчики, например, запрягают пламя напрямую, получают гигантские тяги и мощности, но о крутящих моментах вспоминают лишь в расчетах турбонасосных агрегатов, – да и то, если двигатели не твердотопливные!
Из формулы (1) видно, что для получения достаточной мощности вовсе не обязателен огромный крутящий момент, ведь в произведении два сомножителя.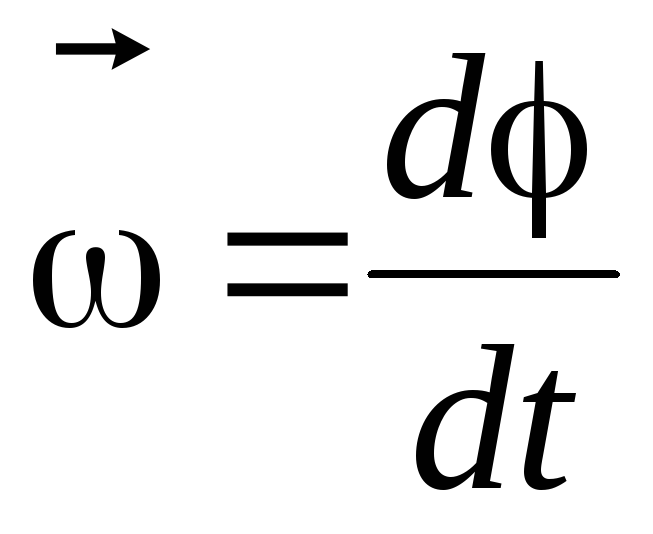 Почему бы, например, не увеличивать мощность при постоянном моменте, наращивая угловую скорость в каком-то диапазоне оборотов? При этом мощность растет по оборотам линейно. А постоянство момента в заданном диапазоне – не чудо, которым некоторые почему-то восторгаются, а всего лишь признак постоянства тяговых сил. Если пренебречь сопротивлением воздуха (к примеру, на первой передаче оно невелико), то и ускорение машины в этом диапазоне постоянное. Это довольно удобно для водителя. Но спросим себя: если бы в начале диапазона момент был таким же, а ближе к пресловутым «верхам» стал больше, стал бы с таким «подхватом» автомобиль хуже? – Вряд ли. Разве только что-нибудь нарушилось бы в смысле экологии.
Почему бы, например, не увеличивать мощность при постоянном моменте, наращивая угловую скорость в каком-то диапазоне оборотов? При этом мощность растет по оборотам линейно. А постоянство момента в заданном диапазоне – не чудо, которым некоторые почему-то восторгаются, а всего лишь признак постоянства тяговых сил. Если пренебречь сопротивлением воздуха (к примеру, на первой передаче оно невелико), то и ускорение машины в этом диапазоне постоянное. Это довольно удобно для водителя. Но спросим себя: если бы в начале диапазона момент был таким же, а ближе к пресловутым «верхам» стал больше, стал бы с таким «подхватом» автомобиль хуже? – Вряд ли. Разве только что-нибудь нарушилось бы в смысле экологии.
Мощность можно менять и при постоянных оборотах. Пример: мы ехали со скоростью 90 км/ч по горизонтальному шоссе, а с началом подъема, дабы сохранить скорость, пришлось больше открыть дроссель. Это увеличение момента в чистом виде.
Итак, имеем дело с формулой (1).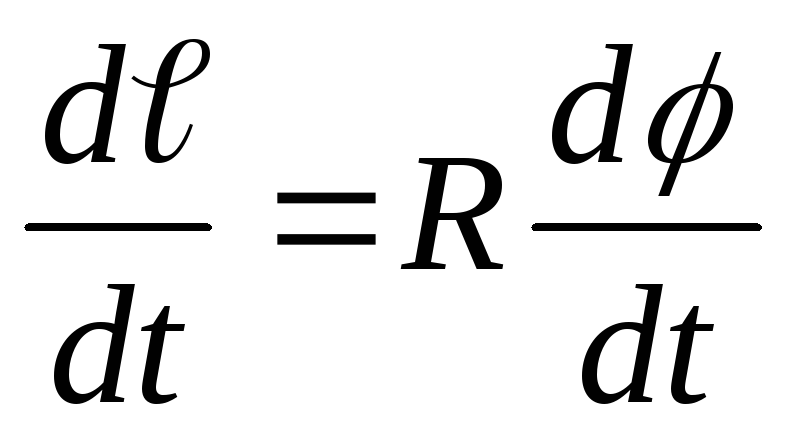 К примеру, перед нами скромный двигатель грузовика с моментом 35 кгм при оборотах 3000 в минуту. Какова мощность? Тут отметим, что в расчетах всегда важен правильный выбор единиц измерений параметров. Угловую скорость измеряют в 1/сек. А момент? – В старых единицах это кгм. Получаем: N = 35 кгм . 0,1047 . 3000 1/сек = 10993 кгм/сек ≈ 146,6 л.с. А в современной системе СИ: 35 кгм = 343,35 Нм. Тогда N = 343,45 Нм • 0,1047 • 3000 1/сек ≈ 107846 Вт.
К примеру, перед нами скромный двигатель грузовика с моментом 35 кгм при оборотах 3000 в минуту. Какова мощность? Тут отметим, что в расчетах всегда важен правильный выбор единиц измерений параметров. Угловую скорость измеряют в 1/сек. А момент? – В старых единицах это кгм. Получаем: N = 35 кгм . 0,1047 . 3000 1/сек = 10993 кгм/сек ≈ 146,6 л.с. А в современной системе СИ: 35 кгм = 343,35 Нм. Тогда N = 343,45 Нм • 0,1047 • 3000 1/сек ≈ 107846 Вт.
На всякий случай напомним, что 1 лс = 75 кгм/сек = 75 • 9,81 Нм/сек = 735,75 Вт. Поэтому 107846 Вт ≈ 146,6 л.с.
А теперь прикинем мощность «формульного» двигателя с таким же скромным моментом, но при оборотах 18 тысяч! Результат – 880 л.с. (647 кВт), которые обеспечивают машине роскошную динамику. Никакого чуда нет: чем больше циклов совершит наш «моментик» за одну секунду, тем больше и совершенная им работа. Еще пример. В авиатехнике ныне практически господствуют газотрубинные двигатели. Повторив наш расчет для небольшого двигателя, с оборотами свободной турбины 40 тысяч в минуту, получим мощность около 1950 л.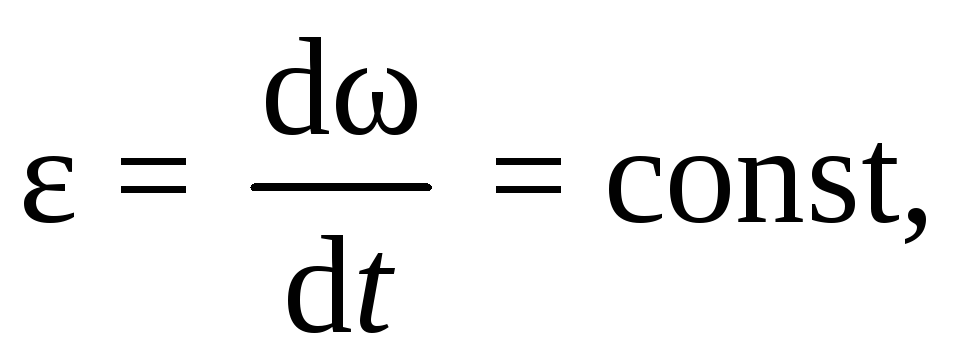 с. или 1438 кВт. Момент турбины невелик, но ведь воздушный винт приводится от нее не напрямую, а через редуктор, – а уж «мощи» ему хватает!
с. или 1438 кВт. Момент турбины невелик, но ведь воздушный винт приводится от нее не напрямую, а через редуктор, – а уж «мощи» ему хватает!
Но вернемся к автомобилю. Как уже сказано, любому комфортней ездить на машине, у которой под капотом достаточно и мощности, и момента. Но многим приходится ездить на скромных авто, возможности коих, как нынче говорят, «очень бюджетные»! Всякий, кто не умеет вовремя переключать передачи, с ними испытывает неприятности. Значит, надо учиться, друзья. Ну а что делать владельцу авто с АКП? На смену недовольству двигателем зачастую приходят претензии к автомату. Нередко – справедливые, ведь у АКПП тоже случаются специфические болячки, требующие ремонта. Но часто они оказываются не обоснованными: современный автомобиль, насыщенный электроникой и настроенный изготовителем на строгое выполнение жестких экологических норм, вовсе не обязан подстраиваться под любую российскую лихость!
Гусеничному трактору дернуться и оборвать сцепку – плевое дело. Это похоже на выстрел из ружья – можно на миг и «формулу I» опередить.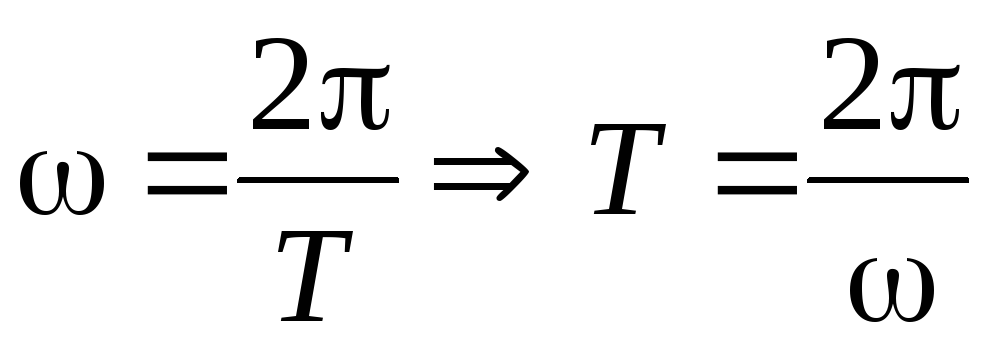 А дольше – никак. Ружье от ракеты отличается принципиально: последняя сохраняет нужное ускорение достаточно долго. В свое время, при стартах к Луне гигант «Сатурн 5» массой свыше 3100 т отделялся от пускового устройства мягко, как пассажирский поезд, – с ускорением чуть больше 1 м/сек2. А минут через пять, по мере выгорания топлива, настолько «терял в весе», что его скорость перед выключением первой ступени составляла 3 км/сек.
А дольше – никак. Ружье от ракеты отличается принципиально: последняя сохраняет нужное ускорение достаточно долго. В свое время, при стартах к Луне гигант «Сатурн 5» массой свыше 3100 т отделялся от пускового устройства мягко, как пассажирский поезд, – с ускорением чуть больше 1 м/сек2. А минут через пять, по мере выгорания топлива, настолько «терял в весе», что его скорость перед выключением первой ступени составляла 3 км/сек.
Низшая передача бульдозера крайне «коротка»: чуть «перекрутил» – тяга упала. А другие не лучше, – вон и «формула» уже растворилась за горизонтом, так что для серьезных игрищ «мощи» на гусеницах маловато.
Если пренебречь разницей в КПД передач (она невелика), то на любой передаче машину движут одни и те же киловатты. Но движут по-разному. Момент и тяговая сила на ведущих колесах подчиняются «золотому правилу»: сколько процентов выиграешь в скорости, столько потеряешь в силе. Это показывают рис. 1 и 2. Если двигатель заведомо слаб, с ним сильно не разгонишься.
Рис. 1. Величины мощности N1 … N5 на ведущей оси не зависят от включенной передачи. Точки пересечения кривой Nсопр с кривыми N3, N4 и N5 дают информацию о максимальных скоростях автомобиля на этих передачах. Здесь самая скоростная на горизонтальной дороге в безветрие – четвертая.
Вся история современной транспортной техники – это непрерывная борьба за большие мощности. У наиболее знаменитых ракетоносителей они давно превысили 100 миллионов кВт. Это не ошибка — именно 100 000 000 000 Вт, или 100 ГигаВатт. И хотя притязания автомобилиста не столь велики, «прохватить» на динамичной машине всякий не прочь.
Главные враги любителя скорости – не гаишники, а силы, тормозящие движение, – от этих не откупишься! Мощность сопротивления воздуха вкупе с мощностью шинных потерь показаны на рис. 1 линией Nсопр.
(Желающие посчитать, могут воспользоваться следующими формулами. Nсопр. = Nw + Nf. Мощность аэродинамических потерь Nw для автомобиля весом 15000 Н при плотности воздуха 1,25 кг/м3, Сх = 0,3 и лобовой площади S = 2 • м2 составляет: Nw = (0,3 • 2 • 1,25)/2 • v3 = 0,375 v3 Вт. А мощность шинных потерь Nf = 0,015 • 15000 • v = 225 v Вт. При 100 км/ч Nсопр составляет лишь 14,5 кВт. А при 200 км/ч – 77 кВт. Разница впечатляет?)
А мощность шинных потерь Nf = 0,015 • 15000 • v = 225 v Вт. При 100 км/ч Nсопр составляет лишь 14,5 кВт. А при 200 км/ч – 77 кВт. Разница впечатляет?)
Колеса автомобиля, борясь с мощностями сил сопротивления, при максимальной скорости полностью расходуют мощность, получаемую от двигателя. Но ее характеристика (например, показанная кривой N4 на рис.1) при полностью открытом дросселе похожа на гору с округлой макушкой, тогда как характеристика мощности сопротивлений Nсопр. поднимается как крутая парабола. Чтобы полностью использовать арсенал мощности двигателя – и получить максимум скорости V4 (на горизонтальной трассе, без ветра), передаточное число трансмиссии и размер шин подбирают так, чтобы кривая Nсопр пересекла кривую N4 возле вершины. Максимальные скорости на третьей и пятой передачах (V3 и V5) существенно ниже. Но на спуске или с ветром вдогон выгодней может стать пятая передача, а на подъеме или с ветром в лоб – третья.
Но на спуске или с ветром вдогон выгодней может стать пятая передача, а на подъеме или с ветром в лоб – третья.
Другие враги скорости – подъем дороги и встречный ветер. Подъем с углом всего 1,5% добавит к потерям в шинах еще столько же. Но еще коварней ветер. Его скорость сложится со скоростью машины относительно дороги, – и уже эту сумму в расчете затрат мощности надо возвести в куб! При скорости по спидометру 36 км/ч (10 м/сек) и ровном встречном ветре 5 м/сек мощность Nсопр вырастет лишь на 0,9 кВт, а вот при 180 км/ч (50 м/сек) – аж на 15,5 кВт. Но придуманный нами автомобиль так ехать не может… Маловато мощи! Максимальная скорость снизится почти на 20 км/ч.
Рис. 2 — Так зависит крутящий момент (М1….М5) или тяговая сила (Fтяг 1 …Fтяг 5) на ведущей оси от включенной передачи. При коэффициенте сцепления шин с дорогой 0,7 ведущая ось, нагруженная половиной веса машины (Gавтом = 15000 н), может создать реальную тяговую силу не больше Fмакс.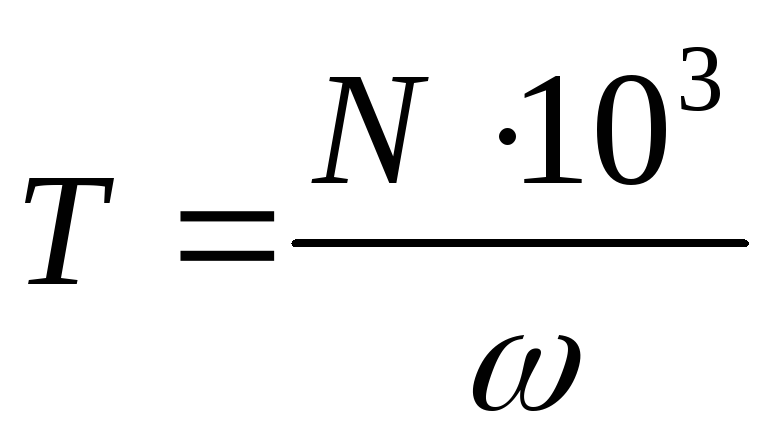 доп. = 5250 Н.
доп. = 5250 Н.
На рис.2 величины крутящего момента М1…М5, а заодно и теоретические тяговые силы F1…F5 на ведущей оси, показаны одними и теми же кривыми, – ведь тяговые силы пропорциональны моментам. Величины сил – на вертикальной оси справа. Но тут важно учесть следующее.
Разгоняет машину не вся тяговая сила, а лишь избыточная – то есть разница между полной тяговой силой колес и сопротивлением воздуха. Отношение этой силы к весу машины академик Чудаков назвал динамическим фактором D. На первой передаче сопротивление воздуха мало, его можно не учитывать – считать, что машину разгоняет полная сила Fтяг.1. Но отталкиваться от дороги сильней, чем позволяет сцепление шин, невозможно! Если, например, ведущая ось несет половину веса машины – 7500 Н, то при коэффициенте сцепления φ = 0,7 тяговая сила не может превысить 35% ее веса. Это неплохо согласуется с такой официальной характеристикой любого автомобиля как предельно возможный угол подъема. С «моноприводом» трудно получить больше. Правда, у машины с задним приводом на подъемах ведущие колеса несколько догружаются весом машины, а вот передний тут невыгоден. Лучшая схема, но сложная и дорогая, – полный привод (конечно, не с такой скромной мощностью, как у «Нивы» или УАЗа!).
С «моноприводом» трудно получить больше. Правда, у машины с задним приводом на подъемах ведущие колеса несколько догружаются весом машины, а вот передний тут невыгоден. Лучшая схема, но сложная и дорогая, – полный привод (конечно, не с такой скромной мощностью, как у «Нивы» или УАЗа!).
Если избыточная сила (на первой передаче, например) слишком велика, машина «шлифует» дорогу. Дело нелепое, нужно перейти на следующую передачу. А вот при разработке нового авто конструктор учитывает высокую мощность двигателя и ее следствие – тяговые силы в передаточных числах трансмиссии. Передачи проектируются как достаточно «длинные», расширяющие диапазон скоростей при достаточных ускорениях. А это значит, что и при более высоких скоростях действуют нужные тяговые силы (или моменты) на колесах. Иначе говоря, реализуется весь арсенал мощности! Значит, она все же важнее.
Споры на тему влияния мощности-момента ведутся давно, и конца им не видно. Вроде бы сто раз уже объясняли самыми разными способами, что тут к чему, а воз и ныне там.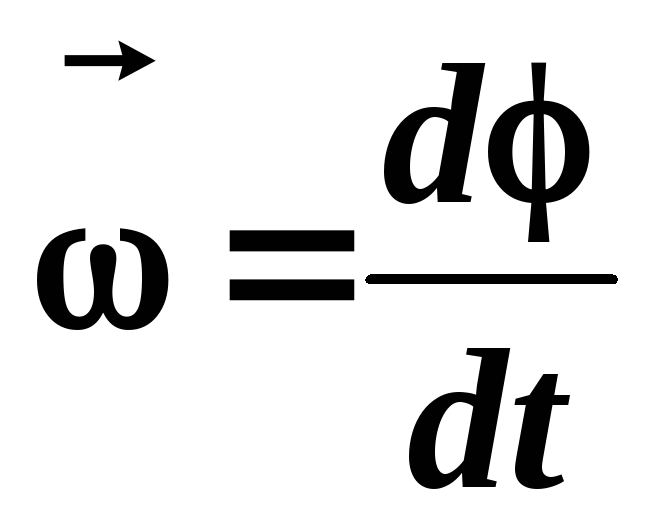 Вызывает неподдельный интерес, откуда все же берется заблуждение и почему оно такое устойчивое?
Вызывает неподдельный интерес, откуда все же берется заблуждение и почему оно такое устойчивое?
Причин видится две. Одна из них в том, что мощность есть функция от момента. Зависимость мощности от момента стоит барьером, который преодолеть оказывается непросто. Что странно. Поскольку очевидность того, что мощность есть функция не только от момента, но и от оборотов, не оспаривается, и тот факт, что у разных двигателей бывает весьма большой разброс по соотношению мощности к моменту, также не подвергается сомнению. То есть существует молчаливое согласие с тем, что мощность есть функция от двух аргументов — оборотов и момента, но при этом зависимость от оборотов как бы игнорируется. Почему?
А в этом и есть вторая, главная причина заблуждения. И ключевая фраза здесь: «Человек совершенно может не иметь понятие про мощность.А вот разницу в ускорении на 3 и 4 передаче он вполне способен почувствовать.» Ясно, что на динамику автомобиля оказывают большое влияние и передаточные числа КПП. На графике 1 видны кривые мощности двигателя, смещенные в зависимости от разных передаточных чисел и кривая сопротивлений. Видно, что с ростом передаточного числа динамика резко возрастает. Это очевидно и вопросов не вызывает. Странно, что не менее очевидный факт, что бОльшая часть времени при разгоне приходится вовсе не на 1 и 2 передачи, а на 3-4, при этом упускается из виду.
На графике 1 видны кривые мощности двигателя, смещенные в зависимости от разных передаточных чисел и кривая сопротивлений. Видно, что с ростом передаточного числа динамика резко возрастает. Это очевидно и вопросов не вызывает. Странно, что не менее очевидный факт, что бОльшая часть времени при разгоне приходится вовсе не на 1 и 2 передачи, а на 3-4, при этом упускается из виду.
При разгоне здравомыслящий водитель пользуется всеми четырьмя передачами и весьма широким диапазоном частот вращения двигателя. При этом редко задумывается о том, что динамика разгона на высокой скорости мала и плохо ощущается, но именно на нее и приходится львиная доля времени разгона (по той простой причине, повторю, что на высших передачах динамика хуже и потому занимает больше времени). Хорошо ощущается динамика разгона на низших передачах, в диапазоне низких и средних оборотов (дальше водитель двигатель раскручивает редко). И что выходит? А выходит, что «низовой», моментный двигатель дает ощущение уверенного и бодрого разгона по той простой причине, что легко и весело страгивает и начинает разгонять автомобиль. А по достижении скорости ощущения становятся слабыми, и оценить разницу в разгоне 100- и 120 сильного моторов на 4-5 передачах, способен не каждый. Потому и кажется, что момент определяет динамику. По ощущениям. А ощущениям человек склонен верить очень сильно, даже вопреки логике и здравому смыслу.
А по достижении скорости ощущения становятся слабыми, и оценить разницу в разгоне 100- и 120 сильного моторов на 4-5 передачах, способен не каждый. Потому и кажется, что момент определяет динамику. По ощущениям. А ощущениям человек склонен верить очень сильно, даже вопреки логике и здравому смыслу.
Проповедующие формулировку «скорость определяется мощностью, а динамика разгона — моментом двигателя» могут убедиться в своем заблуждении, решив простую задачу.
Вводные
1. Равномерный подъем на некоторую высоту равносилен равномерному ускорению, поскольку увеличивает потенциальную энергию тела mgh*. (что можно объяснить — чем с большей высоты упадет, тем сильней ударится).
2. Поднимаем равномерно груз весом 75 кг на высоту 1 м за 1 с.
3. Имеется черный ящик, в котором спрятан мотор неизвестной природы и, возможно, редуктор с КПД=1.
Вопросы.
1. Какая мощность должна быть в моторе, спрятанном внутри черного ящика?
2. Какой момент должен быть в моторе, спрятанном внутри черного ящика?
Подъем указанного груз на нужную высоту за время аналогичен разгону по горизонтали той же массы с ускорением g0. 5.
5.
Если ускорение определяется моментом — просто назовите цифру
Если ускорение определяется мощностью — тоже просто назовите цифру
Если цифру назвать не удается, значит параметр может быть самым разным и роли не играет.
Вы можете разгонять тело с заданным ускорением (или поднимать его вверх), меняя крутящий момент по своей прихоти (и устанавливая каждый раз соответствующий редуктор). Вы можете отталкиваться от параметров редуктора, и всякий раз требуемый момент будет меняться и зависеть от передаточного отношения этого редуктора. Но всегда мощность будет оставаться одной и той же, неизменной величиной — для подъема груза 75 кг на 1 м за 1с понадобится ровно одна лошадиная сила или 0,73549875 кВт
Можно поступить и следующим образом.
Берите любой момент, который причина разгона, берите любой редуктор и разгоните тело 75 кг до скорости 3.13 м/c за 1 с.
Ограничение только по мощности — она не должна превышать 0.9 л.с.
Есть ли решение у этой задачи? Если нет — то почему?
Ответ.
Задача не имеет решения по той простой причине, потому что невозможно обеспечить заданную динамику — для нее не хватит мощности. Каким бы ни был момент.
Вывод. Момент двигателя для разгонной динамики не имеет значения, все решает мощность.
* Пояснение
Вы поднимаете 75 кг получаете от этого энергию mgh. Она преобразуется так:
поскольку a = V2 / 2h, а ускорение а у нас равно g, то V = (2hg)0.5.
Кинетическая энергия тела E = mV2/2 = m2hg/2 = mgh.
Смотри также главу Как движется автомобиль
Как найти угол поворота формула
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α
Вращательное движение, характеристики
| Вращательное движение | Угловая скорость | Угловое ускорение |
|---|---|---|
| Равномерное | Постоянная | Равно нулю |
| Равномерно ускоренное | Изменяется равномерно | Постоянно |
| Неравномерно ускоренное | Изменяется неравномерно | Переменное |
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).
Если
φ — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана
Соотношение между единицами угла
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
( 1 рад = 1 м/ 1 м = 1 ), он не имеет размерности.
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t). Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
ω — угловая частота,
то
Период
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2π:
Угловая скорость
Из формулы для одного оборота следует:
Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного.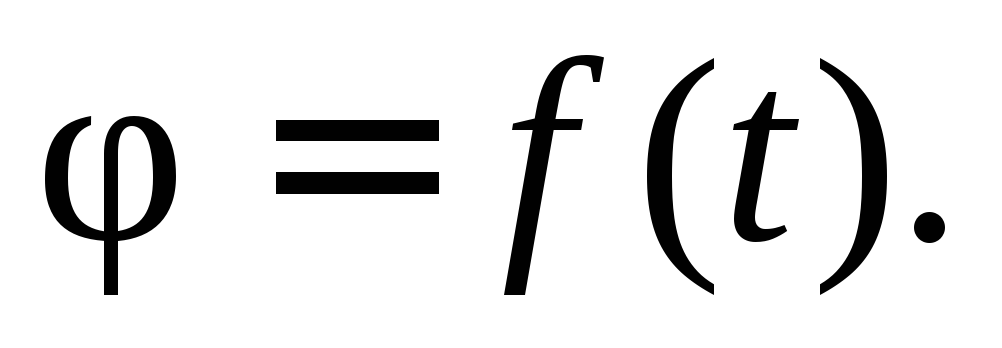 В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.
Движение по окружности – простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
Если угол поворота мал, то ∆ l ≈ ∆ s .
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории – предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости – радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → – v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → – v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
Здесь R → – радиус вектор точки на окружности с началом в ее центре.
Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов – нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 – v 1 – изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) ?,
скорость u — угловая скорость ?,
ускорение a — угловое ускорение ?
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).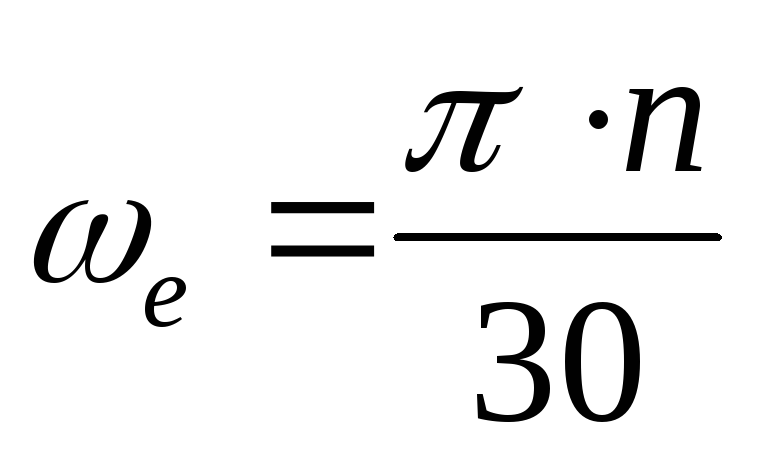
Если
? — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана
Соотношение между единицами угла
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ? от t). Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость ? от t) и график углового ускорения (зависимость ? от t).
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
? — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
? — угловая частота,
то
Период
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2?:
Угловая скорость
Из формулы для одного оборота следует:
Обратите внимание:
• формулы справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного.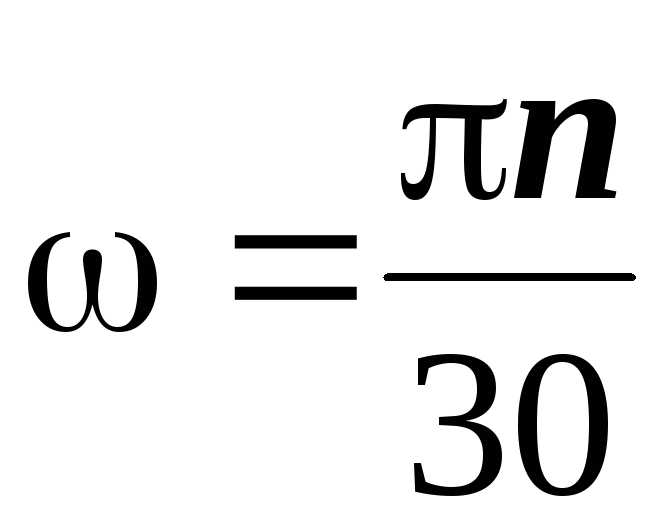 В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.
Равномерное движение тела по окружности
Говорят, что тело движется по окружности равномерно, если его угловая скорость постоянна, т.е. тело за равные промежутки времени поворачивается на один и тот же угол.
? — угловая скорость (постоянная в течение времени t)
? — угловое перемещение
t — время поворота на угол ?
Поскольку на графике угловой скорости площадь прямоугольника соответствует угловому перемещению, имеем:
Постоянная угловая скорость — есть отношение углового перемещения (угла поворота) ко времени, затраченному на это перемещение.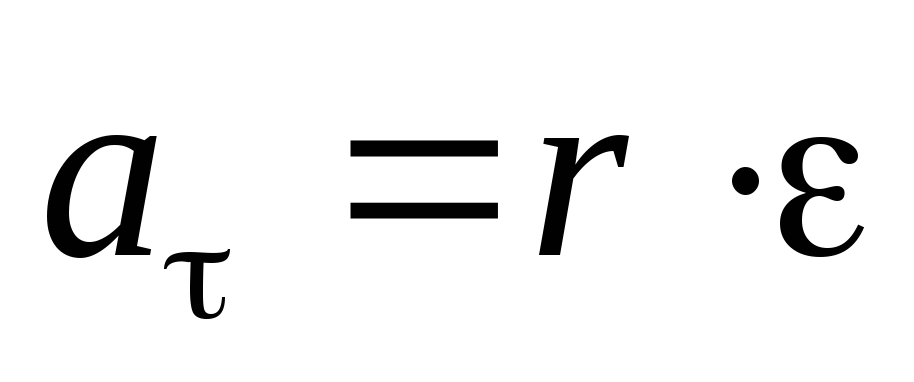
Единица СИ угловой скорости:
Равномерно ускоренное движение по окружности без начальной угловой скорости
Тело начинает двигаться из состояния покоя, и его угловая скорость равномерно возрастает.
? — мгновенная угловая скорость тела в момент времени t
? — угловое ускорение, постоянное в течение времени t
? — угловое перемещение тела за время t, (? в радианах)
t — время
Поскольку на графике скорости угловое перемещение равно площади треугольника, имеем:
Поскольку вращение тела начинается из состояния покоя, изменение угловой скорости ?? равно достигнутой в результате ускорения угловой скорости ?. Поэтому формула принимает следующий вид:
Равномерно ускоренное движение по окружности с начальной угловой скоростью
Начальная скорость тела, равная ?0 в момент t = 0, изменяется равномерно на величину ??. (Угловое ускорение при этом постоянно.)
(Угловое ускорение при этом постоянно.)
?0 — начальная угловая скорость
? — конечная угловая скорость
? — угловое перемещение тела за время t в радианах
t — время
? — угловое ускорение постоянное в течение времени t
Поскольку на графике скорости угловое перемещение соответствует площади трапеции под кривой скорости, имеем:
Так как площадь трапеции равна сумме площадей образующих ее треугольника и прямоугольника, получаем:
Далее из графика скорости следует
Совместив формулы мы получим
После преобразования получаем выражение, не содержащее времени:
Неравномерно ускоренное движение тела по окружности
Движение тела по окружности будет неравномерно ускоренным, если изменение угловой скорости происходит не пропорционально времени, т. е. если угловое ускорение не остается постоянным. В этом случае и угловая скорость и угловое ускорение являются функциями времени.
Связь величин ?, ? и ? представлена на соответствующих графиках.
Мгновенная угловая скорость
Полный угол поворота тела в любой момент времени можно определить по графику углового перемещения. Чем круче график, тем больше в данный момент времени мгновенная угловая скорость.
? — угол между касательной и осью времени t
? — мгновенная угловая скорость
? — угловое перемещение к моменту времени t
Мгновенной угловой скоростью называется первая производная функции ? = ?(t) по времени.
Обратите внимание:
1) чтобы вычислить мгновенную угловую скорость ?, необходимо знать зависимость углового перемещения от времени.
2) формула углового перемещения при равномерном движении тела по окружности и формула углового перемещения при равномерно ускоренном движении по окружности без начальной угловой скорости являются частными случаями формулы (2) соответственно для ? = 0 и ? = const.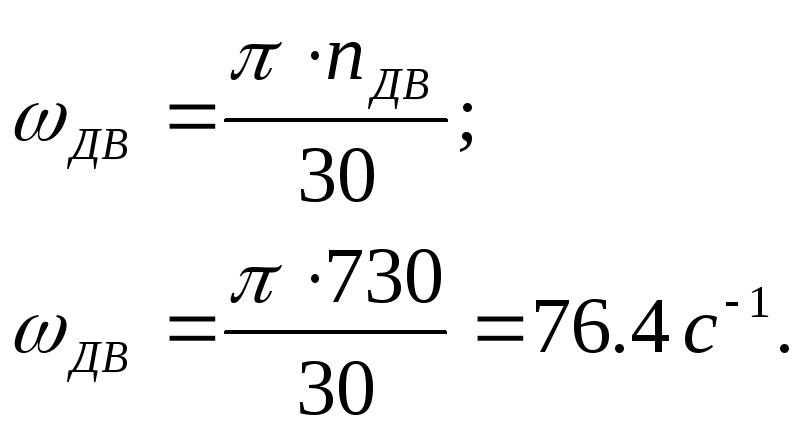
Из формул следует:
Проинтегрировав обе части выражения, получим
Угловое перемещение есть интеграл по времени от угловой скорости.
Обратите внимание:
Для вычисления углового перемещения ? необходимо знать зависимость угловой скорости от времени.
Средняя угловая скорость
Средняя угловая скорость для некоторого интервала времени
Среднее число оборотов определяется аналогично формуле:
Вращательное движение тела, формулы
При вращательном движении твердого тела все элементы его массы, не лежащие на оси вращения, совершают движение по окружности. Аналогично и материальная точка, находящаяся на расстоянии r > 0 от оси вращения, также совершает движение по окружности, как и любое тело, достаточно удаленное от оси вращения.
Линейное перемещение Sл, линейная скорость uл и линейное ускорение aл при таком движении связаны между собой обычными для поступательного движения соотношениями.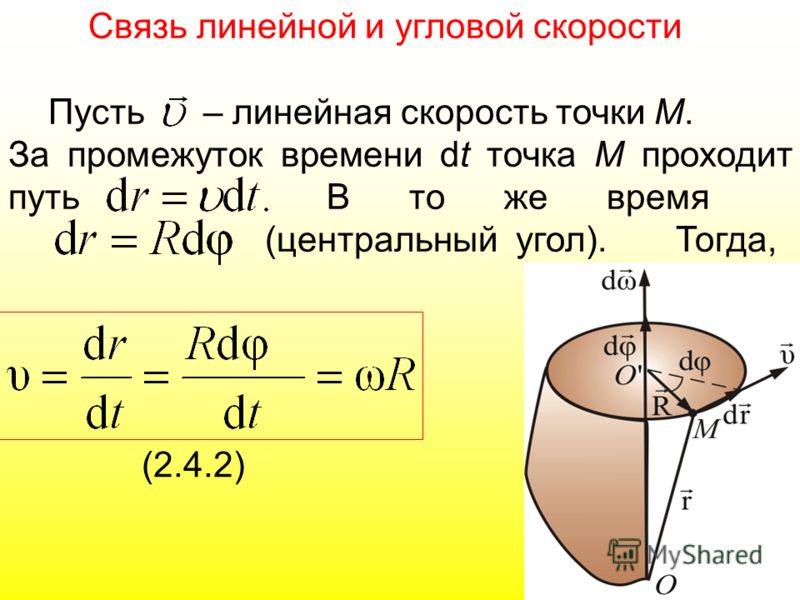
Кроме того, эти величины связаны определенным образом с угловым перемещением ?, угловой скоростью ? и угловым ускорением ?.
| Sл | перемещение тела по траектории, | метр |
|---|---|---|
| Uл | скорость тела при движении по траектории, | метр / секунда |
| aл | ускорение данного тела при движении по траектории, | метр / секунда2 |
| r | радиус траектории, | метр |
| d | диаметр траектории, | метр |
| ? | угловое перемещение тела, | радиан |
| ? | угловая скорость тела, | радиан / секунда |
| ? | угловое ускорение тела, | радиан / секунда2 |
| f | частота, | Герц |
Примечание:Формулы справедливы для постоянных, мгновенных и средних величин, во всех случаях движения тела по окружности.
Векторные величины, характеризующие вращательное движение тела
| Угловая скорость и угловое ускорение тела являются векторными величинами. Эти векторы направлены вдоль оси вращения (аксиальные векторы), а их длина определяет величину соответствующих характеристик вращательного движения. Направление векторов определяется по правилу буравчика, т. е. совпадает с направлением поступательного движения буравчика, рукоятка которого движется в том же направлении, что и тело. |
Определение:Если тело участвует одновременно в нескольких вращательных движениях, то результирующая угловая скорость определяется по правилу векторного (геометрического) сложения:
Величина результирующей угловой скорости определяется по аналогии с формулой (Сложение движений):
или, если оси вращения перпендикулярны друг другу
Примечание: Результирующее угловое ускорение определяется аналогичным образом. Графически результирующую можно найти как диагональ параллелограмма скоростей или ускорений.
Графически результирующую можно найти как диагональ параллелограмма скоростей или ускорений.
Вращательное движение
Вращательное движение — это движение тела, при котором точки описывают окружности, размещенные в параллельных плоскостях, причем центры всех окружностей располагаются на одной прямой, которая обычно определяется как ось вращения.
Вращательное движение представляет траекторию в виде кривой линии, а скорость в каждой точке кривой линии направлена по касательной.
Кинематика вращательного движения характеризуется:
- угловой скоростью и обозначается
- угловым ускорением и обозначается
Угловая скорость — это скорость вращательного движения, которая определяется отношением угла поворота радиуса, соединяющего движущееся тело с центром окружности, к времени, за которое был совершен поворот и записывается формулой: , где — угол поворота радиуса, t — время поворота.
Единицу измерения угла поворота принято считать радианом, но не запрещается выражать его и в градусах. Размерность радиана:
Размерность радиана:
Угловая скорость является векторной величиной, где его угловой вектор скорости направлен в том же направлении, что и поступательное движение правого винта (правило буравчика), где происходит движение по окружности.
Если вращательное движение совпадает с вращением рукоятки буравчика, то поступательное движение буравчика будет указывать на направление угловой скорости и углового ускорения, т.к. они сонаправлены.
Физический смысл угловой скорости при вращательном движении: угловая скорость будет равна углу поворота радиуса за единицу времени.
В Международной системе единиц угловая скорость имеет размерность — рад/с (радиан в секунду).
Связь между угловой и линейной скоростями: так как линейная скорость выражается следующей формулой , а во вращательном движении траектория определена формулой
Скорость во вращательном движении можно также выразить числом оборотов в единицу времени. Через число оборотов легко выразить угловую скорость, которая будет определяться формулой:
Число оборотов есть частота обращения, а величина обратная частоте есть период обращения и определяется формулой: .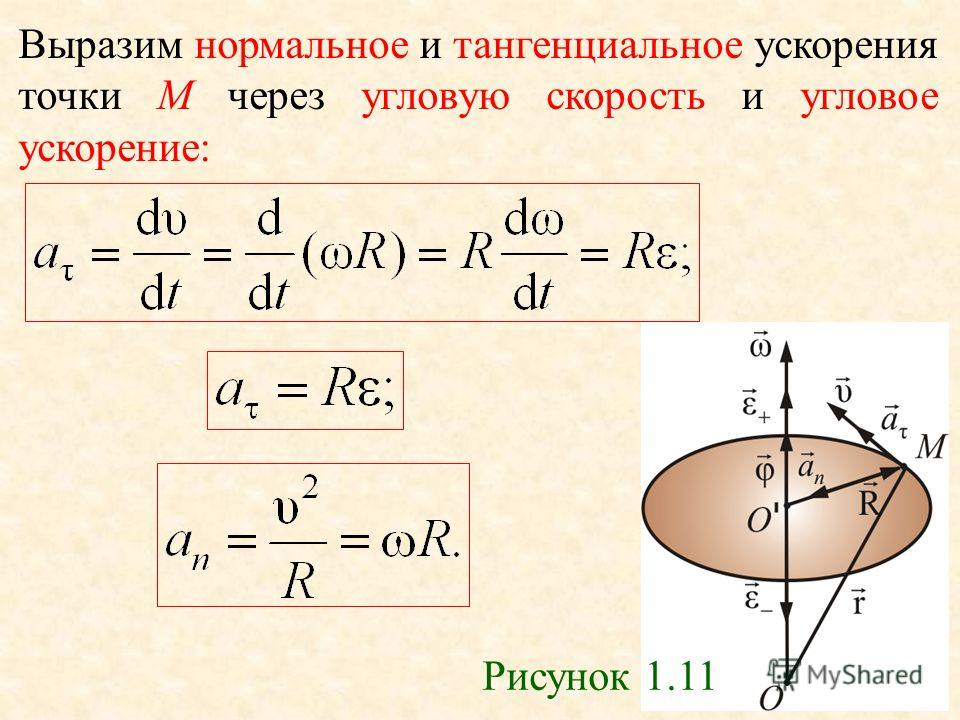
Рассмотрим ускорение во вращательном движении: центростремительное ускорение и угловое ускорение.
Центростремительное ускорение — это такое ускорение, которое образуется при движении тела по окружности и направлено к центру по радиусу окружности. Центростремительное ускорение равно отношению квадрата скорости к радиусу окружности и записывается формулой:
Также центростремительное ускорение выражается в виде произведения линейной и угловой скоростей и записывается формулой:
Угловое ускорение — это ускорение, которое определяется отношением изменения угловой скорости ко времени, за которое произошло изменение этой скорости и записывается в виде формулы: , где — изменение угловой скорости, t — время, за которое произошло изменение угловой скорости.
Физический смысл углового ускорения: при вращательном движении угловое ускорение будет определяться как изменение угловой скорости за единицу времени.
Единицей углового ускорения в международной системе единиц является рад/с (радиан на секунду).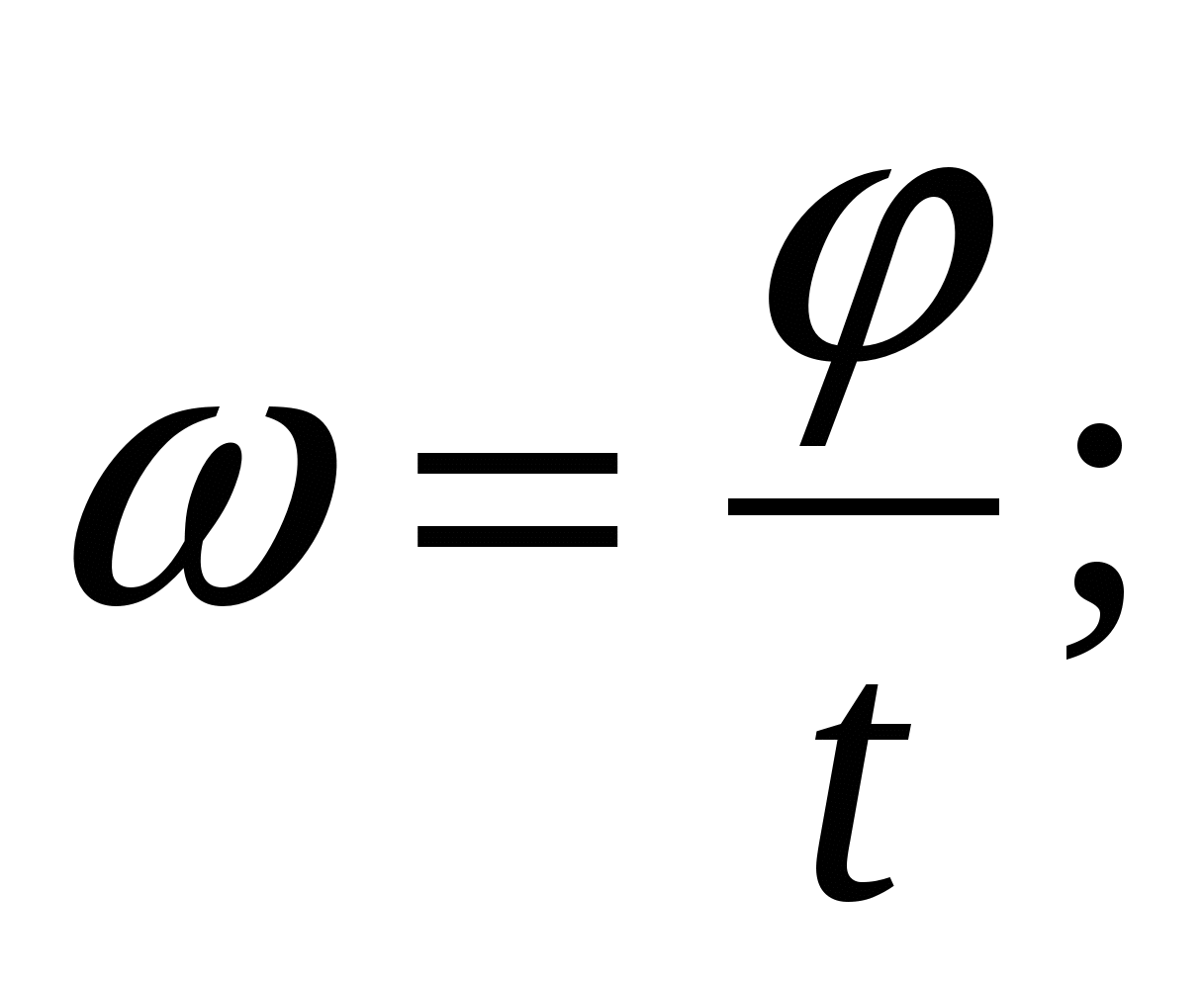
С изменением угловой скорости происходит изменение частоты вращения. Частота вращения характеризуется отношением числа оборотов ко времени и записывается в виде формулы:
Средняя частота вращения определяется соотношением:
являются соответственно начальной и конечной частотой.
Угловое ускорение имеет взаимосвязь с углом поворота. Эта связь определяется следующей формулой:
Вращательные движения — Биомеханика движений фигуриста (Мишин А.Н.)
При рассмотрений обязательных упражнений мы встречались с разновидностями опорных вращательных движений. Мы знаем, что вращательные движения, например повороты, обусловлены главным образом встречным поворотом верхней части тела относительно нижней и не связаны с длительным и быстрым вращением всего тела. Напротив, в произвольном катании наиболее характерными являются движения, связанные с вращением всего тела вокруг продольной оси в 2; 2,5; 3; 3,5 и более оборотов в полете в прыжках, а во вращениях достигают нескольких десятков оборотов.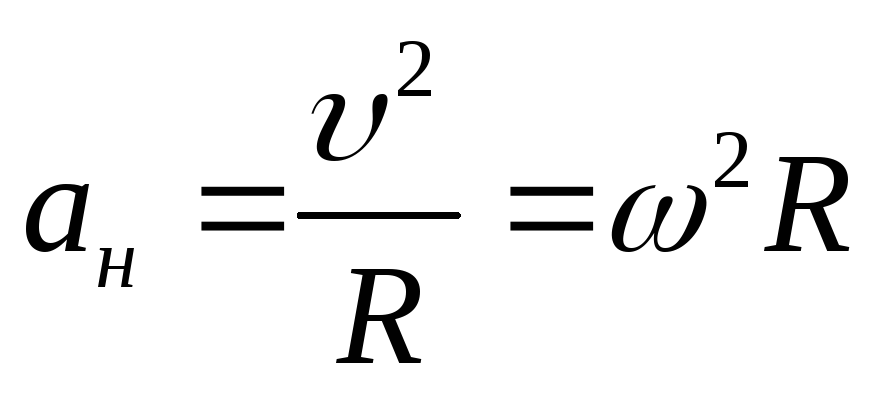 Именно стремительные вращения вокруг вертикальной оси, пожалуй, являются наиболее ярким олицетворением движений произвольного катания.
Именно стремительные вращения вокруг вертикальной оси, пожалуй, являются наиболее ярким олицетворением движений произвольного катания.
Основы механики вращений
В связи с особой важностью вращательных движении в общем комплексе упражнений произвольного катания рассмотрим коротко основные понятия и терминологию механики вращательного движения тела вокруг вертикальной оси.
Характеристики вращательных движений. В качестве пример, вращающегося тела рассмотрим тело фигуриста, выполняющего пируэт на одной ноге (рис. 19, а). Будем условно считать, что вращение его тела происходит вокруг неподвижной оси.
Вращательным движением твердого тела относительно неподвижной оси называется такое движение, при котором две его точки остаются неподвижными. Ось, проходящая через эти точки, называется осью вращения. Вращение тела характеризуется угловой скоростью тела. Величина угловой скорости определяется отношением угла поворота тела к времени, за которое произошел этот поворот:
Угловая скорость характеризуется не только величиной, но и направлением в пространстве, т.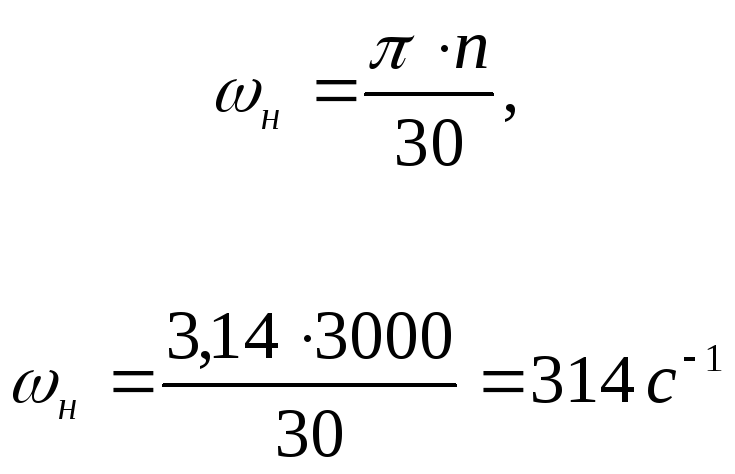 е. является вектором, направленным по оси вращения в ту сторону, откуда вращение наблюдается против часовой стрелки. Различают среднюю угловую скорость, измеряемую в течение нескольких оборотов, и мгновенную угловую скорость тела в данный момент.
е. является вектором, направленным по оси вращения в ту сторону, откуда вращение наблюдается против часовой стрелки. Различают среднюю угловую скорость, измеряемую в течение нескольких оборотов, и мгновенную угловую скорость тела в данный момент.
Если угловая скорость всех точек напряженного тела одинакова, то линейная скорость для каждой точки разная. Зависимость между угловой и линейной скоростями точки выражается формулой:
где R — расстояние точки от оси вращения.
Эта простая зависимость имеет во вращениях важное значение, так как при одной и той же угловой скорости тела со линейные скорости точек тела разные; чем дальше они остоят от оси вращения, тем их линейная скорость больше (рис. 19, б).
Рассмотрим ускорения точки вращающегося тела (рис. 20). Скорость точки является величиной векторной, т. е. может изменяться по величине и направлению в пространстве. Ускорение, вызванное изменением величины вектора скорости, называется касательным или тангенциальным; оно направлено по касательной к траектории движения точки, совпадает с направлением вектора скорости при ускоренном движении и противоположно вектору скорости при замедленном движении. Оно равно:
Оно равно:
При движении точки по окружности ,где — угловое ускорение тела, имеющее размерность
Ускорение, вызванное изменением направления вектора скорости точки, называется нормальным. Оно направлено по нормали в сторону вогнутости траектории и равно при движении точки по окружности . Ускорение точки имеет размерность м/с2.
На рис. 20 приведены векторы касательного и нормального ускорений точки кисти руки фигуриста в пируэте. Таким образом, если вектор скорости изменяется и по величине, и по направлению, то движущаяся точка имеет ускорение, состоящее из касательного и нормального. Геометрическая сумма этих ускорений называется полным ускорением и направлена по диагонали прямоугольника, построенного на векторах касательного и нормального ускорений.
Мерой инертности тела при. поступательном движении является его масса, измеряемая в килограммах. Во вращательном движении особое значение приобретает распределение массы тела относительно оси вращения: удаление массы тела от оси вращения увеличивает инертность тела во вращательном движении вокруг этой оси, а приближение к оси уменьшает.
| Рис. 19. Схема вращения фигуриста |
| Рис. 20. Ускорения точек вращающегося тела |
Мерой инертности тела во вращательном движении является момент инерции, равный сумме произведений масс частей тела на квадраты их расстояний до оси вращения:
где m — массы частей тела; r — расстояние масс тела до оси вращения.
Следует подчеркнуть, что в выражение для величины момента инерции входят расстояния масс частей тела до оси вращения во второй степени, что объясняет значительное изменение момента инерции тела с постоянной массой при перераспределении масс частей тела относительно оси вращения.
Одной из важных характеристик вращающегося тела является количество запасенного им вращательного движения. Она носит название момента количества движения*
или кинетического момента тела К. Величина кинетического момента вращающегося тела измеряется произведением момента инерции тела относительно оси I и угловой скорости, вращения тела вокруг этой оси :
Величина кинетического момента вращающегося тела измеряется произведением момента инерции тела относительно оси I и угловой скорости, вращения тела вокруг этой оси :
Кинетический момент является характеристикой, свойственной вращательному движению.
Закон сохранения момента количества движения
Для анализа вращательных движений фигуриста очень важно знать закон сохранения кинетического момента. Одним из свойств вращающегося тела является стремление сохранить количество приобретенного вращательного движения, или, другими словами, величину кинетического момента. Для рассматриваемого нами случая закон сохранения кинетического момента может быть упрощенно сформулирован следующим образом:
«Кинетический момент тела относительно оси постоянен, если сумма моментов внешних сил относительно оси равна нулю»:
Пренебрегая сопротивлением воздуха и трением конька о лед, можно считать, что при выполнении вращения на тело фигуриста действуют две внешние силы: сила веса и вертикальная составляющая реакции опоры. При хорошем выполнении пируэта эти силы совпадают с осью вращения, поэтому не создают моментов сил относительно оси.
При хорошем выполнении пируэта эти силы совпадают с осью вращения, поэтому не создают моментов сил относительно оси.
Во вращательном движении при выполнении пируэта зависимость проявляется в постоянной взаимосвязи между величинами момента инерции тела и его угловой скоростью вращения. Другими словами, уменьшение одного множителя вызывает увеличение другого настолько, что их произведение остается неизменным. Именно поэтому приближение звеньев тела к оси вращения в процессе группировки, т. е. уменьшение момента инерции, обусловливает увеличение скорости вращения тела и наоборот.
Сравнение моментов инерции тела в различных положениях позволяет, в частности, установить, что группировка рук из положения в стороны может увеличить скорость вращения тела почти вдвое, а переход из положения ласточки в положение стоя с руками вдоль тела—более чем в семь раз. Эти данные не учитывают сил сопротивления, испытываемых телом при вращении, поэтому реальное увеличение угловой скорости всегда меньше и зависит от характера контакта конька со льдом. С этой точки зрения выгодны опора на переднюю треть конька без касания льда зубцами и отсутствие так называемого скобления ребром конька о лед. Наименьшее сопротивление оказывается в случае, если конец опорной ноги во время вращения выполняет петли небольшого размера (3—5 см).
С этой точки зрения выгодны опора на переднюю треть конька без касания льда зубцами и отсутствие так называемого скобления ребром конька о лед. Наименьшее сопротивление оказывается в случае, если конец опорной ноги во время вращения выполняет петли небольшого размера (3—5 см).
Силы инерции при вращениях
Для определения динамической структуры вращательного движения рассмотрим силы инерции, действующие на звенья тела фигуриста при выполнении пируэта.
При анализе ускорений, действующих на точки вращающегося тела, было определено, что в общем случае таких ускорений два: нормальное и касательное. Отсюда на точки вращающегося тела действуют также две силы инерции: нормальная и касательная.
Возьмем систему координат хОу с началом в центре тяжести тела. Ось Oz направим по оси вращения. При равномерном вращении тела вокруг оси Oz с угловой скоростью w на две симметрично расположенные точки A и B будут действовать только нормальные силы инерции, равные по величине направленные противоположно центростремительному ускорению (рис. 21, а). И) формулы видно, что величина этих сил прямо пропорциональна массе точки т, квадрату угловой скорости w и расстоянию r точки от оси вращения.
21, а). И) формулы видно, что величина этих сил прямо пропорциональна массе точки т, квадрату угловой скорости w и расстоянию r точки от оси вращения.
При изменении угловой скорости появляются угловое ускорение и касательные силы инерции, равные по величине и направленные по касательной к траектории точек А и В в стороны, противоположные касательным ускорениям (рис. 21,б). Касательные силы инерции образуют пару сил, лежащую в плоскости, параллельной плоскости хОу. Эта пара сил препятствует вращению фигуриста вокруг оси Oz.
Причины изменения скорости вращения
В различных вращательных движениях и пируэтах фигурист меняет угловую скорость вращения своего тела в значительных пределах. В соответствии с законом сохранения кинетического момента изменение скорости вращения сопровождается изменением момента инерции тела— группировкой или раз-группировкой. Причиной изменения скорости являются определенные силы. Какие же силы вызывают изменение скорости вращения фигуриста?
Пренебрегая силами трения, можно сказать, что внешние силы, как мы уже говорили, не создают значительных моментов относительно оси вращения, т. е. не являются причиной изменений скорости вращения. Следовательно, изменение скорости вращения вызывают силы внутренние —группировки и разгруппировки, т. е. силы активного действия, обусловленные мышечной деятельностью человека.
е. не являются причиной изменений скорости вращения. Следовательно, изменение скорости вращения вызывают силы внутренние —группировки и разгруппировки, т. е. силы активного действия, обусловленные мышечной деятельностью человека.
Рассматривая эти силы, легко убедиться, что линии их действия при группировке и разгруппировке направлены к оси вращения или от нее, т. е., грубо говоря, они не поворачивают тело вокруг оси. Какие же силы непосредственно ускоряют или замедляют вращение тела? Это силы инерции Кориолиса, или, говоря точнее, моменты этих сил. Рассмотрим физическую сущность возникновения сил инерции Кориолиса, определим направление их действия и формулу для определения величины этих сил (рис.22).
В пируэте при группировке и разгруппировке имеют место два движения: вращение тела, которое будем называть переносным, и движение рук и свободной ноги вдоль радиуса к оси или от нее, которое будем называть относительным. Когда руки притягиваются к оси вращения (относительное движение), линейные скорости их частей станут меньше, т.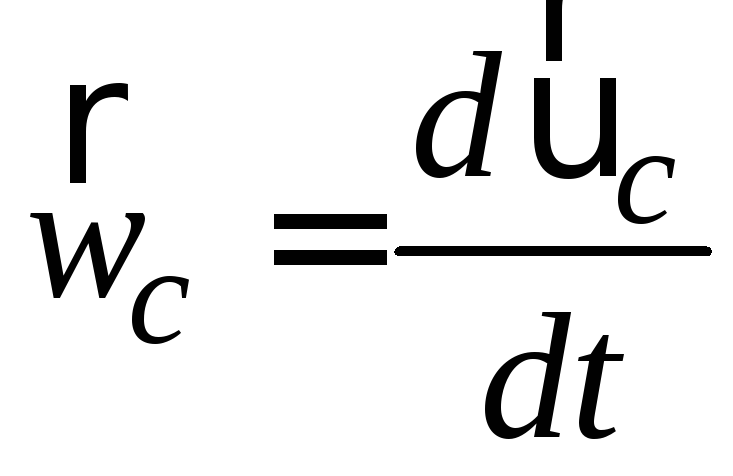 е. звенья тела, участвующие в относительном движении, приобретут отрицательное ускорение (кориолисово). Иными словами —ускорение, направленное против вращения. Так-как всякая сила инерции всегда направлена в сторону, противоположную ускорению, то силы инерции Кориолиса будут направлены по ходу вращения. Они приложены к частям тела, выполняющим группировку, направлены в сторону вращения и увеличивают его угловую скорость.
е. звенья тела, участвующие в относительном движении, приобретут отрицательное ускорение (кориолисово). Иными словами —ускорение, направленное против вращения. Так-как всякая сила инерции всегда направлена в сторону, противоположную ускорению, то силы инерции Кориолиса будут направлены по ходу вращения. Они приложены к частям тела, выполняющим группировку, направлены в сторону вращения и увеличивают его угловую скорость.
Итак, в процессе вращения тела фигуриста, перемещения рук и свободной ноги к оси вращения или от нее возникают силы инерции Кориолиса, которые ускоряют вращение при группировке и замедляют его при разгруппировке. Кориоли-совы силы инерции зависят от величины угловой скорости вращения тела , линейной скорости частей тела при группировке и замедляют его при разгруппировке. Кориолисовы силы инерции зависят от величины угловой скорости вращения тела со, линейной скорости частей тела при группировке и разгруппировке — V, а также от синуса угла между векторами .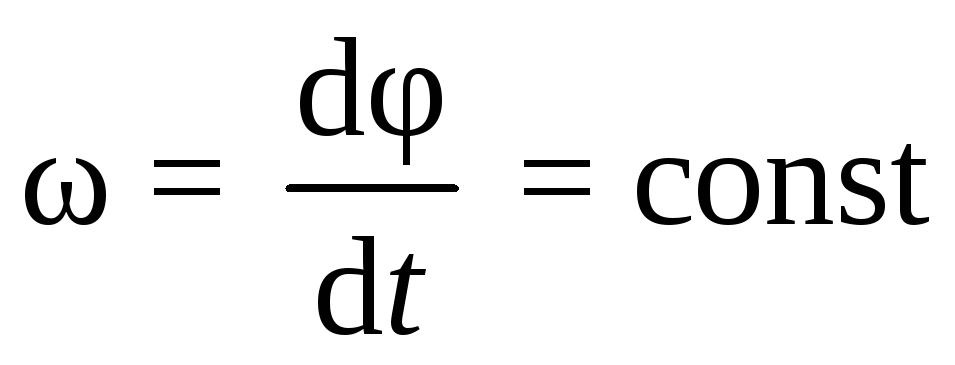 Величина этих сил определяется по формуле:
Величина этих сил определяется по формуле:
На рис.23 приведена совокупность всех сил инерции, действующих на точки А и В вращающегося тела. Необходимо учитывать, что в действительности на каждую из точек тела действует результирующая сила инерции, равная векторной сумме перечисленных сил инерции: нормальной,касательной и кориоли-совой.
| Рис. 21. Силы инерции точек врашающегося тела |
| Рис. 22. Силы инерции Кориолиса, действующие на точки вращающегося тела при группировке |
Прецессия оси вращения
Анализируя вращательное движение, мы говорили, что в процессе вращения о. ц. т. тела находится точно над точкой опоры. В практике фигурного катания встречаются случаи, когда проекция о. ц. г. не совпадает с точкой опоры. В этом случае продольная ось тела z1, проходящая через точку опоры и о. ц. т., начинает вращаться вокруг вертикальной оси z2 с угловой скоростью (рис. 24). Такое движение оси вращающегося тела называют прецессией, а угловую скорость вращательного движения оси — угловой скоростью прецессии. Угловая скорость прецессии может быть определена из следующего выражения:
ц. т., начинает вращаться вокруг вертикальной оси z2 с угловой скоростью (рис. 24). Такое движение оси вращающегося тела называют прецессией, а угловую скорость вращательного движения оси — угловой скоростью прецессии. Угловая скорость прецессии может быть определена из следующего выражения:
где: l-расстояние от точки опоры до о.ц.т. тела; — момент инерции фигуриста относительно оси вращения z1; Р-вес тела фигуриста; — угловая скорость фигуриста вокруг оси z1; —угловая скорость прецессии оси z1.
Прецессионное движение оси вращения нежелательно и с точки зрения качественной оценки пируэта, и, что, пожалуй, главное, с точки зрения управления движением, поскольку ориентация спортсмена, сохранение равновесия резко осложняются.
Из формулы видно, что угловая скорость прецессии обратно пропорциональна угловой скорости вращения фигуриста: чем больше угловая скорость вращения фигуриста, тем меньше угловая скорость прецессии , и наоборот. Отсюда вытекает важный практический вывод: чем больше скорость вращения тела фигуриста в пируэте, тем устойчивее положение оси вращения.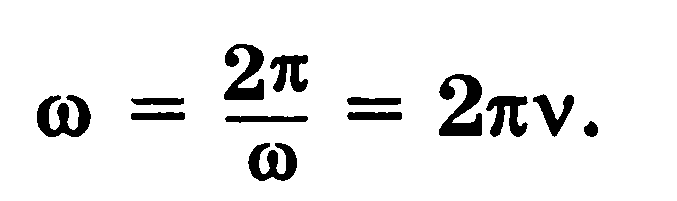
На устойчивость оси вращения положительно влияет также увеличение момента инерции тела относительно оси вращения . Однако наиболее важную роль в устойчивости оси вращения играет положение центра тяжести. Момент силы тяжести относительно точки опоры определяет угловую скорость прецессии. Для уменьшения угловой скорости прецессии следует уменьшить величину этого момента, т. е. стремиться к такому положению, при котором о.ц.т. тела находится над точкой опоры.
Устойчивость вращения к прецессии связана с расстоянием l от о.ц.т. до неподвижной точки вращения. Чем оно меньше, тем при прочих равных условиях меньше угловая скорость прецессии. Не удивительно поэтому, что наиболее устойчивым вращением является волчок —пируэт, в котором расстояние l минимально.
Интересно отметить, что устранение момента силы тяжести приводит к мгновенному устранению прецессии. Дру-гими словами, прецессия не обладает инерцией.
На практике встречаются две основные причины возникновения прецессии в пируэтах.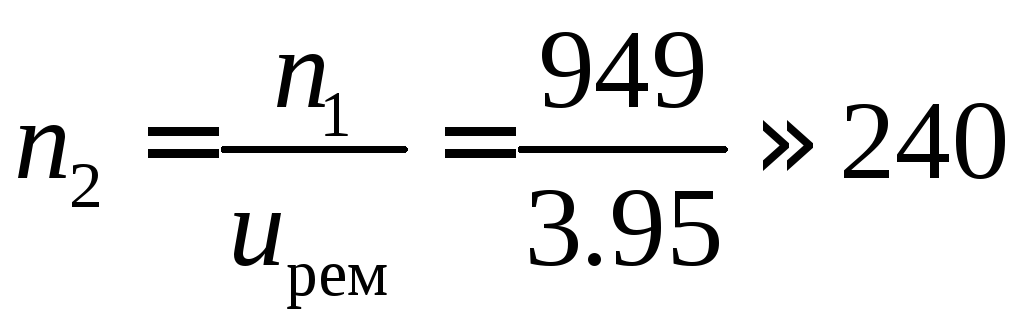 В первом случае несовпадение точки опоры и проекции силы тяжести вызвано несовершенным въездом во вращение, неправильным определением центра вращения. Здесь резкое торможение, раннее начало вращения, неточное маховое движение порождают инерционные силы, отклоняющие о.ц.т. тела от вертикали.
В первом случае несовпадение точки опоры и проекции силы тяжести вызвано несовершенным въездом во вращение, неправильным определением центра вращения. Здесь резкое торможение, раннее начало вращения, неточное маховое движение порождают инерционные силы, отклоняющие о.ц.т. тела от вертикали.
В другом случае смещение о.ц.т. вызвано неправильным перемещением частей тела при смене позы.
Влияние положения тела фигуриста при вращениях на частоту сердечных сокращений*
Влияние положения тела фигуриста на характер кровообращения и частоту сердечных сокращений при вращениях наиболее ярко прослеживается при выполнении таких элементов, как вращение в ласточке, в ласточке со сменой ног, прыжок во вращение ласточка. В это время частота сердечных сокращений оказывается наиболее низка.
Интересна пульсограмма вращения в ласточке. При выполнении данного элемента отмечено заметное уменьшение частоты сердечных сокращений —6—12 уд/мин по сравнению с исходным — фоновым.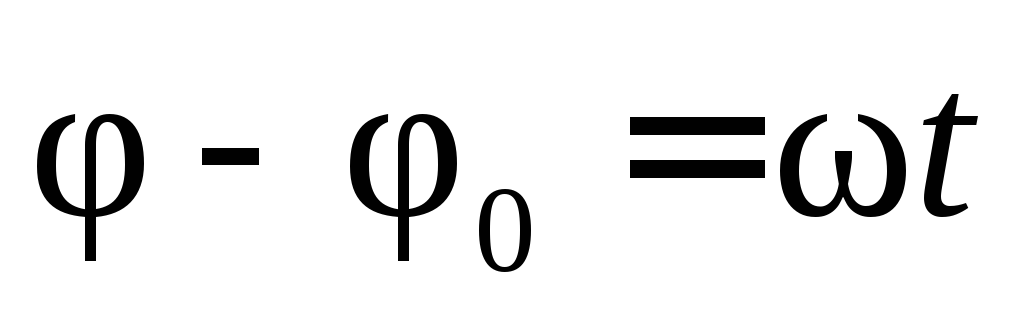
Этот интересный факт требует более глубокого исследования. Однако уже на основании проведенных опытов было высказано предположение, что данное явление может быть объяснено антиортостатической реакцией организма. Имеется в виду практически горизонтальное положение верхней части тела и свободной ноги при вращении. Возможно, что урежение пульса действительно является следствием реакции барорецепторов скаротидных синусов на увеличение венозного возврата крови, вызванного центробежными силами инерции.
| Рис. 23. Совокупность сил инерции, действующих на точки вращающегося тела |
| Рис. 24. Прецессия оси вращения тела фигуриста |
Исследования автора, проведенные под руководством профессора А. Б. Гандельсмана, позволяют предположить более сложную природу такого явления. Не отрицая возможности влияния центробежных сил на характер передвижения масс крови, хочется обратить внимание на два обстоятельства. Вращение в ласточке является пируэтом, в котором, пожалуй, в наибольшей степени выражен статический компонент движения. Вот почему энергетика этого упражнения весьма низкая. Кроме того, характер въезда во вращение и выезда из него не связан с необходимостью глубокого приседания и подъема, как в волчке, или группировки, как во вращении винт. Это также свидетельствует о наиболее низкой энергетической стоимости вращения в простой ласточке. Таким образом, можно предположить, что одной из причин урежения сердечного ритма при вращении в простой ласточке является именно низкая энергетика этого упражнения—более низкая, чем энергетика комплекса различных движений, при которых измеряется фоновый пульс.
Не отрицая возможности влияния центробежных сил на характер передвижения масс крови, хочется обратить внимание на два обстоятельства. Вращение в ласточке является пируэтом, в котором, пожалуй, в наибольшей степени выражен статический компонент движения. Вот почему энергетика этого упражнения весьма низкая. Кроме того, характер въезда во вращение и выезда из него не связан с необходимостью глубокого приседания и подъема, как в волчке, или группировки, как во вращении винт. Это также свидетельствует о наиболее низкой энергетической стоимости вращения в простой ласточке. Таким образом, можно предположить, что одной из причин урежения сердечного ритма при вращении в простой ласточке является именно низкая энергетика этого упражнения—более низкая, чем энергетика комплекса различных движений, при которых измеряется фоновый пульс.
Необходимо также учитывать эмоциональную сторону упражнения. В этом плане следует отметить, во-первых, сравнительную комфортность положения тела при вращении в ласточке и, во-вторых, наиболее низкую из всех вращений угловую скорость, которая и обусловливает относительно спокойный эмоциональный фон упражнения.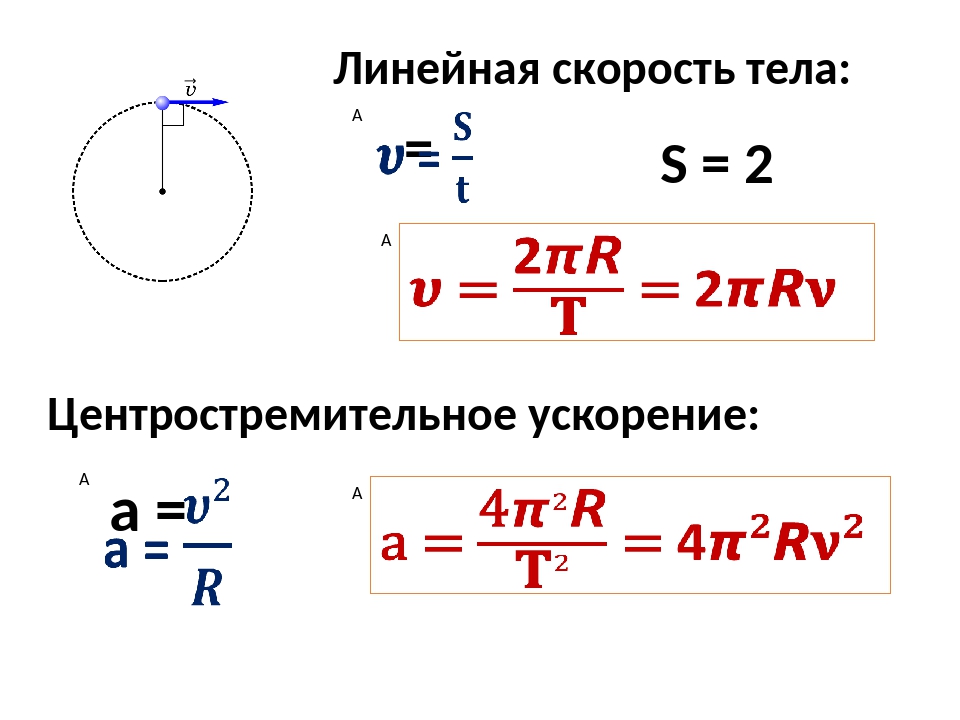
Другие же сходные по биомеханической структуре элементы: вращение в ласточке со сменой ног и прыжок во вращение ласточка —вызывают более выраженную ответную пульсовую реакцию, и феномен уменьшения частоты сердечных сокращений проявляется в меньшей степени. Этот факт связан с тем, что наряду с менее благоприятным эмоциональным фоном при выполнении данных двух элементов фигурист затрачивает дополнительную энергию на отталкивание и смену ног при вращении, что, естественно, увеличивает частоту сердечных сокращений.
Феномен уменьшения частоты сердечных сокращений при простом вращении в положении ласточка может быть использован при составлении произвольных программ.
Рационально включать вращения в ласточке в те места программы, после которых необходим промежуточный отдых, расслабление, снижение эмоционального фона, успокоение.
Анализ техники вращений
Благодаря кривизне лезвия конька в арсенале фигуриста может быть большое количество вращательных движений, возникающих естественно и выполняемых сравнительно легко.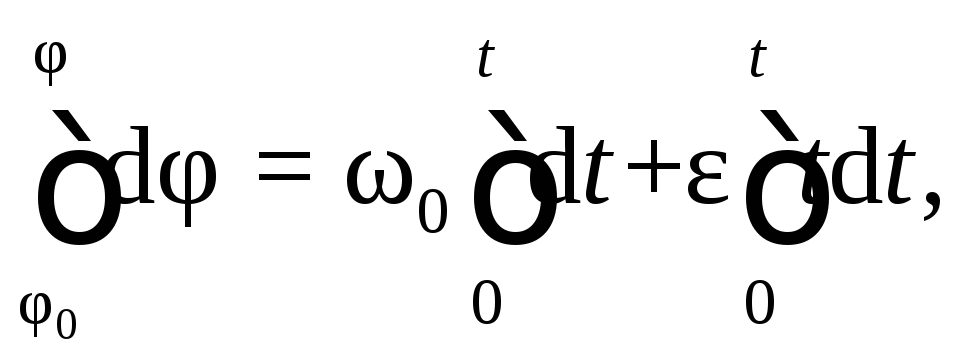 Такими движениями являются опорные вращения — пируэты. Они разнообразят произвольную программу, позволяют спортсмену продемонстрировать способность сохранять равновесие в сложной позиции при быстром вращении.
Такими движениями являются опорные вращения — пируэты. Они разнообразят произвольную программу, позволяют спортсмену продемонстрировать способность сохранять равновесие в сложной позиции при быстром вращении.
Пируэт представляет собой длительное вращательное движение тела вокруг вертикальной оси без заметного перемещения точки опоры. В зависимости от направления вращения различают пируэты вперед (вращение происходит в сторону опорной ноги) и назад (вращение выполняется в сторону свободной ноги).
С точки зрения позы, в которой выполняется пируэт, можно выделить три основные группы: пируэты стоя, пируэты в приседе (волчки) и пируэты в положении ласточка.
Различают простые пируэты, в которых вращение происходит в относительно неизменной позе, и сложные —со сменой позы (например, с переходом из положения стоя в положение сидя).
Пируэты могут выполняться на одной и обеих ногах. В последнем случае понятие «направление вращения» (вперед или назад) теряет смысл, так как обе ноги являются опорными. Поэтому здесь указывают лишь сторону вращения. В произвольных программах сейчас, как правило, встречаются сложные пируэты, состоящие из комбинаций перечисленных пируэтов.
Поэтому здесь указывают лишь сторону вращения. В произвольных программах сейчас, как правило, встречаются сложные пируэты, состоящие из комбинаций перечисленных пируэтов.
Пируэт состоит из подхода, въезда, вращения и выезда. На рис. 25 приведены следы, оставленные при выполнении пируэта вперед. Дуги 1, 2, 3 и 4 соответствуют подходу, дуга 5 —въезду, точка 6—вращению, а дуги .7 и 8 —выезду. Подход. Существует несколько вариантов подходов. Наиболее удобным и поэтому целесообразным для начального обучения является сочетание тройки вперед-наружу с перебежкой назад. Используют подходы в виде тройки вперед-внутрь—назад-наружу, а также ходом вперед-наружу, подходе важно сохранять плавность скольжения, хорошу осанку, чтобы вращение было естественным, а приготовление к нему — незаметным.
Въезд. Это наиболее сложная и ответственная часть пируэта. Именно здесь возникает вращение. Как правило, если фигурист сообщил телу устойчивое вращение, то сохранять и поддерживать его не составляет большой сложности.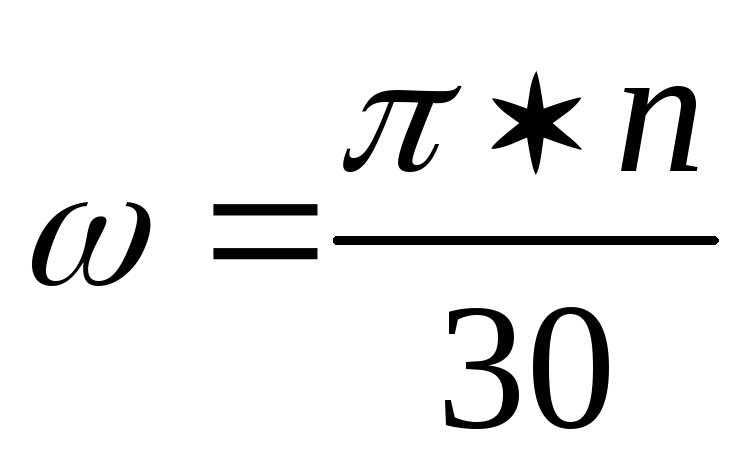 След, оставляемый коньком при въезде, представляет собой кривую с плавно меняющейся кривизной. Выполняют въезд на согнутой ноге и не выпрямляют ее до тех пор, пока не возникнет устойчивое вращение.
След, оставляемый коньком при въезде, представляет собой кривую с плавно меняющейся кривизной. Выполняют въезд на согнутой ноге и не выпрямляют ее до тех пор, пока не возникнет устойчивое вращение.
Вращение телу можно придать двумя способами: толчком ногой при переходе с последней дуги подхода на въездную дугу, а также круговым маховым движением свободной ноги и руки при въезде. Во вращении стоя и в волчках следует использовать оба способа. При вращениях в ласточке маховое движение не всегда эффективно. Здесь оно приводит к выведению свободной ноги вперед, и для принятия положения ласточки фигурист вынужден в конце въезда резко отводить свободную ногу назад. Это движение часто вызывает потерю равновесия. Более простым и надежным является въезд с отведенной назад свободной ногой и одноименной рукой.
Напротив, при въезде в волчок круговое маховое движение весьма целесообразно и эффективно. Необходимо во время подхода сделать сильный мах руками и свободной ногой назад.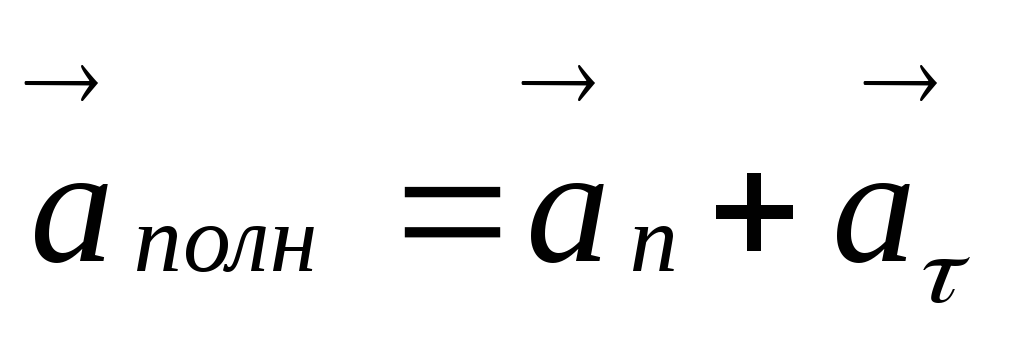 Мах, т. е. выведение рук и ноги вперед, следует начинать только тогда, когда дуга достигнет максимальной кривизны.
Мах, т. е. выведение рук и ноги вперед, следует начинать только тогда, когда дуга достигнет максимальной кривизны.
Въезд во вращение стоя, по существу, не отличается от въезда в волчок. Здесь только опорная нога более выпрямлена. Не следует, однако, выпрямлять ее полностью: это может привести к нарушению равновесия.
Для устойчивости вращения очень важно, как выполнен конечный участок дуги въезда. В пируэтах вперед в конце въезда, когда дуга достигла максимальной кривизны, следует поворот тройкой вперед-наружу, после чего —окружность диаметром 30—40 см, выполняемая ходом назад-внутрь, и только затем начинается вращение.
| Рис. 25. Следы пируэта вперед |
Вращение. В простых пируэтах группировка отсутствует и положение, принятое в начале вращения, сохраняется почти неизменным. Поэтому здесь, как и при выполнении спиралей, важна точность положения тела, стабильность удержания его. Малейшая погрешность, допускаемая на протяжении пяти, шести и более оборотов, портит впечатление.
Малейшая погрешность, допускаемая на протяжении пяти, шести и более оборотов, портит впечатление.
В ласточке необходимо вращаться на плоскости конька, не касаясь льда зубцами. Начинающие фигуристы часто теряют равновесие уже в начале вращения, так как чрезмерно перемещают центр тяжести тела вперед. Чтобы избежать этого, необходимо на протяжении всего вращения, особенно в начале его, оттягивать свободную ногу назад. Она должна быть выпрямлена, развернута, голова направлена вперед, а вытянутые руки на одной линии, находящейся в одной плоскости с опорной и свободной ногами.
В волчке вращение происходит на передней трети конька. Для повышения устойчивости в начале вращения допустимо легкое касание льда зубцами. Наиболее распространенная ошибка здесь—падение назад. Чтобы предотвратить ее, развернутая свободная нога и руки должны быть прямыми и вытянутыми вперед. Опорная нога при этом согнута, голова подтянута, плечи опущены.
Вращение стоя также происходит на передней трети конька с легким касанием льда зубцами.
В сложных пируэтах происходит группировка. Ее можно выполнять в двух вариантах: в первом варианте приближение рук и свободной ноги к оси вращения происходит при неизменном основном положении тела (например, стоя или в приседе), во втором поза меняется —части тела приближаются к оси вращения (например, переход из ласточки в волчок или из волчка в положение стоя). При этом скорость вращения тела возрастает.
Рассмотрим пример группировки в пируэте стоя, называемом винтом. Из положения, когда нога вытянута вперед, правую ногу, не опуская, выводят вперед, сгибают в колене и скрещивают с левой, на которой происходит вращение. Затем правую ногу опускают, скользя задней поверхностью голени по левой. Это движение сопровождается группировкой рук одновременно с группировкой ног или несколько позже. В заключительной фазе руки плотно прижимают к телу, а слегка согнутую опорную ногу выпрямляют, что дает дополнительное увеличение скорости вращения. Необходимо следить за симметрией группировки, ибо неодинаковое движение рук вызывает нарушение равновесия. В этом пируэте скорость вращения наибольшая—до 4 и более оборотов в секунду.
В этом пируэте скорость вращения наибольшая—до 4 и более оборотов в секунду.
Выезд. Выполнению всегда предшествует движение, обратное группировке,— разгруппировка. Делается это для уменьшения скорости вращения, что облегчает выполнение выезда. Здесь важно, чтобы разгруппировка заканчивалась небольшим сгибанием опорной ноги.
Обычно выезд выполняют со сменой ноги: ранее свободная ном становится опорной, и вращение завершается тол-ком, аналогичным толчку в обязательной фигуре № 3, с последующим скольжением назад-наружу. Данный вариант выезда наиболее распространен; его рекомендуют при разучивании пируэтов. В программах мастеров встречаются более сложные выезды (например, вперед-наружу со сменой ноги, назад-внутрь без смены ноги, въезд в остановку, в прыжок). При любом варианте следует стремиться к слитности всех движений, к такому выполнению, при котором выезд является естественным продолжением вращения.
Заклоны. Особой разновидностью пируэтов являются так называемые заклоны.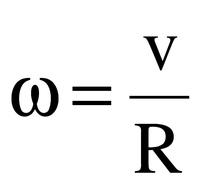 Их выполняют со значительным прогибом назад или в сторону и с откинутой головой. Вращение с необычным положением головы усложняет пространственную ориентировку, вызывает нарушение координации движений, порой сопровождается головокружением. В то же время заклоны —очень ценное упражнение для совершенствования равновесия.
Их выполняют со значительным прогибом назад или в сторону и с откинутой головой. Вращение с необычным положением головы усложняет пространственную ориентировку, вызывает нарушение координации движений, порой сопровождается головокружением. В то же время заклоны —очень ценное упражнение для совершенствования равновесия.
Прежде чем осваивать данную группу пируэтов, фигурист должен научиться уверенно принимать эту позу без коньков. Подход и въезд делают как в обычных вращениях. Положение заклона принимают в тот момент, когда начинается вращение. Далее прогиб рекомендуется увеличить и вместе с тем по возможности (незаметно для наблюдателя) выполнять группировку. Опытные фигуристы иногда поднимают одну руку вверх или опускают вниз, чтобы ее положение совпадало с положением оси вращения: это обеспечивает дополнительную группировку, что вызывает увеличение скорости вращения. С заклонами весьма схожи паузы с захватом свободной ноги одной или двумя руками.
Пируэты назад.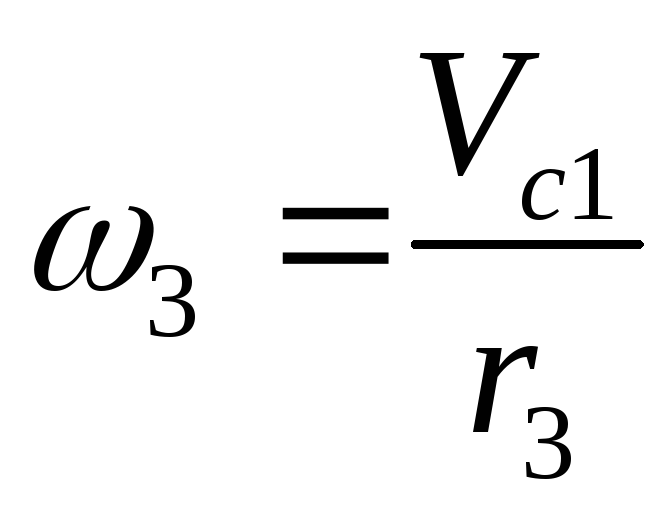 Исключительно ценными для дальнейшего овладения прыжками являются пируэты назад. Их выполняют в тех же позах, что и пируэты вперед. Но есть у них некоторые особенности. Так, несмотря на то, что направление общего вращения тела в пируэте назад и вперед может быть одно и то же, ощущения, испытываемые фигуристом, различны. Пируэты назад наиболее точно имитируют движения тела в полете при выполнении прыжков, поэтому важны как подготовительные упражнения. Они красивы; включают их в различные комбинации.
Исключительно ценными для дальнейшего овладения прыжками являются пируэты назад. Их выполняют в тех же позах, что и пируэты вперед. Но есть у них некоторые особенности. Так, несмотря на то, что направление общего вращения тела в пируэте назад и вперед может быть одно и то же, ощущения, испытываемые фигуристом, различны. Пируэты назад наиболее точно имитируют движения тела в полете при выполнении прыжков, поэтому важны как подготовительные упражнения. Они красивы; включают их в различные комбинации.
При обучении вращениям назад рекомендуется выполнять подход (рис. 26) в виде крутой дуги вперед-внутрь (дута 1). Въезд представляет собой дугу вперед-внутрь на другой ноге (дуга 2), описывая которую фигурист делает энергичное вращательное движение свободной ноги и рук. Вращение (точка 3) может выполняться в любом положении (в ласточке, волчке, стоя), а также в промежуточных положениях. Выезд (дуга 4) лучше всего разучивать на той же ноге, на которой происходило вращение: это помогает совершенствовать выезд из многооборотных прыжков.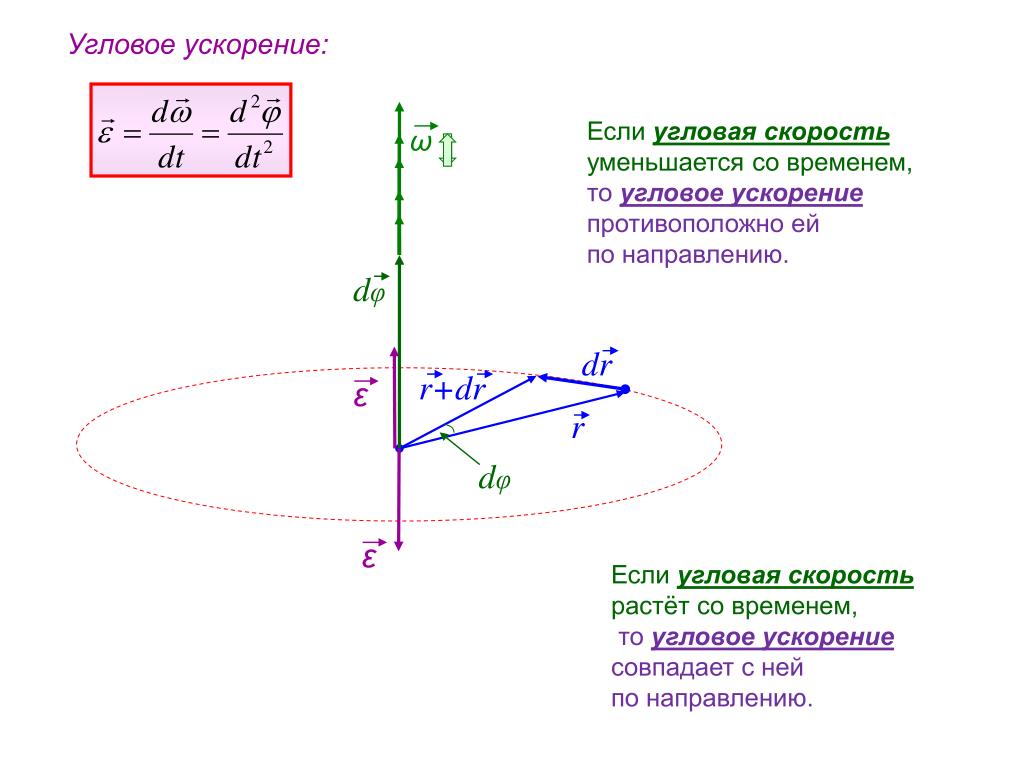
Освоение пируэтов вперед и назад открывает большие возможности для выполнения различных комбинаций: это волчок со сменой ноги, вращение в ласточке со сменой ноги, варианты смены положения тела и ноги.
Для успешного овладения пируэтами важно определить удобную для спортсмена сторону вращения. Большинство фигуристов быстрее овладевают вращениями влево и лучше их переносят. Наиболее простой и верный способ определения «своего» направления вращения —выполнение пируэта назад с выездом без смены ноги. Если этот, пируэт и выезд увереннее и легче получаются на правой ноге, следует лучшие варианты своих вращений планировать влево, и наоборот.
Разучивание пируэтов вперед и назад в различных позах помогает подготовить организм фигуриста к вращательным нагрузкам, которые он постоянно испытывает во время катания.
Специальные упражнения для совершенствования вращений
Одним из важных направлений в тренировке вращений вне льда является работа над гибкостью.
При этом необходимо сочетать традиционные способы развития пассивной гибкости с помощью различных растягиваний, шпагатов, махов и т. п. с развитием активной гибкости. Например, одной из наиболее сложных поз, особенно для мальчиков, является вращение в ласточке. Для ее совершенствования целесообразно применять утяжелитель, прикрепляемый к стопе свободной ноги. Он позволяет добиваться хорошего эффекта при развитии как пассивной гибкости (выполнение махов назад), так и активной (удержание свободной ноги с грузом в требуемой позе).
| Рис. 26. Следы пируэта назад |
Этот же способ эффективен и в занятиях вне льда. Лучшим способом совершенствования положения тела во вращении ласточка, на наш взгляд, является разучивание так называемой качающейся ласточки—поочередно на обеих нoгax.
Целесообразно использовать тренажер «Грация» для совершенствования точности позы и чувства равновесия. Для совершенствования общей выносливости фигуриста к вращательным нагрузкам весьма эффективны специальные тренажеры в виде вращающихся платформ с электроприводом и плавной регулировкой скорости вращения в пределах от ноля до 5 и более оборотов в секунду.
Для совершенствования общей выносливости фигуриста к вращательным нагрузкам весьма эффективны специальные тренажеры в виде вращающихся платформ с электроприводом и плавной регулировкой скорости вращения в пределах от ноля до 5 и более оборотов в секунду.
В тренировках на льду основное внимание следует уделять поиску оптимального варианта въезда во вращение и оптимального контакта конька со льдом во время вращения. Следует анализировать характер следов на льду, обращая главное внимание на отсутствие скоблений, касания льда зубцами.
Хорошим средством совершенствования качества въезда во вращения, повышения стабильности их выполнения являются тренировки с выключением зрения. Надевая специальные непрозрачные очки, фигурист выполняет требуемое вращение. При этом обостряется деятельность двигательного, вестибулярного, тактильного и слухового анализаторов. Опыты показали, что такие упражнения повышают устойчивость навыка, делают выполнение вращений более уверенными, стабильными. Практика показала, что у одних фигуристов принятие требуемой позы происходит с участием зрительного анализатора, выключение зрения у них нарушает точность позы; у других же это происходит практически без участия зрительного анализатора. Сравнение стабильности и качества выполнения вращений показало, что обеспечение позы в основном с помощью двигательного анализатора более совершенно.
Практика показала, что у одних фигуристов принятие требуемой позы происходит с участием зрительного анализатора, выключение зрения у них нарушает точность позы; у других же это происходит практически без участия зрительного анализатора. Сравнение стабильности и качества выполнения вращений показало, что обеспечение позы в основном с помощью двигательного анализатора более совершенно.
| Sл | перемещение тела по траектории, | метр |
|---|---|---|
| Uл | скорость тела при движении по траектории, | метр / секунда |
| aл | ускорение данного тела при движении по траектории, | метр / секунда2 |
| r | радиус траектории, | метр |
| d | диаметр траектории, | метр |
| ? | угловое перемещение тела, | радиан |
| ? | угловая скорость тела, | радиан / секунда |
| ? | угловое ускорение тела, | радиан / секунда2 |
| f | частота, | Герц |
Примечание:Формулы справедливы для постоянных, мгновенных и средних величин, во всех случаях движения тела по окружности.
Векторные величины, характеризующие вращательное движение тела
| Угловая скорость и угловое ускорение тела являются векторными величинами. Эти векторы направлены вдоль оси вращения (аксиальные векторы), а их длина определяет величину соответствующих характеристик вращательного движения. Направление векторов определяется по правилу буравчика, т. е. совпадает с направлением поступательного движения буравчика, рукоятка которого движется в том же направлении, что и тело. |
Определение:Если тело участвует одновременно в нескольких вращательных движениях, то результирующая угловая скорость определяется по правилу векторного (геометрического) сложения:
Величина результирующей угловой скорости определяется по аналогии с формулой (Сложение движений):
или, если оси вращения перпендикулярны друг другу
Примечание: Результирующее угловое ускорение определяется аналогичным образом. Графически результирующую можно найти как диагональ параллелограмма скоростей или ускорений.
Графически результирующую можно найти как диагональ параллелограмма скоростей или ускорений.
- Попроси больше объяснений
- Следить
- Отметить нарушение
Emka1 09.06.2014
Ответ
Угловое ускорение
ε=Δω/t
На участке 0-6: ε=200/6=33.3 рад/с²
На участке 6-8: ε=0
На участке 8-10 (и далее): ε=(0-(-200))/2=100 рад/с²
Строим график ε(t)
Угловой путь
φ=φ₀+εt²/2
На участке 0-6: φ₀=0: φ₁=33.3*6²/2=600 рад
На участке 6-8: φ₀=600 рад: φ₂=600 рад
На участке 8-10: φ₀=600 рад; φ₃=600+100*2²=800 рад
Строим график φ(t)
За первые 6 с угловое ускорение постоянно и равно 33,3 рад/с². Поэтому среднее значение за этот промежуток времени тоже равно 33,3 рад/с²
Кикоин А.К. Формулы кинематики для вращательного движениях //Квант. — 1983. — № 11. — С. 25-26.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Для описания движения материальной точки или поступательного движения твердого тела пользуются следующими кинематическими величинами: перемещением (
vec s), скоростью (
vec upsilon) и ускорением (
vec a). 2_ <0x>= 2 a_x s_x end) .
2_ <0x>= 2 a_x s_x end) .
Но при вращательном движении тела величинами (
vec a) пользоваться неудобно, так как различные точки тела за один и тот же промежуток времени совершают разные перемещения и движутся с различными скоростями и ускорениями. Поэтому для описания вращательного движения вводятся специальные, так называемые угловые величины: угол поворота φ, угловая скорость ω (о них говорится в учебнике «Физика 8») и угловое ускорение (
varepsilon = frac<omega – omega_0> <Delta t>= frac<Delta omega><Delta t>) (о нем в учебнике не говорится). Для различных точек вращающегося тела они одинаковы.
Угловые величины связаны с величинами (
vec a), которые, в отличие от угловых, называют линейными, простыми соотношениями:
egin s = r varphi \ upsilon = r omega \ a = r varepsilon end) .
Здесь s — модуль перемещения данной точки тела (при малых перемещениях s — это длина дуги), r — радиус окружности, по которой она движется, υ — модуль скорости точки, а — модуль касательной проекции ускорения [1] .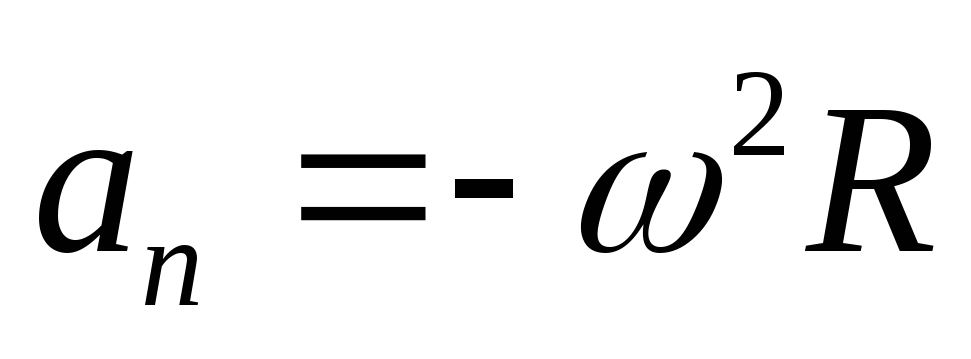 2_0 = 2 varepsilon varphi) .
2_0 = 2 varepsilon varphi) .
Вообще любая формула кинематики вращательного движения тела получается из соответствующей формулы кинематики точки (или поступательного движения тела) простой заменой линейной величины соответствующей угловой.
В заключение отметим (в учебнике «Физика 8» об этом не говорится), что величины φ, ω и ε тоже считаются векторными. (Нужно же отличать повороты или вращения по часовой стрелке от поворотов или вращений против часовой стрелки!) Принимается, что векторы угловых величин направлены вдоль оси вращения тела по правилу правого винта: если мысленно вращать правый винт так, как вращается тело, то направление поступательного движения винта укажет направление соответствующего вектора (см. рисунок). Правда, для углового ускорения это правило несколько усложняется: вектор ускорения совпадает по направлению с направлением движения винта, если угловая скорость возрастает по модулю, и направлен в противоположную сторону, если угловая скорость уменьшается.
об / мин в зависимости от угловой скорости | Sciencing
Число оборотов в минуту (об / мин) и угловая скорость, два показателя скорости вращения точки относительно другой точки, используются для решения задач физики, машиностроения и компьютерного программирования. Часто частота вращения и угловая скорость используются как взаимозаменяемые для моделирования вращения шкивов и качения колес в инженерных симуляторах и видеоиграх.
Использование угловой скорости
Угловая скорость используется для выражения скорости вращения круглого объекта, например колеса.Поскольку в круге 360 градусов, колесо, которое совершает один полный оборот вокруг своего центра за одну секунду, будет иметь угловую скорость 360 градусов в секунду. Поскольку секундная стрелка часов совершает один полный оборот вокруг своего центра за 60 секунд, она имеет угловую скорость 360 градусов каждые 60 секунд или 6 градусов в секунду.
Оборотов в минуту Использует
Оборотов в минуту также используется для выражения скорости вращения круглого объекта, такого как колесо. Поскольку один оборот эквивалентен одному полному обороту или вращению вокруг центральной точки, говорят, что колесо, которое совершает один полный оборот вокруг своего центра за минуту, вращается вокруг своего центра со скоростью 1 оборот в минуту или 1 оборот в минуту. Поскольку секундная стрелка часов совершает один полный оборот вокруг своего центра за 1 минуту, она имеет скорость вращения 1 оборот в минуту или 1 оборот в минуту.
Поскольку один оборот эквивалентен одному полному обороту или вращению вокруг центральной точки, говорят, что колесо, которое совершает один полный оборот вокруг своего центра за минуту, вращается вокруг своего центра со скоростью 1 оборот в минуту или 1 оборот в минуту. Поскольку секундная стрелка часов совершает один полный оборот вокруг своего центра за 1 минуту, она имеет скорость вращения 1 оборот в минуту или 1 оборот в минуту.
Преобразование угловой скорости в число оборотов в минуту
Угловая скорость в градусах в секунду может быть преобразована в число оборотов в минуту путем умножения угловой скорости на 1/6, поскольку один оборот составляет 360 градусов, а это 60 секунд в минуту.Если угловая скорость задана как 6 градусов в секунду, число оборотов в минуту будет 1 оборот в минуту, так как 1/6, умноженное на 6, дает 1.
оборотов в минуту Преобразование угловой скорости
Число оборотов в минуту можно преобразовать в угловую скорость в градусов в секунду, умножив число оборотов на 6, так как один оборот составляет 360 градусов и 60 секунд в минуту. Если частота вращения равна 1 об / мин, угловая скорость в градусах в секунду будет 6 градусов в секунду, так как 6 умноженное на 1 равно 6.
Если частота вращения равна 1 об / мин, угловая скорость в градусах в секунду будет 6 градусов в секунду, так как 6 умноженное на 1 равно 6.
Угловая и линейная скорость и
об / минPurplemath
По некоторым причинам учебники часто обращаются к вопросам угловой скорости, линейной скорости и числа оборотов в минуту (об / мин) вскоре после объяснения секторов круга, их площадей и длины дуги.
Длина дуги — это расстояние до части окружности; и линейное расстояние, которое преодолевает, скажем, велосипед, связано с радиусом шин велосипеда.Если вы отметите одну точку на передней шине велосипеда (скажем, точку напротив клапана шины) и посчитаете количество оборотов колеса, вы сможете найти количество окружностей окружности, на которые переместилась отмеченная точка.
MathHelp.
 com
comЕсли вы «раскрутите» эти окружности, чтобы получить прямую линию, то вы найдете расстояние, которое проехал велосипед.Я думаю, что именно из-за такого рода взаимосвязи между различными показателями эта тема часто возникает на данном этапе исследования.
Во-первых, нам нужна техническая терминология и определения.
«Угловая скорость» — это показатель поворота в единицу времени. Он сообщает вам размер угла, под которым что-то вращается за определенный промежуток времени. Например, если колесо вращается шестьдесят раз за одну минуту, то его угловая скорость составляет 120π радиан в минуту.Затем угловая скорость измеряется в радианах в секунду, греческая строчная омега (ω) часто используется в качестве названия.
«Линейная скорость» — это мера расстояния в единицу времени. Например, если колесо в предыдущем примере имеет радиус 47 сантиметров, то каждый проход по окружности составляет 94π см или около 295 см. Поскольку колесо совершает шестьдесят таких оборотов за одну минуту, общая пройденная длина составляет 60 × 94 & pi = 5640π см, или около 177 метров, за одну минуту.(Это примерно 10,6 км / ч или около 6,7 миль / ч)
«Число оборотов в минуту», обычно сокращенно «об / мин», является мерой вращения за единицу времени, но единица времени — всегда одна минута. И вместо того, чтобы указывать угол поворота, он просто дает количество оборотов. Когда вы смотрите на тахометр на приборной панели автомобиля, вы смотрите на текущие обороты двигателя автомобиля. В приведенном выше примере частота вращения будет просто «60».
«Частота» f — это мера вращения (или вибрации) за единицу времени, но единицей времени всегда является одна секунда.Единицей измерения частот является «герц», который обозначается как Гц.
Соотношение между частотой f (в Гц), об / мин и угловой скоростью ω (в радианах) показано ниже (все элементы в любой строке эквивалентны):
Однако вы можете обнаружить, что «угловая скорость» используется как синонимы (но только неофициально, не учеными) с оборотами в минуту или частотой. Кроме того, некоторые (например, физики) считают, что «угловая скорость» — это векторная величина, а ω — скалярная величина, называемая «угловой частотой».
Пожалуйста, не запоминайте эти потенциальные слияния и не беспокойтесь о том, какими могут быть «векторы» или «скаляры». Я говорю вам об этом, чтобы предупредить вас, что вы должны уделять очень пристальное внимание тому, как ваш конкретный учебник и ваш конкретный преподаватель определяют различные термины для этого конкретного класса. И знайте, что на следующем уроке термины и определения могут быть другими.
Колесо имеет диаметр 100 сантиметров.Если колесо поддерживает тележку, движущуюся со скоростью 45 километров в час, то какова частота вращения колеса с точностью до целого числа оборотов в минуту?
«Об / мин» — это количество оборотов колеса в минуту. Чтобы выяснить, сколько раз это колесо вращается за одну минуту, мне нужно найти (линейное или прямолинейное) расстояние, пройденное (за минуту) при движении со скоростью 45 км / ч. Затем мне нужно найти длину окружности колеса и разделить общее поминутное (линейное) расстояние на это «разовое» расстояние.Количество окружностей, которые умещаются внутри общего расстояния, — это количество оборотов колеса за этот период времени.
Во-первых, я переведу (линейную) скорость тележки из км / ч в «сантиметры в минуту», используя то, что я узнал о преобразовании единиц. (Почему «сантиметры в минуту»? Потому что я ищу «обороты в минуту», поэтому минуты — лучшая единица времени, чем часы. Кроме того, диаметр указывается в сантиметрах, так что это лучшая единица длины, чем километры.)
Итак, расстояние, пройденное за одну минуту, составляет 75 000 сантиметров. Диаметр колеса — 100 см, поэтому радиус — 50 см, а длина окружности — 100π см. Сколько из этих окружностей (или оборотов колеса) умещается внутри 75 000 см? Другими словами, если бы я снял протектор этого колеса с тележки и разложил его ровно, то получилось бы расстояние 100π см. Сколько из этих длин укладывается на все расстояние, пройденное за одну минуту? Чтобы узнать, сколько из (этого) вписывается в такое количество (этого), я должен разделить (это) на (это), поэтому:
Затем, округляя до ближайшего целого числа оборотов (то есть округляя ответ до целого числа), мой ответ:
Примечание. Эта скорость не такая высокая, как может показаться: она чуть меньше четырех оборотов в секунду.Вы можете сделать это на своем велосипеде, не беспокоясь. Вот еще одно примечание: источник, из которого я получил свою схему для вышеупомянутого упражнения, использовал «угловую скорость» и «ω» для «числа оборотов в минуту». Да, в учебнике алгебры использовались неправильные единицы измерения.
Предыдущее упражнение давало информацию о скорости автомобиля и колесе. Отсюда мы нашли количество оборотов в минуту. Мы можем пойти и другим путем; мы можем начать с числа оборотов в минуту (плюс информацию о колесе) и найти скорость транспортного средства.
Велосипедное колесо имеет диаметр 78 см. Если колесо вращается со скоростью 120 оборотов в минуту, какова линейная скорость велосипеда в километрах в час? Округлите ответ до одного десятичного знака.
Линейная скорость — это расстояние по прямой, которое велосипед проходит за определенный период времени.Они дали мне количество оборотов колеса в минуту. Фиксированная точка на шине (скажем, камешек на протекторе шины) перемещает длину окружности за каждый оборот. Раскручивая это расстояние по земле, велосипед будет перемещаться по земле на одинаковое расстояние, по одной окружности за раз, за каждый оборот. Итак, в этом вопросе меня просят найти длину окружности, а затем использовать ее, чтобы найти общее расстояние, пройденное за минуту.
Так как диаметр 78 см, то окружность равна C = 78π см.Разматывая путь шины по прямой линии на земле, это означает, что велосипед перемещается на 78π см вперед за каждый оборот шины. Таких оборотов в минуту 120, итого:
(78π см / об) × (120 об / мин) = 9,360π см / мин
Теперь мне нужно преобразовать это из сантиметров в минуту в километры в час:
Велосипед движется со скоростью около 17,6 км / ч.
… или около одиннадцати миль в час.
Предположим, что орбита Земли круглая с радиусом 93 000 000 миль, и пусть «один год» равен 365,25 дням. В этих условиях найдите линейную скорость Земли в милях в секунду. Округлите ответ до одного десятичного знака.
Скорость — это (линейное или эквивалентное прямолинейное) расстояние, пройденное за одну секунду, деленное на одну секунду.Они дали мне информацию за год, так что я начну с этого. Окружность круга с r = 93 000 000 миль будет линейным расстоянием, которое Земля преодолеет за один год.
C = 2π (93000000 миль) / год = 186000000π миль / год
Это количество миль, пройденных за один год, но мне нужно количество миль, пройденных за одну секунду. В сутках двадцать четыре часа, в часе шестьдесят минут и в минуте шестьдесят секунд, поэтому общее количество секунд в этом году составляет:
Тогда линейная скорость, представляющая собой общее линейное расстояние, деленное на общее время и выраженное в единицах скорости, равна:
Тогда, округленная до одного десятичного знака, линейная скорость Земли равна:
«Эй!» Я слышу, как ты плачешь.»Когда мы собираемся использовать угловые меры для чего-нибудь?» Хотя многие («большинство»?) Упражнений в вашей книге, вероятно, будут аналогичны приведенным выше, иногда вы можете столкнуться с фактическими радианами и градусами.
Поезд движется со скоростью 10 миль в час по кривой радиусом 3000 футов. На какой угол повернется поезд за одну минуту? Округлить до ближайшего целого числа градусов.
«Кривая радиуса 3000 футов» означает, что, если бы я попытался плотно подогнать круг внутри кривой, наилучшим образом подошел бы круг с радиусом r = 3000 футов.Другими словами, я могу использовать факты круга, чтобы ответить на этот вопрос.
Поскольку радиус кривой измеряется в футах и мне нужно найти угол, пройденный за одну минуту, я начну с преобразования скорости миль в час в футы в секунду:
(10 миль / час) (5280 фут / миль) (1 час / 60 мин) = 880 фут / мин
Длина изогнутого пути, который проходит поезд, также является частью окружности круга.Итак, эти 880 футов и есть длина дуги, и теперь мне нужно найти поднятый угол (подразумеваемого) сектора круга:
Но это значение в радианах (потому что это то, что использует формула длины дуги), и мне нужно, чтобы мой ответ был в градусах, поэтому мне нужно преобразовать:
Поезд поворачивает на угол примерно:
Представьте, что вы стоите в центре этого воображаемого круга (то есть на расстоянии трех тысяч футов от поворота, более чем в полумиле) и наблюдаете, как поезд движется по повороту.Если вы протянете руку на расстоянии вытянутой руки, сожмете кулак и, крепко прижав средние пальцы большим пальцем вниз, приподнимите мизинец и указательный пальцы, расстояние между ними составит около пятнадцати градусов. Поезд вряд ли продвинется дальше. Если бы вы держали кулак на расстоянии вытянутой руки и вытянули мизинец и большой палец, расстояние было бы около двадцати пяти градусов. Поезд не выйдет из ваших пальцев в отведенное время.
(Иногда я узнаю самые крутые вещи, когда исследую проблемы со словами.Опять же, мое определение «крутой» может быть немного грустным ….)
URL: https://www.purplemath.com/modules/sectors3.htm
Угол поворота и угловая скорость
Цели обучения
К концу этого раздела вы сможете:
- Определите длину дуги, угол поворота, радиус кривизны и угловую скорость.
- Вычислить угловую скорость вращения колеса автомобиля.
В «Кинематике» мы изучали движение по прямой и ввели такие понятия, как смещение, скорость и ускорение. Двумерная кинематика имеет дело с движением в двух измерениях. Движение снаряда — это частный случай двумерной кинематики, в которой объект проецируется в воздух, находясь под действием силы тяжести, и приземляется на некотором расстоянии. В этой главе мы рассматриваем ситуации, когда объект не приземляется, а движется по кривой.Мы начинаем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.
Угол поворота
Когда объекты вращаются вокруг некоторой оси — например, когда компакт-диск (компакт-диск) на Рисунке 1 вращается вокруг своего центра, — каждая точка объекта следует по дуге окружности. Рассмотрим линию от центра компакт-диска до его края. Каждая лунка , , используемая для записи звука вдоль этой линии, перемещается под одним и тем же углом за одно и то же время. Угол поворота — это величина поворота, аналогичная линейному расстоянию.Мы определяем угол поворота Δ θ как отношение длины дуги к радиусу кривизны: [latex] \ displaystyle \ Delta \ theta = \ frac {\ Delta {s}} {r} \\ [ / латекс]
Рис. 1. Все точки на компакт-диске движутся по дугам окружности. Ямки вдоль линии от центра к краю все перемещаются на один и тот же угол Δθ за время Δt .
Рис. 2. Радиус круга повернут на угол Δθ . Длина дуги Δs описана на окружности.
Длина дуги Δs — это расстояние, пройденное по круговой траектории, как показано на Рисунке 2. Обратите внимание, что r — это радиус кривизны круговой траектории.
Мы знаем, что за один полный оборот длина дуги равна длине окружности радиуса r . Окружность окружности равна 2π r . Таким образом, за один полный оборот угол поворота составляет
[латекс] \ displaystyle \ Delta \ theta = \ frac {2 \ pi {r}} {r} = 2 \ pi \\ [/ latex].
Этот результат является основой для определения единиц, используемых для измерения углов поворота, Δ θ как радиан, (рад), определенное так, что 2π рад = 1 оборот.
Сравнение некоторых полезных углов, выраженных как в градусах, так и в радианах, показано в таблице 1.
| Таблица 1. Сравнение угловых единиц | |
|---|---|
| Степень меры | Мера радиана |
| 30º | [латекс] \ displaystyle \ frac {\ pi} {6} \\ [/ latex] |
| 60º | [латекс] \ displaystyle \ frac {\ pi} {3} \\ [/ latex] |
| 90º | [латекс] \ displaystyle \ frac {\ pi} {2} \\ [/ latex] |
| 120º | [латекс] \ displaystyle \ frac {2 \ pi} {3} \\ [/ latex] |
| 135º | [латекс] \ displaystyle \ frac {3 \ pi} {4} \\ [/ latex] |
| 180º | π |
Рисунок 3. {\ circ}} {2 \ pi} \ приблизительно 57.{\ circ} \\ [/ латекс].
Угловая скорость
Насколько быстро вращается объект? Определим угловую скорость ω как скорость изменения угла. В символах это [латекс] \ omega = \ frac {\ Delta \ theta} {\ Delta {t}} \\ [/ latex], где угловое вращение Δ θ происходит за время Δ t . Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость. Единицы измерения угловой скорости — радианы в секунду (рад / с).
Угловая скорость ω аналогична линейной скорости v . Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся CD. Эта яма перемещается на длину дуги Δ с за время Δ t , и поэтому она имеет линейную скорость [латекс] v = \ frac {\ Delta {s}} {\ Delta {t}} \\ [/ латекс].
Из [latex] \ Delta \ theta = \ frac {\ Delta {s}} {r} \\ [/ latex] мы видим, что Δ s = r Δ θ . Подставляя это в выражение для v , получаем [latex] v = \ frac {r \ Delta \ theta} {\ Delta {t}} = r \ omega \\ [/ latex].
Мы записываем эту связь двумя разными способами и получаем два разных вывода:
[латекс] v = r \ omega \ text {или} \ omega \ frac {v} {r} \\ [/ latex].
Первое соотношение в [latex] v = r \ omega \ text {or} \ omega \ frac {v} {r} \\ [/ latex] утверждает, что линейная скорость v пропорциональна расстоянию от центра вращения, таким образом, он является наибольшим для точки на ободе (наибольшее r ), как и следовало ожидать. Мы также можем назвать эту линейную скорость v точки на ободе тангенциальной скоростью .Вторую взаимосвязь в [latex] v = r \ omega \ text {или} \ omega \ frac {v} {r} \\ [/ latex] можно проиллюстрировать на примере шины движущегося автомобиля. Обратите внимание, что скорость точки на ободе шины такая же, как скорость v автомобиля. См. Рис. 4. Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина — большой v означает большой ω , потому что v = rω . Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ( ω ), будет создавать для автомобиля большую линейную скорость ( v ).
Рис. 4. Автомобиль, движущийся вправо со скоростью v , имеет шину, вращающуюся с угловой скоростью ω. Скорость протектора шины относительно оси составляет v , как если бы автомобиль был поднят. Таким образом, автомобиль движется вперед с линейной скоростью v = r ω, где r — радиус шины. Чем больше угловая скорость шины, тем больше скорость автомобиля.
Пример 1. Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость 0.Автомобильная шина радиусом 300 м при движении автомобиля со скоростью 15,0 м / с (около 54 км / ч). См. Рисунок 4.
Стратегия
Поскольку линейная скорость обода шины такая же, как и скорость автомобиля, мы имеем v = 15,0 м / с. Радиус шины задан равным r = 0,300 м. Зная v и r , мы можем использовать второе соотношение в [latex] v = r \ omega \ text {или} \ omega \ frac {v} {r} \\ [/ latex] для вычисления угловой скорости .
Решение
Для вычисления угловой скорости мы будем использовать следующее соотношение: [latex] \ omega \ frac {v} {r} \\ [/ latex].
Подстановка известных,
[латекс] \ omega = \ frac {15.0 \ text {m / s}} {0.300 \ text {m}} = 50.0 \ text {rad / s} \\ [/ latex].
Обсуждение
Когда мы отменяем единицы в приведенном выше вычислении, мы получаем 50,0 / с. Но угловая скорость должна иметь единицы рад / с. Поскольку радианы на самом деле безразмерны (радианы определяются как отношение расстояний), мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если землеройный комбайн с гораздо большими шинами, скажем, 1.Радиус 20 м, двигался с той же скоростью 15,0 м / с, его колеса вращались медленнее. У них будет угловая скорость [латекс] \ omega = \ frac {15.0 \ text {м / с}} {1.20 \ text {m}} = 12.5 \ text {rad / s} \\ [/ latex].
И ω , и v имеют направления (следовательно, это угловая и линейная скорости соответственно). Угловая скорость имеет только два направления относительно оси вращения — либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается пути, как показано на рисунке 5.
Take-Home Experiment
Привяжите какой-либо предмет к концу веревки и поверните его по горизонтальному кругу над головой (взмахнув запястьем). Поддерживайте равномерную скорость при качании объекта и измеряйте угловую скорость движения. Какая примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости.
Рисунок 5.Поскольку объект движется по кругу, например, муха на краю старинной виниловой пластинки, его мгновенная скорость всегда касается круга. Направление угловой скорости в этом случае — по часовой стрелке.
Исследования PhET: Ladybug Revolution
Присоединяйтесь к божьей коровке и исследуйте вращательное движение. {\ circ} = 1 \ text { революция} \\ [/ латекс].{\ circ} \\ [/ латекс].
Концептуальные вопросы
- Есть аналогия между вращательными и линейными физическими величинами.Какие вращательные величины аналогичны расстоянию и скорости?
Задачи и упражнения
- Грузовики с полуприцепом имеют одометр на одной ступице колеса прицепа. Ступица утяжеляется так, что она не вращается, но она содержит шестерни для подсчета количества оборотов колеса — затем она вычисляет пройденное расстояние. Если колесо имеет диаметр 1,15 м и совершает 200 000 оборотов, сколько километров должен показывать одометр?
- Микроволновые печи вращаются со скоростью около 6 об / мин.6 \ text {m} \\ [/ latex] на его экваторе, какова линейная скорость у поверхности Земли?
- Бейсбольный питчер вытягивает руку вперед во время подачи, вращая предплечье вокруг локтя. Если скорость мяча в руке питчера составляет 35,0 м / с, а мяч находится на расстоянии 0,300 м от локтевого сустава, какова угловая скорость предплечья?
- В лакроссе мяч выбрасывается из сетки на конце клюшки путем вращения клюшки и предплечья вокруг локтя. Если угловая скорость мяча около локтевого сустава равна 30.0 рад / с и мяч находится на расстоянии 1,30 м от локтевого сустава, какова скорость мяча?
- Грузовик с шинами радиусом 0,420 м движется со скоростью 32,0 м / с. Какова угловая скорость вращающихся шин в радианах в секунду? Что это в об / мин?
- Комплексные концепции. При ударе по футбольному мячу игрок, выполняющий удар, вращает ногой вокруг тазобедренного сустава. (а) Если скорость кончика ботинка кикера составляет 35,0 м / с, а тазобедренный сустав находится на расстоянии 1,05 м от кончика ботинка, какова угловая скорость кончика ботинка? (b) Башмак находится в контакте с изначально неподвижным 0.Футбол 500 кг за 20,0 мс. Какая средняя сила прилагается к футбольному мячу, чтобы придать ему скорость 20,0 м / с? (c) Найдите максимальную дальность полета футбольного мяча, пренебрегая сопротивлением воздуха.
- Создайте свою проблему. Рассмотрим аттракцион в парке развлечений, в котором участники вращаются вокруг вертикальной оси в цилиндре с вертикальными стенками. Как только угловая скорость достигает своего полного значения, пол опускается, и трение между стенами и пассажирами препятствует их скольжению.Постройте задачу, в которой вы вычисляете необходимую угловую скорость, которая гарантирует, что всадники не соскользнут со стены. Включите свободную схему тела одного всадника. Среди переменных, которые следует учитывать, — радиус цилиндра и коэффициенты трения между одеждой гонщика и стеной.
Глоссарий
длина дуги: Δ с , расстояние, пройденное объектом по круговой траектории
яма: крошечная выемка на спиральной дорожке, отформованной в верхней части слоя поликарбоната CD
угол поворота: отношение длины дуги к радиусу кривизны на круговой траектории: [latex] \ Delta \ theta = \ frac {\ Delta {s}} {r} \\ [/ latex]
радиус кривизны: радиус круговой траектории
радиан: единица измерения угла
угловая скорость: ω, скорость изменения угла, под которым объект движется по круговой траектории
Избранные решения проблем и упражнения
1.723 км
3. 5 × 10 7 оборотов
5. 117 рад / с
7. 76,2 рад / с; 728 об / мин
8. (а) 33,3 рад / с; (б) 500 Н; (в) 40,8 м
1.4: Скорость и угловая скорость
Длина дуги по окружности
В разделе 1.3 мы узнали, что величина угла в радианах равна длине дуги на единичной окружности, связанной с этим углом. Таким образом, дуга длины 1 на единичной окружности образует угол в 1 радиан. Бывают моменты, когда также будет полезно знать длину дуг на других кругах, которые образуют тот же угол.
Рисунок \ (\ PageIndex {1} \): Дуги, заключенные под углом в 1 радиан.
На рисунке \ (\ PageIndex {1} \) внутренний круг имеет радиус 1, внешний круг имеет радиус \ (r \), а показанный угол имеет меру \ (\ theta \) радиан. . Таким образом, длина дуги на единичной окружности, образуемой углом, равна \ (\ theta \), и мы использовали s, чтобы представить длину дуги на окружности радиуса \ (r \), образуемой этим углом.
Напомним, что длина окружности радиуса \ (r \) равна \ (2 \ pi r \), а окружность круга радиуса 1 равна \ (2 \ pi \).Следовательно, отношение длины дуги \ (s \) на окружности радиуса \ (r \), которая образует угол в \ (\ theta \) радиан к соответствующей дуге единичной окружности, равно \ (\ dfrac {2 \ pi r} {2 \ pi} = r \). Отсюда следует, что
\ [\ dfrac {s} {\ theta} = \ dfrac {2 \ pi r} {\ pi} \]
\ [s = r \ theta \]
Определение
На окружности радиуса \ (r \) длина s дуги, пересекаемая центральным углом с радианами, равна
.\ [s = r \ theta \]
Примечание
Важно помнить, что для расчета длины дуги необходимо измерить центральный угол в радианах.
(Непонятно, почему буква \ (s \) обычно используется для обозначения длины дуги. Одно из объяснений состоит в том, что дуга «расширяет» угол.)
Упражнение \ (\ PageIndex {1} \)
Использование кружков в начале действия для этого раздела:
- Используйте формулу для длины дуги, чтобы определить длину дуги на окружности радиусом 10 футов, которая образует центральный угол в \ (\ dfrac {\ pi} {2} \) радиан. Результат равен одной четверти длины окружности?
- Используйте формулу для длины дуги, чтобы определить длину дуги на окружности радиусом 20 футов, которая образует центральный угол в \ (\ dfrac {\ pi} {2} \) радиан.\ circ}) = \ dfrac {11 \ pi} {90} \) и \ [s = r \ theta = (3ft) \ dfrac {11 \ pi} {90} \] \ [s = \ dfrac {11 \ pi} {30} \] Длина дуги составляет \ (\ dfrac {11 \ pi} {30} \) футов или около \ (1.1519 \) футов.
Почему радианы?
Градус знаком и удобен, так зачем вводить единицу радиан? Это хороший вопрос, но на него есть тонкий ответ. Как мы только что видели, длина \ (s \) дуги на окружности радиуса \ (r \), образуемой углом в \ (\ theta \) радиан, равна \ (s = r \ theta \), поэтому \ (\ theta = \ dfrac {s} {r} \).В результате радиан представляет собой отношение двух длин (отношение длины дуги к радиусу окружности), что делает радиан безразмерной величиной. Таким образом, измерение в радианах можно рассматривать как действительное число. Это удобно для работы с длиной дуги (и угловой скоростью, как мы скоро увидим), а также будет полезно при изучении периодических явлений в главе 2. По этой причине радианная мера повсеместно используется в математике, физике и технике как в отличие от степеней, потому что, когда мы используем градусную меру, мы всегда должны учитывать градусное измерение в вычислениях.Это означает, что радианы на самом деле более естественны с математической точки зрения, чем градусы.
Линейная и угловая скорость
Связь между дугой на окружности и углом, который она образует, измеряемым в радианах, позволяет нам определять величины, связанные с движением по окружности. Объекты, движущиеся по круговой траектории, обладают двумя типами скорости: линейной и угловой скоростью . Подумайте о вращении на карусели. Если вы уроните камешек с края движущейся карусели, он не упадет прямо вниз.Вместо этого он продолжит двигаться вперед со скоростью, которую имела карусель в тот момент, когда камешек был выпущен. Это линейная скорость гальки. Линейная скорость измеряет, как длина дуги изменяется во времени.
Рассмотрим точку \ (P \), движущуюся с постоянной скоростью по окружности радиуса \ (r \). Это называется равномерным круговым движением . Предположим, что P перемещается на расстояние s единиц за время \ (t \). Линейная скорость v точки \ (P \) — это расстояние, которое она проехала, деленное на прошедшее время.То есть \ (v = \ dfrac {s} {t} \). Расстояние s — это длина дуги, и мы знаем, что \ (s = r \ theta \).
Определение: линейная скорость
Рассмотрим точку \ (P \), движущуюся с постоянной скоростью по окружности радиуса \ (r \). Линейная скорость \ (v \) точки \ (P \) определяется как
\ [v = \ dfrac {s} {t} = \ dfrac {r \ theta} {t} \]
где \ (\ theta \), измеренный в радианах, — это центральный угол, образованный дугой длиной \ (s \).
Другой способ измерить, насколько быстро объект движется с постоянной скоростью по круговой траектории, называется угловой скоростью. В то время как линейная скорость измеряет, как длина дуги изменяется во времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол во времени.
Определение: угловая скорость
Рассмотрим точку P, движущуюся с постоянной скоростью по окружности радиуса r по дуге, соответствующей центральному углу измерения \ (\ theta \) (в радианах).Угловая скорость \ (\ omega \) точки — это радианная мера угла \ (\ theta \), деленная на время t, необходимое для того, чтобы вывести этот угол. То есть
\ [\ omega = \ dfrac {\ theta} {t}. \]
Примечание
Символ \ (\ omega \) — это строчная греческая буква «омега». Также обратите внимание, что угловая скорость не зависит от радиуса r.
Это несколько специализированное определение угловой скорости, которое немного отличается от обычного термина, используемого для описания скорости вращения точки по окружности.Этот срок составляет оборотов в минуту или оборотов в минуту . Иногда используется единица оборотов в секунду . Лучший способ представить количество оборотов в минуту — использовать «дробную часть» \ (\ dfrac {rev} {min} \). Поскольку 1 оборот равен \ (2 \ pi \) радианам, мы видим, что если объект min движется со скоростью x оборотов в минуту, то
\ [\ omega = x \ dfrac {rev} {min} \ cdot \ dfrac {2 \ pi rad} {rev} = x (2 \ pi) \ dfrac {rad} {min}. \]
Упражнение \ (\ PageIndex {2} \)
Предположим, круглый диск вращается со скоростью 40 оборотов в минуту.Мы хотим определить линейную скорость v (в футах в секунду) точки, находящейся на расстоянии 3 футов от центра диска.
- Определите угловую скорость \ (\ omega \) точки в радианах в минуту. Совет : Используйте формулу \ [\ omega = x \ dfrac {rev} {min} \ cdot \ dfrac {2 \ pi rad} {rev}. \]
- Теперь мы знаем \ (\ omega = \ dfrac {\ theta} {t} \). Поэтому используйте формулу \ (v = \ dfrac {r \ theta} {t} \), чтобы определить \ (v \) в футах в минуту.
- Наконец, преобразуйте линейную скорость v из футов в минуту в футы в секунду.
- Ответ
1. Мы видим, что
\ [\ omega = 40 \ dfrac {rev} {min} \ times \ dfrac {2 \ pi \ space rad} {rev} \]
\ [\ omega = 80 \ pi \ dfrac {rad} {min} \ ]2. Результат части (а) дает
\ [v = r (\ dfrac {\ theta} {r}) = r \ omega \]
\ [v = (3ft) \ times 80 \ pi \ dfrac {rad} {min} \]
\ [v = 240 \ pi \ dfrac {ft} {min} \]3. Теперь мы переводим футы в минуту в футы в секунду.
\ [v = 240 \ pi \ dfrac {ft} {min} \ times \ dfrac {1 \ space min} {60 \ space sec} \]
\ [v = 4 \ pi \ dfrac {ft} {sec} \ около 12.566 \ dfrac {ft} {sec} \]
Обратите внимание, что в упражнении 1.18 после определения угловой скорости мы смогли определить линейную скорость. То, что мы сделали в этом конкретном случае, мы можем сделать в целом. Существует простая формула, которая напрямую связывает линейную скорость с угловой скоростью. Наша формула для линейной скорости: \ (v = \ dfrac {s} {t} \ dfrac {r \ theta} {t} \). Обратите внимание, что мы можем записать это как \ (v = r \ dfrac {\ theta} {t} \). То есть \ (v = r \ omega \)
Примечание
Рассмотрим точку \ (P \), движущуюся с постоянной (линейной) скоростью \ (v \) по окружности радиуса \ (r \).Если угловая скорость равна \ (\ omega \), то
\ [v = r \ omega \]
Итак, в упражнении 1.18, когда мы определили, что \ (\ omega = 80 \ pi \ dfrac {rad} {min} \), мы могли бы определить v следующим образом:
\ [v = r \ omega = (3 \ space ft) (80 \ pi \ dfrac {rad} {min} = 240 \ pi \ dfrac {ft} {min}). \]
Обратите внимание, что, поскольку радианы «без единиц измерения», мы можем отбросить их при работе с уравнениями, такими как предыдущее.
Пример \ (\ PageIndex {1} \): линейная и угловая скорость
LP (долгоиграющая) или виниловая пластинка со скоростью 331 об / мин является аналоговым носителем для хранения звука и долгое время использовалась для прослушивания музыки.LP обычно имеет диаметр 12 или 10 дюймов. Чтобы работать с нашими формулами для линейной и угловой скорости, нам нужно знать угловую скорость в радианах в единицу времени. Для этого мы переведем \ (33 \ dfrac {1} {3} \) оборотов в минуту в радианы в минуту. Мы будем использовать тот факт, что \ (33 \ dfrac {1} {3} = \ dfrac {100} {3} \)
\ [\ omega = \ dfrac {100} {3} \ dfrac {rev} {min} \ times \ dfrac {2 \ pi \ space rad} {1 \ space rev} = \ dfrac {200 \ pi} {3 } \ dfrac {rad} {min} \]
Теперь мы можем использовать формулу v D r! для определения линейной скорости точки на краю 12-дюймовой пластинки.Радиус 6 дюймов и так
\ [v = r \ omega = (6 \ космических дюймов) (\ dfrac {200 \ pi} {3} \ dfrac {rad} {min}) = 400 \ pi \ dfrac {дюймы} {min} \]
Было бы удобнее выразить это как десятичное значение в дюймах в секунду. Получаем
\ [v = 400 \ pi \ dfrac {дюймы} {мин} \ times \ dfrac {1 \ space min} {60 \ space sec} \ приблизительно 20. 944 \ dfrac {дюймы} {sec} \]
Линейная скорость составляет приблизительно 20,944 дюйма в секунду.
Упражнение \ (\ PageIndex {3} \)
Для этих задач мы предположим, что Земля представляет собой сферу с радиусом 3959 миль.Когда Земля вращается вокруг своей оси, человек, стоящий на Земле, будет путешествовать по кругу, перпендикулярному оси.
- Земля вращается вокруг своей оси каждые \ (24 \) часа. Определите угловую скорость Земли в радианах в час. (Оставьте свой ответ в виде числа �� \ (\ pi \).)
- Когда Земля вращается, человек, стоящий на экваторе, будет путешествовать по кругу с радиусом 3959 миль. Определите линейную скорость этого человека в милях в час.\ circ \) север будет двигаться по кругу радиусом 2800 миль. Определите линейную скорость этого человека в милях в час и футах в секунду.
- Ответ
- Один оборот соответствует \ (2 \ pi \) радианам. Итак, \ [\ omega = \ dfrac {2 \ pi \ space rad} {24 \ space hr} = \ dfrac {\ pi \ space rad} {12 \ space hr}. \]
- Для определения линейной скорости используем формулу \ (v = r \ omega \) \ [v = r \ omega = (3959mi) (\ dfrac {\ pi} {12} \ dfrac {rad} {hr}) = \ dfrac {3959 \ pi} {12} \ dfrac {mi} {hr} \] Линейная скорость приблизительно равна 1036.5 миль в час.
- Для определения линейной скорости используем формулу \ (v = r \ omega \) \ [v = r \ omega = (2800mi) (\ dfrac {\ pi} {12} \ dfrac {rad} {hr}) = \ dfrac {2800 \ pi} {12} \ dfrac {mi} {hr} \] Линейная скорость составляет примерно 733,04 мили в час. Чтобы преобразовать это в футы в секунду, мы используем тот факт, что в одной миле 5280 футов, в часе 60 минут и в минуте 60 секунд. Итак,
\ [v = (\ dfrac {2800 \ pi} {12} \ dfrac {mi} {hr}) (\ dfrac {5280 \ space ft} {1 \ space mi}) (\ dfrac {1 \ space hr } {60 \ space min}) (\ dfrac {1 \ space min} {60 \ space sec}) = \ dfrac {(2800 \ pi) (5280)} {12 \ cdot 60 \ cdot 60} \ dfrac {ft } {сек} \]
Итак, линейная скорость приблизительно равна \ (1075.1 \) футов в секунду.
Сводка
В этом разделе мы изучили следующие важные концепции и идеи:
- На окружности с радиусом \ (r \) длина дуги \ (s \), пересеченная центральным углом с радианами, равна \ [s = r \ theta \]
- Равномерное круговое движение — это когда точка движется с постоянной скоростью по окружности круга. Линейная скорость — это длина дуги, пройденная точкой, деленная на прошедшее время.В то время как линейная скорость измеряет, как длина дуги изменяется во времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол во времени. Угловая скорость точки — это радианная мера угла, деленная на время, необходимое для того, чтобы охватить этот угол.
- Для точки \ (P \), движущейся с постоянной (линейной) скоростью v по окружности окружности радиуса \ (r \), имеем \ [v = r \ omega \], где \ (\ omega \) — угловая скорость точки.
Honors Rotational Kinematics
Радианы и градусы
Обычно люди обсуждают вращательное движение в градусах, где один полный оборот по окружности равен 360 °. Когда речь идет о вращательном движении с точки зрения физики, измерение вращательного движения в единицах, известных как радианы (рад), является гораздо более эффективным. Радиан измеряет расстояние вокруг дуги, равное длине радиуса дуги.
До этого момента вы описывали расстояния и смещения в терминах Δx и Δy.При обсуждении угловых смещений вы должны перейти к описанию поступательного смещения вокруг дуги в терминах переменной s, продолжая использовать символ θ (тета) для обозначения углов и углового смещения.
Расстояние полностью по круговой траектории (360 °), известное как окружность, C, можно найти с помощью ∆s = C = 2𝜋r = 2𝜋 радиан. Следовательно, вы можете использовать это как коэффициент преобразования для перехода между градусами и радианами.
Вопрос: Преобразовать 90 ° в радианы.
Ответ:
Вопрос: Преобразуйте 6 радианов в градусы.
Ответ:
Углы также измеряются в оборотах (полные обходы по кругу). Полный единичный оборот равен 360 °, поэтому вы можете записать коэффициенты пересчета для углов поворота и смещения как 360 ° = 2𝜋 радиан = 1 оборот.
Вопрос: Преобразовать 1.5 оборотов в радианах и градусах.
Ответ:
Скорость и ускорение
Вращательная кинематика очень похожа на поступательную кинематику, все, что вам нужно сделать, это изучить вращательные версии кинематических переменных и уравнений. Когда вы изучали кинематику перевода, смещение обсуждалось с точки зрения Δx. При вращательной кинематике вместо этого вы будете использовать угловую координату θ.Когда в трансляционном мире была введена средняя скорость, вы использовали формулу:
Изучая вращательное движение, вы будете говорить об угловой скорости ω (омега), выраженной в радианах в секунду (рад / с). Поскольку угловая (вращательная) скорость является вектором, определите положительное направление вращения как вращение против часовой стрелки по круговой траектории, а отрицательное направление как по часовой стрелке вокруг траектории.
ПРИМЕЧАНИЕ: Формально направление угловых векторов определяется правилом правой руки.Оберните пальцы правой руки в направлении вращения, скорости или ускорения, а большой палец укажет в направлении вектора.
Вопрос: Рекорд вращается на фонографе со скоростью 33 об / мин (оборотов в минуту) по часовой стрелке. Найдите угловую скорость записи.
Ответ:
Обратите внимание, что вектор угловой скорости отрицательный, потому что запись вращается по часовой стрелке.
Вопрос: Найдите величину угловой скорости Земли в радианах в секунду.
Ответ: Осознавая, что Земля совершает один полный оборот каждые 24 часа, мы можем оценить величину угловой скорости Земли как:
Аналогичным образом, когда вы узнали о поступательном ускорении, вы обнаружили ускорение как скорость изменения поступательной скорости объекта:
Угловое ускорение α (альфа), выраженное в радианах в секунду 2 , представляет собой скорость изменения угловой скорости объекта.Поскольку угловое ускорение также является вектором, вы можете определить его направление как положительное для увеличения угловой скорости в направлении против часовой стрелки и отрицательное для увеличения угловой скорости в направлении по часовой стрелке.
Вопрос: Лягушка едет на одноколесном велосипеде. Если колесо моноцикла начинается в состоянии покоя и равномерно ускоряется против часовой стрелки до угловой скорости 15 об / мин за 6 секунд, найдите угловое ускорение колеса моноцикла.
Ответ: Сначала преобразуйте 15 об / мин в рад / с.
Далее используйте определение углового ускорения.
Снова обратите внимание на положительное угловое ускорение, поскольку колесо велосипеда ускоряется против часовой стрелки.
Вращательные переменные
Объединяя эти определения, вы наблюдаете очень сильную параллель между поступательными кинематическими величинами и вращательными кинематическими величинами.
| Переменная | Трансляционный | Угловой |
|---|---|---|
| Рабочий объем | Δs | Δθ |
| Скорость | v | ω |
| Разгон | а | α |
| Время | т | т |
Довольно просто выполнить перевод между поступательными и угловыми переменными, если вы знаете радиус (r) интересующей точки на вращающемся объекте.
Вопрос: Рыцарь махает булавой радиусом 1 м за два полных оборота. Что такое поступательное смещение булавы?
Ответ:
Вопрос: Проигрыватель компакт-дисков предназначен для изменения скорости вращения диска, так что точка, считываемая лазером, перемещается с линейной скоростью, равной 1.25 м / с. Какова скорость вращения компакт-диска в об / с, когда лазер считывает информацию с внутренней части диска с радиусом 0,03 м?
Ответ:
Вопрос: Какова скорость вращения компакт-диска в предыдущей задаче, когда лазер считывает крайнюю часть диска (радиус = 0,06 м)?
Ответ:
Уравнения вращательной кинематики
Параллели между поступательным и вращательным движением идут еще дальше.Вы разработали набор кинематических уравнений поступательного движения, которые позволили вам исследовать взаимосвязь между смещением, скоростью и ускорением. Вы можете разработать соответствующий набор соотношений для углового смещения, угловой скорости и углового ускорения. Уравнения имеют ту же форму, что и трансляционные уравнения, все, что вам нужно сделать, это заменить трансляционные переменные на вращательные, как показано в следующей таблице.
Уравнения вращательной кинематики можно использовать так же, как вы использовали уравнения поступательной кинематики для решения задач.Когда вы знаете три кинематические переменные, вы всегда можете использовать уравнения для решения двух других.
Вопрос: Плотник вырезает кусок дерева с помощью мощной циркулярной пилы. Пильный диск ускоряется в состоянии покоя с угловым ускорением от 14 рад / с 2 до максимальной скорости 15 000 об / мин. Какова максимальная скорость пилы в радианах в секунду?
Ответ:
Вопрос: Сколько времени нужно пиле для достижения максимальной скорости?
Ответ: Для решения этой задачи можно использовать уравнения кинематики вращения:
Вопрос: Сколько полных оборотов делает пила при разгоне до максимальной скорости?
Ответ:
Вопрос: Предохранительный механизм остановит пильный диск в 0.3 секунды, если рука плотника оторвется от управления пилой. Какое угловое ускорение для этого требуется? Сколько полных оборотов пильное полотно сделает за это время?
Ответ: Начните с воссоздания таблицы кинематики вращения.
Сначала найдите угловое ускорение.
Затем найдите угловое смещение.
Наконец, преобразуйте угловое смещение в число оборотов.
Равномерное круговое движение
Введение
Равномерное круговое движение — это движение объекта, движущегося с постоянной (равномерной) скоростью по круговой траектории. Помимо скорости, есть несколько других переменных, которые используются для характеристики движения. Это радиус движения r , угловая скорость ω , период T и частота вращения f .Период — это время, необходимое для того, чтобы объект совершил один оборот движения. Угловая скорость — это угловое смещение в секунду, и оно связано с частотой следующим образом: с ω в рад / с. Частота вращения — это количество оборотов в секунду и определяется как: с f в Гц или сек -1 . Скорость объекта является касательной к окружности с величиной v = rω .Ускорение , a направлено к центру круга (центростремительное) с величиной, определяемой следующим образом: с a м / с 2 . Для того чтобы объект массой m мог двигаться по окружности с постоянной скоростью, на объект должна действовать чистая центростремительная сила. Величина чистой силы F должна быть постоянной и связана с центростремительным ускорением вторым законом Ньютона: с F в Н. Эта центростремительная сила может быть обеспечена натяжением (как в этой лаборатории), трением (как для автомобиля, движущегося по кривой), нормальной силой (как в петлевых американских горках) или гравитацией (как для движения спутника).В этом эксперименте вы будете измерять период объекта, совершающего равномерное круговое движение с фиксированным радиусом, но с различными значениями F . По периоду можно рассчитать угловую скорость. Используя эти известные значения и приведенные выше уравнения, вы можете найти эмпирическую массу вращающегося объекта и сравнить его со значением массы, полученным путем непосредственного взвешивания его на весах.Аппарат UCM
Аппарат UCM состоит из регулируемой вращающейся платформы .На расстоянии r от центра вращения находится узел боковой стойки , на котором висит объект массой м , называемый вращающейся массой (не путать со статической массой ). Вращающаяся масса прикреплена к пружине на центральной стойке посредством струны и небольшого шкива. Когда платформа вращается, вращающаяся масса будет перемещаться по круговой траектории из-за силы, прилагаемой к ней струной (посредством натяжения пружины).Поскольку невозможно получить мгновенное считывание этой силы натяжения во время вращения платформы, косвенное измерение этой силы будет производиться с использованием веса статической массы, как показано и объяснено ниже.Рисунок 1
Когда платформа не вращается, вращающаяся масса не свешивается вертикально с боковой стойки, а, скорее, втягивается внутрь за счет натяжения струны и пружины. При проведении эксперимента вы будете регулировать скорость вращения платформы до тех пор, пока вращающаяся масса не будет висеть вертикально на радиусе r .Оранжевый индикаторный диск поможет вам определить, когда вращающаяся масса достигла этого положения.Рисунок 2
Период вращения измеряется секундомером . Платформу можно вращать, поворачивая вручную стержень с накаткой.Процедура
Выравнивание предмета
Если платформа неровная, это отрицательно скажется на ваших результатах. Студенты в первой лаборатории недели должны были уже выровнять прибор.Будем надеяться, что с тех пор аппарат не перемещали, и его не нужно будет снова выравнивать. Проверьте, выровнено ли ваше устройство, включив двигатель регулировки скорости и наблюдая за оранжевым индикаторным диском, чтобы увидеть, качается ли он вверх и вниз при вращении платформы. Если ваше устройство необходимо выровнять, выполните следующие действия.1
Чтобы примерно выровнять платформу, поместите пузырьковый уровень в середину платформы и отрегулируйте два регулировочных винта на основании устройства, пока пузырь не будет отцентрирован.2
Поместите дополнительную массу (~ 500 г) на тот же конец вращающейся платформы, что и вращающаяся масса. Если платформа неровная, тяжелый конец будет качаться в низкую сторону.3
Отрегулируйте регулировочные винты на ножках основания до тех пор, пока конец платформы не будет качаться равномерно при легком вращении рукой.
Установка радиуса
1
Осторожно отсоедините вращающуюся массу от струн.Используйте весы, чтобы взвесить его, и запишите значение массы.2
Подвесьте вращающуюся гирю к боковой стойке и подсоедините шнур от пружины к гири. Убедитесь, что эта струна проходит под (а не за) маленьким шкивом на центральной стойке.3
Переместите кронштейн индикатора на центральной стойке в самое нижнее положение.4
Потяните вращающуюся массу в сторону от центральной стойки, пока оранжевый индикатор не окажется в центре кронштейна.Если струна, поддерживающая вращающийся груз, не является вертикальной, когда индикатор совмещен с кронштейном, боковую стойку следует перемещать внутрь или наружу, пока струна не станет вертикальной. Используйте вертикальную линию на боковой стойке, чтобы облегчить это выравнивание. При затягивании боковой стойки, нажмите на платформу, чтобы убедиться, что она надежно удерживается в вертикальном положении, и избегайте чрезмерного затягивания и поломки пластикового винта с накатанной головкой!5
Измерьте и запишите радиус, а также оценку погрешности на основе центровки.6
Теперь ваш аппарат должен быть готов к работе в максимально широком диапазоне центростремительных сил. (Почему это важно?) Центростремительную силу можно изменять, перемещая опору пружины вверх и вниз, при этом другие части устройства остаются на месте. Этот диапазон движение по центральной стойке должно составлять не менее 5 см, что соответствует диапазону натяжения пружины примерно 1,2 Н.
Установка величины центростремительной силы
В этой первой части процедуры вы будете использовать метод static (без вращения) для настройки прибора на известное значение центростремительной силы.1
Прикрепите фиксирующий шкив к концу платформы, ближайшему к вращающейся массе. Прикрепите шнур к вращающейся массе и навесьте известную массу (начиная с 20 г) над зажимным роликом. Отрегулируйте прижимной шкив вверх или вниз по мере необходимости так, чтобы шнур между шкивом и вращающаяся масса расположена горизонтально. (Почему это важно?)2
Запишите значение этой статической массы , которая определит центростремительную силу.3
Отрегулируйте подпружиненную опору по вертикали, пока оранжевый индикаторный диск не окажется в центре держателя индикатора. Теперь устройство должно быть выровнено, чтобы точно знать радиус движения вращающейся массы, когда платформа вращается.
Контрольно-пропускной пункт 1:
Прежде чем продолжить, попросите ТА проверить ваше устройство.
Измерение периода
1
Снимите статическую массу и струну с вращающейся массы. (Почему?)2
Поверните устройство, равномерно повернув стержень с накаткой по часовой стрелке. Уделите минуту, чтобы прочувствовать поворот платформы с постоянной скоростью. Увеличивайте скорость до тех пор, пока оранжевый индикаторный диск не окажется по центру кронштейна индикатора на центральной стойке.Это указывает на то, что струна, поддерживающая вращающуюся массу, вертикальна и, следовательно, масса находится на желаемом радиусе.3
Когда один партнер по лаборатории вращает платформу, другой должен использовать секундомер для измерения времени, необходимого для совершения одного оборота. Сделайте десять таких измерений.4
Альтернативный метод измерения среднего периода заключается в использовании секундомера для измерения времени для N (например, 10) оборотов и деления на N, чтобы получить T .Сделайте это хотя бы для одного испытания и сравните со значением, полученным с помощью процедуры, приведенной в шаге 3. Какой метод, по вашему мнению, более точен?5
Прежде чем продолжить, проверьте свои результаты для этой единственной точки данных и подтвердите, что ваше эмпирическое значение для вращающейся массы является разумным. Если ваш результат не имеет смысла, проанализируйте свою процедуру и исправьте все ошибки, прежде чем брать дополнительные данные.
КПП 2:
Прежде чем продолжить, попросите технический специалист проверить ваши данные и результаты расчетов.
Изменение центростремительной силы
Повторите описанную выше процедуру как минимум с пятью различными статическими массами (и, следовательно, пятью разными силами), которые охватывают максимально широкий диапазон значений (обычно от 40 до 150 г).Анализ
1
Вес статической массы, висящей на шкиве, равен центростремительной силе F , приложенной пружиной. Вычислите эту силу для каждого из пяти испытаний, умножив статическую массу на г , и запишите результаты.2
Для каждой центростремительной силы F вычислите средний период вращения T и его стандартную ошибку.3
Для каждого значения F рассчитайте ω 2 и его неопределенность из4
Постройте график ω 2 против F (с планками ошибок) и выполните аппроксимацию методом наименьших квадратов.5
Определите экспериментальное значение вращающейся массы, м , исходя из наклона вашего графика и уравнения центростремительной силы.Определите пересечение и линейной аппроксимации ваших данных. Это то, чего вы ожидаете?
Обсуждение
Сравните значение м , полученное при подборе кривой, с измеренными значениями вращающейся массы м и радиуса движения r . Есть согласие в пределах неопределенностей? Если вы проведете этот эксперимент осторожно, вы сможете получить результаты с ошибкой менее 3%. Сравните значение интерцепта y с ожидаемым значением.Они согласны? Почему для этого (и большинства других) экспериментов важно получить данные в самом широком диапазоне значений? Каковы потенциальные последствия близкого расположения точек данных? Объясните, как вы собираете данные с помощью этого устройства, чтобы проверить следующую гипотезу: для данного значения величины центростремительной силы F радиус движения r обратно пропорционален квадрату угловой скорости ω .Copyright © 2011 Advanced Instructional Systems, Inc. и Университет Северной Каролины | Кредиты
Угловая скорость Земли — Вселенная сегодня
[/ caption]
Планета Земля совершает три движения: она вращается вокруг своей оси, что дает нам день и ночь; он вращается вокруг Солнца, давая нам времена года, и проходит через Млечный Путь вместе с остальной частью Солнечной системы. В каждом случае ученые пытались рассчитать не только время, необходимое для этого, но и соответствующие относительные скорости.Когда речь идет о вращении Земли вокруг своей оси, процесс, который занимает 23 часа 56 минут и 4,09 секунды, этот процесс известен как звездные сутки, а скорость, с которой она движется, известна как угловая скорость Земли. Это в равной степени относится к Земле, вращающейся вокруг оси Солнца и центра Галактики Млечный Путь.
В физике угловая скорость — это векторная величина, которая определяет угловую скорость объекта и ось, вокруг которой объект вращается. Единица измерения угловой скорости в системе СИ — радианы в секунду, хотя она может измеряться и в других единицах, таких как градусы в секунду, обороты в секунду и т. Д.и обычно обозначается символом омега (ω, реже Ω). Радиан по определению — это единица измерения, которая связывает радиус дуги, длину дуги и угол, образованный дугой. Полный радиан равен 360 градусам, поэтому мы знаем, что Земля совершает два радиана при полном вращении вокруг оси. Однако иногда ее также называют скоростью вращения, и ее величина — скорость вращения — обычно измеряется в циклах или оборотах в единицу времени (например, оборотов в минуту).Кроме того, когда объект вращается вокруг оси, каждая точка объекта имеет одинаковую угловую скорость.
Математически средняя угловая скорость объекта может быть представлена следующим уравнением: ω среднее значение = Δθ / Δt, где ω — радианы / обороты в секунду (в среднем), Δ — изменение количества, θ — скорость, а t — время. При вычислении угловой скорости Земли, когда она совершает полный оборот вокруг своей оси (солнечные сутки), это уравнение представляется следующим образом: ω avg = 2πrad / 1day (86400 секунд), что соответствует умеренным угловым скорость 7.2921159 × 10 -5 радиан / сек. В случае солнечного года, где ω ср. = 2πрад / 1 год (3,2 × 10 7 секунд), мы видим, что угловая скорость составляет 2,0 × 10 -7 рад / с.
Мы написали много статей об угловой скорости Земли для Universe Today. Вот статья об угловой скорости, а вот статья о том, почему Земля вращается.
Если вам нужна дополнительная информация об угловой скорости Земли, ознакомьтесь со следующими статьями:
Угловая скорость Земли
Вращение Земли
Мы также записали эпизод Astronomy Cast, посвященный планете Земля.Послушайте, Эпизод 51: Земля.
Источники:
http://en.wikipedia.org/wiki/Angular_velocity
http://hyperphysics.phy-astr.gsu.edu/hbase/rotq.html
http://hypertextbook.com/facts/2002/ JasonAtkins.shtml
http://en.wikipedia.org/wiki/Earth%27s_rotation#Rotation_period
http://www.livephysics.com/tables-of-physical-data/mechanical/angular-speed-of-earth. html
Нравится:
Нравится Загрузка .

 Вилки и розетки переменного тока .
Вилки и розетки переменного тока .
 и использование твердотельных накопителей в тонких и сверхпортативных ноутбуках. Подобно носителям CD и DVD, количество данных, которые можно сохранить или прочитать для каждого поворота диска, больше на внешнем крае, чем возле шпинделя; однако жесткие диски поддерживают постоянную скорость вращения, поэтому эффективная скорость передачи данных выше на краю (обычно это «начало» диска, в отличие от CD или DVD).
и использование твердотельных накопителей в тонких и сверхпортативных ноутбуках. Подобно носителям CD и DVD, количество данных, которые можно сохранить или прочитать для каждого поворота диска, больше на внешнем крае, чем возле шпинделя; однако жесткие диски поддерживают постоянную скорость вращения, поэтому эффективная скорость передачи данных выше на краю (обычно это «начало» диска, в отличие от CD или DVD).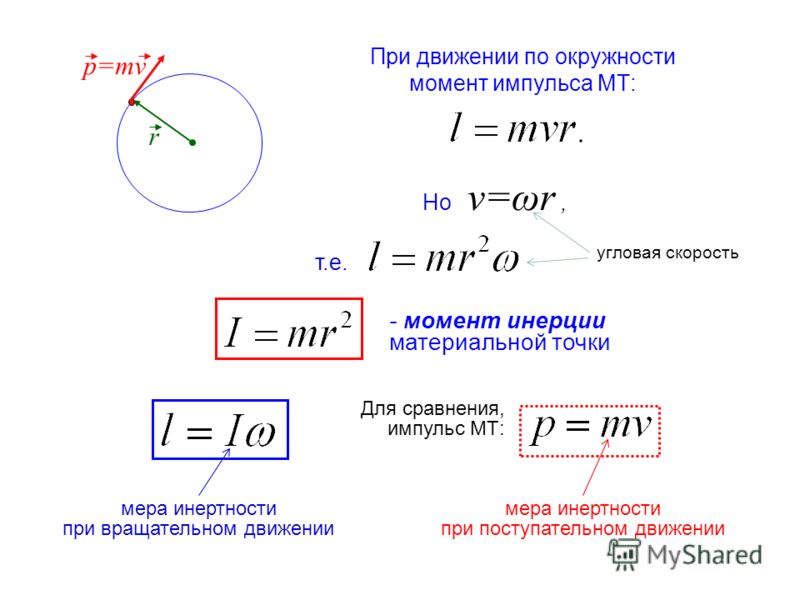 ) — по сравнению с 300 об / мин, 720 КБ и 23 КБ / с (макс.) для дисков двойной плотности в других машинах.
) — по сравнению с 300 об / мин, 720 КБ и 23 КБ / с (макс.) для дисков двойной плотности в других машинах.

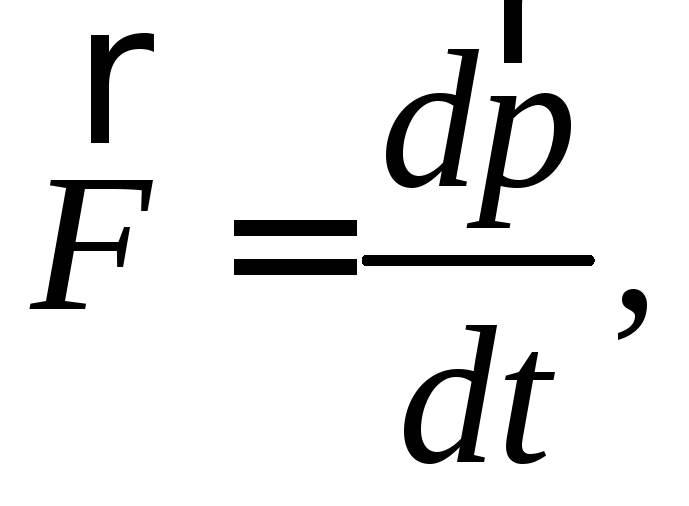
 В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения. 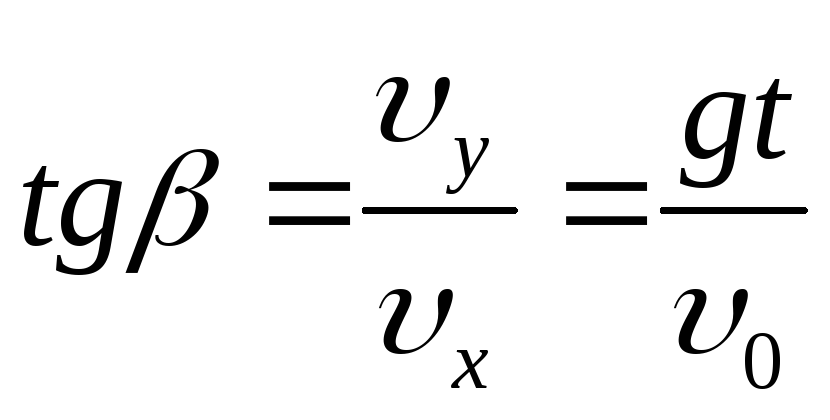
 (Угловое ускорение при этом постоянно.)
(Угловое ускорение при этом постоянно.)