Яркость физика: Яркость, светлота, освещенность. Теория

Яркость, светлота, освещенность. Теория

Напомню основные понятия физической оптики:
1. Сила света. Под силой света понимают величину светового потока, приходящуюся на единицу телесного угла. Источник света предполагается точечный. Сила света измеряется в канделах (кд).
2. Яркость (прямого или отраженного) излучения. Если источник света не точечный, говорят о яркости излучения (или поверхностной яркости). Яркость измеряется в нитах(1нт=1кд/1м2).
3. Освещенность. Освещенностью называется величина светового потока, падающего на единицу поверхности. Освещенность измеряется в люксах (лкс).

В ощущении цвета — яркости соответствует светлота. Яркость падающего или отраженного света — физическая основа светлоты соответствующего цвета. Так же, как и яркость — светлота, освещенность – важное для цветокоррекции понятие физической оптики.

. Освещенность обратно пропорциональна квадрату расстояния до источника света.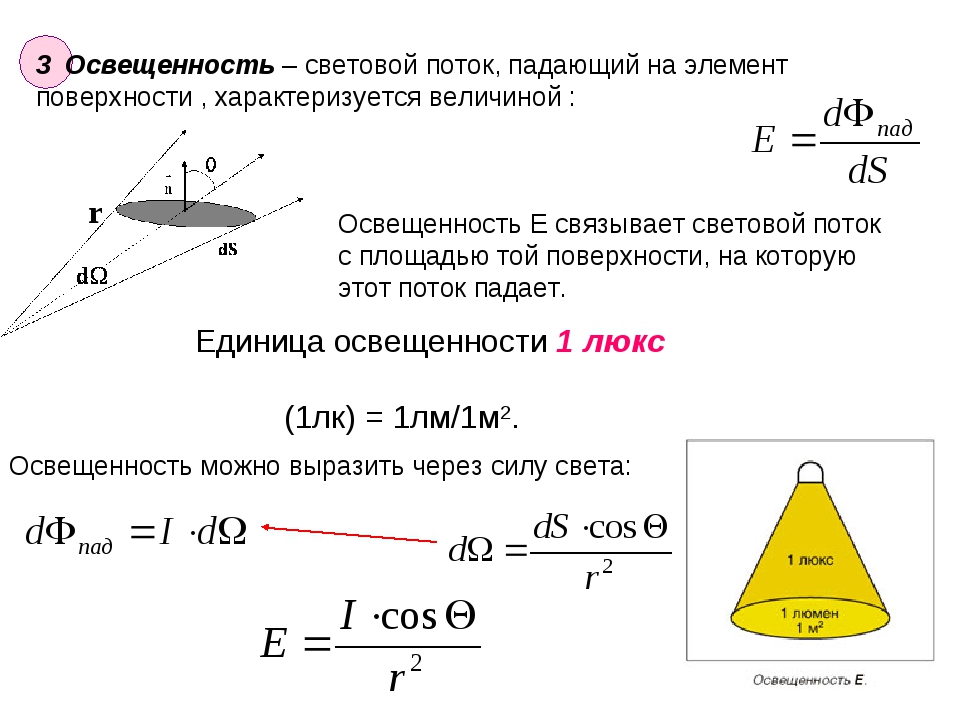

Падение яркости на первом метре и падение яркости между первым и вторым метром

Освещенность солнцем предметов, находящихся по отношению к солнечному лучу под одним углом, равна, так как в ограниченном пространстве данного пейзажа предметы находятся практически на одном расстоянии от солнца. Напротив, освещенность предметов в комнате убывает чрезвычайно быстро по мере удаления от окна или лампы.

Вместе с тем освещенность прямо пропорциональна косинусу угла, составленного падающим лучом и нормалью к поверхности предмета. Следует иметь в виду, что, даже зная яркость излучателя, подсчитать освещенность данного предмета не просто, так как приходится суммировать световой поток, падающий на освещенную площадку от разных точек источника света, учитывая как интенсивность излучения по данному направлению, так и расстояние от площадки до данной точки излучателя и, наконец, угол падения светового потока на площадку.

Как принято говорить в физике, освещенность – есть величина «интегральная». Никто, конечно, не производит расчеты при проведении коррекции изображения — воспринимаемая освещенность сюжета в изображении достигается визуальным контролем и зависит от квалификации цветокорректора.

Полезно иметь в виду, что глаз человека реагирует на яркость излучения, а не на количество световой энергии, в отличии от матрицы фотоаппарата. Величина эффекта от действия света на глаз (интенсивность ощущения света) не зависит от времени действия света. После того как глаз приспособился к свету, мы сохраняем относительно постоянное впечатление яркости. При проведении коррекции мы должны принимать во внимание, что адаптация глаза зрителя по освещенности не происходит для каждого изображения по отдельности — а в основном зависит от яркости освещения «просмотрового» места, а значит свето-теневые отношения изображения для просмотра в галереи, где освещение достаточно низкое по яркости и рассеянное — глаз адаптирован для восприятия в низкой освещенности, когда самым светлым воспринимается самая светлая точка на изображении и глаз «готов» к восприятию деталей в теневой области и «согласен» с отсутствием деталей в крайних тенях.

При подготовке изображения для публикации в книге (журнале) — внешнее освещение просмотра достаточно яркое, а самая светлая точка — белый лист бумаги, на которой напечатано изображение. Из-за этого изображения, подготовленные фотографами, в многостраничном издании выглядят браком — «вуаль» и «чернота». Фотографы сейчас ориентированы на восприятие изображений с экрана монитора (самое светлое — светлая точка изображения и внешнее освещение просмотрового места всегда ниже «излучения» изображения с монитора) — это условия «галереи».

Изображение, подготовленное для комфортного восприятия с монитора или для принта в «галерею».

Изображение в галерее

Изображение подготовленное для печати в издании, альбоме

Свет и цвет — одно и то же? Свет – излучение. Он принадлежит пространству. Цвет принадлежит предмету. Солнце излучает свет.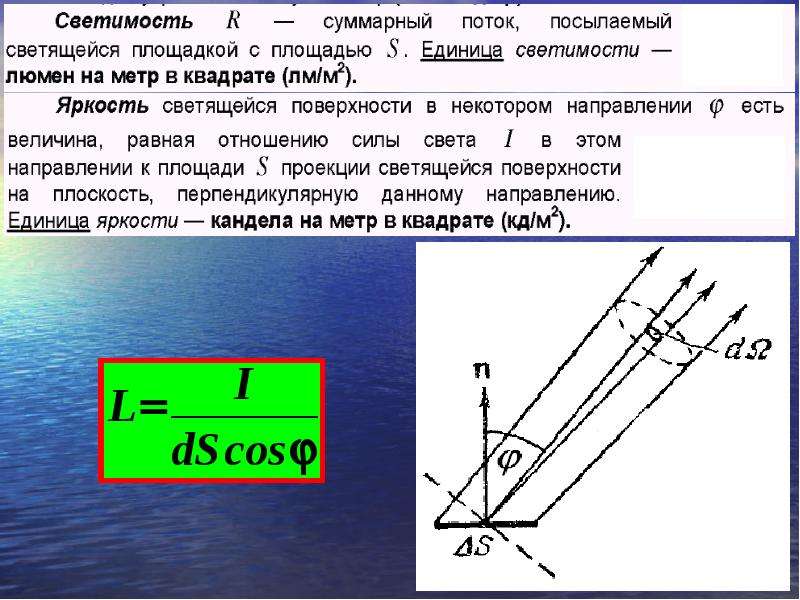

Небо на заре светится, светятся диск луны, лампа. Предметы обычно не светятся, они не источники света. С другой стороны впечатление цвета вызывается именно поступающими в глаз излучениями, и, если отрешиться от эффектов последействия цветового раздражителя, только ими.

Мы противопоставляем свету цвет, не отдавая себе отчета в том, что цвет в конечном итоге также излучение, но менее яркое. Если лист белой бумаги освещен ярким снопом света, охватывающим также и окружающие предметы, мы видим белый цвет. Но если точечно осветить тем же светом один только лист бумаги, вырвав его снопом света из окружения, лист будет казаться светящимся, излучающим белый свет. На самом деле лист бумаги и в первом и во втором случае излучает один и тот же отраженный от него поток световых волн. Относительно слабое излучение мы воспринимаем как цвет, сильное – как свет. Свет, падающий на окружающие нас предметы, вызывает множество градаций тона (светлоты). Первая причина различий тона ослабление светового потока в пространстве, вторая – в разнообразии окраски предметов, то есть в способности вещества сильнее или слабее поглощать световой поток.

Отраженное излучение будет тем ярче и предмет тем светлее, чем менее сильно вещество поглощает падающий на него свет. Отношение между освещенностью предмета и яркостью отраженного от него излучения называют «альбедо»(от album – белое). Идеально белое отражает и рассеивает весь падающий на него световой поток. Альбело идеально белого равно таким образом единице. Альбедо черного приближается к нулю.
Альбедо белой бумаги составляет примерно 0,8. Альбедо порошка титановых белил – около 0,9. Альбедо не меняется при изменении освещения и составляет физическую основу того, что можно было бы назвать светлотой предметного цвета. Предметную светлоту мы видим, а не только помним или знаем. Этому учит весь наш предметный опыт, повседневная практика человека. Если из двух предметов светлый находится в тени, а темный на свету, мы все же можем во многих случаях верно ответить на вопрос, окраска какого из них светлее.

Но мы видим, ожидаем также различия тона, вызванные объективной разницей в яркости отраженного излучения, а эта последняя связана не только с окраской предметов, но и с различной освещенностью. Одни предметы освещены, на другие падает тень. Пространство расчленяется светом и тенью. Разные плоскости предмета освещены сильнее или слабее в зависимости от положения их относительно источника света. Свет и тень формируют на изображении форму предмета. И в то же время окраска (цвет) завязана на освещенность сцены —

цвет должен соответствовать освещенности и освещенность не должна входить в противоречие с цветом (ожидаемым цветом предметов сцены).

Мы видим и непрерывные переходы тона от света к тени и скачки тона. Во всех этих случаях речь идет уже не о предметной светлоте, а о тоне как видимой яркости отраженного излучения. Сюда же относятся и градации тона, связанные с пространством, пространственными планами. Вспомним ряд уходящих вдаль фонарей.

Дальние фонари не светятся. Вспомним сглаживание тональных различий в дальних планах по сравнению с ближним. Всюду здесь имеется в виду тон как видимая яркость излучения. Освещение не только вызывает градации силы тона, вступая в сложное взаимодействие с предметной светлотой, но и объединяет краски по тону, подчиняет их общему тону.

Общий тон – прямое следствие общей освещенности.
Общий тон и освещенность меняются в очень больших пределах не только в зависимости от того, что изображено на изображении- открытое поле, на узкая улица или помещение, не только в зависимости от погоды, времени дня, но и от ряда других причин, например от времени года, от географической широты. Фактическая освещенность рассеянным светом неба на широте Петербурга в час дня в январе в 5 раз меньше освещенности в то же время дня в июне и равна освещенности рассеянным светом неба июньским вечером (в 7 часов вечера). Прямой солнечный свет увеличивает освещенность в июньский полдень еще в 5-6 раз. Несомненно, мы замечаем разницу в общей освещенности. Налетела грозовая туча, и мы говорим: «как потемнело». Но глаз быстро привыкает к изменившейся освещенности. Ее специфика сглаживается.

В комнате при дневном свете освещенность, достаточная для чтения книги, приблизительно в 50 раз меньше освещенности «рассеянным» светом неба в январе в час дня.

И действительно, снег с первых минут слепит нас, когда мы выходим из комнаты на улицу. Однако мы так привыкаем к комнатному освещению, что натюрморт, поставленный в комнате на столе, художник, может быть, напишет почти такими же светлыми красками, как и натюрморт, поставленный в саду при рассеянном свете неба. Что же сказать о темных интерьерах, изображенных в совсем не темных картинах Адрианом ван Остаде, об освещенности свечей в «Снятии с креста» Рембрандта? Освещенность – могучий источник тонального объединения. Она создает диапазон светлот данного куска и состояния природы. Она увеличивает и уменьшает число видимых светлот, вызывая то множество резких различий, то уводя предметы в цветовую неразличимость. Тональное решение изображения должно быть целиком и полностью поставлено в зависимость от содержимого изображения, его сюжета — от контекста.

В свое время физик Гельмгольц, писавший о живописи, пытался дать простое правило для трансформации тонового диапазона реальной сцены в тоновый диапазон изображения, основываясь на том факте, что чувствительность глаза обратно пропорциональна общей освещенности.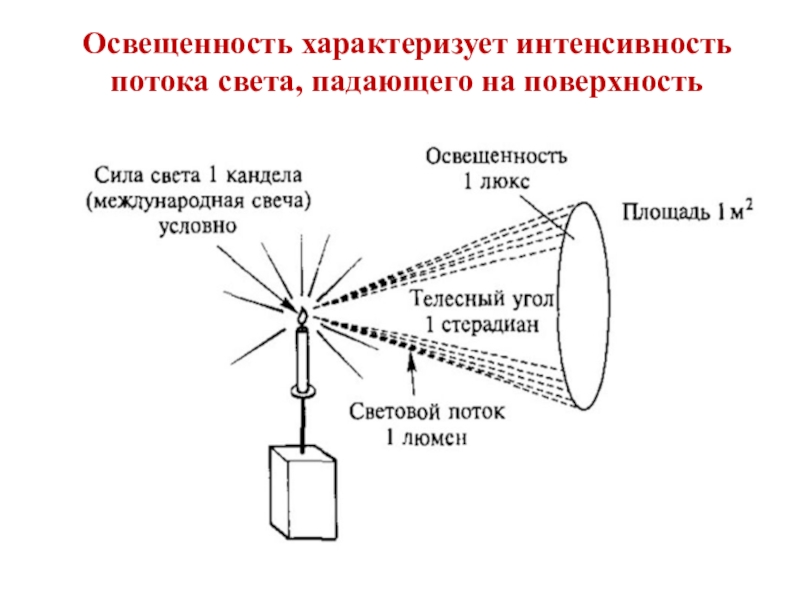 Гельмгольц рекомендовал художникам брать каждое пятно картины во столько раз темнее природного пятна, во сколько освещенность картины меньше общей освещенности в изображаемом природном мотиве. Отношения на картине должны казаться при этом тождественными природным отношениям. В распоряжении художников тоновый диапазон больше, чем тоновый диапазон офсетной печати, с которым имеет дело цветокорректор.

Работая с изображением важно выстроить баланс свето-теневых соотношений отношений, что бы зритель «поверил». И тут присоединяется еще один фактор — подготовленность аудитории к восприятию условностей и символизма изображения. Неискушенный зритель не поймет импресионистских по стилю изображений — увиденное войдет в противоречии с его опытом восприятия изображения, как «кальки» действительности. То, что прощается в семейном фотоальбоме, то чем восторгаются на фото выставках и фото сайтах в печатном многостраничном издании вызывает обычно отторжение и неприятие, но это уже из области психологии. .

Читайте книгу Н. Волкова Цвет в живописи.

Измерение яркости звезд

 — показатель, характеризующий яркость звезды или какого-нибудь другого астрономического объекта.

Существует два вида звездных величин — видимая и абсолютная.
Видимая звездная величина характеризует ту яркость, которую мы видим или можем увидеть. То есть, она определяет условия наблюдения объекта с Земли.
Эта величина берет начало со II века до р.Х., когда Гиппарх предложил делить все звезды по яркости на шесть величин — самые яркие и лучше всего видимые он назвал звездами первой величины, а самые тусклые — шестой.

Разумеется, такой субъективный подход для современных целей неприменим, к тому же, большая часть астрономических объектов невооруженным глазом не видна. При этом характеристика видимой яркости — вещь очень полезная. Поэтому в наше время классификация Гиппарха модернизирована и стала измеримой и объективной — и, несмотря на модернизацию, классы Гиппарха удалось сохранить.

В основе классификации видимой яркости лежат два принципа.
Во-первых, яркость определяется числом квантов излучения объекта, принимаемых глазом или фотоприемником в единицу времени. Это позволяет оценить яркость объективно.
Во-вторых, она учитывает особенность человеческого зрения. Дело в том, что человек оценивает яркость не линейно, а логарифмически — психофизиологический закон Вебера-Фехнера утверждает, что для человека ощущение, вызванное неким раздражителем, изменяется пропорционально логарифму интенсивности раздражителя, то есть, применительно к свету, яркость света воспринимается нами пропорционально логарифму светового потока.
В связи с этим, видимая звездная величина m определяется по формуле:

где I — световой поток, а С — некая константа
Константа С выбирается так, чтобы шкала звездных величин была как можно ближе к гиппарховой, то есть, чтобы для весьма яркой звезды видимая величина m была равна нулю.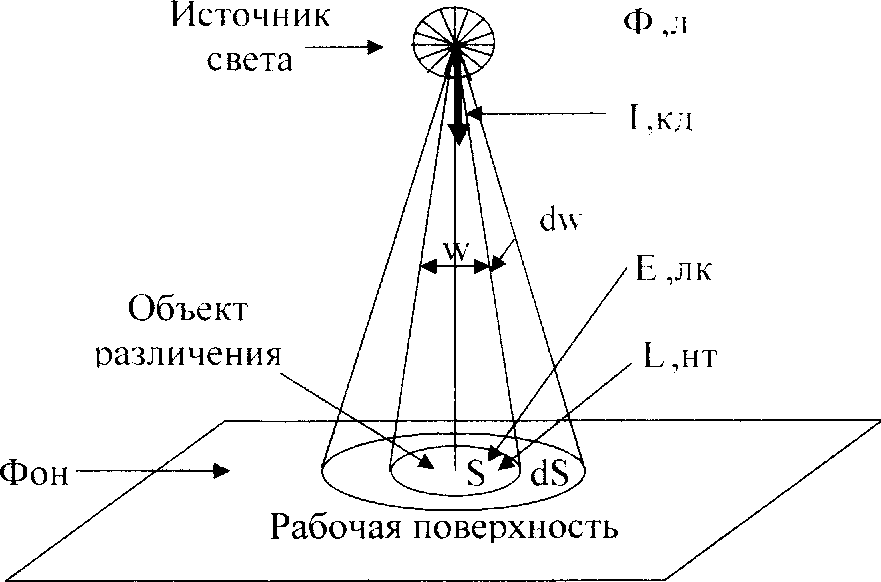 Строго говоря, С выбирается так, чтобы в приведенной формуле m было равно нулю для объекта, создающего (без учета влияния земной атмосферы) освещенность 2,54·10^-6 люкс.
Тогда звезда первой величины создает освещенность, примерно в 2,512 раз ниже указанной, второй величины — в 6,31 раз ниже и так далее. То есть, увеличение (уменьшение) звездной величины на единицу означает уменьшение (увеличение) силы света от источника примерно в 2,512 раза, а на пять единиц — ровно в сто раз. Объекты звездной величины более шести уже практически не видны невооруженным глазом.

Если b₁-кажущаяся яркость звезды 1, а b₂-кажущаяся яркость звезды 2, то разность величин задается выражением:

При этом пока все еще не так просто. Звезда или иной объект излучает (или отражает) свет разных длин волн — а человек их воспринимает по-разному. При одной и той же интенсивности зеленый свет воспринимается ярче, красный — тусклее, а инфракрасный, разумеется, не воспринимается вовсе.  

Абсолютные звёздные величины

Видимый блеск и видимая звёздная величина звезды зависят от её расстояния до наблюдателя – r. Чтобы освободиться от влияния расстояния, введено понятие об абсолютном блеске и абсолютной величине звезды.

Абсолютным блеском звезды L называется тот блеск, который она имела бы, будучи удалена от наблюдателя на расстояние равное 10 парсекам.

Так как освещённость убывает обратно пропорционально квадрату расстояния, то абсолютный блеск L и видимый блеск l связаны соотношением:

L/l = r²/100 = 2,512^m-M 

m – видимая звёздная величина, М – абсолютная звёздная величина, под которой понимают ту звёздную величину, которую бы имела звезда, будучи удалённой на расстояние, равное 10 парсекам.

Из указанного соотношения получаем формулу:

М = m + 5 — 5lg r 

С учётом межзвёздного поглощения:

М = m + 5 — 5lg r — А(r)

где А(r) – поглощение света, пропорциональное расстоянию до звезды.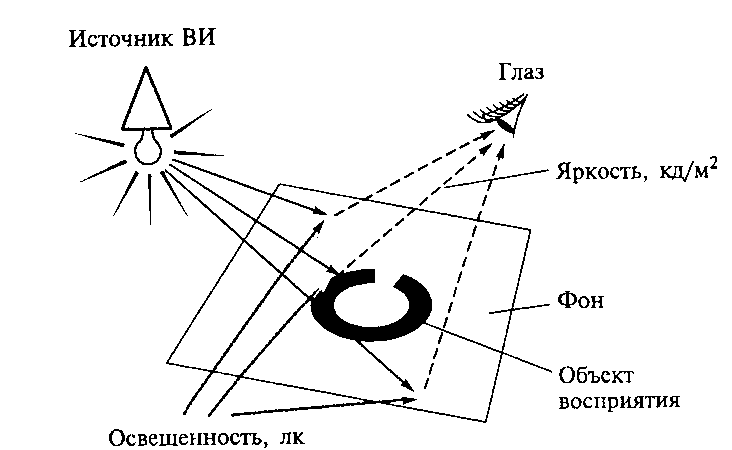

Эта формула позволяет вычислить абсолютную звёздную величину звезды, если известно расстояние, и вычислить расстояние, если известна абсолютная величина, по формуле:

lg r = (m — M)/5 + 1

Абсолютные звёздные величины могут быть болометрическими, визуальными, фотографическими.

Солнце имеет абсолютную звёздную величину +4,7^m.

Часто используют светимость звезды – отношение абсолютного блеска звезды к абсолютному блеску Солнца.

Самые яркие звёзды ярче Солнца на 14^m, они испускают больше энергии в 1 000 000 раз. Самые слабые слабее на 14^m. Они испускают меньше энергии в 300 000 раз.

Отношение светимостей самых ярких и самых слабых звёзд достигает около 100 млрд.

Источник

Светимость (блеск) звезд

Представьте, что где-то в море в ночной тьме тихо мерцает огонек. Если бывалый моряк не объяснит вам, что это, вы часто и не узнаете: то ли перед вами фонарик на носу проходящей шлюпки, то ли мощный прожектор далекого маяка.

В том же положении в темную ночь находимся и мы, глядя на мерцающие звезды. Их видимый блеск зависит и от их истинной силы света, называемой светимостью (полное количествл энергии, излучаемой по всем направлениям), и от их расстояния до нас. Только знание расстояния до звезды позволяет подсчитать ее светимость по сравнению с Солнцем. Так например, светимость звезды, в десять раз менее яркой в действительности, чем Солнце, выразится числом 0,1.

Истинную силу света звезды можно выразить еще иначе, вычислив, какой звездной величины она бы нам казалась, если бы она находилась от нас на стандартном расстоянии в 32,6 светового года, то есть на таком, что свет, несущийся со скоростью 300 000 км/сек, прошел бы его за это время.

где R — радиус звезды, Т — температура.

Принять такое стандартное расстояние оказалось удобным для различных расчетов. Яркость звезды, как и всякого источника света, изменяется обратно пропорционально квадрату расстояния от него. Этот закон позволяет вычислять абсолютные звездные величины или светимости звезд, зная расстояние до них.

Когда расстояния до звезд стали известны, то мы смогли вычислить их светимости, то есть смогли как бы выстроить их в одну шеренгу и сравнивать друг с другом в одинаковых условиях. Надо сознаться, что результаты оказались поразительными, поскольку раньше предполагали, что все звезды «похожи на наше Солнце». Светимости звезд оказались поразительно разнообразными, и их в нашей шеренге не сравнить ни с какой шеренгой пионеров.

Приведем только крайние примеры светимости в мире звезд.

Самой слабой из известных долго являлась звезда, которая в 50 тысяч раз слабее Солнца, и ее абсолютная величина светимости: +16,6. Однако, впоследствии были открыты и ещё более слабые звезды, светимость которых, по сравнению с солнцем, меньше в миллионы раз!

Размеры в космосе обманчивы: Денеб с Земли сияет ярче Антареса, а вот Пистолет — не виден совсем. Тем не менее, наблюдателю с нашей планеты и Денеб и Антарес кажутся просто незначительными точками, по сравнению с Солнцем. Насколько это неверно можно судить по простому факту: Пистолет выпускает в секунду столько же света, сколько Солнце — за год!

На другом краю шеренги звезд стоит «S» Золотой Рыбы, видимая только в странах Южного полушария Земли как звездочка восьмой величины (то есть даже не видимая без телескопа!). В действительности она в 400 тысяч раз ярче Солнца, и ее абсолютная величина светимости: —8,9.

Абсолютная величина светимости нашего Солнца равна +5. Не так уж и много! С расстояния в 32,6 светового года мы бы его плохо видели без бинокля.

Если яркость обычной свечи принять за яркость Солнца, то в сравнении с ней «S» Золотой Рыбы будет мощным прожектором, а самая слабая звезда слабее самого жалкого светлячка.

Итак, звезды — это далекие солнца, но их сила света может быть совершенно иной, чем у нашего светила. Образно выражаясь, менять наше Солнце на другое нужно было бы с оглядкой. От света одного мы ослепли бы, при свете другого бродили бы, как в сумерках.

 

     

Основные формулы [1]

1. Сила света , , .

2. Освещенность ,, .

3. Светимость ,.

4. Яркость ,.

5. Освещенность, создаваемая небом на открытой площади .

6. Коэффициент естественного освещения (к.е.о.) .

Образцы решения задач

1. Найдите освещенность на поверхности Земли вызываемую нормально падающими световыми лучами. Яркость Солнца .

Дано: Решение:

,, где,

.

. — телесный угол Солнца с Земли,

Найти:

.

2. На лист белой бумаги размеромнормально к поверхности падает световой поток. Принимая коэффициент рассеяния бумажного листа, определите для него: освещенность, светимость(S), яркость(L).

Дано: Решение:

, ,

, ,

. ,

Найти:,

,

,

Вопросы и задачи для самостоятельной работы Вопросы

1. Когда небо ниже Земли бывает?

2. Дайте определение освещенности. Запишите законы освещенности. Назовите некоторые числа для освещенности из СНиП.

3. Что такое яркость? Как понятие «яркость» используется в задачах строительной физики?

4. Что такое коэффициент естественного освещения? Значение к.е.о. нормируется в СНиП. Назовите некоторые числа к.е.о. из СНиП.

5. В Череповце в июне после захода солнца за горизонт еще 2-3 часа достаточно светло (белые ночи). Как это можно объяснить? Какого цвета небо в белые ночи: желто-красное, голубое?

6. Что такое визуальная и энергетическая фотометрия? Эквивалентны ли они?

7. Что такое телесный угол? Единицы его измерения.

8. Назовите единицы, принятые в визуальной фотометрии: световой поток, освещенность, сила света. Как они связаны между собой?

9. Чистый стеклянный баллон электролампы накаливания после включения быстро становится горячим. Почему?

10. Поясните физический смысл к.е.о. Его геометрическая интерпретация.

11. Освещенность предметов на земной поверхности может оказаться большей, чем в случае прямого падения солнечных лучей. Как это можно объяснить?

12. Подумайте, насколько важно при установлении законов фотометрии знание, что такое свет:

а) электромагнитные волны;

б) поток фотонов;

в) или еще что-то.

Задачи

4.1. Яркость безоблачного неба в солнечный летний день равна . Оцените освещенность, которая возникает на открытой поверхности Земли в месте, куда не попадают прямые лучи Солнца.

4.2. Как изменятся ваши рассуждения, если говорить об освещенности предметов при ярком безоблачном небе в зимний день, например в декабре или в январе: в степи; в горах. Яркость снега, освещенного Солнцем, .

4.3. Яркость безоблачного неба в солнечный летний день равна . Оцените освещенность, которая возникает на поверхности Земли у стены высотного здания. Считайте, что стена здания характеризуется коэффициентом поглощения света α = 1. Как изменится ваш ответ, если коэффициент поглощения α = 0,4. Дайте приблизительную оценку.

4.4. Электролампочка накаливания, потребляющая мощность 40 Вт, дает световой поток 380 лм. 40 % этого потока направлено на поверхность 5 м². Оцените среднюю освещенность поверхности.

4.5. Какова сила света в канделах для 25-ваттой лампочки накаливания? Какова сила света в канделах для 25-ваттой люминесцентной лампы?

4.6. На лист белой чертежной бумаги падают лучи от лампочки, сила света которой равна 100 св. Определите освещенность, светимостьи яркостьлиста бумаги в точке, находящейся на расстоянии 1,5 м от лампочки, если лучи падают на бумагу перпендикулярно, коэффициент отражения 0,75.

4.7. Вычислите световой поток и силу света, испускаемые шаром, если средняя яркость его внешней поверхности, а диаметр шара.

4.8. Внутри шара из молочного стекла, диаметр которого , помещена лампа накаливания мощностью 200 Вт, работающая при напряжении 220 В, световой поток такой лампы. Определите яркость внешней поверхности шара, если 25% всего потока источника поглощается в стекле.

4.9. Шаровой светильник из молочного стекла, диаметром , при использовании лампы накаливания мощностью 200 Вт, работающей при напряжении 220 В, имеет яркость, световой поток лампы. Найдите КПД светильника.

4.10. Лампа подвешена над столом на высоте 80 см. Освещенность стола в точке под лампой вдвое превышает наиболее благоприятную для чтения освещенность. На каком расстоянии от этой точки по поверхности стола создается нормальная освещенность? Лампу считать точечным источником света.

4.11. Люминесцентная лампа мощностью 20 Вт имеет световую отдачу белого света . Какой мощности надо взять лампу накаливания на напряжение 127 В и 220 В для получения того же светового потока? Во сколько раз люминесцентная лампа будет экономичней лампы накаливания? Потери мощности в дросселе 20 %.

4.12. На экран площадью 3м² (рассеивающий свет с коэффициентом отражения 0,8) падает световой поток 150 лм. Определите светимостьи яркостьэкрана.

4.13. Какой кривой светораспределения (индикатрисой) должна обладать лампа, чтобы давать равномерную освещенность на плоскости стола, над которым она подвешена, а также световой поток, падающий на стол, если ?

4.14. Согласно стандарту лампа мощностью 100 Вт при напряжении 220 В должна давать световой поток 1275 лм. Определите ее удельную мощность (число ватт на канделу), принимая во внимание, что 40 % светового потока лампы падает на поверхность 5 м². Определите среднюю освещенность.

4.15. Точечный источник света находится над поверхностью стола радиусом R. На какую высоту H над поверхностью стола необходимо поднять источник света с тем, чтобы освещенность края стола была максимальной?

4.16. Над серединой круглого стола радиусом R на высоте H от его поверхности висит лампа силой света I . Определите: среднюю освещенность стола; во сколько раз средняя освещенность меньше максимальной; кривую светораспределения (индикатрису) лампы, при которой освещенность по поверхности стола постоянна.

4.17. В центре квадратной комнаты висит лампа. Считая лампу точечным источником света, найдите, на какой высоте от пола должна висеть лампа, чтобы освещенность в углах была максимальной.

4.18. Яркость граней светящегося куба одинакова и равна , ребро куба 20 см. В каком направлении сила света куба максимальна и чему она равна?

4.19. Освещенность поверхности Земли в точке нормального падения лучей . Полагая, что излучение Солнца подчиняется закону Ламберта, и пренебрегая поглощением света в атмосфере, определите яркость Солнца и среднюю освещенность Земли. Расстояние от Солнца до Земли, диаметр Солнца, коэффициент отражения земной поверхности.

Физика цвета. Всю жизнь мы окружены невероятным… | by Mary Sabell | DesignSpot

Что такое свет и цвет

Поскольку цвет — это способность объектов отражать или излучать световые волны отдельной части спектра, начнем с определения того, что же такое свет.

С древних времен люди пытались понять природу света. Так, например, древнегреческий философ Пифагор сформулировал теорию света, в которой утверждал, что непосредственно из глаз испускаются прямолинейные лучи видимого света, которые, попадая на объект и ощупывая его, дают людям возможность видеть. Согласно Эмпедоклу, богиня любви Афродита поместила в наши глаза четыре элемента — огонь, воду, воздух и землю. Именно свет внутреннего огня, считал философ, помогает людям видеть объекты материального мира. Платон же предполагал, что существуют две формы света — внутренняя (огонь в глазах) и внешняя (свет внешнего мира) — и их смешение дает людям зрение.

По мере изобретения и развития различных оптических приборов представления о свете развивались и трансформировались. Так в конце XVII века возникли две основные теории света — корпускулярная теория Ньютона и волновая теория Гюйгенса.

Согласно корпускулярной теории, свет представлялся в виде потока частиц (корпускул), излучаемых светящимся объектом. Ньютон считал, что движение световых частиц подчинено законам механики, то есть, например, отражение света понималось как отражение упругого мячика от поверхности. Преломление света ученый объяснял изменением скорости световых частиц при переходе между разными средами.

В волновой теории, в отличие от корпускулярной, свет рассматривался как волновой процесс, подобно механическим волнам. В основе теории лежит принцип Гюйгенса, по которому каждая точка, до которой доходит световая волна, становится центром вторичных волн. Теория Гюйгенса позволила объяснить такие световые явления, как отражение и преломление.

Таким образом, весь XVIII век стал веком борьбы двух теорий света. В первой трети XIX века, однако, корпускулярная теория Ньютона была отвергнута и восторжествовала волновая теория.

Важным открытием XIX века стала выдвинутая английским ученым Максвеллом электромагнитная теория света. Исследования привели его к выводу, что в природе должны существовать электромагнитные волны, скорость которых достигает скорости света в безвоздушном пространстве. Ученый считал, что световые волны имеют ту же природу, что и волны, возникающие вокруг провода с переменным электрическим током, и отличаются друг от друга лишь длиной.

В 1900 году Макс Планк выдвинул новую квантовую теорию света, согласно которой, свет является потоком определенных и неделимых порций энергии (кванты, фотоны). Развитая Эйнштейном, квантовая теория смогла объяснить не только фотоэлектрический эффект, но и закономерности химического действия света и ряд других явлений.

В настоящее время в науке преобладает корпускулярно-волновой дуализм, то есть свету приписывается двойственная природа. Так при распространении света проявляются его волновые свойства, в то время как при его испускании и поглощении — квантовые.

Но как из света получается цвет? В 1676 году Исаак Ньютон с помощью трёхгранной призмы разложил белый солнечный свет на цветовой спектр, который содержал все цвета кроме пурпурного. Ученый проводил свой опыт следующим образом: белый солнечный свет проходил сквозь узкую щель и пропускался через призму, после чего направлялся на экран, где возникало изображение спектра. Непрерывная цветная полоса начиналась с красного и через оранжевый, желтый, зеленый и синий заканчивалась фиолетовым. Если же это изображение пропускалось через собирающую линзу, то на выходе вновь получался белый свет. Таким образом, Ньютон открыл, что белый свет — это комбинация всех цветов.

Любопытным было и следующее наблюдение: если из цветового спектра убрать один из цветов, например, зеленый, а остальные пропустить через собирающую линзу, то полученный в итоге цвет окажется красным — дополнительным к удаленному цвету.

По сути, каждый цвет создается электромагнитными волнами определенной длины. Человеческий глаз способен видеть цвета с длиной волны в диапазоне от 400 до 700 миллимикрон, где наименьшая длина волны соответствует фиолетовому цвету, а наибольшая — красному. Поскольку каждый цвет спектра характеризуется своей длиной волны, то он может быть точно задан длиной волны или частотой колебаний. Сами по себе световые волны бесцветны, цвет возникает лишь при восприятии волн человеческим глазом и мозгом. Однако механизм, по которому мы распознаем эти волны, до сих пор неизвестен.

Что касается цвета предметов, то он возникает, фактически, в процессе поглощения световых волн. То есть, если мы видим, что предмет зеленого цвета, по сути, это означает, что молекулярный состав его поверхности таков, что он поглощает все волны, кроме зеленых. Сами по себе предметы не имеют никакого цвета и обретают его лишь при освещении.

Магниты разработки ИЯФ СО РАН увеличат яркость синхротрона ESRF

​Ученые Института ядерной физики им Г.И. Будкера СО РАН разработали и изготовили для Европейского центра синхротронного излучения (ESRF) 66 октупольных магнитов. Оборудование станет частью новой магнитной системы, которая позволит увеличить яркость источника синхротронного излучения (СИ) в 30 раз. Общая сумма контракта составила 820 тысяч евро.

Европейский центр синхротронного излучения — это источник СИ, расположенный в Гренобле (Франция). Комплекс представляет собой электронный синхротрон на энергию 6 ГэВ с многочисленными каналами вывода. В настоящее время в Центре проводится модернизация всех систем основного кольца источника синхротронного излучения. Магнитная структура кольца будет полностью изменена, что позволит существенно улучшить параметры пучка СИ.

«Мы изготовили для ESRF партию электромагнитных октупольных линз, основное назначение которых — коррекция нелинейного движения пучка электронов, — рассказывает научный сотрудник ИЯФ СО РАН Михаил Блинов. — Вес каждого магнита составляет 200 кг, гарантийный срок службы — десятки лет. Единственная возможная поломка — повреждение катушек, на этот случай мы поставили два комплекта запасных».

Остальные магниты изготовили специалисты из других стран-членов ESRF, однако, сборкой всей магнитной системы занимаются также сотрудники ИЯФ СО РАН. Сборка, которая началась в октябре 2017 года, продлится до конца 2018 года, затем работа синхротронного центра будет остановлена на год — за это время французские физики установят новую систему в тоннель ускорителя, а также модернизируют пользовательские станции с учетом изменившихся параметров синхротрона.

Одними из основных характеристик источников синхротронного излучения являются яркость и эмиттанс — фазовый объем электронного пучка: чем меньше эмиттанс, тем выше яркость и наоборот. Для пользователя экспериментальной станции увеличение яркости — это, с одной стороны, возможность более детального изучения объекта исследования, а с другой — уменьшение количества образца, необходимое для работы на синхротронном излучении. По словам Жана-Клода Биаши, координатора сборки магнитной системы со стороны ESRF, в результате модернизации горизонтальный эмиттанс пучка уменьшится более чем в 30 раз, что приведет к многократному увеличению яркости синхротрона. В результате у пользователей появятся широкие возможности для исследований вещества на атомарном уровне.

ESRF был построен в 1994 году силами 19 стран. Россия стала участником коллаборации в 2014 году, за реализацию российской научно-исследовательской программы отвечает НИЦ «Курчатовский институт». Комплекс включает в себя более 40 пользовательских станций, на которых проводят исследования ученые, представляющие страны, входящие в коллаборацию, из самых разных областей науки — физики, химии, биологии, геологии, археологии и медицины. Кроме того, на установках Центра регулярно работают сотрудники фармацевтических, нефтедобывающих компаний, а также фирм-производителей электроники.

Работа частично поддержана субсидией Министерства образования и науки РФ в рамках Федеральной целевой программы «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2014 — 2020 годы».

Светимость, яркость, освещенность или двойные стандарты в астрономии — Астрономия — Каталог статей

Продолжение. Начало здесь:

Какие звезды в созвездиях самые яркие?

Что такое блеск и звездная величина светила?

 

Когда мы разбирались с блеском и звездными величинами, то и дело всплывали другие фотометрические величины: светимость, освещенность, световой поток. В этот ряд можно добавить яркость и силу света. В учебнике [1] большинство из них можно встретить в 22 параграфе «Основные характеристики звезд. Светимость». Но определение дается только для светимости L (стр.155): Светимостью называется полная энергия, излучаемая звездой за 1 с. Светимость звезды можно выразить в ваттах, но чаще ее выражают в светимостях Солнца.

Но не все так просто и здесь. Ряд величин имеет не одно значение. В нашем случае приводится определение светимости звезды. А есть еще и просто светимость или, как ее еще называли, светность. В словаре физических и астрономических терминов [3] наряду со светимостью звезды дается формулировка и просто светимости:

Светимость, светность – величина, измеряемая отношением светового потока, испускаемого светящейся поверхностью, к площади этой поверхности. Единица светимости в СИ – люмен на квадратный метр (лм/м²).

Найти такую светимость можно по формуле:

L = dΦ/dS

Где dS – площадь светящейся поверхности.

Это физическое определение светимости. И, к сожалению, в дальнейшем вот такие двойные стандарты встречаются довольно часто. Взять, к примеру, яркость. В астрономии она присутствует во многих выражениях, являясь синонимом блеска. Но, как мы упоминали ранее, под блеском понимается так называемая видимая яркость звезд. А с физической точки зрения, ни о какой яркости звезд не может быть и речи, так как яркость – характеристика светящихся тел, равная отношению силы света в каком-либо направлении к площади проекции светящейся поверхности на плоскость, перпендикулярную к этому направлению. Единица яркости в СИ – кандела на квадратный метр (кд/м²) [3].

B = dI/dS

Но ведь звезды мы представляем как точечные источники света. А точечный источник не имеет площади. Поэтому определение яркости с физической точки зрения неприменимо.

При определении яркости, мы упомянули про силу света.

Сила света – скалярная величина, характеризующая свечение источника света в некотором направлении и равная отношению светового потока, распространяющегося в малом телесном угле, к этому телесному углу. Единица силы света в СИ – кандела [3].

В отличие от предыдущих единиц, единица силы света – кандела (в переводе «свеча»), является основной физической величиной, коих не так много в физике (всего семь).

Если световой поток испускается точечным источником равномерно во всех направлениях, то сила света определяется по формуле:

I = Ф/(4π).

Настала очередь светового потока, который обозначается греческой буквой Φ. Пора нам разобраться и с ним.

Опять в Википедии читаем:

Световой поток — физическая величина, характеризующая «количество» световой энергии в соответствующем потоке излучения. Иными словами, это мощность такого излучения, которое доступно для восприятия нормальным человеческим глазом.

Единица измерения СИ: люмен.

К сожалению, в учебнике нет и определения освещенности, хотя на освещенность ссылаются несколько раз, например, в определении блеска светила. Не нашел я этих величин и в справочнике тех же авторов [2]. Попробуем восполнить этот пробел.

Обратимся к Википедии:

Освещённость — физическая величина, численно равная световому потоку dΦ, падающему на единицу поверхности:

E = dΦ/dσ

dσ – площадь поверхности, на которую падает свет.

Единицей измерения освещённости в системе СИ служит люкс.

А люкс – это лм/м². Но и здесь есть темные стороны. В учебнике Засова [4] есть такое выражение: «Но измерить эту освещенность в абсолютных единицах (например, в Вт/м²) очень сложно» (стр.92). Опять двойные стандарты. 

Представляет интерес закон обратных квадратов Иоганна Кеплера, который устанавливает связь между освещенностью, силой света и расстоянием от источника до объекта (r), а также углом падения лучей относительно нормали к поверхности (i):

E = I cos(i)/r².

Таким образом:

dΦ₁/dΦ₂ = E₁/E₂

Теперь становится понятно, почему  «… звезды 1-й звездной величины создают в 2,5 раза большую освещенность (точнее в 2, 512 раза), чем звезды 2-й звездной величины, которые, в свою очередь, дают световые потоки в 2,5 раза больше, чем звезды 3-й звездной величины, и т.д. Таким образом, за интервал в одну видимую звездную величину (обозначается 1^m) принято отношение освещенностей (Е) в 2,512 раза.… В виде формулы эти отношения выразил Н.Погсон:

E₁/E₂ = 2,512^{m2 – m1} (1).

Измеряя при помощи фотометра отношение блеска звезд, можно определить разность звездных величин по формуле Погсона» [1] (стр.152).  Довольно туманное выражение немного прояснилось.

Но есть в том же параграфе 22 [1] еще одна фраза, заставляющая нас задуматься: Используя формулу (1), можно записать соотношение между светимостями и абсолютными звездными величинами какой-либо звезды и Солнца:

L/L_☼ = 2,512^{M☼ – M} (8)

Выходит: dΦ₁/dΦ₂ = E₁/E₂ = L₁/L₂.

Доказать это можно применив двойные стандарты – воспользовавшись формулой для светимости физической: L = dΦ/dS. Тогда у нас все сходится. А вот для светимости астрономической, все несколько сложнее. Здесь в дело вмешивается цвет звезд. Но это уже совсем другая история.

 

Продолжение следует…

Литература:

1. Галузо, И.В. Астрономия: учеб. пособие для учащихся 11 кл. учреждений, обеспеч. получение общ. сред. образования / И.В. Галузо, В.А. Голубев, А.А. Шимбалев. – Минск: Нар. асвета, 2009.

2. Голубев, В.А. Астрономия: основные понятия, таблицы / И.В. Галузо, В.А. Голубев, А.А. Шимбалев. – Минск: Универсал-Пресс, 2006.

3. Болсун, А.И. Словарь физических и астрономических терминов / А.И. Болсун, Е.Н. Рапанович. – Минск: Нар. асвета, 1986.

4. Засов, А.В. Астрономия: учебник для 11-х кл. средн. общеобраз. шк./ А.В.Засов, Э.В.Кононович. – Минск: Нар. асвета, 1994.

Солнечно-земная физика. Сборник. Выпуск 24 — ISTP SB RAS

I. Исследования эффектов Челябинского метеороида (Research into Chelyabinsk meteoroid effects) Бернгардт О.И., Куркин В.И., Жеребцов Г.А., Кусонский О.А., Григорьева С.А. Ионосферные эффекты в первые два часа после падения метеорита «Челябинск» (Berngardt O.I., Kurkin V.I., Zherebtsov G.A., Kusonskii O.A., Grigoryeva S.A. Ionospheric effects during first two hours after Chelyabinsk meteorite impact) Кутелев К.А., Бернгардт О.И. Моделирование сигнала ВНЗ радара SuperDARN в присутствии движущейся среднемасштабной неоднородности во время падения метеорита «Челябинск» (Kutelev K.A., Berngardt O.I. Modeling of oblique back scatter sounding signal of SuperDARN radar in the presence of travelling medium-sized inhomogeneity during the meteoroid “Chelyabinsk” impact) Ратовский К.Г., Белинская А.Ю., Кусонский О.А., Степанов А.Е. Анализ крупномасштабных ионосферных возмущений, наблюдавшихся в день взрыва Челябинского метеороида на ионозондах в азиатской части России (Ratovsky K.G., Belinskaya A.Yu., Kusonskii O.A., Stepanov A.E. Analysis of large-scale ionospheric disturbances observed with ionosondes in Asian part of Russia on the day of Chelyabinsk meteoroid impact) Козлов В.И., Муллаяров В.А., Корсаков А.А., Каримов Р.Р., Кобякова С.Е., Башкуев Ю.Б., Номинов Г.Б. Эффекты взрыва Челябинского метеороида 15.02.2013 в вариациях параметров ОНЧ-радиосигналов, регистрируемых в Якутске и Улан-Удэ (Kozlov V.I., Mullayarov V.A., Korsakov A.A., Karimov R.R., Kobyakova S.E., Bashkuyev Yu.B., Nominov G.B. Effects of Chelyabinsk meteoroid explosion on 15 February 2013 in variations of parameters of VLF radio signals recorded in Yakutsk and Ulan-Ude) Перевалова Н.П., Шестаков Н.В., Жупитяева А.С., Ясюкевич Ю.В., Воейков С.В., Кутелев К.А. Поведение полного электронного содержания во время пролета и взрыва Челябинского метеороида (Perevalova N.P., Shestakov N.V., Zhupityayeva A.S., Yasyukevich Yu.V., Voeikov S.V., Kutelev K.A. Dynamics of total electron content during the passage and explosion of Chelyabinsk meteoroid) Багров А.В., Леонов В.А., Попеленская Н.В. Оценка происхождения и состава матрицы тела Челябинского болида 2013 г. (Bagrov A.V., Leonov V.A., Popelenskaya N.V. Estimating the origin and composition of the body matrix of 2013 Chelyabinsk bolide) Добрынина А.А., Чечельницкий В.В., Черных Е.Н., Саньков В.А. Челябинский метеороид: сейсмологические наблюдения (Dobrynina A.A., Chechelnitsky V.V., Chernykh E.N., San’kov V.A. Chelyabinsk meteoroid: Seismological observation) Михалев А.В. Яркость ночного неба и собственное излучение верхней атмосферы в регионе Восточной Сибири после падения Челябинского метеорита (Mikhalev A.V. Night sky brightness and intrinsic emission of the upper atmosphere in East Siberia region after Chelyabinsk meteorite fall) Сорокин А.Г. Инфразвуковое излучение Челябинского метеороида (Sorokin A.G. Infrasonic radiation of Chelyabinsk meteoroid) Рахматулин Р.А., Пашинин А.Ю., Липко Ю.В., Хомутов С.Ю., Бабаханов И.Ю. О возможной геоэффективности пролета Челябинского метеороида в магнитосфере Земли (Rakhmatulin R.A., Pashinin A.Yu., Lipko Yu.V., Khomutov S.Yu., Babakhanov I.Yu. On the possible geoefficiency of Chelyabinsk meteorite entering the Earth’s magnetosphere) II. Материалы семинара, посвященного памяти профессора Э.Л. Афраймовича (Materials of the workshop to the memory of Prof. E.L. Afraimovich) Мыльникова А.А., Ясюкевич Ю.В., Демьянов В.В. Определение абсолютного вертикального полного электронного содержания в ионосфере по данным ГЛОНАСС/GPS (Mylnikova A.A., Yasyukevich Yu.V., Demyanov V.V. Estimation of absolute vertical total electron content in the ionosphere from GLONASS/GPS data) Михалев А.В. Среднеширотные сияния в Восточной Сибири в 1991–2012 гг. (Mikhalev A.V. Midlatitude airglows in East Siberia in 1991–2012) Малькова П.Л., Едемский И.К. Исследование широтных особенностей генерации волновых пакетов солнечным терминатором в долготном регионе Америки в течение 2008 г. (Malkova P.L., Edemsky I.K. Investigation of latitudinal peculiarities in generation of wave packets by solar terminator in longitutinal region of America during 2008)

Меры яркости | IOPSpark

Мощность

Квантовая и ядерная | Световой звук и волны

Меры яркости

Повествование о физике для 14-16

Мощность в тракте измеряется в ваттах: видимая мощность в люменах

Мощность обогрева по пути излучения измеряется в ваттах.Это просто и часто называют силой излучения. Более сложно подумать о потоке или потоке через конкретную область — количестве ватт на квадратный метр. Это называется лучистым потоком.

Однако ни один из них не учитывает чувствительность глаза к разным частотам, поэтому они не могут быть мерой яркости. И мощность излучения, и поток излучения могут быть очень высокими, но при этом вы ничего не видите, потому что все частоты выходят за пределы видимого диапазона.Энергия, смещенная фотонами в луче, не соответствует энергии, необходимой для запуска процессов в вашем глазу, которые позволяют вам видеть.

Существует ряд мер (используемых в фотометрии), настроенных на стандартный глаз , с которыми вы можете столкнуться. Это сложная область, и здесь рассматривается значительный выбор.

Мощность света, обнаруживаемая человеческим глазом, — хорошее место для начала, и это аналог мощности излучения, скорректированной для человеческого глаза.Он измеряется в люменах. Приобретая лампочку, вам следует выбрать максимальное количество люмен на ватт, которое вы можете найти, и, таким образом, максимально увеличить соотношение видимых фотонов: невидимых фотонов. Или, как описано в SPT: тема «Энергия и электричество», большая часть энергии будет приходиться на путь освещения и лишь небольшую часть — на путь обогрева.

Люкс — это единица измерения определяемой яркости

Люмен не говорит вам о яркости, потому что яркость — это обнаруживаемый поток фотонов на единицу площади, и есть фотометрический эквивалент лучистого потока (ваттметр ² ) или 1 Вт · м ^-2 ) для выполнения эта функция.Это люкс. Один люкс равен 1 люмен метру ^-2 . Скорее всего, вы встретите его в спецификациях чувствительности электронных устройств обработки изображений (например, видеокамер).

Высокочувствительным сенсорам для работы требуется всего несколько люксов, собирая всего несколько фотонов. Менее чувствительный датчик может компенсировать это за счет увеличения своей площади, как это делает зрачок вашего глаза, когда свет становится тусклым.

люмен — это современный эквивалент мощности свечи

Здесь есть еще один интересный шаг.Так же, как мощность представляет наибольший интерес для людей в практических ситуациях (вспомните блок лошадиных сил и , чтобы показать, сколько лошадей может заменить новомодный паровой двигатель), так и освещение представляет наибольший интерес, когда мы запускаем его в работу. Свеча в течение многих лет выполняла ту же функцию, что и мощность, как единица силы света. Возьмите одну стандартную свечу — фиксированного размера и составляющих — и сравните ее выход с источником, который необходимо калибровать. Сила света источника зависит от мощности, излучаемой в определенном направлении, поскольку мы обычно заинтересованы в освещении чего-либо, а не только освещения.

Современная единица — кандела. Если источник равен 1 канделе, равномерно во всех направлениях, то он излучает силу света 4 люмен на квадратный дюйм. Кандела теперь является одной из шести базовых единиц СИ, к которым относятся все остальные, так что вы проникли в операционно определенную основу, на которой построена вся система единиц. Кажется, это хорошее место, чтобы остановиться — пока все не стало слишком сложным.

Это базовые единицы:

количество	шт.	символ
длина	метр	м
масса	килограмм	кг
время	секунд	с
электрический ток	ампер	A
термодинамическая температура	кельвин	K
количество вещества	моль	моль
сила света	кандела	кд

Кандела используется для определения просвета, а люмен — для определения люкс.

Свечи не совсем изгнаны — астрономы до сих пор ссылаются на стандартных свечей . Это объекты известной яркости. Исходя из этого и по интенсивности, обнаруженной на Земле, они могут определить, как далеко находятся эти объекты, следуя маршруту кандела – люмен – люкс. 2, Вт / стерадиан и т. Д.

Свет измеряется в люменах, а не в ваттах, и для нормальной или так называемой «фотопической» реакции глаза пик видимости глаза при длине волны около 550 нм составляет 680 люмен на ватт. При очень слабом отклике человеческого глаза, адаптированном к темноте, имеется стандартная кривая отклика «Scotopic», которая смещена на разные длины волн на пике.

Итак, вернемся к «яркости», которая обычно не приветствуется в научной работе из-за ее неточности.

Предпочтительным термином является «яркость», который является фотометрическим эквивалентом «яркости», используемого для электромагнитного излучения любой длины волны.

«Сияние» — это Вт на стерадиан на квадратный метр, а «Яркость» — это люмен на стерадиан на квадратный метр.

Вт на стерадиан — это «сила излучения», а люмен на стерадиан — «сила света». Обе единицы подразумевают математический точечный источник. На практике ошибка будет менее 1% при измерении интенсивности источника с мелкими размерами, если расстояние измерения для неточечного источника как минимум в 10 раз превышает диаметр источника.

Таким образом, яркость также может быть выражена как сила излучения на квадратный метр, а яркость — как «кандела» на квадратный метр, где «кандела» — это фотометрическая единица силы света.

Теперь ученые в обычном для них обиходе будут использовать слово «яркость» для самых разных вещей; фактические источники видимого излучения, или источники инфракрасного или ультрафиолетового излучения, или даже для эмиссии электронов, например, термоэлектронным или другим катодом.

Во всех этих случаях они используют термин яркость вместо «Сияния» или «яркости» или подобных единиц, у всех из которых есть размер потока на стерадиан на квадратный метр. Таким образом, «яркость» термоэлектронного или полевого излучателя будет равна амперам на стерадиан на квадратный метр.

В случае фотометрических единиц для видимых «источников света» яркость довольно сложно измерить, потому что вам нужно четко выделить определенную площадь поверхности на источнике, а затем определить очень конкретный телесный угол для излучения, которое попадает в детектор, и это требует некоторой фокусирующей оптической системы.

Яркость

в канделах намного проще измерить, потому что вам не нужно фокусироваться на определенной области источника, но вам нужно проводить измерения на расстоянии не менее 10 диаметров источника, ограниченного с помощью апертур или конечного размера. измерительного детектора.

Это сложная измерительная проблема, и ее нельзя упростить путем вольного использования терминов «яркость» вместо «яркости» или использования слова «свет» для обозначения энергии УФ- или инфракрасного излучения, чего нет. t виден. «свет» — это НЕ излучение; но человеческий глаз откликнулся на это; так что «свет» по определению виден; но только внутри человеческого глаза. Строго говоря, мы НЕ получаем СВЕТа от солнца; наши глаза делают это из видимых частей солнечного излучения.

Но даже после того, как нас предупредили, мы все еще используем слово «яркость» в торговых разговорах; но мы знаем, что на самом деле имеем в виду — это яркость.Иногда вы можете встретить слово «Sterance» вместо «luminance»

.

И используйте яркость, или интенсивность излучения, или энергетическую освещенность (падающие ватты на квадратный метр) или излучательную способность (излучаемые ватты на квадратный метр). Фотометрическими эквивалентами будут «освещенность» для падающих люменов на квадратный метр или световая эмиссия для излучаемых люменов на квадратный метр. метр.

17.1: Яркость звезд

Цели обучения

К концу этого раздела вы сможете:

• Объясните разницу между светимостью и видимой яркостью
• Узнайте, как астрономы определяют яркость с помощью звездных величин

Яркость

Возможно, наиболее важной характеристикой звезды является ее светимость — общее количество энергии на всех длинах волн, которое она излучает в секунду.Ранее мы видели, что Солнце каждую секунду испускает огромное количество энергии. (И есть звезды намного ярче Солнца.) Чтобы упростить сравнение между звездами, астрономы выражают светимость других звезд через светимость Солнца. Например, светимость Сириуса примерно в 25 раз больше, чем у Солнца. Мы используем символ L _Солнце для обозначения светимости Солнца; следовательно, Сириус можно записать как 25 L _Солнце .В следующей главе мы увидим, что если мы сможем измерить, сколько энергии излучает звезда, а также узнать ее массу, то мы сможем вычислить, как долго она может продолжать светить, прежде чем исчерпает свою ядерную энергию и начнет умирать.

Кажущаяся яркость

Астрономы стараются различать светимость звезды (общий выход энергии) и количество энергии, которое достигает наших глаз или телескопа на Земле. Звезды демократичны в том, как они производят излучение; они излучают одинаковое количество энергии во всех направлениях в пространстве.Следовательно, только малая часть энергии, излучаемой звездой, действительно достигает наблюдателя на Земле. Мы называем количество звездной энергии, которое достигает определенной площади (скажем, одного квадратного метра) каждую секунду здесь, на Земле, ее видимой яркостью . Если вы посмотрите на ночное небо, вы увидите широкий диапазон яркости среди звезд. Большинство звезд на самом деле настолько тусклые, что вам понадобится телескоп, чтобы их обнаружить.

Если бы все звезды имели одинаковую светимость — если бы они были похожи на стандартные лампочки с одинаковым световым потоком — мы могли бы использовать разницу в их видимой яркости, чтобы сообщить нам то, что мы очень хотим знать: как далеко они находятся.Представьте, что вы находитесь в большом концертном или танцевальном зале, в котором темно, если не считать нескольких десятков 25-ваттных лампочек, установленных в светильниках вокруг стен. Поскольку все они представляют собой лампочки мощностью 25 Вт, их светимость (выходная энергия) одинакова. Но с того места, где вы стоите в углу, , а не , имеют такую ​​же видимую яркость. Те, кто находится рядом с вами, кажутся ярче (больше их света достигает вашего глаза), тогда как те, кто находится далеко, кажутся более тусклыми (их свет распространился больше, прежде чем достиг вас). Таким образом вы сможете определить, какие лампочки вам ближе всего.Таким же образом, если бы все звезды имели одинаковую светимость, мы могли бы сразу сделать вывод, что самые яркие звезды были рядом, а самые тусклые — далеко.

Чтобы более точно сформулировать эту идею, вспомните из главы «Излучение и спектры», что мы точно знаем, как свет исчезает с увеличением расстояния. Получаемая нами энергия обратно пропорциональна квадрату расстояния. Если, например, у нас есть две звезды одинаковой светимости и одна находится вдвое дальше другой, она будет выглядеть в четыре раза тусклее, чем ближайшая.Если он находится в три раза дальше, он будет выглядеть в девять (три квадрата) более тусклым и так далее.

Увы, не все звезды имеют одинаковую светимость. (На самом деле, мы очень этому рады, потому что наличие множества разных типов звезд делает Вселенную гораздо более интересным местом.) Но это означает, что если звезда выглядит тусклой на небе, мы не можем сказать, кажется ли она тусклой, потому что у нее есть низкая светимость, но относительно близко, или потому, что она имеет высокую светимость, но находится очень далеко.Чтобы измерить светимость звезд, мы должны сначала компенсировать влияние расстояния на затемнение на свет, а для этого мы должны знать, как далеко они находятся. Расстояние — одно из самых сложных астрономических измерений. Мы вернемся к тому, как это определяется, после того, как узнаем больше о звездах. А пока мы опишем, как астрономы определяют видимую яркость звезд.

Шкала звездных величин

Процесс измерения видимой яркости звезд называется фотометрия (от греческого фото означает «свет» и — метрия означает «измерять»).Как мы видели в «Наблюдении за небом: зарождение астрономии», астрономическая фотометрия началась с Гиппарха. Около 150 г. до н. Э. Он построил обсерваторию на острове Родос в Средиземном море. Там он подготовил каталог из почти 1000 звезд, который включал не только их положения, но и оценки их видимой яркости.

У Гиппарха не было телескопа или какого-либо инструмента, который мог бы точно измерить видимую яркость, поэтому он просто делал оценки своими глазами. Он разделил звезды на шесть категорий яркости, каждую из которых назвал величиной звездной величины .Он называл самые яркие звезды в своем каталоге звездами первой величины, тогда как те, которые были настолько слабыми, что он едва мог их видеть, были звездами шестой величины. В девятнадцатом веке астрономы пытались уточнить шкалу, точно установив, насколько видимая яркость звезды шестой величины отличается от яркости звезды первой величины. Измерения показали, что мы получаем примерно в 100 раз больше света от звезды первой величины, чем от звезды шестой величины. На основе этого измерения астрономы затем определили точную систему звездных величин, в которой разница в пять звездных величин точно соответствует соотношению яркости 100: 1.Кроме того, в десятичной форме приведены звездные величины; Например, звезда — это не просто «звезда второй величины», она имеет величину 2,0 (или 2,1, 2,3 и т. д.). Итак, какое это число при пятикратном умножении дает вам множитель 100? Поиграйте на своем калькуляторе и посмотрите, сможете ли вы его получить. Ответ оказывается примерно 2,5, что является корнем пятой степени из 100. Это означает, что звезда с величиной 1,0 и звезда с величиной 2,0 различаются по яркости примерно в 2,5 раза. Так же получаем около 2.В 5 раз больше света от звезды с величиной 2,0, чем от звезды с величиной 3,0. Как насчет разницы между звездой с величиной 1,0 и звездой с величиной 3,0? Поскольку разница в 2,5 раза для каждого «шага» величины, общая разница в яркости составляет 2,5 × 2,5 = 6,25 раза.

Вот несколько практических правил, которые могут помочь новичкам в этой системе. Если две звезды различаются на 0,75 звездной величины, они различаются по яркости примерно в 2 раза. Если они находятся на расстоянии 2,5 звездной величины, они различаются по яркости в 10 раз, а разница в 4 звездной величины соответствует разнице в яркости в 40 раз.В этот момент вы можете спросить себя: «Почему астрономы продолжают использовать эту сложную систему, созданную более 2000 лет назад?» Это отличный вопрос, и, как мы обсудим, сегодня астрономы могут использовать другие способы выразить, насколько яркой выглядит звезда. Но поскольку эта система до сих пор используется во многих книгах, звездных диаграммах и компьютерных приложениях, мы почувствовали, что должны познакомить с ней студентов (хотя нам очень хотелось не упоминать ее).

Ярчайшие звезды, которые традиционно назывались звездами первой величины, на самом деле оказались (при точном измерении) не одинаковыми по яркости.Например, самая яркая звезда на небе, Сириус, излучает нам примерно в 10 раз больше света, чем средняя звезда первой величины. По современной шкале звездной величины Сириусу, звезде с самой яркой видимой величиной, присвоена величина -1,5. Другие объекты в небе могут казаться еще ярче. Венера в самой яркой форме имеет звездную величину -4,4, в то время как Солнце имеет звездную величину -26,8. На рисунке \ (\ PageIndex {1} \) показан диапазон наблюдаемых величин от самых ярких до самых слабых, а также фактические величины нескольких хорошо известных объектов.При использовании звездной величины следует помнить, что система идет в обратном направлении: чем больше, чем больше , тем меньше — звездной величиной, тем слабее , тем больше объект, который вы наблюдаете. {0.{0.7} = 25 \ nonumber \]

(Подсказка: если у вас есть только базовый калькулятор, вы можете задаться вопросом, как довести 100 до 0,7-й степени. Но это то, что вы можете попросить Google сделать. Теперь Google принимает математические вопросы и ответит на них. Так что попробуйте Спросите у Google: «Что такое 100 в степени 0,7?»)

Наши расчеты показывают, что видимая яркость Сириуса в 25 раз больше видимой яркости Полярной звезды.

Другие единицы яркости

Хотя шкала звездных величин по-прежнему используется в визуальной астрономии, она совсем не используется в новых областях науки.Например, в радиоастрономии не определен эквивалент системы звездных величин. Скорее, радиоастрономы измеряют количество энергии, собираемой каждую секунду каждым квадратным метром радиотелескопа, и выражают яркость каждого источника, например, в ваттах на квадратный метр.

Точно так же большинство исследователей в области инфракрасной, рентгеновской и гамма-астрономии используют энергию, приходящуюся на площадь в секунду, а не величины, чтобы выразить результаты своих измерений.Тем не менее, астрономы во всех областях стараются различать светимость источника (даже если эта светимость полностью исчисляется рентгеновскими лучами) и количество энергии, которое достигает нас на Земле. В конце концов, светимость — действительно важная характеристика, которая многое говорит нам о рассматриваемом объекте, в то время как энергия, которая достигает Земли, является случайностью космической географии.

Чтобы упростить сравнение звезд, в этом тексте мы избегаем использования величин, насколько это возможно, и будем выражать светимость других звезд через светимость Солнца.Например, светимость Сириуса в 25 раз больше, чем у Солнца. Мы используем символ L _Солнце для обозначения светимости Солнца; следовательно, Сириус можно записать как 25 L _Солнце .

Сводка

Полная энергия, излучаемая звездой за секунду, называется ее светимостью. Насколько яркой выглядит звезда с точки зрения Земли, зависит от ее видимой яркости. Видимая яркость звезды зависит как от ее светимости, так и от расстояния до Земли.Таким образом, определение видимой яркости и измерение расстояния до звезды дает достаточно информации для расчета ее светимости. Видимая яркость звезд часто выражается в величинах, что является старой системой, основанной на том, как человеческое зрение интерпретирует относительную интенсивность света.

Глоссарий

кажущаяся яркость

мера количества света, полученного Землей от звезды или другого объекта, то есть того, насколько яркий объект кажется на небе по сравнению с его светимостью

светимость

скорость, с которой звезда или другой объект излучает в космос электромагнитную энергию; общая мощность объекта

величина

старая система измерения количества света, который мы получаем от звезды или другого светящегося объекта; чем больше величина, тем меньше излучения мы получаем от объекта

Авторы и ссылки

Светимость и кажущаяся яркость | Астрономия 801: планеты, звезды, галактики и Вселенная

Дополнительная литература с www.Astronomynotes.com

---

Возможно, самым простым измерением звезды является ее видимая яркость. Я намеренно осторожен в выборе слов. Когда я говорю видимой яркости , я имею в виду, насколько яркой кажется звезда для детектора здесь, на Земле. С другой стороны, светимость звезды — это количество света, излучаемого ею с ее поверхности. Разница между светимостью и видимой яркостью зависит от расстояния. Другой способ взглянуть на эти величины состоит в том, что светимость является внутренним свойством звезды, а это означает, что каждый, у кого есть какие-либо средства измерения светимости звезды, должен найти одно и то же значение.Однако видимая яркость составляет , а не как внутреннее свойство звезды; это зависит от вашего местоположения. Таким образом, все будут измерять различную видимую яркость одной и той же звезды, если все они находятся на разном расстоянии от этой звезды.

Для аналогии, с которой вы знакомы, снова рассмотрим фары автомобиля. Когда автомобиль находится далеко, даже если включен дальний свет, свет не будет слишком ярким. Однако, когда машина проезжает мимо вас в пределах 10 футов, ее огни могут казаться ослепляюще яркими.Если подумать об этом по-другому, учитывая два источника света с одинаковой яркостью, более близкий источник света будет казаться ярче. Однако не все лампочки имеют одинаковую яркость. Если вы поместите автомобильную фару на расстоянии 10 футов, а фонарик — на расстоянии 10 футов, фонарик будет тусклее, потому что его яркость меньше.

Звезды имеют широкий диапазон видимой яркости, измеренной здесь, на Земле. Изменение их яркости вызвано как изменением их яркости, так и изменением расстояния до них.По своей природе тусклая ближайшая звезда может казаться нам на Земле такой же яркой, как и сама по себе светящаяся далекая звезда. Существует математическая зависимость, которая связывает эти три величины — видимую яркость, светимость и расстояние для всех источников света, включая звезды.

Почему источники света кажутся слабее в зависимости от расстояния? Причина в том, что по мере того, как свет движется к вам, он распространяется и покрывает большую площадь. Эта идея проиллюстрирована на этом рисунке:

Рис.4.5: Закон обратных квадратов

Опять же, подумайте о светимости — энергии, излучаемой звездой в секунду, — как о внутреннем свойстве звезды. Вы можете представить себе, как эта энергия излучается через сферические оболочки с центром в звезде. На изображении выше вся сферическая оболочка не проиллюстрирована, а только небольшой участок. Каждая оболочка должна получать от звезды одинаковое общее количество энергии в секунду, но, поскольку каждая последующая сфера больше, свет, падающий на отдельную часть более удаленной сферы, будет разбавлен по сравнению с количеством света, падающим на отдельную часть близлежащая сфера.Величина разбавления связана с площадью поверхности сфер, которая определяется по формуле:

A = 4 π d2 Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации». .

Насколько ярким тот же источник света будет казаться наблюдателям, прикрепленным к сферической оболочке с радиусом в два раза большим, чем первая оболочка? Поскольку радиус первой сферы равен d, а радиус второй сферы будет 2 x d, это уравнение не отображается должным образом из-за несовместимого браузера.Список совместимых браузеров см. В разделе «Технические требования в ориентации». , то площадь поверхности большей сферы больше в 4 раза = (22) Это уравнение не отображается должным образом из-за несовместимого браузера. См. Технические требования в разделе «Ориентация» для получения списка совместимых браузеров. Если вы утроите радиус, площадь поверхности большей сферы увеличится в 9 раз = (32) Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации».. Поскольку одинаковое общее количество света освещает каждую сферическую оболочку, свет должен распространяться, чтобы покрыть в 4 раза большую площадь для оболочки, в два раза большего радиуса. Свет должен распространяться, чтобы покрыть в 9 раз большую площадь для снаряда, в три раза большего радиуса. Таким образом, источник света будет казаться в четыре раза слабее, если вы находитесь в два раза дальше от него, чем кто-либо другой, и он будет казаться в девять раз слабее, если вы будете в три раза дальше от него, чем кто-либо другой.

Таким образом, уравнение для кажущейся яркости источника света задается величиной светимости, деленной на площадь поверхности сферы с радиусом, равным вашему расстоянию от источника света, или

F = L / 4 π d2 Это уравнение не отображается должным образом из-за несовместимого браузера.Список совместимых браузеров см. В разделе «Технические требования в ориентации». , где d — ваше расстояние от источника света.

Кажущуюся яркость часто называют потоком и обозначают сокращенно F (как я сделал выше). На практике поток выражается в единицах энергии в единицу времени на единицу площади (например, Джоули / секунда / квадратный метр). Поскольку светимость определяется как количество энергии, излучаемой объектом, она выражается в единицах энергии в единицу времени [e.г., Джоуль / секунда (1 Джоуль / секунда = 1 Ватт) Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации». ]. Расстояние между наблюдателем и источником света равно d и должно указываться в единицах расстояния, например, в метрах. Вы, вероятно, знакомы со светимостью лампочек, выраженной в ваттах (например, лампочка мощностью 100 Вт), и поэтому вы могли бы, например, называть Солнце имеющим светимость 3,9 x 1026 Вт. Это уравнение не отображается должным образом из-за несовместимый браузер.Список совместимых браузеров см. В разделе «Технические требования в ориентации». . При таком значении яркости Солнца и принятии расстояния от Солнца до Земли 1 а.е. = 1,5 x 1011 м. Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации». , вы можете рассчитать поток, получаемый на Земле Солнцем, который составляет:

F = 3,9 x 1026 Вт / 4 π (1,5 x 1011 м) 2 = 1379 Вт на квадратный метр Это уравнение не отображается должным образом из-за несовместимого браузера.Список совместимых браузеров см. В разделе «Технические требования в ориентации».

Это значение обычно называют солнечной постоянной . Однако, как вы могли догадаться, поскольку расстояние между Землей и Солнцем меняется, а яркость Солнца меняется в течение солнечного цикла, существует разброс в несколько процентов вокруг среднего значения солнечной «постоянной» во времени.

Физика света: что такое яркость? — Общие вопросы

Спасибо всем за то, что уловили показатель Ватт = Джоули в секунду.Вы совершенно правы и сожалеете об ошибке.

Однако единицы, которые я дал для интенсивности, верны, scr4 . Я только что перепроверил Modern Astronomy от Carroll & Ostlie на случай, если у меня начался мозговой пук.

Либеральный:

Как заметил Подкайн, если фотон не достигает вашего глаза, его нельзя с полным основанием назвать ярким. Тем не менее, это будет иметь видимую яркость (или поток) для того, чей глаз он действительно достигнет.

Правильно.Один и тот же источник может иметь разную яркость для разных наблюдателей.

Итак, может ли один фотон быть ярче другого по абсолютной яркости? Если да, будет ли это определяться амплитудой каждого?

У меня нет действительно глубокого понимания квантовых тонкостей этого, но я действительно наблюдаю, как фотоны отскакивают от чего-то, зарабатывая себе на жизнь, и вот как я думаю об этом. Фотон имеет энергию, равную E = hf, где h — постоянная Планка, а f — частота фотонов.По крайней мере, с моей точки зрения, амплитуда световой волны — отвлекающий маневр, оставшийся от классической теории. Я не думаю об амплитуде волны, я думаю о количестве фотонов заданной частоты.

Два фотона с одинаковой частотой имеют одинаковую «яркость». Фотон с более высокой энергией будет иметь более высокую «яркость», потому что он дает больше энергии. С точки зрения восприятия, конечно, это не так, поскольку УФ-фотон не имеет для нас яркости, несмотря на то, что он имеет более высокую энергию, чем, скажем, , зеленый фотон.

Какой видимый свет самый яркий из возможных?

Это будет зависеть от того, как быстро ваш глаз сможет обновлять цветные пигменты, а также, потенциально, от того, сколько физических повреждений ваш глаз может получить до того, как вы перестанете видеть. Опять же, на мой взгляд, если один фотон правильной частоты, который случается, ударяет молекулу пигмента в одном из конусов вашего глаза, молекула ломается, и одно из образовавшихся химических веществ запускает нервный импульс, и вы видите свет.Чем больше фотонов находится в соответствующем диапазоне частот для разрушения каждого пигмента, тем больше вы видите, пока ваш глаз не достигнет уровня насыщения и новый пигмент не будет производиться с той же скоростью, что и пигменты разрушаются светом. Тогда, даже если бы источник света был включен и на сетчатку попало больше фотонов, вы бы не увидели более яркий свет, потому что ваш глаз не мог бы уловить более яркий свет.

Итак, не каждый фотон, попадающий в ваш глаз, попадает в молекулу пигмента.Остальные могут быть отражены или поглощены. Поглощенные фотоны будут нагревать ваш глаз. В конце концов, это приведет к поломке.

Есть ли практический предел видимой яркости из-за плотности колбочек на сетчатке? Может ли один человек видеть более яркий свет, чем другой?

Я думаю, что если бы у вас было больше колбочек, они могли бы производить больше пигментов с большей скоростью, и вы могли бы регистрировать более яркий свет. Я не знаю, насколько это варьируется от человека к человеку.

Сколько фотонов может поместиться на квадратный сантиметр под одним и тем же углом и с одних и тех же направлений.(Пожалуйста, без ангельских шуток.) ​​

На самом базовом уровне два фотона могут проходить друг через друга, не изменяя друг друга, потому что они ведут себя как волны. Итак, мой первый инстинкт — сказать, что у вас может быть столько фотонов, сколько захотите.

Однако, если мы выйдем за пределы базового уровня, размещение большого количества энергии в небольшом пространстве может привести к странным эффектам.

Например, если два гамма-фотона с достаточно высокими энергиями сталкиваются, вы производите пару частиц. Я не знаю, можно ли получить такой же эффект, если просто поместить в эфир целую кучу, скажем, фотонов.Это то, что мы называем «физикой высоких энергий», и я боюсь, что Подкайн гораздо больше похож на галактику с низкой энергией, близкую к инфракрасной. Но я уверен, что кто-то другой знает. . .

Яркость изображения простой камеры

На этой странице мы определяем яркость на единицу площади изображение формируется в простой камере или в человеческом глазу. Нам понадобится это для справки, чтобы показать, что оптическая система, состоящая простых линз не может дать ярче изображения в вашем глазу — он может создавать только большее (или меньшее) изображение, самое большее, того же яркость, которую можно увидеть невооруженным глазом.

На рисунке 1 мы показываем изображение в простой камере; см. (изображения линз: случай 1) для описания изображения, сформированного простой позитивной линзой.

Свет из сцены (это пурпурная стрелка на нашей картинке), справа, проходит через объектив камеры (показан синей линией на передней панели камеру) и формирует перевернутое изображение на задней панели камеры, на слева. Тонкие бледно-голубые линии показаны для справки, а проследите два луча от острия стрелки в сцене, один проходящий прямо через центр линзы, другой проходит через передний фокус линзы, а затем выходящий параллельно оси линзы.Лучи пересекаются в острие стрелки на изображении.

янтарные линии на рисунке 1 — это те, которые нас в первую очередь интересуют здесь. Представьте себе крошечный участок сцены общей площадью dv _s , прямо у основания стрелки. Желтые линии, ведущие от сцены к камере, показывают конус света от той части сцены, которая попадает в камеру, а желтые линии внутри камеры показывают конус формируется тем светом, когда он проходит от линзы к изображению, где он формирует изображение крошечной части основания стрелки.Мы сейчас просто нужно определить, сколько света попадает на этот кусок изображение и насколько велик этот фрагмент изображения; от этого мы можем определить яркость на единицу площади изображения.

Рисунок 1: Изображение, сформированное простой камерой (или глазом)

Снова обращаясь к (изображения линз: случай 1) или просто глядя на треугольники, образованные бледно-голубая линия, проходящая через центр линзы на рисунке 1, мы имеем увеличение сцены, равное

(1)

Следовательно, область нашего крошечного фрагмента изображения « dv _e «, который будет пропорционален квадрату увеличения, будет

(2)

До определить, сколько света падает на эту часть изображения, нам нужно знать, сколько света испускает эта часть сцены и где она пошли.Предположим, что часть сцены, dv _s , испускала немного света, dE _s , и что свет распределялся равномерно по полусфере на сторона сцены камеры. Другими словами, мы предполагаем, что сцена плоская , и весь свет от нее выходит вперед. Это предположение на самом деле нереально, поскольку данная область в плоская сцена не распространяется равномерно по всему полушарию, но это здесь достаточно для наших целей.

Количество света от dv _s , которое фактически попадает в камеру, будет количеством, которое проходит через объектив камеры — иными словами, это свет, который движется вниз по конусу, обозначенному желтыми линиями на рисунке 1. часть света от сцены, которая проходит вниз по конусу, будет — телесный угол конуса, делится на телесный угол всей полусферы перед место действия. Предположим, что размер линзы невелик по сравнению с на расстояние до сцены, поэтому мы можем использовать небольшой угол приближение для телесного угла, образованного конусом, приведенное в (телесные углы: уравнение-4).Если мы запишем dE _e для количества света, падающего на область dv _e , тогда у нас будет,

(3)

Яркость изображения — это просто их отношение, или

(4)

Но для малых углов у нас есть

(5)

, поэтому, если расстояние до сцены намного больше, чем радиус линзы, мы можем записать (4) как

(6)

( Н.Б. — Не относитесь к множителю «1/2» слишком серьезно; это зависит от (нереалистичное) предположение, что плоская сцена равномерно излучается полное полушарие. Более точное решение имело бы другое — но все равно постоянный — коэффициент есть.)

Обратите внимание, что яркость функция исходной яркости сцены (очевидно!) и отношение радиуса линзы к расстоянию от линзы до изображения. Фокусное расстояние объектива не включает , а не , равно как и расстояние от сцены до объектива.

Отношение фокусного расстояния к диаметру объектива — это f-число объектива, или, если объектив остановлен вниз, то f-stop — это фокусное расстояние объектива, деленное на диаметр диафрагмы. Если мы напишем « F » для F-остановки, то получим

и Итак, для далекой сцены, где фокусное расстояние приблизительно равно расстояние от линзы до плоскости пленки можно записать (6) как

(7)

Это Интересно, что при некотором конечном, фиксированном F-числе яркость изображение на пленке будет равно поверхностной яркости сцены, а для объективов большего размера она будет на больше, чем на поверхностей. яркость сцены.К сожалению, без более точного модель яркости сцены мы не можем сказать, что это за критическое число F является. Однако наше значение 1/8 в (7), безусловно, слишком мало, поскольку мы предположили, что нет спада яркости сцены в положениях далеко вне оси, что не соответствует действительности; следовательно, мы можем взять (7) в качестве нижняя граница яркости изображения, и мы можем заключить, что F / 0,35 линза будет давать изображение не менее яркое, чем поверхность яркость исходной сцены. (Что бы это ни стоило, «самый светосильный» объектив камеры, который я когда-либо видел, был F / 1, и самый большой слышно было около F / 0.9. Объектив с диафрагмой F / 0,35 был бы чем-то вроде абсурд.)

Должен заметить, что здесь нет противоречия, даже если может нарушиться интуиция. Для достижения имиджа яркость равна яркости сцены, кажется, что нам нужно захватить все света от сцены. Если я сфокусирую Солнце через объектив F / 0,35 яркость изображения действительно будет равна яркость поверхности солнца ?? Судя по всему — но держись Учтите, что камера находится очень далеко от сцены, а изображение очень значительно уменьшился по сравнению с размером Солнца.Почти весь солнечный свет идет в другие места, кроме камеры, и изображение, которое мы создали, крохотный относительно оригинала! Если, с другой стороны, мы спросим, ​​что потребуется для создания больших изображений , одно размером с оригинал, который такой же яркий, как оригинал, то нам нужно переместите камеру очень близко к сцене — и нам нужно отказаться от малоугловую аппроксимацию мы сделали в уравнении (3). Если мы перепишем результаты, используя точное значение угла учащийся, если смотреть с места сцены, тогда, для света, падающего на изображение, мы имеем

(8)

, а для яркости изображения —

(9)

. Теперь, если мы установим размер изображения равным размеру сцены (увеличение 1: 1), затем л ₁ = л _e , и чтобы добиться яркости изображения, равной яркости сцены, мы необходимо, чтобы cos (θ) = 0, что означает θ = π / 2.Но затем подразумевает, что наш объектив покрывает всю полусферу , если смотреть с места съемки! Это, в свою очередь, означает, что объектив бесконечно большой, чего и следовало ожидать.

Опять же, наше уравнение (6) действительно только для объектов, которые находятся на удаленных от диаметра линзы, что является обычным случаем.

Пример: линза солнечного ожога

После написав приведенный выше текст, я все еще чувствовал себя неловко из-за утверждения, что объектив F / 0,35 дает изображение, такое же яркое, как и исходное. место действия.Итак, давайте рассмотрим пример, в котором мы можем легко вычислите правильный ответ и сравните его с приведенными выше результатами.

Радиус Солнца составляет около 700000 километров, а среднее расстояние от расстояние от Солнца до Земли составляет около 150 миллионов километров, по данным Википедия. Он образует угол около 0,0093 радиана, или около полградуса, если смотреть с Земли. Определим

(S-1)

Тогда отношение площади сферы с радиусом, равным орбите Земли, к площади сферы размером с Солнце составит

(S-2).

Следовательно, интенсивность излучения солнечного света у Земли будет около ρ ₁ ² раз меньше, чем интенсивность на поверхности Солнца.Предположим, мы иметь линзу площадью 1 квадратный фут. Для достижения интенсивности, равной яркости поверхности Солнца на изображении, свет, падающий на линза должна быть сконцентрирована в области (1 / ρ ₁ ) ² раз больше площади линзы. Следовательно, радиус пятна, проецируемого линзой, должен быть примерно в 1 / ρ ₁ раз больше радиуса линзы.

изображение солнца, если смотреть из центра линзы, будет тот же угол, что и само Солнце.Поскольку Солнце (по сути) бесконечно удаленный, изображение попадет (по существу) в фокус Объектив. Итак, радиус изображения Солнца будет:

(S-3)

, где мы использовали θ _s вместо более точного загара (θ _s ), так как это очень маленький угол.

Нам нужно, чтобы радиус R _I был в 1 / ρ ₁ раз больше линзы. Пусть R _L будет радиусом линзы. Затем, подставляя желаемое значение для R _I вместе со значением ρ ₁ из уравнения (S-2) и отбрасывая долю R _s / R _o , которая появляется с обеих сторон, мы видим

(С-4)

диаметр будет вдвое больше фокусного расстояния, и нам нужно будет использовать F / 0.5 линза. Если наша линза в 1 квадратный фут будет круглой, ее радиус будет равен около 6,8 дюйма. Если его фокусное расстояние меньше 7 дюймов, это будет объектив с диафрагмой F / 0,5.

Ранее мы пришли к выводу, что объектив с диафрагмой F / 0,35 даст изображение не менее такая же яркая, как исходная сцена; это согласуется с этим результатом. Фактически, в этом случае мы видим, что объектив с F / 0,35 дает изображение значительно ярче, чем поверхность Солнца (если пренебречь затухание атмосферой).

Возможна ли такая «линза солнечного ожога»?

атмосфера довольно серьезно ослабляет солнечный свет, поэтому на самом деле яркость, равная яркости поверхности Солнца, вероятно, потребует площадь линзы в несколько раз больше, чем мы говорили. Однако, если мы пренебрегаем этим вопросом (мы представляем себя на Луне, например), то ответ — да, конечно, это возможно. Квадратная линза Френеля размером 1 фут, которую можно приобрести у Эдмунда и (без сомнения) много других мест, это уже значительная часть пути к тому, чтобы быть этот объектив «супер горелки» сам по себе. В солнечный день можно плавить медь такой линзой (сделал). Однако фокус длина такой линзы может составлять один или два фута, поэтому сама по себе она не даст изображения столь же яркого, как поверхность Солнца, даже на Луна.Либо нам нужно уменьшить фокусное расстояние, либо увеличить эффективный диаметр линзы.

Уменьшение фокусного расстояния как просто сложить две или три линзы вместе. Совокупный фокусное расстояние стопки из N линз будет в 1 / N раз больше фокусного расстояния одного из них. Я не знаю, насколько резким будет изображение такой стопки. производить, но в принципе, по крайней мере, он должен давать действительно крошечный, невыносимо горячая точка.

Объединение четырех линз «параллельно» — это тоже довольно просто; все, что вам нужно, это рамка для них и несколько зеркала передней поверхности для отражения их света в общем фокусе.А для каркаса подойдет лист фанеры с вырезами, а второстепенный зеркала, вероятно, также доступны от Эдмунда.

ПРЕДУПРЕЖДЕНИЕ: Если вы проводите много времени, экспериментируя с большими линзами, фокусирующими солнечный свет — то есть солнечной печью — пользуйтесь средствами защиты глаз. Подойдет маска сварщика. Скрещенные поляризаторы могут быть разумными. Обычные солнцезащитные очки , а не достаточно хорошо. Пятно, создаваемое большой линзой, сильно яркие и тонкие пластиковые линзы Френеля вряд ли сильно отфильтруют ультрафиолет.УФ будет фокусироваться почти так же резко, как и видимый свет, и это может вызвать повреждение глаз, которое может быть незаметным пока гораздо позже.

Фокусировка на близком расстоянии и яркость изображения

Последний момент заслуживает упоминания. Яркость изображения зависит от расстояния от объектива до изображения, , а не . от фокусного расстояния объектива. Человеческий глаз фокусируется, изменяя форму линзы, чтобы отрегулировать ее фокусное расстояние. Следовательно, яркость изображения в глазу составляет , а не . меняется, когда мы смотрим с удаленного объекта на очень близкий.Однако это не относится к обычной камере. В камере фокусировка обычно выполняется путем перемещения объектива на на . Чем ближе мы фокусируемся, тем дальше от пленки отодвигается линза. Поскольку расстояние от объектива до пленки критично, в результате яркость изображения может упасть значительно в экстремальном крупном плане. В макросъемке раньше с появлением линзового замера необходимо было принять счет того, как далеко был перемещен объектив, чтобы рассчитать контакт.Старые сильфоны, бывшие в употреблении (по крайней мере) на Exakta камеры в макрофотографии еще в 1950-х годах Необходимая компенсация выгравирована на направляющих. Вы бы настроили сцену и камеру, вытащите мехи, пока сцена не будет в фокус, а затем прочтите регулировку фокуса на направляющей рядом с объектив и при необходимости отрегулируйте экспозицию.
Стр. Создано 23.09.2007. Исправлены опечатки и переименованы некоторые переменные 24.09.2007.

Яркость лампочки — количественная оценка

Популярная викторина, горячо: яркость лампочки зависит от ее напряжения

(A)

(B) ток

(C) сопротивление

(D) мощность

Ответ: POWER.

Конечно, для * одинаковых * ламп напряжение и / или ток будут зависеть от яркости. Для фиксированного сопротивления уравнения I ² R и В ² / R показывают, что при одинаковом сопротивлении мощность и, следовательно, яркость будут увеличиваться с увеличением тока или напряжения. Однако в конечном итоге у вас возникнут проблемы, если предположить, что лампа с большим током обязательно ярче, чем лампа с меньшим током.

Экспериментально показать, что напряжение не обязательно коррелирует с яркостью лампы, довольно просто.Просто купите кучу миниатюрных лампочек и держателей для фонариков в Radio Shack, Harbour Freight или еще где-нибудь. Обязательно приобретайте лампочки с разным номинальным напряжением и током, чтобы их сопротивление было разным. Подключите их параллельно к батарее — они будут иметь одинаковое напряжение, но НЕ будут такими же яркими, как друг друга.

Майкл Грей, ветеран моего Летнего института AP 2010 г. и частый автор этой колонки, предложил гораздо более умную и тонкую демонстрацию.Он показал с помощью одной лампочки, что яркость лампы зависит от мощности, а не от напряжения или тока. Как? Он измерил яркость лампы напрямую светочувствительным датчиком Вернье. Конечно! Блестяще.

Подключил лампочку к батарее. Он показал, что по уравнению В, ² / R, удвоение напряжения лампы должно не только удвоить яркость лампы, но и четырехкратно увеличить яркость . Он затемнил комнату и поместил датчик освещенности на фиксированном расстоянии от лампочки.Он обнуил датчик внешнего освещения и зажег лампочку. Когда он удвоил напряжение лампы, показания датчика увеличились в четыре раза. Физика работает.

Я обязательно воспользуюсь этой демонстрацией в следующем году. Спасибо, Майкл!

.

No related posts.