Описание параметра «Кривая силы света»
Согласно ГОСТ Р 54350-2011 светильники подразделяют по типу кривой силы света в одной или нескольких характерных меридиональных плоскостях в нижней и/или верхней полусферах — в соответствии с таблицей и рисунком.
| |||||||||||||||||||||||||||||||||||
* Для нижней полусферы отсчет углов ведут от направления на надир, для верхней — на зенит.
Примечание:
Кф
I0 — значение силы света в направлении оптической оси светильника;
Imin, Imax — минимальное и максимальное значения силы света.
При классификации светильника по типу кривой силы света, как правило, указывают, какой полусфере и меридиональной плоскости свойственна данная кривая. При необходимости допускается указывать тип кривых силы света для обеих полусфер и для нескольких меридиональных плоскостей.
Если основная светотехническая характеристика светильника — это его кривая силы света в нижней полусфере, то не указывают, какой полусфере соответствует эта кривая силы света.
Для светильников с круглосимметричным светораспределением в классификации не указывают меридиональную плоскость, для которой дана кривая силы света. Для светильников, светораспределение которых имеет две плоскости симметрии, указывают типы кривых силы света в этих плоскостях.
(главной поперечной) плоскости, если кривая силы света в другой (главной продольной) плоскости — косинусная.
Светильники утилитарного наружного освещения дополнительно классифицируют по типу условной экваториальной кривой силы света в соответствии с таблицей
Здесь и далее под условной экваториальной кривой силы света понимают проекцию на экваториальную плоскость линии пересечения фотометрического тела светильника с соосным круговым конусом, вершина которого совпадает со световым центром светильника, а боковая поверхность проходит через направление максимальной силы света или, если это направление совпадает с осью конуса, через иное характерное направление.
Кривая силы света (КСС или светораспределение): что это, для чего и как правильно использовать при подборе
By Лампа завода Pulsar
|01.03.2016
Кривая силы света (светораспределение) — это графическое изображение распределения света в пространстве.
От того, как свет светильника распределяется в пространстве, зависит его назначение. Светораспределение описывается с помощью кривой силы света. КСС рисуется в виде графика I (a,b), где a и b — углы распространения светового потока в продольной и поперечной плоскостях. По концентричным окружностям откладывают числовые значения силы света в кд (Канде́ла — единица силы света [СИ]).
По КСС можно определить силу света в любом направлении. Для этого проводим радиус под заданным углом до пересечения с кривой силы света. Затем проводим концентрическую окружность из найденной точки на кривой силы света до оси 0-180°, на которой и получаем силу света для данного угла. Так, например, из рисунка видно, что данный светильник излучает в вертикальном вниз направлении силу света, примерно равную 215 кд, а в направлении 50° к вертикали — 120 кд.
Чем больше кривая силы света напоминает овал, вытянутый вдоль вертикальной оси светильника, тем уже считается кривая и тем выше освещенность в центре падения светового пятна. Внешний вид кривой силы света — важнейшая характеристика светового прибора!
Внешний вид кривой силы света — важнейшая характеристика светового прибора!
Распространённые типы кривых силы света
- Узкая кривая силы света светильника говорит о том, что его лучше применять в помещениях с высокими потолками. Это светильники с высокой контрастностью, направленностью, резкими тенями и экономичностью. В основном используются для освещения горизонтальных поверхностей или для акцентированной подсветки картин, скульптур и пр.
- Средняя кривая силы света светильника выбирается для создания общего освещения с мягкими световыми переходами, достаточной насыщенностью светом, умеренной контрастностью и сбалансированным распределением яркости в помещениях с обычной высотой потолков.
- Широкая кривая силы света лучше подходят для общего освещения помещений с низкими потолками и создает хорошую освещённость вертикальных и наклонных поверхностей, обеспечивает равномерное распределение света. Но у светильников с широкой КСС маленький слепой угол и нужно их правильно установить (а лучше заранее это запроектировать), чтобы свет не бил прямо в глаза.

Таблица типов КСС
Тип | Зона направлений максимальной силы света | Коэффициент формы КСС |
кривой силы света | ||
| Концентрированная | 0 — 15° | K>= 3 |
| Глубокая | 0-30°; 180 –150° | 2<=k>3 |
| Косинусная | 0-35°; 180 — 145° | 1,3 |
| Полуширокая | 35-55°; 145- 125° | 1,3<=k —=»k—«> |
| Широкая | 55- 85°; 125 — 95° | 1,3<=k —=»k—«> |
| Равномерная | 0 — 180° | 1,3<K при этом Imin > 0,4 Imax |
| Синусная | 70- 90°; 110 — 90° | 1,3<K при этом I0 < 0,7 Imaх |
Основные светотехнические характеристики светильников:
- Кривые силы света (светораспределение)
- КПД
- Соотношение потоков освещения нижней и верхней полусферы
Поделиться ссылкой:
ПохожееЧто такое КСС — как распределяется свет в линзованных светильниках
На сегодня светодиодные светильники применяются практически повсеместно.
КСС – расшифровывается как кривая силы света и означает графическое отражение распределения света в пространстве, световой поток при этом раскладывается на экваториальные и меридиональные углы. Наиболее популярны 7 типов диаграмм КСС, они прописаны в ГОСТ 17677-82.
Тип кривой силы света — Тип КСС | Угол раскрытия светового потока | Коэффициент формы КСС | ||
Тип | Рисунок | Расшифровка | ||
К | Концентрированная | 0 — 15° | > 3 | |
Г | Глубокая | 0-30°; 180 –150° | 2 – 3 | |
Д | Косинусная | 0-35°; 180 — 145° | 1,3 – 2 | |
Л | Полуширокая | 35-55°; 145- 125° | < 1,3 | |
Ш | Широкая | 55- 85°; 125 — 95° | < 1,3 | |
М | Равномерная | 0 — 180° | Imin > 0,7 Imax | |
С | Синусная | 70- 90°; 110 — 90° | >1,3 при этом I0 < 0,7 Imax | |
- Углом раскрытия светового потока;
- Коэффициентом формы КСС, который является отношением силы света в определенной плоскости к среднеарифметической силе света для данной плоскости.

При подборе определенного светильника наши специалисты обязательно учитывают специфику его применения. Так для освещения склада с высотой около 10-12 метров требуется совершенно другая оптика нежели для освещения магистрали. Какой тип КСС выбрать во многом зависит от освещаемых объектов, производимых работ при этом освещении, назначении помещения и многих других факторов. Благодаря линзам моно получить идеально подходящий тип освещения для вашего объекта.
Разберем несколько примеров:
- При освещении складов, ангаров, цехов с высотой потолка от 10 до 12 метров целесообразно применять светильники с КСС типа «Д» либо «Г». Чем выше подвес, тем более направленный свет должен применяться, так для подвеса на высоте 15 и более метров применяют КСС типа «К».
- Для освещения офисов применяют самую распространенную систему распространения света тип «Д». А для освещения магистралей и автодорог применяют, как правило, линзы для получения КСС типа «Ш».

- При подсветке зданий и архитектурном освещении могут использоваться различные рещения в зависимости от дизайн-проекта. Но наиболее популярны решения с КСС типа «К». Создается направленный пучок света с высокой концентрацией света и большой яркостью. Но при необходимости получить мягкий и приглушенный свет применяют линзы, дающие тип диаграммы «С» и матовый рассеиватель.
- Для освещения дворов, детских площадок, улиц и тротуаров выгодно использовать линзы для получения диаграммы типа «Л» или «Ш».
- Тип «М» применяют при освещении, например, подъездов или парков, небольших подсобных помещений.
В каждом перечисленном варианте могут быть свои особенности, которые будут указывать на совершенно другие линзы. Приведенные нами примеры — это всего лишь статистика применения на основе наших наблюдений.
Ниже приведем наглядное изображение кривых при различных линзах. Высота потолков одна и та же, источник света по мощности и световому потоку идентичен, различие лишь в линзах, применяемых на данных диодах.
На Рис.1 видно, что чем уже световой поток светильника, тем ярче будет световое пятно на освещаемой поверхности, при этом диаметр этого пятна будет меньше.
Рис.1
На данном рисунке видно, что при сужении светового потока, световое пятно на полу будет ярче, а его диаметр меньше. Для кривой типа Ш характерно обширное, растянутое световое пятно.
Рис.2
Ниже, разместив 4 светильника с разными линзами, получим следующую картину освещенности.
Рис.3
Свет при этом распределится следующим образом:
Рис.4
Для КСС типа Ш распределение будет таким:
Рис.5
Также для упрощения понимания ниже приведем стандартную схему применения линз в зависимости от расположения светильника.
Кривые силы света светодиодных светильников | Светодиодные светильники LED
Светодиодные светильники, так же как и традиционные источники света имеют светотехнические характеристики, которые включают в себя несколько видов диаграмм кривых сил света.
названия кривых сил света
Диаграмма КСС в упрощённом понимании это угол распределения светового потока от источника света на предполагаемом участке. Вернёмся к устаревшим осветительным приборам, как пример источником освещения служит люминесцентная лампа, и её конструкция проста, стеклянная трубка, изнутри покрытая люминофором, который начинает светиться при воздействии на него ультрафиолета, данное видимое освещение распределяется на 360 градусов.
кривые силы света светильникакривые силы света светильника
Существуют определённые нормы к осветительной технике для различных задач: будь то чистое помещение, либо сильно загрязнённое, и как вариант взрывоопасное и пожароопасное, все эти приведённые варианты ведут к конструкции светильника. Исходящий свет расположенной внутри люминесцентной лампы ограничен конструкцией светильника, в частности рассеивателем либо высотой боковых и задних стенок, которая намеренно обеспечивает защитный угол от 10 до 15 градусов, для защиты человеческого зрения. При таком варианте создаётся угол распределения видимого излучения. Данный пример верен для традиционной светотехники.
При таком варианте создаётся угол распределения видимого излучения. Данный пример верен для традиционной светотехники.
Для понимания угла распределения светодиода и светодиодного освещения мы рассмотрим отдельно низковольтные источники видимого излучения. Стандартная кривая силы света светодиода равна углу 120 градусов, данный угол задан первичным слоем люминофора определённой формы. Современные технологии позволяют создавать первичные оболочки с разными углами распределения света, и конечно не забываем про вторичную оптику, которая значительно расширяет возможности освещения, помещения и внешней территории, и удешевляет стоимость светильника . Изменить диаграмму кривой силы света светодиодного светильника возможно так же с помощью рассеивателя имеющего форму микропризмы, призмы, колотого льда и т.д. Все данные светотехнические параметры по диаграммам включает в себя ГОСТ 17677—82. Согласно, данного нормативного документа, классификация кривых сил света представлена двумя методами, максимальная сила света направленная на определённую зону и коэффициент формы самой диаграммы ксс.
Типы кривых сил света:
Тип 1 – Концентрированная, обозначение «К», максимальная сила света распределена от 0 до 15 градусов.
Тип 2 – Глубокая, обозначение «Г», максимальная сила света распределена от 0 до 30 градусов и от 150 до 180 градусов.
Тип 3 – Косинусная, обозначение «Д», максимальная сила света распределена поперёк от 0 до 35 градусов и вдоль от 180 до 145 градусов.
Тип 4 – Полуширокая, обозначение «Л», максимальная сила света распределена поперёк от 35 до 55 градусов и вдоль от 145 до 125 градусов.
Тип 5 – Широкая, обозначение «Ш», максимальная сила света распределена поперёк от 55 до 85 градусов и вдоль от 125 до 95 градусов.
Тип 6 – Равномерная, обозначение «М», максимальная сила света распределена от 0 до 180 градусов.
Тип 7 – Синусная, обозначение «С», максимальная сила света распределена вдоль от 70 до 90 градусов и поперёк от 110 до 90 градусов.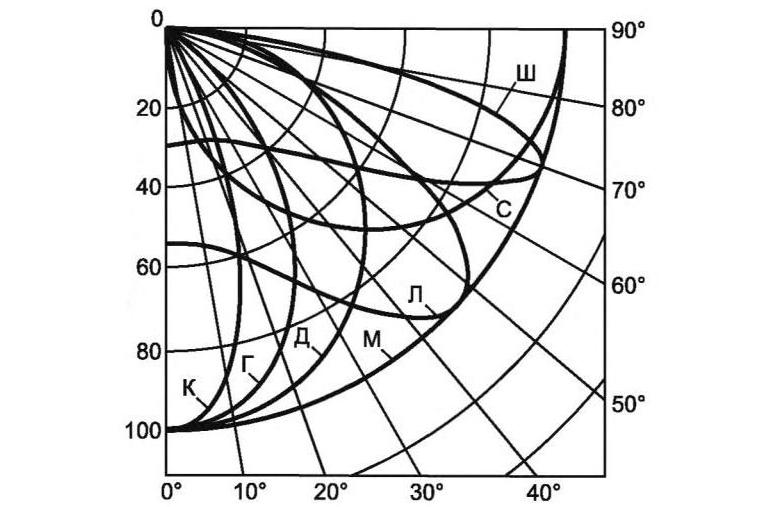
Данные обозначения не являются ограничивающими факторами, как сказано было выше, у каждого светильника своё назначение, эксплуатация и выполняемые функции.
Все типы можно условно разделить по назначению по наружному (внешнему) и внутреннему освещения:
Промышленные помещения – применяются КСС «Г», «К», «Д», в зависимости от силы светового потока необходимо учитывать высоту подвеса для получения нормы освещённости на заданном участке.
Офисные помещения – применяются КСС «Д» и «Л».
Автомобильные дороги – применяются КСС «Ш» и «Д», данные кривые силы света применяются в зависимости от конкретного расстояния между опорами освещения и высоте подвеса.
информационный материал взят с официального ресурса www.antaresled.ru
Светильники Сила света — Кривые распределени
Пример 7.7. Помещение производственно-технического отдела освещается лампой накаливания мощностью 150 Вт, установленной в светильнике типа Шар . Построить кривую распределения силы света указанной лампы.
[c.136]
Построить кривую распределения силы света указанной лампы.
[c.136]Характеристика светильников. Светотехнические свойства светильников характеризуются кривой распределения силы света, защитным углом, коэфициентом полезного действия. [c.526]
Кривая распределения силы света светильника, имеющего ось симметрии, строится в полярной системе координат в пределах от О до 180°. Эта кривая определяет класс светильника, позволяет судить о применимости светильника для заданных условий работы (см. табл. 63) и служит исходным материалом для расчёта освещённости. [c.526]
| Фиг. 21. Примерные кривые распределения силы света светильников а — светильники прямого света 6— светильники отражённого света в — светильники рассеянного света. |
Фиг. 22. Кривые распределения силы света светильников прямого света светильник широкого излучения — — светильник среднего излучения — светильник глубокого излучения.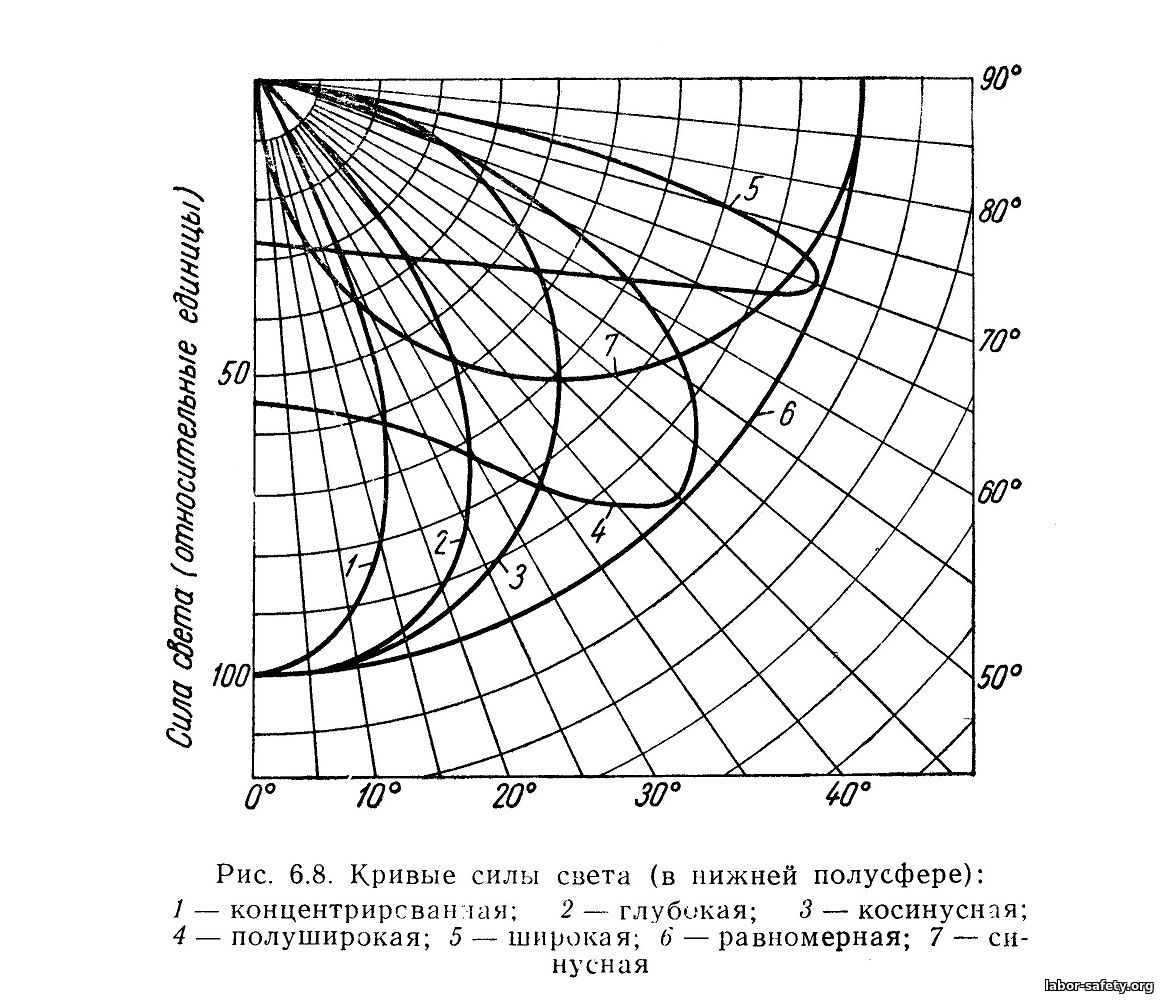
|
Освещенность зр можно определять непосредственными измерениями или расчетом по точечному методу, пользуясь кривой распределения силы света данного светильника [23] [c.61]
| Рис. 7.1. Кривые распределения силы света светильника типа Шар |
 Каждая таблица соответствует конкретному типу светильника и определенному сочетанию коэффициентов отражения потолка, стен и расчетной плоскости. Таблицы составлены для ламп напряжением 220 В при коэффициентах запаса 1,3 (для ламп накаливания) и 1,5 (для люминесцентных ламп). Если конкретные условия отличаются от тех, для которых составлены таблицы, то в значение удельной мощности следует вносить поправочные коэффициенты. Например, при напряжении источников света 127 В (при лампах накаливания) значение удельной мощности, взятое из таблиц, должно быть
[c.126]
Каждая таблица соответствует конкретному типу светильника и определенному сочетанию коэффициентов отражения потолка, стен и расчетной плоскости. Таблицы составлены для ламп напряжением 220 В при коэффициентах запаса 1,3 (для ламп накаливания) и 1,5 (для люминесцентных ламп). Если конкретные условия отличаются от тех, для которых составлены таблицы, то в значение удельной мощности следует вносить поправочные коэффициенты. Например, при напряжении источников света 127 В (при лампах накаливания) значение удельной мощности, взятое из таблиц, должно быть
[c.126]
По кривой распределения силы света заданного светильника определяется сила света / условной лампы для найденного угла а. [c.129]
| Фиг. 7. Кривые распределения силы света светильника Универсаль |
 Употребляется для местного освещения и укрепляется обычно непосредственно на станке или верстаке при помощи шарнирной или гибкой стойки. Светильник изготовляется для ламп до 60 вт. Кривая распределения силы света показана на фиг. 8.
[c.327]
Употребляется для местного освещения и укрепляется обычно непосредственно на станке или верстаке при помощи шарнирной или гибкой стойки. Светильник изготовляется для ламп до 60 вт. Кривая распределения силы света показана на фиг. 8.
[c.327]| Фиг. 11. Кривая распределения силы света светильника наружного освещения |
А — сила света светильника в направлении точки А, полученная из кривой распределения силы света [c.333]
| Рис. 5.7. Светильник СПО-300, его защитный угол (я) и кривая распределения силы света б) |
 1 (на 1000 лм).
[c.25]
1 (на 1000 лм).
[c.25]Распределение силы света светильников в пространстве можно представить в виде таблиц или графиков. В таблицах указываются численные значения силы света в определенном направлении, характеризуемым углом между оптической осью светильника и направлением силы света для условного светильника со световым потоком 100 лм. При графическом изображении кривые распределения силы света строятся в полярной системе координат. Сетка образуется прямыми, которые соответствуют серединам десятиградусных зон (углы 5, 15, 25 и т. д. градусов от вертикали). Величину силы света в направлении угла а — 1а откладывают в масштабе на каждой из таких прямых, после чего полученные точки соединяют плавной кривой. Распределение силы света для светильника типа Шар показано на рис. 7.1 (кривая/). [c.122]
Пример 7.14. Помещение главного механика освещается светильниками типа Люцетта с лампами мощностью 300 Вт (напряжение 220 В). Площадь помещения 8×12 м .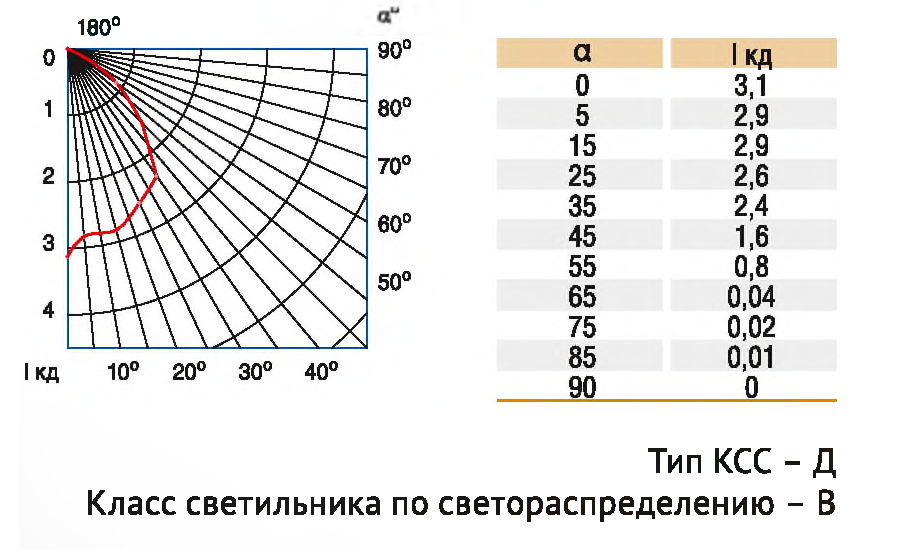 Высота подвеса лампы 4,5 м. Светильники расположены рядами по три светильника в ряд, расстояние между светильниками в ряду 4 м, между рядами 4 м. Определить освещенность горизонтальной поверхности в точке А (рис. 7.9) точечным методом с использованием кривых распределения силы света светильника (см. табл. 7.3).
[c.138]
Высота подвеса лампы 4,5 м. Светильники расположены рядами по три светильника в ряд, расстояние между светильниками в ряду 4 м, между рядами 4 м. Определить освещенность горизонтальной поверхности в точке А (рис. 7.9) точечным методом с использованием кривых распределения силы света светильника (см. табл. 7.3).
[c.138]
По кривой распределения силы света (интерполируя между двумя соседними значениями) находим для светильника типа ОДОР (см. табл. 7.3) силу света условной лампы в направлении а=31°. Она равна 165 кд. [c.140]
| Фиг. 8. Кривая распределения силы света светильника Глубокоизлучатель |
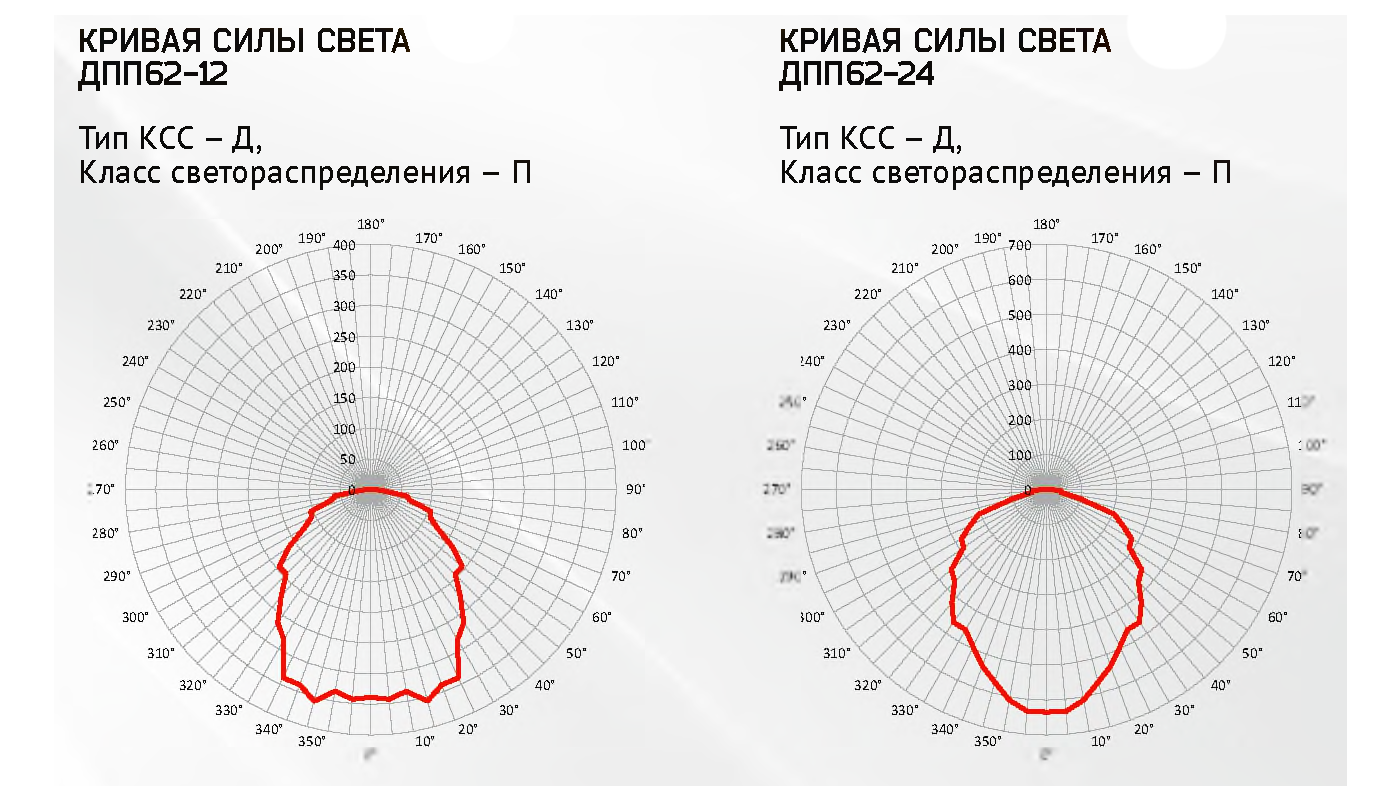
Выбор кривой силы света (КСС) для светодиодных светильников SolidLED.
Все светильники SolidLED могут быть разделены на две общие группы:- Светодиодные светильники без вторичной оптики, где КСС определяют свойства использованных светодиодов.
 Как правило, в применяемых светодиодах производства CREE (USA), Osram (Germany), LG и SEOUL (KOREA), угол раскрытия заключен в рамках от 110 до 120 градусов. Эти светильники cоответствуют КСС типа «Д» согласно ГОСТ 17677-82. В маркировке при заказе (продаже) светильников используется обозначение «R». Например, светильник для АЗС встраиваемый заливающего света: SolidGSL 60 — 74R.50 V.
Как правило, в применяемых светодиодах производства CREE (USA), Osram (Germany), LG и SEOUL (KOREA), угол раскрытия заключен в рамках от 110 до 120 градусов. Эти светильники cоответствуют КСС типа «Д» согласно ГОСТ 17677-82. В маркировке при заказе (продаже) светильников используется обозначение «R». Например, светильник для АЗС встраиваемый заливающего света: SolidGSL 60 — 74R.50 V. - Светодиодные светильники с использованием вторичной оптики (устанавливается непосредственно на светодиоды). Вторичная оптика — это специальные линзы из поликарбоната (или АБС), которые трансформируют «заводскую» КСС светодиода в необходимую наперед заданную. В наших светильниках используются линзы производства LEDIL (Finland) и LEDLINK (TAIWAN) с возможностью формирования практически любой КСС:
- C10…C15 — Концентрированная от 10 до 15 градусов. Используется для подсветки особых, выделенных зон, внутренних архитектурных решений и деталей интерьера.
 В мощных прожекторах серии SolidSLL — это архитектурное освещение, фасадное освещение, а в случае от 120 Вт до 300 Вт — освещение территорий с высоких мачт, освещение спортивных объектов, таких как стадионы. В случае промышленных подвесных светильников серии SolidHBL — освещение цехов с высокими пролетами.
В мощных прожекторах серии SolidSLL — это архитектурное освещение, фасадное освещение, а в случае от 120 Вт до 300 Вт — освещение территорий с высоких мачт, освещение спортивных объектов, таких как стадионы. В случае промышленных подвесных светильников серии SolidHBL — освещение цехов с высокими пролетами. - С25…С90 — Глубокая от 25 до 90 градусов. Применяется в основном в прожекторах серии SolidSLL. Выбор конкретной оптики осуществляется исходя из поставленной задачи. Чем больше высота подвеса, тем уже зона направлений максимальной силы света
- Q40…Q90 — Глубокая для промышленных светильников HiBay. Применяется для направленных прожекторов и для освещения цехов с высокими пролетами. Расстояние подвеса или установки прожектора от освещаемой поверхности от 18 м до 10 м. Точная высота и расстояние рассчитывается нашими специалистами для конкретного объекта. Чем больше высота подвеса, тем уже зона направлений максимальной силы света.

- WA и WS — Широкая асимметричная и широкая симметричная для уличных консольных светодиодных светильников для автодорог серии SolidHWL
Выше приведены типовые популярные КСС, но для решения специальных задач возможно использовать дополнительные не указанные здесь линзы — просьба обращаться к нашим специалистам для дальнейшей консультации.
Стандартные характеристики КСС при заказе светильников SolidLED
Симметричная и асимметричная КСС светильника SolidHWL (и других серий) — сплошная — симметричная, пунктир — асимметричная:
Типовые КСС для дорожных светильников серии
SolidHWLТиповые КСС для прожекторов серии
SolidSLL и промышленных светильников SolidHBLТиповые КСС для светильников серии
SolidGSL — «R120» — см. выше справа.
Внешний вид оптики (примеры) LEDIL и LEDLINK Оптика с обозначением WA и WS в маркировке светильников — оптика размером 2 на 2 светодиода Оптика с обозначениями C30, C60, Q50 — размер 2 на 2 светодиода
Оптика концентрированная с обозначением С10…С15 — одиночная на один светодиод
34.Осветительные приборы. Параметры осветительных приборов.
Осветительные приборы (ОП) — это устройства, перераспределяющие световой поток источников света в пространстве требуемым образом. ОП делятся на три класса: светильники, прожекторы и проекторы.
Проекторы — это ОП,
концентрирующие световой поток источника света на определенной четко
ограниченной площади или в определенном объеме. Наиболее распространенный вид
таких ОП — это известные всем кинопроекторы, создающие заданную освещенность только на определенной площади экрана. Как правило, в проекторах используются сложные оптические системы,
обеспечивающие не только необходимые
уровни и равномерность освещенности по всей заданной поверхности, но и
предельно четкую передачу изображений (их
«проекцию») из одного места в другое с изменением масштаба..
Как правило, в проекторах используются сложные оптические системы,
обеспечивающие не только необходимые
уровни и равномерность освещенности по всей заданной поверхности, но и
предельно четкую передачу изображений (их
«проекцию») из одного места в другое с изменением масштаба..
Прожекторами называются ОП, сосредотачивающие световой поток источников света в достаточно малых телесных углах и освещающие объекты, находящиеся от ОП на расстояниях, значительно превышающих размеры самих ОП (в 20 раз и больше).
Светильники — это ОП, в которых световой поток источников света распределяется внутри больших телесных углов. Как правило, светильники освещают поверхности или предметы, находящиеся от них на достаточно близких расстояниях, соизмеримых с размерами самих светильников (не более 20 размеров светильников).
11.7.1. Светотехнические параметры осветительных приборов
Любой ОП — это устройство, перераспределяющее в пространстве световой
поток источника света. КПД ОП — это отношение светового потока, выходящего
из ОП, к световому потоку источника света:
КПД ОП — это отношение светового потока, выходящего
из ОП, к световому потоку источника света:
кпд =Фоп/Фис
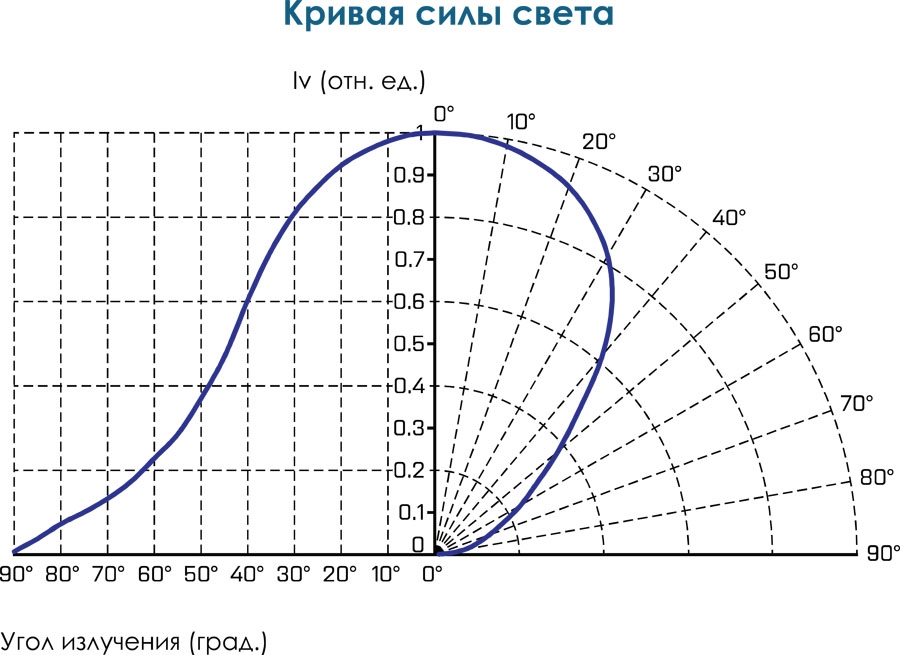
Для того чтобы оценить долю светового потока, попадающую на нужное место, необходимо знать характер распределения светового потока, вышедшего из ОП, в пространстве. Этот характер свето-распределения описывается с помощью кривых сил света, являющихся важнейшим параметром любого ОП.
Кривая сил света (КСС) ОП — это графическое изображение зависимости силы света прибора от направления распространения света. Для удобства пользования в каталогах ОП приводятся условные КСС, рассчитанные для источника света со световым потоком 1000лм
Рис. 11.25. Примеры кривых сил света в полярных (а) и прямоугольных (б) координатах
Реальная сила света ОП определяется для любого источника установленного в данный прибор, с помощью простого соотношения:
Iоп
реал = Iоп
1000 Фис / 1000.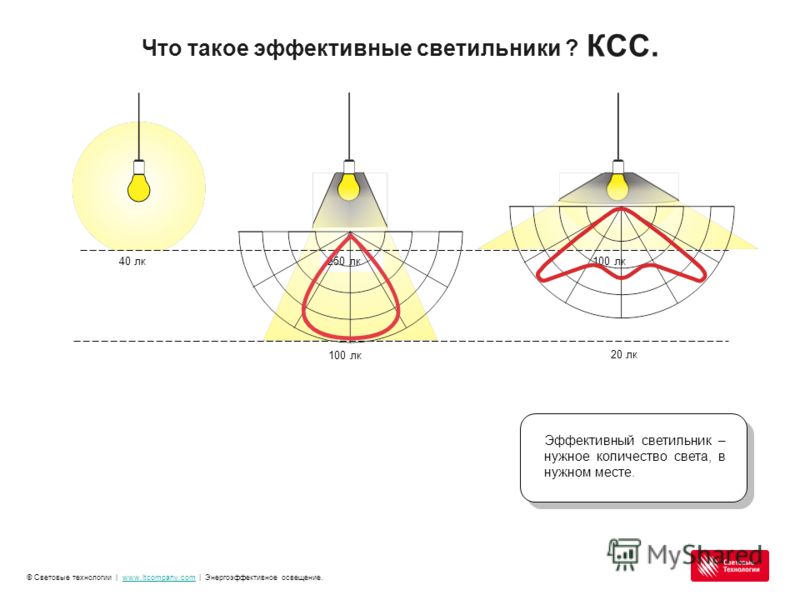
Если ОП многоламповый, то Фис — это сумма световых потоков всех ламп.
По характеру светораспределения ОП делятся на пять классов:
прямое (П), преимущественно прямое (Н), рассеянное (Р), преимущественно
отраженное (В) и отраженное (О). Все ОП прожекторного типа имеют только прямое
светораспределе-ние. Светильники прямого светораспределения — это те, у которых
не менее 80 % светового потока направлено в сторону выходного отверстия.
Преимущественно прямым светораспределением называется такое, при котором в
сторону выходного отверстия направлено от 60 до 80 % светового потока. Если
свет направляется от светильника примерно поровну «вперед» (в сторону
выходного отверстия) и «назад» (в обратную сторону), то такое
светораспределение называется рассеянным. При преимущественно отраженном
светораспределении доля светового потока, направляемого «вперед», составляет
20-40 %, а от 60 до 80 % направляется «назад». Если же «назад» направляется
более 80 %, то такое светораспределение называется отраженным
Если же «назад» направляется
более 80 %, то такое светораспределение называется отраженным
Российским ГОСТ 17677 установлены семь типов КСС: концентрированная (К), глубокая (Г), косинусная или
диффузная (Д), полуширокая (Л),
широкая (Ш), синусная (С) и равномерная (М) (рис. 50). У светильников с кривыми сил света типа К, Г и Д
направление мак симальной силы света совпадает с оптической осью или близко к
ней, у типа С — перпендикулярно
оптической оси. При «широком» типе КСС максимальная сила света создается светильниками в направлениях, лежащих под углом от
55 до 85° к оптической оси, при
«полушироком» — от 35 до 55°. Следует сказать, что КСС типов Ш, Л и Д могут
быть «вывернутыми», поскольку они
присущи светильникам не только с прямым или направленным характером светораспределения, но и с отраженным и
преимущественно отраженным. В этих
случаях направление максимальной силы света
относительно оптической оси соответствует углам 180° (Д), 95 — 125° (Ш) и 125 -
145° (Л).
Рис.11.27. Типы кривых сил света по ГОСТ 17677
К светотехническим параметрам светильников относятся еще две величины: яркость видимых частей светильников и защитный угол.
Задачей ОП является не только перераспределение светового потока, но и защита глаз от воздействия на них высокой яркости.. Поэтому в технической документации часто регламентируется максимально допустимая яркость видимых частей светильников. В частности, такое требование обязательно для светильников, устанавливаемых в помещениях с большим количеством персональных компьютеров.
Совершенно очевидно, что ограничивать яркость надо не по всем направлениям, а только в определенных угловых зонах. Обычно это углы от 0 до 30° к горизонтальному направлению.
Снижение яркости осуществляется путем
экранировки источников
света с помощью отражателей и специальных экранирующих решеток или пластин, а также с помощью
рассеивателей. Угол, в
пределах которого глаз
защищен от попадания на
него прямого света ламп,
называется защитным
углом светильника
(рис. 51).
Угол, в
пределах которого глаз
защищен от попадания на
него прямого света ламп,
называется защитным
углом светильника
(рис. 51).
Осветительные приборы. Параметры осветительных приборов.
Осветительные приборы (ОП) — это устройства, перераспределяющие световой поток источников света в пространстве требуемым образом. ОП делятся на три класса: светильники, прожекторы и проекторы.
Проекторы — это ОП,
концентрирующие световой поток источника света на определенной четко
ограниченной площади или в определенном объеме. Наиболее распространенный вид
таких ОП — это известные всем кинопроекторы, создающие заданную освещенность только на определенной площади экрана. Как правило, в проекторах используются сложные оптические системы,
обеспечивающие не только необходимые
уровни и равномерность освещенности по всей заданной поверхности, но и
предельно четкую передачу изображений (их
«проекцию») из одного места в другое с изменением масштаба. .
.
Прожекторами называются ОП, сосредотачивающие световой поток источников света в достаточно малых телесных углах и освещающие объекты, находящиеся от ОП на расстояниях, значительно превышающих размеры самих ОП (в 20 раз и больше).
Светильники — это ОП, в которых световой поток источников света распределяется внутри больших телесных углов. Как правило, светильники освещают поверхности или предметы, находящиеся от них на достаточно близких расстояниях, соизмеримых с размерами самих светильников (не более 20 размеров светильников).
11.7.1. Светотехнические параметры осветительных приборов
Любой ОП — это устройство, перераспределяющее в пространстве световой
поток источника света. Обычно источники света излучают его во всех
направлениях, а нам часто надо осветить какое-то конкретное место, например,
рабочий стол. В этом случае полезным является световой поток, попадающий на
нужное место (рабочий стол), а остальной — практически бесполезным. Таким
образом, можно говорить о коэффициенте полезного действия (кпд) ОП. КПД
ОП — это отношение светового потока,
выходящего из ОП, к световому потоку источника света:
Таким
образом, можно говорить о коэффициенте полезного действия (кпд) ОП. КПД
ОП — это отношение светового потока,
выходящего из ОП, к световому потоку источника света:
кпд =Фоп/Фис
Однако очевидно, что далеко не весь световой поток, выходящий из ОП, попадает на нужное место. Для того чтобы оценить долю светового потока, попадающую на нужное место, необходимо знать характер распределения светового потока, вышедшего из ОП, в пространстве. Этот характер свето-распределения описывается с помощью кривых сил света, являющихся важнейшим параметром любого ОП.
Кривая сил света (КСС) ОП — это графическое изображение зависимости силы света прибора от направления распространения света. Обычно КСС изображаются в полярных координатах (рис. 46,а), однако для ОП с очень малыми углами излучения иногда используется и прямоугольная система координат (рис. 46,6). Для удобства пользования в каталогах ОП приводятся условные КСС, рассчитанные для источника света со световым потоком 1000лм
Рис. 11.25. Примеры
кривых сил света в полярных (а) и
прямоугольных (б) координатах
11.25. Примеры
кривых сил света в полярных (а) и
прямоугольных (б) координатах
Реальная сила света ОП определяется для любого источника установленного в данный прибор, с помощью простого соотношения:
Iоп реал = Iоп 1000 Фис / 1000.
Если ОП многоламповый, то Фис — это сумма световых потоков всех ламп.
По характеру светораспределения в соответствии с ГОСТ 13828
ОП делятся на пять классов: прямое (П), преимущественно прямое (Н), рассеянное
(Р), преимущественно отраженное (В) и отраженное (О). Все ОП прожекторного типа
имеют только прямое светораспределе-ние. Светильники прямого светораспределения
— это те, у которых не менее 80 % светового потока направлено в сторону
выходного отверстия. Преимущественно прямым светораспределением называется
такое, при котором в сторону выходного отверстия направлено от 60 до 80 %
светового потока. Если свет направляется от светильника примерно поровну
«вперед» (в сторону выходного отверстия) и «назад» (в обратную сторону), то
такое светораспределение называется рассеянным. При преимущественно отраженном
светораспре-делении доля светового потока, направляемого «вперед», составляет
20-40 %, а от 60 до 80 % направляется «назад». Если же «назад» направляется
более 80 %, то такое светораспределение называется отраженным (рис. 48).
Если свет направляется от светильника примерно поровну
«вперед» (в сторону выходного отверстия) и «назад» (в обратную сторону), то
такое светораспределение называется рассеянным. При преимущественно отраженном
светораспре-делении доля светового потока, направляемого «вперед», составляет
20-40 %, а от 60 до 80 % направляется «назад». Если же «назад» направляется
более 80 %, то такое светораспределение называется отраженным (рис. 48).
Рис.11.26. Классы светораспределения
Российским ГОСТ 17677 установлены семь типов КСС: концентрированная (К), глубокая (Г), косинусная или
диффузная (Д), полуширокая (Л),
широкая (Ш), синусная (С) и равномерная (М) (рис. 50). У светильников с кривыми сил света типа К, Г и Д
направление мак симальной силы света совпадает с оптичес- кой осью или близко к
ней, у типа С — перпендикулярно
оптической оси. При «широком» типе КСС максимальная сила света создается светильниками в направлениях, лежащих под углом от
55 до 85° к оптической оси, при
«полушироком» — от 35 до 55°. Следует сказать, что КСС типов Ш, Л и Д могут
быть «вывернутыми», поскольку они
присущи светильникам не только с прямым или направленным характером светораспределения, но и с отраженным и
преимущественно отраженным. В этих
случаях направление максимальной силы света
относительно оптической оси соответствует углам 180° (Д), 95 — 125° (Ш) и 125 -
145° (Л).
Следует сказать, что КСС типов Ш, Л и Д могут
быть «вывернутыми», поскольку они
присущи светильникам не только с прямым или направленным характером светораспределения, но и с отраженным и
преимущественно отраженным. В этих
случаях направление максимальной силы света
относительно оптической оси соответствует углам 180° (Д), 95 — 125° (Ш) и 125 -
145° (Л).
Рис.11.27. Типы кривых сил света по ГОСТ 17677
К светотехническим параметрам светильников относятся еще две величины: яркость видимых частей светильников и защитный угол.
Задачей ОП является не только
перераспределение светового потока, но и защита глаз от воздействия на них
высокой яркости.. Поэтому в технической документации
часто регламентируется максимально допустимая яркость видимых частей
светильников. В частности,
такое требование обязательно для светильников, устанавливаемых в помещениях с
большим количеством персональных компьютеров.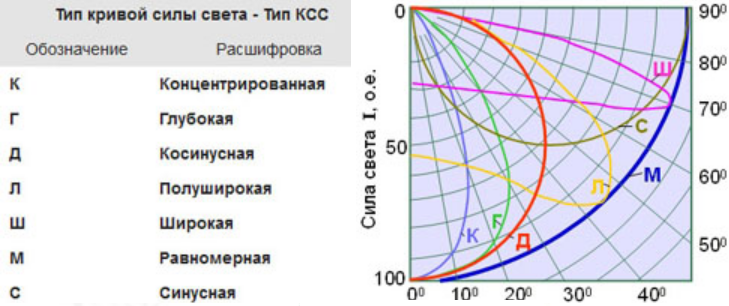
Совершенно очевидно, что ограничивать яркость надо не по всем направлениям, а только в определенных угловых зонах. Обычно это углы от 0 до 30° к горизонтальному направлению.
Снижение яркости осуществляется путем экранировки источников света с помощью отражателей и специальных экранирующих решеток или пластин, а также с помощью рассеивателей. Угол, в пределах которого глаз защищен от попадания на него прямого света ламп, называется защитным углом светильника (рис. 51).
|
Рис. |
кривых распределения света — archtoolbox.com
Производители светильников и ламп предоставляют кривые распределения силы света (или силы света) для своих светильников. Кривые предоставляют дизайнеру важную информацию о том, как свет распространяется от прибора, а также как этот свет падает на поверхность.
Кривая распределения мощности свечей
На изображении ниже представлена кривая распределения мощности свечи, которая дает информацию о том, как свет излучается лампой или осветительной арматурой.Диаграмма представляет собой разрез приспособления и показывает интенсивность света, излучаемого в каждом направлении. Часть графика над горизонтальной линией 90 ° -270 ° указывает свет, который светит над прибором (непрямой), в то время как часть графика ниже представляет свет, падающий вниз (прямой). Прямые линии, исходящие из центральной точки, обозначают угол излучаемого света, а круги обозначают интенсивность. Например, точка А выше показывает, что сила света при 80 ° составляет примерно 110 свечей.Точка B показывает, что при 30 ° вы получите около 225 свечей.
Например, точка А выше показывает, что сила света при 80 ° составляет примерно 110 свечей.Точка B показывает, что при 30 ° вы получите около 225 свечей.
Isochart
Слева находится диаграмма, на которой представлена информация о распределении света в плане. Изохарта (или iso-lux / iso-Candlepower) полезна для определения того, какую площадь может покрыть осветительный прибор. Например, на автостоянке диаграмма слева показывает, что на расстоянии 18-20 футов от центра будет примерно 1/2 футовой свечи света. Если приемлемо 1/2 фута-свечи, то светильники можно разместить на расстоянии 36-40 футов друг от друга.
Файлы фотометрических данных
Информация о распределении света прибора также обычно доступна в формате файла, который можно загрузить в программу анализа или визуализации и использовать для лучшего понимания освещения в пространстве. Существует несколько различных типов файлов, наиболее популярные из которых перечислены ниже.
IES — это тип файла международного стандарта для предоставления информации о распределении света светильника. Стандарт был разработан Обществом инженеров по освещению Северной Америки (IESNA), которое стало просто Обществом инженеров по освещению.Файлы IES имеют расширение .ies.
EULUMDAT — основной формат, используемый в Европе. Стандарт изначально был разработан в Германии, но в настоящее время нет официальной документации по формату. Файлы EULUMDAT имеют расширение .ldt.
CIBSE — это формат, используемый в основном в Великобритании и опубликованный Сертифицированным институтом инженеров по обслуживанию зданий. Файлы CIBSE имеют расширение .cibse.
LTLI — это формат, который иногда используется с продуктами Autodesk, такими как 3ds Max.LTLI был разработан Датской лабораторией освещения и является стандартом, используемым в скандинавских странах. Файлы LTLI имеют расширение . ltli.
ltli.
Зависимость интенсивности света от работы органического солнечного элемента и переключение доминирования между потерями Шокли – Рида – Холла и бимолекулярной рекомбинацией
На рисунке 1 показано систематическое изменение характеристик осциллографа Дж – В в зависимости от интенсивности освещения имитатора солнечной энергии. .Плотность тока короткого замыкания Дж sc и напряжение холостого хода В oc возрастают с увеличением силы света. Однако есть небольшая разница между зависимостью от силы света J sc и V oc . В отличие от J sc , который монотонно увеличивается при любой интенсивности света, скорость увеличения V oc при высокой интенсивности света составляет примерно половину скорости при низкой интенсивности. Кроме того, существует немонотонное изменение «прямоугольности» кривых J – V , которое мы обычно представляем параметрами коэффициента заполнения (FF) 23 .
Кроме того, существует немонотонное изменение «прямоугольности» кривых J – V , которое мы обычно представляем параметрами коэффициента заполнения (FF) 23 .
Зависимость от силы света Дж – В характеристик ОПВ.
Такие вариации в J sc, V oc . И FF в совокупности приводят к зависимости PCE 23 от интенсивности света. Количественно уменьшение FF при высоких интенсивностях достаточно, чтобы противодействовать увеличению как J sc , так и V oc , а также для демонстрации насыщающего поведения PCE после устойчивого увеличения до ~ 13.4%, как показано на рис. 2а. Другие группы ранее связывали изменение наклона полулогарифмического графика V oc от интенсивности света несоответствием в механизмах рекомбинации 12,13,22,24,25,26,27 . Более конкретно, коэффициент идеальности, преобразованный из наклона вышеупомянутых полулогарифмических графиков, должен быть равен 1, если доминирует двухмолекулярная рекомбинация, и 2, если доминирует мономолекулярная рекомбинация.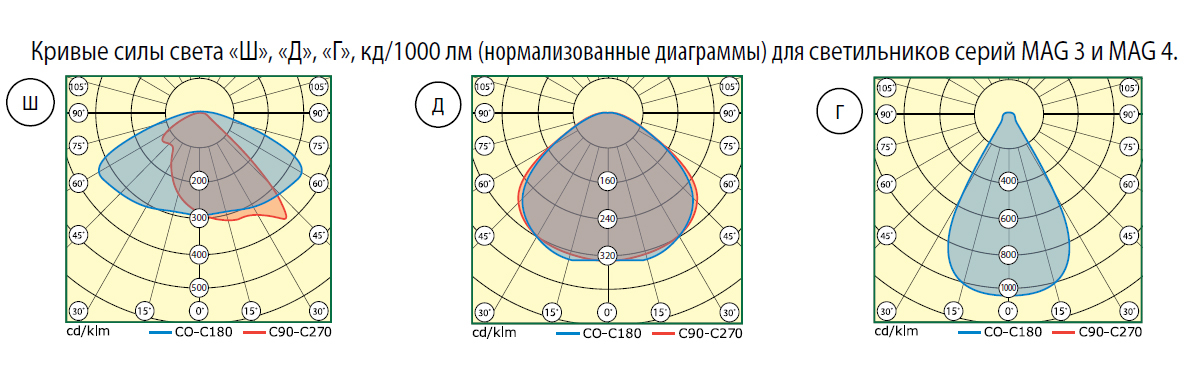 Интересно, что коэффициенты идеальности, соответствующие наклонам двух линейных участков на рис.2b равны 1,12 и 1,86, чтобы предположить такое переключение в механизмах потерь рекомбинации в ответ на увеличение интенсивности света. Двухсегментная особенность также очевидна на графике зависимости FF от интенсивности света на рис. 2c. Однако границы между двумя сегментами для V, , oc, и FF не появляются при одинаковой интенсивности света. Более того, не было сообщений о происхождении систематических изменений в FF 28 . Помимо несоответствия между вариациями V oc и FF, квазилинейный рост J sc на рис.2г показывает, что качественных аргументов, основанных на двух механизмах рекомбинации, недостаточно, чтобы продемонстрировать зависимость работы РЗС от интенсивности света.
Интересно, что коэффициенты идеальности, соответствующие наклонам двух линейных участков на рис.2b равны 1,12 и 1,86, чтобы предположить такое переключение в механизмах потерь рекомбинации в ответ на увеличение интенсивности света. Двухсегментная особенность также очевидна на графике зависимости FF от интенсивности света на рис. 2c. Однако границы между двумя сегментами для V, , oc, и FF не появляются при одинаковой интенсивности света. Более того, не было сообщений о происхождении систематических изменений в FF 28 . Помимо несоответствия между вариациями V oc и FF, квазилинейный рост J sc на рис.2г показывает, что качественных аргументов, основанных на двух механизмах рекомбинации, недостаточно, чтобы продемонстрировать зависимость работы РЗС от интенсивности света.
Параметры солнечного элемента, зависящие от интенсивности света: ( a ) КПД преобразования мощности PCE, ( b ) напряжение холостого хода V oc , ( c ) коэффициент заполнения FF и () d ) плотность тока короткого замыкания J sc .
Мы количественно подтвердили переключение между доминированием би- и мономолекулярной рекомбинации с увеличением интенсивности света с помощью симулятора устройства SCAPS.В этом моделировании мы предполагаем процессы типа SRH для мономолекулярной рекомбинации с нейтральными дефектами. Подробная информация о параметрах моделирования SCAPS указана в таблицах S1 (см. Вспомогательную информацию).
Для надежного моделирования кривой J – V важно использовать правильные профили генерации экситонов, которые показывают зависящие от положения и длины волны скорости генерации экситонов в AL, которая является результатом поглощения фотонов 19 . На рисунке 3a показан набор зависимых от положения спектров поглощения в AL, которые мы смоделировали на основе многослойной структуры OSC на вставке к рис.3b и оптические константы составляющих слоев 21,29 . Интегрирование спектра поглощения по всему диапазону длин волн в каждой позиции привело к глубинному профилю скоростей генерации экситонов на рис. 3b. С другой стороны, интегрирование пространственного профиля поглощения по всей глубине AL дает спектр светособирающей эффективности (LHE) на рис. 3c. Хорошее соответствие между спектрами измеренной эффективности преобразования падающих фотонов в электроны (IPCE) и рассчитанными LHE является убедительным доказательством преобразования всех поглощенных фотонов в экситоны и почти 100% внутренней квантовой эффективности (IQE), что указывает на то, что зарождающаяся рекомбинация крайне маловероятно, и что извлечение носителей заряда почти завершено 21,30 .
3b. С другой стороны, интегрирование пространственного профиля поглощения по всей глубине AL дает спектр светособирающей эффективности (LHE) на рис. 3c. Хорошее соответствие между спектрами измеренной эффективности преобразования падающих фотонов в электроны (IPCE) и рассчитанными LHE является убедительным доказательством преобразования всех поглощенных фотонов в экситоны и почти 100% внутренней квантовой эффективности (IQE), что указывает на то, что зарождающаяся рекомбинация крайне маловероятно, и что извлечение носителей заряда почти завершено 21,30 .
Результаты оптического моделирования: ( a ) зависимые от положения спектры поглощения в активном слое; глубина соответствует расстоянию от границы между ETL и AL, ( b ) глубина профиля скоростей генерации экситонов и многослойной структуры OSC (вставка), и ( c ) сравнение спектров светособирающей эффективности и измеренных эффективность преобразования падающего фотона в электрон.
Серия предварительных расчетов показала, что плотность дефектов является наиболее важным параметром при воспроизведении зависимости интенсивности света измеренных кривых J – V .Напротив, другие параметры не оказали заметного влияния на результаты моделирования до тех пор, пока их порядок величин сохранялся на литературных значениях 31,32,33,34,35 . Рисунок 4 показывает, что неправильный выбор плотности дефектов не позволяет воспроизвести экспериментальные кривые J – V . В частности, разрушение заметно проявляется вблизи точки перегиба в случае темной кривой J – V , и одновременное согласие между смоделированными и измеренными кривыми J – V , соответствующими слабому (0.{- 3} \) сопоставимо с устройствами PM6: Y6, о которых сообщил T-Q Nguyen 33 .
Рисунок 4 Сравнение смоделированных и измеренных кривых J – V . Мы смоделировали набор кривых J – V , соответствующих большим вариациям плотности дефектов, которые охватывают четыре порядка величины. {- 3} \).
{- 3} \).
На рис. 5a, b мы показываем полный набор смоделированных кривых J – V (сплошные линии) вместе с соответствующими данными (символы), измеренными при 9 различных интенсивностях света, а также в темноте. Несмотря на существенные изменения токов короткого замыкания, все смоделированные кривые J – V демонстрируют хорошее согласие с экспериментальными данными, что подтверждает достоверность наших расчетов OSC. Одним из преимуществ моделирования является то, что мы можем определить вклад компонентов генерации ( J gen ) и рекомбинационного тока ( J rec ) в кривые J – V во время работы OSC при интенсивности света L .Более того, мы можем разделить J rec на компоненты SRH-рекомбинации ( J SRH ) и бимолекулярного рекомбинационного тока ( J bi ):
Рисунок 5 Сравнение смоделированных кривых J – V (сплошные линии) с соответствующими данными (символы), измеренными при 9 различных интенсивностях света, а также в темноте: ( a ) от 0,18 до 1,00 солнца и ( b ) ниже 0,09 солнца и в темноте. ( c ) Сравнение смоделированных кривых рекомбинационного тока, J rec — V (сплошные линии), с суммой (символы) измеренного J ( V ) и смоделированного тока генерации J gen ( L ) при каждой интенсивности света L .( d ) Вариации нормированных плотностей тока J norm по отношению к приложенным напряжениям: \ (J_ {norm} = J / J_ {sc} \).
( c ) Сравнение смоделированных кривых рекомбинационного тока, J rec — V (сплошные линии), с суммой (символы) измеренного J ( V ) и смоделированного тока генерации J gen ( L ) при каждой интенсивности света L .( d ) Вариации нормированных плотностей тока J norm по отношению к приложенным напряжениям: \ (J_ {norm} = J / J_ {sc} \).
$$ J \ left (V, L \ right) = {J} _ {rec} (V, L) — {J} _ {gen} \ left (L \ right) = {J} _ {SRH} \ left (V, L \ right) + {J} _ {bi} (V, L) — {J} _ {gen} (L) $$
(1)
J gen , который мы вычисляем путем интегрирования скорости генерации на рис. 3 (b) по глубине AL, не зависит от приложенных напряжений, потому что AL достаточно тонкий, так что все поглощенные фотоны преобразуются в экситоны с ~ 100% IQE 30 .Мы хотим подчеркнуть, что выделение J SRH и J bi важно для количественного выяснения вышеупомянутых вариаций V oc и FF.
Мы сравниваем набор смоделированных кривых J rec –V (сплошные линии) с соответствующей суммой измеренных J ( V ) и смоделированных J gen (символы) на рис. . 5c. В дополнение к темновым токам, которые охватывают 5 порядков величины, весь набор данных фототока хорошо согласуется с смоделированными вариациями J rec .На рис. 5d мы показываем нормализованные плотности тока J norm по отношению к приложенным напряжениям для более легкого распознавания систематических изменений в V oc и FF, независимо от квазилинейного увеличения J sc . : \ ({J} _ {norm} = J / {J} _ {sc} \).
Чтобы показать происхождение отклонения В oc на рис. 2b, мы показываем две компоненты рекомбинационного тока отдельно по отношению к приложенному напряжению на рис. 6a – c. На этих рисунках токи и приложенные напряжения нормированы на J gen и V oc , соответственно, чтобы подчеркнуть систематические изменения в J SRH и J bi и их вклад в В oc . На 1 солнце В oc определяется в основном J bi из-за их доминирования в экспоненциально возрастающих токах, как показано на рис. 6a. Напротив, J SRH доминирует над J bi при 0,01 солнца и определяет J rec . Однако вклады J bi и J SRH становятся сопоставимыми при 0,18 Солнца. Систематические изменения рекомбинационных токов при В oc на рис.6d показывают, что преобладающий механизм потери тока переключается с SRH на бимолекулярную рекомбинацию при температуре около 0,18 Солнца. Соответственно, вариации V oc относительно интенсивности света согласуются с рекомбинацией SRH до 0,18 Солнца, но с бимолекулярной рекомбинацией при более высоких интенсивностях света, как показано на рис. 2b.
На 1 солнце В oc определяется в основном J bi из-за их доминирования в экспоненциально возрастающих токах, как показано на рис. 6a. Напротив, J SRH доминирует над J bi при 0,01 солнца и определяет J rec . Однако вклады J bi и J SRH становятся сопоставимыми при 0,18 Солнца. Систематические изменения рекомбинационных токов при В oc на рис.6d показывают, что преобладающий механизм потери тока переключается с SRH на бимолекулярную рекомбинацию при температуре около 0,18 Солнца. Соответственно, вариации V oc относительно интенсивности света согласуются с рекомбинацией SRH до 0,18 Солнца, но с бимолекулярной рекомбинацией при более высоких интенсивностях света, как показано на рис. 2b.
 Токи рекомбинации нормализованы токами генерации J gen ( L ), а приложенные напряжения нормированы на V oc . ( d ) Вариации токов SRH и бимолекулярной рекомбинации при В oc в зависимости от интенсивности света.
Токи рекомбинации нормализованы токами генерации J gen ( L ), а приложенные напряжения нормированы на V oc . ( d ) Вариации токов SRH и бимолекулярной рекомбинации при В oc в зависимости от интенсивности света. Затем мы расширили анализ вариаций J SRH и J bi , чтобы определить происхождение вариации FF на рис.2c. На рис. 7a, b показаны вариации J SRH и J bi , которые нормированы на J gen по отношению к приложенным напряжениям, нормированным на V oc . Наиболее заметное несоответствие между вариациями J SRH и J bi заключается в систематическом смещении точек перегиба. В случае кривых J SRH — V точки перегиба смещаются в нижнем правом направлении с увеличением силы света.Напротив, точки перегиба кривых J bi — V перемещаются в верхнее левое направление в ответ на увеличение интенсивности света.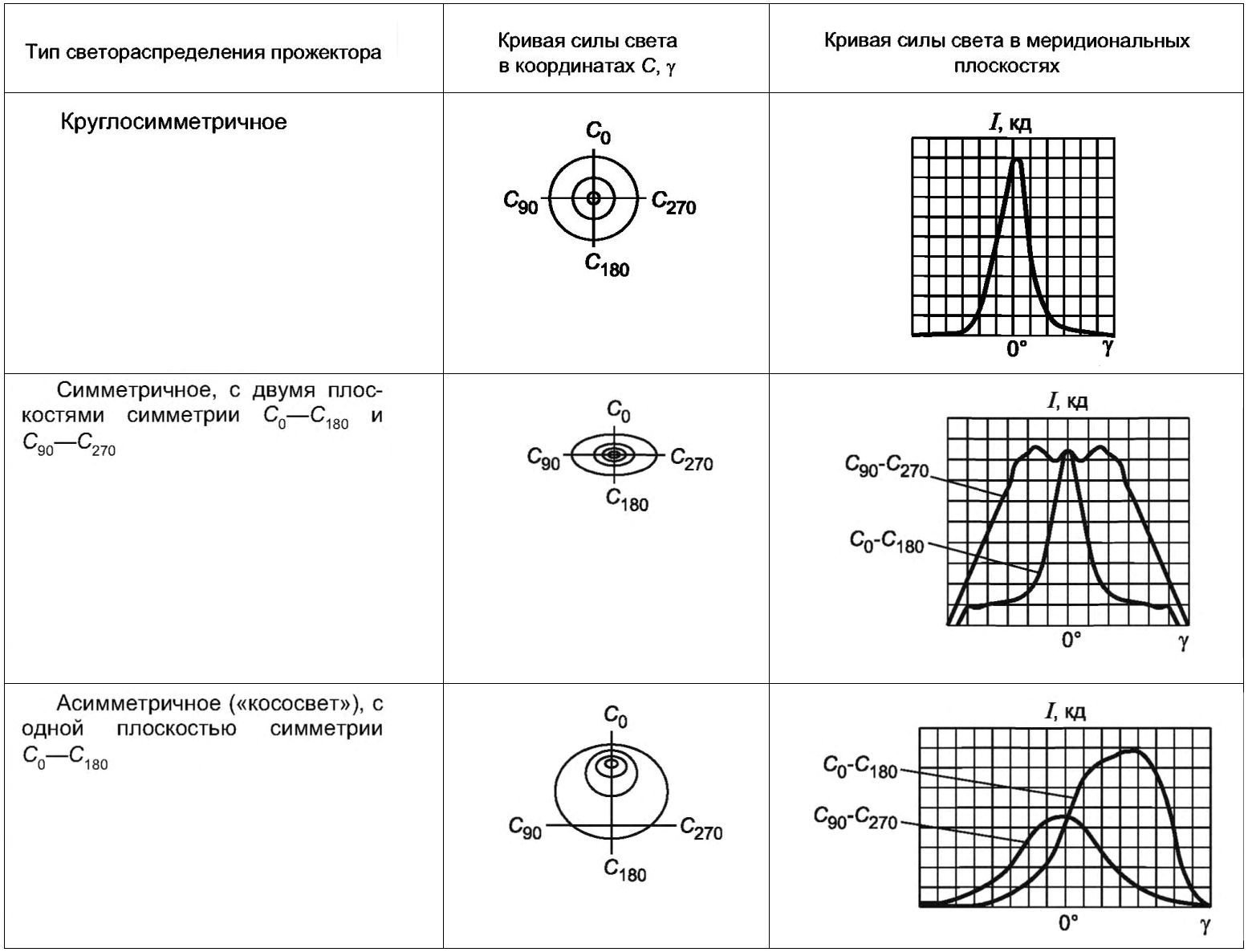 Результатом таких сдвигов являются очевидные изменения прямоугольности кривых J — V в точках максимальной мощности (MPP). Для количественного сравнения вкладов J SRH и J bi в максимальную мощность на рис.8. Все мощности нормированы на P sq , что определяется как произведение J sc и V oc . Несложно увидеть, что разница между генерируемой мощностью ( P gen ) и потерями мощности ( P SRH и P bi ) — это выходная мощность, выдаваемая OSC при каждой интенсивности света. При 0,01 солнца P SRH в 7,1 раза больше, чем P bi в точке MPP, и, соответственно, FF в основном определяется P SRH .С увеличением интенсивности света преобладание P SRH над P bi уменьшается, но P SRH остается в 2,2 раза больше, чем P bi при 0,18 Солнца.
Результатом таких сдвигов являются очевидные изменения прямоугольности кривых J — V в точках максимальной мощности (MPP). Для количественного сравнения вкладов J SRH и J bi в максимальную мощность на рис.8. Все мощности нормированы на P sq , что определяется как произведение J sc и V oc . Несложно увидеть, что разница между генерируемой мощностью ( P gen ) и потерями мощности ( P SRH и P bi ) — это выходная мощность, выдаваемая OSC при каждой интенсивности света. При 0,01 солнца P SRH в 7,1 раза больше, чем P bi в точке MPP, и, соответственно, FF в основном определяется P SRH .С увеличением интенсивности света преобладание P SRH над P bi уменьшается, но P SRH остается в 2,2 раза больше, чем P bi при 0,18 Солнца. Однако P bi становится сопоставимым с P SRH при 0,50 Солнца и в конечном итоге становится в 1,7 раза больше, чем P bi при 1 Солнце.
Однако P bi становится сопоставимым с P SRH при 0,50 Солнца и в конечном итоге становится в 1,7 раза больше, чем P bi при 1 Солнце.
Изменения в зависимости от интенсивности света нормированных токов SRH и бимолекулярной рекомбинации относительно нормированных приложенных напряжений: ( a ) J SRH / J gen по сравнению с V / V oc и ( b ) J bi / J gen по сравнению с V / V oc .
Рисунок 8 Вариации нормированных составляющих мощности относительно нормированных приложенных напряжений, соответствующих интенсивности света ( a ) 0,01, ( b ) 0,18, ( c ) 0,50 и ( d ) 1,00 солнце. Каждый силовой компонент нормализован на P sq , который определяется как произведение J sc и V oc , а приложенные напряжения нормализуются на V oc .
Для более количественного сравнения мы показываем относительные вклады P SRH и P bi в общую потерю мощности P потери в MPP на рис. 9a. P SRH / P потери неуклонно уменьшаются с 86,1% при 0,01 солнца до 37,3% при 1 солнце, и совпадают с P bi / P потерями при 0,50 секунды. Мотивировавшись переключением между P SRH и P bi с преобладанием потерь мощности, мы оцениваем FF, которые возникли бы, если бы только P SRH или P bi были ответственны за потерю мощности:
$$ FF_ {SRH} = \, \ left ({P_ {gen} — \, P_ {SRH}} \ right) _ {max} / P_ {sq} $$
(2)
$$ FF_ {bi} = \ left ({P_ {gen} {-} P_ {bi}} \ right) _ {max} / P_ {sq} $$
(3)
Рисунок 9 ( a ) Вариации относительных вкладов потерь мощности P SRH и P bi в общую потерю мощности P потери в точках максимальной мощности относительно яркости света. ( b ) Вариации коэффициентов заполнения (FF) в зависимости от интенсивности света. FF SRH и FF bi — это FF, которые появились бы, если бы только P SRH или P bi были ответственны за потерю мощности.
( b ) Вариации коэффициентов заполнения (FF) в зависимости от интенсивности света. FF SRH и FF bi — это FF, которые появились бы, если бы только P SRH или P bi были ответственны за потерю мощности.
Интересно отметить, что пересечение вариаций FF SRH и FF bi происходит около 0,50 Солнца, как показано на рис. 9b. Более того, вариация FF близка к вариациям FF SRH для света. интенсивность ниже 0.09 солнце, но следует тенденции FF bi для интенсивности света выше 0,50 солнца. Однако FF не меняется заметно для промежуточных интенсивностей света, в которых FF SRH и FF bi сопоставимы.
Обсуждения, относящиеся к рис. 6 и 8 показывают, что вариации как V, , oc, , так и FF в отношении интенсивности света происходят из-за конкуренции между SRH и механизмами потери бимолекулярной рекомбинации. Поскольку рекомбинационные потери SRH чувствительны к плотности дефектов, мы ожидаем систематического развития J sc , V oc и FF в ответ на изменения плотности дефектов. Серия моделирования, охватывающая 4 порядка изменения плотности дефектов, подтверждает наши ожидания, как показано на рис. S2 и S3 во вспомогательной информации. При низкой (5 × 10 10 см −3 ) и высокой (5 × 10 13 см −3 ) плотностях дефектов V oc и FF демонстрируют относительно простые вариации, поскольку либо J bi или J SRH преобладает над токами потерь. Напротив, более тонкие вариации происходят для плотностей дефектов 5 × 10 11 и 5 × 10 12 см −3 , когда происходит переключение между доминированием J bi и J SRH .Однако J sc демонстрируют квазилинейное изменение интенсивности света независимо от плотности дефектов. Количественно J bi , нормализованное до J gen , составляет всего ~ 1%, и, следовательно, J SRH определяют смещения J sc от J gen .
Серия моделирования, охватывающая 4 порядка изменения плотности дефектов, подтверждает наши ожидания, как показано на рис. S2 и S3 во вспомогательной информации. При низкой (5 × 10 10 см −3 ) и высокой (5 × 10 13 см −3 ) плотностях дефектов V oc и FF демонстрируют относительно простые вариации, поскольку либо J bi или J SRH преобладает над токами потерь. Напротив, более тонкие вариации происходят для плотностей дефектов 5 × 10 11 и 5 × 10 12 см −3 , когда происходит переключение между доминированием J bi и J SRH .Однако J sc демонстрируют квазилинейное изменение интенсивности света независимо от плотности дефектов. Количественно J bi , нормализованное до J gen , составляет всего ~ 1%, и, следовательно, J SRH определяют смещения J sc от J gen . Однако J SRH составляет менее 1% для дефектов с плотностью 5 × 10 10 и 5 × 10 11 см −3 и J sc , нормализованных до J gen. остается близким к 1, чтобы сделать изменение J sc — L почти линейным.Напротив, J SRH , нормализованные до J gen , становятся такими большими, как 7,4% и 21,6% при 0,01 солнечного света для соответствующих плотностей дефектов 5 × 10 12 и 5 × 10 13 см. −3 , а J SRH / J gen монотонно уменьшаются с увеличением интенсивности света. Следовательно, расхождения между J sc и J gen заметны при низкой интенсивности света, а соотношение J sc / J gen монотонно увеличивается с увеличением интенсивности света, в результате в слегка суперлинейных вариантах J sc — L .
Однако J SRH составляет менее 1% для дефектов с плотностью 5 × 10 10 и 5 × 10 11 см −3 и J sc , нормализованных до J gen. остается близким к 1, чтобы сделать изменение J sc — L почти линейным.Напротив, J SRH , нормализованные до J gen , становятся такими большими, как 7,4% и 21,6% при 0,01 солнечного света для соответствующих плотностей дефектов 5 × 10 12 и 5 × 10 13 см. −3 , а J SRH / J gen монотонно уменьшаются с увеличением интенсивности света. Следовательно, расхождения между J sc и J gen заметны при низкой интенсивности света, а соотношение J sc / J gen монотонно увеличивается с увеличением интенсивности света, в результате в слегка суперлинейных вариантах J sc — L .
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.ЯЗЫК}} {{$ select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}границ | Моделирование светового отклика скорости переноса электронов и его распределения для карбоксилирования и оксигенации бифосфата рибулозы
Введение
Интенсивность света ( I ) является одним из наиболее важных факторов окружающей среды, влияющих на поток электронов и его распределение для карбоксилирования по сравнению с оксигенацией бифосфата рибулозы ( RuBP).На уровнях I до достижения интенсивности насыщения непрямоугольная гиперболическая модель (далее модель NH) является подмоделью, которая широко используется для характеристики кривой светового отклика скорости переноса электронов (кривая Дж – I ) и для оценки максимума Дж ( Дж max ) в модели фотосинтеза C 3 (например, Farquhar et al., 1980; Farquhar and Wong, 1984; von Caemmerer, 2000; Farquhar et al., 2001 ; Long and Bernacchi, 2003; von Caemmerer et al., 2009; Bernacchi et al., 2013; Bellasio et al., 2015; Буш и Сейдж, 2017; Walker et al., 2017; Cai et al., 2018) и в модели фотосинтеза C 4 (Berry and Farquhar, 1978; von Caemmerer, Furbank, 1999; von Caemmerer, 2013). При световом насыщении значение J max оценивается с помощью модели фотосинтеза C 3 (Farquhar et al., 1980; von Caemmerer, 2013; Farquhar, Busch, 2017). Точная оценка J max важна для понимания фотосинтеза видов C 3 и C 4 . J max — ключевая величина для представления фотосинтетического статуса растений в различных условиях окружающей среды, когда чистая скорость фотосинтеза ( A n ) ограничена регенерацией RuBP, связанной с разделением потока электронов через фотосистему II. (PSII) для карбоксилирования RuBP ( J C ) по сравнению с таковым для оксигенации RuBP ( J O ) (Farquhar et al., 1980; Long and Bernacchi, 2003).
Путем моделирования кривых светового отклика фотосинтеза ( A n –I кривая) модель NH широко использовалась для получения ключевых фотосинтетических характеристик (например,g., максимальная чистая скорость фотосинтеза, A nmax ; точка компенсации света, когда A n = 0, I c ; частота темнового дыхания, R d ) для различных видов в разных условиях окружающей среды (например, Ögren & Evans, 1993; Thornley, 1998; Ye, 2007; Aspinwall et al., 2011; dos Santos et al., 2013; Mayoral et al., 2015; Sun et al., 2015; Park et al., 2016; Quiroz et al., 2017; Yao et al., 2017; Xu et al., 2019; Ян и др., 2020; Ye et al., 2020). О значительном различии между наблюдаемыми значениями A nmax и оцененными с помощью модели NH для различных видов широко сообщалось (например, Chen et al., 2011; dos Santos et al., 2013; Lobo et al., 2014; Ogawa , 2015; Sun et al., 2015; Quiroz et al., 2017; Poirier-Pocovi et al., 2018; Ye et al., 2020). Эта давняя проблема была решена с помощью модели A n — I , которая принимает неасимптотическую функцию и может точно воспроизводить кривую A n — I в условиях ограниченного освещения, насыщенного света. и фотоингибирующие уровни I (Ye et al., 2013) (далее модель Е.).
Недавно Бакли и Диас-Эспехо (2015) предположили, что модель NH будет переоценивать J max из-за ее асимптотической функции. Срочно необходима надежная модель, которая может точно воспроизвести наблюдаемую кривую J – I и получить J max (Buckley and Diaz-Espejo, 2015). Кроме того, световая характеристика разделения J для карбоксилирования и оксигенации RuBP (кривые J C –I и J O –I ) и ключевые величины для описания кривых (e .g., максимальное значение J C , J C-max и максимальное значение J O , J O-max , а также соответствующие им интенсивности насыщенного света) изучается редко. Между тем, мы впервые сравнили характеристики двух моделей при воспроизведении кривых J C — I и J O — I .
Это исследование было направлено на восполнение этих важных пробелов с использованием подхода взаимного сравнения наблюдений и моделирования.Сначала мы измерили газообмен листьев и флуоресценцию хлорофилла в широком диапазоне уровней I для двух видов C 3 [озимая пшеница ( Triticum aestivum L.) и соя ( Glycine max L.)]. Затем мы включили модель Ye для воспроизведения кривых A n — I , J – I , J C –I и J O –I и клавиши возврата. величин, определяющих кривые, и оценили его производительность в сравнении с моделью NH и наблюдениями.
Материалы и методы
Растительный материал и измерения газообмена в листьях и флуоресценции хлорофилла
Эксперимент проводился на комплексной экспериментальной станции Yucheng Китайской академии наук. Подробные описания почвы и метеорологических условий на этой экспериментальной станции были переданы Ye et al. (2019; 2020). Озимая пшеница была посеяна 4 октября , 2011 г., замеры проводились 23 апреля , 2012.Соя была посеяна 6 мая -го , 2013 г., измерения были выполнены 27 -го числа июля 2013 г. С использованием портативной системы фотосинтеза Li-6400-40 (Li-Cor, Линкольн, Северная Каролина, США) измерения газообмен листа и флуоресценцию хлорофилла одновременно проводили на зрелых полностью разросшихся листьях, подвергшихся воздействию солнца в солнечные дни. J было рассчитано как J = Φ PSII × I × 0,5 × 0,84, где Φ PSII — эффективный квантовый выход PSII (Genty et al., 1989; Кролл и Эдвард, 1992).
Для сои: A n — I Кривые и J — I кривые были сгенерированы путем применения различных значений силы света в порядке убывания 2000, 1800, 1600, 1400, 1200, 1000, 800 , 600, 400, 200, 150, 100, 80, 50 и 0 мкмоль м -2 с -1 . Для озимой пшеницы градиент интенсивности света начинался с максимума 1800 мкмоль · м -2 с -1 в соответствии с доступностью внешнего освещения с октября по апрель.На каждом этапе I ассимиляцию CO 2 отслеживали до достижения устойчивого состояния перед регистрацией показаний. Окружающая концентрация CO 2 в кювете ( C a ) поддерживалась постоянной на уровне 380 мкмоль-моль -1 . Температура листьев в кювете поддерживалась на уровне около 30 ° C для озимой пшеницы и 36 ° C для сои, соответственно. Взаимное сравнение наблюдения и моделирования проводилось внутри каждого вида.
A n –I и J – I Аналитические моделиМодель NH описывает кривую J – I следующим образом (Farquhar and Wong, 1984; von Caemmerer, 2000; von Caemmerer, 2013) :
J = αeI + Jmax− (αeI + Jmax) 2−4αeθJmaxI2θ (1)где α e — начальный наклон кривой J – I , θ — выпуклость кривой, I — интенсивность света, а Дж max — максимальная скорость переноса электронов.Модель
NH описывает кривую A n –I следующим образом (Ögren, Evans, 1993; Thornley, 1998; von Caemmerer, 2000):
An = αI + Anmax− (αI + Anmax) 2−4αθAnmaxI2θ −Rd (2), где α — начальный наклон кривой A n –I , A nmax — максимальная чистая скорость фотосинтеза, а R d — темная частота дыхания при I = 0 мкмоль м -2 с -1 .Модель NH не может возвращать соответствующие интенсивности света насыщения для J max или A nmax из-за своей асимптотической функции.
Модель, разработанная Ye et al. (2013, 2019; далее модель Ye) описывает кривую J – I следующим образом:
, где α e — начальный наклон кривой J – I , а β e и γ e — коэффициент фотоингибирования и коэффициент светонасыщения кривой J – I соответственно.
Насыщенная освещенность, соответствующая J max ( I e — sat ), может быть рассчитана следующим образом:
Ie-sat = (βe + γe) / βe − 1γe (4)Используя модель Ye, J max можно рассчитать следующим образом:
Jmax = αe (βe + γe − βeγe) 2 (5)Модель Ye описывает A n –I кривая следующим образом (Ye, 2007; Ye et al., 2013):
An = α1 − βI1 + γII − Rd (6), где α — начальный наклон кривой A n — I , β и γ — коэффициент фотоингибирования и коэффициент светонасыщения кривой A n — I соответственно.
Энергия насыщения, соответствующая A nmax ( I sat ), может быть рассчитана следующим образом:
Используя модель Ye, A nmax можно рассчитать следующим образом:
Anmax = α ( β + γ − βγ) −Rd (8) J C и J O Оценка и J C –I и J O –I Аналитические моделиКомбинирование измерений газообмена и флуоресценции хлорофилла было надежным и простым в использовании методом, широко используемым для определения J O и J C (e.г., Петерсон, 1990; Comic and Briantais, 1991). У растений C 3 ассимиляция углерода и фотодыхание — два тесно связанных процесса, катализируемых ключевым фотосинтетическим ферментом — карбоксилазой / оксигеназой RuBP. Фотодыхание рассматривается как альтернативный приемник для индуцированных светом фотосинтетических электронов и как процесс, помогающий потреблять дополнительные фотосинтетические электроны при высокой освещенности или других стрессовых факторах, ограничивающих доступность CO 2 в Рубиско (Stuhlfauth et al., 1990; Valentini et al., 1995; Long and Bernacchi, 2003). Когда другие альтернативные стоки электронов игнорируются или остаются постоянными, поток электронов в основном направляется на карбоксилирование RuBP и оксигенацию RuBP (например, Farquhar et al., 1980; von Caemmerer, 2000; Farquhar et al., 2001; Long and Bernacchi, 2003). ; von Caemmerer et al., 2009; Bernacchi et al., 2013; von Caemmerer, 2013) и J C и J O могут быть рассчитаны соответственно следующим образом (Valentini et al., 1995) :
JO = 23 [J-4 (An + Rday)] (10), где R day — дневная частота дыхания, и, следуя Fila et al.(2006), R день = 0,5 R d . В этом исследовании значения J C и J O , рассчитанные по формулам. 9 и 10 рассматривались как экспериментальные наблюдения — для сравнения с смоделированными значениями, полученными из модели NH и модели Ye, соответственно.
Используя ту же структуру моделирования J – I модели Ye, световой отклик J C ( J C –I ) можно описать следующим образом:
JC = αC1 − βCI1 + γCII (11), где α C — начальный наклон кривой J C –I , а β C и γ C — два коэффициента Дж. C –I кривая.Максимальное значение J C ( J C-max ) и яркость насыщения, соответствующая J C-max ( I C — sat ). рассчитывается следующим образом:
JC-max = αC (βC + γC − βCγC) 2 (12) IC-sat = (βC + γC) / βC − 1γC (13)Используя ту же структуру моделирования J – I , Модель Ye, световой отклик J O ( J O –I ) можно описать следующим образом:
JO = αO1 − βOI1 + γOII (14), где α O — начальный наклон кривой J O –I , а β O и γ O — два коэффициента кривой J O –I .Максимальное значение J O ( J O-max ) и яркость насыщения, соответствующая J O-max ( I O — sat ). рассчитывается следующим образом:
JO-max = αO (βO + γO − βOγO) 2 (15) IO-sat = αOβO + γO / βO − 1γO (16)Между тем, модель NH может описывать модель J C –I и J O –I кривые следующим образом:
JC = αCI + JC-max– (αCI + JC-max) 2−4αCθJC-maxI2θ (17)где α C — начальный наклон кривой J C –I , θ — выпуклость кривой, а J C-max — максимальное значение J C и
JO = αOI + JO-max− (αOI + JO-max) 2−4αOθJO-maxI2θ (18)где α O — начальный наклон кривой J O –I , θ — кривая co nvexity, а J O-max — максимальное значение J O .Модель NH — уравнения. 17 и 18 — не может вернуть соответствующие интенсивности насыщенного света для J C-max или J O-max из-за его асимптотической функции.
Статистический анализ
Статистические тесты были выполнены с использованием статистического пакета статистического программного обеспечения SPSS 18.5 (SPSS, Чикаго, Иллинойс). Односторонний дисперсионный анализ был использован для изучения различий между значениями параметров, оцененными с помощью модели NH, модели Ye и наблюдаемых значений каждого параметра ( A nmax , I sat , J max , I e — sat , J C-max , I C — sat , J O-max , I O — сат и т. Д.). Соответствие математической модели экспериментальным наблюдениям оценивалось с помощью коэффициента детерминации ( R 2 = 1 — SSE / SST, где SSE — сумма квадратов ошибок, а SST — общая сумма квадратов).
Результаты
Световой отклик
A n и JСоя и озимая пшеница показали немедленное и быстрое начальное увеличение A n ( α ) и J ( α e ) с увеличением I (рисунок 1 и таблица 1).Увеличение A n и J продолжалось до тех пор, пока I не достигло максимальных значений для конкретного сорта ( A nmax и J max ) при их соответствующей интенсивности насыщенного света ( I sat и I e — sat ) (рисунок 1 и таблица 1). Как модель NH (уравнения 1 и 2), так и модель Ye (уравнения 3 и 6) показали высокий уровень соответствия ( R 2 ) экспериментальным наблюдениям за двумя видами (рисунок 1 и таблица 1).Однако по сравнению с наблюдениями модель NH значительно переоценила значения A nmax и J max ( P < 0,05) как для сои, так и для озимой пшеницы (Таблица 1). Напротив, значения A nmax и J max , полученные с помощью модели Ye, очень хорошо согласуются с наблюдениями для обоих видов (Таблица 1).
Рисунок 1 Кривые светового отклика чистой скорости фотосинтеза (A, B), скорости переноса электронов (C, D), потока электронов для карбоксилирования RuBP (E, F) и потока электронов для RuBP оксигенация (G, H) для озимой пшеницы ( Triticum aestivum L.) и сои ( Glycine max л.) соответственно в диапазоне освещенности от 0 до 2000 мкмоль м -2 с -1 . Сплошные кривые построены с использованием модели Ye, а штриховые кривые — с использованием модели NH. Значения представляют собой средние значения ± стандартная ошибка ( n = 3).
Таблица 1 Установленные (модель Ye и модель NH) и измеренные значения (набл.) Параметров, определяющих кривую светового отклика фотосинтеза ( A n — I кривая), скорость переноса электронов ( J — I кривая ), скорость переноса электронов для карбоксилирования RuBP (кривая J C — I ) и скорость переноса электронов для оксигенации RuBP ( J O — I кривая) для виды пшеницы и сои соответственно.
Световой отклик
J C и J OОба вида показали немедленное и быстрое начальное увеличение J C ( α C ) с увеличением I (Рисунок 1 и Таблица 1). Увеличение J C продолжалось до тех пор, пока I не достигло максимальных значений для конкретного сорта ( J C-max ) при соответствующей интенсивности насыщенного света ( I C — sat ) (Рисунок 1 и Таблица 1).И модель Ye (уравнение 11), и модель NH (уравнение 17) показали высокий уровень соответствия ( R 2 ) экспериментальным наблюдениям за обоими видами (рисунок 1 и таблица 1). Однако по сравнению с наблюдениями модель NH значительно переоценила значение J C-max ( P < 0,05) как для сои, так и для озимой пшеницы (Таблица 1). Напротив, значения J C-max , полученные с помощью модели Ye, очень хорошо согласуются с наблюдениями для обоих видов (Таблица 1).
По сравнению со скоростью светового отклика J C , J O показало гораздо более медленное начальное увеличение ( α O ) с увеличением I (Рисунок 1 и Таблица 1) . Ни один из видов не показал существенной разницы между наблюдаемым значением J O-max и оцененным с помощью модели Ye (уравнение 14) или модели NH (уравнение 18) (таблица 1). Обе модели показали высокий уровень соответствия ( R 2 ) экспериментальным наблюдениям за обоими видами (Рисунок 1 и Таблица 1).
Обсуждение
Результаты данного исследования, оцененные с помощью подхода взаимного сравнения наблюдений и моделирования, подчеркивают надежность модели Ye в точном воспроизведении A n –I , J – I , J C –I и J O –I кривые и возвращение ключевых величин, определяющих кривые, в частности: A nmax , J max , J C-max и J O-max .Напротив, модель NH значительно переоценивает A nmax , J max и J C-max (Таблица 1). В нашем исследовании впервые обнаружено, что ранее широко сообщавшееся завышение J max (и A nmax ) моделью NH связано с его завышением J C-max , но не . J O-макс .
Завышенная оценка A nmax по модели NH, обнаруженная в этом исследовании, согласуется с предыдущими отчетами (например.г., Calama et al., 2013; душ Сантуш и др., 2013 г .; Лобо и др., 2014; Ježilová et al., 2015; Mayoral et al., 2015; Огава, 2015; Park et al., 2016; Quiroz et al., 2017; Пуарье-Покови и др., 2018; Ye et al., 2020). Точное возвращение A nmax по модели Ye, обнаруженное в этом исследовании, согласуется с предыдущими исследованиями с использованием модели Ye для различных видов в различных условиях окружающей среды (например, Wargent et al., 2011; Zu et al., 2011; Xu et al., 2012a; Xu et al., 2012b; Lobo et al., 2014; Сюй и др., 2014; Song et al., 2015; Чен и др., 2016; Ye et al., 2019; Ян и др., 2020; Ye et al., 2020). Устойчивость модели Ye была также подтверждена для наблюдений за микроводорослями, включая четыре пресноводных и три морских вида микроводорослей (Yang et al., 2020). Модель Ye воспроизвела реакцию A n –I для всех видов микроводорослей и произвела I на , близкую к измеренным значениям, чем значения трех широко используемых моделей для микроводорослей (Yang et al., 2020). Между тем, завышенная оценка J max моделью NH, обнаруженная в этом исследовании, поддерживает Бакли и Диас-Эспехо (2015) в подчеркивании недостатков асимптотической функции (т.е. модели NH).
Одной из ключевых новинок настоящего исследования является оценка как асимптотических, так и неасимптотических функций при описании светового отклика распределения электронного потока для карбоксилирования и оксигенации соответственно (т.е. J C — I и J O — I кривые).Насколько нам известно, это первое исследование, которое экспериментально подтвердило устойчивость неасимптотической функции (уравнения 3, 11, 14) при точном (1) воспроизведении J – I , J C –I и J O –I кривые и (2) возвращающие значения J max , J C-max и J O-max , а также как их соответствующие интенсивности света насыщения.Эти новые открытия имеют важное значение для нашего понимания световых реакций ассимиляции углерода растений и фотодыхания, которые катализируются карбоксилазой / оксигеназой RuBP.
Полученные данные и подход к объединяющему эксперименту и моделированию в настоящем исследовании еще предстоит протестировать для (1) видов с разными типами функций растений и / или климатического происхождения, которые могут демонстрировать разные модели реакции (Ye et al., 2020) и (2) реакция растений на взаимодействие множества факторов окружающей среды (например,g., температура, характер осадков, тип почвы) с изменяющимся освещением. Явная и согласованная структура моделирования и определения параметров световых откликов (например, A n –I , J – I , J C –I и J O –I ) — в сочетании с простотой и надежностью — позволяет в будущем прозрачно масштабировать результаты на уровне листа до масштабов всего растения и экосистемы.
Выводы
Модель Ye может точно оценить A nmax , J max и J C-max , что модель NH могла бы переоценить.Принятие четкой и прозрачной аналитической основы и последовательных определений для A n –I , J – I , J C –I и J O –I кривых, это исследование подчеркивает преимущество модели Ye над моделью NH с точки зрения (1) чрезвычайно хорошего воспроизведения J – I , J C –I и J O — I тенденции в широком диапазоне I от интенсивности света ограниченного до подавляющего свет, (2) точное возвращение множества ключевых величин, определяющих J – I , J C –I , и J O –I кривые, в частности J max , J C-max , J O-max и соответствующие им интенсивности насыщенного света (помимо A нмакс и I соответствует из A n –I кривая), и (3) прозрачно раскрывает ранее широко описанную, но плохо объясненную проблему модели NH — завышение J max (и максимальная производительность установки по карбоксилированию) — связана с ее завышением Дж C-max , но не J O-max .Кроме того, модель NH не может получить интенсивность насыщенного света, соответствующую J max , A nmax , J C-max и J O-max из-за своей асимптотической функции. Это исследование важно как для экспериментаторов, так и для разработчиков моделей, работающих над лучшим представлением фотосинтетических процессов в условиях динамического освещения.
Заявление о доступности данных
Необработанные данные, подтверждающие выводы этой статьи, будут предоставлены авторами без излишних оговорок.
Вклад авторов
Все авторы внесли свой вклад в концепцию работы. H-JK в основном проводил эксперимент. Z-PY и S-XZ составили черновик оригинальной рукописи. Все авторы критически рассмотрели и отредактировали рукопись с добавлением новых наборов данных и внесли значительный вклад в завершение настоящего исследования. Все авторы внесли свой вклад в статью и одобрили представленную версию.
Финансирование
Это исследование было поддержано Китайским фондом естественных наук (грант №31960054 и 31560069) и Проект ключевой группы научно-технических инноваций города Вэньчжоу (грант № C20150008).
Конфликт интересов
S-XZ использовался компанией The New Zealand Institute for Plant and Food Research Limited.
Остальные авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Список литературы
Aspinwall, M.Дж., Кинг, Дж. С., Маккинд, С. Е., Домек, Дж. К. (2011). Однородность газообмена на уровне листа и фотосинтетическая способность среди генотипов лоблоловой сосны ( Pinus taeda L.) с контрастирующими врожденными генетическими вариациями. Tree Physiol. 31, 78–91. doi: 10.1093 / treephys / tpq107
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Bellasio, C., Beerling, D. J., Griffiths, H. (2015). Инструмент Excel для получения ключевых параметров фотосинтеза на основе комбинированного газообмена и флуоресценции хлорофилла: теория и практика. Среда растительных клеток. 39, 1180–1197. doi: 10.1111 / pce.12560
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Бернакки, К. Дж., Бэгли, Дж. Э., Сербин, С. П., Руис-Вера, У. М., Розенталь, Д. М., Ванлоок, А. (2013). Моделирование C 3 фотосинтеза из хлоропласта в экосистему. Среда растительных клеток. 36, 1641–1657. doi: 10.1111 / pce.12118
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Берри, Дж.А., Фаркуар, Г. Д. (1978). «Функция концентрации CO2 фотосинтеза C4: биохимическая модель», в Труды Четвертого Международного конгресса по фотосинтезу . Ред. Холл Д., Кумбс Дж., Гудвин Т. (Лондон: Биохимическое общество Лондона), 119–131.
Google Scholar
Буш, Ф. А., Сейдж, Р. Ф. (2017). Чувствительность фотосинтеза к концентрации O 2 и CO 2 указывает на сильный контроль Рубиско выше теплового оптимума. New Phytol. 213, 1036–1051. doi: 10.1111 / nph.14258
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Cai, C., Li, G., Yang, H. L., Yang, J. H., Liu, H., Struik, P. C., et al. (2018). Все ли параметры фотосинтеза листьев риса адаптируются к повышенному CO 2 , повышенной температуре и их сочетанию в средах FACE? Global Change Biol. 24, 1685–1707. doi: 10.1111 / gcb.13961
CrossRef Полный текст | Google Scholar
Calama, R., Пуэртолас, Дж., Мадригал, Г., Пардос, М. (2013). Моделирование реакции окружающей среды на фотосинтез листовой сети у естественного возобновления сосны Pinus pinea L. Ecol. Модель. 51, 9–21. doi: 10.1016 / j.ecolmodel.2012.11.029
CrossRef Полный текст | Google Scholar
Chen, Z. Y., Peng, Z. S., Yang, J., Chen, W. Y., Ou-Yang, Z. M. (2011). Математическая модель для описания кривых светового отклика у nicotiana tabacum l. Photosynthetica 49, 467–471. DOI: 10.1007 / s11099-011-0056-5
CrossRef Полный текст | Google Scholar
Chen, X., Liu, W. Y., Song, L., Li, S., Wu, C. S., Lu, H. Z. (2016). Адаптация эпифитных мохообразных в подлеске за счет корреляций и компромиссов между функциональными признаками. J. Bryol. 38, 110–117. doi: 10.1080 / 03736687.2015.1120370
CrossRef Полный текст | Google Scholar
Comic, G., Briantais, J. M. (1991). Разделение фотосинтетического потока электронов между CO 2 и O 2 сокращение в листе C 3 ( Phaseolus vulgaris L.) при различных концентрациях CO 2 и во время стресса засухи. Planta 183, 178–184. doi: 10.1007 / bf00197786
PubMed Аннотация | CrossRef Полный текст | Google Scholar
душ Сантуш, Дж. У. М., де Карвалью, Дж. Дж. Ф., Фирнсайд, П. М. (2013). Измерение воздействия наводнения на деревья Амазонки: модели фотосинтетической реакции для десяти видов, затопленных плотинами гидроэлектростанций. Деревья 27, 193–210. doi: 10.1007 / s00468-012-0788-2
CrossRef Полный текст | Google Scholar
Farquahr, G.Д., Буш, Ф. А. (2017). Изменения в концентрации CO 2 в хлоропласте объясняют большую часть наблюдаемого эффекта Кока: модель. New Phytol. 214, 570–584. doi: 10.1111 / nph.14512
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Фаркуар, Г. Д., Вонг, С. К. (1984). Эмпирическая модель устьичной проводимости. Aus. J. Plant Physiol. 11, 191–210. doi: 10.1071 / pp9840191
CrossRef Полный текст | Google Scholar
Farquhar, G.Д., фон Каммерер, С., Берри, Дж. А. (1980). Биохимическая модель фотосинтетической ассимиляции CO 2 в листьях видов C 3 . Planta 149, 78–90. doi: 10.1007 / BF00386231
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Fila, G., Badeck, F., Meyer, S., Cerovic, Z., Ghashghaie, J. (2006). Взаимосвязь между проводимостью листьев к диффузии CO 2 и фотосинтезом у микроразмножающихся растений виноградной лозы до и после акклиматизации ex vitro . J. Exp. Бот. 57, 2687–2695. doi: 10.1093 / jxb / erl040
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Дженти, Б., Бриантайс, Дж. М., Бейкер, Н. Р. (1989). Связь между квантовым выходом фотосинтетического транспорта электронов и тушением флуоресценции хлорофилла. Biochim. Биофиз. Acta 990, 87–92. doi: 10.1016 / s0304-4165 (89) 80016-9
CrossRef Полный текст | Google Scholar
Ježilová, E., Nožková-Hlaváčková, V., Духослав, М. (2015). Фотосинтетические характеристики трех уровней плоидности Allium oleraceum L. (Amaryllidaceae), различающихся экологической амплитудой. Завод Спец. Биол. 30, 212–224. doi: 10.1111 / 1442-1984.12053
CrossRef Полный текст | Google Scholar
Krall, J. P., Edward, G. E. (1992). Связь активности фотосистемы II с фиксацией СО 2 в листьях. Physiol. Завод 86, 180–187. DOI: 10.1111 / j.1399-3054.1992.tb01328.x
CrossRef Полный текст | Google Scholar
Lobo, F. D. A., Barros, M. P. D., Dalmagro, H. J., Dalmolin, BC, Pereira, W. E., de Souza, É.C., et al. (2014). Подгонка чистых фотосинтетических кривых световой отдачи с помощью Microsoft Excel — критический взгляд на модели. Photosynthetica 52, 445–456. doi: 10.1007 / s11099-014-0045-6
CrossRef Полный текст | Google Scholar
Лонг, С. П., Бернакки, К. Дж. (2003). Измерения газообмена, что они могут сказать нам об основных ограничениях фотосинтеза? Процедуры и источники ошибок. J. Exp. Бот. 54, 2393–2401. doi: 10.1093 / jxb / erg262
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Майораль, К., Калама, Р., Санчес-Гонсалес, М., Пардос, М. (2015). Моделирование влияния света, воды и температуры на фотосинтез молодых деревьев смешанных средиземноморских лесов. Новое для. 46, 485–506. doi: 10.1007 / s11056-015-9471-y
CrossRef Полный текст | Google Scholar
Огава, К. (2015). Математическое рассмотрение теории модели трубы у древесных растений. Деревья 29, 695–704. doi: 10.1007 / s00468-014-1147-2
CrossRef Полный текст | Google Scholar
Park, K. S., Bekhzod, K., Kwon, J. K., Son, J. E. (2016). Разработка парной фотосинтетической модели базилика сладкого, выращенного на гидропонике на заводах по производству растений. Hortic. Environ. Biotechnol. 57, 20–26. doi: 10.1007 / s13580-016-0019-7
CrossRef Полный текст | Google Scholar
Петерсон, Р. Б. (1990). Влияние облучения на фактор специфичности in vivo CO 2 : O 2 в табаке с использованием методов одновременного газообмена и флуоресценции. Plant Physiol. 94, 892–898. doi: 10.1104 / pp.94.3.892
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Poirier-Pocovi, M., Lothier, J., Buck-Sorlin, G. (2018). Моделирование временного изменения параметров, используемых в двух моделях фотосинтеза: влияние нагрузки плода и опоясания на фотосинтез листьев в плодоносящих ветвях яблони. Ann. Бот. 121, 821–832. doi: 10.1093 / aob / mcx139
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Quiroz, R., Лоайза, Х., Барреда, К., Гавилан, К., Посадас, А., Рамирес, Д. А. (2017). Связывание технологических моделей картофеля с данными светоотражения: повышает ли сложность модели точность прогнозов урожайности? евро. J. Agron. 82, 104–112. doi: 10.1016 / j.eja.2016.10.008
CrossRef Полный текст | Google Scholar
Song, L., Zhang, Y.J., Chen, X., Li, S., Lu, H.Z., Wu, C.S., et al. (2015). Водные отношения и газообмен веерных мохообразных и их адаптация к микропредприятию в азиатских субтропических горных облачных лесах. J. Plant Res. 128, 573–584. doi: 10.1007 / s10265-015-0721-z
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Stuhlfauth, T. R., Scheuermann, R., Foek, H.P. (1990). Рассеяние световой энергии в условиях водного стресса. Вклад реассимиляции и свидетельства дополнительных процессов. Plant Physiol. 92, 1053–1061. doi: 10.1104 / pp.92.4.1053
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Sun, J. S., Sun, J.Д., Фэн З. З. (2015). Моделирование фотосинтеза флаговых листьев озимой пшеницы ( Triticum aestivum ) с учетом изменения параметров фотосинтеза во время развития. Функц. Plant Biol. 42, 1036–1044. doi: 10.1071 / FP15140
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Торнли, Дж. Х. М. (1998). Динамическая модель фотосинтеза листа с акклиматизацией к свету и азоту. Ann. Бот. 81, 431–430. DOI: 10.1006 / anbo.1997.0575
CrossRef Полный текст | Google Scholar
Valentini, R., Epron, D., Angelis, P. D., Matteucci, G., Dreyer, E. (1995). In situ оценка чистого CO 2 ассимиляция, фотосинтетический поток электронов и фотодыхание листьев турецкого дуба ( Q. cerris L.): суточные циклы при разном водоснабжении. Среда растительных клеток. 18, 631–640. doi: 10.1111 / j.1365-3040.1995.tb00564.x
CrossRef Полный текст | Google Scholar
von Caemmerer, S., Фурбанк, Р. Т. (1999). «Моделирование фотосинтеза C4», в C4 Plant Biology . Ред. Сейдж, Р. Ф., Монсон, Р. (Сан-Диего, Калифорния: Academic Press), 169–207.
Google Scholar
фон Каммерер, С., Фаркуар, Г. Д., Берри, Дж. А. (2009). «Биохимическая модель фотосинтеза C3», в Photosynthesis in Silico. Понимание сложности от молекул до экосистем . Ред. Лайск, А., Недбал, Л., Говинджи (Дордрехт, Нидерланды: Springer), 209–230.
Google Scholar
von Caemmerer, S.(2000). Биохимические модели фотосинтеза листьев (Виктория, Австралия: Csiro Publishing).
Google Scholar
Уокер, Б. Дж., Орр, Д. Дж., Кармо-Сильва, Э., Парри, М. А., Бернакки, К. Дж., Орт, Д. Р. (2017). Неопределенность в измерениях точки компенсации фотодыхательного CO 2 и ее влияние на модели фотосинтеза листьев. Photosyn. Res. 132, 245–255. doi: 10.1007 / s11120-017-0369-8
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Wargent, J.Дж., Эльфадли, Э. М., Мур, Дж. П., Пол, Н. Д. (2011). Повышенное воздействие УФ-В-излучения на раннем этапе развития приводит к усилению фотозащиты и улучшенным долгосрочным характеристикам у lactuca sativa. Среда растительных клеток. 34, 1401–1413. doi: 10.1111 / j.1365-3040.2011.02342.x
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Xu, Z. F., Yin, H. J., Xiong, P., Wan, C., Liu, Q. (2012a). Краткосрочные реакции сеянцев Picea asperata разного возраста, выращенных в двух контрастирующих лесных экосистемах, на экспериментальное потепление. Environ. Exp. Бот. 77, 1–11. doi: 10.1016 / j.envexpbot.2011.10.011
CrossRef Полный текст | Google Scholar
Xu, Z. F., Hu, T. X., Zhang, Y. B. (2012b). Влияние экспериментального потепления на фенологию, рост и газообмен саженцев древесной березы ( Betula utilis ), Восточно-Тибетское плато, Китай. Eur. J. For. Res. 131, 811–819. doi: 10.1007 / s10342-011-0554-9
CrossRef Полный текст | Google Scholar
Xu, J. Z., Yu, Y.М., Пэн, С. З., Ян, С. Х., Ляо, Л. X. (2014). Модифицированное уравнение непрямоугольной гиперболы для фотосинтетических кривых светового отклика листьев с различным азотным статусом. Photosynthetica 52, 117–123. doi: 10.1007 / s11099-014-0011-3
CrossRef Полный текст | Google Scholar
Xu, J., Lv, Y., Liu, X., Wei, Q., Liao, L. (2019). Общее непрямоугольное уравнение гиперболы для фотосинтетической кривой светового отклика риса при разном возрасте листьев. Sci. Реп. 9, 9909.doi: 10.1038 / s41598-019-46248-y
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ян, X. L., Liu, L. H., Yin, Z. K., Wang, X. Y., Wang, S. B., Ye, Z. P. (2020). Количественная оценка фотосинтетических характеристик фитопланктона на основе моделей реакции фотосинтеза и освещенности. Environ. Sci. Евро. 32, 24. doi: 10.1186 / s12302-020-00306-9
CrossRef Полный текст | Google Scholar
Yao, X., Zhou, H., Zhu, Q., Li, C.H., Zhang, H.J., Hu, J.J., и другие. (2017). Фотосинтетический ответ листа сои на широкие колебания освещенности в системе посева кукурузы и сои. Фронт. Plant Sci. 8, 1695. doi: 10.3389 / fpls.2017.01695
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ye, Z. P., Suggett, J. D., Robakowski, P., Kang, H. J. (2013). Механистическая модель реакции фотосинтеза на свет, основанная на фотосинтетическом переносе электронов ФС II у видов C 3 и C 4 . New Phytol. 152, 1251–1262. doi: 10.1111 / nph.12242
CrossRef Полный текст | Google Scholar
Ye, Z. P., Liu, Y. G., Kang, H. J., Duan, H. L., Chen, X. M., Zhou, S. X. (2019). Сравнение двух показателей фотодыхания листьев в широком диапазоне интенсивности света. J. Plant Physiol. 240, 153002. doi: 10.1016 / j.jplph.2019.153002
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ye, Z.-P., Ling, Y., Yu, Q., Duan, H.-L., Kang, H.-J., Huang, G.-M., Et al. (2020). Количественная оценка светового отклика эффективности водопользования листовой чешуей и ее взаимосвязи с фотосинтезом и устьичной проводимостью у видов C 3 и C 4 . Фронт. Plant Sci. 11, 374. doi: 10.3389 / fpls.2020.00374
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ye, Z. P. (2007). Новая модель взаимосвязи между освещенностью и скоростью фотосинтеза у Oryza sativa . Photosynthetica 45, 637–640.doi: 10.1007 / s11099-007-0110-5
CrossRef Полный текст | Google Scholar
Zu, Y. G., Wei, X. X., Yu, J. H., Li, D. W., Pang, H. H., Tong, L. (2011). Ответы физиологии и биохимии сосны корейской ( Pinus koraiensis ) на дополнительное УФ-В излучение. Photosynthetica 49, 448–458. doi: 10.1007 / s11099-011-0057-4
CrossRef Полный текст | Google Scholar
Влияние интенсивности света и температуры на кривые реакции фотосинтетического излучения и флуоресценцию хлорофилла у трех штаммов пикоцианобактерий Synechococcus
Albertano, P., Ди Сомма, Д., Капуччи, Э .: Цианобактериальный пикопланктон из Центральной Балтийского моря: классификация размеров клеток с помощью флуоресцентной микроскопии с анализом изображений. — J. Plankton Res. 19 : 1405–1416, 1997.
Статья Google ученый
Антиа, штат Нью-Джерси: Влияние температуры на выживаемость морских микропланктонных водорослей в темноте. — Microb. Ecol. 3 : 41–54, 1976.
CAS PubMed Статья Google ученый
Björkman, O., Деммиг, Б.: Выход фотонов O 2 , эволюция и характеристики флуоресценции хлорофилла при 77 К среди сосудистых растений различного происхождения. — Planta 170 : 489–504, 1987.
PubMed Статья Google ученый
Блэкберн С.И., МакКосленд М.А., Болч С.Дж., Ньюман С.Дж., Джонс Дж. Дж .: Влияние засоления и выработки токсинов в культурах цианобактерий, образующих цветение, Nodularia spumigena из вод Австралии.- Phycologia 35 : 511–522, 1996.
Статья. Google ученый
Каллиери, С., Моро, С., Каравати, Э., Кросби, Н.Д., Вайсс, Т .: Штамм-специфический фотосинтетический ответ пресноводных пикоцианобактерий. — Верх. Междунар. Verein. Лимнол. 29 : 777–782, 2005.
CAS Google ученый
Кэмпбелл, Д., Торри, В., Кларк, А.К., Густафссон, П., Оквист, Г .: Флуоресцентный анализ хлорофилла фотосинтеза и акклиматизации цианобактерий. — Микробиол. Мол. Биол. R. 62 : 667–683, 1998.
CAS Google ученый
Дефью, E.C., Перкинс, Р.Г., Патерсон, Д.М .: Влияние взаимодействий света и температуры на естественный комплекс микрофитобентоса эстуариев. — Биопленки 1 : 21–30, 2004.
Статья. Google ученый
Дринг, М.Дж .: Биология морских растений. 199 стр. Cambridge Univ. Press, Cambridge 1998.
Google ученый
Дубинский А., Стамблер Н .: Фотоакклимационные процессы в фитопланктоне: механизмы, последствия и приложения. — Акват. Microb. Ecol. 56 : 163–176, 2009.
Статья Google ученый
Фишер, Р.А., Йейтс, Ф .: Статистические таблицы для биологических, сельскохозяйственных и медицинских исследований.6-е изд. 138 стр. Оливье и Бойд, Эдинбург, 1963.
Google ученый
Фогг, Г.Э .: Экология океана: свет и ультрафитопланктон. 99 стр. Nature Publishing Group, Лондон 1986.
Google ученый
Фогг, Г.Э., Тэйк, Б.: Культуры водорослей и экология фитопланктона. 269 стр. University of Wisconsin Press, Мэдисон и Милуоки, 1987.
Google ученый
Гловер, Х.Э., Финни Д.А., Йенч К.С.: Фотосинтетические характеристики пикопланктона по сравнению с характеристиками более крупных популяций фитопланктона в различных водных массах в заливе Мэн. — Биологический океаногр. 3 : 223–248, 1985.
Google ученый
Хайду, С., Хёгландер, Х., Ларссон, У .: Вертикальное распределение и состав фитопланктона в цветении цианобактерий в Балтийском море. — Вредные водоросли 6 : 189–205, 2007.
Артикул Google ученый
Хенли, У.Д .: Измерение и интерпретация фотосинтетических кривых светового отклика у водорослей в контексте фотоингибирования и изменений плотности. — J. Phycol. 29 : 729–739, 1993.
Статья Google ученый
Ибелингс, Б.У .: Изменения фотосинтеза в ответ на комбинированное облучение и температурный стресс у цианобактериальных поверхностных водных цветков.- J. Phycol. 32 : 549–557, 1996.
Статья Google ученый
Яссер, И .: Взаимосвязь между автотрофным пикопланктоном (APP) — наименьшим автотрофным компонентом пищевой сети и трофическим статусом и глубиной озер. — Экогидрол. Hydrobiol. 6 : 69–77, 2006.
Статья Google ученый
Яссер, И., Арвола, Л .: Возможное влияние абиотических факторов на численность автотрофного пикопланктона в четырех бореальных озерах.- J. Plankton Res. 25 : 873–883, 2003.
CAS Статья Google ученый
Jodłowska, S., liwińska, S., Latała, A .: Влияние облучения на рост и фотосинтетические пигменты трех балтийских пикоцианобактериальных штаммов Synechococcus. — В: Оланчук-Неймен, К., Мазур-Мажец, Х. (ред.): Микроорганизмы в окружающей среде и экологическая инженерия от экологии к технологии. Стр. 85–92. Монография Komitetu Inżynierii rodowiska PAN, no.64, Zabrze 2010.
Jodłowska, S., Latała, A .: Стратегии фотоакклимации токсичных цианобактерий Nodularia spumigena (Nostocales, Cyanobacteria) — Phycologia 49 : 203–211, 2010.
, статья
, 2010.
Google ученый
Йодловска, С., Латала, А .: Механизмы фотоакклимации на уровне фотосинтеза у цианобактерий. — В: Наджафпур, М. (ред.): достижения в области фотосинтеза — фундаментальные аспекты.Стр. 97–108. InTech, Хорватия, 2012 г.
Google ученый
Jodłowska, S., Latała, A .: Комбинированное влияние света и температуры на рост, фотосинтез и содержание пигментов в цианобактериях, образующих мат, Geitlerinema amphibium . — Photosynthetica 51 : 202–214, 2013.
Статья. Google ученый
Kahru, M., Leppänen, J.-M., Рудь, О., Савчук, О.П .: Цветение цианобактерий в Финском заливе, вызванное притоком соленой воды в Балтийское море. — Mar. Ecol. Прог. Сер. 207 : 13–18, 2000.
Статья Google ученый
Кана, Т.М., Глиберт, П.М.: Влияние освещенности до 2000 мкмоль E m −2 с −1 на морских Synechococcus WH7803-I. Рост, пигментация и клеточный состав. — Deep-Sea Res. 34 : 479–495, 1987.
CAS Статья Google ученый
Кульк, Г., ван де Пол, У. Х., Виссер, Р. Дж. У, Бума, А. Г. Дж .: Отчетливые различия в фотоакклимационном потенциале между прокариотическим и эукариотическим океаническим фитопланктоном. — J. Exp. Mar. Biol. Ecol. 398 : 63–72, 2011.
Статья Google ученый
Латала, А., Йодловска, С., Пневски, Ф .: Коллекция культур балтийских водорослей (CCBA) и характеристика некоторых штаммов методом факторного эксперимента.- Альгологические исследования, 122 : 137–154, 2006.
Статья. Google ученый
Макки, К.Р.М., Пайтан, А., Гроссман, А.Р., Бейли, С .: Стратегия фотосинтеза, позволяющая справиться с ситуацией в условиях яркого света и низкого содержания питательных веществ. — Лимнол. Oceanogr. 53 : 900–913, 2008.
CAS Статья Google ученый
Макинтайр, Х.Л., Кана, Т.М., Эннинг, Т., Гейдер, Р.Дж .: Фотоакклимация кривых реакции фотосинтеза на освещенность и фотосинтетических пигментов в микроводорослях и цианобактериях. — J. Phycol. 38 : 17–38, 2002.
Статья Google ученый
Максвелл К., Джонсон Г. Н .: Флуоресценция хлорофилла — практическое руководство. — J. Exp. Бот. 51 : 659–668, 2000.
CAS PubMed Статья Google ученый
Mouget, J.-Л., Тремблин, Г., Моран-Манко, А., Морансэ, М., Роберт, Ж.-М .: Длительная фотоакклимация Haslea ostrearia (Bacillariophyta): влияние облучения на скорость роста, пигмент содержание и фотосинтез. — Евро. J. Phycol. 34 : 109–115, 1999.
Статья Google ученый
Октаба, В .: [Методы математической статистики в экспериментах]. 488 с. PWN, Warszawa 1986. [на польском языке]
Google ученый
Panosso, R., Гранели, Э .: Влияние растворенного органического вещества на рост Nodularia spumigena (Cyanophyceae), культивируемых в условиях дефицита азота или фосфора. — Мар. Биол. 136 : 331–336, 2000.
Статья Google ученый
Платт Т., Джассби А.Д .: Взаимосвязь между фотосинтезом и светом для природных сообществ прибрежного морского фитопланктона. — J. Phycol. 12 : 421–430, 1976.
Google ученый
Platt.Т., Гальегос, К.Л., Харрисон, У.Г .: Фотоингибирование фотосинтеза в естественных сообществах морского фитопланктона. — J. Mar. Res. 38 : 687–701, 1980.
Google ученый
Презелин, Б.Б .: Световые реакции в фотосинтезе. — Жестяная банка. Б. Рыба. Акват. Sci. 210 : 1–43, 1981.
Google ученый
Рамус Дж .: Захват и преобразование световой энергии.- В: Lobban, C.S., Wynne, M.J. (ed.): The Biology of Seaweeds. Стр. 458–492. Blackwell Scientific, Оксфорд, 1981.
Google ученый
Ричардсон, К., Бирдалл, Дж., Рэйвен, Дж. А .: Адаптация одноклеточных водорослей к облучению: анализ стратегий. — Новый Фитол. 93 : 157–191, 1983.
Артикул Google ученый
Ричардсон, Т.Л., Джексон, Г.О .: Небольшой фитопланктон и экспорт углерода с поверхности океана. — Наука 315 : 838–840, 2007.
CAS. PubMed Статья Google ученый
Rohacek, K .: Параметры флуоресценции хлорофилла: определения, фотосинтетическое значение и взаимоотношения. — Photosynthetica 40 : 13–29, 2002.
CAS. Статья Google ученый
Шесть, К., Финкель, З.В., Ирвин, А.Дж., Кэмпбелл, Д.А.: Изменчивость света указывает на разделение ниш среди морских пикоцианобактерий. — PLOS ONE: doi: 10.1371 / journal.pone. 0001341, 2007.
Snedecor, G.W., Cochran, W.G .: Статистические методы. 703 стр. Iowa State University Press, Ames 1980.
Google ученый
Сталь, Л.Дж., Уолсби, А.Э .: Фотосинтез и фиксация азота при цветении цианобактерий в Балтийском море.- Евро. J. Phycol. 35 : 97–108, 2000.
Статья Google ученый
Сталь, Л.Дж., Альбертано, П., Бергман, Б., и др. : ОСНОВНОЙ: цианобактерии Балтийского моря. Исследование структуры и динамики цветения цианобактерий в Балтийском море — реакция на изменение окружающей среды. — Продолж. Полка Res. 23 : 1695–1714, 2003.
Статья Google ученый
Stanier, R.Y., Kunisawa, R., Mandel, M., Cohen-Bazire, G .: Очистка и свойства одноклеточных сине-зеленых водорослей (порядок Chroococcales). — Бактериол. Ред. 35 : 171–205, 1971.
CAS PubMed Central PubMed Google ученый
Strickland, I.D.H., Parsons, T.R .: Практическое руководство по анализу морской воды. — Бык. Рыба. Res. Bd. Жестяная банка. 167 : 1–310, 1972 г.
Google ученый
Сурош, В., Палинска, К.А .: Ультраструктурные изменения, вызванные выбранными концентрациями Cd и Cu в цианобактериях Phormidium: взаимодействие с соленостью . — J. Plant Physiol. 157 : 643–650, 2000.
CAS Статья Google ученый
Aquation Scientific Equipment Руководство по анализу быстрых кривых блеска
Быстрые кривые блескаможно легко построить с помощью большинства флуорометров PAM, используя программу, поставляемую с прибором, который вы используете.Некоторые флуорометры даже обеспечивают автоматический анализ этих кривых. Однако настройки RLC по умолчанию могут не подходить для вашего исследования, а анализ аппроксимации кривой также может не подходить для ваших целей.
Это руководство призвано помочь вам сделать три вещи:
- правильно настройте флуориметр PAM,
- выберите лучшие настройки RLC для вашего экспериментального плана или режима выборки, а
- проанализируйте ваши кривые, чтобы определить оценки параметров с их оценками погрешности (мы коснемся сравнения между наборами кривых).
Подробное обсуждение интерпретации параметров RLC и RLC выходит далеко за рамки данного Руководства — см. White and Critchley (1999) и Ralph and Gademann (2005) для получения информации об этой важной информации. Номенклатура все еще оспаривается, вы можете использовать Van Kooten and Snel (1990) или более поздние Cosgrove и Borowitzka (2011).
После прочтения этого руководства вы можете ожидать, что узнали:
- Что такое RLC.
- Как и зачем устанавливать флуорометр.
- Как и зачем устанавливать RLC; и как его запустить.
- Как анализировать RLC для определения оценок параметров и их ошибок.
- Как сравнивать RLC между курсами лечения.
PDF-файл этой веб-страницы можно найти здесь: Как анализировать быструю кривую блеска.
Во-первых, немного предыстории…
Что такое быстрая кривая блеска?Типичная быстрая световая кривая (или RLC ) получается в результате быстрой (например, 90-секундной) световой обработки фотосинтетического образца (листа, слоевища, культуры).Во время воздействия лечебного света фотосинтетическая способность (эффективный квантовый выход переноса электронов через фотосистему II (ФСII), или f ФСII ) многократно измеряется с использованием метода импульса насыщения. Обработка кривой может начинаться с измерения насыщающего импульса (f PSII ), за которым следует 10-секундный интервал воздействия низкой интенсивности актиничного света и еще одно измерение f PSII , снова с последующим 10-секундным воздействием немного более сильного актиничного излучения. свет и другое измерение f PSII .Актинический свет — это свет, излучаемый флуорометром, который «управляет» фотосистемой. Может быть всего пять шагов, обычно восемь, а возможно, и больше. Значения f ФСII обычно колеблются от максимального значения около 0,83, что указывает на то, что 83% поглощенной световой энергии направляется на ФСII, до 0%.
Построив график f PSII против PAR, мы можем увидеть, как f PSII постепенно уменьшается с увеличением освещенности. Однако, рассчитав скорость фотосинтеза и построив график зависимости от PAR, мы построим кривую светового отклика, или кривую PE, .Эти кривые существуют уже много лет и показывают, среди прочего, как скорость фотосинтеза достигает максимума при определенной освещенности.
Чтобы оценить скорость фотосинтеза по каждой точке данных, мы вычисляем скорость переноса электронов ( ETR ) путем умножения f PSII и PAR предыдущего интервала, а затем умножаем это на две константы. Если константы неизвестны, просто используйте «1» для определения относительной скорости переноса электронов ( rETR ).Константы: 1) коэффициент поглощения образца и 2) отношение PSII / (PSII + PSI) . Затем значения вычисленных rETR или ETR наносятся на график относительно PAR каждого интервала. Типичная кривая начинается от начала координат (0,0) в виде линии, затем выравнивается (асимптоты) при высокой освещенности, в конечном итоге достигая максимума. Некоторые кривые могут затем снижать ETR с более высоким PAR, что часто называют фотоингибированием. См. Уайт и Кричли (1999) для всестороннего обсуждения RLC, а также более позднюю статью Ральфа и Гадемана (2005).
Важно помнить, что для большинства RLC все измерения проводятся на одном участке образца. Это означает, что каждая точка данных на кривой не является независимой от других точек. Часто это удобно игнорировать, и в некоторых ситуациях это нормально. Однако в конечном итоге это зависит от вас. См. Обсуждение этого вопроса в White and Critchley (1999).
RLC указывают на освещенность, при которой достигается максимальная ETR, а также могут указывать на начало явного фотоингибирования при большей освещенности.
Какие еще измерения мне следует сделать при выполнении быстрой кривой блеска?- Фотосинтетически активное излучение (PAR) : скорость переноса электронов может быть рассчитана только со значением для падающего света. В единицах ммоль кванты м -2 с -1 .
- Поглощение : часто предполагается, что оно составляет 0,84, однако это значение может значительно варьироваться в пределах и между отдельными людьми и видами. Это также используется для расчета скорости переноса электронов
- PSII / (PSI + PSII) : доля энергии, направляемая в фотосистему II, часто принимается равной 0.5, но может отклоняться от этого значения
Эти значения (PAR, абсорбция и PSII (PSI + PSII)) используются с f PSII для расчета скорости переноса электронов (ETR) в соответствии с уравнением Генти (или относительным ETR (rETR), если абсорбция и / или PSII (PSI + PSII) неизвестны):
Какие данные можно получить с помощью быстрой кривой блеска?- ΦPSII сразу после RLC
- ΦPSII при измеренной освещенности окружающей среды, интерполированной по кривой
- ETR , связанный с каждым измерением импульса насыщения, выполненным во время кривой.В единицах ммоль м -2 с -1 .
- ETRmax : максимально достигнутый ETR. В единицах ммоль электронов м -2 с -1 .
- α или альфа; начальный наклон кривой. В единицах электроны / кванты (используйте эти единицы только при определении фактического ETR, а не rETR).
- Ek : минимальная насыщенная освещенность, при которой максимальный ETR был бы достигнут, если бы на кривой не было перегиба (т.е. экстраполировать начальную линейную часть кривой, чтобы пересечь ее с максимальным ETR (или rETR).В единицах ммоль кванты м -2 с -1 .
- β или бета, малоиспользуемый параметр, характеризующий спад кривой после достижения ETRmax.
Теперь, чтобы настроить PAM для достижения оптимальных результатов…
Настройка флуориметра PAMОсвободите место, возьмите флуориметр PAM и тестовый образец или случайный лист, если вы только начинаете привыкать к процедуре.
- Приготовьте тестовый образец для проведения измерений.Предпочтительно выбирать образец, который не подвергался воздействию сильного света.
- Длительность импульса насыщения (SP): Выберите длительность импульса насыщения (часто называемую шириной насыщения): g. При исследовании листа часто используется 800 мс.
- SP интенсивность : выберите интенсивность насыщающего импульса. Часто бывает достаточно настроек по умолчанию. В идеале выберите интенсивность, которая будет обеспечивать кривую насыщения, а не ступенчатую функцию между значениями флуоресценции F и Fm.В последнем случае уменьшайте интенсивность до тех пор, пока не появится кривая.
- AUTOGAIN : Если ваш флуориметр PAM поддерживает эту функцию, выберите AutoGain или аналогичный. Это установит коэффициент усиления флуорометра на подходящий уровень. Если ваш флуорометр требует, чтобы вы устанавливали усиление вручную, выберите значение усиления, при котором значение F для образца без напряжения (т. Е. Собранного рано утром) составляет примерно одну восьмую (0,125) наивысшего допустимого значения Fm. Например, если максимальное значение в PAM составляет 4000 единиц, тогда коэффициент усиления должен быть установлен таким образом, чтобы значение F безударного образца было меньше 400 единиц.Это гарантирует, что максимальное ожидаемое значение Fm не превысит максимум инструмента.
- AUTOZERO : Теперь удалите образец из области измерения флуориметра PAM, убедитесь, что флуориметр не видит ничего, что может флуоресцировать, и выберите AutoZero. F теперь должен быть около нуля. Если флуориметр требует ручной установки нуля, возьмите среднее значение F и вычтите это значение из всех последующих значений
- Тестовое измерение : проведите измерение на свежей части того же листа или образца.Если образец представляет собой зеленый лист без стресса, подвергнутый слабому освещению в течение как минимум часа, можно ожидать, что значение f PSII находится в диапазоне от 0,7 до 0,83. Гораздо меньше, и вы, возможно, захотите повторить процедуру настройки еще раз на новом образце, чтобы быть уверенным.
Теперь, когда вы настроили флуориметр PAM для проведения полезных измерений Φ PSII и Fv / Fm, давайте сосредоточимся на настройках RLC.
- Актинические интервалы: Вам необходимо установить интенсивность актиничного света во время каждого интервала.Различные флуорометры предоставляют разные возможности для установки интенсивности актиничного света. Идеальные настройки будут генерировать несколько точек данных, когда интенсивность света низкая, а кривая представляет собой прямую линию, и несколько точек данных при высокой интенсивности света, чтобы зафиксировать насыщающий характер кривой. Если вас больше интересует, что происходит в условиях низкой освещенности, вы получите лучшую оценку на с большим количеством точек данных при слабом освещении.
- Длительность актинического интервала: Продолжительность каждого интервала или шага обычно может быть изменена от 10 секунд (типично) до 30 секунд или более.Через некоторый промежуток времени быстрые световые кривые перестают быть быстрыми. Функциональное определение термина «быстрый» в значительной степени основано на предположении, что для того, чтобы кривая была быстрой, фундаментальные изменения в фотохимии образца еще не успели произойти. Это неверно, когда речь идет об изменениях энергозависимого нефотохимического тушения (qE), поскольку процессы, описываемые этим параметром, активируются и деактивируются в течение нескольких секунд. Можно предположить, что физиологические процессы, для индукции которых требуется больше времени, во время RLC в значительной степени не изменяются.
Запуск RLC
Это самая легкая часть. Большая часть тяжелой работы выполняется до и после построения кривой!
- Поместите интересующий образец в то место, где он должен быть измерен (либо над окном флуорометра PAM, либо в зажиме держателя образца, либо перед оптоволоконным кабелем, идущим от флуорометра). Убедитесь, что образец не будет двигаться во время процедуры RLC (очень важно).
- Исключить из образца окружающий свет.Полная темнота не обязательна, но лучше всего будет меньше света, чем в течение первого актинического интервала.
- Начните кривую, обеспечивая темноту (кроме света флуорометра). Важно, чтобы образец не двигался в течение всего периода лечения. Если он перемещается, интенсивность флуоресценции, вероятно, изменится, поскольку вы будете смотреть на новый участок образца, и последующие измерения не могут быть связаны с первыми измерениями.
Запуск кривой восстановления после RLC
С увеличением интенсивности света f PSII уменьшается.Когда «легкое давление» снимается в конце лечения RLC, f PSII «приходит в норму», постепенно увеличиваясь до тех пор, пока в темноте не будет достигнуто значение Fv / Fm. Кинетику этого восстановления можно изучить с помощью анализа так называемой кривой восстановления. Восстановление процесса после обработки при сильном освещении лучше всего моделировать с помощью экспоненциальной функции. Восстановление обычно включает два (а иногда и три) процесса, каждый с разным временем полураспада, и это можно смоделировать с помощью двойной экспоненциальной модели.В большинстве случаев выздоровление происходит быстро (в течение нескольких минут), а в оставшейся части может потребоваться много времени для полного восстановления (часы). Таким образом, идеальный режим измерения для фиксации восстановления фотосинтетического образца после обработки при сильном освещении принимает форму множества измерений, проводимых на начальном этапе восстановления, с постепенно менее частыми измерениями, проводимыми с более длительными интервалами.
Как извлечь данные из RLC Подготовка графика RLCПредположим, вы измерили актиническую ФАР на каждом интервале кривой блеска, правильно установили усиление и нулевые настройки флуориметра PAM и убедились, что образец остается фиксированным во время измерений с минимальным освещением, достигающим образца.Флуорометр PAM предоставляет вам значения f PSII , измеренные в конце каждого интервала.
- Соберите значения PAR для каждого интервала в столбце A (начиная с нуля), а в столбце C добавьте соответствующее значение f PSII Первое значение f PSII соответствует нулевому значению PAR. Это значение фактически не используется в большинстве RLC, поскольку предполагается, что транспорт электронов равен нулю в темноте.
- Теперь в столбце B умножьте значения f PSII на значения абсорбции и PSII / (PSII + PSI).Если у вас нет этих значений, вы сможете представить только значения относительного ETR (rETR).
- Создайте линейный график ETR (ось y) и PAR (ось x). Начальная часть линии, идущей от начала координат, должна быть прямой, а последняя часть должна образовывать кривую, которая приближается или достигает максимума (асимптота). Вы можете обнаружить, что кривая затем снова изгибается вниз с еще более высокой освещенностью.
Цель состоит в том, чтобы извлечь из ваших данных значения параметров ETRmax, Ek и a и, возможно, оценки ошибок, связанных с этими значениями.Мы используем просто два столбца: PAR и ETR.
Существует множество моделей, которые использовались для описания RLC и кривых PE в более общем плане. Каждая модель или уравнение предполагает определенное соотношение между параметрами. Некоторые модели вводят новые параметры, которые не имеют прямого биологического значения и должны использоваться только в том случае, если эта модель решает конкретную проблему. В идеале модель должна иметь функции, которые напрямую описывают известные процессы. Например, одно- или многокамерные экспоненциальные модели лучше всего использовать для описания кривых восстановления, поскольку экспоненциальный спад лучше всего описывает релаксацию физиологических процессов, которые были вызваны световой обработкой, и вызывает депрессию в f PSII .
Разработчикикривых PE обычно имеют свои собственные любимые модели, которые они используют для описания RLC. Поскольку многие из моих кривых были либо простыми асимптотами, либо обе были асимптотическими с понижением при более высокой освещенности, я выбрал модель, которая позволила мне проанализировать оба типа кривых. Эта модель включает два члена: один член с двумя параметрами для асимптоты и второй член (с третьим параметром), который может быть добавлен, если кривая также испытала спад. Второй срок можно было исключить, если бы не было спада.Этот подход важен, поскольку можно сравнивать только параметры, полученные из моделей с одной и той же фундаментальной базой, параметры, полученные из принципиально разных моделей, несовместимы и не должны сравниваться напрямую.
Модель, описывающая RLC, которые не имеют спада при высокой освещенности (то есть простая асимптота):
В эту модель добавлен дополнительный член для учета спада ETR:
Где ETRs — это масштабный параметр, определяющий максимальную потенциальную скорость фотосинтеза, а b представляет наклон нисходящей части кривой, часто называемой фотоингибированием.
ETRmax затем рассчитывается по следующей формуле:
См. Frenette et al. (1993) для подробного обсуждения.
Нелинейная регрессия предполагает несколько атрибутов ваших данных; следующие утверждения должны быть верными (или в основном верными):
- Значения PAR (значения оси x) точны, тогда как значения ETR (значения оси y, содержащие f II ) менее точны и содержат интересующую нас изменчивость,
- Вариабельность возможных значений ETR, связанных с определенным значением PAR, будет распределена нормально и следовать колоколообразной кривой — или, другими словами, нет причин ожидать, что значения ETR, связанные с конкретным значением PAR, будут чрезмерно представлены более высокими или более низкими значениями. чем среднее значение.
- Стандартное отклонение каждого остатка в каждой точке данных одинаково по величине на всей кривой, или, если взвешено, то картина предсказуема,
- Каждое значение ETR не зависит от любого другого значения ETR, которое может быть измерено при том же значении PAR.
См. Motulsky and Christopoulos (2013) для доступного и более подробного обсуждения допущений, присущих методам нелинейной регрессии.
Анализ RLC — с использованием электронной таблицыПосле того, как вы выбрали модель, которую хотите использовать (простая асимптотическая модель или модель с спадом), что дальше? Вы можете использовать статистический пакет — ищите «нелинейную регрессию наименьших квадратов», поскольку это используемый метод.В большинстве приложений используется алгоритм Левенберга-Марквардта. Введите свою модель, скопируйте и вставьте набор данных в программу. Вас могут попросить ввести «начальные» значения, которые являются вашими наилучшими оценочными значениями ETRmax, a и Ik (ETRmax и Ik легко получить на глаз из графика RLC, a рассчитывается как ETRmax / Ek). Некоторые приложения могут предлагать только стандартный набор моделей и не позволяют создавать свои собственные.
Возможно, вы захотите избежать расходов на покупку пакета статистики.Электронная таблица с функцией решателя может легко определить оценки параметров (Brown 2001). Однако макрос потребуется, если вы хотите определить оценки ошибок, связанных с каждым параметром. Еще лучше научиться использовать статистическое программное обеспечение с открытым исходным кодом «R» и искать «нелинейную регрессию наименьших квадратов» в качестве руководства. Научившись использовать R, вы сможете решать большинство статистических задач с математической строгостью.
Вместо того, чтобы объяснять детали словами, я создал две таблицы, которые вы можете использовать.Их можно найти на https://aquation.com.au/tools/calculators/. Одна электронная таблица просто вычисляет оценки параметров как для двухпараметрической кривой, так и для трехпараметрической кривой, используя функцию Решателя в Microsoft Excel. Инструкции в электронной таблице. Я предлагаю скопировать один из листов на новый лист в книге и поэкспериментировать с разными моделями, чтобы увидеть, как это работает.
Определение ошибки, связанной с каждой оценкой параметра, сложнее и требует многоступенчатого процесса, который, по-видимому, лучше всего выполнять с помощью макроса.Вместо того, чтобы изобретать велосипед, я предоставил надстройку Excel, любезно предоставленную Леонардо Вольпи и командой Foxes, Италия. Вы можете найти дополнительную информацию, касающуюся этого и другого сложного анализа в Excel, на сайте профессора Роберта де Леви http://www.bowdoin.edu/~rdelevie/excellaneous/.
Запуск модели на основе решателя (только оценки параметров)
Введите свои данные и подходящие оценки для ETRmax и альфа. Выберите Решатель и запустите его, минимизируя сумму квадратов и оптимизируя параметры ETR и альфа.Обратите внимание, что наклон кривой всегда должен быть положительным, это можно вставить в Solver в качестве условия. Обратите внимание на две линии на вашем рисунке, смоделированные данные должны сходиться с наблюдаемыми. Если смоделированные данные внезапно дают кривую, которая совсем не аппроксимирует наблюдения, вам нужно будет выбрать более точные оценки параметров модели.
Если вы настроили его правильно, значения параметров должны колебаться во время итерационной процедуры подбора кривой и быстро устанавливаться, так что только последние десятичные разряды оценок продолжают изменяться в течение нескольких итераций, прежде чем программа остановится.Значение R 2 представляет собой долю данных, которые описывает модель, поэтому значение 1,0 R 2 будет означать, что 100% данных объясняются моделью.
Запуск модели на основе макросов (включает оценки ошибок для параметров)
Введите свои данные и подходящие оценки для ETRmax и альфа. Следуйте инструкциям в электронной таблице, чтобы активировать и запустить макрос Optimiz (с помощью надстроек для Excel). Оценки ошибки для ваших параметров должны быть включены как стандартное отклонение и 95% доверительный интервал.Значение R 2 представляет собой долю данных, которые описывает модель, поэтому значение 1,0 R 2 будет означать, что 100% данных объясняются моделью. Приведенные здесь оценки погрешности и R 2 следует рассматривать как ориентировочные. Вычисление оценок ошибок для параметров и значения R 2 для самой кривой — сложная тема, тонкости которой лучше описать в другом месте.
Как сравнивать RLC между курсами леченияОбъединение и сравнение данных кривых
Можно получить несколько RLC на отдельных репликах растений или листьев в обработке или на участке и пожелать объединить или сравнить эти обработки.Доступно несколько подходов. Вы должны быть окончательным судьей в отношении того, что лучше всего использовать с учетом ваших данных и дизайна эксперимента или опроса. См. Peek et al. (2002) за полезное обсуждение.
Реплика : самый простой метод — объединение данных всех кривых. Если каждая из трех кривых имеет восемь пар данных, то объединенная кривая будет иметь 24-2 = 22 пары данных (начало координат (0,0) не нужно повторять). Один анализ этой кривой предоставит отдельные оценки для ETRmax и альфа, и на их основе можно определить оценку Ek.Ошибка, связанная с оценками параметров, будет отражать изменчивость или разброс точек данных всех кривых. Часто используется альтернативный подход — анализировать каждую кривую отдельно, получать оценки параметров и вычислять среднее значение и ошибку этого набора оценок. Этот подход не рекомендуется, поскольку он не описывает изменчивость, связанную с каждой отдельной кривой. Это связано с тем, что при объединении данных (путем усреднения) из нескольких кривых переносится только оценка параметра.
Сравнения : Часто исследователи выполняют RLC на нескольких образцах, относящихся к лечению, а затем повторяют процесс для образцов от другого лечения с намерением выполнить простой Т-тест (если два лечения) или дисперсионный анализ (или более чем две обработки), чтобы определить, указывают ли кривые на значительную разницу между обработками. Однако, как обсуждалось выше, анализ только оценок параметров из каждой кривой игнорирует степень изменчивости внутри каждой кривой (т.е. количество разброса), и поэтому не является идеальным подходом.
Анализ кривых извлечения
Кривые восстановления получены из многократных измерений насыщающего импульса после световой обработки (например, RLC), но при исключении окружающего света. Восстановление после сильного освещения обычно рассматривается как быстрое увеличение урожайности, которое быстро (в течение нескольких минут) замедляется до более постепенного увеличения урожайности, в конечном итоге достигая максимума через несколько часов или дней, в зависимости от серьезности световой обработки.Как быстро-, так и медленно восстанавливающиеся процессы могут быть описаны экспоненциальными членами, обычно в форме двойной экспоненциальной модели.
Мы уже обсуждали использование нелинейных моделей для анализа RLC. Применение двойной экспоненциальной модели к кривым восстановления очень похоже. В этом случае, вместо того, чтобы адресовать изменения в ETR (которые зависят от наличия положительного значения PAR), мы можем адресовать изменения в ΦII , F или Fm.
Список литературы .КОРИЧНЕВЫЙ, A.M. (2001). Пошаговое руководство по нелинейному регрессионному анализу экспериментальных данных с использованием электронной таблицы Microsoft Excel. Комп. Методы Прог. Биомед. 65, 191-200
FRENETTE, J.-J., DEMERS, S., LEGENDRE, L. & DODSON, J. (1993). Несогласованность моделей оценки фотосинтетических параметров. Лимнол. Oceanogr ., 38 , 679-687.
ГЕНТИ Б., БРИАНТИАС Дж. М. и Бейкер Н. Р. (1989). Связь между квантовым выходом фотосинтетического транспорта электронов и тушением флуоресценции хлорофилла. Biochim. Биофиз. Acta 990, 87-92.
MOTULSKY, H. & CHRISTOPOULOS, A. (2003). Подбор моделей к биологическим данным с использованием линейной и нелинейной регрессии: практическое руководство по подгонке кривой. Издательство Оксфордского университета, Оксфорд.
ПИК, М.С., РАССЕК-КОЭН, Э. УЭЙТ, Д.А., И ФОРСЕТ, И.Н. (2002). Анализ кривой физиологического ответа с использованием смешанных нелинейных моделей. Oecologia 132 , 175–180
РАЛЬФ, П.ДЖ. И ГАДЕМАНН, Р.(2005). Быстрые кривые блеска: мощный инструмент для оценки фотосинтетической способности. Aquat. Бот ., 82 : 222–237.
Уайт, А.Дж., и Критчли, К. (1999). Быстрые кривые блеска: новый метод флуоресценции для оценки состояния фотосинтетического аппарата. Photosynth. Res ., 59 , 63–72.
VAN KOOTEN, O & SNELL, JFH. (1990). Использование номенклатуры флуоресценции хлорофилла в физиологии стресса растений. Photosynth. Res 25 , 147–150
Как рассчитать освещенность — TACHYON Light
Что такое освещенность
Интенсивность освещения — это физический термин, обозначающий световой поток видимого света, приходящийся на единицу площади.Сокращенно освещенность [1], единица люкс (люкс или люкс). Он используется для обозначения интенсивности света и освещенности площади поверхности объекта.
В фотометрии «яркость» — это плотность силы света в определенном направлении, но ее часто неправильно понимают как освещенность. Международная единица светимости — это свет свечи на квадратный метр.
Интенсивность света имеет большое влияние на фотосинтез организмов. Его можно измерить с помощью измерителя освещенности.
Освещенность / освещенность поверхности, освещаемой светом, определяется как световой поток, освещающий единицу площади.
Предположим, что световой поток на элементе поверхности dS равен dΦ, тогда освещенность E на этом элементе поверхности равна: E = dΦ / dS.
1 лк = 1 лм /. Когда объект равномерно освещен светом, когда световой поток, полученный на площади в 1 квадратный метр, составляет 1 люмен, его освещенность составляет 1 люкс. Люмен — это единица светового потока.
Точечный источник света с силой света 1 кандела имеет световой поток «1 люмен» на единицу телесного угла (1 стерадиан).
Candlelight (Candela), транслитерация «Candela». Идея свечей была впервые изобретена британцами, и это единица измерения силы света.
В то время британцы использовали фунт белого воска, чтобы сделать свечу длиной в один фут, чтобы определить единицу света свечи. Но сегодняшнее определение изменилось: нагрев черным светящимся телом размером один кубический сантиметр до тех пор, пока светящееся тело не растворяется в жидкости, 1/60 количества излучаемого света является стандартным источником света, а свет свечи является стандартным источником света.Единица излучаемого света.
Как рассчитать освещенность
Метод расчета освещенности: используйте метод коэффициентов для расчета средней освещенности —
Средняя освещенность (Eav) = общий световой поток источника света (N * Ф) * коэффициент использования (CU) * коэффициент обслуживания (MF) / площадь площади (м2) (применимо для расчета внутреннего освещения или освещения стадиона)
Коэффициент использования: 0,4 для обычных помещений, 0,3 для занятий спортом
Коэффициент обслуживания: обычно 0.7 ~ 0,8
- Пример 1: Внутреннее освещение: комната 4 × 5 м, с использованием 9 комплектов решетчатых светильников 3 × 36 Вт
Средняя освещенность = общий световой поток источника света × CU × MF / площадь
= (2500 × 3 × 9) × 0,4 × 0,8 ÷ 4 ÷ 5
= 1080 люкс
Вывод: средняя освещенность выше 1000 люкс
- Пример 2: Освещение стадиона: площадка 20 × 40 м,
Используйте светодиодный прожектор LedsMaster 1000 Вт, 60 комплектов
Средняя освещенность = общий световой поток источника света × CU × MF / площадь
= (130000 × 60) × 0.3 × 0,8 ÷ 20 ÷ 40 = 2340 Люкс
Вывод: средняя горизонтальная освещенность выше 2000 люкс
- Расчетный корпус средней освещенности футбольного поля:
Расчетные условия: стандартное футбольное поле имеет длину 105 метров, ширину 68 метров, высоту фонарных столбов 18 метров, расстояние между фонарными столбами 36 метров.
Коэффициент использования 0,7, коэффициент обслуживания 0,8, количество ламп 36 комплектов,
Какая средняя освещенность футбольного поля?
Лампа: Лампа использует антибликовый прожектор LedsMaster мощностью 1000 Вт, световой поток 170 000 лм, цветовая температура 5600 К, цветопередача выше Ra90.
По формуле:
Eav = (36 комплектов X 170000 лм X 0,7X0,8) / (105 м X 68 м) = 110880,00 ÷ 196,56 м2 = 480 люкс
Примечания: Проект освещения должен требовать точного коэффициента использования, иначе будут большие отклонения.
Основными факторами, влияющими на коэффициент использования, являются следующие:
* Кривая распределения света ламп
* Коэффициент светоотдачи ламп
* Отражающая способность в помещениях, таких как газоны, стены, трибуны и т. Д.
* Угол луча прожектора
Связанные термины
- 1. Освещение естественное и искусственное
Солнечный свет — это естественное освещение, а световое освещение — это искусственное освещение.
- 2. Световой цикл и световое время
В природе 24 часа в сутки и ночь представляют собой световой цикл. Время со светом — это яркий период, а время без света — это темный период. При естественном освещении время солнечного света (период яркости) обычно рассчитывается как время солнечного сияния; при искусственном освещении время воздействия света — это время освещения, а 24-часовой световой период — это период естественного освещения; длиннее или короче 24 часов называется циклом неестественного освещения; если в течение 24 часов есть только один яркий период и один темный период, это называется однопериодным освещением; если в течение 24 часов есть два или более ярких или темных периода, это прерывистое освещение.Сумма яркого периода в фотопериоде и есть фотопериод.
Количество светового потока, передаваемого источником света в пределах телесного угла в определенном направлении. Единица: кандела (кандела, кд).
Световая энергия, излучаемая источником света в единицу времени, называется световым потоком источника света, и ее единица измерения — люмены (количество света на площади 1 квадратный фут, которая находится на расстоянии 1 фута от источника света 1 свечи, составляет 1 люмен).
Под прямыми солнечными лучами летом интенсивность света может достигать от 60 000 до 100 000 лк, на открытом воздухе от 10 000 до 10 000 лк без солнца, от 100 до 550 лк в помещении ярким летом и 0.2лк ночью при полной луне.
Лампы накаливания могут излучать примерно 12,56 лк света на ватт, но это значение зависит от размера лампы. Маленькие лампочки могут излучать больше люменов, а большие — меньше. Световая отдача люминесцентных ламп в 3-4 раза выше, чем у ламп накаливания, а срок службы в 9 раз больше, чем у ламп накаливания, но цена выше. Из света, излучаемого лампой накаливания без абажура, около 30% люменов поглощается стенами, потолками, оборудованием и т. Д.; плохое качество и темнота лампы уменьшают много люменов, поэтому можно использовать только около 50% люменов.
Как правило, при наличии абажура и высоте лампы 2,0 2,4 м (расстояние между лампами в 1,5 раза больше высоты), лампы мощностью 1 Вт на площадь 0,37 или лампы мощностью 2,7 Вт на 1 области могут обеспечить 10,76 лк. Высота установки лампы и наличие или отсутствие абажура имеют большое влияние на интенсивность света.
Кривая распределения света для светодиодов
Определение кривой светораспределения:
Это относится к распределению силы света источников света (или ламп) во всех направлениях в пространстве.
Кривая, образованная отметкой значений силы света в каждой позиции на графике в полярных координатах, является кривой распределения света лампы.
Как выразить кривую распределения света
Обычно существует три способа выразить кривую распределения света: один — метод полярных координат, другой — метод прямоугольных координат и третий — кривая равной силы света.
а. Кривая распределения света в полярных координатах:
На измерительной плоскости, проходящей через центр источника света, измеряются значения силы света ламп под разными углами.Начиная с определенного направления, интенсивность света под каждым углом отмечается вектором, использующим угол как функцию. Соединение в верхней части вектора представляет собой кривую распределения света в полярных координатах. Если светильник имеет ось симметрии вращения, только кривая распределения силы света на фотометрической поверхности, проходящей через ось, может использоваться для иллюстрации пространственного распределения силы света.
Если распределение света светильника в пространстве асимметрично, необходимы кривые распределения силы света нескольких фотометрических плоскостей, чтобы объяснить пространственное распределение силы света.
г. Кривая распределения света в прямоугольных координатах:
Для концентрирующих ламп, поскольку луч сосредоточен в очень узком телесном угле, сложно выразить пространственное распределение интенсивности его света в полярных координатах, поэтому используется метод представления кривой распределения света под прямым углом, а вертикальная ось представляет карту интенсивности света. I. Используйте горизонтальную ось, чтобы указать угол проекции луча. Если это светильник с симметричной осью вращения, для его представления требуется только одна кривая светораспределения, а если это асимметричный светильник, требуются несколько кривых светораспределения.
г. Кривая силы света:
Кривая, соединяющая вершины векторов с равной силой света, называется кривой равной силы света, и значения соседних кривых силы света расположены в определенном соотношении, а график, состоящий из серии кривых равной силы света, имеет вид называется кривой равной интенсивности. Графики, обычно используемые графы, включают круговые графы, прямоугольные графы и графы с положительной дугой. Поскольку прямоугольная сетевая диаграмма может объяснить как распределение интенсивности света ламп, так и региональное распределение количества света, диаграммы изоинтенсивности прожекторных ламп представляют собой прямоугольные сетевые диаграммы, которые мы здесь не будем вводить.
Коэффициент светоотдачи
Коэффициент светоотдачи, то есть эффективность лампы, означает отношение значения светового потока, излучаемого лампой, измеренного при определенных условиях, к сумме измеренных значений светового потока, излучаемого всеми источниками света в лампе. Существует множество методов классификации осветительных приборов, таких как классификация по назначению, классификация в соответствии с коэффициентом распределения светового потока, рекомендованным CIE, и классификация по пылезащищенности, влагозащищенности и устойчивости к поражению электрическим током.
Основная классификация
Согласно классификации ламп, рекомендованной Международной комиссией по освещению (CIE) (внутреннее освещение)
Согласно рекомендациям Международной комиссии по освещению (CIE), светильники делятся на пять категорий в зависимости от соотношения светового потока в верхнем и нижнем пространствах: прямой тип, полупрямой тип, полностью рассеянный тип (в том числе прямой световой поток). непрямого типа с небольшим горизонтальным освещением) и полупрямого типа.Косвенные и косвенные.
(1) Светильник прямого освещения
Большая часть светового потока (90–100%) этого типа ламп освещается непосредственно снизу, поэтому световой поток ламп имеет самый высокий коэффициент использования.
(2) Светильник полупрямого освещения
Большая часть светового потока (60-90%) этого типа светильников направляется в пространство нижней полусферы, а небольшая часть — вверх. Восходящий компонент снизит жесткость тени, создаваемой окружающей средой освещения, и улучшит коэффициент яркости каждой поверхности.
(3) Рассеянное или прямо-косвенное освещение (светильник рассеянного освещения)
Верхний и нижний световые потоки ламп практически одинаковы (40% -60% каждый).
Наиболее распространенным является сферический абажур из опалесцирующего стекла, а другие закрытые абажуры рассеянной и прозрачной формы имеют аналогичное распределение света. Такой светильник равномерно излучает свет во всех направлениях, поэтому коэффициент использования светового потока низкий.
(4) Светильник полупрямого непрямого освещения
Нисходящий световой поток ламп составляет 10% -40%, и его нисходящая составляющая часто используется только для получения яркости, соизмеримой с потолком.
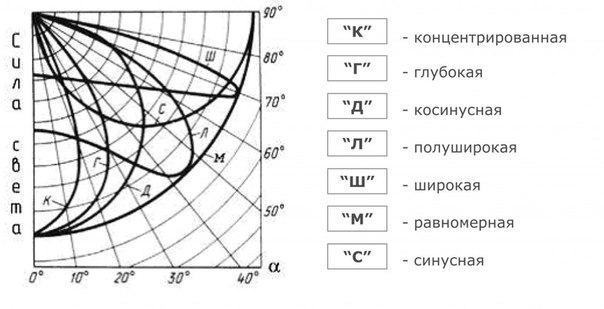
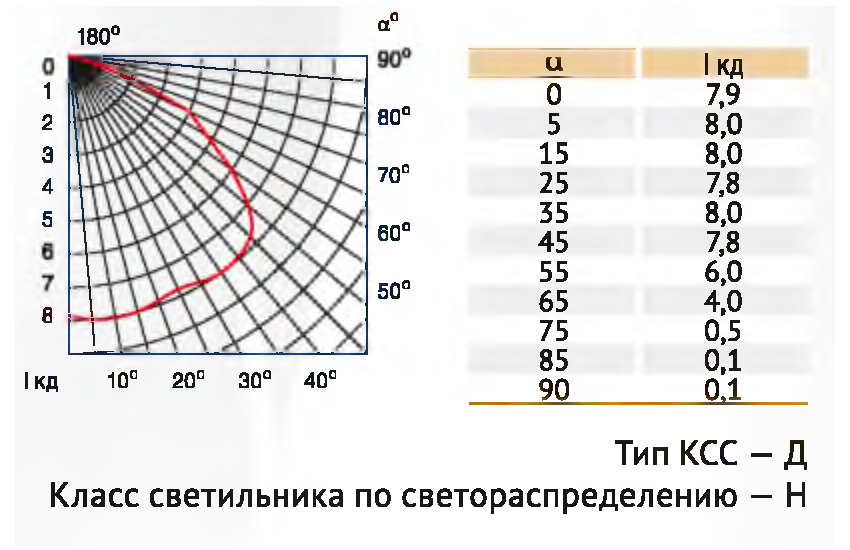

 Как правило, в применяемых светодиодах производства CREE (USA), Osram (Germany), LG и SEOUL (KOREA), угол раскрытия заключен в рамках от 110 до 120 градусов. Эти светильники cоответствуют КСС типа «Д» согласно ГОСТ 17677-82. В маркировке при заказе (продаже) светильников используется обозначение «R». Например, светильник для АЗС встраиваемый заливающего света: SolidGSL 60 — 74R.50 V.
Как правило, в применяемых светодиодах производства CREE (USA), Osram (Germany), LG и SEOUL (KOREA), угол раскрытия заключен в рамках от 110 до 120 градусов. Эти светильники cоответствуют КСС типа «Д» согласно ГОСТ 17677-82. В маркировке при заказе (продаже) светильников используется обозначение «R». Например, светильник для АЗС встраиваемый заливающего света: SolidGSL 60 — 74R.50 V. 
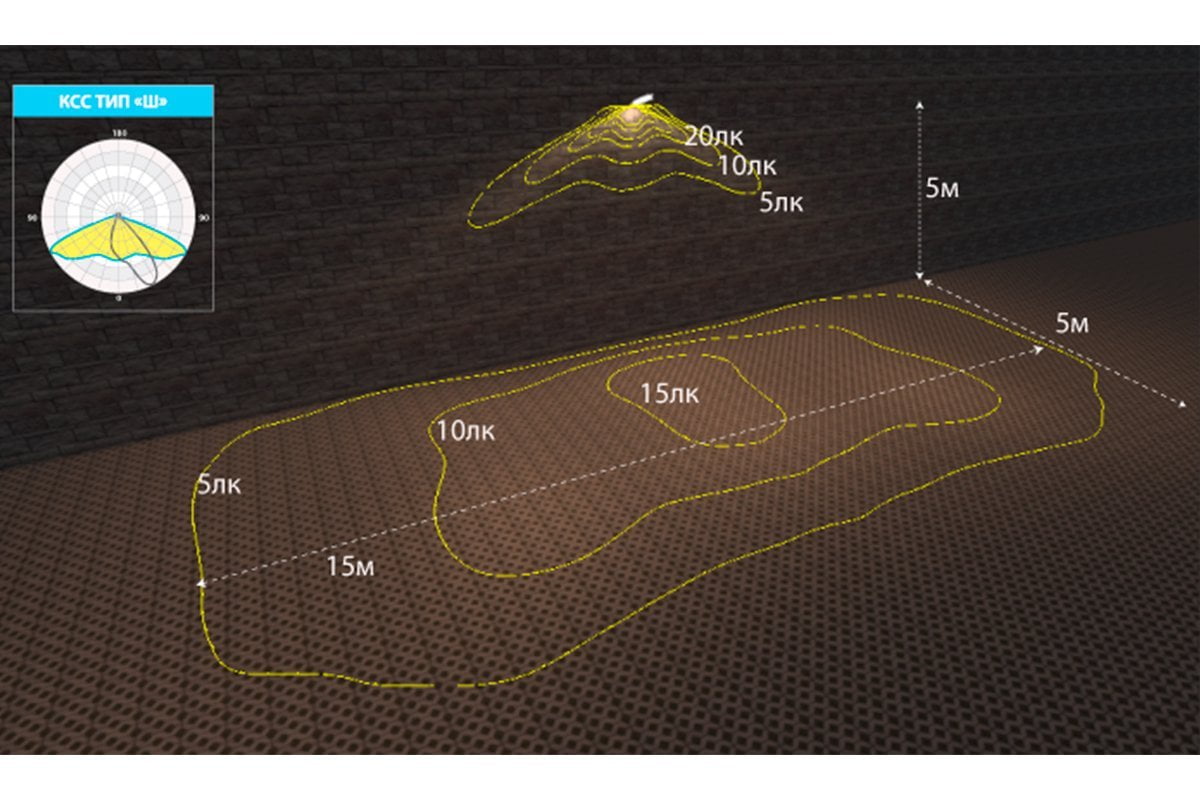 11.28.
Защитные углы осветительных приборов
11.28.
Защитные углы осветительных приборов