Урок 8.3 — Логические элементы
8.3. Логические элементы
Все, абсолютно все электронные компоненты, обрабатывающие цифровые сигналы, состоят из небольшого набора одинаковых «кирпичиков». В микросхемах малой степени интеграции могут быть единицы и десятки таких элементов, а в современных процессорах их может быть очень и очень много. Они называются логические элементы. Логическим элементом называется электрическая схема, предназначенная для выполнения какой-либо логической операции с входными данными. Логический элемент — элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами. Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления.
Тем не менее, принцип работы цифровой логики остается неизменным – на входе логического элемента (входов может быть несколько) должен быть цифровой сигнал (сигналы, если входов несколько), который однозначно определяет сигнал на выходе логического элемента.
Конечно, логические элементы строятся, в свою очередь, из уже рассмотренных в предыдущих уроках резисторов, транзисторов и других электронных компонентов, но с точки зрения разработки цифровых схем именно логический элемент является их «элементарной» частицей.
При анализе работы логических элементов используется так называемая булева алгебра . Начала этого раздела математики было изложено в работах Джорджа Буля – английского математика и логика 19-го века, одного из основателей математической логики. Основами булевой алгебры являются высказывания, логические операции, а также функции и законы. Для понимания принципов работы логических элементов нет необходимости изучать все тонкости булевой алгебры, мы освоим ее основы в процессе обучения с помощью таблиц истинности.
Еще несколько замечаний. Логические элементы (как, впрочем, и другие элементы электронных схем) принято обозначать так, чтобы входы были слева, а выходы справа. Число входов может быть, вообще говоря, любым, отличным от нуля.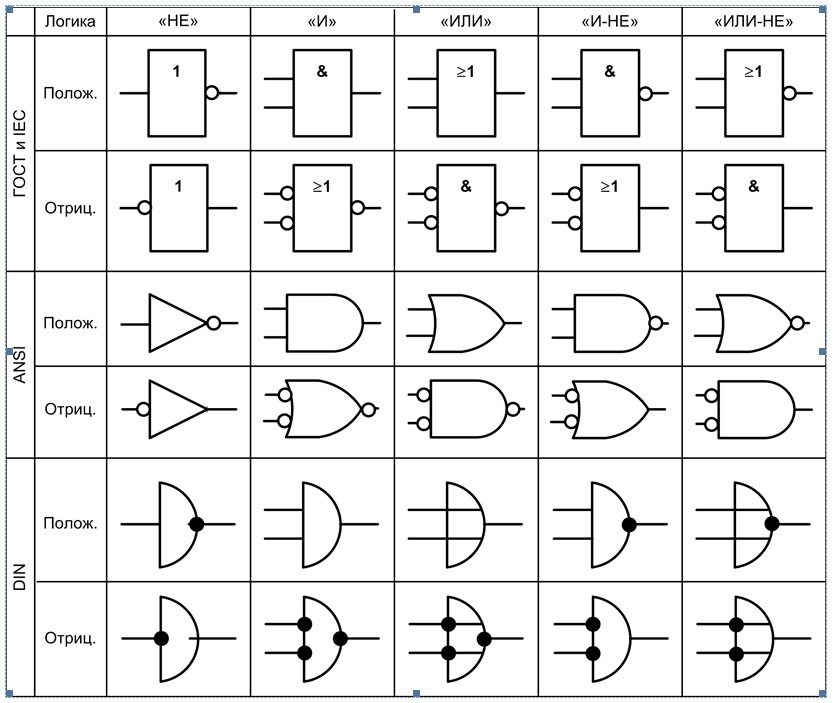 Реальные цифровые микросхемы могут иметь до 8 входов, но мы ограничимся двумя – этого достаточно для понимания. Условные обозначения соответствуют отечественному ГОСТу, в других стандартах они могут быть иными.
Реальные цифровые микросхемы могут иметь до 8 входов, но мы ограничимся двумя – этого достаточно для понимания. Условные обозначения соответствуют отечественному ГОСТу, в других стандартах они могут быть иными.
Какие же бывают логические элементы?
Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.
Элемент «И» (AND), он же конъюнктор, выполняет операцию логического умножения:
Условное обозначение — Таблица истинности
Здесь изображен логический элемент «2И» (цифра перед буквой «И» означает число входов). Знак & (амперсант) в левом верхнем углу прямоугольника указывает, что это логический элемент «И». Первые две буквы обозначения DD1.2 указывают на то, что это цифровая микросхема (Digital), цифра слева от точки указывает номер микросхемы на принципиальной схеме, а цифра справа от точки – номер логического элемента в составе данной микросхемы. Одна микросхема может содержать несколько логических элементов.
Первые две буквы обозначения DD1.2 указывают на то, что это цифровая микросхема (Digital), цифра слева от точки указывает номер микросхемы на принципиальной схеме, а цифра справа от точки – номер логического элемента в составе данной микросхемы. Одна микросхема может содержать несколько логических элементов.
Состояние входов в таблице обозначаются «0» и «1» («ложь» и «истина»). Из таблицы видно, что выход «Y» будет иметь состояние «1» только в том случае, когда на обоих входах «Х1» и «Х2» будут «1». Это легко запомнить: умножение на «0» всегда дает «0».
Элемент «ИЛИ» (OR), он же дизъюнктор, выполняет операцию логического сложения:
Условное обозначение — Таблица истинности
Состояние «1» на выходе будет всегда, пока есть хотя бы одна «1» на входах.
Элемент «НЕ» (NOT), он же инвертор, выполняет операцию логического отрицания:
Условное обозначение — Таблица истинности
Состояние на входе обратно состоянию на входе.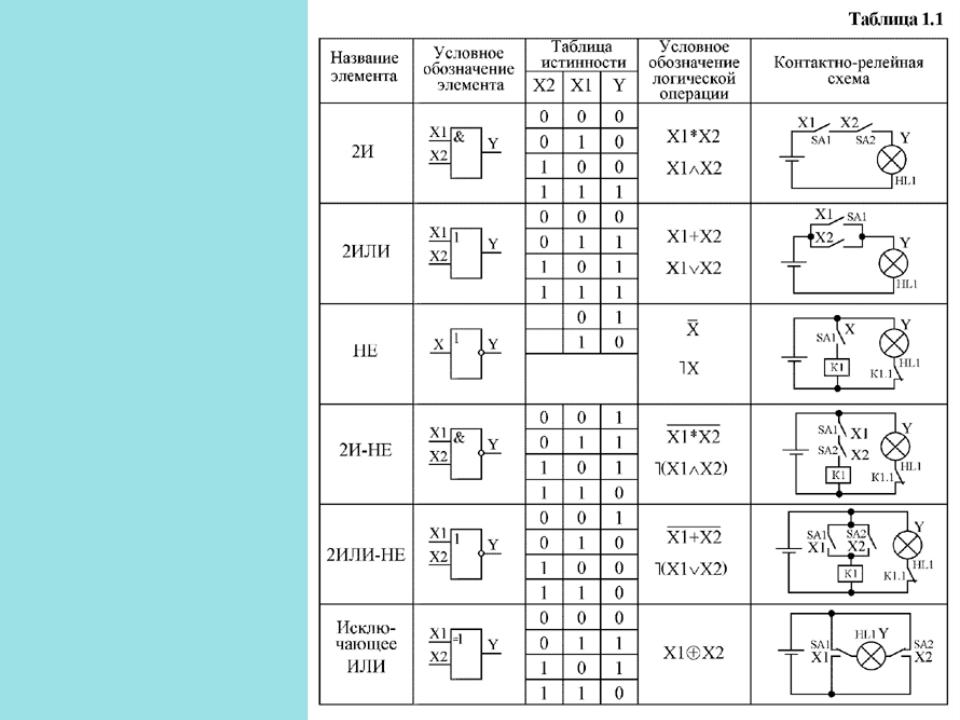
Вот из этих трех элементов строятся все цифровые устройства!
Рассмотрим еще три логических элемента, которые можно получить, комбинируя уже рассмотренные. В силу исторически сложившихся схемотехнических решений эти скомбинированные схемы тоже считаются логическими элементами.
Элемент «И-НЕ» (NAND), конъюнктор с отрицанием:
Условное обозначение — Таблица истинности
Элемент И-НЕ работает точно так же как «И», только выходной сигнал противоположен. Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» будет единица. И наоборот.
Элемент «ИЛИ-НЕ» (NOR), дизъюнктор с отрицанием:
Условное обозначение — Таблица истинности
Элемент работает так же как и «ИЛИ», но с инверсией выхода.
Элемент «Исключающее ИЛИ» (XOR), сумматор по модулю 2:
Условное обозначение — Таблица истинности
В этом элемента «1» на выходе будет только тогда, когда на входах разные состояния.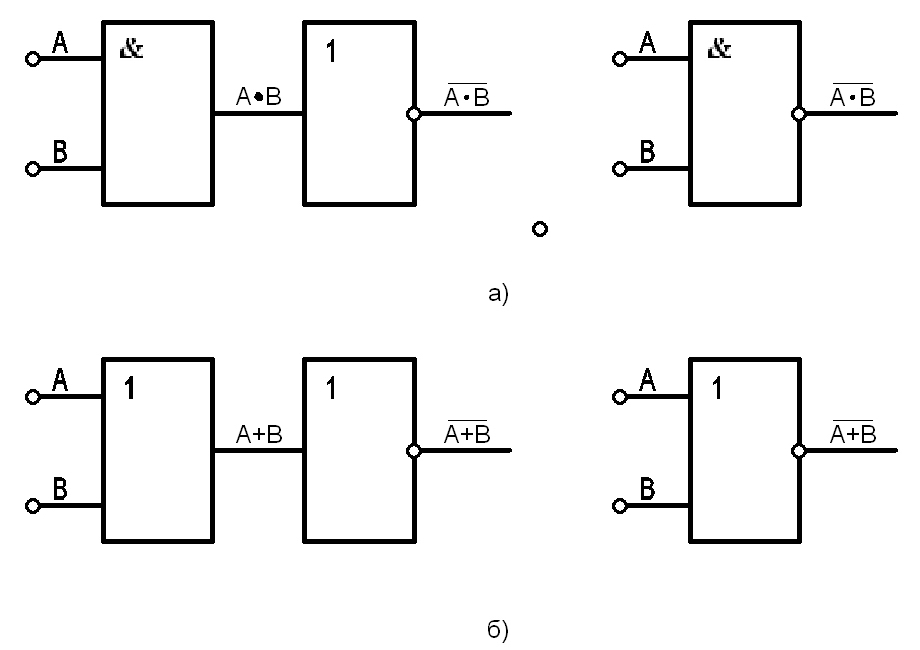
На таких элементах строят сумматоры двоичных многоразрядных чисел. Для этого используется еще один дополнительный выход, на котором при появлении на входах двух «1» появляется сигнал переноса разряда.
Мы рассмотрели логические элементы, которые применяются в цифровой технике для построения логических схем любого уровня сложности, но рассмотренные нами элементы не могут делать одну крайне важную работу – они не умеют хранить информацию. Для хранения используется более сложный класс устройств, называемый элементами с памятью или конечными автоматами. В этот класс входят триггеры, регистры, счетчики, шифраторы (дешифраторы), мультиплексоры (демультиплексоры) и сумматоры. Некоторый из этих устройств мы рассмотрим в следующем уроке.
Цифровые схемы — логические элементы
Цифровые электронные схемы работают с напряжениями двух логических уровней, а именно Logic Low и Logic High. Диапазон напряжений, соответствующий низкому логическому значению, обозначен как «0». Точно так же диапазон напряжений, соответствующий логическому максимуму, обозначен цифрой «1».
Точно так же диапазон напряжений, соответствующий логическому максимуму, обозначен цифрой «1».
Базовая цифровая электронная схема, которая имеет один или несколько входов и один выход, называется логическим вентилем . Следовательно, логические элементы являются строительными блоками любой цифровой системы. Мы можем классифицировать эти логические элементы в следующие три категории.
- Основные ворота
- Универсальные ворота
- Специальные ворота
Теперь давайте поговорим о логических элементах, попадающих в каждую категорию по очереди.
Основные ворота
В предыдущих главах мы узнали, что булевы функции могут быть представлены либо в форме суммы произведений, либо в форме произведения сумм в зависимости от требования. Таким образом, мы можем реализовать эти булевы функции, используя базовые элементы. Основными воротами являются И, ИЛИ И НЕ ворота.
И ворота
Логический элемент И представляет собой цифровую схему, которая имеет два или более входов и производит выход, который является логическим И всех этих входов.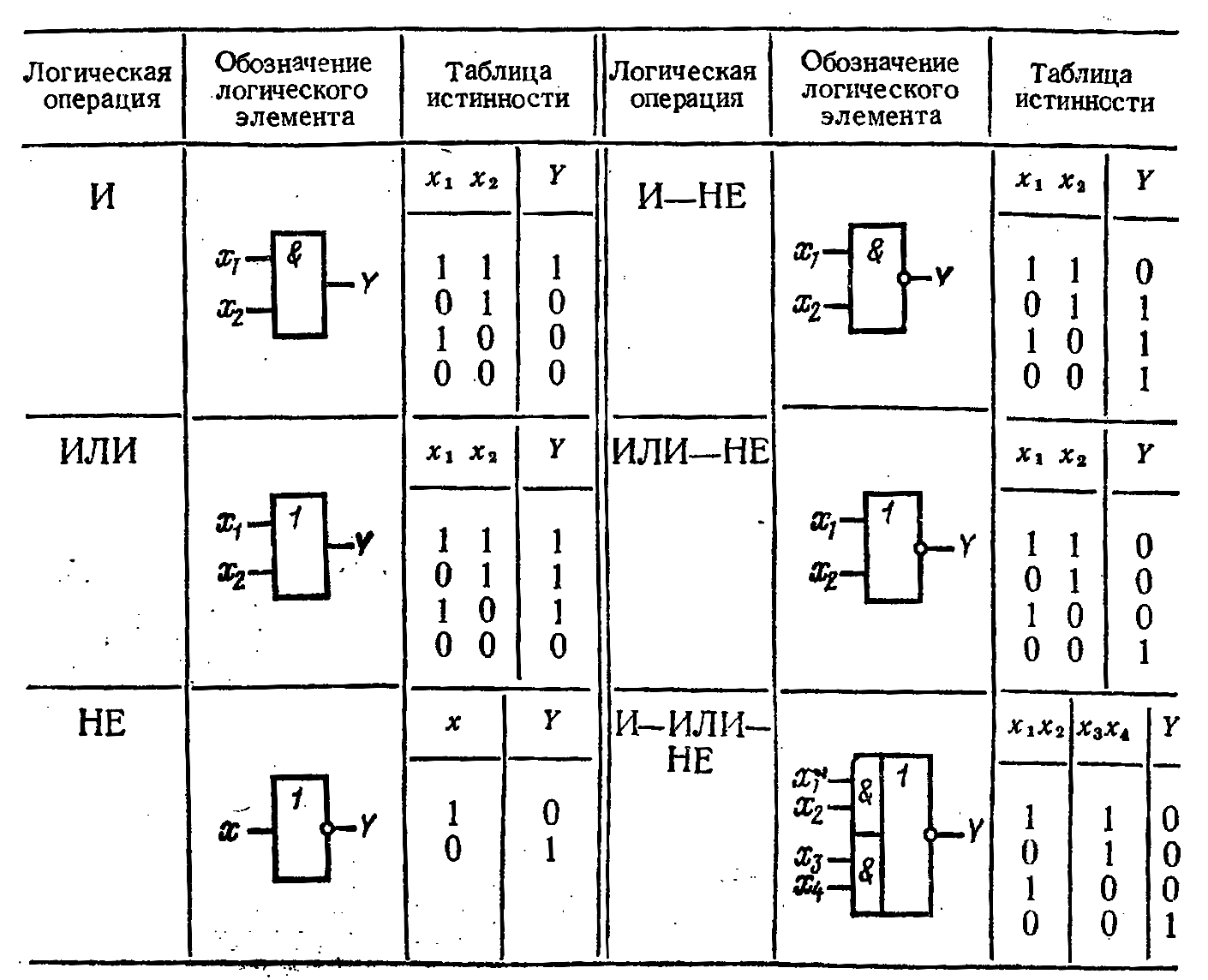 Логическое И необязательно обозначать символом «.».
Логическое И необязательно обозначать символом «.».
В следующей таблице показана таблица истинности 2-входного логического элемента AND.
| В | Y = AB | |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Здесь A, B — входы, а Y — выход двух входных И логических элементов. Если оба входа «1», то только выход, Y «1». Для оставшихся комбинаций входов выход Y равен 0.
На следующем рисунке показан символ логического элемента AND, который имеет два входа A, B и один выход Y.
Этот логический элемент И производит выход (Y), который является логическим И двух входов А, В. Аналогичным образом, если есть ‘n’ входов, то логический элемент И производит выход, который является логическим И всех этих входов.
ИЛИ ворота
Логический элемент ИЛИ — это цифровая схема, которая имеет два или более входов и создает выход, который является логическим ИЛИ всех этих входов. Это логическое ИЛИ обозначается символом «+».
В следующей таблице показана таблица истинности 2-входного ИЛИ вентиля.
| В | Y = A + B | |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Здесь A, B — входы, а Y — выход двух входных логических элементов ИЛИ. Если оба входа «0», то только выход, Y «0». Для остальных комбинаций входов выход Y равен «1».
На следующем рисунке показан символ логического элемента ИЛИ, который имеет два входа A, B и один выход Y.
Этот логический элемент ИЛИ выдает выход (Y), который является
НЕ ворота
Логический элемент NOT — это цифровая схема с одним входом и одним выходом. Выход NOT gate является логической инверсией ввода. Следовательно, вентиль НЕ также называется инвертором.
В следующей таблице показана таблица истинности NOT gate.
Здесь A и Y — вход и выход элемента НЕ соответственно. Если вход A равен 0, то выход Y равен 1. Точно так же, если вход A равен «1», то выход Y равен «0».
Этот НЕ вентиль производит вывод (Y), который является дополнением ввода, A.
Универсальные ворота
Ворота NAND & NOR называются универсальными воротами . Потому что мы можем реализовать любую булеву функцию, которая находится в виде суммы продуктов, используя только вентили NAND. Точно так же мы можем реализовать любую булеву функцию, которая находится в виде суммы сумм, используя только вентили NOR.
NAND ворота
NAND gate — это цифровая схема, которая имеет два или более входов и производит выход, который является
В следующей таблице показана таблица истинности 2-входного вентиля NAND.
| В | Y = (AB) ‘ | |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Здесь A, B — входы, а Y — выход двух входных вентилей NAND. Когда оба входа «1», выход Y равен «0». Если хотя бы один из входов равен нулю, тогда выход Y равен «1». Это прямо противоположно операции ввода-вывода и логического элемента.
Когда оба входа «1», выход Y равен «0». Если хотя бы один из входов равен нулю, тогда выход Y равен «1». Это прямо противоположно операции ввода-вывода и логического элемента.
На следующем изображении показан символ вентиля NAND, который имеет два входа A, B и один выход Y.
Работа шлюза NAND такая же, как и у шлюза AND, за которым следует инвертор. Вот почему символ ворот NAND представлен так.
NOR ворота
NOR gate — это цифровая схема, которая имеет два или более входов и производит выход, который является инверсией логического ИЛИ всех этих входов.
Следующая таблица показывает таблицу истинности 2-входного вентиля NOR
| В | Y = (A + B) ‘ | |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Здесь A, B — входы, а Y — выход. Если оба входа равны 0, то выход Y равен 1. Если хотя бы один из входных данных равен «1», то выходным значением является «0». Это прямо противоположно операции ввода-вывода или логического элемента.
Если оба входа равны 0, то выход Y равен 1. Если хотя бы один из входных данных равен «1», то выходным значением является «0». Это прямо противоположно операции ввода-вывода или логического элемента.
На следующем рисунке показан символ логического элемента NOR, который имеет два входа A, B и один выход Y.
Работа шлюза NOR такая же, как и у шлюза OR, за которым следует инвертор. Вот почему символ ворот NOR представлен так.
Специальные ворота
Ворота EX-OR & Ex-NOR называются специальными воротами. Потому что эти два входа — это особые случаи ворот ИЛИ ИЛИ НЕ.
Бывшие ворота
Полная форма ворот Ex-OR — это ворота Exclusive-OR . Его функция такая же, как у логического элемента ИЛИ, за исключением некоторых случаев, когда входы имеют четное число единиц.
В следующей таблице показана таблица истинности 2-входного вентиля Ex-OR.
| В | Y = A⊕B | |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Здесь A, B — входы, а Y — выход двух входных шлюзов Ex-OR.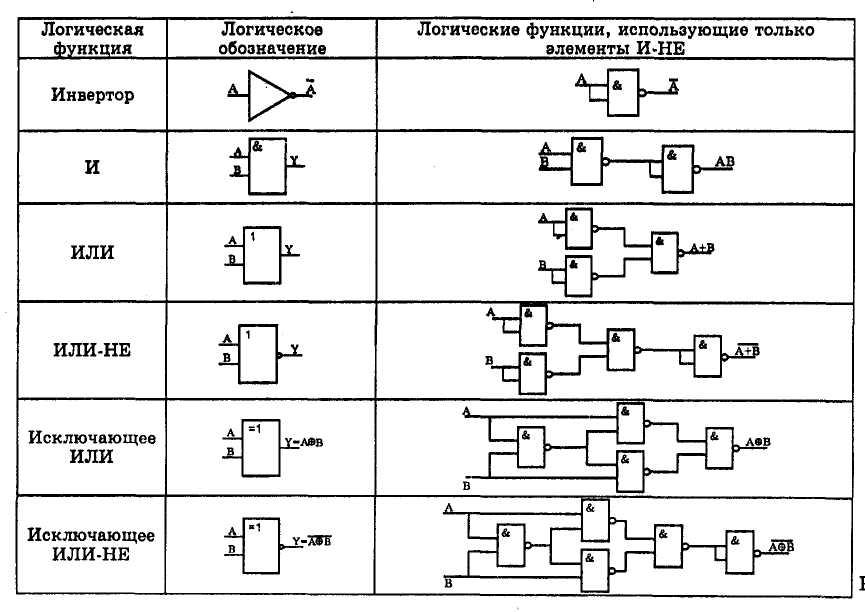 Таблица истинности для шлюза Ex-OR такая же, как и для таблицы ИЛИ для первых трех строк. Единственная модификация находится в четвертом ряду. Это означает, что выход (Y) равен нулю вместо единицы, когда оба входа равны единице, поскольку входы имеют четное число единиц.
Таблица истинности для шлюза Ex-OR такая же, как и для таблицы ИЛИ для первых трех строк. Единственная модификация находится в четвертом ряду. Это означает, что выход (Y) равен нулю вместо единицы, когда оба входа равны единице, поскольку входы имеют четное число единиц.
Следовательно, выход логического элемента «ИЛИ-ИЛИ» равен «1», когда только один из двух входов равен «1». И это ноль, когда оба входа одинаковы.
На следующем рисунке показан символ шлюза Ex-OR, который имеет два входа A, B и один выход Y.
Работа шлюза Ex-OR аналогична работе шлюза OR, за исключением нескольких комбинаций входов. Вот почему символ ворот Ex-OR представлен так. Выход шлюза Ex-OR равен «1», когда на входах присутствует нечетное количество единиц. Следовательно, выход шлюза Ex-OR также называется нечетной функцией .
Бывшие ворота
Полная форма ворот Ex-NOR — это ворота Exclusive-NOR . Его функция такая же, как и у шлюза NOR, за исключением некоторых случаев, когда входы имеют четное число единиц.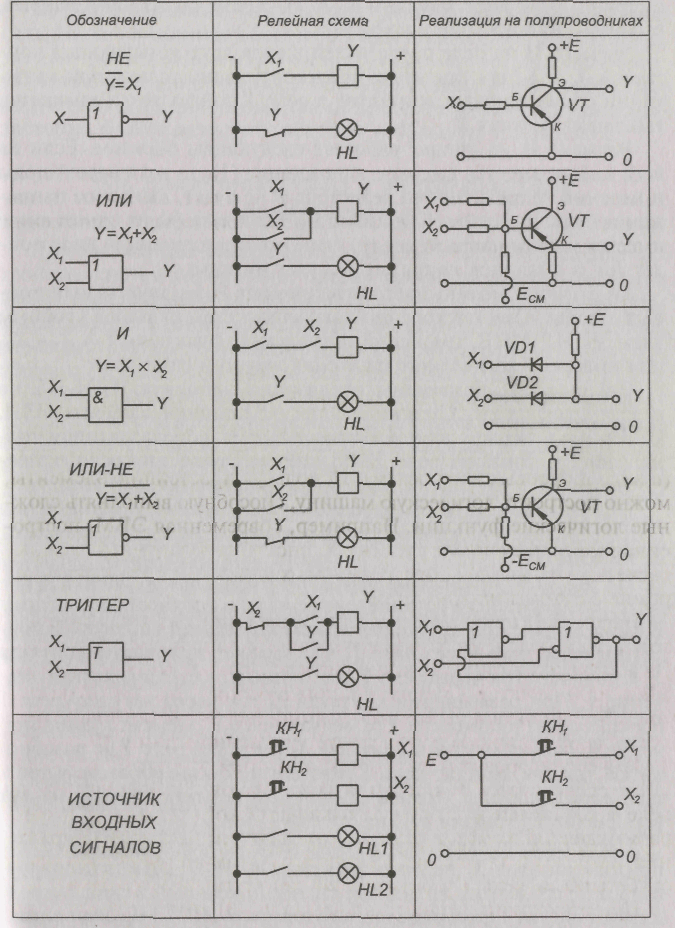
В следующей таблице показана таблица истинности 2-входного вентиля Ex-NOR.
| В | Y = A⊙B | |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Здесь A, B — входы, а Y — выход. Таблица истинности шлюза Ex-NOR такая же, как и у шлюза NOR для первых трех строк. Единственная модификация находится в четвертом ряду. Это означает, что выход равен одному вместо нуля, когда оба входа равны.
Следовательно, выход шлюза Ex-NOR равен «1», когда оба входа одинаковы. И это ноль, когда оба входа разные.
На следующем рисунке показан символ шлюза Ex-NOR, который имеет два входа A, B и один выход Y.
Работа шлюза Ex-NOR аналогична работе шлюза NOR, за исключением нескольких комбинаций входов. Вот почему символ ворот Ex-NOR представлен именно так.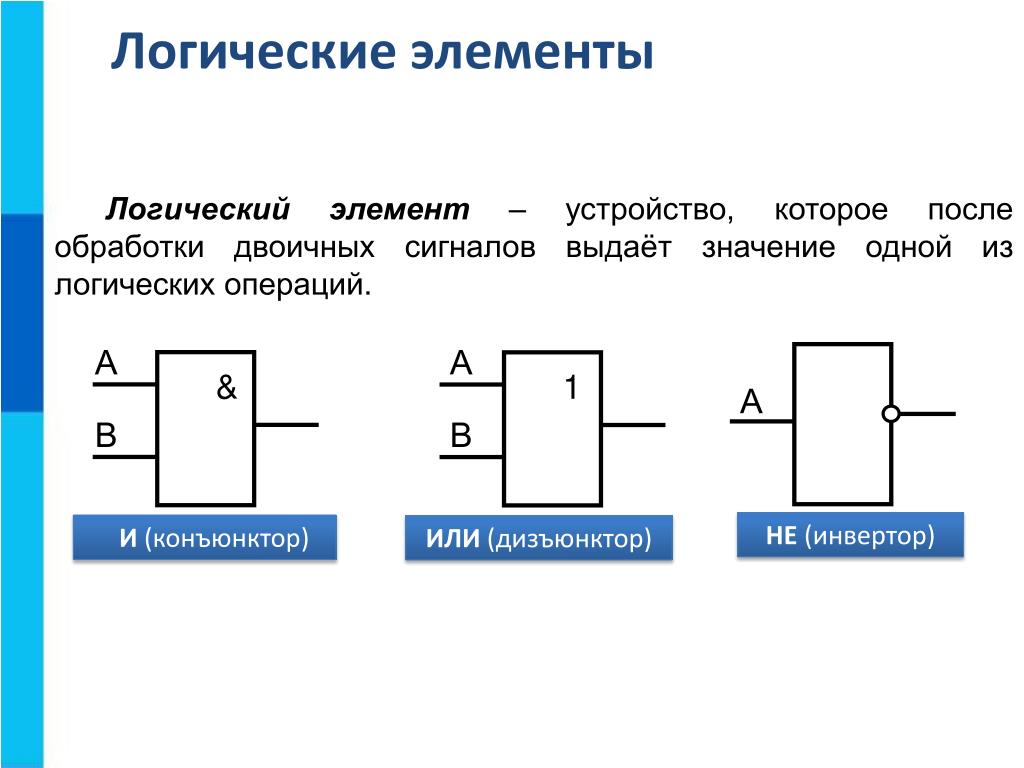 Выход шлюза Ex-NOR равен «1», когда на входах присутствует четное число единиц. Следовательно, выход шлюза Ex-NOR также называется четной функцией .
Выход шлюза Ex-NOR равен «1», когда на входах присутствует четное число единиц. Следовательно, выход шлюза Ex-NOR также называется четной функцией .
Из приведенных выше таблиц истинности логических элементов Ex-OR и Ex-NOR мы можем легко заметить, что операция Ex-NOR является просто логической инверсией операции Ex-OR.
«ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ КОМПЬЮТЕРА. ПОСТРОЕНИЕ ЛОГИЧЕСКИХ СХЕМ» В ШКОЛЬНОМ КУРСЕ ИНФОРМАТИКИ
Михолап Эльвира Леонидовна,
учитель информатики,
ГБОУ Школа №641 имени С. Есенина
Аннотация: Изучение основ логики является одной из ключевых тем школьного курса информатики. Программа углубленного курса информатики в 10-11 классах позволяет показать взаимосвязь теории логики и практики ее применения в компонентах компьютера. В статье рассматриваются инструменты изучения логических элементов компьютера.
Ключевые слова: информатика в школе, логика, логические элементы, логические схемы, схемотехника.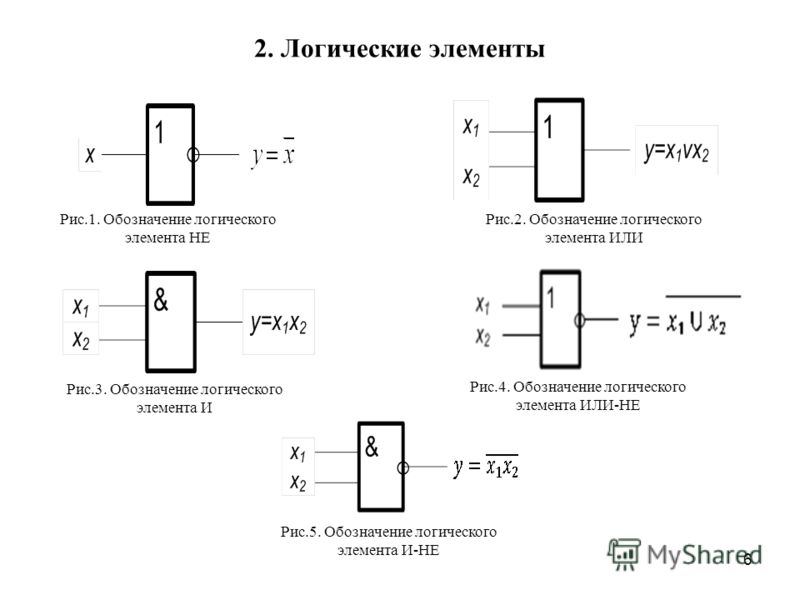
Изучение основ логики является одной из ключевых тем школьного курса информатики. Примерная основная образовательная программа среднего общего образования в предметной области «Информатика» предусматривает изучение темы «Элементы комбинаторики, теории множеств и математической логики» как на базовом, так и на углубленном уровне.
Содержание темы (углубленный уровень):
Операции «импликация», «эквиваленция». Логические функции.
Законы алгебры логики. Эквивалентные преобразования логических выражений. Логические уравнения.
Построение логического выражения с данной таблицей истинности. Дизъюнктивная нормальная форма. Конъюнктивная нормальная форма.
Логические элементы компьютеров. Построение схем из базовых логических элементов.
Дискретные игры двух игроков с полной информацией. Выигрышные стратегии.
Само по себе изучение логических операций, законов логики, логических уравнений очень абстрагировано от практики. И у учеников всегда встает вопрос о применении этой теории в жизни. Да, безусловно, они применяют логические операции в рассуждениях, строят умозаключения, умеют определять истинность высказываний. Но сопоставление логических операций и логических элементов с работой технических устройств для детей остается до конца неясным. Подробнее остановиться на изучении работы логических элементов в работе полусумматора, сумматора, триггера есть возможность в углубленном курсе информатики. На базовом уровне изучения информатики эта тема не рассматривается, но ученикам можно предложить курс по выбору или программу дополнительного образования.
Да, безусловно, они применяют логические операции в рассуждениях, строят умозаключения, умеют определять истинность высказываний. Но сопоставление логических операций и логических элементов с работой технических устройств для детей остается до конца неясным. Подробнее остановиться на изучении работы логических элементов в работе полусумматора, сумматора, триггера есть возможность в углубленном курсе информатики. На базовом уровне изучения информатики эта тема не рассматривается, но ученикам можно предложить курс по выбору или программу дополнительного образования.
Рассмотрим аспекты преподавания темы «Логические элементы компьютера. Построение логических схем».
Цели:
- расширить представление учащихся об устройствах элементной базы компьютера;
- формировать навыки построения логических схем.
- развивать логическое и алгоритмическое мышление;
- формировать конструкторские умения;
- способствовать развитию информационных компетентностей;
- формировать познавательный интерес к предмету информатика;
- воспитывать личностные качества: активность, самостоятельность, аккуратность в работе.

Последовательность изучения:
В начале необходимо ввести систему обозначений логических элементов. А также рассмотреть простые элементы «ИЛИ-НЕ», «И-НЕ».
Изучение типовых логических устройств компьютера целесообразно начать с рассмотрения одноразрядного полусумматора, который учащиеся могут самостоятельно разработать под руководством учителя. Для этого учитель ставит проблему: разработать логическую схему устройства, предназначенного для сложения одноразрядных двоичных чисел. В процессе решения данной проблемы у учащихся активизируются знания правил сложения двоичных чисел. Это достигается за счет постановки перед учащимися наводящих и уточняющих вопросов, позволяющих представить правила сложения двоичных чисел в виде таблицы истинности, самостоятельно записать логические функции для вычисления результатов этого сложения, самостоятельно построить логическую схему разрабатываемого устройства. Проверку правильности работы логической схемы одноразрядного полусумматора для всех возможных комбинаций значений логических аргументов (а также все последующие логические схемы) возможно организовать с помощью взаимопроверки учениками бумажных носителей, с помощью программного обеспечения или с помощью универсальной цифровой логической лаборатории.
Далее рассматриваются одноразрядный сумматор, многоразрядный сумматор и триггер. При этом учащиеся могут самостоятельно составлять логическую схему из уже имеющихся логических элементов и вычислять результаты ее работы, моделировать и тестировать логические схемы устройств компьютера в программной среде и/или на тренажере.
Инструменты:
- Интерактивные программные средства для изучения логических элементов и построения логических схем.
Использование информационных технологий, разнообразных информационных ресурсов, компьютерных программ дает возможность учителю обеспечить гибкость управления учебным процессом, расширить возможность предъявления учебной информации, позволяет учащимся в интерактивном режиме самостоятельно оценить результаты деятельности, а также способствуют интеллектуальному развитию школьника, повышению уровня интереса к обучению.
Примером программы может выступить тренажер «Логика» К.Ю. Полякова (рис. 1). Программа бесплатна для некоммерческого использования.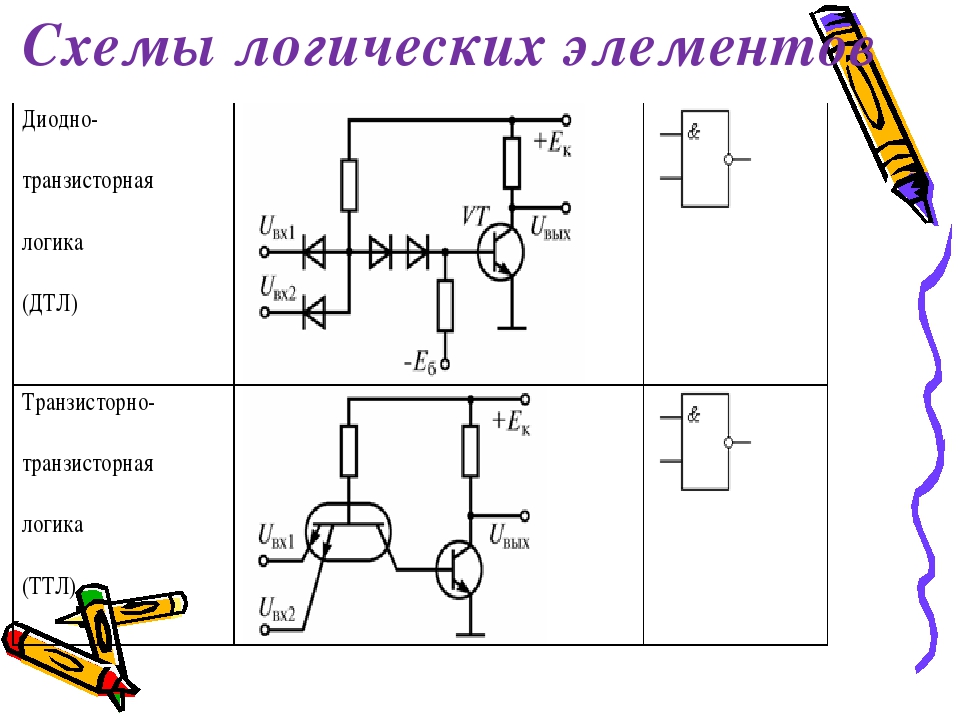 Требуется ее установка на компьютер. Тренажер предназначен для проведения практических занятий в игровой форме.
Требуется ее установка на компьютер. Тренажер предназначен для проведения практических занятий в игровой форме.
Рис. 1. Программа «Логика»
Логические схемы преобразуют входные сигналы по правилам выполнения логических операций НЕ, И, ИЛИ, XOR (исключающее ИЛИ), импликации, эквивалентности. Задача заключается в том, чтобы последовательно передавать кристалл с верхней площадки на нижнюю. Подавая ток на вход механизмов в правой части схемы, можно выдвигать площадки на пути кристалла. Если на входе механизма нет тока, площадка убирается.
Программа также содержит конструктор, позволяющий создавать новые логические схемы и подключать их в качестве уровней. В том числе можно использовать схемы триггеров на элементах «И-НЕ» и «ИЛИ-НЕ».
- Технические средства для изучения логических элементов и построения логических схем.
Использование технических средств обучения дает возможность учителю обеспечить взаимосвязь теории и практики, позволяет учащимся самостоятельно извлекать информацию, анализировать ее, формулировать выводы, способствует повышению уровня мотивации обучения и профориентации школьника.
Примером технического средства является Цифровой логический тренажер ЦЛТ-310. Он входит в комплект оборудования, поставляемого в школы Москвы по проекту «Инженерный класс». ЦЛТ-310 предназначен для изучения основ построения цифровых логических схем и принципов построения микросхем. Тренажер состоит из основного модуля и набора сменных модулей с различными фрагментами электронных схем.
Отталкиваясь от полученных практическим путем (в ходе выполнения лабораторных работ) результатов деятельности ученик сам «добывает» знания и применяет их для решения более сложных задач. Пример первой лабораторной работы с использованием ЦЛТ-310 по теме «Логическая схема ИЛИ-НЕ» — https://drive.google.com/file/d/1zSMrU5pYq76wnXjq_wWJnx5NX5kVbOJc/view?usp=sharing
Пример схемы одноразрядного полусумматора на ЦЛТ-310 — см. рис. 2. На вход поданы два состояния «1», на выходе – индикатор суммы показывает значение «0» (не горит), а индикатор переноса в старший разряд – значение «1» (лампочка горит):
Рис. 2. Схема одноразрядного полусумматора
2. Схема одноразрядного полусумматора
Пример схемы одноразрядного сумматора на ЦЛТ-310 (см. рис. 3):
Рис. 3. Схема одноразрядного сумматора
Рассмотрение схемотехнического аспекта логических основ компьютера позволяет добиться понимания учащимися возможности автоматизации информационных процессов (хранения, обработки и передачи информации) с помощью технических устройств. Для этого школьникам необходимо показать способы единообразного (в виде последовательности нулей и единиц, или состояний включено и выключено) представления различного вида информации и продемонстрировать возможность замены арифметических операций операцией сложения с двоичными числами, а затем выяснить, каким образом элементарные операции (арифметическое сложения, хранение двоичного кода) могут быть реализованы техническими устройствами. Изучение типовых логических устройств компьютера позволит учащимся понять внутренние принципы работы компьютеров, применить знания двоичного кодирования, двоичной арифметики и основных логических операций для самостоятельной разработки отдельных логических компонентов компьютера, соединить теорию с практикой.
ЛИТЕРАТУРА:
- Примерная основная образовательная программа среднего общего образования [электронный ресурс http://fgosreestr.ru/registry/primernaya-osnovnaya-obrazovatelnaya-programma-srednego-obshhego-obrazovaniya/].
- Левченко И.В. Частные вопросы методики обучения теоретическим основам информатики в средней школе. Учебное пособие для студентов педагогических вызов и университетов. — М.: МГПУ, 2007.
- Поляков К.Ю. Логика. Тренажер для логических элементов [электронный ресурс http://kpolyakov.spb.ru/prog/logic.htm].
- Универсальная цифровая логическая лаборатория ЦЛТ-310. Руководство к лабораторным работам. – SAGA Technologies.
Логические основы цифровых схем | Composter 2.0
В некоторых случаях функции электической схемы можно представить с помощью логических операторов Булевой алгебры. Тогда говорят, что схема цифровая, т.е. подчиняется законам, хорошо иллюстрированным логическими операциями — инверсии, логического сложения, конъюнкции, исключающего «ИЛИ» и т. п. Первым исследовал эти законы Клод Шеннон в 1938 г. на примере электрических цепей с ключами. Впрочем, каждому из нас по силам придумать пример, иллюстрирующий физические явления, подчиняющиеся законам формальной логики.
п. Первым исследовал эти законы Клод Шеннон в 1938 г. на примере электрических цепей с ключами. Впрочем, каждому из нас по силам придумать пример, иллюстрирующий физические явления, подчиняющиеся законам формальной логики.
Одной из самых распространенных аналогий является управление водопроводными кранами. Рассмотрим некоторые примеры из этой области, принимая во внимание, что по электрическим схемам тоже «течет ток».
Рис 1. Вентильные схемы работы логических элементов
Во времена первых компьютеров в ходу была диодная логика, по принципу действия в чем-то схожая с работой водопроводных вентилей. Сегодня логические схемы реализуются интегральными микросхемами с высокой плотностью компоновки полупроводниковых элементов, но иногда полезно вспомнить, как формируется один логический элемент с использованием нескольких диодов.
Подключение по схеме «ИЛИ»
Практическую пользу схемы «ИЛИ» трудно переоценить: существует множество схем питания, использующих логику двух входов с диодной коммутацией. Если на одном из входов или на обеих сразу высокий логический уровень, диод (диоды) проводит ток, обеспечивая на выходе Y логическую единицу.
Если на одном из входов или на обеих сразу высокий логический уровень, диод (диоды) проводит ток, обеспечивая на выходе Y логическую единицу.
Рис 2. Логический элемент «ИЛИ», выполненный на двух диодах и подтягивающем резисторе
В логических элементах, основанных на диодной логике возможны состояния, при которых все диоды закрыты: для приведенной схемы «ИЛИ» это состояние, когда на входах A и B присутствует низкий уровень либо они не подключены. В этом случае, элемент «ИЛИ» должен выдавать на выход уровень логического нуля, что и обеспечивается резистором, соединяющим выход с общим проводом.
Подключение по схеме «И»
Диодный элемент «И» состоит из двух входов и выхода (Y). На вход диодной схемы может подаваться логическая единица (ей соответствует высокий уровень сигнала) или логический ноль — коммутация на общий провод («земля»). Замкнутые ключи схемы формируют ноль на выходе. Единицу можно получить только в случае, если не нажат ни один из них: высокий логический уровень на обоих входах дает высокий логический уровень на выходе.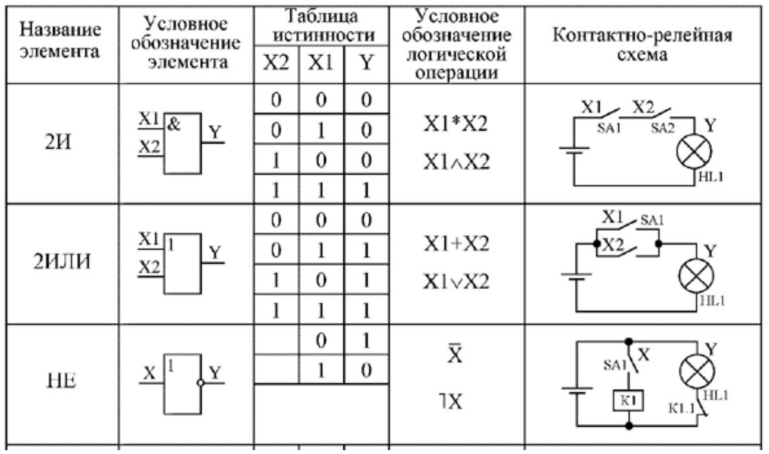
Рис 3. Логический элемент «И», выполненный на двух диодах и подтягивающем резисторе
Для приведенной схемы диодного элемента «И» закрытое состояние обоих диодов возможно при наличии высокого уровня на обоих входах. Аналогичный результат, отсутствие тока через диоды, будет иметь место когда ключи не замкнуты
Если подтягивающие резисторы не устанавливать
Если в схеме логического «ИЛИ» все входные диоды отключены (Рис 2.а) либо в схеме логического «И» все входные диоды отключены (Рис 3.а), на выходе будет так называемое Z-состояние — состояние высокого сопротивления, несущее неопределенность. Его восприятие зависит от схемотехники входных цепей, подключенных к выходу нашего логического элемента. Не исключено, что схема сохранит работоспособность и без подтягивающего резистора, если такой резистор (в явном виде или в виде паразитных цепей утечки) имеется во входной цепи следующего каскада. Рассчитывать на такой «подарок» не следует, поэтому неопределенность устраняется подключением терминирующего резистора.
Выбор номинала для подтягивающего резистора является компромиссом: при низком сопротивлении сигнал будет «просаживаться», при высоком — внешние факторы, такие как паразитные токи утечек, окажут на работу элемента существенное влияние, и требуемый логический уровень не будет гарантирован. Чтобы избежать неопределенности, формированием логического нуля следует считать соединение входа с общим проводом, логической единицы — соединение с плюсом источника питания, а неподключенного состояния следует избегать. Для этого и нужны подтягивающие резисторы. Как видим, приведенные выше схемы на основе кнопок нарушают правила терминации, опираясь на частные случаи и рассчитывая на предсказуемую реакцию диодной логики в неподключенном состоянии (при разомкнутой кнопке).
Вентили на полевых транзисторах
Для построения сложных схем требуются элементы, способные обеспечить развязку между управляющей и ведомой цепями. В качестве таких элементов используются транзисторы.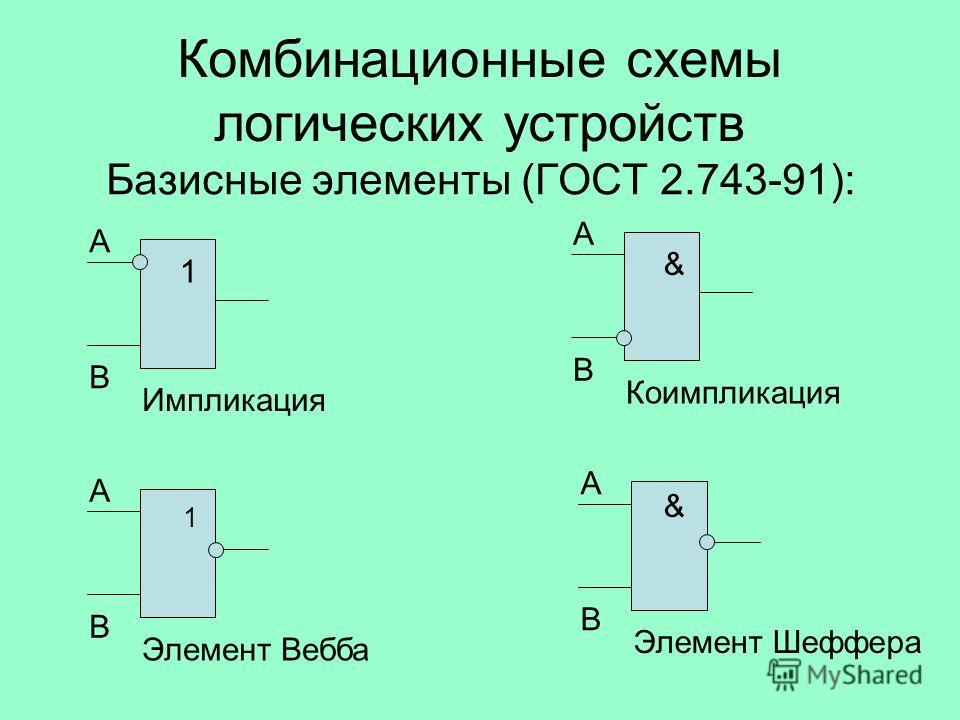 Наиболее продуктивной для логических схем оказалась CMOS-технологиях их изготовления. В качестве основы для этих транзисторов используется комплементарная структура металл-оксид-полупроводник, что и определило название всего семейства.
Наиболее продуктивной для логических схем оказалась CMOS-технологиях их изготовления. В качестве основы для этих транзисторов используется комплементарная структура металл-оксид-полупроводник, что и определило название всего семейства.
Рис 4. N-канальный транзистор закрыт, когда потенциал на затворе равен истоковому
В работе N-канального СMOS-транзистора используется 5-вольтовая логика: ключ на его основе окажется закрытым, если на затвор прибора подать напряжение низкого уровня и открывается при подаче +5V. Напряжение на затворе управляет проводимостью между стоком и истоком «полевика», и этот факт разработчиком схемы может использоваться для реализации заданных возможностей.
Рис 5. N-канальный транзистор откроется, если на затвор подать положительный потенциал
Стоит только изменить уровень напряжения на затворе транзистора, и он откроется, переключаясь в проводимое состояние. Если нулевой уровень запирает логическую схему, то перевести ее в противоположное (открытое) состояние можно только подав относительно истока положительное напряжение. Его уровень должен превышать определенный барьер — threshold voltage. Конструкция транзисторов СMOS-логики такова, что порог срабатывания, как правило, выше 1,5 вольта.
Его уровень должен превышать определенный барьер — threshold voltage. Конструкция транзисторов СMOS-логики такова, что порог срабатывания, как правило, выше 1,5 вольта.
Примечание. Если быть предельно точным, то для надежной работы схемы переключения требуется, чтобы напряжение на затворе превышало коммутируемое напряжение. Именно поэтому в импульсных регуляторах, где ШИМ-контроллер питается от +12V и коммутируемое напряжение равно +12V применяется Boost-цепочка, формирующая напряжение в пределах 20…24V для питания затворов.
базовый логический элемент — Перевод на английский — примеры русский
На основании Вашего запроса эти примеры могут содержать грубую лексику.
На основании Вашего запроса эти примеры могут содержать разговорную лексику.
Предложить пример
Другие результаты
Захват дроида происходит в мини-игре, включающей базовые электрические схемы и логические элементы.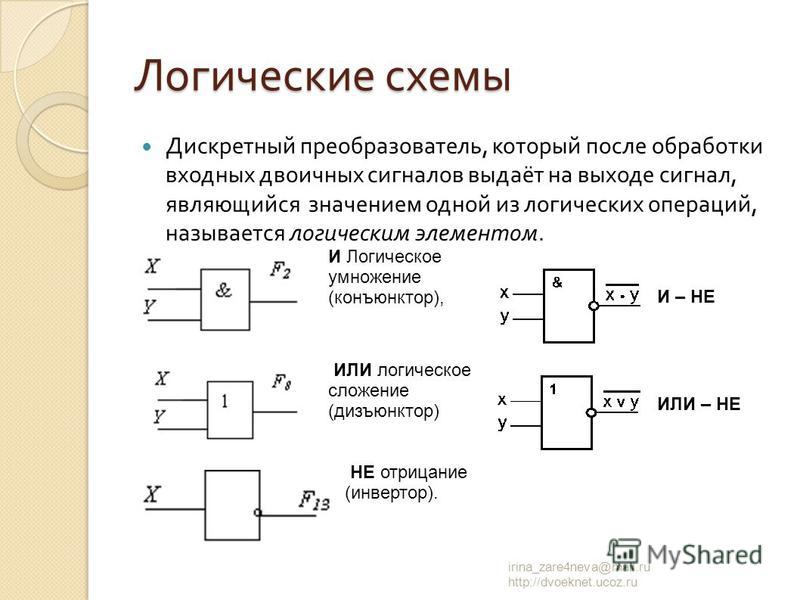
Изобретение относится к области логических элементов, а именно логических элементов на основе биомолекул.
Базовая приемопередающая станция (БППС) состоит из четырёх основных блоков или логических элементов: радиочастотного (РЧ) блока, Модулирующего блока, блока управления и часы, и транспортного блока.
A base transceiver station (BTS) has four main blocks or logical entities: Radio Frequency (RF) block, Baseband block, Control and Clock block, and Transport block. Сущность изобретения заключается в комплексе логического элемента, выполняющем преобразование входных сигналов в выходное воздействие согласно заданной логической функции.
типовое «время задержки основного логического элемента» менее 0,1 нс; или
Рисунок 1: Схема логического элемента двухсигнального мультиплексирования.
Figure 1: Logic gate schematic of a two input mux.В связи с этим использовались две взаимодополняющих версии логических элементов: NPN и PNP.
Consequently, two complementary versions were used: an NPN version and a PNP version.
Wireworld в особенности пригоден для симуляции электронных логических элементов, или «гейтов».
В основе своей он имеет самый фундаментальный строительный блок вычислений, логический элемент цифровой интегральной схемы напрямую в каждой части.
It basically embeds the most fundamental building block of computing, the digital logic gate, directly into your parts.Это делается путем составления цифровых схем, состоящих из логических элементов и триггеров внутри роботов.
This is done by wiring a synchronous digital circuit, consisting of logic gates and flip-flops, inside of the robots. Эта функция является критически важным логическим элементом контроля за доступом.
Предложенный способ вычислений предусматривает, параллельно-последовательную обработку сигнала в блоке триггеров входного регистра; матричном устройстве; блоке логических элементов, преимущественно логических элементов «И»; блоке триггеров выходного регистра.
The proposed computation method comprises parallel and sequential signal processing in a unit of input register triggers, in a matrix device, in a unit of logic elements, preferably AND logic elements, and in a unit of output register triggers.КОМПЛЕКС ЛОГИЧЕСКОГО ЭЛЕМЕНТА НА ОСНОВЕ БИОМОЛЕКУЛ (ВАРИАНТЫ)
Техническое примечание 1 Определение времени задержки основного логического элемента дается, что бы не спутать с временем задержки вход — выход составной монолитной интегральной схемы.
The physical interface which controls the flow of synchronous or asynchronous digital information.
При интеграции всех необходимых систем на один чип и использовании логических элементов малой мощности каждый узел вычисления или ввода/вывода тратит малую мощность (около 17 ватт, включая расходы DRAM).
By the integration of all essential sub-systems on a single chip, and the use of low-power logic, each Compute or I/O node dissipated low power (about 17 watts, including DRAMs).типовое «время задержки основного логического элемента» менее 0,4 нс; или
Техническое примечание 1 Определение времени задержки основного логического элемента дается, что бы не спутать с временем задержки вход — выход составной монолитной интегральной схемы.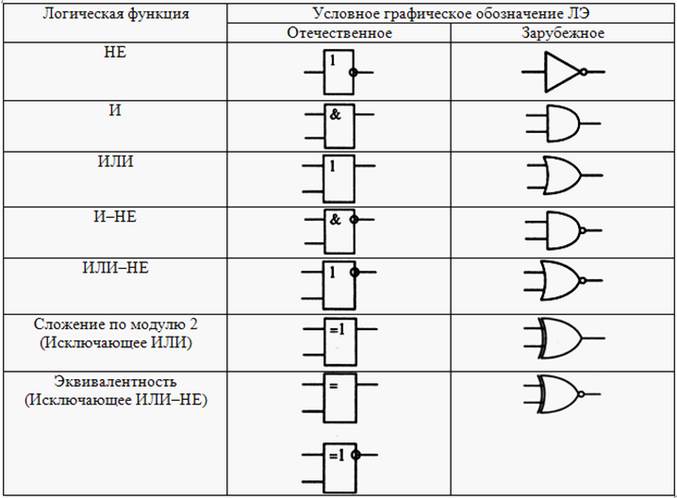
Software, underwater noise reduction Conventional Section: p. 268, 8.D.
Использование: для управления потоками света в оптических логических элементах, оптических компьютерах, оптоволоконных линиях, лазерных затворах, устройствах интегральной оптики.
The invention is used for controlling light beams in optical logic elements, optical computers, optical fibre lines, Q-switches and integrated optics devices.Но, так как каждое новое состояние бита не изменяется по крайней мере в течение 64 раундов, то ещё 64 состояния могут быть сгенерированы параллельно при увеличении количества логических элементов до 5504.
However, because each state bit is not used for at least 64 rounds, 64 state bits can be generated in parallel at a slightly greater hardware cost of 5504 gates.
Изначальный суперкомпьютер Тёга (также известный под названием МТА) оказался неудобным для массового производства из-за агрессивного подхода к упаковке логических элементов и выбранной технологии соединения процессоров.
The original Tera computer (also known as the MTA) turned out to be nearly unmanufacturable due to its aggressive packaging and circuit technology.
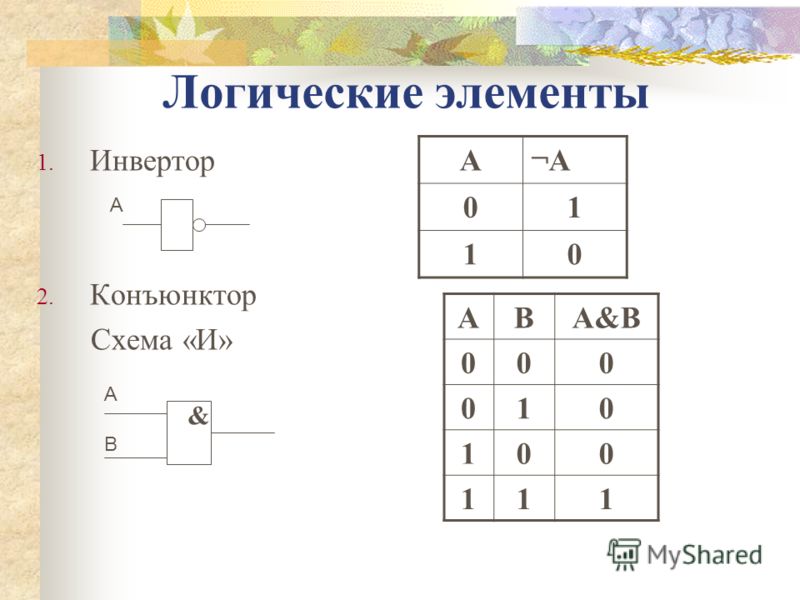
Логические элементы
Логические элементыЛогические элементы
Логическим элементом
называется электрическая схема,
выполняющая какую-либо логическую
операцию (операции) над входными
данными, заданными в виде уровней
напряжения, и возвращающая
результат операции в виде
выходного уровня напряжения. Так
как операнды логических операций
задаются в двоичной системе
счисления, то логический элемент
воспринимает входные данные в виде
высокого и низкого уровней
напряжения на своих входах.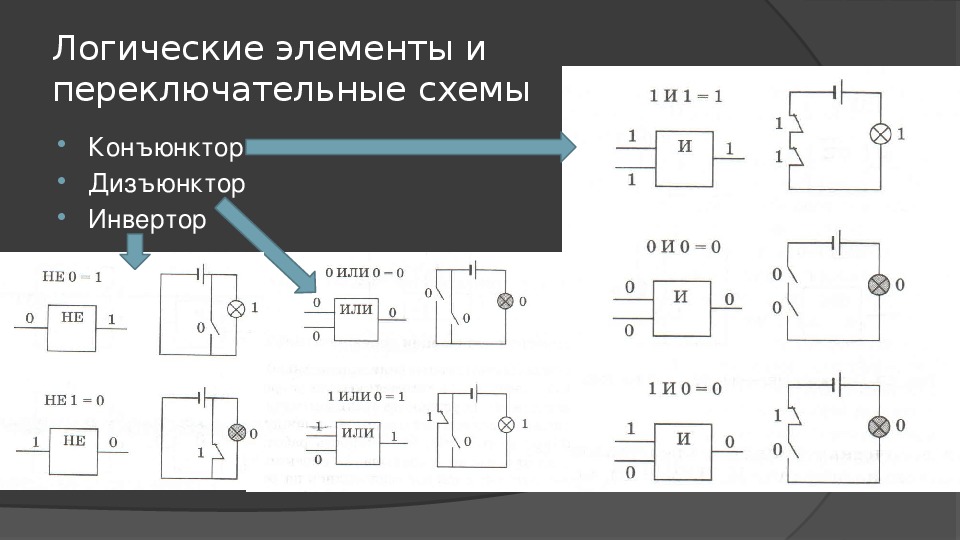 Соответственно, высокий уровень
напряжения (напряжение логической
1) символизирует истинное значение
операнда, а низкий (напряжение
логического 0) — ложное. Значения
высокого и низкого уровней
напряжения определяются
электрическими параметрами схемы
логического элемента и одинаковы
как для входных, так и для выходных
сигналов. Обычно, логические
элементы собираются как отдельная
интегральная микросхема. К числу
логических операций, выполняемых
логическими элементами относятся
конъюнкция (логическое умножение,
И), дизъюнкция (логическое сложение,
ИЛИ), отрицание (НЕ) и сложение по
модулю 2 (исключающее ИЛИ).
Рассмотрим основные типы
логических элементов.
Соответственно, высокий уровень
напряжения (напряжение логической
1) символизирует истинное значение
операнда, а низкий (напряжение
логического 0) — ложное. Значения
высокого и низкого уровней
напряжения определяются
электрическими параметрами схемы
логического элемента и одинаковы
как для входных, так и для выходных
сигналов. Обычно, логические
элементы собираются как отдельная
интегральная микросхема. К числу
логических операций, выполняемых
логическими элементами относятся
конъюнкция (логическое умножение,
И), дизъюнкция (логическое сложение,
ИЛИ), отрицание (НЕ) и сложение по
модулю 2 (исключающее ИЛИ).
Рассмотрим основные типы
логических элементов.
Элемент И
Логический элемент И
выполняет операцию логического
умножения (конъюнкция) над своими
входными данными и имеет от 2 до 8
входов и один выход (как правило,
выпускаются элементы с двумя,
тремя, четырьмя и восемью входами).
На рис. 1. изображены условные
графические обозначения (УГО)
логических элементов И с двумя,
тремя и четырьмя входами
соответственно. Элементы И
обозначаются как NИ, где N —
количество входов логического
элемента (например, 2И, 3И, 8И и т.д.).
Элементы И
обозначаются как NИ, где N —
количество входов логического
элемента (например, 2И, 3И, 8И и т.д.).
| Рис. 1 |
Элемент ИЛИ
Логический элемент ИЛИ выполняет операцию логического сложения (дизъюнкция) над своими входными данными и, также как и логический элемент И, имеет от 2 до 8 входов и один выход. На рис. 2. изображены УГО логических элементов ИЛИ с двумя, тремя и четырьмя входами соответственно. Элементы ИЛИ обозначаются также, как и элементы И (2ИЛИ, 4ИЛИ и т.д.).
| Рис. 2 |
Элемент НЕ (инвертор)
Логический элемент НЕ
выполняет операцию логического
отрицания над своими входными
данными и имеет один вход и один
выход.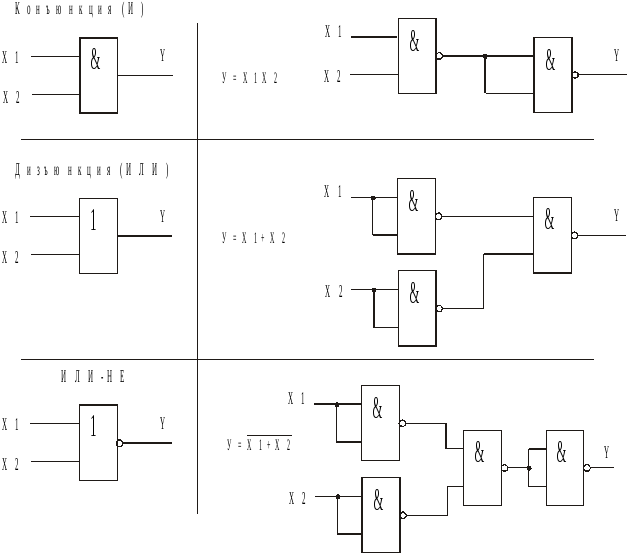 Иногда его называют
инвертор, так как он инвертирует
входной сигнал. На рис. 3 изображено
УГО элемента НЕ.
Иногда его называют
инвертор, так как он инвертирует
входной сигнал. На рис. 3 изображено
УГО элемента НЕ.
| Рис. 3 |
Элемент И-НЕ
Логический элемент И-НЕ выполняет операцию логического умножения над своими входными данными, а затем инвертирует (отрицает) полученный результат и выдаёт его на выход. Таким образом, можно сказать, что логический элемент И-НЕ — это элемент И с инвертором на выходе. УГО элемента 3И-НЕ приведено на рис. 4.
| Рис. 4 |
Элемент ИЛИ-НЕ
Логический элемент ИЛИ-НЕ
выполняет операцию логического
сложения над своими входными
данными, а затем инвертирует
(отрицает) полученный результат и
выдаёт его на выход. Таким образом,
можно сказать, что логический
элемент ИЛИ-НЕ — это элемент ИЛИ с
инвертором на выходе. УГО элемента 3ИЛИ-НЕ
приведено на рис. 5.
Таким образом,
можно сказать, что логический
элемент ИЛИ-НЕ — это элемент ИЛИ с
инвертором на выходе. УГО элемента 3ИЛИ-НЕ
приведено на рис. 5.
| Рис. 5 |
Элемент сложения по модулю 2
Этот логический элемент выполняет логическую операцию сложения по модулю 2 и, как правило, имеет 2 входа и один выход. Такой элемент, в основном, используется в схемах аппаратного контроля. УГО элемента приведено на рис. 6.
| Рис. 6 |
Комбинационные логические элементы
Существуют и более сложные
логические элементы, выполняющие
несколько логических операций над
своими входными данными. Например,
элемент 2И-ИЛИ, УГО и схема которого
приведено на рис. 7, сначала
выполняет операцию логического
умножения над парами операндов x1, x2
и x3, x4, а затем выполняет операцию
логического сложения над
полученными результатами, т.е. y = x1x2
+ x3x4. Можно придумать и более
сложные комбинационные логические
элементы, например 3-2И-ИЛИ-НЕ (рис. 8).
7, сначала
выполняет операцию логического
умножения над парами операндов x1, x2
и x3, x4, а затем выполняет операцию
логического сложения над
полученными результатами, т.е. y = x1x2
+ x3x4. Можно придумать и более
сложные комбинационные логические
элементы, например 3-2И-ИЛИ-НЕ (рис. 8).
| Рис. 7 |
| Рис. 8 |
Универсальные логические элементы
Универсальные логические
элементы могут использоваться для
выполнения разнообразных операций
над своими входными данными.
Конкретная операция зависит от
того, какие сигналы поданы на
управляющие входы. Чтобы
синтезировать такой универсальный
логический элемент, обычно
пользуются СКНФ или СДНФ, как и в
синтезе комбинационных логических
схем.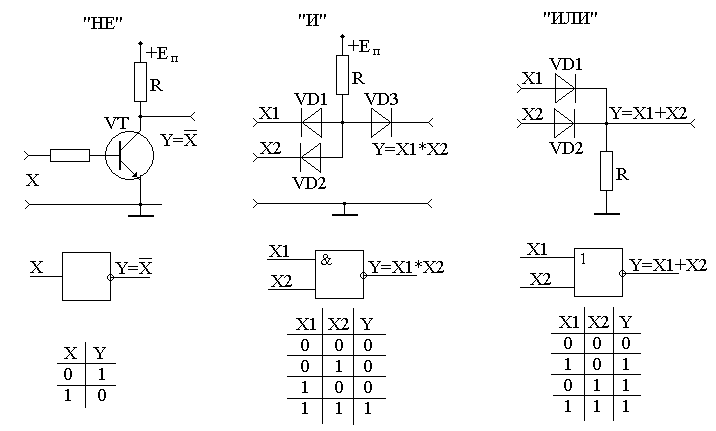
Электрические принципиальные схемы логических элементов
При рассмотрении
электрических принципиальных схем
логических элементов пользуются
термином тип логики. Тип логики
определяет элементную базу, на
которой собран логический элемент,
а также отражает некоторые
особенности отдельных элементов
этой элементной базы и
характеристики самого логического
элемента. Наиболее распространены
следующие типы логик: ТТЛ, ДТЛ, МОП,
КМОП, также существуют типы логик
ЭСЛ, РЕТЛ и некоторые другие. Тип
логики ТТЛ
(транзисторно-транзисторная
логика) определяет элементную базу,
на которой собран логический
элемент, как состоящую
преимущественно из транзисторов,
причём транзисторы используются и
на входе, и на выходе логического
элемента (отсюда и название —
транзисторно-транзисторная). Тип
логики ДТЛ (диодно-транзисторная
логика) определяет элементную базу
как состоящую преимущественно из
транзисторов и диодов (диоды на
входе, транзисторы — на выходе). Типы
логик МОП
(металл-оксид-полупроводник) и КМОП
определяет элементную базу как
состоящую из транзисторов МДП
(металл-диэлектрик-полупроводник),
причём микросхемы этого типа имеют
очень низкую потребляемую
мощность, засчёт особенностей МДП
транзисторов оперировать малыми
токами и имеющими очень малый ток
утечки.
Типы
логик МОП
(металл-оксид-полупроводник) и КМОП
определяет элементную базу как
состоящую из транзисторов МДП
(металл-диэлектрик-полупроводник),
причём микросхемы этого типа имеют
очень низкую потребляемую
мощность, засчёт особенностей МДП
транзисторов оперировать малыми
токами и имеющими очень малый ток
утечки.
Рассмотрим электрические принципиальные схемы логического элемента И-НЕ с n входами — ДТЛ (рис. 9) и логического элемента И-НЕ с n входами — ТТЛ (рис. 10).
| Рис. 9 |
| Рис. 10 |
На рисунках +U обозначает положительный потенциал источника питания, а -U — отрицательный.
Рассмотрим сначала работу
схемы на рис. 9. Если к одному из
входных диодов приложено
напряжение логического 0, то этот
диод открыт и на базу транзистора
подаётся напряжение логического 0. Транзистор закрывается и на выходе y устанавливается напряжение
логической 1. Только когда ко всем
входным диодам будет приложено
напряжение логической 1 транзистор
откроется и на выходе установится
напряжение логического 0.
Оставшиеся каскады на транзисторах
выполняют функцию усиления сигнала
и инвертирования. При подаче на
вход второго транзистора
напряжения логического 0, он
закроется, подключив базы
транзисторов оконечного каскада
через резисторы к плюсу и к минусу
источника питания. Один из
транзисторов оконечного каскада
откроется, а другой — закроется и на
выходе установится напряжение
логической 1. При подаче на второй
транзистор напряжения логической 1,
он откроется. Теперь открытый и
закрытый транзисторы оконечного
каскада поменяются местами и на
выходе установится напряжение
логического 0.
Транзистор закрывается и на выходе y устанавливается напряжение
логической 1. Только когда ко всем
входным диодам будет приложено
напряжение логической 1 транзистор
откроется и на выходе установится
напряжение логического 0.
Оставшиеся каскады на транзисторах
выполняют функцию усиления сигнала
и инвертирования. При подаче на
вход второго транзистора
напряжения логического 0, он
закроется, подключив базы
транзисторов оконечного каскада
через резисторы к плюсу и к минусу
источника питания. Один из
транзисторов оконечного каскада
откроется, а другой — закроется и на
выходе установится напряжение
логической 1. При подаче на второй
транзистор напряжения логической 1,
он откроется. Теперь открытый и
закрытый транзисторы оконечного
каскада поменяются местами и на
выходе установится напряжение
логического 0.
Теперь рассмотрим работу
схемы на рис. 10. Вызывает некоторый
интерес необычный транзистор на
входе и схема его включения. Такие
многоэмиттерные транзисторы
всегда используются на входах
логических элементов ТТЛ. Сам
транзистор выполняет логическую
операцию И. При подаче на один из
входов напряжения логического
нуля, транзистор открывается и,
таким образом, на коллекторе
устанавливается напряжение
логического 0. Напряжение
логической 1 будет на коллекторе
только тогда, когда на всех входах
будет напряжение логической 1.
Подобный транзистор можно
рассматривать как много n-p
переходов, а соответственно, как
много диодов. Таким образом такое
включение транзистора в цепь
эквивалентно диодной сборке на
входе логического элемента И на
рис. 9.
Сам
транзистор выполняет логическую
операцию И. При подаче на один из
входов напряжения логического
нуля, транзистор открывается и,
таким образом, на коллекторе
устанавливается напряжение
логического 0. Напряжение
логической 1 будет на коллекторе
только тогда, когда на всех входах
будет напряжение логической 1.
Подобный транзистор можно
рассматривать как много n-p
переходов, а соответственно, как
много диодов. Таким образом такое
включение транзистора в цепь
эквивалентно диодной сборке на
входе логического элемента И на
рис. 9.
Применение логических элементов
Логические элементы могут
использоваться как
самостоятельные части схемы, так и
входить в состав более сложной
цифровой комбинационной схемы или
схемы с памятью. Как
самостоятельные части схемы,
логические элементы могут
применяться в качестве управляющей
логики какого-либо устройства, а
также в качестве генератора
прямоугольных импульсов с
подключённой ёмкостью или
кварцевым резонатором. В качестве
комбинационных схем логические
элементы используются в составе
микросхем БИС и СБИС, а также в
дешифраторах и шифраторах,
выполненных в виде отдельных
микросхем. Также, логические
элементы могут входить в состав
схем с памятью (триггеры, регистры,
счётчики и т.д.), выполненных в виде
отдельной микросхемы или в составе
других микросхем.
В качестве
комбинационных схем логические
элементы используются в составе
микросхем БИС и СБИС, а также в
дешифраторах и шифраторах,
выполненных в виде отдельных
микросхем. Также, логические
элементы могут входить в состав
схем с памятью (триггеры, регистры,
счётчики и т.д.), выполненных в виде
отдельной микросхемы или в составе
других микросхем.
Комбинированные логические схемы
В цифровых системах для получения требуемых характеристик обычно применяются комбинации логических элементов. Например, последовательное включение логических элементов И и НЕ позволяет получить функцию И-НЕ (рис. 11.13(а)). Таким же образом можно получить логическую функцию ИЛИ-НЕ, объединив элементы ИЛИ и НЕ (рис. 11.13(б)).
В качестве поясняющего примера рассмотрим логическую схему на рис. 11.14. На вход схемы подается сигнал 0111. Нужно определить сигнал на выходе.
Решение.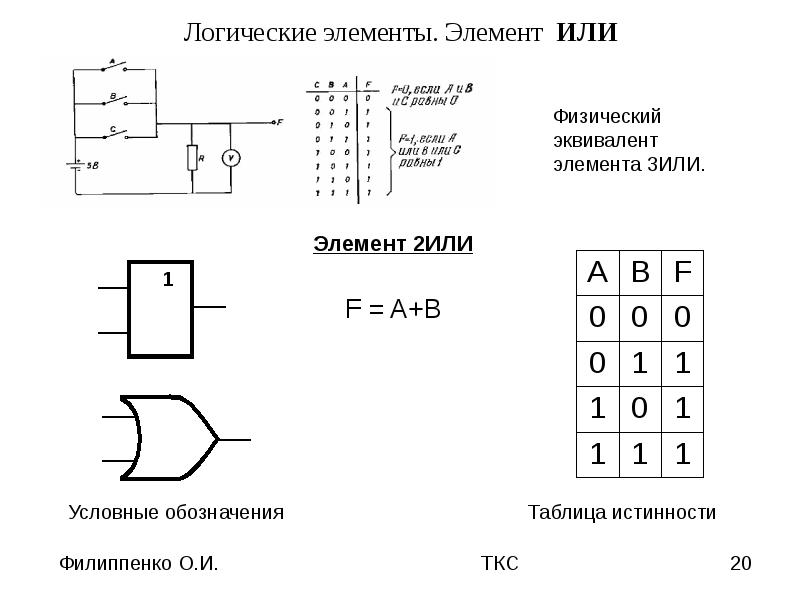 На выходе схемы ИЛИ (i) присутствует 1, а на выходе схемыИ-НЕ (ii) – 0. Следовательно, на входы схемы ИЛИ (iii) подается комбинация 10 и на ее выходе Gдействует логическая 1.
На выходе схемы ИЛИ (i) присутствует 1, а на выходе схемыИ-НЕ (ii) – 0. Следовательно, на входы схемы ИЛИ (iii) подается комбинация 10 и на ее выходе Gдействует логическая 1.
На рис. 11.15 изображена комбинация простых логических элементов для управления сигнализацией. Схема G1является элементом ИЛИ-НЕ, у которого объединены входы. В результате G1 действует как инвертор НЕ. Чтобы сработала сигнализация, на звонок должно быть подано положительное напряжение от источника питания, т. е. на выходе элемента И (схема G2) должна действовать 1. Для этого на оба входа элемента И должны быть поданы 1. Такое может случиться, если ключ S1 разомкнут, а ключ S2 замкнут. Другой комбинации, при которой может сработать сигнализация, нет.
Рис. 11.13. Рис.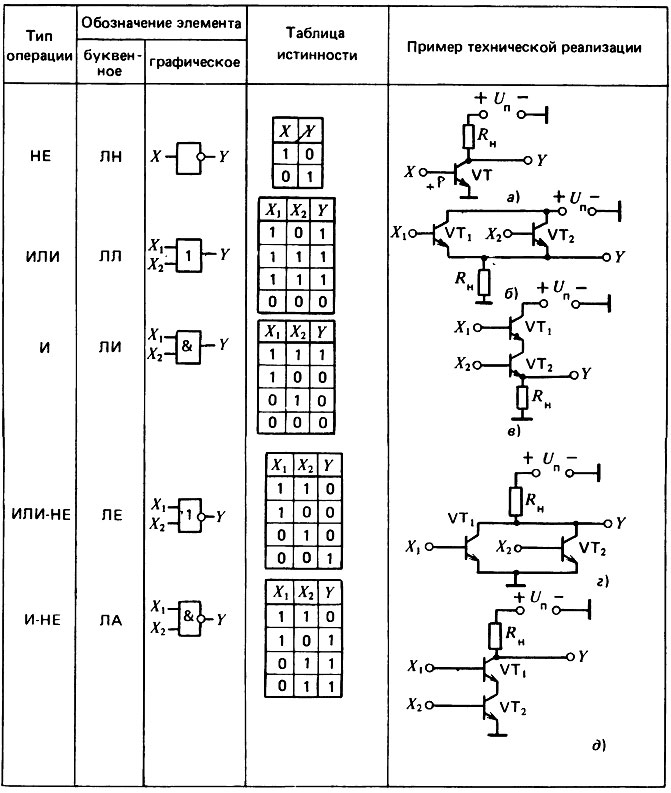 11.14.
11.14.
Рис. 11.15.
Двоичная система счисления
Если в десятичной системе счисления используется десять цифр, то в двоичной их всего две: нуль и единица(0 и 1). Эта система идеально подходит для логических схем и имеет дело именно с ними.
В десятичной системе первый столбец А (табл. 11.9) является столбцом единиц, столбец В — столбцом десятков, С — сотен, D — тысяч и т. д. В двоичной системе каждый столбец может быть представлен либо 0, либо 1. При этом первый столбец А соответствует единицам, В -двойкам, С — четверкам, D — восьмеркам и т. д. Любое число может быть представлено как в десятичной системе, так и в двоичной системе. В табл. 11.10 показано преобразование десятичных чисел от 0 до 7 в двоичные.
Таблица 11.9
|
Десятичные столбцы |
Двоичные столбцы |
||||||
|
D |
C |
B |
А |
D |
C |
B |
А |
|
103 |
102 |
101 |
10° |
23 |
22 |
21 |
2° |
|
Тысячи |
Сотни |
Десятки |
Единицы |
Восьмерки |
Четверки |
Двойки |
Единицы |
Таблица 11. 10
10
|
Десятичные числа |
Двоичные числа |
||
|
С |
В |
А |
|
|
(4) |
(2) |
(1) |
|
|
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
|
2 |
0 |
1 |
0 |
|
3 |
0 |
1 |
1 |
|
4 |
1 |
0 |
0 |
|
5 |
1 |
0 |
1 |
|
6 |
1 |
1 |
0 |
|
7 |
1 |
1 |
1 |
Для чисел, больших 7, нужен четвертый столбец (восьмерки).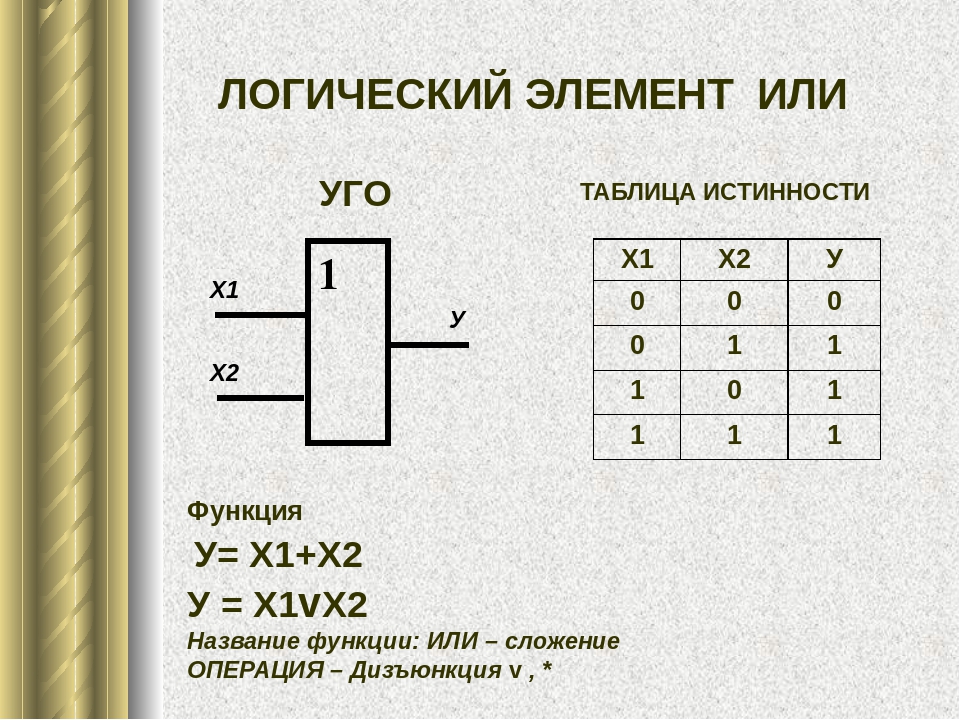 Так, 8 = 1000,9 == 1001, 10 = 1010, 11 == 1011 и т. д.
Так, 8 = 1000,9 == 1001, 10 = 1010, 11 == 1011 и т. д.
В табл. 11.11 приведено несколько примеров преобразования двоичных чисел в десятичные.
Таблица 11.11
|
Двоичные числа |
Двоичные столбцы |
Десятичные числа |
|||||
|
32 |
16 |
8 |
4 |
2 |
1 |
||
|
1110 |
— |
— |
1 |
1 |
1 |
0 |
= 8 + 4 + 2 = 14 |
|
1011 |
— |
— |
1 |
0 |
1 |
1 |
= 8 + 2 + 1 = 11 |
|
11001 |
— |
1 |
1 |
0 |
0 |
1 |
= 16 + 8 + 1 = 25 |
|
10111 |
— |
1 |
0 |
1 |
1 |
1 |
= 16 + 4 + 2 + 1 = 23 |
|
110010 |
1 |
1 |
0 |
0 |
1 |
0 |
= 32 + 16 + 2 = 50 |
Счетчик частоты
Логический элемент И в соединении со счетчиком может применяться для измерения частоты или периода. На рис. 11.16 показана схема измерителя частоты, состоящая из логического элемента И с двумя входами и счетчика. На вход А подается входной сигнал, а на вход В — тактовые импульсы заданной длительности. Сигнальные импульсы будут появляться на выходе схемы И только во время действия тактового импульса. Затем эти импульсы поступают на счетчик, который считает их и таким образом определяет частоту входного сигнала. Например, если длительность тактового импульса равна 10 мс, а длительность входного сигнала при его частоте 1 кГц составляет 1 мс, то за время действия тактового импульса на выходе схемы появятся только 10 импульсов, которые, будучи посчитаны счетчиком, дадут частоту 1 кГц.
На рис. 11.16 показана схема измерителя частоты, состоящая из логического элемента И с двумя входами и счетчика. На вход А подается входной сигнал, а на вход В — тактовые импульсы заданной длительности. Сигнальные импульсы будут появляться на выходе схемы И только во время действия тактового импульса. Затем эти импульсы поступают на счетчик, который считает их и таким образом определяет частоту входного сигнала. Например, если длительность тактового импульса равна 10 мс, а длительность входного сигнала при его частоте 1 кГц составляет 1 мс, то за время действия тактового импульса на выходе схемы появятся только 10 импульсов, которые, будучи посчитаны счетчиком, дадут частоту 1 кГц.
Рис. 11.16. Схема И в качестве измерителя частоты
Цифровой датчик времени (цифровые часы) (рис. 11.17)
Импульсы от кварцевого генератора, имеющего очень высокую стабильность частоты, подаются на цепочку делителей частоты, которая генерирует точную последовательность тактовых импульсов.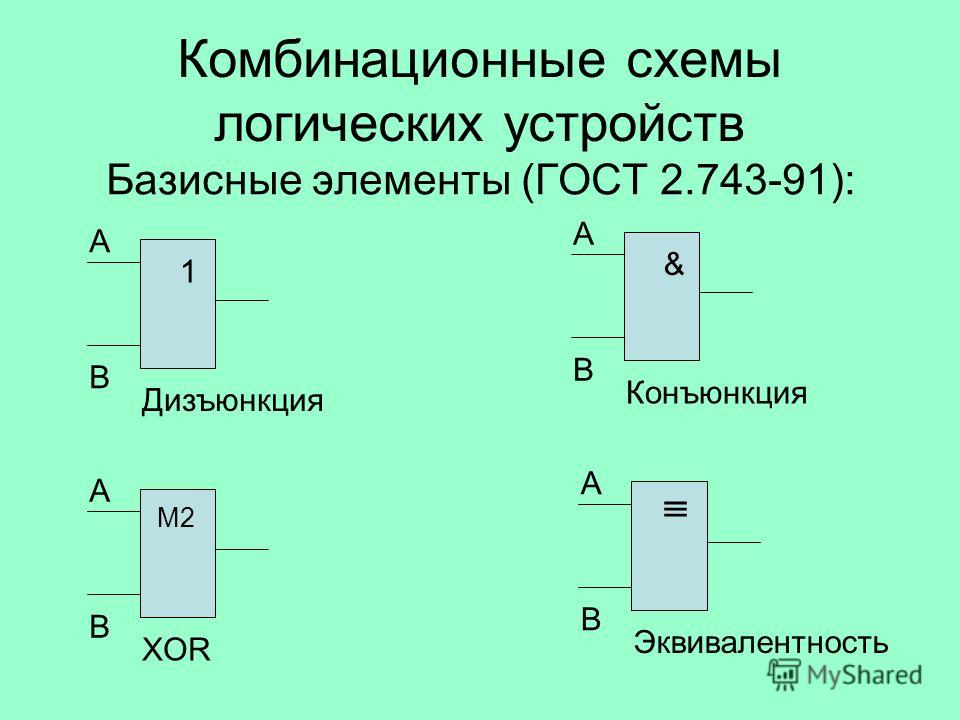 Декодер преобразует тактовые импульсы делителя в соответствующие сигналы, которые поступают на индикатор (см. также гл. 35). Секундный индикатор работает с самой высокой частотой, а часовой – с самой низкой.
Декодер преобразует тактовые импульсы делителя в соответствующие сигналы, которые поступают на индикатор (см. также гл. 35). Секундный индикатор работает с самой высокой частотой, а часовой – с самой низкой.
Рис. 11.17. Блок-схема цифрового датчика времени.
Аналого-цифровой преобразователь (АЦП)
АЦП преобразует входной аналоговый сигнал в цифровой (рис. 11.18). Выходной сигнал представляет собой некоторое число параллельных цифровых разрядов (четыре на рис. 11.18). Каждый разряд это двоичный столбец.
Рис. 11.18.
Цифро-аналоговый преобразователь (ЦАП)
На вход ЦАП поступает параллельный цифровой код. ЦАП преобразует его снова в величину напряжения (или ток), которая была представлена
Рис. 11.19.
в виде двоичного входного сигнала.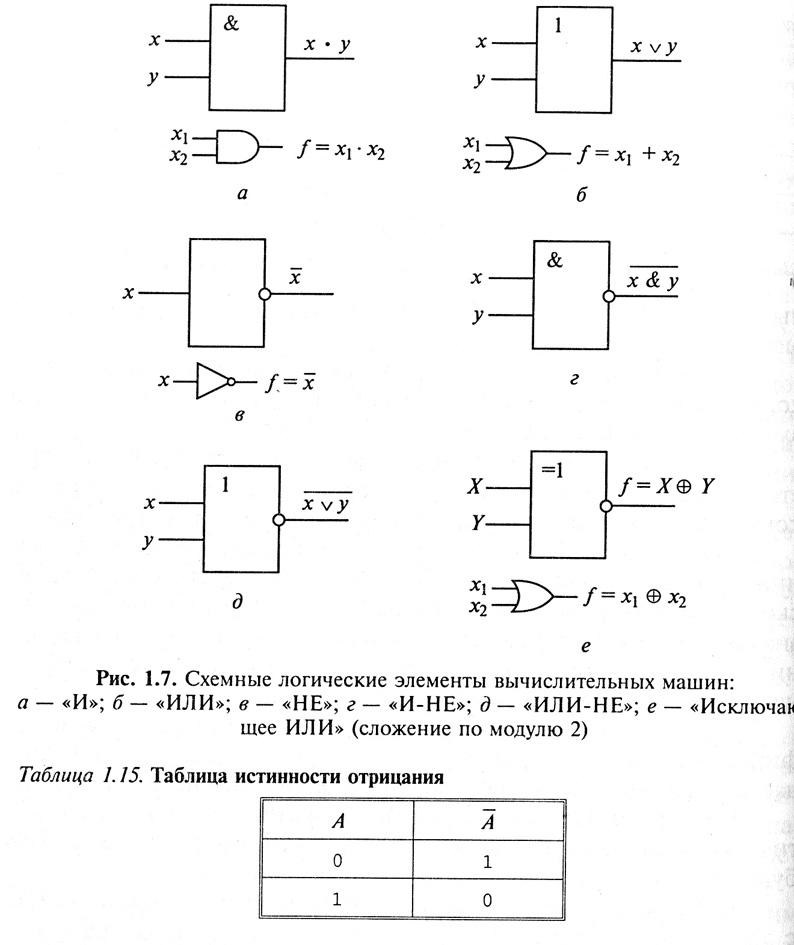 Если это проделать с последовательностью цифровых входных сигналов, то можно восстановить аналоговую форму исходного сигнала (рис. 11.19).
Если это проделать с последовательностью цифровых входных сигналов, то можно восстановить аналоговую форму исходного сигнала (рис. 11.19).
Цифровая обработка сигнала
Большинство сигналов, встречающихся в повседневной жизни, например звук и видео, существуют в аналоговой форме. Прежде чем ввести такие сигналы в цифровую систему, например в цифровой магнитофон, необходимо преобразовать их в цифровую форму с помощью аналого-цифрового преобразователя (рис. 11.20). После соответствующей обработки цифровой сигнал снова преобразуется в исходную аналоговую форму, т. е. в звуковой сигнал, с помощью цифро-аналогового преобразователя.
Рис. 11.20.
В данном видео рассказывается о цифро-аналоговых преобразователях:
Добавить комментарий
Что такое логический вентиль (И, ИЛИ, XOR, NOT, NAND, NOR и XNOR)? Определение с сайта WhatIs.
 com
comЛогический вентиль — это устройство, которое действует как строительный блок для цифровых схем. Они выполняют основные логические функции, которые являются фундаментальными для цифровых схем. В большинстве электронных устройств, которые мы используем сегодня, есть логические вентили. Например, логические вентили могут использоваться в таких технологиях, как смартфоны, планшеты или в устройствах памяти.
В схеме логические вентили будут принимать решения на основе комбинации цифровых сигналов, поступающих с их входов.Большинство логических вентилей имеют два входа и один выход. Логические вентили основаны на булевой алгебре. В любой момент каждый терминал находится в одном из двух двоичных состояний: ложно или истинно . Ложь представляет 0, а истина представляет 1. В зависимости от типа используемого логического элемента и комбинации входов двоичный выход будет отличаться. Логический вентиль можно представить себе как выключатель света, в котором в одном положении выход выключен — 0, а в другом — включен — 1. Логические вентили обычно используются в интегральных схемах (IC).
Логические вентили обычно используются в интегральных схемах (IC).
Существует семь основных логических вентилей: И, ИЛИ, ИСКЛЮЧАЮЩЕЕ ИЛИ, НЕ, ИЛИ, ИЛИ ИЛИ ИСКЛЮЧИТЕЛЬНОЕ ИЛИ.
И | ИЛИ | XOR | НЕ | NAND | NOR | XNOR
Логический элемент И назван так потому, что, если 0 называется «ложным», а 1 называется «истинным», элемент действует так же, как логический оператор «И». На следующей иллюстрации и в таблице показаны символы схемы и логические комбинации для логического элемента И. (В символе входные клеммы слева, а выходные клеммы справа.) Выход «истина», когда оба входа «истина». В противном случае результат будет «ложным». Другими словами, выход равен 1 только тогда, когда оба входа один И два равны 1.
И ворота
| Вход 1 | Ввод 2 | Выход |
| 1 | ||
| 1 | ||
| 1 | 1 | 1 |
Логический элемент OR получил свое название из-за того, что он ведет себя по образцу логического включающего «или».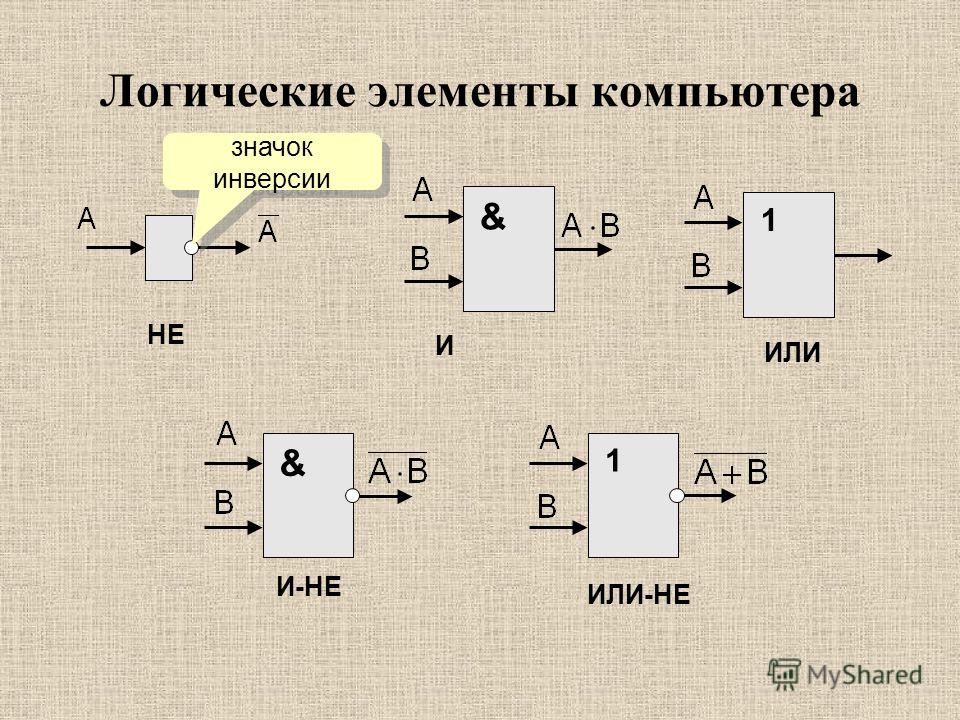 «Выход -« истина », если один или оба входа« истина ». Если оба входа« ложь », то выход« ложь ». Другими словами, для выхода будет 1, по крайней мере, вход один ИЛИ два должны быть 1.
«Выход -« истина », если один или оба входа« истина ». Если оба входа« ложь », то выход« ложь ». Другими словами, для выхода будет 1, по крайней мере, вход один ИЛИ два должны быть 1.
OR ворота
| Вход 1 | Вход 2 | Выход |
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 | 1 |
XOR ( исключающее ИЛИ ) вентиль действует так же, как логическое «или / или». «Выходной сигнал« истина », если один из входов, но не оба,« истина ». Выходной сигнал« ложь », если оба входа« ложь »или если оба входа« истина ». Другой способ взглянуть на это Схема должна следить за тем, чтобы на выходе было 1, если входы разные, и 0, если входы одинаковые.
«Выходной сигнал« истина », если один из входов, но не оба,« истина ». Выходной сигнал« ложь », если оба входа« ложь »или если оба входа« истина ». Другой способ взглянуть на это Схема должна следить за тем, чтобы на выходе было 1, если входы разные, и 0, если входы одинаковые.
Вентиль XOR
| Вход 1 | Ввод 2 | Выход |
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 |
Логический инвертор , иногда называемый вентилем НЕ , чтобы отличать его от других типов электронных инверторных устройств, имеет только один вход. Он меняет логическое состояние на обратное. Если на входе 1, то на выходе 0. Если на входе 0, то на выходе 1.
Он меняет логическое состояние на обратное. Если на входе 1, то на выходе 0. Если на входе 0, то на выходе 1.
Логический элемент И-НЕ работает как вентиль И, за которым следует вентиль НЕ. Он действует как логическая операция «и» с последующим отрицанием. На выходе будет «ложь», если оба входа «истина». В противном случае вывод будет «истина».
вентиль NAND
| Вход 1 | Ввод 2 | Выход |
| 1 | ||
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 |
Логический элемент ИЛИ представляет собой комбинацию логического элемента ИЛИ, за которым следует инвертор. Его выход будет «истина», если оба входа «ложь». В противном случае результат будет «ложным».
Его выход будет «истина», если оба входа «ложь». В противном случае результат будет «ложным».
NOR ворота
| Вход 1 | Ввод 2 | Выход |
| 1 | ||
| 1 | ||
| 1 | ||
| 1 | 1 |
Логический элемент XNOR (исключающее ИЛИ) — это комбинированный вентиль XOR, за которым следует инвертор. Его вывод «истина», если входы одинаковые, и «ложь», если входы разные.
Его вывод «истина», если входы одинаковые, и «ложь», если входы разные.
Ворота XNOR
| Вход 1 | Ввод 2 | Выход |
| 1 | ||
| 1 | ||
| 1 | ||
| 1 | 1 | 1 |
Сложные операции могут выполняться с использованием комбинаций этих логических вентилей. Теоретически нет ограничений на количество ворот, которые могут быть объединены в одно устройство. Но на практике существует ограничение на количество ворот, которые могут быть упакованы в данное физическое пространство. Массивы логических вентилей находятся в цифровых ИС. По мере развития технологии ИС требуемый физический объем для каждого отдельного логического элемента уменьшается, и цифровые устройства того же или меньшего размера становятся способными выполнять все более сложные операции с постоянно увеличивающейся скоростью.
Теоретически нет ограничений на количество ворот, которые могут быть объединены в одно устройство. Но на практике существует ограничение на количество ворот, которые могут быть упакованы в данное физическое пространство. Массивы логических вентилей находятся в цифровых ИС. По мере развития технологии ИС требуемый физический объем для каждого отдельного логического элемента уменьшается, и цифровые устройства того же или меньшего размера становятся способными выполнять все более сложные операции с постоянно увеличивающейся скоростью.
Состав логических вентилей
Высокий или низкий двоичные состояния представлены разными уровнями напряжения.Логическое состояние терминала может и обычно часто изменяется по мере обработки данных схемой. В большинстве логических вентилей низкое состояние составляет приблизительно ноль вольт (0 В), а высокое состояние — приблизительно пять вольт положительного напряжения (+5 В).
Логические вентили могут быть выполнены из резисторов и транзисторов или диодов. Резистор обычно можно использовать как подтягивающий или понижающий резистор. Подтягивающие и понижающие резисторы используются, когда есть какие-либо неиспользуемые входы логических элементов для подключения к логическому уровню 1 или 0.Это предотвращает ложное переключение ворот. Подтягивающие резисторы подключены к Vcc (+ 5 В), а подтягивающие резисторы — к земле (0 В).
Резистор обычно можно использовать как подтягивающий или понижающий резистор. Подтягивающие и понижающие резисторы используются, когда есть какие-либо неиспользуемые входы логических элементов для подключения к логическому уровню 1 или 0.Это предотвращает ложное переключение ворот. Подтягивающие резисторы подключены к Vcc (+ 5 В), а подтягивающие резисторы — к земле (0 В).
Обычно используются логические вентили TTL и CMOS. В ИС TTL, или транзисторно-транзисторной логики, будут использоваться биполярные переходные транзисторы типа NPN и PNP. КМОП, или дополнительные металл-оксидно-кремниевые ИС, построены из полевых транзисторов типа MOSFET или JFET. Микросхемы TTL обычно обозначаются как микросхемы серии 7400, в то время как микросхемы КМОП часто обозначаются как микросхемы серии 4000.
цифровых сигналов и ворот | Логические ворота
Хотя двоичная система счисления представляет собой интересную математическую абстракцию, мы еще не видели ее практического применения в электронике. Эта глава посвящена именно этому: практическому применению концепции двоичных битов к схемам.
Эта глава посвящена именно этому: практическому применению концепции двоичных битов к схемам.
Что делает двоичное счисление таким важным для приложений цифровой электроники, так это легкость, с которой биты могут быть представлены в физических терминах. Поскольку двоичный бит может иметь только одно из двух разных значений, 0 или 1, для представления бита может использоваться любая физическая среда, способная переключаться между двумя состояниями насыщения.
Следовательно, любая физическая система, способная представлять двоичные биты, способна представлять числовые величины и потенциально имеет возможность манипулировать этими числами. Это основная концепция, лежащая в основе цифровых вычислений.
Двоичные и электронные схемы
Двоичный режим транзистора
Электронные схемы — это физические системы, которые хорошо подходят для представления двоичных чисел. Транзисторы, когда работают с предельными значениями смещения, могут находиться в одном из двух различных состояний: отключенном (отсутствие контролируемого тока) или насыщении (максимальный контролируемый ток). Если схема транзистора спроектирована так, чтобы максимизировать вероятность попадания в одно из этих состояний (и не работает в линейном или активном режиме), она может служить физическим представлением двоичного бита.
Если схема транзистора спроектирована так, чтобы максимизировать вероятность попадания в одно из этих состояний (и не работает в линейном или активном режиме), она может служить физическим представлением двоичного бита.
Вход транзистора на «высокий»
Сигнал напряжения, измеренный на выходе такой схемы, также может служить представлением одного бита, при этом низкое напряжение представляет двоичный «0», а (относительно) высокое напряжение представляет двоичную «1». Обратите внимание на следующую схему транзистора:
В этой схеме транзистор находится в состоянии насыщения благодаря приложенному входному напряжению (5 вольт) через двухпозиционный переключатель.Из-за насыщения транзистор очень мало теряет напряжение между коллектором и эмиттером, что приводит к выходному напряжению (практически) 0 вольт.
Если бы мы использовали эту схему для представления двоичных разрядов, мы бы сказали, что входной сигнал — это двоичная «1», а выходной сигнал — двоичный «0». Любое напряжение, близкое к полному напряжению питания (разумеется, по отношению к земле), считается «1», а отсутствие напряжения — «0».
Любое напряжение, близкое к полному напряжению питания (разумеется, по отношению к земле), считается «1», а отсутствие напряжения — «0».
Альтернативные термины для этих уровней напряжения: высокий (то же, что и двоичная «1») и низкий (то же, что двоичный «0»).Общий термин для представления двоичного бита напряжением цепи — логический уровень .
Низкий уровень на входе транзистора
Перемещая переключатель в другое положение, мы прикладываем двоичный «0» к входу и получаем двоичную «1» на выходе:
Что такое логические ворота?
То, что мы создали здесь с одним транзистором, — это схема, известная как логический вентиль или просто вентиль . Затвор — это особый тип схемы усилителя, предназначенный для приема и генерации сигналов напряжения, соответствующих двоичным единицам и нулям.
Таким образом, вентили не предназначены для использования для усиления аналоговых сигналов (сигналов напряжения от 0 до полного напряжения). При совместном использовании несколько вентилей могут применяться к задаче хранения двоичных чисел (схемы памяти) или манипулирования (вычислительные схемы), при этом выход каждого логического элемента представляет один бит многобитового двоичного числа.
При совместном использовании несколько вентилей могут применяться к задаче хранения двоичных чисел (схемы памяти) или манипулирования (вычислительные схемы), при этом выход каждого логического элемента представляет один бит многобитового двоичного числа.
Как это делается, мы поговорим в следующей главе. Сейчас важно сосредоточиться на работе индивидуальных ворот.
Инвертор или НЕ затвор
Показанный здесь вентиль с одиночным транзистором известен как инвертор , или НЕ вентиль, потому что он выводит цифровой сигнал, прямо противоположный входному.Для удобства схемы затвора обычно представлены своими собственными символами, а не составляющими их транзисторами и резисторами. Ниже показан символ инвертора:
Здесь показан альтернативный символ инвертора:
Условное обозначение ворот НЕ
Обратите внимание на треугольную форму символа затвора, очень похожую на форму операционного усилителя. Как было сказано ранее, затворные схемы на самом деле являются усилителями.
Как было сказано ранее, затворные схемы на самом деле являются усилителями.
Маленький кружок или «пузырь», показанный на входной или выходной клемме, является стандартным для представления функции инверсии. Как вы могли догадаться, если бы мы удалили пузырь из символа ворот, оставив только треугольник, получившийся символ больше не означал бы инверсию, а просто прямое усиление.
Такой символ и такой вентиль действительно существуют, и они называются буфером , которому посвящен следующий раздел.
Подобно символу операционного усилителя, входные и выходные соединения показаны как одиночные провода, подразумеваемой точкой отсчета для каждого сигнала напряжения является «земля».В схемах с цифровым затвором заземление почти всегда представляет собой отрицательное соединение одного источника напряжения (источника питания).
Двойные или «раздельные» источники питания редко используются в схемах затвора. Поскольку схемы затвора являются усилителями, для работы им требуется источник питания. Как и в случае с операционными усилителями, разъемы питания для цифровых ворот часто для простоты опускаются на символе.
Как и в случае с операционными усилителями, разъемы питания для цифровых ворот часто для простоты опускаются на символе.
НЕ Ворота в цепях
Если бы мы показали всех необходимых соединений, необходимых для работы этих ворот, схема выглядела бы примерно так:
Проводники источника питания редко показаны на схемах схемы затвора, даже если есть соединения источника питания на каждом затворе.Свернув линии на нашей схеме, мы получим:
«Vcc» обозначает постоянное напряжение, подаваемое на коллектор схемы биполярного переходного транзистора по отношению к земле. Все точки в цепи затвора, отмеченные меткой «Vcc», подключены к одной и той же точке, и эта точка является положительной клеммой источника постоянного напряжения, обычно 5 вольт.
Как мы увидим в других разделах этой главы, существует довольно много различных типов логических вентилей, большинство из которых имеют несколько входных клемм для приема более одного сигнала. Выход любого логического элемента зависит от состояния его входа (ов) и его логической функции.
Выход любого логического элемента зависит от состояния его входа (ов) и его логической функции.
Выражение функций схемы ворот с помощью таблиц истинности
Один из распространенных способов выразить конкретную функцию схемы затвора называется таблицей истинности. Таблицы истинности показывают все комбинации входных условий в терминах состояний логического уровня («высокий» или «низкий», «1» или «0» для каждой входной клеммы логического элемента) вместе с соответствующим выходным логическим уровнем, либо «Высокий» или «низкий».«Для только что проиллюстрированной схемы инвертора или НЕ, таблица истинности действительно очень проста:
Таблицы истинности для более сложных ворот, конечно, больше, чем таблица, показанная для ворот НЕ. Таблица истинности гейта должна иметь столько строк, сколько есть возможностей для уникальных входных комбинаций.
Для элемента с одним входом, такого как элемент НЕ, есть только две возможности, 0 и 1. Для элемента с двумя входами есть четыре возможности (00, 01, 10 и 11), и, следовательно, четыре строки для соответствующих таблица истинности.
Для элемента с двумя входами есть четыре возможности (00, 01, 10 и 11), и, следовательно, четыре строки для соответствующих таблица истинности.
Для вентиля с тремя входами существует восемь возможностей (000, 001, 010, 011, 100, 101, 110 и 111), и поэтому необходима таблица истинности с восемью строками. Те, кто склонен к математике, поймут, что количество строк таблицы истинности, необходимых для элемента, равно 2, возведенному в степень числа входных клемм.
ОБЗОР:
- В цифровых схемах двоичные битовые значения 0 и 1 представлены сигналами напряжения, измеренными относительно общей точки схемы, называемой землей.Отсутствие напряжения представляет двоичный «0», а наличие полного напряжения питания постоянного тока представляет двоичную «1».
- Логический вентиль, или просто вентиль, представляет собой особую форму схемы усилителя, предназначенную для ввода и вывода напряжений логического уровня (напряжения, предназначенные для представления двоичных битов).
 Схемы затвора чаще всего представлены на схемах их собственными уникальными символами, а не составляющими их транзисторами и резисторами.
Схемы затвора чаще всего представлены на схемах их собственными уникальными символами, а не составляющими их транзисторами и резисторами. - Так же, как и в случае с операционными усилителями, соединения источника питания с затворами часто для простоты опускаются на схематических диаграммах.
- Таблица истинности — это стандартный способ представления отношений входа / выхода схемы затвора, в котором перечислены все возможные комбинации входных логических уровней с соответствующими выходными логическими уровнями.
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Введение в логические ворота — GeeksforGeeks
В булевой алгебре есть три основных операции, которые аналогичны дизъюнкции, соединению и отрицанию в логике высказываний.Каждая из этих операций имеет соответствующий логический вентиль. Помимо них есть еще несколько логических ворот.
Логические ворота —
- Элемент AND (.
 ) — Элемент AND дает выход 1, если оба входа равны 1, в противном случае он дает 0.
) — Элемент AND дает выход 1, если оба входа равны 1, в противном случае он дает 0. - Элемент ИЛИ (+) — Элемент ИЛИ дает на выходе 1, если один из двух входов равен 1, в противном случае он дает 0.
- Элемент НЕ (‘) — Элемент НЕ дает выход 1, вход равен 0, и наоборот.
- Элемент XOR () — Элемент XOR дает выход 1, если оба входа различны, он дает 0, если они одинаковы.
Еще три логических элемента получаются, если вывод вышеупомянутых вентилей инвертируется.
- Логический элемент И-НЕ () — Логический элемент И-НЕ (отрицательное И) дает выход 0, если оба входа равны 1, в противном случае он дает 1.
- Элемент ИЛИ-НЕ () — Элемент ИЛИ-НЕ (отрицательное ИЛИ) дает на выходе 1, если оба входа равны 0, в противном случае он дает 0.
- Элемент ИСКЛЮЧАЮЩЕЕ ИЛИ () — Элемент ИСКЛЮЧАЮЩЕЕ ИЛИ (инвертированное ИСКЛЮЧАЮЩЕЕ ИЛИ) дает на выходе 1, оба входа одинаковы и 0, если оба разные.

Каждый логический вентиль имеет графическое представление или связанный с ним символ. Ниже приведено изображение, на котором показаны графические символы и таблицы истинности, связанные с каждым логическим вентилем.
Универсальные логические вентили —
Из семи логических вентилей, описанных выше, NAND и NOR также известны как универсальные вентили , поскольку их можно использовать для реализации любой цифровой схемы без использования каких-либо других вентилей.Это означает, что все ворота могут быть созданы только воротами И-НЕ или И-НЕ.
Реализация трех основных вентилей с использованием вентилей NAND и NOR показана ниже —
Для ворот XOR , реализация NAND и NOR —
- Реализовано Использование NAND —
- Реализовано с использованием NOR —
Примечание — Для реализации логического элемента ИСКЛЮЧАЮЩЕЕ ИЛИ, к указанным выше схемам можно добавить один вентиль ИЛИ или ИЛИ-ИЛИ, чтобы свести на нет выход элемента ИСКЛЮЧАЮЩЕЕ ИЛИ.
GATE CS Corner Questions
Выполнение следующих вопросов поможет вам проверить свои знания. Все вопросы задавались в GATE в предыдущие годы или в пробных тестах GATE. Настоятельно рекомендуется попрактиковаться в них.
1. GATE CS 2013, вопрос 21
2. GATE CS 2012, вопрос 10
3. GATE CS 2007, вопрос 33
4. GATE CS 2005, вопрос 15
Артикул —
Цифровой дизайн, 5-е издание, Моррис Мано и Майкл Силетти
Эта статья предоставлена Chirag Manwani .Если вам нравится GeeksforGeeks, и вы хотели бы внести свой вклад, вы также можете написать статью с помощью provide.geeksforgeeks.org или отправить ее по электронной почте на [email protected]. Смотрите, как ваша статья появляется на главной странице GeeksforGeeks, и помогайте другим гикам.
Пожалуйста, напишите комментарий, если вы обнаружите что-то неправильное, или если вы хотите поделиться дополнительной информацией по теме, обсужденной выше.
Вниманию читателя! Не прекращайте учиться сейчас. Ознакомьтесь со всеми важными концепциями теории CS для собеседований SDE с помощью курса CS Theory Course по доступной для студентов цене и подготовьтесь к работе в отрасли.
Логические ворота
В реальном мире цифровые устройства не являются абстрактными логическими выражениями булевой алгебры, а являются аппаратными реализациями этих выражений. Логические выражения транслируются в структуры устройства, называемые логическими вентилями . Логический вентиль является как символическим представлением логической операции, так и при использовании в цифровой электронике может быть реальной схемой в аппаратном обеспечении. Один логический вентиль обычно состоит из нескольких транзисторов, разделенных пространством со многими другими в интегральной схеме.
Каждый из основных операторов, о которых мы узнали в разделе выражений, имеет символ ворот. Символ занимает место оператора, а переменные являются входными данными для логического элемента. Значение, полученное в результате выражения уравнения, является выходом ворот. Выход элемента может быть конечным результатом или может быть подключен как вход к еще одному элементу.
Символ занимает место оператора, а переменные являются входными данными для логического элемента. Значение, полученное в результате выражения уравнения, является выходом ворот. Выход элемента может быть конечным результатом или может быть подключен как вход к еще одному элементу.
Символы ворот
Логические элементы — это символы, которые могут напрямую заменять выражение в логической арифметике. Каждый из них имеет разную форму, чтобы показать свою особую функцию.Входные данные (логические переменные) вводятся слева от символа, а выходные данные — справа. При объединении несколько ворот могут образовать сложную логическую систему оценки, имеющую множество входов и выходов. Цифровые компьютеры созданы путем соединения тысяч или миллионов этих ворот вместе.
Элемент НЕ
Элемент НЕ представляет собой стрелку вперед с маленьким кружком на выходе. Круглая часть символа говорит о том, что вывод отрицает ввод.
Вентиль ИЛИ
Вентиль ИЛИ имеет изогнутую входную сторону и остроконечный выход.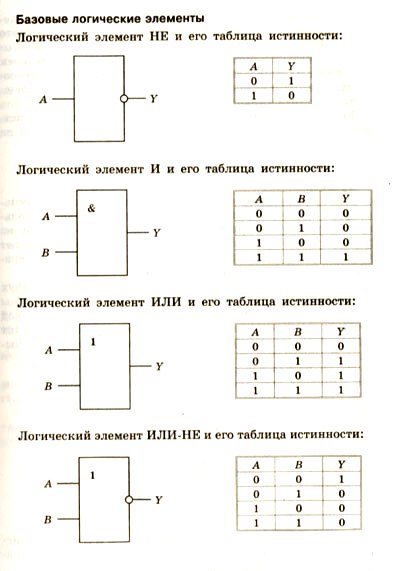
Логический элемент И
Логический элемент И имеет плоскую входную сторону и круглую выходную сторону.
Элемент исключающего ИЛИ (XOR)
Символ логического элемента исключающее ИЛИ аналогичен вентилю ИЛИ, но имеет дополнительную изогнутую линию, пересекающую входы.
Комбинированная логика
Когда вы соединяете несколько вентилей, у вас есть комбинированная логическая система или комбинаторная логика . Для разработки комбинированной логической системы мы можем использовать таблицы истинности для сопоставления логических выходов для различных входных условий.Булевы выражения записываются из условий в таблице. Затем мы можем напрямую преобразовать выражение в схему логических вентилей.
Возможно, вы помните, что еще в булевых элементах мы видели, что в коде для XOR не было оператора. Он был составлен с помощью комбинации операторов AND, OR и NOT:
пусть A = false
пусть B = false
пусть Q = (A || B) &&! (A && B) Давайте сопоставим входные и выходные условия в таблице истинности для комбинированной логической системы для XOR. Мы найдем все условия, которые вызывают результат
Мы найдем все условия, которые вызывают результат истинный , и создадим для них логическое выражение.
| А | B | A ⊕ B |
|---|---|---|
| Ф | F | F |
| Ф | т | т |
| т | F | т |
| т | т | F |
Есть два условия, при которых столбец результата имеет истинных значений.Первое условие: A — false и B — true , что выражается как ~ A · B . Второе условие: A — это истинный , а B — ложный , что выражается как A · ~ B . Наше выражение XOR — true , когда одно из этих условий true , которое записывается как:
A ⊕ B = (~ A · B) + (A · ~ B)
В коде это выражение формируется с помощью следующих логических блоков:
пусть A = false
пусть B = false
пусть Q = (! A && B) || (A &&! B) Покрытие уравнения до логических вентилей дает следующую диаграмму.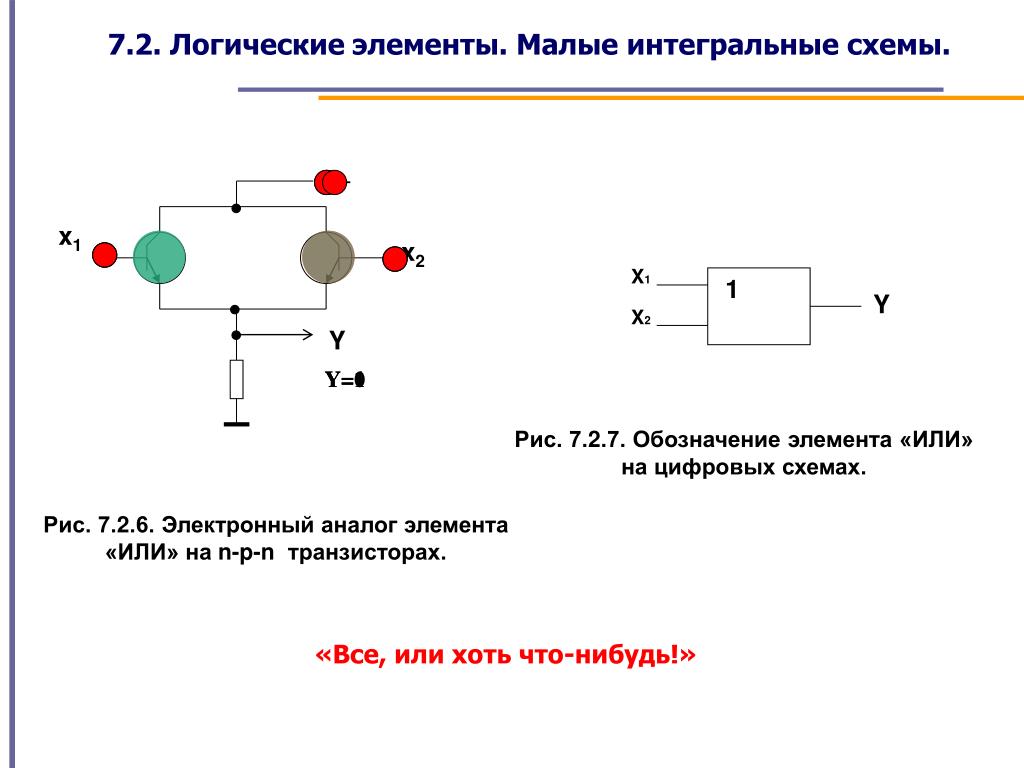 Обратите внимание, как каждый вентиль «связывает» переменные вместе, как и логические блоки в приведенном выше коде.
Обратите внимание, как каждый вентиль «связывает» переменные вместе, как и логические блоки в приведенном выше коде.
Однако, если мы возьмем два других неиспользуемых условия из таблицы истинности, которые делают операцию XOR ложной , мы можем составить отрицательное уравнение для XOR, называемое NXOR:
~ (A ⊕ B) = (~ A · ~ B) + (A · B)
Чтобы вернуться к A ⊕ B , мы должны отрицать это отрицательное уравнение. Затем с помощью Thereom Де Моргана мы получаем другое уравнение для XOR, но оно все еще логически эквивалентно исходному.
A ⊕ B = (A + B) · ~ (A · B)
Когда это уравнение преобразуется в логические вентили, их на один вентиль меньше, чем на первой диаграмме.
Эта диаграмма менее сложна, чем первая. Уменьшение количества вентилей для достижения одного и того же логического результата — одна из основных целей проектирования цифровой логики. Для электронных устройств это позволяет большему количеству вентилей использовать ограниченное пространство на интегральной схеме.
Для электронных устройств это позволяет большему количеству вентилей использовать ограниченное пространство на интегральной схеме.
Как работают логические вентили в цифровой электронике | EAGLE
Бинарный мир единиц и нулей сам по себе не позволяет нам повторно приземлять ракеты посреди океана, доставлять посылки за считанные минуты с помощью дронов или наносить на карту известную физическую вселенную и все ее чудеса.Нет, что делает все это возможным, так это наша способность разрезать двоичные числа во всех их бесконечных возможностях с помощью сложной математики. Наша способность складывать, вычитать, умножать и делить двоичные числа различными способами — вот что позволило нам создать мир цифровой электроники, который мы знаем сегодня. Чтобы перейти от нулей к последним достижениям в медицине, освоении космоса и науке, вам нужно начать с логических ворот.
На ферме
Допустим, вы живете на ферме, и у вас есть стая кур, которых нужно разводить на хорошем участке земли. Каждое утро вы просыпаетесь, открываете ворота на свою ферму и отпускаете цыплят на пастбище. Эти ворота — ваш метод контроля за потоком цыплят на ферму и из нее, а также в достижении ваших целей по созданию счастливых и здоровых существ, которые годами продолжают откладывать яйца.
Каждое утро вы просыпаетесь, открываете ворота на свою ферму и отпускаете цыплят на пастбище. Эти ворота — ваш метод контроля за потоком цыплят на ферму и из нее, а также в достижении ваших целей по созданию счастливых и здоровых существ, которые годами продолжают откладывать яйца.
Выходы бывают разных видов: для кур — для яиц, для электроники — для напряжения!
В компьютере мы также можем использовать ворота для управления потоком и достижения конечной цели, но вместо цыплят мы контролируем поток электрического тока, который проходит по цепи.Этот затвор в мире цифровой электроники известен как транзистор и может находиться в одном из двух состояний: включен или выключен, а также открыт или закрыт, если вы хотите думать о нем как о затворе. Когда транзистор включен или открыт, через него может протекать электрический ток. А когда он выключен, ток не течет.
Когда вы соединяете связку этих транзисторов вместе, вы получаете так называемый логический вентиль , который позволяет вам складывать, вычитать, умножать и делить двоичные числа любым возможным способом. В физической схеме эти логические элементы имеют:
В физической схеме эти логические элементы имеют:
- Входы . Всем логическим элементам требуется какое-то входное значение, чтобы у них были числа для сравнения. Эти цифры представлены в виде напряжений. Когда у вас входное напряжение 0 В, оно считается низким, или 0. А когда на входе напряжение 5 В, оно считается высоким, или 1.
- Выходы . Как только логический вентиль получает возможность обработать ваш ввод, он может принять решение о том, открыть ли его вентиль или оставить его закрытым.Этот выход полностью определяется типом используемого логического элемента, и некоторые из них открываются только при наличии двух высоких напряжений на входе, тогда как другие открываются только при низком напряжении, но не при высоком напряжении на входе. .
Используя комбинацию высокого и низкого напряжения и отправляя их через вход логического элемента, мы можем творить удивительные вещи. Но в конце концов, мы все еще работаем над некоторыми фундаментальными вопросами — хотим ли мы позволить определенному логическому элементу пропускать электрический ток или нет? Хотя на индивидуальном уровне это может показаться упрощенным, объединение всей этой логики и принятия решений воедино — вот как мы пришли к созданию удивительной цифровой электроники за такой короткий исторический период. Но действительно ли логические ворота являются чем-то новым?
Но действительно ли логические ворота являются чем-то новым?
Концепции старше, чем вы думаете
Логические ворота существуют дольше, чем вы живете, в различных формах компьютерных технологий. То, что начиналось как механические релейные переключатели, состоящие из электромагнита и набора контактов, вскоре превратилось в электронные лампы для использования в телевизорах, лампочках и т. Д. В 1900-х годах. И хотя эти электронные лампы были намного быстрее своих релейных аналогов, они были такими же громоздкими и ненадежными, что привело нас к созданию транзистора в 1947 году.
Транзисторы были идеальными. Они были надежны, потребляли меньше энергии, чем электронные лампы и реле, и были невероятно маленькими по размеру. Несмотря на различие в размерах и форме, функции реле, электронных ламп и транзисторов были одинаковыми. Они работали как переключатель для управления потоком электричества на основе некоторого входного напряжения.
Первый транзистор во всей красе, прославленный Bell Labs (Источник изображения)
В 1960-х годах мы начали собирать коллекцию транзисторов, что привело к созданию первой интегральной схемы, положившей начало нашей эре современных компьютеров.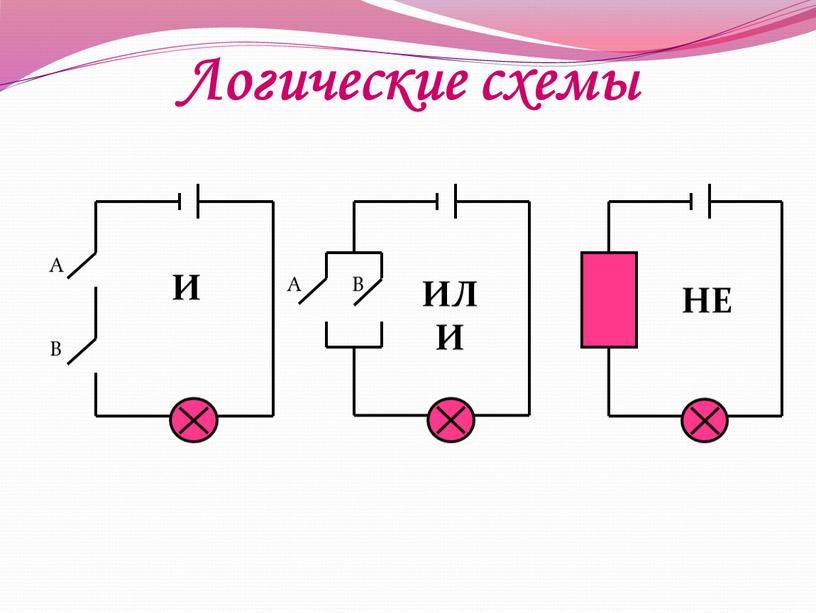 Эти ИС начинались с простого, втиснув примерно 20 транзисторов в кремниевый кристалл квадратной формы 3 мм с другими компонентами, такими как резисторы и диоды. Самые ранние ИС назывались маломасштабными интегрированными (SSI) ИС.
Эти ИС начинались с простого, втиснув примерно 20 транзисторов в кремниевый кристалл квадратной формы 3 мм с другими компонентами, такими как резисторы и диоды. Самые ранние ИС назывались маломасштабными интегрированными (SSI) ИС.
Производство ИС продолжало развиваться, и вскоре в первый микропроцессор, выпущенный Intel в 1974 году, было встроено 4800 транзисторов. Сегодня мы живем в эпоху интегральных микросхем очень большого размера (СБИС), которые могут вместить миллионы и даже миллиарды транзисторов в один крошечный корпус.Все эти интегральные схемы представляют собой математические электростанции, объединяющие головокружительное количество логических вентилей с помощью транзисторов, позволяющих складывать, вычитать, умножать и делить числа по своему усмотрению.
Отличный наглядный пример того, как далеко продвинулись интегральные схемы, теперь упакованные в миллионы транзисторов. (Источник изображения)
Логические ворота и цыплята
Существует множество логических вентилей, включая AND, OR, NOT, XOR, NAND и NOR. У каждого из этих логических элементов есть очень специфический способ обработки входных и выходных данных, которые он производит.Но независимо от того, о каком логическом элементе идет речь, входы и выходы будут разбивать все на два двоичных числа, составляющих цифровую электронику, 1 и 0.
У каждого из этих логических элементов есть очень специфический способ обработки входных и выходных данных, которые он производит.Но независимо от того, о каком логическом элементе идет речь, входы и выходы будут разбивать все на два двоичных числа, составляющих цифровую электронику, 1 и 0.
И Ворота
Вернемся на минутку на нашу ферму. Допустим, мы хотим выпустить одну из наших кур, но только если она будет с петухом, чтобы она могла иметь некоторую защиту на нашем пастбище. В этом случае наши курица и петух зависят друг от друга. Если курица и петух вместе, то мы можем пропустить их через наши ворота на пастбище.
Вот как вентиль И работает в электронной схеме. Единственный способ получить высокий выход 1 — это установить на обоих входах 1 с. Давайте разберемся с этим и посмотрим, как это работает, используя наших цыплят в трех сценариях:
- Если у нас будут курица И петух у наших ворот, тогда мы откроем ворота.
- Если у нас есть курица И нет петуха у ворот, то мы будем держать ворота закрытыми.

- И если у нас не будет курицы И петуха у наших ворот, тогда мы будем держать ворота закрытыми.
Видите здесь шаблон? Оба входа ворот И полностью зависят друг от друга. Вы не можете иметь одно без другого, чтобы получить результат 1. Вот как все это будет разбито на так называемую таблицу истинности, где A и B являются входами, а Q — выходом:
Как видите, единственный способ получить 1 для выхода — это иметь два одинаковых входа. В противном случае затвор в транзисторе останется закрытым, и электричество не сможет проходить через него.Вот как ворота И будут выглядеть на схеме.
Логический вентиль И с двумя входами и одним выходом.
OR Выход
Снова на нашей ферме, допустим, на этот раз мы поставили забор, поэтому мы не слишком беспокоимся о том, что наши куры выйдут с петухом для защиты. В этом примере наша курица и петух не зависят друг от друга, поэтому, если к нашим воротам приблизится курица ИЛИ петух, мы откроем их для них.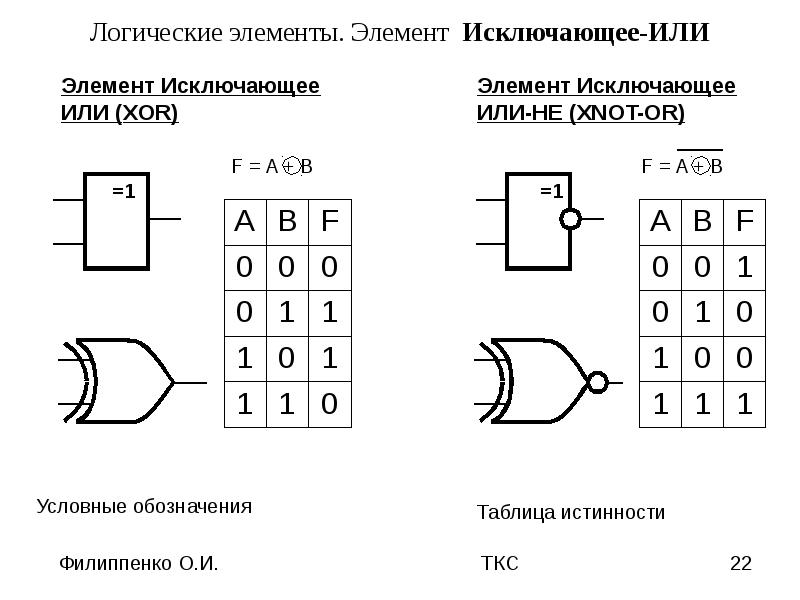
С вентилем OR вам нужно, чтобы только один из ваших входов был 1, чтобы выход также был 1.Вот как это было бы в нашем сценарии с курицей:
- Если у нас будет курица ИЛИ петух у наших ворот, то мы откроем ворота.
- Если у нас есть курица ИЛИ нет петуха у наших ворот, то мы откроем ворота.
- Если у нас нет курицы ИЛИ петуха у ворот, мы будем держать ворота закрытыми.
Картина здесь тоже довольно четкая. Оба наших входа не зависят друг от друга, и пока один из них присутствует, наши ворота открываются.Вот как все это будет выглядеть в таблице истинности, где A и B являются входами, а Q — выходом:
Если вы хотите быстро идентифицировать вентиль OR на схеме, ищите этот символ:
Логический вентиль ИЛИ, для которого требуется только один вход 1.
НЕ Ворота
Гейт НЕ немного усложняет нашу аналогию с курицей, так что давайте попробуем что-нибудь еще. Допустим, у вас на ферме тоже есть козы, но вы никогда не хотите выпускать их за ворота. Так что даже если у нас есть коза у ворот , а НЕ , которая действительно хочет выйти, мы не собираемся открывать ворота. Несмотря на то, что наша коза представляет 1 в нашем логическом элементе в качестве входа, элемент НЕ всегда дает противоположный выход.
Так что даже если у нас есть коза у ворот , а НЕ , которая действительно хочет выйти, мы не собираемся открывать ворота. Несмотря на то, что наша коза представляет 1 в нашем логическом элементе в качестве входа, элемент НЕ всегда дает противоположный выход.
Но предположим, что коза уходит от наших ворот, теперь у нас есть 0 в качестве входных данных, что означает отсутствие козы. Согласно нашим воротам , НЕ , на выходе будет 1, что означает, что мы можем держать ворота открытыми, пока поблизости нет коз.
НЕ ворота немного странны по сравнению с другими воротами, так как они всегда делают полную противоположность любому входному значению, которое вы им предоставляете. Этим воротам также требуется только один вход для выдачи своего выхода, тогда как другим воротам всегда потребуется два входа. Вот как комбинации для ворот НЕ будут выглядеть в таблице истинности, где A является единственным входом, а Q — выходом:
И довольно легко обнаружить вентиль НЕ на схеме, просто найдите логический вентиль только с одним входом и одним выходом.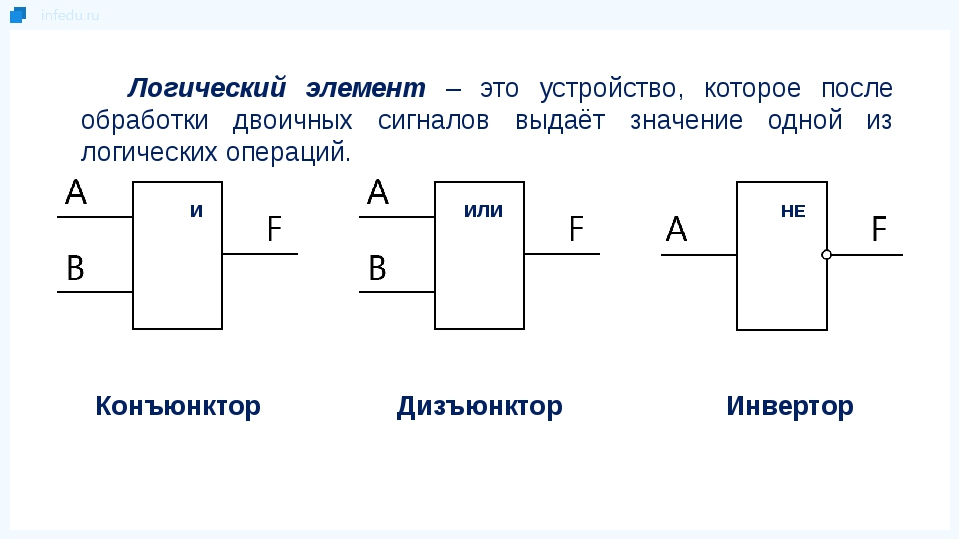
Логический вентиль НЕ обеспечивает в качестве выхода значение, противоположное входному.
Ворота XOR
Возвращаясь к нашей ферме, у нас есть вентиль XOR , который похож на логический элемент ИЛИ, за исключением того, что если присутствуют оба наших входа, то ворота останутся закрытыми. Вы можете думать о воротах XOR как о своего рода ситуации «или / или». Например:
- Если у нас есть ЛИБО курица ИЛИ петух у наших ворот, то мы откроем ворота.
- Если у наших ворот нет курицы или петуха, мы будем держать ворота закрытыми.
- Если у нас есть и цыпленок, и петух у наших ворот, то мы будем держать ворота закрытыми.
Другой способ понять логический элемент XOR заключается в следующем: вы всегда получите на выходе 1, если ваши входы представляют собой смесь 1 и 0. И если у вас есть два одинаковых входа, например 0 и 0 или 1 и 1, тогда вы получите 0 для вывода. Вот как все комбинации элементов XOR будут выглядеть в таблице истинности, где A и B являются входами, а Q — выходом:
И чтобы разместить вентиль XOR на схеме, обратите внимание на этот символ:
Логический вентиль XOR работает так же, как вентиль ИЛИ, за исключением случаев, когда присутствуют оба входа.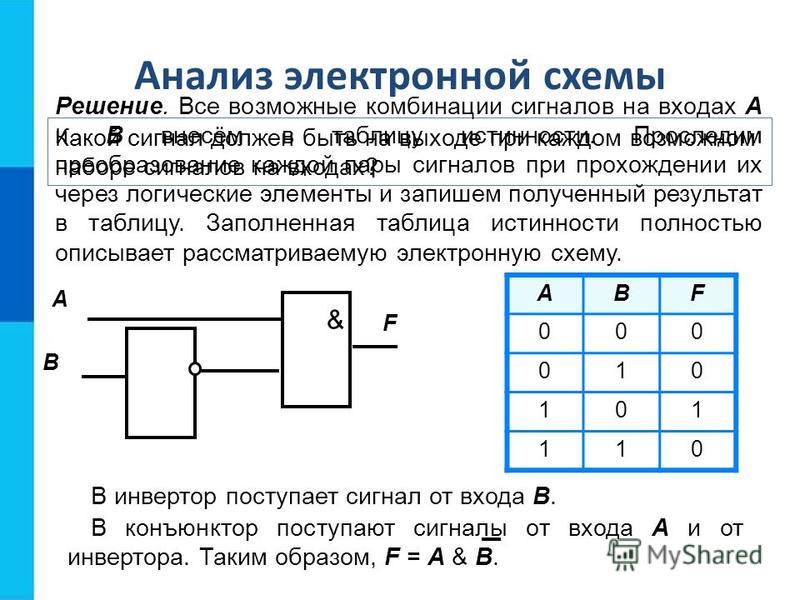
XNOR Ворота
Этот вентиль представляет собой комбинацию вентилей XOR и НЕ . Таким образом, выходы будут равны 1, если входы одинаковы, независимо от того, являются ли они 1 или 0. И если входы разные, на выходе будет 0 или ложь. Для наших цыплят мы можем использовать ворота XNOR, чтобы открывать наши ворота только тогда, когда пара курица и петух отправляется вместе, или если нет курицы или петухов вместе. Например:
- Если у нас будет курица ИЛИ петух у наших ворот, то мы откроем ворота.
- Если у наших ворот будет цыпленок, но нет петуха, то мы будем держать ворота закрытыми.
- Если у нас нет курицы ИЛИ петуха у ворот, то мы ворота откроем.
И вот как все это будет разбито в таблицу истинности, где A и B являются входами, а Q — выходом:
Схематический символ логического элемента XNOR очень похож на логический элемент XOR с добавлением точки в конце вывода:
Логический вентиль XNOR возвращает только 1 выходное значение, если два входа одинаковы.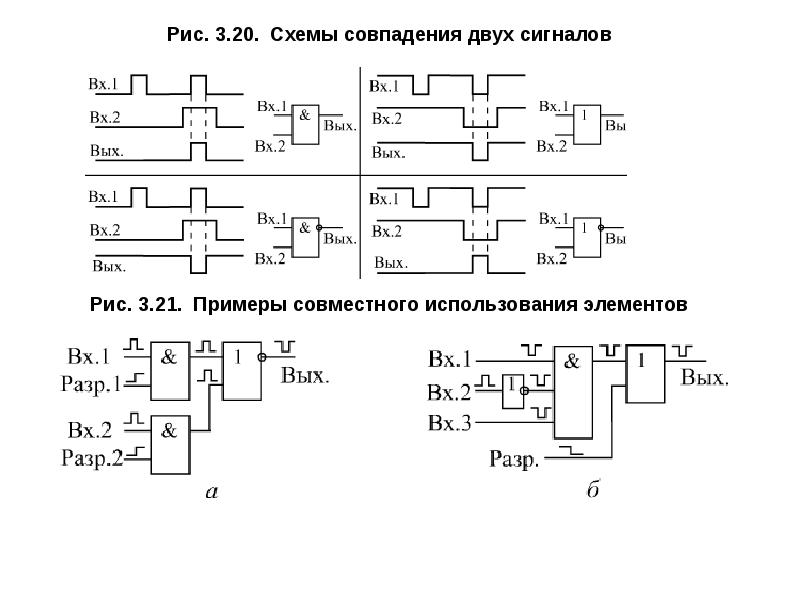
NAND Gate
Этот вентиль работает аналогично вентилю И , за исключением того, что когда у вас есть два входа по 1, вы всегда получите выход 0. Итак, допустим, мы хотим выпускать цыплят только по одному, но не с петухом. Гейт NAND — именно то, что нам нужно для этого:
- Если у нас есть и курица, и петух у наших ворот, то мы НЕ откроем ворота.
- Если у нас есть курица И нет петуха у наших ворот, тогда мы откроем ворота.
- Если у нас не будет курицы и петуха у наших ворот, то мы откроем ворота.
Если вы застряли на этом, то попробуйте думать об этом так: вентиль NAND работает как вентиль И , так и вентиль НЕ . Сначала он сравнивает два значения, используя логику И , а затем выдает противоположный вывод на основе логики И . Вот как все это разбивается на таблицу истинности, где A и B являются входами, а Q — выходом:
И если вам нужно работать с логическим элементом NAND на схеме, вот символ, который нужно искать:
Логический вентиль И-НЕ возвращает выход 0, когда оба входа равны 1.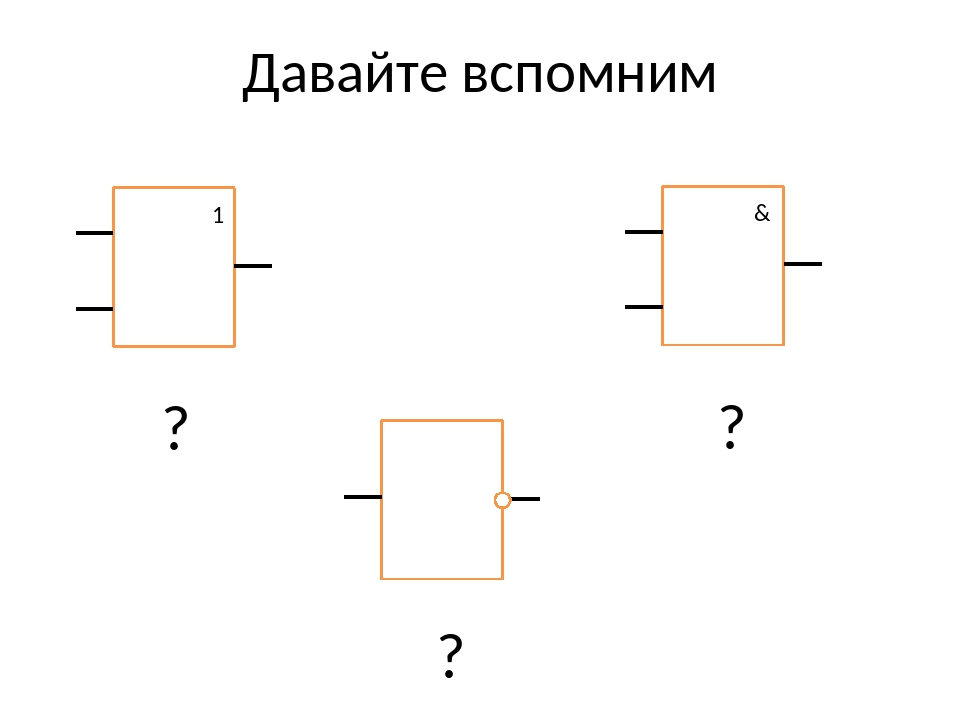
NOR Ворота
Нашими последними и последними воротами для работы на нашей ферме являются ворота NOR , которые похожи на ворота NAND в том, что они имеют выход, противоположный тому, что вы могли ожидать. Вентиль ИЛИ будет работать так же, как вентиль ИЛИ , за исключением того, что его выход противоположен выходу ворот ИЛИ . Например, вернувшись на нашу ферму, предположим, что на улице бушует жестокий шторм, и мы не хотим выпускать цыплят на пастбище.Ворота NOR — именно то, что нам нужно:
- Если у нас будет курица ИЛИ петух у наших ворот, то мы ворота не откроем.
- Если у нас есть курица ИЛИ нет петуха у наших ворот, то мы не откроем ворота.
- Если все наши куры в безопасности в своей курятнике, а не у наших ворот, то мы откроем ворота.
Все еще с нами? Ворота NOR работают как ворота OR , так и ворота NOT . Сначала он сравнивает два значения, используя логику OR , а затем обеспечивает противоположный вывод на основе логики OR . Вот как все это будет разложено в таблице истинности, где A и B являются входами, а Q — выходом:
Вот как все это будет разложено в таблице истинности, где A и B являются входами, а Q — выходом:
И если вы ищете ворота NOR на схеме, найдите этот символ:
Логический вентиль ИЛИ-НЕ работает так же, как вентиль ИЛИ с противоположным выходом.
Они супер калькуляторы
Хотя отдельные логические ворота на своей поверхности все относительно просты и понятны, именно сочетание этих ворот вместе действительно раскрывает их сверхспособности.Используя комбинацию логических вентилей вместе в интегральной схеме, вы можете выполнять невероятно сложные вычисления. И чем больше логических вентилей вы поместите в одно и то же физическое пространство, тем быстрее вы сможете вычислить! Куда бы вы ни посмотрели в мире цифровой электроники, у вас есть логические ворота, которые делают все тяжелые математические операции, чтобы происходить удивительные вещи. Так что в следующий раз, когда вы услышите красивую музыку, льющуюся из ваших динамиков, или вы, не задумываясь, наблюдаете за приземлением ракеты SpaceX посреди океана, помните, что вам нужно благодарить логические ворота, неустанно работая за кулисами.
Готовы экспериментировать со своими собственными логическими воротами? Попробуйте Autodesk EAGLE бесплатно!
Как работает логический вентиль в микрочипе? Затвор кажется устройством, которое должно открываться и закрываться, но микрочипы выгравированы на кремниевых пластинах, у которых нет движущихся частей. Так как же ворота открываются и закрываются?
Ларри Виссел, инженер по приложениям ASIC в IBM Microelectronics, отвечает:«Те из нас, кто разрабатывает логические вентили для компьютеров, редко вспоминают, как термины, которые мы используем для описания технологий, стали использоваться.Видение качающегося назад и вперед затвора явно не отражает буквально структуры на кремниевом кристалле. Но причину использования термина «вентиль» для компьютерной логики можно понять, исследуя основную функцию шлюза: управление потоком.
«На ферме ворота могут использоваться для управления потоком овец или коз между загонами. В этом случае ворота представляют собой физический барьер, положение которого контролируется фермером. Фермер принимает решение о потоке овец или коз. животных, а затем перемещает физический барьер, чтобы обеспечить желаемый поток.
«В компьютере затвор управляет прохождением электрического тока через цепь. Затвор состоит из транзисторов; транзисторы выбираются разработчиком микросхемы из двух основных типов (транзисторы PMOS и NMOS), которые присутствуют в широко распространенных CMOS (дополнительных металл-оксидный полупроводник). Ток, протекающий через затвор, устанавливает напряжение в определенной точке цепи. Это напряжение представляет собой единственный «бит» информации. Напряжение может быть высоким (представляющим значение «1») или низкий (представляющий значение «0»).
«Чтобы установить 1 в цепи, ток направляется в цепь (управляется) путем« включения »транзистора PMOS, подключенного между цепью и положительным напряжением питания. Напряжение питания обычно является стандартным для отрасли значением, например 3,3 или 5,0 В. В течение очень короткого интервала, необходимого для переключения логического элемента (порядка наносекунды или миллиардной доли секунды), ток будет течь через транзистор PMOS от положительного источника питания к цепи. .
«Ток, который заряжает узел схемы до 0, отводится от схемы через другой тип транзистора (NMOS), подключенный между схемой и отрицательным напряжением питания или электрическим заземлением. Опять же, ток будет течь через транзистор NMOS в течение очень короткого интервала, но для NMOS ток находится между цепью и отрицательным источником питания.В любом случае протекание тока приводит к изменению напряжения в цепи, а напряжение в цепи представляет собой бит информации.Итак, когда вентиль управляет потоком тока, он фактически контролирует поток информации.
«Возвращаясь к аналогии между фермой и компьютерным чипом, очевидно, что поток отличается (сельскохозяйственные животные по сравнению с информацией) и что сам затвор отличается (физический барьер по сравнению с транзистором в технологии CMOS). Но Самое важное различие — это средства управления потоком: на ферме фермер сбрасывает местоположение ворот, принимая решение и затем перемещая физический барьер.Поток животных через сложный лабиринт ворот потребует участия фермеров у каждых ворот.
«Но в компьютерном чипе механизмом управления является напряжение на управляющем выводе транзистора. Это напряжение включает транзистор, изменяя его характеристики с разомкнутой цепи (положение« выключено ») на такое, которое может проводить небольшой ток.Это управляющее напряжение, в свою очередь, уже доступно внутри микросхемы как напряжение в точке другой цепи.И, будучи напряжением в цепи, этот механизм управления представляет другой бит информации.
«Подавляющая вычислительная мощность логических вентилей проистекает из того факта, что на выходе любого конкретного логического элемента есть напряжение, которое, в свою очередь, может использоваться для управления другим вентилем. Таким образом, компьютерный чип может быть спроектирован для принятия сложных решений относительно информационного потока внутри Эта способность позволяет создавать сложные системы, соединяя до миллиона ворот в одном чипе. И все это без участия фермеров и движущихся частей ».
Так Нин из IBM T.Исследовательский центр J. Watson добавляет некоторые дополнительные сведения:
«Логический вентиль в микрочипе состоит из определенного расположения транзисторов. Для современных микрочипов используются транзисторы типа, называемые полевым транзистором металл-оксид-полупроводник (MOSFET), а в качестве полупроводника используется кремний. MOSFET имеет три компонента или области: область истока, область стока и область канала, имеющую затвор над ней.Три области расположены горизонтально рядом друг с другом, с областью канала посередине.
«В схеме с логическим затвором каждый из полевых МОП-транзисторов работает как переключатель. Переключатель замкнут или полевой МОП-транзистор включен, если электрический ток может легко течь от истока к стоку. Переключатель разомкнут, или МОП-транзистор включен. отключается, если электрический ток не может течь от источника к стоку.
«Области истока и стока полевого МОП-транзистора изготовлены так, чтобы они были заполнены электронами, которые готовы проводить ток. С другой стороны, область канала спроектирована так, чтобы в нормальных условиях не было электронов, что блокирует движение тока.Следовательно, в нормальных условиях полевой МОП-транзистор выключен (или открыт), и ток не может течь от истока к стоку.
«Если к затвору (который находится наверху области канала) приложено положительное напряжение, то электроны, которые имеют отрицательный заряд, будут притягиваться к затвору. Эти электроны собираются в области канала полевого МОП-транзистора. Напряжение затвора, тем больше концентрация электронов в области канала.Существенная концентрация электронов в канале обеспечивает путь, по которому электроны могут легко перемещаться от истока к стоку.Когда это происходит, полевой МОП-транзистор находится в состоянии «включено» (или «закрыт»), и ток может свободно течь от источника к стоку.
«Таким образом, полевой МОП-транзистор в микрочипе включается путем подачи напряжения на затвор, чтобы привлечь электроны в область канала, и выключается путем подачи напряжения на затвор, чтобы оттолкнуть электроны от области канала. заряды в кремнии, но не задействованы механические движущиеся части ».
Логические ворота | Учебник по компьютерной архитектуре
Двоичная информация представлена в цифровых компьютерах с помощью физических величин, называемых сигналами .Электрические сигналы, такие как напряжение, присутствуют по всему компьютеру в одном из двух распознаваемых состояний. Два состояния представляют собой двоичную переменную, которая может быть равна 1 или 0.
Например, конкретный цифровой компьютер может использовать сигнал 3 вольта для представления двоичного 1 и 0,5 вольта для представления двоичного 0 . Теперь входные клеммы цифровых схем будут принимать двоичные сигналы только 3 и 0,5 В для представления двоичного входа и выхода, соответствующих 1 и 0, соответственно.
Итак, теперь мы знаем, что на уровне ядра компьютер обменивается данными в форме сигналов 0 и 1 , которые представляют собой не что иное, как сигналы напряжения low и high .
Но как разные операции выполняются с этими сигналами? Это делается с использованием другой логики Gates .
Что такое ворота?
Двоичная логика имеет дело с двоичными переменными и операциями, которые имеют логическое значение. Он используется для описания в алгебраической или табличной форме манипуляции, выполняемой логическими схемами, называемыми вентилями .
Шлюзы — это блоки оборудования, которые создают графический символ, и его работа может быть описана с помощью алгебраического выражения. Связь ввода-вывода двоичных переменных для каждого элемента может быть представлена в табличной форме таблицей истинности.
Самыми простыми логическими вентилями являются И и включительно ИЛИ с несколькими входами и НЕ с одним входом.
Каждый вентиль с более чем одним входом чувствителен к входу логического 0 или логической 1 на любом из своих входов, генерируя выход в соответствии с его функцией.Например, вентиль И с несколькими входами чувствителен к логическому 0 на любом из его входов, независимо от любых значений на других входах.
Различные логические ворота:
- И
- ИЛИ
- НЕ
- NAND
- НОР
- XOR
- XNOR
И Ворота
Элемент И создает логическую функцию И, то есть выход равен 1, если вход A и вход B равны 1; в противном случае на выходе будет 0.
Алгебраический символ функции И такой же, как и символ умножения на в обычной арифметике.
Мы можем использовать точку между переменными или объединить переменные без символа операции между ними. Логические элементы И могут иметь более двух входов, и по определению выход равен 1 тогда и только тогда, когда все входы равны 1.
ИЛИ Выход
Элемент ИЛИ производит функцию включающего ИЛИ; то есть выход равен 1, если вход A или вход B, или оба входа равны 1; в противном случае на выходе будет 0.
Алгебраический символ функции ИЛИ — + , аналогично арифметическому сложению .
Логические элементы ИЛИ могут иметь более двух входов, и по определению выход равен 1, если любой вход равен 1.
Инвертор (НЕ) Затвор
Схема инвертора инвертирует логический смысл двоичного сигнала. Он производит функцию НЕ или дополнение.
Алгебраический символ, используемый для логического дополнения, представляет собой штрих или черту над символом переменной.
NAND Gate
Функция И-НЕ является дополнением к функции И, что обозначено графическим символом, который состоит из графического символа И, за которым следует маленький кружок.
Обозначение И-НЕ происходит от сокращения НЕ-И.
NOR Gate
Элемент ИЛИ-НЕ является дополнением элемента ИЛИ и использует графический символ ИЛИ, за которым следует маленький кружок.
Ворота Exclusive-OR
Элемент исключающего ИЛИ имеет графический символ, аналогичный элементу ИЛИ, за исключением дополнительной изогнутой линии на входной стороне.
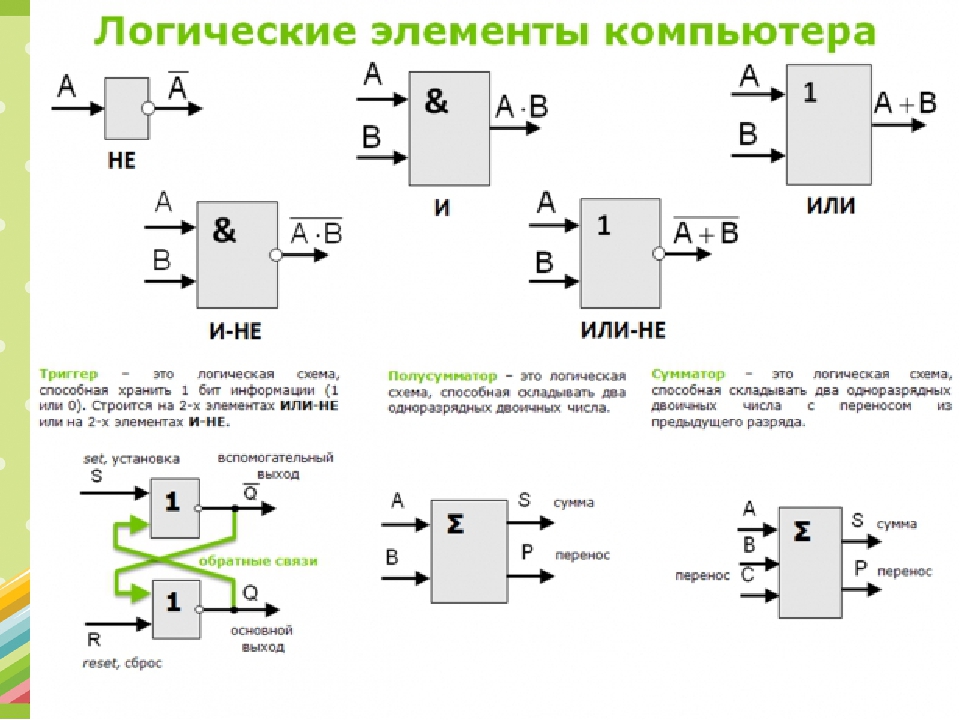
 Схемы затвора чаще всего представлены на схемах их собственными уникальными символами, а не составляющими их транзисторами и резисторами.
Схемы затвора чаще всего представлены на схемах их собственными уникальными символами, а не составляющими их транзисторами и резисторами.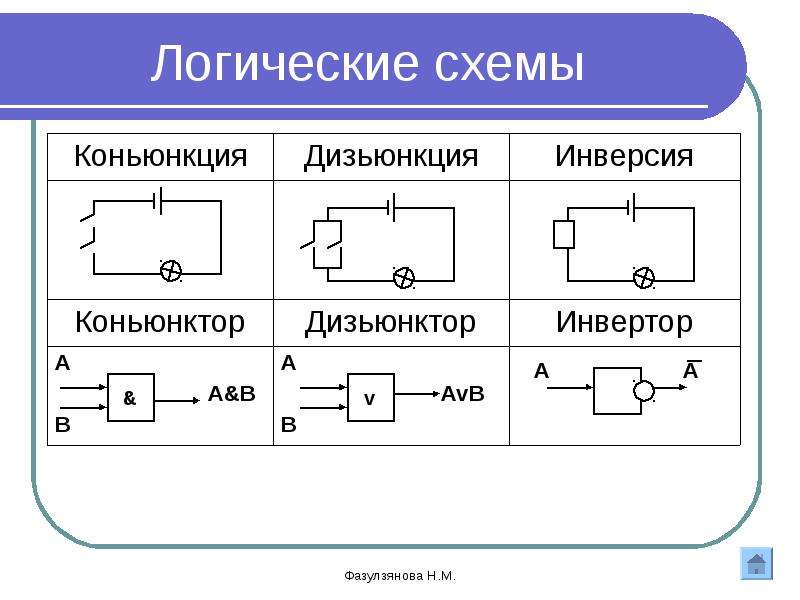 ) — Элемент AND дает выход 1, если оба входа равны 1, в противном случае он дает 0.
) — Элемент AND дает выход 1, если оба входа равны 1, в противном случае он дает 0.